DOI:10.32604/iasc.2020.014192

| Intelligent Automation & Soft Computing DOI:10.32604/iasc.2020.014192 |  |
| Article |
Parallel Equilibrium Optimizer Algorithm and Its Application in Capacitated Vehicle Routing Problem
1College of Computer Science and Engineering, Shandong University of Science and Technology, Qingdao, Shandong, 266590, China
2Faculty of the Built Environment, University of New South Wales, 1466, Australia
*Corresponding Author: JengShyang Pan. Email: jengshyangpan@gmail.com
Received: 04 September 2020; Accepted: 11 October 2020
Abstract: The Equilibrium Optimizer (EO) algorithm is a novel meta-heuristic algorithm based on the strength of physics. To achieve better global search capability, a Parallel Equilibrium Optimizer algorithm, named PEO, is proposed in this paper. PEO is inspired by the idea of parallelism and adopts two different communication strategies between groups to improve EO. The first strategy is used to speed up the convergence rate and the second strategy promotes the algorithm to search for a better solution. These two kinds of communication strategies are used in the early and later iterations of PEO respectively. To check the optimization effect of the proposed PEO algorithm, it is tested on 23 benchmark functions and compared with the Particle Swarm Optimization (PSO), Grey Wolf Optimizer (GWO), Parallel Particle Swarm Optimization (PPSO), and EO as well. The empirical study demonstrates that the abilities of exploration and exploitation of PEO are superior to the above four algorithms in most benchmark functions. Finally, we apply PEO to solve the Capacitated Vehicle Routing Problem (CVRP) in the field of transportation. Experimental results show that PEO can achieve a better driving route.
Keywords: Equilibrium optimizer; parallelism; communication strategy; capacitated vehicle routing problem
Traditional optimization algorithms usually show better performance in solving single-extreme value optimization problems. But in fact, the practical engineering problems are multiple, extreme and complex. The traditional optimization algorithms are difficult to solve these problems. The emergence of intelligent optimization algorithms breaks the above-mentioned bottleneck. When solving complex problems, they can find approximately optimal solutions within an acceptable time and improve efficiency. Therefore, the research of intelligent optimization algorithms is becoming more and more important.
Intelligent optimization algorithms mostly belong to heuristic algorithms. They are mainly used to solve optimization problems, and their inspiration comes from existing phenomena or things [1,2]. As an extension of the heuristic algorithm, the meta-heuristic algorithm given by nature can be roughly split into three categories: swarm intelligence, evolutionary algorithm and physical algorithm. The characteristics of meta-heuristic algorithms based on species behavior are that the optimization process shares the collective information of all individuals. Typical examples are as follows: Cuckoo Search Algorithm (CSA) [3], Artificial Bee Colony (ABC) algorithm [4,5], Bat Algorithm (BA) [6–8], Pigeon-Inspired Optimization (PIO) algorithm [9], and so on. The meta-heuristic algorithms based on evolution are related to the evolution law of organisms. Among such algorithms, there are the Differential Evolution (DE) [10,11], Symbiotic Organism Search (SOS) [12,13], Quasi-Affine Transformation Evolutionary (QUATRE) [14–16], and so on. The DE is an analogy with the early Genetic Algorithm (GA) [17,18]. They are efficient global optimization algorithms with continuous variables and multiple objectives. Finally, the features of meta-heuristic algorithms based on the physical model are that the communication between search agents is described according to the rules in the physical process. The typical algorithms include Simulated Annealing (SA) [19,20], Gravitational Search Algorithm (GSA) [21], Charged System Search (CSS) [22], and so on. The Equilibrium Optimizer (EO) algorithm belongs to the meta-heuristic algorithms based on physics, which is a new intelligent optimization algorithm [23,24].
The EO is enlightened by the model that controls the mass-volume balance and adopts a random exploration mechanism. In EO, each particle updates its position through a candidate particle randomly selected from the equilibrium pool, and the adaptive value of control parameters in the algorithm can reduce the moving speed of particles. The abilities of exploration and exploitation are largely due to this random update strategy and the control parameters in the algorithm. And the tests of EO in benchmark functions and engineering problems prove the practicability and effectiveness of the algorithm [23].
As a new algorithm, the convergence and global search ability of EO need to be further improved. Its balance mechanism leads to the problem of premature convergence. To further advance global search capability and avoid its premature convergence, this paper improves the EO based on parallel ideas. There are many improvement strategies to improve the performance of the meta-heuristic algorithm, like parallel, compact, multi-strategy and space vector improvement [25]. Among them, the parallel strategy is an important algorithm optimization strategy. Parallelized intelligent optimization algorithm expands the original single population into multiple groups, and carries out group communication during the iteration process, which further improves the optimization ability of the algorithm. The most important thing is the communication strategy between groups when designing the parallel algorithm. Up to now, there are many studies on the parallel improvement technology with inter-group communication strategy [26–28]. For instance, parallel Particle Swarm Optimization (PSO) [29–31], parallel Ant Colony Optimization (ACO) [32,33], parallel Cat Swarm Optimization (CSO) [34–36], and so on. Compared with the original algorithms, the parallel strategy improves their optimization ability in solving the problem. Inspired by the idea, a parallel EO algorithm, named PEO, is proposed in this paper. In PEO, two different communication strategies are used to ameliorate the exploitation and search ability of the algorithm. The superiority of PEO is proved by the comparison between PEO and several heuristic algorithms on benchmark functions.
To test the ability of PEO in solving practical problems, the Capacitated Vehicle Routing Problem (CVRP) is treated as an application example of PEO. At present, many scholars have done a lot of research in the field of intelligent transportation information [37–39]. As one of the core issues, the Vehicle Routing Problem (VRP) was first put forward in 1959. Some non-meta-heuristic algorithms, such as the Tabu Search (TS) algorithm [40,41] and Simulated Annealing (SA) algorithm, have been well applied to solve VRP. As the development of meta-heuristic algorithms, like PSO and Sine Cosine Algorithm (SCA) [42], they have also provided better solutions to VRP. The vehicle routing problem is generally depicted as follows: several cities have different demands for goods, and the distribution center provides vehicles to the city to transport goods. Each time the vehicle departs from the distribution center, it transports the goods to the unallocated cities, and finally returns to the distribution center. As a derivative problem of the VRP, the CVRP needs to meet an important constraint: the load weight of each vehicle cannot exceed the maximum load. The contributions of PEO in CVRP are as follows. Firstly, the parallel improvement strategy improves the exploitation and search abilities of EO. Secondly, as far as we know, EO is applied to CVRP for the first time, which broadens the application field of EO in intelligent transportation.
The rest of this paper is organized as follows. Section 2 gives a brief retrospect to the basic concept of EO. Section 3 formally proposes our PEO algorithm with details. Section 4 evaluates the algorithm using extensive experiments. Further application analysis of the proposed PEO algorithm in the CVRP is demonstrated in Section 5. The last section describes the conclusions about the presented work.
In EO, each particle (solution) and its position (concentration) are used as a search agent. During the iteration process, the search agent randomly updates its current position (concentration) according to the equilibrium candidates until the end of the iteration to get the optimal result (equilibrium state). The initialization of EO is similar to the general meta-heuristic algorithm. The initial population consists of randomly distributed particles in the search space, as shown in Eq. (1):
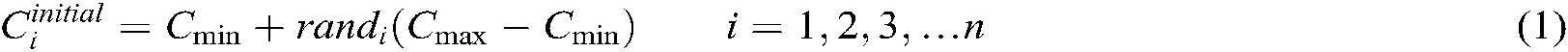
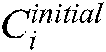 is the initial concentration (position) vector of the
is the initial concentration (position) vector of the 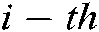 particle,
particle,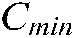 is the minimum dimension,
is the minimum dimension,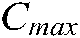 is the maximum dimension,
is the maximum dimension, 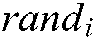 is a random vector in the interval of [0,1], and
is a random vector in the interval of [0,1], and 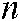 is the whole number of particles.
is the whole number of particles.
The EO expects the final equilibrium state to be globally optimum. To heighten the capabilities of exploration and exploitation, an equilibrium pool is established in EO to update the particles. The five particles in the equilibrium pool are called equilibrium candidates. These five particles are the four particles with the best fitness and their average. The four best candidates are beneficial to improve the exploration ability and their average is beneficial to heighten the exploitation ability. Besides, the number of equilibrium candidates is not fixed and can be adjusted for different application problems, which is similar to the selection of three wolves in GWO [43]. The equilibrium pool vector can be expressed as:
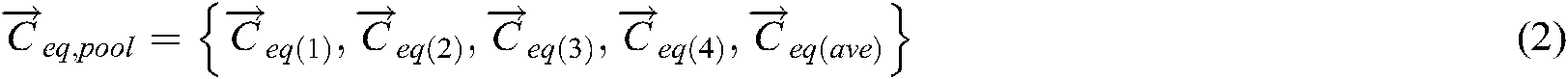
To maintain a balance between exploration and exploitation, the parameter 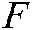 is introduced, and the calculation equation is as follows:
is introduced, and the calculation equation is as follows:

In Eq. (3), the calculation equation of the iterative function 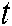 is as follows:
is as follows:

 means the current number of iterations,
means the current number of iterations, 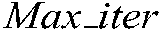 is the maximum number of iterations, and
is the maximum number of iterations, and 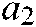 is a constant with a value of 1.
is a constant with a value of 1. 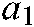 is equal to 2. It should be noted that the values of
is equal to 2. It should be noted that the values of 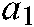 and
and 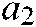 are not fixed to 2 and 1, which can be adjusted according to the problem to be solved.
are not fixed to 2 and 1, which can be adjusted according to the problem to be solved.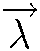 and
and 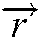 are random vectors in the interval of [0,1].
are random vectors in the interval of [0,1].
The parameter  is introduced into EO to improve the exact solution in the exploitation stage.
is introduced into EO to improve the exact solution in the exploitation stage.  is expressed by the following equation:
is expressed by the following equation:

where:


In Eq. (7), 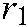 and
and 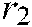 are two random numbers in [0,1], and the parameter
are two random numbers in [0,1], and the parameter 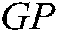 is the generation probability. Experiments show that when the value of
is the generation probability. Experiments show that when the value of  is 0.5, the algorithm can keep a good balance between exploration and exploitation. Finally, the update equation of EO is as follows:
is 0.5, the algorithm can keep a good balance between exploration and exploitation. Finally, the update equation of EO is as follows:
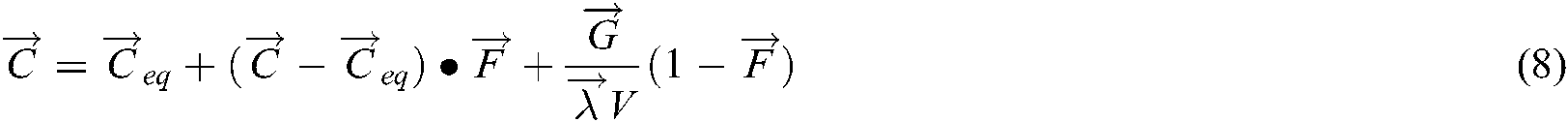
In the Eq. (8),  represents the particle to be updated. The first part
represents the particle to be updated. The first part 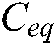 on the right side of the equation is an equilibrium candidate particle obtained in the equilibrium pool. The second and third terms represent a change in the concentration of particles in the population. The second term attempts to find an optimal solution in the solution space, and the third term helps to make the solution more accurate. During the iteration process, each particle is updated through an updated equation to improve the adaptability of the particle and the overall optimization ability of the algorithm.
on the right side of the equation is an equilibrium candidate particle obtained in the equilibrium pool. The second and third terms represent a change in the concentration of particles in the population. The second term attempts to find an optimal solution in the solution space, and the third term helps to make the solution more accurate. During the iteration process, each particle is updated through an updated equation to improve the adaptability of the particle and the overall optimization ability of the algorithm.
3 Parallel Equilibrium Optimizer
In this section, we propose a parallel Equilibrium Optimizer algorithm, named PEO, to improve the optimization capability of EO. In PEO, a multi-group structure is adopted, and each group search strategy is consistent with the original EO. Regularly, particles from different groups communicate with each other to increase cooperation among groups. Two communication strategies are used in PEO. The first strategy of inter-group communication is used for individual mutation of poor particles, which can heighten the convergence speed of the algorithm. The second strategy is to replace the poor particles in each group, which can ameliorate the exploitation capacity of the algorithm. The two strategies are respectively applied in the early and late stages of the algorithm to further improve the convergence results. Besides, the 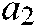 , as an important parameter, affects the exploitation capability of the algorithm. Therefore, the parameter
, as an important parameter, affects the exploitation capability of the algorithm. Therefore, the parameter 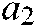 is micro adjusted according to the number of iterations to better heighten the search capacity of the algorithm in the exploitation stage on the parallel mechanism. The evaluation equation of
is micro adjusted according to the number of iterations to better heighten the search capacity of the algorithm in the exploitation stage on the parallel mechanism. The evaluation equation of 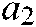 is as follows:
is as follows:

In the initialization phase, the groups are divided according to the predetermined total number of particles. In each group, the fitness values of all particles are calculated and sorted, to get the optimal solution and four equilibrium candidates in the group. Comparing all groups, we can get the global optimal solution  of the entire population and four global optimal equilibrium candidates
of the entire population and four global optimal equilibrium candidates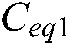 ,
, 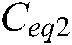 ,
, 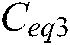 , and
, and 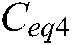 . After that, each group evolves independently. When a certain number of iterations are performed, the above two strategies will be executed to communicate between groups. Concerning the PEO of this paper, the number of groups is set to 6, and the number of communication iteration intervals is set to 20.
. After that, each group evolves independently. When a certain number of iterations are performed, the above two strategies will be executed to communicate between groups. Concerning the PEO of this paper, the number of groups is set to 6, and the number of communication iteration intervals is set to 20.
The first inter-group communication strategy is shown in Fig. 1. In the first 1/3 of the total iteration times, a global optimal equilibrium candidate particle 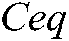 is randomly selected and combined with the global optimal particle
is randomly selected and combined with the global optimal particle . According to Eq. (10), individual mutations are performed on the particles with poor fitness in each group. Through this strategy, the mutant particles quickly approach the average position of the equilibrium candidate
. According to Eq. (10), individual mutations are performed on the particles with poor fitness in each group. Through this strategy, the mutant particles quickly approach the average position of the equilibrium candidate 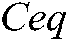 and the optimal particle
and the optimal particle , which further improves the convergence speed of the algorithm. The mutation equation is as follow:
, which further improves the convergence speed of the algorithm. The mutation equation is as follow:

where 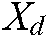 and
and 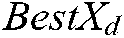 are the
are the 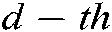 dimensions of the mutated particle and global optimal particle.
dimensions of the mutated particle and global optimal particle. 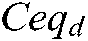 represents the d-dimensional position of the equilibrium candidate particle.
represents the d-dimensional position of the equilibrium candidate particle. 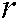 is a random vector between 0 and 1. The value of
is a random vector between 0 and 1. The value of 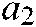 is determined by Eq. (9).
is determined by Eq. (9).
The second inter-group communication strategy is shown in Fig. 2. In the last 2/3 of the whole number of iterations, some particles with poor fitness will be replaced by the average of the optimal particles in this group and the adjacent groups. For example, the average of the optimal particles in the first group and the second group is used to replace the particles with poor fitness in the first group. Repeat this operation until some poor fitness particles in all groups are replaced. This strategy makes the communication between groups more closely, and improves the exploitation ability of the algorithm in the middle and late stages. This operation effectively avoids the premature convergence of the algorithm. In this paper, the number of mutation particles and substitute particles is half of each group. And during the iteration process, the particles are updated according to the structure of EO, regardless of whether component communication has occurred. The particle update equation is shown in Section 2. Figs. 3 and 4 represent the flow chart and pseudo-code of PEO, respectively.
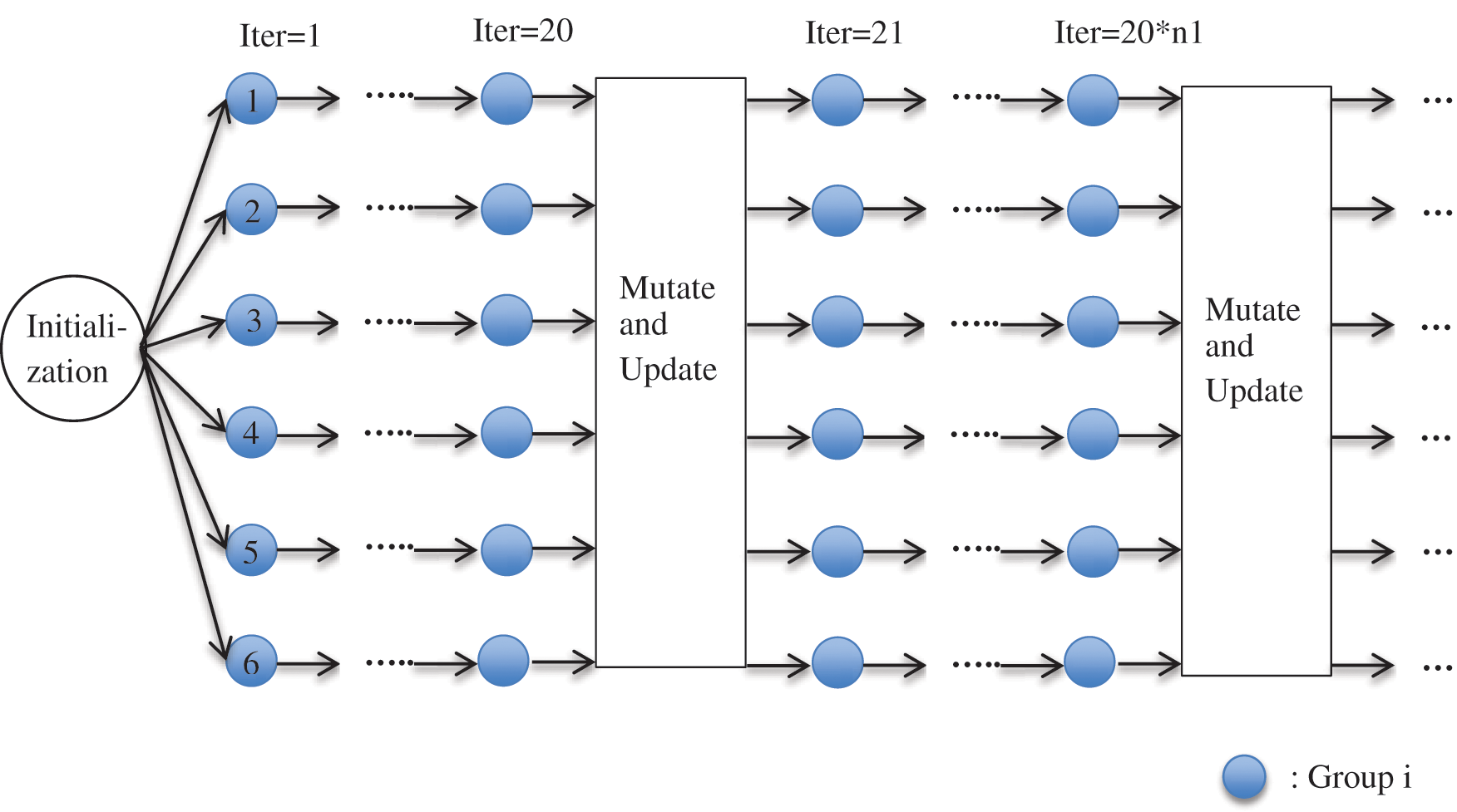
Figure 1: Communication strategy 1

Figure 2: Communication strategy 2
To check the optimization effectiveness of PEO, we test it on 23 benchmark functions and compare it with the PSO, PPSO, GWO, and EO algorithms as well. Among the 23 benchmark functions, F1~F7 represent unimodal functions, F8~F13 represent multimodal functions, and F14~F23 represent fixed-dimensional functions. The detailed description of these functions can be obtained from [21,43]. To make the experiment fair and reasonable, the maximum iteration number of all algorithms is uniformly set as 2000, and the population size is set as 180. Each algorithm is run 10 times independently, and its average (AVG) and standard deviation (STD) are recorded. All simulation experiments are completed in the same experimental environment. The parameter values of the five algorithms are displayed in Tab. 1:
Table 1: The parameter values of five algorithms

Tab. 2 shows the test results of PEO and the other four meta-heuristic algorithms on 23 benchmark functions. The bolded data represents the best average accuracy value of the five algorithms.
Table 2: Results of comparison for the benchmark functions

It can be known from the bold data in Tab. 2 that PEO can obtain the optimal value of the five algorithms on most benchmark functions. This shows that PEO generally has better optimization ability than PSO, PPSO, GWO, and EO algorithms on the whole. In addition, the standard deviation of PEO is generally small, which indicates that the algorithm has better robustness. For the unimodal functions, PEO displays a better global optimal solution than other algorithms on the functions of F1~F5 and F7, followed by EO. On the function F6, EO performs better. The test results on unimodal functions show that the structure of EO makes its convergence value better than other algorithms. Moreover, the parallel mechanism further improves the convergence effect of EO, which makes PEO perform better on most unimodal functions. For multimodal functions, PEO has a slight advantage over the other four algorithms with respect to optimization ability on functions F8~F10. On functions F11~F13, PSO represents a good convergence effect. But the convergence value of PEO is close to the optimal value of PSO on the function F12. This part of the test data shows that compared with EO, PEO uses the strategy of group communication, which to some extent enhances the ability of the algorithm to jump out of the local optimal solution in multivalued functions. For fixed-dimensional functions F14~F23, PEO can be better than or equal to the convergence results of the other four algorithms. According to the data statistics in Tab. 2, PEO can achieve the best average accuracy on 19 functions, while the corresponding numbers of PSO, PPSO, GWO, and EO algorithms are 9, 10, 8, and 11 in turn. To a certain degree, the results in Tab. 2 also prove the effectiveness of the parallel mechanism in improving algorithm optimization capabilities.

Figure 3: Flow chart of parallel equilibrium optimizer

Figure 4: Pseudo-code of parallel equilibrium optimizer
To more intuitively observe the experimental results of the five algorithms, 6 groups are selected from 23 groups of experimental graphs to display. Fig. 5 displays the resulting chart of the five algorithms on the unimodal functions F1 and F3, the multimodal functions F8 and F10, and the fixed-dimensional functions F15 and F22. It can be seen from Fig. 5 that compared to other algorithms, PEO has a faster convergence speed. In the result diagram, the test functions image is on the left, and the algorithm convergence curve is on the right. In the algorithm convergence curve, the x-coordinate is the number of iterations, and the y-coordinate represents the functions convergence value.

Figure 5: Convergence curve of test functions: F1 (a), F3 (b), F8 (c), F10 (d), F15 (e), F22 (f)
5 PEO Algorithm on the Capacitated Vehicle Routing Problem
In this section, we introduce the mathematical model of the Capacitated Vehicle Routing Problem (CVRP) and test the proposed PEO algorithm on the CVRP.
In this paper, the parameter 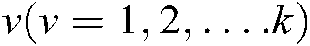 is used to represent the vehicle number, and the parameter
is used to represent the vehicle number, and the parameter 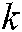 represents the total number of vehicles. The distribution center and task city are respectively represented by 0 and
represents the total number of vehicles. The distribution center and task city are respectively represented by 0 and 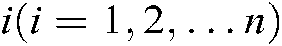 . The variables are defined as follows:
. The variables are defined as follows:
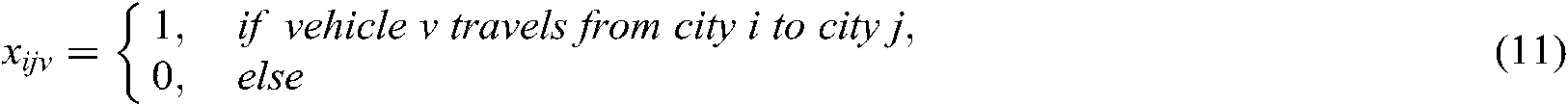
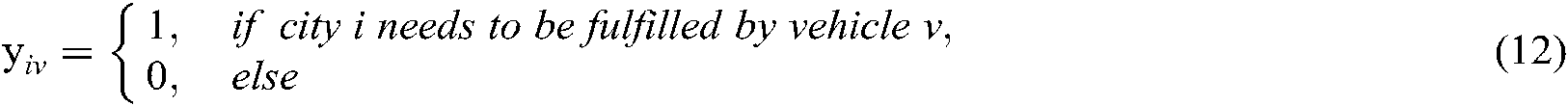
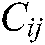 means the distance traveled from city point
means the distance traveled from city point 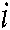 to city point
to city point 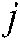 ,
, 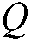 represents the maximum load of the car,
represents the maximum load of the car, 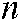 is the total number of city points,
is the total number of city points, 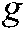 represents the demand for each city point, the distance traveled of the vehicle is represented by
represents the demand for each city point, the distance traveled of the vehicle is represented by 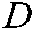 , and the solution of the shortest path
, and the solution of the shortest path 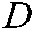 is set as the objective function. Finally, the mathematical model of the CVRP can be obtained as shows:
is set as the objective function. Finally, the mathematical model of the CVRP can be obtained as shows:

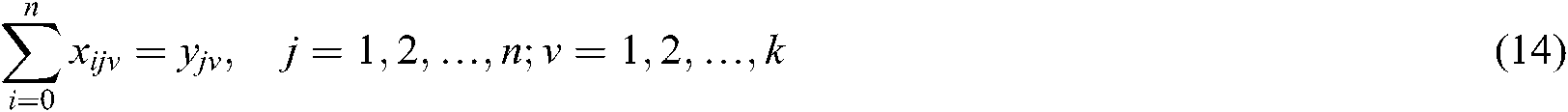
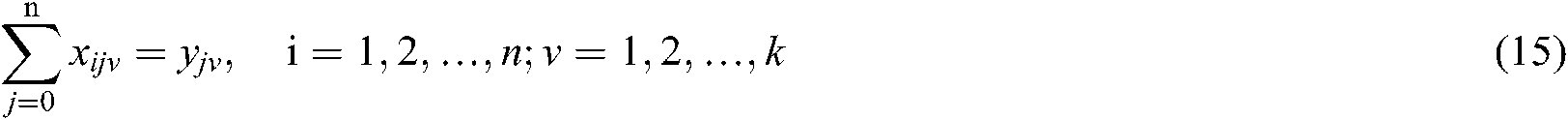


In the mathematical model of the CVRP, Eq. (13) means the shortest path of the objective function. Eqs. (14) and (15) ensure that the task of the city point can be completed. Eq. (16) guarantees that each city point can only be completed by one vehicle. Eq. (17) guarantees that the loading weight of each vehicle must not outnumber the maximum loading capacity, which is the most important constraint condition of the CVRP.
5.2 Simulation and Results Analysis
Firstly, a set of simple data is used to test. The task point coordinate and demand are shown in Tab. 3:
Table 3: The task point coordinates and demand

In this set of simple test cases, 0 is the central warehouse, the maximum load of the car is set to 100, the task distribution is completed by 3 cars, and the known optimal path is 217.8. In the test, the number of iterations is 200, and the particle swarm size is 180, divided into 6 groups. The test result of PEO reveals in Fig. 6. As can be seen from the Fig. 6, it receives the optimal path 217.8 when PEO iterates to the fifth generation. The results show that PEO has the certain optimization ability in solving VRP.

Figure 6: The test result of the PEO algorithm under simple test data
To further test the effect of PEO in the CVRP, we select five groups of test data in the CVRP international standard example VRPLIB and compare the results with EO, MMSCA [44], and PSO algorithms. In this paper, to ensure the fairness of results, the number of iterations for the four algorithms is uniformly set as 3000, and the number of population particles is 180. Tab. 4 records the results of the four algorithms on 5 sets of test data.
Table 4: The result of four algorithms in five test data

Analyzing the data in the Tab. 4, PEO can get a shorter distance than PSO, EO, and MMSCA algorithms on the CVRP under the same experimental conditions. To observe the test results of the four algorithms more intuitively, Fig. 7 shows the change curve of the four algorithms on the CVRP test data A-k32-n5 and A-k33-n6. It can be seen from the Fig. 7 that PEO has a better convergence value than the other three algorithms, yet the convergence speed in the early stage of the iteration is not as fast as other algorithms. Therefore, there is still a lot of room for improvement in the optimization of PEO on the CVRP problem, which can be regarded as the future optimization direction.
In this paper, we developed a parallel paradigm for the EO algorithm, called PEO. Two efficient communication strategies are designed and applied to the set of groups in PEO. Experiments show that our approach outperforms existing approaches in most of 23 benchmark functions. Furthermore, applying the PEO algorithm on CVRP can get a shorter distance than PSO, EO, and MMSCA algorithms, which further testify the effectiveness and superiority of the proposed PEO algorithm.

Figure 7: Convergence curves of A-k32-n5 (a) and A-k33-n6 (b)
Funding Statement: This work is supported by the National Natural Science Foundation of China [Grant No. 61872085], the Natural Science Foundation of Fujian Province [Grant No.2018J01638], and the Fujian Provincial Department of Science and Technology [Grant No. 2018Y3001]. The author who received the grant is J.S. Pan.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
 | This work is licensed under a Creative Commons Attribution 4.0 International License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. |