A Novel Belief Rule-Based Fault Diagnosis Method with Interpretability

1  Introduction

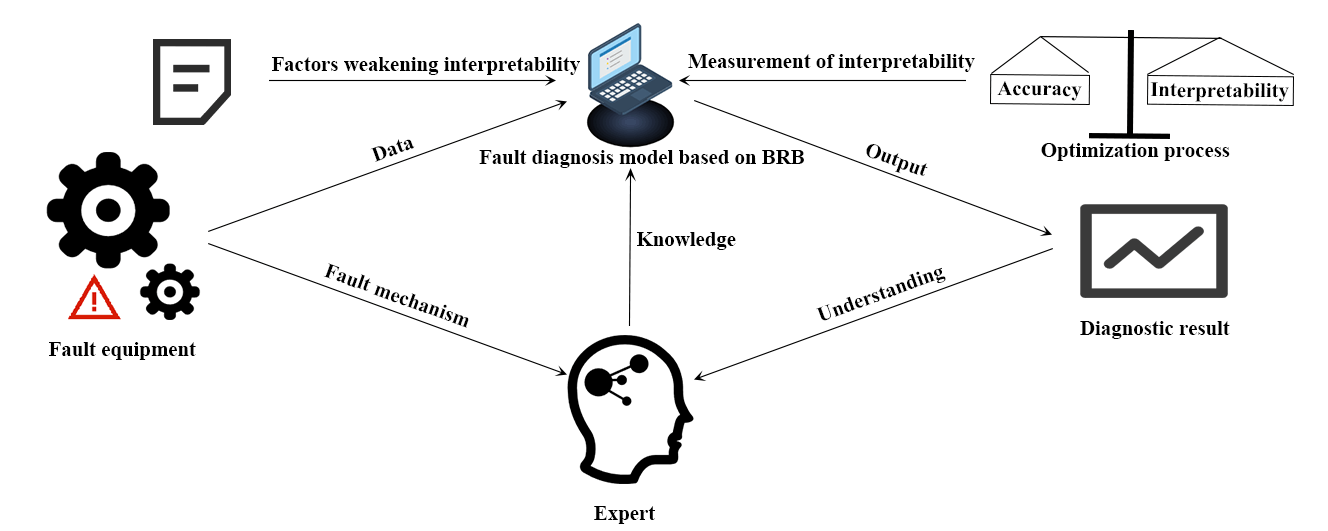
As an effective measure, the fault diagnosis has drawn wide attention to avoid accidents of complex aerospace systems. It is prominent to establish an interpretable and transparent fault diagnosis model for crucial equipment. In this paper, the interpretability of a model indicates that the establishment, reasoning and optimization of the model can be understood by humans, and the diagnostic result is consistent with the cognition of experts. The interpretability of fault diagnosis models can be divided into two classes: post-hoc interpretability and ante-hoc interpretability [1]. The post-hoc interpretability is to establish another model to explain the first black-box model with complex parameters. Sometimes, the explanation of a black-box model is problematic or misleading. The ante-hoc interpretability means that a transparent model is established in an easy-to-understand way, which is inherently interpretable. Accordingly, Rudin [2] pointed out that an interpretable model should be established instead of explaining the black-box model. In this paper, an inherently interpretable model based on the belief rule base (BRB) is established for fault diagnosis.

BRB was proposed by Yang et al. [3], dating back to 2006. BRB is an interpretable expert system with comprehensible knowledge representation and a transparent reasoning process. The rule form of “If-then” is in accordance with the logical rules of human thinking. Belief rules are constructed by experts according to their experience or the fault mechanism of the system, which is considered as the knowledge base. In addition, as the reasoning engine, the evidential reasoning (ER) approach is a generalized form of the traditional Bayesian inference rule [4], which is transparent. The result fused by the ER approach is credible. Thus, the belief rules are consistent with the cognition of experts, and the reasoning process is transparent. Consequently, interpretability is one of the excellent characteristics of BRB. Presently, relevant research on the interpretability of BRB can be found in [5,6]. There is a widespread application of BRB in fields requiring high interpretability, such as the safety and risk assessment [7,8], medical diagnosis [9,10] and fault diagnosis [11,12] during almost two decades. Due to the participation of humans in the modeling process, it is inevitable to bring the subjectivity of experts into the model. To reduce the error caused by subjectivity, an optimization algorithm is employed to update the parameters. However, Zhou et al. [13] found that the interpretability of BRB may be weakened in the optimization process. The optimized rules may be inconsistent with the initial judgment of experts.

There is enormous research on the intelligent optimization of BRB. Yang et al. [14] exploited the differential evolution (DE) algorithm to optimize parameters of BRB on the basis of determining the model structure. Zhang et al. [15] improved the covariance matrix adaption evolution strategy (CMA-ES) optimization algorithm with projection operation and obtained high model accuracy. Also, in addition to evolutionary algorithms, swarm optimization algorithms can be applied to optimize parameters of BRB, such as particle swarm optimization (PSO) algorithm [16], grasshopper optimization algorithm (GOA) [17], bird swarm algorithm (BSA) [18], etc. The common goal of the abovementioned optimization algorithms is to improve the accuracy of the model without considering the interpretability. Through comparisons, it is found that the rules are fine-tuned by the optimization algorithm based on the gradient information, which means the consistencies of initial and optimized rules are strong. For example, Wu et al. [19] proposed the accelerating of gradient algorithm to optimize the initial BRB. Feng et al. [20] proposed a new optimization method based on the method of feasible direction to improve the accuracy of the BRB-based model on the premise of ensuring the modeling transparency and traceability. In fact, the optimization for BRB is a process of solving a nonconvex optimization problem [21]. It is unreasonable to ignore the nonconvex property of BRB as done in the previous works mentioned above. Moreover, it is hard to obtain the gradient information of the complicated objective function formed in the BRB-based fault diagnosis.

To establish an interpretable fault diagnosis model, it is essential to study the interpretability and optimization of BRB. In this paper, for the BRB-based fault diagnosis, the factors for weakening interpretability are analyzed according to the subjective understanding and numerical cases. Deviation from the initial judgement of experts and over-optimization of parameters are the main factors responsible for destroying the interpretability of the model in the optimization. Based on this, three indexes, namely the consistency index of rules, consistency index of the rule base and over-optimization index, are proposed for measuring the interpretability of the optimized model. The consistency index of rules and consistency index of the rule base are utilized to estimate the degree to which the optimized model deviates from the initial judgment of experts. Whether any over-optimization of parameters has occurred is determined by over-optimization index. To consider the accuracy and interpretability of the BRB-based fault diagnosis model simultaneously in the optimization, an improved coordinate ascent (I-CA) optimization algorithm is proposed. The multivariable optimization can be decomposed into multiple univariate optimizations by I-CA. The one-dimensional search algorithm combined with the advance and retreat method and the golden section method is used to replace the operation of solving the gradient information. In addition, due to the nonconvex property of BRB, the random optimization sequence and an adaptive step size are added to I-CA to jump from local optimization solutions as much as possible. Finally, a case of the relay fault diagnosis is conducted to apply the proposed method.

The remainder of this paper is organized as follows. In Section 2, relevant problems of BRB for interpretable fault diagnosis are discussed. In Section 3, the weakening of interpretability for the BRB-based fault diagnosis model in optimization is analyzed, and three indexes are proposed to measure the interpretability of the optimized model. In Section 4, the reasoning process of the fault diagnosis model based on BRB is presented, and an improved coordinate ascent algorithm is proposed to optimize the parameters. The effectiveness of the proposed method is examined in Section 5 through a case study of the relay fault diagnosis. Finally, this paper is concluded in Section 6.

2  Problem Formulation

The BRB-based fault diagnosis model is transparent, which can describe the relationship between fault features x1,x2,…,xM and fault modes D1,D2,…,DN by belief rules. A complete knowledge expression system is contained in BRB. Various types of input information are converted into the belief distribution of fault feature referential grades A1k,A2k,…,AMk(k=1,2,…,K), respectively. The consequent of a belief rule is presented as the belief distribution of fault modes, namely β^1,k,β^2,k,…,β^N,k. The kth rule can be expressed as follows:

Rk:If (x1 is A1k)∧(x2 is A2k)∧⋯∧(xM is AMk), then {(D1,β^1,k),(D2,β^2,k),…,(DN,β^N,k)}with the rule weight θkand fault feature weights δ1,δ2,…,δM(1)

where θk denotes the rule weight of Rk relative to other rules. Similarly, δi is the fault feature weight of xi, and ∧ represents the “AND” logical relationship. The expert knowledge is imbued into the rule base by means of belief rules with the form of “If-then”. The fault knowledge is a key element of the interpretability of BRB. Due to the update of parameters, the implication of rules may be altered in optimization. The optimized rules can not be grasped by experts, which weakens the model’s interpretability. For instance, Chen et al. [22] conducted the case study of fault diagnosis in rolling bearing, where the skewness (x1), mean (x2) and kurtosis (x3) of vibration signals were selected as fault features. The states of Normal (N), Roller fault (R), Inner ring fault (I) and Outer ring fault (O) were regarded as the outcomes of a rule. The partial rules are shown in Table 1, including the initial and optimized rules. The antecedent of a rule is the referential grades of three fault features. The belief degrees of four-fault modes are regarded as the consequence of a rule. Obviously, there is considerable variation between the initial and optimized rules. Generally, the fault mode corresponding to the maximum belief degree is the diagnostic result, which is marked in bold in Table 1. The results of the 2nd–5th rules are inconsistent in the initial and optimized BRB. Although the accuracy of the model was effectively enhanced, the interpretability of BRB was weakened in this optimization.

According to the above, there are some drawbacks with the interpretable fault diagnosis model based on BRB. The accuracy and interpretability of a model are a pair of conflicting performances [23]. It is apparent that the interpretability of the BRB-based fault diagnosis model may be weakened more or less in optimization. However, the accuracy of a model is the unique goal of most current optimization algorithms. To obtain more reliable diagnostic results, the interpretability should be attached significance to fault diagnosis based on BRB. Therefore, this paper focuses on the following problems:

Problem 1: The interpretability of a BRB-based fault diagnosis model may be weakened in optimization. The major influencing factors that weaken the model interpretability should be analyzed. For these factors, the metrics should be put forward to measure the interpretability of the optimized model.

Problem 2: According to the major factors, a new optimization algorithm should be developed for maintaining the trade-off between the accuracy and interpretability of a model.

3  New Measurement Method of Interpretability for BRB-Based Fault Diagnosis Model

In this section, the factors which weaken the interpretability of a BRB-based fault diagnosis model are summarized and illustrated with the help of examples. Afterwards, three indexes are proposed for measuring the retention degree of interpretability.

3.1 Analysis of Interpretability Weakening Factors

With the update of parameters, the interpretability of the model may be lost. In this subsection, the weakening factors are presented from the perspective of humans’ understanding of rules and the basis of parameter optimization. The loss of interpretability is attributed to two aspects, i.e., deviation from the initial judgement of experts and over-optimization of parameters.

1)   Deviation from the initial judgement of experts

The parameters of the initial BRB are assigned by experts so that the belief rules can be grasped by humans. However, due to the change in the rule base, the optimized belief rules may be troublesomely apprehended, and the diagnostic result may become unconvincing. For example, from the case in Section 2, it can be intuitively concluded that the optimized rules deviate from the initial judgement of experts. This deviation is reflected in two aspects. On the one hand, the results of multiple rules vary from those of initial rules. On the other hand, most parameters have been updated in a great measure. The update of some parameters may be unnecessary, and the interpretability of the model may be weakened. In essence, there is a large difference between the initial and optimized BRB, which causes the deviation from the initial judgement of experts. The cause is expressed in a straightforward manner with the help of the following simple example.

Example 1: There is an optimization problem whose objective function is expressed by (2). The functional relationship between z and x, y is described as the surface of the barrel as shown in Fig. 1 where A is the initial point, and the plane z=z∗ in feasible domain is the optimal solution domain. It can be seen that the different optimal solutions can be obtained along the paths from A to B and A to C. Still the number of updated parameters in path P1 is smaller than that in path P2. Also, in P1, the optimal solution is sought by the principle of being as close to the initial point as possible. More specifically, the gradient of z at point A is ∇f(x0,y0)=(∂f/∂x0,∂f/∂y0) where ∂f/∂x0=0 and ∂f/∂y0≠0 can be analyzed from Fig. 1. The optimal solution can be obtained by merely updating the value of y.

minz=f(x,y)(2)

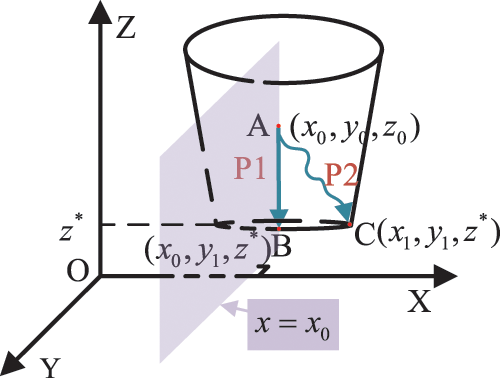
Figure 1: Feasible domain of Example 1

In fault diagnosis, the value of the objective function is calculated by determining the number of fault samples diagnosed correctly or incorrectly. The optimization process is to correct the previous incorrect diagnostic results by updating parameters as shown in Fig. 2. Thus, the parameters related to incorrect diagnostic results should be optimized rather than all parameters. For instance, the updating of the value of y may improve the value of the objective function in Example 1. Although point C is one of the optimal points of f, there is no need to update the value of variable x. The initial values (x0,y0,z0) given by experts are of practical significance in fault diagnosis based on BRB. Optimization of the value of y is based on the change in the objective function value. The updating value of x may result from some kinds of distribution in intelligent optimization algorithms, which is of little significance for the result. However, if the interpretability is taken into account in optimization, the change in the value of x will weaken the interpretability of the model.

Figure 2: Optimization process in fault diagnosis

2)   Over-optimization of parameters

The existing fault features and fault modes of equipment are included in the fault diagnosis model based on BRB, which means that the rule base is complete. A diagnostic result can be obtained when a working sample is given. The partial states of equipment may be contained in the limited fault samples. In other words, in optimization, some belief rules may be activated repeatedly, and others may not be activated even once. The unactivated rules have not participated in the fusion process. In some optimization algorithms, the parameters of unactivated rules are optimized without basis, which means the occurrence of over-optimization of parameters. In this way, the diagnostic results are made untrustworthy. The irrationality of over-optimization of parameters is illustrated in the following example.

Example 2: The objective function is expressed by (2). The plot of f(x,y) is shown in Fig. 3 where D is the initial point located in y=y0 plane, E is the optimal point, and f is the function about x and y. In effect, f is a curve distributed in the X−Z plane. The gradient of f at the point D can be obtained as ∇f(x0,y0)=(∂f/∂x0,∂f/∂y0). ∂f/∂x0≠0 and ∂f/∂y0=0 can be analyzed from Fig. 3. The optimal point E can be searched by applying a suitable optimization algorithm. However, if the population is generated according to a certain distribution, the plane of feasible region may be changed from y=y0 to y=y1, and F may be regarded as the final result. Although the values of the objective function are the same at points E and F, this change in the feasible region cannot improve the value of the objective function. It is clear that the update of y is meaningless. In the context of fault diagnosis based on BRB, y=y0 is determined by the initial judgement of experts, which is credible. However, the trust between humans and the model is weakened by the change in the feasible region without basis, in which the parameter y is over-optimized. It can be seen from this example that finding out the unactivated rules is conducive for reducing the dimension of the objective function and enhancing the efficiency of optimization.

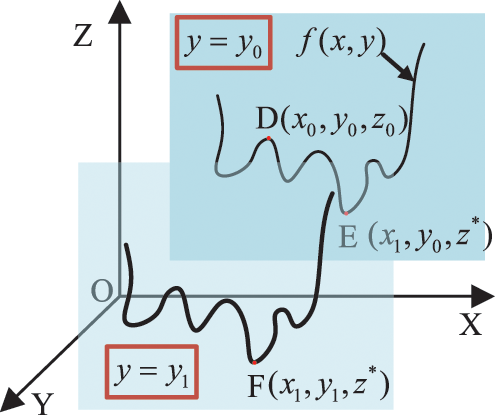
Figure 3: Function of example 2

3.2 Indexes for Measuring Interpretability

According to the factors and influence of weakening interpretability, the measurement of the optimized model’s interpretability is conducted in this subsection. Based on the above analysis, three indexes are proposed for measuring the loss degree of the model interpretability. The overall difference of rule bases and the individual difference of rules in the initial BRB and optimized BRB can describe the degree of the deviation from the experts’ initial judgement in the optimized model. In this connection, two indexes, i.e., consistency index of rules (CIR) and consistency index of the rule base (CIRB), are proposed to represent the degree of deviation. The difference between the initial and optimized parameters in the unactivated rules is calculated as the over-optimization index (OI) to determine whether there is any occurrence of over-optimization. These three indexes are expounded below.

Index 1: Consistency index of rules

In the fault diagnosis model based on BRB, the fault mode corresponding to the maximum of the belief degrees in output is regarded as the diagnostic result. Based on this, the consistency between the initial and optimized rules is studied to reflect the loss degree of the model’s interpretability. CIR is proposed to measure whether the rules in the optimized rule base maintain consistency with the expert’s initial judgement. The specific calculation is as follows:

β^j,i=max{β^1,i,β^2,i,…,β^N,i},β~n,i=max{β~1,i,β~2,i,…,β~N,i},i=1,2,…,K(3a)

Bi={1, if n=j0, Otherwise(3b)

CIR=∑i=1KBi/K,CIR∈[0,1](3c)

where β^o,m denotes the initial belief degree given by experts and β~o,m is the optimized belief degree. Eq. (3a) represents the belief degree corresponding to the output fault mode. If the output of the ith initial and optimized rules is consistent, then Bi=1. Otherwise, Bi=0. CIR can be calculated by using (3c). The larger the value of CIR is, the higher the consistency between the initial and optimized rules will be.

Index 2: Consistency index of the rule base

The consistency between the initial and optimized models is measured by CIR from the perspective of rules. From the perspective of the rule base, CIRB is proposed to measure the difference between the initial and optimized models, which is calculated by (4). The larger the value of CIRB, the smaller the difference, and the smaller degree of deviation from the initial judgement of experts.

CIRB=1−∑i=1K∑j=1N(β^j,i−β~j,i)2/(N×K),CIRB∈[0,1](4)

Index 3: Over-optimization index

The over-optimization is manifested in the parameters of unactivated rules. In other words, the parameters are over-optimized when those of unactivated rules are updated. OI is proposed to judge whether the over-optimization occurs. OI is calculated by using the following equations:

Wk={1,∃wki>0.0010, Otherwise(5a)

OI=∑p∑j=1N(β^j,p−β~j,p)2/(N×S),S=∑p(1+Wp),p∈{k|Wk=0},OI∈[0,1](5b)

where wki is the activation weight of the kth rule corresponding to the ith fault sample. Firstly, the unactivated rules are selected by introducing the activation factor Wk. A rule is not activated when wki≤0.001 [6]. In these rules, the Euclidean distance of the belief degrees is calculated as OI. The larger the value of OI, the greater degree of over-optimization. There is no over-optimization problem when OI=0.

4  Interpretable Fault Diagnosis Method Based on BRB

In this section, the reasoning process of the fault diagnosis model based on BRB is conducted first. Then, a new optimization algorithm is proposed based on the coordinate ascent algorithm by comprehensively considering the interpretability and non-convexity.

4.1 Reasoning Process

In the fault diagnosis based on BRB, the belief rules as in (1) can be given according to the expert knowledge or mechanism of the system. Based on this, the input information is transformed into matching degree to infer the diagnostic result through the reasoning process. There is no doubt that the error between the BRB model and the real system is inevitable due to human intervention. Hence, the optimization is applied to weaken the error caused by the subjectivity of experts. The reasoning process is as follows.

Step 1: Calculation of matching degree

Each fault feature possesses a specific dimension. In BRB, multiple referential values are assigned to fault features, respectively. The values of fault features are uniformly transformed into the belief distribution of referential values. For instance, transforming the value (ςi) of the ith fault feature into the belief distribution of ci the referential values are calculated as follows:

χi,j=Aij+1−ςiAij+1−Aij,Aij≤ςi≤Aij+1(6a)

χi,j+1=1−χi,j,i=1,2,…,M,j=1,2,…,ci−1(6b)

χi,s=0,s=1,2,…,ci,s≠j,j+1(6c)

where χi,j is the matching degree of the input of ith fault feature relative to its jth referential value.

Step 2: Calculation of activation weight

The input for a fault feature lies between two referential values only, which means that all rules are not activated in a reasoning process. The activation weight of the kth rule is calculated by the following equations:

δ¯i=δi/maxl=1,2,…,M{δl},i=1,2,…,M(7a)

ωk=θk×∏i=1M(χik)δ¯i/∑n=1Kθn∏i=1M(χin)δ¯i,χik∈{χi,j},j=1,…,ci(7b)

where is the normalized weight of the ith fault feature. In a reasoning process, at most 2M rules are activated, whose activation weights are greater than 0.

Step 3: ER fusion

The 2M activated rules are fused by the ER algorithm to generate the diagnostic result as shown below:

υ=∑j=1N∏k=12M(ωkβ^j,k+1−ωk∑i=1Nβ^i,k)−(N−1)∏k=12M(1−ωk∑i=1Nβ^i,k)(8a)

βj=∏k=12M(ωkβ^j,k+1−ωk∑i=1Nβ^i,k)−∏k=12M(1−ωk∑i=1Nβ^i,k)υ−∏k=12M(1−ωk)(8b)

where υ is an intermediate variable, and βj denotes the belief degree of occurrence of the jth fault mode

Dj. There is ∑i=1Nβj=1, which means that the uncertainty is not considered. Generally, the fault mode corresponding to the maximum belief degree is taken as the final output.

4.2 Optimization Based on Improved Coordinate Ascent Algorithm

To enhance the accuracy of the fault diagnosis model based on BRB, an appropriate optimization algorithm should be applied, and the objective function should be determined first. In this paper, the accuracy rate of a model is regarded as the objective function. The accuracy of the model is expected to be higher and higher during optimization. Meanwhile, the parameters, including the belief degrees of rules, fault feature weights and rule weights, should be kept within their bounds. The objective function can be expressed as follows:

maxF(Ψ)Ψ={β^1,1,β^2,1,…,β^N,K,δ1,δ2,…,δM,θ1,θ2,…,θK}s.t.0≤θk≤1,0≤δm≤1∑i=1Nβ^i,k=1,0≤β^i,k≤1k=1,2,…,K,m=1,2,…,M(9)

where F(⋅) is the accuracy rate of the BRB-based fault diagnosis model.

Based on the above analysis, an improved coordinate ascent (I-CA) algorithm is proposed for improving the accuracy of the model to avoid weakening the model interpretability as far as possible. The coordinate ascent (CA) is an effective method for transforming multivariable optimization problem into multiple univariate optimization problems. The optimization of each dimensional parameter is done based on the change of the objective function along a better direction. In other words, the parameters that cannot increase the value of the objective function are not updated. The interpretability is effectively maintained by this updating mechanism. Considering the non-convexity of BRB, CA is improved with a random optimization sequence and an adaptive step size. There is a challenge in obtaining the gradient information due to the complex form of the objective function. Hence, a one-dimensional search algorithm, as the search strategy of I-CA, is proposed by combining the advance and retreat method and golden section method. I-CA is presented below in detail.

Step 1: Initialization of model parameters

The initialized parameters are presented in Table 2.

The dimension of Ψ is 1×(M+K+N∗K). The set f−1=f0 is convenient for representing the update of the step size. Let i=0, and start optimization.

Step 2: Generation of random optimization sequence

To avoid the falling into local optimal solutions caused by the fixed optimization order, a random optimization sequence is generated. O[M+K+N∗K] represents the random optimization sequence from 1 to M+K+N∗K. Let i=i+1, j=1.

Step 3: One-dimensional search

The variable Ψi(O(j)) is optimized by a one-dimensional search algorithm as shown in Fig. 4. Ψi(O(j)) satisfies (10) after this optimization.

Ψi(O(j))=argmax f(Ψ(i−1)(1),Ψ(i−1)(2),…,Ψ(O(j)),…,Ψ(i−1)(M+K+N∗K))(10)

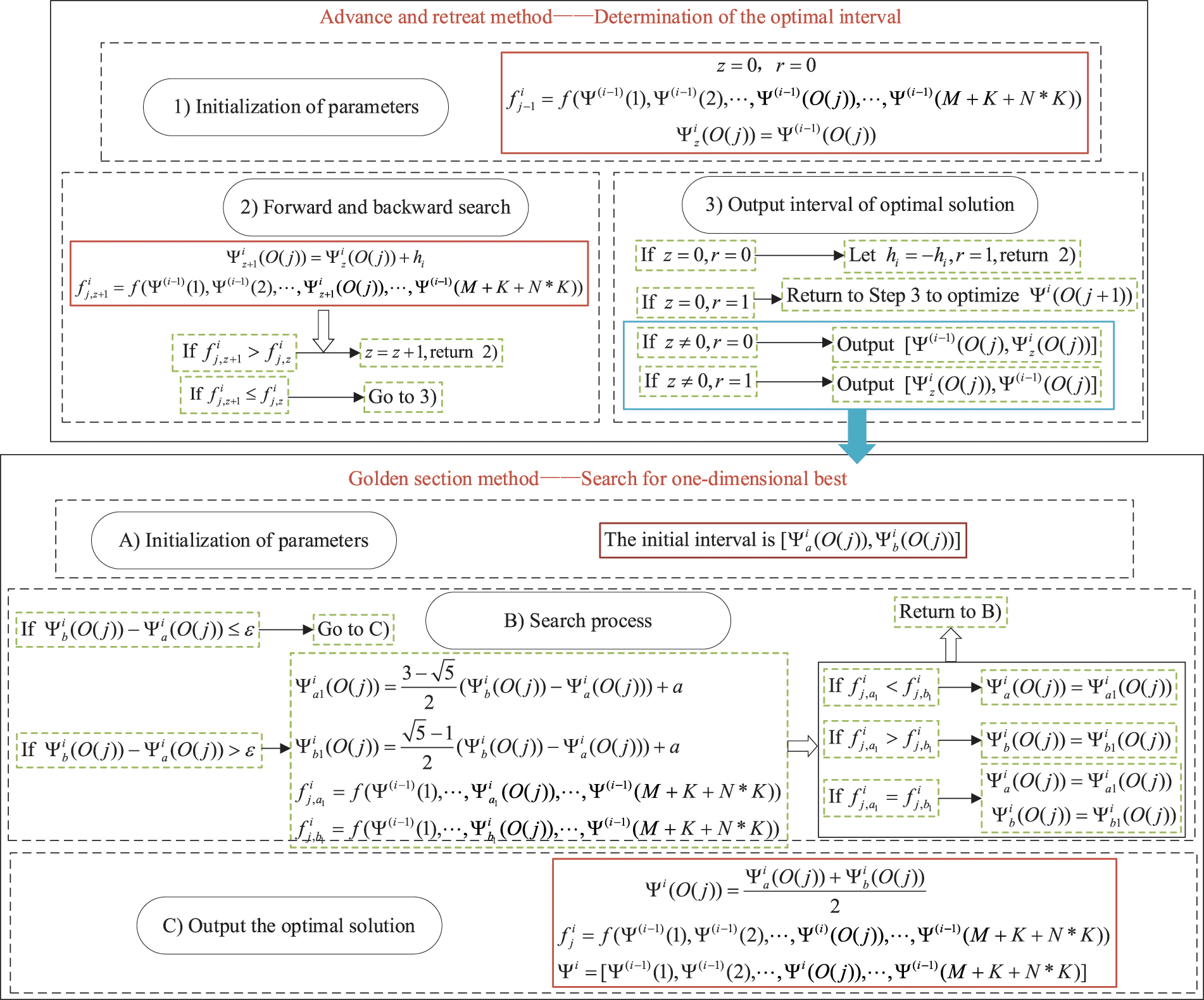
Figure 4: Process of one-dimensional search

Let j=j+1, and continue to update the next parameter. Repeat Step 3 until j>M+K+N∗K.

The advance and retreat method is utilized to find the approximate interval where the optimal solution of the one-dimensional variable is located. In this way, the rising direction of the objective function is found, and the search range is narrowed down. Subsequently, the location of the optimal solution is determined by applying the golden section method.

In Fig. 4, it is necessary to impose boundary constraints to fault feature weights, rule weights and belief degrees, and equality constraints to belief degrees. In the boundary constraint, when a parameter exceeds its threshold value, the parameter is set as the threshold value. The equality constraint conditions are satisfied by normalization.

Step 4: Update of adaptive step size

In this paper, for updating the search range based on the accuracy of the model, the set of hi is related to the value of the objective function, where hi is specifically calculated by (11).

γi=r1er2(fi−2−fi)(11a)

hi+1=γifi(11b)

The acceleration coefficient γi with stretch factor r1 and shrinkage factor r2 is proposed to update the step size based on the historical data. If the value of the objective function value is not changed after two optimization rounds, the step size increases suddenly due to the existence of r1. Based on this, the obtained solution may be able to escape from the local maximum. As the number of iterations increases, hi gets smaller caused by r2 to enhance the ability of the local search. The accuracy of the model can be effectively improved by reasonably selecting r1 and r2.

Step 5: Termination strategy

If i≤T, return to Step 2; otherwise exit optimization.

4.3 Process of Interpretable Fault Diagnosis Model Based on BRB

The modeling, reasoning and optimization of the interpretable BRB-based fault diagnosis model are shown in Fig. 5.

Figure 5: Interpretable fault diagnosis model based on BRB

Step 1: Establishment of initial fault diagnosis model

The existing fault modes are regarded as the outcomes of belief rules. The fault features are determined for using as the input of the model according to the correlation between them and fault modes. Then, the belief rules, reflecting the mapping relationship between the fault features and fault modes, are constructed by adopting the expert experience or fault mechanism of the system. The initial BRB-based fault diagnosis model is established in an understandable way.

Step 2: Reasoning process of fault diagnosis model

In accordance with the established model, the conversion from input to output is conducted in the reasoning process. Firstly, the input information is transformed into the matching degree of referential grades by (6). Then, the activation degree of the belief rule is obtained by calculating the activation weight shown as (7). Based on this, ER is introduced to generate the diagnostic results by fusing the activated rules, the specific calculation of which is shown in (8).

Step 3: Optimization of initial fault diagnosis model based on BRB

Based on the establishment and reasoning of the initial fault diagnosis model, the objective function is constructed, as shown in (9). To avoid the occurrence of factors that weaken the interpretability of the model as much as possible, I-CA optimization algorithm proposed in Subsection 4.2 is used to optimize the parameters of the initial model. The parameters are optimized one by one on the basis of fault samples. During the optimization, the trade-off between the interpretability and the accuracy of BRB-based fault diagnosis model is well adjusted.

Step 4: Measurement of interpretability for the optimized model

The three indexes proposed in Subsection 3.2 are used to measure the interpretability of the optimized model. The performance of the optimization algorithm in balancing interpretability and accuracy can be reflected in this way.

Step 5: Output diagnostic results

The BRB-based fault diagnosis model is constructed through the above process. The diagnostic result can be obtained when the information about the fault features is available at some point of time.

5  Case Study

As the critical switching element of a control circuit, the relay is significant for the reliability of the system [24]. In this paper, the fault diagnosis of the JZX-22F relay is carried out to validate the effectiveness of the proposed method.

5.1 Establishment of Initial BRB-Based Fault Diagnosis

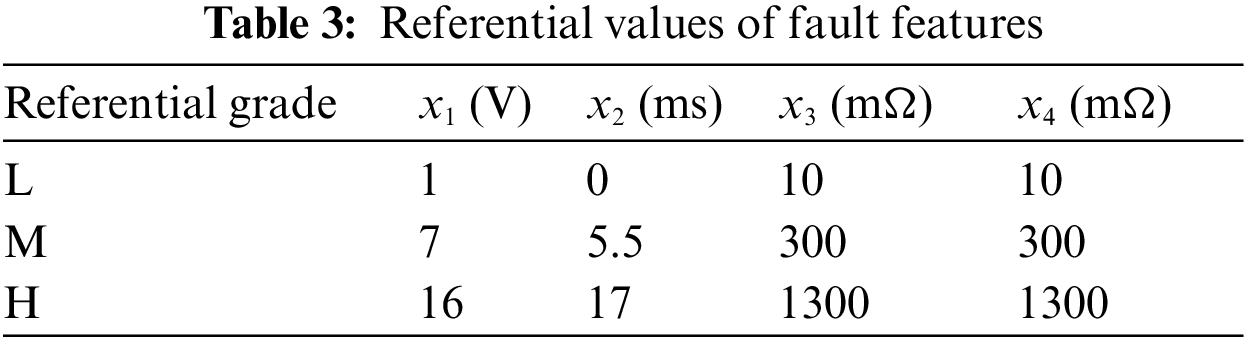
To acquire the samples for experiment, the operation of the fault injection for the relay is conducted. The fault modes, including the contact wear (CW, D1), adhesion of normally open contact (ANOC, D2), adhesion of normally closed contact (ANCC, D3), loose spring (LS, D4) and coil fault (CF, D5) are taken into account. Besides, the normal state (D6) of a relay is one of the outcomes of the rule’s consequence. A total of 200 and 100 samples of each working state are randomly selected for training and testing, respectively. For fully describing the fault modes, the pull-in voltage (PV, x1), pull-in time (PT, x2), resistance of no contact (RNC, x3) and resistance of contact (RC, x4) are taken as the fault features. According to the user manual and experimental samples, 3 referential grades are assigned to each fault feature [25]. The corresponding referential values are listed in Table 3. All the weights of the initial fault features and rules are set as 1. The initial BRB-based fault diagnosis model containing 81 belief rules is given by experts as shown in Table 4.

5.2 Optimization of Initial BRB

The accuracy rate of the initial fault diagnosis model based on BRB is 87.33%. To reduce the error caused by the subjectivity of experts, I-CA is applied to optimize the parameters of the initial model. The parameters of I-CA are shown in Table 5. The objective function is given by (9), where N=6,M=4,K=81.

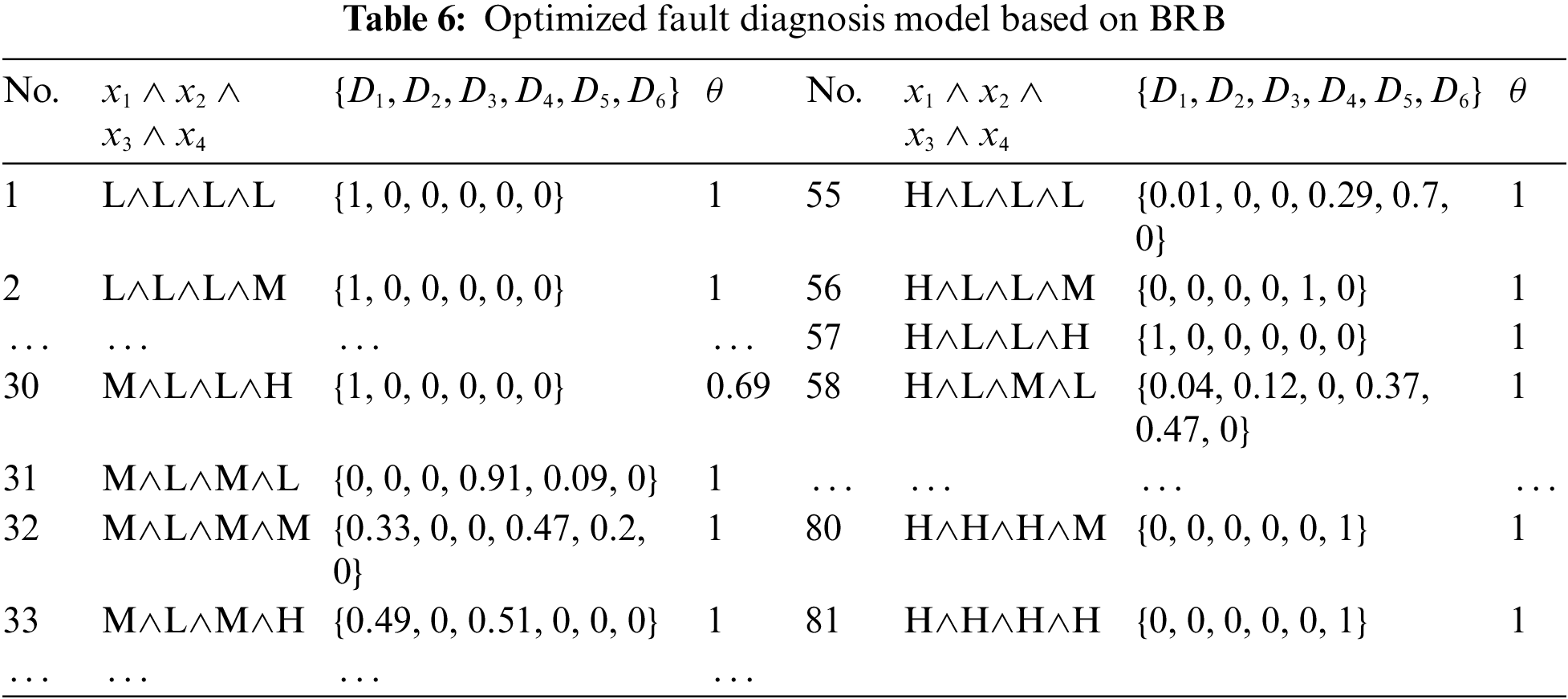
In I-CA, if any change in a parameter can improve the value of the objective function, then the change is regarded to be effective and the update of the parameter is retained; conversely, the update of the parameter is ignored. Therefore, the update of a parameter corresponds to the improvement of the objective function. Due to the normalization process, it should be emphasized that if a certain belief degree in a rule is adjusted, then the belief degrees contained in that rule may be updated. The optimization process is shown in Fig. 6. The optimized BRB-based fault diagnosis model of the relay is shown in Table 6.

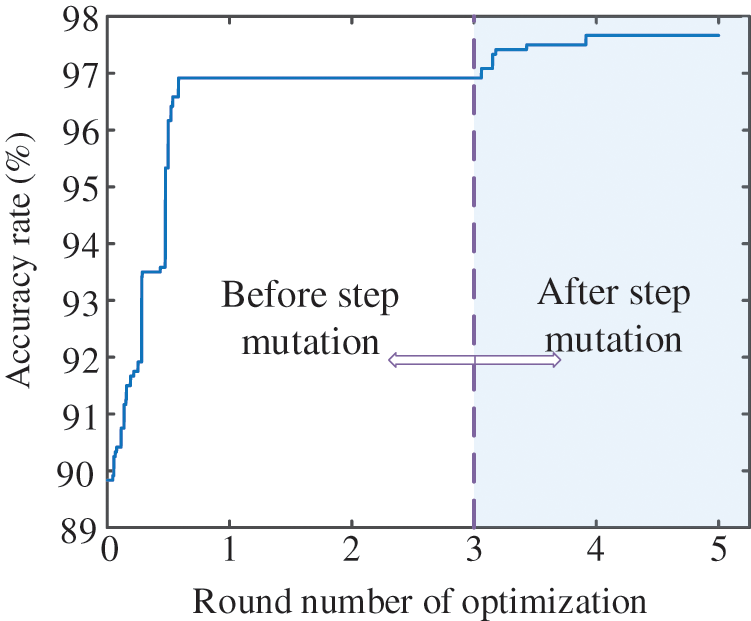
Figure 6: Iteration process of I-CA

The second and third rounds of updates fail to increase the objective function value. Then, the step size changes suddenly to escape from the current local optimal solution and seek better parameter values. The change in the step size is shown in Fig. 7. It can be seen from Figs. 6 and 7 that the value of the objective function increases further thanks to the mutation of the step size.

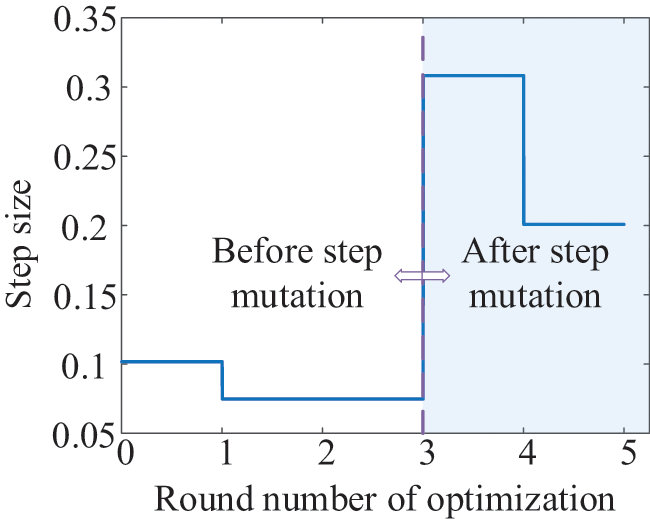
Figure 7: Update of step size

5.3 Comparative Study

In this subsection, the coordinate ascent (CA), the projection covariance matrix adaption evolution strategy (P-CMA-ES), differential evolution (DE) algorithm and particle swarm optimization (PSO) are introduced to optimize the parameters of the initial model for the purpose of examining the effectiveness of I-CA. Since the gradient information of the objective function based on the BRB fault diagnosis method is difficult to solve, the search algorithm of CA is consistent with that of I-CA. The fixed optimization sequence and a fixed optimization step size are employed to carry out the comparative experiment. The step size of CA is set as 0.2. The optimization sequence of parameters is designated to optimize the belief degrees first, then rule weights, and finally, fault feature weights. In addition, the data-driven models, including the back propagation neural network (BPNN), support vector machine (SVM), classification and regression trees (CART) and random forest (RF), are utilized to establish the fault diagnosis model by means of experimental samples. The diagnostic results are listed in Table 7 by dividing them into two parts.

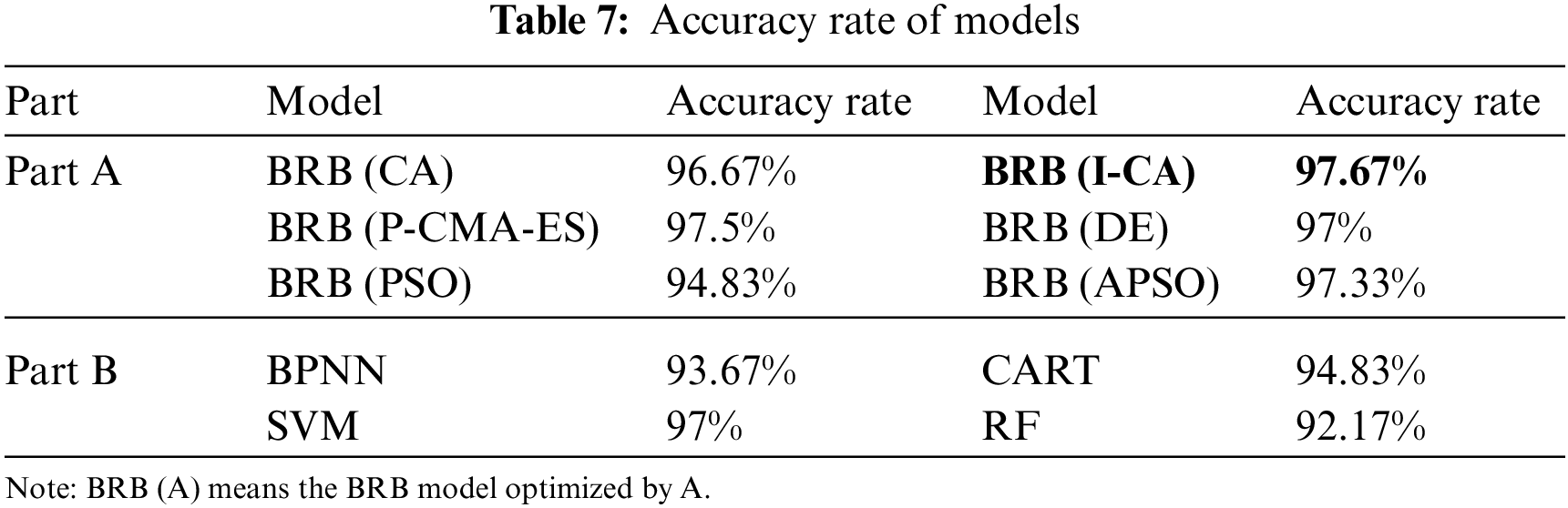
The accuracy rate of the BRB-based fault diagnosis model optimized by I-CA is 97.67%. That is, the diagnostic accuracy is improved by 11.84%. However, the diagnostic accuracy is 96.67% in BRB (CA). The iteration of the optimization based on CA is shown as Fig. 8. It can be concluded from Fig. 8 that the optimization process based on CA has converged to the extreme point in the first round of optimization. In the following rounds, the updating of parameters and improvement of the value of the objective function are at a standstill in BRB (CA), while there are step mutation and further optimization in BRB (I-CA). This may be due to the defects of fixed step size and fixed optimization sequence, which result in the optimization falling the local optimal solution. Therefrom, the effectiveness of the random optimization sequence and the adaptive step size is confirmed by comparing the BRB (CA) and BRB (I-CA). In Part A, the fault diagnosis model based on BRB has higher accuracy after optimization. The reason is that the initial model given by experts reduces the burden of optimization. Due to the non-convexity of BRB, BRB (PSO) falls into local optimal solutions early, and the accuracy is improved by 8.59% only. After several adjustments of super parameters, the accuracy of BRB (PSO) has not been effectively improved. Then, the adaptive particle swarm optimization (APSO) with linearly decreasing inertia weight is introduced to optimize the parameters of BRB. The accuracy of BRB (APSO) is 97.33% through the adjustment of super parameters.

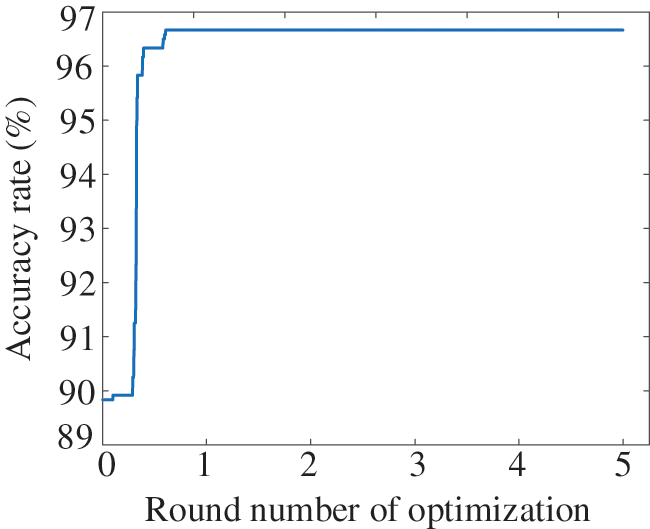
Figure 8: Iteration process of CA

In Part B, compared with BPNN, SVM, CART and RF, the diagnostic accuracy of BRB (I-CA) is improved by 4.27%, 0.69%, 2.99% and 5.97%, respectively. Obviously, SVM has the ability to deal with limited samples compared with other data-driven algorithms. Although the accuracies of BRB (I-CA) and SVM are in the same order of magnitude, the interpretability of the model is an irreplaceable factor for fault diagnosis of critical equipment. Next, the maintenance degree of the model interpretability is analyzed.

Moreover, the time complexity, which is described by the overall time consumption of the optimization, is introduced as an index to compare the computational performance of the optimization algorithm. In the case of the same hardware platform, different optimization algorithms are used to optimize the BRB , and the running time is recorded. In this experiment, the number of iterations of BRB (CA), BRB (P-CMA-ES), BRB (I-CA), BRB (DE) and BRB (PSO) is 5, 200, 5, 100 and 100, respectively. The running time of these models is shown in Table 8.

Comparing the running time of these methods, it can be found that the optimization processes of evolutionary algorithms and swarm algorithms last for a long time. The optimization processes based on CA and I-CA consume approximately the same short time, which means that the time complexity of these methods tends to be stable when the number of iterations is determined. Hence, it can be concluded that the proposed method has an advantage in computational performance.

5.4 Interpretability Analysis

Based on the analysis of interpretability in Section 3, three indexes are used to measure the retention degree of interpretability in the optimized model. To analyze the consistency of rules, CIR is calculated as shown in Table 9. The CIR value of the model optimized by I-CA, i.e., 0.9630, is the highest value. It seemed obvious from the values of CIR that 77 rules are consistent with those of the initial rules among the optimized rules of BRB (CA), and 78 rules of BRB (I-CA) are consistent with those of the initial model. Hence, the consistency of rules is well preserved in BRB (CA) and BRB (I-CA). The CIR value of BRB (PSO) ranks the third, which may result from the untimely falling into the local optimal solution. On the contrary, a serious loss of this consistency arises in the high accuracy model optimized by P-CMA-ES. In other words, the enhancement of accuracy is at the expense of the consistency of rules.

Further, the results of the initial and optimized belief rules are shown in Fig. 9. In BRB (P-CMA-ES), there are only 22 rules in accordance with the initial rules given by experts. In other words, most of the results of rules are inconsistent with the initial judgement of experts. There are 78 rules in BRB (I-CA) in accordance with the initial rules. The remaining three rules, i.e., the 29th, 64th and 65th rules, are inconsistent with those given by experts, which means that the initial judgement may be inaccurate. It just shows that the interpretability and accuracy of a model are contradictory. The weakening of the model interpretability is inevitable in optimization. In comparison, the consistency of rules is maintained well in the proposed method.

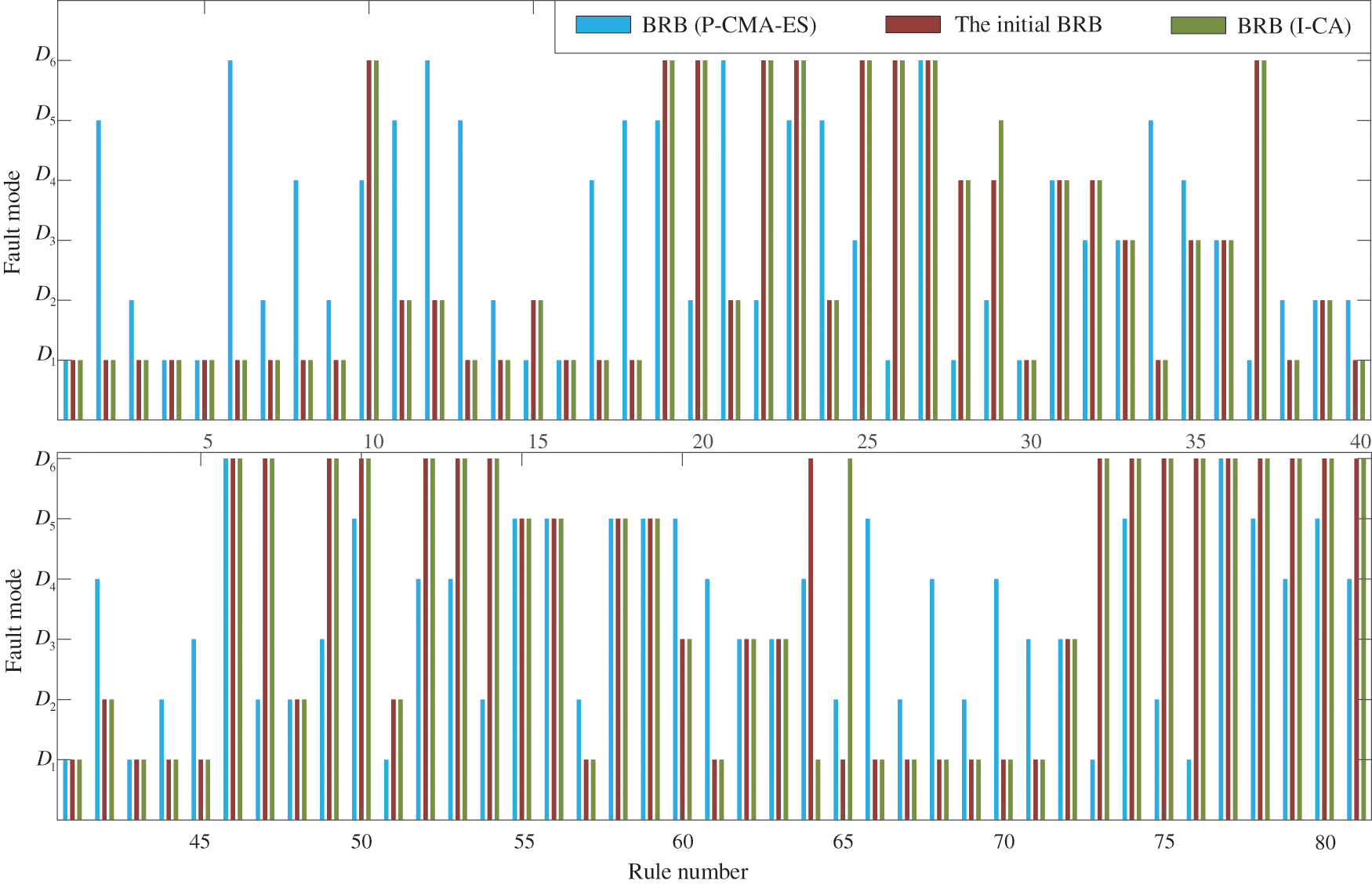
Figure 9: Results of rules

Overall, the degree of deviation of the optimized model from the initial judgement of experts is measured by CIRB as shown in Table 10. The value of CIRB in BRB (CA) model is higher than that of other models, which indicates that the consistency of the rule base is well retained in the optimization process. The CIRB value of BRB (I-CA) is 0.9379, which is higher among these models. The parameters are fine-tuned in CA and I-CA. The partial parameters related to the change in the value of the objective function are optimized. The initial judgement is retained in the remaining parameters as there is no basis for optimization.

To intuitively understand the consistency of the rule base, the difference in the belief degrees between the initial and optimized rule bases is drawn in the point diagram as shown in Fig. 10. It can be seen that the difference between the belief degrees in the initial BRB and the BRB (P-CMA-ES) is randomly distributed in the coordinate. Almost all of the belief degrees are updated in optimization. Compared with the BRB optimized by I-CA, the difference is almost close to 0. That is, only a few parameters are adjusted to enhance the accuracy of the model in optimization. As the consistency of the rule base is retained to the most extent.

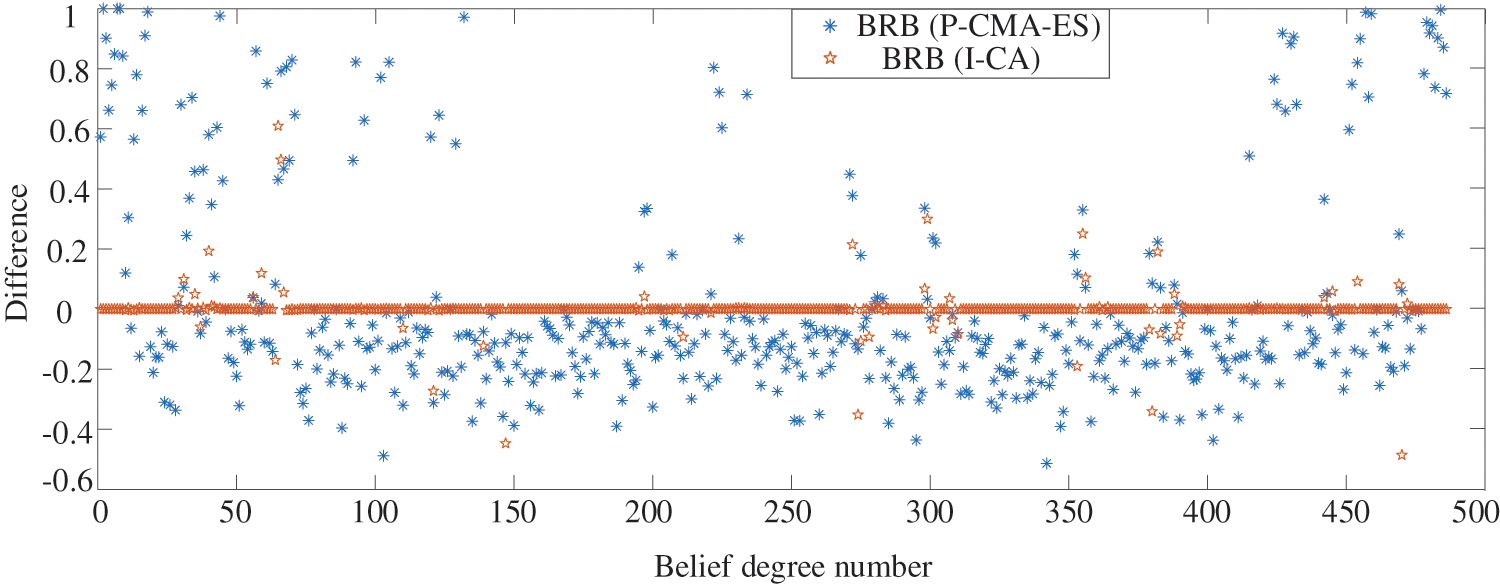
Figure 10: Difference in belief degrees between optimized and initial models

In optimization, whether there is any over-optimization of parameters can be reflected by OI. In this case, there are 5 unactivated rules whose rule numbers are 25, 27, 52, 79 and 81. In the initial BRB-based fault diagnosis model, the results of these rules are that the relay is in a normal state. The parameters of these rules should retain the initial values given by experts, which means OI is 0. The values of OI in the models mentioned above are calculated and shown in Table 11. The values of OI are 0, which means that there is no over-optimization of parameters in BRB (CA) and BRB (I-CA). However, the parameters are over-optimized in other models. In summary, the interpretability of the fault diagnosis model based on BRB can be preserved to a great extent in the I-CA-based optimization.

In short, in the BRB (CA) model, the interpretability of the model is maintained at the expense of loss of accuracy. By comparing BRB (CA) and BRB (I-CA), it can be seen that these two models can better preserve the interpretability of the model. On the basis of introducing the random optimization sequence and the adaptive step size, the accuracy of BRB (I-CA) is effectively improved.

6  Conclusion

In this paper, an interpretable fault diagnosis model based on BRB for crucial equipment is established. To present the loss process of interpretability in optimization, the weakening of interpretability is analyzed and summarized by using two factors. Afterwards, three indexes are proposed for these two factors to measure the interpretability of the optimized model. Finally, the I-CA is proposed to optimize model parameters.

There are mainly three contributions in this paper. One significant contribution is that the weakening factors of interpretability are summarized as the deviation from the initial judgement of experts and over-optimization of parameters in the BRB-based fault diagnosis model. Two numerical examples are examined to illustrate the need to avoid the loss of interpretability. Then, for these two factors, three indexes called the CIR, CIRB and OI are proposed to measure the interpretability of the optimized model. The consistency between the initial and optimized model is measured by CIR from the perspective of individual rules; the consistency between the initial and optimized model is estimated by CIRB from the perspective of the whole rule base. These two indexes reflect the degree to which the optimized BRB deviates from the initial judgment of experts. OI is used to judge whether the parameter is over optimized in the process of optimization. The weakening degree of the fault diagnosis model’s interpretability can be measured by these indexes. The other essential contribution of this paper is the construction of the I-CA optimization algorithm considering the interpretability and accuracy of a model. The random optimization sequence and adaptive step size are created to deal with the local optimal points. Due to the unavailability of gradient information, a one-dimensional search method, combining the advance and retreat method and golden section method, is regarded as the search strategy to replace the operation of solving the gradient. A case of the relay fault diagnosis is conducted to prove that the interpretability of the BRB-based fault diagnosis model is effectively retained in optimization under the premise of the maintenance of accuracy.

In the future, it will be discussed how to establish the fault diagnosis model based on BRB in a reasonable way when there are a large number of fault samples without expert knowledge. Under this circumstance, the interpretability of a model needs to be redefined. Moreover, establishing an incipient fault diagnosis [26] method, which is based on interpretable BRB and fault feature extraction technology, is one of the future works.

Funding Statement: This work was supported by the Natural Science Foundation of China (No. 61833016), the Shaanxi Outstanding Youth Science Foundation (No. 2020JC-34), the Shaanxi Science and Technology Innovation Team (No. 2022TD-24).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. Zhou, Z. J., Cao, Y., Hu, C. H., Tang, S. W., Zhang, C. C. et al. (2021). The interpretability of rule-based modeling approach and its development. Acta Automatica Sinica, 47(6), 1201–1216. DOI 10.16383/j.aas.c200402. [Google Scholar] [CrossRef]

    2. Rudin, C. (2019). Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nature Machine Intelligence, 1(5), 206–215. DOI 10.1038/s42256-019-0048-x. [Google Scholar] [CrossRef]

    3. Yang, J. B., Liu, J., Wang, J., Sii, H. S., Wang, H. W. et al. (2006). Belief rule-base inference methodology using the evidential reasoning approach–RIMER. IEEE Transactions on Systems, Man, and Cybernetics, 36(2), 266–285. DOI 10.1109/TSMCA.2005.851270. [Google Scholar] [CrossRef]

    4. Yang, J. B., Xu, D. L. (2014). A study on generalising Bayesian inference to evidential reasoning. Switzerland: Springer International Publishing Inc. DOI 10.1007/978-3-319-11191-9_20. [Google Scholar] [CrossRef]

    5. You, Y. Q., Sun, J. B., Guo, Y., Tan, Y. J., Jiang, J. (2022). Interpretability and accuracy trade-off in the modeling of belief rule-based systems. Knowledge-Based Systems, 236, 107491. DOI 10.1016/j.knosys.2021.107491. [Google Scholar] [CrossRef]

    6. Cao, Y., Zhou, Z. J., Hu, C. H., He, W., Tang, S. W. (2020). On the interpretability of belief rule based expert systems. IEEE Transactions on Fuzzy Systems, 29(11), 3489–3503. DOI 10.1109/TFUZZ.2020.3024024. [Google Scholar] [CrossRef]

    7. Hu, G. Y., Zhou, Z. J., Zhang, B. C., Yin, X. J., Gao, Z. (2016). A method for predicting the network security situation based on hidden BRB model and revised CMA-ES algorithm. Applied Soft Computing, 48, 404–418. DOI 10.1016/j.asoc.2016.05.046. [Google Scholar] [CrossRef]

    8. Zhang, C. C., Zhou, Z. J., Tang, S. W., Chen, L. Y., Zhang, P. (2022). BR-FRL: A belief rule-based fault recognition and location model for bus network systems. IEEE Transactions on Instrumentation and Measurement, 71, 3513212. DOI 10.1109/TIM.2022.3173638. [Google Scholar] [CrossRef]

    9. Wu, J., Wang, Q. W., Wang, Z. L., Zhou, Z. G. (2022). AutoBRB: An automated belief rule base model for pathologic complete response prediction in gastric cancer. Computers in Biology and Medicine, 140, 105104. DOI 10.1016/j.compbiomed.2021.105104. [Google Scholar] [CrossRef]

  10. Chang, L. L., Fu, C., Zhu, W., Liu, W. Y. (2020). Belief rule mining using the evidential reasoning rule for medical diagnosis. International Journal of Approximate Reasoning, 130(4), 273–291. DOI 10.1016/j.ijar.2020.12.009. [Google Scholar] [CrossRef]

  11. Chang, L. L., Xu, X. J., Liu, Z. G., Qian, B., Xu, X. B. et al. (2020). BRB prediction with customized attributes weights and tradeoff analysis for concurrent fault diagnosis. IEEE Systems Journal, 15(1), 1179–1190. DOI 10.1109/JSYST.2020.2991161. [Google Scholar] [CrossRef]

  12. Xu, X. J., Yan, X. P., Sheng, C. X., Yuan, C. Q., Xu, D. L. et al. (2020). A belief rule-based expert system for fault diagnosis of marine diesel engines. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 50(2), 656–672. DOI 10.1109/TSMC.2017.2759026. [Google Scholar] [CrossRef]

  13. Zhou, Z. J., Cao, Y., Hu, G. Y., Zhang, Y. M., Tang, S. W. et al. (2021). New health-state assessment model based on belief rule base with interpretability. Science China (Information Sciences), 64(7), 209–223. DOI 10.1007/s11432-020-3001-7. [Google Scholar] [CrossRef]

  14. Yang, L. H., Wang, Y. M., Liu, J., Martinez, L. (2018). A joint optimization method on parameter and structure for belief-rule-based systems. Knowledge-Based Systems, 142, 220–240. DOI 10.1016/j.knosys.2017.11.039. [Google Scholar] [CrossRef]

  15. Zhang, B. C., Hu, G. Y., Zhou, Z. J., Zhang, Y. M. (2017). Network intrusion detection based on directed acyclic graph and belief rule base. ETRI Journal, 39(4), 592–604. DOI 10.4218/etrij.17.0116.0305. [Google Scholar] [CrossRef]

  16. Yang, H., Wu, P. Z., Ni, J. L. (2017). Belief rule base parameter training approach based on improved particle swarm optimization. Computer Engineering and Design, 38(2), 400–404. DOI 10.16208/.jissn1000-7024.2017.02.023. [Google Scholar] [CrossRef]

  17. Yan, X. A., Liu, Y., Xu, Y. D., Jia, M. P. (2020). Multistep forecasting for diurnal wind speed based on hybrid deep learning model with improved singular spectrum decomposition. Energy Conversion and Management, 225(4), 113456. DOI 10.1016/j.enconman.2020.113456. [Google Scholar] [CrossRef]

  18. Yan X, A., She, D. M., Xu, Y. D., Jia, M. P. (2021). Deep regularized variational autoencoder for intelligent fault diagnosis of rotor-bearing system within entire life-cycle process. Knowledge-Based Systems, 226(6), 107142. DOI 10.1016/j.knosys.2021.107142. [Google Scholar] [CrossRef]

  19. Wu, W. K., Yang, L. H., Fu, Y. G., Zhang, L. Q., Gong, X. T. (2014). Parameter training approach for belief rule base using the accelerating of gradient algorithm. Journal of Frontiers of Computer Science and Technology, 8(8), 989–1001. DOI 10.3778/j.issn.1673-9418.1403061. [Google Scholar] [CrossRef]

  20. Feng, Z. C., Zhou, Z. J., Hu, C. H., Ban, X. J., Hu, G. Y. (2020). A safety assessment model based on belief rule base with new optimization method. Reliability Engineering System Safety, 203, 107055. DOI 10.1016/j.ress.2020.107055. [Google Scholar] [CrossRef]

  21. Qian, B., Wang, Q. Q., Hu, R., Zhou, Z. J. (2019). An effective soft computing technology based on belief-rule-base and particle swarm optimization for tipping paper permeability measurement. Journal of Ambient Intelligence and Humanized Computing, 10(15), 841–850. DOI 10.1007/s12652-017-0667-1. [Google Scholar] [CrossRef]

  22. Chen, M. L., Zhou, Z. J., Zhang, B. C., Hu, G. Y., Cao, Y. (2022). A novel combination belief rule base model for mechanical equipment fault diagnosis. Chinese Journal of Aeronautics, 35(5), 158–178. DOI 10.1016/j.cja.2021.08.037. [Google Scholar] [CrossRef]

  23. Hu, R., Yi, Z. Y., Qian, B. (2021). Fault diagnosis of oil-immersed transformer based on belief rule base. Journal of Beijing University of Technology, 47(9), 1000–1010. DOI 10.11936/bjutxb2019100015. [Google Scholar] [CrossRef]

  24. Ren, W. B., Zheng, Z. (2022). Experimental investigation of the instantaneous contact welding failure phenomena and mechanisms for general-purpose relays. Engineering Failure Analysis, 135, 106096. DOI 10.1016/j.engfailanal.2022.106096. [Google Scholar] [CrossRef]

  25. Wang, J., Zhou, Z. J., Hu, C. H., Tang, S. W., Cao, Y. (2022). A new evidential reasoning rule with continuous probability distribution of reliability. IEEE Transactions on Cybernetics, 52(8), 8088–8100. DOI 10.1109/TCYB.2021.3051676. [Google Scholar] [CrossRef]

  26. Wu, Y. K., Jiang, B., Wang, Y. L. (2020). Incipient winding fault detection and diagnosis for squirrel-cage induction motors equipped on CRH trains. ISA Transactions, 99, 488–495. DOI 10.1016/j.isatra.2019.09.020. [Google Scholar] [CrossRef]