Open Access

ARTICLE

The Weighted Basis for PHT-Splines

Zhiguo Yong¹, Hongmei Kang¹, Falai Chen^2,*

1 School of Mathematical Sciences, Soochow University, Suzhou, 215006, China
2 School of Mathematical Sciences, University of Science and Technology of China, Hefei, 230026, China

* Corresponding Author: Falai Chen. Email:

(This article belongs to the Special Issue: Integration of Geometric Modeling and Numerical Simulation)

Computer Modeling in Engineering & Sciences 2024, 138(1), 739-760. https://doi.org/10.32604/cmes.2023.027171

Received 17 October 2022; Accepted 03 January 2023; Issue published 22 September 2023

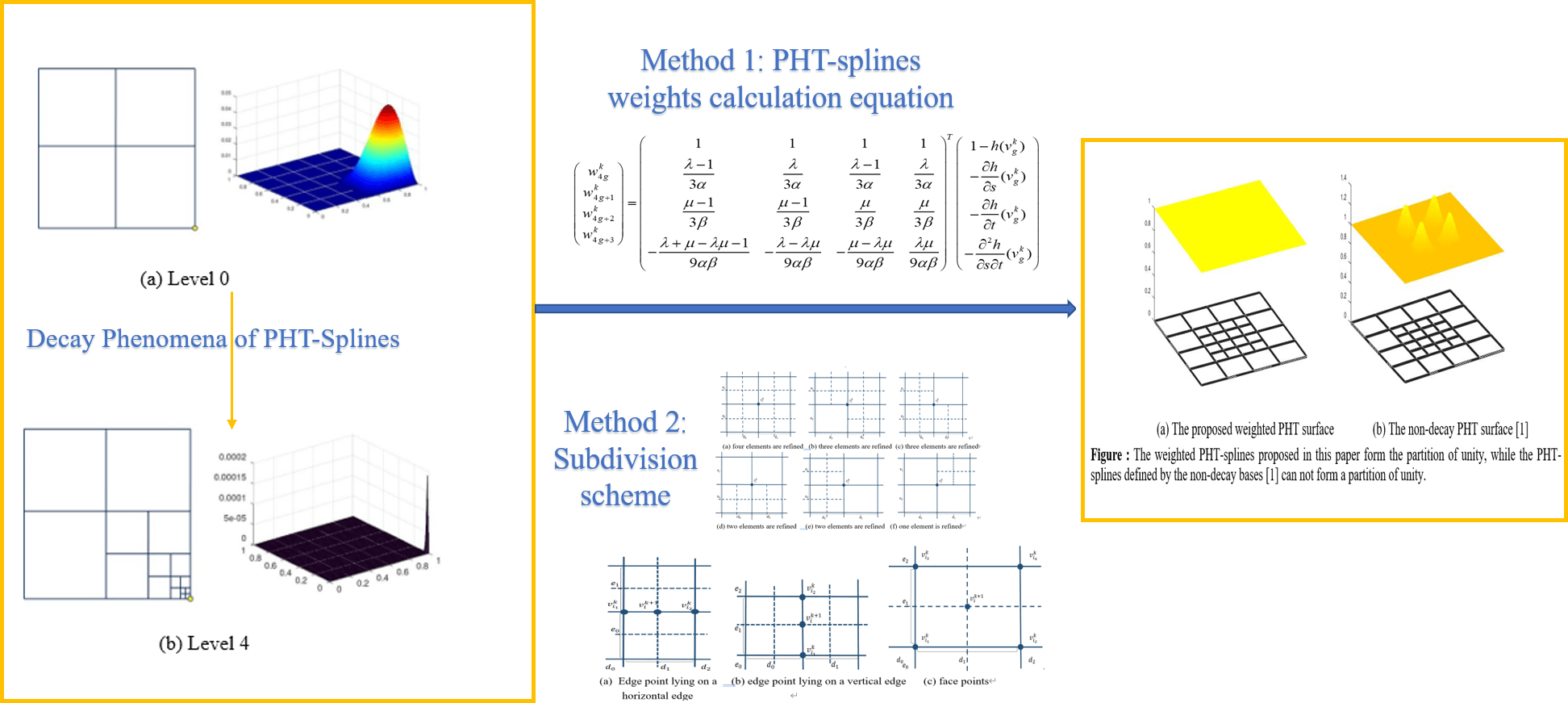
Abstract

PHT-splines are defined as polynomial splines over hierarchical T-meshes with very efficient local refinement properties. The original PHT-spline basis functions constructed by the truncation mechanism have a decay phenomenon, resulting in numerical instability. The non-decay basis functions are constructed as the B-splines that are defined on the 2 × 2 tensor product meshes associated with basis vertices in Kang et al., but at the cost of losing the partition of unity. In the field of finite element analysis and topology optimization, forming the partition of unity is the default ingredient for constructing basis functions of approximate spaces. In this paper, we will show that the non-decay PHT-spline basis functions proposed by Kang et al. can be appropriately modified to form a partition of unity. Each non-decay basis function is multiplied by a positive weight to form the weighted basis. The weights are solved such that the sum of weighted bases is equal to 1 on the domain. We provide two methods for calculating weights, based on geometric information of basis functions and the subdivision of PHT-splines. Weights are given in the form of explicit formulas and can be efficiently calculated. We also prove that the weights on the admissible hierarchical T-meshes are positive.

---

Graphic Abstract

---

Keywords

---