Test Case Prioritization in Unit and Integration Testing: A Shuffled-Frog-Leaping Approach

1  Introduction

Testing is arguably the most empirical and least comprehended part of the software development process [1]. Ever since the inception of contemporary development practices viz continuous integration and deployment (CI and CD), the significance of testing has escalated in industries. Such practices suggest that the entire set of test cases should be executed after every alteration in the code, as this not only guarantees the compatibility of new patches with the existing code but also makes sure that the functionality of the existing code remains intact (regression testing) [2]. Nevertheless, repeated re-execution of the entire test set after each code commit is nearly impossible, particularly in cases where the test suites and the system-under-test (SUT) are enormous [3]. For instance, it was reported that the statistics of per day test execution at Google is nearly 150 million. Such hard-hitting numbers directly point to the mundanity, time-absorbing, and highly-priced (up to 80% of development expense) nature of the regression test execution cycles [4].

The above-stated complications could be precluded through appropriate selection, minimization, and re-ordering of test cases [4]. Among these three, single criterion-based exclusion of test cases during test case selection (TCS) or minimization (TCM) sometimes results in insecure test executions. However, this isn’t a scenario with TCP as it opts for scheduling the test cases’ execution order in a manner that would maximize the detection percentage of regression faults at the earliest [5]. Mathematically, TCP could be elaborated as [6]:

Given: T (any test suite); pT (different permutations of T)

Problem: To find {(pT′∈pT):f(pT′)>f(pT′′)} where pT′′ defines other permutations in pT and f is a function that maps pT to R (real numbers), depicting the prioritization objective.

Categorically, the TCP techniques available today could be studied in two levels, i.e., context-dependent strategies and the heuristic and optimization methodologies [4]. The test cases in context-dependent strategy could be re-ordered according to the obtainable input resources such as requirement, history, coverage, or fault [7,8]. The other perspective chooses to portray the test cases in a specific manner (based on obtainable resources) and then exercise a heuristic or meta-heuristic approach to prioritize them. Despite the fact that these context-dependent strategies acquire 63% of the TCP-related literature, wherein the statistics of coverage-related TCP practices are incredibly high, i.e., 25%, these could lead to scalability issues in the testing environment [9]. Additionally, the percentage of coverage and fault detection acquired by such TCP techniques are also compromised. One potential reason for the same is the scarcity of diversity among the re-ordered test cases.

The kind and the amount of testing information utilized during TCP also plays a vital part in revealing its efficiency. Since most of the current nature-inspired meta-heuristics (NIMs) [10], including Greedy, Genetic algorithm (GA) and its variants [11], consider the single criterion fact for re-ordering system-level test cases, ensuring early coverage of severe faults through them would be difficult. The procedure would become more cumbersome when testers would employ them on real-world applications in unit-level testing environments. Besides this, with the trend of CI, execution of even 100s of unit tests or affected test cases in an order specified by these meta-heuristics after each code commit could become prohibitively expensive.

To address such issues, this research work primarily concentrated on a shuffled-frog-leaping algorithm (SFLA) [12], a population-based, memetics-inspired approach. SFLA assumes global search as a natural evolution process and incorporates information sharing and partitioning hierarchy while targeting the individuals of the populations. Since this property is rare in other NIMs, SFLA could prove to be a strong competitor in handling TCP issues, that too in CI and CD environments. It was noticed that Manaswini et al. [13] also suggested SFLA for TCP; however, the authors haven’t utilized its intrinsic capabilities and skipped the comprehensive clarity on how the approach is being molded to serve TCP with a relevant experimental structure to support.

With the stated facts and the need for a more stable TCP methodology in the practical environment, the major contribution of this study could be enlisted as follows:

•   To propound an SFLA-based TCP approach that could handle regression test cases at the initial and most arduous levels of testing, i.e., unit and integration levels.

•   To incorporate diversity while re-ordering via evaluation of critical testing parameters (multi-objectiveness).

•   To not rely on conventional optimization heuristics and strengthen the proposed-SFLA framework so that it could maximize coverage and fault detection rate, all simultaneously.

•   To assess the efficacy levels of proposed-SFLA against other stable and widely suggested NIMs.

The rest of the study is bifurcated as follows: Section 2 explicates the basic theoretical and mathematical steps of conventional-SFLA along with the inspection of some related works. Section 3 presents the proposed-SFLA framework with a case study. Experimental validation is provided in Section 4, and eventually, Section 5 culminates this study.

2  Background and Related Studies

SFLA algorithm was first proposed by Eusuff et al. in 2006 [12] to merge the search intensification element similar to the memetic approach with the global diversification element inherited from the response surface information exchange in particle swarm optimization (PSO) and shuffled-complex evolution. The basic idea revolved around how frogs leap in a swamp to reach the point of maximal food availability (Fig. 1).

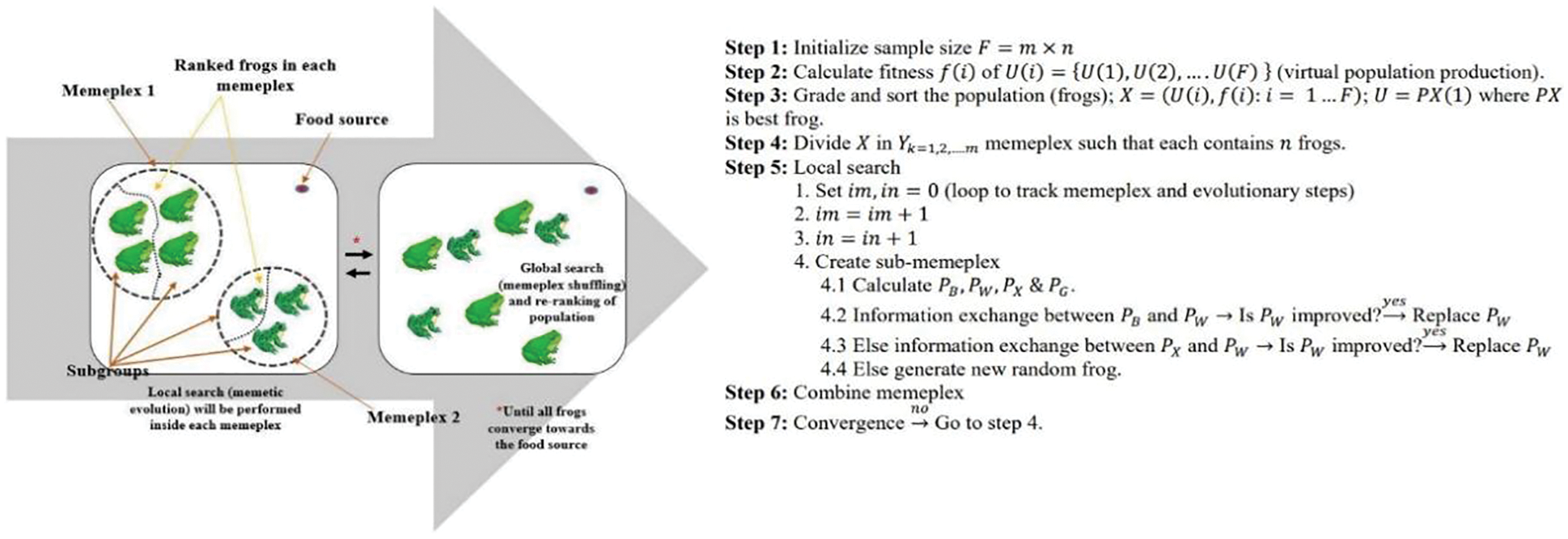
Figure 1: Diagrammatic representation of basic SFLA with pseudo steps [12]

On a broader angle, TCP is a topic of active investigation in the realm of regression testing. Primary heuristics-based TCP techniques are entirely coverage-based and founded on the premise that raising the SUT’s structural test coverage would increase the likelihood of fault discovery. These coverage-based heuristics possess two sub-categories: Overall coverage and Supplementary coverage [14]. Inspired by the latter, Lu et al. [15] suggested an additional-coverage-based (ACB)-heuristic function for TCP problems that blended the additional greedy method’s searching efficiency with the ant colony optimization (ACO) approach’s global searching efficacy. The authors also refined the test solutions obtained by artificial ants using sorting-based-local search methods. Fu et al. [16] combined the clustering and scheduling approaches so that test cases with comparable coverage information in previous executions were clustered and rated, and then execution priorities were assigned to each test case using the scheduling algorithm.

However, Rahman et al. [17] considered that clustering test cases based on similarity could lead to local minima; thus, they proposed a method in which different test cases are clustered and executed at the earliest possible time depending on prior and current fault rates. Apart from coverage, TCP was heavily influenced by user requirements and the complexity of the SUT. Kandil et al. [18] proposed a TCP technique for the agile framework in which parameters such as severity fault detection rates in previous executions and the singularity of user-defined requirements in the stories were used to determine the weighting or priority of each test case. Afzal et al. [19] claimed that the most critical components of TCP practice are the path complexity and branch coverage criterion. The authors employed Halstead’s matrix to determine the difficulty of paths in their investigation.

According to the studies mentioned earlier, it was discovered that the dependence of TCP on some specific input resource (majorly coverage) and the impact of test cases is exaggerated, and solely relying on such notions could jeopardize the TCP’s effectiveness. Research concerning the implementation of GA on TCP issues is extensive and has already carved out a niche in the TCP field [20–22]. Nejad et al. [23] applied discrete versions of the memetic algorithm (GA-base) on model-based testing. The authors utilized the activity diagram of the SUT for TCP that was later converted to CFG with weighted nodes.

Ashraf et al. [24] presented a PSO technique for TCP that is value-based. The authors combined six practical considerations, including requirement volatility, implementation complexity, and traceability, with the customary PSO approach for determining the fitness of test cases. Additionally, this fitness aided them in determining the potential and priority of each test case. They acquired an APFD of 70.3%; however, the factors’ ranking and weighting in their work were not described accurately. Samad et al. [25] also approached PSO, yet the factors considered for allocating priority to test cases were execution time, code coverage, and fault rate.

Noticing the growth in the utilization of state-of-art NIMs for TCP, Bajaj et al. [26] propounded a discrete cuckoo search method in which the traditional cuckoo movement was substituted with the double and 2-opt moves. The authors also proposed asexual genetic reproduction as a new adaptation technique for discretizing the continual cuckoo search. Furthermore, the authors developed a cuckoo search and genetic hybridization for re-ordering purposes. Öztürk [27] adopted a process based on bats’ basic echolocation behavior. The author utilized test case execution time and the number of defects as the primary criteria for test optimization. For comparison and accuracy evaluation, algorithms such as ACO, greedy, and PSO were used, with the suggested framework achieving an APFD of 0.9.

Khatibsyarbini et al. [28] applied the firefly approach to TCP, in which the firefly acted as the test case. The fireflies’ movement was dependent on test disparity and striking similarity weights and distinctiveness, and the brightness remained constant regardless of the distance traveled by the test cases (edit distance). The works cited above have several shortcomings, including the following: (a) by prioritizing fault rate, studies omitted validation of the acquired re-ordered test sequence’s coverage efficiency, (b) increased computational cost of the methodologies due to their inherent behavior and the complex parameter configuration process required to perform TCP, (c) lack of clarity regarding the not-so-defined but utilized testing criteria, and (d) inabilities in addressing conflicted scenarios where the path complexities and the count of faults could be diverse and equal.

Concentrating on the studies that suggest prioritizing test cases in a CI context based on testing characteristics [29–31] are very few, and pointing out their inconsistencies at this stage would be irrelevant. The distinction between this paper and previous work is that this study concentrated on the most extensive levels of testing, namely unit and integration, for TCP, which no previous study has done. This would enable testers to examine modified software modules with the most prominent test sequences. To avoid the problems linked with complex parameter tuning situations that plagued several previous studies, this work presented an SFLA-based technique for TCP. Furthermore, this technique is infused with the five most-effective criteria, including fault, frequency aspects of test statements, and historical details that would help preserve the diversity among the re-ordered test cases.

3  Methodology

Based on the previous studies’ experiences in devising TCP techniques and the prominence of test coverage in optimization strategies, this research work has formulated the regression TCP problem as:

g=maximize{TotalCmc,TotalCmF}

s.t.g(t)>g(t′)

where t and t′ are the permutated versions of T={TC1,TC2,TC3…….TCn}, Cmc and CmF are the cumulative statistics of coverage and fault covered by the test cases in those versions. To have a clarified vision, this section is segmented into two subsections, wherein the algorithmic structure of the proposed-SFLA is discussed in Section 4.1, followed by its gradational execution in Section 4.2.

3.1 Proposed Approach (SFLA)

When it comes to regression testing, historical reporting of each test case is significant as it can truly disclose the flakiness of test cases and could provide the circumstances into which a test case could fail. Without a proper benefit of past test data, the tester could lose visibility into the probabilities that lead to the failure of a system. Sticking to this fact, this study has utilized and filtered some of the major aspects from the regression test execution depositories, such as the test cases’ execution frequencies, their fault detection potentialities, and the extremity of detected faults. A concise depiction of the proposed methodology flow is presented in Fig. 2 with the conceptualization in Algorithm 1.

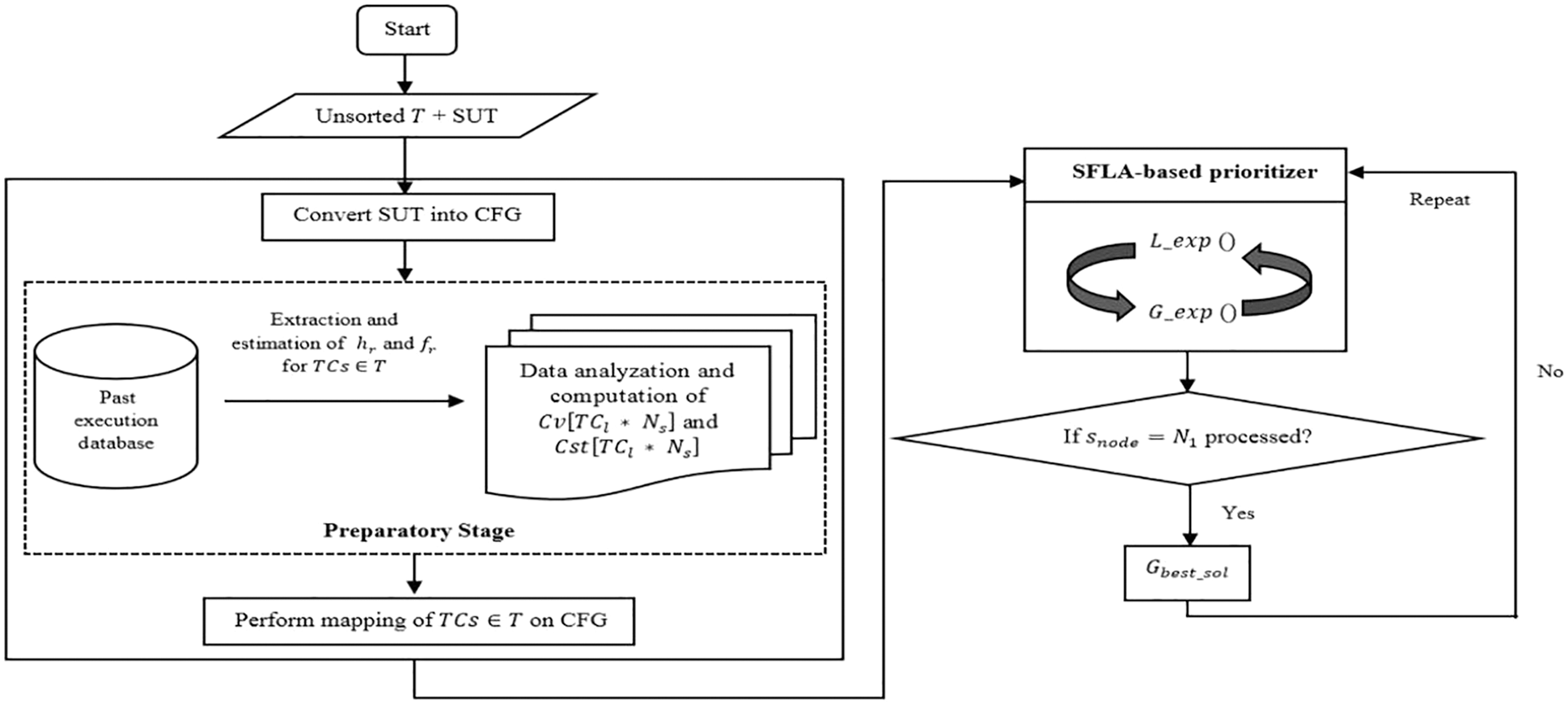
Figure 2: Block schema of the proposed-SFLA

During the initial planning phase, this research study considered numerous source codes for examination, but the practical perspective and evaluation strategies for those are different in the outer environment. Typically, testers rely more on the environment that focuses not only on the program’s logic but also on the program’s flow in the course of the program’s performance or reliability check. Therefore, a control flow graph (CFG) of SUT is utilized in this study, and the paths with new additive information are extracted (independent paths). Considering the gravity of test coverage, Cv[TCl,Ns] in Algorithm 1 is the matrix that describes the coverage particulars of test cases in binary form. Other than Cv[TCl,Ns], the data such as hr(TCl) and fr(TCl) in Algorithm 1 is the extracted data from the depository that interprets the history and fault figures of test cases.

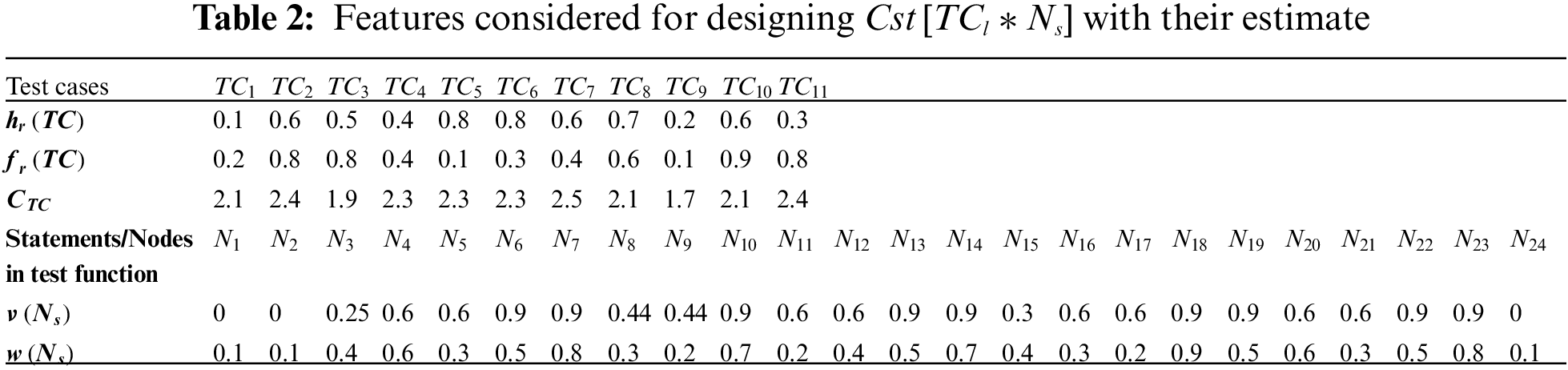
This study has integrated two more essential features that are often neglected during the assessment of data related to test statements and test cases, i.e., the recurrence ratio of test statements in independent test paths (ν(Ns))and the cost of test cases (CTCl) (Eqs. (1) and (2)).

ν(Ns)=Ip(f(Ns))totIp(1)

s.t.if[orgiν(Ns)]={1,setν(Ns)=0<1,variateν(Ns)}

CTCl=∑s=1Maxst(Cv[TCl,Ns]∗w(Ns))(2)

Ip(f(Ns)) in Eq. (1) elucidate the frequency with which a particular statement appeared in the independent paths while totIp is the number of independent paths as a whole. To secure the less frequent statements with crucial data and assign an importance factor based on their prevalence, [orgiν(Ns)] is devised. In Eq. (2), CTClis entirely different from what the actual definition of test cases’ cost means. Basically, it’s the acceptability factor that points to those test cases that cover the statements with critical conditions. To measure this criticality, each statement at its initial is assigned a weightage value (w(Ns)) that is absolutely random yet depends on the complexity of the conditions or functions that the test statements have.

Besides Cv[TCl,Ns], all other features stated till are evaluated to form another informatory packet, i.e., Cst[TCl,Ns] (cost matrix). After the preparatory stage, Algorithm 2 is applied to the mapped CFG (Local Exploration). As the conventional-SFLA [12] starts by forming the memeplexes and dividing the graded population into them, Algorithm 2 assumes the test cases as the population and the mapped CFG as one search space that holds several memeplexes and subgroups within. The individual memeplexes are supposed to be the unit modules within the SUT, while any intra-connection between two unit modules is the point of integration where the interim ordered test cases are allowed to re-shuffle (Global Exploration) (Algorithm 3).

3.2 Experimental Study

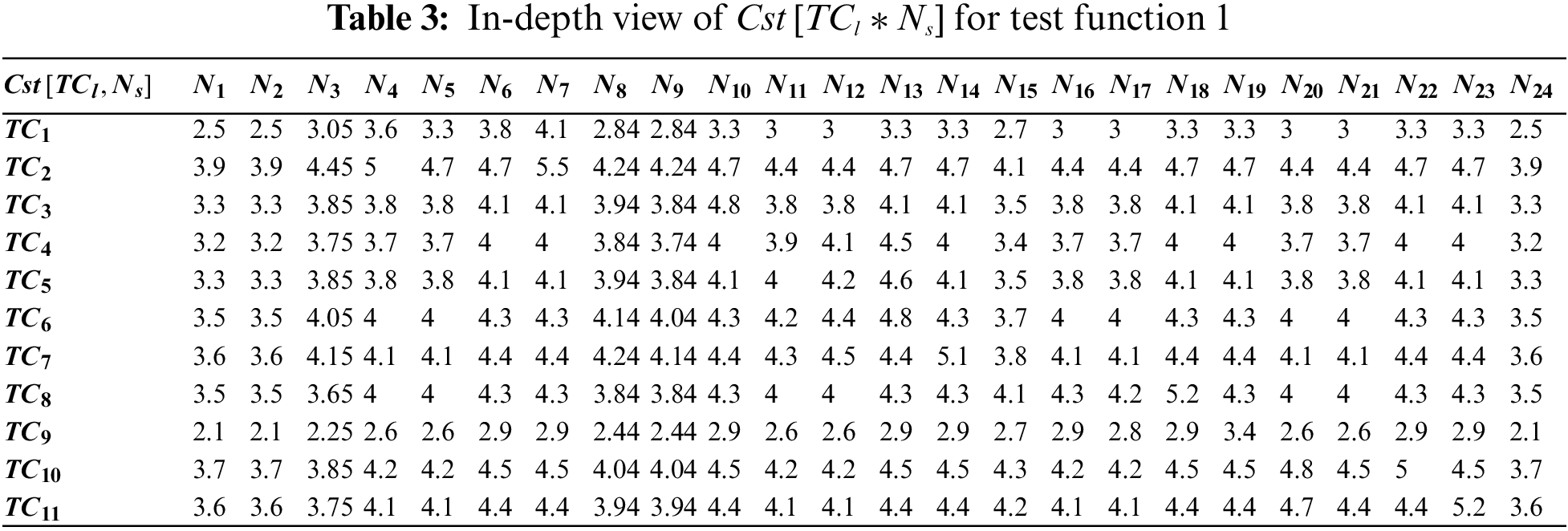
Primarily, this study considered a working module of tax-discount application as the test function (test function 1). On developing its graphical representation (i.e., CFG), it was perceived that the test function comes under a category of high complexity with totIp=9. As there is no specific scale or guidance according to which the parameters of conventional-SFLA [12] could be configured, this work has molded the parameters to conform to the structural delineation of test function and the testing protocols (Table 1).

3.2.1 3.2.1 Construction of Cv[TCl∗Ns] and Cst[TCl∗Ns] (preparatory stage)

The instructions presented in Algorithm 1 are considered for the emergence of Cv[TCl∗Ns] and Cst[TCl∗Ns]. The prior, being the representation of test coverage, would demonstrate the flow of test cases during the implementation of test statements in ‘1’ and ‘0’ format. The value ‘1’ would signify the successful execution of a test statement (Ns) by a test case (TCi); however, ‘0’ is vice versa. Before the demonstration of second-most consequential information, i.e., Cst[TCl∗Ns], the fetched data from the depository needs to be inspected thoroughly. For simplicity purposes, this work has considered a random scale of [0–1] to allot values for features such as hr,fr and w (Table 2). Although this consideration is entirely notional, it is directly proportional to the past behavior of test cases and the seriousness of data residing in the test statements.

The CTC and ν(Ns)values stated in Table 2 are enumerated using Eqs. (1) and (2). For instance, the cost of TC7 would be CTC7=∑s=124(Cv[TC7,Ns]∗w(Ns)) i.e., CTC7=(1×0.1+1×0.1+1×0.4+1.× 0.3 + 1× 0.2 + 1× 0.2 + 1× 0.4 + 0× 0.7 + 1 × 0.1) = 2.5If the values of ν(Ns)are looked, the value of ν(N9) is found to be 0.44 in Table 2. However, in accord with Eq. (1), the value of ν(N9) should be 0.33. This happened because of the broad range that is being set to retain the indispensable yet less-frequent test statements. Such computations (Table 2) and the Cv data would lead to the establishment of Cst[TCl∗Ns] (Table 3).

3.2.2 Local Exploration (memetic-based search)

The central working of the proposed-SFLA starts from here (Algorithm 2). Based on the current execution status, the test cases are plotted on the CFG. This insight would aid in comprehending how the test cases’ population is disseminated over the search space or the test flow that they are adapting (Fig. 3). IndFit(TCq) in Algorithm 2 is responsible for the computation of each test case’s competence linked to a specific path on the search area. Since it utilizes the details from the preparatory stage, this notion would highlight the extremely significant dependencies between the test cases and the test statements. The two most proficient ones with the highest IndFit(TCq) are extracted from Rank1db and the aggregated value of them (BEST) is considered as the termination criteria for the memetic evolution process.

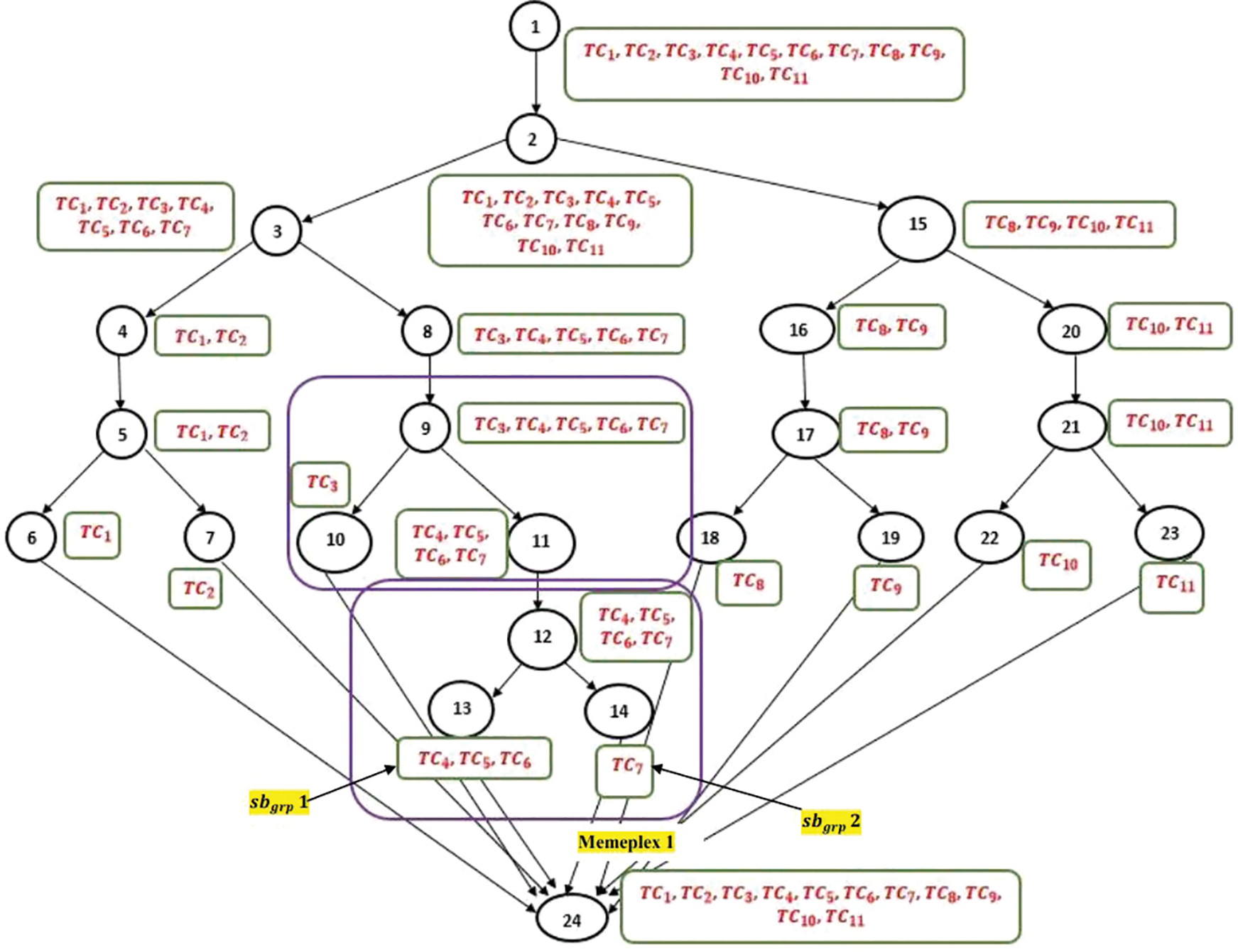
Figure 3: Scattered population of test cases over CFG of test function 1

The mapped CFG in Fig. 3 is scrutinized sequentially in a bottom-to-top manner. The parameter which needs much more concentration while tuning in conventional-SFLA was F [12]; however, this parameter is not necessitated during TCP as there could be several test cases executing a particular unit module and deciding m and even distribution of n on m would be impracticable. In Fig. 3, the combination of the test cases present in sbgrp1 of memeplex1 would be {(TC4,TC5),(TC5,TC6),(TC6,TC4)}. Since the memetic evolution framework that this study adopted is composed of GA and hill-climbing, each test pair from this sequence would undergo a phase of selection, crossover, and mutation.

Selection Operation

Among the test pairs in sequence {(TC4,TC5),(TC5,TC6),(TC6,TC4)} an arbitrary pair is selected initially, and an ‘OR’ operator is applied to the coverage particulars of test cases that are linked with the elected test pair. Fitness in any phase of the genetic approach strictly relies on the coverage of test statements by the offspring. For instance, O1 covers a test statement N1, then Cst[TC4,N1] and Cst[TC4,N1] (parent test cases which are responsible for that coverage) are considered to contribute to the fitness of O1. For this case, Fitness(O1) appeared to be 67.76, which is relatively less, and thus (TC4,TC5) is passed to the crossover phase.

Crossover Operation

In this stage, the swapping is conducted between the 1st bit of TC4 and the 16th bit of TC5 along with 2nd bit of TC4 and the 17th bit of TC5 (2-point crossover), concurrently (Fig. 4). The flow of swapping depends upon the Cst data of parent test cases for the specified bits.

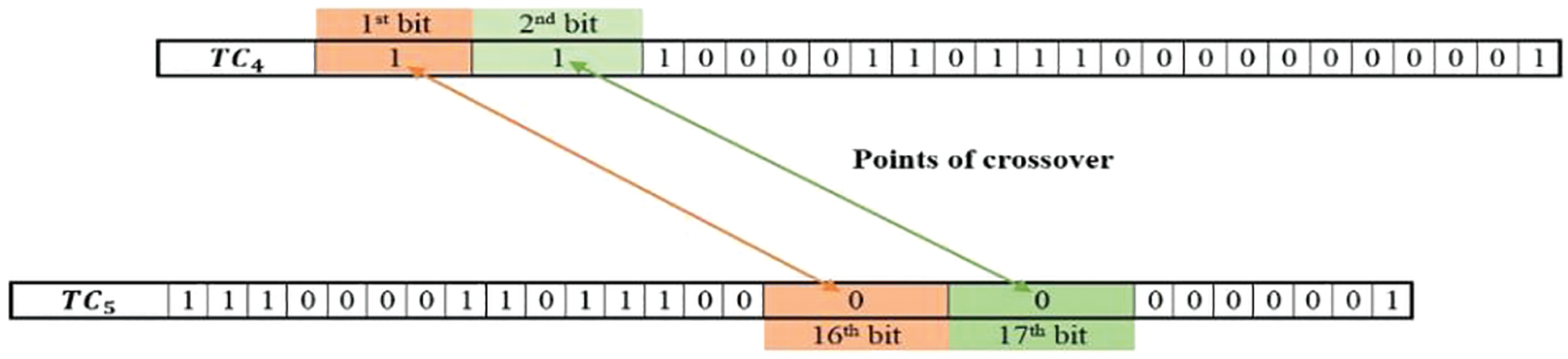
Figure 4: Exemplar view of bit swapping between test case TC4 and TC5 during crossover

After applying the ‘OR’ operator on the swapped versions of TC4 and TC5, the estimate for Fitness(O) noticed to be 68.96. Due to the repeated non-fulfillment of termination criteria (BEST=73.36), the (TC4,TC5) pair is forced to enter the mutation phase.

Mutation Operation

The mutation is the slight alteration to the gene value to have a different trait compared to parents. To acquire this nature, the 21st bit of the chromosomal structure of the offspring test case (here O) is flipped from ‘0’ to ‘1’ based on the statistics of its parent test cases in Cstdata (Table 3). Fitness(O4), after the mutation process, observed to be 72.76. Since in all the phases (TC4,TC5) pair haven’t approved the scale of prescribed termination criteria; therefore, the termination criteria is modified. This study has contemplated 95% of BEST as the second suitable termination criteria for the (TC4,TC5) pair to exercise the genetic cycle.

The genetic cycle is iterated until all the pairs inside {(TC4,TC5),(TC5,TC6),(TC6,TC4)} are covered. Rank2db is the database that keeps track of fitness values of all pairs and is updated every time a new sbgrp is processed. After the generic iterations of the GA cycle, the notion of hill-climbing is initiated. The test pairs are sorted in ascending order of their fitness in the Rank2db and are shifted from snode (sequential node) to cnode (conditional node) of their memeplex according to the adapted triangular probability of the conventional-SFLA [12] (Fig. 5). For such scenarios, the movement and the exploitation rate are managed by another vital information packet, i.e., ρ[TCi=1ton∗Nj=1toMaxst] which is basically the test statement-wise distribution of the fault figures of test cases.

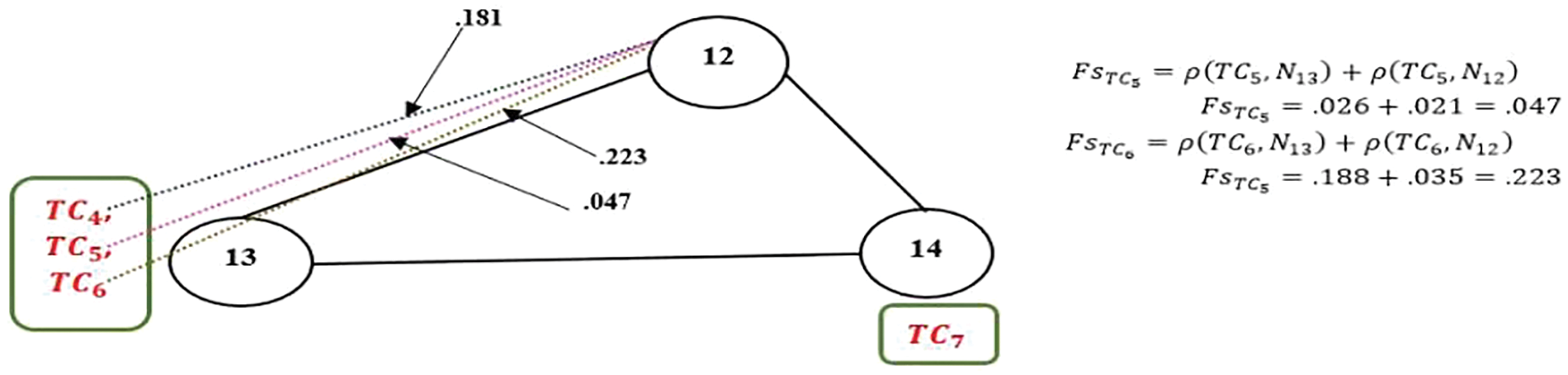
Figure 5: Representation of test cases’ movement during the local search phase

The pair (TC5,TC6) is ordered at first in Rank2db with fitness equal to 75.86. Being the highest fitted test pair in Rank2db, the FsTC value of TC5and TC6 is calculated before TC4. Subsequent to the results depicted in Fig. 5, TC6 is the first test case in sbgrp1that is allowed to climb or move close to cnode=N12. Ultimately, the locally explored solution or the set of re-ordered sbgrp1 and sbgrp2 found at N12 would be {{TC6,TC5,TC4}{TC7}}.

3.2.3 Global Exploration (PSO-based search)

Algorithm 3 is referred to globally re-order the locally procured solution from Algorithm 2. A temporary data storage k[TCs∗Nj] is defined to have a cognizance of the statement-wise coverage and fault figures of each test case that resides at a particular position in the locally prioritized sequence. The exploration rate in k[TCs∗Nj] is controlled by the parameter Smax. Considering the case of {{TC6,TC5,TC4}{TC7}}, initially, the test cases from the sequence are sundered into a 2 layer structure in such a manner that the ρ[TC,Nj] value of each test case at layer 1 should be higher than that of the test cases at the lower layer. This notion is rather identical to the rule that states that the population close to the global best solution is always ahead of the population following or getting influenced by them.

The positions of the test cases within the layers kept changing due to the enumerations (Feval(TC)) at each test statement inside k[TCs∗Nj]. A detailed view with counter (c) information for {{TC6,TC5,TC4}{TC7}} at N12 and N13 is presented in Fig. 6. A similar phenomenon could be observed at N14, however, TC7 with Feval=1.133 took over TC6which is placed at layer 1 in Fig. 6. The final order of test cases at memeplex 1(Gbest_sol), after the computation of Feval at N14, is recorded as {TC4,TC7,TC6,TC5}. Gbest_sol is generally the representation of the prioritized test cases at the integration level and must be revised while handling every new memeplex dynamically. The point where the test cases are integrated to perform verifications of the conditions is different from the point of integration of two memeplexes. For the latter one, the Gbest_sol from cnode of one memeplex is progressed towards the snode of another memeplex if there exists any interdependence between them (Fig. 7).

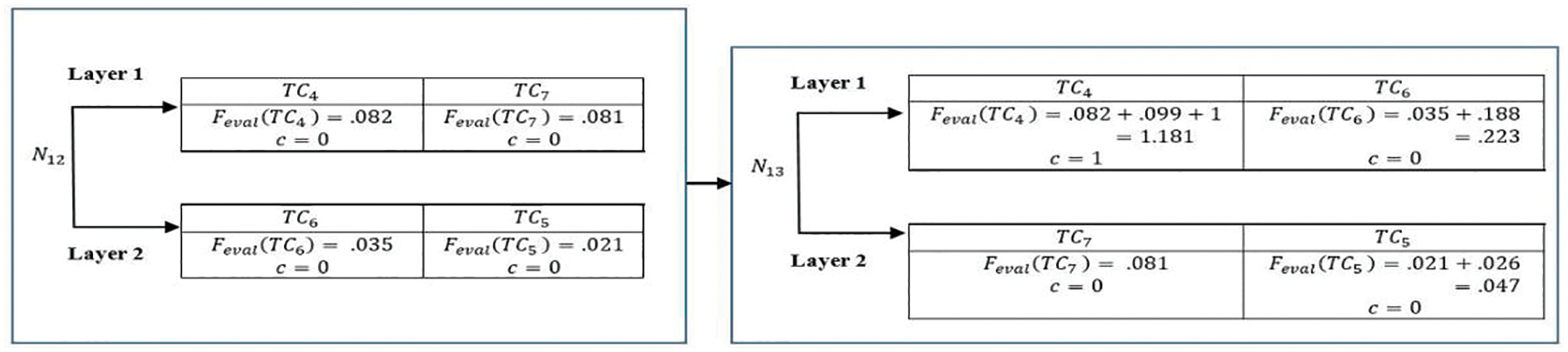
Figure 6: Information exchange and re-shuffling among the locally re-ordered test cases

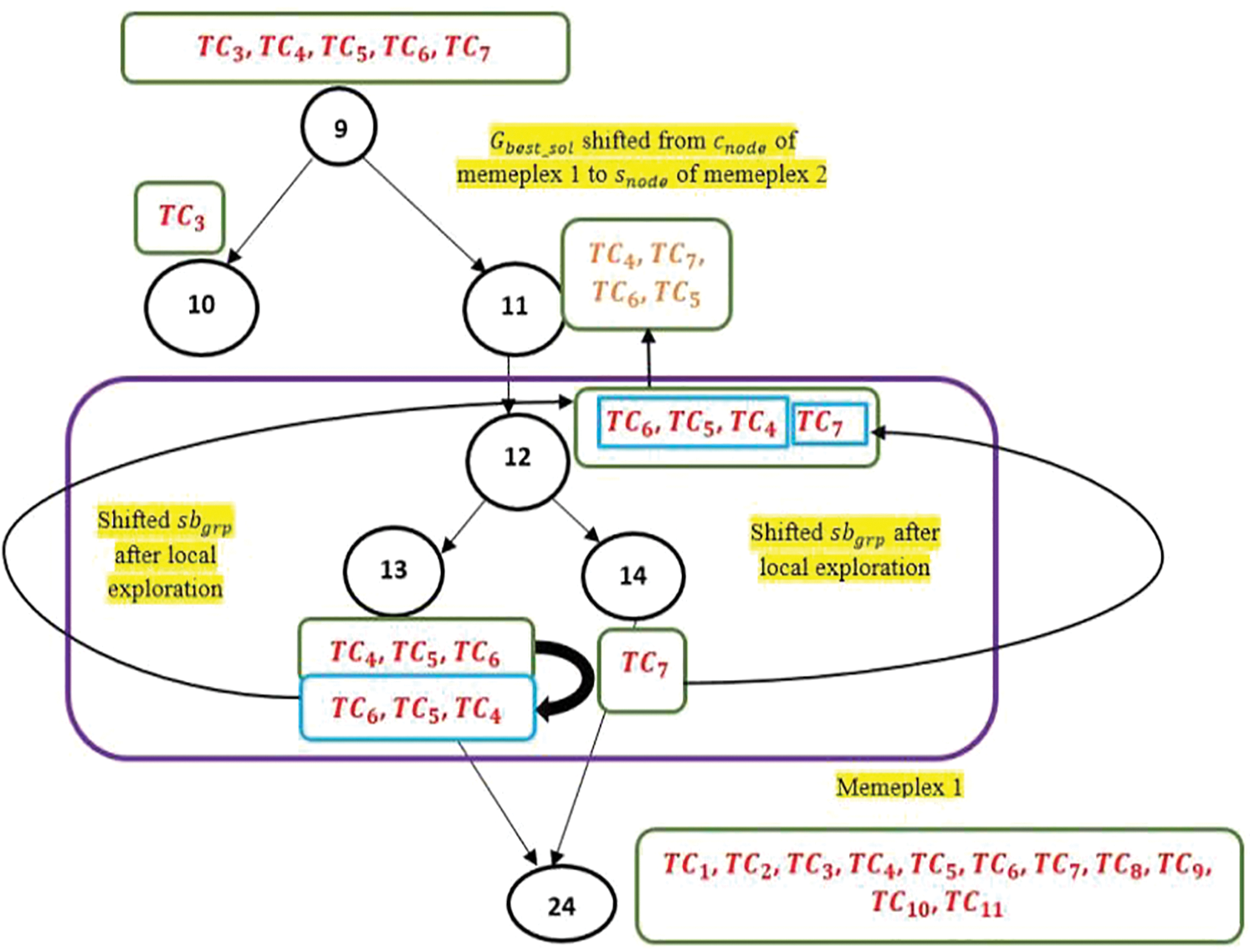
Figure 7: Partial view of test cases advancing towards Gbest_sol

This whole procedure from Algorithm 2 to Algorithm 3 is re-iterated until the search reaches at N1. The final prioritized test sequence attained at N1 is:

Gbest_sol={TC10,TC3,TC2,TC8,TC4,TC11,TC7,TC1,TC9,TC6,TC5}

4  Experimental Inferences and Discussion

This study addressed the following four research questions that prompted the experiments.

RQ1. How efficaciously can the proposed-SFLA re-ordered test cases uncover the faults in contrast to the existing techniques?

RQ2. What is the pace of test coverage by the re-ordered test sequence obtained from proposed-SFLA and other contrasting algorithms? Is the proposed-SFLA efficient enough in tracking the coverage at the earliest?

RQ3. Compared with the original order of the test cases, how productive is the prioritized order presented in the case study in terms of coverage and fault?

RQ4. Taking the case study into reference, does the proposed-SFLA generates encouraging outcomes concerning the APFD?

4.1 Comparative Study

To answer RQ1 and RQ2, apart from test function 1, this study has considered 4 other test functions with high and medium-level complexities. The proposed-SFLA approach is compared with those algorithms that are highly stable in the domain of memetics or are not entirely approaching randomnesses, such as GA-infused-Multi-walk (Optimized Multi-walk) [5], Memetic algorithm [23], PSO [24], and Multi-walk [32].

Through the observations depicted in Fig. 8a, it is seen that the proposed-SFLA achieved the maximum fault rate at ⌈n2⌉th position in Gbest_sol that means at only 54% of the test suite execution, 43% of the faults are already detected. Optimized multi-walk [5] and PSO [24] also yielded a fault detection rate of 40% and 41%, which are near to the results of the proposed-SFLA, respectively. However, the nature shown by the memetic algorithm [23] in covering the potential faults at the earliest is not promising. One reason for the same is the dominance of shielded test cases at the unit level; however, when memetic is practiced at the integration level to attain TCP, this dominance could lower fault rates for prioritized test sequences. To comprehend what a shielded test case is, it is a test case whose execution flow is entirely similar to the other test case in a test suite; nonetheless, the test data that it holds might be different.

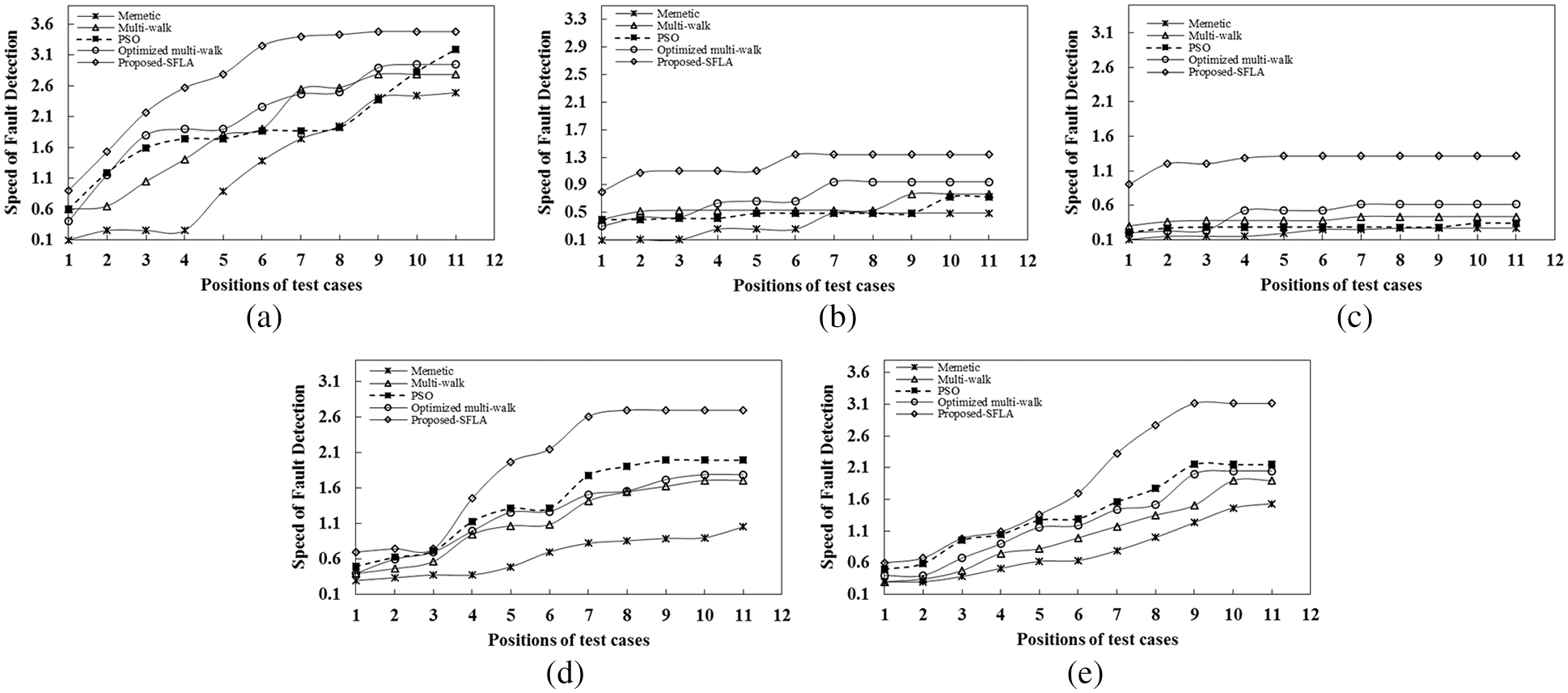
Figure 8: Graphs depicting the growth of fault detection rate among the re-ordered test cases

For cases stated in Figs. 8b and 8c, the fault detection rate by the proposed-SFLA is maximum at ⌊n2⌋, however, in Figs. 8d and 8e, the significant gap could be detected before ⌊n2⌋ and at ⌈n2⌉, respectively. It is also seen that the shieldedness of test cases had a severe impact on the performances of optimized multi-walk [5] and PSO [24]. The performance of basic multi-walk [32] is reasonably satisfactory compared with memetic; nevertheless, this algorithm’s performance is also indirectly proportional to the shieldedness effect.

According to the coverage statistic shown in Fig. 9a, the memetic approach [23] is again the worst performer since it retains only 70% of the coverage of test function when approximately 60% of the re-ordered test cases are executed. Optimized [5] and basic multi-walk [32] performed almost on the same scale, where the first secured the coverage rate of 75% and the latter 79%. PSO [24] appeared to be finer than these 3 algorithms since the coverage rate that it procured is 83% at ⌈n2⌉th position of execution, yet proposed-SFLA outperformed with approximately 88% of attained test coverage at the same position. This could be inferred from Fig. 9 that in 3 out of 5 instances, PSO is the second-best in satisfying the coverage of the test functions. The comparison outcomes in terms of Cmc and CmF for test function 1 are listed in Table 4.

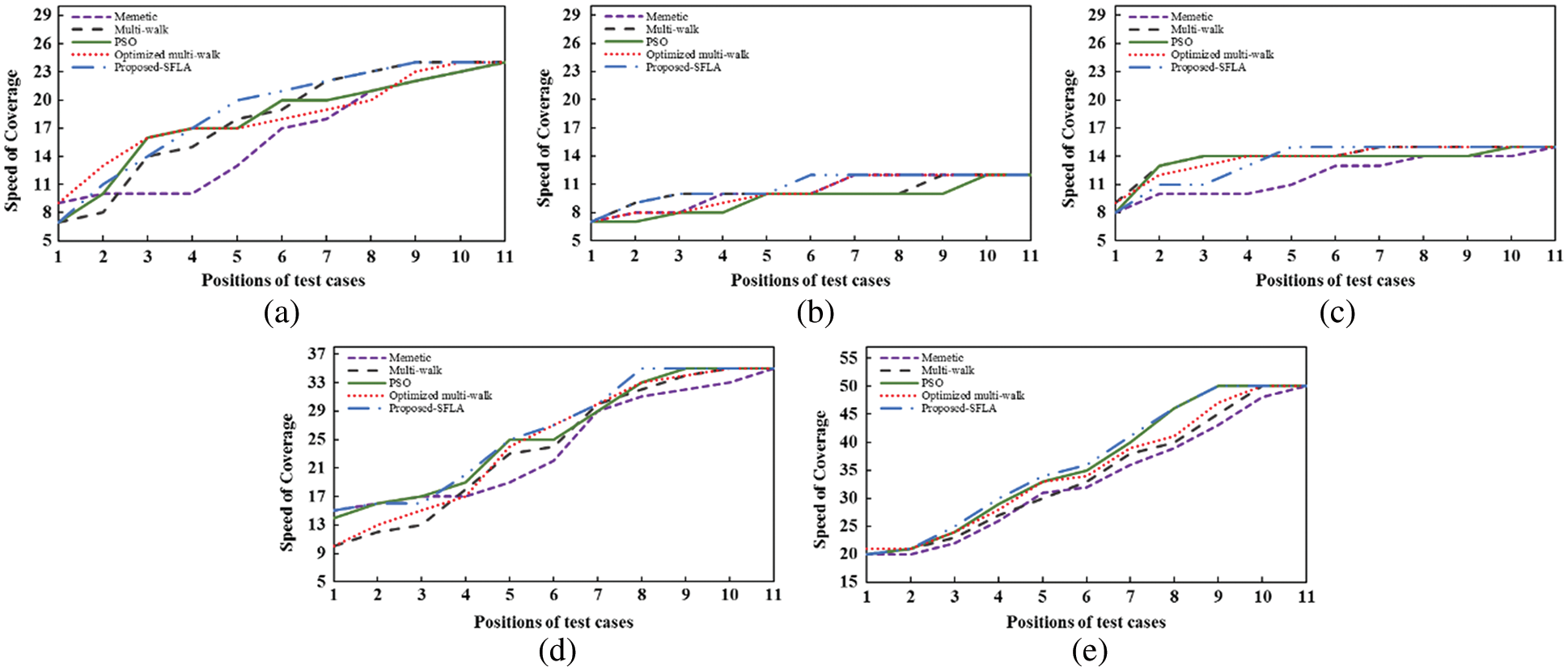
Figure 9: Graphs depicting the growth of coverage rate among the re-ordered test cases

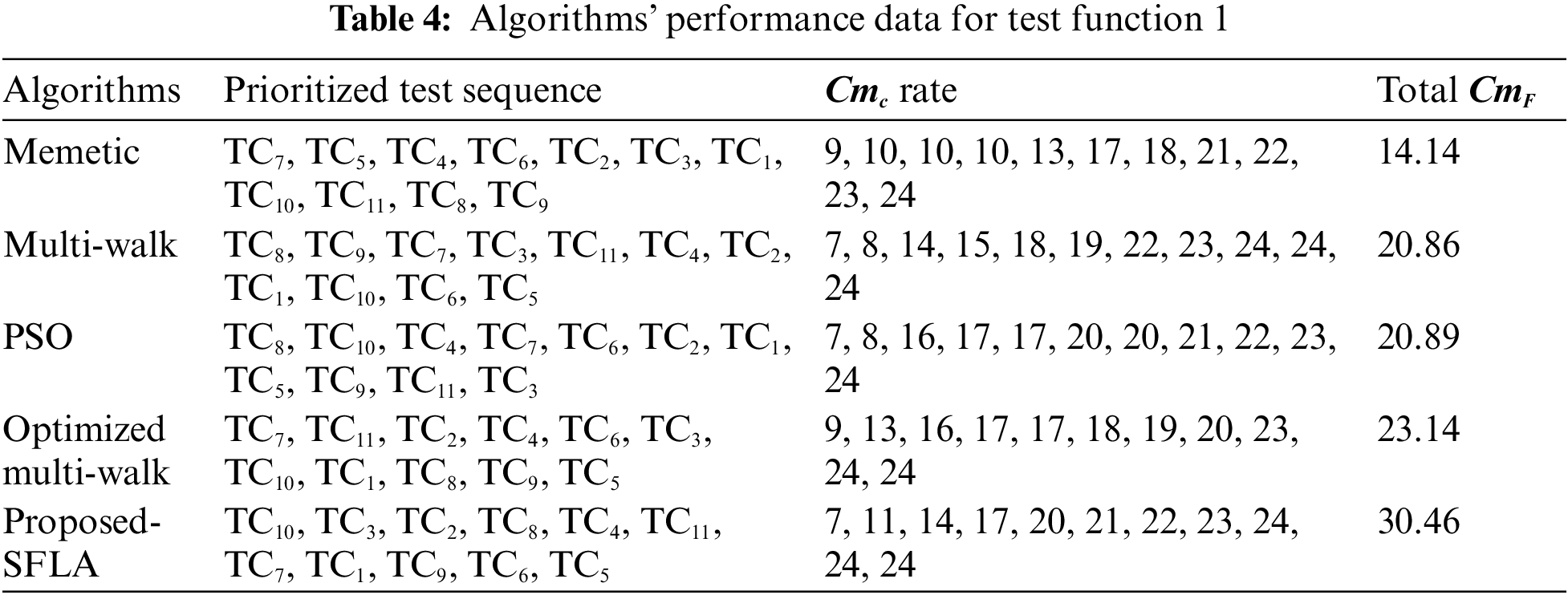
It could be observed from Table 4 that in the case of moderate shieldedness, optimized multi-walk [5] is the second-best in satisfying the coverage and fault at the earliest. This further ensured that optimized multi-walk could be considered the finer option for test codes possessing high complexity and higher or moderate shieldedness effect among the test cases. However, there is no guarantee that the results achieved are optimal since randomness could also affect them in some instances.

With reference to the coverage and fault detection pace of the original order of the test cases and the prioritized order through the proposed-SFLA, Fig. 10 exhibits how the speed drastically changes at the peak, i.e., after ⌊n2⌋−1. The nature of the proposed-SFLA depicted in Fig. 10 also addresses RQ3. The justifications regarding the APFD computation [2] for test function 1 are shown in Fig. 11, which also answers RQ4. In Fig. 11, it is seen that the APFD estimate of optimized multi-walk [5] is slightly lower than basic multi-walk, which in turn is a rare scenario. Since the basic multi-walk [32] incorporates approximately 80% of the randomness, determining its efficiency in terms of the earliest fault and coverage detection for a specific case is almost uncertain as it could even go beneath the efficiency levels of the memetic algorithm [23]. On the contrary, PSO [24] is better in dealing with highly complex code but with a moderate or less shieldedness effect. However, whether the absence of this effect would escalate or de-escalate its efficiency is not yet analyzed. Proposed-SFLA, on the other hand, surpassed all other algorithms by achieving around 70% of APFD with no significant effect of randomness and shieldedness (Fig. 11).

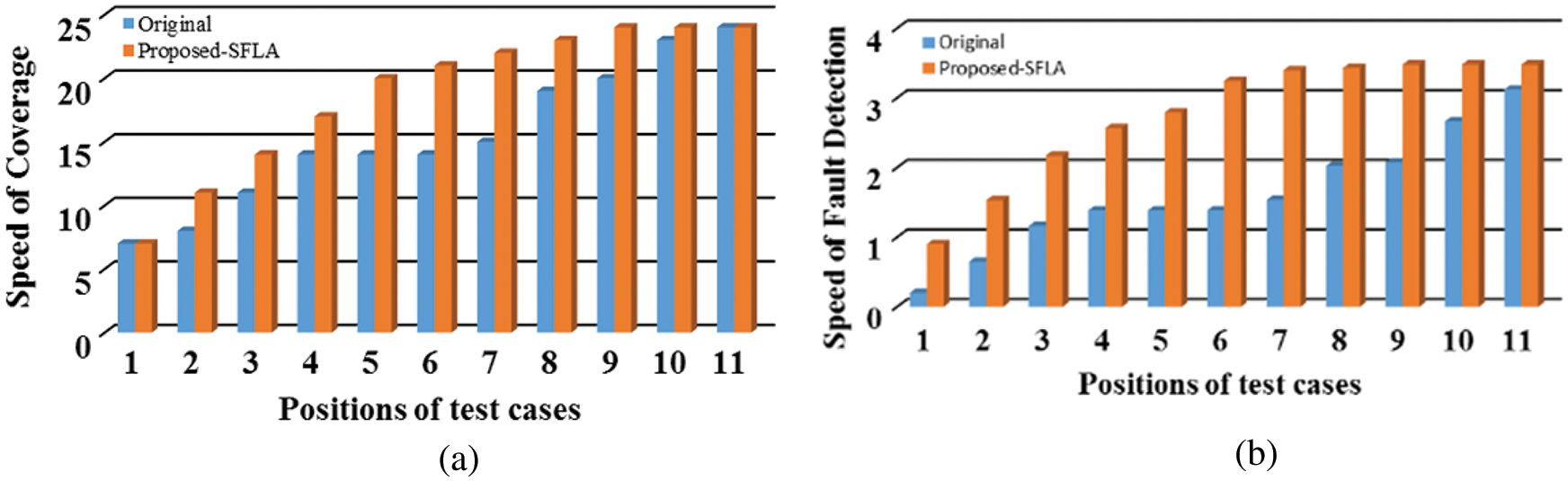
Figure 10: Comparative depiction between original test case order and prioritized test case order by proposed-SFLA for test function 1

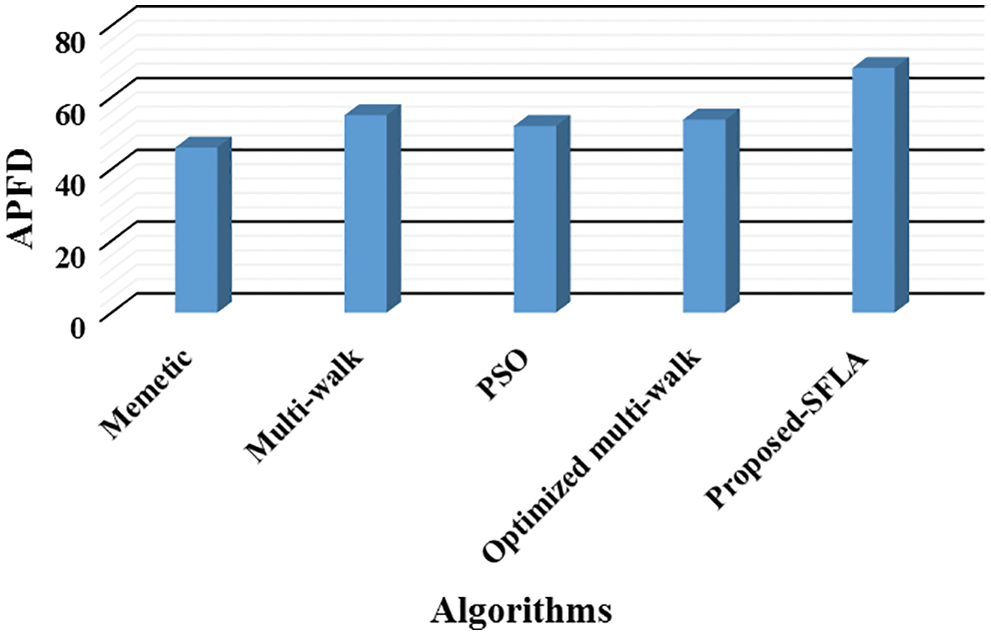
Figure 11: Comparative analysis among algorithms over evaluation metric (i.e. APFD) for test function 1

5  Conclusion

Maximization of either fault or coverage at the earliest is the necessitated prioritization goal in the studies approaching TCP. These studies, using some heuristics or meta-heuristic techniques, prioritize the test cases to attain the specified goal. However, with such a prioritization goal and the lack of multi-objectiveness, one or the other testing information related to test cases or test code gets compromised during TCP. Apart from that, previous research has concentrated their TCP techniques exclusively on the third level of testing, i.e., system. This study tries to shift this focus on the most vulnerable levels of testing, i.e., unit and integration, by proposing a natural memetics-inspired framework (i.e., SFLA) for TCP. The baseline structure of SFLA is infused with the critical parameters to have prioritized sequences of test cases at the unit and integration level of testing of SUT.

The experimental environment was configured to enhance the rate of test coverage and fault, both at the earliest in the prioritized sequence. It could be inferred from experimental data that Gbest_sol (prioritized sequence) acquired through proposed-SFLA suffice total test coverage at 9th position with a total CmF of 30.46 for test function 1. The peak is achieved at ⌈n2⌉th position in Gbest_sol. An average APFD estimate concluded that the proposed-SFLA surpassed optimized multi-walk, PSO, basic multi-walk, and memetic by 11.51%, 12.24%, 13.99%, and 21.7%, sequentially.

Since the Gbest_sol is competent in disclosing faults at the earliest, it could be said that the probability of localizing faults is also improved. However, for future perspective, if additional measures such as fault score, frequency of multi-line faults, and probability of faults in non-weighted statements could be tracked from previous releases of SUT, the ρ[TCi=1ton∗Nj=1toMaxst] database in this study could be further improved and thus could enhance the percentile of fault localization. Additionally, more intricate branching in the CFG and the increased number of leaf nodes (unit nodes) that might be tested by single test cases could make the working of proposed-SFLA susceptible. Since this work is the first to adopt SFLA for TCP in the unit and integration environment, a hybridization of the proposed-SFLA could be practiced for stability.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. Singhal, N. Jatana, B. Suri, S. Misra and L. Fernandez-Sanz, “Systematic literature review on test case selection and prioritization: A tertiary study,” Applied Sciences, vol. 11, no. 24, pp. 12121, 2021. [Google Scholar]

 2.  Y. Lou, J. Chen, L. Zhang and D. Hao, “Chapter one—a survey on regression test-case prioritization,” In: A. M. Memon (Ed.Advances in Computers, vol. 113, pp. 1–46, United States: Elsevier, 2019. [Google Scholar]

 3.  A. Gupta and R. P. Mahapatra, “Multifactor algorithm for test case selection and ordering,” Baghdad Science Journal, vol. 18, no. 2(Suppl.), pp. 1056–1075, 2021. https://doi.org/2021105610.21123/bsj. [Google Scholar]

 4.  H. Hemmati, “Chapter four—advances in techniques for test prioritization,” In: A. M. Memon (Ed.Advances in Computers, vol. 112, pp. 185–221, United States: Elsevier, 2019. [Google Scholar]

 5.  U. Geetha, S. Sankar and M. Sandhya, “Acceptance testing based test case prioritization,” Cogent Engineering, vol. 8, no. 1, pp. 1907013, 2021. [Google Scholar]

 6.  G. Rothermel, R. H. Untch, C. Chu and M. J. Harrold, “Prioritizing test cases for regression testing,” IEEE Transactions on Software Engineering, vol. 27, no. 10, pp. 929–948, 2001. [Google Scholar]

 7.  C. Hettiarachchi and H. Do, “A systematic requirements and risks-based test case prioritization using a fuzzy expert system,” in 2019 IEEE 19th Int. Conf. on Software Quality, Reliability and Security (QRS), Sofia, Bulgaria, pp. 374–385, 2019. [Google Scholar]

 8.  M. Mahdieh, S.-H. Mirian-Hosseinabadi, K. Etemadi, A. Nosrati and S. Jalali, “Incorporating fault-proneness estimations into coverage-based test case prioritization methods,” Information and Software Technology, vol. 121, no. 2, pp. 106269, 2020. [Google Scholar]

 9.  M. Khatibsyarbini, M. Isa, D. Jawawi and R. Tumeng, “Test case prioritization approaches in regression testing: A systematic literature review,” Information and Software Technology, vol. 93, no. 4, pp. 74–93, 2017. [Google Scholar]

10. A. Bajaj and O. P. Sangwan, “A survey on regression testing using nature-inspired approaches,” in 2018 4th Int. Conf. on Computing Communication and Automation (ICCCA), Greater Noida, India, pp. 1–5, 2018. [Google Scholar]

11. A. Bajaj and O. P. Sangwan, “A systematic literature review of test case prioritization using genetic algorithms,” IEEE Access, vol. 7, pp. 126355–126375, 2019. [Google Scholar]

12. M. Eusuff, K. Lansey and F. Pasha, “Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization,” Engineering Optimization, vol. 38, no. 2, pp. 129–154, 2006. [Google Scholar]

13. B. Manaswini and A. Rama Mohan Reddy, “A Shuffled frog leap algorithm based test case prioritization technique to perform regression testing,” International Journal of Engineering and Advanced Technology (IJEAT), vol. 8, no. 5, pp. 671–674, 2019. [Google Scholar]

14. P. Vats, Z. Aalam, S. Kaur, A. Kaur and S. Kaur, “A multi-factorial code coverage based test case selection and prioritization for object oriented programs,” in ICT Systems and Sustainability, Singapore: Springer, pp. 721–731, 2021. [Google Scholar]

15. C. Lu, J. Zhong, Y. Xue, L. Feng and J. Zhang, “Ant colony system with sorting-based local search for coverage-based test case prioritization,” IEEE Transactions on Reliability, vol. 69, no. 3, pp. 1004–1020, 2020. [Google Scholar]

16. W. Fu, H. Yu, G. Fan and X. Ji, “Coverage-based clustering and scheduling approach for test case prioritization,” IEICE Transactions on Information and Systems, vol. E100.D, no. 6, pp. 1218–1230, 2017. [Google Scholar]

17. M. A. Rahman, M. A. Hasan and M. S. Siddik, “Prioritizing dissimilar test cases in regression testing using historical failure data,” International Journal of Computer Applications, vol. 180, no. 14, pp. 1–8, 2018. [Google Scholar]

18. P. Kandil, S. Moussa and N. Badr, “Cluster-based test cases prioritization and selection technique for agile regression testing,” Journal of Software: Evolution and Process, vol. 29, no. 6, pp. e1794, 2017. [Google Scholar]

19. T. Afzal, A. Nadeem, M. Sindhu and Q. uz Zaman, “Test case prioritization based on path complexity,” in 2019 Int. Conf. on Frontiers of Information Technology, Islamabad, Pakistan, pp. 363–3635, 2019. [Google Scholar]

20. D. Di Nucci, A. Panichella, A. Zaidman and A. De Lucia, “A test case prioritization genetic algorithm guided by the hypervolume indicator,” IEEE Transactions on Software Engineering, vol. 46, no. 6, pp. 674–696, 2020. [Google Scholar]

21. P. K. Gupta, “K-step crossover method based on genetic algorithm for test suite prioritization in regression testing,” JUCS—Journal of Universal Computer Science, vol. 27, no. 2, pp. 170–189, 2021. [Google Scholar]

22. D. Mishra, N. Panda, R. Mishra and A. A. Acharya, “Total fault exposing potential based test case prioritization using genetic algorithm,” International Journal of Information Technology, vol. 11, no. 4, pp. 633–637, 2018. [Google Scholar]

23. F. M. Nejad, R. Akbari and M. M. Dejam, “Using memetic algorithms for test case prioritization in model based software testing,” in 2016 1st Conf. on Swarm Intelligence and Evolutionary Computation (CSIEC), Bam, Iran, pp. 142–147, 2016. [Google Scholar]

24. E. Ashraf, K. Mahmood, T. A. Khan and S. Ahmed, “Value based PSO test case prioritization algorithm,” International Journal of Advanced Computer Science and Applications, vol. 8, no. 1, pp. 389–394, 2017. [Google Scholar]

25. A. Samad, H. B. Mahdin, R. Kazmi, R. Ibrahim and Z. Baharum, “Multiobjective test case prioritization using test case effectiveness: Multicriteria scoring method,” Scientific Programming, vol. 2021, pp. e9988987, 2021. [Google Scholar]

26. A. Bajaj and O. P. Sangwan, “Discrete cuckoo search algorithms for test case prioritization,” Applied Soft Computing, vol. 110, no. 3, pp. 107584, 2021. [Google Scholar]

27. M. M. Öztürk, “A bat-inspired algorithm for prioritizing test cases,” Vietnam Journal of Computer Science, vol. 5, no. 1, pp. 45–57, 2018. [Google Scholar]

28. M. Khatibsyarbini, M. A. Isa, D. N. A. Jawawi, H. N. A. Hamed and M. D. Mohamed Suffian, “Test case prioritization using firefly algorithm for software testing,” IEEE Access, vol. 7, pp. 132360–132373, 2019. [Google Scholar]

29. R. Mukherjee and K. S. Patnaik, “Prioritizing JUnit test cases without coverage information: an optimization heuristics based approach,” IEEE Access, vol. 7, pp. 78092–78107, 2019. [Google Scholar]

30. Y. Zhu, E. Shihab and P. C. Rigby, “Test re-prioritization in continuous testing environments,” in 2018 IEEE Int. Conf. on Software Maintenance and Evolution (ICSME), Madrid, Spain, pp. 69–79, 2018. [Google Scholar]

31. J. A. Prado Lima and S. R. Vergilio, “Test case prioritization in continuous integration environments: A systematic mapping study,” Information and Software Technology, vol. 121, pp. 106268, 2020. [Google Scholar]

32. Z. Chi, J. Xuan, Z. Ren, X. Xie and H. Guo, “Multi-level random walk for software test suite reduction,” IEEE Computational Intelligence Magazine, vol. 12, no. 2, pp. 24–33, 2017. [Google Scholar]