Secure and Efficient Data Transmission Scheme Based on Physical Mechanism

1  Introduction

The arrival of 5G (5th generation mobile networks) era will accelerate the development of the Internet of Things (IoT) related industries [1], such as smart city, environmental monitoring, smart home. The broad market prospect of IoT in 5G era increases the demand for security protection and efficient data transmission. The processing speed of asymmetric encryption technology is much lower than that of the symmetric encryption technology, and the latter is much suitable for privacy protection of data transmission. Traditional security technologies are usually based on typical mathematical problems (such as large number factorization, elliptic curve discrete logarithm problem), and their security depends on the computational complexity of reverse attack process, which may not be easy to succeed with the current computing power. With the improvement of computing ability and the progress of attack means, many traditional security algorithms have been proved to be unsafe. The quantum technology will make this situation even worse.

Most IoT application scenarios have the characteristics of limited hardware resources and low power consumption. Traditional security technologies do not consider such resource and power constraints [2]. In order to make the traditional security algorithms adapt to IoT scenario with resource and power constraints, it is usually necessary to simplify these algorithms in terms of key length and number of encryption rounds, which will further reduce the security performance of the traditional security technologies.

In order to address the challenges faced by traditional security technology in the IoT related fields, many physical mechanism based security schemes have been proposed. Their security usually does not depend on the computational complexity of the algorithm. These security schemes usually use the basic characteristics of the physical layer and are designed based on the classical physical principles. For example, the wireless channel based key generation schemes use the reciprocity, time variability and spatial decorrelation of the wireless channel to generate the same key between communication parties [3].

The physical mechanism based security technology urgently needs to overcome the bottleneck of the key generation rate. Due to the resource and power constraints in the IoT related scenarios, lightweight encryption schemes are widely used. Such lightweight algorithms cannot provide the security as the traditional encryption schemes. According to Shannon’s one-time pad theory, in order to realize secure communication, both parties of the communication need to have the same random number as the key, and the key generation rate can neither be lower than the data rate nor be reused. The existing key generation rate based on physical mechanism is far from meeting the needs of the growth of data transmission rate. Taking the wireless channel based key generation schemes as an example, these schemes use wireless channel characteristics as random sources to generate keys. However, However, in IoT applications such as environmental monitoring and vehicle communication, the wireless channel changes very slowly and the randomness of the key source is poor, which cannot meet the need for rapid key generation. According to test results in WiFi [4], vehicle communication [5], wireless sensor [6], body area network [7] and LoRa [8], the key generation rate is generally less than 100 bps. Other technologies, such as quantum based technology and fiber channel based technology, can achieve higher key generation rate, but they are not suitable for most IoT applications.

Superlattice has the physical characteristics and advantages to solve the problem of high-speed symmetric key generation in IoT scenarios. As the ideal elements for sub-THz and THz electronics, superlattices has high signal output rate. The chaotic oscillation of superlattices can be used to generate physical random numbers at high speed [9]. Random number is the basis of all kinds of security algorithms. Under the same excitation signal, the matched superlattice chip can produce chaotic synchronization signal. These chaotic synchronization signals are highly similar to each other [10], which are an ideal signal sources for generating symmetric keys. The inherent random fluctuation of molecular level in the formation process of superlattice materials makes it physically unclonable, which can be used to construct physical unclonable function (PUF) to ensure the security of symmetric keys.

In order to solve the challenge of symmetric key generation in IoT, this paper applies superlattice technology to the security field of IoT, and proposes a high-speed symmetric key generation scheme based on superlattice. This scheme uses the physical characteristics of superlattice materials such as physical non-repetition and high-speed chaotic synchronization to realize the high-speed generation of symmetric key for IoT applications. In addition, in order to improve security and efficiency of IoT data transmission, this paper also proposes a secure and efficient data encoding and decoding scheme based on Superlattice symmetric key and compressed sensing. The main contributions of this paper are summarized as follows:

(1)   We introduce superlattice technology into the security field of Internet of things, and propose a symmetric key generation scheme based on superlattice to solve the secure and high-speed key distribution problem between IoT devices.

(2)   We propose a secure and efficient encoding and decoding scheme based on compressive sensing and superlattice symmetric key to achieve secure and efficient data transmission in IoT.

The rest of this paper is organized as follows. Section 2 contains background knowledge and related works. Section 3 defines the network model and attack models. Section 4 presents the symmetric key generation scheme based on superlattice. Section 5 presents the data transmission scheme based on superlattice and compressive sensing. Section 6 consists of theoretical analyses. Section 7 presents the experimental evaluation. Section 8 is the conclusion.

2  Background and Related Work

2.1 Superlattice and Its Safe Application Value

In order to develop high-frequency oscillators, Esaki and Tsu proposed the concept of semiconductor superlattice. Superlattice is composed of semiconductor thin layers with different components. The thickness of semiconductor thin layer is generally several or tens of nanometers. The number of semiconductor thin layers is very large. Taking GaAs/Al0.45Ga0.55As as an example, the number of thin layers is more than 200. It includes not only the superlattice barrier layer of Al0.45Ga0.55As, but also many quantum well layers with other components. These thin layers alternate to form a periodic band structure. Superlattices are usually fabricated by Molecular Beam Epitaxy (MBE) technology. When the electrons in the superlattice move along the epitaxial direction, they will be affected by the additional periodic potential field. The barrier width between multiple quantum wells in superlattice is small, and electrons can tunnel into adjacent quantum wells. Due to the strong coupling between adjacent quantum wells, the quantized isolated energy levels in the well are coupled to form a superlattice band structure, which shows a series of new quantum physical properties with high safe application value.

Chaotic Oscillation and Random Number: Superlattice is a typical one-dimensional nonlinear system. The continuous resonant tunneling between the thin layers of superlattice leads to negative differential conductance, which induces nonlinear properties. Spontaneous chaotic oscillation is the most representative form of this nonlinear characteristic [9]. Chaotic oscillation in semiconductor superlattices can form a good entropy source for generating physical random numbers at a very high speed. Random number is the basis of all kinds of security algorithms.

High Speed Output Signal: Superlattices are ideal elements for sub-THz and THz electronics, while its signal output rate can match the transmission rate of 5G.

Chaotic Synchronization: There are also chaotic synchronization characteristics in superlattices [10]. Under the same excitation signal, matched semiconductor can produce highly similar output signals. Synchronous chaotic signals can hide the transmission information, which can be applied in secure communication.

2.2 Physical Mechanism Based Key Generation

Such schemes usually generate keys by extracting the common randomness between communication entities. It mainly includes following types.

The first type of schemes is based on the wireless channel, which uses the reciprocity of the wireless channel to extract randomness and generate key. This type of schemes makes full use of the characteristics of wireless channel, and takes into account the influence of noise, fading, interference, dispersion, diversity and so on, so as to ensure that the target user can successfully decode data while preventing eavesdroppers [11]. The key generation technology based on wireless channel has been realized in WiFi [4], vehicle communication [5], wireless sensor [6], body area network [7] and LoRa [8]. The key generation rate of these schemes is generally low, and most of them are less than 100 bps.

The second type of schemes utilizes the randomness of environment sensing to extract a secret key. In order to generate a common secret key, communication entities need physical proximity to obtain similar environmental aware data. For example, Qiu et al. [12] generate secret key from the dynamic geomagnetic field sensing data. Such schemes rely on customized devices, and the key generation rate is also very low.

The third type of schemes is based on the acoustic channel. It exploits fast varying inaudible acoustic channel for generating enough randomness, and improves the key generation rate [13,14]. These schemes have strict requirements on the distance between the two sides of communication. For example, in [14], the best distance is between 50 and 70 cm, and its key generation rate is about 256 bps.

Other representative key generation schemes include quantum based key distribution and laser secure communication [15]. Although these schemes can achieve higher key generation rate, they are not suitable for most Internet of things applications

2.3 Physical Mechanism Based Identity Authentication

Such schemes usually extract some unique characteristic information from the equipment or environment for identity authentication. It mainly includes following types.

The first type of schemes extracts fingerprint from the IoT device itself or the wireless channel. Zheng et al. [16] extract Radio Frequency (RF) fingerprinting for trusted identification of IoT device. DeMiCPU [17] is a stimulation-response-based device fingerprinting technique based on magnetic induction signals emitted from the CPU module. Chen et al. [18] is a lightweight device authentication protocol based on acoustic hardware fingerprint.

The second type of schemes obtains similar information among different devices for mutual authentication. Li et al. [19] authenticate device users by comparing the petting operations sensed by devices and those captured by the user wristband. Yan et al. [20] propose a touch-to-access device authentication scheme using induced body electric potentials caused by the indoor ambient electric field. Han et al. [21] present a proximity-proof based schemes for mobile two-factor authentication by using inaudible acoustic signals. Piano [22] is a proximity-based user authentication method for access control on voice-powered IoT devices.

The third type of schemes extracts user biometrics with device assistance for user identity authentication. Velody [23] leverages the unique and nonlinear hand-surface vibration response to mitigate the vulnerabilities of static biometrics. EchoPrint [24] uses acoustics and vision for user authentication. Taprint [25] leverages the tapping vibrometers as biometrics to authenticate the user, while distinguishing the tapping locations.

3  Network Model and Attack Model

The network model is shown in Fig. 1. It consists of data sender Alice and data receiver Bob. Alice and Bob are common IoT devices. Alice is responsible for data collection, and sends the processed data to Bob through the public communication channel. The transmitted data may be eavesdropped by adversaries.

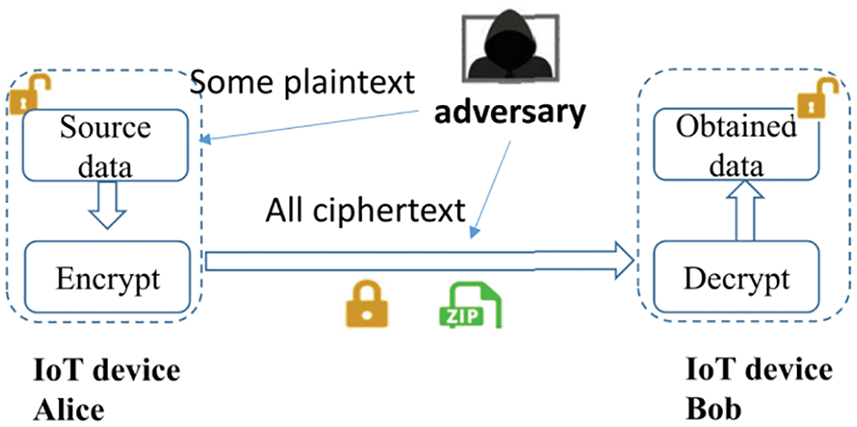
Figure 1: Network model and attack model

In order to improve the efficiency of data transmission, Alice usually needs to compress the data. To ensure data security, Alice also needs to encrypt the data. In this paper, data compression and encryption operations are collectively referred to as data encoding. Bob receives the data from Alice, and decodes it to get the final obtained data. Decoding operation mainly involves decompression and decryption. The communication details such as modulation and demodulation are not involved in the scheme. In reality, IoT devices are usually both data sender and data receiver. The proposed scheme can be extended to this scenario.

This paper focuses on data privacy and transmission efficiency. Other security issues, such as replay attacks, denial of service attacks, data tampering, are not considered. The adversary can implement two kinds of attacks as follows:

Ciphertext Only Attack (COA): As shown in Fig. 1, the adversary can eavesdrop in the public communication channel, and obtain all ciphertext. Therefore, the adversary can launch a ciphertext only attack.

Known Plaintext Attack (KPA): As shown in Fig. 1, the adversary can obtain some plaintext data. For example, IoT devices may be deployed in unattended scenarios and collect environmental data. Adversaries can acquire the required plaintext data by deploying the same sensors near the data sender Alice. As the adversary can obtain all ciphertext, it’s not difficult for him to obtain some plaintext-ciphertext pairs, which means the adversary can perform a known plaintext attack.

4  Symmetric Key Generation Scheme Based on Superlattice

In order to address the challenge of high-speed distribution of symmetric key between IoT devices, we introduce superlattice into IoT field, and build a symmetric key generation scheme based on the chaotic synchronization feature of superlattice. The flow chart of symmetric key generation between IoT devices Alice and Bob is shown in Fig. 2.

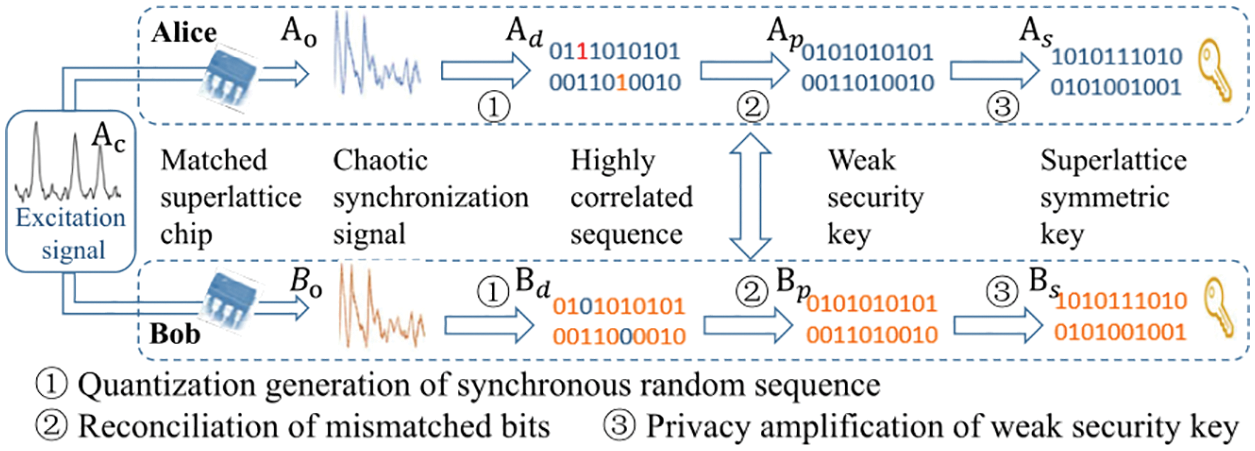
Figure 2: High speed symmetric key generation based on superlattice

The high-speed superlattice symmetric key generation scheme mainly includes four stages: (1) Generation of superlattice chaotic synchronization signal; (2) Quantization generation of synchronous random sequence; (3) Reconciliation of mismatched bits; (4) Privacy amplification of weak security key.

4.1 Generation of Superlattice Chaotic Synchronization Signal

Each IoT device is equipped with superlattice chips. Superlattice chips of Alice and Bob are matched with each other. Under the same excitation signal, there will be superlattice chaotic synchronization between these matched superlattice chips, and the output signals of these matched superlattice chips are similar to each other.

In the chaotic synchronization signal generation stage, the matched superlattice chips carried by Alice and Bob generate highly similar chaotic synchronization (response) signals Ao and Bo under the same excitation signal Ac. Excitation signal Ac is public information. The adversary cannot infer the chaotic signal from the excitation signal. As a result, Alice and Bob can share the excitation signal sequence directly through public communication channel. They can also dynamically generate the same excitation signal by using the same pseudo-random function and the same initialization seed.

4.2 Quantization Generation of Synchronous Random Sequence

Chaotic synchronization signal is an analog signal. It needs to be converted into digital signal sequences Ad and Bd. The rate of quantization will affect the final symmetric key generation rate. There are many ways to improve the quantization generation rate. We can use high speed analog to digital converter (ADC) directly. We can also achieve high-speed quantization generation based on low-speed ADC through parallel technology. The specific implementation needs to be determined according to the requirements of cost budget and symmetric key generation rate.

4.3 Reconciliation of Mismatched Bits

Due to the defects in the fabrication of superlattice chips, digital signal sequences obtained by Alice and Bob are not exactly the same. There will be a certain number of mismatched bits between Ad and Bd. For example, according to Fig. 2, there two mismatched bits in the generated synchronous random sequences, i.e., the 3rd and 16th. In order to generate identical symmetric key, it is necessary to locate and fix mismatched bits in random sequences. Fuzzy extraction [26] is a representative method for reconciliating mismatched bits of synchronous sequences. By using fuzzy extraction, Alice and Bob exchange a certain amount of information, and obtain Ap and Bp, where Ap=Bp.

4.4 Privacy Amplification of Weak Security Key

During the mismatched bit reconciliation stage, Alice and Bob will exchange some auxiliary data in the public communication channel, which will weaken the security key. In order to obtain superlattice symmetric key with information theory security, privacy amplification is necessary [14]. In the proposed scheme, Alice and Bob multiply sequence Ap and Bp with the same Toeplitz-like matrix to obtain the final symmetric key sequence As and Bs, where As=Bs.

5  Data Transmission Scheme Based on Superlattice and Compressive Sensing

In this section, we combine the superlattice and compressive sensing technology to build a secure and efficient data transmission scheme for IoT. The schematic diagram is shown in Fig. 3. Alice and Bob are IoT devices, which represent the sender and receiver of data transmission respectively. Alice performs the data encoding process and sends the encoded result to Bob through the public communication channel. The data decoding process is performed by Bob.

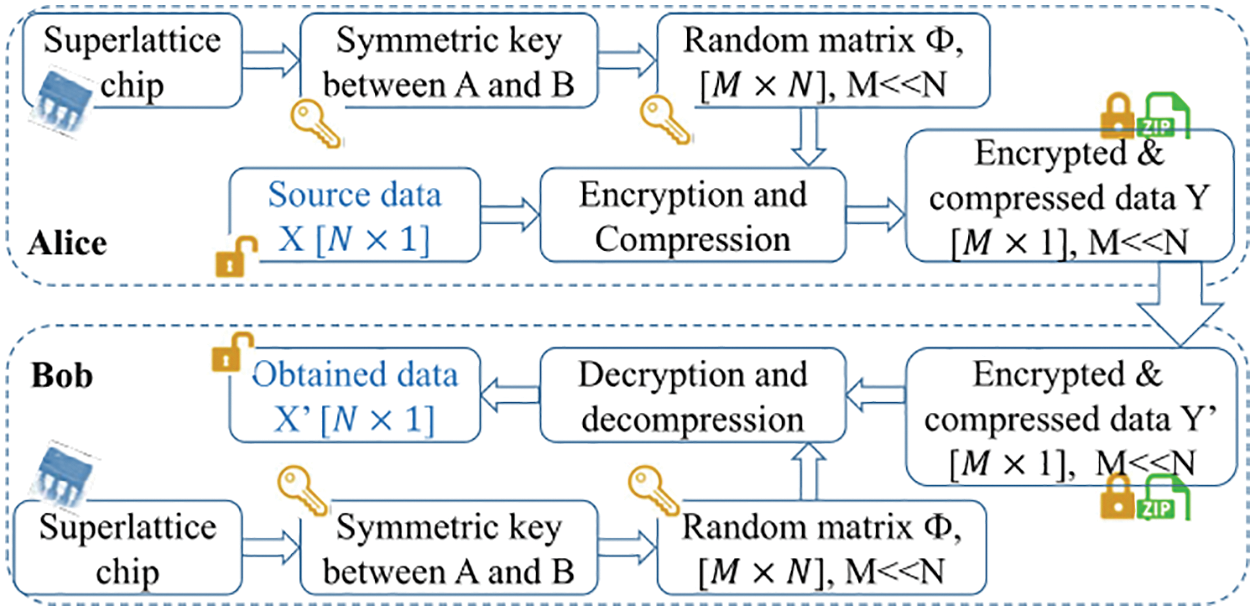
Figure 3: Data transmission based on superlattice and compressive sensing

In order to achieve transmission efficiency and data privacy, the data encoding process consists of both compression and privacy protection. In this scheme, compressive sensing is adopted to realize the efficient data compression [27]. The compressive sensing is also regarded as a lightweight encryption scheme, and the random matrix of compressive sensing is regarded as the secret key. However, as a lightweight encryption scheme, it’s not security enough. In order to improve the privacy protection ability of the proposed data transmission scheme, the superlattice symmetric key is introduced. The random matrix of compressive sensing is generated based on the superlattice symmetric key, and the proposed scheme is in fact a one-time pad encryption based secure communication scheme.

5.1 Data Encoding in Alice

Both data compression and data encryption are performed in the data encoding stage. The detailed encoding process is as follows

Preparation: Alice mainly has two tasks: source data preparation and symmetric key generation. As the data sender, Alice collects the source data, and organizes it into a one-dimensional array X, where its length is N. Both Alice and Bob need to generate the symmetric key between them for next stage. The detail of symmetric key generation scheme based on superlattice has been introduced in the previous section. After this step, the symmetric key sequence As and Bs will be generated synchronously in Alice and Bob, respectively.

Construction of Random Matrix: The random matrix Φ is constructed based on the superlattice symmetric key As. Alice intercepts a small sequence As1 from superlattice symmetric key sequence As, and convert it into a matrix Φ with a size of M×N, where M<<N. The sequence length of As1 can be either MN or not. If the length is MN, we can convert it into Φ in the order of row first or column first. If the length is not MN, we can convert it into a sequence with the length of MN by a pseudo-random number generation method. The seed of pseudo-random algorithm used in Alice and Bob can be generated from As1 and Bs1 in the same way, and thus the newly generated random sequence is still equal to each other.

Encryption and Compression: Both data compression and data encryption are achieved based on compressive sensing measurement. During the compressive sensing measurement, Alice multiplies the random matrix Φ and the source data X to obtain the measurement result Y with length M, i.e., Y=ΦX. The measurement result Y will be send to Bob through the public communication channel. According to Fig. 3, Y is called encrypted compressed data because both data compression and data encryption are achieved in the compressive sensing measurement operation. On the one hand, due to the low rank measurement feature of compressive sensing, the source data are compressed. The length of the measurement result Y is M, which is much smaller than the length of the source data X (i.e., M<<N). On the other hand, different from the traditional compressive sensing technology, the measurement matrix Φ is dynamically generated based on the superlattice symmetric key sequence As. Therefore, the measurement matrix Φ itself is safe. The compressive sensing measurement process performed on the source data X is equivalent to a one-time-pad encryption process. Therefore, the privacy of the source data X is protected.

5.2 Data Decoding in Bob

The data decoding process is performed by the data receiver Bob. It mainly includes the following three stages:

Data Receiving and Extraction: Bob receives the package sent by Alice from the public communication channel. He interprets the packet according to the communication protocol, and obtains the encrypted compressed data Y′. This paper focuses on data privacy protection and data transmission efficiency. It does not involve other security issues such as data integrity protection. For example, the data may not be sent by Alice, or the data may have been illegally tampered with. Therefore, in practical application, it is also necessary to introduce other mechanisms, such as trusted identification [16].

Construction of Random Matrix: Because the received data Y’ is the measurement result of compressive sensing. In order to recover the original data X’ from the compressive sensing measurement results, we need to construct a random matrix at the Bob end, which is the same as that in Alice. The random matrix in traditional compressive sensing technology is usually generated based on pseudo-random function. Different from the traditional compressive sensing technology, in the proposed scheme, the random matrix is not only used for compressive sensing measurement, but also used as the secret key of lightweight data encryption and decryption process. In the ordinary Internet of things scenario, due to the weak anti attack ability of Internet of things devices, the security of the traditional random matrix based on pseudo-random function is usually not guaranteed, and thus it is not suitable to be used as the secret key. In the proposed scheme, Bob constructs the random matrix based on the superlattice symmetric key generation mechanism. The symmetric key sequence Bs obtained by Bob is the same as As. Bob can construct a random matrix Φ with a size of M×N from Bs. If the random matrix construction process is the same as that in Alice, the obtained random matrix Φ of Bob and Alice will equal to each other.

Decryption and Decompression: Both data decryption and decompression are achieved in compressive sensing recovery process. In the proposed scheme, compressive sensing is interpreted as a lightweight symmetric encryption system, where the secure key is the random matrix Φ. Compressive sensing measurement process and recovery process corresponds to encryption and decryption process respectively. Based on encrypted compressed data $Y’$ and random measurement matrix Φ, Bob will construct an optimization problem as θ^=argmin||θ||1, s.t.,y=Aθ,A=ΦΨ∈RM×N. θ is the sparse representation coefficient. Ψ is the sparse transformation basis, which can be either a predefined or a non-predefined. The widely used predefined basis includes DCT and wavelet transform. The non-predefined basis can be obtained from historical data. The final data X′ obtained by Bob can be expressed as X′=Ψθ.

6  Theoretical Analysis

This section analyzes the proposed schemes from three aspects: the security of the superlattice based symmetric key, the security of the data transmission, and the commercial feasibility.

6.1 Security Analysis of Superlattice Based Symmetric Key

Physical Non Clonability of Superlattice Materials: Superlattice materials have physical non-clonal characteristics, which result from random fluctuations at the molecular level. The superlattice materials are fabricated by MBE. According to the theory of thermodynamics and statistical mechanics, molecular level random fluctuations are inevitable in MBE growth process. Molecular level random fluctuations exist widely in various quantum well layers and barrier layers of superlattices, which makes it impossible to replicate superlattice materials manually.

The conditions for generating the chaotic synchronization signal of superlattice are very strict. Generally, it only exists between superlattice chips of the same size and shape from the same semiconductor wafer, which is called matched superlattice. The resonant tunneling current in superlattices is very sensitive to the molecular level fluctuations in the quantum well and barrier layers. Even with the same manufacturing equipment and process conditions, there are significant differences in chaotic oscillation modes between different superlattice chips fabricated from two different semiconductor wafers.

Superlattice chip can be regarded as a physical unclonable function (PUF) [28], which has important security significance. We can ensure the security of the key through the security management system and process of the superlattice chip. The number of superlattice chips processed from the same wafer is limited and cannot be reproduced. Therefore, it is feasible to manage and control the security of the chip at the institutional level.

Unpredictability of Superlattice Chaotic Signal: The pseudo-random number, which is widely used in security algorithms, is essentially a deterministic algorithm. In the case of known pseudo-random number algorithm and initial value, pseudo-random number sequence can be accurately reproduced.

Superlattice based symmetric key is generated based on the chaotic signal of superlattice. The randomness comes from the microphysics level, and the adversary cannot detect the physical generation process of the chaotic signal in superlattice. In theory, as long as the adversary does not own the physical entity of the superlattice chip, even using advanced machine learning methods, the adversary cannot predict the output chaotic signal, as well as the random number sequence.

6.2 Security Analysis of Data Transmission

Ciphertext Only Attack: The encoding process of the proposed scheme is based on compressive sensing technology. In ciphertext only attack, the ciphertext obtained by the adversary is essentially the compressive sensing measurement result.

The random matrix used in the compressive sensing measurement is dynamically generated based on the symmetric key sequence of the superlattice. The symmetric key sequence is shared only by the data sender Alice and the data receiver Bob, so the random matrix is secure.

The compressive sensing measurement is realized by matrix multiplication between random matrix and source data, which is in fact a random obfuscation operation. In theory, it is not feasible to realize the reverse data recovery when the random matrix is unknown.

Known Plaintext Attack: In the known plaintext attack model, the adversary can obtain Y (ciphertext) and a small number of X (plaintext), and try to use these plaintext-ciphertext pairs to crack the decryption key. The symmetric key of the proposed scheme is the random matrix.

In the proposed scheme, the random measurement matrices used in each compressive sensing measurement process are different from each other, and they are constructed dynamically based on a new symmetric key sequence fragment of superlattices. Therefore, even if the adversary can crack the corresponding key according to the known plaintext-ciphertext pair, this key has been invalid due to the dynamic key update mechanism.

The random measurement operation of compressive sensing is a low rank measurement, and there is a dimension compression process [29], which will further increase the difficulty of reverse data recovery of the adversary. In fact, even if the key update frequency is reduced, the security of the proposed scheme can still be guaranteed. The following is a simple quantitative analysis. According to the compressive sensing measurement process Y=ΦX, the number of unknowns in the symmetric key Φ is MN. If we want to solve MN unknowns, we need to construct at least MN linear independent equations. In each plaintext-ciphertext pairs, the size of X is N×1, and the size of Y is M×1.

The number of plaintext-ciphertext pairs required to solve the Φ will be no less than N. Considering the correlation between different equations, the amount of data needed is even larger. In other words, as long as the number of key reuse times is less than N, the proposed scheme is still secure.

7  Experimental Evaluation

In this section, we carry out experimental evaluations. First, we introduce the experimental setting. Then the feasibility of the proposed scheme is demonstrated. Finally, the recovery performance is evaluated.

7.1 Experimental Setting

The material of superlattice chip used in this experiment is GaAs/Al0.45Ga0.55As [9], which has been widely studied. It can maintain sufficient NDC (negative differential conductivity) and can induce spontaneous chaotic current oscillations at room temperature. Its chaotic synchronization phenomena and mechanisms have been deeply studied [10]. The hardware platform for the experiment is commercial embedded development boards equipped with cortex-a9, which is wildly used in IoT application. The software platform is Linux, and the program language adopted for experimental coding is C.

The benchmark schemes adopted in the experimental evaluation include TIFS16 [30]. Two types of datasets used, which are the k-sparse signal and Intel Berkeley Lab dataset. The K-sparse signal is a standard noise-free signal. The performance metric for k-sparse signal is the successful recovery ratio, where the successful recovery has a recovery error that is less than 10−6. The performance metric for real dataset, is the recovery error which is defined as ||x−x^||2||x||2. All recovery performance evaluation experiments were repeated 200 times, and the final result was the average value of them.

7.2 Feasibility Demonstration

In this section, we experimentally demonstrate the feasibility of the key modules of the proposed schemes. In order to deepen the understanding of the scheme, the experimental demonstration will focus on the intuitive results. The concrete demonstration will be carried out from the following two aspects. The first is the experimental demonstration of the chaos synchronization of the superlattice, which is the basis of the construction of the superlattice based symmetric key. The second is the experimental demonstration of secure and compressed encoding and decoding, which is the basis of data transmission scheme.

Chaos Synchronization of Superlattice: The following are experimental demonstration and correlation analyses of the superlattice chaotic synchronization signal, where the experimental results are shown in Fig. 4. Figs. 4a and 4b are chaotic synchronization signals obtained at Alice and Bob, respectively. According to Figs. 4a and 4b, signals A and B are highly similar to each other. Fig. 4c is the autocorrelation analysis result of signal A (which is similar to the one of signal B). The cross-correlation function used in this paper is defined as R12(t)=∫−∞+∞f1(τ)f2(τ−t)dτ. The autocorrelation function has similar definition, where f1 = f2. According to Fig. 4c, when t≠0, the autocorrelation coefficient of signal A is far less than 1, that is, the correlation of any two different time in signal A is very small. This shows that signal A itself is highly dissimilar at any two different time. This also means that signal A has a good randomness, which is conducive to constructing a random matrix that meets the need of compressive sensing. It should be noted that one of the purposes of this experiment is to show the randomness potential of signal A (and B). The random matrix actually used is not directly generated from signal A (and B). After privacy amplification and other operations, the randomness of the secret key will be further improved. In addition, we can also use the secret key as the seed of pseudo-random function to expand the sequence and generate the random matrix. The cross-correlation of A and B is similar to Fig. 4c, due to the high similarity between signals A and B. When t = 0, the cross-correlation of A and B takes the maximum value, which indicates that when signals A and B are in synchronous alignment, they are highly correlated, which is the basis of building a symmetric key between A and B.

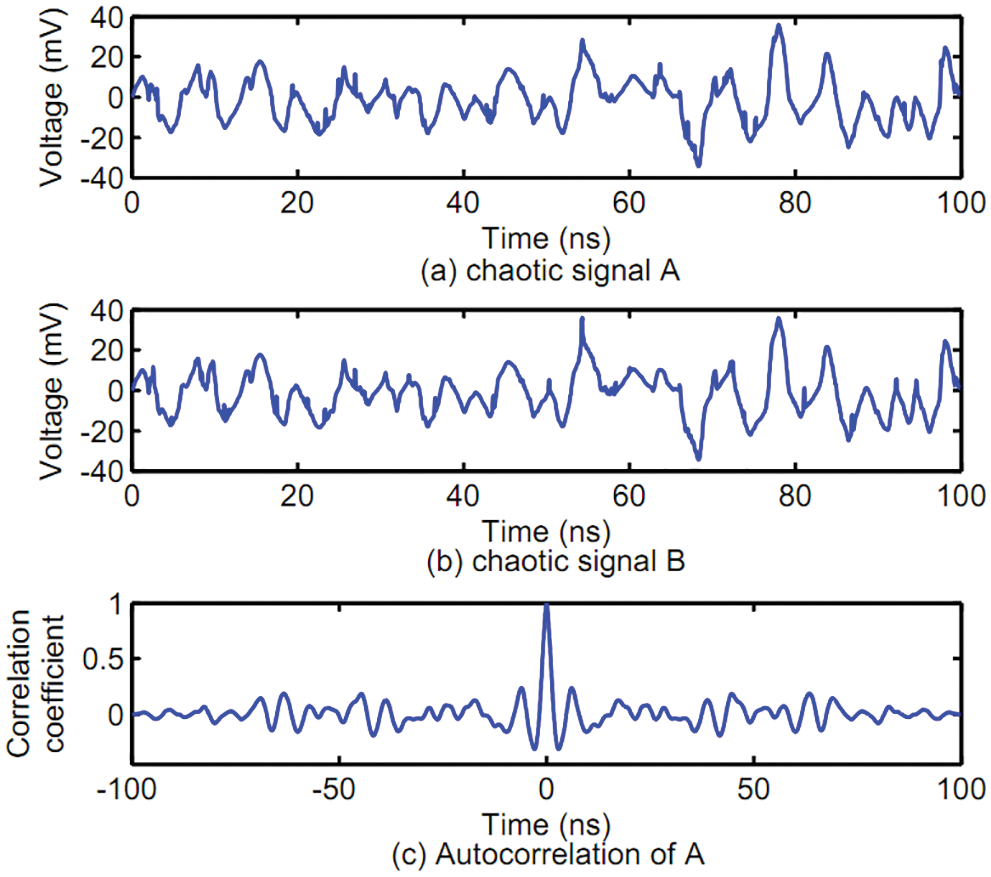
Figure 4: Chaotic synchronization signal of superlattice

Secure and Compressed Encoding and Decoding: In the IoT scenario, image data and sequence data are the two most representative data types. We will demonstrate the feasibility of the proposed scheme based on these two types of data.

Fig. 5 is the experimental demonstration result based on image data from Durlacher-Tor traffic dataset. Fig. 5a is the original image. Fig. 5b is the encoded image, which is an encryption and compression result of the original image. Fig. 5c is the decoded image, which is recovered from the encoded image based on compressive sensing. According to the experimental results, the encoding process realizes two functions: data compression and data privacy protection. Firstly, it performs well in privacy protection. The encoded image has good random characteristics, and the relevant information of the original image is effectively hidden. Secondly, it also performs well in data compression. Although the data amount of the encoded image is less than 40% of the original image, the decoding result can retain most details of the original image.

Figure 5: Encoding and decoding for image data

Fig. 6 shows the experimental demonstration result based on temperature sequence data from Intel Berkeley Lab dataset. Fig. 6a is the original temperature sequence data, Fig. 6b is the encoded result, and Fig. 6c is the decoded result. On the one hand, the encoding process realizes the privacy protection of original data. The encoded result (Fig. 6b) is a series of random sequences, and the detailed information of Fig. 6a has been hidden. On the other hand, the encoding process achieves efficient data compression. Although the length of the encoded data sequence is less than 40% of the original sequence length, the decoded result retains most of the detailed features of the original sequence.

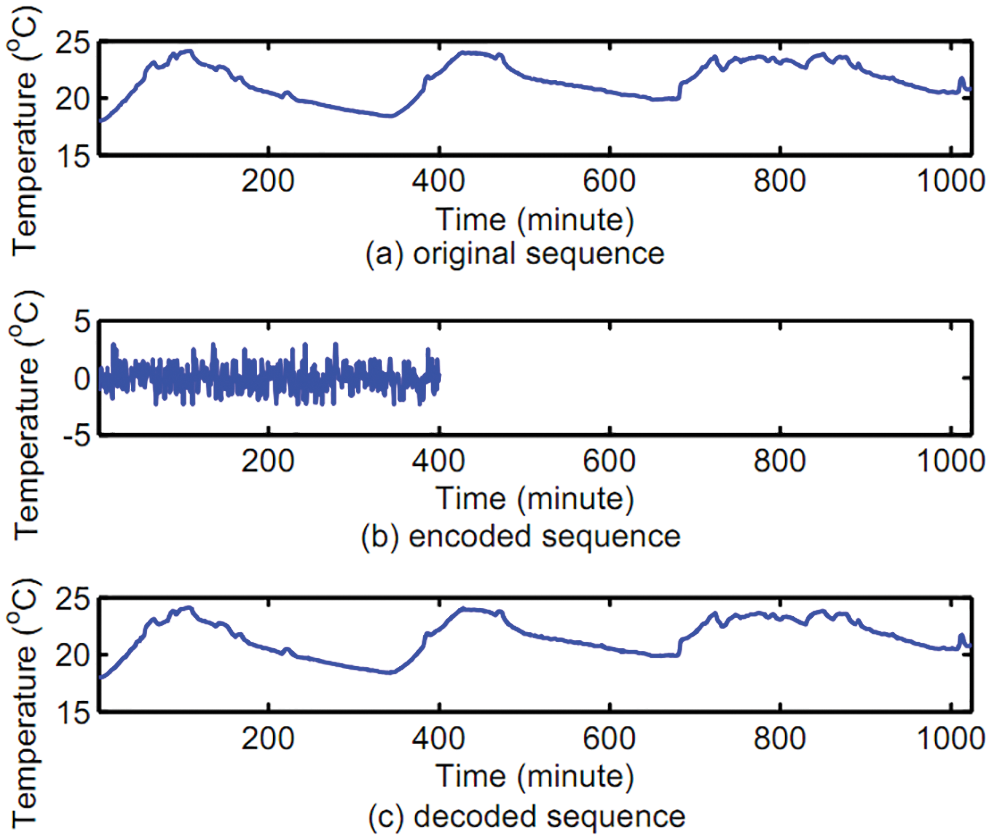
Figure 6: Encoding and decoding for temperature sequence data

7.3 Recovery Performance

In this section, we will conduct the recovery performance evaluation of the proposed scheme based on both k-sparse signals and Intel Berkeley Lab dataset.

(1) k-Sparse Signal

Fig. 7 is the recovery performance evaluation results in k-sparse signals. During the evaluation, we fixed the number of compressive sensing measurements to 68 and 88 respectively. Then, signals with different sparsity are generated, and the recovery performance of the proposed scheme is evaluated in these sparse signals. Two cases of the proposed scheme are evaluated. One is the proposed scheme and the other is the proposed scheme with no privacy amplification (i.e., no PA). The performance of the proposed scheme is basically consistent with that of TIFS16. It should be noted that TIFS16 has been proved to have security challenges in WSN and other IoT scenarios. In the traditional key generation scheme based on physical mechanism, privacy amplify is mainly used to enhance the key security. In the proposed paper, it will also affect the subsequent compressive sensing recovery performance. For the no PA version of the proposed scheme, its recovery performance reduces greatly.

(2) Real World Data

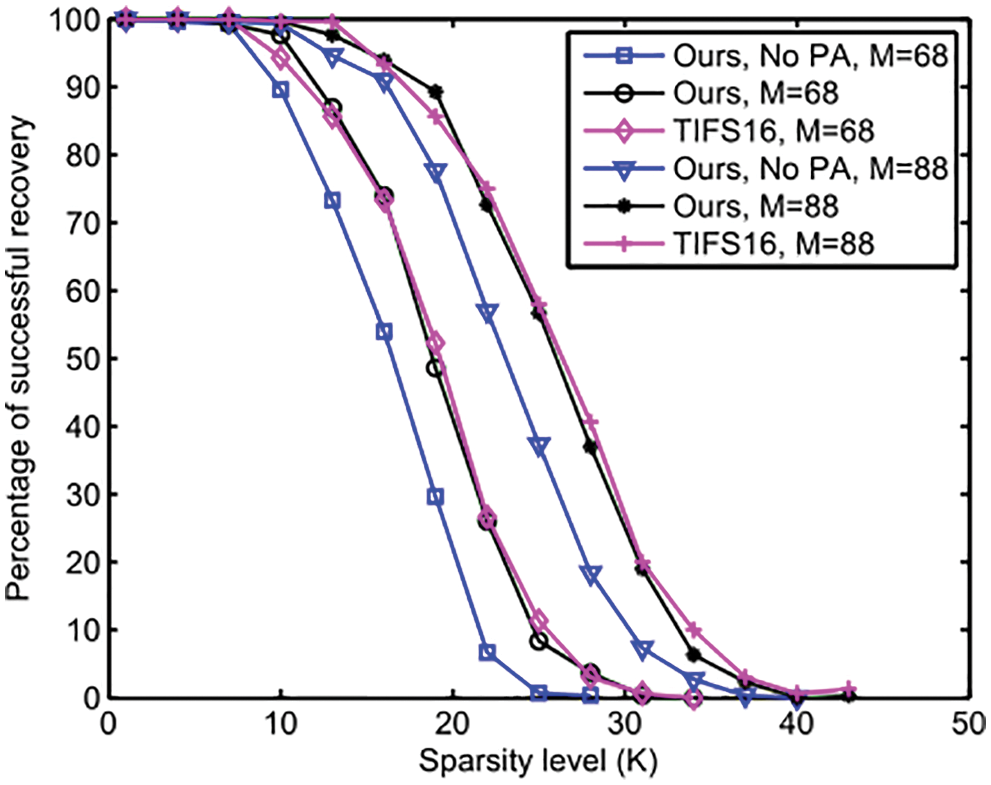
Figure 7: Recovery performance on k-sparse signal

According to the theory of compressive sensing, in order to achieve efficient recovery from compressive sensing measurement results, the signal needs to be sparse or compressible. Therefore, we will perform the sparse testing on the dataset before evaluating the recovery performance of the proposed scheme based on the real dataset. We perform the sparse testing based on the DCT (Discrete Cosine Transform) basis as follows. Firstly, a segment of signal with length of 1024 is randomly selected from the dataset. Then, DCT transformation is performed on it, where Fig. 8a is the transformation coefficients. Finally, we exam its sparse expression ability based on these coefficients. The sparse testing is given in Fig. 8b, where the horizontal axis is the number of coefficients reserved for data recovery, and the vertical axis is the recovery error. According to these results, high recovery accuracy can be achieved by using only a small number of coefficients. Therefore, the dataset meets the sparsity requirements of compressive sensing.

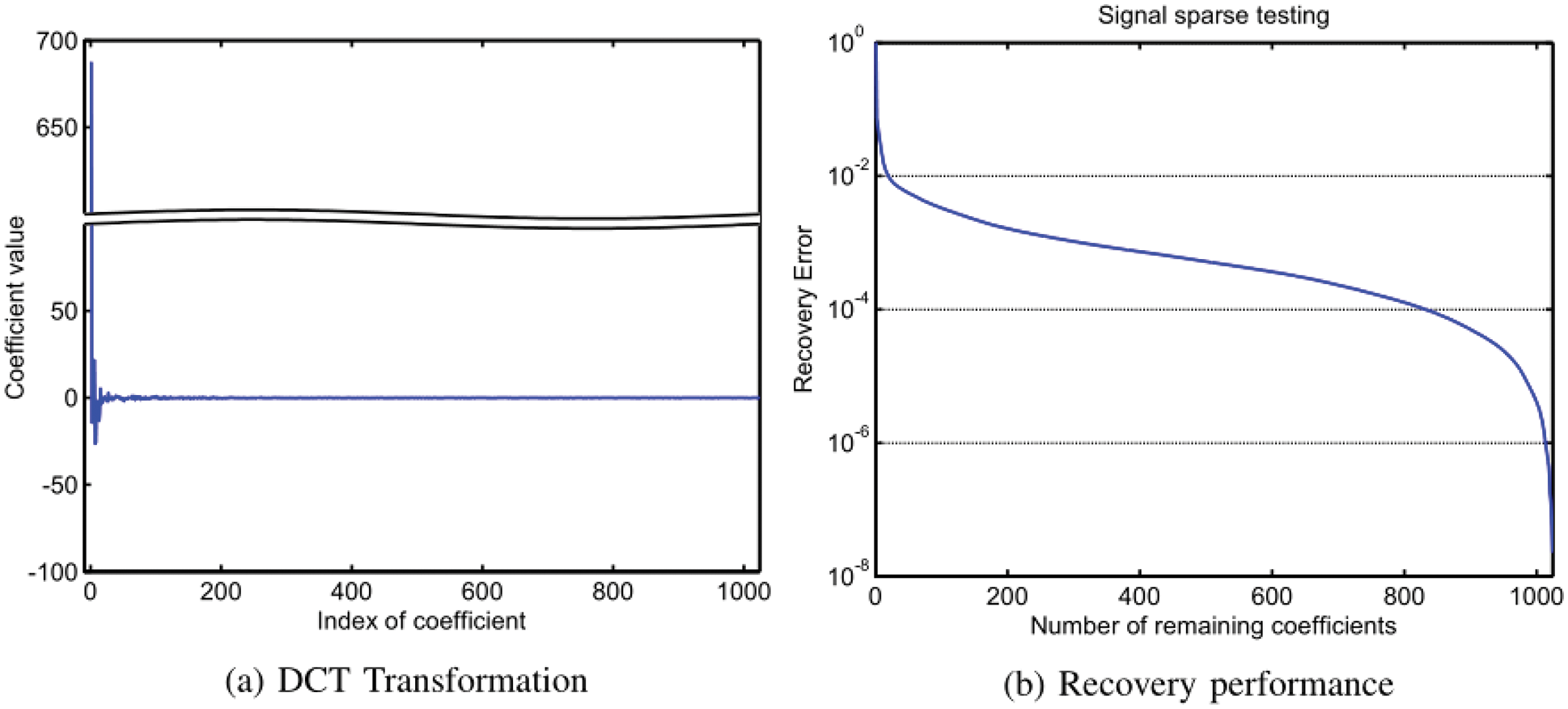
Figure 8: Signal sparse testing

Figs. 9a and 9b are the recovery performance evaluation results in two real data sets of humidity and temperature, respectively. For each dataset, two different sequence length settings (i.e., N = 512 and N = 1024) are adopted. The experimental results show that the recovery performance of the proposed scheme is basically consistent with that of the TIFS16. It should be noted that TIFS16 has been proved to have security challenges in WSN and other IoT scenarios. We can also find that the recovery performance of the proposed scheme is much better than the one without privacy amplify process. Without the privacy amplify process, the random performance of the key sequence is not good enough. Let’s take an example to analyze. Assume that the decimal number is represented by a 3-bit binary number. Taking the decimal number decreasing from 7 to 4 as an example, the leftmost significant bit of the corresponding binary number is kept as 1, while the rightmost significant bit has changed three times between 0 and 1. The change frequency of left significant bit is less than that of right significant bit. In reality, the effective bit length of ADC module is far greater than 3, which makes a large number of bits in random sequence change slowly, thus reducing the random performance of the whole sequence. Since compressive sensing will be implemented based on these random sequences, it will have a bad influence on the compressive sensing recovery performance.

Figure 9: Recovery performance on real world dataset

8  Related Work

9  Conclusion

This paper studies the security and efficiency of data transmission in the IoT. The arrival of 5G era brings new challenges to the IoT data transmission [31]. On the one hand, the widespread use of IoT in 5G era will inevitably lead to the demand for mass data transmission, and thus efficient data transmission scheme is needed. On the other hand, 5G data transmission rate is high, which requires efficient key distribution scheme. However, the traditional key distribution scheme is not suitable for most resource constrained IoT scenarios. This paper proposes the high-speed symmetric key generation scheme based on superlattice. Superlattice is a representative component for sub-THz and THz electronics. It can achieve high symmetric key generation rate, which can match 5G transmission rate. This paper also proposes a lightweight, secure and efficient data transmission scheme based on superlattice and compressed sensing. Efficient data transmission is achieved based on the efficient compression performance of compressive sensing. The compressive sensing is also interpreted as a lightweight encryption scheme, and its security is enhanced by the superlattice based symmetric key generation scheme.

Funding Statement: This work was supported by the Humanities and Social Science Youth Fund of Ministry of Education of China (19YJCZH254), the Innovation driven plan project of Hunan University of Technology and Business in 2020, the Scientific Research Fund of Hunan Provincial Education Department (19B315), and this work was funded by the Researchers Supporting Project No. (RSP-2021/102) King Saud University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. Wang, H. Han, H. Li, S. He, P. K. Sharma et al., “Multiple strategies differential privacy on sparse tensor factorization for network traffic analysis in 5G,” IEEE Transactions on Industrial Informatics, vol. 18, no. 3, pp. 1939–1948, 2022. [Google Scholar]

2. W. Li, S. Zhang, G. Wu, A. Saad, A. Tolba et al., “A sustainable WSN system with heuristic schemes in IIoT,” Computers, Materials & Continua, vol. 72, no. 3, pp. 4215–4231, 2022. [Google Scholar]

3. J. M. Hamamreh, H. M. Furqan and H. Arslan, “Classifications and applications of physical layer security techniques for confidentiality: A comprehensive survey,” IEEE Communications Surveys and Tutorials, vol. 21, no. 2, pp. 1773–1828, 2019. [Google Scholar]

4. H. Zhao, Y. Zhang, X. Huang and Y. Xiang, “An adaptive physical layer key extraction scheme for smart homes,” in TrustCom/BigDataSE’19, Rotorua, New Zealand, IEEE, pp. 499–506, 2019. [Google Scholar]

5. X. Zhu, F. Xu, E. Novak, C. C. Tan, Q. Li et al., “Using wireless link dynamics to extract a secret key in vehicular scenarios,” IEEE Transactions on Mobile Computing, vol. 16, no. 7, pp. 2065–2078, 2017. [Google Scholar]

6. M. Wilhelm, I. Martinovic and J. B. Schmitt, “Secure key generation in sensor networks based on frequency-selective channels,” IEEE Journal on Selected Areas in Communications, vol. 31, no. 9, pp. 1779–1790, 2013. [Google Scholar]

7. Z. Li, Q. Pei, I. Markwood, Y. Liu and H. Zhu, “Secret key establishment via RSS trajectory matching between wearable devices,” IEEE Transactions on Information Forensics and Security, vol. 13, no. 3, pp. 802–817, 2018. [Google Scholar]

8. W. Xu, S. Jha and W. Hu, “Lora-key: Secure key generation system for LORA-based network,” IEEE Internet of Things Journal, vol. 6, no. 4, pp. 6404–6416, 2019. [Google Scholar]

9. W. Li, I. Reidler, Y. Aviad, Y. Huang, H. Song et al., “Fast physical random-number generation based on room-temperature chaotic oscillations in weakly coupled superlattices,” Physical Review Letters, vol. 111, no. 4, pp. 044102, 2013. [Google Scholar] [PubMed]

10. A. E. Hramov, V. V. Makarov, V. A. Maximenko, A. A. Koronovskii and A. G. Balanov, “Intermittency route to chaos and broadband high-frequency generation in semiconductor superlattice coupled to external resonator,” Physical Review E, vol. 92, no. 2, pp. 022911, 2015. [Google Scholar]

11. Y. Wu, A. Khisti, C. Xiao, G. Caire, K. -K. Wong et al., “A survey of physical layer security techniques for 5G wireless networks and challenges ahead,” IEEE Journal on Selected Areas in Communications, vol. 36, no. 4, pp. 679–695, 2018. [Google Scholar]

12. F. Qiu, Z. He, L. Kong and F. Wu, “MAGIK: An efficient key extraction mechanism based on dynamic geomagnetic field,” in IEEE INFOCOM’17, Atlanta, GA, USA, IEEE, pp. 1–9, 2017. [Google Scholar]

13. P. Xie, J. Feng, Z. Cao and J. Wang, “Genewave: Fast authentication and key agreement on commodity mobile devices,” IEEE-ACM Transactions on Networking, vol. 26, no. 4, pp. 1688–1700, 2018. [Google Scholar]

14. Y. Lu, F. Wu, S. Tang, L. Kong and G. Chen, “Free: A fast and robust key extraction mechanism via inaudible acoustic signal,” in MobiHoc’19, Catania, Italy, ACM, pp. 311–320, 2019. [Google Scholar]

15. A. Perez-Resa, M. Garcia-Bosque, C. Sanchez-Azqueta and S. Celma, “Self-synchronized encryption for physical layer in 10 gbps optical links,” IEEE Transactions on Computers, vol. 68, no. 6, pp. 899–911, 2019. [Google Scholar]

16. T. Zheng, Z. Sun and K. Ren, “Fid: Function modeling-based data-independent and channel-robust physical-layer identification,” in IEEE INFOCOM’19, Paris, France, IEEE, pp. 199–207, 2019. [Google Scholar]

17. Y. Cheng, X. Ji, J. Zhang, W. Xu and Y. -C. Chen, “Demicpu: Device fingerprinting with magnetic signals radiated by CPU,” in CCS ‘19, London, UK, ACM, pp. 1149–1170, 2019. [Google Scholar]

18. D. Chen, N. Zhang, Z. Qin, X. Mao, Z. Qin et al., “S2 m: A lightweight acoustic fingerprints-based wireless device authentication protocol,” IEEE Internet of Things Journal, vol. 4, no. 1, pp. 88–100, 2017. [Google Scholar]

19. X. Li, F. Yan, F. Zuo, Q. Zeng and L. Luo, “Touch well before use: Intuitive and secure authentication for iot devices,” in MobiCom ‘19, New York, USA, ACM, pp. 33:1–33:17, 2019. [Google Scholar]

20. Z. Yan, Q. Song, R. Tan, Y. Li and A. W. K. Kong, “Towards touch-to-access device authentication using induced body electric potentials,” in MobiCom ‘19, New York, USA, ACM, pp. 23:1–23:16, 2019. [Google Scholar]

21. D. Han, Y. Chen, T. Li, R. Zhang, Y. Zhang et al., “Proximity-proof: Secure and usable mobile two-factor authentication,” in MobiCom ‘18, New York, USA, ACM, pp. 401–415, 2018. [Google Scholar]

22. N. Z. Gong, A. Ozen, Y. Wu, X. Cao, R. Shin et al., “Piano: Proximity-based user authentication on voice-powered internet-of-things devices,” in ICDCS’17, Atlanta, GA, USA, IEEE, pp. 2212–2219, 2017. [Google Scholar]

23. J. Li, K. Fawaz and Y. Kim, “Velody: Nonlinear vibration challenge-response for resilient user authentication,” in CCS ‘19, London, UK, ACM, pp. 1201–1213, 2019. [Google Scholar]

24. B. Zhou, J. Lohokare, R. Gao and F. Ye, “Echoprint: Two-factor authentication using acoustics and vision on smartphones,” in MobiCom ‘18, New York, USA, ACM, pp. 321–336, 2018. [Google Scholar]

25. W. Chen, L. Chen, Y. Huang, X. Zhang, L. Wang et al., “Taprint: Secure text input for commodity smart wristbands,” in MobiCom ‘19, New York, USA, ACM, pp. 17:1–17:16, 2019. [Google Scholar]

26. G. T. Becker, “Robust fuzzy extractors and helper data manipulation attacks revisited: Theory versus practice,” IEEE Transactions on Dependable and Secure Computing, vol. 16, no. 5, pp. 783–795, 2019. [Google Scholar]

27. P. Zhang and J. Wang, “On enhancing network dynamic adaptability for compressive sensing in WSNs,” IEEE Transactions on Communications, vol. 67, no. 12, pp. 8450–8459, 2019. [Google Scholar]

28. H. Luo, T. Zou, C. Wu, D. Li, S. Li et al., “Lightweight authentication protocol based on physical unclonable function,” Computers, Materials & Continua, vol. 72, no. 3, pp. 5031–5040, 2022. [Google Scholar]

29. P. Zhang, S. Wang, K. Guo and J. Wang, “A secure data collection scheme based on compressive sensing in wireless sensor networks,” Ad Hoc Networks, vol. 70, pp. 73–84, 2018. [Google Scholar]

30. T. Bianchi, V. Bioglio and E. Magli, “Analysis of one-time random projections for privacy preserving compressed sensing,” IEEE Transactions on Information Forensics and Security, vol. 11, no. 2, pp. 313–327, 2016. [Google Scholar]

31. J. Wang, C. Jin, Q. Tang, N. Xiong and G. Srivastava, “Intelligent ubiquitous network accessibility for wireless-powered MEC in UAV-assisted B5G,” IEEE Transactions on Network Science and Engineering, vol. 8, no. 4, pp. 2801–2813, 2021. [Google Scholar]