Output Linearization of Single-Input Single-Output Fuzzy System to Improve Accuracy and Performance

1  Introduction

FS enables human beings to take decisions based on inaccurate information and control real-time applications. In 1965, Zadeh introduced the fuzzy set concept as a means of explaining ambiguity and uncertainty [1]. Afterward, the fuzzy set theory has become the most popular research topic in numerous areas. In FS, the MFs and fuzzy rules have a substantial influence on the fuzzy system’s performance. Therefore, the MF’s tuning has always been the key factor in the design of FS. The current focus of joint FS research is the continuous development of innovative forecasting and optimization methods. Which reduces the consumption of energy and maximizes the level of user comfort. However, the accuracy of the control is the most critical portion that affects FS’s performance, it is generally ignored by most researchers. In many articles, the Mamdani model is utilized because of its efficiency and minimalism. The Mamdani model trusts in the fixed boundary-based MF, which will affect the system’s performance. Because the granularity of MF and its variant will provide different results for a precise value of the input [2,3].

The fuzzy system’s characteristics play a significant role in improving the accuracy and performance of nonlinear systems. The nonlinear reading of FS is pretty much sensitive to the MF’s length and position. The MF’s peak position and base length affect the fuzzy rule’s activating level. The influence of FS on stricture variations might exist in the MF’s suitable settings. Though, despite its major participation, the number of studies is very limited on MFs design. Triangular shaped membership functions are extensively utilized in FSs because they are very simple to implement. The triangular shaped membership functions excel in steady-state conduct, particularly in accumulating preferred positions. Alternatively, the precise input-output MF method improves the compactness of the logic scenario and eventually enhanced the control accuracy [4–6].

Numerous optimization methods for MF optimization have been described in the literature. These optimization techniques include genetic algorithm (GA) [7], ant colony algorithm (ACO) [8], particle swarm optimization (PSO) [9], and artificial neural networks [10]. However, all these algorithms are very time-consuming because the convergence needs complex computations [7–10] and these techniques need extensive prior network training (ANN) or necessitate updating numerous particles in ACO and PSO techniques. There is also a need to calculate the applicability of the GA and eliminate the members of the most inappropriate solution for the candidates after each iteration. Hence, it is not possible to put these methods into practice using commercially available microcontrollers [11,12].

Different technologies have been used for various purposes in various disciplines, based on different algorithms of machine learning and fuzzy logic, but there is no exact way to determine the proper shape, granularity, or spam of MF [13]. The design of MFs and fuzzy rules largely depends on the knowledge of experts in the relevant domain. Hence, it is not straightforward to assess how MFs affect the response of the system if the criteria for MFs change. Due to the lack of auxiliary experimental statistics, the use of precise input and output MF using specific lengths and positions has not been researched, which was the main motivation for this research [14]. It is explained that the performance of FS increases linearly with the precise number of input and output MFs [15]. Though, the need to tune the membership functions further will only exacerbate the convergence issue.

Each section of this article deals with inspiration for the proposed model. This article has the following multiple goals:

1)   Systematically design the input and output MFs of single-input single-output FS to minimize trial-and-error and dependence on expert knowledge. In the proposed method, the position and length of the MFs are critical to obtaining superior outcomes.

2)   In particular, the effect of the proposed relationship of input/output MFs is studied in detail to validate the efficiency of the proposed model. The range of MFs acquired based on the FS’s control accuracy and experimental record is utilized as the criterion valuation. Furthermore, The efficiency and accuracy of the system are improved by applying the precise input/output MFs relationship.

3)   In decision analysis, the grades of the membership are not sufficient to evaluate objects. The addition of reference parameters gives decision-makers the freedom to choose these levels. The proposed approach of SISO FS with correlated reference parameters delivers a robust method for modeling uncertainty.

4)   Since our objective in the MF design is to regulate the steady-state error for the SISO FS because uniformly distributed triangular MFs show superior performance regarding the steady-state behavior, particularly with the cumulative preferred setting.

In this study, the precise input and output MFs with minimum tuning was proposed to enhance the performance and accuracy of the SISO system, which will linearize the system’s output. The outcomes show that precise outcomes can be achieved by designing the effect of relative changes in the precise input and output membership functions and integrating the outcomes into the procedure of defuzzification for a specified monotonic system. In small data scenarios, specifically when the behavior of the target system is known. This also indicates that for a certain number of the output MFs, tuning the first MF only eradicates the requirement of an optimization algorithm. The experimental and simulation results are catered for the precise input and output MFs of the SISO FS.

The architecture overview of the SISO model is presented in Section 2. The specified depiction of the algorithm design is explained in Section 3. The MATLAB simulation setup is explained in Section 4. The experiment setup used to implement the SISO FS is explained in Section 5. Comparative analysis of experimental and simulation results is described in Section 6, whereas the conclusions are given in Section 7.

2  Model Overview

The FS model is proposed for general-purpose systems that take input from a single sensor and generate an output in the form of a pulse width modulation (PWM). The transistor-transistor logic (TTL) facilities are available for most modern sensors. The sensor can synchronize output voltage levels (i.e., 0–5 V). It can be presumed that the sensor can compute any parameter (i.e., humidity, pressure, temperature, etc). The output of the system (PWM) is a form of signal because of its high efficiency and low power consumption when operating under different loads. This PWM is articulated in (%). To define the MF of these fuzzy sets, the isosceles triangles are used in this model. There are two parameters for each MF attribute. For simplicity, existing FSs are designed for systems that display only monotonic behavior.

Fig. 1 shows the block diagram of SISO FS. The FS utilizes a single sensor as an input variable to produce signals proportional to the values of its sensor parameters. The signal is generated after the required signal conditioning is supplied to the fuzzifier, and the fuzzifier produces two variables of a fuzzy set. These variables of the fuzzy sets are then passed to the inference engine. The inference engine is also connected to the rule block which is containing the predefined rules. The inference engine uses the min-AND operation to deliver two outputs to defuzzifier, based on predefined rules and the two fuzzy inputs. The defuzzifier then provides crisp values at its output.

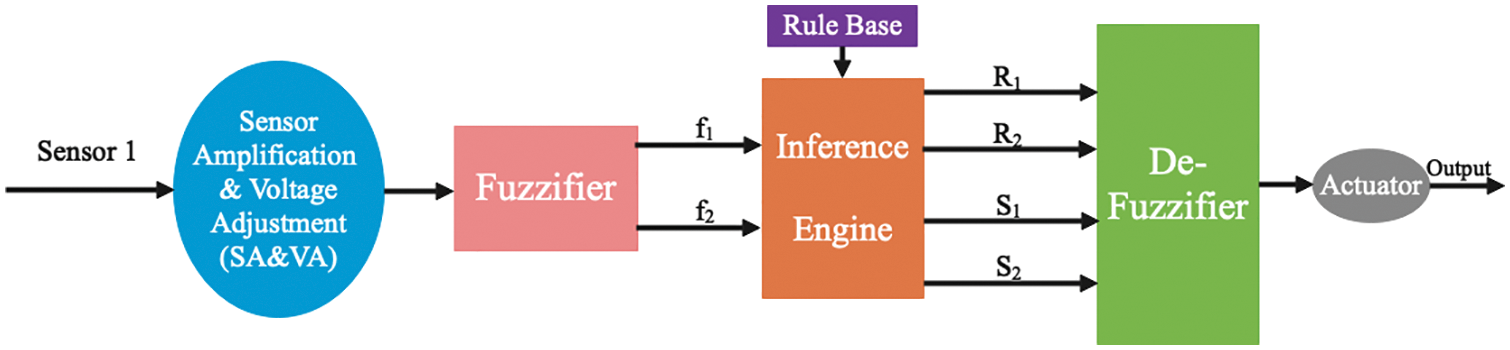
Figure 1: Block diagram of SISO FS

3  Algorithm Design

The proposed FS is designed to define the value of the input sensor in the form of a percentage (0%–100%). In this study, 0–5 volts are considered as 0%–100%, correspondingly. However, this FS is equally appropriate for those systems whose input voltage range is not compatible with TTL. Fig. 1 shows the SA & VA component, which converts the signal (0–5 V) into diverse ranges, which are described in the FS for input parameters.

3.1 Fuzzifier

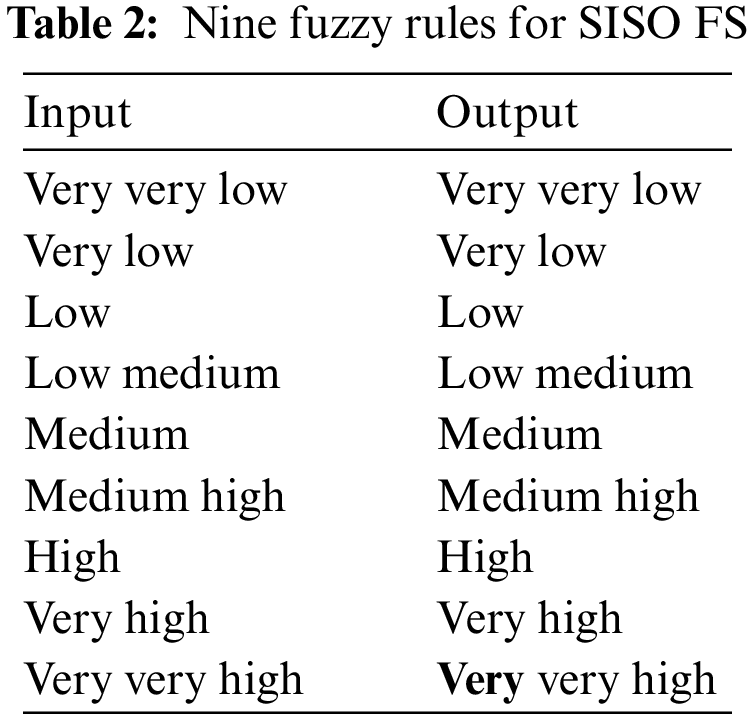
This unit translates fuzzy input as linguistic values and generates output linguistic variables of a fuzzy set. For the entire range of a single input variable, nine triangle MFs are specified, which are classified into eight regions supplementary. Table 1 summarizes the distribution of MF names and their related ranges and regions. Fig. 2 shows a graphical view of the nine MFs of the above classification and the eight regions of the input variables.

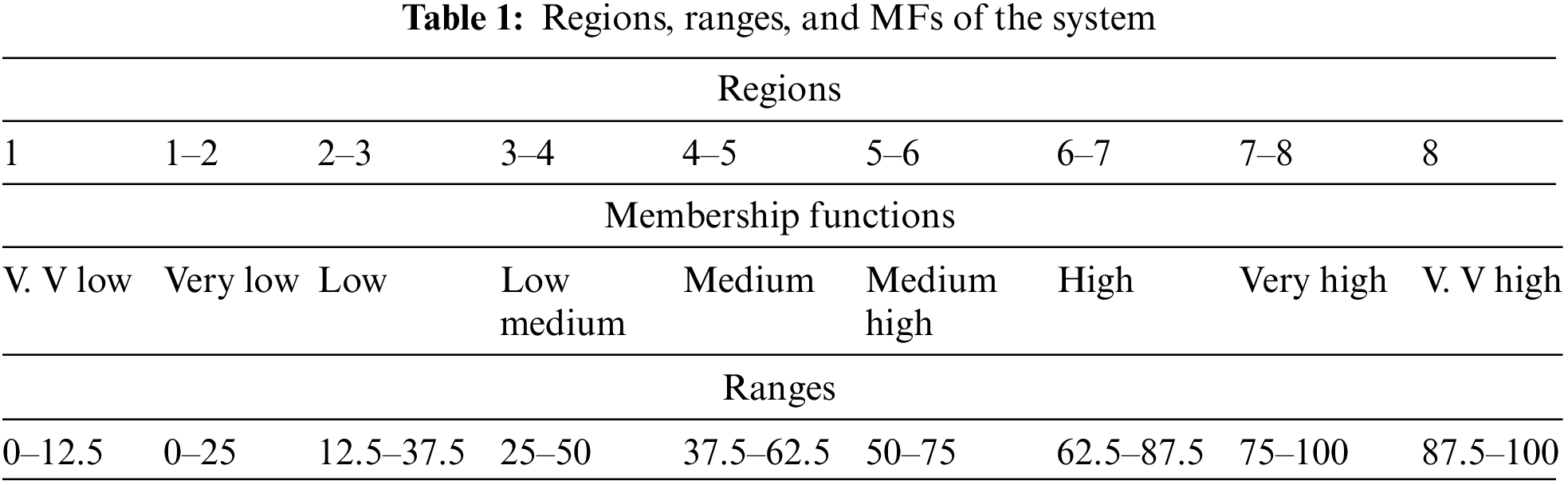
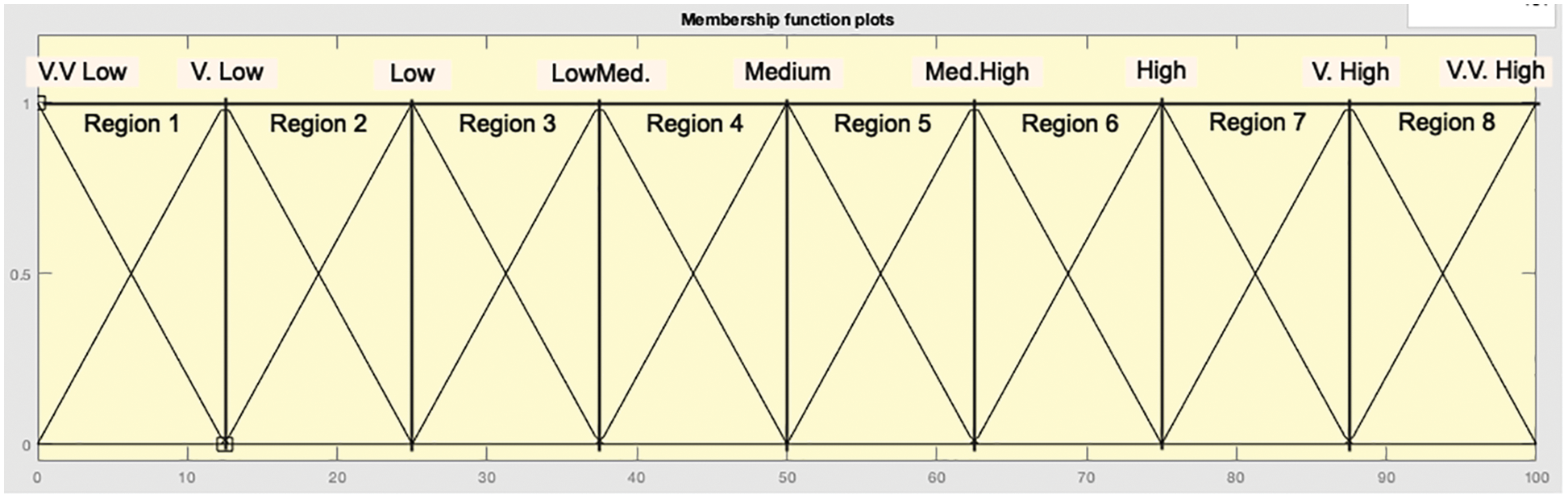
Figure 2: MFs and region distribution

The scheme of different modules’ connectivity in a fuzzifier is shown in Fig. 3, which is used in the FS to produce a single output of the sensor. For the single input variable, the system needs a single fuzzifier unit. Fig. 3 shows that in the range of 0–5 V, the input signal is first multiplied by 12.5 times to simulate the entire range of a single variable in the model. The multiplier’s output is straightforwardly delivered to four subtractors and a region comparator. These subtractors identify the input values by subtracting the boundary of the range value from it. The region comparator equates the input with the range boundary to determine the occupied region. The outputs of all four subtractors are applied as the multiplexer’s input data, and the output of the region comparator is linked to the multiplexer’s selection line. The divider module associated with the multiplexer’s output divides the multiplexer’s outcome by 12.5. The output of the divider produces the f1, and further subtraction from “1” produces f2.

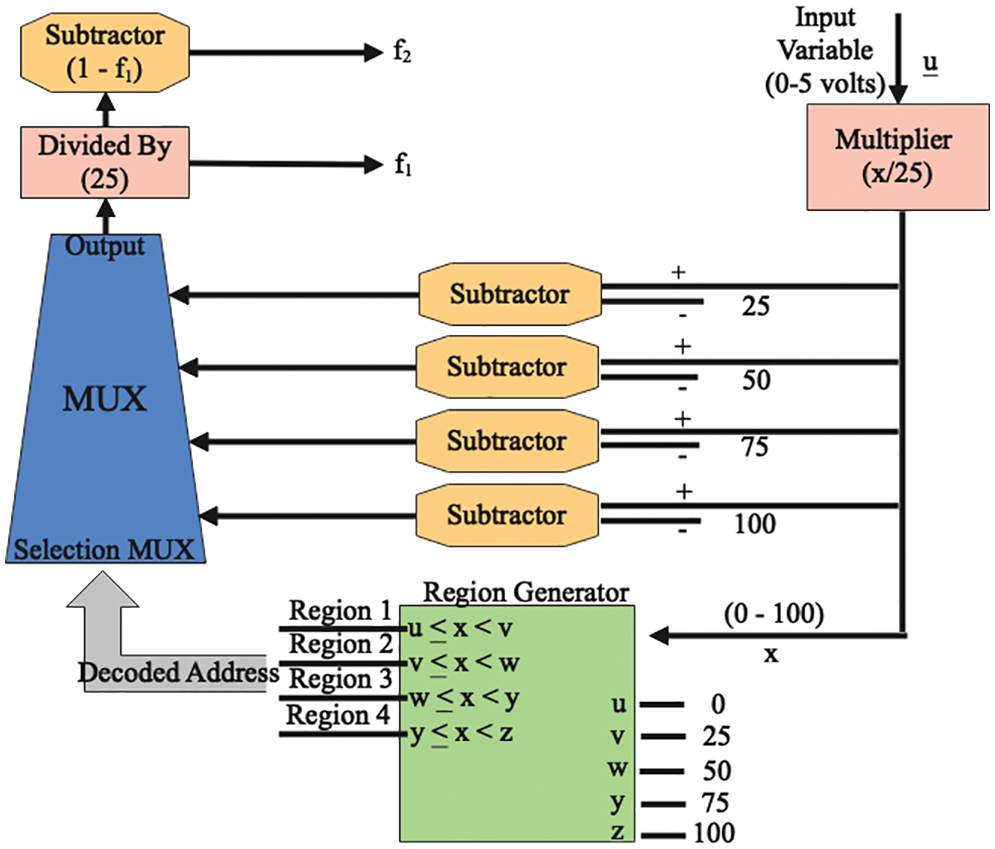
Figure 3: Scheme of different modules connectivity in a fuzzifier

3.2 Inference Engine

Two AND operators are utilized in the inference engine unit. Two inputs deliver to the interface engine from the fuzzifier, and the min-AND configuration has been used by the inference engine to achieve the output “R”. By using the factor mn, the fuzzy rules compulsory for all specified ranges of SISO FS are determined, where n = the number of inputs and m = the number of fuzzy sets. For this SISO FS, n = 1 and m = 9, so the total number of fuzzy rules is nine. Table 2 shows the nine fuzzy rules.

3.3 Fuzzy Rule Block

A single sensor of this FS delivers one crisp value to the rule block. It flexibly outputs a singleton value numeric method according to the principles of the algorithm used in the FS. For a single variable, two fuzzy rules are required to find the matching value of S1 and S2. The rule block acquires an input value and divides the discourse into several regions, each of which limits the two variables of the fuzzy set, activates the rule, and disperses the output.

3.4 DeFuzzifier

The output of any FS is controlled by the defuzzifier, so the defuzzifier has a substantial impact on the system’s control accuracy. Commonly, the similar number of input MFs and output MFs are considered when designing FS. The defuzzification process delivers a crisp output value after assessing the defuzzifier’s input [16,17]. In this case, the defuzzifier received an input value. Two output values R1 and R2, have been generated by the inference engine and two output values S1 and S2 have been generated by the rule block. The defuzzifier calculates a typical output consultation in the route of the center of average (COA) procedure to implement Eq. (1), where i = 1 to 2. The design of output MF comprises nine (9) functions through an identical interpretation of the standard range. Figs. 4 and 5 respectively show the graphical representations of the 9 output MFs distributions, with and without tuning of the first MF.

ΣSi∗Ri/ΣRi(1)

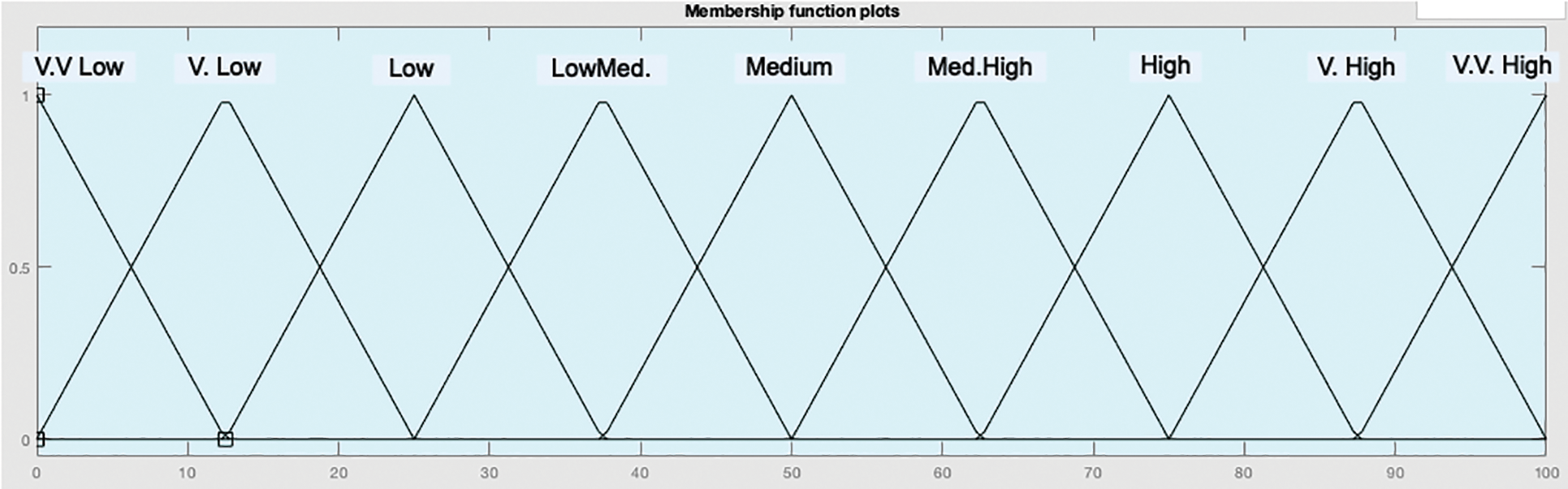
Figure 4: 9 MFs of output

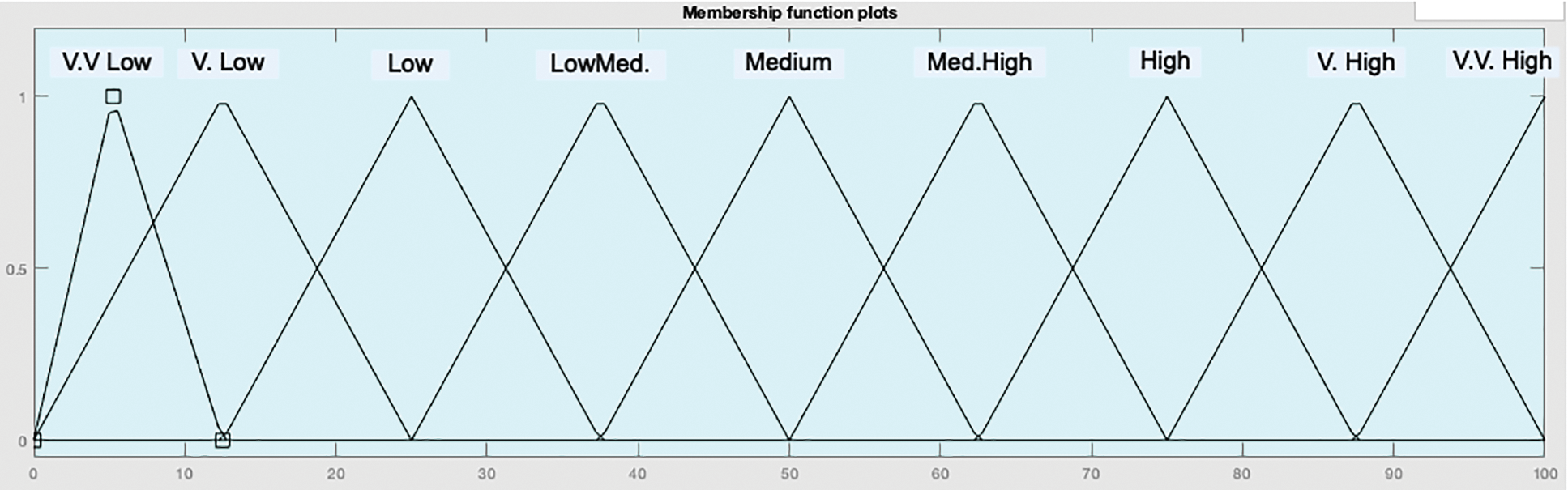
Figure 5: Proposed 9 MFs of output

Four multipliers have been used in the defuzzifier., where two adders are used for Si * Ri, one adder for ΣSi * Ri, the other for ΣRi, and only divider for ΣSi * Ri/ΣRi. Finally, a crisp output has been generated by the defuzzifier [18].

For the model’s performance evaluation, The MAPE is utilized and the root mean square error (RMSE), and mean absolute error (MAE) expressed in Eqs. (2)–(4):

MAPE=1C∑k=0c(Ai−BiAi)(2)

RMSE=1C∑k=0c(Ai−Bi)(3)

MAE=1C∑k=0c(Ai−Bi)(4)

where ‘A’ is the MATLAB Simulated value, ‘B’ is the Measured value, and ‘C’ indicates the No. of observations.

4  Setup of MatLab Simulation

The MatLab Simulink R2016b had been utilized to develop the SISO FS, and verify the reliability of the proposed membership functions through MatLab simulation. For linear systems with different input and output MFs (3, 5, 7, 9), different SISO FS models are simulated, as shown in Table 3. The accuracy of FS simulates many scenarios utilizing identical input values of sensors across the entire range. SISO FS uses a similar number of input and output membership functions which are uniformly distributed in the discourse, and these contiguous MFs coincide with one another by 50%. In all models, similar input values of a sensor are utilized to simulate numerous cases over the entire range to determine the maximum error. Thereafter, utilizing precise 9 input MFs and output MFs and tuning of the only first MF were used and the relative errors have been meaningfully abridged.

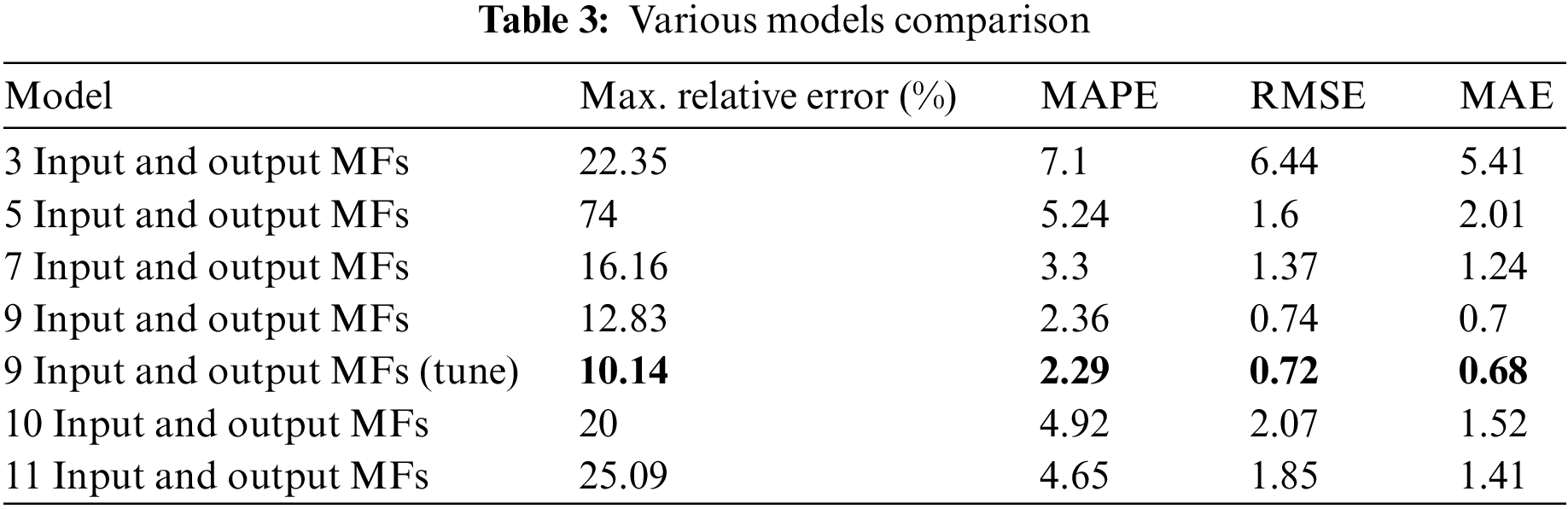
To test the proposed SISO FS’s accuracy, simulations of various SISO FS models of nonlinear systems were performed. Use the exact similar input values for every FS model to simulate numerous scenarios. Table 4 shows the comparative analysis between these models and the proposed method. All SISO FSs with various input and output MFs use a similar number of fuzzy rules and the most appropriate singleton value. After increasing or decreasing the value of the input or output MF, the fuzzy rule and the singleton value configuration should be similar.

5  Implementation of Fuzzy Model

Fig. 6 shows the experimental setup in which all equipment names are mentioned. Input knobs are used to set input values. A microcontroller (ATmega 328P) which is easily available in the market at a low cost, has been utilized to implement our proposed model with a suggested tuning of MF. The analog pins of the microcontroller are suitable for obtaining analog voltage (0–5 volts) which is applied directly to its input analog pins. The integrated analog-to-digital converter converts the analog input to a digital format for advanced processing. The microcontroller works at 16 MHz and produces PWM on its output pins. To simulate the full range of voltages of the signal that a TTL-compatible input sensor can produce, a voltage divider circuit is utilized to deliver variable voltages on the ATmega 328P analog pins. The FS’s output is linked with the microcontroller’s PWM module through Arduino coding, which changes the duty cycle of the output pulse of the microcontroller according to the FS’s output. Use a digital oscilloscope of 100 MHz (MCP model: CQ620A) to measure the exact change in output. Fig. 7 shows the pseudo-code of the system.

Figure 6: Experimental setup

Figure 7: Pseudo code of the system

Fuzzy rules must be translated to an array of numbers to accumulate in memory. The simplest approach is to interpret fuzzy sets to index numbers. Subsequently, every rule needs X numbers in the argument section and a single number in the resulting section. Assume that the index number is accumulated in two bytes. The FS is implemented in hardware by ATmega 328P clocked at 16 MHz, the implementation of instruction takes ten clocks approximately, and afterward, an inference takes almost 65 milliseconds. An inference takes around one millisecond, which is about the speed of 1000 flops. Consequently, inference utilizing rule tables is 65 times quicker than online inference [19,20].

6  Results and Discussion

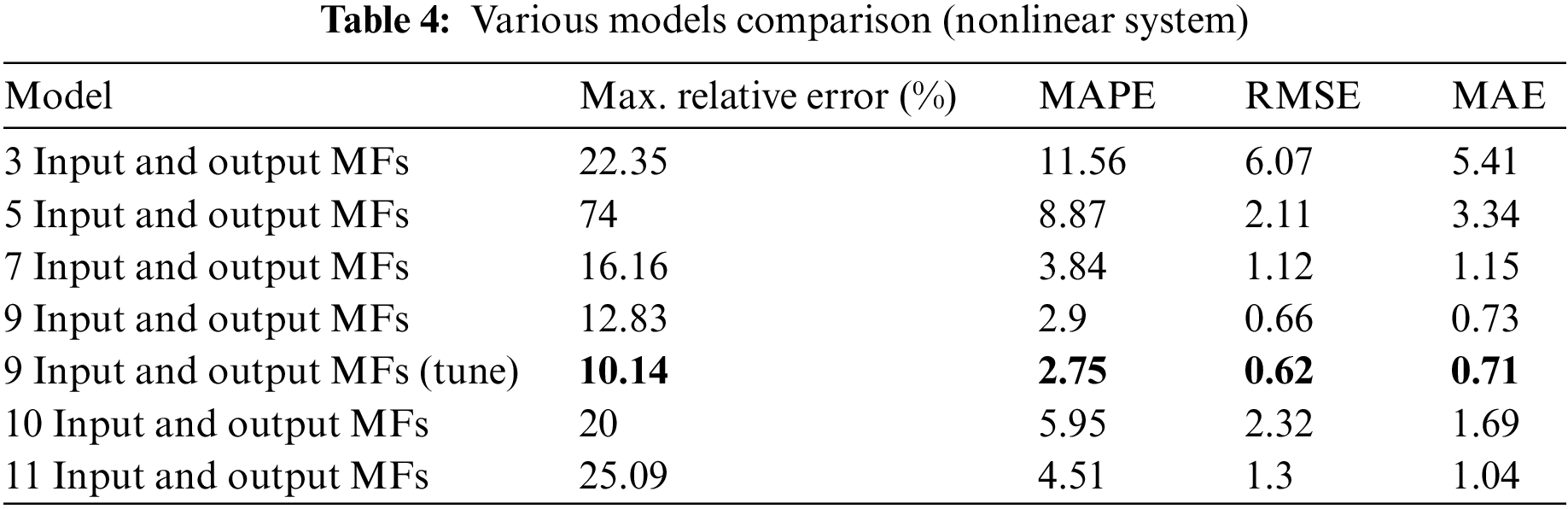
The design of FS is typically based on uniform distribution and the same number of input and output MFs (e.g., 3/3, 4/4, 5/5, 6/6, and 7/7 input/output MF) in the literature [5,15,21–26]. The experimental results in Fig. 8 show that this FS is liable to huge errors even when applied to linear systems. Clearly, in numerous scenarios, relative error values higher than 10% are calculated, eventually resulting in greater MAPE, MAE, and RMSE values for these FS models.

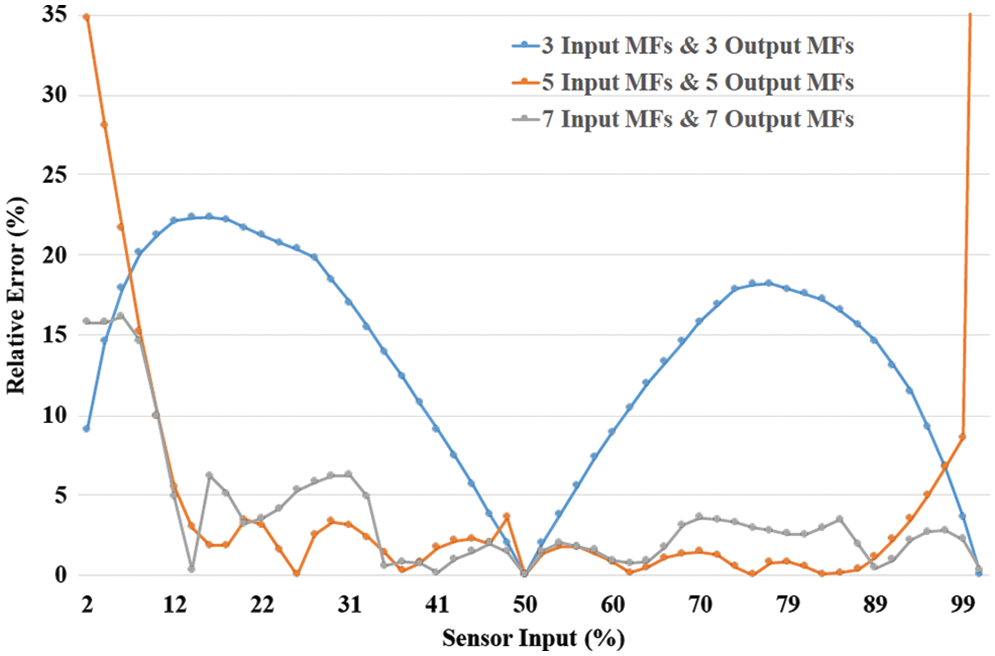
Figure 8: Comparison of relative errors between three SISO systems

By adopting precise nine input and output MFs in the design of the SISO system, the relative error can be significantly reduced. Fig. 9 shows the experimental results of the SISO system’s relative error with even distribution of MFs. The relative error for 9 input and output MFs cases remains less than 10% over the complete input range, except for “v.v. low” input values as compared to 5/7/10/11 input and output MFs.

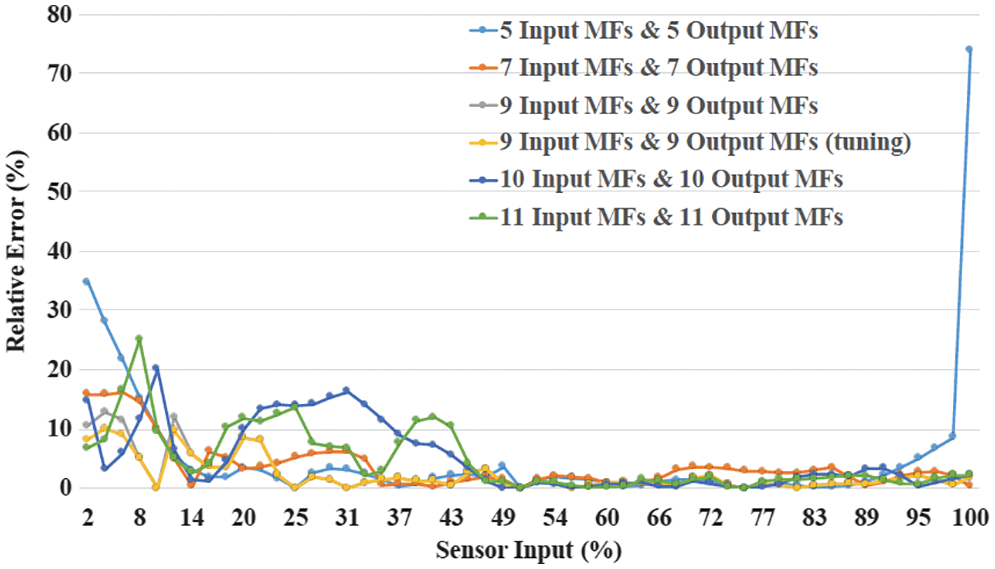
Figure 9: Comparison of relative errors between six SISO systems

For further reduction of relative error in the “v.v. low” region, the first MF needs to be tuned to reduce the relative error within a sufficient range. However, it can be seen from Fig. 10 that the relative error is specifically abridged to 10% after tuning in the “v.v. low” region. Table 3 shows a comparative analysis of the values of MAE, MAPE, and RMSE of the linear system SISO different models utilizing diverse input and output MFs in the discourse. Our proposed method of SISO FS with 9 input and output membership functions and tuning of the only first MF delivers the best results because increasing the input/output MFs to 10 and 11 worsens the value of the relative error compared to the case of 9 input/output MFs.

Figure 10: Comparison of relative errors between SISO systems (with and without tuning)

The effectiveness of our proposed method of designing a perfect SISO system with monotonic behavior and nonlinear output is too confirmed. Similarly, Fig. 11 shows that after tuning only the first output MF of 9 output MFs, the maximum relative error in the SISO system is significantly reduced to ≤10%. The error comparison view given in Table 4 confirms that the proposed 9 input and output MF (tuned with the first MF) method shows better performance even in the scenario of non-linear output values of different models utilizing diverse input and output MFs in the discourse.

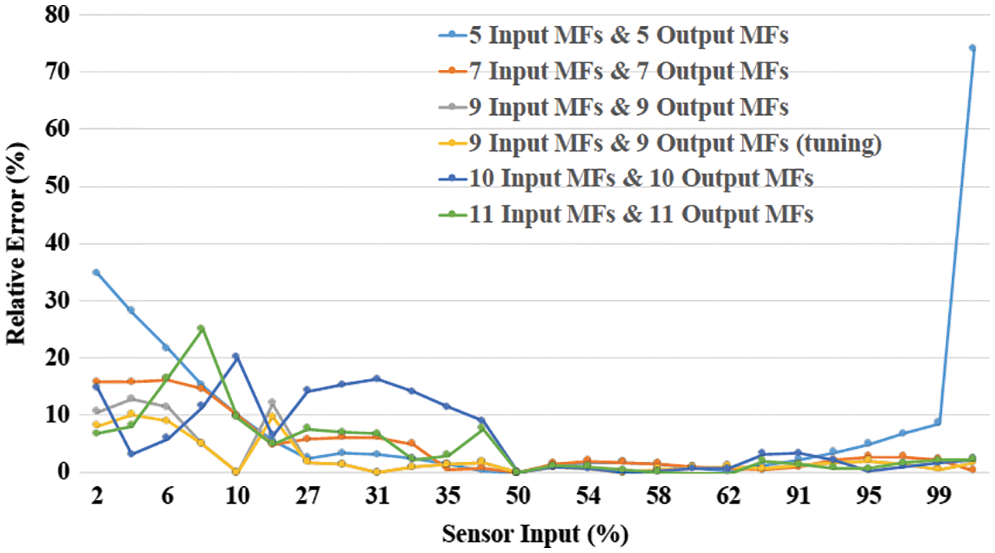
Figure 11: Comparison of relative errors between six SISO systems (non-linear system)

The Mamdani model is one of the most substantial techniques used in fuzzy logic, which has various applications in different modern days fields (e.g., robotics, internet of things, deep learning, etc.) [27]. Even though the Mamdani model used in FSs still has some significant issues to address. The main issue is selecting the precise shape and boundaries of the MFs in the universe of discourse. Its purpose is to control the affiliation between input and output variables by regulating MF to construct a transparent black box of the FS. Based on various algorithms of fuzzy logic and machine learning, numerous methods have been used in diverse areas for numerous purposes [11], but they fail to attain optimized MFs accurately [3].

The proposed method is used to define high-performance fuzzy MFs to minimize the relative error and enhance the accuracy of the FS. The novel approach applies the real-number encoding of the basic length parameters and the peak position of MFs and combines the fuzzy system’s performance assessment to present an applicable MF assessment mechanism to attain the superlative results. A comparison will be given to illustrate the significantly enhanced performance of FS optimized by the proposed method. Precise determination of MFs necessitates not only reducing the relative error but also improving the stability and accuracy of the FS. Different simulations had been performed using the proposed method in similar situations. The results show that the proposed method reduces the MAPE of a SISO FS by more than 66%. Furthermore, reduces MAE and RMSE by nearly 56% and 55% compared to conventional FS [16].

Microcontrollers and nonlinear sensors are utilized in various designs of embedded systems. Since the input/output characteristics of the majority of the sensors are inherently nonlinear, acquiring information from nonlinear sensors utilizing integer microcontrollers has been a design challenge. Another design difficulty in sensor-based applications is exploiting the sensor’s entire range to capture the sensor’s nonlinear behavior in a digital environment. In the literature, numerous linearization techniques have emerged to linearize the sensor response. The analysis and tuning of fuzzy logic controllers (FLCs) is a difficult problem due to the nonlinear control behavior and complexity caused by the multi-parameter nature of FLCs [21,28–30]. Fig. 12 shows the linearization outcomes for the output of SISO FS after using 9 input and output MFs. It is not possible to use 3, 5, and 7 MFs in any SISO FS or any other method used in the literature.

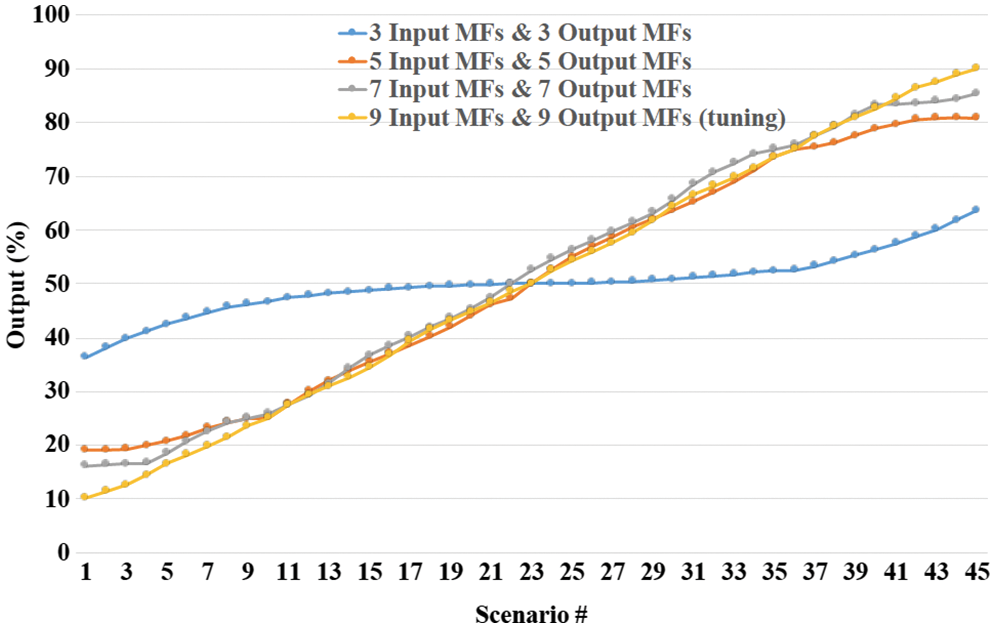
Figure 12: Linearity representation using the Mamdani model

Moreover, the proposed FS yields improved accuracy and stability than any other FS available in the literature. Approximate reasoning techniques based on fuzzy logic (FL) are effectual utensils for producing AI-based systems. Production systems are frequently utilized for the chore of taking decisions and forecasting numerous situations under uncertainty. To evaluate the proposed model’s performance in terms of accuracy utilizing the parameter RMSE; the comparison of achieved outcomes with different FL model outcomes to verify the accuracy of the system.

When examining recent research on univariate modeling, Selvachandran et al. [19]. examines the implementation of six software-based sensor linearization algorithms for low-cost microcontrollers. The linearization algorithm is achieved by utilizing a nonlinear optical ranging sensor. Fayaz et al. [5] introduce a method called Learning Control (LTC) to address the selection of precise shapes and the use of a precise position and length of MFs. The proposed method consists of two different modules. In the control algorithm module, the Mamdani FLC method is utilized, while in the learning algorithm module, the ANN algorithm is used. Sharma et al. [20] analyze the applicability of a self-learning recurrent neural network (NN) with a helical structure of controlled elements and layers. Based on the application and development of NNs, novel schemes and systems for implementing them are proposed. Erdem [21] present an Enhanced Fuzzy Sliding Mode Control (EFSMC) algorithm for monitoring an ambiguous pneumatic artificial muscle (PAM) robotic arm having external instabilities. A novel EFSMC algorithm is defined based on the conventional sliding mode controller, which develops adaptive fuzzy rules based on Lyapunov stability theory and is fuzzified with the Mamdani model. Osipov et al. [22] introduce DynaMut2, a web server that binds normal pattern analysis (NMA) techniques to apprehend protein motility and our graph-based signature to signify the wild-type environment to study the effects of single and multi-point mutations on protein solidity and dynamic effects. Anh et al. [23] shed light on the noise levels of traffic in the Arabian Gulf. Furthermore, it uses an ANFIS to calculate the noise levels of traffic on Kuwait’s ring road. Field measurements were gathered from various measurement points. Rodrigues et al. [24] explained that based on the established 1D convolutional neural network model, the influence of different logging combinations on the prediction of Shearwave velocity was analyzed.

Compared with related research articles available in the literature, the objective of this study is to pretend a new methodology for defining input and output MFs in any SISO FS. The experimental outcomes based on the RMSE criterion are shown in Table 5, and the proposed methodology proved to be the best performer than other modern days approaches (ANN, ANFIS, AFPID, RNN, etc.).

7  Conclusions

The key objective of this study is to find the precise number of input and output MFs to enhance the stability and accuracy of the SISO FS, i.e., the compulsory speed for the SISO system to achieve a steady state. It assists engineers in the field of autonomous systems and robotics improvement insight into the core factors needed for steady system design. The following is a summary of the main points of this study.

1.    The Mamdani model is used to implement our proposed method. The Mamdani model can easily be implemented with a less computational burden. The ANN and GA had been used to optimize MF in different fuzzy systems by most of the authors in the literature. In this study, a SISO fuzzy model based on Mamdani had been used to reduce the MAPE by almost 66.2%, MAE by 56.3%, and RMSE by 54.5%.

2.    Utilizing precise nine input and output MFs in the SISO system will generate nine rules and the tuning of the first MF will provide far better stability and accuracy of the system because a large number of errors had been reduced using the proposed method.

3.    The outcomes of the model show significant progress by perusing the effects of the precise MFs and the productivity of the SISO system, it was witnessed that the proposed method delivers the best SISO fuzzy system (9 input/output MFs with tuning) from the accuracy metrics. Conclusively, this suggests that the proposed SISO system is extra efficient for the controller’s performance index.

The results of measured PWM are in good agreement with simulation results. Consequently, the investigation of the input/output MFs and their allocation over FS can be measured as applicable in this study. Specifically, using the 9 input/output MFs for SISO FS, the desired control accuracy was successfully attained within the range (≤ ± 1%), thus confirming the efficiency of the MF’s design. Hence, the proposed SISO FS can be utilized as a tool of system design for fuzzy logic applications in other sectors of the industry.

For future study, the consequent research recommendations are made based on the fundamental limitations of the article, we plan to apply the proposed method to a multi-output fuzzy system, and we too apply our proposed method to real-life applications related to concepts based on linear diophantine fuzzy set and spherical diophantine fuzzy set.

Acknowledgement: This research work was carried out in the laboratories of the Department of Computer Science and Department of Physics (Electronics), GC University, Lahore, Pakistan. We thank all personnel for their cooperation and participation in facilitating our experiments especially Dr. M. Saleem Khan and Dr. Ali Asif. We are thankful to all the reviewers for their valuable comments because of those comments, we are able to improve the quality of this article.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. L. A. Zadeh, “Fuzzy sets,” Information and Control, vol. 8, no. 3, pp. 338–353, 1965. [Google Scholar]

2. L. K. Sharma, V. Vishal and T. N. Singh, “Developing novel models using neural networks and fuzzy systems for the prediction of strength of rocks from key geomechanical properties,” Measurement, vol. 102, pp. 158–169, 2017. [Google Scholar]

3. S. -U. -D. Khokhar, Q. Peng, A. Asif, M. Y. Noor and A. Inam, “A simple tuning algorithm of augmented fuzzy membership functions,” IEEE Access, vol. 8, pp. 35805–35814, 2020. [Google Scholar]

4. A. Inam, A. Sarwar, A. Atta, I. Naseer S. Y. Siddique et al., “Detection of COVID-19 enhanced by a deep extreme learning machine,” Intelligent Automation & Soft Computing, vol. 27, no. 3, pp. 701–712. 2021. [Google Scholar]

5. M. Fayaz, I. Ullah and D. Kim, “An optimized fuzzy logic control model based on a strategy for the learning of membership functions in an indoor environment,” Electronics, vol. 8, no. 2, pp. 132–148, 2019. [Google Scholar]

6. M. Y. Noor, Q. Peng, U. Khokhar, A. Asif, N. Abid et al., “Low cost and energy efficient fuzzy based kitchen ventilation control system,” in 2019 Int. Conf. on Robotics and Automation in Industry (ICRAI), Rawalpindi, Pakistan, pp. 1–6, 2019. [Google Scholar]

7. K. M. Hamdia, X. Zhuang and T. Rabczuk, “An efficient optimization approach for designing machine learning models based on genetic algorithm,” Neural Computing and Applications, vol. 33, no. 6, pp. 1923–1933, 2021. [Google Scholar]

8. D. Zhao, L. Liu, F. Yu, A. A. Heidari, M. Wang et al., “Ant colony optimization with horizontal and vertical crossover search: Fundamental visions for multi-threshold image segmentation,” Expert Systems with Applications, vol. 167, pp. 114122–114167, 2021. [Google Scholar]

9. X. Zhang, H. Liu and L. Tu, “A modified particle swarm optimization for multimodal multi-objective optimization,” Engineering Applications of Artificial Intelligence, vol. 95, pp. 103905–103914, 2020. [Google Scholar]

10. M. R. C. Qazani, H. Asadi, S. Mohamed and S. Nahavandi, “Prepositioning of a land vehicle simulation-based motion platform using fuzzy logic and neural network,” IEEE Transactions on Vehicular Technology, vol. 69, no. 10, pp. 10446–10456, 2020. [Google Scholar]

11. A. J. Moshayedi, A. S. Roy, L. Liao and S. Li, “Raspberry Pi SCADA zonal based system for agricultural plant monitoring,” in 2019 6th Int. Conf. on Information Science and Control Engineering (ICISCE), Shanghai, China, pp. 427–433, 2019. [Google Scholar]

12. M. Seyedmahmoudian, B. Horan, T. K. Soon, R. Rahmani, A. M. T. Oo et al., “State of the art artificial intelligence-based mppt techniques for mitigating partial shading effects on pv systems–A review,” Renewable and Sustainable Energy Reviews, vol. 64, pp. 435–455, 2016. [Google Scholar]

13. S. Farajdadian and S. H. Hosseini, “Design of an optimal fuzzy controller to obtain maximum power in solar power generation system,” Solar Energy, vol. 182, pp. 161–178, 2019. [Google Scholar]

14. S. K. Jeong, C. H. Han, L. Hua and W. K. Wibowo, “Systematic design of membership functions for fuzzy logic control of variable speed refrigeration,” Applied Thermal Engineering, vol. 142, pp. 303–310, 2018. [Google Scholar]

15. C. Wang, “A study of membership functions on mamdani-type fuzzy inference system for industrial decision-making,” M.S. Dissertation, Lehigh University, USA, 2015. [Google Scholar]

16. S. U. D. Khokhar and Q. Peng, “Utilizing enhanced membership functions to improve the accuracy of a multi-inputs and single-output fuzzy system,” Applied Intelligence, vol. 53, pp. 1–15, 2022. [Google Scholar]

17. S. -U. -D. Khokhar, Q. Peng, R. Touqir and M. S. Khan, “Medical condition monitoring system using fuzzy logic,” in 2020 IEEE Int. Conf. on Artificial Intelligence and Information Systems (ICAIIS), Dalian, China, pp. 211–216, 2020. [Google Scholar]

18. S. Habib, M. Akram and A. Ashraf, “Fuzzy climate decision support systems for tomatoes in high tunnels,” International Journal of Fuzzy Systems, vol. 19, no. 3, pp. 751–775, 2017. [Google Scholar]

19. G. Selvachandran, S. G. Quek, L. T. H. Lan, N. L. Giang, W. Ding et al., “A new design of mamdani complex fuzzy inference system for multiattribute decision making problems,” IEEE Transactions on Fuzzy Systems, vol. 29, no. 4, pp. 716–730, 2019. [Google Scholar]

20. A. K. Sharma, D. Singh, V. Singh and N. K. Verma, “Aerodynamic modeling of attas aircraft using mamdani fuzzy inference network,” IEEE Transactions on Aerospace and Electronic Systems, vol. 56, no. 5, pp. 3566–3576, 2020. [Google Scholar]

21. H. Erdem, “Implementation of software-based sensor linearization algorithms on low-cost microcontrollers,” ISA Transactions, vol. 49, no. 4, pp. 552–558, 2010. [Google Scholar] [PubMed]

22. V. Osipov, V. Nikiforov, N. Zhukova and D. Miloserdov, “Urban traffic flows forecasting by recurrent neural networks with spiral structures of layers,” Neural Computing and Applications, vol. 32, no. 18, pp. 14885–14897, 2020. [Google Scholar]

23. H. P. H. Anh and C. V. Kien, “Hybrid fuzzy sliding mode control for uncertain pam robot arm plant enhanced with evolutionary technique,” Int. J. Comput. Intell. Syst., vol. 14, no. 1, pp. 594–604, 2021. [Google Scholar]

24. C. H. Rodrigues, D. E. Pires and D. B. Ascher, “Dynamut2: Assessing changes in stability and flexibility upon single and multiple point missense mutations,” Protein Science, vol. 30, no. 1, pp. 60–69, 2021. [Google Scholar] [PubMed]

25. S. AlKheder and R. Almutairi, “Roadway traffic noise modelling in the hot hyper-arid Arabian gulf region using adaptive neuro-fuzzy interference system,” Transportation Research Part D: Transport and Environment, vol. 97, pp. 102917–102935, 2021. [Google Scholar]

26. Y. Zhang, C. Zhang, Q. Ma, X. Zhang and H. Zhou, “Automatic prediction of shear wave velocity using convolutional neural networks for different reservoirs in ordos basin,” Journal of Petroleum Science and Engineering, vol. 208, pp. 109252–109264, 2022. [Google Scholar]

27. A. J. Moshayedi, A. S. Roy, S. K. Sambo, Y. Zhong and L. Liao, “Review on: The service robot mathematical model,” EAI Endorsed Transactions on AI and Robotics, vol. 1, pp. 1–19, 2022. [Google Scholar]

28. M. Chenafa, A. Meroufel, A. Mansouri and A. Massoum, “Fuzzy logic control of induction motor with input output feedback,” Acta Electrotechnicaet Informatica, vol. 7, no. 1, pp. 1–8, 2007. [Google Scholar]

29. S. Ayub, M. Shabir, M. Riaz, M. Aslam and R. Chinram, “Linear diophantine fuzzy relations and their algebraic properties with decision making,” Symmetry, vol. 13, no. 6, pp. 945–962, 2021. [Google Scholar]

30. A. Borel, V. Barzd˙enas and A. Vasjanov, “Linearization as a solution for power amplifier imperfections: A review of methods,” Electronics, vol. 10, no. 9, pp. 1073–1097, 2021. [Google Scholar]