An Effective Security Comparison Protocol in Cloud Computing

1  Introduction

Nowadays, due to the continuous progress of network technology, more and more sensitive data needs to be processed over the network [1]. Such a large amount of sensitive data requires collaborative computing in various security fields to solve the privacy and security problems, including edge computing, secure multi-party computing, deep learning, cloud computing, federated learning, the Internet of Things, etc., [2,3]. In collaborative computing, participants need to provide their own sensitive data. This not only exposes the sensitive data of the participants but also makes them vulnerable to malicious adversaries during transmission [4,5]. For example, Cloud computing is a technology that can process and store data on remote cloud servers. It can be combined with secure multi-party computing technology to form a Secure Multi-Party in Cloud Computing (SMCC) scenario, where initially participants need to actually submit their private data to the cloud server due to unknown network environments, malicious adversaries, etc. Therefore, private data is vulnerable to malicious attacks or interception in the transmission process, and the cloud server cannot fully guarantee the data's privacy security after obtaining the data. This paper mainly improves the security comparison protocol proposed by Damard et al. (DGK) [6]. The main idea is to use the additive homomorphism of the homomorphic encryption algorithm to calculate each bit and compare the size of the input from both sides without compromising privacy. That is, each client uses the PHE algorithm to encrypt its secret input and then sends the resulting ciphertext to the cloud server. At the same time, ZKP [7] is used to ensure the protocol’s correctness. Finally, the cloud server performs operations on the ciphertext and sends the comparison results to each client. Compared to the Full Homomorphic Encryption (FHE) scheme, the PHE in this scheme requires lower computational overhead, and the protocol applies to malicious participant models due to the introduction of the ZKP. More importantly, due to the introduction of OT [8] technology, the cloud server knows nothing about data information. The main contributions of this research work are:

(1) This paper proposes a security comparison protocol using ZKP technology, which can not only securely compare sensitive data but also be applied in the malicious party model.

(2) The scheme uses PHE’s addition homomorphism to split the XOR operation of the original protocol so that all computing steps are handed over to the cloud server, which not only ensures the illegal operation of the participants but also ensures the security of the protocol.

(3) The cloud server in this scheme obtains the key bits of clients' data by using OT technology, which not only ensures the sensitive data of clients is not leaked but also ensures the fairness of the protocol.

The organizational structure of this paper is as follows: The second section introduces the related work, and the third section mainly introduces the basic technology used in this paper. The fourth section mainly introduces the details of this scheme. The fourth section is a detailed description of the ZKP algorithm, and the fifth section is an analysis of security and fairness. The sixth section is the conclusion of this paper.

2  Related Work

With the development of 5G technology [9] and the popularity of intelligent mobile devices, although it provides convenience for people’s lives, the massive amount of data also brings severe challenges to various fields [10,11]. Terminal devices cannot process such massive and sensitive data, such as Artificial Intelligence (AI), Internet of Things (IoT), Wireless Sensors (WS), Machine Learning (ML), and so on [12–15]. The emergence of cloud computing effectively solves this problem. Cloud computing is a technology that can process and store data on a remote cloud server and at the same time, allows any device connected to the internet to access data [16]. Cloud computing is not only widely used in computer terminals but can also be applied to mobile terminals [17].

In a cloud computing environment, users’ data and computing are migrated to an external, virtualized “cloud server,” [18], and the cloud server performs data operations and storage. While this method can reduce the maintenance of computer hardware and software [19], it poses many privacy security challenges [20–22]. For example, the unloading of big data causes security problems such as network load and sensitive data loss [23]. There are many studies using blockchain to protect data privacy [24]. However, no matter the public or private chain, there is not only the risk of data leakage but also the easy possibility of malicious attacks [25,26]. Caprolu et al. [27] mainly introduced the advantages and differences of edge computing compared with cloud computing and analyzed data security issues. Qi et al. [28] proposed a category recommendation model for Internet of Things privacy awareness points of interest (POI) based on group preferences. In practical application, this model can not only protect users’ privacy information but also make full use of the information contained in the data set to mine users’ interests. In terms of data security and privacy protection, SMPC based on homomorphic encryption has become an increasingly mainstream data privacy protection method [29]. Derfouf et al. [30] proposed a security protocol based on partial homomorphic encryption, compared the protocol with the complete homomorphic encryption protocol, and analyzed the advantages and disadvantages of the two schemes. An effective response to the challenge of cloud computing is the foundation for building the Industrial Internet of Things (IIoT) [31].

SMPC can effectively address security and privacy issues in cloud computing [32]. Yao [33] first proposed the millionaire problem, which officially launched the SMPC study, in which several participants with secret inputs work together to compute a function and get their output. Still, none of the participants get any information about the inputs [34]. SMPC can be achieved by garbled circuits, secret sharing, and homomorphic encryption [35].

2.1 Secure Multi-party Computation Based on Full-Homomorphic Encryption

Gentry [36] first proposed a FHE scheme that could perform arbitrary operations in ciphertext. However, key storage and generation of fully homomorphic schemes are too heavy on the network, making them impractical. The dynamic unloading algorithm proposed by Chen et al. [37] can effectively improve the user utility function and realize the optimal unloading of dynamic data. Han et al. [38] introduced the multi-key full-homomorphic encryption scheme based on the Learning with Errors (LWE) encryption scheme and the attribute-based multi-key full-homomorphic encryption scheme, which can perform SMPC in an uncertain cloud environment. Mittal et al. [39] discussed the advantages and disadvantages of different FHE schemes in detail and finally gave suggestions on the prospect of FHE application in cloud computing.

Although FHE is suitable for cloud computing environments, the high computational overhead cannot be applied well in reality. And the FHE scheme needs to ensure that participants are semi-honest. The reason is that it is unrealistic to introduce the ZKP to limit malicious behavior among participants when the cost is already high. Therefore, this paper conducts research in the direction of the PHE, and the ZKP can make the scheme in this paper applicable to malicious participant models.

2.2 Secure Multi-party Computation Based on Partially Homomorphic Encryption

Mahmood et al. [40] constructed a hybrid homomorphic encryption scheme using the additive homomorphic Goldwasser Micali (GM) algorithm and the multiplicative homomorphic Rivest-Shamir-Adleman (RSA) algorithm, which not only improved security but also optimized the algorithm’s computational overhead, but still needed to trust the interaction between clients. Tan et al. [41] use Wireless Body Area Network (WBAN) to authenticate nodes, which improves data reliability. This authentication method can reduce storage costs and resource loss during data transmission. Fan et al. [42] propose a secure approach for data sharing between different domains based on edge computing models. The problem of authentication between different domains is solved, effectively ensuring node trust. Ghanem et al. [43] extended the Homomorphic Encryption Library (HElib) to support SMPC is detailed. The performance of the scheme is also analyzed. Becher et al. [44] proposed a SMPC based on a novel approach to random index distribution security. Luo et al. [45] proposed a multi-round SMPC, was built using information entropy, which ensures security between participants and is more suitable for cloud computing.

3  Preliminaries

3.1 AH-ElGamal Encryption Algorithm

Chen et al. [46] is a variant design of the Elgamal [47] encryption algorithm. It has the property of addition homomorphism. That is, given the ciphertext E(m1,r1) and E(m2,r2) under the same public key, the private key holder can obtain the ciphertext sum of m1 and m2 through homomorphism calculation, that is, E(m1,r1)E(m2,r2)=E(m1+m2,r1+r2). The algorithm consists of key generation, encryption and decryption.

Key Generation: Select two large prime numbers a and b randomly, let n=ab, select two generators g and h in Zn∗, select number x in Zn randomly, set the public key to (n,g,h,y), calculate y=hxmodn and set the private key to x.

Encryption: Encrypts the message m, selects the number r randomly, and obtains the ciphertext C=E(m)=(c1,c2)=(gmyr,hr).

Decryption: gm=c1(c2∗)−1 is first computed and then searched according to the pre-computed index table concerning g to obtain plaintext m.

3.2 Zero-Knowledge Proof

ZKP was first proposed by Golfwasser et al. [48] in 1985. It means that the prover proves to the verifier that an event is actual without giving away any relevant information. ZKP system has three characteristics: completeness, reliability, and zero-knowledge. Completeness means that the verifier always accepts a proposition when it is true. Reliability refers to the probability that the proposition will be accepted by any fraudster when the proposition is not standing. Zero-knowledge means that the prover learns nothing new about the proposition from the evidence.

ZKP is divided into interactive and non-interactive. Interactive ZKP means that the prover needs to constantly challenge the prover to verify the “knowledge” of the prover without disclosing the information of the “knowledge.” Non-interactive ZKP does not require repeated challenges but instead uses a random oracle to challenge. The random oracle returns a random output for any input, but for the same input, the random oracle uses one output method each time. In other words, a random oracle is a function that maps all inputs and outputs randomly.

ZKP in this paper replaces all challenges with hash values through a Fiat-Shamir [49] heuristic algorithm, which can be used to transform interactive ZKP into non-interactive ZKP.

3.3 Oblivious Transfer

OT is a cryptographic protocol first proposed by Rabin [50] in 1981. In this protocol, the sender of the message sends a message from the database to the receiver via the Oblivious Transfer technology. However, throughout the transmission process, the sender does not know which message is sent to the receiver, which ensures anonymity in the information query process. Naor et al. [8] proposed a reusable 1-out-of-N OT protocol based on the Diffie-Hellman hypothesis. The following uses 1-out-of-N OT protocol as an example, The Alice inputs strings (X0,X1,X2,…,XN−1), and the Bob gets the output Xr by inputting a bit r. From the perspective of Algorithm 1, the algorithm has two subjects, namely Alice and Bob. Alice has data that Bob wants and the algorithm requires Bob not only to get the data he wants, but also not to disclose any information to Alice. The most essential function of this algorithm for the scheme proposed in this paper is to provide data privacy protection. For details, see the third phase in the next chapter.

3.4 DGK Comparison Protocol

DGK comparison protocol is an efficient and secure comparison protocol under the semi-honest model proposed by Damgard et al. [6]. This protocol uses PHE additive homomorphism to solve the millionaire problem efficiently. DGK protocol starts XOR calculation from a high level until the XOR value is 1. The comparison result of this crucial bit can determine the size of two binary numbers. Suppose two binary numbers are represented by ma and mb, respectively, and 1≤i≤l, where l is the length of the binary number, and i is the ordinal number of the binary number. Under the plaintext, the following formula is calculated to obtain the comparison result. If ci=0, then prove that ma<mb.

ci=1+ma,i−mb,i+3∑j=i+1l(ma,j⊕ma,j)(1)

If the comparison is made in ciphertext, the final result can be obtained by calculating the following formula. For example, [ma,i]=gma,ihra,i mod n indicates the ciphertext that uses the public key of the encryption algorithm to encrypt ma,i.

[ci]=[1+ma,i−mb,i+3∑j=i+1l(ma,j⊕ma,j)]

=[ 1 ]⋅[ ma,i ]⋅[ mb,i ]−1⋅(∏j=i+1l[ma,j⊕ma,j])3(2)

After the server gets the value of [ci], to prevent the client from extrapolating the encryption result through repeated learning, the original protocol adds a blind factor to hide the result (However, it does not affect the final decryption result, because the result of any power of 1 is 1, in other words, any power of g0 is still g0), so the server selects the random blind factor s′ and blinds [ci] by the following formula.

[ ci ]′=[ ci ]s′mod n(3)

Finally, it is decrypted by the client. If 0 exists in the obtained result, it is shown that m1<m2.

4  Improved DGK Comparison Protocol Based on Zero-Knowledge Proof (ZKP-DGK)

The scheme in this article assumes that under the SMCC scenario, for example, as shown in Fig. 1, the clients submit their own encrypted data to the cloud server for calculation and then return the ciphertext data to each client. The cloud server restricts the illegal behavior of clients by using ZKP technology and transferring comparative computing tasks in the original DGK protocol to the cloud service provider, so as long as the cloud server is semi-honest, it will not leak any privacy.

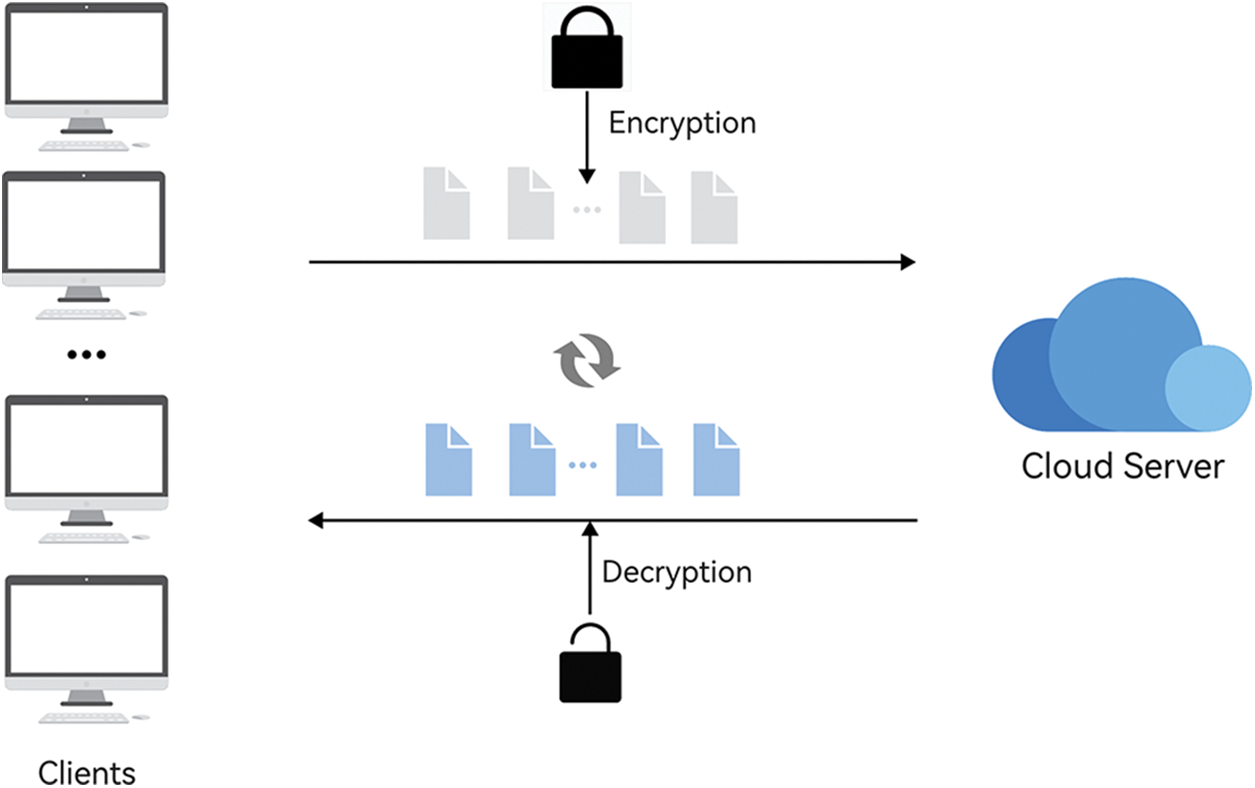
Figure 1: Secure multi-party in cloud computing (SMCC)

4.1 Initialization Phase

The public-private key pair generation mechanism of the participants uses the key generation algorithm in the AH-ElGamal encryption algorithm. After the initialization setting to generate data, suppose there are clients A, B, and server C. The server randomly selects two large prime numbers, a and b, let n=ab, and chooses two generating elements, g and h, from Zn∗. Each client randomly selects the number x in Zn as its private key and satisfies y as the public key, and the public-private key pairs of each subject are denoted as (y1,x1), (y2,x2), and (y3,x3). The encryption form is C=E(m)=(c1,c2)=(gmyr,hr), the decryption form is gm=c1(c2x)−1, and m can be decrypted according to the exponential table. The protocol scheme is broadly implemented in four phases, and each client needs to submit the corresponding ZKP in each phase.

4.2 Exponential Multiplication Phase

The public-private key pair generation mechanism of the participants uses the key generation algorithm in the AH-ElGamal encryption algorithm. After the initialization setting to generate data, suppose there are clients A, B, and server C. The server randomly selects two large prime numbers, a and b, let n=ab, and chooses two generating elements, g and h, from Zn∗. Each client randomly selects the number x in Zn as its private key and satisfies y as the public key, and the public private key pairs of each subject are denoted as (y1,x1), (y2,x2) and (y3,x3), the encryption form is C=E(m)=(c1,c2)=(gmyr,hr), the decryption form is gm=c1(c2x)−1, and m can be decrypted according to the exponential table. The protocol scheme is broadly carried out in four phases, and each client needs to submit the corresponding zero-knowledge proofs in each phase.

Clients A and B use server C’s public key to encrypt their plaintext information ma,i and mb,i respectively, and the encryption format is AH-ElGamal encryption algorithm mentioned above. Similarly, the encrypted ciphertext of client A is Ca,i=E(ma,i)=(c1,i,c2,i)=(gma,iyra,i,hra,i), and the encrypted ciphertext of client B is Cb,i=E(mb,i)=(c1,i′,c2,i′)=(gmb,iyrb,i,hrb,i). ra,i and rb,i are random numbers selected by clients A and B during the encryption, which are visible only to clients. ma,i and mb,i are the comparative plaintext of A and B. ma,i consists of the binary number l bits, where i represents the number of bits in binary. For example, ma,i represents the ith bit of ma , where 0<i≤l . The process at this phase is shown in Fig. 2.

Figure 2: Exponential multiplication phase

First, the client A and B both encrypt their own each bit after getting {Ca,l,Ca,l−1…Ca,1} and {Cb,l,Cb,l−1…Cb,1}, respectively. Then client B sends all the ciphertext to client A. After client A receives all the ciphertext from client B, client A uses its own plaintext value ma,i to perform an exponential operation on the ciphertext of client B and adds a random number r0 to hide ma,i. To ensure the decryption of the encryption algorithm, the second part of the ciphertext is processed in the same way, and finally the ciphertext Ca∗b=(c1,i∗,c2,i∗)=(gma,imb,iyma,irb,i+r0,hma,irb,i+r0) is obtained. The resulting ciphertext is sent to server C, and the discrete logarithm encryption proof is submitted. Then Ca∗b is sent to server C. At last, server C can obtain the value of ma,imb,i through decryption. Find the value ma,imb,i=0 in the result and mark it as kn, where 0<n≤l.

4.3 Additive Homomorphism Phase

Client A multiplies B’s ciphertext kn bit with his ciphertext’s to get Ca,knCb,kn=(c1,kn*c′1,kn,c2,kn*c′2,kn)=(gma,kn+mb,knyra,kn+rb,kn,hra,kn+rb,kn), and client A sends all the results to server C. Server C then decrypts each ciphertext. Obtain ma,knmb,kn from gma,knmb,kn=c1,kn*c′1,kn(c2,kn*c′2,kn)−x3=gma,kn+mb,kny3ra,kn+rb,kn(hra,kn+rb,kn)−x3. Server C then calculates the XOR value c⨁ through formula (4). Finally, server C finds the first sequence number with a value of 1 in the result for c⨁ and records it as the key comparison bit t. The process at this phase is shown in Fig. 3.

Figure 3: Additive homomorphism phase

c⨁=ma,kn+mb,kn−2ma,knmb,kn(4)

4.4 The OT Phase

Before this phase, clients A and B must combine their public keys to generate the common public key y′=y1y2. The common public key here adopts the idea of threshold decryption for the final result to be decrypted and verified in the OT phase jointly by A and B, to avoid the evil of one party. Frist, clients A and B use the joint public key y′ to generate ciphertext C′a,i=E′(ma,i)=(ca,i,c′a,i)=(gma,iy′ra,i,hra,i) and C′b,i=E′(mb,i)=(cb,i,c′b,i)=(gmb,iy′rb,i,hrb,i) respectively, and send the ciphertext to the OT. Then server C enters t into the OT. After OT performs calculation, server C can obtain C′a,t and C′b,t ciphertext. Finally, server C calculates C∗ to get the final comparison result: Finally, server C can get C∗ by formulas (5) and (6) and send C∗ to clients A and B. The process at this phase is shown in Fig. 4.

Figure 4: The OT phase

c1∗=g∗ca,t∗cb,t−1=g1+ma,t−mb,ty′ra,t+rb,t(5)

c2∗=ca,t′∗cb,t′−1=hra,t−rb,t(6)

4.5 Verification Phase

After obtaining the ciphertext comparison result C∗, clients A and B jointly decrypt the result to obtain g1+ma,t−mb,t. If g1+ma,t−mb,t is 1 then ma<mb is proved. The process at this phase is shown in Fig. 5.

Figure 5: Verification phase

The scheme process described above can not only securely compare confidential data but also ensure the security and fairness of each participant. Compared with the original DGK protocol, this paper proposes that this approach can be used to modify any malicious operation under ZKP restrictions and apply it to malicious participant models.

5  Zero-Knowledge Proof

5.1 Binary Format Proof

Because interactive ZKP is highly inconvenient in the use process (data interaction between sender and receiver is required), the ZKP in this paper adopts Fiat-Shamir [49] heuristic algorithm to replace all interactive steps with the random oracle. And this method can be used to transform interactive ZKP into non-interactive ZKP. This algorithm can be simply understood as using a hash function to replace the random challenge value of the data interaction in the interactive ZKP.

Algorithm 2 is described as follows: There is cyphertext Ca,i=E(ma,i)=(c1,c2)=(gma,iyra,i,hra,i). The prover proves to the verifier that ma,i in c1 is the correct binary format [7].

5.2 Proof of Ciphertext Format Correctness

Algorithms 3 and 4 are described as follows: Participants must prove that in Ca,i=E(ma,i)=(c1,c2)=(gma,iyra,i,hra,i) are encrypted following the AH-ElGamal encryption form. The proof is divided into two parts: representation proof and discrete logarithm proof.

(1) Part c1: The ciphertext is Ca,i=E(ma,i)=(c1,c2)=(gma,iyra,i,hra,i),1<i≤l. Prover knows that witness (ma,i, ra,i) and proves that c1=gma,iyra,i holds.

(2) Part c2: The ciphertext is Ca,i=E(ma,i)=(c1,c2)=(gma,iyra,i,hra,i),1<i≤l. Prover knows that witness (ra,i) and proves that c2=hra,i holds.

5.3 Random Number Consistency Proof

The encryption format used in this scheme is (c1,c2)=(gma,iyra,i,hra,i). Since there are two ciphertexts c1 and c2, c2 is used for decryption. If c1 and c2 are inconsistent during the encryption, the decryption operation cannot be performed usually. Therefore, it is necessary to prove that ra,i of c1 and c2 are consistent.

Algorithm 5 is described as follows: There is ciphertext Ca,i=(Ca,l,Ca,l−1,Ca,l−2…Ca,1), where Ca,i=E(ma,i)=(c1,c2)=(gma,iyra,i,hra,i),1<i≤l. The Prover knows witness (ma,i, ra,i) and shows that ra,i=ra,i in (gma,iyra,i,hra,i).

5.4 Ciphertext Consistency Proof

Since this scheme uses multiple rounds of comparison, it is necessary to ensure that the plaintext information contained in the ciphertext submitted by participants in each round is consistent.

Algorithm 6 is described as follows: The encryption format is Ca,i=(Ca,l,Ca,l−1,Ca,l−2…Ca,1), whereCa,i=E(ma,i)=(c1,c2)=(gma,iyra,i,hra,i),1<i≤l. The ciphertext c1=gma,iyra,i in the first round and c′1=gm′a,iyra,i in the second round are set. The participants need to prove that ma,i is consistent with m′a,i.

6  Security and Fairness Analysis

6.1 Security Analysis

Since the objective of this scheme is to apply under the malicious participant model, a security analysis of the zero-knowledge proofs submitted in the scheme is required.

6.1.1 Binary Format Proof

Suppose there exists a malicious adversary A′ that is able to construct a new challenge C′ by mimicking the challenge C of the random oracle and constructs a response s′1,s′2,s′3, while submitting a false proof Proof1,0Ca,i(Ca,i,ma,i,ra,i). Adversary A′ can get c1C−C′=gs1−s′ys2−s′21 and c1C−s1+C′−s′1=g0ys3−s′3 by combining equations, and then the ma,i and ra,i values of the ciphertext can be obtained by equations (s1−s1′)(C1−C1′)−1 and (s2−s2′)(C1−C1′)−1, so the plaintext is completely compromised. However, in the case where the security parameter is large enough, the malicious adversary A′ must guess the same c′ from the random prediction machine under the satisfied condition, which is considered infeasible, and after guessing c′ and to obtain the value of t1 at the same time, the value of t1 needs to be found by discrete logarithm values of λ1 and λ2. The difficulty is to solve the discrete logarithm problem on Gp in polynomial time, which is also considered infeasible, so the hypothesis is not valid.

6.1.2 Proof of Ciphertext Format Correctness

Since the ciphertext encryption format of the participants takes the AH-ElGamal encryption algorithm, the protocol participants need to ensure that the ciphertext is encrypted in the form of Ca,i=E(ma,i)=(c1,c2)=(gma,iyra,i,hra,i). Therefore, this scheme requires the participants to submit two proofs of and respectively. The following is an example of Part c1.

(1) Part c1: Suppose that the malicious client A′ can construct a new challenge c′ by mimicking the challenge C of the random oracle. Then the value of the ciphertext ma,i can be obtained by combining the equation(s1−s1′)(C1−C1′)−1 and the value of the random number ra,i can be obtained by (s2−s2′)(C1−C1′)−1. Thus, ciphertext c1 is breached, resulting in plaintext leakage. In the same way as binary format proof analysis, the cheating client A′ must guess the same c′ from the random oracle under the satisfied condition, which is considered infeasible with sufficiently significant security parameters.

(2) Part c2: It is assumed that cheating participant A′ can forge an identical response to s′, and then the r value of the ciphertext can be obtained by combining the equation s−s′C−C′. Like the above analysis, cheating participant A′ would have to guess the same c′ from the random oracle if the conditions were satisfied, which would be considered infeasible if the security parameters were large enough.

6.1.3 Exponential Multiplication Phase

In the exponential multiplication phase of the ZKP-DGK scheme, client A needs to exponentiate the ciphertext of client B with its plaintext, and then add a random number r0 to construct the ciphertext form of Cb,ima,iy3r0=gma,imb,iy3ma,irb,i+r0. This proof can be analyzed by the discrete logarithm proof, and by the same token, it is infeasible for the client A to attempt to forge false proof. And in the additive homomorphism phase, since the ciphertext is bound using the Pedersen commitment, it is also sufficiently secure for A and B.

6.1.4 Verification Phase

In the third stage, clients A and B need to encrypt with the standard public key y′ and submit proof of correctness, similar to the first stage. Since server C in the ZKP-DGK scheme is a semi-honest model, and neither client A nor client B under the malicious model is involved in the comparison calculation, as long as server C follows the protocol correctly, then even if clients A and B are malicious adversaries, the security of the scheme will not be affected, and the security of the remaining phases can be demonstrated by referring to the security of the DGK protocol.

6.2 Fairness Analysis

Since this scheme assumes that the clients are malicious models and a semi-honest server C is introduced, it is necessary to consider whether there is information leakage in each stage of data interaction and ciphertext computation in this scheme.

6.2.1 Exponential Multiplication Phase

For malicious clients A and B, want to maximize their gains, so this subsection first analyzes whether clients A and B can access each other’s personal input. In the first phase, client A indexes the secret message received from B with its plaintext to obtain Cb,ima,i. To avoid the leakage of A’s plaintext and add a random number r0 to hide ma,i one step deeper to obtain gma,imb,iy3ma,irb,i+r0 and submit proof of correctness of ciphertext format. In this process, client A will not know anything about mb,i, because A only performs the exponential operation on Cb,i. For client B, the value of ma,i cannot be solved from the index table due to the random number r0. For server C, server C can only decrypt the value of ma,i and mb,i multiplied by gma,imb,iy3ma,irb,i+r0, but does not obtain the specific values of ma,i and mb,i.

6.2.2 Additive Homomorphism Phase

At this stage, client A needs to multiply its ciphertext Ca,i with client B’s ciphertext Cb,i to obtain Ca,i Cb,i=(gma,i+mb,iyra,i+rb,i,hra,i+rb,i). This stage is the same as the previous proof stage, where clients A and B cannot obtain explicit information about ma,i and mb,i. For server C, which has information about ma,imb,i and ma,i+mb,i at this point, it is fair for all parties involved since server C cannot to determine the specific, exact value of ma,i or mb,i based on ma,imb,i and ma,i+mb,i.

6.2.3 The OT Phase

This phase of oblivious transfer (OT) refers to the 1-out-of-N model in a black box environment. The server C inputs the sequence number t of the critical comparison bit, and the corresponding ciphertexts C′a,t and C′b,t are obtained by the OT protocol. In this technique, clients A and B cannot know which ciphertext data server C has obtained, and at the same time server C can obtain ciphertexts C′a,t and C′b,t.

6.2.4 Verification Phase

At this stage, clients A and B need to decrypt jointly to get the final comparison result, thus ensuring that A and B cannot decrypt privately. Since clients A and B did not participate in the calculation of the comparison results, and server C needed to verify the submitted zero-knowledge proof, clients could be anything wrong. As for semi-honest server C, as long as the server correctly executes the agreement, the agreement's fairness will not be affected.

Analysis shows that, throughout the scheme, neither client A nor client B nor server C have access to private input data. Therefore, this scheme is fair to the clients. A comparison between this paper and [6] and [51] is shown in Table 1. The DGK comparison protocol can only be compared between participants, which relies heavily on honesty between participants. Yu et al. [51] proposed a scheme constructed with ZKP. Although the scheme can be applied to malicious participant models to some extent, the security and fairness of the scheme still depend on the Trusted Third Party (TTP). In this paper, ZKP-DGK not only protects the user’s private data, but also limits malicious behavior between data parties, which provides the basis for some real-world applications, such as electronic voting, privacy auction, big data fusion, and so on [52]. With the implementation of practical applications, the data will become larger and larger, placing a severe burden on the network [53]. A large number of scholars have researched this aspect so that network overhead will be the next step for this solution.

7  Conclusion

HE-based security comparison protocol provides positive implications for the development of cloud computing. However, distrust between data owners and the expensive computing overhead of a complete homomorphism still pose serious challenges to cloud computing. This paper combines the ZKP and PHE, improves DGK comparison protocol, uses the cloud server in cloud computing to replace the third party, and proposes a security comparison protocol suitable for malicious parties. In this scheme, zero-knowledge proofs are used to curb malicious client behavior. Compared to FHE, PHE not only guarantees the privacy of ciphertext but also has a more minor computational cost. During the entire process, private information will not be leaked to any party, including trusted servers. The final analysis shows that the scheme can achieve the security and fairness of ciphertext comparison. However, all scenarios proposed in this paper are completed under the condition that the cloud server is running normally. That is, although the cloud server cannot obtain any valuable data, its behavior must be guaranteed to be correct. Otherwise, the protocol will not be downright correctly. In future work, we will continue to study ZKP, HE, edge computing, etc., and finally construct a security comparison protocol under a completely malicious model.

Acknowledgement: We are thankful to State Key Laboratory of Public Big Data of Guizhou University for providing an environment for editing manuscripts and experiments.

Funding Statement: This work is financially supported by the National Natural Science Foundation of China under Grant No. (62202118.61962009). And in part by Natural Science Foundation of Shandong Province (ZR2021MF086). And in part by Top Technology Talent Project from Guizhou Education Department (Qian jiao ji [2022]073). And in part by Foundation of Guangxi Key Laboratory of Cryptography and Information Security (GCIS202118).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. Y. Dong, W. J. Wu, Y. Gao, X. X. Wan and P. B. Si, “Deep reinforcement learning based worker selection for distributed machine learning enhanced edge intelligence in internet of vehicles,” Intelligent and Converged Networks, vol. 1, no. 3, pp. 234–242, 2020. [Google Scholar]

2. K. El Makkaoui, A. Beni-Hssane and A. Ezzati, “Cloud-elgamal: An efficient homomorphic encryption scheme,” in 2016 Int. Conf. on Wireless Networks and Mobile Communications (WINCOM), Fez, Morocc, pp. 63–66, 2016. https://doi.org/10.1109/WINCOM.2016.7777192 [Google Scholar] [CrossRef]

3. L. Y. Qi, Y. H. Yang, X. K. Zhou, W. Rafique and J. Ma, “Fast anomaly identification based on multiaspect data streams for intelligent intrusion detection toward secure industry 4.0,” IEEE Transactions on Industrial Informatics, vol. 18, no. 9, pp. 6503–6511, 2022. [Google Scholar]

4. T. Li, Y. L. Chen, Y. L. Wang, Y. L. Wang, M. H. Zha et al., “Rational protocols and attacks in blockchain system,” Security and Communication Networks, vol. 1-11, no. 2020, pp. 1–11, 2020. https://doi.org/10.1155/2020/8839047 [Google Scholar] [CrossRef]

5. L. Z. Kong, G. S. Li, W. Rafique, S. G. Shen, Q. He et al., “Time-aware missing healthcare data prediction based on ARIMA model,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, pp. 1–10, 2022. https://doi.org/10.1109/TCBB.2022.3205064 [Google Scholar] [PubMed] [CrossRef]

6. I. Damgard, M. Geisler and M. Kroigaard, “Homomorphic encryption and secure comparison,” International Journal of Applied Cryptography, vol. 1, no. 1, pp. 22–31, 2008. [Google Scholar]

7. J. Groth and M. Kohlweiss, “One-out-of-many proofs: Or how to leak a secret and spend a coin,” In: E. Oswald, M. Fischlin (Eds. Advances in Cryptology-EUROCRYPT 2015, Berlin Heidelberg: Springer,pp. 253–280, 2015. https://doi.org/10.1007/978-3-662-46803-6_9 [Google Scholar] [CrossRef]

8. M. Naor and B. Pinkas, “Efficient oblivious transfer protocols,” in Proc. of the Twelfth Annual ACM-SIAM Symp. on Discrete Algorithms, ser. SODA ’01., Washington, D.C, USA, pp. 448–457, 2001. https://doi.org/10.1145/365411.365502 [Google Scholar] [CrossRef]

9. Y. Zhang, H. Q. Zhang, J. Cosmas, N. Jawad, K. Ali et al., “Internet of radio and light: 5G building network radio and edge architecture,” Intelligent and Converged Networks, vol. 1, no. 1, pp. 37–57, 2020. [Google Scholar]

10. F. Wang, G. S. Li, Y. L. Wang, W. Rafique, M. R. Khosravi et al., “Privacy-aware traffic flow prediction based on multi-party sensor data with zero trust in smart city,” ACM Transactions on Internet Technology, pp. 1232, 2022. https://doi.org/10.1145/3511904 [Google Scholar] [CrossRef]

11. Y. L. Chen, X. Yang, T. Li, Y. Ren and Y. Y. Long, “A blockchain-empowered authentication scheme for worm detection in wireless sensor network,” Digital Communications and Networks, vol. 8, pp. 111, 2022. https://doi.org/10.1016/j.dcan.2022.04.007 [Google Scholar] [CrossRef]

12. H. Benfenatki, C. F. Da Silva, A. N. Benharkat, P. Ghodous and F. Biennier, “Methodology for semi-automatic development of cloud-based business applications,” in 2014 IEEE 7th Int. Conf. on Cloud Computing, Anchorage, AK, USA, pp. 954–955, 2014. https://doi.org/10.1109/CLOUD.2014.139 [Google Scholar] [CrossRef]

13. A. Al-Fuqaha, M. Guizani, M. Mohammadi, M. Aledhari and M. Ayyash, “Internet of things: A survey on enabling technologies, protocols, and applications,” IEEE Communications Surveys & Tutorials, vol. 17, no. 4, pp. 2347–2376, 2015. [Google Scholar]

14. M. Ayad, M. Taher and A. Salem, “Mobile gpu cloud computing with real time application,” in 5th Int. Conf. on Energy Aware Computing Systems & Applications, Cairo, Egypt, pp. 1–4, 2015. https://doi.org/10.1109/ICEAC.2015.7352209 [Google Scholar] [CrossRef]

15. L. Y. Qi, W. M. Lin, X. Y. Zhang, W. C. Dou, X. L. Xu et al., “A correlation graph based approach for personalized and compatible web apis recommendation in mobile app development,” IEEE Transactions on Knowledge and Data Engineering, pp. 1, 2022. https://doi.org/10.1109/TKDE.2022.3168611 [Google Scholar] [CrossRef]

16. W. Zhang, X. Chen and J. H. Jiang, “A multi-objective optimization method of initial virtual machine fault-tolerant placement for star topological data centers of cloud systems,” Tsinghua Science and Technology, vol. 26, no. 1, pp. 95–111, 2021. [Google Scholar]

17. Y. L. Wang, Tao Li, M. Liu, C. M. Li and H. Wang, “STSIIML: Study on token shuffling under incomplete information based on machine learning,” International Journal of Intelligent Systems, vol. 37, no. 12, pp. 11078–11100, 2022. [Google Scholar]

18. Z. Salman and W. M. Elmedany, “A trustworthy cloud environment using homomorphic encryption: A review,” in 4th Smart Cities Symp. (SCS 2021Online Conf., Bahrain, pp. 31–36, 2021. https://doi.org/10.1049/icp.2022.0308 [Google Scholar] [CrossRef]

19. S. M. Ghanem and I. A. Moursy, “Secure multiparty computation via homomorphic encryption library,” in 2019 Ninth Int. Conf. on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, pp. 227–232, 2019. https://doi.org/10.1109/ICICIS46948.2019.9014698 [Google Scholar] [CrossRef]

20. A. K. Sandhu, “Big data with cloud computing: Discussions and challenges,” Big Data Mining and Analytics, vol. 5, no. 1, pp. 32–40, 2022. [Google Scholar]

21. F. Wang, H. Zhu, G. Srivastava, S. Li, M. R. Khosravi et al., “Robust collaborative filtering recommendation with user-item-trust records,” IEEE Transactions on Computational Social Systems, 2021. https://doi.org/10.1109/TCSS.2021.3064213 [Google Scholar] [CrossRef]

22. L. Z. Kong, L. N. Wang, W. W. Gong, C. Yan, Y. C. Duan et al., “Lsh-aware multitype health data prediction with privacy preservation in edge environment,” World Wide Web Journal, vol. 25, no. 5, pp. 1793–1808, 2021. https://doi.org/10.1007/s11280-021-00941-z [Google Scholar] [CrossRef]

23. Y. L. Chen, J. Sun, Y. Yang, T. Li, X. Niu et al., “Psspr: A source location privacy protection scheme based on sector phantom routing in wsns,” International Journal of Intelligent Systems, vol. 37, no. 2, pp. 1204–1221, 2022. [Google Scholar]

24. K. Lu and C. Y. Zhang, “Blockchain-based multiparty computation system,” in 2020 IEEE 11th Int. Conf. on Software Engineering and Service Science (ICSESS), Beijing, China, pp. 28–31, 2020. https://doi.org/10.1109/ICSESS49938.2020.9237698 [Google Scholar] [CrossRef]

25. T. Li, Z. J. Wang, G. Y. Yang, Y. Cui, Y. L. Chen et al., “Semi-selfish mining based on hidden markov decision process,” International Journal of Intelligent Systems, vol. 36, no. 7, pp. 3596–3612, 2021. [Google Scholar]

26. T. Li, Z. J. Wang, Y. L. Chen, C. M. Li, Y. L. Jia et al., “Is semi-selfish mining available without being detected?,” International Journal of Intelligent Systems, vol. 37, no. 12, pp. 10576–10597, 2022. [Google Scholar]

27. M. Caprolu, R. Di Pietro, F. Lombardi and S. Raponi, “Edge computing perspectives: Architectures, technologies, and open security issues,” in 2019 IEEE Int. Conf. on Edge Computing (EDGE), Milan, Italy, pp. 116–123, 2019. https://doi.org/10.1109/EDGE.2019.00035 [Google Scholar] [CrossRef]

28. L. Y. Qi, Y. W. Liu, Y. L. Zhang, X. L. Xu, M. Bilal et al., “Privacy-aware point-of-interest category recommendation in internet of things,” IEEE Internet of Things Journal, vol. 9, no. 21, pp. 21398–21408, 2022. https://doi.org/10.1109/JIOT.2022.3181136 [Google Scholar] [CrossRef]

29. A. Chouhan, A. Kumari and M. Saiyad, “Secure multiparty computation and privacy preserving scheme using homomorphic elliptic curve cryptography,” in 2019 Int. Conf. on Intelligent Computing and Control Systems (ICCS), Madurai, India, pp. 776–780, 2019. https://doi.org/10.1109/ICCS45141.2019.9065645 [Google Scholar] [CrossRef]

30. M. Derfouf and M. Eleuldj, “Cloud secured protocol based on partial homomorphic encryptions,” in 2018 4th Int. Conf. on Cloud Computing Technologies and Applications (Cloudtech), Brussels, Belgium, pp. 1–6, 2018. https://doi.org/10.1109/CloudTech.2018.8713353 [Google Scholar] [CrossRef]

31. Y. H. Yang, X. Yang, M. Heidari, G. Srivastava, M. R. Khosravi et al., “Astream: Data-stream-driven scalable anomaly detection with accuracy guarantee in IIoT environment,” IEEE Transactions on Network Science and Engineering, pp. 1, 2022. https://doi.org/10.1109/TNSE.2022.3157730 [Google Scholar] [CrossRef]

32. T. Oladunni and S. Sharma, “Homomorphic encryption and data security in the cloud,” in Proc. of 28th Int. Conf. on Software Engineering and Data Engineering, San Diego, California, USA, vol. 64, pp. 129–138, 2019. https://doi.org/10.29007/drnc [Google Scholar] [CrossRef]

33. A. C. Yao, “Protocols for secure computations,” in 23rd Annual Symp. on Foundations of Computer Science (sfcs 1982), Chicago, IL, USA, pp. 160–164, 1982. https://doi.org/10.1109/SFCS.1982.38 [Google Scholar] [CrossRef]

34. Y. L. Chen, S. Dong, T. Li, Y. L. Wang and H. Y. Zhou, “Dynamic multi-key fhe in asymmetric key setting from lwe,” IEEE Transactions on Information Forensics and Security, vol. 16, pp. 5239–5249, 2021. https://doi.org/10.1109/TIFS.2021.3127023 [Google Scholar] [CrossRef]

35. K. Patel, “Secure multiparty computation using secret sharing,” in 2016 Int. Conf. on Signal Processing, Communication, Power and Embedded System (SCOPES), Paralakhemundi, India, pp. 863–866, 2016. https://doi.org/10.1109/SCOPES.2016.7955564 [Google Scholar] [CrossRef]

36. C. Gentry, “Fully homomorphic encryption using ideal lattices,” in Proc. of the Forty-First Annual ACM Symp. on Theory of Computing (STOC ’09), New York, NY, USA, pp. 169–178, 2009. https://doi.org/10.1145/1536414.1536440 [Google Scholar] [CrossRef]

37. Y. Chen, F. Zhao, Y. Lu and X. Chen, “Dynamic task offloading for mobile edge computing with hybrid energy supply,” Tsinghua Science and Technology, 2021. https://doi.org/10.26599/TST.2021.9010050 [Google Scholar] [CrossRef]

38. J. L. Han, Z. L. Wang, Y. Q. Shi, M. J. Wang and H. Dong, “Secure multiparty computation via fully homomorphic encryption scheme,” in 2018 Eighth Int. Conf. on Instrumentation & Measurement, Computer, Communication and Control (IMCCC), Cairo, Egypt, pp. 250–253, 2018. https://doi.org/10.1109/IMCCC.2018.00060 [Google Scholar] [CrossRef]

39. S. Mittal, K. Ramkumar and A. Kaur, “Preserving privacy in clouds using fully homomorphic encryption,” in 2021 Int. Conf. on Smart Generation Computing, Communication and Networking (SMART GENCON), Pune, India, pp. 1–7, 2021. https://doi.org/10.1109/SMARTGENCON51891.2021.9645822 [Google Scholar] [CrossRef]

40. Z. H. Mahmood and M. K. Ibrahem, “New fully homomorphic encryption scheme based on multistage partial homomorphic encryption applied in cloud computing,” in 2018 1st Annual Int. Conf. on Information and Sciences (AiCIS), Fallujah, Iraq, pp. 182–186, 2018. https://doi.org/10.1109/AiCIS.2018.00043 [Google Scholar] [CrossRef]

41. X. Tan, J. L. Zhang, Y. J. Zhang, Z. Qin, Y. Ding et al., “A puf-based and cloud-assisted lightweight authentication for multi-hop body area network,” Tsinghua Science and Technology, vol. 26, no. 1, pp. 36–47, 2021. [Google Scholar]

42. K. Fan, Q. Pan, J. X. Wang, T. T. Liu, H. Li et al., “Cross-domain based data sharing scheme in cooperative edge computing,” in 2018 IEEE Int. Conf. on Edge Computing (EDGE), San Francisco, CA, USA, pp. 87–92, 2018. https://doi.org/10.1109/EDGE.2018.00019 [Google Scholar] [CrossRef]

43. S. M. Ghanem and I. A. Moursy, “Secure multiparty computation via homomorphic encryption library,” in 2019 Ninth Int. Conf. on Intelligent Computing and Information Systems (ICICIS), Cairo, Egypt, pp. 227–232, 2019. https://doi.org/10.1109/ICICIS46948.2019.9014698 [Google Scholar] [CrossRef]

44. K. Becher and T. Strufe, “Efficient cloud-based secret shuffling via homomorphic encryption,” in 2020 IEEE Symp. on Computers and Communications (ISCC), Rennes, France, pp. 1–7, 2020. https://doi.org/10.1109/ISCC50000.2020.9219588 [Google Scholar] [CrossRef]

45. Y. Luo, Y. L. Chen, T. Li, Y. L. Wang, Y. X. Yang et al., “An entropy-view secure multiparty computation protocol based on semi-honest model,” Journal of Organizational and End User Computing (JOEUC), vol. 34, no. 10, pp. 1–17, 2022. [Google Scholar]

46. Z. W. Chen, R. Q. Zhang, Y. T. Yang and Z. C. Li, “A homomorphic elgamal variant based on bgn’s method,” in 2013 Int. Conf. on Cyber-Enabled Distributed Computing and Knowledge Discovery, Beijing, China, pp. 1–5, 2013. https://doi.org/10.1109/CyberC.2013.10 [Google Scholar] [CrossRef]

47. T. Elgamal, “A public key cryptosystem and a signature scheme based on discrete logarithms,” IEEE Transactions on Information Theory, vol. 31, no. 4, pp. 469–472, 1985. [Google Scholar]

48. S. Goldwasser, S. Micali and C. Rackoff, “The knowledge complexity of interactive proof-systems,” in Proc. of the Seventeenth Annual ACM Symp. on Theory of Computing (STOC ’85), New York, NY, USA, pp. 291–304, 1985. https://doi.org/10.1145/22145.22178 [Google Scholar] [CrossRef]

49. M. Bellare and P. Rogaway, “Random oracles are practical: A paradigm for designing efficient protocols,” in Proc. of the 1st ACM Conf. on Computer and Communications Security, ser. CCS ’93, New York, NY, USA, Association for Computing Machinery, pp. 62–73, 1993. https://doi.org/10.1145/168588.168596 [Google Scholar] [CrossRef]

50. M. O. Rabin, “How to exchange secrets by oblivious transfer,” Technical report, Aiken Computation Laboratory. Harvard University, 1981. [Google Scholar]

51. R. C. Yu, “Research on the sealed-bid auction scheme for blockchain based on secure comparison protocols,” M.S. Dissertation, College of Information Engineering, Northwest A&F University, China, 2019. [Google Scholar]

52. J. Z. Wang, Y. Shen and B. C. Wang, “Sealed-bid auction scheme based on blockchain and secure multi-party computation,” in 2021 IEEE 5th Information Technology, Networking, Electronic and Automation Control Conf. (ITNEC), Xi'an, China, vol. 5, pp. 407–412, 2021. https://doi.org/10.1109/ITNEC52019.2021.9587239 [Google Scholar] [CrossRef]

53. H. P. Dai, J. Yu, M. Li, W. Wang, A. Liu et al., “Bloom filter with noisy coding framework for multi-set membership testing,” IEEE Transactions on Knowledge and Data Engineering, pp. 1–14, 2022. https://doi.org/10.1109/TKDE.2022.3199646 [Google Scholar] [CrossRef]