Quantum-Enhanced Blockchain: A Secure and Practical Blockchain Scheme

1  Introduction

Since 2008, when Satoshi Nakamoto proposed Bitcoin [1], blockchain, the underlying technology of Bitcoin has been deeply developed and widely used in various industries [2–6]. However, blockchain development is threatened by the forthcoming quantum computer, as quantum computing attacks can crack vulnerable cryptographic components in blockchain systems, mainly hash functions and public-key digital signatures [7]. Thus, to improve the security level of cryptosystems against quantum computing attacks, post-quantum cryptography (PQC) has arisen, which involves more difficult computational problems that are hard for a quantum computer to solve. Therefore, PQC is widely investigated and has already been adopted in the blockchain system, known as the post-quantum blockchain. The main PQC schemes include lattice-based, code-based, hash-based, multivariate-based, and hybrid cryptosystems [8]. With the increasing complexity of a cryptosystem, the efficiency of blockchain is decreasing accordingly. Although post-quantum blockchain may be quantum-resistant, it will be unsafe when the quantum computing breakthrough occurs, i.e., new quantum algorithms or more powerful computing resources.

Unlike post-quantum blockchain, the quantum blockchain introduces quantum technology into the blockchain system. With the help of quantum physic mechanics, classic cryptography, which is fragile to quantum computing attacks, is replaced by its secure quantum counterpart, avoiding the many attacks toward classic cryptography and enhancing the security level of the blockchain system.

Recently, researchers have conducted extensive research on quantum blockchain, suggesting that the theoretical information security of quantum key distribution (QKD) can be utilized to improve blockchain security [9–12]. Specifically, in 2018 Kiktenko et al. [13] proposed a quantum-secured blockchain scheme based on the QKD network. They used the original Byzantine fault tolerance (BFT) state-machine replication and QKD in the blockchain for secure authentication instead of digital signatures and experimentally evaluated the blockchain scheme in an urban fiber network. However, their scheme is not scalable, as when the number of nodes increases to a certain extent, the efficiency of the BFT consensus mechanism declines rapidly, limiting the scalability of the blockchain system. In 2019, Rajan et al. [14] introduced the concept of a quantum blockchain by utilizing entanglement in time, and in 2020, Gao et al. [15] developed a novel quantum blockchain scheme based on quantum entanglement and a delegated proof of stake (DPoS) consensus mechanism. Nevertheless, [14,15] are not applicable under the existing technology and thus do not have practical value. In 2021, Wen et al. [16] suggested a quantum blockchain scheme combining a QHF, a quantum swap test circuit, and quantum teleportation. However, the quantum swap test circuit fails to judge the equivalence of two different quantum strings with a non-negligible probability. Therefore the QHF wrongly judges the equivalence of two inputs, leading to verifying data consistency inaccurately in the blockchain system. In 2022, El-Latif et al. [17] proposed a blockchain framework by designing a QHF based on a quantum walk model and leveraged the QHF to generate hash values for linking blocks. This blockchain scheme achieves integrity and confidentiality for data in internet of things (IoT) devices. However, the identity authentication security for transaction participants is based on the confidentiality of the QHF parameters. Moreover, their paper does not mention what consensus mechanism is used to guarantee the confidentiality of the QHF parameters.

At the same time, the recent progress in quantum technologies such as QHF and QDS has provided us with new ideas for designing a secure and practical blockchain scheme through quantum methods. In 2013, Li et al. [18] proposed a two-particle controlled interacting quantum walk model and designed a QHF based on the model. As the security of the QHF is guaranteed by the irreversibility of quantum measurement rather than mathematical complexity problems, the quantum walk is considered to be a suitable choice for constructing a QHF. In 2016, Yang et al. [19] designed a QHF based on a two-particle discrete-time quantum walk and it has a wide range of applications such as image encryption and pseudo-random number generation. In 2021, Zhou et al. [20] proposed a QHF based on controlled alternate quantum walk (CAQW) with memory. Their QHF is claimed to be near-ideal in statistical performance. Considering the excellent collision resistance of a QHF, it can be used in a blockchain system to improve the integrity protection of transaction records. As to transaction verification, a quantum signature can be adopted due to its immunity to the threats of quantum computing attacks faced by classic public-key signatures. A quantum signature with a designated verifier allows only the designated verifier to verify a message, providing privacy preservation for the signer. Taking advantage of quantum mechanics, several information-theoretically secure schemes have been proposed in recent years [21–24]. However, the use of a quantum signature in the blockchain is still rare. Adopting a quantum signature in a blockchain system will secure transactions against quantum adversaries. Due to the post-quantum security and high efficiency of quantum cryptography, the adoption of quantum cryptography such as QHF and QDS will enhance both the security and efficiency of a blockchain system.

Inspired by these works and spurred by the promising capabilities of quantum methods, this paper develops a quantum-enhanced blockchain scheme. Specifically, we first discuss the quantum computing attacks against classic blockchains, mainly against fragile components, such as classic hash functions, public-key digital signatures, and consensus mechanisms. Second, to improve the security of a blockchain system through a quantum approach, a QHF based on controlled alternative quantum walk (CAQW) is proposed for hash value generation, and a QDS based on identity is developed for transaction signing. Additionally, a PoA [25] consensus mechanism is adopted to improve the system’s reliability, scalability, and efficiency. Finally, a quantum-enhanced blockchain scheme is proposed by combining QHF, QDS, and a PoA consensus mechanism. All methods adopted are practical technologies that can be implemented under the current technical stage. Therefore, our scheme is feasible and has great value in practical applications.

The main contributions of our work are as follows.

1.    Proposing a QHF scheme based on the CAQW model to generate hash values in the blockchain.

2.    Developing a QDS scheme based on identity for blockchain transactions.

3.    Introducing a quantum-enhanced blockchain scheme based on QHF, QDS, and the PoA consensus mechanism. Unlike the existing concept stating that improving security is achieved by increasing the computational complexity of the cryptographic algorithms, our scheme enhances the security of the blockchain system in a quantum way.

The remainder of this paper is organized as follows. Section 2 discusses the quantum computing attacks against blockchains, and Section 3 proposes a QHF based on CAQW. Section 4 develops a QDS based on identity. Section 5 introduces our quantum-enhanced blockchain scheme, and Section 6 conducts a security analysis of our scheme. Finally, Section 7 concludes this work.

2  Quantum Computing Attacks Against Blockchain

Quantum computing attacks against blockchain are mainly divided into preimage-collision attacks in hash functions implemented by Grover’s searching algorithm [26], forgery attacks in digital signatures implemented by Shor’s algorithm [27], and attacks in the consensus mechanisms.

2.1 Attacks on Hash Functions

Hash functions like secure hash algorithm SHA-256 and Scrypt have been widely used in blockchains for digital signature in transactions, block generation (e.x. Merkle tree), linking blocks, and generating user addresses [8]. As in Bitcoin, each block stores the hash value of its previous block, linking all blocks.

In the classic hash function, the input is a plaintext message m with an unfixed length, and the output is a hash value h of fixed length n. As the input space 2L (L is the maximum length of m) is larger than the output space 2n, there must be collisions in the hash function, i.e., for a hash function h(x), two different inputs exist, x and y, and their hash values are the same.

Compared with classic search algorithms, Grover’s algorithm affords a quadratic speed up in searching, as its complexity is reduced to O(n) from O(n) [26]. This characteristic can be used in the preimage-collision attack against classic hash functions. Take the SHA-256 (used in Bitcoin), for example, to find a certain result, n2 average times are needed for a classic machine, while for a quantum computer running Grover’s algorithm, the number of oracle calls is only π4n [28].

2.1.1 Attack on the Block Based on Hash Collisions

The previous analysis reveals that an attacker with access to quantum computers can implement a preimage-collision attack on classic hash functions using Grover’s algorithm. Therefore, a forgery attack on the block can be implemented. For a specific transaction record, the attackers can use Grover’s algorithm to search for hash conflict and use it to modify the signed data on the block [29]. Taking a specific block, for example, its Merkle tree structure is illustrated in Fig. 1.

Figure 1: The second preimage attack on the block based on Merkle Tree

The hash value of a transaction record Tx is h=h(Tx). The second preimage attack is presented in Fig. 1, where the attacker searches for another input Tx′ (probably a meaningless string) to satisfy h(Tx′)=h(Tx). After the search succeeds, the attacker tampers Tx with Tx′. The final Merkle header remains unchanged if a tampered transaction record does not change its hash value. The second preimage attack on the transaction will destroy the data integrity and consistency of the blockchain. Although classic cryptography is committed to improving the computational complexity and increasing the difficulty for attackers to find the collision, it fails to eliminate the collision’s existence. With the improvement of computing power brought by quantum computing, the vulnerability of classic hash functions against preimage-collision attacks is becoming more prominent. Therefore, it is urgent to find a hash function that resists preimage-collision attacks better to achieve better data integrity protection for blockchain.

2.1.2 Attacks on the Digital Signature Based on Hash Collisions

Based on the collisions of a hash function, the second preimage attack can be performed. If a second preimage Tx′ is found, the attacker will tamper the original information Tx with Tx′. As the hash value remains unchanged, h(Tx)=h(Tx′)=h, and the signature will also remain unchanged sign(Tx,sk)=σ, sign(Tx′,sk)=σ. This demonstrates the vulnerability of the information to tampering.

2.2 Quantum Computing Attacks on Public-Key Digital Signatures Based on Private Key Retrieval

In 1994, Shor [27] proposed Las Vegas algorithms running on a quantum computer, widely known as Shor’s algorithm, which can find discrete logarithms and factor integers in polynomial steps, i.e., cryptosystems based on discrete logarithmic problems and factoring integer problems were fragile from quantum adversaries. Therefore, the public-key signatures based on Rivest-Shamir-Adleman (RSA), digital signature algorithm (DSA), and ellipse curve cryptography (ECC) algorithms will be vulnerable to Shor’s quantum computing attacks [15].

For instance, in a blockchain system with a public-key digital signature, Eve is an attacker with access to a quantum computer, and Alice is a legal user. Alice has several implemented transactions recorded on blocks, and Eve attempts to retrieve Alice’s private key by cracking the digital signature. Eve will collect Alice’s public key and signatures which have been broadcast in the blockchain network, and then Shor’s algorithm can be utilized by Eve to speed up the process of retrieving the private key. If Eve succeeds in the private key retrieval, Eve will be able to publish an illegal transaction in the name of Alice [30]. Considering elliptic curve digital signature algorithm (ECDSA), a quantum computing attack can be conducted with a complexity of 9n+2log2⁡n+10 with n=160 [31]. Using Shor’s algorithm to crack RSA with an n-bit key requires about 2n quantum bits.

2.3 Attacks on the Consensus Mechanism

In a blockchain system with a proof of work (PoW) consensus mechanism, a miner obtains accounting rights by searching for a nonce whose hash value meets specific conditions. The huge advantage of the quantum computer in computing power will break the game’s fairness. Indeed, [32] used quantum parallelism to speed up the mining procedure using the modified Grover’s algorithm and demonstrated that a quantum computer could find a nonce in the Bitcoin network in only 2 s, while a classic computer requires about 465 days. Therefore, quantum competitors would have an overwhelming advantage in the mining game in winning mining rewards. With the emergence of quantum adversaries, the PoW consensus mechanism is not secure anymore.

In a blockchain system with a proof of stake (PoS) consensus mechanism, to obtain the right to validate transactions, stakers are required to perform staking transactions. As the staking transactions are vulnerable to Shor’s attack, the participants will be exposed to losing their assets [30].

3  Quantum Hash Function

Inspired by [19], a QHF based on a discrete quantum walk model is proposed. Specifically, we use a one-dimensional two-particle CAQW on a circle with N nodes to construct the model. The CAQW has two components: a coin and a walker, the walker involves two particles moving in the Hilbert space Hp, and the state of the coin controls the walker’s movement through a conditional shift operator. As the walker moves on a circle with N nodes, the value of x is in {1,2,…, N}.

The coin state in each step is decided by the value of m, where the ith bit in message m controls the ith step of the walker. An M-bit message m=(m1,m2,…, mM)∈{0,1}M will make the walker move M steps. The evolution of CAQW is the product of M unitary transforms:

Um=U(mM)U(mM−1)…U(m1)(1)

U(mi)(i=1,2,…, M) is the transformation of the ith step controlled by mi (the ith bit in m). We define three operators in our CAQW system, C(0), C(1) and C(2), which are coin operators implemented when mi=0, mi=1, and mi is null, respectively. Obviously C(2) is an identity operator.

C(0)=12(1−1−11−11−11−1−1111111),C(1)=12(−11111−11111−11111−1),C(2)=12(1000010000100001)

The working process of QHF is illustrated in Fig. 2 and is described as follows:

Figure 2: QHF based on CAQW

Step 1: Initialize the public parameter N denoting the number of nodes on the circle. Input the QHF parameters (α, β, λ, μ) as the initial state of the walker and input a bit-string message m as the controller of coin states.

Step 2: According to the parameters in Step 1, a CAQW on a circle in one dimension with two particles is performed. Under the control of m, two particles with initial state α|00⟩+β|01⟩+λ|10⟩+μ|11⟩ perform M transformations and generate an N×N probability distribution matrix P, where pij is the element in the ith row and the jth column of matrix P, representing the probability that two particles will finally stop on (i, j).

Step 3: Convert P into a binary string h with a fixed length. By multiplying all elements in P by 10b and then modulo them to 2b, a bN2 bit-string will be generated, where hij denotes the calculating result for pij, h1|h2 denotes the concatenation of string h1 and string h2 and fix(p) denotes the integer part of p.

hij=fix(pij×10b) mod2b, (i=1,2,…, N;j=1,2,…, N)(2)

hi=hi1|hi2|…|hij|…|hiN(3)

h=h1|h2|…|hj|…|hN(4)

Step 4: Calculate the hash value of m, QHF(N,α, β, λ, μ, m)=hm, let l=bN2, and ml denotes the first l bits of m. If the length of m is less than l, then we add “0” to the vacant bits in ml to reach l.

hm=h|(h⊕ml)(5)

The hash value of m by QHF is hm, and the length of hm is 2bN2.

4  Quantum Digital Signature

The detailed process of signing for transaction information is described in the following example. Fig. 3 presents Alice, the signer, Bob, the receiver, and David, the verifier. As a private key generator (PKG), David is a trusted validating node in the blockchain and never exposes the signer’s private key or impersonates the signer to sign the message. Now Alice has a transaction message to send to Bob, which is encoded as a binary bit string m=(m1,m2,…, mi,…, mM),mi∈{0,1}. The signature of the transaction is generated by the proposed QDS, which includes four phases: initialization, key generation, signing, and verification.

Figure 3: QDS structure

4.1 Initialization Phase

Each node participates in a transaction exchange the QHF parameters (α, β, λ, μ) for the intended nodes through a quantum-secured channel.

Let the Hadamard operator be H, the Pauli-y operator be Y, and I is the unit operator.

H=12(111−1),Y=12(0−ii0),I=(1001),|+⟩=12(|0⟩+|1⟩),|−⟩=12(|0⟩−|1⟩)

The symbol “⊕” denotes addition under modulo 2. For two n-bit strings a=(a1,a2,…, an) and b=(b1,b2,…, bn), we define a⊕b=(a1⊕b1,a2⊕b2,…, an⊕bn).

4.2 Key Generation Phase

Alice has a unique identity code in the system, denoted as IDA, IDA=(ID1,ID2,…, IDn)∈{0,1}n. Bob’s identity code is denoted as IDB, IDB∈{0,1}n, G is a one-way function G:{0,1}∗→{0,1}n with uniform output distribution, and F is a one-way function F:{0,1}∗→{0,1}n with uniform output distribution. David generates Alice’s private key KAD in the following steps.

Step 1: David uses the master key G to generate the private key KAD for Alice.

KAD=G(IDA)={ki},i=(1,2,…, n)(6)

Step 2: David and Alice perform the BB84 QKD protocol and share a random key x, x={xi}∈{0,1}n,i=(1,2,…, n). David calculates y by the following formula and publishes y.

y=x⊕KAD(7)

Step 3: Alice obtains her private key KAD by calculating KAD=x⊕y. Alice secretly generates a random n-bit string t={ti}∈{0,1}n,i=(1,2,…, n), and calculates

t′=t⊕KAD(8)

Alice publishes t′ to David. According to t′, David calculates

t=t′⊕KAD(9)

t is used as a shared parameter between Alice and David.

Step 4: Alice secretly holds her secret key KAD and the shared parameter t. David secretly holds the key pair (IDA,KAD,t), where IDA is Alice’s identity code, t is the secret key shared by Alice and David.

4.3 Signing Phase

Step 1: Alice uses her secret parameter (α, β, λ, μ) and the transaction information m to run the QHF and generate the hash value—a 2n-bit string h. QHF(N,α, β, λ, μ, m)=h, h=(h11,h12,…hi1,hi2…, hn1,hn2)∈{0,1}2n.

n=bN2(10)

Step 2: According to Table 1, Alice encodes the 2n-bit h into an n-qubit quantum sequence |h⟩. |h⟩={|h1⟩, |h2⟩, …|hi⟩, …|hn⟩},i=1,2,…, n. The value of |hi⟩ is one of the four states in {|0⟩, |1⟩, |+⟩, |−⟩}.

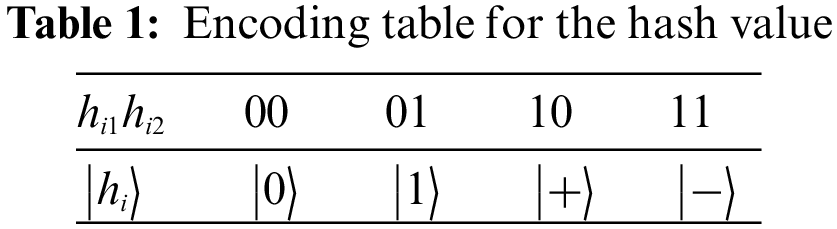
Step 3: Alice and Bob perform the BB84 QKD protocol to share two random keys u and v, u={ui}∈{0,1}n, v={vi}∈{0,1}n, i=(1,2,…, n). Alice secretly generates a random n-bit string r={ri}∈{0,1}n,i=(1,2,…, n), which Alice uses r to calculate r′ and publishes r′ to Bob.

r′=u⊕r(11)

Alice uses Bob’s identity IDB to calculate the shared parameter PAB using the following formula.

PAB=F(IDA⊕IDB)(12)

Alice uses PAB to calculate PAB′ and publishes PAB′ to Bob.

PAB′=v⊕PAB(13)

Step 4: According to r′, Bob obtains r by calculation.

r=r′⊕u(14)

According to PAB′, Bob obtains PAB by calculation.

PAB=v⊕PAB′(15)

r is the shared key of Alice and Bob, PAB is used as a shared parameter between Alice and Bob.

Step 5: By using the H and Y operators, Alice conducts the following operations on |hi⟩, generates |hi¯⟩ and finally gets a new quantum sequence |h¯⟩, denoted as |σ⟩.

|h¯i⟩=HKAD(i)⊕riYPAB(i)⊕ti|hi⟩(16)

Step 6: Alice prepares R decoy particles (R>>2n), which are randomly distributed in (|1⟩, |0⟩, |+⟩, |−⟩). She randomly inserts R decoy particles into the quantum sequence to detect eavesdropping, then |σ′⟩ is generated. After that, Alice sends {Tx,IDA,h,|σ′⟩} to Bob.

Step 7: After receiving {Tx, IDA, h, |σ′⟩}, Alice publishes the positions of decoy particles, and Bob uses the corresponding measurement basis to measure particles at these positions. If there are no errors, Bob proceeds to the next step. Otherwise, he will restart the protocol.

Step 8: After performing the detection operation for eavesdropping, Bob discards all the decoy particles and holds {m, IDA, h, |σ⟩} as Alice’s signature.

4.4 Verification Phase

Step 1: Bob computes the hash value of m with Alice’s parameters and obtains the hash value hB, then Bob compares hB with h. If hB=h, he proceeds to the next step, otherwise he will reject the signature and restart the protocol.

QHF(N,α, β, λ, μ, m)=hB(17)

Step 2: Using the shared parameter PAB and the shared key r, Bob performs the following operations on |hi¯⟩: generates |h^i⟩ and finally obtains a quantum sequence |h^⟩.

|h^i⟩=HriYPAB(i)|h¯i⟩(18)

Step 3: Bob prepares R decoy particles (R>>2n), which are randomly distributed in (|1⟩, |0⟩, |+⟩, |−⟩). He randomly inserts R decoy particles into |h^⟩ and gets the quantum sequence |h^′⟩ to detect eavesdropping. Then Bob sends {IDA,|h^′⟩} to David.

Step 4: After David receives {IDA,|h^′⟩}, Bob announces the positions of the decoy particles. David uses the corresponding measurement basis to measure particles at these positions. If there is no error, David goes to the next step; otherwise, David will restart the protocol.

Step 5: David discards all decoy particles and restores {IDA,|h^′⟩} to {IDA,|h^⟩}.

Step 6: Based on IDA, David recovers the key KAD and the shared parameter t, and performs the following operations on |h^i⟩: generates |hi′⟩ and finally obtains the quantum sequence |h′⟩.

|hi′⟩=HKAD(i)Yti|h^i⟩(19)

Step 7: According to h, the measurement basis is selected for measurement on |h′⟩. Since the h is a 2n-bit string, it can be written in the form of n 2-bit strings. h={h11h12,h21h22,…, hi1hi2,…hn1hn2}. When hi1=0, David selects the {|0⟩, |1⟩} measurement basis and when the measurement result is |0⟩, hi1′hi2′=00. When the measurement result is |1⟩, hi1′hi2′=01. When hi1=1, the measurement basis {|+⟩, |−⟩} is selected for measurement. When the measurement result is |+⟩, hi1′hi2′=10. Finally, when the measurement result is |−⟩, hi1′hi2′=11. After n measurements, h′={h11′h12′,h21′h22′…, hi1′hi2′,…hn1′hn2′}.

Step 8: David compares h′ with h. If h′=h, the verification is successful and the signature will be accepted. Otherwise, the signature is rejected.

The QDS process is illustrated in Fig. 4.

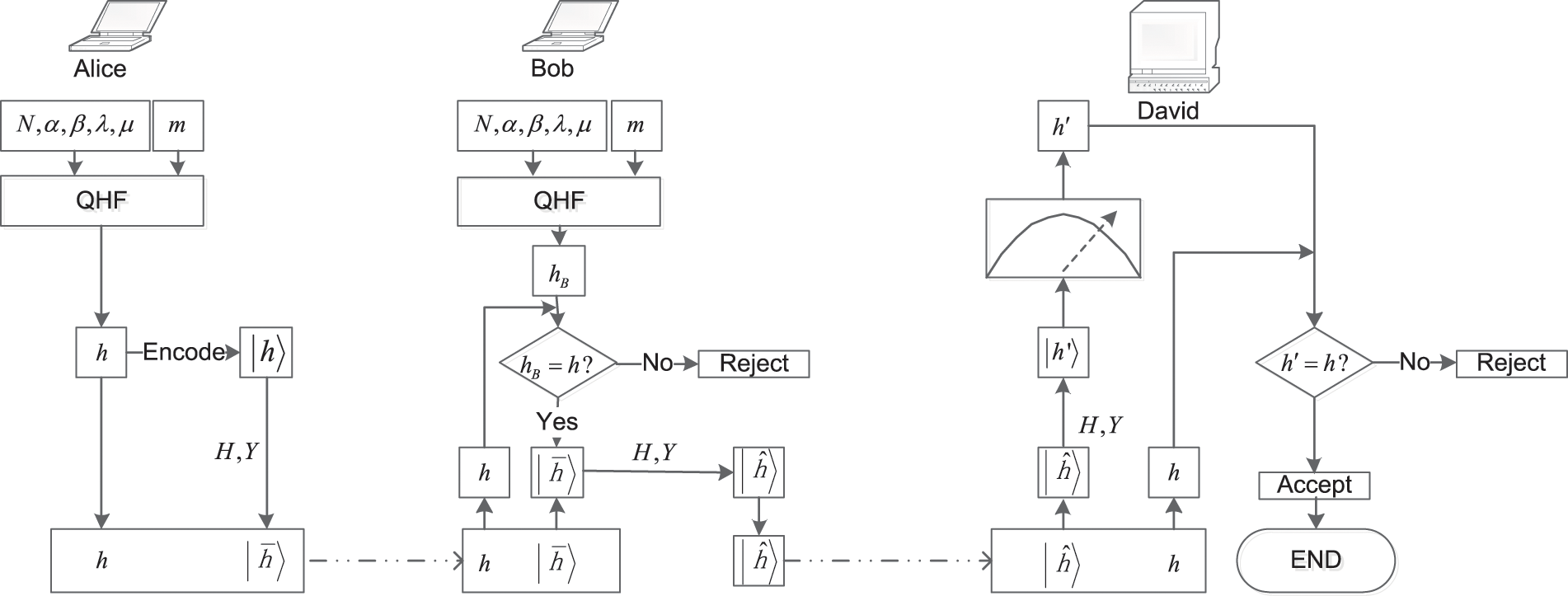
Figure 4: QDS process

5  Quantum-Enhanced Blockchain Scheme

In the proposed scheme, blockchain security is enhanced from three aspects. First, the classic hash function is discarded, as the QHF is utilized to generate hash values, and QHF link blocks by hash values. Second, the classic public-key digital signature is discarded, and the QDS is used. Thus the transactions in a block are signed by QDS. Third, a PoA consensus mechanism is utilized. Additionally, during a transaction, secure QKD protocols like BB84 and one-time pad (OTP) [33] are combined to secure confidential information, such as secret keys and parameters.

5.1 Consensus Mechanism in Quantum-Enhanced Blockchain

The mining process requires excessive computing resources in a blockchain system using PoW, such as Bitcoin. Furthermore, as described in Section 2.3, a miner with access to a quantum computer can use Grover’s algorithm to implement a mining attack and unfairly obtain the right of new block generation. In PoS, staking transactions are fragile to Shor’s attack, and some participants with a stake advantage may acquire a monopoly in the blockchain network, leading to centralization. Regarding the practical Byzantine fault tolerance (PBFT), the efficiency of the consensus will decline when the number of nodes increases to a certain extent.

In conclusion, PoA is a suitable choice for our scheme. Relying on the reputation of validating nodes rather than stakes, PoA can effectively improve the scalability and throughput of the blockchain network [25]. Moreover, PoA efficiently reaches a consensus, generates a new block, is energy-efficient as there is no energy consumption for mining, and is robust against quantum computing attacks due to its computing power independence.

5.2 Structure of Quantum-Enhanced Blockchain

5.2.1 The Generation of a Transaction

Transaction information comprises the signer, the receiver, the verifier, transaction content, and other information, with the most important information placed at the first part of a transaction. As depicted in Fig. 5, a transaction process is as follows.

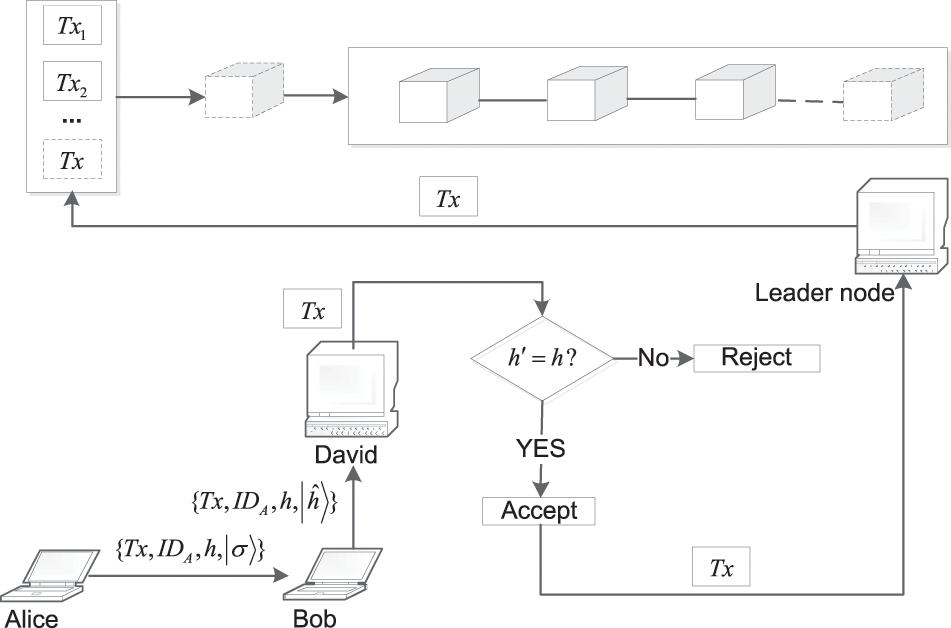
Figure 5: Transaction process in quantum-enhanced blockchain

Alice is the signer, initiates a transaction with the receiver Bob, and David is the verifier designated by Alice. When using PoA, David is a trusted validating node whose identity has already been publicly authenticated. Tx is the transaction, and h is the hash value of Tx generated by QHF with Alice’s parameters. Using QDS presented in Section 4, Alice generates the signature {Tx,IDA,h,|σ⟩} for the transaction and sends it to Bob. If the signature verification succeeds, the message has not been tampered with, and Alice generates the signature. David declares the validity of the signature, accepts the transaction, and submits it to the leader node to be included in a forthcoming new block. Otherwise, it is rejected.

5.2.2 Block Generation Process

In PoA, the validating nodes are trusted nodes whose identity has been authenticated publicly. The blockchain maintains a list of the validating nodes, from which nodes will be elected as the leader node. The leader node is responsible for packaging transactions, proposing, and including a new block in each consensus. At the beginning of a consensus round, the leader node publishes the public QHF parameters (αp,βp,λp,μp) to all validating nodes in a secure quantum channel, which all validating nodes use (αp,βp,λp,μp) to generate hash values for blocks.

The validating node acts as the verifier for a transaction, which will be submitted to the leader node after verification. The leader node will sort all collected transactions based on their timestamp, verify the validity of the transactions one by one, package the valid transactions into a new block, and rejects the invalid ones.

After the valid transactions are accumulated to a certain extent, the leader node proposes a new block and generates the hash value of the new block by QHF with (αp,βp,λp,μp). The new block will be sent to other validating nodes to confirm its validity through voting. The new block will be accepted and added to the blockchain if it gets at least V2+1 affirmative votes (V is the number of validating nodes). Otherwise, it will be rejected. If a validating node fails to generate a valid block for certain times, it will lose the identity of the validating node.

According to PoA, the validating nodes generate new blocks in turn. For instance, the blockchain has T blocks, and David is the current leader node responsible for the new block generation. When legitimate transactions accumulate to a certain amount, David generates a new block—the (T + 1)th block. In the new block, the blockhead contains the hash value of the Tth block, and all other nodes add this new block to their local blockchain. In the next consensus, the (T + 2)th block will store the hash value of the (T + 1)th block in its blockhead, i.e., each blockhead contains the hash value of its previous block, and all blocks are linked to form a complete chain. Fig. 6 illustrates the structure of a block in a quantum-enhanced blockchain.

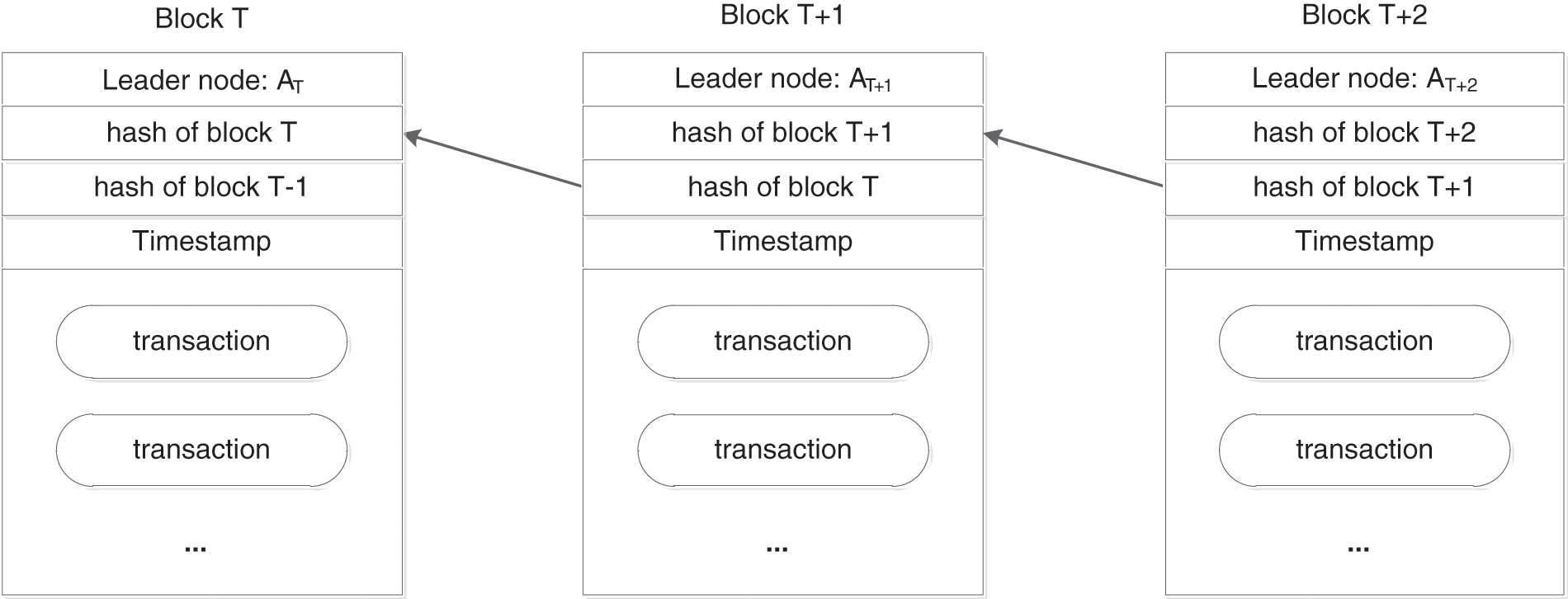
Figure 6: Structure of quantum-enhanced blockchain

6  Security Analysis of Blockchain Scheme

Our scheme is resistant to quantum computing attacks such as the preimage-collision attack in hash functions implemented by Grover’s algorithm, forgery attack in digital signatures implemented by Shor’s algorithm, and mining attack in the consensus mechanism.

6.1 Security Analysis of QHF

The QHF is resistant to the second preimage attack. As depicted in Section 3, the input of QHF includes the public parameter N, secret parameters (α, β, λ, μ), and message m. Since the secret parameters (α, β, λ, μ) are shared between the nodes in a secure quantum channel, these are not available to the adversary. Without knowing the QHF parameters, a quantum attacker cannot perform the preimage searching attack based on Shor’s algorithm. Therefore, the resistance of QHF to quantum computing attacks is guaranteed by the security of quantum communication. Taking a step back, even if the QHF parameters are compromised, and the attacker obtains a hash collision by chance, the effect of data tampering is still limited. This is benefited from the design of Step 4 in the QHF scheme. For instance, m′ is a hash collision for m.

hm=h|(h⊕ml)(20)

hm′=h′|(h′⊕ml′)(21)

It is not difficult to conclude that ml′=ml, which means the first l bits of m′ remain the same with m. This is essential for a transaction, as long as we add the most important information, such as sender, receiver, and amount of coin, in the first l bits of a transaction, the damage of tempering can be limited.

6.2 Security Analysis of QDS Scheme

The QDS is a verifier-designated scheme. Taking advantage of the trust mechanism in PoA, the identity of the validating node is public and trusted, and the validating node will act as the PKG in QDS. The subsequent security analysis is made under the malicious adversary model, which includes the security of the private key and resistance to forgery attacks, repudiation, and interception (eavesdropping).

6.2.1 Security of the Private Key

The QDS scheme is a quantum signature based on identity. The PKG is a trusted validating node whose identity is already authenticated, PKG generates the signer’s private key, and PKG’s trustworthiness guarantees the confidentiality of the private key. Moreover, the attacker has no access to the private key and will try to break the private key from the published information.

Considering the example, first, it is unworkable for the attacker to obtain the KAD value from Alice’s identity IDA. According to formula (6), KAD is generated with David’s secret master key G, which is a one-way function with uniform output distribution. The function set elements for G is 2n! large, while the probability for the attacker to successfully guess G is 12n!, which is negligible. Therefore, obtaining KAD from IDA is unworkable for the attacker.

Second, it is unworkable for the attacker to obtain the KAD value from Alice’s published string y. According to formula (7), y is calculated using KAD and x, where x is a random key generated from the unconditional secure BB84 QKD protocol. Since the BB84 QKD protocol is theoretically information secure to distribute the private key, the keys cannot be eavesdropped during transmission because the sender and the receiver will detect the eavesdropping behavior by measuring and comparing the decoy particles. Thus, it is infeasible for the attacker to obtain the value of x.

Furthermore, we use the OTP to generate x, and y can be seen as ciphertext of KAD. Guaranteed by the unconditional security of OTP, the attacker has no access to obtain the secret pad x, so the attacker has no way to obtain KAD from y without knowing x. In the same way, the attacker cannot obtain r from r′ without knowing u.

Third, the attacker cannot obtain the integral quantum sequence |h¯⟩ containing secret key information KAD. In the signing phase, before a quantum sequence is transmitted, the decoy particles are used to detect an eavesdropping attack, as any eavesdropping attack will disturb the decoy particles, and the receiver will easily detect such attacks through the decoy particles. The no-cloning theorem of quantum mechanics [34] guarantees the security of |h¯⟩, so it cannot be duplicated. Furthermore, the attacker cannot break the secret key from |h¯⟩ even if the attacker obtains the integral quantum sequence |h¯⟩.

In addition, the private key value ranges in {|0⟩, |1⟩, |+⟩, |−⟩}, and the probability of successfully guessing the private key is p=14n. When n is large enough, p is close to 0, i.e., the probability for the attacker to succeed in randomly guessing the private key is negligible. Therefore, cracking the private key by brute force is infeasible.

In a word, the security of the private key KAD is fully guaranteed, and no attacker can break it with a non-negligible probability.

6.2.2 Security Against Forgery Attacks

There are two types of forgery attacks. The first is to forge the signature by using the signer’s transaction information, and the second is to forge the signer’s transaction information. For the former, the signer, Alice, generates the transaction information Tx and uses her IDA and the private key KAD to generate the signature {Tx,IDA,h,|σ⟩}. The attacker intends to generate a forged signature {Tx,IDA,h,|σ′⟩} with |σ′⟩≠|σ⟩ by using Tx and the signer’s private key KAD. The analysis in Section 6.2.1 reveals that an attacker cannot crack the private key KAD with a non-negligible probability. Moreover, the QDS process shows that the security of r and t is guaranteed by the theoretical information security of BB84 QKD protocol and OTP, so the attacker cannot obtain the shared key r, t. Generating a signature requires KAD, PAB, r and t, which the attacker cannot obtain, therefore he cannot forge a valid signature. For the forgery of transaction information, the signer publishes legal transaction information Tx and generates a valid signature {Tx,IDA,h,|σ⟩}. The attacker intends to forge the legal transaction information Tx into illegal transaction information Tx′(Tx′≠Tx) and make the signature of Tx′: {Tx′,IDA,h,|σ⟩} to pass the verification phase. In the verification phase of QDS, the receiver, Bob, computes the hash value of Tx′ and will find QHF(N,α, β, λ, μ, Tx′)≠h, and then the forged signature will be rejected. Obviously, the attacker cannot find a Tx′ that the hash value of Tx′ is h, i.e., QHF(N,α, β, λ, μ, Tx)=QHF(N,α, β, λ, μ, Tx′). As (α, β, λ, μ) are Alice’s secret parameters shared by a quantum secure communication protocol, the attacker cannot obtain Alice’s QHF parameters (α, β, λ, μ), so the attacker cannot find such Tx′ to implement a forgery attack on Tx. Therefore, transaction information cannot be falsified. To sum up, our scheme cannot implement the two types of forgery attacks.

6.2.3 Security Against Repudiation

Repudiation (denial) means the attacker denies (rejects) the signature, so the signer’s signature process fails. According to the signing phase in QDS, if the attacker is the signer Alice, as Alice is not the verifier (a validating node), she cannot participate in the verification phase. Therefore, Alice cannot reject (deny) the signature. David automatically passes the signature if the attacker is the receiver, Bob, and the verification succeeds. In this way, the attacker still cannot reject (deny) the legitimate signature because David is a trusted node and can decide whether the signature passes the verification process.

6.2.4 Security Analysis of Interception (Eavesdropping)

Interception is when an attacker intercepts a message in order to fabricate it. According to the QDS, the adversary can obtain some transaction information, including Tx, IDA, h and the decoy particles’ position distribution.

In the signing phase, the adversary hijacks Tx and submits a tampered transaction Tx′ to the verification phase. The analysis in Section 6.2.2 shows that the tampered transaction Tx′ cannot pass the verification phase because the adversary has no access to the signer’s QHF parameters, and thus, the receiver will reject it by checking the hash value generated by QHF.

6.3 Security Analysis of Quantum-Enhanced Blockchain Scheme

Threats of quantum computing attacks faced by conventional blockchains have been eliminated in our scheme. Our method can also resist popular attacks in blockchain systems, such as man-in-the-middle attacks, double spending attacks, and 51% attacks.

6.3.1 Resistance to Man-in-the-Middle Attack

Our blockchain system has two layers of communication channels for data transmission: the quantum channel and the classic channel. For the quantum channel, the security of quantum communication is guaranteed by the Heisenberg uncertainty principle [35] and quantum no-cloning theorem [34]. Using decoy particles in the BB84 protocol makes eavesdropping impossible because any eavesdropping behavior will disturb the quantum state, exposing the attack behavior. For the classic channel, the integrity of transaction data is protected by QHF and QDS. Since the quantum and classic channels are resistant to a man-in-the-middle attack, a man-in-the-middle attack is not feasible in our scheme.

6.3.2 Resistance to Double-Spending Attack

The double-spending problem arises because, on a P2P network, everyone gets inconsistent transaction information simultaneously. In our scheme, by adopting PoA, the ledger is maintained by trusted validating nodes, and the data is synchronized from the validating nodes. All transactions are verified by trusted validating nodes and will be submitted to the leader node after validation, so the double-spending problem is easy to solve. When generating a new block, the leader node will sort all the transactions by timestamp, and the invalid transactions will be discarded before proposing a new block. Hence, the leader node can deal with the double-spending attack well, and our scheme is resistant to double-spending attacks.

6.3.3 Resistance to 51% Attack

When using PoA, the proposal and package of a block are implemented by the leader node, which is acted by the validating nodes in turn. Block including requires affirmative votes of more than half of the validating nodes. Becoming a validator is difficult. The identity of the validator is public on the line, and the tough process of becoming a validator will reduce the risk of malicious behavior. Therefore, getting more than half of the validating nodes under control is infeasible. In addition, by PoA’s dynamic updating mechanism for validating nodes, malicious nodes will be excluded, which will ensure the reliability of the blockchain system. In conclusion, 51% of attack is not feasible in our scheme.

Table 2 compares six quantum blockchain schemes from four aspects, demonstrating the comprehensive advantages of our scheme.

7  Conclusion

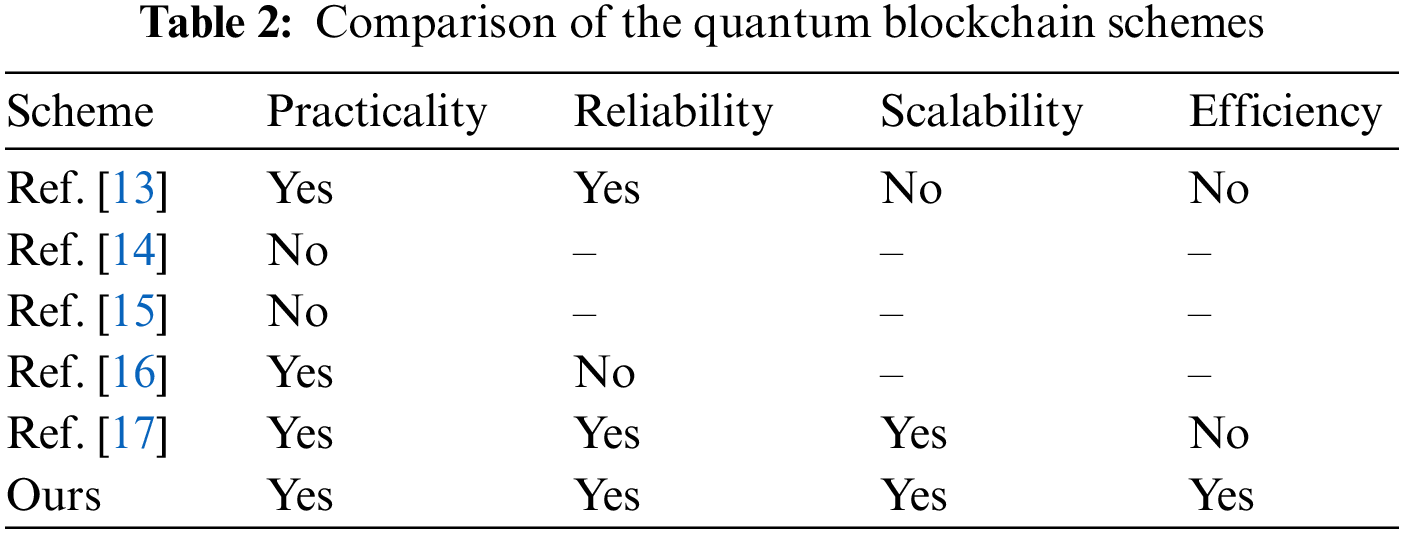
This paper discusses quantum computing attacks toward classic blockchains, including attacks on hash functions, public-key digital signatures, and consensus mechanisms. Moreover, to handle these security threats, we design a QHF and a QDS and propose a quantum-enhanced blockchain scheme that uses the QHF, QDS, and a PoA consensus mechanism. Additionally, our security analysis shows that our scheme has better security against quantum computing and classic attacks. Finally, we compare our scheme with previous works, showing that our scheme has achieved a perfect balance in terms of practicality, reliability, scalability, and efficiency. Overall, this work will contribute to enriching the research on quantum blockchain in the future.

The proposed scheme may be currently expensive, considering communication consumption. However, as quantum communication technology becomes more mature, communication consumption will reduce. More importantly, we present a quantum approach to design a quantum-secured blockchainsecured blockchain system under current technological conditions. Our work will enrich the research of blockchain systems in the quantum era and lay the foundation for optimizing the design of a blockchain system through quantum methods, achieving better security and practicality.

Funding Statement: This work was supported by Research on Satellite Quantum Key Network Security Architecture (No. AHY180500). This work was supported by the Research on Digital Identity Trust System for Massive Heterogeneous Terminals in Road Traffic System (No. 2022YFB3104402). This work was supported in part by National Key RD Program of China (No. 2018YFB0803401), in part by the China Postdoctoral Science Foundation under Grant 2019M650606, in part by First-class Discipline Construction Project of Beijing Electronic Science and Technology Institute (No. 3201012).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Nakamoto, “Bitcoin: A peer-to-peer electronic cash system,” Technical Report, 2019. [Online]. Available: https://bitcoin.org/bitcoin.pdf [Google Scholar]

2. P. Chinnasamy, C. Vinothini, S. A. Kumar, A. A. Sundarraj, S. V. Annlin Jeba et al., “Blockchain technology in smart-cities,” in Blockchain Technology: Applications and Challenges, 1st ed., vol. 203. Cham, Switzerland: Springer Nature Switzerland AG, pp. 179–200, 2021. [Google Scholar]

3. P. Chinnasamy, B. Vinodhini, V. Praveena, C. Vinothini and B. Ben Sujitha, “Blockchain based access control and data sharing systems for smart devices,” Journal of Physics: Conference Series, vol. 1767, no. 1, pp. 012056, 2021. [Google Scholar]

4. S. H. Alsamhi, F. A. Almalki, F. Afghah, A. Hawbani, A. V. Shvetsov et al., “Drones’ edge intelligence over smart environments in B5G: Blockchain and federated learning synergy,” IEEE Transactions on Green Communications and Networking, vol. 6, no. 1, pp. 295–312, 2021. [Google Scholar]

5. R. Sahal, S. H. Alsamhi, K. N. Brown, D. O’Shea and B. Alouffi, “Blockchain-based digital twins collaboration for smart pandemic alerting: Decentralized COVID-19 pandemic alerting use case,” Computational Intelligence and Neuroscience, vol. 2022, no. 7786441, pp. 1–14, 2022. [Google Scholar]

6. S. H. Alsamhi, A. V. Shvetsov, S. V. Shvetsova, A. Hawbani and M. Guizani, “Blockchain-empowered security and energy efficiency of drone swarm consensus for environment exploration,” IEEE Transactions on Green Communications and Networking, vol. 7, no. 1, pp. 328–338, 2022. [Google Scholar]

7. A. H. Lone and R. Naaz, “Demystifying cryptography behind blockchains and a vision for post-quantum blockchains,” in 2020 IEEE Int. Conf. for Innovation in Technology (INOCON), Bangluru, India, pp. 1–6, 2020. [Google Scholar]

8. T. M. Fernandez-Carames and P. Fraga-Lamas, “Towards post-quantum blockchain: A review on blockchain cryptography resistant to quantum computing attacks,” IEEE Access, vol. 8, no. 19313627, pp. 21091–21116, 2020. [Google Scholar]

9. C. H. Bennett and G. Brassard, “An update on quantum cryptography,” In: G. R. Blakley (Ed.CRYPTO, pp. 475–480, Berlin, Heidelberg: Springer, 1984. [Google Scholar]

10. W. McCutcheon, A. Pappa, B. A. Bell, A. McMillan, A. Chailloux et al., “Experimental verification of multipartite entanglement in quantum networks,” Nature Communications, vol. 7, no. 1, pp. 1–8, 2016. [Google Scholar]

11. L. Gyongyosi, S. Imre and H. V. Nguyen, “A survey on quantum channel capacities,” IEEE Communications Surveys & Tutorials, vol. 20, no. 2, pp. 1149–1205, 2018. [Google Scholar]

12. M. Stanley, Y. Gui, D. Unnikrishnan, S. R. G. Hall and I. Fatadin, “Recent progress in quantum Key distribution network deployments and standards,” Journal of Physics: Conference Series, vol. 2416, no. 1, pp. 012001, 2022. [Google Scholar]

13. E. O. Kiktenko, N. O. Pozhar, M. N. Anufriev, A. S. Trushechkin, R. R. Yunusov et al., “Quantum-secured blockchain,” Quantum Science and Technology, vol. 3, no. 3, pp. 035004, 2018. [Google Scholar]

14. D. Rajan and M. Visser, “Quantum blockchain using entanglement in time,” Quantum Reports, vol. 1, no. 1, pp. 3–11, 2019. [Google Scholar]

15. Y. L. Gao, X. B. Chen, G. Xu, K. G. Yuan, W. Liu et al., “A novel quantum blockchain scheme base on quantum entanglement and DPoS,” Quantum Information Processing, vol. 19, no. 12, pp. 1–15, 2020. [Google Scholar]

16. X. J. Wen, Y. Z. Chen and X. C. Fan, “Quantum blockchain system,” Modern Physics Letters B, vol. 35, no. 20, pp. 2150343, 2021. [Google Scholar]

17. A. A. Abd El-Latif, B. Abd-El-Atty, I. Mehmood, K. Muhammad, J. Peng et al., “Quantum-inspired blockchain-based cybersecurity: Securing smart edge utilities in IoT-based smart cities,” Information Processing & Management, vol. 58, no. 4, pp. 102549, 2021. [Google Scholar]

18. D. Li, J. Zhang, F. Z. Guo, W. Huang, Q. Y. Wen et al., “Discrete-time interacting quantum walks and quantum hash schemes,” Quantum Information Processing, vol. 12, pp. 1501–1513, 2013. [Google Scholar]

19. Y. G. Yang, P. Xu, R. Yang, Y. H. Zhou, W. M. Shi et al., “Quantum hash function and its application to privacy amplification in quantum key distribution, pseudo-random number generation and image encryption,” Scientific Reports, vol. 6, no. 1, pp. 1–14, 2016. [Google Scholar]

20. Q. Zhou and S. F. Lu, “Hash function based on controlled alternate quantum walks with memory,” IEEE Transactions on Quantum Engineering, vol. 3, no. 1, pp. 1–10, 2022. [Google Scholar]

21. X. J. Xin, Z. Wang, Q. L. Yang and F. G. Li, “Identity-based quantum designated verifier signature,” International Journal of Theoretical Physics, vol. 59, pp. 918–929, 2020. [Google Scholar]

22. X. J. Xin, L. Ding, C. Y. Li, Y. X. Sang, Q. L. Yang et al., “Quantum public-key designated verifier signature,” Quantum Information Processing, vol. 21, no. 33, pp. 1–16, 2022. [Google Scholar]

23. Z. Wang, J. Li, X. B. Chen and C. Li, “A secure cross-chain transaction model based on quantum multi-signature,” Quantum Information Processing, vol. 21, no. 279, pp. 1–24, 2022. [Google Scholar]

24. X. Xin, L. Ding, Q. Yang, C. Li, T. Zhang et al., “Efficient chain-encryption-based quantum signature scheme with semi-trusted arbitrator,” Quantum Information Processing, vol. 21, no. 246, pp. 1–15, 2022. [Google Scholar]

25. S. Joshi, “Feasibility of proof of authority as a consensus protocol model,” arXiv, 2021. [Online]. Available: https://arxiv.org/pdf/2109.02480.pdf [Google Scholar]

26. L. K. Grover, “A fast quantum mechanical algorithm for database search,” in Proc. of the Twenty-Eighth Annual ACM Symp. on Theory of Computing, Philadelphia PA, USA, pp. 212–219, 1996. [Google Scholar]

27. P. W. Shor, “Algorithms for quantum computation: Discrete logarithms and factoring,” in Proc. 35th Annual Symp. on Foundations of Computer Science, Santa Fe, NM, USA, pp. 124–134, 1994. [Google Scholar]

28. C. Zalka, “Grover’s quantum searching algorithm is optimal,” Physical Review A, vol. 60, no. 4, pp. 2746–2751, 1999. [Google Scholar]

29. J. Zhang, Y. Yuan, X. Wang and F. Y. Wang, “Quantum blockchain: Can blockchain integrated with quantum information technology resist quantum supremacy?” Chinese Journal of Intelligent Science and Technology, vol. 1, no. 4, pp. 409–414, 2019. [Google Scholar]

30. A. M. Khalifa, A. M. Bahaa-Eldin and M. A. Sobh, “Quantum attacks and defenses for proof-of-stake,” in 14th Int. Conf. on Computer Engineering and Systems (ICCES), Cairo, Egypt, 2019, pp. 112–117, 2019. [Google Scholar]

31. M. Roetteler, M. Naehrig, K. M. Svore and K. Lauter, “Quantum resource estimates for computing elliptic curve discrete logarithms,” in Advances in Cryptology–ASIACRYPT 2017: 23rd Int. Conf. on the Theory and Applications of Cryptology and Information Security, Hong Kong, China, pp. 241–270, 2017. [Google Scholar]

32. F. M. Ablayev, D. A. Bulychkov, D. A. Sapaev, A. V. Vasiliev and M. T. Ziatdinov, “Quantum-assisted blockchain,” Lobachevskii Journal of Mathematics, vol. 39, no. 7, pp. 957–960, 2018. [Google Scholar]

33. F. G. Deng and G. L. Long, “Secure direct communication with a quantum one-time pad,” Physical Review A, vol. 69, no. 5, pp. 052319, 2004. [Google Scholar]

34. W. K. Wootters and W. H. Zurek, “A single quantum cannot be cloned,” Nature, vol. 299, no. 5886, pp. 802–803, 1982. [Google Scholar]

35. E. Arthurs and M. S. Goodman, “Quantum correlations: A generalized heisenberg uncertainty relation,” Physical Review Letters, vol. 60, no. 24, pp. 2447–2449, 1988. [Google Scholar] [PubMed]

Appendix