 Open Access
Open Access
ARTICLE
Topology Optimization of Strength-Safe Continuum Structures Considering Random Damage
Beijing University of Technology, Beijing, 10005, China
* Corresponding Author: Jiazheng Du. Email:
(This article belongs to the Special Issue: New Trends in Structural Optimization)
Computer Modeling in Engineering & Sciences 2023, 136(2), 1091-1120. https://doi.org/10.32604/cmes.2023.025585
Received 25 July 2022; Accepted 20 October 2022; Issue published 06 February 2023
Abstract
Spacecraft in the aerospace field and military equipment in the military field are at risk of being impacted by external objects, which can cause local damage to the structure. The randomness of local damage is a new challenge for structural design, and it is essential to take random damage into account in the conceptual design phase for the purpose of improving structure’s resistance to external shocks. In this article, a random damaged structure is assumed to have damages of the same size and shape at random locations, and the random damage is considered as multiple damage conditions of the structure. In order to improve the randomness and comprehensiveness of the multiple damage conditions, the stacking strategy is used to generate the distribution of the damage area. Following this strategy, the topology optimization design of the random damaged structure, which is to minimize the weight of the structure with a constraint on the stress of the structure under multiple damage conditions, is formulated based on the independent continuous mapping (ICM) method. The dual sequence quadratic programming (DSQP) algorithm combined with the stress globalization method is adopted to solve the optimization problem. The numerical examples demonstrate the effectiveness and applicability of the proposed method in the topology optimization of strength-safe continuum structures.Graphic Abstract

Keywords
With the increasing maturity of topology optimization method research and the continuous improvement of engineering structure safety performance requirements [1–3], topology optimization methods considering damage-safety design principle are being used to guide the design of engineering structures. In recent years, with the increasing amount of space junk, the probability of random impacts on spacecraft is increasing. In the military field, the probability of random damage to military equipment such as fighters, missiles and tanks is also increasing. In the aerospace and military fields, the local damage caused by external shocks can result in serious consequences for the structures such as overall failure. To prevent such dangerous accidents, structural designers must take random damage into account in the conceptual design phase in order to improve the resistance of structures to external impacts. Since the shape, size and position of the local damage on the structure are uncertain, how to simulate the local random damage of the continuum structure becomes the key to the research problem in the stage of optimization model establishment.
In 2014, Jansen et al. [4] first proposed a simplified local damage model, which introduced the damage-safety concept into the topology optimization of the continuum structure. They simulated many local damage conditions by covering the base structure with damaged areas of predetermined shape, size and material, but they arranged the damage center on the center of each element, making the number of damage conditions equal to the number of elements, resulting in a very large computational effort. However, Jansen’s pioneering work laid a key foundation for topology optimization of continuum structures considering damage-safety. In 2016, Zhou et al. [5] put forward a hierarchical laying strategy for damaged areas based on Jansen’s research ideas, which greatly reduced the amount of computation. Jansen and Zhou’s work broke through the research bottleneck in this field. After that, many scholars have carried out research on the basis of the above research, and have achieved good research results. Peng et al. [6–8] proposed a damage areas rationality criterion and explored the influence of the shape and size of local damaged areas and the preset distribution of damaged areas on the optimal topology configuration, they used the hierarchical laying strategy to simulate the damage conditions and applied the independent continuous mapping (ICM) method to solve the damage-safety optimization model of the continuum structure with minimal volume under displacement constraints. Utilizing the ICM method, Long et al. [9] proposed a robust design topology optimization method considering local damages and load uncertainty and investigated the effect of changes in input load magnitude, direction and damage location on the optimized design. Du et al. [10–12] simulated the damage conditions based on the level-one laying strategy and solved the damage-safety optimization model of continuum structures with weight minimization under different constraints by using ICM method. The ideal damage-safety structures were obtained, and the damage verification was performed on preset damage regions of the optimal structure, but they did not perform damage verification at random locations. Wang et al. [13] introduced von Mises stress into damage-safety topology optimization, and adaptively selected failure scenarios through the proposed stress criterion. This method effectively controlled the number of failure scenarios in the optimization process, and greatly improved the optimization efficiency. Hederberg et al. [14] used moving morphable components (MMCs) to simulate structural damage and combined with density-based topology optimization method to obtain damage-safety design. Kranz et al. [15] used the maximum length scale method to conduct a damage-safety topology optimization study with the goal of stress minimization. During the optimization process, they evaluated the failure scenarios according to the actual load path, and not only designed the damage-safety design with good performance, but also reduced the calculated cost. Wang et al. [16] introduced the minimization of von Mises stress of damaged structure into the optimization objective, and proposed two topological optimization objectives: the worst-case formulation and the mean-performance formulation, which effectively alleviated the stress concentration problem caused by local failure. Because of the different probabilities of different damages, Cid et al. [17] developed a new optimization strategy to avoid unnecessary structural performance loss caused by low-probability damage. They analyzed different preset damage conditions of the structure, introduced the probability of each damage in the optimization model, and defined the multi-model probabilistic optimization problem. This method is not as conservative as the traditional damage-safety structure optimization method, and the evaluation of damage is closer to the real working environment. Martínez-Frutos et al. [18] calculated the probability of damage occurrence and damage size at the specified position, and explored the optimization of structural boundary, which provided a method for designers to balance structural performance, cost and robustness in the optimization process. In the same year, Martínez-Frutos et al. [19] firstly used the level-set method in the topology optimization design of damage-safety structures. In order to reduce the risk of structural failure, they quantified the unknown risk, and aimed at minimizing the proposed risk aversion formula, and obtained the structural design that was insensitive to random damage.
For the structural topology optimization design in aerospace and military fields, the mechanical structure should not only meet the overall objective condition such as lightweight, but also follow strict mechanical performance constraints. Since permitted stress is a measure of structural strength and a design basis for structural design, solving the problem of optimal design of structures under stress limits is of tremendous scientific relevance. Duysinx et al. [20] adopted the local stress constraint method to optimize the topology of the continuum structure, but this method had huge amount of calculation and low efficiency. Sui et al. [21,22] presented the stress globalization approach as a solution to the enormous computational effort difficulty caused by the local stress constraint. Since then, using the stress globalization approach, Ye et al. [23] explored the topology optimization problem of three-dimensional continuous systems and obtained positive findings. Xuan et al. [24] defined the concept of structural distortion ratio energy constraint based on the stress globalization method and solved the topology optimization of continua structures with minimum weight under stress constraint; Yi et al. [25] extended the SIMP method by referring to the ICM method and the stress globalization method, they established the topology optimization model of plate-shell structure under multiple working conditions with the constraint of structural distortion energy, and obtained good results. The research results of the above scholars have well verified the effectiveness of the stress globalization method. París et al. [26] solved and compared the topology optimization results of local stress constraint method and the global stress constraint method, they concluded that the local stress constraint method was more secure and conservative, but the calculation was huge, so the method required a lot of calculation time, and the global stress constraint method can be used when calculating the structure with more elements and finer meshes, but this method cannot strictly control the local element stress constraint. Chu et al. [27] used the stress penalty approach to address the local problem of stress constraint and established a rational optimal topological structure. Wang et al. [28] proposed an improved bi-directional evolutionary structural optimization method, which effectively solved the topology optimization problem under volume and stress constraints. Long et al. [29] carried out structural topology optimization design based on global dynamic stress constraints, using P-norm to reduce the high computational cost caused by local stress constraints, and they analyzed the necessity of considering stress constraints in structural design. Lüdeker et al. [30] carried out damage-safety optimization of the beam structure under stress constraints, and used P-norm to deal with stress constraints. Meng et al. [31] proposed two stability control schemes by using the stability transformation method, which overcame the difficulties caused by highly nonlinear local stress constraints. Ye et al. [32] proposed a fatigue topology optimization method based on the ICM method and the fatigue analysis method. They used the distortion energy theory to explicitly transform the fatigue life constraints into distortion energy constraints, which provides a new way for fatigue optimization problems. Li et al. [33] proposed a fatigue-constrained topology optimization method based on bidirectional evolutionary structural optimization for high-cycle fatigue caused by non-periodic loads, which solved the problem of topology lightweight with high-cycle fatigue life as the constraint.
With the gradual deepening of research in the field of topology optimization considering damage-safety continuum structures, although many important achievements have been achieved, meeting the design requirements of resistance to random damage and pursuing the resistance of topology to global risks have become the new challenge for structural design. Considering the randomness of the damage location, this paper mainly focuses on improving the damage-safety optimization scheme by adjusting the preset damage area distribution of the continuum structure, and investigates a strength-safe continuum structures topology optimization method considering random damage. The topology optimization model is developed using the ICM technique, with the minimumweight as the objective and the stress as the constraint. The stacking strategy is used to improve the randomness and comprehensiveness of damage conditions, and the stress constraint is expressed by the stress globalization method. The dual sequence quadratic programming (DSQP) algorithm is used to solve the problem. Several examples verify the effectiveness and applicability of the proposed method.
2 Topology Optimization Model Considering Random Damage Based on ICM Method
Although the development of continuum topology optimization research has achieved a lot of remarkable results, most methods still attach high-level topological variables to low-level material, section or shape variables, so they cannot show the characteristics of topology optimization. As a result, the solution efficiency is not high, and sometimes even ill-conditioned problems occur. ICM method is a topology optimization method that characterizes the ‘solid’ and ‘void’ of the element based on the topological variable, independent of the element’s specific physical properties. If the element exists, the element topological variable is 1, and if the element is deleted, the element topological variable is 0. By introducing the filtering function, the discrete 0 and 1 topological variable are transformed into the topological variable in the [0, 1] continuous interval in the optimization process. After solving, the optimal design variable is mapped back to 0 and 1 discrete variable. This method not only restores the independent optimization level of topological variables, but also greatly improves the solving efficiency.
The filter function can identify and filter the performance parameters of each element, the weight and stiffness matrix of the element can be expressed by the corresponding filter function as follows:
where
where the calculation results are generally better when taking
2.2 Expression of Random Damage
This paper mainly studies the second failure reason of structure proposed by Feng [35], that is, the local damage caused by accidental events such as corrosion, technical defects or accidental collision. Since the main factor affecting the optimal topology is the preset distribution of the damaged areas [7], for the convenience of research, this paper studies the square damage area with preset size, and overlaps the damaged areas in the design domain with appropriate interval. In the calculation, elasticity modulus of the damaged area is set to 0.001, which is equivalent to the material ‘disappearance’ when the area is damaged, so each local ‘disappearance’ structure forms a damage condition. Obviously, the number of damage conditions is the same as the number of preset damaged areas, and the random damage event is transformed into the multi-condition problem of the optimization model. The schematic diagram of the local damage of the structure is shown in Fig. 1, and the local damage to a structure can be described using the ICM approach as follows:
where D denotes the design area,

Figure 1: The expression of structural damage
In this paper, the level-one distribution strategy [5] is called the seamless paving distribution strategy, which is to pave the damaged areas of the predetermined shape, size and material seamlessly in the design domain. This paper draws on and develops this idea, and proposes the stacking distribution strategy to simulate random damage conditions, reducing the distance between the centroids of adjacent damaged areas on the basis of the seamless paving distribution strategy, and the damaged areas are still covered in the whole design domain. Therefore, the number of damaged areas increases and the overlap between adjacent damaged areas will occur. The distance between adjacent damaged areas is called the overlay span, which is denoted as S. The conceptual diagram of the stacking distribution strategy is shown in Fig. 2.
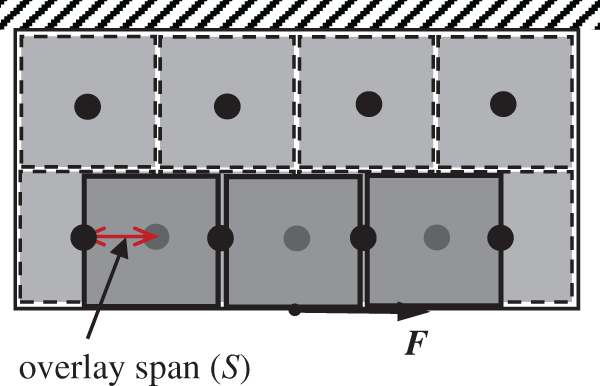
Figure 2: The conceptual diagram of the stacking distribution strategy
2.3 Stress Globalization Method
The following is the topology optimization model based on the ICM technique, using random damage, stress, and minimum weight as constraints and objectives. And it is worth mentioning that the globalization of stress constraints is not related to random damage. The formula derivation in the following chapter is the explicit treatment of stress constraints. Random damage is processed by damage conditions in the software.
where
To improve the efficiency of the solution, the local stress constraint is transformed into a global strain energy constraint using the stress globalization approach. According to the fourth theory of strength, the distortion energy is the primary state variable of material yielding and has the following connection with the permissible stress:
where
where
where
where
2.4 Computation of Permissible Strain Energy
By solving the topology optimization model of minimizing the strain energy with the weight constraint, the permissible strain energy of the structure under a single damage condition may be determined. Solving the permissible strain energy of each damage situation can be computationally prohibitive when the number of damage circumstances is huge. To improve the efficiency of the solution, the permissible structural strain energy of each damage state is determined in two steps: (i) the permissible strain energy of the structure under a particular damage condition is determined initially, and (ii) the allowed structural strain energy of different damage circumstances is evaluated approximately using a numerical fitting method.
Since
where
The damage condition with the maximum structural strain energy is selected, and the strain energy is denoted as
where
where
The ICM method is used to optimize the base structure in Example 1 without considering the damage-safety. The minimum strain energy is pursued with the weight constraint of 30% for the structure, and the minimum strain energy is 2595.7 mJ. The optimal topology is shown in Fig. 3a. The topology optimization of weight minimization is carried out with the strain energy value of 2595.7 mJ as the constraint. The optimal topology is shown in Fig. 3b, and the weight ratio of the structure is 30%. It can be found that the topological results obtained by the two methods are the same, which verifies the validity of the method for calculating the permissible strain energy in this paper.

Figure 3: Topology optimization of the base structure in Example 1 without considering damage-safety
2.5 Establishment and Solution of Strength-Safe Topology Optimization Model
For the topology optimization problem of continuous structures with different damage conditions, with stress as the constraint and lowest weight as the objective, the following topology optimization model is formulated utilizing the stress globalization approach and the filter function:
where
Since the strain energy and the topological variables are negatively correlated, in order to obtain a high-precision linear explicit expression, the inverse variable
where
By introducing the weight coefficient
Following a second-order approximation of the objective function and the omission of the constant term, the following model is obtained:
The coefficients in the model (17) objective function can be written as:
Since the dual problem is simpler than the original problem, the optimization model can be simplified. If the two models are equivalent, the dual problem can be solved instead of the primal problem. Therefore, the dual sequence quadratic programming is utilized to solve the model (17) in order to improve the solution’s efficiency. The dual model looks like this:
where
where
where
Taking the two-dimensional plane stress problem as an example, the topology optimization of continuum structure considering random damage is carried out based on ICM method. In the example, two distribution strategies of paving and stacking are used to simulate random damage conditions, and the optimization results of the two strategies are compared and analyzed. Unless otherwise stated, the elasticity modulus, Poisson’s ratio and physical density of the material is 68.89 GPa, 0.3 and 1 kg/cm3, respectively. It should be pointed out that the global stress constraint is to control the load transfer path, the overall layout of the structure and the thickness of the components in general, although the strain energy of the whole structure can be constrained, the local stress constraint may not be strictly observed, which is manifested in the fact that the stress of a small part of the element will exceed the permissible stress value due to stress concentration and other reasons, and the problem can be solved by low-level optimization in the later stage.
Example 1: As plotted in Fig. 4, the size of the base structure is 100 mm × 200 mm × 6 mm. The concentrated load F = 15.6 kN acts on the midpoint of the right boundary, and the left boundary is the fixed constraint. The permissible stress is 173 MPa. The base structure is meshed into 50 × 100 rectangular elements, which is shown in Fig. 5. In reference [10], based on the same base structure, the seamless paving distribution strategy is used to simulate the damage conditions, where the square damages with side length of d = 50 mm are seamlessly paved in the base structure, and a total of eight preset damage conditions are considered, which is shown in Fig. 6. The topology result obtained by the seamless paving strategy is shown in Fig. 7, and the structure weight after inversion is 54.57 kg.

Figure 4: Basic structure for Example 1

Figure 5: Finite element model for Example 1 (‘123456’ indicates that the left elements are constrained to 6 degrees of freedom)

Figure 6: Seamless paving strategy in [10]

Figure 7: Topology result for in [10]
In reference [10], the eight preset damage areas of the optimization result were verified by damages with the same size and shape respectively, and it was concluded that the structure could resist the damage in the preset areas. However, they did not conduct damage tests at random locations of the structure, so this paper conducts damage tests on their topology result with damages of the same size and shape but random locations. We exemplified four representative random damage conditions that do not meet the strength safety, and the stress distribution results are shown in Fig. 8. It can be observed that when the damage occurs at the important position affecting the force transmission path, the stress of some members far exceeds the permissible stress (at the red circle labeling position), and the failure of the members will lead to the collapse of the whole structure. Therefore, in some structural designs with high safety requirements, the seamless paving distribution strategy cannot meet the requirement of the structure to withstand random damage. Damage occurring outside the preset position can easily lead to the overall collapse of the rod failure, resulting in huge losses.
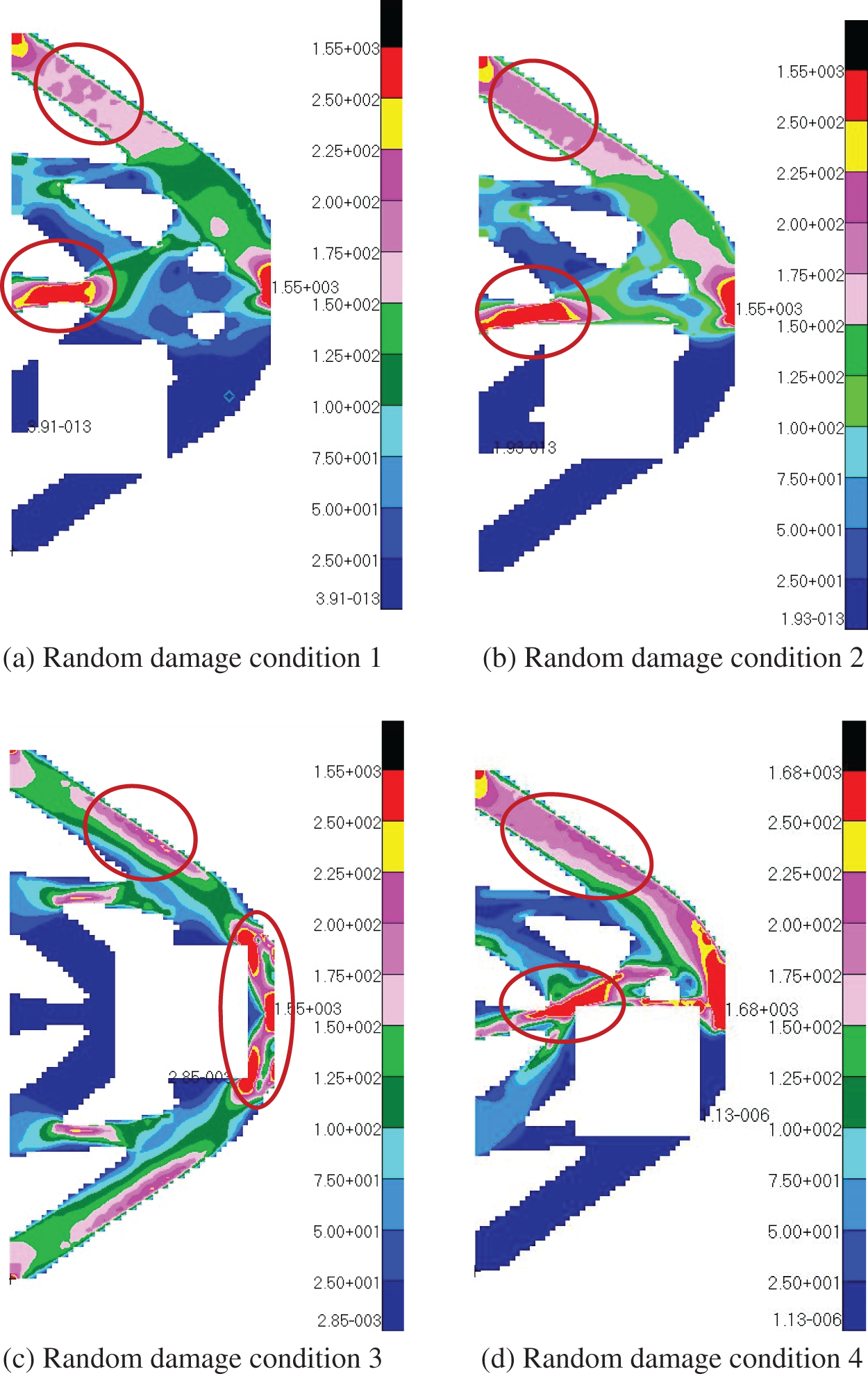
Figure 8: The stress diagrams of four random damage conditions under seamless paving strategy
In order to design a safer and more reliable structure, this paper adopts the damage areas stacking distribution strategy to optimize the topology of the base structure in Fig. 4, and the preset damage areas are laid over the entire design domain in an overlapping manner, with the overlay spanS = 15 mm. As shown in Fig. 9, there are 33 preset damage conditions in total. Due to the overlapping layout of the damaged areas, the graphic description is too complicated. Therefore, the centroid (dot) of the damage area is used to represent the location of each damage area, and the red area is one of the damage areas. In order to make the damage area not affect the force transmission effect of the load, the two areas close to the load and the fixed end are set as non-design areas and are not damaged. Selecting the inversion threshold of 0.2 and the convergence accuracy of 0.001, the topology result considering random damage conditions is shown in Fig. 10, and the structure weight after inversion is 64.8 kg. Fig. 11 shows the iterative curve of structural weight, and Fig. 12 shows the iteration curve of structural strain energy.

Figure 9: The stacking strategy (S = 15 mm)

Figure 10: Topology result for the stacking strategy

Figure 11: The iterative curve of structural weight

Figure 12: The iterative curve of structural strain energy
Compared with the optimization results of the seamless paving strategy, it can be found that the topology structure optimized by the stacking strategy is heavier and more redundant. The structural asymmetry is caused by the increase in the number of damage conditions and the asymmetry of the base structure model. When local damage occurs at different positions, the impact on the structure is different. When the structure is relatively sensitive to the damage condition, the condition is called the hazardous condition, and the condition with less impact on the structure is called the non-hazardous condition. We carried out the damage tests of the optimal structure in the preset damage areas. Due to the large number of damage conditions, only the representative damage test results of hazardous damage conditions are listed, and the stress distribution results in the design area are shown in Fig. 13. It can be seen that except for the very small part of the element stress values caused by stress concentration exceed the permissible stress, most of the elements of the structure meet the stress constraint, and the non-hazardous damage conditions also pass the damage test. And it can be observed that hazardous damage usually occurs in the area near the load, because these positions are most likely to affect the load transfer path. In addition, we also conducted damage tests at random positions and only showed the test results of some random damage conditions. As shown in Fig. 14, it can be observed that most of the element stress values in the design area are lower than the permissible value, indicating that the structure passes the damage tests at random positions. Fig. 15 lists the maximum stress of each damage condition under the stacking strategy and the maximum stress of 1550 MPa under the paving strategy. It is obvious that the stress value of each damage condition under the stacking strategy is greatly reduced compared with that under the paving strategy, and the maximum stress value in each condition is similar, only fluctuating in a small range, indicating that the stacking strategy can better constrain the structural stress, and the stacking strategy is more suitable for the topology optimization design of continua structures considering random damage conditions.

Figure 13: The stress diagrams in the design area of four hazardous preset damage conditions under the stacking strategy

Figure 14: Stress diagrams in the design area of six random damage conditions under the stacking strategy

Figure 15: The maximum stress of each damage condition under the stacking strategy
Example 2: As illustrated in Fig. 16, the base structure is a rectangular plate with the size of120 mm × 40 mm × 1 mm, the left and right ends are both fixed constraints, and a vertical downward force of 500 N acts on the upper boundary of the plate. The permissible stress is 140 MPa. The rectangular plate is meshed into 120 × 40 finite elements, and the finite element model is shown in Fig. 17. Taking the square damage with the size of 20 mm × 20 mm as an example, the topology optimization of the structure is carried out by using the seamless paving distribution strategy and the stacking distribution strategy, respectively. The seamless paving distribution strategy is shown in Fig. 18. The inversion threshold is selected as 0.72 and the convergence accuracy is 0.00025. The topology result obtained by the seamless paving strategy is shown in Fig. 19, and the weight after inversion is 2.61 kg.

Figure 16: Basic structure for Example 2

Figure 17: Finite element model for Example 2 (‘123456’ indicates that the left and right elements are constrained to 6 degrees of freedom)

Figure 18: Seamless paving strategy
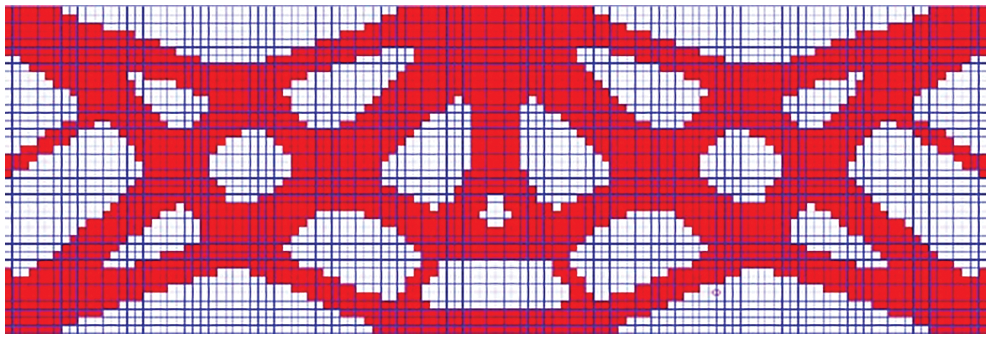
Figure 19: Topology result for seamless paving strategy
Similarly, we found some damage areas that the structure could not bear, as shown in Fig. 20. When the damage occurred at these positions, some of the members of the structure failed, which would lead to the accident that the structure could not bear the normal load and collapsed.

Figure 20: The stress diagrams of two random damage conditions under seamless paving strategy
The stacking distribution strategy is used to optimize the topology of the base structure in Fig. 16. As shown in Fig. 21, the edge areas of the left end, right end and the upper end of the rectangular plate are non-design areas without damage. The same square damage areas of 20 mm × 20 mm are laid in the design area by stacking with the overlay span S = 7.5 mm. The dots in Fig. 21 represent the position of each damage area, and there are a total of 39 preset damage conditions. Selecting the inversion threshold of 0.5 and the convergence accuracy of 0.00025, the topology result is shown in Fig. 22, and the weight after iteration is 3.69 kg. Fig. 23 shows the iterative curve of structural weight, and Fig. 24 shows the iterative curve of structural strain energy.

Figure 21: The stacking strategy (S = 7.5 mm)

Figure 22: Topology results for the stacking strategy

Figure 23: The iterative curve of structural weight

Figure 24: The iterative curve of structural strain energy
Since there are many preset damage conditions and the topology structure is a symmetrical structure, only the damage test results of the hazardous preset damage conditions on the symmetrical side are given. The stress distribution results in the design area are shown in Fig. 25. And the hazardous damage also occurs near the load. The damage test results at random locations are shown in Fig. 26. It can be seen that no matter whether the damage occurs in the preset damage area of the structure or at any random position, most of the element stress values in the structural design area are within the stress constraint range, which means that the structure can work normally in the random damage environment. Fig. 27 lists the maximum stress value of each damage condition under the stacking strategy as much as possible. It can be seen that the maximum stress value under the random damage conditions is similar to the maximum stress value under the preset damage conditions, indicating that the structure is not sensitive to the damage at any position. Compared with the maximum stress values of 547 and 838 MPa in the random damage conditions under the seamless paving strategy in Fig. 20, the maximum stress values by the stacking strategy are lower. In other words, the stacking strategy improves the ability of the structure to resist external shocks. The effectiveness and applicability of the stacking strategy are well verified.

Figure 25: The stress diagrams in the design area of four hazardous preset damage conditions under the stacking strategy
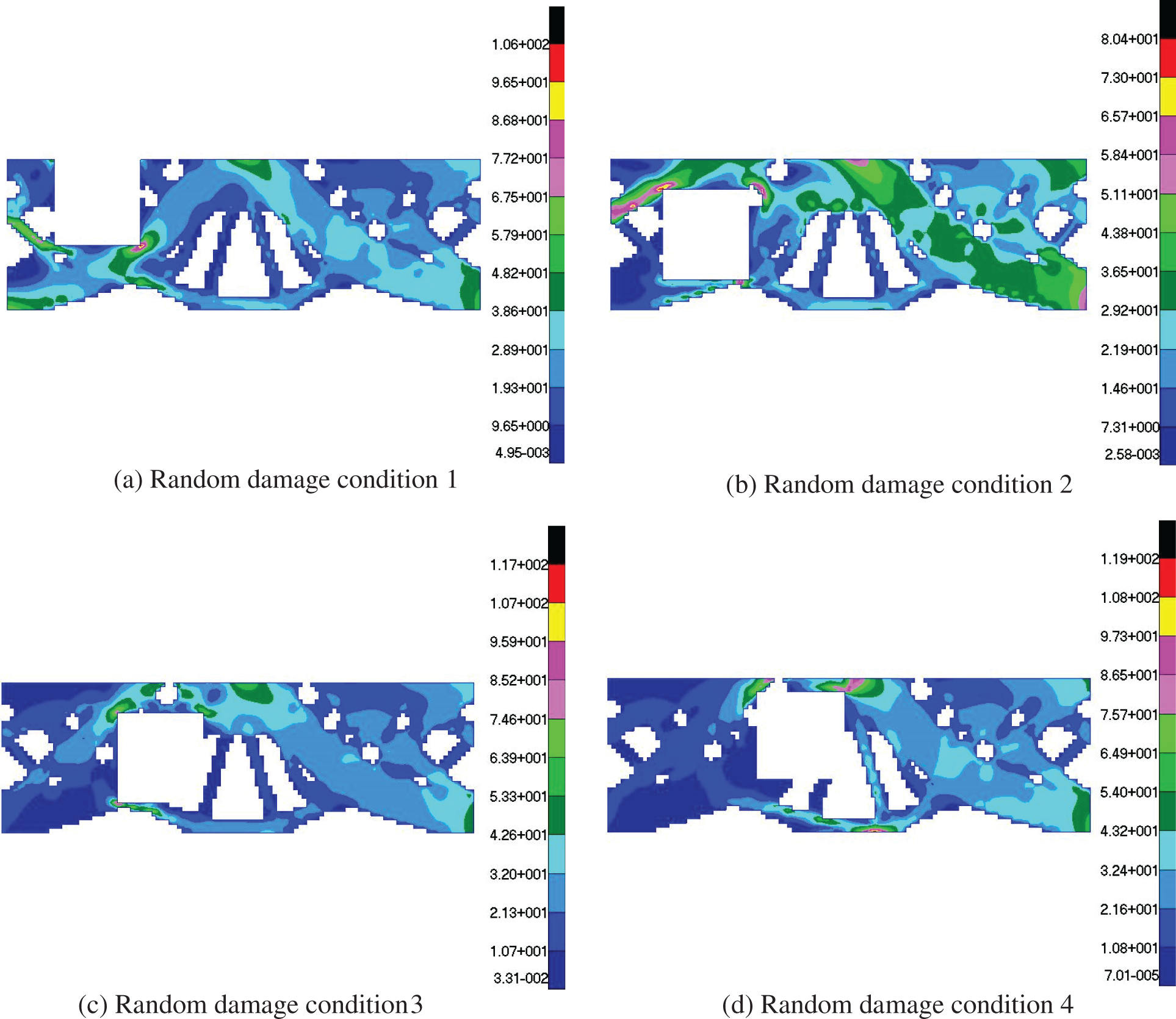
Figure 26: Stress diagrams in the design area of four random damage conditions under the stacking strategy

Figure 27: The maximum stress of each damage condition under the stacking strategy
Example 3: As shown in Fig. 28, the basic structure is a L-shaped beam. The thickness is 2 mm, the upper end of the beam is fixed, and a vertical downward force of 10 N acts on the upper part of the right end. The permissible stress is 140 MPa. The basic structure is meshed into 3420 rectangular elements. The preset distribution of damage areas adopts the stacking strategy. As shown in Fig. 29, the upper end area and right edge area of the L-shaped beam are non-design area without damage. The square damages with size of 12 mm × 12 mm are overlapped and laid in the design domain in turn, and the overlap span is S = 6 mm, a total of 297 damage conditions are considered. Selecting the inversion threshold of 0.46 and the convergence accuracy of 0.001, the topology result is shown in Fig. 30, and the structure weight after iteration is 15.98 kg. The iterative curve of structural weight is shown in Fig. 32, and the iterative curve of structural strain energy is shown in Fig. 33.

Figure 28: Basic structure for Example 3
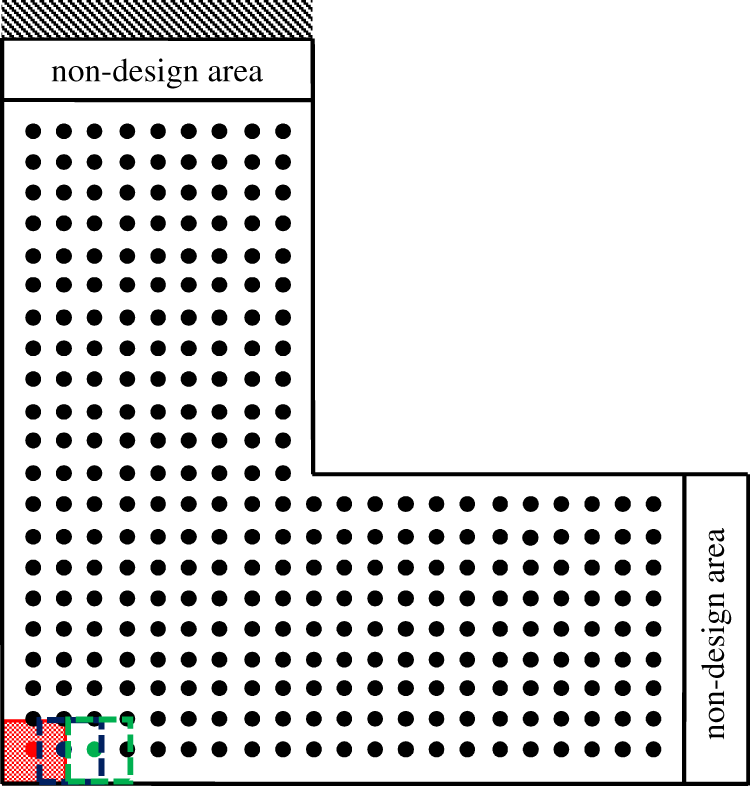
Figure 29: The stacking strategy (S = 6 mm)

Figure 30: Topology result for the stacking strategy

Figure 31: Seamless paving strategy

Figure 32: The iterative curve of structural weight

Figure 33: The iterative curve of structural strain energy
It can be seen from the weight iteration curve and strain energy iteration curve that the optimal solution converges stably after 40 iterations. Due to the numerous damage conditions, the damage test results of all the damage conditions of the structure are not listed one by one, and only the representative damage test results of hazardous damage conditions are listed, which are shown in Fig. 34. Hazardous damage occurs near the corner of the L-shaped beam, where the stress concentration is severe. The damage test results of some random positions are shown in Fig. 35. It can be seen that no matter whether the damage occurs in the preset damage area of the structure or in any random position, the element stress values are within the constraint range, so the structure can resist random damage accidents. Compared with the 85 preset damage conditions under the seamless paving strategy in Fig. 31, the stacking strategy considers more damage conditions and improves the randomness and comprehensiveness of damage conditions. It must be said that the calculation of the optimization process also increases with the increase of the number of damaged conditions. However, in a random damage environment, it is necessary to be as comprehensive as possible, and the stacking distribution strategy is undoubtedly a more reasonable choice.

Figure 34: The stress diagrams in the design area of four hazardous preset damage conditions under the stacking strategy

Figure 35: Stress diagrams in the design area of four random damage conditions under the stacking strategy
Most topology optimization studies on continuum structures that consider damage-safety employ the seamless paving distribution technique for addressing the locations of the damage zones. However, this paper finds that the seamless paving distribution strategy has potential drawbacks when considering the randomness of the damage locations. For examples, the safety of the optimization results is difficult to guarantee, and the structure cannot withstand random damage. The random damage that occurs outside the zone of interest can easily lead to the overall collapse of the structure due to the rod failure. In some fields such as aerospace and military where the safety requirements are high, this design defect in a structure could result in deadly injuries or fatalities.
In order to design topology structures that can withstand random damage, this paper proposes the stacking distribution strategy, which is more secure and conservative than the aforementioned strategy. It can improve the randomness and comprehensiveness of damage conditions, and help the optimized structures avoid the risk of overall collapse resulting from random damage. By comparison, the stacking strategy has more advantages in optimizing the overall layout of the structure, controlling the force transmission path of the load and constraining the stress of the structure. Although this strategy is at the cost of sacrificing the weight of the structure, it ensures that the structure can resist random damage and it thus improves the ability of the structure to resist unknown risks. However, this method has the disadvantage of high computational cost, which will be further studied regarding the optimization efficiency in the future research. The research results of this paper will offer certain benefits to engineering applications. For random damage of a structure in practical engineering applications, the stacking distribution strategy is a good choice for structural designers.
Funding Statement: This work showed in this paper has been supported by the National Natural Science Foundation of China (Grant 11872080).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Zhang, X., Boscolo, M., Figueroa-Gordon, D., Allegri, G., Irving, P. E. (2009). Fail-safe design of integral metallic aircraft structures reinforced by bonded crack retarders. Engineering Fracture Mechanics, 76(1), 114–133. DOI 10.1016/j.engfracmech.2008.02.003. [Google Scholar] [CrossRef]
2. Sheu, J. B., Liu, T., Lee, J. J. (2012). On the fail-safe design of tendon-driven manipulators with redundant tendons. Journal of Mechanical Science and Technology, 26(6), 1911–1920. DOI 10.1007/s12206-012-0409-4. [Google Scholar] [CrossRef]
3. Zhang, L. X., Long, X. H., Fan, J., Chen, B. L. (2017). Seismic performance analysis of isolated continuous girder bridge considering pounding. Engineering Mechanics, 34(S1), 99–104. DOI 10.6052/j.issn.1000-4750.2016.03.S013. [Google Scholar] [CrossRef]
4. Jansen, M., Lombaert, G., Schevenels, M., Sigmund, O. (2014). Topology optimization of fail-safe structures using a simplified local damage model. Structural and Multidisciplinary Optimization, 49(4), 657–666. DOI 10.1007/s00158-013-1001-y. [Google Scholar] [CrossRef]
5. Zhou, M., Fleury, R. (2016). Fail-safe topology optimization. Structural and Multidisciplinary Optimization, 54(5), 1225–1243. DOI 10.1007/s00158-016-1507-1. [Google Scholar] [CrossRef]
6. Peng, X. R., Sui, Y. K. (2018). Rational criterion of pre-estimating failure region distribution for fail-safe topology optimization of continuum structures. Chinese Journal of Solid Mechanics, 39(6), 594–605. DOI 10.19636/j.cnki.cjsm42-1250/o3.2018.024. [Google Scholar] [CrossRef]
7. Peng, X. R., Sui, Y. K. (2018). ICM method for fail-safe topology optimization of continuum structures. Chinese Journal of Theoretical and Applied Mechanics, 50(3), 611–621. DOI 10.6052/0459-1879-17-366. [Google Scholar] [CrossRef]
8. Peng, X. R., Sui, Y. K. (2019). Parameter effect analysis of local failure modes for fail-safe topology optimization. Chinese Journal of Computational Mechanics, 36(3), 317–323. DOI 10.7511/jslx20180201001. [Google Scholar] [CrossRef]
9. Long, K., Wang, X., Du, Y. X. (2018). Robust topology optimization formulation including local failure and load uncertainty using sequential quadratic programming. International Journal of Mechanics and Materials in Design, 15(2), 317–332. DOI 10.1007/s10999-018-9411-z. [Google Scholar] [CrossRef]
10. Du, J. Z., Guo, Y. H., Chen, Z. M., Sui, Y. K. (2019). Topology optimization of continuum structures considering damage based on independent continuous mapping method. Acta Mechanica Sinica, 35(2), 433–444. DOI 10.1007/s10409-018-0807-7. [Google Scholar] [CrossRef]
11. Du, J. Z., Meng, F. W., Guo, Y. H., Sui, Y. K. (2020). Fail-safe topology optimization of continuum structures with fundamental frequency constraints based on the ICM method. Acta Mechanica Sinica, 36(5), 1–13. DOI 10.1007/s10409-020-00988-7. [Google Scholar] [CrossRef]
12. Du, J. Z., Zhang, Y., Meng, F. W. (2021). Fail-safe topology optimization of continuum structures with multiple constraints based on ICM method. Computer Modeling in Engineering & Sciences, 129(2), 661–687. DOI 10.32604/cmes.2021.017580. [Google Scholar] [CrossRef]
13. Wang, H. X., Liu, J., Wen, G. L., Xie, Y. M. (2020). The robust fail-safe topological designs based on the von mises stress. Finite Elements in Analysis and Design, 171, 103376. DOI 10.1016/j.finel.2019.103376. [Google Scholar] [CrossRef]
14. Hederberg, H., Thore, C. J. (2021). Topology optimization for fail-safe designs using moving morphable components as a representation of damage. Structural and Multidisciplinary Optimization, 64(4), 2307–2321. DOI 10.1007/s00158-021-02984-2. [Google Scholar] [CrossRef]
15. Kranz, M., Lüdeker, J. K., Kriegesmann, B. (2021). An empirical study on stress-based fail-safe topology optimization and multiple load path design. Structural and Multidisciplinary Optimization, 64(4), 2113–2134. DOI 10.1007/s00158-021-02969-1. [Google Scholar] [CrossRef]
16. Wang, H. X., Liu, J., Wen, G. L. (2022). A study on fail-safe topological design of continuum structures with stress concentration alleviation. Structural and Multidisciplinary Optimization, 65(6), 174. DOI 10.1007/s00158-022-03259-0. [Google Scholar] [CrossRef]
17. Cid, C., Baldomir, A., Hernández, S. (2020). Probability-damage approach for fail-safe design optimization (PDFSO). Structural and Multidisciplinary Optimization, 62(6), 3149–3163. DOI 10.1007/s00158-020-02660-x. [Google Scholar] [CrossRef]
18. Martínez-Frutos, J., Ortigosa, R. (2021). Robust topology optimization of continuum structures under uncertain partial collapses. Computers & Structures, 257, 106677. DOI 10.1016/j.compstruc.2021.106677. [Google Scholar] [CrossRef]
19. Martínez-Frutos, J., Ortigosa, R. (2021). Risk-averse approach for topology optimization of fail-safe structures using the level-set method. Computational Mechanics, 68(5), 1039–1061. DOI 10.1007/s00466-021-02058-6. [Google Scholar] [CrossRef]
20. Duysinx, P., Bendsøe, M. P. (1998). Topology optimization of continuum structures with local stress constraints. International Journal for Numerical Methods in Engineering, 43(8), 1453–1478. DOI 10.1007/s00158-008-0336-2. [Google Scholar] [CrossRef]
21. Sui, Y. K., Peng, X. R., Ye, H. L. (2006). Topology optimization of continuum structure with globalization of stress constraints by ICM method. Engineering Mechanics, 23(7), 1–7. DOI 10.3969/j.issn.1000-4750.2006.07.001. [Google Scholar] [CrossRef]
22. Sui, Y. K., Zhang, X. S., Long, L. C. (2007). ICM method of the topology optimization for continuum structures with stress constraints approached by the integration of strain energies. Chinese Journal of Computational Mechanics, 24(5), 602–608. DOI 10.3969/j.issn.1007-4708.2007.05.011. [Google Scholar] [CrossRef]
23. Ye, H. L., Sui, Y. K. (2006). ICM-based topological optimization of three-dimensional continuum structure. Acta Mechanica Solida Sinica, 27(4), 387–393. DOI 10.19636/j.cnki.cjsm42-1250/o3.2006.04.011. [Google Scholar] [CrossRef]
24. Xuan, D. H., Sui, Y. K., Tie, J., Ye, H. L. (2011). Continuum structural topology optimization with globalized stress constraint treated by structural distortional strain energy density. Engineering Mechanics, 28(10), 1–8. [Google Scholar]
25. Yi, G. L., Sui, Y. K. (2015). Topology optimization for plate and shell structures based on stress constraint globalization. Engineering Mechanics, 32(8), 211–216. DOI 10.6052/j.issn.1000-4750.2014.01.0015. [Google Scholar] [CrossRef]
26. París, J., Navarrina, F., Colominas, I., Casteleiro, M. (2009). Topology optimization of continuum structures with local and global stress constraints. Structural and Multidisciplinary Optimization, 39(4), 419–437. DOI 10.1007/s00158-008-0336-2. [Google Scholar] [CrossRef]
27. Chu, S., Gao, L., Xiao, M., Luo, Z., Li, H. (2017). Stress-based multi-material topology optimization of compliant mechanisms. International Journal for Numerical Methods in Engineering, 113(7), 1021–1044. DOI 10.1002/nme.5697. [Google Scholar] [CrossRef]
28. Wang, X., Liu, H. L., Long, K., Yang, D. X., Hu, P. (2018). Stress-constrained topology optimization based on improved bi-directional evolutionary optimization method. Chinese Journal of Theoretical and Applied Mechanics, 50(2), 385–394. DOI 10.6052/0459-1879-17-286. [Google Scholar] [CrossRef]
29. Long, K., Wang, X., Liu, H. L. (2019). Stress-constrained topology optimization of continuum structures subjected to harmonic force excitation using sequential quadratic programming. Structural and Multidisciplinary Optimization, 59(5), 1747–1759. DOI 10.1007/s00158-018-2159-0. [Google Scholar] [CrossRef]
30. Lüdeker, J. K., Kriegesmann, B. (2019). Fail-safe optimization of beam structures. Journal of Computational Design and Engineering, 6(3), 260–268. DOI 10.1016/j.jcde.2019.01.004. [Google Scholar] [CrossRef]
31. Meng, Q. X., Xu, B., Wang, C., Zhao, L. (2020). Stress constrained thermo-elastic topology optimization based on stabilizing control schemes. Journal of Thermal Stresses, 43(8), 1040–1068. DOI 10.1080/01495739.2020.1766391. [Google Scholar] [CrossRef]
32. Ye, H. L., Li, Z. H., Wei, N., Su, P. F., Sui, Y. K. (2021). Fatigue topology optimization design based on distortion energy theory and independent continuous mapping method. Computer Modeling in Engineering & Sciences, 128(1), 297–314. DOI 10.32604/cmes.2021.016133. [Google Scholar] [CrossRef]
33. Li, Y. X., Zhou, G. Y., Chang, T., Yang, L. M., Wu, F. H. (2022). Topology optimization with aperiodic load fatigue constraints based on bidirectional evolutionary structural optimization. Computer Modeling in Engineering & Sciences, 130(1), 499–511. DOI 10.32604/cmes.2022.017630. [Google Scholar] [CrossRef]
34. Sui, Y. K., Ye, H. L. (2013). Continuum topology optimization methods ICM. In: Fundamentals of the ICM method, pp. 39–47. China: Science Press. [Google Scholar]
35. Feng, Y. S. (1988). The theory of structural redundancy and its effect on structural design. Computers & Structures, 28(1), 15–24. DOI 10.1016/0045-7949(88)90087-9. [Google Scholar] [CrossRef]
36. Sui, Y. K., Ye, H. L. (2013). Continuum topology optimization methods ICM. In: Topology optimization under stress constraints of continuum structures, pp. 74–76. China: Science Press. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools