Open Access

PROCEEDINGS

Boundary Penalty Method based Acoustic–Structural Coupled Topology Optimization

Tao Liu¹, Yang Liu², Jianbin Du^1,*

1 School of Aerospace Engineering, Tsinghua University, Beijing, 100084, China
2 School of Engineering and Materials Science, Queen Mary University of London, London, E1 4NS, UK

* Corresponding Author: Jianbin Du. Email:

The International Conference on Computational & Experimental Engineering and Sciences 2025, 33(4), 1-2. https://doi.org/10.32604/icces.2025.011595

Abstract

Currently, the application of the Boundary Penalty (BP) method in acoustic-structural coupled multiphysics optimization problems remains unexplored. Within the theoretical framework of BP developed previously, we address acoustic-structural coupled topology optimization problems by proposing a BP-based acoustic-structural coupled topology optimization model. A systematic solution strategy is developed to tackle the challenges encountered during model solving.
The proposed model employs a mixed u/p formulation for finite element analysis and the adjoint method for sensitivity analysis to minimize the acoustic pressure within a specified region (Fig.1 A). During optimization iterations, issues such as topological discretization and iteration oscillations arise. Through an in-depth mechanism analysis, it is found that the acoustic-structural coupled topology optimization problem exhibits strong non-convexity. Additionally, the significant difference in bulk modulus between weak materials (e.g., air) and solid materials during material interpolation exacerbates the ill-conditioned nature of the problem, leading to highly unstable computations and a high likelihood of converging to local optima.
Based on the above analysis, improvements are made to the boundary penalty method for acoustic-structural coupled multiphysics optimization problems. A comprehensive optimization strategy is proposed, combining sensitivity filtering, weak material handling, and adaptive iteration control. Through weak material handling, the absolute magnitude of sensitivity extremes is reduced, while sensitivity filtering alleviates the relative differences in sensitivity between neighboring elements at structural boundaries. This approach achieves stable iterations (Fig.1 B), well-defined topological morphologies, and smooth boundaries in the optimized results (Fig.1 C), and extends the applicability of the BP method to complex multiphysics problems. The corresponding sound pressure level distribution is shown in Fig. 1 D.


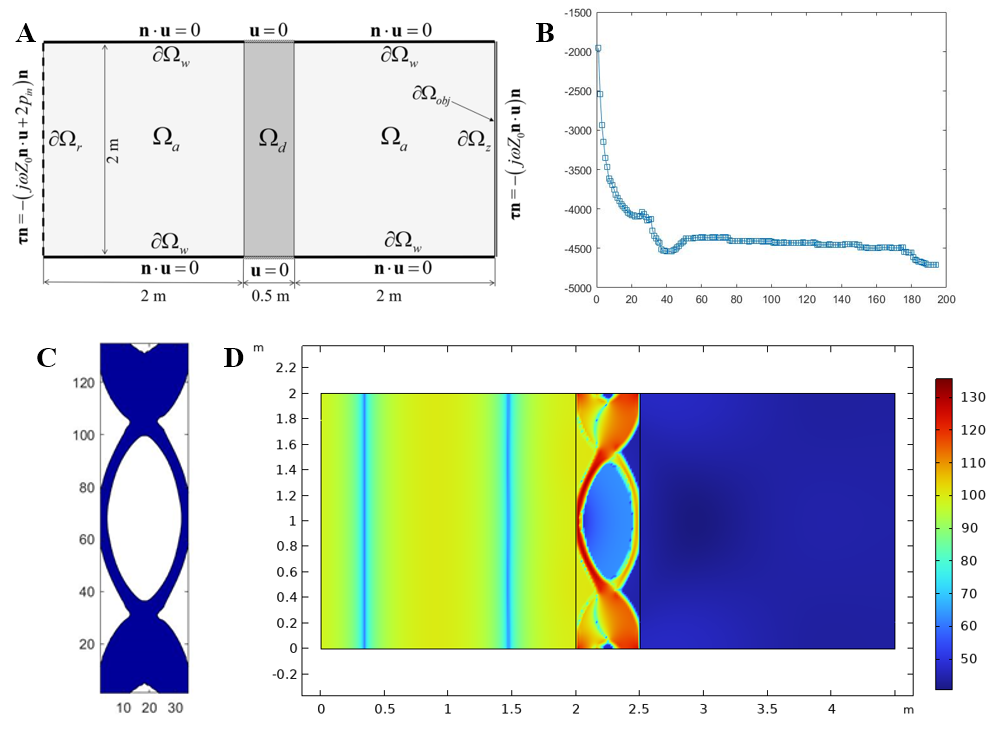
Figure 1: A. Case of acoustic-structural coupled optimization problem: Ωa represents the acoustic domain, Ωd represents the design domain, the left end face is subjected to plane wave radiation, the upper and lower boundaries are acoustic rigid wall conditions, with the optimization objective of minimizing the sound pressure at the right end face. B. Iteration curve of the objective function. C. Optimization result obtained in this work. D. Sound pressure level distribution of the obtained topology result.

---

Keywords

---