New Quantum Color Codes Based on Hyperbolic Geometry

1  Introduction

Channel coding theory is one of the widely used branches of telecommunication, whose purpose is to send information from the sender to the receiver through a physical channel with disturbance. Since the foundation of this theory by Claude Shannon in [1], many efforts have been made to achieve the desired codes and famous codes such as Hamming codes, Golay codes, Reed-Muller codes, convolutional codes, BCH codes, Reed-Solomon codes, turbo codes, and finally Low Density Parity Check (LDPC) codes were proposed. While researching and examining classical codes, researchers also showed interest in quantum codes and in the last few decades, various types of quantum codes have been presented with different methods in the literature. Since the introduction of the first quantum error-correcting code by Shor in [2], Calderbank et al. [3] introduced a systematic way for constructing the QECs from classical error-correcting code. The problem of constructing toric quantum codes has motivated considerable interest in the literature. This problem was generalized within the context of surface codes [4] and color codes [5]. The most popular toric code was proposed for the first time by Kitaev’s [6]. This code defined on a square lattice of size m×m on the torus. Leslie proposed a new type of sparse CSS quantum error correcting codes based on the homology of hypermaps defined on an m×m square lattice [7]. The parameters of hypermap-homology codes are [[(32)m2,2,m]]. These codes are more efficient than Kitaev’s toric codes. This seemed suggests good quantum that is constructed by using hypergraphs. But there are other surface codes with better parameters than the [[2m2,2,m]] toric code. There exist surface codes with parameters [[m2+1,2,m]], called homological quantum codes. These codes were introduced by Bombin et al. [4]. Authors in [8] presented a new class of toric quantum codes with parameters [[m2,2,m]], where m=2(l+1),l≥1. In [9] Families of classes of topological quantum codes from tessellations {4i+2,2i+1}, {4i,4i}, {8i−4,4} and {12i−6,3} on surfaces with genus g≥2 are presented based on hyperbolic tessellations with a specific property. In [10], Yu et al. presented an explicit construction for all the optimal stabilizer codes [[n,k,3]] of distance 3 that saturates the bound n−k≥⌈log2⁡(3n+1)⌉+εn where εn=1 if n=84m−13+{±1,2} or n=4m+2−13−{1,2,3} for some integer m≥1 and εn=0 otherwise. In [11] two new classes of binary quantum codes with minimum distance of at least three presented by self-complementary self-dual orientable embeddings of voltage graphs and Paley graphs. Recently, some research on the construction of quantum color codes has been presented in the literature [12–17]. In these references, various types of quantum color codes have been reported.

The aim of this paper is to present a systematic construction of families of quantum color codes on compact surfaces from hyperbolic tessellations and hyperbolic polygons by pairing the edges. For these quantum codes, the encoding rate is such that kn→1 as n→∞. Moreover, a table of quantum codes which are different parameters in relation to the families previously presented in [9,12–17], among others is presented.

This paper is organized as follows. Section 2 is dedicated to basic concepts on quantum bits and hyperbolic geometry. Section 3 is related to present families of quantum color codes with minimum distance of at least  4. In Section 4, a table of quantum codes comparison is presented. Finally, Section 5 is devoted to conclusion.

2  Reviews on Quantum Bits and Hyperbolic Geometry

In this section, we review some fundamental notions of quantum mechanics and hyperbolic geometry used through the paper. See for detailed descriptions, refer to [18,19].

2.1 Quantum Bits

A quantum bit, qubit for short, is a two-level quantum system. Because there should not be any danger of confusion, we also say that the two-dimensional Hilbert space H2 is a quantum bit. Space H2 is equipped with a fixed basis B={|0⟩,|1⟩}, a so-called computational basis. States |0⟩ and |1⟩ are also called basis states. A general state of a single quantum bit is a vector as:

|ψ⟩=c0|0⟩+c1|1⟩,(2.1)

This vector has a unit length, i.e., |c0|2+|c1|2=1. Numbers c0 and c1 are called amplitudes of |0⟩ and  |1⟩, respectively.

2.2 CSS Codes

The idea of constructing CSS (Calderbank-Shor-Steane) codes from graphs embedded on surfaces has been discussed in a number of papers. See for detailed descriptions e.g., [7,20]. Let X be a compact, connected, oriented surface (i.e., 2-manifold) with genus g. A tiling of X is defined to be a cellular embedding of an undirected (simple) graph G=(V,E) in a surface. This embedding defines a set of faces F, whose each face in this surface, is described by the set of edges on its boundary. This tiling of surface is denoted M=(V,E,F). Dual graph G is the graph G∗=(V∗,E∗) such that:

(i)   One vertex of G∗ inside each face of G,

(ii)   For each edge e of G there is an edge e∗ of G∗ between the two vertices of G∗ corresponding to the two faces of G adjacent to e.

It can easily see that, there is a bijection between the edges of G and the edges of G∗.

The surface code associated with a tiling M=(V,E,F) is the CSS code defined by the matrices HX and HZ such that HX∈M|V|,|E|(Z2) is the vertex-edge incidence matrix of the tiling and HZ∈M|F|,|E|(Z2) is the face-edge incidence matrix of the tiling. Therefore, from (X,G) is constructed a CSS code with parameters [[n,k,d]]. In this code, n is the number of edges of G, k=2g and d is the shortest non-boundary cycle in G or G∗.

2.3 Color Codes

In this section, we recall the quantum color codes introduced by Bombin and Martin-Delgado in [5,14]. A color code is the CSS code defined by the matrices HX=HZ=H∈M|F|,|V|(Z2) such that Hij=1 if the face fi includes the vertex vj. Note that V={vi}i=1|V| and F={fi}i=1|F| are the vertices and the faces of the tiling G respectively. Here, assume that the tiling G=(V,E,F) is trivalent, that is every vertex has third degree and the faces of the G can be 3-colored so that two faces that share a common edge do not wear the same color. In the color codes, unlike in the surface codes the qubits are replaced by vertices instead of the edges and the generators of the stabilizers are the face operators. Given a face f∈F, the face operator Bfσ is defined as the tensor product σi, i∈F with σ=X,Z. Equivalently,

Bfσ=⊗i∈Fσi  σ=X,Z(2.2)

The color code 𝖢 contains the space defined by the operator Bfσ as follows:

𝖢={|ψ⟩:BfX|ψ⟩=|ψ⟩, BfZ|ψ⟩=|ψ⟩}(2.3)

The length of the color code associated with G is  n=|V|, and its dimension is 4−2ℊ. The ℊ denotes the Euler characteristic of the surface. When the tiling is orientable, the dimension of the color code is k=4g, where g is the genus of the surface. The minimum distance of the color code will be the minimum weight of a vector x  in  C∖C⊥. The code Ker H is denoted by  C.

In this paper n is the code length, and dmin is the minimum distance of the code.

2.4 Hyperbolic Geometry

In order to calculate the parameters of quantum color codes, we present some basic concepts of hyperbolic geometry. More information on hyperbolic geometry and shrunk lattices may be found in Refs. [5,9,12,17,19].

A hyperbolic polygon P′ with p′ edges, or a p′-gon, is a convex closed set consisting of p′ hyperbolic geodesic segments. A p′-gon whose edges have the same length and the internal angles are equal, is called a regular p′-gon. A regular tessellation of the Euclidean or hyperbolic plane is a covering of the whole plane by regular polygons, all with the same number of edges, without superposition of such polygons, meeting completely only on edges or vertices. We denote a regular tessellation by {p,q}, where q regular polygons with p edges meet in each vertex. In particular, p=q the tessellation is said to be self-dual.

Every possible tiling {p,q} of the polygon P′ satisfies the following equation:

μ(P′)=nfμ(P)(2.4)

where the hyperbolic tessellations must satisfy the constraint (p−2)(q−2)>4. In (2.4), μ(P′) denotes the area of the polygon P′ associated with the fundamental region of the tessellation {p′,q′}, μ(P) denotes the area of the polygon associated with the fundamental region of the tessellation {p,q}, and nf is a positive integer which denotes the number of faces of the tessellation {p,q}. From the Gauss-Bonnet theorem, the area of a hyperbolic polygon is given by, [9,13],

μ(P′)=4π(g−1)(2.5)

where g is the genus of the surface.

From Eq. (2.5) and the Gauss-Bonnet theorem, Eq. (2.4) may be written as:

4π(g−1)=nf[(p−2)π−2pπq].(2.6)

Hence, the number of faces, nf, associated with the tessellation {p,q} of P′ is given by

nf=4q(g−1)pq−2p−2q(2.7)

For these quantum color codes, the length of the code is n=|V|=nfpq edges, or qubits.

For a fundamental polygon of {4g,4g}, the hyperbolic distance dh between paired sides is calculated as follows, [9],

dh=2a=2arccos⁡h[cos⁡(π/4g)sin⁡(π/4g)],(2.8)

and the edge-length of the tessellation {p,q} is given by, [9],

l(p,q)=arccos⁡h[cos2⁡(π/q)+cos⁡(2π/p)sin2⁡(π/q)],(2.9)

Given a regular polygon of {p,q}, the diameter of its circumscribed circle and an upper bound for an edge of the shrunk lattice are written, respectively as, [12],

D(p,q)=2arccos⁡h[cos⁡(πp)cos⁡(πq)sin⁡(πp)sin⁡(πq)],(2.10)

and

L(p,q)=l(p,q)+D(p,q)(2.11)

Also, a lower bound for the number of the reduced network edges in a non-trivial homology cycle belonging to a shrunk lattice is given as follows, [12],

ne>dhL(p,q),(2.12)

Then, the minimum distance of the code is calculated as follows, [12],

dmin=2⌈dhL(p,q)⌉.(2.13)

In fact, dmin represents the minimum length between paths with non-trivial homology, considering the shrunk lattice.

Using Fig. 1 and by tiling the fundamental polygon P′ of the {8,8} tessellation with the fundamental polygon P of the {8,3} tessellation, the [[16,8,4]] code is obtained. In this tessellation the value of nf is equal to 6.

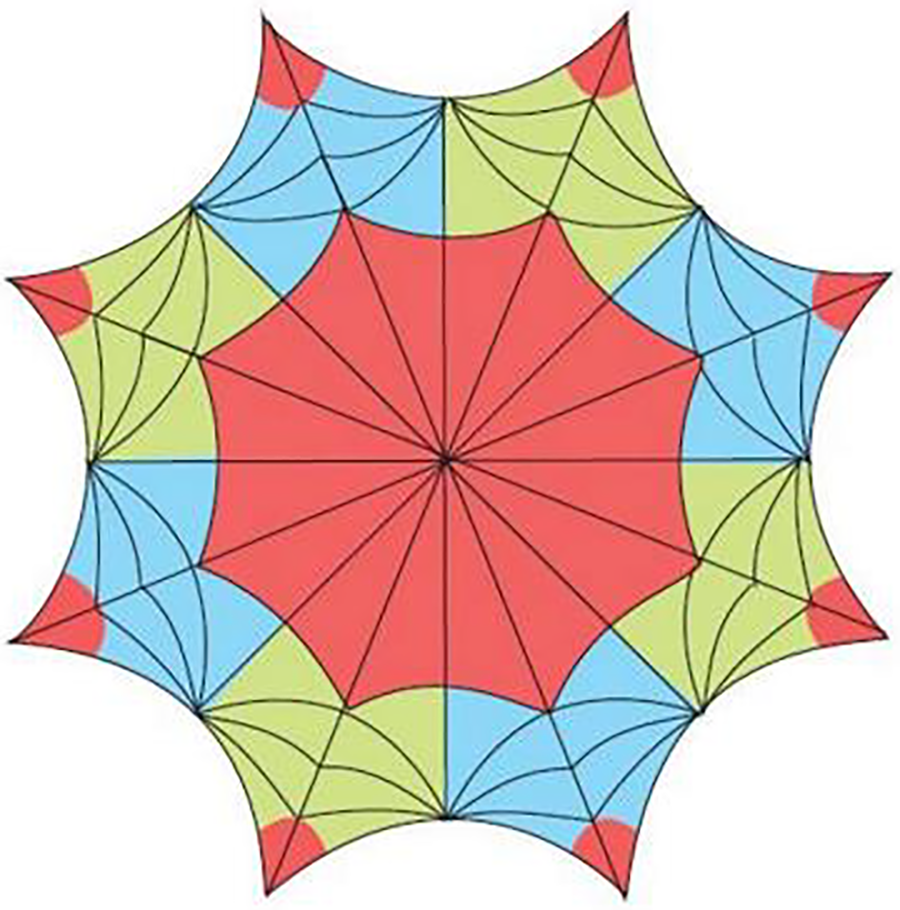
Figure 1: [[16,8,4]] code defined by {8,3} tessellation on 8-gon (g=2) surface

3  New Families of Quantum Color Codes

In this section, we obtain new families of quantum color codes based on the identification of compact surfaces by hyperbolic tessellations.

3.1 Quantum Color Codes from the Tessellation {9+3m,3}

Our goal here is to constructing quantum color codes resulting from the method described in Section 2. Taking q=3 and putting this value in (2.7) for  41−torus, we have:

nf=480p−6,p>6(3.1)

By tiling the fundamental polygon P′ of the {164,164} tessellation with the fundamental polygon P of the {18,3} tessellation, using (2.9) and (2.10), we have

l(18,3)=arccos⁡h[cos2⁡(π/3)+cos⁡(2π/18)sin2⁡(π/3)]≈1.04,

and

D(18,3)=2arccos⁡h[cos⁡(π18)cos⁡(π3)sin⁡(π18)sin⁡(π3)]≈3.71,

Then, by (2.11),

L(18,3)=l(18,3)+D(18,3)≈4.75,

Also, by using (2.13) we have:

dmin=2⌈9.294.75⌉≈4,

Therefore, the quantum color code with parameters [[240,164,4]] is obtained.

Now by tiling the fundamental polygon P′ of the {4g,4g} tessellation with the corresponding edge-pairings, the quantum color codes will be constructed as follows.

According to the color code above, for the minimum distance dmin=4 there were 40 faces of the tessellation. Therefore, by (2.7) with nf=40 and q=3 we have:

nf=12(g−1)p−6,p>6(3.2)

On the other hand, because the length of the code is equal to nf(p/q). Hence, the quantum color codes with parameters [[40m+120,40m+44,4]] for m=3,5,…,230−1 are obtained.

3.2 Quantum Color Codes from the Tessellation {6+34m,3}

In this section, another class of quantum color codes is presented using the approach proposed in Section 2. For this purpose, taking q=3 for  18−torus, we have:

nf=204p−6,p>6(3.3)

By tiling the fundamental polygon P′ of the {72,72} tessellation with the fundamental polygon P of the {40,3} tessellation, using (2.9) and (2.10), we have

l(40,3)=arccos⁡h[cos2⁡(π/3)+cos⁡(2π/40)sin2⁡(π/3)]≈1.19,

and

D(40,3)=2arccos⁡h[cos⁡(π40)cos⁡(π3)sin⁡(π40)sin⁡(π3)]≈5.37,

Then, by (2.11),

L(40,3)=l(40,3)+D(40,3)≈6.56,

Therefore, the minimum distance of the code according to (2.13) will be as follows

dmin=2⌈7.616.65⌉≈4,

Hence, the quantum color code with parameters [[80,72,4]] is obtained.

Now by tiling the fundamental polygon P′ of the {4g,4g} tessellation with the corresponding edge-pairings, for the minimum distance dmin=4 there were 6 faces of the tessellation. By using (2.7) with nf=6 and q=3 we have

nf=12(g−1)p−6,p>6(3.4)

Thus, the quantum color codes with parameters [[68m+12,68m+4,4]] for m≥1 are obtained.

3.3 Quantum Color Codes from the Tessellation {40,3}

In this section, new quantum color codes with minimum distances dmin=4,6,8 from the tessellation {40,3} using the approach proposed in Section 2 are presented. These quantum color codes by considering nf=6m and g=17m+1 for m=1,2,…,20000 are constructed, which are as follows

•   [[80m,68m+4,4]] for m=1,2,…,16

•   [[80m,68m+4,6]] for m=17,18,…,437

•   [[80m,68m+4,8]] for m=438,439,…,20000

From this class, the quantum color codes with minimum distance dmin≥10 are also constructed.

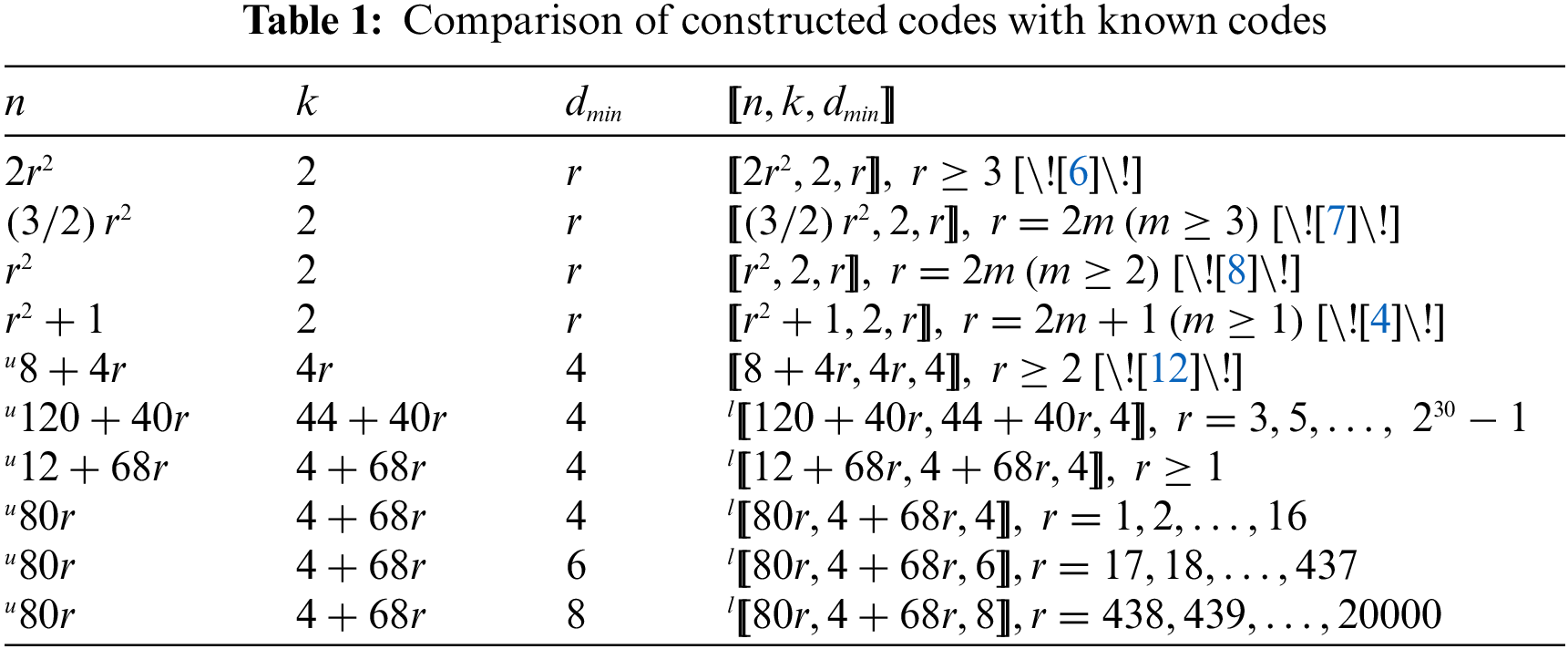
4  Table of Quantum Codes Comparison

In Table 1, the quantum color codes constructed in this paper are compared with the quantum codes constructed in other references. In this table, the first column shows the value of the length of quantum code. The second column shows the value of k. The third column shows the minimum distance of code. The fourth column shows a list of the quantum codes. All the new quantum color codes are labeled with  l. The length of quantum codes having the highest rate kn is labeled with  u.

5  Conclusion

In this paper we have presented a hyperbolic geometry approach to constructing new quantum color codes, based on the identification of compact surfaces by hyperbolic tessellations. We obtained some families of quantum color codes with minimum distances  4, 6 and 8 by new tessellations. For these quantum color codes the encoding rate is such that kn→1 as n→∞. For future study, it would be interesting to investigate the algebraic structure of quantum color codes and their relation to other quantum codes.

Acknowledgement: The authors would like to sincerely thank the referees for a very meticulous reading of this manuscript, and for valuable suggestions which help to create an improved final version.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. C. Shannon, “A mathematical theory of communications,” Bell System Technical Journal, vol. 27, no. 3, pp. 379–423, 623–656, 1948. [Google Scholar]

2. P. W. Shor, “Scheme for reducing decoherence in quantum memory,” Physical Review A, vol. 52, no. 4, pp. 2493–2496, 1995. [Google Scholar]

3. A. Calderbank, E. Rains, P. Shor and N. Sloane, “Quantum error correction via codes over GF(4),” IEEE Transactions on Information Theory, vol. 44, no. 4, pp. 1369–1387, 1998. [Google Scholar]

4. H. Bombin and M. A. Martin-Delgado, “Homological error correction: Classical and quantum codes,” Journal of Mathematical Physics, vol. 48, no. 5, pp. 52105–52140, 2007. [Google Scholar]

5. H. Bombin and M. A. Martin-Delgado, “Topological quantum distillation,” Physical Review Letters, vol. 97, no. 18, pp. 180501–180505, 2006. [Google Scholar] [PubMed]

6. A. Y. Kitaev, “Fault-tolerant quantum computation by anyons,” Annals of Physics, vol. 303, no. 1, pp. 2–30, 2003. [Google Scholar]

7. M. Leslie, “Hypermap-homology quantum codes,” International Journal of Quantum Information, vol. 12, no. 1, pp. 143001–1430040, 2014. [Google Scholar]

8. C. D. de Albuquerque, R. P. Junior and E. B. da Silva, “On toric quantum codes,” International Journal of Pure and Applied Mathematics, vol. 50, no. 2, pp. 221–226, 2009. [Google Scholar]

9. C. D. de Albuquerque, R. Palazzo Jr. and E. B. da Silva, “Families of classes of topological quantum codes from tessellations {4i+2, 2i+1}, {4i, 4i}, {8i−4, 4} and {12i−6, 3},” Quantum Information and Computation, vol. 14, no. 15&16, pp. 1424–1440, 2014. [Google Scholar]

10. S. Yu, J. Bierbrauer, Y. Dong, Q. Chen and C. H. Oh, “All the stabilizer codes of distance 3,” IEEE Transactions on Information Theory, vol. 59, no. 8, pp. 5179–5185, 2013. [Google Scholar]

11. A. Naghipour, M. A. Jafarizadeh and S. Shahmorad, “Topological quantum codes from self-complementary self-dual graphs,” Quantum Information Processing, vol. 14, no. 11, pp. 4057–4066, 2015. [Google Scholar]

12. W. S. Soares Jr. and E. B. da Silva, “Hyperbolic quantum color codes,” Quantum Information and Computation, vol. 18, no. 3&4, pp. 307–318, 2018. [Google Scholar]

13. C. D. Albuquerque, R. Palazzo Jr. and E. B. Silva, “New classes of topological quantum codes associated with self-dual, quasi self-dual and denser tessellations,” Quantum Information and Computation, vol. 10, no. 11&12, pp. 956–970, 2010. [Google Scholar]

14. E. B. da Silva and W. S. Junior, “Construction of color codes from polygons,” Journal of Physics Communications, vol. 2, no. 9, pp. 95011–9523, 2018. [Google Scholar]

15. C. Chamberland, A. Kubica, T. J. Yoder and G. Zhu, “Triangular color codes on trivalent graphs with flag qubits,” New Journal of Physics, vol. 22, pp. 023019, 2020. [Google Scholar]

16. E. D. de Carvalho, W. S. Soares and E. B. da Silva, “Topological quantum codes from lattices partition on the n-dimensional flat tori,” Entropy, vol. 23, pp. 959, 2021. [Google Scholar] [PubMed]

17. C. D. Albuquerque, G. G. La Guardia, R. Palazzo Jr., C. R. de Oliveira, Q. Queiroz et al., “Euclidean and hyperbolic asymmetric topological quantum codes,” Quantum Information Processing, vol. 21, pp. 153, 2022. [Google Scholar]

18. M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information. Cambridge: Cambridge University Press, 2000. [Google Scholar]

19. M. Nakahara, Geometry, Topology and Physics, 2nd ed. UK: IOP Publishing Ltd., 2003. [Google Scholar]

20. D. Gottesman, “Stabilizer codes and quantum error correction,” 1997. www.arxiv.org/abs/quant-ph/9705052 [Google Scholar]