An Intelligent Optimization Method of Reinforcing Bar Cutting for Construction Site

1  Introduction

As societies and economies advance, China has proposed a goal to reach the peak of its total CO2 emissions by 2030, to become carbon neutral by 2060, and to advance new infrastructure development strategies [1]. These objectives promote the development of the construction industry, while proposing higher requirements for sustainable development in the construction industry. Simultaneously, the construction industry, as a pillar industry in the national economy, and the concept of sustainable development is essential. In 2017, building construction and operation accounted for 36% of the global final energy use and nearly 40% of the related CO2 emissions [2]. As the most important building material in construction engineering, steel bars and concrete account for approximately 65% of building greenhouse gases—40% of which are CO2 emissions from concrete [3].

Clark and Bradley’s survey showed that the embodied CO2 (ECO2) contained in an average building is 340 kg-CO2/m2, of which the structure accounts for approximately 60% [4]. In a report by Lee, 95 kg-ECO2/ton for C25/30 concrete was suggested, but the reinforcing bar generated an ECO2 of 872 kg-ECO2/ton. This shows that reducing the ECO2 in the structural framework directly leads to a reduction in greenhouse gases. In addition, in terms of the carbon footprint, reducing the number of steel bars is extremely important because their ECO2 is approximately 9.2 times that of concrete per unit weight [5]. The most effective way to lower carbon emissions is to reduce the steel material from the source. Begum [6] eliminated many problems related to waste disposal. However, steel bar processing and blanking are only combined in a single component at this stage. Workers carry out simple manual control to unload the materials in sequence. Such a method results in low processing efficiency, generates a considerable amount of steel bar waste, causes serious waste of steel bar raw materials. Generally, the steel cutting waste is approximately 3%–5% [7–10] in the design stage, but more than 5% occurs in the construction stage [11–15]. This results from the lack of optimization of cutting technology at the construction site to achieve sustainable construction.

Early research on cutting-stock problems can be traced back to 1939. Based on the cutting-stock problem, economists of the former Soviet Union proposed a mathematical model that uses linear programming to model and solve it by multiplication. Although the method is immature and cannot guarantee an optimal solution, it has far-reaching guiding significance for the solution. Gilmore and Gomory [16] used linear programming methods to build mathematical models. The postponed column generation method, improved in 1963 [17] and 1965 [18], is also applicable to the problem of two-dimensional plate cutting problems and even multidimensional problems.

In particular, for large-scale optimization problems, most linear programming algorithms have low computational efficiency and are difficult to solve. It has been proposed that these problems can be solved using heuristic algorithms. Haessler [19] proposed a new method—the sequential heuristic method, which comprehensively considers loss, consumables, and cutting modes to solve multiple optimization objectives. Haessler et al. [20,21] introduced the variable of the trimming method, and applied it to the “first applicable” first-fit-decreasing and “best applicable” best-fit-decreasing algorithms. For the one-dimensional cutting problem, Wagner [22] proposed adding constraints, such as cutting loss and inventory, and using a genetic algorithm to solve it.

For the one-dimensional cutting problem, Yang et al. [23] improved the tabu search algorithm, solved part of the problem with mixed objective functions, and achieved good results. Moreover, the algorithm can avoid the common defects of traditional heuristic algorithms, i.e., falling into a local optimal situation. Araujo et al. [24] set the objective function as the least remaining material, and used a new heuristic algorithm for the optimization calculation. For small- and medium-scale problems, it has been proposed [25] that simulated annealing algorithms can be used. Cui [26] summarized the one-dimensional cutting problem from the sequential heuristic algorithm, and increased the constraint conditions by setting primary and secondary goals. Based on this method, a computer-aided layout system was developed. Based on the genetic algorithm, Gracia et al. [27] considered the least surplus material as the objective function, and introduced different search strategies to solve the one-dimensional cutting-stock problem. This method sets the cutting from the surplus material to a higher priority. When surplus material is unavailable, a material with a fixed length is considered.

In 2015, Nereu et al. [28] proposed an approach wherein surplus material can be used for other purposes instead of becoming waste. In 2016, Poldi et al. [29] proposed solving the cutting problem using a residual heuristic algorithm. Although various cutting optimization algorithms have been proposed, most are unstable when tested. Most data in reinforcement engineering are extensive and irregular. It is easy to produce nondeterministic polynomial (NP) complete problems when these data are directly used in linear programming and cannot be solved in a feasible amount of time. If other heuristic algorithms are used, it is difficult to set parameters, premature algorithms, and local optimizations. Therefore, it is necessary to study in depth the cutting optimization algorithms suitable for reinforcement engineering. An optimization algorithm for steel bar cutting that can meet the engineering requirements in terms of calculation efficiency and calculation quality is required to improve the application of the material utilization ratio in reinforcement engineering, reduce inefficient labor, and achieve sustainable construction.

In this study, a mathematical model is proposed for minimizing the use of steel materials. An integer programming model is used to solve the problem, and a greedy algorithm is introduced to improve the linearized algorithm to optimize the large-scale steel bar calculation problem. The final design calculation accuracy and calculation efficiency provide an intelligent optimization algorithm for steel bar blanking, and the minimum steel loss is calculated using the cutting plan to achieve sustainable construction.

2  Methodology

To design an optimization algorithm for steel bar blanking, the characteristics of the data in reinforcement engineering were analyzed comprehensively, and the objective function and constraint conditions were defined. A high-quality and high-efficiency solution for rebar blanking was achieved.

2.1 Parameters and Decision Variables

In the case of the same steel bar strength grade and diameter, the essence of the steel-bar-blanking optimization problem is to use the least raw material for the steel bar (i.e., lowest cost) to solve the project planning problem of different lengths and different quantities of blanks. In the optimization model for this type of planning problem, the parameters in Table 1 are used.

Owing to the definite length of the reinforcement, the raw materials of the reinforcement should be minimized (minimum cost). It is necessary to fully utilize the raw materials of each steel bar; i.e., the length of the surplus material after cutting should be less than the shortest length of the blank material. Research has shown that this cutting method is effective. Each effective cutting method uses a steel bar raw material. Steel cutting can be regarded as a combination of many effective cutting methods. The number of times the effective cutting method is used corresponds to the total number of raw materials in this problem. Therefore, the decision variables can be set as in Table 2.

2.2 Model Formulation

2.2.1 Objective Functions

This study aims to meet the requirements of engineering embryo materials, while minimizing cost. For the setting of the objective function, two aspects are considered: minimization of raw material number and loss.

From the perspective of the number of raw materials, the ultimate goal is to minimize the total number of raw materials. To minimize Z (which denotes the total number of raw materials) based on the previously set decision variables, the objective function can be expressed follows:

MinZ=x1+x2+x3+⋯+xn(1)

Z≥0,x≥0

where Z is the total number of steel bars.

The mathematical model for minimizing raw material demand uses the total number of raw materials required for the final calculation as the objective function to evaluate the blanking plan. The mathematical method for minimizing loss summarizes all the remaining material lengths obtained from cutting, sets the remaining material length as an index, and evaluates the cutting plan. The corresponding objective function is as follows:

MinS=LZ−∑i=1n(libi)(2)

where S is the total length of remaining material.

The analysis shows that, if both reach the optimal solution, the material utilization rates corresponding to the two different objective functions are equal. Therefore, the number of raw steel bars used is equal to the material loss. Because the calculation amount of the objective function set by the minimization of raw materials is smaller, in the follow-up study, the number of raw materials is selected to minimize the objective function.

2.2.2 Constraints

Although there exist several objective functions, the final model constraints are mainly based on the number of roots that meet the engineering requirements. Steel bar blanking can be regarded as a combination of multiple effective cutting methods. Each effective cutting method involves blanks of different lengths. The combination of effective cutting methods ensures that the number of blanks with different lengths is equal to the number of blanks required by the project.

For the calculation of effective cutting, the following methods are used [30].

S1: Processing of the blank length set li:{l1,l2,⋯,lm} in descending order, make l1>l2>⋯>lm;

S2: n=1, where n is the number of cutting methods;

an1=min{b1,[L/l1]},

an2=min{b2,[(L−an1l1)/l2]},…

anm=min{bm,[(L−∑i=1m−1anili)/lm]},

The function represents Gaussian rounding, that is, rounding down.

S3: Integrated cutting plan: [an1,an2,⋯,anm];

S4: Iteration based on S3 cutting plan. If there is ani>0 at 1≤i≤m−1, let k be equal to the maximum value of all i that meet the condition ani. If there is no ani>0 at 1≤i≤m−1, the algorithm ends;

S5: n=n+1an1=a(n−1)1,an2=a(n−1)2,⋯,an(k−1)=a(n−1)(k−1),

ank=a(n−1)k−1

an(k+1)=min{bk+1,[(L−∑i=1kanili)/lk+1]}…

anm=min{bm,[(L−∑i=1n−1anili)/ln]]} to S2

Numbered lists can be added as follows.

It is assumed that bi steel bar blanks with a length of li m are required. In the first effective cutting method, a1i steel bars with a length of li meters can be cut. In the second effective cutting method, a2i steel bars with a length of li meters can be cut, and so on. In the n effective cutting method, ani steel bars with a length of li meters can be cut. The following constraints can be obtained.

a1ix1+a2ix2+…+anixn=bi(3)

Assuming that m different lengths of steel bar blanks are required, there are n effective cutting methods, and x1,x2,…,xn represents the number of raw steel bars in the corresponding plan. For all steel bars with different lengths, the following constraints can be obtained.

{a11x1+a21x2+…+an1xn=b1a12x1+a22x2+…+an2xn=b2…a1mx1+a2mx2+…+anmxn=bm(4)

x1,x2,…,xn≥0

where a is the number of steel bars of a certain length that can be cut by various schemes.

2.3 Optimal Algorithm Design of Rebar Cutting

2.3.1 Integer Linear Programming Application

Under the above objective function and its constraints, a mathematical programming algorithm was used to determine the optimal solution. Mathematical planning is an important branch of operations research, and an important branch of mathematical programming is integer programming. Integer linear programming limits the decision variables in linear programming to integers, and its standard form can be expressed as follows:

Minf=cTx(5)

s.t.{Ax=bxj≥0(j=1,2,3,⋯n)xj(j=1,2,3,⋯n;xjis an integer.)(6)

where c=(c1,c2,⋯,cn)T, x=(x1,x2,⋯,xn)T.

For the mathematical model of rebar cutting, the decision variable represents the number of raw materials to be cut, which must be an integer. This exactly matches the principle and idea of integer linear programming, so the integer linear programming algorithm can be used to solve the scheme first.

At this stage, there are mainly exhaustive methods and branch-and-bound methods for solving integer linear programming. Although the exhaustive method is theoretically feasible, it is far greater than the other two algorithms under the same calculation scale. A new method for solving the fully fuzzy system of linear equations using the linear programming problem approach is used.

The branch-and-bound method is one of the main methods for solving integer linear programming problems. It has been widely used in the fields of mixed-integer programming and pure integer programming. The branch-and-bound method first relaxes the original problem into a linear programming problem. Then, it iteratively corrects situations wherein the optimal solution is not all integers. When the algorithm starts to search, the optimal solution currently found is ∅. During solving, the solution space is gradually reduced. At any time, the solution space comprises a subset of the solution space that has not been explored and the optimal solution found thus far. The unsearched subspace is represented as a node in the dynamically generated search tree. The search tree includes only the root node before the algorithm starts. Each iteration of the branch-and-bound method processes a node. The iteration has three parts: branching, boundary calculation, and screening. The branch is generally based on the principle of selecting variables that do not meet the integer constraint, and pick a non-integer variable xn=bn. Let [bn] be an integer rounded down to bn, and the original feasible region is R. R is divided into R1 and R2 by xn= [bn] and xn= [bn] + 1. The non-integer area between [bn] and [bn] + 1 in R is eliminated to reduce feasible domain. The current value divides it into two subproblems for the solution. The boundary calculation aims to solve the subproblems generated by the branch. According to its optimal objective function value, the upper and lower bounds before branching are updated. Screening is based on the relationship between the optimal function value of the branch subproblem and the preset upper and lower bounds. It deletes or rebranches the branch until the optimal objective function value is obtained.

The solution process is as follows.

IL is an integer programming problem that needs to be solved. The linear programming problem corresponding to this problem is called L.

The problem is solved in two stages.

First, to solve problem L, one of the following situations can be obtained.

(1)If there is no feasible solution for L, and there is no feasible solution for the IL, then stop.

(2)There is an optimal solution for L. The solution variables are all integers, so it is also the optimal solution of IL. Then stop.

(3)An optimal solution for L exists. However, it does not meet the integer condition in the IL. Then, f0 is the value of the objective function. If this happens, it must be f≥f0.

Second, iterative operations are performed for the (3) situation in the first stage.

(1)Branch. In the optimal solution of L, a variable is chosen that does not satisfy the integer condition. Assuming that its value is lj, two constraints, xj≤[lj] and xj≥[lj]+1, are established. These conditions are added to question L, and L is divided into two subproblems, L1 and L2. Regardless of the integer condition requirements, L1 and L2 are solved.

(2)Boundary. Each successor subproblem is a branch and indicates the result of the solution. Similar to other results, the smallest value of the optimal objective function is found as the new lower bound, and f0 is replaced simultaneously. From the branches that met the integer condition, the smallest value of the objective function is found as the new upper bound f∗, which is f∗≥f≥f0.

(3)Comparison and pruning. If the optimal objective function of each branch is greater than f∗, it is cut off. If it is less than 1 and does not meet the integer condition, branching steps is repeated until the optimal objective function value f=f∗ is finally obtained. Thus, the optimal integer solution is xj∗(j=1,2,3,⋯,n).

The algorithms were tested. Considering a sample project as an example, the representative data of different scales in the steel bar schedule were extracted. The length of the steel bar raw material was 12 m; there were 23 types of blank that needed to be cut; the length was set li {10.772, 9.888, 9.36, 8.14, 7.66, 6.56, 6.05, 5.82, 5.73, 5.722, 5.684, 3.165, 2.96, 2.885, 2.67, 2.59, 2.565, 2.25, 2.22, 2.146, 1.946, 1.726, 1.44}; and the corresponding quantity set was ai {2, 2, 4, 8, 8, 16, 21, 18, 21, 2, 16, 34, 912, 17, 76, 8, 17, 18, 912, 68, 68, 66, 36}.

An integer linear programming algorithm is used to build the mathematical model. First, it is necessary to calculate all feasible blanking schemes. According to the calculation in Section 2.2.2, there are 3226 feasible blanking methods.

A mathematical model is established based on the cutting method. Solving it by an integer linear programming algorithm took 15.138 s. Finally, 539 12-m-long raw materials were used, with a total length of 12 × 539 = 6468 m. The total length of the blank material required by the project was ∑i=123liai=6397.22 m. The overall utilization rate of the materials was 98.906%. The specific blanking plan is presented in Table 3.

The test calculations revealed that the integer linear programming algorithm could obtain the global optimal solution for small-scale optimization problems. To determine the global optimal solution, it is necessary to enumerate all possible cutting solutions. Thus, the number of cutting plans is equal to the dimensions of the corresponding mathematical model. Numerous blanking options for large-scale optimization problems lead to several mathematical models. The algorithm cannot be solved in polynomial time. Therefore, one of the problems to be solved is how to ensure the calculation effect of the integer programming algorithm as much as possible, while considering the calculation efficiency.

2.3.2 Algorithm Improvement

The cutting-stock problem is an NP problem. It has been shown [31] that no algorithm guarantees the solution of problems of different scales [32]. Approximation algorithms are more suitable for determining acceptable solutions within a reasonable time. Here, it is proposed that the problem of steel bar blanking can be solved by introducing a greedy strategy. A greedy strategy is introduced to solve this problem. Unlike integer programming calculations, this method does not need to calculate all the blanking plans. First, the current optimal blanking plan is calculated. The plan is then reused to the greatest extent, and the completed workload is removed from the engineering requirements. Finally, iteration is performed based on the updated demand cycle. An iteration comprises three parts: calculating the optimal plan, reusing the plan to the greatest extent, and updating the engineering requirements. The original problem is solved when the updated demand is empty. In each sequence, the optimal solution to the original problem is the set of optimal solutions.

Because the number of blanks for each blanking is limited, there is no exponential increase in the number of solutions. The optimal blanking method for each subsequence can be solved using an integer linear programming algorithm. The mathematical model is as follows:

max∑i=1mailisubject to{0≤ai≤biai is an integer∑i=1maili≤L(i=1,2,⋯,m)(7)

The optimal cutting method is calculated as a subroutine of the multilevel sequential linear optimization method, which can be used repeatedly. The overall process is as follows:

S1: Calculate the optimal cutting method.

S2: Calculate the number of repetitions of the cutting method d=Min[b1a1,b2a2,⋯,bmam].

S3: Update the remaining engineering requirements.

S4: If the updated engineering requirement is empty, the calculation is completed; if it is not empty, then cycle steps S1 to S3.

S5: Summarize the optimal cutting method and number of repetitions for each sequence, which is the optimal solution to the original problem.

Introducing a greedy strategy enables the original optimization problem to be divided into multiple sequences, and optimization calculations can be performed sequentially. In the calculation, the scale of the problem is reduced. As the scale of the problem shrinks, the advantages of the greedy strategy are reduced accordingly. Fig. 1 shows the calculation of this case. The integer programming algorithm and introduction of the greedy strategy are used to compare the remaining materials of all the solutions solved by the algorithm. The figure shows that the results based on the greedy strategy are mostly better than the integer programming solution in the initial stage. However, as the data size shrinks, after the 11th solution, the disadvantages of the greedy strategy gradually become apparent. The difference between the quality of the calculation result of the greedy strategy and that of integer programming increase continuously. The main reason for this is analyzed, and the solution is based on the greedy strategy. Although it seems that the optimal solution is selected at each stage, owing to the lack of overall consideration in the early stage to improve the quality of the solution, several short embryos that can be used to fill the gap are employed. Most remaining blanks in the middle and late stages can be optimized to a low degree, resulting in the poor quality of the blanking methods calculated in the middle and later stages, and more surplus materials are generated. However, the integer linear programming algorithm calculates all possible blanking methods in the mathematical model establishment stage. In the solution, one can comprehensively consider the combination of all blanking methods, and the quality of the overall blanking method is relatively average. As shown in Fig. 1, the integer programming algorithm uses a blanking method with a remaining material length of less than 0.2. The only solution with a residual material of 1.228 is when the longest blank is 10.772 and the shortest is 1.44 in the calculation example, which cannot be optimized further. The integer programming algorithm uses less leftover material, which ensures that the quality of the final optimization result of the algorithm is better.

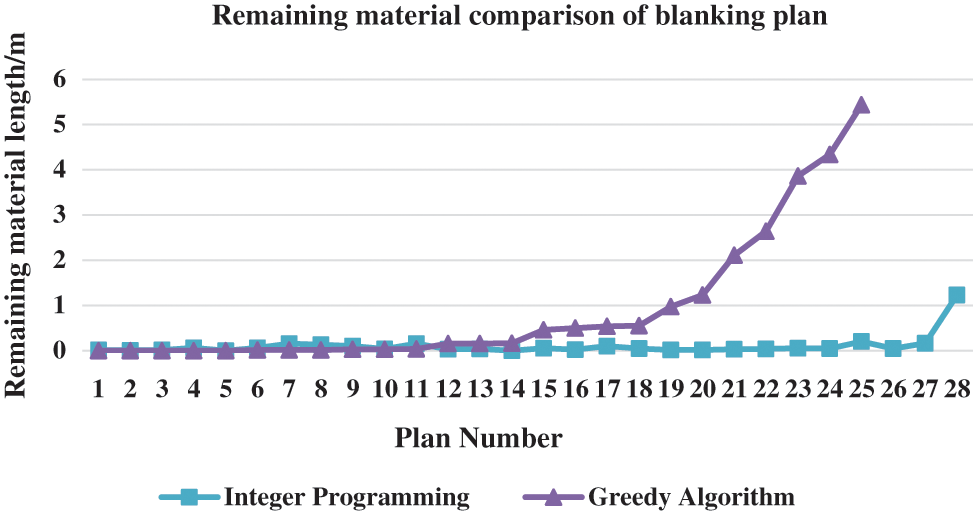
Figure 1: Comparison of the remaining material between the two algorithms

When solving large-scale problems using the greedy strategy, there are serious losses in the later stages of the calculation, as shown in Fig. 1. To consider the efficiency and quality of calculation, a new approach is proposed, combining an integer linear programming algorithm with a greedy strategy. For small-scale problems, the integer programming algorithm is used; for large-scale problems, the greedy strategy is employed first. When the problem size is reduced to a certain extent, an integer programming algorithm is used to solve the cutting problem of the remaining blanks. Finally, the two components are integrated. The phase solution results are the final result.

2.3.3 Critical Threshold Setting

An integer linear programming algorithm is used later. This can compensate for the serious loss in the later calculation of the blanking plan based on the greedy strategy design.

As mentioned above, the quality of the cutting method is directly related to the quality of the final calculation result of the algorithm. The calculation is based on the greedy strategy, and the loss of the scheme used in the early stage is low. The loss of the calculation scheme of this algorithm mainly occurs in the middle and later stages, such as the stage after the 14th scheme in the above calculation example. The greedy algorithm provides a solution every iteration, so the loss is serious after 14 iterations. However, the integer programming algorithm cannot be used to solve the remaining blanks directly after the 14th iteration. The reason for the serious loss is that, in the early stage, to improve the quality of the plan, several short blanks that can be used to fill the gaps are used, and most remaining blanks are in the middle and late stages. The degree of optimization is not high. Therefore, it is necessary to start using the integer linear programming algorithm to solve the problem a few rounds in advance to ensure that the short blanks are included in the blanks that must be cut at that time.

Through calculation, the loss gradually increases after 14 iterations. An integer programming algorithm is used after 6–16 iterations. The raw material consumption of the steel bars is shown in Table 4.

Fig. 2 shows that, after the 14th iteration, if the integer linear programming algorithm is used to solve the problem, 551 raw steel bars are used. Compared with the 552 bars of the greedy algorithm, the optimization effect is not apparent. If seven rounds in advance, after the seventh round, the integer linear programming algorithm is used to solve the problem, and only 539 are required. Consistent with the direct use of the integer programming algorithm, the global optimal solution is calculated, and the calculation efficiency is much higher than that of the integer programming algorithm.

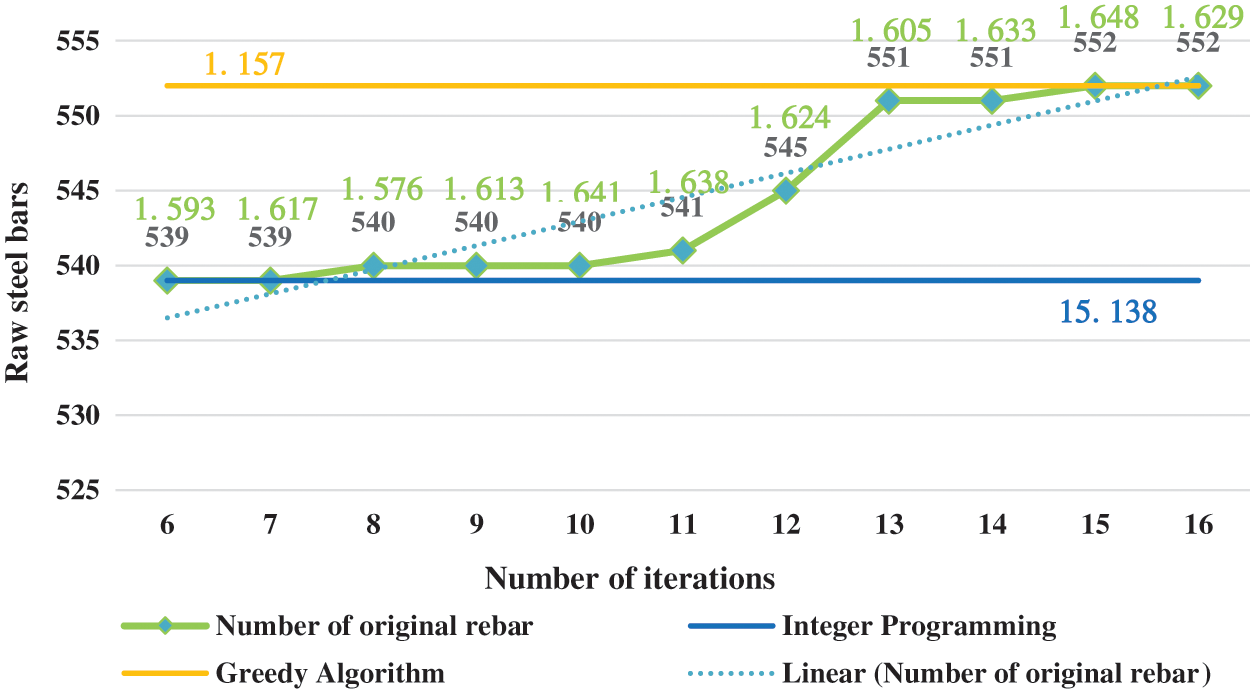
Figure 2: The influence of iteration number on optimization effect

From the actual engineering, 300 groups of steel engineering data of different scales were selected. For the case wherein a cutting method with a serious loss occurs in the Nth round under a different number of advance iterations, the optimal data volume achieved in 300 sets of test data is shown in Fig. 3. The number of early iterations concentrated in interval [7,21] has the most data, accounting for approximately 90%. Therefore, the value range of the final threshold T can be selected in interval [N−20, N−6]; that is, the integer linear programming algorithm is used to solve the problem after the Tth iteration, which can achieve better results.

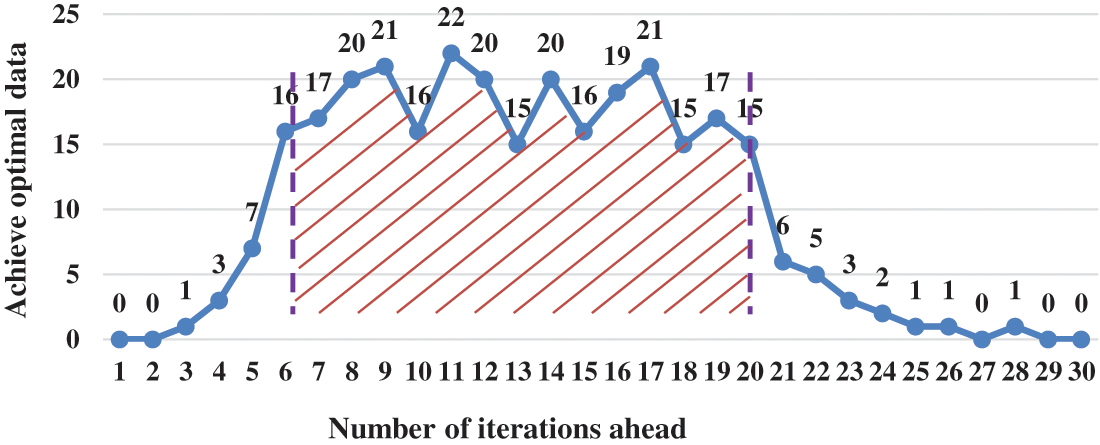
Figure 3: Optimal test data statistics under different number of iterations in advance

2.3.4 Algorithm Flow Setting

Based on the above research and considering the characteristics of steel engineering data, an optimization algorithm for steel blanking is proposed. The specific steps are as follows:

S1: Judge the scale of the problem of rebar blanking.

S2: If it is a small-scale problem, directly call the integer linear programming algorithm to solve it, output the optimization result, and end the algorithm.

S3: If it is a large-scale problem, solve it based on a greedy strategy, and record all the cutting methods used and the number of repetitions, as well as the remaining blank length li and the number of required roots ai after each iteration.

S4: Comprehensively analyze all blanking methods, screening the number of iterations N, where serious losses begin to appear.

S5: Based on the critical threshold setting method, select an appropriate critical threshold T within the threshold interval.

S6: Based on the remaining blank length lis and the number of demand roots ais after the Tth iteration in S3, call the integer linear programming algorithm.

S7: Base synthesis S3 on the greedy strategy to solve the blanking plan before the Tth iteration; S6 uses the integer linear programming algorithm to solve the blanking plan, which is the final blanking plan of the original steel-bar-blanking problem.

The specific algorithm flow chart is shown in Fig. 4.

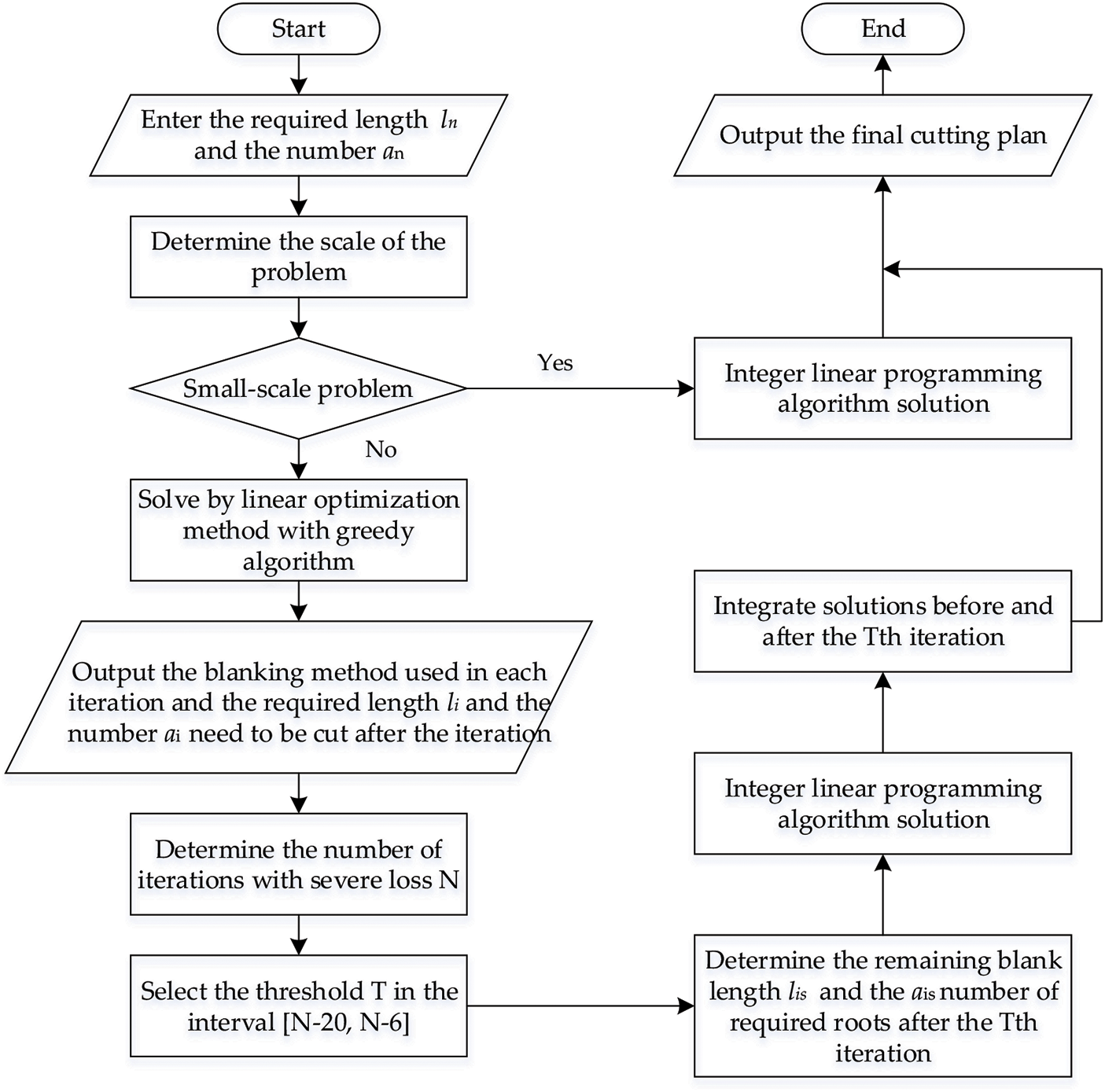
Figure 4: Algorithm flow

3  Algorithm Example Analysis

3.1 Brief Description of the Case Project

The newly built Beijing–Zhangjiakou High-Speed Railway Beijing North EMU is located in the triangle enclosed by the Beijing–Baotou Line, Huanqing Line, and Northeast Ring Line, as shown in Fig. 5. It includes related projects, such as houses behind the station, lighting, HVAC, water supply and drainage, EMU supporting facilities, road pipelines (ditches), communication information, and power. The building area is 59,712 m2, of which the building area of the six-line inspection warehouse is 29,292 m. The length is 492 m, and the width is 61.1 m.

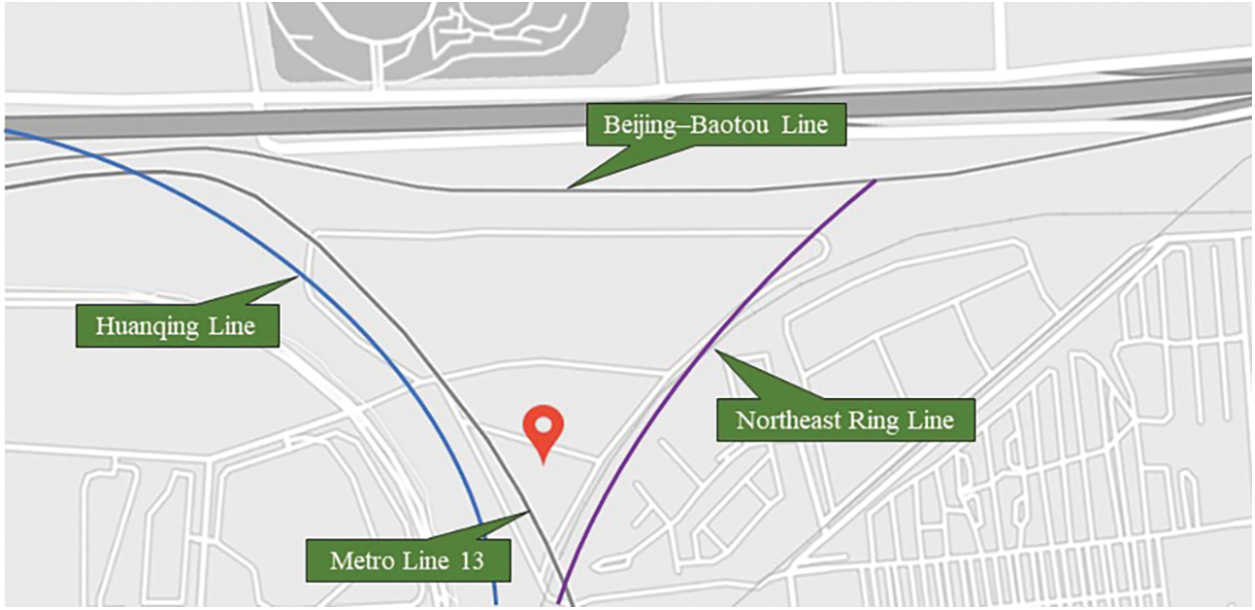
Figure 5: Engineering location map

For the steel bar processing, a centralized processing and distribution method was used. An intelligent centralized processing plant was built near the construction site, and building information modeling technology, computer technology, two-dimensional code technology, and other information technology were used for intelligent processing of steel bars. The number of steel bars in the project was 5764 tons. Because of space limitations, at the focus was on the material warehouse, the comprehensive building of the mechanical engineering area, and the garbage building. Steel bars with a steel bar grade of HRB400 and diameter of 25 were studied for testing.

3.2 Algorithm Application

(1) Engineering requirements

Data extraction was performed on steel bars with grade HRB400 and diameter 25 in the three monomers of the material library, the comprehensive building of the mechanical engineering area, and the garbage building.

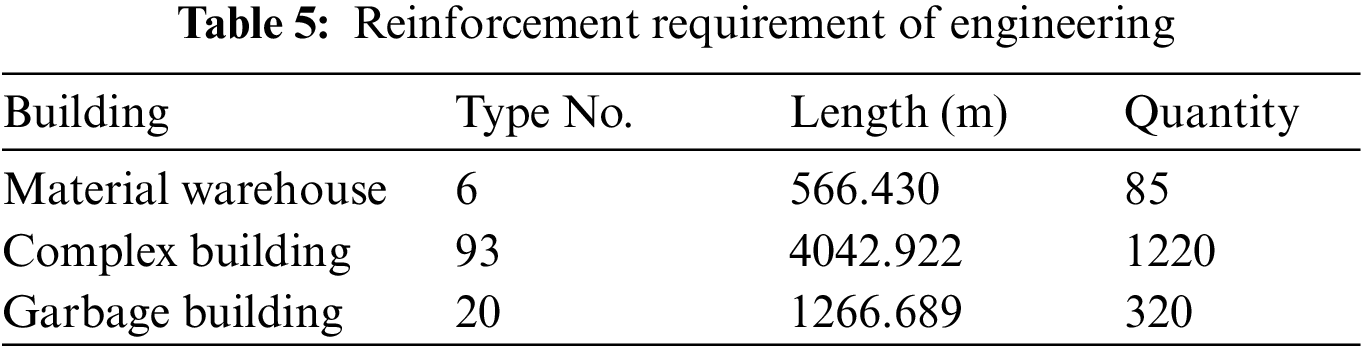
The total length of steel bars shown in the design of the material library was 566.43 m, and the total weight was 2180.55 kg. The total length of the steel bars in the design of the comprehensive building in the mechanical engineering area was 4042.922 m. The total weight was 15565.25 kg. The total length of the steel bars in the design of the garbage building was 1266.689 m, and the total weight was 4876.753 kg. The total length of the steel bars in the figure was 5876.041 m, and the total weight was 22,622.758 kg. The specific requirements are presented in Table 5.

(2) Rebar cutting optimization algorithm test

Through the proposed optimization algorithm for steel bar blanking, the three monomers of the material warehouse, the comprehensive building of the mechanical work area, and the garbage building were cut separately. The calculation results of the blanking plan are as follows.

The material library used 57 steel bars with a length of 12 m. The total length was 12 × 57 = 684 m. The total length of the billet required by the project was 566.43 m. The overall utilization rate of the steel bar raw material was 82.811%. The specific cutting plans are shown in Table 6.

The comprehensive building of the mechanical engineering zone used 342 steel bars with a length of 12 m. The total length was 12 × 342 = 4104 m. The total length of the billet required by the project was 4042.922 m. The overall utilization rate of the steel bar raw material was 98.512%. A part of the blanking plan is shown in Table 7.

The garbage building used 107 12-m steel bars. The total length was 12 × 107 = 1284 m. The total length of the billet required by the project was equal to the total design length of 1266.689 m. The overall utilization rate of the steel bar raw materials was 98.652%. The specific blanking plans are shown in Table 8.

If the three monomers were comprehensively cut, 494 raw materials with a length of 12 m were used. The total length was 12 × 494 = 5928 m. The total length of the billet required by the project was equal to the total design length of 5876.041 m. The overall utilization rate of the materials was 99.124%. A part of the blanking plan is presented in Table 9.

For the three monomers, the results of the calculation of the cutting plan and comprehensive cutting are shown in Table 10.

(3) Analysis of calculation results

Different scales are formed by different combinations. The calculation results are also different. The three projects were individually tailored. To complete the three projects, 506 raw steel bars were required, and the corresponding material loss rate was 3.227%. Compared with the loss rate of approximately 10% of traditional steel bar dispersion processing, the 3.227% loss rate was largely optimized. However, comprehensive tailoring was performed for the data of the three individual projects. The corresponding material loss rate was reduced to 0.876% when using 494 steel bars. These data show that, as the scale of the project increases, the calculation quality of the optimization algorithm for steel bar blanking proposed also increases, while maintaining high calculation efficiency. Overall, the algorithm proposed has a good effect on the optimization of large-scale data.

4  Conclusions

The characteristics of steel engineering data were analyzed comprehensively. An optimization algorithm for steel bar blanking that considers both calculation and calculation efficiency was designed. By using the algorithm influence factors, problems, constants, and variables were defined, and appropriate cutting method calculation methods were set. The integer linear programming algorithm and linear optimization algorithm with a greedy strategy were adopted to solve the problem. To improve the performance of the two algorithms under different data backgrounds, ideas for an optimization algorithm for steel bar cutting were proposed. Based on the number of iterations of the sudden change in loss, the appropriate critical threshold was determined, and the calculation of the steel-bar-blanking plan was divided into two stages. The first stage was solved using the linear optimization method with the greedy algorithm, while reducing the problem scale. The integer programming algorithm was used for subsequent calculations when the number of iterations reached the threshold. A case study involving engineering tests showed that the proposed algorithm is both optimized and time sensitive. It outperforms a single traditional optimization algorithm and is highly applicable to the problem of steel bar cutting.

Acknowledgement: The authors thank China Railway Seventh Group Co., Ltd. for providing the rebar data of the case project to verify the algorithms.

Funding Statement: This research was funded by Nature Science Foundation of China (51878556), the Key Scientific Research Projects of Shaanxi Provincial Department of Education (20JY049), Key Research and Development Program of Shaanxi Province (2019TD-014) and State Key Laboratory of Rail Transit Engineering Informatization (FSDI) (SKLKZ21-03).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Lu, W., Tam, V., Chen, H., Du, L. (2020). A holistic review of research on carbon emissions of green building construction industry. Engineering Construction and Architectural Management, 27(5), 1065–1092. DOI 10.1108/ECAM-06-2019-0283. [Google Scholar] [CrossRef]

 2.  International Energy Agency, the United Nations Environment Programme (2018). 2018 Global Status Report: Towards a Zero-Emission, Efficient and Resilient Buildings and Construction Sector. https://www.worldgbc.org/. [Google Scholar]

 3.  Pacheco-Torgal, F., Cabeza, L. F., Labrincha, J., Magalhaes, A. D. (2014). Eco-efficient construction and building materials (Life Cycle Assessment (LCAEco-Labelling and Case Studies). UK: Woodhead Publishing. [Google Scholar]

 4.  Clark, D., Bradley, D. (2013). Embodied carbon of steel versus concrete buildings. UK: Cundall Johnston and Partners LLP. [Google Scholar]

 5.  Lee, I. J., Yu, H., Chan, S. L. (2016). Carbon Footprint of Steel-Composite and Reinforced Concrete Buildings. https://www.devb.gov.hk/filemanager/en/content_971/7_Carbon_Footprint_for_Steel_Composite_and_Reinforced_Concrete_Buildings.pdf. [Google Scholar]

 6.  Begum, R. A., Siwar, C., Pereira, J. J., Jaafar, A. H. (2006). A benefit–cost analysis on the economic feasibility of construction waste minimisation: the case of malaysia-sciencedirect. Resources, Conservation and Recycling, 48(1), 86–98. DOI 10.1016/j.resconrec.2006.01.004. [Google Scholar] [CrossRef]

 7.  Kim, S. K., Hong, W. K., Joo, J. K. (2004). Algorithms for reducing the waste rate of reinforcement bars. Journal of Asian Architecture and Building Engineering, 3(1), 17–23. DOI 10.3130/jaabe.3.17. [Google Scholar]

 8.  Kim, G. H. (2002). A study on program of minimizing the loss of re-bar (Master Thesis). Seoul, Korea: Korea University. [Google Scholar] [CrossRef]

 9.  Porwal, A., Hewage, K. N. (2012). Building information modeling-based analysis to minimize waste rate of structural reinforcement. Journal of Construction Engineering & Management, 138(8), 943–954. DOI 10.1061/(ASCE)CO.1943-7862.0000508. [Google Scholar] [CrossRef]

10. Nanagiri, Y. V., Singh, R. K. (2015). Reduction of wastage of REBAR by using BIM and linear programming. International Journal of Technology, 5(2), 329–334. DOI 10.5958/2231-3915.2015.00043.7. [Google Scholar]

11. Nadoushani, Z., Hammad, A., Akbar Nezhad, A. (2016). A framework for optimizing lap splice positions within concrete elements to minimize cutting waste of steel bars. Proceedings of the 33th International Symposium on Automation and Robotics in Construction (ISARC 2016), pp. 1–7. Auburn, AL, USA. [Google Scholar] [CrossRef]

12. Zheng, C., Yi, C., Lu, M. (2019). Integrated optimization of rebar detailing design and installation planning for waste reduction and productivity improvement. Automation in Construction, 101(1), 32–47. DOI 10.1016/j.autcon.2019.01.012. [Google Scholar] [CrossRef]

13. Nigussie, T., Chandrasekar, M. K. (2020). Influence of rebar practice in the total cost of building construction projects: The case of Hawassa city, Ethiopia. International Journal of Engineering, Science and Technology, 12(1), 54–65. DOI 10.4314/ijest.v12i1.5. [Google Scholar] [CrossRef]

14. Nadoushani, Z. S. M., Hammad, A. W., Xiao, J., Akbarnezhad, A. (2018). Minimizing cutting wastes of reinforcing steel bars through optimizing lap splicing within reinforced concrete elements. Construction and Building Materials, 185(10), 600–608. DOI 10.1016/j.conbuildmat.2018.07.023. [Google Scholar] [CrossRef]

15. Kwon, K., Kim, D., Kim, S. (2021). Cutting waste minimization of rebar for sustainable structural work: A systematic literature review. Sustainability, 13(11), 5929. DOI 10.3390/su13115929.

16. Gilmore, P. C., Gomory, R. E. (1961). A linear programming approach to the cutting-stock problem. Operations Research, 9(6), 849–859. DOI 10.1287/opre.9.6.849.

17. Gilmore, P. C., Gomory, R. E. (1963). A linear programming approach to the cutting stock problem—Part II. Operations Research, 11(6), 863–888. DOI 10.1287/opre.11.6.863.

18. Gilmore, P. C., Gomory, R. E. (1965). Multistage cutting stock problems of two and more dimensions. Operations Research, 13(1), 94–120. DOI 10.1287/opre.13.1.94.

19. Haessler, R. W. (1971). Application series II a heuristic programming solution to a nonlinear cutting stock problem. Management Science, 17(12), 793–802. DOI 10.1287/mnsc.17.12.B793.

20. Haessler, R. W. (1975). Controlling cutting pattern changes in one-dimensional trim problems. Operations Research, 23(3), 483–493. DOI 10.1287/opre.23.3.483.

21. Haessler, R. W., Sweeney, P. E. (1991). Cutting stock problems and solution procedures. European Journal of Operational Research, 54(2), 141–150. DOI 10.1016/0377-2217(91)90293-5.

22. Wagner, B. J. (1999). A genetic algorithm solution for one-dimensional bundled stock cutting. European Journal of Operational Research, 117(2), 368–381. DOI 10.1016/S0377-2217(98)00244-6.

23. Yang, C., Sung, T., Weng, W. (2006). An improved tabu search approach with mixed objective function for one-dimensional cutting stock problems. Advances in Engineering Software, 37(8), 502–513. DOI 10.1016/j.advengsoft.2006.01.005.

24. Araujo, S. A., Constantino, A. A., Poldi, K. C. (2011). An evolutionary algorithm for the one-dimensional cutting stock problem. International Transactions in Operational Research, 18(1), 115–127. DOI 10.1111/j.1475-3995.2009.00760.x.

25. Jahromi, M., Tavakkoli-Moghaddam, R., Makui, A., Shamsi, A. (2012). Solving an one-dimensional cutting stock problem by simulated annealing and tabu search. Journal of Industrial Engineering International, 8(1), 1–8. DOI 10.1186/2251-712X-8-24.

26. Cui, Y. (2012). A cam system for one-dimensional stock cutting. Advances in Engineering Software, 47(1), 7–16. DOI 10.1016/j.advengsoft.2011.12.004.

27. Gracia, C., Carlos, A., Gracia, L. (2013). A hybrid approach based on genetic algorithms to solve the problem of cutting structural beams in a metalwork company. Journal of Heuristics, 19(2), 253–273. DOI 10.1007/s10732-011-9187-x.

28. Nereu, A. M., Cristina, C. A., Do, N. D. N., Vianna, A. (2015). A new mathematical model for the cutting stock/leftover problem. Pesquisa Operacional, 35(3), 509–522. DOI 10.1590/0101-7438.2015.035.03.0509.

29. Poldi, K. C., Araujo, S. D. (2016). Mathematical models and a heuristic method for the multiperiod one-dimensional cutting stock problem. Annals of Operations Research, 238(1), 497–520. DOI 10.1007/s10479-015-2103-2.

30. Behera, D., Huang, H. Z., Chakraverty, S. (2015). Solution of fully fuzzy system of linear equations by linear programming approach. Computer Modeling in Engineering & Sciences, 108(2), 67–87. DOI 10.3970/cmes.2015.108.067.

31. Gokalp, O. (2020). An iterated greedy algorithm for the obnoxious p-median problem. Engineering Applications of Artificial Intelligence, 92(11), 103674. DOI 10.1016/j.engappai.2020.103674.

32. Wang, C. N., Nhieu, N. L., Tran, T. (2021). Stochastic chebyshev goal programming mixed integer linear model for sustainable global production planning. Mathematics, 9(5), 483–505. DOI 10.3390/math9050483.

Appendix A. Example of appendix

The calculation results of the scheme omitted in the article download and view the URL: https://github.com/XUTMZX996/Appendix.