An Integrated Scheduling Algorithm for the Same Equipment Process Sequencing Based on the Root-Subtree Vertical and Horizontal Pre-Scheduling

1  Introduction

The production scheduling problem has always been the core content and critical technology in manufacturing and composition. It is a constraint satisfaction problem characterized by reasonable use of the limited manufacturing resources and production costs under the condition of satisfying all constraints to ensure the optimal production target selected by the enterprise and maximize efficiency. In general, the solution to the production scheduling problem is NP-hard. It is difficult to form an effective and similar theoretical method to study these scheduling problems. The research of this problem mainly focuses on flow-shop scheduling (flow scheduling for large batches of the same product) [1–3] and Job-shop scheduling (shop scheduling for multi-variety and small-batch products) [4–6]. The integrated scheduling is based on the premise of shortening the production cycle of the products, considering processing and assembly at the same time [7]. Many research results have shown that the integrated scheduling is very outstanding in the production of small or single complex products with tree structure, which is more in line with the actual pro-duction requirements of the large equipment manufacturers. At present, the complex product integrated scheduling algorithm has achieved some results, the literature [8] proposed an integrated scheduling algorithm based on ACPM, which focuses on the vertical structure of the product process tree; The literature [9] proposed a dynamic critical path multi-product manufacturing scheduling algorithm (DCPM) based on the process set, which realizes the scheduling plan that focuses on the vertical while taking into account the horizontal; The literature [10] proposed an integrated scheduling algorithm based on the horizontal layer (DJSSA), which focuses on the horizontal structure characteristics of the product process tree, and on this basis the vertical structure characteristics of the process tree; The literature [11] proposed an integrated algorithm for timing that considers subsequent processes, which starts from the overall structure of the process tree and uses the process sequence sorting strategy to optimize the integrated scheduling result; The literature [12] and the literature [13] (ISA-CPTS) study the solution of the product integrated scheduling problems from the perspective of the intelligent algorithms. However, these scheduling algorithms are based on the overall structure of the process tree analysis but ignored the vertical and horizontal structure of each subtree in the product process tree. The parallel relationship between the subtrees is separated, making the process scheduling of the product not compact enough. It depends too much on the product processing technology structure. At present, there is little research on the integrated scheduling algorithm of the inner structure of the product process tree. Because the product manufacturing total time is limited by the vertical and horizontal aspects of the process tree, the differences of the product structure led to the different vertical and horizontal characteristics of the product process tree. Therefore, it is necessary to study the product process tree's internal vertical and horizontal characteristics for the integrated scheduling problem.

Nowadays, in the customer-oriented personalized and customized production model, the manufacturing methods based on modular design [14–17] are increasingly favored by manufacturing enterprises, which can build the products in parallel and install them integrally. The utility model realizes that the products are easy to maintain and upgrade, improves the diversification of the products, dramatically reduces the construction period and the production and manufacturing cost, and satisfies the customer's personalized demand for products. The schematic diagram of the modular product structure is shown in Fig. 1. In a modular design concept, a product is composed of several component or part modules hierarchically. With the tree structure constraints, each module is completed by dozens or more than hundreds of processing and assembly processes. It associates various product definition data with processing and assembly. Finally, it forms a complete description of product processing and assembly information produces a tree table that can reflect the assembly relationship between product parts or components and the product process tree. It is similar to the idea of the product process tree model in the integrated scheduling. The integrated analysis of the complex large-scale product process trees usually requires a lot of computer resources and time-consuming, which affects the solving efficiency. Therefore, how to effectively pre-process large process trees becomes very important. The process tree pretreatment generally refers to the simplified decomposition operation [18–21]. It decomposes the process tree into multiple independent subtrees according to the specific rules, each subtree is solved independently, and the priority of the subtrees is set. The equipment sequence is used as the grouping to determine the process scheduling order. Finally, all the data information analyzed by the subtrees are recombined to obtain the solution target of the original process tree. This method considers the internal vertical and horizontal characteristic structure of the process tree and considers the overall character of the product process tree itself. To fully reflect the interior characteristics of the process tree, reduce the difficulty of decomposition of the process tree, and conform to the production rules of the product, the process scale of the decomposed components must reach a certain number. Therefore, the decomposition principle of the product process tree is to remove the root node, and splits the process tree into several Root-Subtrees to avoid splitting too many subtrees that are too small, which increases the difficulty of the integrated scheduling algorithm.

Figure 1: The schematic diagram of the product structure

To sum up, this paper presents an integrated scheduling algorithm for the same equipment process sequencing based on the Root-Subtree vertical and horizontal pre-scheduling (ISA-SEPS). Firstly, the algorithm takes component modules or part modules as the basic unit and uses the tree decomposition method of the distributed manufacturing thought to take out the root node. It splits the product process tree into several Root-Subtrees (component modules) to reduce the scale of the process tree. These operations are ready to analyze the vertical and horizontal characteristics of the product process tree. Then, all Root-Subtrees are traversed through the literature [9] with the best vertical scheduling effect “Dynamic Critical Path, Short Time” strategy to obtain the vertical pre-scheduling completion time and the literature [10] with the best horizontal pre-scheduling “Layer Priority, Short Time, Long Path” strategy is traversed to obtain the horizontal pre-scheduling completion time, and the vertical and horizontal pre-scheduling results are compared to determine the vertical and horizontal attributes of each Root-Subtree below the root node of the process tree. The selected pre-scheduling completion time determines the priority of each Root-Subtree, and solves the competition relationship between the Root-Subtree processes in the fusion scheduling process; At the same time, the equipment process pre-start time is obtained by analyzing the vertical and horizontal characteristics of the Root-Subtrees, with the aid of the equipment process pre-start time, the equipment sequence is used as a grouping to determine the scheduling and processing order of all Root-Subtree processes, the purpose of these operations is to solve the problem of the processing conflicts with the same equipment process in the horizontal direction, give full play to the advantages of the vertical and horizontal characteristics of the process tree, and enhance the process scheduling compactness. Finally, it is necessary to perform fusion processing on all Root-Subtree processes to produce a substantial scheduling plan to obtain the final solution, there is no doubt that there will definitely be a phenomenon that destroys the constraint relationship of the product process tree, the dynamic start processing time strategy of the equipment process is proposed to solve the problem of the vertical processing conflict of the process tree in the process of fusion scheduling of the processes, this strategy does not exist to find and compare equipment idle time periods, and will not produce chain reactions caused by the process movement. The proposed algorithm in this paper uses the vertical and horizontal characteristics of the Root-Subtree to enable the process to be processed as soon as possible and shorten the product processing time. So that the algorithm is suitable for the different product structure, and provides a new solution idea for solving the integrated scheduling problem of the complex products.

2  Problem Description and Analysis

2.1 Problem Description and Related Definitions

In the production and processing mode of the integrated scheduling, the complex product process tree model is a directed tree diagram composed of the processes, and these processes have a partial order relationship. The node in the process tree represents the processing or assembly process. There is a one-to-one correspondence between equipment and processes, the root node of the product process tree is the last process of the product processing. When it is finished, it means that the whole product processing and assembly is completed. This paper proposes an integrated scheduling system for the same equipment process sequencing base on the Root-Subtree vertical and horizontal pre-scheduling. The directed graph of the product process tree is divided into several Root-Subtrees by the tree decomposition method, the vertical and horizontal characteristics of each Root-Subtree are evaluated respectively, and based on satisfying the constraint partial order relationship of the process tree, the Root-Subtrees are fused to obtain the final solution, and a reasonable scheduling scheme is sought to reduce the length of the equipment idle time. Due to the parallel relationship between Root-Subtrees, during the fusion scheduling process, there will be a problem that the Root-Subtree processes compete for the processing equipment horizontally. If no reasonable method is found, it will affect the progress of the entire production task. This paper uses the Root-Subtree pre-scheduling strategy to mine the vertical and horizontal characteristics of all Root-Subtrees, determines the priority of each Root-Subtree, and then sorts all Root-Subtree processes by the equipment grouping to solve the horizontal conflict problem of the Root-Subtree processes. On this basis, the dynamic start processing time strategy of the equipment process determines the start processing time of all Root-Subtree processes, the scheduling results of all Root-Subtree process are saved. Getting back the root node produces the actual product process scheduling sequence, solves the vertical conflict problem of the Root-Subtree processes, and finally obtains a reasonable scheduling scheme, which minimizes the product processing completion time. In this paper, the related definitions are described as follows:

Definition 1, Root-Subtree set: The product process tree is divided into several Root-Subtrees by using the tree decomposition method of the graph.

Definition 2, Root-Subtree process set: All the processes in the Root-Subtree.

Definition 3, Vertical pre-scheduling completion time: Through algorithm ① in the literature [9] “Dynamic Critical Path, Short Time” strategy for the completion time of pre-scheduled processing for each Root-Subtree process set.

Definition 4, Horizontal pre-scheduling completion time: Through algorithm ② in the literature [10] “Layer Priority, Short Time, Long Path” strategy for the completion time of pre-scheduling processing for each Root-Subtree process set.

Definition 5, Aspect ratio of Root-Subtree: The ratio of the vertical pre-scheduling completion time to the time of horizontal pre-scheduling.

Definition 6, Virtual root node: If the in-degree of the root node (process) of the product process tree is not greater than 1, it is judged whether the in-degree of the immediately preceding process is greater than 1, and so on. The node with an in-degree greater than 1 is always found, and the node and its immediately following processes are merged to form a new root node.

Definition 7, Root-Subtree priority: During the fusion process, the parameters of the Root-Subtree process scheduling priority level are set from large to small according to the pre-scheduling completion time of the Root-Subtree, use Qrt1,Qrt2,⋯,QrtN from high to low, it indicates the priority of the Root-Subtree.

Definition 8, Equipment process pre-start time: In the analysis of the vertical and horizontal advantages of the Root-Subtree, the start processing time of each Root-Subtree process is obtained according to the selected pre-scheduling plan.

Definition 9, Non-schedulable process: The unprocessed process of the immediately preceding processes.

Definition 10, Scheduling process: The process group that has no immediately preceding processes or all immediately preceding processes have been scheduled.

Definition 11, Schedulable procedure set: The set of all schedulable processes.

2.2 Mathematical Model of the Problem

Assuming that an existing complex product process tree model has N Root-Subtrees, n processes, and m processing equipment, the product needs to meet the following constraints during the processing or assembly process:

1.    The processing time of each process on the processing equipment is determined and independent of other factors;

2.    Each processing equipment can process only one working process at the same time; Once processed, it cannot be interrupted;

3.    There is no equipment with the same function, which allows the processing equipment to wait idle;

4.    There is parallel processing characteristic between Root-Subtrees, there is no restriction relation of the process tree, but there is competition constraint on processing equipment;

5.    Each process must meet the constraints of the product process tree during the processing process, and it must be processed after all the immediately preceding processes have been processed;

6.    After the processes are completed, the processing equipment becomes idle, other dispatchable processes can occupy the equipment.

Under the above conditions, the mathematical model of the integrated scheduling scheme is described as Eqs. (1)–(6):

Cmax=min{max{Fij}},(i=1,2,3…,n;j=1,2,3…,m)(1)

s.t.min{Sij}(2)

Fij=Sij+Ti(3)

Si+1j≥Fij(4)

Sxy≥Fij,(x=1,2,3…,n;y=1,2,3…,m)(5)

VHCrtk=TZrtkTHrtk={>1=1<1(6)

Mathematical model, Cmax represents the maximum completion time of all the product processes, Sij represents the start processing time of the process i on the processing equipment j, Fij represents the completion time of the process i on the processing equipment j, Ti represents the process i continuous processing time, VHCrtk represents the Root-Subtree rtk aspect ratio, rtk is the k Root-Subtree of the product process tree (1≤k≤N), Tzrtk represents the vertical pre-scheduling completion time of the Root-Subtree rtk, THrtk represents the horizontal pre-scheduling completion time of the Root-Subtree rtk. The Eq. (1) is the optimization target of the integrated scheduling algorithm in this paper, that is, the product processing time is as short as possible; The Eq. (2) describes the early processing of each process under the constraints of the process tree; The Eq. (3) describes that the processing end time of the process i on the equipment j is equal to the sum of the processing start time and the continuous processing time for the process i, that is, the processing cannot be interrupted; The Eq. (4) indicates that the start processing time of any process must be greater than or equal to the finishing time of its immediately preceding processes; The Eq. (5) indicates that the processing start time of the post-processing process on the same processing equipment must be greater than or equal to the processing completion time of the processing equipment; The Eq. (6) is the Root-Subtree rtk aspect ratio, and the vertical and horizontal pre-scheduling scheme is selected according to the result.

3  Description and Analysis of Algorithm-Related Strategies

According to the above equation, the description of the proposed algorithm in this paper further explains the main idea of the integrated scheduling algorithm for the same equipment process sequencing base on the Root-Subtree vertical and horizontal pre-scheduling, that is, the process tree is split and merged, it fully mines the internal characteristics of the product process tree, so that each process can be processed as early as possible, optimizes and minimizes the maximum completion time target, and improves the process processing compactness and the efficiency of the solution. The algorithm in this paper can be divided into three steps: The first step is to split the complex product process tree into several Root-Subtrees; The second step is to traverse each Root-Subtree to find the aspect ratio of the Root-Subtree, and analyze the vertical and horizontal characteristics of each Root-Subtree, so as to obtain the Root-Subtree priority, and solve the horizontal equipment competition relationship of the Root-Subtree process in the fusion process; The last step is to use the sorting strategy of the equipment process pre-start time and the dynamic start processing time strategy of the equipment process to perform fusion scheduling for all Root-Subtree processes. In this way, an optimal scheduling algorithm from the whole→part→whole execution process is completed, which considers the internal structure of the product process tree instead of only the overall structure.

3.1 Analysis of the Root-Subtree Pre-Scheduling Strategy

3.1.1 Analysis of the Process Tree Decomposition Strategy

There is a complex product process tree model with N Root-Subtrees. To accurately analyze the vertical and horizontal characteristics of the product process tree, the root node is first taken out and stored in independent storage space. In the process of extracting the root node, it is necessary to reverse the order [22,23] to determine whether the root node is forked, that is, it judges whether the in-degree of the root nodes is greater than 1, if the root node has no bifurcated, then it determines whether there is a bifurcated in the immediately preceding process of the root node, cycle/loop judgment, and always it finds the first bifurcation process node, all processes from this node to the root node are merged into a virtual root node “VR”; According to the simplification principle of the algorithm, the process tree is split into several Root-Subtrees to form a Root-Subtree set, namely {rt1,rt2,rt3,⋯,rtN}.

3.1.2 Analysis of the Root-Subtree Priority Strategy

After the splitting process tree operation is completed, then all Root-Subtrees are traversed respectively by the algorithm ① and the algorithm ② to obtain the vertical pre-scheduling completion time and the horizontal pre-scheduling completion time, and then to obtain the corresponding Root-Subtree aspect ratio. In contrast, this scheduling is not a real production scheduling but only a reference to analyzing the vertical and horizontal characteristics of the process tree. According to the aspect ratio results, it is analyzed that the Root-Subtree has vertical or horizontal advantages. The priority of each Root-Subtree is determined at the same time, to solve the horizontal competition relationship between Root-Subtrees on the processing equipment, and do an excellent job for the subsequent resolution of the process selection conflicts foreshadowing, the choice of which pre-scheduling plan is most suitable directly affects the optimization goal. Because each Root-Subtree is a branch of the product process tree, each Root-Subtree has the same optimization goal as the product process tree itself, which is to minimize the maximum completion time and enhance the scheduling compactness of the process. Using this criterion, the vertical and horizontal advantage of the Root-Subtree is determined by comparing the pre-scheduling completion time of the algorithm ① and the algorithm ② that is, it chooses a scheduling scheme with a short pre-scheduling completion time, min{TZrtk,THrtk},1≤k≤N. At this point, in order to better describe the algorithm solving process and effectively reduce the comparison number of the algorithm, this paper uses the Eq. (6) as the objective function to analyze the vertical and horizontal characteristics of the Root-Subtree, which can be divided into the following three situations for discussion:

Situation 1, when TZrtk<THrtk, that is, VHCrtk<1, which represents the Root-Subtree rtk that has a vertical advantage. Using the algorithm ① to pre-schedule the Root-Subtree process is more compact, so TZrtk is selected as the reference time for setting the priority of the Root-Subtree rtk.

Situation 2, when TZrtk=THrtk, that is, VHCrtk=1, which represents the Root-Subtree rtk with vertical and horizontal balance characteristics, the pre-scheduling completion time TZrtk or THrtk is directly used as the reference time for setting the priority of the Root-Subtree rtk.

Situation 3, when TZrtk>THrtk, that is, VHCrtk>1, which represents the Root-Subtree rtk that has a horizontal advantage. Using the algorithm ② to pre-schedule the Root-Subtree process is more compact, so THrtk is selected as the reference time for setting the priority of the Root-Subtree rtk.

After the analysis of the vertical and horizontal characteristics of the Root-Subtree is completed, this paper uses the idea that the critical path of the product process tree has the greatest impact on the total processing time and that the critical path process is processed first. Compared with the critical path, the Root-Subtree is a branch of the product process tree, the critical path is only the longest path in the process tree. Therefore, using the Root-Subtree pre-scheduling completion time can better explain the lower limit of the product scheduling completion time, that is to say, the selected Root-Subtree with the longer pre-scheduling completion time has a more significant impact on the lower limit of the total product processing time, that is, the longer the pre-scheduling completion time, the higher the priority of the Root-Subtree in the process of fusion scheduling. If there are multiple Root-Subtrees with the same selected pre-scheduling completion time, it follows the principle that the more the number of the Root-Subtree processes, the higher is the priority for processing. The Root-Subtree priority strategy guarantees the flexibility of the Root-Subtree process scheduling, and takes priority to schedule the process of the Root-Subtree with high priority. The Root-Subtree priority strategy uses Qrt1=max{min{TZrt1,THrt1},…,min{TZrtN,THrtN}},…,QrtN=max{{min{TZrt1,THrt1},…,min{TZrtN,THrtN}}−Qrt1−⋯−QrtN−1} to determine the priority of each Root-Subtree, and provides a guarantee for solving the competition problem of the Root-Subtree processes, that is, to make preparations for determining the Root-Subtree process scheduling sequence on the same equipment horizontally.

3.2 Analysis of Fusion Conflict Adjustment Strategy of the Root-Subtree Process Set

3.2.1 Analysis of the Sorting Strategy of the Equipment Process Pre-Start Time

To complete the production scheduling task of a complex product, it is necessary to merge the Root-Subtree process set with the parallel relationships [24]. On the premise of satisfying the constraint relationship of the process tree, it seeks a reasonable scheduling processing sequence for the processes so that all processes can be processed as soon as possible and reduce the idle time of the processing equipment to obtain the final solution. In the process of fusion scheduling of the Root-Subtree processes, there will inevitably be a phenomenon of horizontal processing equipment competition, that is, multiple processes compete for the same processing equipment at the same time, therefore, based on analyzing the vertical and horizontal characteristics of the Root-Subtree, it needs to design the same equipment process conflict adjustment strategy, each process is scheduled in a predetermined order, and it uses the adjustment between the vertical and horizontal, and the equipment sequence is divided into groups to sort the Root-Subtree processes, to solve the problem of the process scheduling and the equipment resource competition. Through the Root-Subtree pre-scheduling strategy in Section 3.1, not only the Root-Subtree priority can be obtained, but also the start processing time of each Root-Subtree process can be determined according to the selected pre-scheduling plan, that is, the equipment process pre-start time. If the aspect ratio of the Root-Subtree VHCrtk=1, the start processing time of any pre-scheduling scheme (vertical or horizontal) is selected as the reference value for the equipment process pre-start time. In this paper, the processing equipment sequence is grouped, and each Root-Subtree process is sorted in ascending order using the equipment process pre-start time to determine the scheduling order. The Root-Subtree process with the highest order is prioritized, so that each Root-Subtree process can be processed as early as possible, giving full play to the vertical and horizontal advantages of the Root-Subtrees, which conforms to the concept of early processing and early end of integrated scheduling. When the Root-Subtree process set are sorted, grouping all Root-Subtree processes are grouped according to their corresponding equipment ID. Firstly, it considers the situation of two processes Pij,Pi+1j on the same equipment and where the corresponding equipment process pre-start time is respectively Sij,Si+1j:

Situation 1, if Sij>Si+1j, the process Pi+1j is ranked first and scheduled first;

Situation 2, if Sij<Si+1j, the process Pij is ranked first and scheduled first;

Situation 3, if Sij=Si+1j, this situation will only occur between different Root-Subtrees, the process with high Root-Subtree priority is scheduled first, the internal characteristics of the process tree are excavated so that subsequent processes can be converted into schedulable processes sooner, which avoids the waste of equipment resources.

The above analysis of the processing of two processes on only one equipment can be extended to the sorting processing of multiple equipment and multiple processes. Finally, the processing equipment is grouped to determine the scheduling processing sequence of the Root-Subtree processes.

3.2.2 Analysis of the Dynamic Start Processing Time Strategy of the Equipment process

In the scheduling process from the decomposition of the product process tree to the integration, the process scheduling needs to meet the constraints of both vertical and horizontal aspects: Horizontally, it must be satisfied that all the immediately preceding processes of the same equipment have been scheduled for processing; Vertically, it must be satisfied that all the immediately preceding processes of the process tree have been scheduled and processed. The sorting strategy of the equipment process pre-start time only solves the problem of the processing sequence of the same equipment process in the horizontal direction, so the dynamic start processing time strategy of the equipment process is proposed to solve the sequential constraint relationship of all processes in the process tree in the vertical direction [25,26]. With the scheduling and processing of equipment processes, according to the constraint relationship between the vertical and horizontal directions of the integrated scheduling, it is necessary to dynamically update the start processing time of the immediately following schedulable process of the same equipment, therefore, the Root-Subtree process is scheduled for processing, it is necessary to determine whether the start processing time of the Root-Subtree process is updated through the final processing completion time of all immediately preceding processes in the process tree, so as to make systematic adjustments in terms of maximum compactness, parallelization, and avoiding falling into the local optima. First, the processing equipment is grouped, and the schedulable processes with the highest sorting priority are determined by the sorting strategy of the equipment process pre-start time, according to the final processing completion time of the scheduled process of the same equipment, it initially determines the start processing time of the immediately following schedulable process of the same equipment. Then, according to the analysis of the vertical constraint relationship of the process tree, it judges whether it is necessary to update the start processing time of the process, and generate the actual scheduled processing operation of all Root-Subtree processes. Finally, it retrieves the root node for scheduling processing to complete the product process tree Scheduling processing tasks. To further explain the strategy better, it supposes there is a schedulable process Pij at a certain moment, the processing completion time of the immediately preceding process of the same equipment is Fi−1j, the immediately following process of the same equipment is Pi+1j, according to the processing completion time of the immediately preceding process scheduled for the same equipment, it is preliminarily determined that the start processing time Sij of the process Pij is equal to Fi−1j, at this time, it is necessary to judge whether the start processing time of the process Pij needs to be updated according to the specific situation, and determine the initial start processing time of the same equipment immediately following process Pi+1j. There are 4 situations as follows:

Situation 1, the process Pij does not have an immediately preceding process restricted by the process tree, which indicates that the process is independent, and there is no need to update the start processing time of the process Pij, and it is determined that the initial start processing time Si+1j of the immediately following process Pi+1j is equal to Sij+Ti.

Situation 2, the process Pij has the immediately preceding process Pxy constrained by the process tree and has been scheduled, the processing completion time of the process Pxy is Fxy, if Sij<Fxy, then the start processing time of the process Pij needs to be updated is Sij=Fxy, to meet the vertical constraints of the process tree, at the same time, It determines that the initial start processing time Si+1j of the process Pi+1j is equal to Fxy+Ti; If Sij≥Fxy, then there is no need to update the start processing time of the equipment process Pij, it determines that the initial start processing time Si+1j of the process Pi+1j is equal to Sij+Ti.

Situation 3, the process Pij has two or more immediately preceding processes {Pxy,Puv,…} that are constrained by the process tree and have been scheduled, the corresponding processing completion time is {Fxy,Fuv,…}, if Sij<max{Fxy,Fuv,…}, it is necessary to update the start processing time Sij of the process Pij is equal to max{Fxy,Fuv,…}; if Sij≥max{Fxy,Fuv,…}, then the start processing time Sij of the process Pij is not updated, after the process Pij is scheduled, it is determined that the initial start processing time of the immediately following process of the same equipment is the same as the situation 2 method.

Situation 4, the process Pij has the immediately preceding process Pxy constrained by the process tree, but the process Pxy is not scheduled for processing, it indicates that the process Pij is a non-schedulable process, and there is no need to update the start processing time Sij of the process Pij. It has been waiting for the immediately preceding process Pxy constrained by the process tree to be scheduled and processed, and then according to situation 1 or situation 2 for the analysis.

4  Algorithm Strategy Design and Complexity Analysis

4.1 Algorithm Strategy Design

Aiming at the complex product integrated scheduling problem with the internal characteristics of the product process tree, this paper uses the Root-Subtree pre-scheduling strategy to split the process tree into several Root-Subtrees and set the priority for each Root-Subtree. On this basis, through the Root-Subtree process set fusion conflict adjustment strategy, the equipment sequence is grouped as the Root-Subtree process set for sorting, and the start processing time of the process is adjusted to produce a substantial scheduling plan. The specific steps of the integrated scheduling algorithm for the same equipment process sequencing based on the Root-Subtree vertical and horizontal pre-scheduling are as follows:

Step 1: Perform data information processing on the complex product model to form a standardized integrated scheduling process tree model; Establish a schedulable process set, and add all schedulable processes in the product process tree to the schedulable process set.

Step 2: According to the simplified pretreatment principle and the process tree decomposition strategy, the root node is taken out and stored in independent storage space, and the process tree is split into several Root-Subtrees to form a Root-Subtree set {rt1,rt2,rt3,…,rtN}.

Step 3: Perform pre-scheduling for each Root-Subtree through the algorithm ① and the algorithm ② and use the pre-scheduling results to obtain the aspect ratio VHCrtk of the Root-Subtree rtk, and analyze the vertical and horizontal characteristics of each Root-Subtree through the aspect ratio, and select a scheduling scheme with a short pre-scheduling completion time. If the pre-scheduled completion time of multiple Root-Subtrees is the same, the number of each Root-Subtree process is calculated and compared. The Root-Subtree with more processes has a higher priority; If the number of the Root-Subtree processes is also the same, then set the priority of such Root-Subtrees by following per under the naming order of the Root-Subtrees.

Step 4: Determine the priority of the Root-Subtree according to the selected pre-scheduling scheme, sort all Root-Subtrees from high to low using the bubble sorting method, and obtain the equipment process pre-start time at the same time. If there are multiple Root-Subtrees with the same pre-scheduled completion time, the priority is determined by the number of the Root-Subtree processes from more to less.

Step 5: All processes are grouped according to the corresponding equipment sequence M1,M2,…,Mm, and the scheduling sequence of the same equipment processes is obtained according to the sorting strategy of the equipment process pre-start time, to solve the process conflict problem of the same equipment in the horizontal direction.

Step 6: Set the processing equipment stack {Stack1,Stack2,…,Stackm}, and put the same equipment processes into the stack from low to high according to the scheduling order obtained in Step 5, that is, the stack-top processes are the process with the highest order. The product start processing time is 0, and the start processing time of the stack-top processes is 0.

Step 7: Judge whether all stacks are empty, if yes, go to Step 11, otherwise go to Step 8.

Step 8: Judge whether the stack-top process is a schedulable process through the schedulable process set. If no, the start processing time of the process is not updated, and the stack-top process is in the waiting stage without being ejected. If yes, the dynamic start processing time strategy of the equipment process is used to determine the start processing time Sij and the processing completion time Fij of the stack-top process, and the stack-top process is unstacked and loaded onto the corresponding equipment for processing.

Step 9: Delete the scheduled processes from the schedulable process set, and add the new schedulable processes to the schedulable process set.

Step 10: Determine the initial start processing time Si+1,j=Fi,j of the current stack-top process of the same equipment through the processing completion time of the process in Step 8, and then go to step (7).

Step 11: Save the results of the essential scheduling sequence of the Root-Subtree process set.

Step 12: Based on the previous Step 11, the root node of the process tree extracted in Step 2 is added to the actual scheduling sequence, and finally the scheduling result of the entire production process tree is formed.

Step 13: Output the Gantt chart according to the scheduling result of the entire production process tree in Step 12.

The proposed algorithm flow chart in this paper is shown in Fig. 2.

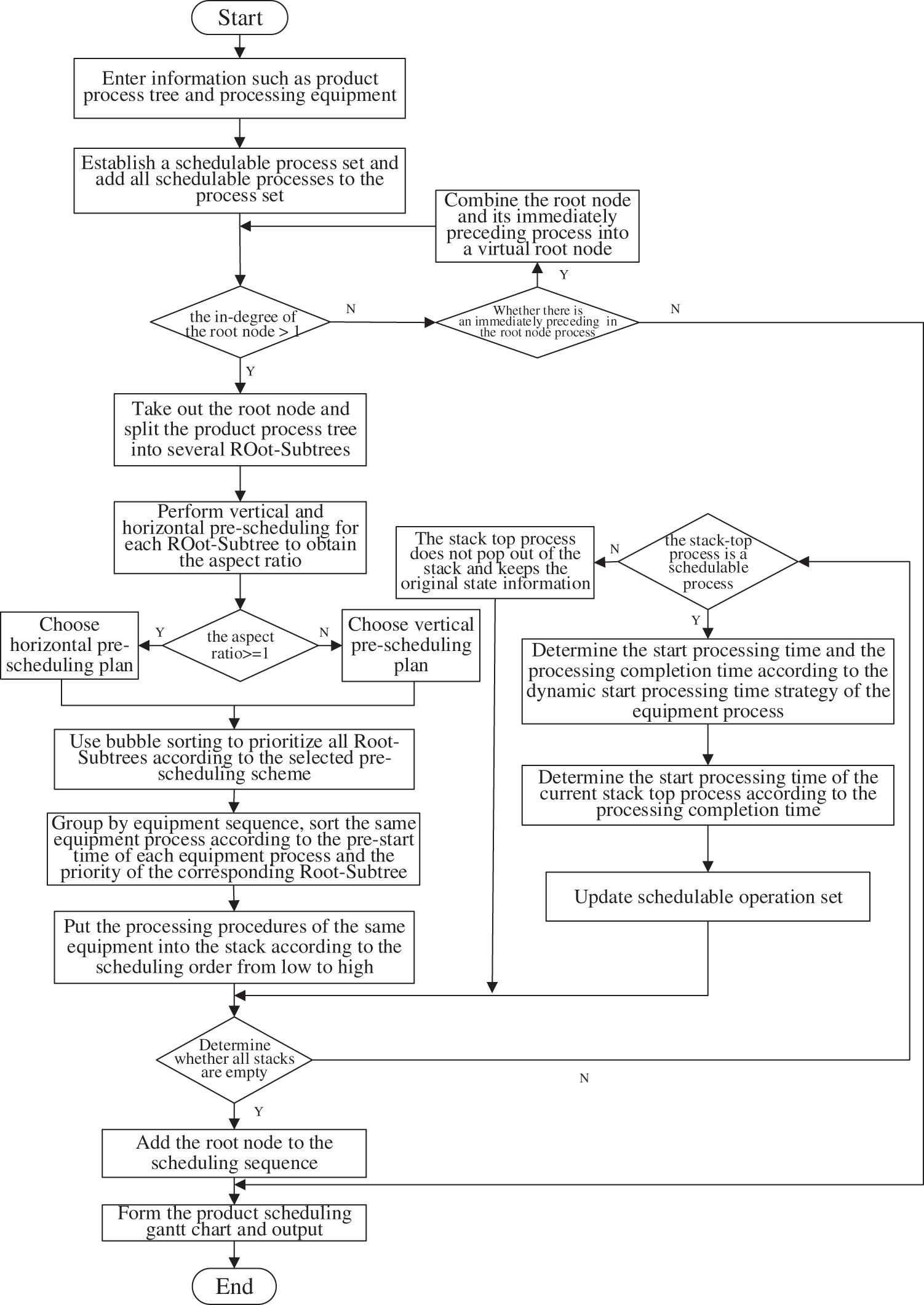
Figure 2: The proposed algorithm flow chart

4.2 Algorithm Complexity Analysis

Assuming that the number of the complex product processes is n, the number of the equipment is m, the number of the Root-Subtrees is N, and the number of the processes in the virtual root node is r. The core of the proposed algorithm is to sort all Root-Subtree processes in equipment sequence grouping, and compactly schedule all processes according to the vertical and horizontal characteristics of the Root-Subtrees. On this basis, the dynamic start processing time strategy of the equipment processes is used to determine the start processing time of each process, which does not require interlocking operations such as inserting, stretching, and moving, thereby reducing the complexity of the algorithm operation. The specific analysis of the entire scheduling process through the above strategy is as follows.

4.2.1 Process Tree Decomposition Strategy

In simplifying and splitting the process tree, it is necessary to reverse the order to determine whether the root node of the process tree has a bifurcation. If so, the root node is directly taken out; if there is no bifurcation, the root node and the immediately preceding process are merged into a virtual root node, cyclically analyze whether there is a bifurcation in the immediately preceding process of the virtual root node. The worst case is that except for a leaf node, the remaining n−1 processes have no forks. Therefore, the complexity of establishing a virtual root node is O(n), taking out the virtual root node and splitting the process tree to form multiple Root-Subtrees is O(1). Therefore, the complexity of merging virtual root node and splitting the process tree is O(n).

4.2.2 Root-Subtree Priority Strategy

The average number of the processes for each Root-Subtree is n−rN, the algorithm ① is used to pre-schedule all Root-Subtrees to get the complexity of the vertical pre-scheduling completion time is N×O((n−rN)2) and the algorithm ② is used to pre-schedule all Root-Subtrees to get the complexity of the horizontal pre-scheduling completion time is N×O((n−rN)2); Through the aspect ratio analysis result, it is determined that the complexity of the selected pre-scheduling scheme is O(N); The complexity of using the pre-scheduled completion time to set the priority of the Root-Subtree is O(N2). In the actual production scheduling process, due to n≫N and n≫r, the complexity of setting the priority of the Root-Subtree is N×O((n−rN)2), that is O(n2).

4.2.3 Sorting Strategy of the Equipment Process Pre-Start Time

The complexity of grouping all Root-Subtree processes with the corresponding processing equipment is O(n), since the average number of each Root-Subtree process is n−rN, according to the equipment process pre-start time, the complexity of the scheduling sequence of the same equipment process is determined to be O((n−rN)2). Therefore, in the horizontal direction, the complexity of determining the process scheduling order by grouping the equipment sequence and pushing the process into the stack in reverse order is O(n2).

4.2.4 Dynamic Start Processing Time Strategy of the Equipment Process

According to the dynamic start processing time strategy of the equipment process, it is necessary to establish and update the schedulable process set. The complexity of finding the current schedulable processes in the process tree for any equipment is O(n2). It determines whether the process of the stack-top is a schedulable process through the schedulable process set, since the number of the schedulable processes for each equipment is at most n−rm, in the worst case, it needs to compare n−rm times, therefore, the complexity of judging whether the stack-top process performs the pop-up operation is O(n−rm). The stack-top process carries out the stack operation and loads it to the corresponding equipment for processing, it needs to meet the constraints of the process tree in the vertical direction, since the scheduled processes are at most n−r−1, the worst case is the complexity of judging whether there is an immediately preceding process and whether to update the start processing time is O(n−r−1). The complexity of fetching the virtual root node and adding it to the scheduling sequence is O(1). Therefore, the complexity of determining the start processing time of the process is O(n2).

The proposed algorithm in this paper involves 4 main strategies, all strategies are connected in series, so the complexity of the algorithm is the sum of the complexity of each strategy. In summary, the complexity of the proposed algorithm is a quadratic polynomial O(n2).

5  Example Analysis and Comparison

5.1 Example Analysis

The proposed algorithm is a theoretical analysis process of the integrated scheduling, which is not based on a specific instance. To facilitate readers to understand the algorithm, and it reflects the universality of the algorithm and evaluates the performance of the algorithm, the following is an example for analysis and comparison. We suppose that a manufacturing company plans to complete an order and record it as the product H, consisting of 22 processes and requiring three processing equipment. The process tree is shown in Fig. 3, each node contains three kinds of data information: the process name, the processing equipment name, and the processing time, in which the unit of the processing time is working hours.

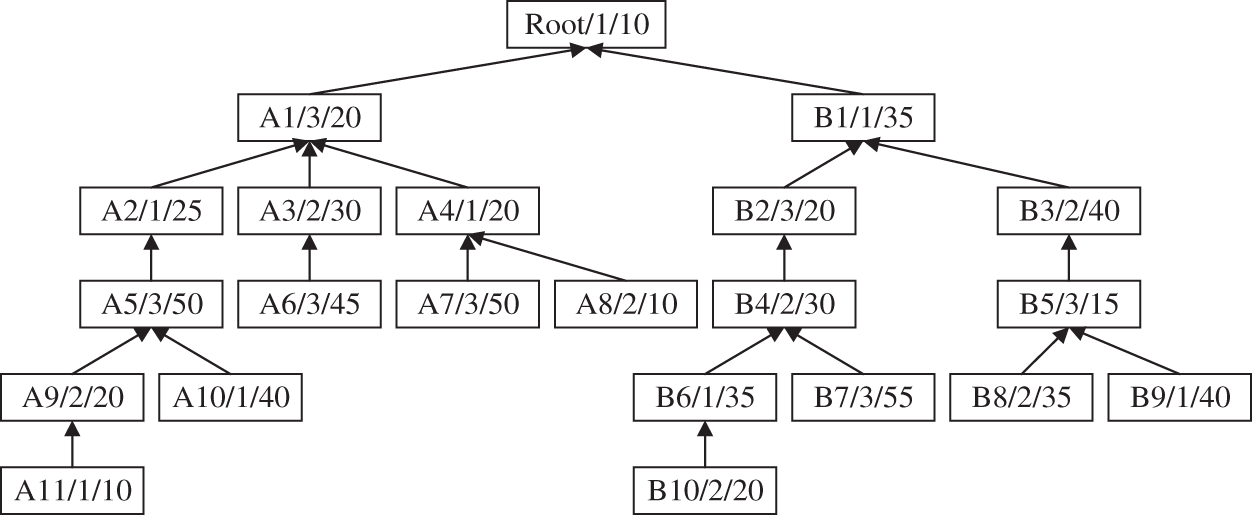
Figure 3: The product process tree H

Firstly, according to the characteristics of the process tree structure of the product H, the process tree decomposition strategy is used to take out the root node “Root”, store it in an independent space, and split the process tree to form two Root-Subtrees, namely rt1 and rt2. The splitting schematic diagram of the process tree of the product H is shown in Fig. 4.

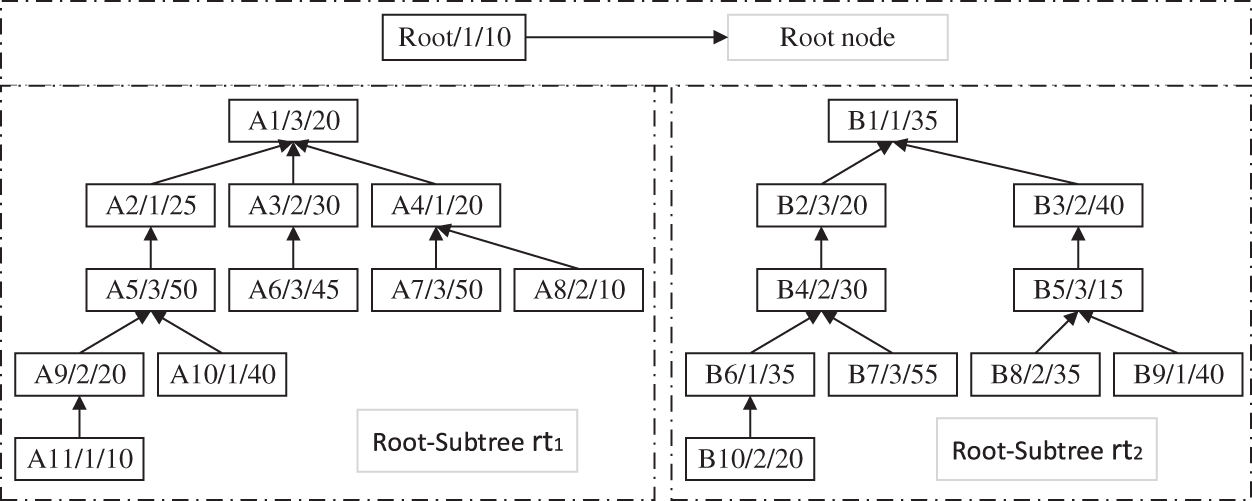
Figure 4: The splitting schematic diagram of the process tree of the product H

Secondly, the algorithm ① and the algorithm ② are used to respectively traverse and pre-schedule each Root-Subtree of the product H, and then obtain the vertical pre-scheduling completion time TZrtk and horizontal pre-scheduling completion time THrtk corresponding to the Root-Subtree, the pre-scheduled Gantt chart of the Root-Subtree rt1 and rt2 is shown in Figs. 5 and 6. The pre-scheduled result is used to calculate the Root-Subtree aspect ratio VHCrtk, and the pre-scheduling scheme is selected based on the aspect ratio result and the priority of the Root-Subtree is set. From Figs. 5 and 6, it can be seen that the Root-Subtree rt1 has horizontal advantages, and the algorithm ② pre-scheduling scheme is selected; The Root-Subtree rt2 has vertical advantages, and the algorithm ① pre-scheduling scheme is selected. To visually describe the analysis of the vertical and horizontal characteristics of the Root-Subtree rt1 and rt2, the specific process of setting the priority of the Root-Subtree rt1 and rt2 is shown in Table 1.

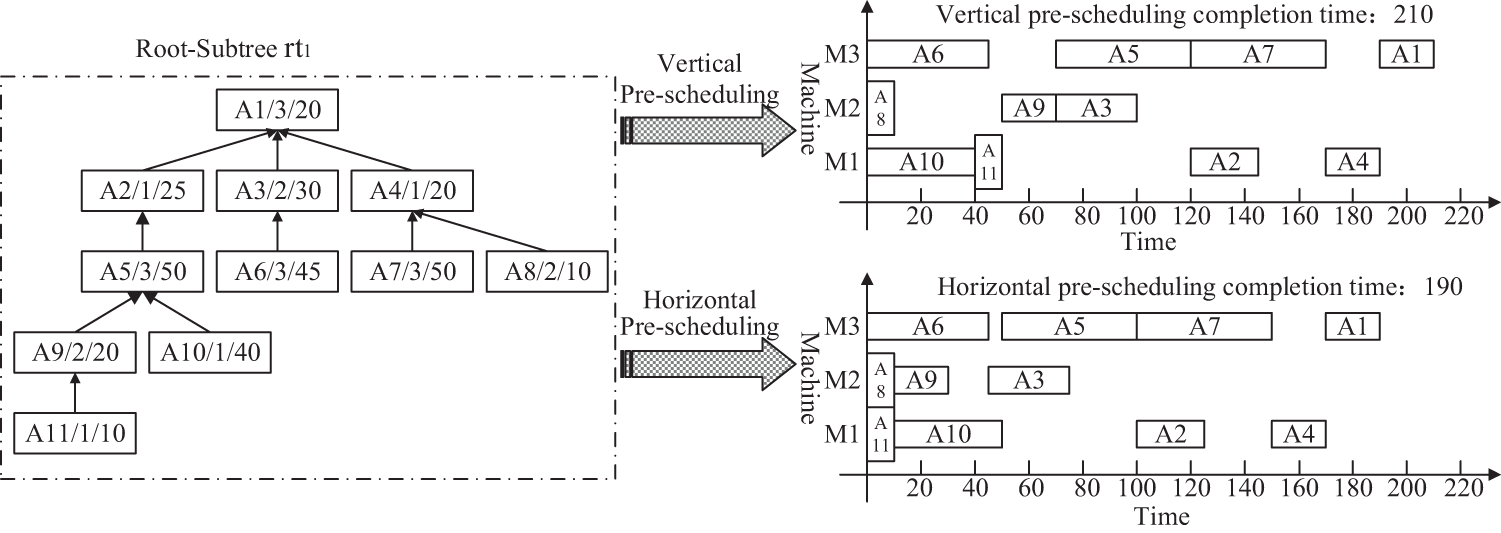
Figure 5: The vertical and horizontal comparison pre-scheduling Gantt chart of Root-Subtree rt1

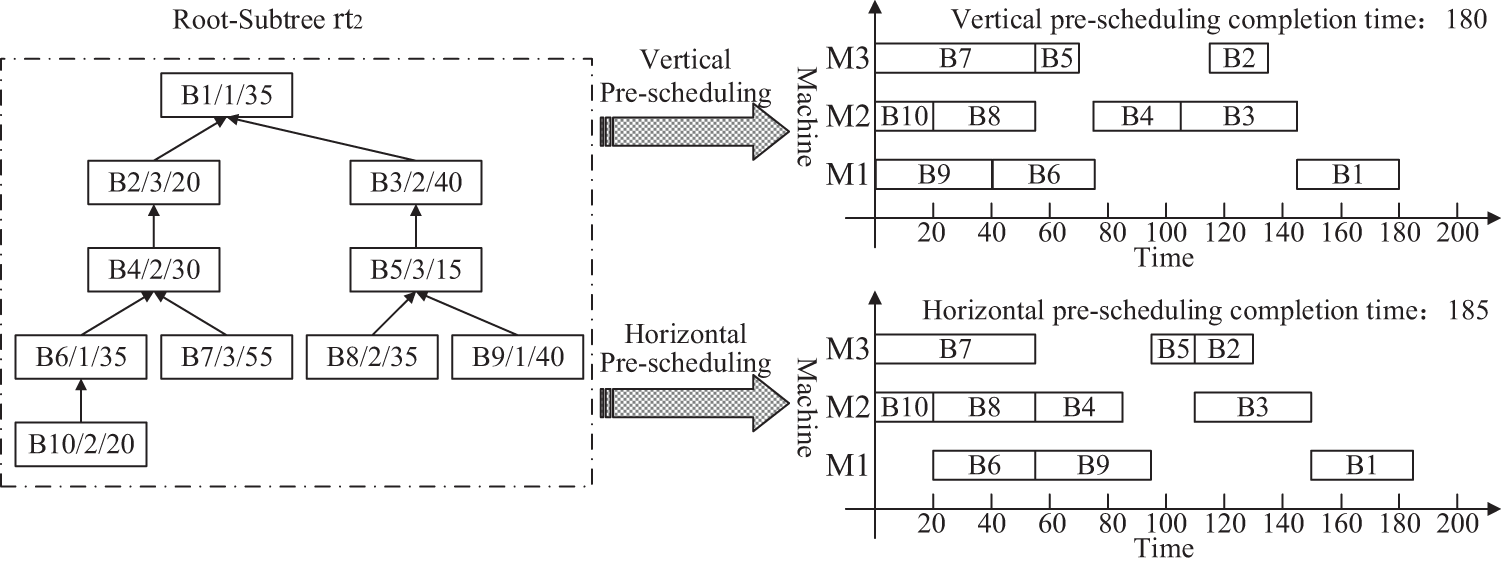
Figure 6: The vertical and horizontal comparison pre-scheduling Gantt chart of Root-Subtree rt2

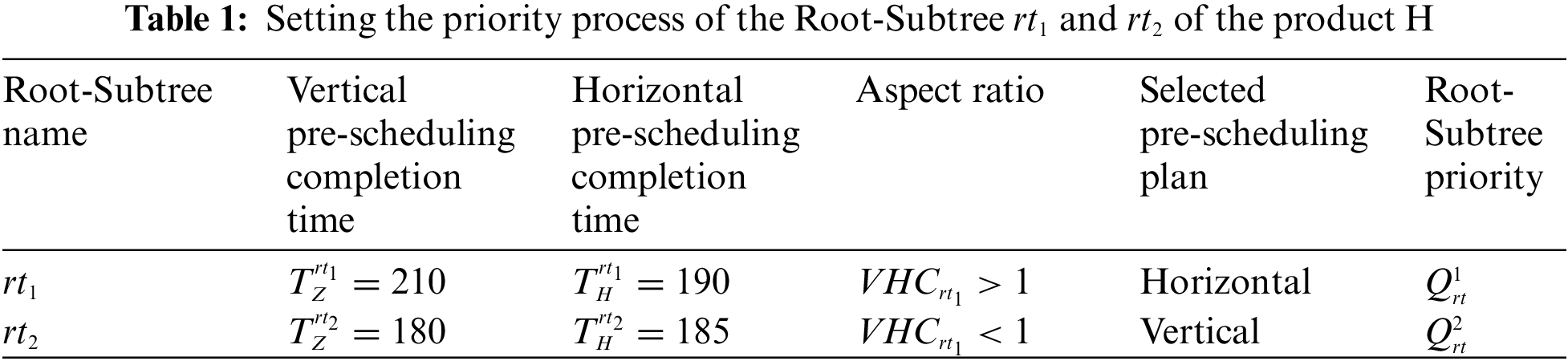
Thirdly, it determines the equipment process pre-start time of all Root-Subtree processes through the selected pre-scheduling scheme in Table 1, and the processes are grouped according to the processing equipment sequence M1, M2 and M3, M1:{A11:0, A10:10, A2:100, A4:150, B9:0, B6:40, B1:145}, M2:{A9:10, A8:0, A3:45, B10:0, B8:20, B4:75, B3:105}, M3:{A7:100, A6:0, A5:50, A1:170, B7:0, B5:55, B2:105}, the Root-Subtree priority strategy and the sorting strategy of the equipment process pre-start time are used to sort all Root-Subtree processes to solve the processing conflict problem of the same equipment process. The sorting process of all Root-Subtree processes grouped by the equipment sequence is shown in Table 2.

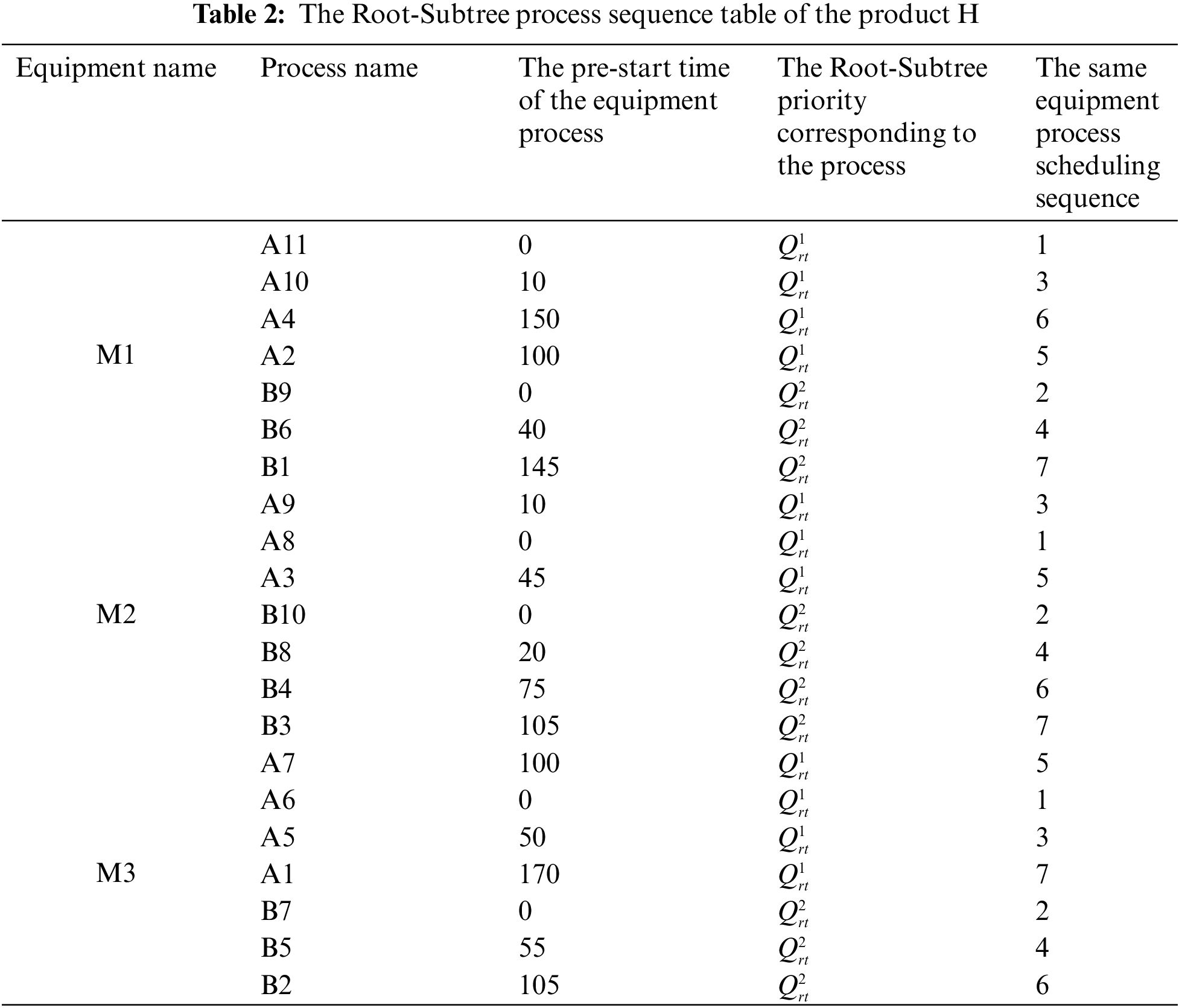
Fourth, the same equipment processes are sequentially pressed into the processing equipment stacks {Stack1,Stack2,Stack3} according to the scheduling order obtained in Table 3, and the stacking order of the Stack1 is B1, A4, A2, B6, A10, B9, A11, and the stacking order of the Stack2 is B3, B4, A3, B8, A9, B10, A8, and the stacking order of the Stack3 is A1, B2, A7, B5, A5, B7, A6. The start-up time of the processing equipment is 0, the schedulable process set at the current moment is {A11, A10, A6, A7, A8, B10, B7, B8, B9}, and the stack-top processes A11, A8 and A6 are the schedulable process and there is no immediately preceding process, that is, the start processing time is 0. The processes A11, A8, and A6 are unstacked and loaded onto the equipment for processing, and the processing completion time FA11,1=10,FA8,2=10,FA6,3=45 corresponding to the processes is obtained. After the first scheduling is completed, according to the dynamic start processing time strategy of the equipment process, the initial start processing time of the new stack-top processes B9, B10 and B7 are SB9,1=FA11,1=10,SB10,2=FA8,2=10,SB7,3=FA6,3=45, through the updated schedulable process set is {A10, A7, A9, A3, B10, B7, B8, B9}, it can be determined that the stack-top processes B9, B10, and B7 are schedulable. There is no immediately preceding process, so the start processing time of the stack-top processes B9, B10, and B7 does not need to be updated, and they are directly out of the stack and processed according to the determined start processing time. After the second scheduling is completed, the schedulable process set is {A10, A7, A9, A3, B6, B8}, the initial processing time of the stack-top processes A10, A9 and A5 are SA10,1=FB9,1=50,SA9,2=FB10,2=30,SA5,3=FB7,3=100, the process A5 is an non-schedulable process, and does not update the start processing time and unstack operations, the processes A10 and A9 are schedulable processes, the process A10 has no immediately preceding processes, and there is no need to update the start processing time, the process A9 has the immediately preceding process A11 and SA9,2>FA11,1, so there is no need to update the start processing time, therefore, the stack-top processes A10 and A9 are removed from the equipment stack and processed according to the determined start processing time. When the immediately preceding processes A9 and A10 of the process A5 are scheduled and processed, the processing completion time of the processes A9 and A10 are respectively FA9,2=50 and FA10,1=90, at this time, the process A5 becomes a schedulable process, and its initial start processing time SA5,3>max(FA9,2,FA10,1), that is, the start processing time of the process A5 does not need to be updated, and it is directly out of the stack for processing. If there is a stack-top process whose initial start processing time is less than its immediately preceding process completion time, it needs to update its start processing time. For example, the initial start processing time of the process B4 is SB4,2 = 115, and the processing completion time of its immediately preceding process B6 and B7 are respectively FB6,1=125 and FB7,3=100, since the initial processing time of the process B4 is SB4,2<max(FB6,1,FB7,3), then the start processing time of the process B4 is updated to SB4,2=125, and the process B4 is popped for processing. Repeating the above operation, the dynamic start processing time strategy of the equipment process is used, until the start processing time of all Root-Subtree processes is determined and scheduled to solve the problem of the process conflicts constrained by the process tree and complete the fusion operation of the Root-Subtree processes. According to the dynamic start processing time strategy of the equipment process, the start processing time of the Root-Subtree processes of the product H is shown in Table 3.

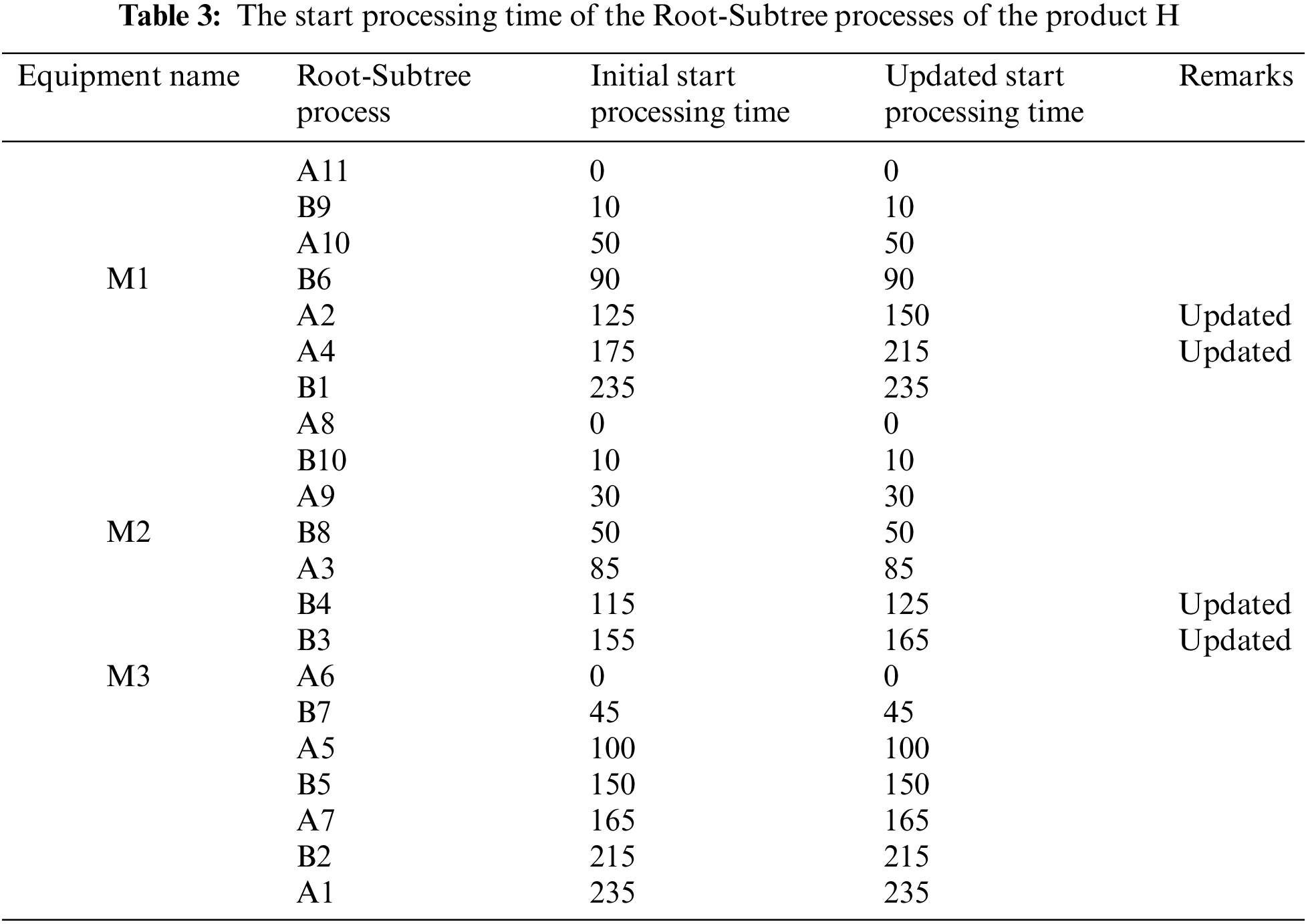
Finally, retrieving the root node “Root” to enter the scheduling sequence to form the actual scheduling plan of the product H and complete the product production scheduling task. The Gantt chart of the scheduling product H using the proposed algorithm is shown in Fig. 7.

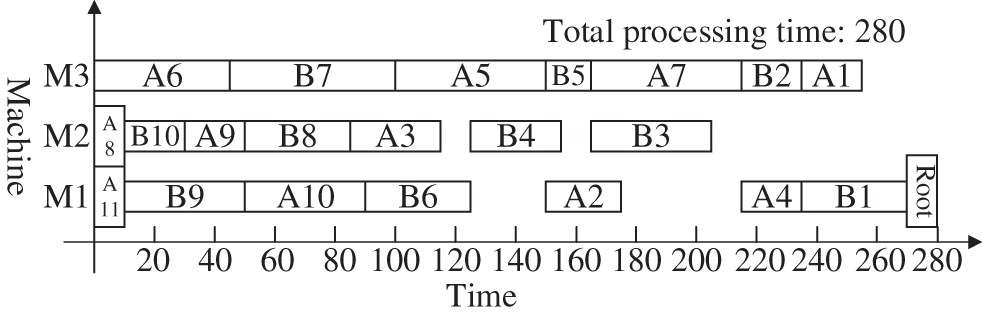
Figure 7: The Gantt chart of the scheduling product H generated by the proposed algorithm

The following uses DCPM, DJSSA and ISA-CPTS to schedule the product H and analyze the scheduling results to illustrate the superiority of the proposed algorithm further. The Gantt chart of DCPM for the overall scheduling of the process tree H mainly in the vertical direction is shown in Fig. 8, the Gantt chart of DJSSA for the overall scheduling of the process tree H mainly in the horizontal direction is shown in Fig. 9, and the Gantt chart of ISA-CPTS for the scheduling of the product process tree H through search and iteration is shown in Fig. 10. From Figs. 7–10, it can be seen that the total product scheduling completion time of the proposed algorithm (ISA-SEPS) is 280, the total product scheduling completion time of DCPM is 290, the total product scheduling completion time of DJSSA is 315, and the total product scheduling completion time of ISA-CPTS is 285. Comparing the scheduling results of DCPM, DJSSA, ISA-CPTS, and ISA-SEPS, it can be seen that ISA-SEPS fully explores the characteristics of the vertical and horizontal structure of the product process tree without increasing the complexity of the algorithm. The production target can be better optimized based on the comprehensive consideration of the horizontal equipment constraints and the vertical process tree constraints in the integrated scheduling process. The main reason is that DCPM and DJSSA both analyze and schedule the process tree as an overall, solidifying the scheduling sequence of certain processes, which delays the processing time of other processes related to it. It is easy to cause idle periods for processing equipment, which leads to poorer compactness between processes, for example, in the scheduling process of DCPM, the dynamic critical path length of the process B9 is 130, and the dynamic critical path length of the process A11 is 125. The “Dynamic Critical Path, Short Time” strategy is used to prioritize the scheduling of the process B9 on the equipment M1, and then schedule the process A11. This scheduling method will cause the subsequent processes A9 and A5 of the process A11 to be delayed, resulting in idle periods on the equipment M3. The proposed algorithm excavates the internal characteristics of the product process tree, when the equipment process pre-start time is the same, according to the Root-Subtree priority strategy, it is determined that the process A11 is scheduled earlier than the same equipment process B9, therefore, the process A9 and the subsequent process A5 can be scheduled as soon as possible, so that no idle time period is generated on the equipment M3; In the scheduling process of DJSSA, the process B5 and A5 have the same priority, and the processing time of the process B5 is shorter than the processing time of the process A5, the “Layer Priority, Short Time, Long Path” strategy is used to prioritize the scheduling of the process B5 on the equipment M3, Which is earlier than the same equipment process A5, which also leads to idle time periods on the equipment M3, however, when the equipment process pre-start time is the same, the Root-Subtree priority strategy of the proposed algorithm is used to determine that the process A5 is processed on the equipment M3 earlier than the same equipment process B5, which avoids the idle time period on the equipment M3; ISA-CPTS searches the product process tree model as a whole, resulting in slow solution efficiency, and it is easy to fall into a local optimum, which limits the scope of the solution space and affects the overall scheduling effect of the product. The above description further illustrates the necessity of analyzing the internal structure of the product process tree in the integrated scheduling process. According to the analysis of the vertical and horizontal characteristics of the Root-Subtree, the most suitable plan is selected to make the scheduling result of the product process tree better and enhance the adaptability of the algorithm to the products of different structures, which reflects the feasibility and superiority of ISA-SEPS in the actual production scheduling.

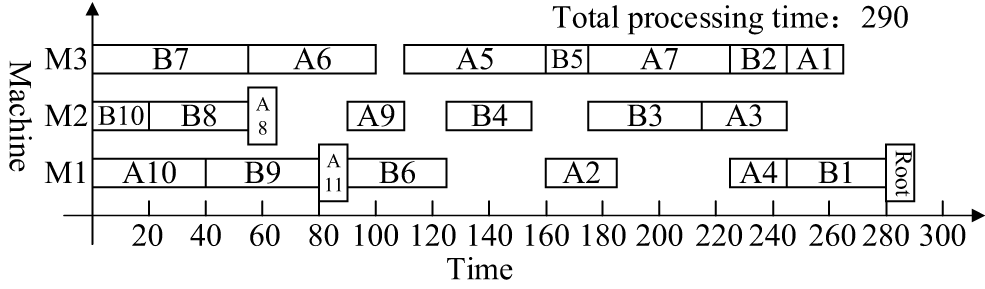
Figure 8: The Gantt chart of the scheduling product H generated by DCPM

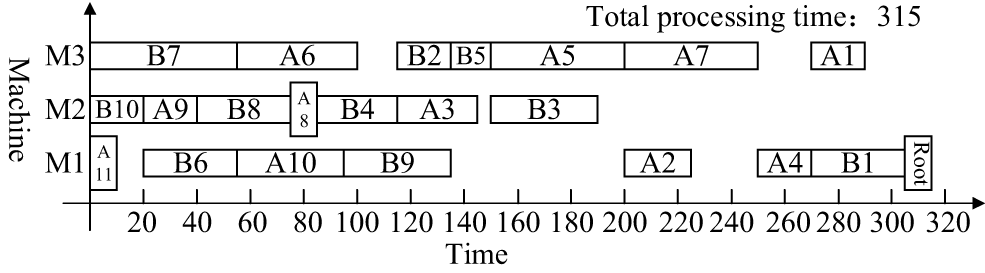
Figure 9: The Gantt chart of the scheduling product H generated by DJSSA

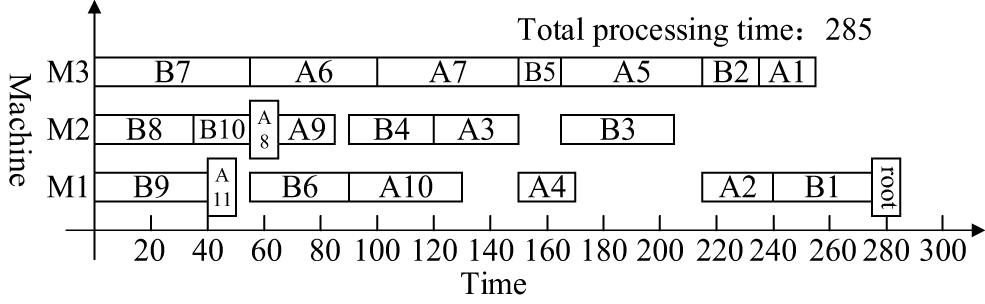
Figure 10: The Gantt chart of the scheduling product H generated by ISA-CPTS

5.2 Experimental Comparison

In order to verify the effectiveness of ISA-SEPS and its adaptability to products with different structures, this paper randomly selects 50 product models with different structures, the selected product instances were used for scheduling analysis using DCPM, DJSSA, ISA-CPTS and ISA-SEPS. The specifications of all process tree model parameters are as follows: the number of the process is [20,50], the number of immediately preceding processes of each process is [0,5], the number of the Root-Subtree is [2,5], and the number of the processing equipment is [3,5], the process processing time is [10,60]. Fig. 11 depicts the comparison of the scheduling results between DCPM, DJSSA, ISA-CPTS and ISA-SEPS for 50 product instances. Fig. 12 depicts the comparison of the average processing time to schedule 50 product instances by above four algorithms. The X-axis represents product instances, and the Y-axis represents the total processing time. The closer to the X-axis, the better the scheduling results. It can be seen from Figs. 11 and 12 that, except the three scheduling results of a product in-stance with a special structure are the same, the scheduling results of ISA-SEPS are better than the scheduling results of DCPM, DJSSA and ISA-CPTS, and it is better applicable to the different structure products.

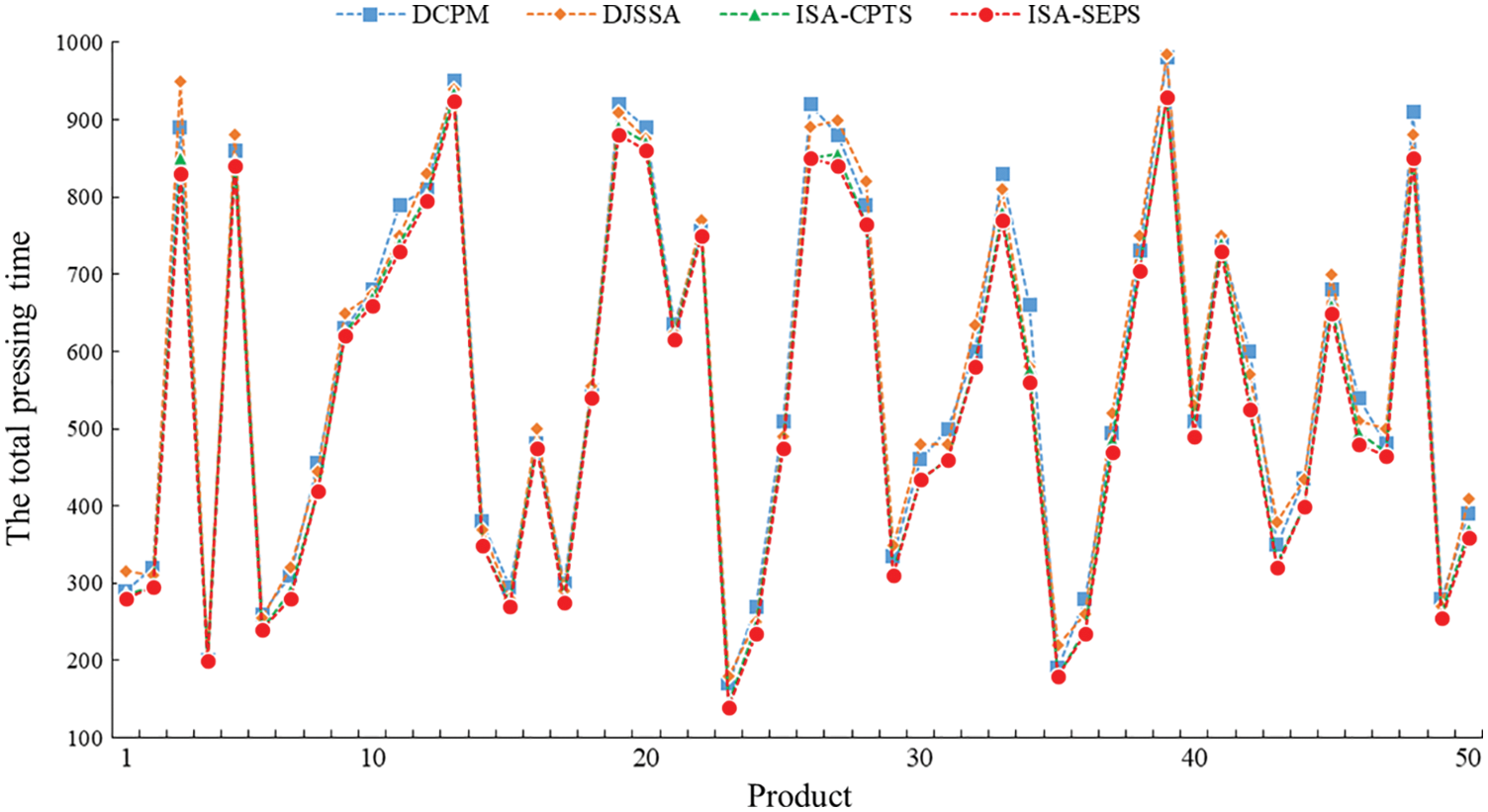
Figure 11: Comparison of the scheduling results between DCPM, DJSSA, ISA-CPTS and ISA-SEPS

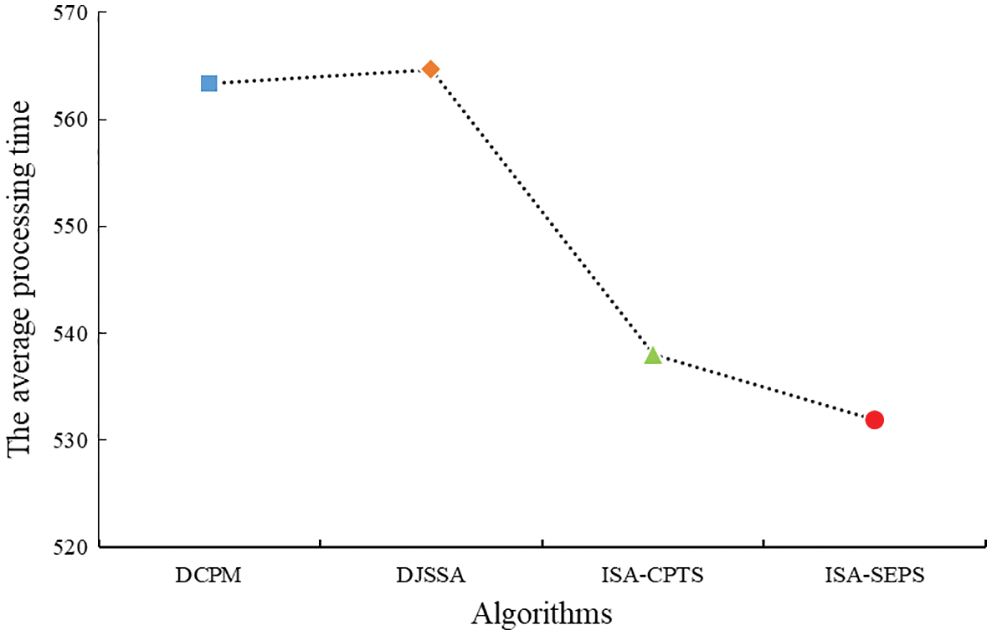
Figure 12: Comparison of the average processing time to schedule 50 product instances by above four algorithms

6  Conclusion

In the field of the integrated scheduling, this paper proposes for the first time an integrated scheduling algorithm for the same equipment process sequencing base on the Root-Subtree vertical and horizontal pre-scheduling. According to the decomposition principle of the product process tree, the process tree is split into several Root-Subtrees, and the vertical and horizontal characteristics of each Root-Subtree are excavated through the pre-scheduling method. On this basis, the sorting strategy of the equipment process pre-start time is used to sort the Root-Subtree process set with the processing equipment sequence as the grouping to solve the horizontal constraint relationship with the same equipment, at the same time, the dynamic start processing time strategy of the equipment process is used to solve the constraint relationship of the vertical process tree, thereby completing an optimized scheduling process considering the internal structure of the product process tree. The test results show that the proposed algorithm is better than the traditional integrated scheduling algorithm for scheduling processes as a whole. It has the following characteristics: (1) It has better adaptability to product instances of different structures; (2) It excavates the vertical and horizontal characteristics of the product process tree, enhances the compactness of equipment process scheduling, and conforms to the principle of early processing and early termination; (3) The scheduling process has better flexibility and reduces the idle time of the processing equipment. In summary, the proposed algorithm ideas can provide a reasonable scheduling scheme for the product process trees with different structural, and expand a new direction for in-depth study of integrated scheduling problems. In addition, the proposed algorithm can be further applied to the field of the dynamic integrated scheduling, so the algorithm has certain theoretical and practical significance.

Funding Statement: This work was supported by the National Natural Science Foundation of China [Grant No. 61772160].

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Wang, L., Pan, Z. X. (2020). Scheduling optimization for flow-shop based on deep reinforcement learning and iterative greedy method. Control and Decision, 10(3), 1–9. DOI 10.3390/machines10030210. [Google Scholar] [CrossRef]

 2.  Qin, W., Zhang, J., Song, D. (2018). An improved ant colony algorithm for dynamic hybrid flow shop scheduling with uncertain processing time. Journal of Intelligent Manufacturing, 29(4), 891–904. DOI 10.1007/s10845-015-1144-3. [Google Scholar] [CrossRef]

 3.  Gruzlikov, A. M., Kolesov, N. V., Skorodumov, I. M., Tolmacheva, M. V. (2017). Using solvable classes in flowshop scheduling. The International Journal of Advanced Manufacturing Technology, 88(5–8), 1535–1546. DOI 10.1007/s00170-016-8828-5. [Google Scholar] [CrossRef]

 4.  Wang, L., Wang, J. J., Wu, C. G. (2018). Advances in green shop scheduling and optimization. Control and Decision, 33(3), 385–391. DOI 10.13195/j.kzyjc.2017.0215. [Google Scholar] [CrossRef]

 5.  Peter, B., Yu, N., Sotskov, F. W. (2007). Complexity of shop-scheduling problems with fixed number of jobs: A survey. Mathematical Methods of Operations Research, 65(3), 461–481. DOI 10.1007/s00186-006-0127-8. [Google Scholar] [CrossRef]

 6.  Brucker, P., Jurisch, B., Sievers, B. (1994). A branch and bound algorithm for the job-shop scheduling problem. Discrete Applied Mathematics, 49(1–3), 107–127. DOI 10.1016/0166-218X(94)90204-6. [Google Scholar] [CrossRef]

 7.  Xie, Z. Q., Zhang, L., Yang, J. (2010). Integrated scheduling algorithm of complex product based on scheduling long-path. Computer Science, 37(2), 150–153. DOI 10.1088/1742-6596/1748/3/032030. [Google Scholar] [CrossRef]

 8.  Xie, Z. Q., Liu, S., Qiao, P. (2003). Dynamic job-shop scheduling algorithm based on ACPM and BFSM. Journal of Computer Research and Development, 40(7), 977–983. [Google Scholar]

 9.  Xie, Z. Q., Yang, J., Zhou, Y., Zhang, D. L., Tan, G. Y. (2011). Dynamic critical paths multi-product manufacturing scheduling algorithm based on operation set. Chinese Journal of Computers, 34(2), 406–412. DOI 10.3724/SP.J.1016.2011.00406. [Google Scholar] [CrossRef]

10. Xie, Z. Q., Yang, J., Yang, G., Tan, G. Y. (2008). Dynamic job-shop scheduling algorithm with dynamic set of operation having priority. Chinese Journal of Computers, 31(3), 502–508. DOI 10.3724/SP.J.1016.2008.00502. [Google Scholar] [CrossRef]

11. Xie, Z. Q., Zhang, X., Xin, Y., Yang, J. (2018). Time-selective integrated scheduling algorithm considering posterior processes. Acta Automatica Sinica, 44(2), 344–362. DOI 10.16383/j.aas.2018.c160562. [Google Scholar] [CrossRef]

12. Guo, W., Lei, Q., Song, Y. C., Lv, X. F., Li, L. (2020). Integrated scheduling algorithm of complex product with no-wait constraint based on virtual component. Journal of Mechanical Engineering, 56(4), 246–257. DOI 10.3901/JME.2020.04.246. [Google Scholar] [CrossRef]

13. Gao, Y. L., Xie, Z. Q., Yu, X. (2020). A hybrid algorithm for integrated scheduling problem of complex products with tree structure. Multimedia Tools and Applications, 79(43), 32285–32304. DOI 10.1007/s11042-020-09477-2. [Google Scholar] [CrossRef]

14. Shao, X., Liu, W., Li, Y., Chaudhry, H. R., Yue, X. G. (2021). Multistage implementation framework for smart supply chain management under industry 4.0. Technological Forecasting and Social Change, 162(4), 120354. DOI 10.1016/j.techfore.2020.120354. [Google Scholar] [CrossRef]

15. Hou, L., Tang, R., Xu, Y. (2004). Review of theory, key technologies and its application of modular product design. Journal of Mechanical Engineering, 40(1), 56–61. DOI 10.3901/JME.2004.01.056. [Google Scholar] [CrossRef]

16. Wang, J., Zhang, L., Han, X., Zhu, C., Wang, L. (2021). Development of green design platform for key components of high-end equipment based on Modularization. Manufacturing Automation, 43(2), 114–117. [Google Scholar]

17. Luo, J. Q., Ma, G. X., Yang, Z. C. (2021). Project task decomposition method for hybrid offerings generation and its application. Industrial Engineering and Management, 26(06), 18–26. DOI 10.19495/j.cnki.1007-5429.2021.06.003. [Google Scholar] [CrossRef]

18. Gui, Z. Y., Yang, J., Xie, Z. Q. (2017). Scheduling algorithm for flexible job shop based on pruning and layering. Control and Decision, 32(11), 1921–1932. DOI 10.13195/j.kzyjc.2016.1018. [Google Scholar] [CrossRef]

19. Shen, J., Ren, Y. F., Mei, D., Yang, M. N. (2019). Heuristic algorithms of tree decomposition based on average degree. Journal of Naval University of Engineering, 31(5), 49–53. [Google Scholar]

20. Song, J. H., Wei, O. (2019). Fault tree module expansion decomposition method based on liner-time algorithm. Computer Science, 46(1), 226–231. [Google Scholar]

21. Chen, X., Yue, X. G., Li, R., Zhumadillayeva, A., Liu, R. (2020). Design and application of an improved genetic algorithm to a class scheduling system. International Journal of Emerging Technologies in Learning, 16(1), 44–59. DOI 10.3991/ijet.v16i01.18225. [Google Scholar] [CrossRef]

22. Ibrahimov, V., Mehdiyeva, G., Yue, X. G., Kaabar, M., Noeiaghdam, S. et al. (2021). Novel symmetric numerical methods for solving symmetric mathematical problems. International Journal of Circuits, Systems and Signal Processing, 15(1), 1545–1557. DOI 10.46300/9106. [Google Scholar] [CrossRef]

23. Xie, Z. Q., Xin, Y., Yang, J. (2013). No-wait integrated scheduling algorithm based on reversed order signal-driven. Journal of Computer Research and Development, 50(8), 1710–1721. [Google Scholar]

24. Chen, M., Xiao, Y. H., Yue, X. G., Yang, H. M., Ubaldo, C. (2021). Innovation of practical teaching mode of marketing major-market research and forecast under the background of big data. Proceedings of 2021 6th International Conference on Intelligent Information Processing, pp. 49–52. New York, USA. [Google Scholar]

25. Luo, Y. M., Liu, W., Yue, X. G., Rosen, M. A. (2020). Sustainable emergency management based on intelligent information processing. Sustainability, 12(3), 1081. DOI 10.3390/su12031081. [Google Scholar] [CrossRef]

26. Teng, H. K., Wang, S. Y., Yue, X. G. (2019). Application of big data technology in emergency decision system. Proceedings of the 2019 3rd International Workshop on Education, Big Data and Information Technology, pp. 93–97. New York, USA. [Google Scholar]