Research on Leak Location Method of Water Supply Pipeline Based on MVMD

1  Introduction

Pipeline transportation is currently the most important transportation method for water resources, and it plays a huge role in urban water supply systems [1]. However, due to the corrosion, aging, welding defects and other phenomena of the pipeline and the destruction of uncontrollable factors by a third party, pipeline leakage accidents often occur in production and life. Pipeline leakage accidents can easily lead to the failure of residents’ normal water needs and cause a certain degree of waste of water resources. At the same time, pipeline leakage points are also potential pollutant intrusion points, which can easily pollute drinking water sources and may harm residents in severe cases life safety. Therefore, locating the leak location quickly and accurately is of great significance for saving water resources and ensuring the safety of residents’ water.

At present, some scholars have proposed many effective algorithms for the leak location of water supply pipelines [2,3]. Among them, the cross-correlation time delay estimation method based on vibration signal has become one of the most commonly used methods due to its low false alarm rate, simple operation, high sensitivity, low cost, and easy implementation [4,5]. It has been widely used in the leak location of water supply pipelines. Use acceleration sensors or hydrophones installed on the upstream and downstream of the water supply pipeline to collect the vibration signals generated when the water supply pipeline leaks, cross-correlate the vibration signals, estimate the signal delay time, and determine the propagation of the leakage signal along the pipeline according to the pipeline material The speed is then combined with the distance between the sensors on both sides to determine the location of the leak [6]. However, the leaked signal is susceptible to interference from common noises in life during the propagation of the pipeline. Moreover, the vibration signal generated by pipeline leakage is a continuous non-stationary signal [7], which exhibits the characteristics of multi-modality and dispersion during the propagation process, and the delay time obtained by direct cross-correlation analysis generally has large error.

In recent years, with the development of related technologies, EMD, WT and other technologies are often used in non-stationary signal analysis [8–11]. Knapp processed the signal based on generalized cross-correlation [12], which pre-filtered the leaked signal before implementing the CC method, So as to enhance the effective signal and reduce the interference of noise signal. Wang et al. used the combined method of EMD and wavelet packet to locate the pipeline leakage [13]. This method uses the method of combining EMD decomposition and wavelet packet to process the leaked signal. The results show that this method is compared with the location without noise reduction the accuracy is significantly improved. Meng et al. proposed a pipeline leak location method based on an improved adjustable Q factor wavelet transform [14]. This method determines the Q factor and the number of decomposition layers by analyzing the peak value. The results show that the location error of the method is all within 1%. Guo et al. [15,16] respectively used EMD adaptive noise reduction method and EEMD pretreatment method to locate pipeline leakage. The former uses EMD to decompose the signal and removes the components that do not contain or less contain leakage related components through correlation coefficients. The results show that the proposed method can effectively reduce the positioning error. The latter uses the method of combining EEMD and correlation coefficient to de-noise the signal, the quadratic correlation time delay estimation method is used to further reduce the leak location error caused by noise, and the error of the results of multiple experiments is less than 1%. Li et al. [17,18] improved the Variational Mode Decomposition (VMD) algorithm and applied it to the leak location of water supply pipelines. The former improves the VMD algorithm. This method can adaptively determine the quadratic penalty term of each band limited intrinsic mode function according to the frequency characteristics of the signal α. The latter proposes to adaptively determine the intrinsic mode function of the leakage vibration signal. The value of parameter k is determined by the number of saddle points and the curvature of the signal. The results show that the average positioning errors of the two methods are 0.92% and 3.85%, respectively. However, the GCC method needs to know the characteristic frequency band of the leaked signal in advance; WT needs to rely on manual experience to select the appropriate wavelet basis and decomposition layer; EMD decomposition has defects such as endpoint effects and mode aliasing; EEMD can suppress mode aliasing to a certain extent However, it is cumbersome to add white noise to calculate the average value many times. Therefore, most of the above algorithms have certain deficiencies.

In summary, this paper proposes a leak location method for water supply pipelines based on Multivariate Variational Mode Decomposition (MVMD) combined with correlation coefficients. The MVMD algorithm expands the traditional VMD algorithm from one-dimensional to multi-dimensional, and this method can ensure that the obtained component frequencies remain consistent when processing multi-channel data, which facilitates the extraction of effective components. Collect the vibration signals during normal operation and leakage of the pipe network for time-frequency domain analysis to determine the characteristic frequency band of the leakage signal. This method combines the two parameters of the energy loss coefficient and the correlation coefficient between adjacent modes, and adaptively determines the decomposition mode number K according to the characteristics of the signal itself. According to the correlation coefficient, the effective component is selected to reconstruct the signal, and perform cross-correlation analysis on the reconstructed signal to achieve water supply precise positioning of the pipeline.

2  Methods

2.1 The Proposed MVMD Algorithm

VMD is a new time-frequency analysis method proposed in 2014, which has been widely used in recent years, which can effectively eliminate the phenomenon of modal aliasing in the process of signal decomposition [19]. MVMD algorithm has certain advantages in dealing with multivariate or multi-channel data, and this method can ensure that the component frequencies are consistent when dealing with multi-channel data. It is a new method to solve the problem of multi-channel data cooperative decomposition. The MVMD algorithm obtains the IMF component based on the common frequency component between the multi-channel input data. At the same time, the variational model is introduced in the data decomposition to transform the problem into the problem of finding the optimal solution of the variational mode. In the whole process, the IMF component of each channel iteratively updates its bandwidth and center frequency at the same time, so as to obtain K narrow-band IMF components. The main goal of the MVMD algorithm is to extract multivariate modulation oscillation uk(t) from the input data x(t) of N data channels. The procedure of MVMD algorithm are as follows:

Step 1. The number of multivariate modulation oscillations is preset as K, then,

x(t)=∑k=1Kuk(t)(1)

where uk(t)=[u1(t),u2(t),⋯uN(t)].

MVMD decomposition is completed when the following two conditions are met:

(1)   Minimum sum of mode bandwidth

(2)   The sum of modes can restore the original signal uk(t)

Step 2. Hilbert transform uk(t) to obtain its analytical signal u+k(t) compare it with the index term e−jwkt. The purpose is to transform the spectrum of each function to the fundamental frequency band, and then modulate it again. The bandwidth of each component uk(t) is roughly estimated by L2 norm. Find the Same frequency component ωk in multiple channels in multivariate oscillation uk(t). So that the sum of IMF components obtained by each channel can reproduce the original signal and minimize the sum of the bandwidth of IMF components, the constrained related optimization problem becomes:

minimize{∑k∑n‖∂t[u+k,n(t)e−jωkt]‖22}subjectto∑kuk,n(t)=xn(t),n=1,2,⋯,N(2)

where u+K,C is the analytical representation of each element in the corresponding channel N and vector uk(t), ∂t represents the time-dependent partial derivative.

Step 3. The solving process of the above problems is complex, so it is convenient to construct an augmented Lagrange for solving:

L({uk,n},{ωk},λn)=α∑k∑n‖∂t[u+k,n(t)e−jωkt]‖22+∑n‖xn(t)−∑kuk,n(t)‖22+∑n⟨λn(t),xn(t)−∑kuk,n(t)⟩(3)

Step 4. Wu et al. [20] used barrier function to find approximate solution. In this paper, Alternate Direction Method of Multipliers (ADMM) is applied to solve the above unconstrained variational problem, and obtain uk(t) and center frequency to obtain the decomposed signal component. The mode is updated according to Eq. (4), and the center frequency is updated according to Eq. (5):

u^k,nc+1(ω)=x^n(ω)−∑i≠ku^i,n(ω)+λ^n(w)21+2α(ω−ωk)2(4)

ωkc+1=∑n∫0∝ω|u^k,n(ω)|2dω∑n∫0∝|u^k,n(ω)|2dω(5)

2.2 Number of Modes K

Through the above introduction of MVMD algorithm, it can be seen that when using MVMD algorithm to decompose the signal, the decomposition number K needs to be set, and the selection of K value affects the accuracy of signal decomposition. In previous studies, Liu et al. [21,22] proposed to judge whether the signal is completely decomposed by using the energy loss coefficient, which is defined as Eq. (6) [21,22]:

δ=‖x(t)−∑uk‖22‖x(t)‖22(6)

where δ represents the energy loss coefficient, x(t) is the collected original signal and ∑uk is the selected reconstructed signal. When the energy loss coefficient is less than a certain threshold, it is considered that the original signal has been decomposed completely and the decomposition operation is no longer carried out according to reference [23], the threshold will be μ1 is set to 0.01). At the same time, set the initial value of the number of modes to K = 2, and calculate the energy loss coefficient according to Eq. (6). If the energy loss coefficient is less than the set threshold μ1, it is considered that the K value at this time is the number of modes. If it is greater than the set threshold μ1. Make K = K + 1 and recalculate the energy loss coefficient until the energy loss coefficient is less than the set threshold μ1. However, for some signals, this method may have over decomposition, resulting in poor signal preprocessing effect. Therefore, this paper uses the correlation coefficient of adjacent modes to detect whether MVMD is over decomposed. Eq. (7) is the formula for calculating the correlation coefficient:

ρi,i+1K=[uiKui+1K]−E[uiK]E[ui+1K]D(uiK)D(ui+1K)(7)

In the above equation, E stands for mathematical expectation and D stands for variance operation uiK is the component whose decomposition mode number is K, ρi,i+1K is the correlation coefficient of two adjacent components. During normal MVMD decomposition, the correlation coefficient between the modal components will be very low. When the signal is decomposed normally, the correlation between the components will be low. However, when MVMD is over decomposed, the adjacent components may overlap partially, so the number of phase relations will increase significantly. In this paper, a mode number K is preliminarily obtained based on the energy loss coefficient, and then MVMD decomposition is carried out to calculate the correlation coefficient between adjacent IMF components, and compare the maximum correlation coefficient ρi,i+1K is it greater than the threshold μ2. According to reference [23], this paper will μ2 is set to 0.2. If ρi,i+1K larger than threshold u2, let K = K − 1, decompose and calculate again ρi,i+1K. If ρi,i+1K specific threshold μ2 is small, then the K value currently is the number of final modes.

2.3 Leak Location Principle

The schematic diagram of leak location is shown in Fig. 1. When a leakage accident occurs in the water supply pipeline, the pressure at the leakage point in the pipe decreases obviously, the water flow in the pipe network impacts outward and forms a vibration signal by friction with the pipe wall. The signal propagates along the downstream direction of the pipe network, and the leakage vibration signal is collected by arranging acceleration sensors upstream and downstream of the suspected leakage point in the pipe network, The time delay of the two collected vibration signals is estimated, and then the propagation speed c of the signal along the pipeline is obtained according to the pipeline material, Then, the location of the leakage point is calculated according to the distance d between the upstream and downstream sensors of the leakage point:

d2=d+cτ2(8)

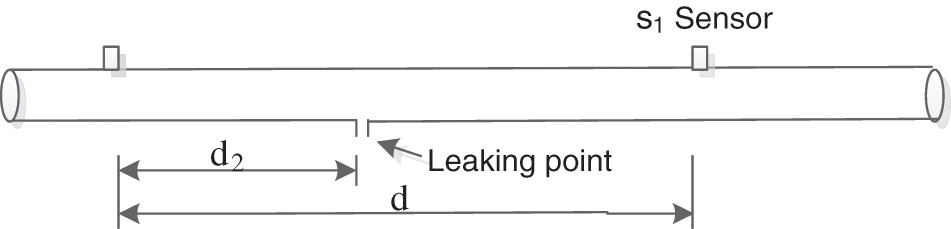
Figure 1: Schematic diagram of water supply pipe leak location

According to Eq. (8), the most important parameter to determine the location of leakage point is the delay time τ of upstream and downstream sensors, and then combined with the sensor distance d, the propagation speed of acoustic signal c can be determined. The propagation velocity c of leakage signal along the pipeline can be calculated by Eq. (9) [18], and the sensor distance d can be measured directly on site. Therefore, the most important problem of pipeline leak location is to obtain accurate delay time. In this paper, the cross-correlation analysis of the two leakage signals is carried out, and the delay time is determined according to the time corresponding to the cross-correlation peak.

c=cw(1+2BαEh)−12(9)

where cw is the propagation velocity of acoustic signal in water, and α is the average radius of the pipe, B is the bulk modulus of water in the pipeline E is the young's modulus of the pipe, and h is the wall thickness of the pipe.

2.4 Leak Location Process of Water Supply Pipeline

Combined with the principle of leak location introduced in Section 2.3, the steps of the location method proposed in this paper are as follows:

Step 1. Perform time-frequency analysis on the collected leakage signals x1(k), x2(k) and no leakage signals x11(k), x22(k) to determine the characteristic frequency band of the leakage signal ω1s1∼ω2s1, ω1s2∼ω1s2;

Step 2. Decompose the leakage signals x1(k), x2(k) by MVMD algorithm to obtain K IMF components, initialize the number of decomposition modes K = 2, and set the penalty parameter α = 2000, and the energy loss coefficient δ is calculated according to Eq. (6);

Step 3. If δ < μ1, preliminarily determine the number of decomposition modes K, if δ > μ1, make K = K + 1 and repeat Step 2 until δ < μ1;

Step 4. Calculate the correlation coefficient of adjacent IMF components ρK. If ρmaxK < μ2, K at this time is deemed to be the number of final decomposition modes, if ρmaxK > μ2, make K = K − 1 to perform MVMD decomposition again and calculate the correlation coefficient of adjacent IMF components ρK, until ρmaxK < μ2;

Step 5. Calculate the correlation coefficient between each IMF component and the characteristic band signal of the leakage signal ρ, the IMF component with correlation coefficient greater than ρmax/2 is selected for reconstruction to obtain the reconstructed signal x1′(t);

Step 6. Similarly, carry out Steps 2∼5 for x2(t) to obtain the reconstructed signal x2′(t), The delay time τ is obtained by cross-correlation of x1′(t) and x2′(t),The leakage position is obtained according to Eq. (8).

3  Results and Discussion

3.1 Experimental Environment

The experimental platform includes two parts: water distribution network and acoustic emission detection system. The pipe is an overhead steel pipe with a diameter of 42 mm and a wall thickness of 4.8 mm. A water pump is installed at the beginning of the pipe network. The start and stop of the water pump can be controlled manually or automatically to control the operation state of the pipe network. In this experiment, the pressure in the pipe network is controlled at about 0.2 MPa. The valve is installed on the pipe network. When the valve is opened, the real leakage of the pipe network is simulated. The acoustic emission detection system includes IEPE acceleration sensor, data acquisition card and host computer. The real water supply platform is shown in Fig. 2. After integrating the working environment, frequency response range, measuring range, cost performance and other factors, this paper selects YK-YD20 IEPE piezoelectric acceleration sensor, which can convert the displacement of vibration signal into voltage output. The working temperature of the sensor is −20°C∼120°C, the working voltage is 18–28 V, the sensitivity is 200 mV/g, the frequency response range is 0.5∼5000 Hz, and the output voltage is −5∼+5 V. The sensor has a small volume. It can be installed by nut and magnetic adsorption. The appropriate mode can be selected according to the actual needs, and the installation operation is relatively simple and convenient. The data acquisition card uses Ni myDAQ. The acquisition card has two analog input channels. The measurement signal range is −10∼10 V. Two analog output channels, and the generated signal range is −10∼10 V. 8 digital I/O channels. By cooperating with NI LabVIEW on the computer, signals can be collected, analyzed and processed. This experiment adopts adsorption installation. When the pipe network is in normal operation, open the water valve simulating leakage, and the water in the pipe will spray outside the pipe to generate a vibration signal. The vibration signal propagates along the upstream and downstream of the water supply pipe and is collected by the acceleration sensor adsorbed on the pipe, uploaded to the upper computer through the data acquisition card and saved to the document, provide basic data for subsequent processing. The basic parameters of the experimental pipeline are shown in Table 1. According to Eq. (8), the propagation velocity c is 1478 m/s.

Figure 2: Acoustic emission acquisition system

3.2 Experimental Process

S1 sensor is placed 3 m upstream of the leakage point, S2 sensor is placed 3.6 m downstream of the leakage point, and the pressure in the pipe network is 0.2 MPa. The duration of data acquisition is 10 s, and the middle stable 3 s is selected for analysis. Suppose the signal collected by sensor S1 is x1(t), the signal collected by sensor S2 is x2(t), and Fig. 3 shows the time domain diagram and frequency domain diagram of the collected leakage signal and non-leakage signal. It can be seen from Fig. 3a that the vibration amplitude of the signal collected during normal operation of the pipe network is small, and the amplitude is relatively large between 0∼600 Hz. Similarly, it can be seen from Fig. 3b that when the pipe network leaks, the amplitude of the vibration signal increases significantly, and the amplitude increases significantly between 1500–1800 Hz. Therefore, it is determined that the leakage signal is mainly distributed in the frequency band of 1500∼1800 Hz.

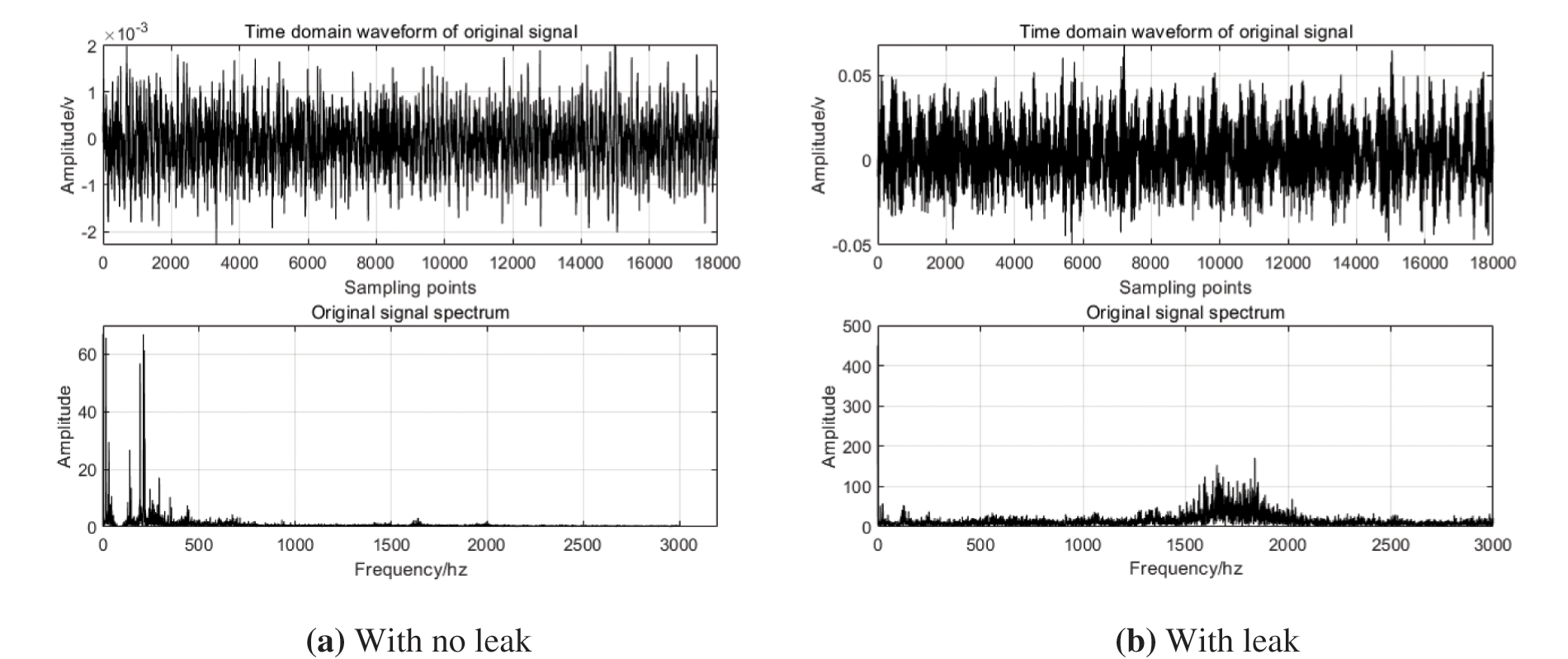
Figure 3: Time domain frequency domain diagram

3.3 Analysis of Leak Location Results

Calculate the energy loss coefficient of MVMD decomposition under different K values according to Eq. (6). Table 2 shows the energy loss coefficient of x1(t) signal decomposition under different K values. It is easy to see from Table 2 that when the value of K is 7, the energy loss coefficient δ is greater than u1, and when K continues to increase to 8, the energy loss coefficient δ is less than u1. Therefore, it is preliminarily determined that the decomposition mode number K is 8. Table 3 shows the maximum correlation coefficients of adjacent components under different K values of x1(t) signal. It can be seen from Table 3 that when K is 8, the maximum correlation coefficients of adjacent components ρmaxK it is greater than u2, it is considered that the decomposition is excessive under the K value at this time, and when the value of K decreases to 6, the maximum correlation coefficient of adjacent components ρmaxK less than u2, so the final mode decomposition number determined is 6.

After determining the pre decomposition scale K, carry out MVMD decomposition for x1(t) and x2(t). Fig. 4 shows the six IMF components decomposed by MVMD of x1(t) signal. The correlation coefficient between each IMF component and the signal in the characteristic frequency band is shown in Fig. 5. The larger the correlation coefficient is, the more leaked information the component contains. Therefore, in this paper, IMF4 and IMF5 whose correlation coefficient is greater than ρmax/2 are selected to obtain x1′(t) through signal reconstruction. The reconstructed signal contains more leakage information. Similarly, the signal x2(t) is decomposed and reconstructed to obtain x2′(t).

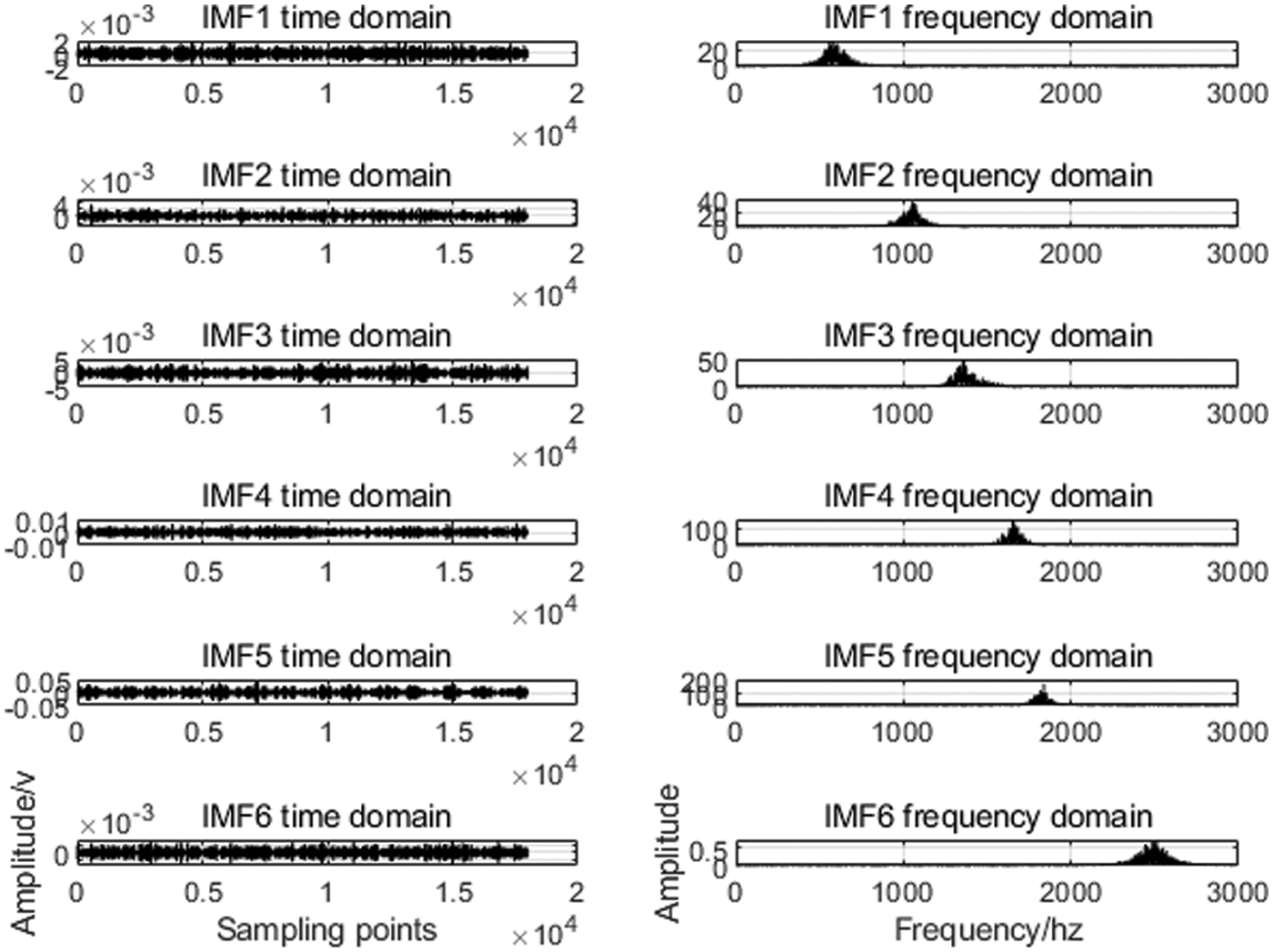
Figure 4: x1(t) MVMD decomposition

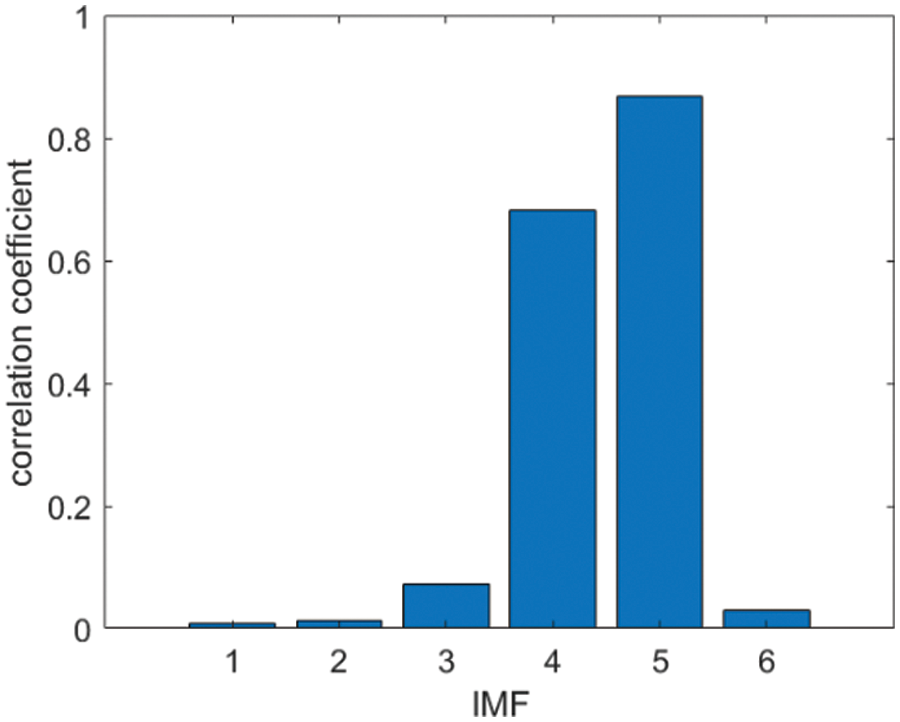
Figure 5: Correlation coefficients between IMF components and characteristic band signals x1(t)

The delay time between upstream and downstream sensors is calculated by MVMD and correlation coefficient combined positioning method, VMD and correlation coefficient combined positioning method, EMD and correlation coefficient combined positioning method and direct cross-correlation positioning method. The results are shown in Fig. 6.

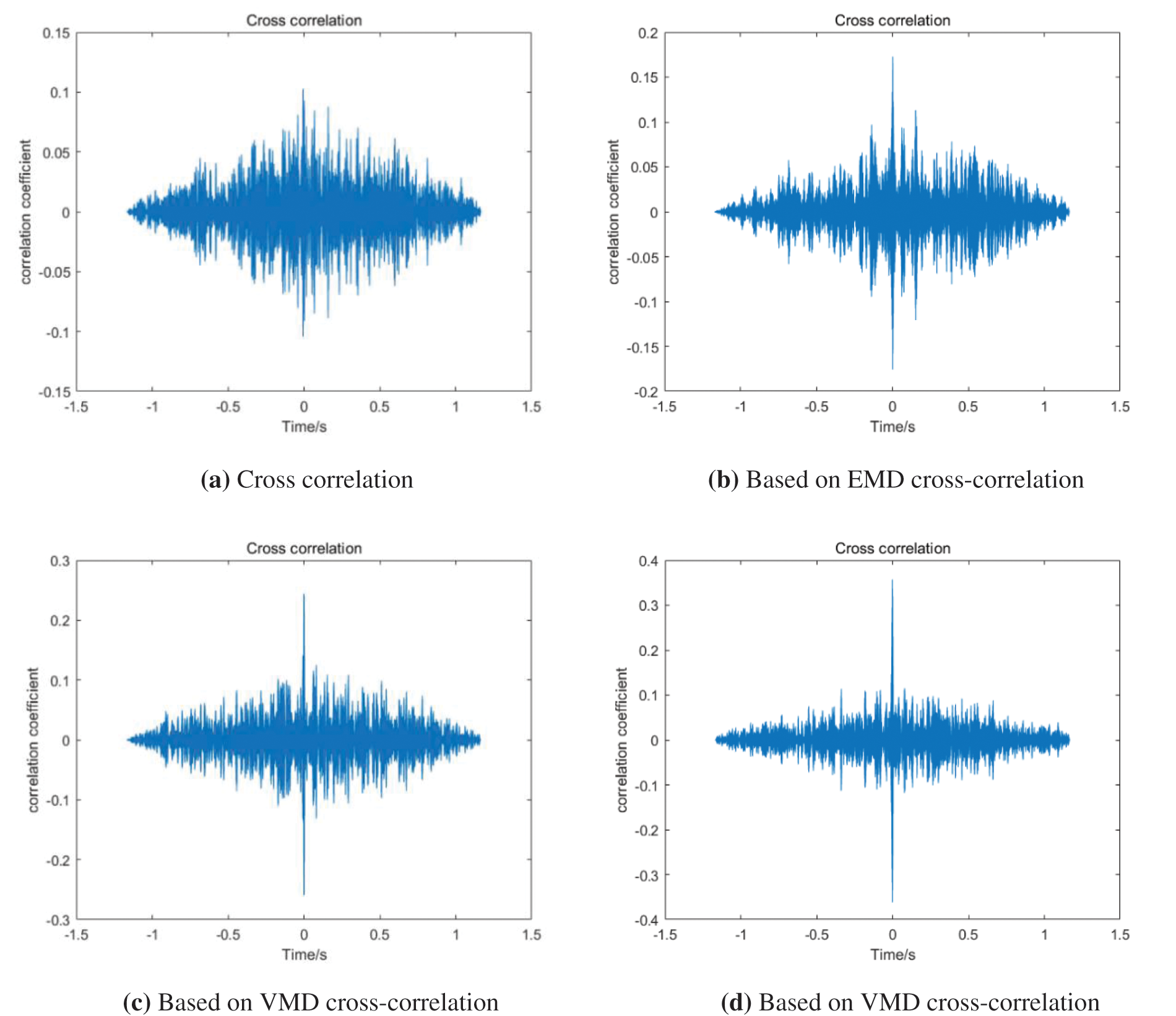
Figure 6: Cross correlation of different positioning methods

Analyzing Fig. 6, it can be seen that due to the existence of interference noise and other factors, directly cross-correlating the leakage signals x1(t) and x2(t) will produce multiple different peaks, and it is difficult to accurately obtain the delay time of the two leakage signals. Since EMD decomposition has problems such as modal aliasing and false components, it is difficult to accurately extract the leakage signal of the original signal, and the resulting positioning error is relatively large. However, the VMD combined with the correlation coefficient method has low recognition for signals with small differences, and the reconstructed signal will contain some noise. The method proposed in this paper can effectively reduce the influence of noise and extract the leakage signal contained in the original signal to the greatest extent, improve the accuracy of the leak location of the water supply pipeline.

According to the direct cross-correlation positioning method, the combination of EMD and correlation coefficient, the combination of VMD and correlation coefficient and the positioning method proposed in this paper, the relative positioning errors are 25.5%, 6.38%, 3.33% and 1.67%, respectively.

The results of a single experiment are accidental and unrepresentative, based on the above experimental platform, 10 groups of data are collected respectively when the position of two sensors on 42 mm pipeline and 32 mm pipeline remains unchanged and the leakage size changes, and 10 groups of data are collected respectively when the position of two sensors on 42 mm pipeline and 32 mm pipeline changes and the leakage size changes, a total of 40 groups of data, The experiments of MVMD and correlation coefficient combined positioning (Algorithm 1), VMD and correlation coefficient combined positioning (Algorithm 2), EMD correlation coefficient combined positioning (Algorithm 3) and direct cross-correlation positioning (Algorithm 4) are carried out and the results are compared. Among them, 1–6 groups of data are collected from the same position of the pipeline with an outer diameter of 42 mm, and 7–12 groups of data are collected from different positions of the pipeline with an outer diameter of 42 mm, 13–18 groups of data are collected from the same position of the pipe with an outer diameter of 32 mm, and 19–24 groups of data are collected from different positions of the pipe with an outer diameter of 32 mm. The statistics of leak location error of water supply pipeline based on four different methods are shown in Table 4. Fig. 7 shows the relative positioning errors of 24 groups of data based on different methods.

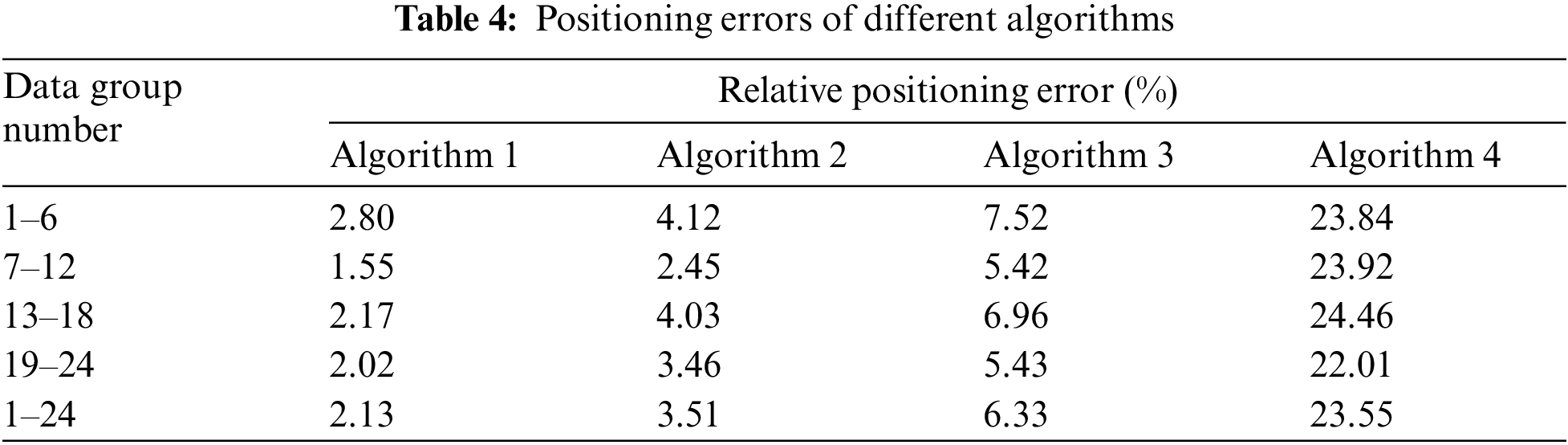
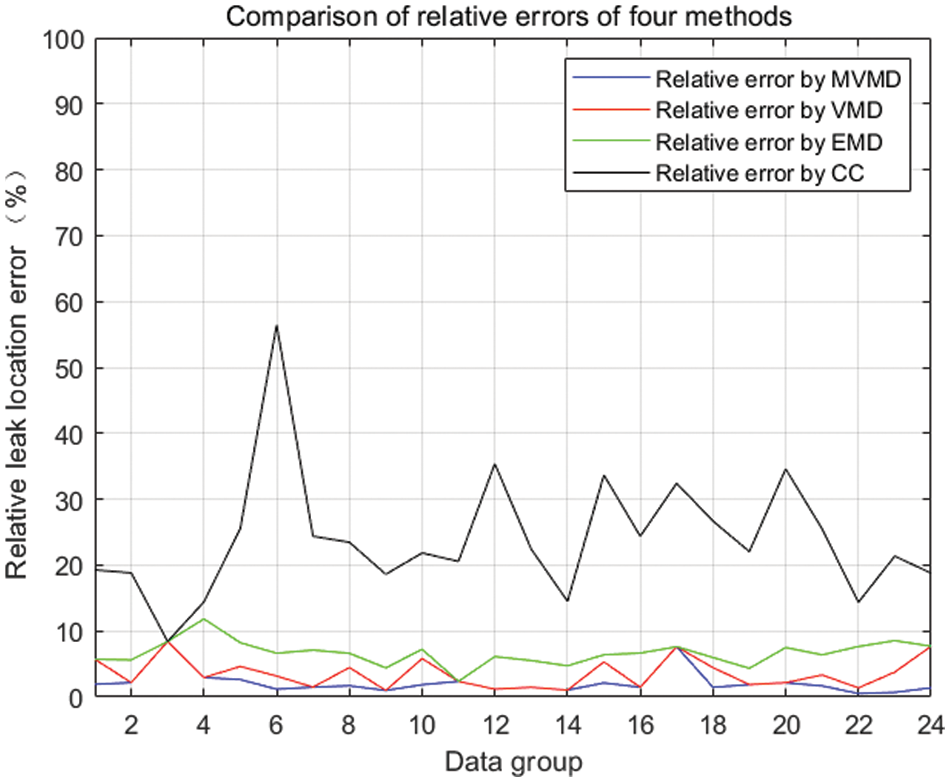
Figure 7: Relative positioning errors of 24 sets of data by different methods

It can be seen from Table 4 and Fig. 7 that under the condition of water supply pipeline leakage with different distance between the two sensors and different pipeline outer diameter, the positioning accuracy of MVMD and correlation coefficient combined algorithm is the highest, and the average relative positioning error is 2.13%. The minimum relative positioning error is 0.12%. The maximum positioning error is 8.41%. The positioning effect of direct cross-correlation algorithm is the worst, and the average relative positioning error is 23.55%. Therefore, for common pipeline leakage accidents, the localization algorithm based on MVMD and correlation coefficient can effectively filter the noise contained in the original signal, so as to improve the positioning accuracy.

4  Conclusion

The traditional non-stationary random signal de-noising method mainly depends on the estimation of noise parameters, ignoring the periodic noise and components unrelated to pipeline leakage. To solve the above problems, this paper proposes a solution based on MVMD. The decomposition mode number k is determined according to the steps in this paper, and the effective component is selected according to the correlation coefficient to reconstruct the signal for cross-correlation time delay estimation to determine the location of pipeline leakage point. The experimental verification is carried out through multiple groups of data collected by the established water supply system experimental platform. The experimental results show that this method has higher accuracy than the other three methods, and the average relative positioning error is less than 2.2%.

This article is an experiment based on the situation that there is only a single leakage point between the two sensors. The influence of multiple leakage points on the experiment is not considered. This can be used as a further research direction.

Funding Statement: This work is supported by the three funds: Industry-University-research Project of Anhui Jianzhu University HYB20210116; National Key Research and Development Project of China No. 2017YFC0704100 (entitled New Generation Intelligent Building Platform Techniques); Research Project of Anhui Jianzhu University jy2021-c-017 (Project Name: Research and Application of Water Distribution Network Leakage Detection System Based on DMA Partition).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Guo, Y., Meng, T., Wang, D., Tan, H., He, R. (2017). Experimental research on the corrosion of X series pipeline steels under alternating current interference. Engineering Failure Analysis, 78, 87–98. DOI 10.1016/j.engfailanal.2017.03.003. [Google Scholar] [CrossRef]

 2.  Xing, Z. X., Zhu, Y. L., Hao, Y. M., Jiang, J. C., Sheng, L. et al. (2019). Multi-point leak location analysis of pipeline based on improved CEEMD. Safety and Environmental Engineering, 26(6), 190–195+208. DOI 10.13578/j.cnki.issn.1671-1556.2019.06.028. [Google Scholar] [CrossRef]

 3.  Liu, J. H., Ji, S. S., Wang, G. M., Keng, X. Y. (2018). Study on location of leakage point in water supply network. Water & Wastewater Engineering, 54(6), 119–122. DOI 10.13789/j.cnki.wwe1964.2018.0180. [Google Scholar] [CrossRef]

 4.  Li, S. Y., Xia, C. Q., Cheng, Z. H., Mao, W. P. (2019). Leak location method in water-supply pipeline based on combination of VMD and cross-spectrum analysis. Chinese Journal of Scientific Instrument, 40(7), 195–205. DOI 10.19650/j.cnki.cjsi.J1905209. [Google Scholar] [CrossRef]

 5.  Hao, Y. M., Qin, N., Xing, Z. X., Lu, G. R. (2018). Pressure pipe leakage location based on of VMD and relative entropy analysis. China Safety Science Journal, 28(10), 124–130. DOI 10.16265/j.cnki.issn1003-3033.2018.10.021. [Google Scholar] [CrossRef]

 6.  Li, H., Tian, L., Lu, J. Y., Liu, Q. Q. (2021). Time delay estimation method of generalized second cross correlation based on VMD. Journal of Jilin University (Information Science Edition), 39(3), 260–266. DOI 10.19292/j.cnki.jdxxp.2021.03.004. [Google Scholar] [CrossRef]

 7.  Li, S. Y., Cheng, Z. H., Mao, W. P., Xia, C. Q., Yang, X. M. (2019). Leak location based on the improved EWT and cross-power phase difference spectrum of vibro-acoustic signal in water-supply pipelines. Chinese Journal of Scientific Instrument, 40(12), 80–91. DOI 10.19650/j.cnki.cjsi.J1905795. [Google Scholar] [CrossRef]

 8.  Kim, M. S., Lee, S. K. (2009). Detection of leak acoustic signal in buried gas pipe based on the time–frequency analysis. Journal of Loss Prevention in the Process Industries, 22(6), 990–994. DOI 10.1016/j.jlp.2008.08.009. [Google Scholar] [CrossRef]

 9.  Ozevin, D., Harding, J. (2012). Novel leak localization in pressurized pipeline networks using acoustic emission and geometric connectivity. International Journal of Pressure Vessels and Piping, 92, 63–69. DOI 10.1016/j.ijpvp.2012.01.001. [Google Scholar] [CrossRef]

10. Guo, C. C., Wen, Y. M., Ping, L., Wen, J. (2015). Enhancement of leak signals using EMD in pipeline. Chinese Journal of Scientific Instrument, 36(6), 1397–1405. DOI 10.19650/j.cnki.cjsi.2015.06.026. [Google Scholar] [CrossRef]

11. Sun, J., Xiao, Q., Wen, J. (2014). Natural gas pipeline small leakage feature extraction and recognition based on LMD envelope spectrum entropy and SVM. Measurement, 55, 434–443. DOI 10.1016/j.measurement.2014.05.012. [Google Scholar] [CrossRef]

12. Knapp, C., Carter, G. (1976). The generalized correlation method for estimation of time delay. IEEE Transactions on Acoustics, Speech, and Signal Processing, 24(4), 320–327. DOI 10.1109/TASSP.1976.1162830. [Google Scholar] [CrossRef]

13. Wang, J. G., Liu, P. Z., Wang, S. F., Gao, L. (2017). Research on the location of the micro pressure pipeline leak based on the EMD and wavelet packet. Journal of Henan Polytechnic University (Natural Science), 36(4), 83–88. DOI 10.16186/j.cnki.1673-9787.2017.04.013. [Google Scholar] [CrossRef]

14. Meng, T., Wang, D., Jiao, J. (2020). Tunable Q-factor wavelet transform of acoustic emission signals and its application on leak location in pipelines. Computer Communications, 154, 398–409. DOI 10.1016/j.comcom.2020.02.047. [Google Scholar] [CrossRef]

15. Guo, C., Wen, Y., Ping, L. (2016). Adaptive noise cancellation based on EMD in water-supply pipeline leak detection. Measurement, 79, 188–197. DOI 10.1016/j.measurement.2015.09.048. [Google Scholar] [CrossRef]

16. Xie, H. Y., Wang, S. X., Guo, Q., Yang, Y. B. (2020). Infrasonic wave method for pipeline leakage locating based on EEMD filter and time delay estimation. Oil & Gas Storage and Transportation, 39(10), 1148–1154+1164. DOI 10.6047/j.issn.1000-8241.2020.10.010. [Google Scholar] [CrossRef]

17. Li, J., Chen, Y., Lu, C. (2020). Application of an improved variational mode decomposition algorithm in leak location detection of water supply pipeline. Measurement, 173(8), 108587. DOI 10.1016/j.measurement.2020.108587. [Google Scholar] [CrossRef]

18. Li, S., Wen, Y., Li, P. (2014). Determination of acoustic speed for improving leak detection and location in gas pipelines. Review of Scientific Instruments, 85(2), 024901. DOI 10.1063/1.4863323. [Google Scholar] [CrossRef]

19. Ding, C. J., Fu, X. Y., Feng, Y. B. (2020). Fault feature extraction method of gearbox based on parameter optimization VMD. Journal of Mechanical Transmission, 44(3), 177–182. DOI 10.16578/j.issn.1004.2539.2020.03.028. [Google Scholar] [CrossRef]

20. Wu, Z., Gao, Q., Jiang, B., Karimi, H. (2021). Solving the production transportation problem via a deterministic annealing neural network method. Applied Mathematics and Computation, 411, 126518. DOI 10.1016/j.amc.2021.126518. [Google Scholar] [CrossRef]

21. Liu, S. K., Tang, G. J., Wang, X. L. (2016). Time frequency analysis method for rotary mechanical fault based on improved variational mode decomposition. Journal of Vibration Engineering, 29(6), 1119–1126. DOI 10.16385/j.cnki.issn.1004-4523.2016.06.022. [Google Scholar] [CrossRef]

22. Lian, J., Zhuo, L., Wang, H. (2018). Adaptive variational mode decomposition method for signal processing based on mode characteristic. Mechanical Systems & Signal Processing, 107, 53–77. DOI 10.1016/j.ymssp.2018.01.019. [Google Scholar] [CrossRef]

23. Li, J., Chen, Y., Qian, Z. (2019). Research on VMD based adaptive denoising method applied to water supply pipeline leak location. Measurement, 151, 107153. DOI 10.1016/j.measurement.2019.107153. [Google Scholar] [CrossRef]