Overview of Earth-Moon Transfer Trajectory Modeling and Design

1  Introduction

The Moon exploration has many scientific and engineering meanings, and trajectory design for the spacecraft transferring from the Earth to the Moon has been the subject of countless works. The conventional transfer trajectory design method began with the Hohmann transfer (Fig. 1) and was improved using the patched conic model (Fig. 2). With the development of the dynamical system, the low-energy ballistic capture trajectory (Fig. 3) was proposed to optimize the fuel requirement. Completely different low-thrust trajectories (Fig. 4) were further developed for other available propulsion systems, like an electric propellant or a solar sail, significantly enhancing the payload capability and enabling high ΔV missions.

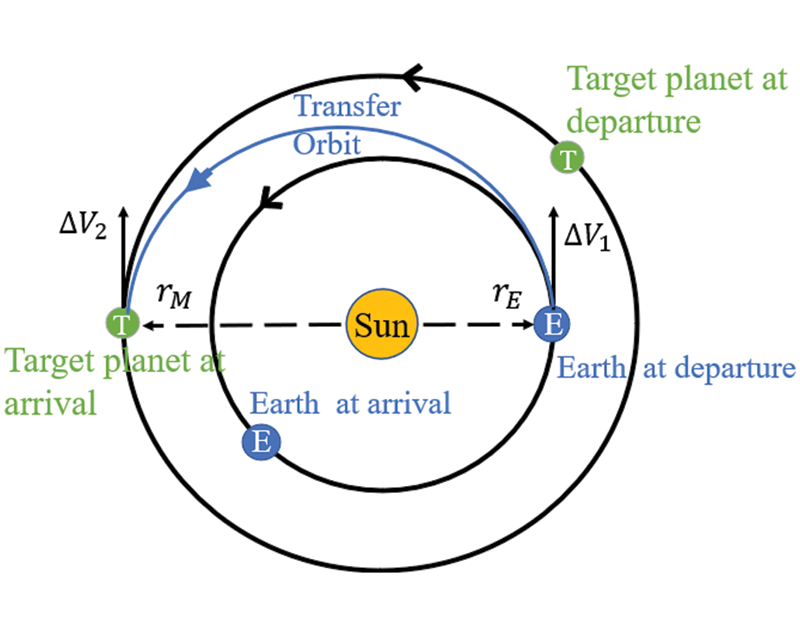
Figure 1: Hohmann transfer geometry

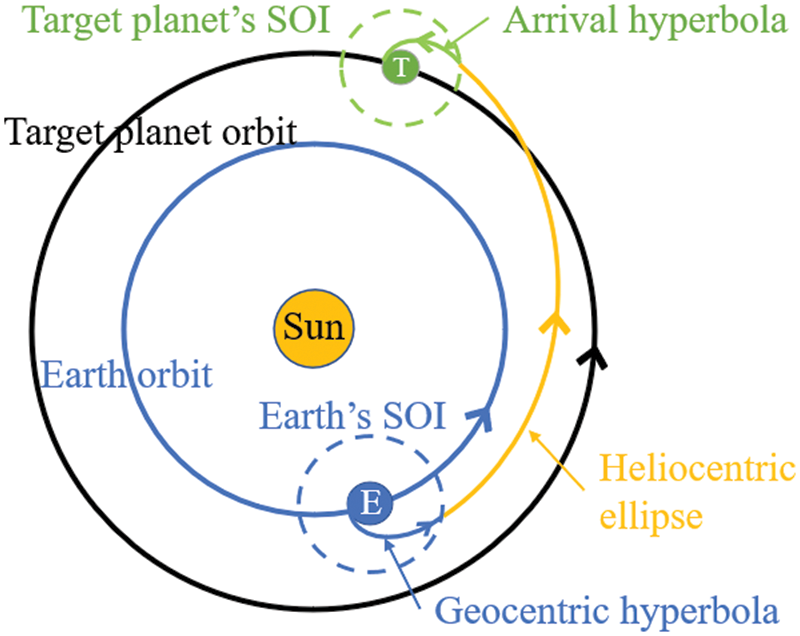
Figure 2: Patched conic method

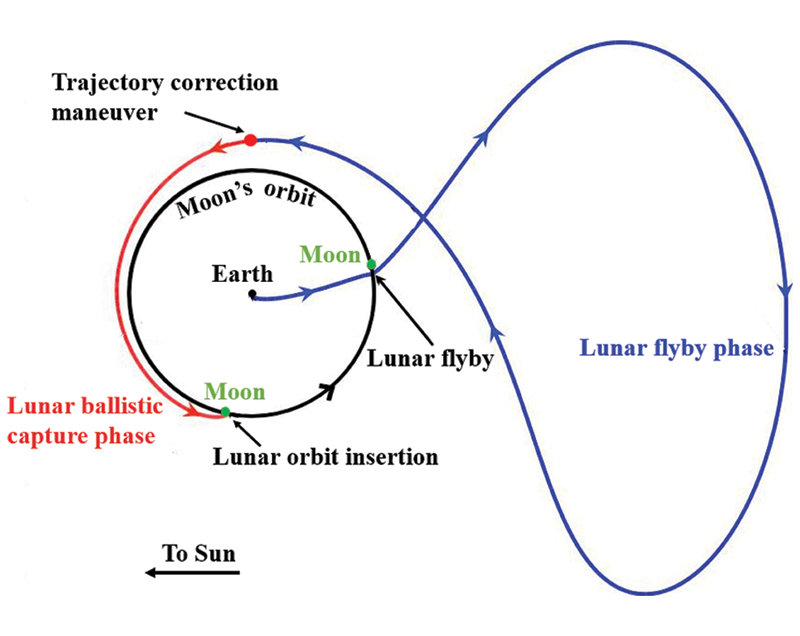
Figure 3: Low-energy lunar trajectory with lunar flyby

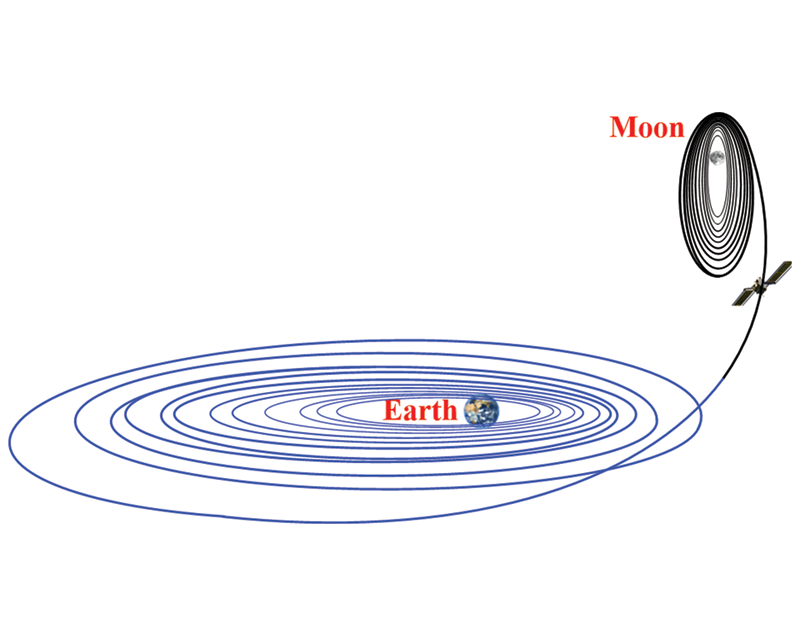
Figure 4: Low-thrust trajectory

The primary transfer approach to the Moon can be broadly classified into four categories: direct transfer, phasing loop transfer (also known as direct, staging), low-energy transfer, and spiral transfer [1]. The direct Moon transfer trajectory is the most commonly used method in engineering tasks [2]. In the framework of the two-body problem, the most straightforward direct transfer trajectory can be obtained by the Hohmann transfer and later a modified patched conic model. Despite the enormous energy requirement and difficulties in searching for proper patching points, the patched conic method was favored in many lunar missions, such as Apollo, Luna, and Chang’E missions, because of its short flight time and simple flight control system. The total ΔV acquired transferring from a 300 km circular Earth parking orbit to a 100 km circular cislunar orbit ranges between 3.5 and 4 km/s. And the typical flight time of a direct transfer varies from two to five days. In general, the most fuel-efficient direct transfer needs about 4.5 days. Any more time-consuming travel typically sends the spacecraft beyond the Moon’s orbit before it falls back and encounters the Moon [3].

In the phasing loop transfer, the trans-lunar injection or the lunar orbit insertion burns are divided into several minor burns to minimize gravity losses. The initial direct and phasing loop trajectories are designed through either the Hohmann transfer or patched conic technique based on an analytical solution to the two-body problem. This approach can provide a chance to verify the operating condition, address the status of the orbiter and correct any anomalies before arriving at the Moon which can be seen in the Chang’E-1 and Chandrayaan-1 missions [4].

However, the analytical two-body model inherently involves hyperbolic approaches upon arrival, which requires a high ΔV maneuver to inject the spacecraft into the final Moon orbit [5]. With the development of the circular restricted three-body problem (CRTBP), some studies showed that hyperbolic velocity is not a necessary condition for a cislunar transfer [6]. By exploiting the concept of temporary ballistic capture, or weak ballistic capture theory, low-energy transfer [7] was proposed to reduce the total energy cost and has been executed in the rescue of the Hiten mission [7,8], and, more recently, in the ARTEMIS [9] and GRAIL missions [10]. For a transfer from a 167 km circular Earth parking orbit to a 100 km circular cislunar orbit, the low-energy transfer yields improvements over Hohmann by 18% but the flight time is quite long up to several months.

Currently, Earth-Moon low-energy transfer trajectories are mainly constructed based on the weak stability boundary (WSB) theory or Lagrangian points and manifold theory [8,11]. According to the trajectory geometry, the low-energy transfer can be classified into the interior (or cislunar) and exterior (or translunar) [5,12]. Trajectories are basically located within the Moon orbit in the interior transfer and are always designed through the Earth-Moon system L1 Lagrangian point or its periodic orbits. As the Lagrangian point and the hyperbolic invariant manifolds of periodic orbits are approached asymptotically, an interior transfer via invariant manifold usually has a pretty long flight duration [13–16]. Moreover, because of the very long flight time, the solar gravity perturbation would cause a significant impact, which can change the invariant manifolds topologically to fail in transiting the L1 point or the periodic orbits [12]. For the exterior transfer, the spacecraft is injected into highly ellipse orbits whose apogee at approximately four Earth-Moon distances. In this region, a small maneuver, combined with the solar perturbation enables an approach to the Moon from the exterior. An exterior transfer could be constructed by using the WSB theory [8,17,18] or the patched manifold technique [6,11,19], which requires more fuel in the accelerating maneuvers but less in the decelerating maneuvers, making it more economical than the direct transfer. However, this kind of transfer heavily depends on the geometry of the Sun, Earth, and Moon. Compared to the interior transfer using the Earth-Moon L1 point, the exterior transfer has fewer opportunities to transit the L2 point. An effective way to increase the transfer opportunities is to transit a periodic orbit near the L2 point instead of the point itself [12].

The spiral approach, a type of low-thrust transfer, is the one subjected to the longest flight time of all methods. The SMART-1 spacecraft reached the Moon following a low-thrust 2-year trajectory, becoming the first successful case using this approach to the Moon [20]. The trajectory, in this case, can be divided into three segments: escaping from the Earth, free flight segment, and capturing by the Moon. The probe can achieve Earth escape and Moon capture through the cumulative effect of low thrust. Defining an (M, N) -loops transit orbit of the ballistic capture, the Moon would capture the probe after it runs M circles from the Earth’s large ellipse with a large semi-major axis and N circles on the Moon’s large ellipse orbit. The whole process is free-flight movement. To this end, the essence of small thrust is to search an (M, N) -loops transit orbit to extend the arc of low-thrust action. Moreover, due to the high energy level of the patched orbit in an exterior transfer, a spacecraft cannot follow an elliptical orbit with a sizeable semi-major axis before escaping from the Earth, which makes it challenging to apply the low-thrust in the exterior transfer. In contrast, the interior transfer based on the L1 point has a stable (M, N) -loops transit orbit, which can make full use of the low-thrust to accumulate energy for a long time to achieve gradual orbit change [21]. A comparison of these four types of transfer is listed in Table 1.

Several review papers are available that discuss the recently proposed low-energy and low-thrust transfer methods and the complex mechanisms of the trajectory design. However, there is a lack of a review enabling readers to grasp the overall development and design principles of the Earth-Moon transfer trajectory construction from a historical and scientific perspective. This paper begins by demonstrating the traditional transfer approach, containing the patched conic and pseudostate methods. Then the low-energy transfer approach is illustrated from two aspects: designing via manifold theory and weak stability boundary theory. Finally, the design of the Earth-Moon transfer trajectory by using the low-thrust technique is also discussed. With no more complex theories and techniques in this paper, essential mechanisms and characteristics of these design methods are discussed to help readers easily grasp the basic overview of the current Earth-Moon transfer orbit design methods.

2  Traditional Transfer Approach

The traditional direct transfer is the most commonly used method in practical engineering tasks. The mainstream design methods to construct this type of transfer, the patched conic method, and the pseudostate technique have been proposed since the era of Apollo and achieved significant development in the past few decades. The patched conic model features a good analytical characteristic due to the multiple-two-body assumption. However, the approach of neglecting the gravitational force of the central celestial body successively may cause non-negligible errors at the patched point. A modified method, i.e., the pseudostate technique was then proposed, whose accuracy is between the patched conic and numerical integration models, owning better practicability in practical engineering missions. In this part, the construction of a direct Earth-Moon transfer trajectory based on these two methods would be reviewed.

2.1 Patched Conic Model

In 1925, Hohmann [22] discussed the double-impulse transfer method between two circular coplanar orbits and concluded that the minimum energy transfer conic would be elliptic, tangent to the inner and outer orbits at perigee and apogee, respectively. When designing an Earth-Moon transfer orbit, the Hohmann transfer can only be used to design a primary trajectory because of its too strict condition, maneuvering at the perigee and neglecting the Moon’s influence on the spacecraft. In 1956, Egorov [2] proposed the patched conic method in the frame of the two-body problem. By introducing the concept of sphere of influence (SOI), a multi-body system can be divided into several two-body systems. Each portion of the trajectory is treated as a two-body trajectory about the most influential body [23]. Then at the boundary of SOI, a transition is made from one central gravity body to the other by matching the relative position and velocity in the appropriated conic trajectories. One of the most commonly used SOI models is the Laplace sphere [24]. For the Earth-Moon system, the radius of the Moon’s SOI can be calculated by

RLaplace=D(mM)2/5,(1)

where, m and M represent the mass of the Moon and the Earth, respectively, and D denotes the average distance between Earth and Moon which follows that RS = 66300 km.

A general interstellar transfer trajectory in the solar system can then be divided into three segments based on the above assumptions [25]: (i) a hyperbola about the departure, (ii) an ellipse about the Sun, and (iii) a hyperbola about the target planet. In the case of the Earth-Moon system, the whole trajectory can be simplified into two segments, i.e., the geocentric segment and selenocentric segment since the Moon’s SOI lies within the Earth’s SOI [26].

Many studies have been carried out based on the patched conic method from the era of Apollo. Penzo [27] impelled the patched conic method further in both theory and computing techniques. He also proposed a free-return orbit design scheme, and determined the effect of the perilune distance and outward/return inclinations to the Moon’s plane on the flight time [28]. It is concluded that the possible launch conditions would be constrained when the perilune distance, flight path, and landing location are fixed. Fig. 5 shows a free-return orbit studied in [28]. It can be seen that the geocentric orbit is an ellipse orbit, and the selenocentric orbit is a hyperbolic one relative to the Moon. An interesting phenomenon is that the SOI entrance velocity is not equal to the SOI exit velocity, due to the velocity combination effect. The phenomenon is also known as the gravity-assist through Moon swing-by [29], which can be further used in an interstellar transfer mission by accelerating the spacecraft.

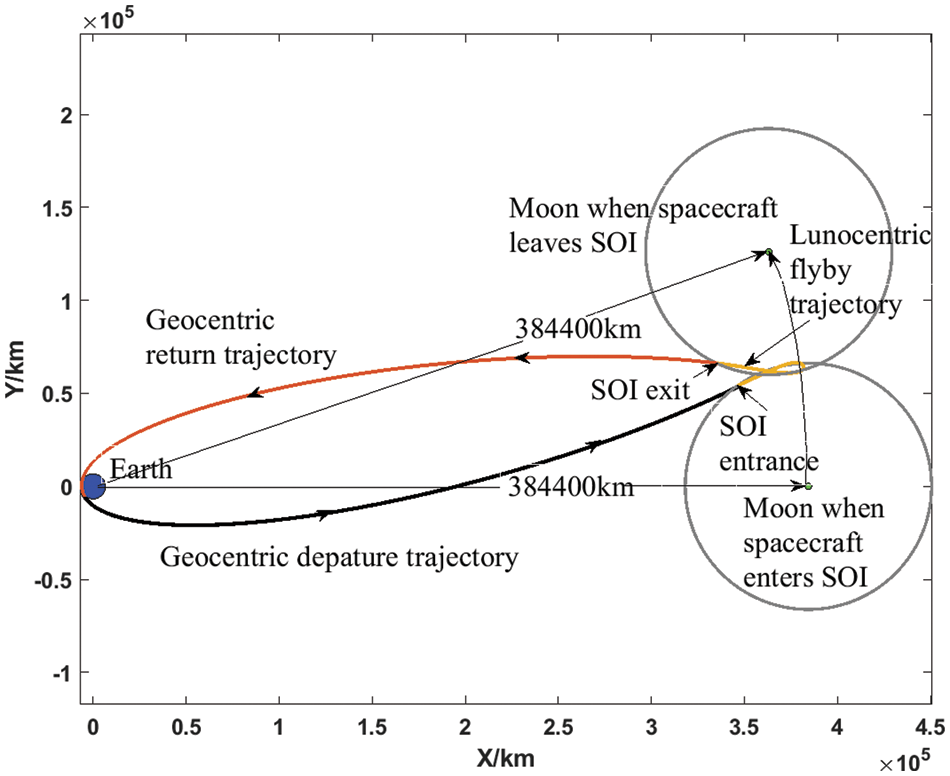
Figure 5: An entire free-return trajectory relative to Earth-centered inertial reference frame

Moreover, Dallas [30] discussed the characteristics of Earth-Moon free-return orbits in more detail. By analyzing the flight time, fuel consumption, and the difficulty of orbit design, he concluded that the counterclockwise class of trajectories is superior to the clockwise ones. To verify the accuracy of the patched conic model, Gibson Jr. [31] compared several parameters (e.g., the velocity (V) and lead angle (ϕ) at injection) between the patched conic model and the 7-body model (considering the gravitational forces of Earth, Moon, Sun, Venus, Mars, Jupiter, and perturbations due to the non-spherical gravitational fields of the Earth and the Moon). The results showed that the patched conic elements can approximate precision elements adequately. He also found that an even better approximation may be obtained by adding constant correction terms to the conic element. In addition, he proposed an iteration scheme that combines the patched conic model in conjunction with the integrated n-body model to obtain any desired integrated trajectory, and a fast convergence can be achieved. Li et al. [32] proposed a multi-segment lunar free-return trajectory when studying the design of a crewed spacecraft's Earth-Moon orbit. They established an analytical model of the multi-segment free-return trajectory using the patched conic technique. The results demonstrated that multi-segment free returns allow a wider range of lunar approach inclinations and free launch windows than free-return profiles. They also found that retrograde Earth returns generally require a higher velocity impulse but lower flight time than posigrade Earth returns which can also offer a wider range of lunar approach inclination.

Salazar et al. [33] studied the problem of determining the optimal flight duration and energy consumption vector for a spacecraft transferring to the Moon. As shown in Fig. 6, λ1 denotes the Moon arrival angle, and the minimum time of flight (TOF) occurs when λ1 = 0° and the minimum total cost (ΔV) occurs when the λ1 = 44°. Qi et al. [34] investigated the two-impulse transfer from the 167 km LEO to the permanent lunar capture orbit with the minimum ΔV in the framework of the planar CRTBP and the two-body model. Different from the traditional method, the Moon ellipse target orbit rather than the circular orbit was used for the sake of less fuel consumption. As an important optimization variable, the height of the perilune of the hyperbolic orbit h determines the optimal transfer and the capture point. As illustrated in Fig. 7, ΔV generally decreases and is followed by a rise with the increase of h. The minimum of ΔV occurs at a height of around 1200 km. The TOF showed a different trend of monotonic increase as h increases. However, the basic assumptions of patched conic, i.e., (i) the Moon acting in a circular motion around the Earth, and (ii) neglecting the gravity of the central body successively, can cause considerable errors. Hence, a more accurate dynamical model containing ephemeris needs to be considered for the practical Earth-Moon mission [35,36]. It should also be noted that, in operations of practical engineering missions, midcourse impulses are always employed to eliminate the initial error in entering the Earth-Moon transfer orbit. For the Chang’E-1 mission, two essential midcourse impulses were planned to perform at the 17th and the 90th h, respectively. An alternative was arranged at the 41st h, which would be performed when the residual error exceeds a certain upper bound after the first midcourse correction. However, due to its ideal flight condition, only one alternative midcourse correction was given at the 41st h of flight duration, and the speed increment used was only 4.8 m/s [37]. Moreover, an important method, the phasing loop method was utilized to link the Earth-Moon transfer orbits in the Chang’E-1 mission. Concretely, the lunar probe ran three circles in the super GTO orbits and operated a small maneuver in the second apogee to increase the height of the perigee to 600 km. The later three impulses were employed at the perigee, changing the orbital period to 24 and 28 h, respectively. A final impulse was given to direct the spacecraft into 114 h Earth-Moon transfer orbit [38]. This method has been proposed since the 1990s which is suitable for limited engine thrust and can reduce midcourse correction increments and widen the launch window [39–41].

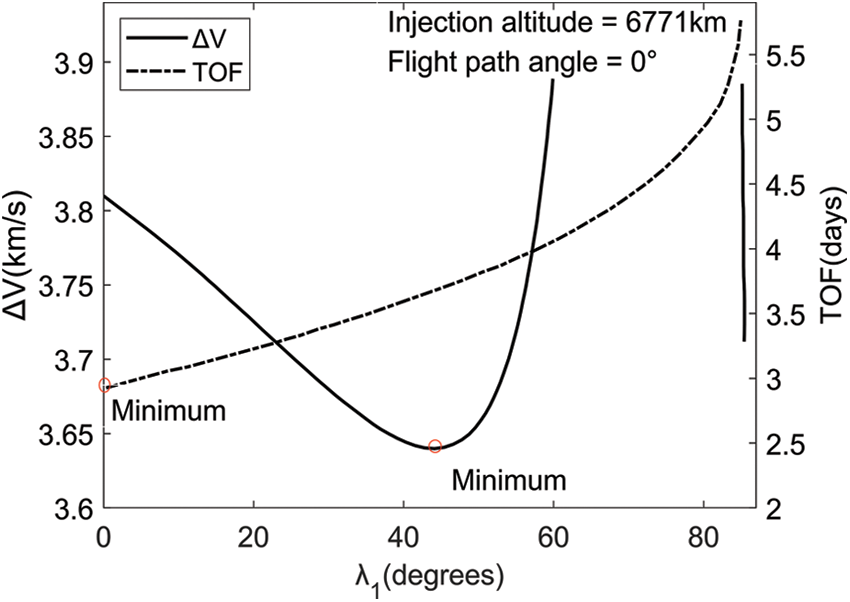
Figure 6: Total ΔV and TOF vs. λ1

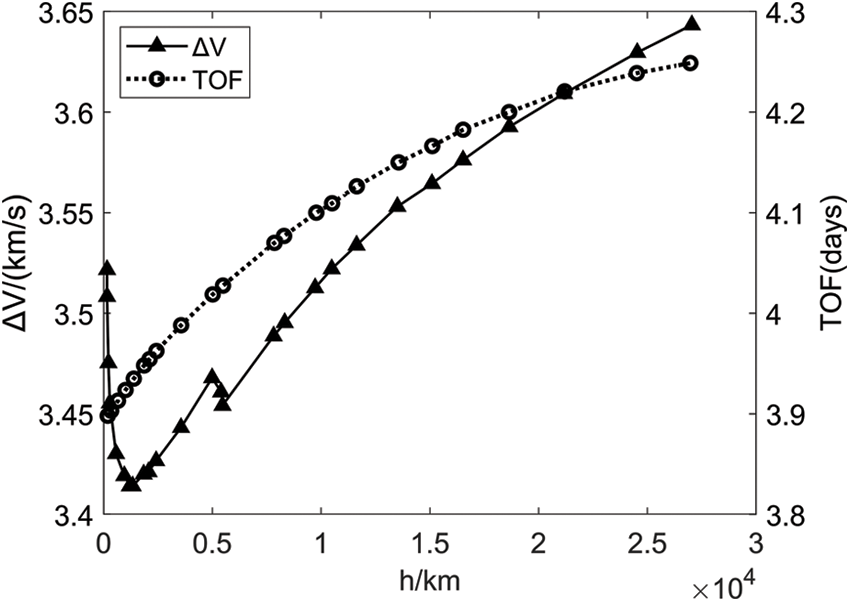
Figure 7: Total ΔV and TOF vs. h

2.2 Pseudostate Model

The patched conic method has a good analytical characteristic, giving a more clear and intuitive view in designing an Earth-Moon transfer trajectory [42]. However, the basic assumptions adopted can cause large errors in both position and velocity at the patched point. Thus, an iterative determination of the intersection at the SOI is necessary, which results in a waste of computing time and instability of the algorithm [43]. In 1970, Wilson [44] proposed the pseudostate model in the study of the Earth-Moon transfer missions, which reduced patched conic errors by 80% without employing a search enabled by numerical integration. As the basis of the pseudostate model, the overlapped conic approximation was firstly derived as a closed-form approximate solution for the restricted three-body problem. For the direct transfer missions, the rectification terms in overlapped conic equations can be omitted to achieve the desired long propagation step. The model then can be simplified into the pseudostate model. Similar to the SOI concept in the patched conic method, a concept of pseudostate transformation sphere (PTS) is introduced in the pseudostate model to define the vicinity of the Moon [45]. Within the PTS, the superimposed effect of the Earth and the Moon is considered. Outside the PTS, only a simple geocentric conic is used [44].

For an Earth-Moon transfer trajectory, the state of the spacecraft’s position at its start and end can be approximated by two instantaneous conics arcs. And the pseudostate theory is then utilized to find a bridge connecting the instantaneous conics at both ends. Suppose the spacecraft’s geocentric states of motion at an initial time ti and an arbitrary time tf are Xi=(ti,Ri,Vi) and Xf=(tf,Rf,Vf), respectively. The selenocentric state at tf is xf=(tf,rf,vf). Let XM=(tf,RM,VM) be the geocentric state of the Moon at tf. The relationship between Xfand xf can be represented by Rf=rf+RM and Vf=vf+VM.

Then, as shown in Fig. 8, the orbit design steps described by the pseudostate theory are as follows [46]:

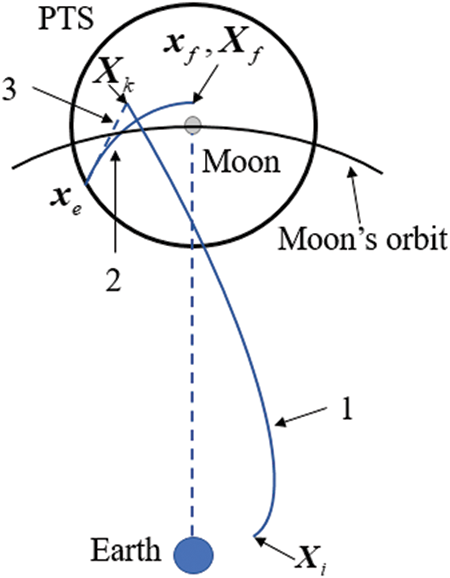
Figure 8: The pseudostate theory

1. Geocentric instantaneous conic: Ignoring the gravitational force of the Moon, then the geocentric motion can be viewed as a two-body problem about the Earth. The pseudostate Xk is obtained by propagating Xi from ti to tf.

2. Linear backward propagation section: Calculate the selenocentric state xk=(tf,rk,vk) corresponding to Xk. The xe=(te,re,ve) can be obtained by linearly backward evolution to te (the PTS spherical moment of arrival) through re=rk+(te−tf)vk and ve=vk.

3. Selenocentric instantaneous conic: The perilune state xf can be obtained by propagating the xe in the central gravitational field of the Moon from te to tf. Then the geocentric state Xf can also be acquired by its relationship with xf.

Based on the pseudostate theory, Luo et al. [46] proposed a preliminary design algorithm for the free-return lunar flyby trajectories. It is a simple iterative algorithm that does not require any prior information and can generate a better initial solution for the free-return lunar flyby trajectory. Zhang et al. [47] proposed a linear approximation-based fast prediction algorithm based on the improved pseudostate theory for the Earth-Moon transfer trajectory. Simulation results showed that the prediction error of this algorithm is 10% of that of the multi-conic technique, and 1% of that of the pseudostate theory. And the algorithm is about 10 times faster than the numerical integration.

Byrnes et al. [48] proposed a multi-conic method that is able to consider a number of complex perturbations in the whole travel. By using a relatively large time step, the method is fast enough and more accurate than the traditional patched conic or pseudostate technique. In this method, the transfer orbit is decomposed into a series of segments and each part could be solved with a similar pseudostate technique. They found that this method’s accuracy is an order of magnitude higher than that of the pseudostate technique, the computation time is two orders of magnitude faster than that of the numerical integration method, and the error is only 1%~5% of that of the patched conic method. For circumlunar flight, errors of the calculated pericynthion and return perigee altitude could be around 20 km; velocity errors be about 0.5 m/s [48]. Byrnes [49] integrated the multi-conic technique into a one-step method, which can be used in a manner analogous to the Lambert method to solve the transfer initial value problem between two planets in an N-body environment. Unlike the multi-conic method, the one-step method associated the pseudostates with the departure and arrival planets through Lambert conic, where the secondary gravity force fields outside the central force field were assumed to be active for a certain flight time. Damario et al. [50] had also shown that such Lambert-like applications of the one-step method may be extended to a flyby problem by combining two such single-step transfers, placed on either side of the flyby celestial body.

To simplify the procedure of the one-step method and improve its computational speed. Sergeyevsky et al. [51] proposed a one-step impact pseudostate technique for direct interplanetary transfer by assuming that the planetary center departure and arrival phase trajectories are rectilinear hyperbolas. This method can avoid the iterations required to obtain approximate hyperbolic trajectory features and the computation of the state transition matrix. Ramanan [52] applied the one-step impact pseudostate technique to generate the one-way Earth-Moon transfer trajectory and developed a comprehensive algorithm. In his paper, the pseudostate was determined by assuming a rectilinear hyperbolic for the arrival phase while the translunar injection state was obtained by solving a Lambert problem. The algorithm can reduce the error of the spacecraft to the target position by more than 95%, which provided a better preliminary value relative to the Lambert conic method with minimal computational effort. However, it is difficult to locate the hyperbolic orbital plane with paralleled position and velocity vectors of the rectilinear hyperbolic employed in the aforementioned algorithm. An undesirable collision with the target could occur in an actual mission scenario. Ramanan et al. [53] developed the one-step pseudostate technique for designing a non-impact Earth-Moon direct transfer trajectory. A simple matching strategy was employed to synchronize the geocentric transfer trajectory with the selenocentric trajectory with no need for computation of the state transition matrix. Characteristics of the nonimpact approaching trajectory were computed from the excess velocity vector. Furthermore, a semi-analytical based targeting technique was proposed to obtain fast and near exact solutions in the frame of three-body problems.

Moreover, it should be noted that the accuracy of both the pseudostate technique and the one-step method depends on the sweep-back duration which is directly relative to the size of PTS. On the one hand, PTS with a small size corresponds to a short sweep-back duration, leading to premature neglect of the secondary gravity force field. On the other hand, too long a sweep-back duration can cause poor approximation accuracy. The selection of the sweep-back duration or the radius of the pseudosphere is vital for transfer trajectory design with the pseudostate technique [45]. In the context of the interplanetary transfer problem, Sweetser [54] and Kiedron et al. [55] established an experienced relationship through multiple simulations and obtained the optimal value of this parameter. The duration of the lunar mission flight is only 3–6 days, so the optimal value can be easily obtained by grid search where a zero sweep-back duration corresponds to the solution of the Lambert conic method [52]. Results show that the achieved periapsis time after propagation is very close to the expected periapsis time when choosing the sweep-back duration of about 75% of the total flight duration. And the optimal percentage value changes with the day of departure.

3  Low-Energy Transfer Based on Lagrangian Point and Manifold Theory

Classical approaches to design the direct transfer from the Earth to the Moon such as Hohmann transfer, patched conic, and pseudostate methods are introduced in the previous section. Although it is desirable to deal with the analytical solution, the fuel consumption is quite high which can render missions infeasible in some circumstances [6]. Fortunately, a new class of low-energy trajectories has recently been discovered and employed, which makes it possible for missions that could not be realized by classical approaches. The low-energy transfer is preferred to direct transfer for its appealing features, such as lower cost, the extended launch window, and the property of allowing for a fixed arrival epoch for many launch dates within the launch window [56–58].

In this part, we will focus on Earth-Moon transfer trajectory design based on Lagrangian point and manifold theory. The trajectory is classified by the Lagrangian point being used. The transfer through the Earth-Moon L1 point is usually located within the Moon’s orbit, and hence it is called interior or cislunar transfer. The Earth-Moon L2 point can also be used to construct the interior transfer, but because the energy of the L2 point is greater than the L1 point, it is not optimal when designing a cislunar transfer trajectory. However, recent studies [6,11,19] showed that with the help of the solar perturbation, the L2 point can be used to design the optimal exterior transfer which is also known as the translunar transfer. Before systematically analyzing and summarizing these two low-energy transfer methods and their development, the fundamental of the problem, the circular restricted three-body problem (CRTBP) will be introduced briefly.

3.1 Basic Theory: CRTBP Problem Sketch Out

The three-body problem dynamic model is attracting ever-growing attention from both academia and industry as its excellent accuracy compared with the traditional two-body and the perturbed two-body models [59]. A restricted three-body problem was then proposed, which can be applied well to practical space missions. A modified model is the circular restricted three-body problem (CRTBP), which provides a high fidelity approximation to the spacecraft motion and can underline the dynamic nature well [60]. In the CRTBP, a spacecraft is considered to be massless. Assume that two primaries are mass points and make circular motions around their common barycenter. The spacecraft’s motion is then described in a rotating frame relative to the two primaries. The non-dimensional motion equations of the third body can be written as [61]

{X¨−2Y˙=ΩXY¨+2X˙=ΩYZ¨=ΩZ,(2)

where the subscripts denote the partial derivatives of the function:

Ω(X,Y,Z)=12(X2+Y2)+1−μR1+μR2+12μ(1−μ),(3)

where

R12=(X+μ)2+Y2+Z2,R22=(X+μ−1)2+Y2+Z2.(4)

with the mass parameter

μ=m2m1+m2,m2<m1.(5)

Five equilibrium points also known as the Lagrangian points L1, …, L5 exist in the CRTBP system, where the gravitational and centrifugal forces are balanced on the spacecraft. For the Earth-Moon system, the mass parameter μ = 0.01214. The Lagrangian points of the Earth-Moon system are summarized in Table 2.

In 1836, the Jacobi constant, C, was discovered under the rotating frame by Jacobi, which is the only constant of energy integral presented in the CRTBP so far [62]. The value can be determined from the initial conditions of the spacecraft’s motion:

C=2Ω(X,Y,Z)−(X˙2+Y˙2+Z˙2).(6)

For a given value of C, the curves of zero velocity are determined by

2Ω(X,Y,Z)−C≥0.(7)

By specifying the spacecraft energy equal to the value at each Lagrangian point, the curves of zero can be plotted as Fig. 9 shows.

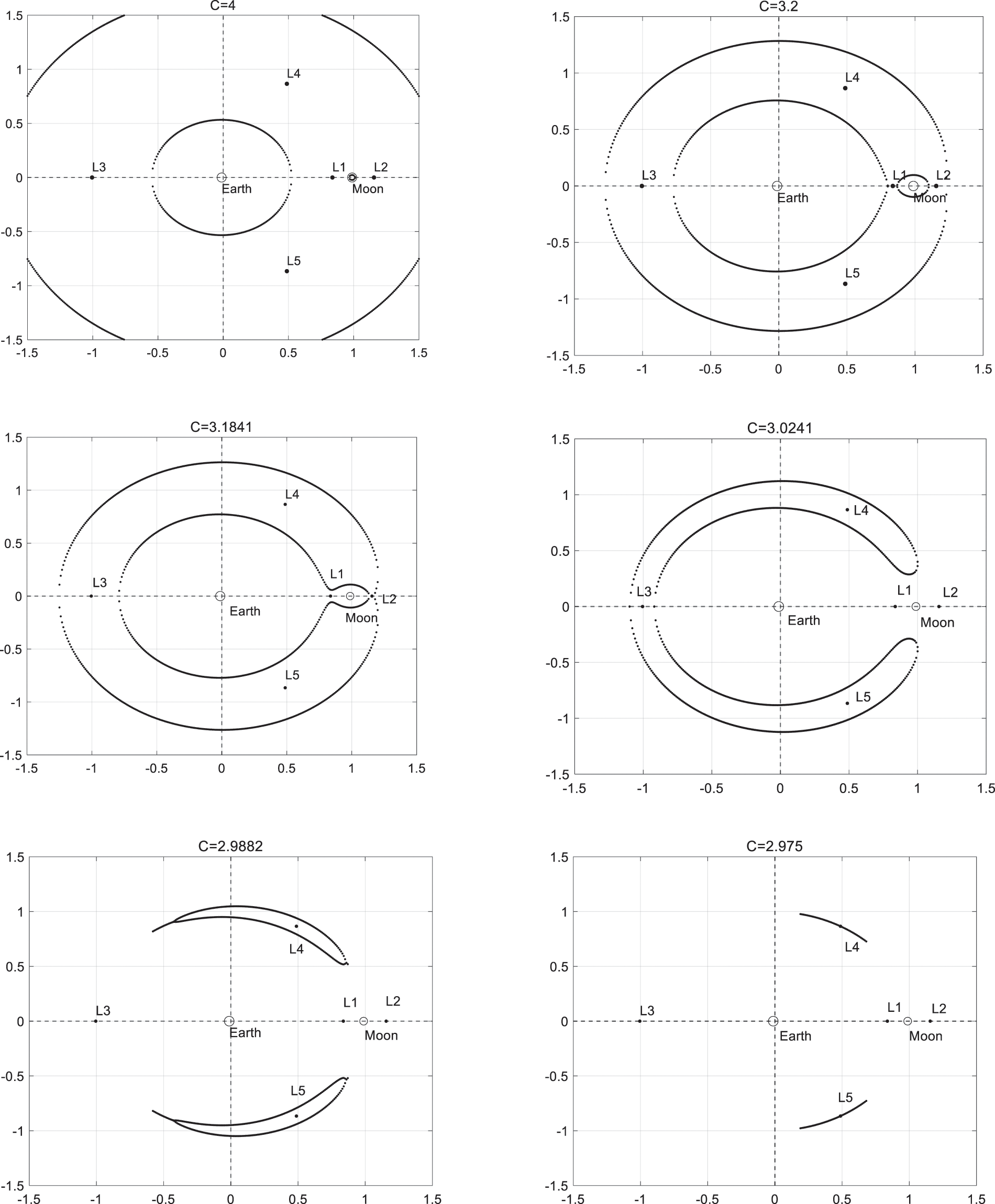
Figure 9: The curves of zero within the Earth-Moon system with different value of Jacobi constant

It is shown that a spacecraft with C equal to that of the L1 point can cross over from Earth to Moon. The one with C of the L2 point can cross the boundary to the exterior, and with C of the L4/L5 point can reach any point in the Earth-Moon system [63]. Moreover, there are abundant periodic and quasi-periodic orbits near the Lagrangian points in the Earth-Moon space, such as Lyapunov orbits, halo orbits, Lissajous orbits and distant retrograde orbits (DROs), etc. [64–66]. For more detail, one can refer to reference [67], where a comprehensive review of periodic orbits in CRTBP has been provided.

In 1968, Conley [68] investigated the phase space structure near Lagrangian points and categorized the motions as (1) periodic orbits, (2) stable/unstable manifolds of periodic orbits, (3) transit orbits, and (4) non-transit orbits, these orbits are shown in Fig.10. Additionally, he thought that the invariant manifolds of a periodic orbit separate transit orbits from non-transit orbits, and the former can be used to construct low-energy cislunar transfer trajectories. McGehee [69] investigated the dynamical behavior of CRTBP and indicated the role of the stable and unstable manifolds of the Lyapunov orbit in understanding the transiting trajectories. To acknowledge the contributions of these authors, Marsden et al. [70] denoted the invariant manifolds as Conley–McGehee tubes (also known as C-M tubes). Yamato [71] then studied the dynamical model considering perturbations and illustrated that most of the tubes would be distorted but few of them could be preserved by small perturbations from the perturbed gravitation of the third celestial body.

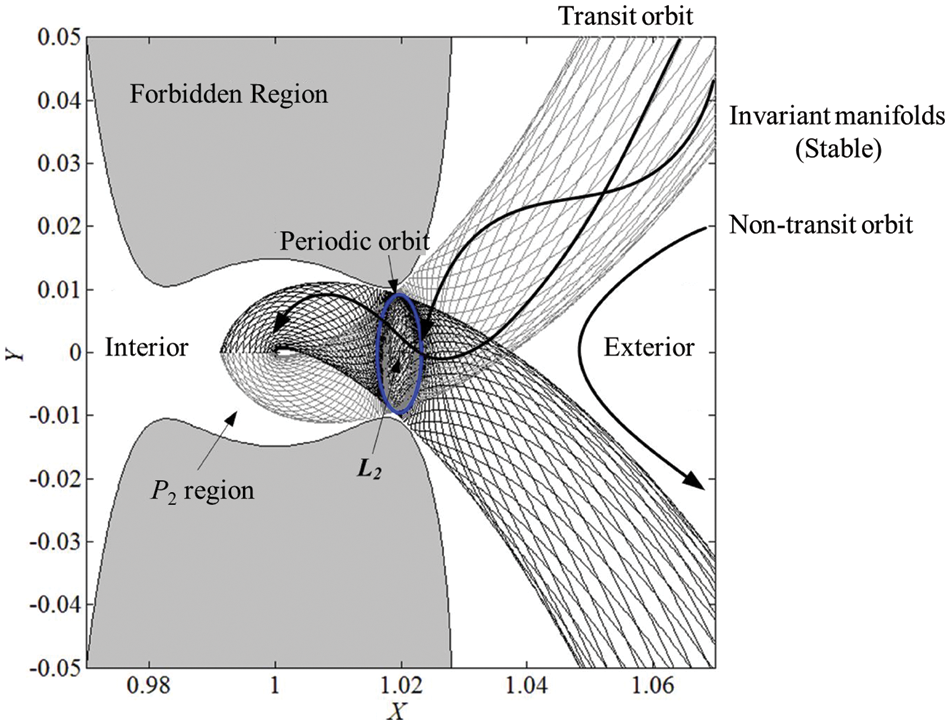
Figure 10: The flow in a collinear Lagrangian point region

3.2 Low-Energy Transfer Based on L1 Point

In the two-body-based classical approaches, direct transfer always needs high energy (C < 2). Theoretically, C < CL1 = 3.2003 is enough for an Earth-Moon transfer, with which a spacecraft could target the neck region around the L1 point. For the planar CRTBP, a planar periodic would separate the interior of the Moon’s region from the rest of the Earth-Moon region. However, the conception above only promoted the possibility of low-energy transfer in theory, and the transfer time tends to be infinite. Based on the author’s knowledge, the design method can be divided into three ways according to the used design tools, i.e., design with (i) chaotic control, (ii) manifold theory and (iii) numerical optimization.

As a systematic and classical method, the design of Earth-Moon transfer based on chaos has been studied since the era of Poincaré [72]. However, very few comprehensive reviews on it can be found. A pioneering work done by Ott et al. [73] on the later developed chaotic-motion-based chaos control theory and illustrated that a small initial perturbation might cause a huge control effect in a chaotic system. The method was come up with to address the local issue of stabilizing the trajectory on unstable periodic orbits embedded into the chaotic system [74]. A further development enables it to solve the global issue and construct a trajectory passing the desired target in a chaotic region known as ‘targeting’, consisting of finding a nearby short trajectory to satisfy the terminal conditions [74]. However, achieving ‘targeting’ in chaotic Hamiltonian systems is always challenging because of their complicated structures [75].

Many efforts have been made in designing chaotic transfer orbits to the Moon via targeting. In 1995, Bollt et al. [13] first obtained a chaotic Earth-Moon transfer orbit which the Moon with this method can ballistically capture. They applied a sequence of small perturbations to the initial condition of the spacecraft motion. Setting the Jacobi constant of C = −3.17948, slightly higher than CL1, and employing eight tiny perturbations, a low energy transfer orbit can be constructed linking with two very high altitude circular orbits of hE = 53,291 km and hM = 12,232 km. Fig. 11 shows a transfer orbit resembling the figure demonstrated by Bollt [13]. The total ΔV = 749.8 m/s whereas the flight time was up to 748 d. To reduce the flight time, Schroer et al. [14] modified the method. They obtained a low-energy transfer orbit that required at least four impulses by targeting a series of unstable periodic orbits. This approach can decrease the flight time to 377.5 d with a ΔV very close to the value in [13]. Macau et al. [15] designed a transfer with a slightly higher ΔV of 767 m/s and considerably cut the transfer time to 287 d. Ross et al. [16] obtained a family of solutions with the best requiring of ΔV = 860 m/s, reducing the transfer time to only 65 d.

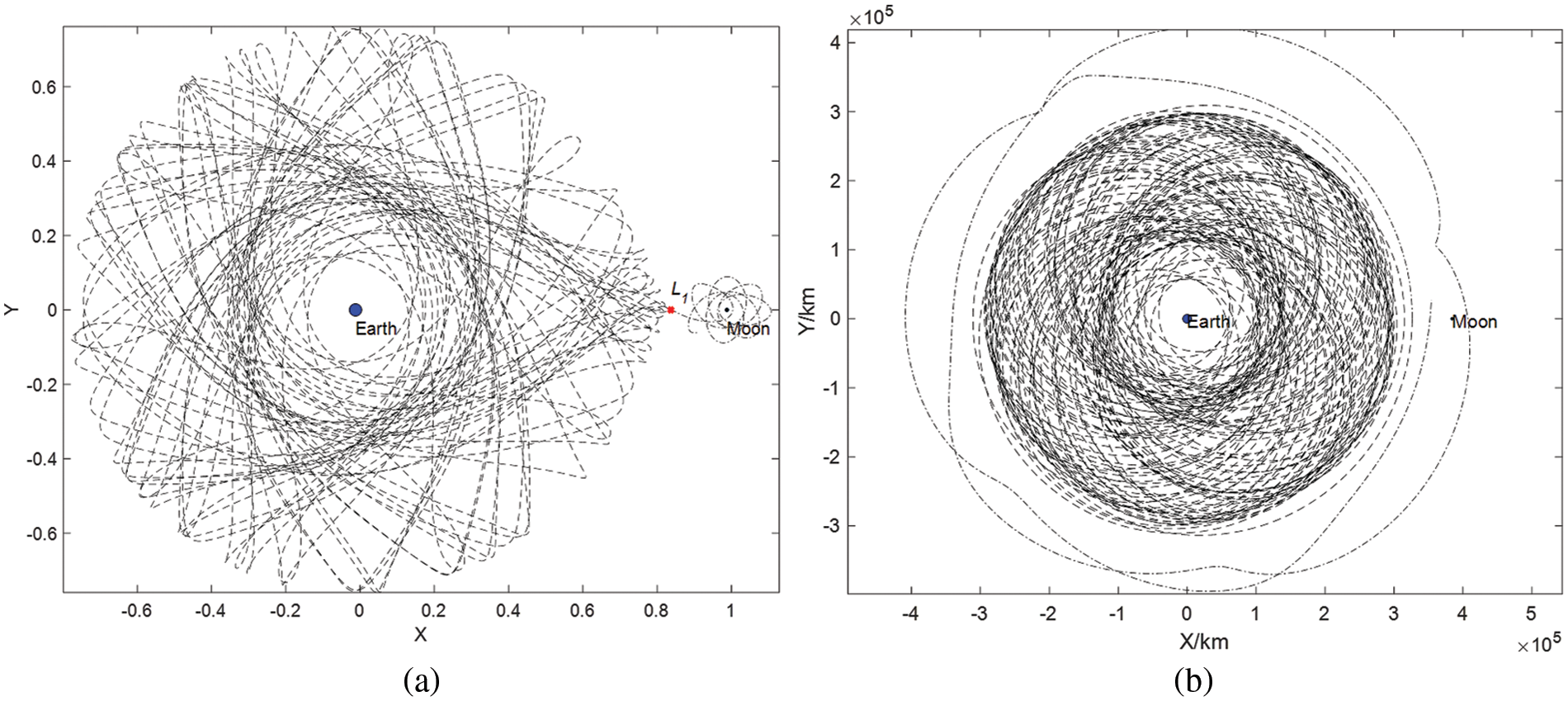
Figure 11: The Earth-Moon low-energy interior transfer trajectory resembling Bollt et al. [13]. (a) Trajectory in the rotating frame. (b) Trajectory in the inertial frame

Recently, Salazar et al. [76] extended Bollt’s method by increasing the pre-assigned distance between two points in the Poincare section. Needless recurrent loops can be removed, and thus, total flight time can be considerably reduced. Moreover, the transfer to triangular equilibrium points was explored in the study. Some studies also combined the targeting method with an optimization approach, which treated the chaotic transfer orbits as a class of multi-constrain fuel problems with multi-dimension decision variables [72,77,78]. With this approach, periodic orbits or random mass search is unnecessary, significantly reducing the transfer time and effectively constructing the low-energy transfer. For example, Wang et al. [72] presented an elitist teaching-learning-based and optimization-based optimal targeting method that can rapidly direct the chaotic series toward the Moon. The optimal transfer orbit they obtained was ΔV = 748.6 m/s and Δt = 213.5 d. Additionally, the trajectory can also be constructed by a hybrid approach using chaos control and invariant manifold simultaneously [79].

The above studies demonstrate that low-energy Earth-Moon transfer is possible when the Jacobi energy of the spacecraft is just a bit higher than CL1, although a long flight time is required. It is worth noting that the low-energy orbit constructed is to link two extremely high looping orbits since the region of chaos could only exist in the vicinity of such two high orbits. This is easy to understand from the invariant manifold perspective. Suppose backward integrate the stable manifold of the L1 point to intersect the low Earth orbit (LEO). In that case, only one impulse from the LEO orbit is needed for sending the spacecraft into the transfer orbit wrapped by the stable manifold. Unfortunately, the stable manifold of the Earth-Moon L1 point cannot reach a position very close to the Earth (about 0.1 Earth-Moon distance). Hence, Conley [68] in 1968 proposed a natural idea of linking the L1 transit orbits with two “looping” orbits around the Earth and the Moon through an impulsive provided at the crossing point. The spacecraft was supposed to transfer from the Earth to the two-dimensional Lyapunov orbit and the Moon’s inner region. This work has laid a theoretical foundation for the low-energy transfer construction by utilizing the Lagrangian point and its invariant manifold. Pernicka et al. then [80] defined a low-energy Earth-Moon transfer from a 167 km Earth parking orbit to a 100 km Moon circular orbit into two parts. One was from the L1 point to lunar orbit, and another from LEO to the L1 point. He applied AVS at the perigee/perilune location to control the orbit period and found a transfer with ΔV = 3824 m/s, Δt = 292 d. Topputo et al. [81] put forward an approach of patching conic-manifold to design a low-energy transfer orbit linking the two same target parking orbits as Pernicka et al. [80] studied. The transfer trajectory was divided into three parts: Earth-L1 leg, transit orbit, and L1-Moon leg. The connection arcs, i.e., the Earth-L1 and L1-Moon leg, were modeled by the three-body Lamber problem and solved separately with the two-point boundary problem. In their study, the amplitude of the hyperbolic transit orbits near L1 was also studied. A patched transfer orbit from a hE = 167 km Earth orbit to a hM = 100 km Moon transfer was found requiring ΔV = 3894.9 m/s and the transfer time Δt = 255.5 d. Again assuming the same two target orbits, Mengali et al. [82] developed a two-impulse optimization method. First, a closed-form approximate expression for the total velocity variation was deduced under the assumption of minimum ΔV bi-impulse maneuver. For a given Jacobi constant, a transit point was selected whose abscissa coincided with the L1 point. Then the amplitude of hyperbolic transit orbits above L1 and the velocity angle was taken as optimization variables. A hybrid methodology of combining genetic algorithms with a deterministic simplex method was employed to refine the solution. The best results of ΔV = 3861 m/s and Δt = 85 d were achieved with the fuel consumption and TOF almost equivalent to those obtained based on WSB theory.

Pontani et al. [83] proposed a geometrical approach for low-energy Earth-Moon mission analysis. They illustrated how isomorphic mapping could be profitably employed to optimize specific cislunar transfers by geometrically determining the desired optimization parameters. Liang et al. [84] systematically discussed both direct and low-energy cislunar trajectories in the context of restricted three-body dynamics. Different transfer trajectories were assessed by considering Jacobi energy and time of flight. They also illustrated the relationship between Jacobi energy, perilune/perigee radius, and the total flight time. The two-body energy with respect to the Moon at perilune and global sketches were accomplished. Xu et al. [12] explored the low-energy transfer of the Earth-Moon equivalent L1 and L2 points under the spatial bi-circular model (SBCM). They divided the transfer into two types: the cislunar transfer transiting the L1 point or its halo orbit, and the translunar transfer transiting the L2 point or its halo orbit. Though the solar perturbation in this model plays a secondary role compared with the Hamiltonian value, it turns the transfer time targeting the L1 point from infinite into finite and makes the low-energy transfer based on a time-dependent manifold possible. They illustrated that the L1 periodic orbit could increase the transfer opportunity by introducing another variable, i.e., serial points of a periodic orbit, but this also means a higher energy consumption. Tan et al. [85] investigated low-energy bi-impulsive transfer using periodic orbits. Two strategies of the direct and indirect methods were proposed. For the direct method, the large amplitude Lyapunov orbits were used to provide the initial value and approximate flight time. The indirect way aimed to design a bi-impulsive low-energy lunar flyby trajectory since lunar gravity can reduce the velocity increments of the Earth-Moon transfer. Concretely, two reference orbits were employed in this strategy, one is the Earth-Moon transfer trajectory which has been designed by the direct method and the other one is a candidate periodic orbit. The basic idea was to patch these two orbits together through differential correction. Both methods were extended into the bi-circular model (BCM) and solved by the optimization algorithm. The results showed that solar perturbation has the potential to further reduce the total cost of the bi-impulsive transfer. Moreover, considering the solar perturbation, Sousa-Silva et al. [86] designed a cislunar transfer by patching the Sun-Earth quasi-periodic orbit with the stable manifold of Earth-Moon L1 periodic orbit which can achieve a faster Earth-Moon transfer with ballistic capture.

Recently, an emerged conception of Earth-Moon transit station in cislunar space such as the Deep Space Gateway brings a lot of attention to the stable periodic orbit in the cislunar space, such as near-rectilinear halo orbits (NRHOs) and distant retrograde orbits (DROs) [87]. Therefore, a brief introduction is also given to the transfer problem based on these two kinds of orbits in the Earth-Moon space. Both NRHOs and DROs have perfect stability, but they also have distinct characteristics. The DROs are planar while the NRHOs are highly inclined. The DROs can cover the Moon entirely within the lunar orbital plane and the NRHO has a small minimum distance to the Moon [88]. Therefore, the NRHOs and DROs have different roles in future space missions.

As for the transfer problem related to the NRHOs, not only the transfers between Earth and NRHOs but also the transfers from NRHOs to the lunar surface and lunar orbits were studied [89–91]. Because of the stability of DROs, the hyperbolic manifolds commonly used in the design of low-energy transfer orbits no longer exist for the DROs. Thus, it is necessary to investigate the transfer orbits based on DROs specifically. For the transfer orbits from the Earth to DROs, Ming et al. [92] designed an indirect transfer to a DRO around the Moon by exploiting the Lyapunov orbits tangential to the DRO. Capdevila et al. [93] presented more solutions for direct transfers from the Earth to the DROs and indirect transfers by Lyapunov orbits associated to L1 or quasi-periodic DROs as bridges. Moreover, Capdebila et al. [94] also obtained direct or indirect transfer orbits based on the optimization approach. For the transfer from DROs to the Moon. Zhang et al. [95] studied the transfer orbits from DROs to low lunar orbits with inclinations between 0° and 90° in both CRTBP and planar bicircular restricted four-body problems. Peng et al. [96] utilized the numerical method to acquire low-energy transfer trajectories to DROs with multiple powered lunar flybys (PLFs) and WSB-like ballistic transfers. The results showed that a single PLF and a WSB-like ballistic arc could further reduce the total cost at the expense of time of flight. The ΔV-Pareto optimal solution could be enhanced and more feasible solutions for low-energy transfer and rendezvous trajectories could be obtained by the double and triple PLFs.

In addition, some studies have been carried out to find multi-impulse (mainly bi-impulsive) transfers under either the three-or four-body model and focused much on dealing with the optimization problems [97–99]. Since our review paid more attention to the characteristic of the dynamical models, relevant results would not be detailly introduced here. Comprehensive reviews of the topic can be seen in [4,5,100].

3.3 Low-Energy Transfer Based on L2 Point

The L2 point in the Earth-Moon system can also provide opportunities to construct low-energy trajectories. However, different from the only type of cislunar transfers based on the L1 point, the transfer trajectories design based on the L2 point contains both the interior cislunar ones and the exterior translunar ones. The former is essentially the cislunar transfer trajectories transiting the Earth-Moon L1 point through a heteroclinic connection which costs more fuel than the cislunar trajectories merely using the L1 point. The latter aims to take full use of the solar gravity and be captured by the Moon ballistically, which has the same geometrical shape in the inertial frame as Belbruno’s result [8,20]. Therefore, considering the former cislunar transfer by using the L2 point is not a fuel-efficient Earth-Moon transfer, the emphasis will be put on the exterior translunar transfer in this section.

The reason why the exterior transfer trajectories can be constructed is the potential of the Sun-Earth system’s stable manifold reaching very close to the Earth enabling a spacecraft to be sent directly to the manifold from the near-Earth space via a single impulse. Then, another impulse is conducted at the transition of the manifold to make the spacecraft enter the stable manifold around the L2 point and be captured by the Moon. This type of transfer trajectory was firstly given by Belbruno [17] based on the Weak Stable Boundary(WSB) theory whose detail will illustrate in the next part. Later in 2001, Koon et al. [11] explained the dynamic mechanism using the invariant manifold theory. Enlightened by the patched conic method to construct the direct transfer trajectories, they developed the patched three-body approach to take advantage of the dynamical structure of the CRTBP to obtain preliminary solutions to the Sun-Earth-Moon-Sc restricted four-body systems. And the foundational idea was to use two solution arcs to connect an initial geocentric orbit to a final selenocentric: one is a non-transit orbit associated to the Lyapunov orbit around L1,2 of the Sun-Earth system; another is a transit orbit associated to the Lyapunov orbit around L2 of the Earth-Moon system. By introducing the tool of the Poincaré section, potential patching points could be found, when integrating forward, the spacecraft will be guided by the L2 Earth-Moon manifold and get ballistically captured by the Moon; when integrating backward, the spacecraft will hug the Sun-Earth manifolds and return to the Earth. The transfer trajectory is shown in Fig.12.

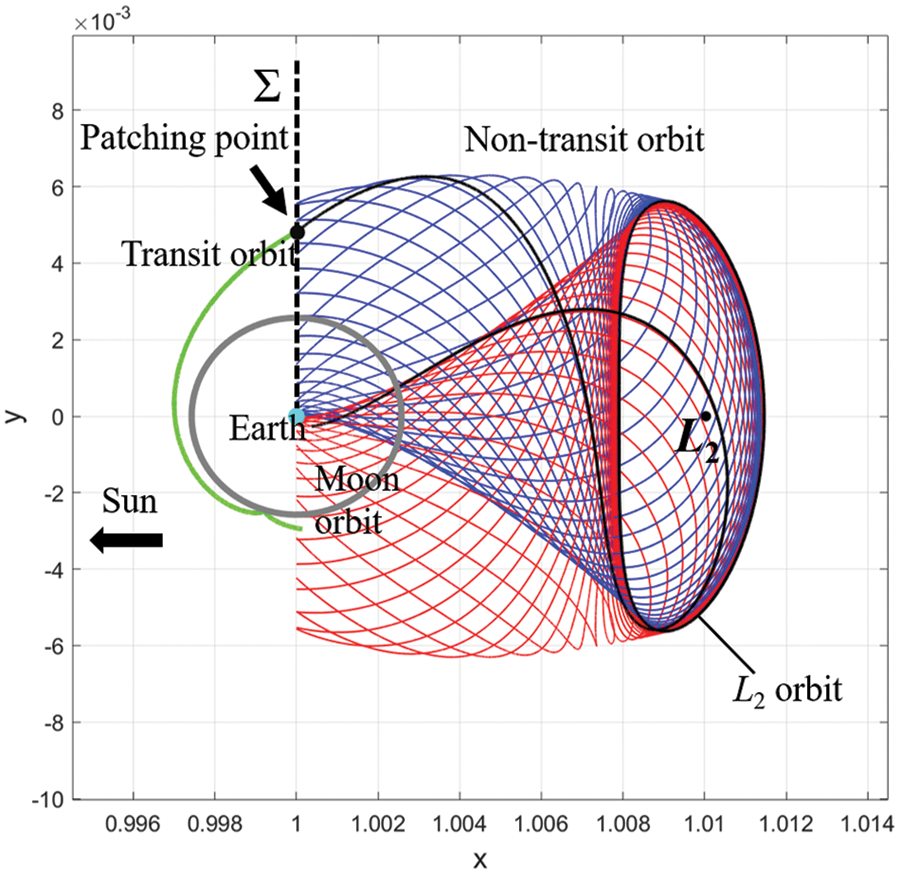
Figure 12: Two legs of a Hiten-like Earth-Moon low-energy exterior transfer trajectory in the Sun-Earth rotating frame

The patched manifold methods introduced above are based on three-body models. However, an expected trajectory is under the four-body or the ephemeris model. Therefore, an effective method is recomputing the Lyapunov orbits and their manifolds in the four-body model to reproduce the low-energy transfer orbit [19]. In addition, the patch point selection was always achieved by the trial and error method by which an optimal solution is not a guarantee. Peng et al. [101] presented an improved DE algorithm and found an optimal patch point. The solution obtained is 92 m/s less than the Hohmann transfer. Gong et al. [102] studied the low-energy Earth-Moon transfer considering the angle between the ecliptic-and lunar orbit planes. They derived the analytical expression describing the relation between the initial ΔV at the parking orbit, the parking orbit’s altitude h, and the Lyapunov orbit’s amplitude Ax. A curve of ΔV to h of the patched manifold was also provided. Compared with the Hohmann transfer, a 20% reduction in ΔV was achieved (3285 m/s vs. 3960 m/s) in a transfer departed from 200 km Earth parking orbit and captured by the lunar ballistically. The flight time in this case is 300 d. However, the utilized periodic orbits were still the planar Lyapunov orbits, and the corresponding invariant manifolds were two-dimensional. Fantino et al. [103] investigated the transfers between LiSE−LjEM(i,j=1,2) connections. Among the four combination types, only L1SE−L2EM and L2SE−L2EM can provide low or zero-cost (if there is a heteroclinic connection) transfers. Moreover, the points of the invariant manifold trajectories, of which the radius vector is orthogonal to the velocity vector of the smaller primary, can effectively confine the unstable points of the WSB region, revealing the relationship between the invariant manifold and the WSB. They also studied the second primary’s capability of temporary capture and illustrated the efficiency of the case when the Jacobi constant of the invariant manifold is large and the amplitude of the periodic orbit is small.

The above studies show that the exterior transfer still costs a long transfer time, usually more than 90 days. This can be attributed to the slow movement of the stable/unstable orbits on the hyperbolic invariant manifolds of Lyapunov orbits, by which the transfer trajectories followed closely, towards the periodic orbits as time goes to plus/minus infinity. To construct a faster Earth-Moon transfer orbit, Sousa-Silva et al. [104] proposed a new strategy that connected the quasi-periodic orbits with the hyperbolic manifold-guided solution. As shown in Fig.13, with the same energy level, the black lines represent the non-transit orbits that follow closely or loosely Ws(Γ2SE) and Wu(Γ2SE) before reaching the selected Poincaré section after about 80 to 300 days. The blue lines are quasi-periodic orbits on two-dimensional tori around the Earth that reach the Poincaré section after less than 40 days. This alternative solution can reduce the total transfer time to about 10 days, while still providing lunar ballistic capture at arrival [105]. However, it is worth noting that the selected departure orbit was a GTO orbit whose energy is considerably higher than that of the traditional Earth parking orbit. Finally, they also explored the superiority of the new method to the conventional direct Earth-Moon transfer method in extending the launch window and decreasing the midcourse maneuver.

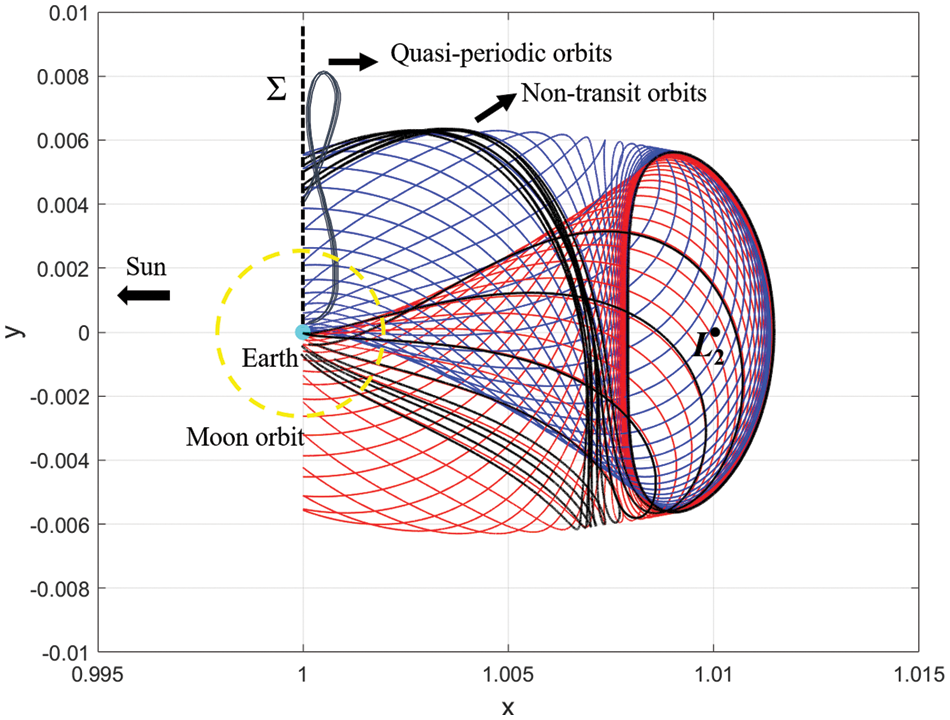
Figure 13: Sample trajectories with the same Jacobi constant CSE = 3.000782. The stable manifold and unstable manifold are shown in red and blue respectively. The black lines represent non-transit orbits while the dark blue lines represent quasi-periodic orbits in the Sun-Earth system

Since solar perturbation is essential in constructing a low-energy exterior transfer, applying a restricted four-body model rather than a three-body one is ideal for achieving higher accuracy of a designed transfer. However, the commonly used plane-restricted four-body model is a non-autonomous system, which challenges much on methods using periodic orbits and their invariant manifolds. In 2005, Shadden et al. [106] used the Lagrangian Coherent Structure (LCS) to find invariant manifolds of 2D non-autonomous systems. Short et al. [107] also calculated the LCS under four-body and ephemeris systems. Then they applied it to designing a transfer orbit from the LEO to the vicinity of the Earth-Moon L1 point. Based on that, Qi et al. [108] proved the existence of a tube-formed time-dependent invariant manifold in the phase space. They also constructed a low-energy transfer trajectory by patching the unstable invariant manifold under Sun-Earth restricted three-body system and the time-dependent stable manifold under the Sun-Earth-Moon system. Same based on the concept of LCS, Onozaki et al. [109] considered the planar four-body model as two coupled three-body with perturbations and constructed a low-energy Earth-Moon transfer trajectory by patching two time-depend manifolds.

Some studies also focused on the Earth-Moon three-dimensional (3D) low-energy transfer problem [57,110–112]. In the two-dimensional planar CRTBP, the interior and exterior regions of their three-dimensional energy surface are well defined. In the spatial case, however, the invariant manifolds of a halo orbit are two-dimensional while the energy space is five-dimensional. Such a manifold cannot define the interior or exterior topologically well, making three-dimensional transfer significantly complex [57,113]. In the Jovian moon system, Gomez et al. [110] designed a trajectory ending in a high inclination around the Europa. Howell et al. [112] obtained the transfers between the Earth-Moon system and Sun-Earth L2 point in three-dimension circumstances. They computed the three-dimensional transit orbit inside the stable Earth-Moon tube to link the exterior and interior regions. The primary solution was then reproduced under the full ephemeris model. In addition, the particular Lissajous trajectories in each system were sought to accomplish the transfer at a low cost. Ren et al. [114,115] analyzed the limitation of the planar manifold assumption and proposed the necessary and sufficient conditions for producing a transit orbit. The statistical character of the natural lunar low-energy transfer orbits and the optimal performance of the artificial lunar transfer orbits were numerically investigated. Similar to the conclusion drawn in [103] under the planar circumstance, in the spatial case, the L2 transit orbit has more opportunities to realize a lunar collision than the L1 transit orbit. They pointed out that the distribution of the elevation angle of the lunar collision velocity vector relative to the lunar surface can be regular with low energy. And individually increasing the energy level is insufficient in improving the transfer ratio. The success of this patched three-body approach depends greatly on the spatial configuration where the invariant manifolds of the three-body subsystems intersect within a reasonable time [104]. Xu et al. [12] studied available transfer opportunities under the spatial bi-circular model. They found that in the case of transiting the L2 point, a whole Earth-Moon transfer trajectory can be achieved only within the solar phasic angle β interval [21.8∘,23.3∘]∪[201.5∘,203∘], while it can be achieved within the pairs(β,τ) of ([85∘,165∘]∪[265∘,330∘])×[0,1] and ([10∘,92∘]∪[192∘,268∘])×([0,0.26]∪[0.57,0.66]) in the case of transiting the halo orbit near the L2 point.

Although showing a relatively long flight duration, the low-energy transfer has many advantages, including the low cost, an extended launch window, and the capability of fixed epoch arrival [5]. Taking the GRAIL mission as an example, the low-energy transfer provided a long launch period (at least 21 days), which is difficult with the direct lunar transfer, whose consecutive launch dates to target a fixed ascending node usually are lower than three. Moreover, in the low-energy case, any launch date within the launch window leads to a fixed lunar orbit insertion date with essentially one certain lunar orbit design, which is also impossible using the direct lunar transfer [56]. Considering the practical trajectory design, Parker et al. [116] proposed a targeting scheme to build 21-day launch trajectories from a 185 km Earth parking orbit to the 100 km circular lunar polar orbit, using up to two midcourse maneuvers. The dynamical model used was JPL’s DE421 planetary Ephemerides. They found that the average cost of 2.5 m/s per day could add a launch period, and the cost of the 288 reference transfers studied was approximately 71.7 ± 29.7 m/s (1σ).

4  Low-Energy Transfer Based on WSB Theory

Section 2 introduced the traditional direct transfer method based on the two-body Keplerian ellipse from the Earth to the Moon. Such transfers have a hyperbolic excess velocity V∞ relative to the Moon which determines another ΔV need to be given to render the spacecraft captured into an elliptic orbit about the Moon.

For the traditional direct transfer orbit, however, the spacecraft cannot reach the moon if the TLI ΔV is eliminated. The only available way is to eliminate the spacecraft velocity in the vicinity of lunar periapsis which means the TLI orbits energy should be similar to the Moon’s orbit. Considering the maneuver at the apogee of the transfer orbit is not provided by the main engine but by the perturbation of the Sun or Moon, theoretically, the total ΔV required can be further reduced. To achieve this, the spacecraft should be sent to the region where the gravitational interactions between Earth, Sun, and Moon tend to balance which is called weak stability boundary (WSB). In this region, a small maneuver can change the spacecraft motion significantly and return the spacecraft for ballistic captured by the Moon. This type of transfer was firstly constructed by Belbruno and utilized by the Japan Hiten probe [18]. By using this method, only one impulse can send the spacecraft to the Moon directly, while two impulses are needed for Hohmann and three for bielliptic. And the energy-saving over Hohmann and bielliptic are 18% and 37% respectively but a longer transfer time is required [8].

4.1 The Weak Stability Boundary

Various definitions have been given to the WSB. The most basic definition according to Belbruno [8] is that WSB is a transition region in the phase space where gravitational interactions between Earth, Sun, and Moon tend to balance. If projected into a three-dimension space, WSB describes a continuous three-dimension space and can be seen as a generalized Lagrangian point or the concept of the sphere of influence. Another definition also given by Belbruno [7] regards WSB as a region in phase space supporting a special type of chaotic motion for a special choice of elliptic initial conditions with respect to m2. Or as “in the CRTBP, WSB is a boundary set in the phase space between stable and unstable motion relative to the second primary. Perturbed by the first primary, Keplerian orbits about the second primary could be stable only if they preserve the character of bound motion after a certain number of revolutions. Yagasaki [97] described WSB as “a transition region between the gravitational capture and escape from the Moon in the phase space”. In this part, we first give three classical definitions of the WSB, i.e., analytical definition, numerical algorithmic definition, and definition given by Garcia and Gomez.

Definition 1: Analytical definition

Reference [7] gives the mathematical definition of WSB in the frame of CRTBP: P3 is captured at the time t = t1, if the solution of CPTBP, φ(t)=(X(t),X˙(t)) satisfies

E2(φ(t1))≤0).(8)

Meanwhile, r2(φ(t))>0, where X and X˙ are position and velocity with respect to P2 in P2 centered inertial coordinate, and the two-body Kepler energy of P3 can be given by

E2(X(t),X˙(t))=12|X˙|2−μr2,(9)

where r2=|X|,0≤μ≤1/2.

We consider the CRTBP and determine the set J−1(C) where E(X,X˙)≤0. In addition, those points are considered where r˙2=0, i.e., local periapsis or apoapsis point. Set

Σ={(X,X˙)|E2(X,X˙)<0},σ={(X,X˙)|X⋅X˙=0}.(10)

Then W=J−1(C)∩Σ∩σ defines a special set where ballistic capture occurs in the restricted problem. W represents the weak stability boundary. The motion of P3 near W is sensitive.

Definition 2: Numerical algorithmic definition

Reference [7] expressed WSB by numerical method. Considering a ray l(θ) from the Moon with perilune distance r lying on the l(θ), the spacecraft performs a stable motion as it follows a full cycle around the Moon without going around the Earth; otherwise, the motion is unstable. When gradually increasing the initial perilune distance along the l(θ), a finite distance r∗ can be found. The eccentricity e is another vital parameter for r∗. Define

W={r∗(θ2,e2)∈R1|θ2∈[0,2π],e2∈[0,1]},(11)

where W has two components. One corresponds to retrograde motion about the Moon and the other to direct motion about P2 after propagation from l.

Definition 3: Definition given by Garcia and Gomez

Reference [117] gave the initial conditions along the l(θ) that must be integrated to determine the stable or unstable regions around P2.

Initial conditions with positive velocity (osculating retrograde motion about P2)

x=−1+μ+r2cos⁡θ,y=r2sin⁡θx˙=r2sin⁡θ−vsin⁡θ,y˙=−r2cos⁡θ+vcos⁡θ.(12)

Initial conditions with negative velocity (osculating direct motion about P2)

x=−1+μ+r2cos⁡θ,y=r2sin⁡θx˙=r2sin⁡θ+vsin⁡θ,y˙=−r2cos⁡θ−vcos⁡θ.(13)

In both cases, v is the modulus of the initial velocity which is given by

v2=μ(2r2−1a)=μ(1+e)r2.(14)

When fixing the value of eccentricity e and the angle θ, all the possible values of the distance r∗ along l are searched for which there is a change in the stability property of the orbit. For a finite number of points (up to a certain precision) r1∗=0,r2∗,…,r2n∗ such that if r2∈[r1∗,r2∗]∪[r3∗,r4∗]∪…∪[r2n−1∗,r2n∗]then the motion is stable and otherwise unstable. The number of ri∗ and their values depend on e,θ and computational precision. Then, WSB can be defined as

W¯={[r2k−1∗(θ,e),r2k∗(θ,e)],k=1,…,n;θ∈[0,2π],e∈[0,1)}.(15)

4.2 Low-Energy Trajectory Design Based on the WSB Theory

According to Dutt [4], there are two common ways to design a ballistic capture transfer trajectory based on WSB theory, i.e., the back-propagation method and forward targeting method [4]. Belbruno et al. [8] first proposed a methodology for producing a WSB-based low-energy trajectory. The dynamical model used is a general restricted four-body problem as given by

mkx¨k=∑i=1i≠k4Gmimk|xi−xk|−3(xi−xk),(16)

where k=1,2,3,4 represents spacecraft, the Sun, the Earth, and the Moon, respectively. And xk denotes the inertial position of the mass point, mk. The initial value xk(0),x˙k(0) for k=2,3,4 can be obtained from an epoch t=0. For convenience, consider a spacecraft’s motion relative to the Earth and introduce a transformation. Let x¯k=xk−x3 denote the relative position of the mass point mk in the Earth-centered non-inertial coordinate. The motion of spacecraft is renewed as

mkx¯¨k=∑i=1i≠k4Gmimk|x¯i−x¯k|−3(x¯i−x¯k)−∑i=1i≠34Gmim3|x¯i|−3x¯i.(17)

Specifically, once the initial value in the WSB region of the Moon is determined, the equation of motion (17) can be integrated back to the trajectory arriving in the WSB3 at approximately 1.5 × 106 km from the Earth. Then for a fixed position relative to the Earth, varying the initial velocity to make the spacecraft leave the Earth and arrive at the target point obtained by previous backward integration. An energy augmentation can be achieved through a lunar gravity assist. The combination of the two trajectory segments is the aimed WSB transfer. Moreover, a differential correction is always needed for targeting, and the equations of motion are solved via a fourth-order Runge-Kutta numerical integration. Yamakawa et al. [118,119] provided a systematic method for trajectory construction and obtained a wide variety of ballistic lunar capture trajectories for different cases. These trajectories were classified into two types: (1) an Earth side approach to the Moon through a geocentric orbit with an initially small semi-major axis and (2) an anti-Earth side approach through a geocentric orbit with an initially large semi-major axis. An analysis of a geocentric orbit considering the solar effect was performed based on simplified Lagrangian’s planetary equation. The investigation of the solar gravity’s influence on the geocentric orbit from the angular momentum viewpoint shows that the perigee distance would increase when the spacecraft location in the second or fourth quadrant in the Sun-Earth rotating frame. A detailed illustration of the solar perturbation effect is shown in Fig.14. Besides, by introducing lunar swing-by, the total flight time can decrease due to the rise of the geocentric orbit’s initial perigee caused by the reduction of the local eccentricity.

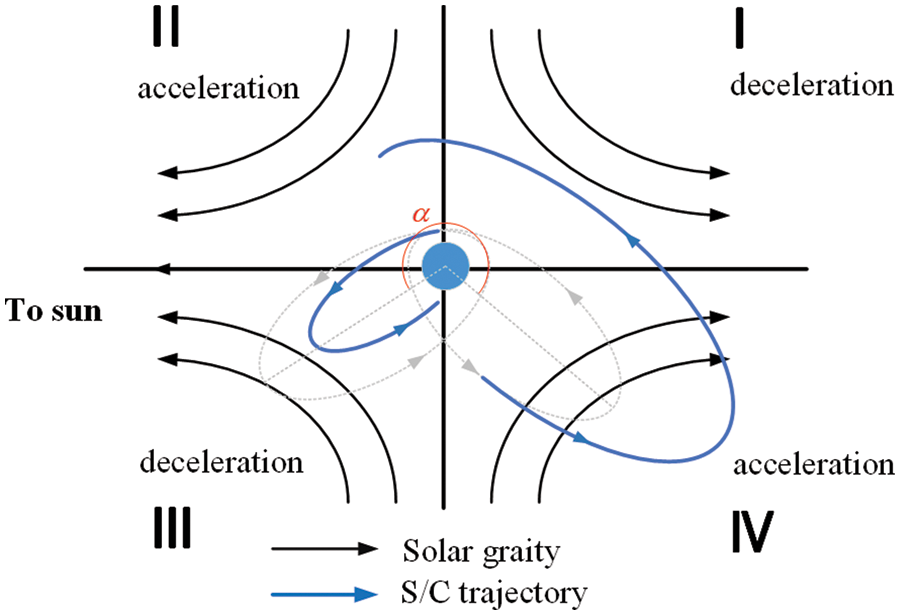
Figure 14: The α angle and the shape of the solar gravity gradient in the surroundings of the Earth. when α is in the II or IV quadrant: the final perigee is higher than the initial one. When α is in the I or III quadrant, the length of the major axis is reduced, leading to a lower perigee

Circi et al. [120] studied the configuration requirement of the WSB transfers. The possibility of the transfers is determined by two important angles: one is the angle between Earth-to-Sun lines and Earth-to-apogee and another is the Sun-Earth-Moon configuration at spacecraft arrival to the Moon. The lunar gravitation capture and solar gravitational effect were analyzed in terms of variations of the Jacobi constant in the Earth-Moon and Earth-Sun systems. They also studied the sensitivity of the lunar encounter region to capture through the parametric analysis. Specific angle values were revealed, under which the lunar capture can be stable. The condition of generating WSB transfers was estimated in the case of the “quasi-ballistically” Moon captured transfer orbits. And the classification substance of the WSB trajectories was explained.

Despite efforts on Earth-Moon transfer orbits design using the WSB theory, the nature of the WSB and associated dynamics has not been well understood until the work done by Garcia and Gomez in 2007 [117]. They proposed a more precise definition of the nth WSB through numerical explorations. The generalized WSB was regarded as a union of the set for n = 1, 2, 3…. A comparison of the stable/unstable regions around the small primary to the stable/unstable invariant manifolds of the periodic orbit about the collinear Lagrangian points was conducted. In the framework of the planar CPTBP, they concluded that for some range of energies, the WSB is located in the closure of the stable manifolds’ union around two of the collinear Lagrangian points. Romagnoli et al. [121] further investigated the lunar WSB in the planar and spatial cases using both the three-and four-body models. The computation of WSB in the study can be divided into single and multiple stable/unstable transitions. The eccentricity of the lunar orbit and the presence of the Sun showed ignorance influence on the WSB geometry. Moreover, a comparison was made between the lunar polar capture and equatorial capture when a stable and safe orbit (no impact on the lunar surface after capture) is required. Results showed the superiority of the equatorial capture in the capture number, although a higher collision risk is found. In addition, the equatorial capture with low perilune altitude presented the ability to achieve the minimum energy transfer. Ceccaroni et al. [122] then proposed a new definition of the WSB consistent with the existing algorithmic definitions. Belbruno et al. [123] also illustrated that for a certain condition of mass ratio and energy level in planar CRTBP, the WSB near the heavier body coincided with a branch of stable manifolds associated to the Lyapunov orbit at one of the collinear Lagrangian points.

Topputo et al. [124] modified the numerical approach proposed in [117]. They defined the motion equations under the polar coordinates to compute the stable sets, and calculate the boundaries through a bisection algorithm. The modified approach was also employed to produce the WSB of the Sun-Jupiter system. The geometry of the stable sets was compared to that in the Earth-Moon system [117,121] in terms of the mass parameter. The study also discussed the possible correlation between the weak stability boundary and the invariant manifolds associated to the Lyapunov orbits. Belbruno et al. [125] also excavated the relationship between weak stability boundary and invariant manifolds. A rigorous definition in the context of the planar CRTBP was given, and a geometric argument based on the separatrix property of the invariant manifolds associated to the Lyapunov orbits was provided. They summarized the following points from numerical experiments’ results. First, with the algorithmic definition of the WSB, a prior knowledge of the Lyapunov orbit is no longer needed in finding trajectories on the stable manifolds of the Lyapunov orbit. Second, they indicated that WSB contained the symmetric homoclinic points in the whole range of Jacobi constants where the WSB is defined, which is different from the results in [7]. Moreover, WSB could also exist in models where the hyperbolic invariant manifolds are inapplicable, such as the elliptic restricted three-body problem and the bicircular restricted four-body problem. Hence, the WSB may be a good substitute for the hyperbolic invariant manifolds in such cases. Besides the expected transitions, Sousa-Silva et al. [126] also found spurious transitions in various types, which was attributed to the separatrix role of the invariant central manifold in the planar CRTBP. The study discussed the spatial distribution of the authentic and spurious transitions along the boundary for sets of initial conditions with high eccentricity. The results showed the regular appearance of spurious transitions and collisional trajectories. In addition, they proposed a new definition of the stability boundary through the investigation of the smooth and fractal-like portions of the boundary. In order to validate the stable solutions in Earth-Moon ballistic capture transfers, Sousa-Silva et al. [127] also investigated the applicability of the initial condition sets generated by the algorithmic definition of WSB within the lunar SOI in the Earth-Moon low-energy capture transfers’ construction. They found subsets of stable conditions which provide feasible Earth-Moon transfers. In the study, an external low-energy Earth-Moon transfer with zero midcourse correction at the patching section was constructed. Griesemer [128] proposed a numerical targeting scheme to design ballistic lunar capture transfers. The initial guesses obtained through a simpler dynamical system were accurate enough to converge to the solution in the numerical targeting scheme. In the algorithm, a particular member of a family of periodic orbits, documented by Makellos [129] as family f 16, was utilized as the initial guess for an Earth-Moon transfer. van der Weg et al. [130] analyzed the lunar orbits and some of the possible contingencies for the European Student Moon Orbiter (ESMO). The operation orbit selected was a highly eccentric one, and the 6 months WSB transfer was obtained. A parameter study was undertaken for the sensitivity investigation of the lunar orbit insertion. And a database of transfer solutions from 2014 to 2015 was used to evaluate the robustness of weak capture and the planetary geometry at lunar arrival. Dutt et al. [131] also constructed the WSB transfer via back-propagation in CRTBP. Concretely, two highly elliptical geocentric orbits about the Earth and the Moon were propagated forward and backward respectively and patched using the Fixed Time of Arrival targeting method. The genetic algorithm was used to find patching points to reduce the required number of patching points. Various selenocentric and geocentric orbits were considered, and eligible candidates for WSB transfers were plotted on the phase space. Moreover, they investigated the fly-by Moon trajectory to show the reduction of the total flight time using this approach.

Additionally, Belbruno [132] proposed a forward targeting algorithm, making the generation of WSB transfers more accessible. In his study, the software package STK/Astrogator was used, and an optimization technique was employed for improving launch opportunities and ΔV saving. Dutt et al. [133] developed a method to find Earth-Moon WSB transfers by forward propagation. The problem was considered as an optimization of the two loops. The outer loop varied the departure parameters from an Earth parking orbit while the inner loop obtained a capture trajectory to the Moon by varying the small impulse given at the WSB of the Earth. Once a lunar capture orbit was obtained, they were able to achieve the minimum eccentricity for circularization.

5  Low-Thrust Method

The low-thrust method typically uses low-thrust propulsion systems such as electric propellants or solar sails. Employing high specific impulse, the fuel efficiency of low-thrust transfers enables the enhancement of payload capability and the potential of achieving high fuel consumption missions. Different from ballistic trajectories mentioned before, a spacecraft that adopted low-thrust transfer would be propelled for long period or even persistent using the low-thrust engine. Therefore, it experiences the gravitational attraction of the primaries and other perturbations along with the change in energy due to thrusters. There are two key problems in the low-thrust method: the dynamic equation under the action of continuous low-thrust has no analytical solution, and the thrust direction, thrust magnitude, and timing of thrust application during a flight are difficult to determine; The low-thrust propulsion system is too powerless to operate instantaneous braking as the high-thrust propulsion system does, hence it is hard for the spacecraft to be captured when it reaches the vicinity of the Moon. The design of low-thrust transfer trajectories can be modeled as a variational problem of optimizing fuel consumption or transfer time, and the method to solve this problem can be divided into the indirect method, direct method, hybrid method, and evolutionary algorithms [134,135]. A graphical illustration of approaches used to solve the spacecraft low-thrust transfer trajectory optimization problems is displayed in Fig. 15.

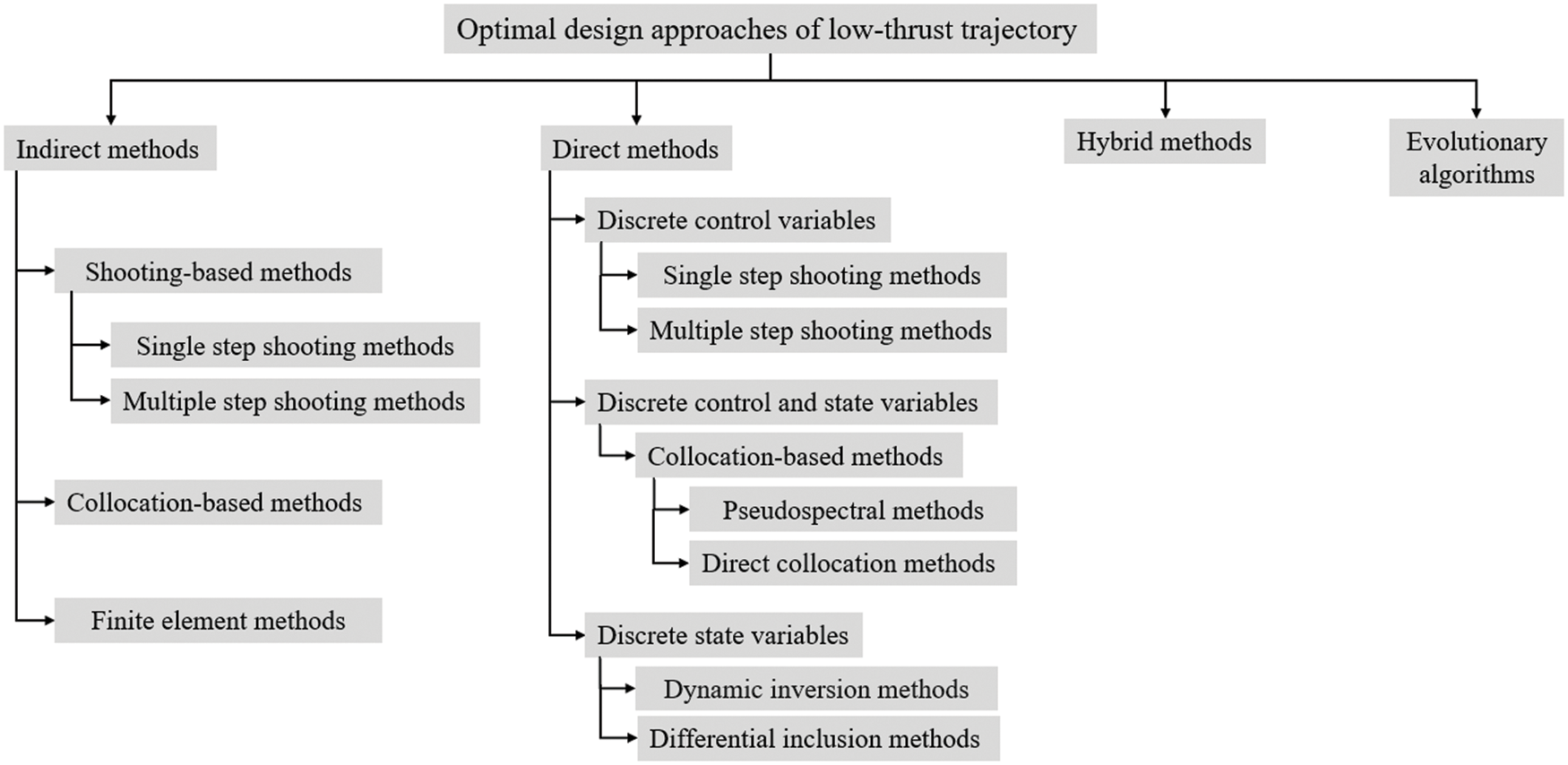
Figure 15: Optimal design approaches of low-thrust trajectory

The indirect method is commonly used in the early study of transfer trajectory optimization. Based on the constraint equations and optimization index of an original problem, the indirect method introduces Lagrangian multipliers to construct the co-state equation and new optimization index to transform the low-thrust transfer trajectory optimization design problem into a two-point boundary value problem (TPBVP) with nonlinear ordinary differential equations. Both the dynamic and boundary constraints include the first-order optimal necessary conditions derived from the calculus of variations and Pontryagin’s Maximum Principle (PMP) [136].

However, deriving the first-order optimal necessary conditions is challenging in this case [137]. For some special low-thrust orbits, Lawden [138] described the first-order optimal necessary conditions based on the primer vector theory. Russell [139] simplified the low-thrust transfer trajectory problem to only a few parameters through the primer vector theory and calculus of variations. Grigoriev et al. [140,141] derived the first-order optimal necessity conditions for complex dynamic models and complex interior point constraints. They also introduced the complementary relaxation and rigidity conditions into inequality constraints.

Moreover, an initial guess is required for the co-state variable. However, in the indirect method, the convergence region is narrow and the results are sensitive to initial guesses [142,143]. Many auxiliary methods have been proposed to release this sensitivity, such as the Adjoint Control Transformation (ACT) [144–147], normalization techniques [148,149], and etc. [142,150,151]. The homotropy method is also emerging in the optimization design of low-thrust Earth-Moon transfer trajectories [152–154]. It was first introduced by Bertrand et al. [155] in 2002. This method can effectively overcome the discontinuous control problem in the fuel optimization problem and can increase the convergence area of the optimization algorithm.

Efforts are also made in the optimal design of the low-thrust transfer trajectory in the cislunar space based on the indirect method. The early studies always divided the whole trajectory into the Earth phase, the middle phase, and the Moon phase, respectively. Then they solved the optimal control problem of each phase separately and patched the trajectories together. Based on this approach, Golan et al. [156] studied the Earth to polar Moon orbit low-thrust transfer problem in both two-and three-dimensional cases. Ranieri et al. [157] used a homotopy process by multiplying a scale factor with the terms due to third-body perturbation and rotational effect and obtained the spatial trajectory in the Earth-Moon rotating frame. To reduce the computational burden, Lee et al. [158] proposed an initial co-state estimation method to construct spiral trajectories directly for an arbitrary initial radius, transfer time, and target-specific energy in the Earth-Moon rotating frame.

Recently, the study on designing the Earth-Moon low-thrust transfer trajectories based on the invariant manifold has been carried out to make full use of the characteristics of three-body dynamics. Senent et al. [159] adopted an indirect method combined with the adjoint control transformation (ACT) to transfer a power-limited spacecraft from an LEO to the stable manifold associated to an unstable periodic orbit in the CRTBP. The guidance algorithm developed was also proven to be capable of dealing with both periodic unmodeled gravitational perturbations and power fluctuations. Oshima et al. [160] studied the global search strategy for low-thrust transfer to the Moon in the planar CRTBP. By implementing the necessary condition of optimality based on the Pontryagin extremum principle, a wide range of Pareto solutions were obtained, many of which exploited high-altitude lunar fly-by to reduce fuel consumption. Pérez-Palau et al. [161] studied the design of minimum fuel low-thrust trajectories from an LEO to a lunar orbit with the BCM model. In their study, two methods were proposed to overcome the numerical difficulties that arose from the huge sensitivity of the state and costate equations. The trajectories found were classified into several families based on orbital shape, transfer duration, and fuel consumption, and a physical interpretation was also given to the different families of trajectories based on invariant manifold theory. Taheri et al. [162] used the indirect method along with Lawden primer vector theory to design low-to high-thrust trajectories from a GTO to a halo orbit of the Earth-Moon L1 point. Considering the challenge caused by the sensitivities of the dynamical models, they introduced the continuous State transition matrix (STM) [163] to calculate the constraint sensitivities. This approach enables them to solve fewer subproblems by changing the continuation parameter at a greater rate when using the homotopy method. Same targeting the extreme sensitivity of the co-state variable when using the indirect method, Hecht et al. [164] combined the heuristic optimization algorithm and the homotopy continuation technique to obtain the effective initial value of the co-state variable. After determining a guess of the co-state variables, a single shooting method was employed to converge to the fuel-optimal solution. The method was then successfully used in a GTO-L1 halo orbit transfer problem. By combining the halo orbit manifolds at the Earth-Moon L1 point, Singh et al. [165] studied the end-to-end low-thrust transfer problem from a GTO orbit to an LLO orbit by exploiting the manifolds associated to the Earth-Moon L1 halo orbit. The homotopy method was still adopted for the final boundary conditions to improve the convergence. Moreover, considering the effect of Sun’s perturbation, they made a comparison between BCM and CRTBP models and achieve some conclusions.

With the development of computer technology and the enhancement of numerical computing capabilities, the direct method has become a widely used method in the optimization design of low-thrust transfer trajectory [166,167]. The direct method [168] discretizes the variational problem and transforms it into a nonlinear optimization problem with multiple nodes and optimization variables. Then the low-thrust transfer trajectory can be obtained by minimizing the performance index by using the nonlinear programming (NLP) algorithm. Different from the indirect method, the direct method does not have high requirements on the initial value. And the decision variables in NLP are directly related to the physical meaning, so its initial value is easier to obtain [169]. However, the computation burden can rapidly increase when dealing with long-term or many-revolution orbital transfers because a large number of nodes are required for numerical iteration [170].

Betts et al. [171] used the transcription method to compute an optimal low-thrust transfer trajectory from an Earth orbit to a specified lunar mission orbit. The SMART-1-like trajectory as shown in Fig. 4 was modeled with three distinct phases as Pierson et al. [172] did. The vehicle dynamics were defined using a set of modified equinoctial coordinates. The solution presented required the solution of a sparse optimization problem with 211031 variables and 146285 constraints. The trajectories presented required two very long thrust arcs which make the overall mission duration shorter than multi-burn trajectories. Herman et al. [173] used the direct method to solve the problem of the shortest flight time of the low-thrust Earth-Moon transfer orbit with the initial acceleration of the spacecraft greater than 1 × 10−3 m/s2. Because of the relatively large initial acceleration, the boundary constraints of the initial orbit were not considered in his study.

Combining low energy and low-thrust approach, Mingotti et al. [174] constructed a WSB-like transfer trajectory shown in Fig.16. They assumed that an initial impulse launched the spacecraft into the stable manifold of the Sun-Earth Lyapunov orbit. Then an attainable set could be defined in the Poincaré section by integrating the controlled dynamic model backward and the whole design can be simplified to the search for a single point on a suitable surface of a section. The first guess obtained from the coupled three-body approximation was then optimized in the controlled four-body dynamics using a direct multiple shooting strategy. The maximal value of the thrust was 0.5N and the backward integration time was set as 6.90 EM in this study. The study was then extended into a lunar fly-by type [175]. Another study carried out by Mingotti et al. [176] also studied the low-thrust Earth-Moon transfer problem, however, the backward propagation time was set to free. The optimal result showed that different from reference. [174], for the global optimal solution, a thrust arc could also be employed when the spacecraft is far from the Earth about six Earth-Moon distances.

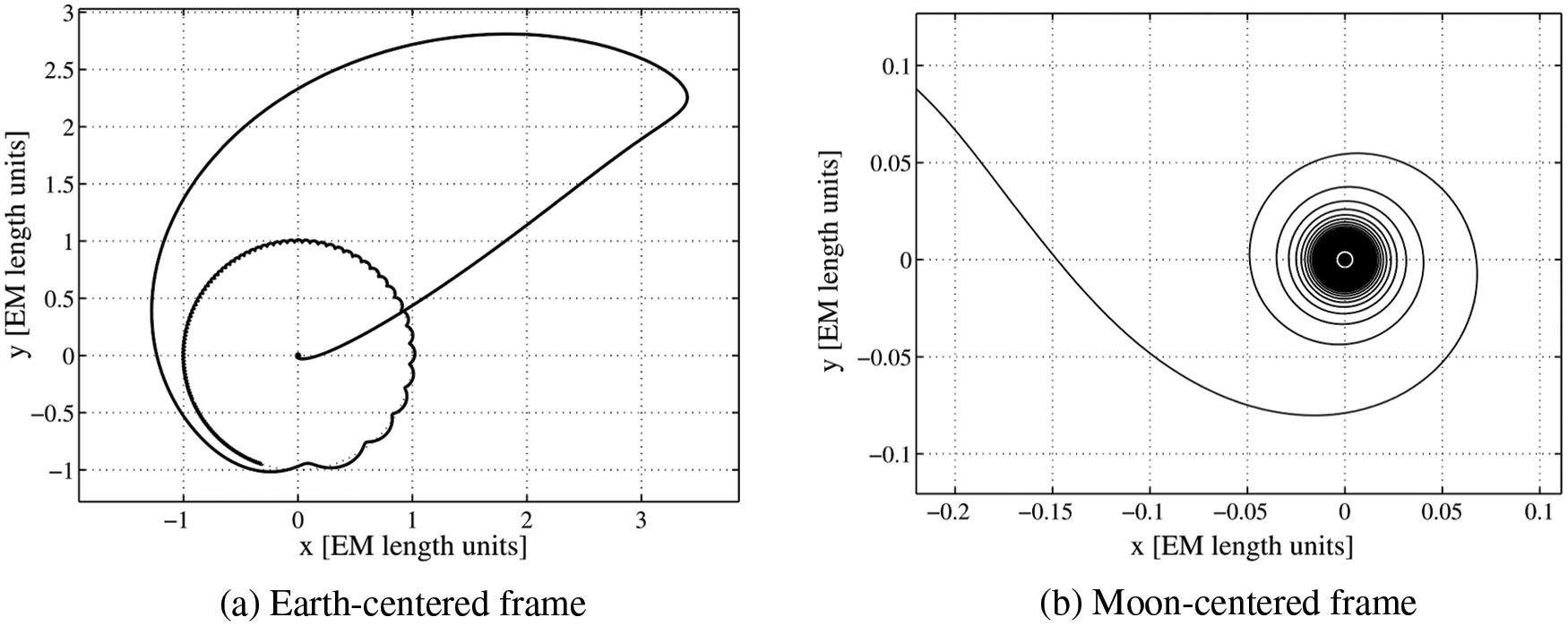
Figure 16: Low-thrust Earth-Moon trajectory in Earth-centered frame and Moon-centered frame [174]

The hybrid method [177] is a mixture of direct and indirect methods. The method uses a co-state variable differential equation and control law in the first-order necessary conditions, but the transversal condition is not adopted. In this frame, the optimization variables are more than constraint conditions, making the optimization problem a non-complete boundary value problem, and generally solved through nonlinear programming. Many early studies are carried out based on the thrust-coast-thrust control strategy. Pierson et al. [172] and Kluever et al. [178] adopted the three-stage approach to decompose the optimal problem from a circular LEO to a circular LMO. The designing variables were parameterized from the indirect method, and sequential quadratic programming (SQP) was employed to solve the TPBVP problem. The discussion in [172] was focused on planar trajectories, while reference [178] also considered three-dimensional trajectories with a Moon orbit inclined 90° to the Earth-Moon plane. Besides the three-stage approach, Kluever et al. [179] also proposed a modified method to develop the minimum-fuel, three-dimensional trajectory from a circular LEO to an inclined circular LMO. Ozimek et al. [177] used both direct single-and multiple-shooting methods to carry out low-thrust transfer trajectory designs from the Earth parking orbit to the Lagrangian point periodic orbits of the Earth-Moon system (including L1 halo orbits, L1 and L2 vertical orbits, and L2 butterfly orbits). The manifolds are utilized in the coast phase of the transfer trajectory. Qi et al. [147] established a low-thrust trajectory optimization problem from both 500 km LEO and 3,629 km medium Earth orbit (MEO) to the L1 halo orbit. By combining the variations approach and direct parameter optimization, the direct and the indirect transfer trajectory considering lunar flybys are obtained, both of which include manifold coasting phases, as shown in Fig. 17. In general, the discretization scale of the hybrid method is much smaller than that of the direct method, and the hybrid method shows higher precision, wider convergence region, and stronger numerical stability than the indirect method. But like the direct method, the quality of the result depends on the size of the discrete and the strength of the optimization algorithm. Moreover, it is usually necessary to assume the control strategy in advance and derive complex first-order necessary conditions.

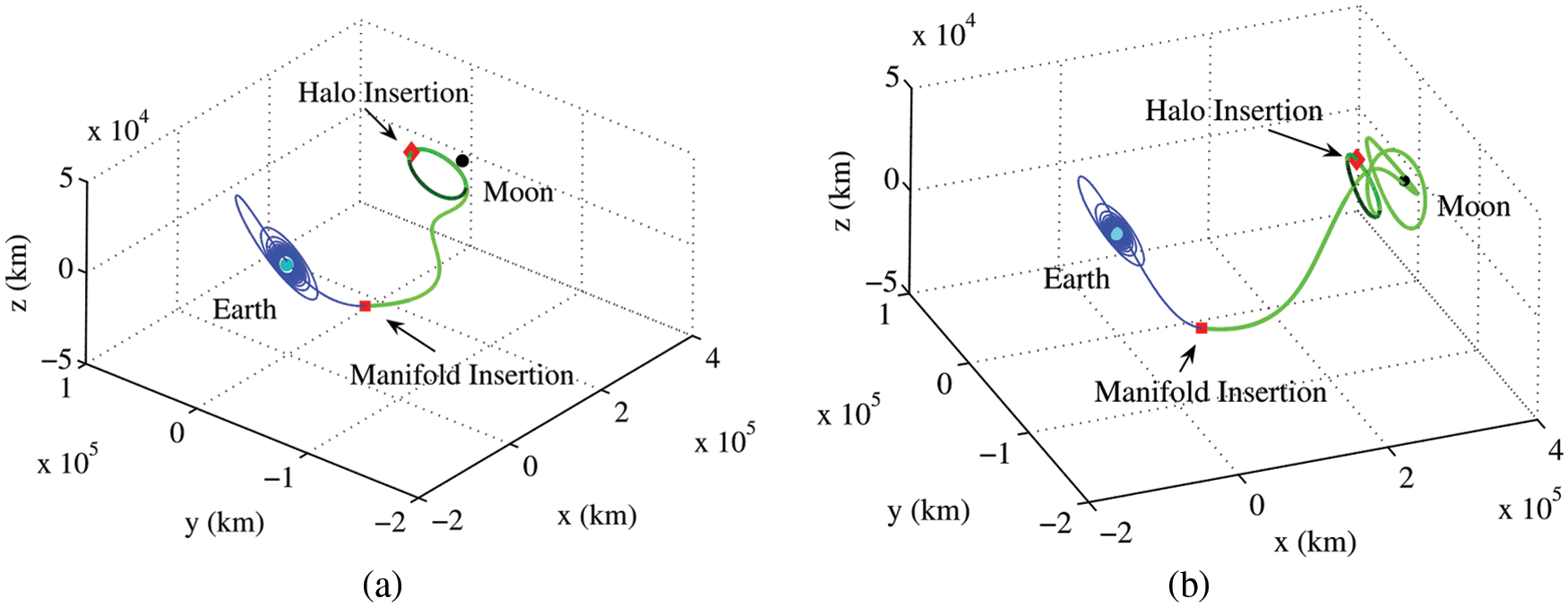
Figure 17: Direct and indirect low-thrust transfer from LEO to a halo orbit in the rotating frame: (a) direct transfer; (b) indirect transfer with a lunar flyby [147]

Evolutionary algorithms optimize discrete variables by simulating the evolutionary process of nature such as the genetic algorithm, ant colony algorithm, and particle swarm algorithm. This method is essentially different from the above three numerical methods: (i) a large number of initial populations are randomly generated as initial guesses during the solution process, with no need for specific initial guesses; (ii) the gradient information of the optimization index is not necessary, and the optimal global solution in the search space relies on the evolution process to iterate. Evolutionary algorithms are mainly used to solve trajectory optimization problems with fewer discrete variables and determine discrete parameters such as mission start/end times, gravitational assistance times, and sequences [180]. It can also be combined with processes like the shape-based method for determining relevant parameters [181,182] and the indirect method for selecting a more reasonable initial guess [149,183].

Besides the optimization methods introduced before, a shape-based method was also presented for initial estimates of low-thrust, gravity-assist trajectories. For the shape-based method, the low-thrust trajectory is parameterized with the basis function. The constraint can be dynamics equations and boundary conditions. The low-thrust trajectory can be obtained by solving the unknown parameters in the transit orbit [181]. Taheri et al. [184] used the finite Flourier series (FFS) to construct the low-thrust trajectories with thrust acceleration constraints in the CRTBP. In their work, the ballistic intermediate arc of a typical low-thrust problem was replaced with a Flourier series approximation. By applying various numbers of revolutions around the primaries, the method demonstrated capability in establishing both prograde and retrograde final orbits. In addition, the method can approximate various shapes of the intermediate phase that does not follow a spiral trajectory. Madhusudan [185] developed a robust Flourier series approach for the fast generation of Earth-Moon trajectories using low thrust. Each component of the position vector was approximated using FFS as a function of time. Approximations were then used to design a trajectory that satisfies the equation of motion and constraints at discrete points, and the problem boundary conditions. Taking advantage of CRTBP characteristics, the thrust-free phase trajectory near L1 was designed and optimized to achieve plane change. Three-dimensional transfers to high lunar orbits, low lunar orbits, and halo orbits can be generated.

6  Conclusion and Scope for Future Work

This paper reviewed various Earth-Moon transfer trajectories modeling and design methods. The engineering favored direct transfer based on the patched conic and the pseudo-state model features high energy consumption but short flight time. Since the gravitational force of two celestial bodies is considered simultaneously in the pseudosphere, the pseudo-state presents higher design accuracy than the patched conic method but is still lower than the three-body model. In comparison, the low-energy transfer effectively reduces the fuel requirement but suffers from a significant drawback of relatively long flight duration. Two commonly used mechanisms of designing low-energy transfer, namely the manifold and the weak stability boundary theory, are presented. The low-energy transfer trajectories obtained through the manifold theory can be varied according to the utilized Lagrangian point. As demonstrated by many groups, transiting through the L1 point enables the energy-minimal interior or cislunar transfer to be acquired, while the energy-minimal exterior or translunar transfer can be obtained by transiting the L2 point, transiting a periodic orbit can increase the chance to realize the Earth-Moon transfer but suffer a high energy consumption. In addition, the chaotic control method of interior transfer basically relies on the exponential amplification of small disturbances in the chaotic motion to reduce the flight time in the chaotic region. Multiple impulses are required in the process, and a series of periodic orbits have to be passed through. A low-energy Earth-Moon interior transfer can be more easily constructed based on the transit orbits surrounded by invariant manifolds, but the method will limit the transfer mode, flight time, and energy consumption of the spacecraft. Since it’s impossible to reach the Earth’s vicinity for the invariant manifold associated to the periodic orbit of the Lagrangian point, neither of the above two methods can directly construct a transfer orbit from LEO to the Moon. Therefore, additional maneuvers are needed for the spacecraft in the LEO to enter the manifold tube. In comparison, with the employment of an exterior transfer, a spacecraft can reach the Moon from the translunar space via the Sun-Earth non-transit orbit as the Sun-Earth manifold can reach the vicinity of the Earth. This method does not require additional connecting arcs, but the results are highly reliant on the geometry configuration of the Sun-Earth-Moon-spacecraft system. Moreover, the solar gravity can cause the distortion of the manifold tube, and the concept of a time-dependent manifold should be introduced to refine the model. The weak stability boundary theory is another important method to construct the low-energy exterior transfer, which has been successfully applied in practical engineering tasks by combining with the planar restricted three-body or four-body problem. However, there is a lack of theoretical support in the spatial case. The direct transcription, which maps an optimal control problem into a nonlinear programming problem, illustrates robustness in solving the optimal trajectory in the multi-body system. More solutions can be obtained when using a global optimization method at the expense of computation time. A common approach is applying the local optimization method for the optimal solution search from a rough initial value. However, this method is not the main topic of this review. The low-thrust transfer method demonstrates efficiency in saving fuel consumption with the conjunction of the manifold theory. Although limited by the difficulties of parameters optimization and lunar capture, the method shows promise in future Earth-Moon exploration missions. It is worth noting that the low-thrust method cannot directly design low-energy external transfer, and an initial impulse is still needed.

Based on the detailed review of Earth-Moon transfer trajectory design methods, a few urgent research topics are identified.

Full lunar surface coverage, high efficiency, and reusability are the three main requirements for the future lunar exploration. Using the invariant manifold of the three-body system can achieve ballistic landing from the Lagrangian point periodic orbit, but the lunar surface coverage is limited using the natural manifold. Also, a contradiction between the transfer time and fuel consumption always exists in the present design methods. Therefore, more efforts are needed in designing the landing orbit to achieve global arrival with minimum fuel consumption. In addition, a flight-based transportation network and an emergency return track are required to realize the transportation of goods and personnel.

In terms of the low-thrust orbit designing method, there are still some unsolved astrodynamics problems for constructing an Earth-Moon transfer trajectory. Although considerable progress has been made in the optimization design of low-thrust transfer based on the two-body and two-body perturbation models under the inertial frame, the method has been barely employed in the three-body dynamic model due to the unsolved theoretical problems. And the optimization algorithm shows poor convergence and low computational efficiency in this case.

Funding Statement: This work was supported by the National Key Research and Development Program of China (No. 2021YFA0717100) and the National Natural Science Foundation of China (Nos. 12072270 and U2013206).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Lee, K. H. (2011). Lunar orbiter trade study and conceptual design of onboard propulsion system. Journal of Spacecraft and Rockets, 48(2), 346–354. DOI 10.2514/1.50459. [Google Scholar] [CrossRef]

 2.  Egorov, V. (1958). Certain problems of moon flight dynamics. The Russian Literature of Satellites, 1, 107–174. [Google Scholar]

 3.  Parker, J. S., Anderson, R. L. (2014). Low-energy lunar trajectory design, pp. 2–3. New York: John Wiley and Sons. [Google Scholar]

 4.  Dutt, P. (2018). A review of low-energy transfers. Astrophysics and Space Science, 363(12), 1–21. DOI 10.1007/s10509-018-3461-4. [Google Scholar] [CrossRef]

 5.  Topputo, F. (2013). On optimal two-impulse Earth-Moon transfers in a four-body model. Celestial Mechanics and Dynamical Astronomy, 117(3), 279–313. DOI 10.1007/s10569-013-9513-8. [Google Scholar] [CrossRef]

 6.  Koon, W. S., Lo, M. W., Marsden, J. E., Ross, S. D. (2006). Dynamical systems, The three-body problem and space mission design, pp. 123–137. Berlin: World Scientific. [Google Scholar]

 7.  Belbruno, E. (2004). Capture dynamics and chaotic motions in celestial mechanics, pp. 103–165. Princeton: Princeton Univ. Press. [Google Scholar]

 8.  Belbruno, E. A., Miller, J. K. (1993). Sun-perturbed Earth-to-Moon transfers with ballistic capture. Journal of Guidance Control and Dynamics, 16(4), 770–775. DOI 10.2514/3.21079. [Google Scholar] [CrossRef]

 9.  Broschart, S., Chung, M., Hatch, S., Ma, J., Sweetser, T. et al. (2009). Preliminary trajectory design for the Artemis Lunar Mission. AAS/AIAA Astrodynamics Specialist Conference, AAS 09-382. Pittsburgh, Pennsylvania, USA. [Google Scholar]

10. Roncoli, R., Fujii, K. (2010). Mission design overview for the gravity recovery and interior laboratory (GRAIL) mission. AAS/AIAA Astrodynamics Specialist Conference, AIAA 2010-9393. Toronto, Ontario, Canada. [Google Scholar]

11. Koon, W. S., Lo, M. W., Marsden, J. E., Ross, S. D. (2001). Low energy transfer to the Moon. Celestial Mechanics and Dynamical Astronomy, 81(1–2), 63–73. DOI 10.1023/A:1013359120468. [Google Scholar] [CrossRef]

12. Xu, M., Wei, Y., Xu, S. J. (2013). On the construction of low-energy cislunar and translunar transfers based on the libration points. Astrophysics and Space Science, 348(1), 65–88. DOI 10.1007/s10509-013-1563-6. [Google Scholar] [CrossRef]

13. Bollt, E. M., Meiss, J. D. (1995). Targeting chaotic orbits to the Moon through recurrence. Physics Letters A, 204(5–6), 373–378. DOI 10.1016/0375-9601(95)00502-T. [Google Scholar] [CrossRef]

14. Schroer, C. G., Ott, E. (1997). Targeting in Hamiltonian systems that have mixed regular/chaotic phase spaces. Chaos: An Interdisciplinary Journal of Nonlinear Science, 7(4), 512–519. DOI 10.1063/1.166277. [Google Scholar] [CrossRef]

15. Macau, E. E. N. (2000). Using chaos to guide a spacecraft to the moon. Acta Astronautica, 47(12), 871–878. DOI 10.1016/S0094-5765(00)00125-9. [Google Scholar] [CrossRef]

16. Ross, S. (2003). Trade-off between fuel and time optimization. New Trends in Astrodynamics and Applications. College Park, MD. http://www.dept.aoe.vt.edu/~sdross/papers/ross-maryland-2003-abstract.pdf. [Google Scholar]

17. Belbruno, E. (1987). Lunar capture orbits, a method of constructing earth moon trajectories and the lunar GAS mission. 19th International Electric Propulsion Conference, AIAA Paper 87-1054. Colorado Springs, CO, USA. [Google Scholar]

18. Belbruno, E., Miller, J. (1990). A ballistic lunar capture trajectory for the Japanese spacecraft hiten. Jet Propulsion Laboratory. IOM 312/90.4-1731. Internal Document, Pasadena, CA. [Google Scholar]

19. Koon, W. S., Lo, M. W., Marsden, J. E., Ross, S. D. (2000). Shoot the moon. https://authors.library.caltech.edu/20290/1/KoLoMaRo2000b.pdf. [Google Scholar]

20. Belbruno, E., Topputo, F., Gidea, M. (2008). Resonance transitions associated to weak capture in the restricted three-body problem. Advances in Space Research, 42(8), 1330–1351. DOI 10.1016/j.asr.2008.01.018. [Google Scholar] [CrossRef]

21. Xu, M. (2010). The occurrence conditions and trajectory constructions for low energy cislunar transfers. Chinese Journal of Theoretical and Applied Mechanics, 42(2), 275–289. DOI 10.6052/0459-1879-2010-2-2008-708. [Google Scholar] [CrossRef]

22. Hohmann, W. (1960). The attainability of heavenly bodies, pp. 76–89. Washington: NASA Technical Translation F-44. [Google Scholar]

23. Crenshaw, J. W. (1963). Sphere of influence in patched-conic methods. AIAA Journal, 1(9), 2168–2170. DOI 10.2514/3.2024. [Google Scholar] [CrossRef]

24. Souami, D., Cresson, J., Biernacki, C., Pierret, F. (2020). On the local and global properties of gravitational spheres of influence. Monthly Notices of the Royal Astronomical Society, 496(4), 4287–4297. DOI 10.1093/mnras/staa1520. [Google Scholar] [CrossRef]

25. Breakwell, J. V. (1966). Matched asymptotic expansions, patched conics, and the computation of interplanetary trajectories. Progress in Astronautics and Aeronautics, 17, 159–182. DOI 10.1016/B978-1-4832-2729-0.50015-6. [Google Scholar] [CrossRef]

26. Bate, R. R., Mueller, D. D., White, J. E., Saylor, W. W. (2020). Fundamentals of astrodynamics, pp. 269–288. New York: Dover Publications. [Google Scholar]

27. Penzo, P. A. (1961). An analysis of Moon-to-Earth trajectories (Report 8976-0008-RU-000). Redondo Beach, California: Space Technology Laboratories, Inc. [Google Scholar]

28. Penzo, P. A. (1963). An analysis of free-flight circumlunar trajectories. Astrodynamics Conference, AIAA Paper 63-404. New Haven, CT, USA. [Google Scholar]

29. Negri, R. B., Sukhanov, A., Prado, A. F. B. D. (2019). Lunar gravity assists using patched-conics approximation, three and four body problems. Advances in Space Research, 64(1), 42–63. DOI 10.1016/j.asr.2019.04.002. [Google Scholar] [CrossRef]

30. Dallas, S. (1963). Moon-to-earth trajectories. Astrodynamics Conference, pp. 391–438. New Haven, CT, USA. [Google Scholar]

31. Gibson Jr, T. (1963). Application of the matched conic model in the study of circumlunar trajectories. https://ntrs.nasa.gov/api/citations/19700026482/downloads/19700026482.pdf. [Google Scholar]

32. Li, J. Y., Gong, S. P., Baoyin, H. X. (2013). Generation of multisegment lunar free-return trajectories. Journal of Guidance Control and Dynamics, 36(3), 765–775. DOI 10.2514/1.58427. [Google Scholar] [CrossRef]

33. Salazar, F. J. T., Macau, E. E. N., Winter, O. C. (2015). Pareto Frontier for the time-energy cost vector to an Earth-Moon transfer orbit using the patched-conic approximation. Computational and Applied Mathematics, 34(2), 461–475. DOI 10.1007/s40314-014-0154-7. [Google Scholar] [CrossRef]

34. Qi, Y., Xu, S. (2016). Minimum ΔV for the transfer to permanent lunar orbits with hyperbolic approach. Acta Astronautica, 119(3), 183–195. DOI 10.1016/j.actaastro.2015.11.016. [Google Scholar] [CrossRef]

35. He, B. Y., Li, H. Y., Zhang, B. (2013). Analysis of transfer orbit deviation propagation mechanism and robust design for manned lunar landing. Acta Physica Sinica, 62(19), 91–98. [Google Scholar]

36. He, B. Y., Li, H. Y., Zhou, J. P. (2017). Solution domain analysis of Earth-Moon quasi-symmetric free-return orbits. Transactions of the Japan Society for Aeronautical and Space Sciences, 60(4), 195–201. DOI 10.2322/tjsass.60.195. [Google Scholar] [CrossRef]

37. Yang, W., Zhou, W. (2008). Analysis on midcourse correction of translunar trajectory for CE-1. Aerospace Control and Application, 34(6), 3–7. [Google Scholar]

38. Yang, W. L. (2010). Phasing orbit design for Chinese lunar satellite CE-1. Chinese Space Science and Technology, 30(1), 18–24. [Google Scholar]

39. Dunham, D. W., Jen, S. C., Uesugi, K., Kawaguchi, J. I., Farquhar, R. W. (1990). A launch window study for GEOTAIL’s double lunar swingby trajectory. Proceedings of 41st Congress of the International Astronautical Federation, IAF-90-309. Dresden, Germany. [Google Scholar]

40. Uesugi, K., Matsuo, H., Kawaguchi, J., Hayashi, T. (1991). Japanese first double lunar swingby mission Hiten. Acta Astronautica, 25(7), 347–355. DOI 10.1016/0094-5765(91)90014-V. [Google Scholar] [CrossRef]

41. Carrington, D., Carrico, J., Jen, J., Roberts, C., Seacord, A. et al. (1993). Trajectory design for the deep space program science experiment (DSPSE) mission. NASA STI/Recon Technical Report A, 95, 157–171. [Google Scholar]

42. Englander, J. A., Conway, B. A., Williams, T. (2012). Automated mission planning via evolutionary algorithms. Journal of Guidance Control and Dynamics, 35(6), 1878–1887. DOI 10.2514/1.54101. [Google Scholar] [CrossRef]

43. Bao, C., Li, J., Baoyin, H. (2018). Two-segment lunar free-return trajectories design using the pseudostate theory. Advances in Space Research, 61(1), 97–110. DOI 10.1016/j.asr.2017.09.026. [Google Scholar] [CrossRef]

44. Wilson, J. S. (1969). A pseudostate theory for the approximation of three-body trajectories. Astrodynamics Conference, AIAA Paper 1970-1061. Santa Barbara, CA, USA. [Google Scholar]

45. Yang, B., Yang, H. W., Li, S. (2019). Pseudostate theory based iterative preliminary design method for powered gravity-assist interplanetary trajectories. Acta Astronautica, 165(11), 139–149. DOI 10.1016/j.actaastro.2019.09.006. [Google Scholar] [CrossRef]

46. Luo, Q. Q., Yin, J. F., Han, C. (2013). Design of Earth-Moon free-return trajectories. Journal of Guidance Control and Dynamics, 36(1), 263–271. DOI 10.2514/1.55910. [Google Scholar] [CrossRef]

47. Zhang, H. L., Luo, Q. Q., Han, C. (2014). Accurate and fast design algorithm for free-return lunar flyby trajectories. Acta Astronautica, 102, 14–26. DOI 10.1016/j.actaastro.2014.05.015. [Google Scholar] [CrossRef]

48. Byrnes, D., Hooper, H. (1970). Multi-conic: A fast and accurate method of computing space flight trajectories. Astrodynamics Conference, AIAA Paper 1970-1062. Santa Barbara, CA, USA. [Google Scholar]

49. Byrnes, D. (1979). Application of the pseudostate theory to the three-body Lambert problem. Journal of the Astronautical Sciences, vol. 37, pp. 221–232. Provincetown, Massachusetts. [Google Scholar]

50. Damario, L. A., Sackett, L., Stanford, R., Byrnes, D. (1979). Optimization of multiple flyby trajectories. American Institute of Aeronautics and Astronautics Conference, pp. 79–162. Provincetown, Massachusetts. [Google Scholar]

51. Sergeyevsky, A., Damario, L. (1983). Application of the rectilinear impact pseudostate method to modelingof third-body effects on interplanetary trajectories. AIAA 21st Aerospace Sciences Meeting, AIAA Paper 1983-0015. Reno, NV, USA. [Google Scholar]

52. Ramanan, R. V. (2002). Integrated algorithm for lunar transfer trajectories using a pseudostate technique. Journal of Guidance Control and Dynamics, 25(5), 946–952. DOI 10.2514/2.4968. [Google Scholar] [CrossRef]

53. Ramanan, R. V., Adimurthy, V. (2005). Nonimpact lunar transfer trajectories using the pseudostate technique. Journal of Guidance Control and Dynamics, 28(2), 217–225. DOI 10.2514/1.7607. [Google Scholar] [CrossRef]

54. Sweetser, T. H. (1988). Some notes on applying the one-step multiconic method of trajectory propagation. Journal of the Astronautical Sciences, 37(3), 233–250. [Google Scholar]

55. Kiedron, K., Sweetser, T. (1988). A comparison between onestep and other multiconic trajectory propagation methods. Astrodynamics, 1987, 532–544. DOI 10.2514/6.1988-4286. [Google Scholar] [CrossRef]

56. Chung, M. K. J., Hatch, S. J., Kangas, J. A., Long, S. M., Roncoli, R. B. et al. (2010). Trans-lunar cruise trajectory design of GRAIL (Gravity Recovery and Interior Laboratory) mission. AAS/AIAA Astrodynamics Specialist Conference, vol. 2010, pp. 1856–1863. [Google Scholar]

57. Parker, J. S., Lo, M. W. (2006). Shoot the Moon 3D. Advances in the Astronautical Sciences, 123, 2067–2086. [Google Scholar]

58. Parker, J. S. (2007). Low-energy ballistic lunar transfers (Ph.D. Thesis). University of Colorado, Boulder. [Google Scholar]

59. Xiangyu, L., Dong, Q., Yu, C. (2021). Progress of three-body orbital dynamics study. Chinese Journal of Theoretical and Applied Mechanics, 53(5), 1223–1245. DOI 10.6052/0459-1879-20-367. [Google Scholar] [CrossRef]

60. Broucke, R. (1969). Stability of periodic orbits in the elliptic, restricted three-body problem. AIAA Journal, 7(6), 1003–1009. DOI 10.2514/3.5267. [Google Scholar] [CrossRef]

61. Szebehely, V. (1967). Theory of orbit: The restricted problem of three Bodies, pp. 16–20. New York and London: Academic Press. [Google Scholar]

62. Jacobi, C. G. J. (1836). Sur le mouvement d’un point et sur un cas particulier du probleme des trois corps. UK: Cambridge University Press. [Google Scholar]

63. Vallado, D. A. (2013). Fundamentals of astrodynamics and applications. California: Microcosm Press. [Google Scholar]

64. Schmidt, D. S. (1974). Periodic solutions near a resonant equilibrium of a Hamiltonian system. Celestial Mechanics, 9(1), 81–103. DOI 10.1007/BF01236166. [Google Scholar] [CrossRef]

65. Celletti, A., Pucacco, G., Stella, D. (2015). Lissajous and halo orbits in the restricted three-body problem. Journal of Nonlinear Science, 25(2), 343–370. DOI 10.1007/s00332-015-9232-2. [Google Scholar] [CrossRef]

66. Hénon, M. (1969). Numerical exploration of the restricted problem, V. Astronomy and Astrophysics, 1, 223–238. [Google Scholar]

67. Zhang, R. (2022). A review of periodic orbits in the circular restricted three-body problem. Journal of Systems Engineering and Electronics, 33(3), 612–646. DOI 10.23919/JSEE.2022.000059. [Google Scholar] [CrossRef]

68. Conley, C. C. (1968). Low energy transit orbits in the restricted three-body problems. SIAM Journal on Applied Mathematics, 16(4), 732–746. DOI 10.1137/0116060. [Google Scholar] [CrossRef]

69. McGehee, R. P. (1969). Some homoclinic orbits for the restricted three-body problem (Ph.D. Thesis). The University of Wisconsin-Madison, Wisconsin. [Google Scholar]

70. Marsden, J. E., Ross, S. D. (2006). New methods in celestial mechanics and mission design. Bulletin of the American Mathematical Society, 43(1), 43–73. DOI 10.1090/S0273-0979-05-01085-2. [Google Scholar] [CrossRef]

71. Yamato, H. (2003). Trajectory design methods for restricted problems of three bodies with perturbations (Ph.D. Thesis). The Pennsylvania State University, Pennsylvania. [Google Scholar]

72. Wang, Y., Pan, B. F., Zheng, Y., Lu, X. (2017). ETLBO based optimal targeting to the moon in the PCR3BP chaotic system. Chaos, Solitons and Fractals, 105(5–6), 21–28. DOI 10.1016/j.chaos.2017.10.009. [Google Scholar] [CrossRef]

73. Shinbrot, T., Ott, E., Grebogi, C., Yorke, J. A. (1990). Using chaos to direct trajectories to targets. Physical Review Letters, 65(26), 3215–3218. DOI 10.1103/PhysRevLett.65.3215. [Google Scholar] [CrossRef]

74. Bollt, E. M. (1995). Controlling chaos, targeting, and transport (Ph.D. Thesis). University of Colorado, Boulder. [Google Scholar]

75. MacKay, R. S., Meiss, J. D., Percival, I. C. (1984). Stochasticity and transport in Hamiltonian systems. Physical Review Letters, 52(9), 697–700. DOI 10.1103/PhysRevLett.52.697. [Google Scholar] [CrossRef]

76. Salazar, F. J. T., MacAu, E. E. N., Winter, O. C. (2015). Chaotic dynamics in a low-energy transfer strategy to the equilateral equilibrium points in the earth-moon system. International Journal of Bifurcation and Chaos, 25(5), 1550077. DOI 10.1142/S0218127415500777. [Google Scholar] [CrossRef]

77. Zheng, Y., Pan, B., Tang, S., Wang, Y. (2018). Multi-step control of chaos in the application of Earth-Moon orbit transfer. Xibei Gongye Daxue Xuebao/Journal of Northwestern Polytechnical University, 36(1), 35–41. DOI 10.1051/jnwpu/20183610035. [Google Scholar] [CrossRef]

78. Zheng, Y., Pan, B., Tang, S. (2018). Chaos control method of earth-moon low energy orbit transfer. Journal of Astronautics, 39(7), 751–759. [Google Scholar]

79. Zheng, Y., Pan, B. F., Tang, S. (2019). A hybrid method based on invariant manifold and chaos control for Earth-Moon low-energy transfer. Acta Astronautica, 163(1), 145–156. DOI 10.1016/j.actaastro.2018.11.038. [Google Scholar] [CrossRef]

80. Pernicka, H. J., Scarberry, D. P., Marsh, S. M., Sweetser, T. H. (1995). A search for low delta-V Earth-to-Moon trajectories. Journal of the Astronautical Sciences, 43(1), 77–88. DOI 10.2514/6.1994-3772. [Google Scholar] [CrossRef]

81. Topputo, F., Vasile, M., Bernelli-Zazzera, F. (2005). Earth-to-Moon low energy transfers targeting L1 hyperbolic transit orbits. Annals of the New York Academy of Sciences, 1065(1), 55–76. DOI 10.1196/annals.1370.025. [Google Scholar] [CrossRef]

82. Mengali, G., Quarta, A. A. (2005). Optimization of biimpulsive trajectories in the Earth-Moon restricted three-body system. Journal of Guidance Control and Dynamics, 28(2), 209–216. DOI 10.2514/1.7702. [Google Scholar] [CrossRef]

83. Pontani, M., Teofilatto, P. (2013). Low-energy Earth-Moon transfers involving manifolds through isomorphic mapping. Acta Astronautica, 91(2), 96–106. DOI 10.1016/j.actaastro.2013.05.009. [Google Scholar] [CrossRef]

84. Liang, Y., Xu, M., Xu, S. (2015). The classification of cislunar trajectories and its applications in the Earth-Moon system. Astrophysics and Space Science, 361(1), 1–19. DOI 10.1007/s10509-015-2577-z. [Google Scholar] [CrossRef]

85. Tan, M., Zhang, K., Wang, J. (2021). Optimization of bi-impulsive Earth-Moon transfers using periodic orbits. Astrophysics and Space Science, 366(2), 1–15. DOI 10.1007/s10509-021-03926-6. [Google Scholar] [CrossRef]

86. Sousa-Silva, P., Terra, M. O., Ceriotti, M. (2018). Fast Earth-Moon transfers with ballistic capture. Astrophysics and Space Science, 363(10), 1–11. DOI 10.1007/s10509-018-3431-x. [Google Scholar] [CrossRef]

87. Howell, K. C., Breakwell, J. V. (1984). Almost rectilinear halo orbits. Celestial Mechanics, 32(1), 29–52. DOI 10.1007/BF01358402. [Google Scholar] [CrossRef]

88. Wang, Y., Zhang, R., Zhang, C., Zhang, H. (2021). Transfers between NRHOs and DROs in the Earth-Moon system. Acta Astronautica, 186(6), 60–73. DOI 10.1016/j.actaastro.2021.05.019. [Google Scholar] [CrossRef]

89. Trofimov, S., Shirobokov, M., Tselousova, A., Ovchinnikov, M. (2020). Transfers from near-rectilinear halo orbits to low-perilune orbits and the Moon's surface. Acta Astronautica, 167(6), 260–271. DOI 10.1016/j.actaastro.2019.10.049. [Google Scholar] [CrossRef]

90. Zimovan, E. M., Howell, K. C., Davis, D. C. (2017). Near rectilinear halo orbits and their application in cis-lunar space. 3rd IAA Conference on Dynamics and Control of Space Systems, pp. 209–228. Moscow, Russia. [Google Scholar]

91. Boudad, K. K., Howell, K. C., Davis, D. C. (2020). Dynamics of synodic resonant near rectilinear halo orbits in the bicircular four-body problem. Advances in Space Research, 66(9), 2194–2214. DOI 10.1016/j.asr.2020.07.044. [Google Scholar] [CrossRef]

92. Ming, X., Xu, S. J. (2009). Exploration of distant retrograde orbits around Moon. Acta Astronautica, 65(5–6), 853–860. DOI 10.1016/j.actaastro.2009.03.026. [Google Scholar] [CrossRef]

93. Capdevila, L., Guzzetti, D., Howell, K. (2014). Various transfer options from Earth into distant retrograde orbits in the vicinity of the Moon. AAS/AIAA Space Flight Mechanics Meeting, pp. 3659–3678. Santa Fe, New Mexico. [Google Scholar]

94. Capdevila, L. R., Howell, K. C. (2018). A transfer network linking Earth, Moon, and the triangular libration point regions in the Earth-Moon system. Advances in Space Research, 62(7), 1826–1852. DOI 10.1016/j.asr.2018.06.045. [Google Scholar] [CrossRef]

95. Zhang, R., Wang, Y., Zhang, H., Zhang, C. (2020). Transfers from distant retrograde orbits to low lunar orbits. Celestial Mechanics and Dynamical Astronomy, 132(8), 1–30. DOI 10.1007/s10569-020-09982-4. [Google Scholar] [CrossRef]

96. Peng, C., Zhang, H., Wen, C., Zhu, Z., Gao, Y. (2022). Exploring more solutions for low-energy transfers to lunar distant retrograde orbits. Celestial Mechanics and Dynamical Astronomy, 134(1), 1–38. DOI 10.1007/s10569-021-10056-2. [Google Scholar] [CrossRef]

97. Yagasaki, K. (2004). Computation of low energy Earth-to-Moon transfers with moderate flight time. Physica D: Nonlinear Phenomena, 197(3–4), 313–331. DOI 10.1016/j.physd.2004.07.005. [Google Scholar] [CrossRef]

98. Yagasaki, K. (2004). Sun-perturbed Earth-to-Moon transfers with low energy and moderate flight time. Celestial Mechanics and Dynamical Astronomy, 90(3–4), 197–212. DOI 10.1007/s10569-004-0406-8. [Google Scholar] [CrossRef]

99. Lei, H., Xu, B., Sun, Y. (2013). Earth-Moon low energy trajectory optimization in the real system. Advances in Space Research, 51(5), 917–929. DOI 10.1016/j.asr.2012.10.011. [Google Scholar] [CrossRef]

100. Guo, Q. W., Lei, H. L. (2019). Families of Earth-Moon trajectories with applications to transfers towards Sun-Earth libration point orbits. Astrophysics and Space Science, 364(3), 1–9. DOI 10.1007/s10509-019-3532-1. [Google Scholar] [CrossRef]

101. Peng, L., Wang, Y. Z., Dai, G. M., Chang, Y. M., Chen, F. J. (2010). Optimization of the Earth-Moon low energy transfer with differential evolution based on uniform design. IEEE Congress on Evolutionary Computation (CEC). pp. 1–8. Barcelona, Spain. [Google Scholar]

102. Gong, S. P., Li, J. F., Baoyin, H. X., Gao, Y. F. (2007). Lunar landing trajectory design based on invariant manifold. Applied Mathematics and Mechanics-English Edition, 28(2), 201–207. DOI 10.1007/s10483-007-0208-1. [Google Scholar] [CrossRef]

103. Fantino, E., Gómez, G., Masdemont, J. J., Ren, Y. (2010). A note on libration point orbits, temporary capture and low-energy transfers. Acta Astronautica, 67(9–10), 1038–1052. DOI 10.1016/j.actaastro.2010.06.037. [Google Scholar] [CrossRef]

104. de Sousa-Silva, P. A., Terra, M. O. (2016). A survey of different classes of Earth-to-Moon trajectories in the patched three-body approach. Acta Astronautica, 123(1–4), 340–349. DOI 10.1016/j.actaastro.2016.04.008. [Google Scholar] [CrossRef]

105. Sousa-Silva, P. A., Terra, M. O. (2014). Dynamical possibilities to design Earth-to-Moon transfers in the patched-three body approximation. AIAA SPACE, 2014 Conference and Exposition, San Diego, CA. [Google Scholar]

106. Shadden, S. C., Lekien, F., Marsden, J. E. (2005). Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Physica D: Nonlinear Phenomena, 212(3–4), 271–304. DOI 10.1016/j.physd.2005.10.007. [Google Scholar] [CrossRef]

107. Short, C. R., Howell, K. C. (2014). Lagrangian coherent structures in various map representations for application to multi-body gravitational regimes. Acta Astronautica, 94(2), 592–607. DOI 10.1016/j.actaastro.2013.08.020. [Google Scholar] [CrossRef]

108. Qi, R., Xu, S., Zhang, Y., Wang, Y. (2012). Earth-to-Moon low energy transfer using time-dependent invariant manifolds. AIAA/AAS Astrodynamics Specialist Conference, pp. 1–11. Minneapolis, USA. [Google Scholar]

109. Onozaki, K., Yoshimura, H., Ross, S. D. (2017). Tube dynamics and low energy Earth-Moon transfers in the 4-body system. Advances in Space Research, 60(10), 2117–2132. DOI 10.1016/j.asr.2017.07.046. [Google Scholar] [CrossRef]

110. Gomez, G., Koon, W. S., Lo, M. W., Marsden, J. E., Masdemont, J. et al. (2001). Invariant manifolds, the spatial three-body problem and space mission design. Proceedings of AAS/AIAA Astrodynamics Specialist Meeting, pp. 3–22. Quebec City, Quebec, Canada. [Google Scholar]

111. Gómez, G., Koon, W. S., Lo, M. W., Marsden, J. E., Masdemont, J. et al. (2004). Connecting orbits and invariant manifolds in the spatial restricted three-body problem. Nonlinearity, 17(5), 1571–1606. DOI 10.1088/0951-7715/17/5/002. [Google Scholar] [CrossRef]

112. Howell, K. C., Kakoi, M. (2006). Transfers between the Earth-Moon and Sun-Earth systems using manifolds and transit orbits. Acta Astronautica, 59(1–5), 367–380. DOI 10.1016/j.actaastro.2006.02.010. [Google Scholar] [CrossRef]

113. Xu, M., Liang, Y. Y., Ren, K. W. (2016). Survey on advances in orbital dynamics and control for libration point orbits. Progress in Aerospace Sciences, 82(10), 24–35. DOI 10.1016/j.paerosci.2015.12.005. [Google Scholar] [CrossRef]

114. Ren, Y., Shan, J. (2012). Numerical study of the three-dimensional transit orbits in the circular restricted three-body problem. Celestial Mechanics and Dynamical Astronomy, 114(4), 415–428. DOI 10.1007/s10569-012-9452-9. [Google Scholar] [CrossRef]

115. Ren, Y., Shan, J. (2014). Low-energy lunar transfers using spatial transit orbits. Communications in Nonlinear Science and Numerical Simulation, 19(3), 554–569. DOI 10.1016/j.cnsns.2013.07.020. [Google Scholar] [CrossRef]

116. Parker, J. S., Anderson, R. L. (2013). Targeting low-energy transfers to low lunar orbit. Acta Astronautica, 84(7), 1–14. DOI 10.1016/j.actaastro.2012.10.033. [Google Scholar] [CrossRef]

117. García, F., Gómez, G. (2006). A note on weak stability boundaries. Celestial Mechanics and Dynamical Astronomy, 97(2), 87–100. DOI 10.1007/s10569-006-9053-6. [Google Scholar] [CrossRef]

118. Yamakawa, H., Kawaguchi, J. I., Ishii, N., Matsuo, H. (1992). Numerical study of gravitational capture orbit in the earth-moon system. Proceedings of the AAS/AIAA Spaceflight Mechanics Meeting, pp. 1113–1132. Colorado Springs, CO, USA. [Google Scholar]

119. Yamakawa, H., Kawaguchi, J. I., Ishii, N., Matsuo, H. (1993). On earth-moon transfer trajectory with gravitational capture. Advances in the Astronautical Sciences, pp. 397–416. Victoria, BC, Can. [Google Scholar]

120. Circi, C., Teofilatto, P. (2001). On the dynamics of weak stability boundary lunar transfers. Celestial Mechanics and Dynamical Astronomy, 79(1), 41–72. DOI 10.1023/A:1011153610564. [Google Scholar] [CrossRef]

121. Romagnoli, D., Circi, C. (2009). Earth-Moon weak stability boundaries in the restricted three and four body problem. Celestial Mechanics and Dynamical Astronomy, 103(1), 79–103. DOI 10.1007/s10569-008-9169-y. [Google Scholar] [CrossRef]

122. Ceccaroni, M., Biggs, J., Biasco, L. (2012). Analytic estimates and topological properties of the weak stability boundary. Celestial Mechanics and Dynamical Astronomy, 114(1–2), 1–24. DOI 10.1007/s10569-012-9419-x. [Google Scholar] [CrossRef]

123. Belbruno, E., Gidea, M., Topputo, F. (2013). Geometry of weak stability boundaries. Qualitative Theory of Dynamical Systems, 12(1), 53–66. DOI 10.1007/s12346-012-0069-x. [Google Scholar] [CrossRef]

124. Topputo, F., Belbruno, E. (2009). Computation of weak stability boundaries: Sun-Jupiter system. Celestial Mechanics and Dynamical Astronomy, 105(1–3), 3–17. DOI 10.1007/s10569-009-9222-5. [Google Scholar] [CrossRef]

125. Belbruno, E., Gidea, M., Topputo, F. (2010). Weak stability boundary and invariant manifolds. SIAM Journal on Applied Dynamical Systems, 9(3), 1061–1089. DOI 10.1137/090780638. [Google Scholar] [CrossRef]

126. Sousa Silva, P. A., Terra, M. O. (2012). Diversity and validity of stable-unstable transitions in the algorithmic weak stability boundary. Celestial Mechanics and Dynamical Astronomy, 113(4), 453–478. DOI 10.1007/s10569-012-9418-y. [Google Scholar] [CrossRef]

127. Sousa Silva, P. A., Terra, M. O. (2012). Applicability and dynamical characterization of the associated sets of the algorithmic weak stability boundary in the lunar sphere of influence. Celestial Mechanics and Dynamical Astronomy, 113(2), 141–168. DOI 10.1007/s10569-012-9409-z. [Google Scholar] [CrossRef]

128. Griesemer, P. R., Ocampo, C., Cooley, D. S. (2011). Targeting ballistic lunar capture trajectories using periodic orbits. Journal of Guidance Control and Dynamics, 34(3), 893–902. DOI 10.2514/1.46843. [Google Scholar] [CrossRef]

129. Markellos, V. V. (1974). Numerical investigation of the planar restricted three-bodyproblem. Celestial Mechanics, 10(1), 87–134. DOI 10.1007/BF01261880. [Google Scholar] [CrossRef]

130. van der Weg, W. J., Vasile, M. (2014). Contingency and recovery options for the European student Moon orbiter. Acta Astronautica, 94(1), 168–183. DOI 10.1016/j.actaastro.2013.08.009. [Google Scholar] [CrossRef]

131. Dutt, P., Anilkumar, A. K., George, R. K. (2016). Dynamics of weak stability boundary transfer trajectories to Moon. Astrophysics and Space Science, 361(11), 1–12. DOI 10.1007/s10509-016-2952-4. [Google Scholar] [CrossRef]

132. Belbruno, E. (2000). Low energy trajectories for space travel using stability transition regions. IFAC Proceedings Volumes, 33(2), 7–12. DOI 10.1016/S1474-6670(17)35540-4. [Google Scholar] [CrossRef]

133. Dutt, P., Anilkumar, A. K., George, R. K. (2018). Design and analysis of weak stability boundary trajectories to Moon. Astrophysics and Space Science, 363(8), 1–10. DOI 10.1007/s10509-018-3378-y. [Google Scholar] [CrossRef]

134. Betts, J. T. (1998). Survey of numerical methods for trajectory optimization. Journal of Guidance Control and Dynamics, 21(2), 193–207. DOI 10.2514/2.4231. [Google Scholar] [CrossRef]

135. Xincheng, Y., Ying, Y., Zhiyong, G. (2009). Near-optimal cumulative longitude low-thrust orbit transfer. Journal of Systems Engineering and Electronics, 20(6), 1271–1277. [Google Scholar]

136. Ranieri, C. L., Ocampo, C. A. (2009). Indirect optimization of three-dimensional finite-burning interplanetary transfers including spiral dynamics. Journal of Guidance Control and Dynamics, 32(2), 445–455. DOI 10.2514/1.38170. [Google Scholar] [CrossRef]

137. Taheri, E., Li, N. I., Kolmanovsky, I. (2017). Co-state initialization for the minimum-time low-thrust trajectory optimization. Advances in Space Research, 59(9), 2360–2373. DOI 10.1016/j.asr.2017.02.010. [Google Scholar] [CrossRef]

138. Lawden, D. F. (1963). Optimal trajectories for space navigation. London: Butterworths. [Google Scholar]

139. Russell, R. P. (2007). Primer vector theory applied to global low-thrust trade studies. Journal of Guidance Control and Dynamics, 30(2), 460–472. DOI 10.2514/1.22984. [Google Scholar] [CrossRef]

140. Grigoriev, I. S., Grigoriev, K. G. (2003). Conditions of the maximum principle in the problem of optimal control over an aggregate of dynamic systems and their application to solution of the problems of optimal control of spacecraft motion. Cosmic Research, 41(3), 285–309. DOI 10.1023/A:1024063317807. [Google Scholar] [CrossRef]

141. Grigoriev, I. S., Zapletin, M. P. (2009). One optimization problem for trajectories of spacecraft rendezvous mission to a group of asteroids. Cosmic Research, 47(5), 426–437. DOI 10.1134/S0010952509050128. [Google Scholar] [CrossRef]

142. Martell, C. A., Lawton, J. A. (1995). Adjoint variable solutions via an auxiliary optimization problem. Journal of Guidance Control and Dynamics, 18(6), 1267–1272. DOI 10.2514/3.21540. [Google Scholar] [CrossRef]

143. Koblick, D., Xu, S. J., Fogel, J., Shankar, P. (2016). Low thrust minimum time orbit transfer nonlinear optimization using impulse discretization via the modified Picard-Chebyshev method. Computer Modeling in Engineering & Sciences, 111(1), 1–27. DOI 10.3970/cmes.2016.111.001. [Google Scholar] [CrossRef]

144. Dixon, L. C. W., Bartholomewbiggs, M. C. (1981). Adjoint-control transformations for solving practical optimal-control problems. Optimal Control Applications and Methods, 2(4), 365–381. DOI 10.1002/oca.4660020405. [Google Scholar] [CrossRef]

145. Ranieri, C. L., Ocampo, C. A. (2005). Optimization of roundtrip, time-constrained, finite burn trajectories via an indirect method. Journal of Guidance Control and Dynamics, 28(2), 306–314. DOI 10.2514/1.5540. [Google Scholar] [CrossRef]

146. Ranieri, C. L., Ocampo, C. A. (2006). Indirect optimization of spiral trajectories. Journal of Guidance Control and Dynamics, 29(6), 1360–1366. DOI 10.2514/1.19539. [Google Scholar] [CrossRef]

147. Qi, R., Xu, S. J. (2015). Optimal low-thrust transfers to lunar L1 halo orbit using variable specific impulse engine. Journal of Aerospace Engineering, 28(4), 04014096. DOI 10.1061/(ASCE)AS.1943-5525.0000432. [Google Scholar] [CrossRef]

148. Gil-Fernandez, J., Gomez-Tierno, M. A. (2010). Practical method for optimization of low-thrust transfers. Journal of Guidance Control and Dynamics, 33(6), 1927–1931. DOI 10.2514/1.50739. [Google Scholar] [CrossRef]

149. Jiang, F. H., Baoyin, H. X., Li, J. F. (2012). Practical techniques for low-thrust trajectory optimization with homotopic approach. Journal of Guidance Control and Dynamics, 35(1), 245–258. DOI 10.2514/1.52476. [Google Scholar] [CrossRef]

150. Yan, H., Wu, H. X. (1999). Initial adjoint-variable guess technique and its application in optimal orbital transfer. Journal of Guidance Control and Dynamics, 22(3), 490–492. DOI 10.2514/2.7631. [Google Scholar] [CrossRef]

151. Wang, D. Y., Li, T. S., Ma, X. R. (2000). Numerical solution of TPBVP in optimal lunar soft landing. Aerospace Control, 3, 44–49. [Google Scholar]

152. Caillau, J. B., Daoud, B., Gergaud, J. (2012). Minimum fuel control of the planar circular restricted three-body problem. Celestial Mechanics and Dynamical Astronomy, 114(1–2), 137–150. DOI 10.1007/s10569-012-9443-x. [Google Scholar] [CrossRef]

153. Picot, G. (2012). Shooting and numerical continuation methods for computing time-minimal and energy-minimal trajectories in the Earth-Moon system using low propulsion. Discrete and Continuous Dynamical Systems B, 17(1), 245–269. DOI 10.3934/dcdsb.2012.17.245. [Google Scholar] [CrossRef]

154. Zhang, C., Topputo, F., Bernelli-Zazzera, F., Zhao, Y. S. (2015). Low-thrust minimum-fuel optimization in the circular restricted three-body problem. Journal of Guidance Control and Dynamics, 38(8), 1501–1509. DOI 10.2514/1.G001080. [Google Scholar] [CrossRef]

155. Bertrand, R., Epenoy, R. (2002). New smoothing techniques for solving bang-bang optimal control problems-numerical results and statistical interpretation. Optimal Control Applications and Methods, 23(4), 171–197. DOI 10.1002/(ISSN)1099-1514. [Google Scholar] [CrossRef]

156. Golan, O. M., Breakwell, J. V. (1994). Minimum fuel lunar trajectories for a low-thrust power-limited spacecraft. Dynamics and Control, 4(4), 383–394. DOI 10.1007/BF01974142. [Google Scholar] [CrossRef]

157. Ranieri, C., Ocampo, C. (2008). Indirect optimization of low Earth orbit to low lunar orbit transfers. AAS/AIAA Astrodynamics Specialist Conference and Exhibit, pp. 2173–2189. Honolulu, Hawaii. [Google Scholar]

158. Lee, D., Bang, H., Kim, H. D. (2012). Optimal Earth-Moon trajectory design using new initial costate estimation method. Journal of Guidance Control and Dynamics, 35(5), 1671–1676. DOI 10.2514/1.55863. [Google Scholar] [CrossRef]

159. Senent, J., Ocampo, C., Capella, A. (2005). Low-thrust variable-specific-impulse transfers and guidance to unstable periodic orbits. Journal of Guidance Control and Dynamics, 28(2), 280–290. DOI 10.2514/1.6398. [Google Scholar] [CrossRef]

160. Oshima, K., Campagnola, S., Yanao, T. (2017). Global search for low-thrust transfers to the Moon in the planar circular restricted three-body problem. Celestial Mechanics and Dynamical Astronomy, 128(2–3), 303–322. DOI 10.1007/s10569-016-9748-2. [Google Scholar] [CrossRef]

161. Pérez-Palau, D., Epenoy, R. (2018). Fuel optimization for low-thrust Earth-Moon transfer via indirect optimal control. Celestial Mechanics and Dynamical Astronomy, 130(2), 1–29. DOI 10.1007/s10569-017-9808-2. [Google Scholar] [CrossRef]

162. Taheri, E., Junkins, J. L. (2020). How many impulses redux. Journal of the Astronautical Sciences, 67(2), 257–334. DOI 10.1007/s40295-019-00203-1. [Google Scholar] [CrossRef]

163. Taheri, E., Kolmanovsky, I., Atkins, E. (2016). Enhanced smoothing technique for indirect optimization of minimum-fuel low-thrust trajectories. Journal of Guidance Control and Dynamics, 39(11), 2500–2511. DOI 10.2514/1.G000379. [Google Scholar] [CrossRef]

164. Hecht, G. R., Botta, E. M. (2022). Heuristic optimization algorithms for initializing indirect minimum-fuel trajectory optimization. AIAA SCITECH 2022 Forum, AIAA 2022-1628. San Diego, CA and Virtual. [Google Scholar]

165. Singh, S. K., Anderson, B. D., Taheri, E., Junkins, J. L. (2021). Exploiting manifolds of L1 halo orbits for end-to-end Earth-Moon low-thrust trajectory design. Acta Astronautica, 183(6), 255–272. DOI 10.1016/j.actaastro.2021.03.017. [Google Scholar] [CrossRef]

166. Betts, J. T. (2000). Very low-thrust trajectory optimization using a direct SQP method. Journal of Computational and Applied Mathematics, 120(1–2), 27–40. DOI 10.1016/S0377-0427(00)00301-0. [Google Scholar] [CrossRef]

167. Mingotti, G., Topputo, F., Bernelli-Zazzera, F. (2007). Combined optimal low-thrust and stable-manifold trajectories to the Earth-Moon halo orbits. AIP Conference Proceedings, pp. 100–112. Omsk, Russia. [Google Scholar]

168. Hull, D. G. (1997). Conversion of optimal control problems into parameter optimization problems. Journal of Guidance Control and Dynamics, 20(1), 57–60. DOI 10.2514/2.4033. [Google Scholar] [CrossRef]

169. Enright, P. J., Conway, B. A. (1992). Discrete approximations to optimal trajectories using direct transcription and nonlinear-programming. Journal of Guidance Control and Dynamics, 15(4), 994–1002. DOI 10.2514/3.20934. [Google Scholar] [CrossRef]

170. Ma, J., Wen, C. X., Zhang, C. (2021). Practical optimization of low-thrust minimum-time orbital rendezvous in sun-synchronous orbits. Computer Modeling in Engineering & Sciences, 126(2), 617–644. DOI 10.32604/cmes.2021.014474. [Google Scholar] [CrossRef]

171. Betts, J. T., Erb, S. O. (2003). Optimal low thrust trajectories to the moon. SIAM Journal on Applied Dynamical Systems, 2(2), 144–170. DOI 10.1137/S1111111102409080. [Google Scholar] [CrossRef]

172. Pierson, B. L., Kluever, C. A. (1994). Three-stage approach to optimal low-thrust Earth-moon trajectories. Journal of Guidance Control and Dynamics, 17(6), 1275–1282. DOI 10.2514/3.21344. [Google Scholar] [CrossRef]

173. Herman, A. L., Conway, B. A. (1998). Optimal, low-thrust, Earth-Moon orbit transfer. Journal of Guidance Control and Dynamics, 21(1), 141–147. DOI 10.2514/2.4210. [Google Scholar] [CrossRef]

174. Mingotti, G., Topputo, F., Bernelli-Zazzera, F. (2011). Optimal low-thrust invariant manifold trajectories via attainable sets. Journal of Guidance Control and Dynamics, 34(6), 1644–1655. DOI 10.2514/1.52493. [Google Scholar] [CrossRef]

175. Mingotti, G., Topputo, F., Bernelli-Zazzera, F. (2012). Efficient invariant-manifold, low-thrust planar trajectories to the Moon. Communications in Nonlinear Science and Numerical Simulation, 17(2), 817–831. DOI 10.1016/j.cnsns.2011.06.033. [Google Scholar] [CrossRef]

176. Mingotti, G., Topputo, F., Bernelli-Zazzera, F. (2009). Low-energy, low-thrust transfers to the Moon. Celestial Mechanics and Dynamical Astronomy, 105(1–3), 61–74. DOI 10.1007/s10569-009-9220-7. [Google Scholar] [CrossRef]

177. Ozimek, M. T., Howell, K. C. (2010). Low-thrust transfers in the Earth-Moon system, including applications to Libration point orbits. Journal of Guidance Control and Dynamics, 33(2), 533–549. DOI 10.2514/1.43179. [Google Scholar] [CrossRef]

178. Kluever, C. A., Pierson, B. L. (1997). Optimal Earth-Moon trajectories using nuclear electric propulsion. Journal of Guidance Control and Dynamics, 20(2), 239–245. DOI 10.2514/2.4058. [Google Scholar] [CrossRef]

179. Kluever, C. A., Pierson, B. L. (1995). Optimal low-thrust three-dimensional Earth-Moon trajectories. Journal of Guidance Control and Dynamics, 18(4), 830–837. DOI 10.2514/3.21466. [Google Scholar] [CrossRef]

180. Wall, B., Conway, B. X. (2005). Near-optimal low-thrust earth-mars trajectories via a genetic algorithm. Journal of Guidance Control and Dynamics, 28(5), 1027–1031. DOI 10.2514/1.11891. [Google Scholar] [CrossRef]

181. Petropoulos, A. E., Longuski, J. M. (2004). Shape-based algorithm for the automated design of low-thrust, gravity assist trajectories. Journal of Spacecraft and Rockets, 41(5), 787–796. DOI 10.2514/1.13095. [Google Scholar] [CrossRef]

182. Wall, B. J., Conway, B. A. (2009). Shape-based approach to low-thrust rendezvous trajectory design. Journal of Guidance Control and Dynamics, 32(1), 95–101. DOI 10.2514/1.36848. [Google Scholar] [CrossRef]

183. Zhu, Z. F., Gan, Q. B., Yang, X., Gao, Y. (2017). Solving fuel-optimal low-thrust orbital transfers with bang-bang control using a novel continuation technique. Acta Astronautica, 137(1), 98–113. DOI 10.1016/j.actaastro.2017.03.032. [Google Scholar] [CrossRef]

184. Taheri, E., Abdelkhalik, O. (2015). Fast initial trajectory design for low-thrust restricted-three-body problems. Journal of Guidance Control and Dynamics, 38(11), 2146–2160. DOI 10.2514/1.G000878. [Google Scholar] [CrossRef]

185. Vijayakumar, M., Abdelkhalik, O. (2022). Shape-based approach for low-thrust Earth-Moon trajectories initial design. Journal of Guidance Control and Dynamics, 45(1), 103–120. DOI 10.2514/1.G006182. [Google Scholar] [CrossRef]