A Modified Bi-Directional Evolutionary Structural Optimization Procedure with Variable Evolutionary Volume Ratio Applied to Multi-Objective Topology Optimization Problem

1  Introduction

Topology optimization aims to produce design solutions of high performance by finding the optimal structural layout in structural design. It has the computational ability to solve great problems and produce reliable solutions to various engineering problems, therefore creating an immense opening for research in applied mechanics. During the last three decades, many gradient- or heuristic based optimization methods have been extensively investigated, according to [1], including density approach, topological derivatives, level set approach, phase field approach and evolutionary approaches. Among them, the convergent and mesh-independent bi-directional evolutionary structural optimization (BESO) developed by Huang et al. [2], iteratively removing inefficient material in addition to add material to the most demanding places, has become a widely adopted methodology for both academic research and engineering application [3,4].

In the classic BESO procedure, the number of elements to be rejected at the current iteration is prescribed by its ratio to the total number of elements at the previous iteration. This ratio is called as Evolutionary Volume Ratio (ER). The rejected elements are removed due to representing unnecessary regions so that their stiffness matrices are deleted. Based on the philosophy, the conventional BESO procedure can produce the following numerical issue due to improper ER. The smaller the value of the evolutionary volume ratio used, the more accurate is the final design, at the expense of larger computation time. The use of larger evolutionary volume ratio will reduce the number of elements of the resulting design more rapidly, whereas it may result in removing efficient elements incorrectly and fail to evolve to optimal solution. To address this issue, SESO (Smoothing Evolutionary Structural Optimization) procedure presents an organization of elements where a defined p% of rejected elements at each iteration are removed and (1 − p%) of them are returned to the structure [5,6]. For an unnecessary element for the structure, its corresponding structural stiffness gradually reduces till it no more contributes to the structure. This procedure can provide a typical characteristic of the continuous optimization. However, the key parameter of p% is selected according to a priori knowledge of optional solution without deterministic formula [7–9]. In this context, this paper applies an alternative topological optimization technique that provides a variable evolutionary volume ratio along the iterative process inside an extended fixed domain for a structure. It is suggested that one could use a high evolutionary volume ratio to sharply decrease the number of elements at early iterations while a low evolutionary volume ratio to obtain the sufficiently precious optimum at final iterations. This technique is an extension of the Morphing ESO methodology by Luo et al. [10]. The present variant of BESO presents advantages over the classical BESO method and these are demonstrated in this work. The numerical examples demonstrate that the improvements included in the formulation provide a compromise between sufficient accuracy and significant time saving.

Attenuation of unwanted vibrations is important in engineering structures as they could have detrimental effects on structural performances. Precious topology optimization focuses mainly on maximizing single dynamic performance like natural frequency [11,12], modal damping [13], or frequency response [14]. Topology optimization minimizing dynamic responses in time domain is another case of more difficulties. The equivalent static load (ESL) method is an increasingly popular approach to solve dynamic response structural optimization problems. By ESL method the dynamic topology optimization of a structure can be transformed into a static one under multiple loading cases [15,16]. Sun et al. [17] performed topology optimization of a three-dimensional flexible multi-body system via equivalent static load in the moving morphable components (MMC) based frame. Xu et al. [18] proposed a method for the concurrent topology optimization of macro-and micro-structural material distribution under dynamic loading based on ESL in the time domain. Up to the present, dynamic stiffness and frequency behavior of structures as two important factors in real-design problems have been deeply studied as separate objective functions. Therefore, achieving a trade-off between these two performances can have vital importance during structural design and analysis related to shipbuilding, automotive and aviation industries.

Over the last decades, a considerable effort has been devoted to single-objective optimization problems. But there may be several objective functions, usually conflicting in many real cases. As such, it is more appropriate to generate a set of optimal solutions which constitute the so-called Pareto set. For example, Simonetti et al. [19] explored the application of an evolutionary optimization technique for multi-objective optimization problems using the stress and strain energy criteria. Xu et al. [20] performed a mixed integer linear programming for multi-objective optimization of tensegrity structures using the ground structure method. Sleesongsom et al. [21] presented a multi-objective reliability-based topology optimization considering uncertain structural parameters using a fuzzy set model. Recently, Teimouri et al. [22] and Zhu et al. [23] have performed multi-objective optimization of continuum structures considering static stiffness and natural frequency. Crescenti et al. [24] generated minimal Pareto sets in multi-objective topology optimization of the wing box structural layout using smart normal constraint method. Lim et al. [25] obtained the optimal topology of a periodic spaceframe structure for maximal effective flexural and torsional stiffnesses along with minimal mass by Genetic Algorithm. Simonetti et al. [26] explored the application of the SESO technique to implement a parallel optimization to minimize the Von Mises stress and the internal strain energy growth.

In the conventional optimal design procedure, the natural frequency and the dynamic stiffness are exclusively considered as two independent factors for practical design problems. Consequently, it is of significance to establish a balance between these two indexes at the conceptual design stage. In this article, a multi-objective optimization scheme is implemented to obtain optimal topologies of a structure considering the natural frequency and the dynamic stiffness. The modified BESO with variable EVR is also introduced to improve the efficiency and stability during optimization.

The remainder of the article is organized as follows. Section 2 introduces the variable evolutionary volume ratio representing the dynamic removal behavior during optimization. Section 3 formulates the mono-objective optimization problem in the natural frequency and the dynamic stiffness. A weighted sum technique according to the sensitivity information obtained from mono-objective optimization is employed to carry out the multi-objective optimization. Section 4 presents several numerical examples to verify the proposed algorithm. Concluding remarks are made in Section 5.

2  Modified BESO with Variable Evolutionary Volume Ratio

Huang et al. [2] treated material removal and addition with a fixed evolutionary volume ratio to impose modifications on the topology of a structure, using the optimality criterion for the gradual removal of the finite elements in the mesh, which do not effectively contribute to a better performance of the structure. According to [2], the target volume for the next iteration (Vk+1) needs to be given first before elements are removed from or added to the current design. The evolution of the volume can be expressed by

Vk+1=Vk(1−ER)(k=1,2,3⋯)(1)

where ER is the evolutionary volume ratio, which is an input datum which is applied to control the evolutionary process of the structure. Vk is the target volume for the previous iteration. Then all the elements, both solid and void are sorted according to the values of their sensitivity numbers (from the highest to lowest). With the optimality criterion, the binary design variables of elements are updated until the constraint volume is achieved and the convergence is satisfied.

The evolutionary volume ratio in the BESO method plays the similar role as the move limit in mathematical programming and the step size in optimality criteria methods. Therefore, it is an important parameter impacting on evolution process and optimal solution. It is expected that a high evolutionary volume ratio is used to significantly decrease the number of inefficient elements at early iterations while a low evolutionary volume ratio to obtain the sufficiently accurate optimum at final iterations. Consequently, a reasonable evolutionary strategy should gradually reduce the evolutionary volume ratio as the iteration proceeds. The evolutionary procedure proposed can be performed by ER(Vk), an evolutionary volume ratio function, using a trigonometric function like sinusoidal and arctan function, an inverse proportional function or a linear function, which are defined by

ER(Vk)=ER0sin⁡[π2(1−V∗/V0)]Vk−V∗V0(1−ERminER0)+ERmin(2)

ER(Vk)=ER0tan⁡[π4(1−V∗/V0)]Vk−V∗V0(1−ERminER0)+ERmin(3)

ER(Vk)=ER0Vk−V∗V0−V∗(1−ERminER0)+ERmin(4)

ER(Vk)=ER0V0V0−V∗(1−V∗Vk)(1−ERminER0)+ERmin(5)

where ER0, ERmin are the initial and minimal evolutionary volume ratio, respectively, where the former is always greater than the latter. V0 is the volume of initial design domain and V∗ the prescribed total structural volume.

These functions are continuous and differentiated with an image varying from 0 to 1, as shown in Fig. 1. Nonetheless, here the sinusoidal function is used to regulate the evolution process. It is noteworthy that for larger value of ER0 and smaller value of ERmin used by the proposed optimization criterion, the optimal process attains a tradeoff between adequate precision and computational cost.

Figure 1: Variable evolutionary volume ratio function

3  Multi-Objective Design Optimization

Topological design considering multiple dynamic characteristics is of great importance for a real engineering structure. A multi-objective topology optimization technique is implemented to obtain optimal topology for Maximizing dynamic stiffness and natural frequency. In this case, weighting factors are imposed on multi-objective sensitivity numbers to reflect the importance of both dynamic stiffness and natural frequency. As a result, using several combinations of weighting factors, the resulting different topology dependent on the level of importance is obtained representing a Pareto-optimal solution.

3.1 Sensitivity Number for Dynamic Stiffness

To attenuate the unwanted vibration, the averaging summation of the dynamic strain energy during the time domain is defined as the objective function for dynamic stiffness in this research. The general formulation can be stated as follows:

MinimizeC(x)=1m∑i=1m12FT(ti)u(x,ti)s.t. V∗−∑i=1NViexi=0  xi=0or1(i=1,⋯,N)(6)

In the above formulation, C(x) is called as dynamic compliance representing structural average strain energy under dynamic load vector F(ti) and u(x,ti) is the displacement response vector corresponding to F(ti). x is the N-dimension vector of design variables in the design domain. The binary design variable xi indicates the corresponding element’s status, namely 1 representing element presence (solid) and 0 representing element absence (void). The volume constraint is formulated with the element volume Vie and the objective volume V∗.

Using the vibration theory with the finite element method, the dynamic behavior of a continuum structure is expressed by the following differential equations:

M(x)u¨(x,ti)+K(x)u(x,ti)=F(ti)(7)

where M(x) is the global mass matrix, K(x) is the global stiffness matrix, the acceleration vector is defined by u¨(x,ti).

Based on equivalent static loads method (ESLM) proposed by Jang et al. [15] for dynamic response topology optimization and verified by Stolpe [16], an ESL set, feq(x,ti) which generates the same displacement filed as dynamic loads at each time step ti, is expressed as

K(x)us(x,ti)=K(x)u(x,ti)=feq(x,ti)(8)

where us(x,ti) is the static displacement vector under the equivalent static loads feq(x,ti) imposed on the structure. It is assumed that the value of us(x,ti) at the initial iteration is equal to that of u(x,ti).

Then the present topology optimization problem can be transformed into that for multiple load cases, which can be rewritten as

MinimizeC~(x)=1m∑i=1m12feqT(x,ti)us(x,ti)s.t. V∗−∑i=1NViexi=0   K(x)us(x,ti)=feq(x,ti)   xi=0or1(i=1,⋯,N)(9)

According to [2,4], the sensitivity number for static stiffness with single load case is generally defined by the following equation:

αj,C¯={12usjT(x,ta)Kj0usj(x,ta)xj=10xj=0(10)

where Kj0 denotes the stiffness matrix of the j-th solid element.

With the static multiple load case in Eq. (9) equivalent to the original one in Eq. (6), the sensitivity of the dynamic strain energy with the design variable can be written as

αj,C∼={12∑a=1musjT(x,ta)Kj0usj(x,ta)xj=10xj=0(11)

3.2 Sensitivity Number for Natural Frequency

For a solid-void design, the topological optimization problem of maximizing the l-th natural frequency ωl(x) can be stated as

Maximizeωl(x)s.t. V∗−∑i=1NViexi=0   xi=0or1(i=1,⋯,N)(12)

Using finite element analysis, the dynamic behavior of a structure may be expressed by the following eigenvalue equation:

K(x)φl(x)=ωl2(x)M(x)φl(x)(13)

where φl(x) is the normalized eigenvector corresponding to the eigenvalue ωl2(x).

The sensitivity number of the j-th element for natural frequency can be formulated as [8]

αj,f={12ωl(x)φlT(x)(Kj0−ωl2(x)pMj0)φl(x)xj=112ωl(x)φlT(x)ωl2(x)pMj0φl(x)xj=0(14)

where p is the penalty factor, Kj0 indicates the stiffness matrix of the j-th solid element and Mj0 the mass matrix of the j-th solid element.

3.3 Multi-Objective Sensitivity Number

Since the obtained multi-objective sensitivity number for dynamic stiffness should be combined with the sensitivity number for natural frequency, it is normalized as follows:

α¯j,C∼=αj,C∼−αmin,C∼αmax,C∼−αmin,C∼(15)

where αmax,C∼ and αmin,C∼ are the maximum and minimum sensitivity numbers for dynamic stiffness, respectively.

In the same way, the sensitivity numbers for natural frequency can be normalized by the following equation:

α¯j.f=αj.f−αmin,fαmax,f−αmin,f(16)

where αmax,f and αmin,f are the maximum and minimum sensitivity numbers for natural frequency, respectively.

The multi-objective sensitivity number for both dynamic stiffness and natural frequency is defined by the following Eq. (17), where the weighting factors of both dynamic stiffness and natural frequency are imposed on sensitivity numbers for them to reflect the importance of dynamic stiffness and natural frequency, respectively.

α~j,multi=λC∗α¯j,C∼+λf∗α¯j,f(17)

where λC∗ and λf∗ are the weighting factors of sensitivity numbers for both dynamic stiffness and natural frequency.

3.4 Checkerboard Elimination

To circumvent the checkerboard pattern, a smoothing filter scheme [4] is implemented to blur the element sensitivities using a low-pass filter of radius rmin. This scheme is briefly summarized into two steps. First the raw element sensitivity α~q,multi is equally distributed to its nodes as α~j,multin, which are called as nodal sensitivities and defined as follows:

α~j,multin=∑q=1MVqα~q,multi/∑q=1MVq(18)

where M denotes the total number of elements connected to the j-th element.

Then the above nodal sensitivity numbers will be converted to smoothed elemental sensitivity numbers by summing up weighted α~j′,multin using a weighting function w(rj′j).

α^j,multi=∑j′=1M′w(rj′j)α~j′,multin/∑j=1M′w(rj′j)(19)

where M′ is the total number of nodes in the subdomain which is a circle of radius rmin centered at the centroid of j-th element. w(rj′j) is the linear weight factor defined as

w(rj′j)={rmin−rj′j(rmin>rj′j)0(rmin≤rj′j)(20)

where rj′j is the distance between the center of the j-th element and j’-th node in the subdomain.

Therefore, in terms of the above discussion, the flowchart of multi-objective topology optimization problem is shown in Fig. 2. To verify the modified BESO method, the multi-objective optimization problem is solved using the classic BESO method compared with the resulting optimal designs generated by the present methodology.

Figure 2: Flowchart for a multi-objective topology optimization

4  Numerical Examples

The design domain and loading condition of a long slender beam is illustrated in Fig. 3. The beam is 140 mm long and 20 mm high. All the degrees of freedom at the left and right sides are fixed. A dynamic force with amplitude 2.0 kN and duration 0.2 s, is applied at the center of the bottom edge. The structure is discretized into 2800 four nods plane stress elements. The Young’s modulus, the Poisson’s ratio, and the density are ρ = 7860 Kg/m3, E = 724 GPa, μ = 0.3, respectively. The final volume is restricted as 50% of the initial design.

Figure 3: A long slender beam with both ends built-in under dynamic load (a) design domain of a long slender beam (b) dynamic load

According to the comprehensive sensitivity number in Eq. (17), the five weighted factors λC∗ for the dynamic stiffness −0, 0.3, 0.5, 0.7 and 1, are considered to obtain the Pareto solutions. The algorithm’s parameters for the present methodology are as follows: initial evolutionary volume ratio ER0=0.06, minimal evolutionary volume ratio ERmin=0.01, penal factor p=3, allowable convergence tolerances ε=0.02, filter radius rmin=3mm. It is convenient for comparison between the present methodology and classic BESO that the two techniques have identical parameters except for the constant evolutionary volume ratio ER=0.04 for the latter.

Figs. 4–8 illustrate the evolution histories of dynamic compliance, natural frequency as well as the volume fraction for various weighted factors using the modified BESO method. In terms of Figs. 4–8, large weighted factor λC∗ for dynamic compliance results in an increasing importance in comprehensive design objective, which guides the optimal topology to a rigid structure with low natural frequency. Once the weighted factor λC∗ reaches one, the multi-objective problem is transformed into a mono-objective problem with the minimal dynamic compliance. As is expected, the weighted factor λf∗ for natural frequency imposes the similar influence on the optimal solution. Fig. 9 shows the resulting optimal topology corresponding to various weighted factors. It is observed that the central beam-like members are significant to improve the structural stiffness and their absence can lead to an increase of the natural frequency. Therefore, a middle optimal topology attains a tradeoff between these two performances, which is of great importance in real-design problems.

Figure 4: Evolutionary histories: weight factor λC∗=1, λf∗=0 by Modified BESO method (a) volume fraction (b) dynamic strain energy and natural frequency

Figure 5: Evolutionary histories: weight factor λC∗=0.7, λf∗=0.3 by Modified BESO method (a) volume fraction (b) dynamic strain energy and natural frequency

Figure 6: Evolutionary histories: weight factor λC∗=0.5, λf∗=0.5 by Modified BESO method (a) volume constraint (b) dynamic strain energy and natural frequency

Figure 7: Evolutionary histories: weight factor λC∗=0.3, λf∗=0.7 by Modified BESO method (a) volume fraction (b) dynamic strain energy and natural frequency

Figure 8: Evolutionary histories: weight factor λC∗=0, λf∗=1 by Modified BESO method (a) volume fraction (b) dynamic strain energy and natural frequency

Figure 9: Pareto-optimal topology solution by Modified BESO method (a) λC∗=1, λf∗=0 (b) λC∗=0.7, λf∗=0.3 (c) λC∗=0.5, λf∗=0.5 (d) λC∗=0.3, λf∗=0.7 (e) λC∗=0, λf∗=1

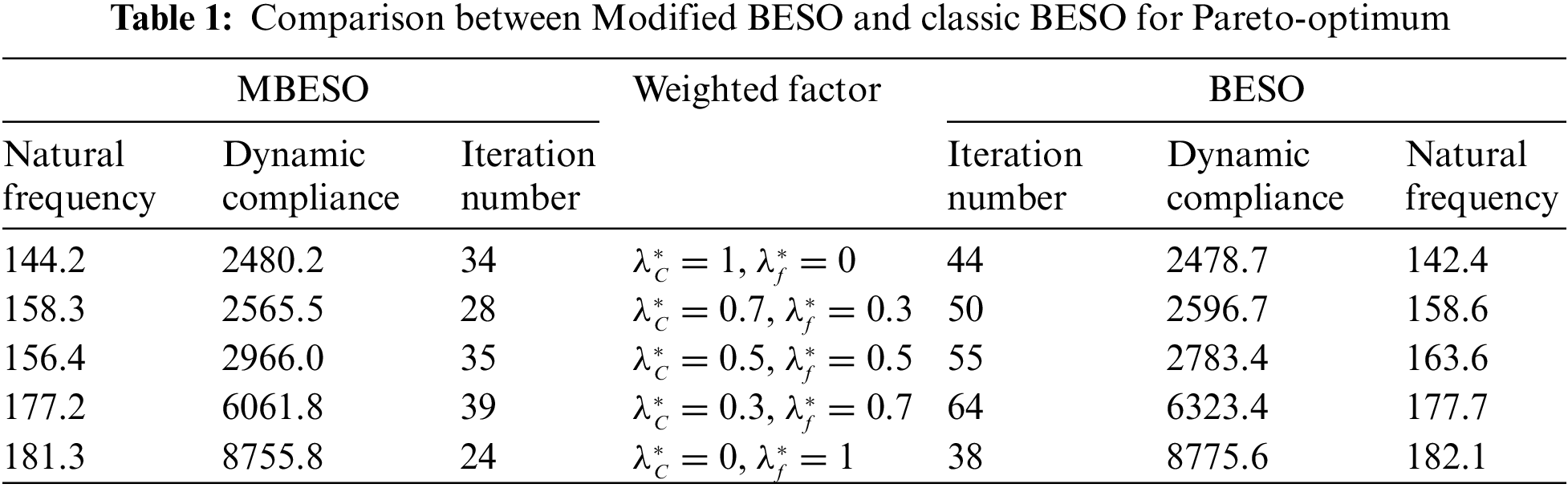
Figs.10–14 show the evolution histories of dynamic compliance, natural frequency as well as the volume fraction for various weighted factors using the classic BESO method with constant EVR. Fig. 15 depicts the resulting optimal topology corresponding to various weighted factors. Table 1 compares the results obtained by the classic BESO with those obtained by the modified BESO. It is evident that the modified BESO method can reproduce the optimal solutions obtained from the classic BESO. It is verified that the dynamic removal strategy with variable EVR substantially saves the computational time when compared with that with constant EVR. It attributes to the fact that high EVR at early iterations is favorable to significantly remove inefficient elements while low EVR at final iterations to obtain the sufficiently accurate optimum.

Figure 10: Evolutionary histories: weight factor λC∗=1, λf∗=0 by classic BESO method (a) volume fraction (b) dynamic strain energy and natural frequency

Figure 11: Evolutionary histories: weight factor λC∗=0.7, λf∗=0.3 by classic BESO method (a) volume fraction (b) dynamic strain energy and natural frequency

Figure 12: Evolutionary histories: weight factor λC∗=0.5, λf∗=0.5 by classic BESO method (a) volume constraint (b) dynamic strain energy and natural frequency

Figure 13: Evolutionary histories: weight factor λC∗=0.3, λf∗=0.7 by classic BESO method (a) volume fraction (b) dynamic strain energy and natural frequency

Figure 14: Evolutionary histories: weight factor λC∗=0, λf∗=1 by classic BESO method (a) volume fraction (b) dynamic strain energy and natural frequency

Figure 15: Pareto-optimal topology solution by classic BESO method (a) λC∗=1, λf∗=0 (b) λC∗=0.7, λf∗=0.3 (c) λC∗=0.5, λf∗=0.5 (d) λC∗=0.3, λf∗=0.7 (e) λC∗=0, λf∗=1

5  Conclusions

The dynamic stiffness and natural frequency are parallelly optimized as a two-objective function in the structural topology by modified BESO method. A weighted sum method is introduced to establish a balance between these two objectives. The numerical results reveal that the optimal topology from the multi-objective optimization problem is provided with a large dynamic stiffness compared with that exclusively from maximization of natural frequency, and a high natural frequency compared with that exclusively from minimization of dynamic stiffness. Any improvement in one objective performance requires a certain amount of compensation with the other objective performance. This type of topology optimization scheme is suitable for structural design in vehicle and aerospace industries where dynamic stiffness and natural frequency are equally important.

The present examples demonstrate that the modified BESO method with variable EVR can produce similar Pareto-optimum sets to those generated by classic BESO method with constant EVR. However, the dynamic removal strategy with the variable EVR presents a low computational cost since it consumes a small number of iterations to capture the accurate optimal topology using the constant EVR. Although only two objective functions are considered in this study, the scheme can be extended to other multiple objectives such as stress, displacement and frequency or even to thermal, fluidic and acoustic applications. These will be investigated and reported in the near future.

Funding Statement: This study was funded by the National Natural Science Foundation of China (Grant No. 51505096), and the Natural Science Foundation of Heilongjiang Province (Grant No. LH2020E064).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Zargham, S., Ward, T. A., Ramli, R., Badruddin, I. A. (2016). Topology optimization: A review for structural designs under vibration problems. Structural and Multidisciplinary Optimization, 53(6), 1157–1177. DOI 10.1007/s00158-015-1370-5. [Google Scholar] [CrossRef]

 2.  Huang, X. D., Xie, Y. M. (2007). Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method. Finite Elements in Analysis and Design, 43(14), 1039–1049. DOI 10.1016/j.finel.2007.06.006. [Google Scholar] [CrossRef]

 3.  Xia, L., Xia, Q., Huang, X., Xie, Y. M. (2016). Bi-directional evolutionary structural optimization on advanced structures and materials: A comprehensive review. Archives of Computational Methods in Engineering, 25(2), 437–478. [Google Scholar]

 4.  Gan, N., Wang, Q. (2021). Topology optimization of multiphase materials with dynamic and static characteristics by BESO method. Advances in Engineering Software, 151, 102928. DOI 10.1016/j.advengsoft.2020.102928. [Google Scholar] [CrossRef]

 5.  Simonetti, H. L., Almeida, V. S., de Oliveira Neto, L. (2014). A smooth evolutionary structural optimization procedure applied to plane stress problem. Engineering Structures, 75(5), 248–258. DOI 10.1016/j.engstruct.2014.05.041. [Google Scholar] [CrossRef]

 6.  Fernandes, W. S., Almeida, V. S., Neves, F. A., Greco, M. (2015). Topology optimization applied to 2D elasticity problems considering the geometrical nonlinearity. Engineering Structures, 100(5), 116–127. DOI 10.1016/j.engstruct.2015.05.042. [Google Scholar] [CrossRef]

 7.  Simonetti, H. L., Almeida, V. S., de Assis das Neves, F. (2018). Smoothing evolutionary structural optimization for structures with displacement or natural frequency constraints. Engineering Structures, 163(2), 1–10. DOI 10.1016/j.engstruct.2018.02.032. [Google Scholar] [CrossRef]

 8.  Simonetti, H. L., Almeida, V. S., de Assis das Neves, F. (2019). Topology optimization: Compliance minimization using SESO with bilinear square element. Numerical Optimization, 19(1), 33–39. [Google Scholar]

 9.  Fernandes, W. S., Greco, M., Almeida, V. S. (2017). Application of the smooth evolutionary structural optimization method combined with a multi-criteria decision procedure. Engineering Structures, 143(6), 40–51. DOI 10.1016/j.engstruct.2017.04.001. [Google Scholar] [CrossRef]

10. Luo, J., Zhang, D. K., Li, H. J., Gong, J. (2015). ESO method based on a kind of dynamic deletion rate. Chinese Journal of Computational Mechanics, 32(2), 274–279. [Google Scholar]

11. Su, W., Liu, S. (2015). Topology design for maximization of fundamental frequency of couple-stress continuum. Structural and Multidisciplinary Optimization, 53(3), 395–408. DOI 10.1007/s00158-015-1316-y. [Google Scholar] [CrossRef]

12. Liu, F. C., Li, W., Zhao, W. G., Zhao, H. B., Lin, G. Y. et al. (2021). Topology optimization based parametric design of balloon borne telescope’s primary mirror. Applied Sciences, 11(11), 5077. DOI 10.3390/app11115077. [Google Scholar] [CrossRef]

13. Alfouneh, M., Tong, L. (2017). Maximizing modal damping in layered structures via multi-objective topology optimization. Engineering Structures, 132(2), 637–647. DOI 10.1016/j.engstruct.2016.11.058. [Google Scholar] [CrossRef]

14. Zhu, J. H., He, F., Liu, T., Zhang, W. H., Liu, Q. et al. (2017). Structural topology optimization under harmonic base acceleration excitations. Structural and Multidisciplinary Optimization, 57(3), 1061–1078. DOI 10.1007/s00158-017-1795-0. [Google Scholar] [CrossRef]

15. Jang, H. H., Lee, H. A., Lee, J. Y., Park, G. J. (2012). Dynamic response topology optimization in the time domain using equivalent static loads. AIAA Journal, 50(1), 226–234. DOI 10.2514/1.J051256. [Google Scholar] [CrossRef]

16. Stolpe, M. (2014). On the equivalent static loads approach for dynamic response structural optimization. Structural and Multidisciplinary Optimization, 50(6), 921–926. DOI 10.1007/s00158-014-1101-3. [Google Scholar] [CrossRef]

17. Sun, J., Tian, Q., Hu, H. (2017). Topology optimization of a three-dimensional flexible multibody system via moving morphable components. Journal of Computational and Nonlinear Dynamics, 13(2), 1–34. [Google Scholar]

18. Xu, B., Huang, X., Xie, Y. M. (2016). Two-scale dynamic optimal design of composite structures in the time domain using equivalent static loads. Composite Structures, 142(12), 335–345. DOI 10.1016/j.compstruct.2016.01.090. [Google Scholar] [CrossRef]

19. Simonetti, H. L., Almeida, V. S., de Assis das Neves, F., Greco, M. (2019). Multi-objective topology optimization using the Boundary Element Method. Structures, 19(3), 84–95. DOI 10.1016/j.istruc.2018.12.002. [Google Scholar] [CrossRef]

20. Xu, X., Wang, Y., Luo, Y. (2017). An improved multi-objective topology optimization approach for tensegrity structures. Advances in Structural Engineering, 21(1), 59–70. DOI 10.1177/1369433217706780. [Google Scholar] [CrossRef]

21. Sleesongsom, S., Bureerat, S. (2020). Multi-objective reliability-based topology optimization of structures using a fuzzy set model. Journal of Mechanical Science and Technology, 34(10), 3973–3980. DOI 10.1007/s12206-020-2207-8. [Google Scholar] [CrossRef]

22. Teimouri, M., Asgari, M. (2019). Multi-objective BESO topology optimization for stiffness and frequency of continuum structures. Structural Engineering and Mechanics, 72(2), 181–190. [Google Scholar]

23. Zhu, N. H., Liu, J. L. (2021). Multiobjective topology optimization of spatial-structure Joints. Advances in Civil Engineering, 2021, 5530644. DOI 10.1155/2021/5530644. [Google Scholar] [CrossRef]

24. Crescenti, F., Kipouros, T., Munk, D. J., Savill, M. A. (2020). Generating minimal Pareto sets in multi-objective topology optimisation: An application to the wing box structural layout. Structural and Multidisciplinary Optimization, 63(3), 1119–1134. DOI 10.1007/s00158-020-02745-7. [Google Scholar] [CrossRef]

25. Lim, J., You, C., Dayyani, I. (2020). Multi-objective topology optimization and structural analysis of periodic spaceframe structures. Materials & Design, 190, 108552. DOI 10.1016/j.matdes.2020.108552. [Google Scholar] [CrossRef]

26. Simonetti, H. L., de Assis das Neves, F., Almeida, V. S. (2021). Multiobjective topology optimization with stress and strain energy criteria using the SESO method and a multicriteria tournament decision. Structures, 30(1), 188–197. DOI 10.1016/j.istruc.2021.01.002. [Google Scholar] [CrossRef]