Algebraic Properties for Molecular Structure of Magnesium Iodide

1  Introduction

The chemical formula MX2 is referred to a chemical compound named magnesium iodide. It has numerous commercial uses and is also valuable to get different organic synthesis, noted that MX2 or magnesium iodide is an inorganic compound. Nanopowder, submicron, high impurity and volumes are the availability measures of MX2. It is a very useful asset in internal medicine. Magnesium iodide may be produced by reacting hydro-iodic acid with magnesium carbonate, magnesium hydroxide, and magnesium oxide. Magnesium iodide is made up of a unique C4-graph pattern, according to molecular graph theory. Multiple heptagons are connected to each other, having each C4-graph inside [1]. For a better understanding of the magnesium iodide molecular graph, we labeled the parameters as follows: m is the number of C4’s of upper sides in a row, and n is the number of lower side C4 in heptagons. The magnesium iodide graph is required to preserve the relationship of m for even and odd values of separately with the relation of m=2(n+1), and m=2n+1, respectively, for all values of n∈Z with n≥1.

In this article, we studied some M-polynomials of magnesium iodide structure for both cases of m. The studied M-polynomials are defined below in Definitions 1.1 to 1.5, with their other fundamentals. Moreover, for a graph χ and their polynomial parameters are x,y, while ξa is the degree of a vertex a and defined by the counting of edges attached to a vertex a.

Definition 1.1. The most famous and first, Hosoya polynomials were introduced by [2] in 1988, and in 2015, Modified-polynomial, also known as M-polynomial, is introduced by [3]. This form of the polynomial has a closed relationship to degree-based topological indices. Topological indices from M-polynomials of a graph may be obtained using a specific format. This M-polynomial may be defined as follows:

M(χ;x,y)=∑i≤jmi,j(χ)xiyj,(1)

where mi,j(χ) is the number of edges of graph χ such that i≤j, are the notation of degrees of a vertex.

Definition 1.2. The symmetric division index SDI of a graph χ was introduced by [4] in 2010. Following are the symmetric division index and its M-polynomials.

SDI(χ)=∑ab∈E(χ)ξa2+ξb2ξa×ξb,(2)

PSDI(χ)=(DxSy+DySx)(M(χ;x,y)),(3)

where Dx,Dy,Sy,Sx are differential and integral operators defined in the Eqs. (10) to (15).

Definition 1.3. Shirdel et al. [5,6] introduced hyper Zagreb index, and given below are topological descriptor and its M-polynomial.

HM(χ)=∑ab∈E(χ)[ξa+ξb]2,(4)

PHM(χ)=2SxJ(M(χ;x,y)).(5)

Definition 1.4. Inverse sum index introduced by [7], and its M-polynomials [8], given below are formulations of its indices and M-polynomial.

IS(χ)=∑ab∈E(χ)ξaξbξa+×ξb,(6)

PIS(χ)=SxJDxDy(M(χ;x,y)).(7)

Definition 1.5. Furtula et al. [9] defined augmented Zagreb index and given below are formulation of index and its M-polynomial.

AZI(χ)=∑ab∈E(χ)(ξa×ξbξa+ξb−2)3,(8)

PAZI(χ)=Sx3Q−2JDx3Dy3(M(χ;x,y)).(9)

where

Dx(f(x,y))=x∂f(x,y)∂x,(10)

Dy(f(x,y))=x∂f(x,y)∂y,(11)

Sx(f(x,y))=∫0xf(z,y)zdz,(12)

Sy(f(x,y))=∫0yf(x,z)zdz,(13)

J(f(x,y))=f(x,x),(14)

Qa(f(x,y))=xaf(x,y).(15)

The researchers in [3] introduced the concept, in combination with numerical descriptors (known as topological indices [10–13]), an algebraic graph theory. The concept is known as the M-polynomials of the graph. It has fundamentals from topological indices. For some basic and important topological indices, we refer to see the articles [14–17]. This subject has been extensively researched in the last half-decade, and there is a wealth of material accessible. We will review a few of the most current papers on this topic.

The study of M-polynomials on nanotubes are available for h-naphthenic nanotube [18], various nanostructures studied in [19], and VC5C7-type of nanotubes are discussed in [20]. Generalized classes and families of the graph are studied with different M-polynomials in [15,21,22], various benzenoid structures are showcased in [23], M-polynomials interaction with statistics probability concept are available in [24]. Metal organic chemical network’s M-polynomials are studied in [25,26]. M-polynomials concept is also studied for various computer related networks and found in [27,28].

The M-polynomials are figured out for the magnesium iodide or MX2 structure for both even and odd cases of parameter m, and such M-polynomials named of augmented Zagreb index, inverse sum index, hyper Zagreb index and the symmetric division index.

2  Results on the M-Polynomials of Magnesium Iodide

Given in this section are some important results of this research work. The idea totally depends on the structural values of the MX2 or magnesium iodide graph, which is defined in Table 1 (for m=odd) and Table 2 (for n=even).

Case 1: For the odd values of m with given n≥1. Let m=2n+1 and n∈Z.

Theorem 2.1. Let Im,n be a magnesium iodide graph, with m=2n+1, n≥1, shown in Fig. 1. Then, its M-polynomial is

M(Im,n,x,y)=x[y3+y4+(n+5)y6]+2x2[y3+y4+4y5+(n+4)y6]+x3[3ny3+y4+12y5+(27n−13)y6].(16)

Figure 1: Magnesium iodide graph for n=4 and m=7

Proof. The construction of magnesium iodide graph from its structure, which is found in Fig. 1. It has six type of vertices, evaluated from the figure and these vertices are described in the vertex set as:

∨1={a∈V(Im,n):ξa=1},∨2={a∈V(Im,n):ξa=2}∨3={a∈V(Im,n):ξa=3},∨4={a∈V(Im,n):ξa=4}∨5={a∈V(Im,n):ξa=5},∨6={a∈V(Im,n):ξa=6}.

The same figure also shows the information of its edge types. It contains eleven types of edges in total and these are described as:

Ξ1,3={ab∈E(Im,n):ξa=1,ξb=3},Ξ1,4={ab∈E(Im,n):ξa=1,ξb=4}Ξ1,6={ab∈E(Im,n):ξa=1,ξb=6},Ξ2,3={ab∈E(Im,n):ξa=2,ξb=3}Ξ2,4={ab∈E(Im,n):ξa=2,ξb=4},Ξ2,5={ab∈E(Im,n):ξa=2,ξb=5}Ξ2,6={ab∈E(Im,n):ξa=2,ξb=6},Ξ3,3={ab∈E(Im,n):ξa=3,ξb=3}Ξ3,4={ab∈E(Im,n):ξa=3,ξb=4},Ξ3,5={ab∈E(Im,n):ξa=3,ξb=5}Ξ3,6={ab∈E(Im,n):ξa=3,ξb=6}.

The cardinality of these edge partitions are |Ξ1,3|=|Ξ1,4|=|Ξ3,4|=1,|Ξ2,3|=|Ξ2,4|=2,|Ξ1,6|=n+5,|Ξ2,5|=8,|Ξ2,6|=2(n+4),|Ξ3,3|=3n,|Ξ3,5|=12, and |Ξ3,6|=27n−13. Then from the Definition 1.1, the M-polynomial of Im,n is

M(Im,n;x,y)=∑i≤jmi,j(Im,n)xiyj=|Ξ1,3|(Im,n)x1y3+|Ξ1,4|(Im,n)x1y4+|Ξ1,6|(Im,n)x1y6+|Ξ2,3|(Im,n)x2y3+|Ξ2,4|(Im,n)x2y4+|Ξ2,5|(Im,n)x2y5+|Ξ2,6|(Im,n)x2y6+|Ξ3,3|(Im,n)x3y3+|Ξ3,4|(Im,n)x3y4+|Ξ3,5|(Im,n)x3y5+|Ξ3,6|(Im,n)x3y6,=x[y3+y4+(n+5)y6]+2x2[y3+y4+4y5+(n+4)y6]+x3[3ny3+y4+12y5+(27n−13)y6].(17)

The 3D plot shown in the Fig. 2, is the general M-polynomial of magnesium iodide graph, for a particular value with n=7 and m=15.

Figure 2: Graphical plot of M-polynomial of magnesium iodide graph

Lemma 2.1. Let Im,n be a magnesium iodide graph, with m=2n+1, n≥1, Then the differential operators are

Dx[M(Im,n;x,y)]=x[y3+y4+(n+5)y6]+4x2[y3+y4+4y5+(n+4)y6]+3x3[3ny3+y4+12y5+(27n−13)y6].(18)

Dy[M(Im,n;x,y)]=x[3y3+4y4+6(n+5)y6]+2x2[3y3+4y4+20y5+3(2n+8)y6]+x3[9ny3+4y4+60y5+6(27n−13)y6].(19)

Proof. Differentiate Eq. (16) with respect to x and multiply the result with x, we get the Dx[M(Im,n;x,y)]. Similarly, differentiate Eq. (16) with respect to y and multiply the result with y, we get the Dy[M(Im,n;x,y)].

Lemma 2.2. Let Im,n be a magnesium iodide graph, with m=2n+1, n≥1. Then the integral operators are

Sx[M(Im,n;x,y)]=x[y3+y4+(n+5)y6]+x2[y3+y4+4y5+(n+4)y6]+13x3[3ny3+y4+12y5+(27n−13)y6].(20)

Sy[M(Im,n;x,y)]=x[13y3+14y4+(n+5)6y6]+x2[23y3+12y4+85y5+(n+4)3y6]+x3[ny3+14y4+125y5+(27n−13)6y6].(21)

Proof. As we know that from Eq. (12), Sx[M(Im,n;x,y)]=∫0xM(Im,n;t,y)tdt uses the general M-polynomial for the Im,n from Eq. (16) in it. After simplification, we obtain Sx[M(Im,n;x,y)]. Similarly, from Eq. (13), Sy[M(Im,n;x,y)]=∫0yM(Im,n;x,t)tdt uses the general M-polynomial for the Im,n from Eq. (16) in it. After simplification, we obtain Sy[M(Im,n;x,y)].

Lemma 2.3. Let Im,n be a magnesium iodide graph, with m=2n+1, n≥1. Then the Eq. (16) is

J[M(Im,n;x,y)]=x4+3x5+(3n+2)x6+(n+8)x7+2(n+10)x8+(27n−13)x9.

Proof. By implementing the operator stated in the Eq. (14) on the main equation defined in Eq. (16), we get the J[M(Im,n;x,y)].

Theorem 2.2. Let Im,n be a magnesium iodide graph, with m=2n+1, n≥1, and PSDI is the M-polynomial of symmetric division index. Then PSDI(Im,n) is

PSDI(Im,n)=x[103y3+174y4+(41+n)6y6]+x2[133y3+5y4+1165y5+20(n+4)3y6]+103x3[10ny3+174y4+3125y5+37(27n−13)6y6].(22)

Proof. The M-polynomial of symmetric division index, given in the Definition 1.2, and the formulas for our structure Im,n can be written as: PSDI(Im,n)=(DxSy+DySx)(M(χ;x,y)). Lemmas 2.1 and 2.2 are the operators and here we used these to find our results for Im,n. We will obtain the M-polynomial of symmetric division index for Im,n after some algebraic simplifications as

PSDI(Im,n)=x[103y3+174y4+(41+n)6y6]+x2[133y3+5y4+1165y5+20(n+4)3y6]+103x3[10ny3+174y4+3125y5+37(27n−13)6y6].

The 3D plot shown in the Fig. 3, is the symmetric division index M-polynomial of magnesium iodide graph, for a particular value with n=7 and m=15.

Figure 3: Graphical plot of SDI M-polynomial of magnesium iodide graph

Theorem 2.3. Let Im,n be a magnesium iodide graph, with m=2n+1, n≥1, and PHM is the M-polynomial of hyper Zagreb index. Then PHM(Im,n) is

PHM(Im,n)=12x4+65x5+(3n+2)3x6+4x7+(n+10)2x8+2(27n−13)9x9.(23)

Proof. The M-polynomial of hyper Zagreb index, given in the Definition 1.3, and the formulas for our structure Im,n can be written as: PHM(Im,n)=2SxJ(M(χ;x,y)). Lemmas 2.2 and 2.3 are the operators and here we used these to find our results for Im,n. We will obtain the M-polynomial of symmetric division index for Im,n after some algebraic simplifications as: PHM(Im,n)=12x4+65x5+(3n+2)3x6+4x7+(n+10)2x8+2(27n−13)9x9.

The 2D plot shown in the Fig. 4, is the hyper Zagreb M-polynomial of magnesium iodide graph. Moreover, all the 2D plots show the M-polynomials of different index containing x values on horizontal scale with different values of n∈{2,3,…,10}.

Figure 4: Graphical plot of HM M-polynomial of magnesium iodide graph

Theorem 2.4. Let Im,n be a magnesium iodide graph, with m=2n+1, n≥1, and PIS is the M-polynomial of inverse sum index. Then PIS(Im,n) is

PIS(Im,n)=34x4+2x5+(9n+8)6x6+(6n+74)7x7+(3n+27)2x8+2(27n−13)3x9.(24)

Proof. The M-polynomial of inverse sum index, given in the Definition 1.4, and the formulas for our structure Im,n can be written as: PIS(Im,n)=SxJDxDy(M(χ;x,y)). Lemmas 2.1, 2.2 and 2.3 are the operators and here we used these to find our results for Im,n. We will obtain the M-polynomial of symmetric division index for Im,n after some algebraic simplifications as

PIS(Im,n)=34x4+2x5+(9n+8)6x6+(6n+74)7x7+(3n+27)2x8+2(27n−13)3x9.

The 2D plot shown in the Fig. 5, is the inverse sum M-polynomial of magnesium iodide graph, for a particular value with n=7 and m=15.

Figure 5: Graphical plot of IS M-polynomial of magnesium iodide graph

Theorem 2.5. Let Im,n be a magnesium iodide graph, with m=2n+1, n≥1, and PAZI is the M-polynomial of augmented Zagreb index. Then PAZI(Im,n) is

PAZI(Im,n)=278x2+11827x3+(243n+128)64x4+(216n+1644)125x5+(432n+3228)216x6+216(27n−13)343x7.(25)

Proof. The M-polynomial of augmented Zagreb index, given in the Definition 1.5, and the formulas for our structure Im,n can be written as: PAZI(Im,n)=Sx3Q2JDx3Dy3(M(χ;x,y)). Lemmas 2.1, 2.2 and 2.3 are the operators and here we used these to find our results for Im,n. We will obtain the M-polynomial of symmetric division index for Im,n after some algebraic simplifications as PAZI(Im,n)=278x2+11827x3+(243n+128)64x4+(216n+1644)125x5+(432n+3228)216x6+216(27n−13)343x7.

The 2D plot shown in the Fig. 6, is the augmented Zagreb index M-polynomial of magnesium iodide graph, for a particular value with n=7 and m=15.

Figure 6: Graphical plot of AZI M-polynomial of magnesium iodide graph

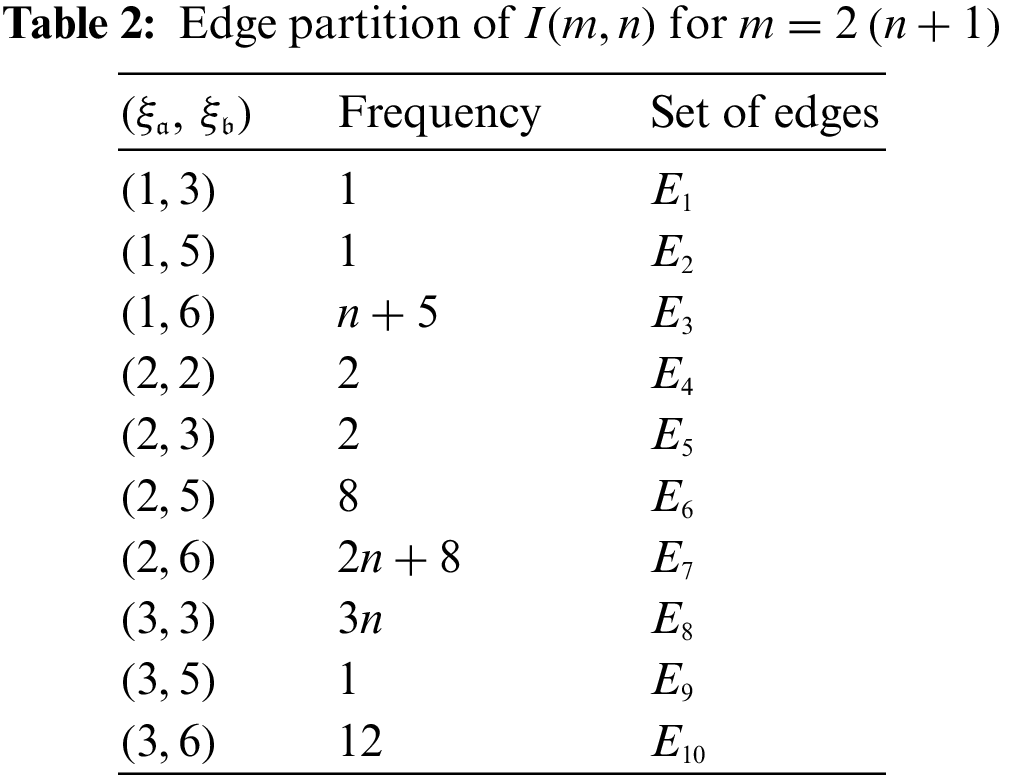
Case 2: For the even values of m with given n≥1. Let m=2(n+1) and n∈Z.

Theorem 2.6. Let Im,n be a magnesium iodide graph, with m=2(n+1), n≥1, shown in the Fig. 1. Then, its M-polynomial is

M(Im,n,x,y)=x[y3+y5+(n+5)y6]+x2[5y2+6y3+2y5+(2n+8)y6]+x3[(3n+1)y3+2y5+(27n+7)y6].(26)

Proof. The construction of magnesium iodide graph from its structure is found in Fig. 1. It has five types of vertices, evaluated from the figure and these vertices are described in the vertex set as

∨1={a∈V(Im,n):ξa=1},∨2={a∈V(Im,n):ξa=2}∨3={a∈V(Im,n):ξa=3},∨5={a∈V(Im,n):ξa=5}∨6={a∈V(Im,n):ξa=6}.

The same figure is also shown the information of its edge types. It contains ten types of edges in total and these are described as

Ξ1,3={ab∈E(Im,n):ξa=1,ξb=3},Ξ1,5={ab∈E(Im,n):ξa=1,ξb=5}Ξ1,6={ab∈E(Im,n):ξa=1,ξb=6},Ξ2,2={ab∈E(Im,n):ξa=2,ξb=2}Ξ2,3={ab∈E(Im,n):ξa=2,ξb=3},Ξ2,5={ab∈E(Im,n):ξa=2,ξb=5}Ξ2,6={ab∈E(Im,n):ξa=2,ξb=6},Ξ3,3={ab∈E(Im,n):ξa=3,ξb=3}Ξ3,5={ab∈E(Im,n):ξa=3,ξb=5},Ξ3,6={ab∈E(Im,n):ξa=3,ξb=6}.

The cardinality of these edge partitions are |Ξ1,3|=|Ξ1,5|=1,|Ξ2,5|=|Ξ3,5|=2,|Ξ1,6|=n+5,|Ξ2,2|=5,|Ξ2,3|=6,|Ξ2,6|=2(n+4),|Ξ3,3|=3n+1, and |Ξ3,6|=27n+7. Then from the definition 1.1, the M-polynomial of Im,n is

M(Im,n;x,y)=∑i≤jmi,j(Im,n)xiyj=|Ξ1,3|(Im,n)x1y3+|Ξ1,5|(Im,n)x1y5+|Ξ1,6|(Im,n)x1y6+|Ξ2,2|(Im,n)x2y2+|Ξ2,3|(Im,n)x2y3+|Ξ2,5|(Im,n)x2y5+|Ξ2,6|(Im,n)x2y6+|Ξ3,3|(Im,n)x3y3+|Ξ3,5|(Im,n)x3y5+|Ξ3,6|(Im,n)x3y6,=x[y3+y5+(n+5)y6]+x2[5y2+6y3+2y5+2(n+4)y6]+x3[(3n+1)y3+2y5+(27n+7)y6].(27)

The 3D plot shown in the Fig. 7, is the general M-polynomial of magnesium iodide graph, for a particular value with n=7 and m=16.

Figure 7: Graphical plot of M-polynomial of magnesium iodide graph

Lemma 2.4. Let Im,n be a magnesium iodide graph, with m=2(n+1), n≥1, then the differential operators are

Dx[M(Im,n;x,y)]=x[y3+y5+(n+5)y6]+2x2[5y2+6y3+2y5+2(n+4)y6]+3x3[(3n+1)y3+2y5+(27n+7)y6].(28)

Dy[M(Im,n;x,y)]=x[3y3+5y4+6(n+5)y6]+2x2[5y2+9y3+5y5+6(n+4)y6]0+x3[3(3n+1)y3+10y5+6(27n+7)y6].(29)

Proof. Differentiate Eq. (26) with respect to x and multiply the result with x, we get the Dx[M(Im,n;x,y)]. Similarly, differentiate Eq. (26) with respect to y and multiply the result with y, we get the Dy[M(Im,n;x,y)].

Lemma 2.5. Let Im,n be a magnesium iodide graph, with m=2n+1, n≥1. Then the integral operators are

Sx[M(Im,n;x,y)]=x[y3+y5+(n+5)y6]+12x2[5y2+6y3+2y5+2(n+4)y6]+13x3[(3n+1)y3+2y5+(27n+7)y6].(30)

Sy[M(Im,n;x,y)]=x[13y3+15y5+(n+5)6y6]+x2[52y2+2y3+25y5+(n+4)3y6]+x3[(3n+1)3y3+25y5+(27n+7)6y6].(31)

Proof. As we know that from Eq. (12), Sx[M(Im,n;x,y)]=∫0xM(Im,n;t,y)tdt uses the general M-polynomial for the Im,n from Eq. (26) in it. After simplification, we obtain Sx[M(Im,n;x,y)]. Similarly, from Eq. (13), Sy[M(Im,n;x,y)]=∫0yM(Im,n;x,t)tdt uses the general M-polynomial for the Im,n from Eq. (26) in it. After simplification, we obtain Sy[M(Im,n;x,y)].

Lemma 2.6. Let Im,n be a magnesium iodide graph, with m=2(n+1), n≥1. Then the Eq. (26) is

J[M(Im,n;x,y)]=6x4+6x5+(3n+2)x6+(n+7)x7+2(n+5)x8+(27n+7)x9.

Proof. By implementing the operator stated in the Eq. (14) on the main equation defined in 11, we get the J[M(Im,n;x,y)].

Theorem 2.7. Let Im,n be a magnesium iodide graph, with m=2(n+1), n≥1, and PSDI is the M-polynomial of symmetric division index. Then PSDI(Im,n) is

PSDI(Im,n)=x[23y3+25y5+n+53y6]+x2[254y2+5y3+y5+5(n+4)6y6]+x3[246n+813y3+1825y5+3429n+8896y6].(32)