Bayesian Computation for the Parameters of a Zero-Inflated Cosine Geometric Distribution with Application to COVID-19 Pandemic Data

Sunisa Junnumtuam; Sa-Aat Niwitpong; Suparat Niwitpong

doi:10.32604/cmes.2022.022098

Table of Content

Open Access

ARTICLE

Bayesian Computation for the Parameters of a Zero-Inflated Cosine Geometric Distribution with Application to COVID-19 Pandemic Data

Sunisa Junnumtuam, Sa-Aat Niwitpong^*, Suparat Niwitpong
Department of Applied Statistics, Faculty of Applied Science, King Mongkut’s University of Technology North Bangkok, Bangkok, 10800, Thailand
* Corresponding Author: Sa-Aat Niwitpong. Email:
(This article belongs to this Special Issue: New Trends in Statistical Computing and Data Science)

Computer Modeling in Engineering & Sciences 2023, 135(2), 1229-1254. https://doi.org/10.32604/cmes.2022.022098

Received 21 February 2022; Accepted 08 June 2022; Issue published 27 October 2022

Abstract

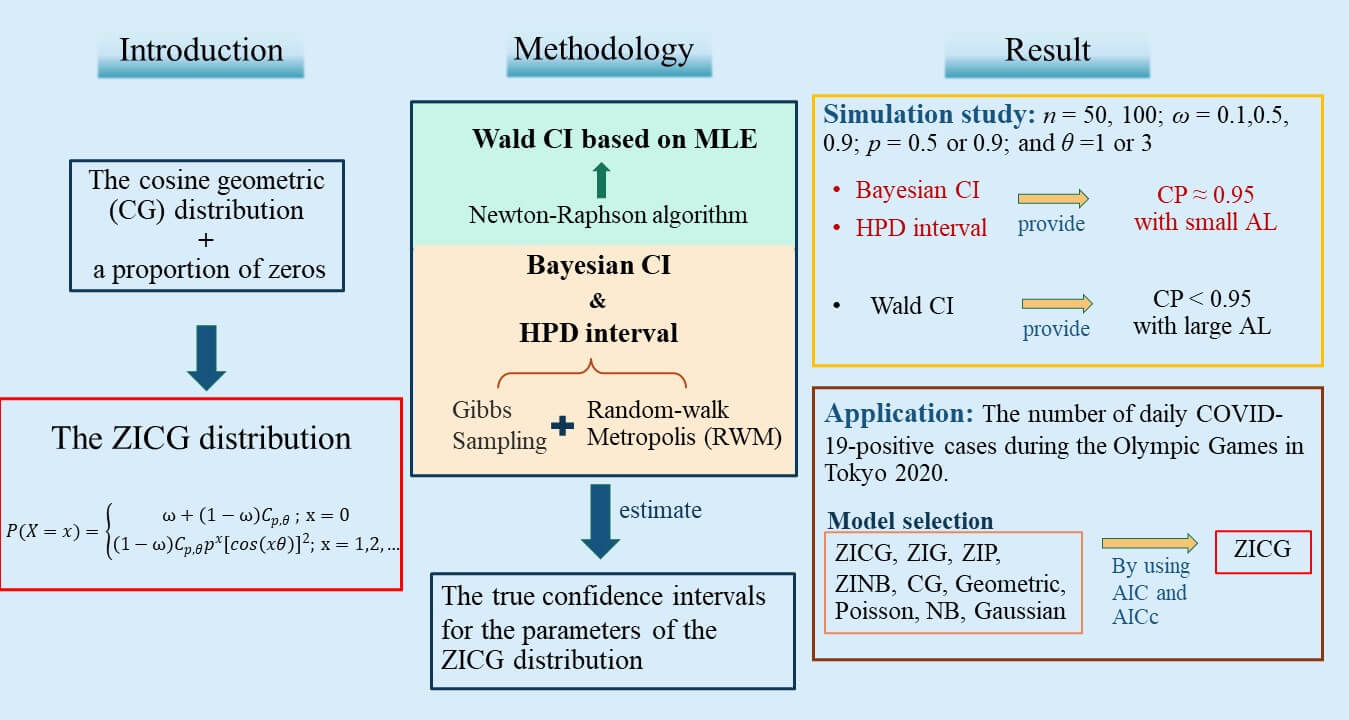
A new three-parameter discrete distribution called the zero-inflated cosine geometric (ZICG) distribution is proposed for the first time herein. It can be used to analyze over-dispersed count data with excess zeros. The basic statistical properties of the new distribution, such as the moment generating function, mean, and variance are presented. Furthermore, confidence intervals are constructed by using the Wald, Bayesian, and highest posterior density (HPD) methods to estimate the true confidence intervals for the parameters of the ZICG distribution. Their efficacies were investigated by using both simulation and real-world data comprising the number of daily COVID-19 positive cases at the Olympic Games in Tokyo 2020. The results show that the HPD interval performed better than the other methods in terms of coverage probability and average length in most cases studied.

Graphical Abstract

Bayesian Computation for the Parameters of a Zero-Inflated Cosine Geometric Distribution with Application to COVID-19 Pandemic Data

Keywords

Bayesian analysis; confidence interval; gibbs sampling; random-walk metropolis; zero-inflated count data

Cite This Article

Junnumtuam, S., Niwitpong, S., Niwitpong, S. (2023). Bayesian Computation for the Parameters of a Zero-Inflated Cosine Geometric Distribution with Application to COVID-19 Pandemic Data. CMES-Computer Modeling in Engineering & Sciences, 135(2), 1229–1254.

This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.