Developments and Applications of Neutrosophic Theory in Civil Engineering Fields: A Review

1  Introduction

The neutrosophic theory was first proposed by Smarandache [1] as a philosophical thought in 1998. After that, Smarandache extended neutrosophic thought to the field of mathematics and proposed a series of neutrosophic mathematical theories, such as neutrosophic logic, neutrosophic probability, statistics, and neutrosophic sets. Then, the neutrosophic theory gradually realized the transformation from philosophy to science and engineering. Since the neutrosophic theory is difficult to express and apply to engineering and science problems, many scholars have generalized and improved the neutrosophic theory and gradually formed engineering neutrosophic theory and methods for convenient applications in engineering and science areas [2–30]. Because of its main advantages in the information expression and analysis of indeterminacy, inconsistency, and incompleteness, which fuzzy sets and (interval-valued) intuitionistic fuzzy sets (IFSs) [31–36] cannot reveal, the engineering neutrosophic theory has been expanded to many different research areas, like decision making, neural network, optimization programming, artificial intelligence, image processing, mechanical fault diagnosis, medical diagnosis and so on. Some of them have also become popular research hotspots in civil engineering.

With the development of current engineering science and technology, the complexity, difficulty, and requirements of civil engineering continue to increase. To adapt to these changes and developments in civil engineering, the theoretical research of civil engineering must become more reasonable and scientific. In terms of the characteristics of civil engineering, traditional theoretical research methods are usually difficult to handle indeterminate and inconsistent problems in civil engineering. Although many theoretical studies of civil engineering have considered the uncertainty in actual engineering issues, most theories and methods are difficult to express the uncertain and inconsistent information contained in civil engineering. Therefore, as a theoretical tool that can effectively express indeterminate, incomplete, and inconsistent information, the neutrosophic theory will play a very crucial role in promoting the development of civil engineering theory and applied methods. Currently, neutrosophic sets, neutrosophic numbers, and neutrosophic possibility and statistics have been applied in rock mechanics and engineering management, gradually forming engineering neutrosophic theory and methods [37–73]. Then, the research progress of the neutrosophic set, the neutrosophic number (NN), and the neutrosophic probability and statistics in civil engineering are shown in Figs. 1–3.

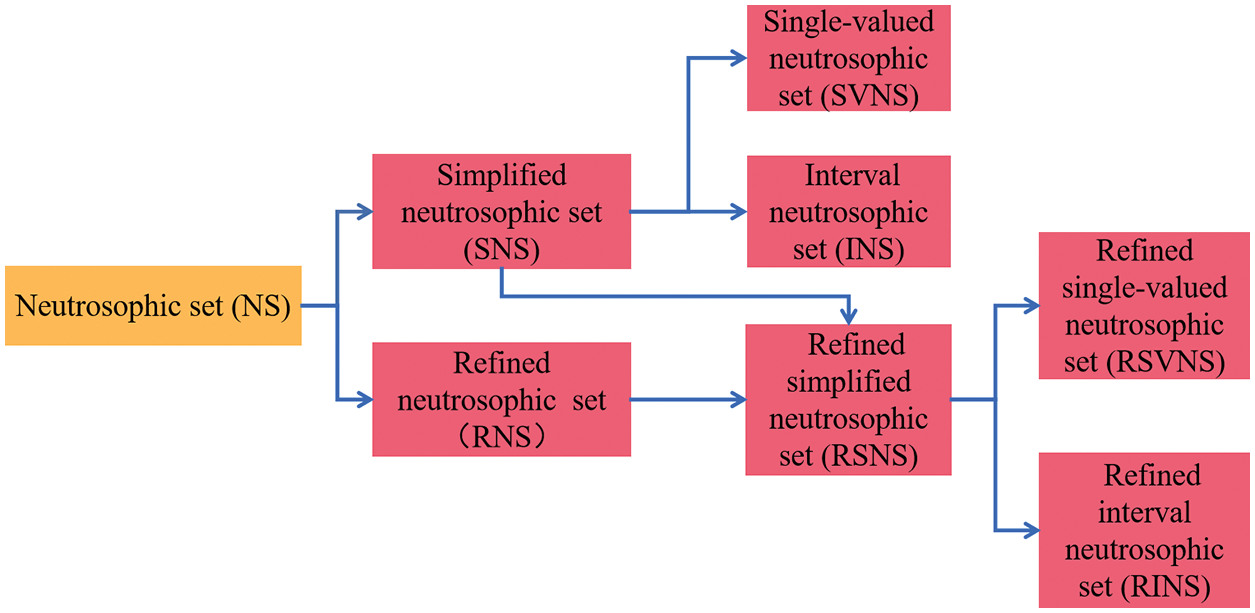
Figure 1: Research progress of neutrosophic sets in civil engineering

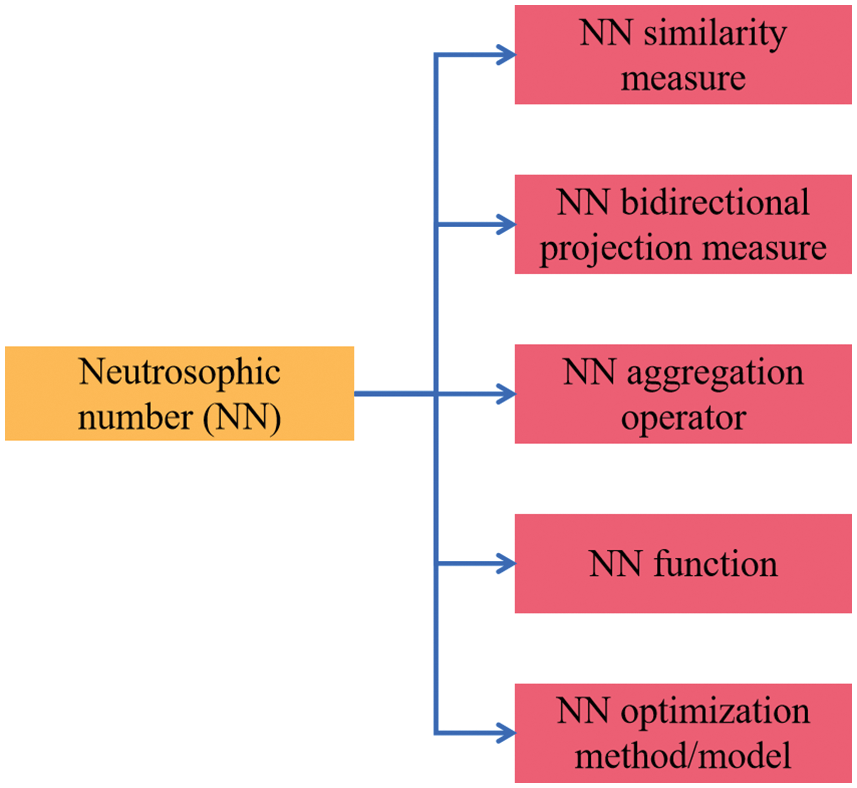
Figure 2: Various algorithms of NNs in civil engineering

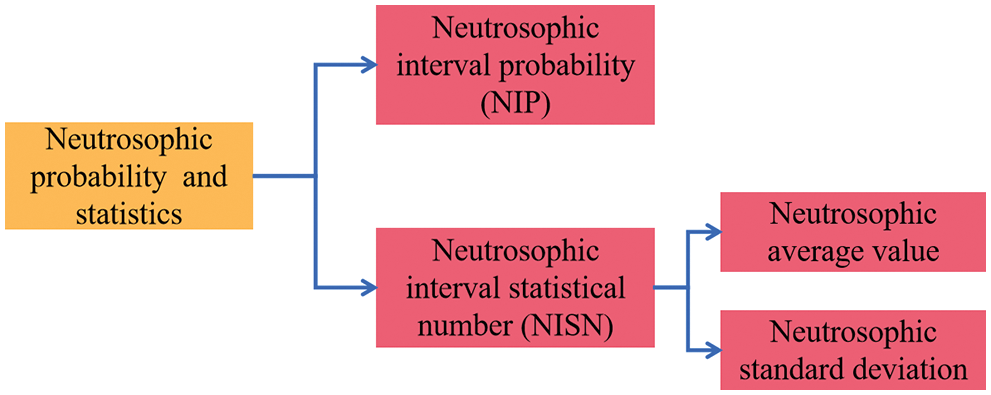
Figure 3: Research progress of neutrosophic probability and statistics

To review developments and applications of neutrosophic theory in civil engineering fields in recent years, the remainder of this review paper first describes the research achievements of engineering neutrosophic theory and applied methods in four main research areas of civil engineering: the neutrosophic decision-making theory and applied methods, the neutrosophic evaluation methods and applications of slope stability, the neutrosophic expressions and analyses of rock joint roughness coefficient, and the neutrosophic structural optimization methods and applications. Then, we perform a literature analysis of published papers in civil engineering. Finally, the research remarks and future research directions in the field of civil engineering are summarized.

2  Neutrosophic Decision-Making Theory and Applied Methods in Civil Engineering Management

Engineering management usually involves various stages of civil engineering projects and then contains various decision-making issues such as engineering contractors, construction design schemes, building materials, engineering maintenance works, and engineering site selection. With the development of civil engineering, decision-making issues in actual project management reflect complexity, vagueness, and indeterminacy, which require neutrosophic decision-making methods to solve them. Therefore, various studies centered on the neutrosophic theory have proved the advantages of describing and handling indeterminate and inconsistent information in actual decision-making problems. Thus, the neutrosophic theory has achieved many important results in the related research on dealing with decision-making problems.

Decision making is an inevitable and important research topic in the construction and management of engineering projects. Because of the complexity of current decision-making problems, they are often filled with uncertain and inconsistent information. It is particularly important to study how to describe and express this information. For this reason, Zadeh [31] proposed fuzzy set theory in 1965. Then, as an extension of the fuzzy set theory, the concepts of intuitionistic fuzzy sets [32] and interval-valued intuitionistic fuzzy sets [33] have been introduced and successfully applied in decision-making areas [34–36]. With the development of the civil engineering field in recent years, the decision-making problems of civil engineering have become increasingly complicated and reflected their indeterminacy, vagueness, and incompleteness. Existing fuzzy set and (interval-valued) intuitionistic fuzzy set theories cannot be able to effectively and reasonably express incomplete, indeterminate, and inconsistent information in complicated decision-making problems. Thus, Smarandache [1] put forward the neutrosophic theory in 1998 to represent the incomplete, indeterminate, and inconsistent information. However, the neutrosophic theory with philosophical thought is difficult to handle engineering and science problems because its truth, falsity, and indeterminacy membership functions are in the non-standard interval ]–0, 1+[. Therefore, many scholars presented the improved neutrosophic theory used for engineering problems to solve complex decision-making problems. In actual engineering decision-making problems, various neutrosophic decision-making theories and methods for decision-making problems have become the research hotspots of civil engineering management.

Regarding complex decision-making problems, multi-attribute/criteria decision-making (MADM/MCDM) is one of the most important research topics. MADM/MCDM is a process of decision makers’ preference assessment of alternatives over multi-attributes and determines the best one among alternatives. In complex MADM problems, how to reasonably express and aggregate relevant information are two main issues that need to be solved. To describe incomplete, indeterminate, and inconsistent information in realistic decision-making problems, Smarandache [1] proposed the concepts of neutrosophic sets and neutrosophic numbers (NNs) as two subclasses of the neutrosophic theory. The neutrosophic set is depicted independently by the membership functions of the truth, falsity, and indeterminacy that belong to subsets of the real standard interval [0, 1] or the non-standard interval ]−0, 1+[. Thus, the neutrosophic set can better express incomplete, indeterminate, and inconsistent information, which fuzzy sets and (interval-valued) IFSs cannot do.

To facilitate science and engineering applications, Ye [37] introduced simplified neutrosophic sets (SNSs) based on the real standard interval [0, 1], which implies single-valued neutrosophic sets (SvNSs) [38] and interval-valued neutrosophic sets (IvNSs) [39], and then defined their operations and weighted aggregation algorithms for MADM problems. SNS is not only a subset of the neutrosophic set, but also the generalization of the fuzzy set and (interval-valued) IFS. Then, Smarandache [1,40,41] proposed NN from symbol theory as another branch of the neutrosophic theory. Under an indeterminate environment, NN can be represented as e = p + qI for p, q ∈ R and I ∈ [inf I, sup I], where p and qI are a certain term and an indeterminate term, respectively. In fact, NN can reflect a family of interval numbers (changeable interval numbers) regarding various indeterminate ranges of I ∈ [inf I, sup I], which reflects its flexible and convenient advantages in expressing indeterminate information.

In construction projects, the choice of building materials is usually a MADM problem. The quality of building materials will affect the safety, economy, and reliability of construction projects. Since the quality of clay bricks is affected by various indicators, the MADM problem of clay bricks based on engineering neutrosophic theory is to choose a high-quality clay brick for construction projects in indeterminate and inconsistent situations.

The traditional method of selecting clay bricks is usually just some rough judgments, such as the color, size, and total cost of the clay bricks, but ignores many complex indeterminate factors/useful information regarding the quality of the clay bricks. Therefore, it is particularly important to establish a scientific decision-making method for the quality assessment of clay bricks. In recent years, some scholars have introduced decision-making methods for clay brick selection problems based on the neutrosophic theory. In 2015, Mondal et al. [42] proposed a MADM method using single-valued neutrosophic grey relational analysis to solve a high-quality clay brick selection problem. In 2016, Chen et al. [43] proposed a MADM method based on the projection model in the NN environment and used it for the selection of clay bricks. In the proposed method, they selected four types of potential clay bricks (alternatives). Then, they are satisfactorily evaluated by the six attributes of solidity, color, size and shape, brick strength, brick cost, and transportation cost corresponding to their different weights. Moreover, the evaluation information of each alternative over the six attributes was expressed by NNs, the four alternatives were sorted through the projection measure between each alternative and an ideal solution, and then the optimal one was finally obtained.

In engineering management, the decision making of engineering projects is a vital research topic. In the MADM problem of engineering projects, we usually consider factors such as functionality, economism, and safety as the main indices/attributes of the decision-making problem. Due to the complexity of decision-making problems, there are often the requirements of attributes and sub-attributes in assessment problems of construction projects, then they are considered by the weights of attributes and sub-attributes. To deal with such a decision-making problem, Chen et al. [44] proposed relevant decision-making methods using the vector similarity measures (the Jaccard, Dice, and cosine similarity measures) of the refined simplified neutrosophic sets (RSNSs) and verified the effectiveness and rationality of these decision-making methods through some examples on selecting the best construction project from four potential engineering projects. After that, Solang et al. [45] proposed the RSNS similarity measures based on tangent and cotangent functions. They then established their MADM methods to solve a decision-making problem of engineering construction projects under the RSNS environment. In the decision-making problem, four construction projects/alternatives must satisfy three basic attributes (budget, quality and delivery) and 8 sub-attributes, and then their assessed information was expressed by RSNSs. Thus, the proposed MADM methods based on the tangent and cotangent similarity measures of RSNSs were used in the decision-making case of engineering construction projects to verify their validity and applicability in RSNS setting. In addition, Gokasar et al. [46] proposed type-2 neutrosophic numbers (T2NNs) and established their MADM method to solve a decision-making problem of engineering maintenance projects. In this study, they ranked five bridge maintenance projects using carbon emissions as the most weighted attribute. The results demonstrated the effectiveness and rationality of this new method. After that, Deveci et al. [47] further proposed advanced type-2 neutrosophic numbers (AT2NNs) and applied them to the decision-making problem of engineering project location selection. This study found the best location from six locations for the construction of an automotive lithium-ion battery remanufacturing facility by building an integrated neutrosophic decision-making model. Further, Bavia et al. [48] applied SvNSs to solve the decision-making problem of engineering project location selection, and then verified the effectiveness of the presented method through examples.

The aforementioned neutrosophic decision-making methods and applications of civil engineering management are shown in Table 1. Then, Fig. 4 shows the number of papers published annually in the field of civil engineering management. As in Fig. 4, the number of papers published annually has been relatively stable over the past seven years.

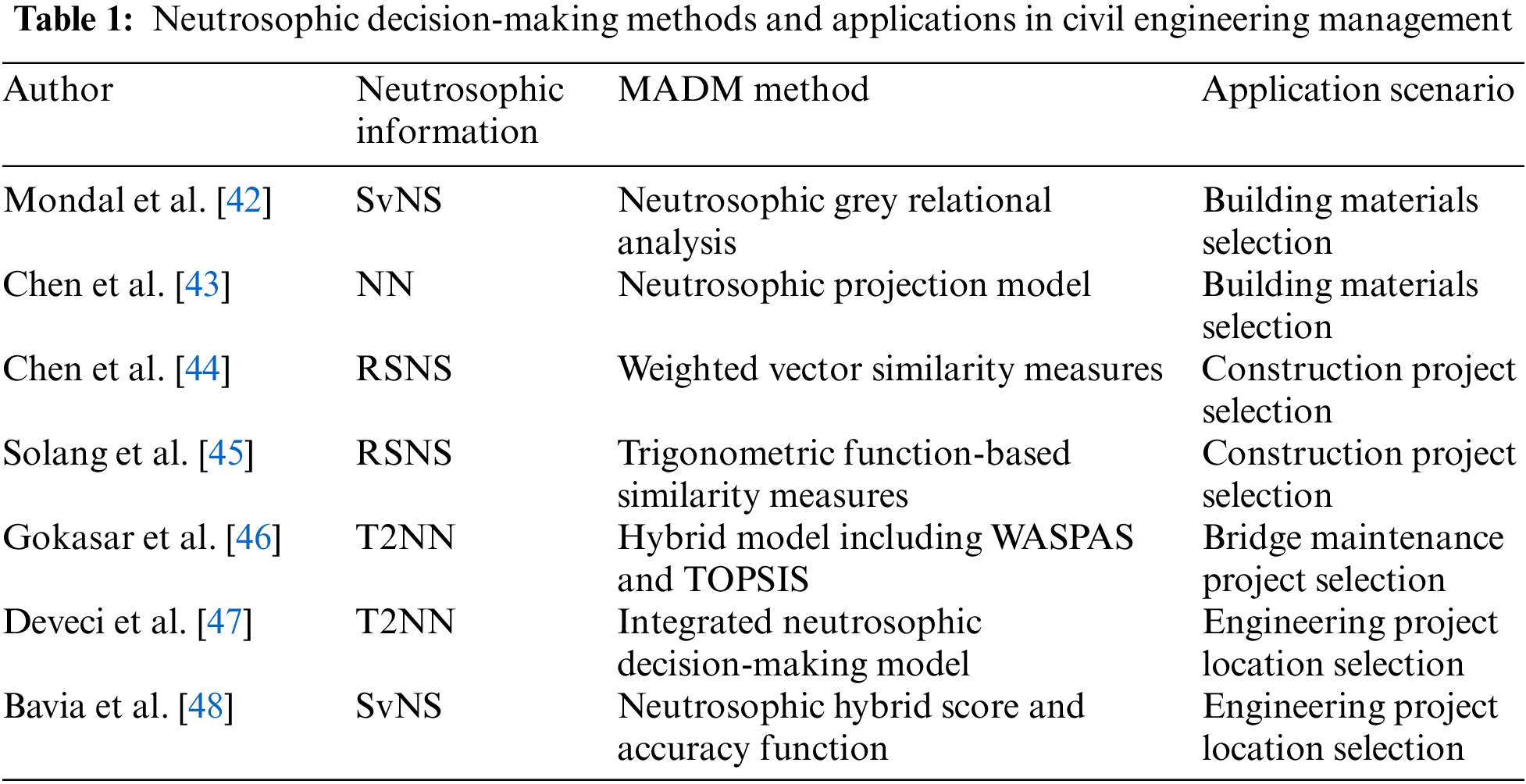
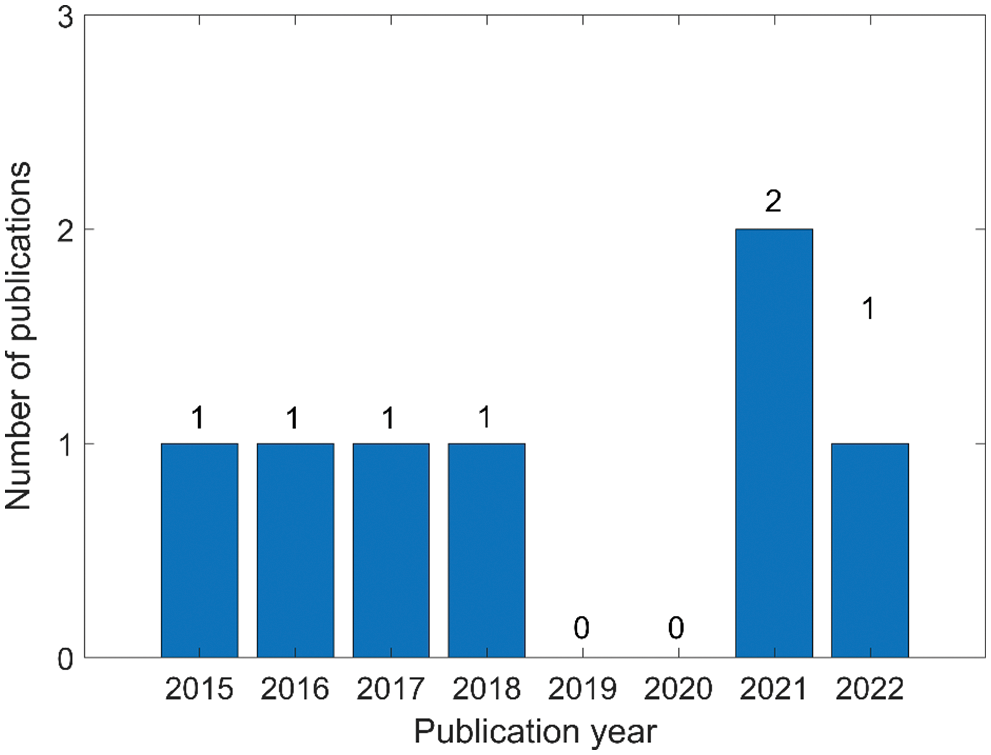
Figure 4: Number of papers published annually in the field of civil engineering management

3  Neutrosophic Evaluation Methods and Applications of Slope Stability

Slope stability is an important research area of civil engineering, involving many engineering constructions such as rail transit, coal mining, and water conservancy projects. According to the composition of the slope, it can be divided into the soil slope and the rock slope. The slope is affected by various factors. Under the action of shear stress, unstable structural planes are produced. The final failure caused by slippage is the instability failure of the slope. Since most of the rock masses and soil masses in slope stability problems are natural rather than artificial, slope stability problems usually include greater randomness and indeterminacy. Hence, the neutrosophic theory is very suitable for slope stability analysis and assessment.

The damage to slopes usually causes serious consequences, such as road burial and construction damage to result in huge damage to the social economy and human safety. In order to avoid slope instability, the evaluation of slope stability is particularly important and necessary. Therefore, the study of slope stability analysis methods has already become an important topic in geotechnical engineering research. When analyzing and evaluating the stability of a slope, it is usually necessary to consider many influencing factors, such as mechanical properties, geological conditions, construction environment, slope geometric parameters, and human factors. Since there are too many factors to be considered during the analysis and evaluation process, it is impossible to accurately measure and judge many influencing factors in actual engineering problems. Therefore, the problem of slope stability is obviously indeterminate and complicated. The existing slope stability analysis methods can generally be divided into deterministic analysis methods and indeterminate analysis methods. The deterministic analysis methods mainly include the limit equilibrium analysis method [74–78] and the numerical analysis method [79–82]. The traditional deterministic analysis method only considers the deterministic information of the slope when calculating or modeling, and regards the stability of the slope as a problem of definite value. Because of its relatively simple calculation and certain usability, it has been widely used in slope stability analysis. To extend the original limit equilibrium method, Yong et al. [83] improved the limit equilibrium method based on the idealized model of rock slope with bedding planes. Then, this method extended a single failure surface to the stability analysis of rock slopes with multiple bedding planes.

In fact, the actual slope stability analysis contains a lot of random, discrete, and nonlinear information, so the information indeterminacy cannot be ignored. To make the analysis of slope stability more reasonable and effective, many indeterminate analysis methods, such as the fuzzy mathematical method [84,85], the grey correlation analysis method [86], and the artificial neural network method [87], have been proposed and applied in the analysis of slope stability. However, the existing indeterminate analysis methods still imply the shortcomings of difficult modeling and complex calculations, which limit the promotion and application of such methods. To solve these issues, some scholars have proposed slope stability analysis methods based on engineering neutrosophic theory.

In 2019, Zhou et al. [49] proposed three similarity measures (the Dice, cosine, and exponential measures) of NNs for slope stability analysis with indeterminate information. Then, the proposed analysis methods based on the Dice, cosine and exponential measures were also used in the stability analysis of actual slope cases in a certain area of Zhejiang, China to verify the effectiveness of the proposed methods. Finally, the standard deviation analysis of the three similarity measures in the proposed methods was used to reflect their different applicable performances.

Since NNs are used to effectively describe the indeterminacy factor in the assessment of slope stability, Li et al. [50] proposed vector similarity measures in the NN environment as an indeterminate analysis method for the rock slope stability assessment. The evaluation method of slope stability based on the vector similarity measures solved the defect of some existing numerical analysis methods that require a large amount of data, and then the evaluation method can be more suitable for the stability analysis of some rock slopes with limited geological data. In the meantime, the proposed method was applied to the slope stability evaluation of rock slopes in Zhejiang Province, China, and the evaluation results were compared with the actual measured results to verify the effectiveness of the proposed method. However, this method indicated its main advantage in analyzing the stability of rock slopes in indeterminate situations.

The stability and reliability of the slope have a very significant impact on the safety and economics of open-pit mines. Therefore, ensuring the slope stability of the open-pit mine is a very critical research topic. Compared with other slopes, the open-pit mine slope has stronger indeterminacy and complexity. In addition to objective factors, various factors affecting slope stability will change as mining activity progress, and subjective perceptions and requirements of slope stability will also change over time. Therefore, some scholars regarded it as a kind of “dynamics” [88] of the open pit slope. For this characteristic, we often need to make dynamic evaluations of slopes. Therefore, Li et al. [51] proposed the arctangent and tangent similarity measures of NNs, and then developed a new slope stability analysis method based on the arctangent and tangent similarity measures. Through 10 actual slope samples, the developed method proved the simplicity and effectiveness of the open-pit slope stability analysis under an indeterminate environment. Compared with NNs (changeable interval numbers), the advantage of SNS (IvNS and SvNS) is that SNS can express the degrees of truth, falsity, and indeterminacy, but NN cannot express the indeterminacy of the truth, falsity, and indeterminacy degrees. Based on the information expression advantages of NN and SNS, Du et al. [52] proposed a simplified neutrosophic indeterminate set (SNIS) to express changeable IvNS/SvNS corresponding to different indeterminate ranges/values of I ∈ [inf I, sup I] and developed two weighted aggregation operators of simplified neutrosophic indeterminate elements (SNIEs) and their MADM method with decision makers’ indeterminate ranges/risks in indeterminate decision-making situations. Through a decision-making example on the choice problem of open pit slope design schemes in an indeterminate environment, the decision results demonstrated the flexibility and applicability of the proposed MADM method. Through the statistics of a large number of slope cases, the machine learning method can effectively obtain the relationship between the influencing factors and the slope stability. Then, the single-valued neutrosophic number (SvNN) can effectively express the truth, indeterminate, and falsity information of the influencing factors of slope stability. In terms of the truth, falsity, and indeterminacy ANFISs (adaptive neuro fuzzy inference systems) and the score function of SvNN, Qin et al. [53] proposed a SvNN adaptive neuro fuzzy inference system (SvNN-ANFIS) method for the stability analysis of open-pit mine slopes. This method used the truth, indeterminacy, and falsity membership functions of SvNN to express the influencing factors of the slope stability and obtained the relationship between the influencing factors and the slope stability through the SvNN-ANFIS and the score function to analyze and evaluate the slope stability of open-pit mines. Then, they used the actual cases of 167 open-pit mine slopes in Zhejiang Province, China, to verify the effectiveness of the proposed method. In the meantime, the proposed method was compared with other machine learning methods to demonstrate its advantage and applicability.

In view of the aforementioned neutrosophic evaluation methods and applications of slope stability, Table 2 shows the existing neutrosophic evaluation methods and applications of slope stability. As can be seen from Fig. 5, the number of papers on the neutrosophic evaluation methods and applications of slope stability reflects more research results in 2019.

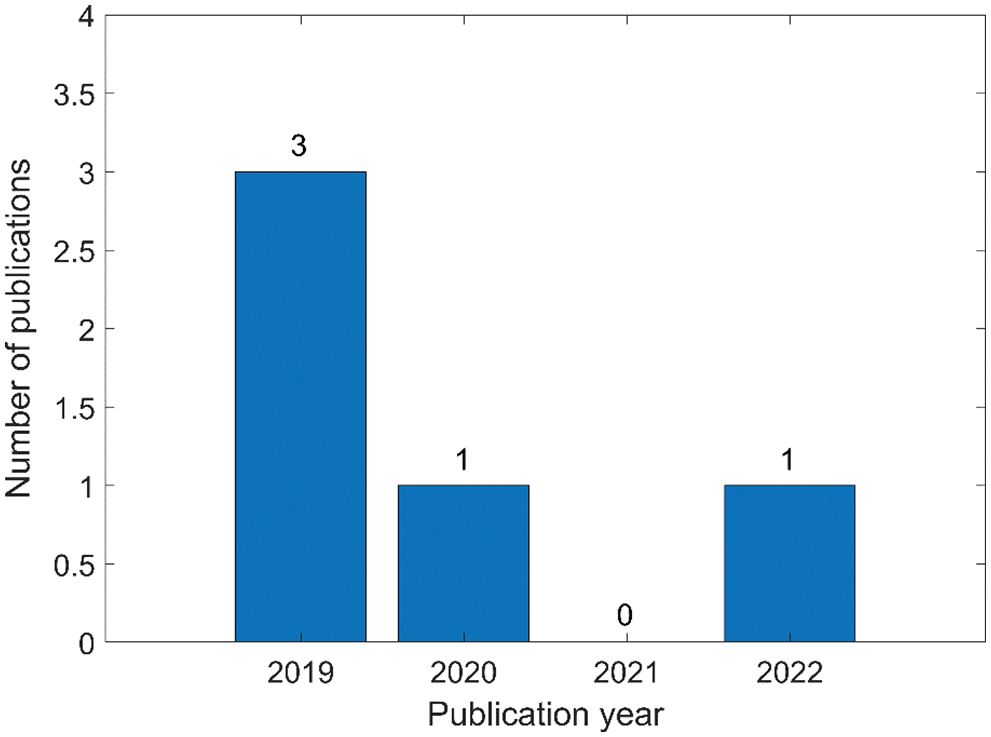
Figure 5: Number of papers published annually on neutrosophic evaluation methods and applications of slope stability

In addition, the related research of engineering neutrosophic theory has also promoted the development of other uncertainty analysis methods. For example, Wang et al. [89] proposed a tangent similarity measure between fuzzy cube sets (FCS) based on the tangent similarity measure of SvNSs proposed by Ye et al. [90] and used it for the slope stability evaluation. This research will promote the extensive applications of FCSs in the slope stability analysis and assessment.

4  Neutrosophic Expression and Analysis of Rock Joint Roughness Coefficient

In rock mechanics, joints usually refer to cracks with no obvious relative displacement on both sides of the crack surface caused by rock cracks. It is obvious that rock joints are often one of the important factors affecting the safety and reliability of slopes. Since rock joints only touch the joint surfaces, their mechanical properties are quite different from those of complete rocks. For this reason, many scholars have conducted comprehensive research on many characteristics of rock joints. In actual engineering, the shear strength of rock joints is very important to evaluate the stability of engineering rock mass. Eq. (1) for estimating the shear strength of rock joints proposed by Barton [91] has been widely recognized in recent decades.

τ=σntan⁡[JRClog10⁡(JCSσn)+ϕb](1)

As shown in Eq. (1), the joint roughness coefficient (JRC) is directly related to its shear strength τ, so JRC is a key parameter in the shear strength of rock joints. In an early study, Barton [91] proposed a method of inverse calculation of JRC through experiments, and then he gave 10 standard JRC profile lines through a large amount of experimental data so that people could get the estimated value of JRC for any joint by comparing with them. In recent research, some scholars have also proposed many methods to determine the JRC values, such as the visual contrast method, the statistical parameter connection method, the fractal dimension connection method, the Barton straight edge method, etc. [92–95].

In the natural environment, the JRC data of the rock joint surface that we can obtain are usually incomplete and uncertain. Therefore, it is very important to study the mechanical properties of the rock joint surface. Barton first discovered and proposed the scale effect of the JRC values in 1977 [96]. After that, through different research methods [97–99], many scholars have shown that the JRC value of the rock joint plane decreases with the increase of the sample size. Numerous studies have shown that anisotropy is also an important property of the JRC values [100–103]. The anisotropy of the JRC values indicates that there are obvious differences in the JRC values in different measurement directions on the same rock joint surface. In addition, the sampling bias will also increase the uncertainty of the JRC values [104,105].

In order to study the scale effect and anisotropy of the JRC values, Tse et al. [92] obtained the linear regression relationship between the JRC values and the root mean square (Z2) for the first time. On this basis, Zhang et al. [106] also obtained an improved root mean square considering the inclination angle, the amplitude of the asperities, and their directions at the same time to calculate the JRC values, and then they proposed a new roughness index (λ). In addition, Chen et al. [107,108] proposed a variogram and a new index to quantify the anisotropy of the JRC values of the joint surfaces by means of digital image processing technology. However, none of these methods can fully consider and express the indeterminacy of JRC values in actual rock engineering. For this reason, many scholars have introduced various research results from engineering neutrosophic theory to solve the indeterminate problem in the study of rock joint roughness and its shear strength.

First, Ye et al. [54] established two neutrosophic functions (interval/thick functions) based on engineering neutrosophic theory to describe the scale effect of the JRC values and the shear strength of the rock joints. The validity and rationality of the proposed neutrosophic functions are verified by using the measured data of four peak samples of volcanic clastic rocks located in Shaoxing City, China. The research results showed that the JRC interval values and the shear strength interval corresponding to joint samples of different sizes could be expressed through the proposed neutrosophic functions, which proved that the established neutrosophic functions could provide a theoretical analysis method for predicting and estimating the JRC values and shear strength of rock joints in a specific area.

Due to the complexity and uncertainty of the JRC value in the actual situation, it is usually impossible to give an accurate JRC value in an uncertain situation. Then, NN is composed of a certain part and an indeterminate part. Therefore, Yong et al. [55] proposed using NN to express JRC data more reasonably, and then proposed two NN functions. One is the JRC anisotropic ellipse parameter equation JRC(θ) obtained by statistical evaluation of JRC values in different directions of the joint section. Another is JRC(L), which is used to quantify the JRC values of joint samples with different sizes and to express the scale effect of the JRC values. On this basis, Ye et al. [56] studied the derivatives of the proposed functions JRC’(θ) and JRC’(L) to describe the change rate of the JRC values in different measurement directions and sample sizes. Then a two-variable neutrosophic function JRC(θ, L) was further proposed to represent the JRC values in an indeterminate environment by considering both the measurement direction and the sample size. The aforementioned NN functions are validated by the sample datasets of large-scale natural rock joint planes located in Changshan County, Zhejiang Province, China. The NN function provided a new and effective way to express and analyze the indeterminate characteristics of JRC values. After that, Yong et al. [57] proposed a new sampling method to more reasonably count the JRC data of large rock joint profiles and used the JRC(L) function to analyze the collected JRC data and the scale effect of the JRC values. Additionally, Wang et al. [58] combined spectral analysis with NN function and proposed a JRC value calculation method based on the neutrosophic function and spectral analysis. Then, they used this method to calculate the JRC values of five sandstone joint samples and verified the validity of this method by comparison with the experimental results.

It is worth mentioning that the NN functions studied above are all fitting functions obtained by fitting the measured value curves. Although they have some fitting accuracy, they still lose 3% to 16% of useful information in the actual fitting process. In addition, the complexity of some fitting functions will also cause inconvenience in practical applications. To make up for the above defects, some scholars have introduced neutrosophic statistics into the uncertainty research of the JRC values. In classic statistical studies on JRC data [109–113], all JRC data are considered to be certain. However, in practical applications, there are often unavoidable errors and interferences in observation, measurement, and calculation. Therefore, actual statistical data are often inaccurate, uncertain, and incomplete. Unlike classical statistics, the neutrosophic statistics proposed by Smarandache [1,40,41] can reflect inaccurate, incomplete, and indeterminate data. Therefore, neutrosophic statistics have been applied in many areas [114–118]. Then, NNs and neutrosophic statistics are also very suitable for the expression of JRC values in an indeterminate environment. Thus, Chen et al. [59] combined NNs with neutrosophic statistics and proposed the neutrosophic statistical analysis of JRC-NNs to analyze the relevant characteristics of the JRC values. They used JRC-NNs to express and calculate the JRC data obtained from actual samples. They also obtained the neutrosophic average values and standard deviations by the neutrosophic statistics to effectively reflect the scale effect and anisotropy of the JRC values. Compared with previous studies, this method not only avoids the loss of useful information, but also makes the information expression simpler and more effective. Further, Aslam et al. also proposed a new approach to determining JRC values called neutrosophic coefficient of variation (NCV) based on neutrosophic exponentially weighted moving average (NEWMA) NNs [60] and introduced the t-test and F-test under neutrosophic statistics [61] to analyze the anisotropy of the JRC values.

In neutrosophic probability and statistics, Smarandache [1,40,41] also proposed the concept of neutrosophic probability. For convenient engineering applications, Chen et al. [62] proposed the neutrosophic interval probability (NIP) based on the truth, falsity, and indeterminacy interval probabilities and defined the confidence degree based on the cosine similarity measure between NIP and an ideal NIP. In view of the defined confidence degree of NIP, the neutrosophic interval statistic number (NISN) was proposed as a new way to express the JRC values. Since NISN is composed of a certain part, an indeterminate part, and a confidence degree of NIP, it is very suitable for the expression of JRC data in actual engineering applications. Then, they also used actual JRC data to verify the effectiveness of this method. To further analyze and express the scale effect and anisotropy of the JRC values, Jiang et al. [63] proposed the neutrosophic average values and neutrosophic standard deviations of NISNs based on the neutrosophic statistics. Finally, the study of actual cases verified that the neutrosophic average values and neutrosophic standard deviations obtained by calculating the JRC values of NISNs can effectively and reasonably express the scale effect and anisotropy of the JRC values. Furthermore, by comparative analysis, it was found that this method can avoid the loss of useful information, so it is more effective and more reasonable in the expression and analysis of the scale effect and anisotropy of the JRC values corresponding to NISNs than the previously proposed JRC-NN method. After that, Song et al. [64] proposed a generalized Dice similarity measure of NISNs to analyze the anisotropy of JRC values and then verified the effectiveness of the presented measure method through the statistical analysis of a group of calcareous slate rock joint samples. In the future work, they will also apply NIP to the expression and analysis of the shear strength of the rock masses.

In general, the expression and analysis studies of JRC data are shown in Table 3. Then, Fig. 6 shows the number of papers published annually on the neutrosophic expression and analysis studies of JRC data.

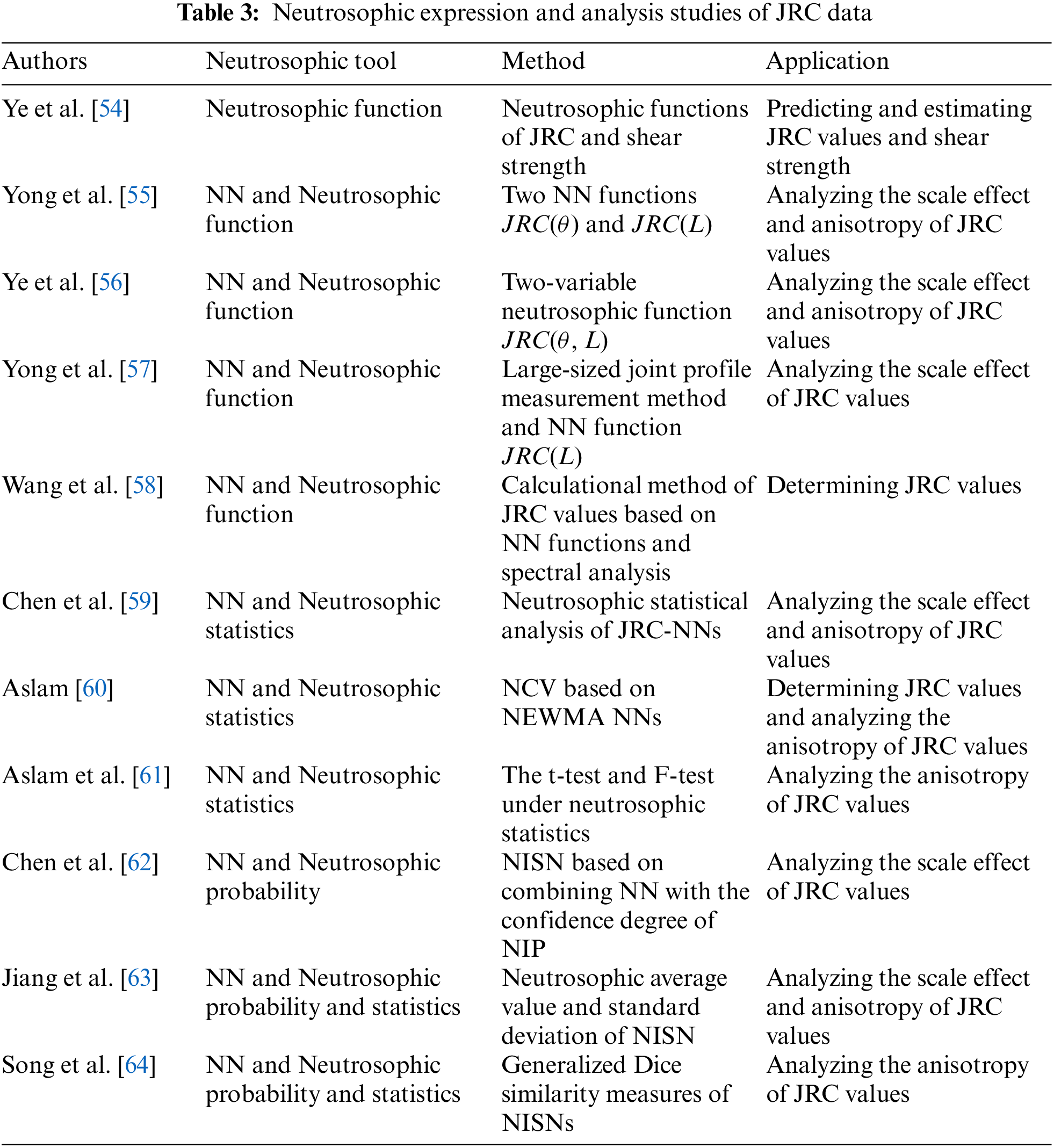
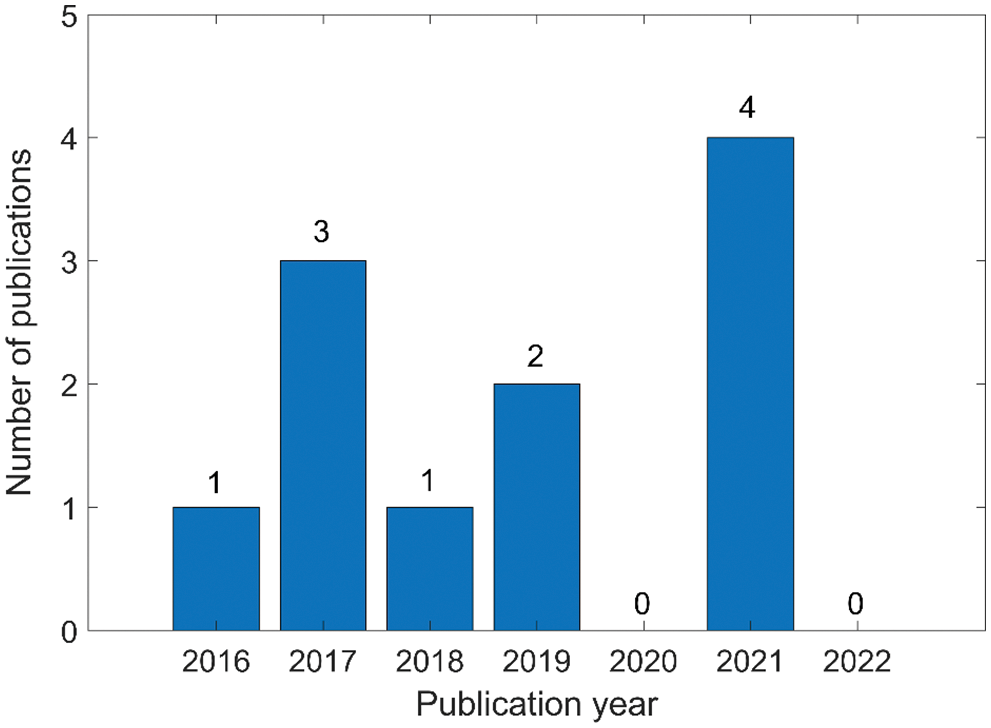
Figure 6: Number of papers published annually on the neutrosophic expression and analysis studies of JRC data

5  Neutrosophic Optimization Methods in Structural Engineering

Practical problems in the civil engineering field usually include the information of inevitable uncertainty, incompleteness, and inconsistency. Then, the structural optimization design in structural engineering usually plays a very important role in improving the economy, safety, and applicability of the structure. To improve the structural optimization design, many structural optimization theories have been proposed, such as structural topology optimization [119], structural ray optimization [120], robust optimization [121,122]. However, to improve the accuracy requirements of complex structural optimization problems, some structural optimization methods use more complex models, making the calculation process more complicated. To solve these problems, many algorithms of structural optimization have been proposed, such as the harmony search algorithm [123] and the artificial bee colony algorithm [124]. However, there are usually unavoidable indeterminate situations in structural optimization problems. For example, uncertainty in material properties primarily refers to a range of uncertain values, such as Young’s modulus, stiffness, and yield stress, rather than a single exact value. Because the existing structural optimization theories and methods usually cannot fully express and describe the uncertain data or information in the actual structural optimization problems, most of these theories and methods have the defects of relatively conservative design and insufficient sensitivity to uncertainty. In addition, the existing indeterminate structure optimization methods usually transform indeterminate objective programming models involving indeterminate variables into crisp objective programming models to find optimal crisp solutions [125–128]. However, from the perspective of the indeterminate problem, the final solution of the uncertain optimization problem should contain the possible ranges of the optimal solution corresponding to different indeterminate ranges to satisfy different design requirements [65,66].

To solve these indeterminate problems in structural optimization design, some scholars have applied engineering neutrosophic theory to structural optimization design. Jiang et al. [65] first proposed that NNs were used to express indeterminate information in structural optimization design, then introduced the concept of NN functions into the structural optimization model, which generally contains objective functions, design variables, and constraints, so as to establish a general nonlinear NN optimization model. Then, they proposed a solution method for this nonlinear NN optimization model in the structural optimization design. Finally, through the optimization design example of the double-bar truss structure under the uncertain environment, the validity and rationality of the proposed optimization model and solution method are proved. In actual applications, some indeterminate range can be specified to meet the actual indeterminate requirements of the truss structure design by the deneutrosophication of the neutrosophic optimization solution. Thus, the optimal design values of the design variables are more suitable for the actual indeterminate requirements. Due to the complexity of indeterminate problems, this solution method is difficult to solve the complex NN optimization model.

To overcome the drawbacks of complex calculation and difficult solution in the existing NN optimization model [65], Ye [67] proposed an improved nonlinear NN optimization method. This method can use the Matlab built-in function “fmincon()” corresponding to the indeterminacy I ∈ [inf I, sup I] and the indeterminate scale λ ∈ [0, 1] to conveniently perform the solution process in the NN optimization models. Therefore, the proposed optimization method showed a certain degree of flexibility and convenience in the solution process. In some specific situations, designers can also specify a suitable indeterminate scale λ to meet specific design requirements. Then, the proposed solution method was applied to the optimization design example of a three-bar plane truss structure with indeterminate information, and then the effectiveness and flexibility of the proposed method were verified through the design example that achieved the minimum weight target under the constraints of stress and deflection.

It is obvious that the improved NN optimization method provides a new and effective way to optimize the truss structure under an indeterminate environment. However, researchers will continue to improve the existing NN optimization methods and extend them to more application fields in indeterminate environments.

Since SvNS contains the advantage of expressing degrees of truth, falsity, and indeterminacy, in addition to NN optimization methods, some scholars have also introduced SvNS into structural optimization design. Das et al. [68] first used SvNS to establish a SvNS optimization method for multi-objective nonlinear programming problems (MONLPP), and then applied it to an actual riser design problem to verify the feasibility of the developed method. After that, Sarkar et al. [69] further introduced the SvNS optimization method into the truss structure optimization design. In the optimal design of a truss structure, the weight of the truss and the deflection of the loaded joint are regarded as objective functions, then the cross section of the truss member and the stress in the member are considered as design variables and constraints, respectively. Sarkar et al. [69] first proposed a SvNS optimization method for single-objective nonlinear programming problems (SONLPP), then the feasibility of the proposed method was verified by a double-bar truss structure under a single load. For comparison, they also provided the optimization method based on intuitionistic fuzzy sets to optimize the design of this double-bar truss structure. Then, the comparative results of the two optimization methods revealed that the SvNS optimization method demonstrated better optimization results than the IFS optimization method. Sarkar et al. [70] further introduced a SvNS truss structure optimization method for MONLPP and verified the effectiveness of the proposed method through an optimization example of a three-bar truss structure. To further study the multi-objective nonlinear optimization design of truss structures, Sarkar et al. [71] also proposed a new neutrosophic optimization method based on generalized single-valued triangular neutrosophic numbers (GSvNNs). In this study, Sarkar et al. first proposed the concept of GSvNN and defined its corresponding total integral values and the ranking method. Then, the applied load and stress parameters were represented by GSvNNs, and the optimization model was solved by the neutrosophic probability operator. By comparing the optimization results of the proposed neutrosophic optimization method for the three-bar truss structure design with the optimization results of the fuzzy optimization method, the neutrosophic optimization method showed its effectiveness.

In addition, the SvNS optimization method has also been extended to the optimization design of welded beam structures. The optimal design of welded beam structures is often constrained by beam internal stresses, loads on rods, and beam deflections to optimize the durability and economy of welded beams. In this respect, Sarkar et al. used SvNS to express the constraints in the design of welded beams and proposed a single-objective nonlinear SvNS optimization method for welded beams [72] and a multi-objective nonlinear SvNS optimization method for welded beams [73]. Through the comparison of the proposed methods with other optimization methods for actual applications, the proposed optimization methods revealed their effectiveness and superiority.

Regarding the above neutrosophic optimization methods and applications in structural engineering, existing neutrosophic tools, methods, and applications are shown in Table 4. Then, Fig. 7 shows the number of papers published each year, which reflects that research in this area has not made new progress since 2018.

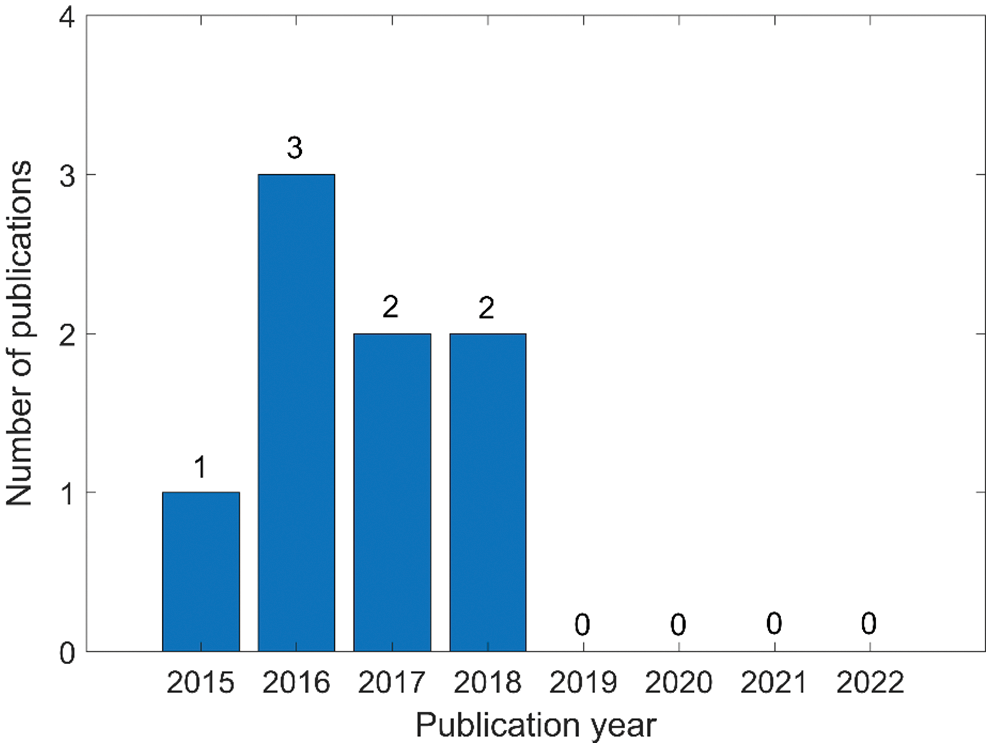
Figure 7: Number of papers published annually on neutrosophic optimization methods and applications in structural engineering

6  Literature Analysis

In the existing literature, 31 papers have been included in civil engineering, as shown in Fig. 8. Except for the small number of papers published in 2015 and 2020, the number of papers in recent years has remained at 4−6.

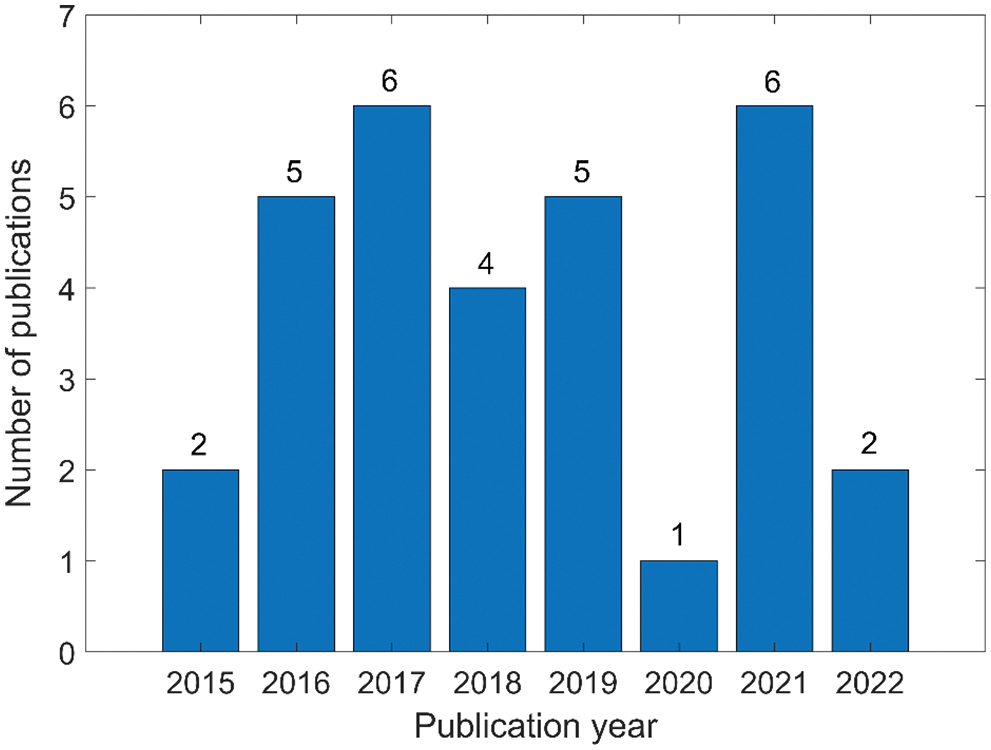
Figure 8: Annual number of papers on research results of engineering neutrosophic theory and methods in the four research areas of civil engineering

Based on research results in the field of civil engineering, we counted the number of publications and researchers in different countries for all 31 papers. As shown in Fig. 9, China and India rank first and second in the number of publications and researchers. It can be seen that Chinese and Indian researchers have made greater contributions to civil engineering. Then, most of the existing engineering neutrosophic theories and methods applied in civil engineering are mainly proposed by Chinese scholars. At the same time, we performed author co-citation analysis on them through VOS viewer, which is shown in Fig. 10. However, Jun Ye contributed the most among these research results. Furthermore, we also found that among the existing research results, there are fewer co-cited authors between countries and regions. Therefore, in the future, the exchanges and cooperation of scholars from various countries should be further strengthened, and the field of civil engineering should further promote/develop neutrosophic theory and applied research.

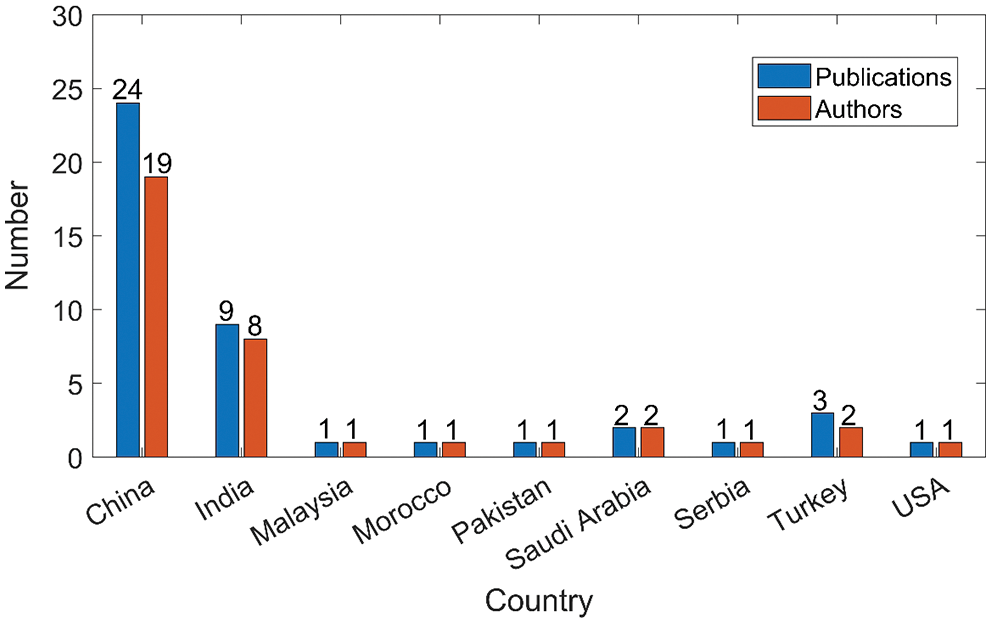
Figure 9: Number of published papers and researchers in different countries in 31 papers

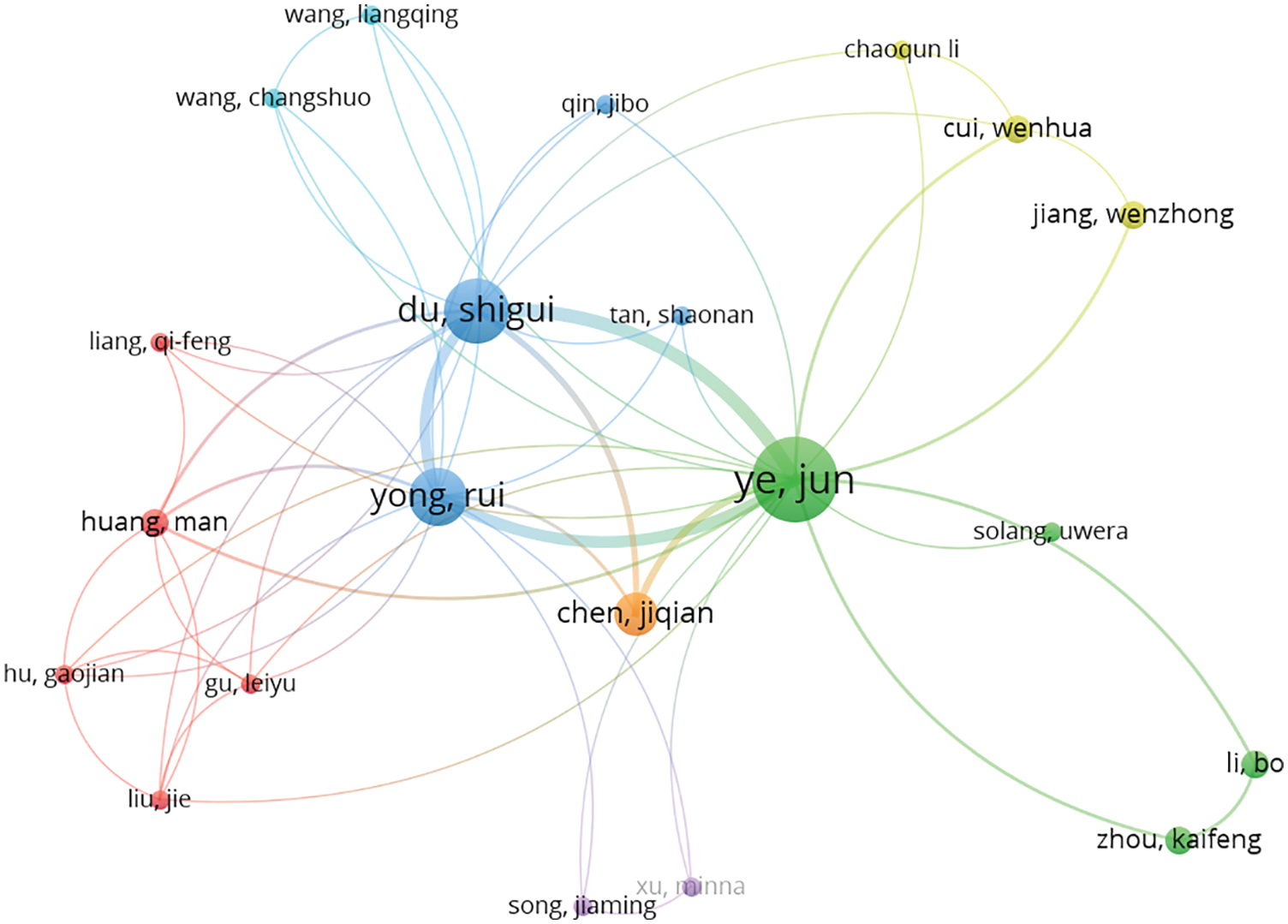
Figure 10: Author co-citation network of neutrosophic theory and applications in civil engineering

Finally, we use VOSviewer to analyze the keyword distribution of 31 papers, and give a corresponding keyword density visualization graph in Fig. 11 and a keyword co-occurrence network graph in Fig. 12. In the keyword density visualization graph, the nodes corresponding to each keyword are represented by different colors according to the item density of the word. Generally, when there are more items around the keyword, the color of the node is closer to yellow, and the fewer items around the keyword, the color of the node is closer to blue. For example, in Fig. 11, the node colors of keywords such as “Neutrosophic number”, “Neutrosophic set”, and “Joint roughness coefficient” are very close to yellow, so we can intuitively find that these keywords are the most important research objects in all 31 papers. The keyword co-occurrence network consists of nodes and connecting lines. The size of the node reflects the weight of the keyword, so the larger the node, the more times the keyword appears. The length of the connecting line reflects the closeness of the relationship between the two keywords. The shorter the connecting line, the stronger the relationship between the two keywords. The thickness of the connecting line reflects the co-occurrence of keywords. The thicker the connecting line, the higher the co-occurrence of the two keywords. Furthermore, closely related keywords are classified into a cluster and represented by the same color. In Fig. 12, we can find that the most frequently occurring keyword in all 31 papers is “Neutrosophic number” with 15 occurrences. Other keywords with high frequency are “Neutrosophic set” with 11 occurrences, “Joint roughness coefficient” with 11 occurrences, “Multi-attribute decision-making” with 8 occurrences, and “Neutrosophic optimization method” with 8 occurrences. Therefore, these keywords reflect their importance in the four research areas of civil engineering. In Fig. 12, we can also find several pairs of keywords with relatively close distances and thicker connecting lines. For example, the two keywords “Neutrosophic number” and “Joint roughness coefficient” indicate that NNs are widely used in the study of JRC values. For another example, the two keywords “Neutrosophic set” and “Single-valued neutrosophic set” indicate that SVNS is an extension of the neutrosophic set and is widely used in civil engineering.

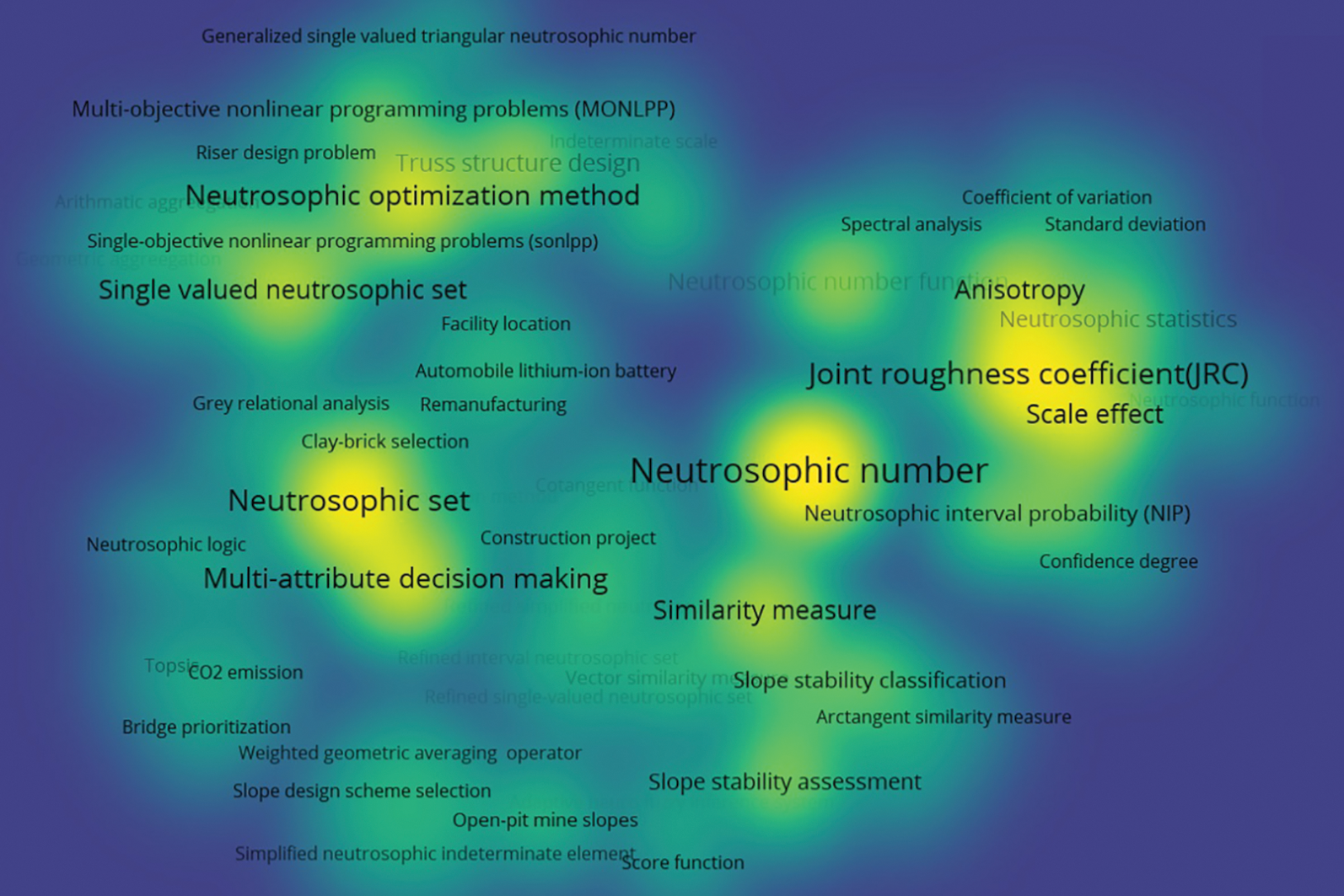
Figure 11: Keyword density visualization graph of published papers

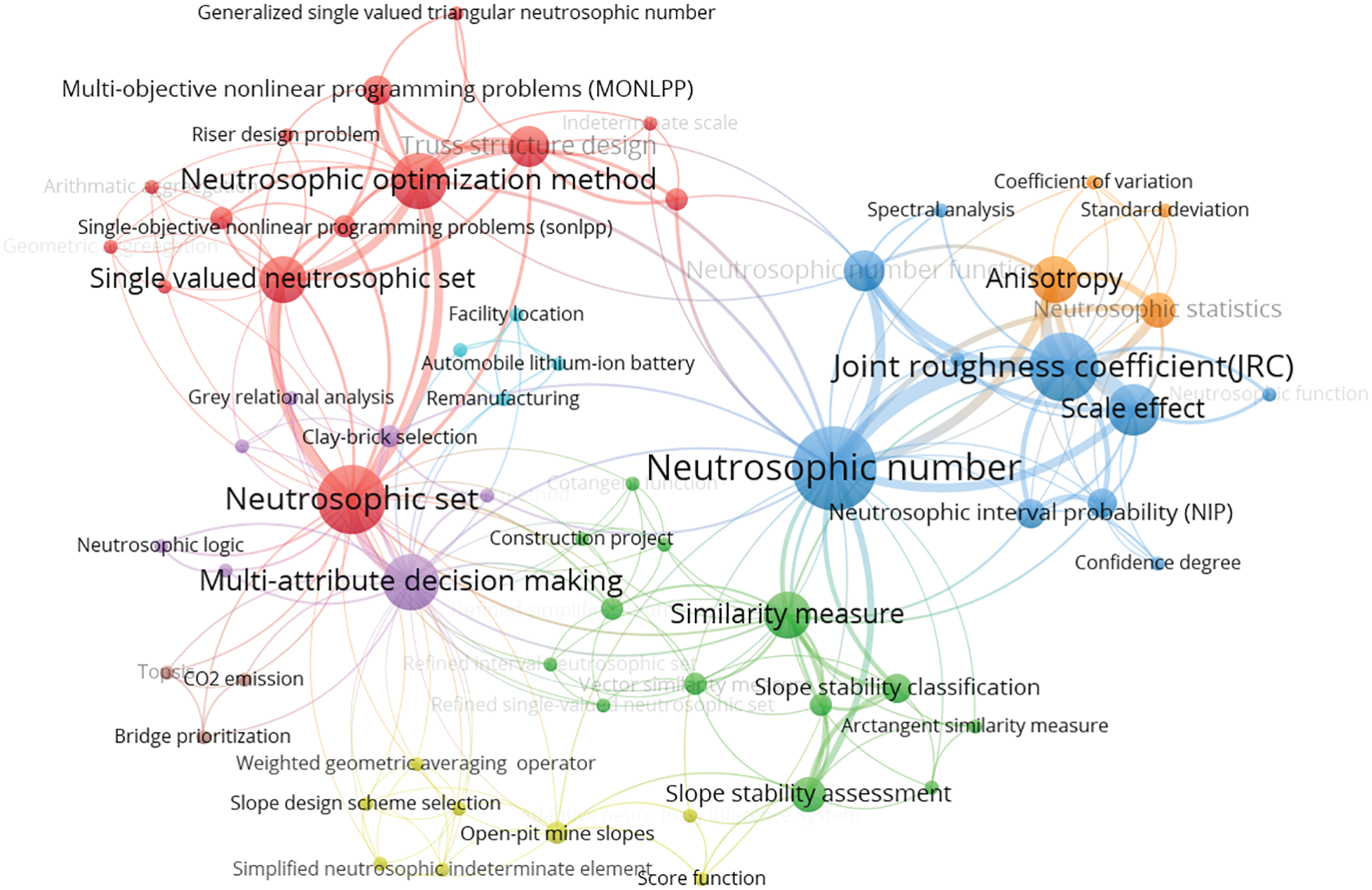
Figure 12: Keyword co-occurrence network of published papers

Through the above analysis, we can find that “Neutrosophic number” and “Neutrosophic set” are the two keywords with the highest frequency and the largest item density in all 31 papers. To clearly and intuitively reflect the relationship between the two keywords and other keywords in the four research areas of civil engineering, we can make a keyword density visualization graph of “Neutrosophic number” related to the published research results in Fig. 13, a keyword co-occurrence network of “Neutrosophic number” related to the published research results in Fig. 14, a keyword density visualization graph of “Neutrosophic set” related to the published research results in Fig. 15, and a keyword co-occurrence network graph of “Neutrosophic set” related to the published research results in Fig. 16. From Figs. 13 and 14, we can find that NNs have made great contributions to the above four fields of civil engineering. From Figs. 15 and 16, we can find that the neutrosophic sets have widely been used for MADM and structural optimization design in civil engineering.

Figure 13: Keyword density visualization graph of “Neutrosophic number” related to the research results published in the four research areas of civil engineering

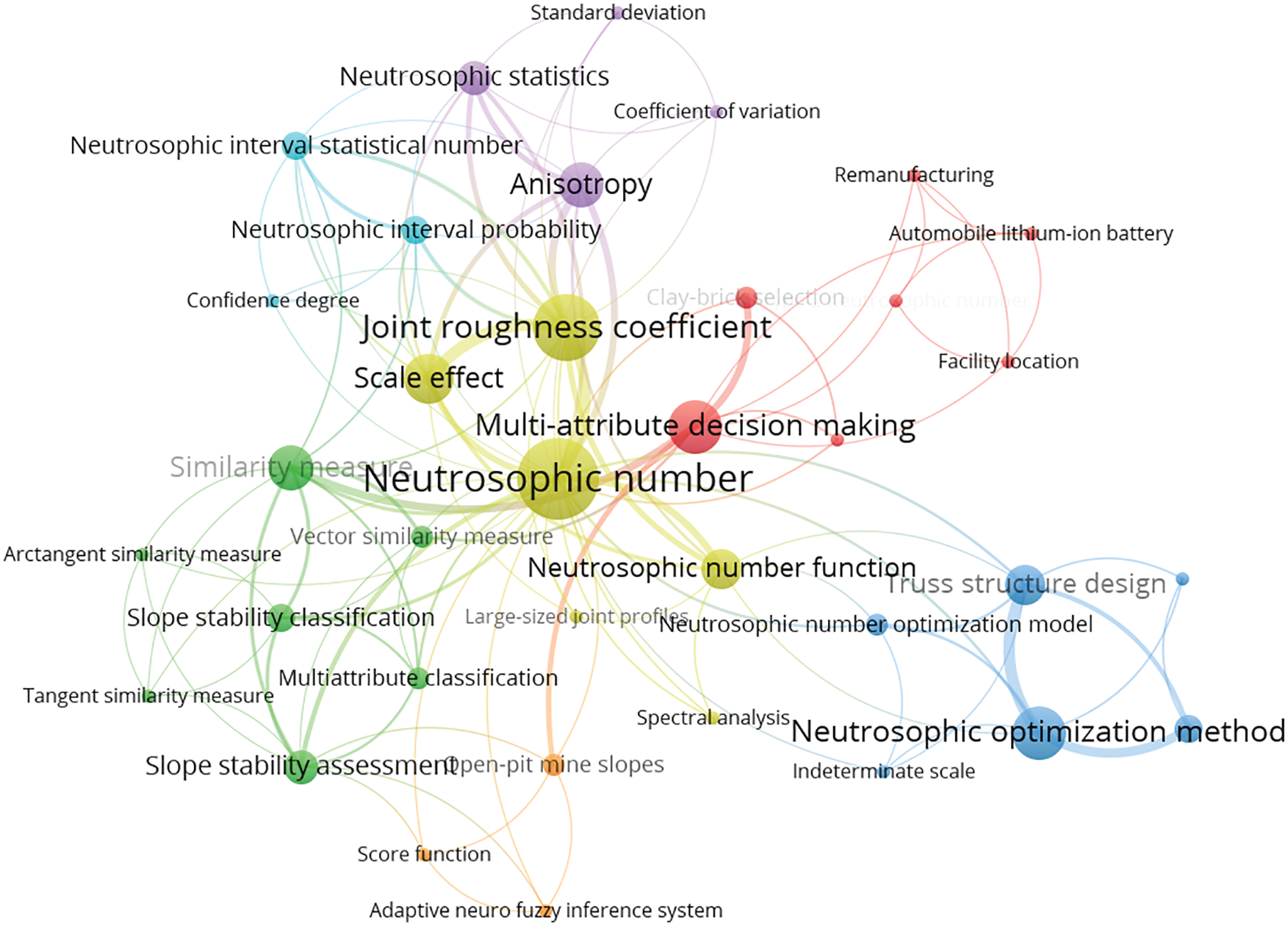
Figure 14: Keyword co-occurrence network of “Neutrosophic number” related to the research results published in the four research areas of civil engineering

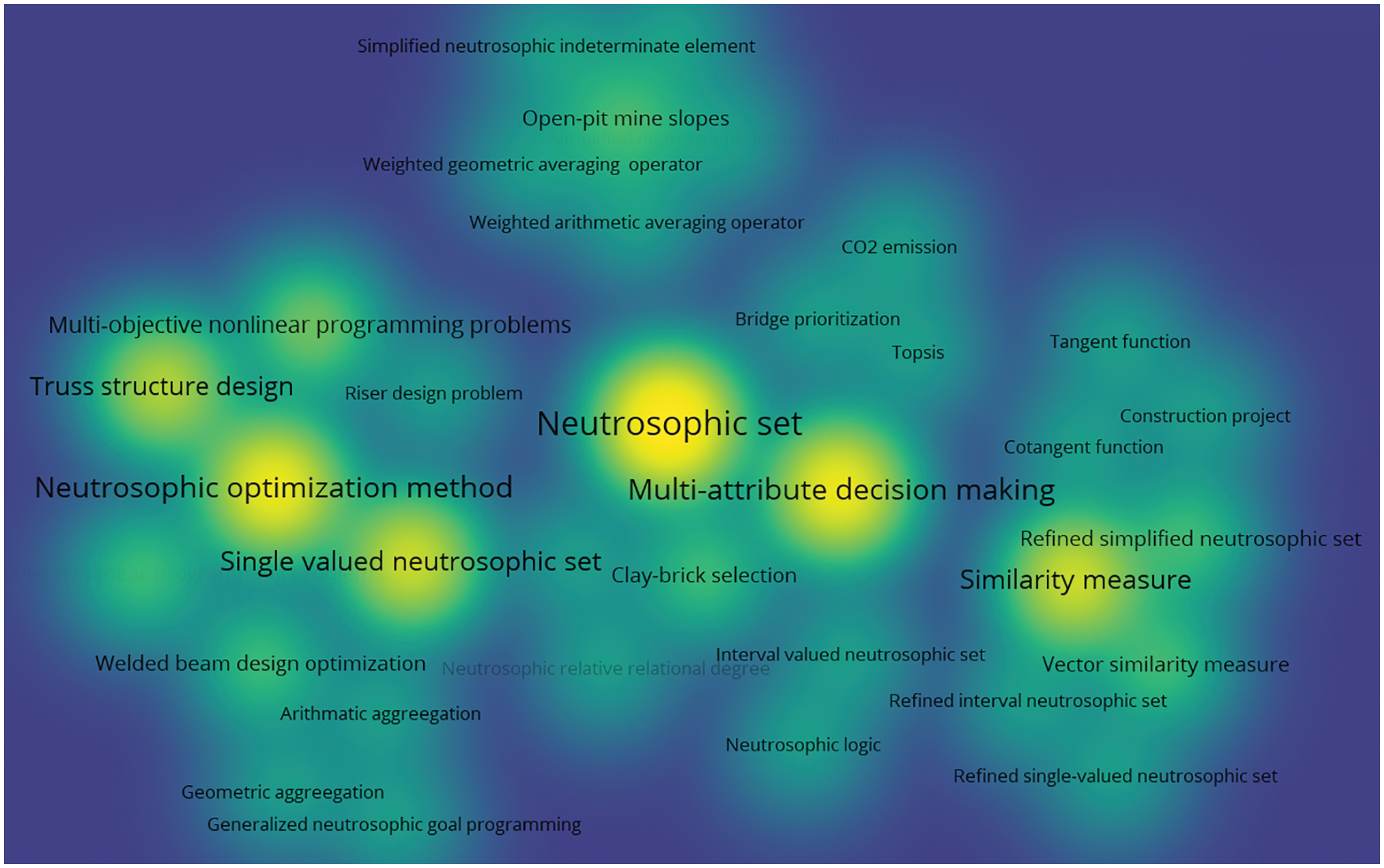
Figure 15: Keyword density visualization graph of “Neutrosophic set” related to the research results published in the four research areas of civil engineering

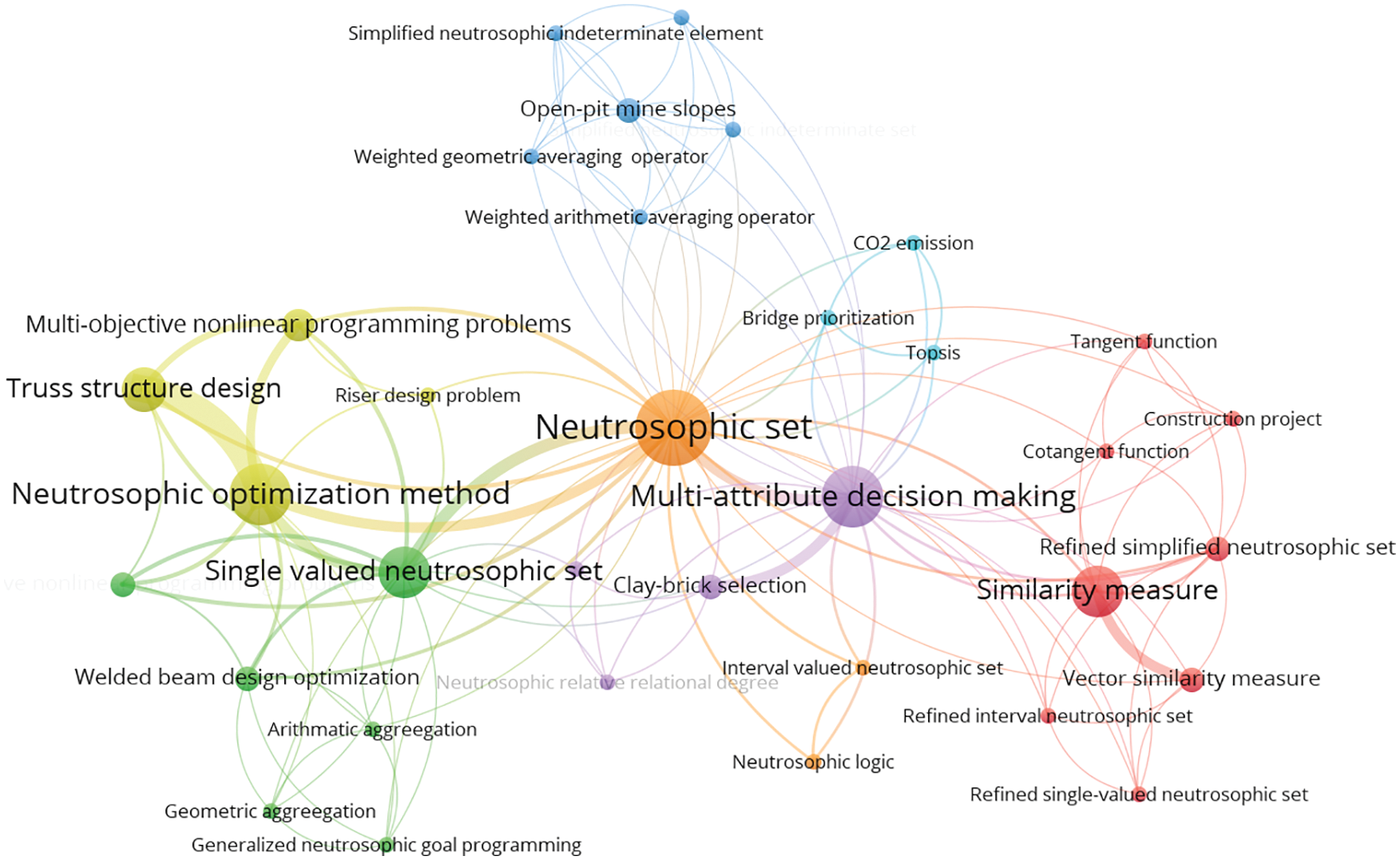
Figure 16: Keyword co-occurrence network graph of “Neutrosophic set” related to the research results published in the four research areas of civil engineering

7  Conclusion

This review paper mainly introduced the research results and applications of engineering neutrosophic theory and methods in four research areas of civil engineering: (1) the neutrosophic decision-making theory and applied methods, (2) the neutrosophic evaluation methods and applications of slope stability, (3) the neutrosophic expressions and analyses of rock joint roughness coefficient, and (4) the neutrosophic structural optimization methods and applications. They demonstrated the important achievements of engineering neutrosophic theory and methods in civil engineering in recent years.

Since most of the real problems involved in civil engineering usually imply indeterminate, incomplete, and inconsistent information, the neutrosophic theory has achieved significant research results in engineering problems. In addition to the civil engineering problems mentioned in this review paper, there are still many uncertain issues in civil engineering that have not been studied by engineering neutrosophic theory. Therefore, the engineering neutrosophic theory in civil engineering has a very broad range of applications, such as construction cost, construction organization and management, rock shear strength, precast concrete structure, etc.

Due to the significant advantages of the engineering neutrosophic theory in civil engineering, the research results based on the engineering neutrosophic theory in civil engineering have increased drastically in recent years. It is obvious that the neutrosophic theory can better solve various indeterminate problems in civil engineering. In future research directions, in addition to further improving the existing research results of civil engineering problems, it is also necessary to propose more advanced engineering neutrosophic theories and methods according to the applicable characteristics of civil engineering problems. With the development of other uncertain research methods in recent years, combining neutrosophic theory with other uncertain theories [129–144] can also become an important research direction to further promote the applications of engineering neutrosophic theory in civil engineering.

In general, the existing research results fully reflect the importance and necessity of neutrosophic theory in engineering, which not only effectively solves practical problems in the field of civil engineering, but also greatly promotes the development of neutrosophic theory itself.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Smarandache, F. (1998). Neutrosophy: Neutrosophic probability, set and logic. Rehoboth, USA: American Research Press. [Google Scholar]

 2.  Guo, Y., Cheng, H. D. (2009). New neutrosophic approach to image segmentation. Pattern Recognition, 42, 587–595. DOI 10.1016/j.patcog.2008.10.002. [Google Scholar] [CrossRef]

 3.  Faraji, M. R., Qi, X. J. (2013). An effective neutrosophic set-based preprocessing method for face recognition. IEEE International Conference on Multimedia and Expo Workshops (ICMEW), pp. 1–4. San Jose, CA, USA. DOI 10.1109/ICMEW.2013.6618251. [Google Scholar] [CrossRef]

 4.  Guo, Y., Zhou, C., Chan, H. P., Chughtai, A., Wei, J. et al. (2013). Automated iterative neutrosophic lung segmentation for image analysis in thoracic computed tomography. Medical Physics, 40(8), 81912. DOI 10.1118/1.4812679. [Google Scholar] [CrossRef]

 5.  Guo, Y., Sengur, A. (2013). A novel color image segmentation approach based on neutrosophic set and modified fuzzy c-means. Circuits, Systems, and Signal Processing, 32, 1699–1723. DOI 10.1007/s00034-012-9531-x. [Google Scholar] [CrossRef]

 6.  Chi, P., Liu, P. (2013). An extended TOPSIS method for the multiple attribute decision making problems based on interval neutrosophic set. Neutrosophic Sets and Systems, 1, 63–70. DOI 10.5281/zenodo.571231. [Google Scholar] [CrossRef]

 7.  Hanafy, I., Salama, A., Mahfouz, M. (2013). Correlation coefficients of neutrosophic sets by centroid method. International Journal of Probability and Statistics, 2(1), 9–12. DOI 10.5923/j.ijps.20130201.02. [Google Scholar] [CrossRef]

 8.  Hanbay, K., Talu, M. F. (2014). Segmentation of SAR images using improved artificial bee colony algorithm and neutrosophic set. Applied Soft Computing, 21, 433–443. DOI 10.1016/j.asoc.2014.04.008. [Google Scholar] [CrossRef]

 9.  Guo, Y., Sengur, A. (2014). A novel image segmentation algorithm based on neutrosophic similarity clustering. Applied Soft Computing, 25, 391–398. DOI 10.1016/j.asoc.2014.08.066. [Google Scholar] [CrossRef]

10. Guo, Y., Sengur, A. (2015). NCM: Neutrosophic c-means clustering algorithm. Pattern Recognition, 48, 2710–2724. DOI 10.1016/j.patcog.2015.02.018. [Google Scholar] [CrossRef]

11. Dey, P. P., Pramanik, S., Giri, B. C. (2015). An extended grey relational analysis based interval neutrosophic multi attribute decision making for weaver selection. Journal of New Theory, 9, 82–93. [Google Scholar]

12. Li, Y., Liu, P., Chen, Y. (2016). Some single valued neutrosophic number heronian mean operators and their application in multiple attribute group decision making. Informatica, 27(1), 85–110. DOI 10.15388/Informatica.2016.78. [Google Scholar] [CrossRef]

13. Elnazer, S., Morsy, M., Eldin, M., Abo-Elsoud, A. (2016). Brain tumor segmentation using hybrid of both neutrosophic modified nonlocal fuzzy c-mean and modified level sets. International Journal of Science and Research, 5(3), 1908–1914. DOI 10.5281/zenodo.232962. [Google Scholar] [CrossRef]

14. Guo, Y., Sengur, A., Tian, J. W. (2016). A novel breast ultrasound image segmentation algorithm based on neutrosophic similarity score and level set. Computer Methods and Programs in Biomedicine, 123, 43–53. DOI 10.1016/j.cmpb.2015.09.007. [Google Scholar] [CrossRef]

15. Heshmati, A., Gholami, M., Rashno, A. (2016). Scheme for unsupervised colour–texture image segmentation using neutrosophic set and non-subsampled contourlet transform. IET Image Processing, 10, 464–473. DOI 10.1049/iet-ipr.2015.0738. [Google Scholar] [CrossRef]

16. Deli, I., Subas, Y. (2017). A ranking method of single valued neutrosophic numbers and its applications to multi-attribute decision making problems. International Journal of Machine Learning and Cybernetics, 8, 1309–1322. DOI 10.1007/s13042-016-0505-3. [Google Scholar] [CrossRef]

17. Han, L., Wei, C. (2017). Group decision making method based on single valued neutrosophic choquet integral operator. Operations Research Transactions, 21, 110–118. DOI 10.15960/j.cnki.issn.1007-6093.2017.02.012. [Google Scholar] [CrossRef]

18. Guo, Y., Xia, R., Sengur, A., Polat, K. (2017). A novel image segmentation approach based on neutrosophic c-means clustering and indeterminacy filtering. Neural Computing and Applications, 28, 3009–3019. DOI 10.1007/s00521-016-2441-2. [Google Scholar] [CrossRef]

19. Guo, Y., Du, G. Q., Xue, J. Y., Xia, R., Wang, Y. H. (2017). A novel myocardium segmentation approach based on neutrosophic active contour model. Computer Methods and Programs in Biomedicine, 142, 109–116. DOI 10.1016/j.cmpb.2017.02.020. [Google Scholar] [CrossRef]

20. Can, M. S., Ozguven, O. F. (2017). PID tuning with neutrosophic similarity measure. International Journal of Fuzzy Systems, 19, 489–503. DOI 10.1007/s40815-015-0136-y. [Google Scholar] [CrossRef]

21. Ali, M., Thanh, N. D., van-Minh, N. (2018). A neutrosophic recommender system for medical diagnosis based on algebraic neutrosophic measures. Applied Soft Computing, 71, 1054–1071. DOI 10.1016/j.asoc.2017.10.012. [Google Scholar] [CrossRef]

22. Pramanik, S., Dalapati, S., Alam, S., Smarandache, F., Roy, T. K. (2018). NS-cross entropy-based MAGDM under single-valued neutrosophic set environment. Information, 9(2), 37. DOI 10.3390/info9020037. [Google Scholar] [CrossRef]

23. Akram, M., Shumaiza, Smarandache, F. (2018). Decision-making with bipolar neutrosophic TOPSIS and bipolar neutrosophic ELECTRE-I. Axioms, 7(2), 33. DOI 10.3390/axioms7020033. [Google Scholar] [CrossRef]

24. Akram, M., Naz, S., Smarandache, F. (2019). Generalization of maximizing deviation and TOPSIS method for MADM in simplified neutrosophic hesitant fuzzy environment. Symmetry, 11(8), 1058. DOI 10.3390/sym11081058. [Google Scholar] [CrossRef]

25. Zhou, L. P., Dong, J. Y., Wan, S. P. (2019). Two new approaches for multi-attribute group decision-making with interval-valued neutrosophic frank aggregation operators and incomplete weights. IEEE Access, 7, 102727–102750. DOI 10.1109/ACCESS.2019.2927133. [Google Scholar] [CrossRef]

26. Abdel-Baset, M., Chang, V., Gamal, A. (2019). Evaluation of the green supply chain management practices: A novel neutrosophic approach. Computers in Industry, 108, 210–220. DOI 10.1016/j.compind.2019.02.013. [Google Scholar] [CrossRef]

27. Guan, H., Dai, Z., Guan, S., Zhao, A. (2019). A neutrosophic forecasting model for time series based on first-order state and information entropy of high-order fluctuation. Entropy, 21, 455. DOI 10.3390/e21050455. [Google Scholar] [CrossRef]

28. Peng, X., Dai, J. (2020). A bibliometric analysis of neutrosophic set: Two decades review from 1998 to 2017. Artificial Intelligence Review, 53, 199–255. DOI 10.1007/s10462-018-9652-0. [Google Scholar] [CrossRef]

29. Tan, R. P., Zhang, W. D. (2021). Decision-making method based on new entropy and refined single-valued neutrosophic sets and its application in typhoon disaster assessment. Applied Intelligence, 51, 283–307. DOI 10.1007/s10489-020-01706-3. [Google Scholar] [CrossRef]

30. Garg, H. (2022). SVNMPR: A new single-valued neutrosophic multiplicative preference relation and their application to decision-making process. International Journal of Intelligent Systems, 37(3), 2089–2130. DOI 10.1002/int.22767. [Google Scholar] [CrossRef]

31. Zadeh, L. A. (1965). Fuzzy sets. Information & Control, 8(3), 338–353. DOI 10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]

32. Krassimir, T. A., Parvathi, R. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87–96. DOI 10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]

33. Atanassov, K., Gargov, G. (1989). Interval valued intuitionistic fuzzy sets. Fuzzy Sets and Systems, 31(3), 343–349. DOI 10.1007/978-3-7908-1870-3_2. [Google Scholar] [CrossRef]

34. Szmidt, E., Kacprzyk, J. (2002). Using intuitionistic fuzzy sets in group decision making. Control and Cybernetics, 31(4), 1055–1057. [Google Scholar]

35. Lin, L., Yuan, X. H., Xia, Z. Q. (2007). Multicriteria fuzzy decision-making methods based on intuitionistic fuzzy sets. Journal of Computer and System Sciences, 73(1), 84–88. DOI 10.1016/j.jcss.2006.03.004. [Google Scholar] [CrossRef]

36. Chen, S. M., Yang, M. W., Yang, S. W., Sheu, T. W., Liau, C. J. (2012). Multicriteria fuzzy decision making based on interval-valued intuitionistic fuzzy sets. Expert Systems with Applications, 39(15), 12085–12091. DOI 10.1016/j.eswa.2012.04.021. [Google Scholar] [CrossRef]

37. Ye, J. (2014). A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets. Journal of Intelligent & Fuzzy Systems, 26(5), 2459–2466. DOI 10.3233/IFS-130916. [Google Scholar] [CrossRef]

38. Wang, H., Smarandache, F., Zhang, Y., Sunderraman, R. (2010). Single valued neutrosophic sets. Multispace and Multistructure, 4, 410–413. [Google Scholar]

39. Wang, H., Smarandache, F., Zhang, Y. Q., Sunderraman, R. (2005). Interval neutrosophic sets and logic: Theory and applications in computing. Phoenix, AZ: Hexis. DOI 10.5281/zenodo.8818. [Google Scholar] [CrossRef]

40. Smarandache, F. (2014). Introduction to neutrosophic statistics. Craiova: Sitech & Education Publishing. [Google Scholar]

41. Smarandache, F. (2013). Introduction to neutrosophic measure, neutrosophic integral, and neutrosophic probability. Craiova: Sitech & Education Publishing. [Google Scholar]

42. Mondal, K., Pramanik, S. (2015). Neutrosophic decision making model for clay-brick selection in construction field based on grey relational analysis. Neutrosophic Sets and Systems, 9(1), 11–11. DOI 10.5281/zenodo.34864. [Google Scholar] [CrossRef]

43. Chen, J., Ye, J. (2016). A projection model of neutrosophic numbers for multiple attribute decision making of clay-brick selection. Neutrosophic Sets & Systems, 12, 139–142. [Google Scholar]

44. Chen, J., Ye, J., Du, S. (2017). Vector similarity measures between refined simplified neutrosophic sets and their multiple attribute decision-making method. Symmetry, 9(8), 153. DOI 10.3390/sym9080153. [Google Scholar] [CrossRef]

45. Solang, U., Ye, J. (2018). Refined simplified neutrosophic similarity measures based on trigonometric function and their application in construction project decision-making. Journal of Soft Computing in Civil Engineering, 2(3), 1–12. DOI 10.22115/scce.2018.126129.1056. [Google Scholar] [CrossRef]

46. Gokasar, I., Deveci, M., Kalan, O. (2022). CO2 emission based prioritization of bridge maintenance projects using neutrosophic fuzzy sets based decision making approach. Research in Transportation Economics, 91, 101029. DOI 10.1016/j.retrec.2021.101029. [Google Scholar] [CrossRef]

47. Deveci, M., Simic, V., Torkayesh, A. E. (2021). Remanufacturing facility location for automotive lithium-ion batteries: An integrated neutrosophic decision-making model. Journal of Cleaner Production, 317, 128438. DOI 10.1016/j.jclepro.2021.128438. [Google Scholar] [CrossRef]

48. Bavia, M. S., Nagarajan, D., Broumi, S., Kavikumar, J., Rajkumar, A. (2022). Neutrosophic in multi-criteria decision making for location selection. Neutrosophic Sets and Systems, 48, 142–153. DOI 10.5281/zenodo.6041399. [Google Scholar] [CrossRef]

49. Zhou, K. F., Ye, J., Li, B. (2019). Similarity measure methods of neutrosophic numbers and their comparative study on the evaluation of slope stability. Journal of Shaoxing University (Natural Science), 39, 11–18. [Google Scholar]

50. Li, B., Zhou, K., Ye, J., Sha, P. (2019). Application of a probabilistic method based on neutrosophic number in rock slope stability assessment. Applied Sciences, 9(11), 2309. DOI 10.3390/app9112309. [Google Scholar] [CrossRef]

51. Li, C., Ye, J., Cui, W., Du, S. G. (2019). Slope stability assessment method using the arctangent and tangent similarity measure of neutrosophic numbers. Neutrosophic Sets and Systems, 27, 98–103. DOI 10.5281/zenodo.3275419. [Google Scholar] [CrossRef]

52. Du, S. G., Ye, J., Yong, R., Zhang, F. (2020). Simplified neutrosophic indeterminate decision making method with decision makers’ indeterminate ranges. Journal of Civil Engineering and Management, 26, 590–598. DOI 10.3846/jcem.2020.12919. [Google Scholar] [CrossRef]

53. Qin, J. B., Du, S. G., Ye, J., Yong, R. (2022). SVNN-ANFIS approach for stability evaluation of open-pit mine slopes. Expert Systems with Applications, 198, 116816. DOI 10.1016/j.eswa.2022.116816. [Google Scholar] [CrossRef]

54. Ye, J., Yong, R., Liang, Q. F., Huang, M., Du, S. G. (2016). Neutrosophic functions of the joint roughness coefficient and the shear strength: A case study from the pyroclastic rock mass in Shaoxing City, China. Mathematical Problems in Engineering, 2016, 1–9. DOI 10.1155/2016/4825709. [Google Scholar] [CrossRef]

55. Yong, R., Gu, L. Y., Ye, J., Du, S. G., Huang, M. et al. (2019). Neutrosophic function with NNs for analyzing and expressing anisotropy characteristic and scale effect of joint surface roughness. Mathematical Problems in Engineering, 2019, 1–11. DOI 10.1155/2019/8718936. [Google Scholar] [CrossRef]

56. Ye, J., Chen, J. Q., Yong, R., Du, S. G. (2017). Expression and analysis of joint roughness coefficient using neutrosophic number functions. Information, 8(2), 69. DOI 10.3390/info8020069. [Google Scholar] [CrossRef]

57. Yong, R., Tan, S. N., Ye, J., Du, S. G., Yang, M. J. (2021). Neutrosophic function for assessing the scale effect of the rock joint surface roughness. Mathematical Problems in Engineering, 2021, 1–11. DOI 10.1155/2021/6611627. [Google Scholar] [CrossRef]

58. Wang, C. S., Wang, L. Q., Du, S. G., Ye, J., Yong, R. (2021). Investigation on the indeterminate information of rock joint roughness through a neutrosophic number approach. Computer Modeling in Engineering & Sciences, 129(2), 973–991. DOI 10.32604/cmes.2021.017453. [Google Scholar] [CrossRef]

59. Chen, J. Q., Ye, J., Du, S. G. (2017). Scale effect and anisotropy analyzed for neutrosophic numbers of rock joint roughness coefficient based on neutrosophic statistics. Symmetry, 9(10), 208. DOI 10.3390/sym9100208. [Google Scholar] [CrossRef]

60. Aslam, M. (2019). A new method to analyze rock joint roughness coefficient based on neutrosophic statistics. Measurement, 146, 65–71. DOI 10.1016/j.measurement.2019.06.024. [Google Scholar] [CrossRef]

61. Aslam, M., Bantan, R. A., Khan, N. (2021). Design of tests for mean and variance under complexity--An application to rock measurement data. Measurement, 177, 109312. DOI 10.1016/j.measurement.2021.109312. [Google Scholar] [CrossRef]

62. Chen, J. Q., Ye, J., Du, S. G., Yong, R. (2017). Expressions of rock joint roughness coefficient using neutrosophic interval statistical numbers. Symmetry, 9(7), 123. DOI 10.3390/sym9070123. [Google Scholar] [CrossRef]

63. Jiang, W. Z., Ye, J., Cui, W. H. (2018). Scale effect and anisotropic analysis of rock joint roughness coefficient neutrosophic interval statistical numbers based on neutrosophic statistics. Journal of Soft Computing in Civil Engineering, 2(4), 62–71. DOI 10.22115/SCCE.2018.143079.1086. [Google Scholar] [CrossRef]

64. Song, J. M., Yong, R., Zhang, Y. Y., Xu, M. N., Ye, J. (2021). Statistical similarity analysis based on neutrosophic interval probability. Neutrosophic Sets and Systems, 46(1). DOI 10.5281/zenodo.5553463. [Google Scholar] [CrossRef]

65. Jiang, W. Z., Ye, J. (2016). Optimal design of truss structures using a neutrosophic number optimization model under an indeterminate environment. Neutrosophic Sets and Systems, 14, 93–97. DOI 10.5281/zenodo.570888. [Google Scholar] [CrossRef]

66. Ye, J. (2018). Neutrosophic number linear programming method and its application under neutrosophic number environments. Soft Computing, 22, 4639–4646. DOI 10.1007/s00500-017-2646-z. [Google Scholar] [CrossRef]

67. Ye, J. (2018). An improved neutrosophic number optimization method for optimal design of truss structures. New Mathematics and Natural Computation, 14(3), 295–305. DOI 10.1142/S1793005718500187. [Google Scholar] [CrossRef]

68. Das, P., Roy, T. K. (2015). Multi-objective non-linear programming problem based on neutrosophic optimization technique and its application in riser design problem. Neutrosophic Sets and Systems, 9(1), 88–95. DOI 10.5281/zenodo.571480. [Google Scholar] [CrossRef]

69. Sarkar, M., Dey, S., Roy, T. K. (2016). Truss design optimization using neutrosophic optimization technique. Neutrosophic Sets and Systems, 13, 62–69. DOI 10.5281/zenodo.570869. [Google Scholar] [CrossRef]

70. Sarkar, M., Dey, S., Roy, T. K. (2016). Multi-objective neutrosophic optimization technique and its application to structural design. International Journal of Computer Applications, 148, 31–37. DOI 10.5120/ijca2016911325. [Google Scholar] [CrossRef]

71. Sarkar, M., Roy, T. K. (2017). Truss design optimization with imprecise load and stress in neutrosophic environment. Advances in Fuzzy Mathematics, 12(3), 439–474. DOI 10.37622/AFM/12.3.2017.439-474. [Google Scholar] [CrossRef]

72. Sarkar, M., Roy, T. K. (2017). Multi-objective welded beam optimization using neutrosophic goal programming technique. Advances in Fuzzy Mathematics, 12(3), 515–538. DOI 10.37622/AFM/12.3.2017.515-538. [Google Scholar] [CrossRef]

73. Sarkar, M., Roy, T. K. (2018). Optimization of welded beam structure using neutrosophic optimization technique: A comparative study. International Journal of Fuzzy Systems, 20(3), 847–860. DOI 10.1007/s40815-017-0362-6. [Google Scholar] [CrossRef]

74. Duncan, J. M. (1996). State of the art: Limit equilibrium and finite-element analysis of slopes. Journal of Geotechnical Engineering, 122(7), 577–596. DOI 10.1061/(ASCE)0733-9410(1996)122:7(577). [Google Scholar] [CrossRef]

75. Yu, H., Salgado, R., Sloan, S., Kim, J. (1998). Limit analysis versus limit equilibrium for slope stability. Journal of Geotechnical and Geoenvironmental Engineering, 124(1), 1–11. DOI 10.1061/(ASCE)1090-0241(1998)124:1(1). [Google Scholar] [CrossRef]

76. Cheng, Y. M., Lansivaara, T., Wei, W. (2007). Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods. Computers and Geotechnics, 34(3), 137–150. DOI 10.1016/j.compgeo.2006.10.011. [Google Scholar] [CrossRef]

77. Wei, W., Cheng, Y. M., Li, L. (2009). Three-dimensional slope failure analysis by the strength reduction and limit equilibrium methods. Computers and Geotechnics, 36(1–2), 70–80. DOI 10.1016/j.compgeo.2008.03.003. [Google Scholar] [CrossRef]

78. Zhou, X., Cheng, H. (2013). Analysis of stability of three-dimensional slopes using the rigorous limit equilibrium method. Engineering Geology, 160, 21–33. DOI 10.1016/j.enggeo.2013.03.027. [Google Scholar] [CrossRef]

79. Wang, C., Tannant, D., Lilly, P. (2003). Numerical analysis of the stability of heavily jointed rock slopes using PFC2D. International Journal of Rock Mechanics and Mining Sciences, 40(3), 415–424. DOI 10.1016/S1365-1609(03)00004-2. [Google Scholar] [CrossRef]

80. Eberhardt, E., Stead, D., Coggan, J. (2004). Numerical analysis of initiation and progressive failure in natural rock slopes—The 1991 randa rockslide. International Journal of Rock Mechanics and Mining Sciences, 41(1), 69–87. DOI 10.1016/S1365-1609(03)00076-5. [Google Scholar] [CrossRef]

81. Stead, D., Eberhardt, E., Coggan, J. (2006). Developments in the characterization of complex rock slope deformation and failure using numerical modelling techniques. Engineering Geology, 83(1–3), 217–235. DOI 10.1016/j.enggeo.2005.06.033. [Google Scholar] [CrossRef]

82. Ning, Y., An, X., Ma, G. (2011). Footwall slope stability analysis with the numerical manifold method. International Journal of Rock Mechanics and Mining Sciences, 48(6), 964–975. DOI 10.1016/j.ijrmms.2011.06.011. [Google Scholar] [CrossRef]

83. Yong, R., Li, C. D., Ye, J., Huang, M., Du, S. (2016). Modified limiting equilibrium method for stability analysis of stratified rock slopes. Mathematical Problems in Engineering, 2016, 8381021. DOI 10.1155/2016/8381021. [Google Scholar] [CrossRef]

84. Ye, H. W., Chang, J. (2009). Choosing mining method based on fuzzy decision and analytic hierarchy process. Journal of Wuhan University of Technology, 31(8), 145–110. DOI 10.1360/972009-1650. [Google Scholar] [CrossRef]

85. Li, L., Li, Y. M. (2003). The design and stability analysis of an adaptive system based on linear TS fuzzy system. Acta Automatica Sinica, 29(6), 815–820. DOI 10.16383/j.aas.2003.06.003. [Google Scholar] [CrossRef]

86. Zhu, Y., Mo, H. (2004). Application of gray correlation analysis to rock slope stability estimation. Chinese Journal of Rock Mechanics and Engineering, 23(6), 915–919. [Google Scholar]

87. He, X., Li, S. J., Liu, Y. X., Zhou, Y. P. (2003). Analyzing method of rock slope stability based on artificial neural network. Rock and Soil Mechanics, 2, 73–76. [Google Scholar]

88. Yang, T., Zhang, F., Yu, Q., Cai, M. F., Li, H. Z. (2011). Research situation of open-pit mining high and steep slope stability and its developing trend. Rock and Soil Mechanics, 32(5), 1437–1451. DOI 10.16285/j.rsm.2011.05.031. [Google Scholar] [CrossRef]

89. Wang, J. M., Cui, W. H., Ye, J. (2019). Slope stability evaluation using tangent similarity measure of fuzzy cube sets. Journal of Soft Computing in Civil Engineering, 3, 27–35. DOI 10.22115/scce.2019.176352.1100. [Google Scholar] [CrossRef]

90. Ye, J., Fu, J. (2016). Multi-period medical diagnosis method using a single valued neutrosophic similarity measure based on tangent function. Computer Methods & Programs in Biomedicine, 123, 142–149. DOI 10.1016/j.cmpb.2015.10.002. [Google Scholar] [CrossRef]

91. Barton, N. (1973). Review of a new shear-strength criterion for rock joints. Engineering Geology, 7(4), 287–332. DOI 10.1016/0013-7952(73)90013-6. [Google Scholar] [CrossRef]

92. Tse, R. (1979). Estimating joint roughness coefficients. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 16(5), 303–307. DOI 10.1016/0148-9062(79)90241-9. [Google Scholar] [CrossRef]

93. Maerz, N. H., Franklin, J. A., Be-Nnett, C. P. (1990). Joint roughness measurement using shadow profilometry. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 27(5), 329–343. DOI 10.1016/0148-9062(90)92708-M. [Google Scholar] [CrossRef]

94. Lee, Y. H., Carr, J. R., Barr, D. J., Haas, C. J. (1990). The fractal dimension as a measure of the roughness of rock discontinuity profiles. International Journal of Rock Mechanics and Mining Science & Geomechanics Abstracts, 27(6), 453–464. DOI 10.1016/0148-9062(90)90998-H. [Google Scholar] [CrossRef]

95. Barton, N., Bandis, S. (1990). Review of predictive capabilities of JRC-JCS model in engineering practice. Proceedings International Symposium on Rock Joints, pp. 603–610. Loen, Norway. [Google Scholar]

96. Barton, N., Choubey, V. (1977). The shear strength of rock joints in theory and practice. Rock Mechanics, 10(1), 1–54. DOI 10.1007/BF01261801. [Google Scholar] [CrossRef]

97. Bandis, S., Lumsden, A., Barton, N. (1981). Experimental studies of scale effects on the shear behaviour of rock joints. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 18(1), 1–21. DOI 10.1016/0148-9062(81)90262-X. [Google Scholar] [CrossRef]

98. Odling, N. (1994). Natural fracture profiles, fractal dimension and joint roughness coefficients. Rock Mechanics and Rock Engineering, 27(3), 135–153. DOI 10.1007/BF01020307. [Google Scholar] [CrossRef]

99. Du, S. G., Fan, L. B. (1999). The statistical estimation of rock joint roughness coefficient. Chinese Journal of Geophysics, 4, 577–580. [Google Scholar]

100. Du, S. G. (1999). Engineering behavior of discontinuities in rock mass. Beijing, China: Seismological Press. [Google Scholar]

101. Du, S. G., Tang, H. M. (1993). A study on the anisotropy of joint roughness coefficient in rock mass. Journal of Engineering Geology, 1(2), 32–42. [Google Scholar]

102. Aydan, Ö., Shimizu, Y., Kawamoto, T. (1996). The anisotropy of surface morphology characteristics of rock discontinuities. Rock Mechanics and Rock Engineering, 29(1), 47–59. DOI 10.1007/BF01019939. [Google Scholar] [CrossRef]

103. Belem, T., Homand-Etienne, F., Souley, M. (2000). Quantitative parameters for rock joint surface roughness. Rock Mechanics and Rock Engineering, 33(4), 217–242. DOI 10.1007/s006030070001. [Google Scholar] [CrossRef]

104. Zhang, G. B., Bao, H., Lan, H. X., Yan, C. G., Tao, Y. (2018). Research on the relationship between joint roughness coefficient and sampling precision of structural plane. Journal of Engineering Geology, 26, 1336–1341. DOI 10.13544/j.cnki.jeg.2018248. [Google Scholar] [CrossRef]

105. Huang, M., Xia, C. C., Sha, P., Ma, C. R., Du, S. G. (2019). Correlation between the joint roughness coefficient and rock joint statistical parameters at different sampling intervals. Advances in Civil Engineering, 2019, 1–9. DOI 10.1155/2019/1643842. [Google Scholar] [CrossRef]

106. Zhang, G. C., Karakus, M., Tang, H. M., Ge, Y. F., Zhang, L. (2014). A new method estimating the 2D joint roughness coefficient for discontinuity surfaces in rock masses. International Journal of Rock Mechanics & Mining Sciences, 2014, 191–198. DOI 10.1016/j.ijrmms.2014.09.009. [Google Scholar] [CrossRef]

107. Chen, S. J., Zhu, W. C., Yu, Q. L., Liu, X. G. (2016). Characterization of anisotropy of joint surface roughness and aperture by variogram approach based on digital image processing technique. Rock Mechanics and Rock Engineering, 49(3), 855–876. DOI 10.1007/s00603-015-0795-x. [Google Scholar] [CrossRef]

108. Chen, S. J., Zhu, W. C., Liu, S. X., Zhang, F., Guo, L. (2015). Anisotropy and size effects of surface roughness of rock joints. Chinese Journal of Rock Mechanics and Engineering, 34(1), 57–66. DOI 10.13722/j.cnki.jrme.2015.01.007. [Google Scholar] [CrossRef]

109. Hsiung, S. M., Ghosh, A., Ahola, M. P., Chowdhury, A. H. (1993). Assessment of conventional methodologies for joint roughness coefficient determination. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 30, 825–829. DOI 10.1016/0148-9062(93)90030-H. [Google Scholar] [CrossRef]

110. Du, S. G. (1994). The directive statistical evaluation of rock joint roughness coefficient (JRC). Journal of Engineering Geology, 2(3), 62–71. [Google Scholar]

111. Du, S. G., Hu, Y. J., Hu, X. F. (2009). Measurement of joint roughness coefficient by using profilograph and roughness ruler. Journal of Earth Science, 20(5), 890–896. DOI 10.1007/s12583-009-0075-3. [Google Scholar] [CrossRef]

112. Jang, H. S., Kang, S. S., Jang, B. A. (2014). Determination of joint roughness coefficients using roughness parameters. Rock Mechanics and Rock Engineering, 47(6), 2061–2073. DOI 10.1007/s00603-013-0535-z. [Google Scholar] [CrossRef]

113. Li, Y. R., Zhang, Y. B. (2015). Quantitative estimation of joint roughness coefficient using statistical parameters. International Journal of Rock Mechanics and Mining Sciences, 100(77), 27–35. DOI 10.1016/j.ijrmms.2015.03.016. [Google Scholar] [CrossRef]

114. Cruzaty, L. E. V., Tomalá, M. R., Gallo, C. M. C. (2020). A neutrosophic statistic method to predict tax time series in Ecuador. Neutrosophic Sets and Systems, 34, 33–39. DOI 10.5281/zenodo.3843289. [Google Scholar] [CrossRef]

115. Aslam, M., Arif, O. H., Sherwani, R. A. K. (2020). New diagnosis test under the neutrosophic statistics: An application to diabetic patients. BioMed Research International, 2020, 2086185. DOI 10.1155/2020/2086185. [Google Scholar] [CrossRef]

116. Aslam, M. (2021). Analyzing wind power data using analysis of means under neutrosophic statistics. Soft Computing, 25, 7087–7093. DOI 10.1007/s00500-021-05661-0. [Google Scholar] [CrossRef]

117. Aslam, M. (2018). Design of sampling plan for exponential distribution under neutrosophic statistical interval method. IEEE Access, 6, 64153–64158. DOI 10.1109/ACCESS.2018.2877923. [Google Scholar] [CrossRef]

118. Aslam, M., Raza, M. A., Ahmad, L. (2019). Acceptance sampling plans for two-stage process for multiple manufacturing lines under neutrosophic statistics. Journal of Intelligent & Fuzzy Systems, 37(6), 7839–7850. DOI 10.3233/JIFS-182849. [Google Scholar] [CrossRef]

119. Sivapuram, R., Dunning, P. D., Kim, H. A. (2016). Simultaneous material and structural optimization by multiscale topology optimization. Structural and Multidisciplinary Optimization, 54(5), 1267–1281. DOI 10.1007/s00158-016-1519-x. [Google Scholar] [CrossRef]

120. Kaveh, A., Khayatazad, M. (2013). Ray optimization for size and shape optimization of truss structures. Computers & Structures, 117, 82–94. DOI 10.1016/j.compstruc.2012.12.01. [Google Scholar] [CrossRef]

121. Wang, S. B., Qing, X. Y. (2016). A mixed interval arithmetic/affine arithmetic approach for robust design optimization with interval uncertainty. Journal of Mechanical Design, 138(4), 41403. DOI 10.1115/1.4032630. [Google Scholar] [CrossRef]

122. Zhou, J. H., Li, M. (2014). Advanced robust optimization with interval uncertainty using a single-looped structure and sequential quadratic programming. Journal of Mechanical Design, 136(2), 21008. DOI 10.1115/1.4025963. [Google Scholar] [CrossRef]

123. Degertekin, S. (2012). Improved harmony search algorithms for sizing optimization of truss structures. Computers & Structures, 92, 229–241. DOI 10.1016/j.compstruc.2011.10.022. [Google Scholar] [CrossRef]

124. Sonmez, M. (2011). Artificial bee colony algorithm for optimization of truss structures. Applied Soft Computing, 11(2), 2406–2418. DOI 10.1016/j.asoc.2010.09.003. [Google Scholar] [CrossRef]

125. Liu, B., Chen, X. (2015). Uncertain multi-objective programming and uncertain goal programming. Journal of Uncertainty Analysis and Applications, 3, 10. DOI 10.1186/s40467-015-0036-6. [Google Scholar] [CrossRef]

126. Schuller, G. I., Jensen, H. A. (2006). Computational methods in optimization considering uncertainties–An overview. Computer Methods in Applied Mechanics & Engineering, 198(1), 2–13. DOI 10.1016/j.cma.2008.05.004. [Google Scholar] [CrossRef]

127. Villa, C., Lozinguez, E., Labayrade, R. (2013). Multi-objective optimization under uncertain objectives: Application to engineering design problem. International Conference on Evolutionary Multi-Criterion Optimization, pp. 796–810. Berlin, Heidelberg: Springer. DOI 10.1007/978-3-642-37140-0_59. [Google Scholar] [CrossRef]

128. Wu, J. L., Luo, Z., Zhang, N., Zhang, Y. Q. (2015). The interval uncertain optimization strategy based on Chebyshev meta-model. In: Advances in global optimization, pp. 203–216. Cham: Springer. DOI 10.1007/978-3-319-08377-3_21. [Google Scholar] [CrossRef]

129. Maji, P. K. (2013). Neutrosophic soft set. Annals of Fuzzy Mathematics and Informatics, 5(1), 157–168. [Google Scholar]

130. Broumi, S., Smarandache, F., Dhar, M. (2014). Rough neutrosophic sets. Neutrosophic Sets and Systems, 3, 60–65. DOI 10.5281/zenodo.571606. [Google Scholar] [CrossRef]

131. Mondal, K., Pramanik, S. (2015). Rough neutrosophic multi-attribute decision-making based on grey relational analysis. Neutrosophic Sets and Systems, 7, 8–17. DOI 10.5281/zenodo.571603. [Google Scholar] [CrossRef]

132. Deli, I., Broumi, S. (2015). Neutrosophic soft matrices and NSM-decision making. Journal of Intelligent & Fuzzy Systems, 28(5), 2233–2241. DOI 10.3233/IFS-141505. [Google Scholar] [CrossRef]

133. Ali, M., Deli, I., Smarandache, F. (2016). The theory of neutrosophic cubic sets and their applications in pattern recognition. Journal of Intelligent & Fuzzy Systems, 30(4), 1957–1963. DOI 10.3233/IFS-151906. [Google Scholar] [CrossRef]

134. Tian, Z. P., Wang, J., Zhang, H. Y., Chen, X. H., Wang, J. Q. (2016). Simplified neutrosophic linguistic normalized weighted Bonferroni mean operator and its application to multi-criteria decision-making problems. Filomat, 30(12), 3339–3360. DOI 10.2298/FIL1508576F. [Google Scholar] [CrossRef]

135. Dey, P. P., Pramanik, S., Giri, B. C. (2016). Neutrosophic soft multi-attribute decision making based on grey relational projection method. Neutrosophic Sets and Systems, 11, 98–106. DOI 10.5281/zenodo.571576. [Google Scholar] [CrossRef]

136. Jun, Y. B., Smarandache, F., Kim, C. S. (2017). Neutrosophic cubic sets. New Mathematics and Natural Computation, 13, 41–54. DOI 10.1142/S1793005717500041. [Google Scholar] [CrossRef]

137. Banerjee, D., Giri, B. C., Pramanik, S., Smarandache, F. (2017). GRA for multi attribute decision making in neutrosophic cubic set environment. Neutrosophic Sets and Systems, 15, 60–69. DOI 10.5281/zenodo.570938. [Google Scholar] [CrossRef]

138. Liu, P. D., Shi, L. L. (2017). Some neutrosophic uncertain linguistic number heronian mean operators and their application to multi-attribute group decision making. Neural Computing and Applications, 28, 1079–1093. DOI 10.1007/s00521-015-2122-6. [Google Scholar] [CrossRef]

139. Pramanik, S., Dey, P. P., Giri, B. C., Smarandache, F. (2017). Bipolar neutrosophic projection based models for solving multi-attribute decision-making problems. Neutrosophic Sets and Systems, 15, 70–79. DOI 10.5281/zenodo.570936. [Google Scholar] [CrossRef]

140. Sahin, R., Liu, P. D. (2017). Correlation coefficient of single-valued neutrosophic hesitant fuzzy sets and its applications in decision making. Neural Computing and Applications, 28, 1387–1395. DOI 10.1007/s00521-015-2163-x. [Google Scholar] [CrossRef]

141. Singh, P. K. (2017). Three-way fuzzy concept lattice representation using neutrosophic set. International Journal of Machine Learning and Cybernetics, 8, 69–79. DOI 10.1007/s13042-016-0585-0. [Google Scholar] [CrossRef]

142. Tian, Z. P., Wang, J., Wang, J. Q., Zhang, H. Y. (2017). Simplified neutrosophic linguistic multi-criteria group decision-making approach to green product development. Group Decision and Negotiation, 26, 597–627. DOI 10.1007/s10726-016-9479-5. [Google Scholar] [CrossRef]

143. Liu, P. D., Cheng, S. F., Zhang, Y. M. (2019). An extended multi-criteria group decision-making PROMETHEE method based on probability multi-valued neutrosophic sets. International Journal of Fuzzy Systems, 21(2), 388–406. DOI 10.1007/s40815-018-0572-6. [Google Scholar] [CrossRef]

144. Zhao, S. P., Wang, D., Liang, C. Y., Lu, W. X. (2019). Induced choquet integral aggregation operators with single-valued neutrosophic uncertain linguistic numbers and their application in multiple attribute group decision-making. Mathematical Problems in Engineering, 2019, 9143624. DOI 10.1155/2019/9143624. [Google Scholar] [CrossRef]