Application of a Parallel Adaptive Cuckoo Search Algorithm in the Rectangle Layout Problem

1  Introduction

With the development of the meta-heuristic algorithm, researchers have paid more and more attention to it. In real life, meta-heuristic algorithms have been widely used in industry, finance, mathematics and other fields, and achieved good results. For example, Particle Swarm Optimization (PSO) is applied to heterogeneous Wireless Sensor Networks (WSN) [1]. PSO is applied to job scheduling algorithm on cloud [2]. Hu et al. improved binary Grey Wolf Optimizer (GWO) to feature selection [3]. Parallel Whale Optimization Algorithm (WOA) is applied to the DV-Hop localization method by Chai et al. [4]. In [5], the improved genetic algorithm is used to solve the job shop scheduling problem. In [6], the researchers used a statistical variable learning strategy to improve the PSO algorithm. Compact Differential Evolution (DE) algorithm is applied in biomedical fields [7], etc. As a relatively new meta-heuristic algorithm, Cuckoo Search (CS) algorithm has fewer parameters and is easy to implement. This algorithm not only has the superior ability of other meta-heuristic algorithms in searching for optimization but also avoids the problem of being easily trapped in local optimization to some extent. Once proposed, this algorithm has been used by many researchers to solve all kinds of practical problems. However, the CS algorithm also shows the shortcomings of relatively slow convergence speed. In view of its shortcomings, researchers improved it through different means, and then applied it to various fields to solve related problems. Walton et al. modified Cuckoo Search (MCS) algorithm to make it perform well at high numbers of dimensions [8]. Wang et al. worked out Chaotic Cuckoo Search (CCS) [9]. Yang et al. came up with Multi-Objective Cuckoo Search (MOCS) for design optimization [10]. Rodrigues et al. came up with Binary Cuckoo Search (BCS) algorithm [11]. Rakhshani applied intelligent multi-search strategy CS algorithm to numerical and engineering optimization problems [12]. Pan et al. came up with compact CS algorithm [13] and Song et al. worked out parallel compact CS algorithm [14], etc. This paper improves the CS algorithm from two aspects: parallel communication strategy and adaptive parameter adjustment. These two improved strategies aim to accelerate the convergence speed and accuracy of the algorithm, and to some extent strengthen the ability of the algorithm to jump out of the local optimal. The effect of the improved algorithm is tested by the test function and compared with the original algorithm and other common meta-heuristic algorithms. The comparison results show that this algorithm has better performance in most cases. Finally, we apply it to the rectangular layout problem.

Layout problems are widely used in the real world, such as stacking of items in warehouse, newspaper text layout, container packing, and so on [15–19]. This kind of problem can be abstracted into a layout problem. The layout problem is to place n known objects in a certain area according to certain rules. During placement, ensure that objects are compact and do not overlap, that is, making the space utilization the highest. Among all kinds of layout problems, rectangular layout problems take up the largest proportion in actual production and life. In many layout problems, the target to be placed is approximated as a rectangle and placed in a large rectangular area. So the rectangular layout problem has become the basis of the layout problem. The solution of rectangular layout is a classic NP-hard problem. Currently, there is no universally recognized fixed optimal solution. Many researchers have applied meta-heuristic algorithms to layout problems and achieved good results [20–22]. For example, Huang et al. further investigated the rectangular part layout problem by using the Genetic Algorithm [23]; Turanoğlu et al. used a bacterial foraging optimization method to solve the dynamic facility layout problem [24]; Liu et al. applied the multi-objective particle swarm optimization algorithm to the dynamic facility layout problem [25]. In this paper, the improved Cuckoo Search algorithm is applied to rectangular layout, aiming to ensure more excellent layout results by combining the superior performance of this algorithm with rectangular layout rules.

The main contributions of this paper include the following four aspects:

1)   A new adaptive parameter strategy is proposed to improve step size and rejection probability respectively and the performance of the algorithm is significantly improved.

2)   Based on the original algorithm, a new parallel communication strategy is applied to enhance the global optimization of the population.

3)   The new improved algorithm is compared with the original algorithm (CS) and several popular algorithms (WOA, SCA, PSO, GWO, ABC, DE) through the CEC-2013 test function.

4)   The improved algorithm is combined with the rule of the lowest horizontal line strategy to expand the practice in the field of the rectangular layout.

The rest of this paper is organized as follows. In Section 2, we mainly introduce the principle of the CS algorithm. In Section 3, the improvement of the CS algorithm is proposed. The comparison between the improved cuckoo search algorithm and other algorithms is discussed in Section 4. Section 5 is mainly about the specific description of the application and the actual simulation experiment results after the combination of the algorithm and the application. The conclusion is given at the end of this paper.

2  Cuckoo Search Algorithm

2.1 Principle of Cuckoo Search Algorithm

Yang et al. proposed the CS algorithm in 2009 [26]. The algorithm is inspired by the breeding behavior of cuckoos in nature. Cuckoos will randomly search for the best nests to lay their eggs on. The algorithm mainly uses the Lévy flight to simulate the random walk of the cuckoo. In nature, the movement patterns of many birds are characteristic of Lévy flight. The Lévy flight process consists of frequent short-distance flights and occasional long-distance flights. The step size of the flight conforms to the Lévy distribution. Frequent short-distance flights can effectively search for the optimal solution in a certain area, while occasional long-distance flights can expand the search range and avoid falling into local optimal values. To describe this behavior, Yang et al. proposed three rules:

(1)   Cuckoo birds randomly choose a nest to lay eggs, and lay only one egg in a nest. At this time, a nest can be abstracted into a solution.

(2)   The best nests will be preserved. That means the best solution is saved for the next iteration.

(3)   The number of nests n is constant, and the probability of cuckoo eggs being found is Pa. The host will abandon the eggs or the nest after finding the abnormality and that means the nest will be replaced with a certain probability. The acquisition of the new nest was made by Lévy flight.

The CS algorithm performs two population updates in one iteration: a random walk update based on the Lévy flight and an update by dropping the probability Pa. Each update has a strong memory. If the fitness of the objective function improves after the update, the update will be accepted. Otherwise, the original value will be maintained. Suppose that the number of nests set by CS algorithm is N, the dimension of the nest, namely the dimension of the solution, is Nd. A nest represents a solution to an objective function. The calculation formula is based on Lévy’s flying random walk:

xit+1=xit+a⊗L(β),i∈(1,2,…,N)(1)

L(β)=s×(xt−xbestt)(2)

In Eq. (1), xi represents the location of nest i at iteration t. In Eq. (2), a is step length coefficient, s is to obey the parameters for the Lévy of β distribution random number, xbestt represents the optimal solution obtained when the algorithm iterates to generation t, symbol ⊗ said dot product.

s=μ|υ|1/β(3)

σ={Γ(1+β)×sin(β×π2)Γ(1+β2)×β×2(β−1)/2}(4)

In Eqs. (3) and (4), μ∼N(0,σ2), υ∼N(0,1), 1≤β≤3.

The random step size based on Lévy distribution has the characteristics of high probability short-distance exploration and occasionally long-distance walking, as shown in Fig. 1.

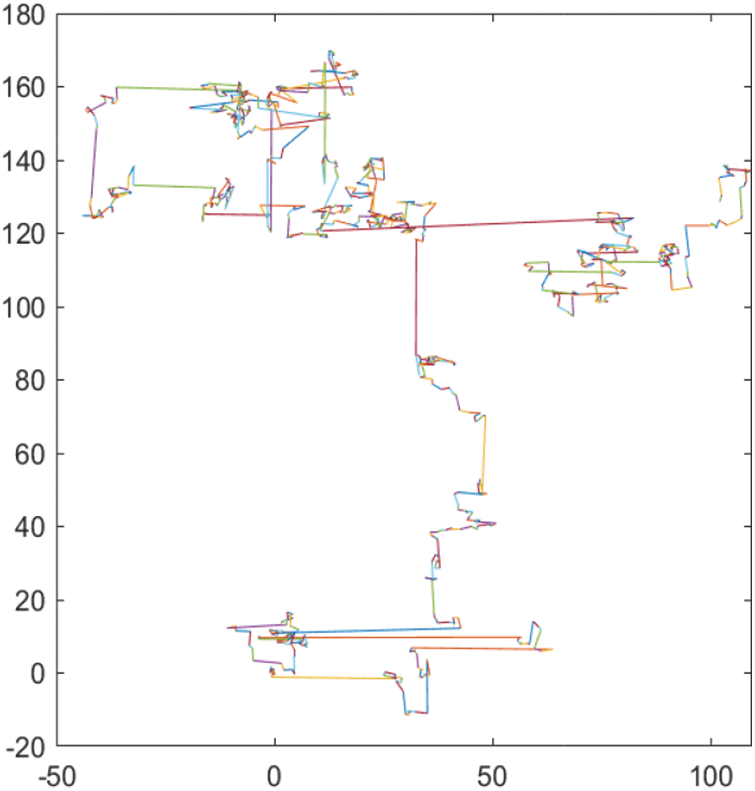
Figure 1: The trajectory generated by Lévy’s flight in two-dimensional space

The second update strategy is as follows: CS algorithm discards partial solutions according to a certain probability of discovery and then adopts preference walk to regenerate the same number of solution.

xit+1=xit+r×(xjt−xkt),j,k∈(1,2,…,N)(5)

In Eq. (5), r follows the uniform distribution of random numbers between [0, 1], and xjt and xkt are any two t generation solutions.

2.2 Specific Algorithm Step Description

Step 1: The number of nests is set to N, that is, the population number was set to N. The search space dimension was set to d, and randomly generated initial population in the bird’s nest location P0=[x10,x20,x30,…,xN0]T.

Step 2: Bird’s Nest location update. The optimal nest location of the previous generation xbi−1, is retained, and the other nest locations were updated using Eq. (1) to obtain a new nest (solution) location. The obtained new position is compared with the current bird’s nest position, and the better solution is reserved.

Step 3: During the solution process, the egg of the cuckoo has a certain probability (Pa) to be found by the host. If the egg is found, it means the current egg is discarded. At this time, the next bird’s nest is found through a specific random function. Otherwise, this situation is not found. The positions of all bird nests in the whole population are Pi=[x1i,x2i,x3i,…,xNi]T.

Step 4: Find the optimal nest location xbt and the optimal fitness value fmin in the final Pi obtained. If the iteration stop condition is reached, the optimal global value fmin and the corresponding global optimal position xbt is output. Conversely, return Steps 2 and 3 to continue the loop body’s iterative update. The iteration stop conditions mentioned here, such as reaching the iteration times, convergence to the precision of the states, etc.

2.3 Advantages and Disadvantages of CS Algorithm

This algorithm has been proved by Yang et al. through many experiments. In general, Pa is set as 0.25, dimension Dim and population number N can meet most of the use scenarios according to their requirements. The algorithm has few parameters, and the variation of parameters has little influence on the experimental results. The existence of Lévy flight mechanism is conducive to jumping out of the optimal local solution and finding the optimal global solution. The algorithm abandons a solution according to the random probability Pa and replaces it with a new solution, which enhances the randomness and helps to find the global optimal solution to a certain extent.

The CS algorithm finds the bird’s nest through the Lévy flight mechanism. Lévy flight is a random walk process consisting of short-distance flight with high probability and long-distance flight with low probability. Therefore, the cuckoo’s nest finding path is easy to jump between different search areas, resulting in the poor local fine search ability of the CS algorithm. After the algorithm is decomposed, it is easy to oscillate in the area near the optimal solution, resulting in low algorithm efficiency.

3  Parallel Adaptive Parameter Cuckoo Search Algorithm

The last section mentioned that the CS algorithm has some advantages over other algorithms but also has some disadvantages. To improve the performance of CS algorithm and expand the application field of CS algorithm, researchers have developed multiple enhanced versions of CS algorithm, such as binary CS algorithm used to replace discrete optimization problem, a chaotic CS algorithm used to improve the performance of CS algorithm [27], adaptive CS algorithm [28] and mixed with other algorithms, CS algorithm used to restore multi-objective optimization, modified cuckoo search algorithm with self-adaptive parameter method [29], and a self-adaptive step size strategy proposed to improve the performance of cuckoo algorithm [30]. In [31], the author adjusted the parameters involved in the algorithm according to the current number of iterations, and improved the performance of the algorithm. In [9], chaotic cuckoo search optimization algorithm was proposed. It is proposed to use chaos theory to improve CS algorithm and to further protect the best cuckoo in the elite protection plan. Experimental results show that chaotic CS has some advantages in accelerating algorithm convergence. In 2011, Tuba et al. [32] and Walton et al. [8] proposed to sort solutions by fitness value size and to exchange information between solutions, some improvements have been made in the performance of the algorithm.

Aiming at the shortcoming of CS algorithm’s low local precision search ability, in this paper, improvements are made from two aspects: on the one hand, population parallel communication strategy is adopted; on the other hand, adaptive parameter strategy is adopted.

3.1 Population Parallel Communication Strategy

Parallel communication strategy can improve the search ability and convergence speed of meta-heuristic optimization algorithms and find better solutions in a better way [33–36]. The parallel meta-heuristic algorithms divide the population into several subgroups. Each subgroup is calculated independently, and the communication and disturbance among the subgroups are carried out after every m iteration. This strategy aims to influence or replace the inferior individuals in this group with the best individuals in the adjacent group. In a parallel communication strategy, many methods can communicate with each subgroup [37–40]. In this paper, two strategies are mainly used to disturb the poor individuals. First, the adjacent subpopulation optimal individual was used to influence the flawed individual of other populations, and the influence weight factor Q from 0 to 1 is randomly generated. The xbi+1 of the next generation of the individual was obtained from the current xbi of the individual and the optimal individual location gbesti of the adjacent population, that is, xbi+1=gbesti∗q+xbi∗(1−q). Secondly, the global optimal individual Gbest is obtained by comparing all optimal individuals of the population. The influence weight factor a and the number of affected individuals l are generated. Disturbing one poor individual in each subpopulation by the optimal individual.

An example is given in Fig. 2, we divide the entire population into 4 small populations according to the parallel strategy. The solid point o in the figure is the ideal optimal point, and the four individuals (a, b, c, d) are the current optimal solutions in each population. Fig. 2a is the communication behavior among the subpopulation individuals. Fig. 2b shows the mutual communication behavior among the subgroups.

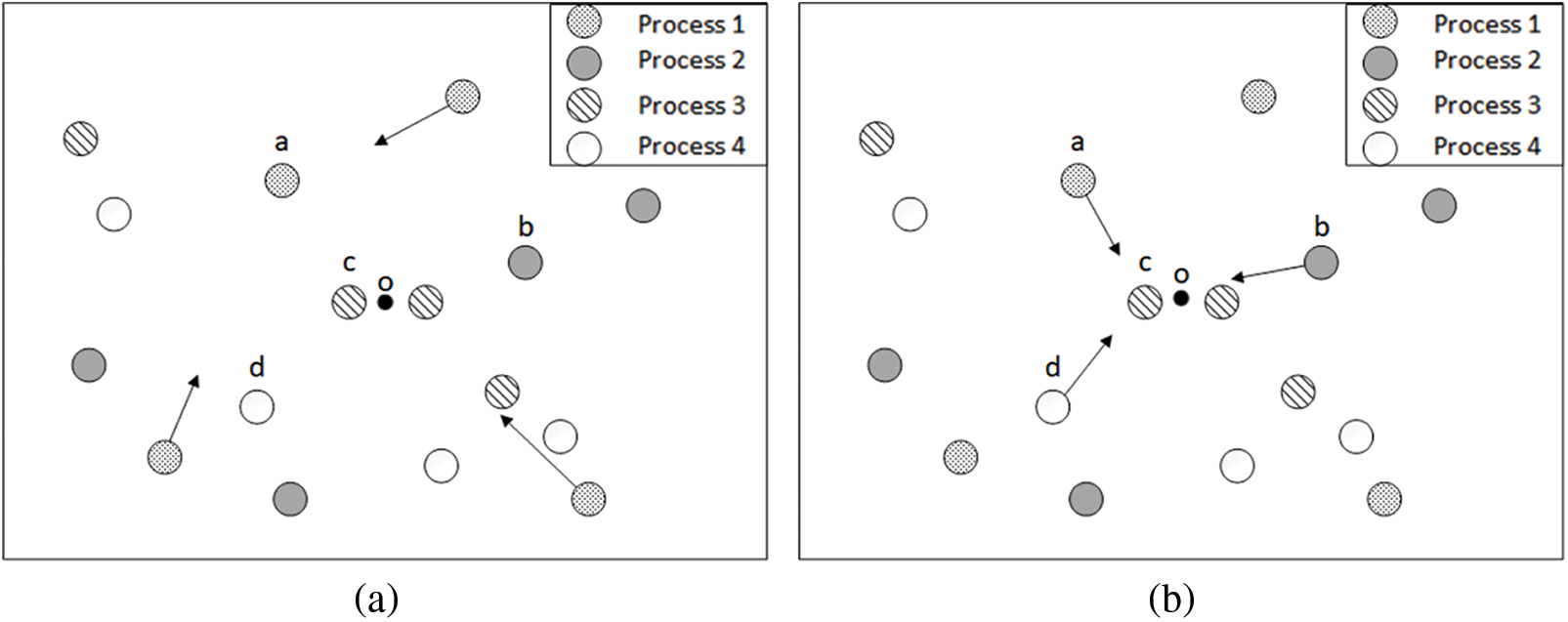
Figure 2: Population parallel communication strategies

The interpopulation communication of the parallel strategy is beneficial to the algorithm to avoid falling into the local optimum and to find the global optimum or its optimal solution with high probability in multiple ranges. Simultaneously, the strategy will accelerate the optimization speed of the population to a certain extent and further improve work efficiency. This can also be proved in the algorithm comparison section.

3.2 Adaptive Parameter Strategy

In this paper, CS algorithm adopts an adaptive parameter strategy, which ensures a large-scale random search in the early stage and a small-scale local precision search in the later stage. In the early stage of the whole process, the CS algorithm is more conducive to finding the global optimal solution or its vicinity by large-scale global random search. In the later stage, frequent local search can more accurately converge to the global optimal solution or approximate global optimal solution, so as to ensure better compliance with the experimental requirements.

The CS algorithm used in this paper involves a few parameters, and the real influential factors are the abandonment probability Pa and Lévy flight step a of the solution. From the previous introduction, we can also see that it is these two parameters that can affect the search scope.

(1) For the problem of abandonment probability Pa, this paper takes the number of iterations as the independent variable and obtains the probability Pa through the linear change in the range from the sine function π/2 to π. The specific changes are shown in Fig. 3a. Thus, the algorithm adaptively matches the appropriate abandonment probability Pa as the number of times increases during iteration. This strategy ensures frequent global long step search in the early stage and reduces the search probability in the later stage. At the same time, this strategy avoids the oscillation phenomenon and enhances the search accuracy. As shown in Eq. (6). Through testing, we concluded that under the adaptive condition of abandoning the parameter Pa, the performance was optimal when the upper bound was 0.7 and the lower bound was 0. The change image of Pa is shown in Fig. 3b.

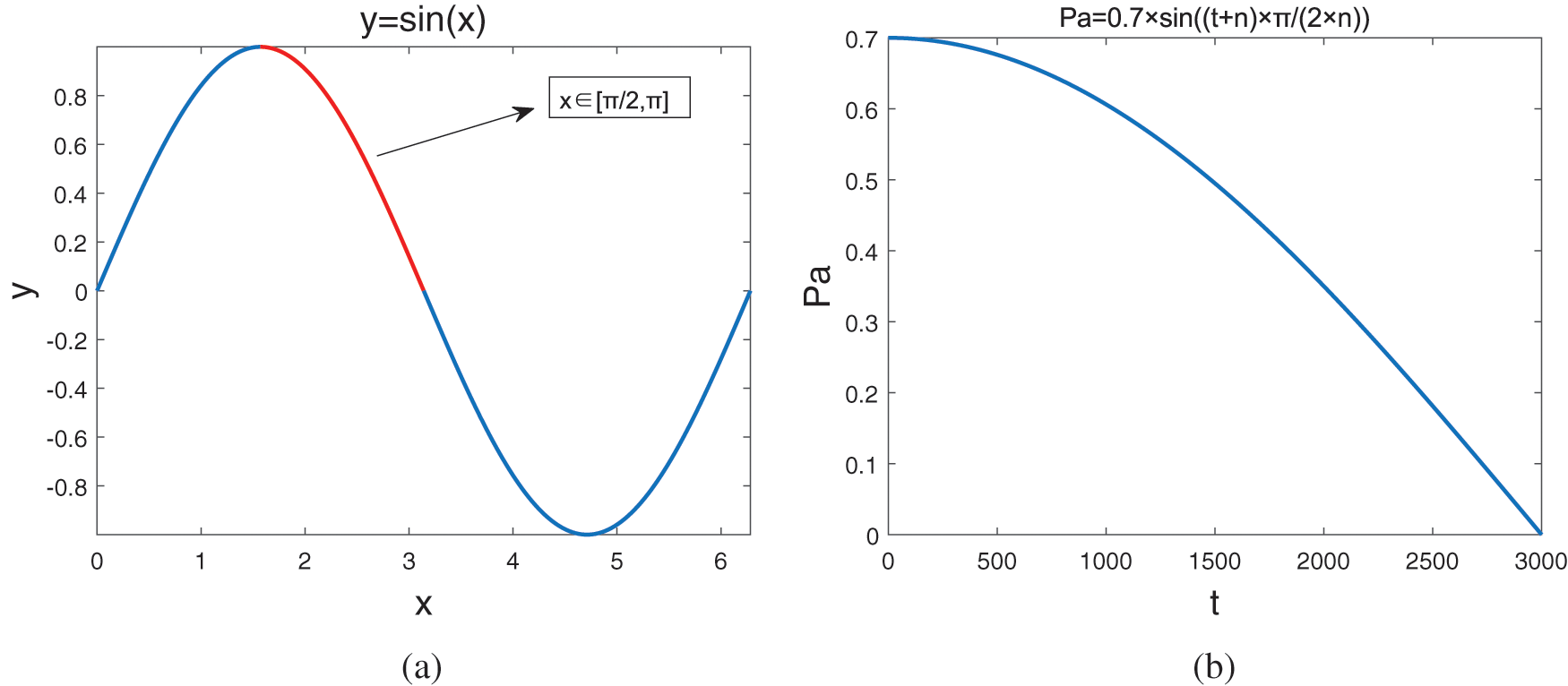
Figure 3: Adaptive parameter Pa

(2) As for Lévy flight step size impact factor a, this paper selects a pattern to generate the step size of the next generation position by determining whether the number of iterations conforms to the standard. One of the two modes is the way of generating the step size of the original algorithm, and the other is to appropriately adjust the Lévy flight step size impact factor according to the number of iterations at this time. In this paper, this strategy avoids the oscillation effect caused by the excessively long step size. As shown in Eq. (7).

Pa=0.7×sin[(t+n)×π/(2×n)](6)

xit+1=xit+a⊗L(β)⊗[1−t/(2×n)]i∈(1,2,…,N)(7)

Parallel Adaptive Cuckoo Search (PACS) algorithm pseudo-code is shown in algorithmic 3.1.

4  Algorithm Contrast

4.1 Experimental Environment

In of 9 this paper, the performance algorithms is compared through 28 benchmark test functions [41], as shown in Table 1. The algorithms for comparison were the CS [26], Parallel Cuckoo Search (PCS), PACS, PSO [42], Sine Cosine Algorithm (SCA) [43], WOA [44], GWO [45], Artificial Bee Colony (ABC) [46], DE [47] performance is analyzed. Set the population number (N) as 100, the dimension (Dim) as 50, and the number of iterations (Max Generation) as 3000. The parameter settings of each algorithm in the experimental comparison are shown in Table 2.

4.2 Analysis of Experimental Results

Combined with the above comparison Figs. 4–6 and Table 3, it can be seen that the CS algorithm has been significantly enhanced in terms of convergence speed and convergence precision after the improvement of population parallel communication and adaptive parameter strategy. The Table 3 is divided into three parts: mean value, standard deviation and optimal value. Among them, the mean value is the result obtained after 30 runs of each algorithm, which more intuitively shows the advantages and disadvantages of each algorithm. The bold part represents the value of the algorithm with the best performance in the test function. The standard deviation is used as an auxiliary function to represent the stability of each algorithm in each test function. PACS outperforms other algorithms in 20 of the 28 tested functions in CEC-2013. To reflect the performance difference of each algorithm more clearly, this paper takes logarithms or reduces the range of the y-axis in some images. As can be seen from the best value in the table, the improved algorithm also shows better performance in precise optimization.

Figure 4: Convergence curves of unimodal benchmark functions

Figure 5: Convergence curves of multimodal benchmark functions

Figure 6: Convergence curves of composite benchmark functions

The first five are unimodal functions, and the performance of the PACS algorithm is the best. Where, in F1, although the final result of CS and PACS is the same, PACS converges faster than CS. In F4, PSO shows good performance. F6 to F20 are multimodal functions. PACS performance is slightly lower than CS performance in F6 and GWO performance in F7 and F9 respectively. Among the other test functions, PACS performed better. F21 to F28 are compound functions. PACS and GWO win or lose half, but the former is more stable. Overall, PACS show better performance in 20 functions, while CS, PSO and GWO all had their strengths in the remaining eight functions. The best performing algorithm in each function is highlighted in bold. Comparing the experimental data of CS and PCS, it can be seen that the parallel strategy works well in improving performance. Comparing the experimental data of PCS and PACS, it can be seen that the performance of the algorithm is significantly improved by the adaptive strategy. As can be seen from Table 4, the running time of the improved algorithm (PACS) does not extend compared with the previous CS algorithm, which also indicates that the improved strategy is effective and does not produce other defects.

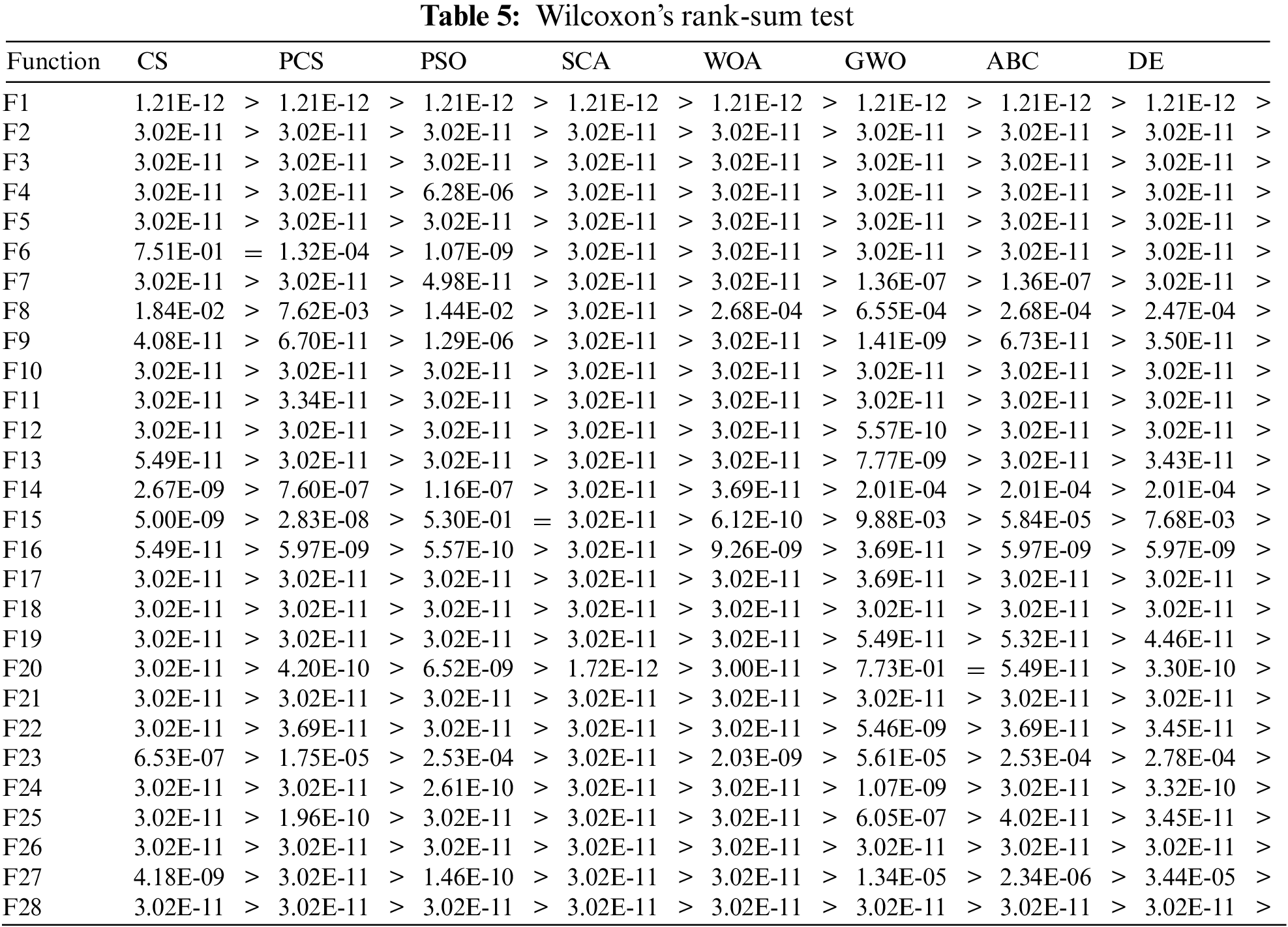
To judge whether the experimental results are statistically significant, Wilcoxon’s rank-sum test is executed at a 5% significance level. The results are shown in Table 5. “=” means that the algorithm is equivalent to those that acquire the best results. “<” shows that the compared algorithm is superior to PACS, “>” indicates that the algorithm is not as good as PACS. At the same time, the table is also attached with the specific results of the test. If the value is less than 5%, PACS is superior to this algorithm. As can be seen from Table 5, at (F6, CS), (F5, PSO), (F20, GWO) the results show “=”, and others show “>”. Combining with Tables 3 and 5, we can see that CS has better performance than PACS in F6 but is similar, and PACS is not much different from PSO and GWO at F15 and F20.

5  Algorithm and Experiment Application Background Analysis

Researchers have conducted some similar case studies in the field of layout. In [48], Lee et al. integrated simulation and ant colony optimization to improve the service facility layout in a station. Motaghi et al. [49] used heuristic algorithms to optimize hospital layout. Heragu et al. [50] carried out an experimental analysis of simulated annealing based algorithms for the layout problem. Gomes de Alvarenga et al. [51] explored out metaheuristic methods for a class of the facility layout problem. Lin et al. [52] integrated systematic layout planning with fuzzy constraint theory to design and optimize the facility layout for operating theatre in hospitals. In different application fields, there are different kinds of rectangular layout problems according to specific requirements. In this paper, PACS is used to solve the rectangular packing problem. The layout problem studied in this paper refers to placing a group of different rectangles in a fixed area and finding out their arrangement to make them as compact as possible. At the same time, there is no clear fixed solution for this kind of problem, and there may be multiple optimal solutions.

5.1 Steps of Algorithm

A group of rectangular (P1,P2,…,PN) and a known length and width and strongly heterogeneous [53]. The width of the raw material is W, the height is H. PACS algorithm and search strategy based on the lowest horizontal line are used to find the optimal solution. In the discharge process, three constraints should be met, namely, no overlap between rectangular parts. Rectangle parts should not exceed the boundary of the plate and the bottom edge of the rectangle parts should be parallel to the bottom edge of the container. hmax is the maximum height after N rectangles are arranged. Y is the utilization ratio of sheet metal, that is, the ratio between the sum of the rectangular area and the area below the maximum height of the layout drawing. Rectangular arrangement decoding consists of two parts: the order and the state of each rectangle. Among them, we numbered each rectangle at the beginning of the experiment and worked out the order at the end of the experiment. The rectangle state is initially set to the horizontal state, meaning that the long side of the rectangle is placed horizontally.

Y=∑i=1nwi×hiW×hmax(8)

There are four commonly used methods about the existing rectangular layout algorithms: the BL algorithm, step down algorithm, the lowest horizontal line algorithm, and improved search algorithm based on the lowest horizontal line. Among them, the BL algorithm has severe defects, some of the best solutions cannot be found. Moreover, the phenomenon of left side height may occur. The descending step algorithm is similar to the BL algorithm, but the difference is that it is easy to produce the sensation of high right side. The lowest horizontal line algorithm generally does not show the sensation that one side is too high, but there are other drawbacks. Stay when the width of the minimum horizontal line is smaller than the width of the rectangular of a row. The method used by the algorithm is to find the current lowest horizontal line and compare the current rectangular blocks to be arranged. However, the height of the lowest level is less than right now to the width of the rectangular of a row, but that doesn’t mean it’s less than the width of all the rectangles. This can make the minimum horizontal lines above small rectangular part of the waste. The search algorithm based on the lowest horizontal line is better than the BL algorithm and the lower step algorithm. Compared with the lowest horizontal line algorithm, this algorithm can solve the waste defect of the small rectangular part above the lowest horizontal line to a certain extent. In this paper, the search algorithm based on the lowest horizontal line is used to arrange the set of rectangular in the determined order.

5.2 Specific Steps of the Application Algorithm

The specific steps are divided into four steps.

Step 1: Set the initial horizontal line queue. The horizontal line queue is arranged in an increasing height. At this time, there is only one horizontal line in the queue with a height of 0 and a length equal to the width of the raw material. Sets the queue of rectangular to be arranged in a known initial order.

Step 2: Whenever a rectangular is placed, select the section with the lowest height from the horizontal line queue. If there are several segments, select the leftmost segment to determine whether the width of the horizontal segment is greater than or equal to the width of the part to be arranged. If the horizontal segment is less than the width of the rectangular, the width of the rectangular state continues to contrast. If still cannot let go of the rectangular, continued to contrast the other block after this block, while the block after all rectangular is unable to meet the conditions. If no block matches the placement criteria, set the lowest horizontal line to the next in the horizontal line queue.

Step 3: Repeat the Step 2 process until a part can be discharged. Each time a part is discharged, the part is removed from the queue of waiting parts.

Step 4: Repeat Step 2 and Step 3 until all parts are discharged. Finally, the maximum height of the upper edge of all rectangular is the required plate’s height.

Fig. 7a is filled with blocks 1, 2, 3, 4, 5, and 6. Assuming these rectangulars of initial order 1, 2, 3, 4, 6, 5, will be encountered in Step 2 mentioned in the case when block 4 into block 6 anyway cannot meet the minimum horizontal line fill-in the rules. You need to block after 5, block 6 continues with the horizontal comparison, at the same time, if the number 5 rectangular is longer than high, wide is placed horizontally, the need to adjust the state can conform to the requirements of the fill in. Fig.7b is the case of filling rectangle 7 after the filling of Fig.7a. When block 7 is filled, the height of the lowest horizontal line is the height of the top edge of block 4. Still, because the horizontal line is too small to fill any rectangular blocks, therefore, it is necessary to change the lowest horizontal line to the lowest horizontal line other than this horizontal line, that is, the top edge of block 1, continue the comparison, and so on. In this paper, the general order and initial state of the rectangular blocks are changed by improving the CS algorithm, and the initial order is iteratively transformed to find the optimal solution.

Figure 7: Rectangular layout diagram

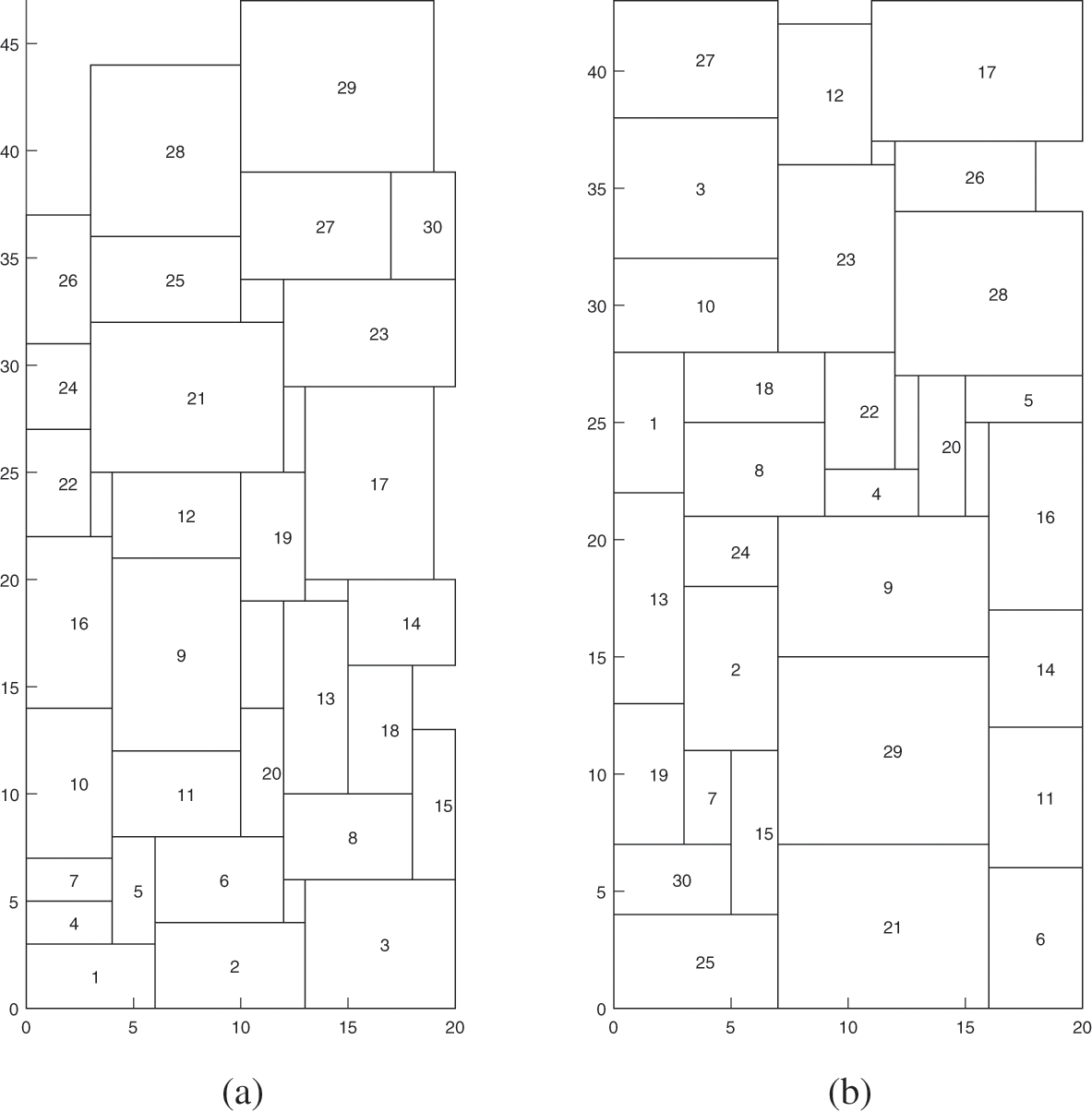
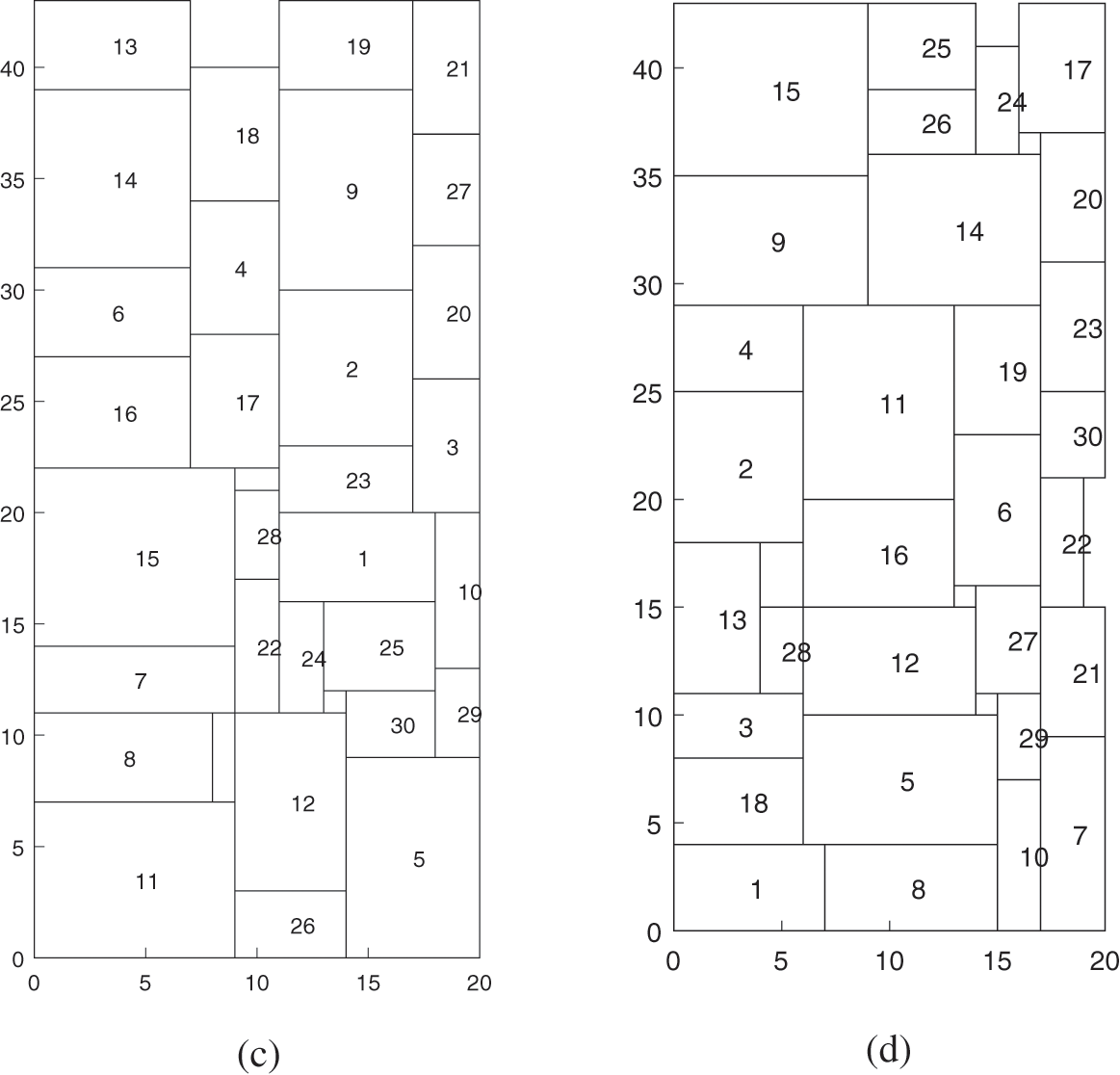
Figure 8: Rectangular layout using legend

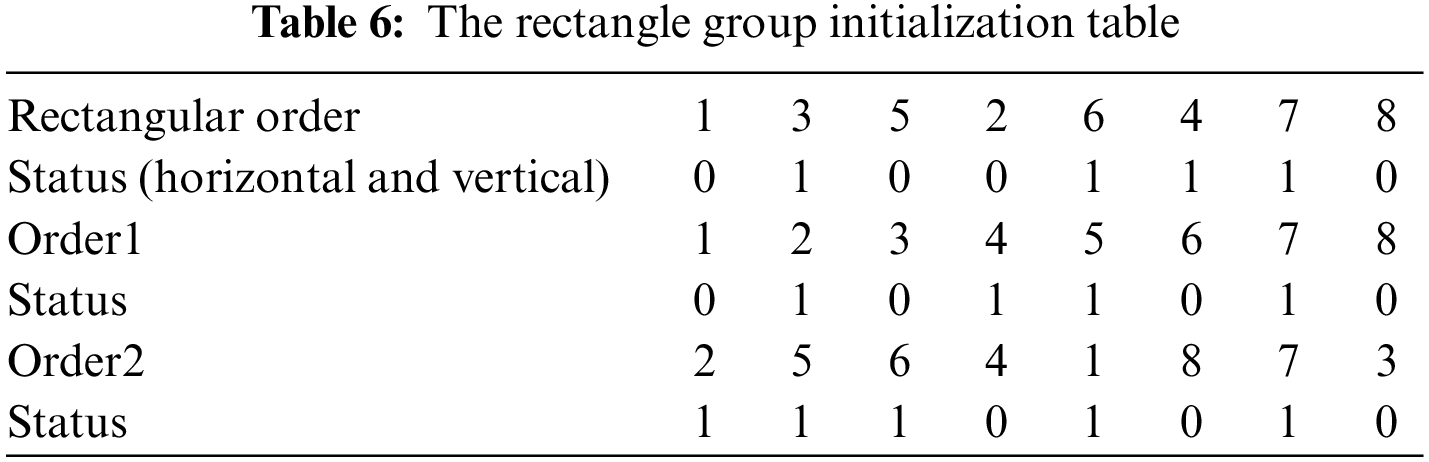
In the experiment, the coding of the solution is divided into two parts: on the one hand, each rectangular block is initially assigned with a number; on the other hand, each rectangular block has its own state (horizontal and vertical), as shown in the first rows of Table 6. In the process of algorithm iteration, the process scheme for building new solutions is as follows. First, randomly initialize the order and state of each rectangular block (horizontal and vertical). Then, in each iteration, some of the other non-optimal solutions choose the variants of the current optimal solution to become the next generation solution, as shown in the following table. The variant is the product of the random transformation order and state of some rectangular blocks selected by the current optimal solution. The other part selects the random transformation order and state of some rectangular blocks on the basis of its own solution. The second and third rows of Table 6 show the transformation order and state of rectangular blocks.

6  Experimental Simulation

Simulation experiment environment: Windows 10, MATLAB R2020a.

Raw material: width is 20, height is 200 rectangle.

The rectangular layout information is shown in Table 7. In Table 7, Order1 is the sequence number of 30 rectangular blocks that have not been explored by the algorithm, Order2 is the sequence number of these rectangular blocks after the exploration of the layout algorithm in this paper.

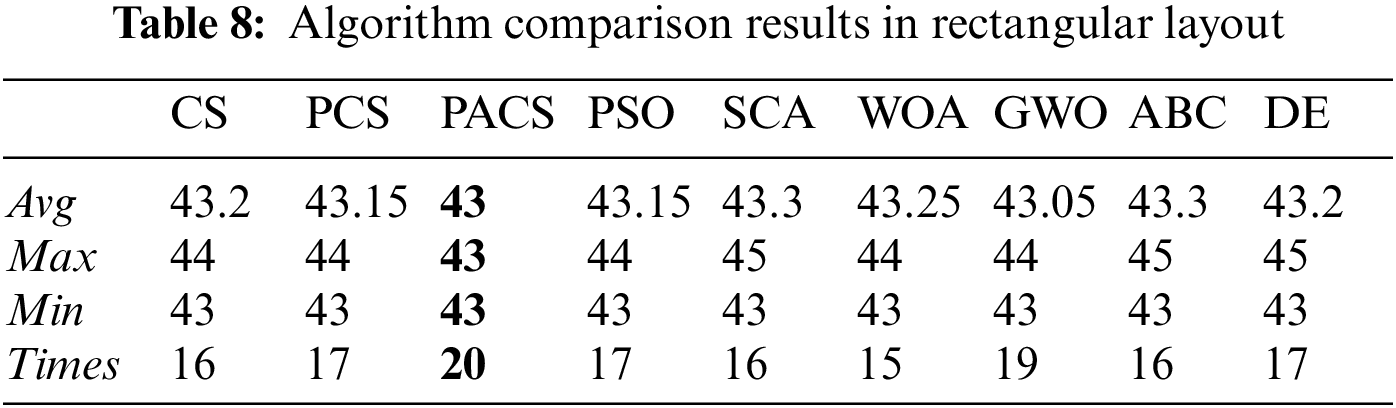
In order to test the superior performance of PACS in the application, this paper also combines other 8 algorithms (CS, PCS, GWO, SCA, WOA, DE, ABC, PSO) with the application to compare their performance. After 20 comparative experiments, the PACS algorithm can find the optimal solution every time, that is, the solution with a height of 43 in the experimental graph. However, other algorithms may not obtain the optimal solution. The specific experimental results are shown in Table 8. In the table, Avg represents the average of the optimal solutions obtained by 20 runs of each algorithm, Max represents the worst result in 20 runs of each algorithm, and Min represents the optimal solution they can obtain. Times represents the number of times each algorithm found the best solution for that application. This also shows that PACS algorithm is more suitable for application and has better performance.

According to the initial sequence, the material height used in the layout results is 47, and the material utilization rate is 841/940 = 89.5%.

The material height of the layout results obtained by combining the improved algorithm is 43, and the material utilization ratio is 841/860 = 97.8%.

7  Conclusion

In this paper, the convergence speed and accuracy of CS algorithm is improved by parallel and adaptive strategies. The performance comparison experiments of PACS, CS, PCS, PSO, GWO, SCA, ABC, DE and WOA are carried out through the CEC-2013 test function set, and the results show that the improvement effect is significant. The optimal layout is a classical NP-hard problem, and the solution set of rectangular layout is huge. In this paper, PACS algorithm is used to obtain the layout order and state of the rectangle. According to the results of application experiments, the material utilization ratio of the improved CS algorithm applied to the layout system is increased from 89.5% to 97.8% compared with the layout algorithm based on the lowest horizontal line algorithm.

In the following research work, we will study Monte Carlo theory [54–57], Fuzzy theory [58], the Taguchi method [59], and Compact technology [60], and explore the connection between them and intelligent algorithms. Through research in this area, we can gain a more comprehensive and systematic understanding of the field of algorithms. At the same time, we can also try to apply evolutionary computing to more aspects, such as, Internet of Things [61], Cognitive Network [62], 5G-IoV Networks [63], and Drone Data Collection [64]. Finally, we can continue to study intelligent algorithms to try to find a more suitable algorithm for rectangular layout applications, further improve efficiency and availability, and play a more important role in industrial production.

Funding Statement: This project was funded by the National Key Research and Development Program of China under Grant No. 11974373.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Wang, J., Gao, Y., Liu, W., Sangaiah, A. K., Kim, H. J. (2019). An improved routing schema with special clustering using pso algorithm for heterogeneous wireless sensor network. Sensors, 19(3), 671. DOI 10.3390/s19030671. [Google Scholar] [CrossRef]

 2.  Xie, X., Liu, R., Cheng, X., Hu, X., Ni, J. (2016). Trust-driven and PSO-SFLA based job scheduling algorithm on cloud. Intelligent Automation & Soft Computing, 22(4), 561–566. DOI 10.1080/10798587.2016.1152770. [Google Scholar] [CrossRef]

 3.  Hu, P., Pan, J. S., Chu, S. C. (2020). Improved binary grey wolf optimizer and its application for feature selection. Knowledge-Based Systems, 195, 105746. DOI 10.1016/j.knosys.2020.105746. [Google Scholar] [CrossRef]

 4.  Chai, Q. W., Chu, S. C., Pan, J. S., Hu, P., Zheng, W. M. (2020). A parallel woa with two communication strategies applied in dv-hop localization method. EURASIP Journal on Wireless Communications and Networking, 2020(1), 1–10. DOI 10.1186/s13638-020-01663-y. [Google Scholar] [CrossRef]

 5.  Sun, L., Cheng, X., Liang, Y. (2010). Solving job shop scheduling problem using genetic algorithm with penalty function. International Journal of Intelligent Information Processing, 1(2), 65–77. [Google Scholar]

 6.  Sun, L., Yoshida, S., Cheng, X., Liang, Y. (2012). A cooperative particle swarm optimizer with statistical variable interdependence learning. Information Sciences, 186(1), 20–39. DOI 10.1016/j.ins.2011.09.033. [Google Scholar] [CrossRef]

 7.  Xue, X., Chen, J. (2021). Matching biomedical ontologies through compact differential evolution algorithm with compact adaption schemes on control parameters. Neurocomputing, 458, 526–534. DOI 10.1016/j.neucom.2020.03.122. [Google Scholar] [CrossRef]

 8.  Walton, S., Hassan, O., Morgan, K., Brown, M. (2011). Modified cuckoo search: A new gradient free optimisation algorithm. Chaos, Solitons & Fractals, 44(9), 710–718. DOI 10.1016/j.chaos.2011.06.004. [Google Scholar] [CrossRef]

 9.  Wang, G. G., Deb, S., Gandomi, A. H., Zhang, Z., Alavi, A. H. (2016). Chaotic cuckoo search. Soft Computing, 20(9), 3349–3362. DOI 10.1007/s00500-015-1726-1. [Google Scholar] [CrossRef]

10. Yang, X. S., Deb, S. (2013). Multiobjective cuckoo search for design optimization. Computers & Operations Research, 40(6), 1616–1624. DOI 10.1016/j.cor.2011.09.026. [Google Scholar] [CrossRef]

11. Rodrigues, D., Pereira, L. A., Almeida, T., Papa, J. P., Souza, A. et al. (2013). Bcs: A binary cuckoo search algorithm for feature selection. International Symposium on Circuits and Systems (ISCAS), pp. 465–468. The Ohio State University, Columbus. [Google Scholar]

12. Rakhshani, H., Rahati, A. (2017). Intelligent multiple search strategy cuckoo algorithm for numerical and engineering optimization problems. Arabian Journal for Science and Engineering, 42(2), 567–593. DOI 10.1007/s13369-016-2270-8. [Google Scholar] [CrossRef]

13. Pan, J. S., Song, P. C., Chu, S. C., Peng, Y. J. (2020). Improved compact cuckoo search algorithm applied to location of drone logistics hub. Mathematics, 8(3), 333. DOI 10.3390/math8030333. [Google Scholar] [CrossRef]

14. Song, P. C., Pan, J. S., Chu, S. C. (2020). A parallel compact cuckoo search algorithm for three-dimensional path planning. Applied Soft Computing, 94, 106443. DOI 10.1016/j.asoc.2020.106443. [Google Scholar] [CrossRef]

15. Zhao, Y., Lu, J., Yan, Q., Lai, L., Xu, L. (2020). Research on cell manufacturing facility layout problem based on improved NSGA-II. Computers, Materials & Continua, 62(1), 355–364. DOI 10.32604/cmc.2020.06396. [Google Scholar] [CrossRef]

16. Wang, R., Zhao, H., Wu, Y., Wang, Y., Feng, X. et al. (2018). An industrial facility layout design method considering energy saving based on surplus rectangle fill algorithm. Energy, 158, 1038–1051. DOI 10.1016/j.energy.2018.06.105. [Google Scholar] [CrossRef]

17. Wu, L., Liu, Q., Wang, F., Xiao, W., Yang, Y. (2018). Heuristic algorithm for rpamp with central rectangle and its application to solve oil–gas treatment facility layout problem. Engineering Applications of Artificial Intelligence, 72, 294–309. DOI 10.1016/j.engappai.2018.04.008. [Google Scholar] [CrossRef]

18. Cui, M., Yang, K., Deng, X., Lyu, S., Feng, M. et al. (2021). Double genes improved genetic algorithm for solving two-dimensional rectangular layout problem. Journal of Physics: Conference Series, 2138(1), 012007. DOI 10.1088/1742-6596/2138/1/012007. [Google Scholar] [CrossRef]

19. Wei, L., Zhu, W., Lim, A., Liu, Q., Chen, X. (2018). An adaptive selection approach for the 2D rectangle packing area minimization problem. Omega, 80, 22–30. DOI 10.1016/j.omega.2017.09.002. [Google Scholar] [CrossRef]

20. Hosseini, S., Al Khaled, A., Vadlamani, S. (2014). Hybrid imperialist competitive algorithm, variable neighborhood search, and simulated annealing for dynamic facility layout problem. Neural Computing and Applications, 25(7), 1871–1885. DOI 10.1007/s00521-014-1678-x. [Google Scholar] [CrossRef]

21. Afshar, M. H., Jabbari, E. (2008). Simultaneous layout and pipe size optimization of pipe networks using genetic algorithm. Arabian Journal for Science and Engineering, 33(2), 391–409. [Google Scholar]

22. Tsao, Y. C., Hung, C. H., Vu, T. L. (2021). Hybrid heuristics for marker planning in the apparel industry. Arabian Journal for Science and Engineering, 1–20. DOI 10.1007/s13369-020-05210-1. [Google Scholar] [CrossRef]

23. Huang, J., Wang, Z., Liu, J., Liao, T. (2020). Research on the layout of rectangular parts based on genetic algorithm. 2020 7th International Forum on Electrical Engineering and Automation (IFEEA), pp. 862–865. Hefei, China. [Google Scholar]

24. Turanoğlu, B., Akkaya, G. (2018). A new hybrid heuristic algorithm based on bacterial foraging optimization for the dynamic facility layout problem. Expert Systems with Applications, 98, 93–104. DOI 10.1016/j.eswa.2018.01.011. [Google Scholar] [CrossRef]

25. Liu, J., Zhang, H., He, K., Jiang, S. (2018). Multi-objective particle swarm optimization algorithm based on objective space division for the unequal-area facility layout problem. Expert Systems with Applications, 102, 179–192. DOI 10.11992/tis.202006042. [Google Scholar] [CrossRef]

26. Yang, X. S., Deb, S. (2009). Cuckoo search via lévy flights. 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), pp. 210–214. Coimbatore, India. DOI 10.1109/NABIC.2009.5393690. [Google Scholar] [CrossRef]

27. Dhal, K. G., Quraishi, M. I., Das, S. (2015). Performance analysis of chaotic lévy bat algorithm and chaotic cuckoo search algorithm for gray level image enhancement. Information Systems Design and Intelligent Applications, New Delhi: Springer. DOI 10.1007/978-81-322-2250-7_23. [Google Scholar] [CrossRef]

28. Mareli, M., Twala, B. (2018). An adaptive cuckoo search algorithm for optimisation. Applied Computing and Informatics, 14(2), 107–115. DOI 10.1016/j.aci.2017.09.001. [Google Scholar] [CrossRef]

29. Li, X., Yin, M. (2015). Modified cuckoo search algorithm with self adaptive parameter method. Information Sciences, 298, 80–97. DOI 10.1016/j.ins.2014.11.042. [Google Scholar] [CrossRef]

30. Mlakar, U., Fister Jr, I., Fister, I. (2016). Hybrid self-adaptive cuckoo search for global optimization. Swarm and Evolutionary Computation, 29, 47–72. DOI 10.1016/j.swevo.2016.03.001. [Google Scholar] [CrossRef]

31. Valian, E., Tavakoli, S., Mohanna, S., Haghi, A. (2013). Improved cuckoo search for reliability optimization problems. Computers & Industrial Engineering, 64(1), 459–468. DOI 10.1016/j.cie.2012.07.011. [Google Scholar] [CrossRef]

32. Tuba, M., Subotic, M., Stanarevic, N. (2011). Modified cuckoo search algorithm for unconstrained optimization problems. Proceedings of the 5th European Conference on European Computing Conference, pp. 263–268. Wisconsin, United States. [Google Scholar]

33. Wang, X., Pan, J. S., Chu, S. C. (2020). A parallel multi-verse optimizer for application in multilevel image segmentation. IEEE Access, 8, 32018–32030. DOI 10.1109/Access.6287639. [Google Scholar] [CrossRef]

34. Pan, J. S., Hu, P., Chu, S. C. (2019). Novel parallel heterogeneous meta-heuristic and its communication strategies for the prediction of wind power. Processes, 7(11), 845. DOI 10.3390/pr7110845. [Google Scholar] [CrossRef]

35. Dao, T. K., Pan, T. S., Pan, J. S. (2018). Parallel bat algorithm for optimizing makespan in job shop scheduling problems. Journal of Intelligent Manufacturing, 29(2), 451–462. DOI 10.1007/s10845-015-1121-x. [Google Scholar] [CrossRef]

36. Chu, S. C., Roddick, J. F., Pan, J. S. (2004). Ant colony system with communication strategies. Information Sciences, 167(1–4), 63–76. DOI 10.1016/j.ins.2003.10.013. [Google Scholar] [CrossRef]

37. Chu, S. C., Roddick, J. F., Pan, J. S. (2005). A parallel particle swarm optimization algorithm with communication strategies. Journal of Information Science and Engineering, 21(4), 809–818. [Google Scholar]

38. Abela, J. (1991). A parallel genetic algorithm for solving the school timetabling problem. Division of Information Technology, CSIRO, Citeseer. [Google Scholar]

39. Kong, L., Pan, J. S., Tsai, P. W., Vaclav, S., Ho, J. H. (2015). A balanced power consumption algorithm based on enhanced parallel cat swarm optimization for wireless sensor network. International Journal of Distributed Sensor Networks, 11(3), 729680. DOI 10.1155/2015/729680. [Google Scholar] [CrossRef]

40. Sun, Y., Pan, J. S., Hu, P., Chu, S. C. (2022). Enhanced equilibrium optimizer algorithm applied in job shop scheduling problem. Journal of Intelligent Manufacturing, 1–27. DOI 10.1007/s10845-021-01899-5. [Google Scholar] [CrossRef]

41. Liang, J., Qu, B., Suganthan, P., Hernández-Díaz, A. G. (2013). Problem definitions and evaluation criteria for the CEC 2013 special session on real-parameter optimization. Technical Report 201212, Computational Intelligence Laboratory, Zhengzhou University, Zhengzhou China; Technical Report, Nanyang Technological University, Singapore. https://www.al-roomi.org/multimedia/CEC_Database/CEC2013/RealParameterOptimization/CEC2013_RealParameterOptimization_TechnicalReport.pdf. [Google Scholar]

42. Kennedy, J., Eberhart, R. (1995). Particle swarm optimization. Proceedings of ICNN’95-International Conference on Neural Networks, 4, 1942–1948. [Google Scholar]

43. Mirjalili, S. (2016). SCA: A sine cosine algorithm for solving optimization problems. Knowledge-based Systems, 96, 120–133. DOI 10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]

44. Mirjalili, S., Lewis, A. (2016). The whale optimization algorithm. Advances in Engineering Software, 95, 51–67. DOI 10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

45. Mirjalili, S., Mirjalili, S. M., Lewis, A. (2014). Grey wolf optimizer. Advances in Engineering Software, 69, 46–61. DOI 10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]

46. Karaboga, D. (2005). An idea based on honey bee swarm for numerical optimization. Erciyes University, Engineering Faculty, Computer Engineering Department. https://abc.erciyes.edu.tr/pub/tr06_2005.pdf. [Google Scholar]

47. Storn, R., Price, K. (1997). Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 11(4), 341–359. DOI 10.1023/A:1008202821328. [Google Scholar] [CrossRef]

48. Lee, H. Y. (2012). Integrating simulation and ant colony optimization to improve the service facility layout in a station. Journal of Computing in Civil Engineering, 26(2), 259–269. DOI 10.1061/(ASCE)CP.1943-5487.0000128. [Google Scholar] [CrossRef]

49. Motaghi, M., Hamzenejad, A., Riyahi, L., Soheili, K. M. (2011). Optimization of hospital layout through the application of heuristic techniques (diamond algorithm) in Shafa hospital. International Journal of Management and Business Research, 1, 133–138. [Google Scholar]

50. Heragu, S. S., Alfa, A. S. (1992). Experimental analysis of simulated annealing based algorithms for the layout problem. European Journal of Operational Research, 57(2), 190–202. DOI 10.1016/0377-2217(92)90042-8. [Google Scholar] [CrossRef]

51. Gomes de Alvarenga, A., Negreiros-Gomes, F. J., Mestria, M. (2000). Metaheuristic methods for a class of the facility layout problem. Journal of Intelligent Manufacturing, 11(4), 421–430. DOI 10.1023/A:1008982420344. [Google Scholar] [CrossRef]

52. Lin, Q. L., Liu, H. C., Wang, D. J., Liu, L. (2015). Integrating systematic layout planning with fuzzy constraint theory to design and optimize the facility layout for operating theatre in hospitals. Journal of Intelligent Manufacturing, 26(1), 87–95. DOI 10.1007/s10845-013-0764-8. [Google Scholar] [CrossRef]

53. Wäscher, G., Haußner, H., Schumann, H. (2007). An improved typology of cutting and packing problems. European Journal of Operational Research, 183(3), 1109–1130. DOI 10.1016/j.ejor.2005.12.047. [Google Scholar] [CrossRef]

54. James, F. (1980). Monte carlo theory and practice. Reports on Progress in Physics, 43(9), 1145. DOI 10.1088/0034-4885/43/9/002. [Google Scholar] [CrossRef]

55. Raychaudhuri, S. (2008). Introduction to monte carlo simulation. 2008 Winter Simulation Conference, pp. 91–100. Miami, USA. [Google Scholar]

56. Jabeen, T., Jabeen, I., Ashraf, H., Jhanjhi, N., Mamoona, H. et al. (2022). A monte carlo based COVID-19 detection framework for smart healthcare. Computers, Materials, & Continua, 70(2), 2365–2380. DOI 10.32604/cmc.2022.020016. [Google Scholar] [CrossRef]

57. Wu, Q., Li, J., Long, L., Liu, L. (2021). Simulating the effect of temperature gradient on grain growth of 6061-T6 aluminum alloy via monte carlo potts algorithm. Computer Modeling in Engineering & Sciences, 129(1), 99–116. DOI 10.32604/cmes.2021.015669. [Google Scholar] [CrossRef]

58. Chu, S. C., Du, Z. G., Peng, Y. J., Pan, J. S. (2021). Fuzzy hierarchical surrogate assists probabilistic particle swarm optimization for expensive high dimensional problem. Knowledge-Based Systems, 220, 106939. DOI 10.1016/j.knosys.2021.106939. [Google Scholar] [CrossRef]

59. Tsai, P. W., Pan, J. S., Chen, S. M., Liao, B. Y. (2012). Enhanced parallel cat swarm optimization based on the taguchi method. Expert Systems with Applications, 39(7), 6309–6319. DOI 10.1016/j.eswa.2011.11.117. [Google Scholar] [CrossRef]

60. Zheng, W. M., Liu, N., Chai, Q. W., Chu, S. C. (2021). A compact adaptive particle swarm optimization algorithm in the application of the mobile sensor localization. Wireless Communications and Mobile Computing, 2021. DOI 10.1155/2021/1676879. [Google Scholar] [CrossRef]

61. Li, J., Zhou, Z., Wu, J., Li, J., Mumtaz, S. et al. (2019). Decentralized on-demand energy supply for blockchain in internet of things: A microgrids approach. IEEE Transactions on Computational Social Systems, 6(6), 1395–1406. DOI 10.1109/TCSS.6570650. [Google Scholar] [CrossRef]

62. Ji, B., Li, Y., Cao, D., Li, C., Mumtaz, S. et al. (2020). Secrecy performance analysis of uav assisted relay transmission for cognitive network with energy harvesting. IEEE Transactions on Vehicular Technology, 69(7), 7404–7415. DOI 10.1109/TVT.25. [Google Scholar] [CrossRef]

63. Duan, W., Gu, J., Wen, M., Zhang, G., Ji, Y. et al. (2020). Emerging technologies for 5G-IoV networks: Applications, trends and opportunities. IEEE Network, 34(5), 283–289. DOI 10.1109/MNET.001.1900659. [Google Scholar] [CrossRef]

64. Goudarzi, S., Kama, N., Anisi, M. H., Zeadally, S., Mumtaz, S. (2019). Data collection using unmanned aerial vehicles for Internet of Things platforms. Computers & Electrical Engineering, 75, 1–15. DOI 10.1016/j.compeleceng.2019.01.028. [Google Scholar] [CrossRef]