 Open Access
Open Access
ARTICLE
Secrecy Outage Probability for Two-Way Integrated Satellite Unmanned Aerial Vehicle Relay Networks with Hardware Impairments
1 College of Public Management, China University of Mining and Technology, Xuzhou, 221116, China
2 School of Space Information, Space Engineering University, Beijing, 101407, China
* Corresponding Author: Kefeng Guo. Email:
(This article belongs to the Special Issue: Recent Advances in Backscatter and Intelligent Reflecting Surface Communications for 6G-enabled Internet of Things Networks)
Computer Modeling in Engineering & Sciences 2023, 135(3), 2515-2530. https://doi.org/10.32604/cmes.2023.024857
Received 09 June 2022; Accepted 14 July 2022; Issue published 23 November 2022
Abstract
In this paper, we investigate the secrecy outage performance for the two-way integrated satellite unmanned aerial vehicle relay networks with hardware impairments. Particularly, the closed-form expression for the secrecy outage probability is obtained. Moreover, to get more information on the secrecy outage probability in a high signal-to-noise regime, the asymptotic analysis along with the secrecy diversity order and secrecy coding gain for the secrecy outage probability are also further obtained, which presents a fast method to evaluate the impact of system parameters and hardware impairments on the considered network. Finally, Monte Carlo simulation results are provided to show the efficiency of the theoretical analysis.Keywords
It is reported that satellite communication (SatCom) is considered to be a wishing way for the sixth generation (6G) and beyond next generation (BNG) wireless communication system for its special characters, such as the wide coverage and particular services [1–5]. Owing to similar reasons, it can make up for the shortage of unmanned aerial vehicle (UAV) networks along with the high data transmission and wide coverage. Based on this foundation, to both utilize the advantage of the SatCom and UAV networks, the framework for the integrated satellite UAV relay network (ISUAVRN) appears, which is considered the major part of the future wireless communication networks [6,7]. Besides, owing to the transmission beam’s wide coverage, many users or relays existed in one beam [7–11]. In [7], a selection scheme based on the threshold was provided to keep the balance between the system performance and system complexity for the considered network. Furthermore, the outage probability (OP) was studied. In [8], one partial selection scheme was utilized to enhance the system performance for the considered networks. In [9], the authors studied the OP for the cognitive networks, which combined the satellite and the terrestrial networks. In [10], the OP was researched for the considered networks along with the secondary network selection scheme under the cognitive technology. In [11], the authors gave a terrestrial and user scheduling scheme based on the maximal performance for the ISUAVRNs in the presence of many terrestrial relays and many users. In [12], the ergodic capacity for the ISUAVRNs with a selection scheme and multiple terrestrial relays was researched. In [13], the OP was investigated for the ISUAVRNs with multiple users and an opportunistic user scheduling scheme. To enhance the spectrum efficiency and time utilization, a two-way relay technique is proposed for the ISUAVRNs [14]. In [15], the OP was researched for the ISUAVRNs with hardware impairments (HIs) and the two-way terrestrial relay. In [16], the OP was analyzed for the ISUAVRs in the presence of many two-way terrestrial relays and a partial selection scheme. In [17], the OP was investigated for the considered ISUAVRNs with multiple terrestrial relays and an opportunistic selection scheme under the non-orthogonal multiple access scenario. However, due to the inherent characters of wireless communications particularly for the SatCom, the secrecy issue has been regarded as the major point for the SatCom [18]. The physical layer security (PLS) is considered as the hopeful method to investigate the difference between the eavesdroppers’ and legitimate channels, which is a popular research issue over recent years [19,20]. In [19], a proposed beamforming (BF) scheme was utilized for the cognitive ISUAVRNs to enhance the secrecy performance. In [21], the authors researched the secrecy-energy efficient hybrid BF scheme for the ISUAVRNs. In [22], the non-ideal channel state information (CSI) and cognitive technology were both investigated for the secrecy ISUAVRNs along with secrecy performance. In practical systems, all nodes are not often ideal, which means they always suffer the I/Q imbalance, phase noise, and amplifier non-linearities [23–25], which results in the HIs in the transmission nodes. In [26], all the HIs issues are concluded, which leads to a general HIs model, widely utilized for many former works [27–31]. Above all, to the authors’ best effort, the investigation for the effects of two-way terrestrial relays on the secrecy ISUAVRNs with HIs is still not published, which motivates our paper.
From the former discussions, by considering the two-way UAV relay and an eavesdropper into our sight, we investigate the secrecy performance for the considered network. The contributions of this paper are presented in the following:
• By utilizing the two-way UAV relay and an eavesdropper into consideration, the framework for the secrecy ISUAVRN is founded. Besides, the decode-and-forward (DF) mode is used in the UAV to help the source to transmit the signals. Due to the heavy fading and other obstacle reasons, no direct link is assumed for the legitimate transmission link for the two sources. In addition, all the nodes are assumed to suffer from the HIs.
• Based on the considered system model, the detailed analysis for the secrecy outage probability (SOP) is obtained, which gives the easy method to investigate the SOP. Besides, these theoretical results can direct the engineering guide.
• To derive the further results of the system parameters on the SOP for the system, the asymptotic behaviors for the SOP are derived, which provide the secrecy diversity and order secrecy coding gain.
The remaining of this paper is shown in the following. A detailed illustration for the considered system is given in Section 2. The analysis for the secrecy OP is derived in Section 3. Some computer simulations namely Monte Carlo (MC) results are given in Section 4 to show the efficiency of the analytical results. The conclusion of the work is provided in Section 5.
Notations:

As plotted in Fig. 1, we consider an ISUAVRN with HIs in this paper, which contains a satellite source
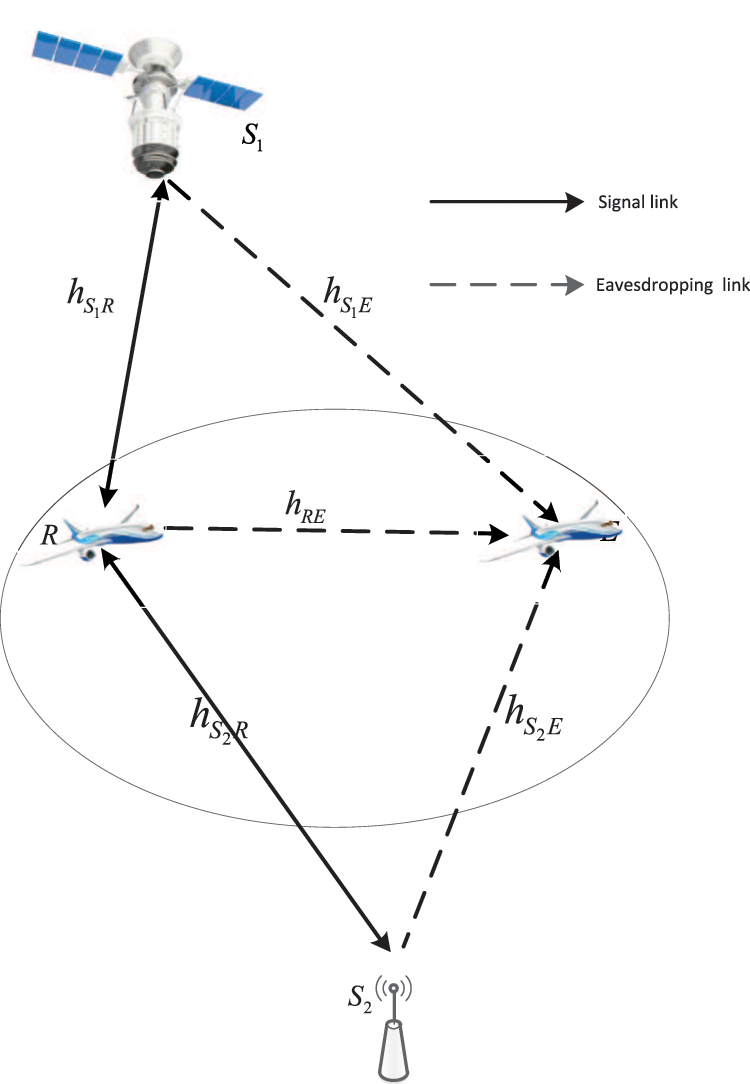
Figure 1: The system model description
It will use two time slots for the whole transmission. During the first time slot,
where
Since E and R are located in the same transmission beam, the overhear signal at E in the first time slot is shown as
where
In the second time slot, owing to the utilized DF protocol, the UAV relay will use some techniques to decode the signals received and then re-transmit the re-encoded signal to
where
As the same assumption, R and E are located in the similar transmission beam. Thus, the obtained signal at E in the second time slot is represented as
where
By utilizing Eqs. (1) and (3), the obtained signal-to-interference-plus-noise ratio (SINR) at R from the p-th source is obtained as
where
The derived signal-to-noise ratio (SNR) at
where
With the help of Eqs. (2) and (4), the obtained SNR at E is, respectively, obtained as
where
According to [32], the capacity for secrecy performance has the definition which is shown as the difference between the capacity of the legitimate users’ channel and the eavesdroppers’ channel. By utilizing Eqs. (5)–(9), the secrecy capacity for the considered network is represented as
where
The detailed analysis for the SOP will be obtained in this part. At first, the channel model for the transmission link is presented.
3.1.1 The Terrestrial Transmission Link
The channel model for the terrestrial transmission link is modeled as independent and identically distribution (i.i.d) Rayleigh fading. From [33], the PDF and CDF of
and
where
3.1.2 The Satellite Transmission Link
The geosynchronous Earth orbit (GEO) satellite is taken for the analysis. In addition, we also consider the satellite having multiple beams for the considered system model. Particularly, time division multiple access (TDMA) [34] scheme is utilized in the considered model, which means that only one UAV R is suitable to forward the information signal at the next time slot.
The channel coefficient
where
where
With help of [35],
where
where
For
With the help of [8], the PDF for
where
Relied on Eq. (17) and utilizing [11], the CDF of
3.1.3 Secrecy Outage Probability
From [18], the SOP defined as
where
For
For
Firstly, with the help of
From Eq. (22), the first consideration is to obtain the CDF for
Then by utilizing Eq. (5), the CDF for
With the help of Eq. (17) with
Then, after some mathematic steps,
Next, with the help of [39],
Then, recalling Eq. (22), Eq. (22) can be re-written as
Then, it should be mentioned that in Eqs. (23) and (24), y should be satisfied with the following condition, which is
where
However, try the authors’ best efforts, it is too hard to obtain the closed-form expression of Eq. (29), then by utilizing [35] and utilizing the Gaussian-Chebyshev quadrature [40], by inserting Eqs. (24) and (23) into Eq. (29), it can be derived as
where
and
By utilizing the similar ways, the closed-form expressions for the
where
and
where
and
where
and
Then, by substituting Eqs. (30)–(33) into Eqs. (19)–(21), respectively. The closed-form expression for the SOP will be obtained, which is omitted here.
In what follows, the asymptotic behaviors for the SOP is obtained. When
and
Then by substituting Eqs. (34)–(37) into Eqs. (19)–(21), the asymptotic expression will be derived.
Then from the final asymptotic SOP expression, the secrecy diversity order and secrecy coding gain are respectively derived as
During this part, some representative MC simulations are provided to prove the efficiency of the theoretical analysis. Through these results, the impacts of channel parameters are evaluated. Without loss of any generality, we set


Fig. 2 examines the SOP vs.
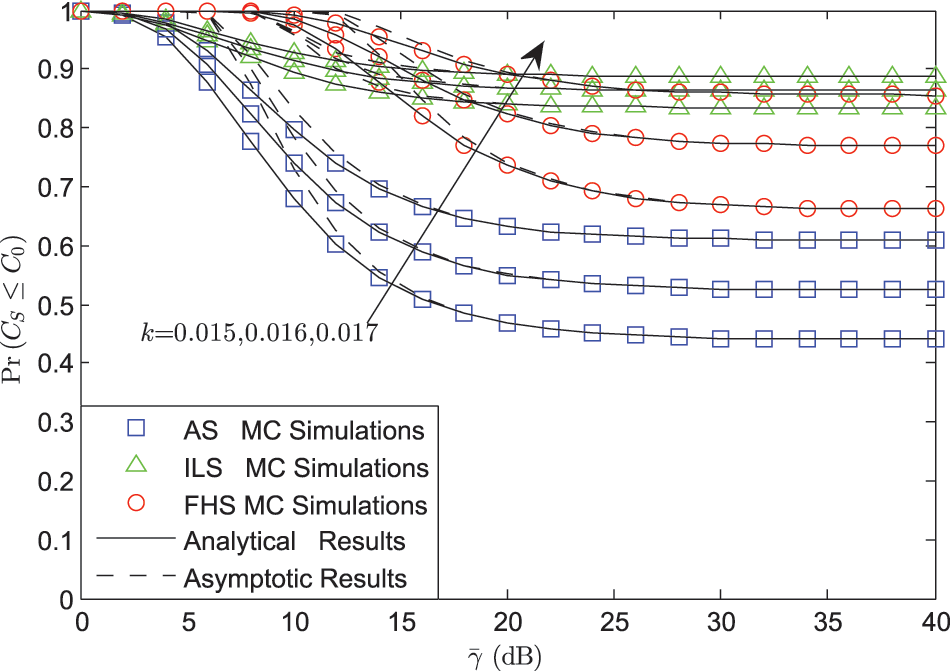
Figure 2: SOP vs.
Fig. 3 represents the SOP vs.
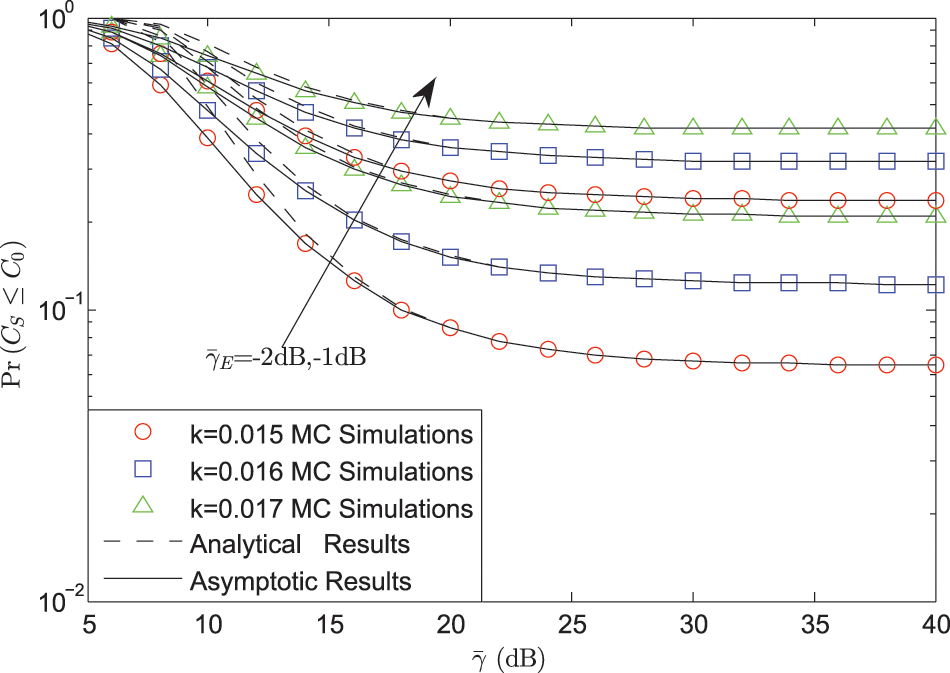
Figure 3: SOP vs.
Fig. 4 plots the SOP vs.
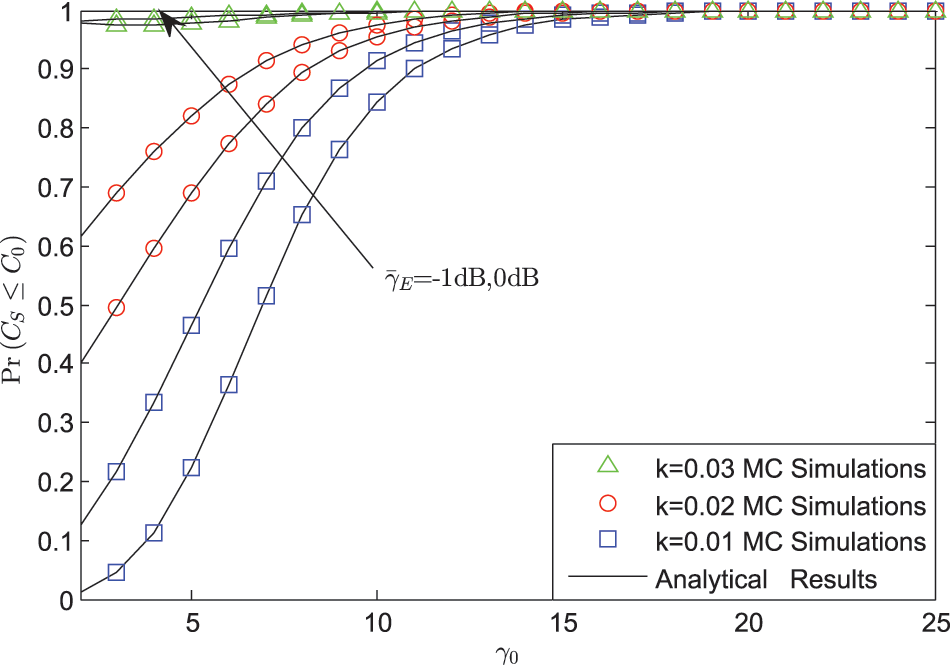
Figure 4: SOP vs.
This paper investigated the SOP for an integrated satellite UAV relay network with HIs. Especially, the closed-form and asymptotic behaviors for the SOP were derived. Firstly, it was derived that the SOP would have worse performance with threshold being larger; Secondly, it was found that the SOP would be larger with a larger
Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.
Funding Statement: This work is supported by the Natural Science Foundation of China under Grant No. 62001517.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1We should know that, during this paper, only one antenna is assumed, however the derived results are still fit for the case with many antennas.
2Although this paper just considers one eavesdropper, the derived results are still fit for the model with multiple eavesdroppers. Besides, the model with multiple eavesdroppers will be investigated in our near future.
3Owing to some reasons, direct transmission link between two sources is not available.
4It should be mentioned that, the SR channel is a famous channel model [8,10], which comes from the practical estimation date [37,38].
References
1. Li, B., Fei, Z., Zhou, C., Zhang, Y. (2020). Physical layer security in space information networks: A survery. IEEE Internet of Things Journal, 69(5), 33–52. DOI 10.1109/JIOT.6488907. [Google Scholar] [CrossRef]
2. Guo, K., Lin, M., Zhang, B., Zhu, W. P., Wang, J. B. et al. (2019). On the performance of LMS communication with hardware impairments and interference. IEEE Transactions on Communications, 67(2), 1490–1505. DOI 10.1109/TCOMM.2018.2878848. [Google Scholar] [CrossRef]
3. Guo, K., Dong, C., An, K. (2022). NOMA-Based cognitive satellite terrestrial relay networks: Secrecy performance under channel estimation errors and hardware impairments. IEEE Internet of Things Journal, 9(18), 17334–17347. DOI 10.1109/JIOT.2022.3157673. [Google Scholar] [CrossRef]
4. Liu, R., Guo, K., An, K., Zhu, S. (2022). NOMA-Based overlay cognitive integrated satellite-terrestrial networks with secondary networks selection. IEEE Transactions on Vehicular Technology, 71(2), 2187–2192. DOI 10.1109/TVT.2021.3122029. [Google Scholar] [CrossRef]
5. Guo, K., An, K. (2022). On the performance of RIS-assisted integrated satellite-UAV-terrestrial networks with hardware impairments and interference. IEEE Wireless Communications Letters, 11(1), 131–135. DOI 10.1109/LWC.2021.3122189. [Google Scholar] [CrossRef]
6. Kodheli, O., Lagunas, E., Maturo, N., Sharma, S. K., Shankar, B. et al. (2021). Satellite communications in the new space era: A survey and future challenges. IEEE Communications Surveys Tutorials, 23(1), 70–109. DOI 10.1109/COMST.9739. [Google Scholar] [CrossRef]
7. Guo, K., Lin, M., Zhang, B., Wang, J. B., Wu, Y. et al. (2020). Performance analysis of hybrid satellite-terrestrial cooperative networks with relay selection. IEEE Transactions on Vehicular Technology, 69(8), 9053–9067. DOI 10.1109/TVT.25. [Google Scholar] [CrossRef]
8. Guo, K., An, K., Zhang, B., Huang, Y., Guo, D. et al. (2019). On the performance of the uplink satellite multi-terrestrial relay networks with hardware impairments and interference. IEEE Systems Journal, 13(3), 2297–2308. DOI 10.1109/JSYST.4267003. [Google Scholar] [CrossRef]
9. An, K., Lin, M., Zhu, W. P., Huang, Y., Zheng, G. (2016). Outage performance of cognitive hybrid satellite-terrestrial networks with interference constraint. IEEE Transactions on Vehicular Technology, 65(11), 9397–9404. DOI 10.1109/TVT.2016.2519893. [Google Scholar] [CrossRef]
10. Sharma, P. K., Upabhat, P. K., da Costa, D. B., Bithas, P. S., Kanatas, A. G. (2017). Performance analysis of overlay spectrum sharing in hybrid satellite-terrestrial systems with secondary network selection. IEEE Transactions on Wireless Communications, 16(10), 6586–6601. DOI 10.1109/TWC.2017.2725950. [Google Scholar] [CrossRef]
11. Upadhyay, P. K., Sharma, P. K. (2016). Max-max user-relay selection scheme in multiuser and multirelay hybrid satellite-terrestrial relay systems. IEEE Communications Letters, 20(2), 268–271. DOI 10.1109/LCOMM.2015.2502599. [Google Scholar] [CrossRef]
12. Zhao, Y., Xie, L., Chen, H., Wang, K. (2017). Ergodic channel capacity analysis of downlink in the hybrid satellite-terrestrial cooperative system. Wireless Personal Communications, 96(3), 3799–3815. DOI 10.1007/s11277-017-4207-2. [Google Scholar] [CrossRef]
13. An, K., Lin, M., Liang, T. (2015). On the performance of multiuser hybrid satellite-terrestrial relay networks with opportunistic scheduling. IEEE Communications Letters, 19(10), 1722–1725. DOI 10.1109/LCOMM.2015.2466535. [Google Scholar] [CrossRef]
14. Tang, X., An, K., Guo, K., Wang, S., Wang, X. et al. (2019). On the performance of two-way multiple relay non-orthogonal multiple access based networks with hardware impairments. IEEE Access, 7, 128896–128909. DOI 10.1109/Access.6287639. [Google Scholar] [CrossRef]
15. Guo, K., Zhang, B., Huang, Y., Guo, D. (2017). Performance analysis of two-way satellite terrestrial relay networks with hardware impairments. IEEE Wireless Communications Letters, 6(4), 430–433. DOI 10.1109/LWC.2017.2700797. [Google Scholar] [CrossRef]
16. Zeng, W., Zhang, J., Ng, D., Ai, B., Zhong, Z. (2019). Two-way hybrid terrestrial-satellite relaying systems: Performance analysis and relay selection. IEEE Transactions on Vehicular Technology, 68(7), 7011–7023. DOI 10.1109/TVT.2019.2916992. [Google Scholar] [CrossRef]
17. Guo, K., An, K., Zhang, B., Guo, D. (2018). Performance analysis of two-way satellite multi-terrestrial relay networks with hardware impairments. Sensors, 18(5), 1–19. DOI 10.3390/s18051574. [Google Scholar] [CrossRef]
18. Guo, K., An, K., Zhang, B., Huang, Y., Tang, X. et al. (2020). Physical layer security for multiuser satellite communication systems with threshold-based scheduling scheme. IEEE Transactions on Vehicular Technology, 69(5), 5129–5141. DOI 10.1109/TVT.2020.2979496. [Google Scholar] [CrossRef]
19. Li, B., Fei, Z., Chu, Z., Zhou, F., Wong, K. K. et al. (2018). Robust chance-constrained secure transmission for cognitive satellite-terrestrial networks. IEEE Transactions on Vehicular Technology, 67(5), 4208–4219. DOI 10.1109/TVT.2018.2791859. [Google Scholar] [CrossRef]
20. Li, B., Fei, Z., Xu, X., Chu, Z. (2018). Resource allocations for secure cognitive satellite-terrestrial networks. IEEE Wireless Communications Letters, 7(1), 78–81. DOI 10.1109/LWC.2017.2755014. [Google Scholar] [CrossRef]
21. Lin, Z., Lin, M., Champagne, B., Zhu, W. P., Naofal, A. D. (2021). Secrecy-energy efficient hybrid beamforming for satellite-terrestrial integrated networks. IEEE Transactions on Communications, 69(9), 6345–6360. DOI 10.1109/TCOMM.2021.3088898. [Google Scholar] [CrossRef]
22. An, K., Lin, M., Ouyang, J., Zhu, W. P. (2016). Secure transmission in cognitive satellite terrstrial networks. IEEE Journal on Selected Areas in Communications, 34(11), 3025–3037. DOI 10.1109/JSAC.2016.2615261. [Google Scholar] [CrossRef]
23. Li, X., Huang, M., Liu, Y., Menon, V. B., Paul, A. et al. (2021). I/Q imbalance aware nonlinear wireless-powered relaying of B5G networks: Security and reliability analysis. IEEE Transactions Network Science and Engineering, 8(4), 2995–3008. DOI 10.1109/TNSE.2020.3020950. [Google Scholar] [CrossRef]
24. Li, X., Zheng, Y., Alshehri, M. D., Hai, L., Balasubramanian, V. et al. (2021). Cognitive AmBC-NOMA IoV-MTS networks with IQI: Reliability and security analysis. IEEE Transactions Intelligent Transportation Systems. DOI 10.1109/TITS.2021.3113995. [Google Scholar] [CrossRef]
25. Li, X., Li, J., Liu, Y., Ding, Z., Nallanathan, A. (2020). Residual transceiver hardware impairments on cooperative NOMA networks. IEEE Transactions on Wireless Communications, 19(1), 680–695. DOI 10.1109/TWC.7693. [Google Scholar] [CrossRef]
26. Bjornson, E., Matthaiou, M., Debbah, M. (2013). A new look at dual-hop relaying: Performance limits with hardware impairments. IEEE Transactions on Communications, 61(11), 4512–4525. DOI 10.1109/TCOMM.2013.100913.130282. [Google Scholar] [CrossRef]
27. Zhang, J., Dai, L., Zhang, X., Bjornson, E., Wang, Z. (2016). Achievable rate of rician large-scale MIMO channels with transceiver hardware impairments. IEEE Transactions on Vehicular Technology, 65(10), 8800–8806. DOI 10.1109/TVT.2015.2504428. [Google Scholar] [CrossRef]
28. Budimir, D., Neskovic, N., Cabarkapa, M. (2016). Hardware impairments impact on fixed-gain AF relaying performance in Nakagami-m fading. Electronics Letters, 52(2), 121–122. DOI 10.1049/el.2015.3378. [Google Scholar] [CrossRef]
29. Duy, T. T., Duong, T. Q., da Costa, D. B., Bao, V. N. Q., Elkashlan, M. (2015). Proactive relay selection with joint impact of hardware impairments and co-channel interference. IEEE Transactions on Communications, 63(5), 1594–1606. DOI 10.1109/TCOMM.2015.2396517. [Google Scholar] [CrossRef]
30. Deng, C., Liu, M., Li, X., Liu, Y. (2021). Residual transceiver hardware impairments on cooperative NOMA networks. IEEE Systems Journal, 19(1), 680–695. [Google Scholar]
31. Li, X., Zhao, M., Zeng, M., Mumtaz, S., Menon, V. G. et al. (2021). Hardware impaired ambient backscatter NOMA system: Reliability and security. IEEE Transactions on Communications, 69(4), 2723–2736. DOI 10.1109/TCOMM.2021.3050503. [Google Scholar] [CrossRef]
32. Guo, K., Lin, M., Zhang, B., Ouyang, J., Zhu, W. P. (2018). Secrecy performance of satellite wiretap channels with multi-user opportunistic scheduling. IEEE Wireless Communications Letters, 7(6), 1054–1057. DOI 10.1109/LWC.2018.2859385. [Google Scholar] [CrossRef]
33. Guo, K., An, K., Zhang, B., Huang, Y., Guo, D. (2018). Physical layer security for hybrid satellite terrestrial relay networks with joint relay selection and user scheduling. IEEE Access, 6, 55815–55827. DOI 10.1109/ACCESS.2018.2872718. [Google Scholar] [CrossRef]
34. Arnau, J., Christopoulos, D., Chatzinotas, S., Mosquera, C., Ottersten, B. (2014). Performance of the multibeam satellite return link with correlated rain attenuation. IEEE Transactions on Wireless Communications, 13(11), 6286–6299. DOI 10.1109/TWC.2014.2329682. [Google Scholar] [CrossRef]
35. Guo, K., An, K., Zhou, F., Theodoros, A. T., Zheng, G. et al. (2021). On the secrecy performance of NOMA-based integrated satellite multipleterrestrial relay networks with hardware impairments. IEEE Transactions on Vehicular Technology, 70(4), 3661–3676. DOI 10.1109/TVT.2021.3068062. [Google Scholar] [CrossRef]
36. Abdi, A., Lau, W. C., Alouini, M. S., Kaveh, M. (2003). A new simple model for land mobile satellite channels: First-and second-order statistics. IEEE Transactions on Wireless Communications, 2(3), 519–528. DOI 10.1109/TWC.2003.811182. [Google Scholar] [CrossRef]
37. Loo, C. (1985). A statistical model for a land mobile satellite link. IEEE Transactions on Vehicular Technology, 34(3), 122–127. [Google Scholar]
38. Loo, C., Butterworth, J. S. (1988). Land mobile satellite channel measurements and modeling. Proceeding of the IEEE, 86, 1442–1463. [Google Scholar]
39. Gradshteyn, I. S., Ryzhik, I. M. (2007). Table of integrals, series and products. Boston, USA: Academic Press. [Google Scholar]
40. Abramowitz, M., Stegun, I. A. (1972). Handbook of mathematical functions with formulas, graphs, and mathematical tables. Florida, USA: CRC Press. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools