The Effects of the Particle Size Ratio on the Behaviors of Binary Granular Materials

1  Introduction

A granular material generally refers to a collection of a large number of discrete solid particles larger than 1 μ m in size, such as sand and soil. The unique mechanical properties of granular materials have attracted the attention of a large number of researchers. In the past two decades, a considerable number of studies have been carried out to investigate and predict the mechanical behaviors of granular materials [1–6]. It has been recognized that the macroscopic behavior of granular materials is controlled by the microstructure characteristics, such as particle packing [1], particle shape [2], and particle size [3,4].

Binary granular materials are a kind of common granular materials composed of particles of two different sizes. Generally, the size ratio of small particles to large particles (PSR) and the volume fraction of small particles (VS) are key factors affecting the properties of binary granular materials [7–13]. The application of binary granular materials with different packing methods is different. For random packing, binary granular materials can be a simplified model of a well-graded mixture [7]. Many studies have reported the mechanical properties of binary particle mixture with random packing based on Discrete Element Method (DEM) [14–26]. Ogarko et al. [8] found that in the case of isotropic compression, any polydisperse mixtures can be replaced by equivalent bidisperse mixtures when the size distribution moments are matched. Wiącek [23] experimentally and numerically studied the effects of the PSR and VS on the geometrical properties of binary granular mixtures, and found a strong relationship between the coordination number and the VS of binary mixtures. Kumar et al. [9], Zhu et al. [24] and Ng et al. [25] found that the modulus is related to PSR and VS. Ueda et al. [7] explored the PSR and VS of the binary mixture to the shear resistance, and identified the threshold VS, which determines whether the mechanical contribution of large or small particles can be negligible. In addition, they found that the contribution of the large particles disappears when their average spacing with respect to the small particle size is around 2. Nie et al. [26] explored the effects of the PSR and VS on the internal stability of binary mixtures, and demonstrated that the internal stability of binary mixtures generally decreases with decreasing PSR and increases with increasing VS.

For regular packing, binary granular materials are called binary granular crystals or metamaterials. At present, the properties of wave or acoustics in binary granular crystals are mainly focused [12,13], which is widely used in building shock absorption and sound insulation. However, in some engineering applications, such as for building exterior walls, a certain bearing capacity of binary granular metamaterials is required. However, there are few reports on the static properties of binary granular metamaterials. Due to the need for contact between adjacent particles and the limitation of geometric space, the PSR of binary granular metamaterials varies within a small range. In this case, whether PSR is a key factor affecting the behavior of binary granular materials remains to be investigated.

In this study, the strength and deformation characteristics of binary granular materials with different packing structures in a quasi-static state are concerned. Which is of great significance for the design of metamaterials and the study of well-graded mixtures. The PSR ranges from 0.5 to 0.9 in binary granular materials according to the actual situation in binary granular crystals. Binary granular materials with different packing structures are focused on, which are regular packing, layered packing, and random packing. Their quasi-static mechanical properties are investigated based on DEM under biaxial loading in 2-dimensional. The effect of PSR on their strength and deformation characteristics at different confining stress are discussed.

2  Discrete Element Method and Numerical Samples

2.1 Discrete Element Method

Discrete element method (DEM) was initiated by Cundall et al. in 1979 [27]. The cores of discrete element method are particle motion equations and contact models between particles.

The motion equation of a particle A can be written according to Newton’s second law as:

mx¨=∑k=1NcFkc+Fe(1)

Iθ˙=∑k=1NcFkc×(Xkc−Xp)+Me(2)

where m and I are the mass and moment of inertia of the particle, respectively, x¨ is the translation acceleration and θ˙ is the angular acceleration, Fkc is the contact force acting on the particle at the kth contact point, and Xkc−Xp the vector connecting the contact point Xkc to the center position Xp, Fe, Me are the external force and external moment acting on the particle A, respectively, Nc is the number of contacts on the particle. The calculation of contact force on the particles is determined by the contact model.

In this study, Hertz-Mindlin contact law is used to calculate the contact force between particles. As shown in Fig. 1, the contact force is resolved into normal force Fnc and shear force Fsc:

Fc=Fnc+Fsc(3)

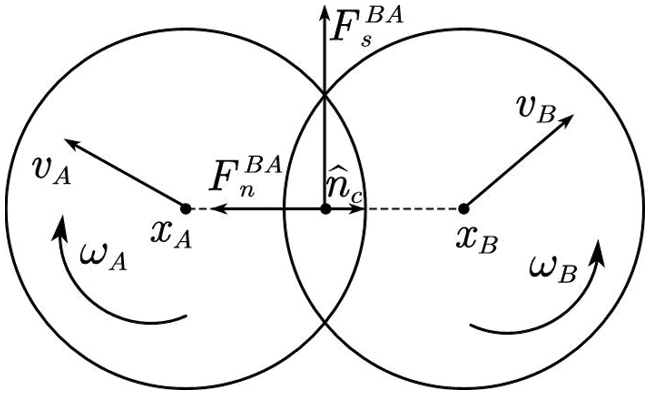
Figure 1: Sketch of contact model between particles

The normal force is related to the overlap of two particles:

Fnc=2G∗2R∗3(1−ν∗)δc3/2(4)

where δc is the normal overlap, R∗, ν∗ and G∗ are the effective contact radius, Poisson’s ratio, and shear modulus, respectively. The effective contact radius, Poisson’s ratio, and shear modulus are computed as:

R∗=(12R(A)+12R(B))−1(5)

v∗=4G′−E′2G′−E′(6)

G∗=2G′(2−v∗)(7)

with

E′=(1−υ(A)2G(A)+1−υ(B)2G(B))−1(8)

G′=(2−υ(A)G(A)+2−υ(B)G(B))−1(9)

where R is the radii of the contacting particle, E, G and υ are the Young’ modulus, the shear modulus and Poisson’s ratio respectively, the superscripts A and B denote the two particles in contact.

The calculation of Fsc is carried out in incremental form. The current shear force Fsc,∗ is obtained by summing the increments ΔFsc:

Fsc,∗=(Fsc)0+ΔFsc(10)

ΔFsc=2G∗2R∗Δδs(2−υ)δc(11)

where Δδs is the relative shear increment. (Fsc)0 is the shear force at last step. In addition, the shear force is restrained by Coulomb’s friction law:

Fsc={Fsc,∗,if‖Fsc,∗‖≤μ‖Fnc‖μ‖Fnc‖Fsc,∗‖Fsc,∗‖,otherwise(12)

where μ is the friction coefficient.

2.2 Numerical Samples

In this section, Numerical samples of binary granular materials with three packing structures were established. The size of the samples is about 1.5 m × 2 m. In all samples, the radius of large particles is R = 0.01 m, and the radius of small particles increases from r = 0.5 R to r = 0.9 R. With the decrease in the regularity of the packing structure, three different packing arrangements are generated, which are regular packing, layered packing, and random packing, as shown in Fig. 2. In the regular packing, we adopted the same packing method as Wang et al. [12], filled the small particles in the square array of large particles to generate regular packing structure, as shown in Fig. 2a. When PSR is 1, the packing structure is hexagonal packing with single particle size. The VS for regular binary mixtures are 18.32%, 25.97%, 32.28%, 38.35% and 44.01% for PSR of 0.5, 0.6, 0.7, 0.8 and 0.9, respectively. In the layered packing, the sample is generated by stacking three large particle layers and two small particle layers, and each particle layer results from a hexagonal packing of particles, as shown in Fig. 2b. And the layered samples with different PSR have the same VS of 40%. In the random packing, the samples are generated by random packing of large and small particles with VS of 50%, and samples with different PSR have the same initial porosity of 0.15, as shown in Fig. 2c.

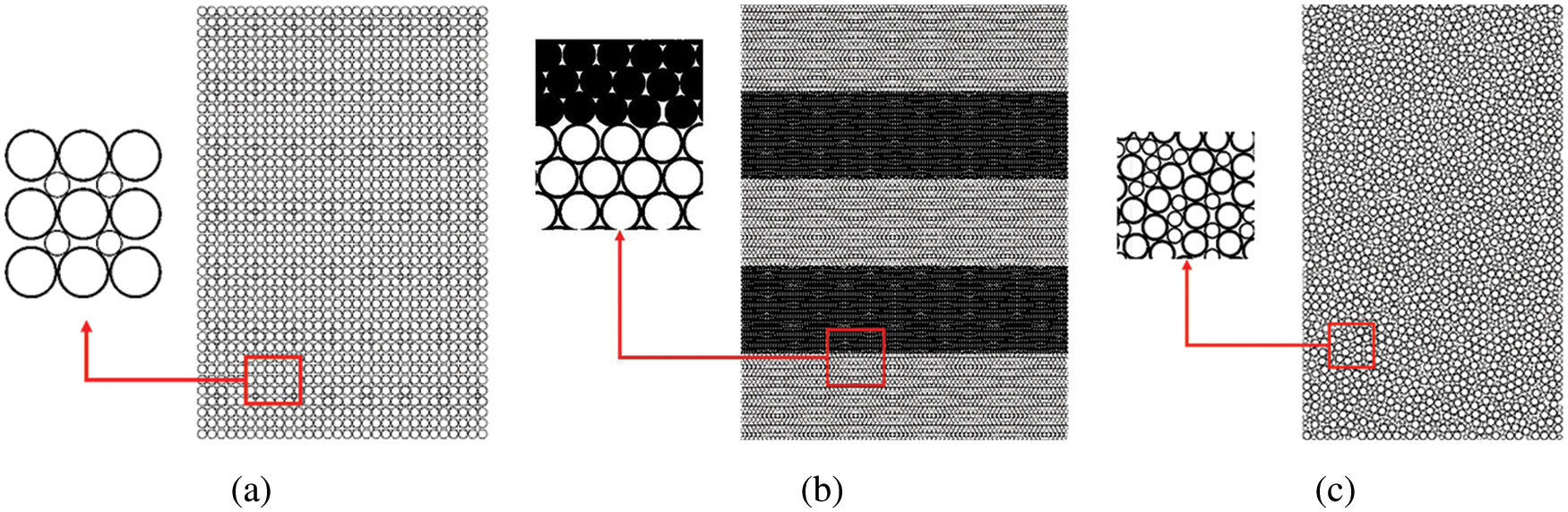
Figure 2: Three arrangement methods: (a) regular packing, (b) layered packing, and (c) random packing

The biaxial test is widely used in the study of granular materials, especially in DEM numerical simulation, as it is easier to visualize particle interactions in two dimensions, and the results are valid for 3-dimensional analysis. The biaxial test is regarded as a simplification of the triaxial test, so a series of biaxial tests for granular samples is performed, as shown in Fig. 3. During biaxial tests based on DEM, firstly rigid plates were manipulated by a servo-controlled mechanism to reach the initial confining pressure and complete the consolidation process. And then the loading was applied by the displacement of the rigid plates at top and bottom, and the rigid plates on the sides keep the confining pressure constant. Loading ends when the target axial strain is reached. The axial strain (ε) is defined as the ratio of the vertical displacement of the rigid plates at top and bottom (Δl) to the height of the sample (l0) after consolidation. In this study, the loading speed of the rigid plates at top and bottom was controlled as v=0.5\% ×l0m/s. Besides, the same microscopic parameters as Wang et al. [12] were used for simulation, as shown in Table 1.

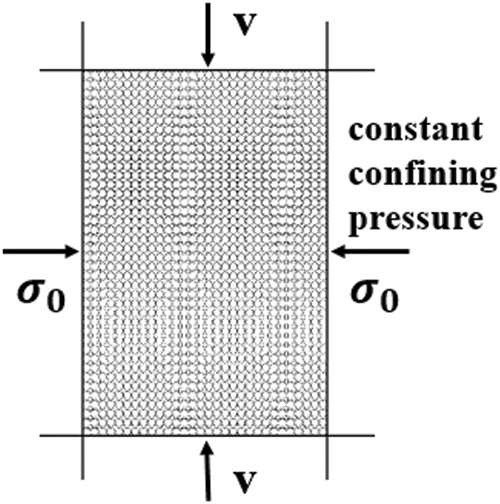
Figure 3: The biaxial compression loading modes

3  Numerical Results and Discussion

The numerical results for each granular sample, including the axial stress-strain curve, axial-volumetric strain curve, and the distribution of the effective strain [28,29] were presented. For the definition of the effective strain, see Appendix A.

3.1 Regular Granular Samples

A series of DEM simulations were carried out for regular granular samples with different PSR at different confining stress. The deviatoric stress-axial strain curves of regular granular samples with different PSR under different confining stress levels are shown in Figs. 4a–4d, and the relationship between peak stress and PSR is shown in Fig. 5a. It can be seen that with the increase of PSR, the peak deviatoric stress and corresponding axial strain increase. After reaching the peak deviatoric stress, with the increase of axial strain, the deviatoric stress decreases rapidly. The initial modulus increases with increasing PSR, and the peak deviatoric stress and corresponding axial strain increase with the increase of confining pressure stress level. Notice that regular granular samples exhibit strong brittle behavior, a similar phenomenon can be found in the study of O’Sullivan et al. [30], which is related to the rapid destruction of regular granular samples.

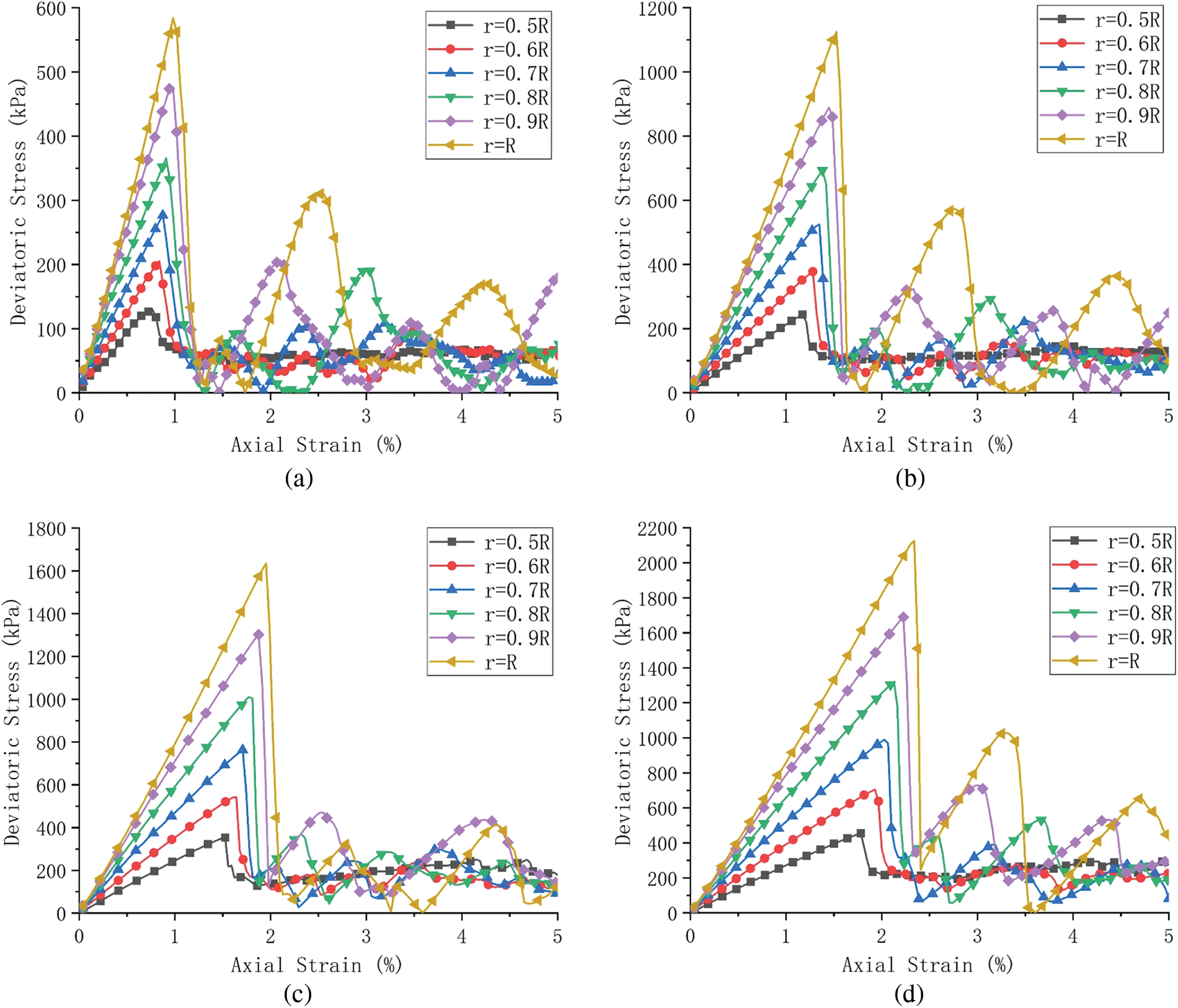
Figure 4: Deviatoric stress-axial strain curves of regular granular samples under different confining stress levels: (a) 100 kPa, (b) 200 kPa, (c) 300 kPa and (d) 400 kPa

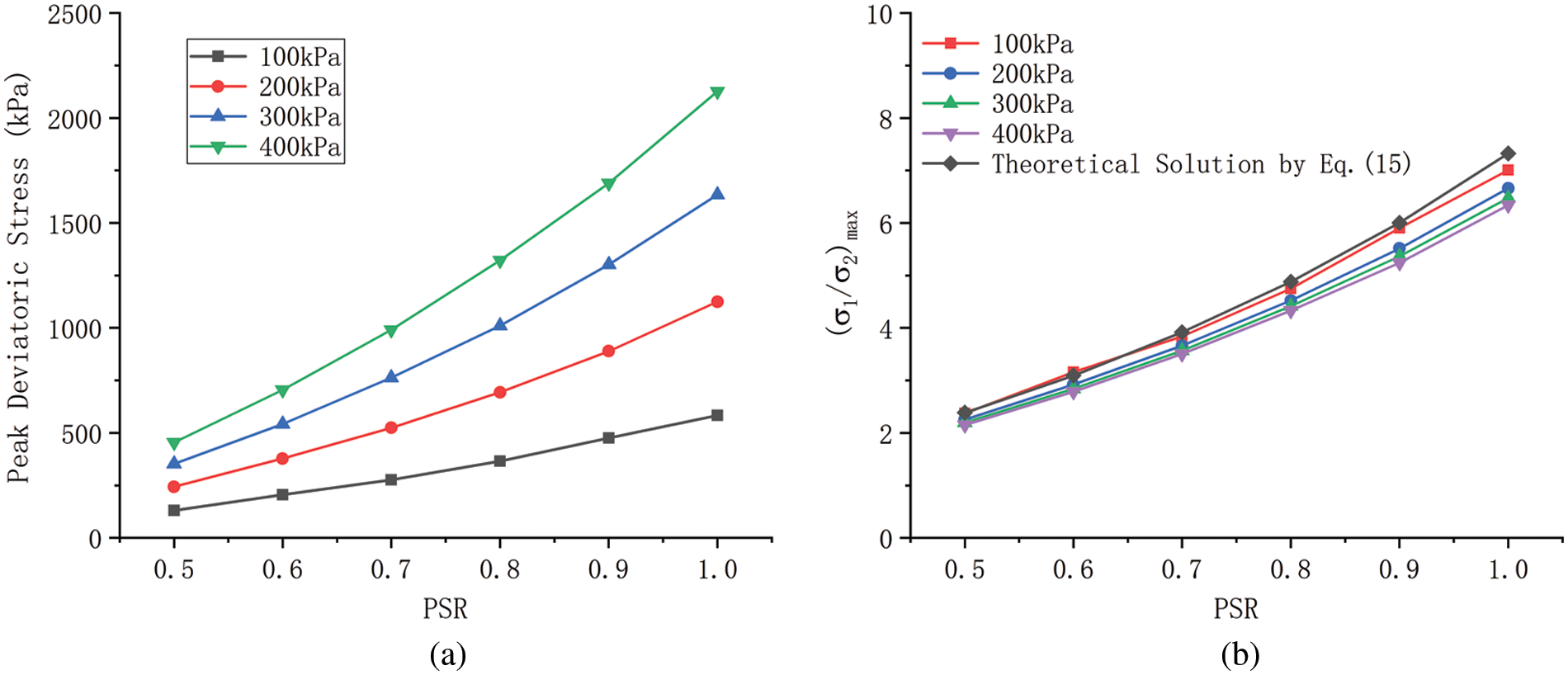
Figure 5: Curve of the relationship between peak deviatoric stress and PSR of regular granular samples: (a) peak deviatoric stress under different confining pressures and (b) theoretical solution by Eq. (15)

For the biaxial tests, there is an analytical solution for the strength of the regular packing structure. Utilizing the condition for sliding at contact points and the symmetry of the packing structure, the analytical solution of the maximum stress ratio was given by Rowe [31]:

σ1σ2|max=tan⁡(ϕu+α)tan⁡α(13)

where σ1 and σ2 are axial stress and lateral stress respectively, tan⁡ϕu is the friction coefficient, and α is the structural slip angle, as shown in Fig. 6. For regular packing structure in Fig. 2a, α can be expressed by PSR as

tan⁡α=γ2+2γ.(14)

where γ is the PSR. According to Eq. (14), the maximum stress ratio of regular packing granular samples is

σ1σ2|max=γ2+2γ(µ+γ2+2γ)1−μγ2+2γ(15)

It can be seen from Fig. 5b, the DEM simulation results agree well with the theoretical solution.

Figure 6: Stress analysis of regular packing structure

Figs. 7a–7d show the relationship between the volumetric strain and the axial strain of the regular granular samples with different PSR under different confining stress. It can be seen that the regular granular samples with different PSR show the phenomenon of first volumetric contraction to volumetric dilation. The peak volumetric contraction increases with the increase of PSR and confining stress level. At the same time, the higher confining stress level and PSR, the higher the axial strain of the regular granular samples at peak volumetric contraction.

Figure 7: Volumetric strain-axial strain curves of regular granular samples under different confining stress levels: (a) 100 kPa, (b) 200 kPa, (c) 300 kPa and (d) 400 kPa

Fig. 8 shows the effective strain distribution of regular granular samples at confining stress level of 100 kPa after peak deviatoric stress. Both of them show that shear bands appear after peak deviatoric stress. In the regular packing structure shown in Fig. 6, the angle between the sliding particles and the loading direction is β when the particles slide, which decreases with the increase of PSR. Therefore, with the increase of PSR, the angle between the main shear band and the loading direction decreases. The formation and shape of the shear band have certain randomness, and there is a bifurcation phenomenon.

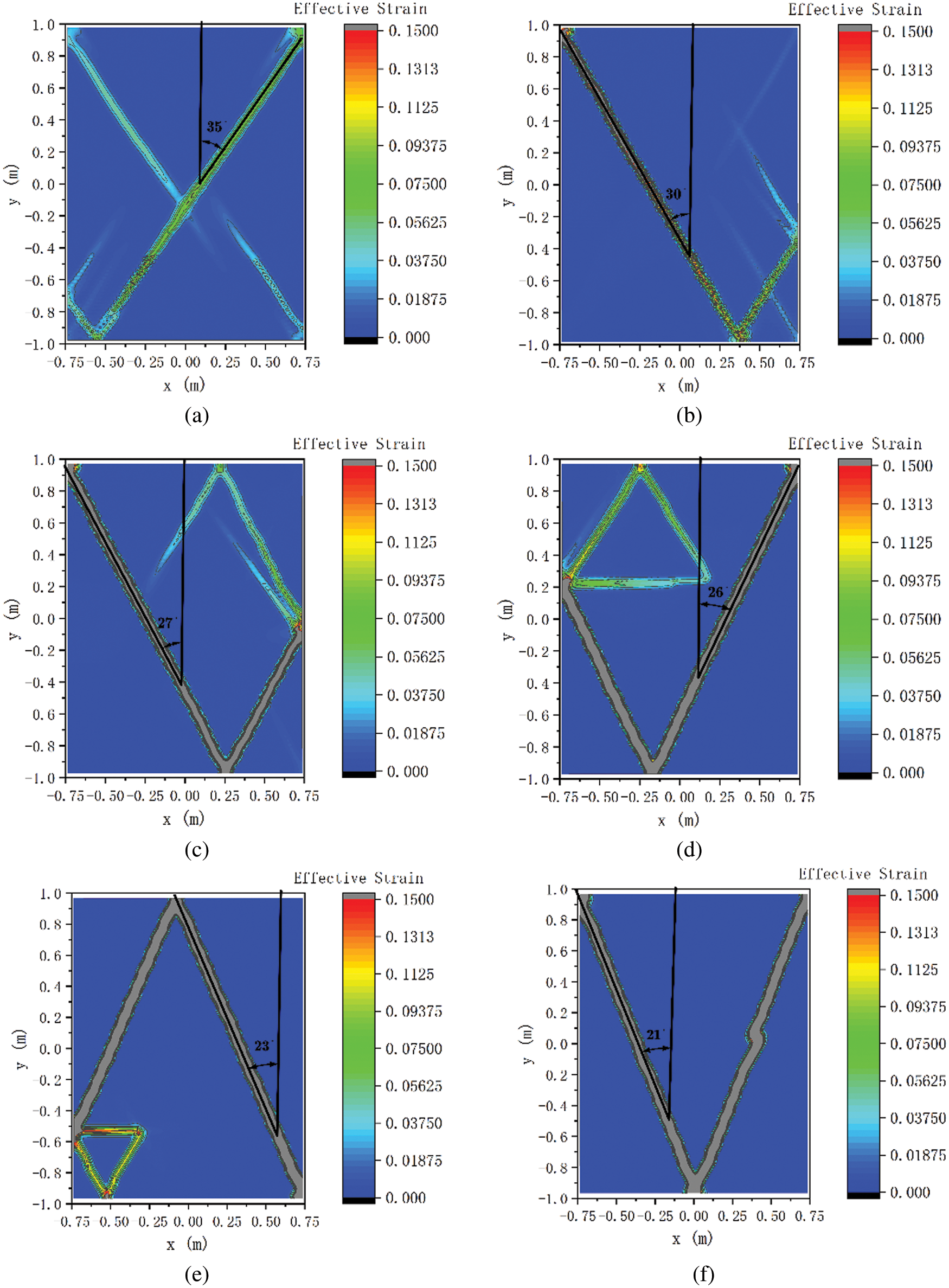
Figure 8: Effective strain distribution of regular granular samples at confining stress level of 100 kPa after peak deviatoric stress: (a) r = 0.5 R, (b) r = 0.6 R, (c) r = 0.7 R, (d) r = 0.8 R, (e) r = 0.9 R and (f) r = R

3.2 Layered Granular Samples

Layered granular samples whose PSR increases from 0.5 to 0.9 are considered, as shown in Fig. 2b. A series of DEM simulations were carried out at different confining stress. The deviatoric stress-axial strain curves of layered granular samples with different PSR under different confining stress levels are shown in Figs. 9a–9d, and the relationship between peak deviatoric stress and PSR is shown in Fig. 10. It can be seen that the layered granular samples with different PSR show similar deviatoric stress-axial strain curves and peak deviatoric stress. It is because although the granular samples are layered packing with different PSR, each particle layer is regularly hexagonal packing. Similar microstructures result in similar strengths for particle slip failure. Note that the modulus of the layered granular samples increases slightly with increasing PSR, a plausible explanation is the effect of Hertz-Mindlin contact law. According to Eq. (4), the normal contact stiffness is

kn=2G∗2R∗3(1−ν∗)δc1/2(16)

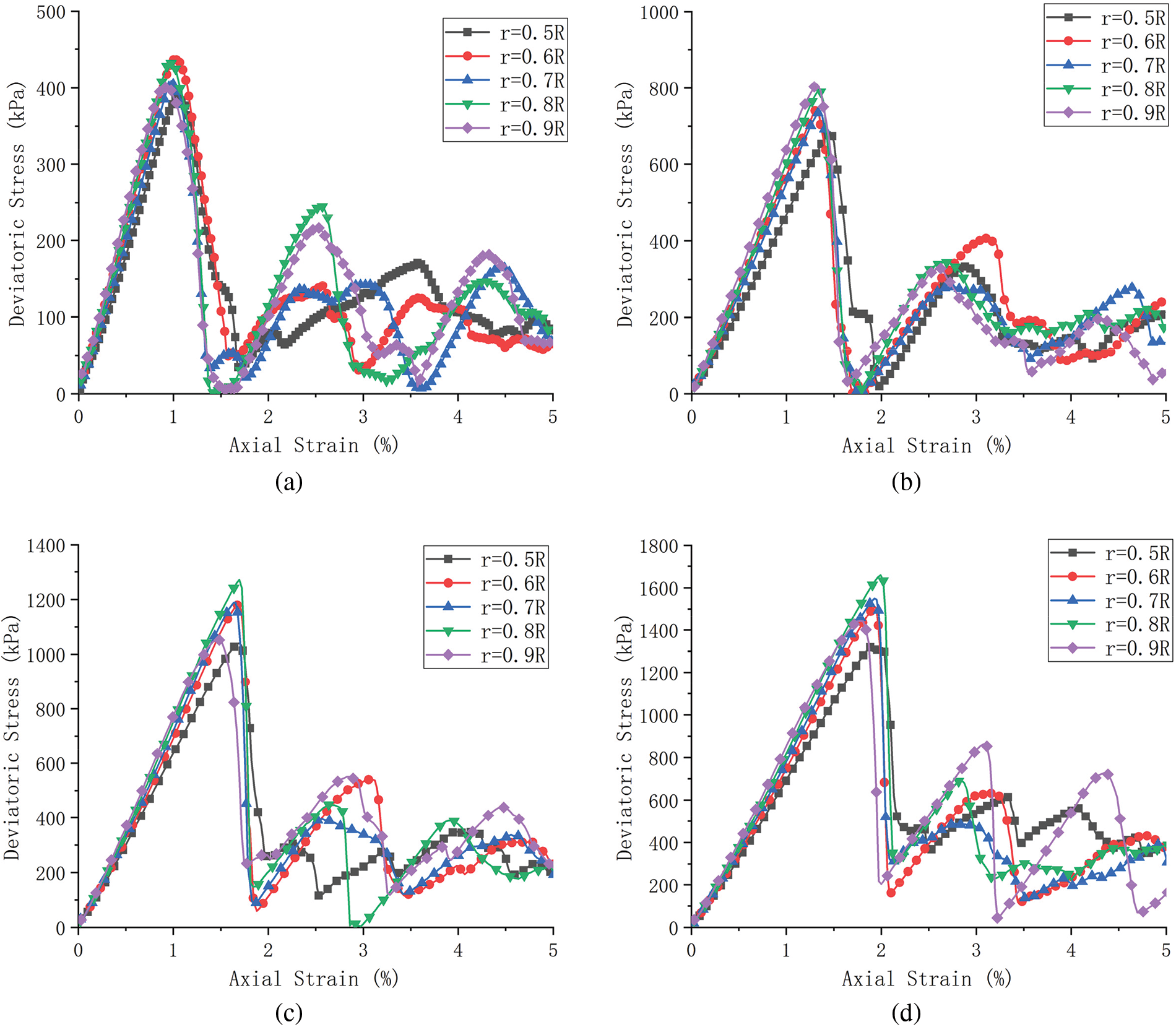
Figure 9: Deviatoric stress-axial strain curves of layered granular samples under different confining stress levels: (a) 100 kPa, (b) 200 kPa, (c) 300 kPa and (d) 400 kPa

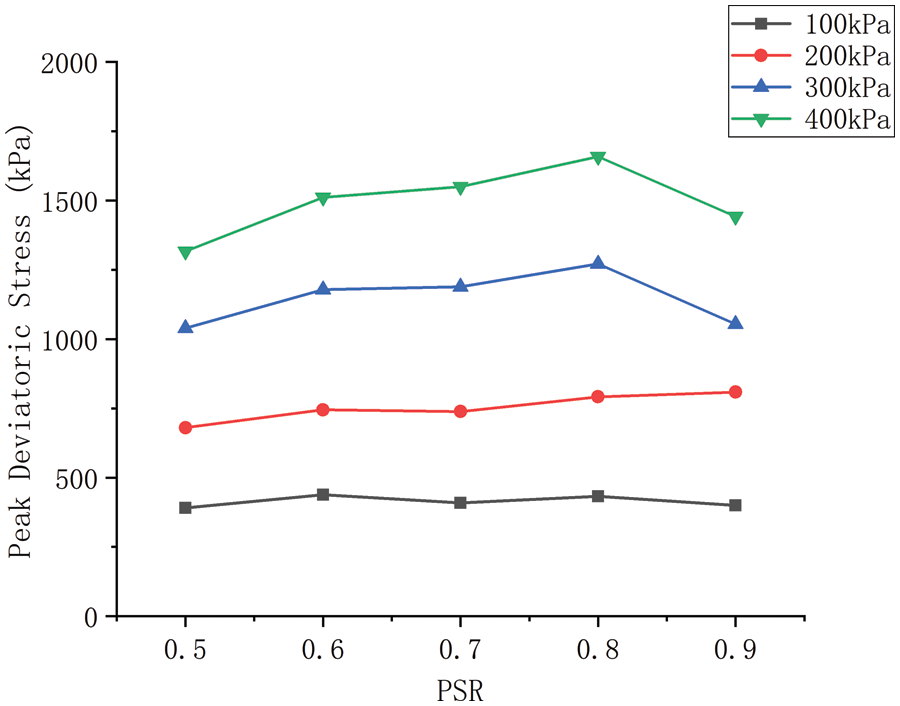
Figure 10: The influence of PSR of layered granular samples on peak deviatoric stress under different confining pressures

It can be seen that the normal contact stiffness is related to particle radius, the larger the particle radius, the greater the normal contact stiffness. With the increase of PSR, the particle radius of small particle increases, and the normal contact stiffness between small particles increase, resulting in a slight increase in modulus. To demonstrate this explanation, we use the linear contact model for layered granular samples with the same contact stiffness kn = 3e7 N/m and ks = 1e7 N/m. The layered granular samples are loaded in the same way at the confining stress of 100 kPa. The result is shown in Fig. 11, it can be seen that the layered granular samples with different PSR have the same modulus, which demonstrated the increase in the modulus of layered granular samples is related to the Hertz-Mindlin contact model.

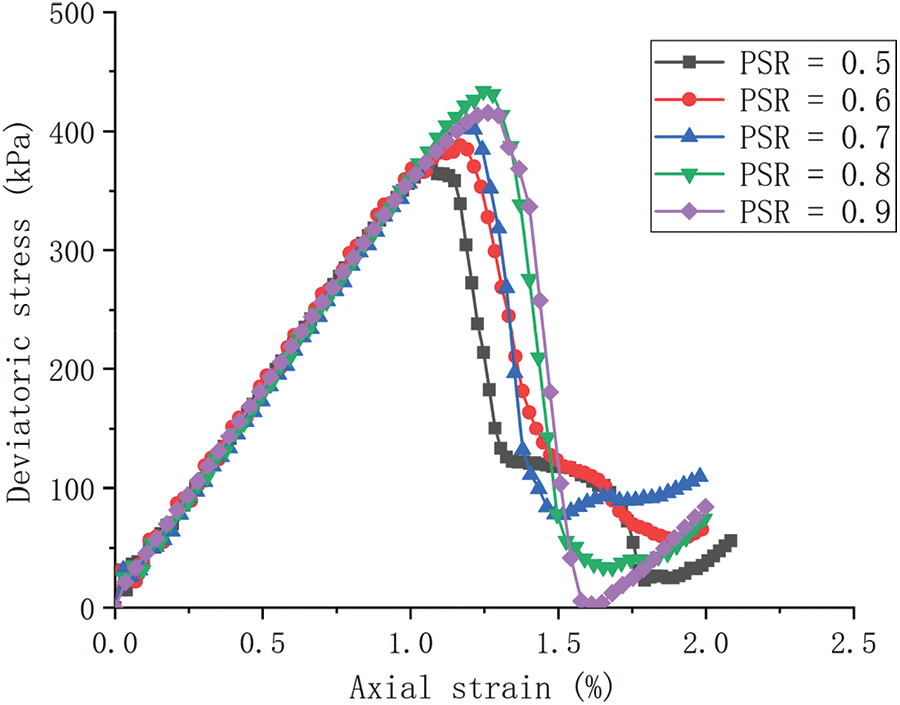
Figure 11: Deviatoric stress-axial strain curves of layered granular samples with linear contact model at confining stress of 100 kPa

Fig. 12 shows the relationship between the volumetric strain and the axial strain of layered granular samples at different confining stress. It can be observed that similar to the regular granular samples, the volumetric contraction occurs first, and with the increase of axial strain, the volumetric dilatation occurs. Similar volumetric strain-axial strain curves are observed for layered granular samples with different PSR.

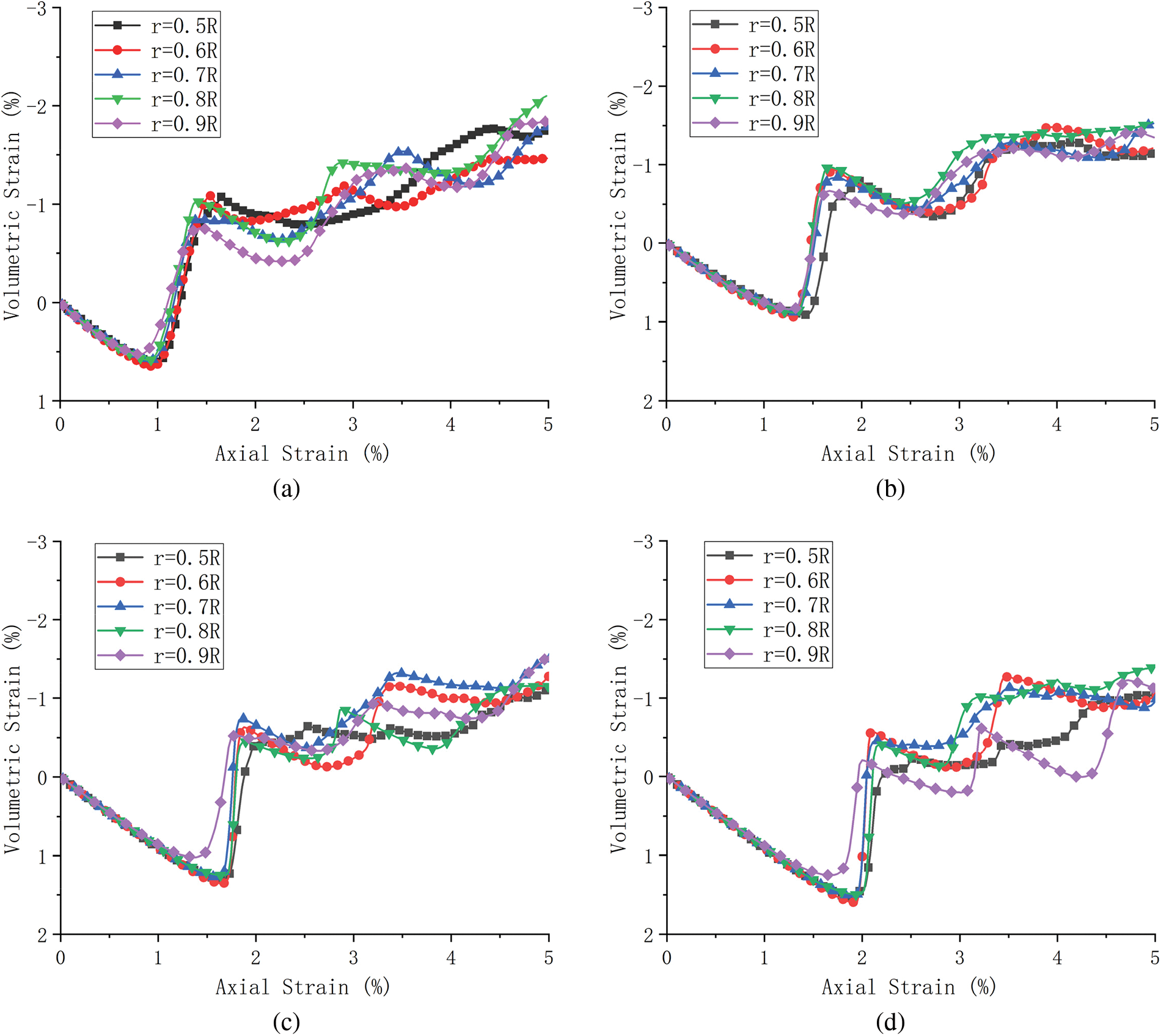
Figure 12: Volumetric strain-axial strain curves of layered granular samples under different confining stress levels: (a) 100 kPa, (b) 200 kPa, (c) 300 kPa and (d) 400 kPa

Fig. 13 shows the effective strain distribution of layered granular samples at confining stress level of 100 kPa at the axial strain of 2%. Both of them show that shear bands appear. The main shear bands run through several grain layers, and several shear bands occur at the layer boundaries. Although the PSR of layered granular samples is different, the angles between the shear band and the loading direction are similar.

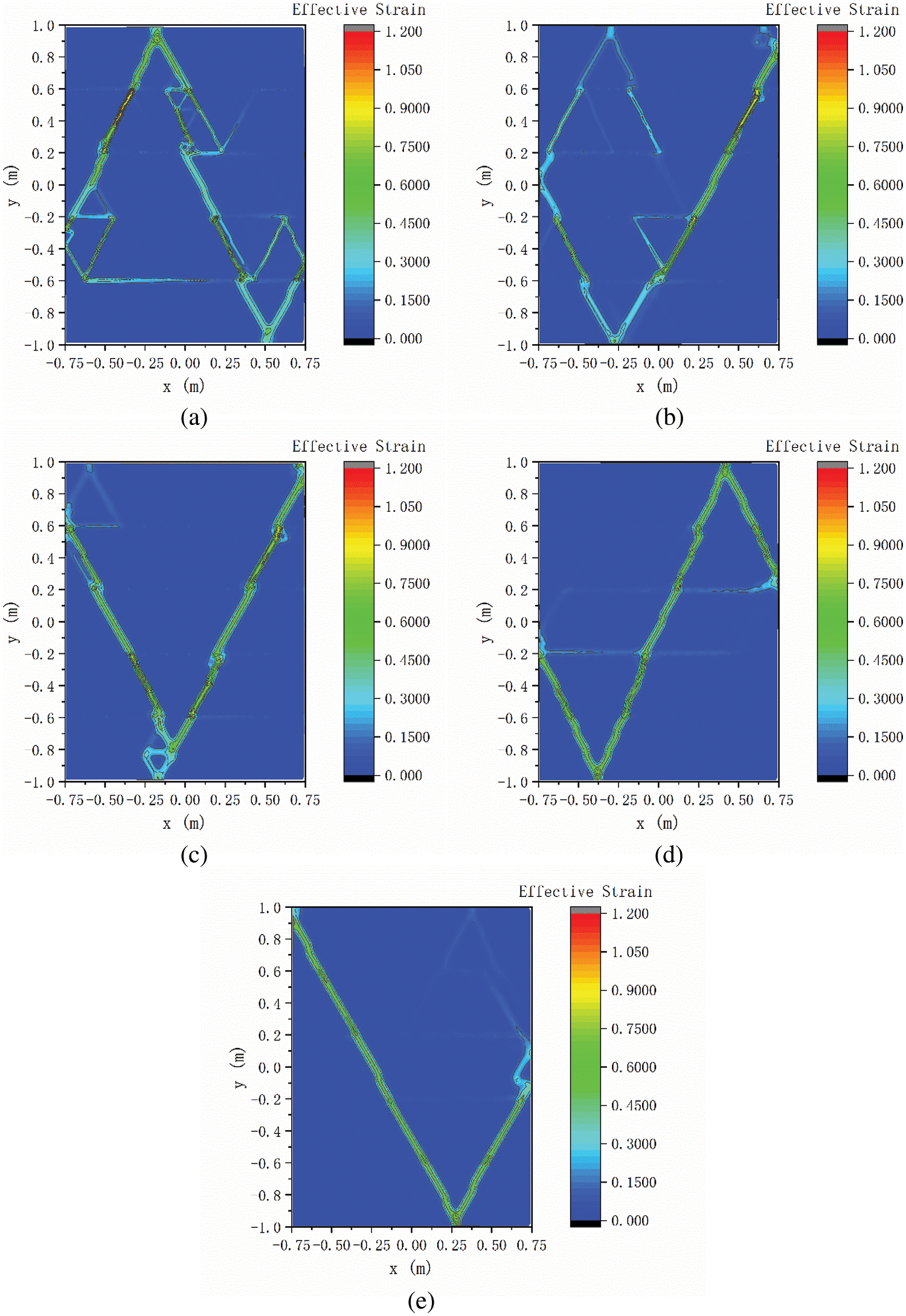
Figure 13: Effective strain distribution of layered granular samples at confining stress level of 100 kPa at axial strain of 2%: (a) r = 0.5 R, (b) r = 0.6 R, (c) r = 0.7 R, (d) r = 0.8 R and (e) r = 0.9 R

In summary, the PSR has little influence on the strength and deformation characteristics of layered granular samples. It may be because although the PSR of the layered granular samples is different, they have very similar microstructures, resulting in similar strength and deformation properties.

3.3 Random Granular Samples

Random granular samples with the same porosity whose PSR increases from 0.5 to 0.9 are considered, as shown in Fig. 2c. And VS of random granular samples is 50%. A series of DEM simulations were carried out at different confining stress. The deviatoric stress-axial strain curves of random granular samples with different PSR under different confining stress levels are shown in Figs. 14a–14d. It can be seen that the particle assemblies show strain softening. The deviatoric stress tends to stabilize with the increase of axial strain.

Figure 14: Deviatoric stress-axial strain curves of random granular samples under different confining stress levels: (a) 100 kPa, (b) 200 kPa, (c) 300 kPa and (d) 400 kPa

Fig. 15 shows the volumetric strain-axial strain curves of random granular samples at different confining stress. Similar to the particle assemblies with the regular and layered arrangement, the volumetric contraction occurs first, and with the increase of axial strain, the volumetric dilatation occurs. Fig. 16 shows the effective strain distribution of randomly arranged particle assemblies at confining stress level of 100 kPa at the axial strain of 15%. Compared with particle assemblies with the regular and layered arrangement, particle assemblies with the random arrangement also show that shear bands appear, but the locations of shear bands are random and not very concentrated.

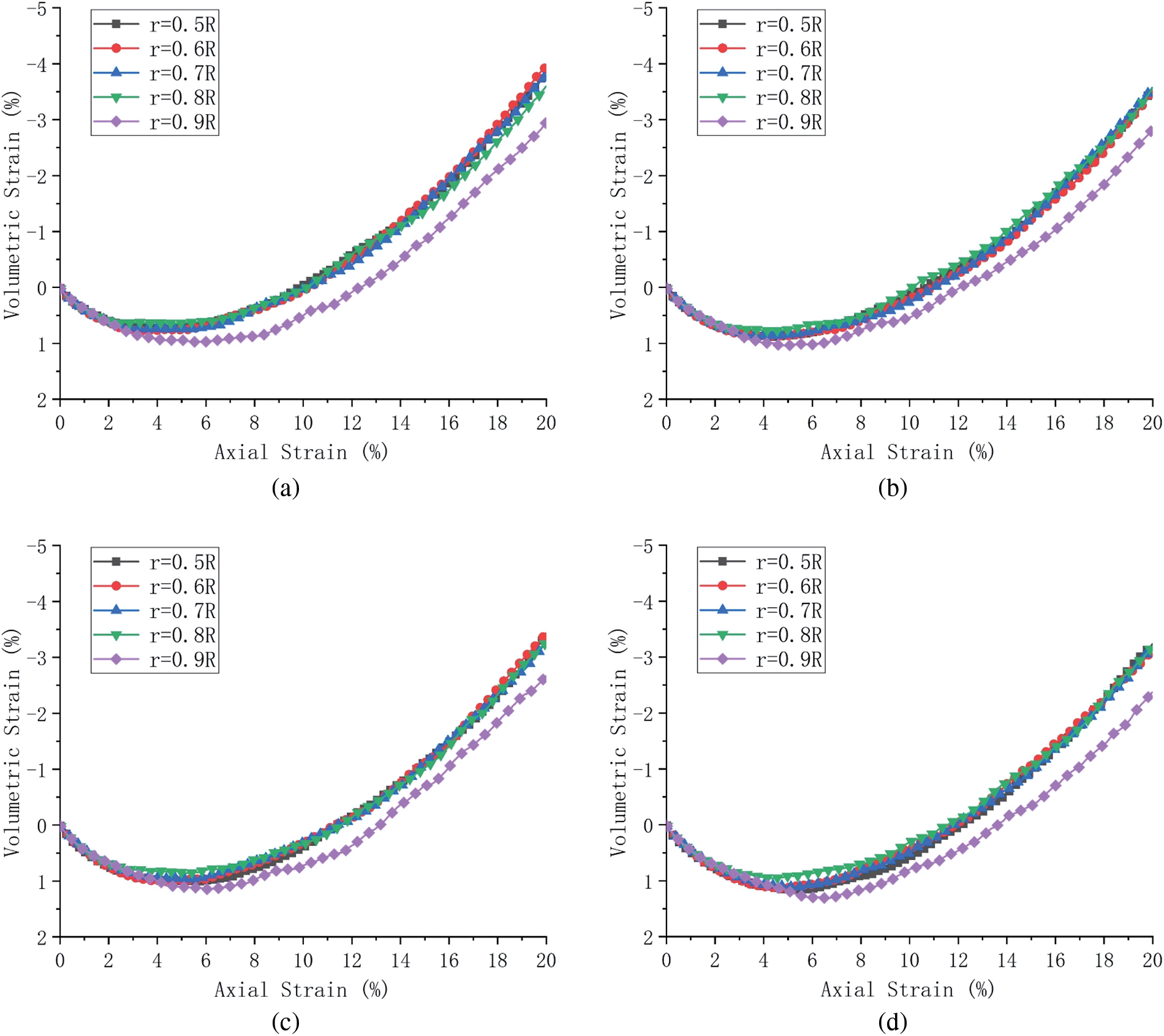
Figure 15: Volumetric strain-axial strain curves of random granular samples under different confining stress levels: (a) 100 kPa, (b) 200 kPa, (c) 300 kPa and (d) 400 kPa

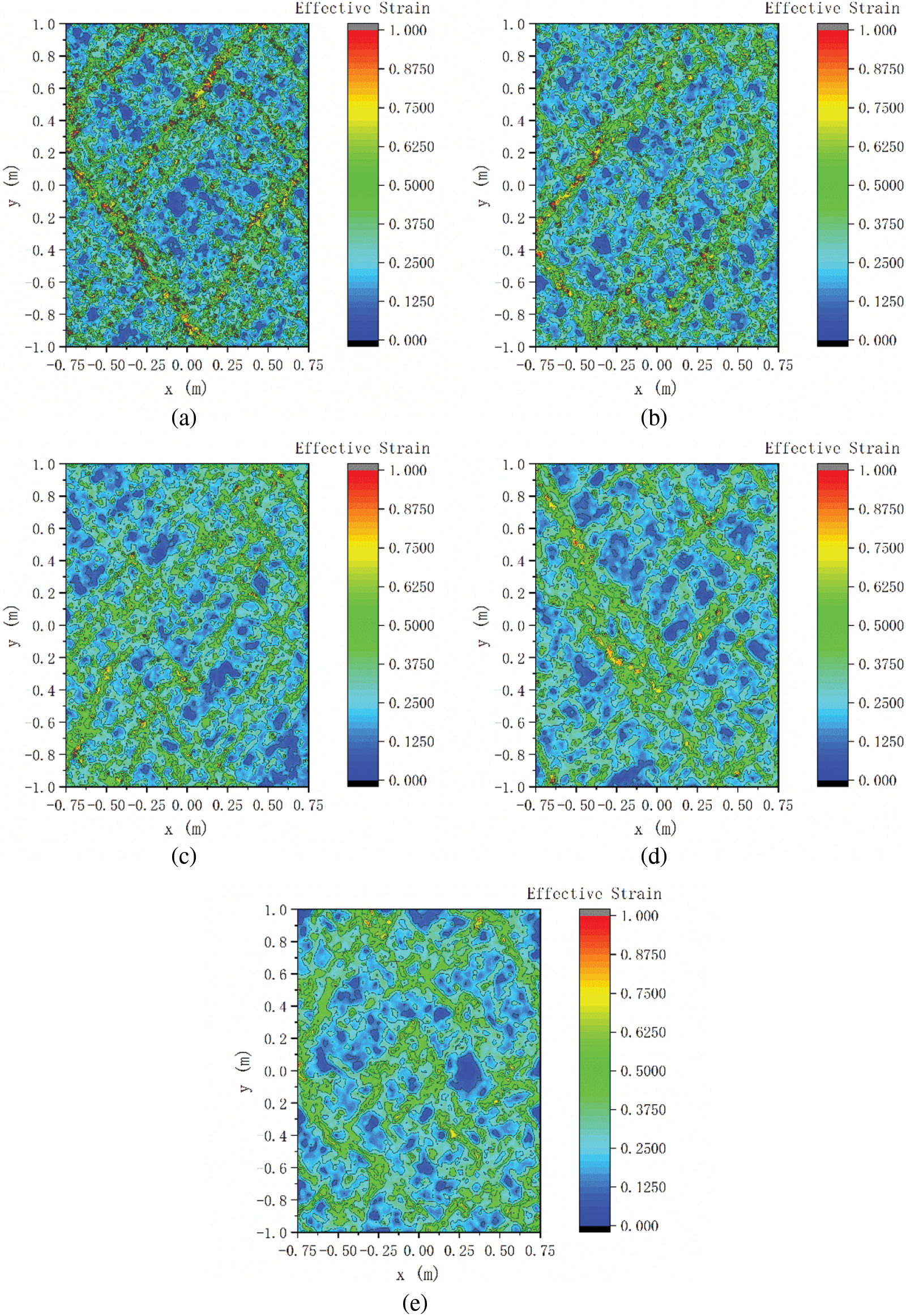
Figure 16: Effective strain distribution of random arranged particle assemblies at confining stress level of 100 kPa at axial strain of 15%: (a) r = 0.5 R, (b) r = 0.6 R, (c) r = 0.7 R, (d) r = 0.8 R and (e) r = 0.9 R

It can be seen that within the range of 0.5–0.9, PSR has little influence on the mechanical and deformation properties of random granular samples. It may be related to the similar microstructure. As indicated by Zhu et al. [24] and Gong et al. [32], Young’s modulus and the shear modulus are strongly linked to the coordination number. In this study, the coordination number Z, mechanical coordination number Zm and volume-weighted coordination number Zv are introduced [33–34], defined as follows:

Z=2C/N(17)

Zm=(2C−N1)/(N−N0−N1)(18)

Zv=1V∑p=1NCpVp(19)

where C is total number of contacts; N is total number of particles; N1 and N0 are numbers of particles with one contact and no contacts, respectively; V is the volume of the particle assembly; Cp is contact number of the particle p, and Vp is the volume of the particle p. The relationship between the PSR and the coordination number Z, the mechanical coordination number Zm and the volume-weighted coordination number Zv at confining stress of 100 kPa is shown in Fig. 17. Similar coordination number Z and mechanical coordination number Zm can be observed, although PSR is different. The volume-weighted coordination number Zv decreases slightly with increasing PSR. In general, the changes in PSR do not lead to significant changes in coordination properties, which may account for similar mechanical and deformation properties of random granular samples with different PSR.

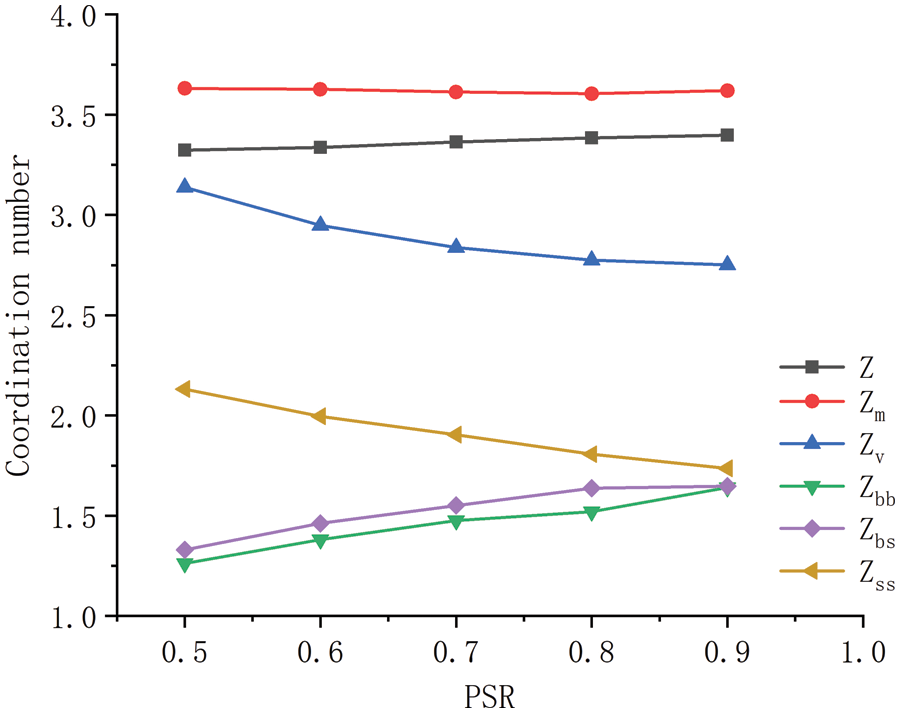
Figure 17: The relationship between PSR and coordination number

Although the mechanical and deformation properties of random granular samples are similar within such a small range of PSR, the contact behavior is changed to some extent. For binary mixture with random packing, the contacts in a particle assembly can be classified as big particle-big particle (bb), big particle-small particle (bs), and small particle-small particle (ss) contacts. The partial coordination numbers which can reflect different contacts are defined as [24]:

Zbb=2CbbNb;Zbs=2CbsN;Zss=2CssNs(20)

where Cbb, Cbs and Css are numbers of bb, bs and ss contacts, respectively, and Nb and Ns are numbers of big particles and small particles, respectively. The relationship between the PSR and the partial coordination at confining stress of 100 kPa is shown in Fig. 17. It can be seen that the increase of PSR leads to greater Zbb and Zbs and smaller Zss, which is consistent with the results of Zhu et al. [24] at VS of 50%. It indicates that as the PSR decreases, bb contacts decrease, and easier to generate bs and ss contacts.

Within a limited range of 0.5–0.9, the microstructure changes caused by PSR are very limited. We generated random granular samples with a larger range of PSR with VS of 50% in the same way, in which PSR is 1/2, 1/4, 1/8, and 1/16, and performed the same loadings at confining stress of100 kPa. If the radius of large particles is fixed, the PSR will cause a large computational cost when the PSR is relatively small, so we fix the radius of small particles to 0.008 m. The deviatoric stress-axial strain curves of random granular samples with different PSR at confining stress of 100 kPa are shown in Fig. 18. It can be seen that the modulus of random granular samples increases with the decrease of PSR, which is consistent with the result obtained by Zhu et al. [24]. They also discussed the contribution of contact type to modulus and found that the bs, and ss contacts accounted for the main contribution in random binary granular mixtures with VS of 50% under small PSR. And it can be well reflected in the force chain distribution, as shown in Fig. 19. When PSR is small, strong force chains are mainly distributed in bs contacts, and the weak chain is distributed in ss contacts which have numerous quantities. Fig. 20 shows the relationship between PSR and the partial coordination numbers. It can be seen that with the increase of PSR, ss contacts decrease, bs and bb contacts increase. It is due to the number of big particles increasing with increasing PSR.

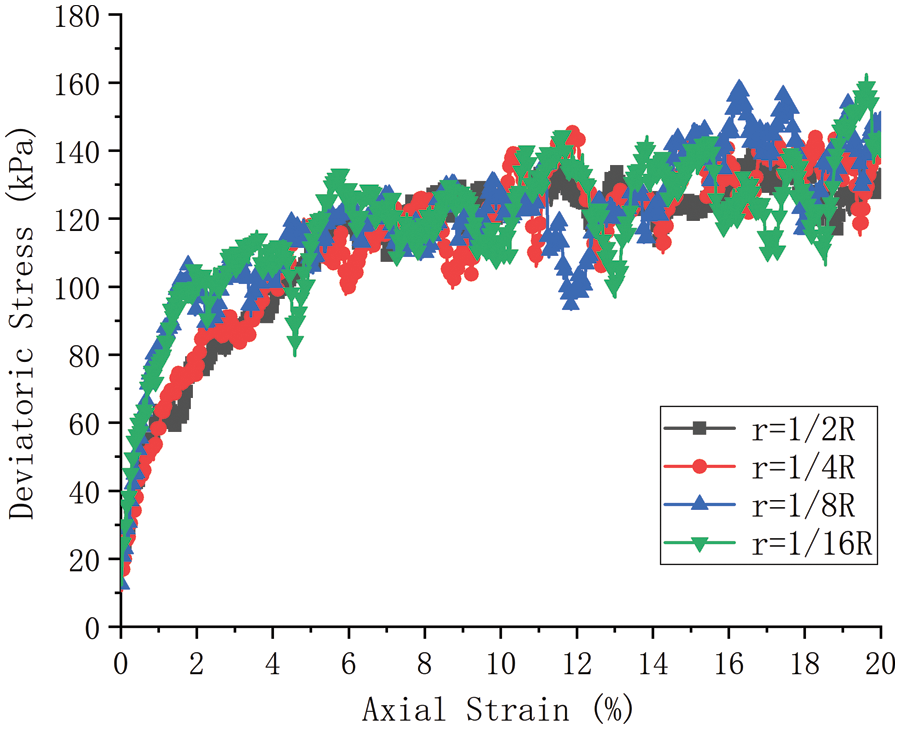
Figure 18: Deviatoric stress-axial strain curves of random granular samples at confining stress of 100 kPa

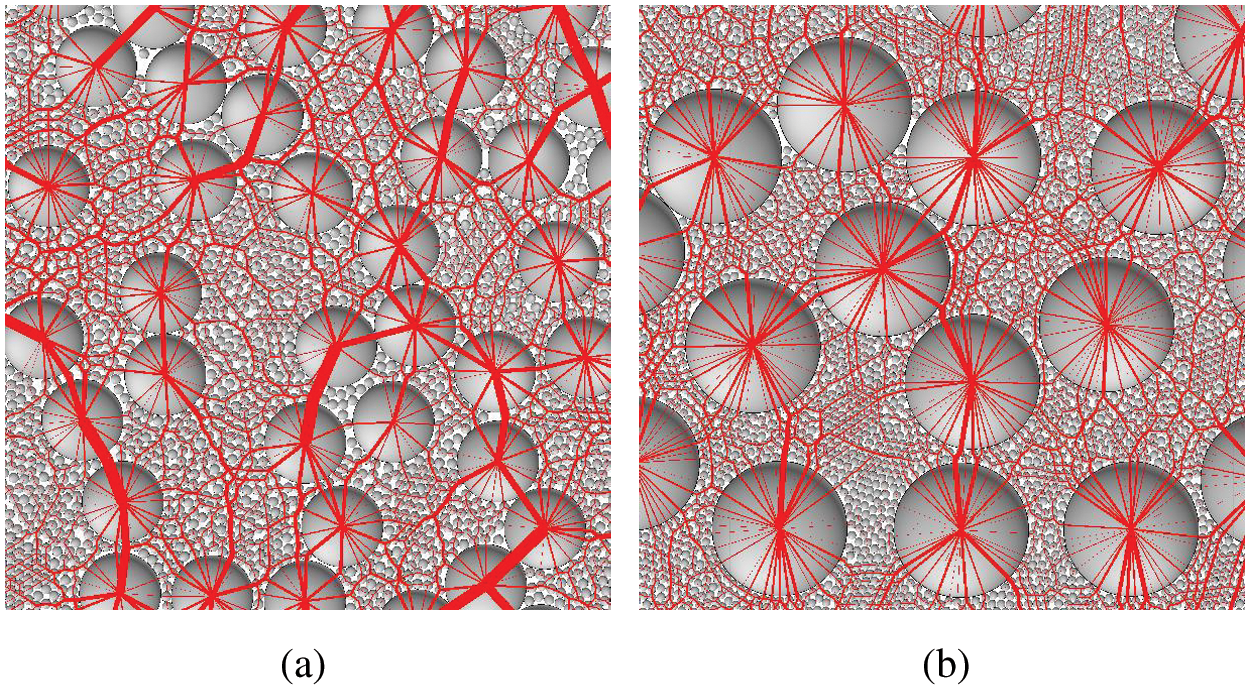
Figure 19: Force chain distribution of (a) PSR = 1/8, (b) PSR = 1/16

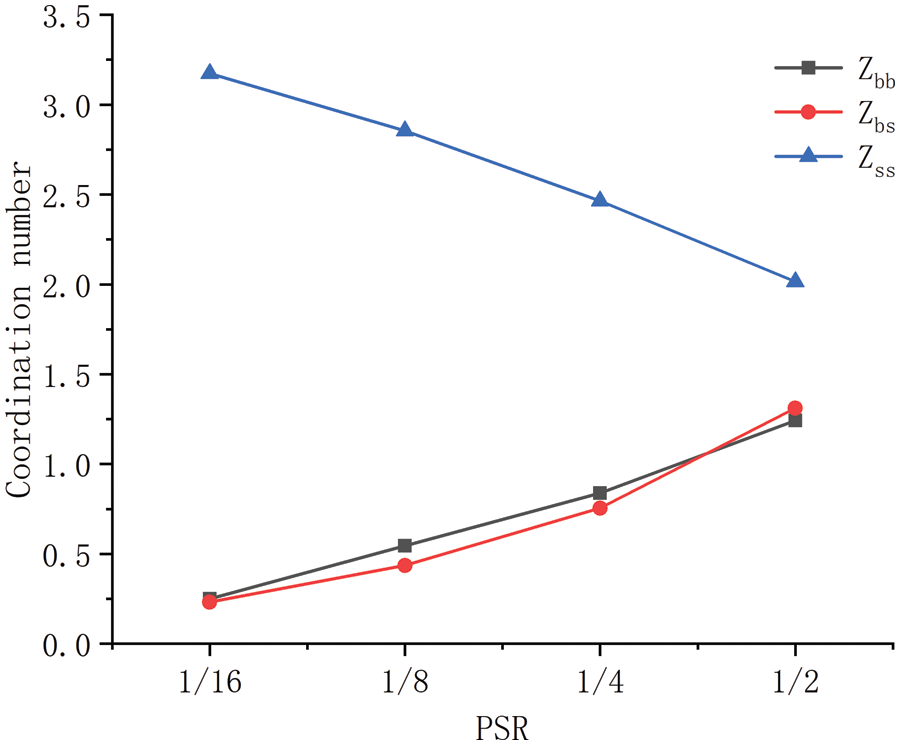
Figure 20: The relationship between PSR and the partial coordination numbers

4  Conclusions

The effect of PSR on the strength and deformation of binary granular materials with different packing methods was studied. PFC2D was used to simulate the influence of PSR on basic mechanical properties such as shear strength, volumetric strain, and so on. Besides, the effective strain distribution and the fabric tensors of the granular materials are analyzed. The main conclusions are as follows:

1)   The macroscopic mechanical properties of binary granular materials with regular packing are greatly affected by the PSR. It is mainly because the effect of PSR mainly comes from the changes in microstructure induced by PSR. The theoretical formula for the peak stress ratio and PSR is obtained, which is in good agreement with the DEM simulation. The strength and modulus of binary granular materials with regular packing increase with increasing PSR, which is mainly due to the change in the structural slip angle. Clear shear bands appear in binary granular materials with regular packing after peak deviatoric stress. With the increase of PSR, the angle between the main shear band and the loading direction decreases.

2)   The PSR has little influence on the macroscopic mechanical properties of binary granular materials with layered packing, which is caused by similar microstructure. The modulus of binary granular materials with layered packing increases with increasing PSR, and we suspect that it is due to the Hertz-Mindlin contact law used in the DEM simulations, which results in greater contact stiffness with an increase of PSR.

3)   For random binary granular materials with VS of 50%, PSR has little effect on mechanical and deformation properties within the range of 0.5–0.9. In the larger range of PSR, with the increase of PSR, the modulus of the random binary granular materials increases. Strong force chains are mainly distributed in bs contacts, and the weak chain is distributed in ss contacts which have numerous quantities.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Nos. 12172263, 11772237).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Chang, C. S., Misra, A. (1990). Packing structure and mechanical-properties of granulates. Journal of Engineering Mechanics, 116(5), 1077–1093. DOI 10.1061/(ASCE)0733-9399(1990)116:5(1077). [Google Scholar] [CrossRef]

 2.  Al-Raoush, R. (2007). Microstructure characterization of granular materials. Physica A: Statistical Mechanics and Its Applications, 377(2), 545–558. DOI 10.1016/j.physa.2006.11.090. [Google Scholar] [CrossRef]

 3.  Hare, C. L., Ghadiri, M. (2013). Influence of measurement cell size on predicted attrition by the distinct element method. Powder Technology, 236(1), 100–106. DOI 10.1016/j.powtec.2012.04.061. [Google Scholar] [CrossRef]

 4.  Obregon, L., Realpe, A., Velazquez, C. (2010). Mixing of granular materials, part II: Effect of particle size under periodic shear. Powder Technology, 201(3), 193–200. DOI 10.1016/j.powtec.2010.03.006. [Google Scholar] [CrossRef]

 5.  Wang, J., Chu, X., Wang, J. (2022). The material deformation and internal structure development of granular materials under different cyclic loadings. Computer Modeling in Engineering & Sciences, 130(2), 653–670. DOI 10.32604/cmes.2022.018207. [Google Scholar] [CrossRef]

 6.  Qu, T., Di, S., Feng, Y. T., Wang, M., Zhao, T. et al. (2021). Deep learning predicts stress-strain relations of granular materials based on triaxial testing data. Computer Modeling in Engineering & Sciences, 128(1), 129–144. DOI 10.32604/cmes.2021.016172. [Google Scholar] [CrossRef]

 7.  Ueda, T., Matsushima, T., Yamada, Y. (2011). Effect of particle size ratio and volume fraction on shear strength of binary granular mixture. Granular Matter, 13(6), 731–742. DOI 10.1007/s10035-011-0292-1. [Google Scholar] [CrossRef]

 8.  Ogarko, V., Luding, S. (2012). Equation of state and jamming density for equivalent bi- and polydisperse, smooth, hard sphere systems. Journal of Chemical Physics, 136(12), 124508. DOI 10.1063/1.3694030. [Google Scholar] [CrossRef]

 9.  Kumar, N., Magnanimo, V., Ramaioli, M., Luding, S. (2016). Tuning the bulk properties of bidisperse granular mixtures by small amount of fines. Powder Technology, 293, 94–112. DOI 10.1016/j.powtec.2015.11.042. [Google Scholar] [CrossRef]

10. Aarons, L. R., Balachandar, S., Horie, Y. (2013). The mixing of cohesive granular materials featuring a large size range in the absence of gravity. Powder Technology, 235(2), 18–26. DOI 10.1016/j.powtec.2012.09.044. [Google Scholar] [CrossRef]

11. Shire, T., O’Sullivan, C., Hanley, K. J. (2016). The influence of fines content and size-ratio on the micro-scale properties of dense bimodal materials. Granular Matter, 18(3), 52. DOI 10.1007/s10035-016-0654-9. [Google Scholar] [CrossRef]

12. Wang, J., Chu, X. H., Zhang, J. B., Liu, H. (2019). The effects of microstructure on wave velocity and wavefront in granular assemblies with binary-sized particles. International Journal of Solids and Structures, 159(2), 156–162. DOI 10.1016/j.ijsolstr.2018.09.026. [Google Scholar] [CrossRef]

13. Wang, J., Chu, X. H., Jiang, Q. H., Xiu, C. X. (2019). Energy transfer and influence of excitation frequency in granular materials from the perspective of Fourier transform. Powder Technology, 356(2), 493–499. DOI 10.1016/j.powtec.2019.08.061. [Google Scholar] [CrossRef]

14. Wang, D. F., An, X. Z., Gou, D. Z., Zhao, H. Y., Wang, L. et al. (2018). DEM construction of binary hard sphere crystals and radical tessellation. AIP Advances, 8(10), 105203. DOI 10.1063/1.5052478. [Google Scholar] [CrossRef]

15. Martin, C. L., Bouvard, D. (2004). Isostatic compaction of bimodal powder mixtures and composites. International Journal of Mechanical Sciences, 46(6), 907–927. DOI 10.1016/j.ijmecsci.2004.05.012. [Google Scholar] [CrossRef]

16. Minh, N. H., Cheng, Y. P., Thornton, C. (2014). Strong force networks in granular mixtures. Granular Matter, 16(1), 69–78. DOI 10.1007/s10035-013-0455-3. [Google Scholar] [CrossRef]

17. Nordstrom, J., Alderborn, G., Frenning, G. (2018). Compressibility and tablet forming ability of bimodal granule mixtures: Experiments and DEM simulations. International Journal of Pharmaceutics, 540(1–2), 120–131. DOI 10.1016/j.ijpharm.2018.02.006. [Google Scholar] [CrossRef]

18. Gong, J., Liu, J. (2017). Mechanical transitional behavior of binary mixtures via DEM: Effect of differences in contact-type friction coefficients. Computers and Geotechnics, 85(4), 1–14. DOI 10.1016/j.compgeo.2016.12.009. [Google Scholar] [CrossRef]

19. Cai, R. H., Xiao, H. Y., Zheng, J. Y., Zhao, Y. Z. (2019). Diffusion of size bidisperse spheres in dense granular shear flow. Physical Review, E, 99(3), 032902. DOI 10.1103/PhysRevE.99.032902. [Google Scholar] [CrossRef]

20. Tunuguntla, D. R., Weinhart, T., Thornton, A. R. (2017). Comparing and contrasting size-based particle segregation models: Applying coarse-graining to perfectly bidisperse systems. Computational Particle Mechanics, 4(4), 387–405. DOI 10.1007/s40571-016-0136-1. [Google Scholar] [CrossRef]

21. Staron, L., Phillips, J. C. (2016). How large grains increase bulk friction in bi-disperse granular chute flows. Computational Particle Mechanics, 3(3), 367–372. DOI 10.1007/s40571-015-0068-1. [Google Scholar] [CrossRef]

22. Tunuguntla, D. R., Thornton, A. R., Weinhart, T. (2016). From discrete elements to continuum fields: Extension to bidisperse systems. Computational Particle Mechanics, 3(3), 349–365. DOI 10.1007/s40571-015-0087-y. [Google Scholar] [CrossRef]

23. Wiącek, J. (2016). Geometrical parameters of binary granular mixtures with size ratio and volume fraction: experiments and DEM simulations. Granular Matter, 18(3), 1–10. DOI 10.1007/s10035-016-0642-0. [Google Scholar] [CrossRef]

24. Zhu, Y. G., Gong, L., Nie, Z. H. (2020). Numerical investigation of the elastic properties of binary mixtures as a function of the size ratio and fines content. International Journal of Geomechanics, 20(9), 04020155. DOI 10.1061/(ASCE)GM.1943-5622.0001792. [Google Scholar] [CrossRef]

25. Ng, T. T., Zhou, W., Ma, G., Chang, X. L. (2018). Macroscopic and microscopic behaviors of binary mixtures of different particle shapes and particle sizes. International Journal of Solids and Structures, 135(3), 74–84. DOI 10.1016/j.ijsolstr.2017.11.011. [Google Scholar] [CrossRef]

26. Nie, Z., Zhu, Y., Zou, J., Gong, J., Liu, S. (2019). DEM study of the microscopic characteristics and internal stability of binary mixtures. Powder Technology, 352, 314–324. DOI 10.1016/j.powtec.2019.04.077. [Google Scholar] [CrossRef]

27. Cundall, P. A., Strack, O. D. L. (1979). A discrete numerical mode for granular assemblies. Géotechnique, 29(1), 47–65. DOI 10.1680/geot.1979.29.1.47. [Google Scholar] [CrossRef]

28. Li, X. K., Chu, X. H., Feng, Y. T. (2005). A discrete particle model and numerical modeling of the failure modes of granular materials. Engineering Computations, 22(8), 894–920. DOI 10.1108/02644400510626479. [Google Scholar] [CrossRef]

29. Tang, H. X., Dong, Y. F., Chu, X. H., Zhang, X. (2016). The influence of particle rolling and imperfections on the formation of shear bands in granular material. Granular Matter, 18(1), 12. DOI 10.1007/s10035-016-0607-3. [Google Scholar] [CrossRef]

30. O’Sullivan, C., Bray, J. D., Riemer, M. (2004). Examination of the response of regularly packed specimens of spherical particles using physical tests and discrete element simulations. Journal of Engineering Mechanics, 130(10), 1140–1150. DOI 10.1061/(ASCE)0733-9399(2004)130:10(1140). [Google Scholar] [CrossRef]

31. Rowe, P. W. (1962). The stress-dilatancy relation for static equilibrium of an assembly of particles in contact. Proceedings of the Royal Society of London A, 269(1339), 500–527. DOI 10.1098/rspa.1962.0193. [Google Scholar] [CrossRef]

32. Gong, J., Wang, X., Li, L., Nie, Z. (2019). DEM study of the effect of fines content on the small-strain stiffness of gap-graded soils. Computers and Geotechnics, 112(124), 35–40. DOI 10.1016/j.compgeo.2019.04.008. [Google Scholar] [CrossRef]

33. Thornton, C. (2000). Numerical simulations of deviatoric shear deformation of granular media. Géotechnique, 50(1), 43–53. DOI 10.1680/geot.2000.50.1.43. [Google Scholar] [CrossRef]

34. Shaebani, M. R., Madadi, M., Luding, S., Wolf, D. E. (2012). Influence of polydispersity on micromechanics of granular materials. Physical Review E, 85(1), 011301. DOI 10.1103/PhysRevE.85.011301. [Google Scholar] [CrossRef]

Appendix A. The Definition of the Effective Strain

To describe the change of relative position between particles, Li et al. [28] and Tang et al. [29] defined the nominal strain based on the change of particle position. Fig. A1 shows the position change of particle A and one of its neighboring particles B.

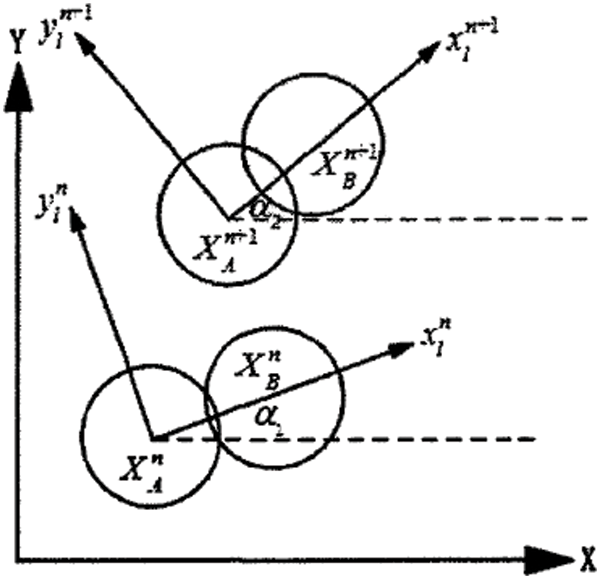
Figure A1: Position change of particle A relating to a neighboring particle [28]

The coordinates of particles A and B at time tn and tn+1 are XAn, XBn and XAn+1, XBn+1 respectively in the global coordinate system.

ΔXBAn=XBn−XAn(A1a)

ΔXBAn+1=XBn+1−XAn+1(A1b)

In the local coordinate system (xln, yln),

ΔxBAn=xBn−xAn(A2a)

ΔxBAn+1=xBn+1−xAn+1(A2b)

where xAn, xBn and xAn+1, xBn+1 are the coordinates of particles A and B at time tn and tn+1 respectively in the local coordinate system (xln, yln). According to the coordination transformation

ΔxABn=TΔXABn(A3a)

ΔxABn+1=TΔXABn+1(A3b)

T=[cosα1sinα1−sinα1cosα1](A3c)

Refer to local coordinate system (xln, yln), deformation gradient fn can be used to describe the relative change of center position of particles A and B.

fn=ΔxBAn+1ΔxBAn=RnUn(A4)

where

Rn=[cos(α2−α1)−sin(α2−α1)sin(α2−α1)cos(α2−α1)];Un=[λAB001](A5a)

λAB=lABn+1lABn;lABn+1=‖ΔxABn+1‖;lABn=‖ΔxABn‖(A5b)

where α1 and α2 correspond to the angle between the local coordinate x-axis and the global coordinate x-axis at tn and tn+1. Substitute Eqs. (A3a) and (A3b) into Eq. (A4).

ΔXABn+1=FXABn(A6)

where

F=TTfnT(A7)

Then the displacement derivative matrix can be defined as

D=F−I(A8)

where I refer to the identity matrix. Then strain between particles A and B can be given as

εAB=[23DijDij]1/2(A9)

where Dij refers to the component of matrix D. Then the nominal strain of particle A with nA neighboring particles can be defined as

εA=1nA∑B=1nAεAB(A10)