Solving Geometry Problems via Feature Learning and Contrastive Learning of Multimodal Data

1  Introduction

Automatically solving geometry problems is a long-standing challenge in artificial intelligence that continues to attract research interest [1–3], which has focused such as on angle and length calculation. Geometry problem solving has been modeled as a process of relation extraction and reasoning [4–6], using a syntax-semantic model to extract geometric relations from problem text, and sending them to an expert system for reasoning and solution. It can also be modeled in terms of submodular optimization [7,8]. The wide application of deep learning methods in natural language processing, computer vision, and vision-language interaction makes it possible to solve geometry problems based on deep learning [9–12]. Whether focusing on problem parsing and relation reasoning or on interpretable presentation, past work has provided important insights.

However, solving geometry problems requires the mapping of human-readable text and visual images into machine-understandable logical forms, followed by reasoning and solution, and not simply by pattern recognition and matching or end-to-end classification [12]. Geometry problems are often presented in multimodal forms such as text, images, and image-text pairs, which brings challenges to their unified representation, which contains multimodal data such as text, symbols, formulas, and images. The different statistical characteristics of modal data lead to a lack of semantic correlation between them. Different modal representations of an entity contain both shared and unique information. If this information is not semantically related, it will affect the understanding of multimodal data, hindering understanding and automatic solution. There is a semantic gap in the multimodal understanding process of geometry problems. Information can describe the same object or event from different angles, and it suffers from a lack of correlation. Although the information on multimodal processing and fusion is rich and detailed [13–15], it is difficult to apply to the solution of geometry problems.

This paper presents an end-to-end, fully automated deep learning method to solve geometry problems via feature learning and contrastive learning of multimodal data. Solving geometry problems by deep learning has the steps of feature extraction, fusion, and reasoning. A shared feature-learning model of multimodal data learns the unified feature representation of text and images, which can solve the heterogeneity problem of multimodal geometry problems. A contrastive learning model of multimodal data enhances the semantic relevance between multimodal features and maps them into a unified semantic space, which can effectively adapt to both single-modal and multimodal downstream tasks. Based on the feature extraction and fusion of multimodal data, a geometry problem solver is proposed, adopting a shared encoder-decoder structure to generate solution sequences. A shared encoder realizes the deep understanding of text and/or images by a multi-headed self-attention mechanism. For multimodal problems, a multilayer Transformer realizes the interaction between cross-modal features. For single-modal problems, the Transformer can adaptively attend to single-modal data. Multimodal contrastive learning addresses the lack of semantic correlation between multimodal data, which can attract relevant text and/or image features, repel irrelevant features in the representation space, and realize the semantic alignment of multimodal data. A shared decoder decodes single-modal contrastive vectors or a series sequence of multimodal contrastive vectors according to the input of the encoder. The encoder and decoder can be cascaded to obtain deeper implicit information. The representation of the decoder is transferred to task-specific heads for geometry relations extraction, theorem reasoning, and problem solution. The proposed algorithm can produce readable solutions. Target programs can assist in problem solution and model diagnosis. Similar to machine translation, beam search produces a better target program. Multiple auxiliary tasks, including puzzle recovery and image element identification, improve the performance of the image embedder. Experiments on two public geometry problem datasets demonstrate the effectiveness of the proposed algorithm.

The main contributions of this paper are as follows:

•   An end-to-end deep learning method to solve geometry problems is proposed, whose input is a geometry problem with text and/or images, and which produces a readable solution procedure. This single framework adaptively solves single-modal and multimodal geometry problems without modifying the model structure;

•   We propose a shared feature-learning model of multimodal data for pretraining geometry problem text and/or images. Because the architecture of multimodal feature learning utilizes a similar network of self-attention masks, extracted multimodal features can be formatted in a unified feature representation, so as to address heterogeneity in multimodal geometry problems;

•   A contrastive learning model of multimodal data is proposed to enhance the semantic relevance between multimodal features and map them into a unified semantic space, which can effectively adapt to both single-modal and multimodal downstream tasks.

The remainder of this paper is organized as follows. Section 2 discusses related research. Section 3 presents our proposed method. Experimental results are given in Section 4, and conclusions are drawn in Section 5.

2  Related Work

Research on feature and contrastive learning can be categorized as single-modal, multimodal, or cross-modal. Single-modal methods are only used to train single-modal tasks, such as for text or image data. Multimodal methods relate to training multimodal tasks, such as for image-text pair data, and cross-modal methods concentrate on the compatibility between single-modal and multimodal tasks.

Single-Modal Learning. Single-modal learning methods focus on the extraction and analysis of text or image features. Most natural language text learning methods are based on the multilayer Transformer architecture. For instance, BERT [16] uses bidirectional representations from Transformers with 24 layers, UniLM [17] uses three types of language modeling tasks to train a shared multilayer Transformer network, RoBERTa [18] optimizes BERT for key hyperparameters and training data size, XLNet [19] uses generalized autoregressive pretraining for a multilayer Transformer, and BART [20] is a language-generating model with a denoising autoencoder. Visual image learning methods are mainly based on the multilayer CNN architecture, such as VGG [21], with 19 weight layers of convolutional networks with very small convolution filters; and ResNet [22], with a 152-layer residual learning framework with less complexity and better performance than VGG. For single-modal problems in different disciplines, both text and image data have the problems of high noise and redundancy. Traditional single-modal methods can perform well only in text or image training; they lack the ability to process multimodal tasks with both text and images, and extracted local and global features cannot be effectively adapted to downstream tasks.

Multimodal Learning. Multimodal learning methods are used, especially in the training of image-text data pairs. There are both one-channel and multi-channel methods. The former uses a single Transformer architecture to train a series sequence of multimodal data. UNITER [23] uses a multilayer Transformer to learn a cross-modal contextualized embedding between visual regions and textual tokens, VisualBERT [24] aligns tokens of the input text and regions in the input image implicitly by Transformer, and VL-BERT [25] extends the Transformer to take both visual and linguistic embedded features as input. Multi-channel methods use multiple Transformer architectures to train different single-modal data. For instance, ViLBERT [26] extends the BERT architecture to parallel models for text and image processing, and uses co-attentional Transformer layers to interact with separate streams. MAGIC [27] leverages three parallel decoders to generate responses in different media. MAS [28] is proposed for awakening the robot without wake words by audiovisual consistency detection and semantic talking intention inference. LARCH [29] performs a conversational image search through a multimodal hierarchical graph-based neural network, multi-form knowledge embedding memory network, and gated neural network. These methods provide some useful ideas for solving geometry problems. On the observation that multimodal information fusion in one-channel methods is proposed earlier than multi-channel methods, which can achieve better performance. Limited to the use of image-text data pairs for training, these multimodal learning methods can only train small-scale data, and cannot be effectively adapted to single-modal downstream tasks.

Cross-Modal Learning. Cross-modal learning methods use text, image, and image-text pairs simultaneously as training data to learn the unified semantic representation of text and images. AttnGAN [30] uses a cross-modal attention learning model, which allows attention-driven, multi-stage refinement for fine-grained text, and can synthesize fine-grained details in different subregions by focusing on relevant words in the natural language description. Contrastive learning is effective for self-supervised representation learning, which attracts relevant text and/or image features to each other in the representation space, and repels irrelevant features, so as to realize the semantic alignment of cross-modal data [31]. UNIMO [32] can effectively adapt to both single-modal and multimodal understanding and generation tasks by using multilayer self-attention Transformers to learn unified semantic representations of cross-modal information, so they can be effectively adapted to downstream tasks.

Geometry Problem Solving. Geometry problem solving efforts are increasing. An automated system, GEOS, solves geometry problems by combining text understanding and image interpretation, where element relations in the text are obtained by machine learning, and the primitive and its relations in the image are obtained by maximizing the consistency of image and text data. An interpretable geometry problem solver (Inter-GPS) parses the problem text and image into formal language by rule-based text parsing and neural object detection, and incorporates theorem knowledge as conditional rules and performs symbolic reasoning [9]. A neural geometric solver (NGS) addresses geometry problems by comprehensively parsing multimodal information and generating interpretable programs [10]. The above work only focuses on multimodal problem solving, and feature representation needs to improve.

This paper proposes an end-to-end deep learning method for solving geometry problems via the feature learning and contrastive learning of Multimodal data, where both the single-modal geometry problems, such as text or images and Multimodal geometry problems, such as image-text pairs are considered. The proposed method shows good performance in solving geometry problems with both single-modal and Multimodal tasks.

3  Proposed Method

We present the proposed method to solve geometry problems via feature learning and contrastive learning of multimodal data. As shown in Fig. 1, the overall framework of this paper is to integrate the encoder and decoder network structure of a multilayer converter. The converter improves the feature representation and problem-solving ability of multimodal data, which can help build an end-to-end deep learning method for solving geometry problems. Figs. 2 and 3 show the two modules for feature representation. This paper considers the text and/or image of a geometry problem as input. The multilayer Transformer in the encoder converts the text and/or image to implicit context features, and features at different levels are semantically aligned and mapped into a unified semantic space through feature and contrastive learning of multimodal data, so as to form a unified feature representation. The multilayer Transformer decodes the unified multimodal features according to task-specific learning embedding to form the shared features of multi-tasks, which are transferred to the head of specific learning tasks, which are learned to solve problems. The multimodal and single-modal learning networks respectively solve image-text and natural language text geometry problems; it should be noted that the networks share the same structure.

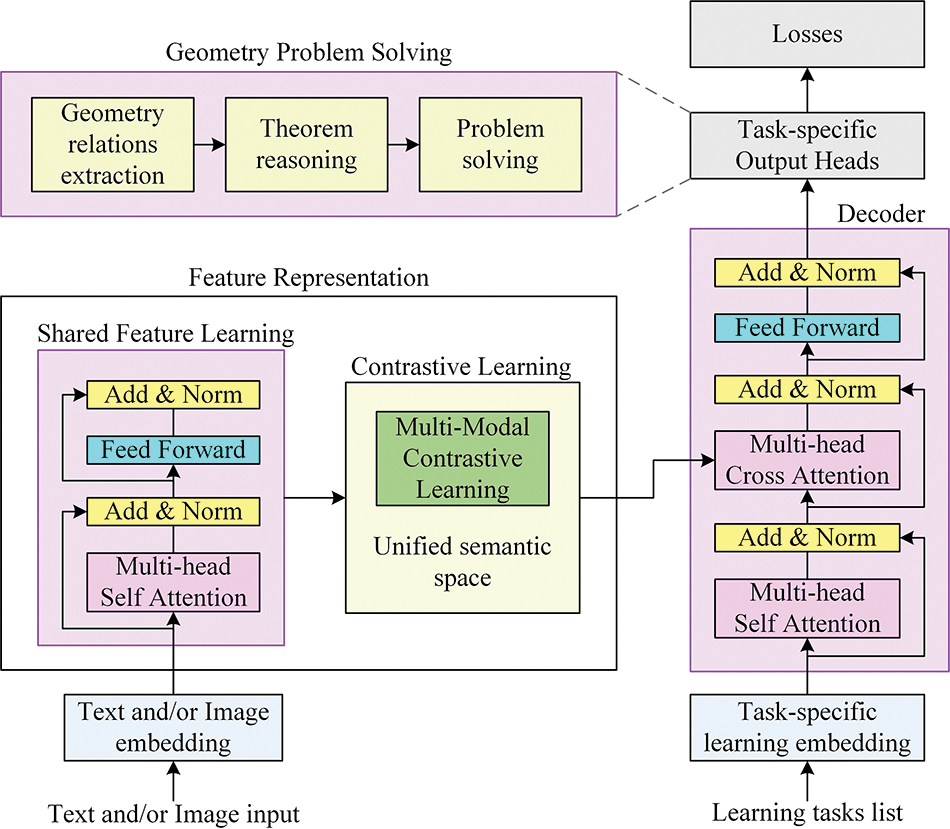
Figure 1: Overall architecture of the proposed method

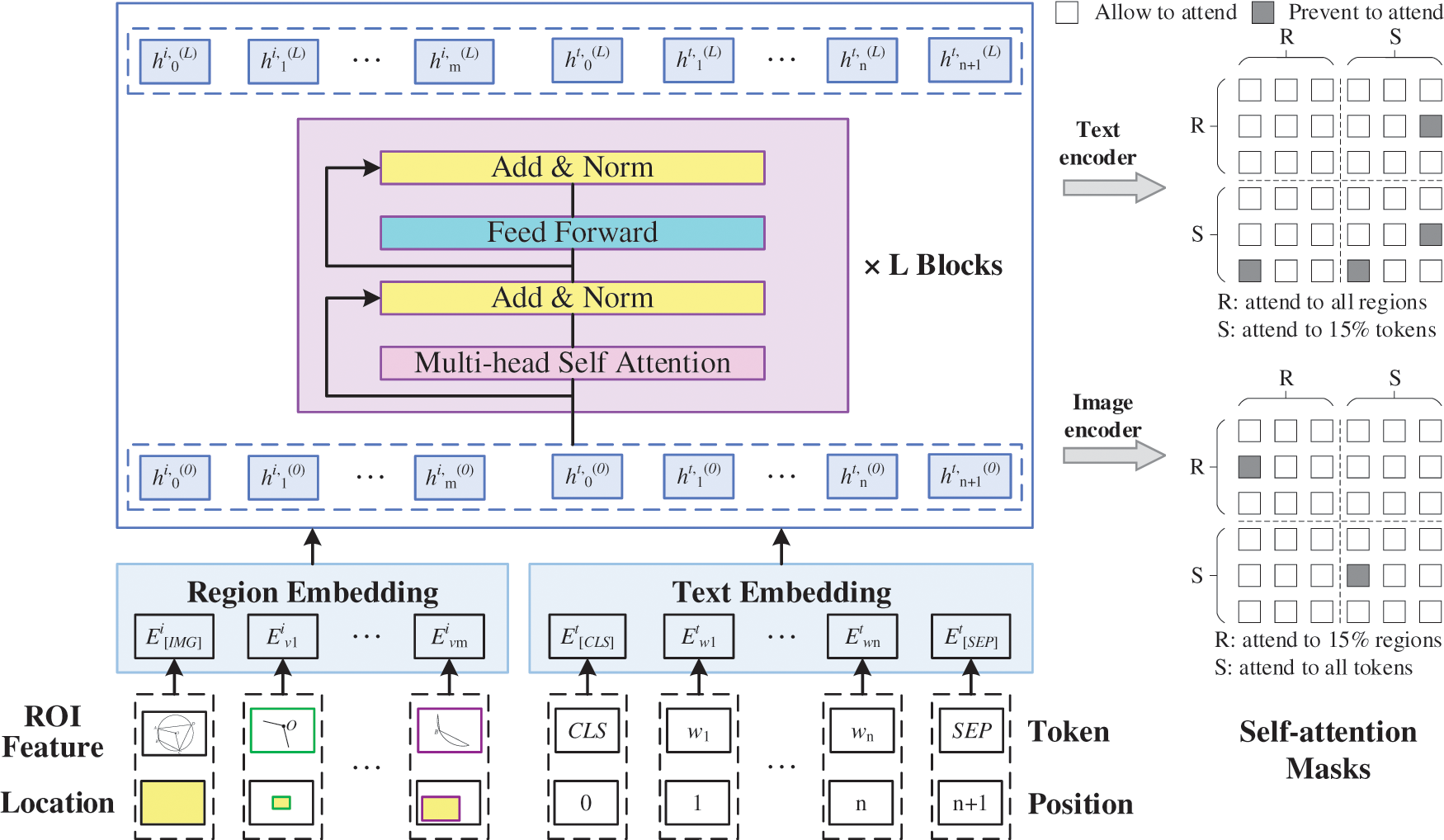
Figure 2: Shared feature-learning model of multimodal data

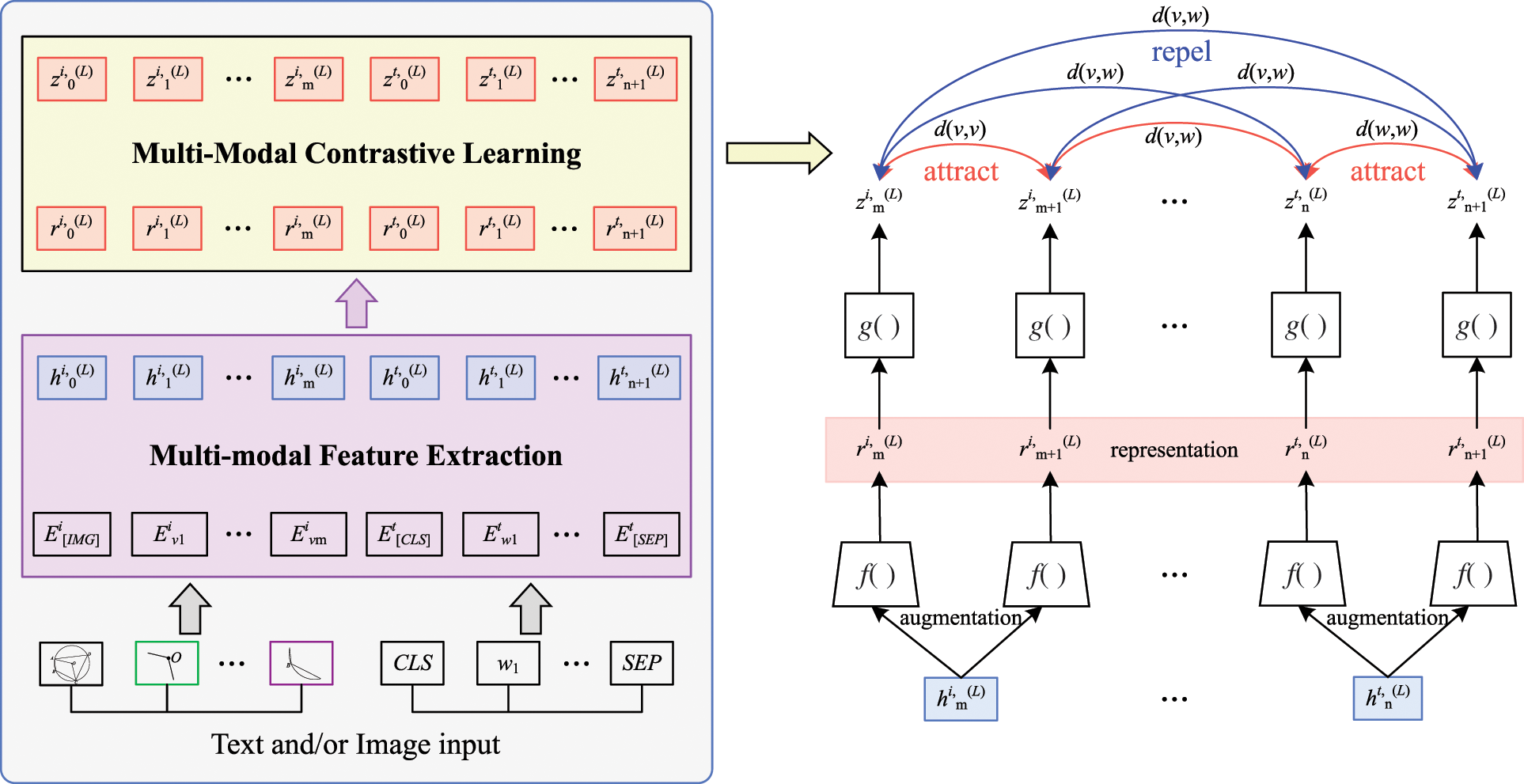
Figure 3: Contrastive learning model of multimodal data which are text and/or image

3.1 Multimodal Feature Learning

Due to the heterogeneity between multimodal geometry problems, the feature distribution of data in each mode is different, which brings difficulties to feature extraction. To model the feature extraction of multimodal problems and deal with various modal data, we establish a shared feature-learning model, which can extract features in single-modal text or image data as well as multimodal image-text data. The model masks text and image features, and realizes the interaction between multimodal data through multilayer Transformers, so as to produce better feature expression of multimodal data and support downstream multimodal tasks.

Fig. 2 shows the shared feature-learning model of multimodal data. For problem text, [CLS] represents the classification mark at the beginning of a sequence, and [SEP] represents the separator mark at the end. For a geometry image, [IMG] represents the classification mark of the start sequence. For the text and image input of multimodal geometry problems, we obtain the respective text tag feature and image region feature embedding sequences, W={E[CLS]t,Ew1t,⋯,Ewnt,E[SEP]t} and V={E[IMG]i,Ev1i,⋯,Evmi}, using the feature embedding module of multimodal data. Then, if the feature learning task is a multimodal problem such as image-text, the two feature embedding sequences are connected into a feature embedding sequence of pairs VW={E[IMG]i,Ev1i,⋯,Evmi,E[CLS]t,Ew1t,⋯,Ewnt,E[SEP]t}, which is input to the multilayer self-attention converter to learn the multimodal feature representation of the text mark and image region, outputting the text feature representation ht={h0t,(L),h1t,(L),⋯,hnt,(L),hn+1t,(L)}, image feature representation hi={h0i,(L),h1i,(L),⋯,hmi,(L)}, or image-text feature representation h={h0i,(L),h1i,(L),⋯,hmi,(L),h0t,(L),h1t,(L),⋯,hnt,(L),hn+1t,(L)}. In particular, considering that learning tasks with different modes may need to extract different types of features, we add a learning task embedding vector wtask to the coding model of the converter to allow it to extract the information of a specific task at the time of output.

Based on the region embedding layer of the image and mark embedding layer of the text, the multilayer self-attention converter realizes the interaction of a single data stream. Each layer is composed of a self-attention mask mechanism and feedforward neural network. The structure of the Transformer encoder is the BERT model [16], which is highlighted in pink in Fig. 2, so the weight can be initialized with the pretrained BERT weight to improve the availability of the original pretraining model. This part uses the text and image encoders of the multilayer self-attention converter to encode the features of the problem text and image, respectively, so as to produce a better context feature representation.

3.1.1 Geometry Problem Text Feature Learning

Similar to the pretraining model BERT and its improved model [16–19] of natural language processing, the text input in the multimodal geometry problem is set as a set of word sequences w={w1,⋯,wn}, which is transformed to a set of text tag embedding sequences W={E[CLS]t,Ew1t,⋯,Ewnt,E[SEP]t} through position, tag, and learning task embedding, where E and t are the text embedded tag and learning task embedded tag, respectively. The multilayer convertor, including a self-attention mask mechanism, is used to train the marked features of the problem text, learn the context marked representation of text features, and output the context marked representation. The learning task embedding vector wttask is added to the text tag embedding sequence as part of the BERT input, and can be separated from the implicit features of the output text ht=BERT(w,wttask) in the downstream task. This vector marks a variety of downstream training tasks and shares implicit features, such as geometry relation extraction, reasoning, and solution.

To better learn the context marked representation of text features, we use two types of language modeling tasks—bidirectional prediction and sequence-to-sequence generation—to train an encoding model of the problem text. The model uses a self-attention mask mechanism to control the context of prediction conditions. To improve the language learning process, we use the proposed syntactic-semantic model [4,6,33] to detect semantically complete phrases in the problem text. In the training process of bidirectional prediction [34] and sequence-to-sequence generation [32], we sample a sequence of complete words or phrases instead of word markers. In the whole training process, we evenly alternate training between bidirectional prediction and sequence-to-sequence generation targets, to obtain the context marked representation of text features.

3.1.2 Geometry Problem Image Feature Learning

Faster-RCNN [35] is used to detect the region of interest of the image to extract visual features. Because the self-attention mechanism in the multilayer converter is disordered, we use a five-dimensional vector, (x1/W,y1/H,x2/W,y2/H,(y2−y1)(x2−x1)/WH), to encode the position features of each region, where (x1,y1) and (x2,y2) are the coordinates of the lower-left and upper-right corner, respectively, and W and H are the respective width and height of the input image. The region feature embedding sequence V={E[IMG]i,Ev1i,⋯,Evmi} is formed by using the first three layers of ResNet101 [22] to extract visual features, and a multilayer converter to fuse visual, location, and learning task features, where E is the image embedding mark of the region feature, and i is the embedding mark of the learning task. The multilayer converter including self-attention mask mechanism is used to train the region features, and to learn and output more realistic context region representation hi={h0i,(L),h1i,(L),⋯,hmi,(L)}. The learning task embedding vector witask is added to the region embedding sequence, and it can be separated from the implicit features of the output image hi=E(v,witask) in the downstream task. This vector marks a variety of downstream training tasks and shares implicit features such as target detection, visual implication, and relational reasoning.

Similar to the self-attention mask modeling of text features, the self-attention mask modeling of image features samples the image region. It uses 15% probability to mask the visual features, which are replaced with 0. The image regions are usually highly overlapped. To avoid information leakage, we mask all high proportion of overlapping regions in the image slices. We randomly select a region as the masking anchor, and mask the region where the anchor receipt is greater than 0.3. The purpose is to reconstruct the masked region vm from the other given region v∖m by using the function LV(θ)=Ev∈Dfθ(vm|v∖m), where θ is a trainable parameter, and each image region v is sampled from training set D. Unlike text tags represented by discrete tags, visual features are high-dimensional and continuous, and the likelihood function cannot be used for supervised learning. Therefore, we use feature regression and region classification to train an encoding model of the geometry problem image, so as to learn a better context region representation of the image.

The process of forwarding propagation of data and the process of predicting the solution sequences are described in detail next. The model can accept single-modal and multimodal data as input. Data is converted to features by text and/or image embedders. As shown in algorithm 1, the input is the text and/or image and the output is a set of text features ht and/or image feature hi.

:

3.2 Multimodal Contrastive Learning

We propose a multimodal contrastive learning model to address the lack of semantic correlation between multimodal geometry data. This model aligns different levels of text and/or image representations and maps them into a unified semantic space. The idea is to attract the relevant text and/or image features to each other and repel irrelevant features in the representation space [31], so as to realize the semantic alignment of multimodal geometry data.

The contrastive learning model of multimodal data is shown in Fig. 3. We transform the feature representation of a text and/or image into the same embedded space through a full connection layer, and calculate the cosine similarity to measure the distance d(V,W) between features. Two text and/or image features, such as hmi,(L) and hnt,(L), are selected randomly, and two pairs of interrelated features are generated for each selected feature using two independent enhancement functions. A basic neural network encoder f(⋅) extracts representation vectors (rmi,(L), rm+1i,(L)) and (rnt,(L), rn+1t,(L)) from the enhanced data. A neural network projection head g(⋅) is used to map the representation vector to the contrastive loss space to obtain contrastive vectors (zmi,(L), zm+1i,(L)) and (znt,(L), zn+1t,(L)). A contrastive loss function is trained for contrastive prediction, so that relevant features attract each other and irrelevant features repel each other.

3.2.1 Single-Modal Contrastive Learning

There is a lack of semantic correlation between the geometry data in a single-modal text or image. To enhance the multiple granularity semantic alignment between single-modal geometry data, we rewrite the semantics of a single-modal text or image using text rewriting technology. We parse the text or image into a scene graph [36] containing objects, attributes, and relations, which are randomly replaced in the geometric vocabulary. For instance, a geometry problem can be parsed into a scene graph of objects (circle, center, radius), attributes (center coordinate is (0, 0), radius is 2 cm) and relations (same radius). Text rewriting can be randomly replaced with other objects, attributes, or relations to generate a large number of negative samples. Because the rewritten text is similar to but different from the original text, it can be used as negative samples. Text rewriting can generate a large number of negative samples instead of randomly extracting negative samples, as in previous methods, so we can help the model learn a more detailed semantic alignment from different levels of a text or image, and a more accurate semantic alignment of features is learned by training the contrastive loss function,

LSMCL=−log⁡exp⁡(d(Z,W+)/τ)∑W′∈{W+,W′}exp⁡(d(Z,W′)/τ),(1)

where W+ and W− represent positive and negative examples, respectively, of text or image Z, and τ represents temperature parameters. so as to realize the unified semantic feature expression of multimodal data.

3.2.2 Cross-Modal Contrastive Learning

For semantic alignment between cross-modal data in geometry problem texts and images, it is not only necessary to connect the scene displayed in the image with the text description in the problem, but also to align the entities in the image and their positional relationships with the description in the text. Many multimodal pretraining methods align visual and text representations by simple image and text matching using a corpus of restricted image and text pairs [23], randomly selecting negative samples of images or texts from the same training batch, and use a classifier to judge whether images and texts match. Because randomly selected negative samples are usually very different from the original images or texts, they can only learn a very rough alignment between text and visual representations. We use text rewriting to create a large number of positive and negative examples from the original image and text pair data instead of randomly extracting negative samples. We translate the description text of an image into another language, and use reverse translation technology [37] to translate it back to the original language, so as to obtain multiple similar description texts of images as positive samples. We retrieve the similarity of image descriptions through TF-IDF technology; the retrieval results are similar to but different from the original description text, so they can be used as negative samples to enhance the semantic alignment of image and text. We use these positive and negative examples to train the contrastive loss function,

LCMCL=−log⁡exp⁡(d(V,W+)/τ)∑W′∈{W+,W′}exp⁡(d(V,W′)/τ),(2)

where W+ and W− represent positive and negative examples, respectively, of image V, and τ is a temperature parameter, to learn a more accurate semantic alignment between image and text representation, and realize the unified semantic feature expression of multimodal data.

The process of multimodal contrastive learning is described in detail next. As shown in algorithm 2, the input is the text and/or image encoded features and the output is a set of contrastive vectors (zmi,(L), zm+1i,(L)) and (znt,(L), zn+1t,(L)).

:

3.3 Geometry Problem Solver

3.3.1 Shared Encoder

We have multimodal information about images and text features or single-modal information to be encoded. Self-attention (SA) units are used to encode both embedded representations of text and images [38]. In the encoder, we concatenate the two kinds of feature vectors (ht and hi) for multimodal features, and feed single-modal features or concatenated multimodal features into six stacked SA units and obtain FP, which are self-attended features.

Self-Attention Units. SA units are used to reconstruct every feature vector by attending all feature vectors. Multi-head is used to enhance generalization. We stack six SA units to reconstruct text-embedded feature ht and image-embedded feature hi. Each internal SA unit takes the output of the previous unit as input. SA units randomly mask hj from ht or hi, and let the encoder explore deeper information from both feature vectors. It is worth noting that the masked feature vectors are not attended. We take the hidden state FP=[f0;…;fn] of the last unit of SA as self-attended features. Most important is sharing parameters when encoding multimodal or single-modal information. Every output feature vector fully considers the entire feature information.

Adaptive Mechanisms. SA units take both text and image embedding as input, whose multimodal or single-modal embedding vector dimensions generally differ. SA can adaptively process vectors with different dimensions, providing the premise to construct a cross-modal information encoder and map them into a unified semantic space.

After features are extracted from the text and/or images, they are encoded for multimodal contrastive learning to map them into a unified semantic space. As described in Algorithm 3, the input is extracted text features ht and/or image features hi and the output is encoding result FP.

:

3.3.2 Shared Decoder

The decoder part has one more cross-attention than SA, which is used to migrate cross-modal features into the shared features of multi-tasks. We stack six of the same structures in the decoder to represent deep information. It takes tokens of embedded learning tasks as input and pays attention to the cross-modal features from the encoder output. The list of learning tasks is manually marked to include all covered tasks. This paper focuses on problem solving in task-specific list. Cross-modal information from shared encoder output is used for cross attention, and it guides the decoder to generate task-specific solution information. Because text and image information is mapped to a unified semantic space, decoders are shared for different modal tasks.

3.3.3 Answer Generator

After obtaining the task-specific features of decoder output, we use a GRU network to generate a target operation tree with attention [39] over Fp. Operation trees are generated by preorder or postorder traversal for different datasets. Operation trees ensure the validity of the generated sequences, generating the current output node to identify the number of child nodes. For example, if the current node is “add,” it has two child nodes, while a current node with a number has no child nodes. At the beginning of target program sequence, the tokens <CLS> and <END> are added to the beginning and end respectively of the sequence. We feed a start token <CLS> concatenated with decoded information into the GRU. For a target program sequence to predict {yt}(1≤t≤T), each prediction step is a classification issue. We can apply the validity of a generated tree to narrow the decision range. For example, in the subsequent tree, if two numbers have been generated, then the next generation must be the operation symbols, and we use this mechanism to improve the performance of the answer generator.

At the training state, after feeding the token <CLS>, we feed GRU hidden state s0 concatenated with decoded information from the shared decoder to a linear layer with a softmax function to produce the probability of predicted next target program token distribution Dt. We feed golden target program token yt concatenated with decoded information at time step t to produce the next prediction. At the final step, we feed the last program token concatenated with decoded information, and train the network to predict the <END> token, which means the predicted process is over. In the training process, the loss of answer sequences is the negative log-likelihood of the generated sequence

ℒa(θ)=1T∑t=1Tlog⁡Pt(yt∣x,y1,…,yt−1;θ),(3)

where θ indicates parameters of the overall model structure without an image embedder, which is trained in auxiliary tasks. x is the input of both the problem text and image. y1,…,yt−1 in training is the target sequence before time step t. For the test mode, it produces sequences in the model. Task-specific output heads can be customized for different tasks. Our answer generator has a geometry program generator.

We found that the model overfit quickly and performance was not increased in the early epoch. Flooding [40] was used to let the model take random walks at the empirical flooding level, which is the training loss of best performance of the model. We change the loss function to

ℒa′(θ)=|ℒa(θ)−b|+b,(4)

where b is the training loss of the best performance of the model. The model will take gradient decrease as normal when training loss is greater than b, and gradient increase if it is less than b.

Algorithm 4 is built for decoding cross-modal information and generating solution sequences. After contrastive learning, the procedure takes the contrastive features zt and/or zi as the input and outputs the set of solution sequence ℛ. The contrastive features are first sent to the decoder, and then the solution sequence is generated by the answer generator.

:

4  Experiments

4.1 Experimental Setup and Implementation

4.1.1 Experimental Setup

We evaluate the multimodal contrastive learning capability of the proposed approach on the datasets of GeoQA [4] which contain 5010 Chinese geometry problems from online education websites. GeoQA contains angle, length, and other types of problems, as described in Table 1. Each problem contains an image and problem text with corresponding problem-solving explanations and an annotated program. The program can be used to model training and generate target sequences. To test the cross-modal contrastive learning ability of the model, it was simultaneously trained on the GeoQA and Math23K datasets [5]. Math23K was collected by Wang et al., and contains 23,162 tagged math word problems (MWPs), which are linear algebra questions with one unknown variable.

We used PyTorch to implement our model. The learning rate was set to 1e−3, with a batch size of 32 and 100 epochs with the Adam optimizer. The beam size was set to 10.

4.1.2 Implementation Details

We measured the multimodal contrastive learning capability of the model. For a fair comparison, we changed the answer generator to LSTM; because LSTM has more parameters than GRU and is more complex, we wanted to test for a corresponding performance improvement. To measure beam size influence in target program sequence generation, we contrasted our model with different beam sizes, so as to measure the performance improvement vs. the amount of computation. During the multimodal fusion experiment, the model converged quickly to the optimal solution, and overfit quickly. To moderate overfitting, the flooding method [3] was used, which let the model take random walks at a certain training loss level.

The cross-modal contrastive learning ability of the model was measured. The model was trained simultaneously on both datasets, and we trained it on a single dataset to see the corresponding performance changes. To measure the importance of the image and answer programs, we used a subset of the datasets for training, discarding images in GeoQA and discarding the solution sequence in GeoQA and Math23K.

For the GeoQA dataset, we calculated the answer accuracy of angle calculation, length calculation, and others such as area and volume calculation. Total problem solving performance was measured without distinction of problem types. For Math23K, we only evaluated the total problem solving performance. The answer accuracy was calculated by executing the predicted sequences to obtain the result compared to the correct answer. The consistency of the solution sequence was measured. The consistency of the marker sequence and model prediction sequence indicated the inference ability of the model, and the gap between consistency and accuracy indicated some inference ability.

For GeoQA, we first resized the image to 224 × 224, which is easy to feed into ResNet101. We fine-tuned ResNet101 to better extract image features, and pretrained it by puzzle recovery and image element identification with a learning rate of 1e−5. In the experiment with cross-modal data, the model was trained by two datasets at the same time. In each epoch, we selected a batch from the dataset in sequential rotation to train the model. At the end of each epoch, the models were evaluated on the validation sets of the two datasets, and the accuracy evaluation metrics were summed to select the model that performed best on both datasets, which was the final training result.

4.2 Experimental Results

4.2.1 Multimodal Contrastive Learning Results

Table 2 compares the result of solving geometry problems with the different methods on the GeoQA datasets. NGS-Auxiliary, Seq2Prog, BERT2Prog, MCL, LSTM Flooding, and MCL Flooding, respectively, refer to the performance of the NGS-Auxiliary method, Sequence-to-Program model using a GRU encoder with an attention mechanism [15], BERT [16] encoder with an attention mechanism, our proposed method, LSTM used to replace the answer generator with flooding, and our approach with flooding. Bolded scores are highest, and “‡” marks the results reported by Chen et al. [10]. Our model overall outperforms NGS-Auxiliary, but has 0.5 percentage point lower accuracy in solving triangle-type questions. At our flooding level setting, model performance has not improved, as MCL Flooding outperforms LSTM Flooding. The performance of Seq2Prog and BERT2Prog is not satisfactory because diagram information is lacking.

Fig. 4 shows the training and validation loss of different models. At the top-left corner, our validation loss begins to increase at the twelfth epoch. Although training loss always decreases, we achieve the best validation accuracy at the 42nd epoch, at 61.7%. We consider that the model is overfitting or the loss function must be improved. So, we try to change the answer generator to LSTM.

Figure 4: Training and validation loss of different models

The graph titled “Replaced by LSTM” (lower-left) shows the LSTM-based answer generator validation loss increase at the twelfth epoch, with the best performance, 63.7% validation accuracy, at the 35th epoch. The two models show almost the same training trends, but the LSTM-based model performs best earlier. LSTM-based model learning curves are smoother than GRU-based, because LSTM is less likely to overfit, with more parameters than GRU. Flooding is used to overcome our model’s tendency to overfit quickly. The training loss of the best-performing model on the validation set is used as the flooding level. For our model, the flooding level is set at 0.0248. For the LSTM-based answer generator, the flooding level is 0.1005. As shown in Table 2, our flooding level settings do not affect the accuracy improvement of the model. However, as seen in the graph titled “Our model with Flooding” (upper-right) in Fig. 4, flooding does alleviate a certain degree of overfitting, slowing down the upward trend of the validation set loss compared to the trend in the upper-left graph. The graph titled “Replaced by LSTM with Flooding” (lower-right) shows that for the LSTM-based answer generator, flooding is used to alleviate overfitting. The validation loss begins to increase at the sixteenth epoch. The best validation accuracy is achieved at 50 epochs with 0.624 accuracy.

The influence of different beam sizes was tested on our model. We set the beam size as 1, 10, and 20. As shown in Table 3, there is a huge accuracy gap between beam sizes 1 and 10. However, when the beam size increases from 10 to 20, the performance increase is not obvious.

4.2.2 Cross-Modal Contrastive Learning Comparison Results

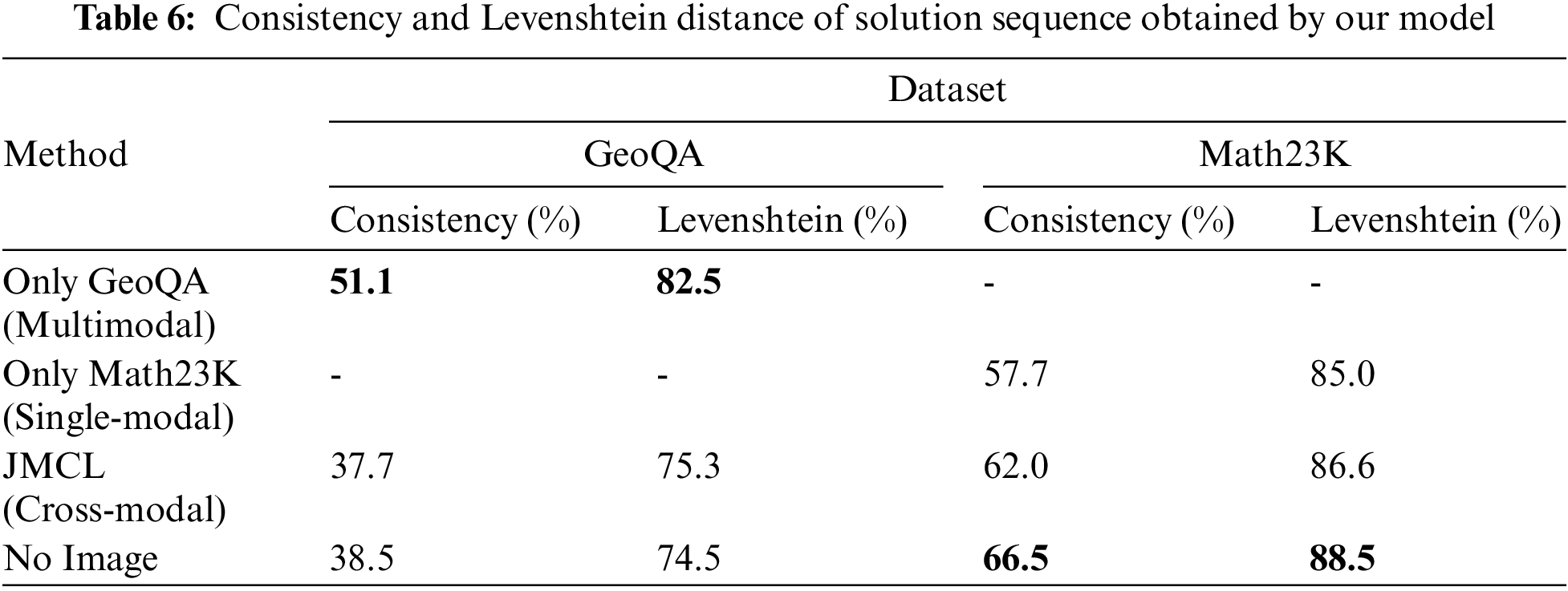
Table 4 shows the answer accuracy of different settings on the two datasets which are GeoQA and Math23K, and “‡” marks the results reported by Wang et al. [41]. To compare model performance changes after cross-modal feature fusion, we used the proposed approach to train GeoQA and Math23K separately. “Only GeoQA,” “Only Math23K,” “Ensemble,” “DNS,” and “JMCL” refer to the performance of the implementation of only training GeoQA on our model, only training Math23K on our model, Wang’s method with the same training set division of our approach, deep neural solver of MWP, and jointly training on the two datasets on our model. The result of JMCL is bolded.

Table 5 shows the performance of using different data subsets to solve the problem. “No Image” and “No Program” refer to not using the image information in GeoQA and not using the program sequence of the two datasets.

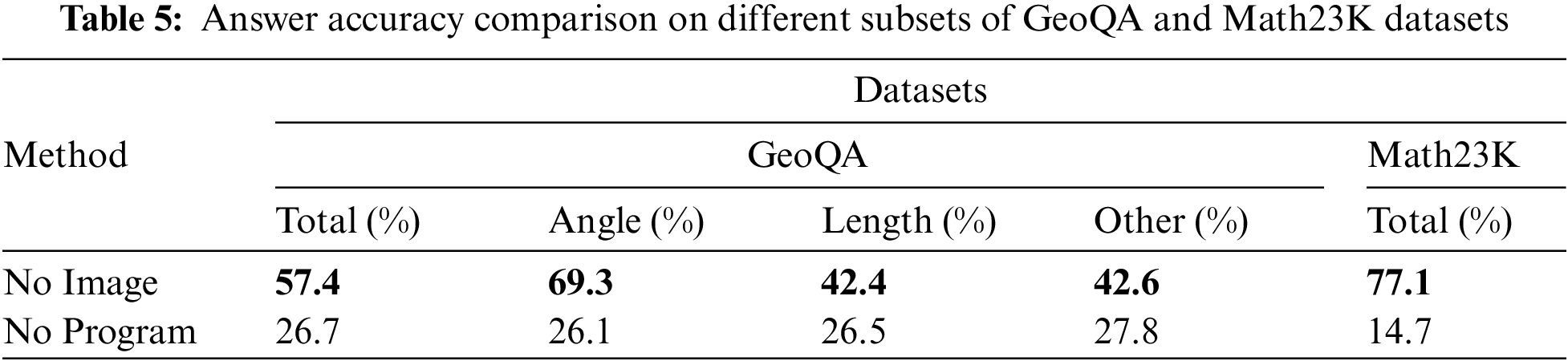
No image information from GeoQA is used to solve the problem, so the model only processes single-modal information from both datasets. The first line, “No Image,” shows that the accuracy is higher than JMCL, as Table 4 confirms, because unimodal information is more effective in contributing to each other’s level of problem comprehension, so there is still much room for improvement in our cross-modal processing. The performance of “No Image” on the GeoQA dataset in Table 5 is less than that of “Only GeoQA” in Table 4 because of the variability between datasets. “No Image” has the best performance, 77.1, on Math23K. “No Program” in Table 5 means the answer is chosen directly from the four options without undertaking any solving steps. The second line, “No Program,” shows that there is a significant drop in performance and the model fails to reason about problems and prove the importance of program sequence.

The consistency and Levenshtein distance of the solution sequence were measured. As Table 6 shows, our cross-modal contrastive learning model has 37.7 consistency on the GeoQA dataset, which is 18.1 different from accuracy, and for Math23K, there is a gap of 9.7. We suggest that the gap occurs because the model is able to generate different solution steps from the labeled sequence to solve the problem. Because a problem does not have a unique solution, the ability to generate different sequences shows some reasoning ability. For a more comprehensive analysis, the Levenshtein distance, a string metric, was measured; this measures the difference between two sequences. The Levenshtein distance of the predicted and labeled sequences was better than the consistency because it only shows the similarity of the sequences. Levenshtein also shows the performance of the model. As Table 6 shows, the Levenshtein distance of the model when trained with Math23K only was 85.0, but it was 86.6 when fusion training of the two datasets was performed. For GeoQA dataset performance, there was no such change.

To explain the performance degradation of GeoQA, we speculate that Math23K has much more data, which increases its impact on the model, and the organization rules of the two datasets labeled with sequences are different. Fig. 5 illustrates that GeoQA and Math23K have different forms of solution sequence construction. In GeoQA, operation symbols include “Minus” and “Half”, and the operands include “N0” and “V1”. For Math23K, operation symbols include “-” and “/”, and operand include “temp_b” and “temp_c”. In the two datasets, different symbols are used for the same operation, making the vocabularies of the model poorly generalized. GeoQA uses preorder trees for operations, while Math23K uses postorder trees. For these reasons, the two datasets do not effectively contribute together to the model’s understanding of the problem.

Figure 5: Examples of solution sequences for GeoQA and Math23K

4.3 Typical Case Analyzing

Two typical cases have been displayed below. Typically, if the predicted program sequence has no match to any of the options, then the model gets no result and we do not let the model make random choices. In Figs. 6 and 7, the operation is predefined such as Minus and Add. Those operations will be executed by pre-defined functions to get a result and the result of each operation is stored in a variable to facilitate the final result. It is worth noting that an operation is generated firstly and secondly, the numbers involved in the operation are generated in annotated program sequences. In programs, N means number in the problem. The serial number is the order in which the numbers appear. V means variables that are operation results labeled by order of execution. C is a constant that has been predefined. The final feature representations of problem are fed into a classifier which transforms features into probability distribution. The position of the maximum value in distribution corresponds to the predicted program. Each time step of classifier will produce a program such as “Minus” until overall program sequences are generated.

Figure 6: Case of our model gets no result

Figure 7: Case of our model gets right answer

In Fig. 6, the model gets the wrong answer sequence and the result is 6.5. At the beginning of the sequence, the model predicts N0−N1 which is 3−10=−7, and −7 is stored in the variable V0. Then the model predicts “Half” and the operation number are V0 and V1 which obtained (−3.5=−7/2). Finally, the answer has been got by Answer=V1+N1(6.5=−3.5+10). We find that in length type questions neither the final result nor the intermediate result will be negative. In future works, we try to avoid negative forecasts and improve the performance of the model by avoiding operations that can generate negative numbers. The model may have failed to effectively perform Multimodal information fusion.

In Fig. 7, the model predicts the right target programs. C2 and C3 are constants that are defined in advance. In our setting, C2 is 90 and C3 is 180. We can get V0=C2−N0=90−70=20, then V1=V0∗2=40. Finally, we get Answer=C3−V1=140. Interestingly, the model can use predefined constants to solve the problem, verifying the validity of the model and demonstrating powerful inference capability.

5  Conclusion

In this work, we focused on solving geometry problems via the feature and contrastive learning of multimodal data. A shared feature-learning model of multimodal data was adopted to learn a unified feature representation of a text and image in order to address the heterogeneity between multimodal geometry problems. A contrastive learning model of multimodal data was proposed to enhance the semantic relevance between multimodal features and map them into a unified semantic space. This model can effectively adapt to both single-modal and multimodal downstream tasks. A shared encoder-decoder structure realized the semantic alignment of multimodal geometry data and generated readable solving sequences of problems. The shared encoder processed text and/or image features masked by self-attention units, and multilayer Transformer was used to realize the interaction between cross-modal features. After encoding, multimodal contrastive learning was proposed to realize the semantic alignment of multimodal geometry data. The shared decoder processed contrastive features and used learning task lists to transform information to generate task-specific features. The method can be used for a variety of applications without changing too much structure. The experimental results showed that the proposed method is promising in the solution of geometry problems.

In future work, we will eliminate the variability in the solution sequences of different datasets to improve the performance of the model, and explore a higher-performance solution framework through methods such as reinforcement learning.

Acknowledgement: The authors gratefully acknowledge the helpful comments and suggestions of the reviewers, which have improved the presentation. We also thank LetPub (www.letpub.com) for its linguistic assistance during the preparation of this manuscript.

Funding Statement: This work is supported by the National Natural Science Foundation of China (No. 62107014, Jian P., 62177025, He B.), the Key R&D and Promotion Projects of Henan Province (No. 212102210147, Jian P.), and Innovative Education Program for Graduate Students at North China University of Water Resources and Electric Power, China (No. YK-2021-99, Guo F.).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. Zhang, J. (2000). Mathematics mechanization and applications. Cambridge: Academic Press. [Google Scholar]

    2. Zhang, D., Wang, L., Zhang, L., Dai, B. T., Shen, H. T. (2019). The gap of semantic parsing: A survey on automatic math word problem solvers. IEEE Transactions on Pattern Analysis and Machine Intelligence, 42(9), 2287–2305. DOI 10.1109/TPAMI.34. [Google Scholar] [CrossRef]

    3. Sachan, M., Dubey, A., Hovy, E. H., Mitchell, T. M., Roth, D. et al. (2020). Discourse in multimedia: A case study in extracting geometry knowledge from textbooks. Computational Linguistics, 45(4), 627–665. DOI 10.1162/coli_a_00360. [Google Scholar] [CrossRef]

    4. Yu, X., Wang, M., Gan, W., He, B., Ye, N. (2019). A framework for solving explicit arithmetic word problems and proving plane geometry theorems. International Journal of Pattern Recognition and Artificial Intelligence, 33(7), 1940005. DOI 10.1142/S0218001419400056. [Google Scholar] [CrossRef]

    5. Gan, W., Yu, X., Wang, M. (2019). Automatic understanding and formalization of plane geometry proving problems in natural language: A supervised approach. International Journal on Artificial Intelligence Tools, 28(4), 1940003. DOI 10.1142/S0218213019400037. [Google Scholar] [CrossRef]

    6. Gan, W., Yu, X., Zhang, T., Wang, M. (2019). Automatically proving plane geometry theorems stated by text and diagram. International Journal of Pattern Recognition and Artificial Intelligence, 33(7), 1940003. DOI 10.1142/S0218001419400032. [Google Scholar] [CrossRef]

    7. Seo, M., Hajishirzi, H., Farhadi, A., Etzioni, O., Malcolm, C. (2015). Solving geometry problems: Combining text and diagram interpretation. Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, pp. 1466–1476. Lisbon. [Google Scholar]

    8. Seo, M. J., Hajishirzi, H., Farhadi, A., Etzioni, O. (2014). Diagram understanding in geometry questions. Proceedings of the AAAI Conference on Artificial Intelligence, pp. 2831–2838. Quebec. [Google Scholar]

    9. Lu, P., Gong, R., Jiang, S., Qiu, L., Huang, S. et al. (2021). Inter-GPS: Interpretable geometry problem solving with formal language and symbolic reasoning. arXiv preprint arXiv:2105.04165. [Google Scholar]

  10. Chen, J., Tang, J., Qin, J., Liang, X., Liu, L. et al. (2021). GeoQA: A geometric question answering benchmark towards multimodal numerical reasoning. arXiv preprint arXiv:2105.14517. [Google Scholar]

  11. Zhong, X., Fu, H., Yu, Y., Liu, Y. (2015). Interactive learning environment based on knowledge network of geometry problems. 10th International Conference on Computer Science & Education (ICCSE), pp. 53–58. Cambridge. [Google Scholar]

  12. Wang, L., Zhang, D., Gao, L., Song, J., Guo, L. et al. (2018). Mathdqn: Solving arithmetic word problems via deep reinforcement learning. Proceedings of the AAAI Conference on Artificial Intelligence, pp. 5545–5552. New Orleans. [Google Scholar]

  13. Nam, H., Ha, J. W., Kim, J. (2017). Dual attention networks for multimodal reasoning and matching. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 299–307. Hawaii. [Google Scholar]

  14. Lu, J., Yang, J., Batra, D., Parikh, D. (2016). Hierarchical question-image co-attention for visual question answering. Advances in Neural Information Processing Systems, 29, 289–297. [Google Scholar]

  15. Amini, A., Gabriel, S., Lin, P., Koncel-Kedziorski, R., Choi, Y. et al. (2019). MathQA: Towards interpretable math word problem solving with operation-based formalisms. arXiv preprint arXiv:1905.13319. [Google Scholar]

  16. Devlin, J., Chang, M. W., Lee, K., Toutanova, K. (2018). BERT: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805. [Google Scholar]

  17. Dong, L., Yang, N., Wang, W., Wei, F., Liu, X. et al. (2019). Unified language model pre-training for natural language understanding and generation. Advances in Neural Information Processing Systems, 32, 12727–12739. [Google Scholar]

  18. Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M. et al. (2019). Roberta: A robustly optimized bert pretraining approach. arXiv preprint arXiv:1907.11692. [Google Scholar]

  19. Yang, Z., Dai, Z., Yang, Y., Carbonell, J., Salakhutdinov, R. R. et al. (2019). XLNet: Generalized autoregressive pretraining for language understanding. Advances in Neural Information Processing Systems, 32, 5571–5581. [Google Scholar]

  20. Lewis, M., Liu, Y., Goyal, N., Ghazvininejad, M., Mohamed, A. et al. (2019). BART: Denoising sequence-to-sequence pre-training for natural language generation, translation, and comprehension. arXiv preprint arXiv:1910.13461. [Google Scholar]

  21. Simonyan, K., Zisserman, A. (2014). Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556. [Google Scholar]

  22. He, K., Zhang, X., Ren, S., Sun, J. (2016). Deep residual learning for image recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778. Las Vegas. [Google Scholar]

  23. Chen, Y. C., Li, L., Yu, L., El Kholy, A., Ahmed, F. et al. (2020). Uniter: Universal image-text representation learning. European Conference on Computer Vision, Glasgow, Scotland, pp. 104–120. [Google Scholar]

  24. Li, L. H., Yatskar, M., Yin, D., Hsieh, C. J., Chang, K. W. (2019). VisualBERT: A simple and performant baseline for vision and language. arXiv preprint arXiv:1908.03557. [Google Scholar]

  25. Su, W., Zhu, X., Cao, Y., Li, B., Lu, L. et al. (2019). VL-BERT: Pre-training of generic visual-linguistic representations. arXiv preprint arXiv:1908.08530. [Google Scholar]

  26. Lu, J., Batra, D., Parikh, D., Lee, S. (2019). Vilbert: Pretraining task-agnostic visiolinguistic representations for vision-and-language tasks. Advances in Neural Information Processing Systems, 32, 1–10. [Google Scholar]

  27. Nie, L., Wang, W., Hong, R., Wang, M., Tian, Q. (2019). Multimodal dialog system: Generating responses via adaptive decoders. Proceedings of the 27th ACM International Conference on Multimedia, pp. 1098–1106. France. [Google Scholar]

  28. Nie, L., Jia, M., Song, X., Wu, G., Cheng, H. et al. (2021). Multimodal activation: Awakening dialog robots without wake words. Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval, pp. 491–500. Canada. [Google Scholar]

  29. Nie, L., Jiao, F., Wang, W., Wang, Y., Tian, Q. (2021). Conversational image search. IEEE Transactions on Image Processing, 30, 7732–7743. DOI 10.1109/TIP.2021.3108724. [Google Scholar] [CrossRef]

  30. Xu, T., Zhang, P., Huang, Q., Zhang, H., Gan, Z. et al. (2018). AttnGAN: Fine-grained text to image generation with attentional generative adversarial networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 1316–1324. Salt Lake City. [Google Scholar]

  31. Zhang, H., Koh, J. Y., Baldridge, J., Lee, H., Yang, Y. (2021). Cross-modal contrastive learning for text-to-image generation. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 833–842. Nashville. [Google Scholar]

  32. Li, W., Gao, C., Niu, G., Xiao, X., Liu, H. et al. (2020). UNIMO: Towards unified-modal understanding and generation via cross-modal contrastive learning. arXiv preprint arXiv:2012.15409. [Google Scholar]

  33. Jian, P., Sun, C., Yu, X., He, B., Xia, M. (2019). An end-to-end algorithm for solving circuit problems. International Journal of Pattern Recognition and Artificial Intelligence, 33(7), 1940004. DOI 10.1142/S0218001419400044. [Google Scholar] [CrossRef]

  34. Joshi, M., Chen, D., Liu, Y., Weld, D. S., Zettlemoyer, L. et al. (2020). Spanbert: Improving pre-training by representing and predicting spans. Transactions of the Association for Computational Linguistics, 8, 64–77. DOI 10.1162/tacl_a_00300. [Google Scholar] [CrossRef]

  35. Ren, S., He, K., Girshick, R., Sun, J. (2015). Faster R-CNN: Towards real-time object detection with region proposal networks. Advances in Neural Information Processing Systems, 28, 91–99. [Google Scholar]

  36. Wang, Y. S., Liu, C., Zeng, X., Yuille, A. (2018). Scene graph parsing as dependency parsing. arXiv preprint arXiv:1803.09189. [Google Scholar]

  37. Edunov, S., Ott, M., Auli, M., Grangier, D. (2018). Understanding back-translation at scale. arXiv preprint arXiv:1808.09381. [Google Scholar]

  38. Yu, Z., Yu, J., Cui, Y., Tao, D., Tian, Q. (2019). Deep modular co-attention networks for visual question answering. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 6281–6290. California. [Google Scholar]

  39. Bahdanau, D., Cho, K., Bengio, Y. (2014). Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473. [Google Scholar]

  40. Ishida, T., Yamane, I., Sakai, T., Niu, G., Sugiyama, M. (2020). Do we need zero training loss after achieving zero training error?. arXiv preprint arXiv:2002.08709. [Google Scholar]

  41. Wang, L., Wang, Y., Cai, D., Zhang, D., Liu, X. (2018). Translating a math word problem to an expression tree. arXiv preprint arXiv:1811.05632. [Google Scholar]

  42. Wang, Y., Liu, X., Shi, S. (2017). Deep neural solver for math word problems. Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, pp. 845–854. Copenhagen. [Google Scholar]