Fairness-Aware Harvested Energy Efficiency Algorithm for IRS-Aided Intelligent Sensor Networks with SWIPT

1  Introduction

Increasing interest from both academia and industry has been drawn to the IRS as a candidate technology for future communication networks. The IRS consists of a variety of intelligent reflecting units that can be automatically changed to reflect signals in different environments to facilitate wireless transmission. In the event that the IRS is affiliated, radio-frequency (RF) signals are able to be transmitted with greater efficiency to intended receivers, and only unintentional receivers can interfere with the transmission. For example, RF signals are reflected in the direction that the transmitters intended for when they are transmitted from the transmitters. In addition, the IRS is an array of passive antennas that consumes substantially less power. In this regard, the IRS is considered to be a cost-effective way for wireless communication networks to improve their spectrum efficiency as well as their energy efficiency due to its cost effective approach.

There have been several previous studies that have investigated active signal transmission via transmitters and shift phase via IRSs in order to enhance the transmission performance for the IRS-assisted communication systems. In particular, Huang et al. [1] investigated sum-rate maximization by optimizing both the transmit power of the transmitter as well as phase shift coefficients the IRS separately. According to [2], the transmission power of a single-user IRS system was optimized using a combination of continuous transmit beamformer and discrete phase shift to minimize the transmission power while taking into account the SINR constraint. There was an investigation in the literature [3] that sought to optimize both the beamforming weights and the phase shifts of IRS in order to maximize the spectral efficiency (SE) of a single antenna user. The work in that article [4] investigated the security of the physical layer for the IRS-aided networks while taking into consideration imperfect CSI corresponding to the presence of multi-antenna potential eavesdroppers. Specially, for transmitter and IRS, beamformers as well as the covariance matrices for the artificial noise are optimized simultaneously as a way of increasing the total transmission rate. It was the authors of [5] who employ convex constraints to approximate the unit modulus constraints of the phase shifters in order to maximize the secrecy rate between several legitimate users and multiple eavesdroppers by using convex constraints to approximate the unit modulus constraints. In spite of the fact that this approach simplifies the design of algorithms in a significant way, there may in fact be a significant performance loss as a result of this approach. In addition, various other setups are also used to study joint transmission and reflection designs, including OFDM [6,7] and NOMA [8,9].

In future wireless systems, one of the most significant concerns is the amount of energy consumed. In order to ensure high energy efficiency, it is possible to harvest energy from ambient radio frequency signals in order to achieve high performance [10–12]. As a result of using the SWIPT, there is the possibility that the user will be able to reap the benefits of both the energy and the information that is being conveyed at the same time. For example, Xu et al. [13] introduced a very interesting transmission scheme for multiuser multiple-input single-output (MISO) SWIPT networks, which comprised a multiantenna transmitter that transmits signals of information to multiple wireless receivers with single antennas and an ER with only one antenna. Besides, a method for achieving robust beamforming was proposed in [14] in which the minimum transmission power of the beam is limited by both the secrecy rate and efficiency of the channel parameters, as both play a critical role in determining the level of robustness of the beamforming. The embodiment of such a concept in practical systems is accomplished by both the PS and time switching (TS) receiver architectures, which are the common user architectures found in SWIPT-enabled systems [15]. When using SWIPT systems, we should be aware that the amount of energy harvested at the user end can be severely dictated by the path losses in long-range data transmissions, which can lead to a performance bottleneck at the user end as a result. With this in mind, multiple antennas and IRSs can be utilized simultaneously in the PS-enabled SWIPT-aided network in order to obtain increased transmission efficiency and to improve beamforming gains at both transmitter and IRS. It is quite evident that both the MISO and IRS can be applied to work together so as to mitigate the attenuation of signals caused by the long distance between the transmitter and energy harvesting receivers.

Recently, there have been a variety of combinations of SWIPT/RIS techniques investigated in order to gain the advantages of SWIPT/RIS and to reap their performance benefits. There are many different forms of communication that can be enhanced through the use of this technology, such as mobile edge computing [16], secure transmission [17], the Internet of Things [18], and heterogeneous networks [19]. For example, the deployment of IRS provides a new way for SWIPT-enabled Communication systems and allows more freedom for optimization. As a result, an increase in the efficiency of the transmission of information and energy can be obtained by combining active and passive beam forming to increase the system’s service coverage. As reported in the literature [20], penalty algorithms are capable of optimizing the active/passive beam forming process to minimize the amount of base-station transmitted power when certain conditions are met, such as satisfying the quality constraint for user service and the IRS modularity constraint. Several studies have been conducted in [21] that demonstrate the optimization of maximum weighted energy as a means of ensuring the fairness of each user’s performance, as well as that base-station’s capability to transmit information beam forming meets the service quality requirements of both users that receive information and those who collect energy. To ensure fairness among multiple users, literature [22] considered the weighting and rate maximization of users receiving information, and proposes an algorithm based on block coordinate descending to alternately optimize the precoding matrix at the AP as well as the phase shift vector to ensure fairness among users. Typically, the receiver of an Internet of Things application must simultaneously decode data and collect energy [22–24]. According to a study published in [22], MISO systems with IRS-assisted downlink SWIPT were examined. In this system, the AP transmits both information and energy simultaneously to the user, who can then decode the data and obtain power through power splitting, where the goal is to minimize the transmitted power of base-station by combining the optimization of beam forming, power splitting factor and reflection phase shift at IRS. Based on literature [23], the IRS-SWIPT system’s performance was compared to the receiver with power splitting mode’s decoding, forwarding, and relaying systems. Additionally, there is a robust beam-forming design that has been proposed in the literature [24]. As a result of the interruption probability constraint, beam forming of AP and phase shift of IRS were combined to minimize the transmitted power by applying SDR and Bernstein type inequality in order to achieve the lowest transmitted power. As stated above, however, in the algorithms discussed above, there is no study on fairness-aware harvested energy efficiency within the confines of module-1 constraint of a SWIPT system based on IRS-assisted [25].

Aiming to resolve the issue of active beamforming as well as passive beamforming in IRS-assisted SWIPT systems, the purpose of this paper is to examine the design and optimization of beamforming based on fairness-aware harvested energy efficiency criteria. Taking the harvested energy efficiency as the optimization objective, we determined the IRS passive beamforming vector of the transmitter as well as the IRS active beamforming vector under power control conditions, and IRS phase shift constraints. To solve the SINR constraints at the receiving end, we propose a method for calculating harvested energy efficiency and apply the alternate direction multiplier method in order to calculate the fairness-aware harvested energy efficiency from the receivers point of view. In this case, it means that the considered problem can be transformed into the standard semi-positive definite problem by performing SDR method for a given IRS-phase shift matrix. Once the active beamforming vector was optimized, the SINR constraint value under the IRS passive condition was calculated, which in turn was transformed into a convex optimization problem for the IRS phase shift matrix. Furthermore, an iterative algorithm of our interested communication systems is developed. The simulation results indicate that the developed RIS-SWIPT network with energy beamformer achieves an impressive performance improvement compared with the conventional transmission schemes.

2  System Model and Problem Formulation

We study the downlink transmission of a MISO-SWIPT network consisting of one transmitter and one IRS as shown in Fig. 1, where the transmitter serves KI information users and KE ERs with aid of the IRS where all the receivers have single antenna. Besides, the transmitter is equipped with M antenna while the IRS has N reflection elements. Assume H represents the complex vector containing the channel coefficients between the M antennas of the transmitter and the IRS, hb,k and gb,i denote the complex vector containing the channel coefficients between the transmitter and the k-th IR and i-th ER, respevtively. hr,k represent the reflective channel between the IRS and k-th IR while gr,i denote the reflective channel from the IRS to i-th ER. We further assume, in this paper, that all information about the channel state is always available at the transmitter, so that we can concentrate more effectively on the design of active beamforming techniques as well as passive beamforming techniques for the purposes of this paper.

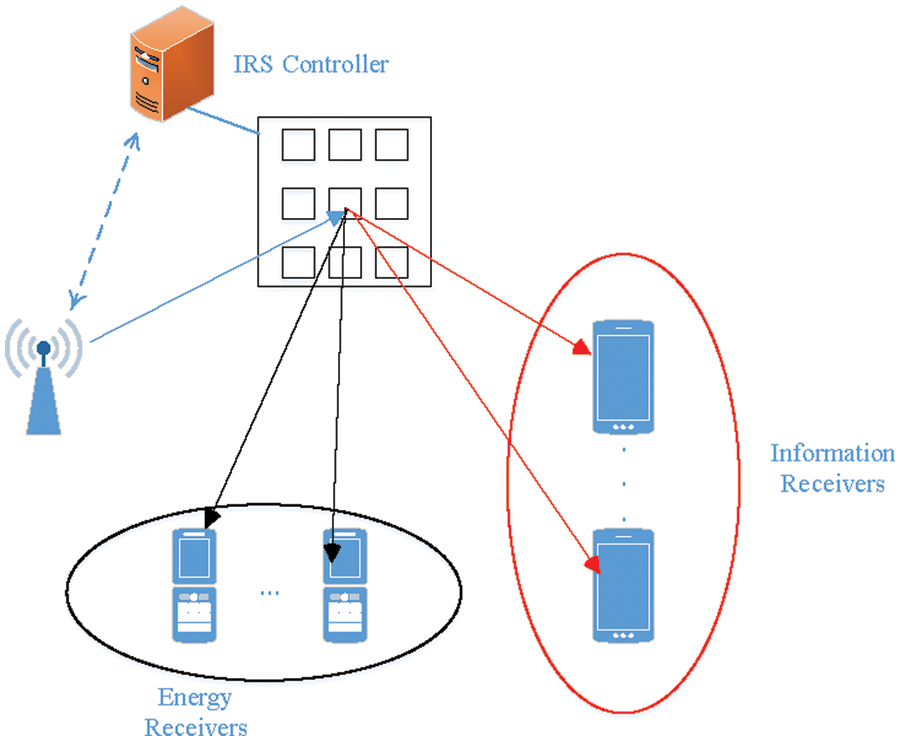
Figure 1: IRS-SWIPT Wireless Sensors System

As a starting point, for the active beam assignment, this work does not only set the traditional information beam assignment at the transmitter, but also adds the energy beam assignment for the ERs for the active beam assignment. Due to the random nature of information, we assume that the signal sk for k-th receivers follow a Gaussian distribution, for example: sk∼CN(0,1), and the corresponding beamforming vector is wk. Because while only the ER needs to capture the beam’s energy and not decode any information, the transmitter is capable of generating pseudo-random sequences of energy signals for transmission through conventional lines. Hence, the energy beamforming vector is set as wE∼CN(0,Z). Specially, Z is the high rank matrix, then there exists rank(Z) separated energy beams in our considered model. Then, the conveyed signal at AP is

x=∑k=1KIwksk+wE(1)

Given that the active beamformer at the transmitter allows a maximum transmitting power of P, then the transmitting power constraint equals ∑k=1KI‖wk‖22+tr(Z)≤P. As a further step, we define the reflective parameters for the IRS based on the passive beamforming at the IRS. In this case, the reflection parameters are primarily comprised of the reflection amplitude and the rotation of the phase of the incident signal. Since the signal coverage problem is inherent, we typically set the reflection amplitude to 1 in order to maximize the reflected signal. Therefore, the reflection phase matrix endowed with passive beams is defined as Θ≜diag(ejθ1,ejθ2,…,ejθN), where θn refers to the reflection phase of the n-th reflection element. By virtue of the above definition, the receivers are capable of simultaneously receiving both the direct signal from the transmitter’s direct path and the reflected signal from the IRS’s reflection path. In the first instance, for each IR, the received signal for the k-th receiver is given by

yk=(hr,kHΘH+hb,kH)x+zk(2)

where zk∼CN(0,σ2) represents the additive white Gaussian noise. Moreover, in view of the fact that the ER only considers the strength of the received signal without regard to the form of the signal, it is possible to generate the energy signal at the transmitter by using a pseudo-random sequence mechanism. As a result, it is perfectly feasible to eliminate the interference caused by the energy signal as soon as the IR has the knowledge of the pseudo-random sequence of the energy signal a prior. After the interference energy signal offset is taken into account, the SINR of the k-th IR can be expressed as

γk(w,Θ)=|(hr,kHΘH+hb,kH)wK|2∑m=1,m≠kKI|(hr,kHΘH+hb,kH)wm|2+σ2(3)

For the ER, the radio-frequency signals it receives are used to charge the battery. Thus, the harvested energy from the i-th ER is provided by

Ei(w,Θ,Z)=(gr,iHΘH+gb,iH)Z(gr,iHΘH+gb,iH)H+∑j=1KI|(gr,iHΘH+gb,iH)wj|2(4)

Herein, PB refers to static energy consumed by the transmitter, while PI refers to the static energy consumed by the IRS. As a result, the total consumed power can be expressed as

Ptotal(w)=ζ(∑k=1KI‖wk‖2)+PB+PI(5)

where ζ indicates the coefficient of the amplifier. In this study, we utilize the novel definition of harvested energy efficiency of i-th ER, which balances the harvested energy and the corresponding power consumption, can be found as follows:

ηi(w,Θ,Z)=Ei(w,Θ,Z)Ptotal(w)(6)

Taking into account the SINR at the IR and the energy receiving power at the ER, it is clear that the level of communication and harvested energy efficiency can be balanced by adjusting the active beam assignment at the transmitter as well as the reflection phase parameter at the IRS to produce a passive beam assignment. As a result, this paper aims to maximize the minimum collected energy efficiency in all ERs so that the harvested energy efficiency level is balanced among ERs in order to achieve this goal under the constraints of the transmitted power at the transmitter, the SINR constraint of all IR, and the reflection phase constraints of the reflective array on the IRS. As a result of the analysis above, the following problem formulation can be modelled:

maxw,Θ,Z  mini∈{1,2,…,KE}  ηi(w,Θ,Z)s.t.  γk(w,Θ)≥γmin,∀k∈{1,2,…,KI}∑k=1KI‖wk‖2+Tr(Z)≤P0≤θn≤2π,∀n∈{1,2,…,N}Z⪰0(7)

where γmin denotes the minimum communication SINR threshold for the i-th IR. As can be seen from optimization problem (7), w and Θ are highly coupled within the objective function and SINR constraints, which prevents the optimization from obtaining the global optimal solution directly. To be able to come up with a globally optimal solution, additional decomposition processes will have to be performed.

3  Design and Optimization of Beamforming Based on Harvested Energy Efficiency

Owing to the fact that the objective function of (7) is a max-min problem, several auxiliary variables are introduced to facilitate further derivation of the objective function, such as t, xk, y. Then, we have

maxw,Z,x,t,y  ts.t.  C1:γk(w,Θ,x,t,y)≥γmin,∀k∈{1,2,…,KI}C2:∑k=1KI‖wk‖2+Tr(Z)≤PC3:0≤θn≤2π,∀n∈{1,2,…,N}C4:Z⪰0C5:xi2y≥t,∀i∈{1,2,…,KE}C6:Ei(w,Θ,Z)≥xi2,∀i∈{1,2,…,KE}C7:Ptotal(w)≤y(8)

Due to the coupling of variables, this paper will use an iterative method to optimize and solve different variables, that is, first fix the passive beam assignment reflection phase variable Θ, and optimize and solve the active beam assignment variable w. When the active beam assignment has been determined, it is then fixed, so that the passive beam assignment variable can be optimized iteratively until convergence is achieved.

3.1 Design Active Beamforming Vectors with Fixed IRS Phase Shift Matrices

In the first instance, after confirming the passive beam assignment Θ, this subsection focuses only on the active beam assignment variable w. Since Θ is coupled to the channel at the time of its creation, when it is fixed, the channel becomes locally invariant. For writing convenience, the superimposed channel of direct path and reflection path at the IR and ER are defined as hk=(hr,kHΘH+hb,kH)H and gi=(gr,iHΘH+gb,iH)H. According to the optimization problem (8) after channel merging, we can deduce the active beamforming optimization problem as follows:

maxw,Z,x,t,y  ts.t.  C1−1:|hkHwk|2γmin≥∑m=1,m≠kKI|hkHwm|2+σ2,∀k∈{1,2,…,KI}C2,C4,C5,C7C6:giHZgi+∑k=1KI|giHwk|2≥xi2,∀i∈{1,2,…,KE}(9)

Since both of the optimization problems C1−1, C5 and C6 have non-convex quadratic constraints on the solution space, one could argue that the optimization problem (9) can be defined as a non-convex quadratic programming problem that cannot be solved directly due to the fact that it involves non-convex quadratic constraints. Here, the SDR method will be used to solve problems such as the one mentioned above. Firstly, the semi-positive definite matrix referred to the active beam is modeled as Wk=wkwkH, whose rank equals to one. Hence, we can find the equivalent form of optimization problem (9) as follows:

maxW,Z,x,t,y  ts.t.  C1−2:Tr(hkhkHWk)γmin≥∑m=1,m≠kKITr(hkhkHWm)+σ2,∀k∈{1,2,…,KI}C2−1:∑k=1KITr(Wk)+Tr(Z)≤PC4:Z⪰0C5:xi2y≥t,∀i∈{1,2,…,KE}C6−1:giHZgi+∑k=1KITr(gigiHWk)≥xi2,∀i∈{1,2,…,KE}C7−1:ζ(∑k=1KITr(Wk))+PB+PI≤yC8:Wk⪰0,∀k∈{1,2,…,KI}C9:Rank(Wk)≤1,∀k∈{1,2,…,KI}(10)

Since (C5) in (10) involves nonconvex constraints, we approximate these constraints around the initial value ({xi(l)},t(l)) using Taylor expansion. Then, the left side of (C5) in (10) can be approximated as

xi2y≥2∗xi(l)xiy(l)−(xi(l))2(y(l))2y(11)

Therefore, the problem (10) can be reformalted as

maxW,Z,x,t,y  ts.t.  C1−2:Tr(hkhkHWk)γmin≥∑m=1,m≠kKITr(hkhkHWm)+σ2,∀k∈{1,2,…,KI}C2−1:∑k=1KITr(Wk)+Tr(Z)≤PC4:Z⪰0C5−1:2∗xi(l)xiy(l)−(xi(l))2(y(l))2y≥t,∀i∈{1,2,…,KE}C6−1:giHZgi+∑k=1KITr(gigiHWk)≥xi2,∀i∈{1,2,…,KE}C7−1:ζ(∑k=1KITr(Wk))+PB+PI≤yC8:Wk⪰0,∀k∈{1,2,…,KI}C9:Rank(Wk)≤1,∀k∈{1,2,…,KI}(12)

Nevertheless, due to the rank constraint (C9), the optimization problem (12) remains non-convex and cannot be solved directly. We can remove the rank-constrained relaxation to obtain the semi-positive definite relaxation form of (12), which can be expressed as

maxW,Z,x,t,y  ts.t.  C1−2,C2−1,C4,C5−1,C6−1,C7−1 and C8(13)

In the case of the optimization problem (13), it should be obvious that the matrix W and E have been selected as variables, and that the optimization problem is a semi-positive definite programming problem (SDP), so it is convex and can be solved directly by using mature optimization tools that are portable [26]. It is supposed that the optimal solution referred to problem (13) is Wk⋆, Z⋆, xi⋆, y⋆, and t⋆. The above assumptions imply that when the rank of Wk is less than or equal to 1, then Wk can only be broken down into a vector form, and the conjugate transpose multiplication optimization problem is a tight semidefinite relaxation problem, while at the same time, the obtained solution is the optimal solution to (9). Fortunately, the following theorem indicates that the Wk is always less than 1. Moreover, we can decompose the optimal solution obtained from the optimization problem (9) into the vector form, i.e., such as wk⋆.

Theorem 3.1. The optimization problem (13) is a tight semidefinite relaxation problem, which means the corresponding solution of (13) always meets Rank(Wk)≤1.

Proof. Firstly, we can obtain the Lagrange function of the optimization problem (13), which is given as follows:

ℒ({Wk},Z,t,y,{xk},{ak},b,C,{di},{ei},f,{Mk})=t+∑k=1KIak(Tr(hkhkHWk)γmin−∑m=1,m≠kKITr(hkhkHWm))+∑k=1KITr(MkWk)+Tr(CZ)+∑i=1KEdi(2∗xi(l)xiy(l)−(xi(l))2(y(l))2y≥t)+b(P−∑k=1KITr(Wk)+Tr(Z))+∑i=1KEei(giHZgi+∑k=1KITr(gigiHWk)−xi2)+f(y−(ζ(∑k=1KITr(Wk))+PB+PI))(14)

where {ak}, b, C, {di}, {ei}, f, and {Mk} are the Lagrangian multipliers and the Lagrangian multipliers matrix, which correspond to constraints C1−2,C2−1,C4,C5−1,C6−1,C7−1 and C8, respectively. As a result, we can obtain the Lagrangian dual function of the optimization problem (13) as follows:

𝒴({ak},b,C,{di},{ei},f,{Mk})=sup{Wk},Z,t,y,{xk} ℒ({Wk},Z,t,y,{xk},{ak},b,C,{di},{ei},f,{Mk})(15)

In this way, we can construct the dual problem of optimization (13) as follows:

min{ak},b,C,{di},{ei},f,{Mk} 𝒴({ak},b,C,{di},{ei},f,{Mk})s.t. ak≥0,b≥0,C⪰0,c,∀k∈{1,2,…,KI}di≥0,ei≥0,f≥0,Mk⪰0,c,∀k∈{1,2,…,KI},∀i∈{1,2,…,KE}(16)

Due to the fact that optimization problem (13) falls into the SDP form, it is compact with the optimal solution of its dual problem (16), that is, the dual gap is zero [27]. Because the strong duality is strictly established and the differentiable objective function is present in the optimization problem (13) along with all its corresponding constraints, optimal solutions are guaranteed to satisfy the Karush–Kuhn–Tucker (KKT) condition. To begin with, let’s assume that the best solution to both the optimization problem (13) and the dual problem (16) is {Wk⋆}, Z⋆, t⋆, {xi⋆}, y⋆ and {ak⋆}, b⋆, C⋆, {di⋆}, {ei⋆}, f⋆, {Mk⋆}. Then, the KKT conditions related to (13) can be written as

ak⋆≥0,b⋆≥0,C⋆⪰0,di⋆≥0,ei⋆≥0,f⋆≥0,Mk⋆⪰0C⋆Z⋆=0,Mk⋆Wk⋆=0∑i=1KEei⋆gigiH+ak⋆hkhkHγmin−(f⋆ζ+b⋆)IM+Mk⋆=0(17)

For the sake of representation, let us define the matrix Fk as ∑i=1KEei⋆gigiH+ak⋆hkhkHγmin. In this case, let the maximum eigenvalue of Fk be λmaxFk. Based on (17), we have

Mk⋆=(f⋆ζ+b⋆)IM−Fk(18)

From (17), we know that Wk⋆’s null space is the span of Mk⋆, which means that the rank relation between them is Rank(Mk⋆)+Rank(Wk⋆)=M. In the following, three cases are discussed: (1) If λmaxFk≤f⋆ζ+b⋆, the ranks of Mk⋆ and Wk⋆ are M and 0, respectively. This implies that, if the transmitter has a non-zero transmitting power constraint, it is not possible to meet the requirements of the SINR constraint, and therefore this case does not represent a valid example. (2) If λmaxFk≥f⋆ζ+b⋆, Mk⋆ becomes a nonsemidefinite matrix. Therefore, there is a conflict between this condition and KKT conditions in (17), so this case cannot be true. (3) According to the analysis above, we can conclude λmaxFk=f⋆ζ+b⋆. Then, the rank of Mk⋆ is M−1, which indicates Rank(Wk⋆)≤1.

Based on the Theorem 3.1, we can determine the optimal active beamforming vector wk⋆ from Wk⋆. More specifically, the SVD decomposition of Wk is Wk=SWkΛWkSWkH, where ΛWk is a diagonal matrix with only one diagonal element λWk⋆, the first column vector of unitary matrix SWk is the corresponding eigenvector. Moreover, the optimal active beamforming vector wk⋆ is λWk⋆SWk⋆(:,1). To derive the passive beam configuration from the energy beam, we need to convert it into vectors in order to make the following calculation. Assume the rank of Z is rZ, then Z⋆=∑m=1rZvm⋆(vm⋆)H.

3.2 The Design of IRS Phase Shift Matrix with Fixed Active Beamforming Vectors

Previously, we discussed how the optimal solution for active beam assignment can be determined by correcting the passive beam assignment reflection phase parameter. Following the fixation of the vectors of the active beam wk⋆ and v⋆, the phase parameters of the endowed reflection of the passive beam will be optimized. In order to simplify the writing, the following variables associated with active beamforming are not designated with ⋆. Accordingly, the passive beam assignment optimization problem can be expressed as follows:

maxθ,t  ts.t.  C1−1:|hkHwk|2γmin≥∑m=1,m≠kKI|hkHwm|2+σ2,∀k∈{1,2,…,KI}C3:0≤θn≤2π,∀n∈{1,2,…,N}C5:giHZgi+∑k=1KI|giHwk|2≥t,∀i∈{1,2,…,KE}(19)

where θ=diag(Θ). From the constraint conditions (C1−1) and (C5) of optimization problem (19), it can be observed that the passive beam assignment vector θ to be optimized is embedded in the diagonal matrix of passive beam assignment, so it cannot be solved directly and must be extracted and decomposed. As a first step, we combine the matrix form shown below:

Rk,i=[rk,irk,iHrk,idk,iHrk,iHdk,i0],∀k∈{1,2,…,KI},∀i∈{1,2,…,KE}

Ti,k=[ti,kti,kHti,kfi,kHti,kHfi,k0],∀k∈{1,2,…,KI},∀i∈{1,2,…,KE}

Oi,k=[oi,koi,kHoi,kqi,kHoi,kHqi,k0],∀k∈{1,2,…,KI},∀i∈{1,2,…,KE}

where rk,i=diag(hr,kH)Hwi, dk,i=hb,kHwi, ti,k=diag(gr,iH)Hwk, fi,k=gb,iHwk, oi,k=diag(gr,iH)Hvk, qi,k=gb,iHvk. Furthermore, we have recombined the variables related to the phase parameters associated with passive beam-endowed reflection into a vector form, such as q={θ,1}H. As soon as algebraic recombination is performed, the optimization problem (19) becomes equivalent to (20), for example:

maxQ,t  ts.t.  C1−1−1:∑k=1KITr(Ti,kQ)+∑k=1rZTr(Oi,kQ)+∑k=1KI|fi,k|2+∑k=1rZ|qi,k|2≥tC5−1:Tr(Rk,kQ)+|dk,k|2≥Γk(∑n=1,n≠kKITr(Rk,nQ))+Γk(∑n=1,n≠k|dk,n|2+σ2)C6:[Q]n,n=1C7:Rank(Q)=1(20)

where Q=qqH. Owing to the rank-1 constraint with Q, the problem still remains difficult to solve. By exploiting the SDR approach, the problem (20) can be reexpressed as

maxQ,t  ts.t.  C1−1−1,C5−1,and C6(21)

It can be obviously seen that the optimization problem (21) is a SDP problem and a convex problem that can be directly solved with convex optimization tools. So we can assume that the solutions are Q⋆ and t⋆. Once Q has been solved in (21), if the rank of Q⋆ equals to 1, θ can be obtain by performing EVD of Q⋆. Otherwise, we are able to obtain θ using the Gaussian randomization method. By using the definition of the phase shift matrix provided by IRS, we are able to obtain the IRS phase shift matrix Θ.

4  Simulation Results

In this section, we will supply several numerical results relating to the harvested energy efficiency performance of the IRS-enabled system via an iterative procedure on the basis of an iterative algorithm created to verify the performance. For the simulation system, since the intelligent reflective surface is often artificially located, its position is relatively fixed, and it can be installed within sight range of the transmitter, we assume that the channel between the transmitter and the intelligent reflecting surface is Rice channel, which can be modeled as

H=βrβr+1HLoS+1βr+1HNLoS(22)

where βr refers to the rice factor. HLoS and HNLoS describe the line-of-sight and non-line-of-sight channel between the transmitter and intelligent reflecting surface, respectively. Due to the ability of receivers to be moved, they may be shielded by obstacles and no LoS path for strong signals exists for intelligent reflecting surface to receiver channels and the transmitter to receiver channels. As a result, we can assume that they are Rayleigh channels. Suppose we have the following channel fading model:

PL=ρ(dd0)−α(23)

where ρ=−30 dB is the channel fading value based on the reference distance d0=1 m, d refers to the distance between two communications devices, α represents the path-loss exponent. In view of the LoS path between the transmitter and the IRS, the path-loss exponent is set as αTI=2. In contrast, the transmitter is usually far away from the receiver and suffers from a large amount of fading, so the path-loss exponent αTR is set as 3.5. Due to the fact that the intelligent reflecting surface is usually installed near the receivers, the path-loss exponent αIR is 2.5. For the ERs to receive high-power wireless signals as much as possible, we set the distance between the transmitter and receiver to 3 meters. The distance between the transmitter and intelligent reflecting surface is dTI=10 meters. We set the distance between the intelligent reflecting surface and receivers is 50 meters.

First, let’s look at Fig. 2, which shows the convergence rate of the iterative algorithm discussed in this study when it comes to solving the optimization problem (7) or (8). Based on Fig. 2, our iterative algorithm ensures that the harvested energy efficiency is monotonous throughout the iterative process of optimizing the minimum amount of harvested energy efficiency. It is also easy to see that in the first 4 iterations, there is a fast convergence rate, which can result in a higher energy efficiency of over 90-percent of the entire system. After 4 iterations, a convergence degree is close to being reached in terms of increase of harvested energy efficiency, which brings the speed guarantee to the real-time adjustment of the intelligent sensors networks.

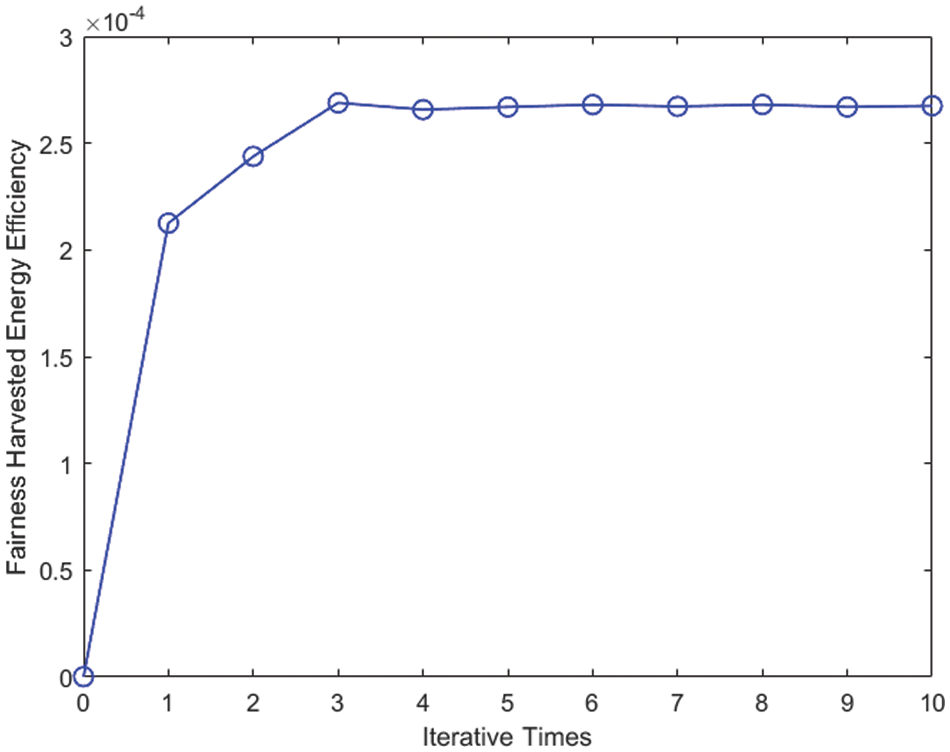
Figure 2: Efficacy of the proposed algorithm in terms of convergence

Fig. 3 presents an experimental simulation that illustrates the changing minimum harvested energy efficiency as a function of the the maximum allowed transmitted power. As part of the setup for the system comparison, four cases were taken into consideration: (1) A system with an energy beamformer and an intelligent reflecting surface is the corresponding system setting for our algorithm. (2) In the system with energy beamformer but no intelligent reflectors, the setup is the same as the traditional system. As far as the AP is concerned, it transmits only information beamformer for SWIPT, which does not offer any IRS services. Then, the solution for the convention problem can be found in the same way as the solution for Section 3. (3) System with no energy beam but intelligent reflector enables the verification of energy beamformer function, by allowing the AP to transmit only the information beamformer configuration to the ER, while the information beamformer transmits energy simultaneously to the ER when the SINR requirements are met. As a consequence, maximum minimum harvested energy efficiency can be expressed as the following constraint optimization problem:

maxwk,Θ min∀j  ∑i=1I|fr,jHΘHBIwi|2∑i=1I‖wi‖2+Pc s.t.   SINRi(wi,Θ)≥γimin∑i=1I‖wi‖2≤Pmax0≤θm≤2π(24)

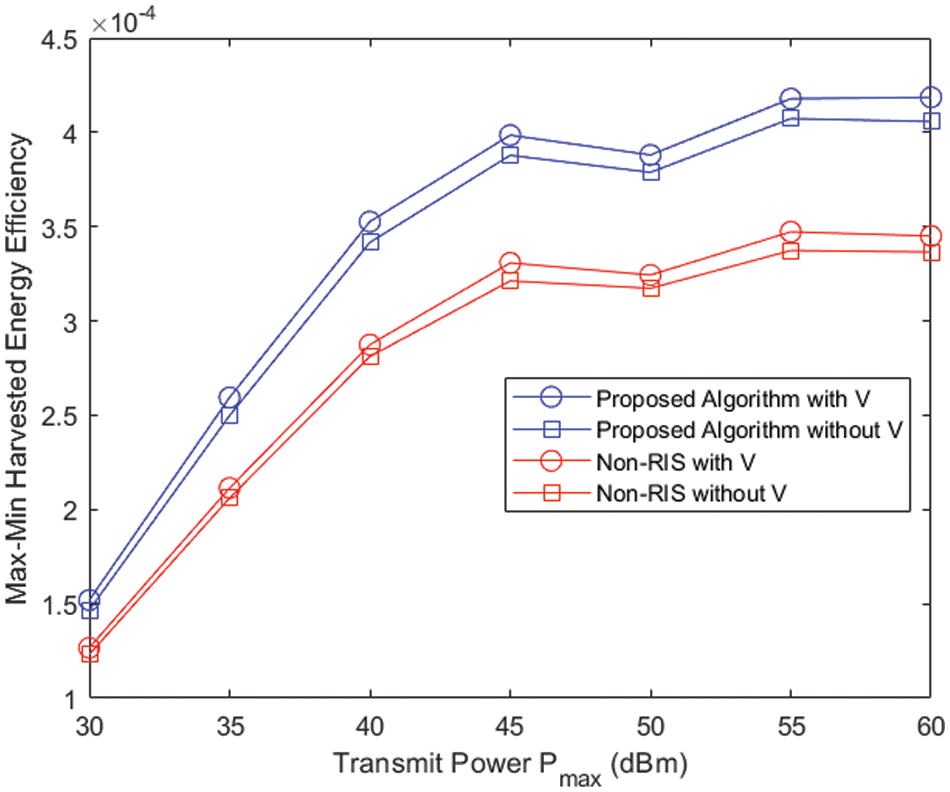
Figure 3: Fairness-aware harvested energy efficiency varies with the maximum allowed transmitted power

Based on the analysis, it appears that the problem (24) has an identical structure as the optimization problem (7) and that the same algorithm can be used to solve them. (4) The system has no energy beam and no intelligent reflective surface. With this system, only information beams are launched to work in conjunction with wireless communication systems of transmission of information and energy. Due to the lack of reflection paths, this problem can be solved by using the iterative algorithm of active beam design. From Fig. 3, we can easily check that there is a practically linear relationship between the fairness-aware harvested energy energy and the transmitter power between 30 and 45 dBm. However, the max-min harvested energy efficiency achieve a constant value. The reason falls into the factthat the adverse effect of the maximum networks power consumption cannot be compensated by any of the schemes. In addition, as compared to (1) and (2) or (3) and (4) system settings, the IRS-aided system performs better than its non-IRS-aided counterpart, which indicates that IRS can increase the range of the transmitter’s signals, improve the performance of fairness-aware harvested energy efficiency in poor channel environments. Furthermore, under the same hardware system conditions, the performance of the system with energy beamformer always exceeds those without, regardless of whether the IRS is equipped or not, which indicates the importance of energy beamformer. The reason is that a targeted design can be performed for the ER’s channel by using the energy beamformer, while in the absence of energy beamformer, the channel of the ER can only be considered at the same time by sacrificing the optimality of the information beamformer, resulting in a decrease in system performance, which is why energy beams are necessary.

Fig. 4 shows how the max-min harvested energy efficiency varies with SINR thresholds at the IR. Here, the maximum allowed transmit power is 40 dBm. With the iterative algorithm in a system setup incorporating IRS and energy beamformers, significant system performance gains can be achieved. The fairness-aware harvested energy efficiency exceeds the experimental values of the other three reference comparison groups. In addition, it can be also checked that the energy beamformer can improve performance gains in systems with or without smart reflectors in the range of entire SINR thresholds. It is because systems with an energy beamformer can better align the beamformer with a channel in the ERs, which offers a greater degree of freedom than systems with only the information beamformer.

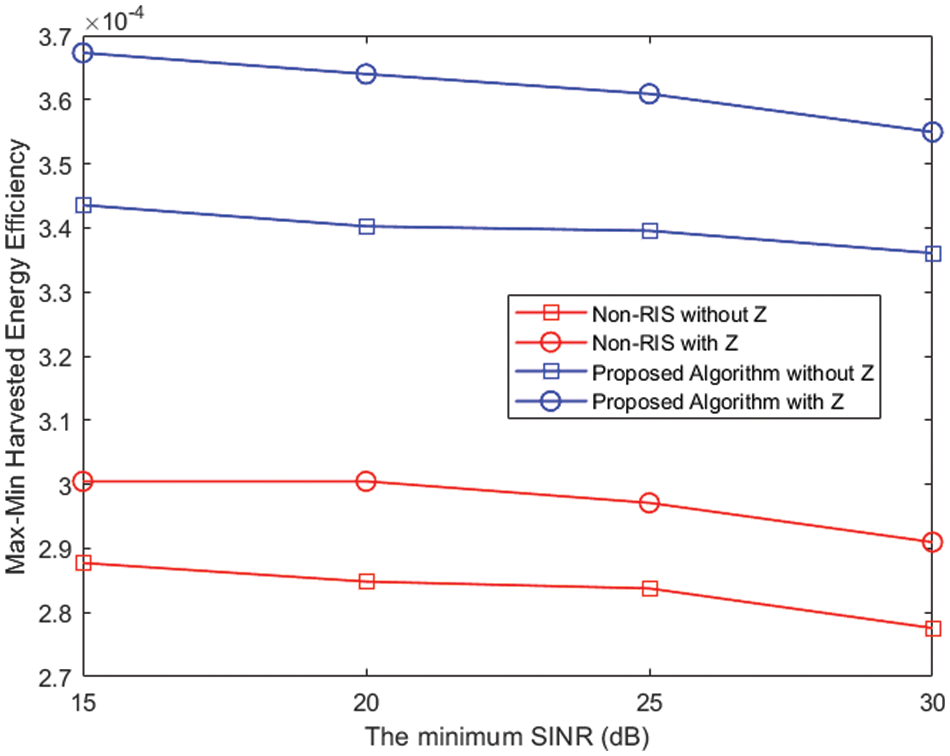
Figure 4: Fairness-aware harvested energy efficiency varies with the minimum required SINR

In Fig. 5, the max-min harvested energy efficiency is shown at different distances between the IRS and the AP. Herein, the distance between the transmitter and the IRS in this experiment is 20 meter, and all individual receivers are arranged on the same plane, which means that the horizontal distance between the receivers and the transmitter or IRS is always the same. In addition, to study the effect of IRS on a system with different number of reflection elements, we have also set up a comparative experiment with a different number of reflection elements as well. Based on Fig. 3, we can draw the following results: Firstly, as long as the receivers are not equipped with an IRS, the energy signals or information signals are mainly transmitted through the active beamformers assignment at the AP. When the horizontal distance between the receivers and the transmitter increases, the fairness-aware harvested energy efficiency will gradually decrease, because the longer the distance, the greater the channel fading. Secondly, it is important to note that as the ERs move away from the transmitter within the first 17 meters of installing IRS, its max-min-harvested-energy-efficiency decreases as the receiver moves away from the transmitter. As a result, it has been observed that if the distance between the transmitter and the IRS is increased from 17 to 19 meters, then the minimum power that can be received by the antenna increases gradually over time as the horizontal distance increases. This is because when the receivers moves away from the transmitter, they are also close to IRS. Hence, the receivers compensates for fading away from AP by receiving the reflected signal. Thirdly, according to the comparison of the experiment with and without intelligent reflectors, the attenuation of minimum energy received power is faster in the system without intelligent reflectors, whereas in the system with intelligent reflectors, the minimum energy received power is always higher than without intelligent reflectors, and the attenuation is slow, indicating that intelligent reflectors can significantly improve system performance gains. Finally, in comparing the gain of fairness-aware harvested energy efficiency between 40 and 80 different reflection elements, it can be found that the greater the number of reflection array elements, the greater is the gain in max-min harvested energy efficiency as compared to the lower number of reflection elements. The reason behind this is that with larger M, more array gain can be achieved, resulting in a greater degree of freedom in the spatial domain.

Figure 5: Fairness-aware harvested energy efficiency varies with the distance between the receivers and the transmitter on a horizontal plane

5  Conclusion

In the MISO SWIPT wireless sensor networks with IRS assistance, a transmitter with multiple antennas is used to simultaneously send energy signals to the ERs and information signals to the IR for a single antenna that is connected to the transmitter. In order to ensure a fair distribution of harvested energy efficiency among all ERs, the system in this study is designed to maximize the minimum energy receiving power in each receiver. In addition, the system has limitations in terms of a constrained SINR at the receivers, a constrained maximum transmitted power at the transmitter, and a constrained reflection phase at the IRS. As a result, both beamformers at the transmitter and the IRS are optimized. As the objective function and SINR constraint are highly coupled between active beamforming vector and passive beamforming, this study uses an iterative approach to fix the passive beamforming, then optimize the active beamforming vector, and finally fix the latter to optimize the former. As a result of simulations, IRS appears to be able to improve energy efficiency while maintaining fairness in harvesting.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This work was supported in part by the Priority Academic Program Development of Jiangsu Higher Education, the National Natural Science Foundation of China under Grant No. 62171119, the Key Research and Development Plan of Xuzhou under Grant Nos. KC20027, KC18079, in part by the Joint Research Fund for Guangzhou University and Hong Kong University of Science and Technology under Grant No. YH202203, the Guangzhou Basic Research Program Municipal School (College) Joint Funding Project.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Huang, C., Zappone, A., Debbah, M., Yuen, C. (2018). Achievable rate maximization by passive intelligent mirrors. 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, IEEE. [Google Scholar]

2. Wu, Q., Zhang, R. (2019). Beamforming optimization for intelligent reflecting surface with discrete phase. 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, IEEE. [Google Scholar]

3. Huang, C., Zappone, A., Alexandropoulos, G., Debbah, M., Yuen, C. (2019). Reconfigurable intelligent surfaces for energy efficiency in wireless communication. IEEE Transactions on Wireless Communications, 18(8), 4157–4170. https://doi.org/10.1109/TWC.2019.2922609 [Google Scholar] [CrossRef]

4. Yu, X., Xu, D., Sun, Y., Ng, D., Schober, R. (2020). Robust and secure wireless communications via intelligent reflecting surfaces. IEEE Journal on Selected Areas in Communications, 38(11), 2637–2652. https://doi.org/10.1109/JSAC.2020.3007043 [Google Scholar] [CrossRef]

5. Chen J., Liang Y. -C., Pei Y., Guo H. (2019). Intelligent reflecting surface: A programmable wireless environment for physical layer security. IEEE Access, 7, 82599–82612. https://doi.org/10.1109/ACCESS.2019.2924034 [Google Scholar] [CrossRef]

6. Jiang, W., Chen, B., Garg, S., Nie, J., Zhao, J. et al. (2021). Joint transmit precoding and reflect beamforming for IRS-assisted MIMO-OFDM secure communications. 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, IEEE. [Google Scholar]

7. Jiang, W., Chen, B., Zhao, J., Xiong, Z., Ding, Z. (2021). Joint active and passive beamforming design for the IRS-assisted MIMOME-OFDM secure communications. IEEE Transactions on Vehicular Technology, 70(10), 10369–10381. https://doi.org/10.1109/TVT.2021.3106351 [Google Scholar] [CrossRef]

8. Li, G., Liu, H., Huang, G., Li, X., Raj, B. et al. (2021). Effective capacity analysis of reconfigurable intelligent surfaces aided NOMA networks. EURASIP Journal on Wireless Communications and Networking, 198(1), 1–16. https://doi.org/10.1186/s13638-021-02070-7 [Google Scholar] [CrossRef]

9. Liu, H., Li, G., Li, X., Huang, G., Liu, Y. et al. (2022). Effective capacity analysis of STAR-RIS assisted NOMA networks. IEEE Wireless Communications Letters, 11(9), 1930–1934. https://doi.org/10.1109/LWC.2022.3188443 [Google Scholar] [CrossRef]

10. Li, S., Zhao, J., Tan, W., You, C. (2020). Optimal secure transmit design for wireless information and power transfer in V2X vehicular communication systems. AEU-International Journal of Electronics and Communications, 118(12), 1–10. https://doi.org/10.1016/j.aeue.2020.153148 [Google Scholar] [CrossRef]

11. Shi, Q., Liu, L., Xu, W., Zhang, R. (2014). Joint transmit beamforming and receive power splitting for MISO SWIPT systems. IEEE Transactions on Wireless Communications, 13(6), 3269–3280. https://doi.org/10.1109/TWC.2014.041714.131688 [Google Scholar] [CrossRef]

12. Song, K., Nie, M., Jiang, J., Li, C., Yin, Y. (2021). On the secrecy for relay-aided SWIPT internet of things system with cooperative eavesdroppers. IEEE Access, 9, 28204–28212. https://doi.org/10.1109/ACCESS.2021.3058504 [Google Scholar] [CrossRef]

13. Xu, J., Liu, L., Zhang, R. (2014). Multiuser MISO beamforming for simultaneous wireless information and power transfer. IEEE Transactions on Signal Processing, 62(18), 4798–4810. https://doi.org/10.1109/TSP.2014.2340817 [Google Scholar] [CrossRef]

14. Wang, X., Feng, W., Chen, Y., Chu, Z., Ge, N. (2017). Energy-efficiency maximization for secure multiuser MIMO SWIPT systems with CSI uncertainty. IEEE Access, 6, 2097–2109. https://doi.org/10.1109/ACCESS.2017.2781717 [Google Scholar] [CrossRef]

15. Clerckx, B., Zhang, R., Schober, R., Ng, D., Kim, D. et al. (2019). Fundamentals of wireless information and power transfer: From RF energy harvester models to signal and system designs. IEEE Journal on Selected Areas in Communications, 37(1), 4–33. https://doi.org/10.1109/JSAC.2018.2872615 [Google Scholar] [CrossRef]

16. Li, B., Wu, W., Li, Y., Zhao, W. (2022). Intelligent reflecting surface and artificial-noise-assisted secure transmission of mec system. IEEE Internet of Things Journal, 9(13), 11477–11488. https://doi.org/10.1109/JIOT.2021.3127534 [Google Scholar] [CrossRef]

17. Li, B., Si, F., Han, D., Wu, W. (2022). IRS-aided SWIPT systems with power splitting and artificial noise. China Communications, 19(4), 108–120. https://doi.org/10.23919/JCC.2022.04.009 [Google Scholar] [CrossRef]

18. Liu, Y., Han, F., Zhao, S. (2022). Flexible and reliable multiuser SWIPT IoT network enhanced by UAV-mounted intelligent reflecting surface. IEEE Transactions on Reliability, 71(22), 1092–1103. https://doi.org/10.1109/TR.2022.3161336 [Google Scholar] [CrossRef]

19. Ntougias, K., Krikidis, I. (2022). Probabilistically robust optimization of IRS-aided SWIPT under coordinated spectrum underlay. IEEE Transactions on Communications, 70(4), 2298–2312. https://doi.org/10.1109/TCOMM.2022.3148425 [Google Scholar] [CrossRef]

20. Wu, Q., Zhang, R. (2020). Joint active and passive beamforming optimization for intelligent reflecting surface assisted SWIPT under QoS constraints. IEEE Journal on Selected Areas in Communications, 70(4), 1735–1748. https://doi.org/10.1109/JSAC.2020.3000807 [Google Scholar] [CrossRef]

21. Wu, Q., Zhang, R. (2020). Weighted sum power maximization for intelligent reflecting surface aided SWIPT. IEEE Wireless Communications Letters, 9(5), 586–590. https://doi.org/10.1109/LWC.2019.2961656 [Google Scholar] [CrossRef]

22. Zargari, S., Farahmand, S., Abolhassani, B. (2021). Joint design of transmit beamforming, IRS platform, and power splitting SWIPT receivers for downlink cellular multiuser MISO. Physical Communication, 48(9), 101413. https://doi.org/10.1016/j.phycom.2021.101413 [Google Scholar] [CrossRef]

23. Masoumi, H., Emadi, M. (2019). Performance analysis of cooperative SWIPT system: Intelligent reflecting surface versus decode-and-forward. AUT Journal of Modeling and Simulation, 51(2), 241–248. https://doi.org/10.22060/MISCJ.2019.16626.5165 [Google Scholar] [CrossRef]

24. Zhu, Z., Xu, J., Sun, G., Hao, W., Chu, Z. et al. (2022). Robust beamforming design for IRS-aided secure SWIPT terahertz systems with non-linear EH model. IEEE Wireless Communications Letters, 11(4), 746–750. https://doi.org/10.1109/LWC.2022.3142098 [Google Scholar] [CrossRef]

25. Tang, Y., Ma, G., Xie, H., Xu, J., Han, X. (2020). Joint transmit and reflective beamforming design for IRS-assisted multiuser MISO SWIPT systems. 2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, IEEE. [Google Scholar]

26. Wang, Q., Zhou, F., Rose Hu, Q., Qian, Y. (2021). Energy efficient robust beamforming and cooperative jamming design for IRS-assisted MISO networks. IEEE Transactions on Wireless Communications, 20(4), 2592–2607. https://doi.org/10.1109/TWC.2020.3043325 [Google Scholar] [CrossRef]

27. Fu, H., Feng, S., Tang, W., Ng, D. (2020). Robust secure beamforming design for two-user downlink MISO rate-splitting systems. IEEE Transactions on Wireless Communications, 19(12), 8351–8365. https://doi.org/10.1109/TWC.2020.3021725 [Google Scholar] [CrossRef]