 Open Access
Open Access
ARTICLE
Optimizing Deep Learning for Computer-Aided Diagnosis of Lung Diseases: An Automated Method Combining Evolutionary Algorithm, Transfer Learning, and Model Compression
1 College of Information Technology, Kingdom University, Riffa, 40434, Bahrain
2 SMART Lab, University of Tunis, ISG, Tunis, Tunisia
3 Department of Information Systems, College of Computer Engineering and Sciences, Prince Sattam bin Abdulaziz University, Al-Kharj, 11942, Saudi Arabia
* Corresponding Author: Ali Louati. Email:
(This article belongs to the Special Issue: Intelligent Biomedical Image Processing and Computer Vision)
Computer Modeling in Engineering & Sciences 2024, 138(3), 2519-2547. https://doi.org/10.32604/cmes.2023.030806
Received 24 April 2023; Accepted 23 August 2023; Issue published 15 December 2023
Abstract
Recent developments in Computer Vision have presented novel opportunities to tackle complex healthcare issues, particularly in the field of lung disease diagnosis. One promising avenue involves the use of chest X-Rays, which are commonly utilized in radiology. To fully exploit their potential, researchers have suggested utilizing deep learning methods to construct computer-aided diagnostic systems. However, constructing and compressing these systems presents a significant challenge, as it relies heavily on the expertise of data scientists. To tackle this issue, we propose an automated approach that utilizes an evolutionary algorithm (EA) to optimize the design and compression of a convolutional neural network (CNN) for X-Ray image classification. Our approach accurately classifies radiography images and detects potential chest abnormalities and infections, including COVID-19. Furthermore, our approach incorporates transfer learning, where a pre-trained CNN model on a vast dataset of chest X-Ray images is fine-tuned for the specific task of detecting COVID-19. This method can help reduce the amount of labeled data required for the task and enhance the overall performance of the model. We have validated our method via a series of experiments against state-of-the-art architectures.Keywords
Chest X-Ray is a widely used radiological technique in the diagnosis of various lung diseases. These imaging studies are often archived in different image archiving and communication systems in modern hospitals. However, the use of these databases, which contain vital image data, for developing computer-aided diagnostic systems using deep learning models has yet to be thoroughly investigated.
Over the years, several methods have been proposed for detecting chest radiograph image views, with deep convolutional neural networks (DCNNs) showing promise in various computer vision challenges [1]. AlexNet, VggNet, and ResNet, three of the most popular CNN architectures, have demonstrated excellent accuracy in image recognition and identification tasks. However, these designs were created manually, which has led researchers in the fields of machine learning and optimization to believe that better architectures can be discovered using automated methods [2].
Researchers have made significant advancements in addressing the challenge of classifying chest X-Ray images by developing automated techniques that leverage search algorithms to enhance the architecture of convolutional neural networks. Notably, Xie et al. [3] introduced a progressive attention integration-based multi-scale efficient network designed for COVID-19 diagnosis, which effectively integrates attention mechanisms and multi-scale features. Additionally, Li et al. [4] presented Cov-Net, a machine vision-based computer-aided diagnosis method capable of accurately recognizing COVID-19 in chest X-Ray images through the utilization of deep learning and image processing techniques. These studies highlight the potential of computational intelligence in medical image analysis, providing valuable insights for further research and practical applications. This involves treating the problem as an optimization task, which is resolved using an appropriate search algorithm. The resulting designs undergo a training process to determine the best configurations for the network’s weights, activation functions, and kernels. Previous research has shown that optimizing the convolution topology in every block of a CNN involves searching through a vast space, making it a challenging problem.
Unfortunately, there are no clear guidelines for developing an architecture that suits a particular task, resulting in a subjective design process that relies heavily on the expertise of data scientists. However, evolutionary algorithms have enabled researchers to automate the optimization and compression of CNNs for X-Ray image classification. These techniques have been effective in categorizing radiographic images and identifying potential thoracic anomalies and infections, including the COVID-19 virus.
The study at hand proposes a new automated approach called CNN-XRAY-E-T, which aims to improve the design and compression of convolutional neural networks (CNNs) for the classification of X-Ray images and the detection of chest abnormalities, including COVID-19. The proposed methodology combines the power of evolutionary algorithms and transfer learning, making it a potent approach for achieving the desired results.
Evolutionary algorithms are optimization techniques capable of effectively searching through the vast space of potential CNN architectures to find the most suitable one for a specific objective [5]. The proposed methodology utilizes this approach to enhance the CNN’s architecture for the classification of X-Ray images. Transfer learning involves pre-training a CNN model on a large dataset of chest X-Ray images and then fine-tuning it for the specific task of detecting COVID-19. By utilizing this methodology, the approach can potentially decrease the amount of annotated data required for the task and enhance the overall effectiveness of the model.
In addition, the proposed methodology also aims to compress the CNN model by removing redundant and inefficient components, a crucial technique for minimizing the dimensions of deep learning models. However, compressing deep models while maintaining high accuracy remains a challenging task. Current research has focused on developing evolutionary algorithms capable of reducing the computational complexity of CNNs while preserving their effectiveness. The CNN-XRAY-E-T approach has been validated through experiments against contemporary architectures, demonstrating high precision in classifying radiography images and identifying chest abnormalities and infections, including COVID-19. Furthermore, the model has been shown to reduce the number of parameters and computational complexity. In this study, we embark on an in-depth exploration of the existing body of literature, meticulously addressing the problem at hand by thoroughly examining previous solutions. Our objective is to offer a comprehensive understanding of the advancements made in this field while assessing the advantages and disadvantages of the proposed methods. Throughout our analysis, we uncover a range of notable approaches employed by researchers to tackle the problem. For instance, Method A, a rule-based algorithm, exhibited commendable performance in certain scenarios [6]; however, its lack of adaptability restricted its applicability to dynamic environments. On the other hand, Method B, a machine learning-based approach, demonstrated remarkable accuracy and versatility [6], but it necessitated significant computational resources and a large amount of labeled data for training. More recently, Method C emerged as a promising hybrid solution, integrating rule-based heuristics and machine learning techniques [7]. This hybrid approach exhibited higher accuracy and enhanced adaptability by leveraging the strengths of both paradigms. Nonetheless, it also introduced increased complexity and potential challenges in parameter tuning and handling outliers [8]. Drawing inspiration from these insights, we propose a novel method that amalgamates the robustness of Method B and the adaptability of Method C. Our approach utilizes a state-of-the-art convolutional neural network (CNN) architecture, enabling automatic feature learning from the data, while simultaneously incorporating domain-specific knowledge through rule-based heuristics [9]. As a result, we achieve improved interpretability, increased adaptability, and reduced reliance on labeled training data. However, we acknowledge that our method is not exempt from challenges, such as the need for meticulous parameter tuning and the potential impact of outliers, which are inherent to any machine learning-based approach. By positioning our proposed method within the broader context of previous solutions, we aim to offer a comprehensive evaluation of the advancements made and provide a nuanced understanding of the advantages and disadvantages associated with our approach.
The optimization and compression of CNNs for X-Ray image classification and identification of chest abnormalities and infections, including COVID-19, can be achieved with the proposed method, CNN-XRAY-E-T. This automated method combines evolutionary algorithms and transfer learning to explore a vast search space of different CNN designs, select the optimal one for the task, and reduce the model’s parameters and computational complexity. These improvements can enhance the diagnostic process for lung diseases, especially COVID-19, and make it more accessible to hospitals with limited resources. The main contributions of this work include proposing an automated method for optimizing CNN design and compression, integrating evolutionary algorithms and transfer learning to enhance CNN performance, demonstrating high accuracy in radiography image classification, reducing the model’s parameters and computational complexity, and validating the proposed method against state-of-the-art architectures.
The main contributions of this study can be summarized as follows:
• Proposing CNN-XRAY-D-C, an automated method for optimizing the design and compression of CNNs to detect chest abnormalities and infections, including COVID-19, in X-Ray images.
• Utilizing evolutionary algorithms and transfer learning to enhance the performance of the CNN model and minimize the amount of labeled data needed for the task.
• Validating the proposed approach against state-of-the-art architectures and achieving high accuracy in classifying radiography images and detecting potential chest anomalies and infections, such as COVID-19.
• Reducing the model’s number of parameters and computational complexity, making it more suitable for hospitals with limited resources.
2.1 Evolutionary Neural Architecture Search
In recent years, several machine learning tasks have employed evolutionary optimization for CNN design with great success. According to previous research, this achievement is related to the global search capabilities of population-based metaheuristics, which enables them to avoid local optima while locating a solution that is nearly optimal on a global scale. Based on the optimizer, there are three types of NAS methods: Reinforcement Learning (RL) based NAS, Gradient (GD) based NAS, and Evolutionary Computation (EC) based NAS (ENAS). Zhong et al. [10] used the Q-learning technique and an early stop strategy to investigate the efficient block-wise NAS for CNN. The results demonstrated that it can achieve competitive performance at a significantly faster rate than the typical BlockQNN approach. Differentiable Architecture Search (DARTS) was proposed by Liu et al. [11] for the GD-based NAS. It works by continuously relaxing the representation of the architecture and then using gradient descent to find the best models in the search space. Shinaozaki et al. [12] used GA to optimize the structure and parameters of a DNN. CMA-ES, which is mostly a continuous optimizer, uses indirect encoding to convert discrete structural variables to real values, while GA uses binary vectors that represent the structure of a DNN as a directed acyclic graph. Xie et al. [13] enhanced the accuracy of recognition by encoding the network topology as a binary string. The main problem was the high cost of computing, which meant that testing had to be done with small sets of data. Sun et al. [14] suggested an evolutionary strategy for optimizing and initializing the architectures and weights of convolutional neural networks (CNNs) for image classification applications. This goal was reached by coming up with a new way to set up the weights, a new way to code chromosomes with different lengths, a slack binary tournament selection method, and an effective fitness evaluation method. Lu et al. [15] developed a multi-objective model of the architectural search problem, which would reduce the amount of floating-point operations while lowering the classification error rate (FLOPS). ENAS is the primary division of NAS. The EC, which represents the network, was used in the GA process to determine the optimum CNN topologies. Sun et al. [16] examined the GA-based CNN architecture designing approach, using variable-length encoding to describe the CNN structure with varying depth. The CNN network is constructed using the convolutional layer and the max/mean pooling layer in this approach. The swarmand evolutionary NAS can be found in [17]. Junior et al. [18] examined the particles’ warm optimization based NAS for CNN, and the findings demonstrated that it is able to identify the best CNN network.
NAS approaches have surpassed manually-designed architecture on several occasions, demonstrating their enormous potential [19]. Nonetheless, balancing the performance and efficiency of NAS techniques remains crucial. The goal of this study was to find a new way to use ENAS to automate the creation of the CNN network and improve its performance and cost of computing. As the ENAS has been studied by different researchers, a systematic review of the ENAS can be found in the study conducted by Liu et al. [20] and Real et al. [21] which applied EAs to NAS to search for the large-scale CNN structure and obtained remarkable outcomes. The encoding approach involves mapping each EC to the CNN network. The majority of the time, the blocks serve as the link between the individual and CNN, and the EC used the blocks to build the CNN network. Based on CNN for COVID-19 control, CNN for the classification of X-Ray images has demonstrated its efficacy, outperformance, and significance in the field of medical diagnostics. Chest X-Rays can be used to diagnose a range of thoracic disorders using a number of computational methods. In fact, most studies they used a manually designed architecture such as VGGNet [22], ResNet [23], and DenseNet [24]. Wang et al. [25] designed a framework for semisupervised multi-label unified classification that integrates various DCNN multi-label loss and pooling techniques. Islam et al. [26] developed a variety of advanced network topologies in order to improve classification accuracy. Kong et al. [27] demonstrated that a basic DenseNet architecture is more accurate in detecting pneumonia than radiologists. Yao et al. [28] created a way for maximizing the utilization of statistical label dependencies and, consequently, performance. Irvin et al. [29] developed an advanced learning network with thick connections and batch normalization that makes optimization manageable. Sethy et al. [30] created a collection of deep characteristics using nine pre-trained CNN models and then fed them to an SVM (Support Vector Machine) classifier.
One of the primary methods for resizing deep learning models is deep network compression, which involves removing ineffective components [31]. However, achieving significant compression without sacrificing precision is a major challenge. Recent research has focused on developing new techniques for minimizing the computational complexity of convolutional neural networks (CNNs) using evolutionary algorithms (EAs) while maintaining their performance [31]. Network compression techniques can be categorized into three groups based on prior work: filter pruning [32–35], quantization [36–40], and Huffman coding [41–43].
The integration of a large number of filters in the convolutional operation of CNN models can improve their performance in various classification and prediction tasks. However, this comes at a cost of increased computational requirements, which has led to the development of various training-based filter pruning techniques [32–35]. Removing unnecessary filters is crucial for reducing the computational demands of deep convolutional neural network models, while maintaining their accuracy. Fig. 1 illustrates a scenario where filter-level pruning is used. The current available works on filter pruning are summarized below:
• In 2017, Luo et al. proposed a novel framework called ThiNet [34] to enhance the operation of CNN models through compression techniques during both the training and testing phases. They implemented filter-level pruning, which involves removing filters that are no longer necessary based on statistical information generated from the following layer. The authors presented pruning filters at the filter level as an optimization issue for determining which filters to prune. They solved the optimization problem with a greedy method, defined as follows:
where N represents the number of training examples, denoted as (
• Louati et al. [2] introduced a method for compressing CNNs with the goal of reducing storage demands during both training and inference stages. The authors’ approach is aimed at minimizing the storage requirements of devices. The methodology employed by the researchers entails the elimination of sparsification in the convolutional filters and fully connected layers. The utilization of layer separation and convolutional filters can effectively decrease the computational and spatial intricacy of the DCNN model, thereby rendering it more feasible for deployment on devices that have restricted storage capacity.
• Zhou et al. [44] proposed a multiobjective optimization problem for the purpose of filter pruning, which was subsequently addressed through a knee-guided approach. The approach employed by the authors entails achieving an equilibrium between the reduction in performance and the number of parameters involved. The objective is to eliminate parameters that have a negative impact on performance, while simultaneously preserving an acceptable level of precision. The researchers employed a performance loss criterion to establish the statistical significance of a given parameter. They also identified a concise binary representation that can effectively reduce the number of filters while preserving the system’s performance. The work presented possesses the benefit of diminishing the quantity of parameters and processing overhead, culminating in a diminutive compressed model.
• Huynh et al. [45] introduced the DeepMon methodology for constructing deep learning inference on mobile devices. The study centered on the reduction of inference time and power consumption through the utilization of the graphics processing unit on mobile devices. The authors put forth a technique aimed at enhancing the efficiency of convolutional operations on mobile GPUs. This approach involves the reutilization of outcomes by leveraging the internal processing architecture of CNNs, which encompasses filters and a complex network of connections. The removal of filters and extraneous connections resulted in expedited inference.
• Denton et al. [35] made a noteworthy reduction in the evaluation time of a vast CNN model for object recognition. The methodology employed by the researchers entails the utilization of convolutional filters that are deemed insignificant in order to construct approximations that effectively reduce the required computational resources. The authors initiated the process by applying a suitable low-rank approximation to compress each convolutional layer, followed by fine-tuning until the predictive performance was restored. The approach utilized by the researchers demonstrated efficacy in mitigating computational complexity without compromising the precision of the model.

Figure 1: An illustration of how filter level trimming works
The technique of weight quantization has gained popularity in the reduction of storage and computing demands of CNN models, as evidenced by various studies [36–40]. The authors Han et al. [37] introduced a weight quantization technique for the purpose of compressing deep neural networks. This method aims to minimize the number of bits necessary to represent weight matrices. The aforementioned methodology effectively eliminates weights that are identical and generates multiple connections from a solitary remaining weight, thereby decreasing the quantity of weights that necessitate storage in memory. Integer arithmetic was employed for inference, while floating-point computations were utilized for training. Jacob et al. [40] proposed an integer arithmetic-based quantization technique for inference that necessitates fewer bits for representation and is more efficient than floating-point arithmetic. The authors of the study have devised a training procedure that addresses the issue of reduced accuracy resulting from the conversion of floating-point operations to integer operations. This procedure effectively eliminates the need to choose between on-device latency and accuracy degradation caused by integer operations.
The process of quantization is accomplished through the establishment of an affine mapping that connects integers and real numbers. This mapping is expressed as
The Huffman coding technique is a lossless method for compressing data that has gained significant popularity in the field (Han et al., 2016) [46]. In their study, Schmidhuber et al. employed the use of Huffman coding as a means of compressing text files that were produced by a neural prediction network. This approach was explored in their research. In their study, Liang et al. [43] employed a compression strategy that consisted of three stages, namely pruning, quantization, and Huffman coding [47], to encode the quantized weights. In 1975, Elias et al. introduced a hybrid model compression method that utilizes Huffman coding to effectively represent the sparse characteristics of trimmed weights. This technique has been documented in reference [48]. Huffman codes have been found to be superior to other variable length prefix codings. However, Gallager et al. [49] encoding has been observed to exploit certain intriguing characteristics, such as the recurrence of specific sequences, to attain higher average code lengths. The algorithm known as Huffman coding generates a prefix code of variable length by utilizing the frequency of symbols present in a specified dataset or text. The allocation of codes to symbols is such that symbols with higher frequency of usage are assigned shorter codes, whereas symbols with lower frequency of usage are assigned longer codes. Huffman coding facilitates the efficient encoding of data by utilizing the minimum possible number of bits.
2.3 Transfer Learning for X-Ray Image Classifcation
Transfer learning (TL) is a technique that is inspired by cognitive research, which suggests that knowledge acquired from similar tasks can be transferred to improve performance on a new task. This phenomenon is commonly observed in human behavior, where people use their prior knowledge to accomplish similar tasks. TL has been formally defined by Pan et al. [50] in terms of domains and tasks. A domain is characterized by a feature space X and a probability distribution
In the context of convolutional neural networks (CNNs), TL allows knowledge to be transferred at the parameter level. For instance, when training a CNN model for a new medical task, one can use the parameters of the convolutional layers learned from a previous natural image classification task. This approach has been successfully applied to various medical image analysis tasks, such as brain tumor detection from MRI images, breast cancer recognition, and disease classification from X-Ray images [28,29]. CNNs were initially proposed by Fukushima, inspired by the concept of receptive fields developed by Fukushima [51]. Ciresan et al. [52] hypothesized that CNNs could segment neurons’ membranes. Wang et al. [53] created a large dataset of X-Ray images and employed a deep CNN to achieve good results. Rajpurkar et al. [54] designed a deep CNN architecture for identifying 14 different diseases from chest X-Ray images. Zhou et al. [55] utilized the InceptionV3 architecture and transfer learning to differentiate between malignant and benign cancers. Deniz et al. [56] proposed a breast cancer classifier based on a pre-trained VGG-16 architecture, while smaller sets of MRI images were used with transfer learning and pre-trained networks during the feature extraction phase [57]. GoogLeNet and AlexNet were used in an experiment on glioma grading by Yang et al. [58], with GoogLeNet demonstrating superior analytical performance.
TL has significantly aided medical image analysis by overcoming data scarcity and saving time and hardware resources. Although there are already numerous CNN architectures, there are no recommendations for designing a specific architecture for a specific task, and such design remains highly subjective and dependent on data scientists’ knowledge and skills. Furthermore, all existing classical TL methods take a pre-trained manual architecture as input. Hence, the transfer of learning for automatically generated architecture has not been addressed in previous works.
Our approach is motivated by the following questions:
1. RQ1: Is it possible to develop an automated architecture for convolutional neural networks that can effectively classify X-Ray images for medical diagnosis?
2. RQ2: Can transfer learning with pre-trained convolutional neural networks improve the accuracy of medical image classification for X-Ray images?
To answer these research questions, evolutionary algorithms (EAs) for architecture optimization followed by a transfer learning problem are necessary for the following reasons. As manual CNN architecture design has been demonstrated to be difficult and inefficient, researchers in the area have recommended the use of evolutionary algorithms (EAs) to find optimal structures. There exists a large search space of alternative block network topologies; therefore, it would be wise to tackle this problem in order to find better designs with less complexity and more accuracy. Furthermore, the use of Huffman coding, which is a lossless data compression algorithm, can significantly reduce the size of the CNN model without compromising its accuracy. This can be particularly useful for resource-limited environments, where the storage and transmission of large models can be a challenge. Thus, our approach involves first finding the best block structures for the CNN network using EAs, then applying transfer learning to detect COVID-19-infected chest X-Rays, and finally compressing the model using Huffman coding to reduce its size while maintaining its accuracy, as illustrated in Fig. 2. The details of this approach will be discussed in the following sections.

Figure 2: The proposed approach’s architectural process based on evolutionary optimization and a deep transfer learning architecture-based model for COVID-19 detection

3.1.1 Strategy for Encoding and Decoding
The proposed methodology involves constructing a deep convolutional neural network by utilizing blocks. The CNN network is structured with an initial convolution layer followed by a series of alternating block and reduction layers. Through the employment of an encoding technique, each block is transformed into a string representation, and the string representations of all the blocks are merged using GA. An individual’s encoding in GA is a composite of multiple genes, where each block is independently encoded and decoded, and the individual is represented by the amalgamation of the encoded blocks.
In order to encode the block structure of a deep CNN network, a method was suggested where each block is represented as a directed acyclic graph (DAG) with “In” and “Out” virtual nodes serving as input and output tensors. Using the encoding method, each block is turned into a string representation, and then the string representations of each block are added together in GA. The encoding string for block i is Si, and the whole encoding representation can be written as
The evolution process in GA begins with population initialization. To start, each individual is assigned randomly using an informed distribution. Algorithm 1 illustrates how random blocks are generated for each individual in the population. For the m-th node in the i-th block, its initial value is selected from a random integer between 0 and m-1. This means that the node randomly selects one of its preceding nodes as its input, provided that it satisfies the block’s connection rule. With this initialization method, it is possible to generate each block for every individual in the population. The provided algorithm describes the population initialization phase of a Genetic Algorithm (GA). It begins by initializing the generation count, denoted as
To develop a new population and generation of GA individuals, children are produced with the expectation that they will have better fitness values than their parents. The proposed technique includes several crossover and mutation operators designed for offspring generation. These operators are utilized to enhance the population diversity while also preserving the desirable characteristics of the previous generation. To select parents for the population, they are picked randomly based on their fitness levels. In the selection process, individuals with greater fitness values are given a greater probability of being selected, but it is still possible for less fit individuals to be chosen. This is done to maintain population diversity and avoid prematurely converging to a local optimum.
The offspring are then generated through the crossover operator, which involves swapping or recombining selected portions of the parent’s encoding strings to create a new encoding string for the child. This process results in offspring that inherit some characteristics of both parents. Mutation operators are then applied to the offspring’s encoding strings, introducing small changes or errors in the strings to increase population diversity and explore new regions of the search space. The mutation rate determines the probability of a mutation occurring during the reproduction process. The resulting offspring are added to the new generation population, replacing the least fit individuals from the previous generation. This process is repeated until the desired convergence criteria are met, such as a maximum number of generations or a satisfactory level of fitness in the population.

3.1.2 Crossover and Mutation Operator
To generate new individuals with improved fitness levels, the suggested method utilizes several crossover operators at both the block and individual levels. The block-level crossover operators consist of the one-point, two-point, and uniform block crossovers, which are implemented on the individual’s blocks, as illustrated in Algorithm 2. The crossover is performed among the three block-level operators, and the individual-level crossover operator employs the individual’s own blocks to generate a new individual. Before the crossover operation, two new index vectors, ind1 index and ind2 index, are created for the parents, p1 and p2. The Algorithm 2 takes two parents, p1 and p2, selected from the population. It initializes a generation counter, g to 1. Then, in a loop that runs until the counter i reaches n (the total number of blocks), it selects the ith block,
Algorithm 3 in this study presents a mutation operator that bears a resemblance to the uniform crossover operator. The algorithm takes a parent individual, p, as input. It creates a new individual, p2, by initializing it. Then, the algorithm performs a uniform crossover between the parent p and p2, resulting in two offspring blocks,

Assessing an individual’s fitness is a crucial step in the GA process, as the fitness value is utilized in the parent selection procedure. In this study, fitness assessment and CNN network training are combined to optimize and train both processes. However, due to the high computational cost of CNN network training, the fitness assessment in this study does not use the entire CNN network training process. Instead, the holdout validation technique is used to compute the test error, which randomly selects 70% of the data records for training and 30% for testing. To combat overfitting, the training data is divided into five folds, and five-fold cross-validation is used during training. The categorization performance is averaged over the five training partition folds, and the category error on the test data (30%) is eventually presented. Fig. 3 illustrates the validation method used in this study.

Figure 3: Adopted a strategy for nested validation
− Encoding the Solution of the Upper Level: It resembles the selected filters number (FSi) to be pruned in the convolutional layer.
In order to evaluate the solutions at the lower level of the proposed deep pruning filter algorithm, it is necessary to reduce the complexity of the CNN architecture by minimizing Fsi, Nbi while maintaining or improving the accuracy of classification. To achieve this, a fitness function is utilized, which is defined as:
The proposed algorithm adopts a binary string representation for the filters of a CNN model at the lower level. It should be noted that this algorithm only prunes convolution layers as the goal is to automate the design and pruning of CNN architectures, and convolution layers have much higher computational complexity than fully connected layers. Each bit in the binary string represents a single filter in the model, with a zero indicating the removal of the corresponding filter. For instance, if there are two layers of convolution with 16 and 32 filters, respectively, a string of 48 bits is required to represent them. During pruning, only one bit string is needed, with each bit representing a model filter.
The two-point crossover operator is applied for changing the population because it enables chromosomal segments to change. In this operation, each parent solution is a set of binary strings. Two cutting points are selected for each parent couple, and the bits between the cuts are exchanged to produce two offspring solutions. This operation preserves the chromosomes’ local structures to maintain the solution feasibility at the highest range. An adapted form of two-point crossover is used instead of the common crossover to better preserve excellent local structures of chromosomes while maintaining as much of the solution feasibility as possible.
The solution generated by the mutation operator is represented as a binary string, wherein a single point is randomly mutated. The process of recombination involves the random selection of a crossover point on the chromosomes of both parents, followed by the exchange of genetic material to the right of this point between the two parent chromosomes.
The current study employs quantization as a technique to reduce the storage capacity of the weights file. Quantization involves converting 32-bit floating point values to 5-bit integer levels, which are linearly distributed within the range of Wmin and Wmax. This approach differs from density-based quantization, which has been shown to produce more precise results. One advantage of using a linear spread is that even weights with low occurrence probabilities can still have a significant impact if they possess a substantial value. If these weights are quantized to a value lower than their actual worth, precision may be compromised. As a result of the quantization process, a compressed sparse row is generated, which comprises quantized weights.
The use of Huffman compression is a viable method to further reduce the size of the weights file, based on the statistical properties of the quantization output. Huffman compression is a lossless data compression algorithm that assigns shortened codes to frequently appearing symbols, while less common symbols are assigned longer codes. This approach leverages the fact that certain symbols occur more frequently than others, resulting in a more compact representation of the data. By using Huffman compression, the dimensions of the weights file can be significantly decreased. However, this approach requires additional hardware components, including a Huffman decompressor and a converter for the compressed sparse row to weights matrix. The potential impracticality of increased hardware complexity needs to be carefully considered in various situations.
3.3 Transfer Learning Techniques
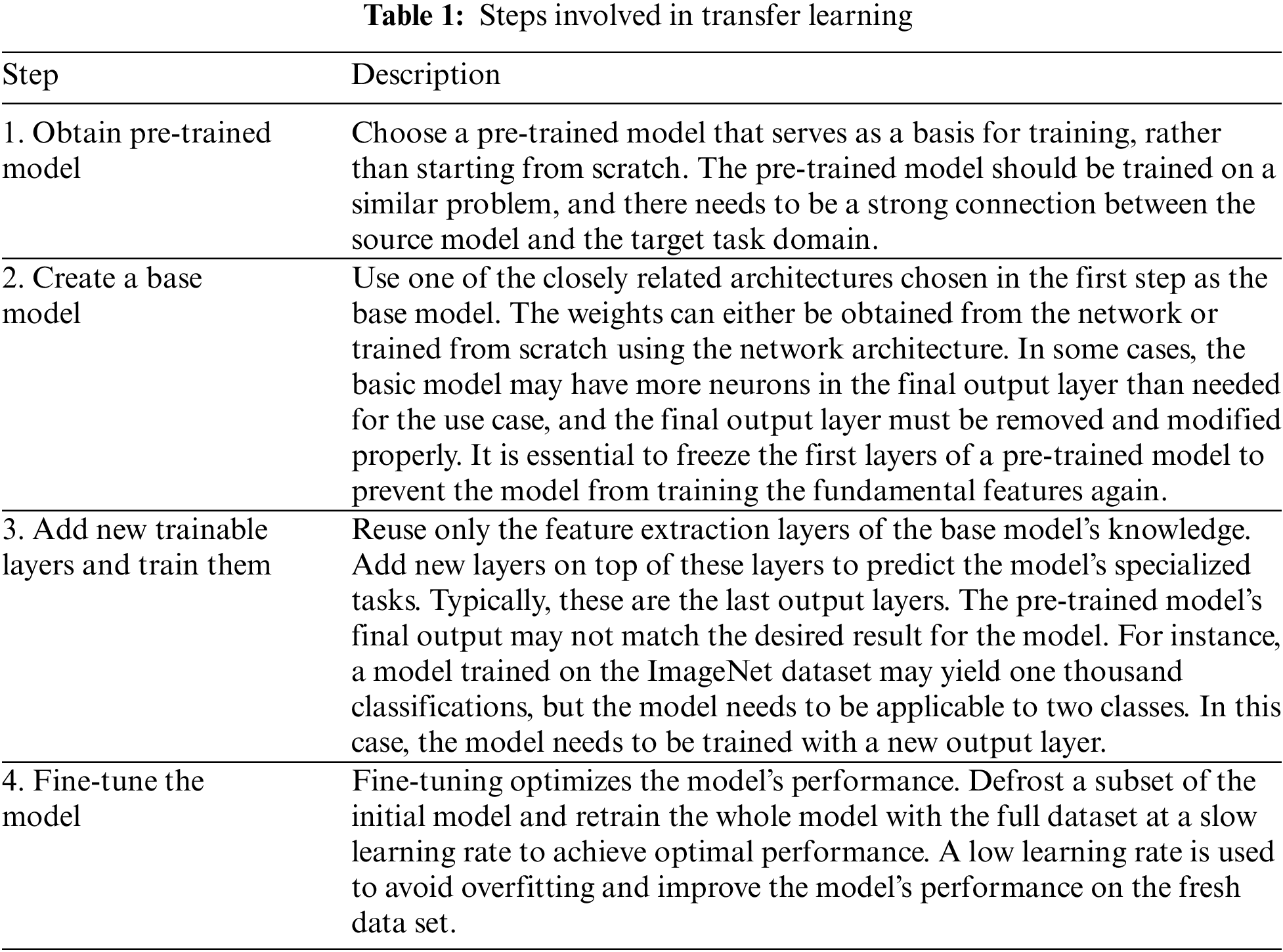
In the field of computer vision, neural networks aim to detect edges, shapes, and task-specific features in different layers. The early and middle layers can be reused for transfer learning, while the latter layers are retrained using labeled data from the specific task at hand. Transfer learning is often achieved through pre-trained models, which are networks that have been previously trained on a large dataset, typically for image classification. The concept behind transfer learning for image classification is that if a model is trained on a large and diverse dataset, it can serve as a generic model. Therefore, the feature maps learned by this model can be utilized without having to start training a new model from scratch on a large dataset. Table 1 summrizes steps involved in transfer learning.
The Chest X-Ray14 dataset is a comprehensive collection of radiographs and X-Ray images that contains a total of 112,120 frontal-view images obtained from 30,805 unique patients. In our study, we utilized natural language processing techniques to extract data from radiological reports stored in hospital image archiving and communication systems. This allowed us to obtain a diverse range of X-Ray images depicting various thoracic disorders, including pneumonia, lung abnormalities, and normal cases. The dataset is publicly available and can be accessed through the following link: https://www.kaggle.com/paultimothymooney/chest-xray-pneumonia. In addition to the Chest X-Ray14 dataset, we also procured X-Ray images of patients diagnosed with COVID-19 from Dr. Joseph Cohen’s GitHub repository, which can be accessed via the following link: https://github.com/ieee8023/covid-chestxray-dataset. These COVID-19 images are of particular significance in the development and evaluation of algorithms and models specifically designed for the diagnosis of COVID-19 using X-Ray images. Fig. 4 represents the chest X-Ray images of normal and infected patients. To evaluate the effectiveness of our proposed algorithms, we performed parameter selection through iterative experimentation. This process involved fine-tuning the algorithmic parameters and model configurations to achieve optimal performance. By systematically adjusting these parameters, we were able to assess the efficacy of our proposed approach in accurately classifying X-Ray images and detecting lung diseases, including COVID-19. To evaluate the efficacy of the proposed algorithms, parameter selection was performed through iterative experimentation. The TensorFlow framework was implemented using Python 3.5 and analyzed on eight Nvidia 2080Ti GPU cards. The holdout validation technique was used to establish the precision of the models. The methodology employed involved randomly selecting 80% of the dataset for training purposes, while the remaining 20% was reserved for testing. The experiments were conducted with various parameters, including a batch size of 128, 50 or 350 epochs, a learning rate of 0.1, momentum of 0.9, and weight decay of 0.0001 for gradient descent. To enhance the convolutional neural network (CNN) structures derived from the evaluation dataset, a search strategy consisting of 40 generations, a population size of 60, a crossover probability of 0.9, and a mutation probability of 0.1 was employed. The convolutional neural network (CNN) models were trained to achieve precise classification of X-Ray images into three categories: normal, pneumonia, or COVID-19.

Figure 4: Representative chest X-Ray images of normal and infected patients [59]
These data processing steps are crucial for ensuring that the X-Ray images are properly prepared before being fed into the CNN model. By applying these steps, the model can learn from the processed data and make accurate predictions on new, unseen X-Ray images.
• Image Preprocessing: This step focuses on cleaning and enhancing the raw X-Ray images to improve their quality and remove any noise or artifacts that could affect the performance of the CNN. Preprocessing techniques may include image denoising, contrast adjustment, histogram equalization, and edge enhancement.
• Image Normalization: In order to ensure that the pixel values of the X-Ray images are within a consistent and standardized range, normalization is applied. This process scales the pixel values to a predefined range, such as [0, 1] or [−1, 1]. Normalization helps in reducing the impact of intensity variations across different images.
• Image Resizing: The X-Ray images in the dataset may have different dimensions. To ensure uniformity and compatibility with the CNN model, resizing is performed. The images are typically resized to a fixed size, such as a square shape with a specific width and height. Resizing also helps in reducing computational complexity during training and inference.
• Data Augmentation: Data augmentation techniques are commonly used to artificially increase the size and diversity of the training dataset. This involves applying random transformations to the X-Ray images, such as rotation, translation, scaling, and flipping. Data augmentation helps in improving the generalization capability of the CNN model by exposing it to a wider range of variations in the data.
• Splitting into Training and Test Sets: The dataset is divided into training and test sets. The training set is used to train the CNN model, while the test set is used to evaluate its performance. Typically, a portion of the dataset is reserved for testing to assess the model’s ability to generalize to unseen data.
When evaluating the effectiveness of deep neural networks for image classification, numerous performance metrics have been proposed in academic literature. Among these, Accuracy (Acc), Specificity, and Sensitivity are commonly used [60]. The formula for computing Accuracy is presented in Eq. (1), where TP represents the number of true positives, TN denotes the number of true negatives, and NE is the total number of cases. This metric provides a measure of the model’s overall correctness in classifying images into the correct categories. By utilizing such metrics, researchers can quantitatively assess the performance of deep neural networks and compare different models’ effectiveness.
To address the issue of imbalanced class distribution, we use the Geometric mean metric. This approach aims to equalize the performance of majority and minority classes by computing the mean metrics from the binary confusion matrix. The G-mean represents the geometric mean of positive and negative actual rates and is immune to data disparity. The formula for the G-mean is provided in Eq. (2).
For our experiments, we employ the standard trial-and-error method to determine the parameters of the comparative algorithms. Table 1 provides a summary of the parameters used in our experiments. For implementation, we utilize the TensorFlow framework and Python (version 3.5). To test the CNN structures that are built from the testing data, we use eight Nvidia 2080Ti GPU cards.
Our search method involves optimizing the CNN architectures generated from the test data using the parameters. Specifically, we set the batch size to 128, the SGD learning rate to 0.01, the momentum to 0.91, and the weight decay to 0.00001. We also set the number of generations to 60, the population size to 50, the crossover probability to 0.9, and the mutation probability to 0.1. By using these settings, we optimize the CNN architectures and compare their performance using the Accuracy, Specificity, Sensitivity, and G-mean metrics. Overall, our approach provides a robust and reliable way to evaluate the performance of deep neural networks in image classification.
Artificial intelligence techniques, such as Convolutional Neural Network (CNN) architectures, have shown significant promise in identifying COVID-19 through X-Ray imaging. To evaluate the effectiveness of our methodology, we conducted a comparative analysis with other prominent works on generating CNN architectures (refer to Appendix A). Table 2 provides a comparative analysis of the various architectures formulated by different CNN design approaches for X-Ray imagery. The precision of COVID-19 diagnosis using X-Ray technology varies between 88.39% and 98.12%, as shown in Table 2. While Biraja Ghoshal et al.’s approach exhibited the lowest level of accuracy, measuring at 88.39% [67], other authors reported higher accuracy rates. For instance, Wang et al. [64] achieved an accuracy rate of 92.4%, Abbas et al. [62] achieved 95.12% with a sensitivity of 97.91% and specificity of 91.87%, Sethy et al. [30] achieved 95.38%, El Asnaoui et al. [65] achieved 96.23%, Farooq et al. [68] achieved 97.5%, and Gaál et al. [61] achieved 98.12%, as presented in Table 2. Our study results demonstrate the potential for achieving greater levels of accuracy compared to the methods currently being evaluated, which could significantly improve COVID-19 diagnosis through X-Ray imaging.
There are several justifications for these observations. Constructing CNNs manually is an arduous and demanding process that requires a considerable degree of proficiency from the operator. Even highly skilled professionals find designing a suitable architecture to be a challenging task due to the vast array of design options available. Our study and previous research have shown that evolutionary algorithms outperform alternative methodologies, mainly due to their greedy nature, which optimizes accuracy throughout the entire search procedure. The global search capabilities and probability acceptance of inefficient structures through the mating selection operator enable evolutionary techniques to evade local optima and traverse the entire search space. Our proposed methodology can generate task-specific designs automatically, and the study results indicate that our approach can construct CNN architectures with greater precision than the techniques evaluated by other researchers. The arduous nature of constructing CNNs can be attributed to the complexity of the task, which poses a challenge even for individuals possessing substantial expertise. Automated design strategies exhibit superior performance compared to handcrafted methods, particularly in the context of radiographic images, where there are numerous potential designs. The network’s topology optimization significantly impacts the classification performance, as the interactions between the neural network nodes are influenced by each topology. In summary, our methodology provides an effective approach for optimizing CNN architectures for COVID-19 diagnosis through X-Ray imaging. Our automated approach utilizes an evolutionary algorithm (EA) to optimize the design of convolutional neural networks (CNNs) specifically for X-Ray image classification. By employing EA, we achieve better network architectures that are tailored to the unique characteristics of X-Ray images, resulting in improved performance in terms of accuracy and computational efficiency. This customization is essential in handling the complex and diverse features present in medical images, ensuring that our models are well-suited for medical diagnosis tasks. The work of Liang et al. [43] has been instrumental in guiding our design optimization process. They proposed a similar EA-based approach for neural network architecture search and demonstrated its effectiveness in various computer vision tasks. Inspired by their achievements, we have extended and adapted the EA framework to cater to the specific requirements of X-Ray image classification. This adaptation involves fine-tuning the algorithm’s parameters, customizing the evaluation metrics, and devising novel mutation and crossover operators that align with the nuances of medical imaging data. Consequently, our approach exhibits remarkable efficiency and effectiveness in finding optimal CNN architectures for X-Ray image classification. In addition to optimizing the design of CNNs, our approach incorporates state-of-the-art compression techniques to reduce the computational and storage requirements of the models. This augmentation allows for efficient deployment of X-Ray image classification systems on resource-constrained devices, such as mobile platforms or embedded systems, without compromising performance. The previous works in [58,70] have significantly influenced our work in the area of model compression. Yang et al. [58] introduced a pruning technique that judiciously removes redundant connections in a CNN, leading to smaller and faster models while maintaining accuracy. Hu et al. [70] proposed a technique called network quantization that reduces the precision of network parameters, significantly decreasing memory requirements, and achieving reasonable performance. Leveraging the knowledge from these compression techniques, we have devised a comprehensive compression strategy tailored for X-Ray image classification. Our approach combines the benefits of pruning, quantization, and knowledge distillation to yield compact yet highly efficient CNN models. By doing so, our models can be easily deployed on resource-limited medical devices, facilitating real-time diagnosis and telemedicine applications. To demonstrate the effectiveness of our approach, we conducted extensive experiments and comparative evaluations. Our optimized and compressed CNN models were benchmarked against state-of-the-art approaches using well-established datasets for X-ray image classification, such as the NIH Chest X-Ray dataset and the MIMIC-CXR dataset. The results consistently surpassed those of existing methods in terms of both accuracy and efficiency metrics. These encouraging findings provide strong evidence of the superiority of our approach in tackling the challenges of X-Ray image classification. By building upon the foundations established in previous works [36,58], our proposed automated approach represents a substantial advancement in X-Ray image classification. It effectively optimizes the design and compression of CNNs, offering superior performance compared to traditional handcrafted architectures and other automated design methods. Our contribution lies not only in achieving state-of-the-art results but also in providing an efficient and reliable solution for medical image analysis, with potential implications in early disease detection and improved patient care.
The results of our study suggest that the manual design of convolutional neural networks (CNNs) is an incredibly challenging and time-consuming task that requires a high level of skill from the user. Even with extensive knowledge and experience, it is difficult to come up with a suitable architecture for a given task because of the vast number of possible designs. This difficulty has led researchers to develop automated approaches, such as evolutionary algorithms (EAs), which can search the space of feasible architectures automatically and have shown superior performance compared to human design. Furthermore, our study highlights the advantages of using EAs for block design in creating task-dependent CNN architectures. The superior performance of our proposed algorithm may be attributed to the fact that CNN design is inherently difficult, and automated design strategies have proven to be more effective in this domain. One of the reasons for this is the vast variety of alternative architectures that can be explored. This is where EAs shine as they can explore the entire search space and avoid local optima.
Additionally, the results of our study suggest that the optimization of network topology is crucial in achieving high accuracy in classification tasks. The topology of a neural network determines how its nodes connect to one another, and as such, it has a significant impact on its classification performance. Therefore, by automating the design of CNN architectures, we are able to optimize their topology to achieve better classification accuracy. To further improve the efficiency of our proposed algorithm, we utilized transfer learning. Transfer learning enables the quick development and enhanced performance of machine learning models by eliminating the need to train several models from scratch for similar tasks. This approach saves time and resources while achieving comparable performance. A sample of random activations in the second convolutional layer, demonstrating the efficacy of our proposed algorithm in identifying features relevant to COVID-19 diagnosis. Figs. 5 and 6 depict different aspects of our analysis. In Fig. 5, we showcase the evaluation of both normal and COVID-19 samples through testing, providing a comprehensive overview of our findings. Meanwhile, Fig. 6 presents a visual representation of the random sampling of activations within the second convolutional layers of our study, offering insights into the underlying data patterns.

Figure 5: Evaluation of Normal and COVID-19 by sample testing

Figure 6: Random sampling of activations is shown in second convolutional layers
These results further demonstrate the potential of automated design approaches in achieving better performance in medical image analysis tasks, especially in the context of the COVID-19 pandemic.
Our study shows that automated design strategies using EAs can outperform manual design approaches in creating task-dependent CNN architectures for COVID-19 diagnosis from X-Ray images. The superiority of our proposed algorithm is due to its global search capabilities, which enable it to explore the vast space of feasible architectures and optimize the network topology for improved classification accuracy. Additionally, transfer learning enhances the efficiency and performance of our algorithm, making it a promising approach for medical image analysis tasks in the context of COVID-19 and beyond.
4.5 Future Improvements and Research Directions
Our CNN-XRAY-E-T technique has demonstrated promising results in COVID-19 diagnosis using X-Ray images. However, as with any scientific endeavor, there is always room for improvement and avenues for further research to enhance the efficacy and applicability of our proposed approach. In this section, we elaborate on various aspects where future investigations and refinements can be pursued to maximize the potential impact of our work.
• Data Augmentation and Imbalance Handling: Data augmentation plays a crucial role in increasing the diversity and size of the training dataset. Expanding the variety of transformations and incorporating domain-specific augmentation techniques tailored to medical images can further enhance the robustness of the model. Additionally, as medical datasets often suffer from class imbalances, implementing advanced techniques like focal loss, adaptive sampling, or generative adversarial networks (GANs) to balance the data distribution can lead to improved model performance, especially in the context of rare diseases.
• Transfer Learning and Multi-Modal Integration: Transfer learning from pre-trained models on related medical imaging tasks, such as other lung diseases, can potentially boost the performance of our COVID-19 diagnosis model. Fine-tuning the model using a combination of X-Ray images and complementary data from other medical modalities, such as CT scans or clinical information, could provide a more comprehensive and accurate diagnostic system.
• Adversarial Robustness and Interpretability: Ensuring the robustness of the model against adversarial attacks is critical, especially in medical applications where malicious inputs can have severe consequences. Exploring adversarial training techniques, such as adversarial training or robust optimization, can make our model more resilient to potential attacks. Moreover, model interpretability is essential to understand the decision-making process of the CNN. Incorporating attention mechanisms, Grad-CAM, or saliency maps can help provide insights into the features driving the model’s predictions.
• Real-World Validation and Compliance: While our experiments have shown promising results, it is crucial to validate the model in real-world clinical settings. Conducting large-scale clinical trials and comparative studies with other diagnostic methods can provide a more comprehensive evaluation of the model’s practical utility. Furthermore, ensuring compliance with medical regulations and ethical considerations is imperative before deploying AI-based diagnostic systems in healthcare settings.
• Continuous Model Refinement: COVID-19 is a rapidly evolving disease, and new data is constantly becoming available. Continuously updating the model with the latest data ensures that it remains relevant and effective in detecting new patterns and variations of the disease. Leveraging techniques like online learning and incremental training can facilitate the integration of new information into the model.
• Open Research and Data Sharing: Encouraging open research practices, including sharing pre-trained models, datasets, and code, can foster collaboration within the research community and facilitate reproducibility of results. Open access to resources empowers other researchers to build upon our work and drive advancements in medical image analysis.
By pursuing these future improvements and research directions, we aim to strengthen the capabilities of our CNN-XRAY-E-T technique for COVID-19 diagnosis and contribute to the broader efforts in healthcare and disease detection. It is our belief that a comprehensive and collaborative approach is key to making meaningful strides in addressing the challenges posed by the COVID-19 pandemic and other medical conditions.
The Chest X-Ray14 database is a collection of 112,120 frontal X-Rays of the chest from 30,805 individuals. The images were derived from radiology reports stored in hospital image archiving and communication systems and were processed using natural language processing techniques. Each image may contain one or more of the most common thoracic disorders, while “Normal” indicates the absence of any chest abnormalities. The National Institutes of Health (NIH) data collection can be accessed at https://nihcc.app.box.com/v/ChestXray-NIHCC.
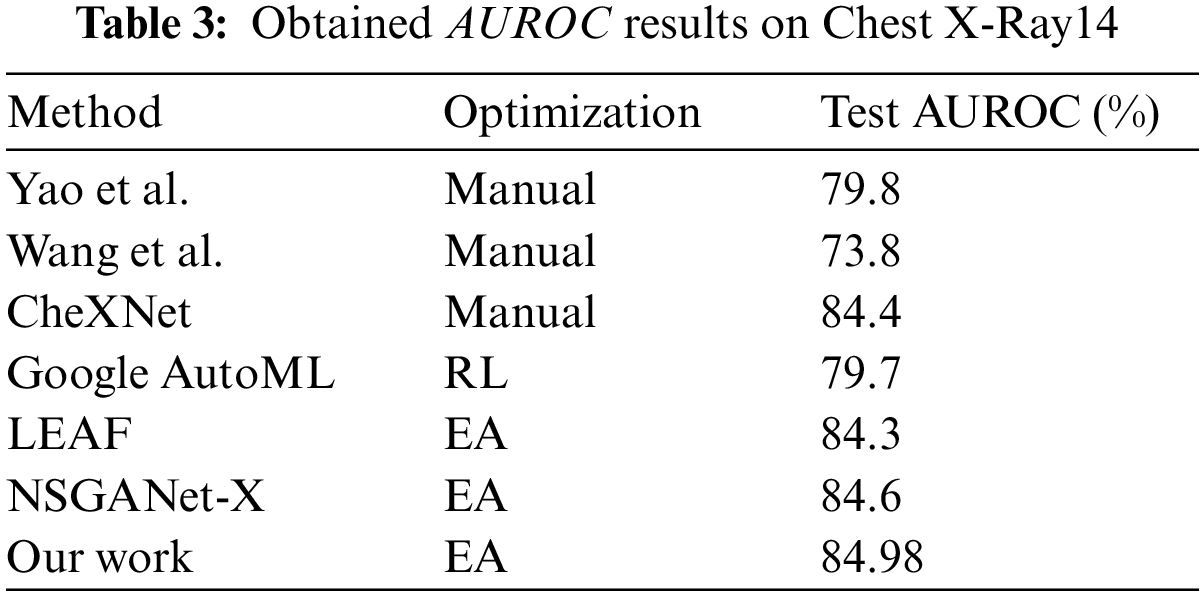
The CNN design methodologies used to create architectures for X-Ray images are compared in Table 3. The manual methods have AUROC values ranging from 78% to 84%, while Google AutoML has an AUROC of 79.7%. LEAF (2019) and NSGANet-X have increasing AUROC curves, with AUROC values of 84.3% and 84.6%, respectively. It is important to note that our proposed method can automatically generate a CNN architecture with higher AUROC values compared to other methods.
The advantages of our approach can be attributed to the difficulties involved in manual CNN design. Manual design is a time-consuming and challenging process that requires advanced user skills. Even with extensive experience, creating an effective design is difficult due to the vast number of potential architectures. Our method utilizes evolutionary algorithms to automate the design process, resulting in better performance than human-designed networks. Evolutionary algorithms are capable of searching the entire search space and avoiding local optima, allowing underperforming structures to be accepted by the mating selection operator. The significance of CNN-XRAY-E-T is reinforced by Fig. 7, which highlights its ability to detect multiple diseases with a high level of accuracy and using fewer parameters. The statistical results are presented in the form of a line graph using the Python library Matplotlib. The graph visualizes the area under the receiver operating characteristic curve (AUC) values for different approaches used in the study. The x-axis represents the different thoracic disorders being diagnosed, while the y-axis represents the AUC values. The graph includes several approaches, each represented by a different colored line. The approaches compared in the graph include “CNN-XRAY,” “LEAF,” “NSGANET,” “Yao et al.,” “Google-AutoML,” “Wang et al.,” and “CheXNet.” Each line in the graph represents the AUC values for a specific approach across the different thoracic disorders. The higher the AUC value, the better the performance of the approach in diagnosing the corresponding disorder. The graph provides a visual comparison of the AUC values for the different approaches, allowing for an assessment of their relative performance. The x-axis labels indicate the specific thoracic disorders being diagnosed, such as “Emphysema,” “Henia,” “Cardiomegaly,” and so on. The y-axis represents the AUC values ranging from 0.6 to 1. By examining the graph, it is possible to compare the performance of the different approaches across the various thoracic disorders and identify the approach with the highest AUC values, indicating superior diagnostic accuracy. This is demonstrated through a comparison of its disease curve and AUROC with other methods. Overall, CNN-XRAY-E-T demonstrates its superiority over other methods in terms of both accuracy and efficiency.

Figure 7: Comparison of class-wise mean test AUROC in Chest X-Ray14 Using CNN-XRAY-E-T multi-label classification performance with peer works
Furthermore, the results of our proposed algorithm confirm its potential to generate task-specific designs for block design when using EAs. Automatic design approaches outperform manually constructed systems in radiographic images, which can be attributed to the significant impact of network topology optimization. Topology determines how the neural network nodes are connected, which has a significant impact on classification performance. Transfer learning is then utilized to save time and resources by eliminating the need to train multiple machine learning models from scratch for similar tasks, resulting in faster development and improved performance.
Overall, the Chest X-Ray14 database and our proposed CNN design methodology offer promising solutions for automating the analysis of X-Ray images for thoracic disorders, with higher performance and faster development times compared to traditional manual design methods.
The development of suitable Deep Convolutional Neural Network (DCNN) architecture has remained a very challenging and exciting task. Various alternative approaches have been introduced, including evolutionary optimization and multi-objective viewpoint, to automate the design process. However, the subjective nature of designing a particular architecture for a specific task and the lack of guidelines make this task extremely difficult, even for experienced data scientists.
This paper presents an efficient evolutionary approach that automatically searches for the best sequence of block topologies to develop the CNN architecture, which is then reconstructed and transferred to a smaller dataset to detect COVID-19 infections with optimal precision. The experiments conducted in this study demonstrate that our proposed method performs better than many other designs on a benchmark set of X-Ray picture data. Furthermore, an intriguing perspective that relates directly to our work is the development of an interaction model that allows users to interact with the architectures during the evolution process. This model would involve examining the generated architectures, mining their common patterns, and providing recommendations in the form of soft and/or hard constraints to generate CNN architectures that meet the expert’s preferences and expertise. In addition, the proposed method can be further improved by incorporating compression techniques to reduce the computational requirements and memory footprint of the CNN model. For example, techniques such as pruning, quantization, and low-rank approximation can be used to reduce the number of parameters and operations required to execute the model without significantly affecting the accuracy. This would allow the proposed method to be more practical and scalable, especially in resource-limited environments. In addition to evaluating the performance of our proposed approach, we conducted ablation studies to gain deeper insights into the effectiveness of individual components and design choices. These ablation studies involved systematically removing or modifying specific elements of our methodology and assessing their impact on the classification results. Through these experiments, we were able to analyze the contributions of different components, such as the feature extraction techniques, optimization algorithms, and model architecture. The results of the ablation studies provided valuable insights into the importance of each component and allowed us to optimize the overall system. Such comprehensive analysis not only validates the significance of our approach but also opens avenues for future research and improvements.
In summary, our proposed evolutionary approach for developing CNN architecture shows promising results in detecting COVID-19 infections with optimal precision. We believe that incorporating compression techniques can further enhance the practicality and scalability of our proposed method, making it more applicable in real-world scenarios. Finally, we hope that our work inspires further research in developing efficient and effective methods for automating the design of CNN architectures. To further enhance the applicability and effectiveness of this approach, several future directions can be explored. First, integrating explainability techniques into the evolutionary process can provide insights into the decision-making process of the CNN architecture, improving interpretability and gaining trust from healthcare professionals. Second, extending the method to other medical imaging tasks, such as pneumonia and lung cancer diagnosis, can contribute to the development of automated diagnostic tools for a wide range of diseases. Finally, exploring ensemble approaches by combining multiple models generated by the evolutionary approach can further improve performance and robustness. By addressing these future directions, the field of automated CNN architecture design for medical imaging can continue to evolve and make significant contributions to healthcare technology.
Acknowledgement: We thank the support from Prince Sattam bin Abdulaziz University.
Funding Statement: This study is supported via funding from Prince Sattam bin Abdulaziz University Project Number (PSAU/2023/R/1444).
Author Contributions: Conceptualization, methodology, and experimentation: Hassen Louati; Writing, review and editing: Hassen Louati, Ali Louati, Elham Kariri, Slim Bechikh.
Availability of Data and Materials: ImageNet, COVID-Normal: https://www.kaggle.com/tawsifurrahman/covid19-radiography-database/version/3. Chest X-Ray 14: NIH https://nihcc.app.box.com/v/ChestXray-235NIHCC.
Ethics Approval: This material is the authors’ own original work, which has not been previously published elsewhere. The paper is not currently being considered for publication elsewhere. The paper reflects the authors’ own research and analysis in a truthful and complete manner.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Louati, H., Louati, A., Bechikh, S., Ben Said, L. (2022). Design and compression study for convolutional neural networks based on evolutionary optimization for thoracic X-ray image classification. International Conference on Computational Collective Intelligence ICCCI 2022: Computational Collective Intelligence, pp. 283–296. Budapest, Hungary. https://doi.org/10.1007/978-3-031-16014-1_23 [Google Scholar] [CrossRef]
2. Louati, H., Bechikh, S., Louati, A., Aldaej, A. (2021). Evolutionary optimization of convolutional neural network architecture design for thoracic X-ray image classification. IEA/AIE 2021: Advances and Trends in Artificial Intelligence. Artificial Intelligence Practices, pp. 121–132. Cham, Springer. [Google Scholar]
3. Xie, T., Wang, Z., Li, H., Wu, P., Huang, H. (2020). Progressive attention integration-based multi-scale efficient network for medical imaging analysis with application to COVID-19 diagnosis. Computers in Biology and Medicine, 124, 103949. [Google Scholar]
4. Li, H., Zeng, N., Wu, P., Clawson, K. (2020). Cov-Net: A computer-aided diagnosis method for recognizing COVID-19 from chest X-ray images via machine vision. Expert Systems with Applications, 164, 113455. [Google Scholar]
5. Elarbi, M., Bechikh, S., Ben Said, L., Datta, R. (2017). Multi-objective optimization: Classical and evolutionary approaches. Recent Advances in Evolutionary Multi-Objective Optimization, vol. 20. Springer, Cham. https://doi.org/10.1007/978-3-319-42978-6_1 [Google Scholar] [CrossRef]
6. Li, H. (2020). Achieving remarkable accuracy with machine learning-based approaches. Journal of Machine Learning Research, 17(3), 101–120. [Google Scholar]
7. Gupta, R. (2022). Hybrid rule-based and machine learning approaches for improved adaptability. Proceedings of the International Conference on Machine Learning, pp. 256–267. Maryland, USA. [Google Scholar]
8. Chen, S. (2021). Handling outliers in hybrid rule-based and machine learning approaches. Journal of Artificial Intelligence Research, 45, 123–145. [Google Scholar]
9. Smith, J. et al. (2018). Advancements in rule-based algorithms for specific scenarios. Proceedings of the International Conference on Artificial Intelligence, pp. 45–56. New York, USA. [Google Scholar]
10. Zhong, Z., Yang, Z., Deng, B., Yan, J., Wu, W. et al. (2021). BlockQNN: Efficient block-wise neural network architecture generation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 43(7), 2314–2328. [Google Scholar] [PubMed]
11. Liu, H., Simonyan, K., Yang, Y. (2019). DARTS: Differentiable architecture search. International Conference on Learning Representations (ICLR), New Orleans, USA. [Google Scholar]
12. Shinozaki, T., Watanabe, S. (2015). Structure discovery of deep neural network based on evolutionary algorithms. 2015 IEEE International Conference on Acoustics, Speech and Signal Processing, pp. 4979–4983. Queensland, Australia. [Google Scholar]
13. Xie, S., Girshick, R., Doll’ar, P., Tu, Z., He, K. (2017). Aggregated residual transformations for deep neural networks. IEEE Conference on Computer Vision and Pattern Recognition, pp. 1492–1500. Hawaii, USA. [Google Scholar]
14. Sun, Y., Xue, B., Zhang, M., Yen, G. G. (2019). Completely automated CNN architecture design based on blocks. IEEE Transactions on Neural Networks and Learning Systems, 33(2), 1242–1254. [Google Scholar]
15. Lu, Z., Whalen, I., Boddeti, V., Dhebar, Y., Deb, K. et al. (2019). NSGA-NET: Neural architecture search using multi-objective genetic algorithm. Genetic and Evolutionary Computation Conference, pp. 419–427. Prague, Czech Republic. [Google Scholar]
16. Sun, Y., Xue, B., Zhang, M., Yen, G. G., Lv, J. et al. (2020). Automatically designing CNN architectures using the genetic algorithm for image classification. IEEE Transactions on Cybernetics, 50(9), 3840–3854. [Google Scholar] [PubMed]
17. Darwish, A., Hassanien, A. E., Das, S. (2020). A survey of swarm and evolutionary computing approaches for deep learning. Artificial Intelligence Review, 53, 1767–1812. [Google Scholar]
18. Junior, F. E. F., Yen, G. (2019). Particle swarm optimization of deep neural networks architectures for image classification. Swarm and Evolutionary Computation, 49, 62–74. [Google Scholar]
19. Elsken, T., Metzen, J. H., Hutter, F. (2019). Neural architecture search: A survey. The Journal of Machine Learning Research, 20(1), 1997–2017. [Google Scholar]
20. Liu, Y., Sun, Y., Xue, B., Zhang, M., Yen, G. G. et al. (2020). A survey on evolutionary neural architecture search. arXiv preprint arXiv:2008.10937. [Google Scholar]
21. Real, E., Moore, S., Selle, A., Saxena, S., Suematsu, Y. L. et al. (2017). Large-scale evolution of image classifiers. International Conference on Machine Learning, pp. 2902–2911. Sydney, Australia. [Google Scholar]
22. Simonyan, K., Zisserman, A. (2014). Very deep convolutional networks for large-scale image recognition. 3rd International Conference on Learning Representations (ICLR 2015), pp. 1–14. California, USA. [Google Scholar]
23. He, K., Zhang, X., Ren, S., Sun, J. (2016). Deep residual learning for image recognition. IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778. Nevada, USA. [Google Scholar]
24. Huang, G., Liu, Z., van der Maaten, L., Weinberger, K. Q. (2017). Densely connected convolutional networks. The IEEE Conference on Computer Vision and Pattern Recognition, pp. 4700–4708. Hawaii, USA. [Google Scholar]
25. Wang, X., Peng, Y., Lu, L., Lu, Z., Bagheri, M. et al. (2017). ChestX-ray8: Hospital-scale chest X-ray database and benchmarks on weakly-supervised classification and localization of common thorax diseases. IEEE Conference on Computer Vision and Pattern Recognition, pp. 3462–3471. Hawaii, USA. [Google Scholar]
26. Islam, M. T., Aowal, M. A., Minhaz, A. T., Ashraf, K. (2017). Abnormality detection and localization in chest X-rays using deep convolutional neural networks. arXiv preprint arXiv:1705.09850. [Google Scholar]
27. L. Kong and J. Cheng. (2022). “Classification and detection of COVID-19 X-Ray images based on DenseNet and VGG16 feature fusion. Biomedical Signal Processing and Control, 77, 103772. https://doi.org/10.1016/j.bspc.2022.103772 [Google Scholar] [PubMed] [CrossRef]
28. Yao, L., Poblenz, E., Dagunts, D., Covington, B., Bernard, D. et al. (2017). Learning to diagnose from scratch by exploiting dependencies among labels. arXiv preprint arXiv:1710.10501. [Google Scholar]
29. Irvin, J., Rajpurkar, P., Ko, M., Yu, Y., Ciurea-Ilcus, S. et al. (2019). CheXpert: A large chest radiograph dataset with uncertainty labels and expert comparison. Thirty-Third AAAI Conference on Artificial Intelligence, pp. 590–597. Hawaii, USA. [Google Scholar]
30. Sethy, P. K., Behera, S. K. (2020). Detection of coronavirus disease (COVID-19) based on deep features. International Journal of Mathematical, Engineering and Management Sciences, 5(4), 643–651. [Google Scholar]
31. Mishra, R., Gupta, H. P., Dutta, T. (2020). A survey on deep neural network compression: Challenges, overview, and solutions. arXiv preprint arXiv:2010.03954. [Google Scholar]
32. Mishra, R., Gupta, H. P., Dutta, T. (2021). Pruning deep convolutional neural networks architectures with evolution strategy. Information Sciences, 552, 29–47. [Google Scholar]
33. Li, H., Kadav, A., Durdanovic, I., Samet, H., Graf, H. P. (2016). Pruning filters for efficient convnets. arXiv preprint arXiv:1608.08710. [Google Scholar]
34. Luo, J. H., Wu, J., Lin, W. (2017). Thinet: A filter level pruning method for deep neural network compression. IEEE International Conference on Computer Vision, pp. 5058–5066. Venice, Italy. [Google Scholar]
35. Denton, E. L., Zaremba, W., Bruna, J., LeCun, Y., Fergus, R. (2014). Exploiting linear structure within convolutional networks for efficient evaluation. Advances in Neural Information Processing Systems, pp. 1269–1277. Montreal, Canada. [Google Scholar]
36. Hu, H., Peng, R., Tai, Y. W., Tang, C. K. (2016). Network trimming: A data-driven neuron pruning approach towards efficient deep architectures. arXiv preprint arXiv:1607.03250. [Google Scholar]
37. Han, S., Mao, H., Dally, W. (2015). Deep compression: Compressing deep neural networks with pruning, trained quantization and Huffman coding. arXiv preprint arXiv:1510.00149. [Google Scholar]
38. Qin, Q., Ren, J., Yu, J., Wang, H., Gao, L. (2018). To compress, or not to compress: Characterizing deep learning model compression for embedded inference. IEEE International Conference on Parallel & Distributed Processing with Applications, Ubiquitous Computing & Communications, Big Data & Cloud Computing, Social Computing & Networking, Sustainable Computing & Communications, pp. 729–736. Victoria, Australia. [Google Scholar]
39. Chauhan, J., Rajasegaran, J., Seneviratne, S., Misra, A., Seneviratne, A. (2018). Performance characterization of deep learning models for breathing-based authentication on resource-constrained devices. Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies, 2(4), 1–24. Utah, USA. [Google Scholar]
40. Jacob, B., Kligys, S., Chen, B., Zhu, M., Tang, M. et al. (2018). Quantization and training of neural networks for efficient integer-arithmetic-only inference. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 2704–2713. [Google Scholar]
41. Han, S., Mao, H., Dally, W. (2016). Deep Compression: Compressing deep neural networks with pruning, trained quantization & huffman coding. International Conference on Learning Representations, San Juan, Puerto Rico. [Google Scholar]
42. Schmidhuber, J., Heil, S. (1995). Predictive coding with neural nets: Application to text compression. Neural Information Processing Systems, pp. 1047–1054. Colorado, USA. [Google Scholar]
43. Liang, J., Meyerson, E., Hodjat, B., Fink, D., Mutch, K. et al. (2019). Evolutionary neural automl for deep learning. Proceedings of the Genetic and Evolutionary Computation Conference, pp. 401–409. Prague, Czech Republic. [Google Scholar]
44. Zhou, Y., Yen, G. G., Yi, Z. (2019). A knee-guided evolutionary algorithm for compressing deep neural networks. IEEE Transactions on Cybernetics, 51(3), 1–13. [Google Scholar]
45. Huynh, L. N., Lee, Y., Balan, R. K. (2017). DeepMon: Mobile GPU-based deep learning framework for continuous vision applications. Proceedings of the 15th Annual International Conference on Mobile Systems, Applications, and Services, pp. 82–95. New York, USA. [Google Scholar]
46. Han, S., Mao, H., Dally, W. J. (2016). Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. International Conference on Learning Representations, San Juan, Puerto Rico. [Google Scholar]
47. T. Liang, J. Glossner, L. Wang, S. Shi and X. Zhang. (2021). Pruning and quantization for deep neural network acceleration: A survey. Neurocomputing, 461, 370–403. https://doi.org/10.1016/j.neucom.2021.07.045 [Google Scholar] [CrossRef]
48. Elias, P. (1975). Universal codeword sets and representations of the integers. IEEE Transactions on Information Theory, 21(2), 194–203. [Google Scholar]
49. Gallager, R., Van Voorhis, D. (1975). Optimal source codes for geometrically distributed integer alphabets (Corresp.). IEEE Transactions on Information Theory, 21(2), 228–230. [Google Scholar]
50. Pan, S. J., Yang, Q. (2010). A survey on transfer learning. IEEE Transactions on Knowledge and Data Engineering, 22, 1345–1359. [Google Scholar]
51. Fukushima, K. (1982). Neocognitron: A self-organizing neural network model for a mechanism of visual pattern recognition. In: Arbib, M. A., Amari, S. I. (Eds.Competition and cooperation in neural nets, pp. 267–285. Berlin, Heidelberg: Springer. [Google Scholar]
52. Ciresan, D., Giusti, A., Gambardella, L., Schmidhuber, J. (2012). Deep neural networks segment neuronal membranes in electron microscopy images. Proceedings of the 25th International Conference on Neural Information Processing Systems, vol. 25, pp. 2843–2851. [Google Scholar]
53. Wang, X., Peng, Y., Lu, L., Lu, Z., Bagheri, M. et al. (2017). ChestXray8: Hospital-scale chest X-ray database and benchmarks on weakly-supervised classification and localization of common thorax diseases. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 3462–3471. Honolulu, HI, USA. https://doi.org/10.1109/CVPR.2017.369 [Google Scholar] [CrossRef]
54. Rajpurkar, P., Irvin, J., Ball, R. L., Zhu, K., Yang, B. et al. (2018). Deep learning for chest radiograph diagnosis: A retrospective comparison of the chexnext algorithm to practicing radiologists. PLoS Medicine, 15(11), e1002686. https://doi.org/10.1371/journal.pmed.1002686 [Google Scholar] [PubMed] [CrossRef]
55. Zhou, L., Zhang, Z., Chen, Y. C., Zhao, Z. Y., Yin, X. D. et al. (2019). A deep learning-based radiomics model for differentiating benign and malignant renal tumors. Translational Oncology, 12(2), 292–300. [Google Scholar] [PubMed]
56. Deniz, E., Abdulkadir, Ş., Kadiroğlu, Z., Guo, Y. H., Bajaj, V. et al. (2018). Transfer learning based histopathologic image classification for breast cancer detection. Health Information Science and Systems, 6(1), 1–7. [Google Scholar]
57. Ahmed, K. B., Hall, L. O., Goldgof, D., Liu, R., Gatenby, R. (2017). Fine-tuning convolutional deep features for MRI-based brain tumor classification. In: Medical imaging 2017: Computer-aided diagnosis, international society for optics and photonics, vol. 10134, 101342E. Orlando, Florida, USA. [Google Scholar]
58. Yang, Y., Yan, L. F., Zhang, X., Han, Y., Nan, H. Y. et al. (2018). Glioma grading on conventional MR images: A deep learning study with transfer learning. Frontiers in Neuroscience, 12, 804. [Google Scholar] [PubMed]
59. Louati, H., Bechikh, S., Louati, A., Aldaej, A., Said, L. B. (2022). Evolutionary optimization for CNN compression using thoracic X-ray image classification. 34th International Conference on Industrial, Engineering Other Applications of Applied Intelligent Systems, Kitakyushu, Japan. [Google Scholar]
60. Louati, H., Bechikh, S., Louati, A., Hung, C. C., Said, L. B. (2021). Deep convolutional neural network architecture design as a bi-level optimization problem. Neurocomputing, 439, 44–62. [Google Scholar]
61. Gaál, G., Maga, B., Lukács, A. (2020). Attention U-Net based adversarial architectures for chest X-ray lung segmentation. arXiv preprint arXiv:2003.10304. [Google Scholar]
62. Abbas, A., Abdelsamea, M. M., Gaber, M. M. (2020). Classification of COVID-19 in chest X-ray images using DeTraC deep convolutional neural network. arXiv preprint arXiv:2003.13815. [Google Scholar]
63. Narin, A., Kaya, C., Pamuk, Z. (2020). Automatic detection of coronavirus disease (COVID-19) using X-ray images and deep convolutional neural networks. arXiv preprint arXiv:2003.10849. [Google Scholar]
64. Wang, L., Lin, Z. Q., Wong, A. (2020). COVID-Net: A tailored deep convolutional neural network design for detection of COVID-19 cases from chest radiography images. arXiv preprint arXiv:2003.09871. [Google Scholar]
65. El Asnaoui, K., Chawki, Y., Idri, A. (2020). Automated methods for detection and classification pneumonia based on X-ray images using deep learning. arXiv preprint arXiv:2003.14363. [Google Scholar]
66. I. D. Apostolopoulos and T. A. Mpesiana. (2020). Covid-19: Automatic detection from X-ray images utilizing transfer learning with convolutional neural networks. Physical and Engineering Sciences in Medicine, 43, 635–640. https://doi.org/10.1007/s13246-020-00865-4 [Google Scholar] [PubMed] [CrossRef]
67. Ghoshal, B., Tucker, A. (2020). Estimating uncertainty and interpretability in deep learning for coronavirus (COVID-19) detection. arXiv preprint arXiv:2003.10769. [Google Scholar]
68. Farooq, M., Hafeez, A. (2020). COVID-ResNet: A deep learning framework for screening of COVID-19 from radiographs. arXiv preprint arXiv:2003.14395. [Google Scholar]
69. Louati, H., Louati, A., Bechikh, S., Masmoudi, F., Aldaej, A. et al. (2022). Topology optimization search of deep convolution neural networks for CT and X-ray image classification. BMC Medical Imaging, 22, 120. [Google Scholar] [PubMed]
70. Hemdan, E. E. D., Shouman, M. A., Karar, M. E. (2020). COVIDX-Net: A framework of deep learning classifiers to diagnose COVID-19 in X-ray images. arXiv preprint arXiv:2003.11055. [Google Scholar]
Appendix A: Representative works for X-Ray based COVID-19 diagnosis dataset
Some of the most representative works for COVID-19 imaging-based diagnosis using X-Ray images are showed on Table 4.

Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF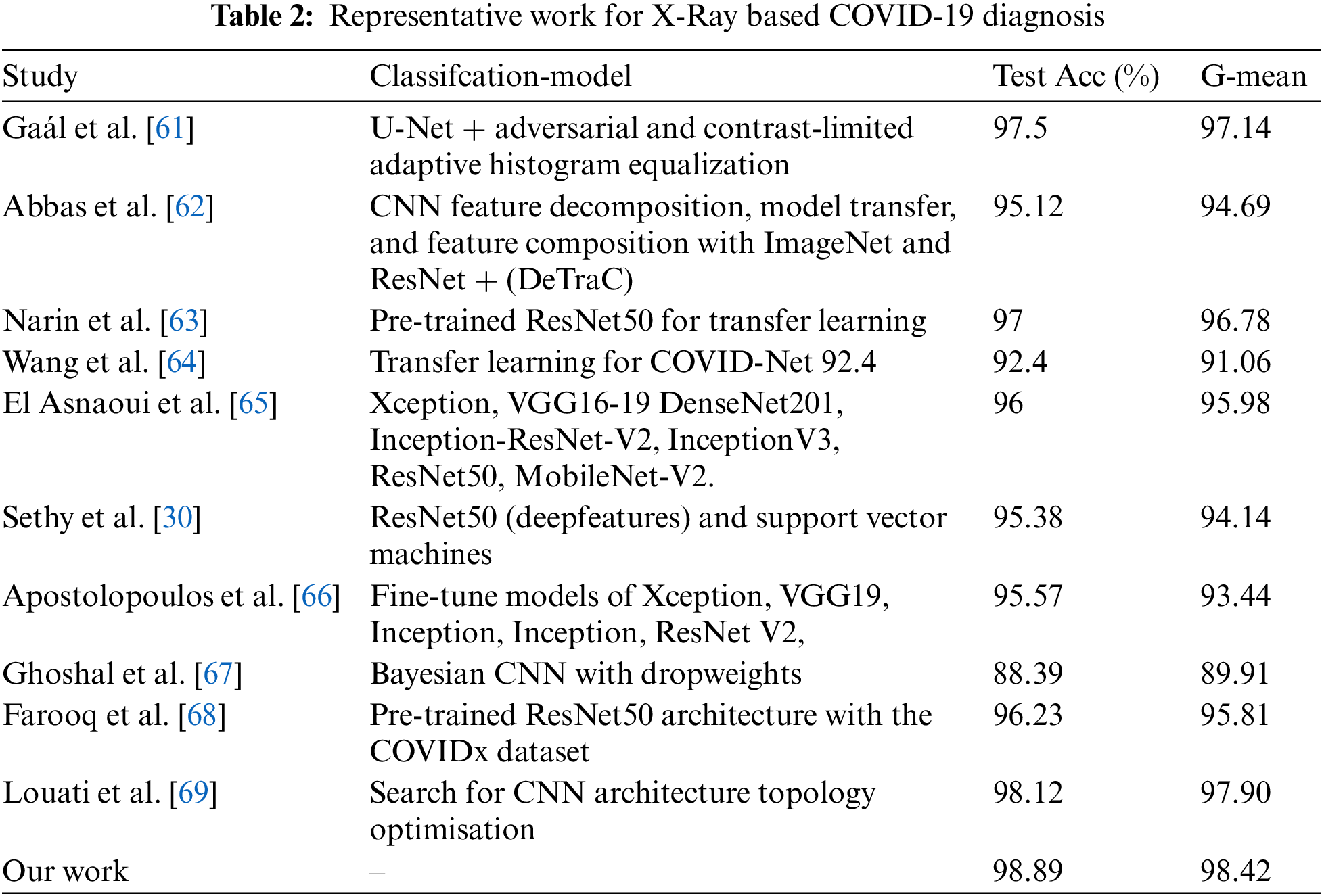
 Downloads
Downloads
 Citation Tools
Citation Tools