 Open Access
Open Access
ARTICLE
Advanced Machine Learning Methods for Prediction of Blast-Induced Flyrock Using Hybrid SVR Methods
1 College of Civil and Environmental Engineering, Hunan University of Science and Engineering, Yongzhou, 425006, China
2 Hunan Provincial Key Laboratory of Intelligent Protection and Utilization Technology in Masonry Artifacts, Hunan University of Science and Engineering, Yongzhou, 425006, China
3 School of Civil Engineering, Guangzhou University, Guangzhou, 510006, China
4 Institute of Research and Development, Duy Tan University, Da Nang, 550000, Vietnam
5 School of Engineering & Technology, Duy Tan University, Da Nang, 550000, Vietnam
* Corresponding Authors: Mahdi Hasanipanah. Email: ,
; Jiandong Huang. Email:
(This article belongs to the Special Issue: Meta-heuristic Algorithms in Materials Science and Engineering)
Computer Modeling in Engineering & Sciences 2024, 140(2), 1595-1617. https://doi.org/10.32604/cmes.2024.048398
Received 06 December 2023; Accepted 06 March 2024; Issue published 20 May 2024
Abstract
Blasting in surface mines aims to fragment rock masses to a proper size. However, flyrock is an undesirable effect of blasting that can result in human injuries. In this study, support vector regression (SVR) is combined with four algorithms: gravitational search algorithm (GSA), biogeography-based optimization (BBO), ant colony optimization (ACO), and whale optimization algorithm (WOA) for predicting flyrock in two surface mines in Iran. Additionally, three other methods, including artificial neural network (ANN), kernel extreme learning machine (KELM), and general regression neural network (GRNN), are employed, and their performances are compared to those of four hybrid SVR models. After modeling, the measured and predicted flyrock values are validated with some performance indices, such as root mean squared error (RMSE). The results revealed that the SVR-WOA model has the most optimal accuracy, with an RMSE of 7.218, while the RMSEs of the KELM, GRNN, SVR-GSA, ANN, SVR-BBO, and SVR-ACO models are 10.668, 10.867, 15.305, 15.661, 16.239, and 18.228, respectively. Therefore, combining WOA and SVR can be a valuable tool for accurately predicting flyrock distance in surface mines.Keywords
Abbreviations
| ANFIS | Adaptive neuro-fuzzy inference system |
| ANFO | Ammonium Nitrate Fuel Oil |
| ACO | Ant colony optimization |
| AI | Artificial intelligence |
| ANN | Artificial neural network |
| BPNN | Back-propagation neural network |
| BBO | Biogeography-based optimization |
| BRT | Boosted regression tree |
| B | Burden |
| R2 | Coefficient of determination |
| DNN | Deep neural network |
| ELM | Extreme learning machine |
| FA | Firefly algorithm |
| GRNN | General regression neural network |
| d | Index of agreement |
| GA | Genetic algorithm |
| GSA | Gravitational search algorithm |
| GWO | Grey wolf optimization algorithm |
| KELM | Kernel extreme learning machine |
| MCPD | Maximum charge per delay |
| MAPE | Mean absolute percentage error |
| NSE | Nash-Sutcliffe efficiency |
| PSO | Particle swarm optimization |
| Q | Quartile |
| RBF | Radial basic function |
| RF | Random forest |
| RMSD | Root mean square deviation |
| RMSE | Root mean square error |
| S | Spacing |
| ST | Stemming |
| SRM | Structural risk minimization |
| SVR | Support vector regression |
| TBM | Tunnel boring machine |
| UCS | Unconfined compressive strength |
| WOA | Whale optimization algorithm |
Drilling and blasting is a frequent and typical method for fragmenting rock masses in surface mines due to its high adaptability and low cost. However, it can produce serious effects, i.e., ground vibration, flyrock, and airblast [1–5]. Among them, flyrock is one of the most dangerous effects, which can result in human injuries. Flyrock poses a significant risk as it has the potential to cause extensive harm to machinery, nearby structures, and individuals, including severe injuries and even fatalities [6]. In other words, excessive flyrock beyond the protected blast zone is identified as the primary cause of numerous fatal and non-fatal accidents related to blasting in surface mining operations. Therefore, precise flyrock prediction is a very significant task before each blasting event. According to previous studies [6–10], some blast design parameters and rock mass properties can be effective parameters on the intensity of flyrock. Reviewing the literature [11–13] found that various empirical studies have been performed to predict and control blast-induced flyrock. The results of these empirical works present empirical equations, and the constructed empirical models were based on the relationship between two or three blast design parameters and flyrock [12]. As a disadvantage of empirical models, they have missed the nonlinear relationship between the blast design parameters and flyrock [13]. Consequently, the performances of empirical models were not in an acceptable range in some cases. Considering the disadvantages of empirical models and improving prediction accuracy, artificial intelligence (AI) methods have been developed in recent decades, which have the advantage of establishing a direct relationship between the effective parameters and the flyrock. In addition, the use of AI methods in different civil [14–18], mining [19–22], and geotechnical fields [23–27] has been underlined.
For the aim of flyrock prediction, Trivedi et al. [28,29] utilized the artificial neural network (ANN) and BPNN, respectively, by using rock mass properties and blast design parameters as the inputs. Their results indicated the good performance of ANN and BPNN in predicting flyrock. In another study, a support vector regression (SVR) was employed by Rad et al. [30] for the same purpose. Extreme learning machine (ELM) and random forest (RF) models were employed by Lu et al. [31] and Ye et al. [32] to predict flyrock. In some studies, the combination of ANN and optimization algorithms has been highlighted. For example, Monjezi et al. [8,33,34] utilized the GA, PSO, and fuzzy Delphi method, respectively, in combination with ANN to predict flyrock. Aside from ANN, the optimization algorithms were also combined with other AI methods to improve the quality of flyrock prediction. A combination of recurrent fuzzy neural networks and PSO was employed in the study by Kalaivaani et al. [35]. Murlidhar et al. [36] adopted a hybrid model based on Harris Hawks optimization (HHO) and a multilayer perceptron model to predict flyrock. In another study, Fattahi et al. [37] predicted the flyrock values using a combination of the grey wolf optimization algorithm (GWO) and ANFIS. Recently, Li et al. [38] discussed the combination of a multi-strategies-based SVR with HHO to predict flyrock. In their study, some other AI methods were also utilized. They concluded that the proposed model can be a powerful prediction tool. The graph and Transformer neural networks are considered novel AI methods with some advantages, especially in the dynamic response process [39–43].
This research develops four SVR models for predicting the flyrock. The main contribution of this research is to develop a new and accurate method to predict flyrock. In this regard, the SVR is combined with the whale optimization algorithm (WOA). To the best of our knowledge, it is the first work that predicts flyrock through the proposed SVR-WOA model. To verify the accuracy of the proposed model, three other algorithms, i.e., gravitational search algorithm (GSA), ant colony optimization (ACO) and biogeography-based optimization (BBO), are combined with SVR. The GSA, BBO, ACO, and WOA are utilized to fine-tune the hyperparameters of the SVR model. Additionally, the GRNN, ANN, and KELM are employed.
The required database was gathered from two surface mines in Kerman Province, Iran, to construct the predictive models. In these mines, the drilling and blasting methods were employed to fragment and displace rock masses using ANFO as the explosive material. The gathered database included 83 sets of data, encompassing four input parameters and one output parameter (flyrock). In this context, the input parameters were designated as the B, S, ST, and maximum charge per delay (MCPD) parameters. These blast design parameters were measured before all 83 blasting events. In addition, the values of flyrock were measured using a handheld Global Positioning System (GPS). Table 1 lists descriptive statistics of all parameters used in this study. The Box-and-whisker plots for all parameters are displayed in Fig. 1, with explanations provided in the figure. Additionally, the relationship between all inputs and output is depicted in Fig. 2. For modeling, the prepared data was divided into two main parts for constructing and verifying the predictive methods. Accordingly, 80% of the datasets were allocated for construction (training) purposes, and the remaining datasets were for verification (testing).
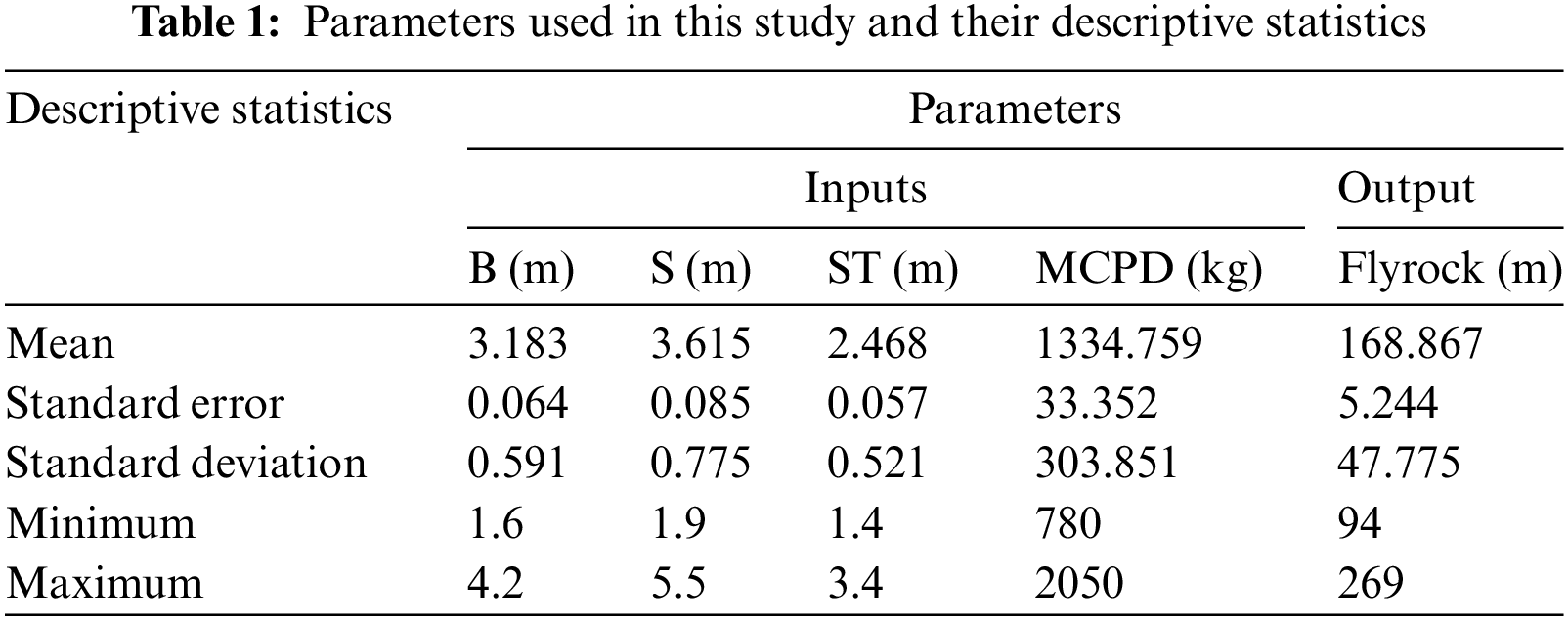
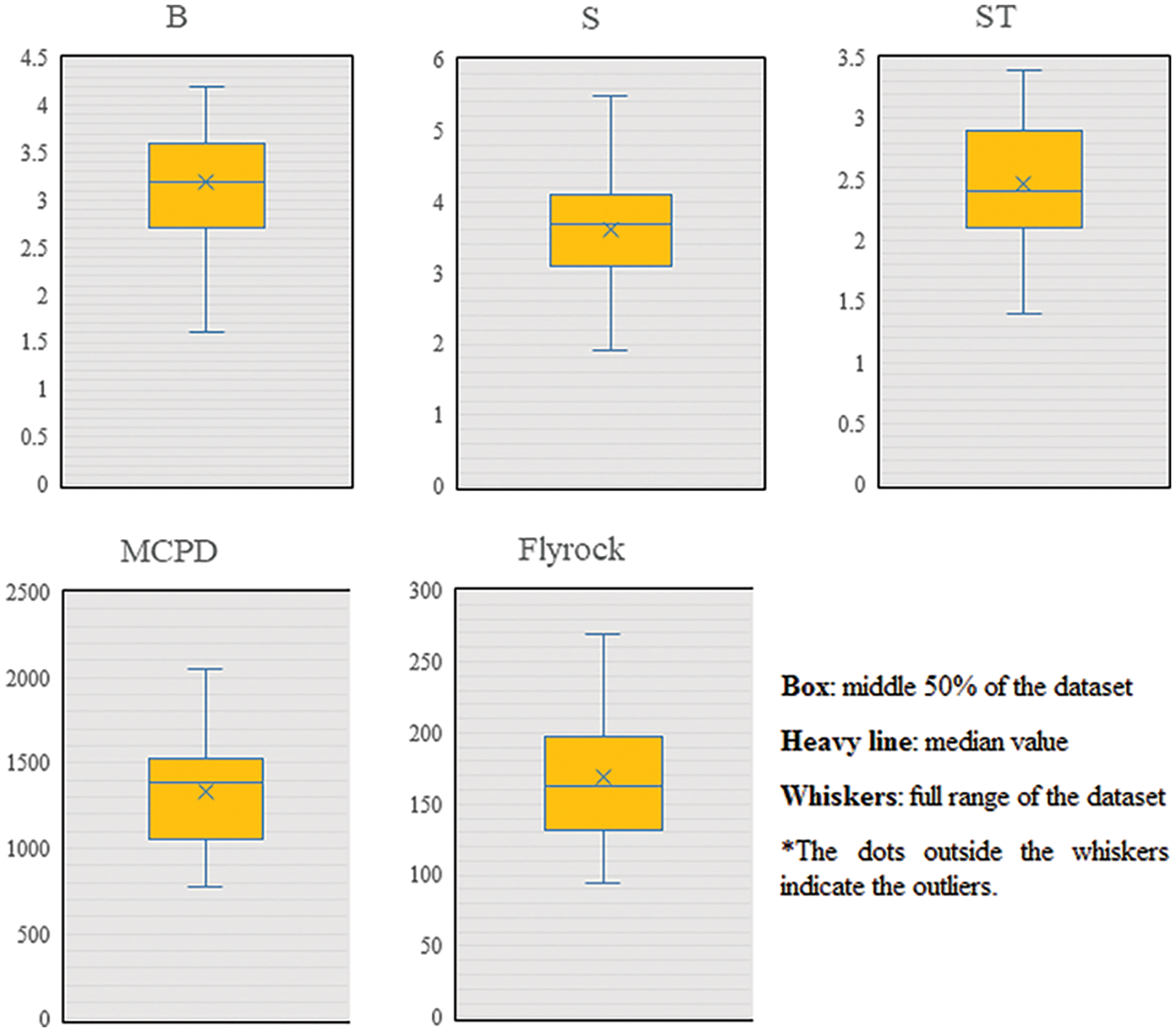
Figure 1: Box-and-whisker plots for all input and output parameters
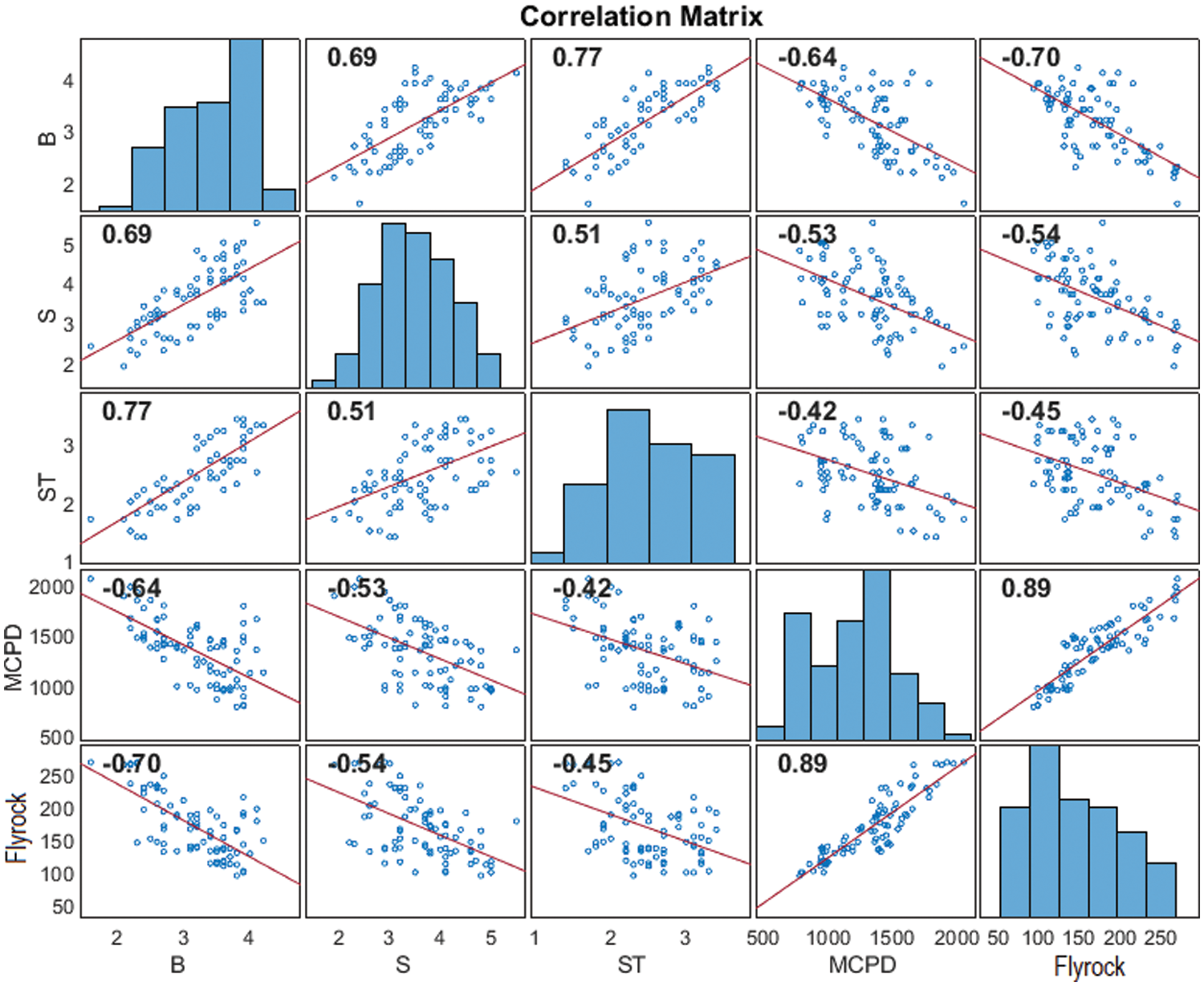
Figure 2: Relationship between all inputs and output parameters
The General Regression Neural Network (GRNN), a type of radial basis function (RBF) network, was first introduced by Specht [44]. The GRNN, based on a standard statistical method known as kernel regression, is notable for its approximation ability and learning speed, mainly when the dataset is large or even when it is small [45]. A GRNN comprises four layers: input, pattern, summation, and output layers. The structure of the GRNN is depicted in Fig. 3 [45]. For detailed explanations regarding the GRNN, some studies [45–47] can be viewed. Owing to its advantages, the application of GRNN has been emphasized in different studies. Ceryan et al. [46] and Singh et al. [47] employed the GRNN to predict unconfined compressive strength (UCS). Ground vibration induced by mine blasting was predicted through GRNN by Xue et al. [48]. The use of GRNN in the field of landslide prediction was investigated by Jiang et al. [49]. Zhang et al. [50] employed the GRNN to predict settlement induced by tunneling. The above studies indicated the acceptability of GRNN for prediction aims with a good performance.
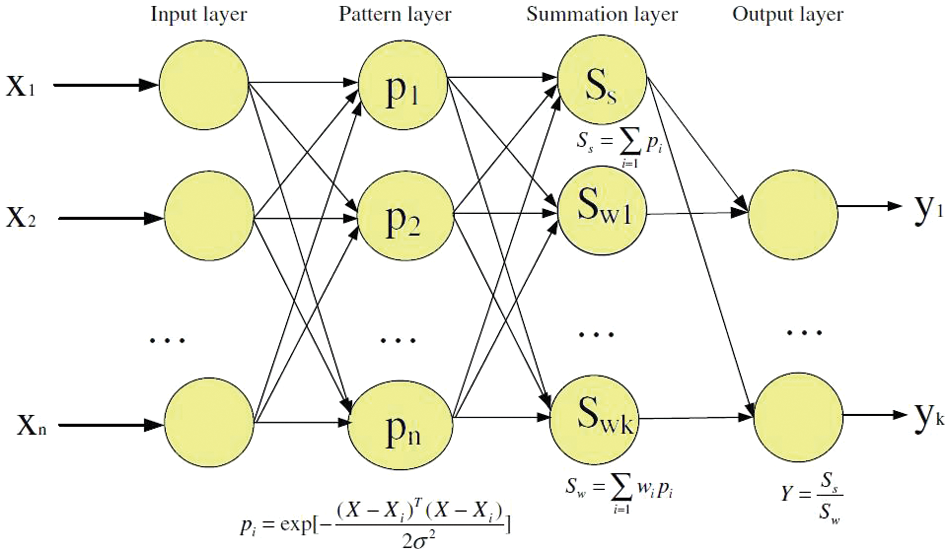
Figure 3: GRNN structure [45]
Support Vector Regression (SVR), a part of the Support Vector Machines (SVM) family, was presented by Vapnik [51]. Structural risk minimization (SRM) is considered the core of the optimizer algorithm to obtain the minimum error [52,53]. According to the literature, the RBF is applied as the kernel function in many studies; therefore, it was also used as the kernel function in this study [52,53]. In the SVR model, three hyperparameters must be demonstrated, including C, ε, and γ [53]. For this purpose, the trial and error method can be employed. Extensive details about SVR can be found in the literature [53–55].
The use of the SVR model for prediction purposes in several mining and civil engineering fields has been underlined. For instance, Xu et al. [54] employed the SVR model to predict shear and uniaxial compressive strength. In their study, the GWO, differential evolution, and artificial bee colony algorithms were applied to select the optimal hyperparameters of the SVR model. The use of GWO in combination with SVR was also utilized by Fan et al. [55] to predict the bond strength of reinforced concrete. Meng et al. [56] employed the SVR model to predict tunnel collapse probability. In another study conducted by Chen et al. [57], the Firefly Algorithm (FA), Particle Swarm Optimization (PSO), and Genetic Algorithm (GA) were combined with SVR to simulate ground vibration. Lawal et al. [58] adopted an SVR model to predict thermal coal ash behavior. The SVR was a valuable tool for prediction purposes in the studies above.
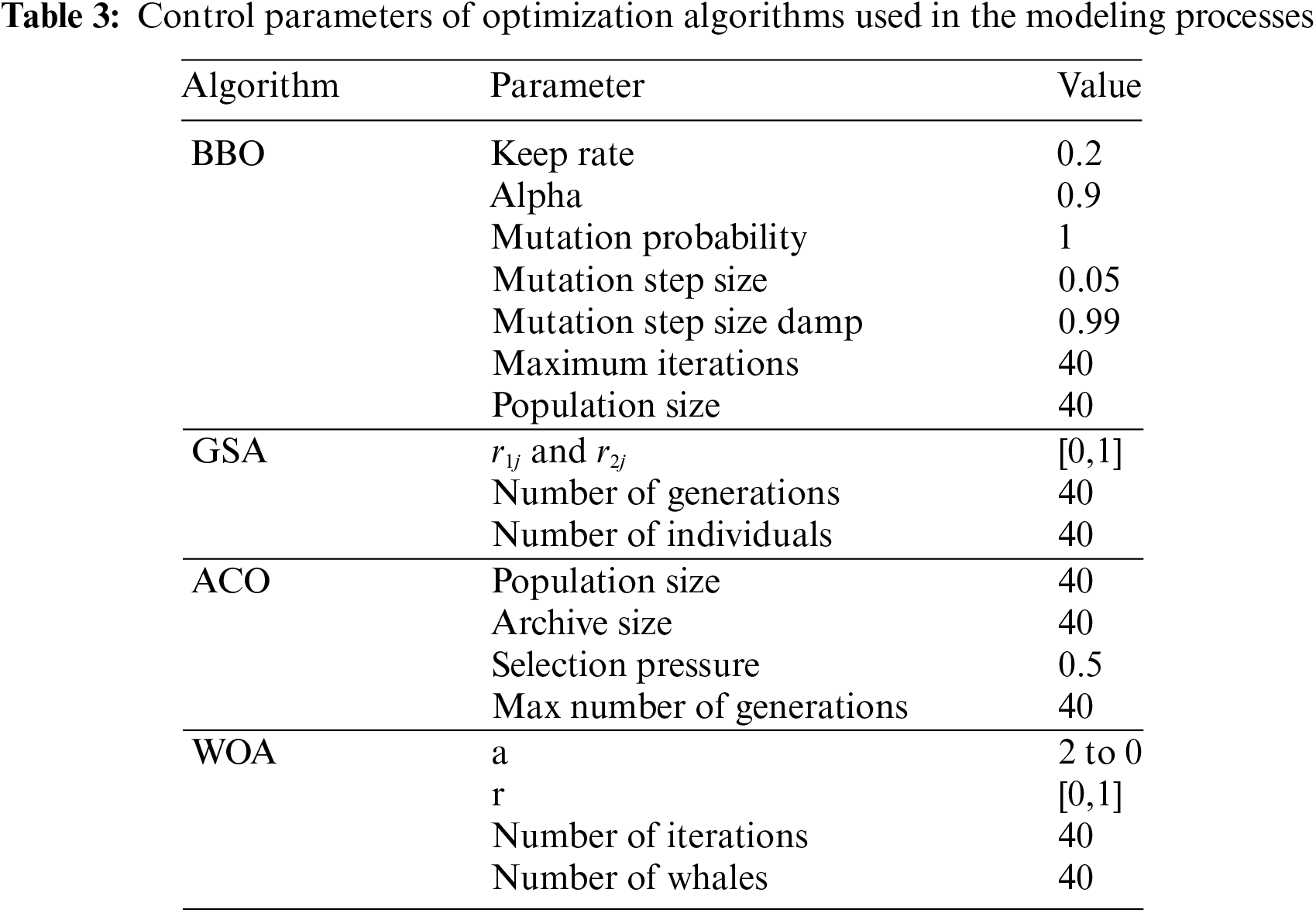
This study uses the GSA, BBO, WOA, and ACO algorithms to select the optimal hyperparameters of the SVR model.
Compared to some evolutionary algorithms, the GSA, as a stochastic local search heuristic, is an effective and successful algorithm. Rashedi et al. [59] first presented the GSA, using it to solve various optimization problems with continuous parameters. Each agent in GSA has four parameters: position, velocity, inertial mass, and gravitational mass. The agent’s location corresponds to the problem’s solution, while its gravitational and inertial mass is determined by a fitness function [60]. Furthermore, the number of generations and individuals are the main parameters in GSA, which can be selected by trial and error methods. Fig. 4 displays the flowchart of GSA [61]. Extensive details about the GSA can be found in [60,62]. A review of previous studies [60–63] revealed that the GSA possesses a satisfying exploration capability compared to other optimization algorithms and has been used in various fields. Adnan et al. [60] combined GSA with least square SVR for river flow prediction. Mehdizadeh et al. [62] employed a hybrid of ANN and GSA (ANN-GSA) for predicting daily soil temperature. In another study, the ANN-GSA was used to simulate the deformation of geogrid-reinforced soil structures by Momeni et al. [63]. In addition, GSA was adopted by Banyhussan et al. [64] to predict the packing density of cementitious pastes in the building engineering field. The use of GSA in these studies indicates its effectiveness for prediction purposes, and therefore, it is used in this study for flyrock prediction.
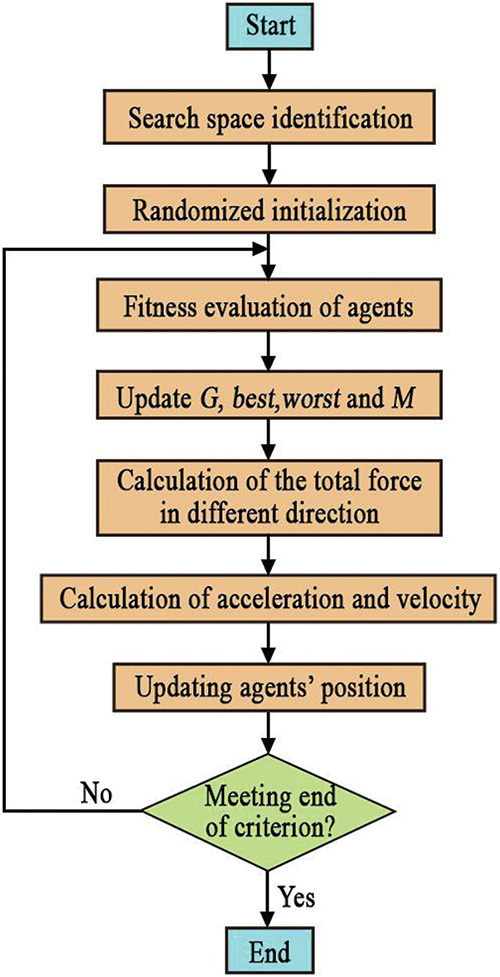
Figure 4: GSA flowchart [61]
Colorni et al. [65] presented the ACO based on the behavior of ant colonies in nature. When ants search for food, they mark their surroundings with a specific pheromone, identifiable by other colonies [66]. Upon discovering it, ants attempt to find food and return to the nest via the closest path. The ant colony members frequently update the path to select the best and closest path. In each ACO model, population size, archive size, selection pressure, and the maximum number of generations are crucial parameters. The flowchart of ACO is shown in Fig. 5 [67]. More details regarding ACO can be found in the literature [68–70].
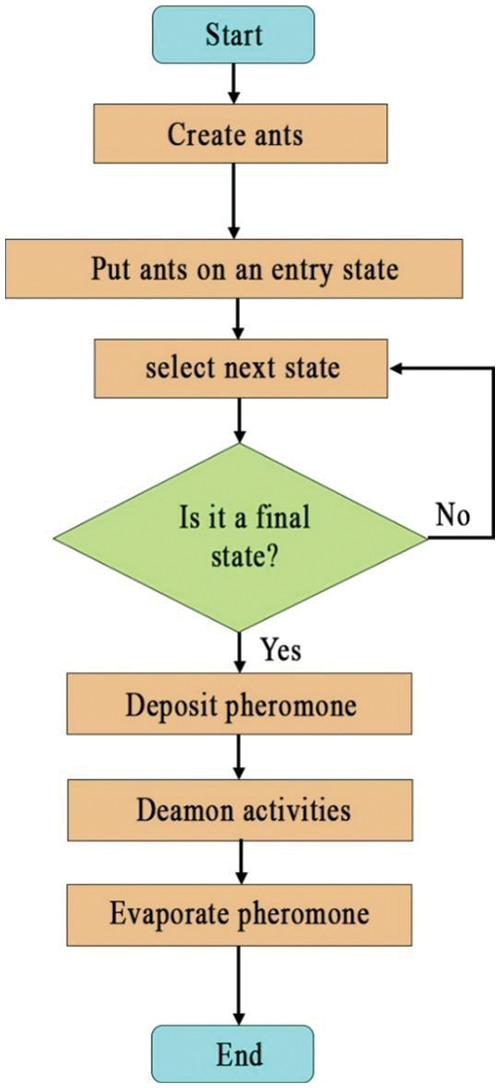
Figure 5: ACO flowchart [67]
ACO has been employed in several studies within the field of engineering for optimization purposes. Saghatforoush et al. [68] combined an ANN and ACO to predict backbreak and flyrock in surface mines. Taghizadeh-Mehrjardi et al. [69] predicted soil particle-size fractions using ACO and ANFIS models. Zhang et al. [70] established a deep neural network (DNN) based on ACO for predicting the capital cost of mining projects. Afradi et al. [71] used ACO to simulate the penetration rate of a TBM. In another study, Xu et al. [72] investigated a hybrid of ANN and ACO to evaluate retaining walls under dynamic conditions. Zhang et al. [67] adopted a boosted regression tree (BRT) optimized by ACO to simulate fragmentation size after mine blasting. These studies indicated that ACO emerged as a powerful and stable algorithm for optimization purposes.
Simon [73] introduced the BBO algorithm, drawing inspiration from the biogeography of species finding the most suitable habitats. This algorithm evaluates each habitat using a habitat suitability index (HSI). Habitats with a high HSI are more likely to attract species, while those with a low HSI tend to acquire characteristics from high HSI habitats [74]. By iteratively performing these evaluations, the algorithm optimizes the problem. BBO relies on two essential operations: migration and mutation, which are vital in the optimization process. Migration is simulated by exchanging habitat features between different habitats, resembling the movement of species between geographical locations. This process allows the exploration of different regions of the search space. A mutation is modeled by perturbing the features of habitats, introducing random changes that promote exploration and prevent premature convergence. The migration and mutation processes in BBO are guided by the concept of “fitness” and the principle of “island biogeography.” Habitats with higher fitness values are more likely to migrate and influence other habitats, while less fit habitats may become extinct. This natural selection mechanism encourages convergence towards better solutions over iterations. The flowchart of BBO is shown in Fig. 6 [75]. A more detailed review of BBO can be found in [74–77].
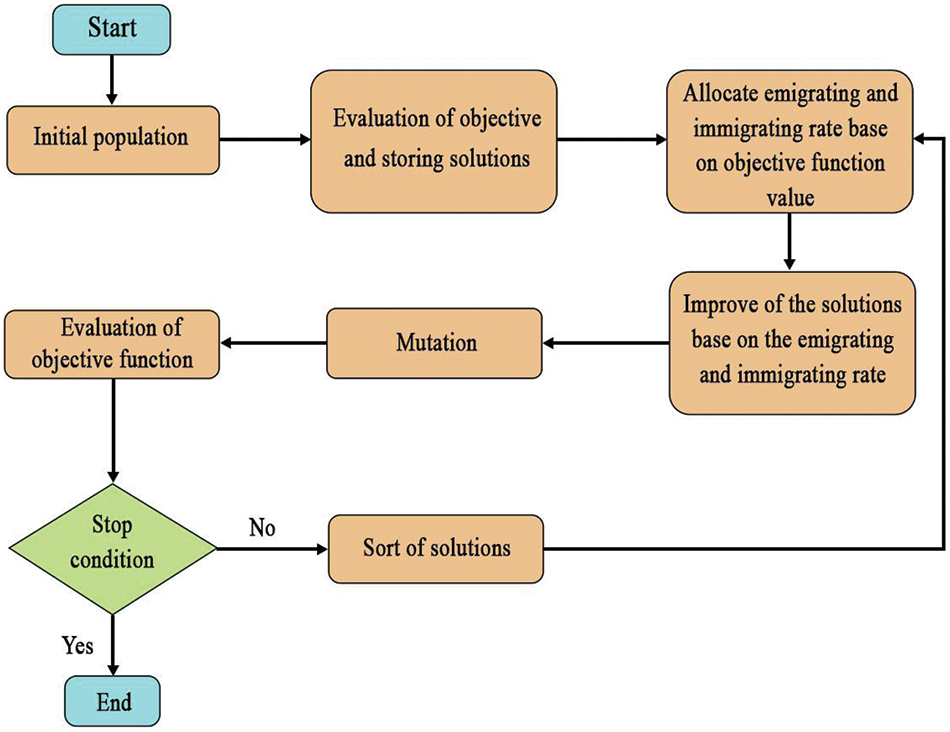
Figure 6: BBO flowchart [75]
BBO’s ability to balance exploration and exploitation, inspired by the principles of biogeography, makes it a promising algorithm for solving complex optimization problems [76–78]. By leveraging the mechanisms of migration and mutation, BBO efficiently explores the search space and seeks optimal solutions. Chen et al. [76] combined ANFIS and BBO to predict groundwater potentiality. Pham et al. [77] predicted the coefficient of soil consolidation using a hybrid of ANN and BBO. A combination of FA and BBO was used for the optimal design of steel frame structures in the study conducted by Farrokh Ghatte [78]. The application of a hybrid ANN and BBO was also developed by Kazemi et al. [79] to evaluate the compressive strength of green concrete. In another study, Jaafari et al. [80] suggested an ANFIS-BBO model to estimate landslide susceptibility. Moayedi et al. [81] utilized an ANN-BBO model for the same purpose. These studies showed the acceptability of BBO to improve ANN and ANFIS performances.
Mirjalili et al. [82] introduced WOA based on the hunting behavior of humpback whales. One significant advantage of WOA is its ability to expedite the optimization rate, making it highly useful for solving various complex problems [83]. In WOA, a population of potential solutions is represented as a group of whales, each corresponding to a candidate solution. The WOA consists of three main stages: encircling the prey (shrinking encircling hunt), bubble-net attacking (exploitation stage), and searching for prey (exploration stage) [66]. These stages guide the search process, aiming to enhance the quality of solutions throughout iterations. WOA systematically explores the search space and converges toward the optimal solution by iteratively updating the positions of potential solutions. During the optimization process, the algorithm updates the search positions of the whales based on their fitness values. Whales with better fitness values are more likely to influence the movement of other whales toward better solutions. Fig. 7 depicts the flowchart of WOA [83]. Further details about WOA are provided in studies such as [83–85].
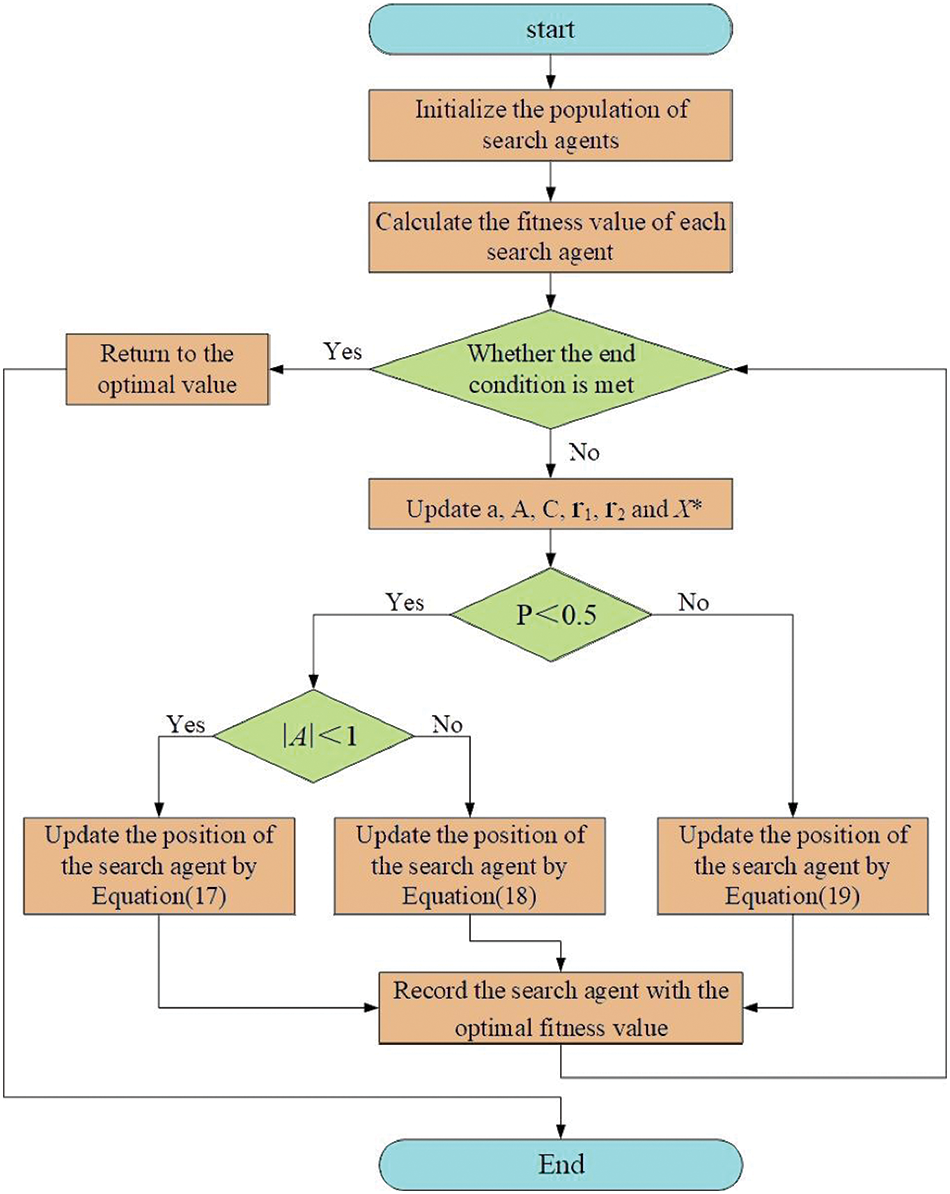
Figure 7: WOA flowchart [83]
WOA has been successfully utilized for various optimization issues, including feature selection, data clustering, scheduling, and engineering design. Its ability to balance exploration and exploitation makes it a promising tool for solving complex problems in civil and mining engineering, where finding optimal solutions is crucial. A hybrid of ANN and WOA was used by Tien Bui et al. [66] to simulate the compressive strength of concrete. The dragonfly algorithm and ACO were also used in their study. Jaafari et al. [84] adopted a group method of data handling model optimized with WOA to simulate landslides. Zhou et al. [85] applied the combination of WOA and SVM to predict tunnel squeezing. Nguyen et al. [86] used WOA and the extreme gradient boosting machine to simulate the bearing capacity of concrete piles. Recently, Liu et al. [87] established a method based on RF and WOA to simulate the invalidation risk of backfilling pipelines. The effectiveness of WOA as an optimization algorithm has been confirmed through the research mentioned above.
Before proceeding with the modeling of the data using the aforementioned data-driven methods, a preliminary step involving data processing was conducted. In this step, the collected data points were normalized between −1 and 1 to enhance the effectiveness of the applied methods and mitigate potential issues related to the learning process. Hence, the following equation was employed for data normalization:
where xi represents the original measurement value, Xn,i denotes the normalized value, and xmax and xmin correspond to the maximum and minimum values of the variable, respectively. The normalization of the database was followed by data-splitting. After normalizing the database, the data was split into two main parts for constructing and verifying the models. Specifically, 80% of the entire dataset was allocated for the construction (training) part, while the remaining datasets were used for verification (testing). This resulted in 67 datasets for the construction part and 17 datasets for the verification part.
As mentioned, two machine learning approaches, namely GRNN and SVR, were employed to model the datasets. It was crucial to select appropriate control parameters to achieve optimal prediction performance with these approaches. The spreading coefficient of GRNN was optimized through a trial-and-error technique, while the three hyperparameters of SVR models were investigated using four nature-inspired algorithms: WOA, BBO, ACO, and GSA. In this study, linear, polynomial, RBF and sigmoid kernels were considered, and the RBF was chosen as the most optimal kernel function. Fig. 8 provides an overview of the main steps involved in developing the models.
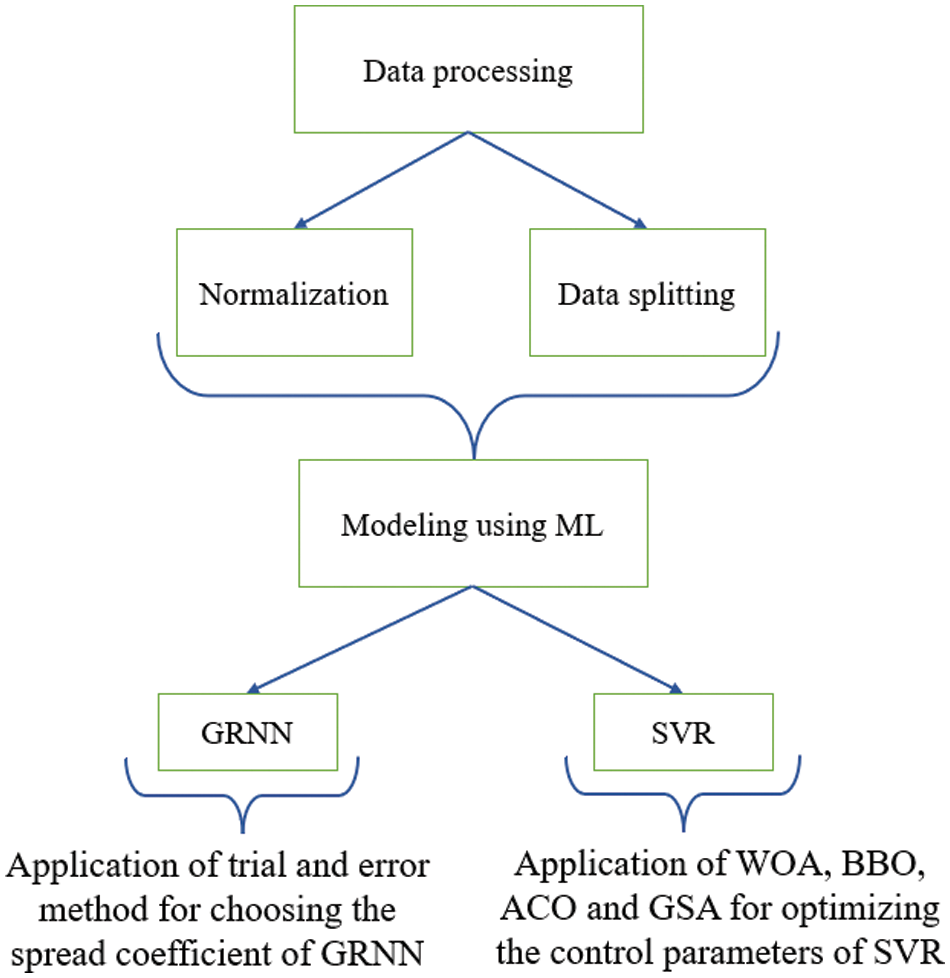
Figure 8: The modeling steps
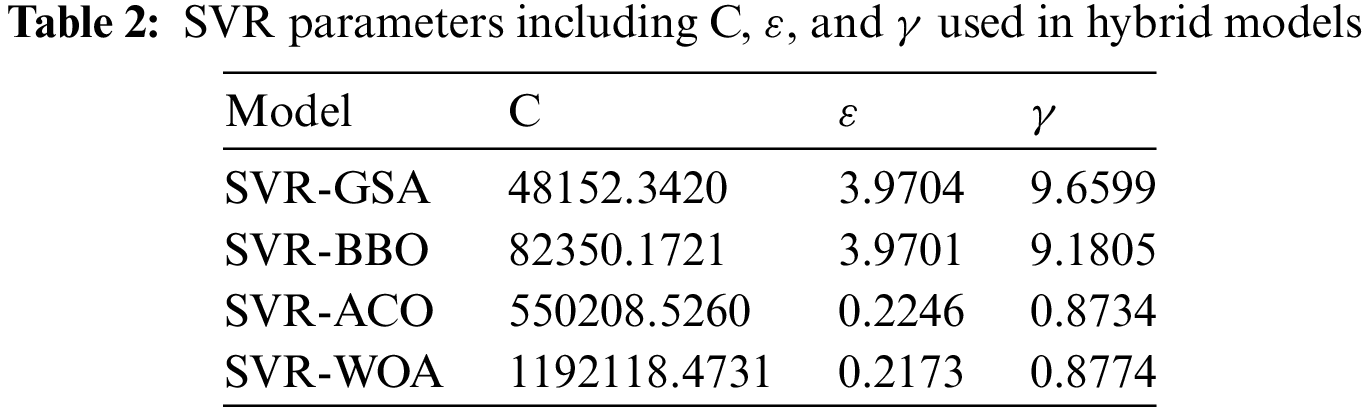
For GRNN modeling, a spread coefficient of 0.075 was chosen. The SVR parameters (C, ε, and γ) utilized in the four hybrid models are presented in Table 2. Additionally, the control parameters of WOA, BBO, ACO, and GSA employed in the modeling processes of SVR-WOA, SVR-BBO-, SVR-ACO, and SVR-GSA are listed in Table 3.
In addition to the models discussed earlier, two traditional models, namely the ANN and KELM, were also utilized in this study. Further information regarding the ANN and KELM can be found in the literature [3,88].
In the ANN modeling, a three-layer structure was implemented, consisting of the input, hidden, and output layers with four, seven, and one neurons, respectively. For the hidden layer, multiple options ranging from 1 to 9 neurons (as suggested by Hecht-Nielsen [89]) were tested, and based on the results, the optimal performance was achieved with seven neurons in the hidden layer. For the KELM, two crucial settings, namely the width of the kernel function and the regularization coefficient, were determined using a trial-and-error technique. The width of the kernel function was set to 30 units, and the regularization coefficient was set to 5,000 units. In this model, the RBF was utilized as the kernel function.
This study utilized four hybrid models, namely SVR-WOA, SVR-BBO, SVR-ACO, and SVR-GSA, for flyrock prediction. Three other models, GRNN, ANN, and KELM, were employed. The accuracy of these models was assessed using six performance indices: MAPE, RMSD, Nash-Sutcliffe efficiency (NSE), RMSE [90–94], index of agreement (d), and R2 [95–97]. A model with the lowest MAPE, RMSD, and RMSE and the highest NSE, d, and R2 values is considered the most optimal model. Table 4 shows the values of these performance indices obtained from all models for the testing part. The table indicates the rank of each model based on its performance indices, and the overall ranks of all models are calculated. As shown in Table 4, SVR-WOA receives the highest rank, followed by GRNN, KELM, SVR-GSA, ANN, SVR-BBO, and SVR-ACO models, respectively. This indicates that SVR-WOA is the most suitable and effective model for flyrock prediction in this study.
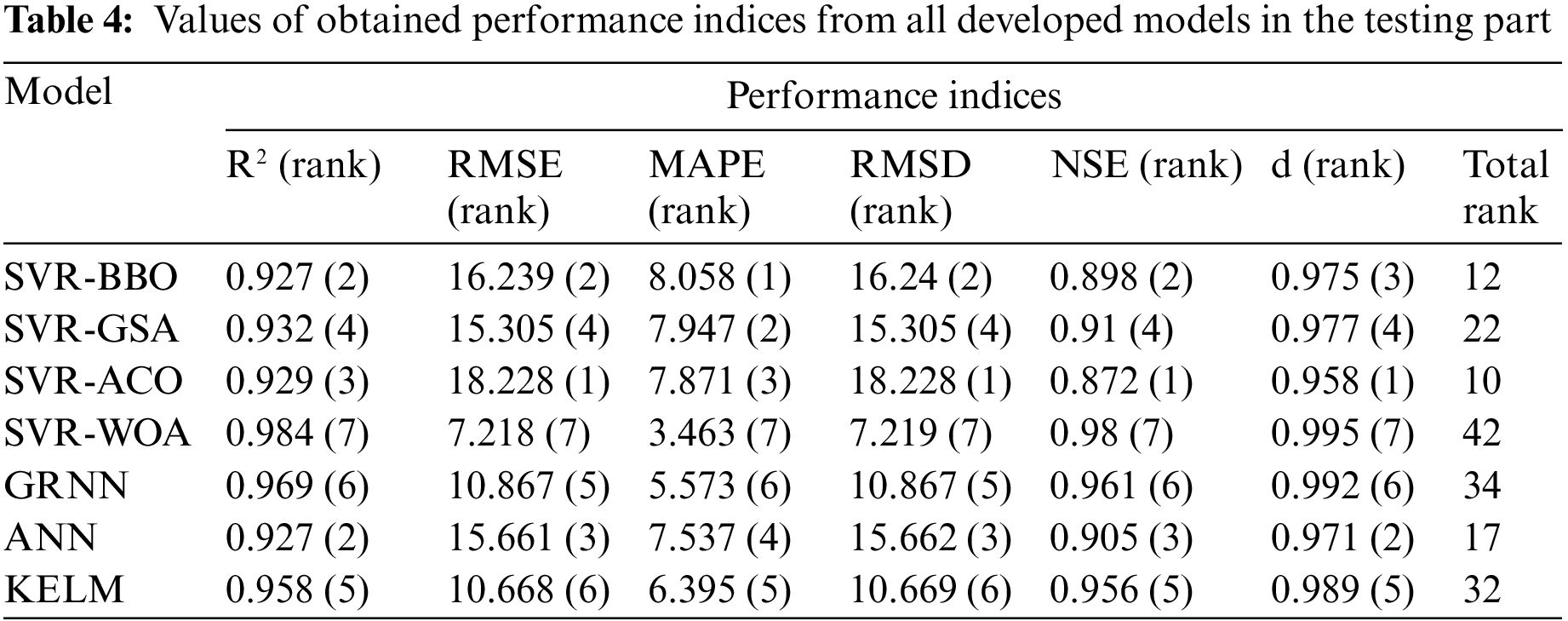
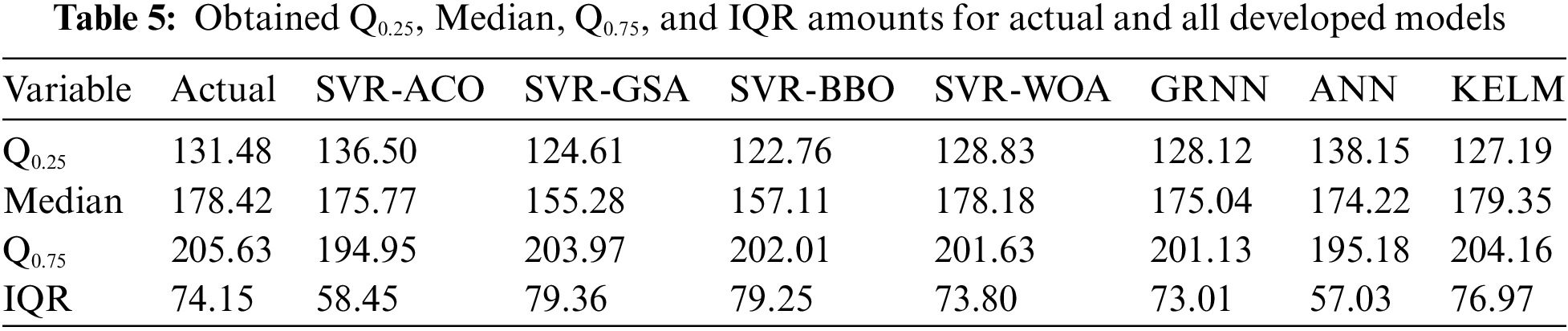
Fig. 9 displays the R2 values of all models for the testing phase, confirming that the SVR-WOA model achieves the best prediction performance and highest accuracy (0.984) among all the models. Furthermore, Fig. 10 depicts an overview of the predicted flyrock values obtained from all models for the testing datasets. It shows that the SVR-WOA model demonstrates superior performance compared to the other models. To further evaluate the models, Fig. 11 presents a Taylor diagram for the testing part of all developed models. Based on this diagram, the SVR-WOA model exhibits highly accurate flyrock predictions that closely align with the actual values. To check the performance of developed models in predicting flyrock, violin box plots comparing the predicted values from all models to the actual flyrock values are presented in Fig. 12. Additionally, Table 5 lists each model’s quartile values, including Q0.25, Q0.75, Median, and interquartile range (IQR). The table indicates that the SVR-WOA exhibits quartile values (Q0.25 and IQR) (128.83 and 73.80) that are closer to the actual values (131.48 and 74.15) compared to other models. In terms of Q0.75 values, KELM, SVR-GSA, SVR-BBO, SVR-WOA, GRNN, ANN, and SVR-ACO demonstrate closer values to the actual amounts. When considering the median values, the SVR-WOA model is found to have a value closer to the actual amount. Based on these findings, it is evident that the developed SVR-WOA model is more robust and provides more accurate flyrock predictions than the other models.
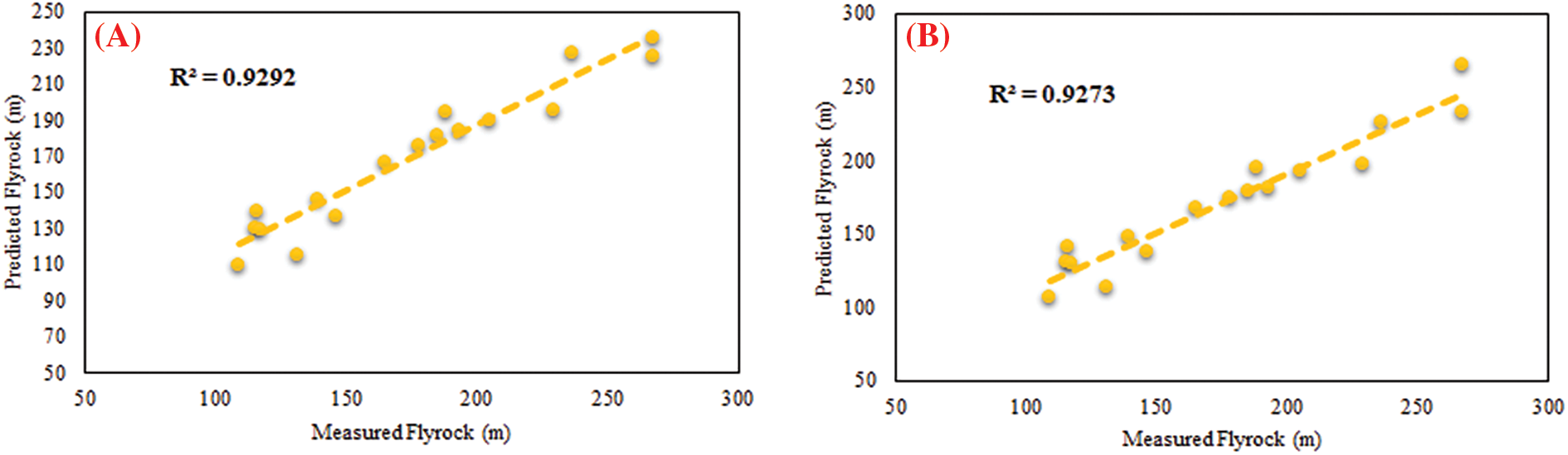
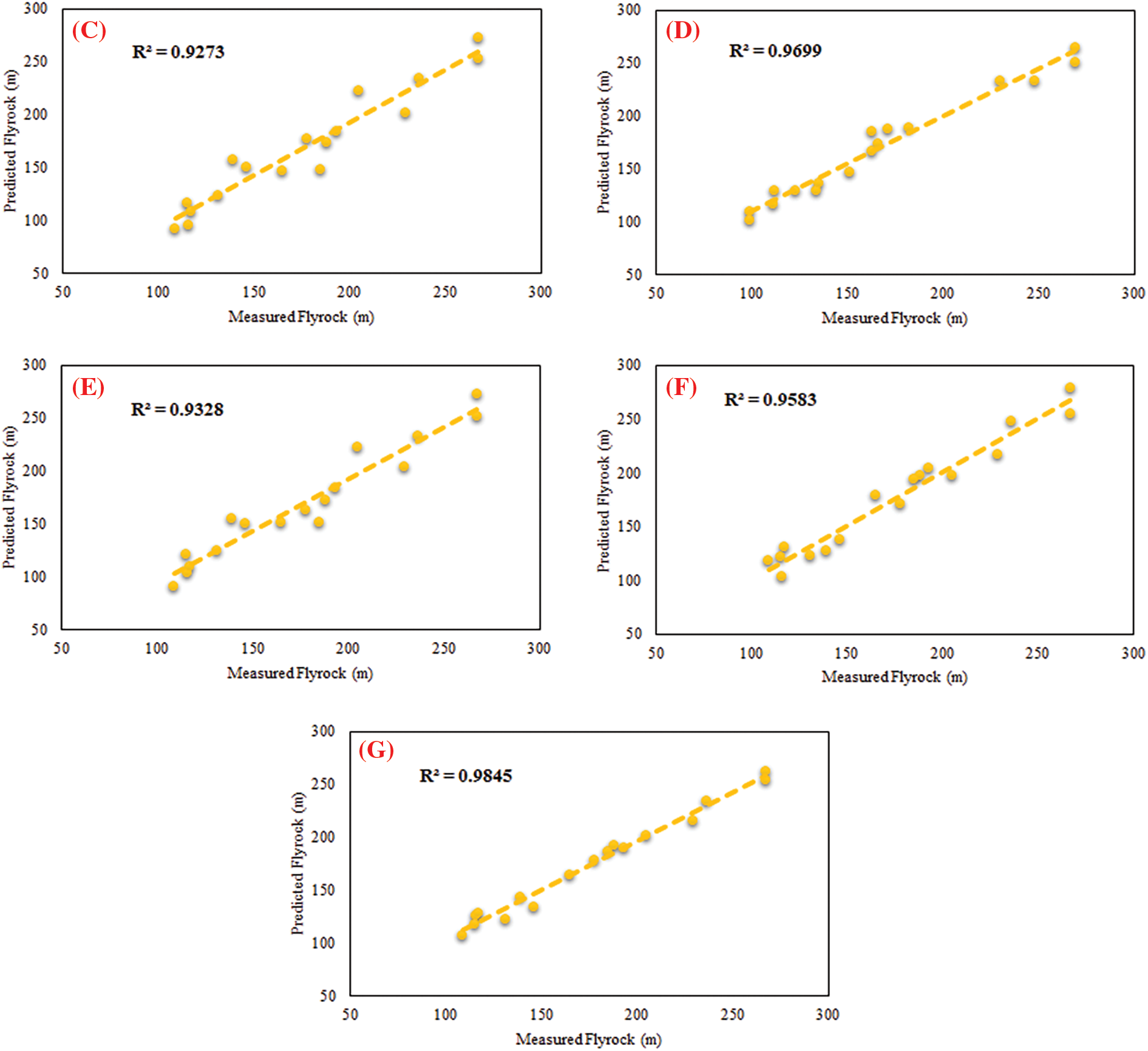
Figure 9: R2 values for all developed models: (A): SVR-ACO, (B): ANN, (C): SVR-BBO, (D): GRNN, (E): SVR-GSA, (F): KELM, and (G): SVR-WOA
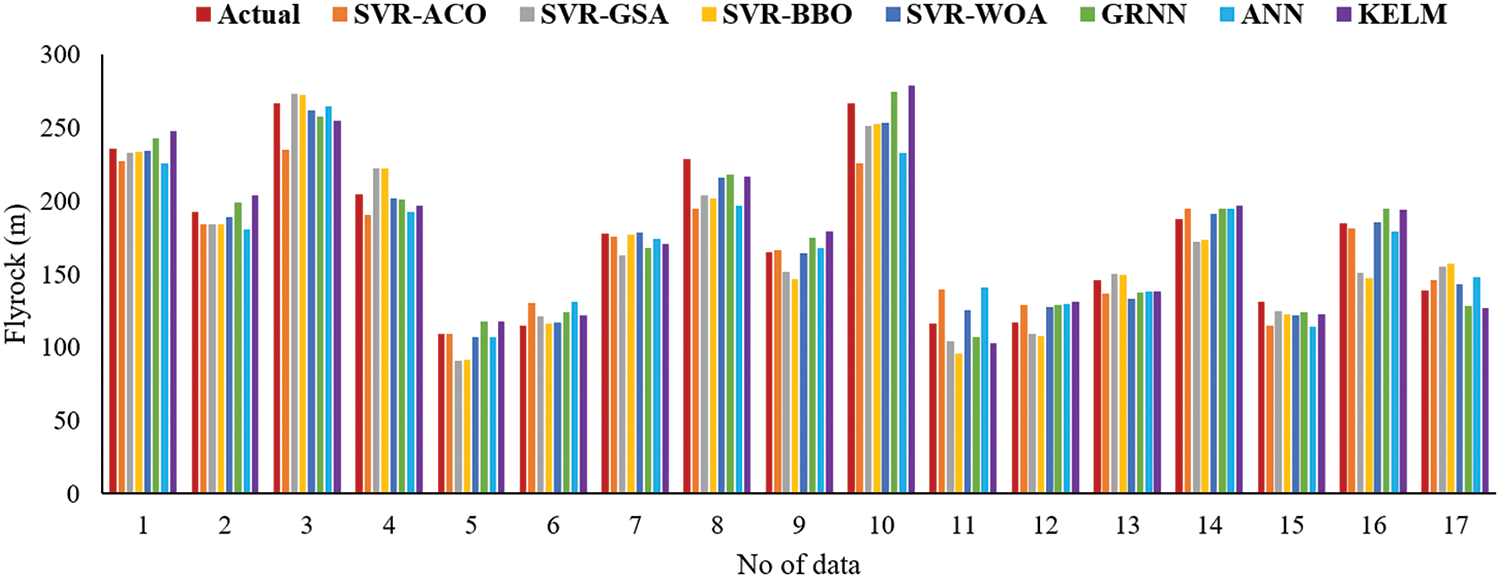
Figure 10: A comparison of measured and predicted flyrock values for all datasets
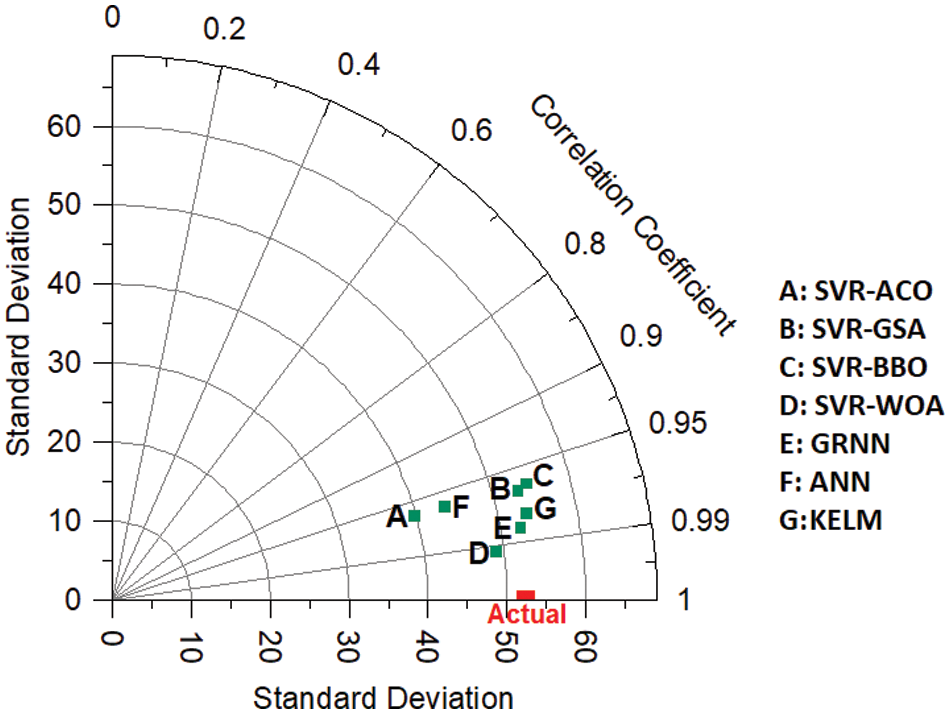
Figure 11: Taylor diagram obtained from all developed models
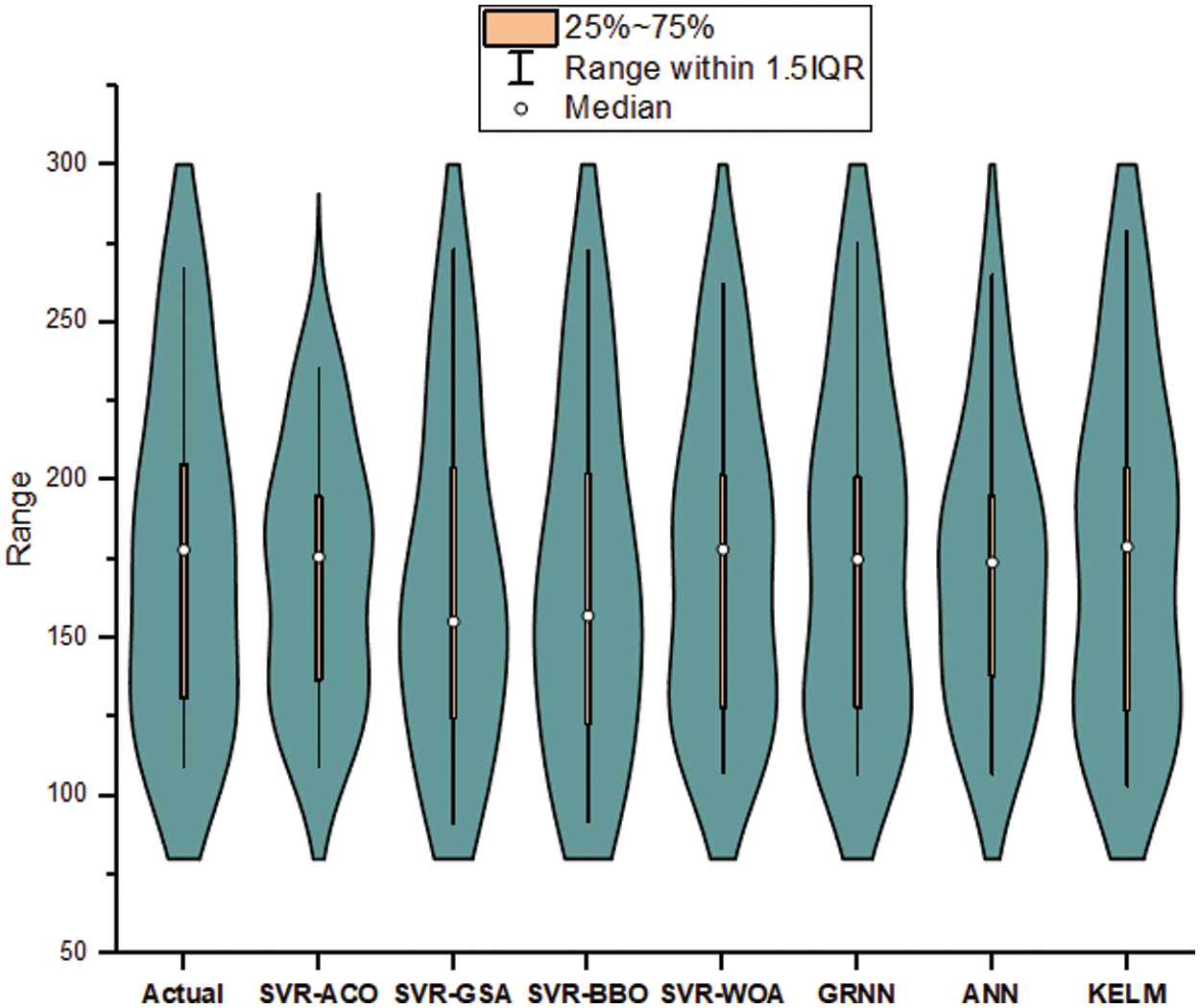
Figure 12: Checking the performance of developed models to predict flyrock through violin box plots
Blasting is considered the most frequent and typical method for fragmenting rocks in surface mines. Among the undesirable effects of blasting, flyrock is unquestionably one of the most dangerous. Therefore, controlling and minimizing flyrock is of paramount importance. In this study, the flyrock distance in two surface mines located in Iran is predicted using four hybrid SVR models: SVR-WOA, SVR-BBO, SVR-ACO, and SVR-GSA, as well as three other models including GRNN, ANN, and KELM. MAPE, RMSE, R2, RMSD, NSE, and d are calculated to test the developed models’ accuracy. The results demonstrated the superiority of SVR-WOA over other models, as it exhibited the lowest MAPE, RMSE, and RMSD values and the highest R2, NSE, and d values. For instance, GRNN, KELM, SVR-GSA, SVR-ACO, ANN, and SVR-BBO predicted flyrock values with an R2 higher than 0.92, which is considered good performance. However, SVR-WOA had the highest accuracy with an R2 of 0.984. Therefore, it can be concluded that WOA optimized SVR performance better than the other employed algorithms and can be generalized. It should be noted that the results yielded in this study are specific to the investigated mines, and for other mines, the modeling processes need to be repeated to select the most accurate model. This study utilized four input parameters (B, S, ST, and MCPD) to model flyrock. These parameters are blast design parameters, while other blast design parameters, particularly rock property parameters, have an influence on the intensity of flyrock. However, due to difficulties in collecting rock properties at our sites, we were unable to incorporate these parameters into our study. Therefore, for future research, it is recommended to consider the inclusion of rock property parameters, such as rock density. In future works, it would be interesting to explore the combination of other metaheuristic algorithms, such as African Buffalo Optimization, Artificial Root Foraging, Bottlenose Dolphin Optimization, and Coral Reefs Optimization algorithms with SVR and ANN models for prediction purposes in various mining and geotechnical fields. Although SVR-WOA demonstrated excellent performance and was selected as this study’s most accurate model, data-driven models have limitations. These models often rely on input-output mapping methods that solely estimate static field parameters, neglecting the capturing of the dynamic response process. Graph and transformer neural networks can be considered valuable approaches to address this limitation.
Acknowledgement: None.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Mahdi Hasanipanah, Jiandong Huang; data collection: Mahdi Hasanipanah; analysis and interpretation of results: Ji Zhou, Yijun Lu, Qiong Tian, Haichuan Liu; draft manuscript preparation: Ji Zhou, Yijun Lu, Qiong Tian, Haichuan Liu, Mahdi Hasanipanah, Jiandong Huang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data of this research can be available from the corresponding author upon request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Khandelwal, M., Singh, T. N. (2005). Prediction of blast induced air overpressure using neural network. Noise & Vibration Worldwide, 36(2), 7–16. https://doi.org/10.1260/0957456053499095 [Google Scholar] [CrossRef]
2. Zhou, J., Shi, X., Li, X. (2016). Utilizing gradient boosted machine for the prediction of damage to residential structures owing to blasting vibrations of open pit mining. Journal of Vibration and Control, 22(19), 3986–3997. https://doi.org/10.1177/1077546314568172 [Google Scholar] [CrossRef]
3. Nguyen, H., Bui, X. N. (2019). Predicting blast-induced air overpressure: A robust artificial intelligence system based on artificial neural networks and random forest. Natural Resources Research, 28(3), 893–907. https://doi.org/10.1007/s11053-018-9424-1 [Google Scholar] [CrossRef]
4. Zhou, J., Asteris, P. G., Armaghani, D. J., Pham, B. T. (2020). Prediction of ground vibration induced by blasting operations through the use of the Bayesian network and random forest models. Soil Dynamics and Earthquake Engineering, 139, 106390. [Google Scholar]
5. Nguyen, H., Bui, X. N. (2020). Soft computing models for predicting blast-induced air over-pressure: A novel artificial intelligence approach. Applied Soft Computing, 92, 106292. https://doi.org/10.1016/j.asoc.2020.106292 [Google Scholar] [CrossRef]
6. Barkhordari, M., Jahed Armaghani, D., Fakharian, P. (2022). Ensemble machine learning models for prediction of flyrock due to quarry blasting. International Journal of Environmental Science and Technology, 19(9), 8661–8676. [Google Scholar]
7. Dai, Y., Khandelwal, M., Qiu, Y., Zhou, J., Monjezi, M. et al. (2022). A hybrid metaheuristic approach using random forest and particle swarm optimization to study and evaluate backbreak in open-pit blasting. Neural Computing and Applications, 34, 6273–6288. https://doi.org/10.1007/s00521-021-06776-z [Google Scholar] [CrossRef]
8. Jahed Armaghani, D., Hajihassani, M., Mohamad, E. T., Marto, A., Noorani, S. A. (2014). Blasting-induced flyrock and ground vibration prediction through an expert artificial neural network based on particle swarm optimization. Arabian Journal of Geosciences, 7(12), 5383–5396. https://doi.org/10.1007/s12517-013-1174-0 [Google Scholar] [CrossRef]
9. Hasanipanah, M., Keshtegar, B., Thai, D. K., Troung, N. T. (2020). An ANN-adaptive dynamical harmony search algorithm to approximate the flyrock resulting from blasting. Engineering with Computers, 38, 1–13. [Google Scholar]
10. Armaghani, D. J., Koopialipoor, M., Bahri, M., Hasanipanah, M., Tahir, M. M. (2020). A SVR-GWO technique to minimize flyrock distance resulting from blasting. Bulletin of Engineering Geology and the Environment, 79(8), 4369–4385. https://doi.org/10.1007/s10064-020-01834-7 [Google Scholar] [CrossRef]
11. Ghasemi, E., Sari, M., Ataei, M. (2012). Development of an empirical model for predicting the effects of controllable blasting parameters on flyrock distance in surface mines. International Journal of Rock Mechanics and Mining Sciences, 52, 163–170. https://doi.org/10.1016/j.ijrmms.2012.03.011 [Google Scholar] [CrossRef]
12. Bakhtavar, E., Nourizadeh, H., Sahebi, A. A. (2017). Toward predicting blast-induced flyrock: A hybrid dimensional analysis fuzzy inference system. International Journal of Environmental Science and Technology, 14, 717–728. https://doi.org/10.1007/s13762-016-1192-z [Google Scholar] [CrossRef]
13. Hasanipanah, M., Jahed Armaghani, D., Bakhshandeh Amnieh, H., Majid, M. Z. A., Tahir, M. (2017). Application of PSO to develop a powerful equation for prediction of flyrock due to blasting. Neural Computing and Applications, 28(1), 1043–1050. [Google Scholar]
14. Yang, H., Koopialipoor, M., Armaghani, D. J., Gordan, B., Khorami, M. et al. (2019). Intelligent design of retaining wall structures under dynamic conditions. Steel and Composite Structures, 31(6), 629–640. [Google Scholar]
15. Hajihassani, M., Abdullah, S. S., Asteris, P. G., Armaghani, D. J. (2019). A gene expression programming model for predicting tunnel convergence. Applied Sciences, 9(21), 4650.https://doi.org/10.3390/app9214650 [Google Scholar] [CrossRef]
16. Asteris, P. G., Mokos, V. G. (2020). Concrete compressive strength using artificial neural networks. Neural Computing and Applications, 32, 1807–11826. [Google Scholar]
17. Asteris, P. G., Lemonis, M. E., Le, T. T., Tsavdaridis, K. D. (2021). Evaluation of the ultimate eccentric load of rectangular CFSTs using advanced neural network modeling. Engineering Structures, 248, 113297. https://doi.org/10.1016/j.engstruct.2021.113297 [Google Scholar] [CrossRef]
18. Asteris, P. G., Armaghani, D. J., Cavaleri, L., Nguyen, H. (2023). Introduction to the special issue on soft computing techniques in materials science and engineering. Computer Modeling in Engineering & Sciences, 135(2), 839–841. https://doi.org/10.32604/cmes.2023.025694 [Google Scholar] [CrossRef]
19. Yang, H., Hasanipanah, M., Tahir, M. M., Bui, D. T. (2020). Intelligent prediction of blasting-induced ground vibration using ANFIS optimized by GA and PSO. Natural Resources Research, 29, 739–750. https://doi.org/10.1007/s11053-019-09515-3 [Google Scholar] [CrossRef]
20. Yang, H., Nikafshan Rad, H., Hasanipanah, M., Bakhshandeh Amnieh, H., Nekouie, A. (2020). Prediction of vibration velocity generated in mine blasting using support vector regression improved by optimization algorithms. Natural Resources Research, 29, 807–830. https://doi.org/10.1007/s11053-019-09597-z [Google Scholar] [CrossRef]
21. Qiu, Y., Zhou, J., (2023). Short-term rockburst damage assessment in burst-prone mines: An explainable XGBOOST hybrid model with SCSO algorithm. Rock Mechanics and Rock Engineering, 56, 8745–8770. https://doi.org/10.1007/s00603-023-03522-w [Google Scholar] [CrossRef]
22. Yari, M., Armaghani, D. J., Maraveas, C., Ejlali, A. N., Mohamad, E. T. et al. (2023). Several tree-based solutions for predicting flyrock distance due to mine blasting. Applied Sciences, 13(3), 1345. https://doi.org/10.3390/app13031345 [Google Scholar] [CrossRef]
23. Liao, X., Khandelwal, M., Yang, H., Koopialipoor, M., Murlidhar, B. R. (2020). Effects of a proper feature selection on prediction and optimization of drilling rate using intelligent techniques. Engineering with Computers, 36, 499–510. https://doi.org/10.1007/s00366-019-00711-6 [Google Scholar] [CrossRef]
24. Yang, H., Wang, Z., Song, K. (2022). A new hybrid grey wolf optimizer-feature weighted-multiple kernel-support vector regression technique to predict TBM performance. Engineering with Computers, 38, 2469–2485. https://doi.org/10.1007/s00366-020-01217-2 [Google Scholar] [CrossRef]
25. Li, C., Zhou, J., Dias, D., Du, K., Khandelwal, M. (2023). Comparative evaluation of empirical approaches and artificial intelligence techniques for predicting uniaxial compressive strength of rock. Geosciences, 13(10), 294. https://doi.org/10.3390/geosciences13100294 https://doi.org/10.3390/geosciences13100294 [Google Scholar] [CrossRef]
26. Zhou, J., Yang, P., Li, C., Du, K. (2023). Hybrid random forest-based models for predicting shear strength of structural surfaces based on surface morphology parameters and metaheuristic algorithms. Construction and Building Materials, 409, 133911. https://doi.org/10.1016/j.conbuildmat.2023.133911 [Google Scholar] [CrossRef]
27. Li, C., Zhou, J., Du, K., Dias, D. (2023). Stability prediction of hard rock pillar using support vector machine optimized by three metaheuristic algorithms. International Journal of Mining Science and Technology, 33(8), 1019–1036. https://doi.org/10.1016/j.ijmst.2023.06.001 [Google Scholar] [CrossRef]
28. Trivedi, R., Singh, T. N., Gupta, N. (2015). Prediction of blastinduced flyrock in opencast mines using ANN and ANFIS. Geotechnical and Geological Engineering, 33(4), 875–891. https://doi.org/10.1007/s10706-015-9869-5 [Google Scholar] [CrossRef]
29. Trivedi, R., Singh, T. N., Raina, A. K. (2016). Simultaneous prediction of blast-induced flyrock and fragmentation in opencast limestone mines using back propagation neural network. International Journal of Mining and Mineral Engineering, 7(3), 237–252. https://doi.org/10.1504/IJMME.2016.078350 [Google Scholar] [CrossRef]
30. Rad, H. N., Hasanipanah, M., Rezaei, M., Eghlim, A. L. (2018). Developing a least squares support vector machine for estimating the blast-induced flyrock. Engineering with Computers, 34(4), 709–717. https://doi.org/10.1007/s00366-017-0568-0 [Google Scholar] [CrossRef]
31. Lu, X., Hasanipanah, M., Brindhadevi, K., Bakhshandeh Amnieh, H., Khalafi, S. (2020). ORELM: A novel machine learning approach for prediction of flyrock in mine blasting. Natural Resources Research, 29(2), 641–654. https://doi.org/10.1007/s11053-019-09532-2 [Google Scholar] [CrossRef]
32. Ye, J., Koopialipoor, M., Zhou, J., Armaghani, D. J., He, X. (2021). A novel combination of tree-based modeling and Monte Carlo simulation for assessing risk levels of flyrock induced by mine blasting. Natural Resources Research, 30(1), 225–243. https://doi.org/10.1007/s11053-020-09730-3 [Google Scholar] [CrossRef]
33. Monjezi, M., Amini Khoshalan, H., Yazdian Varjani, A. (2012). Prediction of flyrock and backbreak in open pit blasting operation: A neuro-genetic approach. Arabian Journal of Geosciences, 5(3), 441–448. https://doi.org/10.1007/s12517-010-0185-3 [Google Scholar] [CrossRef]
34. Li, D., Koopialipoor, M., Armaghani, D. J. (2021). A combination of fuzzy Delphi method and ANN-based models to investigate factors of flyrock induced by mine blasting. Natural Resources Research, 30(2), 1905–1924. https://doi.org/10.1007/s11053-020-09794-1 [Google Scholar] [CrossRef]
35. Kalaivaani, P. T., Akila, T., Tahir, M. M., Ahmed, M., Surendar, A. (2020). A novel intelligent approach to simulate the blast-induced flyrock based on RFNN combined with PSO. Engineering with Computers, 36(2), 435–442. https://doi.org/10.1007/s00366-019-00707-2 [Google Scholar] [CrossRef]
36. Murlidhar, B. R., Nguyen, H., Rostami, J., Bui, X., Armaghani, D. J. et al. (2021). Prediction of flyrock distance induced by mine blasting using a novel Harris Hawks optimization-based multi-layer perceptron neural network. Journal of Rock Mechanics and Geotechnical Engineering, 13(6), 1413–1427. https://doi.org/10.1016/j.jrmge.2021.08.005 [Google Scholar] [CrossRef]
37. Fattahi, H., Hasanipanah, M. (2022). An integrated approach of ANFIS-grasshopper optimization algorithm to approximate flyrock distance in mine blasting. Engineering with Computers, 38, 1–13. [Google Scholar]
38. Li, C., Zhou, J., Du, K., Jahed Armaghani, D., Huang, S. (2023). Prediction of flyrock distance in surface mining using a novel hybrid model of harris hawks optimization with multi-strategies-based support vector regression. Natural Resources Research, 32, 2995–3023. https://doi.org/10.1007/s11053-023-10259-4 [Google Scholar] [CrossRef]
39. Li, Q., Wang, Y., Chen, W., Li, L., Hao, H. (2024). Machine learning prediction of BLEVE loading with graph neural networks. Reliability Engineering & System Safety, 241, 109639. https://doi.org/10.1016/j.ress.2023.109639 [Google Scholar] [CrossRef]
40. Li, Q., Wang, Z., Li, L., Hao, H., Chen, W. et al. (2023). Machine learning prediction of structural dynamic responses using graph neural networks. Computers & Structures, 289, 107188. https://doi.org/10.1016/j.compstruc.2023.107188 [Google Scholar] [CrossRef]
41. Li, Q., Wang, Y., Li, L., Hao, H., Wang, R. et al. (2023). Prediction of BLEVE loads on structures using machine learning and CFD. Process Safety and Environmental Protection, 171, 914–925. https://doi.org/10.1016/j.psep.2023.02.008 [Google Scholar] [CrossRef]
42. Wang, R., Shao, Y., Li, Q., Li, L., Li, J. et al. (2023). A novel transformer-based semantic segmentation framework for structural condition assessment. Structural Health Monitoring, 23(2), 1170–1183. [Google Scholar]
43. Li, Q., Wang, Y., Shao, Y., Li, L., Hao, H. (2023). A comparative study on the most effective machine learning model for blast loading prediction: From GBDT to Transformer. Engineering Structures, 276, 115310. https://doi.org/10.1016/j.engstruct.2022.115310 [Google Scholar] [CrossRef]
44. Specht, D. F. (1991). A general regression neural network. IEEE Transactions on Neural Network, 2(6), 568–576. https://doi.org/10.1109/72.97934 [Google Scholar] [PubMed] [CrossRef]
45. Li, H., Guo, S., Li, C., Sun, J. (2013). A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowledge-Based Systems, 37, 378–387. https://doi.org/10.1016/j.knosys.2012.08.015 [Google Scholar] [CrossRef]
46. Ceryan, N., Okkan, U., Kesimal, A. (2012). Application of generalized regression neural networks in predicting the unconfined compressive strength of carbonate rocks. Rock Mechanics and Rock Engineering, 45, 1055–1072. https://doi.org/10.1007/s00603-012-0239-9 [Google Scholar] [CrossRef]
47. Singh, R., Vishal, V., Singh, T. N., Ranjith, P. G. (2013). A comparative study of generalized regression neural network approach and adaptive neuro-fuzzy inference systems for prediction of unconfined compressive strength of rocks. Neural Computing and Applications, 23, 499–506. https://doi.org/10.1007/s00521-012-0944-z [Google Scholar] [CrossRef]
48. Xue, X., Yang, X. (2014). Predicting blast-induced ground vibration using general regression neural network. Journal of Vibration and Control, 20(10), 1512–1519. https://doi.org/10.1177/1077546312474680 [Google Scholar] [CrossRef]
49. Jiang, P., Chen, J. (2016). Displacement prediction of landslide based on generalized regression neural networks with K-fold cross-validation. Neurocomputing, 198, 40–47. https://doi.org/10.1016/j.neucom.2015.08.118 [Google Scholar] [CrossRef]
50. Zhang, P., Wu, H. N., Chen, R. P., Chan, T. H. T. (2020). Hybrid meta-heuristic and machine learning algorithms for tunneling-induced settlement prediction: A comparative study. Tunnelling and Underground Space Technology, 99, 103383. https://doi.org/10.1016/j.tust.2020.103383 [Google Scholar] [CrossRef]
51. Vapnik, V. (1995). The nature of statistical learning. In: Theory. Springer: Berlin/Heidelberg, Germany. [Google Scholar]
52. Zhou, J., Qiu, Y., Armaghani, D. J., Zhang, W., Li, C. et al. (2021). Predicting TBM penetration rate in hard rock condition: A comparative study among six XGBbased metaheuristic techniques. Geoscience Frontiers, 12(3), 101091. https://doi.org/10.1016/j.gsf.2020.09.020 [Google Scholar] [CrossRef]
53. Zhang, Y., Tang, J., Cheng, Y., Huang, L., Guo, F. et al. (2022). Prediction of landslide displacement with dynamic features using intelligent approaches. International Journal of Mining Science and Technology, 32(3), 539–549. https://doi.org/10.1016/j.ijmst.2022.02.004 [Google Scholar] [CrossRef]
54. Xu, C., Nait Amar, M., Ghriga, M. A., Ouaer, H., Zhang, X. et al. (2022). Evolving support vector regression using Grey Wolf optimization; forecasting the geomechanical properties of rock. Engineering with Computers, 38, 1819–1833. https://doi.org/10.1007/s00366-020-01131-7 [Google Scholar] [CrossRef]
55. Fan, C., Zheng, Y., Wen, Y., Sun, M. (2023). Classification and prediction of deformed steel and concrete bond-slip failure modes based on SSA-ELM model. Structures, 57, 105131. https://doi.org/10.1016/j.istruc.2023.105131 [Google Scholar] [CrossRef]
56. Meng, G., Hongle, L., Bo, W., Liu, G., Ye, H. et al. (2023). Prediction of the tunnel collapse probability using SVR-based monte carlo simulation: A case study. Sustainability, 15(9), 7098. https://doi.org/10.3390/su15097098 [Google Scholar] [CrossRef]
57. Chen, W., Hasanipanah, M., Nikafshan Rad, H., Jahed Armaghani, D., Tahir, M. M. (2021). A new design of evolutionary hybrid optimization of SVR model in predicting the blast-induced ground vibration. Engineering with Computers, 37, 1455–1471. https://doi.org/10.1007/s00366-019-00895-x [Google Scholar] [CrossRef]
58. Lawal, A. I., Onifade, M., Bada, S. O., Shivute, A. P., Abdulsalam, J. (2023). Prediction of thermal coal ash behavior of South African coals: Comparative applications of ANN, GPR, and SVR. Natural Resources Research, 32, 1399–1413. https://doi.org/10.1007/s11053-023-10192-6 [Google Scholar] [CrossRef]
59. Rashedi, E., Nezamabadi-Pour, H., Saryazdi, S. (2009). GSA: A gravitational search algorithm. Information Sciences, 179(13), 2232–2248. https://doi.org/10.1016/j.ins.2009.03.004 [Google Scholar] [CrossRef]
60. Adnan, R. A., Yuan, X., Kisi, O., Anam, R. (2017). Improving accuracy of river flow forecasting using LSSVR with gravitational search algorithm. Advances in Meteorology, 2017, 2391621. https://doi.org/10.1155/2017/2391621 [Google Scholar] [CrossRef]
61. Hemmatian, H., Fereidoon, A., Assareh, E. (2014). Optimization of hybrid laminated composites using the multi-objective gravitational search algorithm (MOGSA). Engineering Optimization, 46(9), 1169–1182. https://doi.org/10.1080/0305215X.2013.832234 [Google Scholar] [CrossRef]
62. Mehdizadeh, S., Mohammadi, B., Pham, Q. B., Khoi, D. N., Thuy Linh, N. T. (2020). Implementing novel hybrid models to improve indirect measurement of the daily soil temperature: Elman neural network coupled with gravitational search algorithm and ant colony optimization. Measurement, 165, 108127. https://doi.org/10.1016/j.measurement.2020.108127 [Google Scholar] [CrossRef]
63. Momeni, E., Yarivand, A., Dowlatshahi, M. B., Jahed Armaghani, D. (2021). An efficient optimal neural network based on gravitational search algorithm in predicting the deformation of geogrid-reinforced soil structures. Transportation Geotechnics, 26, 100446. https://doi.org/10.1016/j.trgeo.2020.100446 [Google Scholar] [CrossRef]
64. Banyhussan, Q. S., Hanoon, A. N., Al-Dahawi, A., Yıldırım, G., Abdulhameed, A. A. (2020). Development of gravitational search algorithm model for predicting packing density of cementitious pastes. Journal of Building Engineering, 27, 100946. https://doi.org/10.1016/j.jobe.2019.100946 [Google Scholar] [CrossRef]
65. Colorni, A., Dorigo, M., Maniezzo, V. (1992). Distributed optimization by ant colonies. Proceedings of the First European Conference on Artificial Life, Cambridge, Massachusetts, USA, MIT Press. [Google Scholar]
66. Tien Bui, D., Abdullahi, M. M., Ghareh, S., Moayedi, H., Nguyen, H. (2021). Fine-tuning of neural computing using whale optimization algorithm for predicting compressive strength of concrete. Engineering with Computers, 37, 701–712. https://doi.org/10.1007/s00366-019-00850-w [Google Scholar] [CrossRef]
67. Zhang, S., Bui, X. N., Trung, N. T., Nguyen, H., Bui, H. B. (2020). Prediction of rock size distribution in mine bench blasting using a novel ant colony optimization-based boosted regression tree technique. Natural Resources Research, 29, 867–886. https://doi.org/10.1007/s11053-019-09603-4 [Google Scholar] [CrossRef]
68. Saghatforoush, A., Monjezi, M., Shirani Faradonbeh, R., Jahed Armaghani, D. (2016). Combination of neural network and ant colony optimization algorithms for prediction and optimization of flyrock and back-break induced by blasting. Engineering with Computers, 32, 255–266. https://doi.org/10.1007/s00366-015-0415-0 [Google Scholar] [CrossRef]
69. Taghizadeh-Mehrjardi, R., Toomanian, N., Khavaninzadeh, A. R., Jafari, A., Triantafilis, J. (2016). Predicting and mapping of soil particle-size fractions with adaptive neuro-fuzzy inference and ant colony optimization in central Iran. European Journal of Soil Science, 67, 707–725. https://doi.org/10.1111/ejss.2016.67.issue-6 [Google Scholar] [CrossRef]
70. Zhang, H., Nguyen, H., Bui, X. N., Nguyen-Thoi, T., Bui, T. T. et al. (2020). Developing a novel artificial intelligence model to estimate the capital cost of mining projects using deep neural network-based ant colony optimization algorithm. Resources Policy, 66, 101604. https://doi.org/10.1016/j.resourpol.2020.101604 [Google Scholar] [CrossRef]
71. Afradi, A., Ebrahimabadi, A., Hallajian, T. (2020). Prediction of tunnel boring machine penetration rate using ant colony optimization, bee colony optimization and the particle swarm optimization, case study: Sabzkooh water conveyance tunnel. Mining Mineral Deposits, 14(2), 75–84.https://doi.org/10.33271/mining [Google Scholar] [CrossRef]
72. Xu, C., Gordan, B., Koopialipoor, M., Jahed Armaghani, D., Tahir, M. M. et al. (2019). Improving performance of retaining walls under dynamic conditions developing an optimized ANN based on ant colony optimization technique. IEEE Access, 7, 94692–94700. https://doi.org/10.1109/Access.6287639 [Google Scholar] [CrossRef]
73. Simon, D. (2008). Biogeography-based Optimization. IEEE Transactions on Evolutionary Computation, 12(6), 702–713. https://doi.org/10.1109/TEVC.2008.919004 [Google Scholar] [CrossRef]
74. Korouzhdeh, T., Eskandari-Naddaf, H., Kazemi, R. (2021). Hybrid artificial neural network with biogeography-based optimization to assess the role of cement fineness on ecological footprint and mechanical properties of cement mortar expose to freezing/thawing. Construction and Building Materials, 304, 124589. https://doi.org/10.1016/j.conbuildmat.2021.124589 [Google Scholar] [CrossRef]
75. Khoshdast, H., Gholami, A., Hassanzadeh, A., Niedoba, T., Surowiak, A. (2021). Advanced simulation of removing chromium from a synthetic wastewater by rhamnolipidic bioflotation using hybrid neural networks with metaheuristic algorithms. Materials, 14(11), 2880. https://doi.org/10.3390/ma14112880 [Google Scholar] [PubMed] [CrossRef]
76. Chen, W., Panahi, M., Khosravi, K., Pourghasemi, H. R., Rezaie, F. et al. (2019). Spatial prediction of groundwater potentiality using anfis ensembled with teaching-learning-based and biogeography-based optimization. Journal of Hydrology, 572, 435–448. https://doi.org/10.1016/j.jhydrol.2019.03.013 [Google Scholar] [CrossRef]
77. Pham, B. T., Nguyen, M. D., Bui, K. T. T., Prakash, I., Chapi, K. et al. (2019). A novel artificial intelligence approach based on multi-layer perceptron neural network and biogeography-based optimization for predicting coefficient of consolidation of soil. Catena, 173, 302–311. https://doi.org/10.1016/j.catena.2018.10.004 [Google Scholar] [CrossRef]
78. Farrokh Ghatte, H. (2021). A hybrid of firefly and biogeography-based optimization algorithms for optimal design of steel frames. Arabian Journal for Science and Engineering, 46, 4703–4717. https://doi.org/10.1007/s13369-020-05118-w [Google Scholar] [CrossRef]
79. Kazemi, R., Naser, M. Z. (2023). Towards sustainable use of foundry by-products: Evaluating the compressive strength of green concrete containing waste foundry sand using hybrid biogeography-based optimization with artificial neural networks. Journal of Building Engineering, 76, 107252. https://doi.org/10.1016/j.jobe.2023.107252 [Google Scholar] [CrossRef]
80. Jaafari, A., Panahi, M., Pham, B. T., Shahabi, H., Bui, D. T. et al. (2019). Meta optimization of an adaptive neuro-fuzzy inference system with grey wolf optimizer and biogeography-based optimization algorithms for spatial prediction of landslide susceptibility. Catena, 175, 430–445. https://doi.org/10.1016/j.catena.2018.12.033 [Google Scholar] [CrossRef]
81. Moayedi, H., Osouli, A., Tien Bui, D., Foong, L. K. (2019). Spatial landslide susceptibility assessment based on novel neural-metaheuristic geographic information system based ensembles. Sensors, 19(21), 4698. https://doi.org/10.3390/s19214698 [Google Scholar] [PubMed] [CrossRef]
82. Mirjalili, S., Lewis, A. (2016). The whale optimization algorithm. Advances in Engineering Software, 95, 51–67. https://doi.org/10.1016/j.advengsoft.2016.01.008 [Google Scholar] [CrossRef]
83. Liu, Y., Yang, S., Li, D., Zhang, S. (2023). Improved whale optimization algorithm for solving microgrid operations planning problems. Symmetry, 15(1), 36. [Google Scholar]
84. Jaafari, A., Panahi, M., Mafi-Gholami, D., Rahmati, O., Shahabi, H. et al. (2022). Swarm intelligence optimization of the group method of data handling using the cuckoo search and whale optimization algorithms to model and predict landslides. Applied Soft Computing, 116, 108254. https://doi.org/10.1016/j.asoc.2021.108254 [Google Scholar] [CrossRef]
85. Zhou, J., Zhu, S., Qiu, Y., Jahed Armaghani, D., Zhou, A. et al. (2022). Predicting tunnel squeezing using support vector machine optimized by whale optimization algorithm. Acta Geotechnica, 17, 1343–1366. https://doi.org/10.1007/s11440-022-01450-7 [Google Scholar] [CrossRef]
86. Nguyen, H., Cao, M. T., Tran, X. L., Tran, T. H., Hoang, N. D. (2023). A novel whale optimization algorithm optimized XGBoost regression for estimating bearing capacity of concrete piles. Neural Computing and Applications, 35, 3825–3852. https://doi.org/10.1007/s00521-022-07896-w [Google Scholar] [CrossRef]
87. Liu, W., Liu, Z., Liu, Z., Xiong, S., Zhang, S. (2023). Random forest and whale optimization algorithm to predict the invalidation risk of backfilling pipeline. Mathematics, 11(7), 1636. https://doi.org/10.3390/math11071636 [Google Scholar] [CrossRef]
88. Jamei, M., Hasanipanah, M., Karbasi, M., Ahmadianfar, I., Taherifar, S. (2021). Prediction of flyrock induced by mine blasting using a novel kernel-based extreme learning machine. Journal of Rock Mechanics and Geotechnical Engineering, 13(6), 1438–1451. https://doi.org/10.1016/j.jrmge.2021.07.007 [Google Scholar] [CrossRef]
89. Hecht-Nielsen, R. (1987). Kolmogorov’s mapping neural network existence theorem. Proceedings of the First IEEE International Conference on Neural Networks, pp. 11–14. San Diego, CA, USA. [Google Scholar]
90. Asteris, P. G., Kolovos, K. G., Douvika, M. G., Roinos, K. (2016). Prediction of self-compacting concrete strength using artificial neural networks. European Journal of Environmental and Civil Engineering, 20, 102–122. https://doi.org/10.1080/19648189.2016.1246693 [Google Scholar] [CrossRef]
91. Yang, H., Liu, X., Song, K. (2022). A novel gradient boosting regression tree technique optimized by improved sparrow search algorithm for predicting TBM penetration rate. Arabian Journal of Geosciences, 15, 461. https://doi.org/10.1007/s12517-022-09665-4 [Google Scholar] [CrossRef]
92. Asteris, P. G., Nikoo, M. (2019). Artificial Bee colony-based neural network for the prediction of the fundamental period of infilled frame structures. Neural Computing and Applications, 31(9), 4837–4847. https://doi.org/10.1007/s00521-018-03965-1 [Google Scholar] [CrossRef]
93. Song, K., Yang, H., Wang, Z. (2023). A hybrid stacking framework optimized method for TBM performance prediction. Bulletin of Engineering Geology and the Environment, 82, 27. https://doi.org/10.1007/s10064-022-03047-6 [Google Scholar] [CrossRef]
94. Xu, H., Zhou, J., Asteris, G. P., Jahed Armaghani, D., Tahir, M. M. (2019). Supervised machine learning techniques to the prediction of tunnel boring machine penetration rate. Applied Sciences, 9(18), 3715. https://doi.org/10.3390/app9183715 [Google Scholar] [CrossRef]
95. Armaghani, D. J., Hatzigeorgiou, G. D., Karamani, C. H., Skentou, A., Zoumpoulaki, I. et al. (2019). Soft computing based techniques for concrete beams shear strength. Procedia Structural Integrity, 17, 924–933. https://doi.org/10.1016/j.prostr.2019.08.123 [Google Scholar] [CrossRef]
96. Ding, X., Jamei, M., Hasanipanah, M., Abdullah, R. A., Le, B. N. (2023). Optimized data-driven models for prediction of flyrock due to blasting in surface mines. Sustainability, 15(10), 8424. https://doi.org/10.3390/su15108424 [Google Scholar] [CrossRef]
97. Asteris, P. G., Armaghani, D. J., Hatzigeorgiou, G. D., Karayannis, C. G., Pilakoutas, K. (2019). Predicting the shear strength of reinforced concrete beams using artificial neural networks. Computers and Concrete, 24(5), 469–488. https://doi.org/10.12989/cac.2019.24.5.469 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools