Dynamic Hypergraph Modeling and Robustness Analysis for SIoT

1  Introduction

Large-scale AI technologies are emerging, and we are in an era of intelligence where AI systems are embedded in everyday life and work. The Internet of Things (IoT) integrates various technologies [1], acting as a bridge between the physical and digital worlds. We assign human social attributes to objects and combine IoT and social networks to create a new paradigm called the Social Internet of Things (SIoT). Artificial intelligence is widely used in the IoT, social networks, and SIoT and has achieved significant results in these areas, such as smart homes, social media analysis, and IoT security. It provides strong support for enabling intelligence, automation, and personalization.

The collaboration of SIoT and AI tech presents new opportunities for intelligent IoT development and research. IoT refers to the connectivity between objects, while social networks connect humans. SIoT encompasses both of these paradigms and expands to include interactions between humans and objects [2]. Fig. 1 demonstrates the convergence of these three relationships. The Internet of Things is composed of physical objects that are connected based on their characteristics. Users are grouped based on similar factors, and the objects associated with these users form a network of relationships. It emphasizes the social attributes of things, involving intelligent connections and autonomous social interactions of objects, achieved through machine learning algorithms for automated control and intelligent management.

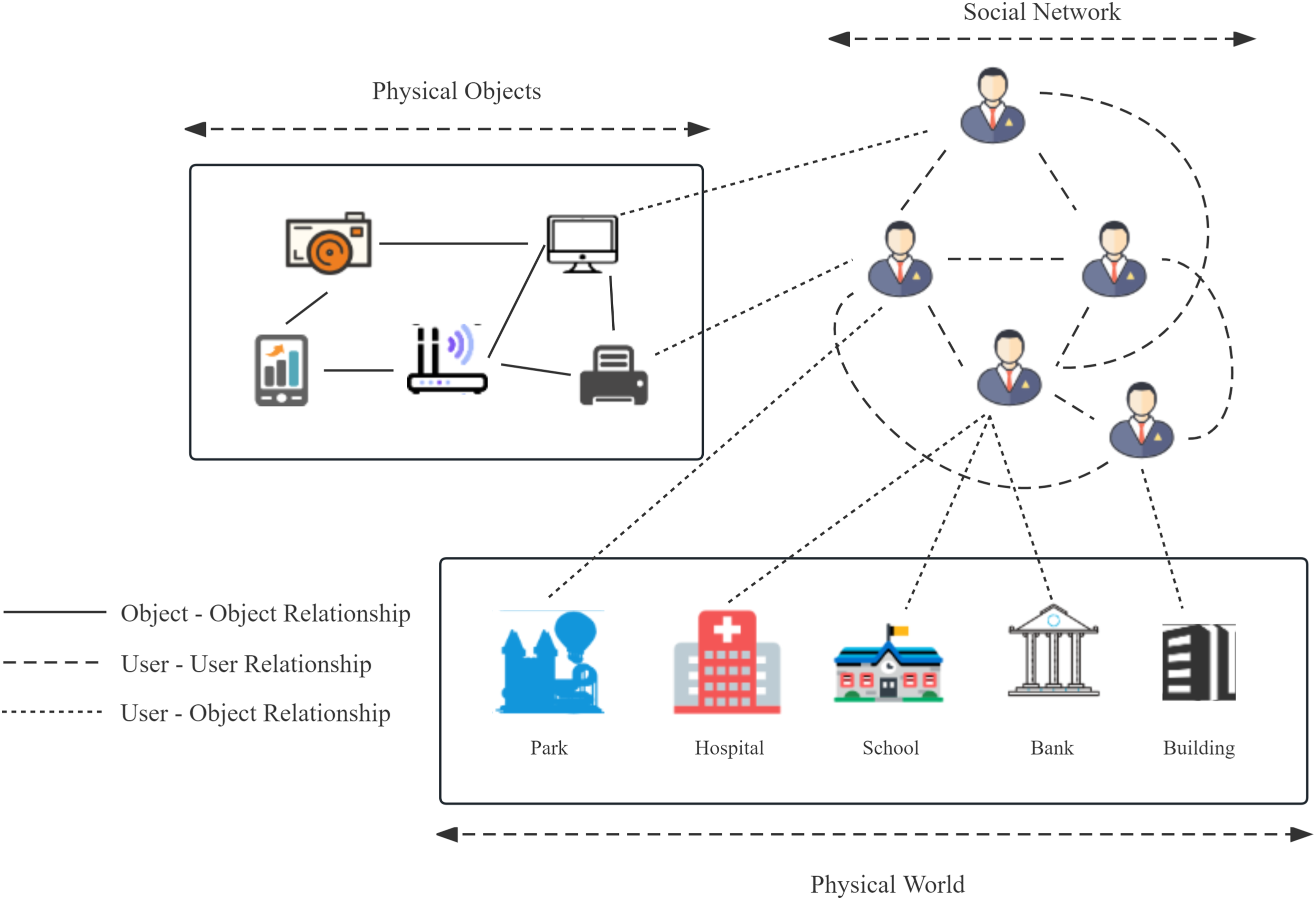
Figure 1: Components of the SIoT

Many efforts have been put into IoT security. To enhance energy transmission efficiency and network robustness. Peng et al. proposed two methods in large-scale wireless sensor networks [3]. Reference [4] proposed security enhancement technology and security control strategies for the security of complex cyber-physical networks. Nevertheless, much of the current research often focuses on single-layer perception networks between objects, neglecting the social attributes of objects. Most of the research in modeling for SIoT is based on complex network theoretical foundations. Lee et al. built a Trust Service Platform to provide trust assessment for any two entities in SIoT [5]. In [6], the routing selection problem for information exchange between nodes in SIoT is investigated. Various classical models for graph generation have been proposed, such as the Erdős-Rényi random (ER) model [7], the Watts-Strogatz model (WS) [8], the Barabási-Albert (BA) model [9], Graph Recurrent Neural Networks (GraphRNN) [10], and the forest fire model [11]. In contrast, the relationships of nodes in many networks today are beyond one-to-one connections, and the above models are based on the complex network theory of traditional graphs. Therefore, hypergraph is a better choice for modeling. HyperNetX is used to model the human gene set and the domain-name system (DNS) for hypergraph generation and topological analysis [12]. This approach is appropriate when both nodes and hyperedges are predetermined. Wang proposed a hypernetwork evolution model where hyperedges are uniformly generated [13]. However, these methods have many constraints that make hypergraph generation difficult to align with the characteristics of real hypernetworks. In the context of intelligent SIoT, generating hypergraph models that consider uncertainty and randomness in real-world node relationships has not yet been explored. In the face of ever-growing data and complex application scenarios, how to build intelligent systems that are trustworthy and transparent has become a crucial issue that needs to be addressed today.

To make the process of communicating, collaborating, and sharing information among objects in the network more transparent, thereby enhancing intelligence and autonomy, we propose a model in this paper, named Hyper-walking Model (HWM). It is a hypergraph generation model, which evolves over time. The hypergraph nodes represent entities in SIoT, and the relationships among them are represented by hyperedges. The Hyper-walking Model consists of two main parts: generating hyperedges and hyperedge expansion, which combines random walk with traditional graph generation models. Unlike traditional methods, HWM only needs to determine the total node number in a hypergraph, which refers to the number of entities in SIoT, without imposing constraints on hyperedge generation. Therefore, the simulated hypernetwork generated by HWM can capture more detailed aspects. The hypergraph updates by adding new nodes, which then move among existing nodes to form new hyperedges. HWM can be subdivided into two models based on different random number generation: the Poisson distribution generating random hypergraph model (HWM-P) and the Equal probability generating random hypergraph model (HWM-E). The forest fire model is used to simulate interactions between hyperedges and aims to establish connections between new and existing hyperedges, thereby mimicking the spread of information in hypernetwork. To evaluate the performance of our proposed model, we compared its pattern characteristics with those of four real-world hypergraphs. The experimental results show that HWM can reproduce the pattern characteristics of real-world hypergraphs, indicating its realism in practical scenarios and significant implications for research. Finally, a robustness analysis is performed to evaluate its resilience under different attack scenarios, providing a comprehensive understanding of the factors affecting the robustness of hypernetworks. This aim is to optimize the hypergraph model and construct a more trustworthy system.

The main contributions of our work are summarized as follows:

•   A new model HWM is proposed, which aims to build a trustworthy intelligence SIoT model that emphasizes the social properties of things. This is the first attempt to build a SIoT hypergraph generation model within AI systems. The HWM possesses the ability to evolve over time, updating nodes and hyperedges in real-time and promptly capturing dynamic changes in the hypergraph, which helps analyze the relationships between nodes and hyperedges.

•   In HWM, we introduce the random walk algorithm to establish connections between new and existing nodes. Thus, the proposed model can simulate node interaction and increase the diversity of hypergraph generation. HWM can be further subdivided into two models depending on different walking end conditions.

•   The experimental results suggest that our proposed model is consistent with real-world hypernetworks, indicating the usefulness of HWM for generating simulated SIoT hypergraph datasets. Moreover, we analyze the robustness of the HWM-generated hypergraph, which can provide theoretical support for enhancing the hypernetwork.

The rest of the paper is organized as follows: Section 2 illustrates our problem and the existing challenges. Section 3 discusses existing relevant studies. Section 4 introduces some notation and background knowledge. Section 5 presents the details of our proposed model. In Section 6, the Hyper-walking Model is characterized for pattern analysis and validated. In Section 7, the model is analyzed for robustness under node and edge attacks. Section 8 concludes this paper.

2  Problem Scope

SIoT is emerging to support the realization of intelligent IoT, which combines the research methodologies of IoT and social networks and emphasizes the social properties of objects. In this paper, we aim to design a new solution to build a hypergraph generation model that changes dynamically with node joining, concerning the idea of traditional graph generation models. The hypergraph’s nodes and hyperedges can simulate the entities and relationships in SIoT. In SIoT, we focus on the connections between entities and represent their interactions as hyperedges. Given that the relationships between entities may involve one-to-many or many-to-many connections, it is necessary to choose a hypergraph as the modeling tool. Although toolkits in some programming languages can be used for hypergraph modeling, they need to determine both the number of nodes and hyperedges and the generated hypergraph frequently overlooks many details present in the real hypergraph. Furthermore, obtaining datasets related to SIoT is difficult, and how to build such networks with hypergraphs and keep them authentic remains challenging. Consequently, we develop a hypergraph generation model that can simulate SIoT datasets and fully investigate the characteristics of SIoT in the real world.

Three challenges are encountered and shall be addressed in our design: 1) how to dynamically update the hypergraph when nodes are added; 2) how to make the connections of newly added nodes both random and reflect the preferential connection mechanism; 3) how to evaluate the performance and realism of the generated hypergraph. To overcome these difficulties, we made the following efforts. The entities’ relationships in SIoT are complex. To increase operational speed at runtime, we use the adjacency list to represent the hypergraph. As new nodes are added, the elements in the adjacency list are continuously updated. In reality, the selection among entities is more consistent with the preferential connection mechanism, but random connections also occur. To increase connection diversity, we introduce a random walk algorithm. Besides updating newly added node’s connections, we also extend the connections of other nodes within hyperedges using a forest fire model. Afterwards, we assess the performance of HWM generated hypergraph by comparing its features with those of real-world hypernetworks, using an improved analysis method based on traditional graph theory.

3  Related Work

Social Internet of Things offers fresh perspectives on the challenges posed by the IoTs [14]. Atzori et al. first proposed the concept of SIoT and investigated ‘socialization in the IoT’ [1]. Guo et al. proposed the concept of ‘opportunistic IoT,’ which focuses on humans, analyzing the coupling between humans and objects [15]. Scholars have put forth various research methodologies on SIoT. Mendes proposed a technique for bridging the physical and virtual worlds [16]. Later, the ‘Socio-Technical Network’ concept emerged, emphasizing connections between objects and interactions among users in both physical and social spaces [17]. As the concept of SIoT matures, many models integrate social network technologies with IoT tehnologies. Social networks can serve as platforms for accessing shared resources in the IoT [18], and enhance collaboration between distributed sensor networks by using social networks as intermediaries [19]. Regarding privacy protection in the IoT, Qiu et al. conducted a review of access control research [20], Qiao et al. proposed a machine learning model based on an adaptive asynchronous clustering algorithm [21]. Additionally, Qiao et al. introduced a summary description model scheme for neighbor information sharing [22]. In the field of cybersecurity, Zhou et al. constructed an open-source dataset (CDTier) [23], which can be utilized for security analysis in the domain of Chinese threat intelligence. Meanwhile, Ren et al. developed a cybersecurity platform equipped with active defense capabilities [24].

Besides exploring existing SIoT, how to generate it deserves further investigation. Graph is a classic approach for studying networks. Several models for generating real-world graphs have been proposed. The classic preferential attachment algorithm [9] provides the fundamental principles for generating graphs, and GraphRNN [10] employs machine learning techniques that can generate graphs with similar structural features to the target set. Leskovec et al. proposed a graph generator named the forest fire model and summarized dynamic patterns in real-world graphs [11]. Hypergraphs are better for modeling SIoT than traditional graphs, a time-changing hypergraph generation model was introduced in [25]. To optimize the generated network a robustness analysis of this network is needed. The most common attack methods include random attacks and deliberate attacks [26] as well as cascading failure models targeting node attacks, which observe the collapse process of the network as nodes are removed [12]. In [27], a 2-hypergraph model is introduced to enhance the robustness of hypergraphs generated from real data. Compared with these studies, our HWM model designs a generative hypergraph model for SIoT that changes dynamically with node joining, which can effectively mimic the features of real datasets and investigate the robustness of this model.

4  Preliminaries

4.1 Hypergraph

A hypergraph H=(V,E), where V is the node set of the hypergraph and E is the hyperedge set. Hyperedges are composed of one or more nodes. Two vertices are considered adjacent if they belong to the same hyperedge, and two hyperedges are adjacent if their intersection is a non-empty set [28]. During the process of generating a hypergraph, at time t, the generated hypergraph is denoted as Ht=(Vt,Et), where |Vt| represents the number of nodes contained in the hypergraph at time t, and |Et| is the number of hyperedges contained in the hypergraph at time t. The degree of a node v is defined as the number of nodes directly adjacent to it, while the hyper degree of a node is determined by the number of hyperedges in which it is contained [29].

4.2 Effective Diameter

The diameter of a hypergraph is defined as the maximum value of the distance between any connected pairs of nodes in the graph since the distance between disconnected pairs of nodes is infinite. The hypergraph’s diameter can be expressed as follows: D=maxi,j⁡d(i,j). The effective diameter of a hypergraph is defined as the minimum distance required for connecting the majority of node pairs [30].

4.3 Clustering Coefficient

In regular graphs, the clustering coefficient is used to measure the degree of connectivity between a node and its neighbors. Also, hypergraphs, it is used to describe the pattern of links between nodes and hyperedges, as well as the density of the node’s neighborhood [31]. A higher clustering coefficient value for a node indicates that the local connectivity within the hypernetwork is strong, which often signifies greater network robustness and is more conducive to information dissemination.

4.4 Heavy-Tailed Distribution

A heavy-tailed distribution, also known as a long-tailed distribution, is a common distribution type characterized by a tail that does not converge to an exponential form but extends further with a slower decline in probability density in the tail region. One of the most common examples of a heavy-tailed distribution is a power-law one.

4.5 2-Section Hypergraph

The 2-section graph of a hypergraph, denoted as H2, is a graph that shares the same set of vertices as the original hypergraph. In the 2-section graph, all vertices that belong to the same hyperedge in the hypergraph are fully connected. If two vertices are part of the same hyperedge in the hypergraph, they are connected by an ordinary edge in the 2-section graph. The hyperedges and nodes of a hypergraph are mapped into two different sets of nodes, where the set of nodes on one side represents the original nodes in the hypergraph and the nodes in the set of nodes on the other side represent the original hyperedges in the hypergraph.

5  Proposed Model

In this section, we will describe a detailed introduction to the Hyper-walking Model used for hypergraph generation. Inspired by Leskovec and others, who proposed the Forest Fire model for regular graph generation, the model introduced in this paper combines random walk methods and the Forest Fire model to generate hypergraphs [11]. The model consists of two main modules. Hyperedge Generation Module: In this module, new hyperedges are generated by initiating random walks from new nodes; the next node is selected according to the preferential attachment in each walk. When the end of the walk condition is reached, a new hyperedge is formed. Hyperedge Expansion Module: In this module, a fire is lit at the nodes in the new hyperedge. This fire spreads through the existing hyperedges, creating connections between the new hyperedge and the hyperedges that are “burned”.

5.1 Model Detail

The pseudocode for the HWM is described in Algorithm 1. Inputs at the beginning of the program: total nodes number N, expansion probability q. The initial hypergraph starts with a single node and no hyperedges. Add a new node at regular intervals of time t, and the following steps are repeated:

(1) The new node v is the starting point, and during the tour, the selection probability of an existing node is related to its degree value. The walk continues until the end of the walk condition is triggered. Two methods are used to generate the random value: the Poisson probability distribution and the equal probability distribution.

(2) All nodes passed by the wandering form a hyperedge et and update each node in the new hyperedge: the node degree is increased by 1.

(3) The nodes in the hyperedge are connected in a fully connected relationship [32], meaning that each pair of nodes in a hyperedge is connected by ordinary edges. To expand the hyperedge, a node in the hyperedge is selected, and its n neighbors are burned in descending order of connection strength until all nodes within the hyperedge are traversed and burning stops. The value of n is sampled from a geometric distribution with an average value of q/(1−q).

This model can be illustrated using a simple example. In Smart Office IoT, a new employee who has just set up a new computer in the office needs to configure it to work with the office printer. However, they are unsure about the optimal printer settings for their specific tasks. The new computer (new node) initiates a process to optimize its printer settings. The new computer decides to seek advice and parameters from other computers that have had a high number of successful interactions with the printer. This selection process mimics the HWM’s choice of neighbors in the hypergraph. The new computer communicates with these selected computers to gather relevant printer configuration parameters, benefiting from their experience in dealing with the printer. This communication can be seen as the “burning” process in the HWM.

5.2 Random Number Generation Methods

In Section 5.1, the termination condition for generating new hyperedges through random walks is when the number of nodes in the hyperedge reaches a predefined value (Algorithm 1, Line 7). The two random number generation methods used to model this paper will be described in detail in this subsection: Poisson distribution generation and equal probability generation.

Poisson distribution generation. Poisson distribution is widely used in various real-world applications for generating random numbers to model the occurrence of events, such as network data packet arrivals, telephone call arrivals, and traffic accidents. In the proposed model HWM-P, the size of the hyperedge is generated according to the Poisson distribution. This is achieved by the following steps:

(1) Determine the parameter λ, which is the average incidence of the event, and set λ=3 directly in the program;

(2) At each time step t, the new nodes select existing nodes to form hyperedges, and the selected node number is denoted as mt, which is a random integer conforming to the Poisson distribution, “k” in (1) represents the number of occurrences of an event (i.e., the selection of existing nodes to form hyperedge).

P{X=k}=λkk!e−λ(k=0,1,2,…)(1)

Equal probability generation. Equal probability generation is the most commonly used method for generating random numbers, which generates random numbers that are uniformly distributed within a given range without significant bias and can avoid uneven sampling to some extent, making it suitable for analog simulations. In the proposed model HWM-E, we limit the size of the hyperedge to vary from 1 to k. At each time step t, the newly added node is selected to form a hyperedge with the existing node. The number of selected nodes ranges from 0 to k−1. The probability density function of this distribution obeys p=1/k.

6  Experiments & Results

This section employs the method described in Section 5 to construct a hypergraph containing 10,000 nodes. Experimental analysis unfolds from two perspectives: the complete hypergraph and the decomposed hypergraph, with the decomposition method based on Manh’s proposal [25]. In Section 5.2, two methods for generating random numbers, HWM-P and HWM-E, were proposed. Pattern feature analyses were performed on hypergraphs generated by both methods, yielding similar experimental results. The following presents only the experimental results of hypergraphs generated by HWM-P due to space limitations.

Complete hypergraph’s pattern feature. In this subsection, it is proven that the generated hypergraph exhibits the same pattern features as real-world hypergraphs. Real-world hypergraphs typically display specific pattern features, including heavy-tailed degree distributions, heavy-tailed hyperedge size distributions, and increasing edge density. This paper conducts an analysis of the degree distribution, hyperedge size distribution, and edge density distribution of the generated hypergraph, as illustrated in Fig. 2. The real-world datasets referenced for the comparison are emails [11,33,34], substances [33], tags [33], and threads [33]. The first two rows intuitively observe that the pattern features of the generated hypergraph have the same trend as those of the real-world hypergraph, following a power-law distribution. The third row plots the hypergraph by displaying the curve of |Et| in relation to |Vt| on a log-log coordinate system over time t. The slope > 1 of the fitted line of the edge density plot indicates that the average degree of the hypergraph increases with the addition of new nodes.

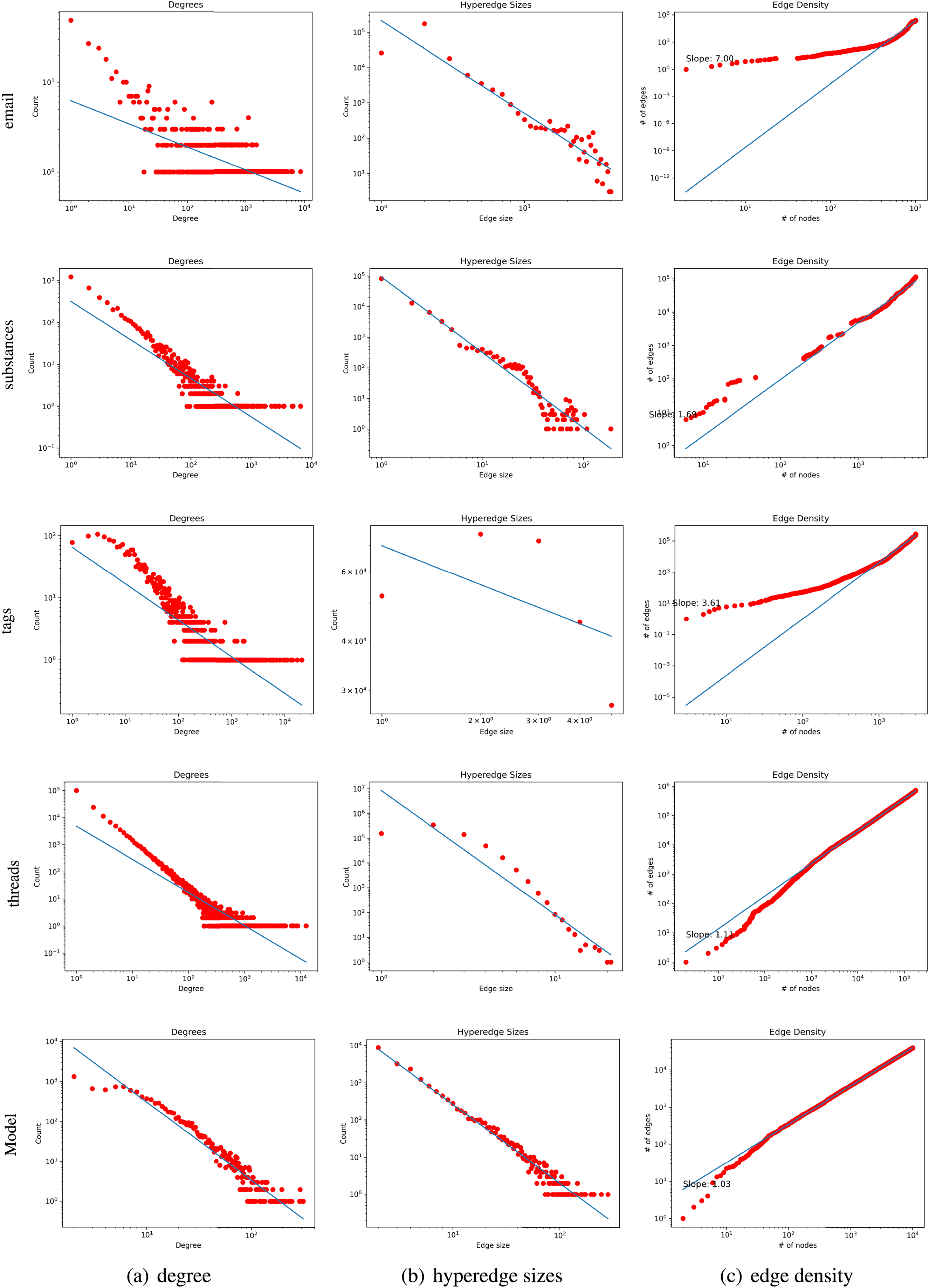
Figure 2: Hypergraph structure analysis of real datasets and model

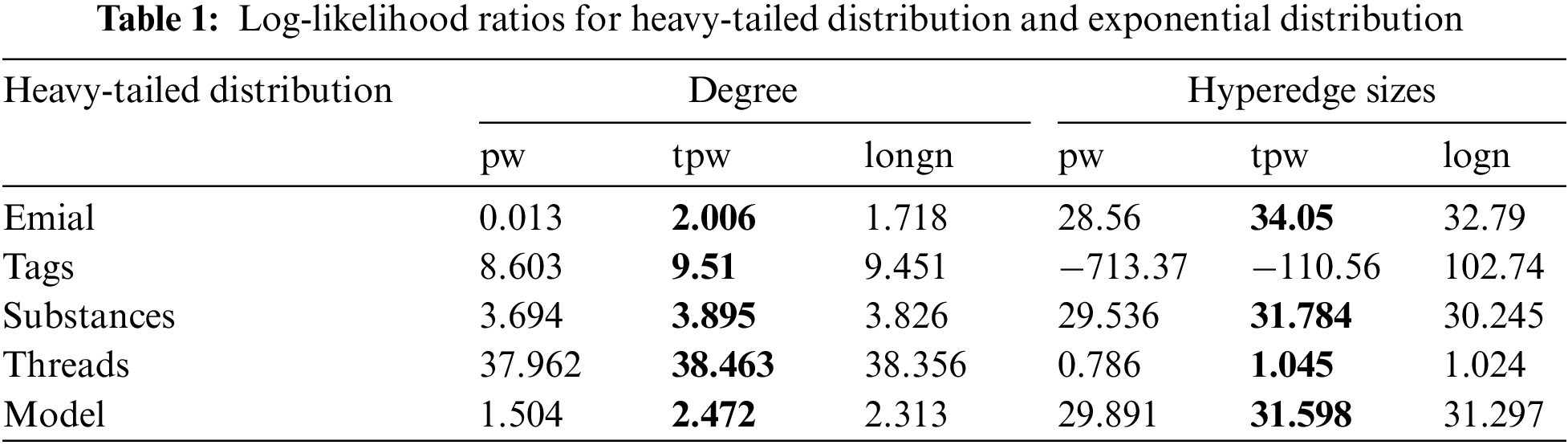
The data shown in Table 1 is the ratios of the three heavy-tailed distributions (pw, tpw, and logn) to the exponential distribution. This ratio represents the log-likelihood ratio (LR) and is calculated as LR=log⁡(LA(D)LB(D)), where A denotes heavy-tailed distribution, B denotes exponential distribution and D denotes dataset. A positive value indicates that the topology is more suitable for a heavy-tailed distribution. The numbers in the ‘Model’ column are all positive. The distribution of the generated hypergraph has the same trend as the real-world hypergraph. In comparison to power-law distributions and lognormal distributions, the degree and hyperedge size of the generated hypergraph is more in line with truncated power-law distributions.

Decomposed hypergraph’s pattern feature. In [25], Do et al. proposed a method for multi-level decomposition of hypergraphs. The hypergraph is decomposed at level k. The higher the level, the simpler the representation of the decomposed hypergraph, and the less detail is retained. The pattern features of the real-world hypergraph remain consistent before and after decomposition.

We decompose the generated hypergraph with the decomposition of degree distribution and singular value distribution to level 3 and the largest connected component to level 4. The different levels of decomposition are as follows: Level 1 (k=1): node-level decomposition; Level 2 (k=2): edge-level decomposition; Level 3 (k=3): triangle-level decomposition; and Level 4 (k=4): 4-clique-level decomposition.

In Fig. 3, both the degree distribution and the singular value distribution of the decomposition of the generative hypergraph and the real-world hypergraph up to level 3 are shown. In degree distribution: In both hypergraphs, at the node-level decomposition (k=1), they follow a heavy-tailed distribution. Deviating more and more from the fitted line as the decomposition level gets higher. In singular value distribution, both hypergraphs exhibit similar trends in the singular value distribution at the node level and edge level and start to deviate from the fitted line at the triangle level. Overall, it is straightforward to observe in Fig. 3 that the decomposition graph of the generated hypergraph replicates the structural pattern of the decomposition graph of the real-world hypergraph.

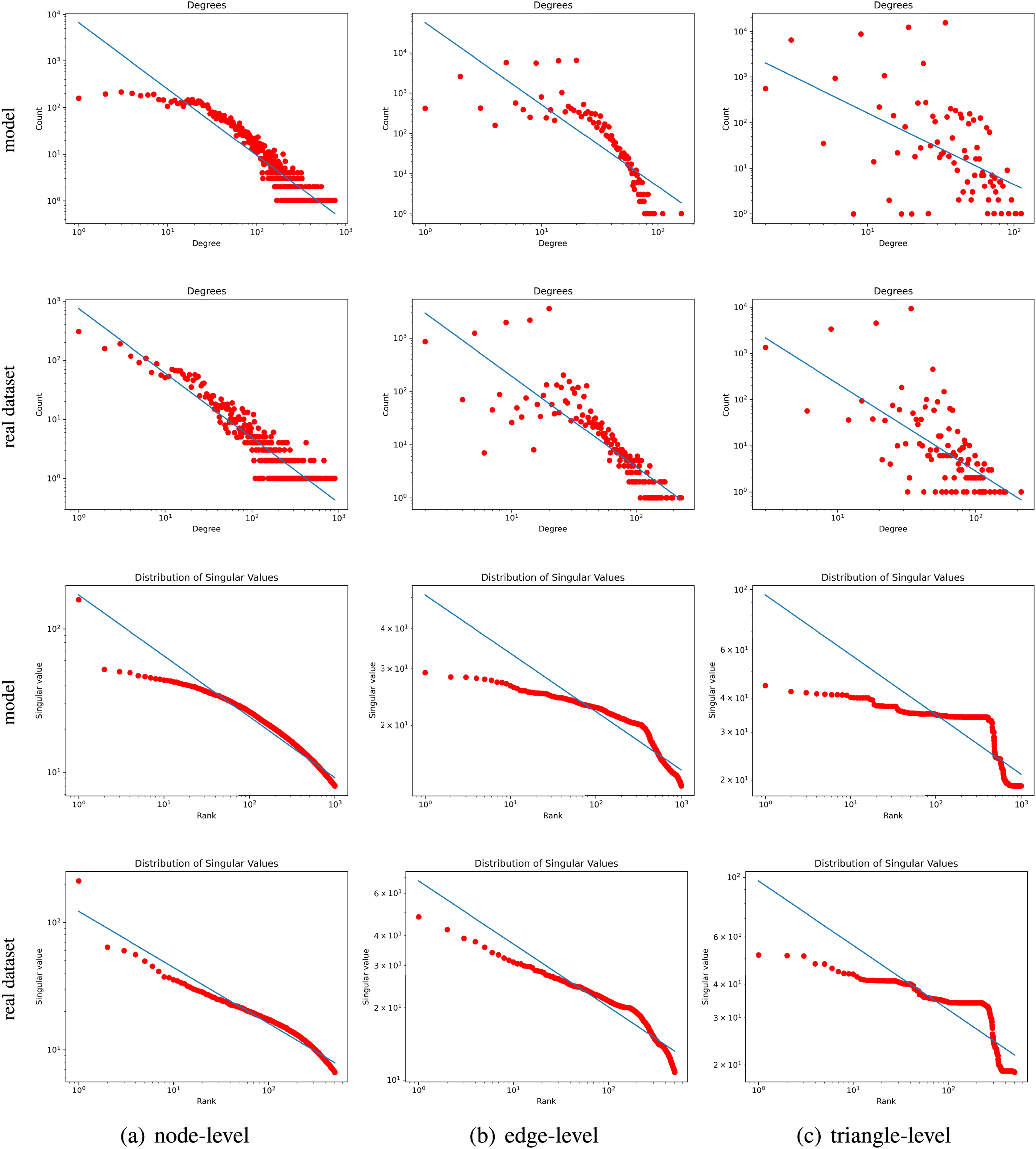
Figure 3: Decomposition graph topology analysis of a real dataset and model

We similarly consider the comparison of clustering coefficients and effective diameters at the node level, as well as analyzing the interconnection of nodes in the decomposition graph. In Table 2, different colors indicate the absence of the largest connected component. Apparent from the data in Table 2, starting from the triangle level, 2/5 of the datasets do not have the largest connected component. By the 4-clique level, only 1/5 of them retain the largest connected component. These phenomena are consistent with some characteristics of real-world hypergraphs. In Table 3, the clustering coefficients and effective diameter in the generated hypergraph exhibit characteristics that align with real-world hypergraphs, which all show small effective diameters and large clustering coefficients at the node level.

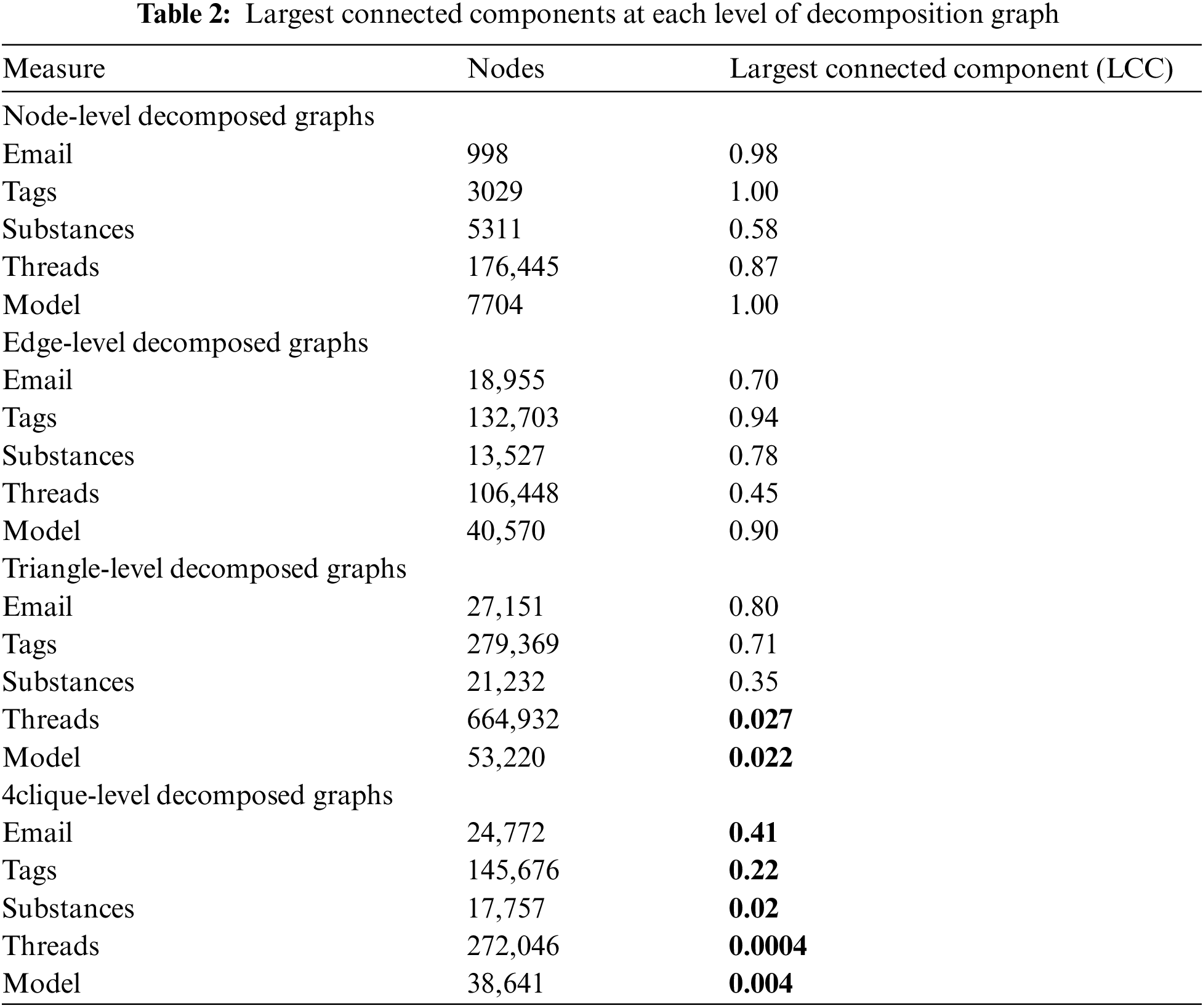
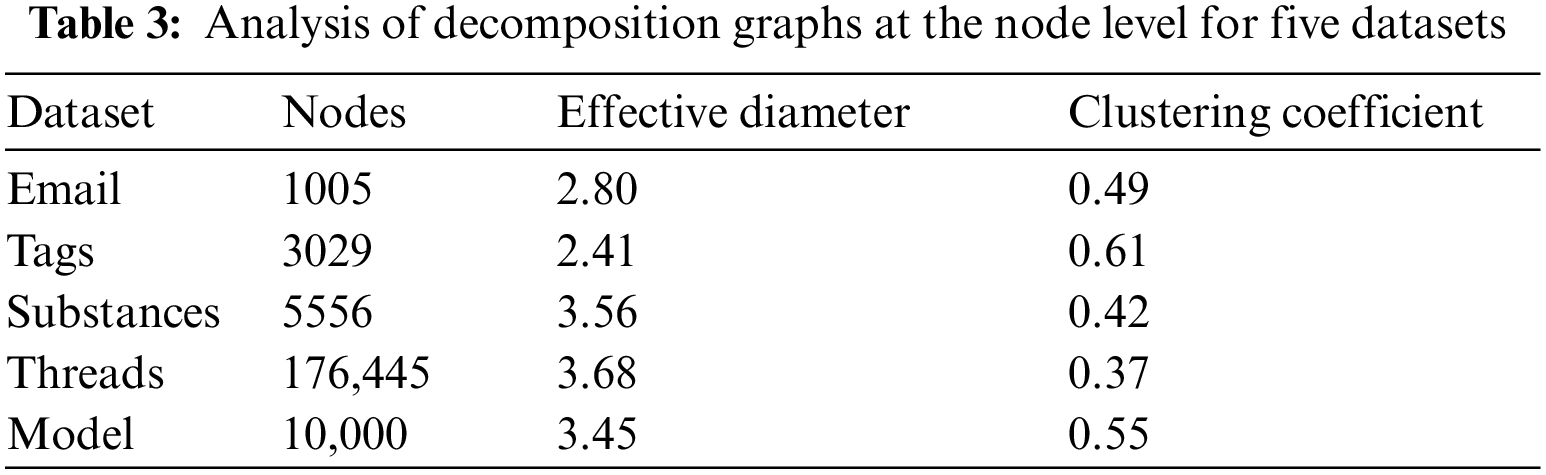
As seen in the pattern feature analysis for complete and decomposed hypergraphs in this section, the model for generating hypergraphs successfully captures the basic features of real-world hypergraphs, which indicates that the model proposed in this paper is consistent with real-world hypergraphs and proves the validity and applicability of the model.

7  Robustness Analysis

Simulating different types of attack scenarios in the robustness analysis can be very helpful in identifying security vulnerabilities and potentially vulnerable parts of SIoT. After simulating the attacks, recovery plans and emergency response strategies can be developed for the problems to better cope with emergencies. In this section, we will assess the robustness of the hypergraph generated in Section 6 by subjecting it to random and deliberate attacks.

7.1 Robustness Index

In this paper, we choose the largest connected component as the robustness assessment index for hypergraphs. The largest connectivity subgraph is a connectivity subgraph that contains the highest number of nodes in the network, which can reflect the overall connectivity of the hypernetwork, and the hypernetwork with higher connectivity has stronger robustness when the hypernetwork is under attack.

The normalized largest connected component is used as the vertical axis in the node and edge attacks effectiveness chart, LCC (norm).

LCC=N0N(2)

N denotes the total number of nodes in the hypergraph, whereas N0 stands for the node count in the largest connected subgraph. The value of LCC ranges from 0 to 1, indicating the relative size of the largest connected subgraph. A value close to 1 indicates that most of the nodes of the hypernetwork are in the largest connectivity subgraph, and the hypernetwork is robust. On the contrary, a value close to 0 indicates the weak robustness of the hypernetwork.

7.2 Attack Strategy

We first convert the hypernetwork generated in Section 6 into its 2-section hypergraph, denoted as H2. According to the definition of the 2-section hypergraph, it can be inferred that the adjacency matrix of the hypernetwork is equal to the adjacency matrix of the corresponding 2-section graph. Thus, when failures in a hypernetwork propagate through nodes, these failures can be viewed as propagating between nodes in their corresponding 2-section hypergraphs [32]. Likewise, in the program based on edge attacks, create a list of edges and use a function to generate the corresponding index list. This ensures consistency in the main body of the attack strategy when dealing with node or edge attacks. In this case, by analyzing the network robustness analysis of the 2-section hypergraph, the robustness characteristics of the hypernetwork based on node attacks and edge attacks are obtained.

7.2.1 Random Attack

Random attacks constitute one of the most prevalent attack patterns when examining network robustness. The attacker randomly selects the target node to attack. This method is usually probabilistic and does not have a clear target. When generating a hypergraph, a new node is introduced at each time step, so each node has its own identity. Three different nodes are randomly selected from the list of nodes to be attacked (deleted), and data is recorded. The process ‘Delete Nodes-Record Data’ loops until all nodes in the hypernetwork are deleted and the attack ends.

7.2.2 Deliberate Attack

Deliberate attacks refer to targeted attacks on hypernetwork nodes. They first measure the centrality of hypernetwork nodes and then select nodes to attack. This attack method is more destructive than random attacks and is one of the two commonly used attack modes.

In this section, we employ four deliberate attack strategies, which are as follows: initial degree attack, initial betweenness attack, recalculated degree attack, and recalculated betweenness attack.

•   Initial degree attack targets nodes with high degree centrality (id). Firstly, the degree centrality of each node DC(vi) in the hypergraph is calculated, and its expression is shown in (3) [35]. Then, the function is called to select the top-k nodes based on their degree of centrality for the attack.

DC(vi)=d(vi)n−1(3)

d(vi) denotes the degree of node vi. In the hypergraph, the nodes in the same hyperedge can be considered to be fully connected. |V|=n represents the number of nodes in the hypergraph. In a hypernetwork, a node’s degree centrality is higher when its degree is larger, indicating that the node is more important in the hypernetwork.

•   Initial betweenness centrality attacks target nodes with high betweenness centrality (ib). First, the betweenness centrality of each node B(vi) in the graph is calculated, as expressed in (4) [35]. Then, nodes with the top k betweenness centrality values are selected for attack.

B(vi)=∑jn∑kngjk(i)gjkn(n−2)2,j≠k≠i,j<k(4)

gjk represents the number of shortest hyperpaths from node vj to node vk, and gjk(i) represents the number of these shortest hyperpaths that pass through node vi. The larger the node betweenness centrality value is, the more short hyperpaths will pass through the node and the greater the influence of the node.

•   Recalculated degree attacks and betweenness (rd, rb) removal attacks are dynamic attack strategies. First, a copy of the hypergraph is made to avoid affecting the initial graph structure during node selection. The remaining steps are similar to id and ib, but in each attack, the attack strategy needs to be updated, i.e., recalculate the degree centrality and betweenness centrality of the nodes.

7.3 Robust Analysis

The hypergraph generated by HWM is subjected to node and edge attacks using the five methods described in Section 7.2. The results of the robustness analysis are shown in Fig. 4. The horizontal axis represents (a) the proportion of nodes removed and (b) the proportion of edges removed.

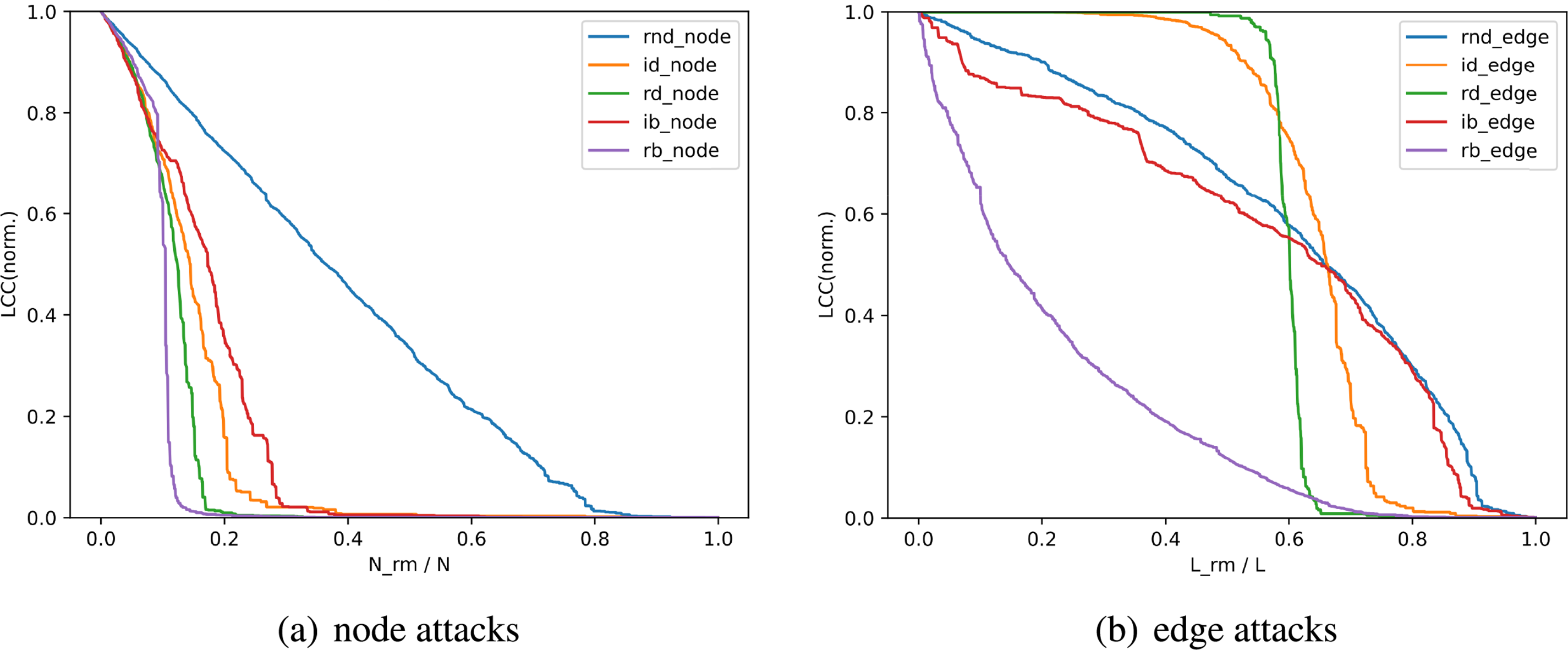
Figure 4: Largest connectivity component based on node and edge attacks

Specifically, regarding node attacks, when the value of LCC decreases to 20% of the initial value, the proportion of nodes to be removed for each attack method is approximately as follows: rb attack about 9.7%, rd attack about 13.3%, id attack about 17.8%, ib attack about 19.5%, and random attack about 61.5%. Similarly, regarding edge attacks, the proportion of edges to be removed is approximately as follows: rb attack about 39.4%, rd attack about 62.1%, id attack about 71.3%, ib attack about 83.3%, and random attack about 85.8%.

Overall, rb attack strategy appears to be the most effective, and the hypernetwork is the most robust against random attacks. Furthermore, it can be seen that the dynamic attack strategy is more effective than the initial attack strategy. This is because they can adapt their attacks to the actual state of the network. With repeated attacks, the hypernetwork’s topology can change, and these dynamic strategies are more likely to target new critical nodes.

In Section 7.2.2, deliberate attack strategies are categorized into two types: those based on degree centrality and those based on betweenness centrality. The effectiveness of these attack strategies can vary depending on factors such as the hypernetwork’s specific topology. However, betweenness-centrality-based attacks are more effective than degree-centrality-based attacks in the hypernetwork proposed in this paper. This is because the former mainly destroys the shortest path of the graph and the latter mainly aims to reduce the number of edges of the graph; one is a global strategy and the other is a local strategy.

8  Conclusions

The Social Internet of Things brings new elaboration on human-object and object-object connections. Constructing a hypergraph model provides a new perspective for studying SIoT, which is of significant importance in understanding their network characteristics. We have proposed a hypergraph generation model based on the context of the Social Internet of Things and studied random hypernetwork evolution models, including Poisson distribution generation and equal probability generation. By analyzing the degree distribution, hyperedge size distribution, and edge density distribution and comparing these patterns with those found in real-world hypergraphs, it has been observed that the proposed hypergraph generation model is capable of replicating the pattern characteristics of real-world hypergraphs effectively. This validation demonstrates the practical significance of the proposed hypergraph generation model in real-world research contexts. This model can successfully generate SIoT simulation datasets, exploring new outlets for building intelligent networks. Furthermore, we conducted a robustness analysis on the generated hypergraphs. We employed five different methods of attacking against nodes, and under node failure, the network showed stronger robustness to random attacks and weakest robustness to attacks based on betweenness centrality. This research contributes to a better understanding of the structural and robustness properties of hypergraphs in the context of the Social Internet of Things. And it provides a theoretical basis for the construction of trustworthy intelligent networks.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception, design, and data collection: Yue Wan, Nan Jiang; analysis and interpretation of results: Yue Wan, Nan Jiang, Ziyu Liu; draft manuscript preparation: Yue Wan, Nan Jiang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data comes from Austin R. Benson datasets, including email-Eu-full as email, tags-ask-ubuntu (tags), NDC-substances-full (substances), and threads-math-sx (threads).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Atzori L, Iera A, Morabito G, Nitti M. The Social Internet of Things (SIoT)–When social networks meet the Internet of Things: concept, architecture and network characterization. Comput Netw. 2012;56(16):3594–608. doi:10.1016/j.comnet.2012.07.010. [Google Scholar] [CrossRef]

2. Tan L, Wang N. Future internet: the internet of things. In: 2010 3rd International Conference on Advanced Computer Theory and Engineering(ICACTE); 2010; Chengdu, China. [Google Scholar]

3. Peng H, Si S, Awad MK, Zhang N, Zhao H, Shen XS. Toward energy-efficient and robust large-scale WSNs: a scale-free network approach. IEEE J Sel Areas Commun. 2016;34(12):4035–47. doi:10.1109/JSAC.2016.2621618. [Google Scholar] [CrossRef]

4. Wen G, Yu W, Yu X, Lü J. Complex cyber-physical networks: from cybersecurity to security control. J Syst Sci Complex. 2017;30(1):46–67. doi:10.1007/s11424-017-6181-x. [Google Scholar] [CrossRef]

5. Lee G, Truong N. A reputation and knowledge based trust service platform for trustworthy social internet of things. In: Innovations in Clouds, Internet and Networks (ICIN); 2016 Mar 1–3; Paris, France. [Google Scholar]

6. Nitti M, Atzori L, Cvijikj IP. Friendship selection in the social internet of things: challenges and possible strategies. IEEE Internet Things J. 2014;2(3):240–7. [Google Scholar]

7. Erdős P, Rényi A. On the evolution of random graphs. Publ Math Inst Hungar Acad Sci. 1960;5:17–61. [Google Scholar]

8. Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature. 1998;393(6684):440–2. doi:10.1038/30918. [Google Scholar] [PubMed] [CrossRef]

9. Barabási AL, Albert R. Emergence of scaling in random networks. Science. 1999;286(5439):509–12. doi:10.1126/science.286.5439.509. [Google Scholar] [PubMed] [CrossRef]

10. You J, Ying R, Ren X, Hamilton W. Graphrnn: generating realistic graphs with deep auto-regressive models. In: Proceedings of the 35th International Conference on Machine Learning; 2018; Stockholm, Sweden. p. 5708–17. [Google Scholar]

11. Leskovec J, Kleinberg J, Faloutsos C. Graph evolution: densification and shrinking diameters. ACM Trans Knowl Discov Data. 2007;1(1):2–42. doi:10.1145/1217299.1217301. [Google Scholar] [CrossRef]

12. Yu Y, Xiao G, Zhou J, Wang Y, Wang Z, Kurths J, et al. System crash as dynamics of complex networks. Proc Natl Acad Sci. 2016;113(42):11726–31. doi:10.1073/pnas.1612094113. [Google Scholar] [PubMed] [CrossRef]

13. Wang JW, Rong LL, Deng QH, Zhang JY. Evolving hypernetwork model. Eur Phys J B. 2010;77:493–8. [Google Scholar]

14. Vahdat-Nejad H, Mazhar-Farimani Z, Tavakolifar A. Social internet of things and new generation computing—A survey. In: Hassanien AE, Bhatnagar R, Khalifa NEM, Taha MHN, editors. Toward social internet of things (SIoTenabling technologies, architectures and applications: emerging technologies for connected and smart social objects. Cham, Switzerland: Springer International Publishing; 2020. p. 139–49. [Google Scholar]

15. Guo B, Yu Z, Zhou X, Zhang D. Opportunistic IoT: exploring the social side of the internet of things. In: Proceedings of the 2012 IEEE 16th International Conference on Computer Supported Cooperative Work in Design (CSCWD); 2012; Wuhan, China. p. 925–9. [Google Scholar]

16. Mendes P. Social-driven internet of connected objects. In: IAB Workshop on Interconnecting Smart Objects with the Internet, 2011; Prague, The Czech Republic. [Google Scholar]

17. Kranz M, Roalter L, Michahelles F. Things that twitter: social networks and the internet of things. In: What can the Internet of Things do for the Citizen (CIoT) Workshop at the Eighth International Conference on Pervasive Computing (Pervasive 2010); 2010; Helsinki, Finland. p. 1–10. [Google Scholar]

18. Guinard D, Fischer M, Trifa V. Sharing using social networks in a composable web of things. In: 2010 8th IEEE International Conference on Pervasive Computing and Communications Workshops (PERCOM Workshops); 2010; Mannheim, Germany. p. 702–7. [Google Scholar]

19. Baqer M. Enabling collaboration and coordination of wireless sensor networks via social networks. In: 2010 6th IEEE International Conference on Distributed Computing in Sensor Systems Workshops (DCOSSW); 2010; Santa Barbara, CA, USA. p. 1–2. [Google Scholar]

20. Qiu J, Tian Z, Du C, Zuo Q, Su S, Fang B. A survey on access control in the age of internet of things. IEEE Internet Things J. 2020;7(6):4682–96. doi:10.1109/JIoT.6488907. [Google Scholar] [CrossRef]

21. Qiao C, Brown KN, Zhang F, Tian Z. Adaptive asynchronous clustering algorithms for wireless mesh networks. IEEE Trans Knowl Data Eng. 2021;35(3):2610–27. [Google Scholar]

22. Qiao C, Qiu J, Tan Z, Min G, Zomaya AY, Tian Z. Evaluation mechanism for decentralized collaborative pattern learning in heterogeneous vehicular networks. IEEE Trans Intell Transp Syst. 2023;24(11):13123–32. doi:10.1109/TITS.2022.3186630. [Google Scholar] [CrossRef]

23. Zhou Y, Ren Y, Yi M, Xiao Y, Tan Z, Moustafa N, et al. Cdtier: a Chinese dataset of threat intelligence entity relationships. IEEE Trans Sustain Comput. 2023;8(4):627–38. doi:10.1109/TSUSC.2023.3240411. [Google Scholar] [CrossRef]

24. Ren Y, Xiao Y, Zhou Y, Zhang Z, Tian Z. CSKG4APT: a cybersecurity knowledge graph for advanced persistent threat organization attribution. IEEE Trans Knowl Data Eng. 2023;35(6):5695–709. [Google Scholar]

25. Do MT, Se Yoon, Hooi B, Shin K. Structural patterns and generative models of real-world hypergraphs. In: Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining; 2020; New York, NY, USA, Association for Computing Machinery. p. 176–86. [Google Scholar]

26. Holme P, Kim BJ, Yoon CN, Han SK. Attack vulnerability of complex networks. Phys Rev E. 2002;65(5):056109. doi:10.1103/PhysRevE.65.056109. [Google Scholar] [PubMed] [CrossRef]

27. Jin T, Yu Z, Gao Y, Gao S, Sun X, Li C. Robust ℓ2—Hypergraph and its applications. Inf Sci. 2019;501:708–23. doi:10.1016/j.ins.2019.03.012. [Google Scholar] [CrossRef]

28. Sarwar M. A theoretical investigation based on the rough approximations of hypergraphs. Am J Math. 2022;2022:1540004. [Google Scholar]

29. M.A.Tao SQ. Review of hypernetwork based on hypergraph. Oper Res Manag Sci. 2021;30(2):232–9. [Google Scholar]

30. Chen G, Wang X, Li X. Fundamentals of complex networks: models, structures and dynamics. Hoboken, New Jersey: John Wiley & Sons; 2014. [Google Scholar]

31. Estrada E, Rodríguez-Velázquez JA. Subgraph centrality and clustering in complex hyper-networks. Physica A. 2006;364:581–94. [Google Scholar]

32. Bretto A. Hypergraph theory: an introduction. Cham, Switzerland: Springer; 2013. [Google Scholar]

33. Benson AR, Abebe R, Schaub MT, Jadbabaie A, Kleinberg J. Simplicial closure and higher-order link prediction. Proc Natl Acad Sci. 2018;115(48):E11221–30. doi:10.1073/pnas.1800683115. [Google Scholar] [PubMed] [CrossRef]

34. Yin H, Benson AR, Leskovec J, Gleich DF. Local higher-order graph clustering. In: Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2017; New York, USA: Association for Computing Machinery. p. 555–64. [Google Scholar]

35. Lü L, Chen D, Ren XL, Zhang QM, Zhang YC, Zhou T. Vital nodes identification in complex networks. Phys Rep. 2016;650(1987):1–63. doi:10.1016/j.physrep.2016.06.007. [Google Scholar] [CrossRef]