 Open Access
Open Access
ARTICLE
GPU-Enabled Isogometric Topology Optimization with Bėzier Element Stiffness Mapping
1 School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan, 430074, China
2 School of Advanced Manufacturing, Nanchang University, Nanchang, 330031, China
* Corresponding Authors: Nianmeng Luo. Email: ; Xianda Xie. Email:
Computer Modeling in Engineering & Sciences 2025, 142(2), 1481-1514. https://doi.org/10.32604/cmes.2024.058798
Received 21 September 2024; Accepted 27 November 2024; Issue published 27 January 2025
Abstract
Due to the high-order B-spline basis functions utilized in isogeometric analysis (IGA) and the repeatedly updating global stiffness matrix of topology optimization, Isogeometric topology optimization (ITO) intrinsically suffers from the computationally demanding process. In this work, we address the efficiency problem existing in the assembling stiffness matrix and sensitivity analysis using Bėzier element stiffness mapping. The Element-wise and Interaction-wise parallel computing frameworks for updating the global stiffness matrix are proposed for ITO with Bėzier element stiffness mapping, which differs from these ones with the traditional Gaussian integrals utilized. Since the explicit stiffness computation formula derived from Bėzier element stiffness mapping possesses a typical parallel structure, the presented GPU-enabled ITO method can greatly accelerate the computation speed while maintaining its high memory efficiency unaltered. Numerical examples demonstrate threefold speedup: 1) the assembling stiffness matrix is accelerated by 10× maximumly with the proposed GPU strategy; 2) the solution efficiency of a sparse linear system is enhanced by up to 30× with Eigen replaced by AMGCL; 3) the efficiency of sensitivity analysis is promoted by 100× with GPU applied. Therefore, the proposed method is a promising way to enhance the numerical efficiency of ITO for both single-patch and multiple-patch design problems.Keywords
Acronyms
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| B-spline | Basis spline |
| COO | Coordinate format |
| CPU | Central processing unit |
| DOF | Degree of freedom |
| ESO | Evolutionary structural optimization |
| EW | Element-wise |
| FEM | Finite element method |
| GPU | Graphics processing units |
| HPC | High performance computing |
| IGA | Isogeometric analysis |
| ITO | Isogeometric topology optimization |
| IW | Interaction-wise |
| NURBS | Non-uniform rational basis spline |
| PDE | Partial differential equation |
| SGRAM | Synchronous graphic random-access memory |
| SIMP | Solid isotropic material with penalization |
| SM | Streaming multiprocessor |
| TO | Topology optimization |
As a new finite element method, Isogeometric analysis (IGA), first proposed by Hughes et al. [1], has great potential in seamless integration between CAD and CAE. Over the last two decades, IGA gradually takes place the traditional Lagrange-based finite element method (FEM) in solving the Partial Differential Equation (PDE), accounting for its merits in high continuity, elimination of geometry discretization error, and high efficiency of high order elements [2,3]. It has been applied to various analysis problems, including fracture mechanics analysis [4,5], structural vibration analysis [6,7], and fluid-structure interaction analysis [8,9]. Naturally, the research topic of IGA was extended to topology optimization (TO), which is an effective tool for implementing innovative structural design with superior structural performance subjected to specified constraints [10]. According to the description of design variables, four major classical TO methods can be categorized into element-based and boundary-based approaches. Through the variation interval of design variables, the element-based TO methods can be further refined into Solid Isotropic Material with Penalization (SIMP) approach [11,12] and Evolutionary Structural Optimization method (ESO) [13,14]. Similarly, boundary-based TO methods can be divided into the implicit Level Set Method [15,16] and the explicit geometric primitive approach [17,18].
Replacing FEM with IGA as the solver in these classical TO methods mentioned above, a series of isogeometric topology optimization (ITO) methods have been put forward over the last decade. Seo et al. first put forward the ITO method with new inner fronts allowed to be created, which can eliminate the post-processing effort as the numerical analysis and design optimization share identical spline information. Qian [19] proposed an implicit filter for TO by parametrizing the density field with NURBS, and Costa et al. [20,21] implemented the minimum and maximum length control for the NURBS-based implicit filter, as well as Yang et al. [22] significantly improve the efficiency of the implicit filter by means of the decomposition of NURBS tensor product structure. Xie et al. [23] proposed an adaptive explicit ITO method based on hierarchical B-splines with much improved computational efficiency for precise, optimized designs, and the numerical accuracy of the adaptive ITO method is significantly improved using truncated hierarchical B-spline under admissible mesh constraint [24]. Zhang et al. used the ITO method to optimize the shell structures under the stress constraint, with the optimized results linked to CAD systems directly. Gupta et al. [25] put forward an adaptive ITO method in terms of PHT splines with complex multi-patch NURBS geometries exported for analysis conveniently. Gao et al. [26] develop an ITO approach to cellular structures on the design domain discretized into multiple IGA patches, where the non-conforming patches are coupled using Nitsche’s method, and apply the ITO method to the innovative design processes of piezoelectric actuators [27] and composite structures [28]. Wang et al. [29] proposed an immersed ITO method for complex design domains with an embedded domain method and accelerated the efficiency by the composite strategies of multilevel mesh, MGCG, and local-update of design variables [30]. Montemurro et al. [31] presented a novel multilevel optimization method for concurrent topology and anisotropy optimization of variable-stiffness structures using NURBS, which was extended into anisotropic materials topology optimization design problems under mixed boundary conditions [32]. Moreover, the ITO method has been applied to the structural design of cross-flow heat exchangers [33], strain gradient materials [34], and sound-absorption materials [35].
Due to the property of NURBS spanning multiple elements [36], stiffness matrix assembly is one of the major efficiency bottlenecks for these ITO methods. To speed up the integration process of IGA, various efficient quadrature techniques are developed for NURBS element, such as reduced quadrature rule [37–39], weighted quadrature [40], sum factorization techniques [41], low-rank approximation [42]. Moreover, Karatarakis et al. [43] first applied the GPU parallelization technique to IGA and drastically accelerated computations of the stiffness matrix assembly process. Based on the adaptive isogeometric-meshfree method, Zhang et al. [44] significantly improved computational cost in the field of fracture resistance topology optimization. Szyszka et al. [45] applied graphics processing units (GPU) to integrate three-dimensional (3D) B-spline functions efficiently for IGA, and a multilevel concurrent integration algorithm was developed to bring extra speed up. Then, similar to the FEM-based TO method using GPU [46–50], Xia et al. [51] applied the GPU parallel strategy to assemble the stiffness matrix assembly process of ITO, causing the parallel assembly race problem. Unlike the FEM-based TO method, the elemental stiffness matrices of IGA for different elements cannot be represented by standard stiffness matrix [52,53], even for rectangular control meshes. Borden et al. [54] present the Bėzier extraction operator and isogeometric Bézier elements for non-uniform rational B-Spline (NURBS)-based isogeometric analysis. Over the last decade, the Bėzier extraction operator has been utilized in T-splines [55], truncated hierarchical B-splines [56], and polar splines [57] in the framework of IGA. More recently, Yang et al. [58] proposed a Bėzier element stiffness mapping technique for the explicit generation of B-spline IGA elements stiffness matrices, where only standard stiffness matrix and Bėzier extraction metrics are required to be pre-computed for rectangular control meshes. Although the Bėzier element stiffness mapping technique can significantly simplify the pre-computation and reduce the memory burden for the ITO method, it inevitably results in more expensive stiffness matrix assembly than the traditional ITO method, as the explicit stiffness matrix computation is required to be performed for each solid IGA element, rather than fetching from memory directly.
To maximize the potential of ITO using Bėzier element stiffness mapping, this work put forward a parallelization paradigm for the explicit stiffness matrix computation and assembling of IGA elements based on the GPU technique. The stiffness matrix assembly processes between six different types of ITO methods are thoroughly compared to illustrate the advanced performance of the presented method. Afterward, we apply the GPU parallelization technique to the sensitivity analysis of ITO, which can promote efficiency in updating the design variables. On the other hand, we extend the parallel framework to a multi-patch design problem to reveal its potential in complex structures. Overall, this work utilizes Bezier element stiffness mapping to further enhance the computing efficiency of ITO while maintaining low memory consumption, thereby verifying the suitability of this method for massively parallel systems with GPUs.
The outline of this work is organized as follows. Section 2 presents several key ingredients of the GPU-enabled ITO method with explicit stiffness matrix generation. In Section 3, the element-wise and interaction-wise approaches are introduced to implement the parallelization of stiffness matrix assembly of ITO using Bėzier element stiffness mapping, and a new parallelization scheme is formulated for sensitivity analysis. The effectiveness of the GPU-enabled ITO method is validated by the numerical examples shown in Section 4. Finally, the conclusions are drawn in Section 5.
In this section, GPU and the programming model CUDA are first introduced, which lays the foundation for the parallelization of ITO. Then, the optimization model of ITO is presented for the structural compliance minimization problem. Lastly, Bėzier element stiffness mapping is illustrated to generate the stiffness matrices of B-spline IGA elements explicitly.
GPU devices are initially designed to fulfill the requirements of graphical and 3D displays, which are extended to the high-performance computing (HPC) field due to their reasonable cost and vast parallel hardware structures. As one of the most, representative GPU devices, NVIDIA [59] and its programming model CUDA have been widely used for HPC. By means of CUDA, developers can treat GPU as a set of computing kernels supporting data parallelization. The kernel functions are the entries for developers to use GPU on the CPU host, which are the C language extension functions essentially. Before using the kernel functions, developers need to configure thread information for the GPU, including the data structures of the thread block on the thread grid and thread on each thread block.
The threads of the GPU have two data access permissions, which are the Synchronous Graphic Random-Access Memory (SGRAM) on GPU devices and Static Random-Access Memory on GPU chips (on-chip SRAM). As depicted in Fig. 1, thread blocks consist of a set of threads sharing data through shared memory. Similarly, the thread grid is made up of thread blocks, for which the execution hardware basis is a Streaming Multiprocessor (SM) with multiple threads, and every thread is allocated to SM, satisfying its execution requirement during the task period.
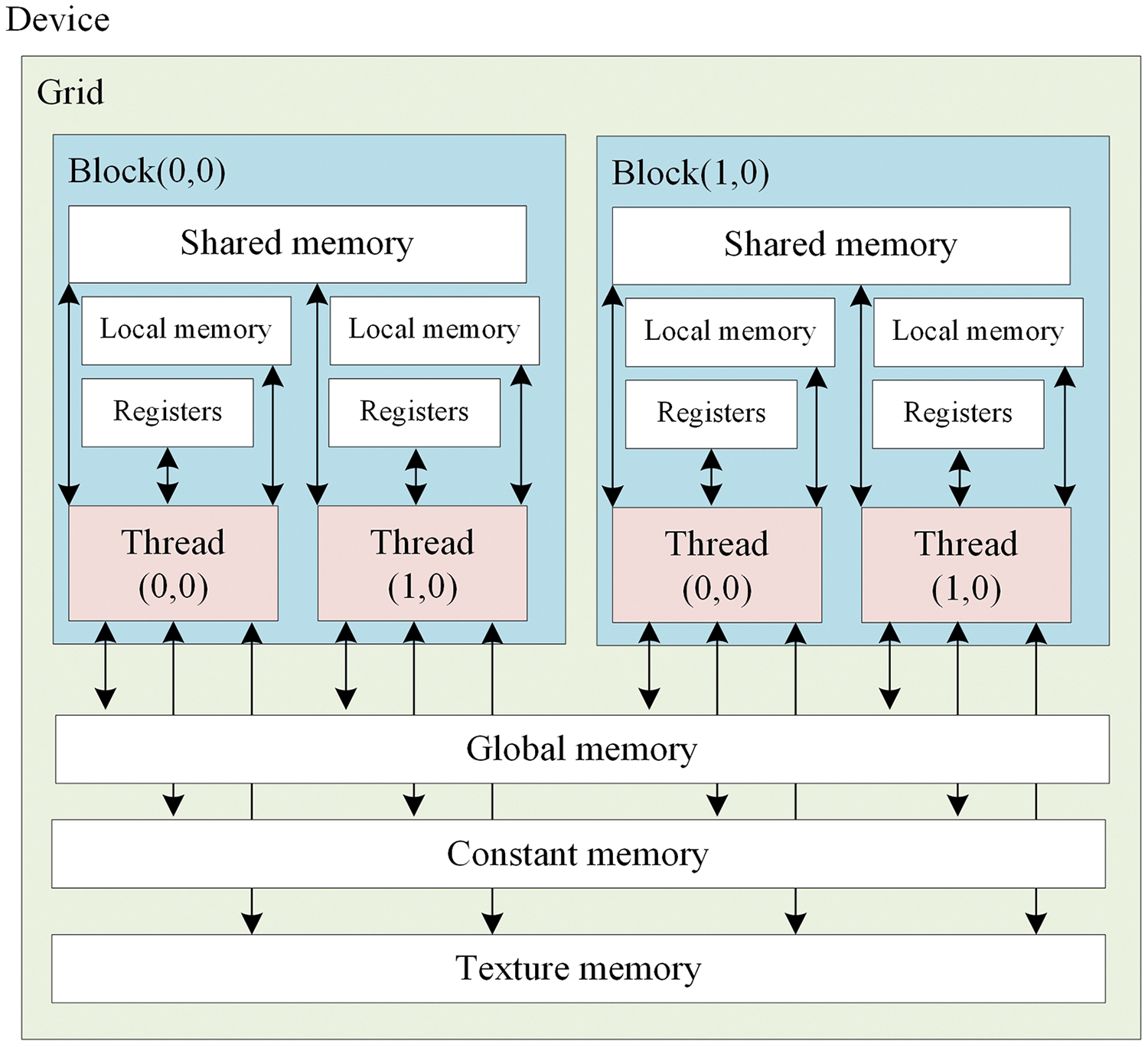
Figure 1: Thread hierarchies and memory model of CUDA
As illustrated in Fig. 2, a set of registers per processor and shared memory are the on-chip memory of each SM, which are used to read constant cache and texture cache only at a high speed. Therefore, the access speed of on-chip GPU memory is much faster than host memory. However, the on-chip GPU memory is shared by the threads on SM, which means that the number of thread blocks executed simultaneously is determined by the number of registers for each thread and the shared memory size for each thread block. Excessive use of shared memory is not conducive to parallel computation of large-scale data, and the constant cache is more suitable for storing the public data with its optimized data broadcast behavior.
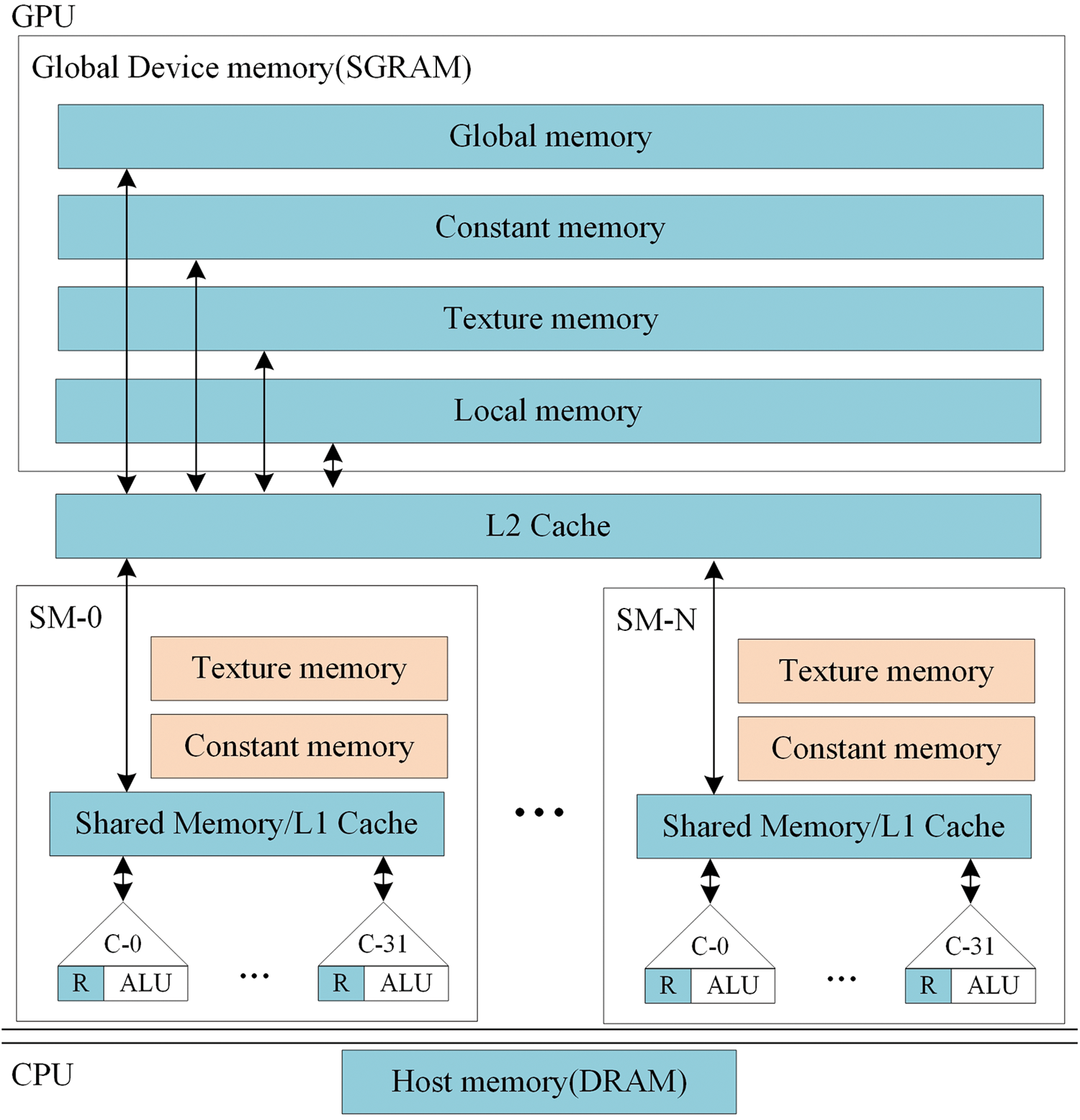
Figure 2: Memory hierarchies of CUDA
2.2 Isogeometric Topology Optimization Method
For the minimization problem of structural compliance, the objective of ITO model is the total structural strain energy obtained from summing all elemental strain energies, which usually equals to the external work of external force and is formulated as:
In Eq. (1),
In Eq. (2), nelx and nely are the number of elements along the parametric directions of IGA mesh,
With the modified SIMP model, the Young’s elastic modulus
where
2.3 Bėzier Element Stiffness Mapping
To bypass the ineffective stiffness matrix computation using Gaussian quadrature in ITO iteration, the stiffness matrices of all solid IGA elements should be pre-computed and stored. However, it leads to prohibitively huge memory burden in turn, especially for 3D design problems, which is undesirable for the designers without high performance server. In [58], instead of performing full Gaussian quadrature, Bėzier element stiffness mapping has been put forward for the explicit generation of IGA elemental stiffness matrix, which makes use of the space-preserving property of Bernstein basis function within an individual IGA element. Through the Bėzier element stiffness mapping, the stiffness matrix
where
In Eq. (7),
where
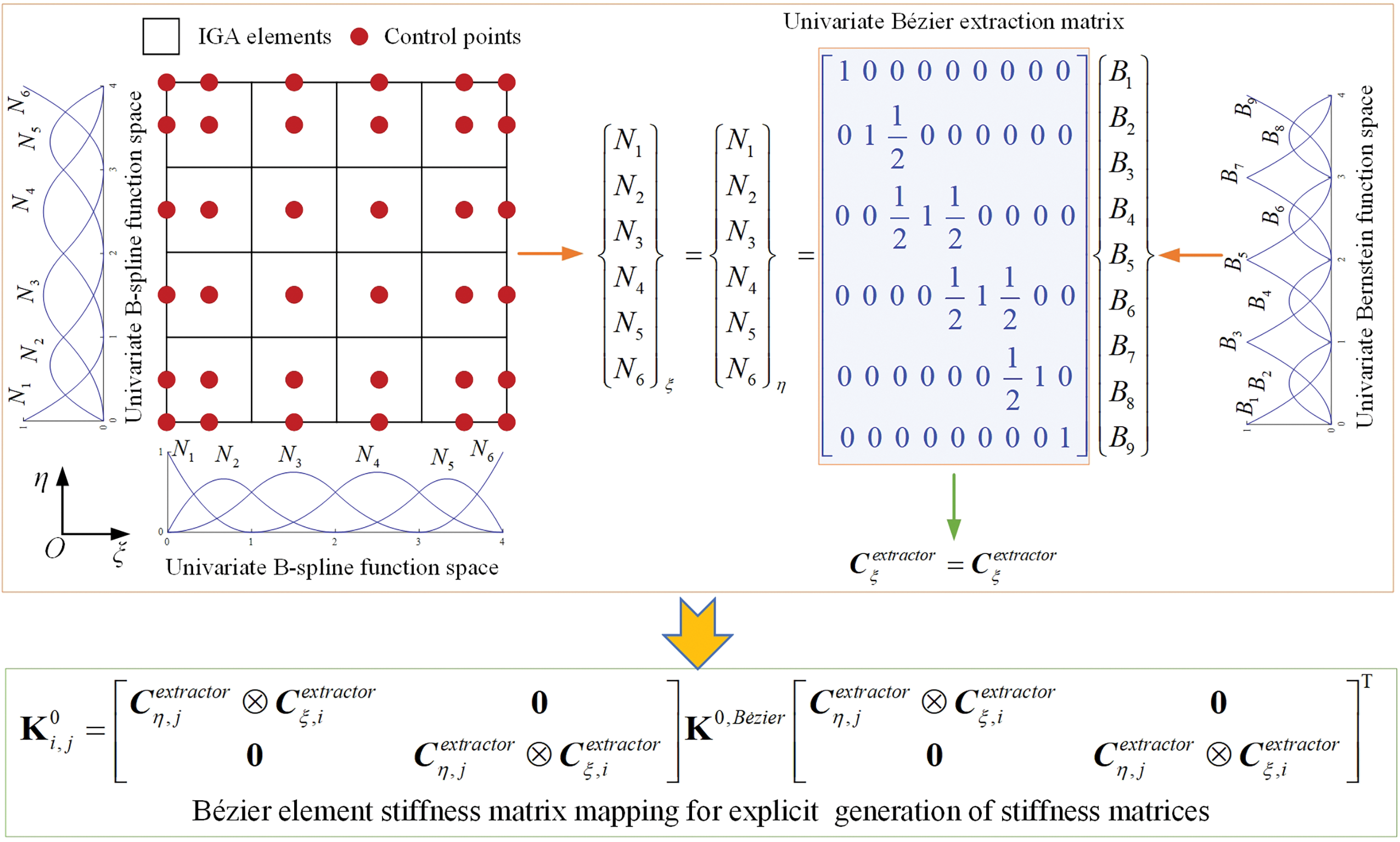
Figure 3: Illustration of Bėzier element stiffness mapping for B-spline IGA control mesh
3 GPU Implementation of Isogeometric Topology Optimization
This section describes the GPU parallel schemes for the stiffness matrix assembly and sensitivity analysis in detail, which are two of the key steps for ITO. With these two parallel schemes, the Bėzier element stiffness mapping will be accelerated to a large extend.
3.1 Parallelization of Stiffness Matrix Assembly
For ITO using Bėzier element stiffness mapping, both Eqs. (3) and (5) are required to be invoked frequently for the purpose of global stiffness matrix assembly at each iterative step. Similar to the parallelization schemes using full Gaussian quadrature presented in [43], both the element-wise and interaction-wise parallelization methods are presented for the global stiffness matrix updating of ITO.
In order to update the global stiffness matrix of ITO using Bėzier element stiffness mapping, the contributions of all calculated B-spline elements stiffness matrices need to be added, which are formulated as:
where
In contrast to the element-wise (EW) method in [43], the proposed element-wise method requires the standard Bėzier element stiffness matrix and the elemental Bėzier extraction matrices formulated as Eq. (10) to be calculated in CPU, rather than computing the shape function derivatives for each non-vanishing B-spline basis functions of every Gauss point. As shown in Fig. 4, the Bėzier element stiffness mapping defined in Eq. (9) is parallelly executed for all elements, and each IGA element is assigned to a thread block with 2(p + 1)(q + 1) threads. The reason for choosing the element stiffness matrix data dimension as the number of threads lies in the maximum number of threads of block in CUDA is limited. To implement the assembly of global stiffness matrix, the atomic operation is executed for all threads. When a thread performs atomic operations, other threads are forbidden to operate the specified memory to avoid data conflict.
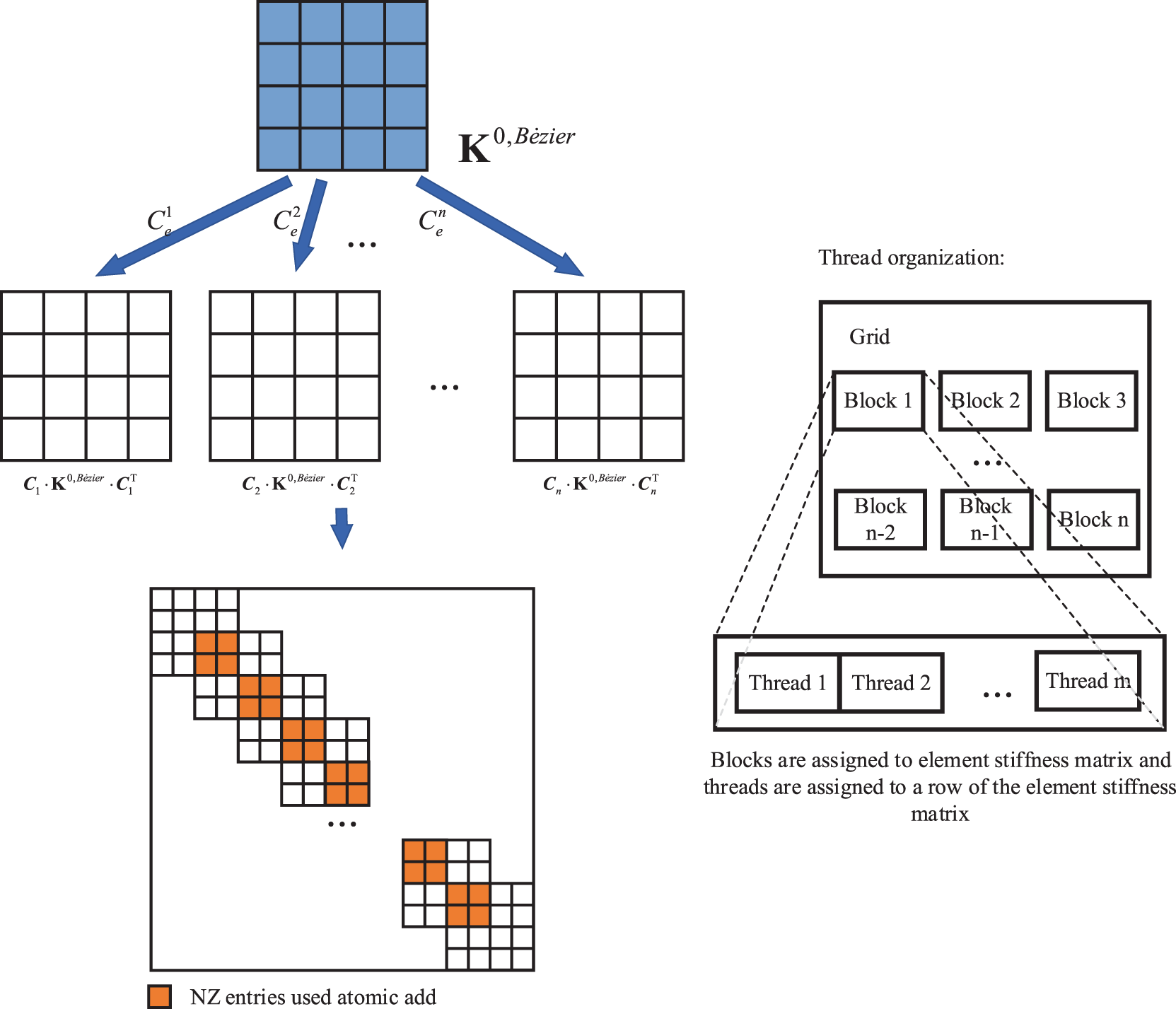
Figure 4: Illustration of EW implementation of ITO using Bėzier element stiffness mapping
As for the CUDA memory layout, Bėzier element stiffness matrix is stored in constant memory which can be accessed by all threads. The shared memory is used to store values like relative densities, the element Bėzier extraction matrix, etc. Other values like the global stiffness matrix are stored in global memory. In order to save more memory, the global stiffness matrix is stored in the form of coordinate format (COO) which is one of typical sparse format.
Considering the GPU amenability to parallelism, the Interaction-wise (IW) method is also efficient in updating the global stiffness matrix of ITO with Bėzier element stiffness mapping. The nonzero entries of the global stiffness matrix are calculated in a control points pair manner and appended to the matrix directly instead of updating the contribution from its influencing elements. In IGA, each Gaussian quadrature point is involved in computations with control points within the surrounding area. In the two-dimensional case, these two mutually influential control points are called control point pairs.
As the basic unit, each control point pair used in the IW approach is assigned to a thread block, and each thread handles the contribution of the associated nonzero values of a shared element. In contrast to the IW method used in [43], the proposed IW method has the following advantages over the traditional method: Firstly, it replaces the calculation of the shape function derivatives with direct matrix computations, which can avoid the time-consuming high-order derivative computation of B-spline; Secondly, it is only required to store the standard stiffness matrix of the Bėzier element and the univariate Bėzier extraction matrices rather than the shape function derivatives and the stiffness matrix coefficients, which greatly improves the storage efficiency. It should be noted that the associated rows and columns in the univariate Bėzier extraction matrices are extracted to compute the contribution value of the shared element for the control point pair, which is different from the approach used in the traditional IW method [43]. Once the contribution values of all shared elements have been computed and stored in the shared memory, the corresponding entries of the global stiffness matrix are summed through a parallel thread reduction strategy. Then, the updated global stiffness matrix will be transferred to the global memory. Fig. 5 presents the flowchart of the proposed IW method, where the partially filled rectangle indicates the control point pairs with idle threads in the thread block. Finally, the CUDA Kernel for the proposed IW approach is described in Algorithm 1. The number of allocated thread blocks is equal to the number of control point pairs, with threads allocated to each thread block, where the maximum number of shared elements for control point pairs is.
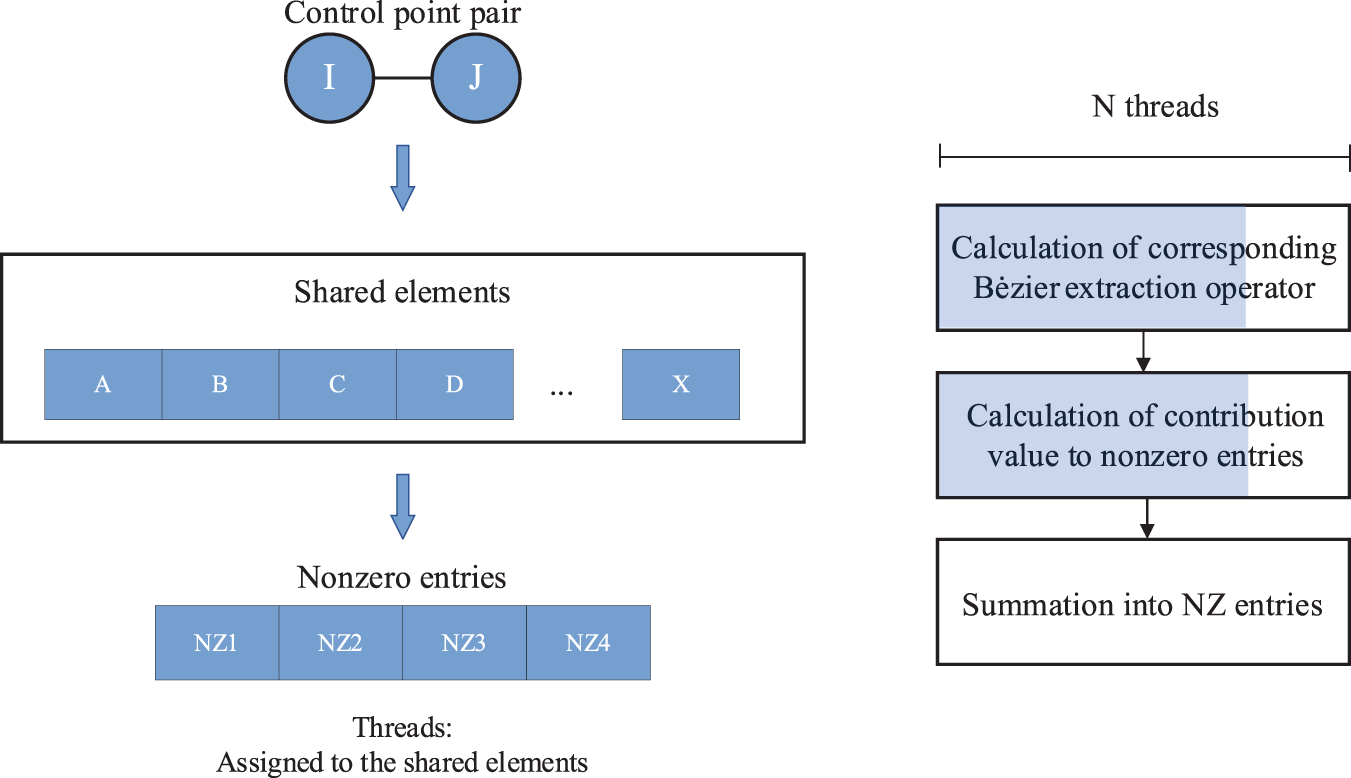
Figure 5: Illustration of IW implementation of ITO using Bėzier element stiffness mapping

3.2 Parallelization of Sensitivity Analysis
According to the mathematical model presented in Eq. (2), we can obtain the sensitivity of objective function as:
with
Since the sensitivity is calculated in terms of the local displacement vector and stiffness matrix as well as the Young’s elastic modulus for each design element, we choose the individual IGA design element as the parallelization unit. Similar to the element-wise stiffness matrix assembly scheme introduced aforementioned, a thread block is assigned to every IGA design element. Therefore, the parallel algorithm for sensitivity calculation of ITO is shown in Algorithm 2. By using the Bėzier element stiffness mapping, the algorithm is only required to store the standard Bėzier element stiffness matrix and the corresponding univariate Bėzier extraction matrices in the efficient updating process of design variables, rather than storing the stiffness matrices for all IGA elements.

The formula for variable iteration update is as follows:
where m is a positive move limit, η ( = 1/2) is a numerical damping coefficient, with
In order to avoid numerical artifacts, it is necessary to apply the sensitivity filter in sensitivity analysis. Similar to the parallel strategy used above, each thread block is assigned to a design element. The criteria for sensitivity filtering are as follows:
where
where
In this section, several classic numerical examples are used to verify the effectiveness of the presented GPU-based ITO implementation with Bėzier element stiffness mapping. The examples are run on the following hardware: AMD Ryzen 7 5700X 8-Core CPU Processor. GPU, NVIDIA GeForce RTX 3060. Windows 10 Operating System, Visual Studio 2019, and CUDA11.2 construct the software environment for all tests. Moreover, the floating point operations are performed in double arithmetic. Single-patch cases are programmed by C++/CUDA, and multi-patch case is programmed by Matlab/CUDA. Besides, the AMGCL library [61,62] is used to solve the linear equations in the ITO process, which greatly reduces the overall optimization time. Unless otherwise specified, all parameters used in this work are treated as dimensionless.
4.1 Messerschmitt–Bolkow–Blohm (MBB) Beam
MBB beam is a typical example that is widely used in topology optimization. We use it as the first numerical example to verify the effectiveness of the proposed parallel ITO methods. Due to symmetric boundary conditions, only half of the design domain is considered. Half of the MBB structure used for the design domain is shown in Fig. 6, of which the aspect ratio is 2, and the volume constraint is prescribed to be 0.4. The left side is fixed in the horizontal direction, the right-bottom corner is simply supported, and an external unit load is applied at the top left corner for the design domain.
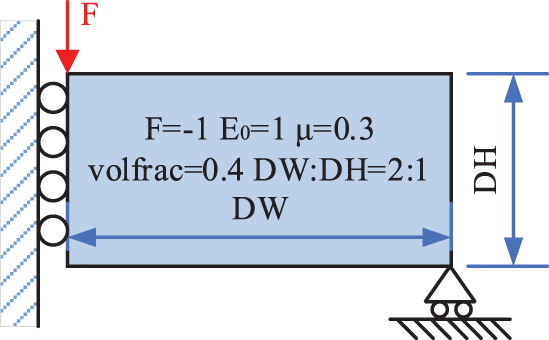
Figure 6: Illustration of problem setting for MBB beam
Taking different mesh resolutions and different basis function degree combinations into consideration, the average stiffness matrix updating time is obtained for the ITO optimization process with different calculation strategies, as illustrated in Fig. 7. The calculation strategies are listed as follows: a) traditional 1-core CPU-based EW method using full Gauss integration; b) the GPU-based EW method with all element stiffness matrices pre-stored; c) GPU-based IW method with all element stiffness matrices pre-stored, d) 1-core CPU-based EW method with Bėzier element stiffness mapping; e) the GPU-based EW method with Bėzier element stiffness mapping; f) GPU-based IW method with Bėzier element stiffness mapping. Four different mesh resolutions with bi-quadratic basis functions are used to compare the assembly time between these six calculation strategies, which are set to 50 × 100, 100 × 200, 150 × 300, and 200 × 400. Fig. 7 illustrates the average updating time in one iteration of the global stiffness matrix by means of all the aforementioned six calculation strategies under different mesh resolutions. According to the results presented in Fig. 7, the GPU-based EW method outperforms the GPU-based IW method, and the GPU-based methods are superior to 1-core CPU-based EW methods for the stiffness matrix updating of ITO, independent of the computing approaches used in stiffness matrices of all solid elements and the IGA mesh resolution. Meanwhile, the GPU-based EW method with Bėzier element stiffness mapping is a more efficient approach than the GPU-based EW method with all element stiffness matrices pre-stored for the ITO method, regardless of the IGA mesh resolution variation. Moreover, the average updating time in one iteration of the global stiffness matrix is compared in Fig. 8 for all aforementioned six calculation strategies under three different basis function degree combinations, where the IGA mesh resolutions are prescribed to 100 × 200. The acceleration effect of GPU-based methods is significant compared to the associated 1-core CPU-based methods observed from Fig. 7, independent of basis function degree, and it becomes more degraded as the increase of basis degree for IW scheme using Bėzier element stiffness mapping rather than storing all element stiffness matrices in advance. The underlying reason for the worst speedup performance lies in the fact that the data coupling between adjacent IGA elements is increased, which complicates the single thread task and increases data competition for the IW scheme using Bėzier element stiffness mapping. The speedup ratios of the proposed two parallel methods compared to the single-core CPU-based EW method are shown in Fig. 9 for the stiffness updating of ITO using Bėzier element stiffness mapping. It can be observed that the stiffness matrix updating process is approximately accelerated by one order of magnitude and three times for EW and IW schemes, respectively. On the other hand, the convergence histories of ITOs using these six different stiffness updating schemes are shown in Figs. 10 and 11, and the history designs under mesh resolutions are shown in Fig. 12. The associated converged results of ITO are shown in Figs. 13 and 14. According to these convergence histories and design results, the equivalence is verified between ITOs with different stiffness matrix updating schemes.
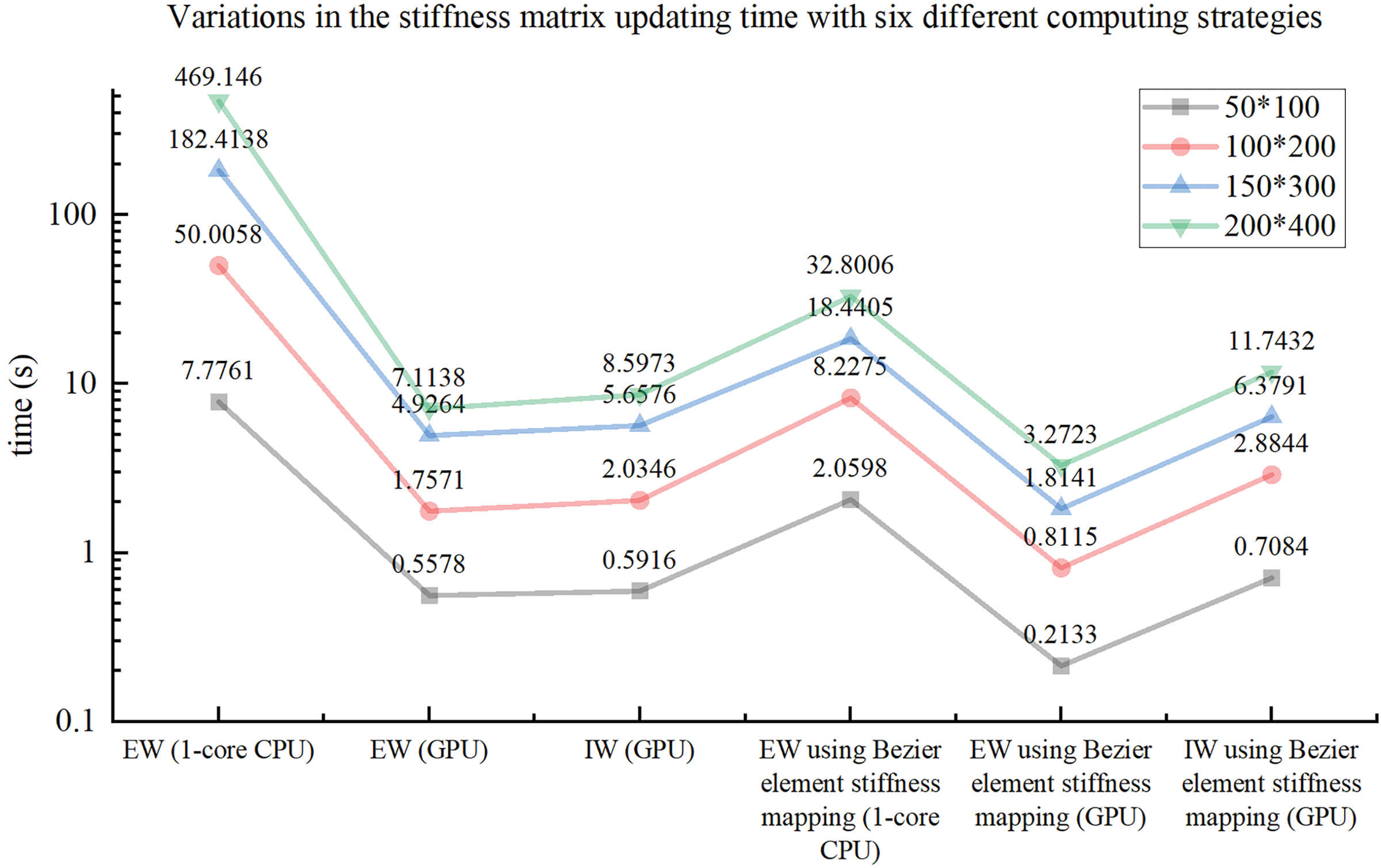
Figure 7: Illustration of variations in average stiffness matrix updating time with six different computing strategies for four different mesh resolutions
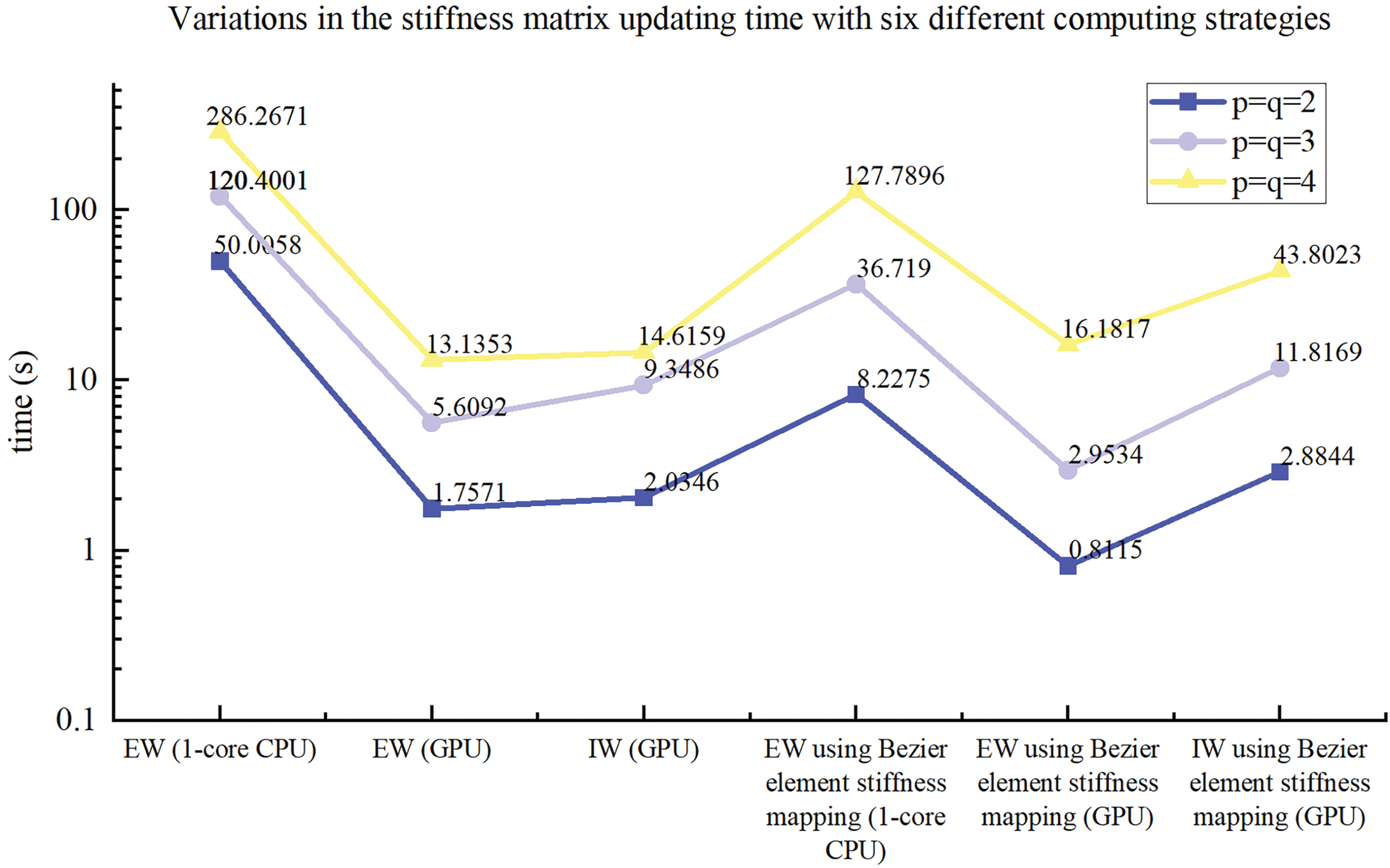
Figure 8: Illustration of variations in average stiffness matrix updating time with six different computing strategies for three different degrees combinations
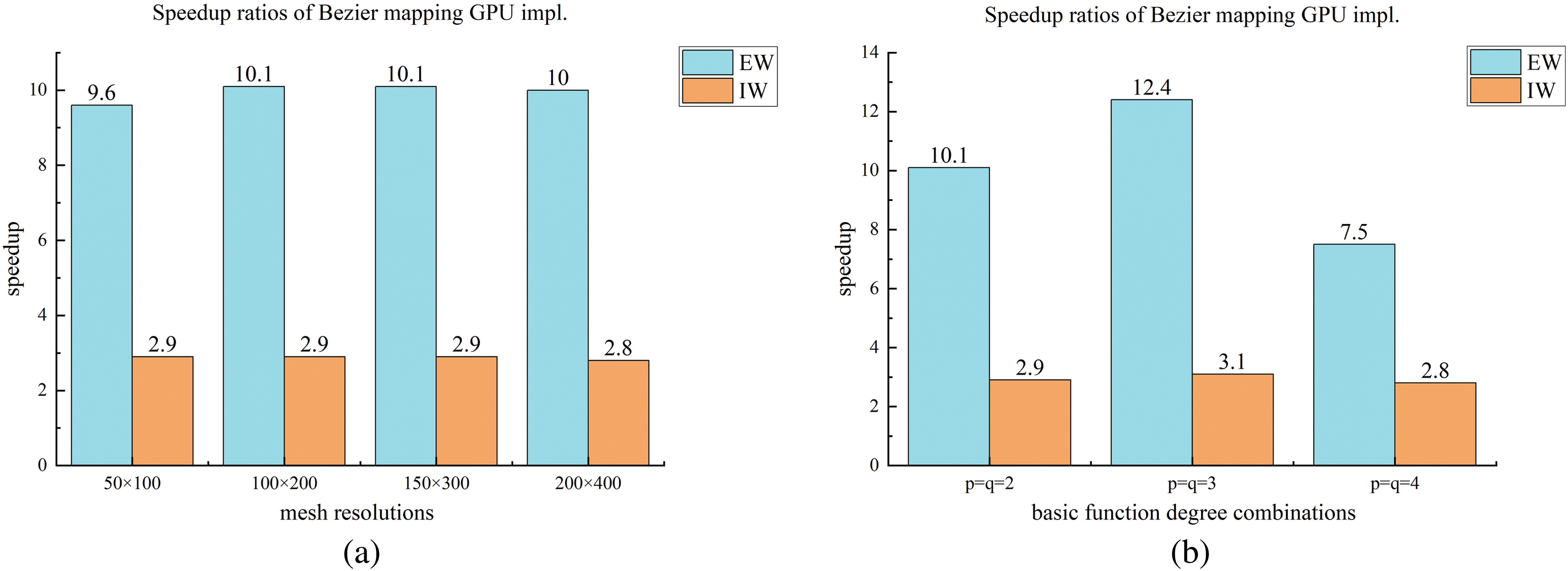
Figure 9: Illustration of speedup ratios of the proposed two parallel methods vs. to the single core CPU-based EW method for ITO using Bėzier element stiffness mapping
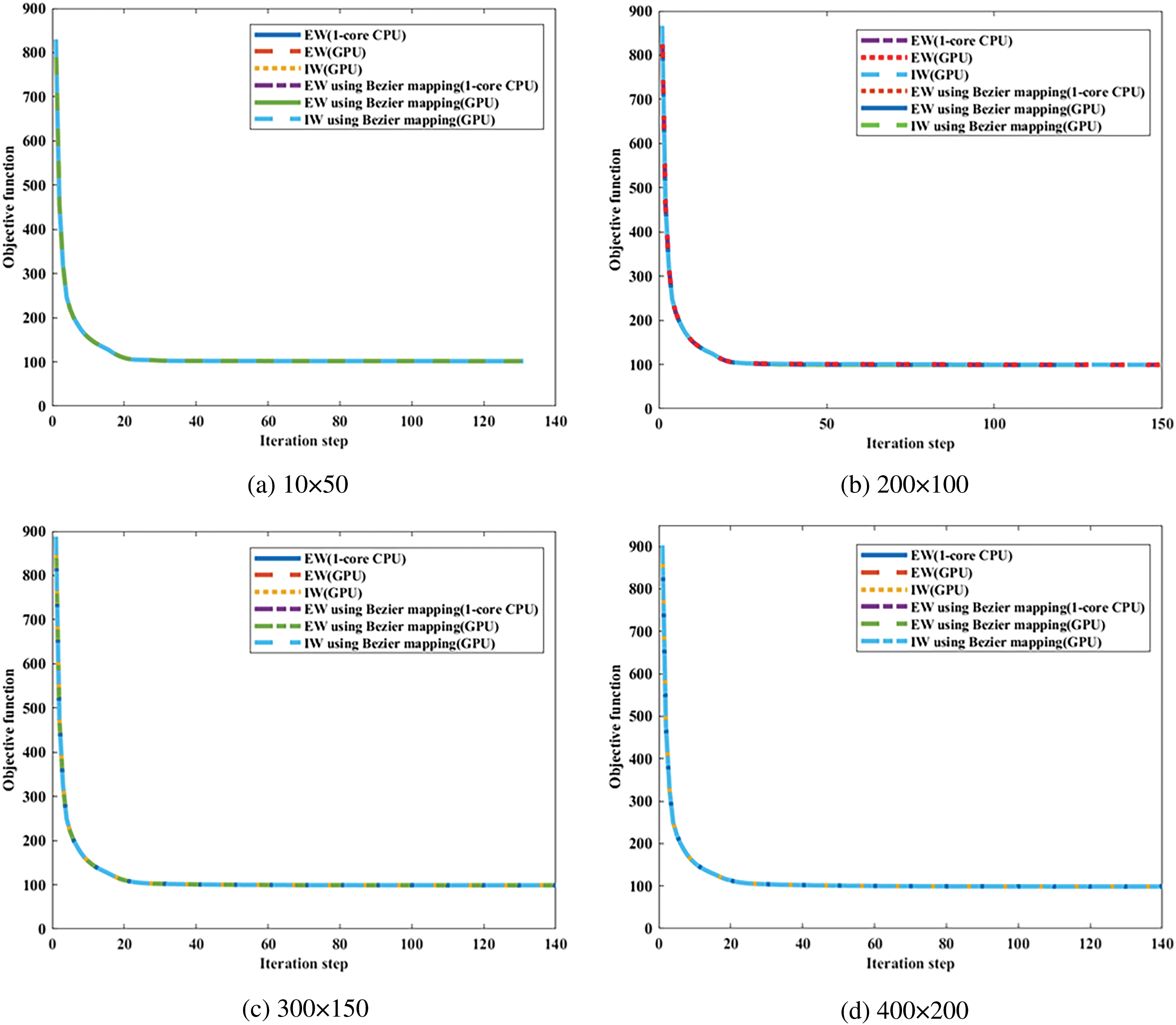
Figure 10: Illustration of convergence histories of ITOs under four different IGA mesh resolutions with bi-quadratic B-spline basis function
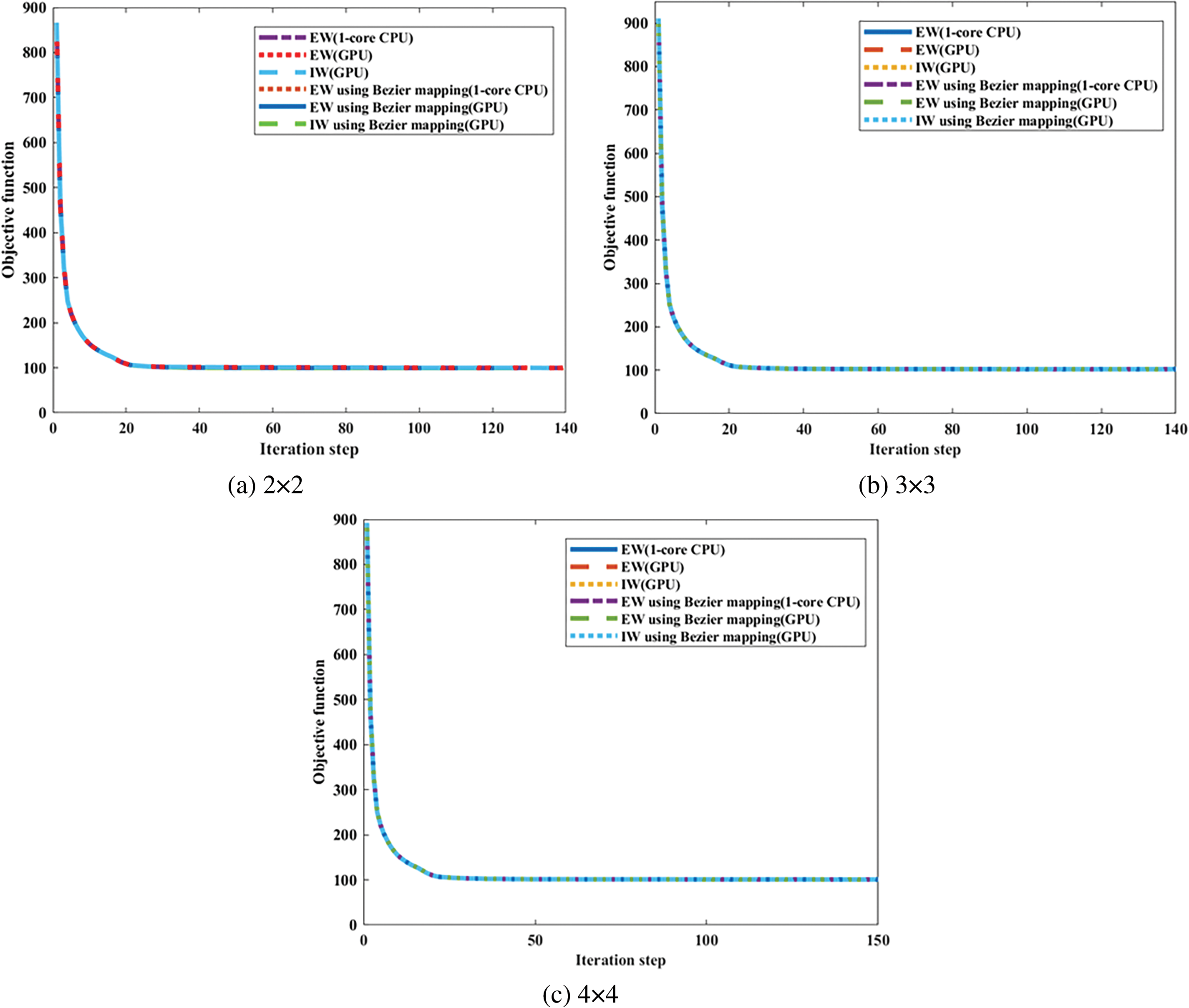
Figure 11: Illustration of convergence histories of ITO under three different degrees combinations with 100 × 200 mesh resolutions
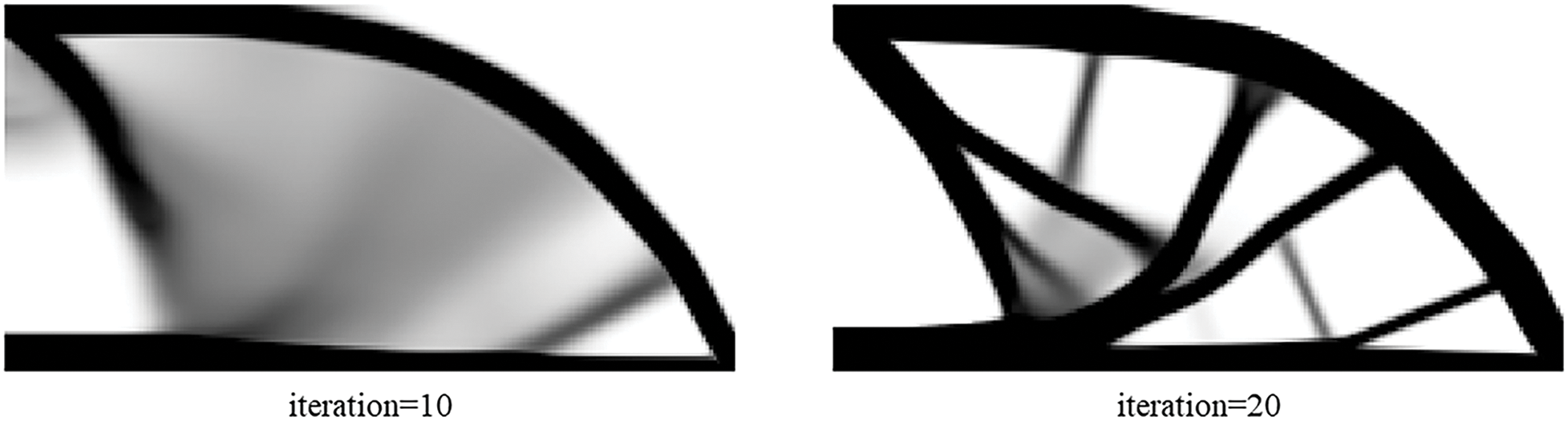
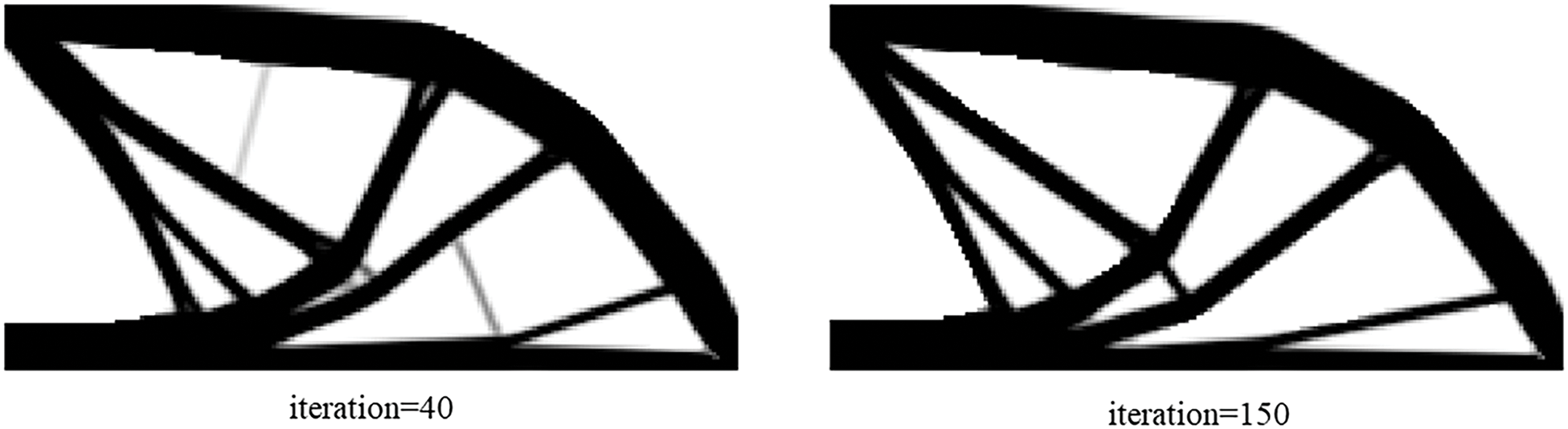
Figure 12: Illustration of history results by ITOs with the proposed and traditional global stiffness matrix updating schemes under
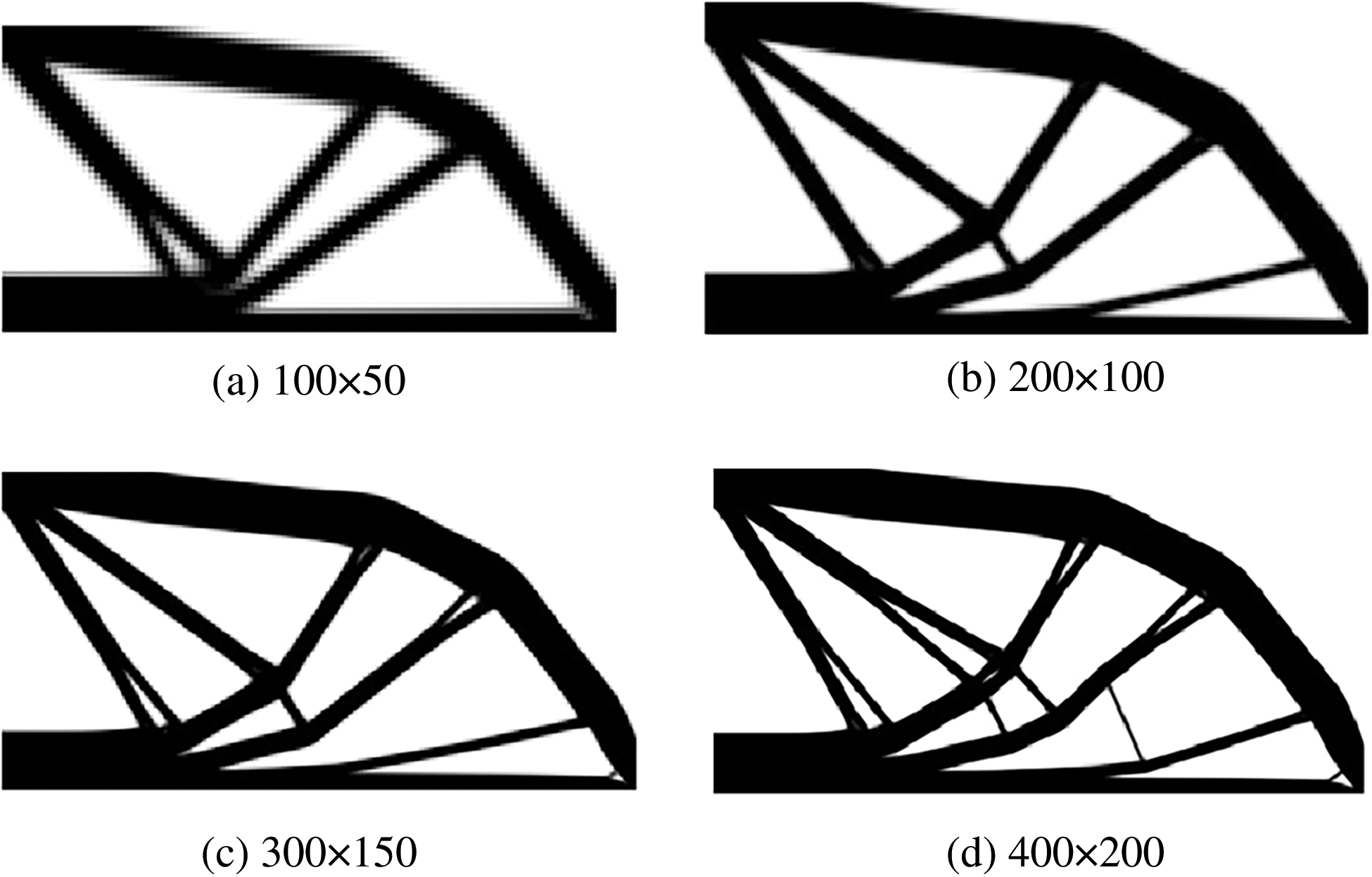
Figure 13: Illustration of optimal results of ITOs under four different mesh resolutions with identical result generated for six different stiffness matrix updating schemes
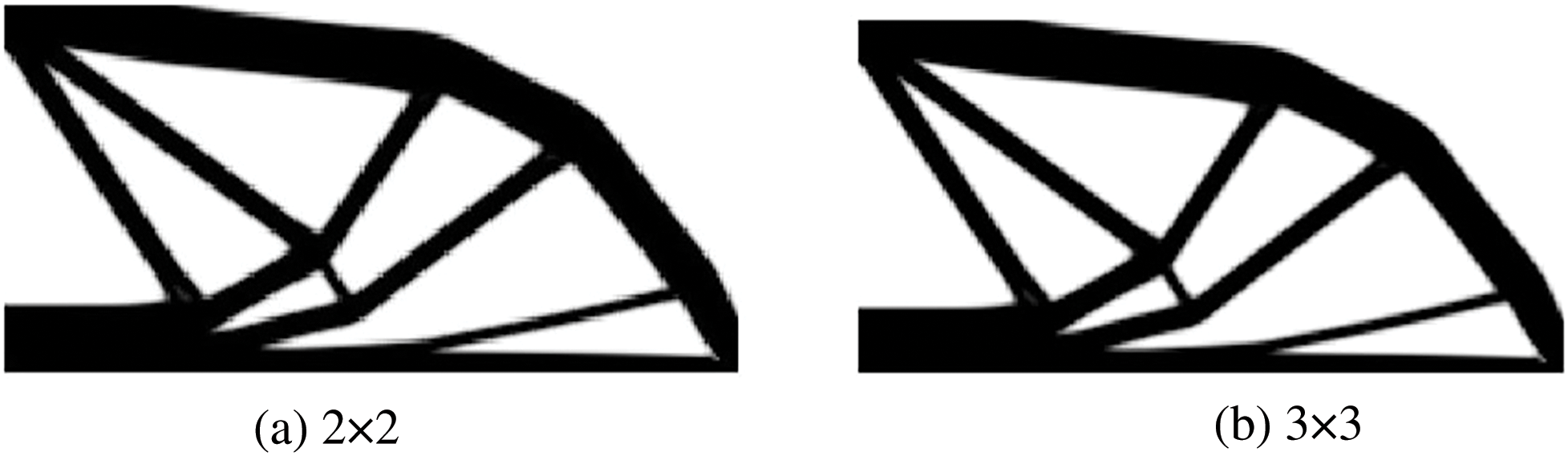
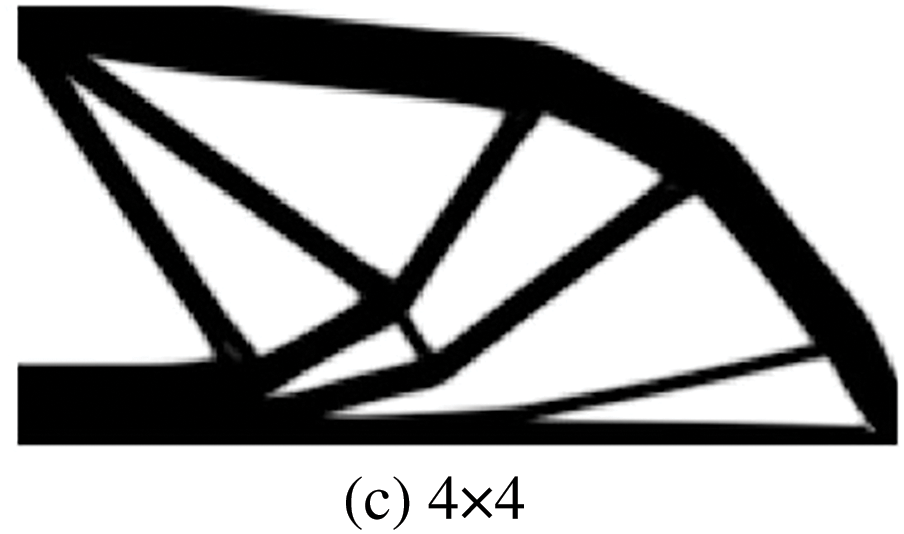
Figure 14: Illustration of optimal results of ITO under three different degrees combinations with identical result generated for six different stiffness matrix updating schemes
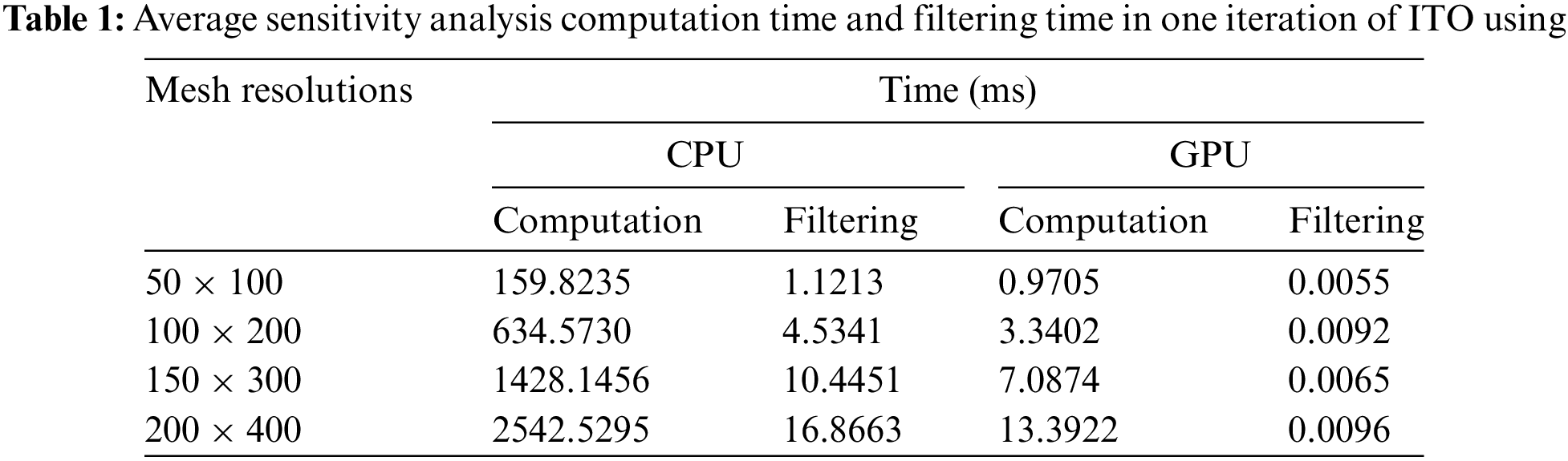
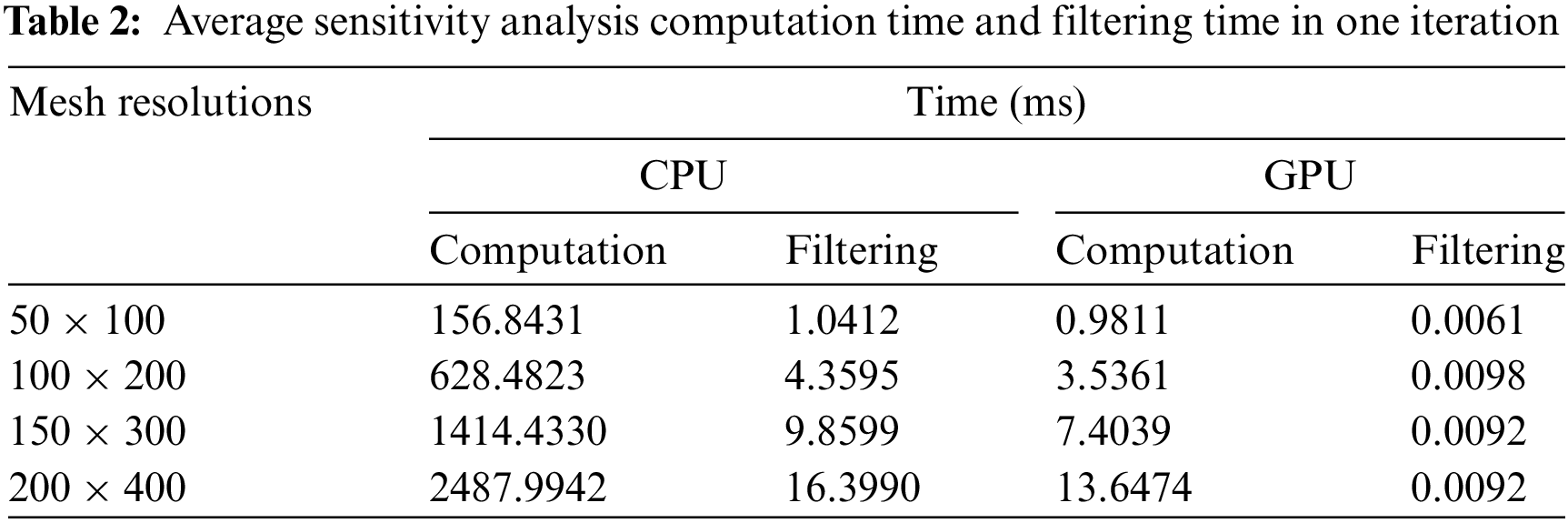
Moreover, the sensitivity analysis parallelization effect is shown in Table 1 for ITOs using Bėzier element stiffness mapping with four different IGA discretization resolutions. According to the experimental results, the parallel acceleration effect of sensitivity filtering becomes more obvious than sensitivity computation with an increase of mesh resolution, and maximum speedup is up to 190 and 1757 for the computation and filtering of sensitivity analysis, respectively. Finally, it is concluded that our proposed GPU-based EW parallel scheme is a much more effective approach than single-core CPU-based scheme for the global stiffness matrix updating and sensitivity analysis of ITO using Bėzier element stiffness mapping, without altering the convergent process and results of 2D design problems.
Michell structure is used as another benchmark to verify the effectiveness of proposed parallel ITO methods. Fig. 15 illustrates the problem setting concerning the Michell structure, where a unit downward vertical load is applied to the middle of the bottom edge, and the lower left corner is fixed, as well as the lower right corner is vertically fixed. The length-width ratio of the design domain is prescribed to 2, and the maximum volume fraction of solid material is set to 0.4.
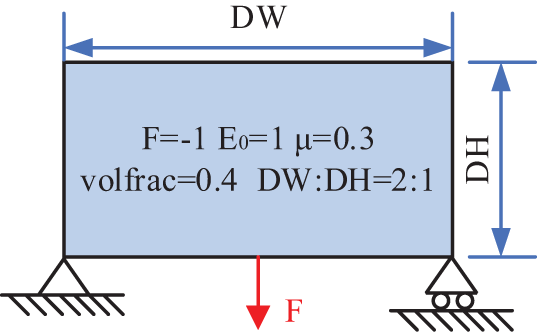
Figure 15: Illustration of problem setting for Michell structure problem [58]
Considering 50 × 100, 100 × 200, 150 × 300, and 200 × 400 mesh resolutions, the average stiffness matrix updating time for the ITO under different computational strategies is obtained as shown in Fig. 16, with bi-quadratic basis functions used. Based on the results presented in Fig. 16, it is concluded that the GPU-based EW method outperforms the GPU-based IW method in terms of stiffness matrix updating in ITO for the Michell structure design problem, independent of the calculation strategy used to obtain the stiffness matrix for each element. Furthermore, the GPU-based approaches have superior computing performance over 1-core CPU-based EW methods, and the GPU-based EW method with Bėzier element stiffness mapping is the most efficient approach among all the GPU-based methods for updating the global stiffness matrix of ITO. To investigate the influence of basis function degree combinations on the proposed parallel methods, Fig. 17 provides a comparison in the average updating time for the global stiffness matrix during one iteration between the six computational strategies under three different degree combinations of basis function, with the IGA mesh resolutions fixed at 100 × 200. According to Fig. 17, the GPU-based methods exhibit significant acceleration compared to the corresponding 1-core CPU-based methods, regardless of the basis function degree combinations. The concerned speedup ratios for GPU-based EW and IW method using Bėzier element stiffness mapping are presented in Fig. 18 in comparison with the 1-core CPU-based EW method, where the observed speedup ratios under various mesh resolutions and basis function degree combinations are comparable to those observed for MBB beam problem. This indicates that the acceleration effect remains consistently effective across different scenarios for 2D TO problems, exhibiting reliable and favorable performance. In order to compare the numerical process of ITOs using different strategies in updating the global stiffness matrix, the convergence histories under different mesh resolutions and degree combinations are presented in Figs. 19 and 20, respectively. The history designs under mesh resolutions are shown in Fig. 21. While the corresponding converged results of ITO are displayed in Figs. 22 and 23. It should be noted that these convergence histories and design results remain unchanged with the variation in the computing strategies used for the global stiffness matrix since the various global stiffness matrix updating schemes in ITO are equivalent numerically.
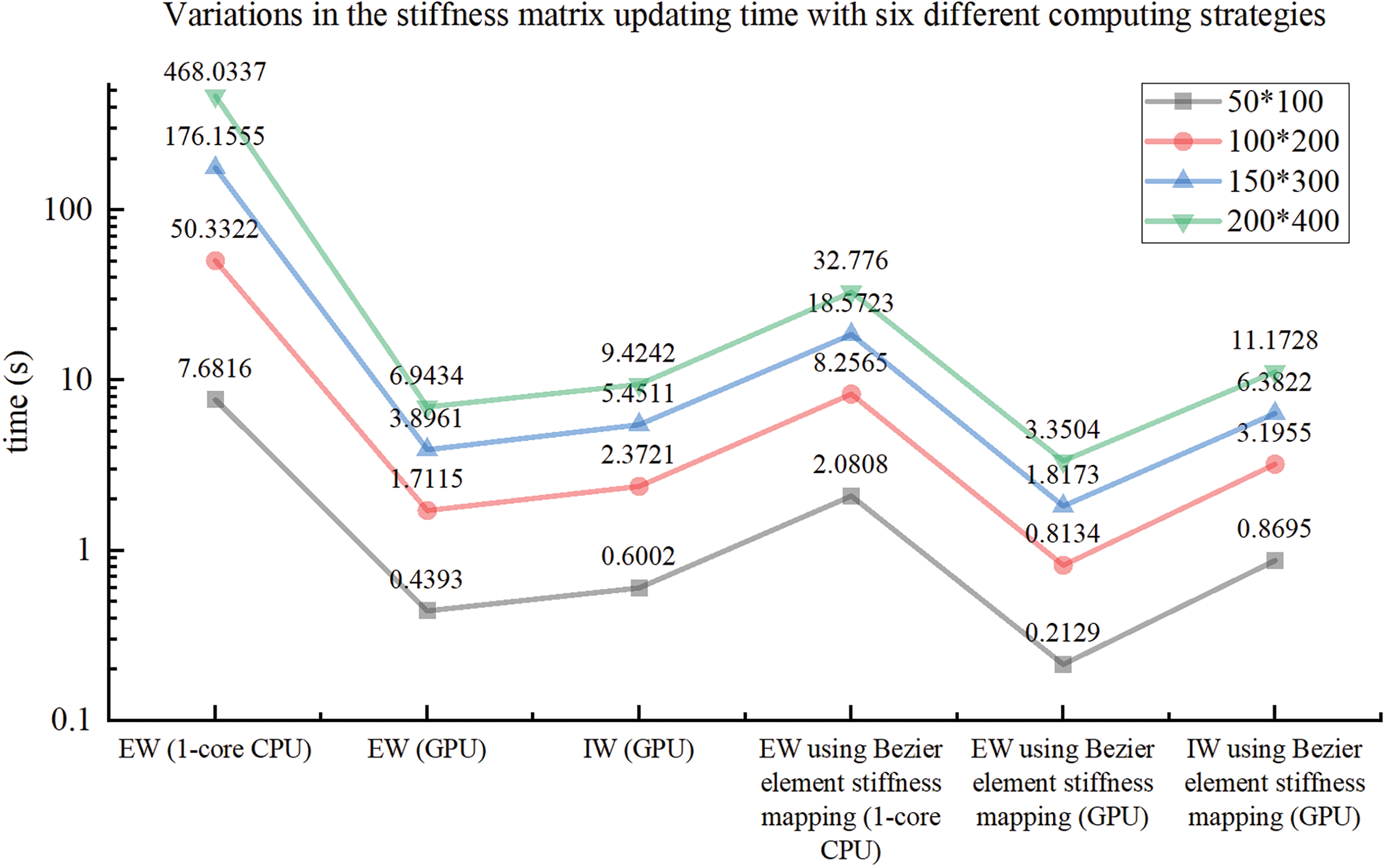
Figure 16: Illustration of variations in the stiffness matrix updating time with six different computing strategies for four different mesh resolutions
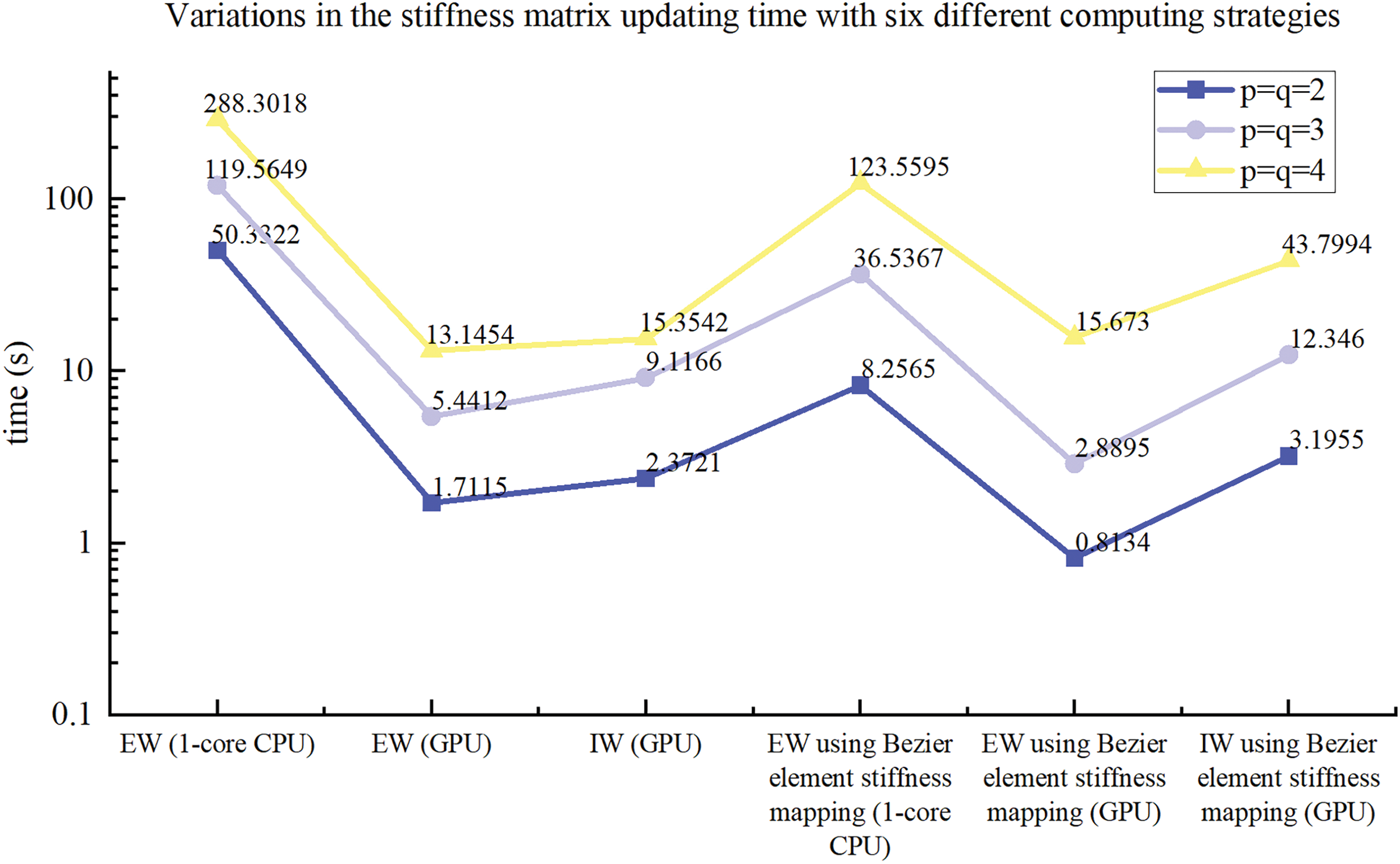
Figure 17: Illustration of variations in the stiffness matrix updating time with six different computing strategies for three different degrees combinations
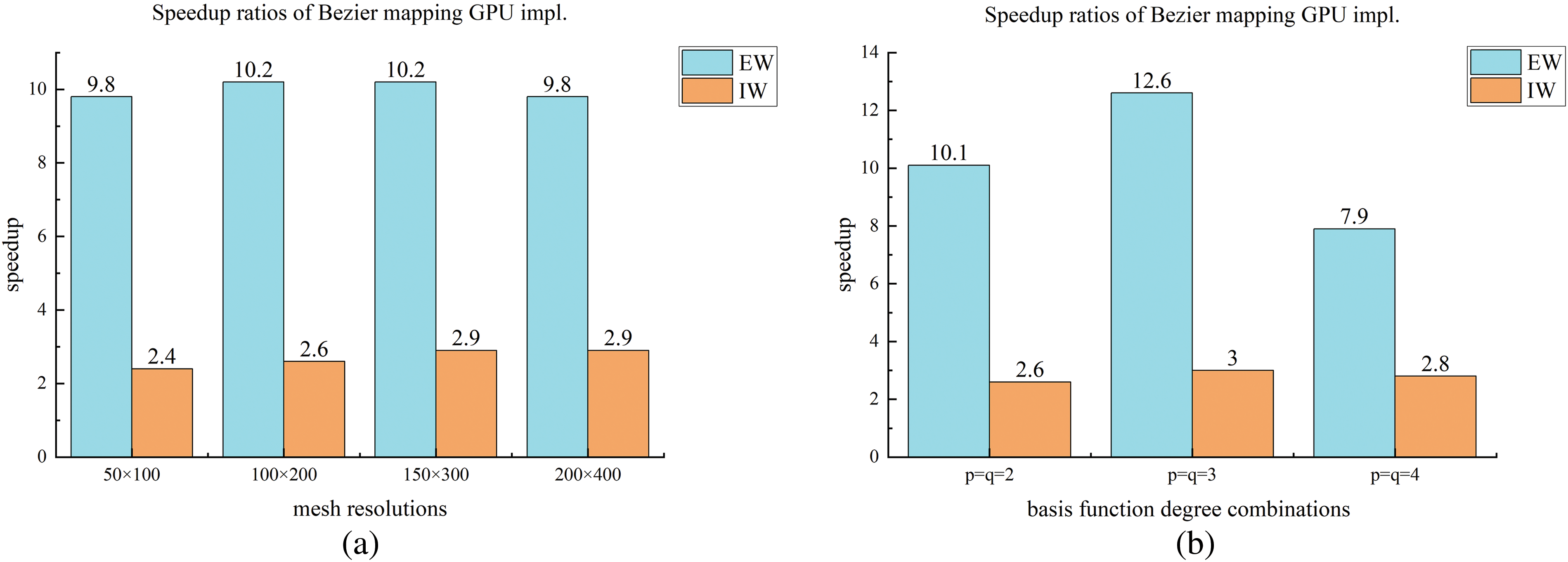
Figure 18: Illustration of speedup ratios of the proposed two parallel methods vs. to the single core CPU-based EW method for ITO using Bėzier element stiffness mapping
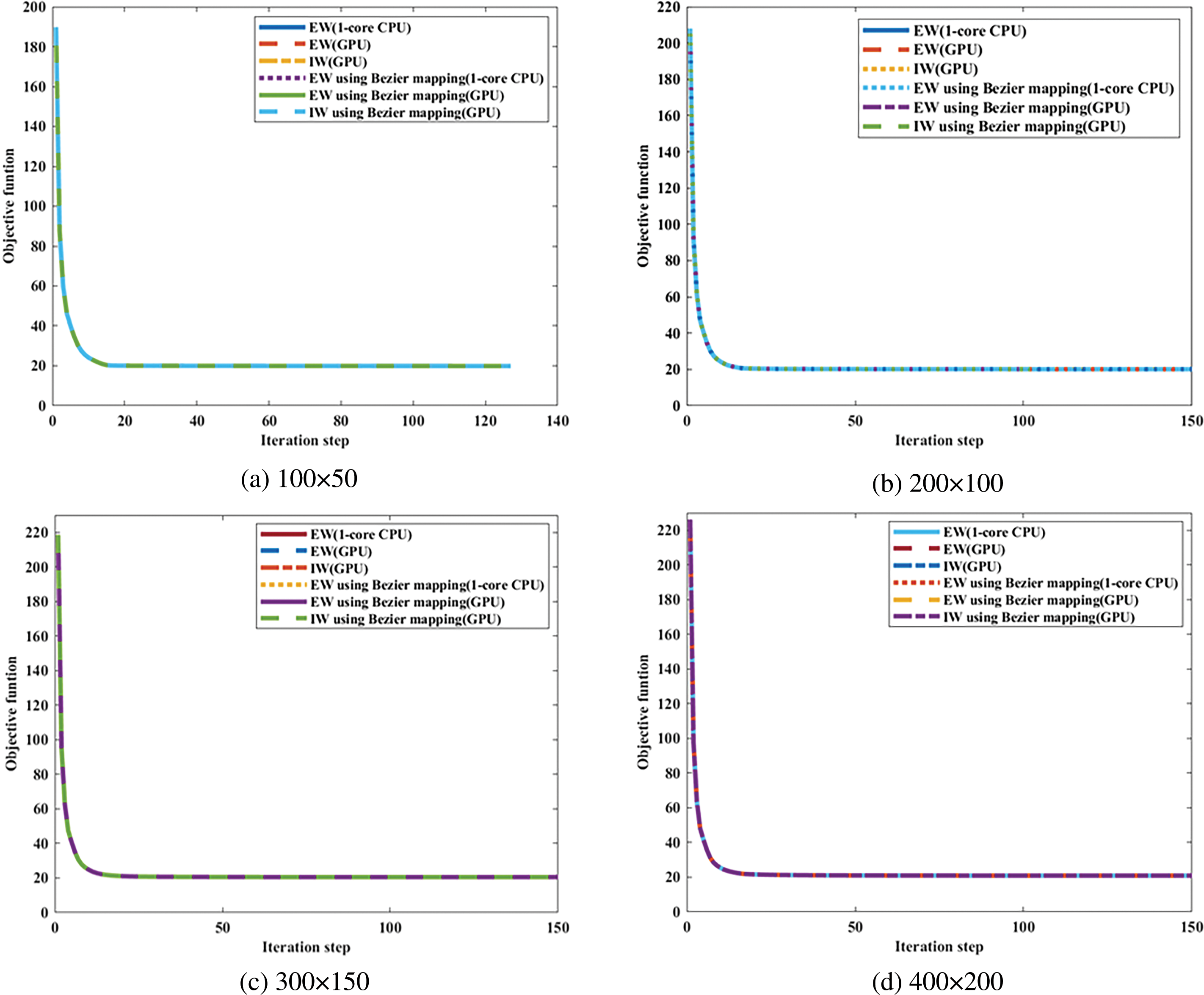
Figure 19: Illustration of convergence histories of ITO under different mesh resolutions with bi-quadratic B-spline basis function order
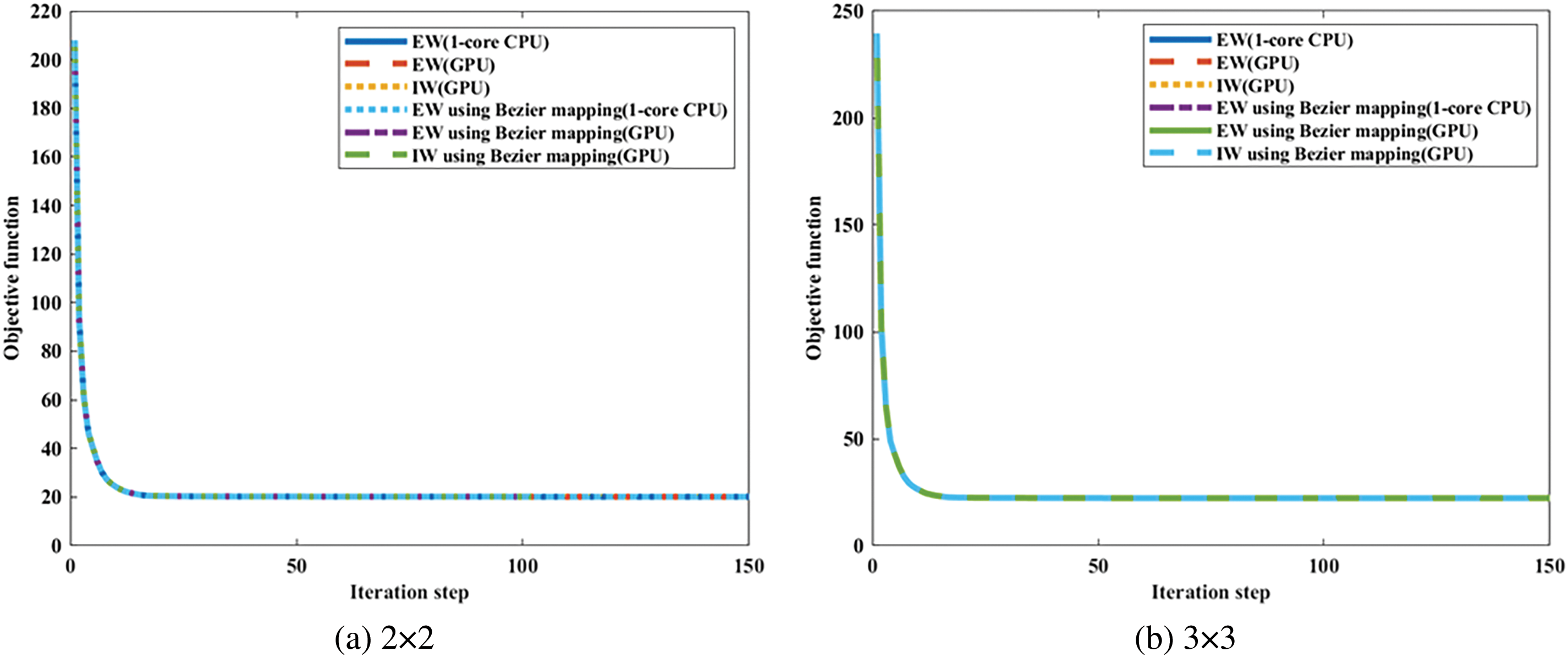
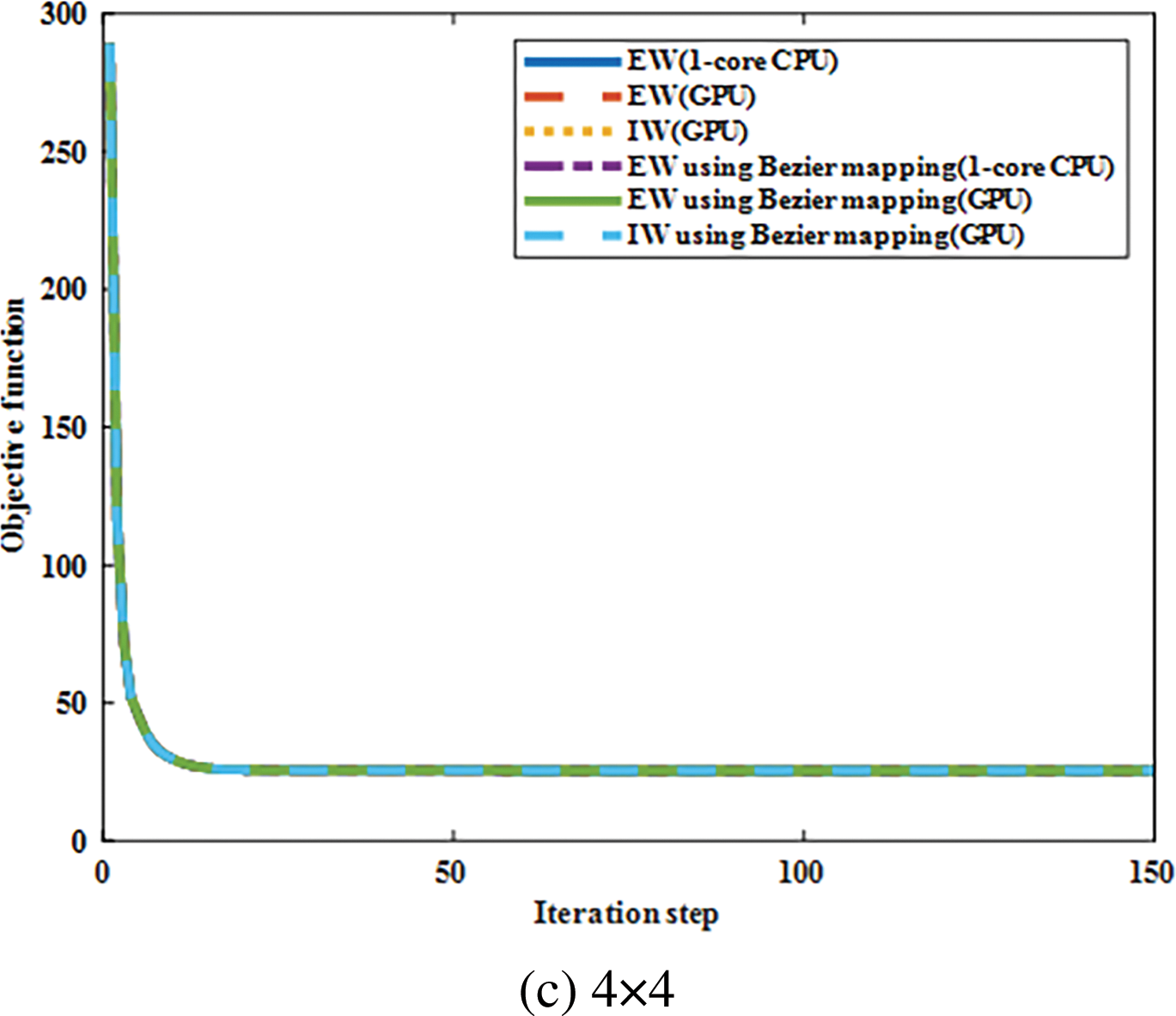
Figure 20: Illustration of convergence histories of ITO under three different degrees combinations with 100 × 200 mesh resolutions
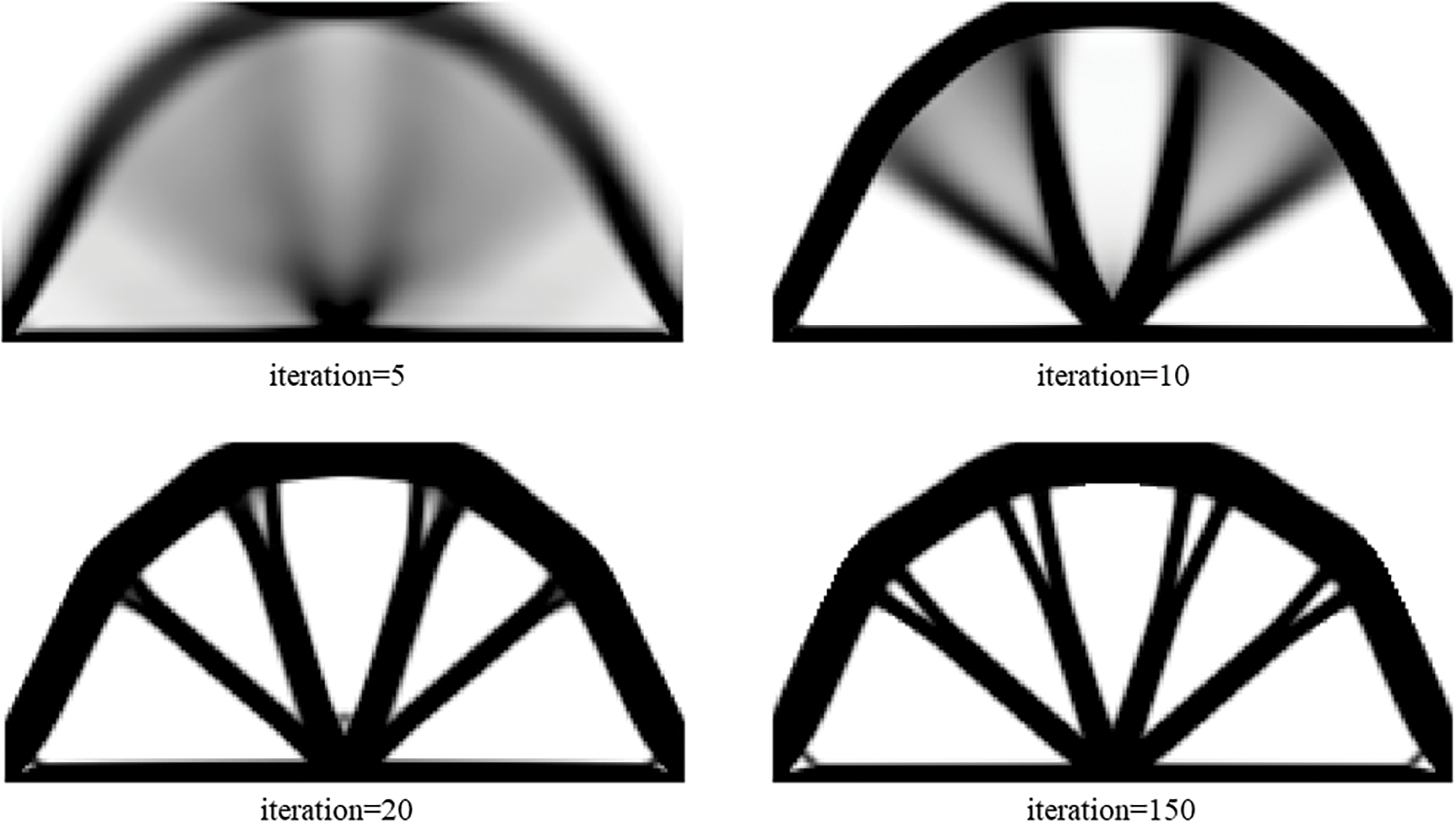
Figure 21: Illustration of history results by ITOs with the proposed and traditional global stiffness matrix updating schemes under
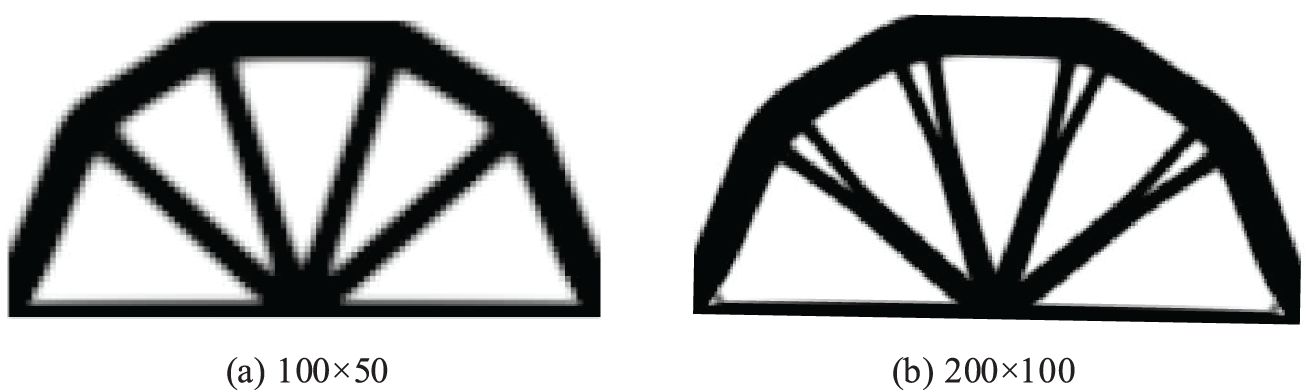
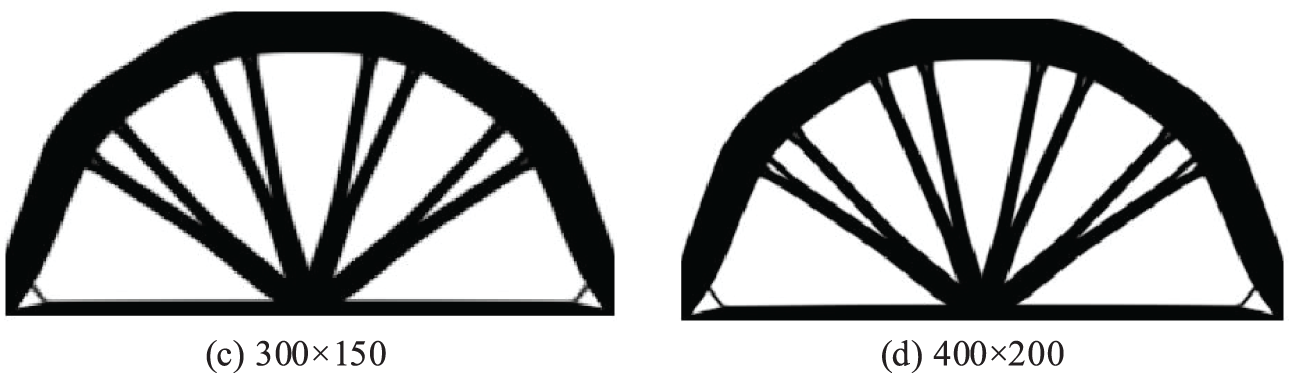
Figure 22: Illustration of optimal results of ITOs under four different mesh resolutions with identical result generated for six different stiffness matrix updating schemes
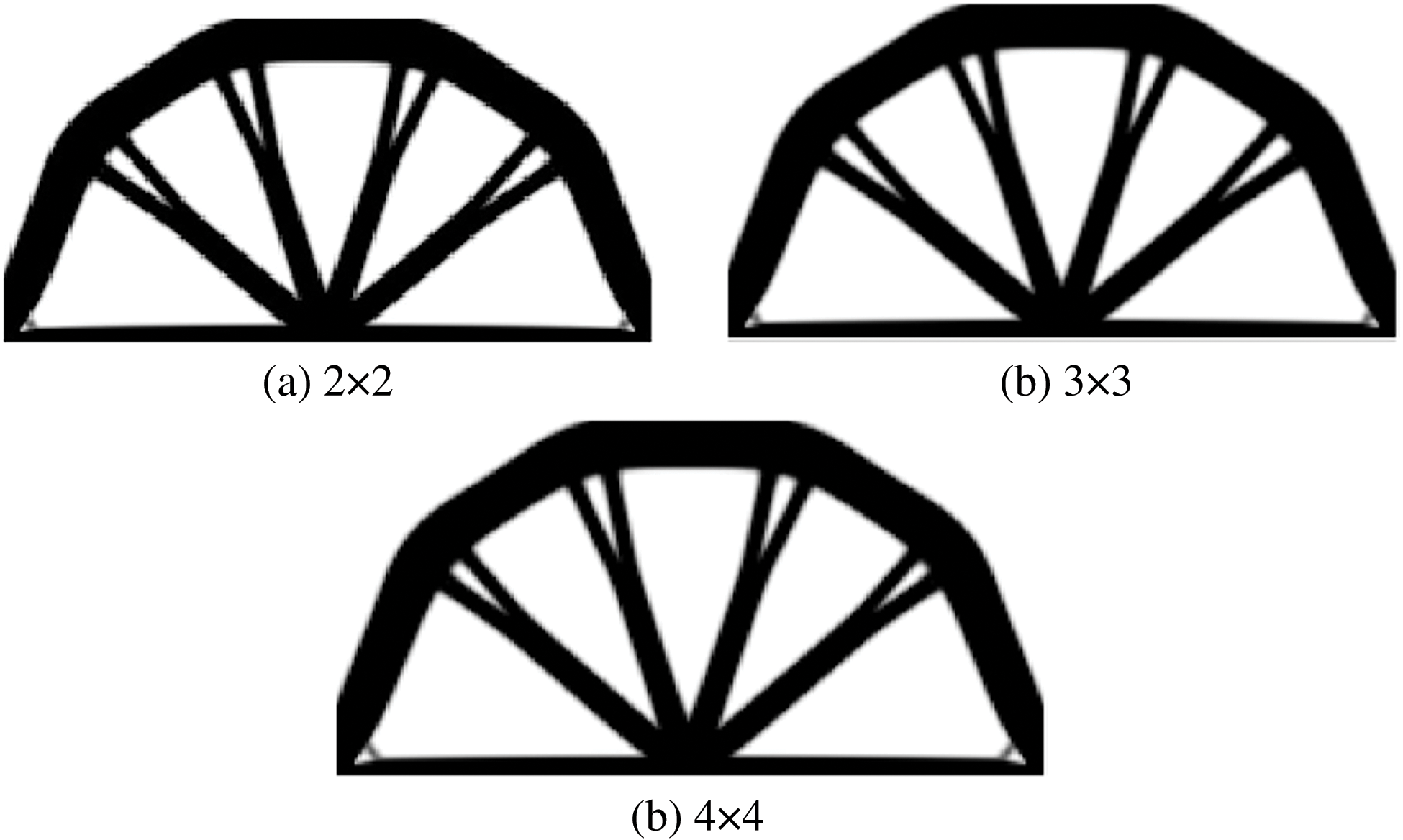
Figure 23: Illustration of optimal results of ITO under three different degrees combinations with identical result generated for six different stiffness matrix updating schemes
For ITO, the solver usually plays a key role in affecting its efficiency, and an appropriate numerical solver can accelerate the sparse matrix-solving process significantly. In this numerical example, we compared the solution time of a sparse matrix in one iteration using Eigen and AMGCL, where the conjugate gradient method is treated as the numerical solver. Besides, the relaxation method of the algebraic multigrid method is Sparse approximate inverse (SPAI) smoother, and the coarsening strategy is smoothed aggregation. As shown in Fig. 24, the AMGCL solver exhibits an increasingly pronounced acceleration effect as the increase of number of IGA elements than the Eigen solver, where the maximum speedup ratio reaches 30.3. The GPU-enabled EW schemes are compared with the 1-core CPU-based scheme in Table 2 for sensitivity analysis of ITO using Bėzier element stiffness mapping, where a significant acceleration effect is obtained by the proposed GPU method. Finally, it arrives at a conclusion that the proposed GPU-based EW parallel scheme with AMGCL treated as a solver is a promising method to improve the numerical efficiency of ITO using Bėzier element stiffness mapping.
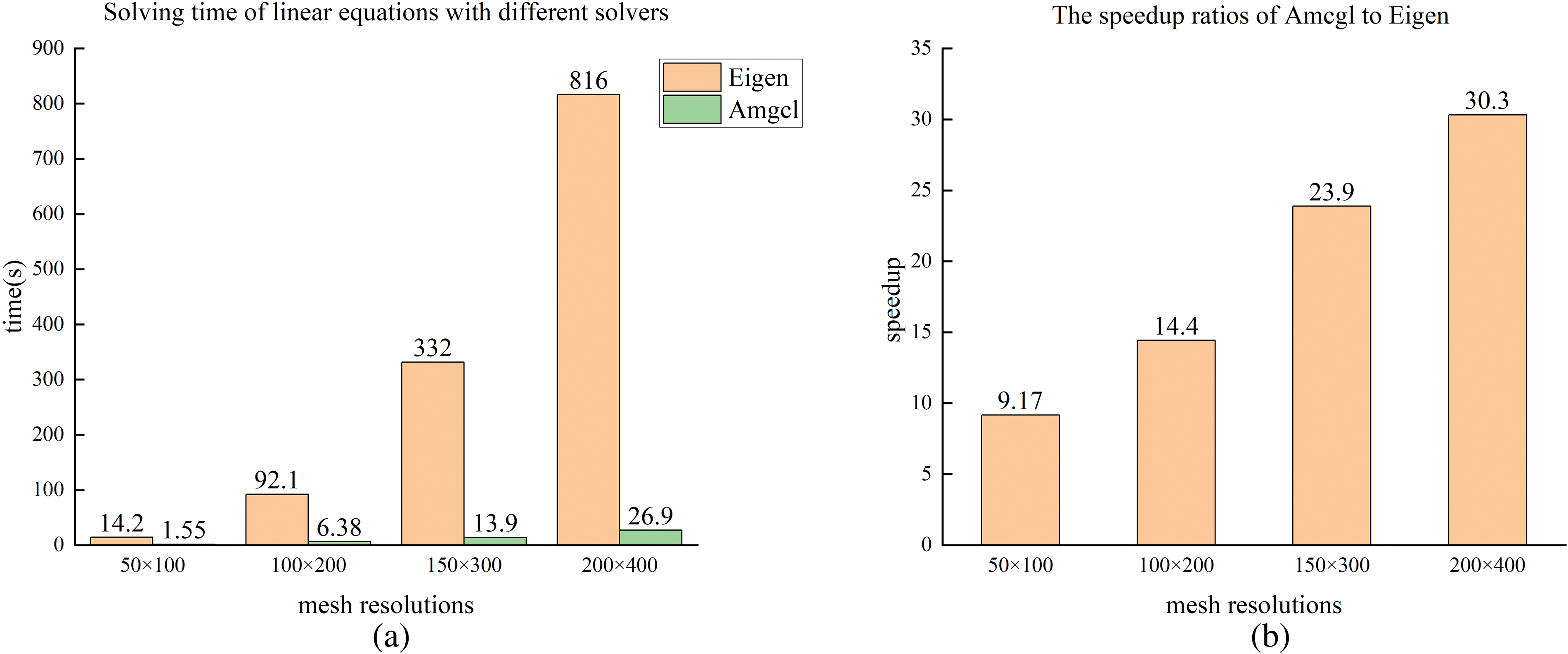
Figure 24: Illustration of solving time for linear equations with Eigen and AMGCL
4.3 L-Shaped Multi-Patch Structure
In this section, we focus on the L-shaped cantilever discretized into multi-patch IGA mesh as presented in Fig. 25a, to validate the extension of the proposed EW parallel scheme from single patch case to multi-patch case for ITO using Bėzier element stiffness mapping. Since the GPU-based EW method outperforms the GPU-based IW method, as shown in the aforementioned benchmarks, only the GPU-based EW scheme is taken into consideration for this multi-patch design problem. As shown in Fig. 25b, a fixed boundary condition is applied to the top edge of the first patch, and an external unit force is vertically downward imposed on the top right corner of the third patch. Additionally, a volume constraint of 0.4 is set for solid material usage.
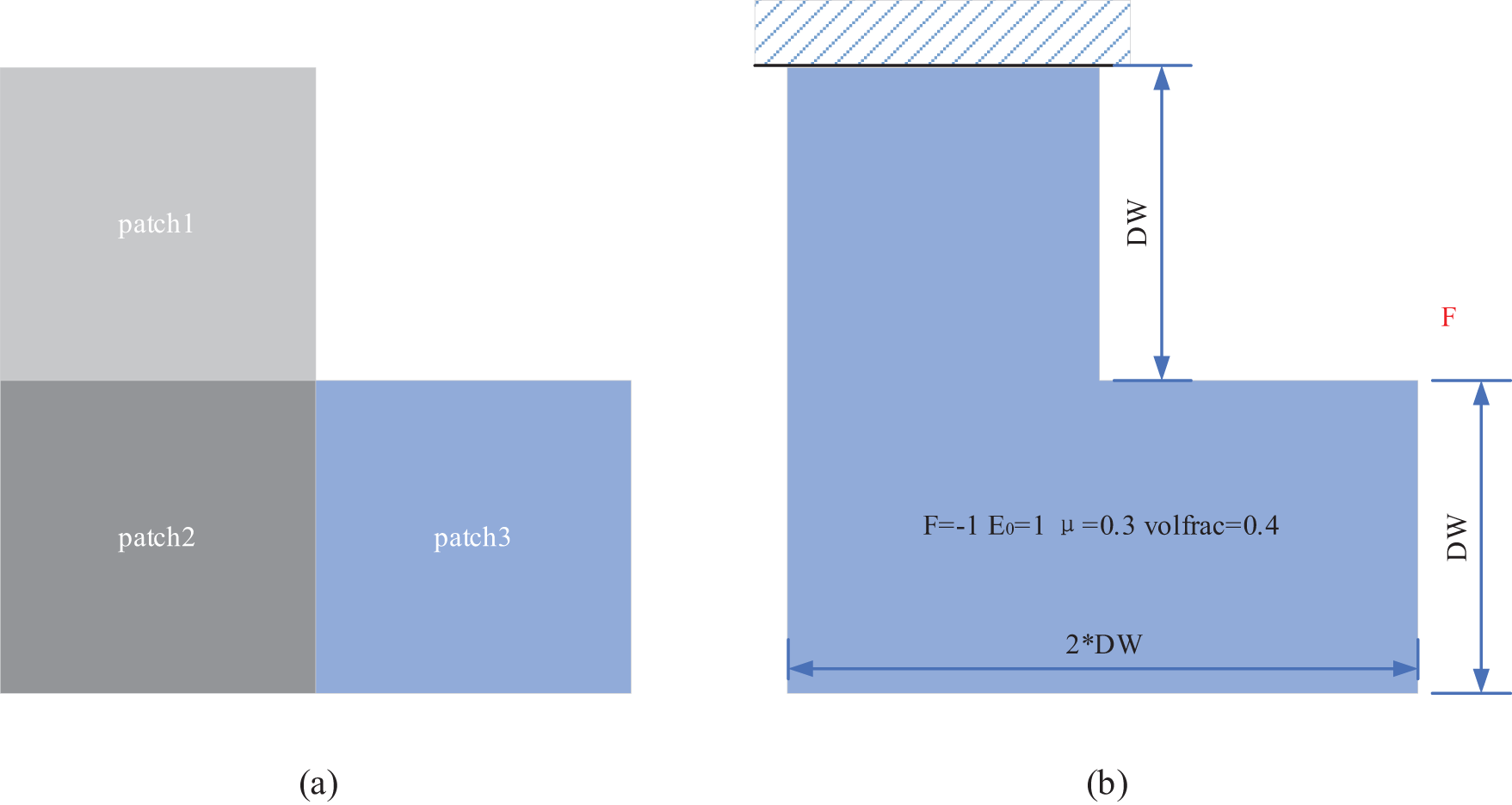
Figure 25: (a) L-shaped computational domain discretized into three IGA patches with regular shape; (b) Problem setting for L-shaped structure
For all IGA patches, the B-spline basis function order is selected as bi-quadratic. The average updating time for the global stiffness matrix updating of ITOs with 1-core CPU and GPU-based EW methods is tabulated. Considering the optimization of computation within Matlab, the acceleration ratio has decreased compared to previous examples written in C++. The difference between the matrix computation environment and data transmission has a certain impact on the results.
Table 3 in one iteration under three different mesh resolutions for all patches. As the number of elements increases for each IGA patch, the acceleration effect of the proposed GPU-based EW method is increasingly improved. Similar to the single patch cases, both the convergence histories and converged designs are illustrated in Figs. 26 and 27, respectively, which advocate the numerical equivalence between the proposed GPU-based and CPU-based methods in updating the global stiffness matrix. The history designs under mesh resolutions per patch are shown in Fig. 28. This indicates that the proposed GPU parallel framework has a promising potential to enhance the numerical efficiency for multi-patch ITO design problems. Considering the optimization of computation within Matlab, the acceleration ratio has decreased compared to previous examples written in C++. The difference between the matrix computation environment and data transmission has a certain impact on the results.
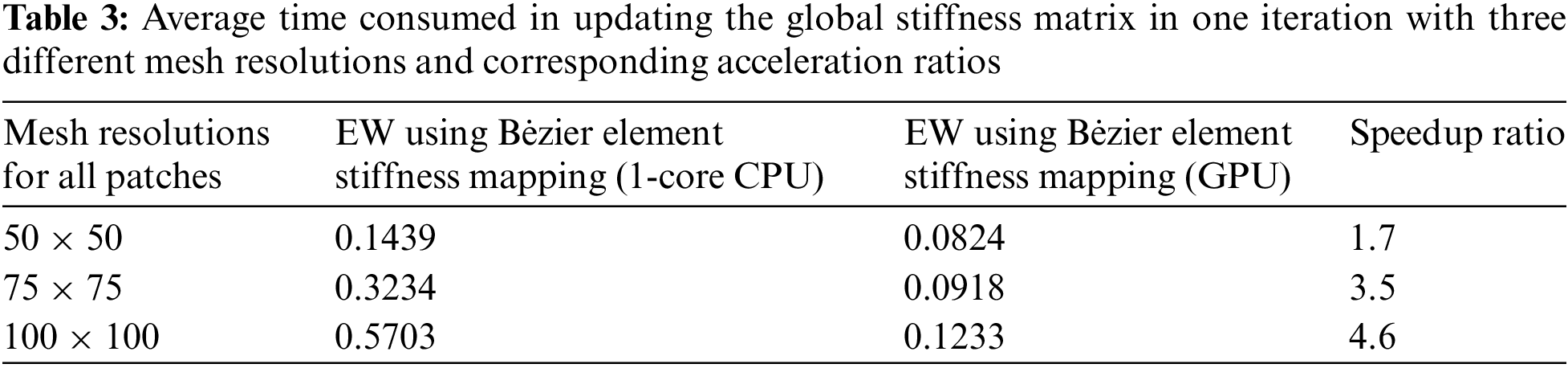
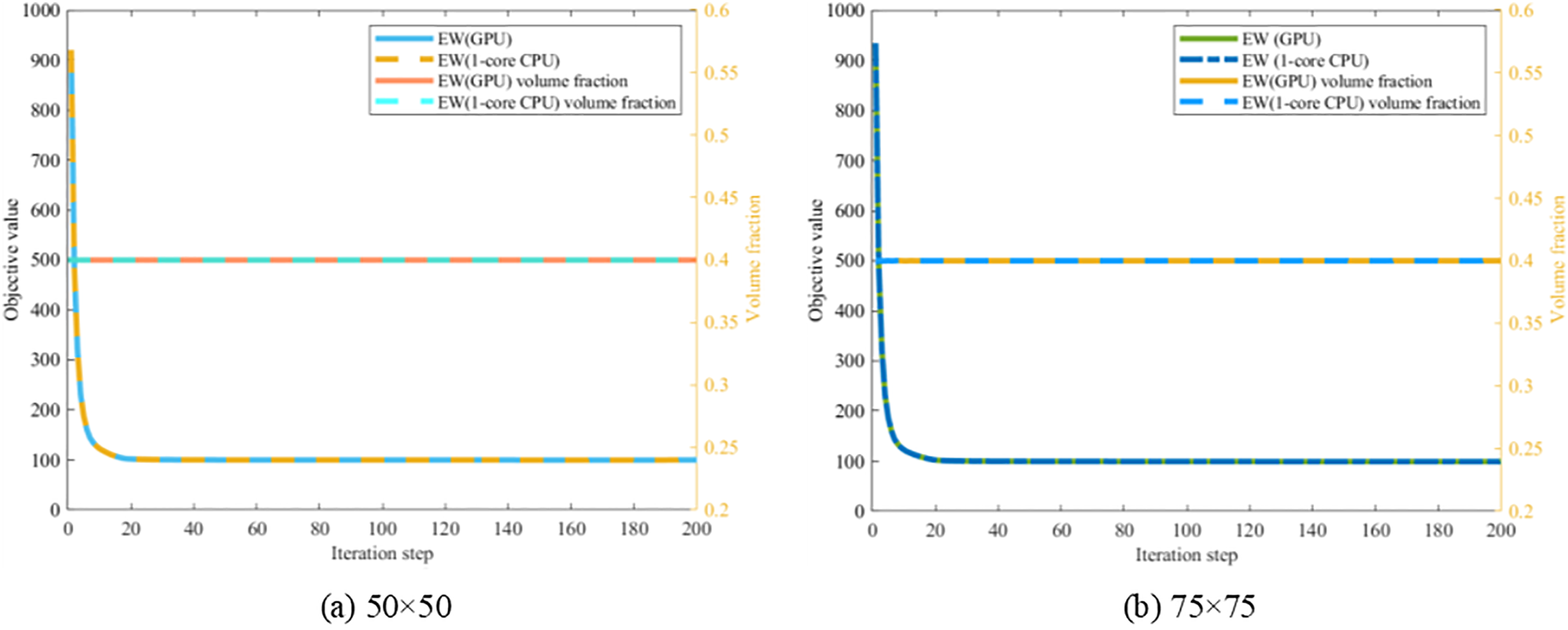
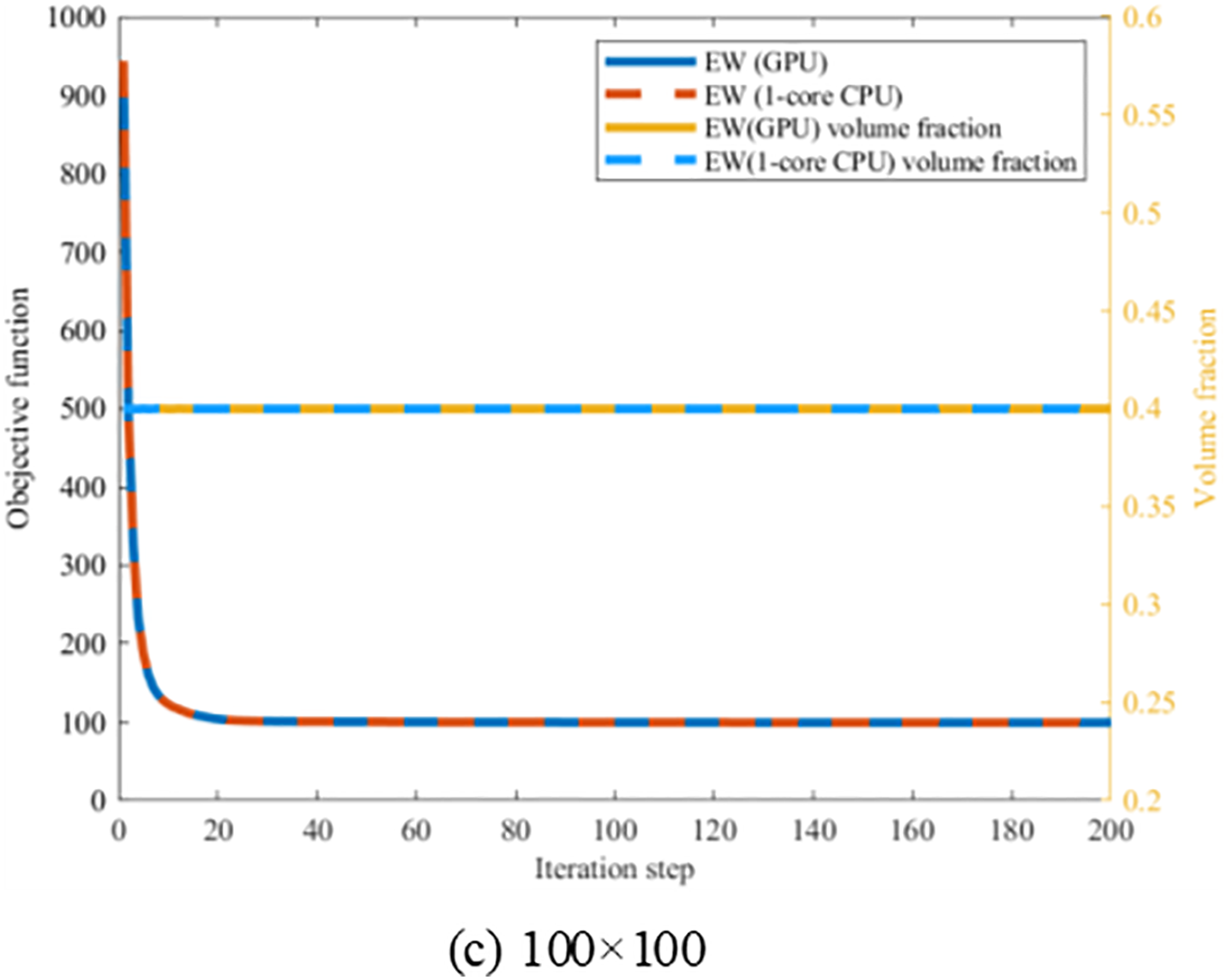
Figure 26: Illustration of convergence histories of ITO under different mesh resolutions per patch with bi-quadratic B-spline basis function
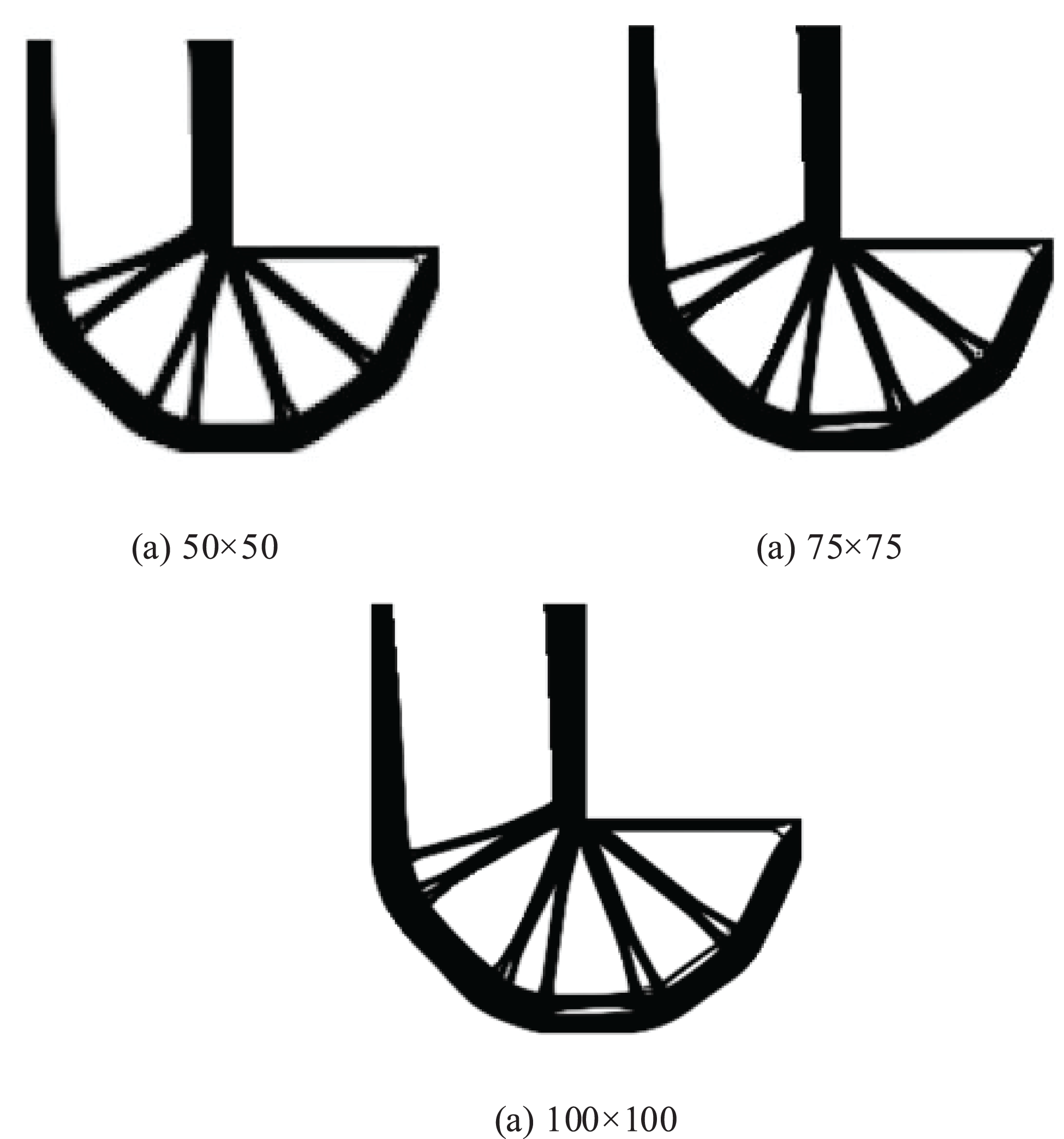
Figure 27: Illustration of the converged design results by ITOs with the proposed and traditional global stiffness matrix updating schemes under different mesh resolutions per patch
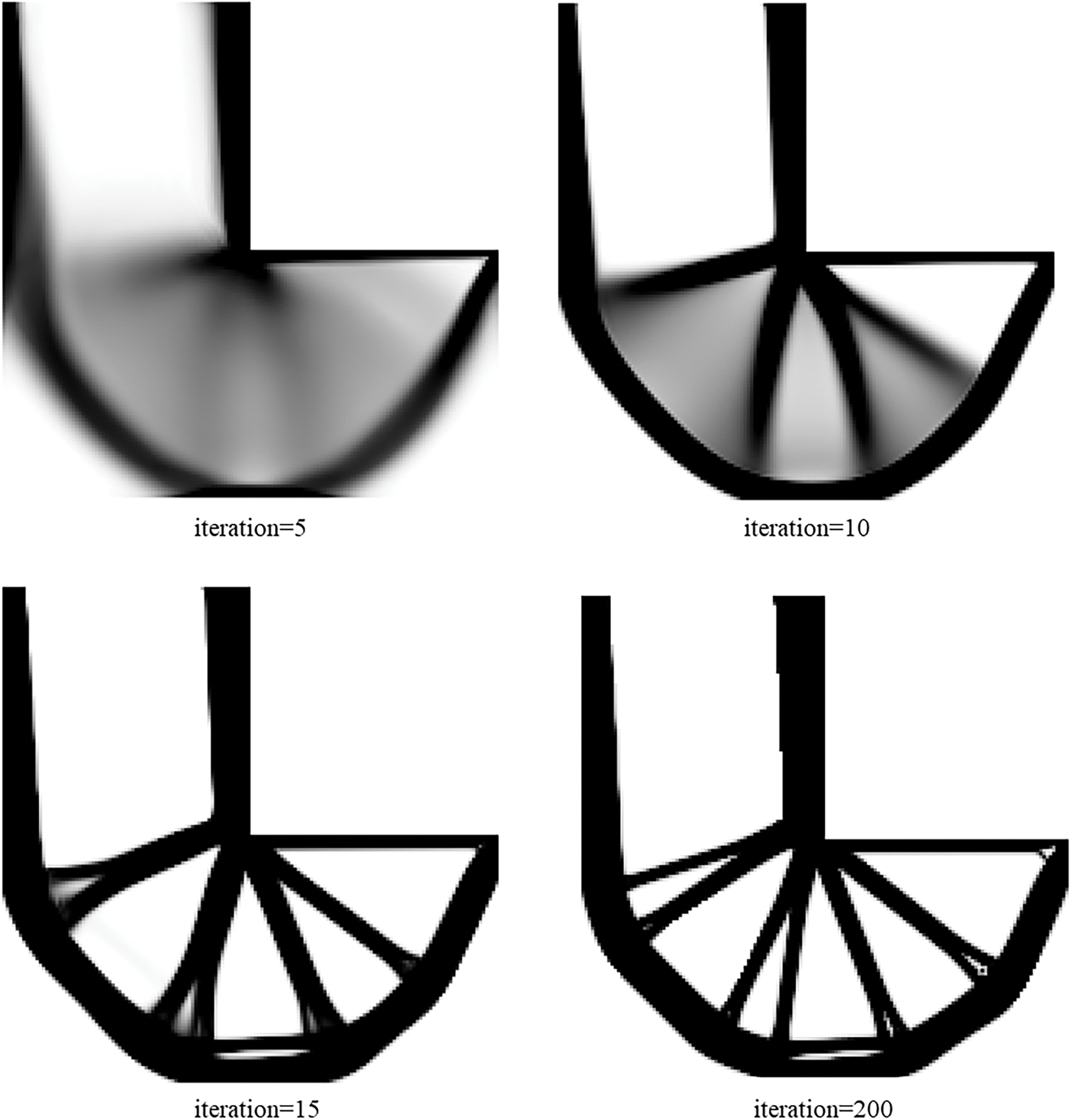
Figure 28: Illustration of history results by ITOs with the proposed and traditional global stiffness matrix updating schemes under
4.4 Three-Dimensional Cantilever Beam
The 3D cantilever beam serves as the final numerical example in this study, demonstrating the effectiveness of the proposed GPU-enabled ITO with Bėzier element stiffness mapping in 3D scenarios. Fig. 29 illustrates the problem setup, where the left face is fixed, and an external unit force is applied in the center of the right side. The volume constraint is set to 0.4.
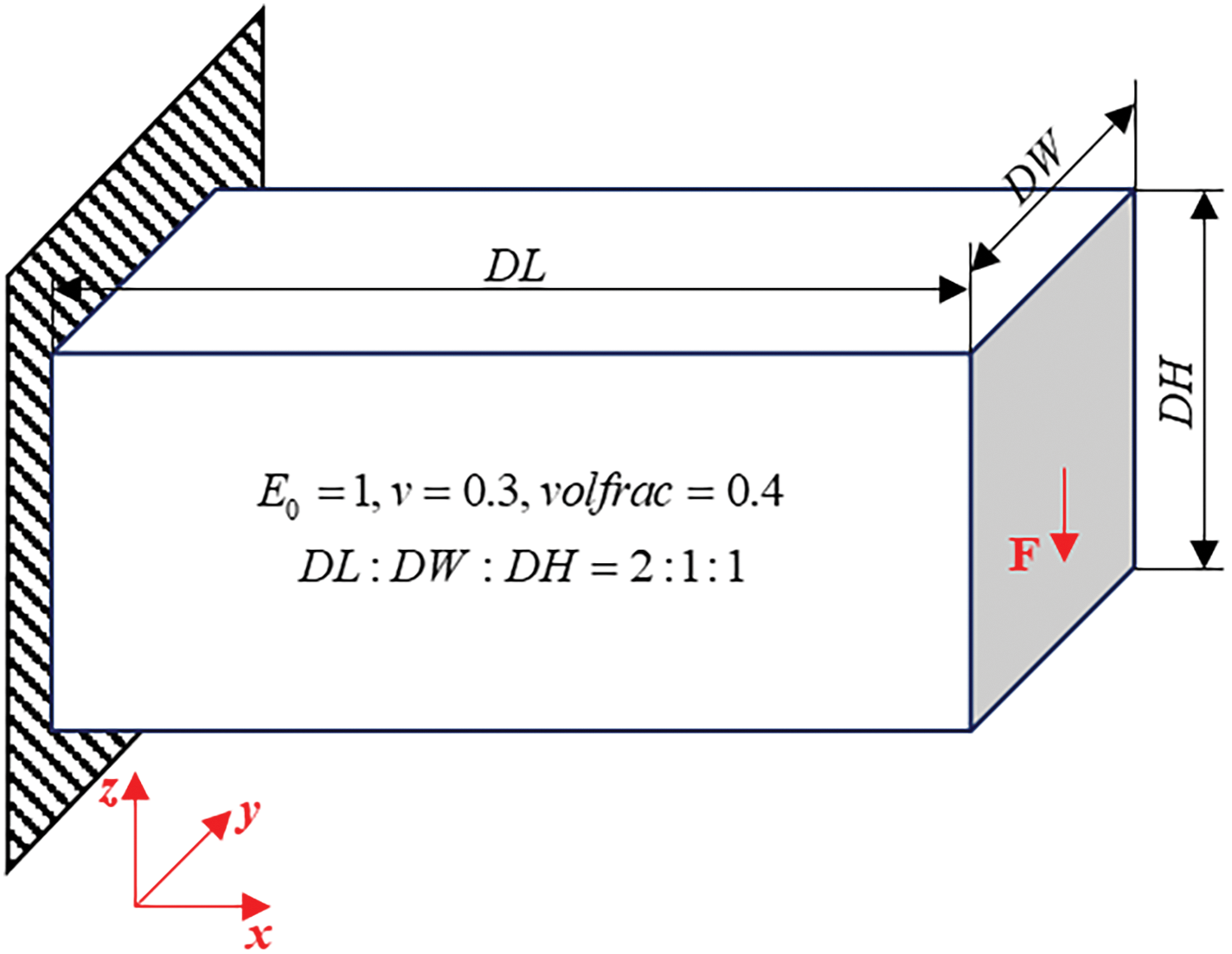
Figure 29: The problem setting for 3D cantilever numerical example
For all IGA elements, the order of the B-spline basis functions is chosen to be bi-quadratic. The average time required for updating the global stiffness matrix of ITOs with 1-core CPU and GPU-based EW methods is presented in Table 4. The convergence histories, history designs and converged designs are illustrated in Figs. 30–32, demonstrating the consistency of the results obtained through the two methods. It can be observed that the maximum speedup ratio is 1.22 in the 3D cantilever beam case, and the acceleration effect increases with the increase of the number of elements. However, compared with the 2D case, the overall acceleration effect is reduced. On the one hand, the data load of each thread in the 3D case is significantly larger, such as the increase in the size of the standard stiffness matrix of Bėzier element
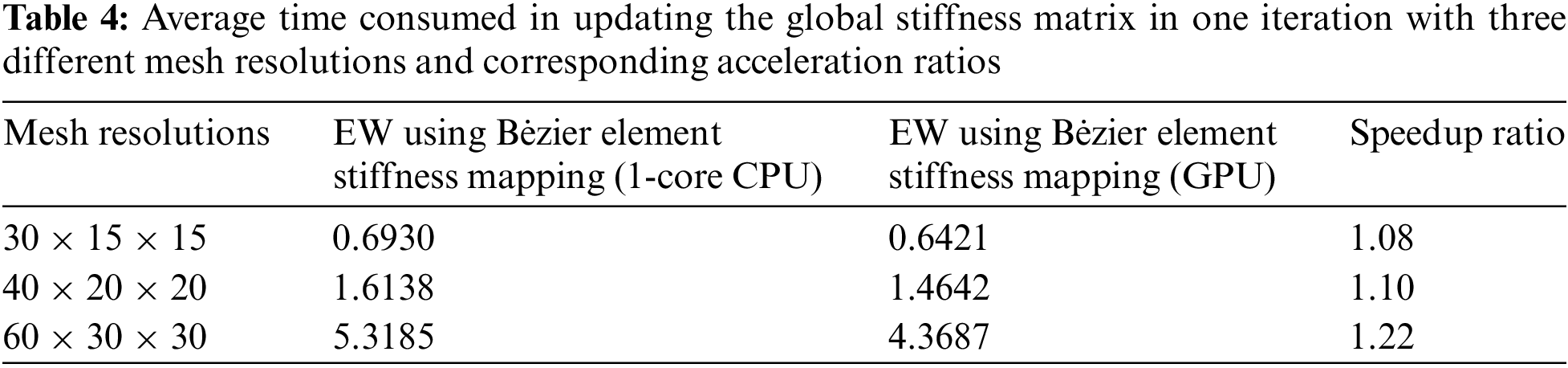
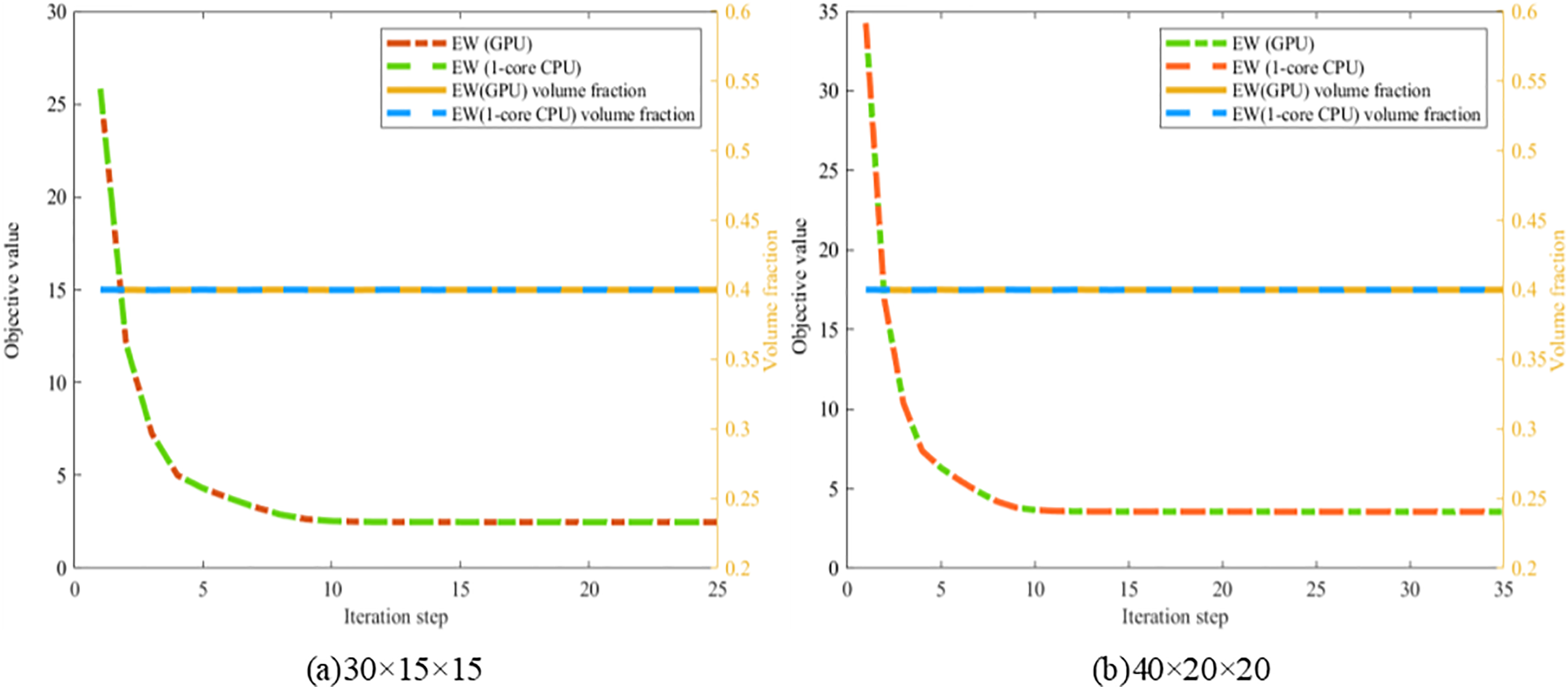
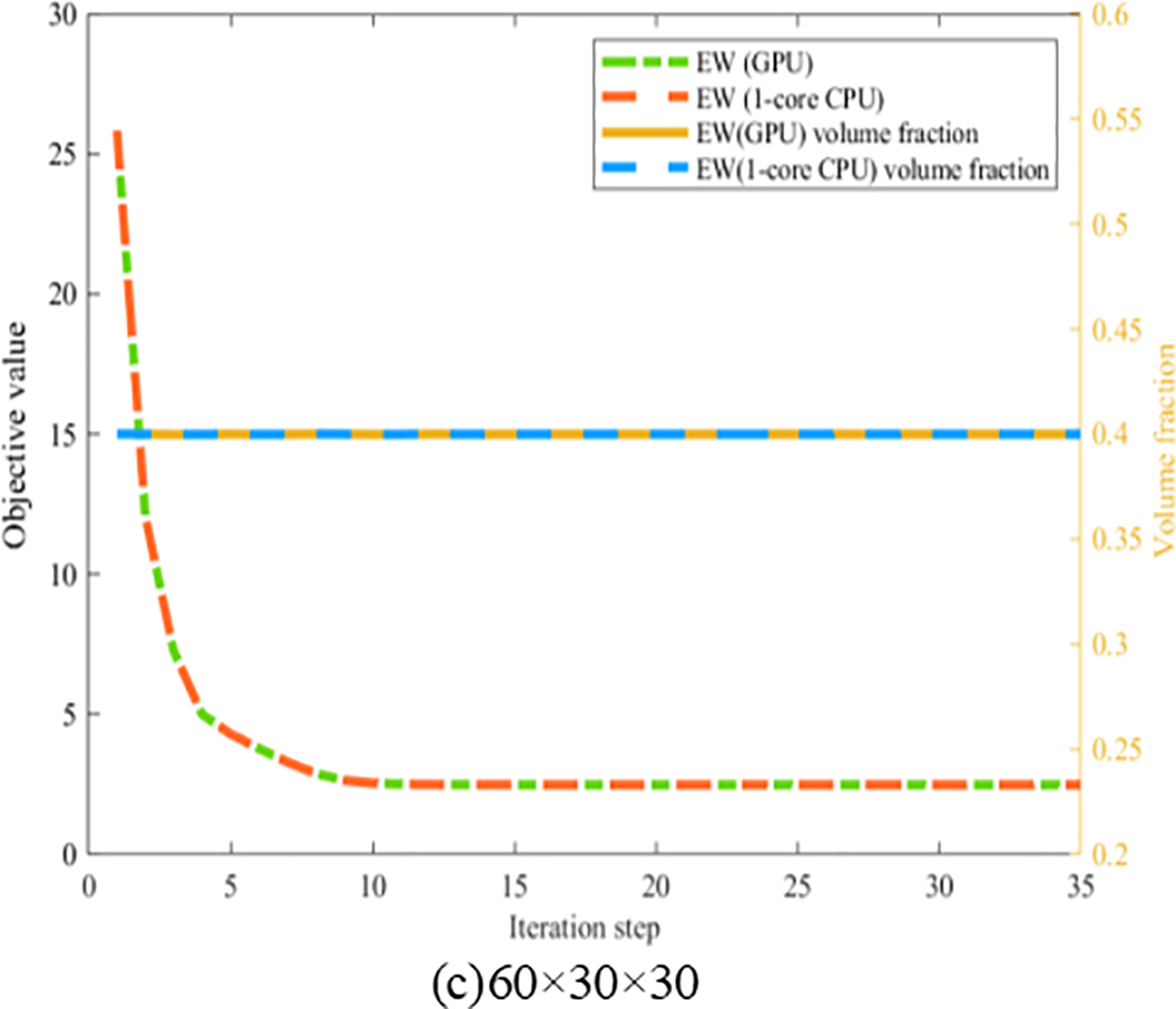
Figure 30: Illustration of convergence histories of ITO under different mesh resolutions per patch with bi-quadratic B-spline basis function
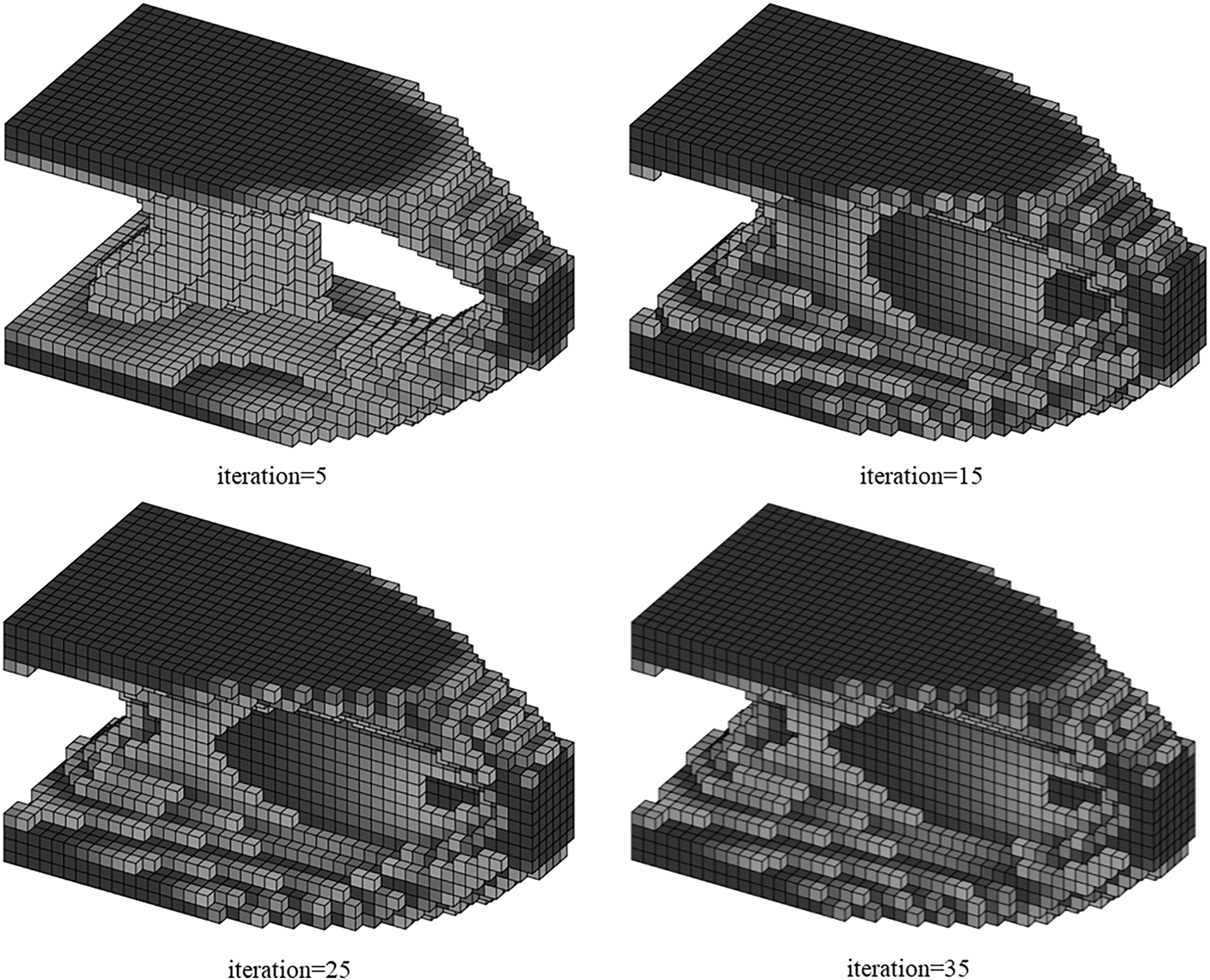
Figure 31: Illustration of history results by ITOs with the proposed and traditional global stiffness matrix updating schemes under
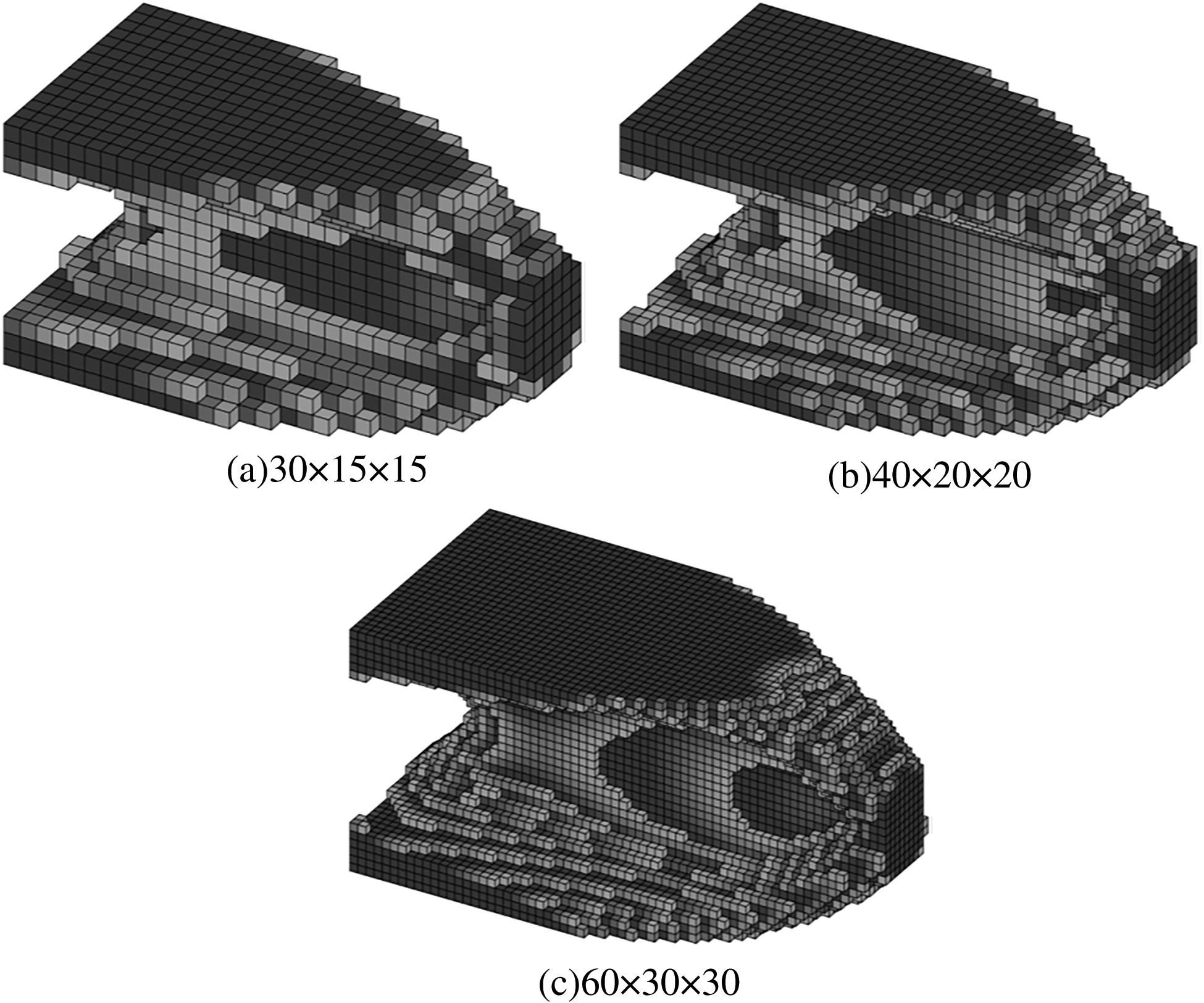
Figure 32: Illustration of the converged design results by ITOs with the proposed and traditional global stiffness matrix updating schemes under different mesh resolutions
To accelerate the computing efficiency of ITO using Bėzier element stiffness mapping, we put forward a parallelization paradigm for the explicit stiffness matrix computation and assembling the global stiffness matrix from all IGA elements in terms of GPU technique, divided into EW and IW methods based on the assembly method of elemental stiffness matrices into global stiffness matrix. Our proposed ITO using Bėzier element stiffness mapping possesses triple acceleration effects as follows:
1. Compared to the traditional single-core CPU updating scheme in an element-wise manner, the GPU-based EW and IW methods exhibit maximum accelerations of 12.6 and 3.1, respectively, with identical convergence history and design results for single-patch design problems.
2. The GPU-based EW parallel strategy is also proposed for sensitivity analysis of ITO using Bėzier element stiffness mapping, considering its characteristics of parallel computing, achieving a significant improvement in numerical efficiency, and the associated speedup is up to 100×.
3. Apart from updating the global stiffness matrix, the solution of the sparse matrix is another step that affects the optimization efficiency of ITO. We replace Eigen with AMGCL as the numerical solver for ITO, by which the speedup of the solver reaches a maximum of 30.3.
Compared to traditional GPU-based EW and IW with stiffness matrices pre-stored for all elements, the proposed schemes in this work may achieve better computing efficiency while maintaining the consumption of hardware memory at an extremely low level. At the same time, we extend the GPU-based EW updating scheme from a single-patch to a multi-patch situation, which can effectively update the global stiffness matrix in a parallel manner.
Since current Bėzier element stiffness mapping is limited to rectangular and circular IGA elements with stricter geometric constraints, it still encounters difficulties in handling other shapes of IGA elements. In the future, we will extend this work to more complex structures and 3D design problems with the immersed isogeometric analysis method in combinations with efficient quadrature rules and considering the anisotropy of the material.
Acknowledgement: None.
Funding Statement: This work has been supported by the National Key R&D Program of China (2023YFB2504601) and National Natural Science Foundation of China (52205267).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Shuting Wang, Xianda Xie, Nianmeng Luo, Aodi Yang; data collection: Xuesong Li, Aodi Yang; analysis and interpretation of results: Xianda Xie, Xuesong Li, Xing Yuan, Aodi Yang; draft manuscript preparation: Xianda Xie, Xuesong Li. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.
Ethics Approval: None.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Hughes TJR, Cottrell JA, Bazilevs Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput Meth Appl Mech Eng. 2005;194:4135–95. doi:10.1016/j.cma.2004.10.008. [Google Scholar] [CrossRef]
2. Cottrell JA, Hughes TJR, Reali A. Studies of refinement and continuity in isogeometric structural analysis. Comput Meth Appl Mech Eng. 2007;196:4160–83. doi:10.1016/j.cma.2007.04.007. [Google Scholar] [CrossRef]
3. Cottrell JA, Hughes TJ, Bazilevs Y. Isogeometric analysis: toward integration of CAD and FEA. John Wiley & Sons; 2009. [Google Scholar]
4. Gu J, Yu T, Tanaka S, Yuan H, Bui TQ. Crack growth adaptive XIGA simulation in isotropic and orthotropic materials. Comput Meth Appl Mech Eng. 2020;365:113016. doi:10.1016/j.cma.2020.113016. [Google Scholar] [CrossRef]
5. Li W, Nguyen-Thanh N, Huang J, Zhou K. Adaptive analysis of crack propagation in thin-shell structures via an isogeometric-meshfree moving least-squares approach. Comput Methods Appl Mech Eng. 2020;358:112613. doi:10.1016/j.cma.2019.112613. [Google Scholar] [CrossRef]
6. Wang D, Pan F, Xu X, Li X. Superconvergent isogeometric analysis of natural frequencies for elastic continua with quadratic splines. Comput Methods Appl Mech Eng. 2019;347:874–905. doi:10.1016/j.cma.2019.01.010. [Google Scholar] [CrossRef]
7. Wang D, Liu W, Zhang H. Novel higher order mass matrices for isogeometric structural vibration analysis. Comput Meth Appl Mech Eng. 2013;260:92–108. doi:10.1016/j.cma.2013.03.011. [Google Scholar] [CrossRef]
8. Bazilevs Y, Hsu MC, Scott MA. Isogeometric fluid-structure interaction analysis with emphasis on non-matching discretizations, and with application to wind turbines. Comput Meth Appl Mech Eng. 2012;249–252:28–41. [Google Scholar]
9. Wu MCH, Kamensky D, Wang C, Herrema AJ, Xu F, Pigazzini MS, et al. Optimizing fluid-structure interaction systems with immersogeometric analysis and surrogate modeling: application to a hydraulic arresting gear. Comput Meth Appl Mech Eng. 2017;316:668–93. doi:10.1016/j.cma.2016.09.032. [Google Scholar] [CrossRef]
10. Bendsoe MP, Kikuchi N. Generating optimal topologies in structural design using a homogenization method. Comput Meth Appl Mech Eng. 1988;71:197–224. doi:10.1016/0045-7825(88)90086-2. [Google Scholar] [CrossRef]
11. Sigmund O. A 99 line topology optimization code written in Matlab. Struct Multidiscip Optim. 2001;21:120–7. doi:10.1007/s001580050176. [Google Scholar] [CrossRef]
12. Ferrari F, Sigmund O. A new generation 99 line Matlab code for compliance topology optimization and its extension to 3D. Struct Multidiscip Optim. 2020;62:2211–28. doi:10.1007/s00158-020-02629-w. [Google Scholar] [CrossRef]
13. Xie YM, Steven GP. A simple evolutionary procedure for structural optimization. Comput Struct. 1993;49:885–96. doi:10.1016/0045-7949(93)90035-C. [Google Scholar] [CrossRef]
14. Huang X, Xie YM. Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method. Finite Elem Anal Des. 2007;43:1039–49. doi:10.1016/j.finel.2007.06.006. [Google Scholar] [CrossRef]
15. Allaire G, Jouve F, Toader AM. Structural optimization using sensitivity analysis and a level-set method. J Comput Phys. 2004;194:363–93. doi:10.1016/j.jcp.2003.09.032. [Google Scholar] [CrossRef]
16. Mei Y, Wang X. A level set method for structural topology optimization and its applications. Adv Eng Softw. 2004;35:415–41. doi:10.1016/j.advengsoft.2004.06.004. [Google Scholar] [CrossRef]
17. Guo X. Doing topology optimization explicitly and geometrically: a new moving morphable components based framework. J Appl Mech-Trans ASME. 2014;81:081009. doi:10.1115/1.4027609. [Google Scholar] [CrossRef]
18. Zhang W, Zhou Y, Zhu J. A comprehensive study of feature definitions with solids and voids for topology optimization. Comput Meth Appl Mech Eng. 2017;325:289–313. doi:10.1016/j.cma.2017.07.004. [Google Scholar] [CrossRef]
19. Qian X. Topology optimization in B-spline space. Comput Meth Appl Mech Eng. 2013;265:15–35. doi:10.1016/j.cma.2013.06.001. [Google Scholar] [CrossRef]
20. Costa G, Montemurro M, Pailhès J. Minimum length scale control in a NURBS-based SIMP method. Comput Meth Appl Mech Eng. 2019;354:963–89. doi:10.1016/j.cma.2019.05.026. [Google Scholar] [CrossRef]
21. Costa G, Montemurro M, Pailhès J, Perry N. Maximum length scale requirement in a topology optimisation method based on NURBS hyper-surfaces. CIRP Ann-Manuf Technol. 2019;68:153–6. doi:10.1016/j.cirp.2019.04.048. [Google Scholar] [CrossRef]
22. Yang A, Wang S, Luo N, Xiong T, Xie X. Massively efficient filter for topology optimization based on the splitting of tensor product structure. Front Mech Eng. 2023;17:54. doi:10.1007/s11465-022-0710-6. [Google Scholar] [CrossRef]
23. Xie X, Wang S, Xu M, Jiang N, Wang Y. A hierarchical spline based isogeometric topology optimization using moving morphable components. Comput Meth Appl Mech Eng. 2019;360:112696. doi:10.1016/j.cma.2019.112696. [Google Scholar] [CrossRef]
24. Xie X, Yang A, Jiang N, Zhao W, Liang Z, Wang S. Adaptive topology optimization under suitably graded THB-spline refinement and coarsening. Int J Numer Methods Eng. 2021;122(20):5971–98. doi:10.1002/nme.6780. [Google Scholar] [CrossRef]
25. Gupta A, Mamindlapelly B, Karuthedath PL, Chowdhury R, Chakrabarti A. Adaptive isogeometric topology optimization using PHT splines. Comput Meth Appl Mech Eng. 2022;395:114993. doi:10.1016/j.cma.2022.114993. [Google Scholar] [CrossRef]
26. Gao J, Wu X, Xiao M, Nguyen VP, Gao L, Rabczuk T. Multi-patch isogeometric topology optimization for cellular structures with flexible designs using Nitsche’s method. Comput Meth Appl Mech Eng. 2023;410:116036. doi:10.1016/j.cma.2023.116036. [Google Scholar] [CrossRef]
27. Gao J, Xiao M, Yan Z, Gao L, Li H. Robust isogeometric topology optimization for piezoelectric actuators with uniform manufacturability. Front Mech Eng. 2022;17:27. doi:10.1007/s11465-022-0683-5. [Google Scholar] [CrossRef]
28. Gao J, Xiao M, Gao L, Yan J, Yan W. Isogeometric topology optimization for computational design of re-entrant and chiral auxetic composites. Comput Meth Appl Mech Eng. 2020;362:112876. doi:10.1016/j.cma.2020.112876. [Google Scholar] [CrossRef]
29. Wang Y, Xiao M, Xia Z, Li P, Gao L. From Computer-Aided Design (CAD) toward Human-Aided Design (HADan isogeometric topology optimization approach. Engineering. 2023;22:94–105. doi:10.1016/j.eng.2022.07.013. [Google Scholar] [CrossRef]
30. Wang Y, Liao Z, Ye M, Zhang Y, Li W, Xia Z. An efficient isogeometric topology optimization using multilevel mesh, MGCG and local-update strategy. Adv Eng Softw. 2020;139:102733. doi:10.1016/j.advengsoft.2019.102733. [Google Scholar] [CrossRef]
31. Montemurro M, Mas A, Zerrouq S-E. Topology and anisotropy optimisation of continua using non-uniform rational basis spline entities. Comput Methods Appl Mech Eng. 2024;420:116714. doi:10.1016/j.cma.2023.116714. [Google Scholar] [CrossRef]
32. Montemurro M. On the structural stiffness maximisation of anisotropic continua under inhomogeneous Neumann-Dirichlet boundary conditions. Compos Struct. 2022;287:115289. doi:10.1016/j.compstruct.2022.115289. [Google Scholar] [CrossRef]
33. Liang X, Li A, Rollett AD, Zhang YJ. An isogeometric analysis-based topology optimization framework for 2D cross-flow heat exchangers with manufacturability constraints. Eng Comput. 2022;38:4829–52. doi:10.1007/s00366-022-01716-4. [Google Scholar] [CrossRef]
34. Li B, Duan Y, Yang H, Lou Y, Müller WH. Isogeometric topology optimization of strain gradient materials. Comput Meth Appl Mech Eng. 2022;397:115135. doi:10.1016/j.cma.2022.115135. [Google Scholar] [CrossRef]
35. Chen LL, Lian H, Natarajan S, Zhao W, Chen XY, Bordas SPA. Multi-frequency acoustic topology optimization of sound-absorption materials with isogeometric boundary element methods accelerated by frequency-decoupling and model order reduction techniques. Comput Meth Appl Mech Eng. 2022;395:114997. doi:10.1016/j.cma.2022.114997. [Google Scholar] [CrossRef]
36. Hughes TJR, Reali A, Sangalli G. Efficient quadrature for NURBS-based isogeometric analysis. Comput Meth Appl Mech Eng. 2010;199:301–13. doi:10.1016/j.cma.2008.12.004. [Google Scholar] [CrossRef]
37. Schillinger D, Hossain SJ, Hughes TJR. Reduced Bézier element quadrature rules for quadratic and cubic splines in isogeometric analysis. Comput Meth Appl Mech Eng. 2014;277:1–45. doi:10.1016/j.cma.2014.04.008. [Google Scholar] [CrossRef]
38. Auricchio F, Calabrò F, Hughes TJR, Reali A, Sangalli G. A simple algorithm for obtaining nearly optimal quadrature rules for NURBS-based isogeometric analysis. Comput Methods Appl Mech Eng. 2012;249-252:15–27. doi:10.1016/j.cma.2012.04.014. [Google Scholar] [CrossRef]
39. Hiemstra RR, Calabrò F, Schillinger D, Hughes TJR. Optimal and reduced quadrature rules for tensor product and hierarchically refined splines in isogeometric analysis. Comput Methods Appl Mech Eng. 2017;316:966–1004. doi:10.1016/j.cma.2016.10.049. [Google Scholar] [CrossRef]
40. Calabrò F, Sangalli G, Tani M. Fast formation of isogeometric Galerkin matrices by weighted quadrature. Comput Meth Appl Mech Eng. 2017;316:606–22. doi:10.1016/j.cma.2016.09.013. [Google Scholar] [CrossRef]
41. Bressan A, Takacs S. Sum factorization techniques in Isogeometric Analysis. Comput Meth Appl Mech Eng. 2019;352:437–60. doi:10.1016/j.cma.2019.04.031. [Google Scholar] [CrossRef]
42. Mantzaflaris A, Jüttler B, Khoromskij BN, Langer U. Low rank tensor methods in Galerkin-based isogeometric analysis. Comput Meth Appl Mech Eng. 2017;316:1062–85. doi:10.1016/j.cma.2016.11.013. [Google Scholar] [CrossRef]
43. Karatarakis A, Karakitsios P, Papadrakakis M. GPU accelerated computation of the isogeometric analysis stiffness matrix. Comput Methods Appl Mech Eng. 2014;269:334–55. doi:10.1016/j.cma.2013.11.008. [Google Scholar] [CrossRef]
44. Zhang Q, Liu Y, Nguyen-Thanh N, Li W, Li S, Zhou K. Adaptive topology optimization for enhancing resistance to brittle fracture using the phase field model. Comput Methods Appl Mech Eng. 2024;431:117237. doi:10.1016/j.cma.2024.117237. [Google Scholar] [CrossRef]
45. Szyszka A, Woźniak M, Schaefer R. Concurrent algorithm for integrating three-dimensional B-spline functions into machines with shared memory such as GPU. Comput Meth Appl Mech Eng. 2022;398:115201. doi:10.1016/j.cma.2022.115201. [Google Scholar] [CrossRef]
46. Munk DJ, Kipouros T, Vio GA. Multi-physics bi-directional evolutionary topology optimization on GPU-architecture. Eng Comput. 2019;35:1059–79. doi:10.1007/s00366-018-0651-1. [Google Scholar] [CrossRef]
47. Herrero-Pérez D, Martínez Castejón PJ. Multi-GPU acceleration of large-scale density-based topology optimization. Adv Eng Softw. 2021;157–158:103006. [Google Scholar]
48. Lin H, Liu H, Wei P. A parallel parameterized level set topology optimization framework for large-scale structures with unstructured meshes. Comput Meth Appl Mech Eng. 2022;397:115112. doi:10.1016/j.cma.2022.115112. [Google Scholar] [CrossRef]
49. Liu J, Xian Z, Zhou Y, Nomura T, Dede EM, Zhu B. A marker-and-cell method for large-scale flow-based topology optimization on GPU. Struct Multidiscip Optim. 2022;65:125. doi:10.1007/s00158-022-03214-z. [Google Scholar] [CrossRef]
50. Träff EA, Rydahl A, Karlsson S, Sigmund O, Aage N. Simple and efficient GPU accelerated topology optimisation: codes and applications. Comput Meth Appl Mech Eng. 2023;410:116043. doi:10.1016/j.cma.2023.116043. [Google Scholar] [CrossRef]
51. Xia Z, Wang Y, Wang Q, Mei C. GPU parallel strategy for parameterized LSM-based topology optimization using isogeometric analysis. Struct Multidiscip Optim. 2017;56:413–34. doi:10.1007/s00158-017-1672-x. [Google Scholar] [CrossRef]
52. Xu G, Kwok T-H, Wang CCL. Isogeometric computation reuse method for complex objects with topology-consistent volumetric parameterization. Comput-Aided Des. 2017;91:1–13. doi:10.1016/j.cad.2017.04.002. [Google Scholar] [CrossRef]
53. Zhuang C, Xiong Z, Ding H. Bézier extraction based isogeometric topology optimization with a locally-adaptive smoothed density model. J Comput Phys. 2022;467:111469. doi:10.1016/j.jcp.2022.111469. [Google Scholar] [CrossRef]
54. Borden MJ, Scott MA, Evans JA, Hughes TJ. Isogeometric finite element data structures based on Bézier extraction of NURBS. Int J Numer Methods Eng. 2011;87:15–47. [Google Scholar]
55. Chen L, de Borst R. Adaptive refinement of hierarchical T-splines. Comput Methods Appl Mech Eng. 2018;337:220–45. doi:10.1016/j.cma.2018.03.032. [Google Scholar] [CrossRef]
56. D’Angella D, Reali A. Efficient extraction of hierarchical B-Splines for local refinement and coarsening of isogeometric analysis. Comput Methods Appl Mech Eng. 2020;367:113131. doi:10.1016/j.cma.2020.113131. [Google Scholar] [CrossRef]
57. Toshniwal D, Hughes TJR. Isogeometric discrete differential forms: non-uniform degrees, Bézier extraction, polar splines and flows on surfaces. Comput Methods Appl Mech Eng. 2021;376:113576. doi:10.1016/j.cma.2020.113576. [Google Scholar] [CrossRef]
58. Yang A, Wang S, Luo N, Xiong T, Xie X. A space-preserving data structure for isogeometric topology optimization in B-splines space. Struct Multidiscipl Optim. 2022;65:281. doi:10.1007/s00158-022-03358-y. [Google Scholar] [CrossRef]
59. Nvidia. Available from: https://wwwnvidiacn/. [Accessed 2024]. [Google Scholar]
60. Piegl LA, Tiller W. The NURBS book. Berlin Heidelberg: Springer; 1997. [Google Scholar]
61. Demidov D. AMGCL—A C++ library for efficient solution of large sparse linear systems. Softw Impacts. 2020;6:100037. doi:10.1016/j.simpa.2020.100037. [Google Scholar] [CrossRef]
62. Demidov D, Mu L, Wang B. Accelerating linear solvers for Stokes problems with C++ metaprogramming. J Comput Sci. 2021;49:101285. doi:10.1016/j.jocs.2020.101285. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools