Multi-Objective Hybrid Sailfish Optimization Algorithm for Planetary Gearbox and Mechanical Engineering Design Optimization Problems

1  Introduction

Multi-objective optimization has gained the attention of researchers in the last decade with the development of improved nature-inspired metaheuristic algorithms. Generally, there are two methodologies for addressing multi-objective optimization problems. The first ones convert the optimization problem with several objectives into a single objective optimization problem by summing all normalized objectives which are then weighted according to a set of predefined values. Despite the extensive application of these classical approaches in addressing multi-objective optimization problems, they exhibit limits in real-world scenarios. These strategies need convex Pareto fronts to obtain a solution, and show significant drawbacks on complex optimization problems [1,2]. Furthermore, the pre-algorithm expert-provided weights have a significant impact on the final solution and biased in their favor [3]. In order to circumvent these limits, researchers developed methods that solve all objectives directly without combining them. Determining a set of solutions that specify the optimal compromise between opposing objectives is one way to tackle such situations. Regarding this, multi-objective Evolutionary Algorithms (MOEAs) can provide solutions that are adequate for practical purposes within an acceptable runtime.

Evolutionary algorithms, or bio-inspired algorithms, are prominent and extensively utilized methods under the category of population-based metaheuristics. The Genetic Algorithm (GA) and its variations are a category of evolutionary algorithms extensively utilized on the practical optimization problems, due to its wide availability in different software packages, and well understood mechanism. The Non-dominated Sorting Genetic Algorithm II (NSGA-II) [4] is a popular multi-objective implementation of GA widely applied in various fields, including engineering design, which is designed to solve optimization problems with multiple conflicting objectives. NSGA-II employs a fast non-dominated sorting approach to classify solutions into different Pareto fronts, and it uses a crowding distance mechanism to ensure diversity among solutions by preserving a spread across the Pareto front. However, NSGA-II has some disadvantages, such as its computational complexity, which can become significant for large populations or problems with many objectives, and its sensitivity to parameter settings, which may require careful tuning for optimal performance.

The majority of practical engineering optimization problems necessitate the presence of multiple constraints of equality and inequality types. Conventional meta-heuristic optimization algorithms are presented for solving unconstrained optimization problems. In order to deal with constraints, various methods have been suggested in the literature. These methods can be grouped into three main categories: penalty functions, addressing constraints using the Multi-Objective Optimization (MOO) problem, and addressing constraints with separate considerations of feasible and infeasible solutions [5]. By adding a penalty term to the objective function associated with the constraints, the most typical method for dealing with constraints is to convert a constrained optimization problem into an unconstrained one. One alternative strategy takes a two-step approach to dealing with constraints: first, the algorithm optimizes the constraints independently of the objective functions; subsequently, once a large number of viable solutions have been found, the optimization of the objective functions is the algorithm’s primary concern. The most up-to-date method involves turning the constrined optimization issue into an unconstrained MOO problem by considering the constraints as additional objectives.

Another widely applied evolutionary optimization algorithm is the Differential Evolution (DE), which, unlike GAs, has not taken inspiration from nature but is designed purely based on mathematical concepts [6]. DE is highly regarded for its robustness and simplicity in solving optimization problems. A key benefit of DE is its effectiveness in tackling intricate optimization problems that involve non-linear relationships and multiple local optima. DE is particularly significant for its strong exploration capabilities, which enable it to effectively search global optimization landscapes and avoid premature convergence to local optima [7]. However, DE has some limitations. The performance of DE is also sensitive to the choice of its control parameters, such as the mutation factor, crossover rate, and population size. Fine-tuning these parameters is often necessary to achieve optimal performance, which can be time-consuming.

The multi-objective version of the DE algorithm extends its optimization capabilities to problems with multiple conflicting objectives, directly incorporating constraints and multi-objectiveness into the evolutionary process [8]. Notable variants include the Multi-Objective Differential Evolution Algorithm (MODEA), which utilizes Opposition-Based Learning for initial population generation and introduces a new selection mechanism for better Pareto front distribution [9], and the Adaptive Chaotic DE, which combines adaptive and chaotic principles for enhanced efficiency [10]. A significant strength of multi-objective DE is its robust exploration ability, efficiently navigating the search space to identify a diverse set of Pareto-optimal solutions. Applications of this algorithm span various fields, including engineering design, power plant control, and chemometrics, where it optimizes trade-offs among multiple objectives effectively [11].

Another category of metaheuristics are swarm optimization algorithms (SO), among which Ant Colony Optimization (ACO), Firefly Algorithm (FA) and Particle Swarm Optimization (PSO) are two approaches commonly used to solve real-world problems. These algorithms are inspired by the collective behavior of decentralized, self-organized systems, typically found in nature, such as bird flocking, fish schooling, and ant colonies. More recently, authors proposed a novel nature-inspired optimization algorithm that belongs to the group of SO algorithms, the Sailfish Optimization (SFO) algorithm, that draws inspiration from the collective hunting behavior of sailfish and sardines. The algorithm maintains two populations simultaneously, e.g., sailfish (predators) and sardines (prey). During the optimization process, SFO alternates between exploration and exploitation phases by having sailfish update their positions based on the elite sailfish and the worst-performing sardines. The movement of sailfish is directed towards the best-known positions, thereby exploiting the search space, while sardines move randomly to explore new areas. This approach ensures a balance between exploration and exploitation, with the aim to efficiently find optimal solutions for various optimization problems.

The SFO algorithm has been widely applied to various optimization problems. The authors in [12] introduced SFO as a novel metaheuristic algorithm for solving constrained engineering optimization problems, demonstrating superior performance in terms of exploration, exploitation, and convergence speed compared to existing algorithms. In the realm of power systems [13] applied SFO for optimal placement and sizing of static synchronous compensator, resulting in improved voltage profiles and reduced power losses. In [14], authors optimized the coverage and connectivity of sensor nodes in a 3D wireless sensor network using SFO, ensuring robust network performance.

These studies collectively highlight the versatility and effectiveness of the SFO algorithm in solving diverse optimization problems. However, the majority of these studies focused on single objective optimization. In [15], authors introduced a multi-objective Sailfish Optimizer combined with a genetic algorithm for expert recommendation in community-based question-answering, demonstrating superior performance in matching questions to experts. In order to design a frequency selective surface for 5G applications, the authors in [16] introduced a hybrid multi-objective optimization technique utilizing the SFO combined with a General Regression Neural Network. However, unlike the multi-objective implementation of SFO algorithm presented in this paper, the proposed algorithm in [16] employed the weighted sum method to balance multiple objectives, which cannot provide satisfactory result on non-convex Pareto fronts.

Despite much investigation using various algorithms, the inquiry into identifying the most appropriate one for a certain challenge remains inadequately addressed. Moreover, preserving the diversity of optimal solutions and preventing premature convergence to local optima remain essential for population-based algorithms. Moreover, the No Free Lunch theorem [17], which established that enhancements in performance for one category of optimization problems result in diminished performance for another, has spurred the advancement and comparative analysis of metaheuristic algorithms for addressing diverse optimization challenges. In general, it is not possible to provide a single algorithm that will successfully solve all problems that can be encountered in practice.

In this regard, researchers proposed a number of hybrid optimization algorithms, with the aim of strategic combination of different optimization techniques to leverage their respective strengths and mitigate their weaknesses, thereby enhancing overall problem-solving efficacy. This approach is performed to improve convergence speed, maintain solution diversity, and adapt to a wide range of problem characteristics, making the optimization process more robust and efficient. In [18], the authors developed a hybrid of the salp swarm algorithm and DE, which improves feature exploitation and demonstrated superior results in big data optimization compared to traditional methods. In [19], the authors introduced an adaptive DE algorithm incorporating a memory mechanism from PSO to adaptively select mutation operators, resulting in competitive performance on benchmark problems. In [20], the authors proposed a hybrid approach combining DE, PSO, and nondominated sorting, improving distributed optimization quality in complex multi-objective problems. Regarding the SFO algorithm, literature reveals numerous studies addressing its enhanced performance, although improvement through various hybridization techniques is seldom. Regarding hybridization, in [21], the authors developed a hybrid model combining SFO with the Whale Optimization Algorithm (WOA) termed SWO-DLSTM (A Hybrid Sailfish Whale Optimization and Deep Long Short-Term Memory). This hybrid model leverages the optimization capabilities of SFO and WOA for feature selection and parameter tuning, which are then utilized by DLSTM (Deep Long Short-Term Memory) for accurate time series predictions in energy demand forecasting, showcasing significant improvements in considered performance metrics. These hybrid methods effectively balance exploration and exploitation, leading to improved solution quality and convergence rates in multi-objective optimization tasks.

The mechanical engineering design problems often involves complex objective functions with numerous variables, a number of complex non-linear constraints. This results into the complex optimization problems, which often require multiple conflicting objectives. The modern requirements, posed on the designer, which require long service life, lightweight but strong construction as well as increased energy efficiency make these design problems even complex. In the area of gearbox design, the objectives are inherently non-linear and non-convex thus making the problem complex to solve. The background part presents a literature review on the development and implementation of several optimization techniques to address difficult gearbox design problems.

The aim of this paper is to explore the suitable choosing of Evolutionary Algorithms (EAs) for hybridization, with the aim to provide an improved optimization algorithm for the established multi-objective planetary gearbox optimization problem. Therefore, it is on researchers to explore the possibilities of application of different algorithms, to establish each of their weaknesses and strengths, and provide the possibilities to hybridize each of the algorithms, in order to obtain the solutions of high accuracy for the considered optimization problem. Based on the literature review and extensive research, we can see that the DE algorithm shows strong exploration capability, if applied with appropriate mutation operator, while the SFO algorithm shows fast convergence towards local optimum. This work presents the HMODESFO algorithm, a hybridization of the DE and SFO algorithms, to enhance the exploration capabilities of the SFO method. The hybridization was executed by integrating the mutation operators DE/rand/1 and DE/rand/2 from the DE algorithm into the equations for updating the locations of the sailfish (predator) and sardine (prey), respectively. The performance of the proposed algorithm is validated against well-known industry benchmarks, e.g., a set of ZDT (Zitzler-Deb-Thiele) and DTLZ (Deb-Thiele-Laumanns-Zitzler) benchmark problems, where the proposed algorithm showed improved performance. This work employs a series of well-recognized multi-objective optimization problems in literature that deal with mechanical engineering to further validate the created hybrid HMODESFO method. Finally, the performance of this algorithm has been validated on the developed multi-objective planetary gear optimization problem, where compared to industry standard it showed improved results.

The primary contributions of the paper can be summarized as follows:

•   The previously developed single stage planetary gearbox optimization problem has been extended to include additional constraints, and increase physical realization of obtained results.

•   To enhance optimization performance, particularly in addressing intricate multi-objective planetary gearbox and mechanical design optimization challenges, a hybrid algorithm combining DE and SFO, termed the HMODESFO algorithm, has been presented. The hybridization of two prominent evolutionary algorithms has been accomplished by integrating the mutation operator of DE into the SFO algorithm. The suggested technique utilizes an adaptive parameter to select a suitable modified mutation operator for the prevailing optimization circumstances.

•   The effectiveness of the proposed HMODESFO algorithm has been evaluated by contrasting it with reputable multi-objective metaheuristic algorithms, including mechanical design benchmark MOO problems, as well as on the recognized ZDT and DTLZ benchmark problems. The experimental results shown that the proposed HMODESFO method greatly surpasses other current algorithms regarding optimization quality, particularly in Pareto solutions and convergence.

The paper is structured as indicated: Section 1 presents the introduction and a survey of the existing literature. Section 2 gives the outline of the background and related work of applying EAs in the area of mechanical design, especially optimal gearbox design. In Section 3, the mathematical formulations of the The Multi-Objective Sailfish Optimization algorithm, Differential evolution algorithm as well as the proposed hybrid algorithm are outlined, with the appropriate pseudo-code that accompanies each algorithm. In Section 4, the formulations of used benchmark test functions as well as the formulated planetary gearbox optimization model are provided. Furthermore, Section 4 also gives the results of the numerical experimental simulations. In Section 5, the conclusions are drawn.

2  Background and Related Work

In mechanical engineering, optimizing gearbox design is a complex and essential task. It requires addressing multiple objectives, such as enhancing performance, improving efficiency, reducing weight, and ensuring long service life. These factors are critical to meeting the stringent requirements of modern gearbox design, which must balance these often-conflicting goals to achieve optimal functionality. The complexity of this task underscores the need for advanced optimization techniques that can handle the intricate trade-offs involved in creating high-performing, efficient, and durable gearboxes. Single-objective optimization has been a fundamental approach in the design and enhancement of gearboxes. Reference [22] proposed a powerful optimization method for the minimal dimensional design of gearboxes. By implementing a PSO algorithm, they achieved significant reductions in gearbox volume, which directly translated to cost savings and material efficiency. In another study [23], authors utilized single-objective optimization to minimize the volume and weight of gearboxes. Their research provided practical graphs and guidelines for deriving optimal gearbox parameters based on different input power, gear ratio, and material hardness. This approach facilitated the design of lightweight and compact gearboxes, which are essential for various industrial applications. In [24], the authors examined an innovative approach to optimizing the transmission efficiency of spiral bevel gears. By integrating PSO with the Gravitational Search Algorithm, they demonstrated significant improvements in gear design performance and efficiency. In [25], the authors explored the use of seven different nature-inspired optimization algorithms to minimize the volume of a two-stage planetary gearbox. This study applied algorithms such as Grey Wolf Optimizer, Artificial Bee Colony, and Multi-verse Optimizer, achieving optimal volume values significantly better than those previously recorded in the literature. The findings highlight the effectiveness of these meta-heuristic approaches in addressing complex engineering optimization challenges.

Given the inherent complexity of gearbox optimization, considering only one objective is often unsatisfactory, especially when aiming to optimize multiple conflicting objectives simultaneously. Multi-objective optimization has emerged as a robust approach to address these conflicting goals, such as minimizing weight while maximizing efficiency and durability. This method effectively balances the trade-offs necessary for optimal gearbox design. Multi-objective optimization techniques have been extensively applied to various types of gearboxes, including spur, helical, and planetary gearboxes. For instance, reference [26] explored the multi-objective optimization of a two-stage spur gearbox by incorporating tribological aspects to minimize weight and power losses. Their study utilized the NSGA-II to achieve significant improvements over traditional single-objective optimization approaches. In another study, the same authors extended their research to a two-stage helical gearbox, again focusing on minimizing volume and power losses while considering tribological constraints [27]. Their findings demonstrated a considerable reduction in power loss and a higher probability of avoiding wear failures when using a multi-objective optimization framework compared to single-objective methods. Additionally, in [28], authors applied the Taguchi method and Grey Relational Analysis to optimize a two-stage helical gearbox, focusing on maximizing efficiency and minimizing mass. Their study identified optimal design parameters, showcasing the effectiveness of combining single-objective and multi-objective optimization phases to achieve superior performance. In [29], the authors developed a multi-objective uncertainty optimization design framework to enhance the performance and reliability of planetary gear trains in electric vehicles. This study incorporates uncertainties in manufacturing size, material properties, and load inputs, optimizing both volume and transmission efficiency using an improved NSGA-II algorithm. The findings demonstrate that the proposed framework offers superior reliability and performance compared to traditional deterministic optimization methods under varying uncertainty. The paper [30] presents a comprehensive framework for enhancing the design of planetary gear sets. By employing advanced optimization algorithms, the authors aim to simultaneously minimize mass and power loss while reducing transmission error. This study achieves significant improvements in efficiency and reliability, offering a balanced trade-off among competing design objectives.

Furthermore, the use of hybrid optimization algorithms has shown promise in optimizing planetary gearboxes. In [31], authors proposed a hybrid algorithm combining particle swarm optimization and differential evolution to tackle the complex multi-objective non-linear optimization problems in planetary gearboxes. Their approach yielded significant improvements in efficiency, weight reduction, and prevention of premature gear failure. A recent research [31] suggested a modified hybrid approach called the Multi-objective Hybrid Butterfly Optimization and Particle Swarm Optimization approach (HMOBPSO), which combines PSO with the Butterfly Optimization Algorithm (BOA). This strategy sought to improve performance by tackling several competing objectives in the optimization of planetary gearboxes. The research has shown notable advancements in gearbox dimensions, efficiency, and spacing relative to traditional techniques.

These studies underscore the advancements and effectiveness of multi-objective optimization in the design and enhancement of gearboxes. By integrating various optimization algorithms and considering multiple performance metrics, researchers continue to push the boundaries of gearbox technology, leading to more efficient, durable, and lightweight designs.

3  The Proposed Hybridization

In this section we will first introduce the Multi-objective SFO and DE algorithms, as the constituents of the proposed hyrbid HMODESFO optimization algorithm.

3.1 The Multi-Objective Sailfish Optimization Algorithm

The Sailfish Optimizer [12] is a nature-inspired meta heuristic algorithm that draws inspiration from the collective hunting behavior of sailfish. Sailfish use their speed, agility, and collaborative strategies to encircle and capture prey, typically sardines. The previous and original implementation of SFO algorithm considered only single objective optimization problems. The Multi-Objective Sailfish Optimization algorithm (MOSFO), presented in this section, extends the original SFO to handle problems with multiple conflicting objectives. In order to do so, MOSFO algorithm incorporates Pareto dominance and an external archive to handle multiple objectives. In the following subsections we will present the main processes of MOSFO algorithm.

In general, the multi-objective optimization problems consider the m=1,2,…,M objectives which are simultaneously optimized. In practical applications the optimization problems require satisfaction of multiple constraints of equality and inequality type. Therefore, the MOO problem can be defined as:

minf→(x)=min[fm],m=1,…,Ms.t.gk(x)≥0,k=1,…,Khl(x)=0,l=1,…,L,(1)

where M is the number of objectives, gk denotes the k-th inequality constraint, K is the total number of inequality constraints, hl is the l-th equality constraint and L is the total number of equality constraints. In order to handle the constraints, in the proposed MOO framework, each constraint is incorporated as an additional objective to be minimized alongside the original objective functions. For each inequality constraint gk(x)≤0 represents the decision variable vector and i = 1, 2, …, we define a constraint violation function as follows:

fgk(x)=max{0,gk(x)}.(2)

This function fgk(x) quantifies the degree to which a candidate solution x violates the k-th inequality constraint. Therefore, in case of gi(x)≤0, then fgk(x)=0 indicates there is no constraint violation.

In case of the equality constraints hl(x)=0, with, these are converted into minimization of objectives by taking the absolute value of the constraint function, according to

fhl(x)=|hl(x)|.(3)

Here, the function fhl(x) measures the absolute deviation from the equality condition, ensuring that both positive and negative deviations contribute equally to the constraint violation. In this way, the introduction of constraints into the objectives, we get the following multi-objective optimization problem:

minf(x)=min[f1,…,fm,…,fM,fhl,…,fhL,fgk,…,fgK].(4)

This formulation enables the optimization algorithm to simultaneously minimize the original objectives and the constraint violation functions. By integrating constraints as additional objectives, we harness the multi-objective nature of the optimization algorithm to discover solutions that not only meet the original objectives but also adhere to the problem’s constraints. This approach enhances the algorithm’s capacity to traverse intricate search spaces where feasible regions may be narrow or fragmented, ultimately resulting in high-quality solutions that fulfill all requirements.

3.1.1 Population Initialization

The MOSFO algorithm operates with two main populations: sailfish (predators) and sardines (prey). To start the iteration process, we generate the initial populations of sailfish and sardines with random positions within the defined search space, was follows:

xSF,i(0)=rand(n)×(xiU−xiL)+xiL,(5)

xS,i(0)=rand(n)×(xiU−xiL)+xiL,(6)

where n is the dimension of the problem, rand is the random number generator in the domain [0,1] and xiL and xiU are the lower and upper bounds of the search space, respectively. The ith position, in the G=0 generation of sailfish is defined as the vector xSF,i(0)=(xSF,i,1(0),xSF,i,2(0),…,xSF,i,j(0),…,xSF,i,n(0))T, while the position of the sardines is defined as xS,i(0)=(xS,i,1(0),xS,i,2(0),…,xS,i,j(0),…,xS,i,n(0))T. In this regard, the initial population of sailfish and sardines can be defined as:

SF(0)=[xSF,1,1(0)xSF,1,2(0)…xSF,1,n(0)xSF,2,1(0)xSF,2,2(0)…xSF,2,n(0)⋮⋮⋱⋮xSF,NP,1(0)xSF,NP,2(0)…xSF,NP,n(0)],(7)

S(0)=[xS,1,1(0)xS,1,2(0)…xS,1,n(0)xS,2,1(0)xS,2,2(0)…xS,2,n(0)⋮⋮⋱⋮xS,NP,1(0)xS,NP,2(0)…xS,NP,n(0)],(8)

where NP is the number of individuals in the population. The initialization ensures a diverse set of starting points, allowing the algorithm to explore the search space effectively.

3.1.2 Elitism and Archive Management

In MOSFO, an elitist strategy is employed to retain the best solutions found during the optimization process. The best sailfish, xelite, and the most injured sardine, xinjured, are preserved across iterations. This preservation ensures that high-quality solutions are not lost and helps in guiding the population towards promising regions of the search space.

An external archive is maintained to store non-dominated solutions. This archive plays a critical role in managing the diversity and quality of solutions, ensuring a comprehensive approximation of the Pareto front. The archive is updated at each iteration with new non-dominated solutions, and dominated solutions are removed. This mechanism helps in maintaining a diverse set of solutions that are spread across the Pareto front.

3.1.3 Attack-Alternation Strategy

The sailfish update their positions based on an alternation strategy inspired by real-world hunting behaviors. In the G-th generation, the new position xSF,i(G) of the i-th sailfish is calculated using the following formula:

xSF,i(G)=xelite−λ(rand(0,1)×(xelite+xinjured)/2−xSF,i(G−1)2),(9)

where rand(0,1) is the random number between [0,1] and λ is a coefficient generated as:

λ=2×rand(0,1)×Pd−Pd.(10)

Here the Pd denotes the prey density, indicating the number of prey at each iteration. As the sailfish progressively hunt and reduce the prey population, the Pd parameter becomes crucial for updating the sailfish positions relative to the prey school, thus the adaptive expressions for this parameter is introduced follows:

Pd=1−mm+n,(11)

where m is the number of sailfish, and n denotes the number of sardines. The attack-alternation strategy allows sailfish to intensify their search around the best solutions while being influenced by the worst solutions. This balance ensures that the population does not converge prematurely to local optima and continues to explore the search space effectively.

3.2 Attack Power—Handling Multiple Objectives

The MOSFO algorithm incorporates Pareto dominance-based selection to handle multiple objectives. After evaluating the objective functions for each individual, non-dominated sorting is performed to identify the Pareto front. The crowding distance metric is employed to maintain diversity among the solutions. This metric ensures that solutions are well-distributed across the Pareto front by favoring solutions that are in less crowded regions.

The updated positions of sardines in the G-th iteration are determined by:

xS,i(G)=rand(0,1)×(xelite−xS,i(G−1)+AP),(12)

where rand(0,1) is the random number between [0,1] and AP is the attack power, introduced as the adaptive parameter that reduces during the generations, with the aim of maintaining the balance between exploration and exploitation capabilities of the algorithm. In this regard, the AP is calculated as:

AP=A×(1−2×FE×ϵmaxFE),(13)

where A is the initial attack power, ϵ is a small constant, FE is the current number of function evaluations, and maxFE is the maximum number of function evaluations. The use of Pareto dominance ensures that only the best trade-offs between objectives are selected, while the crowding distance maintains diversity among the non-dominated solutions.

The presudocode of the MOSFO algorithm is given in Algorithm 1.

3.3 Differential Evolution Algorithm

The DE is an efficient population-based evolutionary algorithm, widely applied in solving practical complex optimization problems [6]. The optimization process is based on four operations, i.e., initialization, mutation, crossover, and selection, which are briefly explained in the following subsections.

3.3.1 Initialization

The DE algorithm is initialized with the random deployment of individuals xi(G), defined as:

xi,j(G)∈[xi,jmin,xi,jmax],∀i∈{1,2,…,NP},∀j=1,2,…,n,(14)

where xi,jmin and xi,jmax denote the lower and upper bound of the solution space, respectively, NP is the population size, and n is the dimension of the considered problem. Therefore, in the initial generation, each component of the vector xi(G) is calculated as:

xi,j(G)=xi,jmin+randj(xi,jmax−xi,jmin),∀j=1,2,…,n,(15)

where randj denotes the random number generator such that randj∈[0,1].

3.3.2 Mutation

Mutation is one of the crucial operators in DE, since it ensures the discoverability of new solutions. The new mutant vector is calculated for each target vector using a number of different strategies, which all possess the necessary traits for solving different types of problems, including [7]:

•   DE/rand/1

vi(G+1)=xr1(G)+F(xr2(G)−xr3(G)),(16)

•   DE/rand/2

vi(G+1)=xr1(G)+F(xr2(G)−xr3(G))+F(xr4(G)−xr5(G)),(17)

•   DE/best/1

vi(G+1)=xbest(G)+F(xr1(G)−xr2(G)),(18)

•   DE/best/2

vi(G+1)=xbest(G)+F(xr1(G)−xr2(G))+F(xr3(G)−xr4(G)),(19)

•   DE/current-to-best/1

vi(G+1)=xi(G)+F(xbest(G)−xi(G))+F(xr1(G)−xr2(G)),(20)

where r1,r2,…,r5 are mutually distinct random numbers drawn from {1,2,…,NP}∖{i}, xbest(G) denotes the individual in the population that achieved the best objective function value, and F is a scale factor, introduced as one of the control parameters of the DE algorithm.

3.3.3 Crossover

In order to increase the diversity of the population, the crossover operator is applied to generate a trial vector ui(G+1), by combining the components of the target vector xi(G) and the appropriate mutant vector viG, as per the expression:

ui,j(G+1)={vi,j(G),if randi,j≤Cr or j=jrand,xi,j(G),otherwise,(21)

where Cr is the crossover rate, the control parameter in the range [0,1], and jrand is a random integer selected from the set {1,2,…,n}.

3.3.4 Selection

The selection operator is applied to choose the individuals with better traits for solving the stated problem to the next generation. The operator works such that the comparison of objective functions is made between trial and target vectors. For the next generation, we select the better one, as follows:

xi(G+1)={ui(G+1),if f(ui(G+1))≤f(xi(G)),xi(G),otherwise.(22)

The pseudo-code of the DE algorithm is given in Algorithm 2.

3.4 Hybrid HMODESFO Algorithm

In this section we present the hybridization between SFO and DE algorithms, named HMODESFO algorithm. The optimization problems in engineering are often complex, requiring to satisfy a number of constraints and multiple conflicting and complex objective functions. Based on the literature research, and on the experimentation on the considered problems, we can conclude that the MOSFO algorithm can suffer for premature convergence and doesn’t maintain the diversity of the solutions. Therefore, the proposed idea in this paper is to include the expressions from the DE algorithm regarding the mutation operator into the SFO algorithm, with the aim to introduce new potential solutions and improve diversity. It has been shown in literature that DE/rand/1 and DE/rand/2 mutation operators are good in exploration and introduction of new solutions into the solution pool. To perform this hybridization we have introduced an adaptive parameter, on which basis the algorithm will decide weather to perform the mutation or not. Then based on the crowding distance operator the algorithm will retain the promising solutions.

In each generation G we calculate the parameter ΔθG according to the expression

ΔθG=θG⋅Δnorm,(23)

where Δnorm denotes the normalized spread metric which is calculated as:

Δnorm=∑i=1M−1|di−d¯|∑i=1M−1di+M⋅d¯,(24)

in which M is the number of Pareto optimal solutions, di is the Euclidean distance between consecutive solutions in the objective space and d¯ is the mean of these distances. The normalized spread metric, indicates the extent of spread achieved among the obtained solutions, such that when Δnorm=0 the algorithm has achieved the perfect uniform spread of solutions along the Pareto front. On the other hand, the second limiting value Δnorm=1 indicates the worst possible spread in the given normalization context. In order control the parameter Δnorm we have introduced the function θG(G) that reduces the value of Δnorm as the generations increase, as follows:

θG=θinit⋅(θfinθinit)GGmax,(25)

where θinit is the starting value of parameter θG and θfin is the final value, in this paper taken as {θinit,θfin}={1,0.1}, while Gmax denotes the maximum number of iterations. We see that the value of this parameter decreases as the generation increases, thus multiplying with Δnorm it will decrease the influence of this parameter as generations are in the later stage, when is expected that the algorithm has converged towards the promising solutions.

As previously pointed out we see that DE/rand/1 and DE/rand/2 mutation operators from DE algorithm can introduce new potential solutions and improve diversity. To select the individuals from the population that we will mutate, we first define cm as the percentage of NP individuals that will be mutated. Then we perform random selection of cm integers from the set {1,2,…,NP} and we thus get the set {Cm,i},i=1,2,…,cm. Then for each individual from the set {Cm,i} we apply the DE/rand/1 or DE/rand/2 mutation operators, as described in Eqs. (16) and (17), respectively, with the random choosing and probability of 0.5. Therefore, we introduce the following mutation operator into the MOSFO algorithm that will introduce new random solutions into the population according to the pseudo-code in Algorithm 3.

In this regard we can observe that in each iteration only one subset of cm solutions are mutated. Furthermore, we mutate individuals only if the spread indicator is showing low diversity and low spread of solutions, thus introducing new solutions into the solution pool. The complete pseudo-code of the proposed HMODESFO algorithm is shown in Algorithm 4.

4  Performance Metrics on Benchmark Tests

To assess the effectiveness of the proposed algorithm and contrast it with established algorithms in the literature, several benchmark tests have been conducted. Firstly, we compare the performance of the proposed method on seven DTLZ and five ZDT benchmark functions for multi-objective optimization [32,33]. Furthermore, two established multi-objective mechanical design optimization problems are used to validate the performance of the proposed modifications. Finally, we employed a multi-objective planetary gearbox optimization model [31], to validate performance. Three well-established performance metrics have been used in this paper including Hypervolume (HV), Spread (SP) and Inverted Generational Distance (IGD) [34] in order to measure the suggested algorithm’s convergence and coverage (diversity).

The HV measures the volume of the objective space dominated by a set of non-dominated solutions, bounded by a reference point r. Formally, the hypervolume indicator for a set of solutions S={s1,s2,…,sn} in the objective space is defined as:

HV(S)=vol(⋃s∈S{z∈Rm∣s⪯z⪯r}),(26)

where s⪯z indicates that solution s dominates or is equal to z, and vol represents the Lebesgue measure of the union of the hyperrectangles formed by each solution s and the reference point r. In this context, z is a point in the objective space, m is the number of objectives, and r is a reference point that is dominated by all solutions in the set S.

The hypervolume metric provides a scalar value that reflects both the convergence and diversity of the solution set by capturing the extent of the dominated objective space.

The SP metric is a crucial measure used to evaluate the distribution and spread of solutions along the Pareto front. It quantifies how well the solutions cover the extent of the Pareto front by considering both the distance between consecutive solutions and the overall extent of the front. The spread metric is formally defined as:

Δ=df+dl+∑i=1n−1|di−d¯|df+dl+(n−1)d¯,(27)

where df and dl are the Euclidean distances from the extreme solutions to the boundary solutions of the Pareto front, di is the distance between consecutive solutions, d¯ is the average of these distances, and n is the number of solutions. This metric ensures that solutions are evenly distributed and cover the entire range of the Pareto front, reflecting both convergence and diversity in the solution set.

The Inverted Generational Distance is a widely used metric in multi-objective optimization for assessing the convergence and diversity of a set of solutions generated by an algorithm with respect to a reference Pareto front. The IGD provides an average distance from the points on the reference front to their closest points in the obtained solution set, thus reflecting how well the solution set covers the true Pareto front. The IGD metric is calculated as:

IGD(S,Pref)=1|Pref|∑y∈Prefminx∈Sd(y,x),(28)

where S is the set of solutions obtained by the algorithm, Pref is the reference Pareto front, |⋅| denotes the cardinality of a set, y is a solution vector in the reference Pareto front Pref, x is a solution vector in the obtained solution set S, d(y,x) is the Euclidean distance between vectors y and x, calculated as:

d(y,x)=∑i=1m(yi−xi)2,(29)

where m is the number of objectives, and yi and xi are the i-th objective values of y and x, respectively. A lower IGD value indicates that the obtained solution set S is closer to the reference Pareto front and provides better coverage of the true Pareto-optimal solutions.

In contrast to the conventional IGD metric, the Inverted Generational Distance Plus (IGD+) [35] metric addresses the shortcomings of the IGD by incorporating a modified distance function that exclusively considers non-dominated vectors. This modification enhances the metric’s sensitivity to both convergence towards the genuine Pareto front and the dispersion of solutions along it, rendering IGD+ a more reliable tool for assessing the efficacy of diverse multi-objective optimization algorithms. The IGD+ metric is defined as:

IGD+(P∗,P)=1|P∗|∑v∈P∗minu∈Pd+(v,u),(30)

where P∗ represents the reference Pareto front (typically the true Pareto-optimal front), P is the set of solutions obtained by the algorithm under evaluation, and |P∗| denotes the number of solutions in P∗. The distance function d+(v,u) calculates the directional distance between vectors v and u, considering only the positive differences in each objective dimension:

d+(v,u)=∑i=1m(max{0,vi−ui})2,(31)

where m is the number of objectives, and vi and ui are the values of the i-th objective for solutions v and u, respectively. The use of the max{0,vi−ui} term ensures that only the distances where vi exceeds ui contribute to the metric, effectively penalizing solutions that are dominated or not well-converged. By averaging the minimal positive distances from each point in the reference set to the obtained solution set, IGD+ provides a comprehensive assessment of how closely and uniformly the algorithm’s solutions approximate the true Pareto front.

In order to perform the statistical comparison between obtained results the Wilcoxon signed rank test and Friedman rank test have been employed.

The Wilcoxon signed-rank test [36] is a non-parametric statistical technique utilized to compare two correlated samples or repeated measurements on a single sample in order to evaluate if their population mean ranks exhibit any differences. The test process entails computing the disparities between paired observations, ordering these disparities ac-cording to their absolute values, and subsequently aggregating the rankings for the positive and negative disparities individually. The lesser of these sums is utilized as the test statistic. The null and alternative hypotheses for the Wilcoxon signed-rank test are stated as follows: H0 states that the median difference between the paired observations is equal to zero, while H1 states that the median difference between the paired observations is not equal to zero. The determination to reject the null hypothesis relies on comparing the test statistic with crucial values obtained from the Wilcoxon signed-rank table or by generating a p-value. If the p-value is less than or equal to the selected significance level (α=0.05), the null hypothesis is rejected, suggesting a statistically significant distinction between the paired observations.

The Friedman test [36], a non-parametric statistical approach, is commonly used in evolutionary optimization to assess the efficiency of various algorithms across several problem occurrences. It is essential in benchmark studies to ascertain whether there are statistically significant disparities in performance indicators among different algorithms. The procedure involves ranking the performance of each algorithm on each problem instance, summing these ranks, and using these sums to compute the test statistic. This statistic follows a chi-squared distribution with k−1 degrees of freedom, where k is the number of algorithms. The null and alternative hypotheses evaluated by the test are: H0: “There are no disparities in the distributions of the performance measures among the algorithms.” H1: “At least one algorithm exhibits significant dissimilarity.” The choice to reject the null hypothesis is determined by comparing the test statistic to the crucial value obtained from the chi-squared distribution table at the selected significance level (α=0.05). If the value of the test statistic exceeds the critical value, it leads to the rejection of the null hypothesis, indicating a significant performance difference among the algorithms.

In the next subsections we present the benchmark problems employed to perform numerical analysis.

4.1 Outline of ZDT and DTLZ Benchmark Problems

In the area of optimization, especially meta-heuristic optimization, the benchmark problems play a crucial role in evaluating the efficiency of algorithms, since in majority of cases the strict mathematical validation is not possible. These benchmarks serve as standardized tests, providing a common ground for researchers to compare the performance of different optimization algorithms. The DTLZ and ZDT test problems are widely recognized benchmarks in the field of multi-objective optimization [32,33]. DTLZ problems are specifically formulated for scenarios involving multiple objectives and can accommodate objective spaces with dimensions greater than two. This poses a challenge for algorithms in identifying a diverse range of Pareto-optimal solutions. In contrast, ZDT problems are specifically formulated for bi-objective optimization tasks, focusing on the consideration of only two objectives. In Table 1, a summary of employed benchmark problems is provided, where the following information are provided such as the number of objectives (M), decision variables (n), and the formulas used to calculate objective functions fi(x), and the auxiliary function g(x). The results of statistical comparison of IGD metric (mean and standard deviation) on different optimization problems described in Table 1 are shown in Table 2. Furthermore, the results of using the IGD+ metric are presented in the Table 3. In these tables for performance comparison we have employed well established algorithms in the literature MO_Ring_PSO_SCD [37], GDE3 [38], NSGA-II [4] and compare their performance to the proposed algorithm. The parameters for the employed algorithms for comparison are outlined in Table 4, and are taken as suggested in the respective cited papers. The population number in each simulation was fixed to NP=100 and the maximum number of iterations to 10,000. The results are presented in the form of mean and standard deviation values of IGD and IGD+ metrics as the outcomes of numerical simulation conducted across 30 independent runs for each of the test problems under consideration.

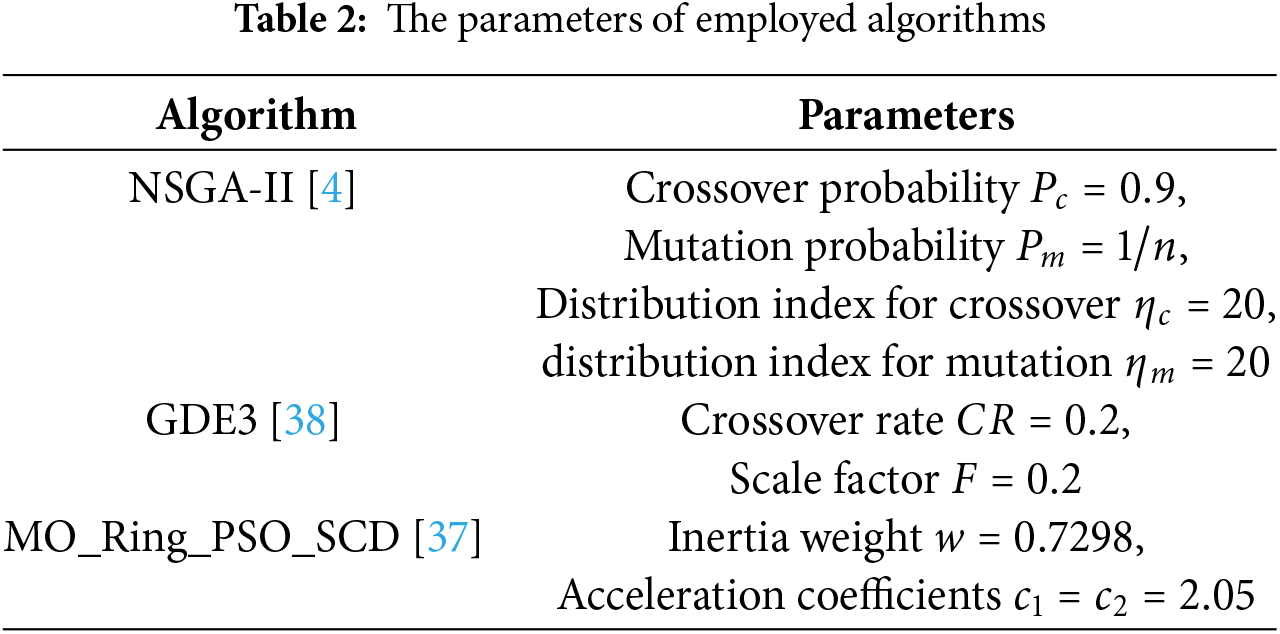
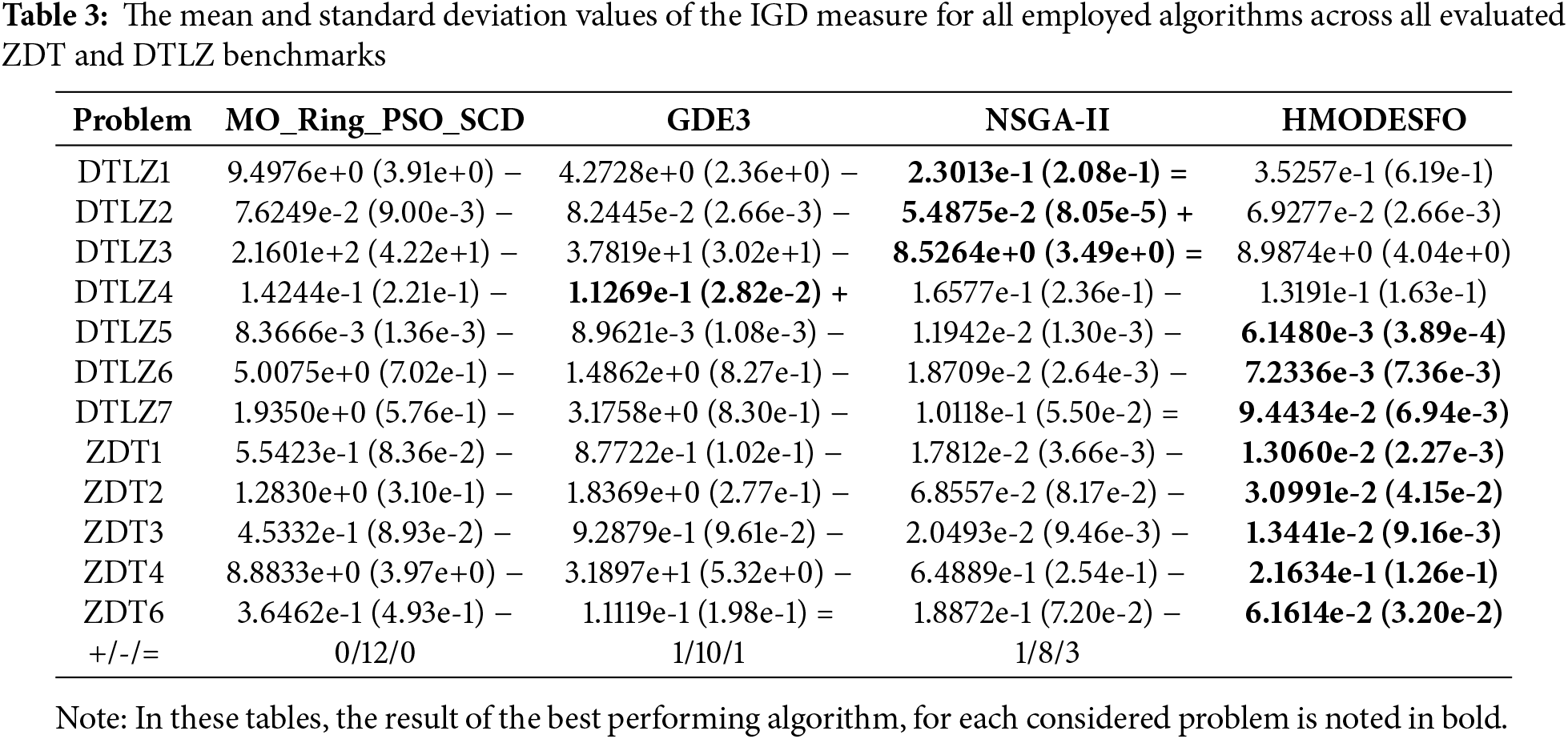
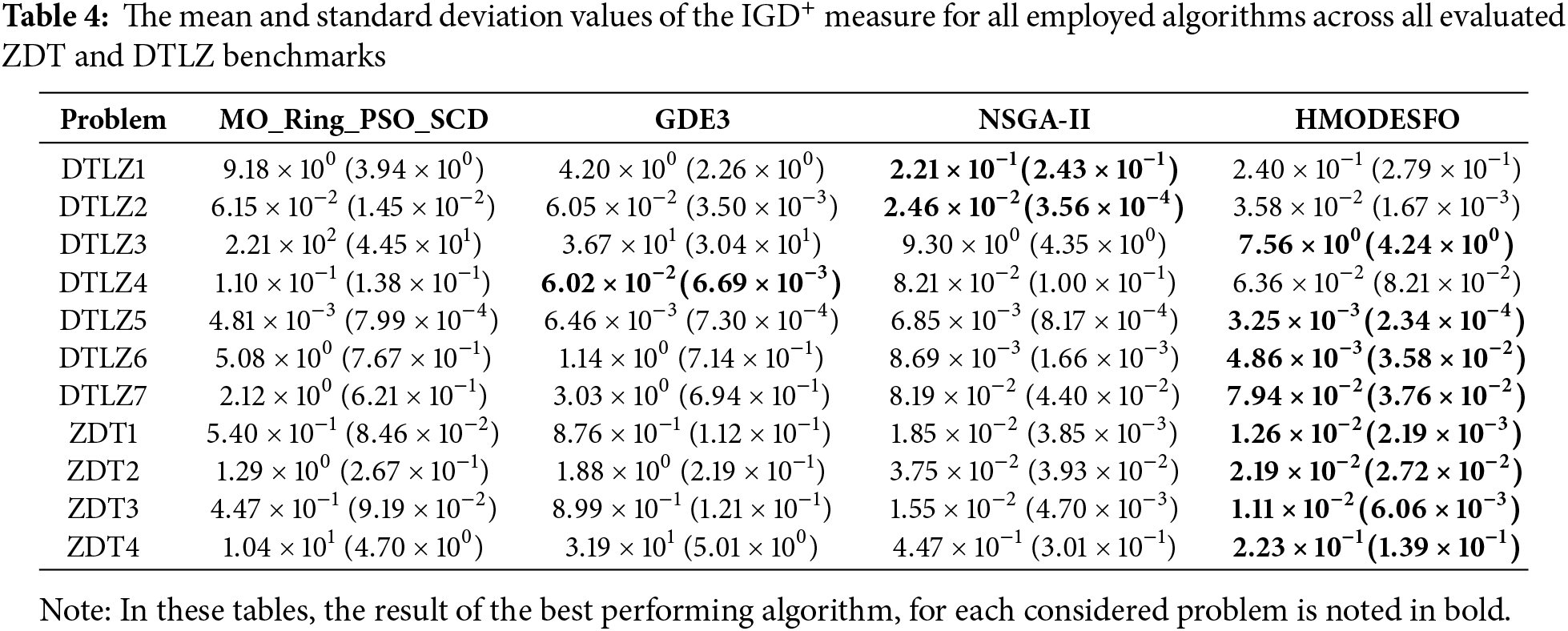
The results presented in Table 3 highlight that for the majority of the test cases, the HMODESFO algorithm achieved the best performance, as indicated by the bold values. In particular, HMODESFO outperforms other algorithms on 9 out of 12 problems.

In contrast, MO_Ring_PSO_SCD and GDE3 exhibit weaker performance, as they were consistently outperformed across all problems, with no observed wins for MO_Ring_PSO_SCD and only one for GDE3. NSGA-II, while competitive in some cases (with three ties), is still largely outperformed by HMODESFO in terms of overall results.

Comparing the results obtained using IGD metric in Table 3 with that in Table 4, we can see that in the case of IGD+ metric the proposed HMODESFO algorithm achieves the similar results, where the NSGA-II algorithm is better only on DTLZ1, DTLZ2 and DTLZ4 problems.

Table 5 displays the statistical results obtained from the application of Wilcoxon’s signed-rank test to the ZDT benchmark issues in this study. This analysis produced results that allowed for the assignment of one of three symbols (+,−,≈) to compare the algorithms. Specifically, the symbol (+) indicates that the first algorithm significantly outperforms the second, while the symbol (−) signifies that the performance of the first algorithm is significantly worse than the second. The symbol (≈) suggests that the two algorithms perform similarly.

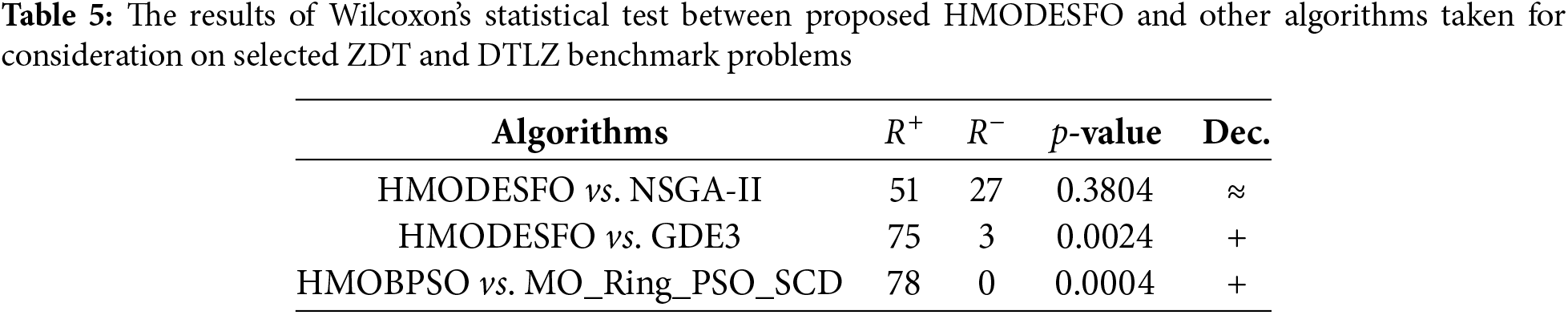
The statistical results presented in Table 5 shows that firstly, the comparison between HMODESFO and NSGA-II yields a p-value of 0.3804, which is greater than the significance threshold of 0.05, indicating that their performance is considered comparable, as denoted by the symbol ≈. In contrast, the comparison between HMODESFO and GDE3 results in a p-value of 0.0024, which is below the significance threshold, indicating a statistically significant difference in favor of HMODESFO. The R+ value of 75 compared to the R− value of 3 further supports this conclusion, and thus, HMODESFO is shown to significantly outperform GDE3, as indicated by the symbol +. Similarly, the comparison between HMOBPSO and MO_Ring_PSO_SCD shows a p-value of 0.0004, also below the threshold of 0.05, indicating a significant difference in favor of HMOBPSO. With R+=78 and R−=0, it is evident that HMOBPSO significantly outperforms MO_Ring_PSO_SCD, as denoted by the symbol +. Table 6 presents the average ranks of the algorithms under analysis across different objective functions of the ZDT and DTLZ benchmark problems, calculated using Friedman’s test. This test was conducted to assess the performance of the proposed algorithm in comparison to other well-established algorithms.

In Table 6, the optimal method for the specified issue is emphasized in bold, whilst the second most effective is underscored. Analyzing the findings reveals that there is a considerable difference in the performance of the algorithms under discussion, as all of the generated p-values fall below the significance level α=0.05. The HMODESFO algorithm attained the highest overall rank, consistent with the findings of the Wilcoxon test. The statistical analysis validates the efficacy of the hybrid algorithm proposed in this paper.

4.2 Benchmark on Mechanical Design Optimization Problems

To evaluate the performance of the proposed algorithm, we have applied it to two real-life mechanical engineering design problems, e.g., welded beam design and pressure vessel design problems, which are widely employed in literature as the benchmarks for multi-objective mechanical engineering design optimization.

4.2.1 Welded-Beam Design Problem

In the field of structural optimization, the welded-beam design problem has been considered as the reference benchmark problem [39]. The main aims of this benchmark problem are to minimize the costs of production while reducing the maximum deflection of the beam, which are conflicting objectives. According to the original problem definition [39], we consider the four design variables: weld thickness (h), beam height (t), beam thickness (b), weld length (l), as shown in Fig. 1. The objectives of the considered problem are formulated as:

minf1=(1+c1)h2l+c2tb(L+l),(32)

minf2=δ,(33)

where f1 is the objective which determines the welding material and working cost, f2 is the beam deflection objective, δ denotes the beam deflection, L=356 mm is the fixed distance between the point of load to the support, and cost coefficients are:

c1=6.3898×10−3$/mm3,(34)

c2=2.9359×10−3$/mm3.(35)

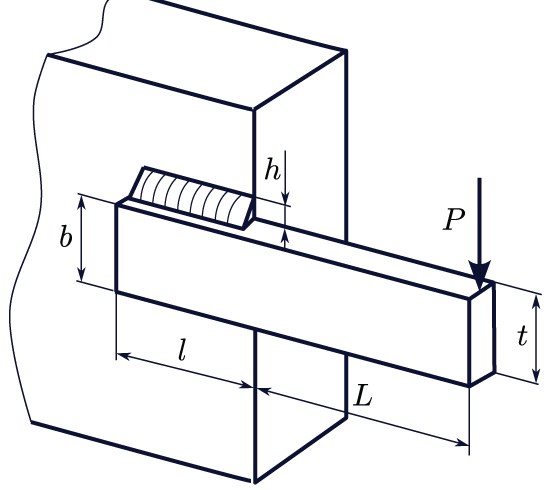
Figure 1: The welded-beam design optimization example

There are numerous constraints that must be met, including the mechanical properties of the weld and the beam, shear and normal stresses, maximal deflection, and the constraints regarding the physical feasibility, including:

g1=τmax−τ≥0,(36)

g2=σmax−σ≥0,(37)

g3=b−h≥0,(38)

g4=l≥0,(39)

g5=t≥0,(40)

g6=Pc−F≥0,(41)

g7=h−0.125≥0,(42)

where τmax is the maximum allowable shear stress of the weld such that τmax=9.38×102 N/mm2, τ is the maximum shear stress in the weld, σmax is the allowable normal stress such that σmax=2.07×102 N/mm2, σ is the maximum normal stress in the beam, Pc is the buckling load, F=26,689 N is the load.

The stresses σ and τ are calculated as follows:

σ=6FLbt2,(43)

τ=F2bt2(2τ′Lbt),(44)

where primary and secondary shear stresses are:

τ1=F2bt2,(45)

τ2=F(L+l)bt2.(46)

and Pc is:

Pc=64746.022(1−0.0282346t)tb2.(47)

4.2.2 Pressure Vessel Design Problem

Another well-established mechanical engineering optimization benchmark problem is the pressure vessel design problem. The main objectives of this problem are to minimize the cost of manufacturing (including the cost of material, forming, and welding) and maximizing the capacity of the pressure vessel [40]. We consider the cylindrical vessel which is closed from the top and bottom with hemispherical heads as depicted in Fig. 2.

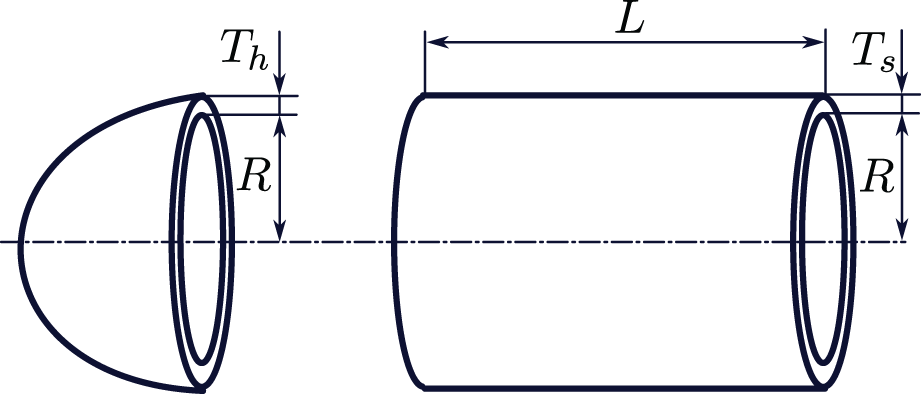
Figure 2: Pressure vessel benchmark design problem

This optimization problem considers four design variables including Ts shell thickness, Th the thickness of the hemispherical heads, R inner radius of the cylindrical part, L the length of the cylindrical part of the vessel. Thus, the objectives can be formulated as:

minf1=0.6224TsLR+1.7781ThR2+3.1661Ts2L+19.84Ts2R,(48)

minf2=−(πR2L+1.333πR3).(49)

To ensure physical feasibility of the solution, there are a number of constraints to satisfy including:

g1=Ts−0.0193R≥0,(50)

g2=Th−0.00954R≥0,(51)

g3=Ts−0.0625≥0,(52)

g4=5−Ts≥0,(53)

g5=Th−0.0625≥0,(54)

g6=5−Th≥0,(55)

g7=R−10≥0,(56)

g8=200−R≥0,(57)

g9=L−10≥0,(58)

g10=240−L≥0.(59)

4.3 Results of Simulation on Welded Beam and Pressure Vessel Problems

This section presents the results of numerical simulations conducted to compare performance and validate the improvements of the proposed HMODESFO algorithm on two mechanical design optimization problems previously described. Based on the conclusions in Section 4.1, in this section we have performed comparison of proposed algorithm to the NSGA-II algorithm. Firstly we have considered welded-beam optimization problem. The obtained Pareto fronts using HMODESFO and NSGA-II algorithms are shown on Fig. 3. From the Fig. 3 we observe that the considered objectives are mutually conflicting, thus validating the need for Pareto optimization. We also observe that the Pareto front obtained by proposed algorithm dominates the one obtained by NSGA-II algorithm.

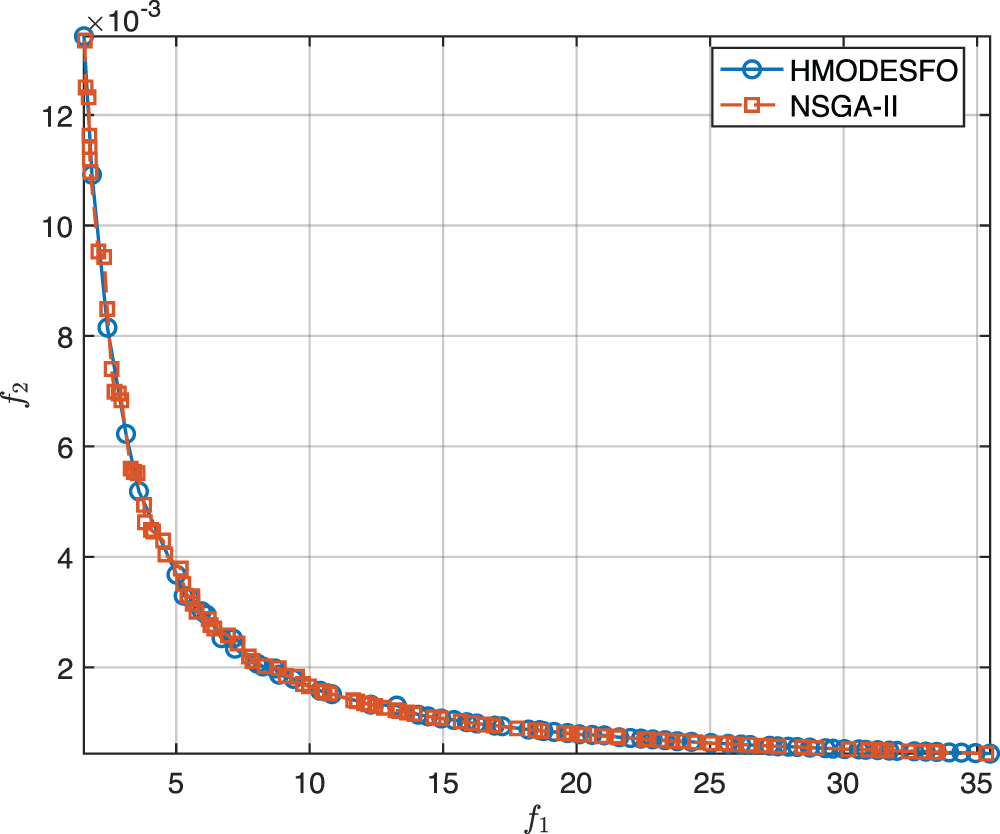
Figure 3: Pareto fronts obtained using HMODESFO and NSGA-II algorithms on welded-beam design problem

Next, we consider the pressure vessel problem described in Section 4.2.2, employing the same algorithms. The obtained Pareto sets for this problem are shown in Fig. 4. Based on the shown Pareto sets from NSGA-II and HMODESFO algorithms, we as in the previous case observe slight improvement in the Pareto front obtained by the proposed algorithm.

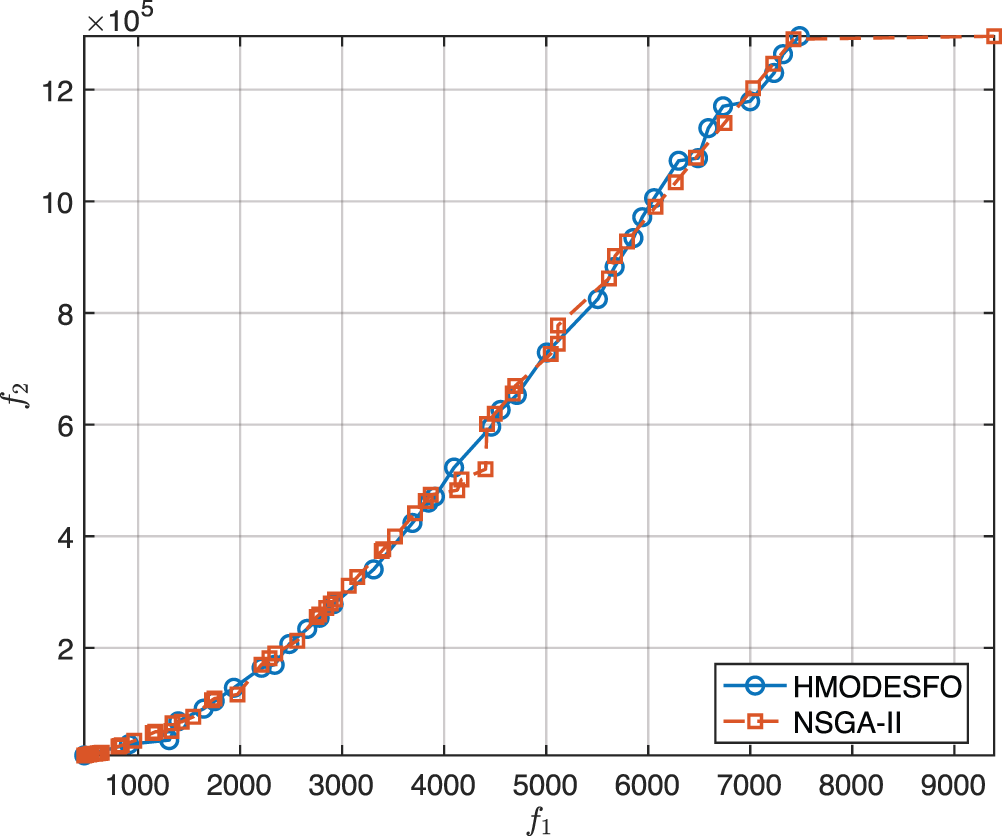
Figure 4: Pareto fronts obtained using HMODESFO and NSGA-II algorithms on pressure vessel design problem

To further validate the performance of two considered algorithms on mechanical engineering problems we have calculated the Hypervolume and Spread metrics using Eqs. (26) and (27), respectively, where the results are presented in Table 7.

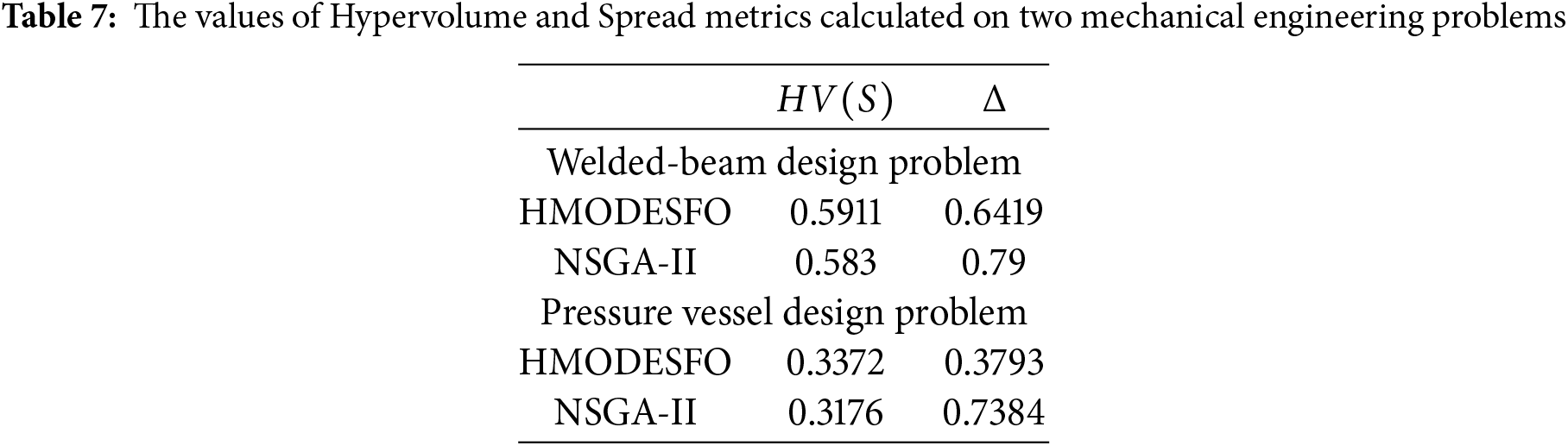
From the results in Table 7 for the welded-beam design problem, HMODESFO achieved a higher hypervolume of 0.5911 compared to hypervolume of NSGA-II algorithm 0.583, indicating that Pareto front obtained by HMODESFO alg. encompasses a larger portion of the objective space, thus demonstrating better convergence. Additionally, HMODESFO attained a lower spread value of 0.6419 vs. NSGA-II 0.79, suggesting a more uniform distribution of solutions along the Pareto front and enhanced diversity. Regarding the pressure vessel design problem, a similar trend is observed. HMODESFO outperformed NSGA-II with a hypervolume of 0.3372 compared to 0.3176. Moreover, spread metric of HMODESFO algorithm is 0.3793 and is significantly lower than that of NSGA-II which is 0.7384, indicating a more evenly spread set of solutions. This shows that the improvements introduced in proposed algorithm lead to better performance on mechanical engineering problems.

4.4 Performance Metrics on Planetary Gearbox Optimization Problem

In order to further compare the performance of the proposed algorithm, the complex multi-objective planetary gearbox optimization problem, formulated by [31,41], has been employed. The considered problem assumes choosing the appropriate parameters for a single stage planetary gearbox with central gear connected with the input, three planet gears on a carrier, and a single stationary rim gear with internal gearing, as shown in Fig. 5.

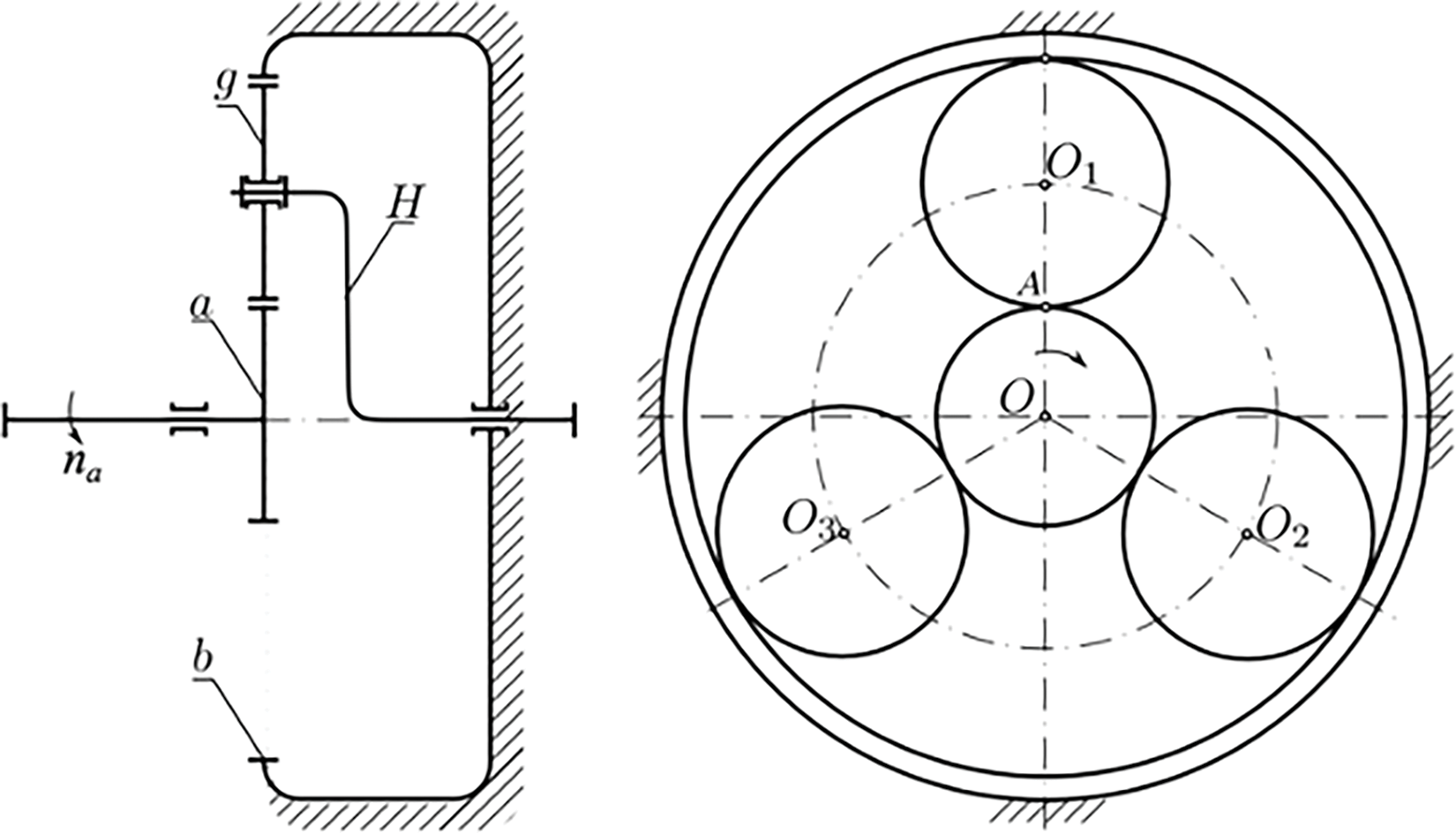
Figure 5: Schematic representation of a single stage planetary gearbox included in the appropriate optimization model [41]

According to the previous works of authors [31,41], the planetary gearbox optimization model uses seven design variables such as the teeth number of central sun gear z3, number of teeth of rim gear with internal teething zr, number of teeth of planet gears zp, module m, x3, xr, and xp which are profile shift coefficients of sun, rim, and planet gears, respectively. The appropriate domains of application for each variable are given in Table 8.

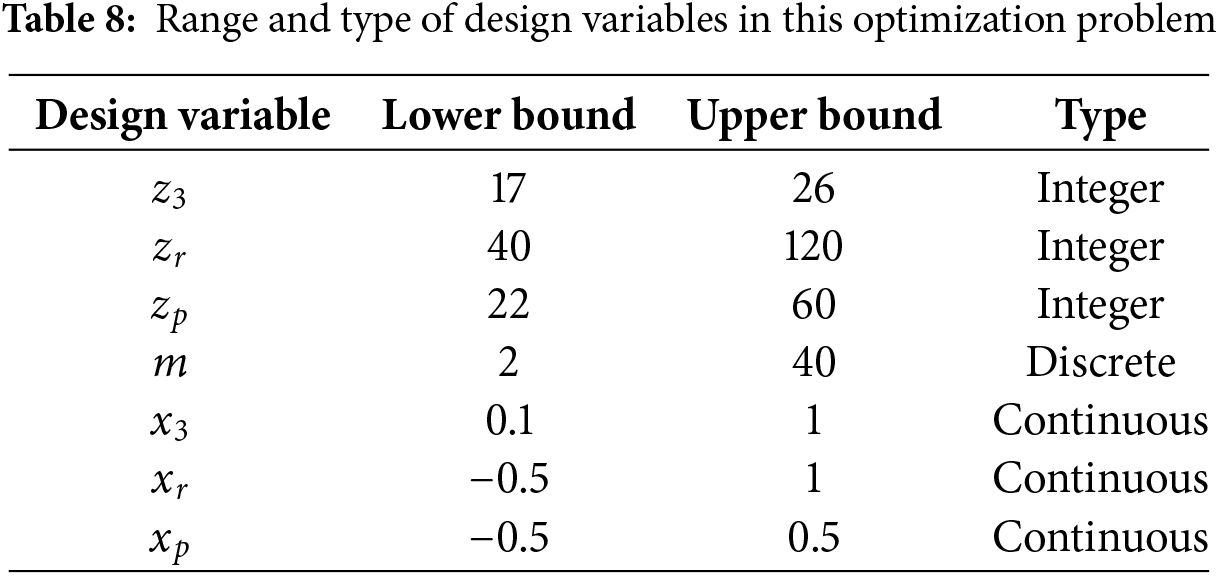
The proposed model assumes a number of different objectives among which, in this study we will employ the gearbox volume, as well as the efficiency calculation of complete gearbox as the two main objectives, which can be defined as

Gears volume

The volume of the gears can be defined under the assumption of uniform density of the gear material and that all gears are produced using the same material as follows:

f1=V(x)=π4b[d(a)2+nw(da(b)2−D2)+(d(g)2−ds2)],(60)

where b is the width of gears, d(a) is the tip circle of the sun gear, nw is the number of planet gears, da(b) is the tip circle of planet gear, D is the outside diameter of ring gear, d(g) is the pitch circle of planet gear and ds is the outside bearing diameter.

Gearbox efficiency

ηaHb=1−ηagHηgbHuabH1−uabH.(61)

where ηaHb, ηagH and ηgbH are the appropriate efficiencies of considered gear pairs and uabH is the overall gearbox gear ratio. To determine the efficiency of a specific gear pair, this paper utilizes the mathematical model established by the authors in [31].

In order to guarantee the viability of the derived optimal solution, and consequently the proper functioning of the planetary gearbox, it is essential to incorporate and fulfill a series of constraints within the proposed optimization model, which include:

Safety against bending

To ensure the proper functioning of gears, we must calculate bending stress and prevent that stress becoming greater than critical stress for material, which is represented with constraint

g1=[σF]cσF−SFmin≥0,(62)

where [σF]c is the critical root stress depending on the material of the gear, SFmin is the factor of safety against bending, such that SFmin=1.25, and root stress is calculated as:

σF=YFYβYϵFtbmnKAKVKH.(63)

where the appropriate factors YF,Yβ,Yϵ,KA,KV,KH are calculated according to the standard [42,43].

Safety against pitting

Another important factor that ensures normal working of gears is ensuring that the contact stress is less than critical contact stress, encompassed with the constraint

g2=[σH]cσH−SHmin≥0,(64)

where [σH]c is the critical contact stress, SHmin is the factor of safety against pitting, taken as SHmin=1.25, and the contact stress is calculated as:

σH=ZHZEZεFtbd(a)u+1uKAKvKHα,(65)

where the appropriate factors ZH,ZE,Zε,KA,Kv,KHα are calculated according to the standard [42,43].

Space requirement

In order to facilitate the proper mounting of gears within the gearbox assembly, it is imperative that an adequate clearance be maintained between the tip circles of the meshing gears. This requirement is addressed through the implementation of the following constraint:

g3=2aagsin⁡(πnw)−fz−da(g)≥0,(66)

where fz=0.5⋅mn is the minimum clearance, and aag is the center distance between sun and planet gears.

Assembly constraint

In order to avert any possible interference of the teeth throughout the meshing process, it is imperative to guarantee that the central sun gear engages with the planet gears in a simultaneous manner consistently. Consequently, the equality constraint is formulated as follows:

h1=za+zbnw−i=0,(67)

where i is the integer which leads to constraint being zero.

4.5 Results on Simulation on Planetary Gearbox Problem

This subsection presents the findings derived from numerical simulations performed on the optimization model of the planetary gearbox, as delineated in Section 4.4.

The system under examination acquires power through the input shaft, which is connected to the sun gear, subsequently disseminating it among the planet gears and transmitting it to the holder, which is connected to the output shaft. In the course of the analysis, the speed of sun gear is maintained at a constant value of na=2750min−1, accompanied by a power output of Pa=175kW. The parameters that remain integral to the design of the considered optimization problem of planetary transmission are enumerated in Table 9.

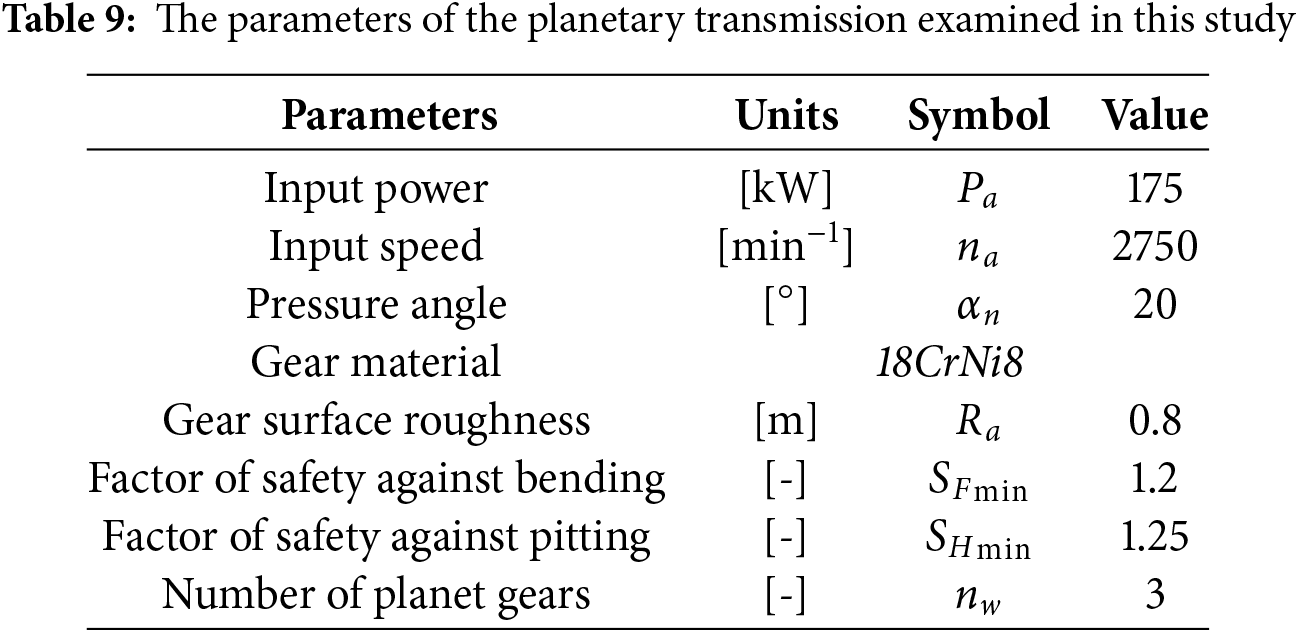
In light of prior benchmark tests conducted for this analysis, we utilized the NSGA-II algorithm to evaluate its performance in comparison to the proposed HMODESFO algorithm. The parameters employed in the simulations consist of NP=100 individuals and a maximum of 10,000 generations. The simulations were conducted utilizing MATLAB software using a computational system featuring a 3.2 GHz central processing unit and 16 gigabytes of random access memory. Considering the presence of conflicting objectives, it is evident that no singular optimal solution can be identified. Consequently, a Pareto set of solutions has been derived and to facilitate comparison, an ideal solution, denoted as xideal=(xideal,1,xideal,2,…,xideal,M), is calculated based on the following expression:

xideal,i=min(fi),∀i=1,2,…,M(68)

here, M denotes the quantity of objectives undergoing optimization. The ideal solution xideal is a theoretical construct that signifies the optimal outcome for each objective, supposing that all objectives can be concurrently reduced. In practical optimization problems, particularly those with competing objectives, such a solution is seldom attainable, as enhancing one goal generally results in the decline of another.

As the optimal solution xideal does not exist in the Pareto set, it functions as a benchmark rather than a realizable outcome. A compromise solution is identified to facilitate practical comparisons. This compromise option is chosen from the Pareto front as the one nearest to the ideal solution, with closeness assessed using the Euclidean distance metric. This guarantees that the compromise solution equilibrates trade-offs among all objectives and embodies the most balanced design option within the framework of the specified challenge. To comprehensively study the issue, many combinations of objectives have been evaluated to encompass diverse aspects of gearbox design optimization, such as

•   Gearbox volume (V) in conjunction with gearbox efficiency (ηgbH) and bending stress (σF), Eqs. (60) and (61), respectively,

•   Gearbox volume V combined with efficiency ηgbH and bending stress σF, and

•   Gearbox volume V in conjunction with efficiency ηgbH and contact stress σH.

An analysis was conducted on the suitable Pareto optimal curves obtained by solving the planetary gearbox multi-objective optimization model, which were derived from both the NSGA-II and the proposed algorithms. The Pareto optimal curves serve as a visual depiction of the trade-offs inherent among various objectives, thereby enabling engineers to identify the most appropriate solution in accordance with their specific needs, rather than being constrained to a singular compromise solution.

We firstly examine the gearbox volume in conjunction with its efficiency as shown in Fig. 6.

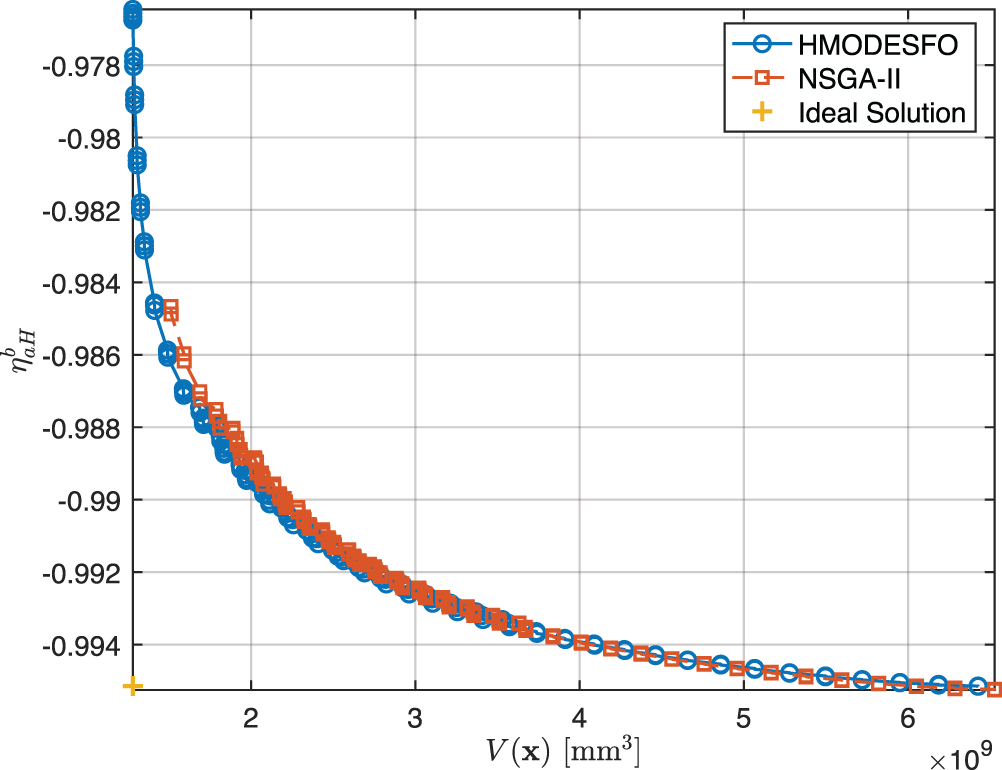
Figure 6: The HMODESFO and NSGA-II algorithms applied to obtained results for the MOO problem with combination of gearbox volume V and gearbox efficiency as the objectives with the appropriate Pareto curves

From the Fig. 6, we can observe that the considered objectives are mutually conflicting. Thus the reduction in one objective leads to the increase in the other. Furthermore, we can see that the Pareto curves obtained by the HMODESFO algorithm dominate the ones obtained by NSGA-II algorithm. To compare two algorithms on the same problem an ideal solution is extracted as a tuple (V,ηgbH)=(1.27×109,0.995) and compromise solution obtained by HMODESFO algorithm is (1.27×109,0.984), as well as the solution obtained by NSGA-II is (1.28×109,0.96).

Furthermore, we consider Pareto curves for three objectives optimization problem, where the objectives are gearbox volume V, gearbox efficiency ηgbH and bending stress σF, as shown in Fig. 7.

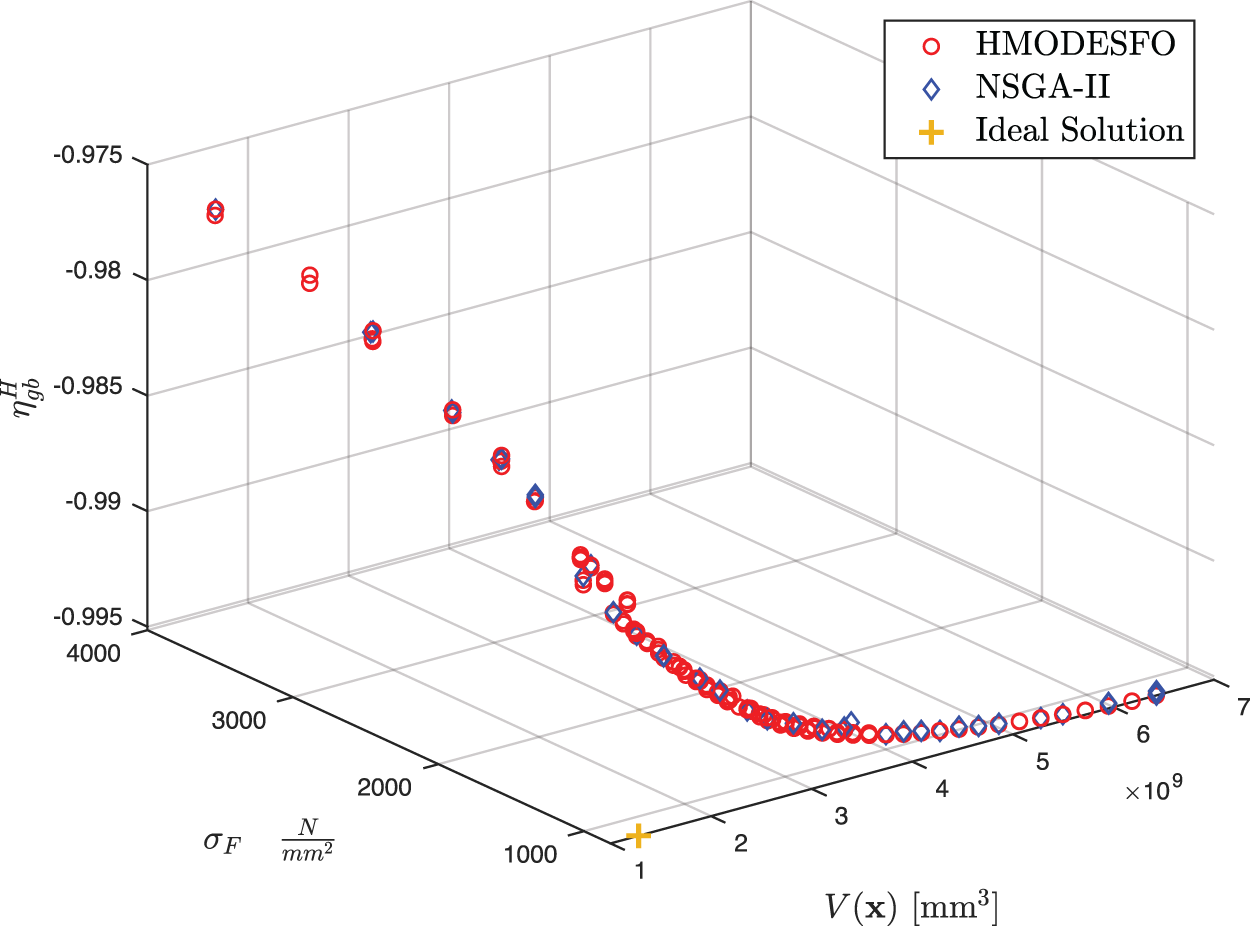
Figure 7: The results of applying HMODESFO and NSGA-II algorithms to obtain solutions for the MOO problem with combination of gearbox volume V, gearbox efficiency and bending stress σF as the objectives with the appropriate Pareto curves

We can see that all the goals that were taken into consideration are in opposition with each other, as shown in Fig. 7. Specifically, when one goal is increased, the other two objectives are decreased. Here, a tuple containing an ideal solution (not part of the Pareto front but minimizing all goals) is extracted for the sake of comparison as (V,σF,ηgbH)=(1.27×109,817.6,0.995) and compromise solution obtained by HMODESFO algorithm is (1.2×109,372,0.97), as well as the solution obtained by NSGA-II is (1.27×109,385,0.96). We see that in the terms of ideal solution in this case both algorithms provide the similar result.

Finally, we consider the following combination of objectives - gearbox volume V, gearbox efficiency ηgbH and contact stress σH as shown in Fig. 8.

Figure 8: The results of applying HMODESFO and NSGA-II algorithms to obtain solutions for the MOO problem with combination of gearbox volume V, gearbox efficiency and contact stress σH as the objectives with the appropriate Pareto curves

Based on the results in Fig. 8 it can be observed that considered objecives are conflicting. In order to make comparison between algorithms, we extracted the ideal and compromise solutions as the following tuples (V,σH,ηgbH)=(1.26×109,614.8,0.995) and compromise solution obtained by HMOBPSO algorithm is (1.27×109,458.5,0.976), as well as the solution obtained by NSGA-II is (1.27×109,473,0.974). This metric again shows similar results, but it’s not the primary metric for deciding the adequatness of the algorithm.

To further validate the performance of HMODESFO and NSGA-II algorithms on considered complex planetary gearbox optimization model, we have calculated the Hypervolume and Spread metrics using Eqs. (26) and (27), respectively, where the results are presented in Table 10.

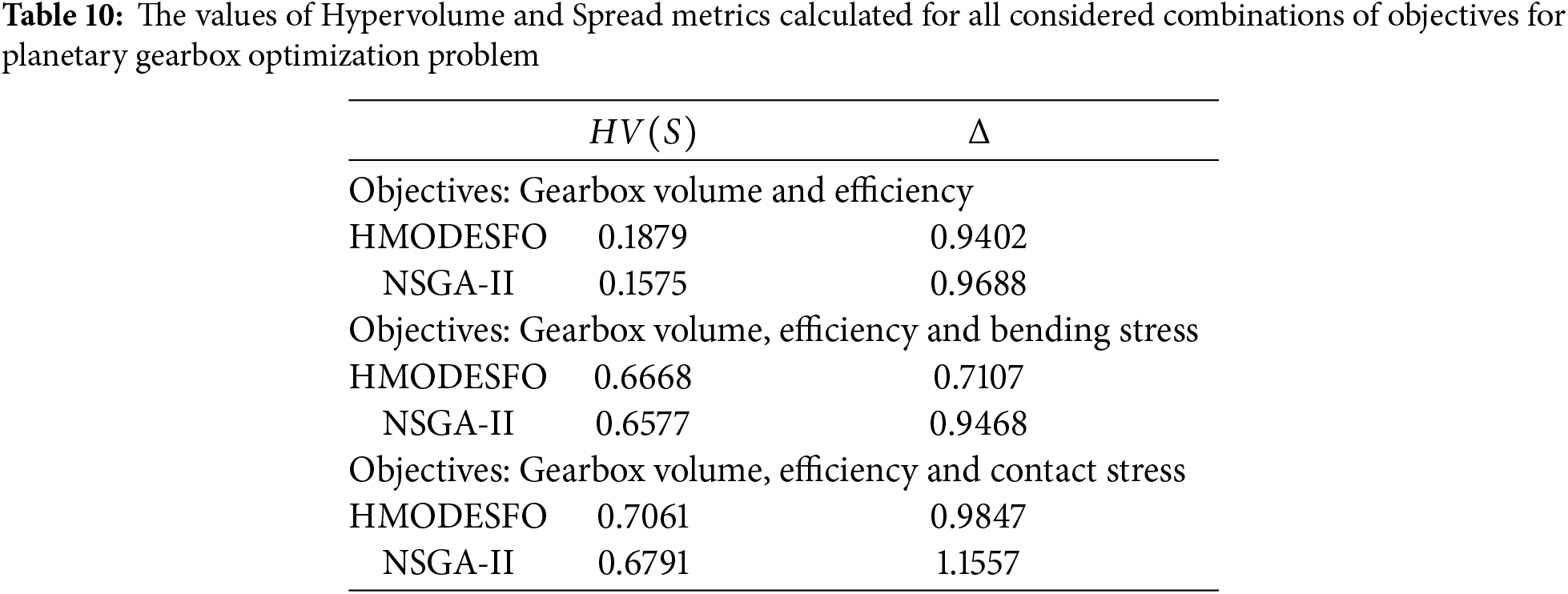
The computed values for each algorithm across different combinations of objectives in the planetary gearbox optimization problem are summarized in Table 10. When considering the objectives of gearbox volume and efficiency, HMODESFO achieved a higher HV of 0.1879 compared to HV value of NSGA-II 0.1575, indicating a better convergence towards the true Pareto front. Additionally, HMODESFO exhibited a lower Spread value (Δ=0.9402) than NSGA-II (Δ=0.9688), suggesting a more uniform distribution of solutions.

For the three-objective optimization involving gearbox volume, efficiency, and bending stress, HMODESFO again outperformed NSGA-II with an HV of 0.6668 vs. 0.6577 and a lower Spread of 0.7107 compared to 0.9468. Similarly, in the case of gearbox volume, efficiency, and contact stress, HMODESFO attained a higher HV of 0.7061 and a lower Spread of 0.9847, whereas NSGA-II recorded an HV of 0.6791 and a Spread of 1.1557. These results consistently demonstrate that HMODESFO not only provides a broader coverage of the objective space but also maintains better solution diversity. Therefore, HMODESFO exhibits superior performance over NSGA-II in optimizing the complex planetary gearbox model across all considered objective combinations.

5  Conclusion

This study has successfully developed and validated the HMODESFO algorithm, a hybrid multi-objective optimization approach that combines the exploratory strengths of DE with the rapid convergence of the SFO algorithm. This integration is specifically designed to tackle the intricate multi-objective optimization challenges encountered in the field of mechanical engineering, concentrating particularly on the optimization of planetary gearboxes. For this purpose, appropriate mechanical optimization problems have been introduced from the literature, and the MOO model has been created for a planetary gearbox, integrating many objectives and multiple constraints, including safety against pitting and bending, assembly and mounting, etc. The integration of mutation strategies from DE algorithm into the SFO framework has notably enhanced the exploration and exploitation phases, thereby preventing premature convergence, a common pitfall in many evolutionary algorithms.

The method in question has effectively produced the non-convex Pareto frontier, which is confirmed with calculated Hypervolume and Spread metrics, thus enabling the designer to have a wider Pareto front and a larger number of solutions to choose from (a larger number of variations of the design). Through comparison with other algorithms on various ZDT and DTLZ benchmark issues, the optimization effectiveness of the HMODESFO approach has been assessed. By producing better results compared to the NSGA-II, the HMODESFO algorithm proved to be more efficient in optimizing the planetary gearbox model. This finding demonstrates how efficient and reliable the suggested approach is for finding best solutions.

Despite its potential, HMODESFO algorithm performance was evaluated on specific benchmark problems and mechanical design optimization scenarios. These scenarios may not fully represent real-world problem domains. Future studies should test the algorithm on a broader range of optimization tasks, including those from unrelated fields.

Secondly, this study derived its parameter settings from established practices and empirical fine-tuning. A more systematic investigation into parameter sensitivity and robustness across different problem types would enhance the algorithm’s generalization and practical implementation.

Building on these findings, future research should extend beyond refining adaptive mechanisms and exploring additional applications. Integrating HMODESFO with emerging computational paradigms can address scalability challenges and enhance performance. The adaptive mechanisms introduced here can serve as a foundation for developing a new class of hybrid meta-heuristic algorithms for diverse fields like supply chain optimization and renewable energy systems.

Collaborations with industrial stakeholders can validate HMODESFO algorithm efficiency on real-world datasets, paving the way for its adoption in different sectors.

Finally, comparative studies with recently developed algorithms in under-explored domains can provide deeper insights into HMODESFO algorithm robustness, adaptability, and versatility. These efforts would strengthen the algorithm’s practical relevance and contribute to advancing multi-objective optimization.

Acknowledgement: Not applicable.

Funding Statement: The research of M. Sedak was supported by the Serbian Ministry of Education and Science under Grant No. TR35006 and COST Action:CA23155—A Pan-European Network of Ocean Tribology (OTC). The research of B. Rosić and M. Rosić was supported by the Serbian Ministry of Education and Science under Grant TR35029.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Miloš Sedak, Božidar Rosić; data collection: Maja Rosić; analysis and interpretation of results: Miloš Sedak, Maja Rosić; draft manuscript preparation: Miloš Sedak. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Wang R, Zhou Z, Ishibuchi H, Liao T, Zhang T. Localized weighted sum method for many-objective optimization. IEEE Trans Evol Comput. 2018 Feb;22(1):3–18. doi:10.1109/TEVC.2016.2611642. [Google Scholar] [CrossRef]

2. Bazgan C, Ruzika S, Thielen C, Vanderpooten D. The power of the weighted sum scalarization for approximating multiobjective optimization problems. Theory Comput Syst. 2022 Feb;66(1):395–415. doi:10.1007/s00224-021-10066-5. [Google Scholar] [CrossRef]

3. Wu Y, Zhang Z, Yuan J, Ma Q. Weight-dependent equilibrium solution for weighted-sum multiobjective optimization. In: Proceedings of the Second International Conference on Intelligent Transportation. Singapore: Springer; 2017. Vol. 53, p. 251–9. [Google Scholar]

4. Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multiobjective genetic algorithm: nSGA-II. IEEE Trans Evol Comput. 2002 Apr;6(2):182–97. doi:10.1109/4235.996017. [Google Scholar] [CrossRef]

5. Mezura-Montes E, Coello CAC. Constraint-handling in nature-inspired numerical optimization: past, present and future. Swarm Evolut Computat. 2011;1(4):173–94. doi:10.1016/j.swevo.2011.10.001. [Google Scholar] [CrossRef]

6. Bilal, Pant M, Zaheer H, Garcia-Hernandez L, Abraham A. Differential evolution: a review of more than two decades of research. Eng Appl Artif Intell. 2020 Apr;90:103479. doi:10.1016/j.engappai.2020.103479. [Google Scholar] [CrossRef]

7. Eltaeib T, Mahmood A. Differential evolution: a survey and analysis. Appl Sci. 2018 Oct;8(10):1945. doi:10.3390/app8101945. [Google Scholar] [CrossRef]

8. Tiemin YU, Dongshu YAN. Differential evolution algorithm for multi-objective optimization. J Changchun Univ. 2006;16(2):77–80. [Google Scholar]

9. Ali M, Siarry P, Pant M. An efficient Differential Evolution based algorithm for solving multi-objective optimization problems. Eur J Oper Res. 2011 Mar;217(2):404–16. [Google Scholar]

10. Niu D, Wang F, Chang Y, He D, Gu D. An improved multi-objective differential evolution algorithm. In: 2012 24th Chinese Control and Decision Conference (CCDC). Taiyuan, China; 2012 May 23–25. p. 879–82. [Google Scholar]

11. Xu B, Tao L, Chen X, Cheng W. Adaptive differential evolution with multi-population-based mutation operators for constrained optimization. Soft Comput. 2018 May;23(10):3423–47. doi:10.1007/s00500-017-3001-0. [Google Scholar] [CrossRef]

12. Shadravan S, Naji HR, Bardsiri VK. The Sailfish Optimizer: a novel nature-inspired metaheuristic algorithm for solving constrained engineering optimization problems. Eng Appl Artif Intell. 2019 Apr;80:20–34. doi:10.1016/j.engappai.2019.01.001. [Google Scholar] [CrossRef]

13. Samal P, Roshan R. Optimal STATCOM allocation and sizing using the sailfish optimizer algorithm. In: 7th IEEE Uttar Pradesh Section International Conference on Electrical, Electronics and Computer Engineering (UPCON). Prayagraj, India; 2020 Nov 27–29. [Google Scholar]

14. Dao TK, Jiang SJ, Ji XR, Ngo TG, Nguyen TT, Tran HT. A coverage and connectivity of WSN in 3D surface using sailfish optimizer. In: Congress on Intelligent Systems: Proceedings of CIS 2020. Singapore: Springer; 2021. Vol. 2, p. 89–98. [Google Scholar]

15. Li M, Li Y, Chen Y, Xu Y. Batch recommendation of experts to questions in community-based question-answering with a sailfish optimizer. Expert Syst Appl. 2021 May;169(9):114484. doi:10.1016/j.eswa.2020.114484. [Google Scholar] [CrossRef]

16. Santos NM, Neto M, Araujo J, Barros F, Cavalcante G, Matos E, et al. A new approach for FSS design in 3.5 GHz based on general neural network model by using multi-objective sailfish optimization algorithm. J Commun Inf Syst. 2022 May;37(1):86–90. doi:10.14209/jcis.2022.9. [Google Scholar] [CrossRef]

17. Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Transact Evolution Comput. 1997;1(1):67–82. doi:10.1109/4235.585893. [Google Scholar] [CrossRef]

18. Abd Elaziz M, Li L, Jayasena KN, Xiong S. Multiobjective big data optimization based on a hybrid salp swarm algorithm and differential evolution. Appl Math Model. 2020 Apr;80(9):929–43. doi:10.1016/j.apm.2019.10.069. [Google Scholar] [CrossRef]

19. Li K, Tian H. Adaptive differential evolution with evolution memory for multiobjective optimization. IEEE Access. 2019;7:866–76. doi:10.1109/ACCESS.2018.2885947. [Google Scholar] [CrossRef]

20. Saveca J, Sun Y, Wang Z. A hybrid multiobjective optimization based on nondominated sorting and crowding distance, with applications to wave energy converters. Int Trans Electr Energy Syst. 2022 Jan;2022(1):8309697. doi:10.1155/2022/8309697. [Google Scholar] [CrossRef]

21. Rajamoorthy R, Saraswathi HV, Devaraj J, Kasinathan P, Elavarasan RM, Arunachalam G, et al. A hybrid sailfish whale optimization and deep long short-term memory (SWO-DLSTM) model for energy efficient autonomy in India by 2048. Sustainability. 2022 Jan;14(3):1355. doi:10.3390/su14031355. [Google Scholar] [CrossRef]

22. Hosseiniasl M, Fesharaki JJ. A heuristic approach for optimization of gearbox dimension. J Modern Process Manufact Product. 2018;7:17–39. [Google Scholar]

23. Golabi S, Fesharaki JJ, Yazdipoor M. Gear train optimization based on minimum volume/weight design. Mech Mach Theory. 2014 Mar;73:197–217. doi:10.1016/j.mechmachtheory.2013.11.002. [Google Scholar] [CrossRef]

24. Hou X, Gao S, Qiu L, Li Z, Zhu R, Lyu SK. Transmission efficiency optimal design of spiral bevel gear based on hybrid PSOGSA (Particle Swarm Optimization-Gravitational Search Algorithm) Method. Appl Sci. 2022 Oct;12(19):10140. doi:10.3390/app121910140. [Google Scholar] [CrossRef]

25. Top N, Dorterler M, Sahin İ. Optimization of planetary gearbox using nature inspired meta-heuristic optimizers. Proc Institut Mech Eng Part C: J Mech Eng Sci. 2023 Oct;238(8):3338–47. doi:10.1177/095440622311960. [Google Scholar] [CrossRef]

26. Patil M, Ramkumar P, Shankar K. Multi-objective optimization of spur gearbox with inclusion of tribological aspects. J Friction Wear. 2017 Nov;38(6):430–6. doi:10.3103/S1068366617060101. [Google Scholar] [CrossRef]

27. Patil M, Ramkumar P, Shankar K. Multi-objective optimization of the two-stage helical gearbox with tribological constraints. Mech Mach Theory. 2019 Aug;138(2):38–57. doi:10.1016/j.mechmachtheory.2019.03.037. [Google Scholar] [CrossRef]

28. Le XH, Vu NP. Multi-objective optimization of a two-stage helical gearbox using taguchi method and grey relational analysis. Appl Sci. 2023 Jun;13(13):7601. doi:10.3390/app13137601. [Google Scholar] [CrossRef]

29. Xu X, Chen J, Lin Z, Qiao Y, Chen X, Zhang Y, et al. Optimization design for the planetary gear train of an electric vehicle under uncertainties. Actuators. 2022 Feb;11(2):49. doi:10.3390/act11020049. [Google Scholar] [CrossRef]

30. Kim BS, Chung WJ, Kim S, Park YJ. Optimum design of planetary gear set using multi-objective optimization considering mass, power loss and transmission error. Mech Based Des Struct Mach. 2024;52(10):7325–48. doi:10.1080/15397734.2023.2297259. [Google Scholar] [CrossRef]

31. Sedak M, Rosić B. Multi-objective optimization of planetary gearbox with adaptive hybrid particle swarm differential evolution algorithm. Appl Sci. 2021 Jan;11(3):1107. doi:10.3390/app11031107. [Google Scholar] [CrossRef]

32. Zitzler E, Deb K, Thiele L. Comparison of multiobjective evolutionary algorithms: empirical results. Evolution Computa. 2000;8(2):173–95. doi:10.1162/106365600568202. [Google Scholar] [PubMed] [CrossRef]

33. Deb K, Thiele L, Laumanns M, Zitzler E. Scalable test problems for evolutionary multiobjective optimization. London: Springer; 2005. [Google Scholar]

34. Riquelme N, Von Lücken C, Baran B. Performance metrics in multi-objective optimization. In: 2015 Latin American Computing Conference (CLEI); 2015 Oct 19–23; Arequipa, Peru. p. 1–11. [Google Scholar]

35. Ishibuchi H, Masuda H, Nojima Y. Sensitivity of performance evaluation results by inverted generational distance to reference points. In: 2016 IEEE Congress on Evolutionary Computation (CEC); 2016 July 24–29; Vancouver, BC, Canada. p. 1107–14. [Google Scholar]

36. Derrac J, García S, Molina D, Herrera F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evolution Computat. 2011;1(1):3–18. doi:10.1016/j.swevo.2011.02.002. [Google Scholar] [CrossRef]

37. Yue C, Qu B, Liang J. A multiobjective particle swarm optimizer using ring topology for solving multimodal multiobjective problems. IEEE Transact Evolution Computat. 2017;22(5):805–17. [Google Scholar]

38. Kukkonen S, Lampinen J. GDE3: the third evolution step of generalized differential evolution. In: 2005 IEEE Congress on Evolutionary Computation; 2005 Sep 2–5; Edinburgh, Scotland, UK; p. 443–50. [Google Scholar]

39. Ravindran A, Reklaitis GV, Ragsdell KM. Engineering optimization: methods and applications. Hoboken, NJ, USA: John Wiley & Sons; 2006. [Google Scholar]

40. Mirzakhani NA, Moradi A. Constrained multi-objective optimization problems in mechanical engineering design using bees algorithm. J Solid Mech. 2011;3(4):353–64. [Google Scholar]

41. Sedak M, Rosić M. Hybrid butterfly optimization and particle swarm optimization algorithm-based constrained multi-objective nonlinear planetary gearbox optimization. Appl Sci. 2023;13(21):11682. doi:10.3390/app132111682. [Google Scholar] [CrossRef]

42. DIN Deutsches Institut für Normung. Calculation of load capacity of cylindrical gears. Berlin, Germany: German Institute for Standardization-DIN; 1987. [Google Scholar]

43. International Organization for Standardization. Calculation of load capacity of spur and helical gears. Geneva, Switzerland: International Organization for Standardization; 1996. [Google Scholar]