 Open Access
Open Access
REVIEW
Unveiling Effective Heuristic Strategies: A Review of Cross-Domain Heuristic Search Challenge Algorithms
1 Faculty of Information Science and Technology, Universiti Kebangsaan Malaysia, Bangi, 43600, Selangor, Malaysia
2 Center for Artificial Intelligence Technology, Universiti Kebangsaan Malaysia, Bangi, 43600, Selangor, Malaysia
3 Faculty of Medicine, Universiti Kebangsaan Malaysia Medical Centre, Cheras, 56000, Kuala Lumpur, Malaysia
4 School of Engineering and Computing, MILA University, Nilai, 71800, Negeri Sembilan, Malaysia
5 School of Computer Science, University of Nottingham-Malaysia Campus, Semenyih, 43500, Selangor, Malaysia
* Corresponding Author: Mohamad Khairulamirin Md Razali. Email:
(This article belongs to the Special Issue: Algorithms, Models, and Applications of Fuzzy Optimization and Decision Making)
Computer Modeling in Engineering & Sciences 2025, 142(2), 1233-1288. https://doi.org/10.32604/cmes.2025.060481
Received 02 November 2024; Accepted 27 December 2024; Issue published 27 January 2025
Abstract
The Cross-domain Heuristic Search Challenge (CHeSC) is a competition focused on creating efficient search algorithms adaptable to diverse problem domains. Selection hyper-heuristics are a class of algorithms that dynamically choose heuristics during the search process. Numerous selection hyper-heuristics have different implementation strategies. However, comparisons between them are lacking in the literature, and previous works have not highlighted the beneficial and detrimental implementation methods of different components. The question is how to effectively employ them to produce an efficient search heuristic. Furthermore, the algorithms that competed in the inaugural CHeSC have not been collectively reviewed. This work conducts a review analysis of the top twenty competitors from this competition to identify effective and ineffective strategies influencing algorithmic performance. A summary of the main characteristics and classification of the algorithms is presented. The analysis underlines efficient and inefficient methods in eight key components, including search points, search phases, heuristic selection, move acceptance, feedback, Tabu mechanism, restart mechanism, and low-level heuristic parameter control. This review analyzes the components referencing the competition’s final leaderboard and discusses future research directions for these components. The effective approaches, identified as having the highest quality index, are mixed search point, iterated search phases, relay hybridization selection, threshold acceptance, mixed learning, Tabu heuristics, stochastic restart, and dynamic parameters. Findings are also compared with recent trends in hyper-heuristics. This work enhances the understanding of selection hyper-heuristics, offering valuable insights for researchers and practitioners aiming to develop effective search algorithms for diverse problem domains.Keywords
Hyper-heuristics are one of the three forms of heuristics as described by Pillay et al. [1]. The other two types are low-level heuristics (often just referred to as heuristics) and metaheuristics. Low-level heuristics make direct changes to the solution, whereas metaheuristics are higher-level methods that guide the search using one or more low-level heuristics [2]. Hyper-heuristics combine multiple low-level heuristics into a framework that explores the heuristic space [3].
Hyper-heuristics can be classified into four categories: selection constructive, selection perturbative, generation constructive or generation perturbative [4]. Selection hyper-heuristics select an existing low-level heuristic (either constructive or perturbative), whereas generation hyper-heuristics evolve a new low-level heuristic at each point of the optimization. Constructive low-level heuristics build a complete solution incrementally, whereas perturbative low-level heuristics are used to iteratively improve an already complete solution, which might be infeasible.
By exploring the heuristic search space, hyper-heuristics achieve a higher level of generality [5]. A method with greater generality can address numerous problem instances, as opposed to tailor-made methodologies that perform well on certain instances but poorly on others [6]. To evaluate the generality of hyper-heuristics, the HyFlex framework was developed [7]. HyFlex provides multiple problem instances with hidden instance-specific low-level heuristics. Users of the framework simply need to design the high-level strategy that decides which low-level heuristic to call at a given decision point. The framework has been used in various research studies and competitions, including the Cross-domain Heuristic Search Challenge (CHeSC) [8]. The inaugural CHeSC drew researchers worldwide to create highly general hyper-heuristics. The final competition includes 20 selection hyper-heuristics of various algorithmic designs. These algorithms have been extensively studied post-competition and remain significant benchmarks in hyper-heuristic research.
One of the main issues in selection hyper-heuristics is the lack of concrete study on which hyper-heuristic components are most crucial to search performance. Hyper-heuristics encompass numerous components, such as feedback, low-level heuristics, solutions (or search points), objectives, move acceptance, and parameter settings [3]. Many hyper-heuristic algorithms have been introduced, each with different features and strategies. Burke et al. [9] reviewed various hyper-heuristic algorithms, categorizing them into selection and generation types. Drake et al. [3] also identified various selection hyper-heuristics with different implementations in components such as feedback mechanisms, move acceptance, and parameter setting. Sánchez et al. [2] examined various hyper-heuristics implemented to solve combinatorial optimization problems. However, existing reviews only conducted comparisons between the algorithms limited to the nature of the heuristic space [9], abstract level [3], or problems addressed [2]. Furthermore, each component of selection hyper-heuristics has different implementation methods [3]. For example, there are three classes of move acceptance: stochastic, non-stochastic basic, and non-stochastic threshold [10]. Comparing performance across different implementations can help in identifying the most effective methods.
Nevertheless, there is a notable absence of a comprehensive analysis on selection hyper-heuristic components. Numerous studies have focused on heuristic selection and move acceptance [10–14], neglecting other crucial components such as feedback mechanisms [15,16], diversification strategies such as Tabu mechanism [16] and search restart [17], as well as parameter settings [16,18]. These overlooked components significantly influence algorithmic performance, with feedback mechanisms enabling adaptive strategies [3,9], diversification techniques promoting exploration of the search space [19–21], and appropriate parameter selection enhancing overall performance [3]. Identifying the best implementation methods for all components can lead to the development of a more effective algorithm.
To address these gaps in the literature, a comprehensive analysis of existing algorithms is needed. The CHeSC algorithms present an ideal case study for addressing these gaps. They remain relevant as they continue to serve as benchmarks in recent studies such as [22–25]. Their use of a standardized framework allows for direct comparisons by ensuring consistent experimental conditions. Additionally, the availability of their design documentation and source codes facilitates in-depth analysis, which is not feasible for more recent HyFlex algorithms. Despite their significance, no comprehensive analysis of the competing algorithms has been conducted. Drake et al. [3] provided a summary and a limited classification of only ten out of the 20 competing algorithms. Furthermore, most algorithms were only inspected by their creators, potentially resulting in a biased analysis. Only the winning algorithm was examined using a complexity analysis to identify features that do not necessarily contribute to algorithmic performance, conducted by Adriaensen et al. [17]. While their analysis method is undoubtedly effective, we contend that it may be too complex to apply to the other 19 algorithms. Moreover, given their diverse algorithmic designs, there is a need to compare the performance of different implementation methods among these algorithms, which remains unexplored.
In this work, a brief summary of ten competing algorithms that were not reviewed in Drake et al. [3] is provided using the information gained from their source codes, design documentation, and extended abstracts. The design documentation offers explanations from the algorithm designers on how their algorithm operates. Then, this study employs a review analysis to investigate eight key components of selection hyper-heuristics among the top twenty competitors from CHeSC: search points, search phases, heuristic selection, move acceptance, feedback, Tabu mechanism, restart mechanism, and low-level heuristic parameters. The review analysis primarily focuses on these components, as they constitute the key components of a selection hyper-heuristic algorithm [26,27]. Within hyper-heuristics, the role of the heuristic selection mechanism is to choose specific low-level heuristics to be employed [28]. The resulting solution then undergoes the move acceptance process to decide whether it should be accepted or rejected. Besides, certain algorithms can learn from feedback to adapt their strategies [3,9]. Tabu and restart mechanisms can promote diversification when the search gets stuck at local optima. Tabu mechanism encourages exploration and avoids short-term cycling by ignoring previously visited solutions [21]. Restart mechanism can move the search to a different region in the search space to escape local optima [19,20]. Hyper-heuristic algorithms may have several parameters that necessitate control within heuristic selection, move acceptance, or low-level heuristics [3]. The selection of appropriate parameter values is essential for achieving increased performance.
This work offers a simpler analysis of all competing algorithms from CHeSC. The main contribution of this study is the identification of effective implementation methods for key components of selection hyper-heuristics by finding the similarities among the top-ranking algorithms. Ineffective strategies are recognized by detecting the similarities among the bottom-ranking algorithms. To achieve this, participating algorithms are categorized based on their similarities in implementation methods for each algorithmic component. The performance of different methods is compared using the average ranking of algorithms employing the same strategy, derived from the final leaderboard of the competition. The algorithms are not subjected to additional execution or re-ranking in this study. Instead, the study relies on the results and rankings provided by the competition organizers.
This study is intended for designers of selection hyper-heuristic algorithms. Although our review focuses on CHeSC algorithms, we ensure the relevance of our findings by relating them to trends observed in recent algorithms. This approach enables our analysis to reflect progress in the field while offering valuable insights for the development of future algorithms. The effective implementation methods identified in this study can serve as focal points for future research aimed at enhancing search performance. By concentrating on these methods, researchers can refine algorithms using proven strategies. The findings can also aid future algorithm designers in creating effective algorithms for solving various optimization problems. The research questions (RQ) of the study are as follows:
RQ1: What are the main characteristics of the proposed algorithms for CHeSC competition?
RQ2: What are the good and bad practices for key components of selection hyper-heuristics, including search points, search phases, heuristic selection, move acceptance, feedback, Tabu mechanism, restart mechanism, and low-level heuristic parameters, observed in the CHeSC algorithms?
RQ3: How do the results obtained from the analysis of the CHeSC algorithms align with the trends identified in recently introduced hyper-heuristics?
RQ4: What are the recommendations for future studies related to selection hyper-heuristics?
The rest of the paper is structured as follows: Section 2 describes related works on core components of selection hyper-heuristic and CHeSC. The methodology for the analysis is described in Section 3. The following sections are structured to answer each research question. The HyFlex framework and the main characteristics of the participating algorithms are summarized in Section 4 (RQ1). Section 5 discusses the classification and implementation of key components of selection hyper-heuristics for the CHeSC algorithms (RQ2). A comparison between the findings from the review with the trends observed in recent algorithms is included in Section 6 (RQ3). Section 7 highlights future research recommendations related to selection hyper-heuristics based on the review findings (RQ4). Finally, Section 8 summarizes the study, discusses limitations and provides suggestions for future work.
The core components of selection hyper-heuristic frameworks are heuristic selection, move acceptance, and a set of low-level heuristics [11]. Within this framework, the selection mechanism determines which low-level heuristic to apply to a working solution, whereas move acceptance establishes whether the resulting solution will replace the existing one. Hyper-heuristics have been explored in a wide array of optimization problems. Related works have been reviewed in various contexts, as summarized in Table 1.
The primary components of selection hyper-heuristics, namely heuristic selection and move acceptance, have been subject to extensive analysis in the literature. Ozcan et al. [11] conducted tests using different combinations from seven heuristic selection methods and five move acceptance methods in solving benchmark functions. Results revealed that the heuristic selection methods exhibit minimal performance differences. In contrast, move acceptance methods significantly affect algorithm performance, with the Improving and Equal strategy proving to be the most effective. Kiraz et al. [13] investigated 35 combinations of five heuristic selection methods and seven move acceptance methods to solve problems in a dynamic environment. Their findings indicated that heuristic selection methods with learning capabilities excel in dynamic settings. Conversely, move acceptance methods with parameters, such as Simulated Annealing (SA), yield poor results, whereas accepting all moves is the least effective. Misir et al. [33] evaluated the generality of different heuristic selection and move acceptance configurations in solving problems with different low-level heuristics sets. Their analysis underscores that the performance of heuristic selection is also influenced by other algorithmic components and runtime. Move acceptance was found to impact performance, but it is essential to ensure compatibility with the chosen heuristic selection method. The set of low-level heuristics employed also affects performance, as they possess varying improvement characteristics that can be leveraged best by different selection strategies.
Zamli et al. [12] assessed the performance of four heuristic selection and move acceptance methods, including the newly developed Fuzzy Inference Selection (FIS), in solving the t-way test generation problem. The results showed that FIS outperforms the Exponential Monte Carlo with counter (EMCQ) and Choice Function (CF), albeit it exhibits slower execution times. Castro et al. [14] focused on the Multi-objective Particle Swarm Optimization Hyper-heuristic, examining four heuristic selection methods, including CF, multi-armed bandit, roulette-based and random approaches. Roulette-based selection emerged as the most effective across 30 instances of multi-objective benchmark problems. Random selection lags behind the other methods, emphasizing the advantages of non-arbitrary selection strategies. Jackson et al. [10] established a taxonomy for move acceptance methods and conducted an empirical study comparing well-known methods. SA was found to be the most effective approach in the context of cross-domain search. Furthermore, they confirmed the contribution of move acceptance methods to algorithmic performance.
In addition to heuristic selection and move acceptance, other components of selection hyper-heuristics impact algorithmic performance, as evidenced in the literature. Several studies explored the role of learning mechanisms in heuristic algorithms. Yates et al. [15] investigated the effect of learning effective heuristic sequences from a set of training instances on the performance of solving cross-domain instances. They showed that offline learning enhances the performance of a sequence-based hyper-heuristic and outperforms the online learning approach. Alanazi et al. [34] compared four approaches for controlling selection probabilities in solving a well-known runtime analysis function. They concluded that learning schemes do not consistently improve performance. Further analysis has shown that the effectiveness of learning schemes is most prominent when there are significant performance variations among the low-level heuristics. This aligns with the findings of Misir et al. [33] that underscore the impact of the set of available low-level heuristics.
Misir et al. [16] investigated whether a learning strategy combined with a Tabu low-level heuristic mechanism can improve algorithmic performance. Experiments on the home care scheduling problem, a variant of VRP, demonstrated that the proposed strategy led to improved outcomes. An additional analysis was conducted to inspect the impact of Tabu duration. The analysis revealed that an optimal range of values exists, and deviating from this range can significantly hinder performance. These findings underscore the importance of carefully tuning algorithmic parameter settings to achieve performance enhancements. This principle is further substantiated by research conducted by Lissovoi et al. [18]. In their study, the impact of using static vs. adaptive values for the learning period (τ) parameter in a random gradient hyper-heuristic algorithm was explored. The comparative analyses on standard unimodal benchmark functions indicated that adaptive parameter values have the potential to enhance algorithmic performance. Furthermore, the research revealed that the optimal parameter value can vary across different problem instances.
Misir et al. [16]’s evaluation has also highlighted the influence of the Tabu mechanism, particularly involving low-level heuristics, on algorithmic performance. The Tabu list, also referred to as a prohibition list, was identified as one of the diversification strategies by Sarhani et al. [35], along with search restart and randomization. Other diversification strategies have also been identified as influential to algorithmic performance. Adriaensen et al. [17] conducted an Accidental Complexity Analysis on the winner of the CHeSC 2011 competition, AdapHH. The analysis delved into the performance contributions of each sub-mechanism within the algorithm. The results of the analysis indicated that the restart mechanism incorporated within the algorithm’s threshold acceptance criterion significantly contributed to its overall performance. However, the Tabu mechanism within the algorithm did not make a substantial contribution to performance. This underlines the importance of understanding how different algorithmic components can impact each other’s performance. Table 2 summarizes the algorithmic components examined in previous studies, emphasizing the novelty of our work in offering a comprehensive review.

The CHeSC 2011 algorithms continue to serve as benchmarks in numerous recent publications, as highlighted in [3]. The selection hyper-heuristics included in the CHeSC 2011 competition have been discussed, analyzed and utilized as benchmarks in other research publications. Burke et al. [9] provided an overview of hyper-heuristics covering the early approaches, classifications, learning components, and research trends in the field. Four algorithms that competed in CHeSC 2011 were included in the survey. Drake et al. [3] focused on extended classification, benchmark frameworks, cross-domain search, and problem domains in selection hyper-heuristics. HyFlex framework and CHeSC 2011 were extensively discussed, and ten of the competing algorithms were described. However, both reviews only provided summaries and lacked an in-depth analysis and comparison. In contrast, Van Onsem et al. [32] produced a report of the CHeSC algorithms, highlighting core concepts such as iterated local search, reinforcement learning, and Tabu search. They concluded that an algorithm’s performance relies on combining various techniques, and no single technique used independently leads to large performance gains.
Adriaensen et al. [36] conducted a comparative study to assess the generality of two CHeSC 2011 algorithms (AdapHH and EPH) in solving three additional problem domains: 0–1 knapsack problem, quadratic assignment problem and max-cut problem. Their experiments showed that AdapHH, the winner of CHeSC 2011, exhibits superior generality and consistency even when considering the extended set of problem domains. The authors also pointed out that AdapHH’s shortcoming is in its complexity, which they examined in detail through the complexity analysis in Adriaensen et al. [17]. The analysis identifies complex algorithmic components that can be eliminated with minimal performance loss to reduce the overall complexity. A less complex variant of the algorithm, Lean-GIHH, is proposed from the analytical results. Drake et al. [37] investigated the crossover control mechanism by substituting the one in AdapHH with another from the literature and using AdapHH’s in a Modified Choice Function-All Moves hyper-heuristic. They concluded that the control strategy has no impact on the algorithm’s performance. Notably, AdapHH has received most of the attention in terms of analysis and comparison, leaving other algorithms overlooked.
The algorithms from CHeSC 2011 have also served as benchmarks in other studies. Numerous works utilize the HyFlex framework to compare their proposed algorithms against CHeSC 2011 algorithms, either with the original problem domains or the extended ones. Table 3 lists the benchmark set used in studies that evaluated algorithms using the HyFlex framework. For a comprehensive summary of works utilizing the HyFlex framework before 2020, refer to Drake et al. [3]. Soria-Alcaraz et al. [38] compared their iterated local search hyper-heuristic to the CHeSC 2011 contestants exclusively on vehicle routing problems. Their algorithm achieved a third-placed ranking among the competitors. Hassan et al. [39] integrated a dynamic heuristic set selection (DHSS) into the Fair-Share Iterated Local Search (FS-ILS) hyper-heuristic [40], which surpassed the performance of all CHeSC 2011 algorithms. The comparison, using the original HyFlex problem domains, showed that DHSS improved FS-ILS. Zhao et al. [41] introduced a hyper-heuristic algorithm that incorporates multi-armed bandit, relay hybridization and a genetic algorithm. The algorithm produced highly competitive results against the top five CHeSC 2011 algorithms in most problem instances and generalized well across the original domains.
In [25], an evolutionary algorithm-based iterated local search (EA-ILS) hyper-heuristic was presented, featuring a novel mutation operator. The study compared the algorithm’s performance in solving all 30 instances of the extended HyFlex problems against seven hyper-heuristics, which included two from CHeSC 2011. The algorithm demonstrated superior generalization compared to other algorithms. Additionally, when applied to address the original HyFlex set, EA-ILS outperformed all algorithms from the competition. Mischek et al. [24] proposed a reinforcement learning approach incorporating different state space representations and an intelligent reset mechanism. The algorithm would have come in second place, beating other reinforcement learning-based algorithms in the competition. Kletzander et al. [23]' large state reinforcement learning-based algorithm managed to outperform all 20 competitors from CHeSC 2011. Gümüş et al. [22] proposed using F-Race as a parameter tuning method for a steady-state memetic algorithm (SSMA) to investigate its efficacy in cross-domain search. They compared the performance of SSMA without tuning [43] with SSMA tuned using the F-Race or Taguchi method in the CHeSC 2011 competition setup. The tuned SSMA ranked higher (fourth place) compared to the untuned variant (22nd of 25 algorithms).
This study conducts a review analysis of the top 20 algorithms that competed in CHeSC 2011, aiming to examine their algorithmic designs. These algorithms are chosen as they continue to be utilized as benchmarks in recent studies such as [22–25], highlighting their relevance. Furthermore, the algorithms utilize the same framework, i.e., the HyFlex framework, streamlining the analysis process. The source codes and supporting documentation for the algorithms are also readily available, enabling us to easily identify the implementation methods for the algorithmic components examined.
More recent selection hyper-heuristics utilizing the HyFlex framework as highlighted in Section 2. However, we excluded these algorithms from our review analysis due to the unavailability of their source codes and to limit the scope of our study. Nevertheless, we provide a brief comparison of the analysis findings from the CHeSC 2011 algorithms to the trends observed in recent algorithms in Section 6. The inclusion and exclusion criteria for the review analysis in this study are summarized in Table 4.

This study examines eight key components of selection hyper-heuristics: search points, search phases heuristic selection, move acceptance, feedback, Tabu mechanism, restart mechanism, and low-level heuristic parameter control. The algorithmic attributes for each component are categorized based on existing classification where available. Otherwise, the attributes are classified based on their similarities. The implementation methods of each algorithm from CHeSC 2011 are identified from the source codes and supporting documentation. We adapt the quality index as in [45,46] to evaluate the performance of the different implementation methods. Quality index

Figure 1: Components of selection hyper-heuristics discussed in this study
The quality index analysis relies on the rankings within the leaderboard, which are determined by the performance metric used to rank the algorithms. In the HyFlex framework, algorithms are ranked using a scoring system inspired by Formula 1 (F1) racing, based on the median values among 31 runs. Recent research has introduced two performance metrics: average rank (
Additionally, statistical tests are conducted to validate the findings. Due to the unavailability of individual algorithmic run results, the tests rely on the normalized median objective function values of 30 HyFlex problem instances, following the approach by Di Gaspero et al. [48]. The normalization is performed using using the formula
4 Main Characteristics of Cross-Domain Heuristic Search Challenge (CHeSC) 2011 Algorithms
CHeSC 2011 competition uses the HyFlex framework to evaluate the competing algorithms based on their ability to find high-quality solutions within given time limits. The HyFlex framework is a Java program that provides a set of problem instances from different domains with varying complexity [7]. There are two distinct sets of problem instances within the framework. The original set consists of 30 instances, encompassing problems from six distinct domains, each comprising five instances. These instances pertain to problems within the field of combinatorial optimization. During the competition, participants are provided with only four problem domains, these being the Boolean satisfiability (SAT) [55], one-dimensional bin packing (BP) [56], personnel scheduling (PS) [57], and permutation flowshop (PFS) [58]. The two hidden domains are the travelling salesman problem (TSP) [59] and the vehicle routing problem (VRP) [60]. The HyFlex instances set was later expanded with three additional domains by Adriaensen et al. [36]: 0–1 Knapsack (KP) [61], Quadratic Assignment (QAP) [62], and Max-Cut Problem (MaxCut) [63]. Each algorithm underwent 31 executions, each with a time limit of 10 min. The competing algorithms were ranked based on the median solution quality achieved in these runs, and the F1 scoring system was employed to assign a score. The scores were then aggregated and used to determine the final rankings on the leaderboard across various problem domains. Readers are referred to the original works by Burke et al. [8] and Ochoa et al. [7] for more information. Table 5 shows the final leaderboard of the CHeSC 2011 competition.

Two notable features of HyFlex that will be discussed throughout this paper are the classes of low-level heuristics and the heuristic parameters. Low-level heuristics are classified into different types: mutational, ruin-recreate, local search, and crossover. Additionally, the behaviour of the low-level heuristics can be controlled using two parameters, namely depth of search (DOS) and intensity of mutation (IM). DOS only applies to local search heuristics, whereas IM is for mutational and ruin-recreate heuristics, both of which specify how much the solution can change. Both parameters have a default value of 0.2 and can increase up to 1.0.
Several algorithms from the competition have been reviewed in Drake et al. [3], including AdapHH [45], VNS-TW [64], ML, PHunter [65], EPH [66], HAHA [67], NAHH [68], ISEA [69], GenHive [70], and AVEG-Nep [48]. Readers are referred to their work for the explanation of those algorithms. The remaining algorithms are examined using their source codes, design documentation, and extended abstracts available at https://github.com/seage/hyflex/tree/master/hyflex-hyperheuristics (accessed on 25 December 2024). The following provides a description of the main characteristics of each algorithm, presented in the order of their rankings in the competition.
KSATS-HH: Achieving a ninth position in the competition, the algorithm demonstrated good performance in solving SAT and VRP problems, while it struggled with PFS and TSP. The algorithm is a hybrid approach that combines reinforcement learning, Tabu search, and simulated annealing. Heuristic selection follows a tournament selection of size two, where heuristics are chosen based on their ranks. Reinforcement learning adjusts the heuristic ranks, increases if heuristic improves the working solution and decreases if it fails. A Tabu mechanism is used, where heuristics that fail to improve the solution are added to the Tabu list with a tenure of seven rounds. Simulated annealing is employed for move acceptance, considering the fitness change relative to the best solution. The cooling schedule resets when the maximum iterations are exceeded, with this value influenced by heuristics’ execution time.
HAEA: Producing the second-best results in solving VRP, contributing to an overall tenth position for the Hybrid Adaptive Evolutionary Algorithm Hyper Heuristic (HAEA). Low-level heuristics are divided into two subsets: one includes a mix of local search and other types of heuristics, whereas the other comprises the remaining local search heuristics. Heuristics from both subsets are applied iteratively, ensuring that a local search heuristic is the last to be applied. Heuristics are selected based on their probabilities, which increase or decrease depending on whether they improve the working solution, employing the roulette wheel strategy. The move acceptance strategy only accepts improving solutions. If a non-improving solution is found, the heuristic receives a penalty (decrease in selection probability), IM and DOS values are adjusted, and the soft replacement policy is applied to assess if a search restart is needed. The soft replacement policy applies local search heuristics using default parameter values and triggers a search restart if the range of DOS has been tested. Upon a search restart, the current solution is changed using random heuristics from the two subsets, and the subsets are updated through random permutation. Additionally, heuristic parameters are adjusted when no improvement is seen, and resets when a maximum value is reached. The value of IM is inversely related to the DOS value, that is, if IM = 0.4, then DOS = 0.6.
ACO-HH: The algorithm performed third best for BP instances and finished eleventh in the competition. It adopted an Ant Colony Optimization (ACO) approach tailored for selection hyper-heuristics [71]. The algorithm employs ants that traverse a path, applying a low-level heuristic at each step. All ants start from the same solution, which is the best solution from the previous iteration. For each iteration, 30 ants search independently by applying low-level heuristics five times. This approach means that the algorithm maintains a population of solutions. Heuristics are selected according to both the pheromone and heuristic information of ACO. The pheromone factor considers the average improvement obtained by a complete path solution, whereas the heuristic information factor considers the average improvement obtained for the component. Heuristics are selection based on their probabilities, following the roulette wheel approach. The algorithm also maintains a different selection probability for the heuristic parameter values. In each application, the heuristic information and its parameter value are updated to reward or penalize the heuristic.
DynILS: This algorithm performed better on BP and TSP than on other problems. DynILS is a dynamic iterated local search that selects perturbative heuristics and their IM value. At each iteration, one perturbative (mutational or ruin-recreate) and one local search heuristic are applied to the incumbent solution, indicating a single-point and iterated search phases approach. Heuristics are selected using the roulette wheel strategy, where the selection probabilities of these heuristics are adjusted based on whether improvement is achieved or not. Heuristic performance is measure by their normalized fitness delta relative to their possible values. The incumbent solution is only replaced when an improvement is found. Additionally, the heuristic parameter values are rewarded or penalized according to their performance. No Tabu or restart mechanisms are employed within the algorithm.
SA-ILS: SA-ILS obtained most of its total score from the personnel scheduling problem, ranking fourth. The algorithm employs two strategies: Iterated Local Search Hyper-heuristic (ILSHH) and Simulated Annealing Hyper-heuristic (SAHH), chosen based on the average execution time of local search heuristics for each problem instance. Before initiating the search process, each local search heuristic once in a random order, and the results guide the choice of strategy and heuristic parameters. For instances with extended execution times, ILSHH is employed, whereas SAHH is utilized for instances with shorter execution times. ILSHH applies one random perturbative heuristic followed by all local search heuristics in a random sequence. The acceptance strategy allows a non-improving solution to be accepted after seven consecutive iterations without improvement. For SAHH, a random local search heuristic is used until no improvements are observed for seven consecutive iterations. The final solution is accepted only if it improves; otherwise, a random perturbative heuristic is applied. Besides, the low-level heuristic parameters differ based on the algorithm: ILSHH uses IM and DOS values of 0.4, whereas SAHH uses IM of 0.8 and DOS of 0.6. These parameters remain constant throughout search process.
XCJ: XCJ (eXplore-Climb-Jump) is a hill climbing-based selection hyper-heuristic that performed best on BP compared to other problem domains. The low-level heuristics are classified into explore heuristics (crossover and ruin-recreate) and exploit heuristics (local search and mutational). The algorithm applies each explore heuristic to the current best solution, generating multiple solutions. Subsequently, each solution undergoes a sequential application of all exploit heuristics, starting from local search to mutational heuristics, until ten consecutive non-improving iterations. After each application of exploit heuristic, the resulting solution is compared to the best solution. An improving solution is always accepted, whereas a worsening solution is accepted only if the fitness delta is less than 0.2. The fitness delta is calculated as one minus the fitness before divided by the fitness after application. The algorithm does not include Tabu mechanism, restart mechanism, or heuristic parameter control.
GISS: Generic Iterative Simulated-Annealing Search (GISS) applies a random heuristic and utilizing simulated annealing move acceptance at each iteration. Heuristics are selected without considering their performance. The move acceptance allows non-worsening solutions, where the simulated annealing temperature is influenced by the heuristic’s execution time and fitness delta. The algorithm incorporates a restart mechanism to reinitialize move acceptance parameters, heuristic parameters, and the working solution. The search restart is triggered when the number of non-accepted iterations exceeds a threshold, calculated as the number of heuristics for the problem instance multiplied by two. This threshold doubles if the current solution is within 1.5 times of the best solution. Upon restart, the temperature resets to its initial value. Heuristic parameter values may be modified, with IM and DOS increased by 1.1 times with a probability of 0.2, and the working solution is updated by applying randomly selected ruin-recreate then mutation heuristics. The algorithm achieves moderate performance for PS and VRP.
SelfSearch: This population-based algorithm adapts its strategy, either explorative or exploitative, depending on the number of expected generations (or iterations) remaining before reaching the time limit. Before initiating the search, each heuristic is applied once to calculate the expected number of generations, based on their execution times and population size. Afterwards, the expected generations are updated after each generation. The two strategies differ in their heuristic selection, search restart methods, and heuristic parameter values to either promote exploration or exploitation. Heuristic selection follows the roulette wheel strategy, which depends on feedback from factors including fitness delta, execution time, usage frequency, frequency of repetitions, and frequency of non-improvements. Besides, the Adaptive Pursuit approach dictates that the explorative strategy prioritizes heuristics with lower frequency of repetition and higher improvement rate, whereas the exploitative strategy only prioritizes higher improvement rate. The selected heuristic is applied to all individuals in the population of solutions. Move acceptance is incorporated into the population update, which follows elitist survival selection while avoiding duplicate solutions. A restart mechanism is triggered when the number of consecutive non-improvement iterations exceeds a threshold, determined by the expected number of generations. Different restart actions are applied depending on the remaining number of generations. During the first half of the search, the DOS value is increased, a ruin-recreate heuristic is applied when DOS reached 1.0 and the current heuristic is applied to all solutions in the population. In the final half of the search, the IM value is increased, a ruin-recreate heuristic is applied when IM reached 1.0, and the heuristic with the highest improvement rate is applied to all solutions in the population. Additionally, different heuristic parameter values are used based on the strategy employed. For the explorative strategy, high IM and low DOS values are used, with IM increasing proportional to the number of local optima reached after a restart. For the exploitative strategy, low IM and high DOS values are used, with DOS increasing proportional to the number of local optima reached after a restart. Tabu mechanism is not incorporated in this algorithm. SelfSearch performed fairly in PS and TSP.
MCHH-S: MCHH-S, a single objective variant of the Markov chain Hyper-heuristic [72], performed well only on SAT. The algorithm utilizes a Markov chain for heuristic selection, considering heuristics’ quality scores derived from fitness delta and execution time. Each iteration involves applying a heuristic to one solution from a population of solutions, updating the quality score and deciding to accept or reject the resulting solution. The quality score is calculated as fitness delta multiplied by one minus the time taken by the heuristic over the maximum time. Improving moves are always accepted, whereas non-improving moves have a gradually increasing probability of acceptance, proportional to the number of consecutive non-accepted iterations, reaching a 100% acceptance chance after five non-accepted iterations. Upon acceptance, a different heuristic (of any type) and solution is selected for the next iteration. Otherwise, a local search heuristic is applied to the current solution in the next cycle. This algorithm does not involve Tabu mechanism, restart mechanism, or heuristic parameter control.
Ant-Q: Ant-Q is a hybridization between an Ant system and Q-learning. In this algorithm, two ants apply heuristics repeatedly, for a total of
5 Effective and Ineffective Strategies among CHeSC 2011 Algorithms
We classify the search point, search phases, heuristic selection methods, move acceptance, feedback, Tabu mechanism, restart mechanism, and low-level heuristic parameters for the CHeSC 2011 competing algorithms as presented in Table 6. Then, the performance of each implementation method is discussed.

Drake et al. [3] classified search points of selection hyper-heuristics into single, population, or mixed. The single-point search involves a continuous process of heuristic selection and move acceptance until termination, applied to a single solution [9]. Population-based (or multi-point) search applies the same process to multiple solutions, whereas mixed-point search combines single and population-based searches sequentially [3].
We illustrate the frequency and average quality index of the search point (see Fig. 2). It shows that the number of algorithms based on single and multi-point searches is equal, with nine each. Mixed-point search is only implemented by two algorithms which produce the highest average quality index. The average quality index for single-point search is slightly higher than for multi-point search algorithms, with 11 and 8.56, respectively. Among the top five performers, Table 6 indicates the distribution among the three approaches is equal with two single-point, two multi-point, and one mixed-point algorithm. Although mixed-point search gives a higher average quality index, its performance gains over the other approaches could not be confirmed as only two algorithms employ this strategy. On the other hand, it can be observed that a single-point search is better than a multi-point search.

Figure 2: Algorithm count and average quality index for search point
Statistical tests revealed a non-normal distribution in the sample for the mixed-point category, necessitating the use of non-parametric tests. The Friedman test identified a significant difference among the groups with a p-value of 0.0022. Subsequent post-hoc Wilcoxon signed-rank tests confirmed significant differences across all pairings, validating the performance variations among the implementation strategies.
Fig. 3 presents the boxplot of normalized median values across 30 HyFlex problem instances, averaged among each group’s algorithms. Lower values indicate better final solutions, whereas a smaller range signifies greater reliability as there is a reduced performance variability across different problem instances. The mixed-point approach demonstrates the best performance but exhibits higher variability.

Figure 3: Boxplot of normalized median values for search point
Fig. 4 displays the average quality index using rankings in individual problem domains in the HyFlex framework. Algorithms employing mixed-point search achieved the highest average quality index in five out of six domains, except for BP, where single-point search is the preferred strategy. Multi-point search was outperformed by single-point search in all domains. Upon further inspection, we found that BP instances are sensitive, where every heuristic application tends to yield an improvement. This observation aligns with findings by Kheiri et al. [73], who emphasized that exploring new search regions significantly enhances performance in BP instances. In time-constrained settings, the single-point approach is advantageous over multi- or mixed-point approaches, as it enables more frequent heuristic applications to a single solution. In contrast, the other approaches must apply heuristics to multiple solutions, selecting the best one for the next iteration while discarding the rest, which may reduce efficiency.

Figure 4: Average quality index in individual problem domains for search points
The single-point search algorithms can further be classified into three different strategies. The first strategy is applying single or multiple heuristics to a single solution. A single heuristic is selected using roulette wheel selection (AdapHH), tournament selection (KSATS-HH), and random selection (GISS). The application of multiple heuristics can be perturbative followed by local search heuristics (HAEA, DynILS, SA-ILS, ML) or relay hybridization (AdapHH). HAEA and DynILS apply only one local search heuristic, whereas SA-ILS and ML apply all local search heuristics after the perturbative one. Relay hybridization in AdapHH chooses a heuristic from a list of efficient heuristics at each step. Adriaensen et al. [17] demonstrated that the combination of single selection and relay hybridization outperformed the variants utilizing only one component. Also, relay hybridization contributes most to the performance.
AVEG-Nep conducts parallel independent searches from three different solutions, which is considered a single-point search supported by Drake et al. [3]. A heuristic type is chosen by reinforcement learning, then one random heuristic is selected from the chosen type to be applied to the solutions. Another strategy is to use multiple algorithm schemata. NAHH runs multiple algorithmic schemata in a race until the best one emerges. Each schema is parametric and contains different heuristic parameter values, acceptance probability, mutation probability, and restart probability. Six algorithmic schemata were included: randomized iterative improvement, probabilistic iterative improvement, variable neighbourhood descent, iterated local search, simulated annealing, and iterated greedy.
Most multi-point search algorithms utilize a population of solutions (VNS-TW, PHunter, EPH, HAHA, ACO-HH, GenHive, XCJ, SelfSearch, MCHH-S, and Ant-Q) in three different ways. The first approach is to maintain a population of solutions where only a single solution is chosen as the working solution for the iteration (VNS-TW, GenHive). VNS-TW selects a solution using tournament selection, which then undergoes shaking and local search stages. The new solution replaces the original solution if an improvement is found. Otherwise, a worse solution from the population is selected for replacement. GenHive conducts searches on a population of solutions, where at each iteration, only the best solution is improved with heuristic sequences. Newly produced solutions always replace the old solution in the population.
The second approach employs search from multiple solutions. In PHunter, EPH, SelfSearch, and MCHH-S, heuristics are applied to different solutions in the population. The population is updated according to the move acceptance strategy. PHunter applies heuristics to different solutions and updates the population upon improvement. EPH applies different heuristic sequences to different solutions. Each resulting solution is compared to the population and placed into the population when it has improved or has a unique fitness value. MCHH-S applies a heuristic to a single solution until the solution is accepted. Once accepted, a different heuristic is applied to a different solution. Conversely, in SelfSearch, all solutions in the population are improved using a heuristic and the population is updated using elitist survival selection. Since SelfSearch ranked poorly in the competition, elitism in population update is undesirable.
The third approach uses multiple solutions derived from a single solution for either local search (HAHA, XCJ) or evaluation (ACO-HH, Ant-Q) on each of these solutions. HAHA follows a mixed-point search, where multiple solutions are generated by applying perturbative heuristics to the solution from the single-point search phase. Each solution is then applied with a local search heuristic. In XCJ, each perturbative heuristic is applied to the current best solution to produce multiple solutions. Then, local search heuristics are used to improve the solutions. ACO-HH and Ant-Q produce multiple solutions for evaluation. Both algorithms follow the strategies from ACO, modified for selection hyper-heuristics [71]. ACO-HH applies heuristics chosen by the Ant system to the previous iteration’s best solution at each iteration. In contrast, Ant-Q only uses the Ant system and Q-learning to determine the first heuristic, with subsequent heuristics chosen randomly. Each heuristic is applied to the best solution among the ones kept by agents.
Agushaka et al. [74] noted the importance of finding the right balance between population size and algorithmic iterations to guarantee optimality. Moreover, Malan et al. [75] found that an algorithm with the same number of function evaluations but different population sizes leads to a significant performance difference. Table 7 summarizes the population sizes of the multi-point search algorithms. It shows that most algorithms limit the number of solutions stored to seven. Only ACO-HH has a large population, but we argue that the performance is maintained since the heuristic reward is updated after each application. EPH only use a large population for problem instances with short heuristic execution times, which we think is the best strategy to achieve greater generality. Two algorithms determine the population size based on the number of heuristics (XCJ and Ant-Q).

A population of heuristic sequences are included in certain algorithms from the competition. A heuristic sequence consists of multiple heuristics to be applied successively to the domain solution. Two algorithms that maintain a population of heuristic sequences, EPH and GenHive, are compared in Table 8. Since EPH outperformed GenHive, several conclusions can be noted. Firstly, an algorithm with predefined sequences of perturbative, followed by local search, heuristics outperforms an algorithm without any rules. A dynamic heuristic sequence length and population size may better suit different problem instances than a fixed one. Next, evolving heuristic parameters alongside the heuristic sequences (co-evolution) presents performance gains. Crossover among heuristic sequences may not lead to a better final solution, and elitism may degrade algorithmic performance compared to evolving every heuristic sequence in the population. A population updated using tournament selection could outperform a population that always accepts offspring. Deploying heuristic sequences to multiple solutions enhances search performance compared to applying the sequences to the same solution. ISEA maintains a population of action sequences which are a series of actions to be applied to a heuristic sequence. The action sequences include adding, removing, moving, swapping, or changing heuristics. The action sequences evolved through crossover and mutation, with an elitist population update strategy. Contrary to the standard evolutionary process, multiple offspring (up to 200) are produced at each generation using the same domain solution.

Population-based algorithms have demonstrated their superiority in achieving global optima [76]. Nevertheless, single-point search strategies can achieve comparable performance by adapting population-based features, such as utilizing multiple starting points [77] or hybridizing with single-point-based algorithms [78]. Within CHeSC 2011 algorithms, VNS-TW utilizes a population of solutions that is reduced to a single solution after 50% of the time limit or when the search stagnates. The search in HAHA is divided into serial and parallel search phases. Parallel search applies perturbative heuristics to produce multiple solutions. Then, one non-Tabu solution is chosen for serial search where local search heuristics are applied to the solution until none of them can improve any further.
The HyFlex framework provides four types of low-level heuristics for each problem instance: mutational, ruin-recreate, local search, and crossover heuristics [7]. Mutational, ruin-recreate, and crossover heuristics are often grouped into perturbative heuristics, including in VNS-TW and ML. Algorithm designers can employ an iterated search strategy where heuristics are applied iteratively between perturbative and local search. Categorizing low-level heuristics or operators by their search capabilities enables control between exploration and exploitation [79]. Algorithms proposed for CHeSC 2011 competition follow one of three strategies for the sequence of heuristic applications: iterated, optional iterated or non-iterated (see categorization in Table 6). Iterated search alternates between phases of applying perturbative and local search heuristics, where some algorithms may only enforce the strategy optionally. Other algorithms may allow any type of heuristics to be applied at any point of the search (non-iterated).
We analyze the search phases by tallying the number of algorithms for each strategy and calculating their average quality index (see Fig. 5). It shows that most algorithms employ the iterated search strategy (10 algorithms), followed by non-iterated search (eight algorithms). The iterated strategy increases algorithm performance, as evidenced by the higher average quality index and six of the top seven algorithms following this strategy (see Table 6). Algorithms with optional iterated search scored marginally lower than ones employing the iterated search strategy, but only two algorithms implemented this strategy. Repeated measure ANOVA confirmed a significant difference among the groups (p = 4.7969E−16). Post-hoc Tukey’s tests showed significant differences across all pairings, with p-values lower than 0.0001. Additionally, the boxplot in Fig. 6 displays normalized median values for different search phases, revealing that the iterated approach has the smallest interquartile range, reflecting higher reliability.

Figure 5: Algorithm count and average quality index for search phases

Figure 6: Boxplot of normalized median values for search phases
The average quality index for iterated search phases in individual domains is consistently high compared to the non-iterated strategy (see Fig. 7), with large differences observed in PS, PFS, TSP, and VRP instances. Notably, both TSP and VRP problems are routing and optimization problems. They often share characteristics of having multiple optima and benefit from similar exploratory strategies for effective solution refinement. PS instances are also characterized as having multiple optimum points [80]. This suggests that iterated search is effective for multi-modal problems. Meanwhile, the optional iterated approach performed well in five domains, except for SAT.

Figure 7: Average quality index in individual problem domains for search phases
The usage of perturbative and local search heuristics can be described as static or dynamic. Most algorithms impose that perturbative heuristics must be followed by the local search heuristics at each iteration. For the iterated search strategy, VNS-TW and ML continue the search until reaching a local optimum using local search heuristics after applying one perturbative heuristic. DynILS and ILSHH of SA-ILS follow one perturbative heuristic with one and all local search heuristics, respectively. PHunter uses perturbative heuristics to escape local optima before improving the solution using local search heuristics with a high DOS. EPH applies every local search heuristic either by a single application or Variable Neighbourhood Descent after the perturbative heuristics. XCJ produce multiple solutions using perturbative heuristics before applying all local search heuristics in sequence. Each step in NAHH involves applying ruin-recreate heuristics followed by local search heuristics. A mutational heuristic is then applied to the resulting solution with a probability.
Meanwhile, HAHA and SAHH of SA-ILS employ the phases in reverse to diversify when no improvement is obtained from the local search heuristics. In the optional iterated search strategy, HAEA and ISEA require starting and ending each iteration’s heuristic sequence with a local search heuristic, but there are no restrictions for the positions in between. Only SelfSearch switches between the search phases dynamically based on the expected number of iterations remaining. For each phase, different heuristic selection rules and parameter values are utilized. Since the algorithm ranked poorly, this feature appears degrading performance.
5.3 Heuristic Selection Methods
Five strategies for selecting heuristics are identified: random, roulette wheel, tournament selection, relay hybridization and sequential (refer to Table 6). Random selection is utilized by SA-ILS, GISS, and VNS-TW in the local search phase and NAHH for the selected heuristic type. Roulette wheel selection based on heuristic performance is the most used strategy, employed by 11 competitors (AdapHH, ML, PHunter, HAHA, HAEA, ACO-HH, DynILS, AVEG-Nep, SelfSearch, MCHH-S, Ant-Q). ACO-HH and Ant-Q obey the principle of Ant systems where selection probabilities are also influenced by pheromone evaporation. AVEG-Nep uses a roulette wheel to select only the heuristic type, and a random heuristic of the type is applied to the solution.
Tournament selection is only used in KSATS-HH using a tournament of size two. AdapHH implements relay hybridization to select heuristic pairings. Relay hybridization involves multiple heuristics working together in a sequence, where the output of one serves as the input for the next heuristic [81]. In AdapHH, the first heuristic is selected by the roulette wheel, and the second is chosen from known good heuristics for the first. XCJ applies all local search heuristics in sequence. On the other hand, EPH, ISEA, and GenHive incorporate heuristic sequences modified using genetic operators or action sequences, negating the need for heuristic selection.
Fig. 8 illustrates the frequency distribution for heuristic selection methods and their average quality index. It suggests that relay hybridization is the most effective heuristic selection strategy, whereas sequential is the least effective. Since these strategies only exist in one algorithm, a deeper inspection is necessary. Kheiri et al. [82] demonstrated the effectiveness of relay hybridization in the HyFlex framework. Zhao et al. [41] also highlighted its capability to form effective heuristics by pairing existing ones. Lepagnot et al. [83] obtained good results using relay hybridization to combine three different metaheuristics, although it may be less effective for simpler problems. The quality index averages indicate a marginally better value for the roulette wheel strategy (10.0) compared to random selection (9.8). We observed high variability between the methods implemented by the random selection algorithms. The use of random selection in VNS-TW and NAHH does not negatively impact search performance as it is used on a small heuristic subset compared to SA-ILS and GISS. Roulette wheel selection was implemented by more algorithms in the top five positions.

Figure 8: Algorithm count and average quality index of heuristic selection methods
Non-parametric statistical tests indicated significant differences among the groups (p = 4.0908E−10). Pairwise comparisons revealed that the top performer, relay hybridization, has significant difference to all other strategies. Interestingly, the sequential approach, which had the lowest average quality index, did not show significant differences with other strategies, whereas other strategies exhibited differences among themselves. The no-selection approach (ranked second) showed no significant difference from tournament selection (ranked third) (p = 0.5999) but was statistically different to both roulette wheel (ranked fourth) (p-value = 3.7243E−05) and random approach (ranked fifth) (p-value = 0.0030). Tournament selection was significantly different from the random approach (p = 0.0350) but not from roulette wheel (p = 0.0571). Roulette wheel selection had no significant difference from the random approach (p = 0.7036).
Fig. 9 illustrates the distribution of normalized median values for six heuristic selection approaches. Relay hybridization demonstrates the best performance but includes multiple high-value outliers. The roulette wheel approach has a narrower interquartile range and a smaller overall range between minimum and maximum values compared to other approaches.

Figure 9: Boxplot of normalized median values for heuristic selection methods
Relay hybridization achieved the highest quality index in four domains: SAT, BP, PFS, and TSP (refer to Fig. 10). The best performers in PS are algorithms that do not employ heuristic selection, relying instead on evolutionary processes to improve solutions. Tournament selection is marginally the best approach for VRP and performs well for BP and TSP. Between the roulette wheel and random selection, the roulette wheel is better in BP, PFS, TSP, and VRP, while random selection is better for SAT and PS. These observations are supported by multiple researchers, noting that search feedback is non-essential for solving SAT [23] and PS instances [73]. Sequential heuristic selection is the worst strategy for the four domains but offers better performance for SAT and BP.

Figure 10: Average quality index in individual problem domains for heuristic selection methods
Move acceptance involves determining whether to accept or reject the outcome of a heuristic application [3]. Move acceptance methods can be broken down into stochastic and non-stochastic methods [10]. Stochastic methods accept a solution with a given probability. In contrast, non-stochastic methods make deterministic decisions about candidate solutions. Within the non-stochastic methods, it can be further divided into basic or threshold methods. Non-stochastic basic utilizes the objective function value of previous solutions, whereas non-stochastic threshold relies on a predetermined value as the criterion for the acceptance threshold. Contrarily, several algorithms deviate from the conventional hyper-heuristic structure by omitting a move acceptance strategy. The categorization of heuristic selection techniques for the participating algorithms can be found in Table 6.
Fig. 11 presents the distribution of algorithm count and the average quality index for each move acceptance method. It shows that most algorithms implemented non-stochastic basic and stochastic move acceptance methods (six algorithms each). Non-stochastic threshold move acceptance was the least frequently employed technique (three algorithms), yet it yielded the highest average quality index. Conversely, algorithms lacking a move acceptance have the lowest quality index. Friedman test demonstrated a significant difference among the groups (p = 4.8205E−12). Post-hoc comparisons showed significant differences in nearly all pairings, except between basic and stochastic move acceptance (p = 0.1414). Furthermore, the boxplot of normalized median values for move acceptance shows lower variability for the basic and threshold approaches (refer to Fig. 12).

Figure 11: Algorithm count and average quality index of move acceptance

Figure 12: Boxplot of normalized median values for move acceptance
Fig. 13 compares the average quality index across problem domains. Threshold move acceptance obtained the best quality index in all domains, whereas not employing move acceptance led to the worst quality index. Non-stochastic move acceptance methods performed significantly better in PS, PFS, TSP, and VRP, indicating a preference for systematic mechanisms. Stochastic move acceptance outperformed non-stochastic basic move acceptance on SAT and BP, suggesting that some degree of randomness is beneficial in these domains. BP instances exhibit sensitivity in objective function changes, leading to all moves being accepted regardless of improvement magnitudes. For SAT instances, escaping local optima is important for better performance. Acceptance criteria that prioritize diversification, such as those integrated with restart mechanisms, are more effective [36,82]. The results suggest that incorporating a move acceptance can enhance search performance, particularly the non-stochastic threshold method.
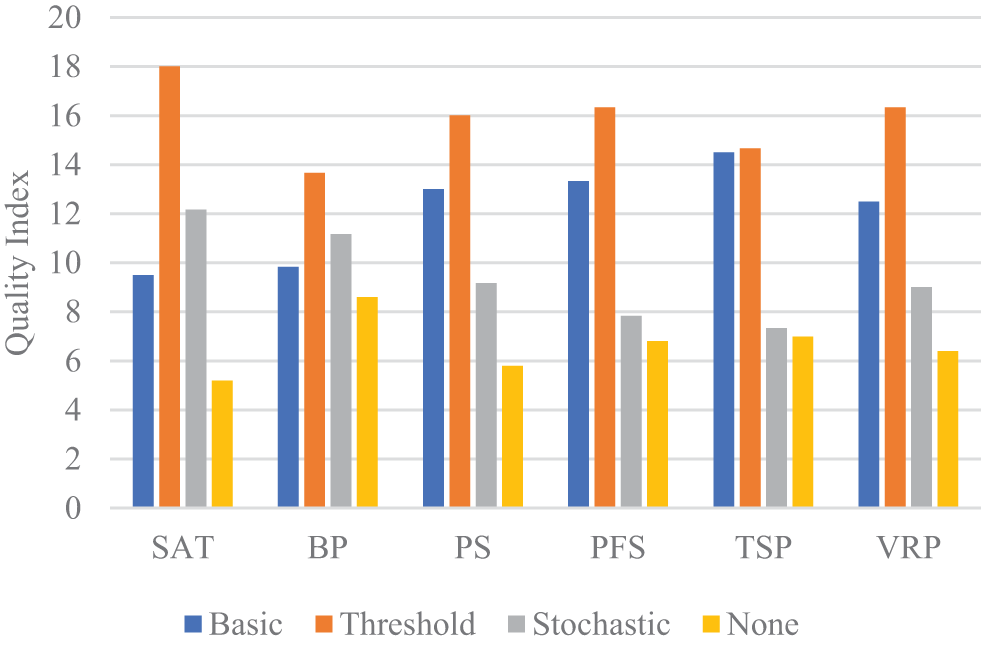
Figure 13: Average quality index in individual problem domains for move acceptance
The two approaches of non-stochastic basic methods are to accept only improving (PHunter, EPH, HAEA, DynILS, and SA-ILS) or accept improving and equal solutions (VNS-TW). Most algorithms accept only improving candidate solutions, including. Notably, EPH follows a unique approach by replacing a solution in its population with only candidate solutions that differ from other solutions within the population.
The non-stochastic threshold method is implemented by the winning algorithm, AdapHH, which compares the candidate solution against the previous best solutions kept in a list. Meanwhile, ML accepts a non-improving solution only if 120 consecutive iterations without improvement have been reached. HAHA rejects worsening solutions unless five consecutive worsening iterations have occurred and a second of execution time has passed since the last acceptance of a candidate solution.
A well-known stochastic move acceptance method is SA [84], which has been used in three algorithms (NAHH, KSATS-HH, and GISS). In NAHH, the move acceptance strategy is different for each algorithmic schemata, with one of them involving SA. NAHH also employs schemata that directly apply probabilities to accept a worsening candidate solution, which is also utilized in ISEA, XCJ, and MCHH-S.
Several algorithms, including ACO-HH, GenHive, AVEG-Nep, SelfSearch, and Ant-Q, do not incorporate a move acceptance strategy. In these algorithms, the solutions are updated every time heuristics are applied. Notably, Di Gaspero et al. [48] highlighted the trust in the reinforcement learning process within AVEG-Nep, leading to the acceptance of every candidate solution, including the worsening ones.
Burke et al. [4] classified hyper-heuristics based on the source of feedback during learning. An algorithm is considered a learning one when it uses feedback from the search process. Learning algorithms process feedback during the search process, influencing the subsequent decisions made at the hyper-heuristic level. Algorithms that do not learn from feedback are considered non-learning ones. Learning can be further divided into online and offline learning. In online learning, the feedback is taken while the algorithm is in the process of solving the problem, whereas offline learning involves collecting knowledge from a set of training instances that are expected to be able to generalize for solving the problem. Drake et al. [3] then extended this taxonomy by adding another category, mixed learning, which combines both offline and online learning approaches.
We classify the algorithms that competed in CHeSC 2011 based on their nature of feedback in Table 6. Fig. 14 shows that most algorithms employ the online learning approach (12 algorithms), followed by the offline learning approach (four algorithms). Notably, the three highest-ranked algorithms implement online learning. However, the bottom three algorithms are also implementing online learning, which causes the average quality index for online learning to be lower than for the offline approach. Upon further investigation, we found no major differences between the online learning strategies utilized by the top three and the bottom three algorithms. In both cases, the performance of heuristics is measured in terms of the solution fitness or fitness improvement to help make decisions in heuristic selection. This could indicate that other features of the algorithm contribute to the performance of the better algorithms. Yates et al. [15] have also observed that offline learning outperforms online learning. Mixed learning has the highest quality index, albeit only one algorithm followed the approach. Three algorithms did not have any element of learning, where they are placed among the worst ten at rank 12, 15, and 17. The significance of learning mechanisms is evident as numerous prior studies have emphasized the notable improvements linked to the inclusion of learning mechanisms [12,13,16]. Statistical tests validated significant differences, with the Friedman test yielding a p-value of 1.8115E−10. Post-hoc Wilcoxon signed-rank tests further validated significant differences across all pairings. In terms of variability, the mixed learning approach exhibits higher variability, as indicated by a larger range of normalized median values in Fig. 15.

Figure 14: Algorithm count and average quality index for nature of feedback

Figure 15: Boxplot of normalized median values for feedback
Regarding the adaptability to different environments, learning approaches are less critical for SAT instances, where algorithm performance relies more on escaping local optima [23]. The slow execution of low-level heuristics in PS and VRP instances limited the benefits of feedback mechanisms, making adaptive or greedy approaches more suitable [73]. Conversely, for PFS instances, feedback mechanisms are crucial in enhancing heuristic effectiveness and guiding the search toward high-quality solutions [23,82]. Overall, learning approaches are well-suited for problems with fast low-level heuristics and large solution space.
Next, we analyze both online and offline learning in terms of the source of feedback (what is measured) and the decisions (or actions) made based on the feedback in Tables 9 and 10. Algorithms with mixed learning are included in both analyses since mixed learning is a combination of online and offline learning. The results show that algorithms with online learning most frequently measure the improvement count (whether the low-level heuristic applied has improved the solution or not), followed by the value of the improvement, with seven and six algorithms, respectively. The execution time of the algorithm (time spent or time left before the time limit) is considered in four algorithms, which influences the heuristic selection and search strategy. VNS-TW checks whether the same solution is produced to disable the low-level heuristic applied. SelfSearch measures low-level heuristics performance in multiple metrics, including the number of the same solution it has produced, the number of non-improvement applications and the total number of applications for the heuristic.

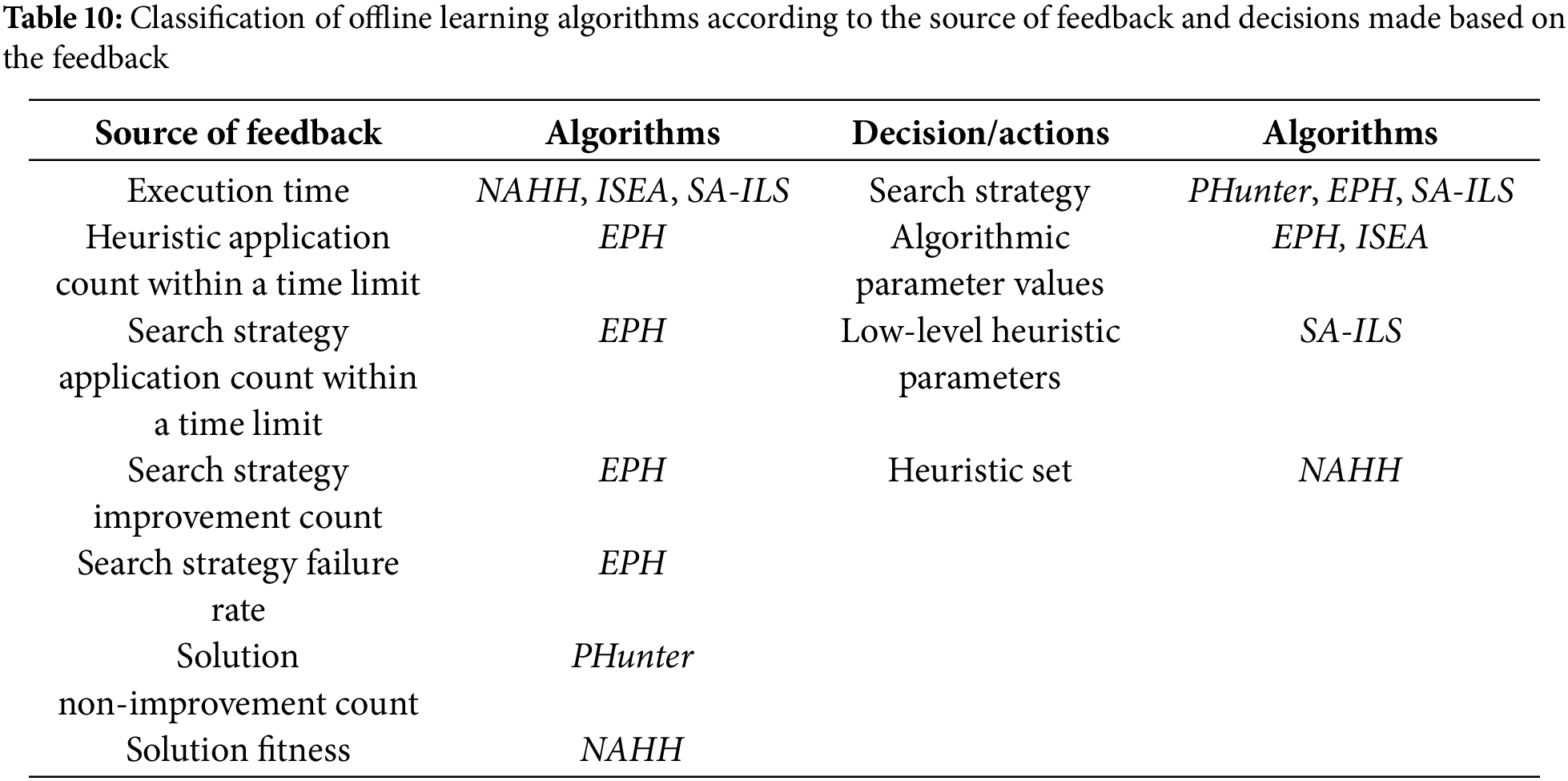
The feedback from the search process is most often used to make decisions in heuristic selection, implemented by 11 algorithms. Two other decisions are within the nature of heuristic selection, which are heuristic order and heuristic type. VNS-TW and HAHA use feedback information to order a set of low-level heuristics to be applied sequentially. Meanwhile, AVEG-Nep determines the type of low-level heuristic (between the four provided in the HyFlex framework) to be applied before randomly choosing one from the selected type. AdapHH alters the low-level heuristic set available for one phase of the search based on the heuristic performance in the previous phase. Finally, SelfSearch controls the search strategy, whether to be more explorative or more exploitative, based on the time left before the time limit is exceeded.
In the context of CHeSC 2011, we observed offline learning as the process of assessing the difficulty of the problem instance. This is achieved by applying the low-level heuristics provided for the selected problem instance before entering the main search process (either loop or other process). Afterwards, feedback from the learning process is used to make some decisions. Among the 20 competitors, offline learning is observed in five algorithms (PHunter, EPH, NAHH, ISEA, and SA-ILS). Most of these are placed in the top half of the competition leaderboard, with SA-ILS being the exception at rank 14.
Our analysis of the source of feedback for offline learning algorithms has shown that most algorithms measure the execution time of the low-level heuristics. Compared to online learning, there is less emphasis on the solution fitness after the heuristic application. Besides, execution time is measured related to the execution time of low-level heuristics instead of the time spent or time left before the time limit. EPH also gauges the execution time of low-level heuristics, but it does so by counting how many times a heuristic is applied within a specified time limit. Moreover, the algorithm tests a local search strategy, namely Variable Neighbourhood Descent (VND), by observing the number of applications within a time limit. The improvement and failure rate of the executions are then measured to influence the decision on which local search strategy to implement in the main phase of the algorithm. PHunter also tests different search strategies in a rehearsal run, which records the number of non-improvement solutions found throughout. Finally, besides execution time, NAHH also considers the solution quality obtained after heuristic application to determine the quality of the particular low-level heuristic.
The feedback from offline learning is most frequently used to determine the search strategy to employ (three algorithms), followed by setting the algorithmic parameter values such as population size (two algorithms). EPH will avoid VND for instances with a low number of applications within the offline learning phase. A single heuristic application strategy will be used in such cases. SA-ILS have two different strategies for local search (SA or iterated local search), determined by the average heuristic execution time. Meanwhile, EPH uses a smaller population when the low-level heuristic has a long execution time and a bigger population when the execution time is shorter. In ISEA, chromosome length and population size are among the parameters adjusted based on the low-level heuristic execution time. Another type of parameter is the one for the low-level heuristics, namely IM and DOS. SA-ILS uses high IM and DOS values for instances with computationally inexpensive low-level heuristics, whereas lower values are used for harder (longer time to solve) instances. NAHH uses the knowledge gathered from the offline learning phase to remove low-level heuristics that are dominated by other ones from being used during the search process.
Only one algorithm (PHunter) uses mixed learning, and it placed fourth in the competition. Their online learning component is similar to other algorithms, where the low-level heuristic performance is measured in terms of solution improvement. Weights are assigned to the heuristics, which will guide heuristic selection. Meanwhile, the offline learning part resembles EPH and SA-ILS, where they test out different local search strategies to be implemented by the main search process. Since the algorithm is placed in the top five of the competition, we argue that mixed learning brings a positive impact on the algorithmic performance. Furthermore, we contend that offline learning is important as different instances have different low-level heuristics with varying execution times, which will affect the search process. This is reasonable as it has been found that parameter adaptation in cross-domain search can increase performance [10], and offline learning is capable of adjusting algorithmic parameters according to the instance difficulty.
The main mechanism of Tabu search [85] is storing information related to the search process [86]. It features a memory mechanism called Tabu list, which stores either solutions or move operators already encountered during the search to avoid cycling to them. Information from the Tabu list can be used to promote diversification by exploring new unvisited areas of the solution space [87]. Talbi [86] gives three representations for the Tabu list, which are visited solutions, moves attributes, and solution attributes. The basic approach in implementing the Tabu mechanism is by storing solutions visited throughout the search process. However, this is computationally expensive and impractical for problems with a large solution space. A simpler approach is to store moves or solution attributes instead, with the former being the most popular of all approaches.
Among the CHeSC 2011 algorithms, we identified two approaches in implementing the Tabu mechanism, which are storing solutions and low-level heuristics. In most cases, the Tabu mechanism with solutions stores domain solutions to ensure it is not revisited, whereas the Tabu mechanism with heuristics prevents ineffective heuristics from being utilized. Besides, several algorithms implement both approaches since they are not mutually exclusive. None of the algorithms implemented a Tabu mechanism based on solution attributes. This omission could be attributed to the fact that the HyFlex framework conceals domain knowledge.
The classification of each algorithm is presented in Table 6, with the frequency distribution and average quality index for Tabu mechanism methods illustrated in Fig. 16. The results indicated that most algorithms, specifically 70% (14 algorithms), do not incorporate any Tabu mechanism. All six algorithms that implement the Tabu mechanism employ the Tabu heuristics approach, with only two of them also implementing the Tabu solutions approach. Notably, the four best-ranked algorithms utilize a Tabu mechanism, whereas none of the bottom half performers have. When comparing the average quality index, the Tabu heuristics approach shows a slightly higher average quality index than the Tabu solutions approach, at 16.83 and 16, respectively. However, the Wilcoxon signed-rank test indicated no significant difference between these strategies (p = 0.1204). Algorithms with no Tabu mechanism has significantly lower value compared to any of the Tabu mechanism methods (at 7.79). Statistical tests confirmed significant differences between the no-Tabu approach and the Tabu-based methods. The existing literature contains conflicting findings regarding the influence of Tabu mechanisms on algorithmic performance. While Misir et al. [16] recognize its positive contribution, Adriaensen et al. [17] dispute this perspective.

Figure 16: Algorithm count and average quality index for Tabu mechanism methods
Fig. 17 presents the boxplot of normalized median values for the Tabu mechanism strategies. It reveals that the Tabu heuristics approach has a smaller variability compared to the Tabu solutions approach. Furthermore, the Tabu solutions approach includes an outlier, exceeding 0.7. Tabu mechanisms can address challenges posed by problem-specific characteristics. The Tabu heuristics approach is closely related to learning mechanisms, since often poorly performing heuristics are excluded from the search. The Tabu solutions approach prevents revisiting previously explored solutions, thereby enhancing solution diversity in problems with complex landscapes. As noted, feedback is advantageous in certain instances (PFS) but not in others (SAT, PS, and VRP). Similarly, the Tabu mechanism is beneficial in problems that gain from feedback, particularly those with fast execution of low-level heuristics and infrequent occurrences of getting trapped in local optima.

Figure 17: Boxplot of normalized median values for Tabu mechanism methods
The implementation of a Tabu mechanism also involves two parameters, which are the Tabu list size and Tabu tenure, which will also be discussed. The Tabu list size plays a significant role in determining the level of restrictions applied to the search process [86]. A smaller Tabu list translates to lower restrictions, reducing the probability of cycling. In contrast, a bigger Tabu list causes higher restrictions, making cycling more likely. Furthermore, the Tabu list size can be classified as static, dynamic, or adaptive [86]. The static type maintains the same list size throughout the search process, whereas the other two types involve variable list sizes. The distinction between dynamic and adaptive is that the former changes without feedback from search, whereas the latter adjusts parameter values according to feedback. On the other hand, Tabu tenure defines the duration, usually measured in the number of iterations, during which a solution or move must remain in the Tabu list [86].
The Tabu heuristics approach is employed by six algorithms (AdapHH, VNS-TW, ML, PHunter, HAHA, and KSATS-HH). AdapHH, the competition winner, excludes low-level heuristics from being utilized in one search phase based on their performance in the preceding phase. At the end of each search phase, the performance of the low-level heuristics, measured by their quality index, is calculated, and the Tabu list is updated. Heuristics with quality indices lower than the average value will make up the Tabu list. Both Tabu list size and Tabu tenure are adaptive, where the former is adjusted based on the quality index, and the latter increases (up to an upper boundary) when the same heuristic is added to the Tabu list for consecutive search phases. An analysis by Adriaensen et al. [17] found that the Tabu mechanism in AdapHH does not significantly improve overall algorithmic performance.
In their iterated local search algorithm [86], VNS-TW implements the Tabu heuristics approach to avoid applying perturbative low-level heuristics that lead to minimal or excessive changes to the solution. Perturbative heuristics that result in a worse solution or no changes to the solution following the local search phase are added to the Tabu list. Otherwise, if a solution with equal fitness is produced, the heuristic is added with a stochastic probability of 0.2. The Tabu list size is static, and heuristics in the Tabu list are released according to the first-in-first-out policy. ML incorporates a Tabu mechanism in its local search phase. Local search low-level heuristics are added to the Tabu list if they fail to improve the incumbent solution. These heuristics are removed from the list as soon as any other heuristic successfully yields an improvement. This approach effectively aids in identifying the local optima, which is the point when none of the heuristics can further enhance the solution.
Other algorithms, including PHunter, HAHA, and KSATS-HH, have varying implementations of the Tabu heuristics approach. PHunter controls the usage of perturbative low-level heuristics using a Tabu mechanism. In HAHA, local search heuristics with a success rate of lower than 1% have a 50% chance of being discarded. KSATS-HH adds low-level heuristics that failed to improve the working solution to the Tabu list, which will only be released after seven algorithmic iterations. Both PHunter and HAHA employ the Tabu solutions approach by storing visited solutions, with HAHA specifically retaining the last 50 solutions.
The restart procedure within a local search algorithm involves the generation of a new solution, in which the search process is reinitialized from the solution [35]. Since the restart mechanism has never been reviewed previously, we provide discussions based on our observations. There are two important dimensions within a restart mechanism: the condition and the method. The restart condition is related to the process of deciding when to trigger the restart, whereas the restart method is the action taken to reinitialize the search. Adapted from the classification of the nature of move acceptance, we categorized the nature of the restart mechanism as threshold and stochastic. Threshold restart involves a restart that is triggered when some conditions are met, whereas stochastic restart is triggered probabilistically.
We classified each algorithm from the competition based on their implementation of the restart mechanism in Table 6. A bar graph of the algorithm count and average quality index is presented in Fig. 18. The results show that there exist more algorithms with no restart mechanism than ones with a restart mechanism from either type (12 compared to eight). One notable observation is that most algorithms in the bottom half of the leaderboard do not implement a restart mechanism. On the other hand, among the eight algorithms with a restart mechanism, only one implements it stochastically.

Figure 18: Algorithm count and average quality index for restart mechanism methods
The quality index analysis shows that algorithms with no restart mechanism give out the lowest average quality index, with 9.42. This implies that a restart mechanism can enhance performance within the HyFlex framework. Adriaensen et al. [17] has demonstrated the significant role of the restart mechanism in increasing AdapHH’s performance. Among the implementations of the restart mechanism, the quality index is higher for stochastic restart, with a value of 14 compared to 11.86 for threshold restart. Friedman test confirmed the results indicating a significant difference among the groups, with a p-value of 4.4139E−7. Post-hoc Wilcoxon signed-rank tests also showed statistical significance across all pairings with p-values smaller than 0.0001. Additionally, the threshold and stochastic approaches exhibit similar variability, as observed in the boxplot of normalized median values in Fig. 19. The no-restart approach shows reduced variability, though it achieves poorer median values.

Figure 19: Boxplot of normalized median values for restart mechanism methods
Within the HyFlex framework, the restart mechanism is particularly effective for SAT instances, helping escape local optima [36,82]. Kheiri et al. [82] highlighted that restart mechanism is required in FSP instances for increased performance. Conversely, PS instances, characterized by their slow low-level heuristics, may gain limited benefits from frequent restarts due to the excessive time spent evaluating heuristic combinations [82]. The restart mechanism proves advantageous for escaping local optima, making it particularly beneficial for multi-modal problems.
Next, the restart conditions and methods for each algorithm that implements a restart mechanism are summarized in Table 11. Among the CHeSC 2011 algorithms, we identified six measures of restart condition: iteration, time, solution quality, heuristic application, heuristic parameters, and probabilistics. Fig. 20 demonstrates that half of the algorithms (four out of eight) use iteration count as the measure for restart condition. AdapHH incorporates a restart mechanism into its move acceptance criterion, known as Adaptive Iteration Limited List-based Threshold (AILLA). In AILLA, there is a threshold level that increases when a move fails to improve the incumbent solution. This implies that re-initialization is initiated after a certain number of consecutive non-improvements. HAHA triggers restart when any one of three conditions is met, with one of them being after six non-improving algorithmic iterations. GISS reinitializes the search when the maximum number of non-accepted iterations has been exceeded. The maximum number of iterations is equal to the square of the number of low-level heuristics. SelfSearch will trigger a search restart after a certain consecutive non-improvement to the best solution. The number of consecutive non-improvement allowed depends on the improving factor and the expected number of generations before the time limit.


Figure 20: Algorithm count and average quality index for restart condition
The second most frequently employed metric for restart conditions is time, used by three algorithms (PHunter, HAHA, and ISEA). PHunter calls the restart mechanism when no new solution is produced after a percentage of the execution time limit has elapsed. One of the other restart conditions for HAHA is the time elapsed since the last improvement, with one minute being the threshold. ISEA also implement a similar time condition as HAHA, with an additional condition that the search has progressed for a certain amount of time after the last restart. Meanwhile, solution quality influences the restart condition in two algorithms: HAHA and GISS. The final restart condition for HAHA is when the algorithm has produced a solution with a fitness value that is 150% of the fitness of the current best solution. The maximum number of iterations in GISS is affected by solution quality, where it doubles when the working solution is within 1.5 times the value of the best solution. Notably, HAHA is placed in the top half of the leaderboard, whereas GISS is at the bottom half. The only difference in the restart condition between the two algorithms is the inclusion of the time metric for HAHA. This suggests that a restart controlled by time can increase the algorithmic performance.
Other restart conditions are implemented only in one algorithm each. ISEA will also trigger a restart when a maximum number of fitness evaluations (heuristic application) has been exceeded. HAEA has a soft replacement policy, which is called when a non-improving solution is found. The policy entails applying local search heuristics to the best solution using default heuristic parameter values. The restart mechanism is triggered if the range of parameter values has been tested, which is determined using a control variable. Finally, NAHH initiates restart using varying probabilities for each of its algorithmic schema.
When comparing the average quality index, it can be observed that the highest value is obtained by the time metric, with 15. Probabilistic and heuristic application conditions have a high average quality index (14 and 13, respectively), albeit only one algorithm implements each approach. The other metric implemented by only one algorithm is heuristic parameters, with a quality index of 11. Iteration and solution quality measurements are the two lowest-scoring approaches, with average quality indices of 10.5 and 9.5, respectively.
Ideally, a search should be reinitialized once a local optimum is reached. Since most algorithms record the time or number of iterations as the restart threshold, this implies that most algorithms consider consecutive non-improvements as local optima. On the other hand, only two of the top five performers implement a restart mechanism, which are AdapHH (rank 1) and PHunter (rank 4). We assume that VNS-TW (rank 2) and ML (rank 3) did not require a restart mechanism since both algorithms performed intensification (applying local search heuristics) until local optima. They define the local optima as the point where all local search heuristics could not improve the solution any further. At this point, exploration will be induced by applying perturbative heuristics to switch the point in the search space. Meanwhile, EPH (rank 5) did not require a restart mechanism since a mutation operator is used as their diversification strategy.
For the restart method, Fig. 21 shows that the most popular actions for restarting the search are reinitializing the solution (using a function provided by HyFlex) or making perturbations to the current solution, with three implementations each. AdapHH, PHunter, and NAHH employ the former. Notably, PHunter applies local search heuristics to the newly produced solution before reinitializing the search process. On the other hand, HAEA applies a random heuristic to the current solution, whereas other algorithms apply different types of heuristics. GISS applies a ruin-recreate heuristic followed by a mutation heuristic to the current solution. SelfSearch applies a heuristic to all solutions in the population, with the type of heuristic determined by the number of expected generations left. When there are more than 50% of the runtime limit, the current heuristic is applied. Otherwise, the heuristic with the highest improvement rate will be applied. Between the two approaches, the average quality index observed by algorithms that reinitialize the solution is higher than algorithms that perturb the current solution, with 17 compared to 6.

Figure 21: Algorithm count and average quality index for restart method
Meanwhile, making perturbations to the best solution and updating low-level heuristic parameters are used to restart the search in two algorithms each. HAHA and ISEA implement the former approach, using ruin-recreate or mutation heuristics. Heuristic parameters are modified when the search is restarted in GISS and SelfSearch. The values for IM and DOS can be increased by 1.1 times with a probability of 0.2 in GISS. For SelfSearch, a different parameter is altered depending on the number of expected generations left. DOS is increased when the search is at the first half of the time limit, whereas IM is increased when it is at the other half. Perturbating the current best solution gives out the second-highest average quality index of 14, whereas updating the heuristic parameters has the lowest quality index of 3.5.
The restart mechanism also involves updating the low-level heuristic set and resetting move acceptance variables in one algorithm each. The quality indices for these approaches are 11 and 4, respectively. HAEA will use a different heuristic set, selected randomly, for the search process after the restart point. Meanwhile, GISS resets the temperature in its move acceptance strategy, i.e., SA, back to the initial value.
Restart mechanism should be included to escape local optima and is especially critical when local optima cannot be identified definitively. This is because the quality index for algorithms with a restart mechanism is higher than those without. Despite this, some of the top-performing algorithms, such as VNS-TW and ML, do not utilize a restart mechanism. It is hypothesized that they may not need such mechanisms because they can detect when a local optimum is reached. Moreover, based on our analysis, it is better to consider execution time rather than algorithmic iteration as the threshold for the restart condition. Meanwhile, the top two restart methods, which are reinitializing the solution and perturbating the best solution, are suggested for future algorithms since they have the highest average quality indices. In contrast, restarting by updating the heuristic parameter values may not be beneficial for algorithmic performance.
5.8 Low-Level Heuristic Parameters
One of the features of the HyFlex framework is the concealment of domain-level knowledge. Nonetheless, the framework offers a method to control the low-level heuristics’ behaviour using two parameters: IM and DOS [7]. IM is for perturbative low-level heuristics, whereas DOS is for local search ones. Parameter setting is a critical facet of heuristic approaches in optimization. It involves defining the values of various parameters that control an algorithm’s behaviour, affecting factors like exploration, exploitation, and convergence. Proper parameter settings can significantly influence an algorithm’s performance and the quality of solutions it produces [88–90]. Furthermore, parameter settings might need adaptation throughout the course of a search since the optimal values for the parameters are different at different stages of the search process [91].
Parameter settings can be classified by their nature into four categories: static, dynamic, adaptive, and self-adaptive [3]. Static parameters indicate the use of a fixed value, determined before the search, throughout the search. The other three approaches involve modification to the parameter values as the search progresses. Dynamic parameters have their values changed based on a predetermined property without considering feedback from the search. Both adaptive and self-adaptive approaches use search feedback to make informed changes to the parameter values. The difference between the two is that the latter simultaneously searches for the best solution and parameter values by having the parameter values encoded into the solution [86].
The algorithms proposed for the CHeSC 2011 competition are classified into four control methods, which are presented in Table 6. Based on our analysis, Fig. 22 demonstrates that static parameter is the most popular low-level heuristic parameter control method (with eight algorithms—ML, NAHH, KSATS-HH, GenHive, SA-ILS, XCJ, MCHH-S, Ant-Q), followed by adaptive parameters (with seven algorithms—AdapHH, VNS-TW, PHunter, HAEA, DynILS, GISS, SelfSearch). The self-adaptive approach is employed by four algorithms, including EPH, ISEA, ACO-HH, and AVEG-Nep. Only one algorithm controls the low-level heuristic parameters dynamically, which is HAHA.

Figure 22: Algorithm count and average quality index for low-level heuristic parameter control methods
In the HyFlex framework, both IM and DOS have default values of 0.2. Six out of the eight algorithms with static parameters utilize the default values throughout the search process. They include ML, KSATS-HH, GenHive, XCJ, MCHH-S, and Ant-Q. On the other hand, NAHH uses different values that are tuned for each of their algorithmic schemata. Furthermore, during its offline learning phase, which involves heuristic applications, both IM and DOS are set to 0.1. In problem instances where the local search heuristics require more than 10 s to execute, the DOS value is configured to 0.1. For SA-ILS, the heuristic parameter values are determined during its offline learning phase. Problem instances with extended heuristic execution times use a lower parameter value of 0.4 for both IM and DOS. For instances with short heuristic execution times, parameter values of 0.8 for IM and 0.6 for DOS are employed.
Next, HAHA is the only algorithm that dynamically manages the low-level heuristic parameters. Random parameter values are used during its serial phase, whereas IM values that correlate with the time since the algorithm started are utilized in the parallel phase. The IM value is controlled so that there is a lower level of mutation towards the end of its execution.
Most algorithms that use adaptive parameter control adjust parameter values according to the solution quality after heuristic applications. The winner of CHeSC 2011, AdapHH, incorporates an adaptive parameter control strategy using a reward-penalty mechanism. The algorithm defined four types of value changes based on the outcome of heuristic applications. Parameter values are increased by 0.01 when a new best solution or by 0.001 when an improvement is found. Conversely, when a heuristic application fails to yield improvement, parameter values are reduced by 0.0005 for obtaining a worse solution or by 0.0001 for obtaining an equal solution. These parameter values are bounded within the range of 0.2 to 1.0. DynILS also employs a reward-penalty mechanism to control the value of IM, which is based on whether an improvement is achieved or not.
Meanwhile, the parameter values are updated when an algorithmic iteration has failed to improve the working solution in HAEA. The DOS value is initialized at 0.1 to promote exploration in the early phases of the search. The DOS value is incremented by a random value between 0 and 0.1, up to the maximum parameter value of 0.5. Upon reaching the maximum value, the parameter value is reset to a random value between 0 and 0.1. Besides, the value of IM is calculated as 1.0 subtracted by the value of DOS, meaning that modifications to DOS value results in an adjustment to the IM value as well. Parameter values are also only adapted at specific intervals in other algorithms. The DOS value in VNS-TW increases by 0.2, up to a maximum of 0.6, when the best solution remains unchanged at the periodical adjustment step. This step is called at intervals during the algorithm’s execution. Parameter value adjustment in GISS can only occur when the search is restarted. In this scenario, both IM and DOS values are increased by 10% with a probability of 0.2.
Parameter values are also adaptable depending on the strategy to be applied in the algorithm. PHunter utilizes one of the different configurations for IM and DOS based on the search state. There are three configurations for IM (low—0.1, medium—0.5, high—1.0) and two configurations for DOS (low—0.1, high—1.0). The lower DOS configuration is used when the search is at a sea trench, which is defined as when the local search heuristic application is prolonged. In SelfSearch, low-level heuristic parameter values are adapted according to the search strategy employed. For explorative strategy, high IM value and low DOS value are employed. The IM value increases in proportion to the number of times local optima are encountered during search restarts. In contrast, when the exploitative strategy is utilized, low IM value and high DOS value are used, with the DOS value being increased proportional to the frequency of local optima encountered when the search restarts.
Self-adaptive is implemented in EPH, where the parameter values evolved together with the heuristic sequences. The parameter values also evolved together with action sequences in ISEA. The initial values, boundaries, and incremental rates of the parameters are established through an offline learning process that considers the execution time of low-level heuristics. For less complex instances, a broader range of parameter values with higher initial values and incremental rates is used, whereas the opposite is true for more challenging instances. Mutation of the action sequences entails a 25% chance of changing the heuristic and a 75% chance of adjusting the parameter values. Changes in parameter values have an equal likelihood of either increasing or decreasing. The amount of adjustment is determined by multiplying the incremental rate by a random value. Meanwhile, in ACO-HH, parameter values evolved alongside the heuristic, though they maintain separate sets of selection probabilities. AVEG-Nep deploys a set of possible values {0.2, 0.4, …, 1.0} for IM and DOS, with one value selected through reinforcement learning.
There have been many arguments that having static parameter values is detrimental to algorithmic performance. Zhang et al. [92] argued that the parameter values may have to be tailored for different types of problems. Even during the search process, different stages of the search may have different optimal parameter values to optimize performance. Jackson et al. [10] have also proven that static algorithm settings perform worse than dynamic or adaptive ones in the context of the move acceptance strategy. Rahman et al. [88] have also highlighted that one of the keys to a successful metaheuristic implementation is adaptive parameter setting.
This sentiment can be observed in Fig. 22 which shows that the static parameter control method has the lowest average quality index of 8.63. The highest quality index belongs to the dynamic approach (15), although only one algorithm implemented this method. Adaptive and self-adaptive approaches outperform the static approach, with the adaptive approach having a slightly higher average quality index than the self-adaptive approach (11.71 and 11, respectively). The Friedman test revealed significant difference between the groups (p-value = 4.3985E-4). However, post-hoc analysis showed that only the static approach differed significantly to other approaches. No statistical differences were found between the dynamic, adaptive, and self-adaptive approaches. Fig. 23 illustrates the distribution of normalized median values for the parameter control strategies. The adaptive approach demonstrates a lower performance variability across different problem instances, indicating a higher reliability.

Figure 23: Boxplot of normalized median values for low-level heuristic parameter control methods
Based on arguments from prior studies and our analysis, which align in highlighting the advantages of adaptive parameter control, we conclude that this approach is the most effective for ensuring adaptability across diverse problem scenarios. Thus, adaptive parameters that evolve with search landscape is recommended. However, parameter configuration should be optimized to avoid wasting computational resources, particularly for problems with slow execution of low-level heuristic, such as PS and VRP instances.
6 Comparison with Trends in Recent Hyper-heuristics
Hyper-heuristics remain highly relevant in current research. Their distinct advantage over other heuristic approaches lies in their greater generality [5].
6.1 Hyper-Heuristics for HyFlex
Many hyper-heuristics employ the HyFlex framework to assess generality. The framework provides multiple instances from nine problem domains, providing a comprehensive platform for evaluating the capabilities of designed algorithms. We direct our attention to algorithms that were implemented in the HyFlex framework for a direct comparison with the algorithms from the CHeSC 2011 competition. We contend that the problem domains provided in the framework are sufficiently robust to assess the cross-domain search performance. Furthermore, the insights derived from the cross-domain search studies have been generalized to encompass all optimization problems, as performed by Jackson et al. [10].
Many algorithms have been proposed to surpass the entries from the CHeSC 2011 competition after its conclusion. It is important to note that critical bugs in one of the original problem domains, namely PS, have rendered comparisons between algorithms developed before and after the bug was fixed on 17th March 2019 incomparable. Several works published after the bug fix have excluded results for PS instances in their comparison, ensuring fair comparison. Table 12 summarizes 26 algorithms, 23 of which were published before the bug fix, whereas the remaining three excluded PS instances results. The table details their chosen benchmark CHeSC 2011 algorithms and corresponding experimental outcomes, sorted by the year of publication.
The HyFlex’s problem instances have been extended after the competition by Adriaensen et al. [36]. Among the algorithms in Table 12, new domains were utilized to assess the generality of NR-FS-ILS, LeanGIHH, SSMA-Best, and EA-ILS. NR-FS-ILS, LeanGIHH, and EA-ILS outperformed the CHeSC 2011 winner, AdapHH, across the extended set. Asta et al. [96], Soria-Alcaraz et al. [102], and Soria-Alcaraz et al. [38] only utilized the VRP instances to evaluate their algorithms, rendering their tests no longer a cross-domain search. Comparisons in Adubi et al. [25] and Adubi et al. [104] excluded the PS domain due to critical bugs affecting the algorithmic process in this domain. The remaining algorithms are benchmarked using the six domains employed in the CHeSC 2011 competition.
Comparisons involving the CHeSC 2011 algorithms typically include all 20 algorithms, with the second most common practice being a comparison with the top five performers. Ferreira et al. [42] compared their proposed algorithm against the top 10 algorithms from the competition. Adriaensen et al. [36] included AdapHH and EPH in their experiments, representing the best single-point and multi-point approaches, respectively. Adriaensen et al. [17] compared LeanGIHH only with AdapHH, as the former is a simplified variant of the latter, aiming to validate the effectiveness of their simplification.
From the algorithms listed in Table 12, ten algorithms have outperformed the CHeSC 2011 competition winner, AdapHH. Notably, GEP-HH and MCTS-HH incorporate multi-point search techniques by maintaining elite solutions to diversify the search. In EA-ILS, a population of elite heuristic sequences is managed, with a sequence undergoing mutation at every iteration to improve the domain solution. This demonstrates that integrating multi-point search with elitism can significantly enhance performance.
Another technique for ensuring diversification is through iterated search phases. The iterated local search principle is a common feature in many effective algorithms, including FS-ILS, NR-FS-ILS, TS-ILS, and EA-ILS, suggesting its beneficial impact on algorithmic performance. These findings are consistent with our analysis of the search phases.
Heuristic selection is implemented based on probability using methods such as multi-armed bandit (in MCTS-HH) or Thompson sampling (in TS-ILS). FS-ILS considers the acceptance rate of the previous candidate solution as the probability for heuristic selection. On the other hand, SSHH and EA-ILS employ a Hidden Markov model in their heuristic selection processes to determine the most appropriate heuristic for the current search state. Based on these observations, it is evident that heuristic selection based on probability and adapted to the current state of the search can enhance performance. The effective utilization of the relay hybridization selection method in MSHH reinforces our findings that this method is a promising heuristic selection approach. Besides, the effectiveness of the dominance-based heuristic selection in MSHH highlights the importance of excluding poor heuristics in certain stages of the search.
The move acceptance methods that are effective are those that incorporate a probability of accepting worsening solutions. However, slightly deviating from our analytical findings, the stochastic approach appears more prominently among the effective algorithms, such as the Metropolis condition in FS-ILS and the Monte Carlo criterion in MCTS-HH.
Recent algorithms frequently apply feedback to improve heuristic selection. For example, GEP-HH uses a probability-based selection mechanism that rewards heuristics leading to improvements. In contrast, SSMA, which lacks a feedback mechanism, could not outperform all CHeSC algorithms. This observation supports our finding that both online and offline learning offer benefits compared to no learning. Asta et al. [96] introduced an apprenticeship learning generation hyper-heuristic to develop an optimal selection hyper-heuristic algorithm. This algorithm operates in two phases. The first phase learns features from an expert algorithm’s behavior while solving a single problem instance, and the second phase applies these learned features to address unseen instances. The features learned include heuristic selection, low-level heuristic parameters, and move acceptance behaviour. In addition to using a heuristic prediction decision tree, ALHH(
Tabu mechanism is also utilized in recent algorithms, including TSHH. However, its failure to outperform all CHeSC algorithms suggests that the Tabu mechanism may provide limited gains. Restart mechanisms are also used in recent algorithms to prevent stagnation. EA-ILS resets the search periodically and outperformed all CHeSC algorithms. In contrast, algorithms with no restart mechanism performed poorly. For instance, TGMA maintained diversity through weak elitism rather than restarts and failed to outperform all CHeSC algorithms. Adriaensen et al. [36] found that the restart mechanism within FS-ILS has outperformed the version without restarts, NR-FS-ILS, although at a small enhancement.
Most recent algorithms focus on algorithmic parameters rather than low-level parameters within the HyFlex framework. Parameters related to move acceptance (FS-ILS, SSHH, GEP-HH), memory (GEP-HH, MCTS-HH, FRAMAB, HHDMAB), and genetic operator (GEP-HH, SSMA-Best) are commonly controlled. Only SSMA-Best adjust low-level parameters, employing offline parameter tuning. This trend emphasizes that controlling algorithmic parameters provide greater benefits over controlling low-level heuristic parameters.
In contrast, most algorithms fell short of surpassing the competition winner, AdapHH. The poor performance of SSMA and TGMA suggests that multi-point search strategies, such as memetic algorithms (MA), suffer from slow convergence. Later research by Gümüş et al. [44] indicated that performance could be enhanced by tuning MA’s parameters, although not sufficiently to outperform AdapHH. Besides, excluding the population of elite solutions in GEP-HH* demonstrates that this mechanism can enhance performance, as GEP-HH, which includes this mechanism, managed to surpass AdapHH. Dempster et al. [101] introduced two Harmony Search hyper-heuristic variants: SP-MA and POP-MA. In both variants, each harmony consists of three heuristics applied sequentially, similar to a memetic algorithm. SP-MA maintains a single solution, whereas POP-MA uses a population of solutions. POP-MA outperformed SP-MA against CHeSC algorithms, indicating that a population-based approach may enhance search effectiveness.
SR-LA employs Simple Random heuristic selection, whereas F1FPS_RUA1-LA uses fitness-proportional roulette wheel selection. With both using the Late Acceptance strategy, F1FPS_RUA1-LA performed better than SR-LA against CHeSC 2011 algorithms, suggesting that fitness-proportional selection may enhance performance over random selection. RHH implements a round-robin neighbourhood selection mechanism, where each low-level heuristic is given equal application time. Heuristic application follows a memetic sequence, progressing from mutation to crossover to hill-climbing heuristics. Additionally, reinforcement learning is integrated into its threshold move acceptance, where the acceptance rate of non-improving moves is adjusted based on solution quality. TeBHA-HH uses random heuristic selection with two move acceptance strategies: naïve and accept improving or equal solutions. It applies tensor analysis to divide heuristics into two subsets, each using a different move acceptance method. The algorithm switches between these subsets in a round-robin manner for set intervals.
TSHH failed to outperform AdapHH despite implementing Thompson sampling similar to EA-ILS. This outcome suggests that the performance boost achieved by EA-ILS is likely attributed to other algorithmic sub-mechanisms, such as its population-based search and adaptive acceptance strategy. Moreover, MCF-AM uses an “accepting all moves” move acceptance strategy, aligning with our analysis that suggests this is one of the less effective implementations of a move acceptance criterion.
Interestingly, the multi-armed bandit strategy employed in FRAMAB, HHDMAB, and HH2DMAB did not yield superior performance compared to AdapHH, despite its effectiveness in MCTS-HH. This suggests that other components within the algorithms may be influencing overall algorithmic performance. Dantas et al. [105] introduced a Deep Q-Network for selecting low-level heuristics, which outperformed two MAB-based algorithms in solving TSP and VRP instances. Among the algorithms discussed, two are generation hyper-heuristics, as they operate at a higher level by designing heuristic selection and move acceptance methods. QHH, which utilizes Q-learning for designing heuristic selection and move acceptance, falls short of surpassing AdapHH in terms of performance. Conversely, Sabar et al. [28] successfully employed Gene Expression Programming (GEP) to design heuristic selection and move acceptance, outperforming AdapHH. This underscores the efficacy of GEP and other sub-mechanisms within GEP-HH, including the multi-solution mechanism.
In addition to the discussed algorithms, we identified four algorithms published after the PS bug fix that utilized the original PS domain results from CHeSC for comparative analysis. These algorithms are listed in Table 13, along with their benchmark set and experimental outcomes, sorted from the earliest to the latest publication.

CMS-HH outperformed AdapHH in three of the five PS instances tested. Excluding the PS domain, the algorithm obtained the best result in 19 out of 25 instances, highlighting its excellent performance in domains unaffected by bugs. LAST-RL achieved the highest score for the PS domain, surpassing all 20 algorithms from the competition. However, its performance is subpar for SAT, BP, and PFS (ranking fourth) and TSP (ranking third). It outperformed CHeSC algorithms only in the VRP domain. This suggests that the algorithm’s overall ranking would either be maintained or potentially decrease if PS results were excluded. Unfortunately, the published article for DHSS and RL lacks detailed results on each problem domain, preventing a conclusive assessment of the PS bug’s impact on overall performance. The impact of the PS bug could potentially either increase or decrease the ranking of the algorithm.
Nevertheless, we are interested in discussing the algorithmic components of these algorithms. CMS-HH employs mixed-point search, utilizing a Genetic Algorithm when diversification in the search is required. This corresponds with our findings, which support the idea that a mixed-point search is the most effective. We also observed that a multi-point strategy is employed when the search requires exploration, as evident in both algorithms from the competition that implement this approach; VNS-TW and HAHA. VNS-TW utilizes a population of solutions in the early phases of the search, intended to facilitate greater exploration. HAHA generates multiple solutions to escape from a local optimum. CMS-HH integrates a multi-armed bandit heuristic selection and relay hybridization selection method to obtain excellent results even in problem domains other than PS. The algorithm also implements a list-based adaptive threshold acceptance method. This highlights the effectiveness of threshold-based move acceptance. The low-level heuristic parameters are tuned using an offline approach.
LAST-RL employs the iterated local search principle and considers multiple features that characterize the search state when making heuristic selections. Both RL and LAST-RL incorporate reinforcement learning, along with the epsilon-greedy approach to have a probability of choosing a random heuristic to allow exploration. In contrast to LAST-RL, RL failed to beat AdapHH, even though both algorithms share the same fundamental principle. This performance difference could be attributed to the absence of iterated search phases in RL. DHSS is primarily characterized by its dynamic adjustment of the heuristic set during the search process. This approach functions similarly to a Tabu mechanism, placing certain low-level heuristics in a Tabu list to exclude them temporarily from the active heuristic set during the search. In contrast, Özcan et al. [106] uses a List of Active Heuristics (LAH), which is the opposite of a Tabu list. A dominance-based strategy updates the active heuristics for the search process by removing low-level heuristics with dominated solution fitness from the LAH.
6.2 Hyper-Heuristics for Other Optimization Problems
Recent research highlights diverse approaches to heuristic selection in hyper-heuristic algorithms, underscoring the impact of tailored selection strategies on performance. For instance, Choong et al. [107] integrated a modified CF within an artificial bee colony algorithm, showing the potential for CF in enhancing algorithm adaptability. Zhang et al. [108] introduced an adaptive bandit-based selection for multi-objective problems, whereas Hou et al. [109] implements multi-armed bandit (MAB) for heuristic selection. Lagos et al. [110] proposed a hyper-heuristic that learns through MAB, specifically Thompson Sampling and Exponential Weights for Exploration and Exploitation algorithms. This suggests that adaptive learning may offer more precise heuristic selection. Zhao et al. [111] and Maashi et al. [112] employed Q-learning and CF methods, respectively, to select heuristics, with learning mechanisms that rank low-level heuristic performance dynamically. Future research could benefit from adaptive selection mechanisms, particularly in dynamic or complex problem domains.
Search strategies are often adapted to problem-specific requirements, where recent work emphasizes structuring search stages for exploration and intensification. For instance, Toledo et al. [113] proposed a two-stage hyper-heuristic algorithm based on Large Neighborhood Search, categorizing fifteen low-level heuristics to systematically explore and refine solutions. Search phases are also implemented to provide more effective control over exploration and exploitation, especially in hyper-heuristics handling a variety of operators. Zhao et al. [114] introduced a framework dividing search operators into hill climber and mutation heuristic pools, managed by an activation system that adjusts according to pool performance. This phase-based approach, coupled with pulsar mechanisms to activate specific pools, enables adaptive control over search stages. On the other hand, Costa et al. [115] proposed a Cluster-based Hyper-Heuristic framework that utilizes a Genetic Algorithm to automatically evolve the exploration space and trim the search space based on the evolution of the solution. The study explored whether an adaptive search space will improve computational time without losing too much quality, compared to having no clusters or fixed ones. This structured approach to defining search points could be particularly useful in balancing exploration with solution refinement.
Adaptive learning mechanisms are key in enhancing hyper-heuristic adaptability across varied problems. Reinforcement learning is implemented in many studies [116,117]. Zhang et al. [118] integrated deep reinforcement learning for heuristic selection and parameter control, whereas Sánchez et al. [119] used a sequence-based selection mechanism with Multi-dimensional Archive of Phenotypic Elites. Ibrahim et al. [120] proposed a two-layer hyper-heuristic paradigm for feature selection, with a Differential Evolution algorithm in the first layer selecting components for various feature selection methods in the second layer. Shao et al. [121] introduced a learning probability model with SA-based move acceptance. Zhang et al. [122] introduced a new effective learning strategy, the perturbation adaptive pursuit strategy, which focuses on improving diversification.
Lissovoi et al. [123] analyzed the performance of simple hyper-heuristics to determine whether sophisticated learning mechanisms are necessary to increase performance. They concluded that single-heuristic observations do not boost performance unless evaluated over a longer period. Additionally, Li et al. [124] showed that a learning automata-based hyper-heuristic outperformed individual algorithms, a traditional online learning, and random selection hyper-heuristic. Gölcük et al. [125] proposed Q-learning hyper-heuristic to control the selection of four bio-inspired metaheuristic algorithms. The algorithm outperformed random and sequential selection. Burke et al. [126] introduced two adaptive variants of a multiple neighborhood iterated local search, using online learning to select perturbations at each step. These variants outperformed a baseline iterated local search with random move selection.
Move acceptance strategies play a pivotal role in handling local optima and encouraging search space exploration. Doerr et al. [127] and Lissovoi et al. [128] evaluated move acceptance strategies that switches between accepting only improving moves and accepting all moves, showing the potential for move acceptance in enhancing solution quality. Shambour et al. [129] and Maashi et al. [130] implemented the late acceptance strategy, whereas Ahmed et al. [131] incorporated reinforcement learning with Q-learning-based memory into the EMCQ framework. Their effectiveness suggests that adaptive move acceptance mechanisms that allow selective non-improving moves could offer a practical approach to escape local optima.
The Tabu mechanism is used to prevent cycles and promote solution diversity in recent hyper-heuristics. Zhang et al. [132] employed Tabu search with a greedy acceptance strategy. The Tabu mechanism employs the first-in-first-out principle to keep track of ineffective low-level operators. This mechanism allows for selective exclusion of heuristics that hinder progress, thus balancing exploration with solution refinement. Besides, the use of adaptive parameter control is increasingly common in hyper-heuristics, allowing real-time adjustment based on the search state. Pukhkaiev et al. [133] defines combination of metaheuristics and its parameters as low-level components and applied a surrogate model for parameter control. Marshall et al. [134] compared adaptive and grammar-based evolutionary hyper-heuristics, focusing on the trade-off between speed and quality. The adaptive hyper-heuristic, a simplified variant of Misir et al. [135], delivered high-quality solutions faster than the grammar-based approach. The algorithm features learning-based selection, relay hybridization, adaptive move acceptance, solution and parameter restarts, and parameter control.
Comparative studies highlight the cross-domain efficacy of hyper-heuristics compared to basic heuristics or metaheuristics. de Carvalho et al. [136] compared several online hyper-heuristics against single metaheuristics, demonstrating superior cross-domain performance for hyper-heuristics. Burke et al. [137] showed the advantage of perturbation-based hyper-heuristic algorithm, which outperformed an iterated local search. Besides, Misir [138] tackled algorithm selection within selection hyper-heuristics, developing a framework that matches algorithms to specific problem instances. This approach is promising for hyper-heuristics designed for cross-domain applications and future research should continue exploring how algorithm selection can improve adaptability and scalability across diverse problem sets.
The field of generation hyper-heuristics focuses on creating new heuristics or hyper-heuristics through automated methods. Burke et al. [139] utilized genetic programming to combine or select heuristic components, whereas Tyasnurita et al. [140] proposed a neural network-based generation hyper-heuristic to design both heuristic selection and move acceptance strategies. These approaches demonstrate the potential of generation hyper-heuristics to create customized strategies for specific problem instances, opening avenues for future research into self-adaptive and generative models in hyper-heuristic design.
7 Recommendations for Future Studies Related to Selection Hyper-Heuristics
This study identified effective methods for search points, search phases, heuristic selection, move acceptance, feedback, Tabu mechanism, restart mechanism, and low-level heuristics parameter control among CHeSC 2011 algorithms. This includes the mixed-point search, iterated search phases, relay hybridization, non-stochastic threshold move acceptance, mixed learning, Tabu mechanism with heuristics list, stochastic restart, and dynamic parameters. Future research should focus on these proven strategies.
Mixed-point search combines single-point and multi-point approaches, leveraging the strengths of each while mitigating their weaknesses. Single-point search can find good solutions but may have poor coverage [89]. Multi-point search offers better coverage but may suffer from poor exploitation and high computation times [141,142]. In the CHeSC 2011 algorithms, mixed-point search is used to promote exploration in the early search phase (VNS-TW) and to escape local optima (HAHA). Future research should identify effective hybridization methods that apply the right approach in the appropriate scenarios, such as using populations for diversification and single-point search to speed up the search process.
Iterated search phases alternate between applying perturbative and local search heuristics, which allows the control of exploration and exploitation. Perturbative heuristics are used for diversification when the algorithm reaches a local optimum [143]. However, excessive diversification can prevent the exploitation of good solutions [91]. Local search heuristics exploit the current solution to find better ones. However, overusing them may lead to premature convergence and an inability to escape local optima. Iterating between these phases leads to better final solutions and speeds up the search [144]. Among the CHeSC 2011 algorithms, many top performers use iterated search phases. Moreover, Choong et al. [103] noted that algorithms based on iterated search phases outperformed traditional ones, cementing the recommendation for new algorithms to employ this strategy. However, classifying heuristics as perturbative or local search types remains challenging. While the HyFlex framework provides predefined types, other optimization problems may not. Further research on classification methods would be beneficial.
Relay hybridization involves multiple heuristics working together in a sequence, where the output of one serves as the input for the next [81]. In the context of heuristic selection, the choice of the second heuristic depends on the first, ensuring compatibility. Applying heuristics individually may be less effective. Certain heuristics may need to be paired to enhance its effectiveness. Zhao et al. [41] highlighted that relay hybridization can form effective heuristics by pairing existing ones. Good pairings of perturbative heuristics can lead to deeper exploration, leading to better solutions [25]. New algorithms should ensure heuristic compatibility and extend the approach to consider longer sequences. However, Lepagnot et al. [83] noted that relay hybridization may be less effective for simpler problems without providing a reason. We recommend further research to improve relay hybridization for low-dimensional problems.
Threshold move acceptance utilizes a predetermined threshold value, which can be static, dynamic, or adaptive, to control solution acceptance. Tuning the threshold value is crucial to balancing exploration and exploitation. Jackson et al. [10] found that non-static methods outperform static ones since the search process fluctuates between needing exploration and exploitation. A threshold value set too high may limit exploration as worsening solutions may never be accepted, whereas a threshold value set too low may lead to poor convergence as too many worsening solutions are accepted. Adriaensen et al. [40] found that Metropolis acceptance, which considers solution quality change and time, outperformed strategies that do not accept worsening solutions or accept all solutions. However, it has not been highlighted that there are various types of threshold values, such as iteration-based (ML, HAHA), time-based (HAHA), and solution quality-based (AdapHH). Certain threshold types may be suited for specific experimental setups. A time-based threshold is more suitable for time-limited experiments such as in the HyFlex framework, whereas an iteration-based threshold works better when iteration count is used as the stopping criterion. Future researchers should choose the appropriate type based on their experimental setup and consider combining them to create more general algorithms.
Mixed learning, which combines both online and offline learning mechanisms, is a promising approach for enhancing algorithm adaptability and robustness. Offline learning pre-tunes an algorithm to better suit a specific problem instance, whereas online learning allows it to adjust based on real-time feedback. Soria-Alcaraz et al. [145] incorporated mixed learning operator probabilities are offline-tuned before applying online updates using credit assignment mechanism. Yates et al. [15] found the offline approach outperforming online approach and recommended hybridization of both. Future research should integrate mixed learning to enhance algorithm robustness across various problem domains.
Incorporating Tabu mechanism of low-level heuristics prevents repeated use of low-performing heuristics within short intervals. Low-level heuristics added to the Tabu list are often ones that performed poorly. The exclusion of these heuristics can avoid time wastage from applying non-improving moves. The tuning of key attributes such as Tabu size list and aspiration criteria [86] is important to prevent cycling while maintaining diverse search options. Future work should focus on designing flexible Tabu lists that adapt based on performance, for better balance of exploration and exploitation.
Restart mechanism is similar to mutation [146]. Stochastic restarts, where the search process periodically reset, encourages exploration. Among CHeSC algorithms, only NAHH employed this, placing seventh in the competition. Further exploration on this approach is needed to confirm its effectiveness. Nevertheless, any form of restart mechanism is useful, especially for problem instances with multiple local optima. Besides, it can be combined into other algorithmic components, such as move acceptance. Restart mechanism also may need the right conditions to be effective [147]. Suitable restart conditions and methods must be employed in future research. In a time-limited setup, time condition would be a better choice compared to iteration condition. Reinitializing the current solution and perturbating the best solution are suggested for future algorithms.
The task of setting algorithm parameters can be classified into parameter tuning and control [90]. When choosing a method, the resource constraints and the trade-off between domain knowledge and the parameter setting approach are considered [148]. Parameter tuning should be used for repetitive problems, whereas parameter control should be used for one-off problems, problems with dynamic fitness function and online adaptation [149]. Dynamic parameter control has shown to be effective, yet only one CHeSC algorithm, HAHA, implements it. Further in-depth studies are needed to validate its impact. Adaptive approaches are generally more effective, as they adjust parameter values based on the current search state. This adaptability is especially valuable for hyper-heuristics, where diverse problem types demand varying parameter intensities for optimal results. Future research should aim to establish adaptive frameworks for dynamic parameter control, enhancing real-time responsiveness to changing problem landscapes.
The HyFlex framework provides valuable insights for future algorithm development as it contains a diverse set of benchmark problems. Our analysis underscores the importance of tailoring algorithmic strategies to specific problem characteristics, including heuristic application sensitivity, speed of the search process, solution space modality, and search landscape complexity. For problems sensitive to objective function changes, such as BP instances, strategies emphasizing exploration are recommended to enhance diversity and performance. Strategies including multi-point search, stochastic move acceptance, Tabu solutions, and restart mechanisms promote exploration.
Speed of the search process, particularly the execution of low-level heuristics, is another critical factor. In slow-execution instances, simpler strategies like single-point search, non-iterated search phases, and basic move acceptance are more effective, as they allow for more frequent heuristic applications. Evidently, PS and VRP instances which have slow execution of low-level heuristics excelled by algorithms with simple strategies. Conversely, faster search process can accommodate more complex strategies, such as online learning, adaptive parameters, or Tabu mechanisms, which enhance algorithm intelligence and adaptability. As evidence, these strategies are more effective in PFS and SAT instances, which have faster processes. Implementation of these strategies in slow-execution instances will lead to wasted computational time.
Search space complexity, especially modality, also influences strategy selection. Multi-modal problems, or problems with multiple optima, require diversification strategies to escape local optima. Strategies like multi-point search, iterated search, threshold or stochastic move acceptance, Tabu and restart mechanisms help diversifying the search by finding solutions that are far from the current one. For example, iterated searches have proven beneficial for PS instances, while restart mechanisms excel in SAT instances. In contrast, learning approaches are less critical in these contexts, as they focus on exploitation. Additionally, hyper-heuristics should prioritize adaptability across diverse scenarios. Incorporating adaptive heuristic selection, online learning, and dynamic parameter control ensures robust performance, addressing the varying demands of different problem domains effectively.
The selection hyper-heuristics from the inaugural CHeSC competition were reviewed in this study. This includes summarizing previously undiscussed algorithms and reviewing critical components of the algorithms, which are the search point, search phases, heuristic selection, move acceptance, feedback, Tabu mechanism, restart mechanism, and low-level heuristic parameter control. The review analysis suggests that heuristic selection using relay hybridization produced the best result, and roulette wheel selection is marginally better than random selection. A mixed-point search can outperform algorithms employing only one type of search point. Searches that are conducted in phases, i.e., perturbation followed by local search, significantly increase algorithm performance. A move acceptance strategy is crucial in enhancing search performance, with a preference for non-stochastic over stochastic methods. A combination of online and offline learning should be incorporated to ensure a highly effective algorithm, whereas ignoring feedback must be avoided. The Tabu mechanism proved to play a critical role in preventing cycling that may degrade search performance. However, maintaining a Tabu list of solutions may not present a remarkable benefit compared to keeping a Tabu list of heuristics only. Including search restarts in algorithm design is crucial for escaping local optima, with a preference for restarts triggered by execution time rather than algorithmic iteration. The best action upon restarting the search is to reinitialize the solution or modify the best solution. Regarding the low-level heuristic parameters, it is recommended not to keep them static throughout the search process. Instead, they should be dynamically or adaptively controlled, with a preference for the former. This implies that algorithms designed without consideration for the control of these parameters will suffer in terms of performance when evaluated within the HyFlex framework. A comparison of the trends among recent hyper-heuristics supported our findings in most cases. Future algorithms should incorporate these beneficial features to ensure high performance and employ them to effectively solve problems in various domains such as remote sensing, biology, and environment networks.
However, the findings could not be confirmed as the algorithms have many dissimilarities in components outside of the comparison scope. Therefore, the analytical results should be verified in future works using a fair comparison technique by having the other components constant. Furthermore, the analysis may yield different results if a different ranking in the leaderboard is considered. The leaderboard is calculated using median values from multiple runs, and each run produces variable results. Therefore, the rankings are highly likely to change if new runs are conducted, especially on contemporary hardware. A positive aspect of research in this field is that the source codes for the CHeSC algorithms are readily available. Future research can utilize these codes to expand the investigation.
Limitations of this study include the lack of complexity analyses or experimental comparisons beyond comparisons using the quality index. This limitation arises from the lack of access to individual algorithmic run records. This study relies on results reported in previous publications. Future research should utilize source codes for the selection of hyper-heuristics to rerun experiments, ensuring results with higher integrity. The analysis could be expanded to include more recent algorithms, provided that the challenges related to the availability of design documentation and source codes are resolved. Further studies could also include more in-depth comparisons of the algorithms’ complexity and utilize more robust performance metrics. Inspecting the compliance of algorithms with competition rules provides an interesting avenue for verifying the integrity of competition results.
Additionally, given the rapid advancements in computer technology, it is recommended to test the algorithms in an environment that leverages this increased computational power, such as extending the execution time limit. This approach could offer fresh perspectives on the challenge of premature convergence. An in-depth analysis of algorithm behaviour throughout the search process, using recorded algorithmic runs, should also be conducted. Convergence analyses could also be employed to observe convergence trends and evaluate algorithms’ ability to achieve optimal or near-optimal solutions. It is also recommended to examine the scalability of the algorithms to larger problem instances to ensure their high generality. Furthermore, the optimization field has grown rapidly in recent years to include multi-objective, multi-task, and multi-factorial optimization. The implementation of selection hyper-heuristic can be explored in these areas, leveraging the insights derived from our analysis as a good starting point.
Acknowledgment: The authors would like to thank the Ministry of Higher Education (MoHE) Malaysia, for the funding and support for this project.
Funding Statement: This research was funded by Ministry of Higher Education (MoHE) Malaysia, under Transdisciplinary Research Grant Scheme (TRGS/1/2019/UKM/01/4/2).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Mohamad Khairulamirin Md Razali, Masri Ayob, Abdul Hadi Abd Rahman, Razman Jarmin, Chian Yong Liu, Muhammad Maaya, Azarinah Izaham; data collection: Mohamad Khairulamirin Md Razali; analysis and interpretation of results: Mohamad Khairulamirin Md Razali; draft manuscript preparation: Mohamad Khairulamirin Md Razali, Masri Ayob, Abdul Hadi Abd Rahman, Graham Kendall. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data and materials that support the findings of this study are openly available in GitHub at https://github.com/seage/hyflex/tree/master/hyflex-hyperheuristics (accessed on 25 December 2024).
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Glossary/Nomenclature/Abbreviations
| ACO | Ant Colony Optimization |
| AILLA | Adaptive Iteration Limited List-based Threshold Accepting |
| ALHH( | Apprenticeship Learning Hyper-Heuristic |
| AVEG-Nep | Hyper-heuristic based on autonomous agents and Epsilon-greedy selection |
| BP | Bin packing |
| CF | Choice Function |
| CHeSC | Cross-domain Heuristic Search Challenge |
| DHSS | Dynamic heuristic set selection |
| DOS | Depth of search |
| EA-ILS | Evolutionary algorithm-based iterated local search |
| EMCQ | Exponential Monte Carlo with counter |
| F1 | Formula 1 |
| FIS | Fuzzy Inference Selection |
| FRAMAB | Fitness-Rate-Average based Multi-armed Bandit |
| FS-ILS | Fair-Share Iterated Local Search |
| GEP | Gene Expression Programming |
| GISS | Generic Iterative Simulated-Annealing Search |
| HAEA | Hybrid Adaptive Evolutionary Algorithm |
| HHDMAB | Hyper-heuristic using Dynamic Multi-armed Bandit |
| HH2DMAB | Hyper-heuristic using Dynamic Multi-armed Bandit 2 |
| ILSHH | Iterated Local Search Hyper-heuristic |
| IM | Intensity of mutation |
| ISEA | Iterated Search Driven by Evolutionary Algorithm |
| KP | Knapsack Problem |
| KSATS-HH | Simulated Annealing and Tabu-Search Hyper-Heuristic |
| LAH | List of Active Heuristics |
| LAST-RL | Large state reinforcement learning hyper-heuristic |
| MA | Memetic algorithm |
| MAB | Multi-armed bandit |
| MaxCut | Max-Cut Problem |
| MCHH-S | Single objective Markov chain Hyper-heuristic |
| MSHH | Multi-stage Hyper-heuristic |
| PFS | Permutation flowshop |
| POP-MA | Population-based memetic algorithm |
| PS | Personnel scheduling |
| QAP | Quadratic Assignment Problem |
| QHH | Q-learning based hyper-heuristic |
| RQ | Research question |
| SA | Simulated Annealing |
| SAHH | Simulated Annealing Hyper-heuristic |
| SAT | Boolean satisfiability |
| SP-MA | Single-point based memetic algorithm |
| SR-LA | Simple Random Late Acceptance |
| SSMA | Steady-state memetic algorithm |
| TGMA | Transgenerational memetic algorithm |
| TS-ILS | Thompson Sampling based Iterated Local Search Algorithm |
| TSP | Travelling salesman problem |
| VND | Variable Neighbourhood Descent |
| VNS-TW | Variable Neighbourhood Search hyper-heuristic |
| VRP | Vehicle routing problem |
| XCJ | EXplore-Climb-Jump |
References
1. Pillay N, Qu R. Hyper-heuristics: theory and applications. 1st ed. (Natural Computing Series). Cham, Switzerland: Springer; 2018. [Google Scholar]
2. Sanchez M, Cruz-Duarte JM, Ortiz-Bayliss JC, Ceballos H, Terashima-Marin H, Amaya I. A systematic review of hyper-heuristics on combinatorial optimization problems. IEEE Access. 2020;8:128068–95. doi:10.1109/ACCESS.2020.3009318. [Google Scholar] [CrossRef]
3. Drake JH, Kheiri A, Özcan E, Burke EK. Recent advances in selection hyper-heuristics. Eur J Oper Res. 2020 Sep 1;285(2):405–28. doi:10.1016/j.ejor.2019.07.073. [Google Scholar] [CrossRef]
4. Burke EK, Hyde M, Kendall G, Ochoa G, Özcan E, Woodward JR. A classification of hyper-heuristic approaches. In: Gendreau M, Potvin J-Y, editors. Handbook of metaheuristics. Boston, MA, USA: Springer; 2010. p. 449–68. [Google Scholar]
5. Qu R, Burke EK. Hybridizations within a graph-based hyper-heuristic framework for university timetabling problems. J Oper Res Soc. 2009;60(9):1273–85. doi:10.1057/jors.2008.102. [Google Scholar] [CrossRef]
6. Ross P. Hyper-heuristics. In: Search methodologies: introductory tutorials in optimization and decision support techniques. Boston, MA, USA: Springer; 2005. p. 529–56. [Google Scholar]
7. Ochoa G, Hyde M, Curtois T, Vazquez-Rodriguez JA, Walker J, Gendreau M, et al. HyFlex: a benchmark framework for cross-domain heuristic search. In: Evolutionary computation in combinatorial optimization. Berlin, Heidelberg: Springer; 2012. p. 136–47. [Google Scholar]
8. Burke EK, Gendreau M, Hyde M, Kendall G, McCollum B, Ochoa G, et al. The cross-domain heuristic search challenge—an international research competition. In: Learning and intelligent optimization. Berlin, Heidelberg: Springer; 2011. p. 631–4. [Google Scholar]
9. Burke EK, Gendreau M, Hyde M, Kendall G, Ochoa G, Özcan E, et al. Hyper-heuristics: a survey of the state of the art. J Oper Res Soc. 2013;64(12):1695–724. doi:10.1057/jors.2013.71. [Google Scholar] [CrossRef]
10. Jackson WG, Özcan E, John RI. Move acceptance in local search metaheuristics for cross-domain search. Expert Syst Appl. 2018;109(13):131–51. doi:10.1016/j.eswa.2018.05.006. [Google Scholar] [CrossRef]
11. Özcan E, Bilgin B, Korkmaz EE. A comprehensive analysis of hyper-heuristics. Intell Data Anal. 2008;12(1):3–23. doi:10.3233/IDA-2008-12102. [Google Scholar] [CrossRef]
12. Zamli KZ, Din F, Kendall G, Ahmed BS. An experimental study of hyper-heuristic selection and acceptance mechanism for combinatorial t-way test suite generation. Inf Sci. 2017 Aug 1;399(12):121–53. doi:10.1016/j.ins.2017.03.007. [Google Scholar] [CrossRef]
13. Kiraz B, Etaner-Uyar AS, Özcan E. Selection hyper-heuristics in dynamic environments. J Oper Res Soc. 2013 Dec 1;64(12):1753–69. doi:10.1057/jors.2013.24. [Google Scholar] [CrossRef]
14. Castro OR, Fritsche GM, Pozo A. Evaluating selection methods on hyper-heuristic multi-objective particle swarm optimization. J Heuristics. 2018 Aug 1;24(4):581–616. doi:10.1007/s10732-018-9369-x. [Google Scholar] [CrossRef]
15. Yates WB, Keedwell EC. Analysing heuristic subsequences for offline hyper-heuristic learning. Paper presented at: Genetic and Evolutionary Computation Conference Companion; 2019; Prague, Czech Republic. doi:10.1145/3319619.3326760. [Google Scholar] [CrossRef]
16. Misir M, Verbeeck K, Causmaecker PD, Berghe GV. Hyper-heuristics with a dynamic heuristic set for the home care scheduling problem. In: IEEE Congress on Evolutionary Computation; 2010 Jul 18–23; New York, NY, USA. p. 1–8. doi:10.1109/CEC.2010.5586348. [Google Scholar] [CrossRef]
17. Adriaensen S, Nowé A. Case study: an analysis of accidental complexity in a state-of-the-art hyper-heuristic for HyFlex. In: 2016 IEEE Congress on Evolutionary Computation (CEC); 2016 Jul 24–29; New York, NY, USA. p. 1485–92. doi:10.1109/CEC.2016.7743965. [Google Scholar] [CrossRef]
18. Lissovoi A, Oliveto P, Warwicker JA. How the duration of the learning period affects the performance of random gradient selection hyper-heuristics. Proc AAAI Conf Artif Intell. 2020 Mar 4;34(3):2376–83. doi:10.1609/aaai.v34i03.5617. [Google Scholar] [CrossRef]
19. Cuccu G, Gomez F, Glasmachers T. Novelty-based restarts for evolution strategies. In: 2011 IEEE Congress of Evolutionary Computation (CEC); 2011 Jun 5–8; New York, NY, USA. p. 158–63. doi:10.1109/CEC.2011.5949613. [Google Scholar] [CrossRef]
20. Mathesen L, Pedrielli G, Ng SH, Zabinsky ZB. Stochastic optimization with adaptive restart: a framework for integrated local and global learning. J Glob Optim. 2021 Jan 1;79(1):87–110. doi:10.1007/s10898-020-00937-5. [Google Scholar] [CrossRef]
21. Baghel M, Agrawal S, Silakari S. Survey of metaheuristic algorithms for combinatorial optimization. Int J Comput Appl. 2012;58(19):10–31. doi:10.5120/9391-3813. [Google Scholar] [CrossRef]
22. Gümüş DB, Özcan E, Atkin J, Drake JH. An investigation of F-Race training strategies for cross domain optimisation with memetic algorithms. Inf Sci. 2023 Jan 1;619(3):153–71. doi:10.1016/j.ins.2022.11.008. [Google Scholar] [CrossRef]
23. Kletzander L, Musliu N. Large-state reinforcement learning for hyper-heuristics. Proc AAAI Conf Artif Intell. 2023 26 Jun;37(10):12444–52. doi:10.1609/aaai.v37i10.26466. [Google Scholar] [CrossRef]
24. Mischek F, Musliu N. Reinforcement learning for cross-domain hyper-heuristics. In: The 31st International Joint Conferences on Artificial Intelligence Organization; 2022 Jul 23–29; Vienna, Austria; p. 4793–9. doi:10.24963/ijcai.2022/664. [Google Scholar] [CrossRef]
25. Adubi SA, Oladipupo OO, Olugbara OO. Evolutionary algorithm-based iterated local search hyper-heuristic for combinatorial optimization problems. Algorithms. 2022;15(11):405. doi:10.3390/a15110405. [Google Scholar] [CrossRef]
26. Drake JH, Özcan E, Burke EK. A case study of controlling crossover in a selection hyper-heuristic framework using the multidimensional knapsack problem. Evol Comput. 2016;24(1):113–41. doi:10.1162/EVCO_a_00145. [Google Scholar] [PubMed] [CrossRef]
27. Ozcan E, Bykov Y, Birben M, Burke EK. Examination timetabling using late acceptance hyper-heuristics. In: IEEE Congress on Evolutionary Computation; 2009 May 18–21; New York, NY, USA. p. 997–1004. doi:10.1109/CEC.2009.4983054. [Google Scholar] [CrossRef]
28. Sabar NR, Ayob M, Kendall G, Qu R. A dynamic multiarmed bandit-gene expression programming hyper-heuristic for combinatorial optimization problems. IEEE Trans Cybern. 2015;45(2):217–28. doi:10.1109/TCYB.2014.2323936. [Google Scholar] [PubMed] [CrossRef]
29. Pillay N. A review of hyper-heuristics for educational timetabling. Ann Oper Res. 2016;239(1):3–38. doi:10.1007/s10479-014-1688-1. [Google Scholar] [CrossRef]
30. Branke J, Nguyen S, Pickardt CW, Zhang M. Automated design of production scheduling heuristics: a review. IEEE Trans Evol Comput. 2016;20(1):110–24. doi:10.1109/TEVC.2015.2429314. [Google Scholar] [CrossRef]
31. Pillay N, Qu R. Assessing hyper-heuristic performance. J Oper Res Soc. 2021 Nov 2;72(11):2503–16. doi:10.1080/01605682.2020.1796538. [Google Scholar] [CrossRef]
32. Onsem WV, Demoen B. Analyse en vergelijking van zestien implementaties uit de CHeSC 2011 competitie. In: CW reports; 2013. [Google Scholar]
33. Mısır M, Verbeeck K, De Causmaecker P, Berghe GV. An investigation on the generality level of selection hyper-heuristics under different empirical conditions. Appl Soft Comput. 2013 Jul 1;13(7):3335–53. doi:10.1016/j.asoc.2013.02.006. [Google Scholar] [CrossRef]
34. Alanazi F, Lehre PK. Runtime analysis of selection hyper-heuristics with classical learning mechanisms. In: 2014 IEEE Congress on Evolutionary Computation (CEC); 2014 Jul 6–11; New York, NY, USA. p. 2515–23. doi:10.1109/CEC.2014.6900602. [Google Scholar] [CrossRef]
35. Sarhani M, Voß S, Jovanovic R. Initialization of metaheuristics: comprehensive review, critical analysis, and research directions. Int Trans Oper Res. 2023;30(6):3361–97. doi:10.1111/itor.13237. [Google Scholar] [CrossRef]
36. Adriaensen S, Ochoa G, Nowé A. A benchmark set extension and comparative study for the HyFlex framework. In: 2015 IEEE Congress on Evolutionary Computation (CEC); 2015 May 25–28; New York, NY, USA. p. 784–91. doi:10.1109/CEC.2015.7256971. [Google Scholar] [CrossRef]
37. Drake JH, Özcan E, Burke EK. A comparison of crossover control mechanisms within single-point selection hyper-heuristics using HyFlex. In: 2015 IEEE Congress on Evolutionary Computation (CEC); 2015 May 25–28; New York, NY, USA. p. 3397–403. doi:10.1109/CEC.2015.7257316. [Google Scholar] [CrossRef]
38. Soria-Alcaraz JA, Ochoa G, Espinal A, Sotelo-Figueroa MA, Ornelas-Rodriguez M, Rostro-Gonzalez H, et al. A methodology for classifying search operators as intensification or diversification heuristics. Complex. 2020;2020:10. doi:10.1155/2020/2871835. [Google Scholar] [CrossRef]
39. Hassan A, Pillay N. Dynamic heuristic set selection for cross-domain selection hyper-heuristics. In: Theory and practice of natural computing. Cham: Springer International Publishing; 2021. p. 33–44. [Google Scholar]
40. Adriaensen S, Brys T, Nowé A. Fair-share ILS: a simple state-of-the-art iterated local search hyperheuristic. Paper presented at: Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation; 2014; Vancouver, BC, Canada. doi:10.1145/2576768.2598285. [Google Scholar] [CrossRef]
41. Zhao F, Di S, Cao J, Tang J, Jonrinaldi. A novel cooperative multi-stage hyper-heuristic for combination optimization problems. Complex Syst Model Simul. 2021;1(2):91–108. doi:10.23919/CSMS.2021.0010. [Google Scholar] [CrossRef]
42. Ferreira AS, Gonçalves RA, Pozo A. A multi-armed bandit selection strategy for hyper-heuristics. In: 2017 IEEE Congress on Evolutionary Computation (CEC); 2017 Jun 5–8; New York, NY, USA. p. 525–32. doi:10.1109/CEC.2017.7969356. [Google Scholar] [CrossRef]
43. Özcan E, Asta S, Altıntaş C. Memetic algorithms for cross-domain heuristic search. In: 2013 13th UK Workshop on Computational Intelligence (UKCI); 2013 Sep 9–11; Guildford, UK. p. 175–82. doi:10.1109/UKCI.2013.6651303. [Google Scholar] [CrossRef]
44. Gümüş DB, Ozcan E, Atkin J. An investigation of tuning a memetic algorithm for cross-domain search. In: 2016 IEEE Congress on Evolutionary Computation (CEC); 2016 Jul 24–29; New York, NY, USA. p. 135–42. doi:10.1109/CEC.2016.7743788. [Google Scholar] [CrossRef]
45. Mısır M, Verbeeck K, Causmaecker PDe, Berghe GV. An intelligent hyper-heuristic framework for CHeSC 2011. In: Learning and intelligent optimization. Berlin, Heidelberg: Springer; 2012. p. 461–6. [Google Scholar]
46. Bilgin B, Demeester P, Misir M, Vancroonenburg W, Berghe GV. One hyper-heuristic approach to two timetabling problems in health care. J Heuristics. 2012 Jun 1;18(3):401–34. doi:10.1007/s10732-011-9192-0. [Google Scholar] [CrossRef]
47. Almutairi A, Özcan E, Kheiri A, Jackson WG. Performance of selection hyper-heuristics on the extended HyFlex domains. In: Computer and information sciences. Cham: Springer International Publishing; 2016. p. 154–62. [Google Scholar]
48. Di Gaspero L, Urli T. Evaluation of a family of reinforcement learning cross-domain optimization heuristics. In: Learning and intelligent optimization. Berlin, Heidelberg: Springer; 2012. p. 384–9. [Google Scholar]
49. Royston P. Approximating the Shapiro-Wilk W-test for non-normality. Stat Comput. 1992;2(3):117–9. doi:10.1007/BF01891203. [Google Scholar] [CrossRef]
50. Park E, Cho M, Ki CS. Correct use of repeated measures analysis of variance. Korean J Lab Med. 2009 Feb;29(1):1–9. doi:10.3343/kjlm.2009.29.1.1. [Google Scholar] [PubMed] [CrossRef]
51. Nanda A, Mohapatra BB, Mahapatra APK, Mahapatra APK, Mahapatra APK. Multiple comparison test by Tukey’s honestly significant difference (HSDdo the confident level control type I error. Int J Stat Appl Math. 2021;6(1):59–65. doi:10.22271/MATHS.2021.V6.I1A.636. [Google Scholar] [CrossRef]
52. Zimmerman DW, Zumbo BD. Relative power of the wilcoxon test, the friedman test, and repeated-measures ANOVA on ranks. J Exp Educ. 1993 Jul 1;62(1):75–86. doi:10.1080/00220973.1993.9943832. [Google Scholar] [CrossRef]
53. Woolson RF. Wilcoxon signed-rank test. In: Wiley encyclopedia of clinical trials. Hoboken, NJ, USA: Wiley; 2007. p. 1–3. [Google Scholar]
54. Wilcoxon F, Katti S, Wilcox RA. Critical values and probability levels for the Wilcoxon rank sum test and the Wilcoxon signed rank test. Select Tables Math Stat. 1970;1:171–259. [Google Scholar]
55. Alyahya TN, Menai MEB, Mathkour H. On the structure of the boolean satisfiability problem: a survey. ACM Comput Surv. 2022;55(3):1–34. doi:10.1145/3491210. [Google Scholar] [CrossRef]
56. Munien C, Mahabeer S, Dzitiro E, Singh S, Zungu S, Ezugwu AES. Metaheuristic approaches for one-dimensional bin packing problem: a comparative performance study. IEEE Access. 2020;8:227438–65. doi:10.1109/ACCESS.2020.3046185. [Google Scholar] [CrossRef]
57. Özder EH, Özcan E, Eren T. A systematic literature review for personnel scheduling problems. Int J Inform Technol Decis Mak. 2020;19(6):1695–735. doi:10.1142/s0219622020300050. [Google Scholar] [CrossRef]
58. Pang X, Xue H, Tseng M-L, Lim MK, Liu K. Hybrid flow shop scheduling problems using improved fireworks algorithm for permutation. Appl Sci. 2020;10(3):1174. [Google Scholar]
59. Arram A, Ayob M. A novel multi-parent order crossover in genetic algorithm for combinatorial optimization problems. Comput Indus Eng. 2019 Jun 1;133(3):267–74. doi:10.1016/j.cie.2019.05.012. [Google Scholar] [CrossRef]
60. Jaradat G, Ayob M, Almarashdeh I. The effect of elite pool in hybrid population-based meta-heuristics for solving combinatorial optimization problems. Appl Soft Comput. 2016 Jun 1;44(2):45–56. doi:10.1016/j.asoc.2016.01.002. [Google Scholar] [CrossRef]
61. Saeed R, Eisa A, Alsaqour R. 0-1 knapsack problem approach for multicast agent in NEMO system. Int J Eng Technol. 2014;6(1):411–7. [Google Scholar]
62. Loiola EM, de Abreu NMM, Boaventura-Netto PO, Hahn P, Querido T. A survey for the quadratic assignment problem. Eur J Oper Res. 2007 Jun 16;176(2):657–90. doi:10.1016/j.ejor.2005.09.032. [Google Scholar] [CrossRef]
63. Festa P, Pardalos PM, Resende MGC, Ribeiro CC. Randomized heuristics for the Max-Cut problem. Optim Methods Softw. 2002 Jan 1;17(6):1033–58. doi:10.1080/1055678021000090033. [Google Scholar] [CrossRef]
64. Ping-Che H, Tsung-Che C, Fu LC. A VNS-based hyper-heuristic with adaptive computational budget of local search. In: 2012 IEEE Congress on Evolutionary Computation; 2012 Jun 10–15; New York, NY, USA. p. 1–8. doi:10.1109/CEC.2012.6252969. [Google Scholar] [CrossRef]
65. Chan CY, Xue F, Ip WH, Cheung CF. A hyper-heuristic inspired by pearl hunting. In: Learning and intelligent optimization. Berlin, Heidelberg: Springer; 2012. p. 349–53. [Google Scholar]
66. Meignan D. An evolutionary programming hyper-heuristic with co-evolution for CHeSC11. In: The 53rd Annual Conference of the UK Operational Research Society (OR53); 2011; Milton Park, Oxfordshire, UK. Vol. 3. [Google Scholar]
67. Lehrbaum A, Musliu N. A new hyperheuristic algorithm for cross-domain search problems. In: Learning and intelligent optimization. Berlin, Heidelberg: Springer; 2012. p. 437–42. [Google Scholar]
68. Mascia F, Stützle T. A non-adaptive stochastic local search algorithm for the CHeSC 2011 competition. In: Learning and intelligent optimization. Berlin Heidelberg: Springer; 2012. p. 101–14. [Google Scholar]
69. Kubalík J. Hyper-heuristic based on iterated local search driven by evolutionary algorithm. In: Evolutionary computation in combinatorial optimization. Berlin, Heidelberg: Springer; 2012. p. 148–59. [Google Scholar]
70. Cichowicz T, Drozdowski M, Frankiewicz M, Pawlak G, Rytwinski F, Wasilewski J. Hyper-heuristics for cross-domain search. Bullet Pol Acad Sci Tech Sci. 2012;60(4):801–8. [Google Scholar]
71. Ferreira AS, Pozo A, Gonçalves RA. An ant colony based hyper-heuristic approach for the set covering problem. ADCAIJ Adv Distrib Comput Artif Intell J. 2015;4(1):1–21. doi:10.14201/adcaij201541121. [Google Scholar] [CrossRef]
72. McClymont K, Keedwell EC. Markov chain hyper-heuristic (MCHHan online selective hyper-heuristic for multi-objective continuous problems. In: Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation; 2011; Dublin, Ireland. doi:10.1145/2001576.2001845. [Google Scholar] [CrossRef]
73. Kheiri A, Keedwell E. A Sequence-based Selection Hyper-heuristic utilising a Hidden Markov Model. Paper presented at: 2015 Annual Conference on Genetic and Evolutionary Computation; 2015; Madrid, Spain. doi:10.1145/2739480.2754766. [Google Scholar] [CrossRef]
74. Agushaka JO, Ezugwu AE. Initialisation approaches for population-based metaheuristic algorithms: a comprehensive review. Appl Sci. 2022;12(2):896. [Google Scholar]
75. Malan KM, Engelbrecht AP. Algorithm comparisons and the significance of population size. In: 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence); 2008 Jun 1–6; Hong Kong, China. p. 914–20. doi:10.1109/CEC.2008.4630905. [Google Scholar] [CrossRef]
76. Prügel-Bennett A. Benefits of a population: five mechanisms that advantage population-based algorithms. IEEE Trans Evol Comput. 2010;14(4):500–17. doi:10.1109/TEVC.2009.2039139. [Google Scholar] [CrossRef]
77. Jaddi NS, Abdullah S. Global search in single-solution-based metaheuristics. Data Technol Appl. 2020;54(3):275–96. doi:10.1108/DTA-07-2019-0115. [Google Scholar] [CrossRef]
78. Arram A, Ayob M, Sulaiman A. Hybrid bird mating optimizer with single-based algorithms for combinatorial optimization problems. IEEE Access. 2021;9:115972–89. doi:10.1109/ACCESS.2021.3102154. [Google Scholar] [CrossRef]
79. Bándi N, Gaskó N. Nested Markov chain hyper-heuristic (NMHHa hybrid hyper-heuristic framework for single-objective continuous problems. PeerJ Comput Sci. 2024 Feb 2;10(4):e1785. doi:10.7717/peerj-cs.1785. [Google Scholar] [PubMed] [CrossRef]
80. Jackson WG, Özcan E, John RI. Tuning a Simulated Annealing metaheuristic for cross-domain search. In: 2017 IEEE Congress on Evolutionary Computation (CEC); 2017 Jun 5–8. p. 1055–62. doi:10.1109/CEC.2017.7969424. [Google Scholar] [CrossRef]
81. Raj B, Ahmedy I, Idris MYI, Noor RM. A hybrid sperm swarm optimization and genetic algorithm for unimodal and multimodal optimization problems. IEEE Access. 2022;10(4):109580–96. doi:10.1109/ACCESS.2022.3208169. [Google Scholar] [CrossRef]
82. Kheiri A, Özcan E. An iterated multi-stage selection hyper-heuristic. Eur J Oper Res. 2016 Apr 1;250(1):77–90. doi:10.1016/j.ejor.2015.09.003. [Google Scholar] [CrossRef]
83. Lepagnot J, Idoumghar L, Brévilliers M, Idrissi-Aouad M. A new high-level relay hybrid metaheuristic for black-box optimization problems. In: Artificial evolution. Cham: Springer International Publishing; 2018. p. 115–28. [Google Scholar]
84. Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by simulated annealing. Science. 1983;220(4598):671–80. doi:10.1126/science.220.4598.671. [Google Scholar] [PubMed] [CrossRef]
85. Glover F. Tabu search—part I. ORSA J Comput. 1989;1(3):190–206. doi:10.1287/ijoc.1.3.190. [Google Scholar] [CrossRef]
86. Talbi EG. Metaheuristics: from design to implementation. Hoboken, NJ, USA: John Wiley & Sons, Inc.; 2009. [Google Scholar]
87. Abdel-Basset M, Abdel-Fatah L, Sangaiah AK. Metaheuristic algorithms: a comprehensive review. Cambridge, MA, USA: Academic Press; 2018. p. 185–231. [Google Scholar]
88. Rahman MA, Sokkalingam R, Othman M, Biswas K, Abdullah L, Kadir EA. Nature-inspired metaheuristic techniques for combinatorial optimization problems: overview and recent advances. Mathematics. 2021;9(20):1–32. doi:10.3390/math9202633. [Google Scholar] [CrossRef]
89. Sabar NR, Ayob M, Kendall G, Qu R. Grammatical evolution hyper-heuristic for combinatorial optimization problems. IEEE Trans Evol Comput. 2013;17(6):840–61. doi:10.1109/TEVC.2013.2281527. [Google Scholar] [CrossRef]
90. Eiben AE, Hinterding R, Michalewicz Z. Parameter control in evolutionary algorithms. IEEE Trans Evol Comput. 1999;3(2):124–41. doi:10.1109/4235.771166. [Google Scholar] [CrossRef]
91. Črepinšek M, Liu S-H, Mernik M. Exploration and exploitation in evolutionary algorithms: a survey. ACM Comput Surv. 2013;45(3):35. doi:10.1145/2480741.2480752. [Google Scholar] [CrossRef]
92. Zhang J, Chen W-N, Zhan Z-H, Yu W-J, Li Y-L, Chen N, et al. A survey on algorithm adaptation in evolutionary computation. Front Electr Electron Eng. 2012 Mar 1;7(1):16–31. doi:10.1007/s11460-012-0192-0. [Google Scholar] [CrossRef]
93. Drake JH, Özcan E, Burke EK. An improved choice function heuristic selection for cross domain heuristic search. In: Parallel problem solving from nature-PPSN XII. Berlin, Heidelberg: Springer; 2012. p. 307–16. [Google Scholar]
94. Jackson WG, Özcan E, Drake JH. Late acceptance-based selection hyper-heuristics for cross-domain heuristic search. In: 2013 13th UK Workshop on Computational Intelligence (UKCI); 2013 Sep 9–11; Guildford, UK. p. 228–35. doi:10.1109/UKCI.2013.6651310. [Google Scholar] [CrossRef]
95. Kheiri A, Özcan E. A hyper-heuristic with a round robin neighbourhood selection. In: Evolutionary computation in combinatorial optimization. Berlin, Heidelberg: Springer; 2013. p. 1–12. [Google Scholar]
96. Asta S, Özcan E. An apprenticeship learning hyper-heuristic for vehicle routing in HyFlex. In: 2014 IEEE Symposium on Evolving and Autonomous Learning Systems (EALS); 2014 Dec 9–12; New York, NY, USA. p. 65–72. doi:10.1109/EALS.2014.7009505. [Google Scholar] [CrossRef]
97. Sabar NR, Ayob M, Kendall G, Qu R. Automatic design of a hyper-heuristic framework with gene expression programming for combinatorial optimization problems. IEEE Trans Evol Comput. 2015;19(3):309–25. doi:10.1109/TEVC.2014.2319051. [Google Scholar] [CrossRef]
98. Sabar NR, Kendall G. Population based Monte Carlo tree search hyper-heuristic for combinatorial optimization problems. Inf Sci. 2015 Sep 1;314(1):225–39. doi:10.1016/j.ins.2014.10.045. [Google Scholar] [CrossRef]
99. Asta S, Özcan E. A tensor-based selection hyper-heuristic for cross-domain heuristic search. Inf Sci. 2015 Apr 1;299(12):412–32. doi:10.1016/j.ins.2014.12.020. [Google Scholar] [CrossRef]
100. Alanazi F. Adaptive thompson sampling for hyper-heuristics. In: 2016 IEEE Symposium Series on Computational Intelligence (SSCI); 2016 Dec 6–9; New York, NY, USA. p. 1–8. doi:10.1109/SSCI.2016.7850086. [Google Scholar] [CrossRef]
101. Dempster P, Drake JH. Two frameworks for cross-domain heuristic and parameter selection using harmony search. In: Harmony search algorithm. Berlin, Heidelberg: Springer; 2016. p. 83–94. [Google Scholar]
102. Soria-Alcaraz JA, Ochoa G, Sotelo-Figeroa MA, Burke EK. A methodology for determining an effective subset of heuristics in selection hyper-heuristics. Eur J Oper Res. 2017 Aug 1;260(3):972–83. doi:10.1016/j.ejor.2017.01.042. [Google Scholar] [CrossRef]
103. Choong SS, Wong L-P, Lim CP. Automatic design of hyper-heuristic based on reinforcement learning. Inf Sci. 2018 Apr 1;436–437(12):89–107. doi:10.1016/j.ins.2018.01.005. [Google Scholar] [CrossRef]
104. Adubi SA, Oladipupo OO, Olugbara OO. Configuring the perturbation operations of an iterated local search algorithm for cross-domain search: a probabilistic learning approach. In: 2021 IEEE Congress on Evolutionary Computation (CEC); 2021 Jun 1–Jul 28; New York, NY, USA. p. 1372–9. doi:10.1109/CEC45853.2021.9504841. [Google Scholar] [CrossRef]
105. Dantas A, Rego AFd, Pozo A. Using deep Q-network for selection hyper-heuristics. Paper presented at: Proceedings of the Genetic and Evolutionary Computation Conference Companion; Lille, France; 2021. doi:10.1145/3449726.3463187. [Google Scholar] [CrossRef]
106. Özcan E, Kheiri A. A hyper-heuristic based on random gradient, greedy and dominance. In: Computer and information sciences II. London: Springer; 2012. p. 557–63. [Google Scholar]
107. Choong SS, Wong L-P, Lim CP. An artificial bee colony algorithm with a Modified Choice Function for the traveling salesman problem. Swarm Evol Comput. 2019 Feb 1;44(4):622–35. doi:10.1016/j.swevo.2018.08.004. [Google Scholar] [CrossRef]
108. Zhang S, Yang T, Liang J, Yue C. A novel adaptive bandit-based selection hyper-heuristic for multiobjective optimization. IEEE Trans Syst Man Cybern Syst. 2023;53(12):7693–706. doi:10.1109/TSMC.2023.3299982. [Google Scholar] [CrossRef]
109. Hou Y, Dang L, Ma H, Zhang C. A selection hyper-heuristic for the multi-compartment vehicle routing problem considering carbon emission. Eng Letters. 2024 Oct 1;32:2002–11. [Google Scholar]
110. Lagos F, Pereira J. Multi-armed bandit-based hyper-heuristics for combinatorial optimization problems. Eur J Oper Res. 2024 Jan 1;312(1):70–91. doi:10.1016/j.ejor.2023.06.016. [Google Scholar] [CrossRef]
111. Zhao F, Liu Y, Zhu N, Xu T, Jonrinaldi. A selection hyper-heuristic algorithm with Q-learning mechanism. Appl Soft Comput. 2023 Nov 1;147:110815. doi:10.1016/j.asoc.2023.110815. [Google Scholar] [CrossRef]
112. Maashi M, Özcan E, Kendall G. A multi-objective hyper-heuristic based on choice function. Expert Syst Appl. 2014 Jul 1;41(9):4475–93. doi:10.1016/j.eswa.2013.12.050. [Google Scholar] [CrossRef]
113. Toledo A, Riff M, Neveu B. A hyper-heuristic for the orienteering problem with hotel selection. IEEE Access. 2020 Jan 1;8:1303–13. doi:10.1109/ACCESS.2019.2960492. [Google Scholar] [CrossRef]
114. Zhao Y, Leng L, Zhang C. A novel framework of hyper-heuristic approach and its application in location-routing problem with simultaneous pickup and delivery. Oper Res. 2021 Jun 1;21(2):1299–332. doi:10.1007/s12351-019-00480-6. [Google Scholar] [CrossRef]
115. Costa JGC, Mei Y, Zhang M. Cluster-based hyper-heuristic for large-scale vehicle routing problem. In: 2020 IEEE Congress on Evolutionary Computation (CEC); 2020 Jul 19–24; New York, NY, USA. p. 1–8. doi:10.1109/CEC48606.2020.9185831. [Google Scholar] [CrossRef]
116. Santiago Júnior VAd, Özcan E, Carvalho VRd. Hyper-heuristics based on reinforcement learning, balanced heuristic selection and group decision acceptance. Appl Soft Comput. 2020 Dec 1;97(12):106760. doi:10.1016/j.asoc.2020.106760. [Google Scholar] [CrossRef]
117. Cao P, Zhang Y, Zhou K, Tang J. A reinforcement learning hyper-heuristic in multi-objective optimization with application to structural damage identification. Struct Multidiscipl Optim. 2022 Dec 28;66(1):16. doi:10.1007/s00158-022-03432-5. [Google Scholar] [CrossRef]
118. Zhang Y, Bai R, Qu R, Tu C, Jin J. A deep reinforcement learning based hyper-heuristic for combinatorial optimisation with uncertainties. Eur J Oper Res. 2022 Jul 16;300(2):418–27. doi:10.1016/j.ejor.2021.10.032. [Google Scholar] [CrossRef]
119. Sánchez M, Cruz-Duarte JM, Ortiz-Bayliss JC, Amaya I. Sequence-based selection hyper-heuristic model via MAP-Elites. IEEE Access. 2021;9:116500–27. doi:10.1109/ACCESS.2021.3106815. [Google Scholar] [CrossRef]
120. Ibrahim RA, Abd Elaziz M, Ewees AA, El-Abd M, Lu S. New feature selection paradigm based on hyper-heuristic technique. Appl Math Model. 2021 Oct 1;98(13):14–37. doi:10.1016/j.apm.2021.04.018. [Google Scholar] [CrossRef]
121. Shao Z, Shao W, Pi D. LS-HH: a Learning-based selection hyper-heuristic for distributed heterogeneous hybrid blocking flow-shop scheduling. IEEE Trans Emerg Top Comput Intell. 2023;7(1):111–27. doi:10.1109/TETCI.2022.3174915. [Google Scholar] [CrossRef]
122. Zhang S, Ren Z, Li C, Xuan J. A perturbation adaptive pursuit strategy based hyper-heuristic for multi-objective optimization problems. Swarm Evol Comput. 2020 May 1;54(1):100647. doi:10.1016/j.swevo.2020.100647. [Google Scholar] [CrossRef]
123. Lissovoi A, Oliveto PS, Warwicker JA. Simple hyper-heuristics control the neighbourhood size of randomised local search optimally for leadingones. Evol Comput. 2020;28(3):437–61. doi:10.1162/evco_a_00258. [Google Scholar] [PubMed] [CrossRef]
124. Li W, Özcan E, Drake JH, Maashi M. A generality analysis of multiobjective hyper-heuristics. Inf Sci. 2023 May 1;627(1):34–51. doi:10.1016/j.ins.2023.01.047. [Google Scholar] [CrossRef]
125. Gölcük İ, Ozsoydan FB. Q-learning and hyper-heuristic based algorithm recommendation for changing environments. Eng Appl Artif Intell. 2021 Jun 1;102:104284. doi:10.1016/j.engappai.2021.104284. [Google Scholar] [CrossRef]
126. Burke EK, Gendreau M, Ochoa G, Walker JD. Adaptive iterated local search for cross-domain optimisation. Paper presented at: Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation; 2011; Dublin, Ireland. 2011. doi:10.1145/2001576.2001843. [Google Scholar] [CrossRef]
127. Doerr B, Dremaux A, Lutzeyer J, Stumpf A. How the move acceptance hyper-heuristic copes with local optima: drastic differences between jumps and cliffs. Paper presented at: Proceedings of the Genetic and Evolutionary Computation Conference; 2023; Lisbon, Portugal. doi:10.1145/3583131.3590509. [Google Scholar] [CrossRef]
128. Lissovoi A, Oliveto PS, Warwicker JA. When move acceptance selection hyper-heuristics outperform Metropolis and elitist evolutionary algorithms and when not. Artif Intell. 2023 Jan 1;314(6):103804. doi:10.1016/j.artint.2022.103804. [Google Scholar] [CrossRef]
129. Shambour MKY, Khan EA. A late acceptance hyper-heuristic approach for the optimization problem of distributing pilgrims over mina tents. J Univ Comput Sci. 2022;28(4):396–413. doi:10.3897/jucs.72900. [Google Scholar] [CrossRef]
130. Maashi M, Kendall G, Özcan E. Choice function based hyper-heuristics for multi-objective optimization. Appl Soft Comput. 2015 Mar 1;28(2):312–26. doi:10.1016/j.asoc.2014.12.012. [Google Scholar] [CrossRef]
131. Ahmed BS, Enoiu E, Afzal W, Zamli KZ. An evaluation of Monte Carlo-based hyper-heuristic for interaction testing of industrial embedded software applications. Soft Comput. 2020 Sep 1;24(18):13929–54. doi:10.1007/s00500-020-04769-z. [Google Scholar] [CrossRef]
132. Zhang C, Zhao Y, Leng L. A hyper-heuristic algorithm for time-dependent green location routing problem with time windows. IEEE Access. 2020;8:83092–104. doi:10.1109/ACCESS.2020.2991411. [Google Scholar] [CrossRef]
133. Pukhkaiev D, Semendiak Y, Götz S, Aßmann U. Combined selection and parameter control of meta-heuristics. In: 2020 IEEE Symposium Series on Computational Intelligence (SSCI); 2020 Dec 1–4; New York, NY, USA. p. 3125–32. doi:10.1109/SSCI47803.2020.9308135. [Google Scholar] [CrossRef]
134. Marshall RJ, Johnston M, Zhang M. A comparison between two evolutionary hyper-heuristics for combinatorial optimisation. In: Simulated evolution and learning. Cham: Springer International Publishing; 2014. p. 618–30. [Google Scholar]
135. Mısır M, Verbeeck K, Causmaecker PD, Berghe GV. A new hyper-heuristic as a general problem solver: an implementation in HyFlex. J Schedul. 2013 Jun 1;16(3):291–311. doi:10.1007/s10951-012-0295-8. [Google Scholar] [CrossRef]
136. de Carvalho VR, Özcan E, Sichman JS. Comparative analysis of selection hyper-heuristics for real-world multi-objective optimization problems. Appl Sci. 2021;11(19):9153. doi:10.3390/app11199153. [Google Scholar] [CrossRef]
137. Burke E, Curtois T, Hyde M, Kendall G, Ochoa G, Petrovic S, et al. Iterated local search vs. hyper-heuristics: towards general-purpose search algorithms. In: IEEE Congress on Evolutionary Computation; 2010 Jul 18–23; New York, NY, USA. p. 1–8. doi:10.1109/CEC.2010.5586064. [Google Scholar] [CrossRef]
138. Misir M. Cross-domain algorithm selection: algorithm selection across selection hyper-heuristics. In: 2022 IEEE Symposium Series on Computational Intelligence (SSCI); 2022 Dec 4–7; New York, NY, USA. p. 22–9. doi:10.1109/SSCI51031.2022.10022078. [Google Scholar] [CrossRef]
139. Burke EK, Hyde MR, Kendall G, Ochoa G, Ozcan E, Woodward JR. Exploring hyper-heuristic methodologies with genetic programming. In: Mumford CL, Jain LC, editors. Computational intelligence: collaboration, fusion and emergence. Berlin, Heidelberg: Springer; 2009. p. 177–201. [Google Scholar]
140. Tyasnurita R, Özcan E, Drake JH, Asta S. Constructing selection hyper-heuristics for open vehicle routing with time delay neural networks using multiple experts. Knowl Based Syst. 2024 Jul 8;295(10):111731. doi:10.1016/j.knosys.2024.111731. [Google Scholar] [CrossRef]
141. Aldeeb BA, Al-Betar MA, Norwawi NM, Alissa KA, Alsmadi MK, Hazaymeh AA, et al. Hybrid intelligent water Drops algorithm for examination timetabling problem. J King Saud Univ-Comput Inf Sci. 2022 Jan 1;34(8):4847–59. doi:10.1016/j.jksuci.2021.06.016. [Google Scholar] [CrossRef]
142. Raghavjee R, Pillay N. A genetic algorithm selection perturbative hyper-heuristic for solving the school timetabling problem. ORiON. 2015;31(1):39–60. doi:10.5784/31-1-158. [Google Scholar] [CrossRef]
143. Almaneea LI, Hosny MI. A two level hybrid bees algorithm for operating room scheduling problem. Intell Comput Proc 2018 Comput Conf. 2019;1(3):272–90. doi:10.1007/978-3-030-01174-1_21. [Google Scholar] [CrossRef]
144. Lourenço HR, Martin OC, Stützle T. Iterated local search. In: Glover F, Kochenberger GA, editors. Handbook of metaheuristics. Boston, MA, USA: Springer; 2003. p. 320–53. [Google Scholar]
145. Soria-Alcaraz JA, Ochoa G, Swan J, Carpio M, Puga H, Burke EK. Effective learning hyper-heuristics for the course timetabling problem. Eur J Oper Res. 2014 Oct 1;238(1):77–86. doi:10.1016/j.ejor.2014.03.046. [Google Scholar] [CrossRef]
146. Koumousis VK, Katsaras CP. A saw-tooth genetic algorithm combining the effects of variable population size and reinitialization to enhance performance. IEEE Trans Evol Comput. 2006;10(1):19–28. doi:10.1109/TEVC.2005.860765. [Google Scholar] [CrossRef]
147. Li X, Li M. Multiobjective local search algorithm-based decomposition for multiobjective permutation flow shop scheduling problem. IEEE Trans Eng Manag. 2015;62(4):544–57. doi:10.1109/TEM.2015.2453264. [Google Scholar] [CrossRef]
148. Phan HD, Ellis K, Barca JC, Dorin A. A survey of dynamic parameter setting methods for nature-inspired swarm intelligence algorithms. Neural Comput Appl. 2020 Jan 1;32(2):567–88. doi:10.1007/s00521-019-04229-2. [Google Scholar] [CrossRef]
149. Karafotias G, Hoogendoorn M, Eiben AE. Parameter control in evolutionary algorithms: trends and challenges. IEEE Trans Evol Comput. 2015;19(2):167–87. doi:10.1109/TEVC.2014.2308294. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF


 Downloads
Downloads
 Citation Tools
Citation Tools