Parameters Estimation of Modified Triple Diode Model of PSCs Considering Charge Accumulations and Electric Field Effects Using Puma Optimizer

1  Introduction

Global attention has been focused on renewable energy sources due to their potential to reduce climate change and address energy security issues stemming from the usage of finite fossil fuels [1]. Promoting the high-penetration of renewable energies like photovoltaic (PV) systems has become an urgent issue for the expansion of modern power grids and accomplished several challenges compared to exited distribution grids. Specifically, solar energy [2] is essential to the shift to sustainable and clean electricity generation. To make solar energy more practical and affordable, the use of solar-generated power in civil applications and connecting it to the grid is still a major issue [3].

Metaheuristic optimization methods could be applied to improve solar cell parameter estimation, which is one way to increase their efficiency [4]. A class of optimization methods known as metaheuristic algorithms is motivated by biological systems, human activity, physical phenomena, or natural events [5–9]. They have been successfully applied in several fields, including computer science, engineering, and biology. Such algorithms are well known for their ability to efficiently search through large solution spaces to find optimal or nearly optimal solutions.

There are various benefits to estimating solar cell parameters using metaheuristic optimization techniques [10]. Because of their versatility, these algorithms can be easily tailored to solve particular optimization issues. They can consider several objective functions at the same time and solve intricate, nonlinear equations. Second, solar cell parameter optimization can be completed in an acceptable period due to the computational efficiency of metaheuristic approaches. This covers both more recent technology, including perovskite solar cells (PSCs) [11], and more traditional silicon-based solar cells [12,13].

Conventional solar cells, which are typically constructed on silicon, have dominated the industry. However, they have a variety of inefficiencies, including relatively high manufacturing costs and limitations on efficiency caused by the materials’ characteristics [14]. The ideality factor, fill factor, open-circuit voltage, short-circuit current density, and other parameters of these solar cells have all been estimated using metaheuristic optimization techniques. These methods, which include Coyote Optimization Algorithm (COA) [15], Improved Equilibrium Optimizer (IEO) [16], Atomic Orbital Search Algorithm (AOSA) [17], Improved Differential Evolution (IDE) [18], A Forensic-Based Investigation Algorithm (FBIA) [19], Particle Swarm Optimization (PSO) [20], Closed Loop PSO [21] and Genetic methods (GA) [22], have demonstrated encouraging outcomes in raising the overall efficiency of traditional solar cells.

On the other hand, PSCs are now a competitive alternative to conventional silicon-based solar cells. PSCs offer several advantages, including higher power conversion efficiency, relatively straightforward construction, and potentially lower production costs [23]. However, many variables, including the operating environment, device architecture, and material composition, affect how well PSCs work [24]. PSCs must have their dynamic behavior precisely modeled and optimized to be used to their best capacity. To do this, the parameters of the dynamic models that explain how PSCs respond in real time to various operating situations must be estimated [25].

Metaheuristic optimization techniques have been used to estimate the PSC’s characteristics and different parameters at different operation conditions. It has been demonstrated that Evolutionary Particle Swarm Optimization (EPSO) [26], COOT optimizer [27], and genetic algorithms [28] are successful at optimizing PSC parameters, leading to significant improvements in the PSCs’ efficient operation. One of these metaheuristic algorithms is the Puma Optimizer (PO) [6], which is a recently proposed algorithm inspired by the hunting behavior of pumas [29]. PO has shown promising performance in solving various optimization problems. This algorithm has improved its performance against a wide range of optimization problems by proposing novel and potent methods at each stage of exploration and exploitation. Furthermore, a novel class of intelligent mechanisms is introduced, namely a kind of phase change hyper-heuristic. The PO method can balance both phases and conduct a phase change operation during the optimization process by using this mechanism. Every stage is automatically modified based on the type of issue. However, its application in the field of PSCs has not been explored extensively. This effort has been made to make sure that PO can solve the PSC dynamic models’ parameter estimate difficulties because, according to the no-free-lunch hypothesis, no optimization method can tackle every problem [30].

This research aims to examine the efficaciousness of the PO algorithm in parameter estimation of PSC dynamic models with hysteresis consideration taking into consideration the electric field effects on operation. The dynamic models used in this study will incorporate hysteresis effects to accurately capture the time-dependent behavior of PSCs.

The main contribution of this paper could be summed up as follows:

1.    A detailed theoretical model of the modified TDM (triple diode model) to consider the effect of electric field and charge accumulation in the perovskite solar cells is presented.

2.    Two forms are presented to consider the effect of charge accumulations,

3.    Developing the PO algorithm for finding the optimal parameter of the derived PV model.

4.    A comparison between the proposed PO and the reported optimization algorithms in the literature

This paper is structured in the following way: Section 2 presents the theoretical model of the PSCs. In Section 3, the development of PO for parameter estimation is presented. In Section 4, the simulation results are reported.

2  Theoretical Model

Because of their low manufacturing costs and high power conversion efficiency, perovskite solar cells, or PSCs, have become a promising technology for next-generation photovoltaics. The foundation of these cells is a perovskite structure, which usually consists of two charge-selective layers encasing a metal halide perovskite substance [31]. Hysteresis, or the system’s reliance on both past and present inputs to determine how to respond to a given input based on whether the scan state is forward or reverse, affects the PSC’s ability to operate [32]. Ion migration and perovskite material defects are the main causes of hysteresis in PSCs, which leads to a highly nonlinear and challenging to precisely predict time-dependent response.

Fig. 1 shows the generic TDM [33] formulation, which is the modification to account for the impact of charge accumulations and the electric field effect as given by the following set of equations [5,34]:

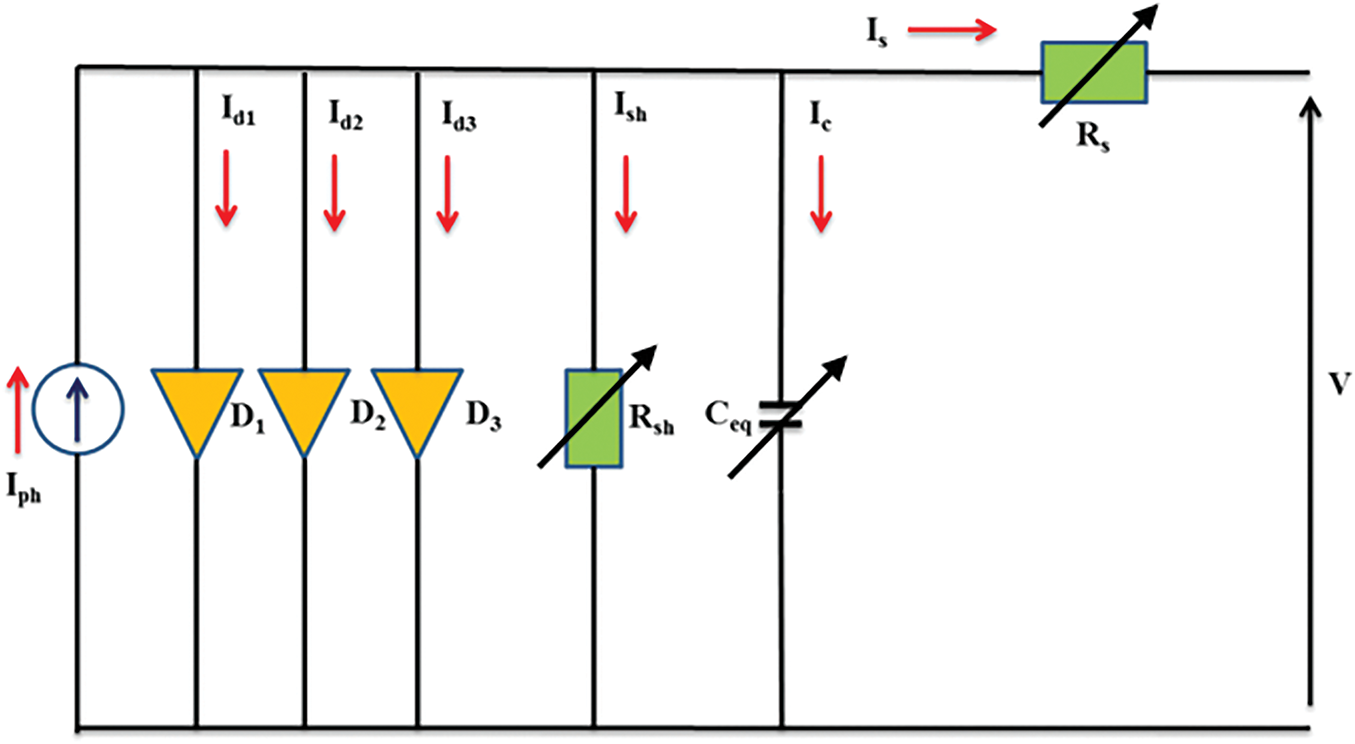
Figure 1: Proposed modified TDM considering the effect of electric field and charge accumulation for PSCs

Is=Iph−Id1−Id2−Id3−Ish−Ic(1a)

Id1=Is1[exp(q(V+Rso(1+Ks.V)Is)(a1.KB.T))−1](1b)

Id2=Is2[exp(q(V+Rso(1+Ks.V)Is)(a2.KB.T))−1](1c)

Id3=Is3[exp(q(V+Rso(1+Ks.V)Is)(a3.KB.T))−1](1d)

Ish=(V+Rso(1+Ks.V)IsRsho(1+KshV))(1e)

Ic=Ceq(d(V+Rso(1+Ks.V)Is)dt)(1f)

where T stands for temperature in Kelvin, Is1, Is2, and Is3 stand for the reverse saturation currents of the three diodes, a1, a2, and a3 stand for ideality factors of three diodes, V stands for the output voltage, and KB stands for Boltzmann’s constant.

The PSCs’ first electrical modeling attempts were inspired by studies on silicon solar cells, notably, Iph is the current generated by incident photons, the first diode (D1) takes into consideration recombination and diffusion in the majority zones and quasi-neutral regions of the emitter. The second diode (D2) is clarifying recombination in the area of space charge. Moreover, the third diode (D3) considers losses, zone recombination, and defects in grain boundaries. The partial current in the short circuit path close to the cell’s borders connected to the semi-conductor, several layers, and non-idealities make up the current leakage of PN junctions is modeled by the resistance (Rsh), in addition to resistance in series (Rs). It considers the effects of silicon, electrode resistance, electrode surface contact, and flowing current resistance. The final capacitors are greatly impacted by the various layer biases; it has been suggested that the varying voltage-dependent capacitances (Ceq) that arise [5] in addition to variable voltage resistors, to consider the implications of the electric field. It has been proposed that Ceq can be determined using either Eqs. (2a) or (2b). For the first representation in Eq. (2a), 3rd order equation has been employed to explain the applied potential and current density.

Another better representation of Ceq is given by Eq. (2b) which uses an exponential form. The terms of Eqs. (2a) and (2b) describe the impact of recombination and generation rates on the properties of hysteresis.

Ceq=a+b(V+RS.Is)+c(V+RS.Is)2+d(V+RS.Is)3(2a)

Ceq=aeb(V+RsIs)−ced(V+RsIs)(2b)

where the model of choice is used to select the positive parameters a, b, c, and d.

The series and shunt resistances are considered to linearly change with output voltage. The values of Rs and Rsh at zero voltage are equal to the fixed resistances Rso and Rsho, respectively. Eqs. (3a) and (3b) describe these relations [34].

Rs=Rso(1+Ks.V)(3a)

Rsh=Rsho(1+Ksh.V)(3b)

where Ks and Ksh are real constants.

A detailed explanation, supported by the previous mathematical derivations in Eqs. (1)–(3) and enhancement issues. For the conventional models like single and double diodes, several assumptions are provided [35,36], for the photogenerated current, ideal diode characteristics and parasitic series, and shunt resistances. However, they fall shortages when applied to PSCs because [36]:

•      Electric field effects in PSCs, arising from ionic migration and polarization, cannot be modeled adequately.

•      Charging accumulation at interfaces due to slow ionic movement is not captured.

•      Dynamic hysteresis observed in PSCs requires more comprehensive modeling of transient effects.

The proposed modified triple-diode model addresses these shortcomings by incorporating additional diodes and terms to represent the complex physics in PSCs as in Eqs. (1a)–(1f). The Charge Accumulation and Electric Field Effects are modeled by the added capacitor to represent interface charge storage as in Eq. (2) [5]. The ionic migration is modeled by including a time-dependent term as in [5]. The resistance time dependent is presented in Eq. (3).

Therefore, the modified model surpasses traditional models by explicitly addressing the unique physical mechanisms of PSCs. It improves accuracy in capturing:

•      Dynamic hysteresis: The inclusion of the time-dependent ionic current and capacitive effects allows the model to capture the hysteresis observed in perovskite solar cells under varying voltage sweep rates.

•      Charge storage: The third diode specifically models the recombination losses and photocurrent suppression caused by the internal electric field due to ion migration and polarization.

•      Electric field effects: Charge storage at the interfaces is directly incorporated, improving the accuracy of transient response predictions.

3     Parameter Estimation of PSCs Using Puma Optimization

3.1 The Parameters of PSCs

The main goal of this study is to investigate the effectiveness of the PO algorithm in parameter estimation of the dynamic PSCs’ models with hysteresis consideration taking into consideration the electric field effects on operation. The optimal values of the parameters of the modified electrical model given in Eq. (1a)–(1f) are extracted using the proposed PO algorithm.

The optimization problem aims to minimize the RMSE, Eq. (4a), that represents the maximum deviation between the current density of the proposed dynamic model and the measured values. Eq. (4a) is solved using the PO algorithm and is subject to the lower and upper bounds of the control variable presented in Eq. (4b). The proposed model of PSCs has fifteen parameters which are considered as the control variables of optimization problem x = [Iph, Is1,Is2, Is3, a1, a2, a3, Ksh, Rsho, Ks, Rso, a, b, c, and d]. The mathematical modeling of parameter estimation as an optimization problem can be expressed as follows:

Min RMSE(4a)

Subject to:LB<x<UB(4b)

where LB and UB refer to the lower and upper bounds of the fifteen control variables, respectively.

3.2 Puma Optimization (PO) Algorithm

The basic ideas of pumas in nature are used to construct a PO algorithm mathematical model, which is according to spontaneous behaviors for hunting and is described and presented. The PO algorithm presents a novel and intentional phase shift method for the first time, which allows the phases switched between exploration and exploitation [6]. That being said, two distinct strategies have been employed to conduct optimization operations throughout both the exploration and exploitation phases. The optimal solution in the PO algorithm is compared to a male puma and the optimization space as a whole to the territory of a puma. Other alternatives (Xi) have also been proposed as the puma in female form. Making use of the phase change process, all of the solutions in this algorithm enter either the exploitation or exploration stages in each iteration. The phases are intelligently and purposefully chosen. Different optimization strategies have been performed in each exploratory step, and two distinct processes have been used in each phase, both of which were motivated by the natural habitat of pumas.

3.2.1 Phase Transition Mechanism (Puma Intelligence)

Pumas are highly clever creatures with excellent memories. Because of their prior experiences, they frequently hunt in areas where hunting is more likely. These focused hunting expeditions may take him to areas where he has already gone hunting and concealed his kill or may go to a more recent location where he hasn’t hunted in earlier phases. Both the discovery phase for visiting new locations and the exploitation phase for puma trips to previously promising locations have been taken into consideration. PO was motivated to alter the phases by the pumas’ intellect and memory as well as a novel and clever mechanism.

The suggested algorithm’s phase change mechanism is a specific type of heuristic choosing method that uses two components to conduct reward and penalty operations for scoring: intensification and diversity. The intellect of cougars served as the model for the phase transition section. It takes two approaches: the first holds that cougars attempt to simultaneously search for prey by exploring uncharted territory since they lack the necessary energy and experience. They ambush in areas that show promise; this is covered in the section on the inexperienced first generation.

Unexperienced Phase

Until the phase change phase’s initialization is completed, PO exploration and exploitation operations are conducted concurrently during the first three iterations. Each step will locate solutions separately developed at the end of the third iteration, which is more than the population as a whole. To address this problem, only the best solutions from the full set of solutions generated are equivalent to the entire population that replaces the present solutions. This is done by computing the total cost of the solutions generated in both phases at the end of the third iteration.

Experienced Phase

Pumas finds that after three generations; it is reasonable to decide to switch phases. As they continue their iterations, they select just one phase for the optimization process. Three distinct functions f1, f2, and f3 are utilized for scoring in this phase. The first function highlights the component of escalation and determines which of the two phases of exploitation and exploration has been chosen and executed more successfully than the other. The exploring phase is given more weight in the first function [6].

3.2.2 Exploration

These puma-related activities have motivated us in the exploratory section to look for food. At this point, pumas roam their region at random in quest of food or approach other pumas at random and utilize their prey. As a result, the puma will occasionally leap into the search area or scavenge for food in the area between them. The population is first arranged in ascending order, then throughout the exploration stage, Puma refines its solutions. Rdim refers to dimensions in Eq. (4), which are randomly generated values between 0 and 1. Another randomly generated integer number between 0 and 1 is called rand1. Solutions Xa,G, Xb,G, Xc,G, Xd,G, Xe,G, and Xf,G are those in the entire population where Faces are chosen at random. G is also computed using Eq. (6) where rand2 is a uniformly distributed random number generated between 0 and 1. Eq. (5) states that one of two equations is chosen to yield a different solution based on the current situation and that new solution is then used to enhance the one that already exists.

Zi,G=RDim∗(Ub−Lb)+LbIf rand1>0.5Xa,G+G⋅(Xa,G−Xb,G)+G⋅(((Xa,G−Xb,G)−(Xc,G−Xd,G))otherwise+((Xc,G−Xd,G)−(Xe,G−Xf,G)))(5)

G=2⋅rand2−1(6)

Xnew={Zi,G, ifj=jrandorrand3≤UXa,G,otherwise(7)

Zi,G in Eq. (7) is presented as the solution produced by Eq. (5). Similarly, rand3 is a randomly generated number between 0 and 1 in a uniform distribution. NC is calculated by applying Eq. (8). U is a parameter that was set before the optimization process and has an integer value between 0 and 1. According to the criterion in Eq. (10), Eqs. (8)–(10) are used to increase the number of dimensions that each iteration replaces with new solutions. In Eq. (9), Npop is the total number of pumas. The improvement of the solution is governed by the condition in Eq. (10); the dimensions of the solutions are altered only when this condition is met.

NC=1−U(8)

p=NCNpop(9)

ifCostXnew<CostXi,U=U+p(10)

The local optimum is avoided as a result of this activity, and there is a good diversity of product solutions. However, the process described in the exploration stage considers the fact that, at the start of each exploration phase iteration, search agents are arranged according to cost, with high-quality solutions coming in first and the Eqs. (8)–(10) in second. Quality solutions do not alter much in the beginning since the U parameter value is minimal. Later on, when this parameter increases, the solutions with greater cost values experience a variety of modifications. As a result, this technique pushes the exploration of less desirable solutions in the problem space to identify meaningful optimal points. The crucial thing is that Eq. (10) won’t be used if the production pumas aren’t superior to the ones that are now in use because improving them would eliminate the necessity for further redundant discoveries. However, high-quality solutions have undergone few modifications and aim solely to evade the trap of local optimality. Finally, using Eq. (11), the present solution is substituted for the newly created solutions.

Xa,G=Xnew,ifXi,new<Xa,G(11)

If the new production solution is more affordable than the current one, it takes the place of the current solution, Eq. (11).

3.2.3 Exploitation

In the exploitation step of the PO algorithm, two different operators are used to enhance solutions; both processes are based on the two hunting habits of pumas: sprinting and ambush hunting. In the wild, pumas attempt to ambush their prey by hiding among bushes, trees, or rocks. It chases after its prey in some situations; this behavior is replicated using Eq. (12) [6].

Xnew={ifrand4≥0.5,Xnew=(mean(Soltotal)Npop)⋅X1r−(−1)β×Xi1+(α⋅rand5)otherwise,ifrand6≥L,Xnew=Pumamale+(2⋅rand7)⋅exp(randn1)⋅X2r−Xiotherwise,Xnew=(2×rand8)×(F1⋅R⋅X(i)+F2⋅(1−R)⋅Pumamale)(2⋅rand9−1+randn2)−Pumamale(12)

The two tactics employed in the PO are indicated in Eq. (12). Given that in pumas, case 1 in Eq. (12) is employed for running and ambush methods during the exploitation phase of hunting, and a division operation performs this operation to mimic pumas’ quick sprint at prey. Eq. (12) states that the fast-running strategy is conducted if rand5, a uniformly distributed, randomly produced number between 0 and 1, is greater than 0.5. If not, the ambush strategy is chosen, which consists of two separate operations: the first is used to simulate pumas making short jumps toward the hunts of other pumas, and second is used to make long jumps toward the best puma. Eq. (12) states that the total number of populations needed to conduct the optimization process is Npop, the mean denotes the mean function, and Soltotal is the sum of all solutions. In the entire population, X1r represents a randomly chosen solution, and b denotes a randomly generated zero or one.

Additionally, Xi represents the current iteration’s solution, and L and A are steady parameters that need to be adjusted before the optimization process. Pumamale is the optimal option for the whole population, and the random numbers generated between zero and one are rand4, rand5, rand6, rand7, rand8, and rand9. Moreover, the exponential function is represented as exp. Regarding the problem size and the normal distribution, randn1 and randn2 are randomly produced numbers, and X2r is a randomly chosen solution that is chosen under Eq. (13).

round(1+(Npop−1)⋅rand10)(13)

Each element of X in Eq. (13), where Npop is the total number of Pumas and rand10 is a number between 0 and 1 that is created at random, is rounded to the nearest integer.

Lastly, using Eqs. (14)–(16), R, F1, and F2 are computed, respectively.

R=2⋅rand11−1(14)

F1=randn3⋅exp(2−Iter⋅(2MaxIter))(15)

Randn2 is a random number in the problem dimensions and the normal distribution in Eq. (15). Iter indicates the current iteration count, whereas MaxIter indicates the iterations total number required to complete the optimization process. The exponential function is denoted by exp.

F2=w×(v)2⋅cos((2×rand12)⋅w)(16)

w=randn4(17)

v=randn5(18)

Both randn4 and randn5, numbers in the normal distribution that are generated at random and the problem’s dimensions, are found in Eqs. (16)–(18). The cosine function is represented by cos, and the number rand12 is a randomly generated integer between 0 and 1. Ultimately, if freshly generated solutions are less expensive than the current solution, they are substituted after this phase. The flowchart shown in Fig. 2 explains the puma optimizer’s general workflow noting that T represents the position of the global best solution and SExplore and SExploit are the scoring of the explore phase and exploit phase based on the function f1, f2, and f3 [6].

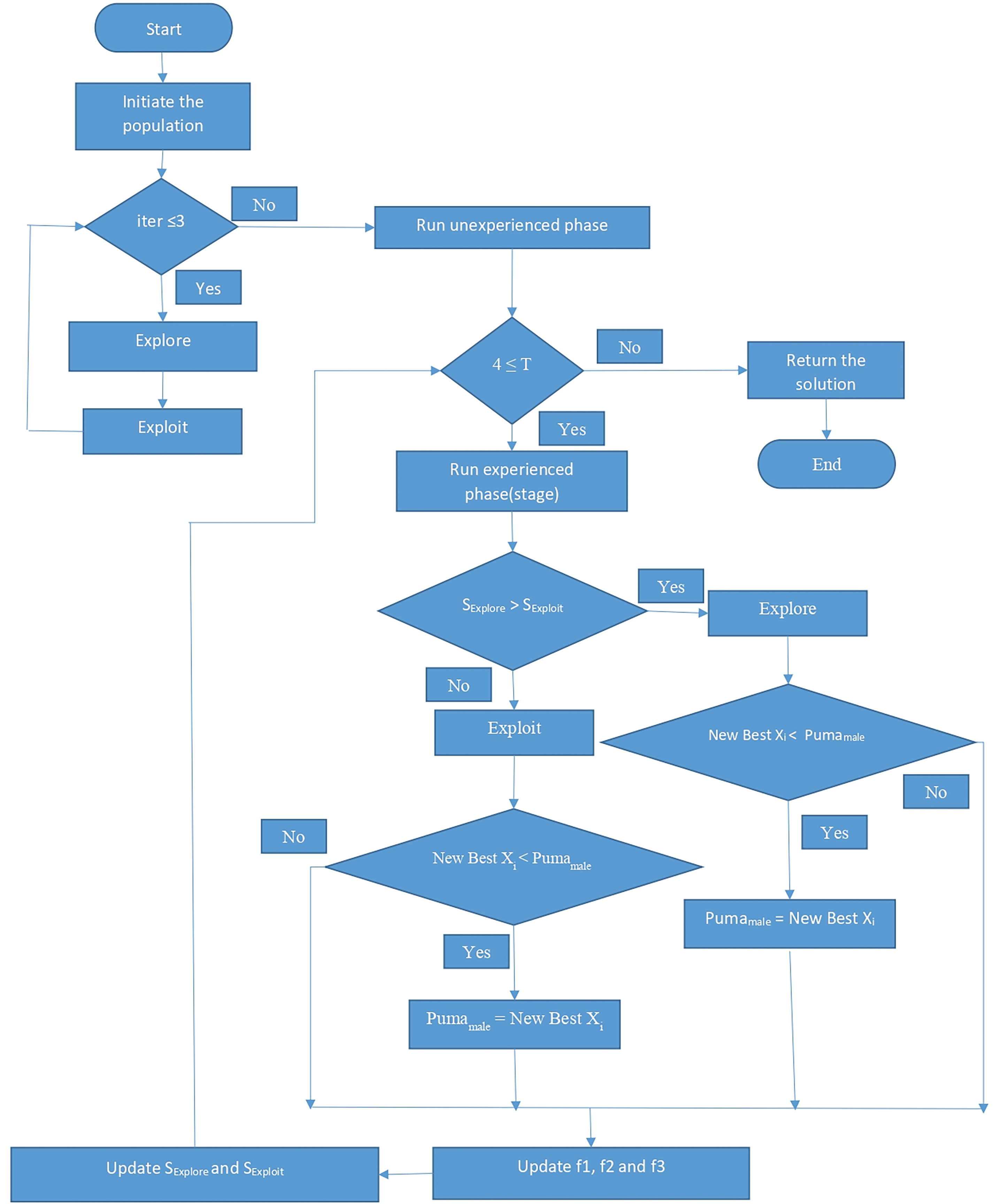
Figure 2: The flowchart of the PO

4  Results and Discussions

4.1 Characteristics of the Tested Perovskite Solar Cells

This study aims to provide a modified model of PSCs considering the effect of charge accumulations, and the variable resistances have been optimally estimated depending on the experimental J-V dataset. Two forms are represented to consider the effect of charge accumulations, Eqs. (2a) and (2b). A comparative analysis is introduced to explain the most efficient formula will be dependent on estimating the behavior of PSCs. The efficient model of PSCs must describe the forward and backward scans of the hysteresis behavior associated with PSCs; this behavior leads to the significant issue of the new PV cells and increases the importance of such an optimal model of the PSCs.

Table 1 illustrates the features recorded for both tracks of PSCs’ scanning in the forward and backward directions. The table shows the open circuit voltage (Voc) for the forward track beside its value at the reverse one. The perovskite cell efficiencies (PCE) reported for the forward and reverse scans are 13.62% and 16.97%, respectively. Also, we notice that the index of hysteresis equals 20%. The filling factors (FF) are 60% and 70% for both the forward and backward track of scanning. Also, from Table 1, the short current densities (Jsc) in both tracks are very close together (23.78 and 23.79 mA/cm2).

4.2 Studied Models of PSCs

In this study, the proposed PO is used to optimize the proposed modified TDMs taking into account the relation between a variable voltage capacitor and resistances (VVCARs) considering the hysteresis behavior. Three studied models are considered to evaluate the modified model: the first model is the proposed model (with VVCARs); the shunt and series resistances are fixed in the second model (VVC only); and the third model is the basic TDM model. The first model has fifteen control parameters (Iph, Is1, Is2, Is3, a1, a2, a3, Ksh, Rsho, Ks, Rso, a, b, c, and d) while the second and third one have thirteen and nine control parameters, respectively (Iph, Is1, Is2, Is3, a1, a2, a3, Rsho, Rso, a, b, c, and d), (Iph, Is1, Is2, Is3, a1, a2, a3, Rsho, Rso).

Three models are studied as follows:

•      The first model: is considered as a modified three diodes model estimated using the polynomial equation (Eq. (2a), (MTDM_PN) and the exponential form, Eq. (2b) (MTDM_EN)).

•      The second model: is termed as MTDM_PO and MTDM_EO, which considered the fixed values of series and shunt resistances.

•      The third mode: is considered as the basic TDM without the effects of Ceq, Rs, and Rsh.

Table 2 shows the upper and lower boundaries of the control variables of the tested models:

4.3 Numerical Simulation

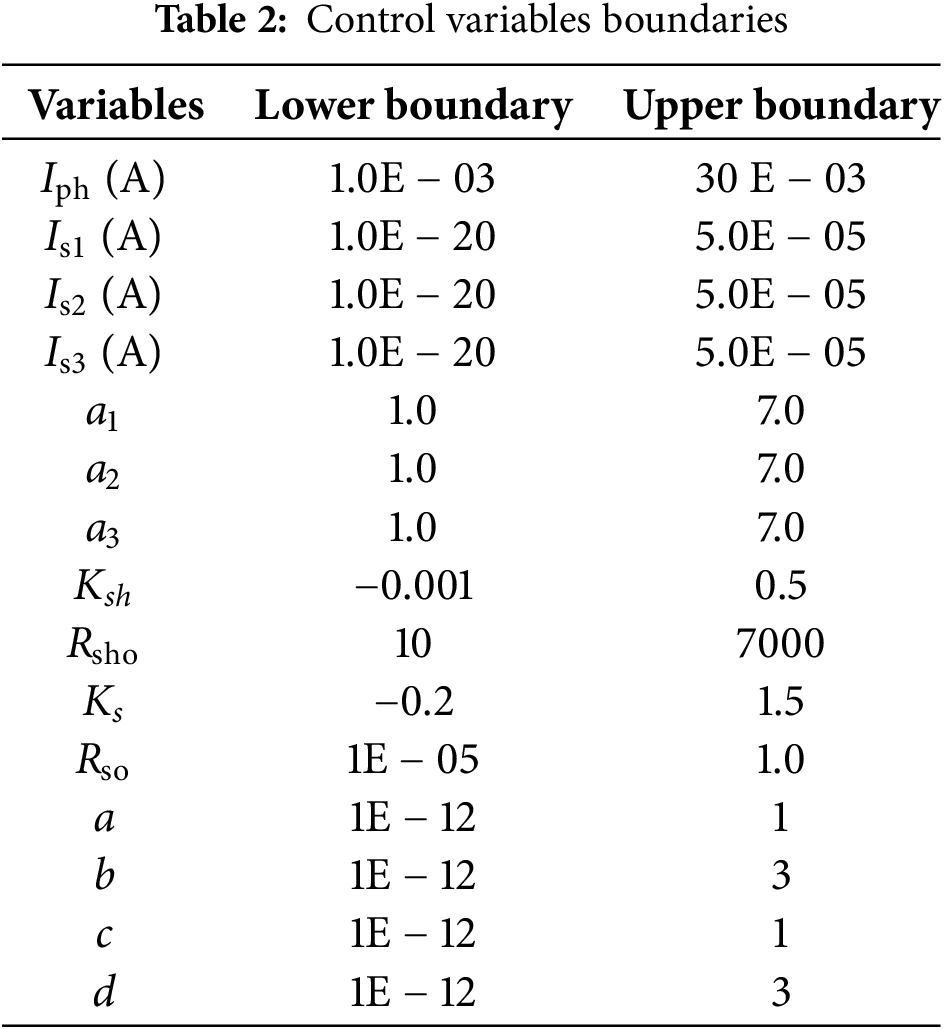
Table 3 reports numerical simulation results of the studied models using the proposed PO algorithm. Simulation results are the optimal estimated parameters and the RMSE. The reported results show that the MTDM_EN model produces optimal control parameters with a lower RMSE value (4.638E − 04) compared to other models. In addition to validating the efficacy of the proposed models, the convergence curves of the first and second models are constructed and explained in Fig. 3a,b. The convergence characteristics besides the minimal RMSE indicate that the exponential formula is more efficient than the polynomial in determining the Ceq value. In Fig. 3c, the convergence rate of all models is illustrated, and it is observed that MTDM_EN outperforms other models.

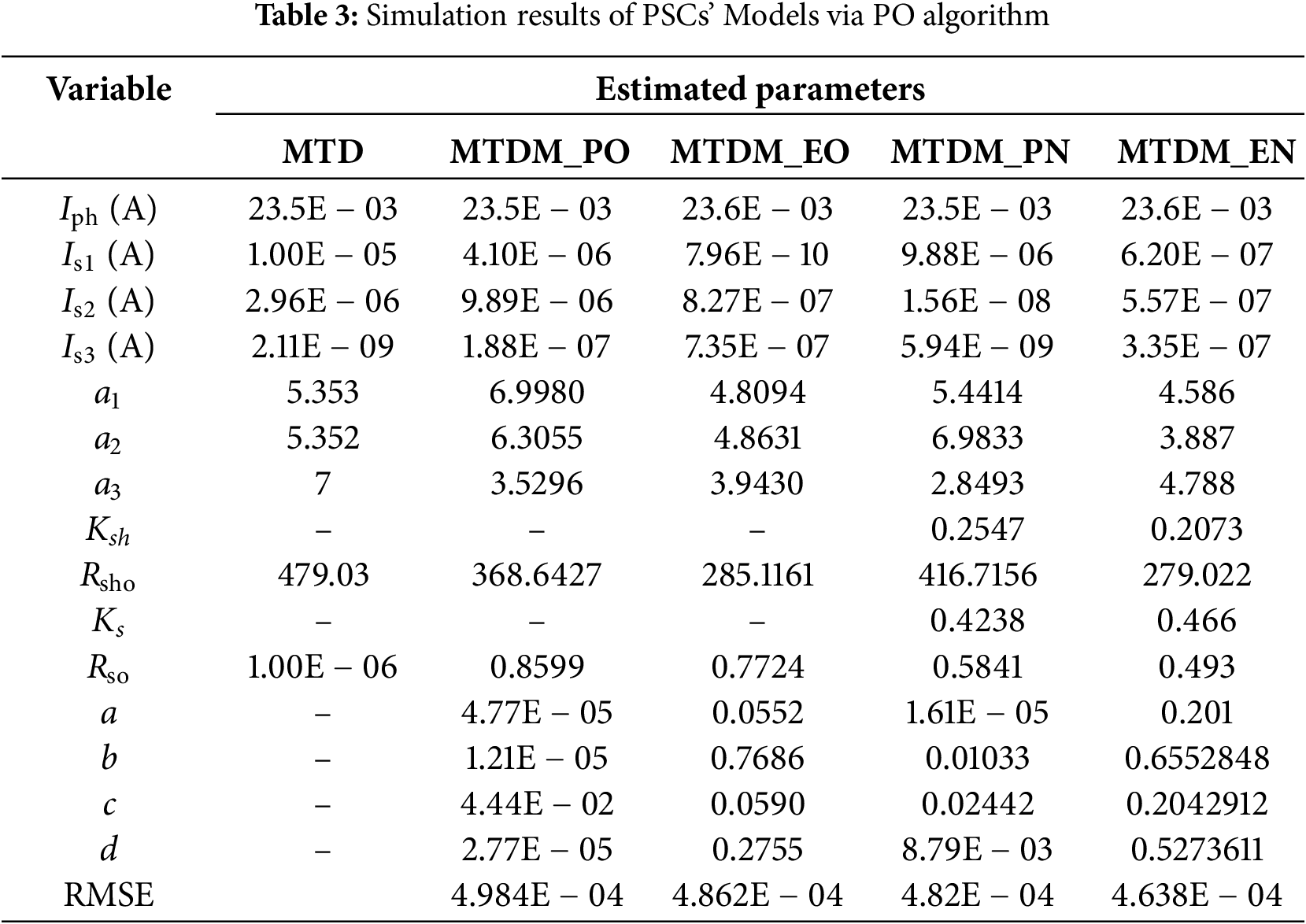
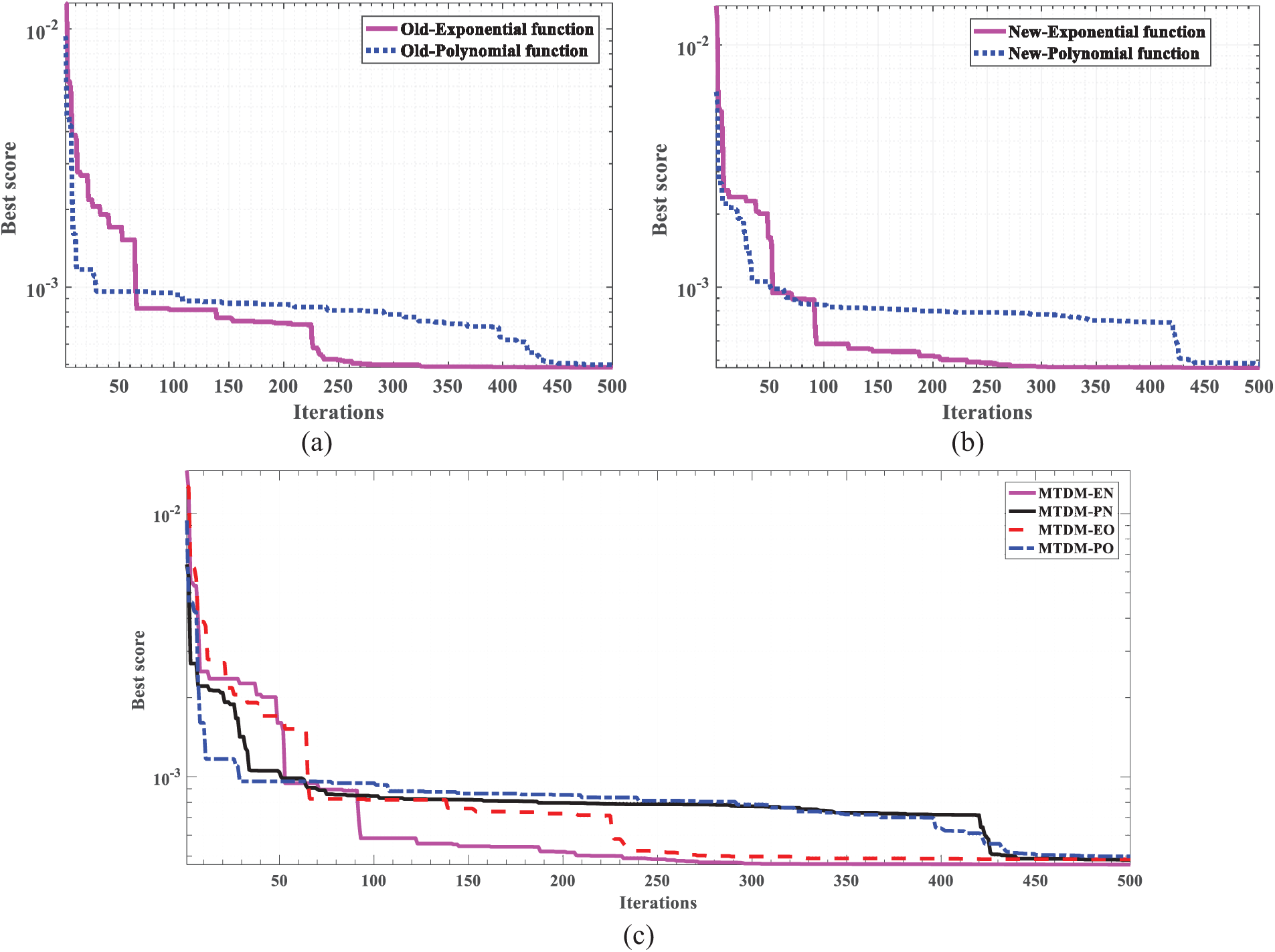
Figure 3: Convergence rates of PSCs: (a) MTDM_EO and MTDM_PO, (b) MTDM_EN and MTDM_PN, (c) All models

The estimated and measured J-V curves are illustrated in Fig. 4a–d. The basic TDM did not adequately emulate the behavior of hysteresis in both forward and backward tracks as in Fig. 4a. Fig. 4d presents the best representation, MTDM_EN, followed by Fig. 4c,b, consistent respectively to the MTDM_PN and MTDM_EO models. From Fig. 4, it can be concluded the following:

(a)   Without capacitor and fixed shunt and series resistances: This model shows significant deviations from experimental data due to its inability to capture dynamic behaviors, such as charge accumulation or hysteresis effects.

(b)   With variable capacitor Eq. (2a) and fixed shunt and series resistances: Improved alignment with experimental data, as the variable capacitor captures charge storage effects, but fixed resistances limit adaptability to real conditions.

(c)   With variable capacitor (Eq. (2a)) and variable shunt and series resistances (Eqs. (3a) and (3b)): Further enhancement in accuracy by accounting for dynamic resistance variations, better reflecting physical processes like recombination and leakage.

(d)   With variable capacitor (Eq. (2b)) and variable shunt and series resistances (Eqs. (3a) and (3b)): The most accurate representation of I–V curves, as the refined capacitor model (Eq. (2b)) improves charge dynamics simulation, combined with adaptable resistances for maximum fidelity to experimental behavior.

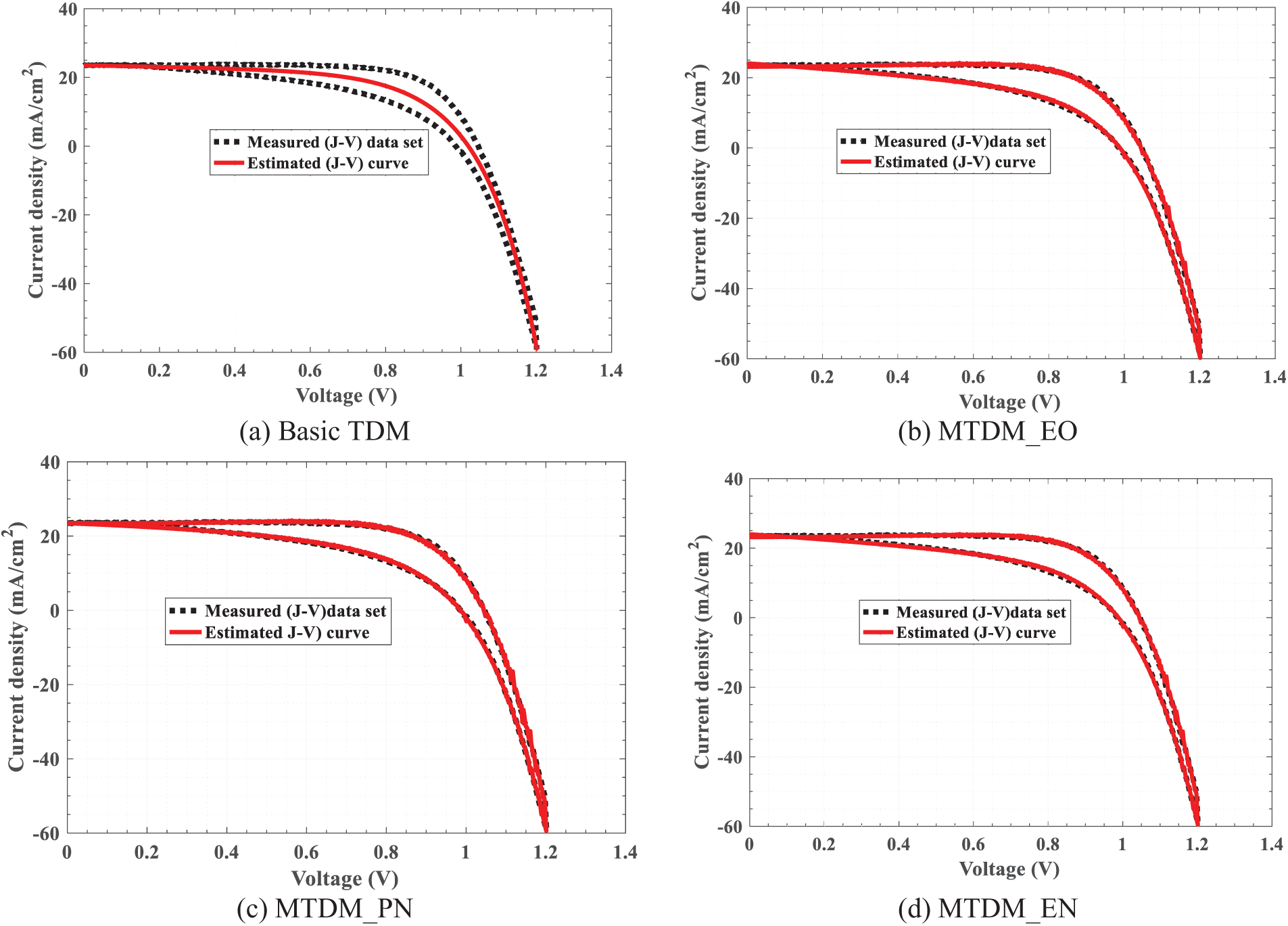
Figure 4: Closeness between estimated and experimental J-V curves for diverse models of perovskite solar cells

Also, the power-voltage curves for both experimental and estimated data corresponding to the models studied are shown in Fig. 5a–d. These remarks confirm the superiority of the MTDM_EN compared to other models of PSCs, and it is tracked by the MTDM_PN model. However, this might be because the exponential form represents the generation and recombination of carriers separately in the two terms of Eq. (2b) more accurately than the overall representation of the polynomial form in Eq. (2a). The previous Figs. 4 and 5 highlight the progressive improvements in modeling accuracy as additional dynamic elements are incorporated.

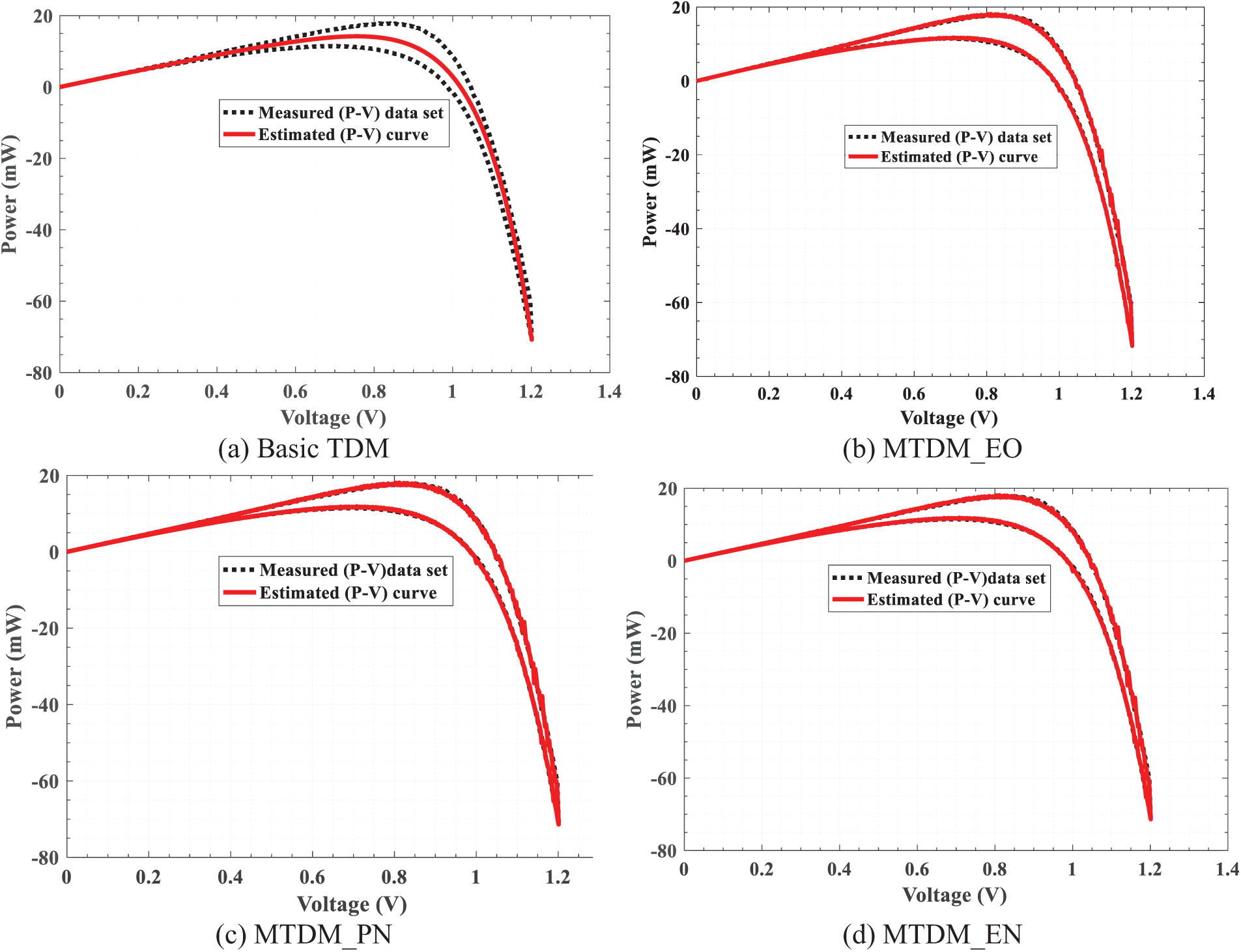
Figure 5: Closeness between estimated and experimental P-V curves for diverse models of perovskite solar cells

4.4 Statistical Indices

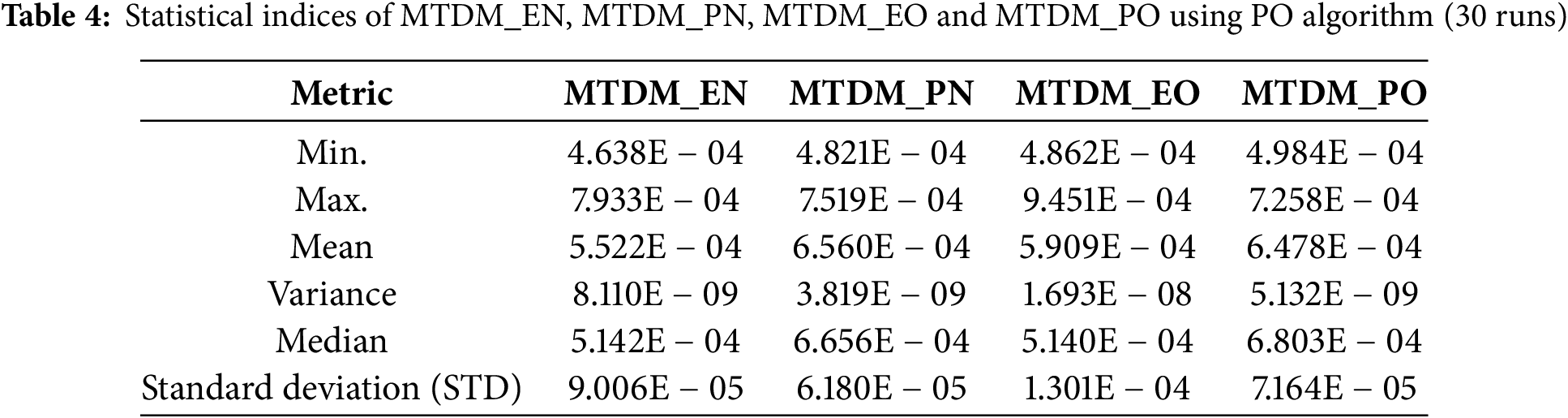
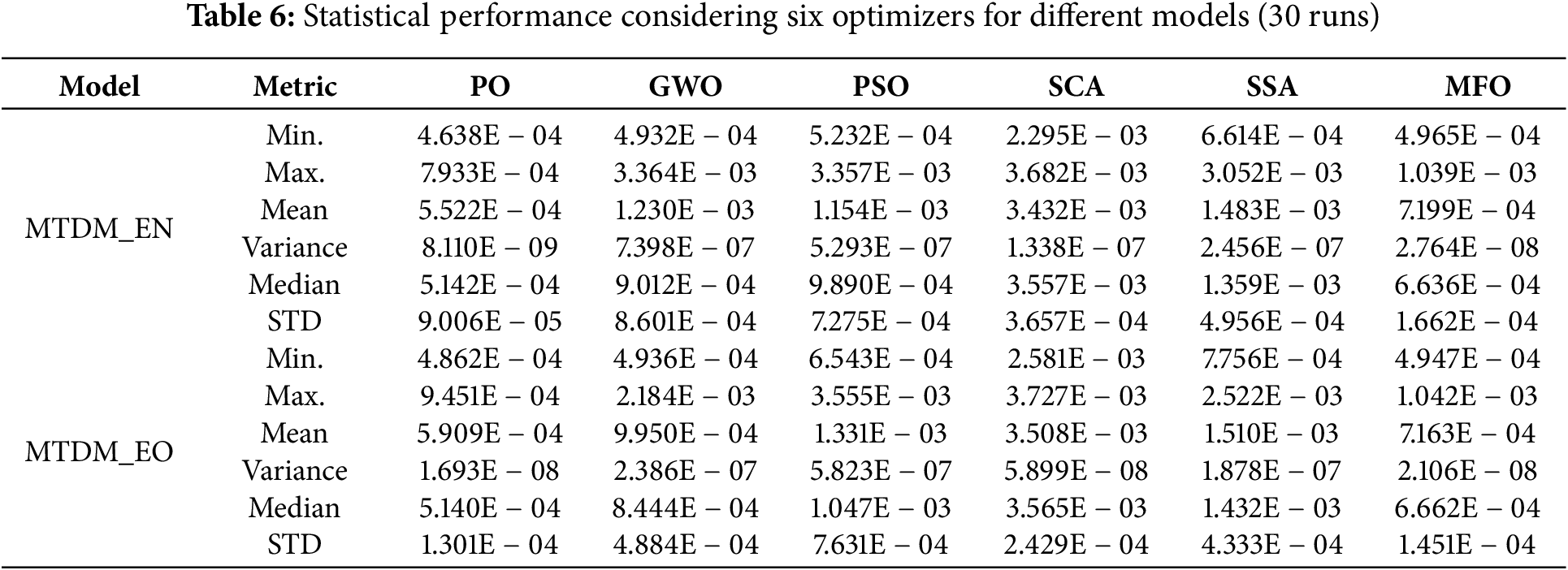
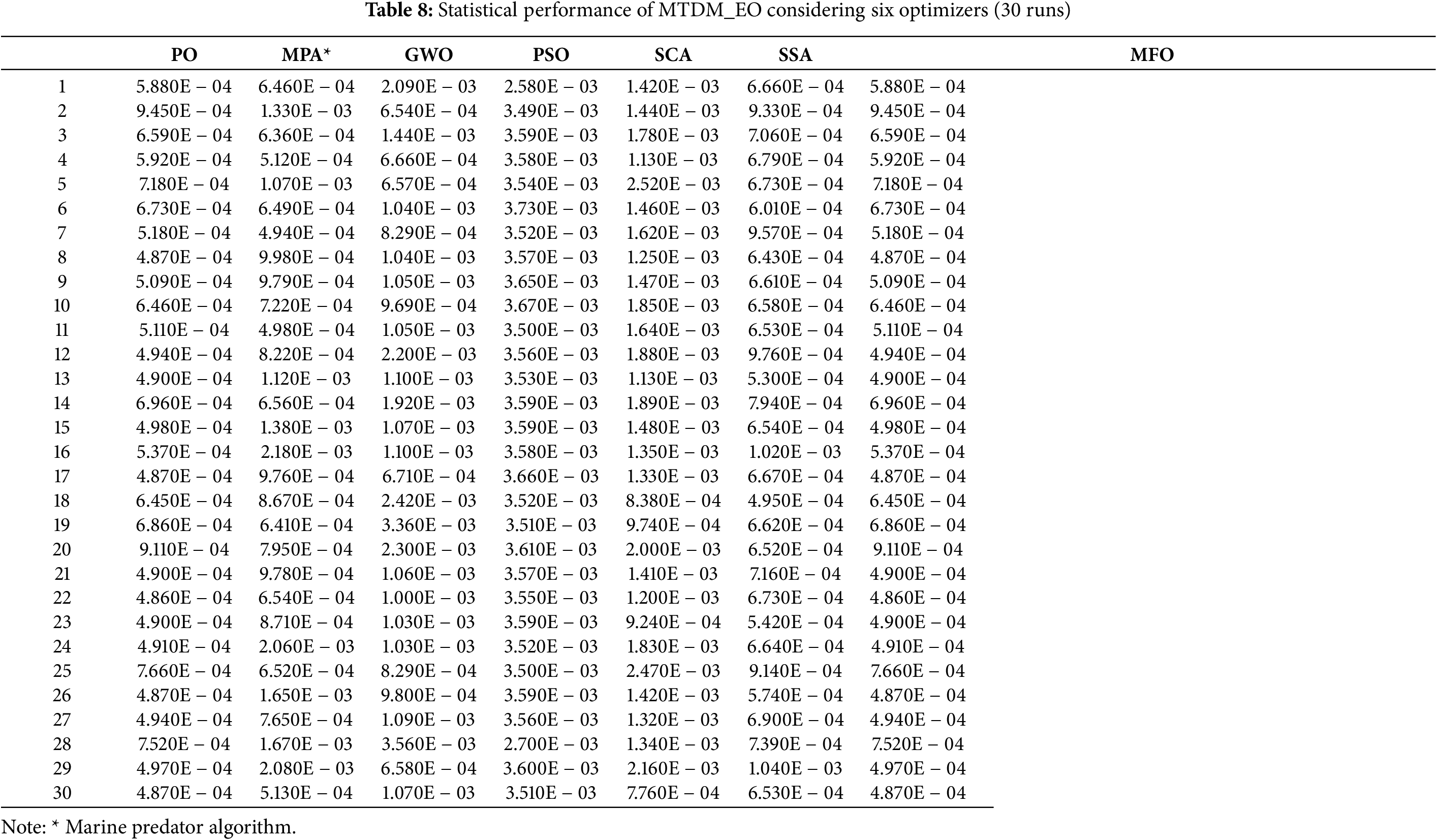
Statistical evaluation employs over 30 runs to validate the proposed models’ precision and efficacy computed by the PO algorithm. Table 4 reports the statistical indices of various PSC models. The MTDM_EN model realizes the lowest RMSE level compared with other models.

4.5 PO Superiority

4.5.1 Comparison Based on Optimized Parameters

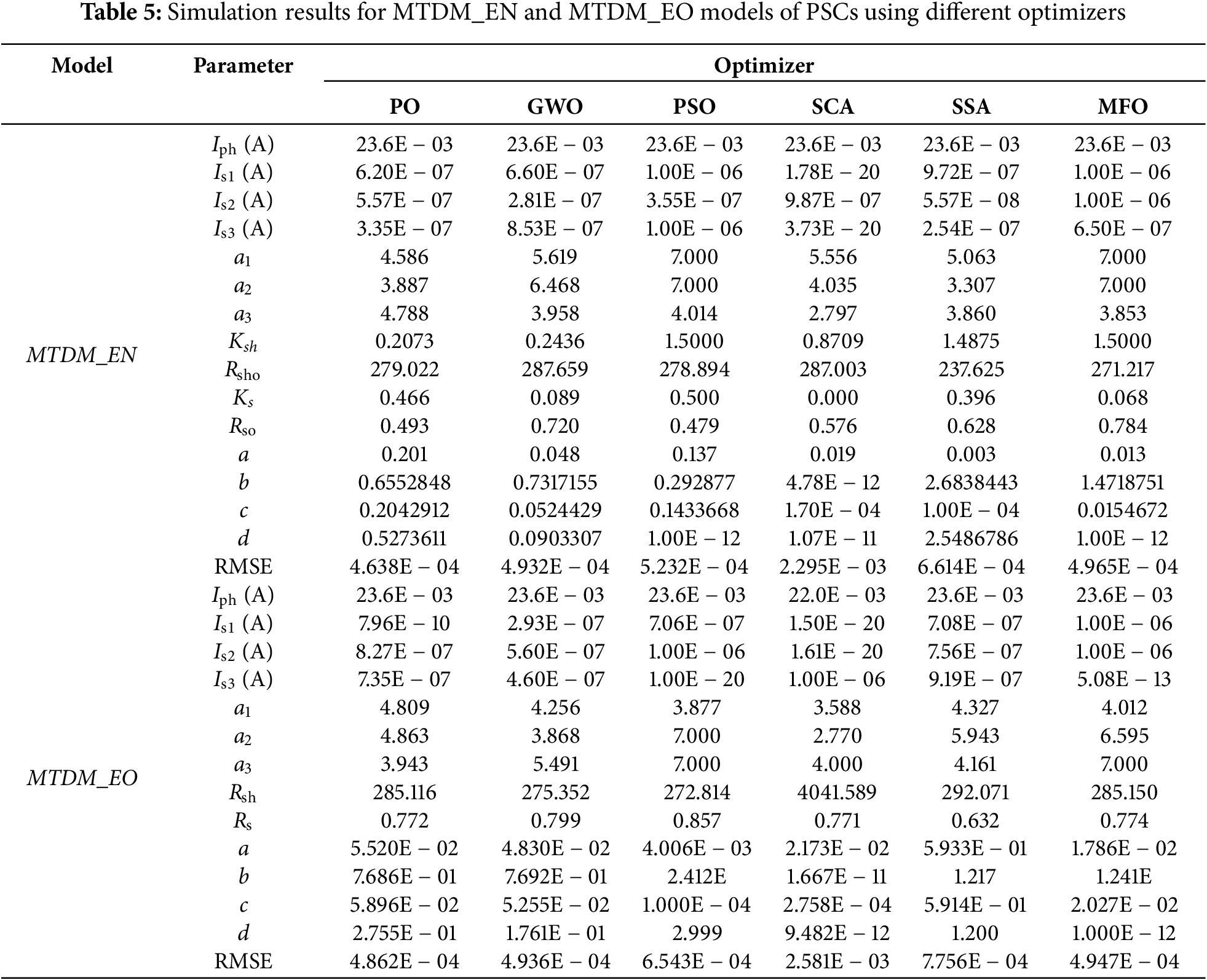
The superiority of the proposed PO algorithm compared to well-known optimizers: grey wolf optimizer (GWO), particle swarm optimizer (PSO), sine cosine algorithm (SCA), salp swarm algorithm (SSA), and moth-flame optimizers (MFO) is clarified in Table 5. These tables introduce the optimal extracted parameters for the MTDM_EN model which is the most precise one compared to MTDM_EO, applying the proposed PO in comparison to the well-known five optimizers. In Table 5, the optimal extracted parameters and the RMSE value are reported for MTDM_EN, and MTDM_EO. The results emphasize that the PO realizes a lower RMSE, which proves its capability and efficacy in finding the best-extracted parameter for these models.

4.5.2 Convergence Assessment

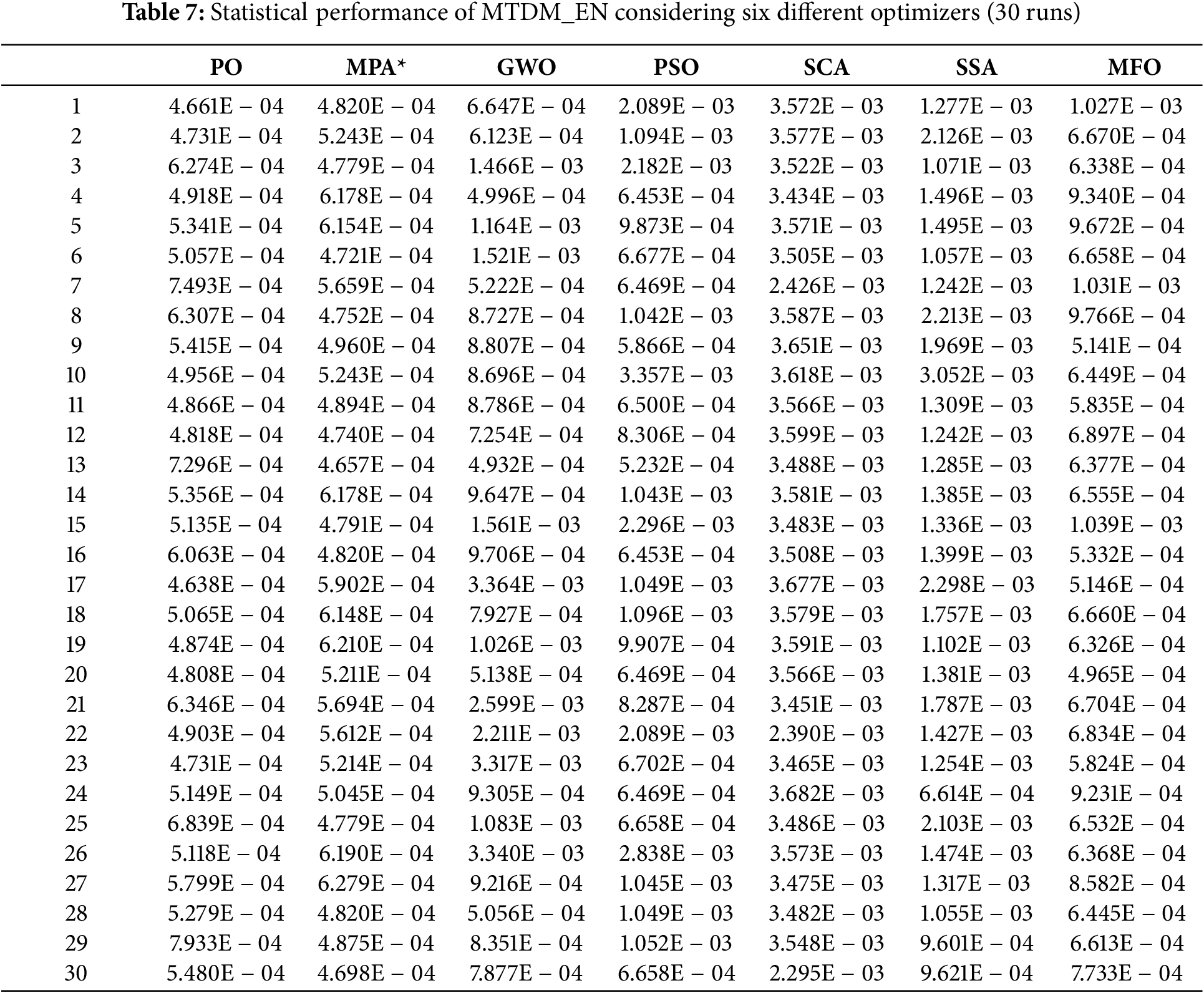
The convergence rates of PO relative to GWO, PSO, SCA, SSA, and MFO for the MTDM_EN and MTDM_EO models are illustrated in Fig. 6. The convergence rates illustrated in Fig. 6 show good, fast, and stable convergence rates with lower RMSE via OP compared to the other five competitive optimizers GWO, PSO, SCA, SSA, and FMO. In addition to the superior performance and efficacy of PO, a statistical analysis is applied to the five competitive optimizers and the proposed PO for the MTDM_EN and MTDM_EO models. The statistical indices resulting are reported in Table 6 over 30 runs. The lower RMSE and STD reflect the good quality of the solution and the high closeness between the extracted and the measured data set. The reported statistical metrics are based on 30 runs, as illustrated in Tables 7 and 8 for both MTDM_EN and MTDM_EO models, respectively. Further, they prove the quality and the robustness of PO are over the other five competitive optimizers.

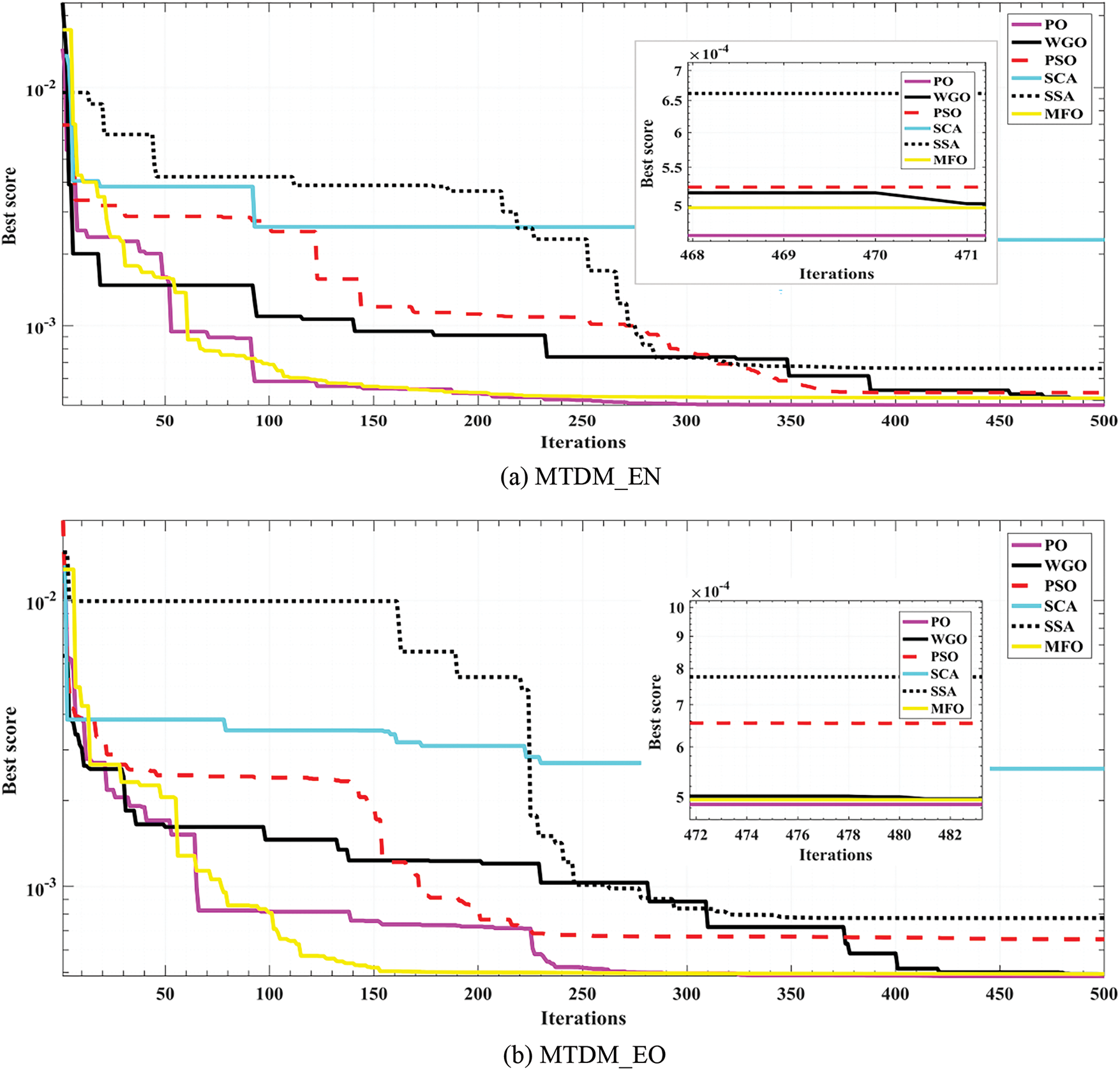
Figure 6: Convergence curves of PSCs for MTDM_EN and MTDM_EO models considering competitive optimizers

4.5.3 Statistical Verifications

For more verification of the quality of PO, the Analysis of variance (ANOVA) test is applied to the statistical results of MTDM_EN and MTDM_EO models alongside the five competitive optimizers and PO. ANOVA test checks if the difference between the mean values of groups realizes a significant variability among groups. The results of the ANOVA test among six optimizers’ statistical analyses reported in Tables 7 and 8 are illustrated in Table 9. The lower value of ρ reflects the realization of the existence of a significant difference between means of optimizers results (null hypothesis (p < 0.05)). Moreover, the lower mean realized via the PO optimizer is illustrated by the box of the plot for all optimizers, as shown in Fig. 7a,b, for both models, MTDM_EN and MTDM_EO. All statistical results emphasize the efficiency and supremacy of the proposed PO compared to the other well-known competing optimizers.

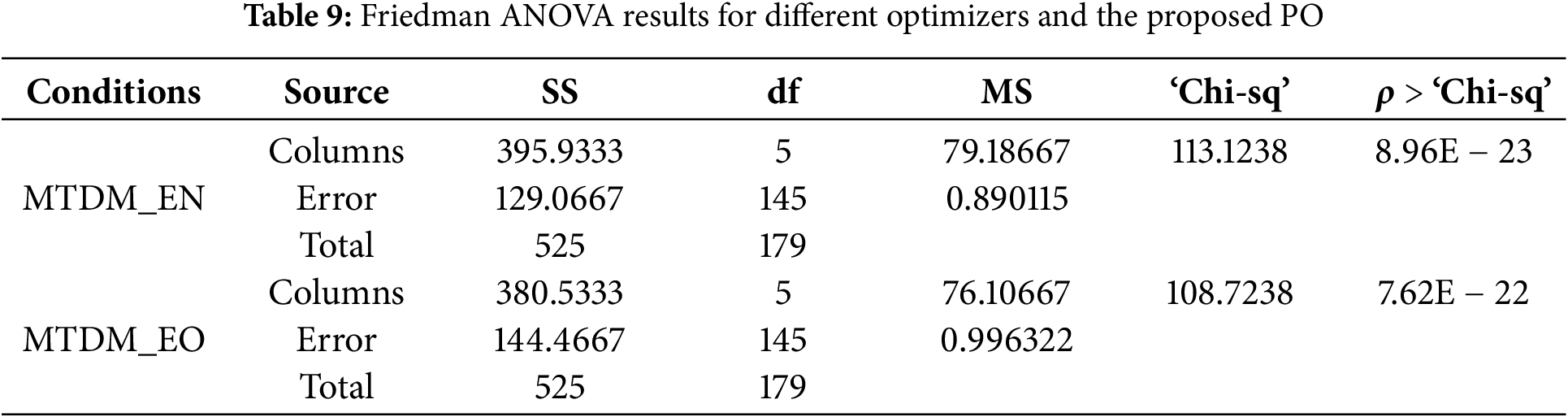
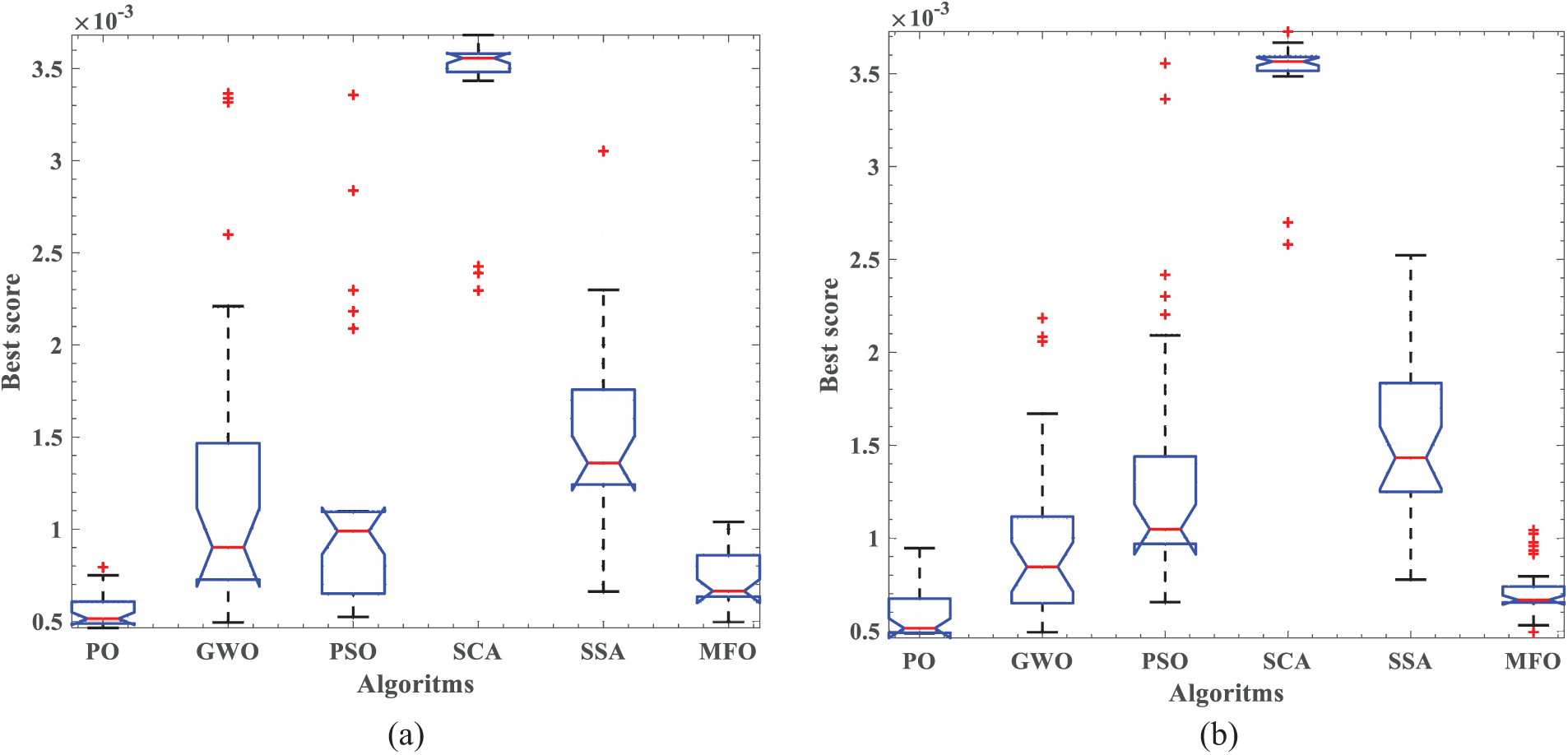
Figure 7: Box plot for the competitive algorithms and the proposed PO; at (a) MTDM_EN, (b) MTDM_EO

5  Assessment and Discussion

5.1 Complexity Problem Computation

The computation complexity of the problem studied is detailed considering the parameter estimation of PV triple diode models. It is indicated by taking into account both the iteration number and the data set size needed for convergence. Three main steps for individual and data set points:

Individual Point Complexity:

For one data point, finding the individual error for the considered error fitness function for the individual data at point (m) needs O (1) unit time. Then calculate the fitness function for all tested data points with size (np) that takes O(np) time.

The iterative PO algorithm aims at minimizing the fitness function (SSE). So, this objective is calculated for all np, as well as the expected PV unknown parameters of the considered models are updated. The total time complexity required by the proposed PO to achieve accepted convergence after number iterations (k) is stated by O(np.k).

5.2 Selection Criteria for PO Algorithm

Based on the numerical simulation results presented in Section 4, the Puma Optimization (PO) Algorithm is chosen because it is an effective tool to overcome the limitations of traditional algorithms, demonstrating robust performance, adaptability, and computational efficiency in solving complex optimization problems. Samples of the gap of previous well-known optimizers such as Genetic Algorithms (GA), Particle Swarm Optimization (PSO), and Ant Colony Optimization (ACO), face specific challenges, including:

•      In terms of convergence: Algorithms like GA and PSO often converge too quickly to suboptimal solutions, especially in complex, multimodal search spaces.

•      In terms of Computational Complexity: Some algorithms, such as ACO or Differential Evolution (DE), can be computationally expensive for high-dimensional or complex optimization problems.

•      In addition to the previous two issues, the traditional algorithms may lack mechanisms to adapt dynamically to changing landscapes in dynamic optimization problems.

5.3 Merits of the PO Algorithm

The main merits of PO that address the above gaps are through its innovative mechanisms inspired by the hunting behavior of pumas. The PO has a simple structure and updating mechanism. The PO algorithm incorporates strategies that mimic puma hunting techniques, such as stalking (exploration) and ambushing (exploitation), ensuring a well-balanced search process. PO strategies allow it to avoid premature convergence and effectively search both locally and globally. PO adapts dynamically to changes in the problem landscape, making it effective in dynamic optimization scenarios. The previous merits lead to fast convergence and low computational costs and based on the statistical analysis we can say that the PO has robust capability to solve high-dimensional optimization problems by leveraging its adaptive exploration and exploitation techniques. PO avoids local optima as it incorporates randomness in movement and decision-making. The PO algorithm’s ability to dynamically adapt its search strategies and balance exploration and exploitation makes it a versatile tool for optimizing various types of solar cells and other complex dynamic systems.

6  Conclusion

In the current research paper, the proposed PO has been optimized for the modified triple diode models with a variable voltage capacitor and resistances considering hysteresis behavior. To extract the optimal PSCs models’ parameters. The output of the proposed theoretical model has been compared to the experimental dataset. The root means square error, which is considered the primary objective function. This comparison represents an optimization problem that aims to minimize RMSE and identify the PSC model’s optimal parameters. Three studied models are considered to evaluate the modified model. To clarify the superiority and effectiveness of the proposed PO algorithm, the simulation results are compared with five competitive optimizers, GWO, PSO, SCA, SSA, and MFO, from the literature. The results emphasize that the PO realizes a lower RMSE, which proves its capability and efficacy in parameter extraction for the models. The statistical results emphasize the efficiency and supremacy of the proposed PO compared to the other well-known competing optimizers. The convergence rates show good, fast, and stable convergence rates with lower RMSE via PO compared to the other five competitive optimizers. Moreover, the lower means realized via the PO optimizer is illustrated by the box of plots for all optimizers. The super performance of the PO is proven. The lower RMSE and STD reflect the good quality of the solution and the high closeness between the extracted and the measured data set.

The PO algorithm’s adaptability and robustness make it a powerful tool for optimizing dynamic models in solar cells and beyond. While computational costs and high-dimensional optimization remain potential challenges, advancements such as parallel computing, surrogate modeling, and meta-optimization can mitigate these limitations. By leveraging its strengths, the PO algorithm can play a critical role in advancing renewable energy technologies, smart grids, and other complex systems.

Acknowledgement: The authors would like to thank Prince Sattam Bin Abdulaziz University for their funding this project.

Funding Statement: This study is supported via funding from Prince Sattam Bin Abdulaziz University project number (PSAU/2025/R/1446).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Amlak Abaza, Ahmed Bayoumi and Ragab A. El-Sehiemy; data collection: Ragab A. El-Sehiemy and Mona Gafar; analysis and interpretation of results: Amlak Abaza, Ahmed Bayoumi and Ragab A. El-Sehiemy; funding: Ragab A. El-Sehiemy and Mona Gafar; draft manuscript preparation: Amlak Abaza, Ahmed Bayoumi and Ragab A. El-Sehiemy; review manuscript draft: Mona Gafar and Ragab A. El-Sehiemy. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data are available upon request by the corresponding author.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Elkhatat A, Al-Muhtaseb S. Climate change and energy security: a comparative analysis of the role of energy policies in advancing environmental sustainability. Energies. 2024;17(13):3179. doi:10.3390/en17133179. [Google Scholar] [CrossRef]

2. Kannan N, Vakeesan D. Solar energy for future world: —a review. Renew Sustain Energy Rev. 2016;62(1):1092–105. doi:10.1016/j.rser.2016.05.022. [Google Scholar] [CrossRef]

3. Akbari Vakilabadi M, Afzalabadi A, Khoeini Poorfar A, Rahbari A, Bidi M, Ahmadi MH, et al. Technical and economical evaluation of grid-connected renewable power generation system for a residential urban area. Int J Low Carbon Technol. 2019;14(1):10–22. doi:10.1093/ijlct/cty053. [Google Scholar] [CrossRef]

4. Bayoumi ASA, El-Sehiemy RA, Abaza A. Effective PV parameter estimation algorithm based on marine predators optimizer considering normal and low radiation operating conditions. Arab J Sci Eng. 2022;47(3):3089–104. doi:10.1007/s13369-021-06045-0. [Google Scholar] [CrossRef]

5. Bayoumi ASA, El-Sehiemy RA, Badawy M, Elhosseini M, Aljohani M, Abaza A. Optimizing multi-layer perovskite solar cell dynamic models with hysteresis consideration using artificial rabbits optimization. Mathematics. 2023;11(24):4912. doi:10.3390/math11244912. [Google Scholar] [CrossRef]

6. Abdollahzadeh B, Khodadadi N, Barshandeh S, Trojovský P, Gharehchopogh FS, El-kenawy EM, et al. Puma optimizer (POa novel metaheuristic optimization algorithm and its application in machine learning. Clust Comput. 2024;27(4):5235–83. doi:10.1007/s10586-023-04221-5. [Google Scholar] [CrossRef]

7. Dehghani M, Trojovská E, Trojovský P. A new human-based metaheuristic algorithm for solving optimization problems on the base of simulation of driving training process. Sci Rep. 2022;12(1):9924. doi:10.1038/s41598-022-14225-7. [Google Scholar] [PubMed] [CrossRef]

8. Alexandros T, Georgios D. Nature inspired optimization algorithms related to physical phenomena and laws of science: a survey. Int J Artif Intell Tools. 2017;26(6):1750022. doi:10.1142/s0218213017500221. [Google Scholar] [CrossRef]

9. Vinod Chandra SS, Anand HS. Nature inspired meta heuristic algorithms for optimization problems. Computing. 2022;104(2):251–69. doi:10.1007/s00607-021-00955-5. [Google Scholar] [CrossRef]

10. Nguyen TT, Nguyen TT, Tran TN. Parameter estimation of photovoltaic cell and module models relied on metaheuristic algorithms including artificial ecosystem optimization. Neural Comput Appl. 2022;34(15):12819–44. doi:10.1007/s00521-022-07142-3. [Google Scholar] [CrossRef]

11. Abdelrazek AS, El-Sehiemy RA, Rezk H, Ghoniem RM, Falaras P, Zaky AA. Dynamic electrical models of perovskite solar cells considering hysteresis and charge accumulations effects by using equilibrium optimizer. IEEE Access. 2022;10(4):104111–22. doi:10.1109/ACCESS.2022.3209795. [Google Scholar] [CrossRef]

12. Bayoumi ASA, El Sehiemy RA, El-Kemary M, Abaza A. Advanced extraction of PV parameters’ models based on electric field impacts on semiconductor conductivity using QIO algorithm. Sci Rep. 2024;14(1):15397. doi:10.1038/s41598-024-65091-4. [Google Scholar] [PubMed] [CrossRef]

13. Sharma A, Sharma A, Averbukh M, Jately V, Rajput S, Azzopardi B, et al. Performance investigation of state-of-the-art metaheuristic techniques for parameter extraction of solar cells/module. Sci Rep. 2023;13(1):11134. doi:10.1038/s41598-023-37824-4. [Google Scholar] [PubMed] [CrossRef]

14. Sui M, Chu Y, Zhang R. A review of technologies for high efficiency silicon solar cells. J Phys: Conf Ser. 2021;1907(1):012026. doi:10.1088/1742-6596/1907/1/012026. [Google Scholar] [CrossRef]

15. Diab AAZ, Sultan HM, Do TD, Kamel OM, Mossa MA. Coyote optimization algorithm for parameters estimation of various models of solar cells and PV modules. IEEE Access. 2020;8:111102–40. doi:10.1109/ACCESS.2020.3000770. [Google Scholar] [CrossRef]

16. Abdel-Basset M, Mohamed R, Mirjalili S, Chakrabortty RK, Ryan MJ. Solar photovoltaic parameter estimation using an improved equilibrium optimizer. Sol Energy. 2020;209(3):694–708. doi:10.1016/j.solener.2020.09.032. [Google Scholar] [CrossRef]

17. Ali F, Sarwar A, Ilahi Bakhsh F, Ahmad S, Ali Shah A, Ahmed H. Parameter extraction of photovoltaic models using atomic orbital search algorithm on a decent basis for novel accurate RMSE calculation. Energy Convers Manag. 2023;277(1):116613. doi:10.1016/j.enconman.2022.116613. [Google Scholar] [CrossRef]

18. Kharchouf Y, Herbazi R, Chahboun A. Parameter’s extraction of solar photovoltaic models using an improved differential evolution algorithm. Energy Convers Manag. 2022;251(8):114972. doi:10.1016/j.enconman.2021.114972. [Google Scholar] [CrossRef]

19. Shaheen AM, Ginidi AR, El-Sehiemy RA, Ghoneim SSM. A forensic-based investigation algorithm for parameter extraction of solar cell models. IEEE Access. 2021;9:1–20. doi:10.1109/ACCESS.2020.3046536. [Google Scholar] [CrossRef]

20. Abdul Hamid NF, Rahim NA, Selvaraj J. Solar cell parameters extraction using particle swarm optimization algorithm. In: 2013 IEEE Conference on Clean Energy and Technology (CEAT); 2013 Nov 18–20; Langkawi, Malaysia. IEEE; 2013. p. 461–5. doi:10.1109/CEAT.2013.6775676. [Google Scholar] [CrossRef]

21. Bayoumi AS, El-Sehiemy RA, Mahmoud K, Lehtonen M, Darwish MMF. Assessment of an improved three-diode against modified two-diode patterns of MCS solar cells associated with soft parameter estimation paradigms. Appl Sci. 2021;11(3):1055. doi:10.3390/app11031055. [Google Scholar] [CrossRef]

22. Saadaoui D, Elyaqouti M, Assalaou K, hmamou Ben D, Lidaighbi S. Parameters optimization of solar PV cell/module using genetic algorithm based on non-uniform mutation. Energy Convers Manag X. 2021;12(2):100129. doi:10.1016/j.ecmx.2021.100129. [Google Scholar] [CrossRef]

23. Ahmed MI, Habib A, Javaid SS. Perovskite solar cells: potentials, challenges, and opportunities. Int J Photoenergy. 2015;2015:592308. doi:10.1155/2015/592308. [Google Scholar] [CrossRef]

24. Velilla E, Ramirez D, Uribe JI, Montoya JF, Jaramillo F. Outdoor performance of perovskite solar technology: silicon comparison and competitive advantages at different irradiances. Sol Energy Mater Sol Cells. 2019;191:15–20. doi:10.1016/j.solmat.2018.10.018. [Google Scholar] [CrossRef]

25. Sanchez RS, Gonzalez-Pedro V, Lee JW, Park NG, Kang YS, Mora-Sero I, et al. Slow dynamic processes in lead halide perovskite solar cells. characteristic times and hysteresis. J Phys Chem Lett. 2014;5(13):2357–63. doi:10.1021/jz5011187. [Google Scholar] [PubMed] [CrossRef]

26. Ghalambaz N, Ganji J, Shabani P. The development of a neural network model for the structural improvement of perovskite solar cells using an evolutionary particle swarm optimization algorithm. J Comput Electron. 2021;20(2):966–73. doi:10.1007/s10825-020-01654-8. [Google Scholar] [CrossRef]

27. Rezk H, Elsenety MM, Ferahtia S, Falaras P, Zaky AA. A novel parameter identification strategy based on COOT optimizer applied to a three-diode model of triple cation perovskite solar cells. Neural Comput Appl. 2023;35(14):10197–219. doi:10.1007/s00521-023-08230-8. [Google Scholar] [CrossRef]

28. Kim E, Bhattacharya I. Material selection method for a perovskite solar cell design based on the genetic algorithm. In: 2020 47th IEEE Photovoltaic Specialists Conference (PVSC); 2020 Jun 15–Aug 21; Calgary, AB, Canada. IEEE; 2020. p. 2631–4. doi:10.1109/pvsc45281.2020.9300498. [Google Scholar] [CrossRef]

29. Knopff KH, Knopff AA, Kortello A, Boyce MS. Cougar kill rate and prey composition in a multiprey system. J Wildl Manag. 2010;74(7):1435–47. doi:10.2193/2009-314. [Google Scholar] [CrossRef]

30. Wolpert DH, Macready WG. No free lunch theorems for optimization. IEEE Trans Evol Comput. 1997;1(1):67–82. doi:10.1109/4235.585893. [Google Scholar] [CrossRef]

31. Bhalla AS, Guo R, Roy R. The perovskite structure—a review of its role in ceramic science and technology. Mater Res Innov. 2000;4(1):3–26. doi:10.1007/s100190000062. [Google Scholar] [CrossRef]

32. Dharmadasa IM, Rahaq Y, Alam AE. Perovskite solar cells: short lifetime and hysteresis behaviour of current-voltage characteristics. J Mater Sci Mater Electron. 2019;30(14):12851–9. doi:10.1007/s10854-019-01759-2. [Google Scholar] [CrossRef]

33. Rezk H, Ali Abdelkareem M. Optimal parameter identification of triple diode model for solar photovoltaic panel and cells. Energy Rep. 2022;8:1179–88. doi:10.1016/j.egyr.2021.11.179. [Google Scholar] [CrossRef]

34. Vellingiri M, Rawa M, Alghamdi S, Alhussainy AA, Althobiti AS, Calasan M, et al. Non-linear analysis of novel equivalent circuits of single-diode solar cell models with voltage-dependent resistance. Fractal Fract. 2023;7(1):95. doi:10.3390/fractalfract7010095. [Google Scholar] [CrossRef]

35. Zaky AA, El Sehiemy RA, Rashwan YI, Elhossieni MA, Gkini K, Kladas A, et al. Optimal performance emulation of PSCs using the elephant herd algorithm associated with experimental validation. ECS J Solid State Sci Technol. 2019;8(12):Q249–55. doi:10.1149/2.0271912jss. [Google Scholar] [CrossRef]

36. Zaky AA, Fathy A, Rezk H, Gkini K, Falaras P, Abaza A. A modified triple-diode model parameters identification for perovskite solar cells via nature-inspired search optimization algorithms. Sustainability. 2021;13(23):12969. doi:10.3390/su132312969. [Google Scholar] [CrossRef]