 Open Access
Open Access
ARTICLE
Integrating Bayesian and Convolution Neural Network for Uncertainty Estimation of Cataract from Fundus Images
1 Department of Informatics and Computer Systems, College of Computer Science, King Khalid University, Abha, 61421, Saudi Arabia
2 Department of Computer Science, King Khalid University, Abha, 61421, Saudi Arabia
* Corresponding Author: Anandhavalli Muniasamy. Email:
(This article belongs to the Special Issue: Advances in AI-Driven Computational Modeling for Image Processing)
Computer Modeling in Engineering & Sciences 2025, 143(1), 569-592. https://doi.org/10.32604/cmes.2025.060484
Received 02 November 2024; Accepted 17 February 2025; Issue published 11 April 2025
Abstract
The effective and timely diagnosis and treatment of ocular diseases are key to the rapid recovery of patients. Today, the mass disease that needs attention in this context is cataracts. Although deep learning has significantly advanced the analysis of ocular disease images, there is a need for a probabilistic model to generate the distributions of potential outcomes and thus make decisions related to uncertainty quantification. Therefore, this study implements a Bayesian Convolutional Neural Networks (BCNN) model for predicting cataracts by assigning probability values to the predictions. It prepares convolutional neural network (CNN) and BCNN models. The proposed BCNN model is CNN-based in which reparameterization is in the first and last layers of the CNN model. This study then trains them on a dataset of cataract images filtered from the ocular disease fundus images from Kaggle. The deep CNN model has an accuracy of 95%, while the BCNN model has an accuracy of 93.75% along with information on uncertainty estimation of cataracts and normal eye conditions. When compared with other methods, the proposed work reveals that it can be a promising solution for cataract prediction with uncertainty estimation.Graphic Abstract
Keywords
A cataract is a clouding of the translucent lens inside the human eye, which typically focuses light as the eye ages and fails to keep up with how much it should be focused on the retina. Cataracts are a significant cause of blindness in older people worldwide, but their development will not damage vision until it is well advanced [1–3]. However, older people continue to suffer from deteriorating sight and can lose their vision altogether after the age of 40. Based on the World Health Organization [4], over 400 million people worldwide are affected by eye problems such as cataracts and glaucoma. Of all today’s eye diseases that pose a serious threat, cataracts are one most often found that can cause total blindness and visual impairment [5,6]. The Global Burden of Disease (GBD) Study reported that the cataract as the primary cause of blindness, accounting for 45% of global blindness [7].
Through AI (artificial intelligence) and deep learning-based techniques, a diagnostic method for eye diseases with fundus images was investigated in some detail, and these images are two-dimensional pictures of one’s eye [8,9]. The traditional approaches can produce errors, which can undoubtedly affect the value of clinical diagnosis [10–12]. An advanced AI system can bring to reality easily accessed equipment that can early screen for conditions in the developed world’s geriatric communities and developing countries where there are few doctors to look after large groups [13]. Modern systems can spot minuscule features of cataracts and learn to do this at all stages, meaning that the disease can be diagnosed far earlier and managed, preventing the progression of the cataract disease and thus reducing its severity [14–16]. Since the healthcare industry is headed toward more individualized patient care with more solution-making shared with patients, Bayesian Neural Networks (BNNs) are going to be increasingly employed as tools for making clinical decision-making processes more reliable and clearer [17] as they apply a probabilistic manner for generating the distributions of potential outcomes and thus making decisions related to uncertainty.
The proposed Bayesian Convolutional Neural Networks (BCNN) follows the structure of a convolutional neural network along with normal distributions imposed on parameters as priors and posterior for model parametrization for uncertainty quantification. The details of the proposed BCNN are obtained simply using Bayesian layers instead of traditional CNN, as better explained in the “experiment” section. The hyper-parameters of these models are tuned, and a suitable one for these models is developed. Finally, the performances of these models are compared in terms of accuracy metrics and the uncertainty quantification results of BCNN for different eye images.
Some of the vital contributions of the designed uncertainty estimation of the cataract condition identification approach with the help of deep learning in fundus images are listed below to bridge the research gap identified from the existing methods:
• Design an integrated Bayesian-CNN framework using fundus images to find cataract conditions in their early stages and start appropriate treatment for the cataract.
• The CNN model is developed to retrieve the necessary features from the input fundus ocular images.
• The Bayesian model is utilized to accurately measure the probability of classification with uncertainty estimation.
• The outcome is verified with other classification techniques to estimate the potential of the Bayesian-CNN-based cataract condition prediction model investigated.
The proposed Bayesian-CNN-based cataract classification and uncertainty estimation approach using ocular fundus images is narrated in the succeeding sections. Section 2 provides the existing works based on cataract disease. In addition, the accuracy of the prior deep learning-based cataract recognition techniques is given in detail. The proposed contract identification technique and the ocular fundus image collection are explained in Section 3. The experimental setup, results, and discussions of the offered cataract identification model using fundus images are given in Section 4. The conclusion of the proposed model is available in Section 5.
For huge medical data and high-risk decisions, AI models tend to offer overconfident predictions [18,19]. Therefore, Bayesian Neural Networks provide key innovations, as they quantify uncertainty, a critical feature for making clinical decisions [20,21]. In addition, relatively recent applications of BNNs have proved that they are increasingly suitable for use in healthcare, for the early detection of diseases, and the drafting of personalized disease treatment plans, which can significantly benefit from the increased reliability of predictions reflecting their uncertainty [22]. Advances in Bayesian mathematics include Dividing Local Gaussian Processes (DLGPs) and Bayesian Long Short-Term Memory (LSTMs), which have expanded the explanatory framework and refined the applicability to hierarchy and times series data, such as that in medical imaging and dealing with chronic diseases [23,24]. Thus, as the healthcare sector evolves, BNNs and related partners will be central to reliable and personalized clinical care.
Problem Statement: Bayesian models, although promising in healthcare, face significant challenges. The first major challenge is computational complexity. Bayesian methods typically require sophisticated and computationally intensive sampling techniques, such as Markov chain Monte Carlo or variational inference. As reported, this challenge is no longer insurmountable, as advances in hardware and the development of optimized and efficient algorithms have made it feasible to deploy these models in a clinical setting [25,26]. Another major challenge is the low interpretability of these models, which is essential for clinician adoption and trust. As understanding of the healthcare processes grows, models such as BNNs and their extensions will play a central role in enabling reliable and personalized clinical care.
A list of studies for identifying and classifying the ocular disease type using fundus images can be found in Table 1. A typical research gap is that while several studies have addressed the classification of cataracts, there appears to be limited research that integrates uncertainty estimation along with classification, particularly to differentiate cataracts from normal eye conditions. Abbas [27] identified, created, and executed a system called Glaucoma-Deep. It entails an unsupervised CNN architecture for automatically extracting features from fundus images. It subsequently employs a DBN model to identify the most discriminative features. Abu-Ein et al. [28] offered a hybrid methodology employing the Support Vector Machine and Naïve Bayes Classifier to identify bright lesions in eye fundus images, potentially aiding in screening various ocular disorders. A deep learning system utilizing a single modality was created based solely on retinal images to identify any disease-related vision impairment and moderate or greater disease-related visual impairment in the literature [29]. This approach underwent internal testing using a novel dataset from the Singapore Epidemiology of Eye Diseases Study and external validation in three population-based studies and two clinical investigations. A CNN-based system for the automated diagnosis of glaucoma using retinal fundus images, integrating transfer learning and data augmentation techniques, was introduced in the literature [30].
Glaucoma was detected in the study [31] using a deep residual learning algorithm applied to fundus images captured by several cameras across many institutions. Diagnosis accuracy was observed when image augmentation was employed to enhance the training dataset. Asaoka et al. [32] proposed a novel architecture for convolutional neural networks: the Tournament-based Ranking CNN. The results indicate significant improvements in performance for detecting the dominant classes, with only a slight reduction in accuracy for the dominant classes. This makes it an effective treatment for cataract grading.
Kim et al. [33] introduced a diagnostic methodology employing machine learning for the early identification of glaucoma in patients, utilizing 3D optical coherence tomography data and color fundus images. The method produced superior accuracy in separate CNN models compared to the combined random forests model, indicating significant promise for enhancing the diagnostic accuracy for glaucoma patients. An et al. [34] examined the effectiveness of deep convolutional neural networks (DCNNs) in identifying glaucoma from color fundus images. The findings demonstrated significant discriminative capability of DCNNs, with the optic disc identified as the most informative region for glaucoma classification.
Phan et al. [35] examined the application of deep convolutional neural networks to differentiate glaucoma in color fundus images. Research demonstrated that Deep Convolutional Neural Networks (DCNNs) can achieve significant discriminative capability, with the optic disc being the most informative region. Diaz-Pinto et al. [36] utilized five distinct ImageNet-trained models for the automatic assessment of glaucoma via fundus images, achieving an average AUC of 0.9605, an average specificity of 0.8580, and an average sensitivity of 0.9346 following comprehensive validation.
In addition, the previous works have not explored the effects of uncertainty on cataract predictions. The present study analyzes the predictions of the classification and prediction of cataract ocular disease and quantifies uncertainties using the BCNN model.
A typical research gap is that no studies have been conducted on classifying cataracts, a common ocular disease. In addition, the previous works have not explored the effects of uncertainty on cataract predictions. The present study analyzes the predictions of the classification and prediction of cataract ocular disease and quantifies uncertainties using the BCNN model.
Table 1 compares different cataract classification methods using accuracy metrics. Diaz-Pinto et al. [36] employed a deep neural network classifier to automatically classify cataract severity. The cataract is classified by the patients through this classifier, which will be normal, mild, medium, or severe. When comparing the results of this study with those of the previous studies [14,37,39–41] that used transfer learning and achieved an accuracy of 92.7%, 97.12%, 99.13%, 95.77%, and 92.48%, respectively, in classifying fundus images. Pratap et al. [42] introduced an automated eye disease recognition system from facial image-based visual content using D-CNN for cataract identification and achieved an accuracy of 92.91%. Imran et al. [43] proposed a pre-trained AlexNet and Support Vector Machine (SVM) cataract classifier, achieving 93.79% accuracy. Cao et al. [44] used a hybrid CNN model and SVM cataract classifier and achieved 92.87% accuracy. Imran et al. [45] applied hybrid CNN for cataract classification with an accuracy of 95.65%. Simanjuntak et al. [46] investigated to compare the effectiveness of four CNN architectures in classifying cataracts using fundus images. The results indicated that the proposed CNN model exhibits the highest level of accuracy and stability, with a score of 92%.
Fig. 1 illustrates the phases of the proposed procedure, which are based on the CNN and Bayesian CNN model for the classification of cataract or normal eye image aspect.
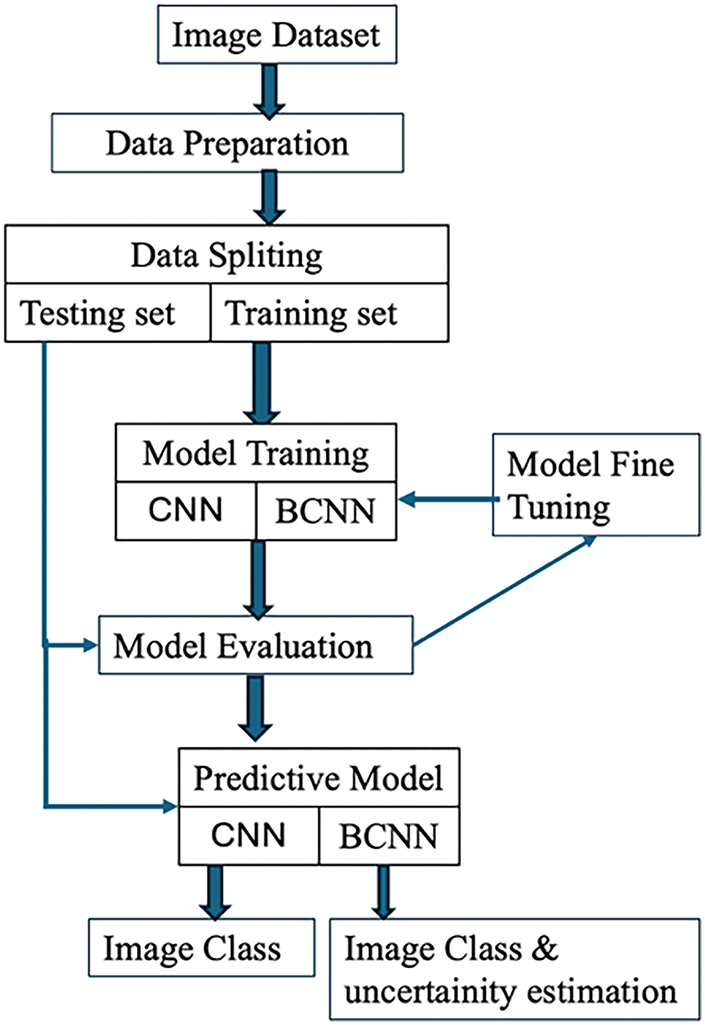
Figure 1: Workflow of the proposed model
Initially, the cataract fundus images are taken from standard data sources. Further, the preprocessed images are given as input to CNN, where the essential features are acquired for classification. Then, the BCNN model is evaluated to predict cataract conditions with uncertainty estimation.
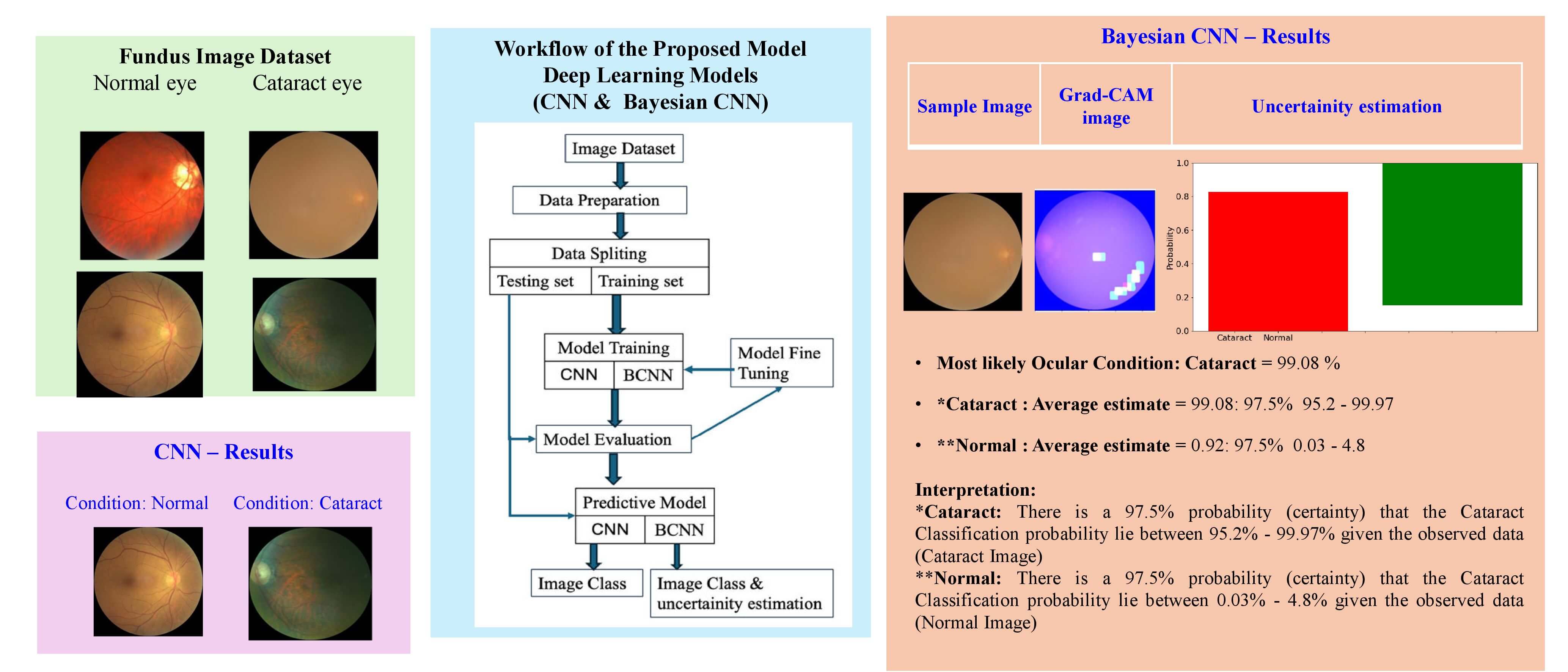
The ODIR [47] (Ocular Disease Intelligent Recognition) dataset contains color retinal photos of 5000 ophthalmic patients’ eyes. This study chooses the dataset options of normal state and cataract for training the model. For this study, the cataract and normal eye condition dataset (Fig. 2) contains 782 images, of which 188 are normal eye images and 594 cataract eye images. Following the experimental procedure, 90% of the image was used for training, and the remaining 10% of the data was employed as a test set. For data preprocessing, rescale and resize operations were made with images. Rescale is a value multiplied by the data before any other processing. The original images consist of RGB coefficients in the 0–255, but such values will be too high for the model to process, so target values between 0 and 1 instead by scaling with a 1/255. All images are resized to (75, 75) size.

Figure 2: Sample ocular fundus images of the (a) normal and (b) cataract condition
3.2.1 Convolutional Neural Network (CNN)
An important advantage of CNN is its automatic feature extraction. This network is also computationally efficient because of special convolution, pooling operations, and parameter sharing. CNN is an NN with a series of convolutional and pooling layers, and it is always possible to start working from randomly initialized weights and biases. The neural network architecture (Fig. 3) is used in all the modeling tasks.

Figure 3: Pictorial representation of the proposed CNN architecture
3.2.2 Bayesian Convolutional Neural Network
Bayesian neural networks involve the concept of treating neural network weights as random variables rather than fixed parameters. This approach enables capturing both parameter uncertainty and prediction variability, which is crucial for healthcare, where uncertainty in decision-making significantly affects patient outcomes.
Bayesian inference in neural networks: In traditional neural networks, the goal is to find weights w that minimize a loss function. In BNNs, the aim is to learn a posterior distribution over the weights p(w|D), conditioned on data D, using Bayes’ theorem in Eq. (1).
Approximations, such as variational inference, are necessary due to the high dimensionality of the weight space. Prediction with uncertainty: Given the approximate posterior, predictions for a new input x∗ are represented as given in Eq. (2).
Monte Carlo sampling is utilized to estimate this integral, providing predictions that account for uncertainty. BNNs quantify two types of uncertainty: Uncertainty due to lack of knowledge, captured by the posterior p(w|D), reducible with more data, is called Epistemic Uncertainty. Aleatoric Uncertainty involves the inherent noise in the data, often modeled as Gaussian noise in the network’s output. The total uncertainty is decomposed into these two components as given in Eq. (3).
Model Training with variational inference: training BNNs involves approximating the posterior p(w|D) using methods such as variational inference (VI). The variational distribution q(w|θ) approximates the posterior by minimizing the Kullback Leibler (KL) divergence in Eq. (4).
Maximizing the Evidence Lower Bound (ELBO) ensures a close approximation of the posterior in Eq. (5).
This Bayesian framework provides a full predictive distribution, incorporating epistemic uncertainty (uncertainty in the model parameters) and aleatoric uncertainty (inherent noise in the data).
Fig. 4 shows the difference between a standard CNN and a Bayesian CNN. CNN has single point estimates as weights, and Bayesian CNN has probability distributions over weights. CNN is an NN with convolutional and pooling layers that can randomly initialize its weights and biases, whereas Bayesian NN takes prior distribution on its weights and biases.

Figure 4: (a) CNN model and (b) Bayesian CNN model
Fig. 5 depicts the integration of the proposed deep CNN and Bayesian CNN models.

Figure 5: Integration of the designed cataract detection (a) CNN model (b) Bayesian CNN model
Therefore, the proposed Bayesian Convolutional Neural Network is a CNN commanded, with typical densities forced on the parameters as priors for multivariate model parametrization (Fig. 5b). CNN is established on the traditional structure. The model utilized the convolutional layer to extract the input features, followed by the fully connected dense layer to process the classification. Eventually, the BCNN can be obtained by applying simple Bayesian layers in the first convolution and the Last dense layer of the CNN model. The reparameterization of the BCNN requires the application of the Multivariate normal distribution, Prior normal distribution, Posterior Kullback-Leibler divergence, and posterior for kernel and bias [48]. A multivariate normal distribution describes any set of sometimes correlated random variables from real values in a frequent way. Statistical technology, which is a method of assumption-based inference, is used in a prior probability distribution of an uncertain quantity, also known as the prior. KL divergence is a difference calculating measure of the distribution of possibilities in one case from those in another. A KL divergence of X from Y is what one expects if the actual distribution is X when using distribution Y as a model instead of the distribution X, which is the excess surprise. An application of Bayes’ rule [49] takes the prior probability and updates it with the probability of the likelihood by applying the prior probability summary into the posterior probability, which forms via an approach.
The model is constructed using the TensorFlow backend and the Keras framework. The primary CNN employed is deep CNN. The model develops the deep CNN and BCNN frameworks. The comprehensive validation and training approach encompasses fine-tuning, training procedures, and testing. The input images are enhanced using a data preprocessing technique. In this study, all experimental data inputs consist of cataract and normal images with a resolution of 75 × 75. The model’s convolution layer is fixed with eight filters, a kernel size of 16, and ‘relu’ for the activation function. When training on the dataset, the number of output channels in the model’s convolutional layers is configured as follows: 32, 32, 64, and 64 for the four convolutional blocks, respectively. Each convolution block is followed by a 2 × 2 MaxPooling operation on the input image matrix. A max-pooling layer picks the largest value in the 2 × 2 window across the input image. The output matrix will be reduced in spatial dimensions by the pooling layer.
When the model is trained with small data, the function is learned inappropriately with no association with the uncertainty of the data. As a result, it is equally incapable of correctly assessing the uncertainty of the network or the model’s prediction. This way, the model has overconfidence in determining the correct classification or prediction. However, one can quantify the uncertainty since the SoftMax function adds up to 1, while using the dropout layer also allows for quantifying the uncertainty of the data in the training dataset. With this, it is possible to estimate the uncertainty in the model’s predictions by providing uncertainty estimates in the form of probability distributions through its parameters.
This study used Normal Priors, indicating that the cataract severity is normally distributed around an average with a known variation. This works when the studied values are expected to be grouped mostly around a known average. The dataset contains information on 594 cataract patients. The average age of the patients is 66.74 years, with a standard deviation of 11.72 years, showing some difference in ages among the patients. The youngest patient is 24 years old, while 25% of the patients are 60 or younger, half are 68, and 75% are 75 or younger. This shows that most patients are older adults.
This study used Spike-and-Slab prior, which was helpful in BCNNs because of its sparsity and flexibility. These prior mixes two Gaussian distributions: one narrow, or spike, and one wider, or slab. The spike has a small standard deviation of 1 to encourage weights to be close to zero and induce sparsity. The slab has a larger standard deviation of 10, is more flexible, and has bigger weight values. These distributions are now combined using a Categorical distribution to create the mixture model, with equal chances (50–50) for each. Fig. 6 shows the Spike-and-Slab distribution, which mixes a sharp peak to encourage many weights to be close to zero with a wide area for bigger weight values. This combination helps balance control and flexibility, making it useful for Bayesian Convolutional Neural Networks. It prevents the model from fitting the data too closely while still identifying important patterns.

Figure 6: Normal prior distribution of BCNN model
The spike-and-slab prior greatly affects how well BCNN works by helping to balance three important things: controlling complexity, allowing the model to learn important patterns, and estimating uncertainty. The spike part helps the model use fewer weights, which prevents it from becoming too complex and overfitting the data. The slab part lets the model use larger weights when needed to focus on important features in the data. Also, the way this prior combined probability makes the BCNN better at estimating uncertainty. This is crucial for making reliable predictions in areas such as medical diagnosis or risk evaluation.
The proposed model uses TensorFlow Probability’s Reparameterization layers such as tfpl. Convolution2DReparameterization and tfpl. DenseReparameterization that handles uncertainties in parameters with probability distributions. Other methods use fixed values for weights, whereas each weight and bias is treated as a probability distribution in this case. This probabilistic approach enables the model to consider changes in learned parameters to make predictions more reliable. It also provides an improved understanding of uncertainty, which is important for improving prediction accuracy.
The Convolution2DReparameterization layer in the code introduces a method to measure uncertainty by treating the weights and biases as probability distributions rather than fixed values. This is achieved using prior and posterior distributions. The prior represents initial assumptions, while the posterior adjusts based on the data. A KL divergence term in the loss function ensures that the learned parameters stay close to the prior, reducing the risk of overfitting. The model can better indicate confidence in its predictions, making it more reliable, especially when working with noisy or limited data, by incorporating uncertainty. This approach enhances the model’s ability to generalize and increases its overall reliability.
DenseReparameterization handles the uncertainty in the output layer, which is considered to be some distribution, for example, OneHotCategorical. It lets the probabilistic prediction be made instead of point predictions, which can further help the model convey uncertainty regarding its classification decisions. The Bayesian methods’ ideas regarding prior and posterior distributions make this model more explainable, and it can also work with uncertain inputs. The KL divergence term ensures that the learned parameters do not move too far away from the prior without strong evidence from the data, improving the model’s performance and giving more reliable predictions, especially in uncertain or complicated situations.
The model summary of the CNN and BCNN used for this research is depicted in Tables 2 and 3.
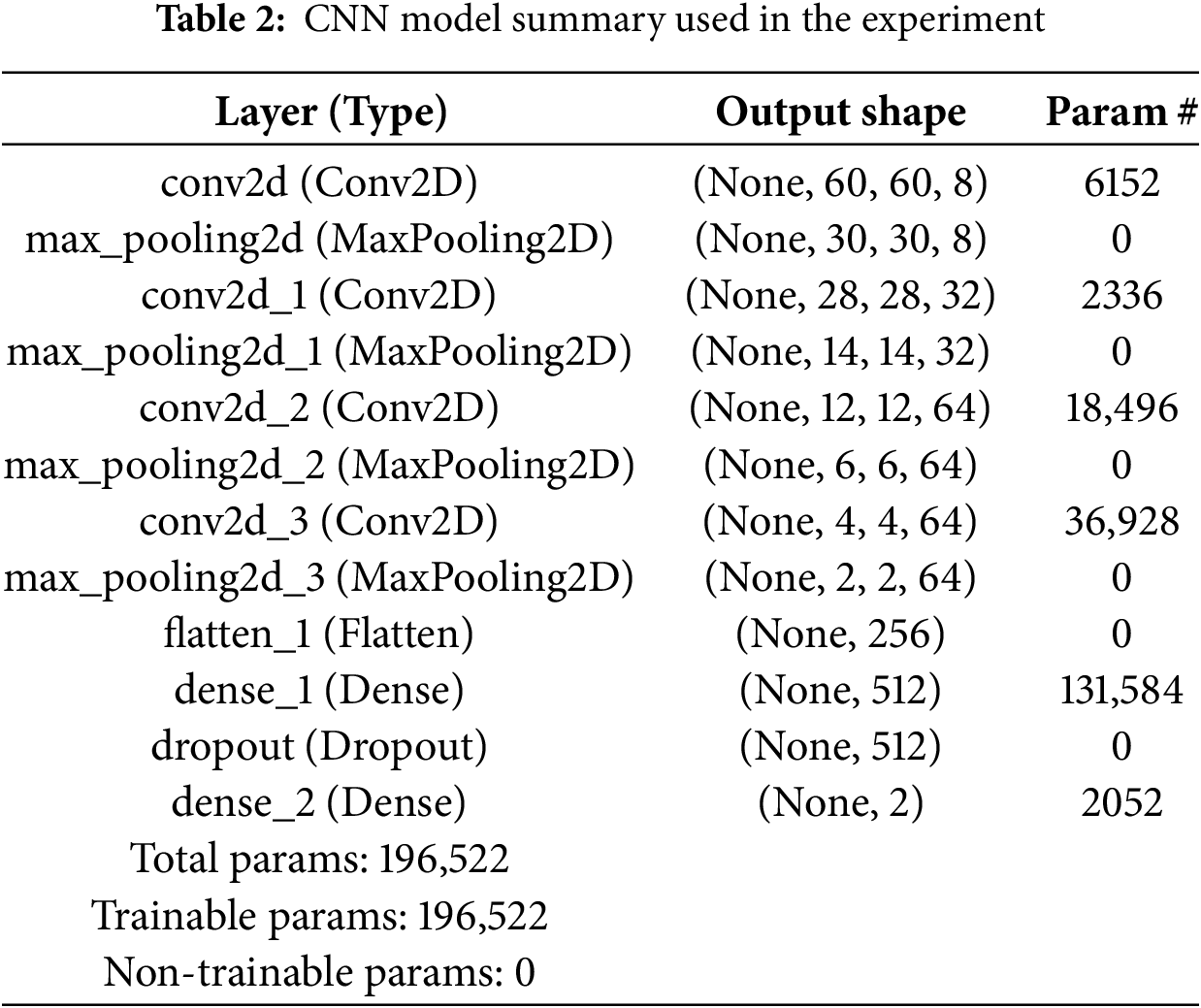
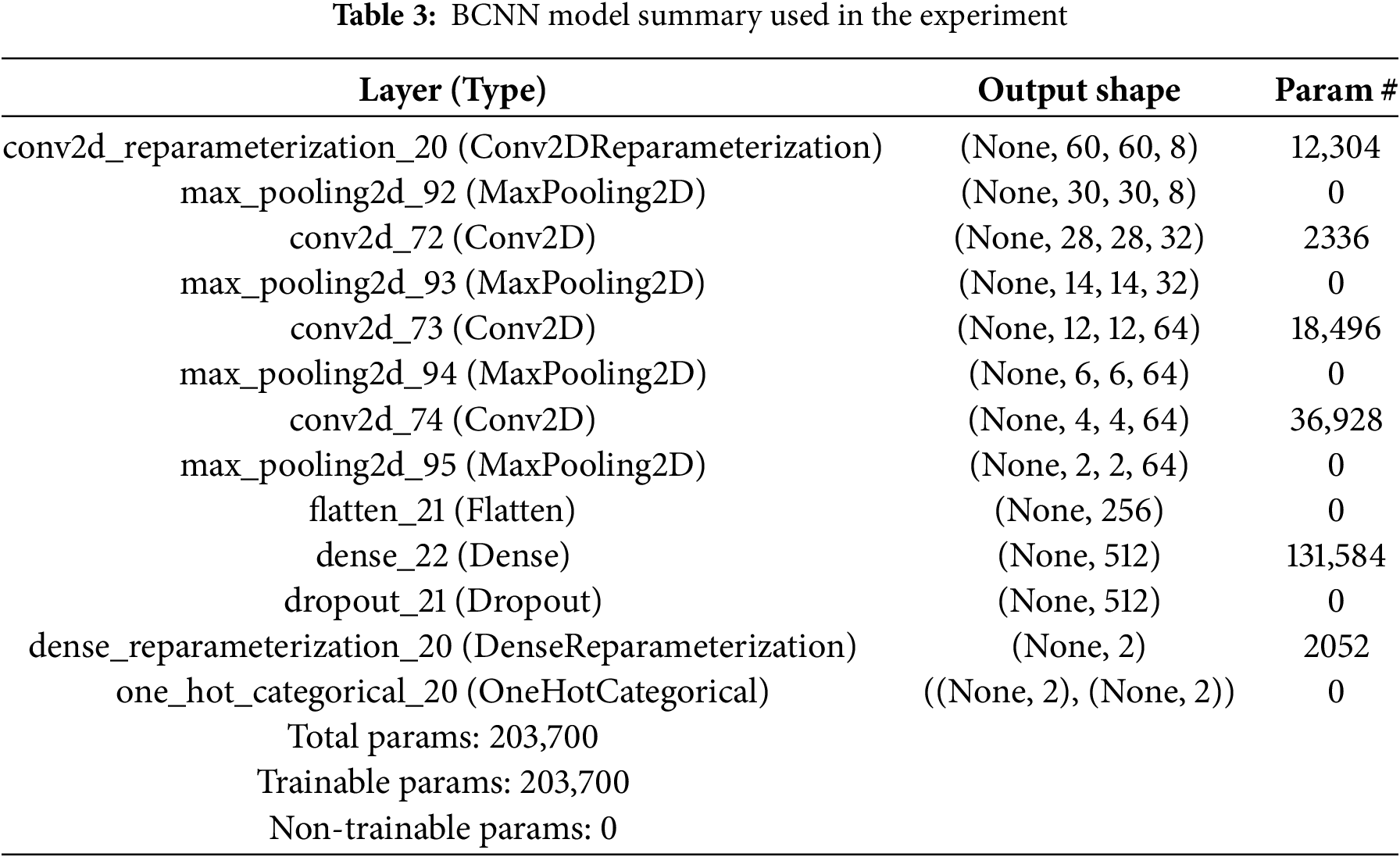
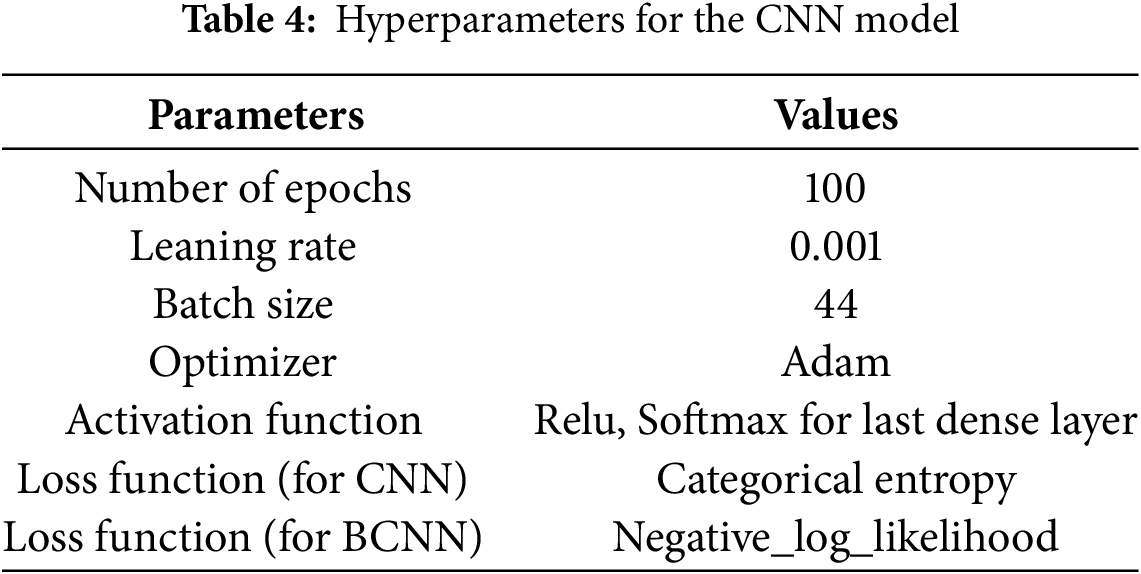
Table 4 lists the different hyperparameters used in this study. The suitable values of these hyper-parameters are achieved by tuning them vigorously. The input image size 75 × 75 for both CNN and BCNN models is used. For batch size, 44 for both models are employed. As an optimizer, the Adam (adaptive learning rate optimization algorithm) optimizer method is utilized. For CNN, the loss function is Categorical entropy and negative_log_likelihood_fpr BCNN model. The number of epochs used is 100 for all models.
The softmax activation function is often placed at the output layer of a neural network. It is commonly used in multi-class learning problems where a set of features can be related to one-of N classes. The loss function is categorical cross-entropy. Categorical cross-entropy is for multi-class classification but works for binary classification. For categorical cross-entropy, categorical data must change using one-hot encoding. The optimizer is Adam. If one wants to train the neural network in less time and more efficiently, then Adam is the best optimizer to select. Since this is a classification problem, the accuracy metric is used, and the data is nearly evenly balanced. Accuracy = Number of correct predictions over the total number of predictions. Validation metric accuracy is employed to get a sense of generalizability. Validation metrics provide a better sense of generalizability. Negative log-likelihood (NLL) is a loss function used in multi-class classification. In deep neural networks, the cross-entropy loss function is commonly used for classification. Minimizing cross-entropy is equivalent to maximizing likelihood under uniform features and class distribution assumptions.
The results of the BCNN model for tuning the number of neurons in each layer for preparing the model are listed in Table 3. Fig. 7 presents the accuracy of the CNN model, and Fig. 8 shows the prediction results of the CNN model. The CNN model achieved the results of testing accuracy of 91.25%.
Figure 7: Performance results of the CNN model
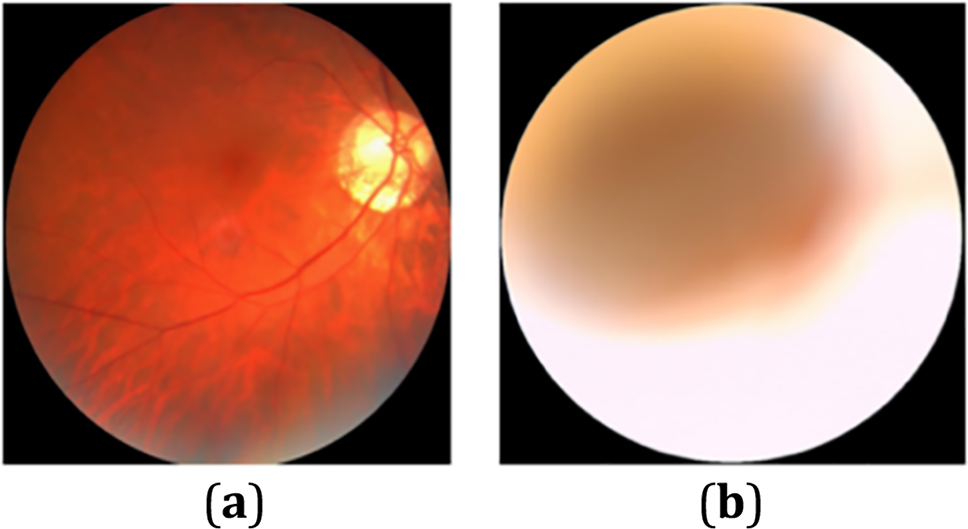
Figure 8: CNN model prediction result: (a) condition: normal (b) condition: cataract
The BCNN model achieved 92.5% accuracy as given in Fig. 9.

Figure 9: Performance results of the BCNN model
Table 5 illustrates the image generated by GRADCAM on the model for various samples of fundus eye images. The brighter yellow color of the image indicates the features in the input image that generate predictions. These visualization models provide insights into the areas where the BCNN model focuses its attention when making predictions.
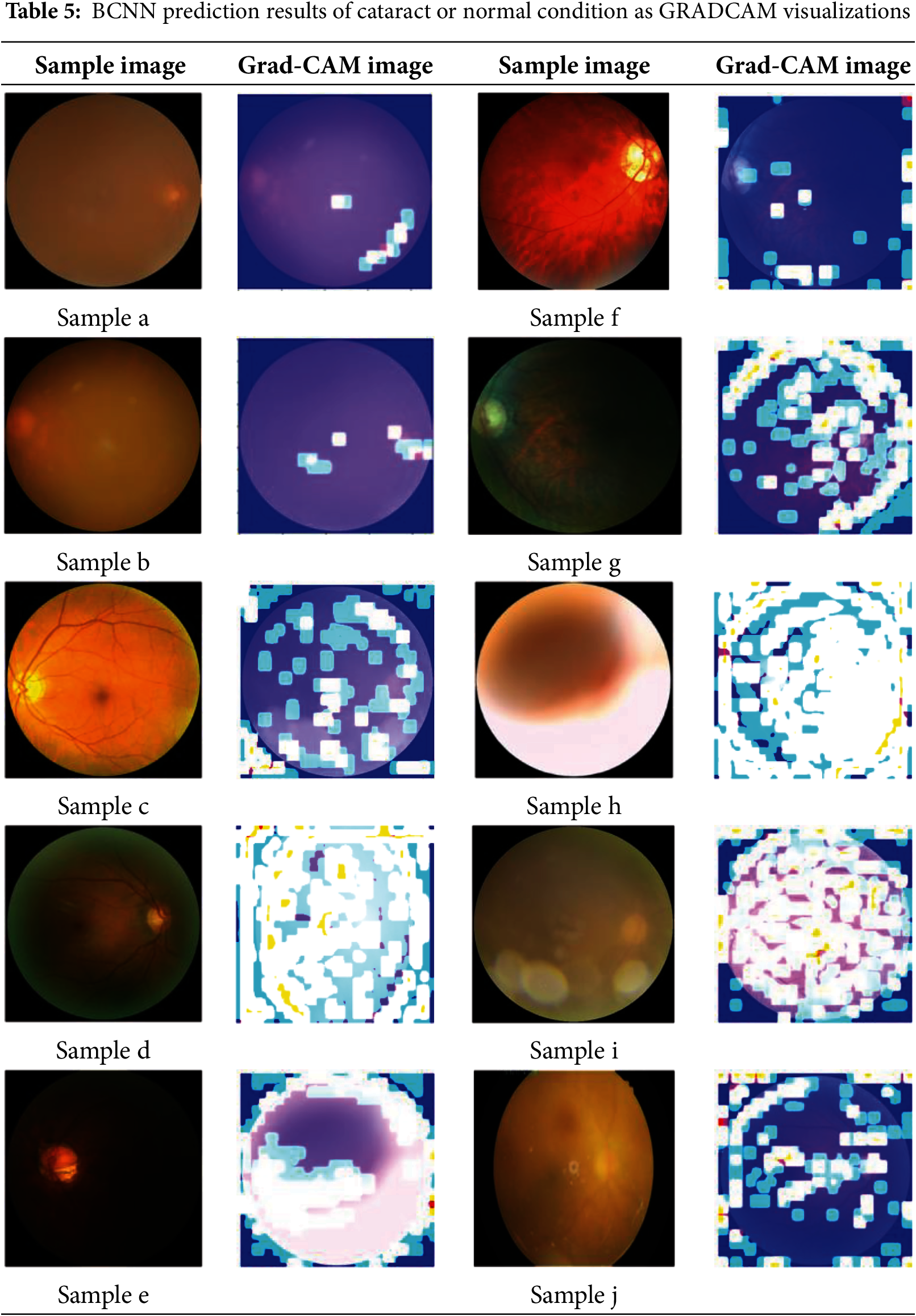
The prediction of various images using BCNN is detailed in Table 6. Since Bayesian methods employ probabilities to represent uncertainty, probabilistic is a neutral way of saying something that comes from a proper interpretation. If the aleatoric and epistemic are indicated in the Bayesian CNN model result (Table 3), both are retained when predicting image cataracts. The same is reflected in the aleatoric uncertainty, and the model now assigns an intermediate probability to the normal class. The model does not know, as shown by the epistemic uncertainty, which means that it is uncertain how large a quantity should be estimated for each ocular disease class (cataract and normal).
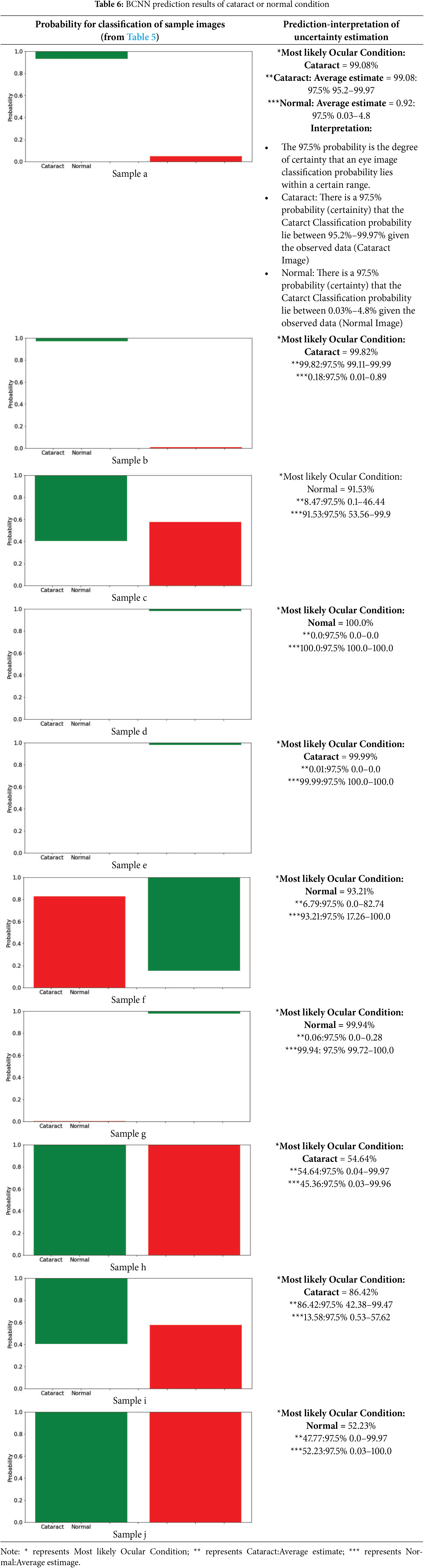
Interpretation of the uncertainty using probability: This study sets the model to iterate 300 times, and then the model will be assigned a single image to predict. From these 300 predictions, a prediction interval for the probabilities will be created (i.e., 97.5% credible interval).
• The 97.5% probability is the confidence level that it can expect a range in which an image classification’s probability lies.
• Cataract: The observed data Cataract Image defines a 97.5% probability (certainty) interval of the Cataract classification probability to be within [43.35%, 58%] (Cataract Image).
• Normal: There is a 97.5% probability (certainty) that the Cataract classification probability lies between 41.4%–56.65%) given in the current observation (Normal Image).
4.2 Performance Estimation among Classifiers
The evaluation results of the BCNN model are detailed in Table 7. It must compare with the recently published works on cataract eye disease recognition work to evaluate the proposed model for cataract eye recognition using uncertainty estimation with BCNN. It was observed that most of the works do not focus on BCNN for uncertainty estimation, which makes it impossible to compare the work of others. However, this study makes some comparisons and finds the result analysis, as shown in Table 5.
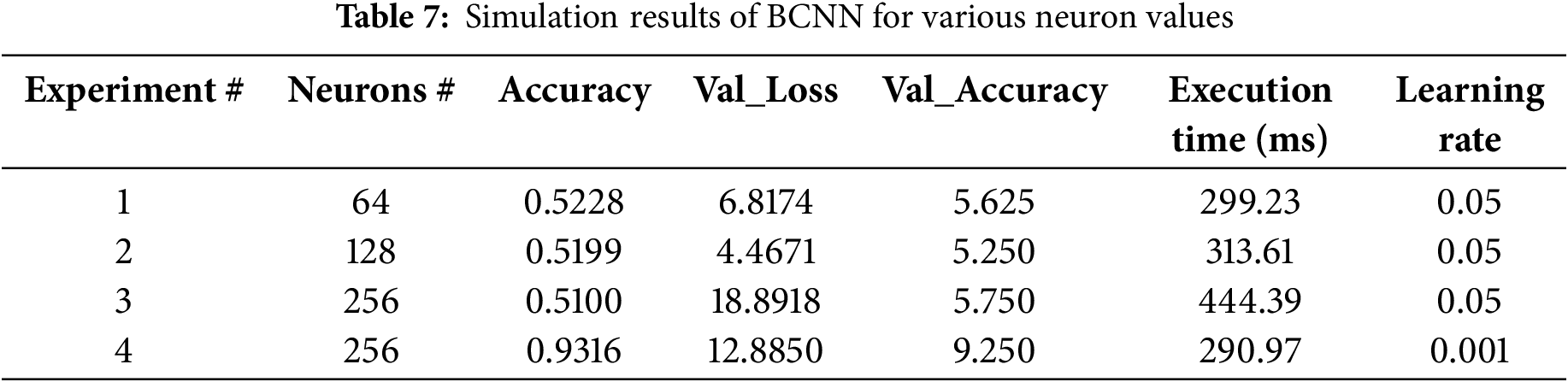
Fig. 10 represents these metrics for both classes, showing how each class performs across precision, recall, and F1 scores.

Figure 10: Performance metrics of cataract class and normal class
Correlation Between Uncertainty and Performance Metrics: Precision shows how accurate the positive predictions are. Higher precision means fewer incorrect positive results. For the Cataract group, the precision is 0.9278, meaning 92.78% of the predictions about cataracts are correct. The Normal group’s precision is 0.8182, meaning 81.82% of the predictions about normal images are accurate. It has been observed that predictions with high precision generally had lower uncertainty bounds. However, the associated uncertainty was higher in cases where false positives were observed. This highlights the model’s ability to quantify ambiguity in its predictions when it struggles to differentiate between classes. Recalling measures how well all positive cases are identified. Higher recall means fewer missed positive cases. The Cataract group has a recall of 0.9184, meaning 91.84% of actual cataract cases were correctly found. The Normal group has a recall of 0.9209, meaning 92.09% of normal images were correctly identified. In cases of lower recall, particularly for ambiguous or borderline images, wider uncertainty intervals have been observed. This suggests that the model captures inherent ambiguities in difficult cases where distinguishing between classes is challenging. F1 score balances precision and recall, giving a combined measure of both. A strong correlation was noted between high F1 scores and narrower uncertainty intervals, implying that when the model achieves a good balance between precision and recall, it also exhibits higher confidence in its predictions.
The proposed model is qualified and evaluated repeatedly (100 epochs) to obtain the result displayed in Table 8. Fig. 11 depicts a visual depiction of the accuracy rate of the proposed classification model at each epoch. A strong fit model is demonstrated by the training and validation accuracy, with the smallest gap between the accuracy values in training and validation sessions.
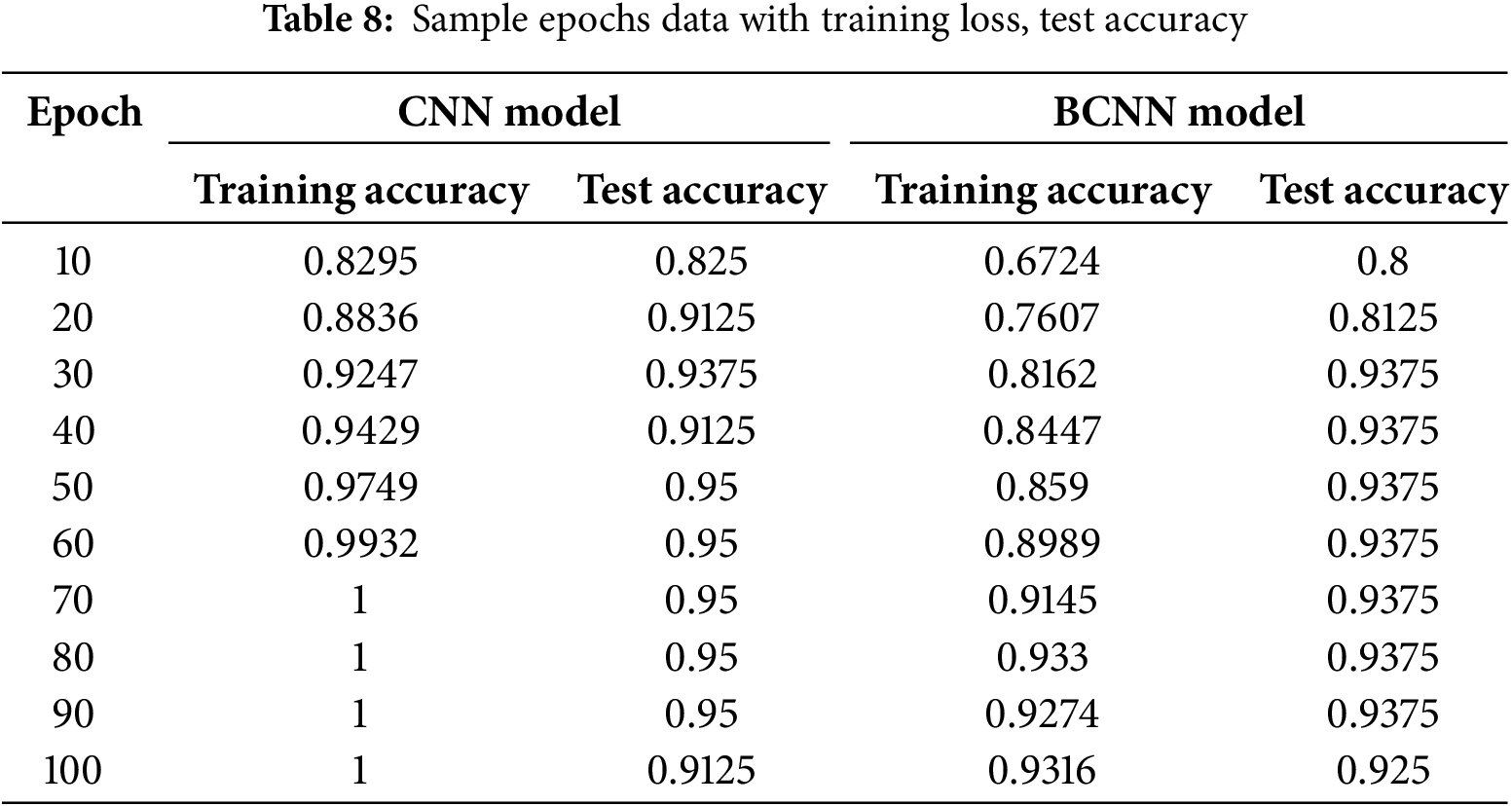

Figure 11: CNN vs. BCNN performance comparison
The best training accuracy during epoch 70 was 100% (training accuracy) and 95% (testing accuracy) for the CNN model, and the BCNN model has 91.45% (training accuracy) and 93.75% (testing accuracy), indicating that the models can provide a reasonable classification result even with appropriate epochs. The testing accuracy curve resembles the training accuracy curve in that the outcome improves as the training progresses. At the 100th epoch, the curve drops to 91.25% for the CNN model and 92.50% for the BCNN model. So, the greatest testing accuracy of CNN was 95% and 93.75% for the BCNN model.
The data in Table 9 demonstrates the proposed methodology’s performance compared to other state-of-the-art methods. In addition, some of the previous studies exhibited higher accuracy than that of the proposed BCNN model. This difference can be attributed to the substantial difference in the dataset size compared to previous studies.
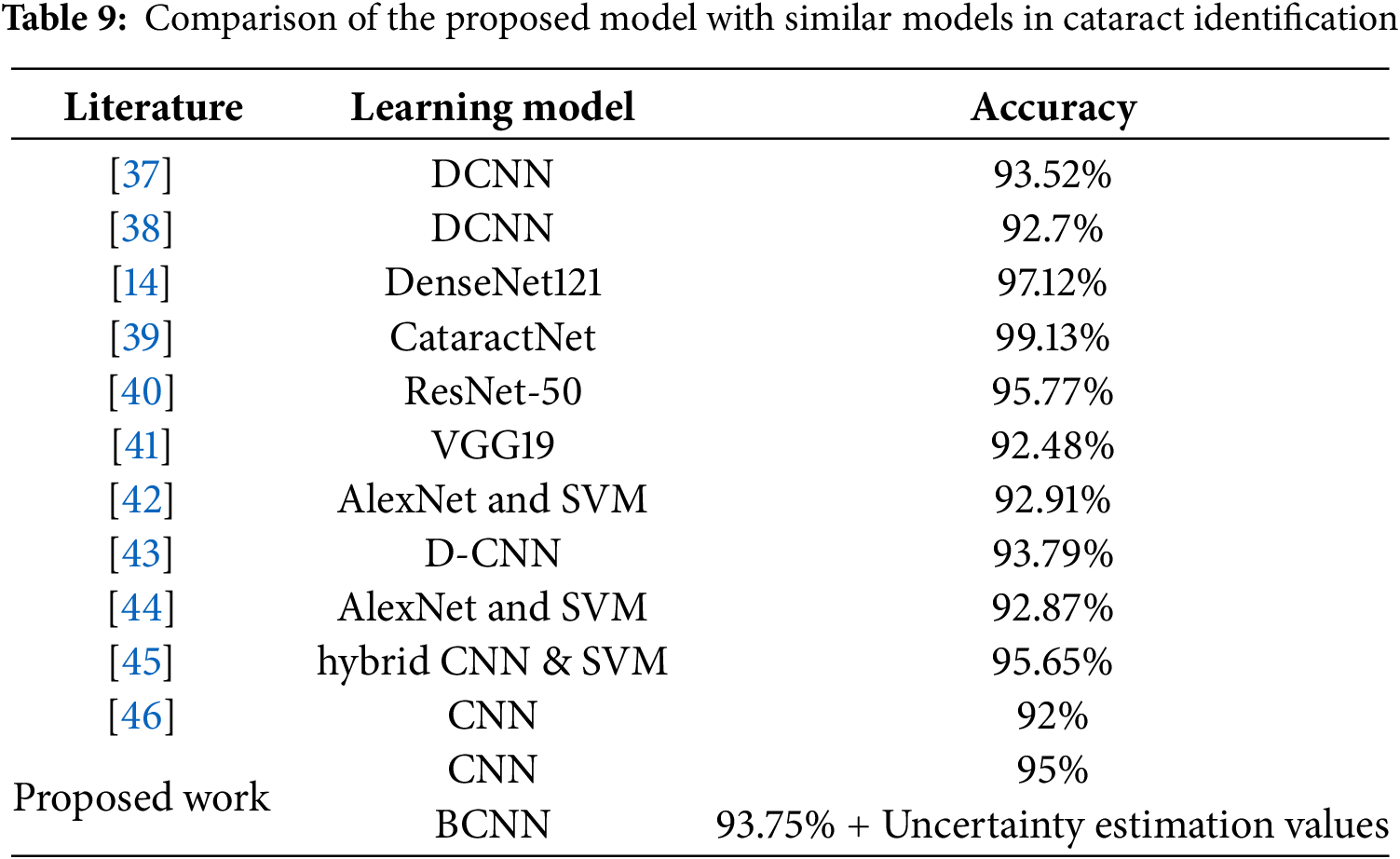
The methodology outlined in [14] demonstrates notable accuracy, which involves four-stage cataract classification and grading (97.12%). The methodology presented in [14] focuses on a classification task encompassing four categories: mild, moderate, severe cataracts, and normal eyes, utilizing a convolutional neural network in conjunction with ensemble learning. Their emphasis is on optimizing accuracy within this multi-class classification framework.
In contrast, our study focuses on a specific dimension of cataract analysis. Our objective is to estimate the uncertainty in predictions for binary classification (cataract vs. normal eye), rather than solely focusing on classification accuracy. While reference [14] focuses on attaining high multi-class accuracy via ensemble learning, our research progresses the field by addressing a significant yet underexplored aspect: the quantification of prediction uncertainty.
This contribution complements methodologies such as [14], as uncertainty-aware systems can function as an initial screening tool to identify high-risk cases for further multi-class analysis. This study does not aim to directly compete with [14] regarding multi-class classification accuracy. This work addresses a significant gap in the field by enhancing the reliability and robustness of cataract detection systems through uncertainty quantification.
The BCNN model for cataract prediction with prediction probability values is developed using fundus images based on deep learning. First, the cataract images needed for the research are collected from the Kaggle data source. Then, the CNN and BCNN frameworks are utilized to classify cataracts and normal eye conditions. The experimental findings of the proposed BCNN model are evaluated with other existing classification models to verify its performance. The accuracy of the performed BCNN-based model is 93.75%, which is 1.25% improved than the CNN model. Also, the implemented BCNN-based cataract detection model provided uncertainty estimation results and a GRAD-CAM visual of the result. The results demonstrate that BCNN outperforms traditional CNN in accuracy and decision-making robustness due to its improved uncertainty handling.
The limitation of the proposed study involves the prediction of only the cataract condition of the ocular diseases. The study suggests that additional data preprocessing and parameter tuning can improve diagnostic accuracy. Future research can focus on applying the BCNN for various ocular disease predictions. Researchers can expand their knowledge by testing various BCNN backbone designs. Looking into the benefits of transfer learning from models trained on bigger medical image datasets and then adjusting them for cataract detection is a good idea. Although this study concentrates on how the methods improve diagnosis, future work should also check how well the suggested method works in practice. This means comparing it to other top methods to ensure it is accurate and valuable in real medical settings.
Acknowledgement: The authors would like to express their gratitude to King Khalid University, Saudi Arabia, for providing administrative and technical support. Also, the authors would like to thank the referees for their comments and suggestions on the manuscript.
Funding Statement: The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University, Saudi Arabia for funding this work through Small Research Group Project under Grant Number RGP.1/316/45.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Anandhavalli Muniasamy; data collection: Anandhavalli Muniasamy; analysis and interpretation of results: Anandhavalli Muniasamy, Aswag Alasmari; draft manuscript preparation: Anandhavalli Muniasamy. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are openly available in Kaggle at https://www.kaggle.com/datasets/andrewmvd/ocular-disease-recognition-odir5k (accessed on 21 August 2024).
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Panda SK, Panjwani N. Cataract detection using deep learning. Res Sq. 2023;69(1):1–12. doi:10.21203/rs.3.rs-3178940/v1. [Google Scholar] [CrossRef]
2. Rana J, Galib SM. Cataract detection using smartphone. In: Proceedings of 3rd International Conference on Electrical Information and Communication Technology (EICT); 2017 Dec 7–9; Khulna, Bangladesh. p. 1–4. [Google Scholar]
3. Gutierrez L, Lim JS, Foo LL, Ng WY, Yip M, Lim GYS, et al. Application of artificial intelligence in cataract management: current and future directions. Eye Vis. 2022;9(1):3. doi:10.1186/s40662-021-00273-z. [Google Scholar] [PubMed] [CrossRef]
4. World report on vision. Geneva, Switzerland: World Health Organization; 2019 [cited 2025 Jan 1]. Available from: https://www.who.int/publications/i/item/9789241516570. [Google Scholar]
5. Abbas Q, Qureshi I, Yan J, Shaheed K. Machine learning methods for diagnosis of eye-related diseases: a systematic review study based on ophthalmic imaging modalities. Arch Comput Meth Eng. 2022;29(6):3861–918. doi:10.1007/s11831-022-09720-z. [Google Scholar] [CrossRef]
6. Tognetto D, Giglio R, Vinciguerra AL, Milan S, Rejdak R, Rejdak M, et al. Artificial intelligence applications and cataract management: a systematic review. Surv Ophthalmol. 2022;67(3):817–29. doi:10.1016/j.survophthal.2021.09.004. [Google Scholar] [PubMed] [CrossRef]
7. Vision Loss Expert Group of the Global Burden of Disease Study, 2019 Blindness and Vision Impairment Collaborators GBD. Global estimates on the number of people blind or visually impaired by cataract: a meta-analysis from 2000 to 2020. Eye. 2024;38(11):2156–72. doi:10.1038/s41433-024-02961-1. [Google Scholar] [PubMed] [CrossRef]
8. Li T, Bo W, Hu C, Kang H, Liu H, Wang K, et al. Applications of deep learning in fundus images: a review. Med Image Anal. 2021;69(3):101971. doi:10.1016/j.media.2021.101971. [Google Scholar] [PubMed] [CrossRef]
9. Taylor M, Liu X, Denniston A, Esteva A, Ko J, Daneshjou R, et al. Raising the bar for randomized trials involving artificial intelligence: the SPIRIT-artificial intelligence and CONSORT-artificial intelligence guidelines. J Investig Dermatol. 2021;141(9):2109–11. doi:10.1016/j.jid.2021.02.744. [Google Scholar] [PubMed] [CrossRef]
10. Zangalli C, Gupta SR, Spaeth GL. The disc as the basis of treatment for glaucoma. Saudi J Ophthalmol. 2011;25(4):381–7. doi:10.1016/j.sjopt.2011.07.003. [Google Scholar] [PubMed] [CrossRef]
11. Divya L, Jacob J. Performance analysis of glaucoma detection approaches from fundus images. Procedia Comput Sci. 2018;143(1):544–51. doi:10.1016/j.procs.2018.10.429. [Google Scholar] [CrossRef]
12. Barros DMS, Moura JCC, Freire CR, Taleb AC, Valentim RAM, Morais PSG. Machine learning applied to retinal image processing for glaucoma detection: review and perspective. Biomed Eng Online. 2020;19(1):20. doi:10.1186/s12938-020-00767-2. [Google Scholar] [PubMed] [CrossRef]
13. Benet D, Pellicer-Valero OJ. Artificial intelligence: the unstoppable revolution in ophthalmology. Surv Ophthalmol. 2022;67(1):252–70. doi:10.1016/j.survophthal.2021.03.003. [Google Scholar] [PubMed] [CrossRef]
14. Yadav S, Yadav JKPS. Enhancing cataract detection precision: a deep learning approach. Traitement Signal. 2023;40(4):1413–24. doi:10.18280/ts.400410. [Google Scholar] [CrossRef]
15. Mahmud Khan MS, Ahmed M, Rasel RZ, Khan MM. Cataract detection using convolutional neural network with VGG-19 model. In: Proceedings of IEEE World AI IoT Congress (AIIoT); 2021 May 10–13; Seattle, WA, USA. p. 209–12. [Google Scholar]
16. Goh JHL, Lim ZW, Fang X, Anees A, Nusinovici S, Rim TH, et al. Artificial intelligence for cataract detection and management. Asia Pac J Ophthalmol. 2020;9(2):88–95. doi:10.1097/01.APO.0000656988.16221.04. [Google Scholar] [PubMed] [CrossRef]
17. Nguyen A, Lee K. Bayesian neural networks for healthcare applications. J Comput Intell. 2023;85:100–15. [Google Scholar]
18. LeCun Y, Bengio Y. Deep learning in healthcare. Artif Intell Med. 2024;98:45–60. [Google Scholar]
19. Hinton G. Neural networks and machine learning. J AI Res. 2024;95:102–17. [Google Scholar]
20. Gal Y, Ghahramani Z. Uncertainty in deep learning models for healthcare applications. J Stat AI. 2025;82:99–115. [Google Scholar]
21. Neal RM. Bayesian methods for machine learning in health informatics. Med Data Sci J. 2024;52:67–89. [Google Scholar]
22. Kumar S, Patel R. Uncertainty quantification in AI-driven diagnostics. Int J Health Inform. 2023;72:33–50. [Google Scholar]
23. Ngartera L, Ali Issaka M, Nadarajah S. Application of Bayesian neural networks in healthcare: three case studies. Mach Learn Knowl Extr. 2024;6(4):2639–58. doi:10.3390/make6040127. [Google Scholar] [CrossRef]
24. Cheng H, Gao S. Bayesian LSTMs for predicting disease progression. J Health Inform Res. 2025;33:25–140. [Google Scholar]
25. Smith J, Taylor R. Early detection of Alzheimer’s disease using Bayesian neural networks. J Med Imaging AI. 2024;61:76–92. [Google Scholar]
26. McDermott M, Mohnson E. Bayesian neural networks for personalized treatment. J Clin Mach Learn. 2024;58:101–20. [Google Scholar]
27. Abbas Q. Glaucoma-deep: detection of glaucoma eye disease on retinal fundus images using deep learning. Int J Adv Comput Sci Appl. 2017;8(6):41–5. doi:10.14569/issn.2156-5570. [Google Scholar] [CrossRef]
28. Abu-Ein AA, Tahat NM, Al-Smadi MM, Al-Nawashi MM. Combining artificial intelligence and image processing for diagnosing diabetic retinopathy in retinal fundus images. Int J Online Eng. 2022;18(13):131–51. doi:10.3991/ijoe.v18i13.33985. [Google Scholar] [CrossRef]
29. Gharaibeh N, Al-hazaimeh OM, Abu-Ein A, Nahar KMO. A hybrid SVM NAÏVE-BAYES classifier for bright lesions recognition in eye fundus images. Int J Electr Eng Inform. 2021;13(3):530–45. [Google Scholar]
30. Tham YC, Anees A, Zhang L, Goh JHL, Rim TH, Nusinovici S, et al. Referral for disease-related visual impairment using retinal photograph-based deep learning: a proof-of-concept, model development study. Lancet Digit Health. 2021;3(1):e29–40. doi:10.1016/S2589-7500(20)30271-5. [Google Scholar] [PubMed] [CrossRef]
31. Maheshwari S, Kanhangad V, Pachori RB. CNN-based approach for glaucoma diagnosis using transfer learning and LBP-based data augmentation. [cited 2025 Jan 1]. Available from: http://arxiv.org/abs/2002.08013. [Google Scholar]
32. Asaoka R, Tanito M, Shibata N, Mitsuhashi K, Nakahara K, Fujino Y, et al. Validation of a deep learning model to screen for glaucoma using images from different fundus cameras and data augmentation. Ophthalmol Glaucoma. 2019;2(4):224–31. doi:10.1016/j.ogla.2019.03.008. [Google Scholar] [PubMed] [CrossRef]
33. Kim D, Jun TJ, Eom Y, Kim C, Kim D. Tournament based ranking CNN for the cataract grading. In: Proceedings of Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC); 2019 Jul 23–27; Berlin, Germany. p. 1630–6. [Google Scholar]
34. An G, Omodaka K, Hashimoto K, Tsuda S, Shiga Y, Takada N, et al. Glaucoma diagnosis with machine learning based on optical coherence tomography and color fundus images. J Healthc Eng. 2019;2019:4061313. doi:10.1155/2019/4061313. [Google Scholar] [PubMed] [CrossRef]
35. Phan S, Satoh S, Yoda Y, Kashiwagi K, Oshika T, Japan Ocular Imaging Registry Research Group. Evaluation of deep convolutional neural networks for glaucoma detection. Jpn J Ophthalmol. 2019;63(3):276–83. doi:10.1007/s10384-019-00659-6. [Google Scholar] [PubMed] [CrossRef]
36. Diaz-Pinto A, Morales S, Naranjo V, Köhler T, Mossi JM, Navea A. CNNs for automatic glaucoma assessment using fundus images: an extensive validation. Biomed Eng Online. 2019;18(1):29. doi:10.1186/s12938-019-0649-y. [Google Scholar] [PubMed] [CrossRef]
37. Sarki R, Ahmed K, Wang H, Zhang Y. Automatic detection of diabetic eye disease through deep learning using fundus images: a survey. IEEE Access. 2020;8:151133–49. doi:10.1109/ACCESS.2020.3015258. [Google Scholar] [CrossRef]
38. Varma N, Yadav S, Yadav JKPS. A reliable automatic cataract detection using deep learning. Int J Syst Assur Eng Manag. 2023;14(3):1089–102. doi:10.1007/s13198-023-01923-2. [Google Scholar] [CrossRef]
39. Junayed MS, Islam MB, Sadeghzadeh A, Rahman S. CataractNet: an automated cataract detection system using deep learning for fundus images. IEEE Access. 2021;9:128799–808. doi:10.1109/ACCESS.2021.3112938. [Google Scholar] [CrossRef]
40. Hossain MR, Afroze S, Siddique N, Hoque MM. Automatic detection of eye cataract using deep convolution neural networks (DCNNs). In: Proceedings of the 2020 IEEE Region 10 Symposium (TENSYMP); 2020 Jun 5–7; Dhaka, Bangladesh. p. 1333–8. [Google Scholar]
41. Chakraborty S, Jana S. Early prediction of cataract using convolutional neural network. In: Proceedings of the 2023 IEEE Devices for Integrated Circuit (DevIC); 2023 Apr 7–8; Kalyani, India. p. 446–50. [Google Scholar]
42. Pratap T, Kokil P. Computer-aided diagnosis of cataract using deep transfer learning. Biomed Signal Process Contr. 2019;53(5):101533. doi:10.1016/j.bspc.2019.04.010. [Google Scholar] [CrossRef]
43. Imran A, Li J, Pei Y, Mokbal FM, Yang JJ, Wang Q. Enhanced intelligence using collective data augmentation for CNN based cataract detection. In: Hung J, Yen N, Chang JW, editors. Frontier computing. Vol. 551. Berlin/Heidelberg, Germany: Springer; 2020. p. 148–60. [Google Scholar]
44. Cao L, Li H, Zhang Y, Zhang L, Xu L. Hierarchical method for cataract grading based on retinal images using improved Haar wavelet. Inf Fusion. 2020;53(34):196–208. doi:10.1016/j.inffus.2019.06.022. [Google Scholar] [CrossRef]
45. Imran A, Li J, Pei Y, Akhtar F, Yang JJ, Dang Y. Automated identification of cataract severity using retinal fundus images. Comput Meth Biomech Biomed Eng Imag Vis. 2020;8(6):691–8. doi:10.1080/21681163.2020.1806733. [Google Scholar] [CrossRef]
46. Simanjuntak RBJ, Fuâ Y, Magdalena R, Saidah S, Wiratama AB, Ubaidah IDS. Cataract classification based on fundus images using convolutional neural network. JOIV: Int J Inform Visualization. 2022;6(1):33. doi:10.30630/joiv.6.1.856. [Google Scholar] [CrossRef]
47. ODIR (Ocular Disease Intelligent Recognition) Dataset. [cited 2025 Jan 1]. Available from: https://www.kaggle.com/datasets/andrewmvd/ocular-disease-recognition-odir5k. [Google Scholar]
48. Lambert B. The posterior—the goal of Bayesian inference. In: A Student’s guide to Bayesian statistic. Thousand Oaks, CA, USA: SAGE Publications Ltd. 2018. p. 121–40. [Google Scholar]
49. Soch J, Maja, Monticone P, Faulkenberry TJ, Kipnis A, Allefeld C, et al. The book of statistical proofs. Geneva, Switzerland: Zenodo; 2023. [Google Scholar]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF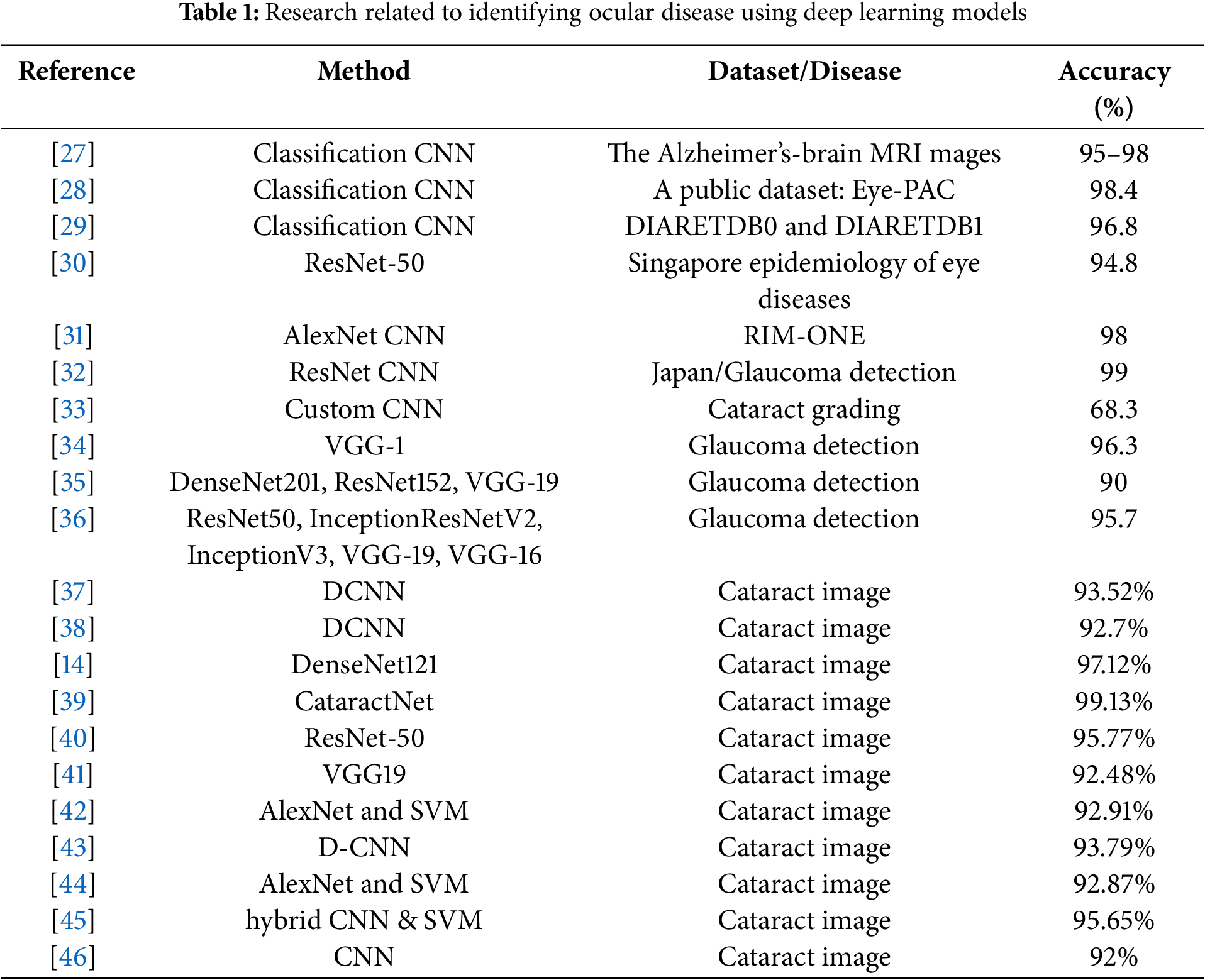
 Downloads
Downloads
 Citation Tools
Citation Tools