 Open Access
Open Access
ARTICLE
Chaos-Based Novel Watermarked Satellite Image Encryption Scheme
1 Applied College of Muhayil Aseer, King Khalid University, Abha, 62529, Saudi Arabia
2 Center for Scientific Research and Entrepreneurship, Northern Border University, Arar, 73213, Saudi Arabia
3 Department of Computer Engineering, College of Engineering, Knowledge University, Erbil, 44001, Iraq
4 Department of Computer Engineering, Al-Kitab University, Altun Kupri, 36001, Iraq
5 Department of Informatics and Its Teaching Methods, Tashkent State Pedagogical University, Tashkent, 100070, Uzbekistan
6 Department of Industrial Engineering, College of Engineering, University of Bisha, Bisha, P.O. Box 001, Saudi Arabia
7 Department of Computer Science, Solent University, Southampton, SO14 0YN, UK
* Corresponding Author: Bacha Rehman. Email:
(This article belongs to the Special Issue: Emerging Technologies in Information Security )
Computer Modeling in Engineering & Sciences 2025, 143(1), 1049-1070. https://doi.org/10.32604/cmes.2025.063405
Received 14 January 2025; Accepted 12 March 2025; Issue published 11 April 2025
Abstract
Satellite images are widely used for remote sensing and defence applications, however, they are subject to a variety of threats. To ensure the security and privacy of these images, they must be watermarked and encrypted before communication. Therefore, this paper proposes a novel watermarked satellite image encryption scheme based on chaos, Deoxyribonucleic Acid (DNA) sequence, and hash algorithm. The watermark image, DNA sequence, and plaintext image are passed through the Secure Hash Algorithm (SHA-512) to compute the initial condition (keys) for the Tangent-Delay Ellipse Reflecting Cavity Map (TD-ERCS), Henon, and Duffing chaotic maps, respectively. Through bitwise XOR and substitution, the TD-ERCS map encrypts the watermark image. The ciphered watermark image is embedded in the plaintext image. The embedded plaintext image is permuted row-wise and column-wise using the Henon chaotic map. The permuted image is then bitwise XORed with the values obtained from the Duffing map. For additional security, the XORed image is substituted through a dynamic S-Box. To evaluate the efficiency and performance of the proposed algorithm, several tests are performed which prove its resistance to various types of attacks such as brute-force and statistical attacks.Keywords
With the technological evolution, satellites are used for various applications such as remote sensing, national security, weather forecasting, deep space research, and navigation purposes [1,2]. The most effective way of satellite communication is through digital images, and these images are exposed to various threats [3]. That is why these images need encryption and digital watermarking to ensure integrity and confidentiality [4]. Masking or concealing the information is encryption, while embedding some information in the digital media to protect it from manipulation and illegal copying is digital watermarking. A digital watermark may be visible or invisible, depending on the scenario. Encryption can be done using different cryptographic techniques. Cryptography deals with the security of information [5]. Confusion and diffusion are the two fundamental mechanisms involved in cryptography. From previous research, it is clear that confusion is changing the values of the pixels dependent on a key, which is obtained via swapping/substituting one value for another [6]. Conventional encryption schemes such as the advanced encryption standard, Rivest-Shamir-Adleman, data encryption standard, and international data encryption algorithm are not suitable for image encryption because of the high correlation of image pixels. Using chaotic maps in cryptography is an emerging field that uses random sequences to encrypt digital images. In addition to being non-linear, these elementary chaotic maps exhibit a variety of strange attractors with variable initial keys, as well as inherent randomness [7]. To design a resilient cryptosystem, it is necessary to use each of these characteristics effectively. These initial conditions serve as secret keys that can only be accessed by authorized individuals. It is impossible to decrypt the system without knowing these keys. In this context, sensitivity to control parameters and initial conditions is critical since it stops unauthorized users and hackers from attempting to decrypt the secured content. Because of the high sensitivity, even minor modifications to the control parameters and initial conditions values result in drastically different weird random numbers, making decryption by hackers nearly impossible.
To consistently enhance the level of encryption security, researchers are persistently engaged in the pursuit of novel high-security techniques to contribute to the encryption process. Therefore, numerous encryption methods have been introduced and presented in the literature, including chaos-based encryption [8–10], visual image encryption [11,12], S-Box-based encryption [13–15], compression and encryption [16,17], and Deoxyribonucleic Acid (DNA) based encryption [18,19]. Authors in [8] use Joseph transforms and discrete Fourier transforms to significantly enhance the security of designed image encryption. In addition to space domain encryption, frequency domain encryption has also been performed. Logistic chaotic map is used for creating chaotic numbers, while Joseph traversals are used for permuting image pixels. As a consequence, it can be concluded that Joseph’s traversal can improve the security of an image, and therefore, the proposed scheme can withstand common attacks. Conventional image encryption algorithms generate encrypted images that include noise-like attributes, drawing potential attackers’ interest. Therefore, to address this issue, visual or meaningful image encryption algorithms are proposed. Su et al. compressed the plaintext image employing sensing, subsequently applying the Arnold transform to induce scrambling and generate a ciphertext image [11]. The ciphertext image is subsequently divided into segments and embedded into a carrier image utilizing shifting intensity levels through Singular Value Decomposition (SVD). To achieve enhanced security, a controllable quantum walk is utilized for the generation of pseudorandom sequences, that are then implemented to determine the embedded image’s positioning within the carrier image and to construct the sensing matrix. In [12], an image encryption algorithm that initially undergoes Vector Quantization (VQ) encoding as a first step, followed by visual encryption by content transformation using Discrete Wavelet Transform (DWT) to produce the resulting meaningful image is developed.
The authors in [20] Multi-Image Encryption (MIE) and Back-Propagation (BP) neural network compression method capable of encrypting color and grayscale images of different sizes. Through the use of BP neural networks, the MI cube is first compressed, then scrambled and finally diffused. The authors in [21] utilized Computational Ghost Imaging (CGI) to design a dual-channel image encryption and authentication algorithm. The pseudo-random sequences are generated using a Logistic map and a 4D chaotic system. Khan et al. present a novel quantum image encryption scheme based on a chaotic confusion-diffusion architecture with two phases [22]. There are four separate confusion-diffusion modules integrated with the proposed architecture, which are capable of simultaneously performing a two-level encryption of both the position of the quantum encoding pixel as well as the intensity of the quantum encoding pixel. Ma et al. utilize Chen’s system and Tabu Search (TS) to design an image encryption scheme that can resist plaintext attacks [23]. Chen’s system key is computed by passing the plaintext image through a hash algorithm. The block permutation technique is used to break the correlation between original adjacent pixels. Kong et al. developed two types of fractional-order memristors for encrypting images on a Field-Programmable Gate Array (FPGA) [24]. It exhibits high dynamic behavior such as extreme multistability, hyperchaos, overclocking, and multiscroll. Substitution boxes (S-Box) are used in image encryption applications for substituting plaintext pixels. Mainly S-Boxes are used for increasing image security via introducing non-linearity [25]. Zhu et al. proposed a robust methodology for constructing a strong and reliable S-Box to encrypt images [13]. The constructed S-Box is based on the utilization of a One-Dimensional (1D) piece-wise quadratic polynomial chaotic Map. Moreover, S-Box substitution and diffusion encryption techniques are combined with pixel segmentation encryption in this encryption algorithm. The authors in [14] proposed a novel approach for developing a chaos-based S-Box that can be incorporated into encryption algorithms. The algorithm’s performance is assessed using various testing procedures.
Contribution
• The designed satellite image encryption scheme has both confusion and diffusion characteristics.
• The Key’s dependence on both the watermark image and the plaintext image, as well as the DNA sequence, makes the scheme resilient to classical attacks.
• The ciphered watermark embedding provides an extra layer of security.
The rest of this article is arranged as follows: Section 2 provides an explanation of the preliminaries, and Section 3 provides a step-by-step description of the proposed watermarked satellite image encryption. Section 4 presents the experimental analysis of the designed scheme. Lastly, the conclusion is drawn in Section 5.
The proposed scheme combines a secure hash algorithm (SHA-512) with multiple chaotic maps and DNA sequences. SHA-512, DNA sequences and chaotic maps are discussed in this section.
Henon Chaotic Map is a two-dimensional dynamic system depicting chaotic behaviour in a discrete domain [26]. Mathematically Henon chaotic map can be written as [26]:
The chaotic nature of this map is based on the values of its control parameters

Figure 1: Sensitivity plots: (a, b) Henon map; (c, d) TD-ERCS map; and (e, f) Duffing map

Figure 2: Random number plots: (a) Henon map; (b) TD-ERCS map; and (c) Duffing map
2.2 Tangent-Delay Ellipse Reflecting Cavity-Map
Li-Yuan et al. proposed TD-ERCS in 2004 [27]. It is a discreet chaotic map belonging to the class of two-dimensional chaotic maps. According to the authors in [28], TD-ERCS maps possess important properties, i.e., zero correlation in the total field, a Lyapunov exponent with a value greater than zero, and an unchangeable equiprobability distribution. Mathematically, the TD-ERCS map can be written as [29]:
whereas
A Holmes map or duffing chaotic map is a discrete-time chaotic system that maps points on a plane
where
2.4 Deoxyribonucleic Acid DNA Sequence
The integral component of chromosomes is Deoxyribonucleic Acid (DNA). A DNA sequence is composed of Adenine (A), Thymine (T), Guanine (G), and Cytosine (C). Adenine, Thymine, Guanine, and Cytosine complement one another according to the Watson-Crick rule [31]. The nucleic acid database has the information of all the known nucleic acids. A permanent and unique ID number is assigned to every sequence known as the sequence code. More than 163 million unique DNA sequences are publicly available [32]. A DNA sequence can act as a natural password so it has its applications in image encryption. In this scheme, the DNA sequence code “NC012920” is used and is selected randomly from the publicly available DNA sequences.
2.5 Secure Hash Algorithm (SHA)
Secure Hash Algorithm abbreviated as SHA is a collection of cryptographic hash functions published by the National Institute of Standards and Technology as a recognized Federal Information Processing Standard (FIPS). Hash functions have their applications in generating pseudo-random numbers, speedy encryption, detection of a computer virus, verification of passwords and storage, etc. [33,34]. The SHA family consists of SHA-0, SHA-1, SHA-2, and SHA-3. SHA-2 is a family of SHA-256 and SHA-512, with the distinction of the word size only. The SHA-256 algorithm uses 32-byte words, while the SHA-512 algorithm uses 64-byte words. In the proposed algorithm SHA-512 is used. SHA-512 generates 512 bits or 128-character hash values.
All the images are grayscale, having pixel values between 0 and 255 for an 8-bit system. A flowchart depicting the proposed scheme is presented in Fig. 3. Each step of the scheme is described in detail as follows:
1. Let P be the plaintext image and W be the watermark image with dimensions
2. The DNA sequence “NC012920”, plaintext image P and watermark image W have been hashed using SHA-512 to generate
3. The hash value
4. The vector
5. The
6. A new vector A is generated by randomly selecting 256 values from the
7. The final ciphered watermarked image
8. To embed the cipher watermark
9. Since embedded image E has values greater than 255 and less than 0, a scaling function (min-max normalization) is applied to limit these values between 0 and 255.
10. The hash
11. The Henon chaotic map is iterated 1024 times to generate two sets of random values that are
12. Using
13. The hash
14. The duffing map is iterated
15. The same functions are applied on vector
16. The shuffled image S and
17. Another

Figure 3: Flowchart detailing the outlined scheme
Numerous security metrics are used to test the efficacy of the designed algorithm. Tests are conducted on a system with Microsoft Windows 10 operating system, 4 GB memory, 1 GHz CPU, and MATLAB 2018a. A Baboon image of size


Figure 4: Results: (a, b, c, d, i, j, and k) are the plaintext Baboon watermark image, Satellite images 1, 2, 3, 4, 5, and 6, while (b, c, d, e, f, g, h, l, m, and n) are the histograms


Figure 5: Results: (a, b, c, d, i, j, and k) are the ciphertext Baboon watermark image, Satellite images 1, 2, 3, 4, 5, and 6, while (b, c, d, e, f, g, h, l, m, and n) are the histograms
4.1 Statistical Attack Analysis
The correlation test determines how similar the two variables are. An encryption scheme’s effectiveness (quality) can be evaluated using this test. Let u and v symbolize a pair of neighbouring grayscale pixels in each plaintext and ciphertext image. It can be mathematically calculated as [35]:
where
The notation


Figure 6: Correlation plots of Sattelite image1: The (a), (b), and (c) are plaintext plots while (d), (e), and (f) are ciphertext plots in horizontal, vertical, and diagonal directions, respectively
A histogram of an image illustrates the dispersion of pixel values using significant statistical features. Histogram analysis is used to find the statistical strength of an image encryption scheme. An efficient encryption algorithm generates an encrypted image with a flat histogram without sharp peaks. The histograms of plaintext and ciphertext watermark Baboon image and six satellite images are generated and displayed in Figs. 4 and 5, respectively. The sharp peaks in histograms are easily visible in Fig. 4 (e, f, g, h, l, m, and n) while Fig. 5 (e, f, g, h, l, m, and n) confirms that the encrypted images histograms are almost flat and uniformly distributed. Accordingly, the proposed scheme conceals all aspects of plaintext images and can withstand statistical attacks.
A key analysis in chaotic image encryption involves examining and evaluating the cryptographic keys used to encrypt the images. A key space analysis and a key sensitivity analysis are therefore conducted and explained in more detail.
In this analysis, a cryptosystem’s resistance to brute-force attacks is calculated. Key space generally means the size of the keys employed in the system. An efficient cryptosystem must have a large key space capable of resisting brute-force attacks. For a cryptosystem, the key space should be greater than
Thus, one can conclude that with the available computational power, the computed key space is fairly large enough to withstand any brute-force attack.
4.2.2 Key Sensitivity Analysis
This analysis is used to assess the effects of modifications to a system’s key variables or input parameters on its output. An image encryption process must undergo sensitivity analysis to be evaluated for security and resilience. Thus, the designed image encryption system must have greater sensitivity so that even a small modification in one of the encryption keys during the encryption and decryption process must produce a dissimilar ciphertext image. For the demonstration of the proposed scheme key sensitivity, let’s change the initial condition

Figure 7: Key sensitivity plots: (a) First ciphertext; (b) second ciphertext with changed key; (c) differential image; (d) histogram of (a); (e) histogram of (b); (f) histogram of (c)
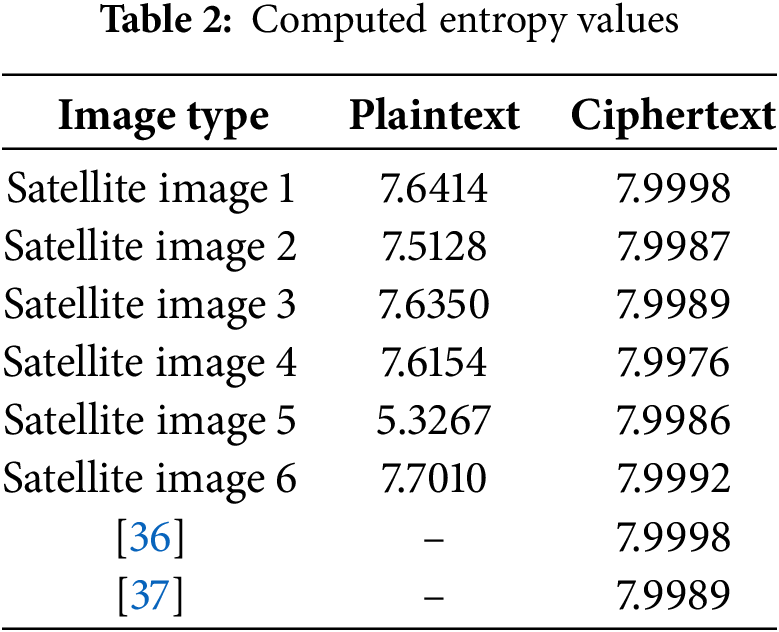
Entropy is a quantitative metric and can be used to assess the level of unpredictability or randomness present in a given dataset or image. Entropy analysis is an essential tool for evaluating how well an encryption technique hides the underlying image data and how resistant it is to brute-force attacks when it comes to image encryption. Strong image encryption techniques require ciphertext images to have a high entropy value, giving them the impression of randomness. On the other hand, if the encryption method is not up to par, the ciphertext image could show recognizable structures or patterns that could be used as a means of recovering the original image data. Shannon entropy
Table 2 displays the results of the proposed scheme entropy evaluation. These high entropy values of the proposed image encryption system have thus made it resistant to possible brute-force attacks.
4.4 Differential Attack Analysis
An image encryption method can undergo evaluation through a differential attack to assess its resilience against changes in the pixel values of the plaintext image. The attacker compares two output images to determine the difference between them, so if the difference is significant, then the designed scheme is resilient to differential attack [39]. There are two tests for the evaluation of differential attack: Number of Pixel Change Rate (NPCR) and Unified Average Change Intensity (UACI). The UACI test evaluates how much the pixel intensities differ between two images that have undergone encryption, rather than focusing on how often the number of pixels changes in the encrypted image when a single pixel in the original image is altered. NPCR measures how frequently the number of pixels changes when one pixel is changed in the plaintext. Mathematically NPCR and UACI can be computed as [39]:
where
The variable

Analyzing the energy distribution of an image can provide insight into the encryption method’s effectiveness and security. In a digital image, each pixel’s intensity or magnitude determines the energy distribution. Therefore, this test identifies the uniformity and predictability of energy distribution in ciphertext images. Mathematically energy can be represented as follows [17]:
where

In image encryption, contrast analysis determines how well images retain contrast. Across different regions of an image, this analysis determines if an image encryption algorithm maintains relative variations in pixel intensities and contrast levels. Mathematically, it is calculated as [17]:
where
Pixel homogeneity is a measure of consistency or uniformity of pixel values. An image is often evaluated by comparing the intensity of pixels within it, especially in examining textures and patterns. A small value is an indication of more variation or heterogeneity in the image, while a larger value indicates a more uniform distribution of pixel intensities. Mathematically, homogeneity can be interpreted as [17]:
where
4.6.1 Occlusion Attack Analyis
Communication over a transmission medium can result in the loss of some part of an image or a change by an attacker. The encryption scheme must have enough robustness to decrypt images that have experienced lossy changes. A cropping attack is illustrated in Fig. 8 by removing

Figure 8: Occlusion attack: (a) occluded encrypted image; (b) decrypted image
Noise interference can affect ciphertext images during transmission and storage. A strong encryption scheme must therefore be immune to noise interference. We evaluated the anti-noise performance of the designed algorithm on one of the encrypted satellite images by adding salt and pepper noise. A noisy satellite image is decrypted, and the result is shown in Fig. 9. Hence, the decrypted image preserves the original data, illustrating how robust the encryption scheme is.

Figure 9: Noise attack: (a) polluted encrypted image; (b) decrypted image
4.6.3 Classical Attack Analysis
This section examines a wide range of attack methodologies at the ciphered image, including known-plaintext, chosen-plaintext, ciphertext-only, and chosen-ciphertext attacks. Three different chaotic maps are employed to produce confusing and diffuse vectors and matrices. SHA-512 hashes of watermark images, plaintext images, and DNA sequences are used to compute the keys (initial conditions and control parameters) of chaotic maps. The Watermark image is then encrypted using the TD-ERCS map and embedded in the plaintext image. The embedded plaintext image is permuted row- and column-wise using the Henon map. Following the permutation, the values from the duffing map are XORed with the permuted image. The XORed image security is further enhanced by applying a dynamic S-Box. A single-pixel change in the plaintext image, watermark image or DNA sequence will alter the resulting keystream, resulting in a completely different ciphertext image. As a result of the reliance on watermark images, plaintext images, and DNA sequences, as well as confusion and diffusion properties, the developed image encryption can resist classical attacks.
4.7 Computational Complexity Analysis
Tests are conducted on a system with the Microsoft Windows 10 operating system, 4 GB memory, 1 GHz CPU, and MATLAB2018a. In addition to the watermark image of 256
A novel satellite watermarked image encryption scheme is proposed. The initial conditions (key) for TD-ERCS, Henon, and Duffing chaotic maps are generated by applying the hash algorithm SHA-512 to watermark images, DNA sequences, and plaintext images, respectively. The Watermark image is encrypted using TD-ERCS and embedded in plaintext. The embedded plaintext image is permuted row-wise and column-wise using the Henon map and then XORed with the random matrix of the same size generated through the Duffing map. A dynamic S-Box was generated and applied to the XORed image to enhance security. To verify the robustness and superiority of the proposed watermarked image encryption scheme, a thorough security analysis is performed. To confirm the robustness and strength of the proposed satellite watermarked image encryption scheme, statistical analyses (correlation and histogram), key analyses (key space and key sensitivity), entropy analyses, differential attack analyses (NPCR and UACI), visual strength analyses (energy, contrast, and homogeneity), robustness analyses (cropping, noise, and classical attacks) are carried out which lead one to the conclusion that the suggested strategy is immune to any prospective attacks. Moreover, a possible limitation of the scheme could be the computational complexity. As the size of images increases, the overall encryption process could take more time.
Acknowledgement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the large group research project under grant number
Funding Statement: This study is supported by the Deanship of Scientific Research at King Khalid University for funding this work through the large group research project under grant number
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Mohamed Medani, Yahia Said, Nashwan Adnan Othman, Mohamed Kchaou; data collection: Mohamed Medani, Yahia Said, Farrukh Yuldashev, Faisal Khaled Aldawood; analysis and interpretation of results: Bacha Rehman, Nashwan Adnan Othman, Farrukh Yuldashev, Mohamed Kchaou; draft manuscript preparation: Mohamed Medani, Yahia Said, Faisal Khaled Aldawood, Bacha Rehman. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Xi Y, Li T, Wang H, Li Y, Tarkoma S, Hui P. Beyond the first law of geography: learning representations of satellite imagery by leveraging point-of-interests. In: Proceedings of the ACM Web Conference 2022; 2022; Lyon, France. p. 3308–16. [Google Scholar]
2. Zhang H, Xu Y, Luo R, Mao Y. Fast GNSS acquisition algorithm based on SFFT with high noise immunity. China Commun. 2023;20(5):70–83. doi:10.23919/JCC.2023.00.006. [Google Scholar] [CrossRef]
3. Banu R, Vladimirova T. Fault-tolerant encryption for space applications. IEEE Transact Aeros Electr Syst. 2009;45(1):266–79. doi:10.1109/TAES.2009.4805278. [Google Scholar] [CrossRef]
4. Singh AK, Thakur S, Jolfaei A, Srivastava G, Elhoseny M, Mohan A. Joint encryption and compression-based watermarking technique for security of digital documents. ACM Transact Inte Technol. 2021;21(1):1–20. doi:10.1145/3414474. [Google Scholar] [CrossRef]
5. Abikoye O, Adewole K, Oladipupo A. Efficient data hiding system using cryptography and steganography. Int J Appl Inform Syst. 2012;4(11):6–11. doi:10.5120/ijais12-450763. [Google Scholar] [CrossRef]
6. Shannon CE. Communication theory of secrecy systems. The Bell Syst Techn J. 1949;28(4):656–715. doi:10.1002/j.1538-7305.1949.tb00928.x. [Google Scholar] [CrossRef]
7. Zhang B, Liu L. Chaos-based image encryption: review, application, and challenges. Mathematics. 2023;11(11):2585. doi:10.3390/math11112585. [Google Scholar] [CrossRef]
8. Wang M, Fu X, Yan X, Teng L. A new chaos-based image encryption algorithm based on discrete fourier transform and improved joseph traversal. Mathematics. 2024;12(5):638. doi:10.3390/math12050638. [Google Scholar] [CrossRef]
9. Zhou S, Wei Y, Zhang Y, Iu HHC, Zhang H. Image encryption algorithm based on the dynamic RNA computing and a new chaotic map. Integration. 2025;101(1):102336. doi:10.1016/j.vlsi.2024.102336. [Google Scholar] [CrossRef]
10. Khan MS, Ahmad J, Al-Dubai A, Pitropakis N, Driss M, Buchanan WJ. A Novel Cosine-modulated-polynomial chaotic map to strengthen image encryption algorithms in IoT environments. Procedia Comput Sci. 2024;246:4214–23. doi:10.1016/j.procs.2024.09.261. [Google Scholar] [CrossRef]
11. Su Y, Wang X. A robust visual image encryption scheme based on controlled quantum walks. Phy A: Statist Mech Applicat. 2022;587:126529. doi:10.1016/j.physa.2021.126529. [Google Scholar] [CrossRef]
12. Zheng S, Liu C, Feng Z, Chen R, Liu X. Visual image encryption scheme based on vector quantization and content transform. Multim Tools Applicat. 2022;81(9):12815–32. doi:10.1007/s11042-022-12583-y. [Google Scholar] [CrossRef]
13. Zhu S, Deng X, Zhang W, Zhu C. Secure image encryption scheme based on a new robust chaotic map and strong S-box. Mathem Comput Simulat. 2023;207(8):322–46. doi:10.1016/j.matcom.2022.12.025. [Google Scholar] [CrossRef]
14. Çavuşoğlu Ü, Kaçar S, Pehlivan I, Zengin A. Secure image encryption algorithm design using a novel chaos based S-Box. Chaos Solit Fract. 2017;95(11):92–101. doi:10.1016/j.chaos.2016.12.018. [Google Scholar] [CrossRef]
15. Khan JS, Kayhan SK, Ahmed SS, Ahmad J, Siddiqa HA, Ahmed F, et al. Dynamic S-box and PWLCM-based robust watermarking scheme. Wireless Pers Commun. 2022;125(1):513–30. doi:10.1007/s11277-022-09562-9. [Google Scholar] [CrossRef]
16. Kadhim Q, Al-Jawher WAM. A new multiple-chaos image encryption algorithm based on block compressive sensing, swin transformer, and wild horse optimization. Multidiscip Sci J. 2025;7(1):2025012–2. doi:10.31893/multiscience.2025012. [Google Scholar] [CrossRef]
17. Khan JS, Kayhan SK. Chaos and compressive sensing based novel image encryption scheme. J Inf Secur Appl. 2021;58(4):102711. doi:10.1016/j.jisa.2020.102711. [Google Scholar] [CrossRef]
18. Zou C, Wang X, Zhou C, Xu S, Huang C. A novel image encryption algorithm based on DNA strand exchange and diffusion. Appl Math Comput. 2022;430(2):127291. doi:10.1016/j.amc.2022.127291. [Google Scholar] [CrossRef]
19. Rahul B, Kuppusamy K, Senthilrajan A. Dynamic DNA cryptography-based Image Encryption Scheme using Multiple Chaotic Maps and SHA-256 hash function. Optik. 2023;289:171253. doi:10.1016/j.ijleo.2023.171253. [Google Scholar] [CrossRef]
20. Gao X, Mou J, Banerjee S, Zhang Y. Color-gray multi-image hybrid compression-encryption scheme based on BP neural network and knight tour. IEEE Transact Cybernet. 2023;53(8):5037–47. doi:10.1109/TCYB.2023.3267785. [Google Scholar] [PubMed] [CrossRef]
21. Guo Z, Chen SH, Zhou L, Gong LH. Optical image encryption and authentication scheme with computational ghost imaging. Appl Mathem Model. 2024;131(6):49–66. doi:10.1016/j.apm.2024.04.012. [Google Scholar] [CrossRef]
22. Khan MS, Ahmad J, Al-Dubai A, Pitropakis N, Ghaleb B, Ullah A, et al. Chaotic quantum encryption to secure image data in post quantum consumer technology. IEEE Trans Consum Electron. 2024;70(4):7087–101. doi:10.1109/TCE.2024.3415411. [Google Scholar] [CrossRef]
23. Ma X, Wang Z, Wang C. An image encryption algorithm based on Tabu Search and hyperchaos. Int J Bifurcat Chaos. 2024;34(14):2450170. doi:10.1142/S0218127424501700. [Google Scholar] [CrossRef]
24. Kong X, Yu F, Yao W, Cai S, Zhang J, Lin H. Memristor-induced hyperchaos, multiscroll and extreme multistability in fractional-order HNN: image encryption and FPGA implementation. Neural Netw. 2024;171(1):85–103. doi:10.1016/j.neunet.2023.12.008. [Google Scholar] [PubMed] [CrossRef]
25. Alexan W, Chen YL, Por LY, Gabr M. Hyperchaotic maps and the single neuron model: a novel framework for chaos-based image encryption. Symmetry. 2023;15(5):1081. doi:10.3390/sym15051081. [Google Scholar] [CrossRef]
26. Hénon M. A two-dimensional mapping with a strange attractor. In: The theory of chaotic attractors. New York, NY, USA: Springer; 1976. p. 94–102. [Google Scholar]
27. Sheng LY, Sun KH, Li CB. Study of a discrete chaotic system based on tangent-delay for elliptic reflecting cavity and its properties. Acta Physica Sinica. 2004;53(9):2871–6. doi:10.7498/aps.53.2871. [Google Scholar] [CrossRef]
28. Sheng LY, Cao LL, Sun KH, Wen J. Pseudo-random number generator based on TD-ERCS chaos and its statistic characteristics analysis. Acta Physica Sinica. 2005;54(9):4031–7. doi:10.7498/aps.54.4031. [Google Scholar] [CrossRef]
29. Zhang K, Fang J-B. Color image encryption algorithm based on TD-ERCS system and wavelet neural network. Math Probl Eng. 2015;2015(11):1–10. doi:10.1155/2015/501054. [Google Scholar] [CrossRef]
30. Dhopavkar TA, Nayak SK, Roy S. IETD: a novel image encryption technique using Tinkerbell map and Duffing map for IoT applications. Multim Tools Applicat. 2022;81(30):43189–228. doi:10.1007/s11042-022-13162-x. [Google Scholar] [CrossRef]
31. Movafegh Ghadirli H, Nodehi A, Enayatifar R. Color image DNA encryption using mRNA properties and non-adjacent coupled map lattices. Multim Tools Applicat. 2021;80(6):8445–69. doi:10.1007/s11042-020-10014-4. [Google Scholar] [CrossRef]
32. Khan JS, Ahmad J, Ahmed SS, Siddiqa HA, Abbasi SF, Kayhan SK. DNA key based visual chaotic image encryption. J Intell Fuzzy Syst. 2019;37(2):2549–61. doi:10.3233/JIFS-182778. [Google Scholar] [CrossRef]
33. Menezes AJ, Katz J, Van Oorschot PC, Vanstone SA. Handbook of applied cryptography. Boca Raton, FL, USA: CRC Press; 1996. [Google Scholar]
34. Stallings W. Cryptography and Network Security. Upper Saddle River, NJ, USA: Prentice-Hall. Inc.; 1999. [Google Scholar]
35. Khan JS, Ahmad J. Chaos based efficient selective image encryption. Multidimens Syst Signal Process. 2019;30(2):943–61. doi:10.1007/s11045-018-0589-x. [Google Scholar] [CrossRef]
36. Kumar A, Dua M. Novel pseudo random key & cosine transformed chaotic maps based satellite image encryption. Multim Tools Applicat. 2021;80(18):27785–805. doi:10.1007/s11042-021-10970-5. [Google Scholar] [CrossRef]
37. Zhao L, Zhao L, Cui F, Sun T. Satellite image encryption based on RNA and 7D complex chaotic system. Visual Comput. 2024;40(8):5659–79. doi:10.1007/s00371-023-03128-x. [Google Scholar] [CrossRef]
38. Alvarez G, Li S. Some basic cryptographic requirements for chaos-based cryptosystems. Internat J Bifurcat Chaos. 2006;16(08):2129–51. doi:10.1142/S0218127406015970. [Google Scholar] [CrossRef]
39. Ullah A, Shah AA, Khan JS, Sajjad M, Boulila W, Akgul A, et al. An efficient lightweight image encryption scheme using multichaos. Secur Commun Netw. 2022;2022(4):680357. doi:10.1155/2022/5680357. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF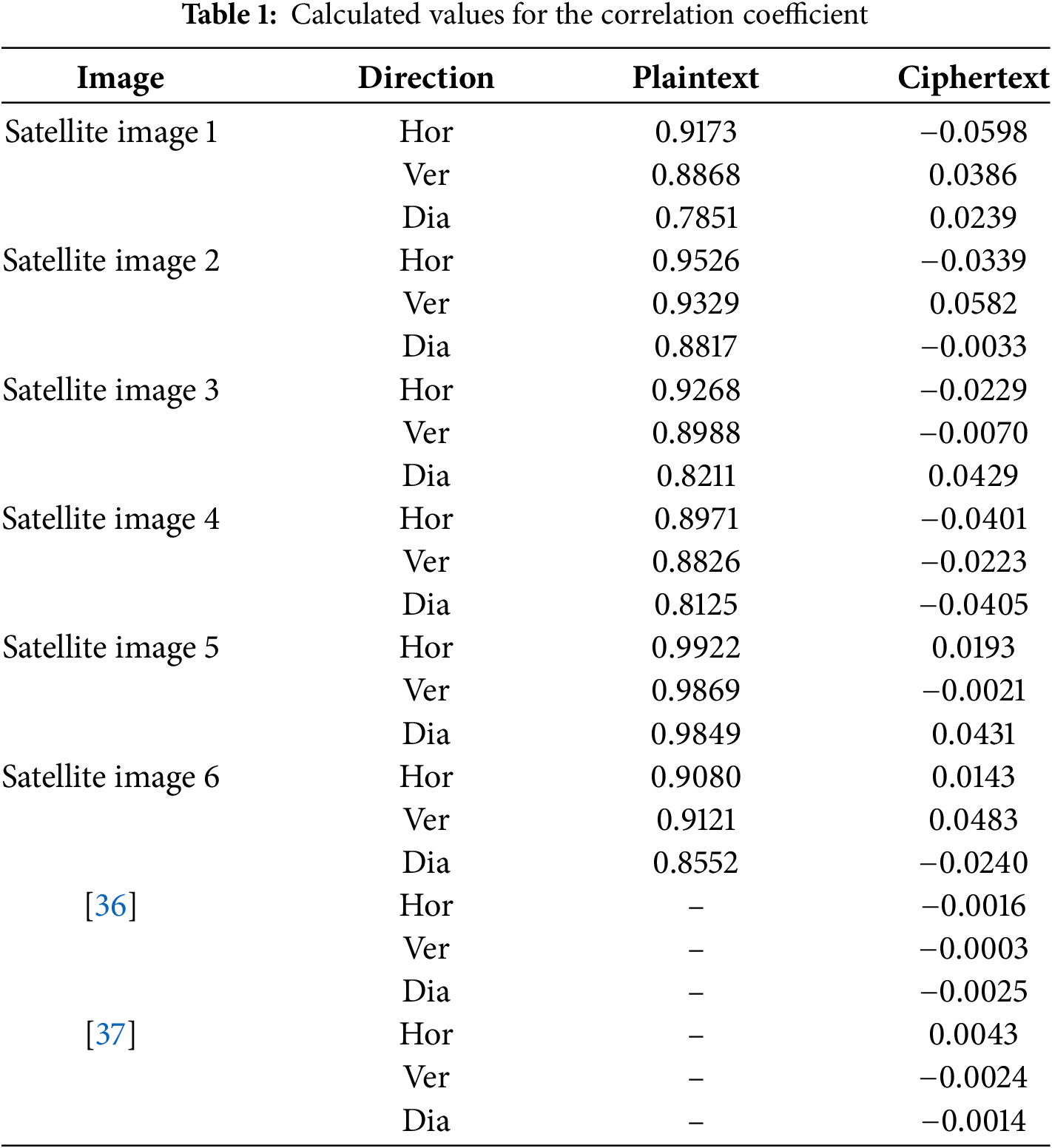
 Downloads
Downloads
 Citation Tools
Citation Tools