A Design of Predictive Intelligent Networks for the Analysis of Fractional Model of TB-Virus

1  Introduction

“Mycobacterium tuberculosis” is the bacterium that causes “tuberculosis” (TB). Although the lungs are usually affected, other organs like the spine, brain, as well as kidneys may also be affected. Droplets containing germs are released into the air and consumed by others when an infected person coughs, sneezes, or talks. The bacteria-containing particles are inhaled by others when an infected person coughs, sneezes or speaks. Once within the body, tuberculosis can spread and lead to an infection. On the other hand, not all TB patients experience active illnesses. A persistent TB infection is typically the result of the immune system suppressing the illness [1]. Congenital tuberculosis patients are asymptomatic and not contagious, but if their immune systems are weakened, the bacteria may stay dormant in their organs and later emerge active. Worldwide TB Burden: By 2020, the World Health Organization (WHO) predicts that 10 million people will get TB globally. The number of TB-related deaths: According to [2], TB claimed the lives of almost 1.5 million people in 2020. People who are actively TB-positive exhibit clinical TB symptoms and run the risk of spreading the illness to others. People who have active tuberculosis may cough up blood or sputum, have a phlegm-producing cough, chest pain, exhaustion, loss of weight, night sweats, and appetite loss. Usually, symptoms get worse with time, but they can also go away on their own and come back. One of the most important methods for characterizing and comprehending systems of various degrees that result from interactions is mathematical modelling [3]. Many mathematical models were created and examined over time to explain the dynamics of tuberculosis epidemiology in the general population. A computational framework was developed in [4] to investigate the dynamics of tuberculosis transmission that takes exogenous re-infection into account. It was demonstrated that the inclusion of exogenous recurrence in the model significantly alters the disease’s qualitative dynamics, increasing the likelihood of several chronic points of equilibrium at the crucial basic reproduction number threshold. Huo et al. [5] developed and examined an unpredictable mathematical model that took into account both hospital and home therapy for TB infectious persons. It was found that home treatment significantly impacted the dynamics of TB transmission. Few research has taken into account the fractional derivative operator while simulating the dynamics of TB epidemiology. Notably, the authors in [6] investigated the issue of optimal control for the fractional-order TB infection model combining diabetic and resistant strains using the Atangana–Baleanu–Caputo (ABC) derivative operator. A discrete fractional framework for tuberculosis in the form of the Caputo derivative was proposed by Altaf Khan et al. [7], who also looked into how the model parameters affected the system’s behavior. A TB model with continuous control measures using the Caputo fractional operator was examined by Owolabi et al. [8]. The scientists concluded that a model that included a fractional order component could provide a good control measure against the spread of tuberculosis in the population after conducting some numerical tests. Using the Laguerre polynomial, the authors in [9] applied fractional-order derivatives of Caputo type to the dynamics of TB transmission. The authors concluded that fractional-order derivatives are more capable of handling real-world scenarios than the typical classical-order models. Ullah et al. [10] analyzed a five-dimensional mathematical model that described the transmission dynamics of tuberculosis in the human population using non-integer-order derivatives of Caputo sense. In a related advancement, Farman et al. [11] used non-integer-order differential equations to create a six-dimensional system of differential equations to investigate how treatment affects the dynamics of tuberculosis transmission. In [12], the authors have done the mathematical analysis of a fractional operator-based TB model. To describe the changing patterns of TB infection in vivo, this work presents a unique model that takes host cell encounters with Mycobacterium tuberculosis into consideration. In addition to the TB virus, fractional derivatives have recently been used to study the dynamics of a recently created co-infection model of the HIV and HCV [13] as well as the dynamic behaviors of the HBV under the influence of cytokines and immune response [14].

An empirical concept called an Artificial Neural Network (ANN) aims to replicate the structure and relationships between neurons in the brain. The basic mathematical model (function) of an ANN begins with an input neuron. Three basic rules: amplification, gathering, and activation—control this model. At the time of termination of an artificial neuron, the sum of the previous weights for connections and selectivity passes through an activation function, also known as a transfer function. When ANNs are connected, their full potential and decoding capability become apparent, even though their physics and basic set of rules may not seem very remarkable. These ANNs are predicated on the idea that variation might result from a few straightforward concepts. Instead of just making the system complex and unmanageable, we often don’t link these artificial neurons carelessly to exactly benefit from the computational demands that may be met by connecting numerous ANs. Several “highly standardised” surface properties for ANNs have previously been produced by researchers. Problem solving may be facilitated by these preset traits, which have the potential to be even more successful. Various problems can be solved more successfully with different ANN topographies. Determine the type of problem that has to be solved before selecting and properly implementing the ANN’s design. It is necessary to modify the architecture and its components. The ANN is a necessary component of every ANN. Its form and function were modelled after the genuine neuron, which is thought to be the basic building component of biological NNs (operations) such as the cerebral cortex, brain stem, and surrounding glands. Recently, ANN approach has been applied to investigate the plant virus [15] and the Stuxnet virus [16].

a) Objective:

All of the above amazing uses encourage authors to explore the machine learning paradigm by developing a Bayesian regularization approach for fractional models of the TB virus (FMTBV) based on neural network (BRA-NNs). The developed determining BRA-NNs plan has the following aims in the future:

•   The findings obtained using the BRA-NNs approach are compared to the exact solutions for six different FMTBV variants.

•   Five suitable fractional-order versions based on the numerical solution of the FMTBV mathematical model, demonstrating the reliability of the BRA-NNs.

•   The outcomes of the FOLotkaVolterra technique’s produced and referenced solutions are compared, and it is shown that they are extremely congruent, proving the correctness of the randomized computationally integrator based on BRA-NNs.

•   The performance of the created BRA-NNs system is assessed using in-depth study on the error histogram, Mean Square Error, regression analysis and transition statistics measures.

b) Layout:

The study is arranged in the form that an orderly and step-by-step introduction of concepts and methods used closely follows after the results and conclusions. Section 2, first of all, a general fundamental overview is needed regarding some definitions of fractional derivatives, which are now considered to be necessary when the modelization of complex dynamic systems requires it, followed then by the introduction of TB virus fractional model, that mathematically frames the subject of the study. The discretization techniques used in the analysis are further explained in Section 3, where the Grünwald-Letnikov scheme for the discretization of fractional derivatives and BRA-NN, how to solve and analyze the model, are also presented. Section 4 states the results and the analysis of the simulation. Finally, Section 5 summarizes key findings and implications of further work that may be achieved for modeling fractional systems such as the TB virus, based on the possible impact of BRA-NN and GL methods.

2  Preliminaries and Mathematical Model

In this section, firstly, we will discuss some basics regarding fractional integral and Caputo fractional order derivative. After we will discuss the methodology that is Bayesian regularization.

a)   Basic Definitions:

Definition 1: For a function g: Ŗ+→Ŗ, the fractional integral of order ᾶ > 0 is defined by

Іʈᾶ(g(ʈ))=1ϓ(ᾶ)∫0ʈ(ʈ−Ẋ)ᾶ−1g(Ẋ) dẊ

The Gamma function is denoted by ϒ here and elsewhere.

Definition 2: The following gives the Caputo fractional order derivative for the function g ϵ ʗn of order ᾶ:

Đʈᾶc(g(ʈ))=Іn−ᾶĐng(ʈ)=1ϓ(n−ᾶ)∫0ʈgn(Ẋ)(ʈ−Ẋ)ᾶ+n−1dẊ

This is clearly defined for functions that are absolutely continuous and n−1<ᾶ<nεÑ. Note that all values of g(n), for Ẋϵ[0,ʈ], are included in the value of the Caputo fractional derivative of the function g at point t. It is obvious that cĐʈᾶ(g(ʈ)) tends to g(ʈ) as ᾶ→1.

Definition 3: The constant ẓ∗ is the system’s equilibrium point in the below-mentioned Caputo fractional dynamical system.

Đʈᾶcẓ(ʈ)=f(ʈ,ẓ(ʈ)),ᾶϵ(1,0)

only if and when, f(ʈ,ẓ∗)=0.

b)   Mathematical Model:

We offer the proposed fractional model to explain the dynamics of TB infection (FMTBV) in this section. The whole human population is separated into five epidemiological sub-divisions to develop the model: susceptible Ș(ʈ), exposed Լ(ʈ), TB active І(ʈ), under treatment Ť(ʈ), and recovered persons after treatment Ŗ(ʈ).

The system of non-linear fractional differential equations that follows provides the transmission model for TB dynamics:

cĐʈᾶȘ=ᴧ−βȘIÑ−ȗȘ 

cĐʈᾶԼ=βȘIÑ−(ȗ+ε)Լ+(1−n)σŤ

cĐʈᾶІ=εԼ+nσŤ−(ȗ+ϓ+σ1)І

cĐʈᾶŤ=ϓІ−(ȗ+σ+σ2+ξ)Ť

cĐʈᾶŖ=ξŤ−ȗŖ

The starting circumstances are

Ș(0)=Ș0,Լ(0)=Լ0,І(0)=І0,Ť(0)=Ť0,andŖ(0)=Ŗ0.

The parameter ᾶ ϵ [0, 1] and the fractional derivatives used in the aforementioned model are both taken in Caputo meaning. All of the functions Ș, Լ, І, Ť, and Ŗ, together with their Caputo fractional derivativses, are considered to be continuous for all ʈ ≥ 0. Table 1 provides a detailed overview of the model parameters and their fitted or estimated numerical values.

3  Methodology

3.1 Fractional Differential Equation’s Stochastic Analyzer Based on Grunwald-Letnikov

The Grünwald-Letnikov (G-L) approach is regularly applied, but the total of the strategy lengthens over time, highlighting the flaw. The factors c v are thorough approaches with properties that improve service, such as being favorable and having a significant attenuation effect. They conclude that the approach offers seamless features although the corrective term causes some disturbance. A discrete version of the Gronwall defense is very helpful in demonstrations. The G-L approximation is used as a numerical tool to study robustness and incorrect predictions related to linear test equations.

Consider generic version of an FDE and its initial circumstances to illustrate the numerical results for FDEs relying on G-L:

Dtβα′. =f(r,s(t)),s(i)(0)=s0(i),i=0,1,…,n−1(1)

Ivo Petras provided a detailed final cyclical prescription of a GL-based solution obtained from Eq. (1):

1hβ∑o=0[(r−a)∗1/h](−1)os(r−oh)(βo)≈f(s(t)t)(2)

To summarize the aforementioned relationship, we obtain

∑o=0[(r−a)∗1/h](−1)os(r−oh)(βo)+r(t)≈h−βf(r,s(t))(3)

In the form of nonlinear input grid systems, the interval tϵ[0,T]=[0,h,2h,…,Kh=T], where h is the step size indicator, [0,T]=t0=0,t1,…,tK=T, as well as any system to collect in the interval were also depicted as tk=kh for k=0,1,2...K. The aforementioned equation is represented as follows in discrete form:

∑o=1k(−1)o(βo)s(rk−oh)+s(rk)=h−βf(rk,s(rk)),k=0,1,2,...,K

In simple usage, the above term is written as:

∑o=1kc0βy(tk−ho)+y(rk)=h−βf(rk,s(rk)),k=0,1,2,...,K

where coβ is defined as:

coβ=(βo)(−1)o

or equivalently with coβ = 1,

coβ=(1−1+βo)co−1β,o=0,1,…

The recursive form of the GL numerical solver is:

s(rk)=−∑o=1kcoβy(rk−o)+h−βf(rk,s(rk)),k=0,1,2,…,k

3.2 Proposed Methodology

As a suitable analogue to such a speculative neural network, we propose a Bayesian regularized artificial neural network (BRA-NNs) with particular properties that relate readily to physiochemical features. The use of BRA-NNs has the benefit of strong predictions without the need for the recognition technique, which in traditional regression algorithms rises as O(N2). Strength training is difficult since it does not require specific validation data to indicate overtraining and instead gives the ideal point at which to cease training. The BRA-NN network architecture is essentially unimportant as long as a minimum design is offered. To properly define the words Bayesian and regularized, basic regression procedures must be presented in Bayesian terms. Because terminology and depictions differ from approach to approach, generating issues, the included depictions are standard but occasionally strange. It is feasible to accomplish at an equilibrium level rather than the generally accepted least amount because the approach employs a gradient decreasing descent or an analogous lowest reported. Five times through this method is all that is necessary, according to observation, to end any unusual behavior. In contrast, embodied ANNs enable trials with hundreds or possibly thousands of repetitions. In addition to avoiding overfitting, it offers a more reliable estimation of the model coefficients. An overview of the Bayesian regularization algorithm is provided below:

1.    Initialize the variables: Define the model coefficients’ previous distribution.

2.    Data preparation: Prepare your dataset, including the input features (X), goal values (Y), and any other relevant information.

3.    Feature standardization (optional): Standardizing the input features to have a zero mean and unit variance is typically a good idea. Although this step is optional, it occasionally can be beneficial.

4.    Model training: Apply Bayesian inference to estimate the model’s parameters. the following steps:

•   Prior Distribution: Define the model coefficients’ previous distribution. The prior is often assumed to be Gaussian with a variance parameter and a mean of zero in Bayesian ridge regression.

•   Likelihood Function: Establish the likelihood function, which, given the model and the input features, provides the likelihood of seeing the target values. The likelihood in linear regression is frequently taken to be Gaussian.

•   Distribution in the rear: Using Bayes’ theorem, combine the prior distribution and likelihood function to get the posterior distribution of the model coefficients.

•   Estimation of the parameter: To estimate the model coefficients from the posterior distribution, use the appropriate technique (for instance, Maximum A Posteriori estimation or Markov Chain Monte Carlo methods).

5.    Model prediction: Use the obtained model coefficients to create predictions about fresh data points.

6.    Model assessment (optional): Use the proper metrics (e.g., mean squared error, mean absolute error, etc.) on a validation set or through cross-validation to assess the performance of the Bayesian regularized model.

7.    Tuning of hyperparameters (optional): Hyperparameters that are part of the Bayesian regularization process, such as the variance parameter, can be tuned using methods like cross-validation to determine the best values that maximize the model’s performance.

8.    Forecast based on new data: You can use the model to generate predictions on fresh, unforeseen data after it has been trained and tweaked.

4  Results and Discussion

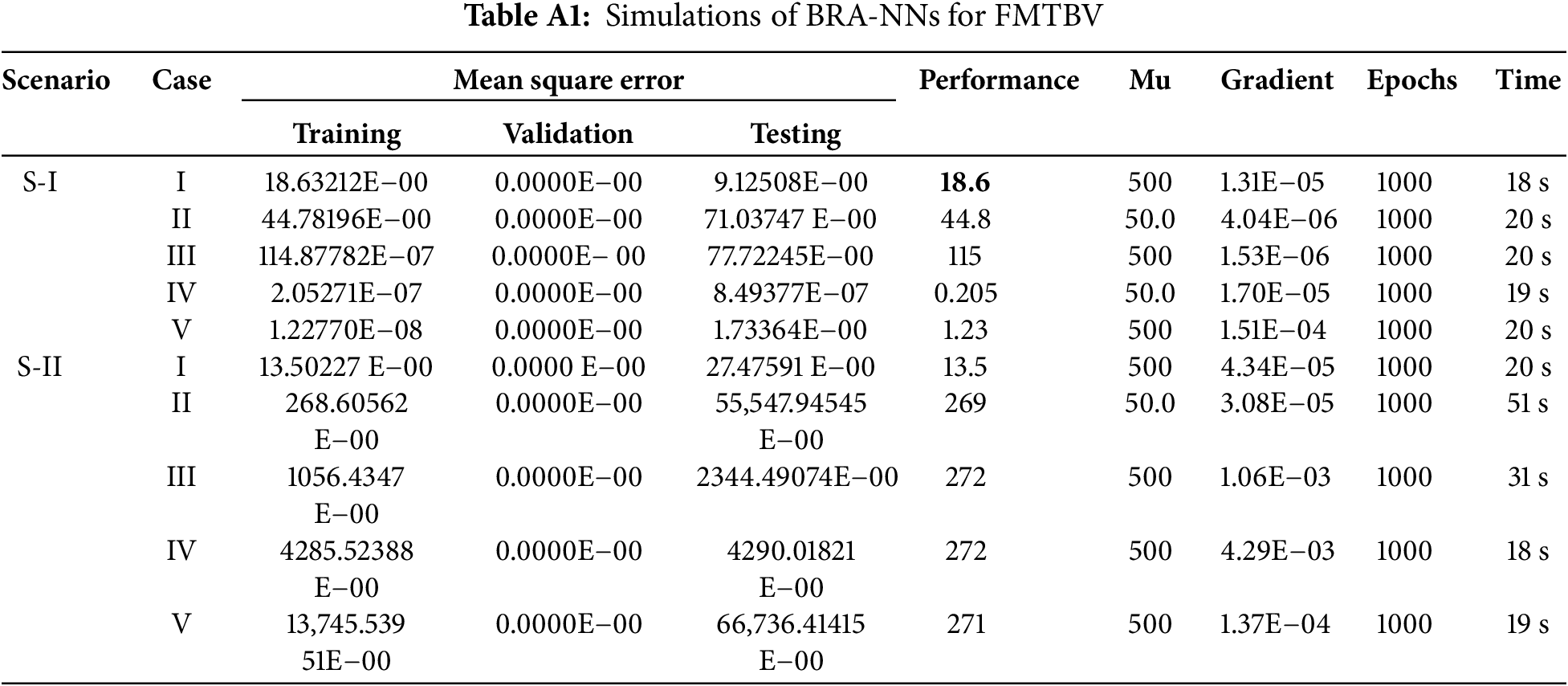
The FMTBV mathematical paradigm is discussed in this section utilizing the recommended BRA-NNs structure. The approach consists of two elements. First, the fundamental BRA-NNs controller discoveries are given. The BRA-NNs implementation approach is also used to resolve the FMTBV mathematical framework. Fig. 1 shows the single-layer layout of neurons. The “nftool” function in MATLAB provides access to the BRA-NNs processes, which use the following data configuration: 90% for training, 5% for testing, and 5% for authorization. Fig. 2 depicts the graphical presentation of the proposed scheme, i.e., BRA-NNs for FMTBV. Table A1 illustrates the simulations of BRA-NNs for FMTBV. Reference datasets are generated using FOLotkavoltera which is based on Grunwald Letnikov method. The data set for scenario I’s case I is presented in Table A2. Complete size of all data sets for each case is 200×5 with step size 0.5.

Figure 1: Single layer neuron formation

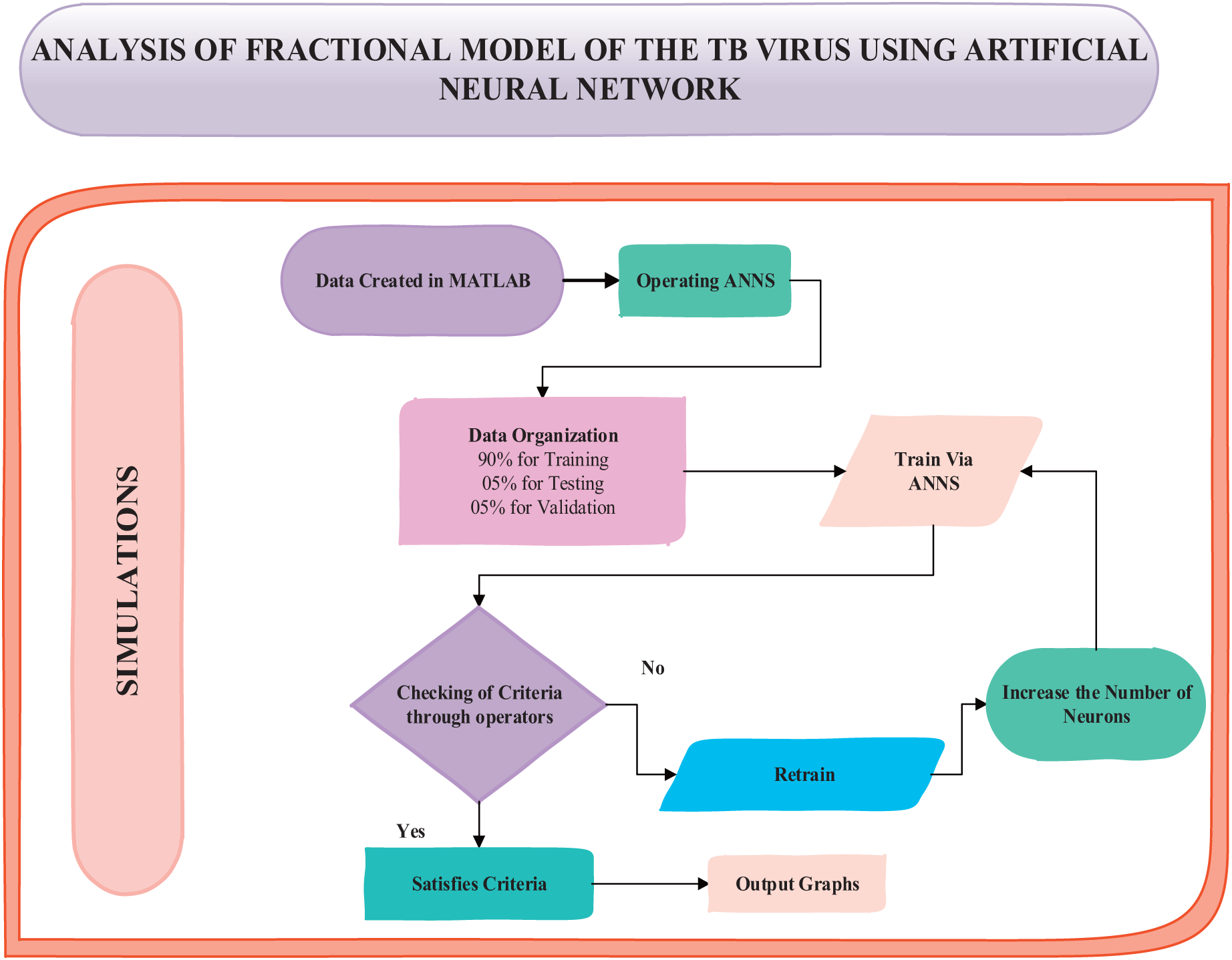
Figure 2: Graphical simulations of BRA-NNs for FMTBV

Figures relating to performance plot, i.e., mean squared error (MSE), transition state (TS), fitness curve (FC), error histogram (EH), and regression analysis (RA) are included in Figs. 3 and 4, which illustrate the BRA-NNs numerical simulation for FMTBV for scenarios I-Case III and II-Case III, respectively. In neural networks, the Mean Squared Error (MSE) loss function is frequently used to calculate the discrepancy between expected and actual output values. It measures the total discrepancy between the predicted values of the network and the exact target values. The neural network’s training function is referred to as “trainFcn”. The network’s training performance and speed can be considerably impacted by the training function that is used. Regularization is a method for keeping neural networks from overfitting. It aids in striking a balance between the network’s capacity (complexity) and adaptability to new inputs. Typically, a regularization parameter with a value between 0 and 1 is indicated. Overfitting may be avoided by using a larger regularization value, prioritizing minimizing squared biases and weights above reducing errors. A preprocessing method called normalization is used to scale data into a particular range. Normalization is used in the context of neural networks to affect the input data and target values. Normalization choices include “no,” “standard,” and “percent.” For BRA-NNs, the transition state consists of five different components: the gradient, Mu, Num parameters, sum squared parameter, and validation check. The vector of a function’s partial derivatives about its inputs is referred to as the gradient. The method of updating the model’s parameters during training is employed in neural network optimization. As a hyper parameter used in optimization methods like gradient descent, Mu often refers to the learning rate. The step size used for parameter updates is determined by the learning rate. The number of learnable weights and biases is represented by the num-parameter in the context of neural networks. In machine learning, the term “sum squared parameter” is not commonly used. Without more information, it’s difficult to give a precise explanation, however, it might be a reference to a certain formula or technique. The process of assessing a trained model’s performance using a different dataset known as the validation set is known as the validation check.

Figure 3: Graphical outputs based on BRA-NNs for scenario 1 case 3

Figure 4: Graphical outputs based on BRA-NNs for scenario 2 case 3

Figs. 5 and 6 show a graphic representation of the FMTBV numerical results and absolute error (AE) for all situations, each with five cases. Despite the behavior of the TB virus model, we see Figs. 5 and 6a,c,e,g,i for α=0.80,0.85,0.90,0.95,1, respectively. We can see from Fig. 5a that the number of sensitive individuals grows as α rises for scenario I, but in Fig. 6a the results fluctuated over time in scenario II. Fig. 5c,e,g,i shows that this tendency alters when α increases, leading to a rapid increase in the population in the latent, infected, treated, and recovered classes. Similarly, in Fig. 6c,e,g, the results have a chaotic behavior whereas Fig. 6i by the increase of fractional order the recovery rate got increased. The simulation’s outputs using BRA-NNs and the FOLotkaVolterra framework are essentially in line with the related AE. As can be observed, the AE for all cases is in the range of 103→10−5. A visual representation of the AEs between actual (ground truth) values and anticipated values in a dataset is called an AE graph. It is frequently employed to assess the effectiveness of a regression model whose objective is to forecast continuous values. We can learn more about the model’s performance by looking at the absolute error graph. It is preferable to have lower absolute errors and a more condensed distribution of vertical lines near 0, which show that the model’s predictions are nearer to the actual values. On the other hand, a wide range of vertical lines with big absolute errors indicates that the model might need to be tweaked or improved.

Figure 5: Dynamical and their corresponding absolute error plots of FMTBV for scenario-I

Figure 6: Dynamical and their corresponding absolute error plots of FMTBV for scenario-II

5  Conclusion

The TB-virus fractional model is discussed in this article. The purpose of this investigation is to supply a fractional order assessment using a mathematical structure with an emphasis on epidemic phenomena to deliver more reliable system efficiency. BRA-NNs are used to solve the FMTBV five-chamber design computationally. While the best under distinct conditions corresponded to different fractional orders, the orders of 0.80 and 0.95 were always the best in a comprehensive context. Such particular orders brought model precision together with computation efficiency, thus describing the subtle dynamics of the TB virus more effectively than other fractional values. The performance at 0.80 and 0.95 indicates that those orders are very well suited to the representation of the complexity inherent in the system, offering strong and reliable predictions across a variety of scenarios for simulations. The elements that follow are the main components of the mathematically calculated FMTBV findings:

•   Using the suggested randomized computing paradigm offered by BRA-NNs, the FMTBV simulated solution has been effectively discovered. Modifications to the settings significantly alter how FMTBV functions.

•   In scenario I, there is proper increase/decrease behavior of performance in all the S,L,I,T,R cases, but in scenario II, there is chaotic behavior with irregular fluctuations.

•   For several circumstances, the AE magnitude ranged from 103→10−5, suggesting accurate validation, testing, and training modeling. The great accuracy, as well as convergence of the developed technique, were proved by evaluations of the projected BRA-NNs findings along with the validated numerical answers provided by the FOLotkaVolterra scheme.

•   Fitness graphs show how well the data was processed and how accurate the results were. Regression matrices, MSE learning curves, and histogram error visualizations show that the resultant BRA-NNs are efficient, reliable, and robust for full computations.

Limitations: The study’s reliance on specific fractional orders (0.80 and 0.95) limits its generalizability to other epidemic models. While BRA-NNs improve computational efficiency, the lack of comparison with other numerical methods leaves uncertainty about its optimality. Additionally, chaotic behavior in Scenario II suggests sensitivity to parameter variations, requiring further stability analysis. The absence of validation with real-world TB data and exploration of alternative AI techniques also restricts the model’s practical applicability.

In the future, the authors intend to implement AI solver based on transfer learning, physics-informing, and deep learning for epidemic systems.

Acknowledgement: The authors would like to thank the supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2024/R/1445).

Funding Statement: This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2024/R/1445).

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Aqsa Zafar Abbasi, Ayesha Rafiq, Muhammad Shoaib; Analysis and interpretation of results: Muhammad Asif Zahoor Raja, Aqsa Zafar Abbasi, Kottakkaran Sooppy Nisar, Muhammad Shoaib; Draft manuscript preparation: Muhammad Asif Zahoor Raja, Aqsa Zafar Abbasi, Kottakkaran Sooppy Nisar, Ayesha Rafiq, Muhammad Shoaib; Validation: Muhammad Asif Zahoor Raja, Kottakkaran Sooppy Nisar; Visualization: Aqsa Zafar Abbasi, Ayesha Rafiq; Supervision: Muhammad Shoaib; Writing—review and editing: Aqsa Zafar Abbasi, Kottakkaran Sooppy Nisar, Muhammad Shoaib. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Nomenclature

Appendix A

References

1. Ai JW, Ruan QL, Liu QH, Zhang WH. Updates on the risk factors for latent tuberculosis reactivation and their managements. Emerg Microbes Infect. 2016;5(2):e10. doi:10.1038/emi.2016.10. [Google Scholar] [PubMed] [CrossRef]

2. Chakaya J, Khan M, Ntoumi F, Aklillu E, Fatima R, Mwaba P, et al. Global tuberculosis report 2020-reflections on the global TB burden, treatment and prevention efforts. Int J Infect Dis. 2021;113(Suppl 1):S7–12. doi:10.1016/j.ijid.2021.02.107. [Google Scholar] [PubMed] [CrossRef]

3. Alade TO, Alnegga M, Olaniyi S, Abidemi A. Mathematical modelling of within-host Chikungunya virus dynamics with adaptive immune response. Model Earth Syst Environ. 2023;9(4):3837–49. doi:10.1007/s40808-023-01737-y. [Google Scholar] [CrossRef]

4. Feng Z, Castillo-Chavez C, Capurro AF. A model for tuberculosis with exogenous reinfection. Theor Popul Biol. 2000;57(3):235–47. doi:10.1006/tpbi.2000.1451. [Google Scholar] [PubMed] [CrossRef]

5. Huo HF, Zou MX. Modelling effects of treatment at home on tuberculosis transmission dynamics. Appl Math Model. 2016;40(21–22):9474–84. doi:10.1016/j.apm.2016.06.029. [Google Scholar] [CrossRef]

6. Sweilam NH, Al-Mekhlafi SM, Baleanu D. Optimal control for a fractional tuberculosis infection model including the impact of diabetes and resistant strains. J Adv Res. 2019;17:125–37. doi:10.1016/j.jare.2019.01.007. [Google Scholar] [PubMed] [CrossRef]

7. Altaf Khan M, Khan K, Safi MA, DarAssi MH. A discrete model of TB dynamics in khyber pakhtunkhwa-Pakistan. Comput Model Eng Sci. 2020;123(2):777–95. doi:10.32604/cmes.2020.08208. [Google Scholar] [CrossRef]

8. Owolabi KM, Pindza E. A nonlinear epidemic model for tuberculosis with Caputo operator and fixed point theory. Healthc Anal. 2022;2(3):100111. doi:10.1016/j.health.2022.100111. [Google Scholar] [CrossRef]

9. Avazzadeh Z, Hassani H, Agarwal P, Mehrabi S, Ebadi MJ, Dahaghin MS. An optimization method for studying fractional-order tuberculosis disease model via generalized Laguerre polynomials. Soft Comput. 2023;27(14):9519–31. doi:10.1007/s00500-023-08086-z. [Google Scholar] [PubMed] [CrossRef]

10. Ullah I, Ahmad S, Arfan M, De la Sen M. Investigation of fractional order dynamics of tuberculosis under caputo operator. Fractal Fract. 2023;7(4):300. doi:10.3390/fractalfract7040300. [Google Scholar] [CrossRef]

11. Farman M, Mehmood Malik S, Akgül A, Ghaffari AS, Salamat N. Analysis and dynamical transmission of tuberculosis model with treatment effect by using fractional operator. Int J Model Simul. 2024;2024(2):1–15. doi:10.1080/02286203.2024.2392222. [Google Scholar] [CrossRef]

12. Khan A, Shah K, Abdeljawad T, Amacha I. Fractal fractional model for tuberculosis: existence and numerical solutions. Sci Rep. 2024;14(1):12211. doi:10.1038/s41598-024-62386-4. [Google Scholar] [PubMed] [CrossRef]

13. Ahmad Naik P, Yeolekar BM, Qureshi S, Yeolekar M, Madzvamuse A. Modeling and analysis of the fractional-order epidemic model to investigate mutual influence in HIV/HCV co-infection. Nonlinear Dyn. 2024;112(13):11679–710. doi:10.1007/s11071-024-09653-1. [Google Scholar] [CrossRef]

14. Ahmad Naik P, Yeolekar BM, Qureshi S, Manhas N, Ghoreishi M, Yeolekar M, et al. Global analysis of a fractional-order hepatitis B virus model under immune response in the presence of cytokines. Adv Theory Simul. 2024;7(12):2400726. doi:10.1002/adts.202400726. [Google Scholar] [CrossRef]

15. Anwar N, Ahmad I, Raja MAZ, Naz S, Shoaib M, Kiani AK. Artificial intelligence knacks-based stochastic paradigm to study the dynamics of plant virus propagation model with impact of seasonality and delays. Eur Phys J Plus. 2022;137(1):144. doi:10.1140/epjp/s13360-021-02248-4. [Google Scholar] [PubMed] [CrossRef]

16. Raja MAZ, Naz H, Shoaib M, Mehmood A. Design of backpropagated neurocomputing paradigm for Stuxnet virus dynamics in control infrastructure. Neural Comput Appl. 2022;34(7):5771–90. doi:10.1007/s00521-021-06721-0. [Google Scholar] [CrossRef]