Promoting Tailored Hotel Recommendations Based on Traveller Preferences: A Circular Intuitionistic Fuzzy Decision Support Model

1  Introduction

The lodging provided for guests is an essential component of any trip. In this context, the hotels that visitors choose significantly influence both their emotions and overall travel experiences. Travelers often rely on various sources to obtain information about hotels in order to select the most suitable option from a wide range of choices [1]. Kwok and Lau [2] recommended that tourism communities foster interaction among members of the general public and other travelers. Xiang et al. [3] and Zhang et al. [4] highlighted the role of online platforms in providing reviews that document hotel guest experiences. Travelers are able to gather comprehensive information about hotels and tourist destinations by engaging with these online communities before planning their trips [5].

A compilation of hotel suggestions from online evaluation platforms serves as a useful resource for travelers [6]. However, these recommendation lists often lack adaptability, making them ineffective in accommodating the individual needs and preferences of visitors. The increasing prevalence of artificial intelligence presents challenges in meeting the diverse needs of travelers. A considerable number of scholars have worked in this domain to identify techniques that could enhance recommendation systems [7,8]. Studies that provide recommendations based on hotel features remain in their preliminary stages, despite numerous advancements in the field over the years. Research focusing on recommendations for tourist groups and traveler types has garnered more attention compared to studies on hotel characteristics influencing individual choices [9,10]. Suggestions are often informed by various types of travelers and tourist groups.

Hou et al. [11] proposed a comprehensive hybrid decision support model for evaluating the service quality of economy hotel websites, addressing the inherent uncertainty and psychological behavior of decision-makers. Unlike traditional evaluation models, this study introduces probabilistic linguistic term sets to capture the hesitancy and subjectivity in human assessments. The authors combine Analytic Network Process with a TODIM-PROMETHEE II approach to construct a MCDM framework that considers both the interdependencies among evaluation criteria and the bounded rationality of users. Their model prioritizes website features across four key dimensions: customer relationship, information value, service competence, and usability. Through a real-world case study involving three economy hotel websites in China, the hybrid model demonstrated robustness, sensitivity, and superiority over traditional MCDM methods. This work significantly contributes to literature by merging fuzzy logic, behavioral decision theory, and outranking methods to support complex web-based service evaluations.

In today’s ever-evolving decision-making environment, characterized by increasing system complexity, decision-makers (DMs) face the significant challenge of selecting the most appropriate solution from a range of possible alternatives. While determining the difficulty of achieving a specific goal is undoubtedly challenging, it is not impossible. Many organizations grapple with motivating their employees, defining objectives, and shaping their worldviews—all of which contribute to the complexity of the decision-making process. As a result, organizational decisions are often laden with multiple implications. Given these constantly shifting factors, it is no surprise that DMs are making considerable efforts to develop reliable methods for solving real-world problems.

1.1 Literature Review

The MCDM method is an efficient cognitive tool, as it enables decision-makers to choose the best option from a limited number of alternatives based on expert judgments. The concept of a “fuzzy set” (FS) was initially introduced by Zadeh [12] in his foundational study, providing a framework specifically designed to represent imprecision. Since then, researchers have developed numerous fuzzy sets and models to address the inherent ambiguity in real-world situations. Atanassov’s intuitionistic fuzzy sets (IFSs) [13] and Yager’s q-rung ortho-pair fuzzy sets (q-ROFSs) [14] are key examples within this category. In 2020, Atanassov extended his research to include the circular domain, in response to increasingly complex decision-making scenarios [15], which led to the development of Circular Intuitionistic Fuzzy Sets (C-IFSs), representing a more advanced methodology.

A significant milestone in computational intelligence (CI) is the evolution of fuzzy set theory from IFS to C-IFS. The circular version of C-IFS offers a more comprehensive representation of uncertainty, particularly useful in situations where categorization is difficult. This nuanced approach allows for the expressive and flexible modeling of complex systems. Due to its distinctive mathematical structure and enhanced representational capacity, C-IFS serves as a powerful tool for managing complex uncertainties. Khan et al. [16] proposed new divergence measures for C-IFS and demonstrated their significance in practical decision-making contexts. Their study illustrated the effectiveness of C-IFS in handling uncertainty, emphasizing its relevance to complex MCDM problems.

Alkan and Kahraman [17] made a significant contribution by demonstrating the application of C-IFS in critical decision-making contexts, specifically in selecting pandemic hospital locations, thereby exemplifying its practical utility. This technique was incorporated into their work related to smart cities. Alsattar et al. [18] contributed to the development of the Internet of Things (IoT) by designing real-time monitoring devices for food supply chains using C-IFS. CRITIC was first proposed by Diakoulaki et al. [19], and since then, it has evolved into a prominent method in MCDM for determining objective weights in complex decision-making situations. CRITIC has developed into a flexible tool applied across various domains. Its effectiveness lies in the systematic approach it uses for weight assignment by organizing the evaluation process and integrating multiple criteria.

Enhancing decision-making in engineering applications, Kizielewicz et al. [20] introduced a fuzzy normalizing-based Multi-Attributive Border Approximation Area Comparison method. Using Stochastic Fuzzy Normalization, Kizielewicz and Salabun [21] demonstrated the effectiveness of benchmark re-identification techniques in engineering decision problems. Further, Kizielewicz et al. [22] compared re-identification techniques in multi-criteria decision analysis, highlighting variations in model performance. Collectively, these studies advance re-identification procedures and normalization strategies, thereby improving decision-making accuracy in engineering and related fields.

New developments, such as the work of Mishra et al. [23], have provided evidence of the method’s adaptability in sophisticated MCDM applications within the field. The unique score functions of Fermatean fuzzy numbers were integrated with CRITIC and GLDS techniques [24]. CRITIC has shown effectiveness in non-traditional sectors, including software selection, 5G industry appraisal [25], and the selection of food waste treatment techniques [26]. All of these applications demonstrate the usefulness of CRITIC across various domains. Market evaluations—such as the assessment of pear varieties in Serbia [27]—and transformations driven by Industry 4.0 [28] also rely on CRITIC to address contemporary challenges. Alterations to criterion weight coefficient computations by Žižović et al. [29] demonstrated that CRITIC is in a continual state of evolution. Liu [30] contributed by incorporating a fuzzy decision-making method for financial risk evaluation. In another study, Zhu et al. [31] employed the CRITIC-TOPSIS method along with multiple machine learning algorithms to evaluate aqueous solubility, making a notable contribution to environmental research. Given the complexities of additive manufacturing, Trivedi et al. [32] proposed a strategy that combines fuzzy WASPAS and fuzzy CRITIC for selecting wire arc additive manufacturing processes. Similarly, Qiu et al. [33] used an integrated spherical fuzzy SWARA-WASPAS technique to accelerate Industry 4.0 implementation in East Africa.

1.2 AROMAN

In 2023, Bošković et al. [34] presented the AROMAN approach, offering a fresh perspective on the decision-making process in the realm of cargo bike delivery concepts. Through their study, which emphasized the system’s flexibility and versatility, they laid the foundation for broader applications in this field. At the same time, Kara et al. [35] introduced the MEREC-AROMAN approach, developed to assess levels of sustainable competitiveness. They achieved this by integrating the MEREC technique with AROMAN through a case study in Turkey, providing valuable insights applicable to real-world situations in socio-economic planning. In a different study, Yalçın et al. [36] proposed an IF-based model focused on port performance assessment. This model aimed to expand existing methodologies. IFSs were incorporated into a comprehensive approach, which was highlighted in a comparison table. The goal of this technique was to assess the sustainability and efficiency of port operations, offering a clearer picture of the uncertainties involved in performance evaluation.

A decision-making problem that considers many criteria seeks to choose the most suitable alternative from a set of options, as opposed to a strategy that only takes one criterion into account. AROMAN [34], when compared to other techniques such as MABAC [37], TOPSIS [38], ARAS [39], MAUT [40], CODAS [41], WASPAS [42], CoCoSo [43], VIKOR [44], and SWARA [45], exhibits notable differences. Most of these methods adhere to the same decision-making principles, the most important of which is the use of an initial decision-making matrix that incorporates a range of alternative options, assessed against a variety of often competing criteria. The outcome of any Multiple Criteria Decision Making (MCDM) approach is a final ranking of the available alternatives, providing decision-makers with a basis for selecting the option that is most suitable for their situation. Table 1 provides a comprehensive presentation of the overall ratings of each strategy, which can be found in full.

The WASPAS approach was developed by Zavadskas et al. [42], who significantly advanced MCDM. By providing decision-makers with a structured and weighted framework for evaluating and ranking alternatives based on multiple criteria, this novel approach is particularly useful when negotiating complex situations. Zavadskas et al. [46] further enhanced decision-making across various domains, offering theoretical support for MCDM while also providing a practical and flexible tool for its application. The domain of MCDM continues to evolve, integrating advanced fuzzy and hybrid models to improve decision-making precision across different fields.

Garg et al. [47] proposed an extended group decision-making method using IFS information distance measures, demonstrating the algorithm’s effectiveness in addressing uncertainty in industrial decision-making contexts. Ayyildiz et al. [48] developed a risk evaluation system for occupational health and safety in pharmaceutical warehouse settings using PyF Bayesian networks, emphasizing the role of probabilistic and fuzzy modeling in risk management. Zheng et al. [49] introduced a novel group decision-making method that combines interval-valued q-rung orthopair fuzzy sets with the CoCoSo approach, enhancing choice robustness in complex evaluation contexts. The study by Chen et al. [50] analyzes over one million TripAdvisor reviews using sentiment analysis and a hospitality-specific lexicon to evaluate hotel attributes across different star ratings. By combining the Kano model with importance-performance analysis, it identifies which features drive positive or negative ratings, showing that key service priorities vary by hotel class. Haseli et al. [51] advanced the MCDM process by incorporating spherical fuzzy sets into the Best-Worst Method, enabling a more sophisticated representation of higher-order uncertainty.

Anum et al. [52] introduced a weighted distance measure for IFS based on a tendency coefficient to demonstrate its application in intelligent control and information processing. Using dual hesitant fuzzy logic, Niaz Khan et al. [53] developed an MCDM model to address problems in the hotel sector. Through a hybrid approach that combines second-order cone programming with multi-criteria decision-making, Tan et al. [54] conducted a cost-benefit analysis in UK hotels, emphasizing the importance of economic efficiency in tourism management. Arıkan Kargı and Cesur [55] identified renewable energy opportunities for hotel buildings using Analytic Hierarchy Process and Multi-Criteria Optimization and Compromise Solution methodologies, thereby enhancing sustainable decision-making in the hotel sector. Research emphasizing the benefits of fuzzy and hybrid MCDM approaches for improving choice accuracy, managing uncertainty, and optimizing complex decision-making processes is driving their increasing adoption across various application domains.

1.3 Motivation and Contribution

The study aims to address the increasing complexity of decision-making processes through a case study focused on hotel selection. In this context, enhanced MCDM approaches are essential to meet the needs of a wide range of tourists. Traditional decision models are often unsuitable in the hotel industry due to the complexity of subjective and ever-changing factors involved in the business. C-IFS provide a solution to the challenges that arise in decision-making situations due to ambiguity and uncertainty. Another key motivation for this study is the need to explore the interaction between three distinct MCDM approaches—namely, CRITIC-AROMAN and CRITIC-WASPAS—within the C-IFS framework. This integration aims to offer decision-makers a combination of tools that are both effective and sophisticated, designed to assist them in navigating the complex process of selecting a hotel.

•   Developed an integrated MCDM framework combining C-IFS with CRITIC, AROMAN, and WASPAS for hotel selection.

•   Enhanced decision-making under uncertainty by leveraging the unique properties of C-IFS to address imprecision in traveler preferences.

•   Contributed methodologically by employing CRITIC for objective criteria weighting, AROMAN for ranking, and WASPAS for comprehensive evaluation.

•   Conducted a case study to validate the effectiveness of the proposed model in a hotel selection context.

•   Performed sensitivity analysis to assess the model’s robustness and adaptability to changes in input parameters.

•   Compared the proposed model with existing MCDM techniques to highlight its superiority and practical applicability.

1.4 Structure of the Paper

Section 2 provides a comprehensive overview of the fundamental concepts of C-IFS, establishing the foundation for the subsequent sections. Section 3 describes the methodology, illustrating how CRITIC emphasizes criteria importance, how AROMAN systematically evaluates alternatives, and how WASPAS conducts an in-depth analysis of the outcomes within the C-IFS framework. After presenting the findings, insights, and applications of the integrated approach, Section 4 effectively addresses the practical aspects by applying the method to a real-world hotel selection scenario. In the ever-evolving field of decision-making, Section 5 summarizes the study, highlighting key issues, implications, and potential directions for future research. Table 2 presents the abbreviations and their full names.

2  Preliminaries

2.1 Intuitionistic Fuzzy Sets

Atanassov [13] expanded fuzzy sets with the introduction of Intuitionistic Fuzzy Sets (IFSs). For IFSs, the sum of the membership and non-membership degrees assigned to each element in a set must be less than or equal to one, ensuring that the sum is a valid whole. Wu et al. [56] outlined the fundamental principles governing the operation of Intuitionistic Fuzzy Numbers (IFNs).

Definition 1: [13] Let U be a non-empty set. An IFS Y in U is given by:

Y={(k,ητYβγ(k),ηηYβγ(k)):k∈U}

where the functions ητYβγ:X→[0,1] and ηηYβγ:X→[0,1] define the degree of membership and the degree of non-membership of the elements in U, respectively, with the condition that

0≤ητYβγ(k)+ηηYβγ(k)≤1,for all k∈U

The degree of hesitancy is computed as follows:

πY(k)=1−ητYβγ(k)−ηηYβγ(k).(1)

Definition 2: [13] Let A=(ητAβγ,ηηAβγ) and B=(ητBβγ,ηηBβγ) be two IFNs, then the addition and multiplication operations on these two IFNs are defined as follows.

A⊕B=(ητAβγ+ητBβγ−ητAβγητBβγ,ηηAβγηηBβγ)(2)

A⊗B=(ητAβγητBβγ,ηηAβγ+ηηBβγ−ηηAβγηηBβγ).(3)

Definition 3: Let A=(ητAβγ,ηηAβγ) be an IFN, then the score function S(A) and accuracy function H(A) of A can be defined as as follows:

S(A)=ητAβγ−ηηAβγ(4)

H(A)=ητAβγ+ηηAβγ.(5)

Definition 4: [56] Let AY=(ητAYβγ,ηηAYβγ) (i=1,2,…,n) be a set of IFNs and w=(w1,w2,…,wn)J be the weight vector of AY with ∑i=1nwY=1, then an IF weighted geometric (IFWG) operator is:

IFWG⁡(A1,A2,…,An)=(∏i=1nητAYwYβγ,1−∏i=1n(1−ηηAYβγ)wY).(6)

Definition 5: [57] Let A=(ητAYβγ,ηηAYβγ) and B=(ητBYβγ,ηηBYβγ) be two IFNs. The following is the formula for calculating the normalised Euclidean distance between these two C-IFNs:

=12n∑i=1n(ητAYβγ−ητBYβγ)2+(ηηAYβγ−ηηBYβγ)2+(πAY−πBY)2¯(7)

2.2 Circular Intuitionistic Fuzzy Sets

Research has proposed several expansions of IFSs, such as Pythagorean fuzzy sets (PyFSs) and q-q rung orthopair fuzzy sets (q-ROFSs). A significant expansion of IFS, the concept of circular IFS (C-IFS), was introduced by Atanassov [15]. In this section, we provide a brief overview of the fundamentals of C-IFSs. Each element in a C-IFS is represented by a circle that indicates its membership status. The following definition clarifies what C-IFS is.

Definition 6: [15] Let U be the universe. A C-IFS Yr in U is an object with the form

Yr={⟨k,ητYβγ(k),ηηYβγ(k);rβγ⟩:k∈U},(8)

where 0≤ητYβγ(k)+ηηYβγ(k)≤1, and r∈[0,1] is the radius of the circle around each element x∈U. The functions ητYβγ:E→[0,1] and ηηYβγ:E→[0,1] represent the degree of membership and the degree of non-membership of the elements x∈U, respectively.

The degree of indeterminacy is calculated as follows:

πY(k)=1−ητYβγ(k)−ηηYβγ(k).(9)

In contrast to standard IFSs, where each element is represented by a point, in C-IFSs, each element is represented by a circle with center ⟨ητYβγ(k),ηηYβγ(k)⟩ and radius r.

Definition 7: For an IFS ZY, where i is the number of IFS ZY that include kY IF pairs, the IF pairs may be expressed as {⟨mi,1,ni,1⟩,⟨mi,2,ni,2⟩,…}. Next, we find the C-IFS by following these steps. To begin, Eq. (10) is used to compute the arithmetic average of the IF pairings.

⟨ητβγ(ZY),ηηβγ(ZY)⟩=⟨∑j=1kYmi,jkY,∑j=1kYni,jkY⟩,(10)

where kY is the number of pairs in ZY. Then, the radius of ⟨ητβγ(ZY),ηηβγ(ZY)⟩ is the maximum of the Euclidean distances given in Eq. (11).

rYβγ=max1≤j≤kY(ητβγ(ZY)−mi,j)2+(ηηβγ(ZY)−ni,j)2.(11)

For a universe X={Z1,Z2,…}, the C-IFS can be expressed as follows.

Ar={⟨ZY,ητβγ(ZY),ηηβγ(ZY);rβγ⟩:ZY∈X}={⟨ZY,Or(ητβγ(ZY),ηηβγ(ZY))⟩:ZY∈U}(12)

Fig. 1 gives the geometric explanation of C-IFS and IFS.

Figure 1: Graphical explanation of C-IFS and IFS

Definition 8:

L∗={⟨c,d⟩:c,d∈[0,1] & c+d≤1}.(13)

Therefore, Yr can be rewritten in the form:

Yr∗={⟨k,O(ητYβγ(k),ηηYβγ(k));rβγ⟩:k∈U},(14)

where O is a function representing a circle, whose radius is r and center is (ητYβγ(k),ηηYβγ(k)).

O(ητYβγ(k),ηηYβγ(k))={⟨c,d⟩:c,d∈[0,1],(ητYβγ(k)−a)2+(ηηYβγ(k)−b)2≤r}∩L∗={⟨c,d⟩:c,d∈[0,1],(ητYβγ(k)−c)2+(ηηYβγ(k)−d)2≤r,c+d≤1}.

Thus C-IFS has the form C={(⟨k,O(ητYβγ(k),(ηηYβγ(k))⟩:k∈U)}. Note that each IFS is a C-IFS with radius 0. But its converse is not true.

3  Algorithm

Step 1: Presenting the C-IFNs dataset, where AATT (for k=1,2,…,p) signifies alternatives assessed across various criteria CCRT (for k=1,2,…,q). A mathematical statement that characterises our dataset, which is referred to as C-IFNs, is CCRij=(BYij,BYij;Rij). This dataset contains information on alternatives evaluated based on various DM criteria. These alternatives are identified by indices i and j, where i is a range of 1,2,…,p and j is a range of 1,2,…,q. Table 3 provides an overview of eight unique linguistic terms that are used to characterise each criteria under consideration. The linguistic terms that are related with competence are shown in Table 4. In addition, we complement these words with others. In order to provide a thorough information assessment process, this collection of diverse linguistic terms is providing it.

Step 2: Calculate the weights of the DM by using the scoring function outlined in Eq. (4). Include the scores into the Equation that has been specified 15 once they have been evaluated.

ℶij−=∑Yn(ητYβγ−ηηYβγ+2rβγ(2s−1)3)∑j3(∑YnητYβγ−ηηYβγ+2rβγ(2s−1)3)(15)

Step 3: Calculate the aggregated decision matrix shown as M=[Mij]q×p using the method detailed in Eq. (16). This entails using the stated formula in a methodical manner in order to gather together the pertinent data, which ultimately results in the production of a complete decision matrix.

=(1−11+{∑i=1nθνγi(ξνγi1−ξνγi)m}1m,11+{∑i=1nθνγi(1−ωνγiωνγi)m}1m)(16)

Step 4: CRITIC Method

The method is divided into the following parts so that we may evaluate the relative importance of the MCDM process’s contained criteria:

Step 4.1: Utilising Eq. (17), get the score value of the combined choice matrix.

ητYβγ−ηηYβγ+2rβγ(2s−1)3(17)

Step 4.2: Apply Eq. (18) to convert SScc into normal matrix.

SScc~ij={SSccij−SSccj−SSccj+−SSccj−,j∈CCRbSSccj+−SSccijSSccj+−SSccj−,j∈CCRc(18)

where SSccj+=maxiSSccij,SSccj−=miniSSccij,CCRb and CCRc represents the benefit-type and cost-type criteria, respectively.

Step 4.3: Estimating the standard deviations for the criterion by use of Eq. (19).

σj=∑i=1n(SSccij−SScc¯j)2n.(19)

where SScc¯j=∑i=1nSScc~ij/n

Step 4.4: The correlation coefficient of the criteria concerned is determined by means of the Eq. (20).

rjt=∑i=1n(SSccij−SScc¯j)(SSccij−SScct¯)∑i=1n(SSccij−SScc¯j)2(SSccij−SScc¯t)2(20)

Step 4.5: Perform a thorough analysis of the data pertaining to every criteria by using Eq. (21).

ZZj=σ∑t=1m(1−rjt)(21)

Step 4.6: Use the Eq. (22) to determine the objective weight that each criteria.

wj=ZZj∑j=1mZZj(22)

Step 5: AROMAN

To standardise the data input into the decision-making matrix, normalisation must be conducted. After creating the matrix with the input data, the next step involves normalising the data within the intervals of 0 to 1 by using Eqs. (23) and (24).

Step 5.1: Normalization 1 (Linear):

ℶμij=βηij−βηijβηij−βηij,Y=1,2,…,p; j=1,2,…,q(23)

Step 5.2: Normalization 2 (Vector):

ℶμij∗=βηij∑i=1mβηij2,Y=1,2,…,p; j=1,2,…,q(24)

Step 6: For the purpose of standardising the information that has been provided, do the Averaged Aggregation Normalisation.

For the purpose of carrying out the procedure of aggregated averaged normalisation, Eq. (25) is used accordingly.

ℶμijnorm=βℶμij+(1−β)ℶμij∗2,Y=1,2,…,p;j=1,2,…,q(25)

The phrase ℶμijnorm where β acts as a weighting factor within the range of 0 to 1 reflects the aggregated average normalisation. With regard to our specific circumstances, the variable β gets a value of 0.5.

Step 7: The decision-making matrix, which has been processed by aggregated averaging to achieve normalisation, should be multiplied by the weights of the corresponding criteria. As shown by Eq. (26), this procedure results in the production of a weighted decision-making matrix.

ℶμij^=Wij⋅ℶμijnorm,Y=1,2,…,p; j=1,2,…,q(26)

Step 8: Eq. (27) must be employed to distinctly express the normalised weighted values for the criteria type min(ξνγi) and the maximum type (ηηi) under consideration.

ξνγ=∑j=1nℶμij^(min),Y=1,2,…,p; j=1,2,…,qηηY=∑j=1nℶμij^(max),Y=1,2,…,p; j=1,2,…,q(27)

Step 9: Determine the final ranking of alternatives:

R^Y=ξγβη+ηηY(1−βη),Y=1,2,…,p(28)

Step 10: WASPAS method

Step 10.1: Normalise the cost and benefit criterion using Eq. (29).

WWSij={SKijmaxYSKij,j∈CCRbmaxYSKijSKij,j∈CCRc(29)

Step 10.2: Eq. (30) allows one to obtain the additive relative significance in the weighted normalised data for every alternative.

Q1Y=∑j=1nWWSij⋅βηj,(30)

where Q1Y indicates the additive relative importance of each alternative.

Step 10.3: Calculate the multiplicative relative significance of the weighted normalised data for each alternative using Eq. (31).

Q2Y=∏j=1nWWSijβηj.(31)

Step 10.4: The joint generalized criteria (Q) described as follows to combine and generalise additive and multiplicative methods:

QQY=12(∑j=1nWWSij⋅βηj+∏j=1nWWSijβηj).(32)

In addition, apply Eq. (33) to improve ranking accuracy as:

QQY=λ∑j=1nWWSij⋅βηj+(1−λ)∏j=1nWWSijβηj.(33)

4  Case Study

This case study has been influenced by the evolving needs of modern travelers, who are increasingly seeking unique and superior hotel selections. Contemporary travelers exhibit a wide range of motivations and interests, including a commitment to environmental sustainability, cultural immersion, as well as more traditional reasons such as business trips and romantic getaways. As a result, there is a need for an alternative decision-making approach that can address the various factors involved in hotel reservations comprehensively. This case study is particularly important given the complexity of transportation options available today. Planning a trip now requires considering numerous factors, such as preferences for facilities, attractions, pricing, sustainability, safety, and opportunities for cultural engagement. Understanding the intricacies of these challenges is crucial for hotel operators who aim to meet the ever-changing expectations of their guests, as well as for travelers seeking to make choices that align with their individual preferences and tastes.

This case study demonstrates the practical application of the decision-making framework, helping travelers identify the alternatives that best align with their specific needs. It serves as a crucial resource for addressing the evolving demands of the hospitality sector. Moving beyond theoretical discussions, this work introduces a flexible decision-making model that can be easily adapted to meet the requirements of both hotel owners and guests. By doing so, it enables informed decision-making that aligns with the complexities of contemporary travel preferences.

4.1 Definition Machine Learning Models (Alternatives)

1.    Hotel A-Luxury Boutique Hotel in the City Center (AAT1):

Hotel A stands as an urban sanctuary, offering a tailored experience amidst the vibrant pulse of the city. Catering to discerning travelers, it goes beyond traditional accommodation by providing personalized concierge services, bespoke interiors crafted by renowned designers, and a selection of amenities that redefine luxury.

2.    Hotel B-Resort with Scenic Views and Recreational Facilities (AAT2):

Hotel B serves as the perfect retreat, offering complete privacy alongside breathtaking views of the surrounding landscape. The establishment combines the traditional resort experience with a variety of recreational activities, complemented by rejuvenating spa services and serene natural surroundings.

3.    Hotel C-Budget-Friendly Accommodations with Essential Amenities (AAT3):

Hotel C sets a new standard for cost-effective accommodations by offering a unique blend of affordable pricing and essential amenities. It goes beyond simple lodging, presenting a practical choice for pragmatic travellers.

4.    Hotel D-Business-Focused Hotel with Conference Facilities (AAT4):

Hotel D is tailored to meet the needs of modern professionals. The facility boasts state-of-the-art meeting amenities, high-speed internet access, and a streamlined design that promotes efficiency, making it the perfect choice for productive business travel.

5.    Hotel E-Eco-Friendly Accommodations Emphasizing Sustainability (AAT5):

Hotel E goes beyond traditional accommodation by embracing a vacationing philosophy focused on environmental and social responsibility. The hotel actively engages in sustainability initiatives, including energy-efficient systems and waste reduction measures, making a positive impact on both the environment and the community.

4.2 Definition of Criteria

Location Proximity (CCR1):

This criterion evaluates the hotel’s proximity to public transportation and key tourist attractions. The goal is to offer guests a luxurious all-inclusive experience, with easy access to the city’s top destinations, ensuring a seamless and memorable stay.

Amenities and Services (CCR2):

This criterion goes beyond mere assessment by evaluating the hotel’s in-room facilities, which are both comprehensive and of exceptional quality. A thorough analysis of the available alternatives must take into account factors such as personalized concierge services and meticulously designed interiors.

Pricing and Affordability (CCR3):

In an era where financial savings are paramount, this criterion evaluates the total cost of the stay, factoring in any applicable discounts or promotions. This analysis goes beyond simple price assessment to encompass the overall value of the accommodation.

Customer Reviews and Ratings (CCR4):

This criterion goes beyond aggregated evaluations by incorporating qualitative analysis derived from specific feedback provided by previous visitors, based on their individual experiences.

Environmental Impact (CCR5):

This criterion emphasizes the fundamental principles of ethical travel by highlighting the hotel’s commitment to environmental sustainability. The assessment includes environmentally responsible actions and evaluates certifications for sustainable practices.

Safety and Security (CCR6):

To ensure the hotel’s physical safety, this criterion evaluates the immediate surroundings of the establishment, including data on the local crime rate. Additionally, it assesses the safety procedures followed by the hotel.

Step 1: Experts employ the C-IFNs dataset, integrating linguistic terms from Table 3 for each alternative AATr (where p=1,2,…,r), considering diverse criteria CCR, as specified in Table 5.

Step 2: To determine the weights of decision-makers (DMs), it is necessary to use the scoring function that is defined in Eq. (4). After that, the scores that were acquired should be applied to Eq. (15), and the values that are obtained should be shown in Table 6.

Step 3: Utilising Eq. (16), do the calculation of the aggregated decision matrix M=[Mij]q×p. The results of this calculation should be shown in Table 7.

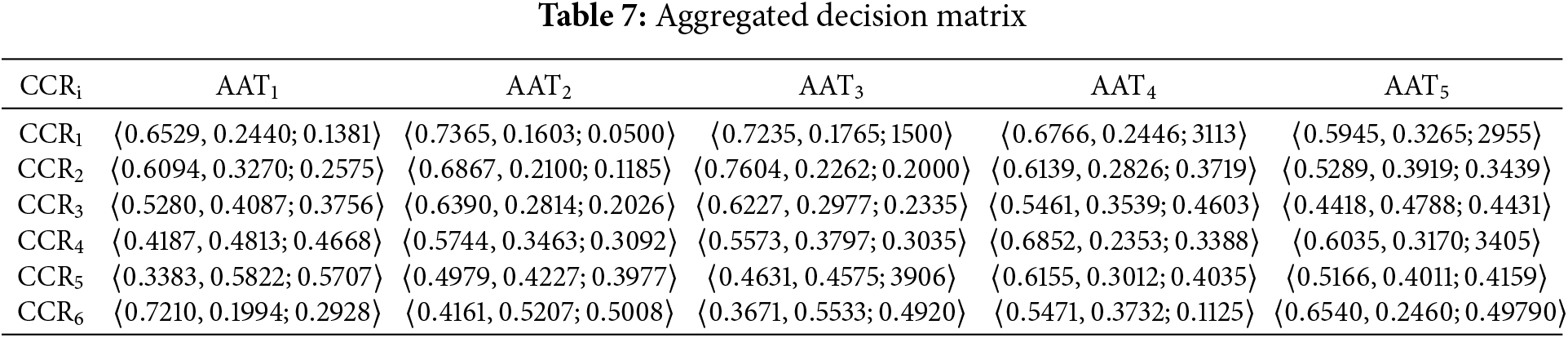
Step 4.1: To obtain the score of the choice matrix, use Eq. (4) in Table 8 through calculation.

Step 4.2: Convert the matrix ℶ¯− into a C-IFNs matrix utilising Equation (refttt1) from Table 9.

Step 4.3: Utilise the formula presented in Eq. (19) in Table 10 to compute an estimate of the standard deviations for the criteria.

Step 4.4: To determine the correlation coefficient for the criteria enumerated in Table 11, employ Eq. (20) supplied.

Step 4.5: Evaluate the details of each criterion using Eq. (21) as specified in Table 12.

Step 4.6: Calculate the desired weight for each criteria using Eq. (22), as shown in Table 13. Evaluate each criteria using Eq. (21), as shown in Table 12.

Step 5:

Step 5.1: Normalization 1 (Linear) utilizing Eq. (23).

T(i,j)=[0.22910.44090.46000010.66720.887110.48050.50590.1381110.94090.36330.357600.90280.90850.8599110.24810000.64280.60420.9662]

Step 5.2: Normalization 2 (Vector) utilizing Eq. (24)

F(i,j)=[0.40350.40900.39390.25410.18030.65430.45800.48230.51940.42560.42460.23380.49930.50080.50570.38370.35300.16640.48730.48580.48680.61100.66320.28750.37510.33670.28700.48350.47210.6378]

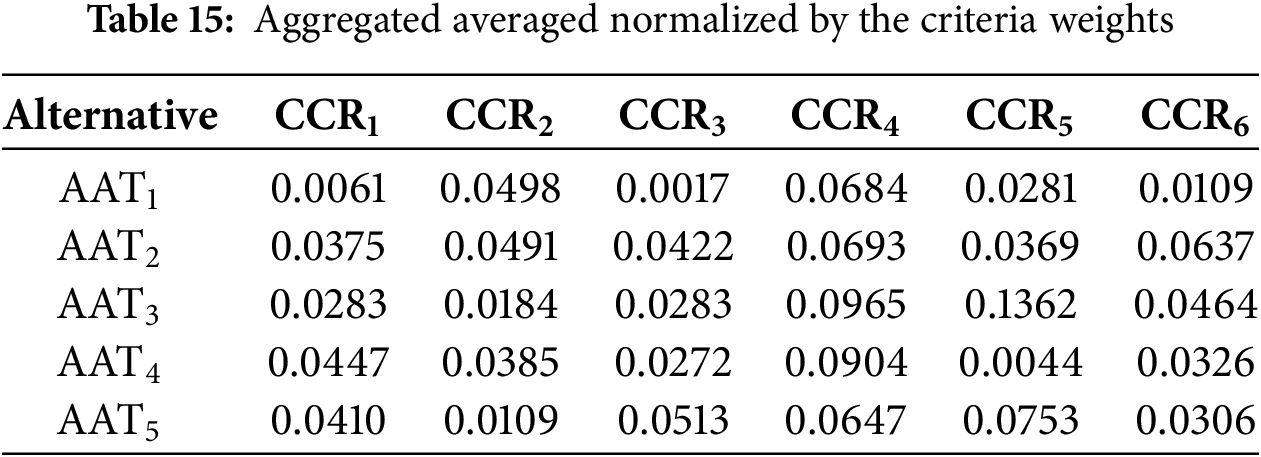
Step 6: Table 14 shows how we use Eq. (25) for aggregated averaged normalisation.

The variation in β from 0.1 to 0.8 is depicted in Fig. 2.

Figure 2: The variation in β from 0 to 1

Step 7: To obtain a weighted decision-making matrix as given in Eq. (26), multiply the aggregated averaged normalised decision-making matrix by the criteria weights (Table 15).

Step 8: Using Eq. (27) with parameter βη=0.5 express the normalised weighted values distinctively for the criterion type min(βηi) and the max type (βηi). Using Eq. (28) in Table 16 get the last ranking of the choices.

Step 9: Use Eq. (29) to normalise the cost and benefit criterion. Table 17 shows values after normalisation.

Steps 10.1–10.3: To determine the additive relative significance, multiplicative relative importance, and joint generalised criterion (Q) in the weighted normalised data for each option, use the Formulae (30)–(32). The acquired values are shown in Table 18.

4.3 Sensitivity Analysis

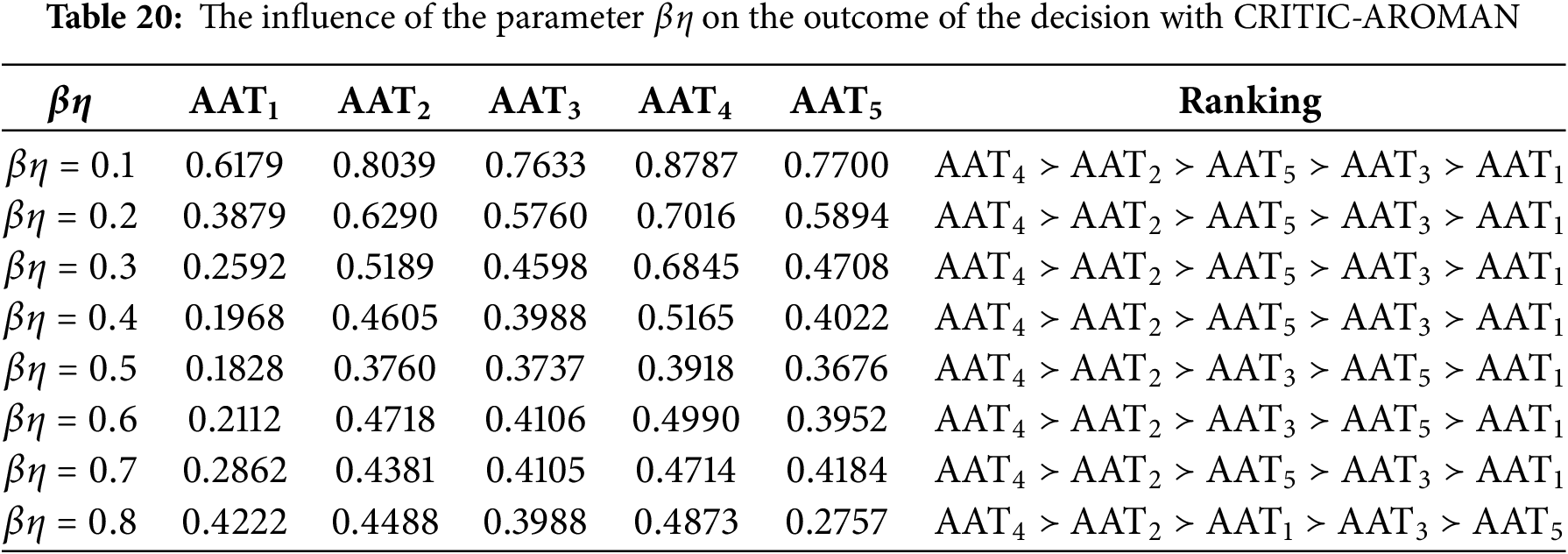
Within the C-IFS framework for hotel selection, the sensitivity analysis conducted in this study aims to assess the reliability and robustness of the combined CRITIC-WASPAS techniques (Fig. 3) and CRITIC-AROMAN techniques (Fig. 4). By systematically varying key factors βη, the sensitivity analysis provides insights into the stability of the decision outcomes. This analysis explores how changes in these criteria influence the final selection of the best hotel option, thereby offering a deeper understanding of the model’s responsiveness to variations in decision inputs. The sensitivity analysis of decision outcomes, presented in Table 19, shows a consistent ranking of alternatives by the CRITIC-WASPAS method, denoted as AAT1 to AAT5, as the parameter βη changes from 0.1 to 0.8. In contrast, Table 20 reveals an inconsistent ranking of alternatives by the CRITIC-AROMAN method.

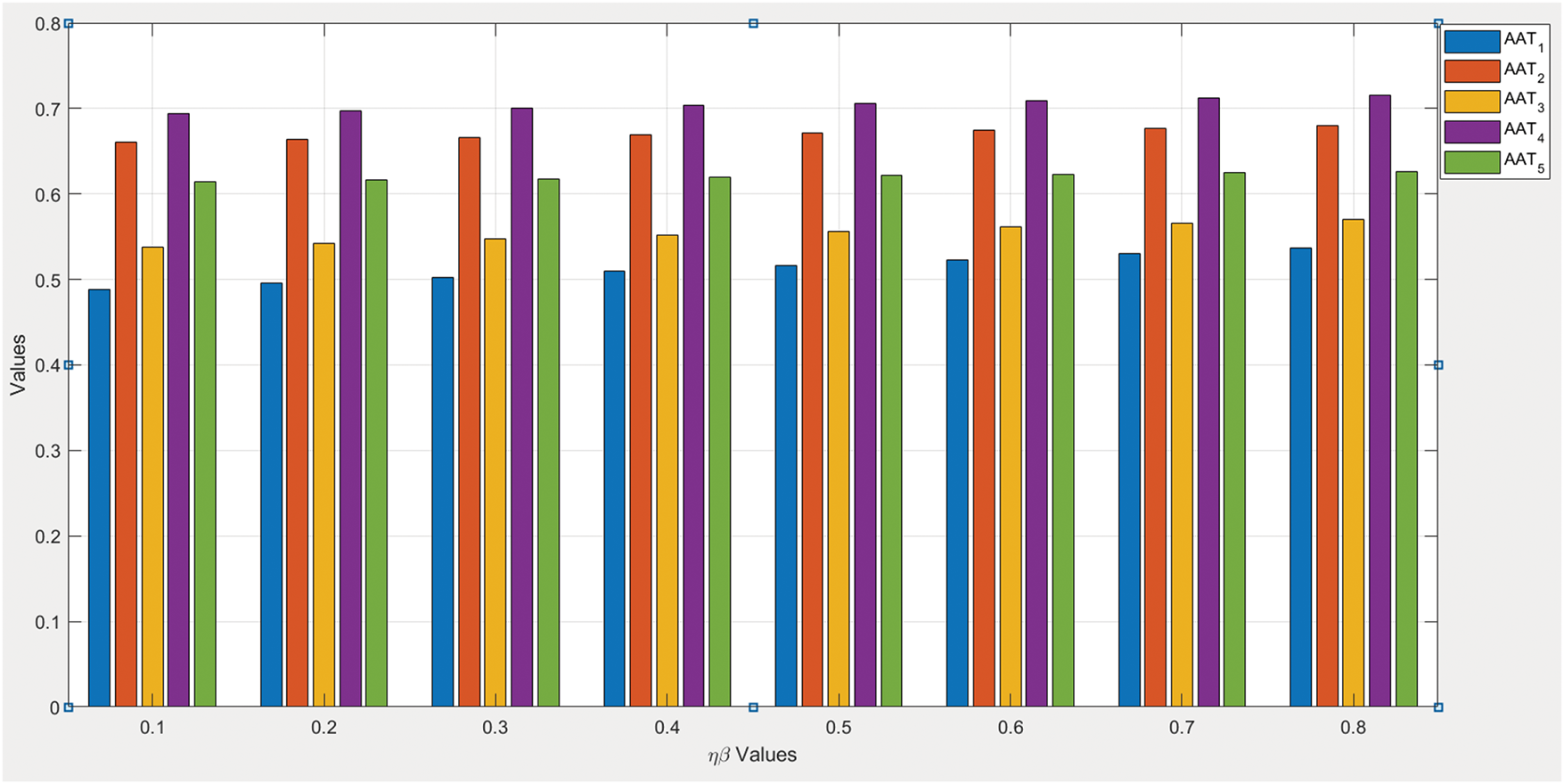
Figure 3: Visualizing variations with changing parameter (βη) in CRITIC-WASPAS

Figure 4: Visualizing variations with changing parameter (βη) in CRITIC-AROMAN

4.4 Comparative Analysis

Throughout our comprehensive comparative study, we conducted a systematic investigation into the practicality and efficiency of decision-making processes within C-IFNs. Moreover, the reliability and consistency of our findings are significantly enhanced by the thorough examination of each component, coupled with rigorous validation and robustness tests performed throughout the research. These methodological elements not only contribute to the comprehensive nature of our study but also form the foundation upon which our conclusive insights are based. The key findings are succinctly summarized in Table 21, which offers a compelling overview of our work. Our in-depth analysis has provided valuable insights that have allowed us to fully understand the strengths and weaknesses associated with the various decision-making techniques employed within IFNs. At the heart of our study is the provision of reliable insights for decision-makers, which strategically guide the integration of IFs and enhance our collective understanding of decision-making within the IF framework.

4.5 Discussion

The study investigates the outcomes, implications, and overall insights gained from applying the C-IFS framework for hotel selection in conjunction with the integrated CRITIC-AROMAN and CRITIC-WASPAS methodologies. The comprehensive research conducted in a real-life scenario led to valuable findings, with Hotel D, a commercial hotel offering conference rooms, being identified as the most suitable alternative.

The CRITIC method, by effectively determining the importance of criteria, reveals that business-oriented amenities, particularly conference facilities, are critical to the decision-making process. The thorough evaluation conducted by AROMAN further underscores the significance of Hotel D and its ability to meet the specific needs of corporate guests. The complete analysis provided by WASPAS considers both the positive and negative aspects of the evaluated alternatives, enhancing the robustness of the decision-making process.

The selection of Hotel D illustrates a strong awareness of factors such as amenity availability, safety, and the specific requirements of business travel. In addition to addressing the practical constraints of the decision-making problem, the result highlights the efficacy of the integrated approach in identifying subtle aspects across multiple criteria. This application provides decision-makers with tailored insights that align with their specific needs, showcasing the potential of the integrated methodology to address complex decision scenarios.

By demonstrating how these approaches, when applied within a C-IFS framework, can benefit situations such as hotel selection, the study contributes to the growing body of knowledge in decision science. The discussion concludes with reflections on the research findings, their implications for hotel decision-making, and potential future directions for MCDM research.

4.6 Limitations

While the proposed C-IFS-based decision-making model demonstrates strong applicability in hotel selection, several limitations must be addressed to improve methodological transparency and practical implementation:

1.    The integration of multiple methodologies, including C-IFS, CRITIC, AROMAN, and WASPAS, increases the computational burden, particularly for large-scale decision problems.

2.    The determination of fuzzy set parameters, especially hesitation and membership degrees in C-IFS, may introduce subjectivity, potentially affecting the model’s consistency.

3.    Sensitivity analysis reveals that small fluctuations in input data can influence ranking outcomes. A more extensive robustness check is necessary to assess the model’s stability in varying conditions.

4.    The model’s accuracy depends heavily on the availability and quality of input data. In data-scarce environments, hybrid approaches that combine expert judgment with machine learning-driven imputation techniques could enhance the model’s reliability.

5.    While the model has been validated in a hotel selection scenario, broader applicability across industries such as healthcare, energy, and supply chain management requires further empirical testing to confirm its effectiveness.

6.    The complexity of integrating multiple methodologies may reduce interpretability for decision-makers. Enhancing model transparency through visual analytics and explainable AI techniques could facilitate its practical adoption in real-world decision support systems.

5  Conclusion

In conclusion, this research introduces a novel approach to MCDM in hotel selection, utilizing the C-IFS framework in conjunction with the CRITIC-AROMAN and CRITIC-WASPAS methodologies. The study delves into the complexities of hotel selection and the evolving preferences of tourists through a detailed classification approach. The systematic application of this integrated method in a real-world scenario reveals that Hotel D, which caters to business travelers and provides conference facilities, emerges as the most suitable choice. This finding demonstrates the effectiveness of the integrated approach in providing decision-makers with unique insights tailored to diverse contexts, underscoring its practical significance in identifying subtle distinctions.

The research highlights the effective application of each methodology, emphasizing their roles in assessing alternatives, conducting comprehensive analyses, and establishing the importance of various criteria. The paper contributes to the field of decision science by demonstrating the efficacy of these strategies within the C-IFS framework and their relevance to complex decision-making problems, such as hotel selection. The sensitivity analysis further illustrates the model’s responsiveness to variations in input parameters, showcasing its adaptability.

However, the integration of multiple methodologies and the C-IFS framework may demand significant computational resources, potentially limiting scalability for larger datasets. The accuracy and reliability of the proposed algorithm are influenced by several important constraints. Notably, the subjectivity in determining fuzzy parameters, such as expert assessments and pre-defined membership functions, can introduce biases, potentially compromising the accuracy of decision results. Furthermore, the model’s sensitivity to minor changes in input parameters can lead to variations in the final rankings, affecting the stability of the decision-making process. The model’s performance is also heavily dependent on the availability and quality of data, which may impact its effectiveness in data-scarce environments.

To address these limitations, future research can focus on the following areas:

•   Developing computationally efficient algorithms to enhance the scalability of the model for handling larger decision problems, ensuring applicability in more complex scenarios.

•   Exploring alternative parameter determination techniques to reduce subjectivity, improving the reliability and robustness of the decision outcomes by minimizing biases in expert judgments.

•   Extending the framework to other industries, such as healthcare, transportation, and sustainable energy, to validate its broader applicability and demonstrate its versatility in diverse decision-making contexts.

•   Investigating hybrid decision-support models that integrate machine learning with fuzzy logic-based MCDM approaches to enhance decision accuracy and adapt to dynamic environments.

•   Enhancing interpretability by simplifying the integration of multiple methodologies, providing more user-friendly decision-support tools to practitioners and decision-makers, making the model more accessible and easier to apply in real-world settings.

By addressing these aspects, future research can further refine and expand the applicability of the proposed MCDM model, enhancing its adaptability to a wider range of complex decision-making scenarios across various industries.

Acknowledgement: This research was supported by the Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2025R259), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This research was also supported by the Researchers Supporting Project Number (UM-DSR-IG-2023–07), Almaarefa University, Riyadh, Saudi Arabia.

Funding Statement: This research was supported by the Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2025R259), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This work was also supported by the Researchers Supporting Project Number (UM-DSR-IG-2023–07), Almaarefa University, Riyadh, Saudi Arabia.

Author Contributions: Conceptualization, Sana Shahab and Vladimir Simic; methodology, Ibtehal Alazman and Mohd Anjum; software, Sana Shahab and Mohd Anjum; validation, Ashit Kumar Dutta and Nouf Abdulrahman Alqahtani; formal analysis, Mohd Anjum, Nouf Abdulrahman Alqahtani and Željko Stević; resources, Sana Shahab, Ibtehal Alazman and Ashit Kumar Dutta; data curation, Nouf Abdulrahman Alqahtani; writing—original draft preparation, Sana Shahab and Mohd Anjum; writing—review and editing, Ashit Kumar Dutta, Vladimir Simic and Željko Stević; visualization, Ibtehal Alazman, Ashit Kumar Dutta and Vladimir Simic; funding acquisition, Sana Shahab, Ibtehal Alazman and Ashit Kumar Dutta. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Roy G. Travelers’ online review on hotel performance—analyzing facts with the Theory of Lodging and sentiment analysis. Int J Hosp Manage. 2023;111:103459. doi:10.1016/j.ijhm.2023.103459. [Google Scholar] [CrossRef]

2. Kwok PK, Lau HY. Hotel selection using a modified TOPSIS-based decision support algorithm. Decis Support Syst. 2019;120:95–105. doi:10.1016/j.dss.2019.02.004. [Google Scholar] [CrossRef]

3. Xiang Z, Du Q, Ma Y, Fan W. A comparative analysis of major online review platforms: implications for social media analytics in hospitality and tourism. Tour Manage. 2017;58:51–65. doi:10.1016/j.tourman.2016.10.001. [Google Scholar] [CrossRef]

4. Zhang CX, Zhao M, Cai MY, Xiao QR. Multi-stage multi-attribute decision making method based on online reviews for hotel selection considering the aspirations with different development speeds. Comput Ind Eng. 2020;143:106421. doi:10.1016/j.cie.2020.106421. [Google Scholar] [CrossRef]

5. Hou Z, Cui F, Meng Y, Lian T, Yu C. Opinion mining from online travel reviews: a comparative analysis of Chinese major OTAs using semantic association analysis. Tour Manage. 2019;74:276–89. doi:10.1016/j.tourman.2019.03.009. [Google Scholar] [CrossRef]

6. Ahani A, Nilashi M, Ibrahim O, Sanzogni L, Weaven S. Market segmentation and travel choice prediction in Spa hotels through TripAdvisor’s online reviews. Int J Hosp Manage. 2019;80:52–77. doi:10.1016/j.ijhm.2019.01.003. [Google Scholar] [CrossRef]

7. Nilashi M, Ibrahim O, Yadegaridehkordi E, Samad S, Akbari E, Alizadeh A. Travelers decision making using online review in social network sites: a case on TripAdvisor. J Comput Sci. 2018;28:168–79. doi:10.1016/j.jocs.2018.09.006. [Google Scholar] [CrossRef]

8. Chang YC, Ku CH, Chen CH. Social media analytics: extracting and visualizing Hilton hotel ratings and reviews from TripAdvisor. Int J Inf Manage. 2019;48:263–79. doi:10.1016/j.ijinfomgt.2017.11.001. [Google Scholar] [CrossRef]

9. Cheng SH. Autocratic decision making using group recommendations based on hesitant fuzzy sets for green hotels selection and bidders selection. Inf Sci. 2018;467:604–17. doi:10.1016/j.ins.2018.08.014. [Google Scholar] [CrossRef]

10. Radojevic T, Stanisic N, Stanic N, Davidson R. The effects of traveling for business on customer satisfaction with hotel services. Tour Manage. 2018;67:326–41. doi:10.1016/j.tourman.2018.02.007. [Google Scholar] [CrossRef]

11. Hou Z, He S, Liang R, Li J, Huang R, Wang J. Evaluating economy hotel website service quality: a hybrid bounded rationality behavioral decision support model. Mathematics. 2023;11(12):2776. doi:10.3390/math11122776. [Google Scholar] [CrossRef]

12. Zadeh LA. Information and control. Fuzzy Sets. 1965;8(3):338–53. [Google Scholar]

13. Atanassov KT. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986;20(1):87–96. [Google Scholar]

14. Yager RR. Generalized Orthopair Fuzzy sets. IEEE Trans Fuzzy Syst. 2017;25(5):1220–123. [Google Scholar]

15. Atanassov KT. Circular intuitionistic fuzzy sets. J Intell Fuzzy Syst. 2020;39(5):5981–6. [Google Scholar]

16. Khan MJ, Kumam W, Alreshidi NA. Divergence measures for C-IFSs and their applications. Eng Appl Artif Intell. 2022;116:105455. doi:10.1016/j.engappai.2022.105455. [Google Scholar] [CrossRef]

17. Alkan N, Kahraman C. Circular intuitionistic fuzzy TOPSIS method: pandemic hospital location selection. J Intell Fuzzy Syst. 2022;42(1):295–316. doi:10.3233/JIFS-219193. [Google Scholar] [CrossRef]

18. Alsattar HA, Mourad N, Zaidan AA, Deveci M, Qahtan S, Jayaraman V, et al. Developing IoT sustainable real-time monitoring devices for food supply chain systems based on climate change using circular intuitionistic fuzzy set. IEEE Internet Things J. 2024;11(16):26680–9. doi:10.1109/JIOT.2023.3305910. [Google Scholar] [CrossRef]

19. Diakoulaki D, Mavrotas G, Papayannakis L. Determining objective weights in multiple criteria problems: the CRITIC method. Comput Oper Res. 1995;22(7):763–77. doi:10.1016/0305-0548(94)00059-H. [Google Scholar] [CrossRef]

20. Kizielewicz B, Więckowski J, Sałabun W. Fuzzy normalization-based multi-attributive border approximation area comparison. Eng Appl Artif Intell. 2025;141:109736. doi:10.1016/j.engappai.2024.109736. [Google Scholar] [CrossRef]

21. Kizielewicz B, Sałabun W. Benchmark study of re-identification methods based on Stochastic Fuzzy Normalization and their application to decision-making problems in engineering. Facta Univ Series Mech Eng. 2025. doi:10.22190/FUME240916004K. [Google Scholar] [CrossRef]

22. Kizielewicz B, Wiȩckowski J, Franczyk B, Wa̧tróbski J, Sałabun W. Comparative analysis of re-identification methods of multi-criteria decision analysis models. IEEE Access. 2025;13:8338–54. doi:10.1109/ACCESS.2024.3524672. [Google Scholar] [CrossRef]

23. Mishra AR, Chen SM, Rani P. Multi-criteria decision-making based on novel score function of Fermatean fuzzy numbers, the CRITIC method, and the GLDS method. Inf Sci. 2023;623:915–31. doi:10.1016/j.ins.2022.12.031. [Google Scholar] [CrossRef]

24. Tuş A, Aytaç Adalı E. The new combination with CRITIC and WASPAS methods for the time and attendance software selection problem. Opsearch. 2019;56:528–38. doi:10.1007/s12597-019-00371-6. [Google Scholar] [CrossRef]

25. Mohamed M, Ali A, Abdel-Basset M, Abouhawwash M, Askar S, Tantawy A. Extension of simple multi-attribute rating technique in uncertainty environment for 5G industry evaluation: egyptian new administrative capital as a case study. Heliyon. 2024;10(7):e29033. doi:10.1016/j.heliyon.2024.e29033. [Google Scholar] [PubMed] [CrossRef]

26. Rani P, Mishra AR, Krishankumar R, Ravichandran KS, Kar S. Multi-criteria food waste treatment method selection using single-valued neutrosophic-CRITIC-MULTIMOORA framework. Appl Soft Comput. 2021;111:107657. doi:10.1016/j.asoc.2021.107657. [Google Scholar] [CrossRef]

27. Puška A, Nedeljković M, Prodanović R, Vladisavljević R, Suzić R. Market assessment of pear varieties in Serbia using fuzzy CRADIS and CRITIC methods. Agriculture. 2022;12(2):139. doi:10.3390/agriculture12020139. [Google Scholar] [CrossRef]

28. Kamali Saraji M, Streimikiene D, Kyriakopoulos GL. Fermatean fuzzy CRITIC-COPRAS method for evaluating the challenges to Industry 4.0 adoption for a sustainable digital transformation. Sustainability. 2021;13(17):9577. doi:10.3390/su13179577. [Google Scholar] [CrossRef]

29. Žižović M, Miljković B, Marinković D. Objective methods for determining criteria weight coefficients: a modification of the CRITIC method. Decis Making Appl Manage Eng. 2020;3(2):149–61. doi:10.31181/dmame2003149z. [Google Scholar] [CrossRef]

30. Liu H. Enhanced CoCoSo method for intuitionistic fuzzy MAGDM and application to financial risk evaluation of high-tech enterprises. Informatica. 2024;48(5):1–14. doi:10.31449/inf.v48i5.5169. [Google Scholar] [CrossRef]

31. Zhu T, Chen Y, Tao C. Multiple machine learning algorithms assisted QSPR models for aqueous solubility: comprehensive assessment with CRITIC-TOPSIS. Sci Total Environ. 2023;857:159448. doi:10.1016/j.scitotenv.2022.159448. [Google Scholar] [PubMed] [CrossRef]

32. Trivedi P, Vansjalia R, Erra S, Narayanan S, Nagaraju D. A fuzzy CRITIC and fuzzy WASPAS-based integrated approach for wire arc additive manufacturing (WAAM) technique selection. Arab J Sci Eng. 2023;48(3):3269–88. doi:10.1007/s13369-022-07127-3. [Google Scholar] [CrossRef]

33. Qiu YJ, Bouraima MB, Kiptum CK, Ayyildiz E. Strategies for enhancing industry 4.0 adoption in East Africa: an integrated spherical fuzzy SWARA-WASPAS approach. J Ind Intell. 2023;1(2):87–100. doi:10.56578/jii010202. [Google Scholar] [CrossRef]

34. Bošković S, Švadlenka L, Dobrodolac M, Jovčić S, Zanne M. An extended AROMAN method for cargo bike delivery concept selection. Decis Mak Adv. 2023;1:1–9. doi:10.31181/v120231. [Google Scholar] [CrossRef]

35. Kara K, Yalçın GC, Acar AZ, Simic V, Konya S, Pamucar D. The MEREC-AROMAN method for determining sustainable competitiveness levels: a case study for Turkey. Socio-Econ Plann Sci. 2024;91:101762. doi:10.1016/j.seps.2023.101762. [Google Scholar] [CrossRef]

36. Yalçın GC, Kara K, Toygar A, Simic V, Pamucar D, Köleoǧlu N. An intuitionistic fuzzy-based model for performance evaluation of EcoPorts. Eng Appl Artif Intell. 2023;126:107192. doi:10.1016/j.engappai.2023.107192. [Google Scholar] [CrossRef]

37. Pamućar D, Ćirović G. The selection of transport and handling resources in logistics centers using Multi-Attributive Border Approximation area Comparison (MABAC). Expert Syst Appl. 2015;42(6):3016–28. doi:10.1016/j.eswa.2014.11.057. [Google Scholar] [CrossRef]

38. Yoon KP, Hwang CL. Multiple attribute decision making: an introduction. London, UK: Sage publications; 1995. [Google Scholar]

39. Turskis Z, Zavadskas EK. A novel method for multiple criteria analysis: grey additive ratio assessment (ARAS-G) method. Informatica. 2010;21(4):597–610. doi:10.15388/Informatica.2010.307. [Google Scholar] [CrossRef]

40. Keeney RL, Raiffa H. Decisions with multiple objectives: preference and value tradeoffs. New York, NY, USA: Wiley; 1976. [Google Scholar]

41. Keshavarz Ghorabaee M, Zavadskas EK, Turskis Z, Antucheviciene J. A new combinative distance-based assessment (CODAS) method for multi-criteria decision-making. Econ Comput Econ Cybern Stud Res. 2016;50(3):25–44. [Google Scholar]

42. Zavadskas EK, Turskis Z, Antucheviciene J, Zakarevicius A. Optimization of weighted aggregated sum product assessment. Elektron Elektrotech. 2012;122(6):3–6. doi:10.5755/j01.eee.122.6.1810. [Google Scholar] [CrossRef]

43. Yazdani M, Zarate P, Kazimieras Zavadskas E, Turskis Z. A combined compromise solution (CoCoSo) method for multi-criteria decision-making problems. Manage Decis. 2019;57(9):2501–19. doi:10.1108/MD-05-2017-0458. [Google Scholar] [CrossRef]

44. Opricovic S, Tzeng GH. Extended VIKOR method in comparison with outranking methods. Eur J Oper Res. 2007;178(2):514–29. doi:10.1016/j.ejor.2006.01.020. [Google Scholar] [CrossRef]

45. Keršuliene V, Zavadskas EK, Turskis Z. Selection of rational dispute resolution method by applying new step-wise weight assessment ratio analysis (SWARA). J Bus Econ Manage. 2010;11(2):243–58. doi:10.3846/jbem.2010.12. [Google Scholar] [CrossRef]

46. Zavadskas EK, Antuchevičienė J, Šaparauskas J, Turskis Z. MCDM methods WASPAS and MULTIMOORA: verification of robustness of methods when assessing alternative solutions. Econ Comput Econ Cybern Stud Res. 2013;47(2):5–20. [Google Scholar]

47. Garg H, Dutta D, Dutta P, Gohain B. An extended group decision-making algorithm with intuitionistic fuzzy set information distance measures and their applications. Comput Ind Eng. 2024;197:110537. doi:10.1016/j.cie.2024.110537. [Google Scholar] [CrossRef]

48. Ayyildiz E, Erdogan M, Gul M. A comprehensive risk assessment framework for occupational health and safety in pharmaceutical warehouses using Pythagorean fuzzy Bayesian networks. Eng Appl Artif Intell. 2024;135:108763. doi:10.1016/j.engappai.2024.108763. [Google Scholar] [CrossRef]

49. Zheng Y, Qin H, Ma X. A novel group decision making method based on CoCoSo and interval-valued Q-rung orthopair fuzzy sets. Sci Rep. 2024;14(1):6562. doi:10.1038/s41598-024-56922-5. [Google Scholar] [PubMed] [CrossRef]

50. Chen Y, Zhong Y, Yu S, Xiao Y, Chen S. Exploring bidirectional performance of hotel attributes through online reviews based on sentiment analysis and Kano-IPA model. Appl Sci. 2022;12:692. doi:10.3390/app12020692. [Google Scholar] [CrossRef]

51. Haseli G, Sheikh R, Ghoushchi SJ, Hajiaghaei-Keshteli M, Moslem S, Deveci M, et al. An extension of the best-worst method based on the spherical fuzzy sets for multi-criteria decision-making. Granul Comput. 2024;9(2):40. doi:10.1007/s41066-024-00462-w. [Google Scholar] [PubMed] [CrossRef]

52. Anum MT, Zhang H, Ejegwa PA, Feng Y. Tendency coefficient-based weighted distance measure for intuitionistic fuzzy sets with applications. In: 2024 12th International Conference on Intelligent Control and Information Processing (ICICIP); 2024 Mar; Nanjing, China. p. 54–61. [Google Scholar]

53. Niaz Khan R, Sajjad Ali Khan M, Mashwani WK, Ibrar M, Senapati T, Moslem S. Multi-criteria decision making model for hotel selection problem under complex dual hesitant fuzzy information. Appl Artif Intell. 2024;38(1):2300215. doi:10.1080/08839514.2023.2300215. [Google Scholar] [CrossRef]

54. Tan Y, Park S, de Medeiros AMA, Wanke P. Cost-benefit analysis in UK hotels: a hybrid SOCP-MCDM approach. Tour Manage. 2025;106:105034. doi:10.1016/j.tourman.2024.105034. [Google Scholar] [CrossRef]

55. Arıkan Kargı VS, Cesur F. Renewable energy technology selection for hotel buildings: a systematic approach based on AHP and VIKOR methods. Buildings. 2024;14(9):2662. doi:10.3390/buildings14092662. [Google Scholar] [CrossRef]

56. Wu J, Cao Q. Same families of geometric aggregation operators with intuitionistic trapezoidal fuzzy numbers. Appl Math Model. 2013;37:318–27. doi:10.1016/j.apm.2012.03.001. [Google Scholar] [CrossRef]

57. Szmidt E, Kacprzyk J. Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000;114(3):505–18. doi:10.1016/S0165-0114(98)00244-9. [Google Scholar] [CrossRef]

58. Ashraf S, Iqbal W, Ahmad S, Khan F. Circular Spherical Fuzzy Sugeno weber aggregation operators: a novel uncertain approach for adaption a programming language for social media platform. IEEE Access. 2023;11:124920–41. doi:10.1109/ACCESS.2023.3329242. [Google Scholar] [CrossRef]

59. Garg H, Ünver M, Olgun M, Türkarslan E. An extended EDAS method with circular intuitionistic fuzzy value features and its application to multi-criteria decision-making process. Artif Intell Rev. 2023;56(Suppl 3):3173–204. doi:10.1007/s10462-023-10601-5. [Google Scholar] [CrossRef]

60. Kahraman C. Proportional picture fuzzy sets and their AHP extension: application to waste disposal site selection. Expert Syst Appl. 2024;238:122354. doi:10.1016/j.eswa.2023.122354. [Google Scholar] [CrossRef]

61. Krohling RA, Pacheco AG, Siviero AL. IF-TODIM: an intuitionistic fuzzy TODIM to multi-criteria decision making. Knowl Based Syst. 2013;53:142–6. [Google Scholar]

62. Liu P, Liu J. Some q-rung orthopai fuzzy Bonferroni mean operators and their application to multi-attribute group decision making. Int J Intell Syst. 2018;33:315–47. [Google Scholar]