A Shuffled Frog-Leaping Algorithm with Competition for Parallel Batch Processing Machines Scheduling in Fabric Dyeing Process

1  Introduction

Batch processing is a typical production mode and has been widely applied in the manufacturing processes of textiles, chemicals, minerals, pharmaceuticals, semiconductors, and others. Batch processing machines (BPM) can simultaneously process multiple jobs in a batch. Parallel batch and serial batch are often considered, the processing time of the former being the maximum processing time of all jobs in a batch and the processing time of the latter being the sum of the processing time of all jobs in a batch. BPM scheduling problems have attracted much attention [1–5].

Parallel batch processing machines scheduling problem (PBPMSP) is an extended version of the parallel machines scheduling problem [6] and has attracted much attention in the past decades. Koh et al. [7] designed a genetic algorithm (GA) for the problem in a multi-layer ceramic capacitor production line. Su and Wang [8] proposed weighted nested partitions based on differential evolution (DE) for the problem in semiconductor production lines. Zhou et al. [9] developed a multi-objective DE algorithm to solve the problem considering electricity cost. Zhang et al. [10] solved the problem in cloud manufacturing with an efficient algorithm and improved particle swarm optimization (PSO). Gahm et al. [11] handled parallel serial-batch processing machine scheduling by using some heuristics. Zhang et al. [12] presented a mixed integer linear programming (MILP) model and an improved biased random key GA for the problem with two-dimensional bin packing constraints. Ou et al. [13] considered an efficient polynomial time approximation scheme with near-linear-time complexity. Uzunoglu et al. [14] provided a new multi-start construction heuristic with controlled batch urgencies and a local search mechanism with advanced termination criteria for solution improvement. Kucukkoc et al. [15] dealt with the problem of batch delivery by using a discrete DE algorithm hybridized with GA.

There are some works on uniform PBPMSP. Jula and Leachman [16] gave three algorithms based on linear programming, integer programming, and heuristic for solving the problem in semiconductor manufacturing. Li et al. [17] proposed several heuristics, including an algorithm batching rule and a heuristic assignment rule, to solve the problem of dynamic job arrivals. Some meta-heuristics are applied, which are the Pareto-based ant colony system (Xu et al. [18]), non-dominated sorting genetic algorithm-II (NSGA-II), and multi-objective imperialist competitive algorithm [19], DE [20], ant colony optimization [21,22], artificial immune system [23] and evolutionary algorithm [24].

Non-identical PBPMSP is also solved by PSO [25], GA [26], and fruit fly optimization algorithm [27]. Many results on unrelated PBPMSP were also obtained. Shahidi-Zadeh et al. [28] presented a multi-objective harmony search algorithm. Lu et al. [29] developed a hybrid ABC with tabu search for the problem with maintenance and deteriorating jobs. Zhou et al. [30] solved the problem with different capacities and arbitrary job sizes by a random key GA. Sadati et al. [31] proposed fuzzy multi-objective discrete teaching learning-based optimization and fuzzy NSGA-II. Zarook et al. [32] constructed a MILP model and provided six heuristics and a random key GA. Fallahi et al. [33] studied the problem in production systems under carbon reduction policies, presented a MILP model, NSGA-II and multi-objective gray wolf optimizer. Kong et al. [34] applied a shuffled frog-leaping algorithm (SFLA) with variable neighborhood search for the problem with nonlinear processing time. Xiao et al. [35] proposed a tabu-based adaptive large neighborhood search algorithm, which updates the best-known solutions of 55 instances.

PBPMSP is widely found in various manufacturing processes such as casting [36], food and chemical production [37], semiconductors [38], metal packaging [39], and others. In recent years, PBPMSP in the fabric dyeing process has also received some attention. Zhang et al. [40] proposed a multi-objective artificial bee colony algorithm with an elite retention strategy to simultaneously minimize total tardiness and total completion time. Huynh and Chien [41] studied a hybrid multi-subpopulation GA with heuristic rules. Li et al. [42] proposed a two-objective evolutionary algorithm with the constructive generation of an initial solution and cluster-based environmental selection strategy. Demir [43] developed a lexicographic multi-objective GA to simultaneously minimize total tardiness, total washing times, and total machine fixed costs. Srinath et al. [44] proposed two meta-heuristics to solve multi-objective problems considering SDST and preferences.

Machine eligibility is often investigated in parallel machine scheduling problems [45–47], and there are limited works on PBPMSP with machine eligibility. Li et al. [48] presented a hybrid DE algorithm with chaos theory and two local search algorithms for the problem considering different colors, sequence-dependent setup time (SDST), and machine eligibility. Wang et al. [49] solved a fuzzy energy-efficient problem with machine eligibility and SDST by using a dynamic teaching-learning-based optimization. Lei and Dai [50] dealt with the problem of machine eligibility in the fabric dyeing process by using an adaptive SFLA.

Accordingly, PBPMSP has been studied fully in the last three years, and most of the existing works are related to the usage of heuristics and meta-heuristics; however, PBPMSP with machine eligibility is seldom considered [48–50]. Machine eligibility often exists in real-life manufacturing processes such as fabric dyeing and PBPMSP, with machine eligibility often exhibiting different features compared to the classical PBPMSP. For example, a machine set is used when a machine assignment is done for a job. The inclusion of machine eligibility can make PBPMSP closely resemble the actual situations of manufacturing processes. As a result, the corresponding optimization results hold high application value, so it is necessary to focus on PBPMSP with machine eligibility in fabric dyeing shops.

Compared to PSO, DE, and GA, SFLA has fast convergence speed and effective algorithm structure containing local search and global information exchanges; in addition, as an effective method for BPM scheduling [34,50], distributed scheduling [51,52], flexible job shop scheduling [53], and flow shop scheduling [54], SFLA has been successfully applied to solve PBPMSP [34,50] and the corresponding results show that has advantages on solving PBPMSP. On the other hand, the integration of new optimization mechanisms and SFLA is an effective way to intensify the search ability of SFLA. Q-learning and cooperation are proven to be useful mechanisms and can improve search advantages of SFLA [52,53]; however, competition among memeplexes is seldom considered. After the competition is added to SFLA, parameters or search strategies can be adjusted in the search process, the search ability can be intensified effectively, and optimization results on PBPMSP can be significantly improved. The advantages of SFLA on PBPMSP and the great impact of competition demonstrate that the shuffled frog-leaping algorithm with competition (CSFLA) is particularly suited for PBPMSP, so it is necessary to focus on CSFLA.

This study considers PBPMSP with machine eligibility in the fabric dyeing process, and a new CSFLA is presented to minimize makespan. The competitive search of memeplexes is composed of two phases to produce high-quality solutions, and the initial population is produced in a heuristic and random way. Competition between any two memeplexes is executed in the first phase, then iteration times are adjusted based on competition, and search strategies are adjusted adaptively based on the evolution quality of memeplexes. An adaptive population shuffling is given. Several computational experiments are conducted on 100 instances. The computational results demonstrate that the new strategies of CSFLA are effective and that CSFLA has promising advantages in solving the PBPMSP considered.

The remaining parts of the paper are organized as follows. The problem description is given in Section 2. CSFLA for PBPMSP is shown in Section 3. Computational results and analyses are provided in Section 4. The conclusions are drawn, and the future research topics are reported in the final section.

2  Problem Description

PBPMSP in fabric dyeing process is composed of n jobs J1,J2,…,Jn and m BPM M1,M2,…,Mm.

Each Mk has a capacity Qk. There are F families for n jobs in terms of the dyeing color. wi,di,Θi and fi are weight, due date, the set of machines and job family for Ji. All jobs with the same family have the same processing time, pg indicates processing time of each job in family g. Machine eligibility is considered, which means that at least one machine is not eligible for at least one job, that is, at least one job Ji has Θi⊂{M1,M2,…,Mm}.

All jobs in a batch are processed simultaneously on BPM. Families are incompatible, and jobs within different families cannot be processed in the same batch. Each batch is formed with jobs in the same family. When jobs of family g are applied to form a batch allocated on Mk, job Ji with Mk∈Θi can be chosen and added into batch Bh if the following condition is met.

wi+∑j∈Bhwj≤Qk

The above equation is used described capacity constraint, that is, the sum of weight of job Ji and all jobs in batch Bh cannot exceed Qk.

All jobs in the same batch are processed with the same beginning time and completion time. When BPM is required to switch from one batch with family g to other batch with family h, setup time is incurred because dyeing machines need cleaning before a different color is handled. stgh indicates setup time between families, which means that after a batch of family g is processed, the cleaning time is required to process a batch of family h, if two adjacent batches belong to the same family, that is, g=h, BPM does not need cleaning.

There are some constraints on jobs and machines.

Each BPM can only process one batch at a time.

No job can be processed in different batches on more than one BPM.

Operations cannot be interrupted.

All BPMs and jobs are always available.

The goal of the problem is to minimize makespan when all constraints are satisfied and three sub-problems are solved.

Cmax=max{Ci|i=1,2,…,n}

where Ci is completion time of Ji and Cmax is maximum value of C1,C2,⋯,Cn.

The above formula is applied to compute Cmax.

Table 1 lists an illustrative example with 10 jobs, 3 job families and 3 BPMs, Q1=40, Q2=70, Q3=90, p1=5, p2=10, p3=15. The setup time matrix is shown below.

(stge)3×3=[013402510]

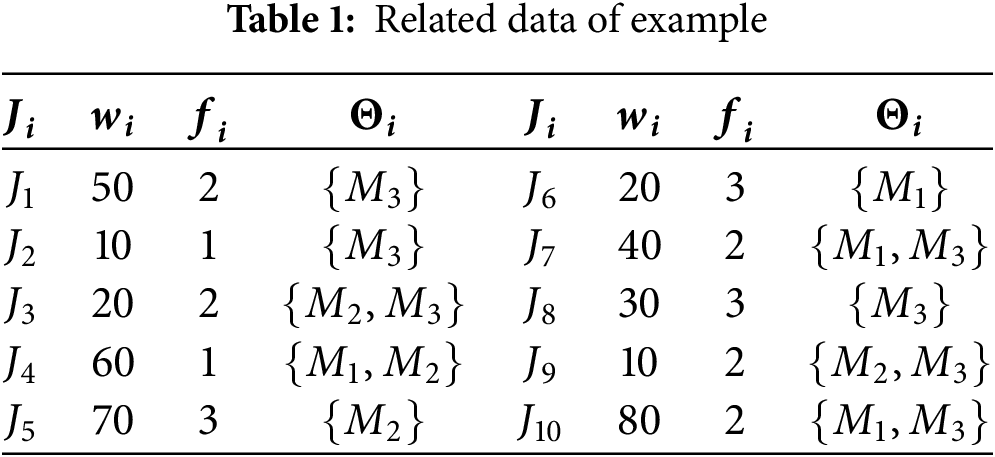
In the above equation, st12=1, this setup time exists for the batch of family 1 and batch of family 2, after batch of family 1 is processed, the setup time on batch of family 2 is st12.

3  CSFLA for PBPMSP in the Fabric Dyeing Process

There are s memeplexes ℳ1,ℳ2,⋯,ℳs in SFLA and the search within each memeplex is implemented independently in most of the previous SFLAs [35,48]. In this study, competition among memeplexes is added, and CSFLA is presented to PBPMSP in the fabric dyeing process.

3.1 Initialization

Zhang et al. [40] presented a two-string representation. For PBPMSP with n jobs, m BPM and F families, its solution is represented as a scheduling string [π1,π2,…,πn] and a machine assignment string [θ1,θ2,…,θn] for batches, where πi∈{1,2,…,n}, θi∈{1,2,…,m}.

With respect to [θ1,θ2,…,θn], if η(<n) batches are formed, then only θ1,θ2,…,θη are used, other elements are not considered; however, the number of the formed batches is not fixed, so a string with the length of n is used and optimized.

The decoding procedure of [40] is directly adopted. For the example in Table 1, a possible solution is [10, 1, 8, 4, 9, 6, 2, 5, 3, 7] and [2, 1, 3, 3, 2, 3, 3, 1, 1, 2]. After two strings are decoded, a schedule in Fig. 1 is obtained. B1={J1,J9},B2={J8},B3={J10},B4={J2,J4},B5={J5},B6={J6},B7={J3,J7}. The processing sequence of batches on each BPM is shown in Fig. 1.

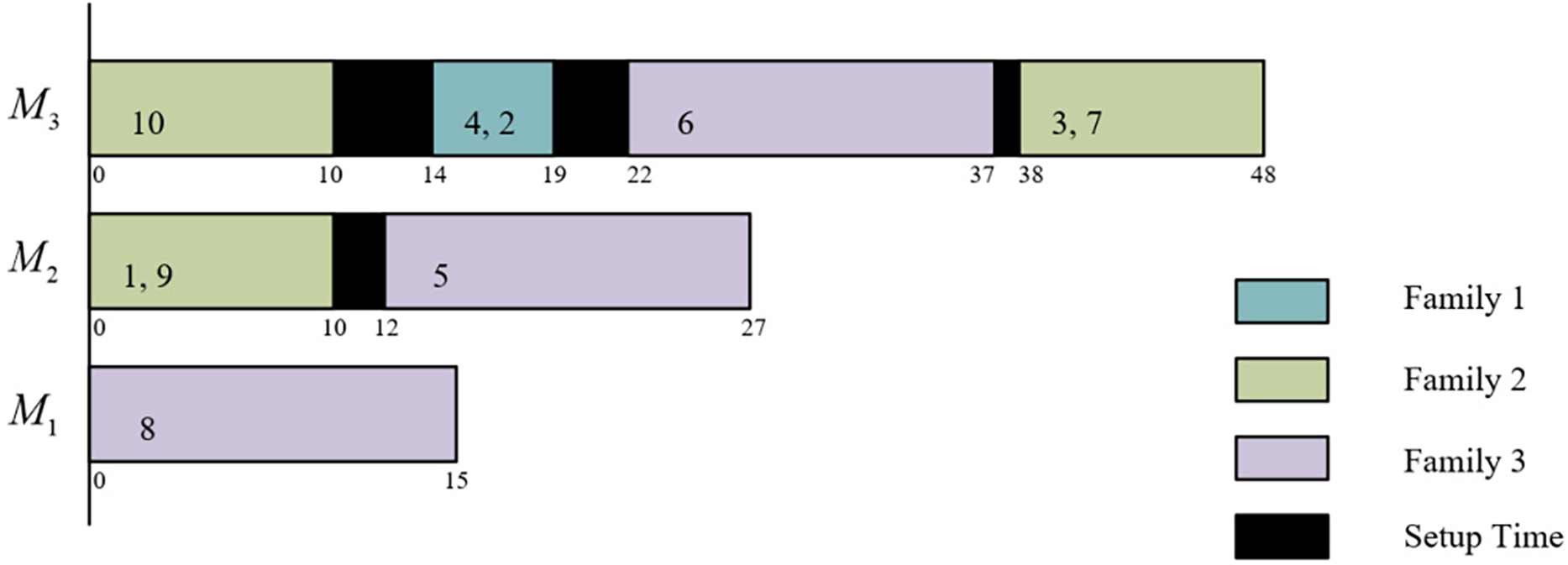
Figure 1: A schedule of the example

Initial population P is composed of x1,x2,⋯,xN. For each xi,i=1,2,⋯,n, if random number rand< ε, then xi is produced randomly; otherwise, xi is obtained by using a heuristic, where ε is probability, rand follows uniform distribution on [0, 1].

The heuristic is shown below.

(1)   Produce scheduling string by sorting all jobs in the ascending order of wi.

(2)   Calculate the average weight w¯ of all jobs, let t=1.

(3)   Repeat the following steps until t>n/2: stochastically generate an integer 1≤r≤m, if Qr>w¯, then let θt=r; otherwise, randomly chose one from m,m−2,m−1 with the same probability, and let θt be the chosen one, t=t+1.

(4)   Repeat the following steps until t>n: randomly select an integer from [1,m] and let θt be the chosen one, t=t+1.

As stated above, jobs with smaller weight are given higher priority to be assigned into the first half of scheduling string, machines with Qr>w¯ are given bigger probability to be allocated in the first half of machine assignment string, so jobs with smaller weight can be formed into a batch and processed on machine with bigger capacity, as a result, the number of the formed batches can be diminished, so maximum completion time can be improved.

Population division is an important step of SFLA. In this study, population P¯ is divided into s¯ memeplexes in the following way: sort all solutions in P¯ in the descending order of Cmaxxi, suppose that Cmaxx1≤Cmaxx2≤⋯≤CmaxxN, then allocate each xi,i=1,2,⋯.n into memeplex i(mods)+1, finally, s memeplexes ℳ1,ℳ2,⋯,ℳs are formed, where i(mods) is the remainder of i/s, Cmaxxi is makespan of xi.

Initially, P¯=P,N¯=N,s¯=s.

3.2 Search Operators

Three global search operators GS1,GS2,GS3 are used. GS1 is described below. For solutions x,y, randomly select k1,k2∈[1,n],k1 < k2, machines between positions k1,k2 on machine assignment string of y substitute for those at the same position on machine assignment string of x. GS2 is shown as follows. For solutions x,y, order crossover [51] is performed on scheduling string of x,y. GS3 is depicted below. For solutions x,y, GS1,GS2 are executed sequentially.

For solution x with η batches, six neighborhoods’ structures are used. Neighborhood structure 𝒩1 is described below: randomly select a πg and insert it into a newly decided position. 𝒩2 is insertion operator on machine assignment string as done in 𝒩1 𝒩3,𝒩4 are swap operator on scheduling string and machine assignment string, respectively. 𝒩5 is inversion operator for those genes of scheduling string between two randomly decided k1,k2,k1 < k2. 𝒩6 is described below. Decide a machine Mk with the biggest completion time, for each θl,l=1,2,⋯,η, if θl=k, then a randomly chosen integer from [1,m] substitutes for θl.

Three search strategies SO1,SO2,SO3 are produced by using global search operators and neighborhood search operators. SO1 is described below. For solutions x,y, perform GS1 between x,y and obtain a new solution z1, if z1 is better than x, then x=z1, else if z1 is better than y, then y=z1, else produce z2∈𝒩1(z1), then compare z2 with x,y and replace x or y with the above procedure on z1,x,y, if z2 cannot substitutes for y, then generate z3∈𝒩1(z2), compare z2 with x,y and replace x or y with the above procedure on z1,x,y. Where 𝒩g(x) indicates the set of neighborhood solutions of x produced by 𝒩g.

When GS2,𝒩3,𝒩4 are replaced with GS1,𝒩1,𝒩2 in the above procedure, SO2 is obtained. SO3 is also similar with SO1; however, in SO3, GS3,𝒩5,𝒩6 are used sequentially like GS1,𝒩1,𝒩2 of SO1.

The initial set S of search strategies consists of SO1,SO2,SO3. The alternate set AS is empty.

3.3 Competitive Search of Memeplexes

In existing SFLAs [34,53], search within memeplex is often done independently; in CSFLA, the competitive search of memeplexes is composed of two phases. In the first phase, any two memeplexes compete with each other. The second phase is done based on the data from the first phase and the adaptive adjustment of search strategies.

Algorithm 1 describes competitive search of memeplexes, where xnearb,i is the best solution of ℳi∖{xb,i}, xb,i is the best solution of ℳi, Mei indicates solution quality of ℳi.

Mei=∑x∈ℳi|{y∈P|Cmaxx<Cmaxy}|

In the above equation, for each x∈ℳi, the number of solutions of P with smaller Cmax than x is computed, then all numbers of all solutions of ℳi are added together and Mei is obtained.

In line 9, For ℳi,ℳj, let γi=γj=0, when SOl is executed on xb,i(xb,j) and xb,i(xb,j) is updated with new solution produced by SOl, γi=γi+1(γj=γj+1), after SO1−SO3 are executed, if γi<(>)γj, then cnti=cnti+1,cntj=cntj−1(cntj=cntj+1,cnti=cnti−1).

In line 9, with respect to Ωl, when SOl acts on xb,i and xb,i is updated with new solution, then Ωl=Ωl+1.

In line 12, ℳ1 is given more iteration times by using some iteration times of ℳs because ℳ1 wins in the first phase, which is shown in line 9, the search strategy with biggest Ω1 is used for ℳ1.

In lines 17–27, when conditions in lines 17 or 20 are met, evolution difference among memeplexes occurs and is avoided by adjusting search strategies for memeplexes.

In the above procedure, competition can lead to more iteration times and SO1 with the biggest Ω1 for ℳ1, the extra iteration times comes from memeplex ℳs, as a result, ℳ1 is used fully and the usage of ℳs is limited, however, in the second phase beginning with line 13, the adjustment on search operator is done to diminish evolution difference among memeplexes, and global search can be improved.

3.4 Algorithm Description

The detailed steps of CSFLA are described as follows.

(1)   Produce initial population by using heuristic and random way, for each memeplex ℳi, cnti=0.

(2)   Execute population division.

(3)   Perform a competitive search of memeplexes.

(4)   Execute adaptive population shuffling.

(5)   If the termination condition is not met, then go to step (2); otherwise, stop the search.

The flowchart of CSFLA is shown in Fig. 2.

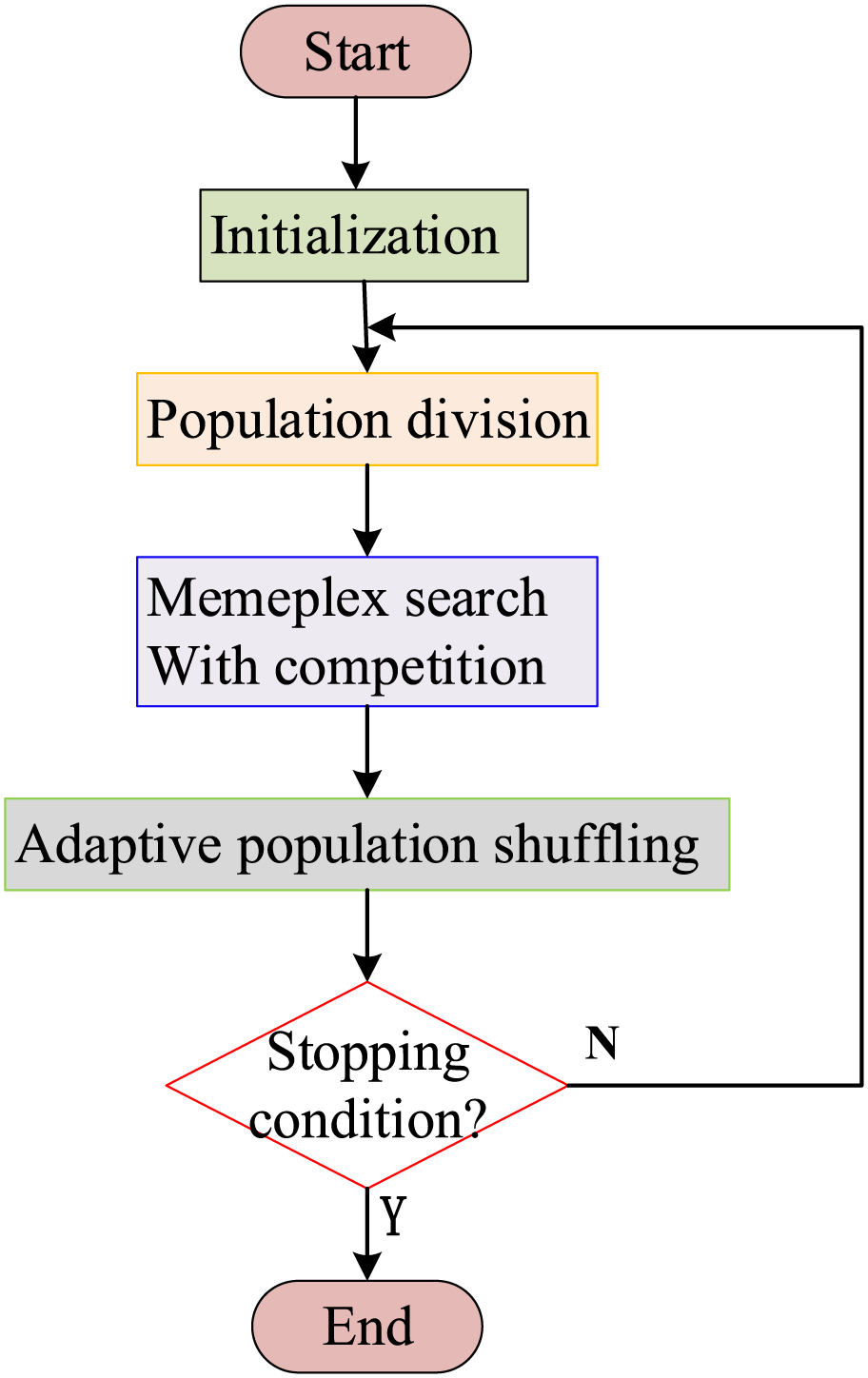
Figure 2: Flowchart of CSFLA

As the main step of SFLA, population shuffling is utilized to form a new population by using all memeplexes, and it is done in each generation. Adaptive population shuffling is proposed and described below. Compute Mei for each memeplex ℳi,i=1,2,⋯,s, suppose that memeplex ℳ1 has the highest Mei, then let cnti=0 for each memeplex ℳi,i≠1, construct a population P¯ with all memeplexes except ℳ1.

In the above process, a memeplex is decided with Mei and excluded from population P¯ and not all memeplexes are utilized to form a new population.

Unlike the existing SFLA [51–54], CSFLA has the following features: (1) Each memeplex ℳi is assigned evi,cnti, and each strategy SOl is given Ωl, these data are utilized to adjust iteration times and search strategy in an adaptive way. (2) Search procedure of memeplexes is composed of two phases, and the results of the first phase affect the second phase. Competition is implemented in the first phases, and then excessive evolution differences among memeplexes are avoided. (3) An adaptive population shuffling is performed by excluding memeplexes with the highest Mei.

Competition, Ωl on SOl, evi,cnti for ℳi are added to improve performance of CSFLA, so the implementation of CSFLA using programming language will become more difficult; however, the increasing of implementation difficulty is limited because the newly added things of CSFLA are easily achieved.

4  Computational Experiments

Extensive experiments are conducted to test the performance of CSFLA for the considered PBPMSP. Experiments are implemented by using Microsoft Visual C++ 2019 and run on 8.0 G RAM 2.4 GHz CPU PC.

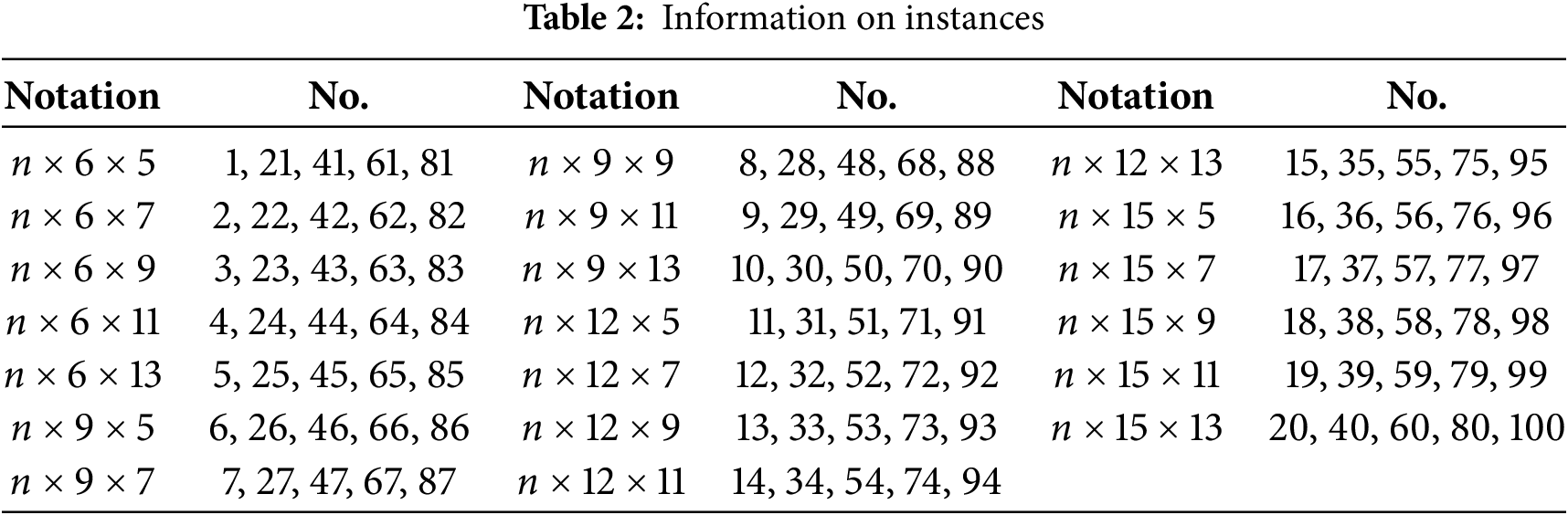
4.1 Instances and Comparative Algorithms

One hundred instances are generated based on the data refined from the dyeing factory in China. The related data are shown below. n∈{100,200,300,400,500}, m∈{5,7,9,11,13}, F∈{6,9,12,15}, pg∈[15,45], stgh∈[4,9], wi∈[15,75], Qk=50+10k. Each instance is indicated as n×F×m. Table 2 describes information on instances.

CSFLA is compared to three existing methods, which are the random key genetic algorithm (RKGA, [30]), RKGA [32], and orthogonal biased random-key genetic algorithm (OBRKGA, [12]) to show the search advantages of CSFLA. RKGA (Zhou et al. [30]) is called as RKGA1, and RKGA (Zarook et al. [32]) as RKGA2 for convenience. These GAs are utilized to solve PBPMSP with the minimization of makespan and can be directly applied to solve the PBPMSP; in addition, three GAs have promising advantages on solving the problems in references [12,30,32], so they are chosen.

SFLA was constructed to show the impact of new strategies of CSFLA on its performance. The steps of SFLA are identical with the general SFLA, when memeplex search is done, one of SO1,SO2,SO3 is randomly selected as search strategy between two solutions, for example, xw,xb. Where xw,xb are the worst solutions and the best ones in a memeplex.

4.2 Parameter Settings

CSFLA has the following parameters: N, s, μ, α and stopping condition. In this study, CPU time is used as a stopping condition. The study found through experiments that CSFLA, SFLA, and three comparative algorithms can converge fully on all instances when 0.05×n s CPU time reaches, so this CPU time is used as a stopping condition.

Taguchi method [55] is applied to obtain the settings of parameters. Instance 50 is used. Table 3 describes the levels of each parameter. The orthogonal array L16(44) is executed. 16 parameter combinations are tested. CSFLA with each parameter combination runs 10 times for the chosen instance.

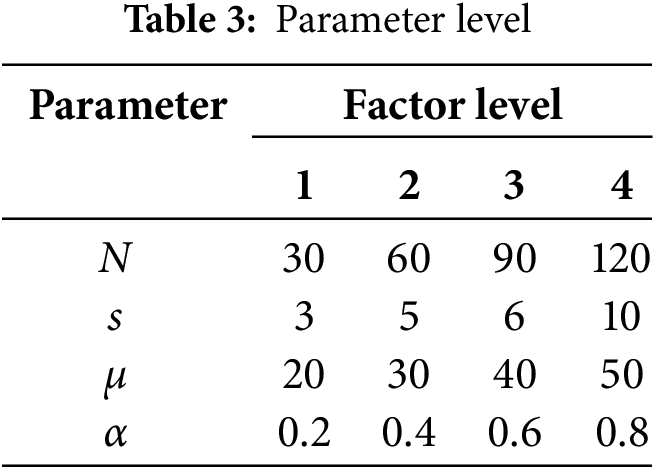
Fig. 3 shows the results of MIN and S/N ratio, which is defined as −10log10⁡(MIN2). CSFLA runs 10 times for the selected instance. In the run, an elite solution is obtained. MIN is the best one of 10 elite solutions obtained in 10 runs. Fig. 3 indicates that CSFLA with following combination N=90, s=10, μ=50, α=0.2 can obtain better results than CSFLA with other combinations, so the above parameter settings are used.

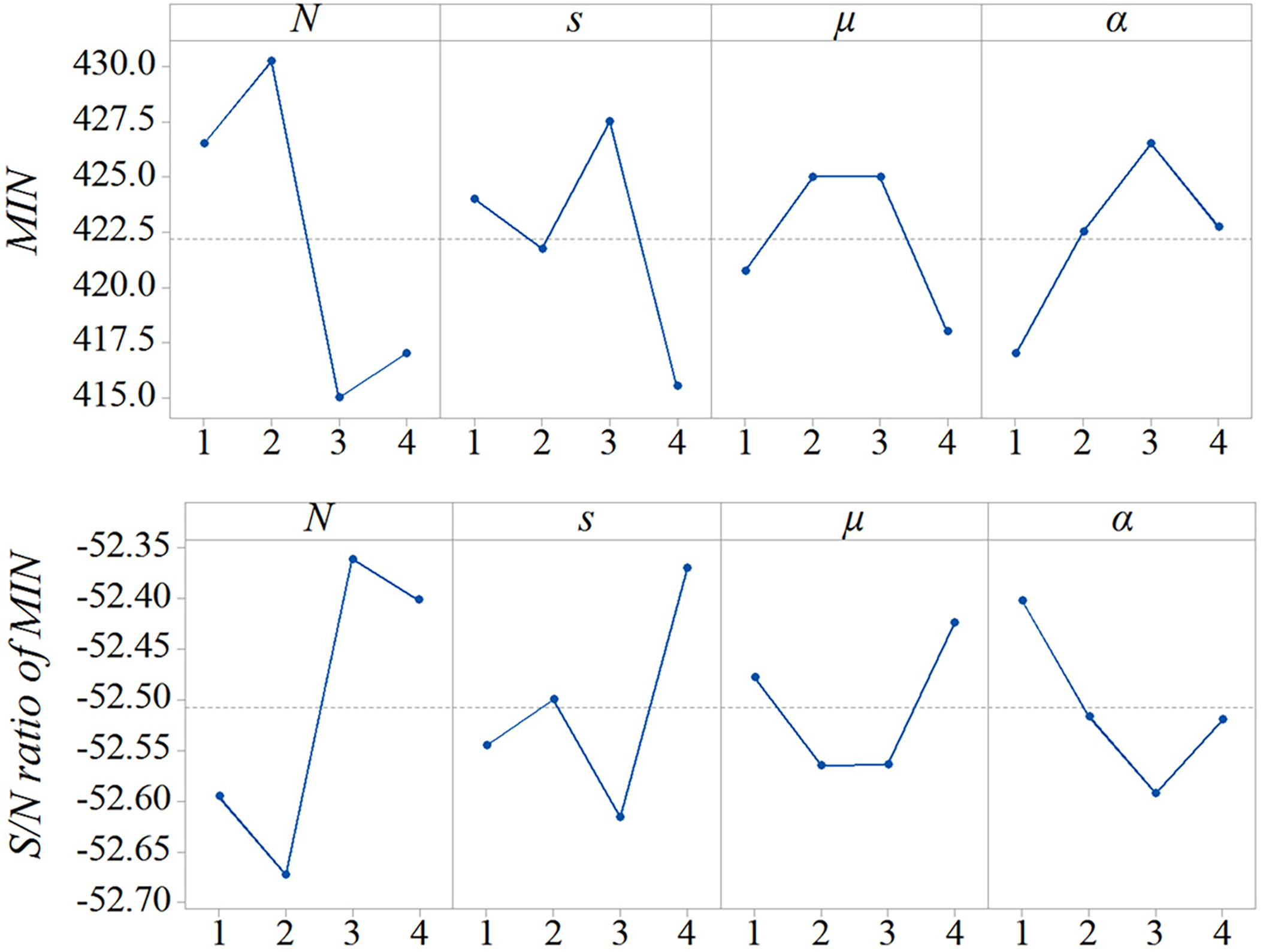
Figure 3: Main effect plot for MIN and S/N ratio

SFLA has N=90, s=10, μ=50 and the above stopping condition.

With respect to RKGA1, RKGA2, and OBRKGA, their parameter settings, except the stopping condition, are directly used in this study. The experimental results show that these settings of each comparative algorithm are still effective, so they are kept. Three GAs are given the same stopping condition as CSFLA.

4.3 Results and Analyses

CSFLA, SFLA, and three RKGA are compared, each of which randomly runs 10 times on each instance. In a run, an elite solution is obtained, MAX indicates the worst one of 10 elite solutions, and AVG denotes the average value of 10 elite solutions. Tables 4–6 show the computational results of five algorithms. CS, SF, RK1, RK2, OB indicate CSFLA, SFLA, RKGA1, RKGA2, OBRKGA. Fig. 4 describes the convergence curves of all algorithms, and Fig. 5 provides a box plot.

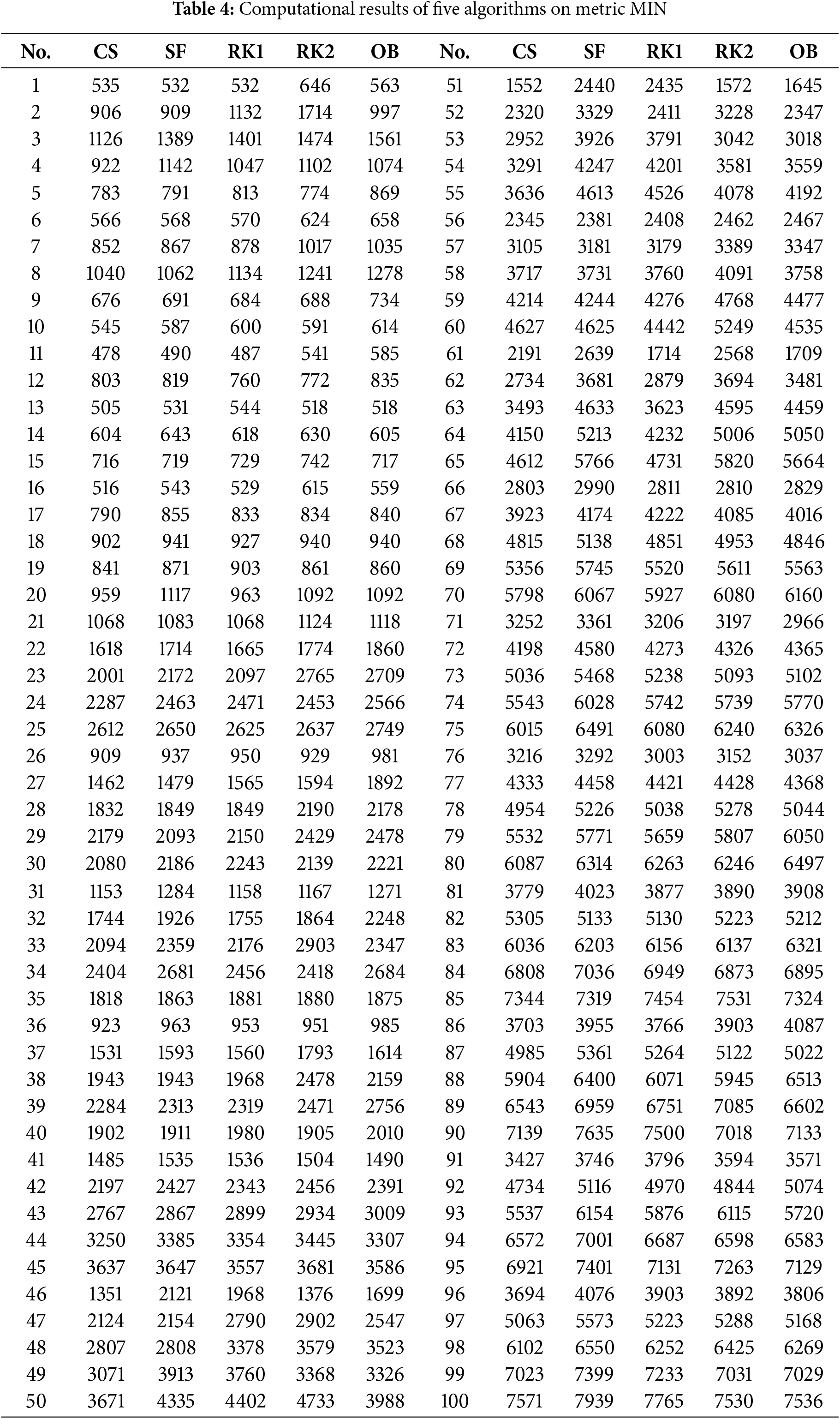
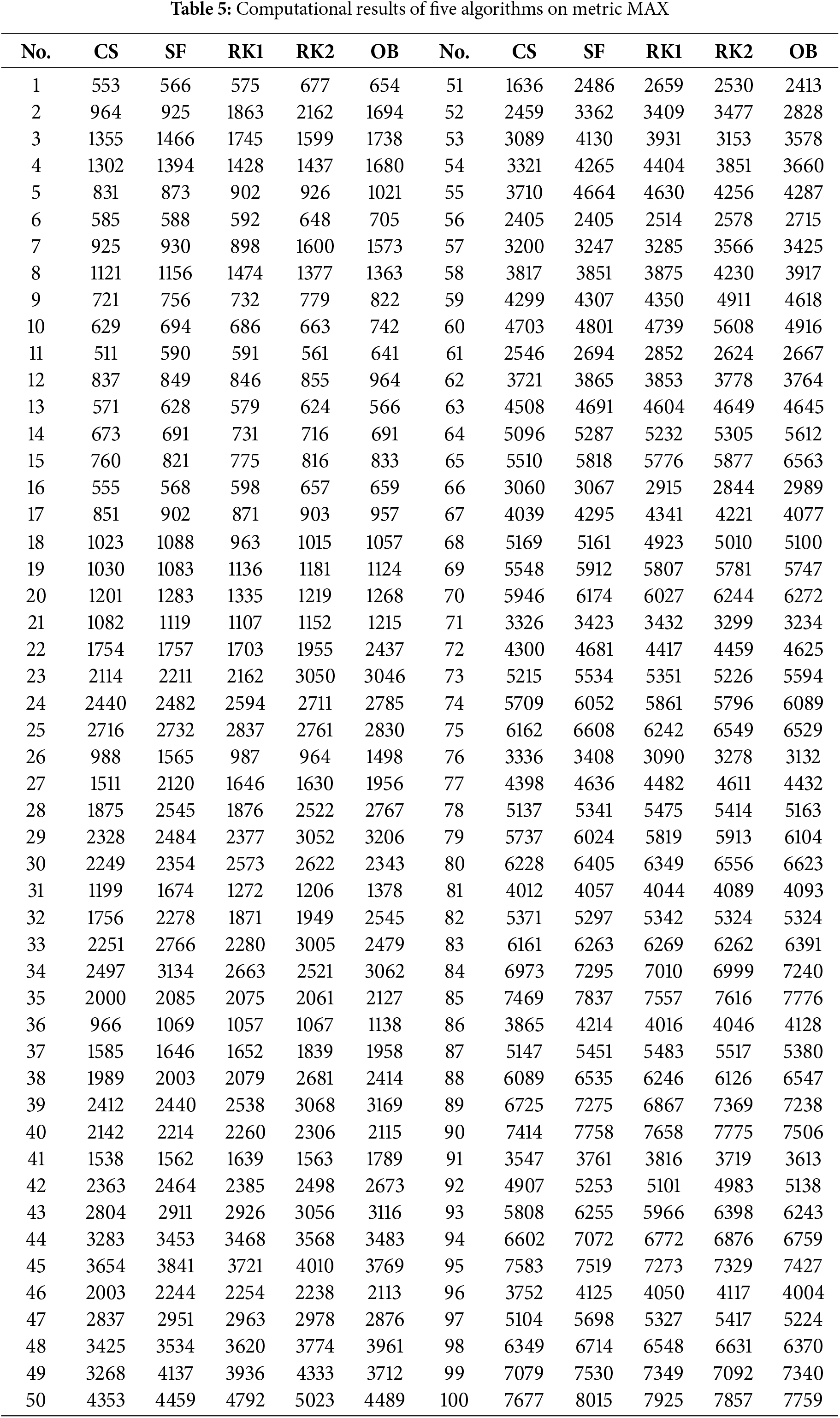
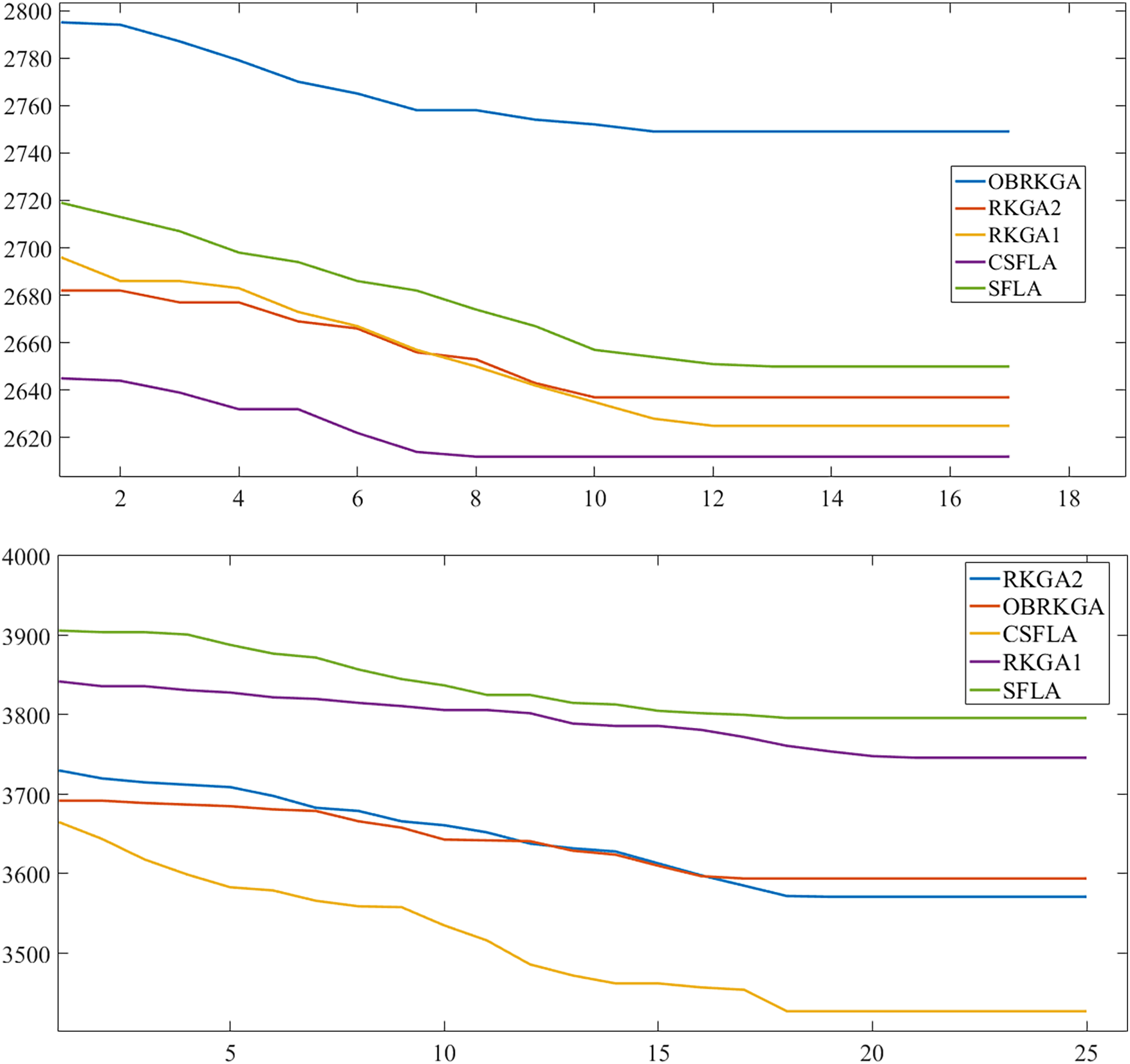
Figure 4: Convergence curves of five algorithms

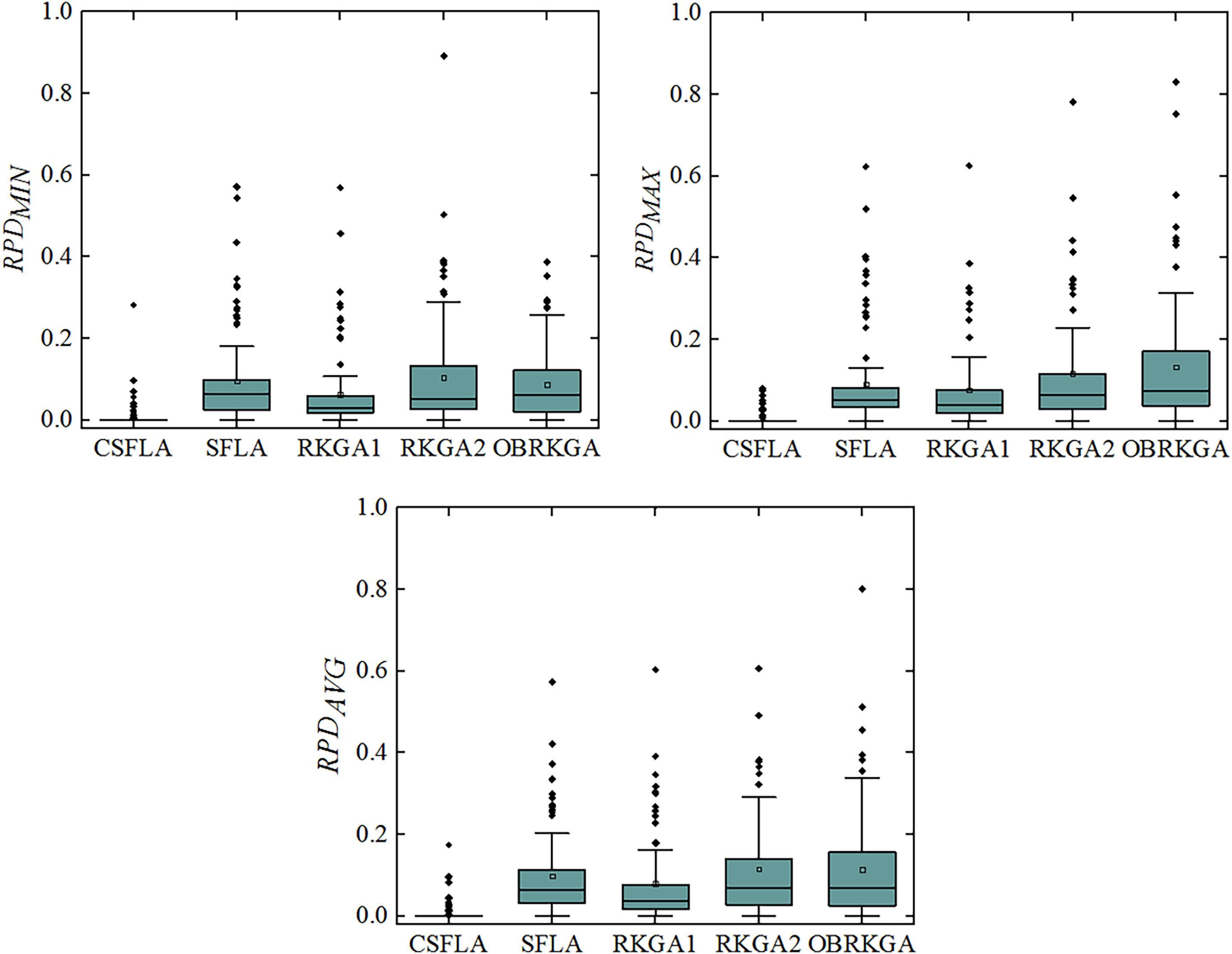
Figure 5: Box plot of all algorithms

Table 4 indicates that CSFLA obtains a smaller MIN than SFLA on 94 instances, and the MIN of CSFLA is bigger than that of SFLA just on 5 instances; in addition, the MIN of CSFLA is less than by at least 100 on 57 instances. CSFLA significantly outperforms SFLA on convergence. The convergence curves in Fig. 4 and RPDmin in Fig. 5 also reveal that CSFLA converges better than SFLA.

Tables 5 and 6 indicate that CSFLA performs better than SFLA on MAX and AVG. SFLA just produces a smaller MAX than CSFLA in 4 instances, and there are differences between the MAX of CSFLA and SFLA. CSFLA obtains smaller AVG on 93 instances. The performance advantages of CSFLA on MAX and AVG also can be observed in Fig. 5. The above analyses show new strategies.

When CSFLA is compared to RKGA1, it can be found that CSFLA produces better results than RKGA1. RKGA1 obtains a smaller MIN than CSFLA in six instances; however, the MIN of RKGA1 is worse than that of CSFLA in 94 of 100 instances. Obviously, CSFLA converges better than RKGA1.

Competition and excessive evolution differences really have a positive impact on the performance of CSFLA. Thus, these new strategies are effective.

Convergence differences between CSFLA and RKGA1 also can be observed in Figs. 4 and 5. Tables 5 and 6 indicate that CSFLA performs better than RKGA1 on MAX, AVG, MAX of CSFLA is less than that of RKGA1 by at least 100 on 54 instances, and CSFLA also obtains smaller AVG than RKGA1 on 93 instances.

Tables 4–6 exhibit that CSFLA has a smaller MIN than RKGA2 and OBRKGA on 89 instances, the MAX of CSFLA is smaller than that of RKGA2 and OBRKGA on 91 instances, and CSFLA has better average results than RKGA2 and OBRKGA more than 85 instances. CSFLA really performs better than RKGA2 and OBRKGA, and this conclusion can also be concluded from Figs. 4 and 5. Based on the above analyses, it can be concluded that CSFLA outperforms three GAs on three metrics.

The above analyses show that the superiority of CSFLA lies in the performance between CSFLA and its comparative algorithm. The advantage of CSFLA results from its adaptive adjustment of search strategies and iteration times by using competition and avoiding excessive evolution differences. With the inclusion of these new strategies, global search ability can be intensified, and a good solution structure can be kept in the memeplex. As a result, search efficiency is significantly improved. Thus, CSFLA is a competitive method for solving PBPMSP.

5  Conclusion

This study considers PBPMSP with machine eligibility in the fabric dyeing process and presents a new algorithm called CSFLA to minimize makespan. Population initialization is implemented in a heuristic and random way. A competitive search of memeplexes is composed of two phases. Competition between any two memeplexes is done in the first phase, then iteration times are adjusted based on competition, and search strategies are adjusted adaptively based on the evolution quality of memeplexes. An adaptive population shuffling is also given. Computational experiments are conducted, and experimental results validate the effectiveness of new strategies and the promising advantages of CSFLA in solving the considered PBPMSP in the fabric dyeing process.

BPM extensively exists in many real-life manufacturing industries, and the BPM scheduling problem has higher complexity than the classical scheduling problem. Shortly, it will focus on PBPMSP, a hybrid flow shop scheduling problem with BPM. In recent years, learning, cooperation, feedback, and competition have been included in meta-heuristics. Meta-heuristics with new optimization mechanisms for scheduling problems are also future research topics.

Acknowledgement: Thanks to anonymous reviewers and the editors for providing valuable suggestions for the paper.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Grant Number 61573264).

Author Contributions: The authors confirm their contribution to the paper as follows: Conceptualization: Deming Lei; methodology, formal analysis, original draft preparation: Mingbo Li; writing—review and editing: Deming Lei. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data generated in this paper are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Azizoglu M, Webster S. Scheduling a batch processing machine with non-identical job sizes. Int J Prod Res. 2000;38(10):2173–84. doi:10.1080/00207540050028034. [Google Scholar] [CrossRef]

2. Shi ZS, Huang ZW, Shi LY. Customer order scheduling on batch processing machines with incompatible job families. Int J Prod Res. 2018;56(1–2):795–808. doi:10.1080/00207543.2017.1401247. [Google Scholar] [CrossRef]

3. Trindade RS, de Araujo OCB, Fampa MHC, Muller FM. Modelling and symmetry breaking in scheduling problems on batch processing machines. Int J Prod Res. 2018;56(22):7031–48. doi:10.1080/00207543.2018.1424371. [Google Scholar] [CrossRef]

4. Zheng SX, Xie NM, Wu Q, Liu CJ. Novel mathematical formulations for parallel-batching processing machine scheduling problems. Comput Oper Res. 2025;173(20):106859. doi:10.1016/j.cor.2024.106859. [Google Scholar] [CrossRef]

5. Wang J, Lei DM, Tang HT. A multi-objective dynamical artificial bee colony for energy-efficient fuzzy hybrid flow shop cheduling with batch processing machines. Expert Syst Appl. 2025;259(2):125244. doi:10.1016/j.eswa.2024.125244. [Google Scholar] [CrossRef]

6. Esfandiari S, Mashreghi H, Emami S. Coordination of order acceptance, scheduling, and pricing decisions in unrelated parallel machine scheduling. Int J Ind Eng Prod Res. 2019;30(2):195–205. [Google Scholar]

7. Koh SG, Koo PH, Ha JW, Lee WS. Scheduling parallel batch processing machines with arbitrary job sizes and incompatible job families. Int J Prod Res. 2004;42(19):4091–107. doi:10.1080/00207540410001704041. [Google Scholar] [CrossRef]

8. Su GJ, Wang XH. Weighted nested partitions based on differential evolution (WNPDE) algorithm-based scheduling of parallel batching processing machines (BPM) with incompatible families and dynamic lot arrival. Int J Comput Integ Manuf. 2011;24(6):552–60. doi:10.1080/0951192X.2011.562545. [Google Scholar] [CrossRef]

9. Zhou SC, Li XL, Du N, Pang Y, Chen HP. A multi-objective differential evolution algorithm for parallel batch processing machine scheduling considering electricity consumption cost. Comput Oper Res. 2018;96(1):55–68. doi:10.1016/j.cor.2018.04.009. [Google Scholar] [CrossRef]

10. Zhang H, Li K, Chu CB, Jia ZH. Parallel batch processing machines scheduling in cloud manufacturing for minimizing total service completion time. Comput Oper Res. 2022;146(2):105899. doi:10.1016/j.cor.2022.105899. [Google Scholar] [CrossRef]

11. Gahm C, Wahl S, Tuma A. Scheduling parallel serial-batch processing machines with incompatible job families, sequence-dependent setup times and arbitrary sizes. IntJ Prod Res. 2022;60(17):5131–54. doi:10.1080/00207543.2021.1951446. [Google Scholar] [CrossRef]

12. Zhang XP, Shan MJ, Zeng J. Parallel batch processing machine scheduling under two-dimensional bin-packing constraints. IEEE Trans Reliab. 2023;72(3):1265–75. doi:10.1109/TR.2022.3201333. [Google Scholar] [CrossRef]

13. Ou JW, Lu LF, Zhon XL. Parallel-batch scheduling with rejection: structural properties and approximation algorithms. Euro J Oper Res. 2023;310(3):1017–32. doi:10.1016/j.ejor.2023.04.019. [Google Scholar] [CrossRef]

14. Uzunoglu A, Gahm C, Wahl S, Tuma A. Learning-augmented heuristics for scheduling parallel serial-batch processing machines. Comput Oper Res. 2023;151(3):106122. doi:10.1016/j.cor.2022.106122. [Google Scholar] [CrossRef]

15. Kucukkoc I, Keskin GA, Karaoglan AD, Karadag S. A hybrid discrete differential evolution—genetic algorithm approach with a new batch formation mechanism for parallel batch scheduling considering batch delivery. Int J Prod Res. 2024;62(1–2):460–82. doi:10.1080/00207543.2023.2233626. [Google Scholar] [CrossRef]

16. Jula P, Leachman RC. Coordinated multistage scheduling of parallel batch-processing machines under multiresource constraints. Oper Res. 2010;58(4):933–47. doi:10.1287/opre.1090.0788. [Google Scholar] [CrossRef]

17. Li XL, Chen HP, Du B, Tan Q. Heuristics to schedule uniform parallel batch processing machines with dynamic job arrivals. Int J Comput Integ Manuf. 2013;26(5):474–86. doi:10.1080/0951192X.2012.731612. [Google Scholar] [CrossRef]

18. Xu R, Chen HP, Li XP. A bi-objective scheduling problem on batch machines via a Pareto-based ant colony system. Int J Prod Econo. 2013;145(1):371–86. doi:10.1016/j.ijpe.2013.04.053. [Google Scholar] [CrossRef]

19. Abedi M, Seidgar H, Fazlollahtabar H, Bijani R. Bi-objective optimisation for scheduling the identical parallel batch-processing machines with arbitrary job sizes, unequal job release times and capacity limits. Int J Prod Res. 2015;53(6):1680–711. doi:10.1080/00207543.2014.952795. [Google Scholar] [CrossRef]

20. Zhou SC, Liu M, Chen HP, Li XP. An effective discrete differential evolution algorithm for scheduling uniform parallel batch processing machines with non-identical capacities and arbitrary job sizes. Int J Prod Econo. 2016;179(1):1–11. doi:10.1016/j.ijpe.2016.05.014. [Google Scholar] [CrossRef]

21. Jia ZH, Yan JH, Leung JYT, Li K, Chen HP. Ant colony optimization algorithm for scheduling jobs withfuzzy processing times on parallel batch machines with different capacities. Appl Soft Comput. 2019;75(9–10):548–61. doi:10.1016/j.asoc.2018.11.027. [Google Scholar] [CrossRef]

22. Jia ZH, Huo SY, Li K, Chen HP. Integrated scheduling on parallel batch processing machines with non-identical capacities. Eng Optim. 2020;52(4):715–30. doi:10.1080/0305215X.2019.1613388. [Google Scholar] [CrossRef]

23. Li CH, Wang F, Gupta JND, Chung T. Scheduling identical parallel batch processing machines involving incompatible families with different job sizes and capacity constraints. Comput Ind Eng. 2022;169(5):108115. doi:10.1016/j.cie.2022.108115. [Google Scholar] [CrossRef]

24. Li K, Zhang H, Chu CB, Jia ZH, Chen JF. Abi-objective evolutionary algorithm scheduled on uniform parallel batch processing machines. Exp Syst Appl. 2022;204(6):117487. doi:10.1016/j.eswa.2022.117487. [Google Scholar] [CrossRef]

25. Liu M, Chu F, He JK, Yang DP, Chu CB. Coke production scheduling problem: a parallel machine scheduling with batch preprocessings and location-dependent processing times. Comput Oper Res. 2019;104(7):37–48. doi:10.1016/j.cor.2018.12.002. [Google Scholar] [CrossRef]

26. Hulett M, Damodaran P, Amouie M. Scheduling non-identical parallel batch processing machines to minimize total weighted tardiness using particle swarm optimization. Comput Ind Eng. 2017;113(8):425–36. doi:10.1016/j.cie.2017.09.037. [Google Scholar] [CrossRef]

27. Wang R, Jia ZH, Li K. Scheduling parallel-batching processing machines problem with learning and deterioration effect in fuzzy environment. J Intel Fuzzy Syst. 2021;40(6):12111–24. doi:10.3233/JIFS-210196. [Google Scholar] [CrossRef]

28. Shahidi-Zadeh B, Tavakkoli-Moghaddam R, Taheri-Moghadam A, Rastgar I. Solving a bi-objective unrelated parallel batch processing machines scheduling problem: a comparison study. Comput Oper Res. 2017;88(6):71–90. doi:10.1016/j.cor.2017.06.019. [Google Scholar] [CrossRef]

29. Lu SJ, Liu XB, Pei J, Thai MT, Pardalos PM. A hybrid ABC-TS algorithm for the unrelated parallel-batching machines scheduling problem with deteriorating jobs and maintenance activity. Appl Soft Comput. 2018;66(2):168–82. doi:10.1016/j.asoc.2018.02.018. [Google Scholar] [CrossRef]

30. Zhou SC, Xie JH, Du N, Pang Y. A random-keys genetic algorithm for scheduling unrelated parallel batch processing machines with different capacities and arbitrary job sizes. Appl Math Comput. 2018;334(8):254–68. doi:10.1016/j.amc.2018.04.024. [Google Scholar] [CrossRef]

31. Sadati A, Moghaddam RT, Naderi B, Mohammadi M. Abi-objective model for a scheduling problem of unrelated parallel batch processing machines with fuzzy parameters by two fuzzy multi-objective meta-heuristics. Iran J Fuzzy Syst. 2019;16(4):21–40. [Google Scholar]

32. Zarook Y, Rezaeian J, Mahdavi I, Yaghini M. Efficient algorithms to minimize makespan of the unrelated parallel batch-processing machines scheduling problem with unequal job ready times. Performa Analy Intel Syst Oper. 2021;55(3):1501–22. doi:10.1051/ro/2021062. [Google Scholar] [CrossRef]

33. Fallahi A, Shahidi-Zadeh B, Niaki STA. Unrelated parallel batch processing machine scheduling for production systems under carbon reduction policies: nSGA-II and MOGWO metaheuristics. Soft Comput. 2023;27(22):17063–91. doi:10.1007/s00500-023-08754-0. [Google Scholar] [CrossRef]

34. Kong M, Wang WZ, Deveci M, Zhang YJ, Wu XZ, Coffman D. A novel carbon reduction engineering method-based deep Q-learning algorithm for energy-efficient scheduling on a single batch-processing machine in semiconductor manufacturing. Int J Prod Res. 2024;62(18):6449–72. doi:10.1080/00207543.2023.2252932. [Google Scholar] [CrossRef]

35. Xiao X, Ji B, Yu SS, Wu GH. A tabu-based adaptive large neighborhood search for scheduling unrelated parallel batch processing machines with non-identical job sizes and dynamic job arrivals. Flex Serv Manuf J. 2024;36(2):409–52. doi:10.1007/s10696-023-09488-9. [Google Scholar] [CrossRef]

36. Zhang W, Tang HT, Wang WY, Zhuang M, Lei D, Wang XV. A multi-objective hybrid algorithm for the casting scheduling problem with unrelated batch processing machine. Compl Syst Model Simul. 2024;4(3):236–57. doi:10.23919/CSMS.2024.0011. [Google Scholar] [CrossRef]

37. Mageed G, Sharareh T. Dynamic shop-floor scheduling using real-time information: a case study from the thermoplastic industry. Comput Oper Res. 2023;152(4):106134. doi:10.1016/j.cor.2022.106134. [Google Scholar] [CrossRef]

38. Hu KX, Che YX, Ng TS, Deng J. Unrelated parallel batch processing machine scheduling with time requirements and two-dimensional packing constraints. Comput Oper Res. 2024;162(3):106474. doi:10.1016/j.cor.2023.106474. [Google Scholar] [CrossRef]

39. Fu LL, Aloulou MA, Triki C. Integrated production scheduling and vehicle routing problem with job splitting and delivery time windows. Int J Prod Res. 2017;55(20):5942–57. doi:10.1080/00207543.2017.1308572. [Google Scholar] [CrossRef]

40. Zhang R, Chang PC, Song SJ, Wu C. A multi-objective artificial bee colony algorithm for parallel batch-processing machine scheduling in fabric dyeing processes. Knowl-Based Syst. 2017;116(7):114–29. doi:10.1016/j.knosys.2016.10.026. [Google Scholar] [CrossRef]

41. Huynh NT, Chien CF. A hybrid multi-subpopulation genetic algorithm for textile batch dyeing scheduling and an empirical study. Comput Ind Eng. 2018;125(2):615–27. doi:10.1016/j.cie.2018.01.005. [Google Scholar] [CrossRef]

42. Li K, Zhang H, Chu CB, Jia ZH, Wang Y. A bi-objective evolutionary algorithm for minimizing maximum lateness and total pollution cost on non-identical parallel batch processing machines. Comput Ind Eng. 2022;172(3):108608. doi:10.1016/j.cie.2022.108608. [Google Scholar] [CrossRef]

43. Demir Y. An efficientlexicographic approach to solve multi-objective multi-port fabric dyeing machine planning problem. Appl Soft Comput. 2023;144(2):110541. doi:10.1016/j.asoc.2023.110541. [Google Scholar] [CrossRef]

44. Srinath N, Yilmazlar IO, Kurz ME, Taaffe K. Hybrid multi-objective evolutionary meta-heuristics for a parallel machine scheduling problem with setup times and preferences. Comput Ind Eng. 2023;185(5–6):109675. doi:10.1016/j.cie.2023.109675. [Google Scholar] [CrossRef]

45. Lee DH, Park IB, Kim K. An incremental learning approach to dynamical parallel machine scheduling with sequence-dependent setups and machine eligibility restrictions. Appl Soft Comput. 2024;164(21):112002. doi:10.1016/j.asoc.2024.112002. [Google Scholar] [CrossRef]

46. Santoro MC, Junqueira L. Unrelated parallel machine scheduling models with machine avaiability and eligibility constraints. Comput Ind Eng. 2023;179(1–2):109219. doi:10.1016/j.cie.2023.109219. [Google Scholar] [CrossRef]

47. Zheng FF, Jin KY, Xu YF, Liu M. Unrelated parallel machine scheduling with processing cost, machine eligibility and order splitting. Comput Ind Eng. 2022;171(3):108483. doi:10.1016/j.cie.2022.108483. [Google Scholar] [CrossRef]

48. Li DB, Wang J, Qiang R, Chiong R. A hybrid differential evolution algorithm for parallel machine scheduling of lace dyeing considering colour families, sequence-dependent setup and machine eligibility. Int J Prod Res. 2021;59(9):2722–38. doi:10.1080/00207543.2020.1740341. [Google Scholar] [CrossRef]

49. Wang J, Li DB, Tang HT, Li XX, Lei DM. A dynamical teaching-learning-based optimization algorithm for fuzzy energy-efficient parallel batch processing machines scheduling in fabric dyeing process. Appl Soft Comput. 2024;167(9):112413. doi:10.1016/j.asoc.2024.112413. [Google Scholar] [CrossRef]

50. Lei DM, Dai T. An adaptive shuffled frog-leaping algorithm for parallel batch processing machines scheduling with machine eligibility in fabric dyeing process. Int J Prod Res. 2024;62(21):7704–21. doi:10.1080/00207543.2024.2324452. [Google Scholar] [CrossRef]

51. Cai JC, Lei DM. A cooperated shuffled frog-leaping algorithm for distributed energy-efficient hybrid flow shop scheduling with fuzzy processing time. Comple Intel Syst. 2021;7(5):2235–53. doi:10.1007/s40747-021-00400-2. [Google Scholar] [CrossRef]

52. Cai JC, Lei DM, Wang J, Wang L. A novel shuffled frog-leaping algorithm with reinforcement learning for distributed assembly hybrid flow shop scheduling. Int J Prod Res. 2022;61(4):1233–51. doi:10.1080/00207543.2022.2031331. [Google Scholar] [CrossRef]

53. Yang YF, Song YH, Guo WF, Lei Q, Sun AH, Fan LH. Guided shuffled frog-leaping algorithm for flexible job shop scheduling with variable sublots and overlapping in operations. Comput Ind Eng. 2023;180(19):109209. doi:10.1016/j.cie.2023.109209. [Google Scholar] [CrossRef]

54. Wu PL, Yang QY, Chen WB, Mao BY, Yu HN. An improved genetic-shuffled frog-leaping algorithm for permutation flowshop scheduling. Complexity. 2020;1(14):3450180. doi:10.1155/2020/3450180. [Google Scholar] [CrossRef]

55. Taguchi G. Introduction to quality engineering: designing quality into products and processes. Tokyo, Japan: Asian Productivity Organization; 1986. 191 p. [Google Scholar]