Experimental and Peridynamic Numerical Study on the Opening Process of the Soft PSD in Pulse Solid Rocket Motors

1  Introduction

Pulse solid rocket motors (SRMs) offer significant advantages over traditional solid propulsion systems, including enhanced velocity, extended range, and improved flight control capabilities. As one of the key technologies of pulse SRMs, the isolation device plays a critical role in realizing their engineering implementation. There are mainly two modes of isolation devices: compartment mode and layer mode. The layer mode has the characteristics of simple structure, light weight, and small space occupation, which helps significantly reduce the inert mass of the pulse SRM. Moreover, it offers ease of manufacturing and simplified assembly procedures. Therefore, the layered pulse SRM shows strong potential for practical engineering applications. The isolation device of the layered pulse SRMs usually employs a soft pulse separation device (PSD), which must exhibit both high pressure-bearing capacity and effective thermal insulation, while also ensuring safe and reliable opening. The ability of the PSD to open reliably under operating conditions directly impacts the overall performance of the pulse SRM and represents a key technical challenge in PSD design. Therefore, investigating the opening process, failure mechanisms, and influencing factors of soft PSDs is of great significance for optimizing their structural design and ensuring the reliable operation of pulse SRMs.

A large body of research has been conducted by scholars and researchers regarding layered pulse solid rocket motors. Stadler et al. [1] designed an axial-radial hybrid layered dual-pulse engine and measured its pressure and thrust curves through ground static testing, followed by two successful flight tests. Gao et al. [2] developed an integrated soft PSD for pulse SRMs, which simplifies the molding process, effectively reduces the inert mass, and improves the overall mass efficiency of the engine. Zhang et al. [3] designed a radial PSD structure aimed at reducing the circumferential strain in the PSD of a dual-pulse solid rocket motor. Liu et al. [4] designed and conducted a fast-loading test to evaluate the deformation behavior of the pulse charge and soft PSD during ignition and pressure build-up in the first-stage combustor of an axial layered dual-pulse engine. The results showed that the axial deformation of the soft PSD was significant and closely matched the finite element predictions. Yang et al. [5] employed the MpCCI coupler to facilitate data exchange between FLUENT and ANSYS, enabling the simulation of ignition delay characteristics in a layered multi-pulse SRM, as well as the ignition gas filling and PSD deformation processes. Li et al. [6] adopted fluid-structure interaction simulations to study the transient process of the second pulse ignition in the axial-radial hybrid layered dual-pulse engine, solving large deformation issues using nested grid techniques. Fan et al. [7] established a viscoelastic constitutive model for Ethylene-propylene-diene Monomer (EPDM) soft interlayers under finite deformation and validated its predictive capability using experimental data under various loading conditions. Subsequently, Fan et al. [8,9] investigated the failure behavior of soft PSDs during operation. Based on the viscoelastic constitutive model, an energy limiter with a content-related term was introduced to establish a constitutive model that can effectively predict the failure behavior of EPDM under uniaxial tension. Chong et al. [10] designed a novel adhesive-based soft PSD structure to investigate the opening performance of dual-pulse solid rocket motors. By inverting the data of mechanical experiments and finite element simulations, the constitutive parameters and the fracture mechanics parameters of EPDM material were obtained. The pressure opening process of the soft interlayer was simulated via the method of explicit dynamics, indicating that the interlayer can be safely opened at the predetermined adhesive zone of the interlayer. Wang et al. [11] conducted research on the rupture and stress distribution of soft PSD in dual-pulse engines, designing a soft PSD with prefabricated defect and conducting ignition tests. The results indicate that during the operation of the engine, the soft PSD ruptures on time, which is consistent with the simulated location of the soft PSD rupture. Fu et al. [12] utilized the ABAQUS/Explicit module to simulate the reverse opening process of the EPDM soft insulation layer in the axial-radial hybrid compartmentalized dual-pulse engine, obtaining the contour of stress distribution and opening process in the weak area of the EPDM soft PSD. Wang et al. [13,14] further designed PSDs to support pulse start–stop functionality and verified their performance through simulations and experiments.

These existing studies have achieved certain results, but also have certain limitations or shortcomings. At present, research on the soft PSD rubber materials mainly includes experimental methods and numerical simulation methods. The results obtained from experimental research methods are reliable, but they are time-consuming and expensive. Therefore, the corresponding advantages of numerical simulation can be reflected. The finite element method, as the most mature numerical analysis method, is widely used in the field of engineering. However, there are some limitations in using this method to study the soft PSD of the layered pulse solid rocket motor. The soft PSD is usually made of rubber material, which is a typical hyperelastic material. Unlike metal materials, rubber material is a nonlinear material with complex constitutive relationships, and its material properties cannot be described by a few coefficients like metal materials. The deformation and failure process of rubber under stress is very complex. Its deformation is accompanied by large displacement and strain. When dealing with large deformations or failure problems, the finite element method may encounter mesh singularities, making calculations impossible. In addition, the commercial software widely used in engineering, such as ABAQUS, only includes certain constitutive model and failure criteria, so it may not simulate the failure process of the soft PSD rubber materials well.

In recent years, peridynamics (PD) [15] has emerged as a meshless computational framework grounded in a novel nonlocal theory. It fundamentally reformulates classical continuum mechanics by removing the assumption of spatial continuity. Unlike traditional methods that rely on spatial continuity and differential equations, PD discretizes a solid body into a set of material points and governs their interactions via spatial integral equations. This allows it to naturally handle discontinuities such as cracks without encountering singularities. Therefore, PD offers distinct advantages in modeling discontinuities such as crack propagation, effectively addressing the limitations of traditional finite element methods (FEM) [16]. As a result, it has attracted increasing attention from researchers in various engineering fields [17–20]. Bobaru et al. [21] systematically investigated the fracture behavior of brittle materials using the PD method and analyzed the influence of stress waves on crack propagation and branching. Tupek et al. [22] incorporated a viscoplastic constitutive model and a metal toughness degradation law to simulate the failure of aluminum plates under impact loading. Fan et al. [23] employed the critical stretch failure criterion to simulate the mechanical response of soil under explosive loading. In recent years, PD has also been extended to the modeling of rubber-like materials. Bang et al. [24] proposed a bond-based strain energy formulation to simulate the tensile behavior of polymeric materials. Silling et al. [25] simulated the tearing of polymer materials using bond-based peridynamics in conjunction with a Neo-Hookean constitutive model. Chen et al. [26] developed a neural network (NN) non-ordinary state-based peridynamics (NOSB PD) method to model the large deformation and failure behavior of rubber-like materials.

Considering the advantages of peridynamics, it is employed in this study to simulate the opening and failure processes of the soft PSD. The paper is organized as follows: we first overview the theory of peridynamics and the hyperelastic constitutive model for soft PSD in Section 2. And then, according to the measured performance data of the soft PSD rubber material, the Mooney–Rivlin constitutive model of the soft PSD rubber material was established based on the peridynamics method in Section 3. In Section 4, the opening process of the soft PSD is simulated based on the failure criterion of fracture stretch via peridynamics, and its strain field distribution, failure mode, and opening pressure value were obtained. Meanwhile, a single-opening test of the soft PSD was designed, and the experimental results were compared with the numerical simulation results to verify the rationality of the calculation method and the design of the soft PSD. After that, the influence of the distribution and depth of defects in the prefabricated soft PSD on the failure mode and opening pressure of the soft PSD was explored in Section 5. Finally, the conclusions drawn based on these study findings are presented in Section 6.

2  Methodology

2.1 Overview of Peridynamics

Peridynamics (PD) is a nonlocal continuum theory of solid mechanics that replaces conventional partial differential equations with integral equations. In non-ordinary state-based peridynamics, a continuum body Ω is discretized into individual material particles XA with associated volume VXA and density ρXA, where A = 1, 2, …, n denotes the index of each particle. The material particle XA is assumed to be only interacted with other material particles in a certain horizon HXA, which is defined as circle in 2D or a sphere in 3D. In this study, the horizon size is set to δ=3.015Δ, where Δ represents particle spacing.

The governing equation of motion in PD is given by

ρAu¨=∫HXA[T(XA,XA→B)−T(XB,XB→A)]dVXB+bA,(1)

where T(XA,XA→B) denotes the force state acting on particle XA due to the interaction with particle XB within horizon HXA, and T(XB,XB→A) is the force state acted on particle XB due to particle XA. u and b represent the displacement and external body force of particle XA, respectively.

The discretized form of the peridynamic equation is expressed as

ρAu¨=∑XB∈HXA[T(XA,XA→B)−T(XB,XB→A)]dVXB+bA.(2)

The force state can be represented in terms of the first Piola-Kirchhoff stress tensor P, by establishing an equivalence between the strain energy densities in PD and classical continuum mechanics. The correspondence equation can be written as

T(XA,XA→B)=w(|XA→B|)PXA⋅KXA−1⋅XA→B,(3)

XA→B=XB−XA,(4)

where XA→B is the relative position vector pointing from particle XA to particle XB in the reference configuration. w(|XA→B|) is the influence function associated with the distance of particle XA and particle XB. If the distance between particles is smaller than the horizon size, the influence function is equal to 1; if the distance exceeds the horizon size, it is equal to 0. KXA is the reference shape tensor of particle XA, defined as

KXA=∫HXAw(|XA→B|)XA→B⊗XA→BdVXB=∑XB∈HXAw(|XA→B|)XA→B⊗XA→BdVXB.(5)

The relationship between the first Piola–Kirchhoff stress tensor PXA and Cauchy stress σXA follows classical continuum mechanics and is given by

PXA=JσXAFXA−T,(6)

where J=det(FXA), FXA is the deformation gradient tensor at particle XA, which can then be applied to the constitutive relation in classical continuum mechanics, defined as

FXA=∫HXAw(|XA→B|)YA→B⊗XA→BdVXB⋅KXA−1=∑XB∈HXAw(|XA→B|)YA→B⊗XA→BdVXB⋅KXA−1,(7)

YA→B=xB−xA=(uB+XB)−(uA+XA),(8)

where YA→B is the deformation state, which is the relative position vector pointing from particle XA to particle XB in the current configuration.

Non-ordinary state-based peridynamics (NOSBPD) suffers from the zero-energy mode problem. To address this issue, several control strategies have been proposed in the literature. Among them, the method proposed by Li et al. [27] does not require any control parameters, making it attractive for practical implementation. Accordingly, this control method is adopted in the present study to suppress unphysical oscillations. In this method, the force state associated with non-uniform deformation is given by

Ts(XA,XA→B)=12w(|XA→B|)[CXAzA→B−(∫HXAw(|XA→B|)CXAzA→BXA→BdVXB)]KXAXA→B,,(9)

where the correction vector is defined as

zA→B=YA→B−FXAXA→B,(10)

and the influence coefficient tensor CXA is given by

CXA=c0XA→B⊗XA→B|XA→B|3.(11)

The scalar micro-modulus c0 for the bond-based peridynamic model (BBPD) is expressed as

c0={12Eπδ43D9Eπhδ32D (plane stress)48Eπhδ32D (plane strain)2EAδ21D,(12)

where E is Young’s modulus, h is the thickness in the 2D case, and A represents the cross-sectional area for the 1D case.

By combining Eq. (3) with Eq. (4), the corrected force state Tc with zero-energy mode suppression is obtained as

Tc(XA,XA→B)=T(XA,XA→B)−Ts(XA,XA→B).(13)

2.2 Hyperelastic Constitutive Model

Numerous hyperelastic material models have been developed to characterize the mechanical behavior of soft polymer-based PSD materials. Among these, the Mooney–Rivlin model is one of the most widely used due to its capability to capture large deformations and its relatively simple form of strain energy density function. Accordingly, the Mooney–Rivlin model is adopted in this study to describe the nonlinear constitutive behavior of the soft PSD material. The strain energy density function W of the Mooney–Rivlin model under nearly incompressible conditions is defined as

W(I1¯,I2¯,J)=C10(I1¯−3)+C01(I2¯−3)+1D1(J−1)2,(14)

I1¯=tr(B¯),(15)

I2¯=12[(tr(B¯))2−tr(B¯2)],(16)

where J is the determinant of deformation gradient (J=det(F)), I1¯ and I2¯ are invariants of isochoric left Cauchy-Green deformation tensor B¯=F¯⋅F¯T. F¯ is the isochoric deformation gradient, expressed as F¯=J−1/3F. In this model, C10 and C01 are material constants governing the isochoric (distortional) response, and D1 is a penalty parameter associated with volumetric deformation, used to enforce near-incompressibility. The initial bulk modulus is given by K0=2/D1, and the infinitesimal-strain shear modulus is G0=2(C10+C01). When G0/K0≪1, the material exhibits quasi-incompressible behavior, as is typical for elastomers.

The corresponding Cauchy stress σ can be derived from strain energy density function, expressed as

σ=1J[2(C10+C01I1¯)B¯−2C01B¯⋅B¯−23(C10I1¯+2C01I2¯)I]+21D1(J−1)I,(17)

where I is the second-order identity tensor.

3  Mechanical Properties of the Soft PSD

3.1 Constitutive Model

In this study, the soft PSD is made of a typical hyperelastic material, which has the advantages of low density, erosion resistance, and excellent electrical insulation performance. To obtain the constitutive model of the soft PSD, uniaxial tensile tests were conducted on the specimens made of PSD materials using a universal testing machine. The specimens were fabricated into dumbbell-shaped configurations in accordance with aerospace industry standards. Multiple repeated tests were conducted to ensure data reliability, and the stress–strain curve with the highest repeatability was selected for constitutive model fitting. The selected experimental data were fitted using the two-parameter Mooney–Rivlin model through least-squares regression implemented in ABAQUS. The stress-strain curves for fitting and testing are presented in Fig. 1, and the calibrated material parameters are summarized in Table 1.

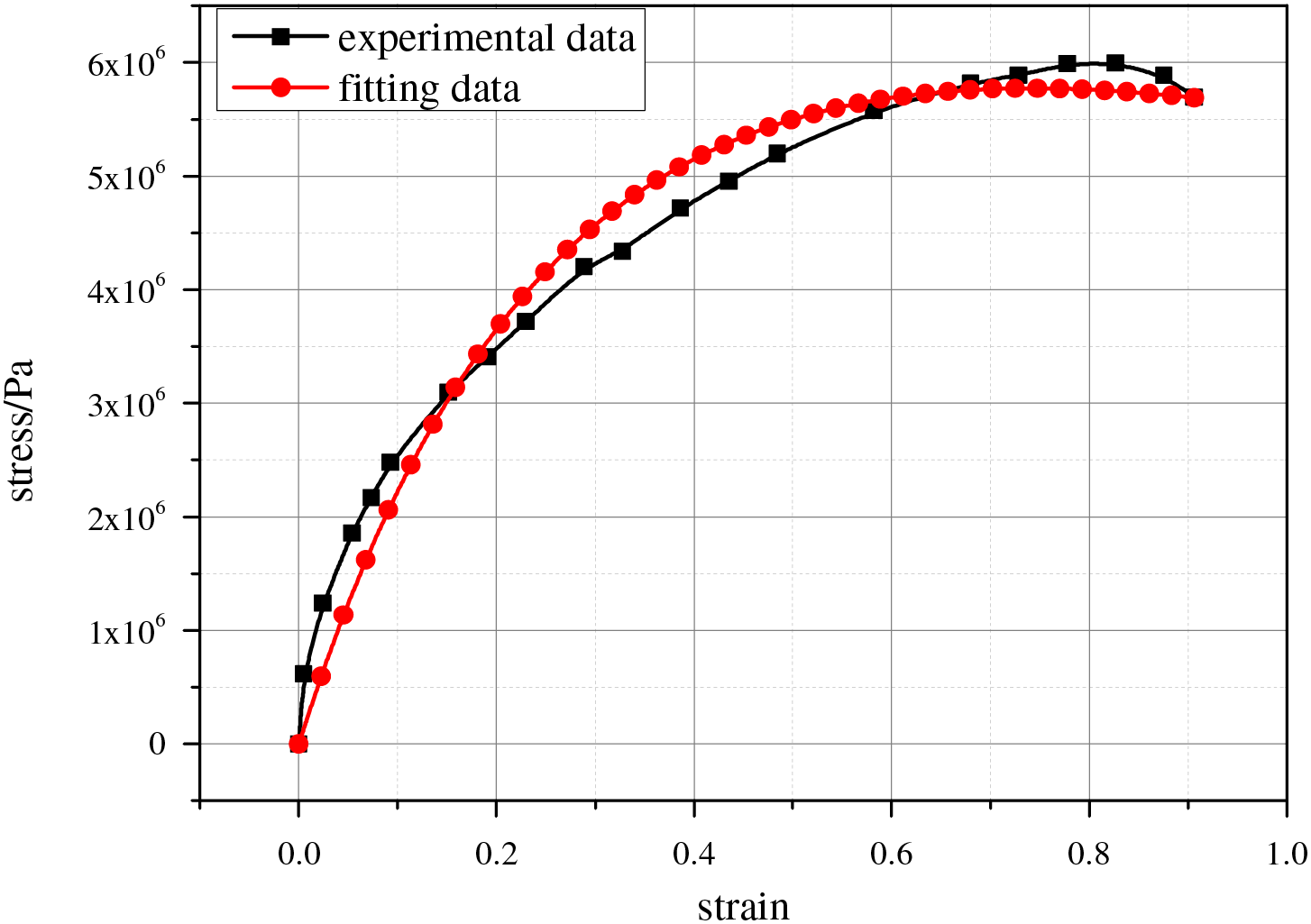
Figure 1: Comparison of experimental and fitted stress–strain curves for soft PSD

3.2 Failure Criterion

In peridynamics, crack initiation and propagation are simulated by breaking bonds (interactions) between material points. The bonding between particles can be removed based on failure criteria, such as criteria based on critical stretch, strain energy density, or stress thresholds. For linear elastic materials, the value of critical stretch can be expressed based on its critical energy release rate. However, such an approach is not suitable for rubber-like materials due to their highly nonlinear constitutive behavior. Several studies have reported that rubber-like materials exhibit a fundamentally different stress state near the crack tip compared to linear elastic solids. Specifically, the dominant stress field near the crack tip in rubber is uniaxial tension rather than the plane strain condition typically assumed in linear fracture mechanics. Moreover, because strain can be directly measured through experimental techniques such as digital image correlation (DIC), without needing to rely on a specific constitutive model, strain-based failure criteria are widely adopted for rubber-like materials. In this study, a critical stretch criterion is adopted: when the bond stretch between two peridynamic particles exceeds a critical uniaxial value, the bond is irreversibly broken. Similar criteria have been proposed by Ayatollahi et al. [28].

The value of bond critical stretch scr can be determined by the critical uniaxial stretch obtained from uniaxial tensile tests. According to the uniaxial tensile testing of soft PSD materials described in Section 3.1, the specimen stretches to fracture when the strain reaches 0.91, indicating a critical uniaxial stretch of scr=0.91. This value is therefore used as the bond-breaking threshold in the subsequent peridynamic simulations. Once the stretch between two particles exceeds this value, the bond is considered broken, and damage initiates in the soft PSD material. The bond stretch can be expressed as follows:

s=|YA→B−XA→B||XA→B|,(18)

where XA→B and YA→B are the relative position vectors in the reference and current configurations, respectively.

4  Numerical Simulation and Experimental Analysis of the Opening Process of the Soft PSD

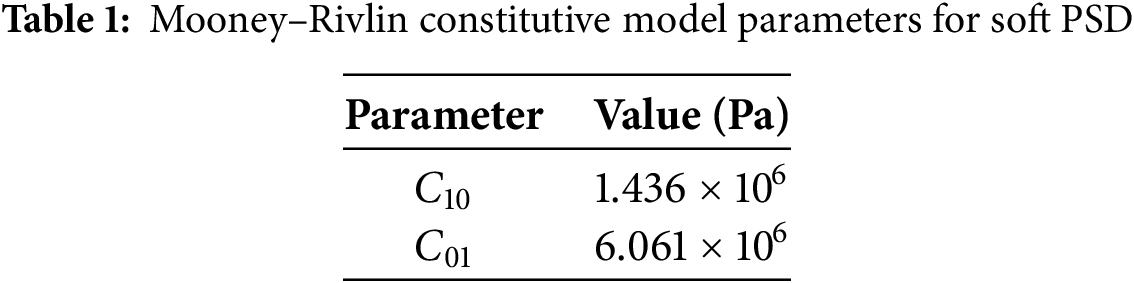
The working principle of the soft PSD is that during the I pulse operation, the soft PSD relies on the structural support provided by the II pulse charge to resist the gas pressure generated in the I pulse chamber, while also playing a role in insulation and sealing. During the II pulse operation, the soft PSD fractured and opened in the designed weak area due to the gas pressure from the II pulse chamber. According to the different isolation directions of the II pulse charge, the soft PSD can be divided into three types: axial PSD, radial PSD, and axial-radial hybrid PSD, as shown in Fig. 2. In this study, both numerical simulation and experimental analysis are conducted for the opening process of axial PSD.

Figure 2: Different types of PSD: (a) axial PSD; (b) radial PSD; (c) axial-radial hybrid PSD

4.1 Numerical Simulation Analysis

In this section, numerical simulations of the opening process of the soft PSD are performed based on peridynamics. The soft PSD consists of a cylindrical shell segment and an end face, in which the end face is deliberately weakened by introducing a “star-shaped” defect composed of three intersecting notches at 60° angles. The outer diameter of the soft PSD is 192 mm, and the thickness is 6 mm. The notches comprising the star defect have a depth of 2 mm and a length of 140 mm. To simplify the modeling process, the soft PSD is simplified as a 2D “hat-shaped” structure, as shown in Fig. 3. And the calculation model of the soft PSD is shown in Fig. 4, which is discretized into uniformly distributed particles with a particle spacing of Δx=1mm, and the peridynamic horizon is defined as δ=3.015Δx. Time step size is set as Δt=2×10−6, which satisfies the stability condition imposed by the Courant–Friedrichs–Lewy (CFL) criterion. The front end of the cylindrical segment is subjected to a fixed boundary condition, while the inner surface is loaded with a linearly increasing internal pressure, ramping up to a peak value of 2 MPa. The hyperelastic constitutive behavior of the PSD material is modeled using the Mooney–Rivlin model, with material parameters calibrated from mechanical tests described in Section 3.1 and summarized in Table 1.

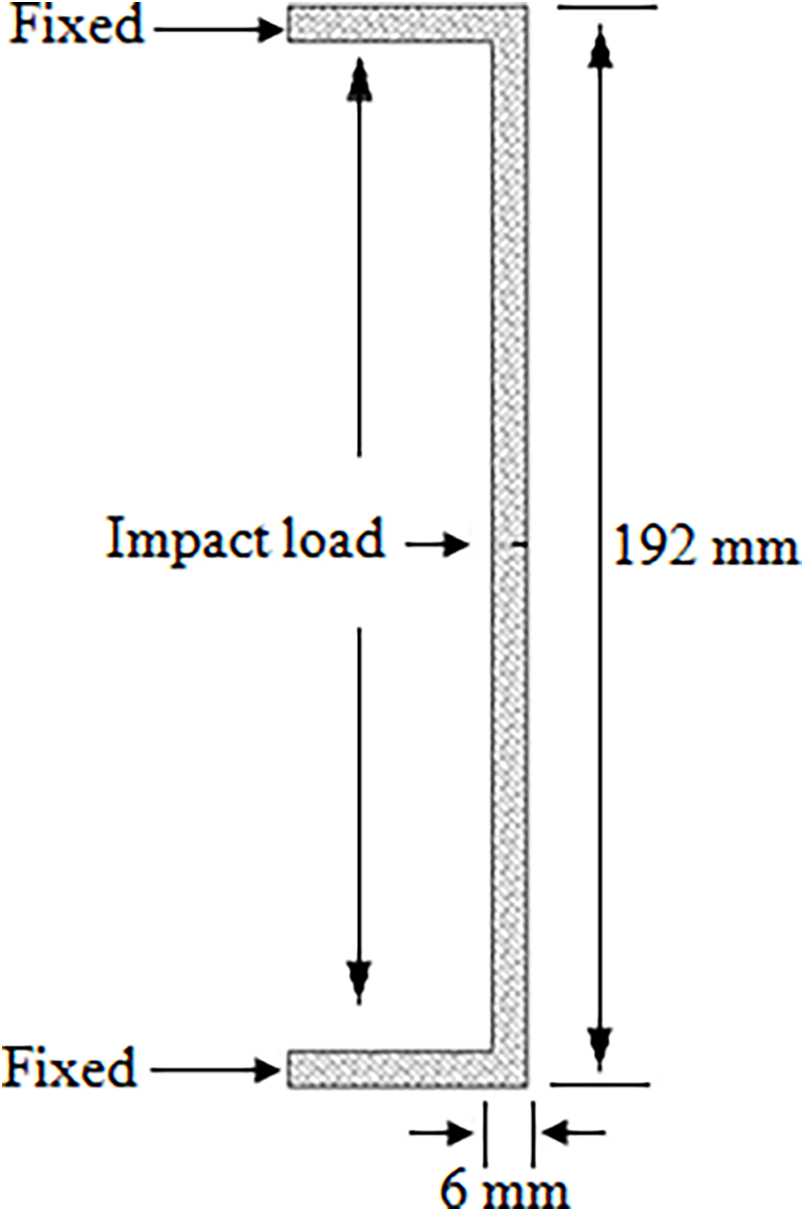
Figure 3: Configuration of the soft PSD in 2D

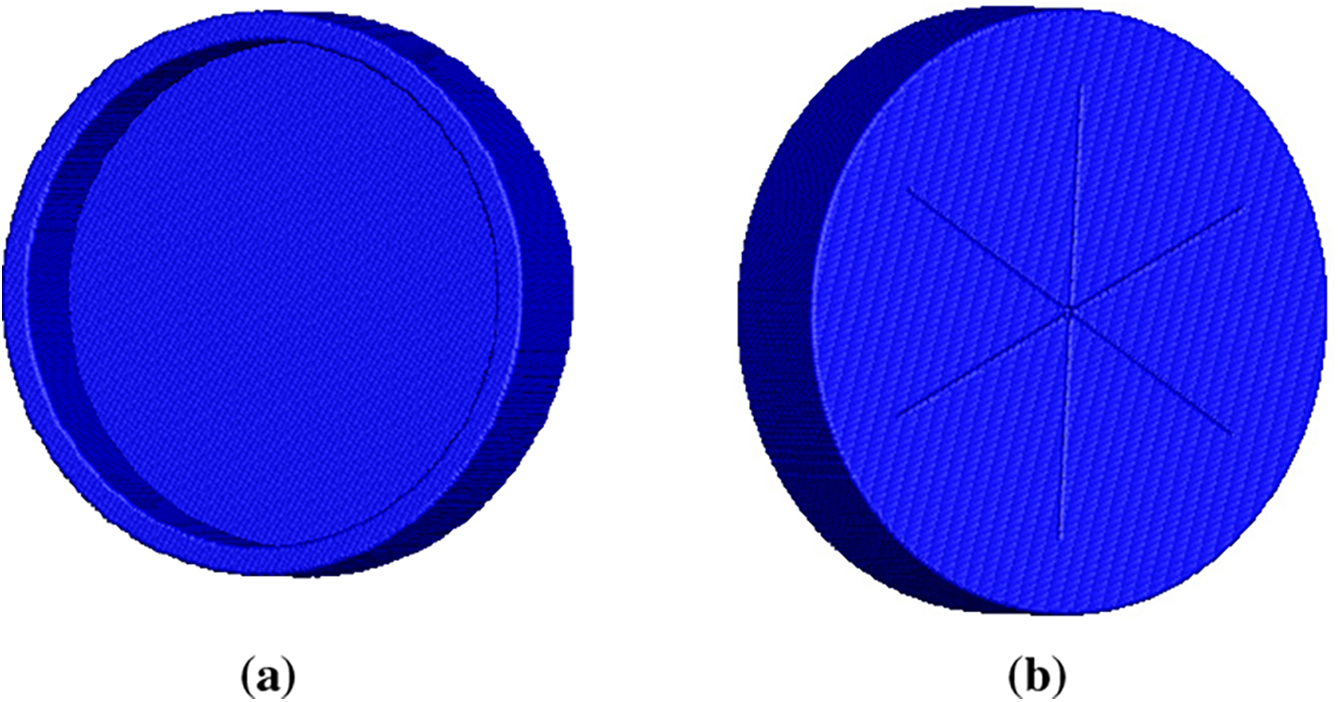
Figure 4: Numerical model of the soft PSD: (a) front view; (b) back view

The numerical simulation results of the soft PSD opening process based on peridynamics are presented as follows. Fig. 5 shows the displacement contours of the side view of the soft PSD at various time steps during the pressure impact load applied on the inner surface of the soft PSD. It can be seen from the figure that the soft PSD undergoes a sequential process of expansion and failure under increasing pressure. As the load is applied continuously, the soft PSD exhibits outward deformation, with displacement magnitudes increasing over time. The largest displacement is observed in the central region of the PSD structure. As the deformation progresses, a crack initiates in the pre-defined weak region and propagates along the prefabricated defect path. The simulation successfully captures both the initiation and evolution of failure during the opening process of the soft PSD.

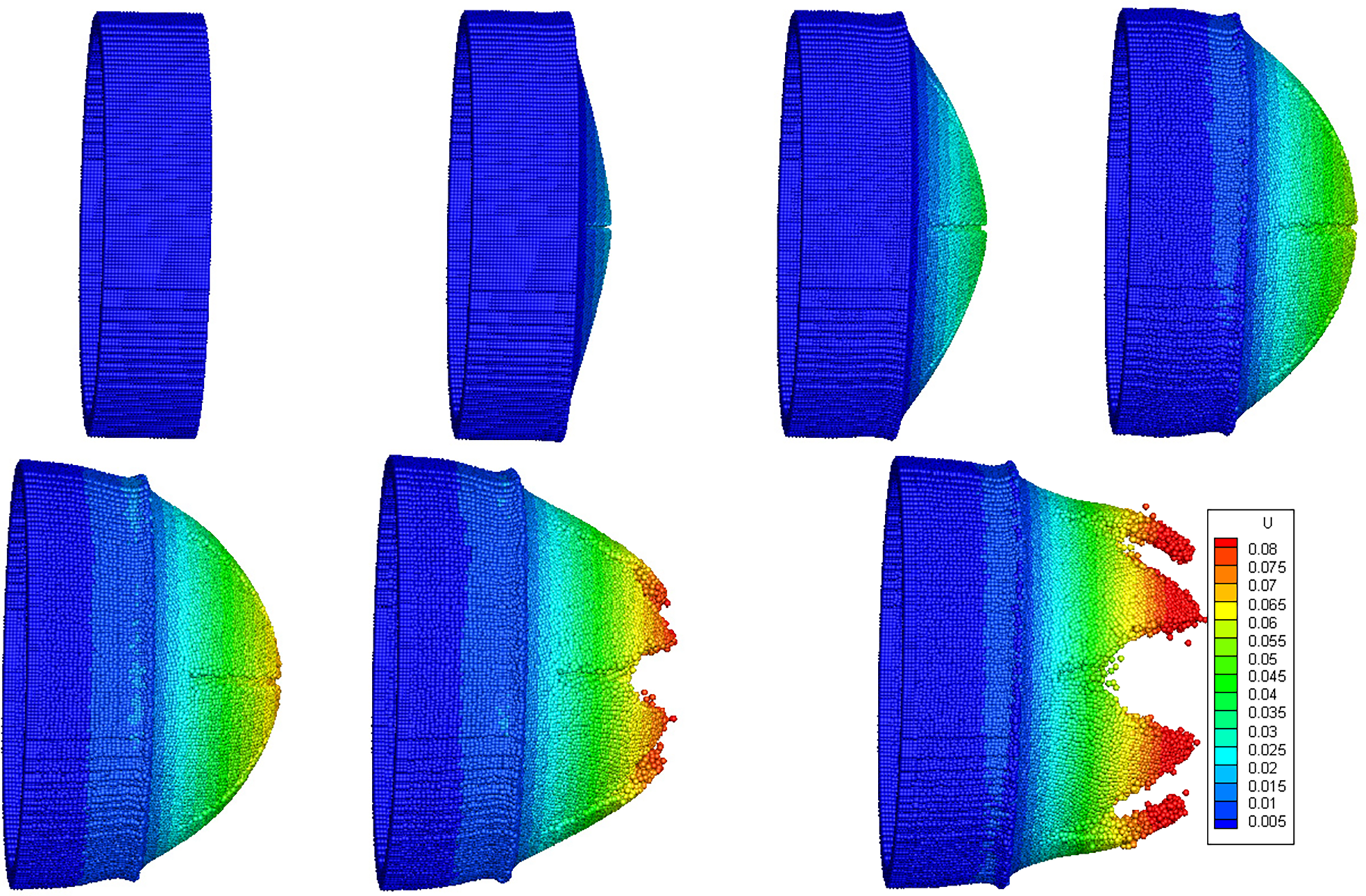
Figure 5: Side-view displacement contours of the soft PSD during the deformation and opening process

Fig. 6 shows the damage contour of the soft PSD during the opening process, as predicted by the peridynamics simulation. It can be observed that during the opening process of the soft PSD, when the pressure reaches 1.34 MPa, fracture initiates at the central region of the star-shaped prefabricated defect. As the pressure continues to increase, the crack propagates along the predefined defect paths, resulting in the formation of three distinct long cracks. Consequently, the damaged area of the soft PSD expands progressively throughout the loading process.

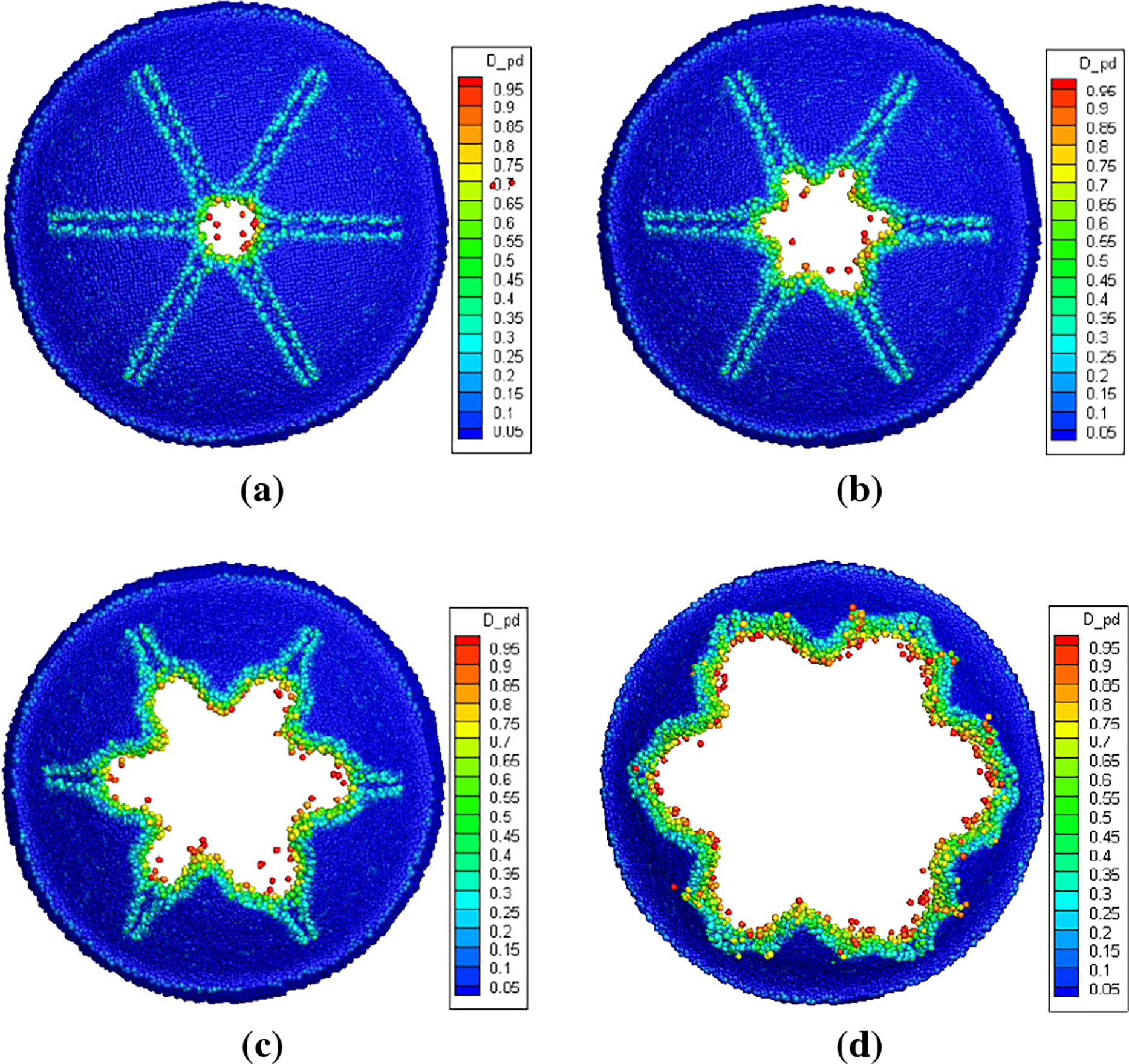
Figure 6: Back-view damage contours of the soft PSD during the opening process. (a) 1.341 MPa; (b) 1.345 MPa; (c) 1.349 MPa; (d) 1.354 MPa

4.2 Monomial Opening Test Analysis

The monomial opening test of the soft PSD is an essential process in the design of solid rocket engines, which can assess the opening performance of the soft PSD. To validate the structural design and numerical simulation results of the soft PSD, a test device was developed based on the structure and working principle of the axial PSD used in dual-pulse solid rocket engines. In the test, the instantaneous pressure generated by the second pulse of the engine is simulated by rapidly supplying high-pressure nitrogen gas. The test setup consists of three main parts: a nitrogen pressurization system, a pressure measurement system, and a test engine. The test engine assembly includes the gas generator, soft PSD, front head, and other structural components. The schematic diagram of the test engine is shown in Fig. 7. The real object of the test engine is shown in Fig. 8a, and the real object of soft PSD is shown in Fig. 8b.

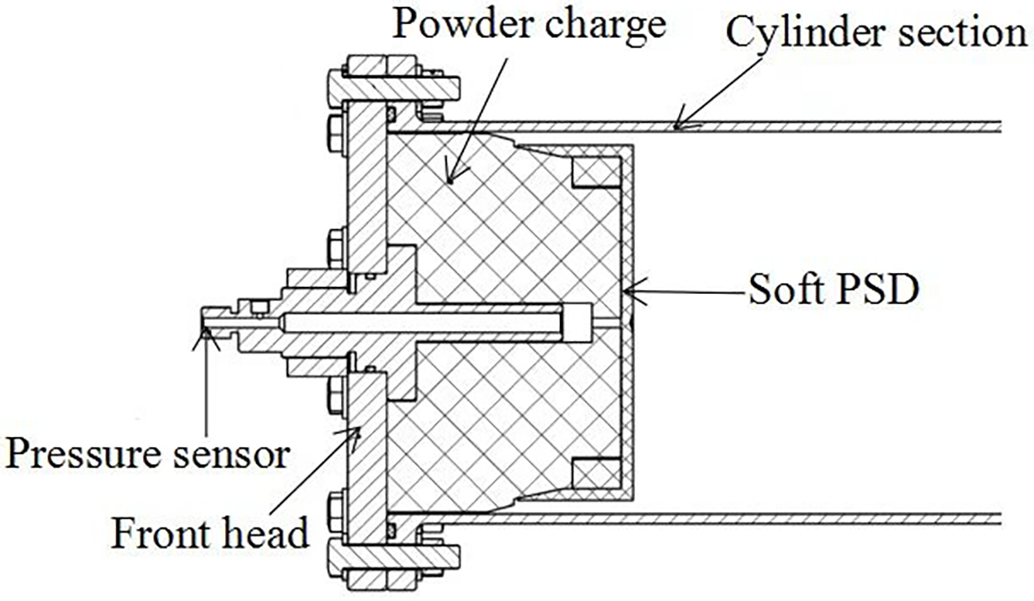
Figure 7: Schematic diagram of the test engine structure

Figure 8: Physical drawing structure: (a) physical drawing of test engine; (b) physical drawing of soft PSD

In the monomial opening test of the soft PSD, the pressure sensor was employed to monitor the internal pressure during the opening process. The recorded pressure-time curve is shown in Fig. 9.

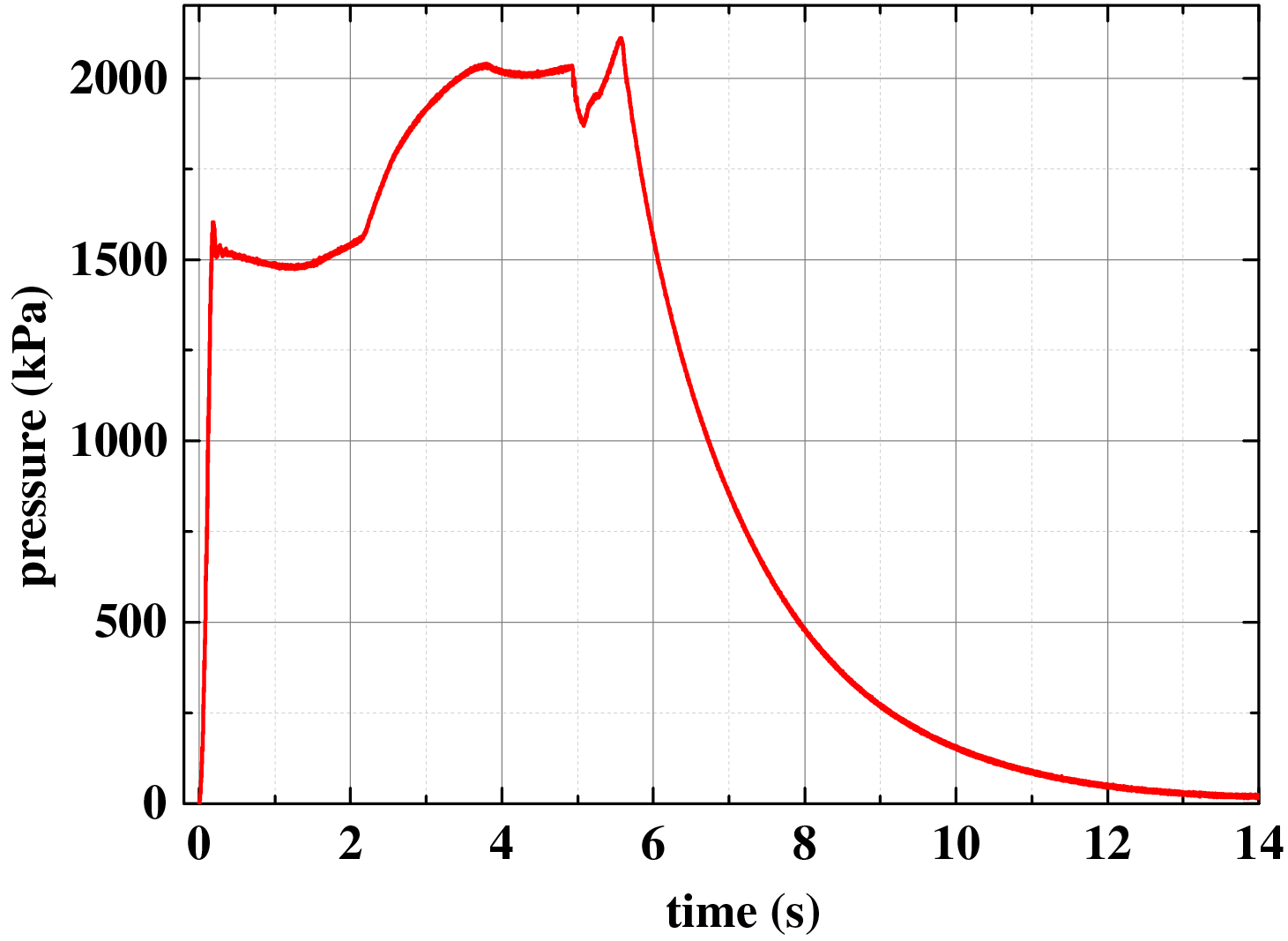
Figure 9: Pressure test curve during the opening process of the soft PSD

By analyzing the pressure test curve, it can be seen that the nitrogen pressurization system began to supply the high-pressure nitrogen at 0 s. With the continuous supply of high-pressure nitrogen, the pressure at the measuring point monitored by the pressure sensor began to increase continuously. At approximately 185 ms, a sudden pressure fluctuation was observed, which can be attributed to nitrogen leakage initiated by the formation of cracks in the soft PSD. These cracks formed due to the structure’s inability to withstand the impact of the high-pressure nitrogen. This moment corresponds to the opening pressure, which was measured to be 1.6 MPa. Since the nitrogen supply system remained active after fracture initiation, the pressure continued to fluctuate and slightly increased. At 5.57 s, the nitrogen pressurization system was shut down and stopped supplying gas, resulting in a downward trend in pressure.

Fig. 10 presents the post-test state of the soft PSD. The image shows that the fracture occurred at the pre-defined weak zone, and the damage propagated along the prefabricated notch, resulting in the formation of a single long crack. This confirms that the partition ruptured as intended, validating the effectiveness of the weak-point design.

Figure 10: Fracture condition of the soft PSD after the monomial opening test

From the comparison between the calculation results and the experimental results, it can be seen that the hyperelastic constitutive model and the failure criterion of fracture stretch established based on the peridynamics method can effectively predict the opening process of the soft PSD. The numerically predicted opening pressure closely matches the measured value of 1.6 MPa, and the failure mode is generally consistent with failure model obtained from test (the soft PSD can be opened at the predetermined weak position, and the crack propagated along the notch), which verifies the effectiveness of the soft PSD design and the established simulation method. Minor discrepancies between simulation and experimental results in terms of crack path and opening pressure are likely due to manufacturing imperfections in the three prefabricated notches. These variations may have caused asymmetric failure resistance, leading to crack propagation along only one notch during the test, instead of simultaneous propagation along all three. As a result, the total opening pressure observed in the test differed slightly from the ideal numerical prediction.

5  Analysis of Factors Affecting the Opening Performance of Soft PSD

The opening performance of the soft PSD is directly determined by the structural design of the soft PSD, which is influenced by various factors, among which the prefabricated defect of the soft PSD is the key factor. Understanding how these defects affect the opening behavior is of great importance for optimizing the design of soft PSDs in engineering applications.

Based on the validated hyperelastic constitutive model and fracture criterion developed in Section 4, which can accurately simulate the deformation and failure process from expansion to rupture, this chapter investigates the influence of prefabricated defect geometry, specifically the form and depth, on the opening performance of the soft PSD through numerical simulations.

5.1 The Influence of Prefabricated Form on the Opening Performance of the Soft PSD

The purpose of introducing prefabricated defects on the soft PSD is to reduce the opening pressure of the soft PSD and increase the uniformity of cracks when the soft PSD ruptures. This ensures that the soft PSD opens safely and reliably under operating conditions. Considering the structural symmetry of the soft PSD and assuming that the internal gas pressure is uniformly distributed along its inner surface, the prefabricated defect must also exhibit either central or axial symmetry to ensure a balanced rupture pattern. Based on the above considerations, symmetric models of soft PSD were developed to investigate the influence of defect geometry on opening performance. Three types of defect forms were considered: a straight notch (Type I, “−”), two perpendicular notches intersecting at 90° (Type II, “+”), and three notches intersecting at 60° (Type III, “star”). To isolate the effect of geometry, the defect length and depth were kept constant across all models, and each model was subjected to the same loading conditions. Specifically, the front-end face of the soft PSD was fixed, and the inner surface was subjected to a linearly increasing internal pressure up to 2 MPa.

The damage contours of the soft PSDs with different defect forms under impact loading are shown in Figs. 11–13. It can be observed that, under identical loading and with a consistent defect depth of 2 mm, the failure modes vary depending on the defect type. The PSD with a Type I defect exhibits a straight-line fracture; the Type II defect produces a cross-shaped crack pattern; and the Type III defect results in a star-shaped fracture extending along all three notches. In all cases, the crack initiates at the central intersection point of the prefabricated defect and propagates along the notch direction. Moreover, a greater number of notches leads to a larger initial weak area, which facilitates rupture and reduces the opening pressure. The simulation results indicate that the opening pressures for the Type I, Type II, and Type III defects are 1.652, 1.634, and 1.341 MPa, respectively. This trend confirms that as the number of notches increases, the structural resistance to impact loading decreases. The larger cumulative weakened area introduced by multiple notches reduces the local stiffness of the soft PSD, resulting in earlier failure under the same loading conditions.

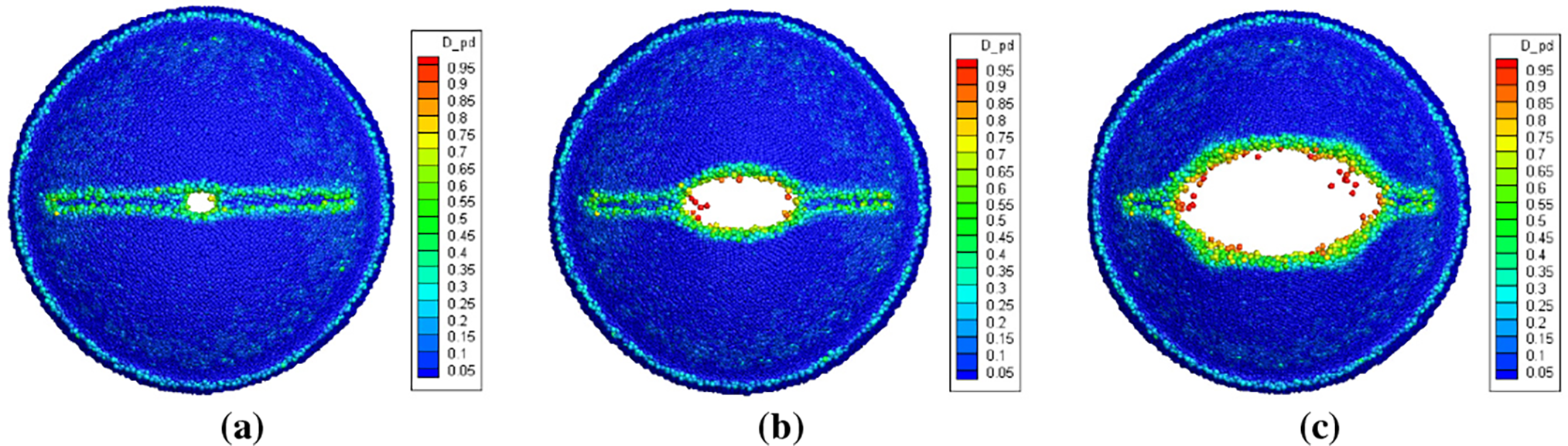
Figure 11: Damage contours of the soft PSD with Type I (“−”) defect form during opening process (back view). (a) 1.652 MPa; (b) 1.656 MPa; (c) 1.661 MPa

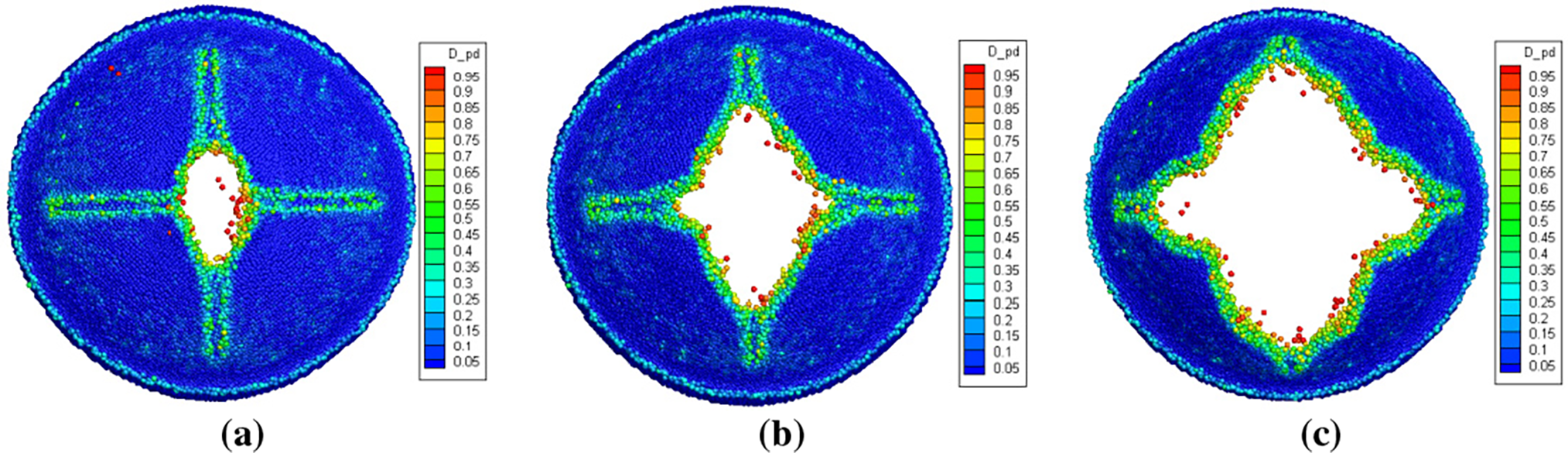
Figure 12: Damage contours of the soft PSD with Type II (“+”) defect form during opening process (back view). (a) 1.634 MPa; (b) 1.639 MPa; (c) 1.643 MPa

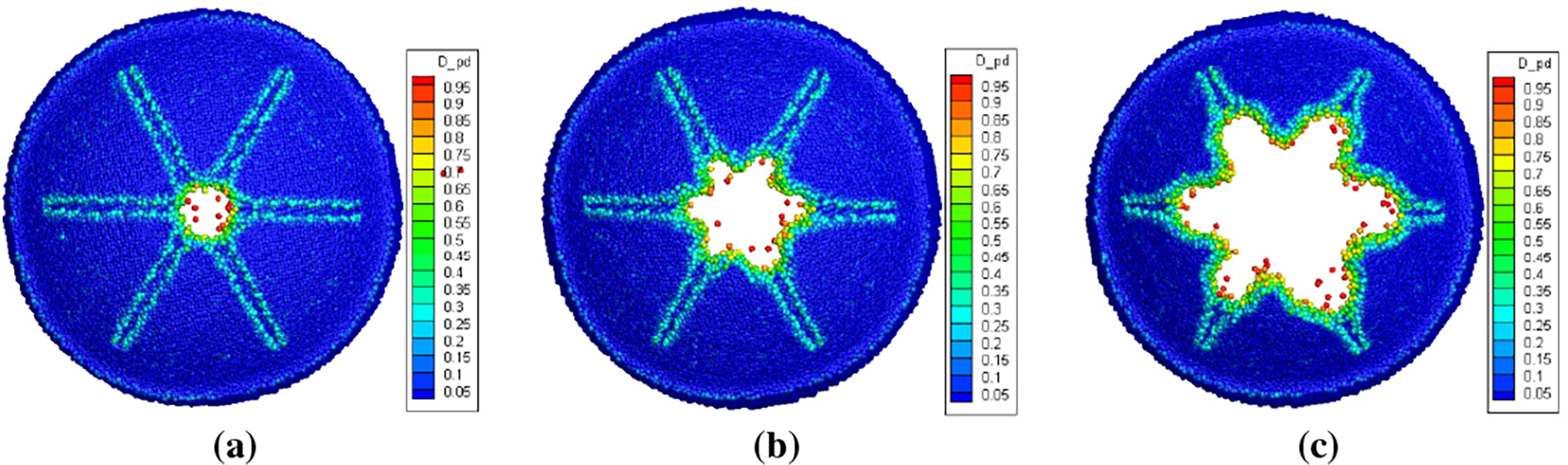
Figure 13: Damage contours of the soft PSD with Type III (“star”) defect form during opening process (back view). (a) 1.341 MPa; (b) 1.345 MPa; (c) 1.349 MPa

5.2 The Influence of Prefabricated Defect Depth on the Opening Performance of the Soft PSD

To further investigate the effect of prefabricated defect depth on the opening performance of the soft PSD, a parametric study was conducted using the method of controlled variables. Only the defect depth was varied, while all other conditions were held constant. Numerical models of the soft PSD were developed with defect depths of 1, 2, and 3 mm, respectively. The prefabricated defect form is the same as the Type I prefabricated defect. All models were subjected to identical boundary and loading conditions: the front-end face of the PSD was constrained, and the internal surface was loaded with a linearly increasing pressure up to 2 MPa. The damage contours of soft PSDs with different defect depths under impact loading are presented in Figs. 14–16.

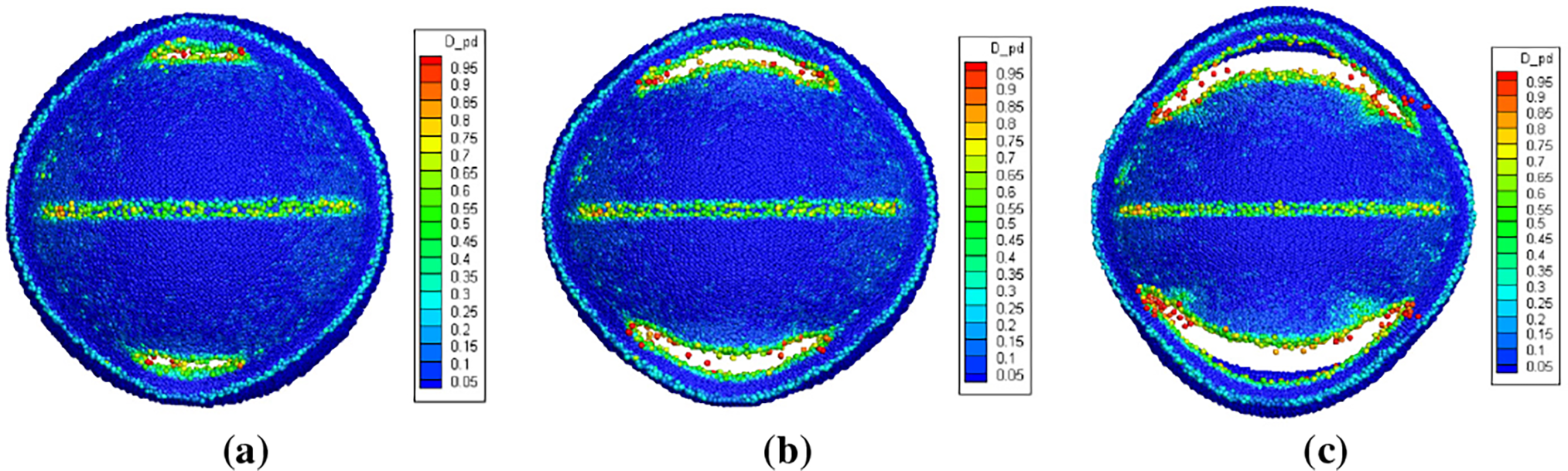
Figure 14: Damage contours of the soft PSD with defect depth of 1 mm during opening process (back view). (a) 1.682 MPa; (b) 1.687 MPa; (c) 1.691 MPa

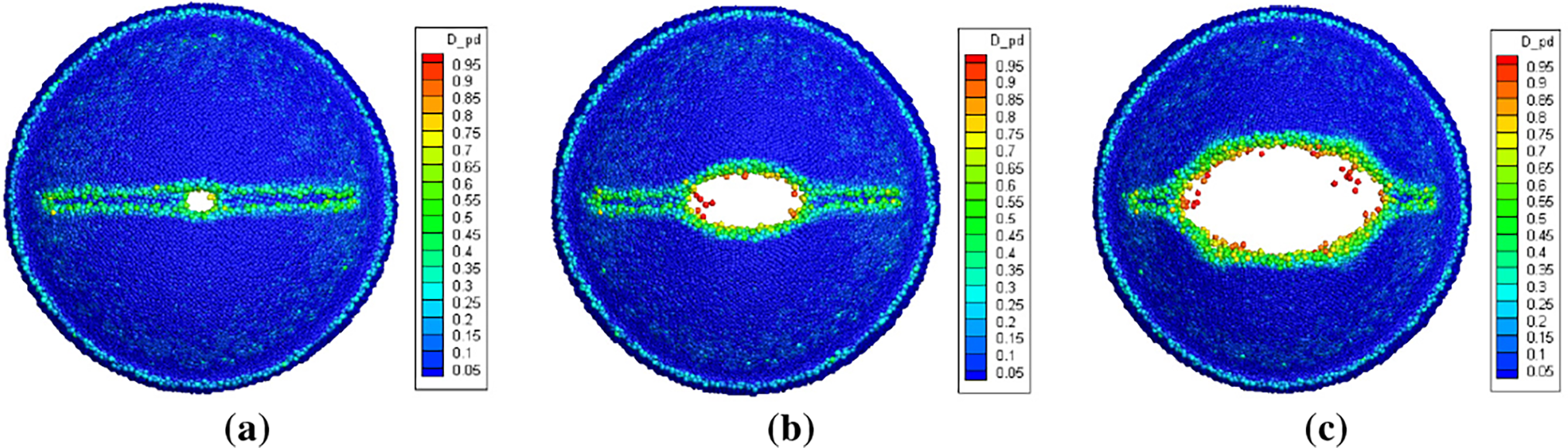
Figure 15: Damage contours of the soft PSD with defect depth of 2 mm during opening process (back view). (a) 1.652 MPa; (b) 1.656 MPa; (c) 1.661 MPa

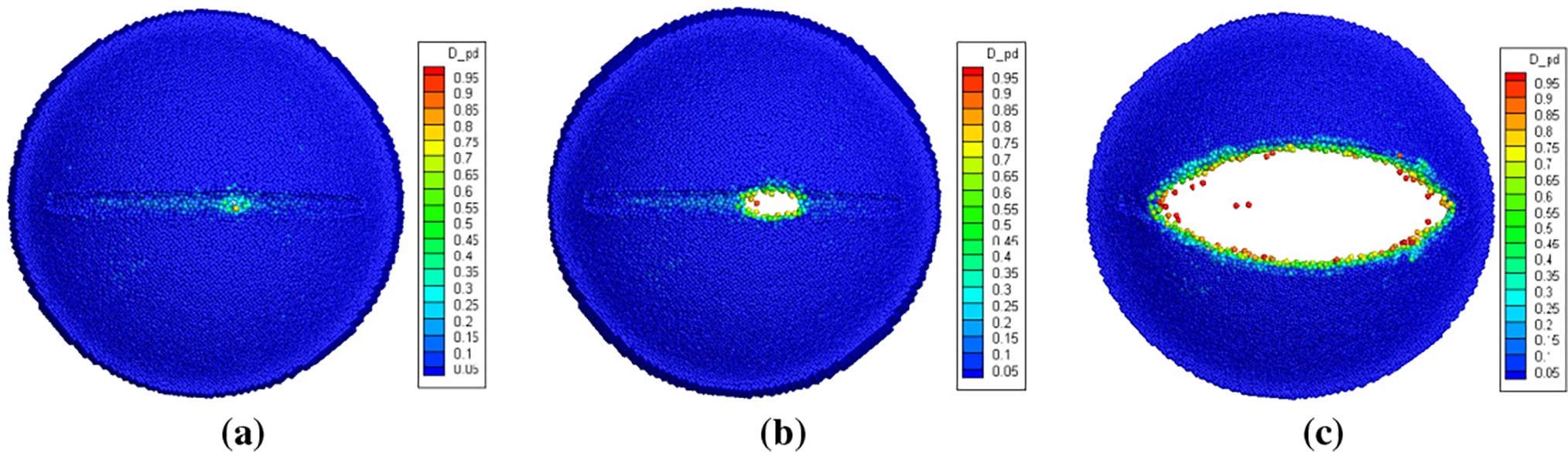
Figure 16: Damage contours of the soft PSD with defect depth of 3 mm during the opening process (back view). (a) 0.882 MPa; (b) 0.895 MPa; (c) 0.908 MPa

It can be observed from Figs. 14–16, under the same defect form and loading conditions, the failure modes of the soft PSD vary with different defect depths. When the defect depth is 1 mm, the initial failure occurs at the corners, and the opening pressure reaches 1.682 MPa. As the pressure increases, the damaged zone extends along the curved edge of the PSD, eventually forming a circumferential crack. This behavior may be attributed to the relatively weak stress concentration generated by shallow defects compared to the intensified stress field around geometric corners, which makes the corner regions more susceptible to failure. In contrast, with deeper defects (2 and 3 mm), crack initiation occurs at the central region of the notch. As the pressure increases, the damage propagates along the notch direction, forming a linear crack path. Additionally, the opening pressure decreases significantly with increasing defect depth, showing an inverse relationship between defect depth and opening resistance. This trend can be explained by the reduced load-bearing capacity of the PSD due to increased local weakening, which lowers its resistance to impact-induced fracture.

6  Conclusion

This study investigates the opening performance of the soft PSD in pulse solid rocket motors. A soft PSD structure with a star-shaped prefabricated defect was designed, and the constitutive model and failure model of the soft PSD based on peridynamics were established using the experimental data of the uniaxial tensile test of the soft PSD material. The opening process of the soft PSD was numerically simulated via the peridynamic method, yielding the strain field evolution, failure mode, and opening pressure. At the same time, the monomial opening test of the soft PSD was designed and conducted to verify the rationality of the design of the soft PSD structure and calculation method. Furthermore, the effects of defect geometry and defect depth on the opening performance were systematically explored. The main conclusions are as follows:

(1)   The peridynamic simulation successfully predicts the opening pressure and failure mode of the soft PSD, showing good agreement with experimental results. This demonstrates that peridynamics provides an effective numerical framework for modeling the opening process of PSDs in pulse engines.

(2)   The opening process of the soft PSD involves a sequence of deformation stages, including initial expansion, failure initiation in the weakened region, crack propagation, and eventual rupture.

(3)   The opening pressure and failure mode are significantly influenced by the depth of the prefabricated defect. As the defect depth increases, the opening pressure decreases due to reduced structural resistance.

(4)   The failure mode and opening pressure of the soft PSD vary with different defect forms. A greater number of surface notches enlarges the weakened area of the PSD, leading to lower opening pressure and altered crack propagation behavior.

Meanwhile, it is worth noting that the current model does not consider the effect of a high-temperature gas thermal environment. In the actual working process, the soft PSD is exposed to the high-temperature thermal environment of the combustion chamber. The temperature change of the soft PSD will affect its structural deformation, having a thermo-mechanical coupling effect between them, which may influence the actual opening state of the soft PSD. The relevant discussion and analyses will be further provided in the forthcoming research.

Acknowledgement: The authors would like to thank anonymous reviewers, associate editor, and editor-in-chief for their constructive comments on earlier versions of the manuscript.

Funding Statement: The study was supported by the National Natural Science Foundation of China (No. 12202011), the Youth Research fund of Shanghai Academy of Spaceflight Technology (KJW-KT-QNKYJJ-2022-25), and China Postdoctoral Science Foundation (Nos. 2024T170009, 2022M710190).

Author Contributions: Study conception and design: Wenxia Cheng, Qinliu Cao; data collection and experimental design: Bin Yuan, Qinliu Cao; analysis and interpretation of results: Wenxia Cheng, Qinliu Cao, Jiale Yan; draft manuscript preparation: Wenxia Cheng, Jiale Yan; review and editing: Jiale Yan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data and related programs are available from the first and corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Stadler L, Hoffmann S, Niedermaier H, Hacker A, Bénayon G, Trouillot P, et al. Testing and verification of the LFK NG dual pulse motor. In: 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit; 2006 Jul 9–12; Sacramento, CA, USA. doi:10.2514/6.2006-4765. [Google Scholar] [CrossRef]

2. Gao AT, Yang Y, Zhang P, Zhao F, Zu YR, Li Yinventors, et al. An integrated dual pulse solid motor soft interlayer. China patent CN201811635726.7; 2019 Mar 8. [Google Scholar]

3. Zhang XY, Li FX, Gan XS, Guo YQ, Gao WW, Li QPinventors, et al. An interlayer structure for reducing the strain of the interlayer of double pulse solid motor. China patent CN201910769809.3; 2019 Dec 20. [Google Scholar]

4. Liu HC, Fu TT, Wang CG, Hua LH, Yao D. Axial deformation of soft PSD in the speed punching test of double pulse solid rocket motor. J Solid Rocket Technol. 2012;35(5):608–12. (In Chinese). [Google Scholar]

5. Yang CQ, Wei ZJ, Zhang L, Wang NF. Numerical simulation of ignition delay for elastomeric barrier multi-pulse solid rocket motor. J Propuls Technol. 2014;35(4):514–22. (In Chinese). doi:10.13675/j.cnki.tjjs.2014.03.009. [Google Scholar] [CrossRef]

6. Li Y, Chen X, Cheng H, Zhao Z. Fluid-structure coupled simulation of ignition transient in a dual pulse motor using overset grid method. Acta Astronaut. 2021;183(4):211–26. doi:10.1016/j.actaastro.2021.03.008. [Google Scholar] [CrossRef]

7. Fan XG, Xu JS, Chen X, Du HY, Li YK, Zhang ZS. A visco-hyperelastic constitutive model for EPDM soft PSD of dual-pulse motors. Acta Aeronaut Astronaut Sin. 2018;39(11):222307. (In Chinese). doi:10.7527/S1000-6893.2018.22299. [Google Scholar] [CrossRef]

8. Fan XG, Xu JS, Chen X. A visco-hyperelastic constitutive model of EPDM soft PSD of dual-pulse SRM with rate-dependent energy limiter. J Solid Rocket Technol. 2019;42(3):308–13. (In Chinese). [Google Scholar]

9. Fan XG, Xu JS, Chen X, Wang SX, Hu SQ. Investigation on failure properties and constitutive modeling of EPDM used for pulse separation device. Mech Mater. 2019;137:103127. doi:10.1016/j.mechmat.2019.103127. [Google Scholar] [CrossRef]

10. Chong F, Chen X, Xu JS. Material characterization and numerical analysis of soft PSD in dual-pulse motors. J Ordnance Equip Eng. 2022;43(6):102–7,40. [Google Scholar]

11. Wang CH, Liu Y, Liu YB. Design and experimental studies on ceramic port cover for dual pulse motor. Acta Astronaut. 2011;68(11–12):1881–90. doi:10.1016/j.actaastro.2010.12.012. [Google Scholar] [CrossRef]

12. Fu P, Song XY, Sun LQ, Yao D. Investigation on the reverse opening process of the soft insulator of double pulse solid rocket motor. J Solid Rocket Technol. 2017;40(2):146–50,63. [Google Scholar]

13. Wang CG, Tian WP, Ren QB, Yang DM, Chen C. Numerical analysis and test on work process of pulse separation device in pulse motor. J Propuls Technol. 2012;33(5):790–4,830. doi:10.13675/j.cnki.tjjs.2012.05.020. [Google Scholar] [CrossRef]

14. Wang S, Wang YB, Chen Z, Cao XW, Liu Y. Fracture test of soft-clapboard in dual-pulse solid rocket motor. Aerosp Shanghai. 2017;34(1):116–20. doi:10.19328/j.cnki.1006-1630.2017.01.019. [Google Scholar] [CrossRef]

15. Silling SA. Reformulation of elasticity theory for discontinuities and long-range forces. J Mech Phys Solids. 2000;48(1):175–209. doi:10.1016/S0022-5096(99)00029-0. [Google Scholar] [CrossRef]

16. Oh M, Koo B, Kim JH, Cho S. Shape design optimization of dynamic crack propagation using peridynamics. Eng Fract Mech. 2021;252(2):107837. doi:10.1016/j.engfracmech.2021.107837. [Google Scholar] [CrossRef]

17. Zhang X, Ding J, Zhang Y. A rate-dependent peridynamic model of reinforced concrete subjected to explosive loading. Eng Fract Mech. 2023;292:109666. doi:10.1016/j.engfracmech.2023.109666. [Google Scholar] [CrossRef]

18. Kan X, Wang J, Yan J, Wang C, Wang Y. Numerical analysis of ice-breaking effects induced by two interacting bubbles using the coupled boundary element method and peridynamics model. Phys Fluids. 2024;36(9):097110. doi:10.1063/5.0218632. [Google Scholar] [CrossRef]

19. Li S, Lai X, Liu L. Peridynamic modeling of brittle fracture in mindlin-reissner shell theory. Comput Model Eng Sci. 2022;131(2):715–46. doi:10.32604/cmes.2022.018544. [Google Scholar] [CrossRef]

20. Yan J, Li S, Kan X, Lv P, Zhang AM, Duan H. Updated Lagrangian particle hydrodynamics (ULPH) modeling for free-surface fluid flows. Comput Mech. 2024;73(2):297–316. doi:10.1007/s00466-023-02368-x. [Google Scholar] [CrossRef]

21. Bobaru F, Zhang G. Why do cracks branch? A peridynamic investigation of dynamic brittle fracture. Int J Fract. 2015;196(1):59–98. doi:10.1007/s10704-015-0056-8. [Google Scholar] [CrossRef]

22. Tupek MR, Rimoli JJ, Radovitzky R. An approach for incorporating classical continuum damage models in state-based peridynamics. Comput Meth Appl Mech Eng. 2013;263(6):20–6. doi:10.1016/j.cma.2013.04.012. [Google Scholar] [CrossRef]

23. Fan H, Bergel GL, Li S. A hybrid peridynamics—SPH simulation of soil fragmentation by blast loads of buried explosive. Int J Impact Eng. 2016;87(11):14–27. doi:10.1016/j.ijimpeng.2015.08.006. [Google Scholar] [CrossRef]

24. Bang DJ, Madenci E. Peridynamic modeling of hyperelastic membrane deformation. J Eng Mater Technol. 2017;139(3):031007. doi:10.1115/1.4035875. [Google Scholar] [CrossRef]

25. Silling SA, Bobaru F. Peridynamic modeling of membranes and fibers. Int J Non Linear Mech. 2005;40(2–3):395–409. doi:10.1016/j.ijnonlinmec.2004.08.004. [Google Scholar] [CrossRef]

26. Chen Y, Yang Y, Liu Y. A neural network peridynamic method for modeling rubber-like materials. Int J Mech Sci. 2024;273(4):109234. doi:10.1016/j.ijmecsci.2024.109234. [Google Scholar] [CrossRef]

27. Li P, Hao ZM, Zhen WQ. A zero-energy mode control method of non-ordinary state-based peridynamics. Chin J Theor Appl Mech. 2018;50(2):329–38. doi:10.6052/0459-1879-17-386. [Google Scholar] [CrossRef]

28. Ayatollahi MR, Heydari-Meybodi M, Dehghany M, Berto F. A new criterion for rupture assessment of rubber-like materials under mode-I crack loading: the effective stretch criterion. Adv Eng Mater. 2016;18(8):1364–70. doi:10.1002/adem.201600046. [Google Scholar] [CrossRef]