Fatigue Resistance in Engineering Components: A Comprehensive Review on the Role of Geometry and Its Optimization

1  Introduction

A critical concern in engineering design is the persistent issue of fatigue failure in structural components. This phenomenon frequently occurs in dynamic systems where parts endure fluctuating or rotating loads. Historically, research has primarily focused on material properties and stress-life analysis, often neglecting the subtle yet substantial influence of geometry on fatigue behavior. However, it has become increasingly clear that geometry can no longer be considered a secondary factor. Rather, it must be recognized as a key parameter capable of either intensifying or alleviating fatigue failure mechanisms. A systematic classification of existing works reveals that geometric aspects, from the smallest microstructural inclusions to large-scale design transitions, powerfully affect fatigue resistance by altering local stress concentration and crack growth pathways. Even though these geometric triggers were thought to be detrimental by default, contemporary studies demonstrate that geometry can be strategically optimized to enhance component service life.

The subsequent sections in this review synthesize findings from extensive investigations, with a particular focus on the geometric dimensions of fatigue. This includes an assessment of specific features such as graphite nodules, defects, and layering in additive manufacturing (AM). Special attention is dedicated to design frameworks like topology and shape optimization, as well as to advanced techniques in reliability-based and machine learning-driven methods.

Microstructural geometry (nodules, inclusions) concentrates stress, impacting fatigue failure [1]. Nodule morphology affects crack deflection [2]. Topology optimization redistributes stress, extending fatigue life [3]. Nodule size/spacing influence crack onset [4]. Graphite geometry shifts fatigue responses [5]. Thermal distortion near discontinuities exacerbates crack formation [6]. Principal stress reorients cracks under non-proportional loading [7]. Nodule geometry “pulls” cracks [8]. Geometric characteristics are central to inspection/design [9]. Topology optimization emphasizes geometric control [10]. Geometric complexity links to early crack detection [11]. Reshaping components reduces stress singularities [12]. Geometry reflects microstructural inhomogeneities [13]. Surface geometry correlates with fatigue scatter [14]. Geometry-based methods shape stress concentrations [15]. Matrix-phase geometry (austempering) affects fatigue resistance [16]. Geometry and mechanical features influence fatigue limit [17]. Simulations remain sensitive to geometry [18]. Crack paths follow geometric stress maxima [19]. Geometry is integral to fatigue-based topology optimization [20].

Surface geometry (notches, roughness) amplifies stress, initiating fatigue cracks [21]. Angular nodules initiate cracks [22]. Topology optimization lowers mass, raises fatigue life [23]. Geometric misalignments affect fatigue [24]. Print-induced surfaces have severe geometric discontinuities, accelerating crack initiation [25]. Local geometry outweighs material properties in strain energy concentration [26]. Interlayer voids create crack sites [27]. Geometry alignment enhances fatigue life [28,29]. Geometry control minimizes stress risers [30]. Smoother geometry improves fatigue life [31]. Raster angle refines internal geometry, maximizing fatigue life [32]. Polygonal meshes adapt geometry to fatigue constraints [33]. Geometry evolves with damage [34]. Fatigue crack propagation incorporated into design [35]. Internal bonding geometry overshadows reinforcement [36]. Geometry and probabilistic elements reduce fatigue risk [37,38]. Minor geometric changes reduce fatigue hotspots [39]. Internal voids/raster control early crack emergence [40].

Additive manufacturing (AM) (geometric freedom) can introduce geometry-driven weaknesses [41]. Circular pores outperform triangular [41]. Topology optimization refines implant geometry [42]. ±45° grids improve fatigue [43]. High infill density, flatter orientations extend fatigue life [44]. Nodule clustering parallels voids/pores, accelerating fatigue crack nucleation [45]. Geometry-based features predict crack onset [46]. Fillet, transition, and bored hole geometry define fatigue vulnerability [47]. Raster orientations, heat treatment improve fatigue [48]. Cracks follow geometry-driven boundaries [49] and poor interlayer adhesion [50]. Asymmetric loading complicates geometry-based fatigue [51]. Blade twist geometry alters fatigue life [52]. Heat treatments reshape boundaries, affecting life [53,54]. Crack propagation follows internal geometry [55]. Nodule clustering reduces fatigue life [56]. Vermicular graphite accelerates crack growth [57]. Printing orientation, internal void geometry, shape bending fatigue strength [58]. Penalized fatigue topology optimization realigns material [59]. Support-induced geometric transitions are early crack initiation sites [60].

Topology optimization (TO) transforms geometry for weight reduction, load path alteration, and enhanced fatigue durability [61]. Shape refinement increases fatigue life [61]. Spatial geometry dominates mean stress [62]. TO smooth stress flows [63]. Reliability-based topology is crucial for geometric design with probabilistic fail-safety [64]. Infill geometry relates to early failures [65]. Geometric features aligned with principal stress extend fatigue life [66]. Raster orientation, infill ratios affect fatigue crack behavior, notch effects [67,68]. Local strain energy density ties notch root radius to crack onset [69]. Layering transitions are the primary crack path [70]. Local geometry modifies crack growth rates [71,72]. Geometry-induced instability under out-of-phase loads [73]. Probabilistic methods account for geometric variability [74]. Defect shape is critical for fatigue vulnerability [75]. Iterative TO reduces fatigue damage [76]. Large transitions initiate crack formation [77]. Geometric alignment steers fatigue life [78]. Higher nodule count leads to quicker crack coalescence [79]. Nodule geometry dictates fatigue response [80].

Geometry, manufacturing imperfections, and load variabilities necessitate reliability-based/probabilistic models for fatigue failure [81]. Integrating fatigue, manufacturing uncertainty in topology optimization ensures geometric robustness [81]. Nodule shape/randomness governs fracture toughness, cyclic strength [82]. Embedding reliability targets shapes designs against stress extremes, geometric variations [83]. Incorporating time-dependent degradation adapts the geometry at risk [84]. Defect distribution-focused design is more precise for AM fatigue [85]. Probabilistic capture of local shape complexities needed for crack initiation [86]. Bolt hole geometry is a fatigue hotspot instigator under reliability-based design [87]. Combining notch geometry, improper layer orientation lowers fatigue thresholds [88]. Geometry-based discontinuities control failure onset [89]. Targeting geometry, avoiding stress peaks [90]. Controlling maximum stress amplitude fosters smoother geometries [91]. Geometry, orientation drive crack formation more than defect size [92]. Nodular misalignments probabilistically guide crack trajectories [93]. Surface patterning, layer fusion key to fatigue endurance [94]. Random vibration, local geometry transitions dictate fatigue damage [95]. Micromechanical void models relevant for cyclic crack initiation [96]. Refining geometry optimizes suspension brackets [97]. Local defect shape stronger effect than average area [98]. Integrating directional geometry alignment manages crack growth [99]. Surface discontinuities are potent even with finishing [100].

Geometric adaptation is crucial for biomedical/automotive design. Tuning geometric transitions is critical [101]. Continuous-time modeling in topology optimization for lightweight designs with strict fatigue requirements [101]. Under-optimized fillet geometry leads to crankshaft cracks [102]. Streamlined geometry benefits damped structures [103]. Machine learning identifies microstructural geometry as a critical fatigue feature [104]. Subtle phase geometry alters fatigue response [105]. Geometric design influences resonance modes [106]. Geometry’s influence is magnified under mixed loading [107,108]. Local boundary shapes affect fatigue resistance [109]. Geometric waviness lowers fatigue limits [110]. Geometry shapes crack initiation under torsion [111]. Refining load arm geometry extends life [112]. Fatigue strength depends on infill geometry, layer transition smoothness [113]. Raster layout shapes anisotropy, voids [114]. Geometry of interfacial boundaries pivotal [115]. Geometry-driven hotspots correlate with cracks [116]. Geometric forms alleviate fatigue accumulation [117]. Casting skin alters fatigue life [118]. Geometric scaling, inclusion probability reduce long-life fatigue [119]. Layering directs crack growth [120].

Micromechanical simulations, AI, and multiscale modeling emphasize geometry’s role in fatigue design [121–123]. Algorithms show geometry’s role in dampening stress [124]. Statistical methods show the importance of spatial irregularities [125]. Strain energy density approaches incorporate notch tip geometry [126]. Non-local fatigue life models link micro-defect geometry with macro loading [127,128]. Geometry-based stress fields steer crack plane orientation [129]. Wall thickness, mold geometry influence fatigue [130]. Computational optimization refines fatigue-constrained topology evolution [131,132]. Reliability-based design extends to microscale geometry [133]. Augmented Lagrangian approaches control notch/corner shapes [134]. Geometry smoothing postpones fatigue cracks [135]. Multiaxial fatigue criteria reflect principal stress, geometric plane alignment [136]. Neglected geometry (pores, roughness) reduces fatigue life in AM metals [137]. Precise blade shaping counters cyclic stress [138]. Internal pore shapes link to early failure [139]. Unfavorably oriented defects act as cracks [140].

Geometric factors in origami fatigue life analyzed by AI (ANN) [141]. Predicting notch fatigue life merges physics-based models with Machine Learning (ML) (geometric parameters) [142]. Geometric assessment with AE via AI (CNN) estimates crack length [143]. ANN with damage parameters predicts fretting fatigue crack initiation life [144]. AI predicts fatigue resistance in AM metals using geometric defects [145,146]. Some AI focuses on hardness, defect size [147], others on surface roughness (geometric factor) [148]. PINN integrates physical fatigue models, capturing geometry-related stress [149]. Geometric features enhance fatigue life prediction using physics-guided ML [150]. ML frameworks could benefit from geometric factors [151]. μCT defect characterization with ML improves fatigue life prediction using geometric features [152].

Overview of the Study

In sum, the collective body of research strongly indicates that geometry—across multiple scales—fundamentally dictates where and how fatigue failures arise. Rather than treating geometry as a static boundary condition, modern design strategies recognize it as a powerful, designable factor. This recognition has prompted widespread investigation into geometry-based optimization frameworks, advanced simulation, and integrated reliability approaches.

Section 2 outlines direct geometric influences on fatigue resistance, capturing micro-level flaws, surface notches, and layered anisotropy.

Section 3 discusses geometry-oriented optimization methods—topology, shape, and microstructure—that systematically reduce fatigue vulnerabilities.

Section 4 highlights cross-domain aspects, including industrial implementations and references back to additive manufacturing.

Section 5 identifies persisting research gaps and draws conclusions on how geometric insights pave the way for next-generation, fatigue-resistant designs.

For each category, Table 1 outlines the principal impact of the specific geometry type on fatigue resistance, identifies the key underlying mechanisms (such as localized stress concentration and optimized load distribution), and cites representative references from the literature. Together, these classifications provide a detailed overview of how geometry is intrinsically linked to fatigue behavior and offer a valuable resource for researchers aiming to design more durable materials and structures.

To point out critical criteria:

•   Fatigue failure, common in dynamic systems under cyclic loading, has been historically studied, focusing on material properties and stress-life methods, often neglecting geometric influence.

•   Geometry exerts a profound influence over fatigue resistance, from microstructural inclusions to macro-scale notches and shape transitions, by altering stress concentration and crack paths.

•   Geometry should no longer be treated as a secondary factor but as a highly influential and designable variable for fatigue life enhancement.

•   Recent advances integrate topology optimization, additive manufacturing, and AI-driven methods to optimize geometry for fatigue resistance.

•   The shift from viewing geometry as a weakness to a proactive design variable marks a key evolution in fatigue engineering.

•   There remains a need for unified frameworks that link geometry effects across scales and incorporate manufacturing realities and AI-based predictive methods.

2  Micro to Macro Geometry

Fatigue resistance in engineering components arises from more than just material composition and strength: geometry—in its many guises—shapes the local stresses that ultimately foster or forestall crack initiation. Whether the focus is on micro-level features (e.g., inclusions, graphite nodules, or interphase boundaries) or meso- and macro-scale design elements (e.g., fillets, notches, infill raster patterns in additive manufacturing, or topological transitions), extensive research confirms that how and where cracks form is heavily influenced by geometric considerations. This section explores these geometric impacts in detail, providing examples from cast irons, polymers, and additive-manufactured parts.

2.1 Microstructural Geometry

The geometry of graphite nodules plays a foundational role in fatigue crack development within spheroidal graphite cast iron. Rather than behaving as inert inclusions, these nodules act as stress amplifiers whose shape and spatial configuration define micro-crack paths.

Micromechanical evaluation under cyclic loading conditions has revealed that cracks rarely propagate uniformly; instead, they navigate through regions of angular graphite morphology, emphasizing the role of nodule shape in directing fatigue paths [2]. This behavior is vividly illustrated in Fig. 1, where SEM imagery captures the step-wise advancement of cracks through deformed graphite regions.

Figure 1: SEM micrograph showing fatigue crack path traversing through deformed and angular graphite nodules. The image highlights the influence of non-spherical graphite on local stress intensification and deflection of fatigue cracks [2]

Because graphite nodules can be large relative to microscopic plastic zones, the authors suggest classical LEFM parameters ΔK and R alone are insufficient descriptors:

“For lower ΔK and R values, the material cannot be considered homogeneous; moreover, overload tests reveal the presence of a ‘damaged zone’ rather than a simple ‘plastic zone’ at the crack tip”.

Therefore, fatigue crack growth rate (dNda) must be described by a multiscale function:

(dNda)=F(Kmax,R,dn,fn,microstructure)

where fn is volume fraction of nodules, clearly relating microstructural geometry dn and distribution to fatigue response, incorporating experimental inputs such as:

•   Matrix-nodules interface debonding prevalence,

•   Internal cracking,

•   Compressive reversed plastic zone activation,

•   Overload-induced secondary cracks.

Instead of simply following the path of maximum principal stress, cracks in ductile cast iron often get steered by internal features, acting almost like “crack guides.” Research has shown that graphite nodules can attract cracks, encouraging them to grow along their clusters [8] (as illustrated in Fig. 2).

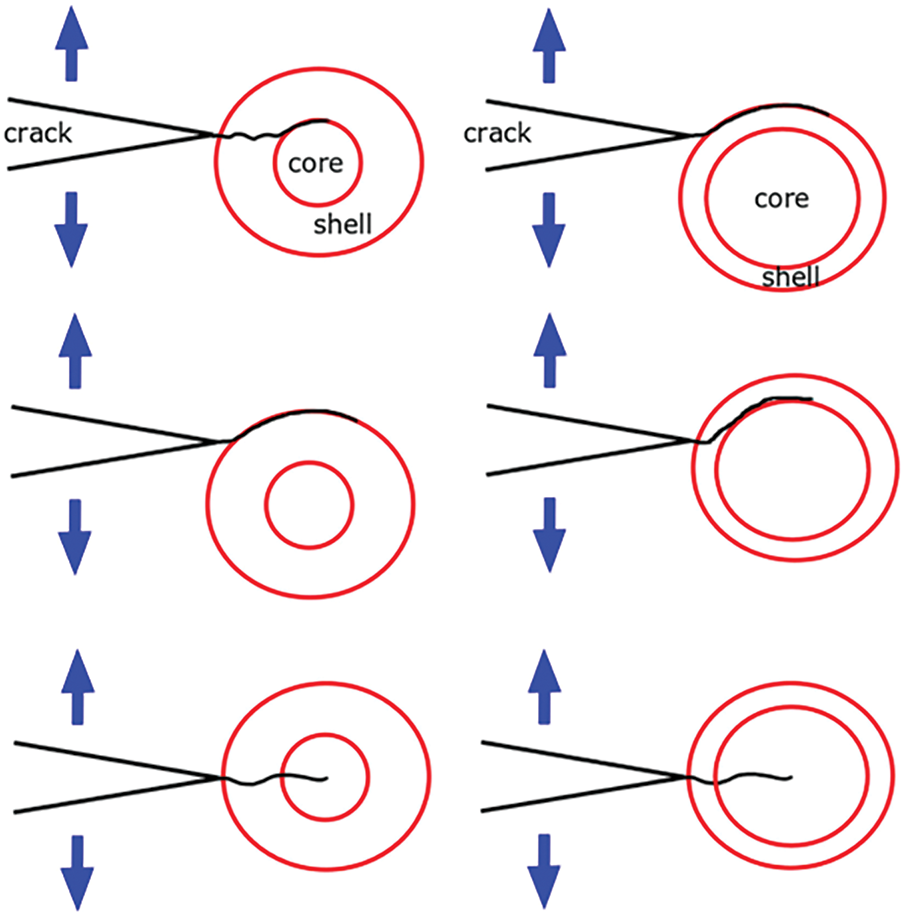
Figure 2: Fatigue crack profiles revealing step-wise propagation through nodule-dense zones. The crack trajectory is observed to align with the spatial layout of graphite nodules, rather than following a uniform direction [8]

The shape and size of these graphite nodules are key players in determining how well a ductile cast iron resists fatigue. Larger and more irregular nodules tend to concentrate stress in their vicinity, making these areas more likely to be where cracks start under repeated loading. The thickness of the shell surrounding the nodule is also important. Thicker shells can help spread the stress out more evenly, delaying the breakdown or separation processes that speed up crack growth. On the flip side, thinner shells are more susceptible to failure, creating tiny voids that act as easy pathways for cracks to spread.

Furthermore, how the nodules are distributed and whether they clump together affects fatigue life. Regions with large clusters or unevenly sized nodules create localized stress “hotspots” that weaken the material’s overall durability. Even variations within the nodules themselves, such as differences in the mechanical properties of their core vs. their shell, can influence how damage occurs. These differences can lead to phenomena like onion-like layering, debonding, or disaggregation, which make it easier for cracks to grow when the microstructure contains large or poorly formed nodules.

The three-dimensional shape and arrangement of the nodules also play a role in the path a crack takes, often causing it to deviate. This increases the roughness of the fracture surface, which in turn affects how the crack closes during cyclic loading.

Overall, the microscopic geometry of graphite nodules is a crucial factor in how ductile cast iron behaves under fatigue. Generally, larger, irregular, or thin-shelled nodules tend to reduce fatigue life, while a more uniform distribution of smaller nodules enhances resistance by minimizing localized stress concentrations.

When nodules are packed closely together, it becomes more likely that tiny cracks will merge early on. This concentration of crack paths was particularly noticeable in fatigue studies of thick-section cast iron, where fractures often started in areas with the smallest distances between nodules [4]. Fig. 3 clearly demonstrates the link between reduced spacing between nodules and premature failure.

Figure 3: Fractographic analysis marking fracture origins in regions of clustered graphite nodules [4]

The impact of microstructural geometry on fatigue behavior is fundamentally tied to how stress concentrates within the material. Features like the size, shape, and distribution of graphite nodules act as localized stress concentrators within the metal matrix. Larger or irregularly shaped nodules, especially when they are clustered closely, can be the starting points for micro-cracks because the stress is amplified at their edges. This localized stress increase speeds up crack initiation and propagation under cyclic loading, thus weakening the material’s resistance to fatigue. In contrast, a more uniform microstructure with smaller, well-dispersed inclusions helps to distribute the applied stresses more evenly, minimizing stress concentrations and improving fatigue resistance. Understanding this relationship between geometric features and stress distribution is essential for predicting how long a material will last under fatigue conditions and for designing microstructures that offer improved durability.

2.2 Surface Geometry: Notches, Fillets, and Fatigue Initiation

Geometric transitions at the surface level—particularly notches, fillets, and ridges—serve as high-risk fatigue crack initiation zones. These features distort stress fields and introduce localized plasticity under cyclic loading. Real-world fatigue failures in railway brake discs have been linked to thermal-mechanical deformation that sharpens geometric features over time. Fig. 4 showcases how fatigue performance varies with raster angle, clearly indicating that a 30° orientation offers the best compromise between load path continuity and geometric stability [32].

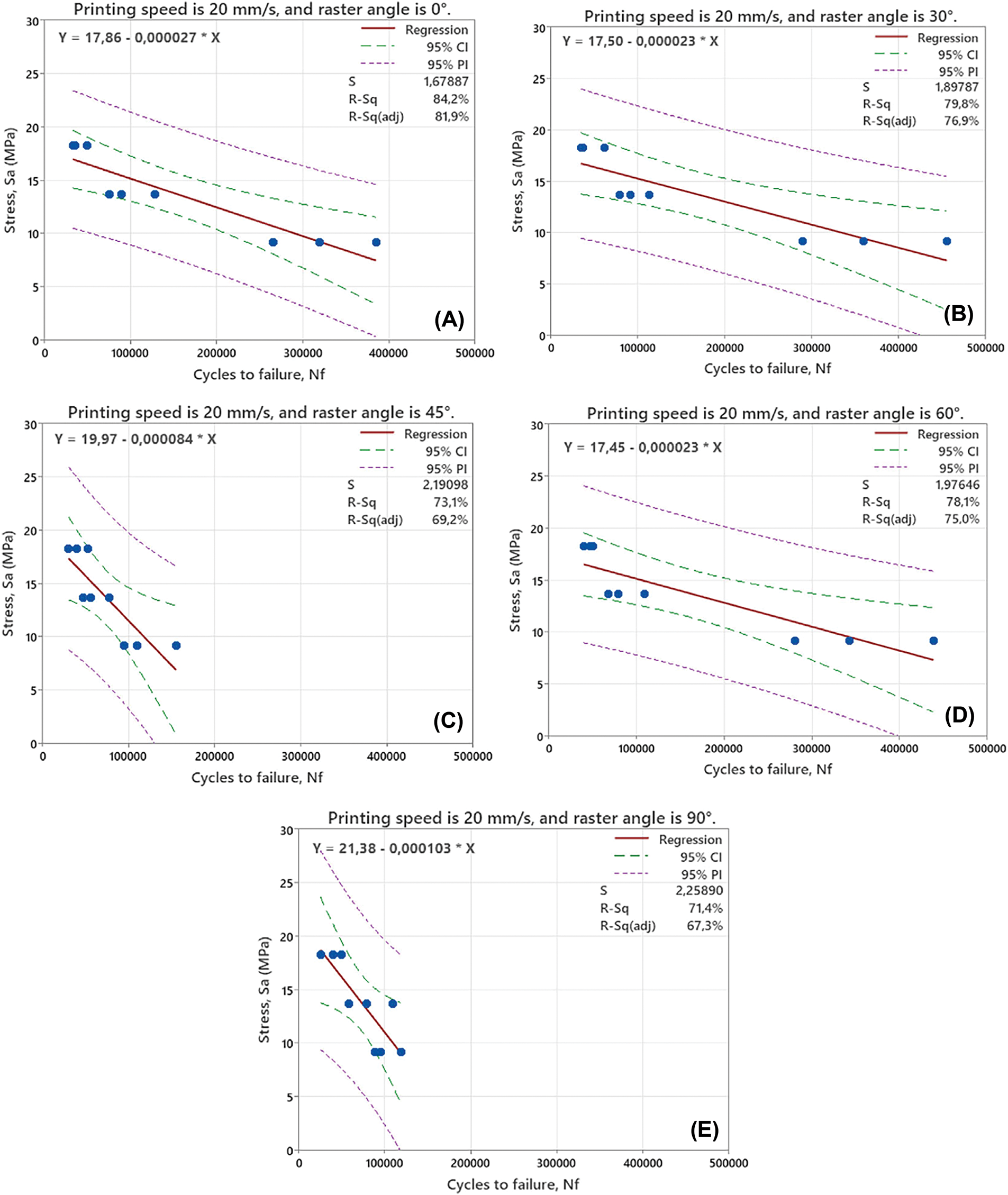
Figure 4: S-N curves for different raster angles, (A) 0°, (B) 30°, (C) 45°, (D) 60°, (E) 90° in 3D-printed PLA. The figure demonstrates how raster-induced surface geometry modifies fatigue endurance, with a 30° raster performing best [32]

The fatigue life of a material under cyclic loading depends strongly on the local stress state within the material. In FDM 3D prints, the anisotropic filament deposition creates directional mechanical properties that vary with raster angle θ, the angle between the loading direction and the filament orientation.

If the applied bending stress amplitude is σa, the effective stress experienced along the filament direction can be approximated using the transformation of stresses:

σθ=σacos⁡2θ+τasin⁡θcos⁡θ

where τa is the shear stress component induced by bending, which also depends on θ. This means that different raster angles lead to different effective normal and shear stresses along filaments.

Fatigue life Nf is commonly expressed by Basquin’s law for high-cycle fatigue:

σa=σf′(2Nf)b

where σf′ is the fatigue strength coefficient, and b is the fatigue strength exponent. These parameters depend on the microstructural features, including filament orientation.

The article reports that the slope of the Stress–Number of Cycles (S-N) curves (related to b) decreases with increasing printing speed, reflecting more rapid fatigue degradation at higher speeds. Similarly, raster angle was shown to affect fatigue strength by altering internal stress distribution and defect orientation, which modulates σf′(θ) and b(θ).

Given that raster angle θ affects the effective stresses σθ, the corresponding fatigue parameters can be expressed as functions of θ, i.e., σf′(θ) and b(θ), reflecting how geometry impacts the material fatigue response.

The boundaries between printed filaments and layers can be treated as interfaces with distinct mechanical properties and imperfect bonding. The fracture mechanics parameter, e.g., stress intensity factor K, may be influenced by the raster geometry:

KI=Yσθπa

where a is the crack size initiated at weak interfacial sites, and Y is a geometric factor depending on crack orientation and shape.

Higher raster angles (e.g., 90°) tend to have weaker interlayers bonding perpendicular to the loading direction, increasing the stress intensity factor and promoting earlier crack growth, thus reducing fatigue life.

Printing speed affects the degree of filament bonding and microvoid formation, changing the effective cross-sectional area Aeff and the local stress concentration factor Kt:

σlocal=KtFAeff

Higher printing speeds generally reduce molecular diffusion at interfaces, increasing porosity and defects, thereby raising Kt and accelerating fatigue damage accumulation.

Microscopic surface imperfections, even when barely visible, act as fatigue initiators when located at critical curvature zones. In Fig. 5, it shows casting defect and its relation with fatigue strength via defect size [110] (Fig. 5). Based on the formulation-focused evaluation of the manuscript’s content, the study primarily employs the √area parameter model as the foundational quantitative tool for fatigue strength assessment of ductile cast iron (DI) with casting surfaces. This model quantifies the influence of defects and surface roughness through an “effective defect size” parameter (√areaeff), integrating geometrical defect size and surface irregularities into a unified metric impacting fatigue limits.

Figure 5: Casting defects and its size to evaluate fatigue strength [110]

The fatigue limit (σw) is linked to the defect size by correlating the stress intensity factor threshold (ΔKth) with √area. Empirical relationships derived from fracture mechanics principles govern these correlations, for example:

ΔKth=C × (area)α

where C and α are material-dependent constants calibrated from fatigue tests incorporating various defect sizes and microstructural conditions. This relation captures the critical crack size below which cracks remain non-propagating up to 107 cycles, establishing the fatigue endurance limit concerning casting surface defects [T1].

Moreover, the study refines the assessment by defining an equivalent hardness value that accounts for transitional microstructure layers near casting surfaces, influencing local mechanical properties central to fatigue resistance. This hardness is combined with the effective defect size in fatigue life predictions, effectively representing microstructure-property interactions without directly modeling microstructural mechanics:

σw′=f(HVequiv,areaeff)

where σw′ is the adjusted fatigue limit based on equivalent hardness (HVequiv) and effective defect size. This empirical formulation allows practical fatigue strength estimation considering geometrical (defect and roughness) and microstructural factors.

Statistically, the manuscript utilizes extreme value distribution approaches to estimate the maximum defect size (√areaD,max) within specimens, which is then used to predict the lower bound of fatigue strength scatter, thus incorporating variability in defect population into the fatigue limit formulation.

In summary, the manuscript’s formulation-centric methodology couples fracture mechanics-based defect size parameters with equivalent hardness representations and statistical modeling to quantitatively predict fatigue limits in ductile cast iron. Although the fundamental mechanics underlying the influence of geometry on fatigue are implicitly incorporated via the √area parameter model, an explicit mechanistic formulation linking microstructural-scale geometries to fatigue crack initiation and propagation could further enhance the theoretical rigor of the study.

2.3 Raster Orientation and Infill Geometry in Additive Manufacturing

In fused deposition modeling (FDM), the internal structure is more than an artifact of manufacturing—it is a deliberate geometric configuration that governs mechanical behavior under fatigue. Raster angles, layer orientation, and infill architecture define the paths along which stress is transmitted and redistributed.

The influence of raster angle on stress flow is further supported by fatigue testing with different infill orientations. Data from Stress–Number of Cycles (S-N) curve analyses confirm that optimized raster configurations (such as 0°/30°/45°) substantially improve fatigue life by reducing geometric discontinuities in load-bearing zones [29] (see Fig. 6).

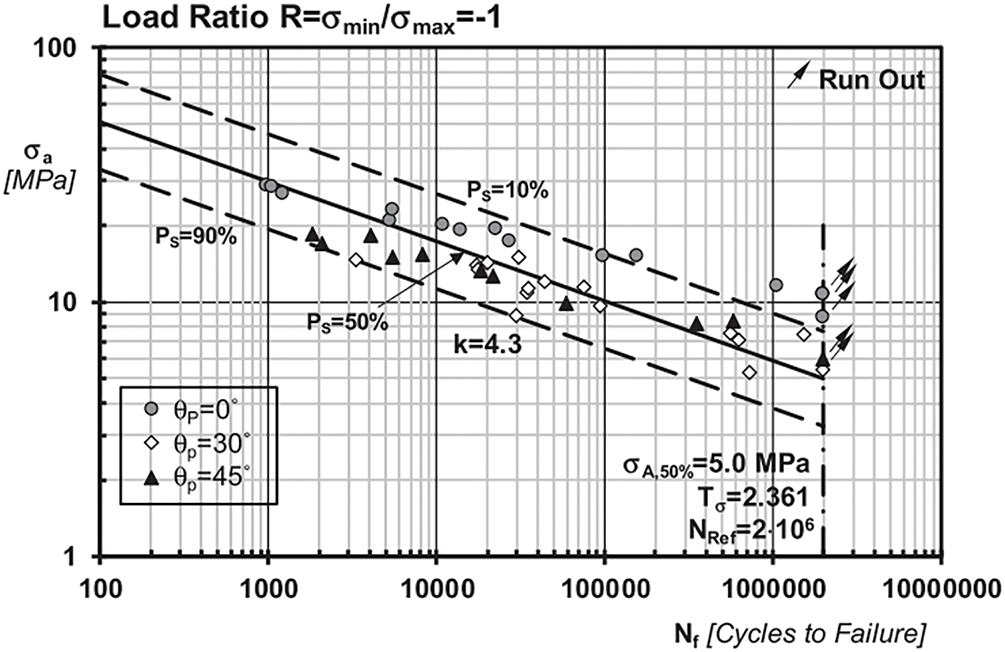
Figure 6: S-N curves for PLA specimens printed at different raster angles [29]

Build orientation affects the fatigue behavior, with upright orientations exhibiting reduced resistance compared to flat and on-edge configurations.

Post-processing can further enhance interlayer adhesion and geometry-induced stress mitigation. Thermal treatment following a 0°/45°/−45° raster build has been shown to reduce crack propagation, as demonstrated by fracture pattern visualizations in Fig. 7 [48].

Figure 7: Crack path visualizations across different raster configurations [48]

The study presents empirical and statistical formulations that relate the geometric parameter, namely the raster direction angle (RDA), to hardness, fatigue life, and crack propagation in 3D-printed PLA parts. While it does not propose a fundamental mechanical theory, it provides several mathematical models based on experimental data, as follows:

Hardness (HSD) is modeled as a quadratic function of RDA and heat treatment temperature (HT), expressed by the surface regression equation:

HSD=29.68+0.92⋅RDA+2.37×10−2⋅HT−7.12×10−3⋅RDA2+6.4×10−5⋅HT2+2.72×10−4⋅(RDA×HT)

This model achieves an R-squared of 0.97, indicating a strong fit.

The fatigue life NFL (number of cycles to failure) is linearly related to RDA:

NFL=11236.43+101.28⋅RDA

Despite the stochastic nature of fatigue, this model explains approximately 60% of the fatigue life variation, as indicated by an R-squared of ~0.608.

The crack length aRDA,N as a function of RDA and fatigue cycles N is modeled by a nonlinear ratio of polynomials:

aRDA,N=P1(RDA,N)P2(RDA,N)

Although exact forms of P1 and P2 polynomials are not provided here, this model represents crack growth dynamics under cyclic loading at constant stress amplitude.

Alternatively, a quadratic polynomial model describing crack length as a function of RDA and N is given by:

aRDA,N=0.68⋅RDA−3.6×10−4⋅N+8.5×10−5⋅RDA2+9.4×10−8⋅N2+2.0×10−6⋅(RDA×N)

The crack growth rate dN/da shows a change in slope at crack lengths about 0.30 mm, indicating different fatigue mechanisms for RDAs greater than 40°. This behavior is in accordance with fracture mechanisms such as intra-layer and inter-layer cracking influenced by the printing pattern and presence of porosity/microvoids.

Directional mismatch between notches and raster lines has been confirmed as a critical factor in early fatigue failure. When notch tips intersect print paths at unfavorable angles, cracks initiate prematurely at stress-amplified transition zones [88]. The fatigue resistance of 3D-printed PLA is significantly influenced by the geometry of the component, particularly the presence and sharpness of notches. The study shows that:

•   Notches decrease fatigue strength, with sharper notches (higher notch sharpness) leading to greater reductions in fatigue resistance.

•   The size and shape of the notch, along with its sharpness, are critical in determining the local stress concentration, which governs crack initiation and propagation.

•   Broader or blunt notches tend to have a less severe effect on fatigue life compared to sharp notches.

•   The fatigue cracking behavior is governed mainly by the local stress amplification around the notch tip, which follows the material’s response to maximum stress cycles.

The application of the Theory of Critical Distances (TCD) allows for the reliable prediction of fatigue life, considering these geometric effects, enabling more accurate design against fatigue failure in geometrically complex or notched 3D-printed PLA parts.

The fracture surfaces in Fig. 8 depict how print orientation governs fatigue failure progression. Here, raster-aligned cracks follow interlayer boundaries, confirming that internal geometric layout, not bulk strength, is the primary fatigue limiter [120].

Figure 8: Fatigue fracture surfaces under varying print orientations [120]

2.4 Defect Geometry and Void Morphology

Defects in both cast and additively manufactured components often possess non-trivial geometry—elongated voids, jagged edges, and irregular surfaces—that dominate fatigue crack nucleation under cyclic loading.

High-resolution imaging has revealed that in FDM parts, internal voids often align with the direction of print, forming weak zones along raster boundaries. Fracture surface analysis confirms that cracks initiate at these locations, especially in vertically printed samples (see Fig. 9) [58].

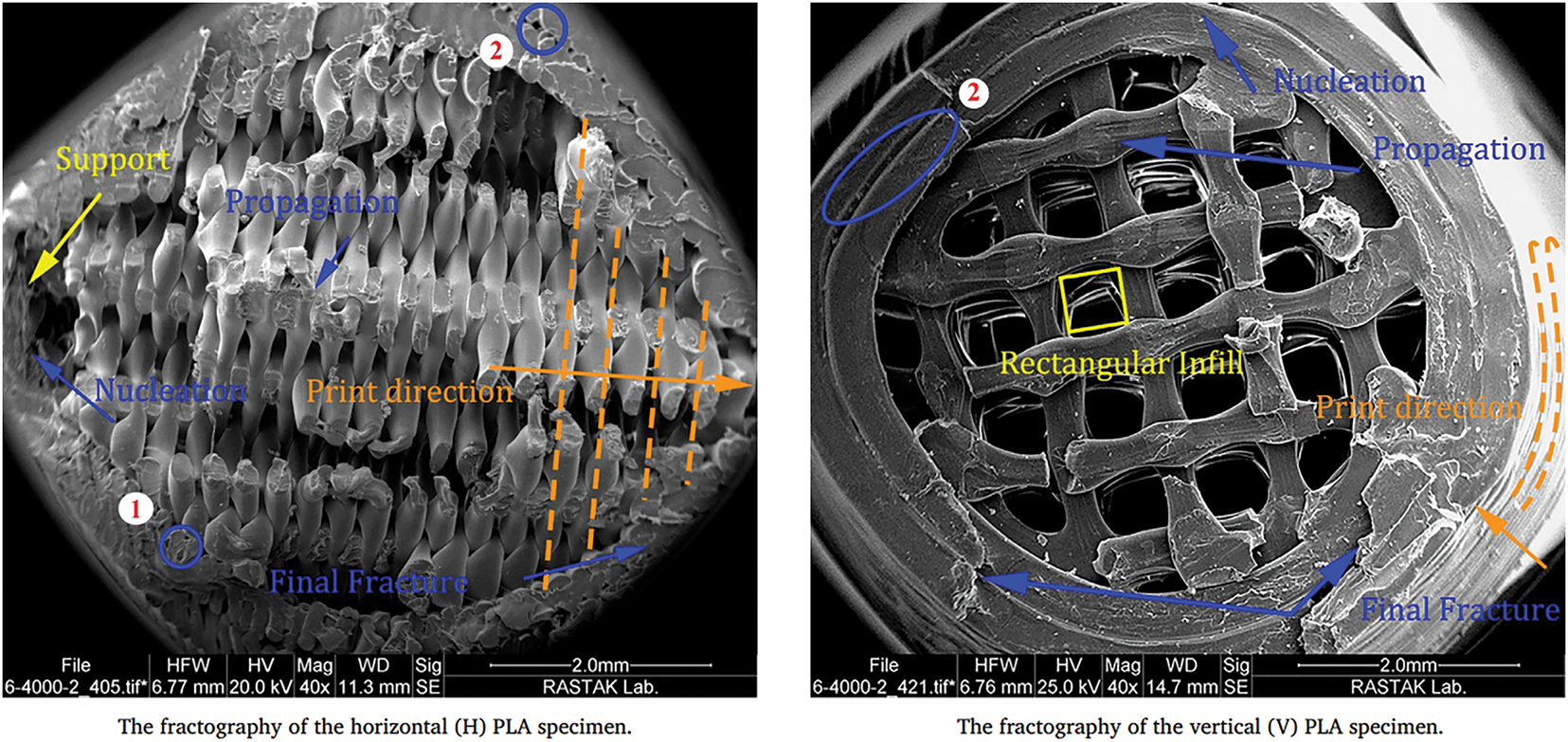
Figure 9: Fracture surfaces of PLA specimens showing void-induced crack initiation in vertically printed layers [58]

Fatigue life Nf under cyclic loading can be related to stress amplitude σa by Basquin’s equation:

Nf=(σf′σa)b

where σf′ is the fatigue strength coefficient, and b is the fatigue strength exponent.

In additive manufacturing (AM) polymers fabricated by FDM, the effective stress amplitude σaeff experienced within the material depends on the intrinsic geometry induced by printing, notably:

•   Layer orientation and thickness (t),

•   Filament alignment,

•   Inter-layer porosity and defects,

•   Surface roughness (Ra).

These geometrical factors influence local stress concentration sites, which can be modeled by a stress concentration factor Kt:

σaeff=Ktσa

here, Kt is a function of geometric discontinuities such as layer interfaces and voids formed during the printing process:

Kt=f(θ,t,Ra,Vd)

where:

•   θ is the print direction angle relative to the loading axis,

•   t is the layer thickness,

•   Ra is the surface roughness,

•   Vd is the volumetric density or void fraction.

Considering these effects, the fatigue life expression modifies as:

Nf=(σf′Ktσa)b

This formulation indicates that geometrical characteristics intrinsic to the AM process effectively amplify the applied stress amplitude through stress concentrations, reducing the fatigue life. For example, vertically printed samples exhibit more orthogonal interfaces to bending stresses, increasing Kt, thereby lowering Nf compared to horizontally printed samples. Additionally, the transition between crack initiation and propagation phases is influenced by the microscale geometry, where factors such as filament bonding and layer adhesion determine the crack path and resistance, often modeled in fracture mechanics by stress intensity factors KI related to crack size and geometry. In summary, geometry influences fatigue behavior by modifying local stress states in AM polymers, which can be quantitatively incorporated into fatigue life models through stress concentration factors dependent on print parameters and specimen geometry.

Modeling work on casting defects has reinforced that defect sharpness and alignment with stress axes are more detrimental than size alone. Elliptical and crescent-shaped voids have been shown to reduce life expectancy far more than smooth, spherical ones [98]. The fatigue resistance of a material is strongly influenced by the geometry of surface defects. Smaller defects tend to generate lower stress concentration factors, reducing the local stress intensity at the defect tip and thereby delaying crack initiation and growth. Conversely, larger defects increase the stress concentration, making the material more susceptible to fatigue failure. Additionally, the shape of the defect plays a crucial role; defects with sharp or elongated shapes produce higher stress concentration factors, which accelerate crack propagation and diminish fatigue life. Therefore, controlling defect size and shape—favoring smaller, more rounded imperfections—helps enhance the material’s resistance to fatigue failure.

2.5 Geometric Transitions in Structural Components

Abrupt transitions in geometry—such as from thick to thin sections, or sharp fillet radii—are universally recognized as fatigue-critical zones. These discontinuities elevate local stress amplitudes and serve as crack initiation hotspots. Detailed fracture surface analysis in compact tension specimens has shown that fatigue cracks frequently initiate at zones where microstructural and geometric transitions intersect, such as at the border between nodule-rich and nodule-sparse areas [2]. In low-cycle fatigue environments, even subtle geometric changes can dominate crack behavior. Experimental testing has shown that parts with sharper shoulder transitions exhibit concentrated plasticity and shorter fatigue lives [5]. To mitigate such effects, topology optimization techniques have been employed to smooth out abrupt changes and maintain uniform stress distribution. One such approach penalized geometric sharpness under random vibration loading, effectively smoothing corners and reducing stress singularities [12]. Micromechanical modeling has revealed that stress redistribution favors crack redirection toward internal notches—geometric features that arise naturally from phase misalignment or solidification-induced inclusions [19].

2.6 Geometry under Multiaxial and Non-Proportional Loading

When cyclic loads vary in direction or phase, the geometry of structural features becomes even more critical. Fatigue response under such conditions is no longer governed solely by material strength or nominal stress but by the spatial orientation of geometric entities relative to evolving stress axes.

Crack paths under non-proportional loading do not follow traditional maximum principal stress lines. As phase angles increase, the directional dependence of fatigue cracks diminishes, leading to more complex propagation behavior—a phenomenon rooted in geometry–load misalignment [7] (see Fig. 10). The fatigue phase shift angle (δ) critically influences crack growth and fatigue life in nodular cast iron under multiaxial cyclic loading. When δ approaches 0°, the load acts more like uniaxial loading with lower stress amplitudes and longer fatigue life. As δ nears 90°, the principal stress amplitude increases significantly, leading to higher crack growth rates—up to eight times greater than at small phase shifts—and consequently shorter fatigue lives. The analytical and microscopic analyses reveal that maximum principal stresses are higher for δ < 90°, promoting Mode I crack propagation and accelerating fatigue failure. Conversely, at phase shifts approaching 180°, the stress state varies, leading to more complex crack propagation modes with no strong preferential directions, as principal stress directions rotate continuously. Overall, the phase shift angle governs the stress amplitudes and crack modes, dictating the fatigue behavior where non-symmetrical effects around δ = 90° are observed, with fatigue life decreasing markedly as the phase shift approaches 90°.

Figure 10: Evolution of fatigue crack direction under different phase shift angles [7]

Chiocca et al. [129] investigate the fatigue resistance of ductile cast iron components with complex geometries, such as notches, under multiaxial and non-proportional loading conditions. It highlights that geometric irregularities like notches and casting defects (e.g., pores) significantly influence fatigue life by creating localized stress concentrations. The Effective Critical Plane (ECP) approach, which accounts for stress and strain averaging within a defined control volume around critical locations, enhances the accuracy of fatigue life predictions for these geometries. By integrating this method with multiaxial and non-proportional loading scenarios, the research demonstrates improved assessment of how complex geometrical features affect fatigue resistance, enabling more reliable design and lifetime estimation of large, irregularly shaped ductile cast iron components subjected to real-world loading complexities.

The Effective Critical Plane (ECP) approach revolves around integrating stress and strain averaging within a defined control volume to better capture localized damage mechanisms in complex geometries under multiaxial loading. Specifically, the ECP method combines the critical plane hypothesis—identifying the plane within the material where damage most likely initiates—with volumetric averaging of the stress and strain tensors over a small, material-specific process volume characterized by a control radius. This averaging process, based on concepts introduced by Neuber, mitigates issues caused by stress singularities and high gradient effects near geometric features like notches or pores. It evaluates the local stress and strain fields within this process volume, effectively smoothing out peaks and capturing the actual damaging stress state more accurately. Subsequently, the method computes a critical plane factor, such as Smith-Watson-Topper or Fatemi-Socie, based on these averaged tensors, rather than point-wise values, leading to more realistic fatigue damage predictions. Calibration of the control radius (rc)—specific to the material—is performed using experimental fatigue data, enabling the method to be adapted to various geometries without extensive additional testing. During life prediction, the method iteratively searches for the critical plane and local stress states, considering geometrical and loading complexities, resulting in a robust, computationally efficient approach that inherently accounts for local stress concentrations and defect effects.

Insights on fatigue resistance from micro to macroscale geometry:

•   Geometry controls fatigue crack initiation and propagation across multiple scales—from microscale features like graphite nodules to macroscale fillets and holes.

•   At the microscale, the shape, spacing, and orientation of microstructural inclusions and nodules create localized strain concentrations that serve as fatigue nucleation sites.

•   Mesoscale features, including surface notches, curvature transitions, and layer interfaces (especially in additive manufacturing like FDM), act as stress concentrators that dominate fatigue life independently of bulk material strength.

•   On the macroscale, geometric transitions such as fillets or varying thicknesses, though unavoidable, can be controlled through deliberate smoothing and stress redistribution to delay crack onset.

•   These findings emphasize that geometry is a primary driver of fatigue behavior, necessitating design interventions at every scale.

3  Optimization Approaches

Geometry optimization has matured into a powerful approach for enhancing fatigue resistance, not merely through shape refinement, but by fundamentally redesigning stress paths, removing failure-prone material, and embedding crack-deflecting microstructures. Across a spectrum of methodologies—from topology optimization to reliability-informed models—geometry is being re-engineered as the primary driver of durability under cyclic loads.

3.1 Topology Optimization with Fatigue Constraints

Topology optimization (TO) has expanded far beyond stiffness and compliance; it is now fully integrated with fatigue-based performance metrics. By embedding fatigue damage or life constraints directly into the objective function, TO has become a cornerstone of proactive durability design.

Graded lattice optimization has shown promise in aligning material density with stress exposure [10]. Functionally graded topologies, refined through penalization techniques targeting fatigue-specific metrics, have been shown to effectively redirect loads and delay fatigue failure. Among various penalization methods—stress, SN-intercept, yield—stress penalization emerged as the most damage-efficient, leading to the optimized lattice shown in Fig. 11.

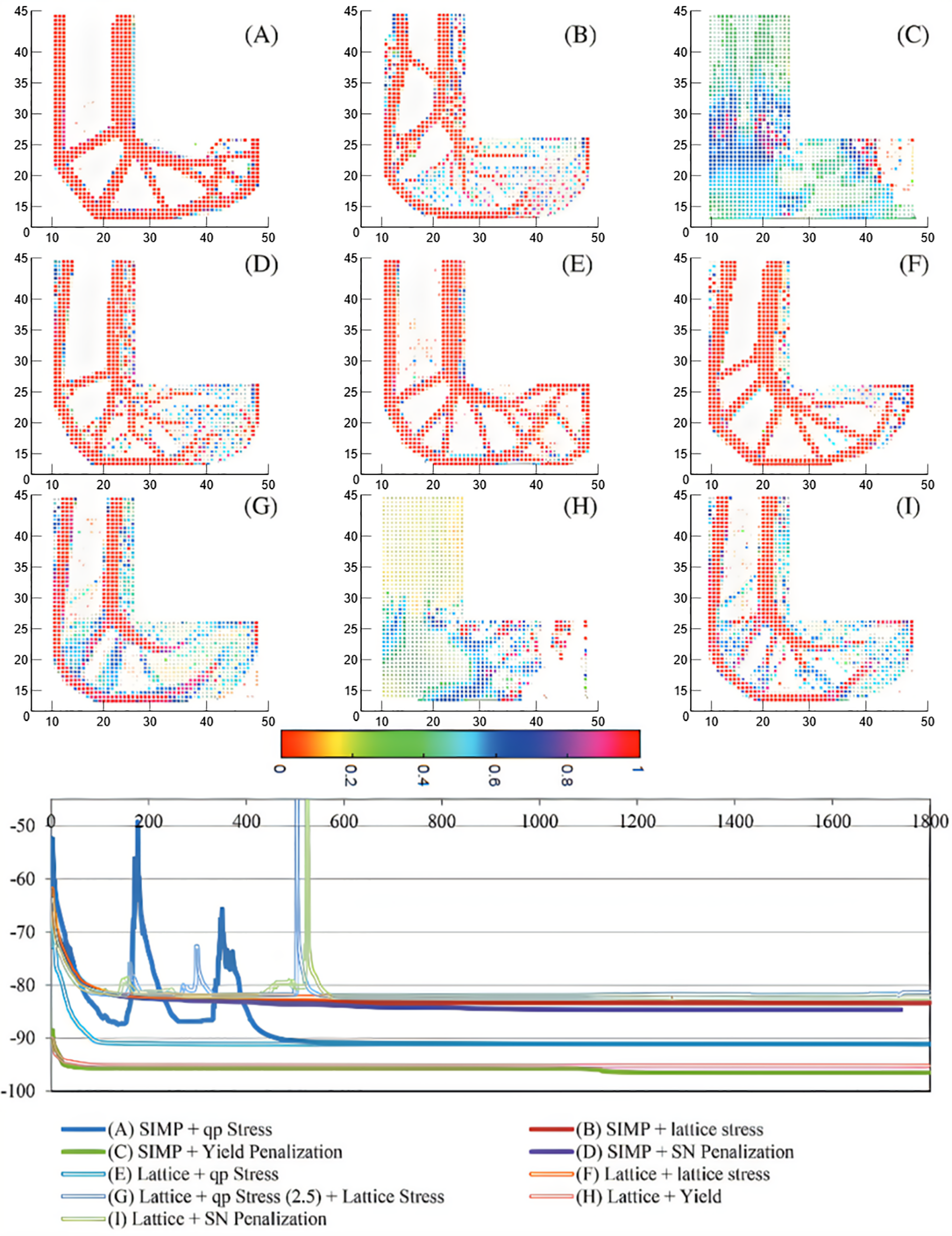
Figure 11: Optimized lattice-based structure with minimized fatigue damage using stress penalization, (A) SIMP + qp Stress, (B) SIMP + lattice stress, (C) SIMP + Yield Penalization, (D) SIMP + SN Penalization, (E) Lattice + qp Stress, (F) Lattice + lattice stress, (G) Lattice + qp Stress (2.5) + Lattice Stress, (H) Lattice + Yield, (I) Lattice + SN Penalization [10]

Let the design domain be discretized into finite elements, each characterized by a design variable ρe representing the relative density or material volume fraction, encoding geometric features such as porosity or lattice topology.

The projected element density ρe~ is obtained as a weighted average over neighboring element densities to introduce geometric smoothness and control feature size:

ρe~=∑i∈Neωeiρi∑i∈Neωei

where ωei is a convolution weight depending on the distance between element centers, and Ne denotes the neighborhood of element e.

The mechanical properties—stiffness E(ρe~), yield strength σy(ρe~), and fatigue SN-curve parameters—are homogenized and depend on the local geometry via ρe~, capturing the geometry–material interplay. Fatigue damage accumulation at element e over time is modeled by a cumulative damage variable He, which depends on local stress amplitudes σa,e influenced by geometry-dependent stiffness and stress distribution, as well as on local material fatigue parameters:

He=k∑i=1ni(σa,i(ρ~e).ν(ρ~e)σSN(ρ~e))bνSN,i(ρ~e)

where k and b are material constants, ϑ is a geometry-dependent correction factor for stress response, and σSN encapsulates SN-curve characteristics also influenced by ρe~. Thus, by controlling ρe through topology optimization, the geometry is adjusted to influence local stress states and fatigue damage accumulation, establishing a fundamental connection between geometric design variables and fatigue life.

Geometry penalization via cumulative fatigue damage filters can focus optimization efforts on crack-prone regions. p-norm aggregation methods help filter critical zones while modifying local geometry to redistribute loads, as seen in the comparative geometries shown in Fig. 12 [59].

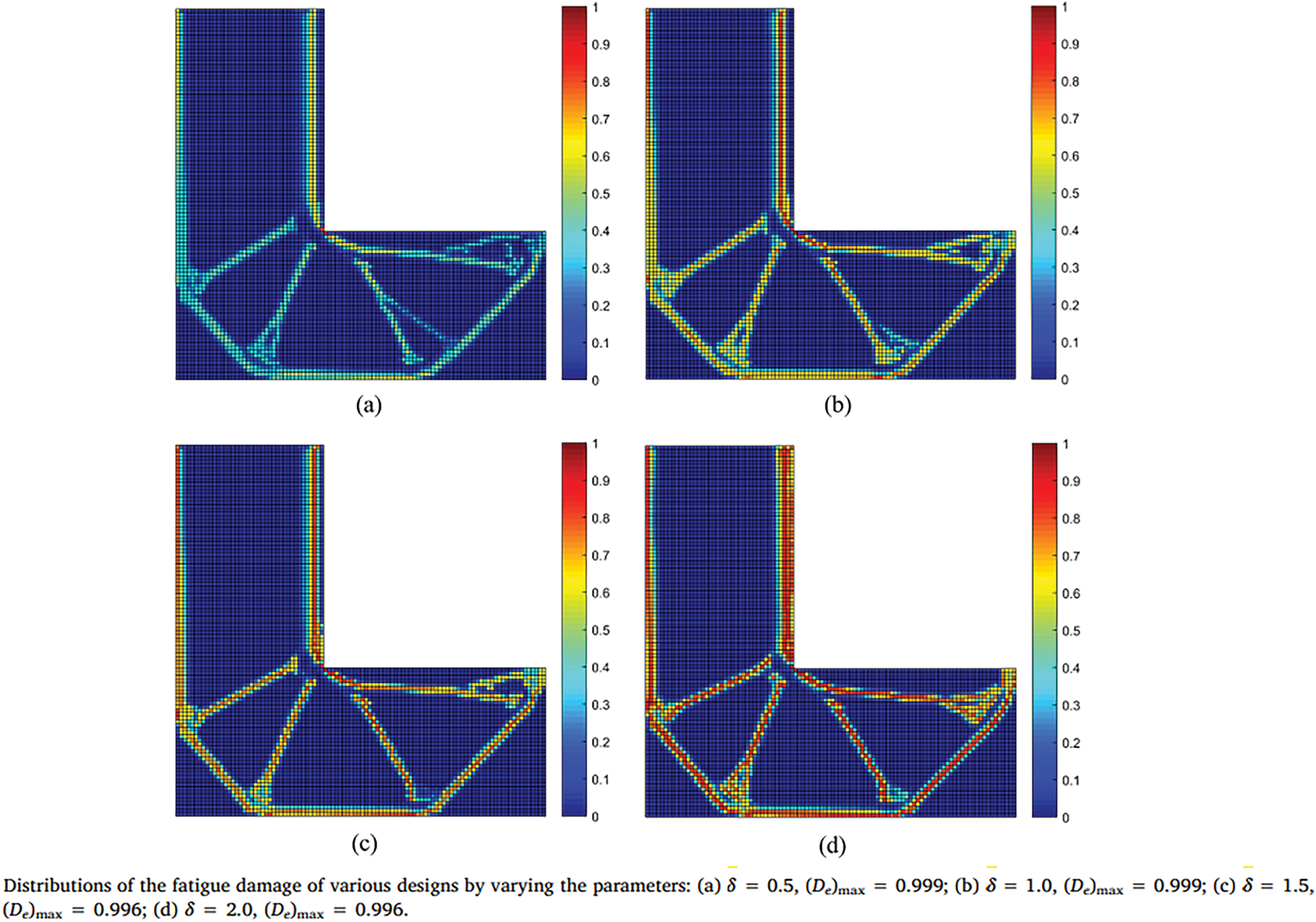
Figure 12: Geometry comparison between traditional and penalized fatigue-driven optimization [59]

The core theoretical concept relies on modeling the cumulative fatigue damage at the elemental level within a discretized design domain. Each finite element e undergoes cyclic stresses σe(t) due to applied time-varying loads. The fatigue damage De~ is computed through a combination of local stress responses and fatigue damage accumulation laws (e.g., Miner’s rule), accounting for mean stress effects via Goodman correction if needed.

Formally, the cumulative fatigue damage De~ of element e can be represented as:

De~=∑hDeh=∑hnhNf(σeh,σm)

where:

•   nh is the number of cycles in load cycle h,

•   Nf(σeh,σm) is the fatigue life estimate for element e under cycle h with stress amplitude σeh and mean stress σm,

•   Fatigue life Nf is typically related to the S-N curve adjusted by mean stress correction.

The topology optimization problem imposes constraints on these elemental fatigue damages to keep their maxima below a permissible threshold. Because local constraints are numerous, a p-norm aggregation function is employed to combine these into a single, differentiable constraint for computational tractability:

g=(∑e=1NeD~ep)≤Dallow

here, the cumulative fatigue damage De~ depends implicitly on the geometry through the design variables ρe~, which affect local stiffness and stress distribution via the SIMP interpolation scheme.

Therefore, geometry influences fatigue behavior through:

1.    Local stress modulation: Elemental material distribution ρe~ modifies stiffness and thus local stress fields σe.

2.    Fatigue damage coupling: The local stress amplitude σeh and mean stress σm govern the element-wise fatigue damage.

3.    Penalization and aggregation: Integrating fatigue damage into the optimization objective/constraints guides material to be allocated in geometrically favorable positions to minimize or uniformly distribute fatigue damage.

In conclusion, the paper’s theoretical framework links geometry to fatigue by embedding fatigue damage accumulation into the element-wise constraints of the topology optimization problem. This coupling is mediated by finite element stress analysis and penalization schemes, enabling geometry to adapt to fatigue requirements indirectly via local stress states.

3.2 Shape and Parametric Optimization for Fatigue Improvement

Shape optimization targets the refinement of structural boundaries—smooth transitions, curvature, and hole radii—to reduce peak stress concentrations. It is particularly effective where topology is fixed or when precise surface control is necessary, such as in machined or cast components.

Parametric studies of connecting rod geometry have demonstrated that even minor adjustments—such as increased web thickness or pin-hole edge radius—can yield substantial fatigue life improvements. Such refinements redistribute stress and eliminate crack initiation sites at geometric transitions [61].

Optimization of bearing housings has followed similar principles. Instead of bulk reinforcement, material was redistributed along curved load paths, reducing stiffness gradients that typically cause stress intensification under cyclic bending [63].

In vibration-sensitive designs, fatigue performance has been enhanced by suppressing resonant frequencies through strategic geometric modifications. These include changing wall curvature and thickening localized transition areas to minimize modal amplification [106].

Reshaping structural transitions in hooks and cranes has proven particularly effective in lowering stress concentrations. A case study on lifting hooks demonstrated that enlarging the curvature at load entry and smoothing the junction between arm and hook body preserved its fatigue life with a certain reduction of mass (see Fig. 13) [112].

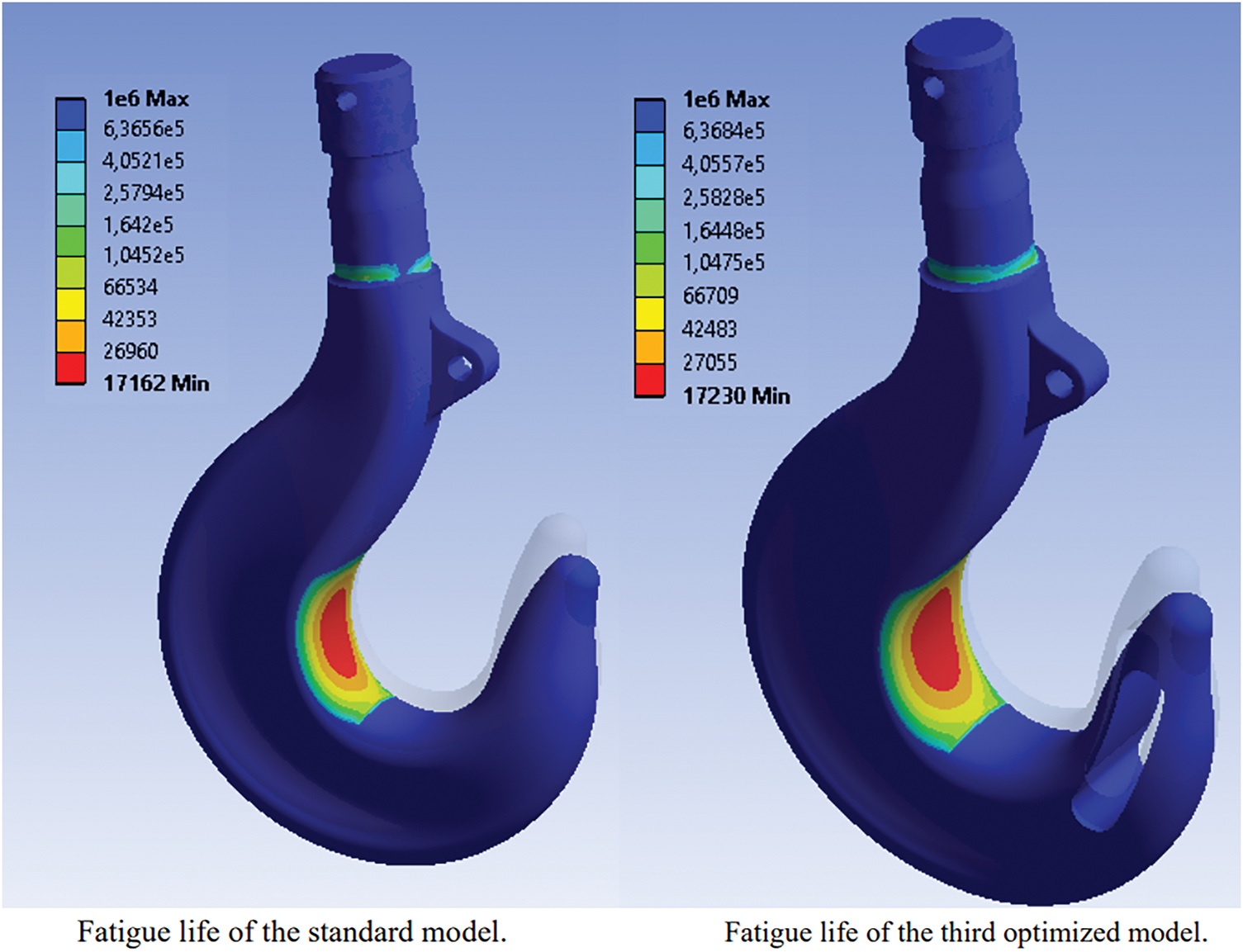
Figure 13: Fatigue life distribution before and after shape optimization of lifting hook [112]

The same principles have been applied to suspension systems. In MacPherson arms, fatigue resistance was notably improved by blending weld zones and controlling the rate of change in section geometry across load paths [135].

3.3 Fatigue-Oriented Microstructure and Lattice Geometry Optimization

The optimization of internal geometry—particularly in additively manufactured or lattice-based structures—has opened a new frontier in fatigue design. Here, microstructure is no longer treated as fixed, but as a tunable geometry with direct impact on crack paths.

Pedranz et al. [128] applied the strain energy density method to large cast iron components, linking multiaxial fatigue life to internal microstructural configurations. Their results showed that adjusting casting parameters to promote more uniform nodule distribution resulted in significant fatigue life gains, as shown in Fig. 14, which correlates fatigue damage evolution with nodule spacing geometry.

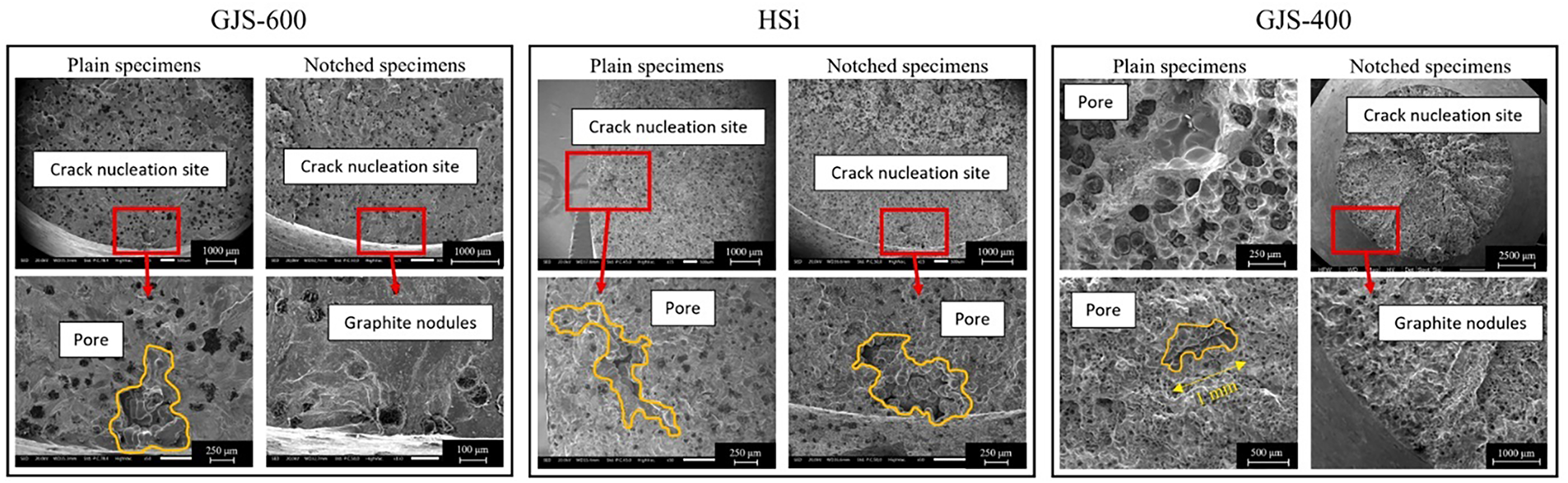
Figure 14: Damage evolution plots over nodular distributions [128]

The fatigue behavior of ductile cast iron (DCI) components is intrinsically linked to the interplay between microstructural features and geometric stress concentrators, which collectively define the highly stressed volume (HSV) where fatigue damage initiates. The fundamental mechanics governing this relationship are captured via a volumetric strain energy density (SED) approach, as expressed by the following formulation:

kϕ(W1,eq+W3,eq)=(1−f)W1∗+fW3∗

where W1,eq and W3,eq are the equivalent strain energy densities associated with axial and torsional loadings, respectively, W1∗ and W3∗ are critical strain energy densities characteristic of the material microstructure, f is a material-dependent weighting factor, and kϕ accounts for loading phase effects. Geometry influences fatigue behavior by governing the size and distribution of the HSV, which determines the volume over which the strain energy is averaged. Notches and other geometric discontinuities amplify local stresses, increasing the volumetric SED within their associated control volumes of radius R (e.g., R1 for mode I and R3 for mode III loadings). These radii represent material-dependent characteristic lengths encompassing microstructural heterogeneities such as graphite nodules and shrinkage pores. The heterogeneous distribution of critical defects implies that for larger HSVs, typical of unnotched or plain specimens, the probability of containing a harmful shrinkage pore increases, leading to fatigue initiation at such defects. Conversely, in specimens with stress concentrators (e.g., notches), the smaller HSV reduces the likelihood of pore-dominated initiation; instead, fatigue cracks initiate at more frequently occurring microstructural features like graphite nodules near the notch tip. This probabilistic effect of geometry on defect interaction is fundamental to understanding fatigue design in DCI.

Therefore, by integrating volumetric SED over geometry-dependent control volumes that reflect the microstructure-defect scale, the proposed criterion unites geometric effects and material microstructural response within a scalar energy-based fatigue parameter. This formulation inherently incorporates stress gradient effects and links macroscopic geometry to microscopic fatigue initiation mechanisms, providing a unified theoretical framework to predict fatigue performance across different geometries and loading scales.

3.4 Fatigue Optimization under Uncertainty and Reliability Constraints

Fatigue performance in service conditions is governed not only by deterministic stress fields but also by stochastic variability in loads, defects, and material properties. Geometry optimization under these uncertainties has become a focal point in reliability-based design.

Probabilistic models now integrate geometric tolerances—such as variable fillet radii or casting shrinkage zones—into fatigue predictions. One such model for military vehicle components accounted for weld variability and thickness tolerance, resulting in more robust structural layouts [38].

Topology optimization under probabilistic fatigue constraints uses sampling-based methods like Monte Carlo to identify and reinforce statistically vulnerable geometric zones. These designs exhibit higher resilience under service variability and manufacturing imperfections [39].

Hybrid reliability frameworks combine deterministic geometry with probabilistic life estimation. By embedding Weibull-distributed life constraints and assigning geometric design variables, engineers can tune curvature, notch depth, and alignment for optimal robustness [66].

Time-dependent degradation models now use geometry-aware functions to track life consumption across inspection intervals. These models account for weld toe transitions and geometrical stress concentrators, helping extend the predicted service life through shape redesign [84].

Probabilistic life predictions based on casting defect shape and alignment outperform average-based models. Angular defects exhibit markedly lower fatigue endurance under both tension and torsion, emphasizing the importance of geometric fidelity in uncertainty modeling [98].

Localized optimization techniques like augmented Lagrangian enforcement allow detailed refinement of notch zones while maintaining global design constraints. These methods help apply local fatigue improvements in high-risk regions without compromising the larger structural integrity [134].

Recent studies highlight the critical role of geometric factors in fatigue lifespan across various applications, from origami-inspired designs to additively manufactured (AM) metals and notched aerospace alloys [141,142,145,146]. For origami structures, radius and thickness are key, with length ratios modulating height’s impact [141]. In notched components, the notch root radius is a significant geometric determinant of fatigue resistance [142]. Geometric defects like pores and surface roughness are crucial in AM metals, complicating traditional fatigue modeling [145,146]. Even machining-induced surface roughness significantly affects aluminum alloy fatigue life [148].

Artificial Intelligence (AI), particularly Artificial Neural Networks (ANN) and other Machine Learning (ML) techniques, offers precise and efficient alternatives to traditional fatigue analysis by effectively incorporating these complex geometric features [141,145]. AI models trained on Finite Element Method (FEM) data achieve high prediction accuracy in origami fatigue [141]. Physics-informed ML (PIML) frameworks, integrating physical understanding with ML models like SVR, Random Forest, and XGBoost, enhance fatigue life prediction in notched materials by considering key geometric parameters [142].

The integration of geometric assessment with acoustic emission (AE) signal analysis using AI enables accurate fatigue crack length estimation [143]. Similarly, ANN models combined with damage parameters can predict fretting fatigue crack initiation life by accurately estimating critical geometric distances [144]. In AM metals, ML models correlate defect characteristics and process parameters with fatigue life, outperforming classical models [145,146]. Incorporating detailed geometric features of critical defects in AM materials further enhances prediction accuracy in physics-guided ML frameworks [150]. Micro-computed tomography (μCT) combined with optimized ML models also improves fatigue life prediction in AM alloys by using key geometric defect features [152].

While some AI-based methods focus on material properties and intrinsic defect size [147] or machining parameters influencing surface roughness [148], the trend emphasizes the increasing importance of integrating explicit geometric parameters into AI frameworks for more accurate and reliable fatigue life predictions across diverse materials and structural configurations [142–144,150,152]. Physics-informed neural networks (PINNs) also show promise by embedding physical fatigue models, implicitly capturing geometry-related stress influences [149]. Knowledge-based ML frameworks, while effective, could further benefit from the explicit inclusion of geometric characteristics [151]. Overall, the synergy of AI and geometric analysis marks a significant advancement in fatigue assessment, facilitating optimized designs and improved structural health monitoring. Table 2 classifies and summarizes recent advances in fatigue performance modeling, emphasizing the integration of geometric factors and AI techniques, as referenced throughout the text.

4  Reliability & Future Trends

Fatigue behavior, once thought to be governed predominantly by material composition and external loads, is now increasingly understood as a geometry-driven phenomenon. Across micro-, meso-, and macro-scales, geometry dictates the onset, direction, and propagation of fatigue cracks, turning it from a passive descriptor into an active design variable. This section synthesizes the findings to generalize key insights and outline how fatigue resistance can be engineered through geometric intervention.

4.1 Geometry as a Multiscale Fatigue Driver

From graphite nodules at the microscale to fillet transitions at the macroscale, geometry consistently emerges as the initiation site of fatigue damage. It is not simply the presence of defects or features, but their shape, orientation, spacing, and alignment with stress fields that dictate failure progression.

At the microstructural level, non-spherical graphite nodules, irregular inclusion boundaries, and sharp-edged lamellae have been shown to concentrate local strain energy, serving as fatigue nuclei. These findings were consistently observed in nodular cast irons [1,2,45,104], where SEM and tomography revealed that crack initiation aligns with nodule shape and distribution rather than with random stress maxima.

Zooming out to mesoscale phenomena, surface geometries such as notches, curvature transitions, and layer interfaces in FDM parts introduce stress amplifiers that dominate fatigue life [29,32,40,100,110]. These geometrical triggers are often design-imposed or process-induced, and their effect persists regardless of the material’s nominal strength.

On the macro scale, geometric transitions such as fillets, holes, and varying wall thicknesses have proven to be unavoidable but controllable contributors to fatigue risk [5,102,112]. Studies across automotive, aerospace, and civil engineering have emphasized that these regions require deliberate smoothing or stress redistribution to prevent early crack formation.

4.2 Optimization as a Tool for Geometric Control

Optimization has shifted geometry from a passive to an actively controllable fatigue determinant. Whether through removing excess material, smoothing transitions, or designing internal lattice architectures, geometry can now be intentionally tailored for fatigue performance.

Topology optimization frameworks—initially focused on stiffness and compliance—now incorporate fatigue-based constraints, ensuring that geometry evolves to distribute loads more uniformly and avoid crack-prone regions. Local constraint models, cumulative damage penalization, and p-norm filtering techniques have all proven effective in reshaping geometry to extend fatigue life [3,15,33,59,90].

Parametric shape optimization has targeted fillet radii, curvature continuity, and cross-sectional thickness, which are all known fatigue hotspots. Improvements in suspension arms, crankshafts, and connecting rods demonstrate how subtle boundary refinements can yield large fatigue benefits without compromising weight or manufacturability [61,63,106,135].

Within additive manufacturing, infill pattern design and raster angle selection provide direct control over internal geometry. Lattice tuning and graded cell density approaches allow designers to embed fatigue resistance into the structure’s core, not just its surface [10,65,104].

4.3 Reliability and Manufacturing Integration

While deterministic models provide a solid foundation, real-world fatigue performance is often dictated by variability in manufacturing, loading, and environmental conditions. Several reviewed studies emphasize the integration of reliability into fatigue-aware geometry design.

Reliability-Based Design Optimization (RBDO) frameworks now incorporate geometry-specific uncertainties, including variations in fillet radius, weld geometry, defect positioning, and surface roughness. These methods have demonstrated the ability to maintain fatigue performance across production batches and loading scenarios [38,66,84].

Stochastic optimization has also been used to identify the statistically vulnerable regions within a geometry. Monte Carlo–based methods and Weibull-distributed life predictions have helped reshape geometry where it matters most—at risk-prone interfaces or likely defect zones [39,98,140].

Importantly, the shift toward as-built condition optimization is gaining momentum. Instead of designing for ideal geometry, designers are beginning to incorporate manufacturing flaws (such as lack-of-fusion voids or casting porosity) directly into their optimization constraints. This enables preemptive reinforcement or geometry realignment that offsets expected imperfections [115,130,140].

4.4 The Geometry–Fatigue Nexus: From Passive to Active Control

Traditional fatigue design often treated geometry as a source of weakness—an unavoidable feature to be mitigated post hoc. Today, geometry is increasingly understood as a designable, tunable variable capable of enhancing fatigue life when used deliberately.

Evidence from micromechanics, topology optimization, and additive manufacturing converges on the same conclusion: geometry governs fatigue, and design tools now exist to manipulate it at every scale.

Instead of reacting to failure, modern approaches advocate predicting and preventing fatigue through front-loaded design—whether by optimizing internal print paths, reshaping outer boundaries, or embedding robustness against manufacturing uncertainty. This evolution reflects a broader trend: from “damage tolerance” to damage avoidance by design.

To conclude the discussion on fatigue resistance:

•   Fatigue behavior is increasingly recognized as geometry-driven at micro-, meso-, and macro-scales. Geometry influences crack initiation sites and propagation paths by altering local strain and stress fields.

•   Probabilistic models now integrate geometric tolerances such as fillet radius variation, weld geometry, and surface roughness into fatigue life predictions, enhancing robustness.

•   Stochastic optimization methods identify statistically vulnerable regions for targeted geometric reinforcement.

•   Hybrid reliability frameworks embed Weibull-distributed life constraints into geometric design variables, optimizing features like curvature, notch depth, and alignment for fatigue performance.

•   Time-dependent degradation models that include geometry-aware stress concentrators (e.g., weld toes) enable fatigue life extension through shape redesign.

•   Additive manufacturing also plays a pivotal role by allowing internal geometry control through infill patterning, lattice structures, and raster orientation, which can be optimized for fatigue improvement.

•   Real-world variability in manufacturing and loading necessitates reliability-based design optimization (RBDO) frameworks to ensure fatigue performance is consistent across production batches and service conditions.

•   Localized refinement in high-risk geometric zones can be achieved without compromising overall structural integrity using methods such as augmented Lagrangian enforcement.

4.5 Research Gaps

Despite major advances in understanding and optimizing fatigue resistance through geometric approaches, several critical research gaps remain unaddressed. These limitations, observed across all geometry scales and modeling domains, highlight the challenges that still need to be overcome for geometry-driven fatigue design to become fully integrated and predictive.

4.5.1 Fragmentation between Scales

While significant insights have been gained at individual scales—such as the microscale behavior of nodules [1,2], mesoscale effects of raster paths [29,32], and macroscale shape transitions [5,102]—there is a lack of unified multiscale frameworks that link these together. Most studies either treat geometry at a single scale or assume idealized conditions across others, limiting the fidelity of fatigue life predictions for complex components.

4.5.2 Neglect of As-Built Manufacturing Geometry

Many optimization methods assume idealized geometry, disregarding real-world manufacturing artifacts. However, recent studies show that fatigue failures often initiate at as-built features, such as FDM layer ridges, casting porosity, or unmelted powder zones [58,110,140]. Incorporating these geometric imperfections into optimization pipelines remains underexplored.

4.5.3 Underuse of AI-Driven Fatigue Prediction

Artificial intelligence—especially deep learning trained on microstructural images—has shown promising results in predicting fatigue behavior based on geometry [104]. Yet, its use remains rare. Current models are often data-poor or lack generalization capability across materials and manufacturing methods. Expanding AI frameworks to include geometry-informed fatigue modeling is a clear opportunity for advancement.

4.5.4 Limited Adoption of Reliability-Centered Design

While reliability-based design optimization (RBDO) frameworks exist, few studies integrate them seamlessly with geometry-focused fatigue models. As shown in select works [38,39,66,84], including probabilistic treatment of geometric uncertainty—like weld variability, surface texture, and nodule spacing, can greatly enhance predictive accuracy. Broader implementation of these methods is needed.

4.5.5 Absence of Standardized Benchmark Problems

Benchmarking across different fatigue optimization methods remains a challenge due to non-uniform testing protocols, material systems, and loading profiles. Without agreed-upon geometry-focused fatigue test cases, it is difficult to compare outcomes or validate new modeling approaches. Establishing a standardized set of fatigue-geometry benchmark problems would enhance reproducibility and foster community-wide progress.

5  Conclusion

This review offers the first comprehensive and systematic examination of geometry-focused fatigue resistance across multiple length scales. Key novel contributions include:

•   A unified framework contrasting geometry-optimization strategies at micro-, meso-, and macro-scales, elucidating their specific fatigue initiation and propagation mechanisms.

•   Identification of the critical role and underutilization of reliability-based design optimization (RBDO) and probabilistic geometric uncertainty quantification in fatigue life prediction.

•   The proposal of standardized, geometry-centric benchmark problems and evaluation criteria to enhance reproducibility and comparative assessments across research efforts.

•   Highlighting the transformative potential of additive manufacturing to control internal lattice and microstructural geometries for fatigue improvement, balanced against challenges such as print-path anisotropy.

•   Establishing a clear path forward, integrating multiscale, manufacturing-aware, and AI-driven methods to realize predictive and proactive fatigue life optimization.

By reframing geometry as a controllable, designable variable rather than an uncontrollable liability, this work lays the groundwork for next-generation fatigue-resistant component design, shifting from reactive damage tolerance to proactive fault prevention grounded in shape and topology.

To reinforce the paper’s contribution and provide a clearer path for future research, the following Table 3 summarizes the specific unresolved challenges per geometry scale (micro, meso, macro) identified within the preceding discussion, along with possible future directions.

As this transition matures, the language of fatigue will increasingly be written in geometric terms, where curves, patterns, and voids are not liabilities, but deliberate decisions.

Acknowledgement: The authors would like to acknowledge that this paper is submitted in partial fulfilment of the requirements for PhD degree at Bursa Technical University.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Ibrahim T. Teke and Ahmet H. Ertas; methodology, Ibrahim T. Teke and Ahmet H. Ertas; software, Ibrahim T. Teke; validation, Ibrahim T. Teke; formal analysis, Ibrahim T. Teke; investigation, Ibrahim T. Teke; resources, Ibrahim T. Teke; data curation, Ibrahim T. Teke; writing—original draft preparation, Ibrahim T. Teke; writing—review and editing, Ahmet H. Ertas and Ibrahim T. Teke; visualization, Ibrahim T. Teke and Ahmet H. Ertas; supervision, Ahmet H. Ertas; project administration, Ahmet H. Ertas. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article. In other words, all data underlying the results are available as part of the article and no additional source data are required.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Yaacoub Agha H, Béranger AS, Billardon R, Hild F. High-cycle fatigue behaviour of spheroidal graphite cast iron. Fatigue Fract Eng Mater Struct. 1998;21(3):287–96. doi:10.1046/j.1460-2695.1998.00293.x. [Google Scholar] [CrossRef]

2. Di Cocco V, Iacoviello F, Rossi A, Cavallini M, Natali S. Graphite nodules and fatigue crack propagation micromechanisms in a ferritic ductile cast iron. Fatigue Fract Eng Mater Struct. 2013;36(9):893–902. doi:10.1111/ffe.12056. [Google Scholar] [CrossRef]

3. Sherif K, Witteveen W, Puchner K, Irschik H. Efficient topology optimization of large dynamic finite element systems using fatigue. AIAA J. 2010;48(7):1339–47. doi:10.2514/1.45196. [Google Scholar] [CrossRef]

4. Čanžar P, Tonković Z, Kodvanj J. Microstructure influence on fatigue behaviour of nodular cast iron. Mater Sci Eng A. 2012;556:88–99. doi:10.1016/j.msea.2012.06.062. [Google Scholar] [CrossRef]

5. Petrenec M, Tesařová H, Beran P, Šmíd M, Roupcová P. Comparison of low cycle fatigue of ductile cast irons with different matrix alloyed with nickel. Procedia Eng. 2010;2(1):2307–16. doi:10.1016/j.proeng.2010.03.247. [Google Scholar] [CrossRef]

6. Šamec B, Potrč I, Šraml M. Low cycle fatigue of nodular cast iron used for railway brake discs. Eng Fail Anal. 2011;18(6):1424–34. doi:10.1016/j.engfailanal.2011.04.002. [Google Scholar] [CrossRef]

7. Kachit M, Verdu C. Cracking behavior in nodular graphite cast iron under non-proportional cyclic loading. Int J Fatigue. 2020;140(4):105840. doi:10.1016/j.ijfatigue.2020.105840. [Google Scholar] [CrossRef]

8. Iacoviello F, Di Cocco V, Bellini C. Fatigue crack propagation and damaging micromechanisms in ductile cast irons. Int J Fatigue. 2019;124(1–2):48–54. doi:10.1016/j.ijfatigue.2019.02.030. [Google Scholar] [CrossRef]

9. Zou G, Faber MH, González A, Banisoleiman K. A holistic approach to risk-based decision on inspection and design of fatigue-sensitive structures. Eng Struct. 2020;221(1–2):110949. doi:10.1016/j.engstruct.2020.110949. [Google Scholar] [CrossRef]

10. Trudel E, ElSayed MSA. Penalization techniques for fatigue-based topology optimizations of structures with embedded functionally graded lattice materials. Int J Numer Meth Eng. 2022;123(9):1991–2011. doi:10.1002/nme.6924. [Google Scholar] [CrossRef]

11. Hosseini SM, Azadi M, Ghasemi-Ghalebahman A, Jafari SM. Fatigue crack initiation detection in ductile cast iron crankshaft under rotating bending fatigue test using the acoustic emission entropy method. Eng Fail Anal. 2023;144:106981. doi:10.1016/j.engfailanal.2022.106981. [Google Scholar] [CrossRef]

12. Zhao L, Xu B, Han Y, Xue J, Rong J. Structural topological optimization with dynamic fatigue constraints subject to dynamic random loads. Eng Struct. 2020;205(6):110089. doi:10.1016/j.engstruct.2019.110089. [Google Scholar] [CrossRef]

13. Ricotta M. Simple expressions to estimate the Manson–Coffin curves of ductile cast irons. Int J Fatigue. 2015;78(5):38–45. doi:10.1016/j.ijfatigue.2015.03.025. [Google Scholar] [CrossRef]

14. Jamalkhani Khameneh M, Azadi M. Reliability prediction, scatter-band analysis and fatigue limit assessment of high-cycle fatigue properties in EN-GJS700-2 ductile cast iron. MATEC Web Conf. 2018;165(4):10012. doi:10.1051/matecconf/201816510012. [Google Scholar] [CrossRef]

15. Oest J, Lund E. Topology optimization with finite-life fatigue constraints. Struct Multidiscip Optim. 2017;56(5):1045–59. doi:10.1007/s00158-017-1701-9. [Google Scholar] [CrossRef]

16. Bendikiene R, Ciuplys A, Cesnavicius R, Jutas A, Bahdanovich A, Marmysh D, et al. Influence of austempering temperatures on the microstructure and mechanical properties of austempered ductile cast iron. Metals. 2021;11(6):967. doi:10.3390/met11060967. [Google Scholar] [CrossRef]

17. Costa N, Machado N, Silva FS. A new method for prediction of nodular cast iron fatigue limit. Int J Fatigue. 2010;32(7):988–95. doi:10.1016/j.ijfatigue.2009.11.005. [Google Scholar] [CrossRef]

18. Suresh S, Lindström SB, Thore CJ, Klarbring A. Acceleration of continuous-time, high-cycle fatigue constrained problems in topology optimization. Eur J Mech A Solids. 2022;96:104723. doi:10.1016/j.euromechsol.2022.104723. [Google Scholar] [CrossRef]

19. Andriollo T, Zhang Y, Fæster S, Kouznetsova V. Analysis of the correlation between micro-mechanical fields and fatigue crack propagation path in nodular cast iron. Acta Mater. 2020;188:302–14. doi:10.1016/j.actamat.2020.02.026. [Google Scholar] [CrossRef]

20. Collet M, Bruggi M, Duysinx P. Topology optimization for minimum weight with compliance and simplified nominal stress constraints for fatigue resistance. Struct Multidiscip Optim. 2017;55(3):839–55. doi:10.1007/s00158-016-1510-6. [Google Scholar] [CrossRef]

21. Czekaj K, Mazurek B, Owsiński R, Niesłony A. Complexity of determining the fatigue strength of real structures under random vibration conditions-two case studies. Appl Sci. 2024;14(21):10051. doi:10.3390/app142110051. [Google Scholar] [CrossRef]

22. Gebhardt C, Zhang J, Bezold A, Broeckmann C. Microscale fatigue mechanisms in high silicon alloyed nodular cast iron. Int J Fatigue. 2023;168(3):107402. doi:10.1016/j.ijfatigue.2022.107402. [Google Scholar] [CrossRef]

23. Marjan A, Huang L. Topology optimisation of offshore wind turbine jacket foundation for fatigue life and mass reduction. Ocean Eng. 2023;289(9):116228. doi:10.1016/j.oceaneng.2023.116228. [Google Scholar] [CrossRef]

24. Slebioda M, Giele R, Langelaar M. Topology optimization for infinite fatigue life of cyclic symmetric structures subjected to non-proportional loading. Comput Struct. 2023;286:107113. doi:10.1016/j.compstruc.2023.107113. [Google Scholar] [CrossRef]

25. Padzi MM, Bazin MM, Muhamad WMW. Fatigue characteristics of 3D printed acrylonitrile butadiene styrene (ABS). IOP Conf Ser Mater Sci Eng. 2017;269(1):012060. doi:10.1088/1757-899X/269/1/012060. [Google Scholar] [CrossRef]

26. Gebhardt C, Chen G, Bezold A, Broeckmann C. Influence of graphite morphology on static and cyclic strength offerritic nodular cast iron. MATEC Web Conf. 2018;165:14014. doi:10.1051/matecconf/201816514014. [Google Scholar] [CrossRef]

27. Vanaei HR, Shirinbayan M, Vanaei S, Fitoussi J, Khelladi S, Tcharkhtchi A. Multi-scale damage analysis and fatigue behavior of PLA manufactured by fused deposition modeling (FDM). Rapid Prototyp J. 2021;27(2):371–8. doi:10.1108/rpj-11-2019-0300. [Google Scholar] [CrossRef]

28. Su PF, Ye HL, Wang WW, Sui YK. Fatigue topology optimization based on global stress constraint method. IOP Conf Ser Mater Sci Eng. 2019;531(1):012048. doi:10.1088/1757-899X/531/1/012048. [Google Scholar] [CrossRef]

29. Ezeh OH, Susmel L. Fatigue strength of additively manufactured polylactide (PLAeffect of raster angle and non-zero mean stresses. Int J Fatigue. 2019;126(15):319–26. doi:10.1016/j.ijfatigue.2019.05.014. [Google Scholar] [CrossRef]

30. Hassan AA, Biswas B. Topology optimization of an automotive seatbelt bracket considering fatigue. Designs. 2024;8(5):99. doi:10.3390/designs8050099. [Google Scholar] [CrossRef]

31. Popescu D, Baciu F, Vlăsceanu D, Marinescu R, Lăptoiu D. Investigations on the fatigue behavior of 3D-printed and thermoformed polylactic acid wrist-hand orthoses. Polymers. 2023;15(12):2737. doi:10.3390/polym15122737. [Google Scholar] [PubMed] [CrossRef]

32. Horasan M, Sarac I. The fatigue responses of 3D-printed polylactic acid (PLA) parts with varying raster angles and printing speeds. Fatigue Fract Eng Mater Struct. 2024;47(10):3693–706. doi:10.1111/ffe.14406. [Google Scholar] [CrossRef]

33. Teng X, Wang C, Jiang X, Chen X. Structural topology optimization with local finite-life fatigue constraints. Mathematics. 2023;11(5):1220. doi:10.3390/math11051220. [Google Scholar] [CrossRef]

34. Sartorti R, Möcker T, Kriegesmann B, Pedersen CBW. On non-parametric fatigue optimization. Int J Numer Meth Eng. 2023;124(5):1168–92. doi:10.1002/nme.7158. [Google Scholar] [CrossRef]

35. Habashneh M, Movahedi Rad M. Optimizing structural topology design through consideration of fatigue crack propagation. Comput Meth Appl Mech Eng. 2024;419(1):116629. doi:10.1016/j.cma.2023.116629. [Google Scholar] [CrossRef]

36. Müller M, Šleger V, Kolář V, Hromasová M, Piš D, Mishra RK. Low-cycle fatigue behavior of 3D-printed PLA reinforced with natural filler. Polymers. 2022;14(7):1301. doi:10.3390/polym14071301. [Google Scholar] [PubMed] [CrossRef]

37. Chen Y, Monteiro E, Koutiri I, Favier V. Aggregation-free fatigue constrained topology optimization using the constrained natural element method. In: 15th International Conference on Evolutionary and Deterministic Methods for Design, Optimization and Control; 2023 Jun 1–3; Chania, Greece. p. 300–14. doi:10.7712/140123.10206.18876. [Google Scholar] [CrossRef]

38. Choi KK, Tang J, Hardee E, Youn BD. Application of reliability-based design optimization to durability of military vehicles. In: SAE technical paper. Warrendale, PA, USA; 2005. doi:10.4271/2005-01-0530. [Google Scholar] [CrossRef]

39. Logo J, Tauzowski P, Blachowski B. Optimal topologies considering fatigue with reliability constraint. Comput Struct Technol Conf Proc. 2023;3:1–5. doi:10.4203/ccc.3.2.5. [Google Scholar] [CrossRef]

40. Hassanifard S, Behdinan K. Effects of voids and raster orientations on fatigue life of notched additively manufactured PLA components. Int J Adv Manuf Technol. 2022;120(9):6241–50. doi:10.1007/s00170-022-09169-1. [Google Scholar] [CrossRef]

41. Gong B, Cui S, Zhao Y, Sun Y, Ding Q. Strain-controlled fatigue behaviors of porous PLA-based scaffolds by 3D-printing technology. J Biomater Sci Polym Ed. 2017;28(18):2196–204. doi:10.1080/09205063.2017.1388993. [Google Scholar] [PubMed] [CrossRef]

42. Al-Ali MA, Al-Ali MA, Takezawa A, Kitamura M. Topology optimization and fatigue analysis of temporomandibular joint prosthesis. World J Mech. 2017;7(12):323–39. doi:10.4236/wjm.2017.712025. [Google Scholar] [CrossRef]

43. Dudescu MC, Racz L, Popa F. Effect of infill pattern on fatigue characteristics of 3D printed polymers. Mater Today Proc. 2023;78(3):263–9. doi:10.1016/j.matpr.2022.11.283. [Google Scholar] [CrossRef]

44. Cerda-Avila SN, Medellín-Castillo HI, Cervántes-Uc JM, May-Pat A, Rivas-Menchi A. Fatigue experimental analysis and modelling of fused filament fabricated PLA specimens with variable process parameters. Rapid Prototyp J. 2023;29(6):1155–65. doi:10.1108/rpj-10-2022-0354. [Google Scholar] [CrossRef]

45. Shiraki N, Usui Y, Kanno T. Effects of number of graphite nodules on fatigue limit and fracture origins in heavy section spheroidal graphite cast iron. Mater Trans. 2016;57(3):379–84. doi:10.2320/matertrans.f-m2015841. [Google Scholar] [CrossRef]

46. Szmytka F, Charkaluk E, Constantinescu A, Osmond P. Probabilistic low cycle fatigue criterion for nodular cast-irons. Int J Fatigue. 2020;139(8):105701. doi:10.1016/j.ijfatigue.2020.105701. [Google Scholar] [CrossRef]

47. Kyling H, Siddiqui MO. Full-scale fatigue testing of acast-iron wind turbine rotor shaft. Forsch Im Ingenieurwesen. 2023;87(1):235–46. doi:10.1007/s10010-023-00649-8. [Google Scholar] [CrossRef]

48. Mayén J, Gallegos-Melgar ADC, Pereyra I, Poblano-Salas CA, Hernández-Hernández M, Betancourt-Cantera JA, et al. Descriptive and inferential study of hardness, fatigue life, and crack propagation on PLA 3D-printed parts. Mater Today Commun. 2022;32:103948. doi:10.1016/j.mtcomm.2022.103948. [Google Scholar] [CrossRef]

49. Iacoviello F, Di Cocco V, Cavallini M. Fatigue crack propagation and overload damaging micromechanisms in a ferritic-pearlitic ductile cast iron. Fatigue Fract Eng Mater Struct. 2016;39(8):999–1011. doi:10.1111/ffe.12443. [Google Scholar] [CrossRef]

50. Ambhore N, Dhumal A, Borawake O, Marathe V, Nalawade D. Fatigue analysis of polylactide manufactured by fused deposition method of 3D printing. J Mines Met Fuels. 2024;2024:957–64. doi:10.18311/jmmf/2024/45449. [Google Scholar] [CrossRef]

51. Vechet S, Kohout J, Hanzlikova K, Hruby V. Fatigue behaviour of nodular cast iron at various loading cycle asymmetry. Komunikácie. 2006;8(4):42–6. doi:10.26552/com.c.2006.4.42-46. [Google Scholar] [CrossRef]

52. Tawade SV, Todkar SB, Hade AS. Fatigue life optimization of wind turbine blade. Int J Res Eng Technol. 2014;3(15):843–50. doi:10.15623/ijret.2014.0315160. [Google Scholar] [CrossRef]

53. Ghodrat S, Kestens LAI. Microstructural dependence of tensile and fatigue properties of compacted graphite iron in diesel engine components. Steel Res Int. 2016;87(6):772–9. doi:10.1002/srin.201500219. [Google Scholar] [CrossRef]

54. Trampert S, Gocmez T, Pischinger S. Thermomechanical fatigue life prediction of cylinder heads in combustion engines. J Eng Gas Turbines Power. 2008;130(1):012806. doi:10.1115/1.2771251. [Google Scholar] [CrossRef]

55. Iacoviello F, Di Cocco V, Cavallini M. Fatigue crack tip damaging micromechanisms in a ferritic-pearlitic ductile cast iron. Frat Ed Integrità Strutturale. 2015;9(33):111–9. doi:10.3221/igf-esis.33.15. [Google Scholar] [CrossRef]

56. Čanžar P, Tonković Z, Bakić A, Kodvanj J. Experimental and numerical investigation of fatigue behaviour of nodular cast iron. Key Eng Mater. 2011;488-9:182–5. doi:10.4028/www.scientific.net/kem.488-489.182. [Google Scholar] [CrossRef]

57. Hosdez J, Limodin N, Najjar D, Witz JF, Charkaluk E, Osmond P, et al. Fatigue crack growth in compacted and spheroidal graphite cast irons. Int J Fatigue. 2020;131(12):105319. doi:10.1016/j.ijfatigue.2019.105319. [Google Scholar] [CrossRef]

58. Azadi M, Dadashi A, Dezianian S, Kianifar M, Torkaman S, Chiyani M. High-cycle bending fatigue properties of additive-manufactured ABS and PLA polymers fabricated by fused deposition modeling 3D-printing. Forces Mech. 2021;3(1):100016. doi:10.1016/j.finmec.2021.100016. [Google Scholar] [CrossRef]

59. Chen Z, Long K, Wen P, Nouman S. Fatigue-resistance topology optimization of continuum structure by penalizing the cumulative fatigue damage. Adv Eng Softw. 2020;150(2):102924. doi:10.1016/j.advengsoft.2020.102924. [Google Scholar] [CrossRef]

60. Nakhaei M, Sterba M, Foletti JM, Badih L, Behr M. Experimental analysis and numerical fatigue life prediction of 3D-printed osteosynthesis plates. Front Bioeng Biotechnol. 2023;11:1133869. doi:10.3389/fbioe.2023.1133869. [Google Scholar] [PubMed] [CrossRef]

61. Lee TH, Jung JJ. Metamodel-based shape optimization of connecting rod considering fatigue life. Key Eng Mater. 2006;306–308:211–6. doi:10.4028/www.scientific.net/kem.306-308.211. [Google Scholar] [CrossRef]

62. Ulewicz R, Nový F, Selejdak J. Fatigue strength of ductile iron in ultra-high cycle regime. Adv Mater Res. 2014;874:43–8. doi:10.4028/www.scientific.net/amr.874.43. [Google Scholar] [CrossRef]

63. Kabus S, Pedersen CBW. Optimal bearing housing designing using topology optimization. J Tribol. 2012;134(2):021102. doi:10.1115/1.4005951. [Google Scholar] [CrossRef]

64. Habashneh M, Movahedi Rad M. An investigation of the recent developments in reliability-based structural topology optimization. Period Polytech Civil Eng. 2023;67(3):765–74. doi:10.3311/ppci.22107. [Google Scholar] [CrossRef]

65. Domingo-Espin M, Travieso-Rodriguez JA, Jerez-Mesa R, Lluma-Fuentes J. Fatigue performance of ABS specimens obtained by fused filament fabrication. Materials. 2018;11(12):2521. doi:10.3390/ma11122521. [Google Scholar] [PubMed] [CrossRef]

66. Yaich A, Kharmanda G, El Hami A, Walha L, Haddar M. Reliability based design optimization for multiaxial fatigue damage analysis using robust hybrid method. J Mech. 2018;34(5):551–66. doi:10.1017/jmech.2017.44. [Google Scholar] [CrossRef]

67. Kianifar M, Azadi M, Heidari F. Evaluation of stress-controlled high-cycle fatigue characteristics in PLA-wood fused deposition modeling 3D-printed parts under bending loads. PLoS One. 2024;19(4):e0300569. doi:10.1371/journal.pone.0300569. [Google Scholar] [PubMed] [CrossRef]

68. Yankin A, Serik G, Danenova S, Alipov Y, Temirgali A, Talamona D, et al. Optimization of fatigue performance of FDM ABS and nylon printed parts. Micromachines. 2023;14(2):304. doi:10.3390/mi14020304. [Google Scholar] [PubMed] [CrossRef]

69. Pelizzari J, Campagnolo A, Dengo C, Meneghetti G. A master curve for fatigue design of notched nodular cast iron components based on the local averaged strain energy density. Materials. 2024;17(19):4807. doi:10.3390/ma17194807. [Google Scholar] [PubMed] [CrossRef]

70. Jimenez-Martinez M, Varela-Soriano J, Carreón JJR, Torres-Cedillo SG. Mechanical fatigue of PLA in additive manufacturing. Eng Fail Anal. 2023;149(3):107273. doi:10.1016/j.engfailanal.2023.107273. [Google Scholar] [CrossRef]

71. Dahlberg M. Fatigue crack propagation in nodular graphite cast iron. Int J Cast Met Res. 2004;17(1):29–37. doi:10.1179/136404604225012398. [Google Scholar] [CrossRef]

72. Iacoviello F, Di Cocco V, Rossi A, Cavallini M. Fatigue crack tip damaging micromechanisms in pearlitic ductile cast irons. Fatigue Fract Eng Mater Struct. 2015;38(2):238–45. doi:10.1111/ffe.12215. [Google Scholar] [CrossRef]

73. Akrache R, Lu J. Three-dimensional calculations of high cycle fatigue life under out-of-phase multiaxial loading. Fatigue Fract Eng Mater Struct. 1999;22(6):527–34. doi:10.1046/j.1460-2695.1999.00172.x. [Google Scholar] [CrossRef]

74. Chantier I, Bobet V, Billardon R, Hild F. A probabilistic approach to predict the very high-cycle fatigue behaviour of spheroidal graphite cast iron structures. Fatigue Fract Eng Mater Struct. 2000;23(2):173–80. doi:10.1046/j.1460-2695.2000.00228.x. [Google Scholar] [CrossRef]

75. Mendez N, Beranger R. Fatigue life assessment of nodular cast iron containing casting defects. Fatigue Fract Eng Mater Struct. 2001;22(4):289–300. doi:10.1046/j.1460-2695.1999.00162.x. [Google Scholar] [CrossRef]

76. Holmberg E, Torstenfelt B, Klarbring A. Fatigue constrained topology optimization. Struct Multidiscip Optim. 2014;50(2):207–19. doi:10.1007/s00158-014-1054-6. [Google Scholar] [CrossRef]

77. Månsson T, Nilsson F. Fatigue life estimation of cast components. Int J Cast Met Res. 2001;13(6):373–8. doi:10.1080/13640461.2001.11819418. [Google Scholar] [CrossRef]

78. Čanžar P, Tonković Z. Nodular cast iron-fatigue crack measurement and simulation. Key Eng Mater. 2013;577–578:473–6. doi:10.4028/www.scientific.net/kem.577-578.473. [Google Scholar] [CrossRef]

79. Caldera M, Chapetti M, Massone JM, Sikora JA. Influence of nodule count on fatigue properties of ferritic thin wall ductile iron. Mater Sci Technol. 2007;23(8):1000–4. doi:10.1179/174328407X185910. [Google Scholar] [CrossRef]

80. Collini L, Nicoletto G. Determination of the relationship between microstructure and constitutive behaviour of nodular cast iron with a unit cell model. J Strain Anal Eng Des. 2005;40(2):107–16. doi:10.1243/030932405x7692. [Google Scholar] [CrossRef]

81. Zhao D, Wang H. Topology optimization of compliant mechanisms considering manufacturing uncertainty, fatigue, and static failure constraints. Processes. 2023;11(10):2914. doi:10.3390/pr11102914. [Google Scholar] [CrossRef]

82. Hübner S, Trubitz P, Henschel S, Krüger L. Influence of microstructure on static and cyclic fracture toughness of EN-GJS-600-3 nodular cast iron. Int J Met. 2023;17(2):1217–28. doi:10.1007/s40962-022-00849-y. [Google Scholar] [CrossRef]

83. Gottschalk H, Schmitz S. Optimal reliability in design for fatigue life. SIAM J Control Optim. 2014;52(5):2727–52. doi:10.1137/120897092. [Google Scholar] [CrossRef]

84. Rathod V, Yadav OP, Rathore A, Jain R. Reliability-based design optimization considering probabilistic degradation behavior. Qual Reliab Eng Int. 2012;28(8):911–23. doi:10.1002/qre.1281. [Google Scholar] [CrossRef]

85. Boursier Niutta C, Tridello A, Paolino DS. Fatigue design of additive manufacturing components through topology optimization: comparison of methodologies based on the defect distribution and on the stress gradient. Fatigue Fract Eng Mater Struct. 2023;46(9):3429–45. doi:10.1111/ffe.14082. [Google Scholar] [CrossRef]

86. Lukhi M, Hütter G, Kuna M. A novel micromechanics approach for understanding of fatigue in nodular cast iron. Procedia Struct Integr. 2018;13(4):607–12. doi:10.1016/j.prostr.2018.12.100. [Google Scholar] [CrossRef]

87. Hou J, Zhu J, Wang J, Zhang W. Topology optimization of the multi-fasteners jointed structure considering fatigue constraints. Int J Simul Multidisci Des Optim. 2018;9:A4. doi:10.1051/smdo/2018003. [Google Scholar] [CrossRef]

88. Ezeh OH, Susmel L. On the notch fatigue strength of additively manufactured polylactide (PLA). Int J Fatigue. 2020;136(5):105583. doi:10.1016/j.ijfatigue.2020.105583. [Google Scholar] [CrossRef]

89. Hassanifard S, Hashemi SM. On the strain-life fatigue parameters of additive manufactured plastic materials through fused filament fabrication process. Addit Manuf. 2020;32(3):100973. doi:10.1016/j.addma.2019.100973. [Google Scholar] [CrossRef]

90. Sartorti R, Kriegesmann B, Hawla D, Pedersen CBW. Topology optimization for fatigue reserve factors. Struct Multidiscip Optim. 2024;67(8):141. doi:10.1007/s00158-024-03849-0. [Google Scholar] [CrossRef]

91. Nabaki K, Shen J, Huang X. Effect of different fatigue constraints on optimal topology of structures with minimum weight. Eng Struct. 2023;288(2):116149. doi:10.1016/j.engstruct.2023.116149. [Google Scholar] [CrossRef]

92. Singh R, Matsuo T, Hayashi K, Endo M. High-cycle fatigue strength prediction of ductile Ni-resist cast iron containing casting defects. Int J Fatigue. 2022;163(6):107015. doi:10.1016/j.ijfatigue.2022.107015. [Google Scholar] [CrossRef]

93. Iacoviello F, Di Cocco V, Cavallini M. Ductile cast irons: microstructure influence on fatigue crack propagation resistance. Frat Ed Integrità Strutturale. 2010;4(13):3–16. doi:10.3221/igf-esis.13.01. [Google Scholar] [CrossRef]

94. El Magri A, Vanaei S, Shirinbayan M, Vaudreuil S, Tcharkhtchi A. An investigation to study the effect of process parameters on the strength and fatigue behavior of 3D-printed PLA-graphene. Polymers. 2021;13(19):3218. doi:10.3390/polym13193218. [Google Scholar] [PubMed] [CrossRef]

95. Saga M, Kopas P, Vasko M. Some computational aspects of vehicle shell frames optimization subjected to fatigue life. Commun Sci Lett Univ Zilina. 2010;12(4):73–9. doi:10.26552/com.c.2010.4.73-79. [Google Scholar] [CrossRef]

96. Steglich D, Brocks W. Micromechanical modelling of damage and fracture of ductile materials. Fatigue Fract Eng Mater Struct. 1998;21(10):1175–88. doi:10.1046/j.1460-2695.1998.00078.x. [Google Scholar] [CrossRef]

97. Saoudi A, Bouazara M, Marceau D. Study of the fatigue life and weight optimization of an automobile aluminium alloy part under random road excitation. Shock Vib. 2010;17(2):107–21. doi:10.1155/2010/845609. [Google Scholar] [CrossRef]

98. Nasr A, Bouraoui C, Fathallah R, Nadot Y. Probabilistic high cycle fatigue behaviour of nodular cast iron containing casting defects. Fatigue Fract Eng Mater Struct. 2009;32(4):292–309. doi:10.1111/j.1460-2695.2009.01330.x. [Google Scholar] [CrossRef]

99. Suresh S, Lindström SB, Thore CJ, Torstenfelt B, Klarbring A. Topology optimization using a continuous-time high-cycle fatigue model. Struct Multidiscip Optim. 2020;61(3):1011–25. doi:10.1007/s00158-019-02400-w. [Google Scholar] [CrossRef]

100. Gróza M, Váradi K. Fatigue design of ferritic-pearlitic nodular cast iron components with surface discontinuities. J Mech Eng. 2018;64(6):356–64. doi:10.5545/sv-jme.2017.5120. [Google Scholar] [CrossRef]

101. Suresh S, Lindström SB, Thore CJ, Klarbring A. Topology optimization for transversely isotropic materials with high-cycle fatigue as a constraint. Struct Multidiscip Optim. 2021;63(1):161–72. doi:10.1007/s00158-020-02677-2. [Google Scholar] [CrossRef]

102. Aliakbari K. Failure analysis of ductile iron crankshaft in four-cylinder diesel engine. Int J Met. 2021;15(4):1223–37. doi:10.1007/s40962-020-00550-y. [Google Scholar] [CrossRef]

103. Gonçalves LKS, Rosa UL, de Lima AMG. Fatigue damage investigation and optimization of a viscoelastically damped system with uncertainties. J Braz Soc Mech Sci Eng. 2019;41(9):382. doi:10.1007/s40430-019-1879-4. [Google Scholar] [CrossRef]

104. Gebhardt C, Trimborn T, Weber F, Bezold A, Broeckmann C, Herty M. Simplified ResNet approach for data driven prediction of microstructure-fatigue relationship. Mech Mater. 2020;151(3):103625. doi:10.1016/j.mechmat.2020.103625. [Google Scholar] [CrossRef]

105. Vaško A. Comparison of mechanical and fatigue properties of SiMo- and SiCu-types of nodular cast iron. Mater Today Proc. 2020;32:168–73. doi:10.1016/j.matpr.2020.04.184. [Google Scholar] [CrossRef]

106. Lee JW, Yoon GH, Jeong SH. Topology optimization considering fatigue life in the frequency domain. Comput Math Appl. 2015;70(8):1852–77. doi:10.1016/j.camwa.2015.08.006. [Google Scholar] [CrossRef]

107. Endo M, Iseda K. Prediction of the fatigue strength of nodular cast irons under combined loading. Int J Mod Phys B. 2006;20(25n27):3817–23. doi:10.1142/s0217979206040428. [Google Scholar] [CrossRef]

108. Jimenez-Martinez M, Alfaro-Ponce M. Effects of synthetic data applied to artificial neural networks for fatigue life prediction in nodular cast iron. J Braz Soc Mech Sci Eng. 2021;43(1):10. doi:10.1007/s40430-020-02747-y. [Google Scholar] [CrossRef]

109. Vaško A, Uhríčik M, Belan J, Pastierovičová L, Kaňa V. Fatigue behaviour of NiCr-type of austenitic nodular cast iron. Procedia Struct Integr. 2023;51:129–34. doi:10.1016/j.prostr.2023.10.078. [Google Scholar] [CrossRef]

110. Yamabe J, Kobayashi M. Influence of casting surfaces on fatigue strength of ductile cast iron. Fatigue Fract Eng Mater Struct. 2006;29(6):403–15. doi:10.1111/j.1460-2695.2006.01017.x. [Google Scholar] [CrossRef]

111. Ferreira CM, Vicente CMS, Sardinha M, Leite M, Reis L. Characterization of 3D printed ABS specimens under static and cyclic torsional loadings. Procedia Struct Integr. 2021;34(825):205–10. doi:10.1016/j.prostr.2021.12.030. [Google Scholar] [CrossRef]

112. Teke IT, Akbulut M, Ertas AH. Topology optimization and fatigue analysis of a lifting hook. Procedia Struct Integr. 2021;33(12):75–83. doi:10.1016/j.prostr.2021.10.011. [Google Scholar] [CrossRef]

113. Frascio M, Avalle M, Monti M. Fatigue strength of plastics components made in additive manufacturing: first experimental results. Procedia Struct Integr. 2018;12(3):32–43. doi:10.1016/j.prostr.2018.11.109. [Google Scholar] [CrossRef]

114. Hassanifard S, Behdinan K. Anisotropy and internal flaws effects on fatigue response of notched 3D-printed PLA parts. Mater Today Commun. 2023;35(1):105734. doi:10.1016/j.mtcomm.2023.105734. [Google Scholar] [CrossRef]

115. Gebhardt C, Nellessen J, Bührig-Polaczek A, Broeckmann C. Influence of aluminum on fatigue strength of solution-strengthened nodular cast iron. Metals. 2021;11(2):311. doi:10.3390/met11020311. [Google Scholar] [CrossRef]

116. Ahmadi R, D’Andrea D, Santonocito D, Risitano G. Fatigue investigation of 3D-printed notched PLA specimens by thermographic methods with FEM simulation integration. Procedia Struct Integr. 2024;53(3):97–111. doi:10.1016/j.prostr.2024.01.013. [Google Scholar] [CrossRef]

117. Gu X, Cao Y, Zhu J, Wang J, Zhang W, Moumni Z. Shape optimization of SMA structures with respect to fatigue. Mater Des. 2020;189(1):108456. doi:10.1016/j.matdes.2019.108456. [Google Scholar] [CrossRef]

118. Scacco F, Campagnolo A, Franceschi M, Meneghetti G. Strain-controlled fatigue behavior of a nodular cast iron in real off-highway axles: effects of casting skin and strain ratio. Metals. 2022;12(3):426. doi:10.3390/met12030426. [Google Scholar] [CrossRef]

119. Shirani M, Härkegård G. Fatigue life distribution and size effect in ductile cast iron for wind turbine components. Eng Fail Anal. 2011;18(1):12–24. doi:10.1016/j.engfailanal.2010.07.001. [Google Scholar] [CrossRef]

120. Jap NSF, Pearce GM, Hellier AK, Russell N, Parr WC, Walsh WR. The effect of raster orientation on the static and fatigue properties of filament deposited ABS polymer. Int J Fatigue. 2019;124(4):328–37. doi:10.1016/j.ijfatigue.2019.02.042. [Google Scholar] [CrossRef]

121. Vaško A, Uhríčik M, Kuchariková L, Tillová E. Microstructure, mechanical and fatigue properties of SiMo- and SiCu- nodular cast irons. Procedia Struct Integr. 2018;13:1527–32. doi:10.1016/j.prostr.2018.12.312. [Google Scholar] [CrossRef]

122. Lee J, Huang A. Fatigue analysis of FDM materials. Rapid Prototyp J. 2013;19(4):291–9. doi:10.1108/13552541311323290. [Google Scholar] [CrossRef]

123. Vaško M, Vaško A. Correlation between charge composition and fatigue properties of nodular cast irons. Appl Mech Mater. 2014;474:291–6. doi:10.4028/www.scientific.net/amm.474.291. [Google Scholar] [CrossRef]

124. Sága M, Vaško M, Ságová Z, Handrik M. Effective algorithm for structural optimization subjected to fatigue damage and random excitation. Sci J Silesian Univ Technol Ser Transp. 2018;99:149–61. doi:10.20858/sjsutst.2018.99.14. [Google Scholar] [CrossRef]

125. Vaara J, Väntänen M, Laine J, Kemppainen J, Frondelius T. Prediction of the fatigue limit defining mechanism of nodular cast iron based on statistical microstructural features. Eng Fract Mech. 2023;277(433):109004. doi:10.1016/j.engfracmech.2022.109004. [Google Scholar] [CrossRef]

126. Pedranz M, Fontanari V, De Biasi R, Berto F, Santus C, Benedetti M. A simplified strain energy density approach for multiaxial fatigue predictions. Int J Mech Sci. 2025;288(3):109961. doi:10.1016/j.ijmecsci.2025.109961. [Google Scholar] [CrossRef]

127. Matpadi Raghavendra A, Kalkur A, Maurel V, Marcin L, Proudhon H. Fatigue life prediction at mesoscopic scale of samples containing casting defects: a novel energy based non-local model. Int J Fatigue. 2024;179(1–2):108485. doi:10.1016/j.ijfatigue.2024.108485. [Google Scholar] [CrossRef]

128. Pedranz M, Fontanari V, Santus C, Lusuardi D, Berto F, Benedetti M. A strain energy density design approach for large cast iron components: from microstructural analysis to multiaxial fatigue response. Int J Fatigue. 2023;175:107824. doi:10.1016/j.ijfatigue.2023.107824. [Google Scholar] [CrossRef]

129. Chiocca A, Pedranz M, Zanini F, Carmignato S, Fontanari V, Benedetti M, et al. Application of the effective critical plane approach for the fatigue assessment of ductile cast iron under multiaxial and non-proportional loading conditions. Int J Fatigue. 2025;192(1):108716. doi:10.1016/j.ijfatigue.2024.108716. [Google Scholar] [CrossRef]

130. Bleicher C, Pittel C, Kansy A, Niewiadomski J, Kaufmann H. Strain-life behavior of thick-walled nodular cast iron. Mater Test. 2024;66(4):459–77. doi:10.1515/mt-2023-0307. [Google Scholar] [CrossRef]

131. Ye H, Li Z, Wei N, Su P, Sui Y. Fatigue topology optimization design based on distortion energy theory and independent continuous mapping method. Comput Model Eng Sci. 2021;128(1):297–314. doi:10.32604/cmes.2021.016133. [Google Scholar] [CrossRef]

132. Li Y, Zhou G, Chang T, Yang L, Wu F. Topology optimization with aperiodic load fatigue constraints based on bidirectional evolutionary structural optimization. Comput Model Eng Sci. 2022;130(1):499–511. doi:10.32604/cmes.2022.017630. [Google Scholar] [CrossRef]

133. Wang Q, Zhang X. Fatigue reliability based optimal design of planar compliant micropositioning stages. Rev Sci Instrum. 2015;86(10):105117. doi:10.1063/1.4933387. [Google Scholar] [PubMed] [CrossRef]

134. Lino CE, Ferreira ALS, Silva CE. Topology optimization for local fatigue constraints: a solution using the augmented Lagrangian method. In: Proceedings of the joint XLV Ibero-Latin-American Congress on Computational Methods in Engineering (CILAMCE); 2024 Nov 24–27; Vitória, Brazil. [Google Scholar]

135. Marzbanrad J, Hoseinpour A. Structural optimization of MacPherson control arm under fatigue loading. Teh Vjesn. 2017;24(1):289–95. (In Croatian). doi:10.17559/tv-20150225090554. [Google Scholar] [CrossRef]

136. Mrzygłód MW, Kurek M, Łagoda T. The application of the criteria of multiaxial fatigue in the critical plane for the topology optimization of a structure. AIP Conf Proc. 2016;1780(1):040003. doi:10.1063/1.4965944. [Google Scholar] [CrossRef]

137. Solberg K, Guan S, Razavi N, Welo T, Chan KC, Berto F. Fatigue of additively manufactured 316L stainless steel: the influence of porosity and surface roughness. Fatigue Fract Eng Mater Struct. 2019;42(9):2043–52. doi:10.1111/ffe.13077. [Google Scholar] [CrossRef]

138. Ingersoll B, Ning A. Efficient incorporation of fatigue damage constraints in wind turbine blade optimization. Wind Energy. 2020;23(4):1063–76. doi:10.1002/we.2473. [Google Scholar] [CrossRef]

139. Avanzini A. Fatigue behavior of additively manufactured stainless steel 316L. Materials. 2022;16(1):65. doi:10.3390/ma16010065. [Google Scholar] [PubMed] [CrossRef]

140. Hu YN, Wu SC, Withers PJ, Zhang J, Bao HYX, Fu YN, et al. The effect of manufacturing defects on the fatigue life of selective laser melted Ti-6Al-4V structures. Mater Des. 2020;192(3):108708. doi:10.1016/j.matdes.2020.108708. [Google Scholar] [CrossRef]

141. Moshtaghzadeh M, Bakhtiari A, Izadpanahi E, Mardanpour P. Artificial neural network for the prediction of fatigue life of a flexible foldable origami antenna with Kresling pattern. Thin Walled Struct. 2022;174(5):109160. doi:10.1016/j.tws.2022.109160. [Google Scholar] [CrossRef]

142. Hao WQ, Tan L, Yang XG, Shi DQ, Wang ML, Miao GL, et al. A physics-informed machine learning approach for notch fatigue evaluation of alloys used in aerospace. Int J Fatigue. 2023;170:107536. doi:10.1016/j.ijfatigue.2023.107536. [Google Scholar] [CrossRef]

143. Garrett JC, Mei H, Giurgiutiu V. An artificial intelligence approach to fatigue crack length estimation from acoustic emission waves in thin metallic plates. Appl Sci. 2022;12(3):1372. doi:10.3390/app12031372. [Google Scholar] [CrossRef]

144. Wang C, Li Y, Tran NH, Wang D, Khatir S, Wahab MA. Artificial neural network combined with damage parameters to predict fretting fatigue crack initiation lifetime. Tribol Int. 2022;175(2020):107854. doi:10.1016/j.triboint.2022.107854. [Google Scholar] [CrossRef]

145. Zhan Z, He X, Tang D, Dang L, Li A, Xia Q, et al. Recent developments and future trends in fatigue life assessment of additively manufactured metals with particular emphasis on machine learning modeling. Fatigue Fract Eng Mater Struct. 2023;46(12):4425–64. doi:10.1111/ffe.14152. [Google Scholar] [CrossRef]

146. Wang H, Gao SL, Wang BT, Ma YT, Guo ZJ, Zhang K, et al. Recent advances in machine learning-assisted fatigue life prediction of additive manufactured metallic materials: a review. J Mater Sci Technol. 2024;198:111–36. doi:10.1016/j.jmst.2024.01.086. [Google Scholar] [CrossRef]

147. Schneller W, Leitner M, Maier B, Grün F, Jantschner O, Leuders S, et al. Artificial intelligence assisted fatigue failure prediction. Int J Fatigue. 2022;155(6):106580. doi:10.1016/j.ijfatigue.2021.106580. [Google Scholar] [CrossRef]

148. Reza Kashyzadeh K, Ghorbani S. New neural network-based algorithm for predicting fatigue life of aluminum alloys in terms of machining parameters. Eng Fail Anal. 2023;146(1):107128. doi:10.1016/j.engfailanal.2023.107128. [Google Scholar] [CrossRef]

149. He G, Zhao Y, Yan C. Multiaxial fatigue life prediction using physics-informed neural networks with sensitive features. Eng Fract Mech. 2023;289(8):109456. doi:10.1016/j.engfracmech.2023.109456. [Google Scholar] [CrossRef]

150. Wang L, Zhu SP, Luo C, Liao D, Wang Q. Physics-guided machine learning frameworks for fatigue life prediction of AM materials. Int J Fatigue. 2023;172(1):107658. doi:10.1016/j.ijfatigue.2023.107658. [Google Scholar] [CrossRef]

151. Lian Z, Li M, Lu W. Fatigue life prediction of aluminum alloy via knowledge-based machine learning. Int J Fatigue. 2022;157(2):106716. doi:10.1016/j.ijfatigue.2021.106716. [Google Scholar] [CrossRef]

152. Horňas J, Běhal J, Homola P, Senck S, Holzleitner M, Godja N, et al. Modelling fatigue life prediction of additively manufactured Ti-6Al-4V samples using machine learning approach. Int J Fatigue. 2023;169:107483. doi:10.1016/j.ijfatigue.2022.107483. [Google Scholar] [CrossRef]