Magneto Thermosolutal-Aiding Free Convection in a Nanofluid-Filled-Non-Darcy Porous Annulus under Local Thermal Non-Equilibrium Approach

1  Introduction

Thermosolutal convection describes the fluid flow generated by the combined influence of temperature and salinity gradients, which induce two separate diffusion processes. The study of double-diffusive natural convection has gained significant importance across numerous scientific and engineering disciplines, such as medicine, astrophysics, biology, geosciences, chemical engineering, as well as applications such as solar ponds, thermal energy storage, petroleum extraction, food processing, and material manufacturing. Within saturated porous media, this phenomenon is particularly relevant to key technological operations like geothermal reservoir fluid dynamics, hydrocarbon recovery, grain preservation, evaporative cooling systems, and drying techniques. To better understand the interplay of heat and mass transfer under these conditions, extensive research has been conducted on a variety of enclosure geometries and sizes in porous media environments [1–3].

Siavashi et al. [4] explored non-Darcy thermosolutal free convection within an inclined permeable cavity, emphasizing how the configurations of heat and solute sources affect their transfer rates and system irreversibilities to identify the optimal source arrangement. He et al. [5] examined natural convection-driven heat and mass transfer inside an irregular permeable enclosure, focusing on how porosity and buoyancy ratio influence the transport processes, concluding that these parameters strongly affect temperature and concentration profiles as well as fluid flow patterns. Li et al. [6] utilized a numerical technique coupled with the Newton-Raphson technique to model double diffusion convective flow in a permeable parallelogram domain. Akbal and Baytas [7] conducted Computational Fluid Dynamics (CFD) simulations on combined thermal and solutal free convection in a square Darcian permeable cavity, identifying notable leakage phenomena, assuming uniform properties. Reddy et al. [8] studied the influence of cross-diffusion effects on unsteady heat and solute transfer during double-diffusion buoyancy-driven convection in an inclined porous domain with nonuniformly varying thermo-solutal boundaries, finding that cross-diffusion terms reduce sensitivity to changes in inclination angle. Additionally, Alluguvelli et al. [9] explored bioconvective nanofluid containing oxytactic microorganisms within a porous square cavity, accounting for viscous dissipation. In their CFD investigation of thermosolutal convection involving an electrically conducting fluid mixture, Rebhi et al. [10] showed that fluid velocity and the rates of heat and mass transmission inside porous media are markedly impacted by the combined impacts of inertial forces and magnetic fields.

Most numerical and analytical studies on porous materials assume Local Thermal Equilibrium (LTE), where the fluid and solid phases share the same temperature. However, this assumption breaks down in many real applications due to Local Thermal Non-Equilibrium (LTNE) effects. For instance, Straughan [11] showed that incorporating Cattaneo heat flux in the solid phase reveals new oscillatory convection modes not captured by standard LTNE models. Sunil et al. [12] also highlighted the importance of LTNE in thermally unstable porous systems with complex fluid behavior. Tayebi et al. [13] and Ahmed et al. [14] demonstrated that LTNE-based modeling significantly improves accuracy in non-Newtonian and mixed convection flows. Kouki et al. [15] emphasized the role of interfacial heat transfer between fluid and solid, while Straughan [16] reinforced the theoretical necessity of LTNE in advanced porous flow analyses. Such considerations are vital in drying, food preservation, electronics cooling, and other applications where fluid and solid temperatures diverge. The LTNE framework is especially advantageous for modeling heat transmission in penetrable media where there is a considerable disparity in thermal conductivities between the solid structure and the saturating fluid [17,18].

Relatively few studies have addressed thermosolutal free convection phenomena incorporating the LTNE model in porous media. A stability examination was done by Chen et al. [19] for thermosolutal convection under LTNE conditions, considering solute properties dependent on temperature. Bera et al. [20] investigated the impact of LTNE on double-diffusive buoyancy-driven convection in a rectangular domain loaded by porous media saturated by fluid, reporting that LTNE significantly alters heat transfer rates and temperature fields but has minimal impact on mass transmission and concentration distribution. Lakshmi et al. [21] studied thermosolutal free convection in circular annuli and rectangular enclosures filled with porous materials using a modified Darcy model under LTNE assumptions. Harzallah et al. [22] examined the influence of opposing thermal and solutal buoyancy forces in free convection within a vertically oriented porous cavity with finite-thickness walls, applying both Darcy and LTNE models to delineate the validity range of the LTE hypothesis for various controlling parameters. Zhuang et al. [23] employed CFD to analyze thermosolutal free convection of non-Newtonian liquids inside a permeable chamber, with the inclusion of thermal production in the solid matrix and chemical reactions, based on the non-Darcy and LTNE frameworks.

Tayebi [24] studied double-diffusive free convection and associated irreversibilities within a porous container via the Darcy-Brinkman-Forchheimer model combined with LTNE conditions, introducing a novel dimensionless parameter defined as the ratio of thermal production rates between fluid and solid phases. Further, Tayebi et al. [25] examined magnetohydrodynamic thermosolutal free convection of nanoliquid-saturated media containing an undulating permeable cylinder under LTNE, demonstrating that increasing Rayleigh number, Darcy number, and porosity enhances heat and mass transfer, while reductions in Hartmann and Lewis numbers produce similar effects. Bera et al. [26] applied the LTNE hypothesis with the Darcy model to investigate thermosolutal free convection in square and thin cavities, highlighting the profound efficacy of thermal non-equilibrium on thermal and solutal transport. In their study, Carvalho et al. [27] adopted the LTNE model to examine laminar magnetohydrodynamic (MHD) convection driven via thermal and solutal buoyancy in a porous square domain, finding that solid-to-fluid thermal conductivity ratio and porosity notably affect heat and mass transmission processes. Altawallbeh et al. [28] employed the LTNE assumption in Darcy flow analysis to examine double-buoyancy convection within an anisotropic, fluid-saturated permeable medium containing internal heat sources and Soret effects. Their results indicated that double diffusion induces convective instability manifested as oscillatory behavior rather than stationary convection, with the Soret coefficient exerting limited influence on oscillation characteristics.

In the present work, a classical engineering configuration is adopted to investigate double-diffusive free convection inside a porous concentric annulus under LTNE conditions using an extended Darcy-Brinkman-Forchheimer model. The study considers a nanofluid as the working fluid, owing to its well-documented enhancements in thermal performance across various applications [29–32], attributed to its elevated thermal conductivity. Empirical correlations are employed to estimate the nanofluid’s thermophysical properties [33]. The computational domain accounts for internal heat generation within both the nanofluid and the solid matrix. Moreover, the presence of a magnetic field serves as an external control mechanism, influencing convective patterns through Lorentz forces and as a result modulating the overall heat transmission performance [34–38]. Accordingly, the system is subjected to an applied magnetic field, including the effects of Joule heating. This investigation contributes originality by integrating these aspects to deepen the understanding of thermal transport phenomena in porous media, with potential implications for energy-efficient thermal system design.

2  Problem Formulation

Under an LTNE situation, consider a non-Darcy porous medium loaded via a nanofluid and confined between two horizontal cylindrical concentric cylinders of radius ratio RR = 2 with a horizontally directed magnetic field acting. The inner impermeable cylinder is at a high level of solute and temperature, while the outer impermeable cylinder is kept at a low level of solute and temperature. Consequently, thermosolutal natural convection impacted by a magnetic field and governed by the Boussinesq approximation is induced within the annulus. The flow is steady, laminar, and the nanofluid is treated as incompressible. The Joule heating effect due to the magnetic field, and the internal heat production within the nanofluid phase (qnf) and the solid phase (qs) of the porous annulus are considered, while the coupling effects between thermal and solutal gradients, thermal radiation, and viscous dissipation are disregarded. Fig. 1 graphically depicts the problem design.

Figure 1: The physical domain

2.1 Governing Equations

The governing mathematical model for this problem, based on the aforementioned assumptions, can be expressed as:

∂u∂x+∂v∂y=0(1)

ρnfε2(u∂u∂x+v∂u∂y)=−∂p∂x+μnfε(∂2u∂x2+∂2u∂y2)−(μnfKu+1.75150ε3/2ρnfuu2+v2K)(2)

ρnfε2(u∂v∂x+v∂v∂y)=−∂p∂y+μnfε(∂2v∂x2+∂2v∂y2)−(μnfKv+1.75150ε3/2ρnfvu2+v2K)+(ρβ)nfg(T−Tc)+(ρβc)g(c−cc)−σhnfB02v(3)

u∂c∂x+v∂c∂y=Df(∂2c∂x2+∂2c∂y2)(4)

The LTNE model requires two heat equations, for the fluid phase and solid phase in the porous medium:

u∂Tnf∂x+v∂Tnf∂y=ελnf(ρCp)nf(∂2Tnf∂x2+∂2Tnf∂y2)+h(Ts−Tnf)(ρCp)nf+σhnfB02v2(ρCp)nf+εqnf(ρCp)nf(5)

(1−ε)λs(∂2Ts∂x2+∂2Ts∂y2)=h(Ts−Tnf)+(1−ε)qs(6)

Stream function, ψ expression given as:

{u=∂ψ∂yv=−∂ψ∂x(7)

The non-dimensional form of the governing equations is derived via the following characteristic scale:

(X,Y)=(xR2−R1,yR2−R1),(U,V)=(u(R2−R1)αf,v(R2−R1)αf),P=p(R2−R1)2αf2ρf,ΔT=(Th−Tc),ΔC=(ch−cc),θnf=Tnf−TcΔT,θs=Ts−TcΔT,C=c−ccΔC,Ψ=ψαf

γ=ελf(1−ε)λs,H=h(R2−R1)2ελf,F=1.75(R2−R1)ε3/2150K

Ra=(R2−R1)3gβf(Th−Tl)υfαf,Le=αfDf,N=βcΔCβfΔT,Pr=υfαf,Ha=(R2−R1)B0σf/μf,Da=K(R2−R1)2,J=Ha2αf2μf(R2−R1)2ΔTελf,Qnf=qnf(R2−R1)2ΔTλf,Qs=qs(R2−R1)2ΔTλs

Thus, the Eqs. (1)–(7) become, respectively:

∂U∂X+∂V∂Y=0(8)

1ε2(U∂U∂X+V∂U∂Y)=−∂P∂X+ρfρnfμnfμfPrε(∂2U∂X2+∂2U∂Y2)−ρfρnfμnfμfPrDaU−FU2+V2U(9)

1ε2(U∂V∂X+V∂V∂Y)=−∂P∂Y+μnfμfρfρnfPrε(∂2V∂X2+∂2V∂Y2)−μnfμfρfρnfPrDaU−FU2+V2V+(ρβ)nfρnfβfRaPr(θnf+NC)−ρfρnfσhnfσfHa2PrV(10)

u∂C∂X+v∂C∂Y=1Le(∂2C∂X2+∂2C∂Y2)(11)

1ε(U∂θnf∂X+V∂θnf∂Y)=λnfλf(ρCp)f(ρCp)nf(∂2θnf∂X2+∂2θnf∂Y2)+(ρCp)f(ρCp)nfH(θs−θnf)+(ρCp)f(ρCp)nfJV2+(ρCp)f(ρCp)nfQnf(12)

∂2θs∂X2+∂2θs∂Y2=γH(θs−θnf)+Qs(13)

{U=∂Ψ∂YV=−∂Ψ∂X(14)

The influence of incorporating Al2O3 nanoparticles on the overall thermophysical properties of the nanofluid is quantified using the following expressions:

ρnf=(1−ϕ)ρf+ϕρp(15)

(ρCp)nf=(1−ϕ)(ρCp)f+ϕ(ρCp)p(16)

(ρβ)nf=(1−ϕ)(ρβ)f+ϕ(ρβ)p(17)

σnf=σp(1+3(σpσf−1)ϕ/(σpσf)−(σpσf)ϕ)(18)

Adopting Corcione’s correlations [33], μnf and λnf are estimated as:

μnf=μf/(1−34.87(dp/df)−0.3ϕ1.03)(19)

λnf=λf(1+4.4Re0.4Pr0.66(Tnf/Tfr)10(λp/λf)0.03ϕ0.66)(20)

Re=2kbρfT/πμf2dp(21)

The thermo-physical properties of the host liquid (H2O) and Al2O3 nanomaterials are extracted from tables in [39,40].

The dimensionless thermosolutal boundary conditions would be:

C = θnf = θs = 1 and Ψ = 0; at the internal surface

C = θnf = θs = 0 and Ψ = 0; at the external surface

2.2 Evaluation of Heat and Solutal Transfer

The Nusselt and Sherwood numbers are employed to quantify the rates of heat and solute transfer from the heated and solute-enriched surface to the nanofluid and solid phases within the porous annulus:

{Nunf=(∂θnf∂X)2+(∂θnf∂Y)2|nNus=(∂θs∂X)2+(∂θs∂Y)2|nSh=(∂C∂X)2+(∂C∂Y)2|nNuavg_nf=1S∫0sNufdsNuavg_s=1S∫0sNusdsShavg=1S∫0sSh ds(22)

where: n represents the coordinate direction normal to the inner surface, S is the dimensionless length along the inner surface, and s is the coordinate along the inner surface.

3  Numerical Process and Validation

The finite volume technique utilizing the second-order upwind procedure is implemented to discretize governing Eqs. (8)–(13) along with their related boundary conditions, and they are then solved utilizing the SIMPLE (Semi-Implicit Method for Pressure-Linked Equations) algorithm, considering the convergence standard to be 10−6. Various grid resolutions are employed to ensure grid-independent results and to achieve sufficient resolution that avoids inaccuracies in the numerical outcomes. The established grid for the domain under consideration is portrayed in Fig. 2. To show the accuracy of the present results, a comparison of current findings with those of Matin and Pop [41] and Abu-Nada et al. [42], in the presence of nanofluid, along with the experimental findings of Kuehn and Goldstein [43] (see Figs. 3–5). Furthermore, further comparison of the outcomes with those of Bera et al. [20] for double-diffusion NC under LTNE situation was done as illustrated in Fig. 6 and Table 1.

Figure 2: Mapping generation of the computational domain

Figure 3: Our outputs, Ref. [41] for the isotherms and streamlines at ϕ = 0.03 (water-Cu), RR = 2.5, and Pr = 6.21

Figure 4: Our outputs, Refs. [41] and [42] for Nuavg

Figure 5: Our results besides those of Kuehn and Goldstein [43] for an annulus filled with air at Ra = 4.7 × 104 and RR = 2.6

Figure 6: Validation of the current code outputs against those of [20], (a): Ra = 104, Da = 10−2, ε = 0.97, H = 10, γ = 10, Le = 0.1, N = 1, and (b): Ra = 106, Da = 10−4, ε = 0.97, H = 10, γ = 10, Le = 0.1, N = 1

4  Results and Interpretation

The results are given through contour plots of the stream function, concentration, and temperature fields of both the nanofluid and solid phases within the porous annulus, considering aiding buoyancy flow (N > 1). The porous annulus, characterized by a porosity ε = 0.5 and a Darcy number Da = 10−3, consistently operates under LTNE conditions for an inter-phase heat transfer coefficient H = 10, and a conductivity ratio, γ = 10. In this study, the following parameters were varied: Ra = 102 to 105; Le = 0.1 to 10; Ha = 10 to 50; N = 1 to 5; and Q=Qnf=Qs= 0 to 20. The nanoparticle volume fraction ϕ was held constant at 0.04 throughout the analysis.

Fig. 7a demonstrates patterns of streamlines, isotherms for both nanofluid and solid phases, and isoconcentrations in the porous annulus considering LTNE conditions for various Rayleigh numbers (Ra = 102, 103, 104, 105) when Q = 0, N = 1, Le = 1, and Ha = 30. The streamlines illustrate that the flow within the annulus is organized into vortices, with one rotating in the clockwise direction and the other in the counterclockwise direction. This configuration is typical in natural convection scenarios where buoyancy-driven flows create symmetric counter-rotating vortices. At low Ra, the streamlines are weak, indicating minimal double-diffusive convective flow with relatively simple and concentric contours showing weak circulation. As Ra increases, the streamlines become more pronounced, indicating stronger convection with increasingly complex patterns and stronger circulation. At the highest Ra value, the streamlines indicate very strong convection with highly intricate and vigorous flow patterns. The flow remains symmetric within the annulus for all Ra values. The isotherms for the solid and nanofluid phases are relatively smooth and symmetric at low Ra, indicating a more diffusive temperature distribution with minimal convective influence. Both fluid and solid phase isotherms show increasing distortion with higher Ra values, indicating stronger convective heat transfer. The differences between the isotherms of the nanofluid and solid phases reflect LTNE conditions, where the solid and fluid phases’ temperatures are not similar. It is also noticed that the formation of an inert and cold region at the bottom of the annulus at a large Rayleigh number with high-temperature and concentration gradients on the annulus’s surfaces reflects high thermal and mass exchange rates. Additionally, the isoconcentration and nanofluid isotherms are comparable at this Lewis number (Le = 1), reflecting similar heat and mass diffusion rates. Fig. 7b indicates that the additional heat source within the annulus affects the temperature distribution. In the absence of internal heating, maximum temperatures were near the hot wall, but they became concentrated in the middle of the annulus and headed to the top with high Ra. Weak temperature gradients on the annulus’s surfaces are observed in comparison to a case in which Q = 0. Moreover, the existence of the internal heat source limits the inert area formed when Q = 0. Overall, internal heating promotes natural convective flow circulation. Fig. 8a,b illustrates the impact of Ha on the flow and transport features of the nanoliquid within the porous domain, considering LTNE. Without internal heat generation (Fig. 8a), increasing Ha suppresses convective flow due to the damping action of Lorentz forces, which oppose the buoyancy-driven motion. This results in a weakening of the streamlines, evidenced by the reduced intensity of circulation and an observable upward displacement and expansion of the vortex cores. This behavior reflects the resistance imposed by the magnetic field on the motion of fluid, which alters the flow structure by stabilizing it and reducing flow mixing. When internal heat generation is introduced (Fig. 8b), a similar suppression trend is observed, but with slightly more pronounced effects on circulation due to the enhanced buoyancy competing with the Lorentz forces. The streamlines show weaker circulation and a further shift of the vortex structure, confirming the magnetic field’s role in reshaping the flow dynamics under thermal excitation.

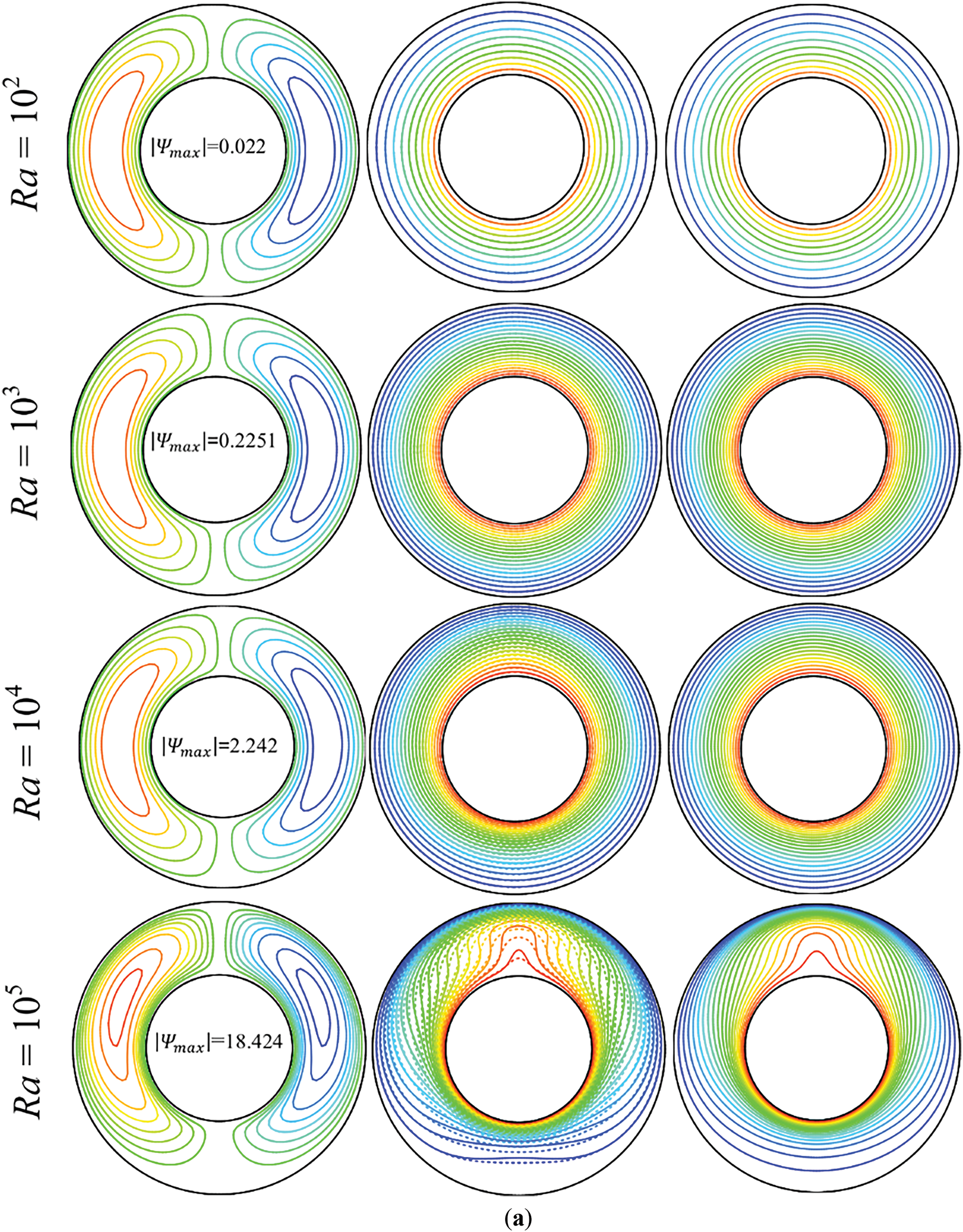
Figure 7: Effect of Ra on the streamline, nanofluid and solid phases isotherms, and isoconcentrations, (a): Q = 0, (b): Q = 10 (Ha = 30, N = 1, and Le = 1)

Figure 8: Effect of Ha on the streamline patterns, nanofluid and solid phases isotherms, and isoconcentrations (a): Q = 0, (b): Q = 10 (Ra = 105, N = 1 and Le = 1)

Regarding thermal transport, the temperature gradients along the inner cylinder diminish with increasing Ha in the absence of internal heat production, indicating reduced heat transfer rates due to weakened convective motion. However, considering internal heat generation, increasing Ha causes the hot region within the annulus to expand, and the temperature gradients near the inner surface to widen. This behavior suggests a complex interaction between internal heating and magnetic damping that can lead to enhanced thermal gradients despite reduced fluid motion. The concentration distributions, on the other hand, appear relatively insensitive to variations in Ha.

Fig. 9a,b illustrates the impact of varying buoyancy ratios (N) on the flow behavior in a scenario where only aiding flows are considered (N > 0). As the N increases, the solutal buoyancy force, which is proportional to N, reinforces the thermal buoyancy, resulting in a concerted flow direction. This cooperation between thermal and solutal buoyancies would lead to a notable increment in stream function values as N rises, indicating enhanced flow effects. Further, as the N increases, both nanofluid and solid isotherms and isoconcentrations are developed more and represent higher gradients of concentration and temperature in the direction normal to the surface, which in turn imply increased rates of heat and mass transfer within the annular region. Additionally, it is noted that in the case of Q = 10, a thermal layer forms on the inner cylinder’s upper surface, resulting in the division of the hot zone at the top of the annulus into two side portions.

Figure 9: Effect of N on the streamline patterns, nanofluid and solid phases isotherms, and isoconcentrations, (a): Q = 0, (b): Q = 10 (Ha = 30, Ra = 105, and Le = 1)

The efficacy of the Le on the flow, θ, and concentration contours in the annulus is illustrated in Fig. 10a,b. The Le, which would measure the ratio of thermal diffusivity to mass diffusivity of the nanofluid, was varied between 0.1 and 10 in this investigation. The other parameters were held constant at Q = 0 (Fig. 10a), Q = 10 (Fig. 10b), Ha = 30, Ra = 105, and N = 1. For Le = 0.1, at both values of Q, the mass diffusivity would be more than the thermal diffusivity, leading mass transfer primarily to occur through diffusion, while convection dominates thermal transfer. As the Lewis number increases, the scenario shifts. The thermal diffusion forces (thermal resistance) surpass the mass diffusion forces (mass resistance). Consequently, heat transfer begins to occur more through diffusion, reducing nanofluid circulation, while mass transfer becomes predominantly driven by natural convection, as evidenced by the increased distortion of the isoconcentration lines. It should also be noted that, in contrast to the situation when Q = 0, when Q = 10, the temperature gradients around the inner cylinder increase progressively with higher Lewis numbers. This indicates greater heat transfer rates at elevated Lewis values.

Figure 10: Effect of Le on the streamline patterns, nanofluid and solid phases isotherms, and isoconcentrations, (a): Q = 0, (b): Q = 10 (Ha = 30, Ra = 105 and N = 1)

The fields portrayed in Fig. 11 demonstrate the significant influence of internal heat generation on the thermal and flow behavior within the porous annulus. At low internal heating (Q = 5), a localized hot zone develops near the upper region of the annulus, leading to weak thermal gradients along the inner cylinder and, consequently, a reduced heat transfer rate. As Q increases, the thermal energy supplied to the system intensifies, causing the hot region to expand and the temperature gradients near the inner surface to widen, indicating enhanced heat transfer. Correspondingly, the strength of the nanofluid circulation rises due to the increased thermal energy input, as reflected by higher absolute stream function (Ψ) values. Additionally, the isoconcentration contours reveal that mass convection weakens with increasing Q, attributed to the altered thermal distribution, which modifies the interaction between solutal and thermal buoyancy forces under LTNE conditions.

Figure 11: Effect of Q on the streamline patterns, nanofluid and solid phases isotherms, and isoconcentrations (Ha = 30, Ra = 105, N = 1 and Le = 1)

An important finding presented in Fig. 12, which displays the efficacy of the internal heat production parameter (Q) on mass and heat transfer rates for diverse Le, is that the rate of heat transfer for both the solid and nanofluid phases within the porous medium initially decreases with increasing Q up to Q = 5, and then increases with further increases in Q. This behavior could be attributed to the impact of internal heat on the temperature distribution in the porous annulus, as previously mentioned. The amounts of Nuavg_nf and Nuavg_s for different Lewis numbers (Le) also confirm this trend. After Q = 7, the rate of heat transfer increases with rising Le after it had decreased with Le. Additionally, the influence of Q on the Shavg would be more highlighted at higher Le amounts. The difference between the Nuavg_nf and Nuavg_s values reflects the LTNE condition in the porous system. Fig. 13 illustrates how the thermal Rayleigh (Ra) affects the mass and heat transfer rates from the inner heated and salted cylinder to the solid and nanofluid phases inside the porous annulus for different Lewis numbers (Le) when heat generation is absent (Q = 0) and Q = 10. For Ra < 104 and no internal heat generation, both Nuavg_nf and Nuavg_s are less sensitive to variations in Ra. However, the sensitivity increases as Ra grows. Shavg starts to increase with Ra at a value of 103. The mass transfer rate grows with increasing Le while the heat transfer rates decrease. At Q = 10, the behavior of Nuavg_nf and Nuavg_s is completely inverted, with both decreasing as Ra increases. The mass transfer rate reduces considering internal heat production, but maintains the same behavior with respect to Ra and Le.

Figure 12: Q effects on Nuavg_nf, Nuavg_s, and Shavg for various Le

Figure 13: Ra effects on Nuavg_nf, Nuavg_s, and Shavg for various Le at Q = 0 and Q = 10

Fig. 14 revealed that, in the absence of a heating source, Nuavg_nf and Nuavg_s drop when the magnetic field increases, whereas they improve when Q = 10. This trend reflects the combined effects of the Lorentz forces, which act in the opposing direction of both buoyancy forces and internal heat generation, leading to enhancements in heat transfer. However, it was discovered that Shavg decreases independently of Q value when the magnetic field intensity increases. Fig. 15 exhibits the change of Nuavg_nf, Nuavg_s, and Shavg with buoyancy ratio (N) for diverse Le for Ra = 105, Ha = 30, at Q = 0 and 10. Without internal heat production in the porous matrix, as N increases from 1 to 5, Nuavg_nf, Nuavg_s, and Shavg improve for all Le values, indicating increased heat and mass transfer rates. However, the extent of the increase in heat transfer rates decreases as the Lewis number increases. Higher Le values, on the other hand, provide more significant increases in mass transfer with increasing N. The introduction of internal heat alters the behavior of heat transfer rates with N and Le, causing the heat transfer rate to decline with less impact by buoyancy variations, particularly at large Le. Lower Le indicates more sensitivity to changes in N.

Figure 14: Ha effects on Nuavg_nf, Nuavg_s, and Shavg for various Le at Q = 0 and Q = 10

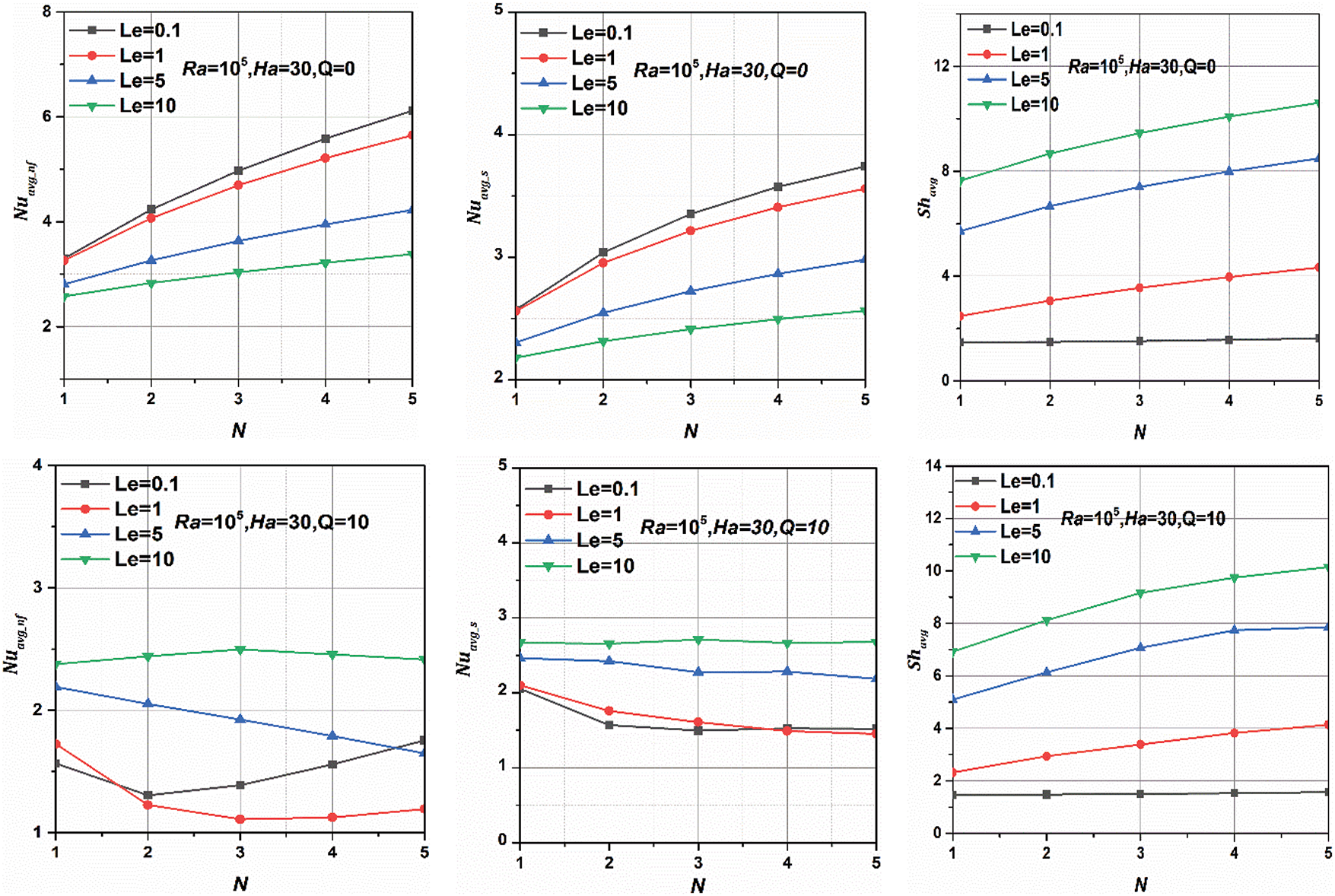
Figure 15: N effects on Nuavg_nf, Nuavg_s, and Shavg for various Le at Q = 0 and Q = 10

5  Conclusion

This paper investigates magneto-aided thermosolutal natural convection in a nanofluid-filled porous annulus, employing the Darcy-Brinkman-Forchheimer extended model under the LTNE state. The study incorporates heat production in both phases of the porous medium as well as Joule-heating effects. After a robust validation of the numerical code, the analysis of the phenomenon and its interaction with governing parameters reveals several important and unexpected results, summarized as follows:

•   As predicted, increasing Ra and N enhances the double-diffusive convective circulation of the nanofluid, while increasing Le and Ha suppress it. This trend holds both in the absence and presence of internal heat generation.

•   Introducing an interior heat generation in both phases, which is under LTNE conditions, significantly alters the heat transport mechanism and promotes double-diffusive convective circulation.

•   The rate of heat transmission for both the solid and nanofluid phases initially decreases with increasing Q up to Q = 5, and then increases with further increments in Q. Conversely, the mass transfer rate generally decreases as Q increases.

•   Another significant finding is that the Lewis number (Le) causes the heat transfer rates for the solid and fluid phases to reduce when Q = 0 or when Q ≤ 7. However, when Q > 7, increasing Le would lead to a growth in heat transfer rates. The mass transfer rate is consistently noticed to grow with Le.

•   It was found that the Ra effects are positive on Nuavg_nf, and Nuavg_s without internal heat generation, and negative with internal heat generation. Shavg is found to be increased as Ra increases.

•   Applying a magnetic field to the system lessens the heat transfer rates from the hot cylinder for both phases in the absence of internal heat, while enhancing it in the presence of internal heat. The mass transfer rate decreases as Ha increases.

•   Aiding buoyancy flow tends to augment both heat and mass transfer rates. However, its behavior varies when internal heat generation is present and is influenced by the Lewis number.

This study is limited to steady-state, two-dimensional analysis, assuming a uniform magnetic field and ideal nanofluid behavior without accounting for particle agglomeration, sedimentation, or thermophoresis. Future work could address unsteady, three-dimensional effects, complex magnetic fields, and more advanced nanofluid models for enhanced realism.

Acknowledgement: The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, Saudi Arabia, for funding this research work through the project number NBU-FFR-2025-2193-15.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, Saudi Arabia, for funding this research work through the project number NBU-FFR-2025-2193-15.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and mathematical formulation, data collection: Abdelhakim Lahrech, Tahar Tayebi; analysis and interpretation of results: Abdelhakim Lahrech, Tahar Tayebi, Mohamed Kallel, Mehdi Hashemi-Tilehnoee; draft manuscript preparation: Abdelhakim Lahrech, Tahar Tayebi, Mohamed Kallel, Mehdi Hashemi-Tilehnoee, Ali J. Chamkha; writing—review and editing: Tahar Tayebi, Mohamed Kallel, Mehdi Hashemi-Tilehnoee, Ali J. Chamkha. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Das D, Roy M, Basak T. Studies on natural convection within enclosures of various (non-square) shapes—a review. Int J Heat Mass Transf. 2017;106:356–406. [Google Scholar]

2. Izadi S, Armaghani T, Ghasemiasl R, Chamkha AJ, Molana M. A comprehensive review on mixed convection of nanofluids in various shapes of enclosures. Powder Technol. 2019;343:880–907. [Google Scholar]

3. Kouki M, Nayak MK, Irshad K, Al Mesfer MK, Danish M, Pasha AA, et al. Analysis of thermosolutal buoyancy-driven suspension comprising nano-encapsulated phase change materials using finite element method and ANN-based MLP algorithm. J Taiwan Inst Chem Eng. 2025;168(7):105912. doi:10.1016/j.jtice.2024.105912. [Google Scholar] [CrossRef]

4. Siavashi M, Bordbar V, Rahnama P. Heat transfer and entropy generation study of non-Darcy double-diffusive natural convection in inclined porous enclosures with different source configurations. Appl Therm Eng. 2017;110(Part 1):1462–75. doi:10.1016/j.applthermaleng.2016.09.060. [Google Scholar] [CrossRef]

5. He B, Lu S, Gao D, Chen W, Lin F. Lattice Boltzmann simulation of double diffusive natural convection in heterogeneously porous media of a fluid with temperature-dependent viscosity. Chin J Phys. 2020;63(5):186–200. doi:10.1016/j.cjph.2019.10.027. [Google Scholar] [CrossRef]

6. Li PW, Chen W, Fu ZJ, Fan CM. Generalized finite difference method for solving the double-diffusive natural convection in fluid-saturated porous media. Eng Anal Bound Elem. 2018;95:175–86. doi:10.1016/j.enganabound.2022.04.038. [Google Scholar] [CrossRef]

7. Akbal S, Baytaş F. Effects of non-uniform porosity on double diffusive natural convection in a porous cavity with partially permeable wall. Int J Therm Sci. 2008;47(7):875–85. doi:10.1016/j.ijthermalsci.2007.07.007. [Google Scholar] [CrossRef]

8. Reddy ES, Panda S, Nayak MK, Makinde OD. Cross flow on transient double-diffusive natural convection in inclined porous trapezoidal enclosures. Heat Transfer. 2021;50(1):849–75. doi:10.1002/htj.21908. [Google Scholar] [CrossRef]

9. Alluguvelli R, Balla CS, Naikoti K, Makinde OD. Nanofluid bioconvection in porous enclosure with viscous dissipation. Indian J Pure Appl Phys (IJPAP). 2022;60(1):78–89. [Google Scholar]

10. Rebhi R, Hadidi N, Bennacer R. Non-Darcian effect on double-diffusive natural convection inside aninclined square Dupuit-Darcy porous cavity under a magnetic field. Therm Sci. 2021;25(1 Part A):121–32. [Google Scholar]

11. Straughan B. Porous convection with local thermal non-equilibrium temperatures and with Cattaneo effects in the solid. Proc R Soc A Math Phys Eng Sci. 2013;469(2157):20130187. doi:10.1098/rspa.2013.0187. [Google Scholar] [CrossRef]

12. Sunil, Choudhary S, Mahajan A. Conditional stability for thermal convection in a rotating couple-stress fluid saturating a porous media with temperature- and pressure-dependent viscosity using a thermal non-equilibrium model. J Non-Equilib Thermodyn. 2014;39(2):61–78. doi:10.1515/jnetdy-2013-0025. [Google Scholar] [CrossRef]

13. Tayebi T, Ali R, Kouki M, Nayak MK, Galal AM. Neural network modeling of non-Newtonian NEPCMs suspension in a non-Darcy porous medium under LTNE conditions. J Taiwan Inst Chem Eng. 2025;167(5):105897. doi:10.1016/j.jtice.2024.105897. [Google Scholar] [CrossRef]

14. Ahmed SE, Raizha ZAS, Alsubaie F. Artificial neural network and CBS-FEM techniques for mixed convection in lid-driven tank heated by triangular fins and filled with permeable medium: two-energy equations model. J Taiwan Inst Chem Eng. 2025;167(19):105850. doi:10.1016/j.jtice.2024.105850. [Google Scholar] [CrossRef]

15. Kouki M, Pasha AA, Nayak MK, Algarni S, Alqahtani T, Irshad K. Buoyancy-driven nano-suspension subject to interstitial solid/nanofluid heat transfer coefficient: role of local thermal non-equilibrium (LTNE). J Taiwan Inst Chem Eng. 2024;165(5):105702. doi:10.1016/j.jtice.2024.105702. [Google Scholar] [CrossRef]

16. Straughan B. Convection with local thermal non-equilibrium and microfluidic effects. Vol. 32. Cham: Springer; 2015. [Google Scholar]

17. Malashetty MS, Swamy M, Heera R. Double diffusive convection in a porous layer using a thermal non-equilibrium model. Int J Therm Sci. 2008;47(9):1131–47. [Google Scholar]

18. Esfe MH, Bahiraei M, Hajbarati H, Valadkhani M. A comprehensive review on convective heat transfer of nanofluids in porous media: energy-related and thermohydraulic characteristics. Appl Therm Eng. 2020;178(1):115487. doi:10.1016/j.applthermaleng.2020.115487. [Google Scholar] [CrossRef]

19. Chen X, Wang S, Tao J, Tan W. Stability analysis of thermosolutal convection in a horizontal porous layer using a thermal non-equilibrium model. Int J Heat Fluid Flow. 2011;32(1):78–87. doi:10.1016/j.ijheatfluidflow.2010.06.003. [Google Scholar] [CrossRef]

20. Bera P, Pippal S, Sharma AK. A thermal non-equilibrium approach on double-diffusive natural convection in a square porous-medium cavity. Int J Heat Mass Transf. 2014;78:1080–94. doi:10.1016/j.ijheatmasstransfer.2014.07.041. [Google Scholar] [CrossRef]

21. Lakshmi KM, Laroze D, Siddheshwar PG. Natural convection of a binary liquid in cylindrical porous annuli/rectangular porous enclosures with cross-diffusion effects under local thermal non-equilibrium state. Int J Heat Mass Transf. 2022;184(9):122294. doi:10.1016/j.ijheatmasstransfer.2021.122294. [Google Scholar] [CrossRef]

22. Harzallah HS, Jbara A, Slimi K. Double-diffusive natural convection in anisotropic porous medium bounded by finite thickness walls: validity of local thermal equilibrium assumption. Transp Porous Media. 2014;103(2):207–31. doi:10.1007/s11242-014-0298-3. [Google Scholar] [CrossRef]

23. Zhuang YJ, Yu HZ, Zhu QY. A thermal non-equilibrium model for 3D double diffusive convection of power-law fluids with chemical reaction in the porous medium. Int J Heat Mass Transf. 2017;115(12):670–94. doi:10.1016/j.ijheatmasstransfer.2017.08.068. [Google Scholar] [CrossRef]

24. Tayebi T. Analysis of the local non-equilibria on the heat transfer and entropy generation during thermal natural convection in a non-Darcy porous medium. Int Commun Heat Mass Transf. 2022;135(5):106133. doi:10.1016/j.icheatmasstransfer.2022.106133. [Google Scholar] [CrossRef]

25. Tayebi T, Dahmane F, Jamshed W, Chamkha AJ, El Din SM, Raizah Z. Double-diffusive magneto-natural convection of nanofluid in an enclosure equipped with a wavy porous cylinder in the local thermal non-equilibrium situation. Case Stud Therm Eng. 2023;43:102785. [Google Scholar]

26. Bera P, Pippal S, Khan A. A thermal non-equilibrium approach on thermo-solutal natural convection due to the lateral flux of heat and solute on enclosure walls: multi-solutions and oscillations. Int J Heat Mass Transf. 2019;128:1322–43. doi:10.1016/j.ijheatmasstransfer.2018.08.076. [Google Scholar] [CrossRef]

27. Carvalho PH, de Lemos MJ. Double-diffusive laminar free convection in a porous cavity simulated with the two-energy equation model. Int Commun Heat Mass Transf. 2017;82(7):89–96. doi:10.1016/j.icheatmasstransfer.2017.02.005. [Google Scholar] [CrossRef]

28. Altawallbeh A, Bhadauria BS, Hashim I. Linear and nonlinear double-diffusive convection in a saturated porous layer with Soret effect under local thermal non-equilibrium model. J Porous Media. 2018;21(13):1395–413. [Google Scholar]

29. Saidur R, Leong KY, Mohammed HA. A review on applications and challenges of nanofluids. Renew Sustain Energ Rev. 2011;15(3):1646–68. [Google Scholar]

30. Wang X, Song Y, Li C, Zhang Y, Ali HM, Sharma S, et al. Nanofluids application in machining: a comprehensive review. Int J Adv Manuf Technol. 2024;131(5):3113–64. [Google Scholar]

31. Wen D, Lin G, Vafaei S, Zhang K. Review of nanofluids for heat transfer applications. Particuology. 2009;7(2):141–50. [Google Scholar]

32. Mahian O, Kianifar A, Kalogirou SA, Pop I, Wongwises S. A review of the applications of nanofluids in solar energy. Int J Heat Mass Transf. 2013;57(2):582–94. [Google Scholar]

33. Corcione M. Empirical correlating equations for predicting the effective thermal conductivity and dynamic viscosity of nanofluids. Energy Convers Manag. 2011;52(1):789–93. doi:10.1016/j.enconman.2010.06.072. [Google Scholar] [CrossRef]

34. Izadi M, Oztop HF, Sheremet MA, Mehryan SAM, Abu-Hamdeh N. Coupled FHD–MHD free convection of a hybrid nanoliquid in an inversed T-shaped enclosure occupied by partitioned porous media. Numer Heat Transfer, Part A: Appl. 2019;76(6):479–98. doi:10.1080/10407782.2019.1637626. [Google Scholar] [CrossRef]

35. Mahesh R, Mahabaleshwar US, Kumar PV, Öztop HF, Abu-Hamdeh N. Impact of radiation on the MHD couple stress hybrid nanofluid flow over a porous sheet with viscous dissipation. Results Eng. 2023;17(3):100905. doi:10.1016/j.rineng.2023.100905. [Google Scholar] [CrossRef]

36. Armaghani T, Kolsi L, Khashi’ie NS, Rashad AM, Mansour MA, Salah T, et al. Unsteady flow of hybrid nanofluid with magnetohydrodynamics-radiation-natural convection effects in a U-shaped wavy porous cavity. Comput Model Eng Sci. 2024;141(3). doi:10.32604/cmes.2024.056676. [Google Scholar] [CrossRef]

37. Majeed AH, Mahmood R, Eldin SM, Saddique I, Saleem S, Jawad M. Natural convection and irreversibility of nanofluid due to inclined magnetohydrodynamics (MHD) filled in a cavity with Y-shape heated fin: FEM computational configuration. Comput Model Eng Sci. 2024;139(2):1505–19. doi:10.32604/cmes.2023.030255. [Google Scholar] [CrossRef]

38. Karthik S, Iranian D, Al-Mdallal QM. Numerical simulation of magneto-hydrodynamic fluid flow with heat sink, chemical diffusion and Powell Eyring fluid behavior using Cattaneo-Christov source term. Int J Thermofluids. 2024;22(2):100616. doi:10.1016/j.ijft.2024.100616. [Google Scholar] [CrossRef]

39. Tayebi T, Chamkha AJ. Entropy generation analysis during MHD natural convection flow of hybrid nanofluid in a square cavity containing a corrugated conducting block. Int J Numer Methods Heat Fluid Flow. 2020;30(3):1115–36. [Google Scholar]

40. Tayebi T, Öztop HF, Chamkha AJ. Natural convection and entropy production in hybrid nanofluid filled-annular elliptical cavity with internal heat generation or absorption. Ther Sci Eng Prog. 2020;19:100605. [Google Scholar]

41. Matin MH, Pop I. Natural convection flow and heat transfer in an eccentric annulus filled by copper nanofluid. Int J Heat Mass Transf. 2013;61(4):353–64. doi:10.1016/j.ijheatmasstransfer.2013.01.061. [Google Scholar] [CrossRef]

42. Abu-Nada E, Masoud Z, Hijazi A. Natural convection heat transfer enhancement in horizontal concentric annuli using nanofluids. Int Commun Heat Mass Transf. 2008;35(5):657–65. doi:10.1016/j.icheatmasstransfer.2007.11.004. [Google Scholar] [CrossRef]

43. Kuehn TH, Goldstein RJ. An experimental and theoretical study of natural convection in the annulus between horizontal concentric cylinders. J Fluid Mech. 1976;74(4):695–719. doi:10.1017/S0022112076002012. [Google Scholar] [CrossRef]