Multi-Kernel Bandwidth Based Maximum Correntropy Extended Kalman Filter for GPS Navigation

1  Introduction

The Filtering techniques for state estimation in dynamic state-space models have a broad range of applications in real-world engineering fields, including target tracking, navigation, attitude determination, robotics, telecommunications, and system identification [1–4]. For linear Gaussian systems, the ideal estimators are well-known, and the Kalman filter (KF) is commonly used for this purpose. Nevertheless, the optimal or systematic solution of the posterior probability density functions (PDFs) for a nonlinear Gaussian system is often rarely accessible. The relative resemblance of two random variables into the kernel width is measured using the technique called correentropy, in which the kernel bandwidth controls the “observational insights” like a zoom lens [5]. It is utilized as a resilient cost for state estimation, adaptable filtering, regression, and machine learning techniques [6] since it is naturally resistant to outliers. A linear estimator called the Kalman filter (KF) gives an ideal recursive solution for linear systems [7]. The fields of navigation, target tracking, sensor fusion, and many more have made extensive use of it. Its performance could, however, deteriorate in the presence of unknown disturbances and non-Gaussian noises. To deal with heavy-tailed measurement disturbances, Huang et al. [8] designed a maximum correntropy Kalman filter (MCKF) based on the concept of mixture Correntropy (MC).

Afterward, several extensions of KF were derived under maximum correntropy criterion (MCC), including the cubature Kalman filter (CKF) [9], extended Kalman filter (EKF) [10], Chandrasekhar-based Kalman filter [11], distributed Kalman filter (DKF) [12], interacting multiple model Kalman filter (IMMKF) [13], and the unscented Kalman filter (UKF) [14]. In general, these filters can withstand measurement outliers with ease. When faced with unknown disturbances and non-Gaussian process sounds, they might not perform well. One explanation for this is that these filters manage multivariate non-Gaussian noises by using a uniform kernel bandwidth. An additional explanation is that precisely modeling disturbances is challenging. To enhance learning performance, the mixture correntropy was thus introduced. Here, the kernel function is constructed as a linear combination of multiple zero-mean Gaussian kernels, each having a distinct width [15]. The MCC algorithm still has a flaw, though, in that it can only combine zero-mean Gaussian kernels, which might lead to subpar performance when dealing with complex non-Gaussian disturbances like multimodal distributions. Recently, correntropy has been employed to handle non-Gaussian format noise to overcome the issues related to this noise [16]. One information-theoretic quantity that has been exploited recently to produce significant performance gains across several industries is correntropy [17]. It can record higher-order loss statistics. Additionally, modeling noise followed by a Gaussian distribution, multiple-model filters, and EKF can aid the boosting robustness against outliers, while computing the difficulty and efficacy will always be a limitation [18,19].

Additionally, the MCC solution is commonly achieved through iterative techniques. The most widely used methods are gradient-based algorithms, as they are straightforward to understand. However, they require a free parameter, the step size, and have a slow rate of convergence. Another effective approach is the fixed-point iteration (FPI) technique, which has a small step size with a faster rate of convergence. MC-based KF ignores the recurrence of covariance matrices, which may have an impact on the accuracy of their estimations [20]. In addition, investigations using robust filters illustrate the computational cost in a high-noise environment. Heavy-tailed noises have several practical applications, including radar measuring systems and global positioning systems (GPS). More specifically, the motivation also includes the optimization criterion for correntropy is adjusted into information-theoretic learning (ITL) [21]. The multi-kernel bandwidth maximum correntropy extended Kalman filter (MCEKF) is an advanced filtering method aimed at improving GPS navigation accuracy. By using multiple kernel bandwidths, this approach enhances the traditional maximum correntropy framework, enabling it to more effectively handle non-Gaussian noise. Tackling the issues of unknown measurement noise covariance and measurement outliers in a vision/dual-inertial measurement unit (IMU) integrated attitude determination system. Adaptive filters presume the absence of measurement outliers, whereas robust filters depend on precise knowledge of the measurement noise covariance matrices [22–24]. Numerous studies on robustness and adaptivity filters against heavy-tailed non-Gaussian sounds have been conducted, and they have been widely applied to GPS navigation [25–27].

The contributions of this study are that we introduced a novel multi-kernel maximum correntropy extended Kalman filter (MKMC-EKF), where each Gaussian kernel in the mixture is centered at distinct locations, enhancing learning performance in GPS navigation. The use of the MKMC-EKF in our work is primarily aimed at addressing non-Gaussian noise in both the state and measurement vectors, rather than compensating for system nonlinearity alone. While the EKF inherently handles model nonlinearity through linearization, its performance degrades under heavy-tailed or impulsive noise. The MKMC-EKF enhances robustness by incorporating a multi-kernel correntropy (MKC) criterion in the measurement update, allowing it to better suppress the influence of outliers and adapt to complex noise distributions. The MKC improves adaptability to varying noise conditions, making GPS systems more robust against measurement disturbances. Optimizing noise parameters in MKC is addressed by minimizing the difference between the error PDF and a mixed-Gaussian function. The proposed MKMC-EKF enhances filtering performance by integrating multi-kernel bandwidth selection, ensuring robust state estimation in non-Gaussian noise. Unlike traditional methods, it leverages PDFs to model complex noise variations, improving accuracy in GPS navigation. Fixed-point iteration prevents divergence, optimizing kernel selection for stability. While computationally more intensive than EKF, its complexity remains feasible for real-time applications. Simulations confirm superior performance over EKF and MCC-EKF, particularly in heavy-tailed noise, demonstrating its reliability in dynamic environments. Moreover, it offers a significant deal of promise for application in numerous domains other than GPS navigation, involving complicated noise disturbances, including biomedical engineering, remote sensing, autonomous systems, and many more, because of its superior adaptability and stability.

The outline for the remaining content of the article is arranged as follows. We define and present numerous features of the MKMC-EKF in Section 2. We offer a formulation overview in Section 3 for MKC conceptualization. Following that, Section 5 presents the simulation results and discussion, and Section 6 provides the conclusion.

2  Notations in Mathematical Formulation

The notations used in this proposed study are as follows; E[.] represents expectation operator, κ(x,y) is the Mercer kernel with shift-variation, σ is the kernel bandwidth, Gσ is the Gaussian kernel, X and Y denote the random variables, FXY(x,y) is the joint probability function of X and Y, p is number of subkernels, N is number of samples in series, ei=xi−yi represents the i-th error, k is discrete-time index, Bp and Br are the covariances matrices, Pk− is prior error covariance matrix, JLMCC is the cost function for MCC, ep and er are process and measurement errors, xk, x^k−, and x^k,t+ are the real, predicted, and estimation states, and P^k,t is the posterior error covariance, M~p and M~r are diagonal matrices, σp,σr are the process and measurement bandwidths, K~t,k−1 is Kalman gain, dk represents the unknown state disturbance, qk and rk are Gaussian noises for system model, γ denotes the mapping matrix for unknown disturbance, m, n, and K are the dimensions of state, measurement, and small number of Kernels, respectively, used for time complexity analysis.

3  Methodologies

3.1 Multi-Kernel Correntropy (MKC)

Correntropy serves as a similarity measure for signal which are mapped nonlinearly into a featured space. Essentially, it generalizes the concept of autocorrelation into nonlinear domains. The relationship between two random variables X and Y with their joint PDF is FXY(x,y), the correntropy between them can be expressed as

V(X,Y)=E[κ(X,Y)]=∫κ(x,y)FXY(x,y)(1)

where E[⋅] is the expectation operator, and κ(x,y) is the Mercer kernel with shift-variation. The Gaussian kernel function is κ(x,y)=Gσ(e)=exp⁡(−e22σ2); where σ denotes the kernel bandwidth and the error is e=x−y. Here, FXY(x,y) is often unknown due to the limited availability of data. In such cases, correntropy can be estimated using a sample mean estimator as follows:

V(X,Y)=∑i=1pE[κ¯(Xi−Yi)]=∑i=1p∫κ¯(xi,yi)dFXiYi(xi,yi)(2)

where

κ¯(xi,yi)=σi2exp⁡(−ei22σi2)(3)

where the Gaussian function is represented by κ¯(xi,yi), σi denotes ith element of the kernel bandwidth, and the ith error is ei=xi−yi. It can be noted from (2) the kernel size σ=[σ1,σ2,......,σp]′, which controls both the weighted and observational pathway coefficients.

Further, the finite number of samples required for estimating the MKC [20,21] is

V(X,Y)=1N∑k=1N∑i=1pσiexp⁡(−ei2(k)2σi2)(4)

where the error for ith element at kth sample is ei(k)=xi(k)−yi(k), and the number of samples is N.

3.2 Derivation of System Model Algorithm

In this section, the core methodology for the proposed novel multi-kernel EKF is outlined.

[x^k−yk]=[f(xk)h(xk)]+ϑk(5)

where

ϑk=[x^k−−xkrk](6)

with

E[ϑkϑkT]=[P^k−00Rk]=[BpBpT00BrBrT]=BkBkT(7)

The prior error and the measurement noise covariance matrices are Pk− and Rk. Bk can be obtained from Cholesky decomposition method.

Multiplying Bk−1 at both sides of the Eq. (7) by, we will get

Φk=d(xk)+ek,(8)

where we got

Φk=Bk−1[x^k−yk],d(xk)=Bk−1[f(xk)h(xk)],ek=Bk−1ϑk(9)

The MCC-based cost function JMCC can be written as

JLMCC(xk)=1L∑i=1LGσ(Φk,i−di(xk))(10)

where the dimension L=n+m. The ith element of Φk is Φk,i. di(xk) is the ith row of d(xk), and error at k time step is ek,i=zk,i−di(xk).

Next, select the ideal estimation state based on MCC corresponding to xk is calculated as

xk+=arg⁡maxxkJLMCC(xk)=arg⁡maxxk∑i=1LGσ(ek,i)(11)

Therefore, the optimal solution of xk can be

(∂d∂xk)TMk(d(xk)−Φk)=0(12)

Further, by taking the linerization of d(xk) arround the estimation x^k,t+ through the fixed point iteratiion at every step, we obtained

x^k,t+=(DT(x^k,t−1+)Mk,t−1D(x^k,t−1+))−1DT(x^k,t−1+)Mk,t−1×(DT(x^k,t−1+)x^k,t−1+−d(x^k,t−1+)+Φk)(13)

Then,

D(x^k,t−1+)=∂d∂x|x=x^k,t−1+(14)

M~p=diag[Gσp(ep)],M~r=diag[Gσr(er)](15)

ep=Bp−1(x^k−−f(xk)),er=Br−1(yk−h(xk))(16)

We know that the process bandwidth vector is σp=[σ1,σ2,……,σn]′, and the measurement bandwidth vector can be expressed as σr=[σn+1,σn+2,……,σn+m]′, where ep and er are the process and measurement errors.

From Eqs. (7), (9) and (13), we got

(DT(x^k,t−1+)Mk,t−1D(x^k,t−1+))−1=((Bp−1)TM~pBp−1+HT(x^k,t−1+)×(Br−1)TM~rBr−1H(x^k,t−1+))−1(17)

Now considering matrix inversion lemma

(Bp−1)TM~pBp−1→A,HT(x^k,t−1+))−1→B,H(x^k,t−1+)→C,(Bp−1)TM~rBr−1→D(18)

Then we obtained

(DT(x^k,t−1+)Mk,t−1D(x^k,t−1+))−1=(Bp)T(M~p)−1BpT−Bp(M~p)−1BpTHT(x^k,t−1+)×(Br(M~r)−1BrT+H(x^k,t−1+)Bp)×(M~pBpTHT(x^k,t−1+))−1×H(x^k,t−1+)Bp(M~p)−1BpT(19)

Furthermore, we got

(DT(x^k,t−1+)Mk,t−1(D(x^k,t−1+)x^k,t−1+−d(x^k,t−1+)+Φk)=(Bp)TM~p)−1BpTx~k+HT(x^k,t−1+)(Br−1)TM~rBr−1×(yk+H(x^k(t−1))x^k,t−1+−h(x^k,t−1+))(20)

Finally, combining Eqs. (13), (19), (20), we found

x^k,t+=x^k−+K~k,t−1(yk−h(x^k,t−1+)−H(x^k,t−1+)(x^k−−x^k,t−1+))(21)

Again

H(x^k,t−1+)=∂h∂x|x=x^k,t−1+K~k,t−1=P^k,t−1−HT(x^k,t−1+)×(H(x^k,t−1+)P^k,t−1−HT(x^k,t−1+)+Rk,t−1)−1(22)

P^−k,t−1=Bp(M~p)BpT(23)

Rk,t−1=Br(M~p)BrT(24)

Additionally, the updated matrix of posterior error covariance is

P^k,t=(I−K~k,t−1H(x^k,t−1+))P^k−(I−K~k,t−1H(x^k,t−1+))T+K~k,t−1Rk(K~k,t−1)T(25)

It is noted that in (21), xk is in relation with the fixed-point equation of P^k,t−1− and Rk,t−1, which can be used in the algorithm. For avoiding the singularities of diagonal matrices, Mp and Mr, we have as follows:

M~p≥αIn×n, and M~r≥βIm×m(26)

where α and β represents two small positive numbers.

3.3 System Model with Non-Gaussian Noise and Disturbances

The model with process noise is

xk+1=φxk+γdk+qk,yk=h(xk)+rk(27)

where the unknown state disturbance is dk, qk and rk are the Gaussian noises and γ is the mapping matrix for the state disturbance. Further the derivations of state and measurement disturbances (see Ref. [21]).

Then, the model with measurement noise is

xk+1=φxk+qk,yk=h(xk)+γdk+rk(28)

In the simulation, we have considered the following non-Gaussian noises for process and measurement, such as

q1,k∼0.9N(0,0.1)+0.1N(0,20)q2,k∼0.9N(0,0.3)+0.1N(0,60)rk∼N(0,0.04)(29)

Then, the Gaussian noises are

q1,k∼N(0,0.1),q2,k∼N(0,0.1),rk∼N(0,0.4)(30)

Further, we assumed the disturbance is given by

dk(t)={10sin⁡(0.45πt)+rk,50≤t≥60rk otherwise(31)

4  MK (Multi-Kernel) Based Maximum Correntropy EKF (MKMC-EKF)

The MKMC-EKF approach offers further performance enhancements for the estimation process and control. Fig. 1 presents a flow chart outlining a singular series of the EKF that utilizes the MCC. The MCC-EKF can be viewed as a specific instance of the broader maximum MKC (MMKC) framework. Here, a novel robust KF based on the concept of MKMC, MKMC-EKF has been discussed to effectively address unusual disturbances and complexity, non-Gaussian noise distributions in satellite navigation.

Figure 1: Close-loop flow diagram for the MKMC-EKF

The proposed MKMC-EKF significantly enhances filtering performance in GPS navigation by improving adaptability to varying and non-Gaussian noise conditions. This is achieved through a multi-kernel correntropy framework that models complex noise distributions more accurately than traditional methods. Instead of assuming fixed noise characteristics, the filter optimizes kernel parameters by minimizing the discrepancy between the empirical error PDF and a mixed-Gaussian model. To ensure stability and prevent divergence, a fixed-point iteration strategy is employed for kernel selection. Although the approach introduces additional computational cost compared to the standard EKF, the complexity remains manageable for real-time implementation, offering a practical and robust solution for GPS systems operating in challenging noise environments. Techniques such as covariance-matching and correlation leverage innovation sequences for estimating noise covariances. The core principle of the covariance-matching method is to align the actual covariance of the residual with its theoretical value, ensuring consistency between the observed and expected covariance.

The steps involved for the computation of MKMC-EKF is summarized below:

(1)   Initializing x^0, P^0.

(2)   Then choose σp, σr, α, β with small positive value for the tolerance, and ε a threshold value.

(3)   Prediction, x^k−=f(x^k−1+), P^k−=Ψk−1P^k−1+Ψk−1T+Qk−1.

(4)   Calculate Bp and Br with P^−k,t−1=Bp(M~p)BpT and Rk,t−1=Br(M~p)BrT.

(5)   Updating, x^k,0+=x^k−.

(6)   Iteration loop: Calculating x^k,t+ from steps bellow:

i)   x^k,t+=x^k−+K~k,t−1(yk−h(x^k,t−1+)−H(x^k,t−1+)(x^k−−x^k,t−1+))

ii)   K~k,t−1=P^k,t−1−HT(x^k,t−1+)×(H(x^k,t−1+)P^k,t−1−HT(x^k,t−1+)+Rk,t−1)−1

iii)   P^−k,t−1=Bp(M~p)BpT

iv)   Rk,t−1=Br(M~p)BrT

v)   M~p=diag(Gσp(ep))

vi)   M~r=diag(Gσr(er))

vii)   ep=Bp−1x^k−−Bp−1x^k,t−1+

viii)   er=Br−1yk−Br−1x^k,t−1+

ix)   P^k,t=(I−K~k,t−1H(x^k,t−1+))P^k−(I−K~k,t−1H(x^k,t−1+))T+K~k,t−1Rk(K~k,t−1)T

(7)   If ‖x^k+−x^k,t−1+‖‖x^k,t+‖>ε, where t starts from 1. Do M~p≥αIn×n, M~r≥βIm×m, or else, set t=t+1, and repeat from the step 3.

Notably, the MKMC-EKF algorithm leverages a multi-kernel bandwidth framework, which helps to improve the estimation accuracy. As the kernel bandwidth increases, the influence of higher-order moments in the correntropy measure is reduced, causing the MKMC-EKF to gradually align with the behavior of the iterated EKF (IEKF). In this regime, the filter’s sensitivity to non-Gaussian noise diminishes, and it effectively reverts to a form dominated by the Gaussian assumptions, resembling the iterative refinement process characteristic of the IEKF.

5  Results and Discussion

Fig. 1 illustrates the schematic flow for the MKMC-EKF algorithm. The simulation aims to assess the proposed method’s effectiveness in managing time-varying satellite signal quality by comparing it with a standard GPS navigation approach. This study utilizes MATLAB® codes within commercially available software, specifically the Inertial Navigation System (INS) Toolbox and Satellite Navigation (SatNav) Toolbox, both developed by GPSoft LLC [28,29]. The INS Toolbox is used to create the trajectory of the vehicle, while the SatNav Toolbox provides satellite orbits and pseudoranges, supporting the implementation of different navigational filters, including EKF, MCC-EKFs, and MKMC-EKF.

Fig. 2 illustrates the simulated test trajectory, depicting the movement of the vehicle within the defined navigation scenario. The positions of the eight available GPS satellites are represented as red stars in Fig. 3, each labeled with its unique GPS ID. The spatial distribution of these satellites yields a geometry dilution of precision (GDOP) of approximately 2.5, signifying a well-conditioned positioning geometry that enhances the stability and accuracy of the navigation solution. This favorable GDOP suggests that geometric amplification of measurement errors is minimized, ensuring that the estimated position remains robust against minor variations in pseudorange observations. By maintaining this optimal satellite configuration, the experiment isolates the impact of pseudorange errors arising from signal propagation effects such as multipath interference and atmospheric delays on the positioning accuracy, providing a controlled framework for evaluating the performance of different filtering algorithms. The simulation of the vehicle is positioned roughly 100 m from the Earth’s surface.

Figure 2: The simulated vehicle trajectory

Figure 3: The satellite skyplot

To assess the impact of outliers due to multipath interruptions, multiple intentional and randomly generated errors were introduced into the GPS pseudorange observation data while the vehicle was in motion. The GPS measurements were distorted by various error sources, including ionospheric and tropospheric delays, multipath effects, and receiver noise. To minimize errors, it was assumed that differential GPS (DGPS) mode was active; however, this setup did not completely mitigate multipath effects and receiver thermal noise. Navigating in urban environments or areas with non-line-of-sight (NLOS) and multipath reception presents significant challenges for vehicles, as these conditions introduce erroneous data that can disrupt the GPS sensor’s positioning accuracy. This study conducted various error analyses to achieve a cleaner signal for GPS navigation, calculating metrics such as Mean Error (ME) and Root Mean Square Error (RMSE) at each time step, using statistical measurements across 100 Monte Carlo runs. The formulas are as follows used for these calculations:

ME(k)=1M∑m=1M(xk−x^k), m=1, …, M(32)

RMSE(k)=1K∑k=1K(xk−x^k)2,k=1,…,K(33)

where M is the total number of Monte Carlo runs and K is total time steps for one Monte Carlo run.

In this scenario, the altitude, velocity, and ballistic coefficient of a vertically falling body are estimated using a suitable tracking model derived from the equations of motion under aerodynamic drag. The model is formulated through rectangular (Euler) integration with a discrete sampling period of ΔT, ensuring numerical propagation of the system state over time (sec). Given that radar data is recorded at 1-s interval, the tracking system updates state estimates sequentially, incorporating new measurements to refine altitude and velocity estimates. The ballistic coefficient, which encapsulates the body’s aerodynamic properties and governs its deceleration due to atmospheric drag, is also inferred as part of the estimation process. This setup provides a basis for assessing the accuracy and stability of different filtering techniques in real-time tracking applications.

Fig. 4a–c displays the Mean Error precision across four filtering approaches such as EKF, MCC-EKF1, MCC-EKF2, and MKMC-EKF are used for various positioning comparisons. In this study, all EKF-based methods incorporate the MCC framework, while MKMC-EKF uniquely combines the MCC with a multi-kernel technique. The impact of time-varying noise strength is more pronounced with EKF compared to the other filters. Integrating the MCC mechanism enhances EKF’s adaptability to varying noise conditions by dynamically adjusting to non-Gaussian disturbances. The MCC-based multi-kernel approach in MKMC-EKF not only improves computational efficiency but also refines state estimation by effectively suppressing the influence of outliers. By leveraging multiple kernel functions, MKMC-EKF provides a more flexible and accurate representation of the underlying error distribution, leading to improved robustness against time-varying measurement noise. Additionally, the adaptive weighting of the Kalman gain ensures that updates remain stable even in the presence of abrupt noise variations. As a result, MKMC-EKF achieves positioning accuracy comparable to MCC-enhanced EKFs while offering superior efficiency in handling complex noise environments. Table 1 summarizes the performance of each algorithm in MEs for different positions. Furthermore, with only a slight increase in execution time compared to MCC-EKF1 and MCC-EKF2, MKMC-EKF achieves the highest positioning accuracy among the tested methods.

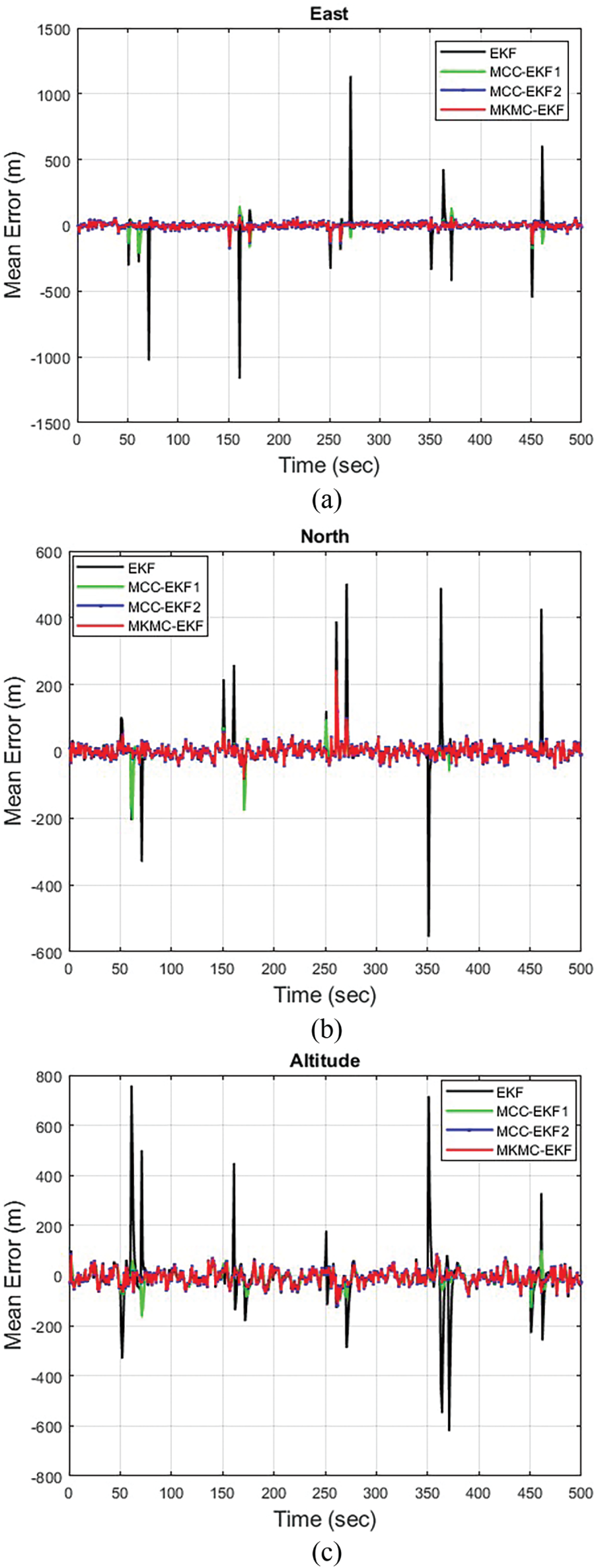
Figure 4: The different positional errors (a) East, (b) North, and (c) Altitude for MKMC-EKF in terms of ME

Fig. 5a–c depicts the Root Mean Square Error precision across distinct filtering techniques such as EKF, MCC-EKF1, MCC-EKF2, and MKMC-EKF are evaluated for various positioning scenarios. Table 2 compares the performance of these algorithms, showing that MCC-EKF1 and MCC-EKF2, where MKMC-EKF achieve the highest positioning accuracy among the methods analyzed. Notably, the fixed-point MKMC-EKF algorithm is designed to converge for the optimal results within a few iterations, significantly improving its efficiency for real-time GPS satellite navigation. By leveraging a multi-kernel approach, it adapts dynamically to varying noise distributions, ensuring stable and accurate state estimation even in challenging conditions. The fixed-point iteration method refines the Kalman gain updates, reducing computational complexity while maintaining high precision. Additionally, the algorithm’s ability to suppress outliers and mitigate the effects of non-Gaussian noise enhances its robustness, making it well-suited for applications requiring rapid and reliable positioning. This combination of fast convergence, adaptability, and noise resilience makes MKMC-EKF a highly effective solution for modern navigation systems. Moreover, the Kalman gain in Figs. 4 and 5 are primarily derived from the MKMC-EKF framework, but their optimization depends on the adaptive tuning of kernel width or different filtering methods are applied. Optimization technique Monte Carlo simulations is used to enhance estimation accuracy and stability under non-Gaussian noise.

Figure 5: The different positional errors (a) East, (b) North, and (c) Altitude for MKMC-EKF in terms of RMSE

Fig. 6a–c shows the probability density functions (PDFs) with small process and measurement noises for various filtering methods, such as EKF, MCC-EKF1, MCC-EKF2, and MKMC-EKF are evaluated across different positioning scenarios. The results highlight that MKMC-EKF provides the highest positioning accuracy among the methods tested. With a limited number of samples per iteration, outliers are more likely to be chosen as centers. To mitigate this, abnormal centers are set to zero when errors exceed a predefined threshold. The PDFs of MCC-EKF1, MCC-EKF2, and EKF outperform in estimation accuracy, while the proposed MKMC-EKF achieves the best results among all compared methods. EKF, relying on Gaussian assumptions and the minimum mean square error (MMSE) criterion, is highly sensitive to outliers, leading to deviations in state updates. In contrast, MCC-EKF and MKMC-EKF, based on MCC and MMKC, respectively are more robust to outliers. The use of a Gaussian kernel function to weight the Kalman gain helps suppress outlier influence during state updates. Additionally, the fixed-point MKMC-EKF algorithm is designed to converge to optimal results in just a few iterations, which improves its applicability in GPS satellite navigation. The PDF offers several advantages in the context of evaluating filtering methods, particularly in positioning and navigation applications.

Figure 6: The probability densities of estimation errors (a) East, (b) North, and (c) Altitude, under non-Gaussian noise. PDFs estimated via kernel density over 100 Monte Carlo runs for different filter with small process and measurement noises at various positions

The PDF is evaluated in Fig. 7a–c under large process and measurement noise conditions for different filtering methods such as EKF, MCC-EKF1, MCC-EKF2, and MKMC-EKF to represent various positioning scenarios. The results remain consistent with those in Fig. 6, with robust mean square error (MSE)-based algorithms maintaining their stability. Among them, MKMC-EKF performs better than MCC-EKFs and EKF, while the proposed method achieves the highest accuracy. Results show that MKMC-EKF achieves the highest positioning accuracy among the tested methods. Further, the fixed-point MKMC-EKF algorithm efficiently converges to optimal results within a few iterations, enhancing its suitability for GPS satellite navigation. PDFs play a key role in assessing filtering performance in positioning and navigation. They offer a detailed view of error distributions, providing insights into system behavior under varying noise and uncertainty conditions. Unlike metrics like mean or RMSE, PDFs illustrate the spread and probability of different error magnitudes, enabling a deeper understanding of a filter’s stability and reliability.

Figure 7: The probability densities of estimation errors (a) East, (b) North, and (c) Altitude, under non-Gaussian noise. PDFs estimated via kernel density over 100 Monte Carlo runs for different filter with large process and measurement noises at various positions

In contrast to adaptive EKFs, which rely on adjusting noise covariances, this method modifies the influence function itself using a mixture of kernels. The MKMC-EKF enhances robustness by integrating a multi-kernel correntropy measure in the measurement update, allowing the filter to better model heavy-tailed, impulsive, or multi-modal noise. This is particularly useful in GPS environments affected by multipath, signal blockage, or sensor degradation.

The calculation power of MCC-EKF variants depends on their robustness and adaptability. MCC-EKF operates at due to matrix inversion and kernel computations, making it more demanding than EKF but manageable. MKMC-EKF increases memory usage by storing past estimates, while MCC-EKF1 and MCC-EKF2 add overhead through adaptive kernel updates. MKMC-EKF significantly raises complexity with iterative variational inference for noise estimation. Table 3 indicates that the EKF achieves the fastest computation time, followed by MCC-EKF1, MCC-EKF2, and MKMC-EKF. In comparison, MKMC-EKF takes longer to execute due to the additional effort required to compute multiple kernel functions and fine-tune free parameters for improved robustness and accuracy. It is worth noting that the computation time of MKMC-EKF is directly affected by the number of kernel widths considered. The computation time for MKMC-EKF is influenced by kernel evaluations, fixed-point iterations, batch-mode regression, and covariance updates. While it is more computationally demanding than a standard EKF, its robustness against non-Gaussian noise justifies the additional processing cost, making it suitable for high-precision applications with optimized hardware support. MKMC-EKF benefits from a system with at least 16–32 GB RAM and a multi-core CPU (≥3.0 GHz). Parallel Computing Toolbox is recommended to speed up simulations and multi-kernel evaluations by utilizing multiple CPU cores efficiently. Moreover, MKMC-EKF adds computational steps beyond EKF, but its fixed-point iteration and multi-kernel MCC framework maintain a balance between efficiency and robustness. With a less time complexity, it remains suitable for real-time applications like GPS satellite navigation while enhancing estimation accuracy in non-Gaussian noise environments [30].

Furthermore, the convergence analysis of the MKMC-EKF focuses on its robustness and stability in non-Gaussian and time-varying noise environments. By leveraging multiple kernels, MKMC-EKF effectively captures diverse noise characteristics, improving estimation accuracy. In mathematics, the contraction mapping theorem (or Banach fixed-point theorem), is a key principle used to demonstrate the convergence of fixed-point algorithm [31]. Convergence is evaluated using ME, RMSE, and correntropy-based metrics, ensuring the estimation error remains bounded and decreases over time. However, stability can be analyzed using Lyapunov criteria and eigenvalue distribution of the system matrix, confirming that the filter maintains consistent performance [32,33]. Additionally, the evaluation has been carried out by analyzing the convergence behavior of the a posteriori error covariance matrix within the MKMC-EKF framework. The trace of this covariance matrix stabilizes, indicating that the filter maintains bounded estimation uncertainty even in the presence of time-varying and non-Gaussian noise. To further validate consistency and convergence, we examined the normalized innovation squared (NIS), which remained within the expected statistical bounds. This confirms that the MKMC-EKF achieves stable performance and reliable state estimation, demonstrating convergence in both a covariance-optimal and projection-normalized sense. The proposed MKMC-EKF was compared with the error modeling approaches in [34,35], which use conventional navigation error dynamics and adaptive filtering techniques. While adopting a similar state structure, our method introduces a multi-kernel correntropy framework that better captures non-Gaussian noise characteristics. Simulation results confirm that MKMC-EKF maintains lower estimation errors and faster recovery during and after signal outages, demonstrating its enhanced resilience in challenging environments.

Fig. 8a–c shows the analysis of different filter performance with varying noise levels, including process (Q) and measurement (R) noise covariance ratios (Q/R) ranging from low to high noise intensity, dynamic transitions noise, and normalized innovation squared (NIS) values over time under varying noise intensities. The results clearly demonstrate that the proposed MKMC-EKF exhibits consistently stable estimation performance across a variety of noise scenarios, including those involving abrupt changes in noise intensity and distribution. Unlike the conventional EKF, which tends to diverge or degrade significantly in the presence of non-Gaussian or time-varying noise, the MKMC-EKF maintains reliable state estimates with lower error and improved convergence behavior. Additionally, compared to the single-kernel MCC-EKF, the multi-kernel approach in MKMC-EKF provides enhanced flexibility to model complex error distributions more accurately, allowing the filter to adapt dynamically to noise characteristics. This leads to significantly improved robustness and accuracy in GPS navigation applications, especially in challenging environments with high uncertainty or outliers in the measurements.

Figure 8: The RMSEs for different filter at multiple noise scenarios (a) Q/R Ratio, (b) Dynamic noise, and (c) NIS

6  Conclusion

This paper presents an extended Kalman filter variant, the MKMC-EKF, developed for GPS navigation and positioning. The approach extends traditional correntropy by introducing a mixture of correntropy, which combines multiple kernel functions with the EKF to form a multi-kernel filtering algorithm. The proposed filter, designed through an optimized cost function, demonstrates superior robustness and estimation accuracy compared to traditional correntropy-based filters and other EKF variants. In standard correntropy methods, the kernel width plays a vital role in determining performance, yet lacks a definitive selection rule. To overcome this limitation, the MKC framework introduces a more adaptable structure by integrating multiple kernel bandwidths, enabling greater modeling flexibility and algorithmic versatility. By leveraging an FPI scheme, the filter effectively handles Gaussian noise while maintaining robustness to outliers, thus preventing instability or divergence caused by poorly chosen bandwidths. The interaction between kernel width and filter behavior is central to achieving reliable performance. Simulation results validate that the MKMC-EKF outperforms various MCC-EKF approaches when the kernel parameters are appropriately set. Further, PDF provides a versatile framework for representing diverse noisy data distributions, including non-Gaussian and mixed-Gaussian noise, which frequently arise in real-world systems. Unlike traditional statistical methods that assume fixed noise models, PDFs offer a dynamic approach to characterizing uncertainties by capturing intricate variations in measurement errors. This capability is particularly beneficial in navigation and positioning applications, where environmental factors, sensor imperfections, and multipath effects introduce complex noise patterns. Unlike traditional methods, it leverages PDFs to model complex noise variations, improving accuracy in GPS navigation. Fixed-point iteration prevents divergence, optimizing kernel selection for stability. The MKMC-EKF determines the error covariance matrix of its state estimates using the total influence function, leading to improved filtering performance. Additionally, an innovative filtering strategy is introduced to streamline computational processes. It is worth noting that, MKMC-EKF incorporates additional computations compared to EKF, but its fixed-point iteration and multi-kernel MCC approach optimize both accuracy and efficiency. The complexity has been verified, which remains feasible for real-time GPS satellite navigation, ensuring greater robustness and accuracy in non-Gaussian noise environments. The MKMC-EKF ensures robust convergence by leveraging multiple kernels to handle non-Gaussian and time-varying noise.

Simulation results using realistic GPS trajectory scenarios and measurement models demonstrated that the MKMC-EKF outperforms both standard EKF and MCC-EKF in terms of positioning accuracy and robustness. Specifically, the MKMC-EKF achieved up to 35% reduction in root mean square (RMS) positioning error during periods of GNSS multipath and maintained stable estimation during signal outages. Furthermore, analysis of the a posteriori covariance matrix and NIS showed the confidence bounds within 95% of the filter’s convergence and statistical consistency under dynamic noise conditions. These findings confirm that the MKMC-EKF is a viable and practical solution for real-time navigation applications, especially in challenging environments where traditional filters struggle. Future work will focus on hardware implementation and testing with real GNSS/INS data to further validate real-world performance and computational feasibility. Further, the evaluation can be carried out by applying the MKMC-EKF to the real-world GNSS/IMU datasets and also the field experiments by using a GNSS receiver integrated with a micro-electro-mechanical system (MEMS)-grade IMU, that will help to assess real-world performance under actual multipath, signal outage, and sensor drift scenarios.

Acknowledgement: Not applicable.

Funding Statement: The author gratefully acknowledges the support from National Science and Technology Council, Taiwan under grant numbers NSTC 113-2811-E-019-001 and NSTC 113-2221-E-019-059.

Author Contributions: Conceptualization, Amita Biswal; methodology, Amita Biswal; software, Amita Biswal; validation, Amita Biswal; writing—original draft preparation, Amita Biswal; writing—review and editing, Amita Biswal and Dah-Jing Jwo; supervision, Dah-Jing Jwo. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Simon D. Optimal state estimation: Kalman, H infinity, and nonlinear approaches. New York: John Wiley & Sons; 2006. [Google Scholar]

2. Anderson BD, Moore JB. Optimal filtering. Mineola, NY, USA: Courier Corporation, Dover Publications, Inc.; 2005. [Google Scholar]

3. Bar-Shalom Y, Li XR, Kirubarajan T. Estimation, tracking and navigation: theory, algorithms and software. New York: John Wiley & Sons, Inc.; 2001. [Google Scholar]

4. Abdelrahman M, Park SY. Sigma-point Kalman filtering for spacecraft attitude and rate estimation using magnetometer measurements. IEEE Trans Aerosp Electron Syst. 2011;47(2):1401–15. doi:10.1109/taes.2011.5751266. [Google Scholar] [CrossRef]

5. Liu W, Pokharel PP, Principe JC. Correntropy: properties and applications in non-Gaussian signal processing. IEEE Trans Signal Process. 2007;55(11):5286–98. doi:10.1109/tsp.2007.896065. [Google Scholar] [CrossRef]

6. Liu X, Ren Z, Lyu H, Jiang Z, Ren P, Chen B. Linear and nonlinear regression-based maximum correntropy extended Kalman filtering. IEEE Trans Syst, Man, Cybern: Syst. 2019;51(5):3093–102. doi:10.1109/tsmc.2019.2917712. [Google Scholar] [CrossRef]

7. Huang Y, Zhang Y, Zhao Y, Shi P, Chambers JA. A novel outlier-robust Kalman filtering framework based on statistical similarity measure. IEEE Trans Automat Contr. 2020;66(6):2677–92. doi:10.1109/tac.2020.3011443. [Google Scholar] [CrossRef]

8. Huang Y, Zhang Y, Shi P, Wu Z, Qian J, Chambers JA. Robust Kalman filters based on Gaussian scale mixture distributions with application to target tracking. IEEE Trans Syst, Man, Cybern: Syst. 2017;49(10):2082–96. doi:10.1109/tsmc.2017.2778269. [Google Scholar] [CrossRef]

9. Liu X, Qu H, Zhao J, Yue P. Maximum correntropy square-root cubature Kalman filter with application to SINS/GPS integrated systems. ISA Trans. 2018;80(1):195–202. doi:10.1016/j.isatra.2018.05.001. [Google Scholar] [PubMed] [CrossRef]

10. Liu X, Qu H, Zhao J, Chen B. Extended Kalman filter under maximum correntropy criterion. In: 2016 International Joint Conference on Neural Networks (IJCNN); 2016; Vancouver, BC, Canada. p. 1733–7. [Google Scholar]

11. Kulikova MV. Chandrasekhar-based maximum correntropy Kalman filtering with the adaptive kernel size selection. IEEE Trans Automat Contr. 2019;65(2):741–8. doi:10.1109/tac.2019.2919341. [Google Scholar] [CrossRef]

12. Wang G, Xue R, Wang JA. Distributed maximum correntropy Kalman filter. Signal Process. 2019;160(1):247–51. doi:10.1016/j.sigpro.2019.02.030. [Google Scholar] [CrossRef]

13. Fan X, Wang G, Han J, Wang Y. Interacting multiple model based on maximum correntropy Kalman filter. IEEE Trans Circuits Syst II: Express Briefs. 2021;68(8):3017–21. doi:10.1109/tcsii.2021.3068221. [Google Scholar] [CrossRef]

14. Wan EA, Van Der Merwe R. The unscented Kalman filter. In: Kalman filtering and neural networks; 2001. p. 221–80. doi:10.1002/0471221546.ch7. [Google Scholar] [CrossRef]

15. Li S, Li L, Shi D, Zou W, Duan P, Shi L. Multi-kernel maximum correntropy Kalman filter for orientation estimation. IEEE Robot Autom Lett. 2022;7(3):6693–700. doi:10.1109/lra.2022.3176798. [Google Scholar] [CrossRef]

16. Lu C, Zhang Y, Ge Q. Kalman filter based on multiple scaled multivariate skew normal variance mean mixture distributions with application to target tracking. IEEE Trans Circuits Syst II: Express Briefs. 2020;68(2):802–6. doi:10.1109/tcsii.2020.3015905. [Google Scholar] [CrossRef]

17. Liu X, Liu X, Yang Y, Guo Y, Zhang W. Variational Bayesian-based robust cubature Kalman filter with application on SINS/GPS integrated navigation system. IEEE Sens J. 2021;22(1):489–500. doi:10.1109/jsen.2021.3127191. [Google Scholar] [CrossRef]

18. Biswal A, Jwo D-J. Maximum correntropy extended Kalman filtering with nonlinear regression technique for GPS navigation. Appl Sci. 2024;14(17):7657. doi:10.3390/app14177657. [Google Scholar] [CrossRef]

19. He J, Sun C, Zhang B, Wang P. Variational Bayesian-based maximum correntropy cubature Kalman filter with both adaptivity and robustness. IEEE Sens J. 2020;21(2):1982–92. doi:10.1109/jsen.2020.3020273. [Google Scholar] [CrossRef]

20. Principe JC. Information theoretic learning: Renyi’s entropy and kernel perspectives. Germany: Springer Science & Business Media; 2010. [Google Scholar]

21. Li S, Shi D, Zou W, Shi L. Multi-kernel maximum correntropy Kalman filter. IEEE Control Syst Lett. 2021;6:1490–5. doi:10.1109/lcsys.2021.3114137. [Google Scholar] [CrossRef]

22. He R, Hu B, Yuan X, Wang L. Robust recognition via information theoretic learning. Berlin, Germany: Springer International Publishing; 2014. [Google Scholar]

23. Jwo D-J, Cho T-S, Biswal A. Geometric insights into the multivariate gaussian distribution and its entropy and mutual information. Entropy. 2023;25(8):1177. doi:10.3390/e25081177. [Google Scholar] [PubMed] [CrossRef]

24. Zhao S, Chen B, Principe JC. Kernel adaptive filtering with maximum correntropy criterion. In: The 2011 International Joint Conference on Neural Networks. San Jose, CA, USA; 2011. p. 2012–7. [Google Scholar]

25. Jwo D-J, Chen Y-L, Cho T-S, Biswal A. A robust GPS navigation filter based on maximum correntropy criterion with adaptive kernel bandwidth. Sensors. 2023;23(23):9386. doi:10.3390/s23239386. [Google Scholar] [PubMed] [CrossRef]

26. Wang G, Zhu Z, Yang C, Ma L, Dai W, Chen X. Distributed multi-kernel maximum correntropy state-constrained kalman filter under deception attacks. IEEE Trans Netw Sci Eng. 2024;12(1):533–46. doi:10.1109/tnse.2024.3506553. [Google Scholar] [CrossRef]

27. Wang G, Fan X, Zhao J, Yang C, Ma L, Dai W. Iterated maximum mixture correntropy Kalman filter and its applications in tracking and navigation. IEEE Sens J. 2024;24(17):27790–802. doi:10.1109/jsen.2024.3429365. [Google Scholar] [CrossRef]

28. GPSoft LLC. Satellite navigation toolbox 3.0 user’s guide. Athens, OH, USA; 2003. [Google Scholar]

29. GPSoft LLC. Inertial navigation system toolbox 3.0 user’s guide. Athens, OH, USA; 2007. [Google Scholar]

30. Hu C, Chen B. An efficient distributed Kalman filter over sensor networks with maximum correntropy criterion. IEEE Trans Signal Inf Process Over Netw. 2022;8:433–44. doi:10.1109/tsipn.2022.3175363. [Google Scholar] [CrossRef]

31. Agarwal RP, Meehan M, O’regan D. Fixed point theory and applications. Vol. 141. Cambridge, England: Cambridge University Press; 2001. [Google Scholar]

32. Lian B, Wan Y, Zhang Y, Liu M, Lewis FL, Chai T. Distributed Kalman consensus filter for estimation with moving targets. IEEE Trans Cybern. 2020;52(6):5242–54. doi:10.1109/tcyb.2020.3029007. [Google Scholar] [PubMed] [CrossRef]

33. Feng Z, Wang G, Peng B, He J, Zhang K. Distributed minimum error entropy Kalman filter. Inf Fusion. 2023;91(2):556–65. doi:10.1016/j.inffus.2022.11.016. [Google Scholar] [CrossRef]

34. Nourmohammadi H, Keighobadi J. Fuzzy adaptive integration scheme for low-cost SINS/GPS navigation system. Mech Syst Signal Process. 2018;99(6):434–49. doi:10.1016/j.ymssp.2017.06.030. [Google Scholar] [CrossRef]

35. Doostdar P, Keighobadi J, Hamed MA. INS/GNSS integration using recurrent fuzzy wavelet neural networks. GPS Solut. 2020;24(1):29. doi:10.1007/s10291-019-0942-z. [Google Scholar] [CrossRef]