IECC-SAIN: Innovative ECC-Based Approach for Secure Authentication in IoT Networks

1  Introduction

The exponential growth in Information and Communication Technology (ICT) has revolutionized the way we interact with and utilize data, facilitating seamless connectivity and empowering myriad applications across various sectors [1]. Central to this evolution is the Internet of Things (IoT), a paradigm that interconnects countless devices, enabling efficient automation, enhanced productivity, and enriched service delivery in both consumer and industrial contexts [2]. From smart homes that adjust environments based on occupant behavior to industrial sensors that optimize manufacturing processes in real-time, the IoT not only has streamlined operations but also has elevated standards of living and service provision [3].

However, this rapid digitization has been paralleled by a surge in cybersecurity threats, amplifying concerns about data integrity, privacy breaches, and system vulnerabilities. Cryptography emerges as a cornerstone in mitigating these risks, offering robust mechanisms to secure sensitive information and communications. The IoT Threat Report 2023 by Securelist, backed by Kaspersky, underscores the importance of effective authentication mechanisms in the IoT space, revealing a 30% surge in attacks and over 1.5 billion incidents in the first half of 2023 [4]. This highlights the critical need for robust security measures to protect data exchanges across potentially insecure networks.

For instance, IoT authentication ensures that only authorized devices can communicate and access resources within a network. This authentication process hinges significantly on the efficiency and security of cryptographic protocols. Elliptic curve cryptography has emerged as a pivotal solution, offering superior performance advantages with shorter key lengths compared to traditional cryptographic methods. ECC’s ability to provide equivalent security with smaller key sizes reduces computational overhead, making it particularly well-suited for resource-constrained IoT devices [5].

Against this backdrop, this paper presents a novel IoT authentication approach based on our previously proposed mapping and reverse operations [6] on elliptic curves over prime fields. We select NIST curves (192, 256, 384, 521) for their efficient arithmetic and low resource requirements [7]. It is worth noting that we also go beyond the 521-bit security level to demonstrate the scalability of our approach. Unlike existing benchmarks that rely heavily on point multiplication and suffer from significant performance degradation as security increases, our method maintains efficiency even at higher security levels. Our method focuses on optimizing authentication speed across varying key sizes, surpassing conventional point multiplication techniques that often bottleneck ECC-based systems [8]. Furthermore, we conduct a comprehensive security evaluation using AVISPA and BAN logic, supported by informal proofs against potential attacks. Through empirical assessments covering storage, communication, and computational costs, we demonstrate the efficiency and effectiveness of our proposed system in real-world scenarios.

2  Related Works

The Internet of Things (IoT) heavily depends on wireless networks for data collection by authorized users. Typically, communication happens between a central platform and various terminal nodes, where the platform sends commands to the nodes to gather and transmit data back. Mutual authentication between the platform and terminal nodes is crucial to ensure network security. Without this, unauthorized individuals could exploit the network for data theft or malicious activities. Moreover, terminal nodes need to authenticate themselves to other nodes to prevent unauthorized access, which could disrupt the network and deceive both the platform and legitimate nodes [9]. Therefore, mutual identity authentication is vital for maintaining the security of IoT systems. In scenarios where processing power and memory are constrained, ECC as a form of public key cryptography, is particularly suitable. ECC offers an efficient solution for secure communication in resource-limited environments, making it a viable option for enhancing IoT security [10].

The various ECC-based authentication schemes proposed in the literature utilize different methods, such as time-stamp techniques and certificate-based mutual authentication. However, certificate-based methods can be costly, as they require additional computational resources for servers and users to authenticate each other’s identities. In contrast, the authors in [11] proposed an ECC-based authentication and key agreement scheme specifically for IoT environments. Their protocol facilitates secure communication between embedded devices and cloud servers by providing mutual authentication, allowing both the user and server to negotiate encryption keys collaboratively. They assert that their scheme meets all necessary security requirements and offers robust resistance to various well-known IoT attacks.

Despite the author’s claim, studies in [12–15] identified significant security flaws and structural issues in their protocol. These issues include the failure of mutual authentication, ambiguity in session key establishment, vulnerability to offline password guessing, and susceptibility to insider and traceability attacks. In response, each of these researchers proposed enhanced protocols, asserting that their improvements effectively address the identified vulnerabilities and fulfill the necessary security requirements. Further advancements include the work in [16], which proposed an anonymous authentication scheme that integrates a password validator to defend against known temporary information and DoS attacks. This scheme showcased ECC’s potential in fortifying IoT devices against sophisticated attacks while maintaining a lightweight footprint. Another significant contribution is from [17] proposed a novel lightweight anonymous authentication protocol (LAAP) to meet security and efficiency requirements. This protocol uses ECC and dynamic pseudonyms to prevent traceable attacks caused by fixed identity identification and employs symmetric encryption to optimize the server’s search for anonymous device information, reducing the time complexity from O(n) to O(1). Very recently, the authors in [18,19] proposed a mutual authentication scheme based on ECC and the U-Quark light hash function, which is known for its collision resistance. This approach not only retains the essential security features of ECC but also enhances performance, making it well-suited for the IoT environment. Despite continuous efforts, designing a resource-efficient and secure ECC-based authentication protocol for IoT edge devices remains a significant challenge. Similarly, in 2024, the authors in [6] proposed an innovative hash-based technique that embeds messages into an elliptic curve (EC) points before encryption, using a random parameter and a shared secret point from the generated through elliptic curve Diffie–Hellman protocol. The method’s security was evaluated against various attack models, and its complexity and sensitivity were analyzed. A tag ensures message integrity, and the scheme meets criteria such as the strict avalanche criterion and linear complexity. Comprehensive analysis confirmed its effectiveness in maintaining data security and integrity. Another recent study, the authors in [20] proposed a two-factor authentication protocol for IoT-enabled Wireless Sensor Networks (WSNs), integrating ECC with a fuzzy verifier to enhance both security and usability in resource-constrained environments. Instead of relying on traditional deterministic password hashes, their scheme employs a fuzzy verifier approach, introducing randomness that enhances resistance to common attacks while preserving authentication reliability. Formal security validation using the Real-or-Random model and comparative analysis confirmed the scheme’s efficiency, achieving a computation cost of 8.9569 ms, outperforming existing protocols in both performance and protection metrics. In a related contribution, the authors in [21] designed an authentication protocol optimized for military Internet of Drones (IoD) scenarios, addressing the need for secure, real-time communication under resource constraints. Their approach leverages Elliptic Curve Cryptography and independently managed session keys across various communication links to contain potential breaches and reduce computational load. To further strengthen security, the protocol integrates trust anchors, group key exchanges, and position verification techniques, ensuring resistance to attacks such as replay and denial-of-service. In 2025, the authors in [22] introduced a lightweight authentication protocol specifically designed for the Internet of Medical Things (IoMT), addressing both security and user privacy in resource-constrained medical environments. Their approach ensures secure communication between body-connected devices while preserving patient confidentiality, and it is formally verified using the AVISPA tool. By leveraging smaller key sizes and efficient cryptographic techniques, the proposed protocol achieves 5 to 6 times greater computational efficiency compared to conventional methods such as ElGamal and Rivest–Shamir–Adleman (RSA), while resisting common threats found in existing schemes. Building on the work proposed in [6], we introduce a novel ECC-based mutual authentication protocol for IoT environments. Our protocol is designed to provide lightweight communication with reduced computational and storage costs while maintaining strong security properties. The security of our protocol has been formally verified using AVISPA and BAN logic, chosen based on a survey of 40 authentication protocols, which revealed that 25% use AVISPA and 36% use BAN logic [10]. Furthermore, our protocol has been tested informally against various attacks, including Distributed Denial of Service (DDoS), forward secrecy, impersonation replay attacks, and so on, demonstrating its robustness and reliability. Our proposed ECC-based authentication protocol addresses existing security and efficiency gaps by enhancing cryptographic techniques and optimizing computational processes. This ensures robust mutual authentication with minimal resource consumption, making it well-suited for IoT applications. Overall, ECC-based authentication schemes effectively secure IoT devices by balancing strong security and computational efficiency. Our scheme builds on these principles, introducing improvements to meet the evolving security demands of IoT environments.

3  Elliptic Curves Cryptography and Secure Embedding Approach

This section provides essential background on ECC required to understand the proposed scheme. It covers key concepts such as point multiplication, solving modular quadratic equations, and data embedding into elliptic curve points.

3.1 Introduction to Elliptic Curve Cryptography over Prime Fields

Elliptic Curve Cryptography uses the algebraic structure of elliptic curves over finite fields for secure communication. An elliptic curve over a prime field Fp (where p is a large prime) is defined by the equation:

y2=x3+ax+b(modp)

where a and b are constants fulfills −16(4a3+27b2)≠0.

3.1.1 Points on Elliptic Curves

Points on the elliptic curve E(Fp) are pairs (x,y) that satisfy the curve equation, along with a point at infinity, 𝒪.

3.1.2 Key Operations

1.   Point Addition: Given two points P and Q, their sum R = P + Q is another point on the curve. The point −P denotes the symmetric of P and verifies P+(−P)=𝒪.

2.   Point Doubling: Doubling a point P results in another point R=2P.

3.   Point Multiplication (PM): Multiplying a point P by an integer k (denoted kP) involves repeatedly adding P to itself. Efficient PM computation significantly impacts both performance and security. A comprehensive overview of PM algorithms optimized for resource-constrained devices is provided in [23].

3.1.3 Generator Point

A generator point G is a specific point on the elliptic curve used to generate all or almost all other points in the elliptic curve group through repeated addition. Table 1 describes various elliptic curve parameters used in alongside this paper.

Comprehensive details on ECC can be found in [24].

3.2 Modular Quadratic Equation

The proposed mapping and reverse mapping operations require solving a modular quadratic equation of the form

x2+bx+c≡0(modp),(1)

with discriminant Δ=b2−4c(modp). A solution exists if and only if Δ is a quadratic residue modulo p. For NIST prime fields where p≡3(mod4), this can be efficiently verified by evaluating the Legendre symbol [25]:

(Δp)=Δp−12modp.(2)

If (Δp)=1, then solutions exist and can be computed as x=−b±r2modp, where r=Δp+14modp. This procedure benefits from the arithmetic efficiency of NIST elliptic curve defined over prime fields, ensuring lightweight and fast computation within the proposed protocol.

3.3 Elliptic Curve Embedding Approach

In this section, we explore a secure method for embedding information into elliptic curves, originally proposed in [6], and it is applied in a novel way to support efficient and secure authentication. The approach focuses on integrating data within the curve’s structure while ensuring robust security measures. Upon establishing an agreement between the server and the device on the elliptic curve domain parameters, as detailed in the forthcoming setup phase Section 4.1, we define

Mapp:Fp→E(Fp),

which converts a given element m of the prime field Fp into a point Pm on the elliptic curve E(Fp). This process involves using a secret point Ps=(xs,ys) on the curve E(Fp). A line passing through Ps with slope S=(ys−m)xs−1 is defined. One of the intersection points between this line and the elliptic curve is chosen as the mapping point Pm for m. If there are no intersection points other than Ps and −Ps, m is incremented by one, and the process is repeated until a point Pm∈E(Fp)∖{±Ps} is found. As highlighted in [6], the problem of finding the point Pm is equivalent to solving the following equation:

x2+(xs−S2)x+xs−1(−b+m2)≡0(modp).(3)

Once a solution xm≠xs to Eq. (3) is found, the point Pm is defined as (xm,ym), where the y-coordinate ym is computed as ym≡Sxm+m. It is crucial to ensure that xm≠xs to guarantee that Pm≠±Ps. Algorithm 1 provides comprehensive details on the embedding process.

Now we explore how to reverse the mapping process. This method complements the secure embedding approach detailed previously, ensuring that the original integer m∈Fp can be accurately retrieved from a mapping point Pm elliptic curve E(Fp). We denote that process by:

Reverse:E(Fp)→Fp

Given the shared elliptic curve E(Fp), a mapping point Pm=(xm,ym), and the secret point Ps=(xs,ys) used during Pm computation. To determine the original integer m, the reverse mapping process involves computing the slope of the line between the secret point and the mapping point, and then determining m from the computed slope and coordinates.

The reverse mapping process follows these steps:

1.   Slope Calculation: The slope S of the line passing through the points Ps=(xs,ys) and Pm=(xm,ym) is computed as:

S≡(ym−ys)(xm−xs)−1(modp)

2.   Computing m′: Use the slope S and the x-coordinate of the secret point Ps to compute the value m′ as:

m′≡ym−Sxm(modp)

3.   Removing the Last 8 Bits: Convert m′ to its binary form and remove the last 8 bits, which were appended during the secure embedding process to ensure a unique mapping. The truncated value represents the original integer m. Another way

m=Integer(Bin(m′)∖{last 8 bits})

The algorithm for this reverse mapping approach is detailed in Algorithm 2.

4  Our Protocol Explanation

Our protocol consists of four main phases: the setup phase, the registration phase, the login phase, and the authentication phase. Implemented using the Charm framework, it employs elliptic curve cryptography for secure key exchange and authentication. Data transmission from the embedded devices D and the server is assumed to occur over a secure channel during the registration phase. In the following, we detail each phase and the corresponding steps involved in the protocol execution as depicted in Fig. 1. The parameters used in our protocol and their corresponding definitions are listed in Table 2.

Figure 1: Proposed ECC-based authentication scheme for IoT.

4.1 Setup Phase

In the setup phase, both the server and the device agree on an elliptic curve to use, such as the standardized NIST curve prime192v1. In the proposed method, we specifically use elliptic curves defined over prime fields with characteristics greater than or equal to 5. The domain parameters for the chosen elliptic curve are detailed in Table 1.

4.2 Registration Phase

In the Registration Phase, the device Di begins by sending its identifier IDi to the server S. Both the device and the server create a counter (cpt) initialized to 0. Upon receiving IDi, the server selects a random number k within the range [2,n−1], and their private key X. The server then performs a series of computations:

R=kG,(4)

Ti=h(X)⊕IDi⊕Exp_Timemodp,(5)

Ps=Mapp(Ti,Ri)∈E(Fp),(6)

Hi=h(IDi||cpt+1).(7)

The server then stores the values (Ps,IDi,Exp_Time,cpt,Hi) in its database and sends Ps back to the device Di. The device stores (Ps,IDi,cpt) in its database for future use.

4.3 Login and Authentication Phase

The authentication phase involves mutual verification between the device and the server through a sequence of cryptographic operations and exchanges of various values.

During the Login and Authentication Phases, the device Di initiates the process by updating its counter cpt and choosing a random number Vr from the finite field Fp. It computes:

cpt←cpt+1,(8)

V1=IDi⊕Vr⊕cptmodp,(9)

Pd=Mapp(V1,Ps)∈E(Fp),(10)

Hi=h(IDi||cpt).(11)

The device then sends Hi and Pd to the server S. Upon receiving Hi and Pd, the server checks its database for a record of Hi. If it does not exist, the server rejects the request and returns a failure indicator (⊥). Otherwise, the server proceeds to compute:

V1′=Reverse(Pd,Ps).(12)

Additionally, the server updates its counter (cpt) to ensure synchronization with the device and then calculates:

cpt←cpt+1,(13)

A1=Mapp(V1′⊕IDi⊕cpt,Ps)∈E(Fp).(14)

The server then sends A1 back to the device. Once the device receives A1 it computes:

Vr′=Reverse(A1,Ps).(15)

If Vr′ does not match Vr, the device resets its counter to the previous state by setting cpt←cpt−1, rejects the authentication, and returns a failure indicator (⊥). If Vr′ matches Vr, the device proceeds to compute:

A2=h(V1),(16)

and sends A2 to the server. The device also derives the session key:

Sk=KDF(Vr),(17)

where KDF is a key derivation function. Upon receiving A2, the server computes:

A2′=h(V1′).(18)

If A2′ does not match A2, the server resets its counter to the previous state by setting cpt←cpt−1, rejects the authentication, and returns a failure indicator (⊥). If A2′ matches A2, the server updates Hi to h(IDi||cpt+1) and calculates:

Vr=V1′⊕IDi⊕cpt,(19)

and derives the session key:

Sk=KDF(Vr).(20)

By adhering to these carefully structured steps, our ECC-based authentication protocol ensures robust mutual authentication between IoT devices and the central server, capitalizing on the computational efficiency and security strengths of elliptic curve cryptography.

5  Security Analysis and Performance Analysis of the Elliptic Curve Embedding Approach

In this section, we delve into the rigorous evaluation of the security and performance aspects of our proposed Elliptic Curve Embedding Approach (ECEA) for IoT authentication. Our approach builds upon the foundation laid by our previously proposed ElGamal ECC-based encryption [6], leveraging its inherent security properties and extending them to authenticate IoT devices securely.

Lemma 1. Let E(Fp) an elliptic curve. For all elements m in Fp and a point Ps in E(Fp). There exist an embedding point Pm=Mapp(m,Ps)∈E(Fp) if and only if there exist a third point Pm′ in E(Fp) such that:

Pm=−(Ps+Pm′).(21)

Proof: Let Pm=Mapp(m,Ps) be the embedding point of m∈Fp based on a Ps point on the elliptic curve E(Fp). By construction, Pm is the intersection point of the line passing through Ps, where m is the y-intercept, such that Pm≠±Ps. Given that the line already intersects the elliptic curve at Ps and Pm, Pm can be viewed as the sum of −Ps and a point −Pm′, where Pm′ is the third intersection point of the line with the curve. Hence,

Pm=−(Ps+Pm′).

On the other hand, suppose there exists a point Pm′ that satisfies Eq. (21). Let S≡(ys−ym)(xs−xm)−1modp and m≡ym−Sxmmodp. Then, Pm=Mapp(m,Ps) is the embedding point of m on the elliptic curve E(Fp) with respect to Ps. This is due to the fact that −Pm=Ps+Pm′. Hence, −Pm is the symmetric point of Pm with respect to the x-axis. By the definition of point addition on an elliptic curve, −Pm is the intersection point of the line passing through Ps and Pm′ with the elliptic curve. This confirms that Pm is indeed the correct embedding point of m on the curve. ◻

Theorem 1. Let E(Fp) be an elliptic curve, G the generator point of order n, and k a random number in [1,n−1]. The embedding approach acts as ElGamal ECC-based encryption with less computational overhead.

Proof: Consider G to be the generator point of E(Fp) with order n, and let k be a random number in [1,n−1]. Let Pa=aG represent the public key of a receiver with a private key a. Suppose a message m<p is encoded as an integer and embedded into a point Pm=Mapp(m,R), where R=kPa. By Lemma 1, there exists a point Pm′ such that:

Pm=−(Pm′+R)(22)

=−(Pm′+kPa)(23)

=Pm′′+k′Pa,(24)

where k′≡−k(modn) and Pm′′=−Pm′ acts as another embedding point of the message m. The ElGamal ECC-based encryption of Pm′′ using the key k′ calculated as Enc(m,k′)=Pm′′+k′Pa. Thus, the process of embedding m into Pm mirrors the ElGamal encryption scheme, where the ciphertext comprises components dependent on the recipient’s public key and a random key. This establishes the fundamental similarity between our proposed embedding approach and ElGamal ECC encryption. However, ElGamal ECC encryption requires additional operations after embedding the message in a point, specifically point multiplication and point addition. ◻

As discussed in [6], the embedding approach successfully encodes a message (integer m<p) into a point on the curve with an average of two rounds. The algorithm’s complexity has been demonstrated to be 𝒪(1) in terms of message size. Furthermore, sensitivity analysis reveals that small changes in m or the key (Point Ps) result in a 50% change rate, illustrating that the proposed scheme satisfies both the confusion property and the strict avalanche criterion [26,27]. Moreover, the proposed method successfully passes the NIST statistical test suite, ensuring the randomness of the ciphertext from an adversary’s perspective. By Theorem 1, we demonstrate how the embedding approach shares similarities with Elgamal ECC-based encryption. Thus, the embedding approach utilized in our proposed authentication method inherits the security properties of our previously proposed encryption scheme [6], particularly as elaborated in Section 5 for a comprehensive security analysis.

To demonstrate the authentication system’s sensitivity to small changes in its inputs, ensuring security through significant variations in authentication parameters, we set an initial ID as a random number, then created 10 different IDi values by changing one bit in the original ID, each linked to a device Di. We kept all other parameters fixed (k,X,cpt,Exp_time, EC-parameters, Vr). The resulting plot (see Fig. 2) illustrates distinct communication pathways for each device Di based on normalized values of (xs,xd,xA1,A2), where xs,xd,xA1 represent the x-coordinates of exchanged points Ps,Pd,A1. This highlights that multiple devices with almost identical IDs, but with one-bit difference, exhibit significant and unpredictable variations in the exchanged messages while interacting with a server having fixed parameters. This property holds for all inputs, thereby ensuring the integrity and robustness of the authentication protocol by preventing predictable outcomes from slight alterations. The empirical analysis of cryptographic operations using NIST curves demonstrates that our proposed mapping and reverse operations offer significantly higher efficiency compared to traditional point multiplication, which was implemented using the double-and-add algorithm exactly as in the tinyec library. Across all key sizes—192-bit, 256-bit, 384-bit, and 521-bit—mapping and reverse operations consistently achieve minimal execution times, as illustrated in Fig. 3. In contrast, point multiplication exhibits the highest execution times, especially noticeable even with smaller key sizes like 192-bit.

Figure 2: Normalized Data Pathways in Device-Server Communication during Authentication Protocol

Figure 3: Comparative Analysis of Execution Times for Cryptographic Operations: Mapping, Reverse, Multiplication, Addition

The computational overhead, assessed across the NIST elliptic curve with various key sizes compared to secp192r1 as illustrated in Table 3, which highlights how the execution time growth ratio for reverse and mapping operations remains manageable yet notably faster compared to the substantial growth observed with point multiplication. This disparity leads to slower authentication processes when relying on point multiplication. Conversely, our proposed mapping operations maintain a more linear growth pattern, ensuring efficiency even as key sizes increase.

Additionally, we compared the computational cost of point multiplication and our embedding algorithm on the NIST curve secp192r1. Point multiplication using the double-and-add algorithm requires up to 23,857 field operations with affine coordinates and 2500 with mixed coordinates (Jacobian and affine), reduced to 718 using the Fixed-Base Comb method, which trades off the storage of approximately 30 points [24]. In contrast, our embedding approach, which involves solving the quadratic Eq. (3) using the square root of the discriminant Δp+14 [28], requires about 412 field operations on average without any additional storage requirements.

Note that the previously established comparison is motivated by the fact that all ECC-based authentication schemes rely on point multiplication as a core operation. While these schemes successfully enhance performance and security compared to those leveraging other cryptographic techniques like RSA, the point multiplication operation remains the most computationally intensive aspect. Our proposed embedding scheme is designed to offer improved performance while maintaining high security.

The findings show that our method is particularly suitable for reducing computational complexity in elliptic curve cryptographic applications, such as authentication, in resource-constrained IoT environments. By maintaining a delicate balance between security and performance while addressing the scalability challenges posed by larger key sizes, our method is well-suited for deployment in these environments.

6  Threat Model and Assumptions

This section outlines the security assumptions, attacker capabilities, and environmental constraints considered in the design of the proposed authentication protocol for IoT environments. We target typical IoT scenarios, where devices operate in open and potentially untrusted settings, often with limited computational, memory, and energy resources.

We assume that an adversary has full control over the communication channel between the device and the server. This includes the ability to intercept, eavesdrop, replay, inject, or alter transmitted messages. The adversary may act passively (observing protocol flows) or actively (modifying or forging messages). However, the adversary cannot break standard cryptographic assumptions, such as the collision resistance of SHA-256 or the intractability of the Elliptic Curve Discrete Logarithm Problem (ECDLP) over ECC-256. Moreover, it is assumed that the adversary cannot access the secure internal memory of honest IoT devices.

A stronger adversarial model is also considered, in which long-term secrets from the server side may become exposed. In such a setting, the focus shifts to assessing whether past session keys remain confidential. These assumptions are particularly relevant for environments that require session-level security guarantees even under partial compromise.

The IoT devices are assumed to be constrained in terms of processing power and storage, and the initial registration phase is performed in a trusted and secure environment. Communications take place over insecure and asynchronous wireless networks. To maintain freshness and prevent replay without requiring strict time synchronization, we assume the use of a monotonically increasing counter (cpt) shared between the device and server. The server is trusted and possesses sufficient computational capacity to manage authentication requests from numerous devices simultaneously. This threat model establishes the foundation upon which the protocol’s security properties—such as resistance to replay, impersonation, and man-in-the-middle attacks—will be rigorously evaluated in the subsequent formal and informal analysis sections.

7  Security Analysis of the Proposed Authentication

In this section, we aim to rigorously demonstrate the resilience of our proposed secure ECC-based authentication scheme against a range of prevalent attacks targeting the Internet of Things (IoT). To accomplish this, we will employ both informal and formal security analysis methodologies. Specifically, we will leverage the Automated Validation of Internet Security Protocols and Applications (AVISPA) tool and Burrows–Abadi–Needham (BAN) logic to thoroughly validate and verify our scheme’s security properties. Through these methods, we will comprehensively assess the scheme’s ability to withstand potential security threats.

7.1 Informal Security Analysis

This subsection provides an informal security analysis of our authentication scheme, demonstrating its resilience against several common threats: replay attacks, impersonation attacks, and man-in-the-middle attacks. Additionally, we discuss how the scheme ensures Perfect Forward Secrecy. We will show how our scheme effectively mitigates these threats, ensuring robust and secure authentication.

7.1.1 Device Anonymity

Threat: Tracking a specific IoT device over multiple sessions.

Mitigation: In the logging and authentication phases, it is essential for the server to identify which device is attempting to log in, enabling the authentication process based on the corresponding data of that identity. Some existing schemes [16] transmit the hash value of the device ID (h(IDi)). While this technique obscures the device’s true identity, it still allows an adversary to track and gather information related to the same device whenever the same hashed ID is observed. This could enable the adversary to mount attacks, such as offline password guessing attacks, to deduce the original device ID or other sensitive information. In [15], the authors propose an approach to achieve anonymity by defining PIDi=(Xi⊕IDi) during the registration phase. In the login and authentication phase, a random number N1 is selected to compute P1=N1×G, where G is the generator point of the curve. Subsequently, PPIDi=PIDi×P1 and P1 are transmitted to the server. The server identifies the logging device by finding the corresponding record PIDi that relates to PPIDi in its database. This is done by checking each existing PIDi record to verify if PPIDi=?PIDi×P1. While this procedure effectively obscures the identity and achieves device anonymity, it incurs significant computational costs. In the proposed scheme, the device Di sends Hi=h(IDi||cpt) to the server, which allows the server to retrieve the corresponding records from its database. Importantly, this value is never retransmitted by the device because the counter (cpt) is incremented with each successful authentication, leading to a new Hi value every time. It is worth noting that even small changes in the counter (cpt) result in a completely different Hi, a property ensured by the cryptographic hash function used. As a result, even if an adversary intercepts Hi, they cannot track the device across multiple sessions, thereby preserving the device’s anonymity in our proposed scheme.

Effectiveness: Ensures unlinkability and anonymized authentication.

7.1.2 Perfect Forward Secrecy

Threat: Recovering past session keys after long-term key compromise.

Mitigation: The proposed authentication protocol ensures resilience against attacks targeting perfect forward secrecy (PFS) by protecting past session keys even if long-term keys are compromised. The protocol uses a unique random value Vr generated for each session, which is crucial for deriving session-specific values Pd, A1, and A2, all of which contribute to computing the session key. Since Vr is neither stored nor transmitted, an attacker cannot recover past Vr values or session keys, even if they possess the server’s private key X and stored values Ps and IDi. Additionally, new values Pd, A1, and A2 cannot be used to derive or recompute older ones or Vr. Consequently, the proposed method ensures that each session key is independently derived and isolated, maintaining the security of past communications.

Effectiveness: Achieves strong session isolation and confidentiality over time.

7.1.3 Replay Attack

Threat: Reusing previously captured messages to gain unauthorized access.

Mitigation: Our authentication scheme is secured against replay attacks through the use of a counter (cpt) that is incremented with each authentication attempt. During the login phase, both the device and the server update their counters, which are then incorporated into the computation of the messages Pd and A2. This ensures that each session is uniquely identified by the current counter value. If an attacker intercepts and replays Pd and A2, the server’s counter will not match the outdated counter value used in the replayed messages, resulting in a mismatch during the verification and subsequent rejection of the replayed attempt. Thus, the counter mechanism effectively invalidates replayed messages, providing robust security against replay attacks.

Effectiveness: Replay attempts are rejected due to counter mismatch.

7.1.4 Impersonation Attack

Threat: An attacker impersonates a legitimate device or server.

Mitigation: In our scheme, an attacker cannot impersonate either the device or the server due to the reliance on specific cryptographic values and session-specific information. To impersonate the device, the attacker would need the legitimate user’s IDi and the point Ps, a valid random number Vr, and the current counter value cpt, which are unknown to them. Consequently, the attacker cannot compute the correct Pd or generate a valid A2. To impersonate the server, the attacker would need to generate a valid A1, which requires knowledge of the server’s secret values and the correct computation of Pd. Without these, the attacker cannot produce a valid response to the device’s challenge. Thus, our scheme effectively prevents both device and server impersonation, ensuring secure authentication.

Effectiveness: Prevents both client-side and server-side impersonation through cryptographic binding of session-specific secrets.

7.1.5 Man-in-the-Middle Attack

Threat: Intercepting, modifying, or forging messages between device and server.

Mitigation: A Man-in-the-Middle (MitM) attack occurs when an attacker secretly intercepts and possibly alters the communication between two parties to gain unauthorized access or manipulate the data. For MitM attacks, the scheme’s use of random values and counters ensures that each session is unique and secure. During the exchange, the counter cpt and random number Vr are securely embedded in an elliptic curve point Pd and incorporated in the hash value A2. Similarly, A1 securely embeds Vr with the help of the shared secret point Ps. This ensures the integrity and confidentiality of the exchanged values. An attacker cannot alter or forge the messages without being detected, as they would need the same cryptographic keys and session-specific information. Thus, our scheme effectively prevents MitM attacks.

Effectiveness: Ensures message integrity and authenticity under active adversary conditions.

As shown in Table 4, the comparative analysis of the proposed scheme with other relevant schemes demonstrates comprehensive security coverage, outperforming other schemes in several critical areas. This comprehensive security performance underlines the effectiveness and robustness of theproposed scheme in various attack scenarios.

7.2 Formal Security Analysis

This subsection demonstrates the formal security analysis of the proposed methods utilizing the AVISPA tool and BAN Logic.

7.2.1 AVIPSA Tool

The Automated Validation of Internet Security Protocols and Applications tool is a comprehensive framework designed to rigorously assess network protocol security against well-known attack vectors. In our evaluation, we explicitly analyzed the resilience of the proposed protocol against Man-in-the-Middle (MITM) attacks, replay attacks, interception, and message modification attacks.

Utilizing the High-Level Protocol Specification Language (HLPSL), AVISPA allows for precise specification of protocol participants’ actions and interactions. HLPSL, a role-based language, enables detailed specification of the behavior and roles of protocol entities. This high-level description is translated into an Intermediate Format (IF), which serves as the input for AVISPA’s backend analyzers. This translation is essential for systematically analyzing the protocol’s security properties.

The backend of the AVISPA tool comprises four main components, each using different methodologies to analyze the protocol. These are the SAT-based Model-Checker (SATMC), which uses satisfiability-solving techniques; the Tree-Automata-based Protocol Analyzer (TA4SP), which employs tree automata; the On-the-Fly Model-Checker (OFMC), which performs dynamic analysis; and the Constraint Logic-based Attack Searcher (CL-AtSe), which uses constraint-solving techniques to identify potential attacks. For protocols involving XOR operations, such as ours, OFMC and CL-AtSe are particularly suitable, as SATMC and TA4SP do not support XOR operations.

The AVISPA tool produces an Output Format (OF) that provides a detailed security analysis of the protocol. A result indicating that the protocol is SAFE confirms its robustness against specified attacks, such as MITM and replay attacks, thereby validating the protocol’s security properties.

In our proposed protocol, we utilized HLPSL to define the protocol’s roles, environment, and security objectives as depicted in Fig. 4. This includes specifying the actions and interactions of each participant, setting up instances of each role, constructing the entire protocol session, and establishing goals such as confidentiality to ensure sensitive information remains protected, and authentication to verify the legitimacy of the data exchanged between entities.

Figure 4: HLPSL Code Specification for our proposed authentication protocol analyzed by the AVISPA tool.

The security goals are integral to the protocol’s design and are articulated using HLPSL constructs such as secrecy and authentication. These constructs ensure that secret values remain undisclosed and unauthorized access to sensitive information is prevented, while also validating the legitimacy of the entities involved.

As illustrated in Fig. 5, the OFMC and CL-AtSe backends verified that the protocol is SAFE under the specified analysis conditions. The OFMC backend’s statistics demonstrate its efficiency by detailing the parse time, search time, visited nodes, and search depth. Meanwhile, the CL-AtSe backend provides metrics on the number of analyzed and reachable states. These results indicate that our protocol has undergone a comprehensive analysis and has been deemed secure against the potential threats evaluated by the AVISPA tool.

Figure 5: Analysis result of OFMC and CL AtSc security checkers on our protocol.

7.2.2 BAN Logic

To complement the automated validation, we employed BAN logic to formally reason about the mutual authentication, session key establishment, and message integrity properties of our protocol.

We present the constructs and primary postulates of BAN logic in Tables 5 and 6, respectively.

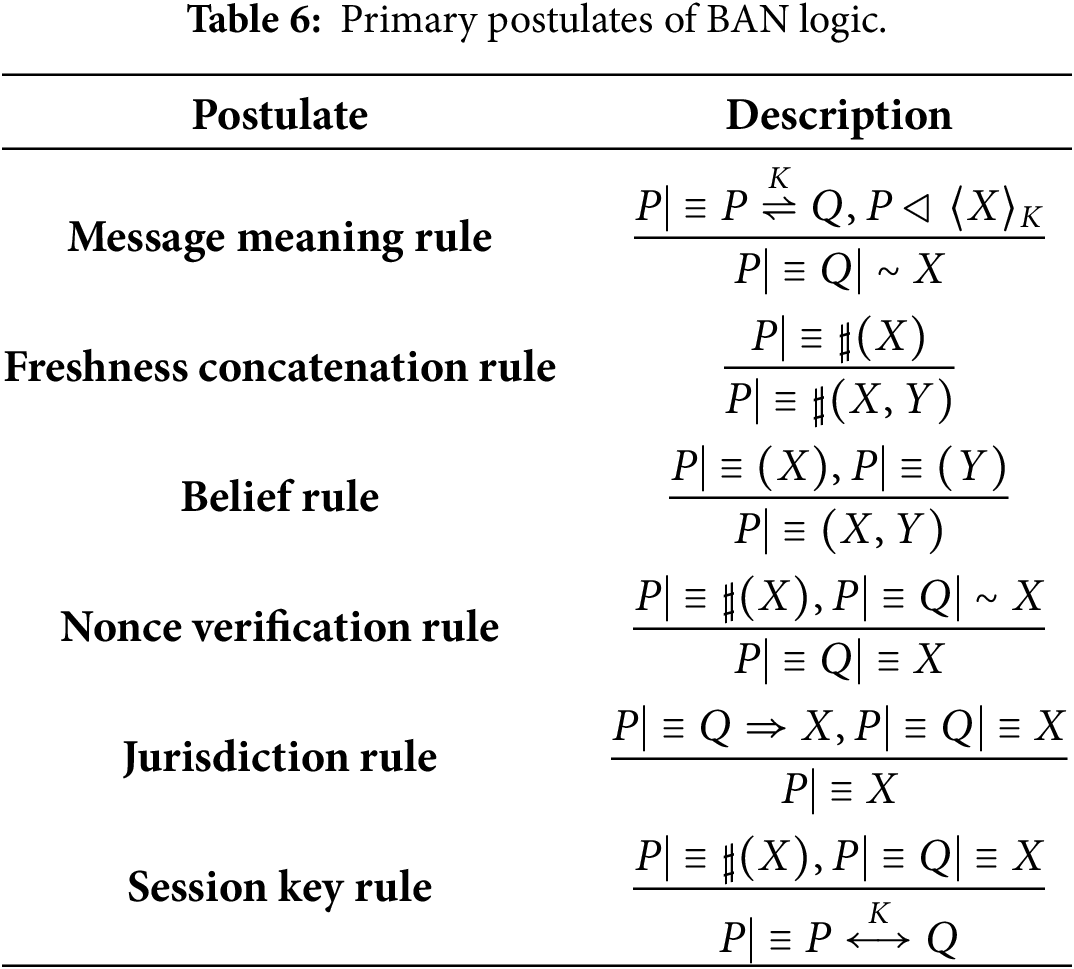
The process to prove the authentication protocol using BAN logic is as follows:

1.   Define the goals, which need to be achieved by the authentication system.

2.   The proposed authentication protocol should be idealized in the formal language of BAN logic.

3.   Set the initial state of the protocol by mentioning the various assumptions.

4.   Apply BAN logic constructs and postulates to prove or achieve the goals set in the first step.

The proof of the proposed authentication protocol using BAN logic is described as follows:

Goals:

Goal 1:S|≡S⟷𝒮𝒦DiGoal 2:S|≡Di|≡S⟷𝒮𝒦DiGoal 3:Di|≡S⟷𝒮𝒦DiGoal 4:Di|≡S|≡S⟷𝒮𝒦Di

—The idealized form of the authentication phase of the proposed protocol is given by:

M1:Di→S:{IDi,Pd,A2}M2:S→Di:{Ps,A1}

—The following are the assumptions made to achieve the defined goals:

A1:S|≡♯(Vr)A2:Di|≡♯(h(V1))A3:S|≡S⟷PsDiA4:Di|≡S⟷PdDiA5:S|≡Di⇒VrA6:S|≡Di⇒V1A7:S|≡S⟷𝒮𝒦DiA8:Di|≡S⟷𝒮𝒦DiA9:S|≡Di|≡S⟷𝒮𝒦Di

—The above-mentioned postulates and assumptions are applied to the idealized form: M1 and M2 to achieve the defined goals as follows.

M1: Di→S:{IDi,Pd,A2}:{IDi,V1,A2}

According to the assumption A1 and the freshness concatenation rule:

S|≡♯({IDi,V1,A2})

Using the assumptions A4, A6, and the message meaning rule:

S|≡Di|∼({IDi,V1,A2})

Using the assumptions A5 and A9 and the jurisdiction rule:

S|≡h(V1′)

M2: S→Di:{Ps,A1}

Using the assumptions A2, A3, and the nonce verification rule:

Di|≡S|≡h(V1′)

According to the session key rule:

Di|≡Di⟷𝒮𝒦S

From the goal definition:

Di|≡S⟷𝒮𝒦Di

This completes the proof. The BAN logic analysis confirmed that both communication parties can trust the established session key and are mutually authenticated, reinforcing the results obtained through AVISPA. This dual-layer verification provides strong assurance of the protocol’s ability to withstand critical security threats in IoT environments.

8  Performance Analysis

The proposed ECC-based authentication protocol was rigorously evaluated to assess its computational efficiency, communication overhead, storage requirements, and security robustness. To ensure consistency and rigor in the evaluation, the proposed protocol employs a 256-bit elliptic curve (ECC-256) alongside SHA-256 for cryptographic operations. The selection of SHA-256 is based on recommendations from NIST, which highlight its suitability for IoT environments due to its optimal balance between computational efficiency and cryptographic strength, particularly in resource-constrained devices. Although NIST has not deprecated SHA-256 in favor of SHA-3—both being considered secure—SHA-256 remains the most practical and efficient option for the majority of current IoT deployments [29]. Similarly, all relevant recent protocols included in the comparative analysis were standardized to use ECC-256 and SHA-256. When evaluating computational complexity, lightweight operations such as exclusive OR (XOR) and string concatenation were excluded.

8.1 Experimental Setup

The results presented here were obtained following the implementation of the protocols on a system with the following specifications as shown in Table 7: Ubuntu 16 and Python 2.6 in a virtual machine (VM) adapted to the Charm framework. Web sockets were employed for communication between the embedded device D and the server S. All experiments were conducted on a MacBook Air with a 1.6 GHz Intel i5 processor, 8 GB of RAM, running macOS 12.2. Notably, all experiments were performed on a single core of the processor.

8.2 Computational Cost

In our analysis of the computation cost, we define the execution times of various cryptographic operations as follows:

•   Tp: Time required for a point multiplication operation.

•   TMapp: Execution time for mapping and processes using ECC.

•   TRev: Execution time for reverse processes using ECC.

•   T⊕: Duration needed to perform an XOR operation.

•   T||: Time taken for data concatenation.

•   Th: Execution time for performing a hash operation.

Our experimental findings indicate the following execution times for Tp, TMapp, TRev, and Th: 0.0326, 0.0001347, 0.00000905, and 0.0074 s, respectively. During the execution of the protocol, the registration phase incurs a computation cost of 2Th+Tp+TMapp. In the login and authentication phase, the session key Sk=KDF(Vr) is treated as a hash function due to its fixed output length and deterministic nature. Consequently, the computation cost for this phase is 6Th+2TMapp+2TRev. Therefore, the overall computational cost of the proposed protocol is 8Th+Tp+3TMapp+2TRev, which corresponds to approximately 92.22 ms. A detailed breakdown of the computational costs is provided in Table 8.

Based on the comparison Table 8, our proposed protocol demonstrates a significant improvement in computational efficiency relative to other recent protocols. With a total computation overhead of 92.22 ms, our protocol is markedly more efficient than those listed in the comparison. Specifically, it achieves a reduction of approximately 61.1% compared to the average total computation cost of the other protocols.

The registration phase of our protocol incurs a cost of 47.53 ms, which is more efficient compared to some other protocols. Notably, the efficiency gains are particularly evident in the login and authentication phase, where our protocol’s computation overhead is only 44.68 ms, significantly lower than that of other protocols. For example, the protocol by [16] has a computation cost of 316.3012 ms, and Ref. [15] shows 256.0705 ms for the same phase.

This reduction is primarily attributable to our protocol’s design, which incorporates only a single point multiplication Tp in the registration phase, unlike other protocols that may involve more complex operations.

This efficiency is further illustrated in Fig. 6, which shows that our protocol achieves the lowest computation overhead values in both the registration and authentication phases. This reduced overhead is crucial for time-sensitive applications, as it enables faster and more responsive authentication processes. In comparison, other schemes exhibit higher computation overheads, which can result in delays or increased resource consumption. Thus, the streamlined design of our protocol not only improves computational efficiency but also makes it a more optimal choice compared to existing solutions.

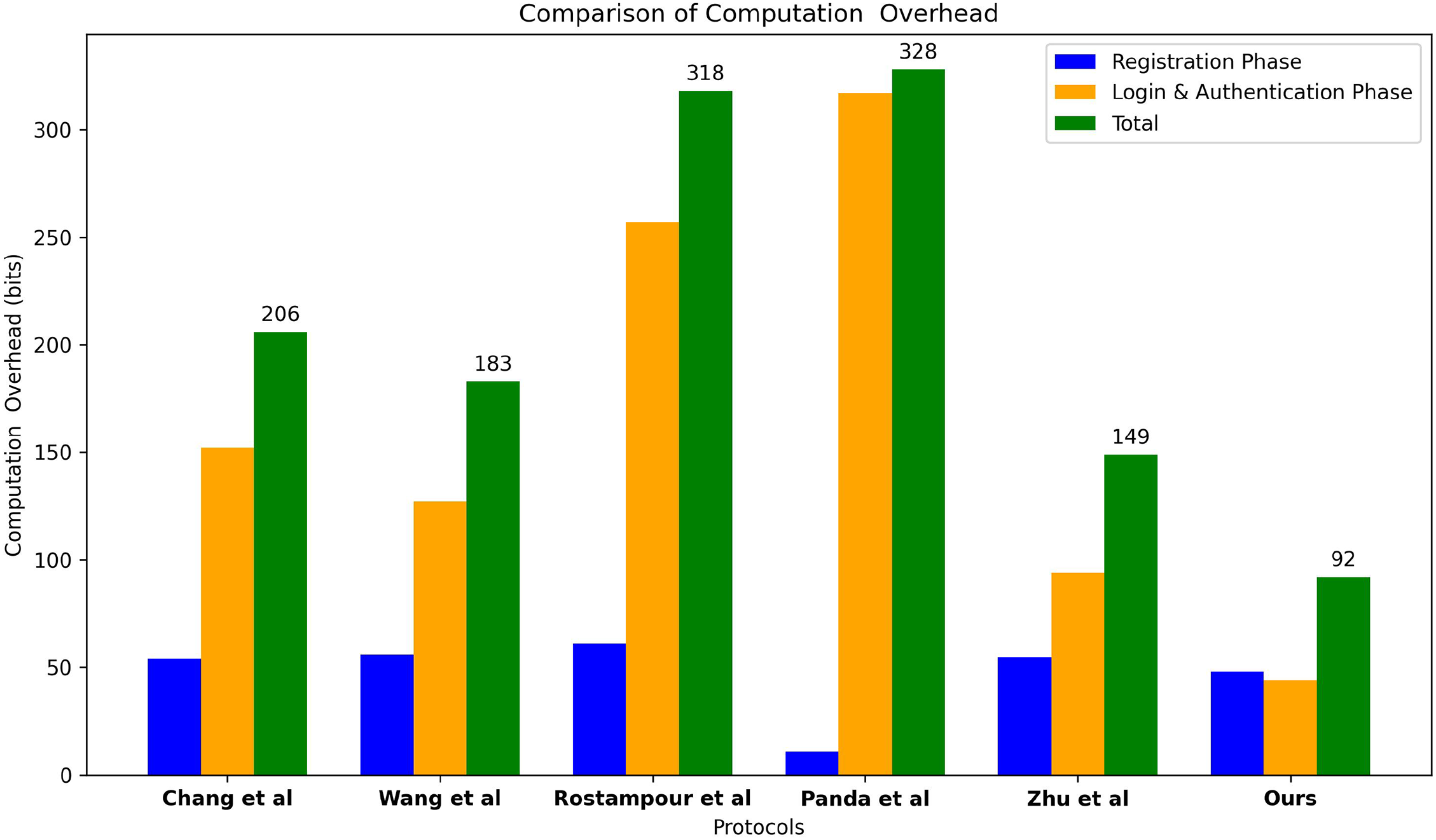
Figure 6: Performance comparison of different schemes in terms of computational overheads: Chang et al. [12], Wang et al. [13], Rostampour et al. [15], Panda and Chattopadhyay [16], and Zhu et al. [17].

8.3 Communication Overhead

The communication overhead was assessed by measuring the size of the authentication messages exchanged between IoT devices and the server during the registration, login, and authentication phases. In our proposed authentication protocol, the data transmitted between the device and the server consists of three types of messages:

1.   Registration Phase:The message msg1 includes ID and Ps. The size of ID used in our protocol is 160 bits. The size of Ps, representing the elliptic curve point (xs,ys), is 512 bits (256 bits for each coordinate). Therefore, the total communication cost for this phase is:

• msg1 = 160 bits+512 bits=672 bits.

2.   Login and Authentication Phase: Two messages are transmitted:

• —msg2=h(ID||cpt)+Pd, where h(ID||cpt) is a hash function output of 256 bits (using SHA-256) and Pd is an elliptic curve point of 512 bits. Thus, the total size of msg2 is 256 bits+512 bits=768 bits.

• —msg3=A1+A2, where A1 and A2 are both elliptic curve points of 512 bits each. Therefore, the total size of msg3 is 512 bits+512 bits=1024 bits.

The total communication overhead for both phases is the sum of the sizes of all transmitted messages: msg1+msg2+msg3=672 bits+768 bits+1024 bits=2464 bits.

Based on the comparison Table 9, our proposed protocol exhibits superior performance in terms of communication overhead compared to other recent protocols. Specifically, our protocol achieves the lowest registration phase communication overhead, totaling 672 bits. This is notably more efficient than the protocol by [13], which has a registration phase overhead of 768 bits.

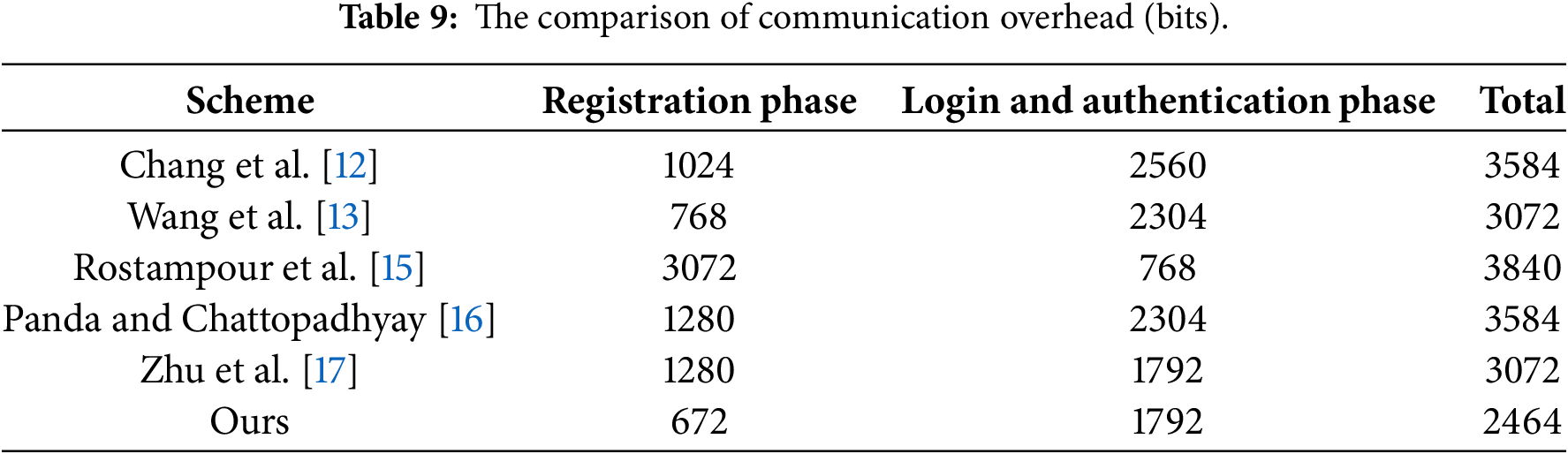
In the login and authentication phase, our protocol’s communication overhead is 1792 bits, which aligns with the protocol size presented by [17]. However, our protocol achieves a lower total communication overhead of 2464 bits, compared to 3072 bits in theirs. This represents a reduction of approximately 19.8% in total communication cost when compared to the protocol by [17].

Overall, the reduced registration phase overhead and competitive login and authentication phase size contribute to the lower total communication cost of our protocol. This reduction in message size is critical for IoT environments, where bandwidth and energy efficiency are of utmost importance as illustrated in Fig.7, making our protocol a more efficient choice relative to existing solutions.

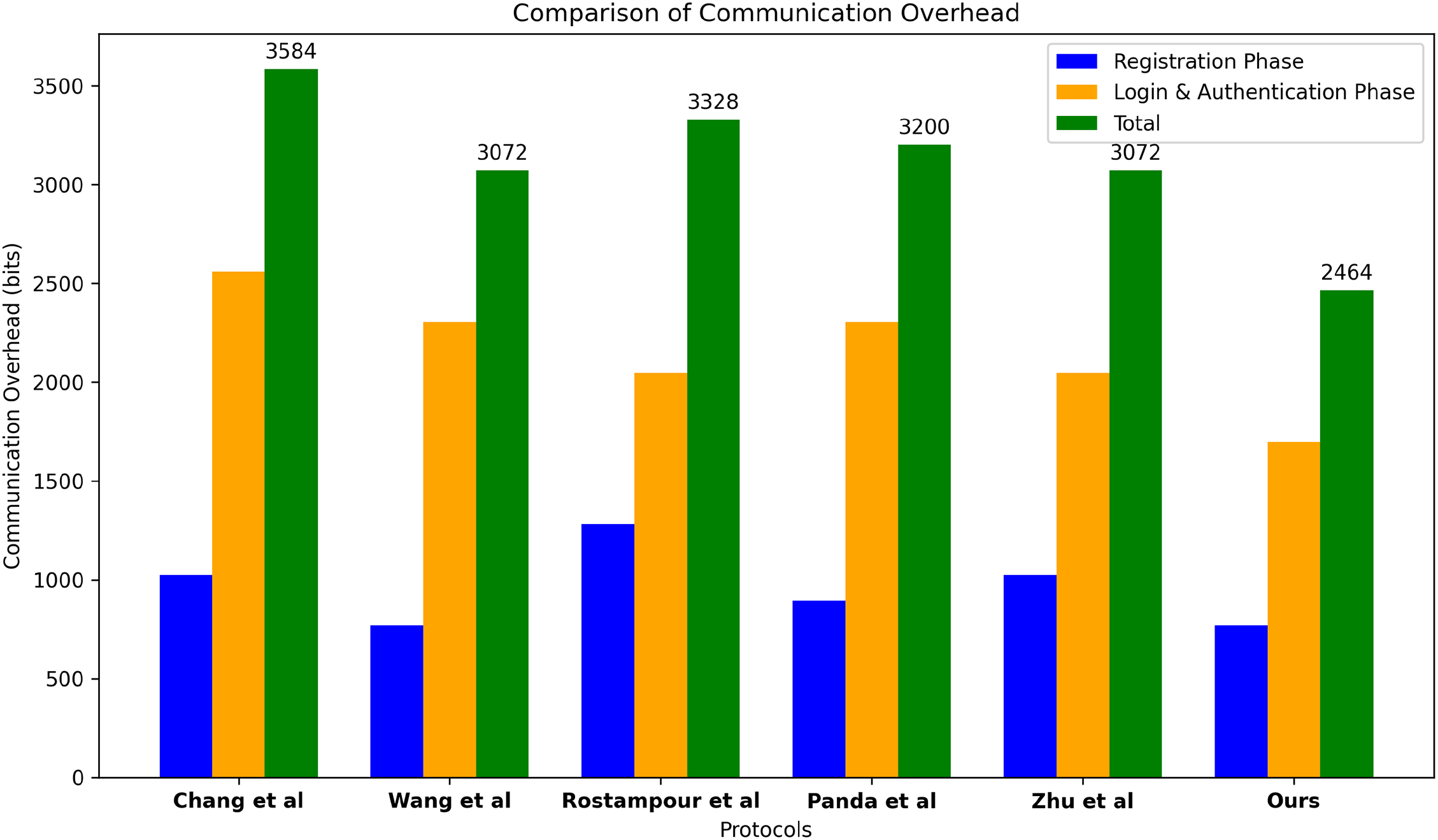
Figure 7: performance of different schemes in terms of communication overheads: Chang et al. [12], Wang et al. [13], Rostampour et al. [15], Panda and Chattopadhyay [16], and Zhu et al. [17].

8.4 Storage Cost

For our proposed protocol, the storage cost is analyzed in two phases: the registration phase and the login and authentication phase.

1.   Registration Phase:

-   Device: During the registration phase, the device stores the identity ID (160 bits) and the value of Ps (512 bits) received from the server, resulting in a total storage cost of 672 bits.

-   Server: Concurrently, the server stores the values of Ps (512 bits), ID (160 bits), and EXP_time (160 bits) in its database, totaling 832 bits.

2.   Login and Authentication Phase:

-   Device: In this phase, the device temporarily stores the values of Vr (160 bits), V1 (160 bits), and Sk (256 bits), leading to a total temporary storage cost of 576bits.

-   Server: The server temporarily stores the values Ps (512 bits), Pd (512 bits), Vr′ (512 bits), ID (160 bits), h(ID||cpt) (256 bits), A2 (256 bits), Vr (512 bits), and Sk (256 bits), leading to a total storage cost of 2976 bits.

The overall total storage cost for both the device and the server across all phases is 5056 bits.

However, in the relevant literature [13,16,17], the focus is typically on the storage cost of the device rather than the server, due to the limited memory capacity of IoT devices compared to the vast storage resources of cloud servers. Therefore, to ensure a fair and accurate comparison with other protocols, we consider only the device’s storage cost in our analysis. The detailed results, highlighting the device’s storage requirements, are presented in Table 10.

As shown in Fig. 8, our proposed protocol offers notable improvements in device storage overhead compared to other recent protocols, both during the registration and login/authentication phases. The reduction in storage requirements is critical for IoT devices, where memory capacity is typically limited. This efficiency allows our protocol to effectively minimize storage usage while maintaining robust security and functionality

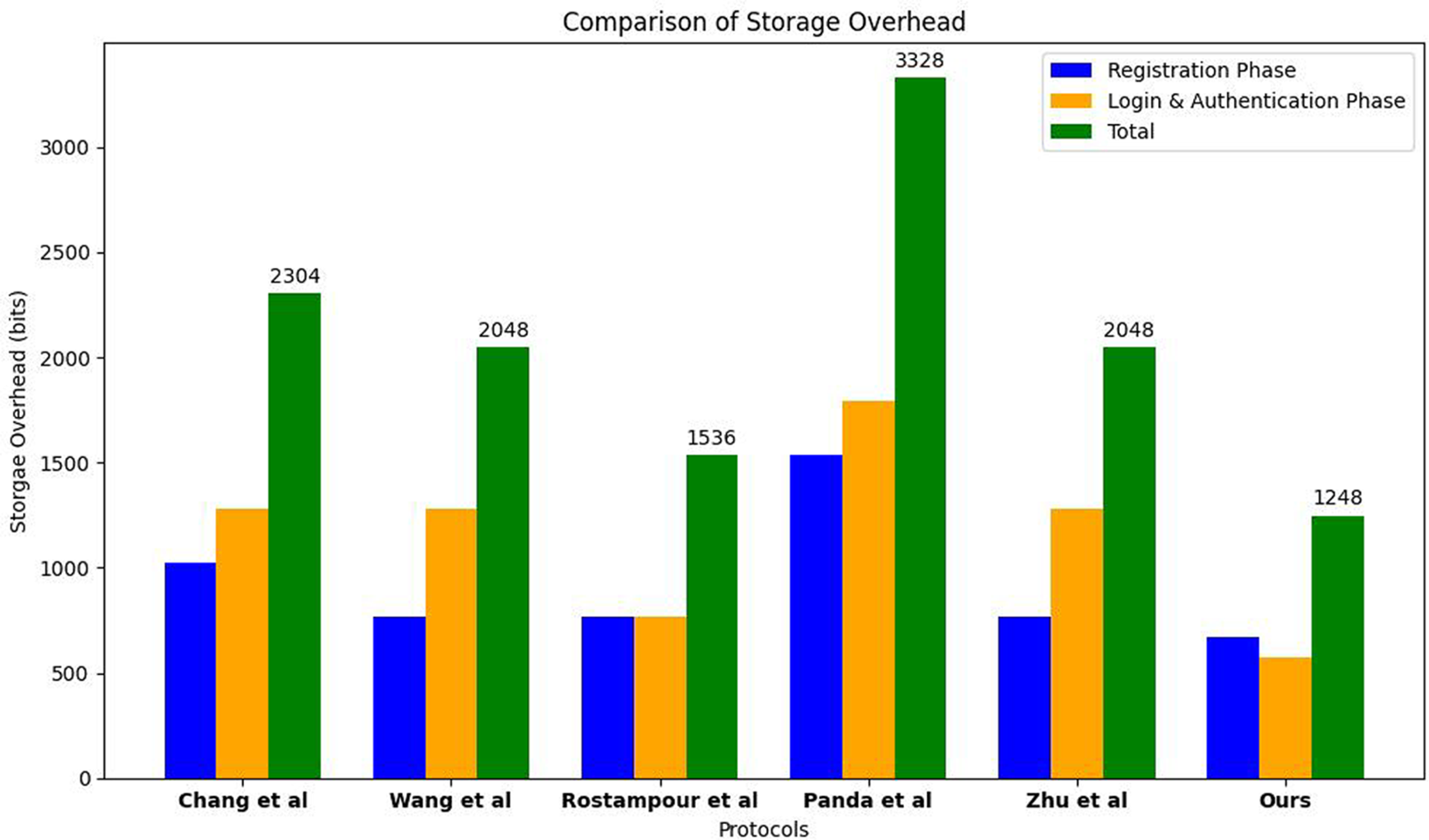
Figure 8: performance of different schemes in terms of device storage overheads: Chang et al. [12], Wang et al. [13], Rostampour et al. [15], Panda and Chattopadhyay [16], and Zhu et al. [17].

The evaluation of our proposed authentication protocol highlights its significant advantages in both security and lightweight performance compared to existing protocols. By effectively reducing communication, computation, and storage overheads, our scheme not only ensures robust protection against a variety of attacks but also maintains user anonymity and service availability. These attributes make it particularly well-suited for secure authentication in practical deployment scenarios.

Furthermore, the protocol’s efficiency in resource-constrained environments, achieved through substantial reductions in overheads, underscores its practicality. This balance of security and performance positions our protocol as an optimal solution for applications where both resource efficiency and strong security measures are critical, making it a superior choice for modern authentication needs.

9  Conclusion and Perspectives

This article introduces a novel ECC-based authentication protocol for IoT designed to enhance security while optimizing performance. Through the application of ECC, our protocol achieves superior security with reduced computational, communication, and storage overheads. A thorough security analysis, conducted both informally and formally using AVISPA and BAN logic, confirms the protocol’s resilience against various attacks.

Our performance evaluation underscores the protocol’s efficiency, demonstrating significantly lower computational, communication, and storage costs compared to existing relevant authentication protocols. These findings highlight that our protocol is not only secure but also highly practical for real-world applications, particularly in IoT environments where resource constraints are a significant concern.

Future work will focus on applying our authentication protocol in real-world scenarios to validate its practical effectiveness and reliability. Additionally, we aim to extend our protocol for integration with blockchain technology, leveraging its decentralized nature to further enhance security and trust in various applications. By continually refining and adapting our approach, we aim to advance secure and efficient authentication mechanisms in an increasingly interconnected digital landscape.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Younes Lahraoui and Jihane Jebrane; methodology, Younes Lahraoui and Jihane Jebrane; software, Younes Lahraoui and Jihane Jebrane; validation, Younes Lahraoui, Jihane Jebrane, Youssef Amal, Saiida Lazaar and Cheng-Chi Lee; formal analysis, Younes Lahraoui and Jihane Jebrane; investigation, Younes Lahraoui, Jihane Jebrane; writing—original draft preparation, Younes Lahraoui, Jihane Jebrane; writing—review and editing, Younes Lahraoui, Jihane Jebrane, Youssef Amal, Saiida Lazaar and Cheng-Chi Lee; funding acquisition, Cheng-Chi Lee. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Chauhan A, Sharma A, Sikhwal OP. Opportunities created by digital technology and increased data. ECS Trans. 2022;107(1):8071–8076. doi:10.1149/10701.8071ecst. [Google Scholar] [CrossRef]

2. Sharma J, Sangwan A, Singh RP. A review on evolving domains of internet of things: architecture, applications, and technical challenges. Int J Commun Syst. 2023;36(18):e5613. doi:10.1002/dac.5613. [Google Scholar] [CrossRef]

3. Zanella A, Bui N, Castellani A, Vangelista L, Zorzi M. Internet of things for smart cities. IEEE Internet Things J. 2014;1(1):22–32. doi:10.1109/JIOT.2014.2306328. [Google Scholar] [CrossRef]

4. Securelist. IoT threat report 2023. 2023. [cited 2025 Jun 20]. Available from: https://securelist.com/iot-threat-report-2023/110644/. [Accessed June 20, 2025]. [Google Scholar]

5. Zhang L, Tang S, Luo H. Elliptic curve cryptography-based authentication with identity protection for smart grids. PLoS One. 2016;11(3):e0151253. doi:10.1371/journal.pone.0151253. [Google Scholar] [PubMed] [CrossRef]

6. Lahraoui Y, Lazaar S, Amal Y, Nitaj A. Securing data exchange with elliptic curve cryptography: a novel hash-based method for message mapping and integrity assurance. Cryptography. 2024;8(2):23. doi:10.3390/cryptography8020023. [Google Scholar] [CrossRef]

7. Brown M, Hankerson D, López J, Menezes A. Software implementation of the NIST elliptic curves over prime fields. In: Naccache D, editor. Lecture notes in computer science. Topics in cryptology—CT-RSA 2001. Vol. 2020. Berlin/Heidelberg: Springer; 2001. p. 250–65. doi:10.1007/3-540-45353-9_19. [Google Scholar] [CrossRef]

8. Verri Lucca A, Mariano Sborz GA, Leithardt VRQ, Beko M, Albenes Zeferino C, Parreira WD. A review of techniques for implementing elliptic curve point multiplication on hardware. J Sensor Actuator Networks. 2021;10(1):3. doi:10.3390/jsan10010003. [Google Scholar] [CrossRef]

9. Zhao G, Si X, Wang J, Long X, Hu T. A novel mutual authentication scheme for internet of things. In: Proceedings of the 2011 International Conference on Modelling, Identification and Control; Shanghai, China; 2011. p. 563–6. doi:10.1109/ICMIC.2011.5973767. [Google Scholar] [CrossRef]

10. Ferrag MA, Maglaras LA, Janicke H, Jiang J, Shu L. Authentication protocols for internet of things: a comprehensive survey. Secur Commun Netw. 2017;2017(4):562953. doi:10.1155/2017/6562953. [Google Scholar] [CrossRef]

11. Kalra S, Sood SK. Secure authentication scheme for IoT and cloud servers. Pervasive Mob Comput. 2015;24(1):210–23. doi:10.1016/j.pmcj.2015.08.001. [Google Scholar] [CrossRef]

12. Chang CC, Wu HL, Sun CY. Notes on ‘secure authentication scheme for IoT and cloud servers’. Pervasive Mob Comput. 2017;38(15):275–8. doi:10.1016/j.pmcj.2015.12.003. [Google Scholar] [CrossRef]

13. Wang KH, Chen CM, Fang W, Wu TY. A secure authentication scheme for internet of things. Pervasive Mob Comput. 2017;42(15):15–26. doi:10.1016/j.pmcj.2017.09.004. [Google Scholar] [CrossRef]

14. Kumari S, Karuppiah M, Das AK, Li X, Wu F, Kumar N. A secure authentication scheme based on elliptic curve cryptography for IoT and cloud servers. J Supercomput. 2018;74(4):6428–53. doi:10.1007/s11227-017-2048-0. [Google Scholar] [CrossRef]

15. Rostampour S, Safkhani M, Bendavid Y, Bagheri N. ECCbAP: a secure ECC-based authentication protocol for IoT edge devices. Pervasive Mob Comput. 2020;67(2018):101194. doi:10.1016/j.pmcj.2020.101194. [Google Scholar] [CrossRef]

16. Panda PK, Chattopadhyay S. A secure mutual authentication protocol for IoT environment. J Reliab Intell Environ. 2020;6(2):79–94. doi:10.1007/s40860-020-00098-y. [Google Scholar] [CrossRef]

17. Zhu X, Ren Z, He J, Ren B, Zhao S, Zhang P. LAAP: lightweight anonymous authentication protocol for IoT edge devices based on elliptic curve. Wirel Commun Mob Comput. 2022;2022(1):8768928. doi:10.1155/2022/8768928. [Google Scholar] [CrossRef]

18. Jebrane J, Lazaar S. ILAPU-Q: an improved lightweight authentication protocol for IoT based on U-quark hash function. Recent Adv Comput Sci Commun. 2024;17(2):78–87. doi:10.2174/0126662558274597231204114801. [Google Scholar] [CrossRef]

19. Jebrane J, Lazaar S. An enhanced and verifiable lightweight authentication protocol for securing the internet of medical things (IoMT) based on CP-ABE encryption. Int J Inf Secur. 2024;1(1):1–15. doi:10.1007/s10207-024-00906-z. [Google Scholar] [CrossRef]

20. Sudhakar T, Praveen R, Natarajan V. An efficient ECC and fuzzy verifier based user authentication protocol for IoT-enabled WSNs. Sci Rep. 2025;15(1):9974. doi:10.1038/s41598-025-16694-3. [Google Scholar] [CrossRef]

21. Choe H, Kang D. ECC-based authentication protocol for military internet of drones (IoDa holistic security framework. IEEE Access. 2025;13(1):21503–21519. doi:10.1109/ACCESS.2025.3536014. [Google Scholar] [CrossRef]

22. Samal K, Sunanda SK, Jena D, Patnaik S. A lightweight privacy preservation authentication protocol for IoMT using ECC based blind signature. Int J Eng Bus Manag. 2025;17(4):1–13. doi:10.1177/18479790251318538. [Google Scholar] [CrossRef]

23. Sabbry NH, Levina AB. An optimized point multiplication strategy in elliptic curve cryptography for resource-constrained devices. Mathematics. 2024;12(6):881. doi:10.3390/math12060881. [Google Scholar] [CrossRef]

24. Hankerson D, Vanstone S, Menezes A. Guide to elliptic curve cryptography. New York, NY: Springer Professional Computing; 2004. doi:10.1007/b97644, 978-0-387-95273-4 [Google Scholar] [CrossRef]

25. Szepieniec A. On the use of the Legendre symbol in symmetric cipher design. Cryptology ePrint Archive, Paper 2021/984. 2021. [cited 2025 Jun 20]. Available from: https://eprint.iacr.org/2021/984. [Google Scholar]

26. Webster AF, Tavares SE. On the design of S-Boxes. In: Lecture notes in computer science (including subseries lecture notes in artificial intelligence and lecture notes in bioinformaticsVol. 218. LNCS; 1986. doi:10.1007/3-540-39799-X_41. [Google Scholar] [CrossRef]

27. Kam L, Davida G. Structured design of substitution-permutation encryption networks. IEEE Trans Comput. 1979;28(10):747–53. doi:10.1109/TC.1979.1675242. [Google Scholar] [CrossRef]

28. Adiguzel-Goktas E, Ozdemir E. Square root computation in finite fields; 2024. arXiv:2206.07145. [Google Scholar]

29. Dang Q. NIST special publication 800-107 revision 1: recommendation for applications using approved hash algorithms. Natl Inst Stand Technol. 2017. doi:10.6028/NIST.SP.800-107r1. [Google Scholar] [CrossRef]