A Novel Approach Based on Recuperated Seed Search Optimization for Solving Mechanical Engineering Design Problems

1  Introduction

Nature-inspired algorithms have gained significant popularity among researchers and scientists for addressing a wide range of challenges in engineering fields, including medical image processing, signal processing, cloud computing, feature selection, deep learning, text mining, photovoltaic models, and urban planning [1]. These algorithms are categorized into swarm intelligence (SI), physics-based, and evolutionary algorithms (EA). Notably, swarm-based optimization algorithms are renowned for their ability to mimic the social behaviour of organisms found in nature [2,3].

Swarm-based optimization algorithms excel in solving real-world optimization problems due to several key characteristics: (i) The search process mimics natural phenomena, which are inherently random. This randomness enables swarm-based optimization algorithms to avoid getting trapped in local optima; (ii) these algorithms, also known as population-based optimization, explore all potential solutions by updating the positions of individuals within the search space to achieve the global optimal solution. Notable swarm-based optimization algorithms include the particle swarm optimizer (PSO) [4], arithmetic optimization algorithm (AOA) [5], ant lion optimizer (ALO) [6], dragonfly algorithm (DA) [7], grey wolf optimization (GWO) [8], moth-flame optimization (MFO) [9], multi-verse optimization (MVO) [10], salp swarm algorithm (SSA) [11], rabbits optimization algorithm (ROA) [12] and sine cosine algorithm (SCA) [11]. Sperm swarm optimization, a novel approach proposed by Shehadeh et al. [13], emulates the movement of sperm or seed during fertilization.

In recent years, researchers have been focused on developing innovative methods to enhance the performance of swarm-based optimization algorithms. These mechanisms include the hybridization of two algorithms, the incorporation of an opposition-based concept, the addition of various mutation strategies, and the application of weightage during position updating. For example, Wang et al. [14] improved kill herd optimization by integrating OBL and heavy-tailed CM to boost the convergence rate of the basic kill herd. Kumari et al. [15] enhanced the chimp optimization algorithm by incorporating elements from the spotted hyena optimizer, aiming to improve both the exploration and exploitation phases of the optimization process. Kaucic et al. [16] tackled the limitations of basic optimization techniques for high-dimensional problems by combining the level-based learning swarm optimizer (LLSO) with PSO. Alruwais et al. [17] hybridized the moth flame optimization (MFO) with deep learning concepts for automatic fabric inspection. Zhou et al. [18] refined the slime mould algorithm (SMA) by incorporating mutation and neighborhood search strategies, enhancing both exploration and exploitation capabilities, especially for complex combinatorial functions. Yu et al. [19] integrated grey wolf optimization (GWO) and differential evolution (DE) to improve UAV path planning. Vashishtha and Kumar [20] utilized AO to determine the optimal filter length for minimum entropy deconvolution (MED), a technique used to diagnose bearing defects in Francis turbines. Chauhan et al. [21] explored various mutation strategies within a diversity-driven multi-parent evolutionary algorithm to address area coverage issues in wireless sensor networks. Wang et al. [22] enhanced the Golden Jackal Optimization algorithm with multi-strategy mixing, incorporating chaotic initialization, dynamic inertia weight, and Gaussian mutation. It outperforms existing methods on benchmark functions and industrial problems, effectively balancing exploration and exploitation, avoiding local optima, and demonstrating high robustness and applicability for complex real-world optimization challenges.

Swarm-based optimization algorithms offer numerous advantages, yet no single algorithm can efficiently and effectively solve all optimization problems. This notion is supported by the no-free-lunch (NFL) theorem, which underscores the importance of developing innovative and unique algorithms for different optimization challenges. This insight has inspired a modification to the existing sperm swarm optimization (SSO), which mimics the movement of sperm toward fertilizing an egg. While the basic SSO is adept at handling a range of optimization problems, it does face limitations, such as slow convergence and a tendency to get trapped in local optima when addressing high-dimensional problems. To tackle these issues, OBL and CM strategies have been integrated into the basic SSO. The OBL enhances the diversity of SSO solutions by generating a new solution that is the opposite of the current one, thereby accelerating convergence. Meanwhile, the CM strategy balances the exploration and exploitation search capabilities.

The quality of solutions and the convergence rate of the basic SSO were improved by competitively incorporating the benefits of OBL and CM operators throughout the exploratory phase. The innovations of this study are summarized as follows:

1.    The basic SSO was refined using OBL and CM strategies to boost its performance. This enhanced algorithm is called recuperated seed swarm optimization (RSSO).

2.    The fundamental SSO was enhanced through the application of OBL and CM strategies to improve its performance. This upgraded algorithm is known as recuperated seed swarm optimization (RSSO).

3.    To demonstrate its effectiveness, RSSO was compared with other popular optimization algorithms developed in recent years. This comparison highlights RSSO’s advantages and showcases its potential to outperform existing methods.

The rest of this paper is organized as follows. Section 2 provides the background information for this research. Section 3 describes the proposed RSSO-based optimization algorithm. Section 4 presents experimental results, analysis, and discussion. Section 6 summarizes the key conclusions and findings of this study.

2  Background

2.1 Sperm Swarm Optimization (SSO)

Shehadeh et al. [13] introduced the SSO algorithm, inspired by the natural process of sperm fertilization. This algorithm mimics the journey of sperm as they move from the cooler cervix to the warmer fallopian tubes in search of the egg. In this optimization model, the ‘sperm’ or ‘seed’ seeks the ‘egg’ or ‘ovum’ within an optimal environment. Numerous seeds, or solutions, exist within the search space, but only one successfully fertilizes an egg, becoming the winner or global solution. However, this optimization faces certain limitations, such as the seeds not having a low pH level during fertilization. Therefore, it is recommended to maintain a pH value between 7 and 14 to ensure an alkaline and non-toxic environment for ovulation. This concept is represented by Eq. (1).

vini=DF×vseed×log10(ph_r1)(1)

where the parameter DF represents the damping factor of velocity which is randomly generated in the range of [0, 1], the parameter vseed is the velocity of the seed. And, the parameter ph_r1 indicates the pH value in the range of 7 to 14.

The algorithm keeps track of the best solution found thus far, which is represented by the position of the most successful ‘seed.’ To identify the best seed, the algorithm constantly compares the current position of the best seed with its previously recorded position of the best seed. Thus, the current position replaces the previous position if the latest seed provides a superior solution to that of the last seed. The solution of the best seed can be obtained by Eq. (2).

SCB=log10⁡(ph_r2)×log10⁡(T_r1)×(SB−SC)(2)

where the parameter SB indicates the best solution, ph_r2 is the pH value of the visited area in the range of 7 to 14. Whereas the parameter T_r1 randomly generated between 35.1 to 38.5 indicating the temperature of the visited area. The global best solution obtained from the seed can be computed using Eq. (3).

SG=log1⁡(ph_r3)×log10⁡(T_r2)×(SGB−SC)(3)

where the parameter SGB represents the global best solution obtained by the seed. The parameter ph_r3 indicates the pH value of the visited area generated in the range of 7 to 14 and the T_r2 indicates the temperature of the visited area generated in the range of 35.1 to 38.5. The SC represents the current solution of the seed which can be calculated through Eq. (4).

SC=SC+vseed(4)

where the velocity of the seed is represented by vseed that can be obtained by Eq. (5).

vseed=vini+SCB+SG(5)

2.2 Cauchy Mutation (CM) Strategy

The algorithm uses a mathematical technique called Cauchy mutation to introduce randomness into the search process. Cauchy mutation is a type of probability distribution that depends on two factors: location (x) and scaling (t) [23,24]. These factors determine the shape of the Cauchy distribution, which is defined by the following density function: f(x).

f(x)=1π(tt2+x2),−∞<x<∞(6)

where the parameter t > 0 is a scaling parameter. Whereas, Cauchy distribution function Ft(x) is defined as:

Ft(x)=12+1πarctan(xt)(7)

The CM operator increases the probability of not being trapped in a local optimum solution and overcomes premature convergence problems by performing small controlled steps in the search space. The solution of the Cauchy distributed random number C(x) is computed by Eq. (7), whereas the mutation in the proposed methodology is performed through Eq. (8).

Xit+1=Xi+C(x)×ΔXit+1(8)

where ΔXit+1 is the step vector.

2.3 Opposition-Based Learning (OBL)

Every optimization algorithm starts by randomly choosing a starting point for the solution. The positions of the individual elements within the algorithm are then updated based on their ‘intelligence’ (meaning their ability to improve the overall solution). This means that the initial guess significantly affects the time required by the algorithm to find a solution. To improve the speed and efficiency, the algorithm can explore both the initial guess and its opposite. This implies calculating the solution based on the initial guess and then calculating the solution based on the opposite of that guess. A better solution of these two is then used to start the optimization process, which leads to faster convergence. This process of exploring both the initial guess and its opposite is repeated throughout the optimization process. Eq. (9) outlines the specific method used for initializing the solution within the algorithm.

xi+NP,jt=xjmin+xjmax−xijt(i=1,2,…,NP;j=1,2,…,D),(9)

where NP is the population size and D is the dimension of the search space.

3  Proposed Algorithm

The concept of OBL and CM has been incorporated in the basic SSO to develop RSSO whose pseudo-code is given in Algorithm 1. Along with the OBL and CM, the weighting factor has also been introduced while computing the current solution. The proposed algorithm is accomplished through the following steps which are also shown in Fig. 1.

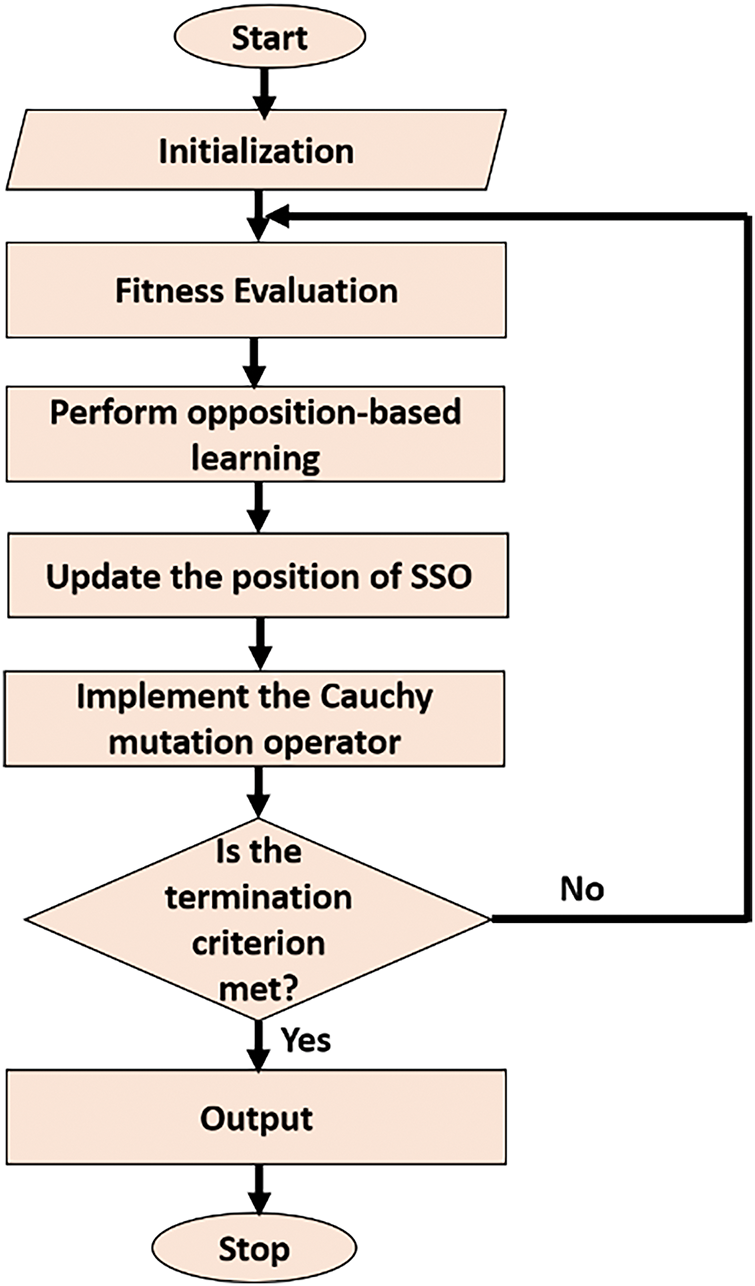
Figure 1: Proposed RSSO algorithm

Step 1. Initialization

The population is the RSSO has been initialized randomly through Eq. (10).

Xij=Xjmin+rij(Xjmax+Xjmin);(i=1,2,…,NP;j=1,2,…,D)(10)

where Xij is the initial population having an upper bound Xjmax and lower bound Xjmin, respectively. The parameter rij is uniformly and randomly distributed number between [0, 1].

Step 2. Incorporating the OBL

The opposite solution has also been explored to improve the diversity in the population which increases the convergence rate. This step can be attained through Eq. (9).

Step 3. Position clamping in RSSO

The velocity of the “seed” (representing a potential solution) is crucial in finding the optimal solution within the RSSO algorithm, as outlined in Algorithm 1. To enhance the algorithm’s exploration capabilities, a weighting factor has been introduced. The current position of the seed (SC) is updated using Eq. (11) within the RSSO framework.

SC=SC×0.3+vseed×0.7(11)

Step 4. Utilizing the CM operator

Finding the optimal solution in any optimization algorithm requires a delicate balance between exploration (searching for new areas of the solution space) and exploitation (refining existing solutions). An effective balance helps to speed up the convergence process and prevents the algorithm from getting stuck in suboptimal solutions (local optima). The Cauchy Mutation (CM) operator has been incorporated into the algorithm to address this balance. Eq. (8) demonstrates how CM is implemented to achieve this balance.

4  Results and Discussion

4.1 Classical Benchmark Functions

Three sets of classical benchmark functions viz., unimodal, multi-modal, and fixed-dimensional multi-modal have been used to evaluate the RSSO’s performance. Applying the one best global solution of each approach to the unimodal benchmark functions F1–F7 improves their capabilities. Alternatively, optimizers can test their algorithms’ diversification capabilities using fixed-dimension multi-modal benchmark functions F14–F23 and multimodal benchmark functions F8–F13. Tables 1–3 present the definitions of the three types of benchmark functions.

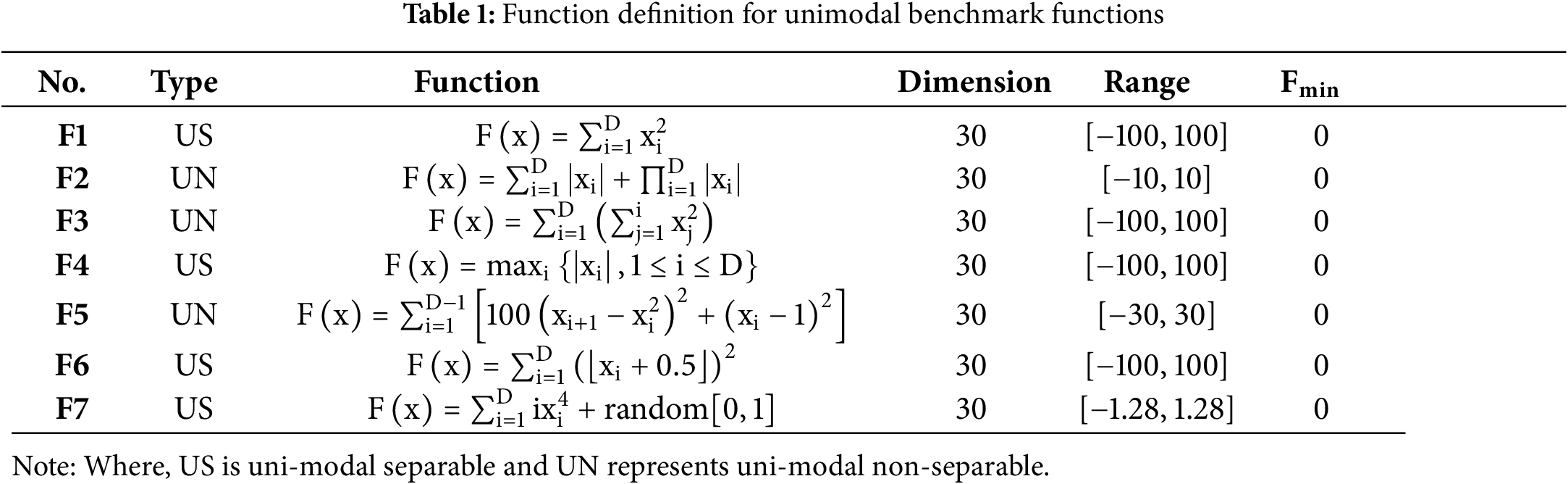
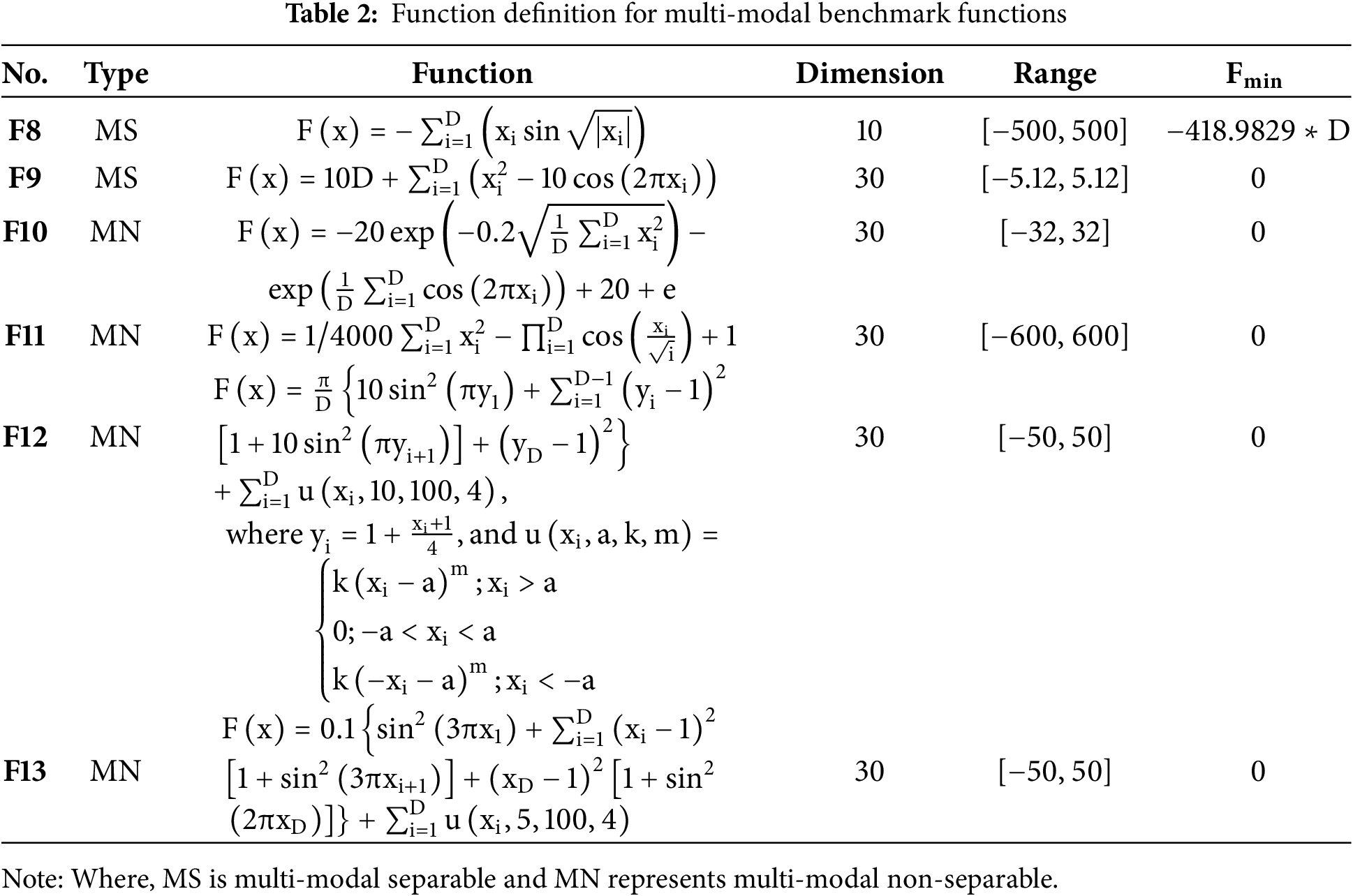
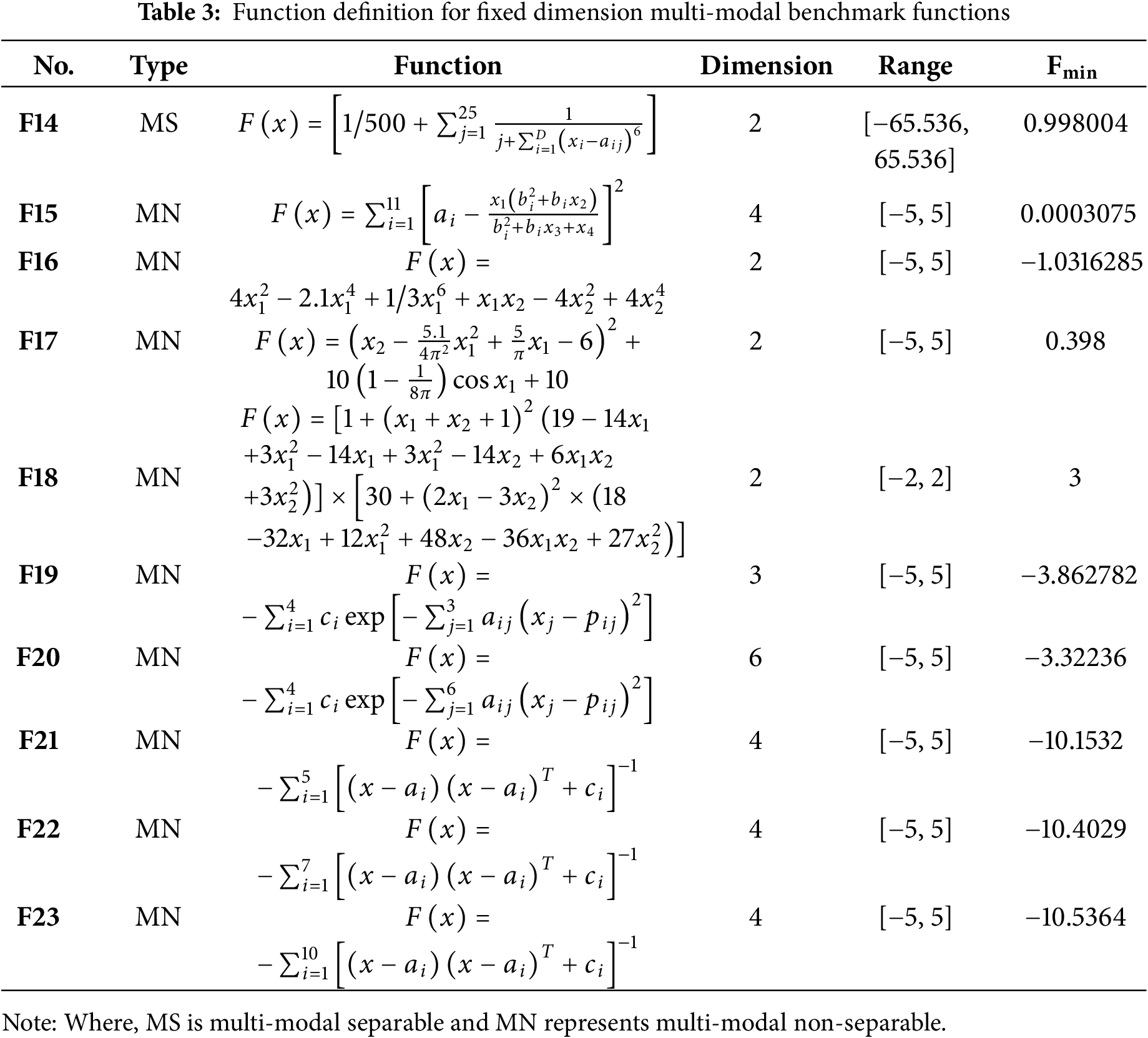
The results obtained by RSSO at benchmark functions have been compared with well-known algorithms of recent times.

4.2 Parametric Settings

The research was conducted using MATLAB 2019b software on a specific computer with the following specifications: processor: AMD Ryzen 5 4600 with Radeon graphics 3.00 GHz, RAM: 8.00 GB and operating system: 64-bit Windows 11. For all the algorithms tested, the population size was set to 30 and the maximum number of iterations was set to 1000. The specific settings for each algorithm are summarized in Table 4.

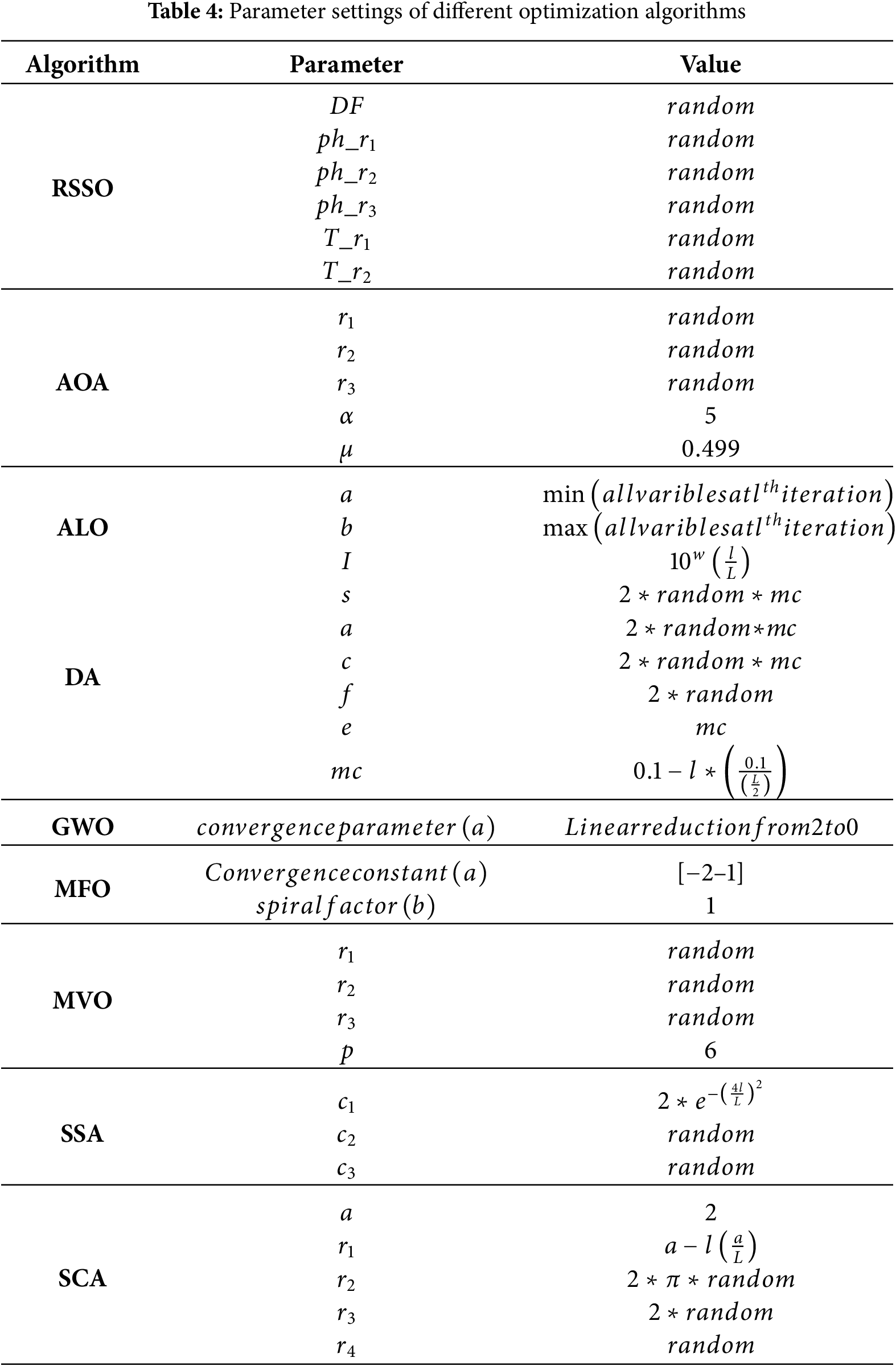
4.3 Quantitative Analysis of RSSO

The proposed RSSO algorithm was compared against other recently developed optimization algorithms using standard benchmark functions. The comparison focused on the average and standard deviation of the results, which are presented in a Table 5.

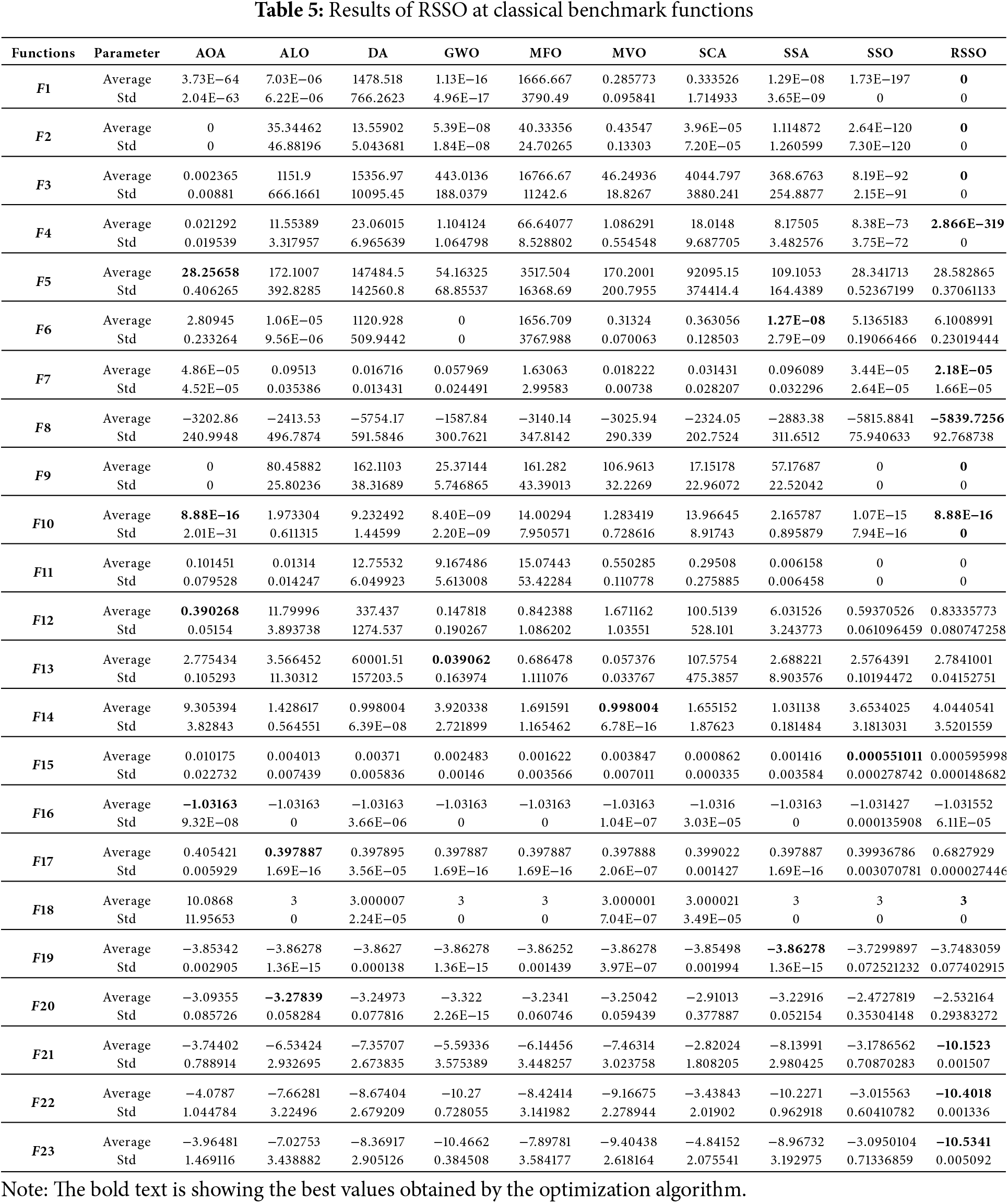
4.4 Statistical Analysis of Proposed Optimization RSSO

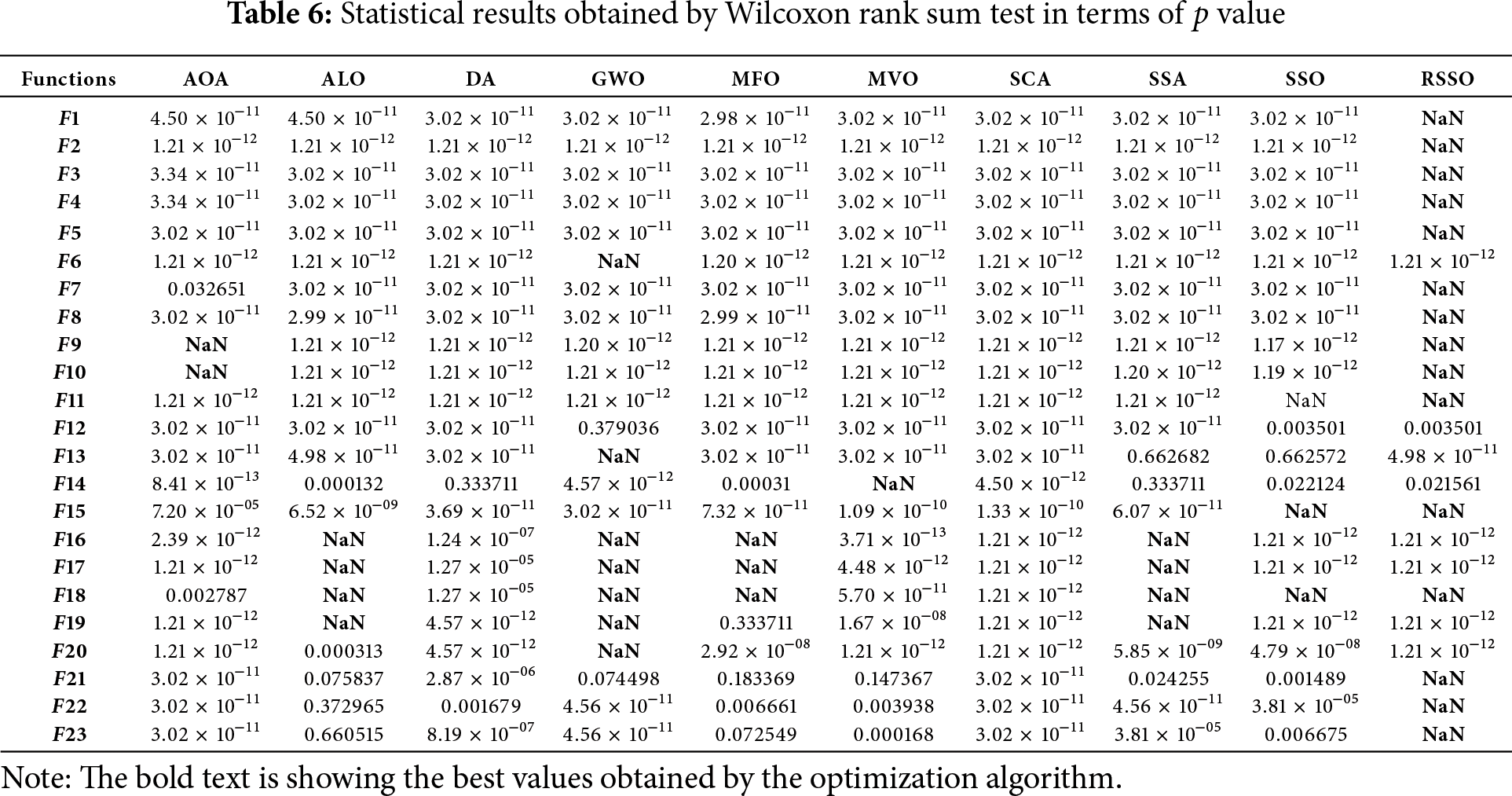
While no direct comparison of RSSO with other optimization algorithms has been published independently, the study conducted 30 independent runs of RSSO and compared its performance (in terms of average and standard deviation) to other algorithms. To rule out the possibility that the superior performance of RSSO was simply due to chance, a statistical test called the Wilcoxon rank-sum test was performed. Table 6 summarizes the p-values obtained from this test for each benchmark function. A p-value less than 0.05 indicates strong support for the hypothesis that RSSO is significantly better than the other algorithms. Since RSSO cannot be compared to itself, “N/A” (Not Applicable) is used in these cases.

4.5 Qualitative Analysis of the RSSO

Using convergence analysis and box plots, the suggested RSSO has been qualitatively analyzed. Fig. 2 displays the RSSO algorithm’s convergence graphs for the classical benchmark functions. Comparing it to the basic SSO and other algorithms, it appears that the RSSO approach demonstrates faster convergence. Due to the stochastic character of metaheuristic algorithms, Box plots have been used to verify RSSO’s stability by comparing the means obtained by various algorithms, as shown in Fig. 3. To further compare RSSO outcomes to different optimization procedures, box plots of the top individuals’ fitness from the last generation are provided. This further demonstrates RSSO’s superior performance and convergence capabilities. If all trials yield the same result, the RSSO algorithm can strike a balance between the exploration and efficiency phases.

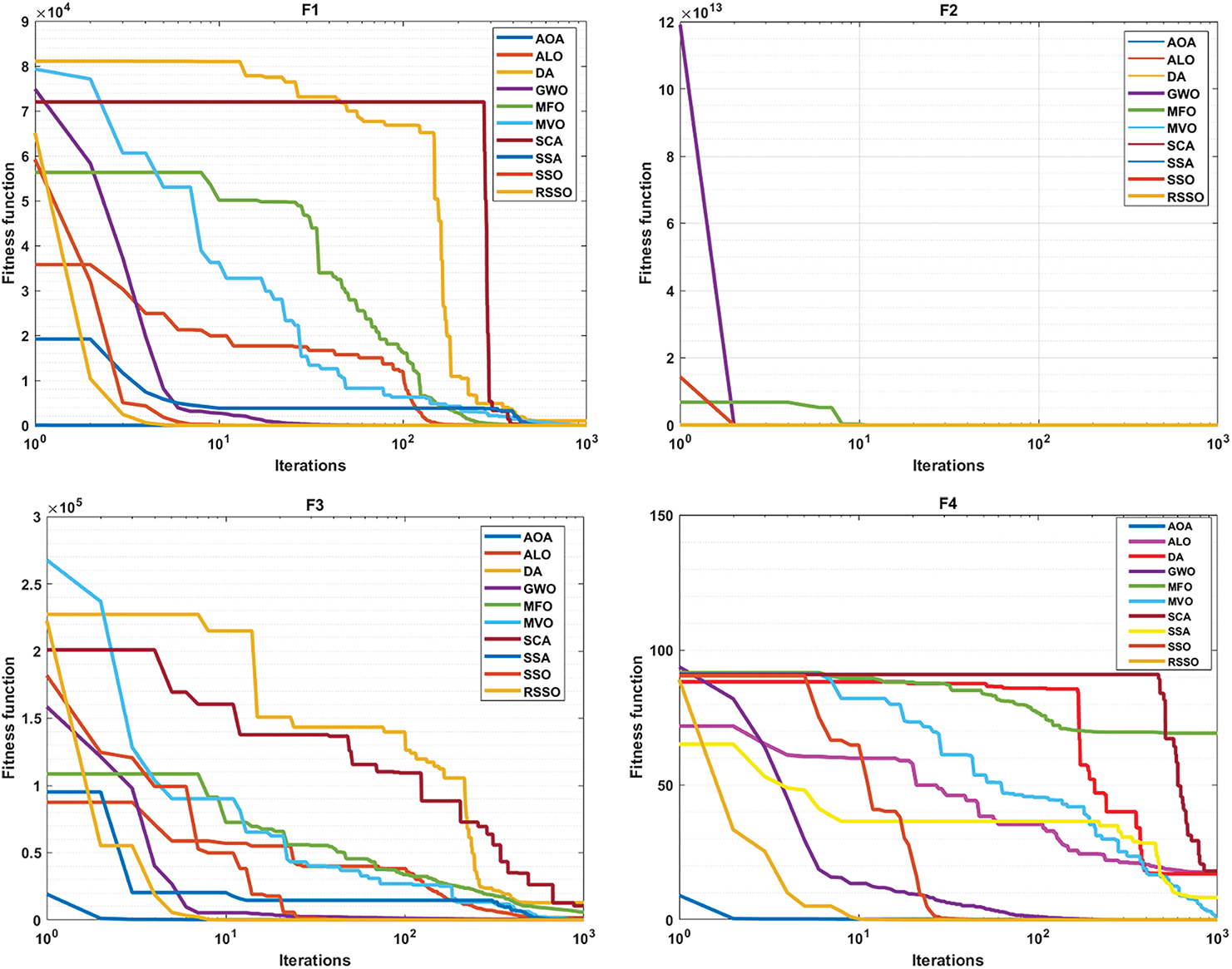
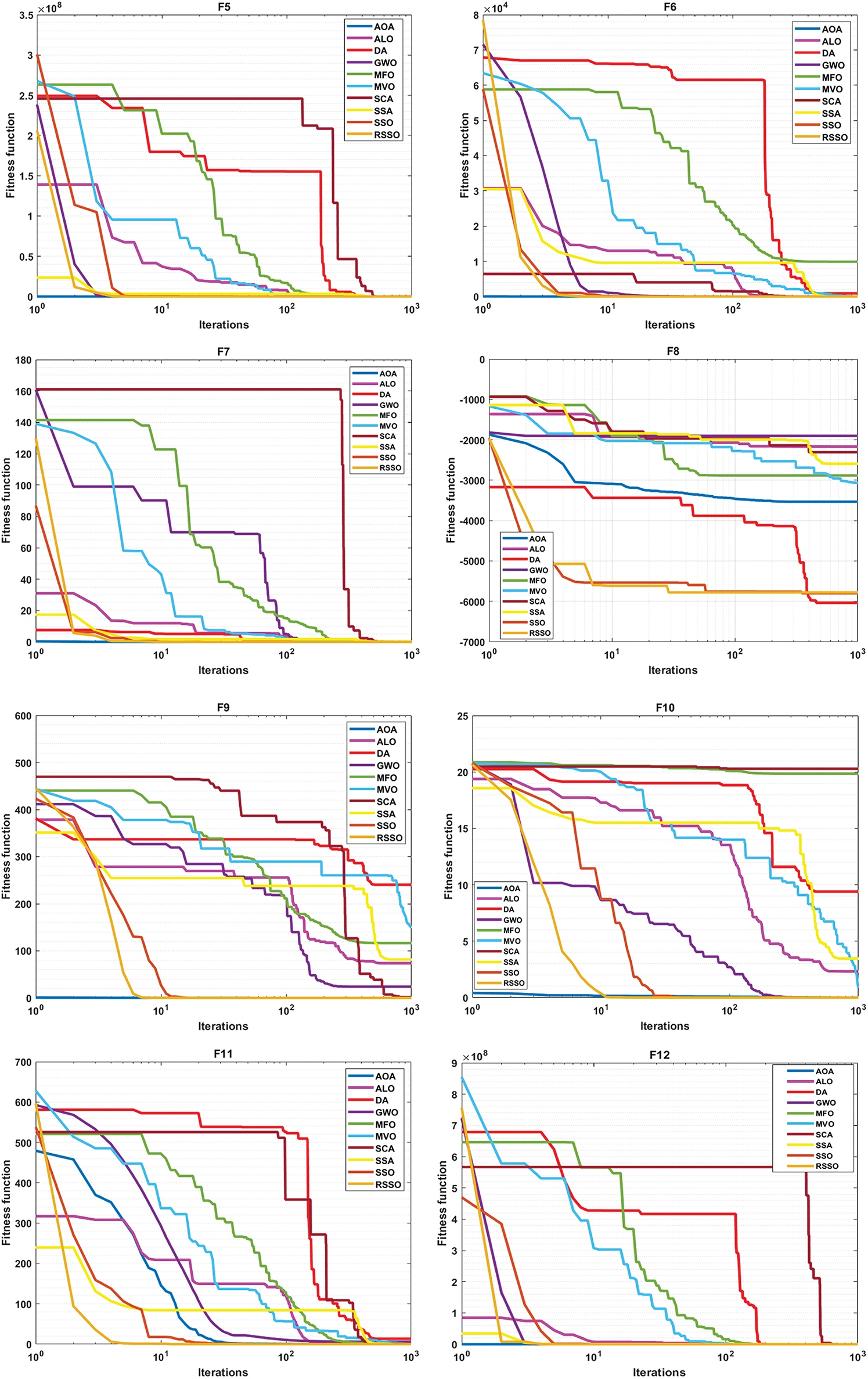
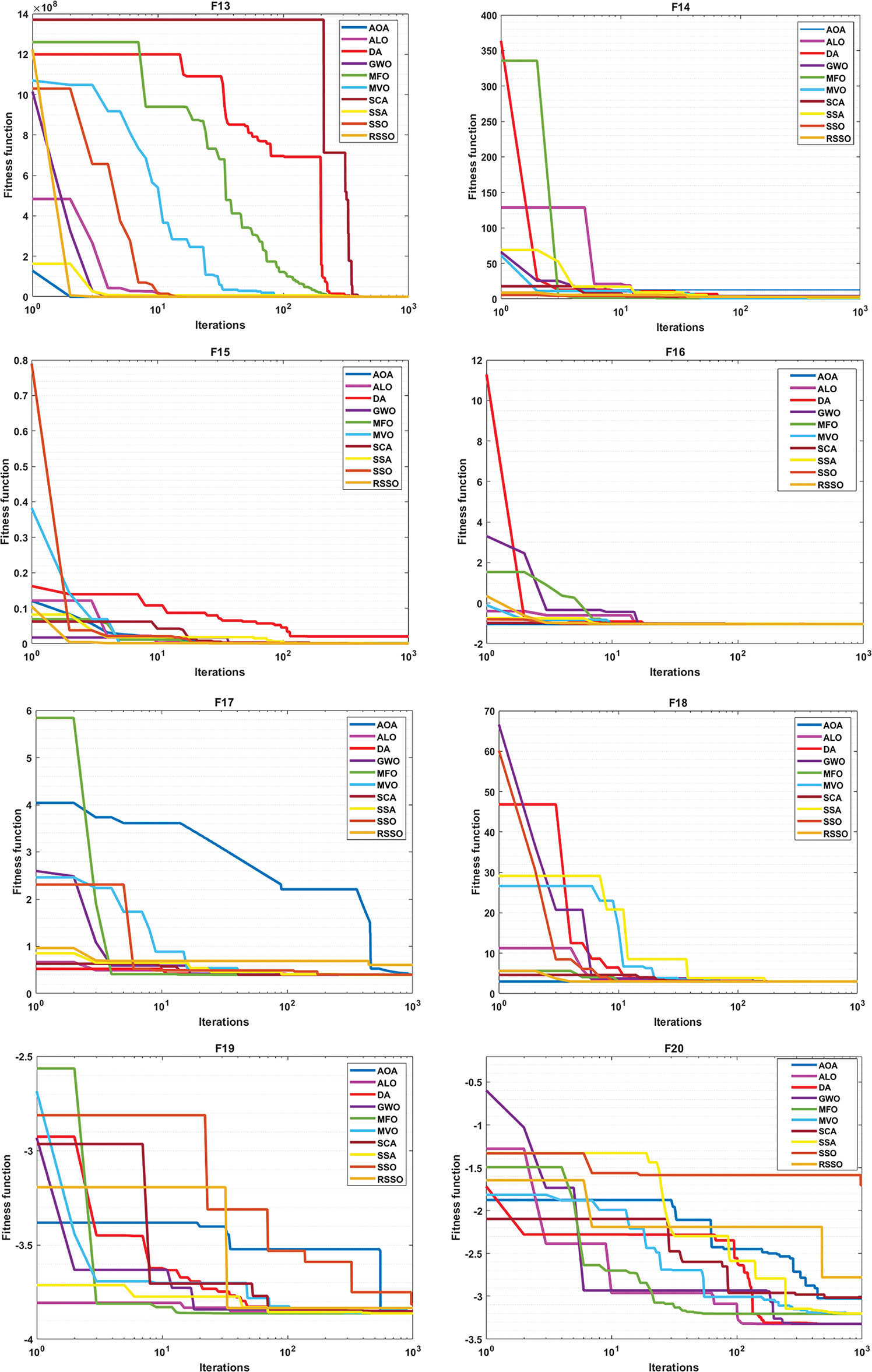
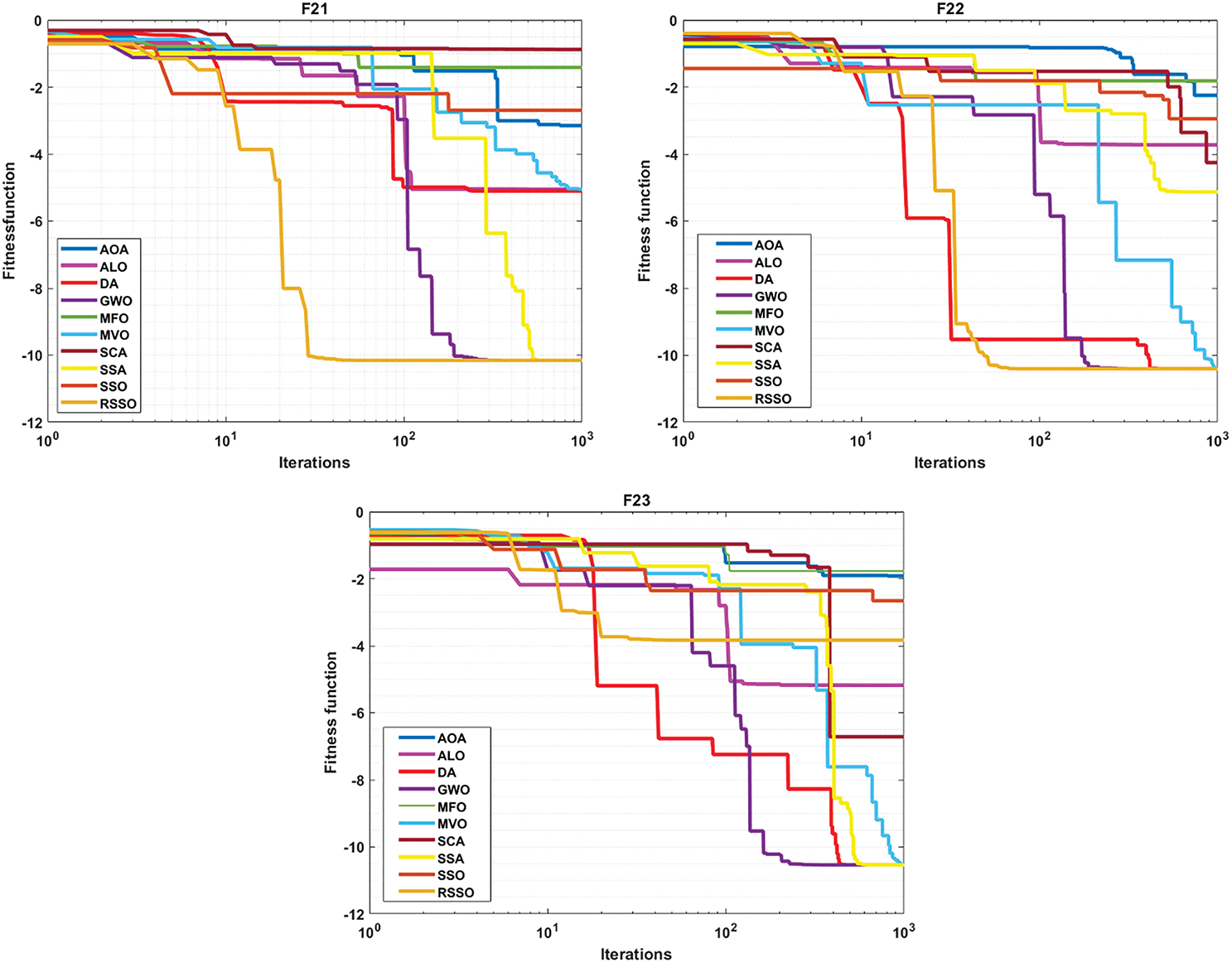
Figure 2: Convergence behaviour for functions F1–F23

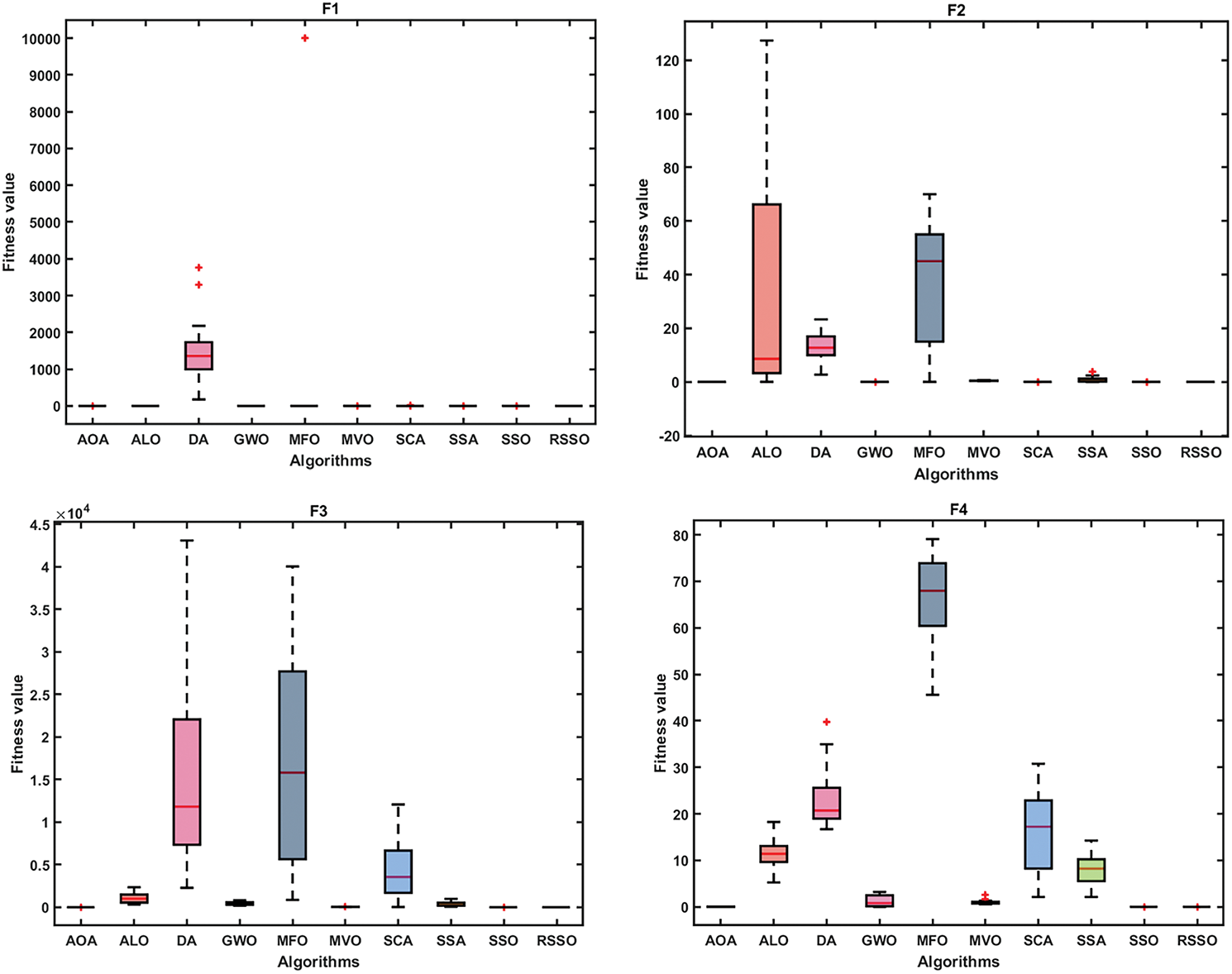
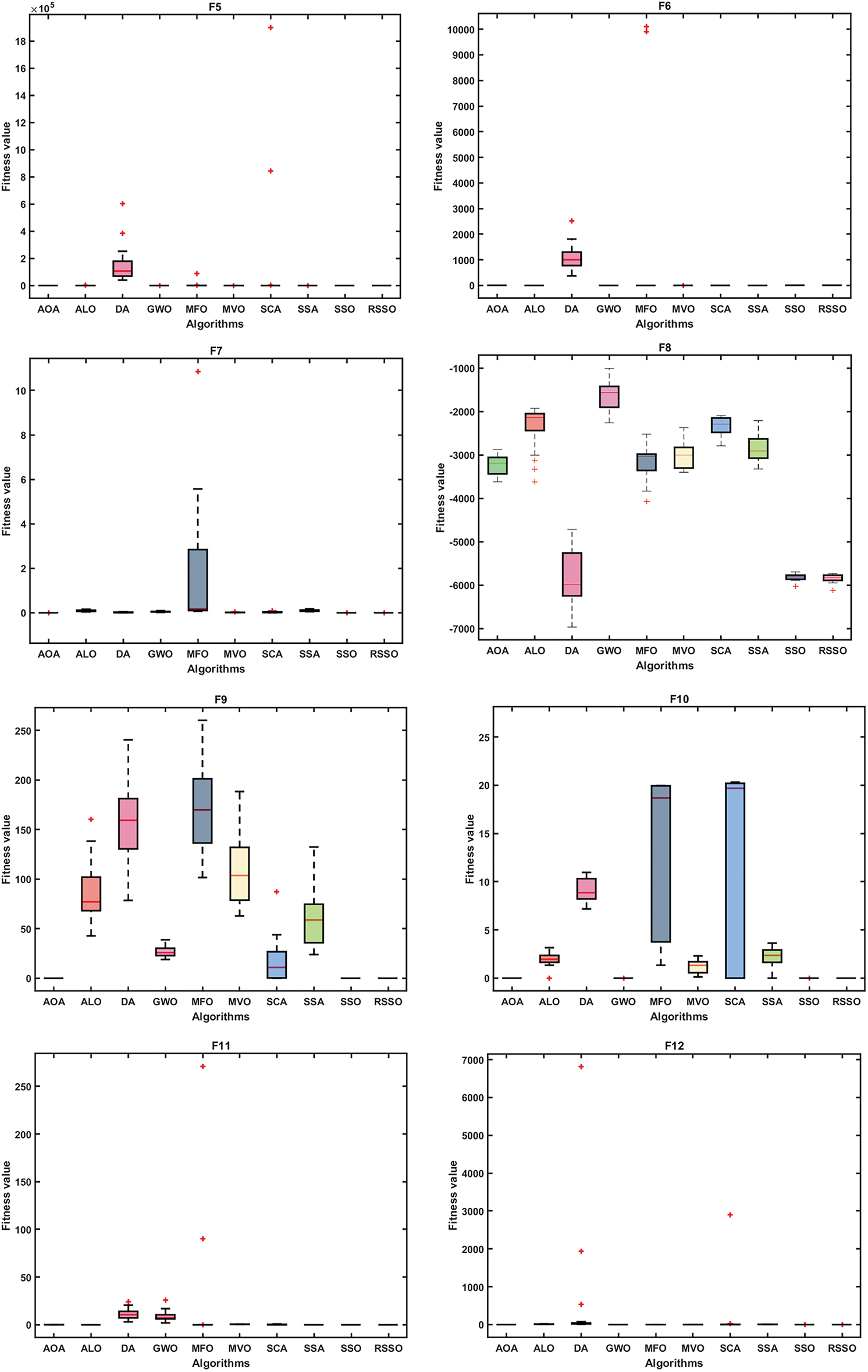
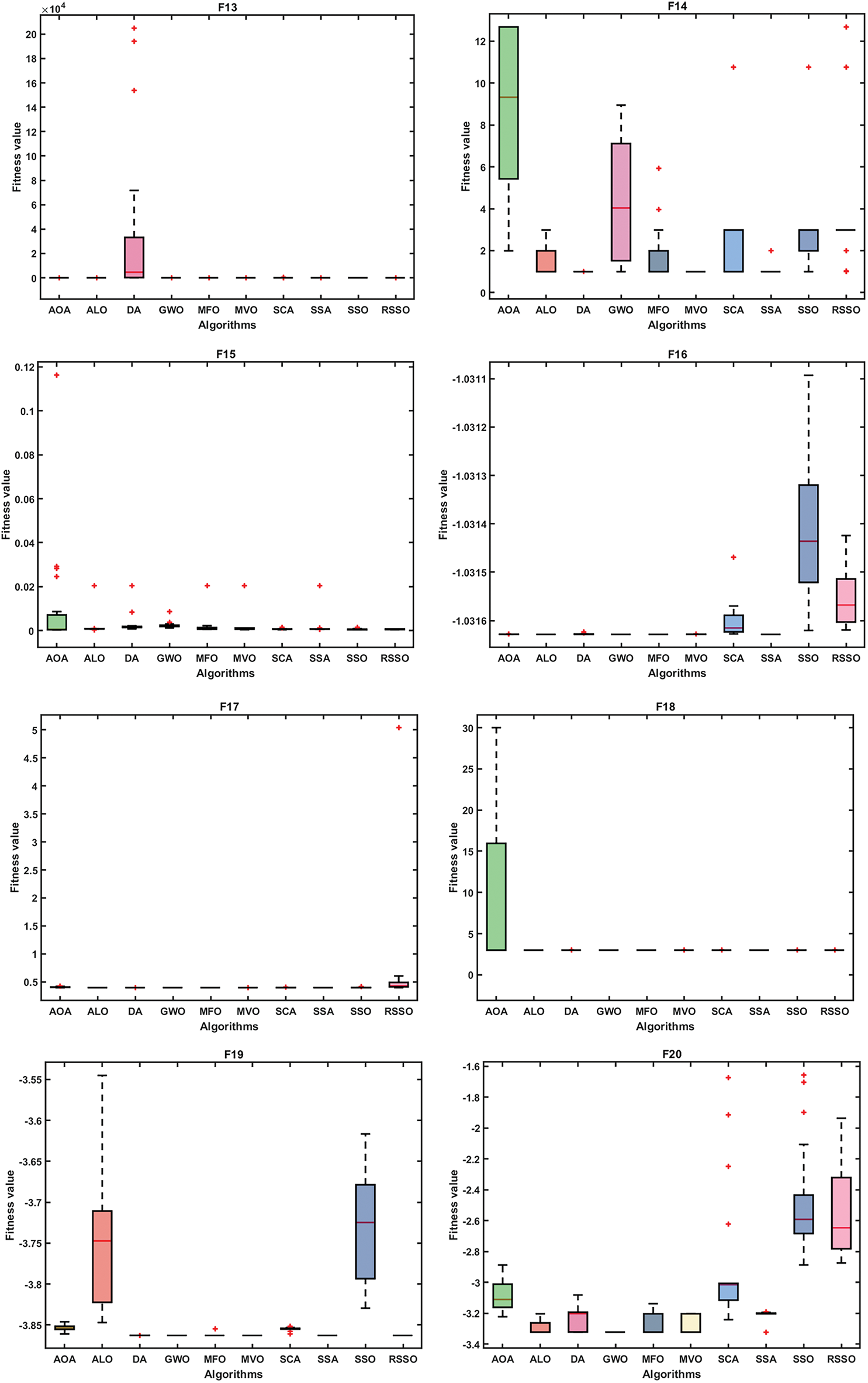
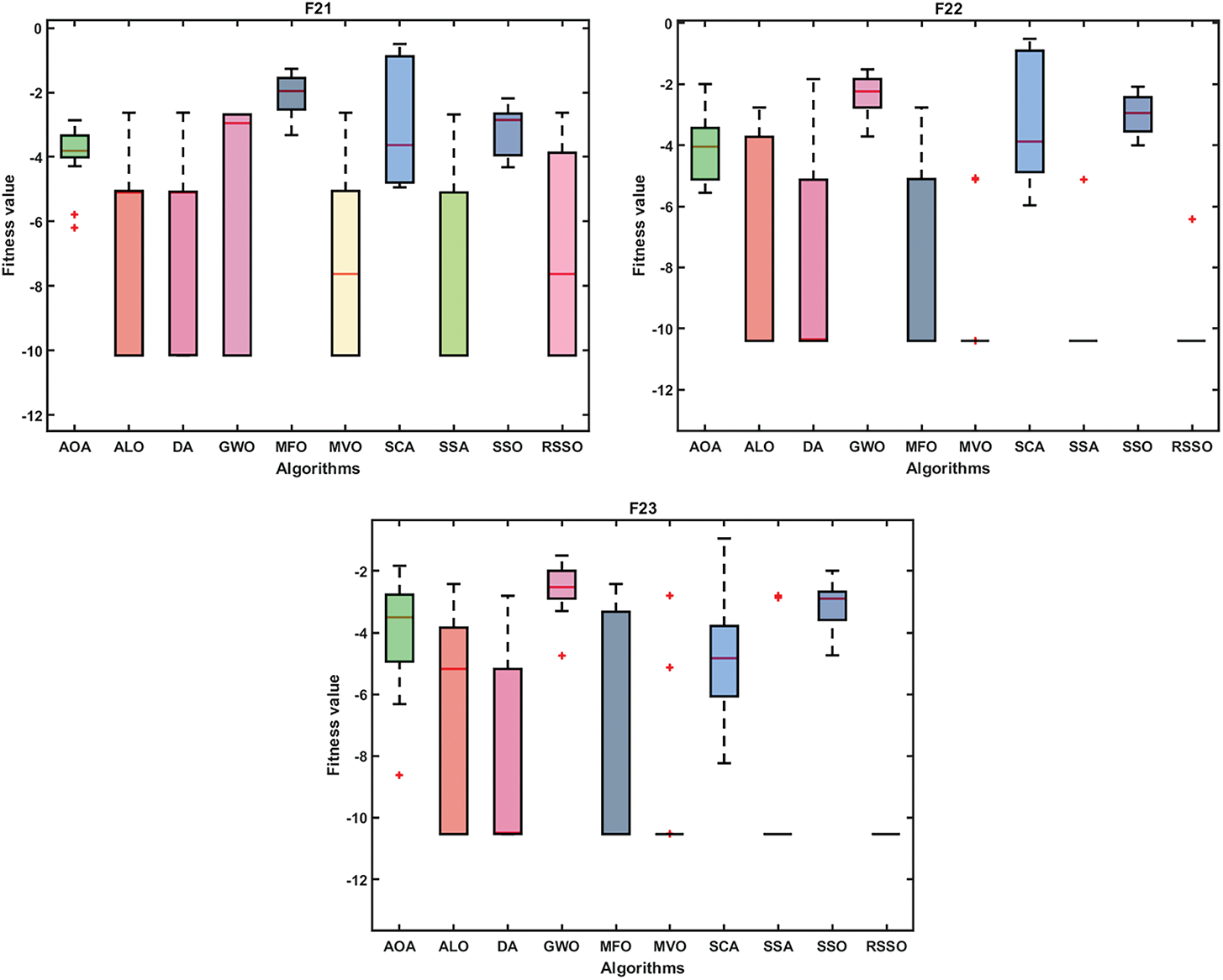
Figure 3: Box plots for functions F1–F23

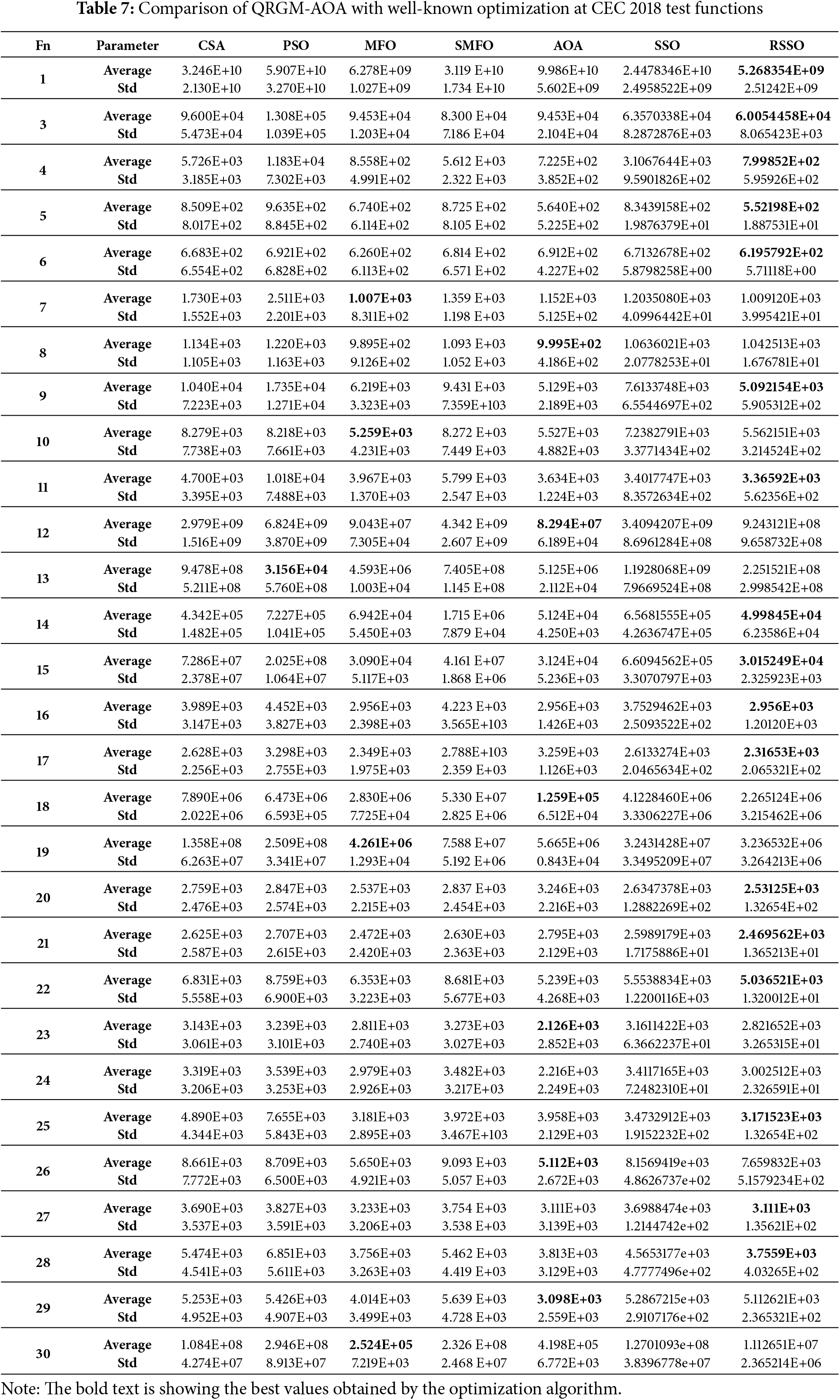
4.6 Quantitative Analysis of CEC 2018 Test Functions

The robustness of the proposed algorithms has been evaluated using the CEC 2018 test functions. Additionally, these algorithms have been compared with other contemporary algorithms, with results sourced from Ref. [25]. As shown in Table 7, RSSO delivers optimal results for most functions, including F1, F3–F6, F9, F11, F14–F17, F20–F22, F25, and F27–F28. In contrast, MFO achieves optimal results for functions such as F7, F10, F19, and F30. Meanwhile, AOA provides optimal outcomes for F8, F12, F18, F23, F26, and F29.

4.7 Comparison of Computational Complexity

The computational complexity of the RSSO algorithm has been analyzed using Big-O notation and compared to the basic SSO algorithm. The results, presented in Table 8, show that both algorithms have similar time complexity. In other words, they take roughly the same amount of time to execute.

The computational complexity is evaluated based on Algorithms 1 and 2 using the following Eq. (12).

O(NP×D×max_iter)(12)

5  Application of the Proposed RSSO Algorithm to the Real-World Application

The proposed algorithm proved its efficiency efficient through quantitative and qualitative analysis of the benchmark problems. The efficacy of the proposed algorithm has also been validated on real-world optimization problems through well-known engineering design problems.

5.1 Gear Train Design Problem

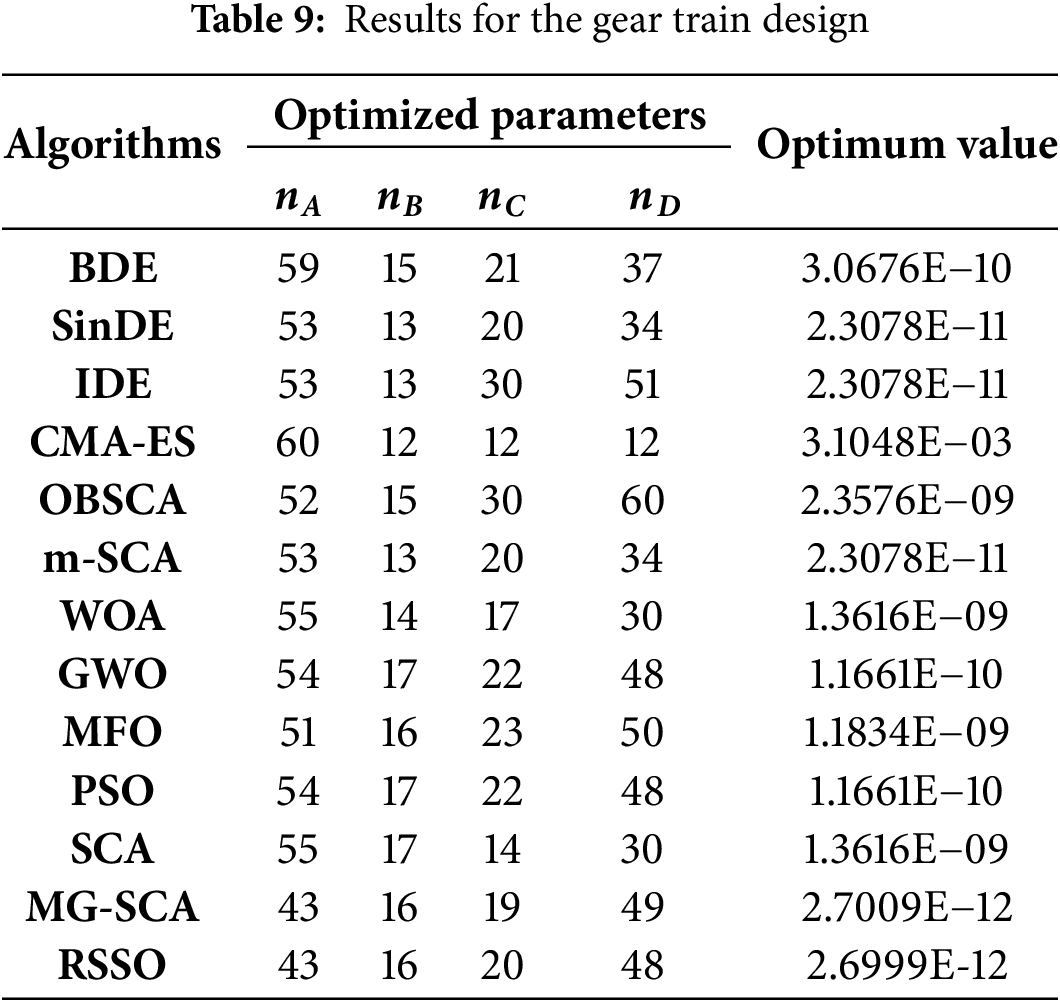
Fig. 4 depicts the gear train design problem as an unconstrained case study with decision variables with discrete values. The following is a mathematical representation of these choice variables as train gears.

Minimize f(n)=(16.931−nCnDnAnB)2(13)

subjected to

12≤nA,nB,nC,nD≤60

Figure 4: Gear train design problem

The obtained results are tabulated in Table 9. The parameters in each optimization algorithm are set to similar values for fair comparison. From Table 8, it can be observed that the proposed RSSO algorithm gives superior results when compared to other algorithms.

5.2 Speed Reducer Design Problem

Speed reducer as shown in Fig. 5 is designed to minimize the weight of the reducer. The face width (n1), a module of teeth (n2), number of teeth on the pinion (n3), length of the first shaft between bearings (n4), length of the second shaft between bearings (n5), the diameter of the first shaft (n6), and the diameter of the first shaft (n7) are the key variables to be optimized.

Minimize f(n)7=0.785n1n22(3.333n32+14.9334n3−42.0934)−1.508n1(n62+n72)+7.4777n1(n63+n73)+1.508n1(n4n62+n5n72)(14)

subject to:

g1(n)=21n1n22n3−1≤0;(15)

g2(n)=397.5n1n2n32−1≤0;(16)

g3(n)=1.93n43n1n3n64−1≤0;(17)

g4(n)=1.93n43n1n3n74−1≤0;(18)

g5(n)=1110n63(745n4n2n3)2+16.9×106−1≤0;(19)

g6(n)=185n73(745n4n2n3)2+157.5×106−1≤0;(20)

g7(n)=n2n340−1≤0;(21)

g8(n)=5n2n1−1≤0;(22)

g9(n)=n112n2−1≤0;(23)

g10(n)=1.5n6+1.9n4−1≤0;(24)

g11(n)=1.1n7+1.9n5−1≤0;(25)

variable range:2.6≤n1≤3.6;0.7≤n2≤0.8;17≤n3≤28;

7.3≤n4≤8.3;7.8≤n5≤8.3;2.9≤n6≤3.9;5≤n7≤5.5.

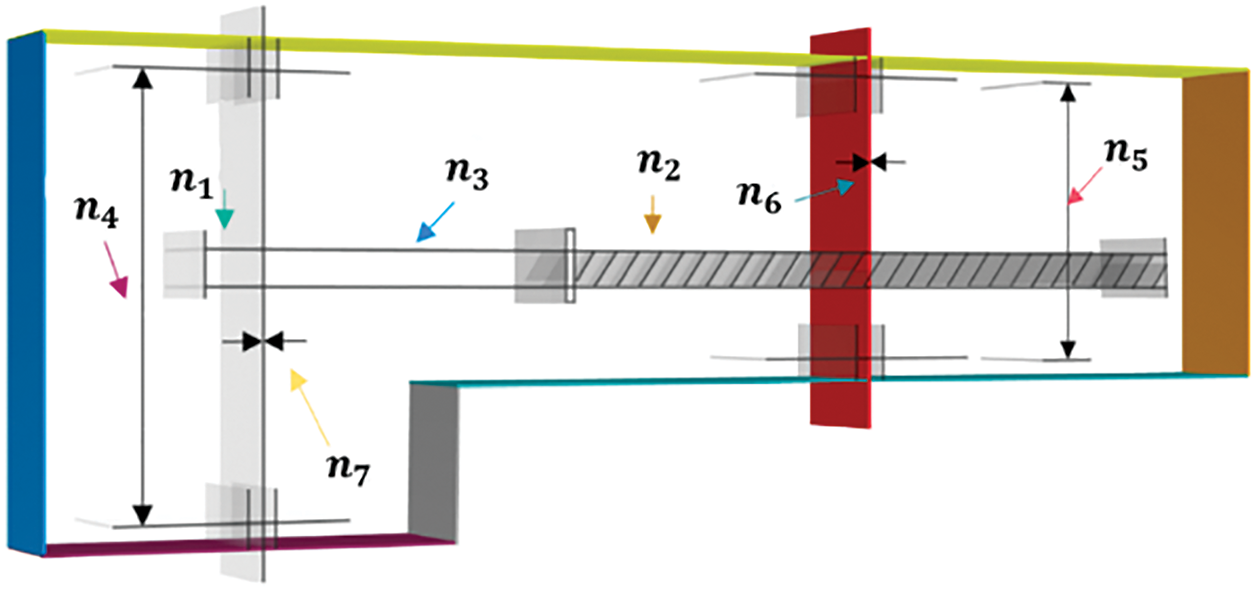
Figure 5: Speed reducer design problem

The performance of the proposed RSSO algorithm was compared to several other optimization algorithms, including MBFPA, WCA, PSODE, MDE, HEAA, and PVS. Table 10 shows that RSSO consistently produces superior solutions, particularly when dealing with complex constraints.

5.3 Parameter Estimation for Frequency-Modulated Synthesizer

The decision variables of a frequency-modulated synthesizer are estimated in this problem. This is an unconstrained, multimodal, complicated problem which contains six decision variables, a1,a2,a3,n1,n2 and n3. The problem is formulated in the following manner

Minimize f(x)=∑t=1100(X(t,x→)−X0(t,x→))2;(26)

x→=a1,a2,a3,n1,n2,n3 and

x¯=(1,5,1.5,4.8,2,4.9)

subjected to −6.4≤a1,a2,a3,n1,n2,n3≤6.35

where

X(t,x→)=a1sin⁡(n1tθ+a2sin⁡(n2tθ+a3sin⁡(n3tθ))),(27)

X0(t,x¯)=sin⁡(5t×2π100+1.5sin⁡(4.8t×2π100+2sin⁡(4.9t×2π100))).(28)

A comprehensive comparison was conducted to evaluate the performance of the proposed RSSO algorithm against various other optimization techniques, including BDE, SinDE, IDE, CMA-ES, OBSCA, m-SCA, WOA, GWO, MFO, PSO, SCA, and MG-SCA. The comparison considered several metrics: best solution, worst solution, standard deviation, and average performance. All algorithms were tested using 105 function evaluations, a population size of 30, and 30 independent runs. The results consistently showed that RSSO outperforms all other optimization algorithms tested as shown in Table 11.

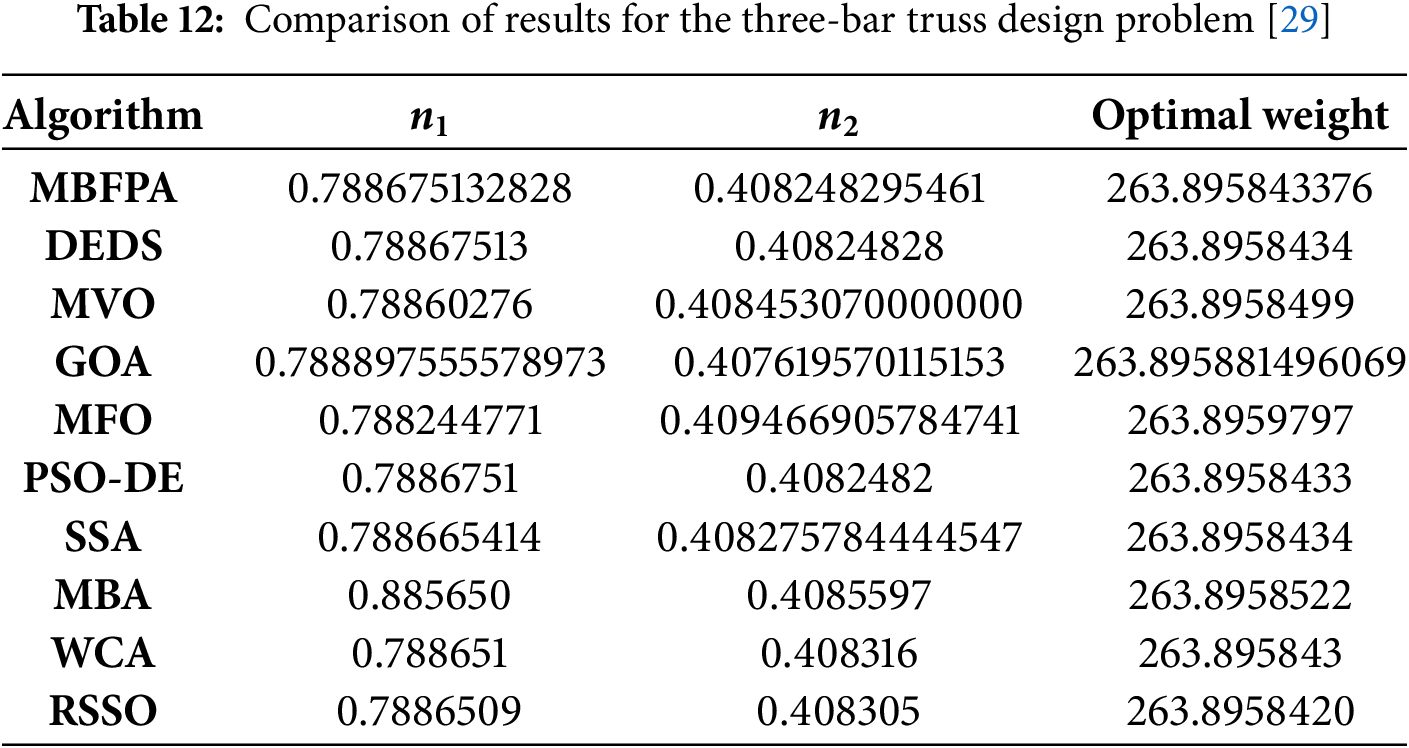
5.4 Three-Bar Truss Design Problem

Fig. 6 illustrates the three-bar truss design problem, which involves minimizing the weight of a three-bar truss structure. This optimization problem includes constraints related to stress, deflection, and buckling, ensuring that the final design meets structural integrity requirements.

[n]=[n1,n2]=[A1,A2](29)

Minimize f(n)=(22n1+n2)×l.(30)

Figure 6: Three-bar truss design problem

Subject to:

g1(n)=2n1+n2/2n12+2n1n2P−σ≤0;(31)

g2(n)=n2/2n12+2n1n2P−σ≤0;(32)

g3(n)=1/2n2+n1P−σ≤0;(33)

variable range 0≤n1,n2≤1.

where l=100cm;P=2 kN/cm2;r=2 kN/cm2.

The results are tabulated in Table 12 which suggests that the RSSO perform better in this problem when compared to other algorithms.

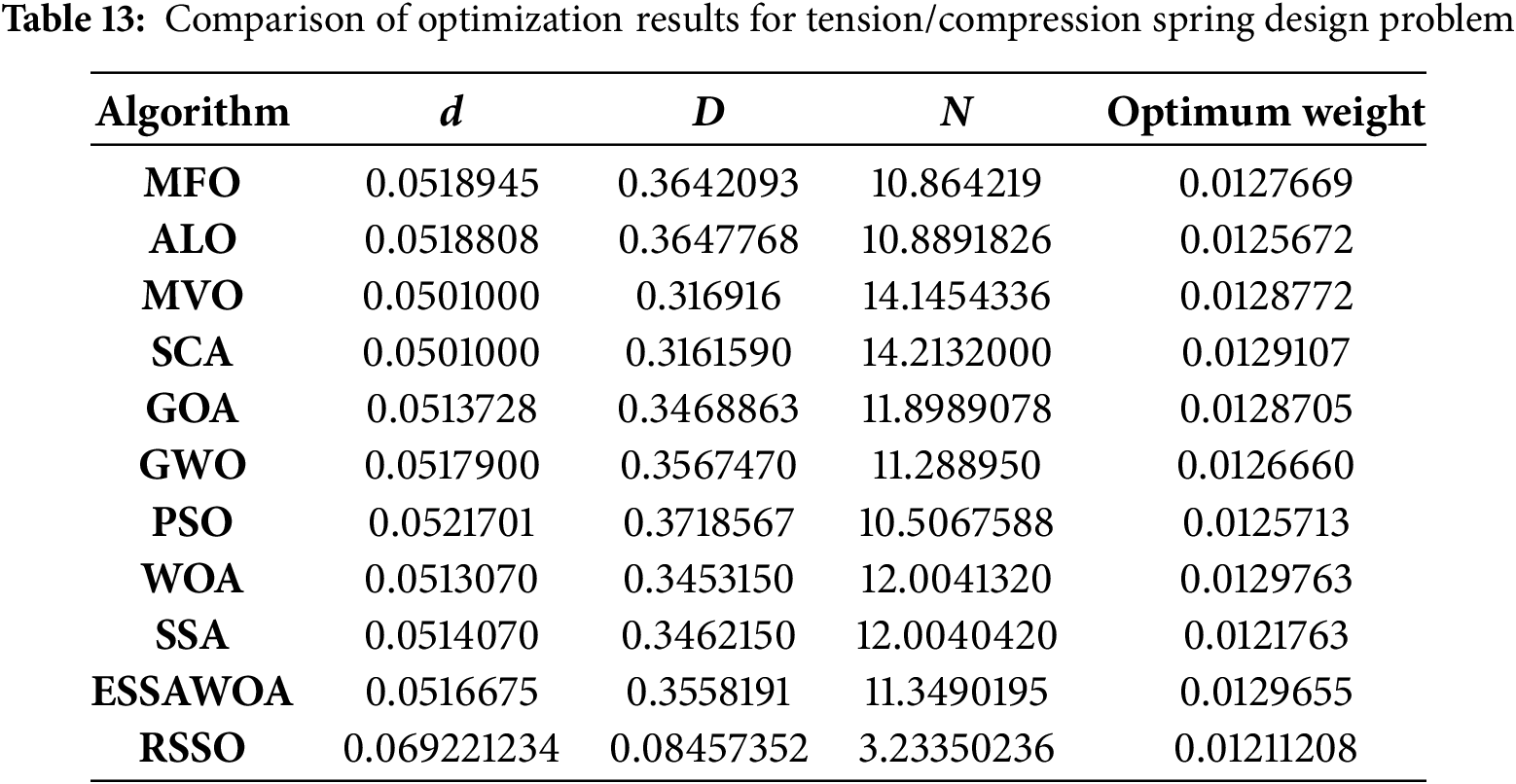
5.5 Tension/Compression Spring Design

The suggested RSSO lightens the tension/compression spring’s load in this case. Shear stress, frequency, and deflection must all be considered when designing the ideal spring configuration. Wire diameter (d), mean coil diameter (D), and number of active coils (N) are the design characteristics displayed in Fig. 7. Subsequent sections outline the challenge of minimization.

X=[x1,x2,x3]=[dDN](34)

Minimize f(X)=(x3+2)x2x12(35)

Subject to g1(X)=1−x23x371785x14≤0(36)

g2(X)=4x22−x1x212566x14(x2x32−x14)+15108x12≤0(37)

g3(X)=1−140.45x1x22x3≤0(38)

g4(X)=x1+x21.5−1≤0(39)

where x1, x2 and x3 are in the range of:

0.05,≤x1≤2.00;0.05≤x2≤1.30;2.00≤x3≤15.

Figure 7: Tension/Compression spring design problem

The findings of the proposed RSSO along with other algorithms considering both tension and compression of the spring are shown in Table 13 which suggests that the proposed RSSO outperforms the other research.

5.6 Pressure Vessel Design

In order to minimize the total cost while taking material, forming, and welding limits into account, the RSSO is employed to address the design issues associated with pressure vessels. Fig. 8 shows the pressure vessel’s structural design, with design parameters such shell thickness (t), head thickness (T), inner radius (R), and length of the head-free cylindrical portion (L) shown. The following is the mathematical formulation of the four restrictions that the design is subject to:

X=[x1,x2,x3,x4]=[Ts,Th,R,L],(40)

f(X)=0.6224x1x3x4+1.7781x2x32+3.1661x12x4+19.84x12x3.(41)

Figure 8: Pressure vessel design problem

Subject to

g1(X)=−x1+0.0193x3≤0,(42)

g2(X)=−x3+0.00954x3≤0,(43)

g3(X)=−πx32x4−43πx33+1296000≤0,(44)

g4(X)=x4−240≤0.(45)

variable range: 0≤x1,x2≤99, 10≤x3,x4≤200.

Table 14 displays the outcomes produced by the suggested method in addition to other optimization techniques. The optimal solution was attained by the proposed RSSO at the lowest cost.

5.7 Welded Beam Design

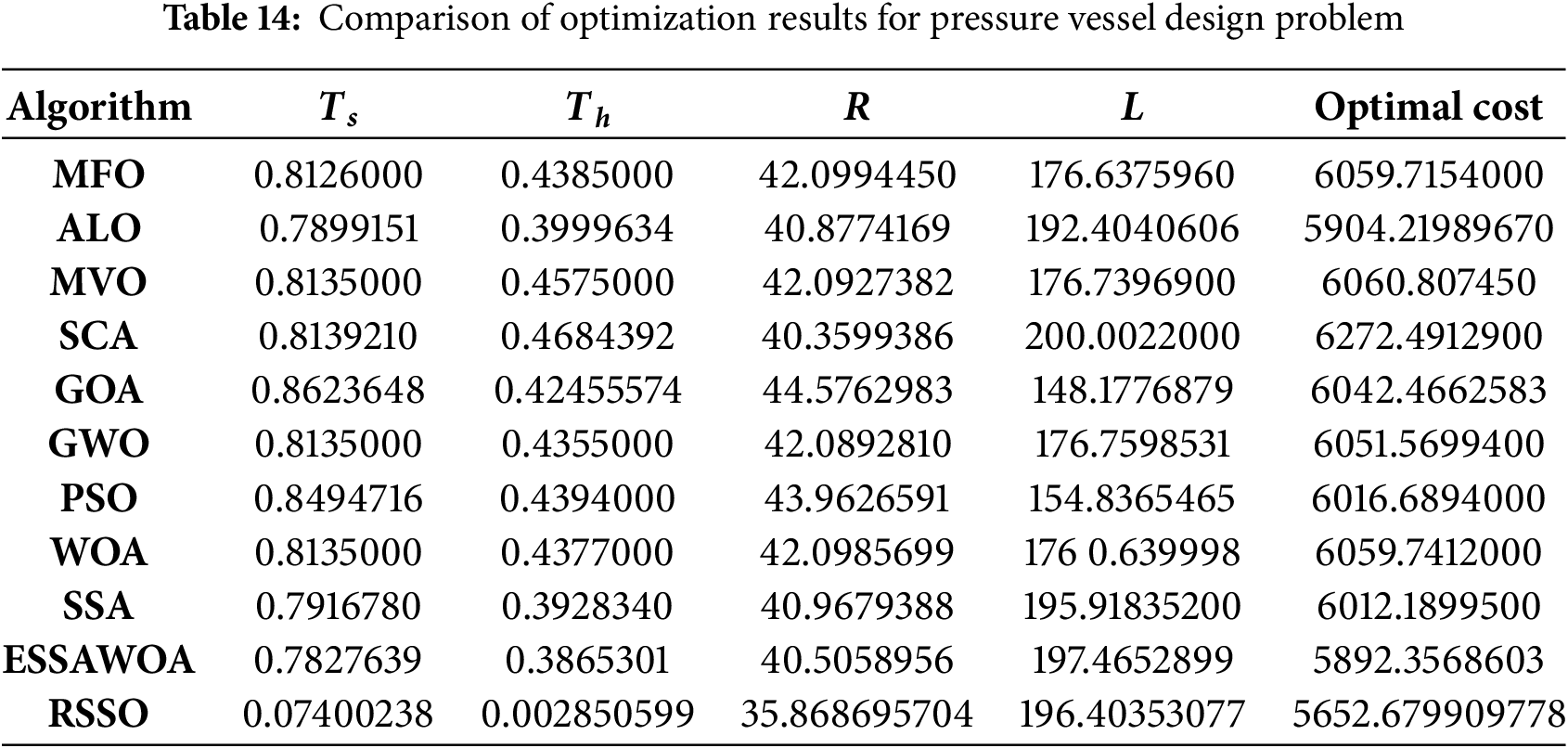
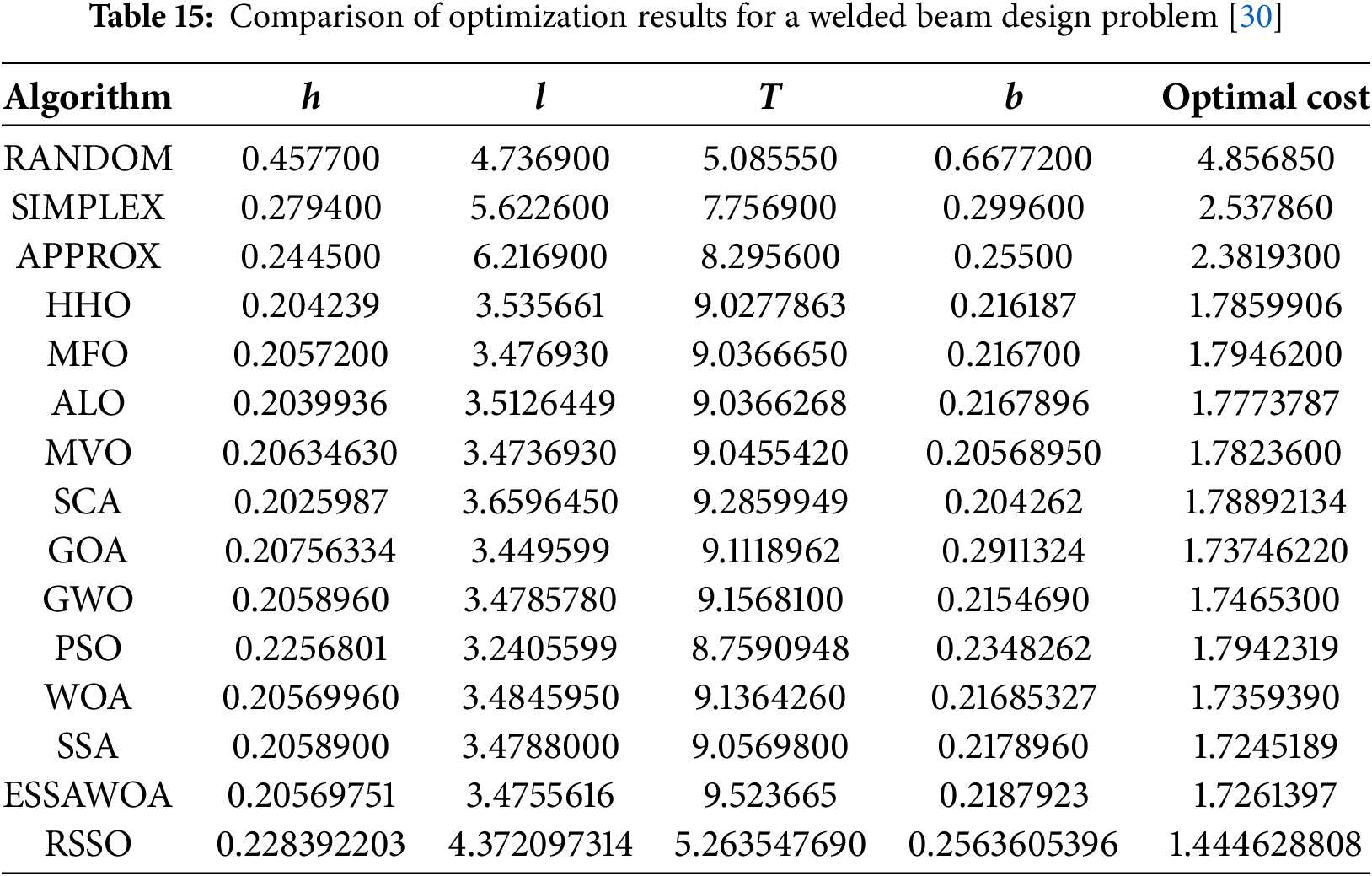
Fig. 9 illustrates how the proposed RSSO algorithm is used to optimize the design of a welded beam, with the goal of minimizing its fabrication cost. By optimizing various design parameters, such as shear stress (τ), bending stress (σ), buckling load (Pc), deflection (δ), and side constraints, the overall production cost can be reduced. This optimization problem involves four key design variables: bar thickness (b), height (t), length (l), and weld thickness (h).

X=[x1,x2,x3,x4]=[hlTb](46)

f(X)=1.10471x12x2+0.04811x3x4(14.0+x2)(47)

Figure 9: Welded beam design problem

Subject to

g1(X)=τ(X)−τmax≤0(48)

g2(X)=σ−σmax≤0(49)

g3(X)=δ−δmax≤0(50)

g4(X)=x1−x4≤0(51)

g5(X)=P−PC(X)≤0(52)

g6(X)=0.125−x1≤0(53)

g7(X)=1.10471x12+0.04811x3x4(14+x2)−5.0≤0(54)

The variable range is taken as follows 0.1≤x1,x4≤2 and 0.1≤x2,x3≤10, where

τ(X)=(τ′)2+2τ′τ′′x22R+(τ′′)2(55)

τ′=P2x1x2(56)

τ′′=MRJ(57)

M=P(L+x22)(58)

R=x224+(x1+x32)2(59)

J=2{2x1x2[x224+(x1+x32)2]}(60)

σ(X)=6PLEx32x4(61)

δ(X)=6PL3Ex32x4(62)

PC(X)=4.013Ex32x4636L2(1−x32LE4G)(63)

P=6000lb,L=14 in,E=30×106psi,G=12×106psi,

δmax=0.25in,τmax=13600psi,σmax=30000psi.

The results of the proposed algorithm and other optimization are tabulated in Table 15 which indicates proposed RSSO outperforms the majority of the existing methods.

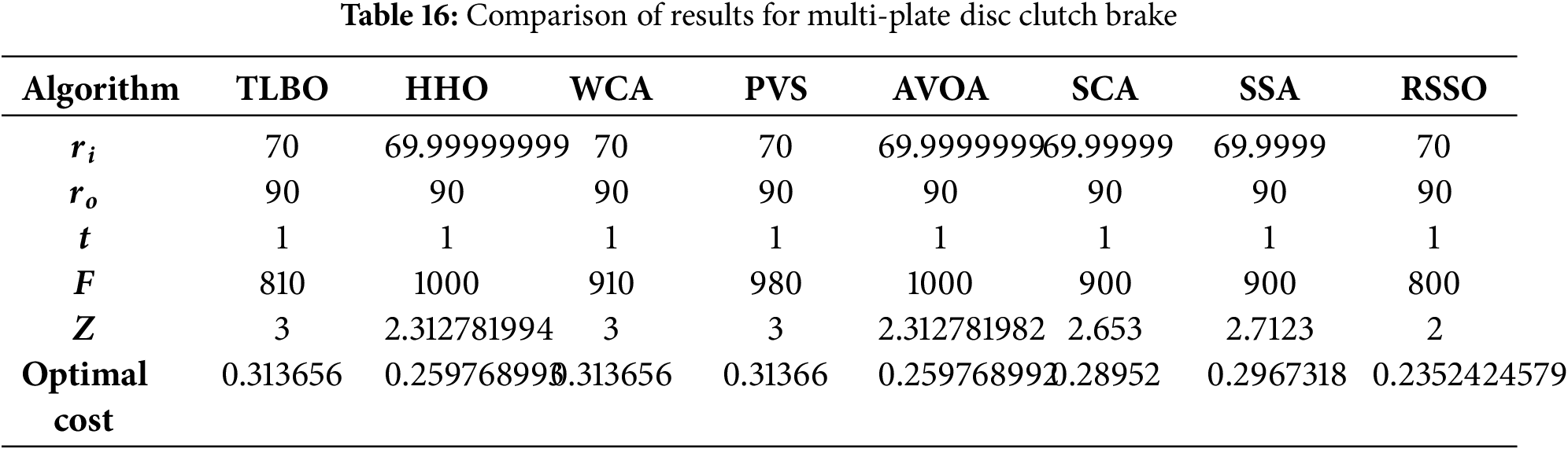
5.8 Multi-Plate Disc Clutch Brake Design Problem

The research also focused on optimizing the design of a multi-plate disc brake system to reduce its weight. The optimization targeted minimizing several factors, including the actuation force required to engage the brakes, the inner and outer radii of the discs, the friction surfaces, and the thickness of the discs. Fig. 10 provides a visual representation of a multi-plate disc clutch, which serves as an analogy for the disc brake system being optimized. The mathematical formulation of this optimization problem is provided below.

[n]=[n1,n2,n3,n4,n5]=[ri,ro,t,F,Z](64)

Minimize f(n)=π(n22−n12)n3(n5+1)ρ(65)

Figure 10: Multi-plate disc clutch brake design problem

Subject to:

g1(n)=n2−n1−ΔR≥0(66)

g2(n)=Lmax−(n5+1)(n3+δ)≥0(67)

g3(n)=Pmax−Prz≥0(68)

g4(n)=Pmaxvsrmax−Przvsr≥0(69)

g5(n)=vsrmax−vsr≥0(70)

g6(n)=Tmax−T≥0(71)

g7(n)=Mh−sMs≥0(72)

g8(n)=T≥0(73)

where Mh=2/3μn4n5n23−n13n22−n12,w=πnq30rad/s;

A=π(n22−n12)mm2, Prz=n4ANmm2, vsr=πRrsnq30 mm/s,

Rsr=2/3n23−n13n22n12, T=Izπnq30(Mh+Mf)mm, ΔR=20 mm, Lmax=30 mm,

μ=0.6, Tmax=15s, δ=0.5 mm, s=1.5, Ms=40 Nm, Pmax=1 MPa,

ρ=0.0000078 kg/mm3, vsrmax=10m/s, Tmax=15s, nq=250 rpm,

Iz=55 kg m2, Ms=40 Nm, Mf=3 Nm,

variable range 60≤n1≤80;90≤n2≤110;1≤n3≤3;

60≤n4≤1000;2≤n5≤9;i=1,2,3,4,5.

As shown in Table 16, the suggested RSSO is included with the results obtained by several algorithms, including TLBO, HHO, WCA, PVS, and AVOA. When compared to the other optimization techniques, the RSSO clearly came out on top.

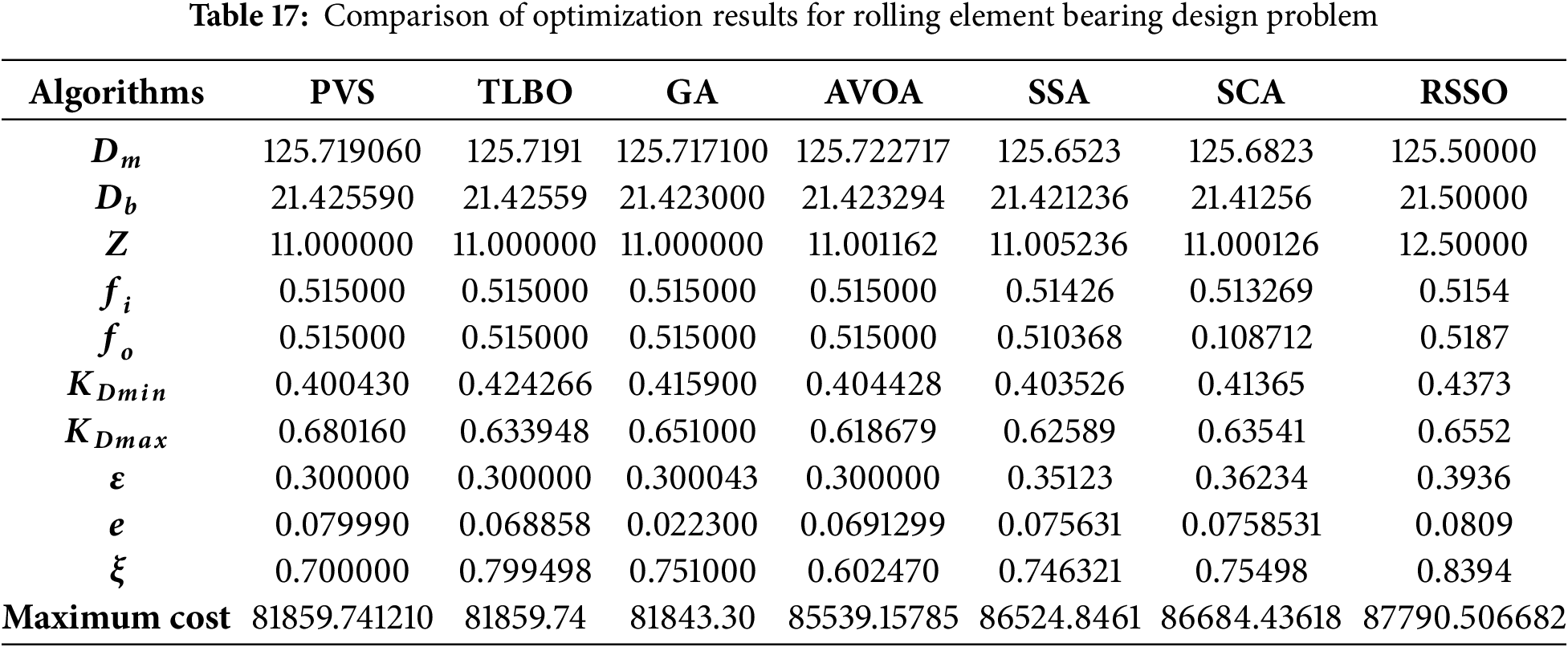
5.9 Rolling Element Bearing Design Problem

The research also investigated the optimization of rolling element bearings, which are commonly used in various mechanical systems. This design problem involved optimizing ten variables while adhering to nine constraints, as shown in Fig. 11. The objective was to maximize the load-carrying capacity of the bearing, which was calculated using a specific formula.

Maximize Cd={fcZ2/3Db1.8, if D≤25.4 mm3.647fcZ2/3Db1.4, if D>25.4 mm(74)

Figure 11: Rolling element bearing design problem

Subject to:

g1(z→)=φ02sin−1(Db/Dm)−Z+1≥0(75)

g2(z→)=2Db−KDmin(D−d)>0(76)

g3(z→)=KDmax(D−d)−2Db≥0(77)

g4(z→)=ζBw−Db≤0(78)

g5(z→)=Dm−0.5(D+d)≥0(79)

g6(z→)=(0.5+e)(D+d)−Dm≥0(80)

g7(z→)=0.5(D−Dm−Db)−ϵDb≥0(81)

g8(z→)=fi≥0.515(82)

g9(z→)=fo≥0.515(83)

where

fc=37.91[1+{1.04(1−γ1+γ)1.72(fi(2fo−1)fo(2fi−1))0.41}10/3]−0.3×[γ0.3(1−γ)1.39(1+γ)1/3][2fi2fi−1]0.41,

x=[{(D−d)/2−3(T/4)}2+{D/2−T/4−Db}2−{d/2+T/4}2],

y=2{(D−d)/2−3(T/4)}{D/2−T/4−Db},

φ0=2π−cos−1(xy),

γ=DbDm,fi=riDb,fo=roDb,T=D−d−2Db,

D=160,d=90,Bw=30,ri=ro=11.0330,

0.5(D+d)≤Dm≤0.6(D+d),

0.15(D−d)≤Db≤0.45(D−d),

4≤Z≤50, 0.515≤fiandfo≤0.6,

0.4≤KDmin≤0.5, 0.6≤KDmax≤0.7,

0.3≤ϵ≤0.4, 0.02≤e≤0.1,

0.6≤ζ≤0.85.

The suggested RSSO has been compared to other algorithms’ outputs, including AVOA, PVS, TLBO, and GA. Table 17 displays the results of the comparison, which indicate that the SSCA outperformed the other algorithms.

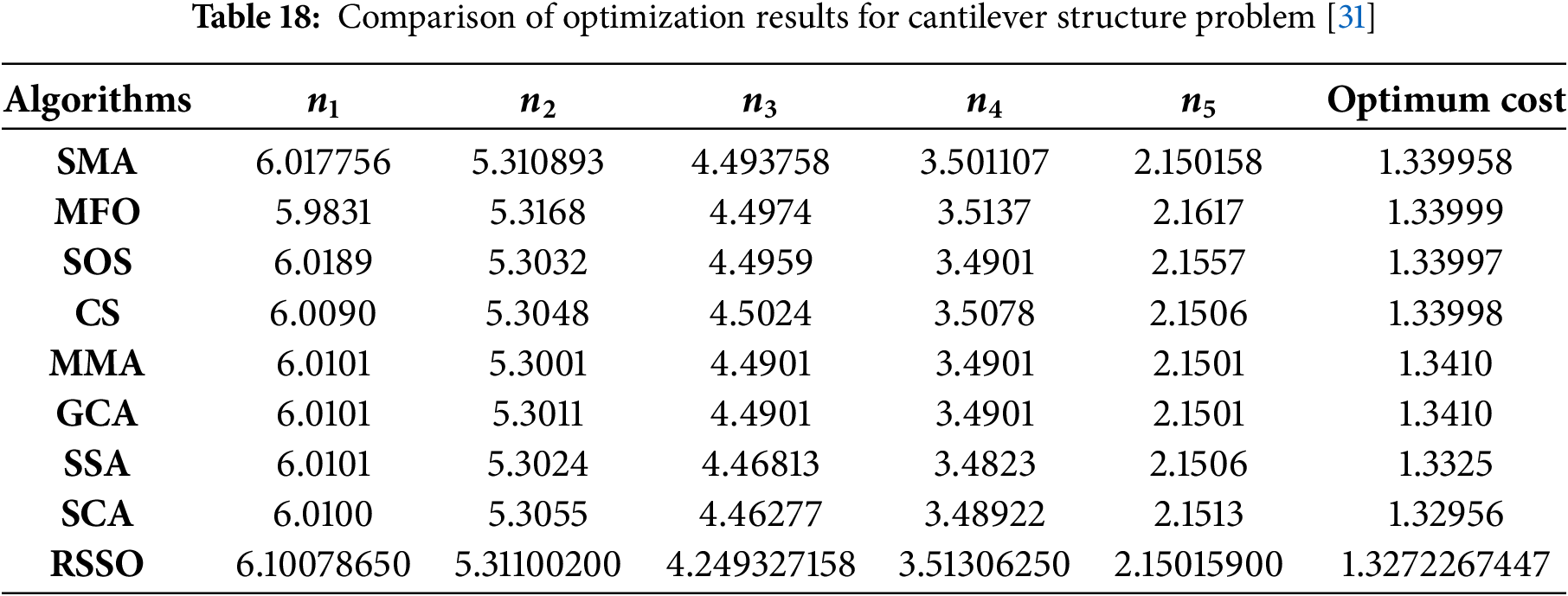
5.10 Cantilever Structure Problem

The cantilever beam used in this work has five hollow square cross-sections, as shown in Fig. 12. To find the most economical solution, we’ll assume that the thickness is constant and look at the other six parameters in Fig. 12. Following are the mathematical concepts used in this design issue:

Minimize f(n)=0.6224(n1+n2+n3+n4+n5)(84)

Figure 12: Cantilever design problem

Subject to:

g(n)=61n13+37n23+19n33+7n43+1n53≤1(85)

variable range 0.01≤n1,n2,n3,n4,n5≤100.

Table 18 shows the results of comparing the proposed RSSO with different optimization strategies. The superior performance of the RSSO compared to the other optimization techniques is clearly demonstrated in Table 18.

6  Conclusion

This research focused on enhancing the search and convergence capabilities of the SSO algorithm. To achieve this, three key modifications were made to the original algorithm. The following conclusions have been drawn from the above research.

•   The proposed optimization method incorporates three key features: OBL, the Cauchy mutation strategy, and position clamping. These features enhance the balance between exploration and exploitation phases compared to the basic SSO algorithm, resulting in a more effective search process.

•   The proposed RSSO algorithm demonstrated superior performance compared to other leading optimization techniques when evaluated on various benchmark functions, including unimodal, multi-modal, and fixed-dimensional multi-modal functions. The results, measured by average and standard deviation, showed that RSSO effectively avoids getting stuck in local optima (exploitation) while simultaneously exploring a wider range of potential solutions (exploration).

•   RSSO proves to be a powerful tool for solving complex optimization problems. Both qualitative and statistical analyses demonstrate that RSSO outperforms other algorithms in terms of both speed of convergence and quality of the final solution. This makes RSSO a valuable tool for computer-aided design and engineering applications.

•   The effectiveness of the RSSO algorithm has been validated not only on theoretical benchmark problems but also on a range of real-world engineering design problems. In all these cases, RSSO has demonstrated superior performance compared to other algorithms, highlighting its broad applicability and potential for solving complex engineering challenges.

•   Future research directions could include investigating adaptive parameter tuning mechanisms to further enhance RSSO’s performance across diverse problem domains. Developing hybrid algorithms that integrate RSSO with other metaheuristic techniques to capitalize on their respective strengths. Applying RSSO to emerging fields such as machine learning hyperparameter optimization and quantum computing optimization problems.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Sumika Chauhan: Conceptualisation, Investigation, Data curation, Writing—original draft. Govind Vashishtha: Conceptualisation, Investigation, Writing—original draft. Riya Singh: Conceptualisation, Investigation, Supervision, Writing—original draft, review & editing. Divesh Bharti: Supervision, Writing—review & editing. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data will be available on reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Ding Z, Huang Z, Pang M, Bai G, Wang Q, Han B. Optimized design of uniform-field coils system with a large uniform region by particle swarm optimization algorithm. Measurement. 2024;234(2):114614. doi:10.1016/j.measurement.2024.114614. [Google Scholar] [CrossRef]

2. Li D, Li C, Yang J, Chen Z, Liu X, Wang X, et al. Bayesian optimization-attention-feedforward neural network based train traction motor-gearbox coupled noise prediction. Measurement. 2024;238:115323. doi:10.1016/j.measurement.2024.115323. [Google Scholar] [CrossRef]

3. Lu J, Yue J, Zhu L, Wang D, Li G. An improved variational mode decomposition method based on the optimization of salp swarm algorithm used for denoising of natural gas pipeline leakage signal. Measurement. 2021;185(454):110107. doi:10.1016/j.measurement.2021.110107. [Google Scholar] [CrossRef]

4. Khunkitti S, Siritaratiwat A, Premrudeepreechacharn S, Chatthaworn R, Watson NR. A hybrid DA-PSO optimization algorithm for multiobjective optimal power flow problems. Energies. 2018;11(9):2270. doi:10.3390/en11092270. [Google Scholar] [CrossRef]

5. Abbassi A, Ben Mehrez R, Touaiti B, Abualigah L, Touti E. Parameterization of photovoltaic solar cell double-diode model based on improved arithmetic optimization algorithm. Optik. 2022;253(2):168600. doi:10.1016/j.ijleo.2022.168600. [Google Scholar] [CrossRef]

6. Vashishtha G, Kumar R. Feature selection based on gaussian ant lion optimizer for fault identification in centrifugal pump. In: Gupta VK, Amarnath C, Tandon P, Ansari MZ, editors. Recent advances in machines and mechanisms. Singapore: Springer Nature; 2023. p. 295–310. doi:10.1007/978-981-19-3716-3_23. [Google Scholar] [CrossRef]

7. Chen J, Aurangzeb M, Iqbal S, Shafiullah M, Harrison A. Advancing EV fast charging: addressing power mismatches through P2P optimization and grid-EV impact analysis using dragonfly algorithm and reinforcement learning. Appl Energy. 2025;394(2):126157. doi:10.1016/j.apenergy.2025.126157. [Google Scholar] [CrossRef]

8. Gai J, Shen J, Hu Y, Wang H. An integrated method based on hybrid grey wolf optimizer improved variational mode decomposition and deep neural network for fault diagnosis of rolling bearing. Measurement. 2020;162:107901. doi:10.1016/j.measurement.2020.107901. [Google Scholar] [CrossRef]

9. Anslam Sibi S, Sherly Puspha Annabel L. Network lifetime improvement in wireless sensor networks using energy-efficient bat-moth flame optimization technique. Sci Rep. 2025;15(1):18065. doi:10.1038/s41598-025-88550-y. [Google Scholar] [PubMed] [CrossRef]

10. Grisales-Noreña LF, Botero-Gómez V, Bolaños RI, Moreno-Gamboa F, Sanin-Villa D. An effective parameter estimation on thermoelectric devices for power generation based on multiverse optimization algorithm. Results Eng. 2025;25(1):104408. doi:10.1016/j.rineng.2025.104408. [Google Scholar] [CrossRef]

11. Neggaz N, Ewees AA, Elaziz MA, Mafarja M. Boosting salp swarm algorithm by sine cosine algorithm and disrupt operator for feature selection. Expert Syst Appl. 2020;145(1181):113103. doi:10.1016/j.eswa.2019.113103. [Google Scholar] [CrossRef]

12. Özbay F, Özbay E, Gharehchopogh F. An improved artificial rabbits optimization algorithm with chaotic local search and opposition-based learning for engineering problems and its applications in breast cancer problem. Comput Model Eng Sci. 2024;141(2):1067–110. doi:10.32604/cmes.2024.054334. [Google Scholar] [CrossRef]

13. Shehadeh HA, Ahmedy I, Idris MYI. Sperm swarm optimization algorithm for optimizing wireless sensor network challenges. In: Proceedings of the 6th International Conference on Communications and Broadband Networking. New York, NY, USA: Association for Computing Machinery; 2018. p. 53–9. doi:10.1145/3193092.3193100. [Google Scholar] [CrossRef]

14. Wang GG, Deb S, Gandomi AH, Alavi AH. Opposition-based krill herd algorithm with Cauchy mutation and position clamping. Neurocomputing. 2016;177:147–57. doi:10.1016/j.neucom.2015.11.018. [Google Scholar] [CrossRef]

15. Kumari CL, Kamboj VK, Bath SK, Tripathi SL, Khatri M, Sehgal S. A boosted chimp optimizer for numerical and engineering design optimization challenges. Eng Comput. 2022;39(4):2463–514. doi:10.1007/s00366-021-01591-5. [Google Scholar] [PubMed] [CrossRef]

16. Kaucic M, Piccotto F, Sbaiz G, Valentinuz G. A hybrid level-based learning swarm algorithm with mutation operator for solving large-scale cardinality-constrained portfolio optimization problems. Inf Sci. 2023;634(4):321–39. doi:10.1016/j.ins.2023.03.115. [Google Scholar] [CrossRef]

17. Alruwais N, Alabdulkreem E, Mahmood K, Marzouk R, Assiri M, Abdelmageed AA, et al. Hybrid mutation moth flame optimization with deep learning-based smart fabric defect detection. Comput Electr Eng. 2023;108(3):108706. doi:10.1016/j.compeleceng.2023.108706. [Google Scholar] [CrossRef]

18. Zhou X, Chen Y, Wu Z, Heidari AA, Chen H, Alabdulkreem E, et al. Boosted local dimensional mutation and all-dimensional neighborhood slime mould algorithm for feature selection. Neurocomputing. 2023;551(6):126467. doi:10.1016/j.neucom.2023.126467. [Google Scholar] [CrossRef]

19. Yu X, Jiang N, Wang X, Li M. A hybrid algorithm based on grey wolf optimizer and differential evolution for UAV path planning. Expert Syst Appl. 2023;215:119327. doi:10.1016/j.eswa.2022.119327. [Google Scholar] [CrossRef]

20. Vashishtha G, Kumar R. Autocorrelation energy and aquila optimizer for MED filtering of sound signal to detect bearing defect in Francis turbine. Meas Sci Technol. 2021;33(1):15006. doi:10.1088/1361-6501/ac2cf2. [Google Scholar] [CrossRef]

21. Chauhan S, Singh M, Aggarwal AK. Investigative analysis of different mutation on diversity-driven multi-parent evolutionary algorithm and its application in area coverage optimization of WSN. Soft Comput. 2023;27(14):9565–959. doi:10.1007/s00500-023-08090-3. [Google Scholar] [CrossRef]

22. Wang J, Wang W, Chau K, Qiu L, Hu X, Zang H, et al. An improved golden jackal optimization algorithm based on multi-strategy mixing for solving engineering optimization problems. J Bionic Eng. 2024;21(2):1092–115. doi:10.1007/s42235-023-00469-0. [Google Scholar] [CrossRef]

23. Abualigah L, Elaziz MA, Khasawneh AM, Alshinwan M, Ibrahim RA, Al-Qaness MAA, et al. Meta-heuristic optimization algorithms for solving real-world mechanical engineering design problems: a comprehensive survey, applications, comparative analysis, and results. Neural Comput Appl. 2022;34(6):4081–110. doi:10.1007/s00521-021-06747-4. [Google Scholar] [CrossRef]

24. Das A, Namtirtha A, Dutta A. Lévy-Cauchy arithmetic optimization algorithm combined with rough K-means for image segmentation. Appl Soft Comput. 2023;140(1):110268. doi:10.1016/j.asoc.2023.110268. [Google Scholar] [CrossRef]

25. Nadimi-Shahraki MH, Zamani H, Fatahi A, Mirjalili S. MFO-SFR: an enhanced moth-flame optimization algorithm using an effective stagnation finding and replacing strategy. Mathematics. 2023;11(4):862. doi:10.3390/math11040862. [Google Scholar] [CrossRef]

26. Savsani P, Savsani V. Passing vehicle search (PVSa novel metaheuristic algorithm. Appl Math Model. 2016;40:3951–78. doi:10.1016/j.apm.2015.10.040. [Google Scholar] [CrossRef]

27. Shehadeh HA. A hybrid sperm swarm optimization and gravitational search algorithm (HSSOGSA) for global optimization. Neural Comput Appl. 2021;33(18):11739–52. doi:10.1007/s00521-021-05880-4. [Google Scholar] [CrossRef]

28. Gupta S, Deep K, Mirjalili S, Kim JH. A modified sine cosine algorithm with novel transition parameter and mutation operator for global optimization. Expert Syst Appl. 2020;154(3):113395. doi:10.1016/j.eswa.2020.113395. [Google Scholar] [CrossRef]

29. Wang S, Liu Q, Liu Y, Jia H, Abualigah L, Zheng R, et al. A hybrid SSA and SMA with mutation opposition-based learning for constrained engineering problems. Comput Intell Neurosci. 2021;2021(1):6379469. doi:10.1155/2021/6379469. [Google Scholar] [PubMed] [CrossRef]

30. Wang Y, Cai Z, Zhou Y, Fan Z. Constrained optimization based on hybrid evolutionary algorithm and adaptive constraint-handling technique. Struct Multidiscip Optim. 2009;37(4):395–413. doi:10.1007/s00158-008-0238-3. [Google Scholar] [CrossRef]

31. Li S, Chen H, Wang M, Heidari AA, Mirjalili S. Slime mould algorithm: a new method for stochastic optimization. Future Gener Comput Syst. 2020;111:300–23. doi:10.1016/j.future.2020.03.055. [Google Scholar] [CrossRef]