Optimized Deployment Method for Finite Access Points Based on Virtual Force Fusion Bat Algorithm

1  Introduction

With the continuous development of sophisticated information technology, strategies such as Industry 4.0 and Made in China 2025 have been put forward one after another. As a critical infrastructure for intelligent manufacturing systems, the Industrial Internet aims to achieve comprehensive interconnection among all elements of production systems. Among various wireless technologies, WiFi stands out due to its significant advantages in mobility, flexibility, data transmission rates, and deployment costs (Industrial Internet is the crucial infrastructure of an intelligent manufacturing system, aiming to realize the interconnection of all elements of the production system. WiFi, as one of the widely used wireless technologies, has major advantages in terms of mobility, flexibility, data transmission rate and deployment cost). For a WiFi network, the spatial deployment location of the AP will directly affect the signal strength distribution. Therefore, the AP deployment problem is of great significance for the network performance optimization of WiFi.

In the wave of Industry 4.0 and education digital transformation, smart factories and smart campuses put forward stringent requirements for wireless network coverage. Intelligent factories with collaborative manufacturing and predictive maintenance of equipment, and campuses with large-scale online teaching and real-time interaction of knowledge resources all rely on stable network coverage as a digital base. However, the limited number of AP nodes has significant shortcomings in coverage. On the one hand, subject to the physical coverage radius constraints, traditional AP nodes deployment methods are difficult to meet the demand for full coverage of the signal of the factory workshop and campus buildings, which is prone to the formation of signal blind zones; on the other hand, in face of the factory equipment and the campus high density terminal access demand, the limited number of AP nodes is difficult to guarantee the density of coverage, which results in the lack of signal strength in some areas, the unstable connection of terminal equipment, and the decline in data transmission rate. Therefore, optimizing the coverage strategy of limited AP nodes and improving coverage range and intensity have become the core propositions for guaranteeing the network quality in the intelligent field, which is of great significance for promoting the digital transformation of industries and the modernization process of education.

The deployment of nodes belongs to an NP-hard problem, which is essentially a nonlinear, multi-objective, multi-constraint optimization problem. There are three optimization algorithms for node deployment, one is the deployment optimization grounded in the virtual force algorithm [1], the second is the deployment relying on a geometric graph [2]. Additionally, the third category is the optimization using meta-heuristic algorithms [3], such as the multi-group dragonfly algorithm [4], whale algorithm [5], grey wolf algorithm [6] that have become common methods in multi-objective solving problems.

To enhance the coverage capacity with a finite number of wireless AP nodes while conserving energy and minimizing coverage redundancy, this paper presents a virtual force fusion bat algorithm. The factors affecting the performance of AP nodes, such as coverage, coverage efficiency, and energy consumption, are combined and optimized to establish a joint optimization decision formula to select the best node deployment location.

2  Related Work

As wireless network rapidly advances, the rational deployment of wireless AP has become a key issue to ensure network performance and enhance user experience. AP deployment not only affects signal strength, network coverage, but also closely related to energy efficiency, cost control and other aspects. Many scholars have conducted research in this area and proposed a series of innovative strategies and methods.

Kong et al. [7] proposed to optimize the AP location and transmit power with multi-objective particle swarm algorithm, and combined with greedy algorithm to eliminate redundant APs, so that the transmit power of the AP can be reduced and energy efficiency can be improved. Chen et al. [8] proposed a save energy deployment method for AP relyed on the improved golden jackal, on premise of ensuring effective coverage, energy consumption is reduced by optimizing the position, status and transmission power of the AP. Liu et al. [9] proposed particle swarm-Lévy-double subgroup fruit fly algorithm to solve the problem of energy and efficient AP deployment for WLANs in a three dimensional environment, but did not further explore the possibility of minimizing the number of APs. Yang et al. [10] proposed the fine-grained strategy for AP deployment, that significantly improves the coverage efficiency and flexibility through ray tracing modeling and iterative fruit fly optimization algorithm. Marinho et al. [11] effectively promoted the AP coverage extension problem under high frequency communication by combining intelligent routing with AI techniques. Kumar et al. [12] proposed a bit error rate (BER) based multi-sector switching beam antenna synthesis schemez aimed at improving reliable communication coverage and system capacity of APs. But hardware complexity is high. Vijayaraghavan et al. [13] proposed the PlaciFi infrastructure, systematic optimization of the 3D spatial location of APs, through accurate planning layout of the APs, and ultimately achieve synergistic optimization of network capability and cost. Dao and Nguyen [14] focused on the whale algorithm, drawing on the logic of siege behavior, and combined chaotic initialization technology, but parameters adjustment there are still optimization space. Qi et al. [15] used rectangular layout and mathematically calculated the minimum number of nodes required to achieve full coverage of the monitored area, reducing the network energy consumption. Zheng et al. [16] proposed a square layout strategy in wireless networks. The strategy aimed to address the coverage problem of the monitoring area, leveraging distance calculations between nodes. However, scholars did not conduct a comparison across multiple deployment strategy types, which constituted a critical gap. Yang et al. [17] optimized distribution of node to improve detection rate under limited node conditions. It concluded that the diamond deployment strategy outperforms random deployment in detection rate, but lacks a discussion on the optimization mechanism of energy consumption.

The virtual force algorithm (VFA), as the most effective algorithm for node deployment, has been studied by many scholars. Zhang et al. [18] aimed at the problems of insufficient number of drones and unpredictable user movement during the deployment of Unmanned Aerial Vehicle (UAV) station, the arrangement of communication nodes can be dynamically optimized by using the virtual force model. Wang and Guo [19] improved the parameters of the virtual force to realize the adaptive division of the water monitoring area, which effectively improves the coverage quality in sparse node scenarios. Li et al. [20] proposed the algorithm of extending virtual force, which effectively improves the network deployment performance under different communication range to sensing range ratios by designing the force model in separate scenarios.

Li et al. [21] proposed a mongoose algorithm to settle the deployment optimization of network nodes with consideration of data fusion techniques and environmental randomness. Yao et al. [22] on a basis of ant lion optimization algorithm oriented toward virtual force, Yao et al. [23] based on the improvement of the moth flame search algorithm to solve the node coverage problem, while did not consider the redundancy of nodes. Mohar et al. [24] mixed fruit fly olfaction and bat echoes for optimizing node deployment to improve the coverage, but the computation time is long. Muhammad et al. [25] introduced an adaptive search factor into the velocity update formula of the Particle Swarm Optimization (PSO) algorithm, this allows particles to dynamically adjust both the magnitude and direction of velocity update during the search process. However, there is still a trap of falling into the local optimum. Sun et al. [26] proposed genetic algorithm (GA) fused with whale optimization algorithm (WOA), and solved the coverage redundancy problem in wireless sensor networks due to the random deployment of nodes. But cross-variation introduces more parameters, making parameter tuning difficult. Zhao et al. [27] transformed the node deployment problem into a mixed integer linear problem, and applied the simulated annealing (SA) algorithm to solve the problem, but the convergence speed is slow. Liu et al. [28] used the trapping mechanism of the Gray Wolf optimization algorithm (GWO) to assign pilot to ensure coverage of users while minimizing signal interference during node deployment. Saranya and Karthik [29] combined the mayfly and ant colony algorithm to solve the energy consumption problem of nodes in wireless sensor networks.

The main contributions of this study are as follows:

(1)   Joint coverage, node redundancy and node movement distance multi-factor objective function is established, and the weighting idea is used to assign weights to each factor to attain synergistic enhancement and balanced optimization of comprehensive network performance.

(2)   The Lévy flight is embedded in the global search framework of the bat algorithm to enhance its cross-scale exploration capacity, while the virtual force algorithm is introduced in the local fine-tuning part to construct a dynamic force model, to attain the efficient optimization of the spatial layout of the AP nodes and guarantee the performance through the organic coupling of the global-local optimization process and the synergy of the strategies.

(3)   The quantitative performance evaluation of the algorithm proposed in this paper is carried out by using the test function, comparing the final results of regular deployment with the deployment effect of this algorithm in multiple indexes, and analyzing the results of simulation experiments in a systematic way.

The rest of the paper is as follows: Section 2 analyzes the current state of research on the AP node deployment problem. Section 3 describes the AP model and objective function. Section 4 analyzes the fusion algorithm. Section 5 analyzes the proposed algorithm through simulation experiments. Section 6 makes conclusions.

3  Basic Theory

3.1 Network Model

Today, the field of wireless communications is undergoing rapid changes, gradually replacing wired communications, making industrial centralized control a reality. However, for the commonly used wireless communication technologies, Bluetooth technology has a short transmission distance and few connectable devices; Zigbee technology has a low transmission rate; and Wi-Fi is a high-speed WLAN designed based on the IEEE 802.11 standard. The structure of the WLAN system is shown in Fig. 1 and consists of four parts, including the personal computer (PC), gateway (GW), access points (APs) and sensors, and each sensor device can be connected to one or more access devices to ensure reliable data transmission. The PC sits at the top of the entire system and is used to set up and monitor the entire network as well as manage data. As a key node of network connection, GW performs network layer protocol conversion to realize seamless data forwarding between networks with different communication protocols, ensuring smooth data interaction and compatibility between heterogeneous networks. The access device receives data from the sensors by means of a wireless link and forwards the data to the gateway by means of a wired link, which is connected to the host computer via a fieldbus.

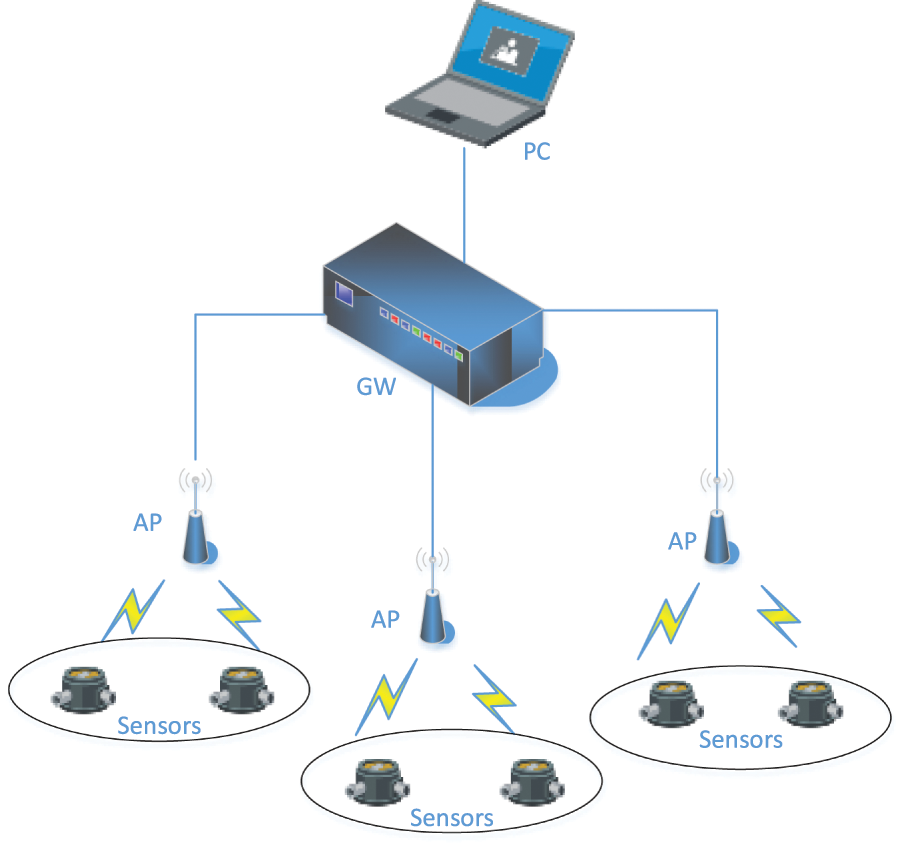
Figure 1: Network model

3.2 AP Perception Model

The perception model of the AP is shown in Fig. 2. Where S represents the position coordinates, R represents the perceived node radius, V→ is the perceived direction, θ represents the angle of rotation of the node, and α is the perceived half-angle, 2α is the perceived angle of the AP. C is the center of mass point of the node, P is the target point, here represents the grid points in the monitoring area.

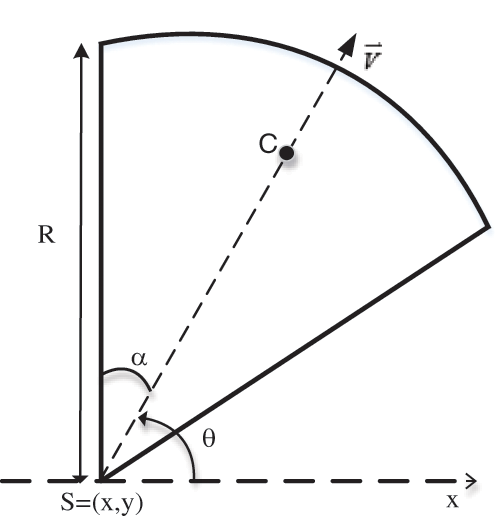
Figure 2: Perception model

With the adoption of the Boolean perception model, the constraint conditions for point Pj to be covered by Si are given by Eq. (1).

{‖SiPj→‖≤RSiPj→∙V→≥‖SiPj→‖∙cos⁡α(1)

where ‖SiPj→‖ represents the euclidean distance between Pj and Si.

It is possible for multiple nodes to sense an arbitrary grid point. Consequently, the probability that a set of nodes collectively senses a grid point can be expressed by Eq. (2).

p(S,Pj)=1−∏i=1N[1−p(Si,Pj)](2)

3.3 Objective Function

The coverage quality evaluation in this paper includes three indicators.

(1) Coverage Cr. Supposed the monitoring region is square and its sides are divided into m equal parts, then the square region is discretized into K mesh points. The network coverage rate of area can be measured by constructing a mathematical relationship between the number of target points covered by all nodes and the number of mesh points in the area. The coverage rate is shown in Eq. (3).

Cr=∑j=1Kp(S,Pj)K(3)

(2) Coverage efficiency Ce. It can characterize the uniformity degree of node distribution, the ratio is the quotient of the effective coverage region to the total region covered by all nodes. The more evenly distributed the nodes are, the larger the value, the smaller the redundancy. The coverage efficiency is shown in Eq. (4).

Ce=∑j=1Kp(S,Pj)N×(π×2α×R2)(4)

(3) Total moving distance dtmd. The energy consumption during deployment is from node mobility, so the energy costs of a node is measured based on node movement distance. After node deployment, the total moving distance of the node is given by Eq. (5).

dtmd=∑i=1Ndi(5)

where di is the distance that node i has traveled through the deployment period.

The objective function adopts the concept of weights and is formulated as Eq. (6).

f(x)=ω1Cr+ω2Ce+ω31dtmd(6)

where ω1, ω2, ω3 are weighting factors that satisfy ω1+ω2+ω3=1. Cr as a core measure of wireless network quality of service, with a weighting of 0.5, Ce is critical for efficient deployment, as the next highest weighting of 0.3, and dtmd is a relatively low priority, as a low weighting of 0.2.

4  Fusion Algorithm

In this section, the basic bat algorithm and the virtual force algorithm are introduced, to optimize the wireless network coverage, the Lévy flight strategy and the virtual force are used as the perturbation factors for the bat global position and local position updating, and the fused algorithm improves the convergence speed and optimization seeking ability.

4.1 Traditional Algorithm

4.1.1 Traditional Bat Algorithm

The Bat Algorithm (BA), a prominent meta-heuristic optimization, derives its inspiration from the echolocation mechanisms exhibited by bats in nature. Individual bat searches by adjusting its frequency, speed and position, while the loudness and pulse frequency change dynamically with iterations. At the beginning of the search, bats have a large loudness and a small pulse frequency, which allows the algorithm to search globally over a large solution space to explore potentially optimal solution regions; as the iteration progresses, the loudness decreases, the pulse frequency increases, and the algorithm focuses on localized regions to perform a fine search. This mechanism ensures that the bat algorithm does not search blindly, but progressively advances in the direction of a more optimal solution. Compared with PSO [27], GAWOA [28] and SA [29], the bat algorithm is less prone to local optimum traps, has concise parameters, and converges quickly. The bat schematic diagram is shown in Fig. 3. The bat algorithm position, frequency update and velocity update equations are as in Eqs. (7)–(9).

xi(t)=xi(t−1)+vi(t)(7)

fi=fmin+(fmax−fmin)β(8)

vi(t)=vi(t−1)+(xi(t)−x∗)fi(9)

where xi(t) is the position of the i-th bat at time t, vi(t) is the velocity of the i-th bat at time t, fi is the frequency of the i-th bat, fmin and fmax limit the range of variation of frequency, and β is in the interval [0, 1]. x∗ is the currently found global optimum. To generate a locally optimal solution, the bat performs random flights around the current optimal solution, the position updating is given by Eq. (10).

xnew=xold+εAt(10)

where ε is a random value in the interval [−1, 1], xold representing the current global optimum, and also is the center point of bat around the flight, and At is the average loudness at iteration t.

Figure 3: Bat schematic diagram

The loudness and pulse frequency update equations are as in Eqs. (11) and (12).

Ai(t+1)=αAi(t)(11)

ri(t+1)=R0(1−exp⁡(−γ×t))(12)

where α is loudness debilitation factor in the interval (0, 1), γ is pulse frequency strengthening factor, γ > 0, and R0 is pulse frequency at start, which takes the value of 0.7.

Since the local movement direction of the bat depends on the random number ε, it leads to ambiguous direction of local position update and many invalid searches. But the virtual force algorithm accurately captures the location of voids and redundancies through attractive and repulsive forces, providing a clear direction for local optimization at later stage.

4.1.2 Virtual Force Algorithm

Every node experiences repulsive forces from other nodes in its neighborhood, while coverage blind region where the perception points around itself are located acts gravitationally on the node. All the nodes rotate under the joint action of repulsion as well as gravitational force, thus making the nodes adjust to the appropriate position, reducing the node redundancy coverage while reducing the coverage hole, maximizing the coverage of the entire region.

When the center of mass point cj of sj is inside an area centered on node si and twice the radius R as a radius circle, the overlapping portion between the sensed regions of nodes si and sj is achievable. In the network, nodes whose euclidean distance between nodes does not exceed two times the perceived radius are defined as neighboring nodes. Once nodes si and sj are determined to be neighboring nodes to each other, then there is a repulsive force acting at the center of mass point of these two nodes, and the magnitude of the repulsive force is shown in Eq. (13).

Fij→={(∑j=1mKRdij2,δij)dij≤2R0otherwise(13)

where dij is the euclidean distance between ci and cj, KR is the coefficient of repulsion; the angle denoted as δij corresponds to the repulsive force direction, which points from cj to ci.

When the perception point fk around node si is not covered, the point fk exerts gravitational effect on the center of mass point ci, node si approaches the region of fk by changing the location of ci. When the perception point is covered by a neighboring node sj, the fk is marked as 0, which indicates that the region is covered, it does not exert gravitational force on the center of mass point; when the perception point is not covered by any node, which indicates that there is a coverage void in the region, the fk is marked as 1, which means that it exerts gravitational force on the center of mass point. The magnitude of gravitational force of the sensing point on the center of mass point is shown in Eq. (14).

Fik→={(∑k=1f_max1dik2,δik)fk=10otherwise(14)

where f−max=max−integer(2π/α−3) denotes the maximum integer value of the number of perception points that can be taken, dik denotes the euclidean distance between fk of node si and the center of mass point ci, and δik denotes the gravitational direction of the center of mass point.

The combined force on the node center of mass point is the vector sum of the repulsive forc between the node and its neighbors and gravitational force on its own perception point, as shown in Eq. (15).

Fi→=∑j=1,j≠iNFij→+∑k=1f_maxFik→(15)

The combined force at the center of mass point of the nodes is shown in Fig. 4. There are four nodes in the figure, where F1→, F2→ and F3→ are repulsive forces acting on neighboring nodes, and f1→, f2→ and f3→ are gravitational forces acting on perception points.

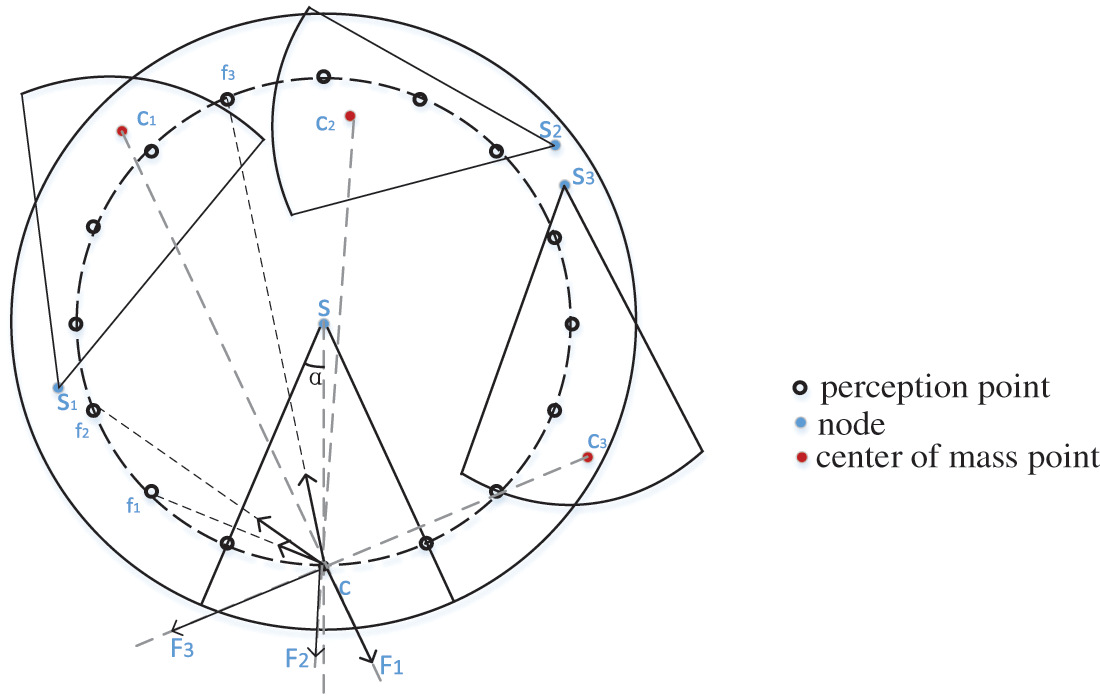
Figure 4: Combined force at the center of mass point

4.2 VFBA Algorithm

4.2.1 Global Quick Search

To boost the bat algorithm global optimization performance, the Lévy flight strategy [30] is adopted to modify the global position update mechanism for bat individuals, enhancing exploration efficiency. Lévy flight has a power-law step size distribution proprety, which can generate intermittent long-distance jumps and break the limitation of individual local search in the traditional bat algorithm. When updating position, the randomly generated step size and direction of Lévy flight are used to guide the bat to escape from the local traps, especially in the complex multimodal function optimization problems, and its advantages are more obvious. In calculating the search path of Lévy flight, the formula is given by Eq. (16).

Levy(λ)=μ|ν|1β(16)

where β∈(0,2), μ and ν are normally distributed random numbers. μ∼N(0,σμ2), ν∼N(0,σν2).

σμ and σν are given by given Eq. (17).

{σμ=(τ(1+β)sin⁡(πβ/2)βτ((1+β)/2)2(β−1)/2)σν=11/β(17)

where τ is the Gamma function and β takes the value 1.5.

To update the bat positions, the Lévy flight strategy is incorporated, and its update equation is given by Eq. (18).

xi(t+1)=xi(t)+ζ∙Levy(λ)(18)

where ζ is the scaling factor, which controls the jump amplitude and takes the value of 0.01. As shown in Fig. 5, when ζ takes the value of 1, the step size of each position update is too large, the algorithm is prone to jump too much in the solution space, miss the local optimal region, and fail to converge; while ζ takes the value of 0.001, the step size is too tiny, the algorithm will converge very slowly, and fall into the local optimum can not be jumped out of the algorithm.

Figure 5: Scaling factor value

The flight trajectory is shown in Fig. 6. The randomness of the flight trajectory and its long step size enables the bat to make a larger range of jumps in the feasible domain. This helps the algorithm to escape from the local optimum and explore broader regions within the search space, thus increasing the possibility of finding the overall optimal solution.

Figure 6: Lévy flight trajectory

4.2.2 Local Precision Optimization

Although the BA can achieve network coverage to a certain extent, there may be some uncovered areas, which are also known as coverage blind zones. The virtual force algorithm can fill the coverage holes by developing a simulation model for inter-node gravitational and repulsive forces, which steers the node to migrate into blind zones, thus making the network coverage more comprehensive and uniform. The bat position fusion virtual force is given by Eq. (19).

{xnew=xold+Fix→Fi→×Maxstep×e−1/Fi→ynew=yold+Fiy→Fi→×Maxstep×e−1/Fi→(19)

where (xold,yold) is the original coordinates of the individual and the updated coordinates are (xnew,ynew), Maxstep represents maximum movement step of the node, assuming that the combined force on the i-th node is Fi→, and the combined forces in the horizontal and vertical directions are Fix→ and Fiy→, respectively. Maxstep is usually a fixed step, but there is also a need to focus on the accuracy of the local solution while taking into account the global optimization process, Maxstep is set to a dynamic step size for adaptive tuning. Maxstep is given by Eq. (20).

Maxstep=(φmax−φmin)×e−(λ1×t/T+λ2×(t/T)2)(20)

where φmax takes the value of 0.1, and φmin takes the value of 0.01, λ1 and λ2 are positive constant parameters.

λ1 accelerates the rate of pre-decay with a value of 1, λ2 regulates the stability of post-decay with a value of 0.5.

The decay curve of the iterative step size is shown in Fig. 7. The curve at the beginning of the iteration shows an almost linear downward trend, indicating that the mobile step size adaptive adjustment speed is faster, which is more consistent with the iterative mechanisms in swarm intelligence algorithm. Fixed step size cannot regulate the search phase, if the step size is too large in the later local optimization, the nodes sway sharply around the optimal solution, if the step size is too small will lead to very low efficiency in the early global search. At the beginning of the iteration, Maxstep is maintained at a relatively large value to ensure the global exploration ability and accelerate the convergence rate of algorithm; at the late iteration, it should decreases to refine local optimization precision and ensure solution quality.

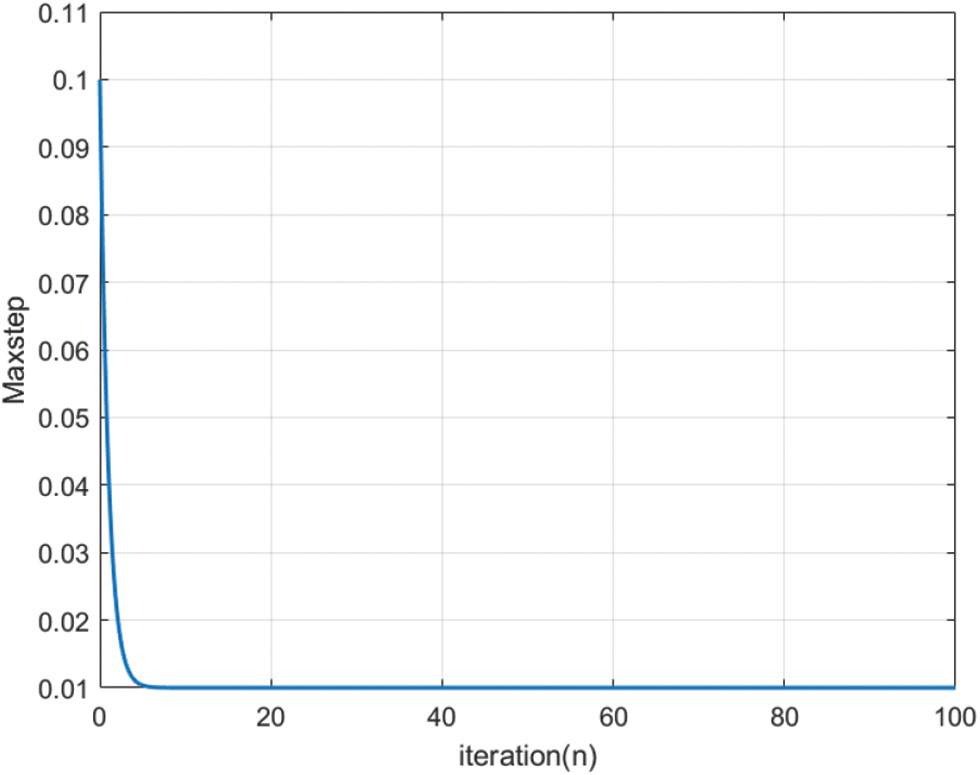
Figure 7: Dynamic step decay

The flowchart of the VFBA is shown in Fig. 8.

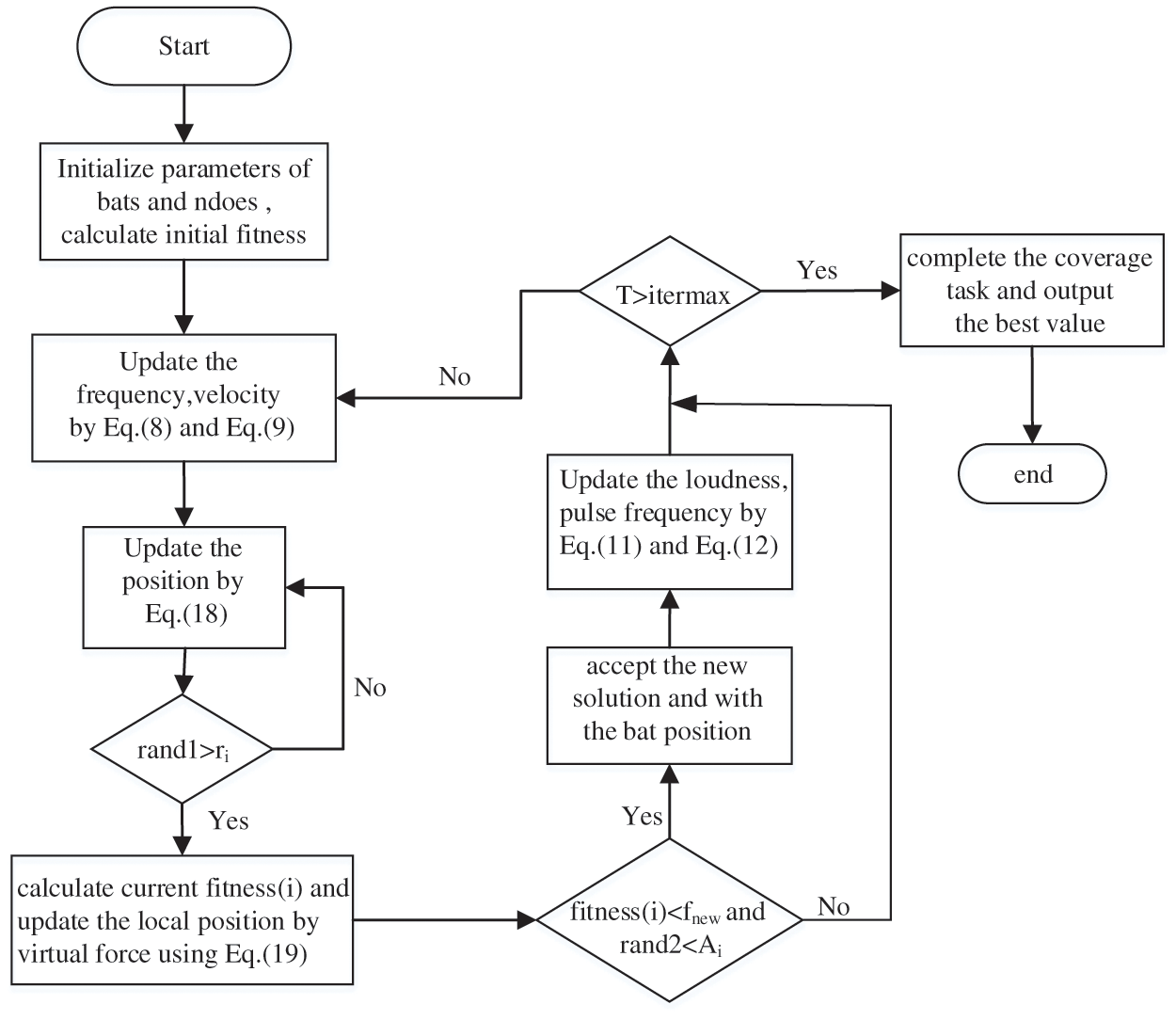
Figure 8: Flowchart of VFBA

The VFBA pseudocode is shown in the Algorithm 1.

5  Result Analysis

Aiming to validate the solution applicability of the virtual force fusion bat optimization algorithm for the coverage problem, the simulation uses an Intel Core i5-13500H processor (12 cores, 16 threads, 1.45 GHz) and 16 GB of RAM, the environment is MATLAB 2021b. Since the number of nodes N for virtual force computation is fixed and smaller than the population size n, the time and space complexity of the algorithm is determined by the population size n, the number of iterations T, and the problem dimension D, and is of the same order of magnitude as the complexity of the standard bat algorithm, which is O (T × n × D) in time complexity and O (n × D) in space complexity. The experimental parameters are tabulated in Table 1.

5.1 Benchmark Test Function Simulation

To assess the effectiveness of the VFBA, four benchmark functions are selected to test the simulation result. The configurations of the benchmark functions are tabulated in Table 2. f1(x) is the single-peak high dimensional function, while f9(x), f10(x) and f11(x) are the multi-peak high dimensional functions.

Comparison of the convergence curves of VFBA with the VFA and the BA are shown in Fig. 9. Which shows the VFBA has a better ability to find the optimum of the extremum of the four benchmark functions than VFA and BA, there is only one extremum of the single-peaked function Sphere, thus the convergence rate is fast. For the multi-peak function, owing to the presense of multiple local optimal solutions, the VFBA algorithm is slower to converge than the single-peak function and requires more iterations to find the global optimal solution, thus proving the feasibility and superiority of the VFBA in solving optimization problems.

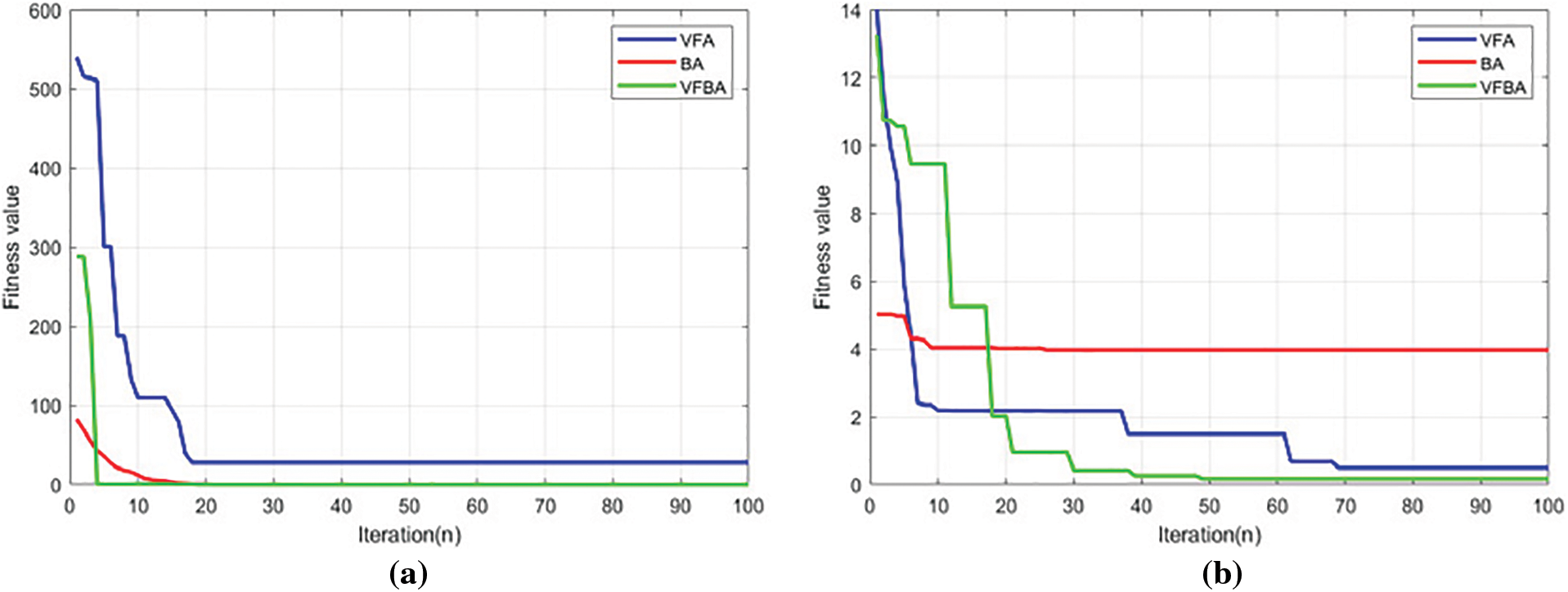
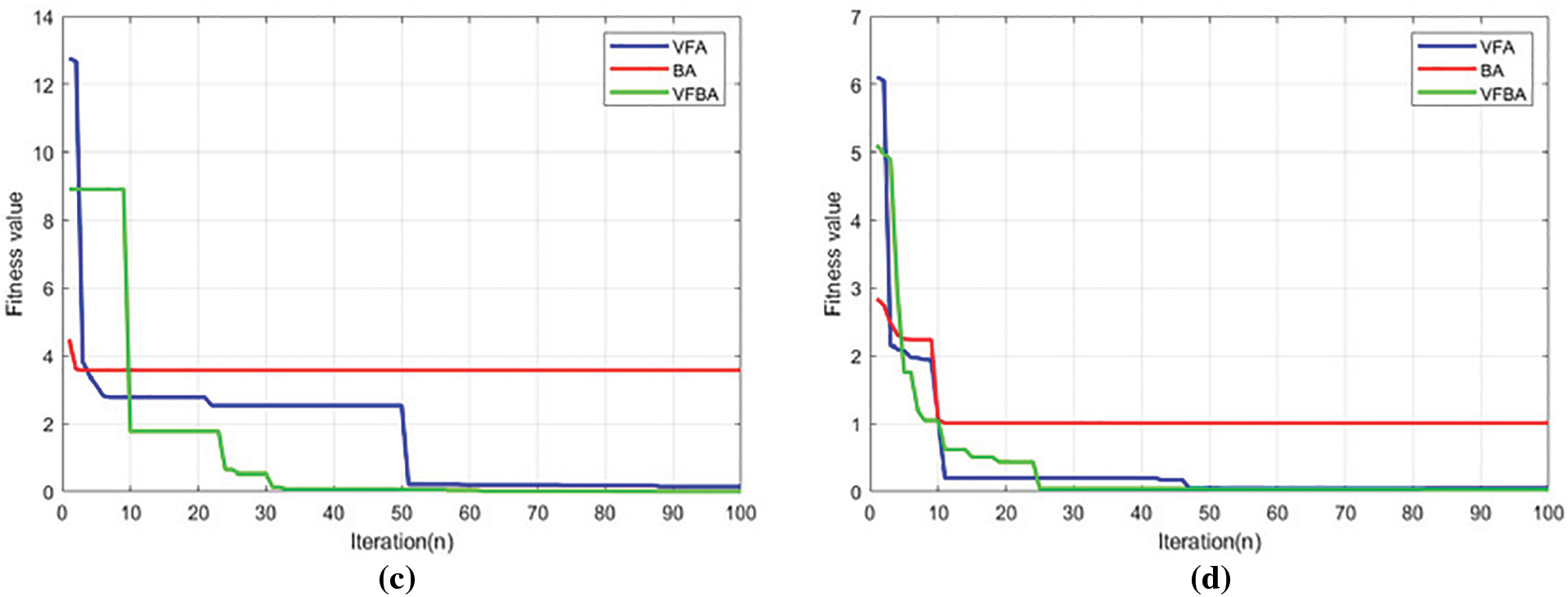
Figure 9: (a) Iteration of Sphere; (b) Iteration of Rastrigin; (c) Iteration of Ackley; (d) Iteration of Griewank

5.2 AP Node Coverage Simulation

5.2.1 Coverage Analysis in Monitoring Area

A right-angle coordinate system is established with the area to be monitored as the target, in which the positive x-direction is eastward, and the positive y-direction is northward. The measurement range is 500 m × 500 m, and taking three typical four-node rule layouts as an example, the APs are laid in the area according to the positions shown in Fig. 10. In the square layout, four APs (labeled A, B, C, and D) are located at the four corners of the monitoring area. The diamond layout places the APs on the vertical and horizontal centerlines of the monitoring area boundaries. The rectangular layout places the four APs on the upper and lower boundaries in three equal parts.

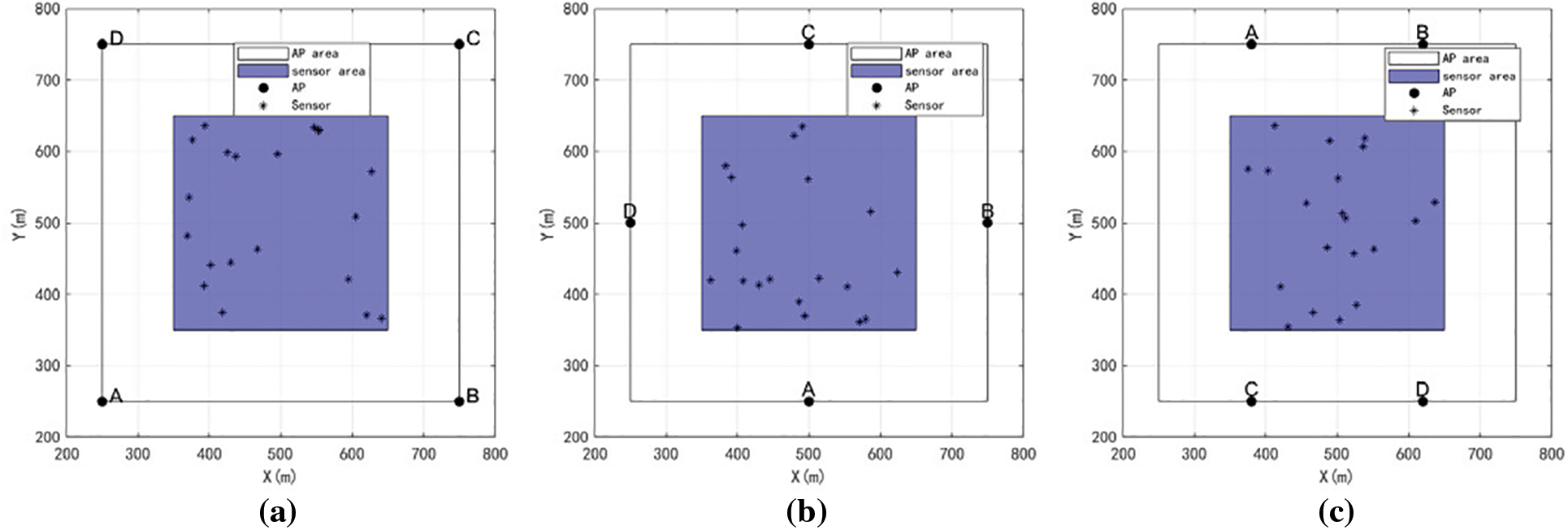
Figure 10: (a) Square layout; (b) Diamond layout; (c) Rectangular layout

The final coverage visualization results are shown in Fig. 11. Compared with rectangular layout [15], square layout [16] and diamond layout [17], due to these three methods of layout are based on simple geometric shapes for node layout, and these layout methods can only achieve locally better coverage, the coverage map of the three rules of layout has a larger coverage blind zone. In contrast, the algorithm in this paper adds Lévy flight to the bat position update, and further incorporates virtual force for optimization, resulting in a more uniform layout, smaller coverage blind zone, and a significant increase in the coverage rate.

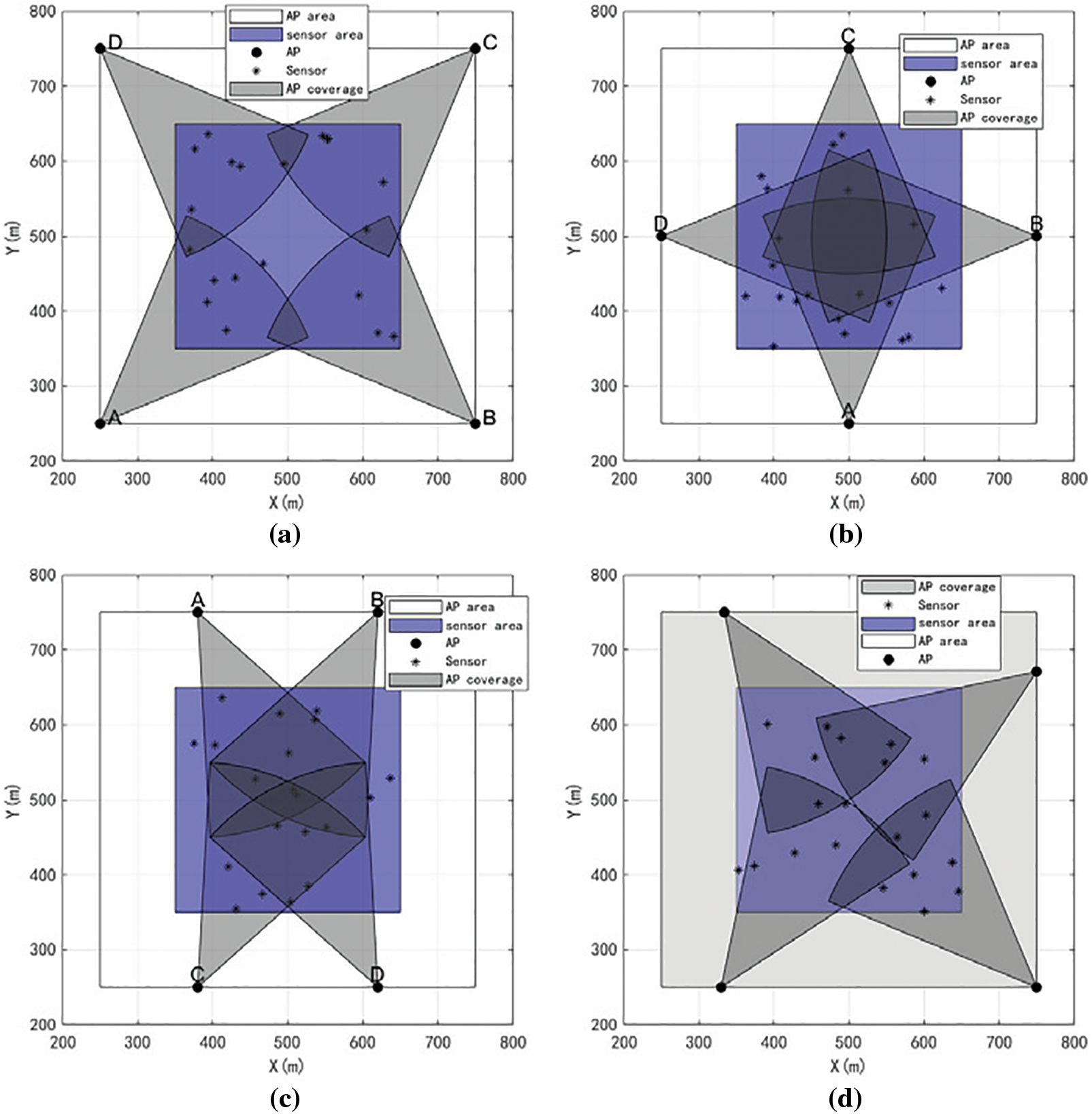
Figure 11: (a) Coverage of square layout; (b) Coverage of diamond layout; (c) Coverage of rectangular layout; (d) Coverage of VFBA algorithm

To validate the discrepancy in coverage performance between our algorithm and the conventional node layout method, the convergence curves are as shown in Fig. 12, the VFBA achieves 41.06% coverage at an early stage and has the fastest convergence speed. With the iterations increasing, the coverage effect is gradually close to the optimum under the fusion algorithm. Upon reaching 40 iterations, the algorithm has stabilized and achieves an optimal coverage of 91.99%. Diamond layout starts with a coverage of 30%, which grows slowly throughout the process, and later in the iteration the coverage is only 59%, which is a limited increase in coverage. The coverage of square layout is 84.75% and the coverage of rectangular layout is 73.64%. The VFBA has the highest coverage relative to other methods.

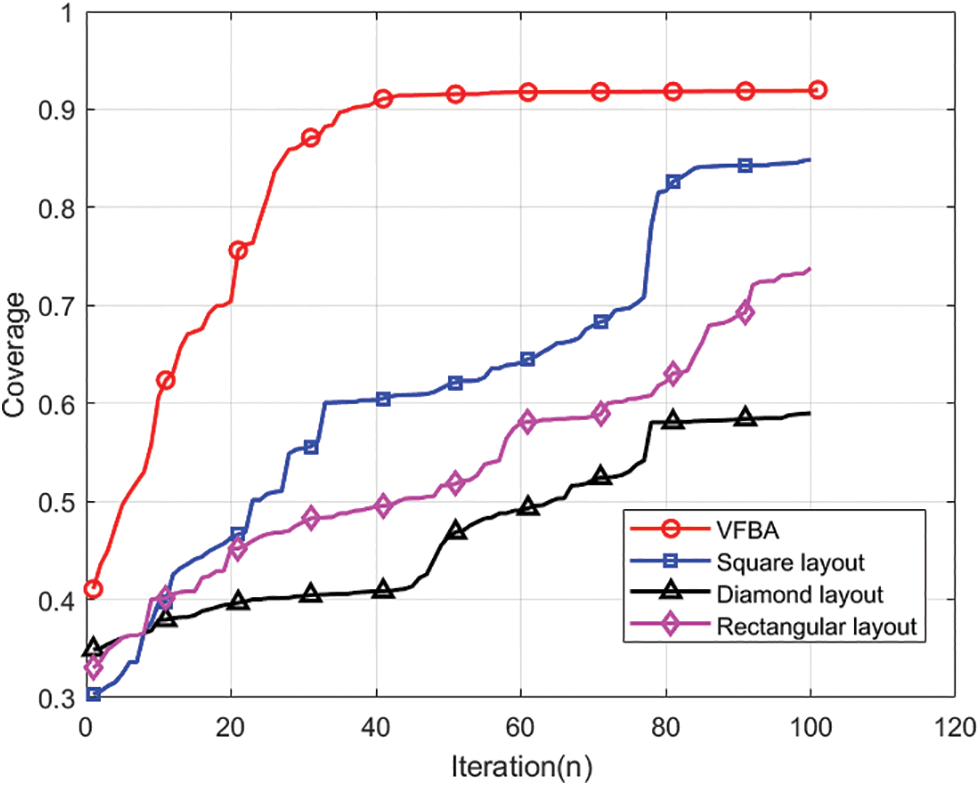
Figure 12: Coverage comparison

The node movement trajectory is shown in Fig. 13. The red dots represent the initial node positions determined by applying the bat algorithm, the initially deployed nodes may have coverage blind zones or coverage overlap is too high, bat algorithm is affected by its own search mechanism and parameter settings and other factors, it is difficult to eliminate these problems, the final node position is determined by the position of the end of the colored dotted line.

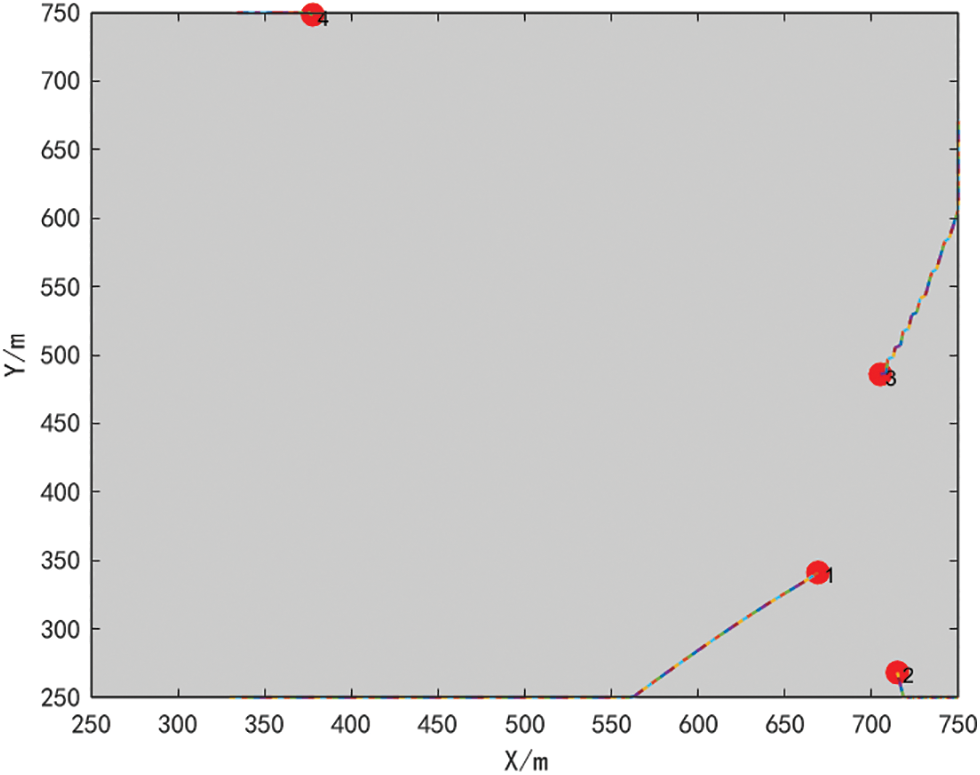
Figure 13: Node movement trajectory

To remove the errors due to randomness, every result underwent 30 runs for analysis under identical conditions, as shown in Table 3.

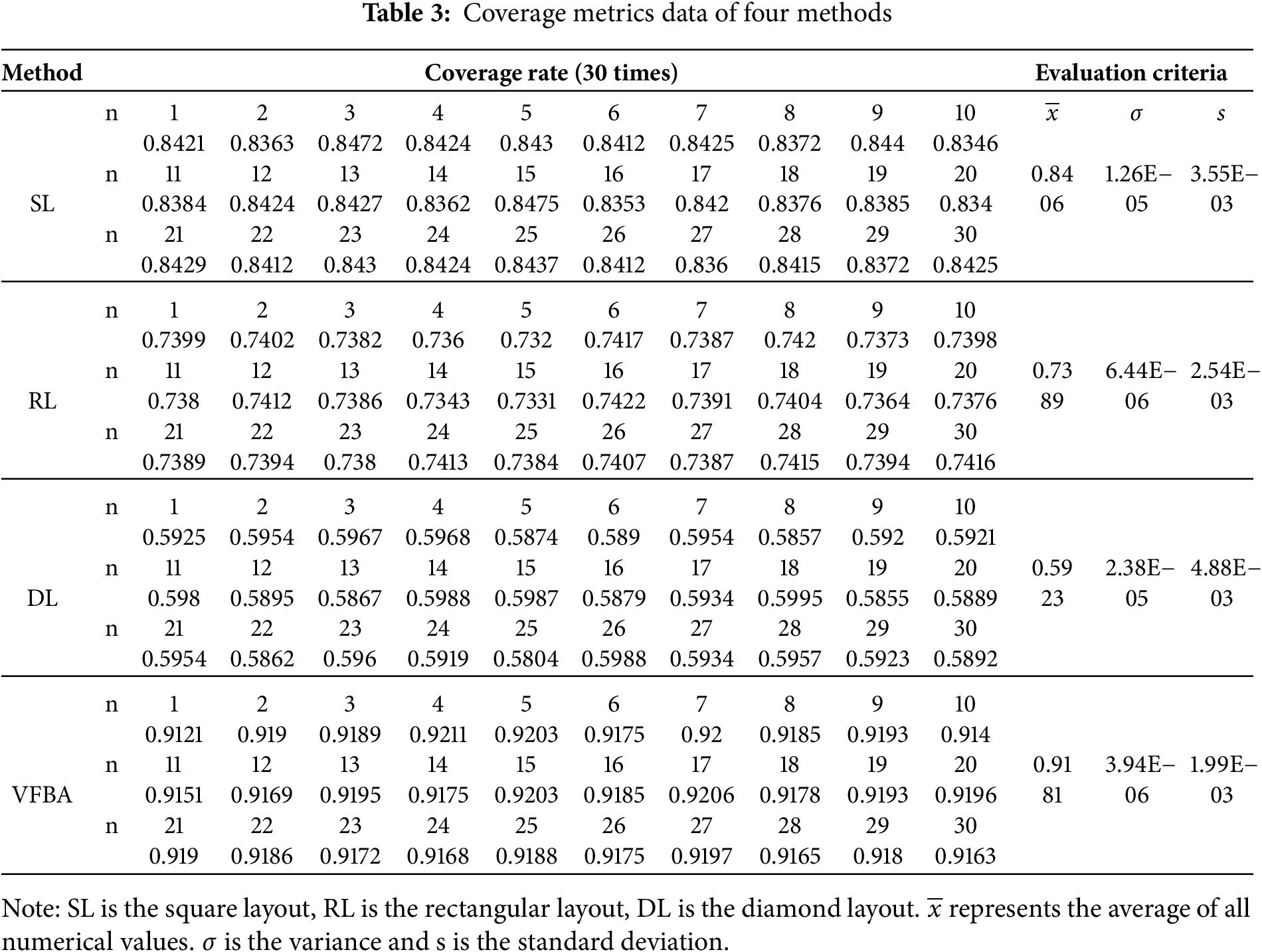
The table proves the average coverage of VFBA algorithm is 91.81% under the same conditions, which improved by 7.75% compared with the square layout method; by 32.6% compared with the diamond layout; and by 17.9% compared with the rectangular layout method. The variance and standard deviation of the algorithm in this paper are minimal compared to other layout methods, which proves that the VFBA is more stable. These prove that the VFBA significantly surpasses other methods in coverage performance.

The simulation results of coverage efficiency of nodes under the four methods are shown in Fig. 14. The coverage efficiency attained by VFBA reaches a high level at a low number of iterations and stabilizes at 88.46% as the iterations proceed. This indicates that when using the VFBA, the nodes can be distributed quickly and efficiently to achieve a large coverage area, and effectively reducing the coverage redundancy. The square layout has a low coverage efficiency at the beginning, it improves significantly in the later stages, and the coverage efficiency eventually reaches 91.67%, but the convergence speed is slightly slower compared to VFBA. The overall improvement ability of the diamond and rectangular layout is weaker, especially the diamond layout, under the same number of iterations, the coverage efficiency is much lower than VFBA and square layout, and the rectangular layout is the second.

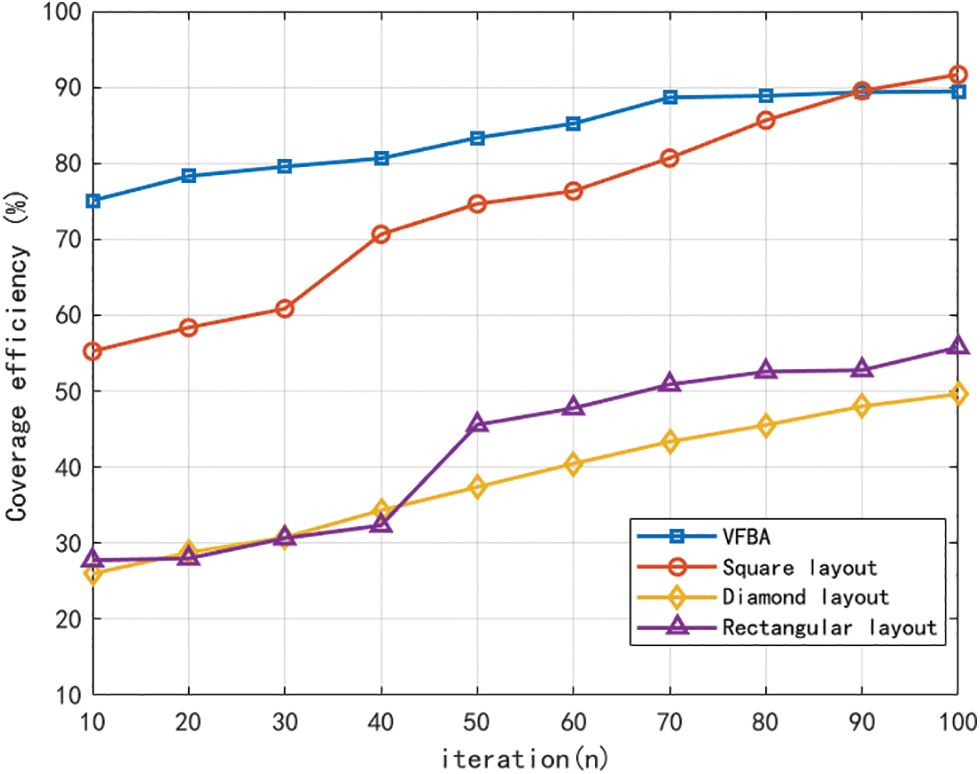
Figure 14: Coverage efficiency comparison

Since the radio signal propagation attenuation can be calculated using the free space model in the environment without obstacles in the campus outfield, the path loss from each location in the region to the signal source is shown in Fig. 15. The high signal strength area of VFBA is widely distributed and has the largest coverage, the high signal area of the diamond and rectangular layout is concentrated and unevenly distributed, and the signal attenuation in the center area of the square layout is serious and not conducive to stable communication. The feasibility of VFBA is proved by comparison.

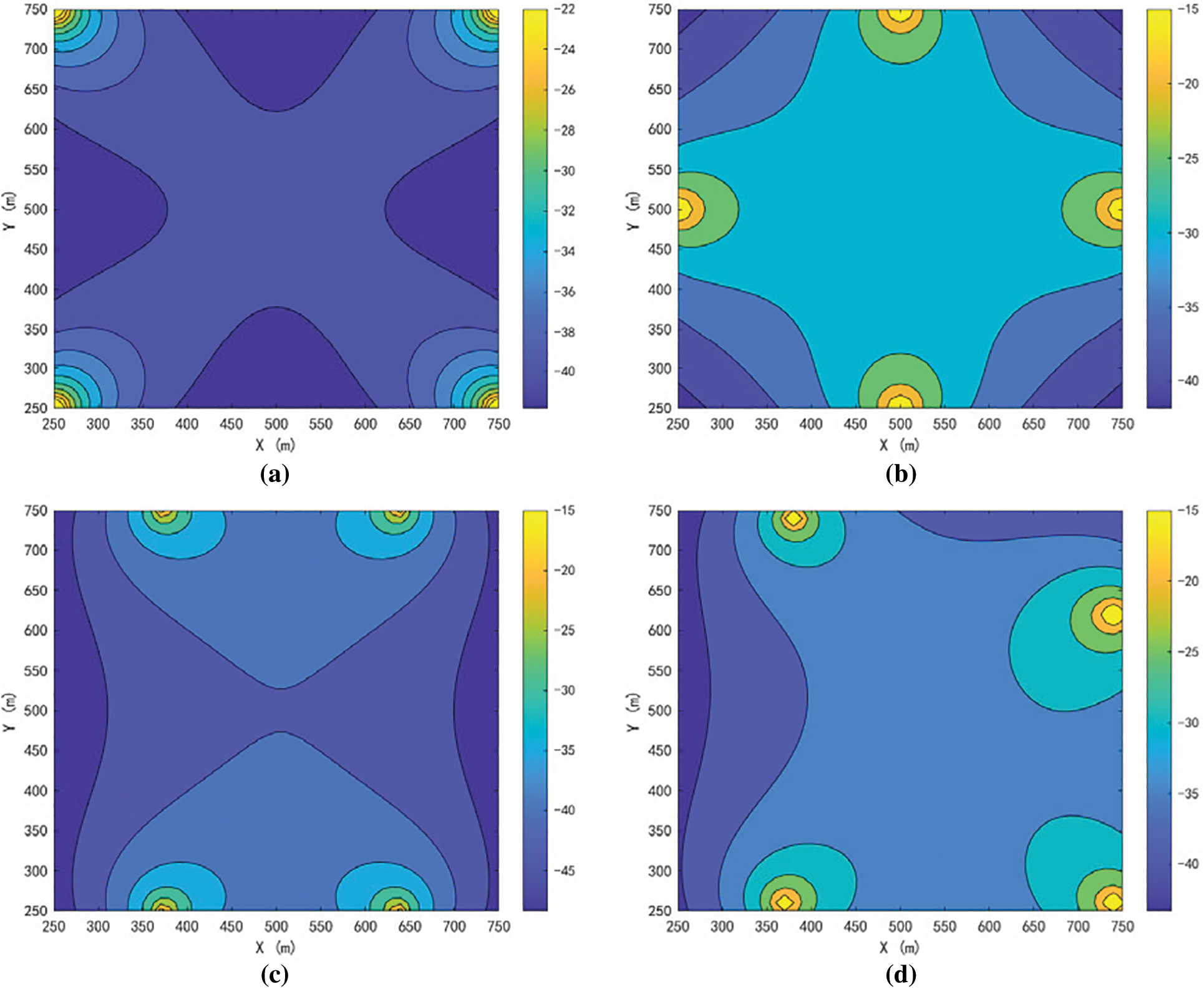
Figure 15: (a) Path loss of square layout; (b) Path loss of diamond layout; (c) Path loss of rectangular layout; (d) Path loss of VFBA algorithm

Across the four methods, the movement distance of every node is shown in Fig. 16a. The movement distance of the four nodes of VFBA, square, diamond and rectangular layout are shown from right to left. The maximum moving distance of a node of VFBA is 321.4 m, the maximum moving distance of a node of square, diamond and rectangular layout is 455.78, 494.25 and 511.08 m, respectively. In comparison with the other methods, the VFBA demonstrates a reduction in moving distance. And the total distance traveled by all nodes of the four methods is shown in Fig. 16b. The total movement distance using the VFBA is 930.26 m, which is the least movement distance among all methods. It shows that the VFBA is more efficient in resource utilization, reducing unnecessary mobile consumption and improving overall layout efficiency.

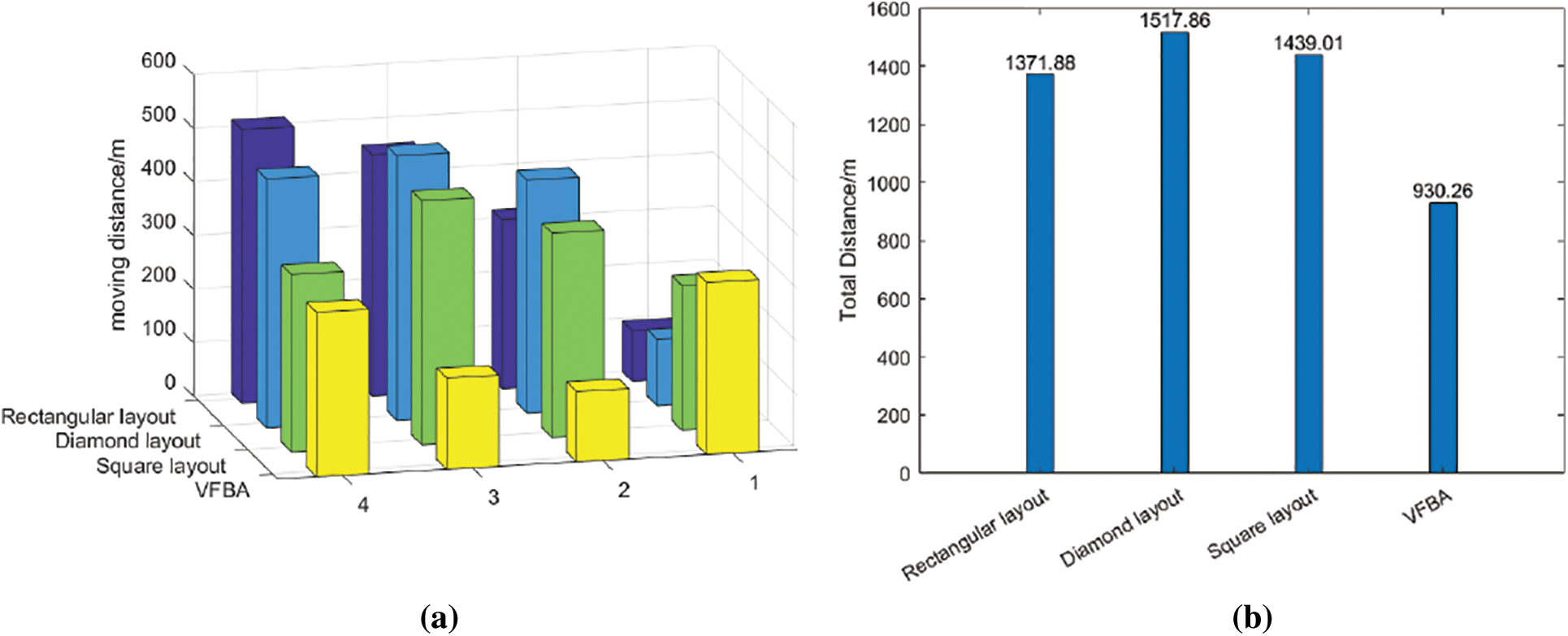
Figure 16: (a) Single node movement distance; (b) Total nodes movement distance

To validate the coverage applicability of VFBA in large areas, two groups of extended simulation experiments are designed, and the coverage curves are shown in Fig. 17. One group is carried out in an area of 1000 m × 1000 m, the radius of the nodes is set to 600m; the other group expands the area to 1500 m × 1500 m and adjusts the radius of the nodes to 800 m. Except for the two parameters of area and radius of the nodes in these two groups of experiments, the other parameters are unchanged as in the previous basic experiments to ensure the comparability of the experiments. For two larger regional deployments, the VFBA has a higher coverage than the other three layout methods. In a 1000 m × 1000 m monitoring area, VFBA achieves a final coverage of 85.92%, while square, diamond, and rectangular layouts have coverage of 80.55%, 58.6%, and 68.17%, respectively.

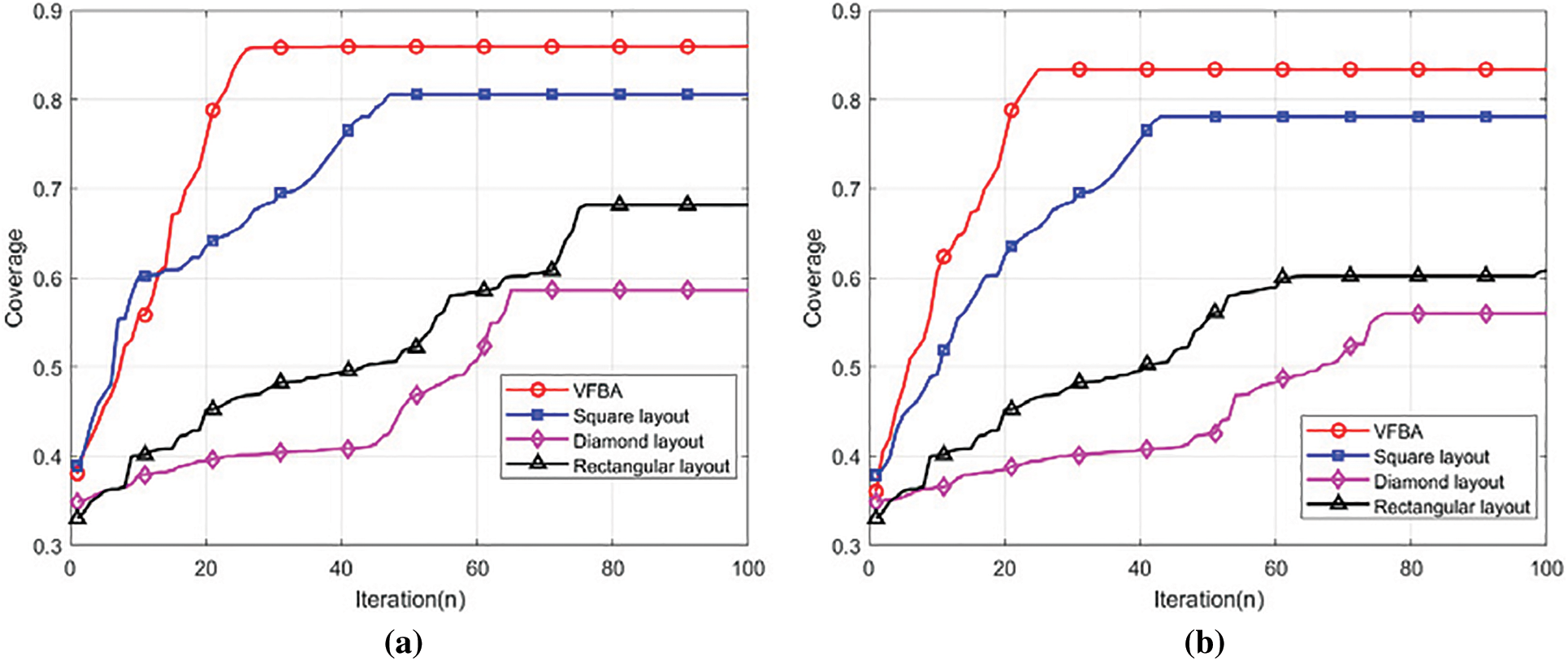
Figure 17: (a) Coverage of 1000 m × 1000 m; (b) Coverage of 1500 m × 1500 m

5.2.2 Coverage Analysis in Different Algorithms

Comparison of the coverage of different algorithms in the iterative optimization process is shown in Fig. 18. The node coverage of VFBA is 91.9%, GAWOA is next with a coverage value of 85%, SA has a coverage of 71.1%, and PSO has the worst coverage of 68.1%. VFBA is able to quickly approach the optimal solution at start and converge to the optimal solution quickly. Although PSO converges faster, in terms of node coverage, PSO falls into the optimum value at the later stage and it is difficult to jump out. Compared with VFBA, the final network coverage obtained by GAWOA is lower and the convergence speed is slower. Taken together, VFBA outperforms other algorithms in the node coverage optimization problem.

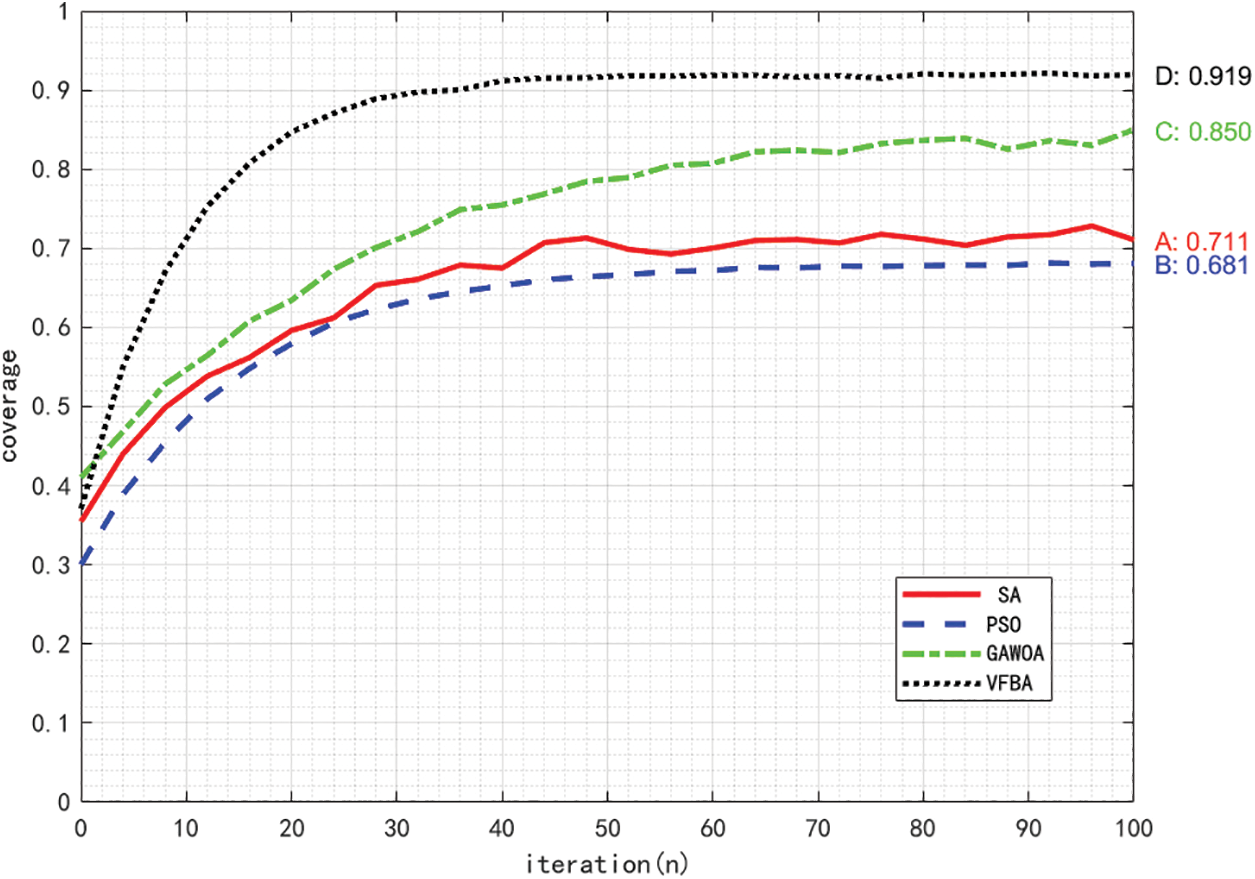
Figure 18: Coverage of different algorithms

6  Conclusion

In this paper, we study the key technology of wireless coverage enhancement for a finite number of AP nodes and propose a virtual force fusion bat algorithm. For the purpose of raising the coverage effect, the Lévy flight strategy is incorporated, and the position update mechanism of the bat is improved so that the individuals can make long-distance jumps with a large probability in each iteration to promote the ability of global search. At post-algorithmic to enhance the bat search accuracy, virtual force is combined with the feature that the traveling step size decreases gradually with the number of iterations, and the virtual force is introduced as a disturbance factor in the position update process of bats as a way to improve the accuracy of the local search. The results indicate that when compared to diamond, rectangular, and square layout methods, VFBA substantially promotes the coverage and coverage efficiency of AP nodes. The VFBA makes the nodes well distributed and reduces energy consumption. In addition, the coverage of VFBA is also significantly improved compared to SA, PSO, and GAWOA. However, this study is limited to the deployment of AP in 2-D space, after which a more realistic monitoring environment will be simulated to extend the deployment optimization to 3-D space.

Acknowledgement: The authors thank all funding agencies for their support of this work, as well as teachers and students for their help.

Funding Statement: This work is supported in part by the National Natural Science Foundation of China under Grant No. 62271453, in part by the National Natural Science Foundation of China No. 62101512, in part by the Central Support for Local Projects under Grant No. YDZJSX2024D031, in part by Project supported by the Shanxi Provincial Foundation for Leaders of Disciplines in Science, China under Grant No. 2024Q022, and in part by Shanxi Province Patent Conversion Special Plan Funding Projects under Grant No. 202405004.

Author Contributions: Conceptualization, Jian Li, Qing Zhang, Tong Yang, Yu’an Chen and Yongzhong Zhan; methodology, Jian Li, Qing Zhang, Tong Yang and Yu’an Chen; investigation, Jian Li, Qing Zhang and Tong Yang; writing, Jian Li and Qing Zhang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The original data that support the findings of this study are available from the corresponding author, Jian Li, upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Liu S, Zhang R, Shi Y. Design of coverage algorithm for mobile sensor networks based on virtual molecular force. Comput Commun. 2020;150(3):269–77. doi:10.1016/j.comcom.2019.11.001. [Google Scholar] [CrossRef]

2. Karimi-Bidhendi S, Guo J, Jafarkhani H. Energy-efficient node deployment in heterogeneous two-tier wireless sensor networks with limited communication range. IEEE Trans Wirel Commun. 2021;20(1):40–55. doi:10.1109/TWC.2020.3023065. [Google Scholar] [CrossRef]

3. Nematzadeh S, Torkamanian-Afshar M, Seyyedabbasi A, Kiani F. Maximizing coverage and maintaining connectivity in WSN and decentralized IoT: an efficient metaheuristic-based method for environment-aware node deployment. Neural Comput Appl. 2023;35(1):611–41. doi:10.1007/s00521-022-07786-1. [Google Scholar] [CrossRef]

4. Wang X, Chu SC, Chao HC, Pan JS. A multi-group dragonfly algorithm for application in wireless sensor network deployment problem. Int J Ad Hoc Ubiquitous Comput. 2021;37(4):227. doi:10.1504/ijahuc.2021.10040654. [Google Scholar] [CrossRef]

5. Zulfiqar R, Javed T, Anwar Ali Z, Alkhammash EH, Hadjouni M. Selection of metaheuristic algorithm to design wireless sensor network. Intell Autom Soft Comput. 2023;37(1):985–1000. doi:10.32604/iasc.2023.037248. [Google Scholar] [CrossRef]

6. Seyyedabbasi A, Kiani F, Allahviranloo T, Fernandez-Gamiz U, Noeiaghdam S. Optimal data transmission and pathfinding for WSN and decentralized IoT systems using I-GWO and Ex-GWO algorithms. Alex Eng J. 2023;63(12):339–57. doi:10.1016/j.aej.2022.08.009. [Google Scholar] [CrossRef]

7. Kong Z, Wu D, Jin X, Cen S, Dong F. Improved AP deployment optimization scheme based on multi-objective particle swarm optimization algorithm. KSII Trans Internet Inf Syst. 2021;15(4):1568–89. doi:10.3837/tiis.2021.04.021. [Google Scholar] [CrossRef]

8. Chen L, Xu F, Jin K, Tang Z. Energy-saving access point configurations in WLANs: a swarm intelligent approach. J Supercomput. 2023;79(17):19332–64. doi:10.1007/s11227-023-05402-0. [Google Scholar] [CrossRef]

9. Liu P, Hu Q, Jin K, Yu G, Tang Z. Toward the energy-saving optimization of WLAN deployment in real 3-D environment: a hybrid swarm intelligent method. IEEE Syst J. 2022;16(2):2425–36. doi:10.1109/JSYST.2021.3065434. [Google Scholar] [CrossRef]

10. Yang Y, Zhou A, Ma H. FineAP: fine-grained access point deployment strategy for 60 GHz millimeter-wave wireless networks. IEEE Commun Lett. 2023;27(1):381–5. doi:10.1109/LCOMM.2022.3213578. [Google Scholar] [CrossRef]

11. Marinho RP, Vieira LFM, Vieira MAM, Loureiro AAF. CAIN: an energy-aware and intelligent increasing coverage area routing protocol for future 6G networks. Comput Netw. 2023;228(2):109733. doi:10.1016/j.comnet.2023.109733. [Google Scholar] [CrossRef]

12. Kumar S, Jain S, Sharma A. A BER-conscious synthesis of switched-beam antenna to maximize reliable coverage in WSN applications. IEEE Sens J. 2022;22(4):3785–95. doi:10.1109/JSEN.2022.3142137. [Google Scholar] [CrossRef]

13. Vijayaraghavan H, Von Mankowski J, Mas-Machuca C, Kellerer W. PlaciFi: orchestrating optimal 3D access point placement for LiFi-WiFi heterogeneous networks. IEEE Access. 2023;11:115415–29. doi:10.1109/access.2023.3325097. [Google Scholar] [CrossRef]

14. Dao TK, Nguyen TT. An optimal node localization in WSN based on siege whale optimization algorithm. Comput Model Eng Sci. 2024;138(3):2201–37. doi:10.32604/cmes.2023.029880. [Google Scholar] [CrossRef]

15. Qi C, Huang J, Liu X, Zong G. A novel mobile-coverage scheme for hybrid sensor networks. IEEE Access. 2020;8:121678–92. doi:10.1109/access.2020.3007267. [Google Scholar] [CrossRef]

16. Zheng J, Huang Y, Wang Y, Xiao Y. Deterministic deployment based on information coverage in wireless sensor networks. Wirel Commun Mob Comput. 2014;14(18):1657–71. doi:10.1002/wcm.2304. [Google Scholar] [CrossRef]

17. Yang L, Liang J, Liu W. Graphical deployment strategies in radar sensor networks (RSN) for target detection. EURASIP J Wirel Commun Netw. 2013;2013(1):55. doi:10.1186/1687-1499-2013-55. [Google Scholar] [CrossRef]

18. Zhang S, Wu D, Jiang L, Jin X, Cen S. Research on UAV access deployment algorithm based on improved virtual force model. KSII Trans Internet Inf Syst. 2022;16(8):2606–26. doi:10.3837/tiis.2022.08.008. [Google Scholar] [CrossRef]

19. Wang J, Guo H. Virtual force field coverage algorithms for wireless sensor networks in water environments. Int J Sens Netw. 2020;32(3):174. doi:10.1504/ijsnet.2020.105564. [Google Scholar] [CrossRef]

20. Li J, Zhang B, Cui L, Chai S. An extended virtual force-based approach to distributed self-deployment in mobile sensor networks. Int J Distrib Sens Netw. 2012;8(3):417307. doi:10.1155/2012/417307. [Google Scholar] [CrossRef]

21. Li S, Zhou Y, Luo Q. Enhanced multi-object dwarf mongoose algorithm for optimization stochastic data Fusi on wireless sensor network deployment. Comput Model Eng Sci. 2025;142(2):1955–94. doi:10.32604/cmes.2025.059738. [Google Scholar] [CrossRef]

22. Yao Y, Li Y, Xie D, Hu S, Wang C, Li Y. Coverage enhancement strategy for WSNs based on virtual force-directed ant lion optimization algorithm. IEEE Sens J. 2021;21(17):19611–22. doi:10.1109/JSEN.2021.3091619. [Google Scholar] [CrossRef]

23. Yao Y, Hu S, Li Y, Wen Q. A node deployment optimization algorithm of WSNs based on improved moth flame search. IEEE Sens J. 2022;22(10):10018–30. doi:10.1109/JSEN.2022.3166804. [Google Scholar] [CrossRef]

24. Mohar SS, Goyal S, Kaur R. Optimum deployment of sensor nodes in wireless sensor network using hybrid fruit fly optimization algorithm and bat optimization algorithm for 3D Environment. Peer Peer Netw Appl. 2022;15(6):2694–718. doi:10.1007/s12083-022-01364-x. [Google Scholar] [CrossRef]

25. Muhammad H, Nam H. Sensor node deployment optimization for continuous coverage in WSNs. Sensors. 2025;25(12):3620. doi:10.3390/s25123620. [Google Scholar] [PubMed] [CrossRef]

26. Sun S, Chen Y, Dong L. An optimization method for wireless sensor networks coverage based on genetic algorithm and reinforced whale algorithm. Math Biosci Eng. 2024;21(2):2787–812. doi:10.3934/mbe.2024124. [Google Scholar] [PubMed] [CrossRef]

27. Zhao J, Zhang Z, Yi Z, Ma X, Zhang Q. Deployment of edge computing nodes in IoT: effective implementation of simulated annealing method based on user location. China Commun. 2024;21(1):279–96. doi:10.23919/jcc.fa.2021-0034.202401. [Google Scholar] [CrossRef]

28. Liu Z, Xu F. Joint AP selection and grey wolf optimization based pilot design for cell-free massive MIMO systems. IEICE Trans Fundamentals. 2024;E107.A(7):1011–8. doi:10.1587/transfun.2023eap1085. [Google Scholar] [CrossRef]

29. Saranya VG, Karthik S. Bio-inspired intelligent routing in WSN: integrating mayfly optimization and enhanced ant colony optimization for energy-efficient cluster formation and maintenance. Comput Model Eng Sci. 2024;141(1):127–50. doi:10.32604/cmes.2024.053825. [Google Scholar] [CrossRef]

30. Alghamdi AS, Zohdy MA, Aldoihi S. Enhancing renewable energy integration: a Gaussian-bare-bones levy cheetah optimization approach to optimal power flow in electrical networks. Comput Model Eng Sci. 2024;140(2):1339–70. doi:10.32604/cmes.2024.048839. [Google Scholar] [CrossRef]