 Open Access
Open Access
ARTICLE
MHD Convective Flow of CNT/Water-Nanofluid in a 3D Cavity Incorporating Hot Cross-Shaped Obstacle
1 Department of Industrial and Systems Engineering, College of Engineering, Princess Nourah Bint Abdulrahman University, P.O. Box 84428, Riyadh, 11671, Saudi Arabia
2 Laboratory of Metrology and Energy Systems, University of Monastir, Monastir, 5000, Tunisia
3 Department of Physics, College of Sciences, Princess Nourah Bint Abdulrahman University, P.O. Box 84428, Riyadh, 11671, Saudi Arabia
4 Department of Mechanical Engineering, College of Engineering, University of Ha’il, Ha’il, 81451, Saudi Arabia
* Corresponding Author: Lioua Kolsi. Email:
(This article belongs to the Special Issue: Computational Methods in Mono/hybrid nanofluids: Innovative Applications and Future Trends)
Computer Modeling in Engineering & Sciences 2025, 145(2), 1839-1861. https://doi.org/10.32604/cmes.2025.071678
Received 10 August 2025; Accepted 28 October 2025; Issue published 26 November 2025
Abstract
Current developments in magnetohydrodynamic (MHD) convection and nanofluid engineering technology have have greatly enhanced heat transfer performance in process systems, particularly through the use of carbon nanotube (CNT)–based fluids that offer exceptional thermal conductivity. Despite extensive research on MHD natural convection in enclosures, the combined effects of complex obstacle geometries, magnetic fields, and CNT nanofluids in three-dimensional configurations remain insufficiently explored. This research investigates MHD natural convection of carbon nanotube (CNT)-water nanofluid within a three-dimensional cavity. The study considers an inclined cross-shaped hot obstacle, a configuration not extensively explored in previous works. The work aims to elucidate the combined effects of CNT nanofluid concentration, magnetic field strength, and obstacle inclination on fluid flow patterns and heat transfer characteristics. Numerical simulations are performed using the finite element method (FEM) based on the Galerkin Weighted Residual approach. The analysis systematically considers variations in Rayleigh number (Ra), Hartmann number (Ha), nanoparticle volume fraction (Φ), and obstacle inclination angle (θ). Results show that increasing Ra from 103 to 106 enhances convective heat transfer by up to 228%, while raising the CNT volume fraction to 4.5% improves heat transfer by about 64%. In contrast, strengthening the magnetic field from Ha = 0 to Ha = 100 suppresses fluid motion and reduces heat transfer by nearly 67%, whereas varying the obstacle inclination from 0° to 45° leads to a 4.6% decrease in efficiency. The addition of nanoparticles slightly increases viscosity, reducing flow intensity by 8.3% when Ha = 0. Furthermore, a novel multiparametric correlation is proposed, accurately predicting the average Nusselt number as a function of Ra, Ha, ϕ, and θ, with an R2 of 0.98. These findings provide new insights into the role of geometry, magnetic effects, and nanofluids in heat transfer enhancement, offering practical guidance for the design and optimization of advanced thermal systems.Keywords
The study of magnetohydrodynamics with obstacles is a significant area of research with numerous practical applications. This field investigates how electroconductive fluids behave in environments where magnetic fields play a crucial role in fluid flow and thermal processes. Implementing MHD in areas with physical barriers is essential. It allows for effective control and optimization of fluid movement and thermal characteristics. This approach is particularly relevant in various industries, such as enhancing cooling in advanced nuclear power plants and managing temperatures in confined compartments within the space industry. These diverse applications highlight the crucial importance of MHD in technological advancement. The investigation of nanofluids’ behavior under the influence of external magnetic fields, especially in the presence of complex obstacles, represents a significant and burgeoning field of research. This area has various applications across various industries. In electronics cooling, it enhances heat dissipation in high-performance devices. In aerospace, it optimizes thermal management systems for aircraft and spacecraft. Solar energy systems benefit from improved thermal efficiency and energy capture. Advanced heat exchangers utilize these findings to increase heat transfer rates and efficiency. In metal processing, it aids in precise temperature control during manufacturing processes. Additionally, cooling systems for cross-shaped beams and columns during construction can be optimized for better structural integrity and safety. This interest arises from the unique effects of magnetic fields on the thermal and fluid properties of nanofluids. When a magnetic field is present, the conductive particles in nanofluids restructure and interact with the field, influencing their thermal conduction capacity and viscosity. This phenomenon is crucial in several engineering sectors, including strengthening cooling systems in electronics, improving heat transfer in nuclear power plants, and optimizing thermal management in aerospace. Advances in these areas are essential, especially when precise thermal regulation and efficient heat dissipation are required. Mohseni et al. [1] explored the dynamics of ferro-nanofluids under the effect of magnetic fields. They focused on the analysis of nanofluids composed of water and Fe2O3, contained in an L-shaped tank with internal partitions. Their research focused on evaluating the impact of varying magnetic field strengths, different Rayleigh number levels and changes to the tank structure. They observed that increasing the Rayleigh number promoted better heat dissipation and greater entropy production, while adjustments to the vessel structure had a less pronounced impact. This study provides essential insights into the important implications in the engineering and healthcare sectors. Mliki et al. [2] performed a comprehensive investigation on the thermal behavior inside an inclined C-shaped chamber filled with a nanofluid consisting of CuO and water, influenced by magnetohydrodynamic forces. This research applies the Lattice Boltzmann Method (LBM) to analyze the dynamics of nanoparticles in Brownian motion. It investigates in detail the effect of various factors, including the Rayleigh number (Ra), Hartmann number (Ha), inclination angle, nanoparticle volume concentration, and aspect ratio. This study reveals a significant increase in heat transfer efficiency through Brownian motion, although this is partially offset by a magnetically induced slowing of convection processes. Sannad et al. [3] analyzed the heat transfer and MHD flow of copper-water nanofluid in a cubic enclosure. The originality of their approach lies in adopting a non-homogeneous dynamic model for a more faithful representation of the nanofluid. Their research focused on evaluating the influence of several parameters, including nanoparticle diameter, magnetic field intensity, solid phase concentration and Ra on Nu. The results revealed a direct correlation between Nu and Ra as well as the solid phase concentration, and an inverse relationship with the diameter of the nanoparticles. This research enriches the understanding of heat transfer mechanisms in nanofluids and opens prospects for practical applications, such as developing more compact heat exchangers and improving cooling systems in nuclear reactors. It highlights the complex interactions between magnetic fields and nanofluids and their impact on heat transfer. The authors adopt an integrated approach that considers both the size and concentration of nanoparticles. This method provides a detailed perspective on the heat transfer characteristics in nanofluids. It also has significant implications for advancing nanotechnology in thermal engineering, particularly for optimizing cooling systems in electronics and improving thermal management in industrial processes. Khan et al. [4] studied the properties of the boundary layer that surrounds fractional Maxwell-like viscoelastic nanofluids and their composite mixtures, specifically on a permeable vertical surface. The analysis meticulously assessed the impact of magnetic forces (Lorentz effect) and gravity (buoyancy effect), adopting distributed-order fractional time derivatives to regulate both fluid dynamic behavior and the dynamics of heat transfer. This study provides crucial knowledge for improving heat dissipation and fluid control, key factors for optimizing thermal systems in various applications, including cooling systems and heat exchange devices. Asha and Molla [5] focused on the investigation of natural convection, emphasizing the use of nanofluids in a Bingham-type magnetohydrodynamic context within a C-shaped cavity. To carry out his research, he opted for the Boltzmann simulation technique on a multiple relaxation time network. His analysis delves into the influence of several crucial parameters, such as the Bingham number, Ra, Ha, and nanoparticle concentration. This research is important for elucidating the behaviors of nanofluids in complex structures and in the presence of magnetic fields, opening the way to new perspectives in areas related to heat transfer. Tasnim et al. [6] studied the behavior of a TiO2-water nanofluid circulating in an oblique square container equipped with heat-producing devices. This research used finite element analysis techniques to examine the influence of Ra, Pr and Ha, as well as the effect of Joule heating. Emphasis was placed on analyzing flow patterns and thermal profiles, evaluating the average Nusselt number and internal fluid temperature. The study also quantified overall entropy generation and thermal efficiency, taking into account the angle of inclination of the container and the effect of the nanoparticles on heat transfer. Sajjadi et al. [7] explored the dynamics of natural convection in a magneto-hydrodynamic (MHD) environment within cubic space. This study looks specifically at a wall that has a sinusoidal temperature profile, examining the use of a nanofluid composed of copper and water. They adopted a state-of-the-art Lattice Boltzmann method (LBM) with a dual Multi-Relaxation-Time (MRT) system. This process made it possible to analyze the influence of variations in Ra (Rayleigh number) and Ha (Hartmann number), as well as the concentration of nanoparticles. The findings highlight the notable effect of these factors on heat transfer efficiency. These insights are essential for optimizing nanofluid circulation and thermal regulation in MHD applications. The research carried out by Vijaybabu and Dhinakaran [8] explored convective heat transfer in a square-shaped cavity. Their attention focused on the study of a porous triangular cylinder immersed in a nanofluid composed of alumina and water. This detailed analysis examined how magnetohydrodynamic forces interact with permeability parameters and porous structure orientation, thereby influencing fluid movement and convective heat transfer. Their results highlight the critical importance of permeability and magnetic field strength in regulating the characteristics of fluid motion and heat exchange. These findings provide valuable data for the development of more sophisticated thermal control methods for use in heat exchange systems and thermal management applications. Nabwey et al. [9] conducted extensive research on magnetohydrodynamic (MHD) fluid dynamics in a porous and wavy environment. This research focuses on the dynamics of hybrid nanofluids composed of aluminum oxide, copper and water flowing in an inclined and undulating cavity containing a square-shaped obstacle. The study highlights the impacts of thermal radiation, heat production and absorption, while examining variables such as the porosity of the medium, the concentration of nanoparticles, and the influence of Ha. The main objective of this work is to improve the efficiency of heat transfer in complex thermal systems, focusing on specific configurations and conditions. Saha et al. [10] studied the impact of a heating fin on the MHD natural convection movement inside a square enclosure, with an undulated upper wall. They focused on using a nanofluid composed of Al2O3 and H2O. Their methodology was based on finite element analysis, particularly adopting the weighted Galerkin residuals approach. Their results revealed notable variations in fluid flow patterns and heat distribution in relation to factors such as Rayleigh number, nanoparticle concentration, and Hartmann number. This study provided insight into improving heat transfer efficiency by manipulating the characteristics and varieties of nanoparticles.
Selimefendigil and Öztop [11] numerically studied natural convection in a cavity divided by a corrugated, thermally conductive partition, with different fluids on each side. One domain contained a CNT–water nanofluid subjected to an inclined magnetic field. Using the Galerkin finite element method, the authors examined the influence of key parameters, including the Rayleigh number, Hartmann number, magnetic field angle, nanoparticle concentration, corrugation geometry (triangular waves with varying heights), and thermal conductivity ratio. Their findings indicated that CNT addition significantly enhanced heat transfer, while higher Hartmann numbers reduced it. Increasing the number or height of corrugations also lowered the average heat transfer. Finally, a predictive model combining Proper Orthogonal Decomposition (POD) and an Adaptive-Network-Based Fuzzy Inference System (ANFIS) was introduced, providing highly accurate results with low computational cost. A numerical investigation was conducted by Aghaei et al. [12] to examine how the orientation of elliptic baffles influences mixed convection, heat transfer, and entropy generation in a square cavity filled with MWCNT–water nanofluid. The thermophysical properties of the nanofluid were determined experimentally at different temperatures and particle concentrations. Using a finite volume approach with the SIMPLER algorithm, the authors simulated flow and thermal fields for various Richardson numbers and nanoparticle loadings. They found that positioning the heated elliptic baffle horizontally enhanced the average Nusselt number and promoted more efficient heat exchange compared to the vertical orientation, although it also increased entropy generation. The optimal condition was reported at a volume fraction of 1% and a Richardson number of 0.01, corresponding to the highest heat transfer performance. Sajjadi et al. [13] explored the mechanisms of natural magnetohydrodynamic (MHD) convection in a porous medium, focusing on the use of a novel hybrid nanofluid composed of Multi-Walled Carbon Nanotubes (MWCNT)-Fe3O4 and water. They employed a sophisticated simulation technique based on the lattice Boltzmann method with double temporal relaxation. The analysis focused on the influence of several key parameters such as Da (Darcy number), Ra (Rayleigh number), porosity rate, nanoparticle concentration, and Ha (Hartmann number) on heat transfer efficiency. They mentioned that an increase of Ra improves heat transfer, and that adding nanoparticles improves the average Nusselt number. This study represents a significant advancement in the application of nanofluids for MHD convection in porous environments. Al-Farhany et al. [14] performed a careful analysis of fluid movements caused by thermal convection and buoyancy in a U-shaped container containing a porous structure saturated with nanofluids. Their approach included the use of an advanced finite element-based technique. It accounted for periodic temperature variations on the bottom edge and fixed cryogenic temperature conditions on the bulkheads and internal surfaces of the enclosure. The study examined a wide range of factors, such as the intensity of the magnetic field, the permeability of the porous matrix (Darcy number), the strength of thermal convection, the geometric shape of the particles and their orientation in the magnetic field. The results demonstrated that improved thermal buoyancy and average permeability, combined with a higher concentration of nanoparticles, significantly increased heat transfer efficiency. However, the intensity of the magnetic field negatively influenced this process. The optimal shapes and concentrations of the nanoparticles were determined, providing crucial data for optimizing natural convective heat transfer mechanisms. The effect of nanoparticle shape has also been extensively investigated. Asifa Anwar et al. [15] studied particle shapes and flow effects, including porosity, Lorentz force, and radiation, using a Caputo–Fabrizio fractional derivative and the Laplace transform. Their results indicated a thermal conductivity enhancement of approximately 67% and a shear stress reduction of 11.2%, with lamina-shaped particles showing the best performance. Similarly, Darvesh et al. [16] examined the influence of particle size and spacing on MHD flow of copper-based nanofluids in a dual-stretching frame. Numerical simulations and artificial neural network analyses revealed that smaller particles increase velocity. Thermal radiation and thermophoresis elevate temperature, while suction or chemical reactions reduce concentration, providing valuable insights for optimizing nanofluid heat transfer. Gitte et al. [17] studied the effects of a thin conductive baffle and a first-order chemical reaction on liquid flow in an upright double-passage channel. Using regular perturbation analysis, they showed that increasing the perturbation parameter and Grashof numbers enhances temperature, velocity, and micro-rotational fields, while microporous material properties tend to suppress flow. The Brinkman number was found to promote flow. Analytical and numerical results agreed well, highlighting practical relevance for engineering applications. The study carried out by Hashemi et al. [18] explored in detail natural convection in magnetohydrodynamics (MHD) within a porous environment using a micropolar nanofluid. For their simulations, they adopted the Galerkin finite element method, allowing an in-depth assessment of the impact of Da-Ra number, Ha, porosity and nanoparticle concentration. The results obtained are crucial to optimizing thermal performance in systems governed by MHD. Hassen et al. [19] were interested in MHD mixed convection and the production of entropy in a partitioned porous cavity. This study evaluated the effect of variables such as Ra, Ha, Da and magnetic field orientation. Through numerical simulations, the authors studied flow dynamics, heat transfer and entropy production, highlighting the complex interactions and potential improvements in heat transfer under various conditions. Other interesting references related to the subject can be found in the literature [20,21]. In another publication, Kolsi et al. [22] presented a 3D computational analysis of the effects of a magnetic field on thermocapillary free convection within a cavity containing a CNT-water nanofluid. This research investigated the effect of magnetic field orientation and Marangoni number on the heat transfer process. The vertical magnetic field was found to be particularly effective, especially at high values of the Hartman number, and the presence of CNTs improved heat transfer due to optimized thermophysical properties. Javed et al. [23] investigated the magnetohydrodynamic (MHD) lid-driven flow of a bi-viscosity fluid in a differentially heated I-shaped cavity. The governing equations, based on the Navier-Stokes equations and energy balance equations with a bi-viscosity model, are solved using a finite element method with a penalty function to eliminate the pressure term. The results show that increasing the bi-viscosity parameter and Reynolds number enhances the fluid velocity and heat transfer rate, respectively. The Nusselt number along the bottom lid decreases significantly with an increasing Hartmann number, highlighting the influence of magnetic fields on heat transfer. Geridonmez and Oztop [24] extensively explored the nanofluid flow dynamics and heat transfer mechanisms within a cavity affected by partially intersecting magnetic fields. This study focuses on the impact of these magnetic fields combined with selective heating on fluidic behaviors. To analyze these phenomena, techniques based on radial functions and retrograde Euler approaches were used for the resolution of the governing equations. The results of this research highlight how the position of heat sources and the presence of magnetic fields modify flow patterns and the heat transfer process. Islam et al. [25] conducted an in-depth study on the dynamics of natural magnetohydrodynamic convection within a prismatic-shaped cavity using a hybrid nanofluid composed of Cu, TiO2 nanoparticles in water (H2O). This analysis focused on the influence of several key parameters: Ra, Ha, and concentration of nanoparticles on the phenomena of heat transfer and fluid movement. To carry out this study, the team adopted an innovative approach using simulation techniques based on weighted residual Galerkin finite element methods, complemented by sensitivity analysis using response surface methodology. This research is crucial for understanding and improving heat transfer processes via the use of hybrid nanofluids, particularly in complex spatial configurations and under the effect of magnetic fields. Finally, Al-Khaleel et al. [26] conducted an in-depth analysis on Ostwald-de Waele nanofluid dynamics in the presence of mixed magnetohydrodynamic (MHD) convection within a corrugated-walled cavity driven by a moving lid. This study focuses on crucial elements of heat transfer, with particular relevance to applications such as nuclear power plants and solar thermal energy collection devices. Through the use of the Galerkin method for finite elements, this research evaluates the complex interaction between various factors, including the thermal Grashof numbers, the influence of the magnetic field (represented by the Hartmann numbers), Reynolds numbers, and Darcy numbers, as well as the physical characteristics of nanofluids. The conclusions highlight the significant impact of various physical parameters, such as the transition to a turbulent flow regime, the increase in porosity, the resilience of nanoparticles, and the dimensions of these particles, on the behavior of the fluid flow.
The novelty of this work lies primarily in the investigation of a specific three-dimensional cross-shaped obstacle that has not been extensively studied in a 3D context under the influence of magnetic fields and CNT nanofluids. This study also introduces a new and unique complex multiparametric correlation to determine the average Nusselt number as a function of the obstacle inclination, Rayleigh number, Hartmann number, and the volume fraction of the nanofluid. This correlation is highly valuable in the engineering field, as it facilitates the estimation of convective transfer efficiency, thereby aiding in the optimization of energy systems incorporating this type of obstacle. The study focuses on a geometry widely used in industry but not thoroughly explored. By leveraging the Finite Element Method, the study delves into the optimization and sensitivity of key parameters, including the effects of Ha and Ra. Additionally, it examines the impact of CNT nanoparticle concentration on heat transfer and fluid dynamics.
This study bridges the gap between theoretical research and practical applications, offering innovative insights into heat transfer efficiency in complex and novel configurations. It underscores the potential benefits of CNT nanofluids, known for their high thermal conductivity, in enhancing natural convection within MHD systems. The remainder of the paper is organized as follows: After the bibliographic review in the introduction, Section 2 covers the physical problem, governing equations, and numerical methods. The results and discussion are presented in Section 3. Finally, Section 4 summarizes our findings.
2 Methodology and Mathematical Modeling
The configuration examined in this study is a cubic enclosure with dimensions L3, filled with CNT-Water nanofluid which incorporates an inclined cross-shaped hot obstacle (Fig. 1). This obstacle has a height H = L/2 and a length Y = 0.6L. The flow is incompressible and is governed by the influences of the buoyancy force (Boussinesq approximation) and the magnetic field (
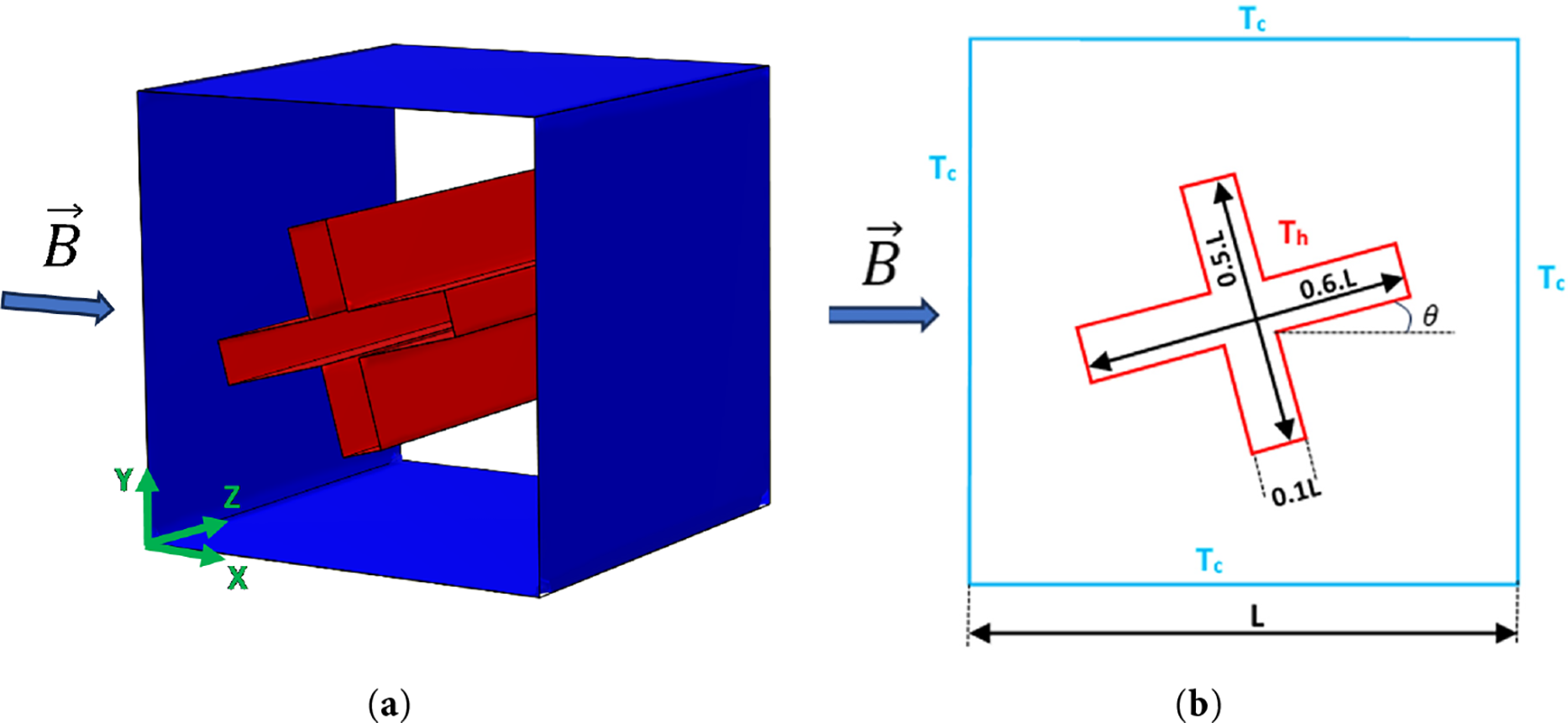
Figure 1: (a) 3D configuration, and (b) Z = 0.5 plan
Under these aforementioned assumptions, the governing equations can be expressed as follows [27,28]:
The non-dimensional variables are as follows:
The dimensionless governing equations become:
With:
Dimensionless boundary conditions:
• X = 0, X = 1, Y = 0 and Y = 1, T =
• Z = 0 and Z = l,
• On obstacle: T =
•
•
The local Nusselt number evaluated on the cold wall is expressed as follows:
The properties of the nanofluid (Table 1) are expressed as [29]:
The dimensionless governing Eqs. (6)–(10) of magnetohydrodynamic (MHD) natural convection in a 3D cavity filled with a carbon nanotube (CNT)–water nanofluid are solved using the finite element method (FEM) based on the Galerkin weighted residual approach. Spatial discretization is performed using trilinear hexahedral elements with Lagrange interpolation functions of polynomial order 1 for all variables. The velocity and pressure fields are stabilized using a consistent formulation. The time derivative is discretized using a second-order backward differentiation formula (BDF) which ensures a robust framework for addressing time-dependent dynamics. The resulting system of algebraic equations is solved using an iterative solver the Generalized Minimal Residual (GMRES) method. In this context, the Lagrangian interpolation functions, characterized by their polynomial form, serve as the foundational elements for constructing the spatial solution, facilitating the precise representation of the physical variables involved:
The following conditions are imposed to ensure the convergence of the solution:
2.3 Verification of the Numerical Model and Analysis of Mesh Dependency
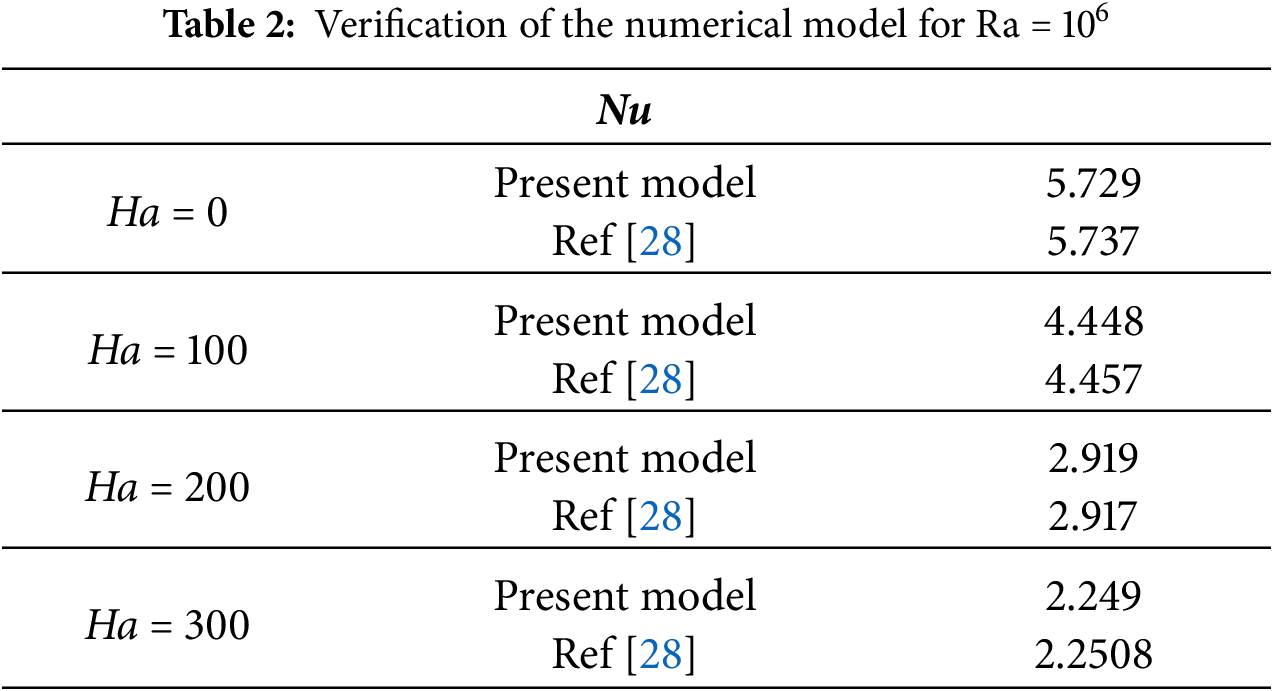
The proposed numerical model is evaluated by directly comparing it with the reference data established by Ozoe and Okada [28], as illustrated in Table 2. This comparison focuses specifically on the values of Nu. Four Hartmann numbers ranging from 0 to 300 are considered. The difference between the results for the all Ha values is less than 0.2%, indicating excellent agreement between the numerical model and the reference data. The very small disparity observed between the results of the current model and those reported by Ozoe and Okada [28] not only confirms the validity of the numerical model but also suggests its relevance for in-depth studies in MHD fluid dynamics and heat transfer.
The grid sensitivity analysis, as presented in Table 3, examines the impact of mesh density on the results calculated for Ra = 106, ϕ = 0.045, Ha = 100 and θ = 75°. This analysis highlights the relationship between the Nu and the density of the mesh elements. Four different mesh configurations, namely M1, M2, M3 and M4 are used to represent the varying mesh densities.
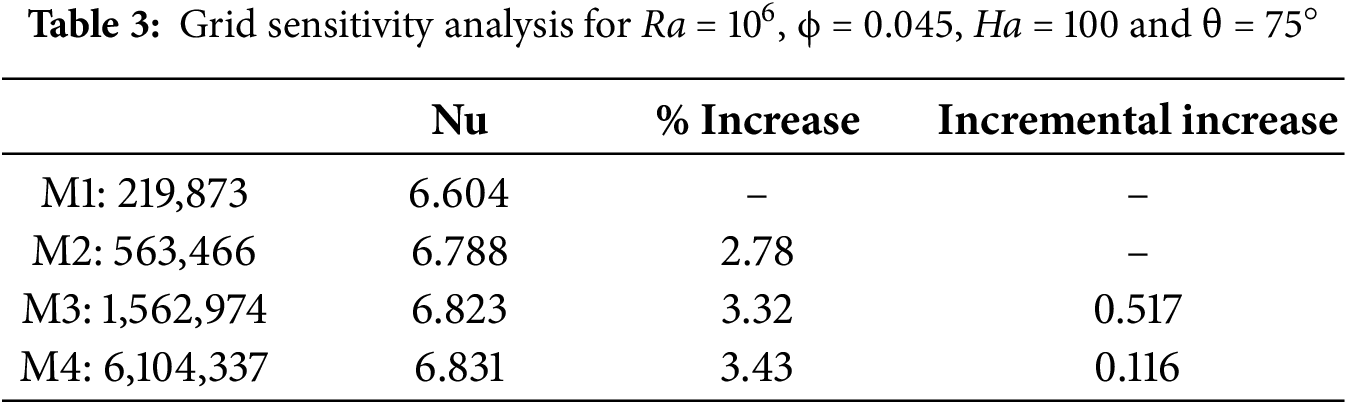
For configuration M1, with 219,873 mesh elements, the Nusselt number is recorded as 6.604. When the mesh density is increased to 563,466 elements for M2, the Nusselt number increases slightly to 6.788, representing a 2.78% increase compared to M1. This variation indicates that the model is sensitive to mesh refinement and highlights the importance of mesh density in accurately calculating heat transfer. The transition from M2 to M3, with the number of mesh elements rising to 1,562,974, leads to a Nusselt number of 6.823, an additional 3.32% increase compared to M1, with an incremental increase of 0.517% compared to M2. This marginal increase suggests that although mesh refinement continues to affect the results, the impact becomes less pronounced as mesh density increases. Finally, for the densest mesh configuration, M4, with 6,104,337 elements, the Nusselt number reaches 6.831, marking a total increase of 3.43% compared to M1, with a small incremental increase of 0.116% compared to M3. This observation indicates that the model reaches convergence, where further increases in mesh density result in only marginal improvements in the calculated results. In conclusion, this grid sensitivity analysis demonstrates that mesh refinement influences the calculation of the Nusselt number, particularly in the initial stages of increasing mesh density. However, beyond a certain threshold, the benefits for improving result precision of the results become progressively minimal, highlighting the existence of an optimal balance between result precision and computational efficiency. Consequently, for subsequent numerical simulations, the choice was made to use the M3 mesh, in order to strike a balance between result precision and saving computational resources.
In this study, the Rayleigh number was varied from 103 to 106 to span from weak to strong natural convection regimes as widely used in benchmark studies [30]. The Hartmann number range 0–100 covers the transition from no field to strong magnetic damping effects in line with MHD convection literature [29]. Inclination angles from 0° to 75° are considered since partial rotations significantly influence flow and heat transfer, while 90° is geometrically symmetric to the baseline case [31]. The nanoparticle volume fraction was limited to ϕ = 0.045 to avoid transition to non-Newtonian behaviour and ensure stability and consistency with practical CNT–water nanofluid studies [32].
Figs. 2 and 3 show the 3D flow structures as well as the streamlines in the central plane (z = 0), respectively, for different Hartmann numbers and volume fractions of carbon nanotubes. These figures provide a comprehensive visualization of the flow, thereby enhancing our understanding of the fluid’s behaviour under various applied magnetic field magnitudes. In fact, the motion of the fluid is driven by a density gradient resulting from an uneven temperature distribution. The hotter layers, characterized by lower specific gravity, experience upward buoyancy forces, thus causing the fluid near the obstacle to move upwards. In contrast, the colder regions of the fluid exhibit downward currents. As a result, recirculation patterns occur within the cavity, leading to the formation of a four-compartment flow. In other words, the shape of the obstacle divides the cavity into four sections, with vortices rotating clockwise on the right side and counterclockwise on the left side. It is observed that the vortices at the top of the cavity are 70% stronger than those at the bottom. In fact, in the lower compartment of the enclosure, the hot obstacle is positioned at the top of the fluid layer, which obstructs the flow. On the contrary, in the upper section, the hot block is at the bottom, allowing the fluid to flow freely. The increase in the Ha value indicates that magnetic effects are stronger than viscous forces and thermal buoyancy forces. Consequently, this leads to a significant 85% reduction in thermal convection movements, which contributes to the stabilization of the fluid and inhibits the formation of convective structures. The presence of nanoparticles, with volume fractions ranging from 0 to 0.045, leads to an increase in fluid viscosity. This increase in the viscosity impacts the dynamics of the convective movement and slightly hinders the movement of the fluid. As a result, the flow intensity experiences an approximate decrease of 8.3% for Ha = 0.
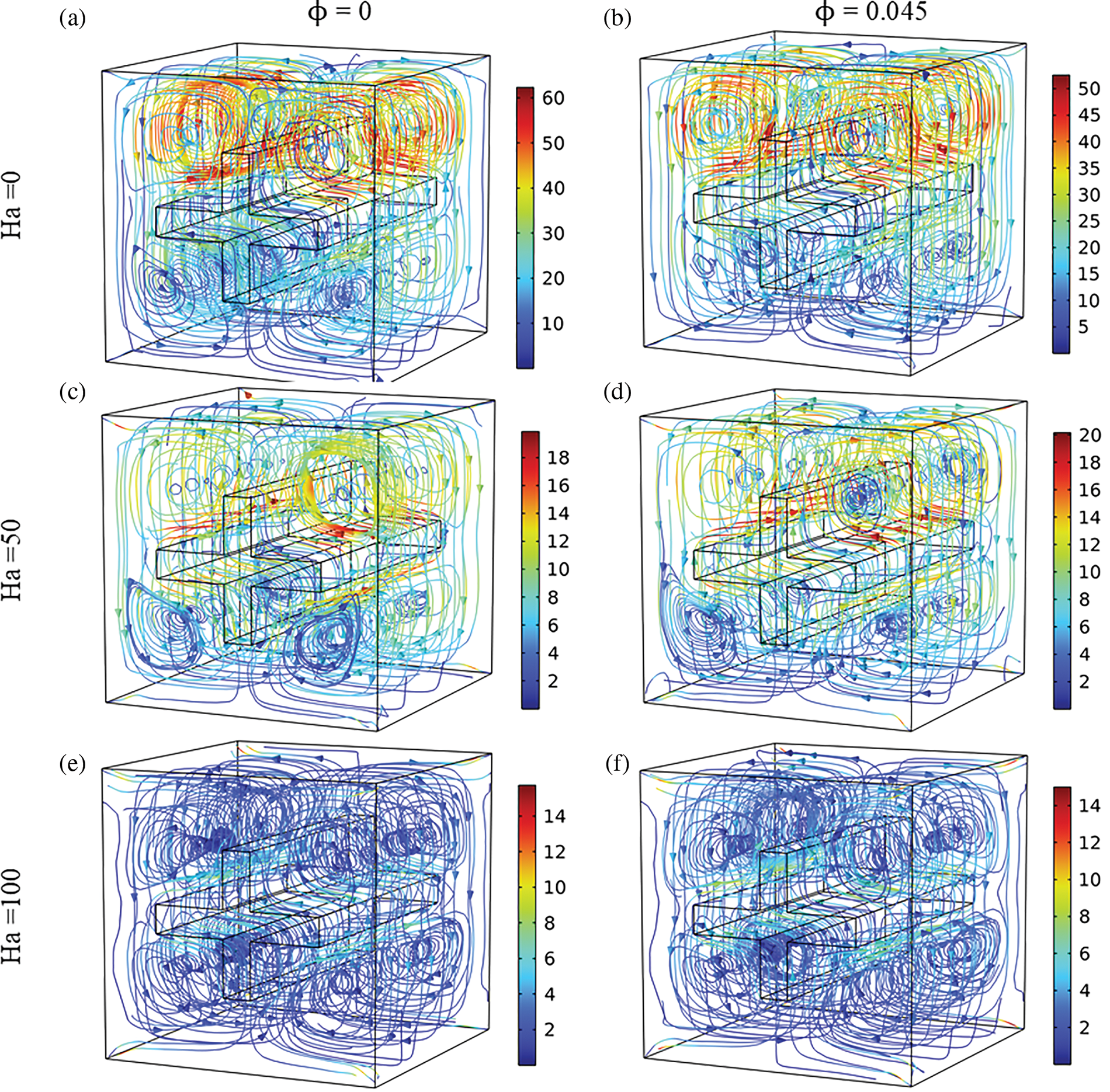
Figure 2: 3D flow structures for various Ha and nanoparticles volume fractions for Ra = 105 and θ = 0°. (a) Ha = 0, ϕ = 0; (b) Ha = 0, ϕ = 0.045; (c) Ha = 50, ϕ = 0; (d) Ha = 50, ϕ = 0.045, (e) Ha = 100, ϕ = 0; (f) Ha = 100, ϕ = 0.045
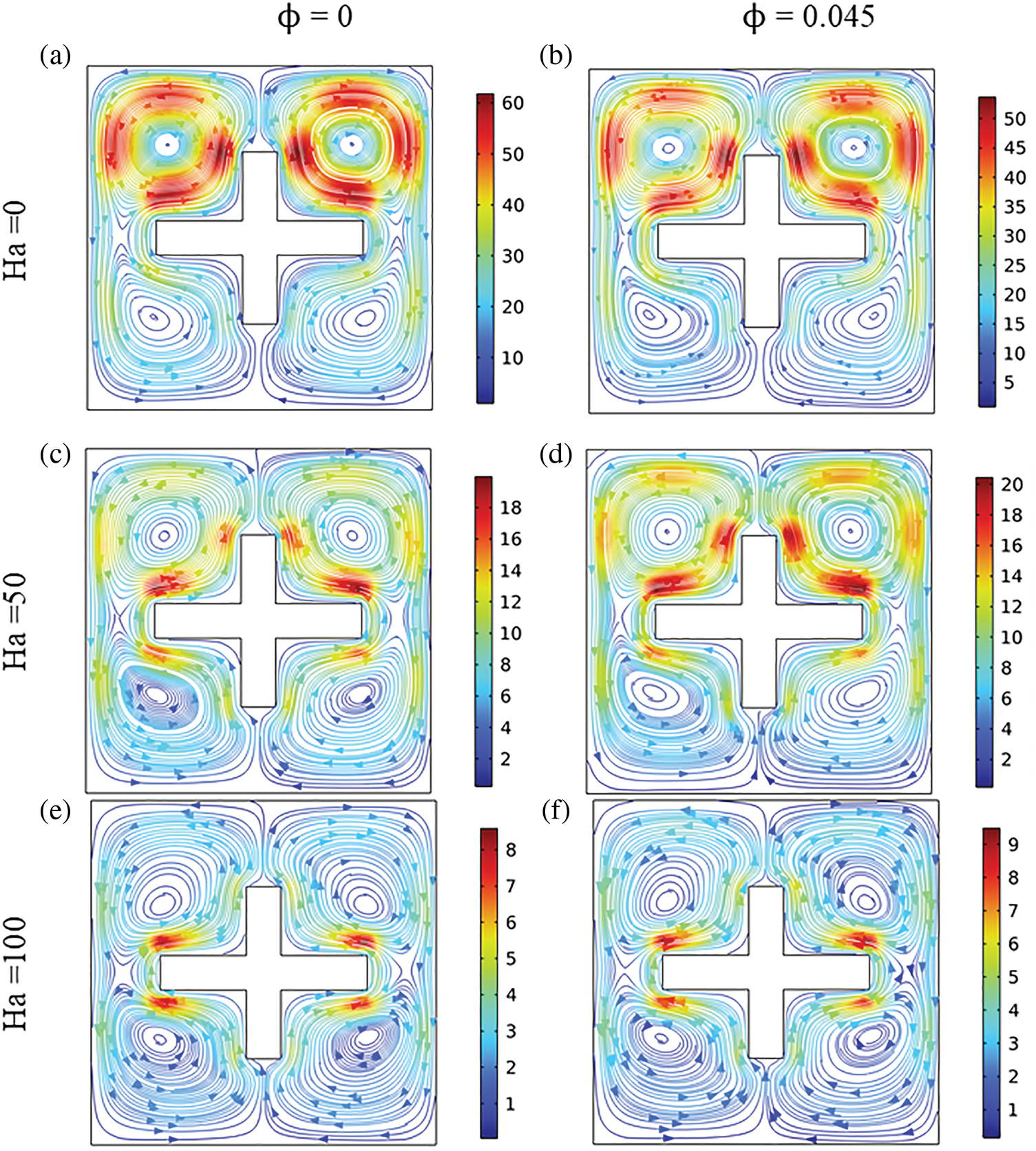
Figure 3: Flow field at Z = 0.5 plane, for Ra = 105 and θ = 0° for various Ha numbers and nanoparticles volume fractions ((a) Ha = 0, ϕ = 0; (b) Ha = 0, ϕ = 0.045; (c) Ha = 50, ϕ = 0; (d) Ha = 50, ϕ = 0.045, (e) Ha = 100, ϕ = 0; (f) Ha = 100, ϕ = 0.045)
Fig. 4 shows the 3D iso-surfaces of temperature and the 2D isotherms in the central plane z = 0.5. The temperature distribution demonstrates good penetration of the hot fluid at the top and center of the cavity, as expected, thanks to thermal buoyancy forces. However, a deficient exchange zone known as the “dead zone” is observed at the bottom of the cavity, with some hot pockets of fluid, also called hot spot, are trapped just below the cavity. The distortions of the isotherm lines become more pronounced at low Hartmann numbers. The addition of nanoparticles, which have good thermal conductivity, allows for better thermal propagation and diffusion. The presence of a thermal boundary layer at the lateral ends of the obstacle has also been recorded. For Ha = 100, a conductive regime is established. In this regime, layers of hot fluid spread uniformly in all directions and remain parallel to each other. In fact, the presence of the magnetic field inhibits the convective motions.
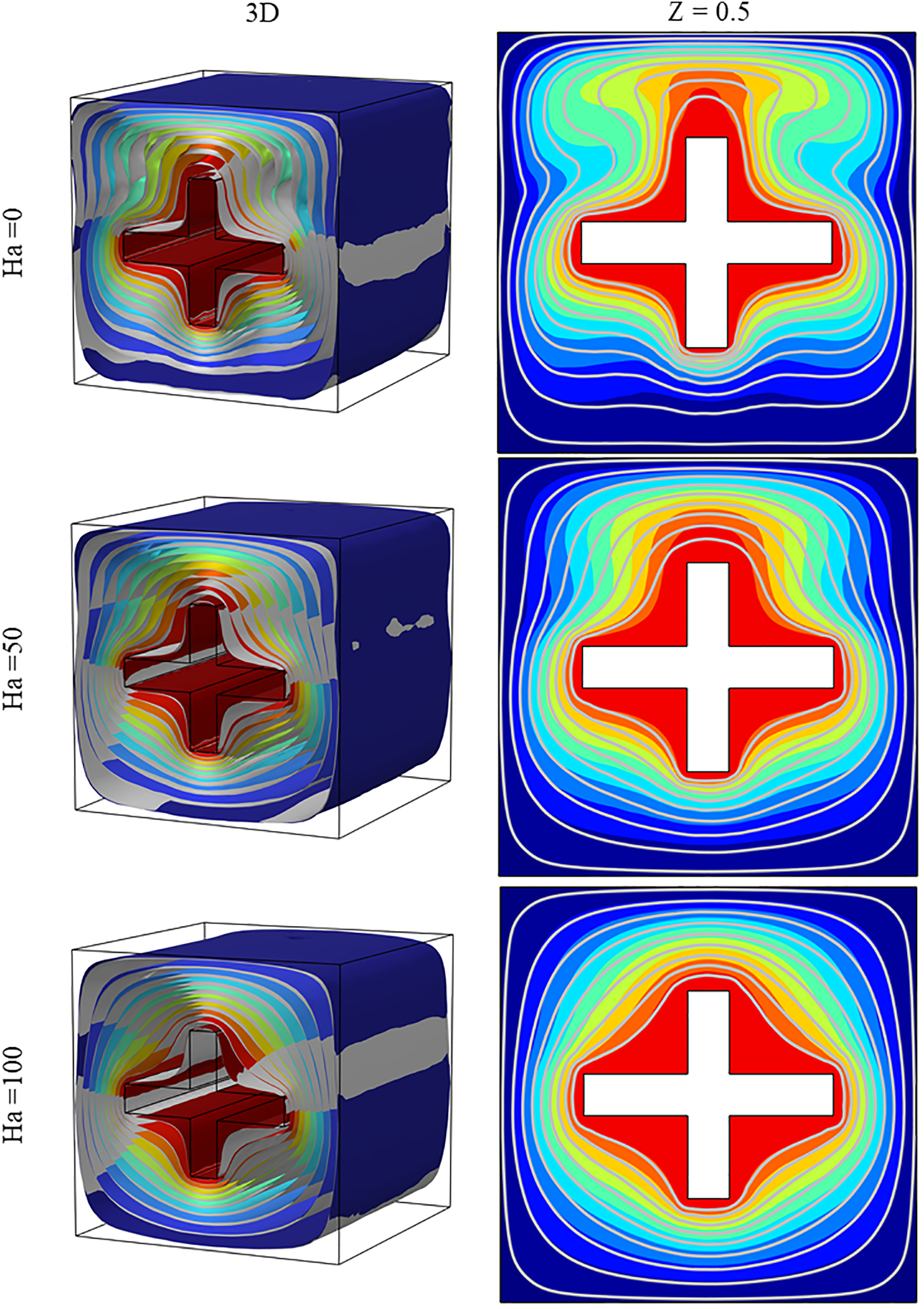
Figure 4: Temperature fields (3D on the left and central plane on the right) for Ra = 105, Ha equal respectivily to 0, 50, 100. Coloured (
The effects of the obstacle’s inclination on the flow and temperature distributions are illustrated in Fig. 5. Once the obstacle is rotated, the symmetry of the flow and temperature distributions is lost. Regardless of the tilt angle, the temperature profile consistently exhibits a significant penetration of hot fluid into the upper central part of the cavity. The dead zone, characterized by poor heat exchange, persists at the bottom of the cavity. However, the rotation leads to a decrease in the presence of a hot spot region under the obstacle. Regarding the flow, the rotation of the obstacle allows for a modification of the streamline topography, as well as the position and shape of the vortices. Specifically, when the angle θ increases by 15° and 30°, the cells in the upper right and bottom left corners elongate in the longitudinal direction, while the other vortices tend to elongate vertically. As θ surpasses 45°, two additional vortices form near the centre of the vertical walls at x = 0 and x = L. It should be noted that for an angle θ less than 45°, the streamlines are predominantly strong in the upper part of the cavity, near the vertical walls and the obstacle. Conversely, when θ exceeds 45°, the flow intensity extends to the bottom of the cavity while remaining near the obstacle.
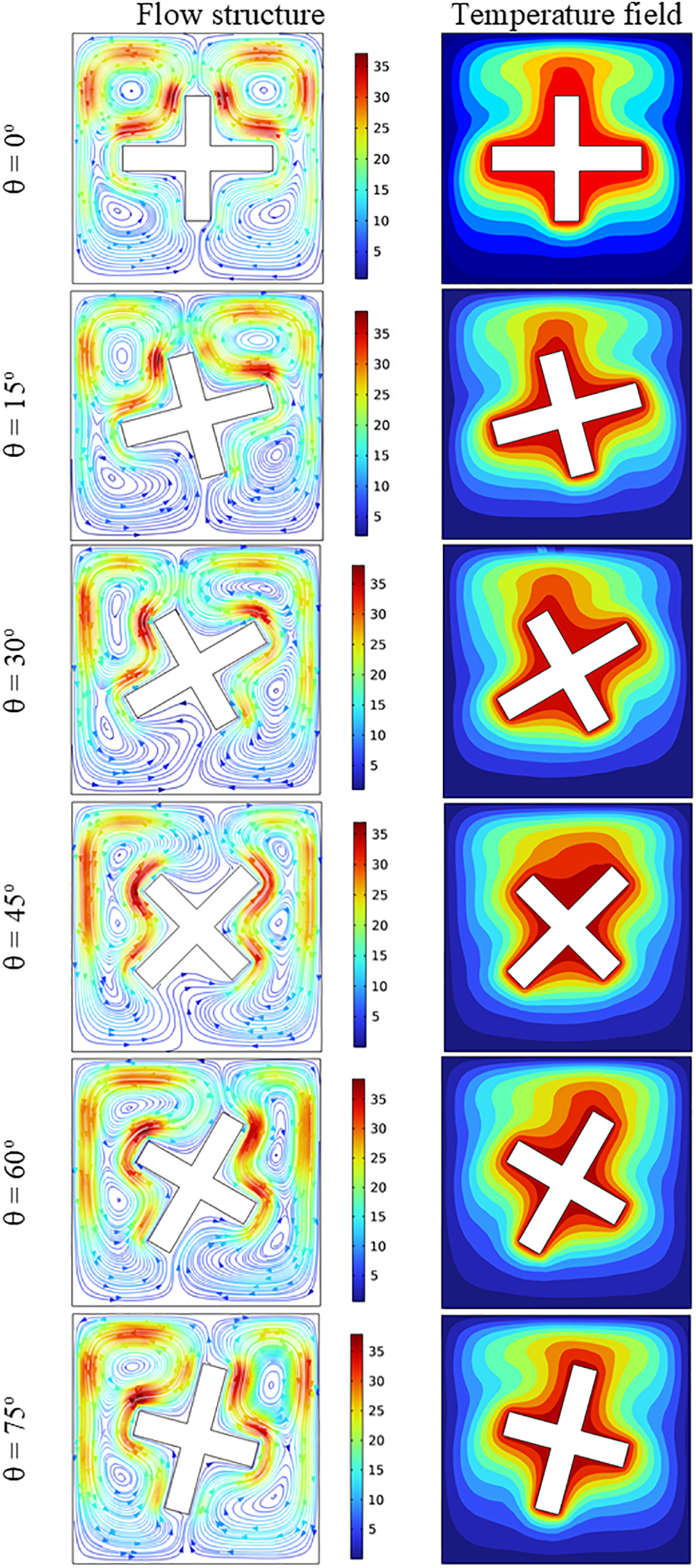
Figure 5: Effect of θ on the flow field (left) for θ = 0°, 15°, 30°, 45°, 60 and 75 and temperature field (right) for Ra = 105, Ha = 25, and
Based on Figs. 2–5, it is worth to mention that the strengthening or weakening of vortices is governed by the competition between buoyancy forces and the Lorentz force induced by the applied magnetic field: stronger buoyancy (high Ra) enhances circulation, whereas higher Hartmann numbers damp fluid motion, reducing vortex intensity. Also, the “dead zone” that appears at the bottom of the cavity arises from both the cross-shaped geometry, which obstructs upward motion, and magnetic damping, which suppresses mixing and prolongs the presence of hot fluid pockets. From an application standpoint, these stagnant regions are highly relevant, since they resemble localized hot spots in electronic cooling devices or confined enclosures in nuclear and aerospace systems. Understanding the mechanisms that create and reinforce such zones provides guidance for obstacle design and magnetic field control to either mitigate or exploit these effects in thermal management systems.
Fig. 6a depicts a three-dimensional surface illustrating Nu in relation to Ha and ϕ. The Nusselt number increases as ϕ rises, indicating that the inclusion of nanoparticles improves convective heat transfer. This enhancement is attributed to the increased conductivity of the fluid when nanoparticles are present. Additionally, the graph demonstrates that the Nu decreases with higher Ha. This implies that a stronger magnetic field hampers fluid movement, consequently diminishing convective heat transfer. This phenomenon aligns with the stabilizing effect of a magnetic field on the movement of a fluid that suppresses convective motions. Therefore, convective heat transfer benefits from higher ϕ values and is impeded by a more intense magnetic field. It should be mentioned that optimizing the Nusselt number requires a delicate balance. This involves improving heat transfer through the nanoparticles while also suppressing convection motion caused by the magnetic field. Fig. 6b shows the variation of the variation of Nu as a function of Ra and ϕ. It is evident that, for low Ra values, increasing ϕ has only a minor impact on Nu. This suggests that, in a weak natural convection regime, the addition of nanoparticles minimally affects heat transfer. However, as Ra increases, indicating an enhancement of natural convection, the effect of adding nanoparticles becomes more pronounced. The curve rises sharply, indicating a significant rise in Nu as ϕ increases. This rise implies that under strong natural convection conditions, the presence of nanoparticles can significantly improve heat transfer. This highlights that the highest Nu values are achieved at both high Ra values and at increased nanoparticle volume fractions. Therefore, higher Ra values, coupled with a higher concentration of nanoparticles, can significantly improve the convective heat transfer.
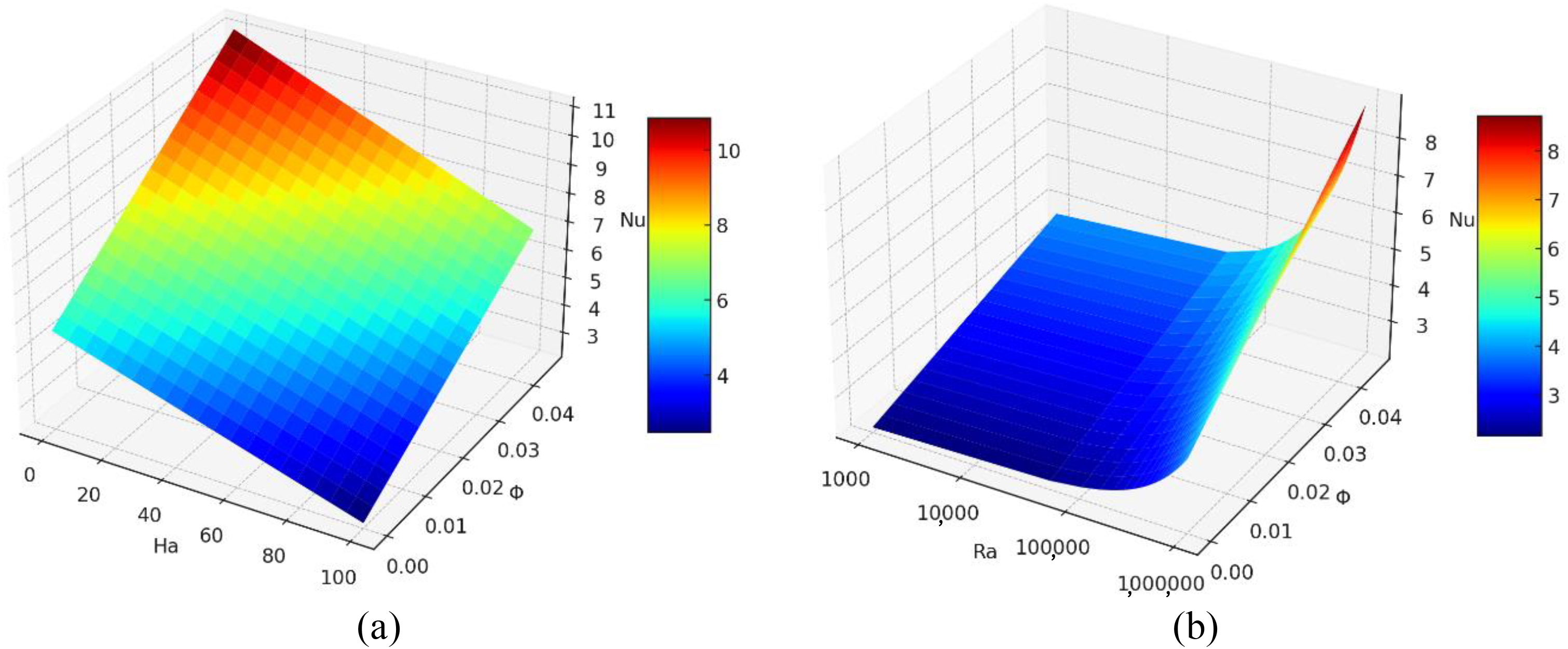
Figure 6: Variations of Nu for θ = 0: (a) vs. Ha and ϕ for Ra = 106, and (b) vs. Ra and
Fig. 7 shows the variations of Nu as a function of the inclination angle of the internal hot block for three different values of Ha. For Ha = 0 (no magnetic field), the curve shows a slight decrease in Nu as θ increases up to about 30°, followed by a progressive increase. This indicates that initially, the tilting of the block has a negative impact on convective heat transfer, which then improves with a larger tilt. Nu decreases overall when Ha reaches to 50, suggesting that a moderate magnetic field reduces the efficiency of convective heat transfer. The trend with the inclination angle θ is quite similar to that observed for Ha = 0, although the values of Nu are lower overall. Further increasing Ha to 100 decreases Nu, highlighting the inhibiting effect of a strong magnetic field on the heat transfer. The curve also shows a dependence on the inclination angle θ, but with significantly reduced Nu values compared to cases with lower Ha values. Results indicate that an increase in Ha reduces heat transfer efficiency, while the effect of hot block tilt is more complex and depends on the magnetic field strength.
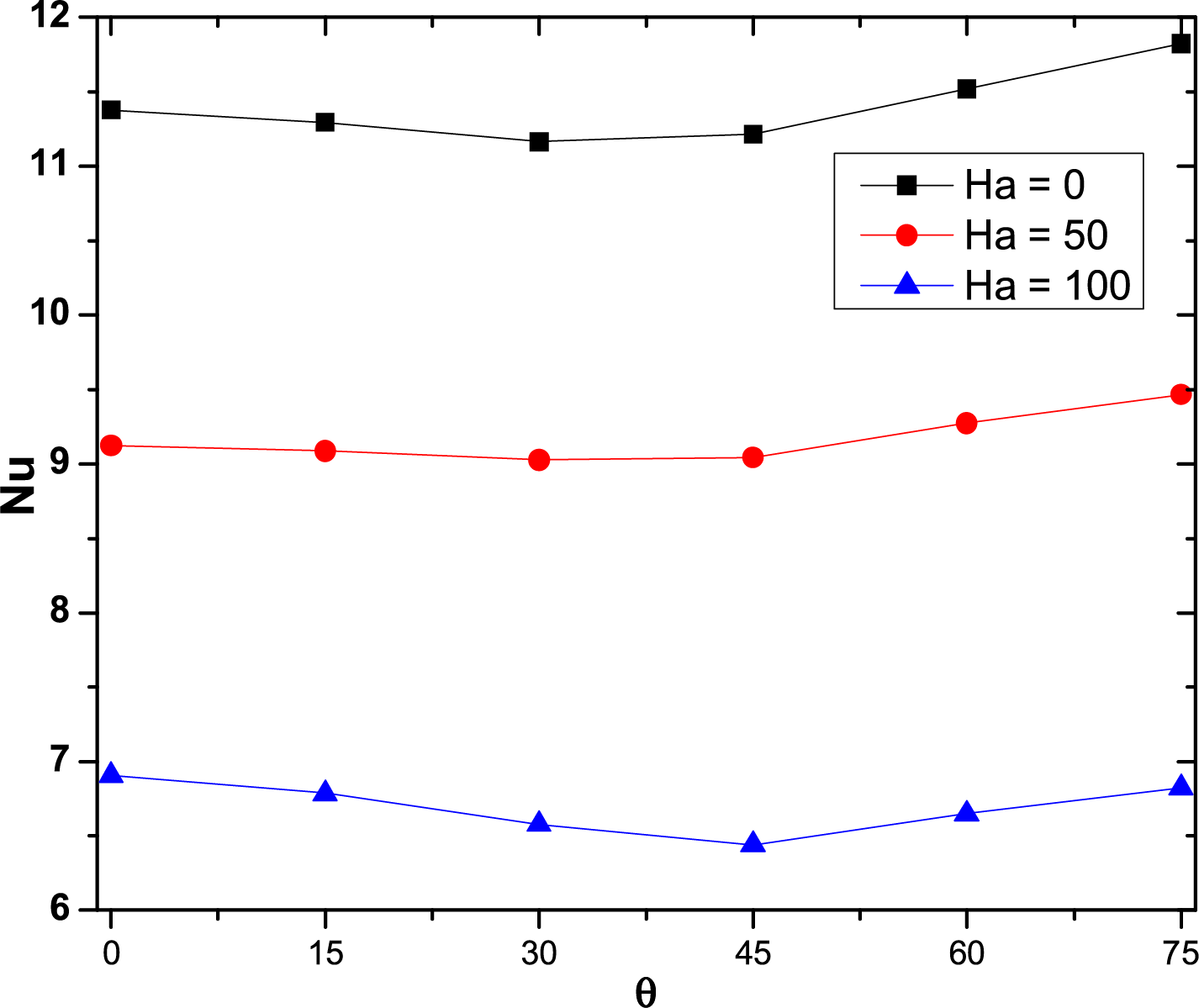
Figure 7: Influence of internal block inclination on the Nu for various Ha values at Ra = 106 and ϕ = 0.045
In order to establish a correlation allowing the direct calculation of Nu, the Lasso regression model is used. This model predicts Nu based on the independent variables θ, Ra, Ha and ϕ as well as their interaction terms:
The R2 value is 0.980, indicating that the used regression model is very precise. The model particularly highlights the strong positive influence of ϕ on Nusselt.
Fig. 8a shows the predicted Nu vs. the actual Nu number for the 480 simulation cases. There is no systematic offset between predicted and the actual values and the points mostly align along the y = x line. This is an indication on the accuracy of the correlation regardless of the input variations. Fig. 8b corresponds to the residual plot, displaying the prediction error (actual Nu minus predicted Nu) vs. the predicted Nu. The points are distributed roughly symmetrically around the zero line, with no clear trend or curvature and there is no concentration of positive or negative errors at any particular range of predicted Nu. The residuals do not consistently skew upward or downward for larger predicted values; indicating the absence of systematic bias. In addition, the spread of the residuals is relatively uniform, meaning that the error magnitude remains fairly constant. This figure demonstrates that the Lasso-based correlation for the average Nusselt number is performing well and that the model is both accurate and reliable within the tested parameters.
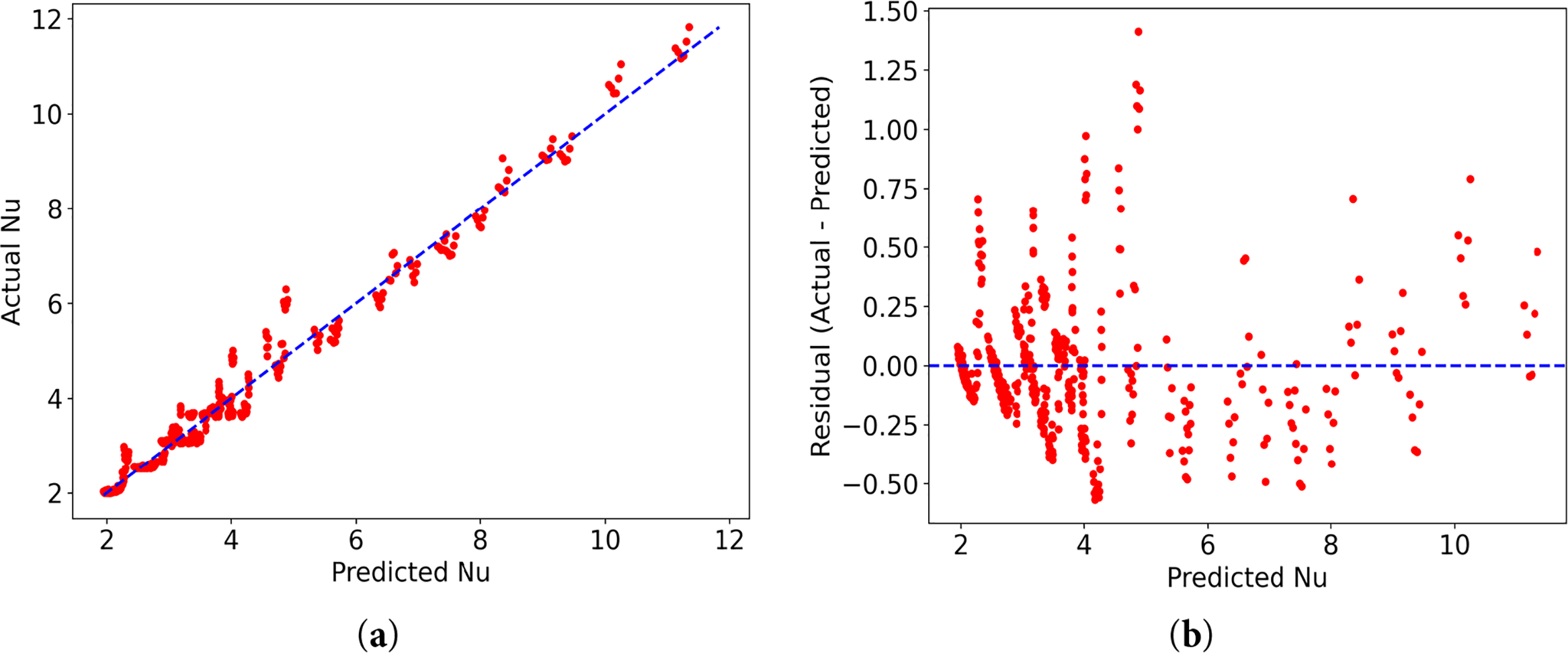
Figure 8: (a) Actual vs. predicted and (b) Residual plot
Fig. 9 represents the iso-surfaces of the electric potential in the cavity. For θ = 0°, the iso-surfaces of the electric potential show a symmetrical distribution around the block. This indicates a uniform distribution of the electric field in the cavity. As the inclination of the internal block increases to θ = 30°, the electric potential iso-surfaces start to tilt, following the position of the block. This change in geometry affects the distribution of the electric potential, making it more complex due to the block’s inclination. At an even steeper tilt of θ = 75°, the iso-surfaces become significantly asymmetric. This asymmetry is caused by the block’s altered orientation, which further disturbs the electric field and, consequently, the natural convection flow within the cavity. For all block inclinations, the plot clearly shows that the electrical potential is relatively low near the obstacle located at the central region, indicating that the magnetic field has minimal impact in this particular area. It can be mentioned that the inclination of the internal block is a key parameter that significantly modifies the configuration of the generated electric field in the cavity.
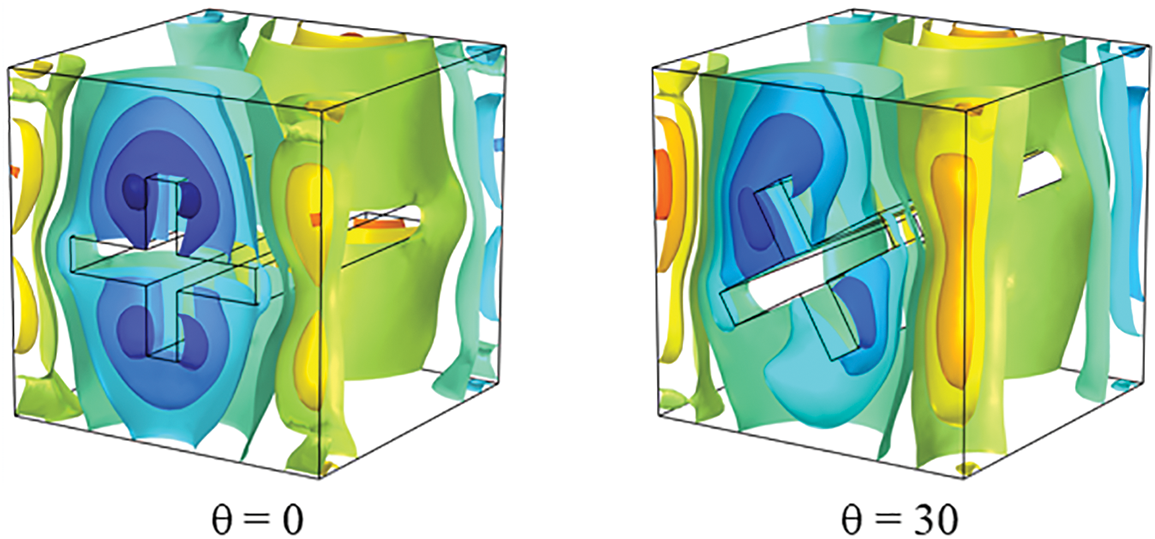
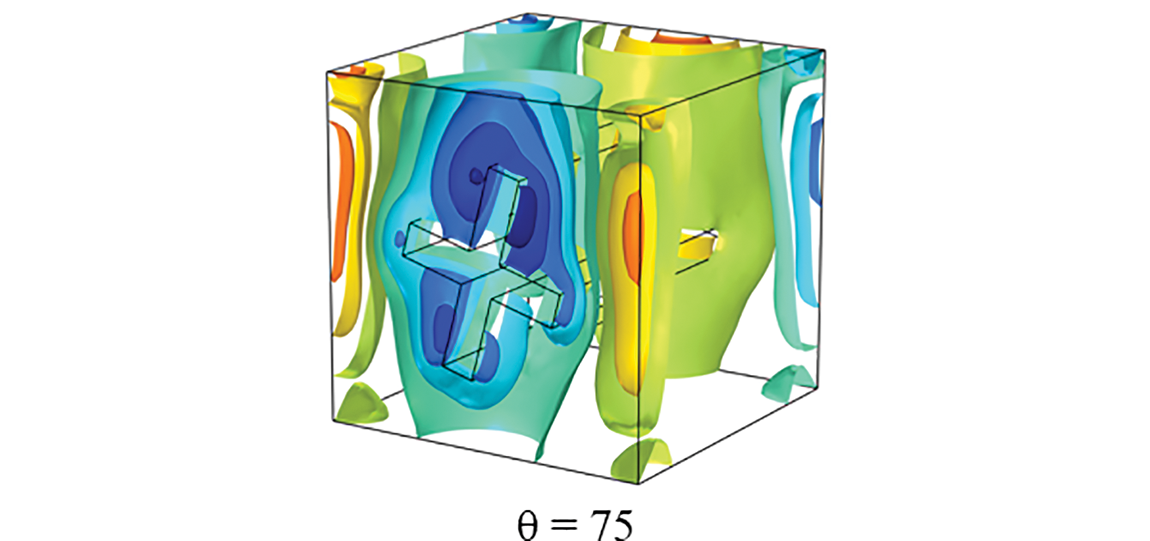
Figure 9: Electrical potential iso-surfaces for Ra = 105, Ha = 50 and ϕ = 0.045
Fig. 10 illustrates the electric current density generated by the interaction between the magnetic field and the motion of the nanofluid. For θ = 0 and ϕ = 0, the current lines are mostly horizontal and uniform, indicating a stable distribution of electric current density in a pure fluid. When ϕ is increased to 0.045, a slight increase in the complexity of the current lines is observed, suggesting that the nanoparticles influence the behaviour of the electric current in the fluid. With a tilt of the block at θ = 30° and ϕ = 0, the current density lines show a noticeable deviation, reflecting the effect of tilt on the distribution of the electric current. This effect is even more pronounced when nanoparticles are added (ϕ = 0.045), where current lines become more irregular and dispersed, indicating a significant impact of nanoparticles on the electric current density. At an even larger inclination of θ = 75°, the current line for ϕ = 0 reveals an even greater influence of block inclination on the electric current. When nanoparticles are added (ϕ = 0.045), the current lines become very irregular, implying that the current density is strongly modified by the tilt of the block. The results show that the electric current density is affected by the inclination of the heating block and the presence of nanoparticles. These factors, in turn, modify the electrical and hydrodynamic behaviours in the cavity.
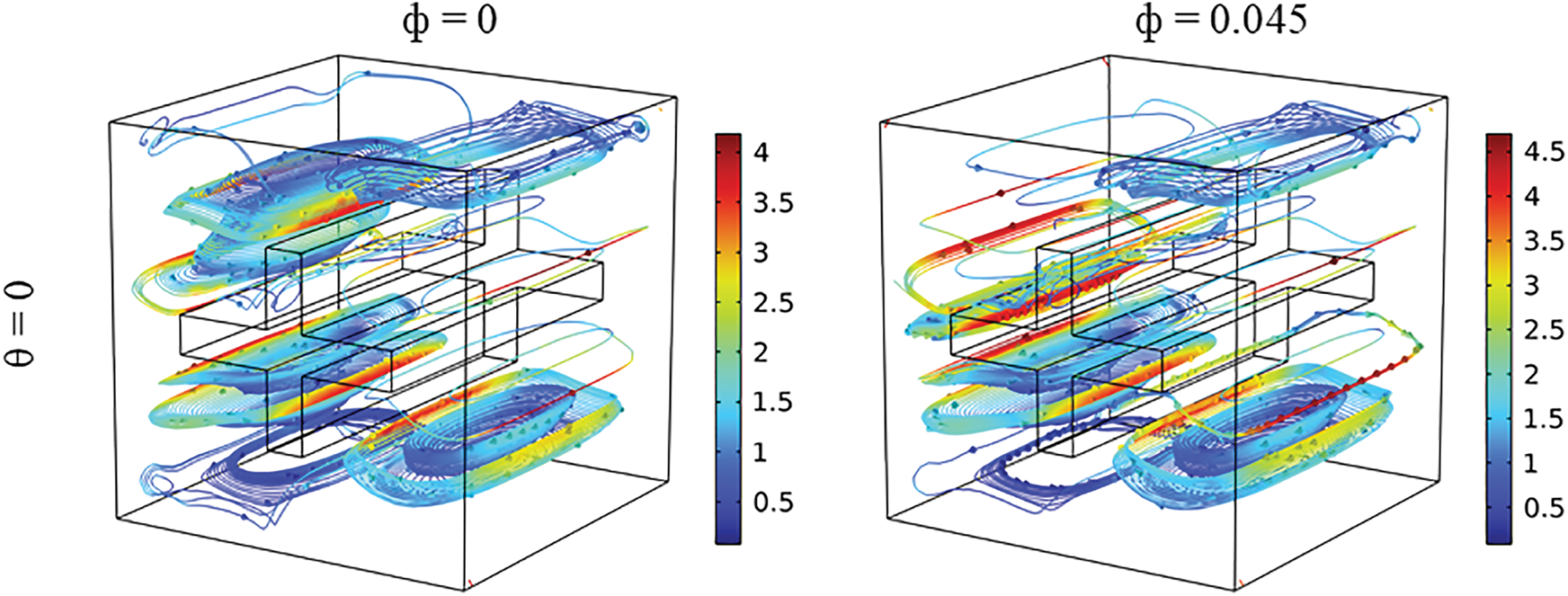
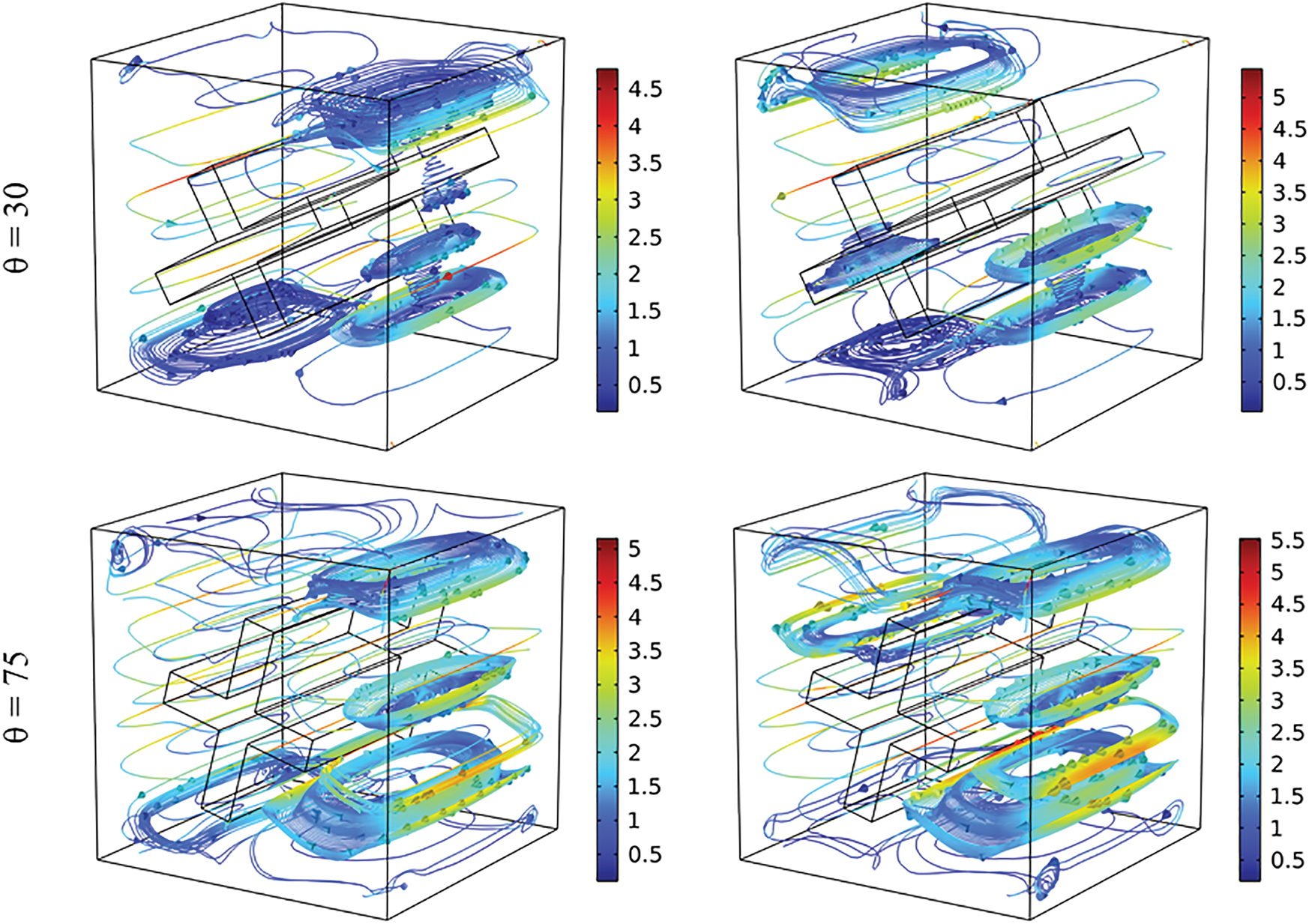
Figure 10: 3D current density at θ equal respectively to 0, 30 and 75, Ra = 105 and Ha = 100 (left ϕ = 0. Right ϕ = 0.045)
The study aimed to investigate the magnetohydrodynamic (MHD) behaviour of carbon nanotube (CNT)-nanofluid natural convection in a 3D cavity with a hot cross-shaped obstacle. The research focused on understanding the MHD effects on the nanofluid flow and heat distribution in the presence of an inclined obstacle. The main findings are as follows:
• Increasing Rayleigh number enhances heat dissipation by 228% from 103 to 106.
• The concentration of nanoparticles (ϕ), the Hartman number (Ha), and the inclination of the obstacle (θ) significantly impact fluid flow patterns and heat transfer efficiency. Specifically, increasing the nanoparticle concentration from 0% to 4% enhances heat transfer by 64%. In contrast, raising the Hartmann number from 0 to 100 reduces heat transfer by 67%. Furthermore, adjusting the obstacle’s inclination angle from 0° to 45° leads to a 4.6% decrease in heat transfer.
• The increase in the nanoparticle fraction from 0 to 0.045 leads to a slight rise in fluid viscosity. Consequently, the flow intensity decreases by approximately 8.3% for Ha = 0.
• The temperature distribution demonstrates effective penetration of the hot fluid towards the top and centre of the cavity. However, there is a problematic exchange zone, commonly referred to as the “dead zone,” at the bottom region. This area shows the presence of pockets of hot fluid that are trapped at the bottom of the cavity.
Further investigation are needed to explore the effects of different obstacle shapes and sizes on fluid flow and heat transfer characteristics. Additionally, the study focused on a specific range of parameters, and it would be beneficial to explore a wider range of operating conditions to assess the generalizability of the findings. Further experimental validation of the numerical results would also contribute to the robustness of the study.
The findings have practical engineering applications, practically the combined use of CNT nanofluids and magnetic field control may be benefic in electronics cooling systems, nuclear reactor safety, and aerospace thermal regulation. The insights into obstacle geometry and flow control can guide the design of compact and adaptive thermal management solutions in these advanced technologies.
It should be noted that the present study is limited to a single nanofluid type (CNT–water), laminar natural convection, and specific ranges of Ra, Ha, ϕ, and θ. The effects of turbulence, nanoparticle agglomeration, and experimental validation were not considered and remain for future investigation.
Acknowledgement: Not applicable.
Funding Statement: The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number RI-44-0451.
Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Faiza Benabdallah, Kaouther Ghachem, Walid Hassen, Lioua Kolsi; methodology, Faiza Benabdallah, Kaouther Ghachem, Walid Hassen, Haythem Baya, Hind Albalawi, Lioua Kolsi; validation, Faiza Benabdallah, Kaouther Ghachem, Walid Hassen, Lioua Kolsi; formal analysis, Faiza Benabdallah, Kaouther Ghachem, Walid Hassen, Haythem Baya, Hind Albalawi, Lioua Kolsi; investigation, Faiza Benabdallah, Kaouther Ghachem, Walid Hassen, Haythem Baya, Hind Albalawi, Lioua Kolsi; writing—original draft preparation, Faiza Benabdallah, Kaouther Ghachem, Walid Hassen, Haythem Baya, Hind Albalawi, Lioua Kolsi; writing—review and editing, Faiza Benabdallah, Kaouther Ghachem, Walid Hassen, Haythem Baya, Hind Albalawi, Lioua Kolsi; funding acquisition, Faiza Benabdallah. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Nomenclature
| Dimensionless magnetic field | |
| Cp | Specific heat capacity, kJ·kg−1·K−1 |
| Direction of the magnetic field | |
| Dimensionless electric field | |
| Dimensionless Lorentz force | |
| Gravitational acceleration, m·s−2 | |
| Ha | Hartmann number |
| Dimensionless density of electrical current | |
| k | Thermal conductivity, kW·m−1·K−1 |
| Nu | Nusselt number |
| p | Dimensionless pressure |
| Pr | Prandtl number |
| Ra | Rayleigh number |
| T | Dimensionless temperature |
| t | Dimensionless time |
| Dimensionless velocity vector | |
| x, y, z | Dimensionless cartesian coordinates |
| Greek Characters | |
| α | Thermal diffusivity, m2·s−1 |
| β | Thermal expansion coefficient, K−1 |
| Φ | Nanoparticle volume fraction |
| μ | Dynamic viscosity, Pa·s |
| ν | Kinematic viscosity, m2·s−1 |
| ρ | Density of the fluid, kg·m−3 |
| σ | Electric conductivity, Ω−1·m−1 |
| Subscripts | |
| av | Average |
| c | Cold |
| h | Hot |
| nf | Nanofluid |
| s | Solid nanoparticles |
References
1. Mohseni J, Haratian M, Toghraie D. Analysis of the first and second laws of thermodynamics for MHD two-phase natural convection of water/Fe2O3 ferro-nanofluids in a 3D baffled enclosure. Eng Anal Bound Elem. 2023;155(9):371–400. doi:10.1016/j.enganabound.2023.06.015. [Google Scholar] [CrossRef]
2. Mliki B, Abbassi MA, Omri A, Belkacem Z. Lattice Boltzmann analysis of MHD natural convection of CuO-water nanofluid in inclined C-shaped enclosures under the effect of nanoparticles Brownian motion. Powder Technol. 2017;308(1):70–83. doi:10.1016/j.powtec.2016.11.054. [Google Scholar] [CrossRef]
3. Sannad M, Hussein AK, Abidi A, Homod RZ, Biswal U, Ali B, et al. Numerical study of MHD natural convection inside a cubical cavity loaded with copper-water nanofluid by using a non-homogeneous dynamic mathematical model. Mathematics. 2022;10(12):2072. doi:10.3390/math10122072. [Google Scholar] [CrossRef]
4. Khan M, Rasheed A, Anwar MS, Hussain Shah ST. Application of fractional derivatives in a Darcy medium natural convection flow of MHD nanofluid. Ain Shams Eng J. 2023;14(9):102093. doi:10.1016/j.asej.2022.102093. [Google Scholar] [CrossRef]
5. Asha NEJ, Molla MM. MRT-lattice Boltzmann simulation of MHD natural convection of Bingham nanofluid in a C-shaped enclosure with response surface analysis. Heliyon. 2023;9(12):e22539. doi:10.1016/j.heliyon.2023.e22539. [Google Scholar] [PubMed] [CrossRef]
6. Tasnim S, Mitra A, Saha H, Islam MQ, Saha S. MHD conjugate natural convection and entropy generation of a nanofluid filled square enclosure with multiple heat-generating elements in the presence of Joule heating. Res Eng. 2023;17(11–12):100993. doi:10.1016/j.rineng.2023.100993. [Google Scholar] [CrossRef]
7. Sajjadi H, Delouei AA, Atashafrooz M, Sheikholeslami M. Double MRT Lattice Boltzmann simulation of 3-D MHD natural convection in a cubic cavity with sinusoidal temperature distribution utilizing nanofluid. Int J Heat Mass Transf. 2018;126(2009):489–503. doi:10.1016/j.ijheatmasstransfer.2018.05.064. [Google Scholar] [CrossRef]
8. Vijaybabu TR, Dhinakaran S. MHD natural convection around a permeable triangular cylinder inside a square enclosure filled with Al2O3–H2O nanofluid: an LBM study. Int J Mech Sci. 2019;153–154(23–24):500–16. doi:10.1016/j.ijmecsci.2019.02.003. [Google Scholar] [CrossRef]
9. Nabwey HA, Rashad AM, Reddy PBA, Jakeer S, Mansour MA, Salah T. Radiative effects on unsteady MHD natural convection flow in an inclined wavy porous cavity using hybrid nanofluid containing a square obstacle. Alex Eng J. 2023;65(5):921–37. doi:10.1016/j.aej.2022.10.004. [Google Scholar] [CrossRef]
10. Saha T, Islam T, Yeasmin S, Parveen N. Thermal influence of heated fin on MHD natural convection flow of nanofluids inside a wavy square cavity. Int J Thermofluids. 2023;18(6):100338. doi:10.1016/j.ijft.2023.100338. [Google Scholar] [CrossRef]
11. Selimefendigil F, Öztop HF. Corrugated conductive partition effects on MHD free convection of CNT-water nanofluid in a cavity. Int J Heat Mass Transf. 2019;129:265–77. doi:10.1016/j.ijheatmasstransfer.2018.09.101. [Google Scholar] [CrossRef]
12. Aghaei A, Sheikhzadeh GA, Goodarzi M, Hasani H, Damirchi H, Afrand M. Effect of horizontal and vertical elliptic baffles inside an enclosure on the mixed convection of a MWCNTs-water nanofluid and its entropy generation. Eur Phys J Plus. 2018;133(11):486. doi:10.1140/epjp/i2018-12278-4. [Google Scholar] [CrossRef]
13. Sajjadi H, Amiri Delouei A, Izadi M, Mohebbi R. Investigation of MHD natural convection in a porous media by double MRT lattice Boltzmann method utilizing MWCNT-Fe3O4/water hybrid nanofluid. Int J Heat Mass Transf. 2019;132:1087–104. doi:10.1016/j.ijheatmasstransfer.2018.12.060. [Google Scholar] [CrossRef]
14. Al-Farhany K, Abdulkadhim A, Hamzah HK, Ali FH, Chamkha A. MHD effects on natural convection in a U-shaped enclosure filled with nanofluid-saturated porous media with two baffles. Prog Nucl Energy. 2022;145(4):104136. doi:10.1016/j.pnucene.2022.104136. [Google Scholar] [CrossRef]
15. Asifa Anwar T, Kumam P, Almutairi KS, Watthayu W. Thermophysical dynamics of mineral oil-based hybrid nanofluids under multiple flow conditions and radiation effects; Individual, synergistic, and shape impacts analysis. Comput Model Eng Sci. 2025;180(1):1748. doi:10.1016/j.jrras.2025.101748. [Google Scholar] [CrossRef]
16. Darvesh A, Maiz FM, Santisteban LJC, Anwar T, Almutairi K. Particle size and inter-particle spacing effect on thermal performance of MHD copper nanofluid flow over dual-stretching rectangular frame: ANN-based simulations. Case Stud Therm Eng. 2025;40(3–4):106682. doi:10.1016/j.csite.2025.106682. [Google Scholar] [CrossRef]
17. Gitte GT, Kalyan S, Saraswathi H, Kulkarni V, Jameel M, Tawade JV, et al. Thermal and solutal performance analysis featuring fully developed chemically reacting micro-rotational convective flow in an open-ended vertical channel. Comput Model Eng Sci. 2025;65(2):105603. doi:10.1016/j.csite.2024.105603. [Google Scholar] [CrossRef]
18. Hashemi H, Namazian Z, Zadeh SMH, Mehryan SAM. MHD natural convection of a micropolar nanofluid flowing inside a radiative porous medium under LTNE condition with an elliptical heat source. J Mol Liq. 2018;271(12):914–25. doi:10.1016/j.molliq.2018.09.010. [Google Scholar] [CrossRef]
19. Hassen W, Selimefendigil F, Ben Khedher N, Kolsi L, Borjini MN, Alresheedi F. Control of magnetohydrodynamic mixed convection and entropy generation in a porous cavity by using double rotating cylinders and curved partition. ACS Omega. 2021;6(51):35607–18. doi:10.1021/acsomega.1c05334. [Google Scholar] [PubMed] [CrossRef]
20. Menni Y, Chamkha AJ, Zidani C, Benyoucef B. Heat and nanofluid transfer in baffled channels of different outlet models. Math Model Eng Probl. 2019;6(1):21–8. doi:10.18280/mmep.060103. [Google Scholar] [CrossRef]
21. Maouedj R, Menni Y, Inc M, Chu YM, Ameur H, Lorenzini G. Simulating the turbulent hydrothermal behavior of oil/MWCNT nanofluid in a solar channel heat exchanger equipped with vortex generators. Comput Model Eng Sci. 2021;126(3):855–89. doi:10.32604/cmes.2021.014524. [Google Scholar] [CrossRef]
22. Kolsi L, Algarni S, Mohammed HA, Hassen W, Lajnef E, Aich W, et al. 3D magneto-buoyancy-thermocapillary convection of CNT-water nanofluid in the presence of a magnetic field. Processes. 2020;8(3):258. doi:10.3390/pr8030258. [Google Scholar] [CrossRef]
23. Javed T, Iftikhar B, Siddiqui MA. MHD mixed convection non-isothermal flow and heat transfer analysis of non-Newtonian fluid saturated in I-shaped cavity. Numer Heat Transf Part B. 2023;83(6):395–409. doi:10.1080/10407790.2022.2164531. [Google Scholar] [CrossRef]
24. Geridonmez BP, Oztop HF. MHD natural convection in a cavity in the presence of cross partial magnetic fields and Al2O3-water nanofluid. Comput Math Appl. 2020;80(12):2796–810. doi:10.1016/j.camwa.2020.10.003. [Google Scholar] [CrossRef]
25. Islam MS, Islam S, Siddiki MNAA. Numerical simulation with sensitivity analysis of MHD natural convection using Cu-TiO2-H2O hybrid nanofluids. Int J Thermofluids. 2023;20(23):100509. doi:10.1016/j.ijft.2023.100509. [Google Scholar] [CrossRef]
26. Al-Khaleel M, Abderrahmane A, Younis O, Jamshed W, Guedri K, Safdar R, et al. A Galerkin finite element-based study of MHD mixed convective of Ostwald-de Waele nanofluids in a lid-driven wavy chamber. Results Phys. 2024;56(10):107232. doi:10.1016/j.rinp.2023.107232. [Google Scholar] [CrossRef]
27. Gal S, Kolsi L, Hassen W, Ben Ali N, Ben Khedher N, Chamkha AJ. Three-dimensional study of magnetohydrodynamic natural convection, entropy generation, and electromagnetic variables in a nanofluid filled enclosure equipped with inclined fins. ACS Omega. 2022;7(14):12365–73. doi:10.1021/acsomega.2c00923. [Google Scholar] [PubMed] [CrossRef]
28. Ozoe H, Okada K. The effect of the direction of the external magnetic field on the three-dimensional natural convection in a cubical enclosure. Int J Heat Mass Transf. 1989;32(10):1939–54. doi:10.1016/0017-9310(89)90163-4. [Google Scholar] [CrossRef]
29. Ghasemi B, Aminossadati SM, Raisi A. Magnetic field effect on natural convection in a nanofluid-filled square enclosure. Int J Therm Sci. 2011;50(9):1748–56. doi:10.1016/j.ijthermalsci.2011.04.010. [Google Scholar] [CrossRef]
30. De Vahl Davis G. Natural convection of air in a square cavity: a benchmark numerical solution. Int J Numer Methods Fluids. 1983;3(3):249–64. doi:10.1002/fld.1650030305. [Google Scholar] [CrossRef]
31. Ben-Nakhi A, Chamkha AJ. Effect of length and inclination of a thin fin on natural convection in a square enclosure. Numer Heat Transf Part A Appl. 2006;50(4):381–99. doi:10.1080/10407780600619907. [Google Scholar] [CrossRef]
32. El Hattab M, Boumhaout M, Oukach S. MHD natural convection in a square enclosure using carbon nanotubewater nanofluid with two isothermal fins. Sigma J Eng Nat Sci. 2024;42(4):1075–87. doi:10.14744/sigma.2024.00089. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools