Numerical Modelling of Oblique Wave Interaction with Dual Curved-LEG Pontoon Floating Breakwaters

1  Introduction

Over the past few decades, the gradual rise in sea levels has significantly impacted coastlines and communities in various coastal nations. Coupled with this phenomenon, the accelerated urbanization and expansion of human activities in countries such as Singapore, Japan, and the Netherlands have placed substantial demands on land resources [1–2]. To address these challenges, the utilization of marine space through the development of very large floating structures along coastlines and in harbors has emerged as a promising solution. These very large floating structures, which include applications such as bridges, airports, offshore platforms, wave energy systems, military installations, aquaculture protection structures, and ship navigation aids, offer distinct advantages such as reduced construction costs, efficient water exchange, and ease of construction compared to traditional bottom-standing breakwaters [3–6]. However, despite these advantages, Very Large Floating Structures (VLFS) are vulnerable to extreme ocean conditions such as storm waves and tsunamis. Therefore, it is essential to design new hybrid VLFS models capable of improving hydrodynamic performance and ensuring long-term structural safety.

Many floating breakwaters have been proposed to improve hydrodynamic performance. According to their structural features and applications, floating breakwaters are categorized into various configurations, such as box-type, pontoon-type, frame-type, mat-type, tethered float-type, and horizontal plate-type [7]. Noteworthy advancements in this domain have been reported in the literature. For instance, Mei and Black [8] explored the wave reflection and transmission coefficient of rectangular obstacles employing the eigenfunction expansion approach, with their findings corroborated through experimental and analytical comparisons. Williams and Abul-Azm [9] studied a twin pontoon leg floating breakwater using the eigenfunction expansion approach. Neelamani and Rajendran [10] investigated a T-type floating breakwater, demonstrating that an increase in the vertical sectional area enhanced wave reflection and overall wave attenuation. Subsequently, Esmaeel [11] provided numerical insights into the same breakwater type, highlighting its lower wave transmission compared to rectangular designs and emphasizing the role of draft in wave attenuation. Pena et al. [12] evaluated the hydrodynamic characteristics of a rectangular structure with a slotted barrier, reporting improved wave transmission coefficients. Masoudi et al. [13] carried out a detailed parametric investigation into the hydrodynamic behavior of a two-legged rectangular floating breakwater. Their findings indicated that this configuration offered superior performance compared to conventional rectangular floating breakwaters, and that the legs play an efficient role in the structural response. Similarly, Ruol et al. [14] and Sharma et al. [15] investigated π-type breakwaters incorporating vertical thin plates, which effectively reduced transmission coefficients. Recently, Sujana et al. [16] examined the phenomena of scattering and radiation associated with inverted F-type and slanted floating breakwaters in the context of arbitrary trench configurations.

Complex structural geometries have attracted significant attention due to their capacity to improve wave attenuation, blocking efficacy, and energy dissipation, thereby offering enhanced solutions for coastal defense and offshore stability [17–19]. Jain et al. [20] introduced floating breakwaters with arc-shaped wings and opening-pass structures, reporting 8.2%–17.8% lower transmission coefficients compared to traditional designs. Hussein et al. [21] conducted both experimental and numerical analyses on curved breakwaters, comparing convex and concave semi-circular configurations, and found that concave configurations provided superior energy dissipation. Further, El Saie et al. [22] demonstrated the hydrodynamic efficiency of a structure with a curved design, noting that increased concavity enhances energy absorption with respect to wave height and steepness. He et al. [23] studied single-wing floating breakwaters using the matching eigenfunction expansion method to analyze convex, concave, and inclined wing geometries. It was noted that the wing model reduced wave transmission compared to the rectangular structure and the heave plate. The authors later extended the study to investigate double-wing floating breakwaters [24]. They found that the double-wing floating breakwater effectively blocked the waves and dissipated the wave energy compared to the single-wing floating breakwater. Therefore, the effects of wave blocking and energy dissipation mainly affects the presence of a dual-curved leg floating structure. For this reason, the present study focuses on the dual-curved floating breakwaters.

Recent advancements in the technology of floating structures have facilitated the emergence of VLFS, which are currently being investigated for a broader range of marine applications. The potential applications of such large floating structures extend far beyond conventional uses such as airports, bridges, or platforms for sea-to-land transportation. Research by various authors, including [25–28], emphasizes their versatility. For instance, Lee et al. [29] analyzed rectangular floating platforms integrated with tuned liquid column dampers, demonstrating an effective reduction in wave forces. Wang and Yung [30] examined a pontoon-type very large floating breakwater incorporating hydro-elastic plates, highlighting their capacity to mitigate wave-induced responses on platforms. Sun et al. [31] studied a pontoon-type floating bridge under regular wave conditions and discovered that nonlinear hydroelastic effects greatly impact bending moments, which must be considered in design. Numerical investigations into the hydrodynamic properties of coastal bridge decks by Qu et al. [32] revealed that wave loads on bridge decks increase with wave heights. Experimental studies by Luo et al. [33] examined the impact of freak wave actions and air gap variations on floating platforms, concluding that reduced air gaps increase tether forces. Khan et al. [34] examined a submerged structure placed near a floating dock using the boundary element method. They found that the submerged structure shielded the floating dock. Further, the multi-flat leg attached to a very large floating breakwater was investigated in [35] and [36]. The results revealed that the multi-flat legs protected the floating structure. Moreover, the above studies focused on the elastic plate, separated structures, and flat legs used to protect the very large floating structures. As a novelty contribution, the present study deals with a curved leg directly attached to a floating breakwater, which forms the main focus of the research.

Previous studies have established that structural modifications, such as a single horizontal thick attachment [37] and two-leg extensions [13], can significantly affect the hydrodynamic performance of a rectangular floating breakwater. To the best of the author’s knowledge, no systematic study has investigated rectangular floating breakwaters equipped with curved-leg geometries, despite their potential to enhance wave blocking, flow direction, energy dissipation, and structural resilience. To address this gap, the present study analyzes four novel curved-leg pontoon floating breakwater models with different curvatures and configurations. The objective is to determine which configuration offers the most effective wave attenuation and structural protection, with potential applications in platforms, bridges, and coastal protection systems.

In the present study, the mathematical model for the proposed physical problem is described in Section 2, followed by the presentation of the Boundary Element Method(BEM)-based numerical technique to solve the associated boundary value problem in Section 3. In Section 4, the current study is validated against previously published results, and an analysis of various curved-leg models is carried out. Finally, Section 5 provides concluding remarks and insights derived from the study.

2  Mathematical Formulation

This section presents the mathematical model for oblique wave scattering by dual curved-leg pontoon floating breakwaters, analyzed under the assumptions of small-amplitude linear wave theory. The current study analyzes four different configurations of floating breakwaters. The present problem is formulated in a three-dimensional Cartesian coordinate system with the x−z plane representing the horizontal plane and the y-axis denoting the vertical direction, oriented positively upwards. Assume that the water depth is h, the height of the curved-leg pontoon floating structure is d, the height of the floating rectangle is da, the space between the two curved-leg pontoons is b, and the height of the curved-leg is dr. The entire fluid domain can be subdivided into two regions, namely, the unbounded regions (Ω1:−∞<x<−l0 and Ω2:r0<x<∞) and the bounded region restricted to R:−l0<x<r0.

Further, assume that the fluid is inviscid and incompressible and that the flow is represented as irrotational. The incident wave travels at an oblique angle θ relative to the x-axis, and the fluid motion is simple harmonic in time with an angular frequency ω. There exists a velocity potential function. Φ(x,y,z,t)=Re[ϕ(x,z)e−i(kyy−ωt)] for the bounded region R, where ky=k0sin⁡θ, k0 is the wavenumber, and ϕ(x,z) is the spatial velocity potential, which satisfies the Helmholtz equation in bounded domain, expressed as:

(∂2∂x2+∂2∂z2−ky2)ϕ=0.(1)

The boundary notations corresponding to those given in Fig. 1 are explained below:

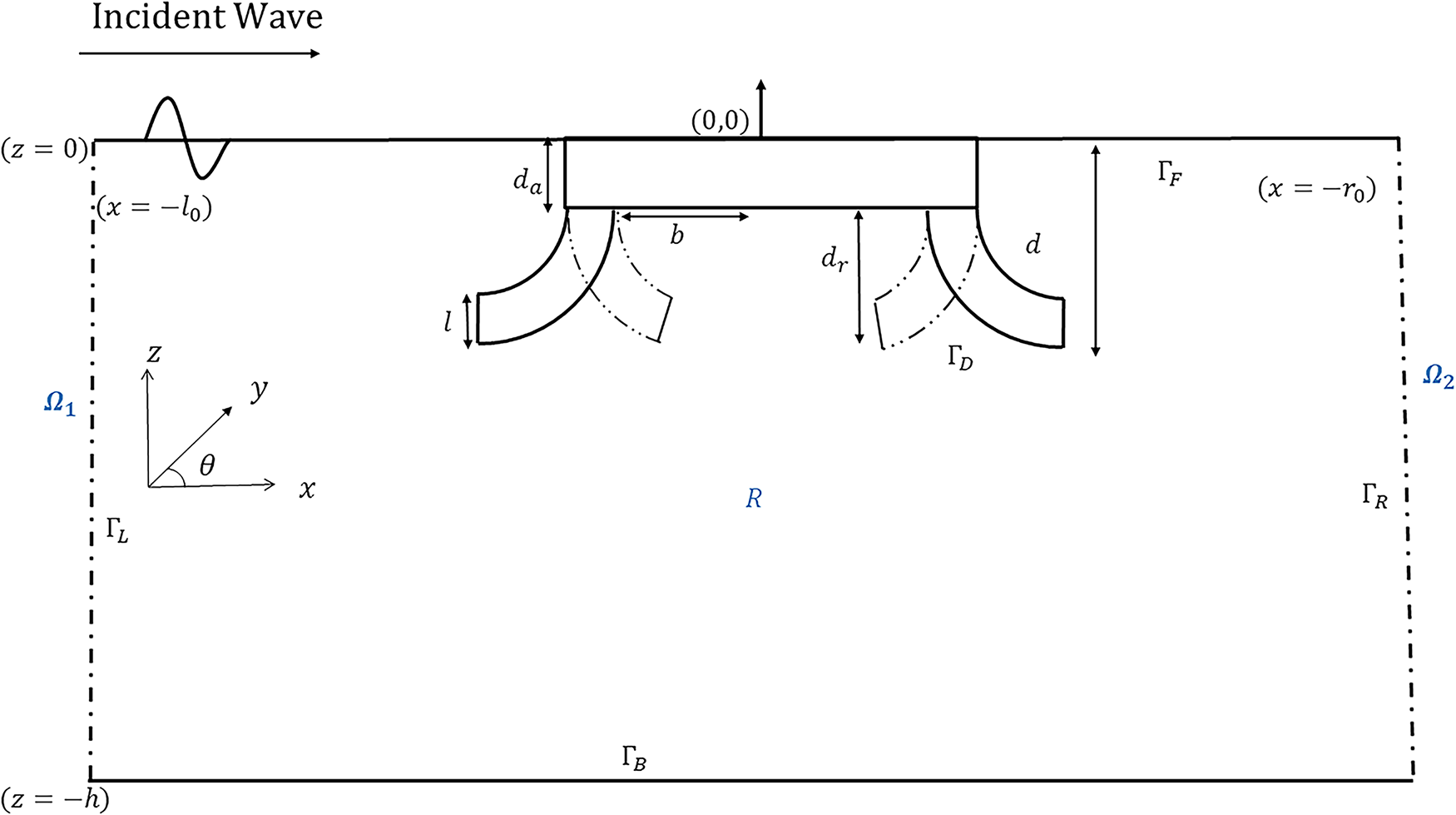
Figure 1: Schematic sketch of dual curved pontoon floating structure: BEM formulation

ΓL:x=−l0,−h≤z≤0,

ΓB:z=−h,−l0≤x≤r0,

ΓR:x=r0,−h≤z≤0,

ΓF:z=0,{r0≤x≤l+b} ∪ {−l−b≤x≤−l0}.

Model-1:

ΓD:{x=b+l,z=da≤z≤0} ∪ {x=(b+dr)+(dr−l)cos⁡θ,z=−da+(dr−l)sin⁡θ}

      ∪ {x=b+dr,−d≤z≤(−d+l)} ∪ {x=(b+dr)+drcos⁡θ,z=−da+drsin⁡θ}

      ∪ {b≤x≤−b,z=−da} ∪ {x=(−b−dr)+drcos⁡θ,z=−da+drsin⁡θ} ∪ {x=−b−dr,

      −d≤z≤(−d+l)} ∪ {x=(−b−dr)+(dr−l)cos⁡θ,z=−da+(dr−l)sin⁡θ}

      ∪ {x=−b−l,−da≤z≤0}.

Model-2:

ΓD:{x=b+l,z=da≤z≤0} ∪ {x=(b−dr)+drcos⁡θ,z=−da+drsin⁡θ}

      ∪ {x=b−dr,−d≤z≤(−d+l)} ∪ {x=(b−dr)+(dr−l)cos⁡θ,z=−da+(dr−l)sin⁡θ}

      ∪ {b≤x≤−b,z=−da} ∪ {x=(−b+dr)+(dr−l)cos⁡θ,z=−da+(dr−l)sin⁡θ}

      ∪ {x=−b+dr,−d≤z≤(−d+l)} ∪ {x=(−b+dr)+drcos⁡θ,z=−da+drsin⁡θ}

      ∪ {x=−b−l,−da≤z≤0}.

Model-3:

ΓD:{x=b+l,z=da≤z≤0} ∪ {x=(b−dr)+drcos⁡θ,z=−da+drsin⁡θ}

      ∪ {x=b−dr,−d≤z≤(−d+l)} ∪ {x=(b−dr)+(dr−l)cos⁡θ,z=−da+(dr−l)sin⁡θ}

      ∪ {b≤x≤−b,z=−da} ∪ {x=(−b−dr)+drcos⁡θ,z=−da+drsin⁡θ} ∪ {x=−b−dr,

      −d≤z≤(−d+l)} ∪ {x=(−b−dr)+(dr−l)cos⁡θ,z=−da+(dr−l)sin⁡θ}

      ∪ {x=−b−l,−da≤z≤0}.

Model-4:

ΓD:{x=b+l,z=da≤z≤0} ∪ {x=(b+dr)+(dr−l)cos⁡θ,z=−da+(dr−l)sin⁡θ}

      ∪ {x=b+dr,−d≤z≤(−d+l)} ∪ {x=(b+dr)+drcos⁡θ,z=−da+drsin⁡θ}

      ∪ {b≤x≤−b,z=−da} ∪ {x=(−b+dr)+(dr−l)cos⁡θ,z=−da+(dr−l)sin⁡θ},

      ∪ {x=−b+dr,−d≤z≤(−d+l)} ∪ {x=(−b+dr)+drcos⁡θ,z=−da+drsin⁡θ}

      ∪ {x=−b−l,−da≤z≤0}..

Further, the impermeable bottom boundary has zero flux as defined by

∂ϕ∂z=0 on ΓB.(2)

The free surface is governed by the linearized kinematic and dynamic conditions, which combine to yield the free surface boundary condition as:

∂ϕ∂z−Kϕ=0 on ΓF,(3)

where K=ω2/g, with g denoting the acceleration due to gravity. The no-flow condition for the floating rigid breakwater is represented as a Neumann boundary condition, enforcing zero normal velocity at the breakwater surface, as given by:

∂ϕ∂z=0 on ΓD.(4)

Subsequently, the far-field conditions are described as

{ ϕ(x,z)=(igω)[e−iq0x+R0eiq0x](cosh⁡k0(z+h)cosh⁡k0h) as x→−∞, ϕ(x,z)=T0(gω)e−iq0x(cosh⁡k0(z+h)cosh⁡k0h) as x→∞,(5)

where q0=k02−ky2, R0 and T0 are the reflection and transmission coefficients, respectively. By applying these boundary conditions, the velocity potential is determined using a combination of semi-analytical and numerical methods, as described in the following section.

3  Mathematical Solution

In this section, the boundary value problem along with its associated boundary conditions is formulated using the eigenfunction expansion approach for the velocity potential in the unbounded region, and the boundary element method is applied in the bounded region.

3.1 Eigenfunction Expansion Method in the Unbounded Domain

The spatial velocity potential function in the unbounded regions Ω1 and Ω2 can be expressed the eigenfunction expansion method [38] as follows

ϕΩ1=I0e−iq0(x+l0)ψ0(k0,z)+∑n=0∞Rneiqn(x+l0)ψn(kn,z) on ∂L,(6)

ϕΩ2=∑n=0∞Tne−iqn(x−r0)ψn(kn,z) on ∂R,(7)

where ψn(kn,z) for n=0,1,2,… are defined by

ψn(kn,z)=(igω)cosh⁡kn(z+h)cosh⁡ (knh),(8)

and the dispersion relation is satisfied by kn, given

ω2=gkntanh⁡(knh).(9)

The eigenfunctions ψn(kn,z) satisfy the orthogonal relation

⟨ψm(km,z),ψn(kn,z)⟩=Pnδmn,(10)

where δmn is the Kronecker delta function, and the normalization constant Pn is

Pn=∫−h0ψn2(kn,z)dz=(−g2ω2)knh+sinh⁡ (knh)cosh⁡ (knh)2kncosh2⁡ (knh).

The undetermined coefficients Rn and Tn are calculated employing the orthogonality of the eigenfuction eigenfunction ψn in the outer domain as

Rn+δn0=1Pn∫−h0ϕΩ1(z)ψn(kn,z)dz,(11)

Tn=1Pn∫−h0ϕΩ2(z)ψn(kn,z)dz.(12)

The normal derivatives associated with the potential function are defined as

∂ϕΩ1∂n|x=−l0=−∂ϕΩ1∂x|x=−l0=iq0ψ0(k0,z)−∑n=0∞Rniqnψn(kn,z),(13)

∂ϕΩ2∂n|x=r0=∂ϕΩ2∂x|x=r0=−∑n=0∞Tniqnψn(kn,z).(14)

Substituting the unknown coefficients Rn and Tn in (13) and (14), respectively, after truncating the series to N terms, we obtain

∂ϕΩ1∂n|x=−l0=Q1[ϕΩ1]+2iq0ψ0(k0,z),(15)

where Q1[ϕΩ1] is defined by

Q1[ϕΩ1]=−∑n=0N(iqnPn)(∫−h0(ϕΩ1(s)ψn(kn,s) ds))ψn(kn,z),

∂ϕΩ2∂n|x=r0=Q2[ϕΩ2],(16)

where Q2[ϕΩ2] is given by

Q2[ϕΩ2]=−∑n=0N(iqnPn)(∫−h0(ϕΩ2(s)ψn(kn,s) ds))ψn(kn,z).

These aforementioned two normal derivatives of the potential function constitute the boundary conditions for the left and right lateral boundaries.

3.2 Boundary Element Method in the Bounded Region

Applying Green’s second identity to the spatial velocity potential ϕ(x,z) and the free-space Green’s function G(x,z;x0,z0) along the closed boundaries, we obtain

(−ϕ(x,z)12ϕ(x,z))=∫Γ(ϕ∂G∂n−G∂ϕ∂n)dΓ, (if (x,z)∈∂Γ if (x,z)∈Γ,(x,z)∉∂Γ),(17)

where the fundamental solution G that satisfies the Helmholtz equation

(∇2−ky2)G=δ(x−x0)δ(z−z0),(18)

where δ is the Dirac delta function. It is well known that the Laplace equation in cylindrical coordinates is given by,

∇2=∂2∂r2+1r∂∂r.(19)

Substituting the above expression into (18), we obtain [39]

∂2G∂r2+1r∂G∂r−ky2G=δ,

which gives

r2∂2G∂r2+r∂G∂r−r2ky2G=δr2.

Now, let kyr=x so that r=xky. Substituting, we obtain

x2ky2∂2G∂x2ky2+xkyky∂G∂x−x2ky2ky2G=x2ky2δ.

Finally, it reduces to

x2∂2G∂x2+x∂G∂x−(x2−02)G=0.

The above equation corresponds to the general form of the Bessel equation. Its solution is given by

G=J0(x) and G=K0(x).

The modified Bessel fuction of the first kind, J0(x) grows exponentially for large x,

J0(x)≈ex asx→∞,

while the modified Bessel function of the second kind, K0(x), exponentially for large x

K0(x)≈e−x as x→∞.

Further, as the origin x→0, K0(x) has a logarithmic singularity given as

K0(x)≈−ln(x)−γ+ln(2).

Thus, G=aK0(x), G=aK0(kyr) where a is a proportionality constant depending on the physical problem. Now, integrating (18) over a surface S, we obtain

∬S∇2G(r)ds−ky2∬SG(r)ds=∬Sδ(r)ds=1.

Using the divergence theorem, the first term can be expressed as

∬S∇2G(r)ds=∬S∇.(∇G)ds=∮∇G.n^dl.

Consequently, we further deduce that

∮∂G∂ndl=∮∂∂r(−ln(x)−γ+ln(2))ar^dl =−2πa.

Next, the second kind of equation is given by

ky2∬SG(r)ds=ky2∫02π∫0ϵG(r)rdrdθ=2πky2∫0ϵG(r)rdr=2πaδ24[1−2γ+ln4−2ln(δ)].

The above expression tends to zero as x=0. Thus, we get

−2πa−0=1 ⟹ a=−12π

Substituting the value of a into the solution gives

G(x,z,x0,z0)=−12πK0(kyr),

which is the fundamental solution of the Helmholtz equation, where r=(x−x0)2+(z−z0)2 is the Euclidean distance between the integration point (source point) (x0,z0) and the field point (x,z).

Further, the Bessel function of the recurrence formula is employed to determine the normal derivative of G, providing

∂G∂n=ky2πK1(kyr)∂r∂n,(20)

where K1 represents the modified Bessel function of the second kind and first order. The integration point (x0,z0) congruent with the field point (x,z), i.e., r→0 gets the asymptotic behavior

K0(kyr)=−γ−ln⁡(kyr2),(21)

where γ=0.5772 is the Euler constant. Substituting the boundary conditions (2)–(4) into the Green’s identity (17), then the integral equations in every boundary domain are obtained by

12ϕ(x,z)+∫ΓL(ϕ∂G∂n−G∂ϕ∂n)dΓ+∫ΓB(ϕ∂G∂n)dΓ+∫ΓR(ϕ∂G∂n−G∂ϕ∂n)dΓ+∫ΓF(∂G∂n−KG)ϕ   dΓ+∫ΓD(ϕ∂G∂n)dΓ=0.(22)

To solve the aforementioned boundary integral equation, the region is discretized into a limited number of boundary elements, with assumed values ϕ and ∂ϕ constant across all elements (Wang and Meylan [40]). Furthermore, a set of linear algebraic systems is calculated using the point-collocation technique. The integral Eq. (22) is expressed as

∑j=1NLHijϕ−Gij∂ϕ∂n|ΓL+∑j=1NBHijϕ|ΓB+∑j=1NRHijϕ−Gij∂ϕ∂n|ΓR(23)

+∑j=1NF(Hij−KGij)ϕ|ΓF+∑j=1NDHijϕ|ΓD=0.(24)

Here, NL and NR are the number of elements along the lateral boundary, NB represents the number of elements along the bottom boundary, ND refers to the number of elements on the structure boundary, and NF indicates the number of elements on the free surface boundary. The terms Hij and Gijij are denote influence coefficients, which are defined as

Hij=−12δij+∫Γj∂G∂ndΓandGij=∫ΓjGdΓ,

when i≠j, the points (x,z) and (x0,z0) are located on various boundary elements. For this case, the required influence coefficients are calculated numerically using the Gauss-Legendre quadrature technique. On the other hand, when i=j, the field and integration points lie within the same boundary element, and the influence coefficients are evaluated analytically. The corresponding algebraic system is assembled into matrix form and evaluated using the Gauss elimination method to get the potential velocity and its normal derivatives on each boundary element. Furthermore, the reflection coefficient Kr, the transmission coefficient Kt, surface elevation η, vertical force FV, and horizontal force FH are calculated using the expressions provided in

Kr=|R0|,(25)

Kt=|T0|.(26)

The elevation of the free surface is represented by

η(x,0)=−iωg(ϕ(x,0).(27)

The wave forces exerted on the breakwater are defined by

FH=−iωgh2∫ϕ(x,z)nxdz,(28)

FV=−iωgh2∫ϕ(x,z)nzdx.(29)

4  Results and Discussions

In this section, the impacts of a floating dual curved-leg pontoon breakwater on surface wave scattering are examined for different physical parameters. The eigenfunction expansion approach is used on semi-infinite regions, and the boundary element method is employed on closed regions, enabling computational efficiency. Throughout the discussion, the following fixed physical parameters are used, unless stated otherwise: water depth h=10 m, height of the pontoon legs dr/h=0.35, height of the floating rectangle da/h=0.15, structure height d=dr+da, width of the pontoon legs l/h=0.15, space between the two curved-leg pontoons 2b/h=2, and incident wave angle θ=10∘.

The curved-leg geometry of the floating breakwater satisfies the circular equation:

(x−x0)2+(z−z0)2=dr2,(30)

where x0=±(b+dr), z0=−da, x=drcos⁡θ, z=drsin⁡θ. Here, the concave and convex legs on the seaside correspond to the circles of arcs in the fourth and third quadrants, respectively, and are positioned oppositely on the leeside, as shown in Fig. 2. Four structural models are compared to identify the most efficient design and analyze their hydrodynamic performance under varying conditions.

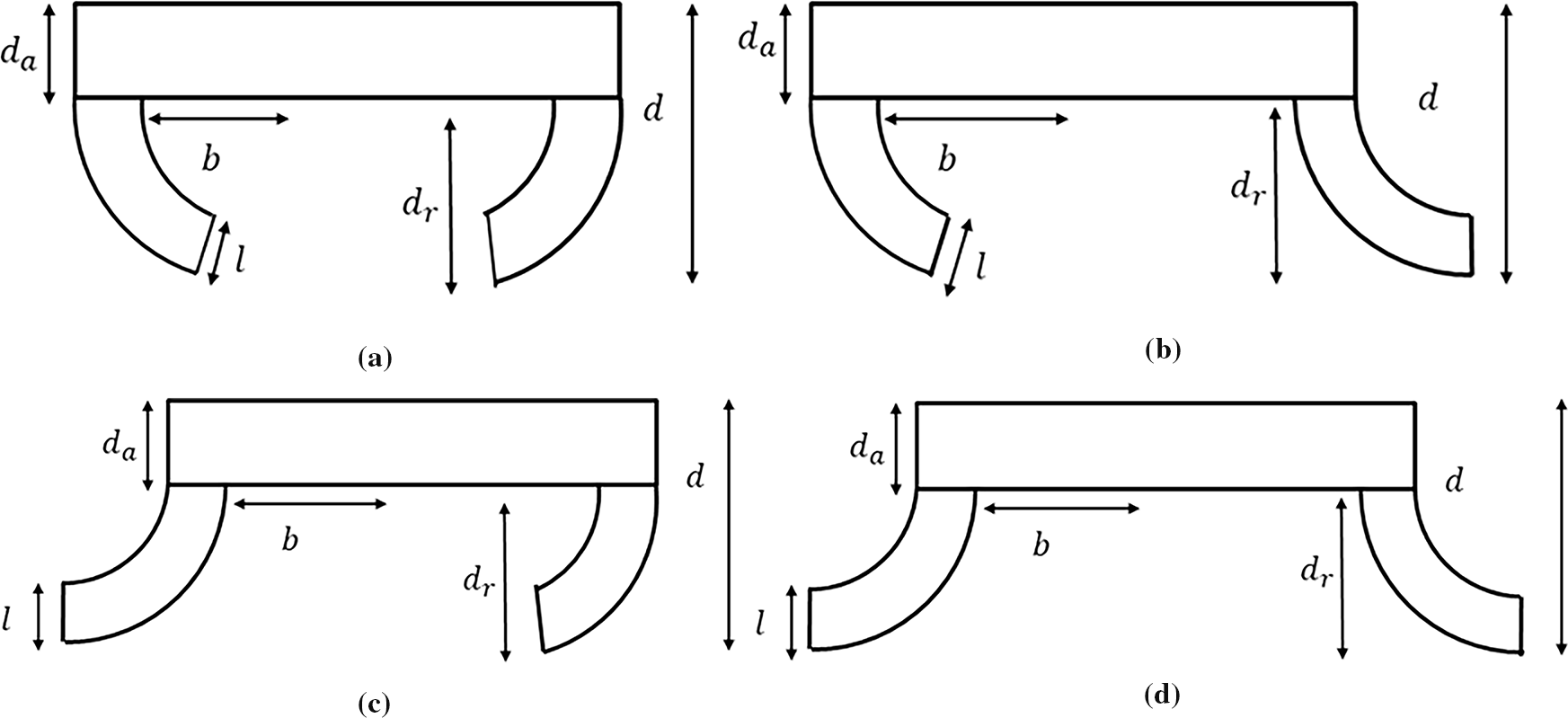
Figure 2: Various types of curved-leg pontoon floating breakwater: (a) Model-1, (b) Model-2, (c) Model-3, (d) Model-4

4.1 Convergence Study

The convergence of the numerical solutions derived via BEM depends on the dimensions of the panels employed to discretize the boundaries in the closed domain. The panel size ps is determined as follows [40]

ps=1κk0,(31)

where κ represents a constant of proportionality derived through convergence analysis. Table 1 illustrates the convergence behavior of the numerical solutions for different curved-leg geometries. From Table 1, it is evident that for κ=30 and ps=0.39, the computed wave reflection Kr and the transmission coefficient Kt converge accurately to the three decimal places.

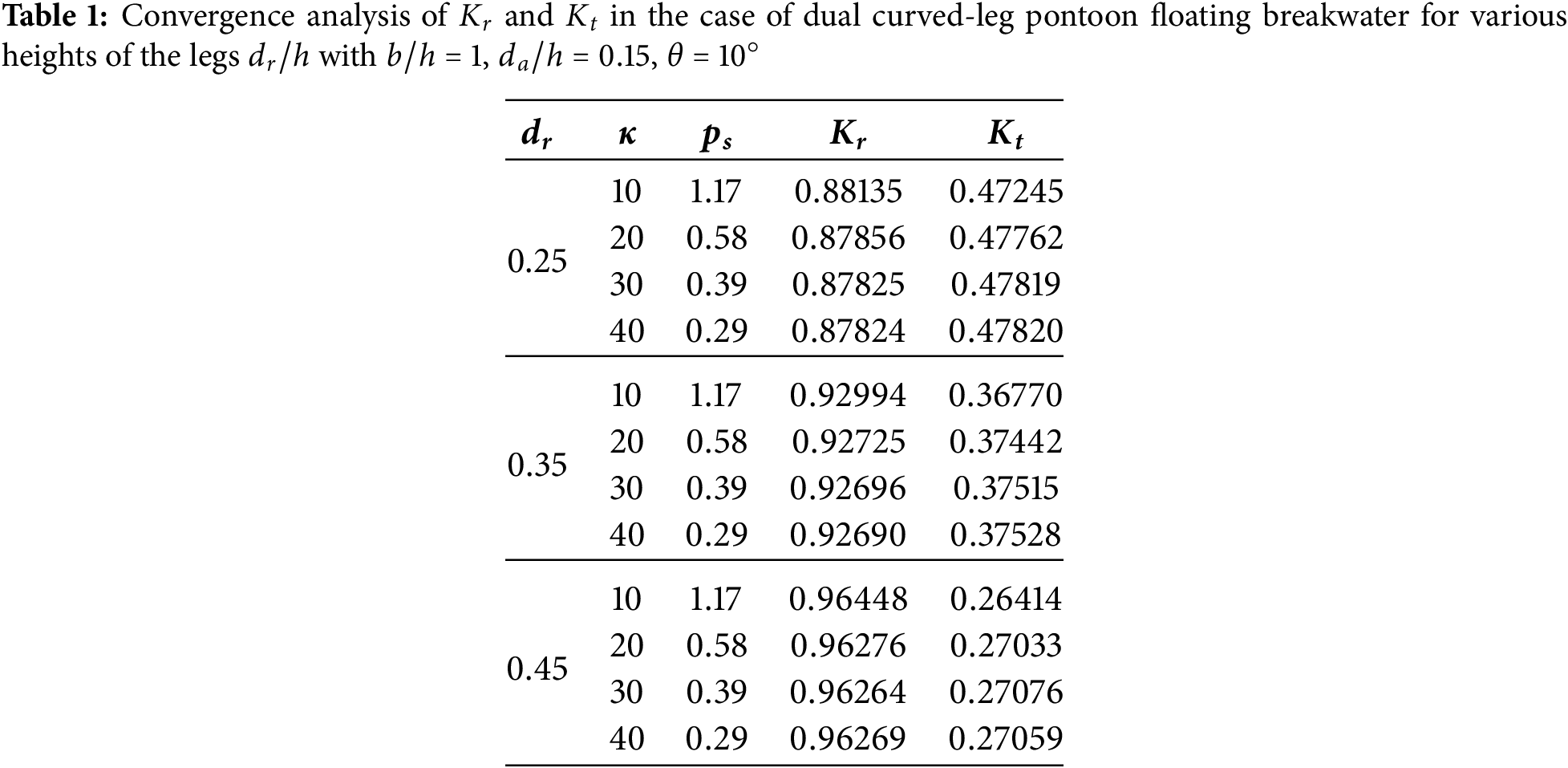
4.2 Model Validation and Numerical Results on Dual Curved-Leg Pontoon Breakwaters

The present section determines the wave reflection and transmission coefficients employing the boundary element method and compares them with previous research on rectangular structures. As the height of the curved-leg geometries approaches zero, the dual curved-leg pontoon floating structure effectively transforms into a rectangular configuration. Fig. 3a illustrates the reflection coefficient vs. the dimensionless height of the structure k0a. The present problem is reduced to the surface wave scattering by a rectangular structure, investigated analytically by Mei and Black [8] and experimentally in [41]. The present results are clearly shown to correlate with the analytical and experimental findings. The boundary element method is more accurate, as the results of the current problem agree well with those of previous studies.

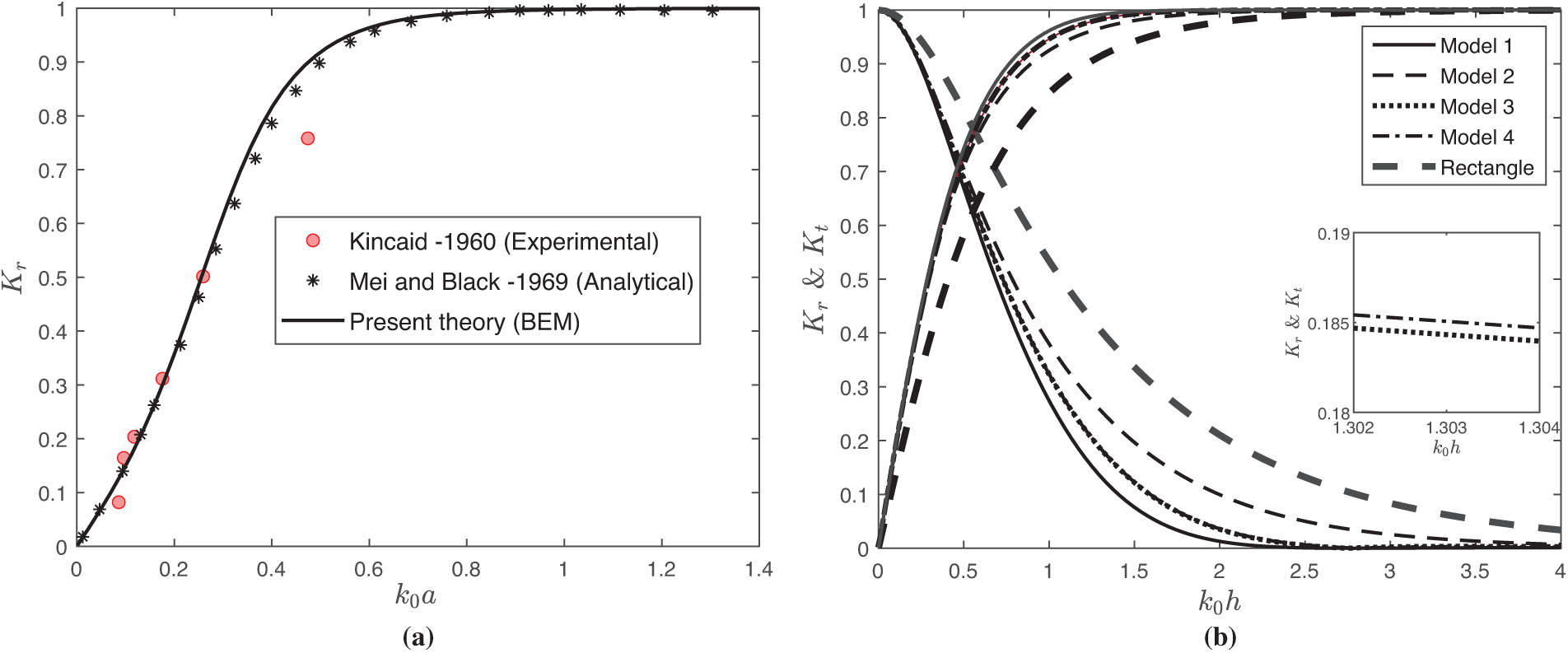
Figure 3: Comparison of Kr and Kt vs. (a) k0a for the scattering of a single rectangle dock with dr=0, h/a=6.17, b/a=1. vs. (b) k0h for different curved model and rectangle with dr/h=0.35, da/h=0.15, l/h=0.15, b/h=1, θ=10∘

Fig. 3b depicts the wave reflection Kr and the transmission coefficient Kt vs. for different models of the curved pontoon legs and the rectangle. The wave reflection increases by more than 5% for different dual curved-leg pontoon models when compared to the rectangular model, whereas the transmission decreases by more than 15%, as shown in Table 2. This attenuation of wave transmission is due to the attachment of the dual legs, which reduces transmitted wave energy by altering wave propagation patterns. Similar phenomena were observed in the T-shaped floating structure by Neelamani and Rajendran [10]. Also, Ruol et al. [14] discussed this for the π-shaped floating structure. Therefore, the wave-blocking performance of the curved legs is superior to that of the rectangular structure. A similar conclusion was drawn when comparing single-wing and box-type structures [23]. In addition, it is observed that the wave transmission of Model-2 increases significantly, whereas it decreases for Models 1, 3, and 4. This is due to the small area between the pontoon legs; as a result, higher wave transmission occurs. The transmission coefficient of Model-1 decreases, and the reflection increases relative to Models 2 and 3 due to the larger area between the legs, a phenomenon also observed in [24]. The flow direction changes due to the seaside of the concave leg. The same phenomenon was analyzed by Hussein et al. [21] while studying the concave and convex semi-circular barriers. Moreover, in Model 1, wave reflection increases by over 8% and wave transmission decreases by more than 27% compared to the rectangular model as shown in Table 2. This phenomenon is attributed to wave diffraction, which increases the wave height in front of the structure while decreasing it behind; a similar observation was analyzed in the experimental work on wing-shaped structures [42].

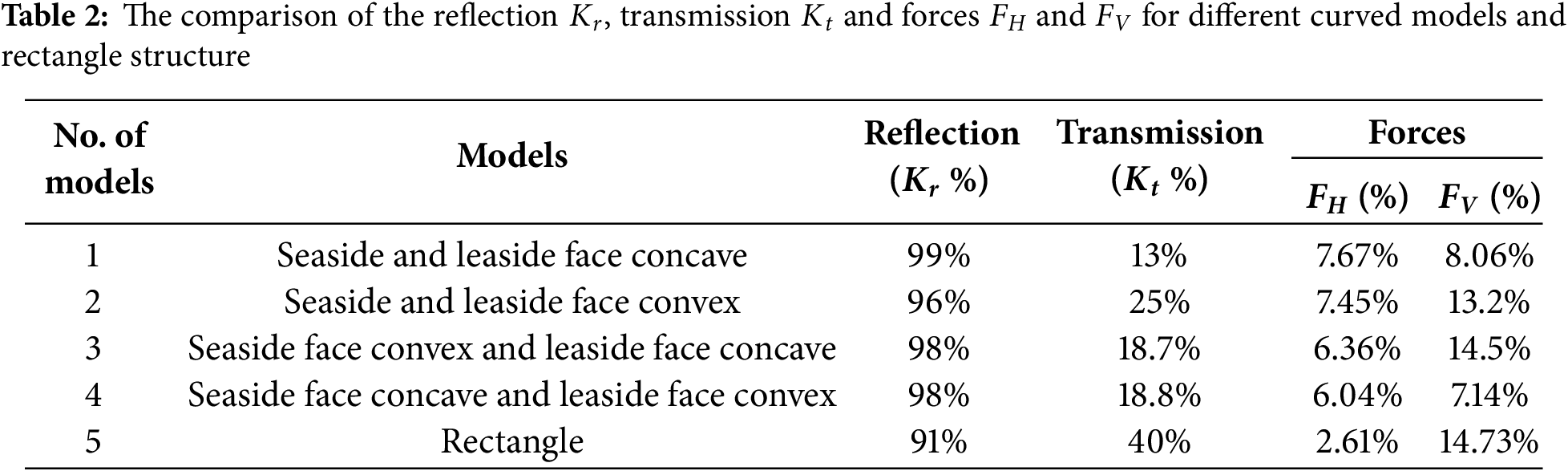
Fig. 4 presents the wave variation of wave-induced forces on the curved-leg pontoon breakwater vs. wave number k0h for various types of curved-leg models and a rectangular one. From Fig. 4a, it is noted that the horizontal force FH acting on the curved models increases compared to the rectangular structure. This higher force is attributed to wave slamming and breaking on the curved legs. This effect was reported by Ji et al. [43] when comparing wing-type and box-type structures. The force exerted on Model-1 increases because the seaside concave and leeside convex leg of the breakwater enhances wave trapping and reflection, resulting in greater reflected energy that increases the horizontal force. The vertical force FV acting on the rectangular structure increases relative to the other models, as shown in Fig. 4b. Additionally, the wave force FV for Model-1 and Model-4 eventually approaches zero due to the energy dissipation that occurs between the legs.

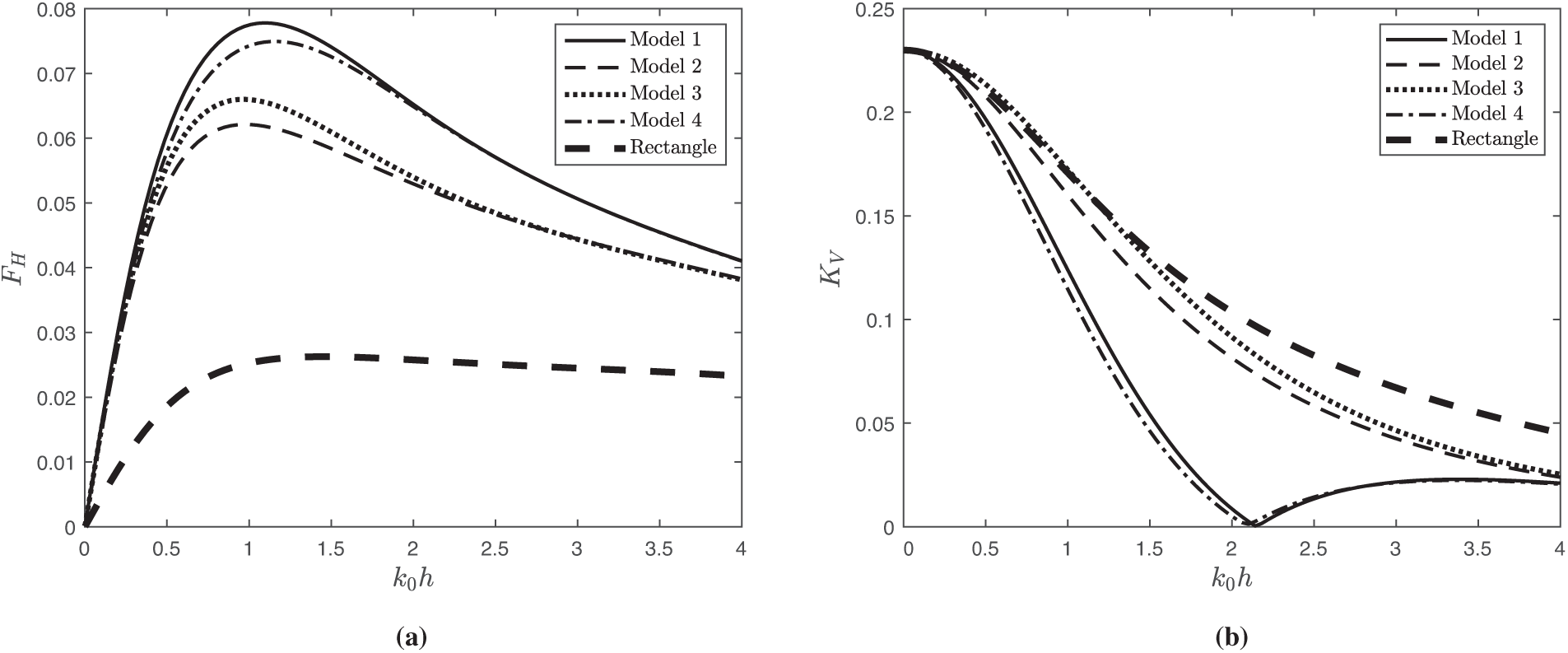
Figure 4: Variation of (a) KH and (b) KV vs. wave number k0h for different model with dr/h=0.35, da/h=0.15, l/h=0.15, b/h=1, θ=10∘

Fig. 5 illustrates the distribution of free surface elevation for different models and different heights of the curved-leg geometries. Fig. 5a depicts that the surface elevation of the rectangular model increases on both the seaside and leeside, whereas Model-1 shows a decrease on both sides. This reduction is attributed to the presence of the attached curved-leg pontoons, which increase the wave blocking effect. Furthermore, it is observed that the surface elevation on both the leeside and seaside of the breakwater is lower in Model-1 compared to other models due to the larger area between the legs. He et al. [24] reported a similar trend while comparing the different floating curved wing structures. From Table 2, it can be concluded that Model-1 is the most effective structure for attenuating waves compared to the other models. Therefore, Model-1 is considered more favorable for establishing a floating platform or supporting additional coastal activities. As a result, the rest of the discussion will focus primarily on Model-1. Fig. 5b shows that the surface elevation diminishes with increasing dr on the leeside of the structure due to the longer length of the legs, while it increases on the seaside.

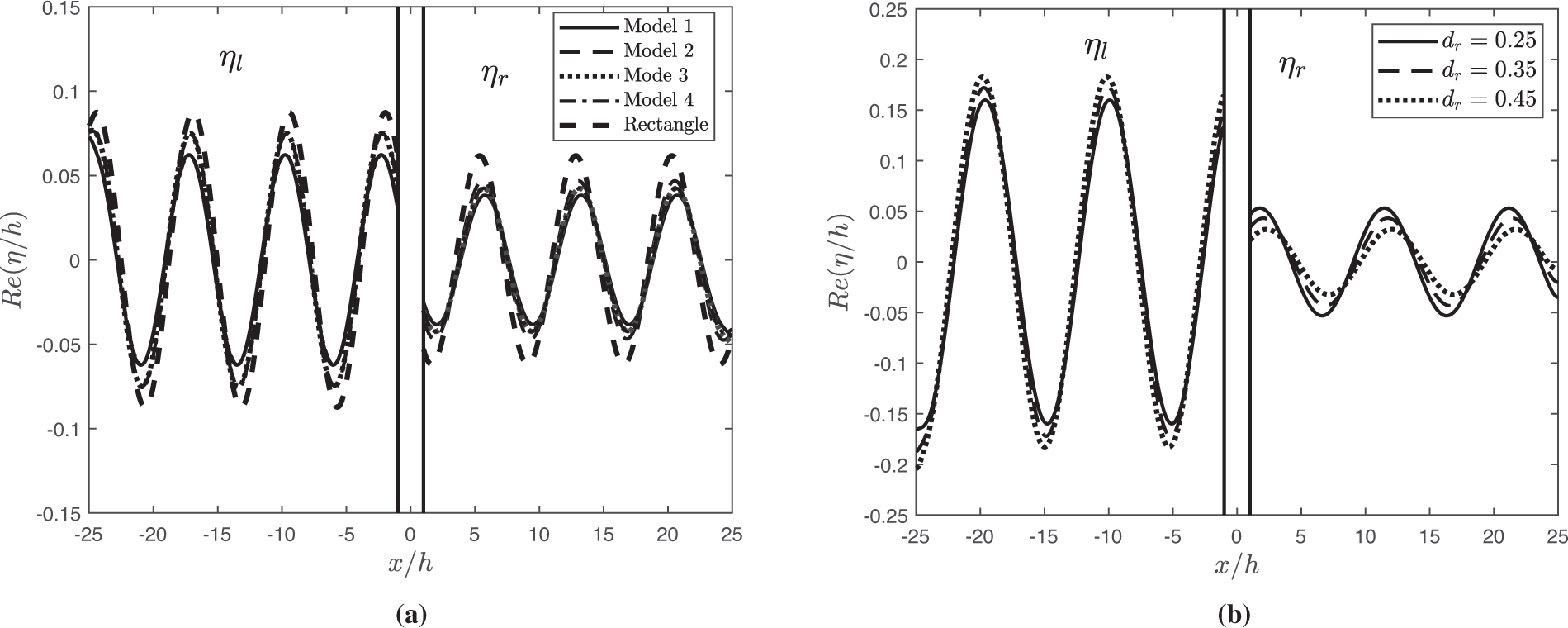
Figure 5: Variation of surface elevation Re(η/h) for different (a) Models, (b) dr/h along with da/h=0.15, b/h=1, θ=10∘

Fig. 6 demonstrates the reflection coefficient Kr and the transmission coefficient Kt as a function of the wavenumber k0h for varying values of dr/h and da/h. Fig. 6a presents that wave reflection increases with increasing height of the curved-leg for k0h<1.5, and transmission is observed in the opposite trend for k0h<2. This is due to the blocking of waves by the larger curved-leg, which is similar to that noticed in [23] for a single-wing floating structure. Further, the wave transmission approaches zero. In Fig. 6b, for k0h<1.2, the wave reflection reduces as the height of the rectangular floating structure da/h decreases. It also illustrates that transmission decreases with increasing height da/h due to the more wave energy concentrated by the larger pontoon.

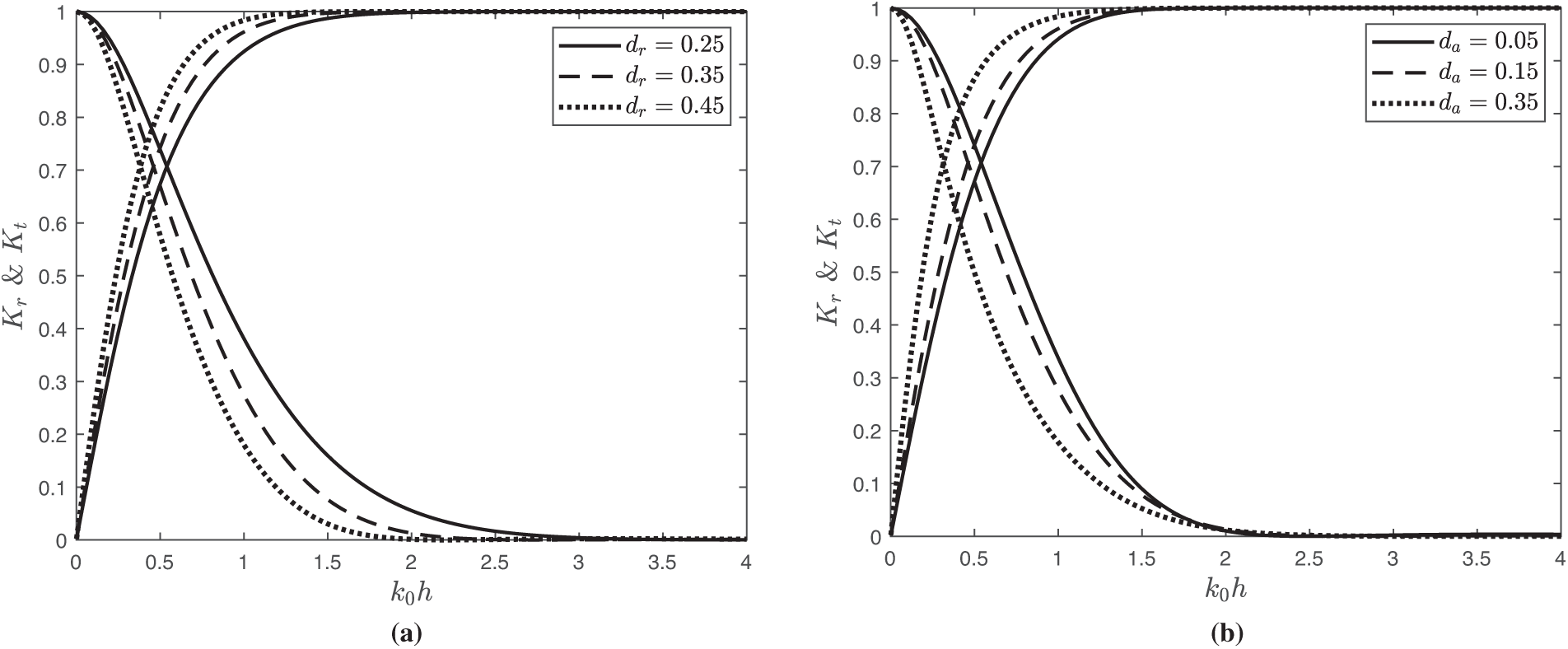
Figure 6: Variation of Kr and Kt vs. wave number k0h for various values of (a) dr/h with da/h=0.15 (b) da/h with dr/h=0.35 and the other parameters kept constant

Fig. 7 demonstrates the wave reflection Kr and the wave transmission Kt vs. the wave number k0h for varying of b/h and l/h. In Fig. 7a, the reflection coefficient increases with increasing distance between the two legs because larger areas occur between the legs. In addition, the transmission decreases as b/h increases. This is due to the wave trapping between the legs. Fig. 7b shows that the wave reflection increases with increasing width of legs l/h and the transmission coefficient attains an opposite behavior. This can be attributed to the greater wave blocking by the larger width of the legs.

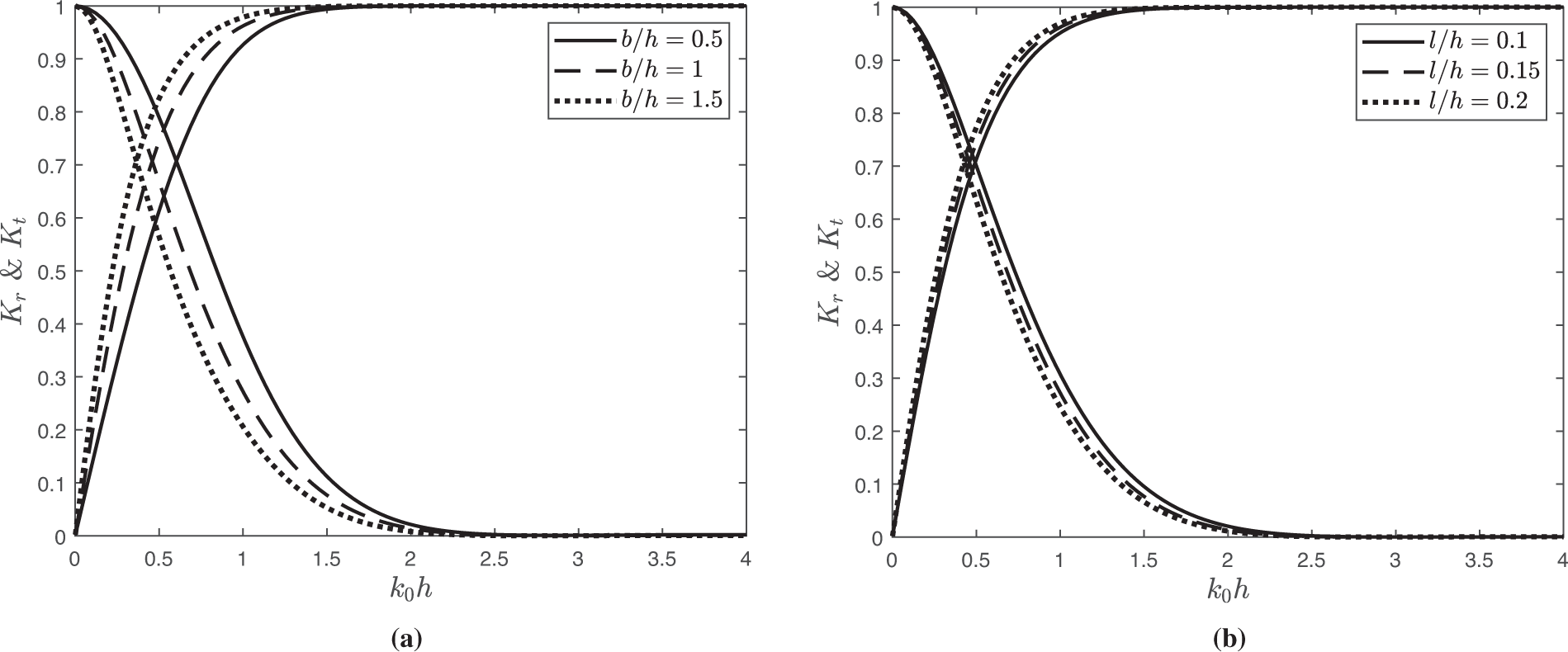
Figure 7: Variation of Kr and Kt vs. wave number k0h for various values of (a) b/h with l/h=0.15 (b) l/h with b/h=1 and the other parameters kept constant

Fig. 8 illustrates the horizontal and vertical forces, FH and FV, excitation on the structure against the dimensionless wavenumber k0h for various heights of the legs dr/h. Fig. 8a shows the horizontal force FH increases to its maximum at k0h=0.8 and then gradually diminishes as the wavenumber k0h increases for all values of dr/h. As the leg height increases, the breakwater interacts with more wave energy, resulting in stronger wave loading and a corresponding rise in horizontal force. Fig. 8b reveals that as dr/h increases, the vertical force FV initially diminishes, reaching zero at k0h=1.6, and then gradually increases to attain stability due to enhanced wave pressure on the structure base.

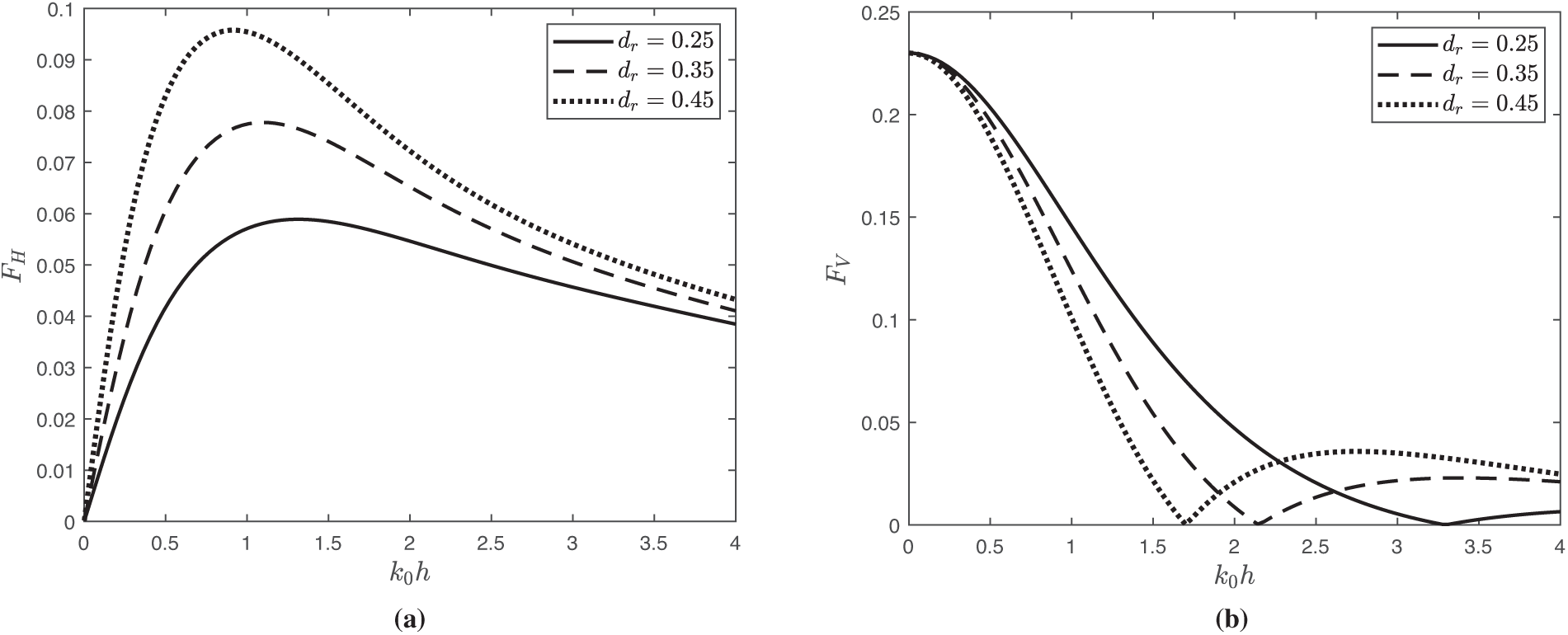
Figure 8: Variation of force (a) FH and (b) FV vs. wave number k0h for various values of dr/h with da/h=0.15, b/h=1

Fig. 9 depicts the horizontal wave force FH and the vertical wave force FV as a function of the wavenumber k0h for varying rectangular height da/h and b/h, respectively. Fig. 9a demonstrates that the horizontal force FH attains a similar pattern as shown in Fig. 8a. It is noticeable that, for higher values of the da/h, the force increases with the larger area of the pontoon. Fig. 9b shows that for k0h<2, the vertical force FV increases as b/h increases due to the larger surface area between the legs that interacts with the incident wave, resulting in a higher wave force, and then zero force occurs at k0h=2.

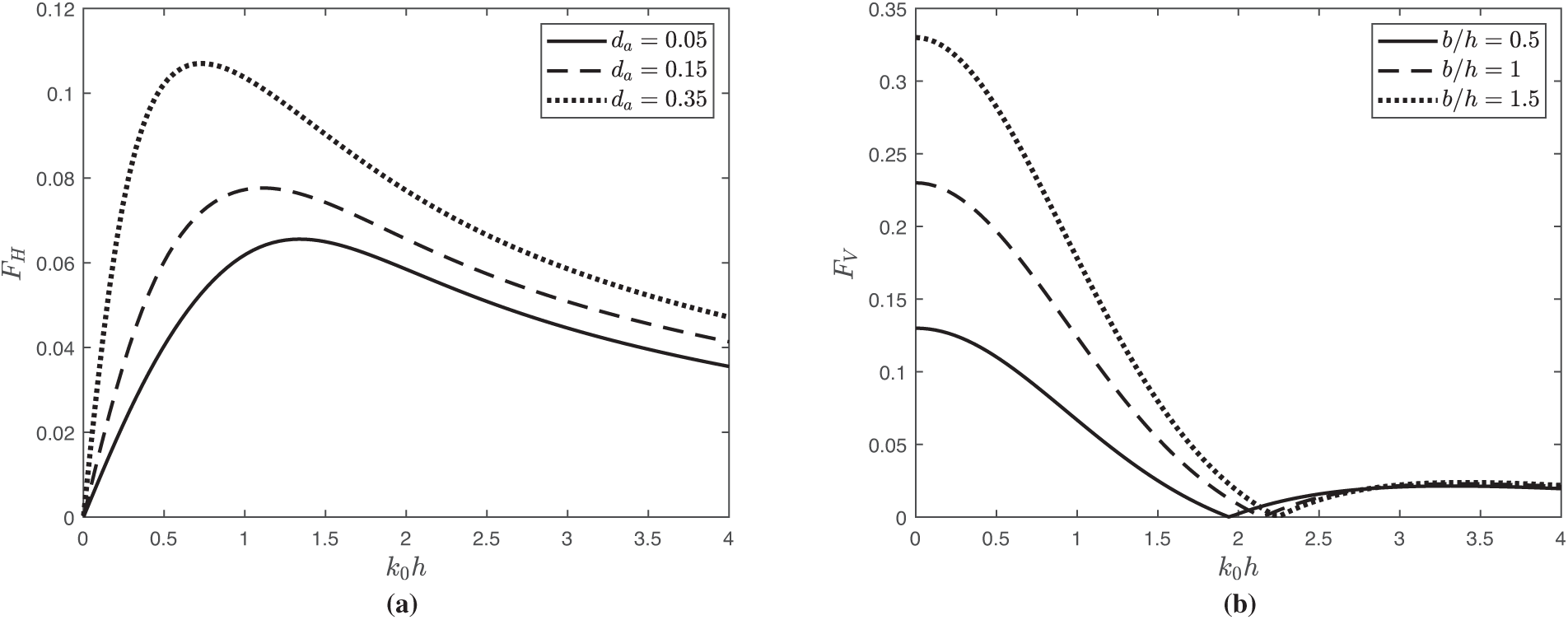
Figure 9: Variation of wave force FH and FV vs. wave number k0h for various values of (a) da/h with b/h=1 (b) b/h with da/h=0.15 and other fixed parameters are dr/h=0.35, l/h=0.15, θ=10∘

Fig. 10 demonstrates the horizontal force FH and the vertical force FV as a function of the wavenumber k0h for the variation of l/h. In Fig. 10a, as the width of the dual curved-leg l/h increases, the horizontal force FH increases. This phenomenon arises from the effect of the slamming wave, resulting in an increase in the pressure on the structure. Further, Fig. 10b depicts that the vertical force FH reduces with increasing l/h, then reaches zero force at k0h=2.1 after FV increases. The reduction in force occurs because the larger width of the legs decreases the vertical pressure.

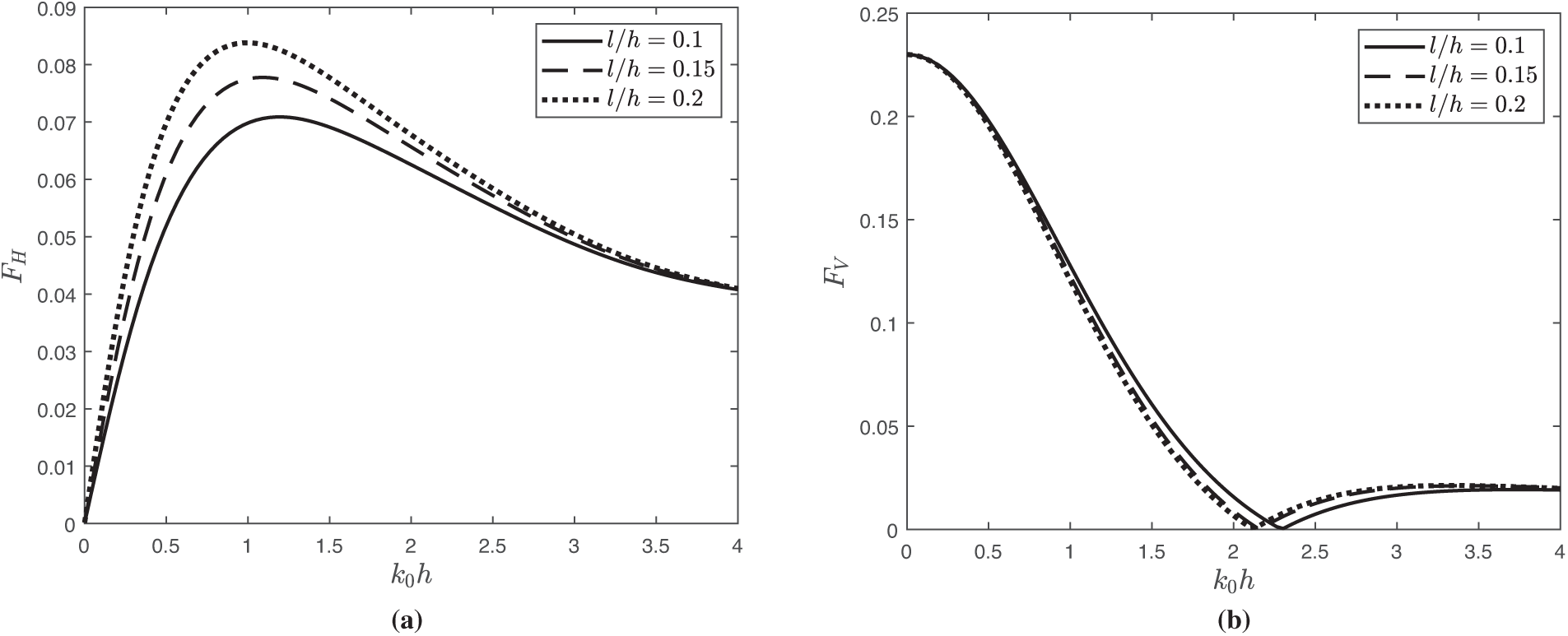
Figure 10: Variation of wave force (a) FH and (b) FV vs. wave number k0h for various values of l/h and other fixed parameters are b/h=1, da/h=0.15, dr/h=0.35, θ=10∘

The variation of the wave reflection Kr and wave transmission Kt is plotted as a function of wave angle θ for different values of dr/h and b/h, as shown in Fig. 11. Fig. 11a depicts that the reflection coefficient increases with increasing incident angles θ and wave transmission exhibits the opposite behavior. This phenomenon can be attributed to the wave blocking by the larger legs. Further, in Fig. 11b, the transmission coefficient diminishes with an increase in distance between the two legs, and the reflection increases. This occurs because the wider rigid breakwater intercepts more of the incoming wave energy, thereby enhancing wave reflection and limiting the transmission beyond the structure.

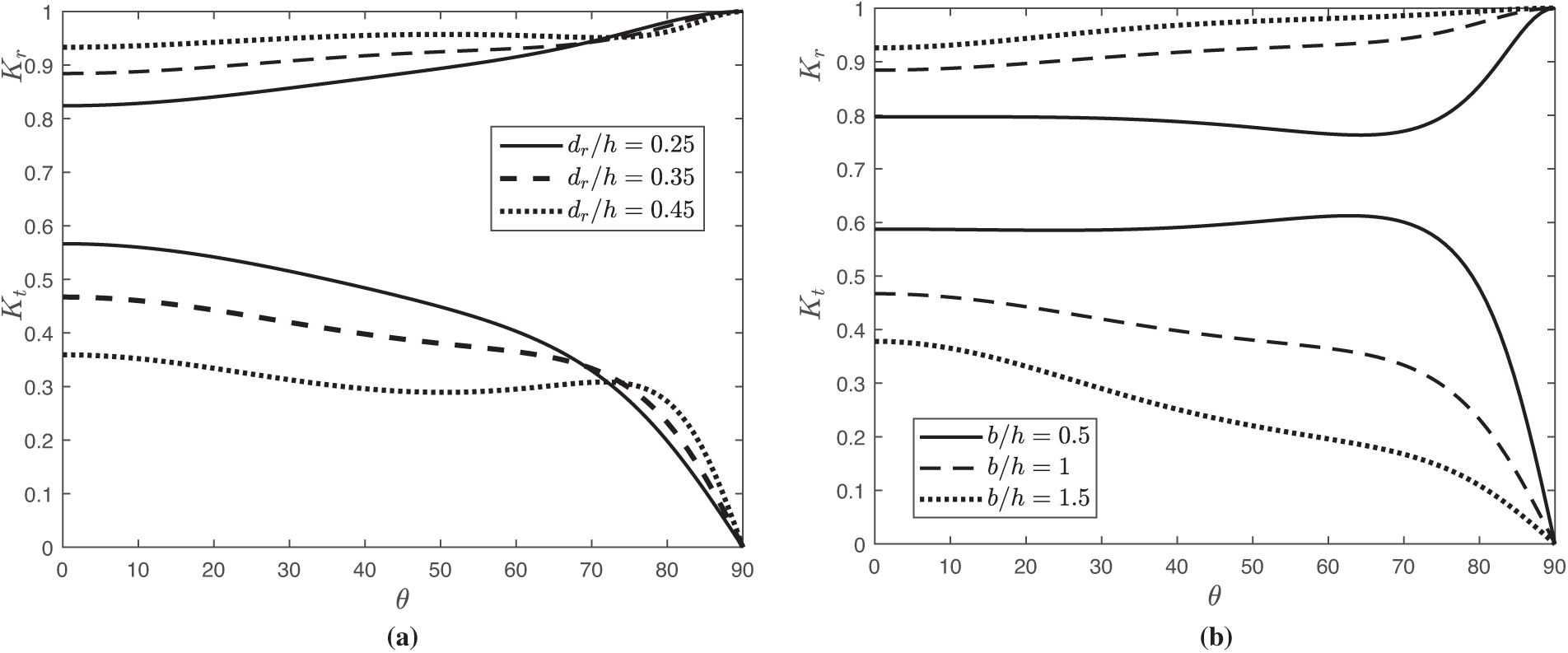
Figure 11: The Kr and Kt vs. θ for various values of (a) dr/h with da/h=0.15 (b) da/h with dr/h=0.35 and other parameters kept constant

Fig. 12 shows that the reflection coefficient Kr and transmission coefficient Kt against the wave angle θ for various values of da/h and l/h. Fig. 12a presents that Kr increases and transmission decreases, whereas for da/h increases owing to the larger height of the pontoon structure. On the other hand, in Fig. 12b, the reflection increases with increasing l/h. As l/h increases, the transmission decreases for θ<70∘ due to blockage of the waves.

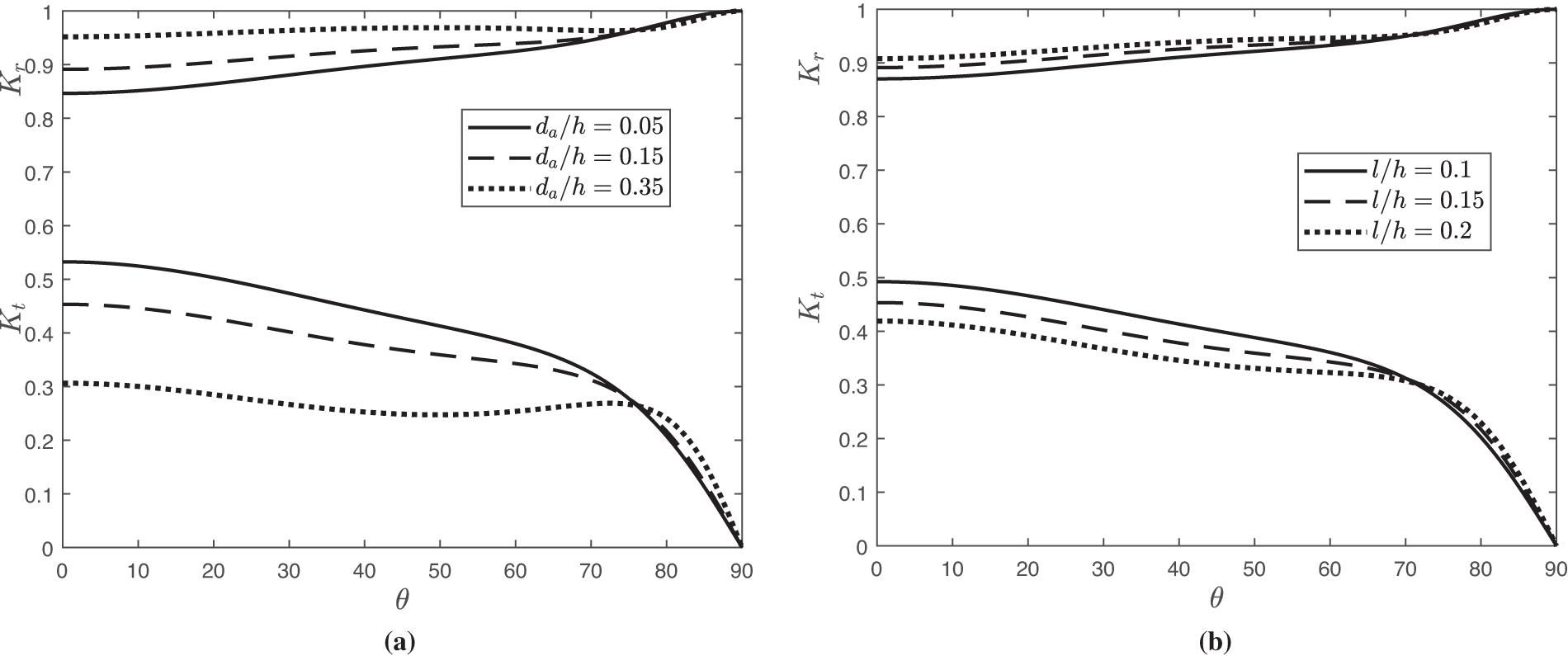
Figure 12: The Kr and Kt vs. θ for various values of (a) da/h with l/h=0.15 (b) l/h with da/h=0.15 and other parameters kept constant

Fig. 13 illustrates the horizontal force FH and vertical wave force FV against the wave angle θ for changes in dr/h. As shown in Fig. 13a, the horizontal force FH decreases as the dual leg height reduces because of the reduction of the wave reflection. Fig. 13b shows that the vertical force dramatically reduces to reach θ=90∘. Further, the vertical force decreases with increasing dr/h. This is because the greater wave energy is reflected and lesser energy is transmitted below the larger leg of the structure, leading to reduced vertical force.

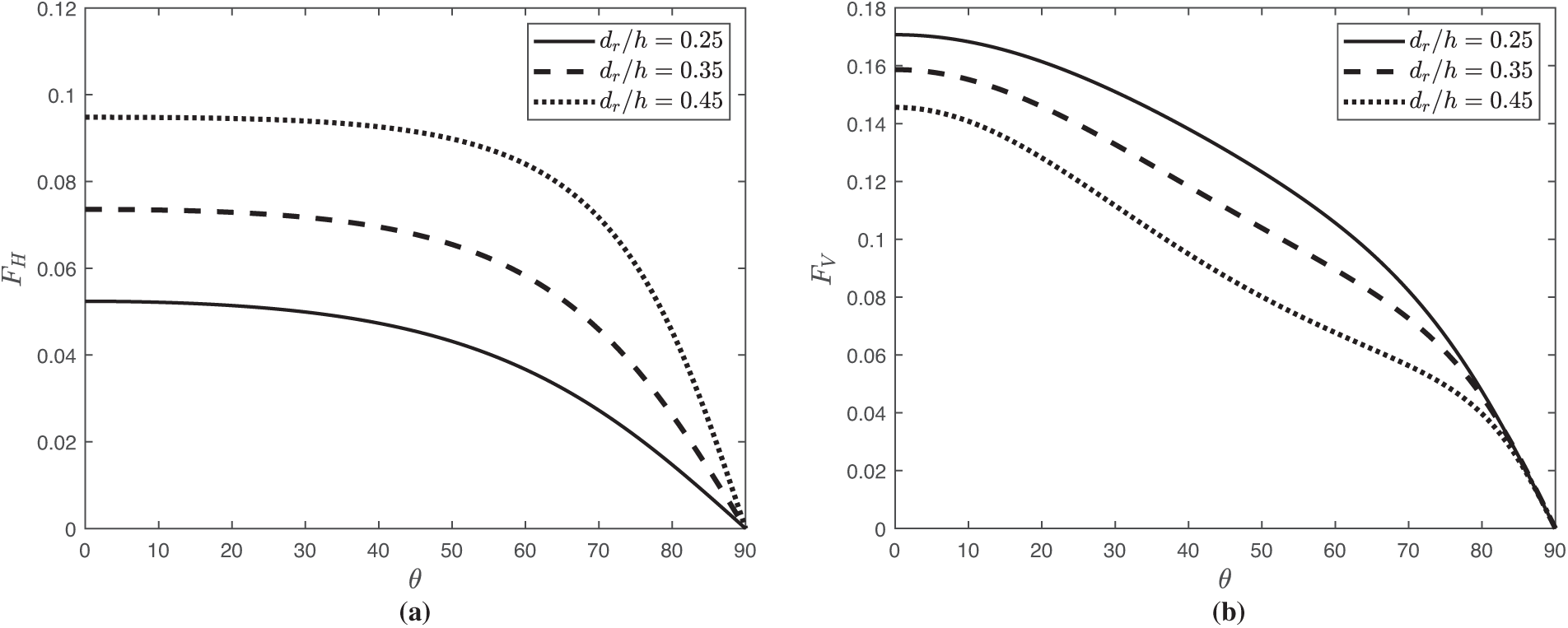
Figure 13: Variation of wave force (a) FH and (b) FV vs. θ for various values of dr/h with other fixed parameters are b/h=1, da/h=0.15, k0h=0.75

Fig. 14 presents the wave forces on the structure FH and FV against θ for varying b/h. Fig. 14a shows that the horizontal force decreases with increasing b/h for θ<60∘ and increases for higher incident angles. The reduction of the wave force is due to the redirection of wave energy around the structure. Fig. 14b shows that the vertical force increases as the gap between the dual legs increases. As the larger surface area of the beneath structure interacts with the incident wave, it leads to a greater vertical force due to the higher pressure acting on the structure.

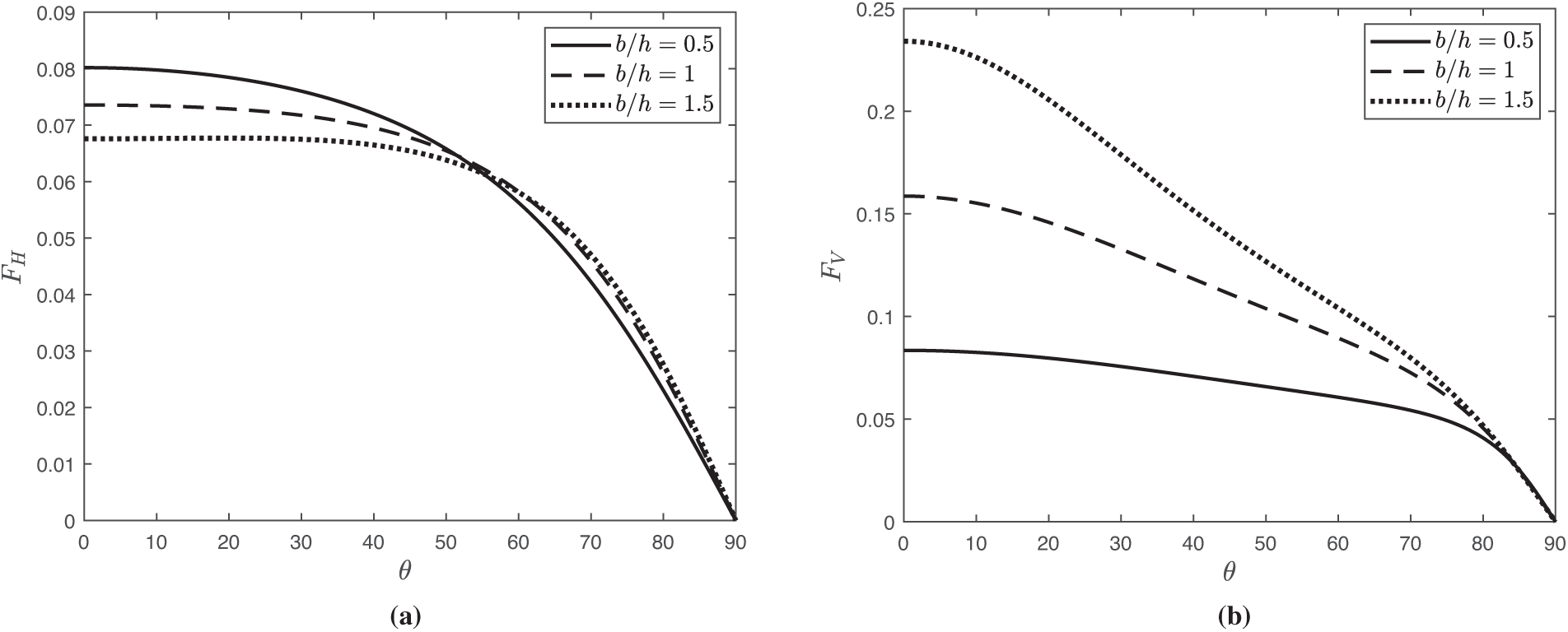
Figure 14: Variation of wave force (a) FH and (b) FV vs. wave angle θ for various values of dr/h with other fixed parameters are b/h=1, da/h=0.15, k0h=0.75

The surface plots showing the variation of horizontal force FH and vertical force FV, on the structure are presented in Fig. 15. In Fig. 15a, the horizontal force FH initially increases and reaches a maximum at k0h=1, after which it decreases monotonically as the wave number increases. The increase in wave force is due to higher wave reflection, as shown in Fig. 4. In addition, the FH becomes more stable with an increase in the incident wave angle θ and eventually approaches zero for larger angles. In Fig. 15b, as the k0h increases, the FV initially decreases; after attaining the zero force at k0h=2.1, it increases.

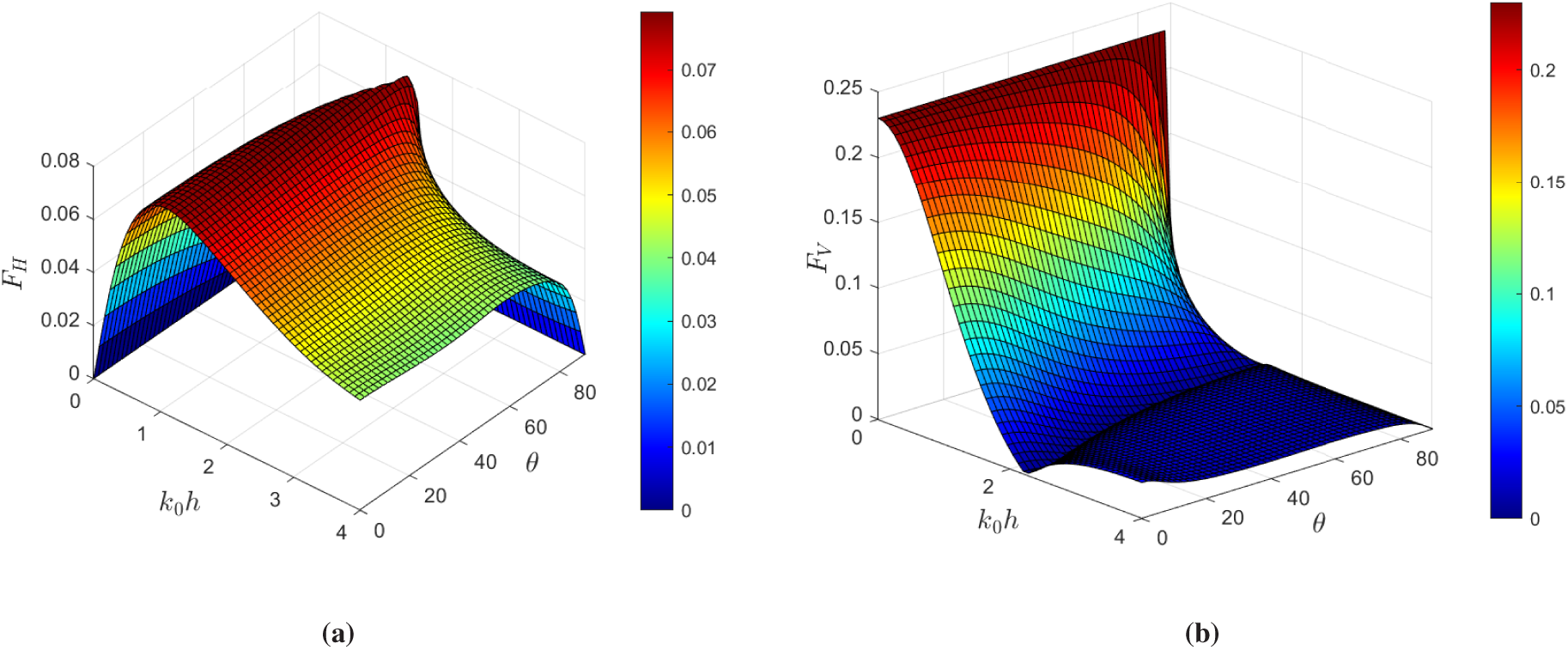
Figure 15: The surface plot of wave force (a) FH and (b) FV vs. (k0h,θ) with other fixed parameters are b/h=1, da/h=0.15, dr/h=0.35, l/h=0.15, k0h=0.75, θ=10∘

5  Conclusion

This study investigates the performance of dual-curved-leg pontoon floating breakwaters in finite water depth, based on linear water wave theory. Four different curved-leg models are analyzed using the boundary element method.

•   The results demonstrate that curved-leg pontoons are more effective in attenuating 15% wave transmission compared to traditional rectangular designs. Among the models examined, Model-1 shows superior hydrodynamic performance. Specifically, it exhibits a lower wave transmission coefficient and a higher reflection coefficient compared to the other curved-leg models.

•   Additionally, the horizontal force acting on Model-1 increases, and the vertical force acting on Model-1 and Model-4 decreases. The study indicates that the surface elevation of Model-1 decreases both on the leeward and windward sides compared to the others.

•   Finally, the results reveal that the hydrodynamic characteristics of Model-1 efficiently attenuate waves compared to other models. Moreover, the study concluded that Model-1 is considered more useful for establishing a platform and auxiliary coastel activities.

•   Further analysis of Model-1 reveals that as the leg height dr/h increases, the wave reflection coefficient increases, while an inverse trend is observed in the transmission behavior. A similar trend is observed when varying the height of the floating rectangular section da/h. The results also indicate that wave reflection improves with increased leg height, leg width, and spacing between the legs, while wave transmission decreases accordingly.

Overall, this study highlights the importance of optimizing structural parameters, such as leg dimensions and spacing, for the effective design and performance of a floating breakwater system. The BEM is restricted to problems for which a fundamental solution exists, which makes the treatment of nonlinear and inhomogeneous problems difficult. Future work may focus on extending the present formulation to incorporate nonlinear wave effects, inhomogeneous boundary conditions, and coupling with numerical methods such as computational fluid dynamics to overcome these limitations.

The complex pontoon breakwater investigated in this study can be further examined for all six degrees of freedom (surge, sway, heave, roll, pitch, and yaw) using high-fidelity computational fluid dynamics simulations and experimental setups, providing a more realistic representation of its dynamic behavior. Future research will address these limitations, which define the scope of the study. Additionally, future research may extend the current model by incorporating additional energy-harvesting mechanisms, such as an integrated oscillating water column system.

Acknowledgement: The authors gratefully acknowledge the valuable insights and stimulating discussions contributed by Dr. R. Gayathri of the Department of Mathematics, School of Advanced Sciences, Vellore Institute of Technology, Vellore, India, which have substantially enhanced the development of this work.

Funding Statement: This work is supported by Vellore Institute of Technology, Vellore, under a SEED grant (Sanction Order No. SG20230081).

Author Contributions: Conceptualization, Jothika Palanisamy, Chandru Muthusamy, and Higinio Ramos; methodology, Jothika Palanisamy, Chandru Muthusamy, and Higinio Ramos; validation, Jothika Palanisamy, Chandru Muthusamy, and Higinio Ramos; formal analysis, Jothika Palanisamy, Chandru Muthusamy, and Higinio Ramos; writing—original draft preparation, Jothika Palanisamy; writing—review and editing, Chandru Muthusamy and Higinio Ramos; visualization, Jothika Palanisamy and Chandru Muthusamy; supervision, Chandru Muthusamy and Higinio Ramos. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data supporting the findings of this study are provided within the article, as detailed in the figure captions and their corresponding discussions.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Koh HS, Lim YB. The floating platform at the Marina Bay, Singapore. Struct Eng Int. 2009;19(1):33–7. doi:10.2749/101686609787398263. [Google Scholar] [CrossRef]

2. Lamas-Pardo M, Iglesias G, Carral L. A review of Very Large Floating Structures (VLFS) for coastal and offshore uses. Ocean Eng. 2015;109:677–90. doi:10.1016/j.oceaneng.2015.09.012. [Google Scholar] [CrossRef]

3. Ohmatsu S. Numerical calculation method for the hydroelastic response of a pontoon-type very large floating structure close to a breakwater. J Marine Sci Technol. 2000;5(4):147–60. doi:10.1007/s007730070001. [Google Scholar] [CrossRef]

4. Jiang D, Wu B, Peng B, Shao Y. Dynamic response analysis of pontoon-type floating bridges subjected to wave and traffic loads. In: Proceedings of the Fourth World Conference on Floating Solutions: WCFS 2024; 2025 Dec 2–4; Hong Kong, China. Singapore: Springer Nature. p. 477–86. doi:10.1007/978-981-96-4569-5_50. [Google Scholar] [CrossRef]

5. Wang CM, Han M, Lyu J, Duan W, Jung K. Floating forest: a novel breakwater-windbreak structure against wind and wave hazards. Front Struct Civil Eng. 2021;15(5):1111–27. doi:10.1007/s11709-021-0757-1. [Google Scholar] [CrossRef]

6. Wang CM, Tay ZY. Very large floating structures: applications, research and development. Procedia Eng. 2011;14:62–72. doi:10.1016/j.proeng.2011.07.007. [Google Scholar] [CrossRef]

7. Dai J, Wang CM, Utsunomiya T, Duan W. Review of recent research and developments on floating breakwaters. Ocean Eng. 2018;158(1):132–51. doi:10.1016/j.oceaneng.2018.03.083. [Google Scholar] [CrossRef]

8. Mei CC, Black JL. Scattering of surface waves by rectangular obstacles in waters of finite depth. J Fluid Mech. 1969;38(3):499–511. doi:10.1017/s0022112069000309. [Google Scholar] [CrossRef]

9. Williams AN, Abul-Azm AG. Dual pontoon floating breakwater. Ocean Eng. 1997;24(5):465–78. doi:10.1016/S0029-8018(96)00024-8. [Google Scholar] [CrossRef]

10. Neelamani S, Rajendran R. Wave interaction with T-type breakwaters. Ocean Eng. 2002;29(2):151–75. doi:10.1016/S0029-8018(00)00060-3. [Google Scholar] [CrossRef]

11. Masoudi E. Hydrodynamic characteristics of inverse T-type floating breakwaters. Int J Maritime Technol. 2019;11:13–20. doi:10.29252/ijmt.11.13. [Google Scholar] [CrossRef]

12. Peña E, Ferreras J, Sanchez-Tembleque F. Experimental study on wave transmission coefficient, mooring lines and module connector forces with different designs of floating breakwaters. Ocean Eng. 2011;38(10):1150–60. doi:10.1016/j.oceaneng.2011.05.005. [Google Scholar] [CrossRef]

13. Masoudi E, Gan L. Diffraction waves on general two-legged rectangular floating breakwaters. Ocean Eng. 2021;235(4):109420. doi:10.1016/j.oceaneng.2021.109420. [Google Scholar] [CrossRef]

14. Ruol P, Martinelli L, Pezzutto P. Formula to predict transmission for π-type floating breakwaters. J Waterway Port Coastal Ocean Eng. 2013;139(1):1–8. doi:10.1061/(asce)ww.1943-5460.0000153. [Google Scholar] [CrossRef]

15. Sharma P, Roy R, De S. Water wave scattering by π-shaped and inverted π-shaped porous breakwaters. Cambridge, UK: Cambridge University Press; 2025. [Google Scholar]

16. Sujana Praisilin S, Gayathri R, Chandru M. Effect of trench configuration on the scattering and radiation of surface gravity waves by different floating breakwaters. Phy Fluids. 2025;37(8):087225. doi:10.1063/5.0278889. [Google Scholar] [CrossRef]

17. Rahman S, Baeda AY, Achmad A, Jamal RF. Performance of a new floating breakwater. IOP Conf Ser Mater Sci Eng. 2020;875(1):012081. doi:10.1088/1757-899x/875/1/012081. [Google Scholar] [CrossRef]

18. Lyu X, Yang Y, Mi C, Tang CM, Adeboye L, Farhan M, et al. A symmetric experimental study of the interaction between regular waves and a pontoon breakwater with novel fin attachments. Symmetry. 2024;16(12):1605. doi:10.3390/sym16121605. [Google Scholar] [CrossRef]

19. Yuan H, Zhang H, Wang G, Tu J. A numerical study on a winglet floating breakwater: enhancing wave dissipation performance. Ocean Eng. 2024;309:118532. doi:10.1016/j.oceaneng.2024.118532. [Google Scholar] [CrossRef]

20. Jain S, Bora SN. Oblique water wave scattering by a floating bridge fitted with a rectangular porous structure and the resulting waveload mitigation. Ocean Eng. 2023;275(4):114132. doi:10.1016/j.oceaneng.2023.114132. [Google Scholar] [CrossRef]

21. Hussein KB, Ibrahim M. Experimental and numerical study on the hydrodynamic performance of suspended curved breakwaters. Int J Maritime Sci Technol. 2022;69(3):123–31. doi:10.17818/nm/2022/3.2. [Google Scholar] [CrossRef]

22. El Saie Y, El Sayed A, Ehab H, Balah A. The hydrodynamic performance examination of a new floating breakwater configuration. Int J Adv Eng. 2023;9(1):1–8. doi:10.22161/ijaems.91.1. [Google Scholar] [CrossRef]

23. He Y, Han B, Han X, Xie H. Diffraction wave on the single wing floating breakwater. Appl Ocean Res. 2024;146(1):103941. doi:10.1016/j.apor.2024.103941. [Google Scholar] [CrossRef]

24. He Y, Han B, Han X, Xie H. Wave blocking performance of the symmetrical double-wing floating breakwater. Ocean Eng. 2024;303:117852. doi:10.1016/j.oceaneng.2024.117852. [Google Scholar] [CrossRef]

25. Doss A. Impact of box-type floating breakwater on motion response of hydrodynamically coupled floating platforms downstream [master’s thesis]. Delft, The Netherlands: Delft University of Technology; 2020. [Google Scholar]

26. Watanabe E, Wang CM, Utsunomiya T, Moan T. Very large floating structures: applications, analysis and design. Centre for Offshore Research and Engineering. National University of Singapore. Core report 2004-02 (2004). p. 1–30. [cited 2025 Sep 15]. Available from: https://scholar.google.com/scholar?hl=en&as_sdt=0%2C5&q=Watanabe+E%2C+Wang+CM%2C+Utsunomiya+T%2C+Moan+T.+Very+large+floating+structures%3A+applications%2C+analysis+and+design.++Centre+for+Offshore+Research+and+Engineering.+National+University+of+Singapore.+Core+report+2004-02+%282004%29.+p.++1%E2%80%9330.&btnG=. [Google Scholar]

27. Xue S, Xu Y, Xu G, Wang J, Chen Q. A novel tri-semicircle shaped submerged breakwater for mitigating wave loads on coastal bridges part I: efficacy. Ocean Eng. 2022;245:110462. doi:10.1016/j.oceaneng.2021.110462. [Google Scholar] [CrossRef]

28. Samuel SP, Gayathri R, Koley S, Muthusamy C. Motion responses with hydrodynamic factors in designing a floating breakwater and wave energy converter: a review. J Ocean Eng Mari Energy. 2025;11(1):233–63. doi:10.1007/s40722-024-00372-8. [Google Scholar] [CrossRef]

29. Lee HH, Wong SH, Lee RS. Response mitigation on the offshore floating platform system with tuned liquid column damper. Ocean Eng. 2006;33(8–9):1118–42. doi:10.1016/j.oceaneng.2005.06.008. [Google Scholar] [CrossRef]

30. Wang CM, Tay ZY. Hydroelastic analysis and response of pontoon-type very large floating structures. In: Fluid structure interaction II. Berlin/Heidelberg, Germany: Springer; 2010. p. 103–30. doi:10.1007/978-3-642-14206-2_5. [Google Scholar] [CrossRef]

31. Sun J, Jiang P, Sun Y, Song C, Wang D. An experimental investigation on the nonlinear hydroelastic response of a pontoon-type floating bridge under regular wave action. Ships Offshore Struct. 2018;13(3):233–43. doi:10.1080/17445302.2017.1356438. [Google Scholar] [CrossRef]

32. Qu K, Sun WY, Ren XY, Kraatz S, Jiang CB. Numerical investigation on the hydrodynamic characteristics of coastal bridge decks under the impact of extreme waves. J Coast Res. 2021;37(2). doi:10.2112/jcoastres-d-20-00045.1. [Google Scholar] [CrossRef]

33. Luo M, Rubinato M, Wang X, Zhao X. Experimental investigation of freak wave actions on a floating platform and effects of the air gap. Ocean Eng. 2022;253(1):111192. doi:10.1016/j.oceaneng.2022.111192. [Google Scholar] [CrossRef]

34. Khan MBM, Gayathri R, Behera H. Wave attenuation properties of rubble mound breakwater in tandem with a floating dock against oblique regular waves. Waves Rand Complex Med. 2024;34(4):2707–25. doi:10.1080/17455030.2021.1967512. [Google Scholar] [CrossRef]

35. Wu Q, Xu G, Xue S, Wang J, Li Y. Experimental and numerical investigation of combined countermeasure for mitigating tsunami forces on typical coastal T-girder bridge deck. Ocean Eng. 2023;268(6):113419. doi:10.1016/j.oceaneng.2022.113419. [Google Scholar] [CrossRef]

36. Hemanth S, Karmakar D. Hydroelastic analysis of VLFS integrated with multiple porous vertical barriers. Ships Offshore Struct. 2025;10(2):1–22. doi:10.1080/17445302.2025.2466107. [Google Scholar] [CrossRef]

37. Sharma P, Sarkar B, De S. Comparative hydrodynamic analysis of T and inverse T-shape floating breakwater in oblique wave. European J Mechan-B/Fluids. 2025;113(2):204274. doi:10.1016/j.euromechflu.2025.204274. [Google Scholar] [CrossRef]

38. Sahoo H, Gayathri R, Khan MBM, Behera H. Hybrid boundary element and eigenfunction expansion method for wave trapping by a floating porous box near a rigid wall. Ships Offshore Struct. 2023;18(8):1148–58. doi:10.1080/17445302.2022.2108227. [Google Scholar] [CrossRef]

39. Jins MM, Vijay KG, Venkateswarlu V, Behera H. Oblique wave interaction with a floating dock in the presence of inverted trapezoidal pile-rock breakwaters. Eng Anal Bound Elem. 2025;172(3):106111. doi:10.1016/j.enganabound.2024.106111. [Google Scholar] [CrossRef]

40. Wang CD, Meylan MH. The linear wave response of a floating thin plate on water of variable depth. Appl Ocean Res. 2002;24(3):163–74. doi:10.1016/S0141-1187(02)00025-1. [Google Scholar] [CrossRef]

41. Kincaid, Gary Allan. Effects of natural period upon the characteristics of a moored floating breakwater [Ph.D. dissertation]. Cambridge, MA, USA: Department of Civil Engineering, Massachusetts Institute of Technology; 1960. [cited 2025 Sep 15]. Available from: journals.cambridge.org/abstract_S0022112069000309. [Google Scholar]

42. Ji C, Bian X, Lu L, Guo J, Xu S, Lv F. 3D experimental investigation of floating breakwater with symmetrical openings and wing structures. Ocean Eng. 2024;313:119624. doi:10.1016/j.oceaneng.2024.119624. [Google Scholar] [CrossRef]

43. Ji C, Bian X, Huo F, Guo J, lian Z, Yuan Z. Experimental study on hydrodynamic characteristics of a new type floating breakwater with opening pass and wing structure. Ocean Eng. 2022;259:111923. doi:10.1016/j.oceaneng.2022.111923. [Google Scholar] [CrossRef]