Forecasting Performance Indicators of a Single-Channel Solar Chimney Using Artificial Neural Networks

1  Introduction

Nowadays, buildings are significant energy consumers, particularly for heating, cooling, and lighting. The International Energy Agency reports that the building and industrial sectors together account for more than 90% of global electricity consumption [1]. Furthermore, the construction sector accounts for 40% and 39% of total energy consumption in Europe and the United States, respectively [2,3]. Moreover, buildings account for one-third of global Greenhouse Gas emissions, which are considered a significant contributor to global warming [4]. In response, new measures for energy efficiency and conservation have been implemented worldwide to reduce energy consumption.

Building energy efficiency is a key focus of the United Nations Sustainable Development Goals [5]. Specifically, Sustainable Development Goal 7 (Affordable and Clean Energy) aims for a significant improvement in global energy efficiency by 2030. Meanwhile, Sustainable Development Goals 11 (Sustainable Cities and Communities) and 13 (Climate Action) emphasize the need to develop sustainable urban infrastructure and reduce emissions to address climate change [6]. In this line, passive systems improve the energy performance of buildings through passive and low-carbon design strategies, aligning with global efforts to promote sustainable, resilient, and low-emission communities. Additionally, energy-efficient buildings enhance indoor environmental quality and help alleviate pressure on energy infrastructure by smoothing out electricity demand peaks. The Solar Chimney (SoCh), a passive system, has emerged as an environmentally friendly and economically viable alternative to active mechanical systems [7–9]. SoCh uses solar radiation to induce natural ventilation, enhancing air circulation without mechanical assistance. This way, solar chimneys significantly improve thermal comfort while reducing energy consumption. Consequently, SoCh is becoming increasingly essential in the design of sustainable buildings, e.g., zero-energy buildings [10].

The performance of SoCh is affected by several design parameters, including height, width, depth, construction materials, and their orientation in relation to the sun [11,12]. Additionally, environmental conditions such as solar irradiance, ambient temperature, and wind speed are crucial to the design of SoCh. Therefore, accurately predicting SoCh performance across various configurations and climatic scenarios is essential for making informed design decisions [13,14]. This way, modeling the thermal and fluid-dynamic behavior of a SoCh poses significant challenges due to its inherently nonlinear and transient characteristics [15,16]. Factors such as time-dependent boundary conditions, variable heat transfer coefficients, and the complex thermophysical properties of building materials introduce significant uncertainty into the modeling process. High-fidelity simulations based on Computational Fluid Dynamics (CFD) can accurately capture complex phenomena [17,18]. However, CFD methods are often computationally intensive, making them impractical for iterative design processes or optimization under uncertainty. On the other hand, alternative methods employ optimization techniques to integrate hybrid systems, leveraging multi-objective evolutionary optimization and machine learning models, thereby significantly enhancing the efficiency, cost-effectiveness, and operational reliability of hybrid solar chimney power plants [19]. Therefore, there is growing interest in using surrogate modeling techniques or approximation methods that require fewer computational resources while maintaining accuracy comparable to CFD solutions, e.g., Global Energy Balance (GEB) models [20]. The approximation methods provide quick and reasonably accurate estimates of system behavior without requiring the solution of complex physical equations [21].

In this line of work, the main contributions of this article are: (i) the development of ANN models tailored to predict key performance indicators of Single-Channel Solar Chimneys (SC-SoCh), including ACH, FVOL, and FMAS; (ii) the integration of a comprehensive set of geometric, material, and environmental variables into a unified predictive framework; (iii) the generation and use of a novel dataset comprising 2784 SC-SoCh configurations to ensure robust generalization across diverse design and climate scenarios; (iv) rigorous validation of the ANN models against both GEB simulations and experimental data, demonstrating predictive accuracy with R2 values up to 0.990, outperforming a baseline regression method, and replacing computationally intensive simulations with near-instant forecasts that are highly practical for iterative design, rapid prototyping, and sustainable building applications. The results demonstrate that the ANN models outperform a baseline regression method and offer physically meaningful, computationally efficient alternatives for assessing solar chimney performance.

The problem addressed in this article was also studied in our previous article [21]. This article presents the following contributions: (i) an extended related work; (ii) an extended methodology based on a supervised learning-based ANN technique; (iii) a new dataset of performance indicators of SC-SoCh configurations, including ACH, FVOL, and FMAS; and (iv) a comprehensive experimental evaluation of the proposed ANN models, featuring a comparison with a linear regression model and validation against a GEB model.

This article is organized as follows: Section 2 describes the GEB model applied to SC-SoCh and describes the related work. Section 3 outlines the proposed computational intelligence approach, which utilizes a supervised learning-based ANN method, and data sources used to solve the problem. Section 4 reports the experimental evaluation of the proposed approach and discusses the results obtained. Finally, Section 5 presents the conclusions and formulates the main lines for future work.

2  Single-Channel Solar Chimney

This section describes the GEB model for the SC-SoCh performance indicators and reviews the related work.

2.1 GEB Model for SC-SoCh

An SC-SoCh can achieve significant performance indicators while maintaining minimal design complexity compared to double-channel or hybrid systems, resulting in lower computational costs for large-scale parametric studies. In addition to its modeling simplicity, the SC-SoCh offers practical advantages for architectural integration, as single-channel configurations are easier to incorporate into building facades and are less constrained by spatial or structural limitations than more complex alternatives [22]. Furthermore, the SC-SoCh effectively provides significant airflow rates with relatively straightforward construction and modeling requirements [7]. By simplifying the modeling geometry, the SC-SoCh reduces complexity, resulting in more accurate surrogate models and faster computation. Additionally, experimental prototypes reported in the literature can be used to validate the SC-SoCh design [8], allowing controlled testing and direct comparison with simulation results.

2.1.1 Summary Physical Model

The GEB model for SC-SoCh is based on our previous study [9]. The physical model of the SC-SoCh comprises several elements and envelopes, including a cover glass, an air channel, two absorber plates incorporating Phase Change Material (PCM), and thermal insulation.

Fig. 1 presents a visual summary of the physical model of the SC-SoCh, which can be described as follows. The SC-SoCh is installed on the building’s lateral side. Fortunately, the SC-SoCh can be applied in several facade or wall configurations. The amplified cross-section is presented for analysis of its functioning. The solar chimney is exposed to incident solar radiation (αg∗ Gsolar), convective gains with the environment due to high level of outdoor temperature (Tout), and the radiative transfer with the sky which its temperature (Tsky) depends on the outdoor conditions and the cloudiness. Then, in the physical model the heat exchange by natural convection through outdoor air (qconv−out) and radiative exchange with the sky (qrad-out) due to the temperature difference between the glass cover and the sky (Tsky>Tg) are evaluated through the mathematical model proposed, these termal gains are the principal energy source for the SC-SoCh to induce natural ventilation. The heat is conducted through the external glass cover (Hxg represents the glass cover thickness) into the air channel (qcond). Inside the channel, there is heat convection due to the air channel (qconv) resulting from the temperature difference between the glass cover and the air channel (Tg>Tf), and the heat convection is also present between the air channel and the absorber plate. Meanwhile, there is radiative Exchange between the glass cover Surface and the absorber plate surface (qrad,g−p). The convective transfer and radiative exchange between the air channel and the glass cover are independent effects of the absorption of the solar radiation transmitted by the glass cover (αp∗τg∗Gsolar), which is the main thermal gain to increase the temperature of the absorber plate and, subsequently, increase the temperature change inside the air channel.

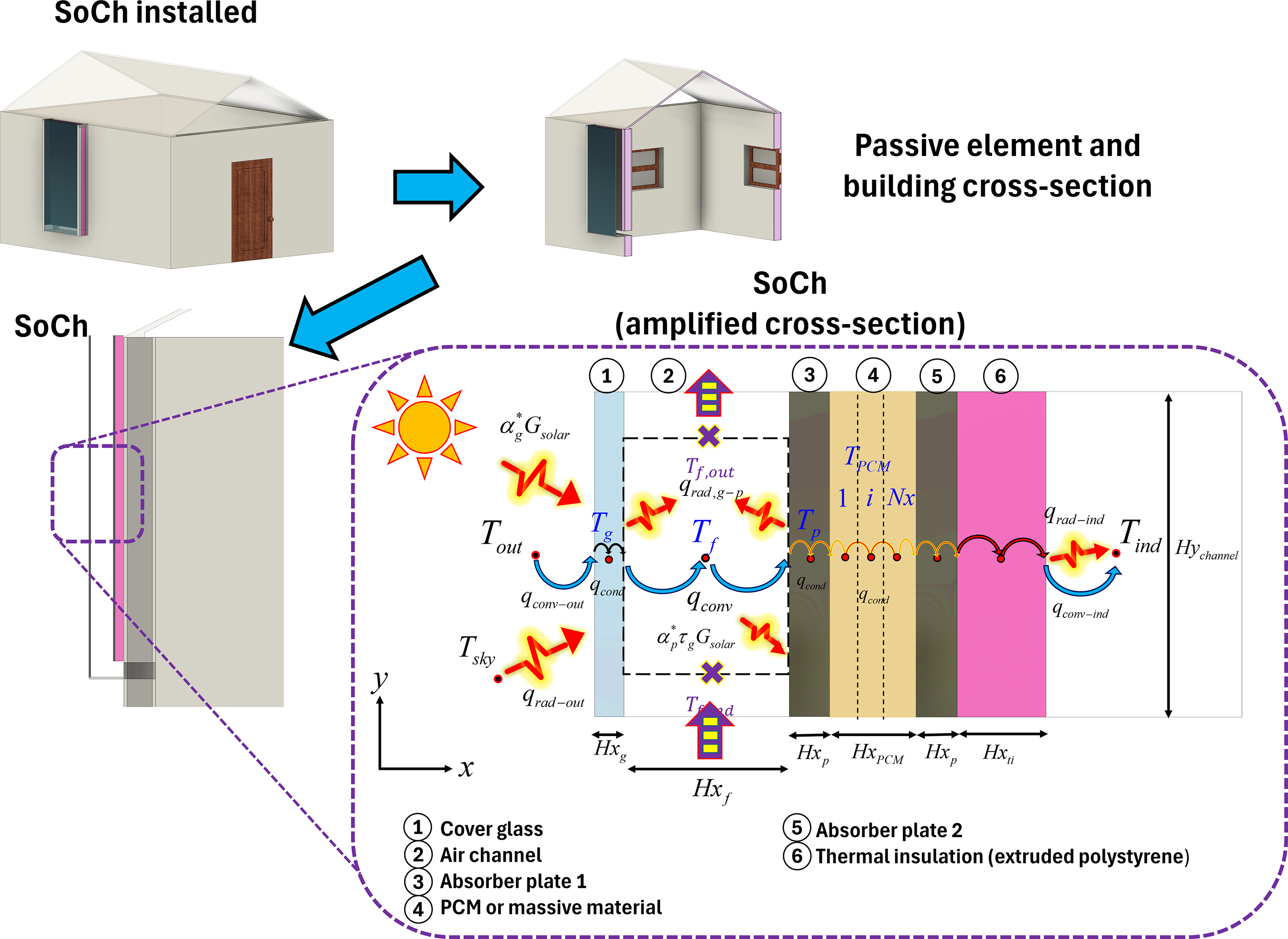
Figure 1: Physical model of a solar chimney

From indoors, the physical model works as follows. From the air channel of the SC-SoCh to the building the heat is transferred through the absorber plate (with thickness Hxp), the PCM or massive material (which can be conformed of several layers and has a thickness of HxPCM), the absorber plate 2 (with thickness Hxp) and the thermal insulation (with thickness Hxti). Then the heat is transferred to the inner part of the building by convection through air (qconv−ind) and radiation (qrad−ind) due to the temperature difference between indoor and the thermal insulation (Tind<Tins). Hy represents the height of the channel. The installation of PCM is needed to increase thermal storage and extend ventilation time during the night shift. The use of PCM increases sensible heat storage and permits latent heat storage. The induced ventilation results from all the effects described.

2.1.2 Mathematical Model

Unlike previous studies that only examined south or west orientations [9,23], the current GEB model permits any cardinal orientation of the SC-SoCh. Additionally, the GEB model evaluates heat transfer at any time step, as the heat transfer mechanism has been assessed in an unsteady state. The GEB model evaluates heat transfer along the air channel using a two-dimensional approach, whereas other elements adopt a one-dimensional analysis. The GEB model is validated with data from a SC-SoCh prototype developed under controlled conditions. Next, each component of the GEB model is described.

Glass cover (g): Eq. (1) represents the heat transfer through the thin glass cover, with the j subscripts denoting a node in the y−direction due to the two-dimensional effect in the air channel. Eq. (1a) defines the heat transfer process occurring through the thin glass cover, and Eq. (1b) describes the thermal resistance associated with each heat transfer process. The glass cover absorbs only a proportion of incident solar radiation (αg∗ Gsolar), the radiation emitted by the absorber plate (qrad,g−p), the heat exchange by natural convection to outdoor air (qconv−out) and radiative exchange to the sky (qrad-out). In contrast to the models proposed by Ong [24] and Tariq et al. [23], this model incorporates heat conduction in thin layers (qcond,g). R denotes the thermal resistance derived from the analogy of the law of Kirchhoff for electrical circuits; the subscript of every R in Eq. (1b) refers to the phenomenon evaluated in the energy balance.

qcond,g+qconv−out+qrad-out+qrad,g−p1+αg∗ Gsolar=ρg,jCP,g,jHxg,jdTg,jdt(1a)

(Text−Tg,j)(Rconv−out+Rcond,g)Ag,j+(Tsky−Tg,j)(Rrad-out)Ag,j+αg∗GsrAg,i−(Tg,j−Tf,j)(Rcond,g+Rconv,g)Ag,j−(Tg,j−Tp1,j)(Rrad,g−p1)Ag,j=(ρg,jCP,g,jHxg,jAg,j)dTg,jdt(1b)

Air channel (f): Eq. (2) describes the GEB of the air channel. The GEB model considers the natural convection between the glass cover and metal plate (qconv,g−f and qconv,f−p1) along the height of the channel through the mass flow rate effect (m˙CPfTf). The air is a transparent medium for the radiative exchange in the air channel. The thermal resistances Rconv are determined as a function of flow regime (laminar or turbulent) from the experimental correlations reported in the literature [9].

qconv,g−f+m˙inletCPf,inletTf,ind+qconv,f−p−m˙outCPf,outTf,out=ρf,jCP,f,jHxf,jdTf,jdt(2a)

(Tg,j−Tf,j)(Rcond,g+Rconv,g−f)Ag,j+m˙inletCPf,inletTf,inlet−(Tf,j−Tp1,j)(Rconv,f−p1+Rcond,p1)Ap1,j−m˙outCPf,outTf,out=(ρf,jCP,f,jHxf,jAf,j)dTf,jdt(2b)

Metal plate 1 (p1): p1 is part of the container of the absorber plate, which is a thermal massive material or phase change material (PCM), a metal sheet with high thermal conductivity to improve the thermal storage. The GEB model for the p1 considers the heat conduction (qcond,p1), the absorption of the solar radiation transmitted by the glass cover (αp∗τg∗Gsolar), the heat convection with the air channel (qconv,f−p) and the radiative exchange to the glass cover (qrad,g−p). Eq. (3) describes the heat transfer with the air channel and the PCM.

qconv,f−p1+qcond,p1+qrad,g−p1+αp∗τg∗Gsolar=ρp1,jCP,p1,jHxp1,jdTp1,jdt(3a)

αp1∗τg∗GsrAp1,i+(Tf,j−Tp1,j)(Rconv,f−p1+Rcond,p1)Ap1,j+(Tg,j−Tp1,j)(Rrad,g−p1)Ap1,j−(Tp1,j−TPCM,j)(Rcond,p1+Rcond,PCM)Ap1,j=(ρp1,jCP,p1,jHxp1,jAp1,j)dTp1,jdt(3b)

Absorber plate (PCM): The absorber plate is the only element in the GEB model that requires more nodes, enabling the model to store thermal energy. The PCM in the absorber plate stores latent and sensible heat as only sensible energy. In this context, the number of nodes to be applied was evaluated in a previous analysis similar to a grid independence analysis. The GEB model divides the materials of the physical model (Fig. 1 ) into 21 distinct nodes. The PCM equation considers only heat conduction (qcond,PCM) due to the arrangement of layers. The “effective” specific heat (CP,eff) method is employed to account for latent and sensible heat storage during heat transfer processes. Eq. (4) describes the GEB of the PCM, and Eq. (5) describes the “effective” specific heat (CP,eff), which considers the temperature of solid and liquid phase (Tliq, Tsol), the specific heat of solid and liquid phase (CP,liq, CP,sol), and the phase change enthalpy (hls). If the material stores only sensible heat, the “effective” specific heat is a constant value and the relations presented in Eq. (5) are not required. The specific heat is used to calculate the PCM or absorber material’s thermal diffusivity (αPCM), a parameter of the SC-SoCh analyzed for forecasting. Eq. (4) is split into three equations for three possible locations (PCM1, PCMi, and PCMNx); these equations correspond to a multilayer method for analyzing thick materials. Eq. (6) describes the thermal diffusivity (αp) calculated for the absorber plate.

qcond,PCM=ρPCM,jCP,eff,PCM,jHxPCM,jdTPCM,jdt(4a)

(Tp1,j−TPCM1,j)(Rcond,p1+Rcond,PCM1)APCM1,j−(TPCM1,j−TPCM2,j)(Rcond,PCM1+Rcond,PCM2)APCM1,j=(ρPCM1,jCP,PCM1,jHxPCM1,jAPCM1,j)dTPCM1,jdt(4b)

(TPCMi−1,j−TPCMi,j)(Rcond,PCMi−1+Rcond,PCMi)APCMi,j−(TPCMi,j−TPCMi+1,j)(Rcond,PCMi+Rcond,PCMi+1)APCMi,j=(ρPCMi,jCP,PCMi,jHxPCMi,jAPCMi,j)dTPCMi,jdt(4c)

(TPCMNx−1,j−TPCMNx,j)(Rcond,PCMNx−1+Rcond,PCMNx)APCMNx,j−(TPCMNx,j−Tp′′,j)(Rcond,PCMNx+Rcond,p2)APCMNx,j=(ρPCMNx,jCP,PCMNx,jHxPCMNx,jAPCMNx,j)dTPCMNx,jdt(4d)

CP,eff,p,j=CP,sol−CP,liq2+hlsTsol−Tliq(5)

αPCM=λPCM,jρPCM,jCP,eff,PCM,j(6)

Metal plate 2 (p2): p2 is the right side of the container for the thermal massive material or PCM. The GEB model for p2 considers the heat conduction (qcond,p2) with the PCM and the thermal insulation. Eq. (7) describes the heat transfer phenomenon.

qcond,p2=ρp2,jCP,p2,jHxp2,jdTp2,jdt(7a)

(TPCMNx,j−Tp2,j)(Rcond,PCMNx+Rcond,p2)Ap2,j−(Tp2,j−Tti,j)(Rcond,p2+Rcond,ti)Ap2,j=(ρp2,jCP,p2,jHxp2,jAp2,j)dTp2,jdt(7b)

Thermal insulation (ti): The GEB model of thermal insulation is expressed in Eq. (8). Thermal insulation considers the heat conduction with the metal plate which is the next element (qcond,ti), the heat convection with the indoor air of the building room (qconv,ti−ind) and the radiative exchange with the indoor air (qrad,ind).

qcond,ti+qconv,ti−ind+qrad,ind=ρti,jCP,ti,jHxti,jdTti,jdt(8a)

(Tp2,j−Tti,j)(Rcond,p2+Rcond,ti)Ati,j−(Tti,j−Tint)(Rcond,ti+Rconv−int)Ati,j−(Tti,j−Tint)(Rrad−int)Ati,j=(ρti,jCP,ti,jHxti,jAti,j)dTti,jdt(8b)

2.2 Related Work

A solar chimney is an essential feature in sustainable building design, as it enhances ventilation without requiring mechanical energy. SoCh operates exclusively on renewable solar heat; it does not consume electricity for fans. As a result, SoCh provides a cost-effective, low-carbon solution for improving indoor environmental conditions. In literature, research in SoCh has demonstrated that passive systems effectively remove indoor pollutants and introduce fresh air, thereby improving indoor air quality. SoCh operates reliably in sunny climates without requiring an external power supply [25]. This way, SoCh provides a passive strategy that promotes natural ventilation and thermal comfort in buildings. Next, recent related work is described.

In recent years, researchers have increasingly applied Artificial Intelligence (AI) techniques to optimize SoCh performance. Several studies have demonstrated that a hybrid workflow combining physics-based simulations with AI can forecast the complex behavior of systems. A standard methodology involves first generating a dataset of SoCh performance results utilizing validated simulations (e.g., CFD or GEB models) or experimental data. Then, AI models learn the relationships between design input variables and performance indicators for forecasting. Then, AI models serve as predictive surrogates, enabling the rapid evaluation of new designs without the need for numerous simulations. For instance, Mandal et al. [26] implemented an approach by conducting a series of CFD simulations on a prototype SoCh power plant with different geometric configurations. The approach used the performance indicators of the SoCh power plan to train an ANN model that could then predict the power plant’s performance across different geometries. The proposed approach highlights the potential of ANN tools for solar chimney design.

Tariq et al. [27] developed a digital twin model for a SoCh ventilation system in a building. The proposed model used a multilayer perceptron ANN trained on a dataset (derived from simulations or experiments) to predict key performance indicators such as the number of ACH delivered by the SoCh, as well as metrics of energy efficiency and environmental impact under different design and climate scenarios. The ANN significantly outperformed a traditional multivariate regression model in predictive precision, achieving higher coefficients of determination (R2) and lower errors effectively. Then, the ANN predictions were used to perform a multi-objective optimization of the SoCh design by coupling the ANN with a Non-dominated Sorting Genetic Algorithm II as a decision-making procedure. The experimental evaluation used a SoCh geometry across four climatic zones, aiming to maximize ventilation and energy efficiency while minimizing environmental impact. Results showed that ACH improved by 71%–87% compared to the baseline design, without the addition of any additional energy source. The proposed approach presented a solution for the rapid exploration of SoCh design alternatives.

Ali et al. [28] explored the optimization of conventional chimney designs by integrating a SoCh with a humidification system that utilizes water spray for evaporative cooling in a hot climate, specifically in Kirkuk, Iraq. The experiments and CFD simulations demonstrated that water spray cooling reduces the incoming air temperature by 5∘C to 10∘C, resulting in significantly improved summer comfort. However, increased humidity reduced air buoyancy, resulting in lower airflow rates. Experimental analysis showed that the optimal chimney height was approximately 0.5 m, which maximized the ACH before the adverse effects of moisture became problematic. To enhance the design process, a multilayer perceptron ANN was applied to predict indoor ACH and room temperature based on design variables, including water spray rate and chimney dimensions (height and width). The results demonstrated that the ANN achieved robust accuracy, with high regression coefficients (R2≈0.9566 for ACH and 0.9505 for room temperature), when compared with the CFD data. The proposed method provided valuable guidance for the design and control of evaporative-cooled solar chimney systems.

Xiao et al. [29] proposed an AI technique that integrates thermal energy storage using PCM to improve the performance of a SoCh. The proposed strategy was implemented through transient numerical simulations of a building that incorporated PCM in its envelope, combined with an enhanced ventilation strategy that increased airflow during peak thermal load periods. An ANN was trained to learn the complex heat transfer characteristics of the PCM-augmented SoCh system. Key performance metrics, including wall and roof surface temperatures and cooling load reductions, were analyzed. The results indicated that the ANN closely matched the detailed simulation outcomes, achieving coefficients of determination of 0.991 for wall temperature predictions and 0.979 for roof temperature predictions. The proposed strategy demonstrated that the ANN effectively captured the intricate thermal behavior resulting from the interaction between PCM and ventilation. Furthermore, the ANN was able to predict indoor comfort benefits and energy savings for various PCM deployment scenarios without the need to perform time-consuming simulations for each case.

Barghi Jahromi et al. [30] developed a hybrid solar air ventilator that combines a Trombe wall with a SoCh and incorporates PCM to enhance natural ventilation in buildings. An ANN with a 2-4-1 architecture was used to predict the outlet air velocity of the SoCh under various conditions, comparing scenarios with and without the PCM in operation. The ANN predictions showed a strong correlation with experimental measurements (R2> 0.96) and a low relative error <2.8%. Additionally, an evolutionary polynomial regression model demonstrated even slightly higher accuracy (R2> 0.99), although the performance difference between the evolutionary polynomial regression and ANN models was minimal. Results showed the sustainability benefits of PCM-enhanced SoCh, demonstrating that ANNs accurately estimate the performance improvements achieved by incorporating thermal storage into passive ventilation systems.

Tariq et al. [31] extended the digital twin concept to include a double-skin façade that incorporates a SoCh and PCM for building cooling. The double-skin SoCh is a complex system where the cavity between the façade layers acts as a solar-heated chimney, while the PCM provides thermal storage to smooth out temperature fluctuations. An aANN model was used for a detailed physical simulation of the system. However, the high-fidelity simulation of a double-skin façade with PCM is computationally expensive. Experimental analysis showed that the ANN significantly reduces computation time while maintaining high accuracy. The ANN accurately estimated the performance indicators of the physical model, achieving R2 values ranging from 0.921 to 0.999 across various performance metrics. Furthermore, the ANN was employed within a multi-objective optimization framework, allowing the identification of optimal design settings for the double-skin façade that balance natural ventilation, thermal comfort, and energy efficiency.

The literature review identified a growing interest in AI techniques, particularly ANNs, for predicting SoCh performance. ANN models have shown better computational efficiency than CFD and other surrogate models, significantly reducing computation time. Additionally, ANN models offer scalability and generalization through their learning strategies, enabling them to predict the performance of solar chimneys for new configurations without re-running simulations across diverse design and climate scenarios. The performance of solar chimneys depends on complex, nonlinear interactions among geometry, materials, and environmental conditions. This way, ANNs are particularly well-suited for modeling nonlinear systems, often outperforming regression models in terms of accuracy and precision. In this line of work, this article presents an ANN-based approach for forecasting SC-SoCh’s performance indicators. The next section describes the proposed ANN approach.

3  The Proposed Approach for Forecasting the Solar Chimney Performance

This section describes the proposed computational intelligence approach for forecasting the SC-SoCh’s performance indicators. A supervised learning-based ANN method is introduced for predicting the performance indicators. Finally, the considered dataset is described, along with a detailed description of the preparation process.

3.1 Artificial Neural Networks for Regression Problems

An Artificial Neural Network is a nonlinear computational model inspired by the structure and function of the human brain. ANN is a machine learning technique composed of layers of interconnected nodes, called neurons, which process data by learning patterns and relationships, providing a dynamic, adaptable, and increasingly intelligent system. Neurons communicate with one another by transmitting information through activation signals along specific, directed connections. This way, ANN enables machines to perform tasks such as natural language understanding, image recognition, and decision-making. The learning mechanism in ANNs offers a practical approach for training multilayer feedforward networks. A widely used learning algorithm is backpropagation, a supervised learning algorithm. The backpropagation algorithm trains feedforward neural networks, especially multilayer perceptrons, by minimizing the difference between the ANN’s predicted output and the target output.

An ANN consists of an input layer, one or more hidden layers, and an output layer. Each neuron in the ANN is connected to the neurons in the previous layer through adjustable synaptic weights. The knowledge within the ANN is stored as a set of connection weights associated with specific neurons. During training, the connection weights are updated using a learning algorithm, such as the backpropagation algorithm. The ANN learns from labeled data in the input dataset by comparing the actual output with the estimated output it generates. It then adjusts the weights of the neurons until the difference between the real and estimated data is minimized. The difference in error is managed by a loss function that is associated with the ANN [32].

ANN techniques are particularly valuable for regression problems, where the goal is to predict a continuous output, especially in real-world scenarios with complex, nonlinear relationships between inputs and outputs. ANNs approximate any continuous function given an appropriate architecture with enough layers, neurons, and activation functions [33].

3.2 Data Sources

The research studied data from numerical simulations and meteorological observations. The GEB model uses parameter data related to physical properties, thermodynamics, and geometry. The GEB model was first used to run a parametric study covering 2784 SC-SoCh configurations. We performed each configuration using meteorological conditions for Mexico City, and we recorded the GEB outputs (air changes per hour, volumetric flow rate and mass flow rate). From these GEB runs, we constructed a single, consolidated dataset comprising selected SC-SoCh geometric/thermophysical parameters, as well as meteorological features. Geometric parameters included the chimney height (Hyf), air channel thickness (Hxf), and glass thickness (Hxg). Material properties comprised the absorptance of the surface coating (αP∗) and thermal diffusivity (αPCM∗) of the absorber plate; the materials considered for the absorber plate that stores only sensible heat were aluminum sheet metal, brick, concrete, while the PCM evaluated were RT25-HC, RT28-HC, RT35-HC, RT42, Mg29 and parafine 46–50. Fig. 2 shows the property values considered for the parametric study with the GEB model. In addition, climatic data were considered, including ambient temperature (Text,m), solar irradiance (Gsolar,m), relative humidity (RHm), wind speed (Vwind,m), atmospheric pressure (Patm,m), the evaluated day of the year (Nday,m), and chimney orientation (Orientation). Climatic data were obtained from a meteorological station operated by the National Water Commission (CONAGUA) in Mexico City. The data were averaged daily to reflect the typical conditions for each day from 01 January to 31 December 2024. The average data ensured temporal consistency between the environmental inputs and the thermal performance predictions of the solar chimney model. This way, the GEB model performs detailed physical simulations using a broader set of thermodynamic and geometric variables.

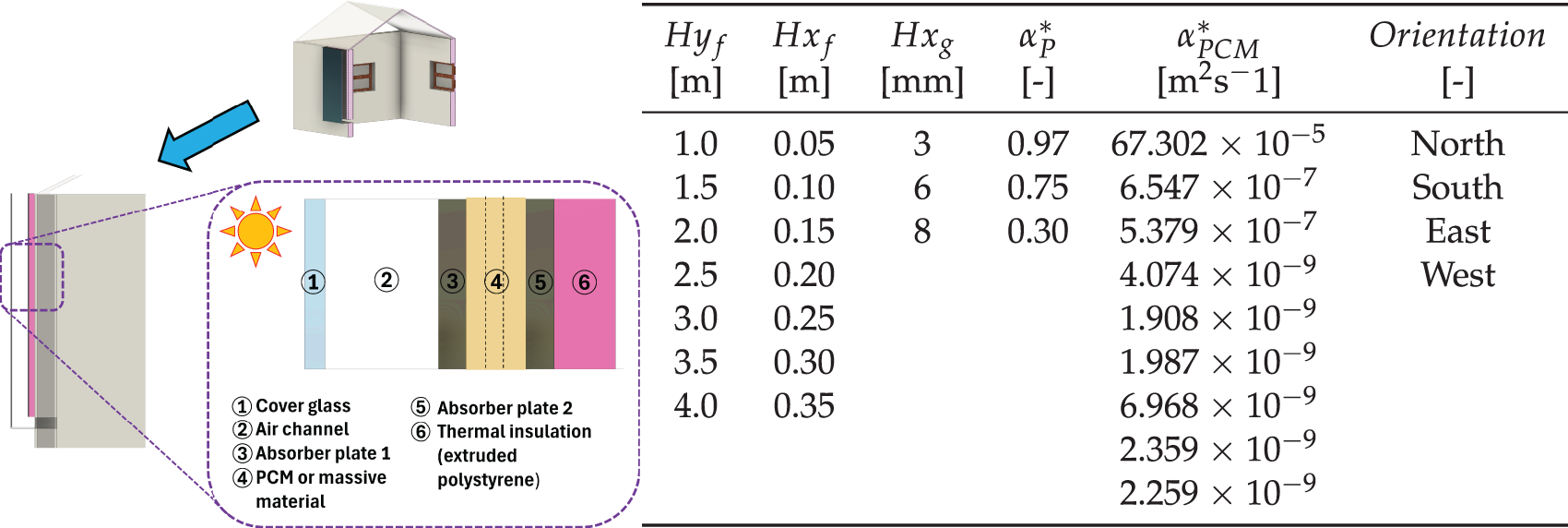
Figure 2: SC-SoCh components modeled and material properties

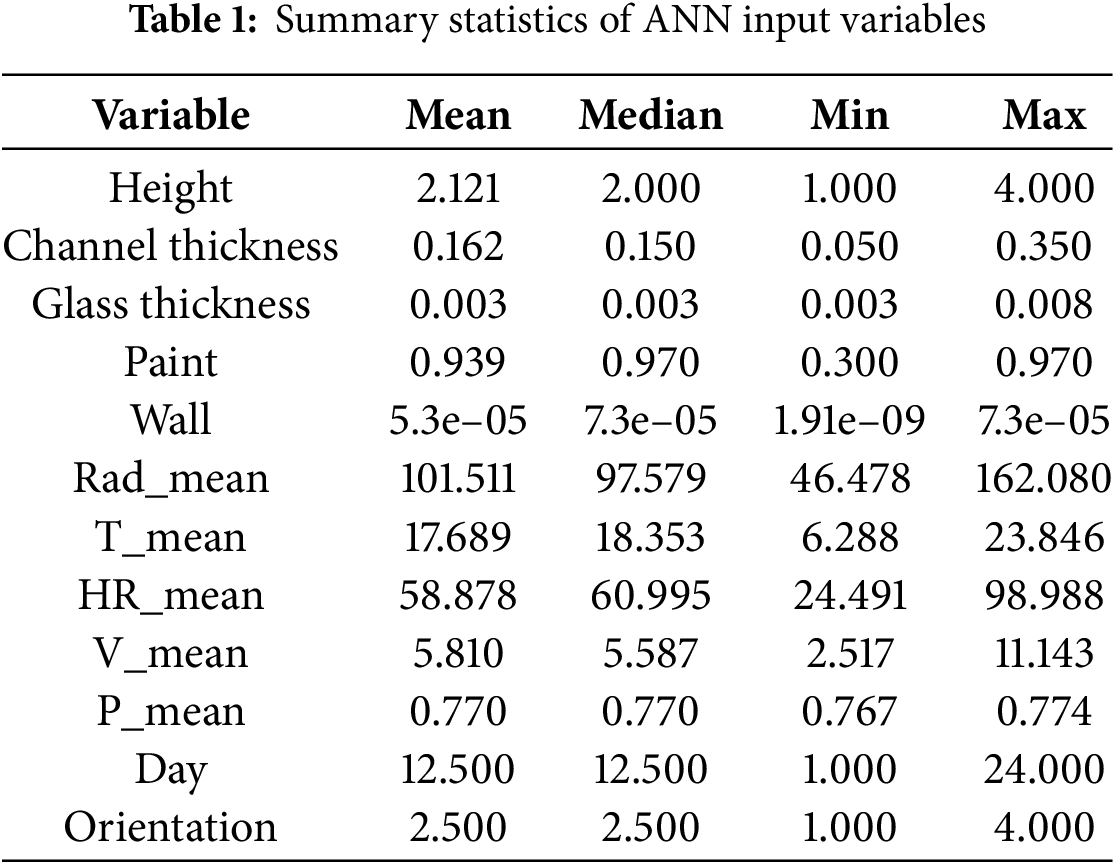
The ANN model uses a simplified and normalized dataset of 12 variables derived from GEB simulations and meteorological data. These variables form the input vector utilized to train the ANN for each solar chimney configuration. The dataset is used to simulate the environmental conditions necessary for forecasting performance indicators, i.e., ACH, FVOL, and FMAS. The variables are: i) Height, which refers to the height of the SoCh; ii) Channel thickness, which refers to the thickness of the air channel in the SoCh; iii) Glass thickness, which refers to the thickness of glass used in the SoCh; iv) Paint, which refers to the absorptivity of the surface coating applied to the absorber plate; v) Wall, which refers to the kind of material used for the absorber wall, e.g., brick, concrete; vi) Rad_mean, which refers to the solar irradiance for the evaluated day, averaged from meteorological data; vii) T_mean, which refers to the mean ambient temperature for the evaluated day; viii) HR_mean, which refers to the mean relative humidity for the evaluated day; ix) V_mean, which refers to the mean wind velocity for the evaluated day; x) P_mean, which refers to the mean atmospheric pressure for the evaluated day; xi) Day, which refers to the specific day of the year, and xii) Orientation, which refers to the cardinal direction of the solar chimney. The labeled data used for training and validating the supervised learning approach vary from 2784 SC-SoCh configurations. Table 1 presents the summary statistics for each numeric variable in the dataset.

3.3 Data Preparation

The available data was pre-processed to analyze historical conditions from 2024. The dataset includes the dimensions of the SC-SoCh, properties of the absorber plate, and meteorological data from Mexico City. Variables were pre-processed using a parametric study based on transient simulations conducted with the GEB model. The GEB model incorporated temperature and humidity-dependent properties of construction materials and established boundary conditions. It accounted for the effects of ambient temperature, atmospheric pressure, and relative humidity on air density while treating the air as a non-participating medium. The enthalpy data for PCM corresponding to the phase transition range were utilized as reported in the literature. The set of configurations was defined based on commonly reported ranges for SoCh: chimney heights from 1 to 4 m, air channel thicknesses from 0.05 to 0.35 m, glass thicknesses from 0.003 to 0.008 m, surface absorptance of the absorber plate ranging from 0.30 to 0.97, and thermal diffusivity values varying between 1.91×10−9 and 7.30×10−5 m2/s.

The ANN model was then trained using a labeled dataset derived from these GEB simulations. Each simulation combined geometric, material, and environmental variables to compute the performance indicators (ACH, FVOL, FMAS). While surrogate models typically employ uniform or random distributions to enforce independence among input variables, this study utilized environmental variables sourced from real meteorological data, which naturally exhibit correlations, and design variables that incorporated practical dependencies reflecting realistic construction choices. The SoCh data were analyzed to identify the most significant changes across variables. Fig. 3 shows the correlation matrix of the input variables used in the ANN model.

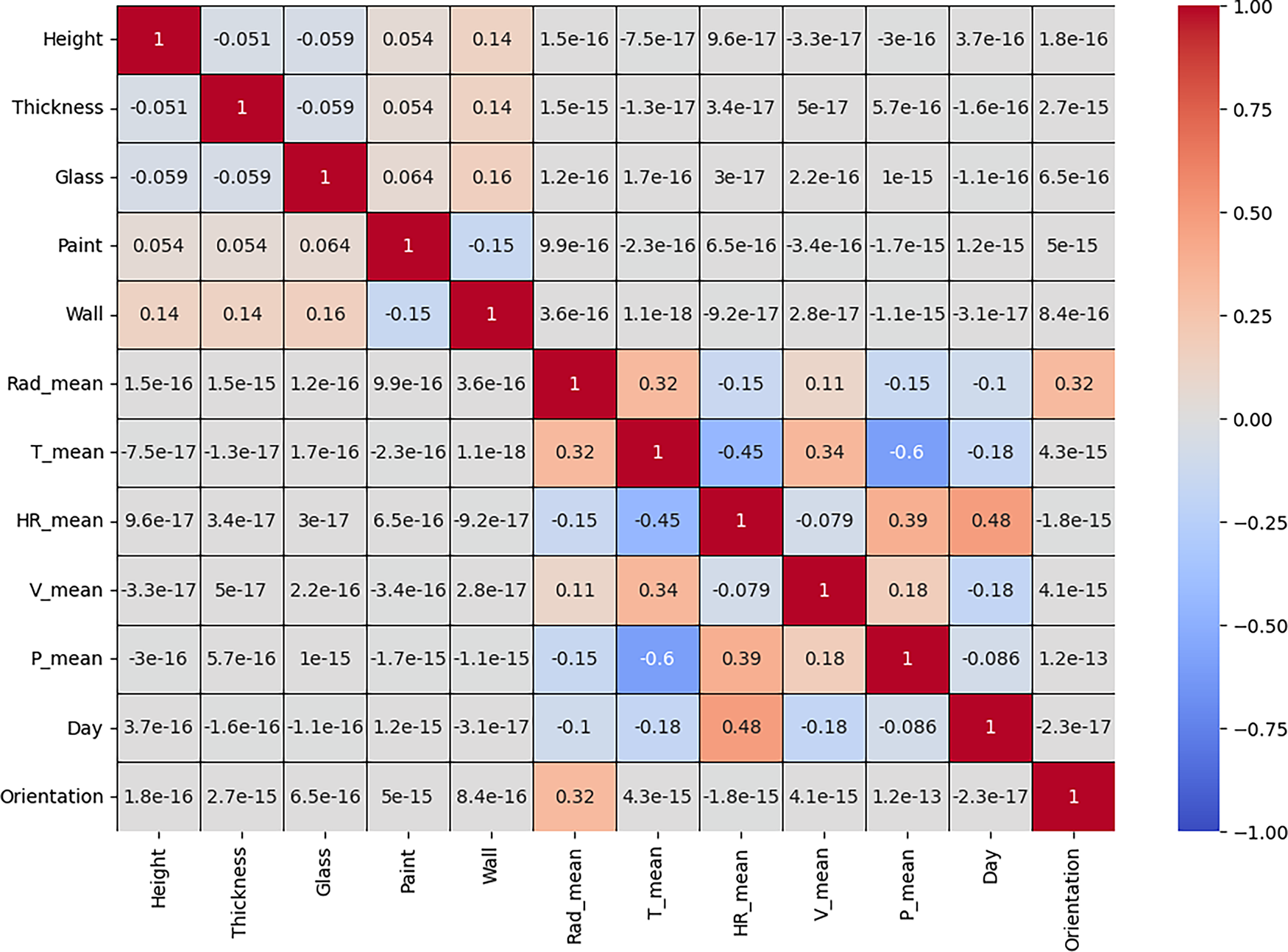
Figure 3: Correlation matrix of the input data

Fig. 3 revealed several statistically significant Pearson correlation coefficients among all the input features. The important relationships between variables that influence the design and performance of the ANN model are: Paint–Wall, with a correlation coefficient of -0.15, T_mean–HR_mean, with a correlation coefficient of -0.45, T_mean–P_mean, with a correlation coefficient of -0.60, and Day–V_mean, with a correlation coefficient of +0.48. The correlation coefficient values indicate moderate to strong linear relationships, particularly between T_mean and P_mean, demonstrating a strong negative correlation.

The simulation time step for the GEB model was set to 30 s. The cardinal directions, North, South, East, and West, were represented by the values 1, 2, 3, and 4, respectively. The selected days for evaluation were the warmest and coldest of each month, yielding a total of 24 representative days for the year. This approach preserved climatic variability while keeping dataset size manageable.

3.4 Supervised Learning Regression Algorithm

The supervised learning regression algorithm is trained using labeled data, indicating the performance indicators AHC, FVOL, and FMAS used in each SC-SoCh configuration. The proposed algorithm applies four steps:

1.   Determine the performance indicators ACH, FVOL, and FMAS related to each SC-SoCh configuration through the GEB model.

2.   Create three datasets, one for each performance indicator.

3.   For each performance indicator, a vector with 12 variables is built, featuring the following characteristics: chimney height, channel thickness, glass thickness, paint, wall material, temperature, radiation, relative humidity, wind velocity, atmospheric pressure, day of the month, and orientation. A matrix with the row vectors for each SC-SoCh configuration is used to train the supervised learning regression algorithm.

4.   An ANN is proposed as a regression algorithm with an input layer comprising 12 neurons, corresponding to the 12 features of the SC-SoCh configuration and the performance indicator value. Three to four hidden layers with varying numbers of neurons, each utilizing the Rectified Linear Unit activation function, were implemented. The output layer consisted of a single neuron with a Linear activation function for every performance indicator.

The diagram in Fig. 4 presents the flowchart of the supervised regression algorithm. The model inputs include the SC-SoCh configuration for each performance indicator.

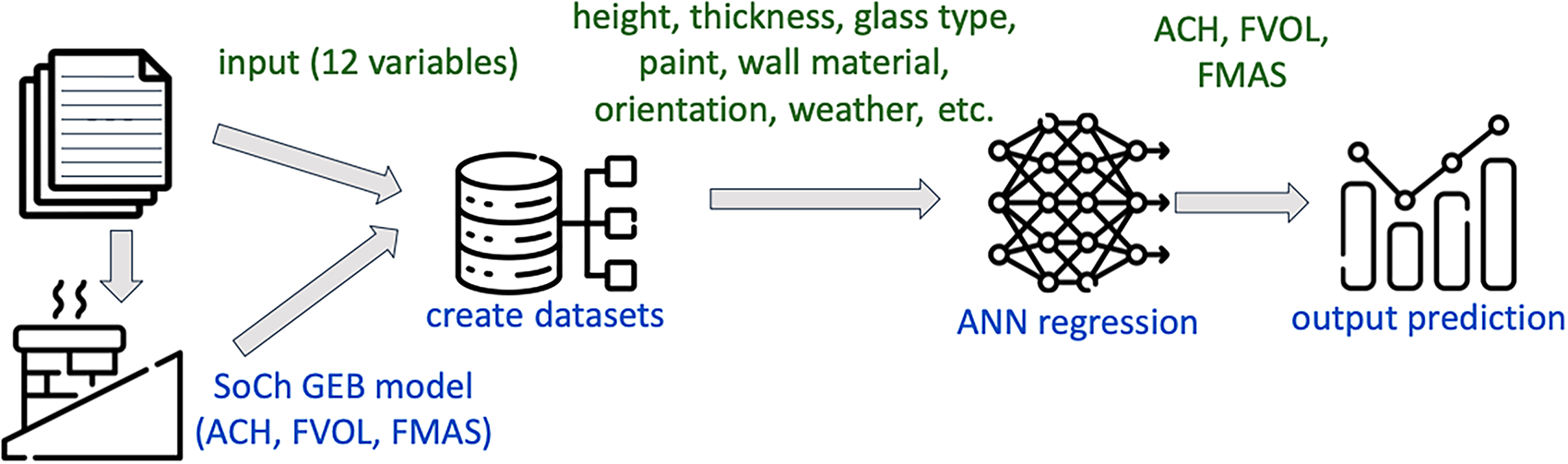
Figure 4: Flowchart of the supervised regression algorithm

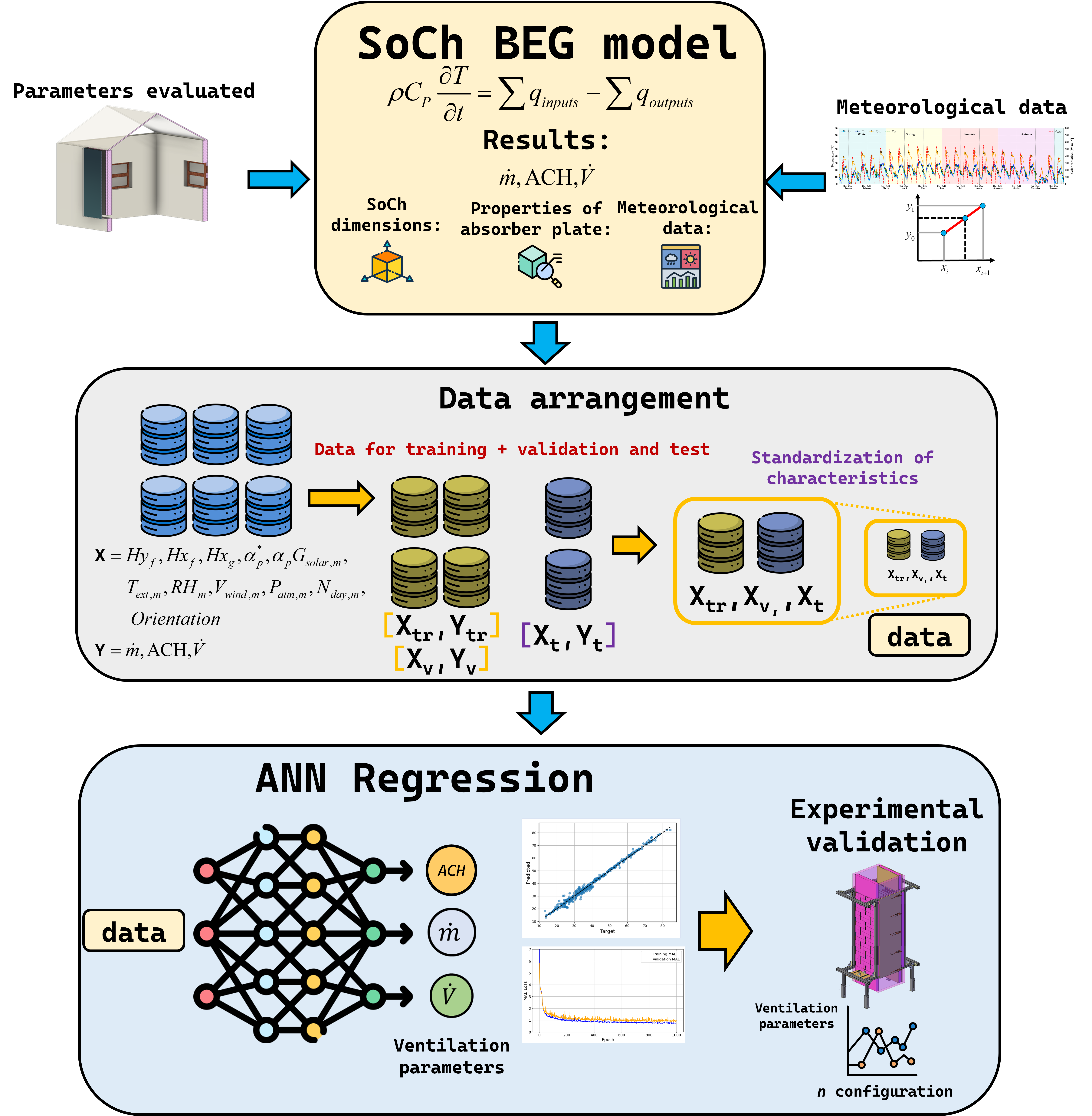
Twelve input features were normalized using a standard scaling method during both the training and testing processes. The normalization method was implemented to enhance model convergence and to prevent variables with larger numeric ranges from dominating the results. Fig. 5 shows the complete methodology employed for the proposed ANN approach in forecasting the performance of the SC-SoCh system.

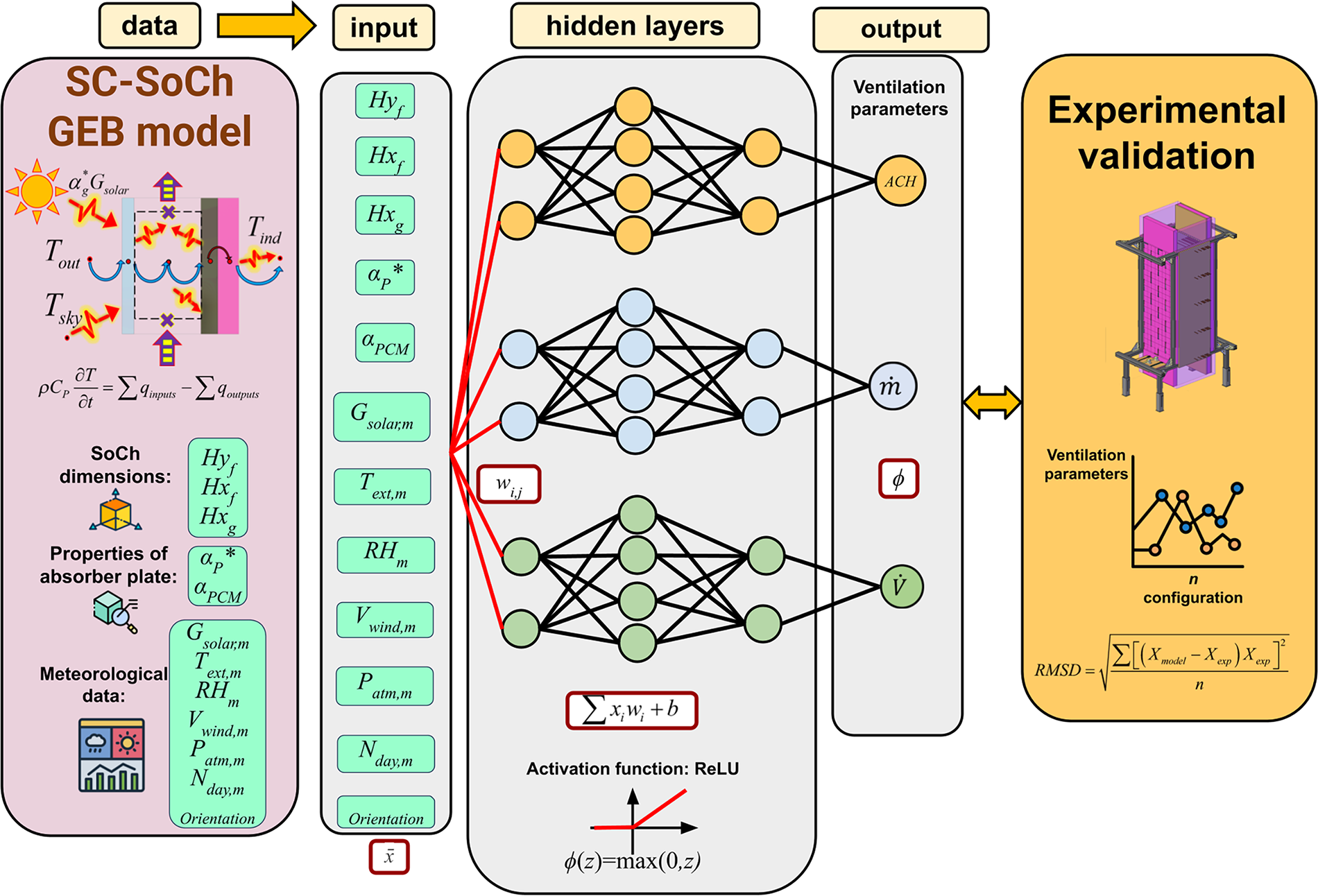
Figure 5: Methodology of the proposed ANN approach

Fig. 5 illustrates the comparison of the ANN output with experimental data obtained from a full-scale prototype of the SC-SoCh. The comparison evaluates the accuracy of the proposed ANN model and the underlying GEB simulations. By comparing the ANN predictions with real-world performance metrics, the study verifies the predictive capabilities of both the ANN and the simulation model. It ensures that the trained ANN model reflects physically meaningful behavior and provides reliable predictions across various configurations and environmental conditions.

The next section presents the experimental analysis and discusses the results.

4  Experimental Analysis and Discussion

This section describes the evaluation of a computational intelligence technique and discusses the results for forecasting performance indicators of an SC-SoCh.

4.1 Development and Execution Platform

The GEB model was developed in ANSI C and compiled with GCC 7.5.0. The supervised learning regression algorithm was implemented in Python, utilizing scientific libraries such as Pandas, Matplotlib, and NumPy. The ANN was developed, trained, and evaluated with TensorFlow. The experimental evaluation was performed on an Intel(R) Xeon(R) Gold 6138 processor (20 cores) with 124 GB of RAM at the National Supercomputing Center (Cluster-UY), Uruguay.

The GEB model has been previously validated against experimental data [8], showing deviations below 12% under controlled conditions. Therefore, it is considered reliable for generating the dataset used to train the ANN.

4.2 Hyperparameter Tunning

The parameter tuning was performed using the Grid Search method. Grid search is a brute-force method that identifies the best hyperparameter configuration in the architecture search space for machine learning models [34]. Grid Search evaluates different combinations of hyperparameters of the training algorithm to find the optimal combination that yields the best model performance.

Hyperparameter testing is performed separately for each performance indicator (ACH, FVOL, and FMAS) of the SC-SoCh. It is necessary due to the distinct output ranges and physical behaviors of each indicator. Additionally, ANNs are sensitive to scale and the output domain, such as hours, cubic meters per second, or kilograms per second. Additionally, the performance indicators exhibit different physical dependencies and respond differently to inputs such as temperature, pressure, and radiation. A single hyperparameter set does not effectively capture the nuances. Additionally, the normalization process is recommended because a dataset without normalization affects the scale of the output data, which in turn affects the model, prioritizing the reduction of errors in variables with the largest scale, leading to poor performance in the ANN.

Table 2 provides a statistical comparison of the ACH, FVOL, and FMAS target variables from the SC-SoCH datasets, including the median, first and third quartiles, interquartile range (IQR), minimum, and maximum.

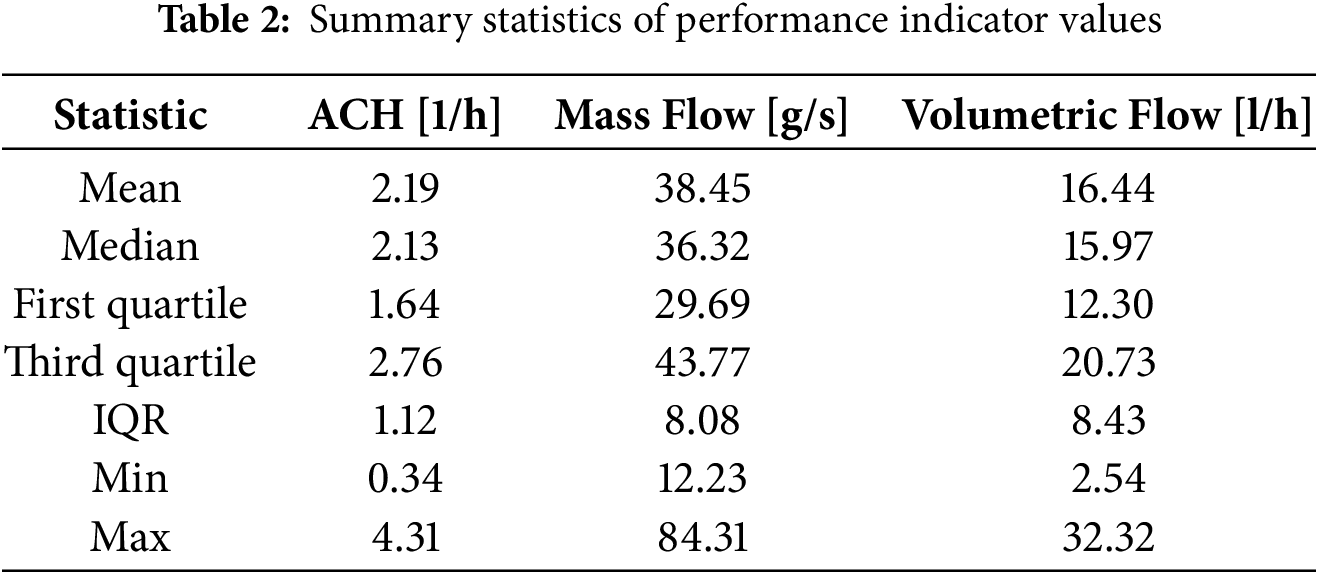
Table 2 shows different output ranges for performance indicators. The varying scales of output affect the learning process of the ANN. Thus, a shared model may become biased toward minimizing error on larger-scale outputs. Fig. 6 illustrates the distribution and spread for the target variables related to the performance indicators of the SC-SoCh datasets.

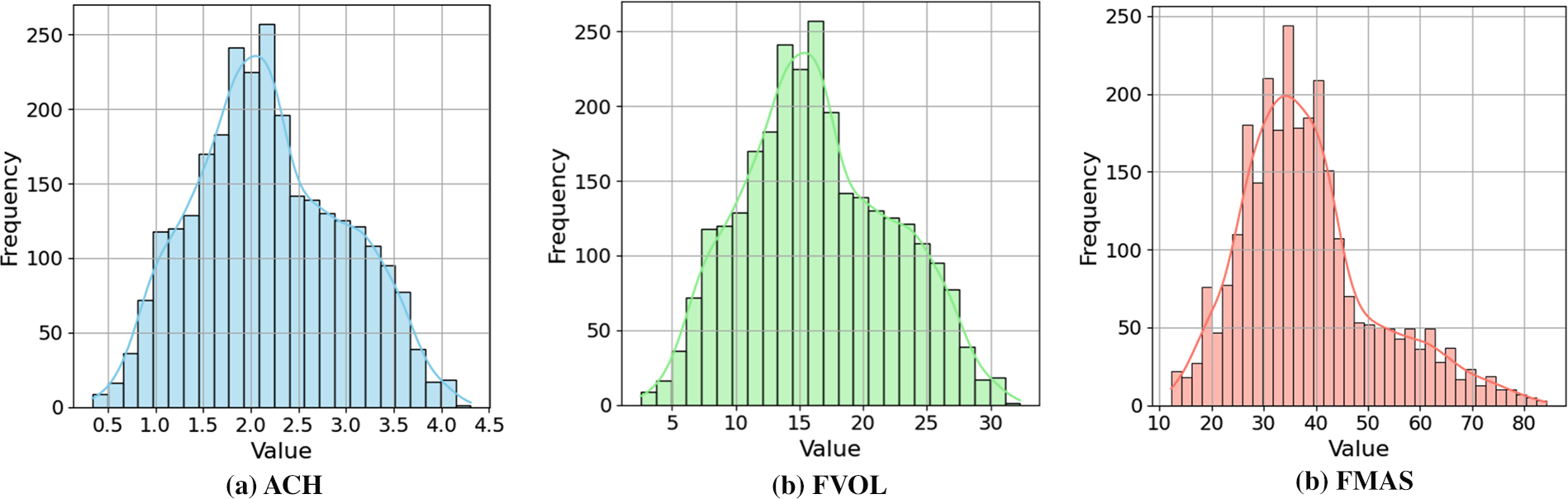
Figure 6: Histograms of performance indicators

Fig. 6a displays an ACH narrow spread, indicating consistent air change rates. In contrast, FVOL (Fig. 6b) and FMAS (Fig. 6c) exhibit wider spreads, suggesting greater variability in airflow performance. Additionally, the mean and median values are close for all variables, indicating that the distributions are roughly symmetric.

The hyperparameter values studied in the grid search for each performance indicator (ACH, FVOL, and FMAS) of the SC-SoCh included batch size = {16, 32, 64}, epochs = {20, 50, 100, 300, 500, 1000}, learning rate = {0.0001, 0.005, 0.001, 0.01}, neurons Layer 1 = {64, 32, 16}, neurons Layer 2 = {32, 16, 12}, neurons Layer 3 = {8, 6, 4, 2}, neurons Layer 4 = {4, 2}, and optimizers = {adam, rmsprop}.

Grid search results revealed the optimal ANN configuration of hyperparameters for the AHC performance indicator, using three hidden layers, was a batch size of 16, 500 epochs, a learning rate of 0.01, an architecture of 64-32-8, and the Adam optimizer, resulting in a mean test score of 0.869. In a separate configuration using a four-layer architecture, the optimal setup was determined with a batch size of 16, 300 epochs, a learning rate of 0.01, and Adam optimizer, with an architecture of 32-12-8-4, yielding a mean test score of 0.889.

The optimal configuration of hyperparameters for the FVOL performance indicator with three hidden layers was a batch size of 32, 500 epochs, a learning rate of 0.005, and the Adam optimizer, yielding an architecture of 32-12-6 and a mean test score of 0.889. In a separate configuration using a four-layer architecture, the optimal setup was determined with a batch size of 16, 1000 epochs, and a learning rate of 0.005 using the Adam optimizer. The resulting architecture had 32-12-4-4, yielding a mean test score of 0.890.

Finally, the optimal configuration of hyperparameters for the FMAS performance indicator using a three-layer architecture was determined to have a batch size of 16, 1000 epochs, a learning rate of 0.005, and the Adam optimizer. The resulting setup had an architecture of 32-12-2, achieving a mean test score of 0.989. In a different configuration using a four-layer architecture, the optimal setup also had a batch size of 16 and 1000 epochs, but utilized a learning rate of 0.001 with the RMSPROP optimizer. This configuration yielded an architecture of 32-12-4-4, with a mean test score of 0.987.

4.3 Metrics Evaluated

Evaluation metrics for regression problems using ANNs are essential for assessing model performance. The standard evaluation metrics for ANN regression include the following:

•   Mean Absolute Error (MAE) measures the average magnitude of errors in a set of predictions. The MAE equation is expressed as MAE=1n∑i=1n|yi−y^i|

•   Mean Absolute Percentage Error (MAPE) measures the average absolute percentage difference between the predicted and actual values. It expresses the prediction error as a percentage of the total. The MAPE equation is expressed as MAPE=100%n∑i=1n|yi−y^iyi|

•   Mean Squared Error (MSE) calculates the average of the squares of the errors between the estimated values and the actual values. The MSE equation is expressed as MSE=1n∑i=1n(yi−y^i)2

•   Root Mean Squared Error (RMSE) computes the square root of the mean of the squared errors, giving more weight to significant errors. The RMSE equation is expressed as RMSE=1n∑i=1n(yi−y^i)2

•   R-Squared (R2), also known as the coefficient of determination, indicates the proportion of variance in the dependent variable that is predictable from the independent variables. A value closer to 1 signifies a better fit. The R2 equation is expressed as R2=1−∑i=1n(yi−y^i)2∑i=1n(yi−y¯)2

4.4 Methods for Comparison

The performance of the ANN models was compared against a multivariate linear regression baseline and experimental data. Despite its simplicity, multivariate linear regression has demonstrated reasonable effectiveness in predicting solar chimney performance [21]. The regression model was implemented using the Python library scikitlearn, with 20% of the dataset reserved for testing.

4.5 Results and Discussion

An experimental evaluation was performed using an 80-20 data split for training and testing. Eighty percent of the training data was split into 80-20 for training and validation, respectively. The performance of the ANN model was compared against a linear regression baseline method using test data for each performance indicator. Table 3 reports the metric results on test data for each performance indicator of the SC-SoCh, utilizing the best ANN architecture and configuration reported in the hyperparameter tuning section. The MAE, MAPE, and MSE are reported as specific performance measures of the ANN, whereas RMSE and R2 are employed to compare the ANN with the PREG model. In this comparison, the percentage improvement achieved by the ANN over PREG is also reported.

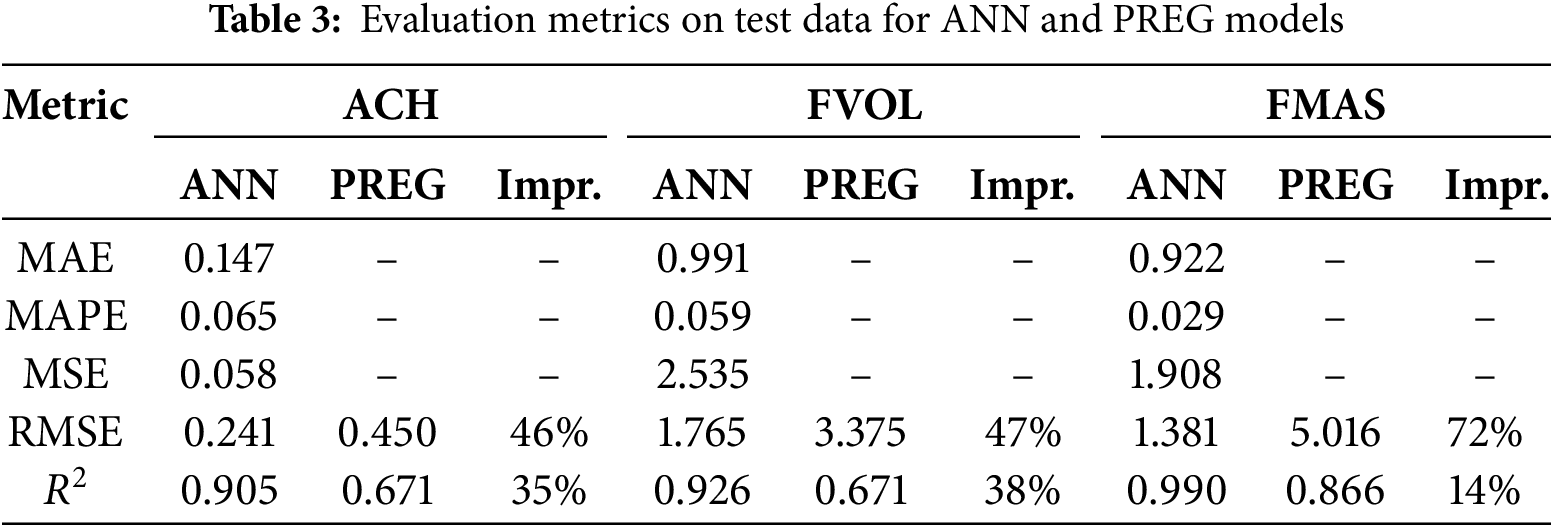
Results in Table 3 showed that show that the ANN model demonstrated strong performance in predicting the ACH indicator of the SC-SoCh system across both the training and test datasets. Regarding the RMSE, the ANN achieved an average improvement of 56%, with the best improvement on FMAS (72%). Regarding R2, the ANN achieved an average improvement of 29%, with the best improvement on FVOL (38%).

Fig. 7 illustrates the behavior of the loss function for both training and validation data, using MSE (Fig. 7a) and MAE (Fig. 7b) metrics. Additionally, Fig. 7 compares the predicted ACH values from the ANN (Fig. 7c) and PREG (Fig. 7d) against the GEB-computed target ACH values.

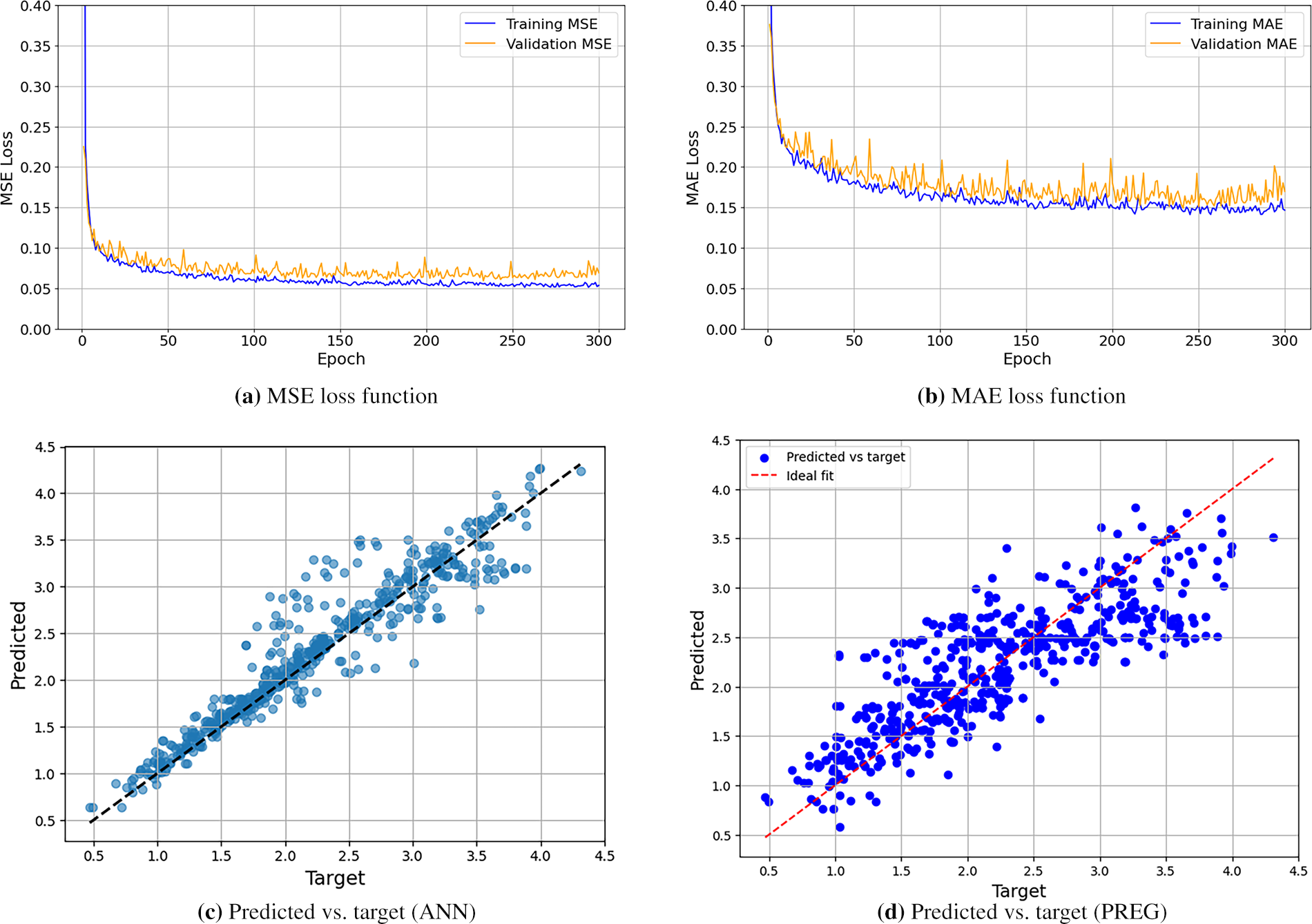
Figure 7: ACH-Comparison of loss functions and prediction accuracy for ANN and PREG models

In Fig. 7c, the data points are closely aligned with the ideal diagonal line, signifying a strong correlation between the predicted and actual values. This proximity suggests that the ANN model generalizes effectively, exhibiting minimal overfitting and high predictive accuracy. Furthermore, the ANN model for the ACH indicator significantly outperforms the PREG model, achieving over 90% accuracy in ACH predictions.

The ANN model significantly outperforms the PREG model in forecasting the FVOL indicator, achieving over 91% accuracy compared to 67% for the PREG model. Fig. 8 illustrates the behavior of the loss function for both training and validation data, using MSE (Fig. 8a) and MAE (Fig. 8b) metrics. Additionally, Fig. 8 provides a comparison between the predicted and actual FVOL values obtained from the ANN (Fig. 8c) and PREG (Fig. 8d) models.

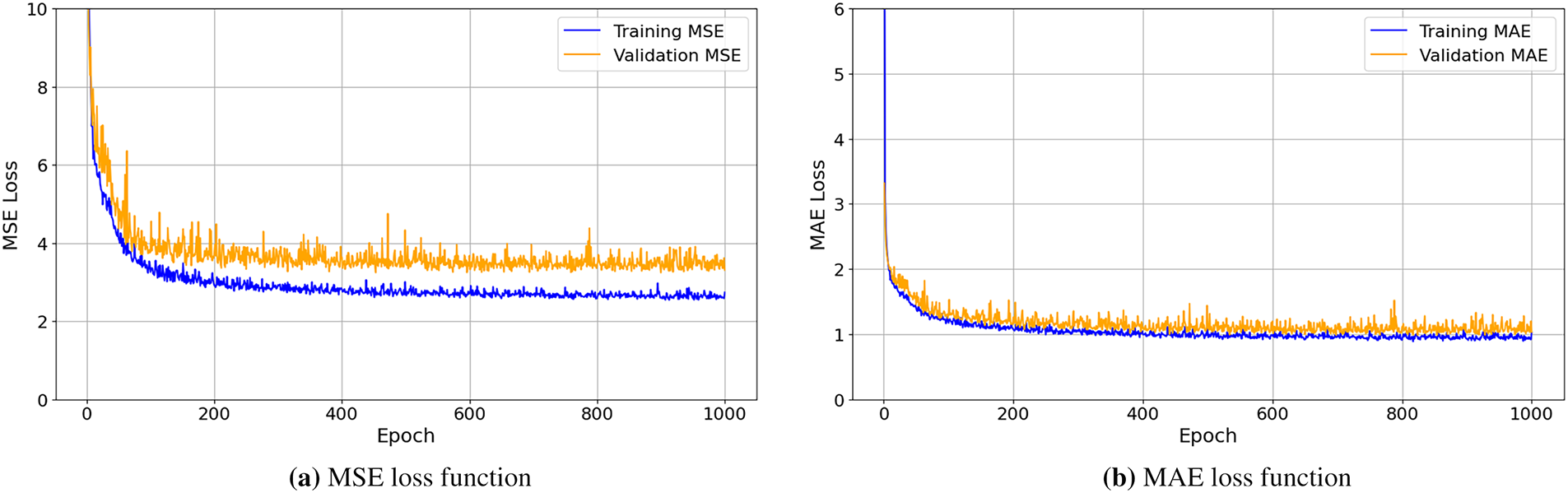
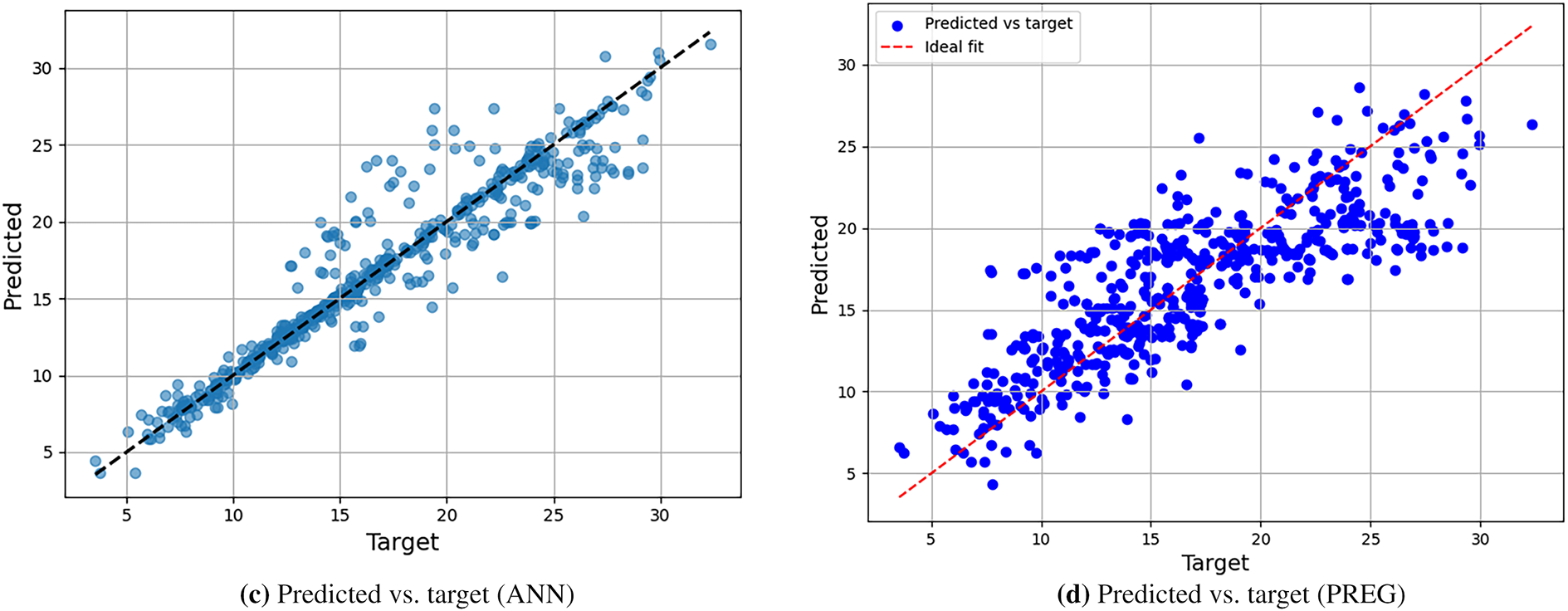
Figure 8: FVOL-Comparison of loss functions and prediction accuracy for ANN and PREG models

The ANN model significantly outperforms the PREG model in forecasting the FMAS indicator, accounting for over 99% in FMAS predictions compared to 86.6% of the PREG model. The ANN model also achieves a substantially lower RMSE, indicating much more accurate predictions. Additionally, the low MAPE of 2.9% further supports the precision of the ANN model in predicting FMAS rates. Fig. 9 illustrates the behavior of the loss function for both training and validation data concerning the FMAS performance indicator, specifically for the MSE (Fig. 9a) and MAE (Fig. 9b) metrics. Additionally, Fig. 9 compares the predicted FMAS values with the actual values obtained from the ANN (Fig. 9c) and PREG (Fig. 9d) models.

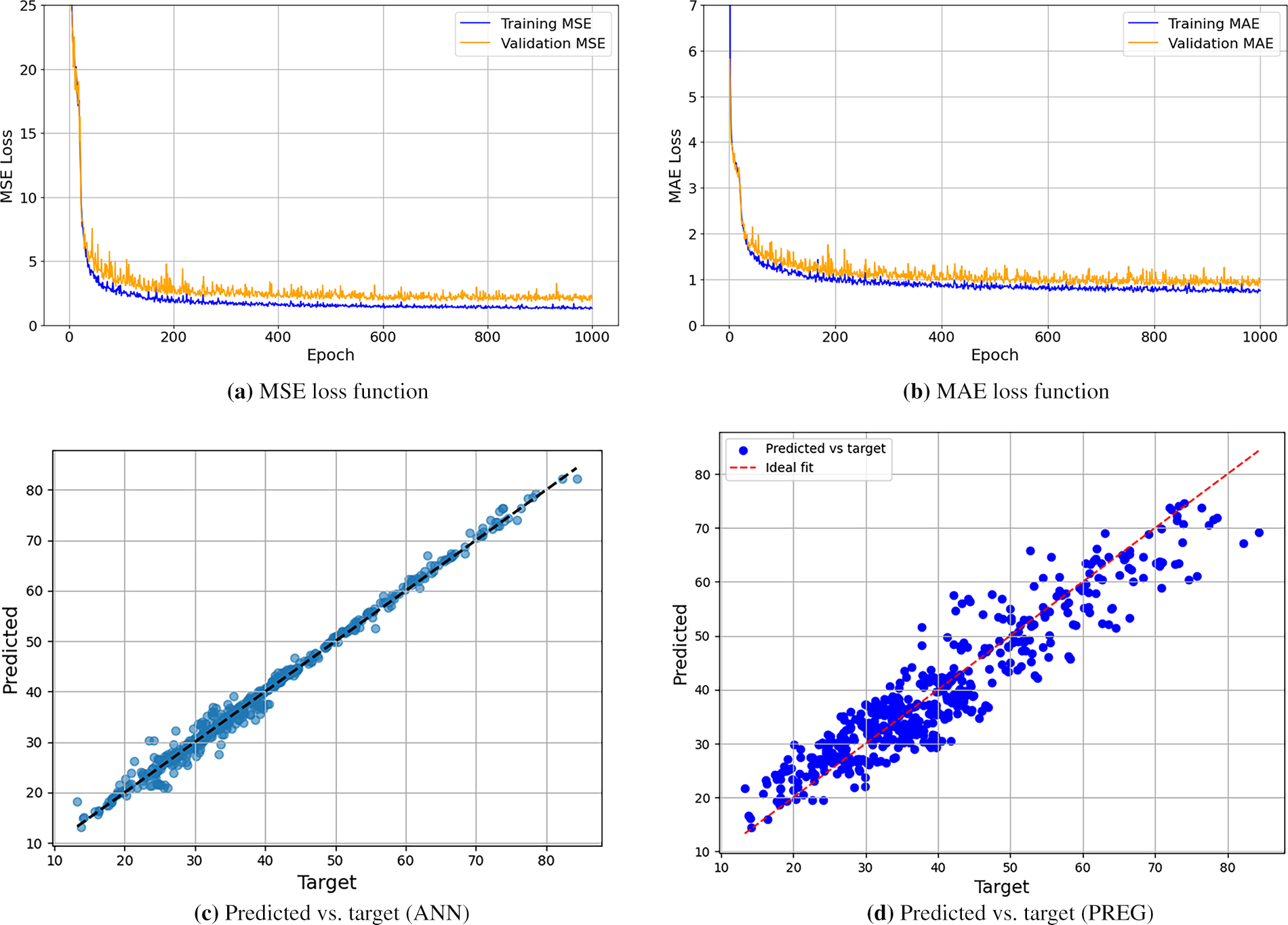
Figure 9: FMAS-Comparison of loss functions and prediction accuracy for ANN and PREG models

The average percentage difference between the predicted and target FMAS values in the test dataset is approximately 2.88%, indicating high accuracy in forecasting the FMAS rate for the SC-SoCh system. The average percentage difference between the predicted and actual ACH values in the test dataset is approximately 6.45%, indicating a relatively high level of accuracy for regression problems. Additionally, the average percentage difference between the predicted and actual FVOL values in the test dataset is around 6.71%, reflecting reasonably accurate performance.

The ANN model training time using the ACH performance indicator was 55.4 s, achieved with the optimal parameter configuration identified in the previous hyperparameter analysis. In comparison, the execution time for the GEB model with the ACH indicator was 10368 s. For the FVOL performance indicator, the ANN model took 185 s to train, while the FMAS performance indicator required 179.4 s. The execution time for the GEB model for the FVOL indicator was 10188 s, and the FMAS performance indicator took 9360 s.

The ANN model shows superior accuracy, generalization, and robustness in predicting the performance indicators of the SC-SoCh system when compared to the PREG baseline method. The ability of ANN models to capture complex nonlinear relationships makes them highly effective tools for forecasting ACH, FVOL, and FMAS behavior in SoCh systems, particularly for modeling dynamic natural ventilation systems.

The behavior of the loss function for the ANN models exhibits a sharp decline during the initial training epochs, indicating rapid learning and effective weight updates early in training. Additionally, in the early epochs, the losses stabilize and remain consistently low, suggesting that the model has reached a steady state. Overall, this behavior indicates that the ANN models are well-trained, stable, and possess strong generalization capabilities.

Finally, the ANN model’s performance indicator values were validated against experimental data by comparing the FMAS rate under steady-state conditions. The ANN-based predictions deviated by less than 9.5% from the measured values, supporting the use of the ANN model for forecasting airflow rates in practical solar chimney configurations. Overall, the validation results indicate that both the GEB and ANN models can reliably reproduce the dynamic ventilation behavior of solar chimneys under controlled thermal loads.

5  Conclusions

This article presents computational intelligence models based on artificial neural networks for forecasting performance indicators of a SC-SoCh system, including air change per hour, volumetric flow, and mass flow. GEB models were applied, using information from 2784 SC-SoCh configurations to create the input datasets. The SC-SoCh configurations encompass various factors, including chimney height, channel thickness, glass thickness, paint, wall material, measurement date, and orientation.

Three ANN models were evaluated in a real case study in Mexico City, using a linear regression as the baseline method. The results showed that the proposed ANN consistently outperformed the baseline, achieving higher R2 values and lower RMSE. On average, the ANN improved RMSE by 56% (reaching up to 72% for FMAS) and R2 by 29% (with a maximum of 38% for FVOL), demonstrating both greater accuracy and enhanced generalization. In addition, the ANN predictions were validated against experimental data by comparing FMAS rates under steady-state conditions, with deviations remaining below 9.5%. This supports the applicability of ANN models for forecasting airflow rates in practical solar chimney configurations. Overall, the findings confirm that ANN-based methods provide a robust and reliable approach for modeling the complex dynamics of SoCh systems.

The proposed models serve as practical tools for companies focused on sustainable building design, enhancing decision-making processes during the design phase of solar chimneys in sustainable architecture.

The main lines for future work involve enhancing the ANN models to accommodate more complex building geometries and additional climatic regions. Furthermore, these models need to be integrated with optimization frameworks, such as metaheuristic methods, to tackle larger problems and account for a wider range of real-world scenarios.

Acknowledgement: This work acknowledges Juan Manuel Hurtado Ramírez of the Biotechnology Institute, Universidad Nacional Autónoma de México (UNAM) for the bibliography support.

Funding Statement: This research received no external funding.

Author Contributions: Conceptualization, Carlos Torres-Aguilar and Pedro Moreno; methodology, Carlos Torres-Aguilar, Pedro Moreno and Diego Rossit; software, Carlos Torres-Aguilar and Pedro Moreno; validation, Carlos Torres-Aguilar, Pedro Moreno, Diego Rossit and Sergio Nesmachnow; formal analysis, Carlos Torres-Aguilar and Diego Rossit; investigation, Carlos Torres-Aguilar, Pedro Moreno and Diego Rossit; resources, Luis Hernández-Callejo; data curation, Carlos Torres-Aguilar and Pedro Moreno; writing—original draft preparation, Carlos Torres-Aguilar, Pedro Moreno, Diego Rossit, Karla M. Aguilar-Castro and Edgar V. Macias-Melo; writing—review and editing, Carlos Torres-Aguilar, Pedro Moreno, Diego Rossit, Sergio Nesmachnow, Karla M. Aguilar-Castro, and Edgar V. Macias-Melo; visualization, Carlos Torres-Aguilar, Pedro Moreno and Diego Rossit; supervision, Sergio Nesmachnow and Luis Hernández-Callejo; project administration, Sergio Nesmachnow and Luis Hernández-Callejo. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data and results are available upon request. Datasets are available in the GitHub repository https://github.com/CarlosETA/Sc-SoCh_ANN (accessed on 28 October 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. International Energy Agency. Electricity market report. Paris, France: IEA; 2023. [Google Scholar]

2. Ahmad A, Hassan M, Abdullah M, Rahman H, Hussin F, Abdullah H, et al. A review on applications of ANN and SVM for building electrical energy consumption forecasting. Renew Sustain Energy Rev. 2014;33(10):102–9. doi:10.1016/j.rser.2014.01.069. [Google Scholar] [CrossRef]

3. Amasyali K, El-Gohary N. Building lighting energy consumption prediction for supporting energy data analytics. Procedia Eng. 2016;145:511–7. doi:10.1016/j.proeng.2016.04.036. [Google Scholar] [CrossRef]

4. Wei Y, Zhang X, Shi Y, Xia L, Pan S, Wu J, et al. A review of data-driven approaches for prediction and classification of building energy consumption. Renew Sustain Energy Rev. 2018;82(3):1027–47. doi:10.1016/j.rser.2017.09.108. [Google Scholar] [CrossRef]

5. Alawneh R, Ghazali FEM, Ali H, Asif M. Assessing the contribution of water and energy efficiency in green buildings to achieve United Nations Sustainable Development Goals in Jordan. Build Environ. 2018;146(31):119–32. doi:10.1016/j.buildenv.2018.09.043. [Google Scholar] [CrossRef]

6. United Nations. Sustainable development goals report. New York, NY, USA: UN; 2025. [Google Scholar]

7. Zavala-Guillén I, Xamán J, Hernández-Pérez I, Hernández-Lopéz I, Jiménez-Xamán C, Moreno-Bernal P, et al. Ventilation potential of an absorber-partitioned air channel solar chimney for diurnal use under Mexican climate conditions. Appl Therm Eng. 2019;149:807–21. doi:10.1016/j.applthermaleng.2018.12.074. [Google Scholar] [CrossRef]

8. Torres-Aguilar CE, Arce J, Xamán J, Macias-Melo EV. Experimental study and numerical analysis of radiative losses of single-channel solar chimney. J Build Phys. 2022;46(3):340–71. doi:10.1177/17442591221127279. [Google Scholar] [CrossRef]

9. Torres-Aguilar CE, Moreno-Bernal P, Nesmachnow S, Aguilar-Castro KM, Cisneros-Villalobos L, Arce J. Annual evaluation of natural ventilation induction in solar chimneys under tropical, dry, and temperate climates of mexico: a case study. Sustainability. 2023;15(23):16399. doi:10.3390/su152316399. [Google Scholar] [CrossRef]

10. Belussi L, Barozzi B, Bellazzi A, Danza L, Devitofrancesco A, Fanciulli C, et al. A review of performance of zero energy buildings and energy efficiency solutions. J Build Eng. 2019;25:100772. doi:10.1016/j.jobe.2019.100772. [Google Scholar] [CrossRef]

11. Dahire H, Kannan S, Saw S. Effect of humidity on the performance of rooftop solar chimney. Therm Sci Eng Progress. 2022;27(10):101026. doi:10.1016/j.tsep.2021.101026. [Google Scholar] [CrossRef]

12. Wei T, Li H, Sun R, Yu CW, Luo X. Evaluation of photovoltaic-based solar chimney-assisted stack ventilation within a large space hall: a case study. Indoor Built Environ. 2023;33(4):741–56. doi:10.1177/1420326x231220527. [Google Scholar] [CrossRef]

13. Salari A, Shakibi H, Alimohammadi M, Naghdbishi A, Goodarzi S. A machine learning approach to optimize the performance of a combined solar chimney-photovoltaic thermal power plant. Renew Energy. 2023;212(1):717–37. doi:10.1016/j.renene.2023.05.047. [Google Scholar] [CrossRef]

14. de Araujo L, Ceha T, Baldi S, De Schutter B. Model predictive control of a thermal chimney and dynamic solar shades for an all-glass facades building. Energy. 2023;264:126177. doi:10.1016/j.energy.2022.126177. [Google Scholar] [CrossRef]

15. Lahimer AA, Razak AA, Sopian K. Mathematical modeling and validation of solar-induced ventilation system for vehicle cabin cooling in hot parking conditions. J Adv Res Fluid Mech Therm Sci. 2023;110(1):200–26. [Google Scholar]

16. Belfegas B, Tayebi T, Larbi S. Analysis of a hybrid system solar chimney-air soil heat exchanger for natural ventilation. Int J Eng Res Afr. 2023;66(1–2):91–110. doi:10.4028/p-3elgvg. [Google Scholar] [CrossRef]

17. Zavala-Guillén I, Xamán J, Álvarez G, Arce J, Hernández-Pérez I, Gijón-Rivera M. Computational fluid dynamics for modeling the turbulent natural convection in a double air-channel solar chimney system. Int J Modern Phy C. 2016;27(8):1–19. doi:10.1142/s0129183116500959. [Google Scholar] [CrossRef]

18. Rodríguez-Vázquez M, Hernández-Pérez I, Xamán J, Chávez Y, Gijón-Rivera M, Belman-Flores JM. Coupling building energy simulation and computational fluid dynamics: an overview. J Build Phys. 2020;44(2):137–80. doi:10.1177/1744259120901840. [Google Scholar] [CrossRef]

19. Mandal DK, Gupta KK, Biswas N, Manna NK, Santra S, Benim AC. Optimization of hybrid solar chimney power plants (HSCPPsa review of multi-objective approaches. Appl Energy. 2025;396:126214. doi:10.1016/j.apenergy.2025.126214. [Google Scholar] [CrossRef]

20. Torres-Aguilar C, Moreno-Bernal P, Xamán J, Nesmachnow S, Cisneros-Villalobos L. Global energy balances for energy analysis in buildings. In: V Ibero-American congress of smart cities. Berlin, Germany: Springer Nature; 2022. p. 306–20. [Google Scholar]

21. Torres-Aguilar C, Moreno-Bernal P, Nesmachnow S, Rossit D, Aguilar-Castro KM, Macias-Melo EV. Regression analysis for prediction of solar chimney performance. In: Ibero-American congress of smart cities. Berlin, Germany: Springer Nature; 2024. p. 229–43. [Google Scholar]

22. Zhang H, Tao Y, Shi L. Solar chimney applications in buildings. Encyclopedia. 2021;2(2):409–22. doi:10.3390/encyclopedia1020034. [Google Scholar] [CrossRef]

23. Tariq R, Bassam A, Orozco M, Ricalde L, Carvente O. Sustainability framework of intelligent social houses with a synergy of double-façade architecture and active air conditioning systems. Energy Convers Manag. 2023;288:117120. doi:10.1016/j.enconman.2023.117120. [Google Scholar] [CrossRef]

24. Ong KS. A mathematical model of a solar chimney. Renew Energy. 2003;28:1047–60. [Google Scholar]

25. Maghrabie HM, Abdelkareem MA, Elsaid K, Sayed ET, Radwan A, Rezk H, et al. A review of solar chimney for natural ventilation of residential and non-residential buildings. Sustain Energy Technol Assess. 2022;52:102082. doi:10.1016/j.seta.2022.102082. [Google Scholar] [CrossRef]

26. Mandal DK, Biswas N, Manna NK, Gayen DK, Benim AC. An application of artificial neural network (ANN) for comparative performance assessment of solar chimney (SC) plant for green energy production. Sci Rep. 2024;14(1):979. doi:10.1038/s41598-023-46505-1. [Google Scholar] [PubMed] [CrossRef]

27. Tariq R, Torres-Aguilar CE, Xamán J, Zavala-Guillén I, Bassam A, Ricalde LJ, et al. Digital twin models for optimization and global projection of building-integrated solar chimney. Build Environ. 2022;213:108807. doi:10.1016/j.buildenv.2022.108807. [Google Scholar] [CrossRef]

28. Ali MH, Mawlood MK, Jalal RE. Experimental and numerical investigation of the cooling performance of a solar chimney integrated with a humidification system. J Build Phys. 2025;48(5):767–93. doi:10.1177/17442591241276392. [Google Scholar] [CrossRef]

29. Xiao X, Hu Q, Jiao H, Wang Y, Badiei A. Simulation and machine learning investigation on thermoregulation performance of phase change walls. Sustainability. 2023;15(14):11365. doi:10.3390/su151411365. [Google Scholar] [CrossRef]

30. Barghi Jahromi MS, Kalantar V, Akhijahani HS, Salami P. Application of artificial neural network, evolutionary polynomial regression, and life cycle assessment techniques to predict the performance of a new designed solar air ventilator with phase change material. Appl Therm Eng. 2025;269(7):126117. doi:10.1016/j.applthermaleng.2025.126117. [Google Scholar] [CrossRef]

31. Tariq R, Recio-Garcia JA, Cetina-Quiñones AJ, del Castillo MGO, Bassam A. Explainable artificial intelligence twin for metaheuristic optimization: double-skin facade with energy storage in buildings. J Comput Des Eng. 2025 Mar;12(3):16–35. doi:10.1093/jcde/qwaf015. [Google Scholar] [CrossRef]

32. Kalogirou SA, Bojic M. Artificial neural networks for the prediction of the energy consumption of a passive solar building. Energy. 2000;25(5):479–91. doi:10.1016/s0360-5442(99)00086-9. [Google Scholar] [CrossRef]

33. Hornik K, Stinchcombe M, White H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989;2(5):359–66. doi:10.1016/0893-6080(89)90020-8. [Google Scholar] [CrossRef]

34. Liashchynskyi P, Liashchynskyi P. Grid search, random search, genetic algorithm: a big comparison for NAS. arXiv:1912.06059. 2019. [Google Scholar]