Neuro-Fuzzy Computational Dynamics of Reactive Hybrid Nanofluid Flow Inside a Squarely Elevated Riga Tunnel with Ramped Thermo-Solutal Conditions under Strong Electromagnetic Rotation

1  Introduction

The thermophysical behavior of working fluids is a decisive factor in advanced engineering and industrial applications, particularly with the rapid evolution of nanotechnology. Nanoparticles (NPs) (generally smaller than 100 nm) are now widely utilized as additives to boost the thermal performance of working base fluids such as water, ethylene glycol (EG), EG-water mixture, engine oils, kerosene, and biological fluids (e.g., blood, mucus, and plasma). When evenly suspended, the resulting colloidal dispersions, known as nanofluids (NFs), display markedly improved transport properties compared to the host fluids. A large body of theoretical and experimental research has demonstrated that the effective thermal conductivity of nanofluids is strongly dependent on the nanoparticle characteristics, including geometry, dimensions, concentration, and intrinsic material properties. Because of these enhancements, nanofluids are increasingly deployed in a variety of sectors–ranging from solar energy harvesting, heat exchangers, and thermal storage systems to biomedical treatments such as hyperthermia and cryosurgery, as well as electronic cooling, batteries, chemical processing, and renewable energy platforms. The pioneering work of Choi [1] first articulated the idea of dispersing nanoparticles in a base liquid to improve heat transport, establishing that nanoparticle volume fraction (NVF) plays a central role in dictating thermophysical properties. Later, Buongiorno [2] refined this perspective by attributing nanofluid transport to nanoscale mechanisms such as Brownian diffusion and thermophoresis. Recent studies have further deepened understanding of nanofluid transport phenomena under complex physical conditions. Boujelbene et al. [3] examined the thermodynamics of hydromagnetic boundary-layer flow of a Prandtl nanofluid past a heated stretching cylinder with interfacial slip, while Asiri et al. [4] analyzed the influence of thermal relaxation and non-Fickian diffusion in ferromagnetic nanofluids through the Cattaneo-Christov framework. Khan et al. [5] studied radiative Prandtl nanofluid transport in a tapered peristaltic channel, highlighting nanoparticle-driven thermal enhancement coupled with electromagnetic and viscous dissipation effects. Uddin and Rasel [6] further investigated MHD nanofluid convection influenced by radiative heat flux and exothermic chemical reactions. Complementing these advances, the foundational review by Uddin et al. [7] systematically outlined the evolution, theoretical basis, and applications of nanofluids. These works underscore the vast potential of nanofluids in modern energy systems, materials processing, and thermal transport technologies.

Hybrid nanofluids (HNFs), formed by combining two or more types of nanoparticles in a base liquid, provide superior performance compared to conventional nanofluids. These multiphase suspensions allow for enhanced thermal conductivity, tunable viscosity, and improved convective behavior. Such fluids have attracted applications in aerospace, electronics cooling, power engineering, and biomedical systems [8,9]. Copper (Cu) nanoparticles are notable for their exceptional electrical and thermal conductivity, antimicrobial activity, and catalytic properties. They are integral in printed electronics, cooling technologies, biomedical coatings, catalysis, and energy storage systems (batteries, capacitors, and fuel cells). Titanium dioxide (TiO2) nanoparticles, by contrast, are well known for their photocatalytic activity, strong UV absorption, and high refractive index, supporting applications in pollution remediation, pigments, protective coatings, sunscreen formulations, and self-cleaning surfaces. Driven by these advantages, Cu–TiO2 hybrid nanofluids have been extensively investigated. Ahmad et al. [10] demonstrated substantial thermal enhancement in TiO2–Cu/ethylene glycol suspensions. Manigandan et al. [11] reported notable increases in skin friction and solutal diffusion for TiO2–Cu/water flows under thermal radiation. Meena and Sharma [12] found that chemical reactivity and radiation strongly affect velocity and thermal layers in HNFs over rotating disks. Islam et al. [13] studied magnetically influenced convection of Cu–TiO2/water, highlighting sensitivity to nanoparticle concentration. Pattnaik et al. [14] considered porous drag and found both Cu and TiO2 to be effective contributors to heat and mass transfer. Together, these works affirm the technological promise of Cu–TiO2 HNFs in advanced transport applications.

Ramped thermal and concentration (RTC) profiles, where wall temperature or solute concentration vary in space or time, provide a practical means of regulating thermal and solutal transport. Such conditions are particularly useful in polymer processing, chemical synthesis, and food engineering, where precise control of energy and mass fluxes enhances process efficiency and prevents thermal stresses. Kataria and Patel [15] explored ramped temperature and concentration effect on unsteady magneto-Casson fluid flow through porous plates, considering chemical reactivity and heat generation/absorption. Asogwa et al. [16] analyzed reactive Casson fluid flow over inclined Riga plates subject to ramped vs. isothermal regimes. More recently, Nagaraju et al. [17] addressed radiative and chemical reactive second grade fluid transport near an infinite rotating vertical plate under ramped thermo-solutal conditions.

Porous media, composed of interconnected voids within a solid matrix, enable fluid, solute, and gas transport and are widely encountered in fields such as groundwater hydrology, petroleum recovery, chemical processing, and materials engineering. The Darcy model, which postulates a linear dependence between pressure drop and velocity, provides the classical framework for describing such flows at low Reynolds numbers. At higher velocities, however, inertial corrections, commonly termed Forchheimer effects, become necessary to capture deviations from Darcy’s law [18]. Heat and mass transfer in porous environments has been extensively analyzed under diverse physical influences. Khalid et al. [19] studied magneto-thermal convection of Casson fluids in porous absorptive layers driven by oscillatory boundaries. Kataria et al. [20] derived solutions for radiative, chemically reactive Casson flows through porous domains subject to oscillatory heating and magnetic fields, while their subsequent work [21] highlighted MHD effects under ramped thermal conditions and Soret diffusion. Kumar et al. [22] analyzed double stratification and reactivity in porous-driven MHD flows, and Narahari et al. [23] studied thermal responses under radiative heating with variable wall temperatures. More recently, Gulle and Kodi [24] examined radiative-reactive Jeffrey fluids in porous inclined geometries, accounting for thermophoretic and magnetic effects.

Thermal radiation, the transport of heat via electromagnetic emission (predominantly in the infrared band), strongly influences temperature distributions in radiating and ionized fluids. The interaction of radiative flux with viscous fluids depends on material absorption, scattering properties, and flow geometry. To model such systems, the Rosseland diffusion approximation [25] is widely used, simplifying radiative flux to a diffusion-type term valid in optically thick regimes. Cess [26] pioneered its use in radiative convection problems. Narahari [27] extended these ideas to reactive flows between parallel plates under ramped heating. Prakash and Muthtamilselvan [28] analyzed MHD non-Newtonian fluids through porous media subject to third-kind thermal conditions. Sheikholeslami et al. [29] explored radiation in magneto-nanofluids in rotating tunnels, while Thriveni and Mahanthesh [30] highlighted its impact on mixed convection in annular HNF-filled domains.

Chemical reactivity plays a critical role in modifying transport in nanofluid and hybrid nanofluid flows, with applications ranging from catalysis to biomedical systems. In particular, first-order homogeneous reactions alter concentration distributions and strongly influence solutal boundary layer development. Recent studies confirm this influence. Ali et al. [31] modeled chemically reactive trihybrid Casson NF transport in porous rotating plate under strong magnetization. Famakinwa et al. [32] demonstrated chemical reactivity impact on MHD HNFs flow inside parallel plates. Xia et al. [33] demonstrated that activation energy driven chemical reactions substantially elevate species concentration in hybrid nanofluid flow. Khan and Alzahrani [34] explored non-Newtonian reactive flows with activation energy. Manigandan et al. [35] studied chemically reactive HNFs flow over inclined surfaces.

In rotating systems, Coriolis forces significantly influence magnetohydrodynamic (MHD) transport, dominating viscous and inertial contributions. These effects are important in geophysics, astrophysics, and rotating industrial devices. Chauhan and Rastogi [36] studied Coriolis-driven flows in porous tunnels under MHD forcing. Seth et al. [37] examined gravity-modulated unsteady rotating tunnel flows, highlighting wall conductivity. VeeraKrishna and Reddy [38] considered reactive non-Newtonian flows in rotating porous tunnels. Hayat et al. [39] analyzed hybrid nanofluid transport with internal heat generation in rotating frames. Ahammad and VeeraKrishna [40] investigated rotating transport with Soret and Dufour effects. Sharma et al. [41] studied rotating Riga-disk nanoflows under radiation and chemical effects.

Ionized fluids such as plasmas, electrolytes, and liquid metals exhibit unique conduction mechanisms, where Hall and ion-slip currents significantly alter electrical transport and fluid motion. The Hall effect suppresses cross-field currents, induces anisotropic conductivity, and generates secondary flow structures, while ion-slip currents arise from ion-neutral drift under electric fields. These effects are critical in Hall thrusters, plasma accelerators, and energy generation systems. Jana and Kanch [42] studied Hall currents in unsteady plasma Couette flows. Ghosh [43] analyzed Hall-influenced MHD Couette flows in rotating systems. Jha and Apere [44] examined combined Hall and ion-slip effects in transient Couette flows. Das et al. [45] addressed Hall and ion-slip electromotive forces on low-ionization fluid flow via rotating riga channel.

The Riga plate, introduced by Gailitis and Lielausis [46], is an electromagnetic actuator composed of alternating electrodes and magnets that generate a spatially decaying Lorentz force parallel to the plate surface. This enables precise control of low-conductivity flows where magnetic fields alone are ineffective. Applications of Riga plates span marine propulsion, electrochemical systems, sensors, and heat transfer devices. Grinberg [47] modified governing equations to incorporate exponentially decaying wall forces. Ahmad et al. [48–50] explored their role in nanofluid flows, demonstrating reductions in skin friction and altered heat transport. Rasool et al. [51] included buoyancy and magnetization, while Loganathan and Deepa [52] highlighted velocity amplification near oscillating Riga plates. Khatun et al. [53] reported that strong EM forcing reduces shear stress in radiative Bingham flows. Nasrin et al. [54,55] examined Riga-plate nanoflows under Hall currents and ramped boundary conditions. Asogwa et al. [56] showed enhanced momentum transport in HNFs, and Upreti et al. [57] linked Hartmann numbers to entropy production.

Artificial Intelligence (AI) methods such as artificial neural networks (ANNs), adaptive neuro-fuzzy inference systems (ANFIS), and deep learning are increasingly being used to complement analytical and numerical fluid dynamics. These methods address nonlinear multiphysics problems that are often computationally expensive or analytically intractable. Ali and Das [58] combined fractional-order modeling with ANN to simulate electroosmotic nanoblood flow. Karmakar et al. [59] developed ANN-based models for transient electromagnetized nanoblood flows. Karmakar and Das [60] applied AI-assisted modeling to reactive convection over Riga plates. Maddina et al. [61] compared ANFIS-PSO and ANN in Casson fluid modeling, while Kumar et al. [62] applied ANFIS-PSO to MHD radiative tetra-hybrid nanoblood. Together, these works underscore AI’s growing role in predictive fluid mechanics.

Objectives and Novelty

The study of hybrid nanofluid flows in electromagnetically actuated tunnels has gained increasing importance due to its relevance in naval propulsion, industrial cooling systems, and advanced thermal management technologies. In this context, Riga-type tunnels provide a promising configuration for flow control, as they combine electromagnetic actuation with boundary layer modulation. The present work focuses on the unsteady transport of reactive Cu–TiO2/water based hybridized nanofluid in a squarely elevated Riga tunnel embedded in a homogeneous porous medium. The model accounts for ramped and uniform wall temperature and concentration conditions (RWTC and UWTC), enabling the examination of transient thermal and solutal responses. Additional physical mechanisms considered include Hall and ion-slip currents within a rotating reference frame, thermal radiation effects, and homogeneous first-order chemical reactivity. The porous matrix resistance is modeled using Darcy’s formulation. The governing equations are transformed into dimensionless form and solved analytically using the Laplace Transform technique. Parametric studies highlight the influence of key dimensionless numbers such as magnetic interaction parameters, Hall and ion-slip coefficients, thermal/solutal Grashof numbers, nanoparticle volume fraction, and reaction rate on velocity, temperature, and concentration distributions. Results for shear stress are further tabulated, comparing RWTC and UWTC regimes. To complement the analytical treatment, numerical datasets are generated in Mathematica and subsequently used to develop predictive machine learning frameworks. An Artificial Neural Network (ANN) trained via the Levenberg-Marquardt algorithm (ANN-LMBPA) is constructed to estimate shear stress (SS), heat transfer rate (HTR), and mass transfer rate (MTR), achieving high accuracy as validated through regression metrics, error histograms, and performance plots. Furthermore, an Adaptive Neuro-Fuzzy Inference System (ANFIS) is employed to enhance prediction of HTR, exploiting its capability to capture nonlinear relationships and provide interpretability through fuzzy logic rules. To the best of the authors’ knowledge, a comprehensive integration of Riga-plate-induced electromagnetic forcing, porous drag, radiative transport, Hall/ion-slip effects, first-order chemical reactivity, and AI-assisted predictive modeling has not yet been reported. This gap provides the central motivation for the present investigation.

The novel contributions of the current work can be summarized as follows:

•   Development of a new model for the unsteady, rotating flow of Cu–TiO2/water hybrid nanofluid in a squarely elevated Riga tunnel, incorporating both RWTC and UWTC settings.

•   Integration of multiple physical mechanisms including Hall and ion-slip currents, thermal radiation, first-order chemical reaction, and Darcy resistance to provide a realistic representation of complex transport processes.

•   Explicit inclusion of the Riga plate’s exponentially decaying Lorentz force in the governing formulation, highlighting its role in momentum modulation.

•   Derivation of closed-form solutions using the Laplace Transform method, offering insights into the transient transport phenomena.

•   Construction of a machine learning framework using ANN-LMBPA to accurately predict shear stress, heat transfer, and mass transfer characteristics.

•   Deployment of ANFIS for forecasting nonlinear dependencies in heat transfer rates, thus combining predictive precision with enhanced interpretability.

2  Mathematical Model

We analyze the transient, two-dimensional motion of a copper–titania–water hybrid nanofluid bounded by two infinitely extended vertical Riga plates separated by a distance h. The coordinate system is oriented such that the x-axis lies along the streamwise direction parallel to the plates and the y-axis is normal to them. The entire system undergoes rigid-body rotation with angular speed Ω about the z-axis. At the initial state (t≤0), the tunnel fluid is quiescent with uniform reference temperature Th and solute concentration Ch. For t>0, the plate at y=0 initiates motion with a squarely elevating velocity profile u0(t/t0)2, where u0 is a reference velocity and t0 a characteristic time. During the ramping interval 0<t≤t0, the left wall temperature and concentration vary linearly with time according to Tw(t)=Th+(T0−Th)t/t0,Cw(t)=Ch+(C0−Ch)t/t0, with T0≠Th and C0≠Ch. Beyond t>t0, both quantities relax back to their initial values Th and Ch. The right wall at y=h is fixed and maintained at constant thermal and solutal states. In addition, the fluid is influenced by a suddenly imposed axial pressure gradient, exponentially decaying Lorentz forces generated by the Riga actuator array of magnets and electrodes, and radiative heat flux. These effects jointly govern the coupled momentum, thermal, and solutal transport. A schematic of the physical setup is shown in Fig. 1.

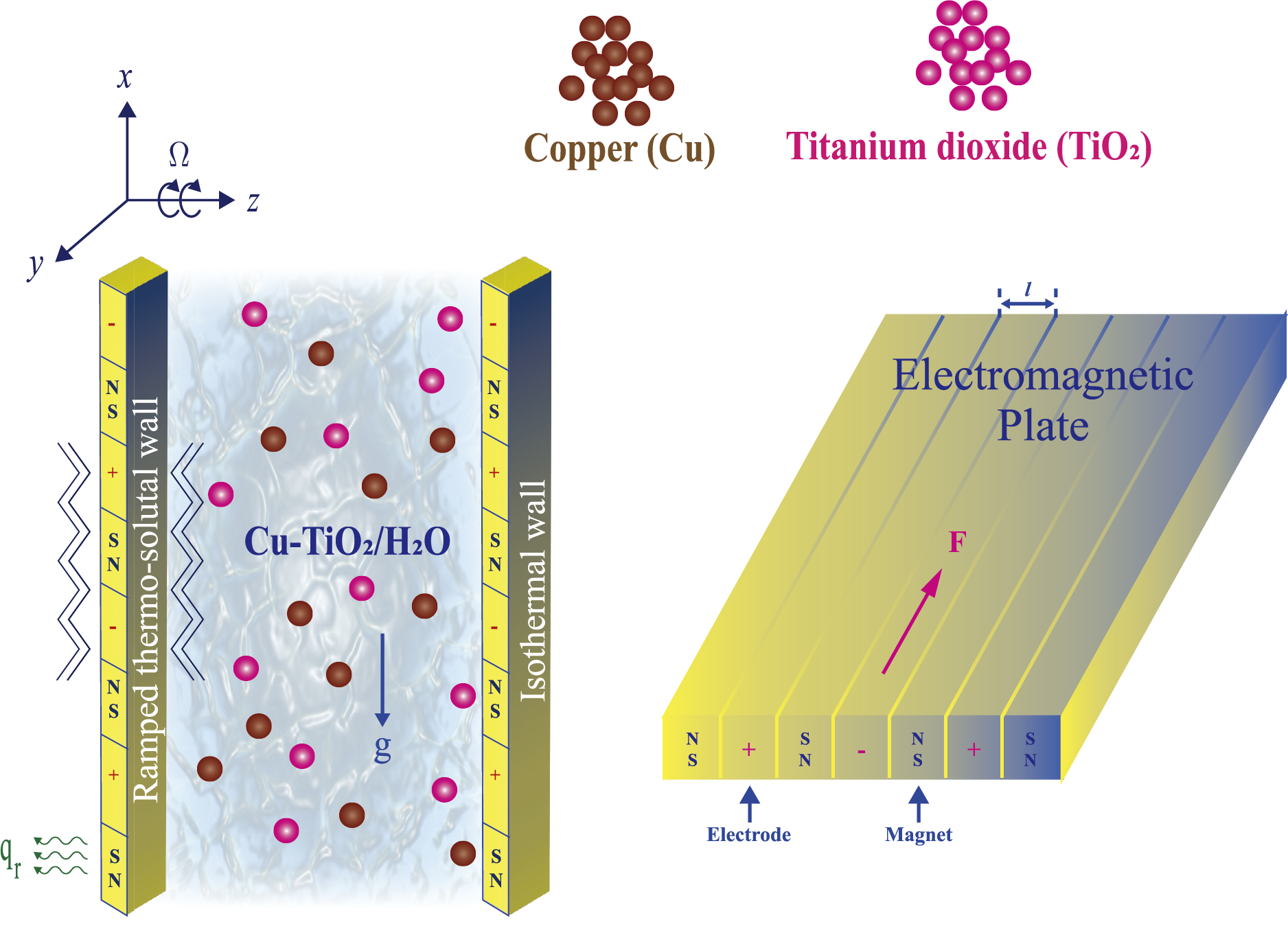
Figure 1: Physical configuration of flow

2.1 Model Hypotheses

The formulation is constructed on the following physical premises:

•   The working medium is a single-phase hybrid nanofluid composed of uniformly dispersed Cu and TiO2 NPs in water. The suspension is considered incompressible, weakly conductive, and chemically reactive.

•   Flow is laminar, unsteady, and two-dimensional.

•   The isotropic and homogeneous porous matrix filling the domain is assumed.

•   Nanoparticle diameters are much smaller than the typical pore scale, thereby avoiding pore blockage or slip effects at the fluid-solid interface.

•   A first-order homogeneous chemical reaction takes place, with a rate proportional to the local solute concentration.

•   Thermal equilibrium holds among the fluid, nanoparticles, and porous medium throughout the tunnel.

•   Owing to the infinite extent of the plates, variations occur only in the transverse coordinate y and time t.

2.2 Governing Equations

Using the Boussinesq approximation, the coupled momentum, energy, and species equations are formulated for a weakly conducting hybrid nanofluid in a rotating Riga tunnel, accounting for porous resistance, electromagnetic forcing, Hall and ion-slip effects, radiation, and chemical reaction [45,63]:

(ρ)hnf(∂u∂t−2Ωv)=μhnf∂2u∂z2+g(ρβT)hnf(T−Th)+g(ρβC)hnf(C−Ch)−μhnfK∗u+πJ0m08(1+βe−βeβi)e−πlz,(1)

(ρ)hnf(∂v∂t+2Ωu)=μhnf∂2v∂z2−μhnfK∗v+πJ0m08(1−βe−βeβi)e−πlz,(2)

(ρcp)hnf∂T∂t=khnf∂2T∂z2−∂qr∂z−Q0(T−Th),(3)

∂C∂t=Dhnf∂2C∂z2−K1(C−Ch).(4)

In Eqs. (1) and (2), the terms πJ0m08(1+βe−βeβi)e−πlz and πJ0m08(1−βe−βeβi)e−πlz, referred to as the Grinberg terms, are significant in the context of Riga tunnel setups, especially in studies of plasma dynamics under the influence of Hall and ion-slip electric fields. These terms encapsulate the interaction of several key factors in a Riga plate configuration. Here, m0 represents the magnetism strength of the permanent magnets on the Riga plate’s surface, l is the width between the magnets and electrodes, and J0 denotes the applied current density in the electrodes. The term m0 indicates the magnetic field’s intensity, crucial in influencing the behavior of the ionic fluid over the Riga plate. The geometric factor l determines the magnetic field’s spatial reach, affecting the fluid’s behavior-a smaller l implies a more concentrated magnetic repercussion, while a larger l leads to a more dispersed field. The current density J0 in the electrodes significantly impacts the electromagnetic forces on the fluid, where higher J0 values intensify these forces and modify the fluid dynamics. Incorporated within the Grinberg term are the Hall parameter βe and the ion-slip parameter βi. βe accounts for the impact of Hall currents, generated by the orthogonal interaction between the magnetic field and electric currents in the fluid, leading to a transverse electric field that markedly influences the charged particles’ behavior. The ion-slip parameter βi reflects the relative motion of ions within the fluid due to collisions and interactions, significantly affecting momentum exchange and flow patterns. Furthermore, the exponential term e−πlz indicates a diminishing effect with increasing distance z from the tunnel left wall, signifying the decreasing influence of magnetic and electric fields with distance from the Riga plate [55]. This aspect is crucial in understanding the spatial variability of these forces’ effects in Riga tunnel setups.

The corresponding initial and boundary conditions (IBCs) are [63]:

t=0:u=0=v, T=Th,  C=Ch  for all  0≤z≤h,t>0:u=u0(tt0)2, v=0  at  y=0,T={Th+(T0−Th)tt0,0<t≤t0Th,t>t0  at  z=0,C={Ch+(C0−Ch)tt0,0<t≤t0Ch,t>t0  at  y=0,t>0:u=0=v,  T=Th,  C=Ch  at  z=h.(5)

2.3 Rosseland Approximation

The Rosseland approximation [25] offers a tractable method for modeling radiative heat transfer in optically thick media, where radiation transport occurs primarily through absorption, scattering, and re-emission of photons. This approach is particularly applicable when the mean free path of photons is significantly smaller than the characteristic length scale of the temperature gradient, allowing the radiative flux to be expressed in a diffusion-like form. While widely used in astrophysical and high-temperature engineering applications, such as stellar interiors and thermally insulated enclosures, its accuracy diminishes in optically thin or semi-transparent media with sharp thermal gradients. Under the Rosseland diffusion approximation, the radiative heat flux qr in an optically dense fluid is expressed as [63]:

qr=−4σ∗3k∗∂T4∂y,(6)

where σ∗ is the Stefan-Boltzmann constant and k∗ denotes the Rosseland mean absorption coefficient.

To facilitate mathematical treatment and ensure linearity in the governing energy equation, the term T4 is linearized around a reference (free-stream) temperature Th using a first-order Taylor series expansion:

T4=Th4+3Th3(T−Th)+6Th2(T−Th)2+⋅⋅⋅(7)

to

T4≈4Th3T−3Th4.(8)

Substituting into Eq. (3), we obtain:

(ρcp)hnf∂T∂t=(khnf+16σ∗3k∗Th3)∂2T∂y2−Q0(T−Th).(9)

2.4 Thermo-Physical Correlation and Properties of Hybrid Nanofluid (HNF)

The macroscopic behavior of a hybrid nanofluid (HNF) is governed by its effective thermo-physical attributes, which are obtained through standard mixture-based correlations. The key quantities considered include viscosity, density, heat capacity, coefficients of thermal and solutal expansion, and thermal conductivity. A summary of the adopted formulations is reported in Table 1. In the present case, the suspension is prepared by combining copper (Cu) and titanium dioxide (TiO2) nanoparticles within water, serving as the host fluid. The volumetric share of Cu is represented by ϕ1, while ϕ2 denotes the proportion of TiO2. The notation s1, s2, and f correspond to Cu, TiO2, and the pure fluid, respectively, whereas nf designates the single-particle nanofluid (Cu–H2O) and hnf the combined system (Cu–TiO2–H2O). The nanofluid formulation proceeds sequentially: Cu particles are initially incorporated into water with a volume fraction up to ϕ1=2%. The hybrid configuration is obtained by subsequently introducing TiO2 particles at ϕ2=2%. The case ϕ1=ϕ2=0 recovers the base fluid, while setting ϕ2=0 yields the Cu–H2O nanofluid.

For completeness, Table 2 lists the inherent thermophysical constants of the three constituents (Cu, TiO2, and water). These parameters form the baseline for calculating the effective properties of the nanofluid and hybrid nanofluid models applied in this study.

2.5 Non-Dimensional Form

To facilitate the mathematical analysis, the governing equations are transformed into their dimensionless form by introducing appropriate non-dimensional variables. This non-dimensionalization simplifies the physical interpretation of the system parameters and reduces the number of governing variables. The following dimensionless quantities are employed, as adopted in recent studies [56,63]:

η=yh, τ=tνfh2, (u1,v1)=(uu0,vu0), θ=T−ThT0−Th, ϕ=C−ChC0−Ch.(10)

Considering (10), the dimensionless versions of Eqs. (1), (2), (4), and (9) can be succinctly expressed as follows:

x1(∂u1∂τ−2K2v1)=x0∂2u1∂η2+x2Grθ+x3Gcϕ−x0σu1+E(1+βe−βeβi)e−Sη,(11)

x1(∂v1∂τ+2K2u1)=x0∂2v1∂η2−x0σv1+E(1−βe−βeβi)e−Sη,(12)

x4Pr∂θ∂τ=(x5+Ra)∂2θ∂η2−Qrθ,(13)

∂ϕ∂τ=x6Sc∂2ϕ∂η2−Krϕ,(14)

where the non-dimensional parameters are: K2=Ωh2νf, Gr=(gβT)f(T0−Th)h2νfu0, Gc=(gβC)f(C0−Ch)h2νfu0, E=πJ0m0h28μfu0, S=πhl, σ=k∗h2, Ra=kfk∗4σ∗Th3, Qr=Q0h2kf, Pr=(μfcp)fkf, Kr=K1h2νf, Sc=νfDf.

The dimensionless IBCs are:

τ=0:u1=0=v1,  θ=0,  ϕ=0  for all  0≤η≤1,τ>0:u1=τ2, v1=0  at  η=0,θ={τ,0<τ≤11,τ>1=τH(τ)−(τ−1)H(τ−1)  at  η=0,ϕ={τ,0<τ≤11,τ>1=τH(τ)−(τ−1)H(τ−1)  at  η=0,τ>0:u1=0=v1,  θ=0,  ϕ=0  at  η=1,(15)

where H(τ) represents the Heaviside step function.

It is advantageous to consolidate Eqs. (11) and (12) into a single comprehensive equation. This is accomplished by initially multiplying Eq. (12) by i and then adding it to Eq. (11), leading to the following unified equation:

x1(∂Ψ∂τ+2iK2Ψ)=x0∂2Ψ∂η2+x2Grθ+x3Gcϕ−x0σΨ+E[(1+βe−βeβi)+i(1−βe−βeβi)]e−Sη,(16)

where Ψ(=u1+iv1) is the unified fluid velocity, and i=−1.

The IBCs for (Ψ, θ, ϕ) are expressed as follows:

τ=0:Ψ=0,  θ=0,  ϕ=0  for all  0≤η≤1,τ>0:Ψ=τ2  at  η=0,θ={τ,0<τ≤11,τ>1=τH(τ)−(τ−1)H(τ−1)  at  η=0,ϕ={τ,0<τ≤11,τ>1=τH(τ)−(τ−1)H(τ−1)  at  η=0,τ>0:Ψ=0,  θ=0,  ϕ=0  at  η=1.(17)

2.6 Method of Solution

The Laplace Transform (LT) is an effective analytical method for solving linear differential equations, particularly in time-dependent and dynamic systems. Its strength lies in converting complex time-domain problems into simpler algebraic forms in the Laplace domain, especially through its linearity and ability to transform convolutions into multiplications. This makes LT especially suitable for initial- and boundary-value problems in linear time-invariant systems.

In the present study, the LT method is employed to obtain semi-analytical solutions for the governing Eqs. (13), (14) and (16), subject to the initial and boundary conditions given in (15). The corresponding Laplace-transformed formulations are derived as follows [63]:

a1ξΨ¯=d2Ψ¯dη2+a2θ¯+a3Φ¯−a4Ψ¯1+a5ξe−Sη,(18)

a6ξθ¯=d2θ¯dη2−a7θ¯,(19)

a8ξϕ¯=d2ϕ¯dη2−a9ϕ¯,(20)

where Ψ¯=L{Ψ}, θ¯=L{θ}, ϕ¯=L{ϕ}, and ξ(>0) stands for the LT parameter, Moreover, a1, a2, a3, a4, a5, a6, a7, a8, and a9 are given in the Appendix A.

The corresponding BCs for Ψ¯, θ¯, and ϕ¯ are:

Ψ¯=0,  θ¯=0,  ϕ¯=0  for  0≤η≤1,Ψ¯=2s3, θ¯=1ξ2(1−e−ξ),  ϕ¯=1ξ2(1−e−ξ)  at  η=0,Ψ¯=0,  θ¯=0,  ϕ¯=0  at   η=1.(21)

Applying the boundary conditions (21), the solution to Eqs. (18)–(20) is formulated in the following manner:

ϕ¯(η,ξ)=1ξ2(1−e−ξ)sinh⁡(a8ξ+a9)1/2(1−η)sinh⁡(a8ξ+a9)1/2,(22)

θ¯(η,ξ)=1ξ2(1−e−ξ)sinh⁡(a6ξ+a7)1/2(1−η)sinh⁡(a6ξ+a7)1/2,(23)

Ψ¯(η,ξ)=2ξ3sinh⁡(a1ξ+a4)1/2(1−η)sinh⁡(a1ξ+a4)1/2+Υ1ξ2(ξ−β1)(1−e−ξ)[sinh⁡(a1ξ+a4)1/2(1−η)sinh⁡(a1ξ+a4)1/2−sinh⁡(a6ξ+a7)1/2(1−η)sinh⁡(a6ξ+a7)1/2]+Υ2ξ2(ξ−β2)(1−e−ξ)[sinh⁡(a1ξ+a4)1/2(1−η)sinh⁡(a1ξ+a4)1/2−sinh⁡(a8ξ+a9)1/2(1−η)sinh⁡(a8ξ+a9)1/2]+Υ3ξ(ξ−β3)[e−Sη−sinh⁡(a1ξ+a4)1/2(1−η)sinh⁡(a1ξ+a4)1/2−e−Ssinh⁡(a1ξ+a4)1/2ηsinh⁡(a1ξ+a4)1/2],(24)

where expressions Υ1, Υ2, Υ3, β1, β2, and β3 are given in the Appendix A.

By applying the inverse Laplace Transforms to Eqs. (18)–(20), the analytical expressions for the concentration, temperature, and velocity distributions within the Riga tunnel are derived. These closed-form solutions are presented below and follow the methodologies outlined in [63]:

ϕ(η,τ)=∑n=0∞[f~1(aa8,γ1,τ)−f~1(ba8,γ1,τ)−H(τ−1){f~1(aa8,γ1,τ−1)−f~1(ba8,γ1,τ−1)}],(25)

θ(η,τ)=∑n=0∞[f~1(aa6,γ2,τ)−f~1(ba6,γ2,τ)−H(τ−1){f~1(aa6,γ2,τ−1)−f~1(ba6,γ2,τ−1)}],(26)

Ψ(η,τ)=∑n=0∞[f~2(aa1,γ3,τ)−f~2(ba1,γ3,τ)]+Υ1∑n=0∞[{f~3(aa1,γ3,β1,τ)−f~3(ba1,γ3,β1,τ)−f~3(aa6,γ2,β1,τ)+f~3(ba6,γ2,β1,τ)}−H(τ−1){f~3(aa1,γ3,β1,τ−1)−f~3(ba1,γ3,β1,τ−1)−f~3(aa6,γ2,β1,τ−1)+f~3(ba6,γ2,β1,τ−1)}]+Υ2∑n=0∞[{f~3(aa1,γ3,β2,τ)−f~3(ba1,γ3,β2,τ)−f~3(aa8,γ1,β2,τ)+f~3(ba8,γ1,β2,τ)}−H(τ−1){f~3(aa1,γ3,β2,τ−1)−f~3(ba1,γ3,β2,τ−1)−f~3(aa8,γ1,β2,τ−1)+f~3(ba8,γ1,β2,τ−1)}]+Υ3f~4(η,τ),(27)

where the functions f~1, f~2, and f~3 are provided in the Appendix A, and

f~4(η,τ)=1β3(eβ3τ−1)e−Sη+1β3[e−Ssinh⁡σ1ηsinh⁡σ1+sinh⁡σ1(1−η)sinh⁡σ1]−1β3[e−Ssinh⁡σ2ηsinh⁡σ2+sinh⁡σ2(1−η)sinh⁡σ2]eβ3τ+∑n=1∞nπ(−1)nAnsin⁡nπη,An=2(e−S−1)eξ1τa1ξ1(ξ1−β3), a=2n+η, b=2n+2−ηξ1=−1a1(n2π2+a4).(28)

Moreover, expressions a1, a2, a3, ..., a9; β1, β2, β3; γ1, γ2, γ3; σ1, and σ2 are given in the Appendix A.

Eq. (27) represents the unified expression for flow field of an electrically conductive and thermally radiative hybrid nanofluid confined between two vertically extended infinite Riga plates in an intense electromagnetic rotational framework, invoking the existence of Hall and ion-slip currents, and occurrence of stepped up wall temperature and concentration. On separating into a real and imaginary parts one can easily obtain the velocity components (u1, v1) from Eq. (27).

2.7 Engineering Quantities

The evaluation of key engineering parameters, such as shear stress, heat transfer rate, and mass transfer rate is crucial for a wide range of industrial and mechanical processes. These quantities directly influence thermal management, fluid transport efficiency, and chemical reactivity at boundaries, thereby playing a central role in optimizing operational performance. Accurate prediction and control of these parameters are essential not only for ensuring process stability and energy efficiency but also for enhancing the reliability, safety, and durability of engineering systems. Consequently, their rigorous assessment is indispensable during both the design and operational stages of technological applications.

2.7.1 Heat and Mass Transfer Rates

The nondimensional heat and mass transfer rates at the left wall of the tunnel (η=0) are derived from Eqs. (25) and (26). These quantities, representing the wall heat flux nd mass flux, are expressed as:

ϕ′(0)=∂ϕ∂η)η=0=∑n=0∞[h~1(ca8,γ1,τ)−h~1(da8,γ1,τ)−H(τ−1){h~1(ca8,γ1,τ−1)−h~1(da8,γ1,τ−1)}],(29)

θ′(0)=∂θ∂η)η=0=∑n=0∞[h~1(ca6,γ2,τ)−h~1(da6,γ2,τ)−H(τ−1){h~1(ca6,γ2,τ−1)−h~1(da6,γ2,τ−1)}],(30)

where c=2n, d=2n+2, and the expression of the known function h~1 is given in the Appendix A.

2.7.2 Shear Stresses

The non-dimensional shear stresses at the left wall of the tunnel (η=0) are evaluated using the expression derived in Eq. (27). These shear stress values characterize the tangential momentum transfer induced by the hybrid nanofluid flow along the wall and are presented as follows:

τx0R+iτy0R=∂Ψ∂η)η=0=∑n=0∞[h~2(ca1,γ3,τ)−h~2(da1,γ3,τ)]+Υ1∑n=0∞[{h~3(ca1,γ3,β1,τ)−h~3(da1,γ3,β1,τ)−h~3(ca6,γ2,β1,τ)+h~3(da6,γ2,β1,τ)}−H(τ−1){h~3(ca1,γ3,β1,τ−1)−h~3(da1,γ3,β1,τ−1)−h~3(ca6,γ2,β1,τ−1)+h~3(da6,γ2,β1,τ−1)}]+Υ2∑n=0∞[{h~3(ca1,γ3,β2,τ)−h~3(da1,γ3,β2,τ)−h~3(ca8,γ1,β2,τ)+h~3(da8,γ1,β2,τ)}−H(τ−1){h~3(ca1,γ3,β2,τ−1)−h~3(da1,γ3,β2,τ−1)−h~3(ca8,γ1,β2,τ−1)+h~3(da8,γ1,β2,τ−1)}]+Υ3h~4(0,τ),(31)

where the functions h~2, and h~3 are provided in the Appendix A.

h~4(0,τ)=−Sβ3(eβ3τ−1)+1β3[e−Sσ1sinh⁡σ1−σ1cosh⁡σ1sinh⁡σ1]−1β3[e−Sσ2sinh⁡σ2−σ2cosh⁡σ2sinh⁡σ2]eβ3τ+∑n=1∞n2π2(−1)nAn.(32)

2.8 Solutions under UWT and UWC Conditions

Under uniform wall temperature (UWT) and uniform wall concentration (UWC) conditions, the dimensionless boundary initial conditions in Eq. (21) are modified by setting θ(0,τ)=1 and ϕ(0,τ)=1 for τ>0, respectively. Closed-form expressions for velocity, temperature, and concentration fields are derived at the left wall of the tunnel based on these conditions as follows:

ϕ(η,τ)=∑n=0∞[f~6(aa8,γ1,τ)−f~6(ba8,γ1,τ)],(33)

θ(η,τ)=∑n=0∞[f~6(aa6,γ2,τ)−f~6(ba6,γ2,τ)],(34)

Ψ(η,τ)=∑n=0∞[f~2(aa1,γ3,τ)−f~2(ba1,γ3,τ)]+Υ1∑n=0∞[{f~5(aa1,γ3,β1,τ)−f~5(ba1,γ3,β1,τ)−f~5(aa6,γ2,β1,τ)+f~5(ba6,γ2,β1,τ)}]+Υ2∑n=0∞[{f~5(aa1,γ3,β2,τ)−f~5(ba1,γ3,β2,τ)−f~5(aa8,γ1,β2,τ)+f~5(ba8,γ1,β2,τ)}]+Υ3f~4(η,τ),(35)

where the expressions of the known functions h~5 and h~6 are given in the Appendix A.

For UWT and UWC situations, the dimensionless MTR ϕ′(0,τ), HTR θ′(0,τ), and shear stresses (SS) are evaluated as:

ϕ′(0)=∑n=0∞[h~6(ca8,γ1,τ)−h~6(da8,γ1,τ)],(36)

θ′(0)=∑n=0∞[h~6(ca6,γ2,τ)−h~6(da6,γ2,τ)],(37)

τx0U+iτy0U=∂Ψ∂η)η=0=∑n=0∞[h~2(ca1,γ3,τ)−h~2(da1,γ3,τ)]+Υ1∑n=0∞[{h~5(ca1,γ3,β1,τ)−h~5(da1,γ3,β1,τ)−h~5(ca6,γ2,β1,τ)+h~5(da6,γ2,β1,τ)}]+Υ2∑n=0∞[{h~5(ca1,γ3,β2,τ)−h~5(da1,γ3,β2,τ)−h~5(ca8,γ1,β2,τ)+h~5(da8,γ1,β2,τ)}]+Υ3h~4(0,τ),(38)

where the expressions of the known functions h~5 and h~6 are given in the Appendix A.

In order to understand the effectiveness of stepped up wall temperature and concentration (RWTC, UWTC) conditions. A comparative analysis is conducted sketchily on the (HNF, NF) flows within a moving thermal Riga tunnel.

3  Validation

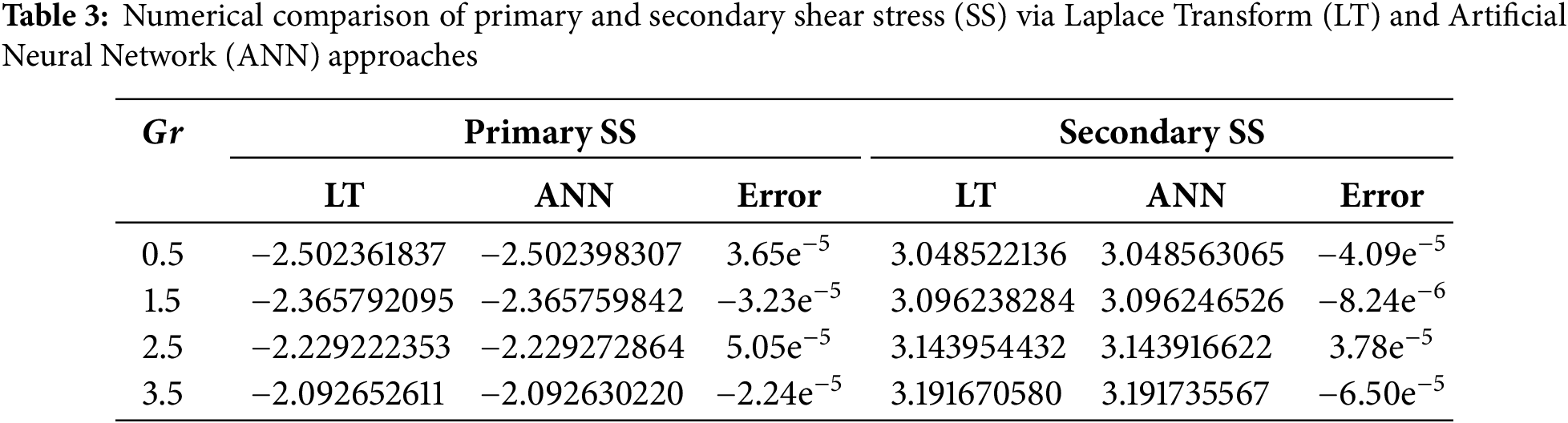
In the limiting case, where the effects of rotation, Hall, and ion-slip currents are neglected, the present analytical formulation precisely reduces to the benchmark solutions reported by Ali et al. [63] (see Fig. 2). This convergence not only verifies the mathematical consistency and accuracy of the current analytical model but also extends the theoretical framework of electromagnetically actuated hybrid nanofluid dynamics to more complex rotating environments incorporating Hall and ion-slip phenomena. Moreover, the comparative results presented in Table 3 reveal excellent concordance between the left-wall shear stress values computed using the Laplace Transform (LT) technique and those predicted by the Artificial Neural Network (ANN) model for both primary and secondary shear stress components. The observed discrepancies are minimal, with relative errors on the order of 10−6 to 10−5, highlighting the predictive capability and robustness of the ANN framework.

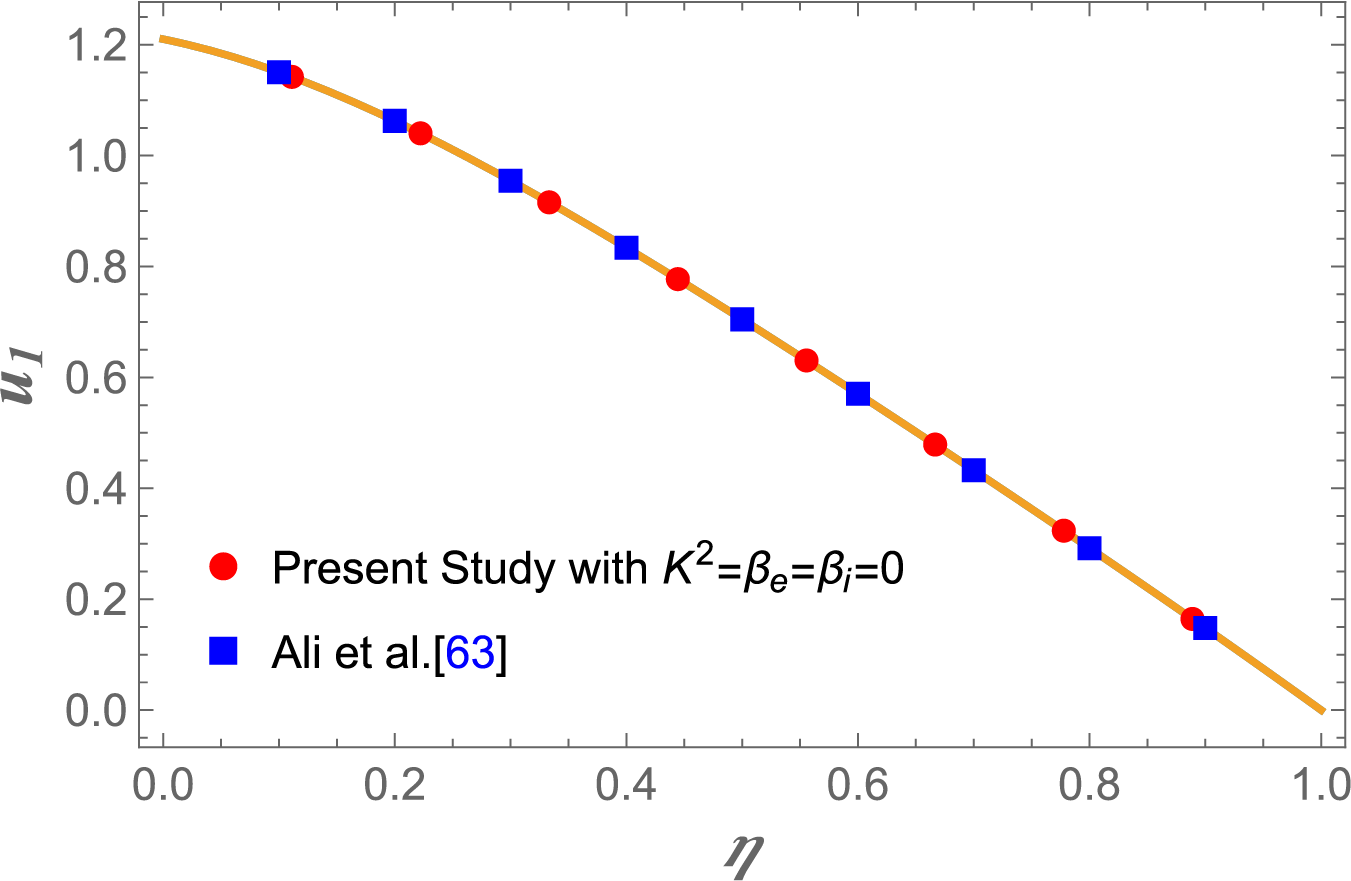
Figure 2: Comparison of velocity profile

4  Results and Discussion

This section investigates the influence of key physical parameters on the essential flow features of the system. The numerical results, derived from comprehensive computational simulations, are presented in Figs. 3–29. These figures demonstrate how variations in thermal, geometric, and transport parameters affect fundamental flow fields and associated transport rates. The parameter ranges employed in this study are selected based on relevant literature and are systematically summarized in Table 4. All graphical outputs have been generated using Mathematica, ensuring high numerical accuracy and clarity in visual representation. This analysis provides a detailed understanding of how individual and combined effects of critical parameters shape the fluid dynamics and transport phenomena, offering valuable physical insights into the behavior of the hybrid nanofluid system under various conditions.

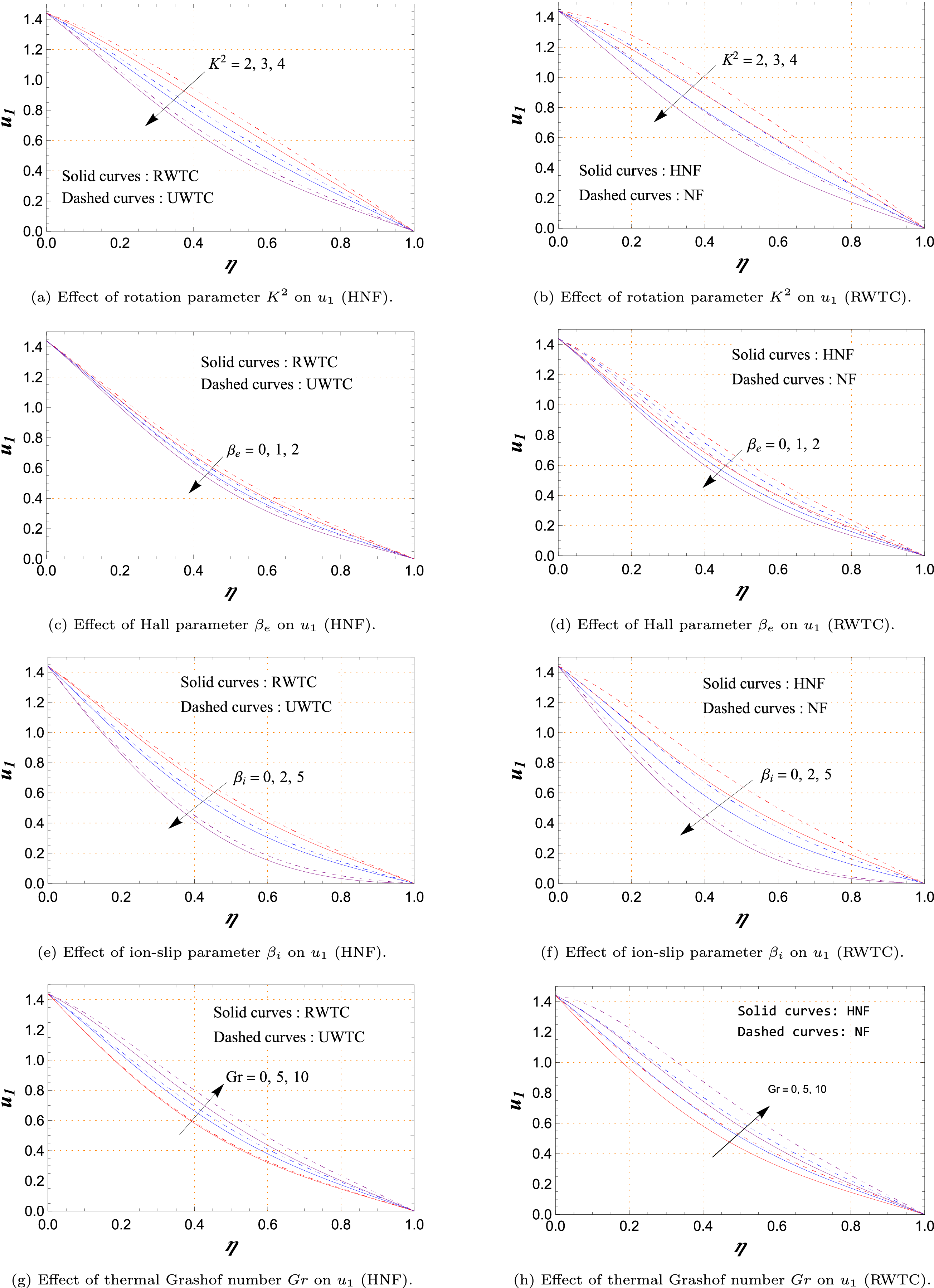
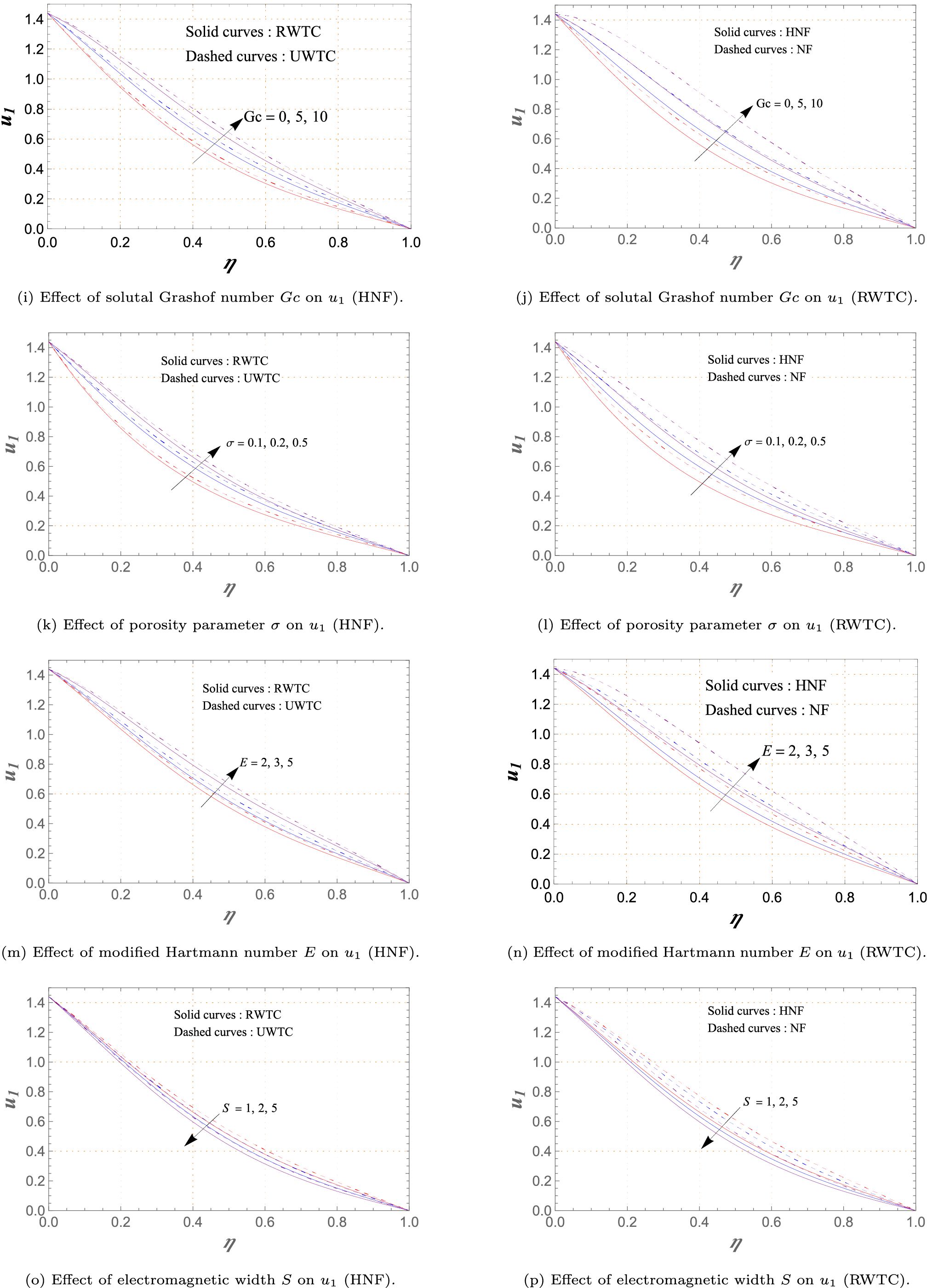
Figure 3: Variations of primary velocity u1 under different controlling parameters

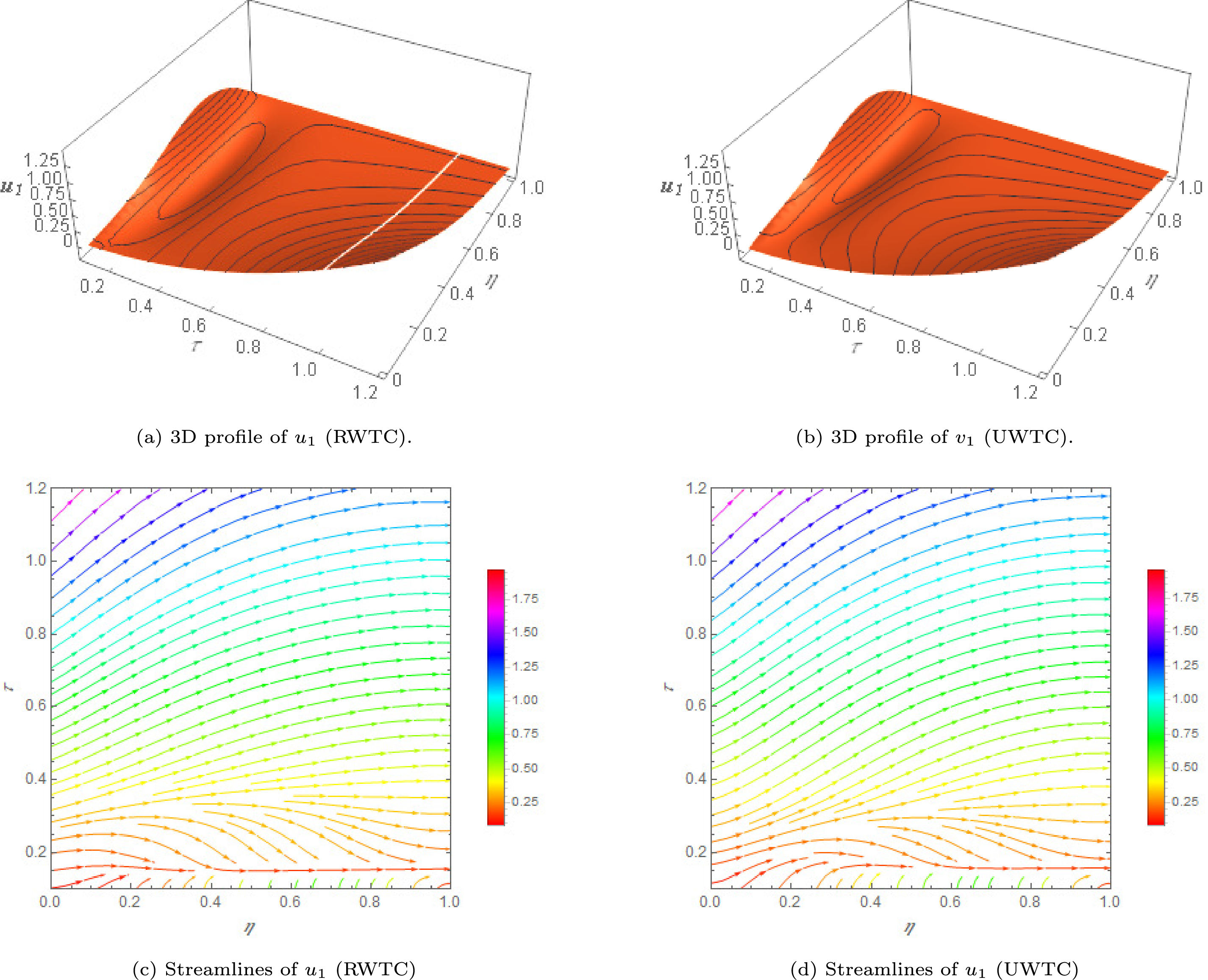
Figure 4: 3D visualization of the profile u1 and streamlines

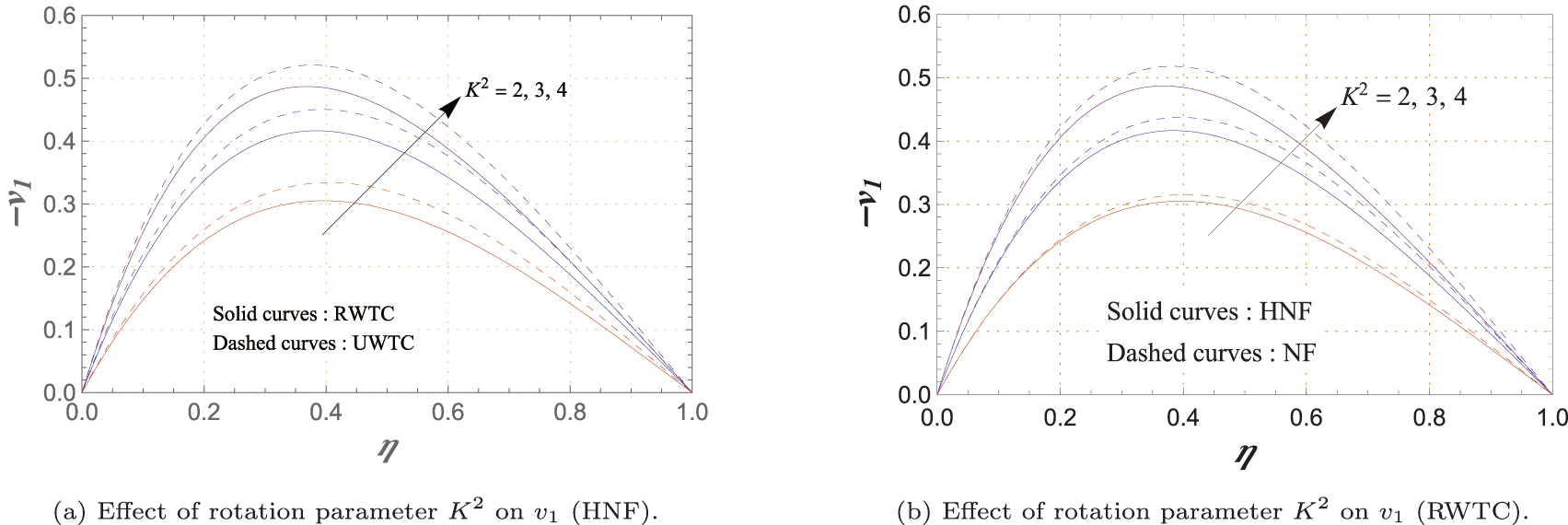
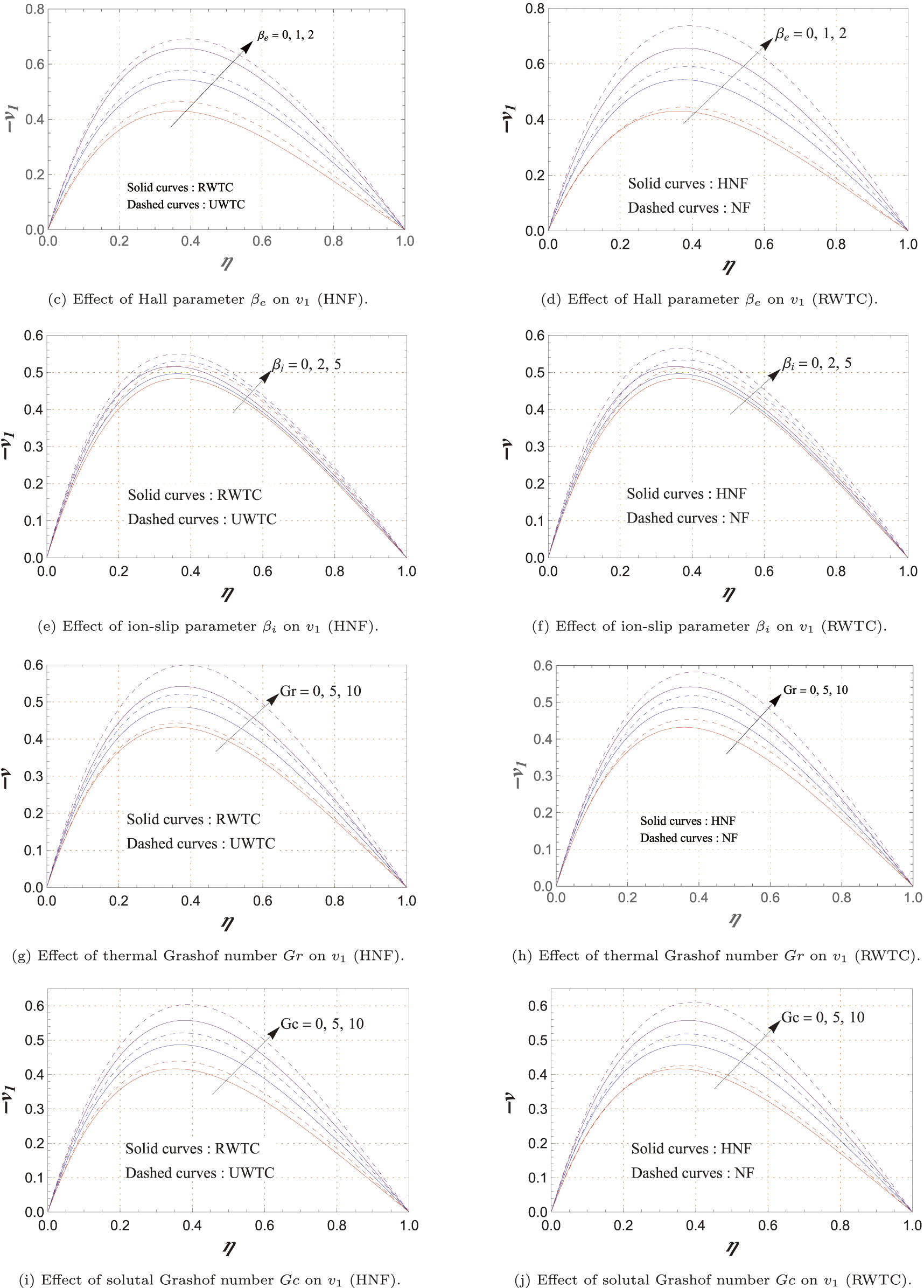
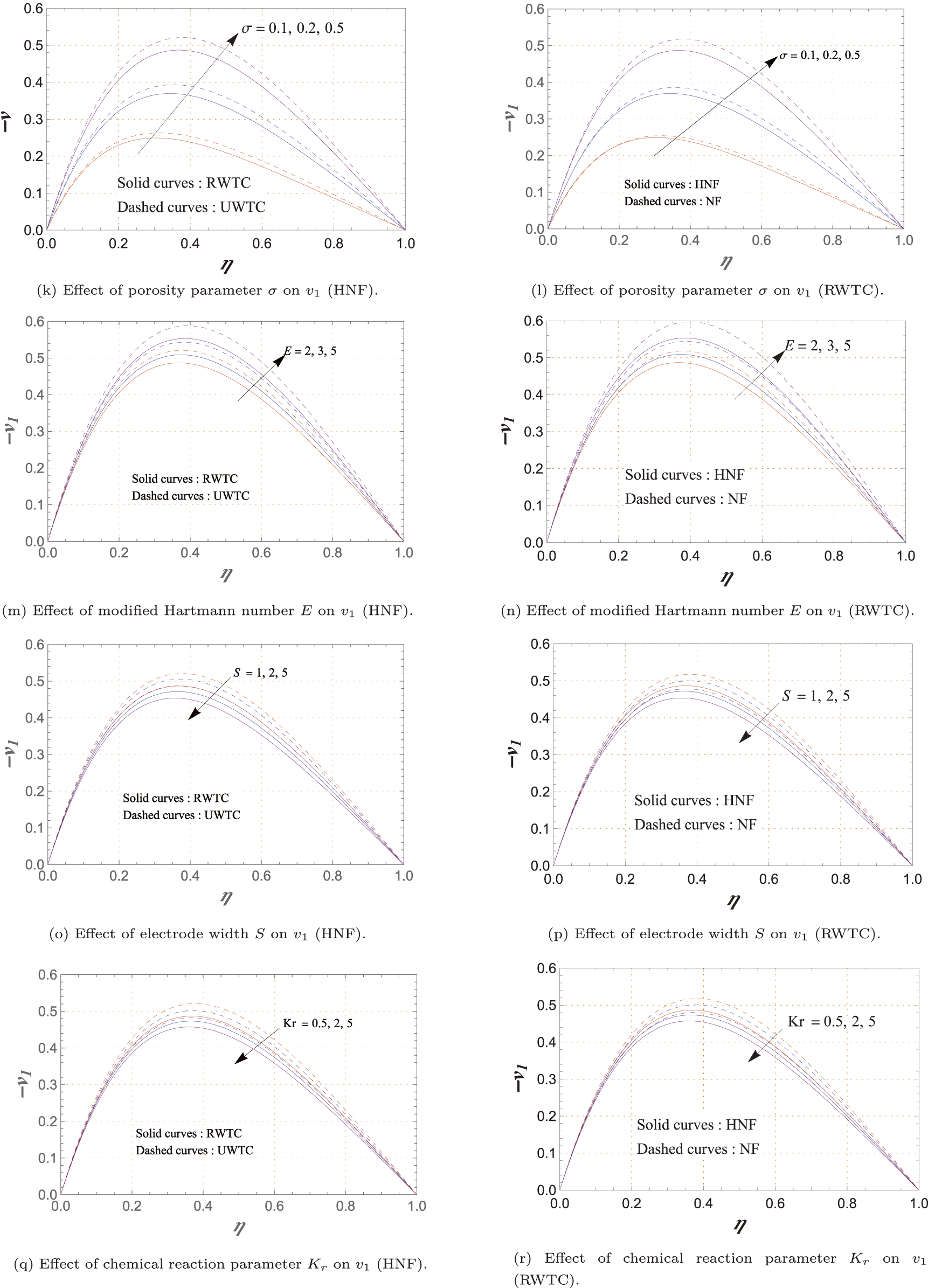
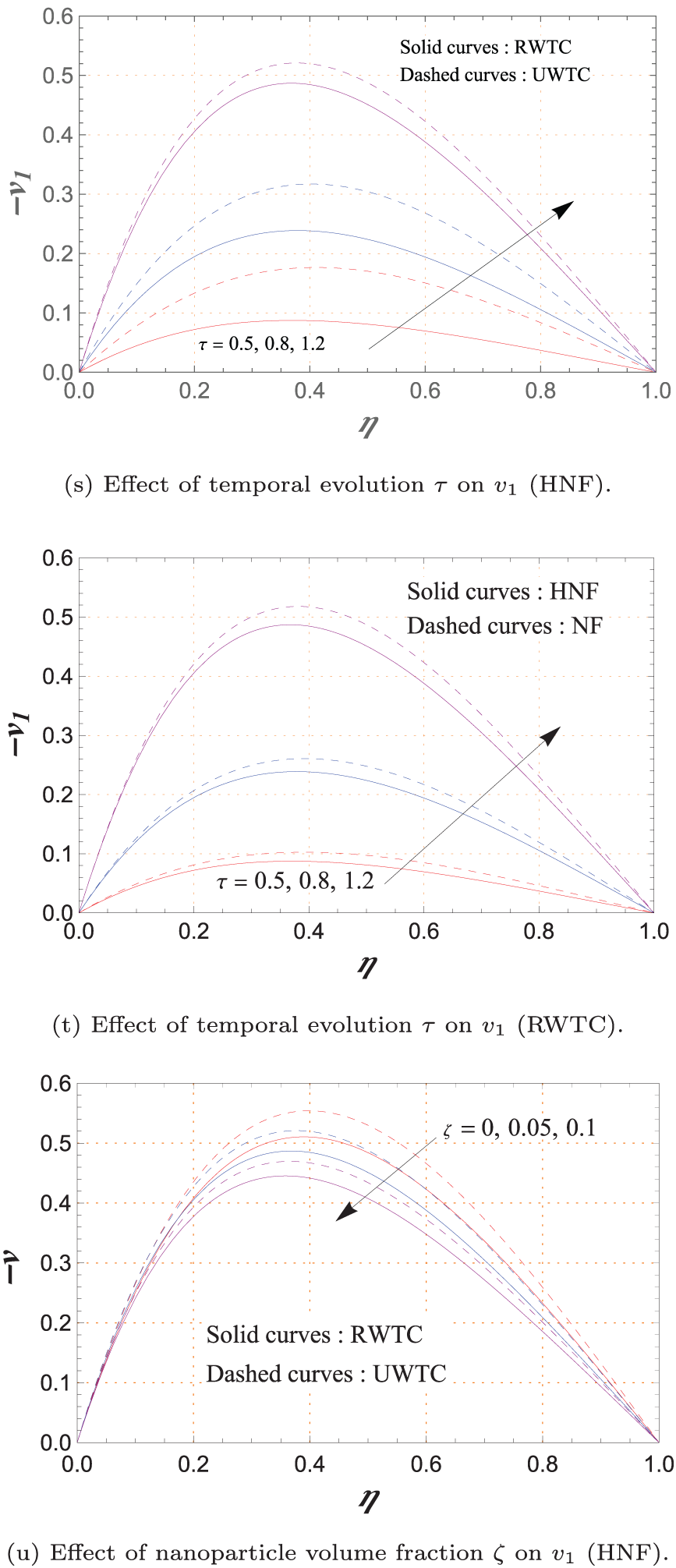
Figure 5: Variations of secondary velocity v1 under different controlling parameters

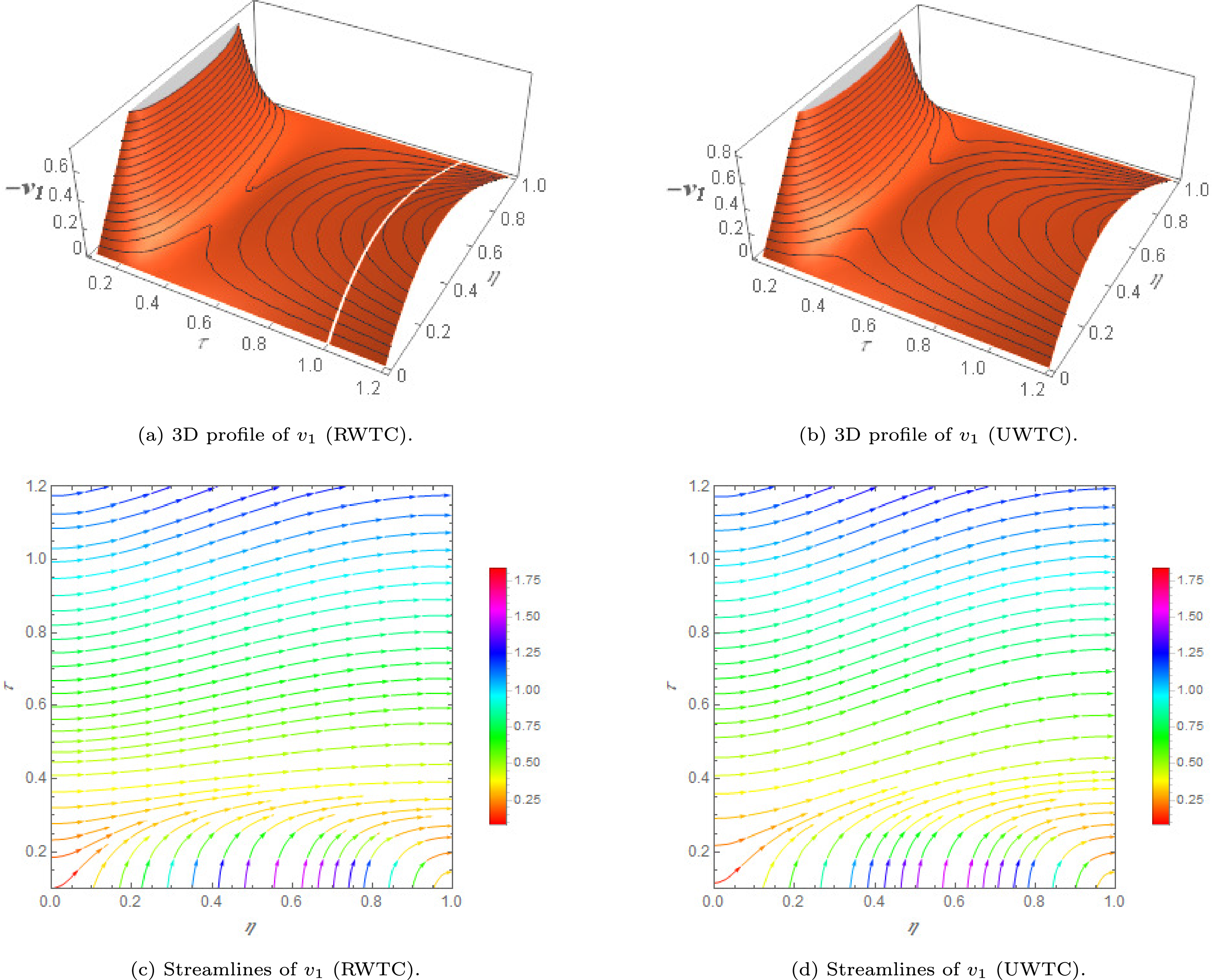
Figure 6: 3D visualization of secondary velocity v1 and streamlines

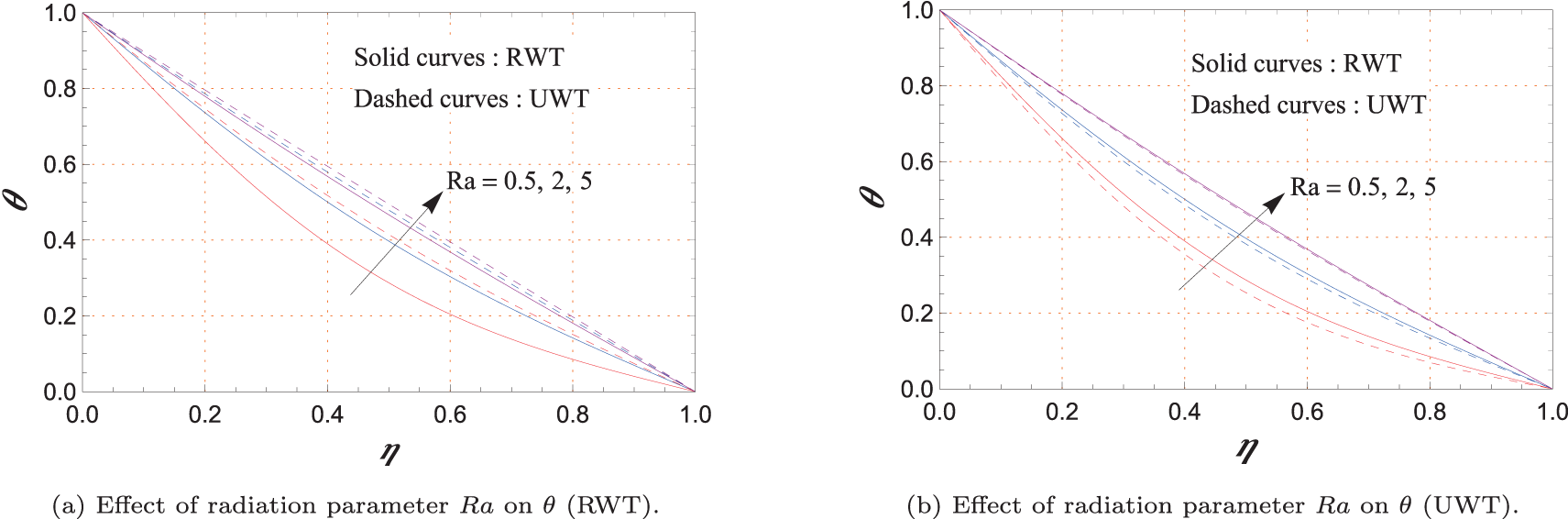
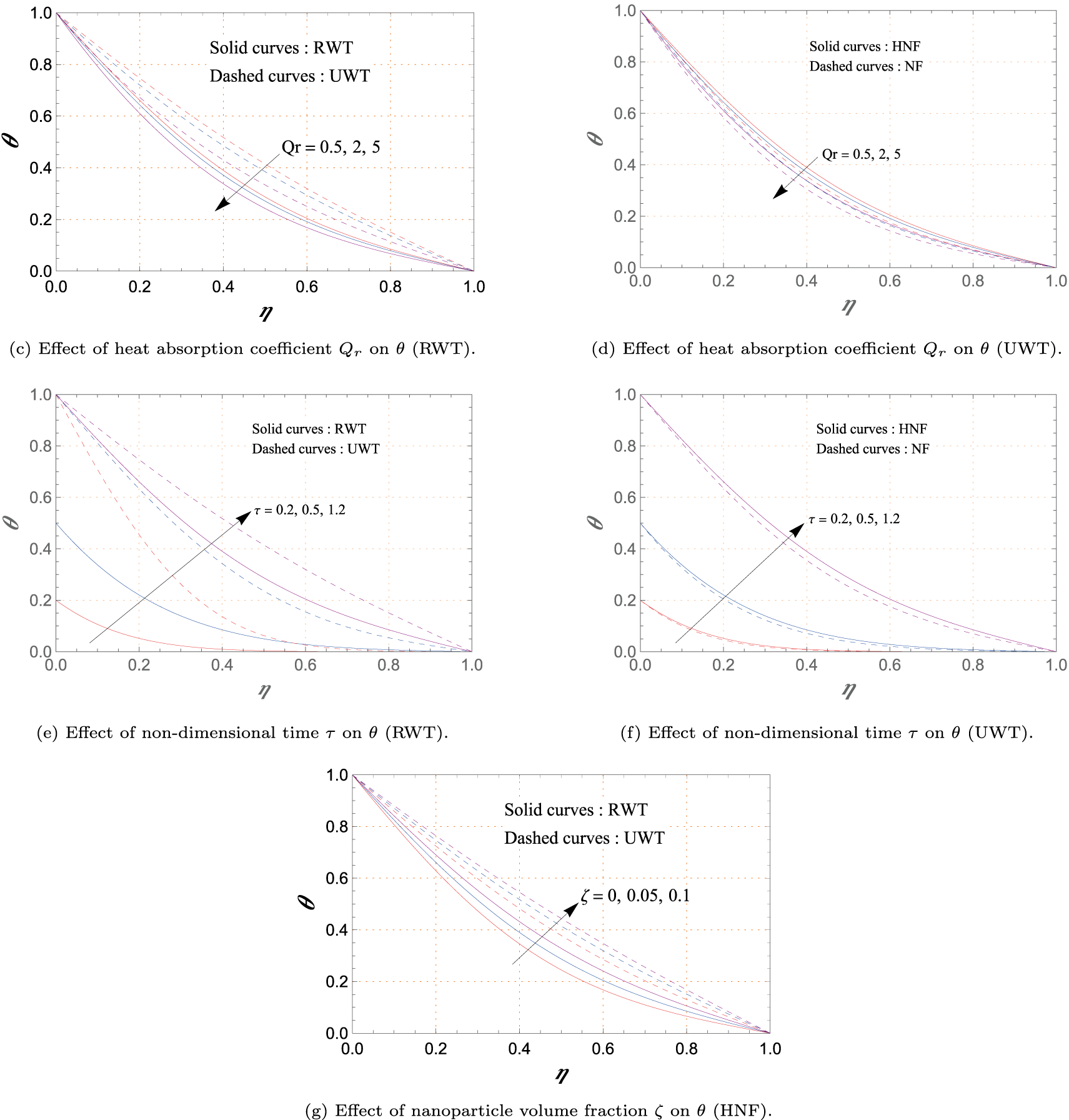
Figure 7: Variations of temperature profile θ under different controlling parameters

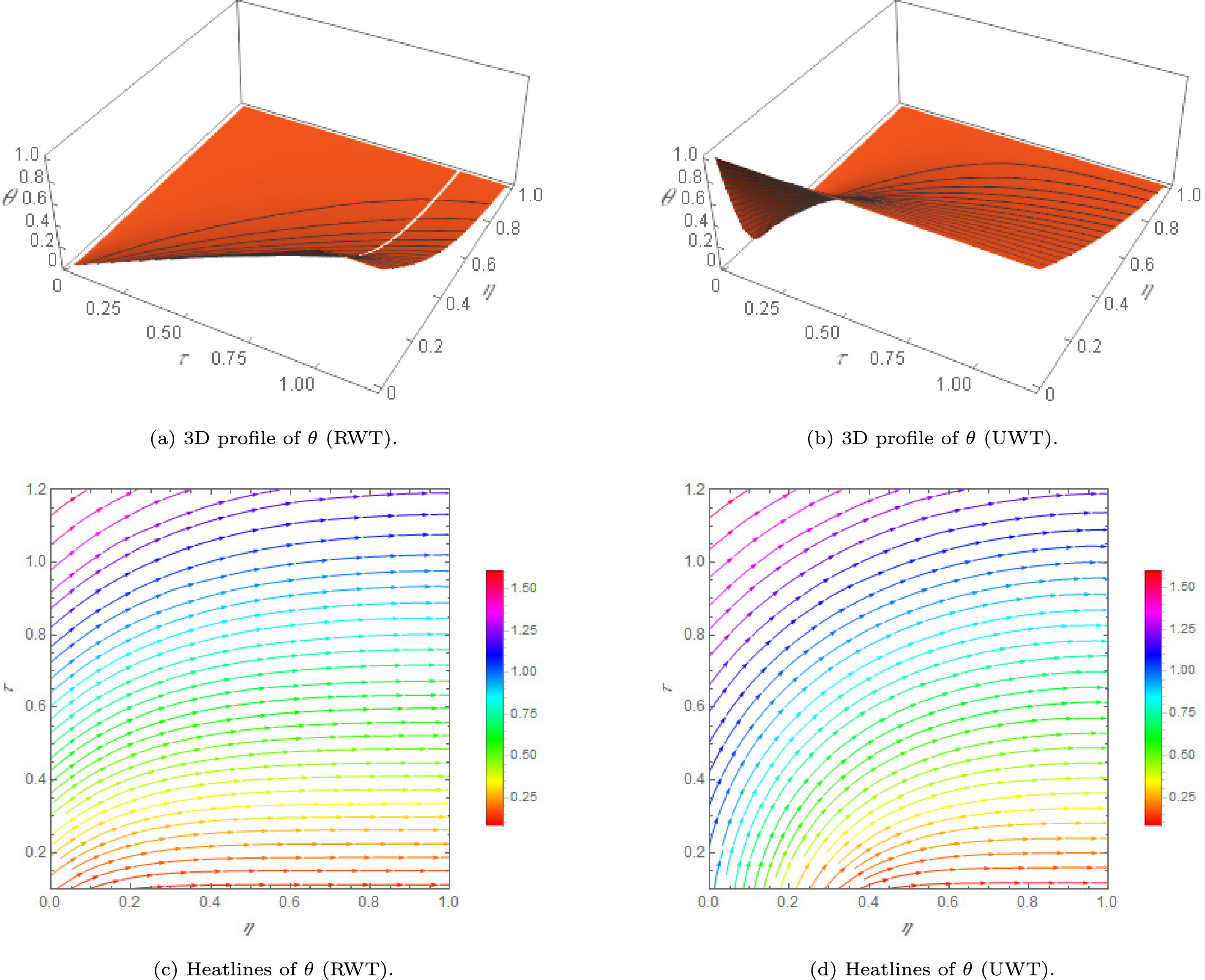
Figure 8: 3D visualization of temperature profile θ and heatlines

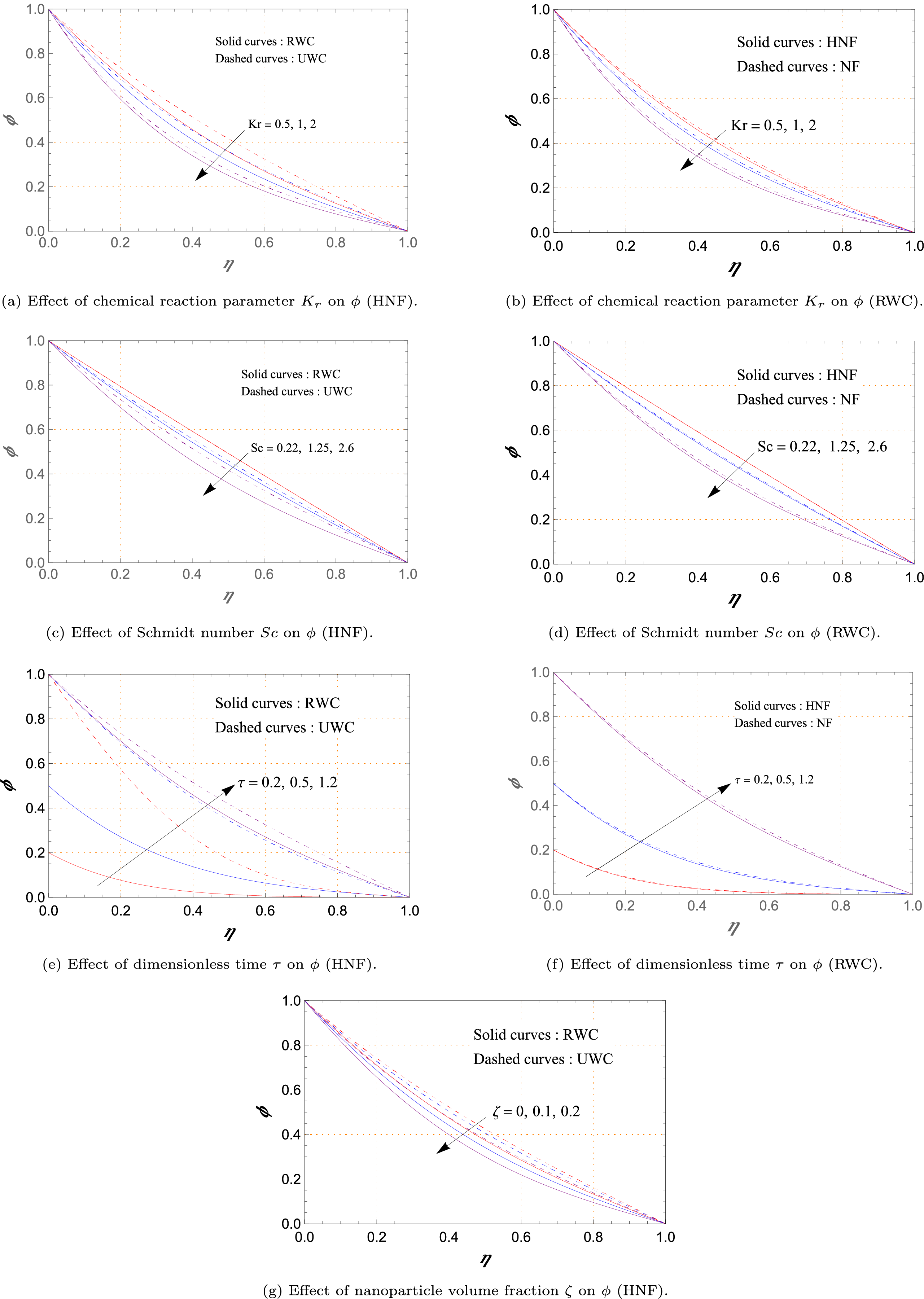
Figure 9: Variations of concentration profile ϕ under different controlling parameters

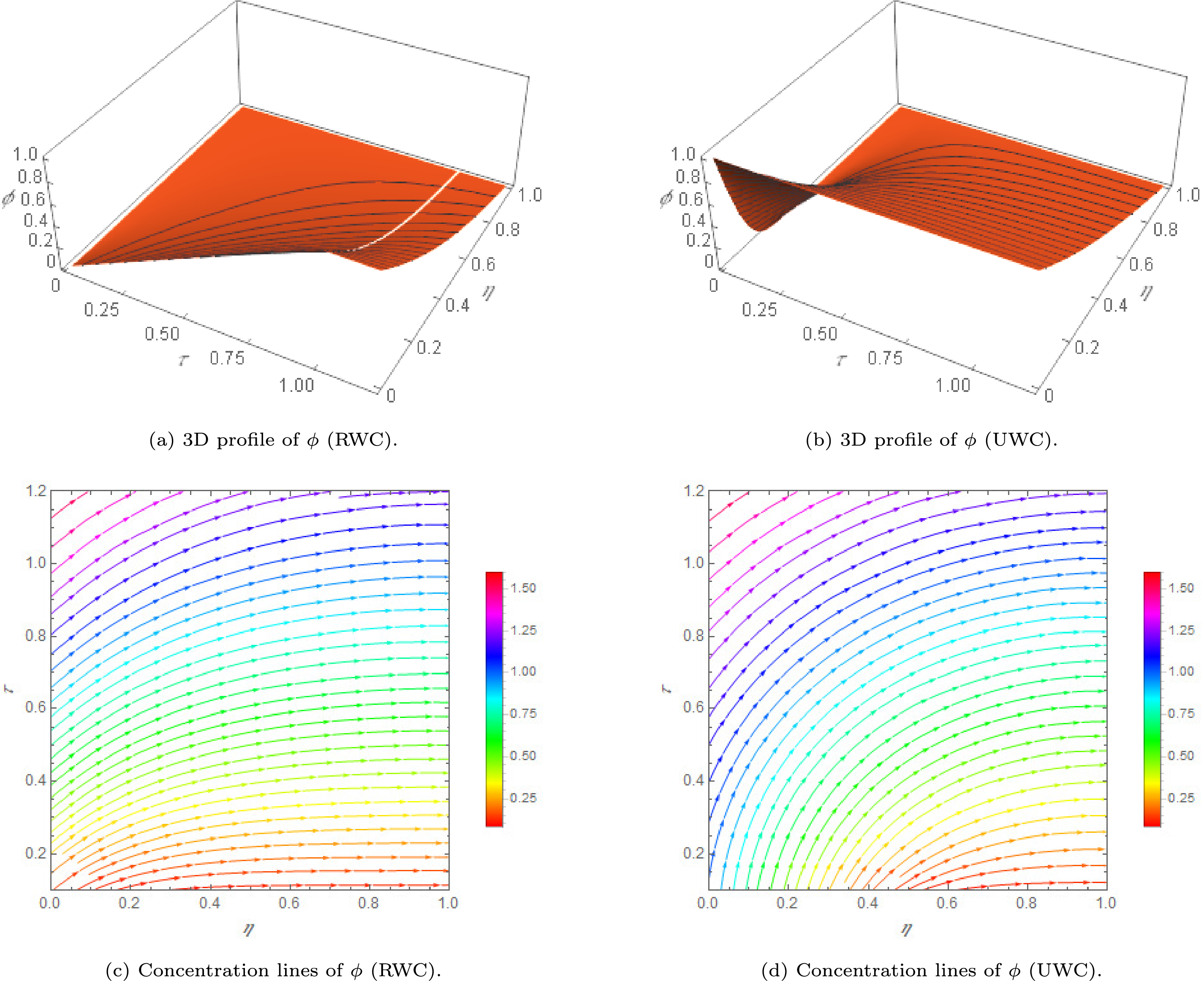
Figure 10: 3D visualization of the profile ϕ and concentration lines

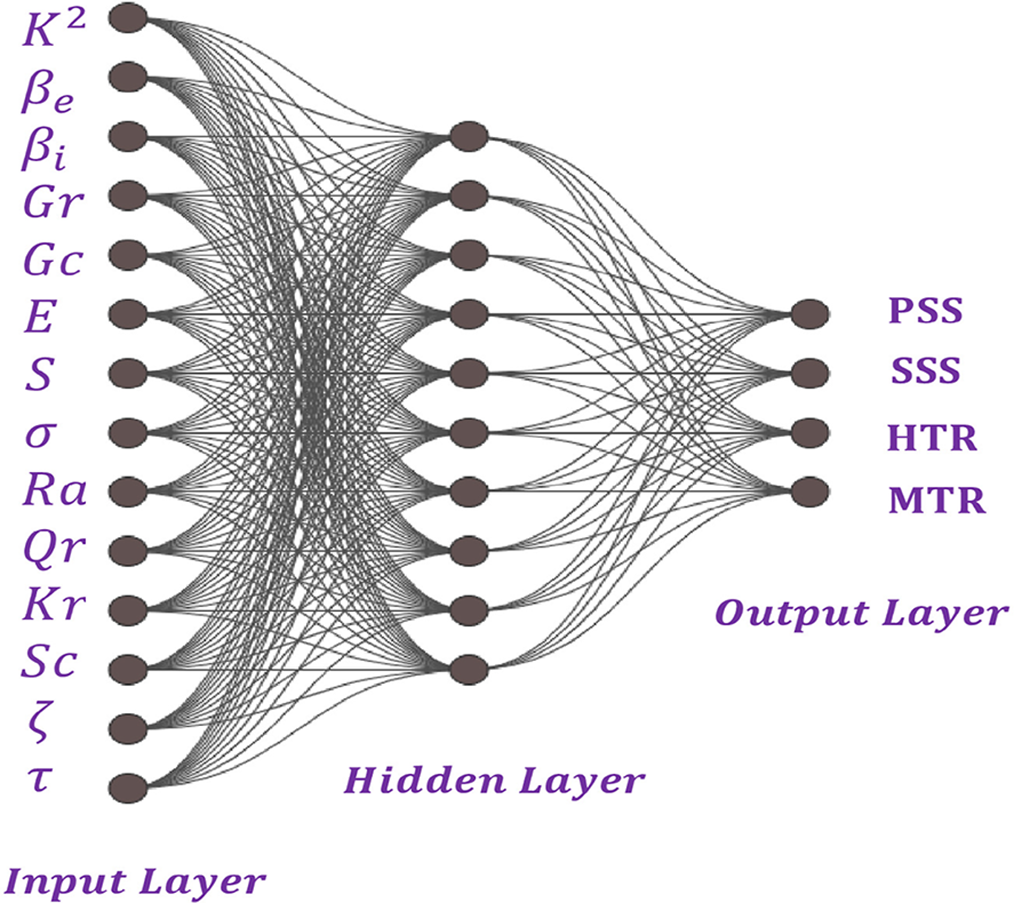
Figure 11: Schematic architecture of ANNs

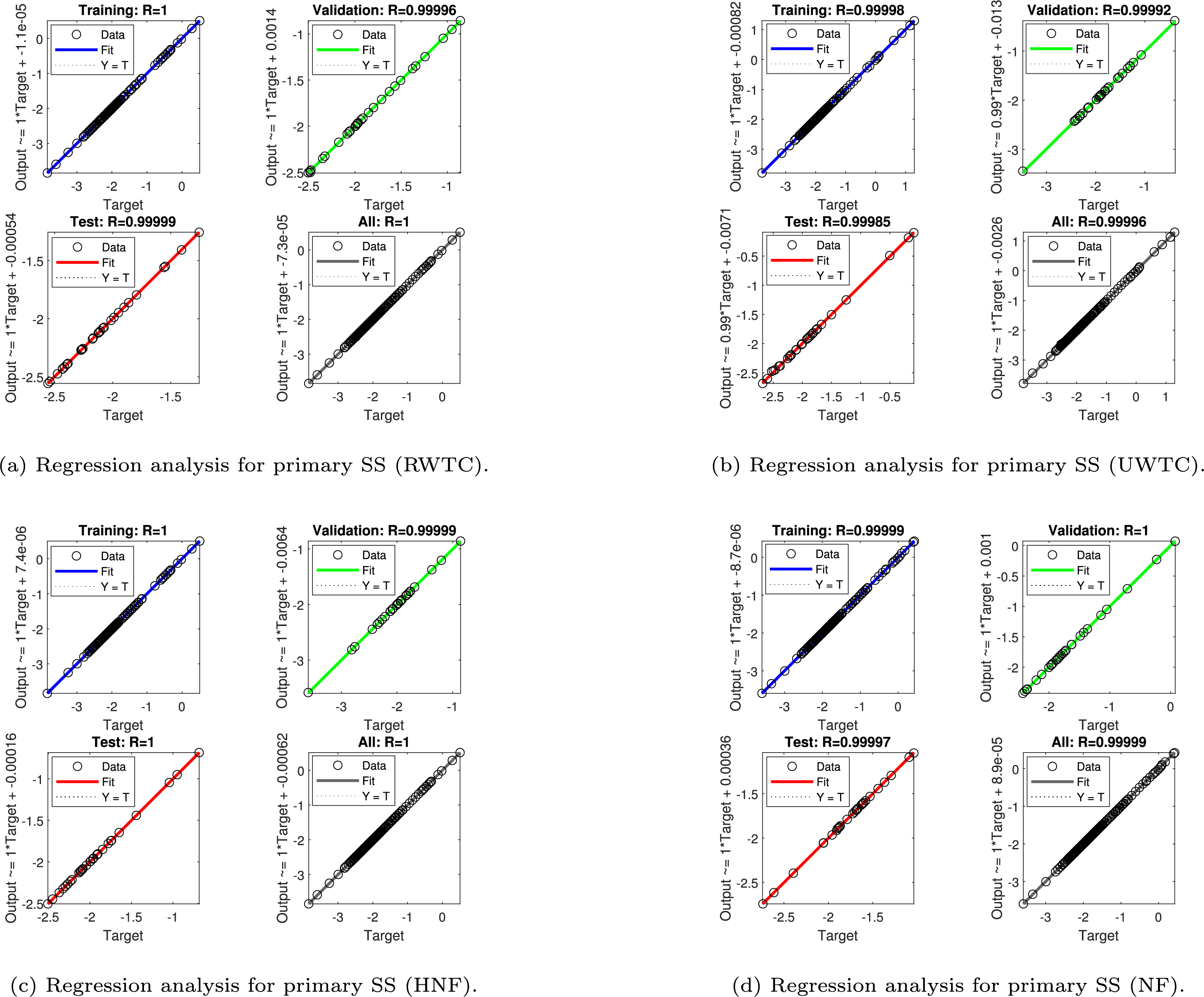
Figure 12: Regression analysis for primary shear stress (SS)

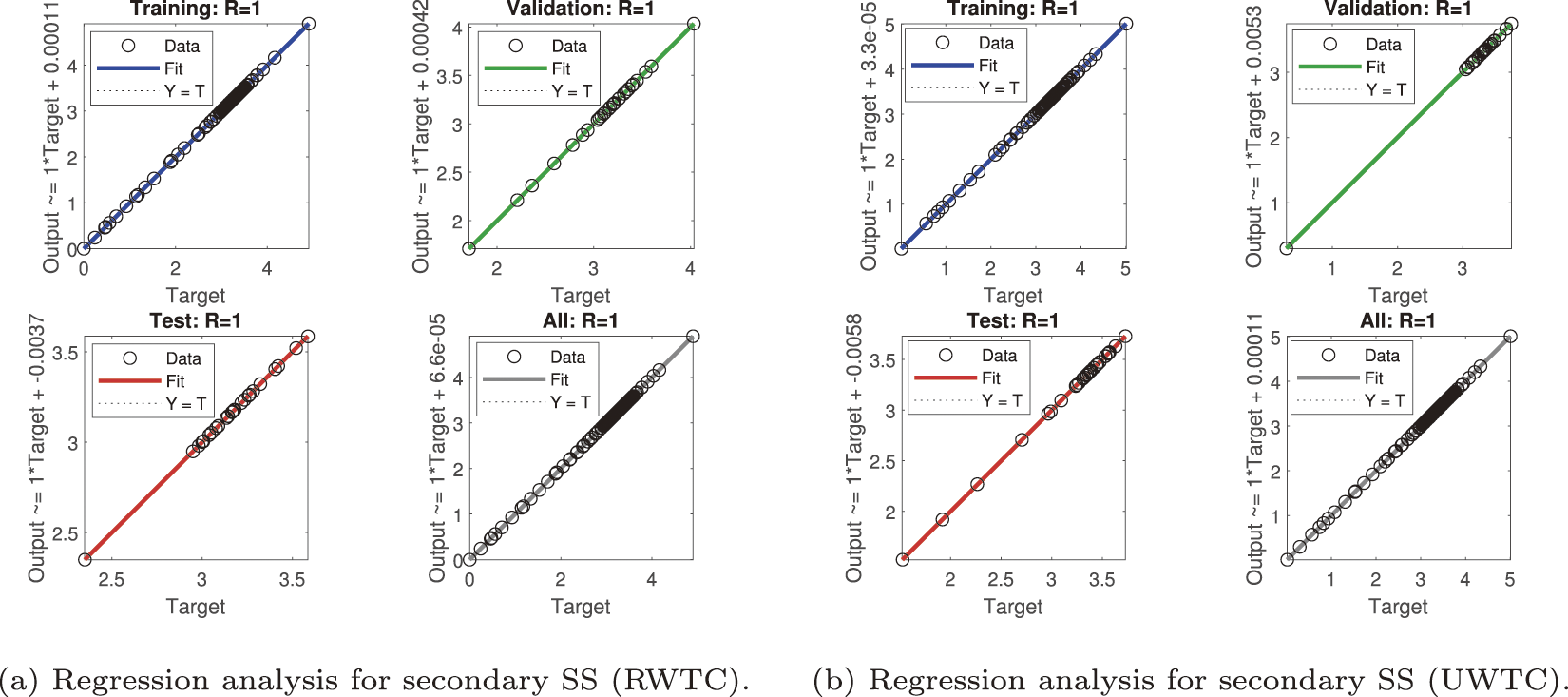
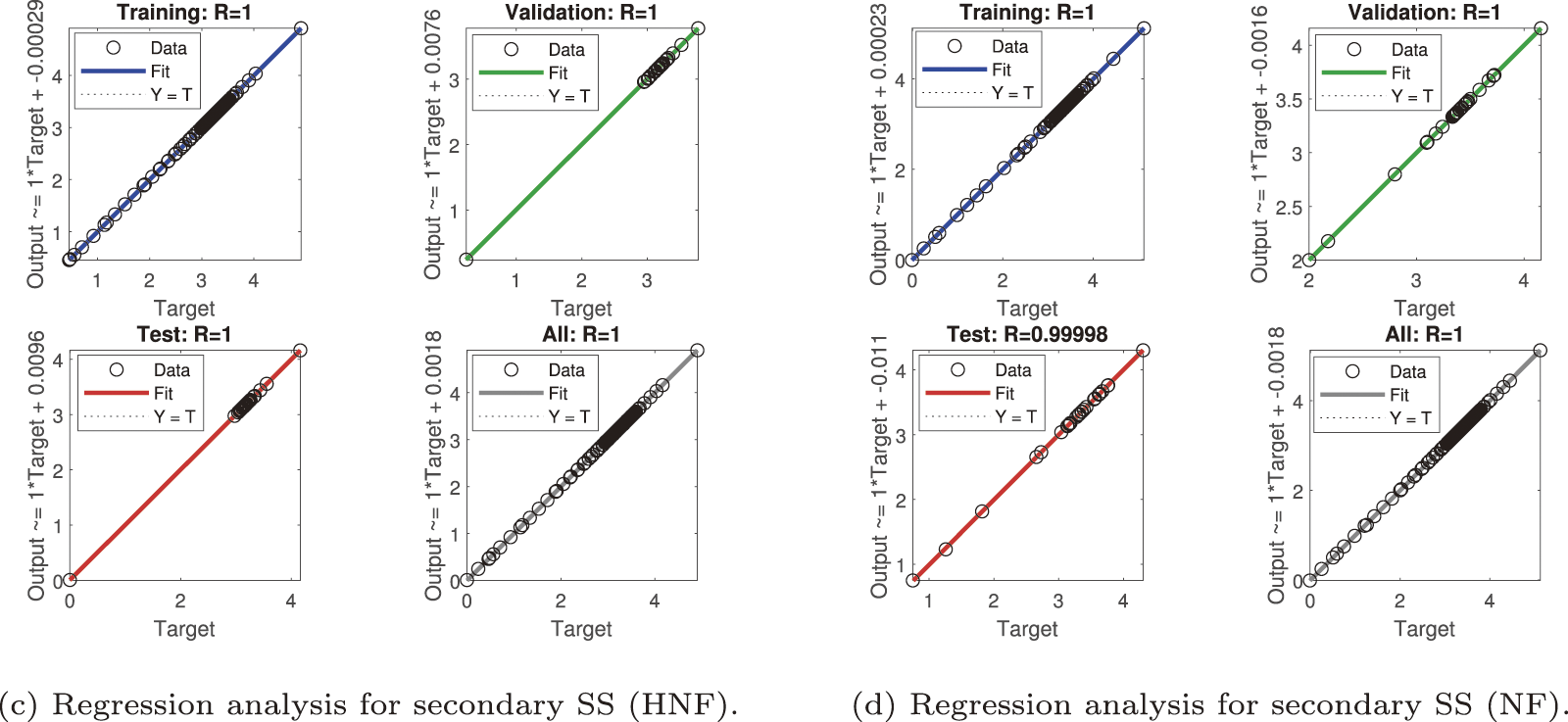
Figure 13: Regression analysis for secondary shear stress (SS)

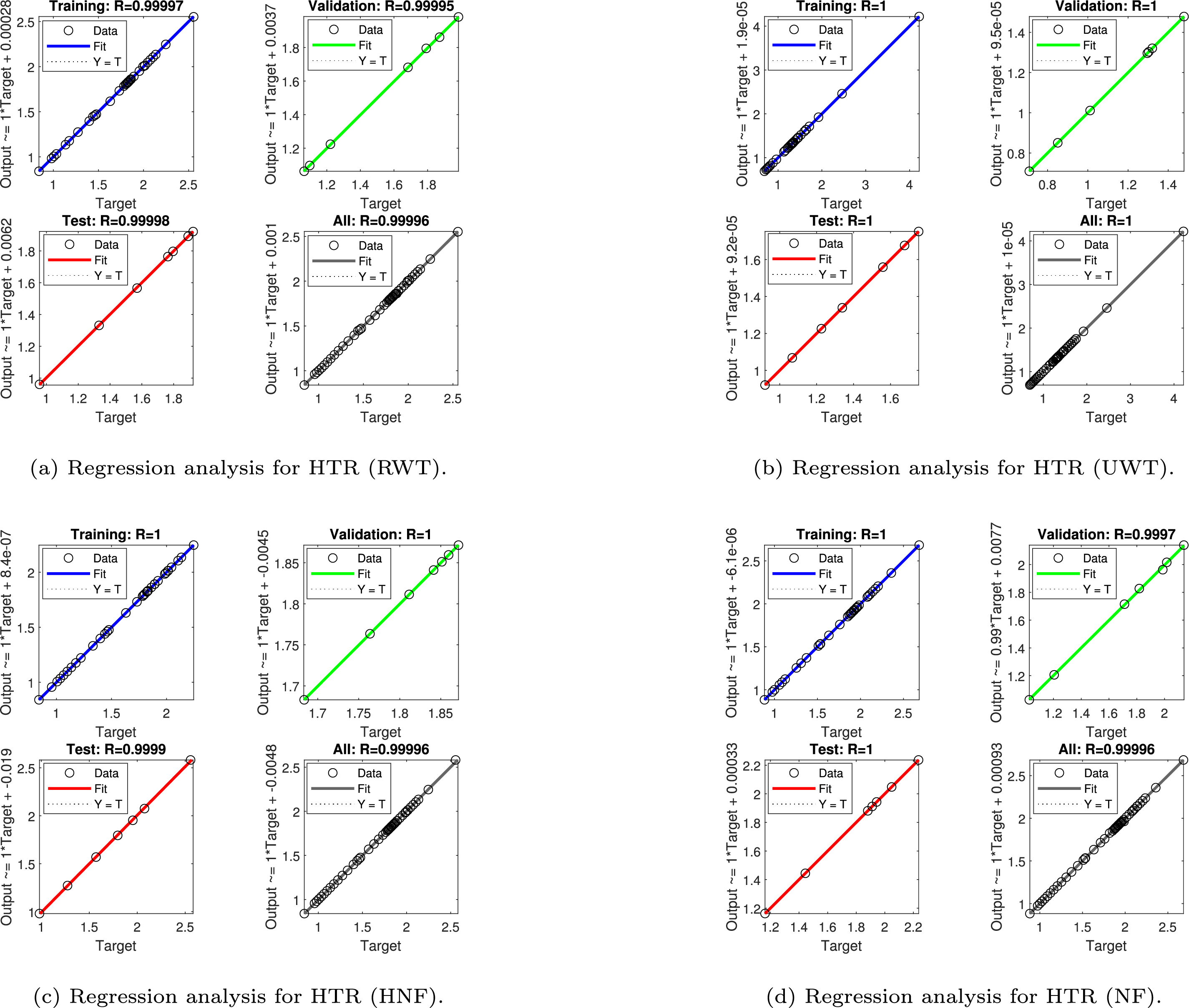
Figure 14: Regression analysis for heat transfer rate (HTR)

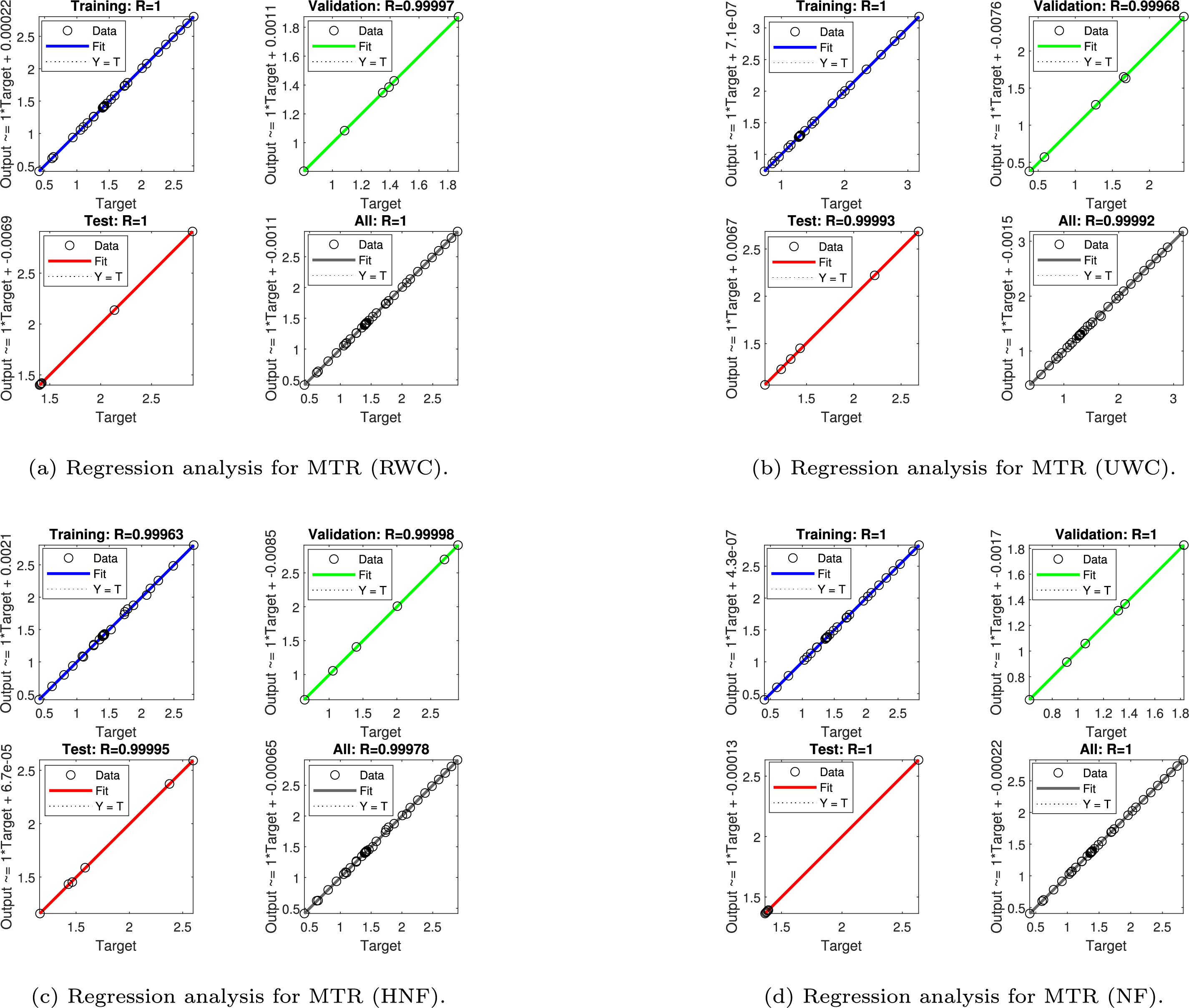
Figure 15: Regression analysis for mass transfer rate (MTR)

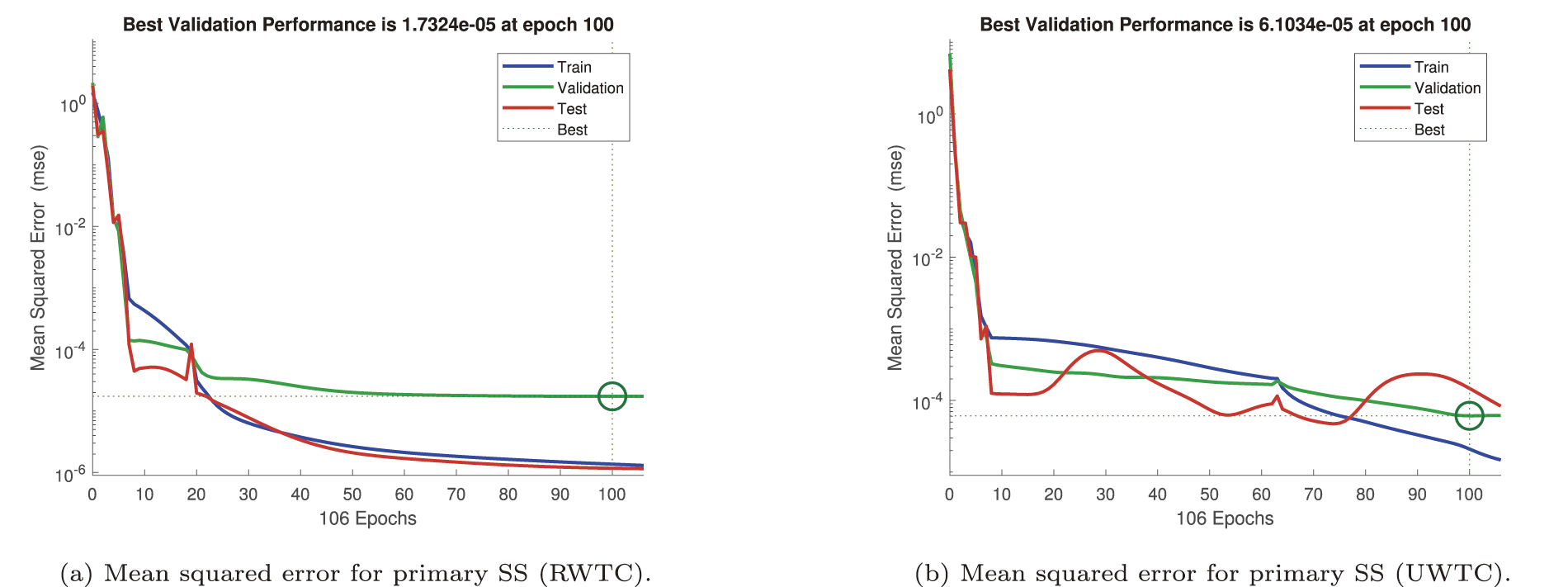
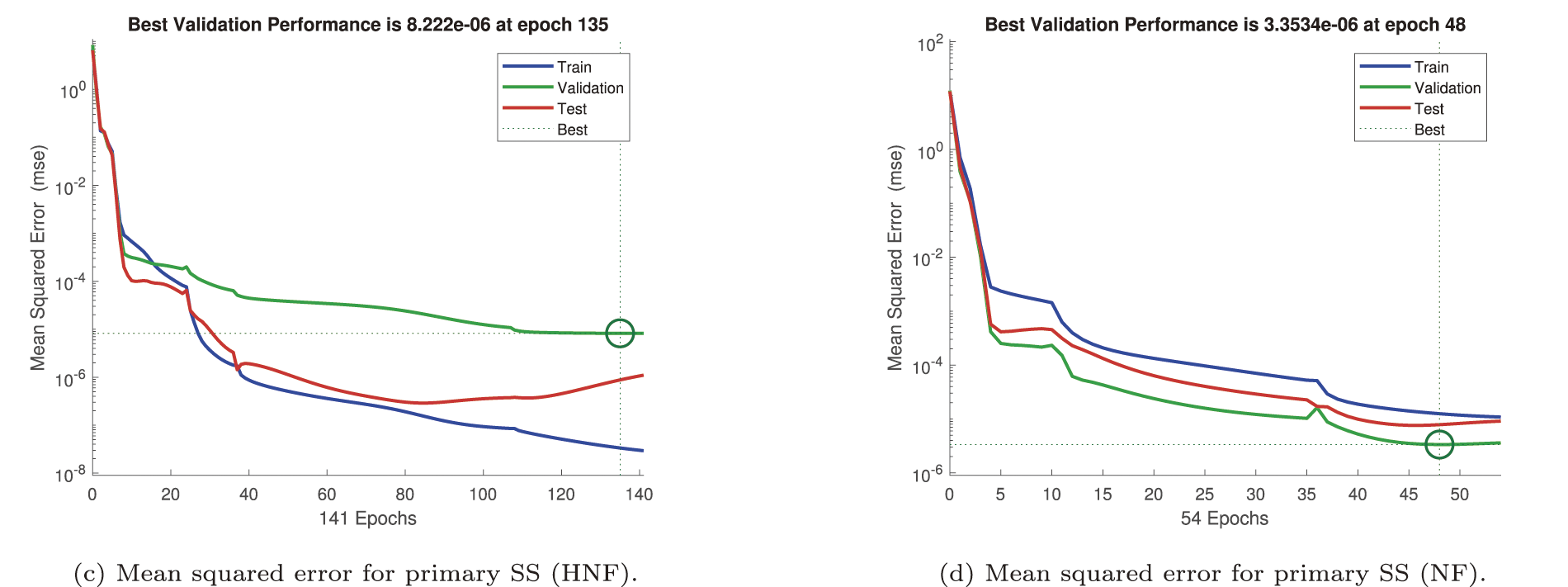
Figure 16: Mean squared error (MSE) for primary shear stress (SS)

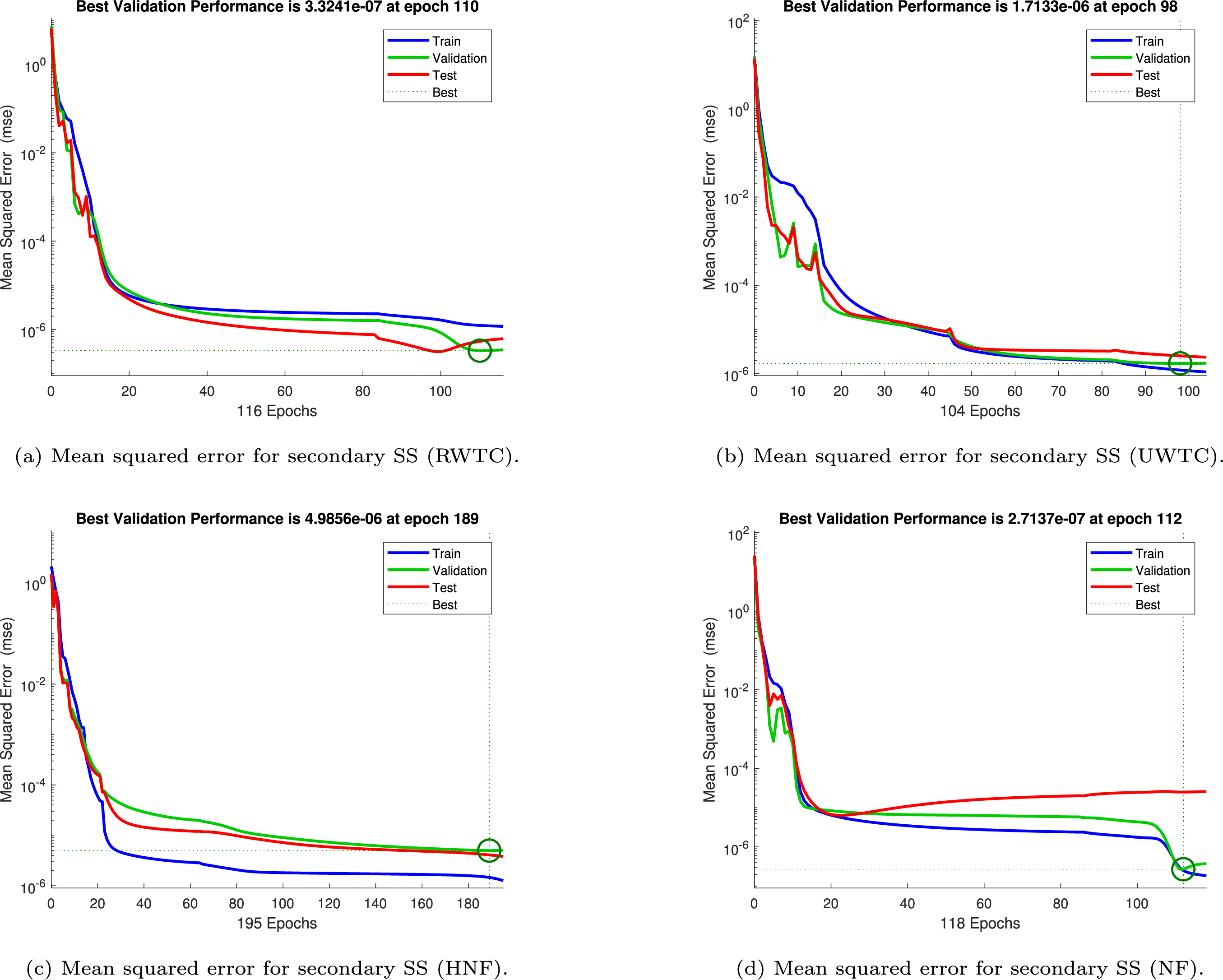
Figure 17: Mean squared error (MSE) for secondary shear stress (SS)

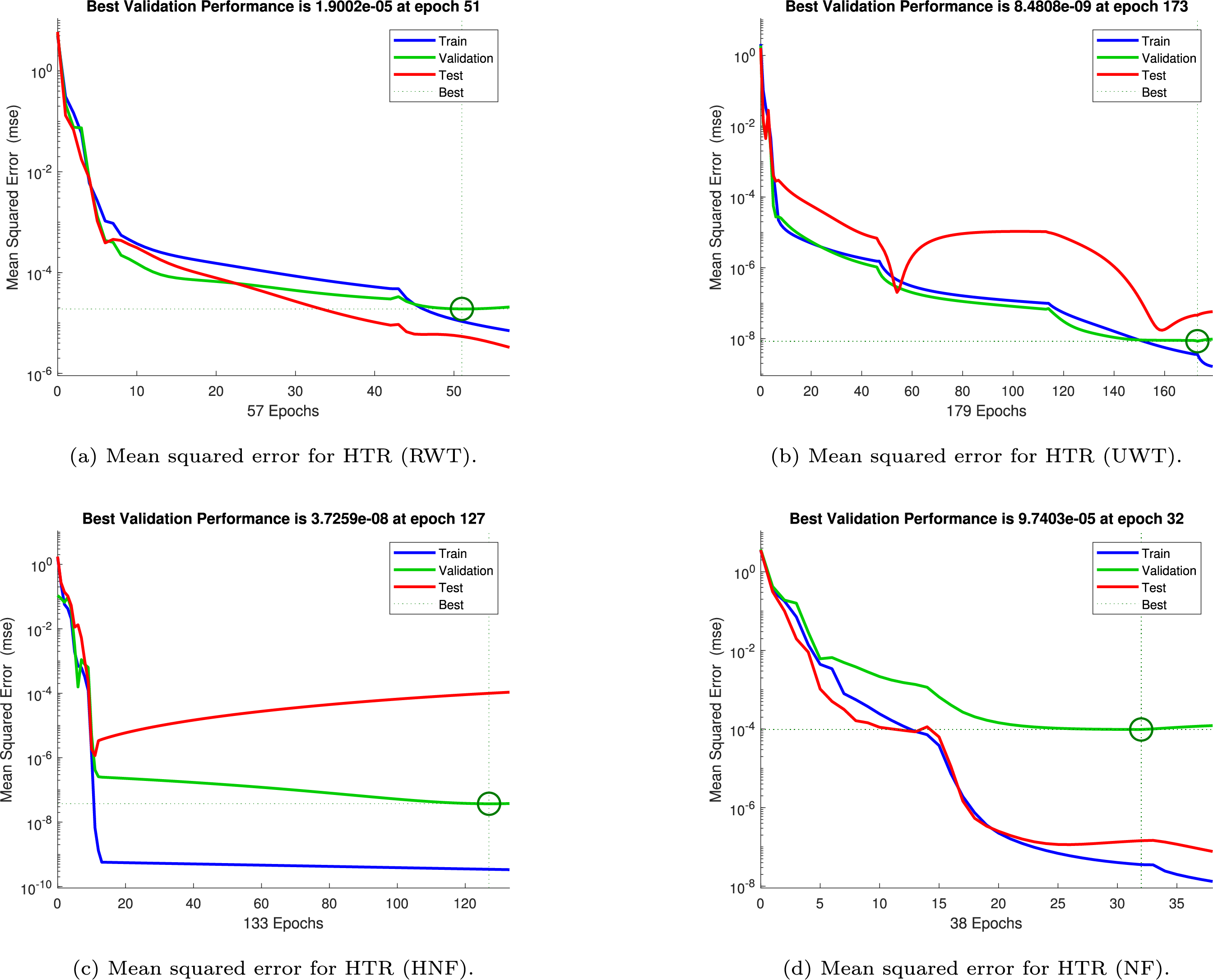
Figure 18: Mean squared error (MSE) for heat transfer rate (HTR)

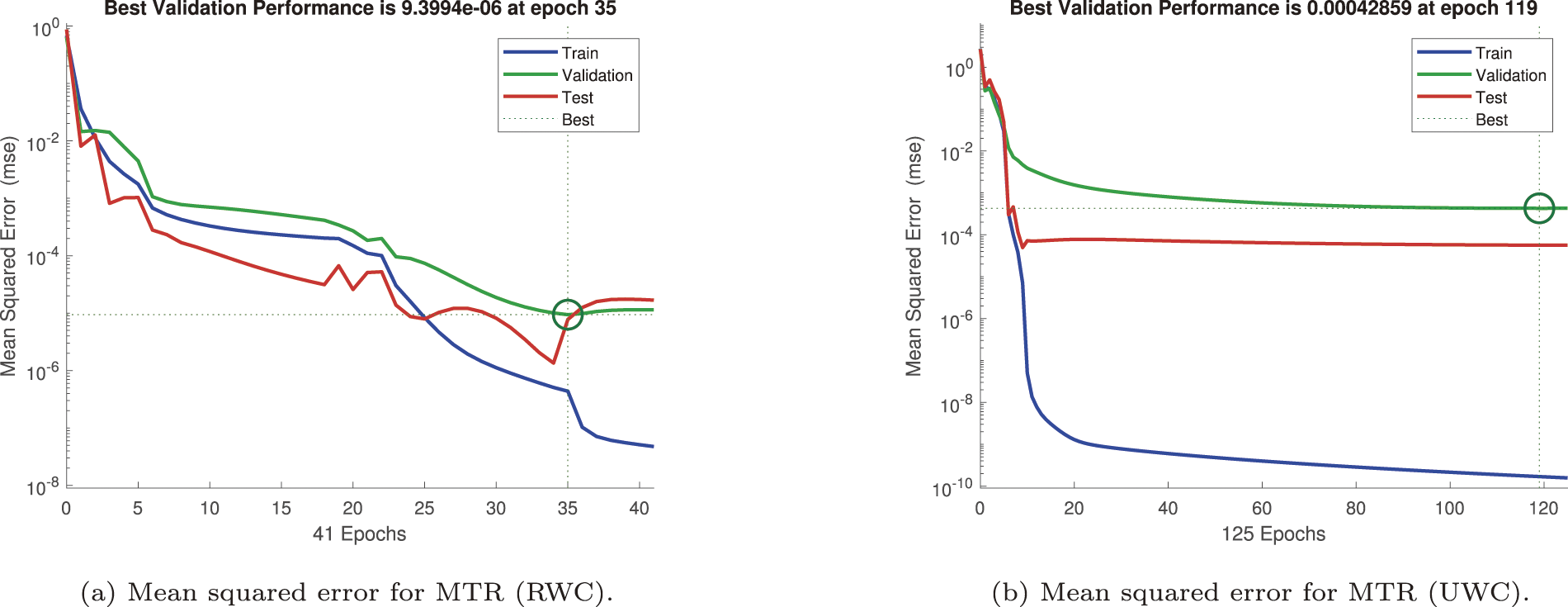
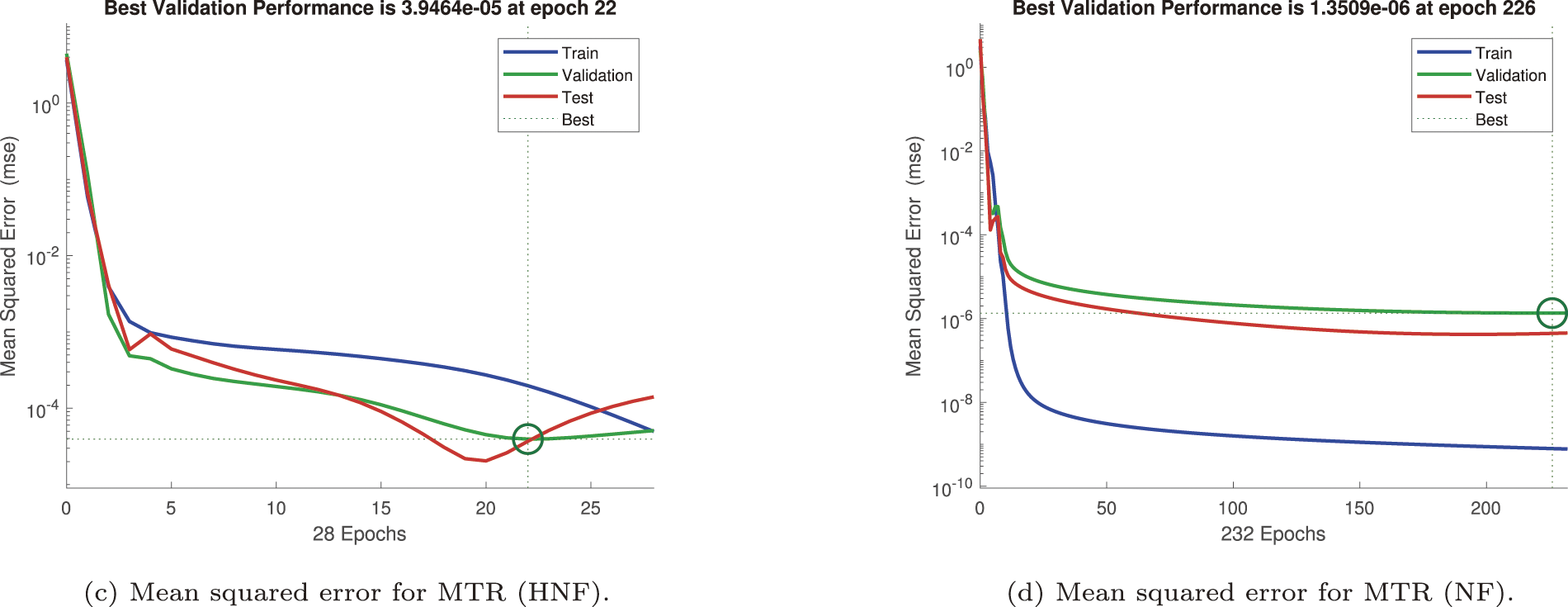
Figure 19: Mean squared error (MSE) for mass transfer rate (MTR)

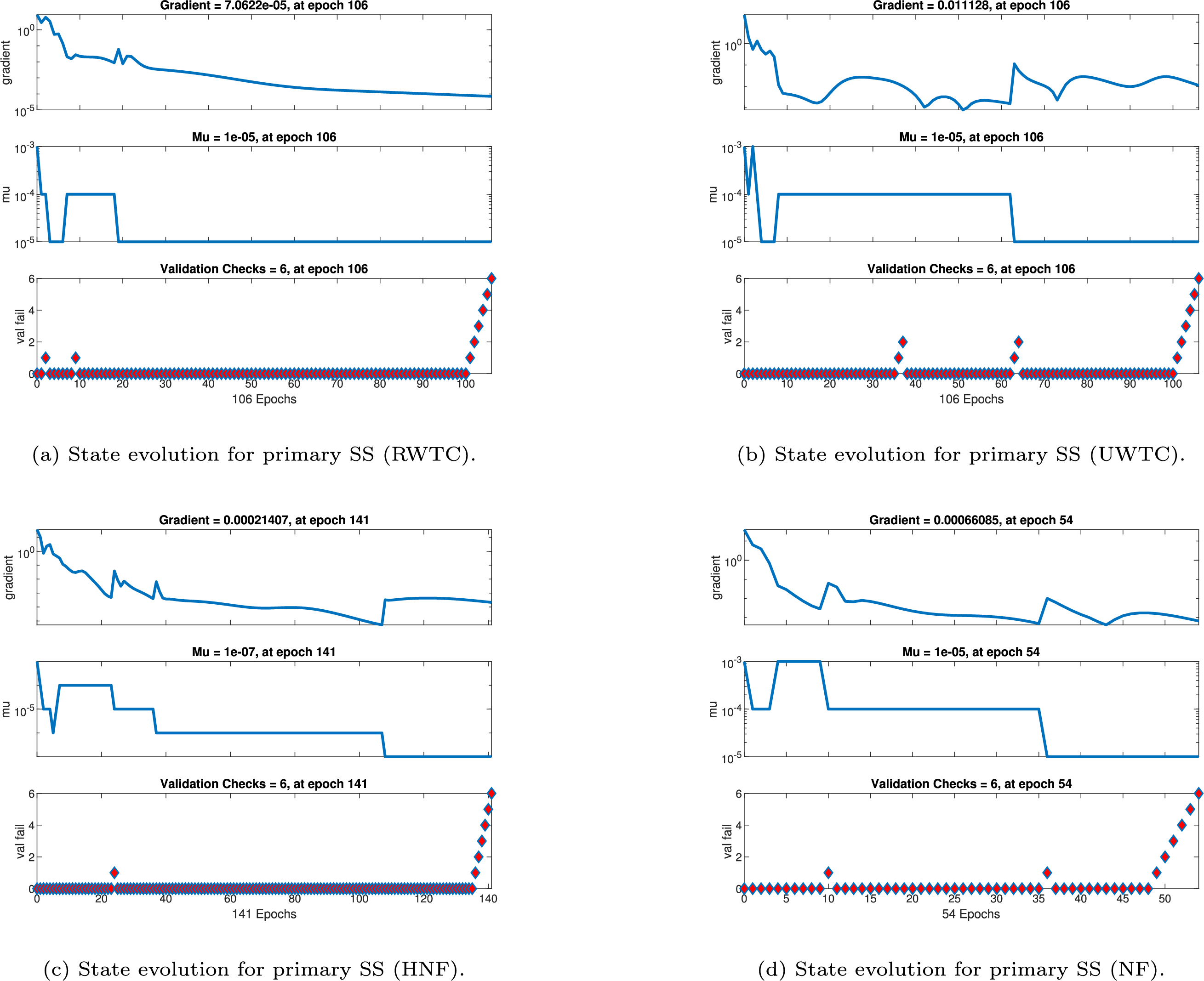
Figure 20: State evolution of primary shear stress (SS)

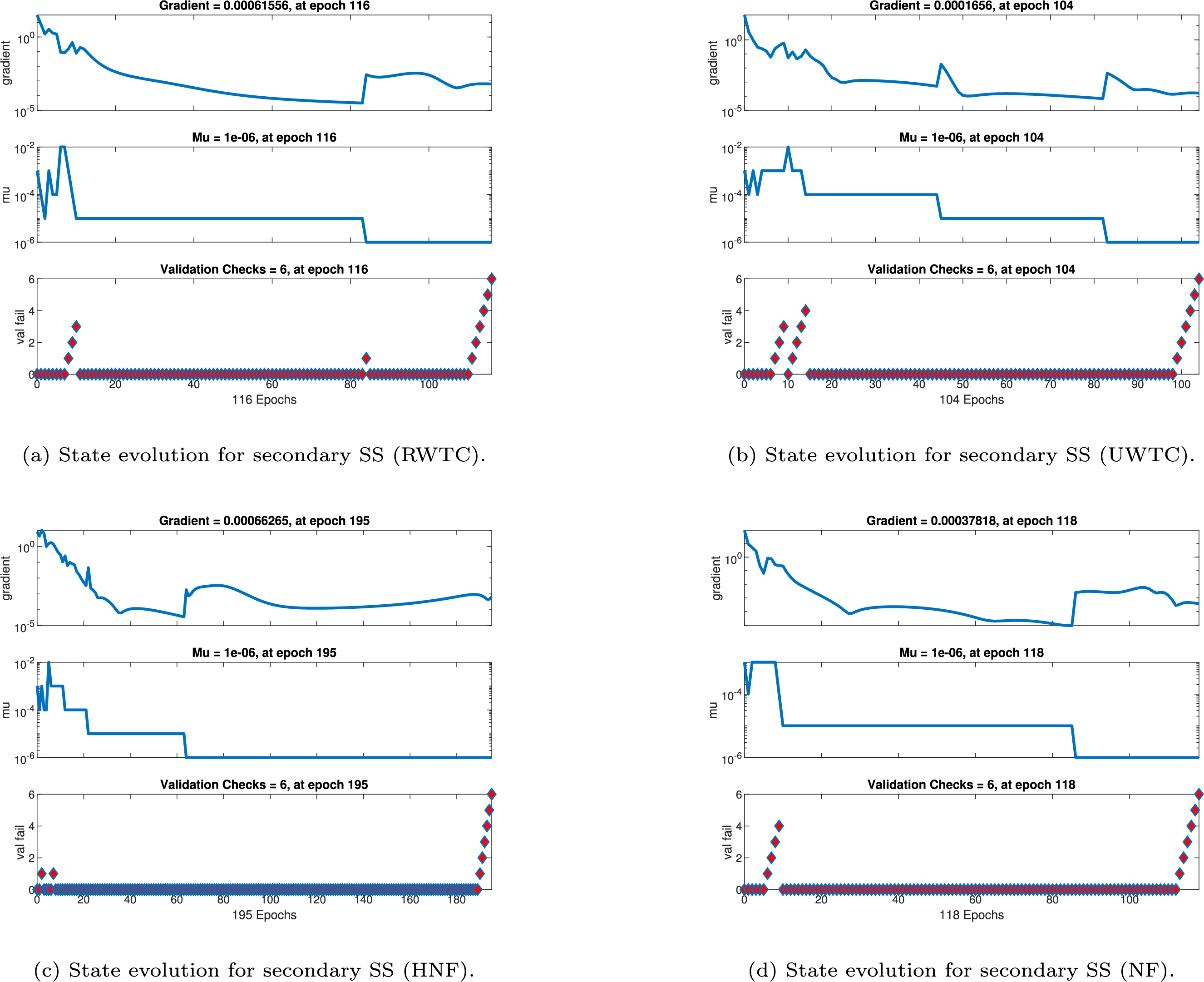
Figure 21: State evolution of secondary shear stress (SS)

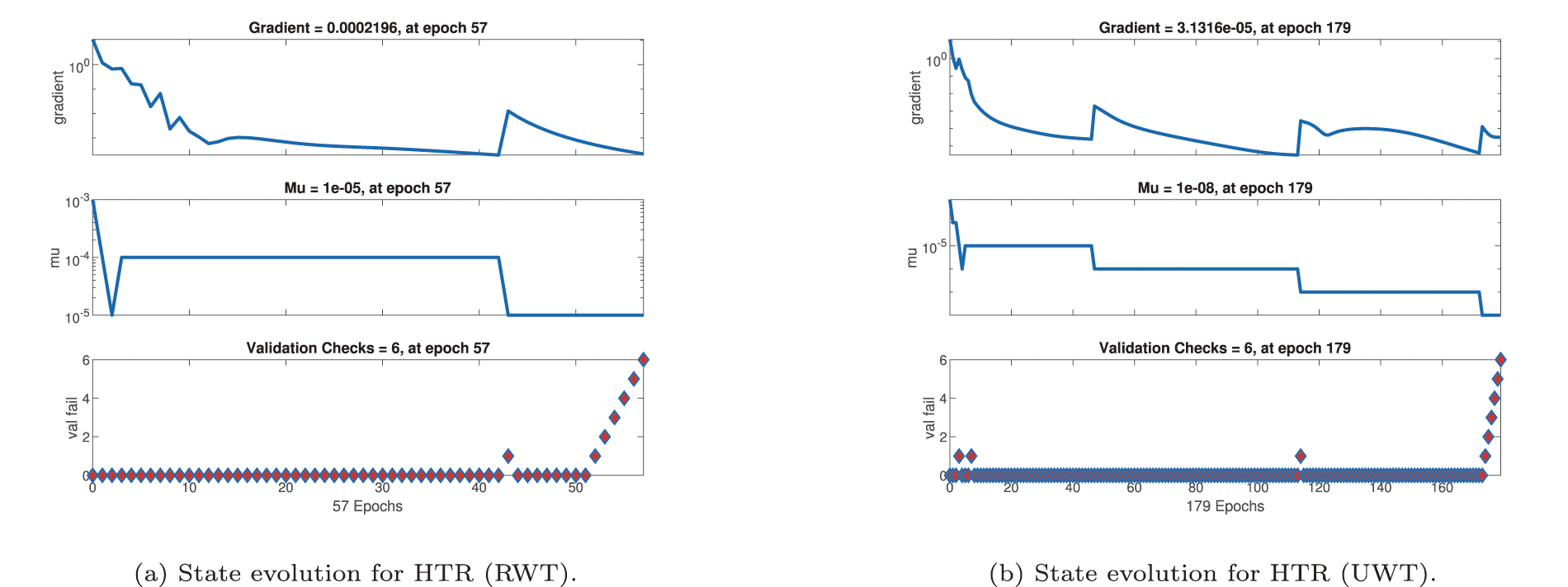
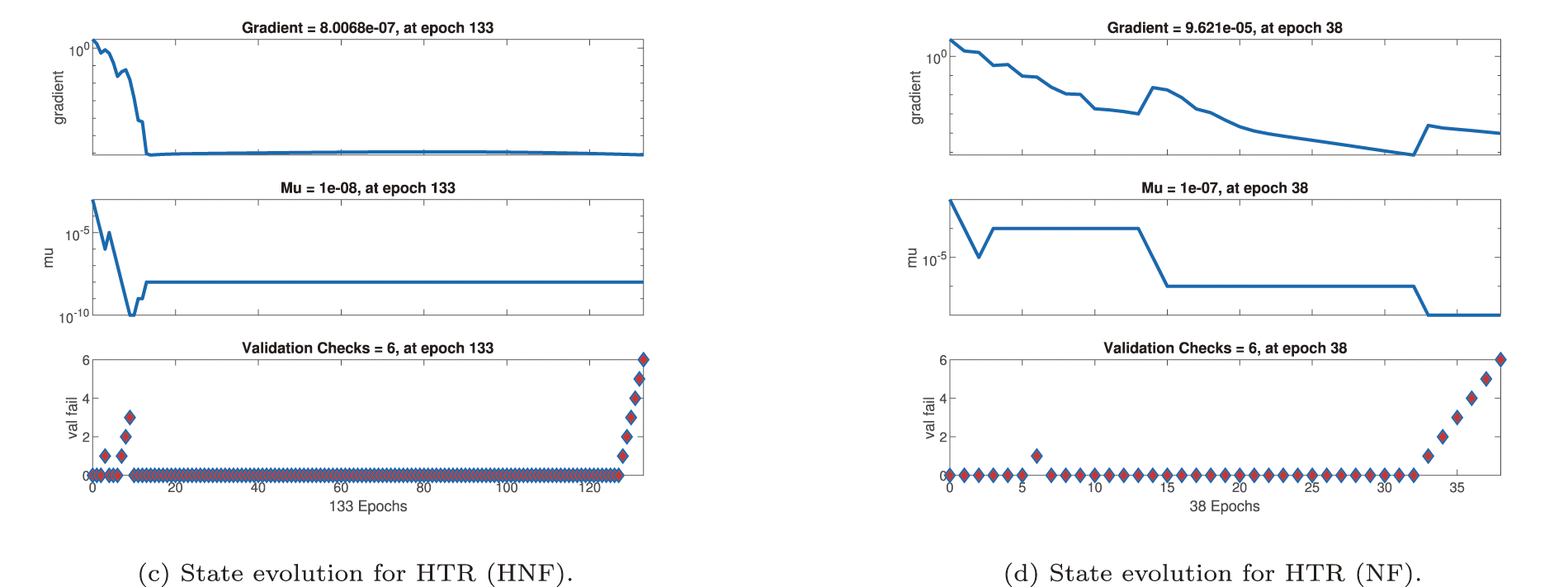
Figure 22: State evolution of heat transfer rate (HTR)

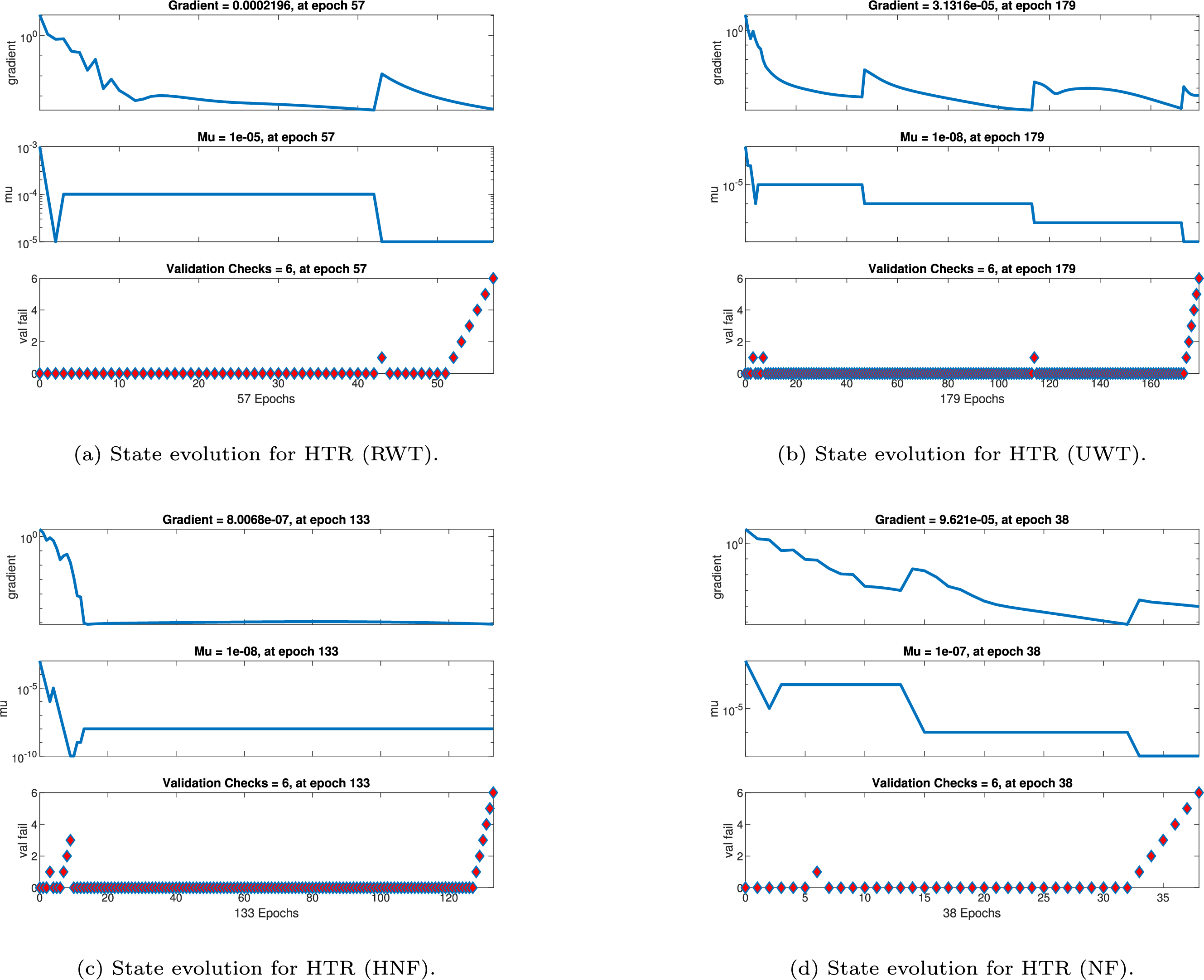
Figure 23: State evolution of mass transfer rate (MTR)

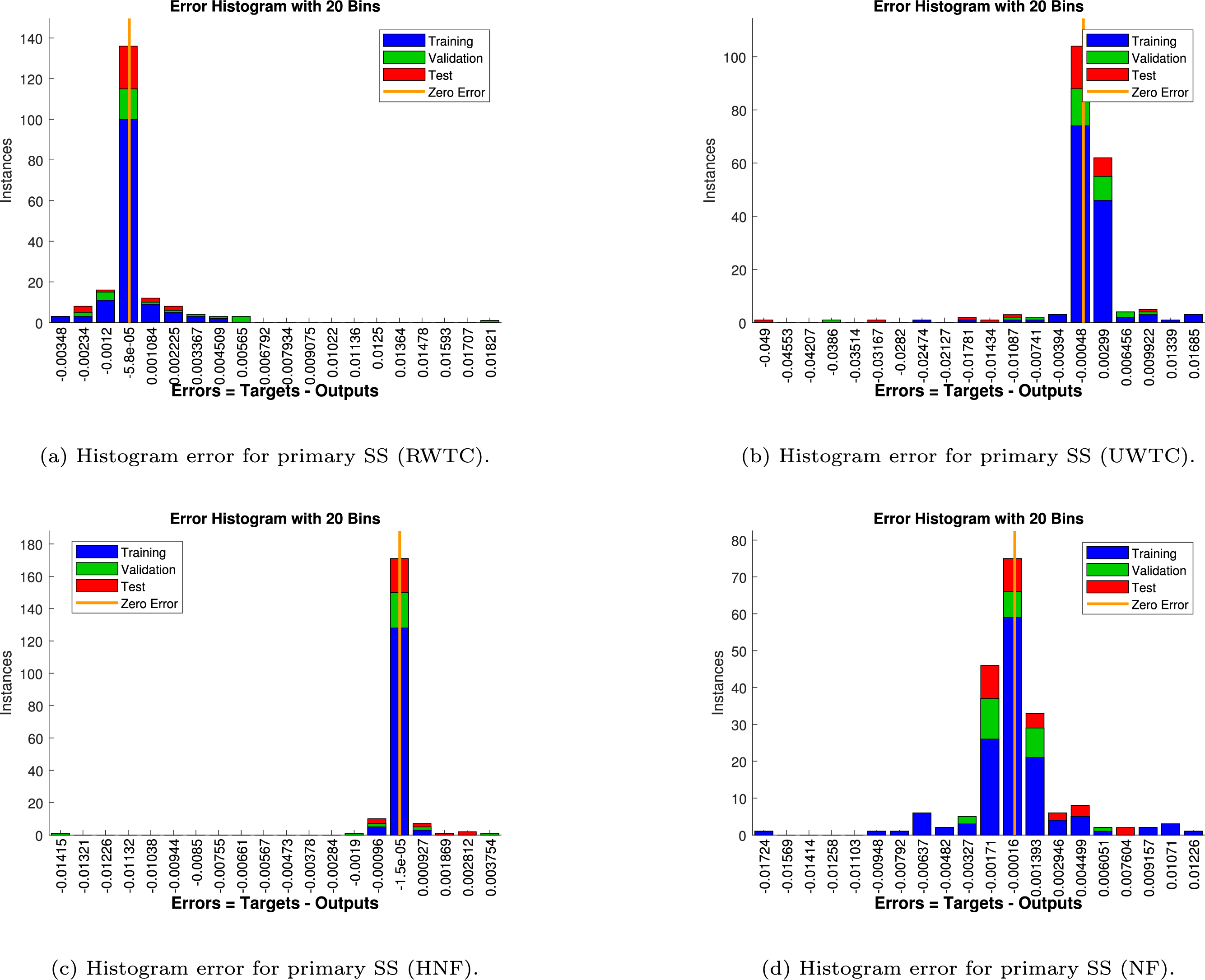
Figure 24: Histogram error analysis for primary shear stress (SS)

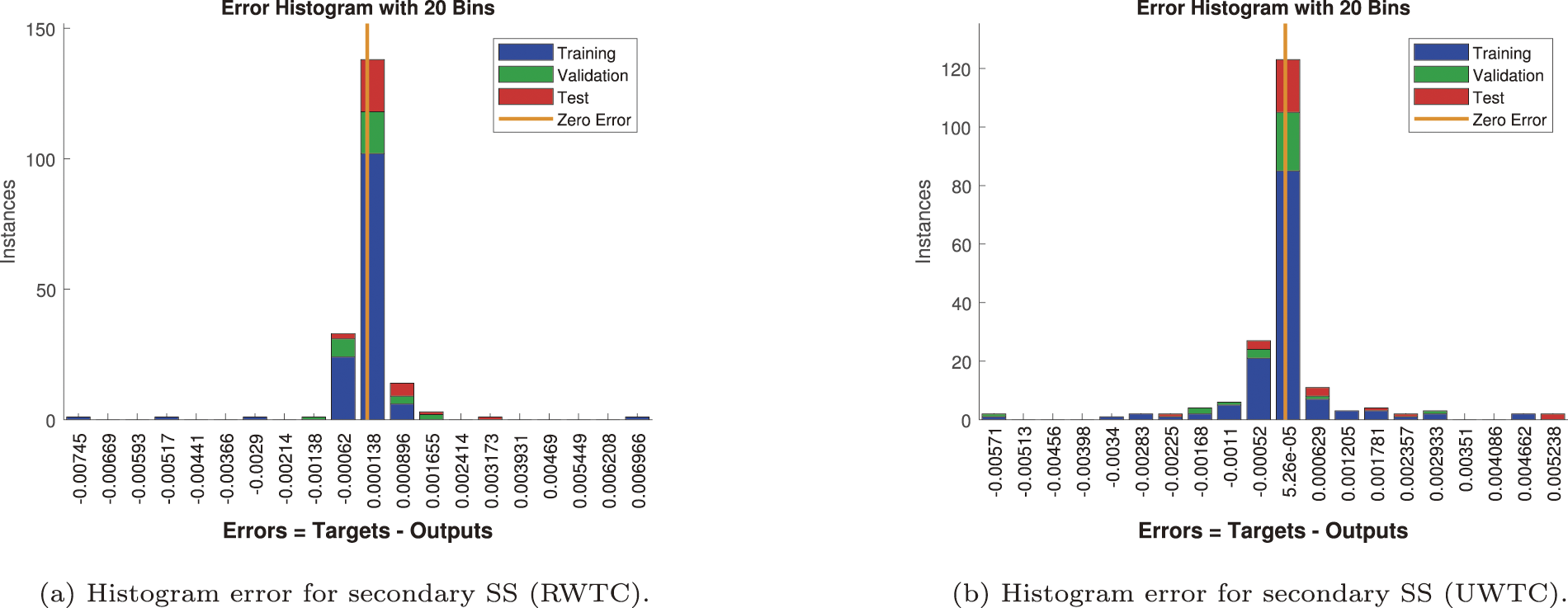
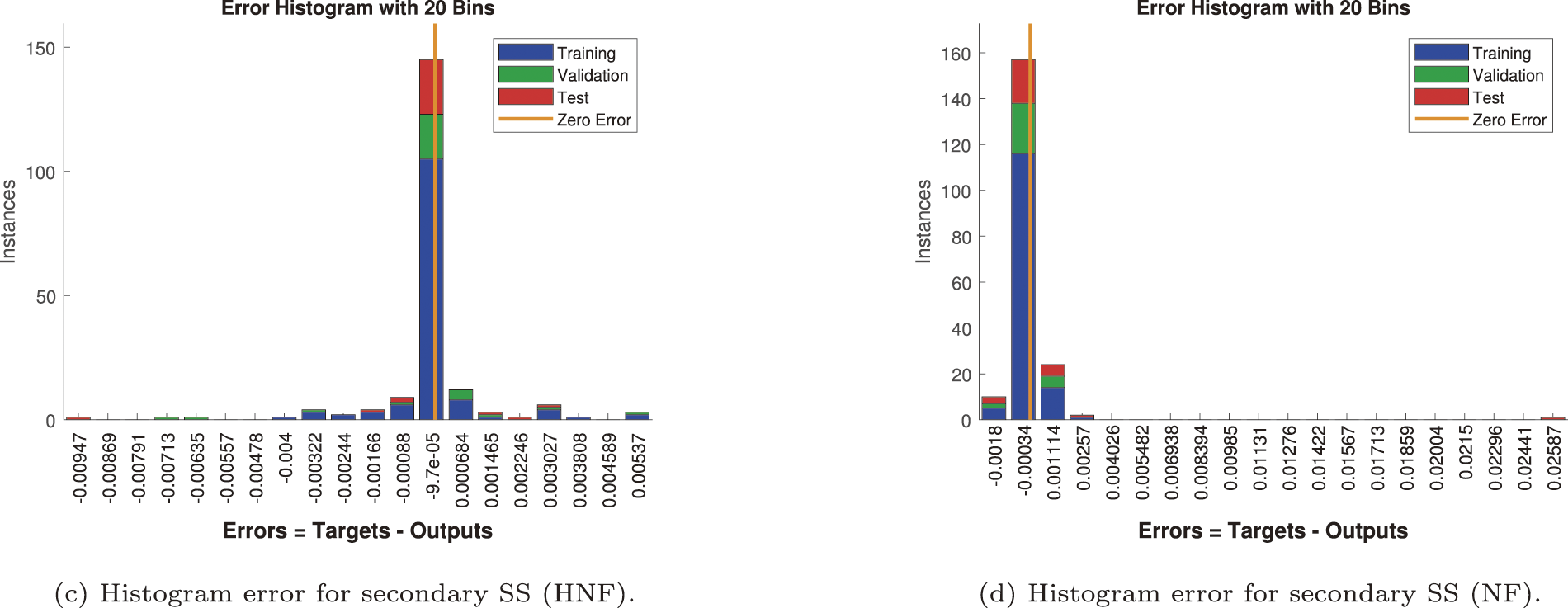
Figure 25: Histogram error analysis for secondary shear stress (SS)

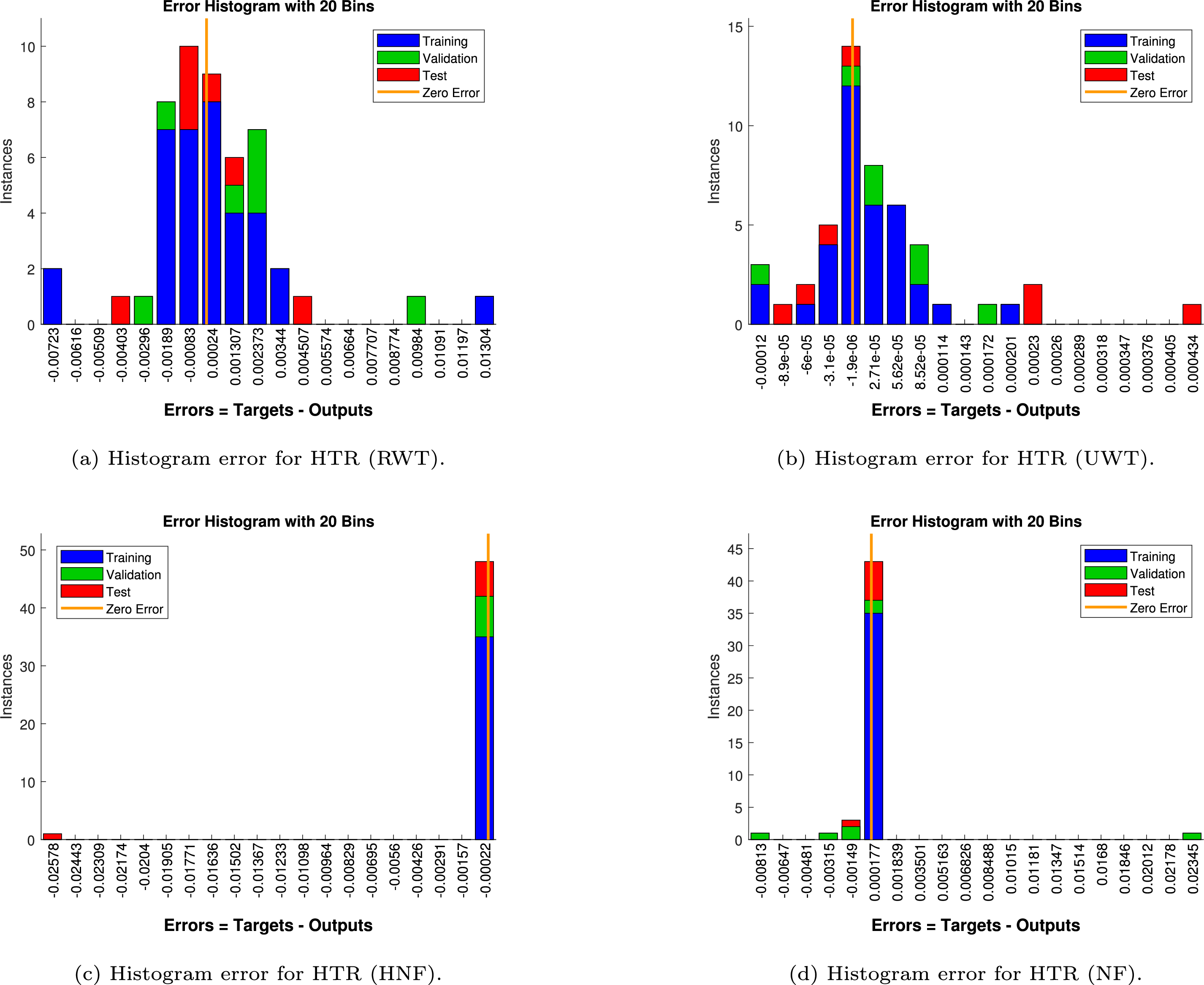
Figure 26: Histogram error analysis for heat transfer rate (HTR)

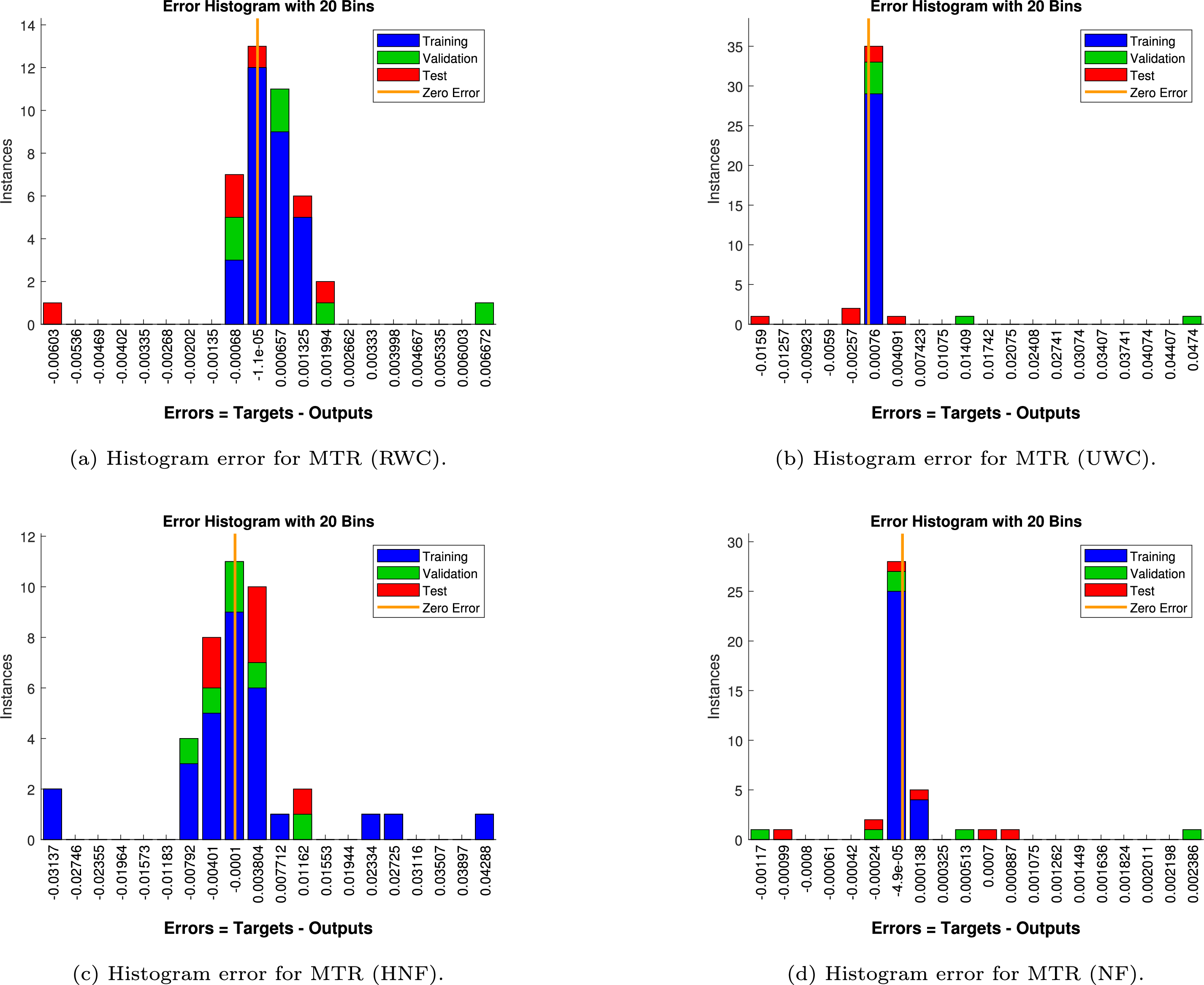
Figure 27: Histogram error analysis for mass transfer rate (MTR)

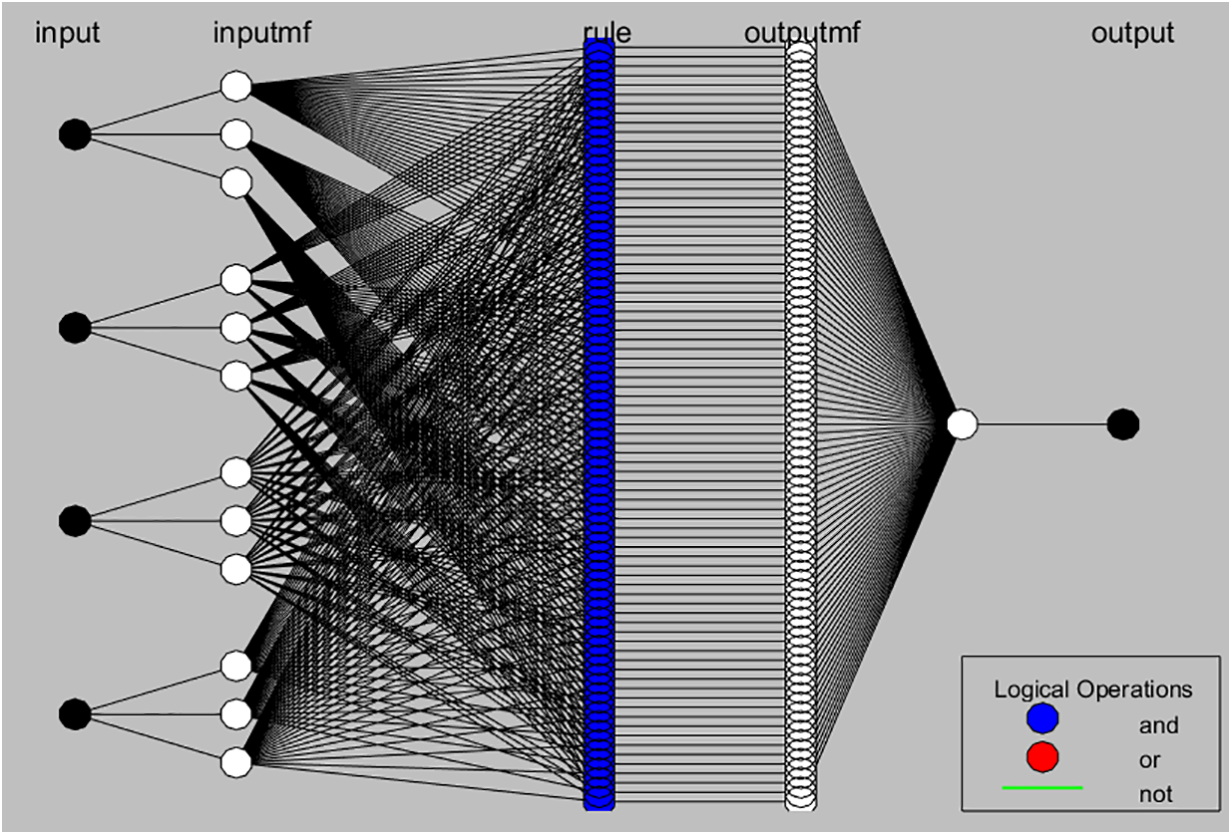
Figure 28: Adaptive Neuro-Fuzzy Inference System (ANFIS) training performance

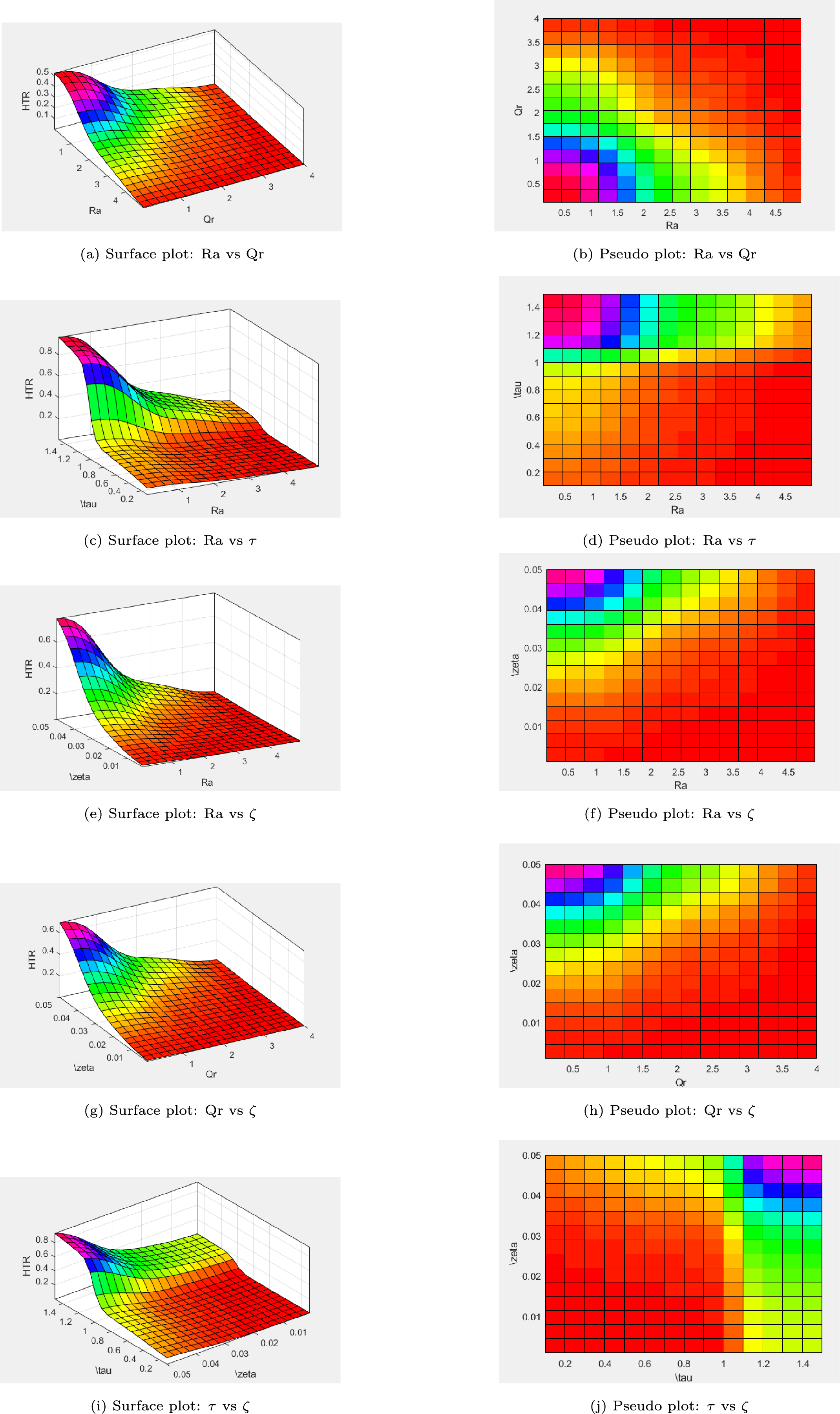
Figure 29: Surface and pseudo plots showing the influence of different pairs of parameters on HTR

4.1 Main Flow (Primary Velocity Profiles)

Fig. 3a–u presents the response of the non-dimensional velocity component u1 to a range of governing parameters for both the base nanofluid (NF: Cu–H2O) and the hybrid nanofluid (HNF: Cu–TiO2–H2O), under two thermal and solutal boundary scenarios: ramped wall temperature and concentration (RWTC) and uniform wall temperature and concentration (UWTC).

In Fig. 3a,b, the rotation parameter K2 is varied. Since K2 quantifies the rotational intensity of the system, higher values amplify the Coriolis acceleration acting perpendicular to the flow and the rotation axis. This lateral force interferes with axial momentum transport, thereby lowering the velocity magnitude across both boundary conditions. The suppression of u1 with increasing K2 reflects the fact that stronger rotation enhances resistance to axial transport, a hallmark of rotating magnetohydrodynamic tunnels driven by electromagnetic actuators such as the Riga plate.

Fig. 3c,d highlights the influence of the Hall parameter βe. The Hall effect introduces an additional transverse electric field through the coupling of magnetic fields and induced currents. Larger βe values strengthen this coupling, redirecting part of the current away from the primary flow and thus reducing axial momentum. Consequently, the velocity distribution flattens as βe grows, demonstrating that Hall currents have a stabilizing but momentum-suppressing impact on electro-magnetohydrodynamic transport.

The variation of u1 with ion-slip parameter βi is shown in Fig. 3e,f. Ion-slip originates from collisions between charged and neutral particles in a partially ionized fluid. Increasing βi indicates stronger slippage, which introduces a resistive drift relative to the bulk motion. This manifests as a uniform reduction in velocity in both RWTC and UWTC cases, underscoring the importance of ion-neutral interactions in limiting effective momentum transfer within ionized nanofluids.

Fig. 3g,h reports the influence of the thermal Grashof number Gr. Since Gr measures the ratio of buoyancy to viscous forces, larger values correspond to stronger thermally induced convection. As Gr increases, the upward buoyancy force accelerates fluid particles, yielding higher velocity profiles for both NFs and HNFs. Thus, thermal gradients counteract viscous drag, leading to more vigorous flow in the Riga tunnel.

The solutal Grashof number Gc is varied in Fig. 3i,j. Similar to Gr, but arising from concentration differences, higher Gc strengthens solutal buoyancy forces. This accelerates the fluid, raising u1 across both boundary condition types. Hence, solutal buoyancy enhances transport in species-driven flows, reinforcing the role of concentration gradients in coupled mass–momentum systems.

Fig. 3k,l depicts the effect of the porosity parameter σ. As σ rises, the porous resistance weakens, allowing fluid to pass more freely through the medium. This reduction in drag increases the velocity throughout the domain, showing that permeability enhancement facilitates stronger motion, particularly in the presence of electromagnetic forcing.

The modified Hartmann number E, shown in Fig. 3m,n, reflects the interaction of the applied magnetic field with the conducting nanofluid. Contrary to classical Hartmann suppression, here the specific electromagnetic configuration of the Riga plate enhances the flow. As E increases, Lorentz forces streamline the motion, aligning particle trajectories and thereby raising u1.

Fig. 3o,p shows the role of S, a measure of the electrode and magnet width. Broader electrodes spread the applied electromagnetic field over a wider region, lowering its local intensity. This reduces the Lorentz driving force and consequently diminishes velocity. Thus, geometric optimization of electrode placement is crucial in maximizing electromagnetic pumping efficiency.

The impact of the chemical reaction parameter Kr is demonstrated in Fig. 3q,r. Stronger chemical activity consumes species and modifies effective viscosity, both of which act as sinks for momentum. As a result, velocity decreases with increasing Kr, indicating that chemical reactions contribute an additional damping mechanism to the transport process.

Fig. 3s,t captures the temporal development of u1. With increasing dimensionless time τ, the fluid accelerates due to sustained action of buoyancy and electromagnetic forces. The time-dependent growth illustrates the transient buildup of momentum in response to external driving, consistent for both NF and HNF cases.

Panels Fig. 3b,d,f,h,j,l,n,p,r,t provide side-by-side comparisons of NF and HNF. The hybrid fluid consistently yields a lower u1 than the base NF. This outcome arises from the combined effects of enhanced viscosity and altered electromagnetic susceptibility imparted by the TiO2 nanoparticles. Their magnetic response increases internal drag, while the overall density of the suspension grows, leading to reduced axial transport compared to pure Cu-based NF.

Fig. 3a,c,e,g,i,k,m,o,q,s compares RWTC with UWTC boundary conditions. In all scenarios, RWTC produces a smaller velocity. Non-uniform wall heating and solutal ramping introduce gradients in viscosity and density, increasing resistance to motion. Conversely, uniform conditions minimize such gradients, allowing faster flow. This illustrates how thermal and solutal boundary modulation directly shapes hydrodynamic performance.

Finally, Fig. 3u demonstrates the impact of nanoparticle volume fraction ζ. Increasing ζ raises the effective viscosity and density of the suspension, leading to stronger resistance and hence lower u1. While higher ζ improves heat conduction, it also dissipates kinetic energy more efficiently, reducing the net velocity. Therefore, volume fraction provides a design parameter to balance thermal and momentum transport in HNFs.

Surface Plots and Streamlines

Fig. 4a,b displays three-dimensional representations of the primary velocity field u1 for both RWTC and UWTC settings. These plots provide an effective way to interpret how the flow develops simultaneously in the spatial (η) and temporal (τ) domains. The surfaces highlight that as the fluid moves away from the wall (larger η) and evolves in time, the velocity u1 gradually intensifies. This acceleration is a direct response to the imposed boundary heating and solutal driving forces, which weaken viscous resistance and promote stronger momentum transport. Physically, the 3D view reveals how the interaction between wall forcing and transient effects gives rise to layered velocity structures, thereby offering a holistic understanding of the flow dynamics that is not immediately apparent from 2D profiles alone.

Fig. 4c,d shows the corresponding streamline distributions under RWTC and UWTC scenarios. Streamlines act as instantaneous trajectories of fluid particles, thereby illustrating the overall circulation pattern within the Riga tunnel. Near the right wall, the streamlines exhibit a rapid reorientation and tend to bend almost orthogonally toward the boundary. This distinctive turning indicates the strong local influence of Lorentz forces generated by the electromagnetic actuation of the Riga surface, which dominate viscous diffusion in this region. Such perpendicular alignment of streamlines signifies the suppression of tangential motion close to the wall and the emergence of intensified cross-tunnel momentum transport. From a physical standpoint, these streamline transformations clearly highlight how electromagnetic forcing coupled with thermal-solutal boundary conditions alters near-wall fluid organization, which is of practical importance in applications where wall-driven flow control is essential.

4.2 Cross-Flow (Secondary Velocity Profile)

The variation of the secondary velocity component v1 under different nondimensional controls is illustrated in Fig. 5a–u for Cu–H2O nanofluid (NF) and Cu–TiO2–H2O hybrid nanofluid (HNF), considering both RWTC and UWTC settings. Fig. 5a,b shows that stronger rotation (K2) enhances v1. Physically, rotation introduces Coriolis acceleration perpendicular to the main flow, which strengthens the transverse momentum transport. With larger K2, centrifugal forces redistribute energy from the streamwise motion into the cross-flow, producing higher v1.

Fig. 5c,d indicates that an increase in βe promotes v1 under both instantaneous and steady magnetic actuation. The Hall effect generates a transverse electromotive force that modifies charge transport in conducting fluids. Larger βe amplifies this interaction, alters current density distribution, and thereby magnifies the Lorentz force contribution in the cross-flow direction, leading to stronger v1.

As shown in Fig. 5e,f, v1 rises as βi grows. Ion-slip accounts for imperfect coupling between ions and neutrals during collisions. Larger βi weakens ion-neutral momentum balance, generating additional shear stresses that divert flow away from the primary stream. This results in noticeable growth in the secondary velocity.

Fig. 5g–j reveals that both Gr (thermal buoyancy) and Gc (solutal buoyancy) enhance v1. When buoyant driving exceeds viscous resistance, transverse motion is intensified. For higher Gr, temperature-induced density gradients accelerate fluid layers, whereas elevated Gc produces similar enhancement via concentration gradients. The combined buoyancy interacts constructively with magnetic and rotational effects, thereby raising v1.

Fig. 5k,l shows that higher σ corresponds to increased v1. A larger porosity reflects lower drag within the porous substrate, easing cross-flow passage and enabling stronger velocity magnitudes.

From Fig. 5m,n, v1 increases with E. A stronger electromagnetic field intensifies Lorentz forcing, aligning fluid motion with the field and assisting the momentum transfer in the cross direction. This effect demonstrates the capacity of electromagnetic actuation to enhance secondary circulation.

Fig. 5o,p illustrates that larger S suppresses v1. Increasing the electrode and magnet span disperses the Lorentz force over a broader area, reducing local intensity of electromagnetic pumping. As a result, the driving action weakens, lowering cross-flow strength.

In Fig. 5q,r, v1 decreases as Kr grows. Stronger chemical reactions may either consume energy or increase fluid resistance by altering concentration fields, both of which diminish the momentum available for transverse acceleration.

Fig. 5s,t shows that v1 amplifies with increasing τ. As the system evolves, the cumulative influence of Coriolis, buoyancy, and Lorentz forces strengthens secondary flow. For RWTC, the gradients in wall heating and solute release add spatial variability, while in UWTC the growth is smoother but generally higher. The hybrid nanofluid responds more strongly because of its enhanced conductivity and inertia.

In Fig. 5b,d,f,h,j,l,n,p,r,t, the HNF generally produces lower v1 values compared to NF. The presence of TiO2 in Cu–TiO2–H2O increases effective viscosity and density, producing higher resistance to secondary motion. This synergistic modification stabilizes the flow but reduces its magnitude.

Fig. 5a,c,e,g,i,k,m,o,q,s reveals that UWTC leads to greater v1 than RWTC. Non-uniform ramped heating and solute release in RWTC introduce additional viscous resistance and damping, whereas uniform boundary conditions maintain smoother gradients, allowing larger cross-flow velocity.

Finally, Fig. 5u shows that higher ζ reduces v1. Increasing nanoparticle concentration raises viscosity and density, intensifying drag forces. Although thermal conductivity improves, the added resistance dominates, yielding suppressed cross-flow velocity. This indicates a trade-off between enhanced heat transfer and reduced fluid mobility at elevated particle loadings.

Surface Plots and Streamlines

Fig. 6a,b displays the three-dimensional distribution of the velocity component v1 for both RWTC and UWTC settings. These plots reveal how the flow evolves in the (η,τ) space, where η represents the spatial coordinate across the tunnel and τ denotes the non-dimensional time. As time progresses, the imposed wall actuation gradually injects momentum into the system, leading to a noticeable amplification of v1 throughout the domain. The growth in velocity is more prominent near the accelerating wall, consistent with the squarely moving wall, and diminishes away from it due to viscous resistance and porous drag. Physically, this indicates that thermal and solutal ramping enhances buoyancy-driven acceleration, thereby promoting a stronger velocity field compared to the uniform case at later times.

Fig. 6c,d illustrates the associated streamline topologies under the same boundary conditions. Streamlines depict the instantaneous direction of particle motion and thus provide a complementary perspective on the spatial organization of the flow. Near the right-hand wall of the tunnel, the streamlines undergo a sharp turning and tend to align nearly perpendicular to the surface. This behavior signifies that strong electromagnetic forcing from the Riga actuator modifies the near-wall dynamics, producing local zones of intensified momentum exchange. Such reorientation reflects the interplay between Lorentz forces, wall ramping effects, and viscous diffusion. In the RWTC case, these distortions are more pronounced because of the combined influence of time-dependent heating and solutal gradients, whereas the UWTC condition yields comparatively smoother streamline patterns. Overall, the visualization underscores how boundary condition type governs both global acceleration of the fluid and localized structural adjustments in the flow field.

4.3 Temperature

Fig. 7a–g highlights how the temperature distribution θ inside the Riga tunnel is shaped by the radiation parameter (Ra), the heat absorption coefficient (Qr), the non-dimensional time (τ), and the nanoparticle volume fraction (ζ). These influences are examined under both RWT and UWT settings for nanofluid (NF) and hybrid nanofluid (HNF) suspensions.

Fig. 7a,b shows the response of θ to variations in Ra. Since Ra measures the extent of radiative energy exchange, a larger value increases the effective thermal flux throughout the medium. This elevates fluid temperature by allowing more radiative energy to be absorbed and redistributed. The effect is more pronounced in HNFs because the combined Cu and TiO2 particles improve radiative absorption and thermal conductivity, leading to steeper heating and smoother gradients near the tunnel boundaries. Physically, this represents a radiative preheating process, where suspended nanoparticles facilitate enhanced particle-fluid interactions and intensify the rise in temperature.

The outcome of increasing Qr is illustrated in Fig. 7c,d. In this case, θ consistently decreases, since higher Qr represents stronger internal energy extraction, effectively acting as a volumetric sink that suppresses temperature growth. While both NF and HNF exhibit this cooling, the decline is less severe in HNF because the greater conductivity of hybrid suspensions partially offsets the imposed absorption, helping the fluid retain more heat. This mechanism is particularly relevant in electromagnetic tunnels, where internal absorption can control overheating by limiting thermal build-up.

Fig. 7e,f captures how temperature evolves over time. As τ grows, θ rises across all configurations, which is expected because the fluid accumulates energy continuously from the heated wall. Under UWT, the wall delivers a constant supply of heat, leading to a steady rise in the bulk temperature. In contrast, the RWT case provides a gradually increasing boundary input, producing a slower but progressive growth in θ. Hybrid nanofluids adapt more quickly and achieve higher temperatures owing to their enhanced energy storage and conduction pathways, which allow them to spread the absorbed heat more effectively than conventional nanofluids.

The role of nanoparticle loading is demonstrated in Fig. 7g. Increasing ζ results in higher θ, reflecting the superior thermal conduction pathways created by densely packed nanoparticles. Copper and TiO2, when combined, form a network of high-conductivity tunnels that improve heat dispersion and homogenize temperature across the fluid. This effect underscores how particle concentration is a critical design parameter for maximizing the efficiency of nanofluid-based heat transport systems.

Comparisons in Fig. 7b,d,f between Cu–H2O NF and Cu–TiO2–H2O HNF confirm that hybrid suspensions consistently maintain higher temperatures. The reason lies in their enhanced transport properties: TiO2 contributes to improved conductivity and modifies electromagnetic coupling with the Riga plate, while Cu provides excellent conduction. Together, they yield superior thermal storage and redistribution, keeping the HNF temperature above that of NF under identical operating conditions.

A final consistent observation from Fig. 7a,c,e,g is that UWT cases always yield higher θ than RWT. This can be explained physically: UWT applies a constant high wall temperature, ensuring continuous and uniform energy transfer into the fluid. RWT, however, introduces a gradient where heating grows with distance, reducing the average heat absorbed over a given length. As a result, UWT produces a more intense and uniform heating effect compared to the ramped counterpart.

Surface Plots and Heatlines

A 3D visualization of the dimensionless temperature profile θ under RWT and UWT settings is presented in Fig. 8a,b. These visualizations serve not only as graphical representations but also as critical tools to elucidate the nuanced thermal behavior of the system. The temperature profile exhibits spatiotemporal modulations across both the similarity variable η and the dimensionless time τ. These fluctuations indicate that thermal responses are governed jointly by spatial positioning and temporal evolution, reflecting the non-steady nature of heat propagation within the fluid medium. A significant observation is the notable rise in fluid temperature, which closely corresponds to the boundary constraints imposed at the tunnel walls. For the RWT case, the wall temperature increases over time, resulting in a gradual rise in fluid temperature near the wall. In contrast, the UWT condition enforces a constant thermal boundary, leading to a steady thermal diffusion pattern. The temperature field in both scenarios demonstrates predictable evolution, emphasizing the deterministic influence of the imposed thermal conditions on the overall heat transfer process.

Fig. 8c,d depicts the heatline distributions for both RWT and UWT cases, offering a detailed perspective on the thermal transport mechanisms. Heatlines, analogous to streamlines in fluid flow analysis, are employed here to trace the direction and path of thermal energy transport. The curvature and density of these heatlines provide valuable insights into the thermal gradients within the tunnel. Notably, regions with steeper temperature gradients exhibit tighter and more curved heatlines, signaling intensified heat transfer activity. This curvature arises from the intrinsic thermodynamic drive to equalize temperature differences across the domain. The pronounced bending of heatlines near the walls underscores the system’s tendency to redistribute thermal energy and progress toward thermal equilibrium, governed by spatially varying temperature fields.

4.4 Species Concentration

Fig. 9a–g illustrates how the concentration field ϕ responds to variations in four controlling parameters: the chemical reaction coefficient (Kr), Schmidt number (Sc), dimensionless time (τ), and nanoparticle volume fraction (ζ). The behavior is examined for both RWC and UWC settings in Cu–H2O nanofluid (NF) and Cu–TiO2–H2O hybrid nanofluid (HNF).

Fig. 9a,b reveals that concentration consistently diminishes as Kr rises. A stronger chemical reaction rate accelerates the consumption of solute, reducing its persistence in the tunnel. This effect is physically expected: faster molecular conversion or degradation reduces the accumulation of species, leaving a thinner concentration boundary layer. Such trends are important for reactive transport modeling in catalytic and biomedical flows, where adjusting reaction intensity directly controls residual species distribution.

The influence of Sc is shown in Fig. 9c,d. Larger Sc values (implying reduced mass diffusivity relative to momentum diffusivity) lead to lower ϕ levels. In practice, this means solute spreading is hindered, and transport relies more on convection rather than diffusion. This interplay is essential in pollutant dispersion and biochemical separation processes, where high-Sc fluids tend to suppress lateral mixing and yield sharper concentration gradients.

Fig. 9e,f demonstrates the temporal development of ϕ. As τ increases, the concentration grows across the tunnel because cumulative transport allows species to diffuse more extensively from the walls into the fluid core. This highlights the role of unsteady effects, where prolonged interaction time facilitates stronger penetration of mass into the domain. Such observations are critical for transient mixing in biological tissues or chemical reactors.

The outcome of varying nanoparticle volume fraction ζ is shown in Fig. 9g. Adding nanoparticles reduces concentration, with higher ζ producing steeper declines. Physically, nanoparticles offer additional sites for adsorption or catalytic reactions, which consume solute more efficiently. Furthermore, ζ modifies fluid viscosity and effective diffusivity, restricting solute spread. This indicates that tailoring nanoparticle loading can be an effective design tool in drug delivery or wastewater treatment systems.

Fig. 9b,d,f indicates that the Cu–TiO2–H2O HNF generally exhibits slightly lower concentration levels compared to Cu–H2O NF. The inclusion of TiO2 improves thermal conductivity and modifies electromagnetic interactions under Riga plate forcing, enhancing convective and reactive mass transfer. As a result, hybrid suspensions accelerate solute depletion relative to their single-particle counterparts.

A consistent distinction between boundary scenarios emerges from Fig. 9a,c,e,g: UWC supports higher concentration values than RWC. With UWC, the wall injects species uniformly, maintaining a continuous supply across the domain. In contrast, RWC enforces a gradient at the wall, leading to weaker near-wall replenishment and overall lower concentrations. This comparison emphasizes how boundary modulation can be strategically used to regulate solute delivery in electro-magnetically controlled tunnels.

Surface Plots and Concentration-Lines

Three-dimensional plots in Fig. 10a,b provide a broader view of ϕ variation across both space (η) and time (τ). These demonstrate that concentration grows progressively with τ, reflecting the sustained diffusion of solute from the wall into the bulk flow.

The iso-concentration maps in Fig. 10c,d further clarify the distribution pattern. Contour lines curve asymmetrically towards the right wall, showing how electromagnetic forcing from the Riga plate biases mass flux. This asymmetric distortion highlights the combined action of imposed concentration gradients and Lorentz forces, which tunnel solute transport preferentially across the width of the domain. Such asymmetry is particularly relevant in designing EMHD-assisted mixing and targeted solute delivery systems.

4.5 Primary Shear Stresses

Table 5 illustrates the variation of the primary wall shear stresses, denoted by −τx0R and −τx0U, under RWTC and UWTC settings, for both the hybrid nanofluid (HNF: Cu–TiO2–H2O) and the conventional nanofluid (NF: Cu–H2O).

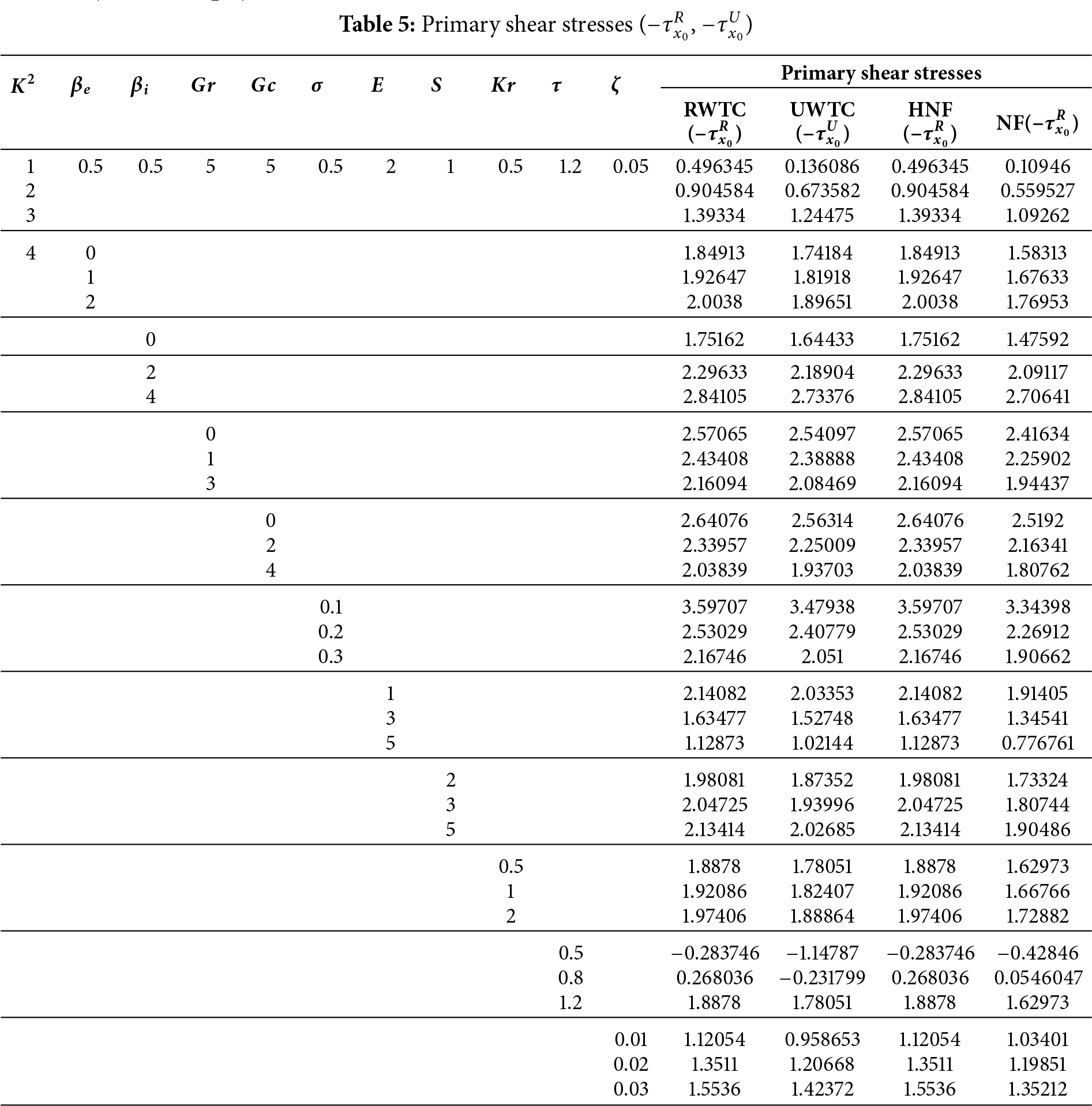
The rotation parameter K2 plays a dominant role: increasing K2 intensifies the Coriolis acceleration, which strengthens rotational motion in the tunnel and thus steepens the velocity gradient at the wall, raising the shear stress for both boundary types. A rise in the Hall parameter βe enhances cross-field currents and secondary velocity components, which effectively increase the wall drag. Likewise, larger ion-slip parameter values βi indicate stronger ion–electron decoupling in the magnetized fluid, which promotes momentum transport near the boundary and augments the shear response.

In contrast, buoyancy-related parameters show the opposite tendency. Higher thermal (Gr) and solutal (Gc) Grashof numbers generate upward or outward motion driven by buoyant forces, redistributing fluid away from the surface and thereby diminishing wall shear. The porous medium parameter σ also acts to reduce shear: increasing permeability eases fluid seepage through the matrix, thereby lowering resistance at the solid–fluid interface.

Electromagnetic effects exhibit contrasting influences. An increase in the modified Hartmann number E strengthens Lorentz damping, which suppresses wall-adjacent velocity gradients and lowers shear stress. Conversely, a wider electrode span S broadens the electromagnetic actuation zone, aligning fluid motion more effectively with the forcing and producing higher shear stress.

Other physical parameters further modulate the shear behavior. A stronger chemical reaction rate Kr enhances molecular diffusion and species activity, increasing viscous drag at the wall. The temporal parameter τ reflects the evolution of boundary layers; with increasing time, momentum diffusion intensifies and elevates the wall shear. Nanoparticle volume fraction ζ also has a positive contribution: higher loading augments effective viscosity and heat capacity, strengthening near-wall momentum exchange.

Overall, −τx0R consistently exceeds −τx0U, as the ramped boundary conditions impose spatio-temporal gradients that generate sharper velocity variations near the wall. Furthermore, HNFs display larger shear stresses compared to NFs under the same conditions. This arises from the synergistic enhancement of viscosity and conductivity by Cu and TiO2 nanoparticles, which improves energy and momentum diffusion. Hence, hybrid suspensions yield more pronounced shear responses, marking their advantage in flow control and thermal management.

4.6 Secondary Shear Stresses

Table 6 reports the dependence of the secondary wall shear stresses, τy0R and τy0U, on key parameters for both hybrid and conventional nanofluids. The rotation parameter K2 again emerges as a strengthening factor: greater Coriolis action reinforces cross-flow components, thereby raising the secondary wall drag. Both Hall current (βe) and ion-slip (βi) contributions modify the electromagnetic force balance, amplifying secondary circulation and yielding larger shear stresses for both RWTC and UWTC cases.

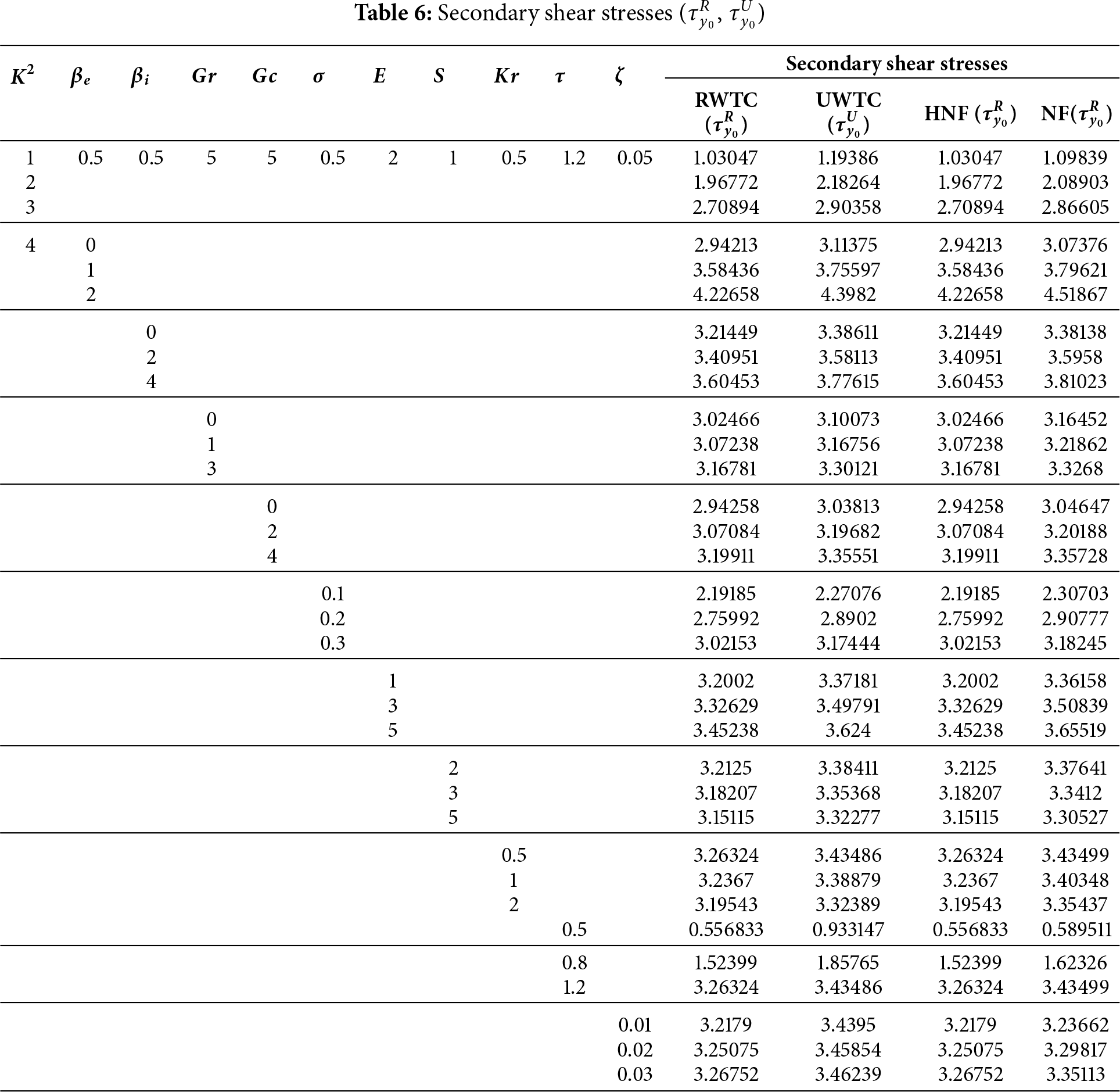
Unlike the primary stress, buoyancy through Gr and Gc promotes secondary flow intensities near the surface, which enhances wall shear. Similarly, higher porous medium permeability σ allows stronger penetration of flow into the matrix, sharpening velocity gradients and thus increasing shear. The Hartmann number E also supports secondary shear in this case, as stronger magnetic coupling redistributes velocities and elevates near-wall stresses. However, the electrode width S acts oppositely: broader electrodes dilute the local electromagnetic forcing and slightly suppress the secondary motion, thereby lowering the shear stress.

The chemical reaction parameter Kr tends to reduce secondary shear. Stronger reactive effects limit solutal diffusion near the boundary, weakening cross-flow development. With time τ, inertia and convective interactions grow, naturally intensifying secondary drag. The nanoparticle volume fraction ζ once again elevates shear by raising effective viscosity and conductive pathways, enhancing the transfer of momentum toward the wall.

Comparisons between boundary conditions reveal that τy0R is generally smaller than τy0U. The gradual build-up in ramped thermal and solutal conditions moderates velocity gradients during early stages, producing slightly weaker wall drag than the uniform case. In terms of fluid type, NFs show marginally higher secondary shear than HNFs. This counterintuitive result is linked to the higher viscosity of hybrid suspensions, which damps localized cross-flow structures. Nevertheless, hybrid nanofluids exhibit superior transport characteristics overall, offering stable boundary layers and improved energy exchange, even if their instantaneous secondary shear values are lower.

4.7 Heat Transfer Rate (HTR)

The variations of the non-dimensional heat transfer rate (HTR) with respect to selected control parameters are summarized in Table 7. The analysis focuses on the effects of the radiation parameter (Ra), internal heat generation (Qr), time (τ), and nanoparticle concentration (ζ), under both RWT and UWT heating. Results are contrasted between a hybrid nanofluid (HNF: Cu–TiO2–H2O) and a conventional nanofluid (NF: Cu–H2O).

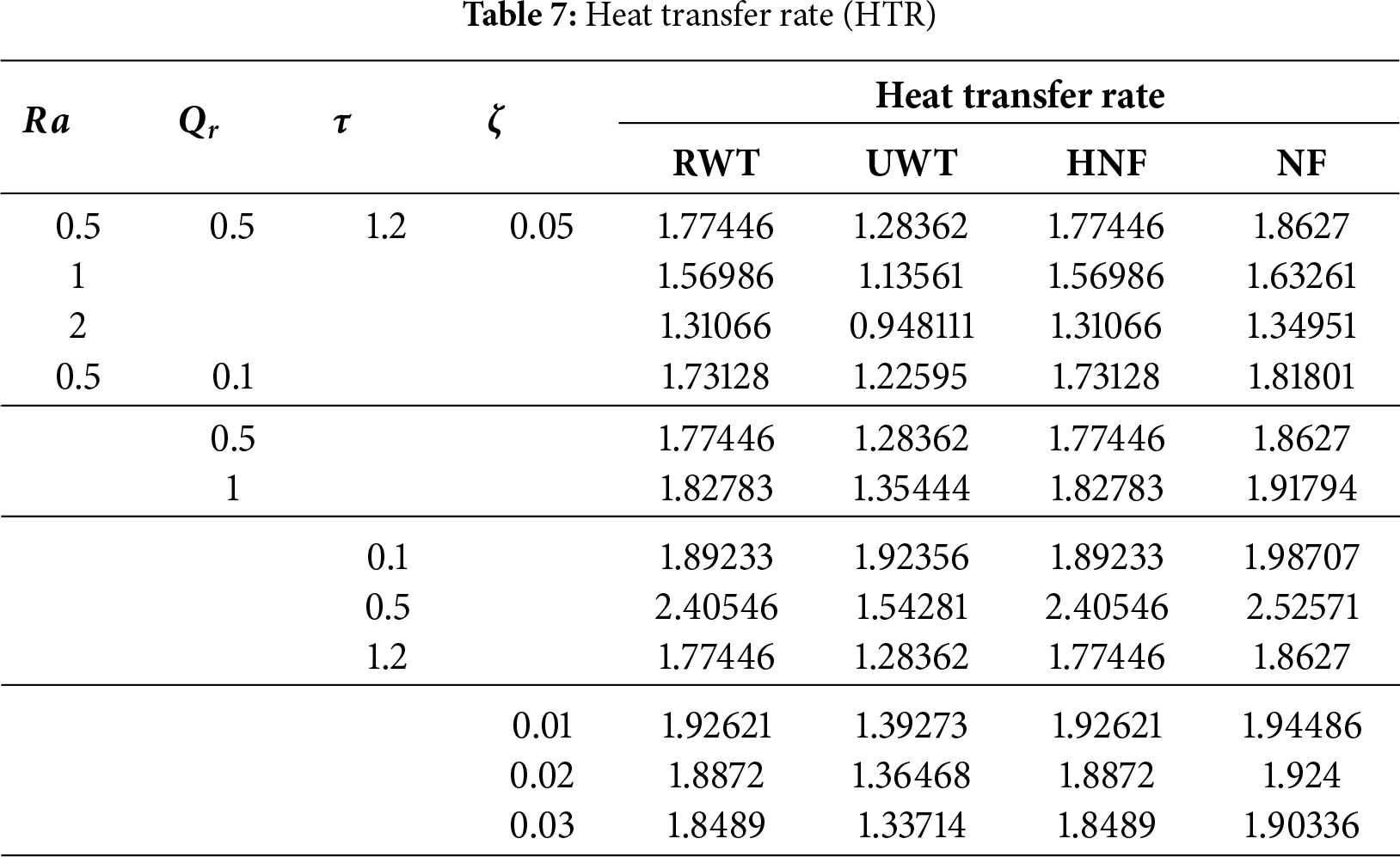
An increase in Ra reduces the magnitude of HTR across both boundary conditions. This occurs because radiative transport acts as an alternative pathway for thermal energy, which diminishes the net conductive heat flux at the wall. From a physical perspective, stronger radiative losses spread thermal energy more evenly in the fluid domain, leading to a weaker temperature gradient at the solid-fluid interface.

Conversely, larger Qr enhances the HTR in all cases. Additional volumetric heat input raises the fluid’s internal energy, which intensifies the near-wall temperature gradient and thereby drives a stronger heat flux. The effect is particularly evident in UWT, where the wall temperature is maintained at a constant high value, continuously sustaining conduction into the bulk fluid.

The temporal behavior of HTR shows distinct characteristics under RWT and UWT. In the UWT case, the heat transfer rate steadily decreases with τ, a signature of the system gradually approaching thermal equilibrium as the fluid warms up and the wall-fluid temperature gradient diminishes. In contrast, under ramped heating, the wall temperature itself grows with time; this initially strengthens the gradient and raises HTR for τ<1. At later times, the increase saturates, and the system transitions to a quasi-steady state with a declining heat transfer rate. These contrasting outcomes emphasize how temporal modulation of boundary heating governs transient energy transport.

The impact of nanoparticle concentration is somewhat counterintuitive. As ζ increases, HTR decreases for both fluids. While nanoparticles boost thermal conductivity, they also raise viscosity and suppress fluid motion, which thickens the thermal boundary layer and reduces the effective wall gradient. Thus, the overall convective contribution is weakened. Across all cases, RWT maintains a higher HTR than UWT, highlighting the benefit of time-dependent heating. Moreover, NF (Cu–H2O) consistently shows slightly stronger heat transfer than HNF (Cu–TiO2–H2O), a consequence of the higher viscous resistance associated with TiO2 in the hybrid mixture.

4.8 Mass Transfer Rate (MTR)

Table 8 outlines the sensitivity of the non-dimensional mass transfer rate (MTR) to the chemical reaction rate constant (Kr), Schmidt number (Sc), dimensionless time (τ), and nanoparticle volume fraction (ζ). Two wall concentration scenarios are considered: RWC and UWC, for both the hybrid nanofluid and the conventional nanofluid.

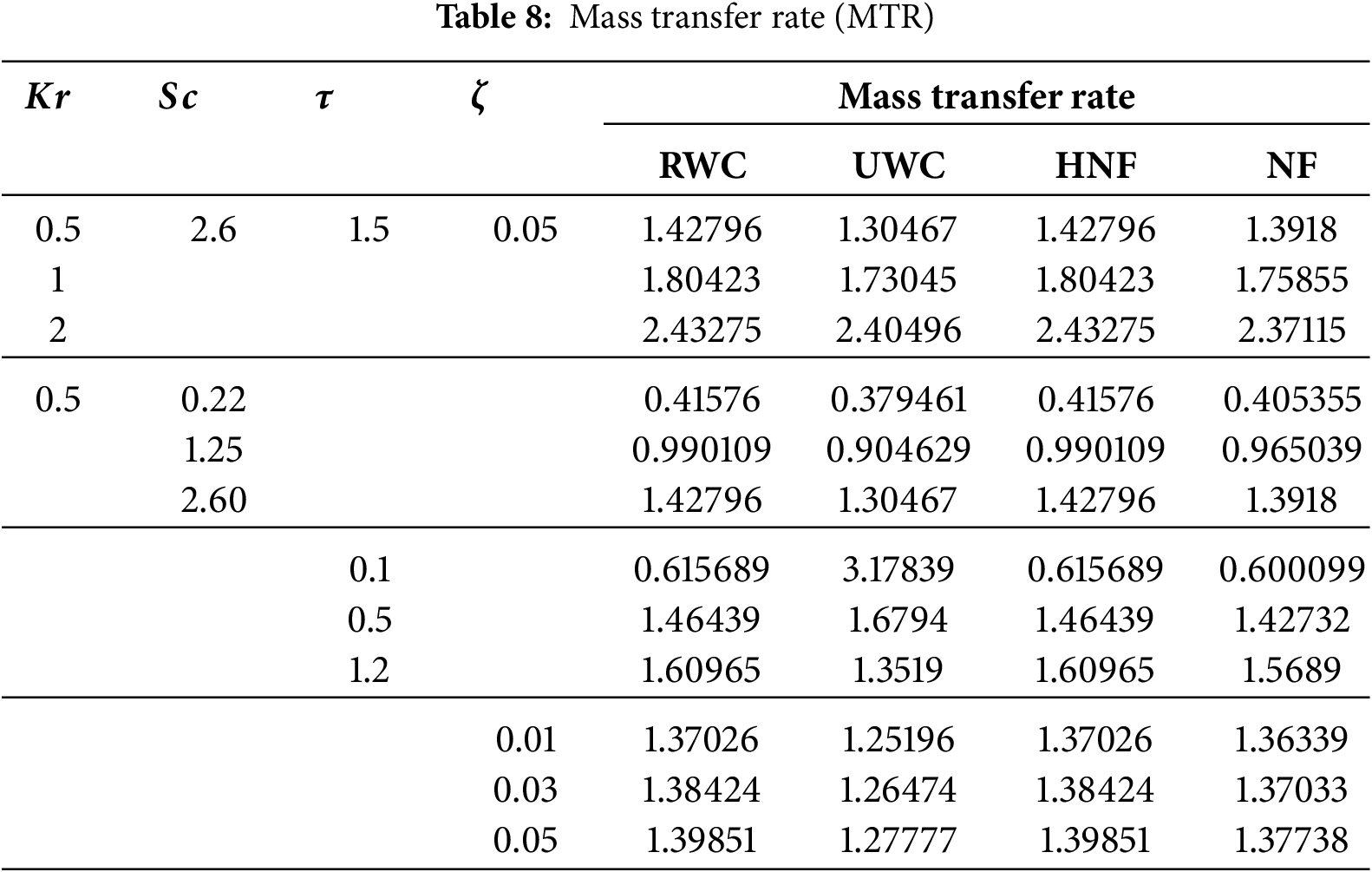
Increasing Kr strengthens MTR under both wall conditions. Faster reaction kinetics act as a sink for solute species at the boundary, steepening the concentration gradient and intensifying diffusive flux. This effect reflects the direct coupling between chemical consumption at the wall and enhanced mass transport through the boundary layer.

The Schmidt number also plays a critical role: higher Sc leads to higher MTR. Since Sc is inversely related to molecular diffusivity, larger values reduce the rate of solute spreading in the bulk fluid. This produces a thinner solutal boundary layer and sharper gradients at the wall, which in turn promotes stronger mass flux.

Temporal evolution again depends on the imposed boundary. In UWC, the mass transfer rate declines with time, as the initially strong gradient at the wall relaxes when diffusion progresses toward equilibrium. Under RWC, however, the imposed time-dependent concentration increases the gradient continuously, causing MTR to rise with τ. This opposite behavior highlights the critical role of dynamic boundary conditions in controlling transient solute transport.

Finally, the effect of nanoparticle loading shows a positive contribution: larger ζ enhances MTR for all cases. Unlike thermal transport, where viscosity effects dominate, here the presence of nanoparticles promotes micro-convection and surface interaction mechanisms that facilitate solute dispersion. The hybrid nanofluid consistently produces slightly higher MTR than the single-component NF, attributable to the complementary roles of copper and titania nanoparticles in enhancing solutal diffusion.

Overall, RWC conditions consistently generate stronger mass transfer than UWC, and hybrid suspensions provide marginally improved performance compared to conventional nanofluids. These findings underline how both reactive kinetics and nanoparticle synergy can be harnessed to control solutal transport in advanced nanofluid systems.

4.9 Artificial Neural Network (ANN) Framework

Artificial Neural Networks (ANNs) offer a flexible data-driven strategy for approximating highly nonlinear input-output relations that are often difficult to capture using classical analytical or regression techniques. Inspired by the connectivity of biological neurons, ANNs can map multiple interacting parameters to physical outcomes with remarkable precision. In the present analysis, the ANN serves as a surrogate model for predicting transport quantities obtained from a hybrid nanofluid system.

The learning process is carried out using the Levenberg-Marquardt backpropagation (LMBP) scheme. This hybrid optimization technique effectively merges the fast convergence properties of Newton-like algorithms with the stability of gradient descent. As a result, the method ensures rapid adjustment of synaptic weights even in scenarios where the error surface is highly nonlinear. Such efficiency is especially advantageous in fluid mechanics applications, where the governing equations involve several coupled nonlinearities associated with buoyancy forces, electromagnetic stresses, and nanoparticle interactions.

The ANN structure used in this study consists of three key components (See Fig. 11):

•   An input layer encoding dimensionless control parameters such as the thermal Grashof number (Gr), solutal Grashof number (Gc), Modified Hartmann number (E), Schmidt number (Sc), and nanoparticle loading (ζ), etc.

•   A hidden layer activated by a nonlinear transfer function. Here, the Tan-Sigmoid function is selected since it compresses large variations of input into a bounded interval, thereby enabling the network to approximate threshold-like phenomena.

•   An output layer with a linear activation rule, producing continuous predictions of wall shear stress, heat transfer, or solute flux.

The governing activation laws are:

fTS(x)=11+e−x,flin(x)=x,

where fTS mimics nonlinear saturation effects often present in physical processes, while flin preserves dimensional scaling in the outputs.

To prevent overfitting and ensure robustness, the dataset is partitioned into training, validation, and testing subsets. Training focuses on minimizing the mean squared deviation between ANN predictions and reference data. Validation continuously checks the model,s ability to generalize, while testing evaluates performance on unseen cases, thereby ensuring predictive reliability.

The ANN predictive performance is quantified through the following indicators:

Mean Squared Error (MSE)=1N∑i=1N(Xref(i)−XANN(i))2,Correlation Coefficient (R)=[1−∑i=1N(Xref(i)−XANN(i))2∑i=1N(Xref(i))2]1/2,Relative Error (%)=(Xref−XANNXref)×100.(39)