Analysis on D2D Heterogeneous Networks with State-Dependent Priority Traffic

1  Introduction

Device-to-device (D2D) communication is a modern communication method that allows direct communication between nearby users, which is considered to be one of the key technologies of 5G communication system [1,2]. It provides new opportunities for proximity-based business services, including the development of social networks [3,4]. Due to D2D communication may bring many advantages, such as improved spectrum efficiency, expanded cellular coverage, improved energy efficiency, and reduced backhaul requirements [3]. Unlike self-organizing networks, D2D communication is usually established under the control of a base station (BS) [3].

In [5], Zhong et al. employed queuing theory and Poisson point process (PPP) to study the necessary and sufficient conditions for queuing stability in static Poisson networks. In [6], Zhong et al. considered the randomly generated data flow and further analyzed the packet delay in the cellular heterogeneous network. They evaluated the delay performance of three scheduling schemes: Random Selection (RS), first-in first-out (FIFO) scheduling and round-robin (RR) protocol. However, because the signal-to-interference ratio (SIR) analysis and queue status are not decoupled, only the boundary of the network delay distribution under a fixed base station can be obtained. In [7], Yang et al. assumes that the number of users in each BS is fixed. On this basis, the delay interruption of PPP distributed small cell network using RS or RR is derived.

Existing works have applied the priority jump queue model to wireless packet networks or cognitive radio networks [8–10]. According to the inherent characteristics of multiple traffic types, the system parameters are derived under the premise of satisfying Quality of Service (QoS) to optimize the network architecture. In [8], Balapuwaduge et al. established two queues for secondary users in a multi-channel wireless cognitive network with heterogeneous traffic. The two queues analyzed and stored real-time and elastic data. The work allocated priority service to high-level real-time data through channel access strategies, while establishes a queuing scheme based on delay threshold for elastic data. In addition, a continuous-time Markov chain model is established to evaluate the performance of the proposed channel allocation strategy. The correctness and accuracy of the derived theoretical model is verified through extensive simulations. In [9], Walraevens et al. proposed a spatial merging method in the packet switching network to study the queue model with limited buffer and jump priority. When a call with a low priority arrives, it is assumed that such a call is transferred to the end of the high priority call queue. The transition probability depends on the status of the heterogeneous call queue. The algorithm calculates the service quality index of this type of queuing model and analyzes the results of numerical experiments. In addition, the dynamic priority jump model is also applied to wireless body area networks. In [10], Zhao et al. considered combining the priority transmission of medical data packets in the wireless body area network with the dynamic priority queuing model. Based on the analysis of a delay-dependent dynamic priority transmission scheduling scheme, a queuing principle with buffer overflow is studied, which is approximated as the jump strategy in the priority transmission scheduling criterion, and the delay is analyzed. The tail characteristics of the distribution. So far, few papers apply the priority shifting model to the D2D cellular heterogeneous network.

So far, few papers have applied the priority queue model to the D2D cellular heterogeneous network. Reference [11] models two priority data transmission processes, assuming that two priority data have independent caches. There is no mutual constraint between the two caches. when the arrival rate of one type is low, it will cause a great waste of the cache space of the queue. Moreover, HP data transmission is always met first. If there is a large amount of LP data, there will be a large amount of LP data that cannot be sent. This situation will cause excessive delay and packet loss of LP data. In order to solve this problem, in our paper, we assume that the high and low priority data are stored in the common cache space. We allocate the public cache to the high and low priority data storage space in proportion. This strategy can maximize the utilization of the public buffer area and ensure the packet loss rate of low-priority data. In order to further optimize the data transmission process of high and low priority queues, we consider adding a priority jump strategy to the priority queuing model. Priority jump strategy allow low priority data packets to be sent as high priority data with a certain jump probability. The jump probability is determined by the queue leader status of high and low priority queues, so it is called state dependent priority jump strategy.

This paper focuses on the multi-class service transmission model in the D2D underlying cellular network. Combined with queuing theory and Stochastic geometry, a spatiotemporal model is proposed to analyze the performance of cellular users in heterogeneous networks. First, we consider the transmission mode of potential D2D users in the cellular network which adopts a distance-based D2D mode selection strategy. At the same time, considering that the interference is caused by users who use non-empty buffers, we use the thinning Poisson point process to model the spatial distribution of cellular users and obtain the probability of successful transmission. Second, we consider the priority transmission status of multiple business models, which can make full use of the buffer space. The priority jump strategy with a common buffer area in the queuing theory is adopted to provide more transmission opportunities for low-priority data, thereby alleviating the starvation state of low-priority data under high load. A two-dimensional Geo/G/1 Markov chain is established to describe the queue model with priority switching strategy for each cellular user, and the quasi-birth and death (QBD) method is used to evaluate the queuing behavior. When calculating the steady-state probability distribution, the iterative solution is used to calculate the steady-state probability distribution and obtain the expression of performance indicators.

The rest of this paper is organized as follows. The Section 2 describes the system model and performance indicators. The queuing model analysis framework with priority jumping is established in the Section 3. Queue stability analysis and performance parameters are introduced in Section 4. Section 5 provides numerical and simulation results, followed by the conclusions of Section 6.

2  System Model

As shown in Fig. 1, we consider a hybrid network, including cellular users and D2D users, and focus on the user’s uplink communication. Assuming that the location distribution of base stations follows independent PPPs ΦB with the density is λb.They are randomly distributed in the regular hexagonal grid-like area and the area of the hexagonal cell is 1λb, where λb is the average number of BSs per unit area. In this paper, A is used to denote the coverage area of the hexagonal macro cell. We approximate A by a spherical disk with the same area as the hexagonal cell with a radius of R, R=1πλb. In addition, we assume that the cellular users are evenly distributed in the coverage area A, and the location of the cellular user constitutes a PPP ΦC of λc. Cellular users communicate with the base station closest to it. For typical uplink transmission, the interference of other cellular users comes from outside area A. We make reasonable assumptions of λc>>λb.

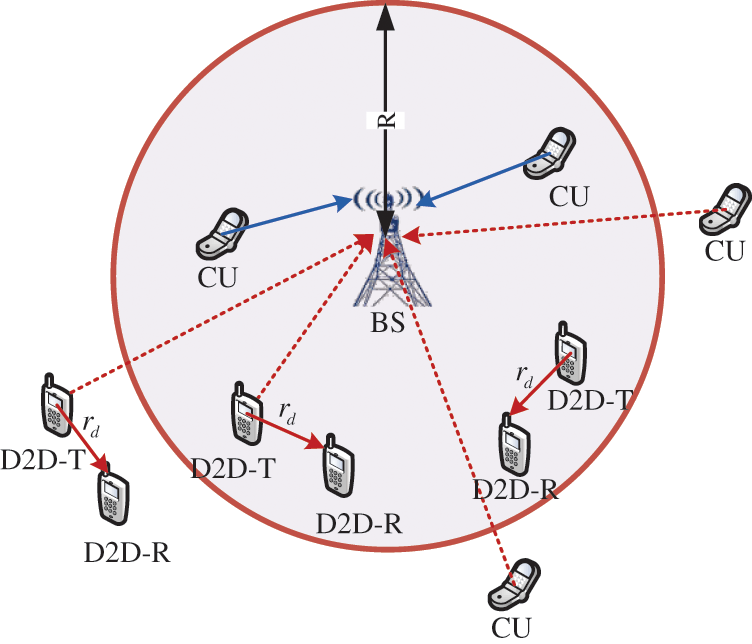
Figure 1: D2D underlying cellular heterogeneous network

This paper considers that the uplink spectrum resources in the cell are orthogonally allocated to different cellular users. Potential D2D users reuse the channel in an underlay manner. It is assumed that the cellular network is in a fully loaded state, that is, all uplink sub-channels in the cell are allocated to different cellular users. We adopt a mode selection strategy for potential D2D users. When the distance between the D2D transmitter and the target receiver is less than the preset threshold, the potential D2D user will work in D2D mode, that is, sharing channel resources with cellular users for direct communication. At this time, D2D communication will cause interference to the cellular link of the shared channel. When the distance between the D2D transmitter and the receiver exceeds the threshold, the D2D user enters the sleep mode [12,13]. In addition, it is assumed that each D2D transmitter is equipped with a limited buffer for storing sporadic arriving data packets, in which only non-empty queues will cause interference to other links in the shared channel. Assuming that potential D2D users obey PPPs ΦD with density of λd, only some users can cause interference to the cellular link. The position distribution of these users constitutes a thinned PPP ΦD′, and the density λd′ can be expressed as

λd′=P(rd<μ)ηλd(1)

where rd represents the distance from the D2D transmitter to its target receiver and μ is the preset distance threshold. η represents the probability of non-empty queue status.

We assume that each potential D2D receiver is randomly distributed around its potential transmitter, and the distance from the transmitter to the receiver rd obeys the Rayleigh distribution. Its probability density function (PDF) is as follow:

frd(x)=2πςxe−πςx2,x≥0(2)

We consider the path loss plus block fading channel model [14], The received power of the cellular user is ptgd−α, where pt is the transmit power of the cellular user, g represents the small-scale fading of the communication link, which follows the exponential distribution of the normalized mean. d is the distance from the transmitter to the receiver and α is the path loss factor.

Additionally, as we consider the uplink transmission, power control is necessary. Uplink power control is used to adjust the transmit power to keep the base station receiving the signal power from the cellular user at a certain value, we employ the full channel inversion for uplink power control [15]. Then the transmit power of the cellular user is ρBSdk,BSαC, where ρBS is the minimum required power at the BS. dk,BS is the distance from cellular user k to its serving base station. αC represents the path loss factor of the cellular link.

According to the above assumptions, cellular users k is subjected to intra-layer interference from cellular users in other cells IaggC, as well as inter-layer interference IaggD from D2D users sharing channels inside and outside the cell due to non-orthogonal spectrum access strategies. Then the interference received by the serving base station of cellular user k can be expressed as

IaggC+IaggD=∑i∈ΦC∖{k}ρBSdk,BSαCdi,BS−αCgi,BS+∑j∈ΦD′Pdgj,BSdj,BS−αD(3)

where gi,BS and gj,BS respectively represent the fading power gain of the interference link from cellular user i and the D2D user j to the BS. These two parameters are assumed to be independent and identically distributed. Considering that the cellular link and the D2D link may experience different propagation channels, αC and αD are defined as the path loss factors of cellular and D2D link. di,BS and dj,BS respectively represent the distance from CU i and D2D users j to the BS. Pd is the D2D transmit power.

Considering the interference limited system, we can get the expression of the signal to interference and noise ratio of cellular user i to the BS as:

SINRk=gk,BSρBSIaggC+IaggD+δ2(4)

where gk,BS is the fading power is gain between CU k and BS, and δ2 is the noise power.

3  Queuing Model and Priority Jump Strategy

In this section, we build a dynamic priority queuing model with a common buffer area, and discuss state-dependent priority jump strategies.

3.1 Queuing Model

We use the two-dimensional Geo/G/1 Markov chain to establish a priority queue model for cellular users, where Geo represents the arrival process that obeys the geometric distribution, and G represents the service time, which is a non-negative random variable. Taking into account the actual interference received by cellular users in the D2D underlying cellular network, the service process is determined by the SINR value of each time slot. For the convenience of analysis, this paper takes two types of priority data as examples. For the case of multiple types of priority, the derivation process is similar. By setting the jumping probability γi(j), the relationship between high and low priority queue is expressed.

(1) Data packet arrival process

It is assumed that the data packets arrival of the cellular user obeys the Bernoulli distribution with the parameter α, in which the high priority (HP) service data is generated with probability pHP, and the low priority (LP) service data is generated by pLP, pLP=1−pHP. Then HP data packet arrival probability is apHP, and the LP data packet arrival probability is a(1−pHP).

(2) Service process

Assuming that the cellular user is sending at the maximum rate, the sending rate is R(t)=Blog2⁡(1+SINRk(t)). We set the time slot length is T0 and each data packet has a fixed length L0. Then the lowest average sending rate to send a data packet is R0=L0T0. The expression of probability that the sending rate exceeds the lowest average sending rate is the probability of successful transmission of a data packet, then

b=P(R(t)>R0)=P(Blog2⁡(1+SINRk(t))>L0T0)=P(SINRk(t)>2L0BT0−1)(5)

The complementary cumulative distribution function (CCDF) of the cellular link SINR can be expressed as

P[SINRk>2L0BT0−1]=Er[P[SINRk>2L0BT0−1|r]]=∫0RP[SINRk>2L0BT0−1|r]fr(r)dr=∫0R2R2e−2L0BT0−1ρBS⋅δ2⋅LIaggD(2L0BT0−1ρBS)⋅LIaggC(2L0BT0−1ρBS)rdr(6)

where LIaggD(s) and LIaggC(s) are the Laplace transform of IaggC and IaggD, respectively. Their expressions are as follow:

LIaggD(s)=exp⁡(−2πλd∫0∞(1−Egd[11+sPdv−αD])vdv)(7)

Formula (7) is established based on the independent and identical distribution of gd and the probability generating function (PGFL) from PPP.

LIaggC(s)=exp⁡(−2πλc∫R∞(1−Egc[11+sρBSdk,BSαCdi,BS−αCgc])vdv)(8)

The derivation of LIaggC(s) is mostly the same as LIaggD(s), except that the value range of the integral variable v refers to the distance between a cellular user in other cells and its serving base station. By substituting Eqs. (6)--(8) into Eq. (5), the probability that the CU transmission rate is greater than is obtained, that is, the closed expression of the probability of successful transmission.

3.2 Priority Jump Queuing Strategy

In this discrete-time queuing system, we assume that each cellular user can only send one data packet in one time slot. In the transmission process of multiple data types, services such as video or telephony, which require high delay, need to be transmitted first and set as HP data. Data services like short messages have lower latency requirements and are set as LP services. The priority queuing model used in this paper always meets the transmission of HP data first. If there is a large amount of LP data, there will be a large amount of LP data that cannot be sent. This situation will lead to excessive delay and packet loss of LP data. We consider adding a priority jump strategy to the priority queuing model to allow low priority data packets to be sent as high priority data with a certain jump probability. The jump probability is determined by the number of data packets in the high and low priority queues. it is called state dependent priority jump strategy.

As shown in Fig. 2, we consider a model with a common buffer in which two types of data traffic are stored. The buffer size is L. In this model, the state-dependent priority jump strategy is adopted and there are the following definitions.

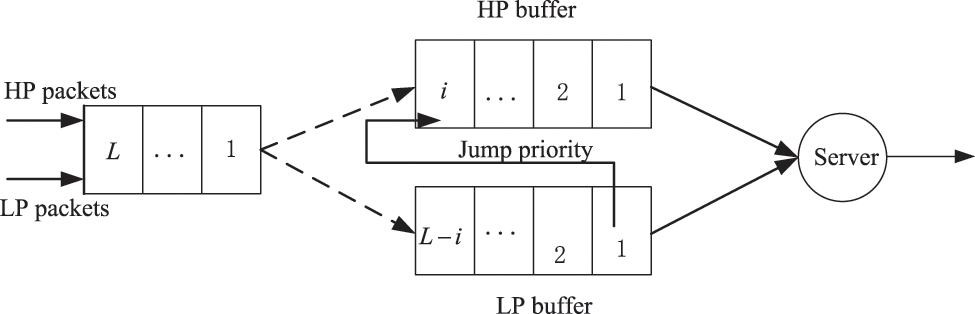
Figure 2: Structure of queuing system with priority jump

First, as long as there is high priority data in the queue, high priority data will be sent first, and LP data will be sent when the HP buffer is empty. Secondly, if there is only high priority data in the queue and the queue is not full, the packets will enter the queue with probability 1 and to be transmitted. If the queue is full, the arriving HP data will be discarded with probability 1. Third, when the number of data packets in the buffer of the HP queue is i, i<L and the number of data packets in the LP queue is j, j<L−i,The newly arrived low-priority data can be transmitted as high-priority data with probability γi(j). There is no need to wait for transmission in the low-priority queue. Fourth, if the common buffer area is full, the low priority data that arrives is discarded with probability 1.

In this queuing system, we consider a State-dependent-based priority jump strategy as follow

γi(j)=i+j+β2cos⁡(πi/I)−cos⁡(πj/J)β2I+J(9)

where β2,β2>1 is the adjustment parameter.

4  QBD Process and Matrix Geometry Method

4.1 Quasi-Birth and Death Process Method

In order to analyze the transmission behavior of high and low priority data under the jump strategy respectively, we regard the two types of data entering the same buffer as two virtual queues. We use a two-dimensional Markov chain to model the data transmission of cellular user. The system state can be represented by the number of data packets (i,j) in the two queues in the system. The state process is defined as {X(t),t≥0} where i represents the number of HP data packets, and j represents the number of LP data packets. Fig. 3 shows state transition diagram. The behavior of queuing is evaluated by QBD. We rearrange (i,j) the state of the queue length and treat it as a one-dimensional process. Definition, where is named level and is phase.

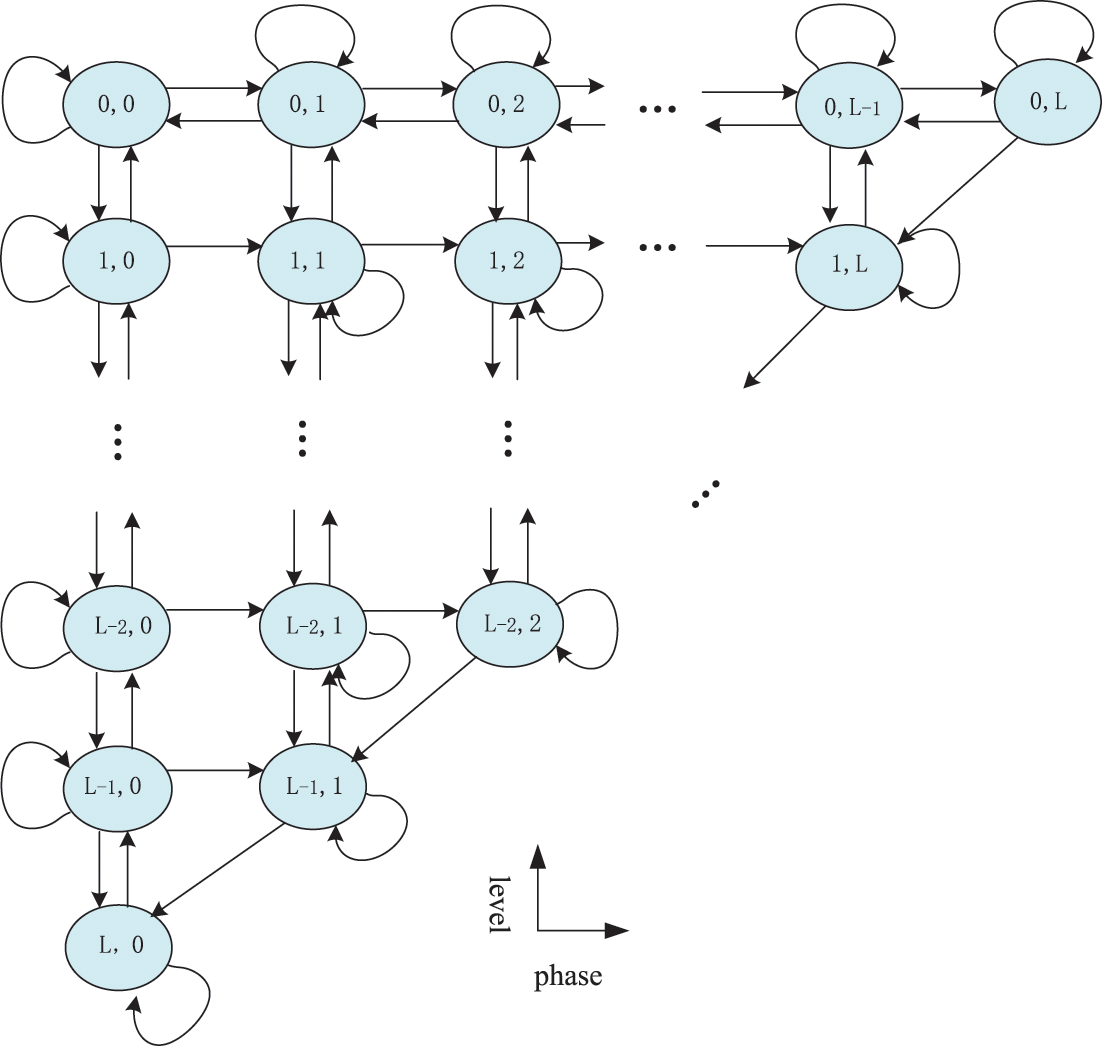
Figure 3: State transition diagram of priority queuing model with common buffer

The transition probability matrix P is given in the form of a block matrix, as follows:

P=[B0C0000…0A0B1C100⋱⋮0A1B2C20⋱⋮00⋱⋱⋱⋱⋮⋮⋮⋱⋱⋱⋱0⋮⋮⋱⋱AL−1BL−1CL−10………0ALBL](10)

where the sub-matrix represents the transfer between levels, the sub-matrix on the diagonal Bi represents the set of events in which the level (HP queue length) remains unchanged after the data packet arrives and is served in a time slot, while the phase (LP queue length) plus 1, minus 1, or remains unchanged, Li→Li,i∈[0,L]. The expressions of the elements in all sub-matrix ∈RL×L are as follows:

B0=[B0,00,0B0,00,10⋯⋯0B0,10,0B0,10,1B0,00,10⋯00B0,20,1B0,20,2B0,00,1⋱⋮00⋱⋱⋱⋮⋮⋱⋱B0,L−10,L−2B0,L−10,L−1B0,L−10,L0⋯⋯⋯B0,L0,L−1B0,L0,L](11)

where B0,k0,k represent the situation of the high priority queue length is 0, and the low priority queue remains unchanged, expressed as:

B0,k0,k={1−a,k=0(1−a)(1−b)+ba(1−μHP)(1−γ0(k)),1≤k≤L−11−b+ba(1−μHP)(1−γ0(L)),k=L(12)

The high priority queue length is 0, and the phase (LP queue length) plus 1 or minus 1, expressed as:

B0,k+10,k={(1−a)b,0≤k<L−1b,k=L−1(13)

B0,k−10,k={a(1−μHP)(1−γ0(0)),k=1a(1−μHP)(1−γ0(k−1))(1−b),,1≤k≤L−2(14)

For 1≤i≤L−1, because the high and low priority data share the same buffer, that is i+j≤L, so the element in Bi exceeds the line of L−i is 0.

Bi=(i,0)(i,1)⋮(i,L−i−1)(i,L−i)⋮(i,L)[Bi,0i,0Bi,0i,100⋯000Bi,1i,1Bi1i,20⋱⋱⋮00⋱⋱⋱⋱⋮⋮⋱⋱Bi,L−i−1i,L−i−1Bi,L−i−1i,L−i000⋱⋱0Bi,L−ii,L−i00⋮⋱⋱⋱⋱⋮⋮0⋯⋯⋯000](15)

where

Bi,ki,k={(1−a)(1−b)+b[aμHP+a(1−μHP)γi(k)],0≤k<L−i(1−a)(1−b),k=L−i(16)

Bi,k−1i,k=(1−b)[a(1−μHP)(1−βi(k−1))],0≤k≤L−i(17)

For the boundary conditions i=L of the sub-matrix,

BL=[(1−aμLP)(1−b)00⋯000⋱⋯⋮0⋱⋱⋱0⋮⋱0⋱00⋯⋯00](18)

The sub-matrix Ci indicates Li−1→Li,i∈[1,L], which contains all the events of adding a HP data packet. The added data packet may be an arriving HP data packet, or a data packet from the LP queue with probability γi(j). The boundary condition C0 represents the state transition situation of L0→L1, since the initial queue length of the HP queue is 0, the LP queue length will j→j−1.

C0=(0,0)(0,1)⋮(0,L−1)(0,L)[C0,01,000⋯0C0,11,0C0,11,10⋯⋮0⋱⋱⋱⋮⋮⋱C0,L−11,L−2C0,L−11,L−100⋯⋯C0,L1,L−10](19)

where

C0,k1,k={aμHP+a(1−μHP)γ0(0),k=0[aμHP+a(1−μHP)γ0(k)](1−b),1≤k≤L−1(20)

C0,k1,k−1=[aμHP+a(1−μHP)β0(k)]bLP,1≤k≤L(21)

For 1≤i≤L−2, the HP queue length i≥1. Based on the principle that HP data is sent first, there is no transfer of j→j−1, the elements except the diagonal are all 0.

Ci=(i,0)(i,1)⋮(i,L−i−1)(i,L−i)⋮(i,L)[Ci,0i+1,0000⋯000Ci,1i+1,100⋱⋱⋮00⋱⋱⋱⋱⋮⋮⋱⋱Ci,L−i−1i,L−i−10000⋱⋱0Ci,L−ii,L−i00⋮⋱⋱⋱⋱⋮⋮0⋯⋯⋯000](22)

where

Ci,ki+1,k=[aμHP+a(1−μHP)γi(k)](1−b),0≤k≤L−i−1(23)

For boundary conditions of i=L−1,

CL−1=(L−1,0)(L−1,1)⋮(L−1,L−1)(L−1,L)[aμHP(1−b)00⋯0000⋯⋮0⋱⋱⋱⋮⋮⋱⋱⋱000⋯00](24)

The sub-matrix Ai below the diagonal indicates that the HP queue adds a data packet after a service period, namely Li→Li−1,i∈[1,L]. For 0≤i≤L−1, Ai means that the packet with no probability is added to the HP queue.

Ai=(i+1,0)(i+1,1)⋮(i+1,L−1)(i+1,L)[b(1−a),a(1−μHP)(1−γ0(k−1))b00b(1−a)a(1−μHP)(1−γ1(k−1))b0⋱⋱⋮⋱⋱0⋯⋯⋯0⋯⋮⋱0b(1−a)a(1−μHP)(1−γL−1(k−1))b00](25)

4.2 Matrix Geometry Method to Solve Two-dimensional Markov Chain

The steady-state solution of the quasi-birth-death process can be obtained by solving the linear balance equations, which is the column matrix of steady-state probability. In order to use the regular structure of the block matrix, we will divide the quasi-birth-death process into:

Π=[Π0,Π1,⋯,ΠLmax](26)

where

Πi=[Πi,0,Πi,1,Πi,2,⋯Πi,Lmax],i∈[0,Lmax](27)

From the linear balance equation, in order to solve the steady-state probability Π from (26), the transition probability matrix P is required. The analysis of the Section 3.1 shows that it depends on the arrival rate, transmission probability and jump probability. Among them, the D2D user density of the non-empty queue and the potential D2D mode selection determine the following parameters, which are the average arrival rate of HP and LP data, the probability of successful transmission and the jump probability. In particular, the probability of successful transmission depends on the interference from non-empty queue users, and the interference is related to the steady-state probability distribution of HP and LP. It can be clearly seen that there is an interactive relationship between the steady-state distribution of the queuing model and the successful transmission probability calculated by the thinned PPP. We use the fixed-point iteration method to solve the causal relationship to obtain the steady-state probability distribution, as shown in Algorithm 1.

4.3 Performance Parameters

After the steady-state probability distribution is obtained by Algorithm 1, performance parameters such as average queue length, average throughput, average delay and packet dropping probability can be expressed as the following expressions. The expressions of the average captain of HP and LP are given as:

QHP=∑i=0L∑j=0L−i(i−γi(j))Πi,j(28)

QLP=∑j=0L∑i=0L−j(j+γi(j))Πi,j(29)

Given the steady-state probability distribution and the probability of successful transmission, the average throughput of HP and LP queues can be derived as:

ThrHP=(1−∑j=0LΠ0,j)⋅b(30)

ThrLP=(1−∑i=0LΠi,0)⋅∑j=0LΠ0,j⋅b(31)

In addition, Little’s law can be used to evaluate the average waiting time DelHP and DelLP required before sending HP and LP packets in the queue.

DelHP=∑i=0L∑j=0L−i(i−γi(j))Πi,j(1−∑j=0LΠ0,j)⋅b(32)

DelLP=∑j=0L∑i=0L−j(j+γi(j))Πi,j(1−∑i=0LΠi,0)⋅∑j=0LΠ0,j⋅b(33)

Furthermore, we can give the closed-form expressions of the packet dropping probability as:

pdropHP=aμHP∑j=0LΠL,j(34)

pdropLP=aμLP∑i=0LΠi,L(35)

5  Numerical and Simulation Results

In this section, we use MATLAB to analyze and verify the correctness of the mathematical expressions of the above performance parameters, and explore the system performance by changing the parameters in Tab. 1. In the following numerical simulations, unless otherwise specified, we consider a simulation area 20km×20km where the base station is located in a circular area with R=500m, and the cellular users are evenly distributed among them. The D2D transmitter is distributed uniformly in accordance with the density of PPP. All links experience independent and identically distributed Rayleigh fading with unit variance. In order to show the impact of changes in the proportion of HP data cache in the total cache on performance, we define high priority cache ratio as ϕ. The simulation results are carried out by using MATLAB and repeat for over 10,000 iterations.

Fig. 4 is a three-dimensional graph of the LP queue length in the cache with the average arrival rate and the ratio of the HP data cache to the total cache capacity under the priority jump queuing strategy (PJQS) scheme. We set pHP=0.2. It can be seen from the figure that with the increase of the data arrival rate, the captain of the LP gradually increases. When the high-priority cache occupies a relatively small amount, that is, when the low-priority data has more space to enter the queue, the LP queue length grows faster and the curve is steeper. On the contrary, when the high-priority queue cache space increases, for example, the proportion is 80%, most of the low-priority data cannot enter the cache, resulting in a reduction of the queue length to 10. Then the LP packet dropping probability will increase sharply.

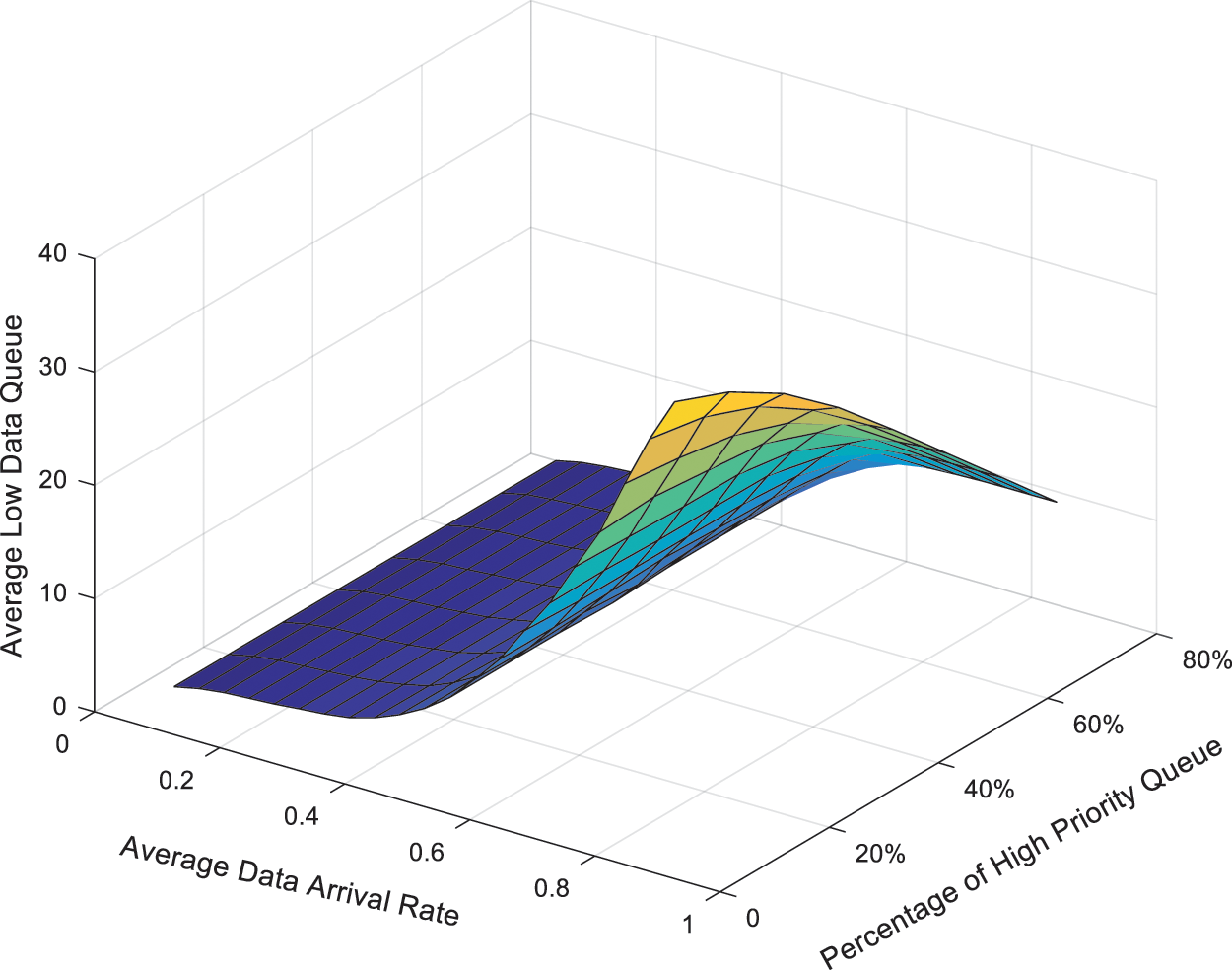
Figure 4: The LP data queue length with PJQS scheme

Fig. 5 shows the curve of queue length of the LP queue with the data arrival rate under different HP buffer ratios. We set pHP=0.2. It can be seen from the small backlog of low-data queue that PJQS has better performance than non-PJQS overall. We compare the curves where is ϕ=0.5 and ϕ=0.8. If the HP cache ratio ϕ is low, more LP data enters the cache, and the queue length is larger. When ϕ=0.5, and the data arrival rate reaches 0.6 under the no-jumping strategy, the LP queue quickly saturates, because the HP queue helps alleviate the transmission pressure of a large amount of LP data. When the arrival rate is close to 1 and ϕ=0.8, all curves tend to overlap which is because the limited LP data cache space. When the data arrival rate is large, the PJQS has no effect on the queue length.

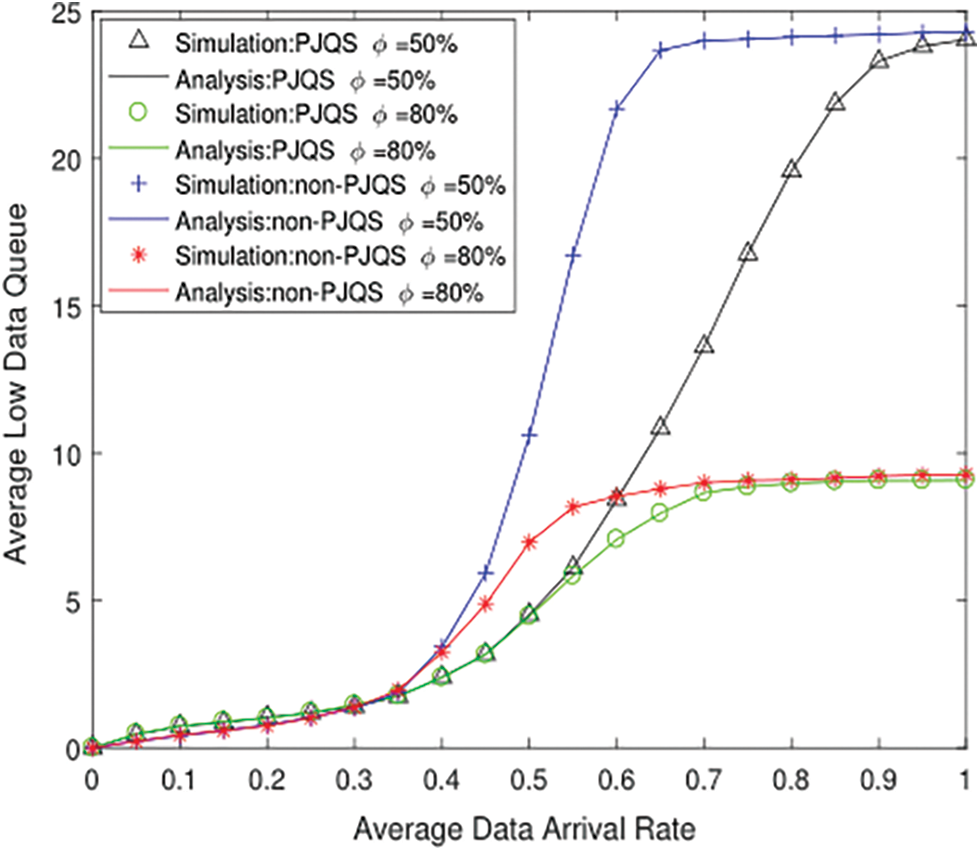
Figure 5: The LP data queue length under different ϕ

Fig. 6 is a figure of LP data packet dropping probability under PJQS and non-PJQS. Fig. 6a is PJQS scheme and Fig. 6b is non-PJQS scheme. The x-axis represents the average data arrival rate, the y-axis represents the proportion of the buffer allocated for the HP queue in the total buffer. It can be seen from Fig. 6a that when HP cache part is small, the increase in the average arrival rate has little effect on LP packet loss rate. The backlog of priority queues can maintain a very low dropping probability even if the arrival rate is large. When the proportion of HP buffers increases, especially when they account for more than 60% of the total buffer, the dropping probability increases sharply. It is because LP queue has insufficient buffer space, which causes overflow and packet loss. Therefore, the proportion of high-and LP buffers in the total buffer should be appropriately allocated to maximize the use of buffer capacity. In Fig. 6b, no matter how much the HP cache occupies, the increase in data arrival rate has a huge impact on dropping probability. When the arrival rate reaches 0.4, the dropping probability increases sharply. However, the buffer ratio has little effect on the change of the curve. This is because without the help of the jump queuing strategy, the LP queue is saturated when the arrival rate is 0.4, and the HP data is sent first and LP data cannot be sent. Comparing the two figures, we can see that the cache strategy reduces the maximum packet loss rate of LP queue from 0.25 to 0.05, which clearly shows the effectiveness of the jump queuing strategy.

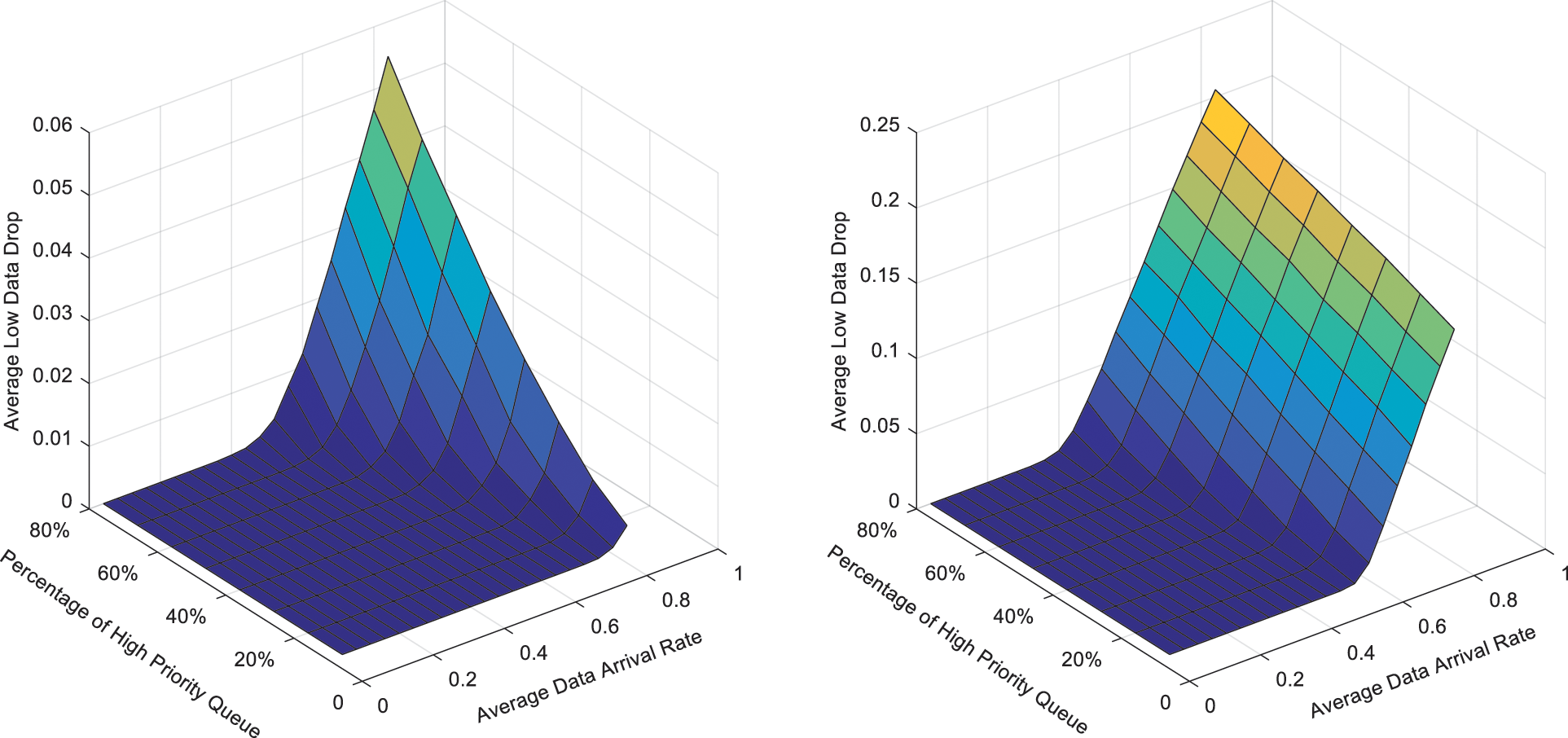
Figure 6: The LP data drop of PJQS and non-PJQS

Fig. 7 shows the delay of low priority queue vs. arrival rate.It can be seen that the numerical results coincide with the simulation results. When the data arrival rate is less than 1, on the premise of the same proportion, the delay of the priority jump queuing strategy is lower than that of non jump queuing strategy. As the data arrival rate is close to 1 and the capacity of both queues is close to full, the advantages of the jump strategy are gradually disappearing, and the curve of whether there is a jump strategy is close to the same. In the case of non jump queuing strategy, the delay curve of ϕ=0.5 is higher than ϕ=0.8, because the smaller the cache capacity allocated to low priority data, the shorter the queue length of low priority, and the less time required for transmission, the smaller the delay. There is the same trend in the curve with the priority jump queuing strategy.

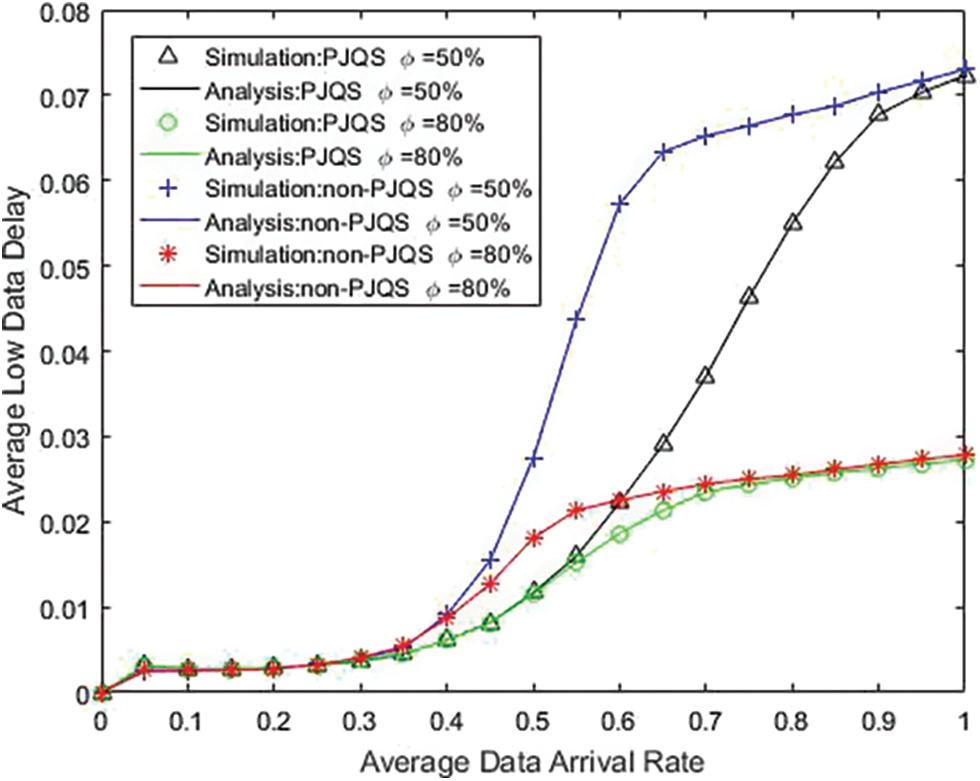
Figure 7: The LP data delay with data arrival rate

Fig. 8 is a three-dimensional graph of the low-priority data delay as a function of the average arrival rate and the proportion of high-priority data caches in the total cache under PJQS scheme. When the high-priority data cache occupies a small amount of total cache space, it is allocated to the low-priority data cache. The high-level data space is large, and more low-priority data can be accommodated at this time. When the arrival rate is high, the longer the queue length of the low-priority queue is, the longer the sending delay is, and when the high-priority data cache occupies a large proportion, with the increase of the average arrival rate, the increase of the delay slows down. This is because the limited low-priority data buffer space prevents the arriving data from entering the queue.The queue length is shorter, the delay is lower.

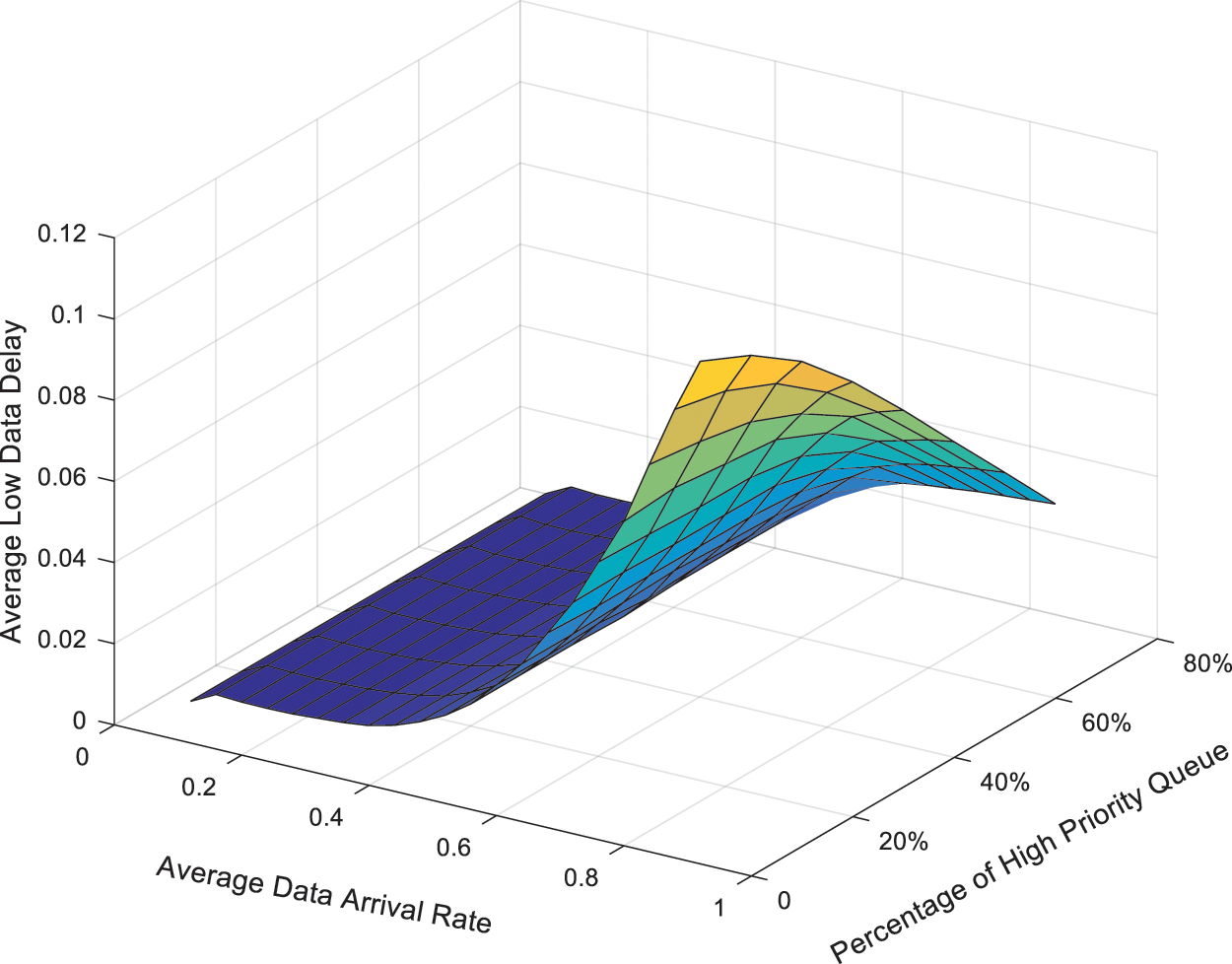
Figure 8: The LP data delay with PJQS scheme

Fig. 9 shows the average throughput of HP and LP vs. arrival rate. It can be seen that the numerical results coincide with the simulation results. Since data arrival rate of HP is much smaller than its maximum transmission capacity, HP data throughput increases linearly. As the data arrival rate increases, the throughput of LP first rises rapidly and then decreases. This is because the two queues store less data. The HP queue sends some LP data with probability γi(j) to increase the LP throughput. As the both queue lengths increase, the HP queue needs to send arriving HP data. When the transmission capacity is not enough to continue sending data packets from the LP queue, and the LP throughput will decrease. The numerical results are basically coincide with the simulation results.

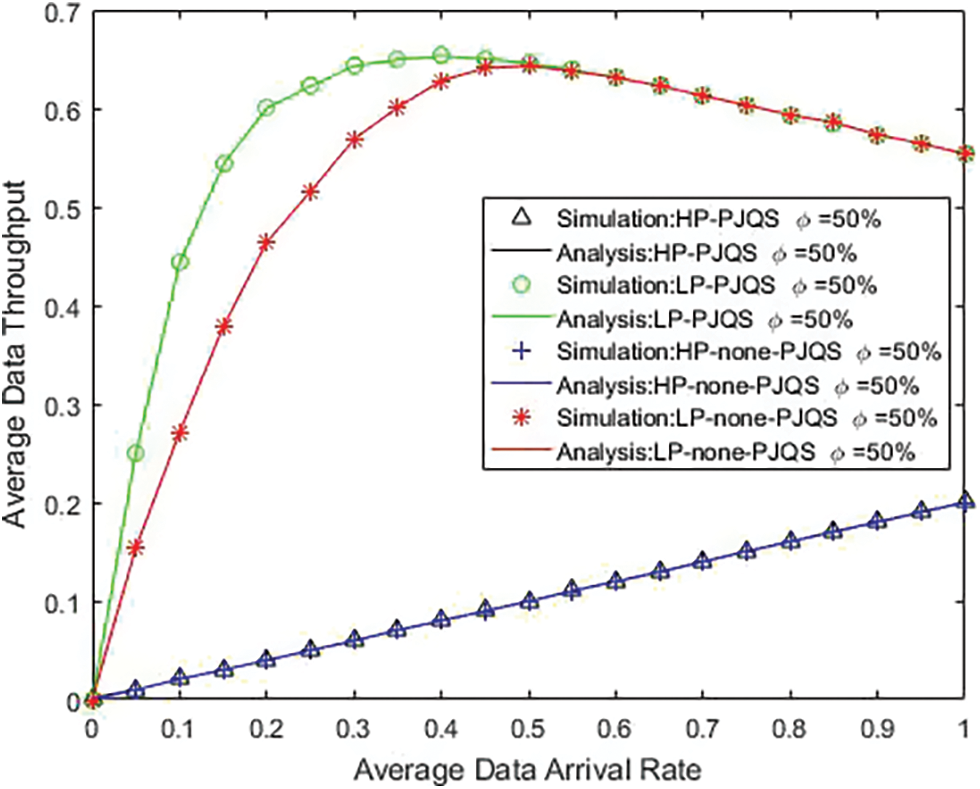
Figure 9: The average throughput with data arrival rate

6  Conclusions

A spatiotemporal mathematical model in the D2D underlying cellular network was proposed. Different from the existing results, we focus on the multi-priority business mode. Stochastic geometry and priority queuing theory are adapted in this network. We set a priority jump strategy to provide transmission opportunities for LP data and reduce the packet dropping probability of the LP queue. In addition, considering the transmission mode of potential D2D users in the cellular network, we adopt a distance-based D2D mode selection scheme. To show the relationship between the D2D user queues, we model the positions of D2D users with Non-empty queue buffers using a thinned Poisson point process to derive the CCDF of the D2D receiving SINR. Secondly, we use a two-dimensional Geo/G/1 Markov chain to describe the queue model with priority jumps for D2D users, and the QBD method evaluates the queue state transition process. Finally, a series of expressions of performance parameters are derived, such as average queue length, average throughput, average delay and packet dropping probability. Simulation analysis confirmed the correctness of the numerical analysis. In addition, by comparing the packet loss rate of priority queues with and without jump strategy, the rationality of the model proposed in this paper is explained. In future work, we can apply the queuing model and analytical approach presented in this paper to conducting performance studies on D2D-assisted wireless caching networks. Specially, we can discuss the service transmission model of D2D heterogeneous cellular network in full duplex mode, and further analyze various types of jump strategies. We can also consider D2D equipment powered by pre-charged batteries from the perspective of green communication.The harvested energy can signifificantly improve the lifetime of the device and the network. we will concentrate on using more realistic assumptions to build a dynamic model in further research. We hope our work can provide a more accurate theoretical basis for the design of the actual system.

Acknowledgement: Guangjun Liang and Jianfang Xin conceived and designed the experiments; Guangjun Liang and Lingling Xia performed the experiments; Xueli Ni and Yi Cao analyzed the data; Guangjun Liang wrote the paper. All authors have read and agreed to the published version of the manuscript.

Funding Statement: The work is supported by 2020 Major Natural Science Research Project of Jiangsu Province Colleges and Universities: Research on Forensic Modeling and Analysis of the Internet of Things (20KJA520004), 2020 Open Project of National and Local Joint Engineering Laboratory of Radio Frequency Integration and Micro-assembly Technology: Research on the Security Performance of Radio Frequency Energy Collection Cooperative Communication Network (KFJJ20200201), 2021 Jiangsu Police Officer Academy Scientific Research Project: Research on D2D Cache Network Resource Optimization Based on Edge Computing Technology (2021SJYZK01), High-level Introduction of Talent Scientific Research Start-up Fund of Jiangsu Police Institute (JSPI19GKZL407).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  T. Ahmad, I. Khan, A. Irshad, S. Ahmad, A. T. Soliman et al., “Spark spectrum allocation for D2D communication in cellular networks,” Computers, Materials & Continua, vol. 70, no. 3, pp. 6381–6394, 2022. [Google Scholar]

 2.  X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]

 3.  F. Jameel, Z. Hamid, F. Jabeen, S. Zeadally and M. A. Javed, “A survey of device-to-device communications: Research issues and challenges,” IEEE Communications Surveys & Tutorials, vol. 3, no. 3, pp. 2133–2168, 2018. [Google Scholar]

 4.  X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

 5.  Y. Zhong, M. Haenggi, T. Q. S. Quek and W. Zhang, “On the stability of static poisson networks under random access,” IEEE Transactions on Communications, vol. 64, no. 7, pp. 2985–2998, 2016. [Google Scholar]

 6.  Y. Zhong, T. Q. S. Quek and X. Ge, “Heterogeneous cellular networks with spatio-temporal traffic: Delay analysis and scheduling,” IEEE Journal on Selected Areas in Communications, vol. 35, no. 6, pp. 1373–1386, 2017. [Google Scholar]

 7.  H. H. Yang, Y. Wang and T. Q. S. Quek, “Delay analysis of random scheduling and round robin in small cell networks,” IEEE Wireless Communications Letters, vol. 7, no. 6, pp. 978–981, 2018. [Google Scholar]

 8.  I. A. M. Balapuwaduge, L. Jiao, V. Pla and F. Y. Li, “Channel assembling with priority-based queues in cognitive radio networks: Strategies and performance evaluation,” IEEE Transactions on Wireless Communications, vol. 13, no. 2, pp. 630–645, 2014. [Google Scholar]

 9.  J. Walraevens, B. Steyaert and H. Bruneel, “Performance analysis of a single-server ATM queue with a priority scheduling,” Computers & Operations Research, vol. 30, no. 12, pp. 1807–1829, 2003. [Google Scholar]

10. Z. Zhao, C. Yi, J. Cai and H. Cao, “Queueing analysis for medical data transmissions with delay-dependent packet priorities in WBANs,” in Int. Conf. on Wireless Communications & Signal Processing, Yangzhou, pp. 24–37, 2016. [Google Scholar]

11. J. F. Xin, Q. Zhu and G. J. Liang, “Performance analysis of D2D underlying cellular networks based on dynamic priority queuing model,” IEEE Access, vol. 7, no. 1, pp. 27479–27489, 2020. [Google Scholar]

12. A. K. Hamid, F. N. Al-Wesabi, N. Nemri, A. Zahary and I. Khan, “An optimized algorithm for resource allocation for D2D in heterogeneous networks,” Computers, Materials & Continua, vol. 70, no. 2, pp. 2923–2936, 2022. [Google Scholar]

13. R. Z. Ahamad, A. R. Javed, S. Mehmood, M. Z. Khan, A. Noorwali et al., “Interference mitigation in D2D communication underlying cellular networks: Towards green energy,” Computers, Materials & Continua, vol. 68, no. 1, pp. 45–58, 2021. [Google Scholar]

14. S. Huang, B. Liang and J. Li, “Distributed interference and delay aware design for D2D communication in large wireless networks with adaptive interference estimation,” IEEE Transactions on Wireless Communications, vol. 16, no. 6, pp. 3924–3939, 2017. [Google Scholar]

15. H. Elsawy and E. Hossain, “Analytical modeling of mode selection and power control for underlay D2D communication in cellular networks,” IEEE Transactions on Communications, vol. 62, no. 11, pp. 4147–4161, 2014. [Google Scholar]