Non-Negative Adaptive Mechanism-Based Sliding Mode Control for Parallel Manipulators with Uncertainties

1  Introduction

In recent years, parallel manipulators have been widely deployed in various industry fields. Examples can be found in flight simulators, machine tools, micro-mechanisms, haptic devices, etc. [1,2]. In real applications, parallel manipulators have high stiffness, huge overload-driven capability, and high accuracy [2]. Unfortunately, this robot always faces many complex uncertainties and external disturbances caused by unknown dynamic systems, external noises, and nonlinear frictional forces. Hence, the design of the trajectory tracking control for parallel manipulators presents unique challenges, specifically while high-speed motions, high accuracy, and high acceleration are required. In the literature, various approaches for parallel mechanisms have been proposed to enhance tracking control, for example, PID [1], adaptive control [2], backstepping control [3], optimal control [4], sliding mode control [5], etc. Among them, robust control techniques are used to cancel complex uncertainties and external disturbances as well as provide higher robustness. Based on computational intelligence like neural networks, fuzzy systems, robust tracking control strategies have been proposed in [6–12]. However, the learning techniques always need a huge computation because of the training complication in fuzzy rules or neural weights. Then they may have a computational burden in implementation.

In order to guarantee the performance of the tracking controller, the terminal sliding mode control (TSMC) scheme has been developed and discussed as an efficient methodology [13,14]. The TSMC approach has many properties such as robustness, higher precision, rapid response, and finite-time stable equilibrium. The essential philosophy of TSMC is to design a terminal attractor sliding surface that guarantees finite-time convergence of the states. In the literature, TSMC has been successfully applied in various industrial fields, for example, switched reluctance motor [13], uncertain robot systems [14], etc. However, those approaches have three potential disadvantages: 1) singular problem, 2) slow convergence to the equilibrium, 3) chattering phenomenon problem, and hence limits its performance in practical applications. In order to overcome the above-mentioned drawbacks and to guarantee the performance of TSMC approaches, various approaches have been developed in the literature. Firstly, to overcome the singular problem, nonsingular terminal sliding mode control (NTSMC) has been analyzed in [15,16] separately. Secondly, in order to resolve the problem of slow convergence, fast terminal sliding mode control (FTSMC) is widely employed, such as in [17,18]. However, NTSMC or FTSMC has just only resolved one problem and neglected the other aspects of TSMC. To cope with both singular problems and slow convergence speed, integral terminal sliding mode control (ITSMC) [19,20] and nonsingular fast terminal sliding mode control (NFTSMC) [21–26] are developed. However, ITSMC is designed based on TSMC, and then, the above feebleness of TSMC may still exist. On the contrary, it is well known that NFTSMC has many outstanding advantages like robustness, rapid response, nonsingular, and fast convergence to the globally stable equilibrium. In the literature, various advanced methods based on NFTSMC have also been developed for control theory studies and practical applications; for example, robot manipulators [21–23], and induction motors [24–26]. Thirdly, to address the chattering problems, various approaches have been discussed based on either the disturbance estimation method [27] or the boundary layer saturation method [28]. Among them, the saturation method is widely used in implementation because it provides both chattering elimination and high accuracy. Generally, the corresponding suitable approaches [15–28] can overcome some drawbacks of TSMC. However, none of these approaches can resolve all of the problems of TSMC simultaneously. From the economic point of view, the control system of parallel manipulators requires easy implementation, low complexity, real-time control, computer-implementable, and effectiveness with high-speed motions with complex uncertainties and disturbances. Thanks to those promising features of NFTSMC as mentioned above, in this study, adaptive nonsingular fast terminal sliding mode control (ANFTSMC) is proposed not only to resolve all drawbacks of TSMC but also to enhance the performance of finite-time and high-speed trajectory tracking control of parallel robots in the case of high-speed motions and unknown bounded complex uncertainties and external disturbances. The several contributions of the study are highlighted as follows.

1)   The online non-negative adaptive mechanism (NAM) is used to estimate the uncertainties and disturbances. Hence, unlike the existing TSMC [13–26], the proposed approach does not require prior knowledge about the bounds of the complexity of external disturbances and complex uncertainties.

2)   In this approach, the tracking differentiator (TD) is adopted to cope with the high-speed motions. It can be found that the tracking control performance at high-speed motions can be better in a real-time fashion because all control parameters are online updated based on TD and NAM.

3)   The proposed controller has possessed advantages such as simple structure, easy implementation, chattering-free, high precision, robustness, singularity avoidance, and finite-time convergence. Besides, the proposed approach has superior tracking control performance and disturbance rejection ability. The stability and finite-time convergence of the parallel mechanisms are ensured by the Lyapunov theory.

2  Related Work

The stability of a robotic system with the NFTSMC controller [21–26] is proven with an assumption that the disturbances and uncertainties are required to be bounded. The boundness is hard to be estimated in advance because of the complexity of disturbances and uncertainties. To address this drawback, there are other modifications to the adaptive laws in NFTSMC approaches. For example, in [29], a robust NFTSMC control strategy is proposed based on computational intelligence (CI) techniques such as fuzzy systems and neural networks. In [30,31], an NFTSMC scheme is developed to improve control precision and response rapidity of nonlinear systems by extended state observer (ESO). Also, in [32,33], based on time delay estimation (TDE), an adaptive NFTSMC is designed. In the above approaches, generally, those CI, ESO, or TDE techniques are employed to handle the estimation of complex uncertainties and external disturbances. Hence, these approaches may increase the computational burden of the systems.

To address this issue, in [34], based on the backstepping technique, an adaptive backstepping NFTSMC controller is proposed for tracking control of robot manipulators. In [35], a robust NFTSMC scheme is developed for the tracking problem of the robotic manipulator subject to uncertainty and disturbances. Also, in [36], a robust adaptive NTSMC control scheme is designed for the position and the velocity tracking control of the automatic train operation system. In [34–36], the upper bound of the complex uncertainties and external disturbances is estimated via a NAM. The NAM adjusts the gain of the control automatically and enables the tracking protocol to work well without prior knowledge of the robot system. Hence, these control methodologies cannot only hold the advantageous features of NFTSMC but also have low complexity and real-time control. However, those approaches neglect the stability of the closed-loop systems while operating at high-speed motions, especially in the cases of complicated mixture noises. To enhance the performance in high-speed motions, recently, an additional TD based NFTSMC has been developed and discussed in [37,38]. TD is used to estimate the target tracking signal and the derivative quickly and accurately. However, although ESO is used to handle the uncertainties in those approaches, it increases the computational burden of the systems. It is shown in this study that combining NFTSMC, NAM and TD together is feasible and promising for finite-time and high accuracy as well as high-speed tracking control.

3  Problem Formulation and Preliminaries

3.1 Dynamic Model of Parallel Manipulators

From [2] and [28], the parallel mechanisms dynamic model in the active joint space is presented by

M(q)q¨+C(q,q˙)q˙+G(q)+F(q,q˙)=τ,(1)

where q,q˙,q¨∈Rn are the vectors of the active joints position, velocity, and acceleration, respectively. τ∈Rn is the vector of the corresponding forces. G(q)∈Rn is the matrix of the gravitational forces. F(q,q˙)∈Rn is the vector of the complex uncertainties and external disturbances and is expressed as

F(q,q˙)=ΔM(q)q¨+ΔC(q,q˙)q˙+ΔG(q)+f(q)+d(q,q˙),(2)

where f(q)∈Rn is the active joints friction models, d(q,q˙)∈Rn is the disturbances force, and ΔM(q), ΔC(q,q˙) and ΔG(q) are actual components caused by uncertainties and disturbances.

The parallel mechanisms dynamic is represented in a second-order differential equation as

q¨=M−1(q)τ+D(q,q˙)+ΔF(q,q˙),(3)

where ΔF(q,q˙)=−M−1(q).F(q,q˙) is the unknown uncertainties and disturbances in the nominal model. D(q,q˙)=M−1(q)[−C(q,q˙)q˙−G(q)] is the known nominal parallel mechanisms dynamic.

3.2 Notations, Preliminaries, and Useful Assumptions

The Euclidean norm of a vector that has K elements is as

‖v‖=∑i=1K|vi|2(4)

To avoid any possible confusion, a variable vector x=[x1,…,xn]∈Rn, sigc(x) and its derivative are presented as

sigc(x)=|x|csign(x)=[|x1|csign(x1),…,|xn|csign(xn)]T,c>0(5)

ddt(sigc(x))=c|x|c−1x˙,(6)

sign(x)={1ifx>00ifx=0−1ifx<0.(7)

Assumption 1 The sum of the unknown uncertainties and disturbances is bounded as

‖ΔF(q,q˙)=−M−1(q).F(q,q˙)‖≤m0.(8)

4  Controller Design

Define qa∈Rn as the desired state vector and e=q−qa as the vector of the tracking error. According to [21–26], the NFTSMC surface function and its derivation are expressed as

s=e+α|e|φsign(e)+β|e˙|a/bsign(e˙),(9)

s˙=e˙+αφ|e|φ−1e˙+βab|e˙|(a/b)−1(q¨−q¨a),(10)

where the positive odd numbers a and b are satisfied by the rules 1<a/b<2 and φ>a/b, α=diag{α1,…,αn};αi>0, β=diag{β1,…,βn};βi>0, |e|φ−1=diag{|e1|φ−1,…,|en|φ−1}, |e|φ=diag{|e1|φ,…,|en|φ}, |e˙|(a/b)=diag{|e˙1|(a/b),…,|e˙n|(a/b)}, and |e˙|(a/b)−1=diag{|e˙1|(a/b)−1,…,|e˙n|(a/b)−1}, i=1,…,n.

Let Ψ(e,e˙)=e˙+αφ|e|φ−1e˙ and Ξ(e˙)=β(a/b)|e˙|(a/b)−1. From (3) and (10), we have

s˙=Ψ(e,e˙)+Ξ(e˙).[M−1(q)u+D(q,q˙)+ΔF(q,q˙)−q¨a].(11)

Under Assumption 1, modifications of the NFTSMC design have also been proposed in the literature [21–26,29–36]. For example, in [23] and in [32], the NFTSMC control law is expressed as

u=ueq+usw=−M(q)[Ψ(e,e˙)Ξ−1(e˙)+D(q,q˙)−q¨a+(m0+ξ)sign(s)].(12)

In [24], the NFTSMC control law is presented by

u=ueq+usw=−M(q)[Ψ(e,e˙)Ξ−1(e˙)+D(q,q˙)−q¨a+ξs+m0sign(s)].(13)

In (12) and (13), ξ is a known small positive constant. ueq=−M(q)[Ψ(e,e˙)Ξ−1(e˙)+D(q,q˙)−q¨a] is the equivalent control law which ensures fast finite-time convergence no matter the system states are near the sliding surface. usw=−M(q)(m0+ξ)sign(s) or usw=−M(q)(ξs+m0sign(s)) is the switching control law that can make the parallel mechanisms system more robust against complex uncertainties and disturbances. It should be noted that ξ is manually set in the above NFTSMC controllers, and thus, the robot dynamics model is not compensated. The controller structures can considerably be simplified and make the controller attractive. However, the stability of the robot system at a high speed may have problems, especially in the cases of complex mixture noises. Besides, the stability of the parallel mechanisms system with the use of the NFTSMC controller is proven with an assumption that the bounds of the uncertainties and disturbances are known (Assumption 1). However, the assumption is difficult to be satisfied in practical applications with the complexity of the complex uncertainty and external disturbance.

To address these issues, in this study, an online NAM is used to estimate the upper bounds of complex uncertainties and external disturbances of parallel manipulator systems. The proposed controller does not require prior knowledge about the bounds of uncertainties and disturbances. Besides, the TD is adopted to deal with the transition process and to decrease the initial impulse of the manipulative variable. Combining NFTSMC, TD, and online NAM together in this study, the proposed ANFTSMC law is expressed as

u=ueq+uAsw=−M(q)[Ψ(e,e˙)Ξ−1(e˙)+D(q,q˙)−q¨a+K^p.s+(m^0+K^d)sign(s)],(14)

K^p={k^p|e|λ1−1for|e|>δ1k^p|δ1|λ1−1for|e|≤δ1,k^p>0,(15)

K^d={k^d|e˙|λ2−1for|e˙|>δ2k^d|δ2|λ2−1for|e˙|≤δ2,k^d>0.(16)

The NAM law of the parameters m^0 is

m^˙0=c|s||e˙|(a/b)−1,c>0.(17)

Theorem 1 Supports that the parallel manipulators are described by (1) with the complex uncertainties and external disturbances as (2). Under the sliding mode surfaces (9), the control inputs (14), and the online adaptive update laws (15)–(17), it is concluded that the system trajectories can move fast to zero in a finite time without any singularity.

Proof Consider a Lyapunov function candidate as

V(t)=12sTs+abβ2c(m^0−m0)2,(18)

V˙(t)=sTs˙+abβc(m^0−m0)m^˙0.(19)

Substituting (11) and (17) into (19) and with Ξ(e˙)=β(a/b)|e˙|(a/b)−1, we have

V˙(t)=sT(Ψ(e,e˙)+Ξ(e˙).(M−1(q)u+D(q,q˙)+ΔF(q,q˙)−q¨a))+Ξ(e˙)|s|(m^0−m0).(20)

In combination with the control input (14), it yields

V˙(t)=sT.Ξ(e˙).(ΔF(q,q˙)−K^P.s−(m^0+K^d)sign(s))+Ξ(e˙)|s|(m^0−m0)=−Ξ(e˙).(K^ps2+K^d|s|)+Ξ(e˙)(ΔF(q,q˙)s−m0|s|)≤−Ξ(e˙).(K^ps2+K^d|s|)≤−∑i=1nΞ(e˙i).[k^p|ei|λ1−1.si2+k^d|e˙i|λ2−1.|si|]≤0.(21)

Hence, the parallel mechanisms states converge to the sliding surfaces asymptotically. To show that the system trajectories can move fast to zero in a finite time, V˙(t) in (19) can be rewritten as

V˙(t)=dV(t)dt≤−Ξ(e˙).(K^ps2+K^d|s|)=−ρ1V(t)−ρ2V1/2(t),(22)

where ρ1=2Ξ(e˙)K^p>0 and ρ2=2Ξ(e˙)K^d>0. Hence, it yields

dt≤−dV(t)ρ1V(t)+ρ2V1/2(t)=−V−1/2(t)dV(t)ρ1V1/2(t)+ρ2=−2dV1/2(t)ρ1V1/2(t)+ρ2.(23)

Define tr as the reaching time. It is certain that V(tr)=0. Taking integral of both sides of (23), it yields

∫0trdt≤∫V(0)V(tr)−2dV1/2(t)ρ1V1/2(t)+ρ2=[−2ρ1ln⁡(ρ1V1/2(t)+ρ2)]|V(0)V(tr)tr≤−2ρ1ln⁡(ρ1V1/2(0)+ρ2ρ2).(24)

Following the Lyapunov stability theorem, the sliding surface in (9) can converge fast to zero in the amount of time tr≤2ρ1ln⁡(ρ1V1/2(0)+ρ2ρ2). It can be concluded that the system trajectories can move fast to zero in a finite time. It completes the Proof.

Remark 1 The structure of the ANFTSMC scheme is given in Fig. 1. In practical applications, the desired reference may be a square wave signal or a step signal, which always includes jump points. The system may not be able to track the reference signal in real-time. Specifically, when the initial tracking error e is large, the control gain should be large to have a fast-tracking response. It may generate large overshoots and large initial impulses. To address this issue, TD designed in (15) and (16) is employed to have a suitable transition process. According to (15) and (16), it should be emphasized that TD provides transitive desired input signals and those noise-free differential signals. Besides, the TD gains are very simple.

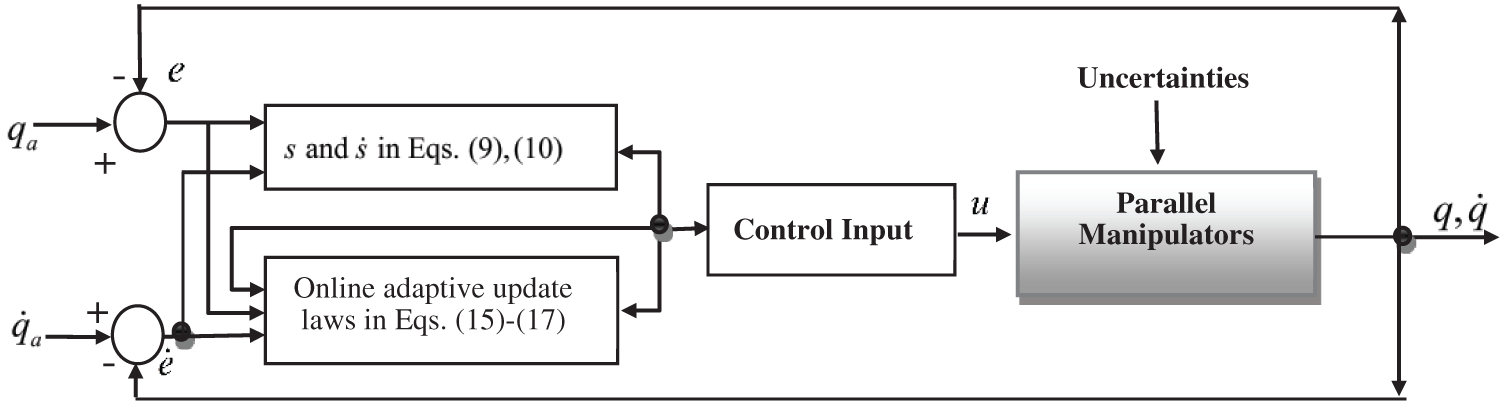
Figure 1: ANFTSMC scheme

Remark 2 In TD gains (15) and (16), δ1,δ2>0 are the positive threshold parameters of the errors and the errors rate, respectively, and are selected in between the maximum error and close to zero. The parameters λ1,λ2>0 are tuned in practice. With TD, the errors can reach zero much more quickly in a finite time. To improve the error curve further, the value of the parameters λ1 and kp should be decreased at the same time, because the term kp|ei|λ1−1 or kp|δ1|λ1−1 makes the proportional control much more sensitive, especially with small errors. The differentiation term kd|e˙i|λ2−1 or kd|δ2|λ2−1 prevents overshooting output through a transient period when the error is sufficiently large. k^p and k^d can be selected by a trial and error manner [28]. The nonlinear gains under these selections also have the following properties: a huge gain for large error rates and a little gain for small error rates; on the contrary, a huge gain for small errors and a little gain for large errors. This design makes a rapid conversion of the dynamic systems with advantageous damping. Thus, the control approach is highly suitable for high-speed motions of parallel mechanisms systems.

Remark 3 From (17), it can be deduced that m^˙0≥0. Hence, the optimal value m^0 can be obtained via the NAM for the unknown bounded component m0. Besides, the NAM law in (17) does not require the symmetric and regression properties, which are used in most of the adaptive update laws for controlling robot systems in previous approaches [29–36]. Hence the proposed control laws are applicable to any mechanical systems, including parallel manipulators.

Remark 4 The approximation learning techniques based on computational intelligence such as fuzzy systems, neural networks, etc. are used to approximate the unknown bounded component m0 as that in [29]. However, such learning techniques are computationally expensive.

Remark 5 The discontinuous function sign(⋅) in the control input (14) may cause chattering phenomena. To cope with this, the sign(⋅) function is replaced by a saturation function

sign(s)=s‖s‖+ρ,(25)

where ρ is a positive constant, ||s|| is the Euclidean norm of the vector s. As stated in [32], the stability and finite-time convergence of the saturation function are proved based on the Lyapunov approach.

Remark 6 To implement the ANFTSMC controller, the desired state of the position, and the acceleration of the active joints should be known. Unfortunately, the dynamic model of parallel manipulators is only available with position measurement. In this paper, based on the backward differentiator technique [32], the measurement of the acceleration can be calculated as

q¨¯a(t)=1N∑i=0N−1q¨a(t−i)=qa(t)−2qa(t−L)+qa(t−2L)L2.(26)

The acceleration signals defined by (26) can reduce the noises on the sensor signal. Besides, it achieves finite time error convergence no matter what the input signals are.

Remark 7 Compared with state-of-the-art approaches [13–26], the proposed approach does not require the upper bound of uncertainties, which is almost impossible to obtain in many real applications. Besides, the proposed control scheme has superior tracking control performance such as convergence fast to the finite-time stable equilibrium, the non-singularity, rapid response, and the strong robustness with complex uncertainties and external disturbances.

5  Demonstrative Example

In this section, the performances of the proposed controller are verified for a 2-DOF parallel mechanisms as shown in Fig. 2. Its kinematics parameters are as in [2,8,28]. To show the strong robustness of the proposed controller, the unknown modeling ΔM(q) and ΔC(q,q˙), the nonlinear frictions forces f(q˙) and the external disturbances d(q,q˙) are

ΔM(q)=0.25M(q);ΔC(q,q˙)=0.25C(q,q˙),(27)

f(q˙)=[0.4976000.4570].[sign(q˙1)sign(q˙2)]+[2.9936002.7617].[q˙1q˙2],(28)

d(q,q˙)cases1,2=0.1[sin⁡(0.2t)+1+0.8q˙1cos⁡(0.3t)+0.8q˙2],(29)

d(q,q˙)case3=1.0[sin⁡(2t)+1+q˙1cos⁡(3t)+1.2q˙2].(30)

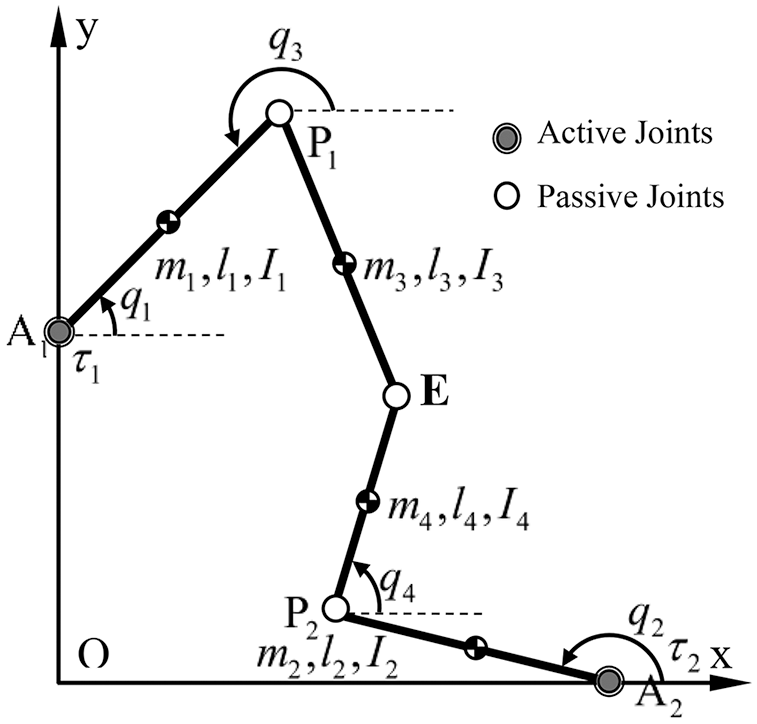
Figure 2: The 2-DOF redundant parallel manipulator

It is noted that the parallel manipulator is influenced by the uncertainties F(q,q˙)=ΔM(q)q¨+ΔC(q,q˙)q˙+f(q)+d(q,q˙) and such uncertainties and their derivative may be unbounded.

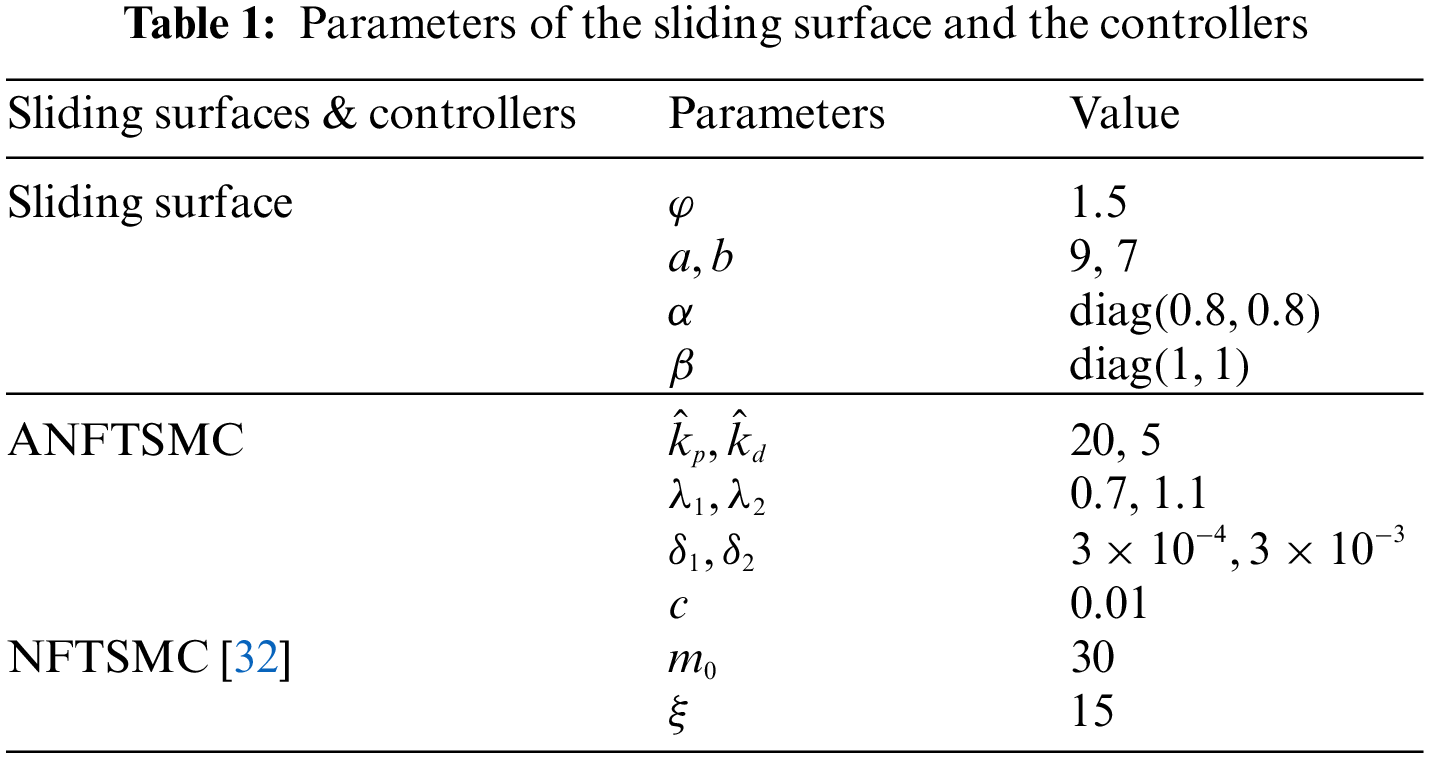
In order to show the improvement in performance, the ANFTSMC control scheme is compared with the NFTSMC [32]. The NFTSMC sliding surfaces are selected in (9). The NFTSMC input control law is obtained in (12).

To overcome the chattering problem, the sign(⋅) function in ANFTSMC (in (14)), and in NFTSMC (in (12)) are both replaced by the saturation function given in (25), where ρ=0.001. In all simulations, the reference trajectories tracking are chosen as: xE=0.006+0.02×cos⁡(ω.t)and yE=0.0785+0.02×sin⁡(ω.t). The initial positions of the parallel mechanisms are set as: q1=−0.2235, q2=3.517, q3=3.655, q4=2.395 [rad]; and q˙1=0, q˙2=0 [rad/s]. The initial values of the adaptive update laws are as K^pi=0, K^di=0(i=1,2) and m^0=0. The sliding surface parameters and the control parameters are set in Tab. 1. To show the accuracy improvement in the case of high-speed motions of the proposed controllers, we have tested in three different cases as follows

Case 1 Low-speed motion (the maximum velocity is 0.2 [m/s] and ω=7 [rad/s]) with uncertainties and disturbances designed in (27)–(29).

Case 2 High-speed motion (the maximum velocity is 0.48 [m/s] and ω=17 [rad/s]) with uncertainties and disturbances designed in (27)–(29).

Case 3 High-speed motion (the maximum velocity is 0.48 [m/s] and ω=17 [rad/s]) with significantly enlarged uncertainties and disturbances designed in (27), (28) and (30).

The simulation results in case 1 are given in Figs. 3–6. The position tracking errors of the active joints q1 and q2 are shown in Fig. 4. These velocity tracking errors are given in Fig. 5. The sum of the unknown modeling, the nonlinear friction forces, and the external disturbances in the low-speed trajectory tracking motions is given in Fig. 6. From Figs. 4 and 5, it demonstrates that those two controllers can make the parallel manipulator system track the desired trajectory under complex uncertainties and external disturbances and the proposed controller has better performance as expected.

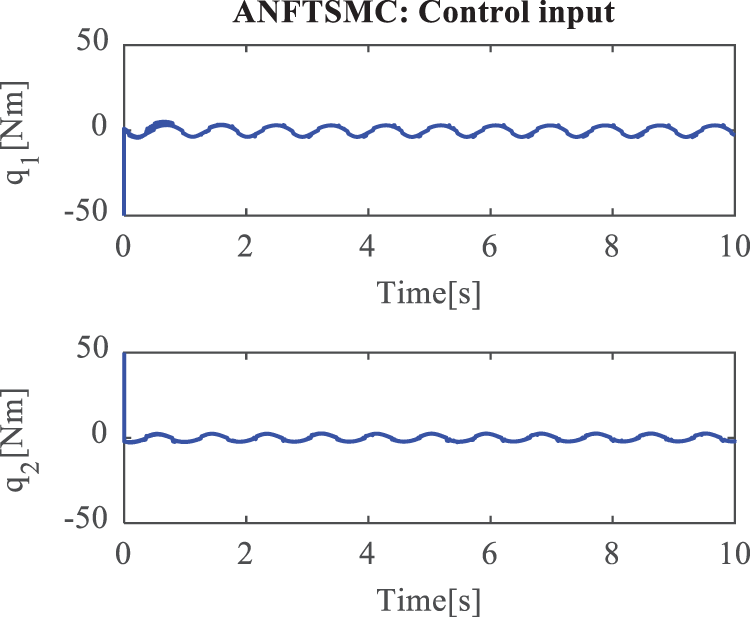
Figure 3: Control torques of the active joints in case 1 under ANFTSMC

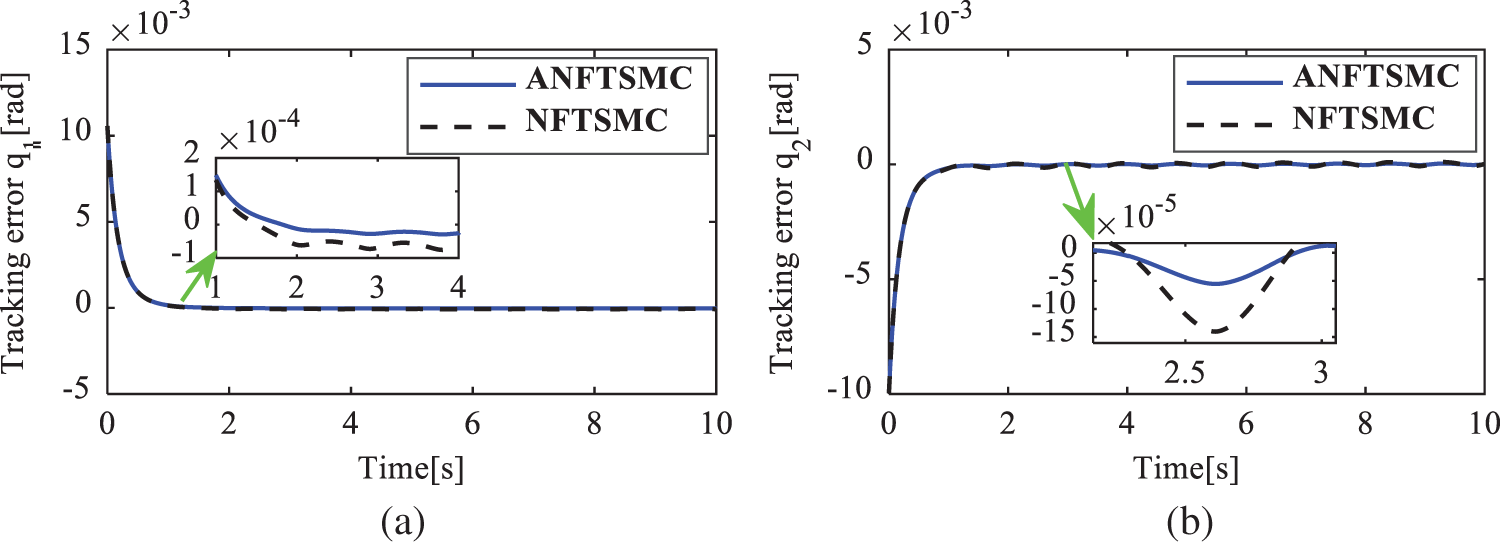
Figure 4: Position tracking error of the active joints in case 1. (a) q1. (b) q2

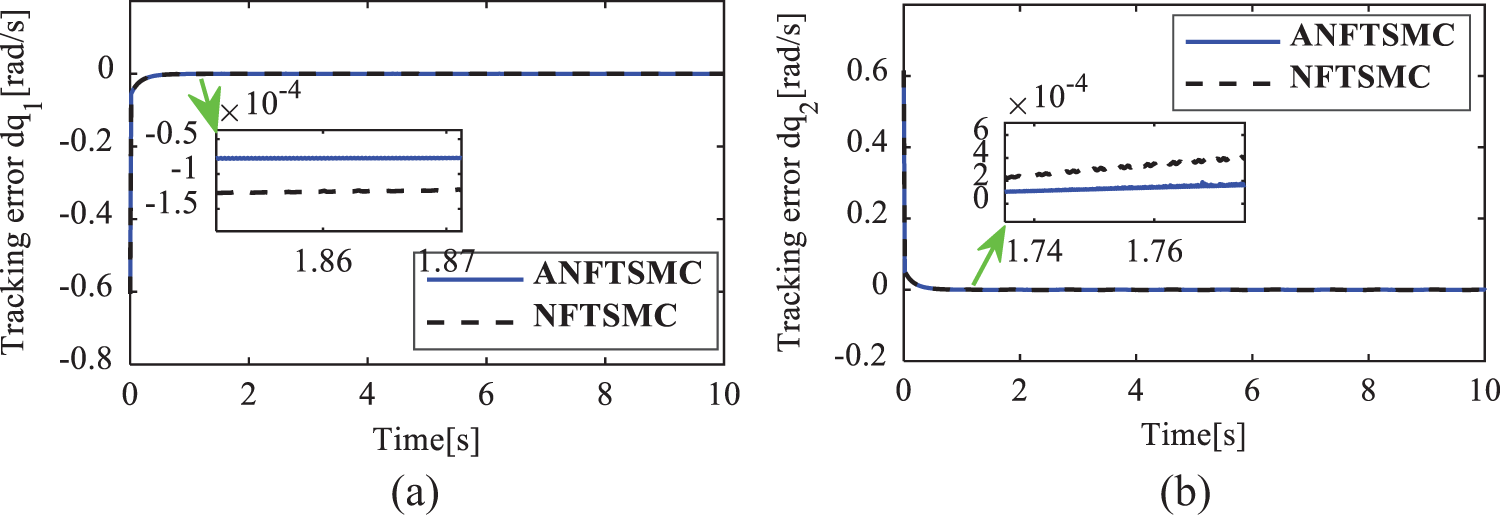
Figure 5: Velocity tracking error of the active joints in case 1. (a) q˙1. (b) q˙2

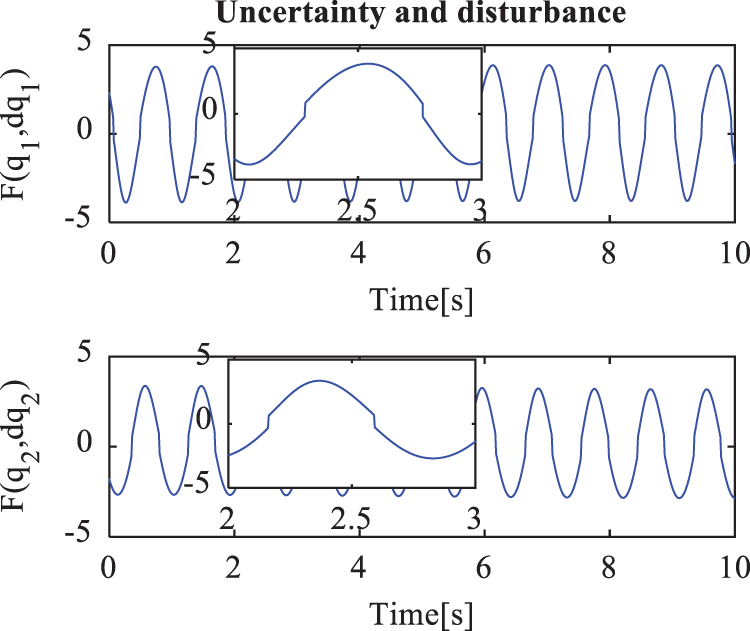
Figure 6: Total of the unknown modeling, the frictions forces, and the disturbances in case 1

Figs. 7–14 show the simulation results for cases 2 and 3. Figs. 10 and 14 show the sum of the unknown modeling, the nonlinear friction forces, and the external disturbances, respectively. Figs. 6, 10, and 14 show the results when the velocity of the end effector increases from 0.2 m/s to 0.48 m/s, and both the amplitude and the frequency oscillation of F(q,q˙) defined in (2) increase significantly. The values of F(q1,q˙1) are {−3.9≤F(q1,q˙1)≤3.9} in case 1, {−9.1≤F(q1,q˙1)≤8.1} in case 2, and {−9.2≤F(q1,q˙1)≤27.8} in case 3. Similarly, the respective values of F(q2,q˙2) are {−2.8≤F(q2,q˙2)≤3.4}, {−6.1≤F(q2,q˙2)≤7.3}, and {−16.2≤F(q2,q˙2)≤17.2}. As shown in Figs. 8, 9, 12 and 13, it can be observed that the peaks of the motion and velocity tracking errors under NFTSMC [32] are related largely in cases 2 and 3, for example, in case 2: {−1.02×10−3≤e(q1)≤−2.4×10−4} and {−9.1×10−4≤e(q2)≤5.5×10−4}, and in case 3: {−2.52×10−3≤e(q1)≤1.35×10−4} and {−2.63×10−3≤e(q2)≤2.08×10−3}. Specifically, NFTSMC [32] becomes unstable with case 3. However, these peaks are reduced dramatically with the tracking errors close to zero in the proposed ANFTSMC controller. It is because the online NAM in the proposed controller can speed up the convergence rate. From Figs. 4, 5, 8, 9, 12 and 13, it can be seen that the finite-time convergence is approximate 1s with the use of ANFTSMC. According to these figures, it can be seen that the ANFTSMC controller has the smallest tracking errors in comparison with that using the NFTSMC controller in both low-speed and high-speed motions. The corresponding control torques of the active joints for cases 1, 2, and 3 are given in Figs. 3, 7, and 11, respectively. It is also clear that the chattering phenomenon is significantly reduced by using the saturation function (25). Therefore, it is evident that the proposed control is suitable to deal with tracking control problems of parallel manipulator systems.

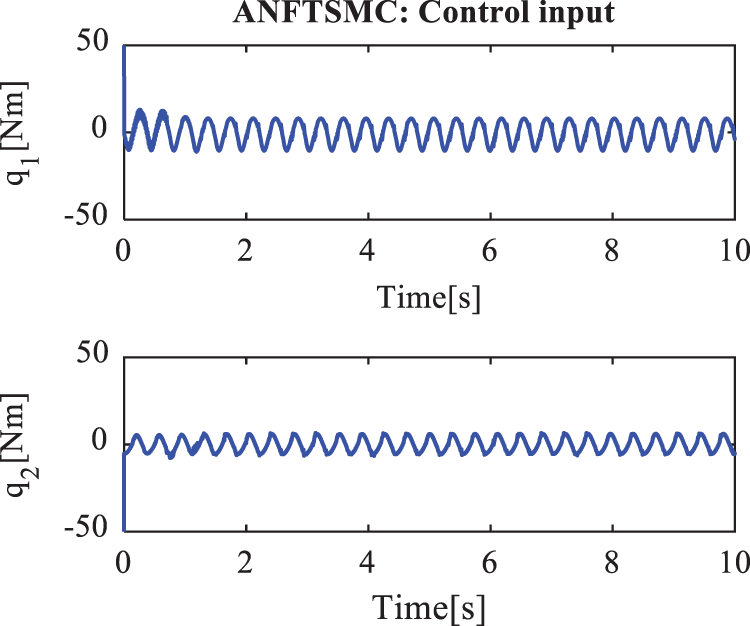
Figure 7: Control torques of the active joints in case 2 under ANFTSMC

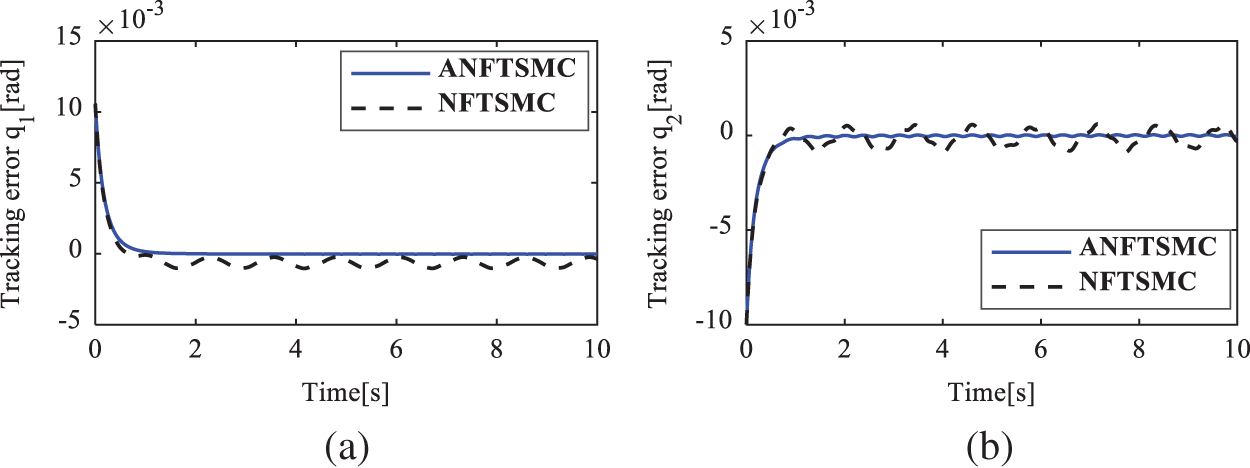
Figure 8: Position tracking error of the active joints in case 2. (a) q1. (b) q2

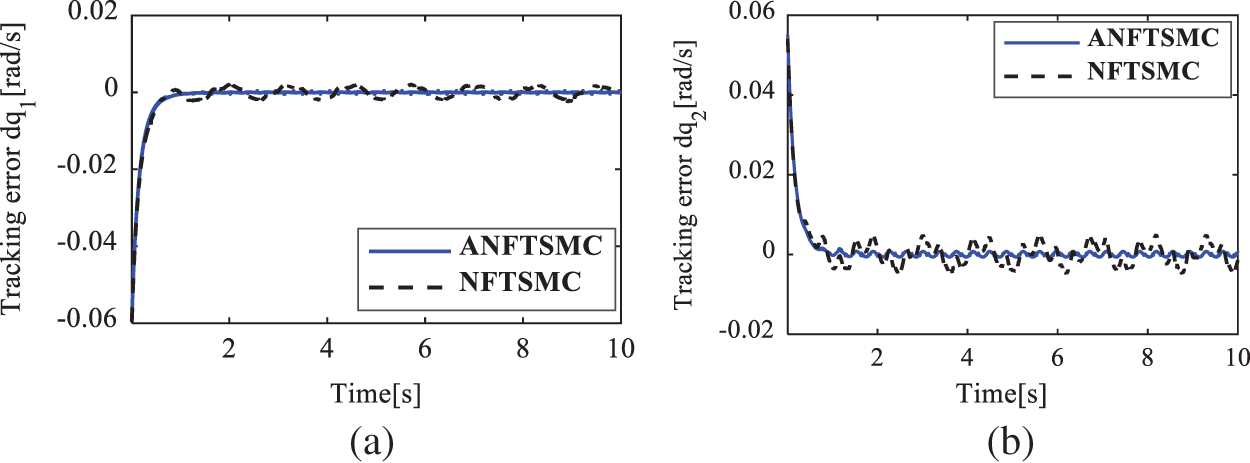
Figure 9: Velocity tracking error of the active joints in case 2. (a) q˙1. (b) q˙2

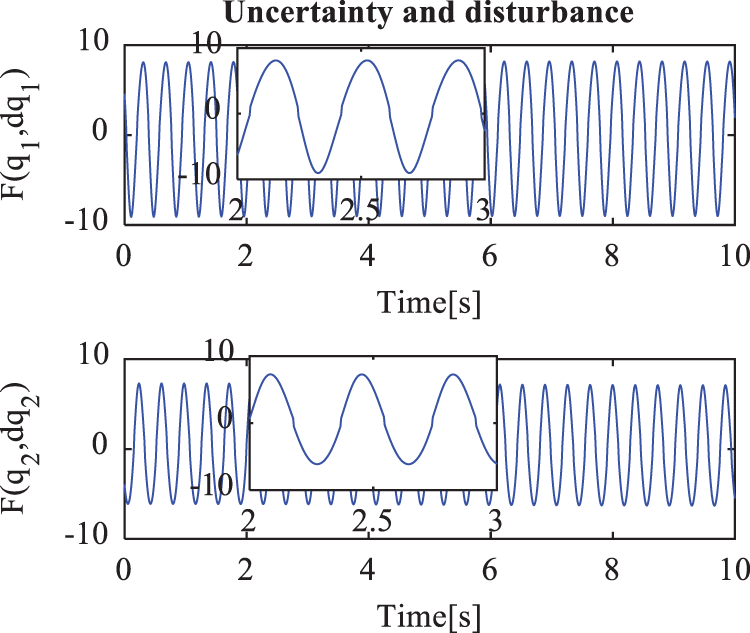
Figure 10: Total of the unknown modeling, the frictions forces, and the disturbances in case 2

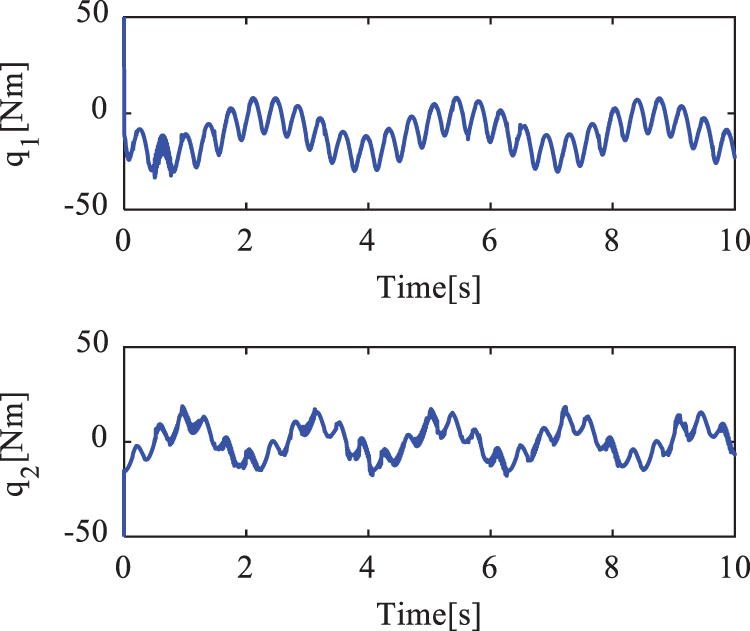
Figure 11: Control torques of the active joints in case 3 under ANFTSMC

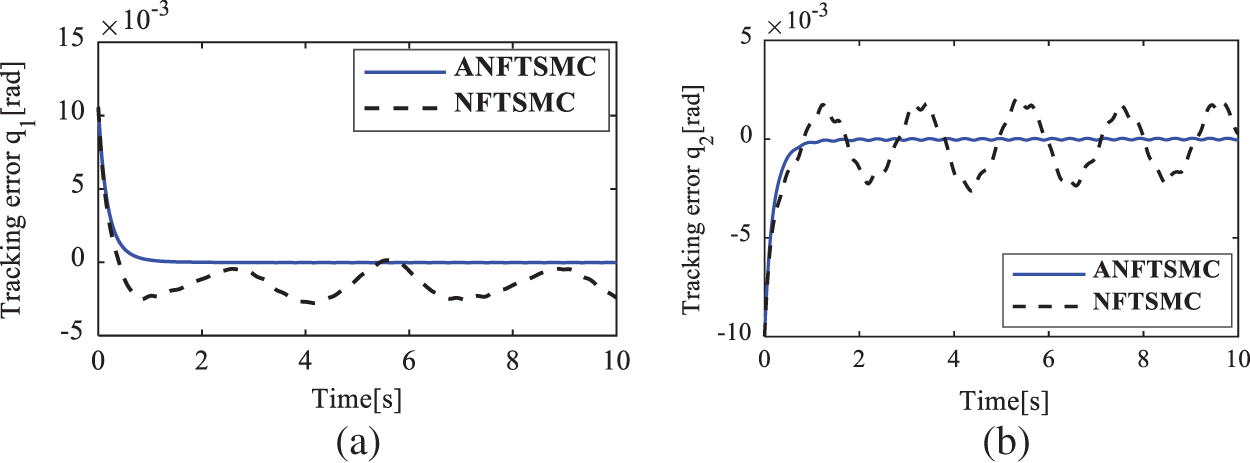
Figure 12: Position tracking error of the active joints in case 3. (a) q1. (b) q2

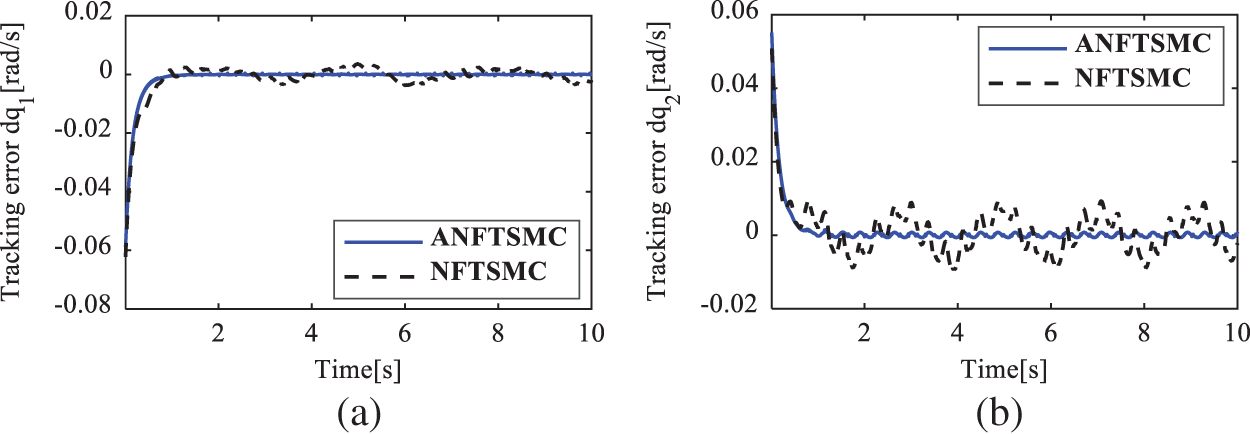
Figure 13: Velocity tracking error of the active joints in case 3. (a) q˙1. (b) q˙2

Figure 14: Total of the unknown modeling, the frictions forces, and the disturbances in case 3

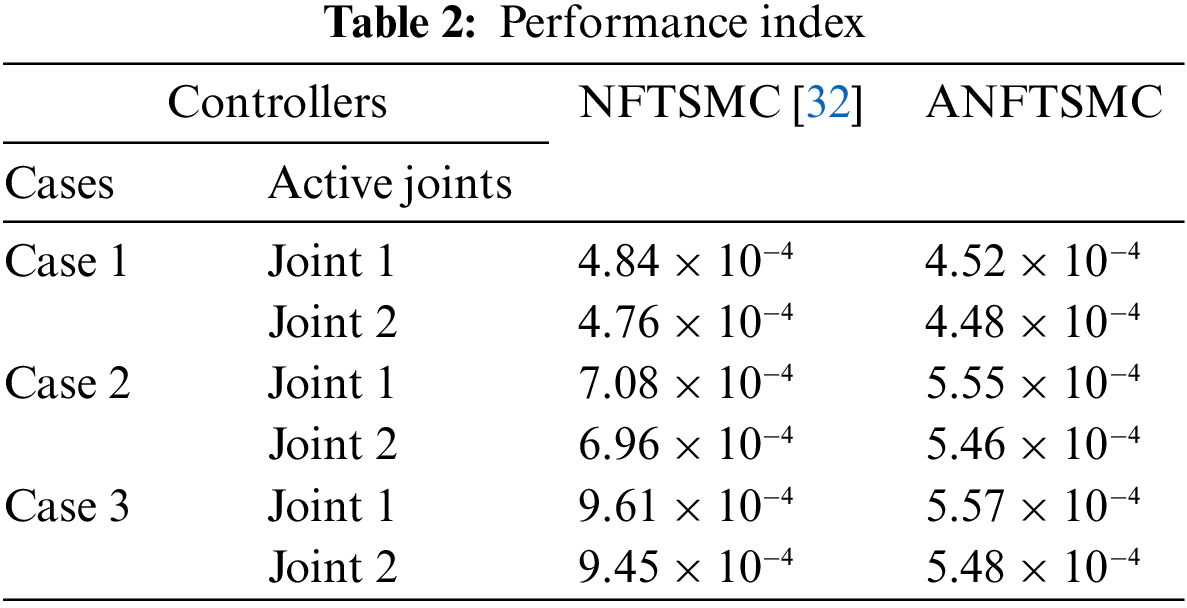
To show the quantitative comparison, the root square mean error (RSME) of the position tracking errors of the active joints is chosen as the performance index. Tab. 2 summarizes the quantitative comparisons between ANFTSMC and NFTSMC [32] under those three different tests. This table also indirectly shows the robustness and the precision level of individual control strategies. From the table, it can be seen that in comparison with the NFTSMC scheme, the ANFTSMC controller has 5.88%, 21.55%, and 42.01% position accuracy improvements in cases 1, 2, and 3, respectively. It can be concluded that the proposed ANFTSMC controller indeed has a smaller position tracking error in the case of having complex uncertainties and external disturbances as well as in the high-speed tracking motion. Furthermore, when the velocity of the end effector increases from 0.2 to 0.48 m/s and the complexity of significantly enlarged uncertainties and disturbances are changed from case 1 to case 3, the position tracking errors of the NFTSMC scheme increase significantly (The active joint q1 is 49.64%, and the active joint q2 is 49.63%, respectively). In contrast, it is a small increase in the position tracking error by using the ANFTSMC scheme (18.85% for q1, and 18.25% for q2). Indeed, the proposed ANFTSMC controller can achieve good performance and is highly suitable for practical applications in the case of unknown bounded complex uncertainties and external disturbances as well as high-speed motions for parallel manipulators.

6  Conclusion

This paper reports our study on the adaptive nonsingular fast terminal sliding mode finite-time tracking control for parallel manipulators with the existence of complex uncertainties and external disturbances in the case of high-speed motions. The proposed control scheme is successfully designed based on the tracking differentiator, the non-negative adaptive mechanism, and the nonsingular fast terminal sliding mode control. The non-negative adaptive law is employed to handle the real-time estimation of the total of complex uncertainties and external disturbances. This control scheme does not require prior knowledge of bounded uncertainties and disturbances. Simulation results show that the proposed scheme has superior tracking control performance, and the tracking error converges fast to zero in a finite time without any singularity. Possible future work can be to choose the optimal control parameters by using optimization algorithms.

Funding Statement: This project was funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED), Vietnam under Grant No. (107.01-2019.311). Sponsors’ Websites: https://nafosted.gov.vn/en/.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  H. Goud, P. C. Sharma, K. Nisar, M. R. Haque, A. A. A. Ibrahim et al., “Metaheuristics algorithm for tuning of PID controller of mobile robot system,” Computers, Materials & Continua, vol. 72, no. 2, pp. 3481–3492, 2022. [Google Scholar]

 2.  V. T. Nguyen, C. Y. Lin, S. F. Su, W. Sun and M. J. Er, “Global finite time active disturbance rejection control for parallel manipulators with unknown bounded uncertainties,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 51, no. 12, pp. 7838–7849, 2021. [Google Scholar]

 3.  M. Stölzle and C. D. Santina, “Piston-driven pneumatically-actuated soft robots: Modeling and backstepping control,” IEEE Control Systems Letters, vol. 6, pp. 1837–1842, 2022. [Google Scholar]

 4.  G. Rigatos and M. Abbaszadeh, “Nonlinear optimal control for a five-link parallel robotic manipulator,” Journal of Vibration and Control, 2022. https://doi.org/10.1177/10775463211051449. [Google Scholar]

 5.  D. V. Le and C. Ha, “Finite-time fault-tolerant control for a stewart platform using sliding mode control with improved reaching law,” IEEE Access, vol. 10, pp. 43284–43302, 2022. [Google Scholar]

 6.  I. Aldarraji, A. Kakei, A. G. Ismaeel, G. Tsaramirsis, F. Q. Khan et al., “Takagi-sugeno fuzzy modeling and control for effective robotic manipulator motion,” Computers, Materials & Continua, vol. 71, no. 1, pp. 1011–1024, 2022. [Google Scholar]

 7.  A. Ibrahim, S. Mirjalili, M. El-Said, S. S. M. Ghoneim, M. Al-Harthi et al., “Wind speed ensemble forecasting based on deep learning using adaptive dynamic optimization algorithm,” IEEE Access, vol. 9, pp. 125787–125804, 2021. [Google Scholar]

 8.  V. T. Nguyen, S. F. Su, N. Wang and W. Sun, “Adaptive finite-time neural network control for redundant parallel manipulators,” Asian Journal of Control, vol. 22, no. 6, pp. 2534–2542, 2020. [Google Scholar]

 9.  S. Diao, W. Sun and S. F. Su, “Neural-based adaptive event-triggered tracking control for flexible-joint robots with random noises,” International Journal of Robust and Nonlinear Control, vol. 32, no. 5, pp. 2722–2740, 2022. [Google Scholar]

10. V. T. Nguyen, C. Y. Lin, S. F. Su and W. Sun, “Finite-time adaptive fuzzy tracking control design for parallel manipulators with unbounded uncertainties,” International Journal of Fuzzy Systems, vol. 21, no. 2, pp. 545–555, 2019. [Google Scholar]

11. W. Sun, S. Diao, S. F. Su and Z. Y. Sun, “Fixed-time adaptive neural network control for nonlinear systems with input saturation,” IEEE Transactions on Neural Networks and Learning Systems, 2021. https://doi.org/10.1109/TNNLS.2021.3105664. [Google Scholar]

12. W. Sun, J. W. Lin, S. F. Su, N. Wang and M. J. Er, “Reduced adaptive fuzzy decoupling control for lower limb exoskeleton,” IEEE Transactions on Cybernetics, vol. 51, no. 3, pp. 1099–1109, 2021. [Google Scholar]

13. X. Sun, L. Feng, Z. Zhu, G. Lei, K. Diao et al., “Optimal design of terminal sliding mode controller for direct torque control of SRMs,” IEEE Transactions on Transportation Electrification, vol. 8, no. 1, pp. 1445–1453, 2022. [Google Scholar]

14. T. Song, L. Fang and H. Wang, “Model-free finite-time terminal sliding mode control with a novel adaptive sliding mode observer of uncertain robot systems,” Asian Journal of Control, vol. 24, no. 3, pp. 1437–1451, 2022. [Google Scholar]

15. D. Cruz-Ortiz, I. Chairez and A. Poznyak, “Non-singular terminal sliding-mode control for a manipulator robot using a barrier lyapunov function,” ISA Transactions, vol. 121, pp. 268–283, 2022. [Google Scholar]

16. H. Li and Y. Cai, “Fixed-time non-singular terminal sliding mode control with globally fast convergence,” IET Control Theory & Applications, 2022. https://doi.org/10.1049/cth2.12299. [Google Scholar]

17. H. Du, X. Chen, G. Wen, X. Yu and J. Lü, “Discrete-time fast terminal sliding mode control for permanent magnet linear motor,” IEEE Transactions on Industrial Electronics, vol. 65, no. 12, pp. 9916–9927, 2018. [Google Scholar]

18. H. Ghadiri, A. Mohammadi and H. Khodadadi, “Fast terminal sliding mode control based on SDRE observer for two-axis gimbal with external disturbances,” Journal of the Brazilian Society of Mechanical Sciences and Engineering, vol. 44, no. 2, pp. 1–23, 2022. [Google Scholar]

19. Y. Ma, D. Li, Y. Li and L. Yang, “A novel discrete compound integral terminal sliding mode control with disturbance compensation for PMSM speed system,” IEEE/ASME Transactions on Mechatronics, vol. 27, no. 1, pp. 549–560, 2022. [Google Scholar]

20. H. Karami, K. A. Alattas, S. Mobayen and A. Fekih, “Adaptive integral-type terminal sliding mode tracker based on active disturbance rejection for uncertain nonlinear robotic systems with input saturation,” IEEE Access, vol. 9, pp. 129528–129538, 2021. [Google Scholar]

21. Y. Hu, H. Yan, H. Zhang, M. Wang and L. Zeng, “Robust adaptive fixed-time sliding-mode control for uncertain robotic systems with input saturation,” IEEE Transactions on Cybernetics, 2022. https://doi.org/10.1109/TCYB.2022.3164739. [Google Scholar]

22. V. C. Nguyen, A. T. Vo and H. J. Kang, “A finite-time fault-tolerant control using non-singular fast terminal sliding mode control and third-order sliding mode observer for robotic manipulators,” IEEE Access, vol. 9, pp. 31225–31235, 2021. [Google Scholar]

23. S. S. Xu, C. Chen and Z. Wu, “Study of nonsingular fast terminal sliding-mode fault-tolerant control,” IEEE Transactions on Industrial Electronics, vol. 62, no. 6, pp. 3906–3913, 2015. [Google Scholar]

24. J. Zheng, H. Wang, Z. Man, J. Jin and M. Fu, “Robust motion control of a linear motor positioner using fast nonsingular terminal sliding mode,” IEEE/ASME Transactions on Mechatronics, vol. 20, no. 4, pp. 1743–1752, 2015. [Google Scholar]

25. Z. Yang, D. Zhang, X. Sun, W. Sun and L. Chen, “Nonsingular fast terminal sliding mode control for a bearingless induction motor,” IEEE Access, vol. 5, pp. 16656–16664, 2017. [Google Scholar]

26. K. Zhang, L. Wang and X. Fang, “High-order fast nonsingular terminal sliding mode control of permanent magnet linear motor based on double disturbance observer,” IEEE Transactions on Industrial Electronics, vol. 58, no. 3, pp. 3696–3705, 2022. [Google Scholar]

27. K. Liao and Y. Xu, “A robust load frequency control scheme for power systems based on second-order sliding mode and extended disturbance observer,” IEEE Transactions on Industrial Informatics, vol. 14, no. 7, pp. 3076–3086, 2018. [Google Scholar]

28. V. T. Nguyen, C. Y. Lin, S. F. Su and Q. V. Tran, “Adaptive chattering free neural network based sliding mode control for trajectory tracking of redundant parallel manipulators,” Asian Journal of Control, vol. 21, no. 3, pp. 1–16, 2019. [Google Scholar]

29. M. Van, “An enhanced robust fault tolerant control based on an adaptive fuzzy PID-nonsingular fast terminal sliding mode control for uncertain nonlinear systems,” IEEE/ASME Transactions on Mechatronics, vol. 23, no. 3, pp. 1362–1371, 2018. [Google Scholar]

30. H. Wang, L. Shi, Z. Man, J. Zheng, S. Li et al., “Continuous fast nonsingular terminal sliding mode control of automotive electronic throttle systems using finite-time exact observer,” IEEE Transactions on Industrial Electronics, vol. 65, no. 9, pp. 7160–7172, 2018. [Google Scholar]

31. C. C. Hua, K. Wang, J. N. Chen and X. You, “Tracking differentiator and extended state observer-based nonsingular fast terminal sliding mode attitude control for a quadrotor,” Nonlinear Dynamics, vol. 94, pp. 343–354, 2018. [Google Scholar]

32. M. Van, S. S. Ge and H. Ren, “Finite time fault tolerant control for robot manipulators using time delay estimation and continuous nonsingular fast terminal sliding mode control,” IEEE Transactions on Cybernetics, vol. 47, no. 7, pp. 1681–1693, 2017. [Google Scholar]

33. S. Ahmed, H. Wang and Y. Tian, “Model-free control using time delay estimation and fractional-order nonsingular fast terminal sliding mode for uncertain lower-limb exoskeleton,” Journal of Vibration and Control, vol. 24, no. 22, pp. 5273–5290, 2018. [Google Scholar]

34. M. Van, M. Mavrovouniotis and S. S. Ge, “An adaptive backstepping nonsingular fast terminal sliding mode control for robust fault tolerant control of robot manipulators,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 49, no. 7, pp. 1448–1458, 2019. [Google Scholar]

35. M. Boukattaya, N. Mezghani and T. Damak, “Adaptive nonsingular fast terminal sliding-mode control for the tracking problem of uncertain dynamical systems,” ISA Transactions, vol. 77, pp. 1–19, 2018. [Google Scholar]

36. X. Yao, J. H. Park, H. Dong, L. Guo and X. Lin, “Robust adaptive nonsingular terminal sliding mode control for automatic train operation,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 49, no. 12, pp. 2406–2415, 2019. [Google Scholar]

37. H. Zhang, Y. Xie, G. Xiao, C. Zhai and Z. Long, “A simple discrete-time tracking differentiator and its application to speed and position detection system for a maglev train,” IEEE Transactions on Control Systems Technology, vol. 27, no. 4, pp. 1728–1734, 2019. [Google Scholar]

38. X. Chang, L. Liu, W. Ding, D. Liang, C. Liu et al., “Novel nonsingular fast terminal sliding mode control for a PMSM chaotic system with extended state observer and tracking differentiator,” Journal of Vibration and Control, vol. 23, no. 15, pp. 2478–2493, 2015. [Google Scholar]