DNA Computing with Water Strider Based Vector Quantization for Data Storage Systems

1  Introduction

With the development of digital systems for storage, generation, and broadcast of data, there increases require to ongoing and active maintenance of digital media. With the huge amount of digital information that needs that storing to further utilize, a problem arises from the storage of irresistible number of information [1]. Yearly the storage need is increased by 50% [2]. Nowadays, most of the digital data is storing with a technique that only will last long for a minimum duration. Chips and Memory cards are sustainable for five years from their primary purpose [3]. However solid-state drive operates better when compared to hard drives, when not operated for long duration, they have the tendency of losing data [4]. Thus, researcher dedication has been driven toward the advancement of storage methods that successfully overcome the abovementioned problems. Fig. 1 illustrates the process involved in DNA data storage.

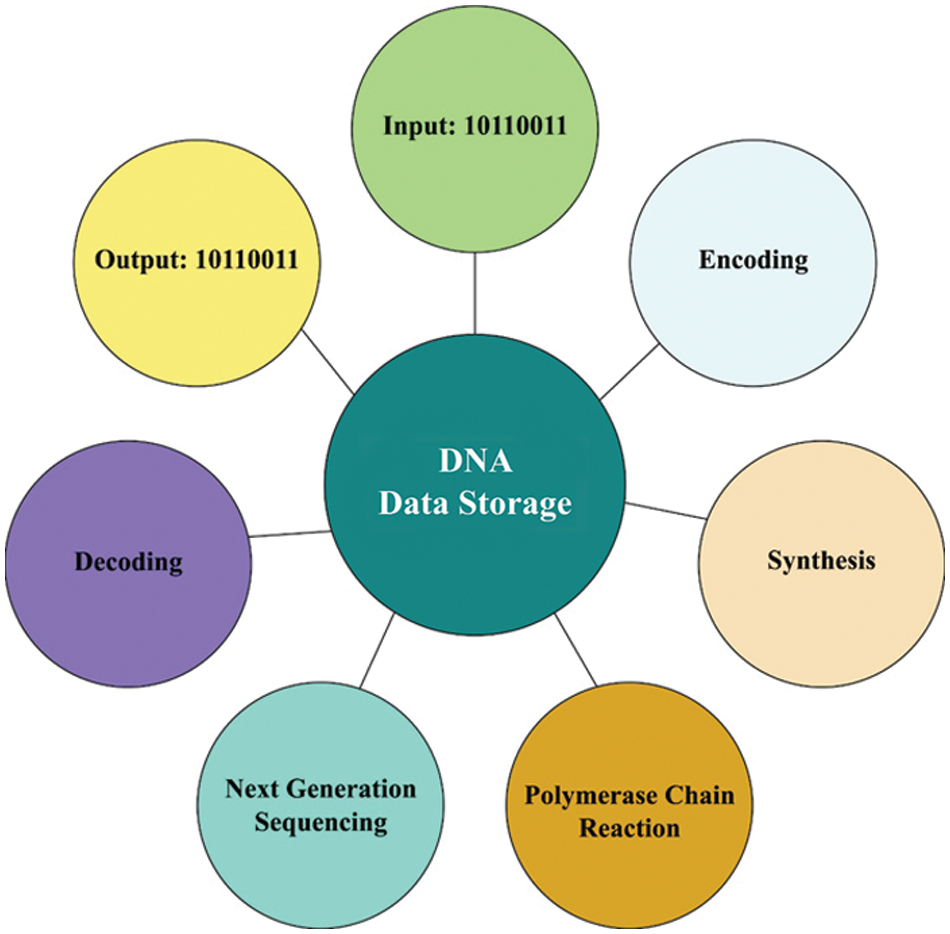
Figure 1: Process in DNA data storage

Furthermore, the environment might be polluted with non-biodegradable and silicon materials that are constrained in resources and will drain someday. File sharing systems are preferred for moving to new technology since the present storage technology is incapable of handling it effectively [5]. Any organism that is composed of 2 stranded spirals of nucleotides has cells named Deoxyribonucleic Acid (DNA) cells. Cytosine, Adenine, Thymine, and Guanine form these nucleotides that comprise one phosphate group, 5 carbon sugar, and 4 nitrogen bases. A massive number of data is stored in DNA to exploit considerable amount of combinatory questions, DNA registering methodology is used. It is possible that some grams of DNA have the opportunity of storing each information across the world. As well, this DNA could be preserved in dark and dry cold environments. Since it come for storage problems, there is several reasons to utlized DNA because of its very small size and ubiquity [6,7].

Currently, development of image compression (IC) technique with regenerated image quality is a challenging and crucial tasks for the researcher [8]. It aims at transmitting the image using lower bits. Detection of redundancy in image, suitable and perfect encoding techniques and conversion technology are the major factor for IC. Quantization consist of: vector and scalar quantization. Vector quantization (VQ) has been a non-transformed compression system, is an efficient and effective mechanism for lossy IC [9]. The primary objective of VQ is to develop an effective codebook that comprises a collection of codeword where input image vector has been allocated according to the minimal Euclidean distance. The most used and primary VQ method is Linde Buzo Gray (LBG) approach [10].

This article introduces a new DNA Computing with Water Strider Algorithm based Vector Quantization (DNAC-WSAVQ) technique for Data Storage Systems. The proposed DNAC-WSAVQ technique allows data encoding by the use of DNA computing and then compresses it for effective data storage. Moreover, the DNAC-WSAVQ model initially performs DNA encoding on the input images to generate a binary encoded form. Furthermore, a Water Strider algorithm with LBG (WSA-LBG) model is utilized to accomplish effective compression process and thereby storage area can be considerably minimized. For generating an optimum codebook for LBG, the WSA is applied to it. The performance validation of the DNAC-WSAVQ model is carried out and the results are examined under several measures.

2  Related Works

The authors in [11] presented Cuckoo search (CS) metaheuristic optimization method which enhances the LBG codebook through levy flight distribution process which follows the Mantegna algorithm in place of Gaussian distribution. Dimopoulou et al. [12] proposed an end-to-end storage system for effective storage of images to synthetic DNA. This system employs an encoding approach that serves the need for IC while being strong to the biological error that might corrupt the encoding. Kumar et al. [13] proposed a biomedical IC method from the cloud computing (CC) platform with Harris Hawks Optimization (HHO)-based LBG approaches. The presented method accomplishes a smooth transition amongst exploitation and exploration.

Guo et al. [14] designed a bat algorithm based adopted separation search mode to enhance the codebook design with the mean square error (MSE) as the adaptation values. The presented method employs pulse emission rate for switching the loudness and the search mode to define the searching range, however, it continued suffering from a deficiency of searching ability. Thus, adoptive separation rule is presented for enhancing the global exploration ability and for avoiding earlier convergence. Khan [15] examined several executions of IC techniques which utilize approaches like artificial neural networks (ANNs), Residual Learning, Fuzzy Neural Networks (FNN), convolution neural network (CNNs), deep learning (DL), and genetic algorithm (GA). This work also explains an execution of VQ utilizing GA for generating codebook that is utilized for Lossy IC. In [16], a new DNA based fast and secured data access control method was established in the cloud environments. During this presented method, a long 1024-bit DNA based password or confidential key was utilized for encrypting user secret or personal information.

Wu et al. [17] considered DNA computation based image encryption method that executes to cloud CCTV model. In several distinct image encryption studies, the artefact hyperchaotic map is utilized. It is presented an image encryption technique dependent upon DNA coding and hyperchaotic map that employs the chaotic property of hyperchaotic map on maximum of DNA calculating. In [18], VQ was utilized that employs the local binary pattern technique. While a novel purpose, the codebooks were optimized by an enhanced optimized technique. During this method, the database image was primarily divided as to a group of blocks, namely, pixels, and these groups of blocks were mentioned that vectors. Afterward, an appropriate codeword was chosen for all the vectors such that is neighboring representation of input vectors. To obtain an optimum IC result, the codebook was optimized utilizing the Best Fitness Updated Rider Optimized technique.

3  The Proposed Model

In this objective, a new DNAC-WSAVQ technique has been developed for effective data storage systems. The proposed DNAC-WSAVQ technique mainly intends in data encoding via DNA computing and then compresses it for effective data storage. Moreover, the DNAC-WSAVQ model primarily carried out DNA encoding on the input images for producing binary encoded form. Furthermore, a WSA-LBG model is utilized for the compression process and thereby storage area can be considerably minimized.

3.1 DNA Computing for Data Encoding

A DNA sequence is comprised of 4 nucleic acid bases, such as adenine (A), cytosine(C), guanine (G), and thymine (T), where A andT, and G and C are complements. The researcher uses the binary values 00, 01, 10, and 11 to denote four bases [19]. An overall of 24 kinds of coding could be listed; but based on the complementary relationship among 0 and 1 in binary. Thus, 8 out of 24 coding rules are carefully chosen for satisfying the base complementary condition. The pixel value of image lies among [0,255], and comprises eight-bit binary numbers. The present image encryption algorithm depends on DNA coding are nearly inseparable in this coding rule or deforming according to the coding rule. Fig. 2 depicts the components in DNA.

Figure 2: Components in DNA

Two DNA sequence complements are available namely single base direct complement approach and the method that employs the principle of single base and double base complementary pairing in biotechnology to implement the complement process.

{T=complement(A)A=complement(T)G=complement(C)C=complement(G)(1)

where complement (⋅) denotes the function of complement. The complement rule is determined according to the double helix model; a nucleoside is paired based on the double helix model [19]. Assuming the complementary conversion is D, each nucleoside xi fulfills the subsequent formula:

{xi≠D(xi)≠D(D(xi))≠D(D(D(xi)))xi=D(D(D(D(xi))))(2)

Whereas xi and D(xi) denotes complementary, that is xi and D(xi) indicates a pair of base pairs.

3.2 Design of WSA-LBG Model

The compression of input images is implemented utilizing VQ on co-efficient of sub-bands b∈{1,2,…,B}, with B=3i+1 created by i-level discrete wavelet transform (DWT) decompositions. The benefit of utilizing VQ rather than scalar quantization is that it gives optimum compression efficiency but is connected to a set length code. During this case, the selection of utilizing a set length code instead of variable length one is simulated as the detail it can be effectual manner that further robust to sequence noise [20].

The drive of VQ is for mapping n dimension vectors from the vector space Rn as to finite group of vectors Σ (the codebook) whereas Σ={Vj∈Rn|j=1,2,…,K}. The vector set Σ has the centroid vector which is calculated then clusters a group of trained vectors based on generalization Lloyd technique is projected.

3.2.1 LBG Algorithm

The LBG approach is an iterative method that requires a primary codebook to initiate with. At this point, the generation of codebook was completed utilizing a trained group of images, whereas the set specifies the distinct types of images that are compressed. This codebook (initial) was obtained by “splitting method”’ from the LBG method. During this approach, a primary code vector was set as a mean of every trained sequence and is then separated as to two [20]. The compression method is investigated by particular performances such as compression rate, peak signal to noise ratio (PSNR). The set of points at quantize outcome was named as codebook of quantizing and the process of placing this resultant points is named as “codebook design”.

LBG approach was demonstrated from the subsequent steps.

1.    Start with a primary group of reconstruction values {Ri(o)}i=1W. Allocate iteration p=0, H(o)=0. Select a threshold ∈.

2.    Determine regions of quantization as per Eq. (3).

Vi(p)={U:h(U,Ri)<h(U,Rj)∀j≠i}j=1,2..M(3)

3.    Estimate distortion as per Eq. (4).

H(p)=∑i=1W∫Vi(p)‖U−Ri(p)‖2fx(U)dU(4)

4.    If(H(p)−H(p−1))H(p)< ∈, terminating or continuing.

5.    p=p+1. Determine novel creating values {Ri(p)}i=1W that are centroids of {Vi(p−1)}. Continue step2.

These method procedures are the root of popular VQ techniques. It is generally recognized as the LBG manner. A primary codebook to 2level VQ is obtained by incorporating the resultant point to 1level quantizing and 2nd resultant point was achieved by summing up existing perturbation vector. Moreover, the LBG method is utilized for obtaining the 2 levels VQ. Fig. 3 portrays the process flow of LBG.

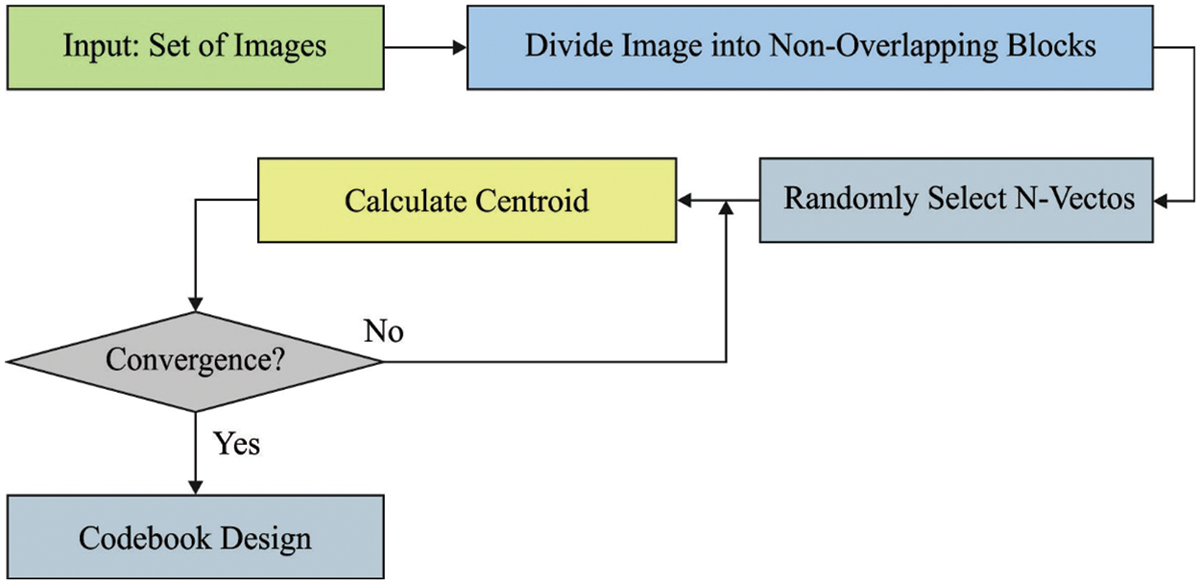
Figure 3: Process in LBG

The 2 codebook vectors were exploited for attaining a primary codebook to 4level VQ if the technique converges. A primary 4level codebook includes 2 codebook vectors in the final codebook of 2 levels VQ and other 2 vectors were obtained by summing up to 2 codebook vectors. The LBG method is utilized still this 4level VQ converges. Thus, the level is doubled still the optimum amount of levels are achieved. This technique was continued still the distortion drives under a particular lesser threshold.

The size of codebook was higher exponentially with rate of VQ that in order improves the quality of reform; but, the encoder time increases because of the increase from the computation essential for discovering the neighboring match. On integrating the preceding codebook of previous stage at all the divisions, it is certain that codebook then separating is an optimum as the codebook earlier to separating.

3.2.2 Optimal Codebook Construction Using WSA

In recent times, a new metaheuristic approach was stimulated from the behavior of Water Strider (WS) bugs [21] that is named WSA. It provides the best solution for complex optimization problems [22–24]. The process starts with initial random generating individual that is named Birth phase. Now, the male WS (keystone) gets mate with female WS for generating a population initialization (eggs). It can be expressed as follows.

Xi(0)=Lb+r×(Ub−Lb)(5)

i=1,2,…,n.

Whereas, r determines an arbitrary number within [0,1],Xi(0) defines the first location of ith individual, n indicates the candidate number, and Lb and Ub represent the lower and the upper limits, correspondingly. To generate n territories using n WSs, the objective value of WS is sorted and saved according to their cost value. Next, the mating begins with larger attempts, energy utilization, and search of the male WSs to achieve the female WS. Due to the stronger shield of females on their body, the male WS cannot do mating even with force that is

{Xi(t+1)=Xi(t)+R×r,if mating happensXi(t+1)=Xi(t)+R×(1+r),Otherwise(6)

Whereas, Xi(t) describes the location for ith WS and R defines the distance among the male WS position (Xi(t)) and the female territory (XF(t)) endpoint that is expressed by the following:

R=XF(t)−Xi(t)(7)

Next, the foraging procedure initiates. Because of consuming a longer time of male WS to search the female WS gets laid, they must reenergize itself to recover their body. It can be performed by searching for new location with high food sources. When the candidate objective values are lesser when compared to the previous position, it moves to the optimal territory using the maximum fitness(XBL(t)).

Xi(t+1)=Xi(t)+2×rand×(XBL(t)−Xi(t))(8)

Here, the succession and death of individuals are simulated so that the solution would be saved when they are determined in the predetermined boundary and they would be removed when they move beyond the constraint. This implies, when stranger WSs enter new territory, the male WS behaves brutally with him such that killing him or bringing him out. In this method, when the novel population is an appropriate solution when compared to the old one, it would be a substitute and the old one would be eliminated and killed.

Xi(t+1)=Lbj(t)+r×(Ubj(t)−Lbj(t))(9)

Whereas, Lb(t)and Ub(t) describe the minimal and the maximal value of the position of the WS in jth territory. Eventually, the process ends when the ending criteria are satisfied. The objective model of presented WSA based VQ model is for minimizing the rate of compression and consequently, the error variance amongst the decompressed as well as original images have that minimizing as illustrated by Eq. (10). In Eq. (10), Erepresents error variance among the decompressed and novel images, and CI represents the compression ratio.

Min=E+CI(10)

CI=Size of Compressed imageSize of original image(11)

4  Performance Validation

This section inspects the data storage efficiency of the DNAC-WSAVQ model using benchmark test images. The results are inspected under several aspects and measures. Some sample images are illustrated in Fig. 4.

Figure 4: Sample images

Tab. 1 and Fig. 5 reports the compression ratio (CR) examination of the DNAC-WSAVQ model with other methods on distinct test images [25]. The results indicated that the DNAC-WSAVQ model has resulted in effective outcomes with increased CR on all test images. For instance, on test image 1, the DNAC-WSAVQ model has obtainable higher CR of 3.6746 whereas the L2LBG methodology, CSLBG system, FFLBG approach, and JPEG2000 models have obtained lower CR of 2.2456, 2.1274, 1.7819, and 1.5268 respectively. Besides, on test image 4, the DNAC-WSAVQ model has provided increased CR of 3.2269 whereas the L2LBG methodology, CSLBG system, FFLBG approach, and JPEG2000 models have provided reduced CR of 2.5347, 2.2133, 1.7860, and 1.5148 respectively.

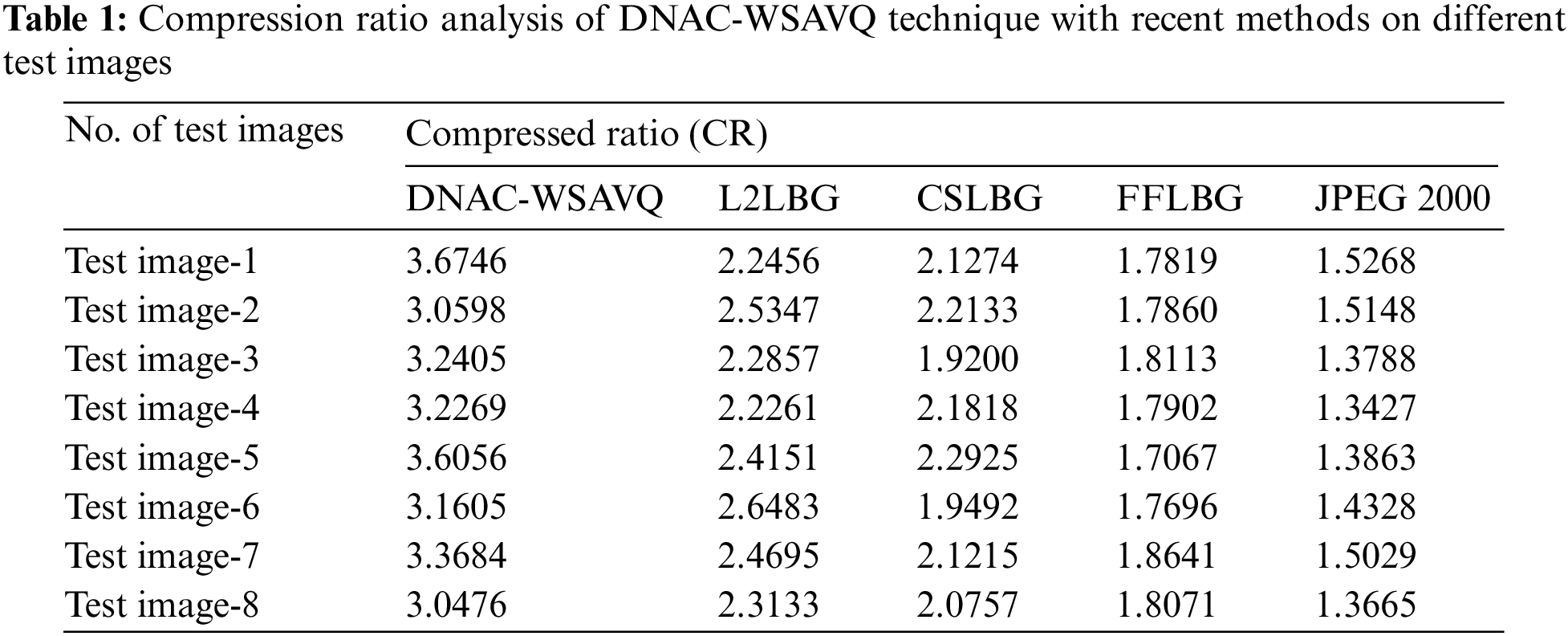
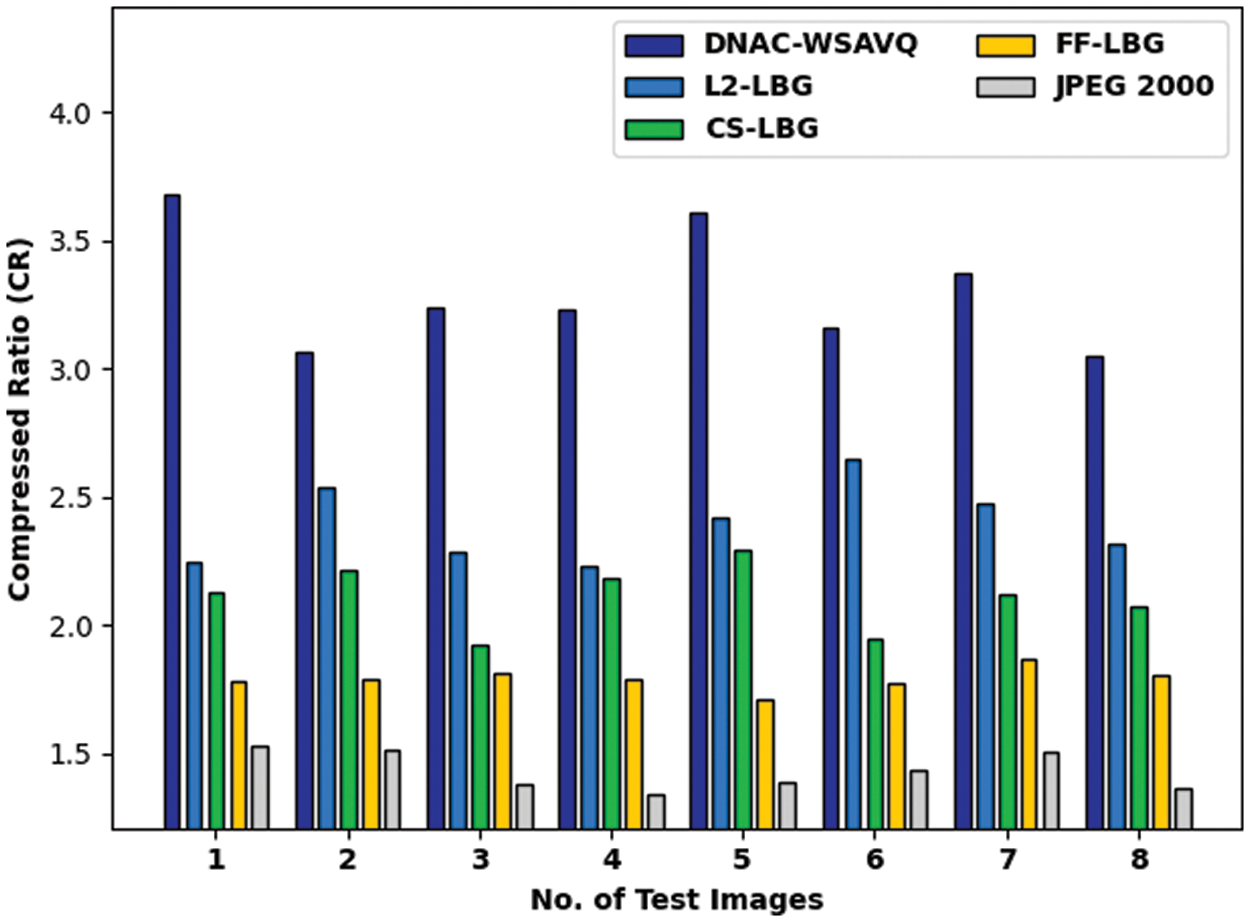
Figure 5: CR analysis of DNAC-WSAVQ technique with recent approaches

A detailed compression factor (CF) assessment of the DNAC-WSAVQ model with recent methods is provided in Tab. 2 and Fig. 6. The experimental results reported that the DNAC-WSAVQ model has resulted in proficient results with least values of CF. For instance, on test image 1, the DNAC-WSAVQ model has attained decreased CF of 0.2721 whereas the L2LBG methodology, CSLBG system, FFLBG approach, and JPEG2000 models have achieved increased CF of 0.4453, 0.4701, 0.5612, and 0.6549 respectively. Concurrently, on test image 5, the DNAC-WSAVQ model has resulted to minimal CF of 0.2773 whereas the L2LBG methodology, CSLBG system, FFLBG approach, and JPEG2000 models have obtained maximum CF of 0.4141, 0.4362, 0.5859, and 0.7214 respectively.

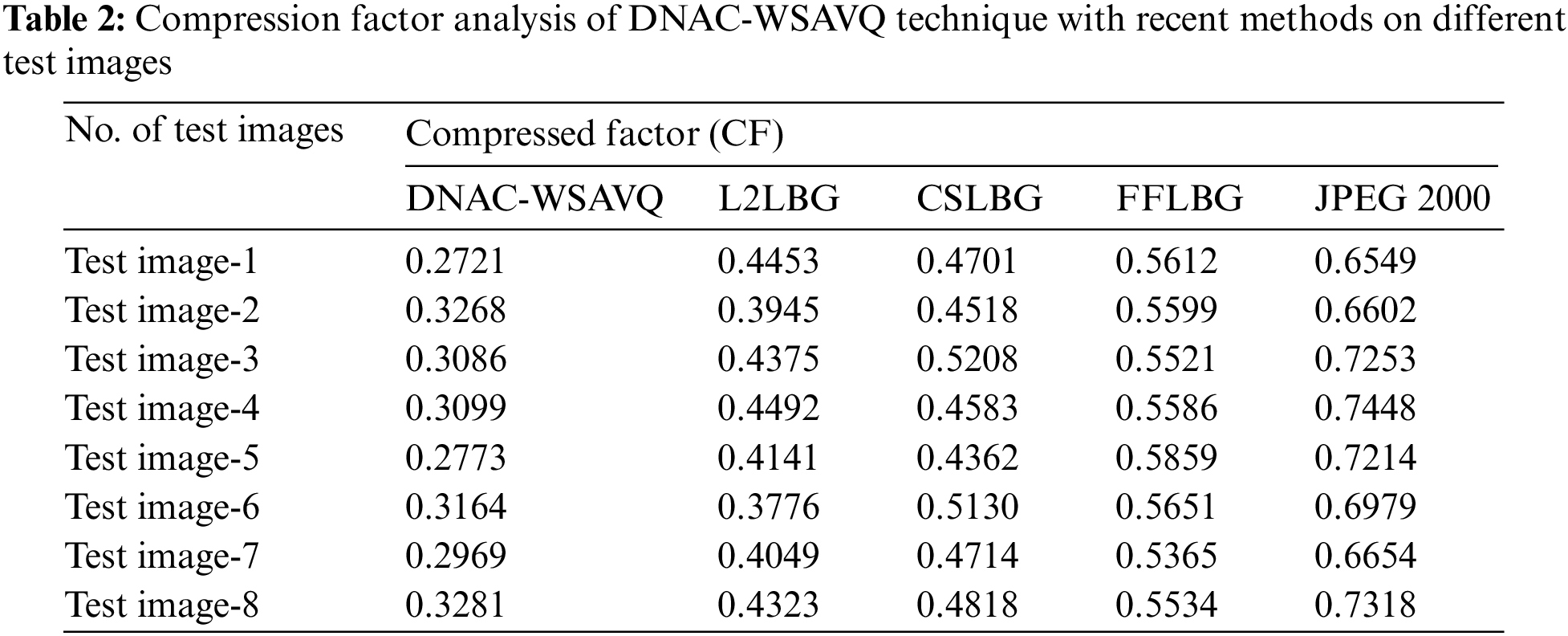
Figure 6: CF analysis of DNAC-WSAVQ technique with recent approaches

A comprehensive bit rate per pixel (BRPP) assessment of DNAC-WSAVQ system with current approaches is shown in Tab. 3 and Fig. 7. The experimental result reports that the DNAC-WSAVQ system has resulted in proficient outcomes with least values of BRPP. For example, on test image 1, the DNAC-WSAVQ approach has accomplished decreased BRPP of 2.177 while the L2LBG methodology, CSLBG system, FFLBG approach, and JPEG2000 methods have accomplished increased BRPP of 13.091, 8.444, 9.551, and 9.336 correspondingly. Simultaneously, on test image 5, the DNAC-WSAVQ technique has resulted in minimal BRPP of 2.219 while the L2LBG methodology, CSLBG system, FFLBG approach, and JPEG2000 methods have attained maximal BRPP of 11.944, 8.428, 10.746, and 9.849 correspondingly.

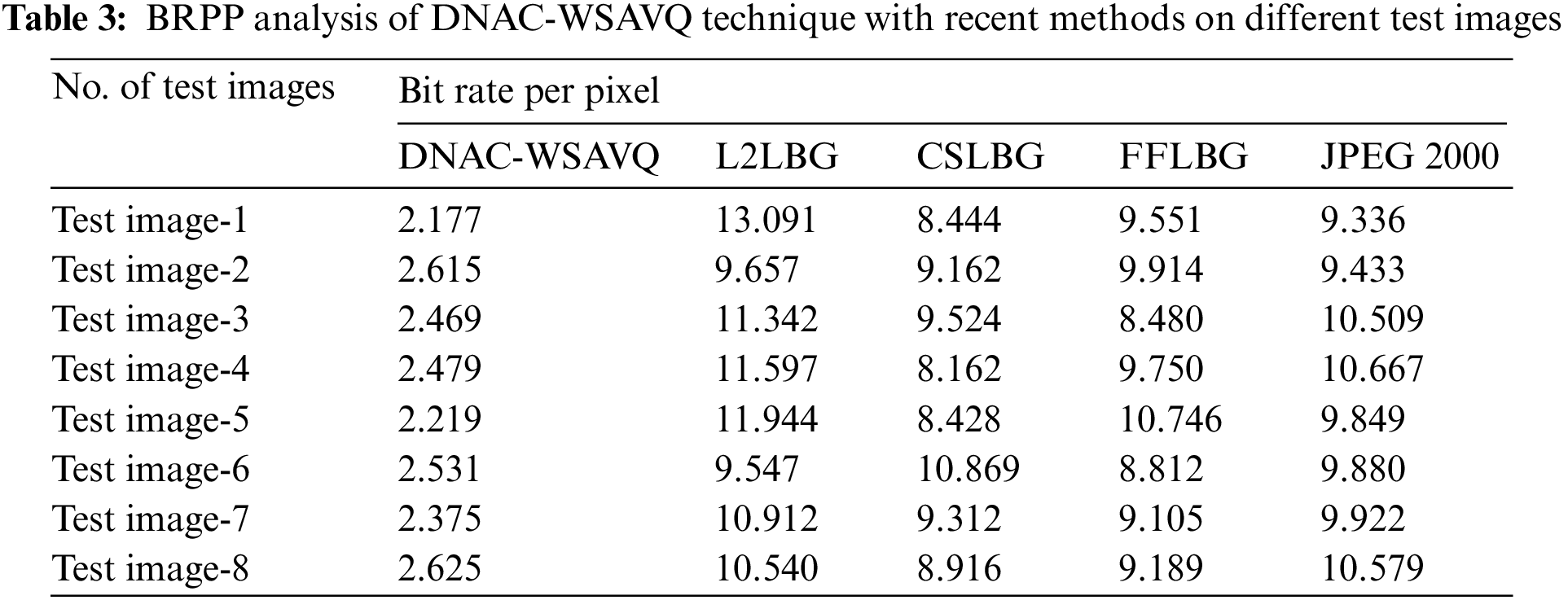
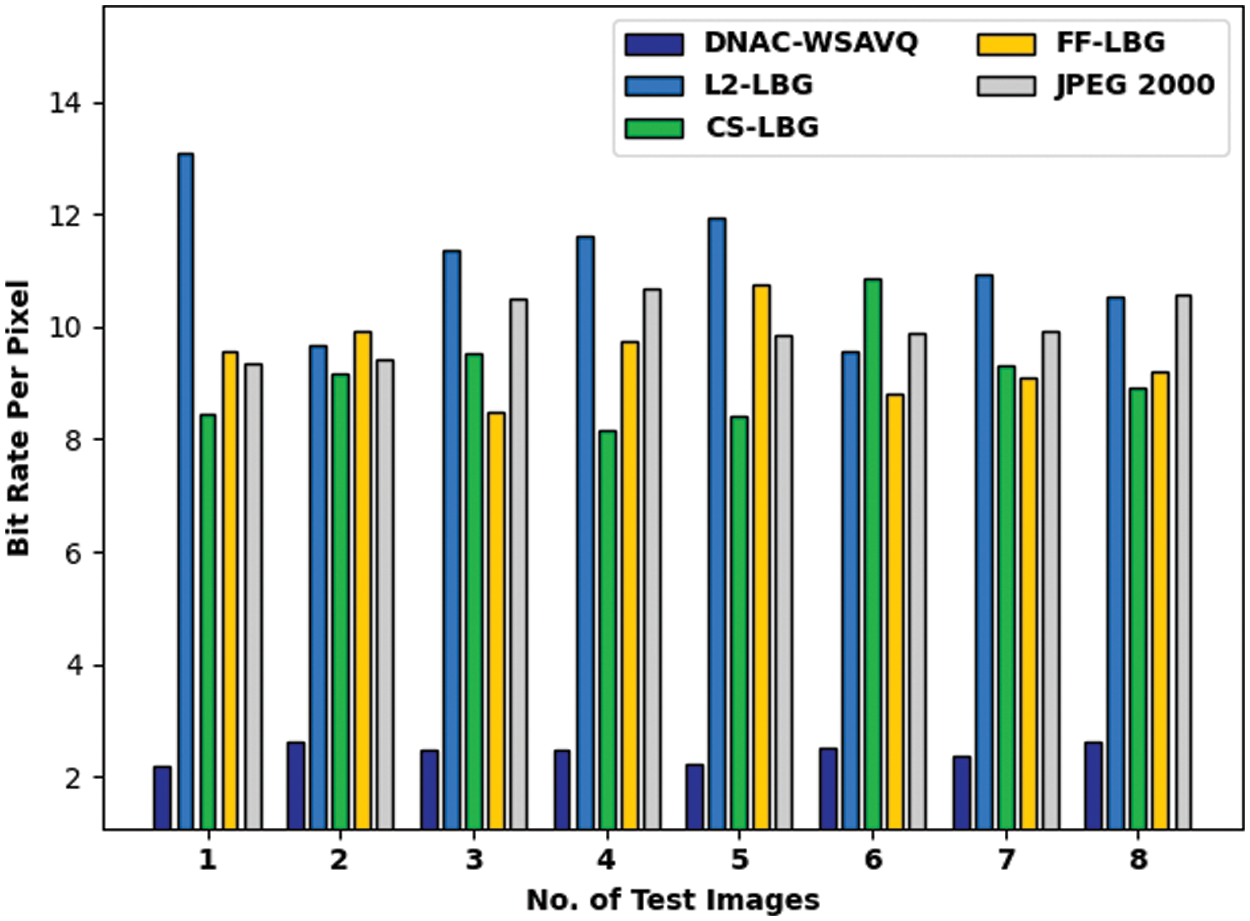
Figure 7: BRPP analysis of DNAC-WSAVQ technique with recent approaches

A detailed MSE assessment of DNAC-WSAVQ approach with current approaches is given in Tab. 4 and Fig. 8. The experimental results show that the DNAC-WSAVQ technique has resulted in proficient outcomes with minimum values of MSE. For example, on test image 1, the DNAC-WSAVQ algorithm has gained reduced MSE of 0.160 while the L2LBG methodology, CSLBG system, FFLBG approach, and JPEG2000 methods have reached improved MSE of 1.370, 1.300, 1.510, and 2.300 correspondingly. Synchronously, on test image 5, the DNAC-WSAVQ method has resulted in least MSE of 0.120 while the L2LBG methodology, CSLBG system, FFLBG approach, and JPEG2000 techniques have attained maximal MSE of 1.360, 1.370, 1.550, and 2.200 correspondingly.

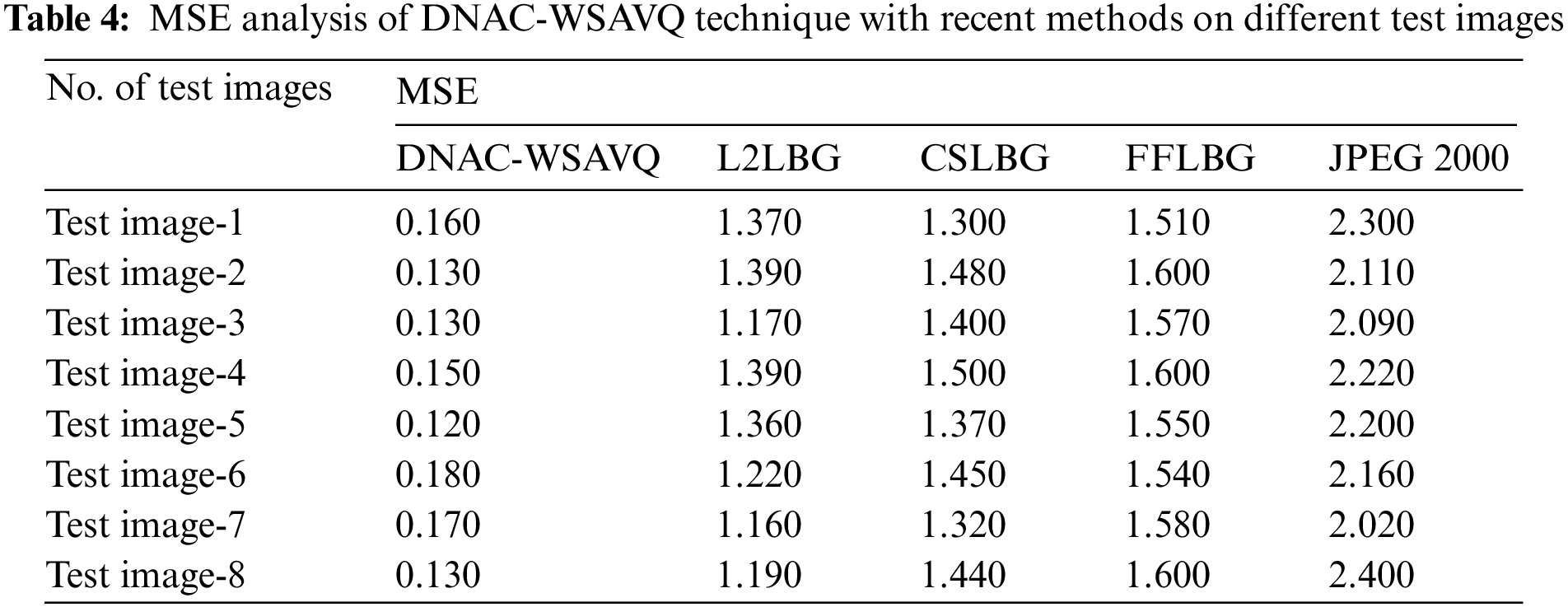
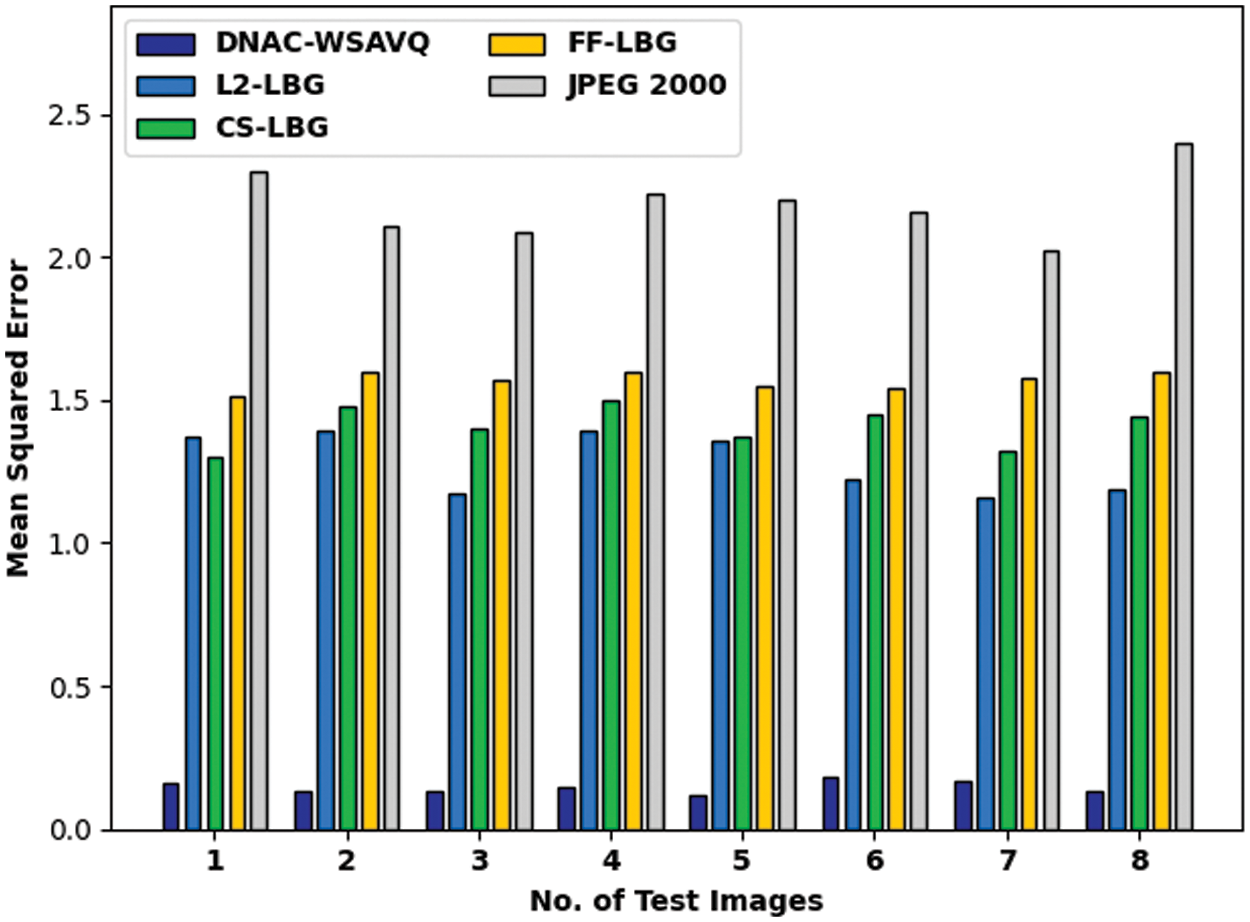
Figure 8: MSE analysis of DNAC-WSAVQ technique with recent approaches

A detailed root mean square error (RMSE) assessment of the DNAC-WSAVQ models with current approaches is given in Tab. 5 and Fig. 9. The experimental results show that the DNAC-WSAVQ technique has resulted in proficient outcomes with minimum values of RMSE. For example, on test image 1, the DNAC-WSAVQ method has accomplished reduced RMSE of 0.400 while the L2LBG methodology, CSLBG system, firefly based LBG (FFLBG) approach, and JPEG2000 techniques have accomplished improved RMSE of 1.170, 1.140, 1.229, and 1.517 correspondingly.

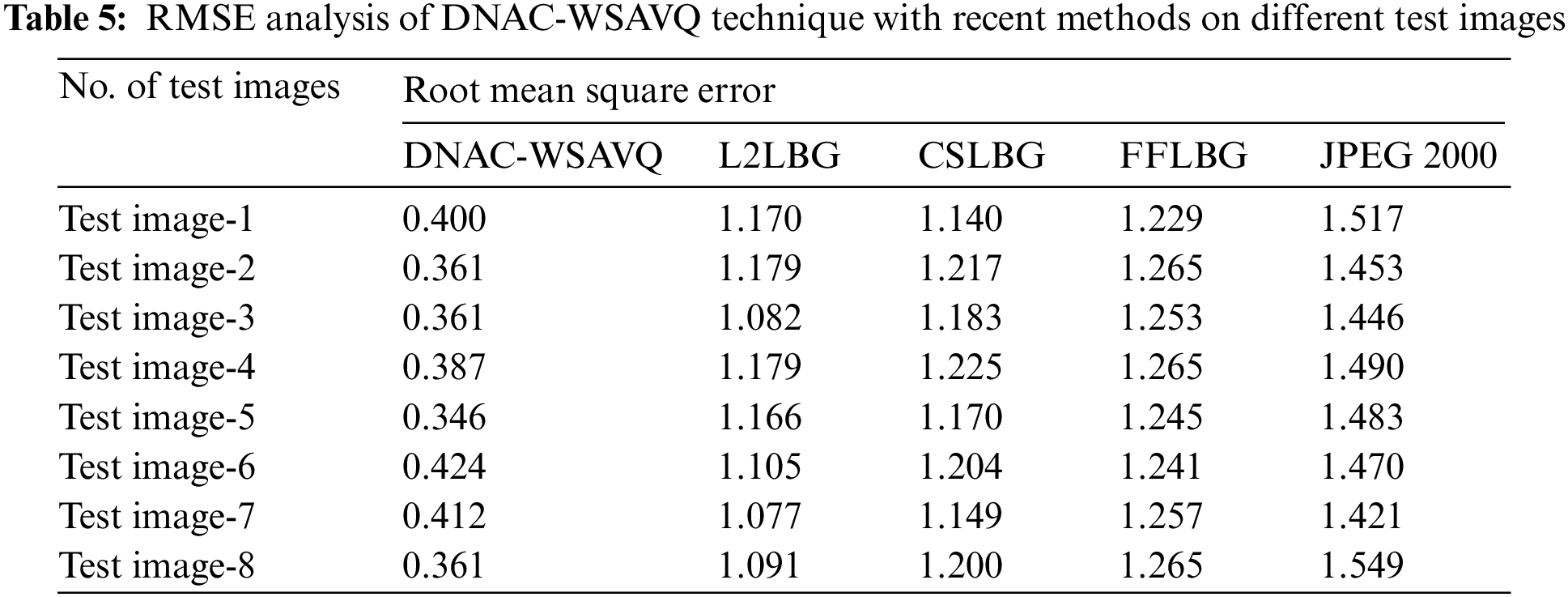
Figure 9: RMSE analysis of DNAC-WSAVQ technique with recent approaches

Simultaneously, on test image 5, the DNAC-WSAVQ method has resulted in least RMSE of 0.346 while the L2LBG methodology, CSLBG system, FFLBG approach, and JPEG2000 systems have attained maximal RMSE of 1.166, 1.170, 1.245, and 1.483 correspondingly.

Tab. 6 and Fig. 10 show the PSNR examination of the DNAC-WSAVQ approach with other approaches on distinct test images. The results show that the DNAC-WSAVQ system has resulted in effective outcomes with improved PSNR on all test images.

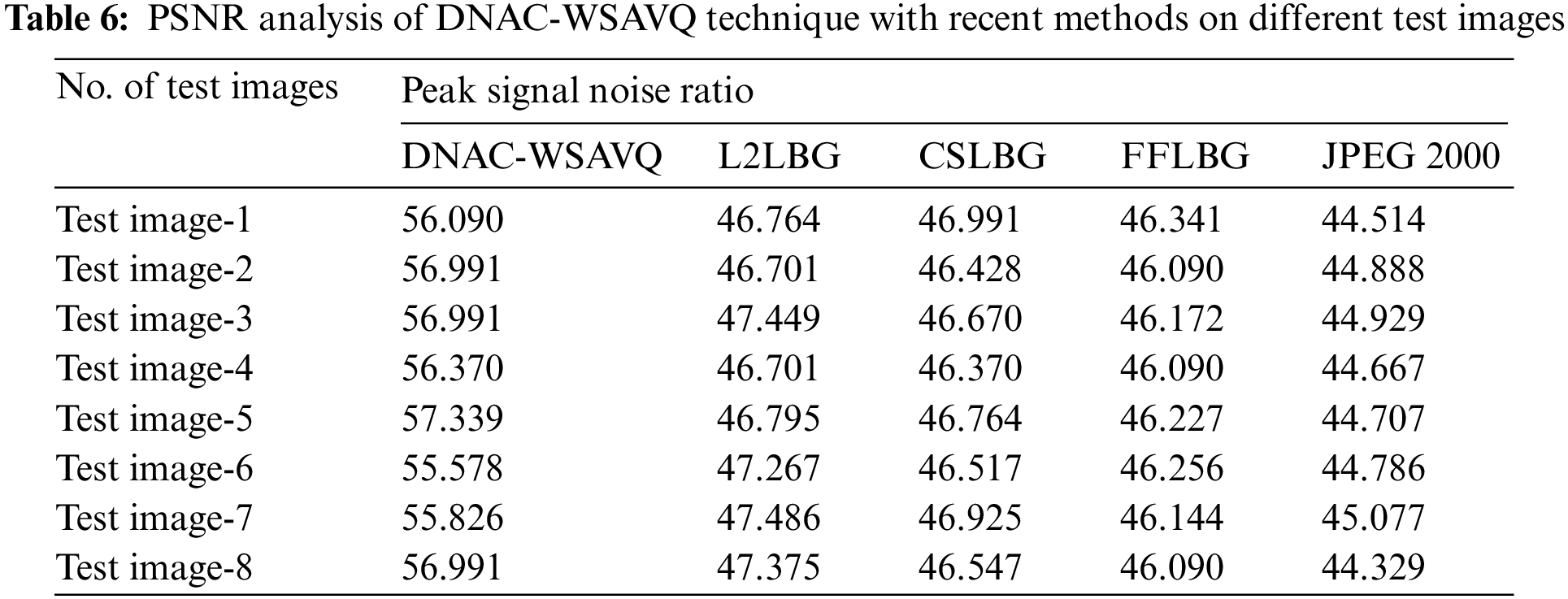
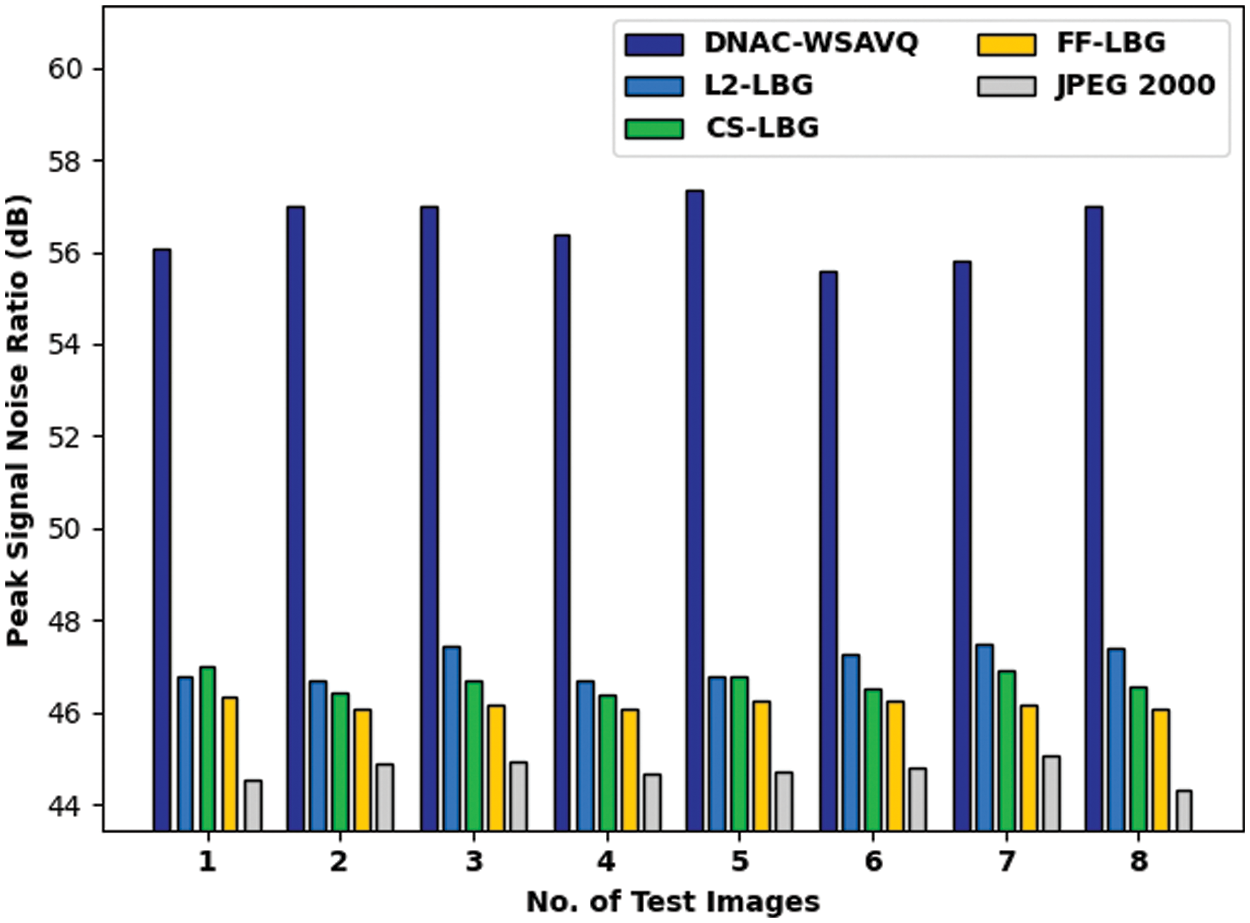
Figure 10: PSNR analysis of DNAC-WSAVQ technique with recent approaches

For example, on test image 1, the DNAC-WSAVQ model has accessible high PSNR of 56.090 dB while the L2LBG methodology, CSLBG system, FFLBG approach, and JPEG2000 models have accomplished lower PSNR of 46.764 dB, 46.991 dB, 46.341 dB, and 44.514 dB correspondingly. As well, on test image 4, the DNAC-WSAVQ approach has provided increased PSNR of 56.370 dB while the L2LBG methodology, CSLBG system, FFLBG approach, and JPEG2000 methods have provided reduced PSNR of 46.701 dB, 46.370 dB, 46.090 dB, and 44.667 dB correspondingly.

5  Conclusion

In this objective, a new DNAC-WSAVQ technique was developed for effective data storage systems. The proposed DNAC-WSAVQ technique mainly intends in data encoding via DNA computing and then compresses it for effective data storage. Moreover, the DNAC-WSAVQ model primarily carried out DNA encoding on the input images for producing binary encoded form. Furthermore, a WSA-LBG model is utilized for the compression process and thereby storage area can be considerably minimized. For generating an optimum codebook for LBG, the WSA is applied to it. The performance validation of the DNAC-WSAVQ model is applied and the outcomes are examined under several measures. The comparative study highlighted the improved outcomes of the DNAC-WSAVQ model over the existing methods.

Funding Statement: This research was supported in part by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education (NRF-2021R1A6A1A03039493), in part by the NRF grant funded by the Korea government (MSIT) (NRF-2022R1A2C1004401), and in part by the 2022 Yeungnam University Research Grant.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. Shrivastava and R. Badlani, “Data storage in DNA,” International Journal of Electrical Energy, vol. 2, pp. 119–124, 2014. [Google Scholar]

 2.  P. Y. De Silva and G. U. Ganegoda, “New trends of digital data storage in DNA,” BioMed Research International, vol. 2016, pp. 1–14, 2016. [Google Scholar]

 3.  F. Akram, I. ul Haq, H. Ali and A. T. Laghari, “Trends to store digital data in DNA: An overview,” Molecular Biology Reports, vol. 45, no. 5, pp. 1479–1490, 2018. [Google Scholar]

 4.  D. Carmean, L. Ceze, G. Seelig, K. Stewart, K. Strauss et al. “DNA data storage and hybrid molecular–electronic computing,” Proceedings of the IEEE, vol. 107, no. 1, pp. 63–72, 2019. [Google Scholar]

 5.  N. M. Nasrabadi, H. Kwon, and M. Venkatraman, “Object-based SAR image compression using vector quantization,” IEEE Transactions on Aerospace and Electronic Systems, vol. 36, no. 4, pp. 1036–1046, 2000. [Google Scholar]

 6.  Q. Ma, C. Zhang, M. Zhang, D. Han and W. Tan, “DNA computing: Principle, construction, and applications in intelligent diagnostics,” Small Structures, vol. 2, no. 11, pp. 2170030, 2021. [Google Scholar]

 7.  S. Namasudra, G. C. Deka and R. Bali, “Applications and future trends of DNA computing,” in Advances of DNA Computing in Cryptography, New York: Chapman and Hall/CRC, pp. 166–176, 2018. [Google Scholar]

 8.  A. Saha, D. Dewan, L. Ghosh and A. Konar, “Fuzzy vector quantization with a step-optimizer to improve pattern classification,” Expert Systems with Applications, vol. 188, pp. 115941, 2022. [Google Scholar]

 9.  S. Othman, A. Mohamed, A. Abouali and Z. Nossair, “Performance improvement of lossy image compression based on polynomial curve fitting and vector quantization,” in Information and Communication Technology for Competitive Strategies (ICTCS 2020Lecture Notes in Networks and Systems Book Series, Springer, Singapore, vol. 190, pp. 297–309, 2021. [Google Scholar]

10. S. M. Darwish and A. A. J. Almajtomi, “Metaheuristic-based vector quantization approach: A new paradigm for neural network-based video compression,” Multimedia Tools and Applications, vol. 80, no. 5, pp. 7367–7396, 2021. [Google Scholar]

11. K. Chiranjeevi and U. R. Jena, “Image compression based on vector quantization using cuckoo search optimization technique,” Ain Shams Engineering Journal, vol. 9, no. 4, pp. 1417–1431, 2018. [Google Scholar]

12. M. Dimopoulou and M. Antonini, “Image storage in DNA using vector quantization,” in 2020 28th European Signal Processing Conf. (EUSIPCO), Amsterdam, Netherlands, pp. 516–520, 2021. [Google Scholar]

13. T. S. Kumar, S. Jothilakshmi, B. C. James, M. Prakash, N. Arulkumar et al., “HHO-Based vector quantization technique for biomedical image compression in cloud computing,” International Journal of Image and Graphics, pp. 2240008, 2021. https://doi.org/10.1142/S0219467822400083. [Google Scholar]

14. J. R. Guo, C. Y. Wu, Z. L. Huang, F. J. Wang and M. T. Huang, “Vector quantization image compression algorithm based on bat algorithm of adaptive separation search,” in International Conference on Advanced Intelligent System and Informatics, Lecture Notes on Data Engineering and Communications Technologies book series, Springer, Cham, vol. 100, pp. 174–184, 2021. [Google Scholar]

15. M. M. Khan, “An implementation of vector quantization using the genetic algorithm approach,” arXiv preprint arXiv:2102.08893, 2021. [Google Scholar]

16. S. Namasudra, S. Sharma, G. C. Deka and P. Lorenz, “DNA computing and table based data accessing in the cloud environment,” Journal of Network and Computer Applications, vol. 172, pp. 102835, 2020. [Google Scholar]

17. T. Y. Wu, X. Fan, K. H. Wang, C. F. Lai, N. Xiong et al. “A DNA computation-based image encryption scheme for cloud CCTV systems,” IEEE Access, vol. 7, pp. 181434–181443, 2019. [Google Scholar]

18. P. P. Chavan, B. S. Rani, M. Murugan and P. Chavan, “A novel image compression model by adaptive vector quantization: Modified rider optimization algorithm,” Sādhanā, vol. 45, no. 1, pp. 232, 2020. [Google Scholar]

19. X. Xue, D. Zhou and C. Zhou, “New insights into the existing image encryption algorithms based on DNA coding,” PLoS ONE, vol. 15, no. 10, pp. e0241184, 2020. [Google Scholar]

20. S. Zheng, C. Liu, Z. Feng, R. Chen and X. Liu, “Visual image encryption scheme based on vector quantization and content transform,” Multimedia Tools and Applications, vol. 81, no. 9, pp. 12815–12832, 2022. [Google Scholar]

21. Y. P. Xu, P. Ouyang, S. M. Xing, L. Y. Qi, M. khayatnezhad et al. “Optimal structure design of a PV/FC HRES using amended water strider algorithm,” Energy Reports, vol. 7, pp. 2057–2067, 2021. [Google Scholar]

22. K. Shankar, D. Taniar, E. Yang and O. Yi, “Secure and optimal secret sharing scheme for color images,” Mathematics, vol. 9, no. 19, pp. 1–20, 2021. [Google Scholar]

23. M. Elhoseny and K. Shankar, “Reliable data transmission model for mobile ad hoc network using signcryption technique,” IEEE Transactions on Reliability, vol. 69, no. 3, pp. 1077–1086, 2020. [Google Scholar]

24. M. H. S. Saša, Z. Adamović, V. A. Miškovic, M. Elhoseny, N. D. Maček et al. “Data encryption for internet of things applications based on Catalan objects and two combinatorial structures,” IEEE Transactions on Reliability, vol. 70, no. 2, pp. 819–830, 2021. [Google Scholar]

25. K. Geetha, V. Anitha, M. Elhoseny, S. Kathiresan, P. Shamsolmoali et al. “An evolutionary lion optimization algorithm-based image compression technique for biomedical applications,” Expert Systems, vol. 38, no. 1, 2021. https://doi.org/10.1111/exsy.12508. [Google Scholar]